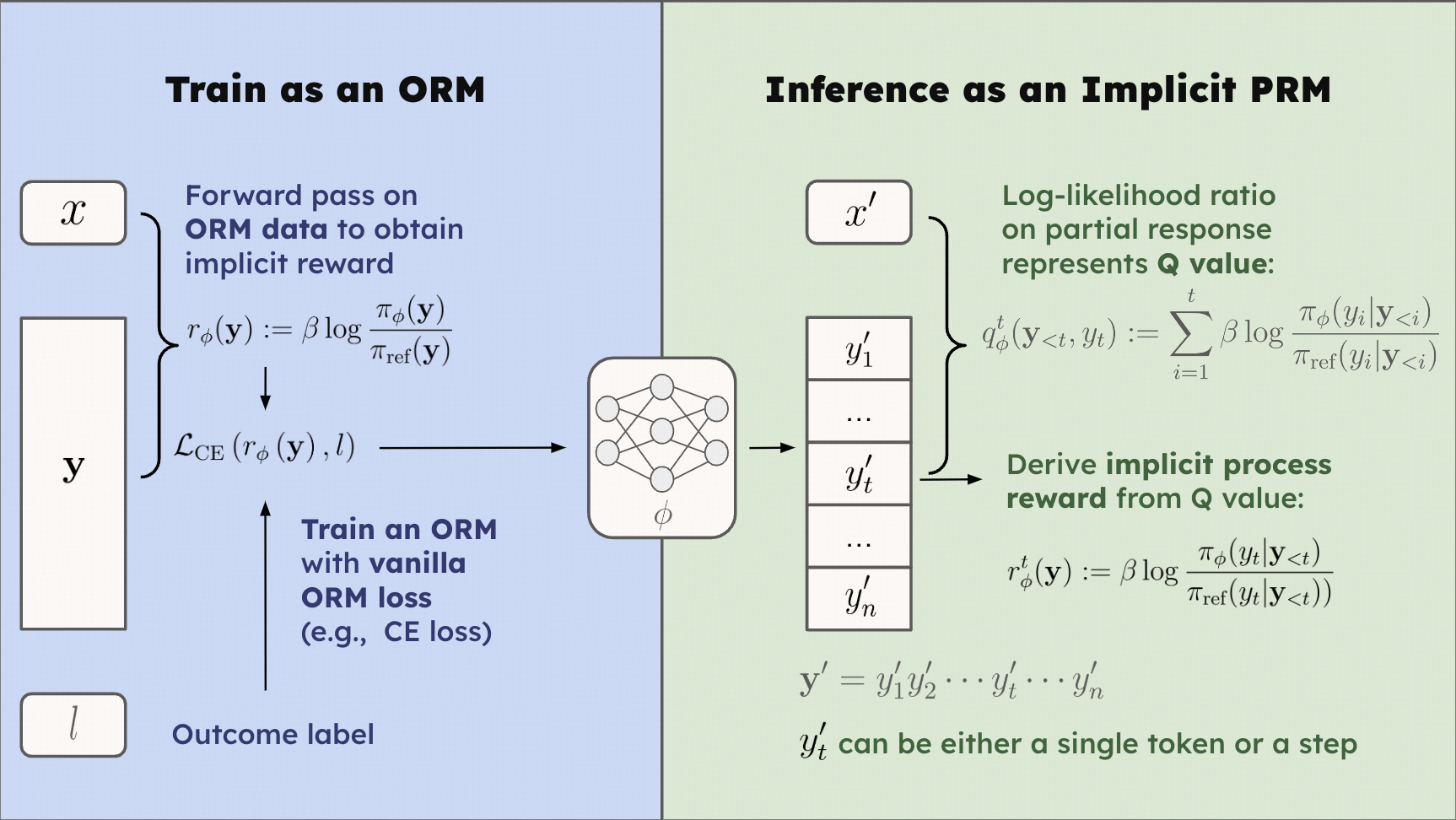
The key ingredient of Implicit PRM is the reward representation, as demonstrated below:
✨
Proposition
r ϕ ( y ) : = β log π ϕ ( y ) π ref ( y ) . r ϕ ( y ) := β log π ref ( y ) π ϕ ( y ) .
Define
q ϕ t ( y < t , y t ) : = ∑ i = 1 t β log π ϕ ( y i ∣ y < i ) π ref ( y i ∣ y < i ) . q ϕ t ( y < t , y t ) := i = 1 ∑ t β log π ref ( y i ∣ y < i ) π ϕ ( y i ∣ y < i ) .
is the exponential average of r θ r θ t t
q ϕ t ( y < t , y t ) = β log E π ref ( y ∣ y ≤ t ) [ e 1 β r ϕ ( y ) ] q ϕ t ( y < t , y t ) = β log E π ref ( y ∣ y ≤ t ) [ e β 1 r ϕ ( y ) ]
Hence, q θ t q θ t r θ r θ t t
The proposition indicates that when modeling
r ϕ ( y ) : = β log π ϕ ( y ) π ref ( y ) r ϕ ( y ) := β log π ref ( y ) π ϕ ( y )
to train an ORM with the standard pipeline, where β β ϕ ϕ r ϕ t r ϕ t
r ϕ t : = q ϕ t − q ϕ t − 1 = β log π ϕ ( y t ∣ y < t ) π ref ( y t ∣ y < t ) . r ϕ t := q ϕ t − q ϕ t − 1 = β log π ref ( y t ∣ y < t ) π ϕ ( y t ∣ y < t ) .
Therefore, we can indeed obtain PRMs simply by collecting response-level data and training an ORM, without any burden of annotating step labels.
The proposition is agnostic to specific choices of the training objective of ORMs . It can be instantiated with different objectives as vanilla ORM training, with the only difference being substituting the r ϕ ( y ) r ϕ ( y ) β log π ϕ ( y ) π ref ( y ) β log π ref ( y ) π ϕ ( y )
For example, DPO already meets our assumption and serves as a strong variant, while in this work, we instantiate our implicit PRM with cross entropy (CE) loss due to memory efficiency:
L C E = l ⋅ log σ ( β log π ϕ ( y ) π ref ( y ) ) + ( 1 − l ) ⋅ log [ 1 − σ ( β log π ϕ ( y ) π ref ( y ) ) ] L CE = l ⋅ log σ ( β log π ref ( y ) π ϕ ( y ) ) + ( 1 − l ) ⋅ log [ 1 − σ ( β log π ref ( y ) π ϕ ( y ) ) ]
We applied the above L C E L CE
Usage
We show an example leveraging EurusPRM-Stage1 below:
import torch
from transformers import AutoTokenizer,AutoModelForCausalLM
coef=0.001
d = {'query' :'Convert the point $(0,3)$ in rectangular coordinates to polar coordinates. Enter your answer in the form $(r,\\theta),$ where $r > 0$ and $0 \\le \\theta < 2 \\pi.$' ,
'answer' :[
"Step 1: To convert the point (0,3) from rectangular coordinates to polar coordinates, we need to find the radius (r) and the angle theta (\u03b8)." ,
"Step 2: Find the radius (r). The radius is the distance from the origin (0,0) to the point (0,3). Since the x-coordinate is 0, the distance is simply the absolute value of the y-coordinate. So, r = |3| = 3." ,
"Step 3: Find the angle theta (\u03b8). The angle theta is measured counterclockwise from the positive x-axis. Since the point (0,3) lies on the positive y-axis, the angle theta is 90 degrees or \u03c0\/2 radians." ,
"Step 4: Write the polar coordinates. The polar coordinates are (r, \u03b8), where r > 0 and 0 \u2264 \u03b8 < 2\u03c0. In this case, r = 3 and \u03b8 = \u03c0\/2.\n\nTherefore, the polar coordinates of the point (0,3) are (3, \u03c0\/2).\n\n\n\\boxed{(3,\\frac{\\pi}{2})}"
]
}
model = AutoModelForCausalLM.from_pretrained('PRIME-RL/EurusPRM-Stage1' )
tokenizer = AutoTokenizer.from_pretrained('PRIME-RL/EurusPRM-Stage1' )
ref_model = AutoModelForCausalLM.from_pretrained('Qwen/Qwen2.5-Math-7B-Instruct' )
input_ids = tokenizer.apply_chat_template([
{"role" : "user" , "content" : d["query" ]},
{"role" : "assistant" , "content" : "\n\n" .join(d["answer" ])},
], tokenize=True , add_generation_prompt=False ,return_tensors='pt' )
attention_mask = input_ids!=tokenizer.pad_token_id
step_last_tokens = []
for step_num in range (0 , len (d["answer" ])+1 ):
conv = tokenizer.apply_chat_template([
{"role" :"user" , "content" :d["query" ]},
{"role" :"assistant" , "content" :"\n\n" .join(d["answer" ][:step_num])},
], tokenize=False , add_generation_prompt=False )
conv = conv.strip()
if step_num!=0 and step_num!=len (d['answer' ]):
conv+='\n\n'
currect_ids = tokenizer.encode(conv,add_special_tokens=False )
step_last_tokens.append(len (currect_ids) - 2 )
inputs = {'input_ids' :input_ids,'attention_mask' :attention_mask,'labels' :input_ids}
label_mask = torch.tensor([[0 ]*step_last_tokens[0 ]+[1 ]*(input_ids.shape[-1 ]-step_last_tokens[0 ])])
step_last_tokens = torch.tensor([step_last_tokens])
def get_logps (model,inputs ):
logits = model(input_ids=inputs['input_ids' ], attention_mask=inputs['attention_mask' ]).logits
labels = inputs['labels' ][:, 1 :].clone().long()
logits = logits[:, :-1 , :]
labels[labels == -100 ] = 0
per_token_logps = torch.gather(logits.log_softmax(-1 ), dim=2 , index=labels.unsqueeze(2 )).squeeze(2 )
return per_token_logps
with torch.no_grad():
per_token_logps = get_logps(model, inputs)
ref_per_token_logps = get_logps(ref_model,inputs)
raw_reward = per_token_logps - ref_per_token_logps
beta_reward = coef * raw_reward * label_mask[:,1 :]
beta_reward = beta_reward.cumsum(-1 )
beta_reward = beta_reward.gather(dim=-1 , index=step_last_tokens[:,1 :])
print (beta_reward)
Evaluation
Evaluation Code
We use codes in Implicit PRM to evaluate the performance of EurusPRM. The reference model is Qwen2.5-Math-7B-Instruct .
Evaluation Base Model
We adopt Eurus-2-7B-SFT , Qwen2.5-7B-Instruct and Llama-3.1-70B-Instruct as generation models to evaluate the performance of our implicit PRM. For all models, we set the sampling temperature as 0.5, p of the top-p sampling as 1.
Best-of-N Sampling
We use Best-of-64 as our evaluation metric. The weighting methods are different for several PRMs below.
For Skywork-o1-Open-PRM-Qwen-2.5-7B , we use simple average reward across all steps.
For EurusPRM-Stage 1, we use the minimum reward across all steps.
For EurusPRM-Stage 2, we use the accumulative rewards.
Eurus-2-7B-SFT
Method
Reward Model
MATH
AMC
AIME_2024
OlympiadBench
Minerva Math
Avg
Greedy Pass @ 1
N/A
65.1
30.1
3.3
29.8
32.7
32.2
Majority Voting @ 64
N/A
65.6
53.0
13.3
39.1
22.4
38.7
Best-of-64
Skywork-o1-Open-PRM-Qwen-2.5-7B
47.2
45.8
10.0
32.3
16.2
30.3
EurusPRM-Stage 1
44.6
41.0
6.7
32.9
17.3
28.5
EurusPRM-Stage 2
47.2
43.4
13.3
33.8
19.2
31.4
Weighted Best-of-64
Skywork-o1-Open-PRM-Qwen-2.5-7B
64.6
55.4 13.3
41.3
23.2
39.6
EurusPRM-Stage 1
66.0 54.2
13.3
39.6
29.0 40.4
EurusPRM-Stage 2
66.0 54.2
13.3
39.7 29.0 40.4
Llama-3.1-70B-Instruct
Method
Reward Model
MATH
AMC
AIME 2024
OlympiadBench
Minerva Math
Avg
Greedy Pass @ 1
N/A
64.6
30.1
16.7
31.9
35.3
35.7
Majority Voting @ 64
N/A
80.2
53.0
26.7
40.4
38.6
47.8
Best-of-N @ 64
Skywork-o1-Open-PRM-Qwen-2.5-7B
77.8
56.6
23.3
39.0
31.6
45.7
EurusPRM-Stage 1
77.8
44.6
26.7 35.3
41.5
45.2
EurusPRM-Stage 2
80.6
59.0 20.0
37.6
44.9
48.4
Weighted Best-of-64
Skywork-o1-Open-PRM-Qwen-2.5-7B
81.2 56.6
23.3
42.4 38.2
48.3
EurusPRM-Stage 1
80.4
53.0
26.7 40.9
46.7 49.5
EurusPRM-Stage 2
80.4
53.0
26.7 41.0
46.3
49.5
Qwen2.5-7B-Instruct
Method
Reward Model
MATH
AMC
AIME 2024
OlympiadBench
Minerva Math
Avg
Greedy Pass @ 1
N/A
73.3
47.0
13.3
39.4
35.3
41.7
Majority Voting @ 64
N/A
82.0
53.0
16.7
43.0
36.4
46.2
Best-of-N @ 64
Skywork-o1-Open-PRM-Qwen-2.5-7B
85.2
60.2 20.0 44.7 32.7
48.6
EurusPRM-Stage 1
81.8
47.0
16.7
40.1
41.5
45.4
EurusPRM-Stage 2
86.0 59.0
16.7
41.4
41.5
48.9
Weighted Best-of-64
Skywork-o1-Open-PRM-Qwen-2.5-7B
83.6
55.4
13.3
43.7
36.8
46.6
EurusPRM-Stage 1
82.6
53.0
16.7
42.7
45.2
48.0
EurusPRM-Stage 2
84.8
53.0
16.7
43.2
45.6 48.7
Citation
@article{cui2025process,
title={Process reinforcement through implicit rewards},
author={Cui, Ganqu and Yuan, Lifan and Wang, Zefan and Wang, Hanbin and Li, Wendi and He, Bingxiang and Fan, Yuchen and Yu, Tianyu and Xu, Qixin and Chen, Weize and others},
journal={arXiv preprint arXiv:2502.01456},
year={2025}
}
@article{yuan2024implicitprm,
title={Free Process Rewards without Process Labels},
author={Lifan Yuan and Wendi Li and Huayu Chen and Ganqu Cui and Ning Ding and Kaiyan Zhang and Bowen Zhou and Zhiyuan Liu and Hao Peng},
journal={arXiv preprint arXiv:2412.01981},
year={2024}
}