problem
stringlengths 5
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 4
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 5
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 10k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:
$$
\frac{a_{1}}{k^{2}+1}+\frac{a_{2}}{k^{2}+2}+\frac{a_{3}}{k^{2}+3}+\frac{a_{4}}{k^{2}+4}+\frac{a_{5}}{k^{2}+5}=\frac{1}{k^{2}} \text { for } k=1,2,3,4,5
$$
Find the value of $\frac{a_{1}}{37}+\frac{a_{2}}{38}+\frac{a_{3}}{39}+\frac{a_{4}}{40}+\frac{a_{5}}{41}$. (Express the value in a single fraction.)
|
Let $R(x):=\frac{a_{1}}{x^{2}+1}+\frac{a_{2}}{x^{2}+2}+\frac{a_{3}}{x^{2}+3}+\frac{a_{4}}{x^{2}+4}+\frac{a_{5}}{x^{2}+5}$. Then $R( \pm 1)=1$, $R( \pm 2)=\frac{1}{4}, R( \pm 3)=\frac{1}{9}, R( \pm 4)=\frac{1}{16}, R( \pm 5)=\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get $Q(k)=R(k) P(k)=\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get
$$
P(x)-x^{2} Q(x)=A\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)
$$
Putting $x=0$, we get $A=\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields
$$
1-x^{2} R(x)=1-x^{2} \frac{Q(x)}{P(x)}=-\frac{1}{120} \cdot \frac{\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)}{\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)}
$$
and hence that
$$
1-36 R(6)=-\frac{35 \times 32 \times 27 \times 20 \times 11}{120 \times 37 \times 38 \times 39 \times 40 \times 41}=-\frac{3 \times 7 \times 11}{13 \times 19 \times 37 \times 41}=-\frac{231}{374699}
$$
which implies $R(6)=\frac{187465}{6744582}$.
Remark. We can get $a_{1}=\frac{1105}{72}, a_{2}=-\frac{2673}{40}, a_{3}=\frac{1862}{15}, a_{4}=-\frac{1885}{18}, a_{5}=\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.
|
\frac{187465}{6744582}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ be real numbers satisfying the following equations:
$$
\frac{a_{1}}{k^{2}+1}+\frac{a_{2}}{k^{2}+2}+\frac{a_{3}}{k^{2}+3}+\frac{a_{4}}{k^{2}+4}+\frac{a_{5}}{k^{2}+5}=\frac{1}{k^{2}} \text { for } k=1,2,3,4,5
$$
Find the value of $\frac{a_{1}}{37}+\frac{a_{2}}{38}+\frac{a_{3}}{39}+\frac{a_{4}}{40}+\frac{a_{5}}{41}$. (Express the value in a single fraction.)
|
Let $R(x):=\frac{a_{1}}{x^{2}+1}+\frac{a_{2}}{x^{2}+2}+\frac{a_{3}}{x^{2}+3}+\frac{a_{4}}{x^{2}+4}+\frac{a_{5}}{x^{2}+5}$. Then $R( \pm 1)=1$, $R( \pm 2)=\frac{1}{4}, R( \pm 3)=\frac{1}{9}, R( \pm 4)=\frac{1}{16}, R( \pm 5)=\frac{1}{25}$ and $R(6)$ is the value to be found. Let's put $P(x):=\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)$ and $Q(x):=R(x) P(x)$. Then for $k= \pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get $Q(k)=R(k) P(k)=\frac{P(k)}{k^{2}}$, that is, $P(k)-k^{2} Q(k)=0$. Since $P(x)-x^{2} Q(x)$ is a polynomial of degree 10 with roots $\pm 1, \pm 2, \pm 3, \pm 4, \pm 5$, we get
$$
P(x)-x^{2} Q(x)=A\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)
$$
Putting $x=0$, we get $A=\frac{P(0)}{(-1)(-4)(-9)(-16)(-25)}=-\frac{1}{120}$. Finally, dividing both sides of $(*)$ by $P(x)$ yields
$$
1-x^{2} R(x)=1-x^{2} \frac{Q(x)}{P(x)}=-\frac{1}{120} \cdot \frac{\left(x^{2}-1\right)\left(x^{2}-4\right)\left(x^{2}-9\right)\left(x^{2}-16\right)\left(x^{2}-25\right)}{\left(x^{2}+1\right)\left(x^{2}+2\right)\left(x^{2}+3\right)\left(x^{2}+4\right)\left(x^{2}+5\right)}
$$
and hence that
$$
1-36 R(6)=-\frac{35 \times 32 \times 27 \times 20 \times 11}{120 \times 37 \times 38 \times 39 \times 40 \times 41}=-\frac{3 \times 7 \times 11}{13 \times 19 \times 37 \times 41}=-\frac{231}{374699}
$$
which implies $R(6)=\frac{187465}{6744582}$.
Remark. We can get $a_{1}=\frac{1105}{72}, a_{2}=-\frac{2673}{40}, a_{3}=\frac{1862}{15}, a_{4}=-\frac{1885}{18}, a_{5}=\frac{1323}{40}$ by solving the given system of linear equations, which is extremely messy and takes a lot of time.
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "(Solution)"
}
|
149fe16f-5e4d-586c-aea5-aafc6a7e9dea
| 605,313
|
Let three circles $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}$, which are non-overlapping and mutually external, be given in the plane. For each point $P$ in the plane, outside the three circles, construct six points $A_{1}, B_{1}, A_{2}, B_{2}, A_{3}, B_{3}$ as follows: For each $i=1,2,3, A_{i}, B_{i}$ are distinct points on the circle $\Gamma_{i}$ such that the lines $P A_{i}$ and $P B_{i}$ are both tangents to $\Gamma_{i}$. Call the point $P$ exceptional if, from the construction, three lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ are concurrent. Show that every exceptional point of the plane, if exists, lies on the same circle.
|
Let $O_{i}$ be the center and $r_{i}$ the radius of circle $\Gamma_{i}$ for each $i=1,2,3$. Let $P$ be an exceptional point, and let the three corresponding lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ concur at $Q$. Construct the circle with diameter $P Q$. Call the circle $\Gamma$, its center $O$ and its radius $r$. We now claim that all exceptional points lie on $\Gamma$.
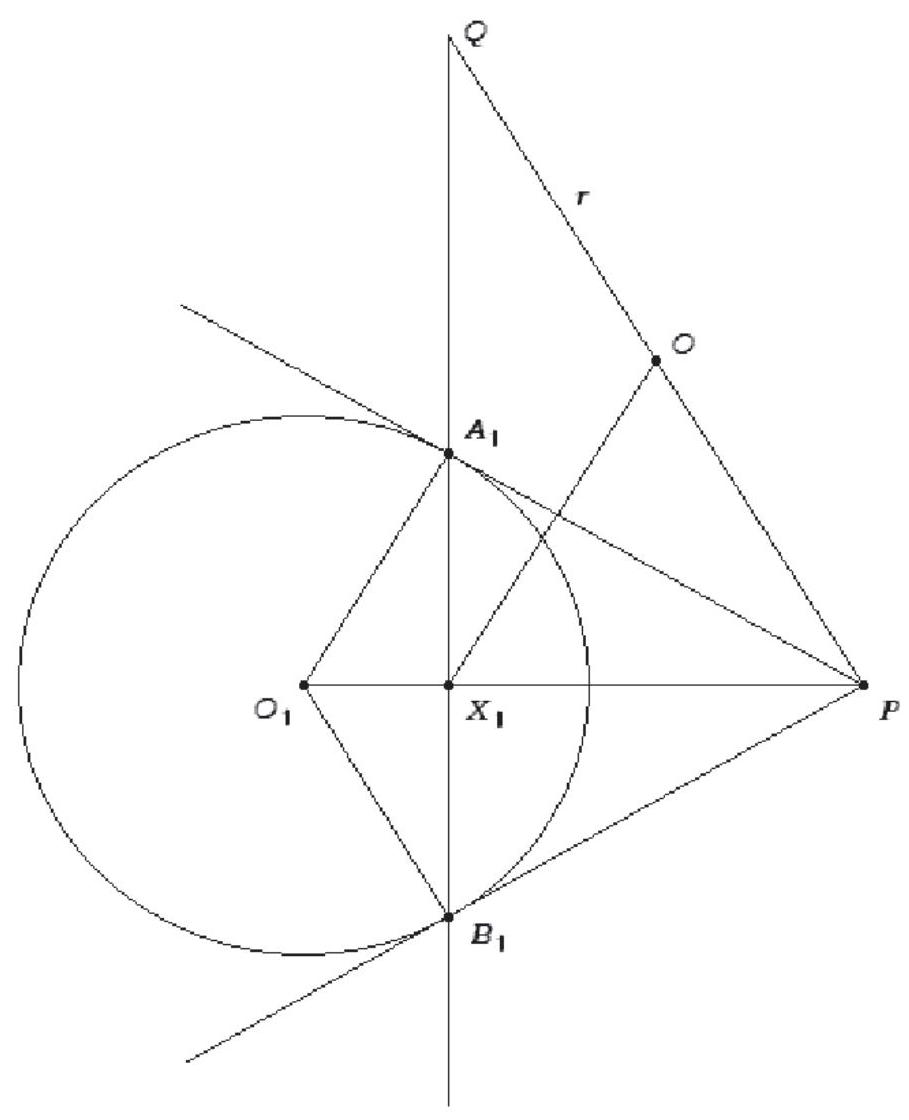
Let $P O_{1}$ intersect $A_{1} B_{1}$ in $X_{1}$. As $P O_{1} \perp A_{1} B_{1}$, we see that $X_{1}$ lies on $\Gamma$. As $P A_{1}$ is a tangent to $\Gamma_{1}$, triangle $P A_{1} O_{1}$ is right-angled and similar to triangle $A_{1} X_{1} O_{1}$. It follows that
$$
\frac{O_{1} X_{1}}{O_{1} A_{1}}=\frac{O_{1} A_{1}}{O_{1} P}, \quad \text { i.e., } \quad O_{1} X_{1} \cdot O_{1} P=O_{1} A_{1}^{2}=r_{1}^{2}
$$
On the other hand, $O_{1} X_{1} \cdot O_{1} P$ is also the power of $O_{1}$ with respect to $\Gamma$, so that
$$
r_{1}^{2}=O_{1} X_{1} \cdot O_{1} P=\left(O_{1} O-r\right)\left(O_{1} O+r\right)=O_{1} O^{2}-r^{2}
$$
and hence
$$
r^{2}=O O_{1}^{2}-r_{1}^{2}=\left(O O_{1}-r_{1}\right)\left(O O_{1}+r_{1}\right)
$$
Thus, $r^{2}$ is the power of $O$ with respect to $\Gamma_{1}$. By the same token, $r^{2}$ is also the power of $O$ with respect to $\Gamma_{2}$ and $\Gamma_{3}$. Hence $O$ must be the radical center of the three given circles. Since $r$, as the square root of the power of $O$ with respect to the three given circles, does not depend on $P$, it follows that all exceptional points lie on $\Gamma$.
Remark. In the event of the radical point being at infinity (and hence the three radical axes being parallel), there are no exceptional points in the plane, which is consistent with the statement of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let three circles $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}$, which are non-overlapping and mutually external, be given in the plane. For each point $P$ in the plane, outside the three circles, construct six points $A_{1}, B_{1}, A_{2}, B_{2}, A_{3}, B_{3}$ as follows: For each $i=1,2,3, A_{i}, B_{i}$ are distinct points on the circle $\Gamma_{i}$ such that the lines $P A_{i}$ and $P B_{i}$ are both tangents to $\Gamma_{i}$. Call the point $P$ exceptional if, from the construction, three lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ are concurrent. Show that every exceptional point of the plane, if exists, lies on the same circle.
|
Let $O_{i}$ be the center and $r_{i}$ the radius of circle $\Gamma_{i}$ for each $i=1,2,3$. Let $P$ be an exceptional point, and let the three corresponding lines $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ concur at $Q$. Construct the circle with diameter $P Q$. Call the circle $\Gamma$, its center $O$ and its radius $r$. We now claim that all exceptional points lie on $\Gamma$.

Let $P O_{1}$ intersect $A_{1} B_{1}$ in $X_{1}$. As $P O_{1} \perp A_{1} B_{1}$, we see that $X_{1}$ lies on $\Gamma$. As $P A_{1}$ is a tangent to $\Gamma_{1}$, triangle $P A_{1} O_{1}$ is right-angled and similar to triangle $A_{1} X_{1} O_{1}$. It follows that
$$
\frac{O_{1} X_{1}}{O_{1} A_{1}}=\frac{O_{1} A_{1}}{O_{1} P}, \quad \text { i.e., } \quad O_{1} X_{1} \cdot O_{1} P=O_{1} A_{1}^{2}=r_{1}^{2}
$$
On the other hand, $O_{1} X_{1} \cdot O_{1} P$ is also the power of $O_{1}$ with respect to $\Gamma$, so that
$$
r_{1}^{2}=O_{1} X_{1} \cdot O_{1} P=\left(O_{1} O-r\right)\left(O_{1} O+r\right)=O_{1} O^{2}-r^{2}
$$
and hence
$$
r^{2}=O O_{1}^{2}-r_{1}^{2}=\left(O O_{1}-r_{1}\right)\left(O O_{1}+r_{1}\right)
$$
Thus, $r^{2}$ is the power of $O$ with respect to $\Gamma_{1}$. By the same token, $r^{2}$ is also the power of $O$ with respect to $\Gamma_{2}$ and $\Gamma_{3}$. Hence $O$ must be the radical center of the three given circles. Since $r$, as the square root of the power of $O$ with respect to the three given circles, does not depend on $P$, it follows that all exceptional points lie on $\Gamma$.
Remark. In the event of the radical point being at infinity (and hence the three radical axes being parallel), there are no exceptional points in the plane, which is consistent with the statement of the problem.
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "(Solution)"
}
|
fcc2aa8b-17ae-5861-a9ef-182d467cfc53
| 260,914
|
Prove that for any positive integer $k$, there exists an arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of rational numbers, where $a_{i}, b_{i}$ are relatively prime positive integers for each $i=1,2, \ldots, k$, such that the positive integers $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{k}, b_{k}$ are all distinct.
|
For $k=1$, there is nothing to prove. Henceforth assume $k \geq 2$.
Let $p_{1}, p_{2}, \ldots, p_{k}$ be $k$ distinct primes such that
$$
k<p_{k}<\cdots<p_{2}<p_{1}
$$
and let $N=p_{1} p_{2} \cdots p_{k}$. By Chinese Remainder Theorem, there exists a positive integer $x$ satisfying
$$
x \equiv-i \quad\left(\bmod p_{i}\right)
$$
for all $i=1,2, \ldots, k$ and $x>N^{2}$. Consider the following sequence:
$$
\frac{x+1}{N}, \frac{x+2}{N}, \quad, \ldots, \frac{x+k}{N}
$$
This sequence is obviously an arithmetic sequence of positive rational numbers of length $k$. For each $i=1,2, \ldots, k$, the numerator $x+i$ is divisible by $p_{i}$ but not by $p_{j}$ for $j \neq i$, for otherwise $p_{j}$ divides $|i-j|$, which is not possible because $p_{j}>k>|i-j|$. Let
$$
a_{i}:=\frac{x+i}{p_{i}}, \quad b_{i}:=\frac{N}{p_{i}} \quad \text { for all } i=1,2, \ldots, k
$$
Then
$$
\frac{x+i}{N}=\frac{a_{i}}{b_{i}}, \quad \operatorname{gcd}\left(a_{i}, b_{i}\right)=1 \quad \text { for all } i=1,2, \ldots, k
$$
and all $b_{i}$ 's are distinct from each other. Moreover, $x>N^{2}$ implies
$$
a_{i}=\frac{x+i}{p_{i}}>\frac{N^{2}}{p_{i}}>N>\frac{N}{p_{j}}=b_{j} \quad \text { for all } i, j=1,2, \ldots, k
$$
and hence all $a_{i}$ 's are distinct from $b_{i}$ 's. It only remains to show that all $a_{i}$ 's are distinct from each other. This follows from
$$
a_{j}=\frac{x+j}{p_{j}}>\frac{x+i}{p_{j}}>\frac{x+i}{p_{i}}=a_{i} \quad \text { for all } i<j
$$
by our choice of $p_{1}, p_{2}, \ldots, p_{k}$. Thus, the arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of positive rational numbers satisfies the conditions of the problem.
Remark. Here is a much easier solution :
For any positive integer $k \geq 2$, consider the sequence
$$
\frac{(k!)^{2}+1}{k!}, \frac{(k!)^{2}+2}{k!}, \ldots, \frac{(k!)^{2}+k}{k!}
$$
Note that $\operatorname{gcd}\left(k!,(k!)^{2}+i\right)=i$ for all $i=1,2, \ldots, k$. So, taking
$$
a_{i}:=\frac{(k!)^{2}+i}{i}, \quad b_{i}:=\frac{k!}{i} \quad \text { for all } i=1,2, \ldots, k
$$
we have $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ and
$$
a_{i}=\frac{(k!)^{2}+i}{i}>a_{j}=\frac{(k!)^{2}+j}{j}>b_{i}=\frac{k!}{i}>b_{j}=\frac{k!}{j}
$$
for any $1 \leq i<j \leq k$. Therefore this sequence satisfies every condition given in the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for any positive integer $k$, there exists an arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of rational numbers, where $a_{i}, b_{i}$ are relatively prime positive integers for each $i=1,2, \ldots, k$, such that the positive integers $a_{1}, b_{1}, a_{2}, b_{2}, \ldots, a_{k}, b_{k}$ are all distinct.
|
For $k=1$, there is nothing to prove. Henceforth assume $k \geq 2$.
Let $p_{1}, p_{2}, \ldots, p_{k}$ be $k$ distinct primes such that
$$
k<p_{k}<\cdots<p_{2}<p_{1}
$$
and let $N=p_{1} p_{2} \cdots p_{k}$. By Chinese Remainder Theorem, there exists a positive integer $x$ satisfying
$$
x \equiv-i \quad\left(\bmod p_{i}\right)
$$
for all $i=1,2, \ldots, k$ and $x>N^{2}$. Consider the following sequence:
$$
\frac{x+1}{N}, \frac{x+2}{N}, \quad, \ldots, \frac{x+k}{N}
$$
This sequence is obviously an arithmetic sequence of positive rational numbers of length $k$. For each $i=1,2, \ldots, k$, the numerator $x+i$ is divisible by $p_{i}$ but not by $p_{j}$ for $j \neq i$, for otherwise $p_{j}$ divides $|i-j|$, which is not possible because $p_{j}>k>|i-j|$. Let
$$
a_{i}:=\frac{x+i}{p_{i}}, \quad b_{i}:=\frac{N}{p_{i}} \quad \text { for all } i=1,2, \ldots, k
$$
Then
$$
\frac{x+i}{N}=\frac{a_{i}}{b_{i}}, \quad \operatorname{gcd}\left(a_{i}, b_{i}\right)=1 \quad \text { for all } i=1,2, \ldots, k
$$
and all $b_{i}$ 's are distinct from each other. Moreover, $x>N^{2}$ implies
$$
a_{i}=\frac{x+i}{p_{i}}>\frac{N^{2}}{p_{i}}>N>\frac{N}{p_{j}}=b_{j} \quad \text { for all } i, j=1,2, \ldots, k
$$
and hence all $a_{i}$ 's are distinct from $b_{i}$ 's. It only remains to show that all $a_{i}$ 's are distinct from each other. This follows from
$$
a_{j}=\frac{x+j}{p_{j}}>\frac{x+i}{p_{j}}>\frac{x+i}{p_{i}}=a_{i} \quad \text { for all } i<j
$$
by our choice of $p_{1}, p_{2}, \ldots, p_{k}$. Thus, the arithmetic sequence
$$
\frac{a_{1}}{b_{1}}, \quad \frac{a_{2}}{b_{2}}, \ldots, \quad \frac{a_{k}}{b_{k}}
$$
of positive rational numbers satisfies the conditions of the problem.
Remark. Here is a much easier solution :
For any positive integer $k \geq 2$, consider the sequence
$$
\frac{(k!)^{2}+1}{k!}, \frac{(k!)^{2}+2}{k!}, \ldots, \frac{(k!)^{2}+k}{k!}
$$
Note that $\operatorname{gcd}\left(k!,(k!)^{2}+i\right)=i$ for all $i=1,2, \ldots, k$. So, taking
$$
a_{i}:=\frac{(k!)^{2}+i}{i}, \quad b_{i}:=\frac{k!}{i} \quad \text { for all } i=1,2, \ldots, k
$$
we have $\operatorname{gcd}\left(a_{i}, b_{i}\right)=1$ and
$$
a_{i}=\frac{(k!)^{2}+i}{i}>a_{j}=\frac{(k!)^{2}+j}{j}>b_{i}=\frac{k!}{i}>b_{j}=\frac{k!}{j}
$$
for any $1 \leq i<j \leq k$. Therefore this sequence satisfies every condition given in the problem.
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "(Solution)"
}
|
65d2cd32-d74b-5aa1-9ed5-cdb332a0343a
| 605,340
|
Larry and Rob are two robots travelling in one car from Argovia to Zillis. Both robots have control over the steering and steer according to the following algorithm: Larry makes a $90^{\circ}$ left turn after every $\ell$ kilometer driving from start; Rob makes a $90^{\circ}$ right turn after every $r$ kilometer driving from start, where $\ell$ and $r$ are relatively prime positive integers. In the event of both turns occurring simultaneously, the car will keep going without changing direction. Assume that the ground is flat and the car can move in any direction.
Let the car start from Argovia facing towards Zillis. For which choices of the pair $(\ell, r)$ is the car guaranteed to reach Zillis, regardless of how far it is from Argovia?
|
Let Zillis be $d$ kilometers away from Argovia, where $d$ is a positive real number. For simplicity, we will position Argovia at $(0,0)$ and Zillis at $(d, 0)$, so that the car starts out facing east. We will investigate how the car moves around in the period of travelling the first $\ell r$ kilometers, the second $\ell r$ kilometers, ..., and so on. We call each period of travelling $\ell r$ kilometers a section. It is clear that the car will have identical behavior in every section except the direction of the car at the beginning.
Case 1: $\underline{\ell-r \equiv 2(\bmod 4)}$. After the first section, the car has made $\ell-1$ right turns and $r-1$ left turns, which is a net of $2(\equiv \ell-r(\bmod 4))$ right turns. Let the displacement vector for the first section be $(x, y)$. Since the car has rotated $180^{\circ}$, the displacement vector for the second section will be $(-x,-y)$, which will take the car back to $(0,0)$ facing east again. We now have our original situation, and the car has certainly never travelled further than lr kilometers from Argovia. So, the car cannot reach Zillis if it is further apart from Argovia.
Case 2: $\ell-r \equiv 1(\bmod 4)$. After the first section, the car has made a net of 1 right turn. Let the displacement vector for the first section again be $(x, y)$. This time the car has rotated $90^{\circ}$ clockwise. We can see that the displacements for the second, third and fourth section will be $(y,-x),(-x,-y)$ and $(-y, x)$, respectively, so after four sections the car is back at $(0,0)$ facing east. Since the car has certainly never travelled further than $2 \ell r$ kilometers from Argovia, the car cannot reach Zillis if it is further apart from Argovia.
Case 3: $\quad \ell-r \equiv 3(\bmod 4)$. An argument similar to that in Case 2 (switching the roles of left and right) shows that the car cannot reach Zillis if it is further apart from Argovia.
Case 4: $\quad \ell \equiv r(\bmod 4)$. The car makes a net turn of $0^{\circ}$ after each section, so it must be facing east. We are going to show that, after traversing the first section, the car will be at $(1,0)$. It will be useful to interpret the Cartesian plane as the complex plane, i.e. writing $x+i y$ for $(x, y)$, where $i=\sqrt{-1}$. We will denote the $k$-th kilometer of movement by $m_{k-1}$,
which takes values from the set $\{1, i,-1,-i\}$, depending on the direction. We then just have to show that
$$
\sum_{k=0}^{\ell r-1} m_{k}=1
$$
which implies that the car will get to Zillis no matter how far it is apart from Argovia.
Case $4 \mathrm{a}: \underline{\ell \equiv r \equiv 1(\bmod 4)}$. First note that for $k=0,1, \ldots, \ell r-1$,
$$
m_{k}=i^{\lfloor k / \ell\rfloor}(-i)^{\lfloor k / r\rfloor}
$$
since $\lfloor k / \ell\rfloor$ and $\lfloor k / r\rfloor$ are the exact numbers of left and right turns before the $(k+1)$ st kilometer, respectively. Let $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ be the remainders of $k$ when divided by $\ell$ and $r$, respectively. Then, since
$$
a_{k}=k-\left\lfloor\frac{k}{\ell}\right\rfloor \ell \equiv k-\left\lfloor\frac{k}{\ell}\right\rfloor \quad(\bmod 4) \quad \text { and } \quad b_{k}=k-\left\lfloor\frac{k}{r}\right\rfloor r \equiv k-\left\lfloor\frac{k}{r}\right\rfloor \quad(\bmod 4),
$$
we have $\lfloor k / \ell\rfloor \equiv k-a_{k}(\bmod 4)$ and $\lfloor k / r\rfloor \equiv k-b_{k}(\bmod 4)$. We therefore have
$$
m_{k}=i^{k-a_{k}}(-i)^{k-b_{k}}=\left(-i^{2}\right)^{k} i^{-a_{k}}(-i)^{-b_{k}}=(-i)^{a_{k}} i^{b_{k}} .
$$
As $\ell$ and $r$ are relatively prime, by Chinese Remainder Theorem, there is a bijection between pairs $\left(a_{k}, b_{k}\right)=(k(\bmod \ell), k(\bmod r))$ and the numbers $k=0,1,2, \ldots, \ell r-1$. Hence
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=1 \times 1=1
$$
as required because $\ell \equiv r \equiv 1(\bmod 4)$.
Case $4 \mathrm{~b}: \underline{\ell \equiv r \equiv 3(\bmod 4)}$. In this case, we get
$$
m_{k}=i^{a_{k}}(-i)^{b_{k}}
$$
where $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ for $k=0,1, \ldots, \ell r-1$. Then we can proceed analogously to Case 4a to obtain
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=i \times(-i)=1
$$
as required because $\ell \equiv r \equiv 3(\bmod 4)$.
Now clearly the car traverses through all points between $(0,0)$ and $(1,0)$ during the first section and, in fact, covers all points between $(n-1,0)$ and $(n, 0)$ during the $n$-th section. Hence it will eventually reach $(d, 0)$ for any positive $d$.
To summarize: $(\ell, r)$ satisfies the required conditions if and only if
$$
\ell \equiv r \equiv 1 \quad \text { or } \quad \ell \equiv r \equiv 3 \quad(\bmod 4)
$$
Remark. In case $\operatorname{gcd}(\ell, r)=d \neq 1$, the answer is :
$$
\frac{\ell}{d} \equiv \frac{r}{d} \equiv 1 \quad \text { or } \quad \frac{\ell}{d} \equiv \frac{r}{d} \equiv 3 \quad(\bmod 4)
$$
|
\ell \equiv r \equiv 1 \quad \text { or } \quad \ell \equiv r \equiv 3 \quad(\bmod 4)
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Larry and Rob are two robots travelling in one car from Argovia to Zillis. Both robots have control over the steering and steer according to the following algorithm: Larry makes a $90^{\circ}$ left turn after every $\ell$ kilometer driving from start; Rob makes a $90^{\circ}$ right turn after every $r$ kilometer driving from start, where $\ell$ and $r$ are relatively prime positive integers. In the event of both turns occurring simultaneously, the car will keep going without changing direction. Assume that the ground is flat and the car can move in any direction.
Let the car start from Argovia facing towards Zillis. For which choices of the pair $(\ell, r)$ is the car guaranteed to reach Zillis, regardless of how far it is from Argovia?
|
Let Zillis be $d$ kilometers away from Argovia, where $d$ is a positive real number. For simplicity, we will position Argovia at $(0,0)$ and Zillis at $(d, 0)$, so that the car starts out facing east. We will investigate how the car moves around in the period of travelling the first $\ell r$ kilometers, the second $\ell r$ kilometers, ..., and so on. We call each period of travelling $\ell r$ kilometers a section. It is clear that the car will have identical behavior in every section except the direction of the car at the beginning.
Case 1: $\underline{\ell-r \equiv 2(\bmod 4)}$. After the first section, the car has made $\ell-1$ right turns and $r-1$ left turns, which is a net of $2(\equiv \ell-r(\bmod 4))$ right turns. Let the displacement vector for the first section be $(x, y)$. Since the car has rotated $180^{\circ}$, the displacement vector for the second section will be $(-x,-y)$, which will take the car back to $(0,0)$ facing east again. We now have our original situation, and the car has certainly never travelled further than lr kilometers from Argovia. So, the car cannot reach Zillis if it is further apart from Argovia.
Case 2: $\ell-r \equiv 1(\bmod 4)$. After the first section, the car has made a net of 1 right turn. Let the displacement vector for the first section again be $(x, y)$. This time the car has rotated $90^{\circ}$ clockwise. We can see that the displacements for the second, third and fourth section will be $(y,-x),(-x,-y)$ and $(-y, x)$, respectively, so after four sections the car is back at $(0,0)$ facing east. Since the car has certainly never travelled further than $2 \ell r$ kilometers from Argovia, the car cannot reach Zillis if it is further apart from Argovia.
Case 3: $\quad \ell-r \equiv 3(\bmod 4)$. An argument similar to that in Case 2 (switching the roles of left and right) shows that the car cannot reach Zillis if it is further apart from Argovia.
Case 4: $\quad \ell \equiv r(\bmod 4)$. The car makes a net turn of $0^{\circ}$ after each section, so it must be facing east. We are going to show that, after traversing the first section, the car will be at $(1,0)$. It will be useful to interpret the Cartesian plane as the complex plane, i.e. writing $x+i y$ for $(x, y)$, where $i=\sqrt{-1}$. We will denote the $k$-th kilometer of movement by $m_{k-1}$,
which takes values from the set $\{1, i,-1,-i\}$, depending on the direction. We then just have to show that
$$
\sum_{k=0}^{\ell r-1} m_{k}=1
$$
which implies that the car will get to Zillis no matter how far it is apart from Argovia.
Case $4 \mathrm{a}: \underline{\ell \equiv r \equiv 1(\bmod 4)}$. First note that for $k=0,1, \ldots, \ell r-1$,
$$
m_{k}=i^{\lfloor k / \ell\rfloor}(-i)^{\lfloor k / r\rfloor}
$$
since $\lfloor k / \ell\rfloor$ and $\lfloor k / r\rfloor$ are the exact numbers of left and right turns before the $(k+1)$ st kilometer, respectively. Let $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ be the remainders of $k$ when divided by $\ell$ and $r$, respectively. Then, since
$$
a_{k}=k-\left\lfloor\frac{k}{\ell}\right\rfloor \ell \equiv k-\left\lfloor\frac{k}{\ell}\right\rfloor \quad(\bmod 4) \quad \text { and } \quad b_{k}=k-\left\lfloor\frac{k}{r}\right\rfloor r \equiv k-\left\lfloor\frac{k}{r}\right\rfloor \quad(\bmod 4),
$$
we have $\lfloor k / \ell\rfloor \equiv k-a_{k}(\bmod 4)$ and $\lfloor k / r\rfloor \equiv k-b_{k}(\bmod 4)$. We therefore have
$$
m_{k}=i^{k-a_{k}}(-i)^{k-b_{k}}=\left(-i^{2}\right)^{k} i^{-a_{k}}(-i)^{-b_{k}}=(-i)^{a_{k}} i^{b_{k}} .
$$
As $\ell$ and $r$ are relatively prime, by Chinese Remainder Theorem, there is a bijection between pairs $\left(a_{k}, b_{k}\right)=(k(\bmod \ell), k(\bmod r))$ and the numbers $k=0,1,2, \ldots, \ell r-1$. Hence
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=1 \times 1=1
$$
as required because $\ell \equiv r \equiv 1(\bmod 4)$.
Case $4 \mathrm{~b}: \underline{\ell \equiv r \equiv 3(\bmod 4)}$. In this case, we get
$$
m_{k}=i^{a_{k}}(-i)^{b_{k}}
$$
where $a_{k}(\equiv k(\bmod \ell))$ and $b_{k}(\equiv k(\bmod r))$ for $k=0,1, \ldots, \ell r-1$. Then we can proceed analogously to Case 4a to obtain
$$
\sum_{k=0}^{\ell r-1} m_{k}=\sum_{k=0}^{\ell r-1}(-i)^{a_{k}} i^{b_{k}}=\left(\sum_{k=0}^{\ell-1}(-i)^{a_{k}}\right)\left(\sum_{k=0}^{r-1} i^{b_{k}}\right)=i \times(-i)=1
$$
as required because $\ell \equiv r \equiv 3(\bmod 4)$.
Now clearly the car traverses through all points between $(0,0)$ and $(1,0)$ during the first section and, in fact, covers all points between $(n-1,0)$ and $(n, 0)$ during the $n$-th section. Hence it will eventually reach $(d, 0)$ for any positive $d$.
To summarize: $(\ell, r)$ satisfies the required conditions if and only if
$$
\ell \equiv r \equiv 1 \quad \text { or } \quad \ell \equiv r \equiv 3 \quad(\bmod 4)
$$
Remark. In case $\operatorname{gcd}(\ell, r)=d \neq 1$, the answer is :
$$
\frac{\ell}{d} \equiv \frac{r}{d} \equiv 1 \quad \text { or } \quad \frac{\ell}{d} \equiv \frac{r}{d} \equiv 3 \quad(\bmod 4)
$$
|
{
"resource_path": "APMO/segmented/en-apmo2009_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "(Solution)"
}
|
5835d794-b56d-5f8d-957e-536e413e708d
| 260,929
|
Let $A B C$ be a triangle with $\angle B A C \neq 90^{\circ}$. Let $O$ be the circumcenter of the triangle $A B C$ and let $\Gamma$ be the circumcircle of the triangle $B O C$. Suppose that $\Gamma$ intersects the line segment $A B$ at $P$ different from $B$, and the line segment $A C$ at $Q$ different from $C$. Let $O N$ be a diameter of the circle $\Gamma$. Prove that the quadrilateral $A P N Q$ is a parallelogram.
|
From the assumption that the circle $\Gamma$ intersects both of the line segments $A B$ and $A C$, it follows that the 4 points $N, C, Q, O$ are located on $\Gamma$ in the order of $N, C, Q, O$ or in the order of $N, C, O, Q$. The following argument for the proof of the assertion of the problem is valid in either case. Since $\angle N Q C$ and $\angle N O C$ are subtended by the same arc $\widehat{N C}$ of $\Gamma$ at the points $Q$ and $O$, respectively, on $\Gamma$, we have $\angle N Q C=\angle N O C$. We also have $\angle B O C=2 \angle B A C$, since $\angle B O C$ and $\angle B A C$ are subtended by the same arc $\widehat{B C}$ of the circum-circle of the triangle $A B C$ at the center $O$ of the circle and at the point $A$ on the circle, respectively. From $O B=O C$ and the fact that $O N$ is a diameter of $\Gamma$, it follows that the triangles $O B N$ and $O C N$ are congruent, and therefore we obtain $2 \angle N O C=\angle B O C$. Consequently, we have $\angle N Q C=\frac{1}{2} \angle B O C=\angle B A C$, which shows that the 2 lines $A P, Q N$ are parallel.
In the same manner, we can show that the 2 lines $A Q, P N$ are also parallel. Thus, the quadrilateral $A P N Q$ is a parallelogram.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle B A C \neq 90^{\circ}$. Let $O$ be the circumcenter of the triangle $A B C$ and let $\Gamma$ be the circumcircle of the triangle $B O C$. Suppose that $\Gamma$ intersects the line segment $A B$ at $P$ different from $B$, and the line segment $A C$ at $Q$ different from $C$. Let $O N$ be a diameter of the circle $\Gamma$. Prove that the quadrilateral $A P N Q$ is a parallelogram.
|
From the assumption that the circle $\Gamma$ intersects both of the line segments $A B$ and $A C$, it follows that the 4 points $N, C, Q, O$ are located on $\Gamma$ in the order of $N, C, Q, O$ or in the order of $N, C, O, Q$. The following argument for the proof of the assertion of the problem is valid in either case. Since $\angle N Q C$ and $\angle N O C$ are subtended by the same arc $\widehat{N C}$ of $\Gamma$ at the points $Q$ and $O$, respectively, on $\Gamma$, we have $\angle N Q C=\angle N O C$. We also have $\angle B O C=2 \angle B A C$, since $\angle B O C$ and $\angle B A C$ are subtended by the same arc $\widehat{B C}$ of the circum-circle of the triangle $A B C$ at the center $O$ of the circle and at the point $A$ on the circle, respectively. From $O B=O C$ and the fact that $O N$ is a diameter of $\Gamma$, it follows that the triangles $O B N$ and $O C N$ are congruent, and therefore we obtain $2 \angle N O C=\angle B O C$. Consequently, we have $\angle N Q C=\frac{1}{2} \angle B O C=\angle B A C$, which shows that the 2 lines $A P, Q N$ are parallel.
In the same manner, we can show that the 2 lines $A Q, P N$ are also parallel. Thus, the quadrilateral $A P N Q$ is a parallelogram.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution:"
}
|
28b834bc-001b-53aa-b86b-5010753075aa
| 260,815
|
For a positive integer $k$, call an integer a pure $k$-th power if it can be represented as $m^{k}$ for some integer $m$. Show that for every positive integer $n$ there exist $n$ distinct positive integers such that their sum is a pure 2009-th power, and their product is a pure 2010-th power.
|
For the sake of simplicity, let us set $k=2009$.
First of all, choose $n$ distinct positive integers $b_{1}, \cdots, b_{n}$ suitably so that their product is a pure $k+1$-th power (for example, let $b_{i}=i^{k+1}$ for $i=1, \cdots, n$ ). Then we have $b_{1} \cdots b_{n}=t^{k+1}$ for some positive integer $t$. Set $b_{1}+\cdots+b_{n}=s$.
Now we set $a_{i}=b_{i} s^{k^{2}-1}$ for $i=1, \cdots, n$, and show that $a_{1}, \cdots, a_{n}$ satisfy the required conditions. Since $b_{1}, \cdots, b_{n}$ are distinct positive integers, it is clear that so are $a_{1}, \cdots, a_{n}$. From
$$
\begin{aligned}
a_{1}+\cdots+a_{n} & =s^{k^{2}-1}\left(b_{1}+\cdots+b_{n}\right)=s^{k^{2}}=\left(s^{k}\right)^{2009} \\
a_{1} \cdots a_{n} & =\left(s^{k^{2}-1}\right)^{n} b_{1} \cdots b_{n}=\left(s^{k^{2}-1}\right)^{n} t^{k+1}=\left(s^{(k-1) n} t\right)^{2010}
\end{aligned}
$$
we can see that $a_{1}, \cdots, a_{n}$ satisfy the conditions on the sum and the product as well. This ends the proof of the assertion.
Remark: We can find the appropriate exponent $k^{2}-1$ needed for the construction of the $a_{i}$ 's by solving the simultaneous congruence relations: $x \equiv 0(\bmod k+1), x \equiv-1(\bmod k)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $k$, call an integer a pure $k$-th power if it can be represented as $m^{k}$ for some integer $m$. Show that for every positive integer $n$ there exist $n$ distinct positive integers such that their sum is a pure 2009-th power, and their product is a pure 2010-th power.
|
For the sake of simplicity, let us set $k=2009$.
First of all, choose $n$ distinct positive integers $b_{1}, \cdots, b_{n}$ suitably so that their product is a pure $k+1$-th power (for example, let $b_{i}=i^{k+1}$ for $i=1, \cdots, n$ ). Then we have $b_{1} \cdots b_{n}=t^{k+1}$ for some positive integer $t$. Set $b_{1}+\cdots+b_{n}=s$.
Now we set $a_{i}=b_{i} s^{k^{2}-1}$ for $i=1, \cdots, n$, and show that $a_{1}, \cdots, a_{n}$ satisfy the required conditions. Since $b_{1}, \cdots, b_{n}$ are distinct positive integers, it is clear that so are $a_{1}, \cdots, a_{n}$. From
$$
\begin{aligned}
a_{1}+\cdots+a_{n} & =s^{k^{2}-1}\left(b_{1}+\cdots+b_{n}\right)=s^{k^{2}}=\left(s^{k}\right)^{2009} \\
a_{1} \cdots a_{n} & =\left(s^{k^{2}-1}\right)^{n} b_{1} \cdots b_{n}=\left(s^{k^{2}-1}\right)^{n} t^{k+1}=\left(s^{(k-1) n} t\right)^{2010}
\end{aligned}
$$
we can see that $a_{1}, \cdots, a_{n}$ satisfy the conditions on the sum and the product as well. This ends the proof of the assertion.
Remark: We can find the appropriate exponent $k^{2}-1$ needed for the construction of the $a_{i}$ 's by solving the simultaneous congruence relations: $x \equiv 0(\bmod k+1), x \equiv-1(\bmod k)$.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution:"
}
|
3720b38c-4edb-5765-88ad-6277b0bfb140
| 605,389
|
Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?
|
When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\frac{(n-1)(n-2)}{2}=\frac{n^{2}-3 n+2}{2}$.
Let us show that $\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \in T$ and $B \in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.
Let us now call a set of participants a group if it satisfies the following 2 conditions:
- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \leq i \leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.
- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.
In view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.
Lemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.
Proof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.
The lemma implies that there are at most $\frac{n(n-1)}{2}-(n-1)=\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\frac{n^{2}-3 n+2}{2}$.
Remark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.
Alternate Solution 1: The construction of an example for the case for which the number $\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.
Suppose, then, $n$ participants are separated into $k(k \geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\sum_{i=1}^{k} a_{i} C_{2} \leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From
$$
{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\frac{n^{2}-n}{2}=\left(a_{1}-\frac{n}{2}\right)^{2}+\frac{n^{2}-2 n}{4}
$$
it follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\sum_{i=1}^{k}{ }_{a} C_{2} \leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\frac{n^{2}-3 n+2}{2}$.
Alternate Solution 2: Construction of an example would be the same as the preceding proof.
For a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.
Suppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.
Then the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since
$$
e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\frac{n^{2}-3 n+2}{2}
$$
the number we seek is at most $\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.
|
\frac{n^{2}-3 n+2}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. $n$ people take part in a certain party. For any pair of the participants, either the two are acquainted with each other or they are not. What is the maximum possible number of the pairs for which the two are not acquainted but have a common acquaintance among the participants?
|
When 1 participant, say the person $A$, is mutually acquainted with each of the remaining $n-1$ participants, and if there are no other acquaintance relationships among the participants, then for any pair of participants not involving $A$, the two are not mutual acquaintances, but they have a common acquaintance, namely $A$, so any such pair satisfies the requirement. Thus, the number desired in this case is $\frac{(n-1)(n-2)}{2}=\frac{n^{2}-3 n+2}{2}$.
Let us show that $\frac{n^{2}-3 n+2}{2}$ is the maximum possible number of the pairs satisfying the requirement of the problem. First, let us observe that in the process of trying to find the maximum possible number of such pairs, if we split the participants into two non-empty subsets $T$ and $S$ which are disjoint, we may assume that there is a pair consisting of one person chosen from $T$ and the other chosen from $S$ who are mutual acquaintances. This is so, since if there are no such pair for some splitting $T$ and $S$, then among the pairs consisting of one person chosen from $T$ and the other chosen from $S$, there is no pair for which the two have a common acquaintance among participants, and therefore, if we arbitrarily choose a person $A \in T$ and $B \in S$ and declare that $A$ and $B$ are mutual acquaintances, the number of the pairs satisfying the requirement of the problem does not decrease.
Let us now call a set of participants a group if it satisfies the following 2 conditions:
- One can connect any person in the set with any other person in the set by tracing a chain of mutually acquainted pairs. More precisely, for any pair of people $A, B$ in the set there exists a sequence of people $A_{0}, A_{1}, \cdots, A_{n}$ for which $A_{0}=A, A_{n}=B$ and, for each $i: 0 \leq i \leq n-1, A_{i}$ and $A_{i+1}$ are mutual acquaintances.
- No person in this set can be connected with a person not belonging to this set by tracing a chain of mutually acquainted pairs.
In view of the discussions made above, we may assume that the set of all the participants to the party forms a group of $n$ people. Let us next consider the following lemma.
Lemma. In a group of $n$ people, there are at least $n-1$ pairs of mutual acquaintances.
Proof: If you choose a mutually acquainted pair in a group and declare the two in the pair are not mutually acquainted, then either the group stays the same or splits into 2 groups. This means that by changing the status of a mutually acquainted pair in a group to that of a non-acquainted pair, one can increase the number of groups at most by 1 . Now if in a group of $n$ people you change the status of all of the mutually acquainted pairs to that of non-acquainted pairs, then obviously, the number of groups increases from 1 to $n$. Therefore, there must be at least $n-1$ pairs of mutually acquainted pairs in a group consisting of $n$ people.
The lemma implies that there are at most $\frac{n(n-1)}{2}-(n-1)=\frac{n^{2}-3 n+2}{2}$ pairs satisfying the condition of the problem. Thus the desired maximum number of pairs satisfying the requirement of the problem is $\frac{n^{2}-3 n+2}{2}$.
Remark: One can give a somewhat different proof by separating into 2 cases depending on whether there are at least $n-1$ mutually acquainted pairs, or at most $n-2$ such pairs. In the former case, one can argue in the same way as the proof above, while in the latter case, the Lemma above implies that there would be 2 or more groups to start with, but then, in view of the comment made before the definition of a group above, these groups can be combined to form one group, thereby one can reduce the argument to the former case.
Alternate Solution 1: The construction of an example for the case for which the number $\frac{n^{2}-3 n+2}{2}$ appears, and the argument for the case where there is only 1 group would be the same as in the preceding proof.
Suppose, then, $n$ participants are separated into $k(k \geq 2)$ groups, and the number of people in each group is given by $a_{i}, i=1, \cdots, k$. In such a case, the number of pairs for which paired people are not mutually acquainted but have a common acquaintance is at most $\sum_{i=1}^{k} a_{i} C_{2}$, where we set ${ }_{1} C_{2}=0$ for convenience. Since ${ }_{a} C_{2}+{ }_{b} C_{2} \leq{ }_{a+b} C_{2}$ holds for any pair of positive integers $a, b$, we have $\sum_{i=1}^{k} a_{i} C_{2} \leq{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}$. From
$$
{ }_{a_{1}} C_{2}+{ }_{n-a_{1}} C_{2}=a_{1}^{2}-n a_{1}+\frac{n^{2}-n}{2}=\left(a_{1}-\frac{n}{2}\right)^{2}+\frac{n^{2}-2 n}{4}
$$
it follows that ${ }_{a} C_{2}+{ }_{n-a_{1}} C_{2}$ takes its maximum value when $a_{1}=1, n-1$. Therefore, we have $\sum_{i=1}^{k}{ }_{a} C_{2} \leq{ }_{n-1} C_{2}$, which shows that in the case where the number of groups are 2 or more, the number of the pairs for which paired people are not mutually acquainted but have a common acquaintance is at most ${ }_{n-1} C_{2}=\frac{n^{2}-3 n+2}{2}$, and hence the desired maximum number of the pairs satisfying the requirement is $\frac{n^{2}-3 n+2}{2}$.
Alternate Solution 2: Construction of an example would be the same as the preceding proof.
For a participant, say $A$, call another participant, say $B$, a familiar face if $A$ and $B$ are not mutually acquainted but they have a common acquaintance among the participants, and in this case call the pair $A, B$ a familiar pair.
Suppose there is a participant $P$ who is mutually acquainted with $d$ participants. Denote by $S$ the set of these $d$ participants, and by $T$ the set of participants different from $P$ and not belonging to the set $S$. Suppose there are $e$ pairs formed by a person in $S$ and a person in $T$ who are mutually acquainted.
Then the number of participants who are familiar faces to $P$ is at most $e$. The number of pairs formed by two people belonging to the set $S$ and are mutually acquainted is at most ${ }_{d} C_{2}$. The number of familiar pairs formed by two people belonging to the set $T$ is at most ${ }_{n-d-1} C_{2}$. Since there are $e$ pairs formed by a person in the set $S$ and a person in the set $T$ who are mutually acquainted (and so the pairs are not familiar pairs), we have at most $d(n-1-d)-e$ familiar pairs formed by a person chosen from $S$ and a person chosen from $T$. Putting these together we conclude that there are at most $e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e$ familiar pairs. Since
$$
e+{ }_{d} C_{2}+{ }_{n-1-d} C_{2}+d(n-1-d)-e=\frac{n^{2}-3 n+2}{2}
$$
the number we seek is at most $\frac{n^{2}-3 n+2}{2}$, and hence this is the desired solution to the problem.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution:"
}
|
8217e940-8b0a-5b7b-b8b8-51d1b25d50a6
| 65,014
|
Let $A B C$ be an acute triangle satisfying the condition $A B>B C$ and $A C>B C$. Denote by $O$ and $H$ the circumcenter and the orthocenter, respectively, of the triangle $A B C$. Suppose that the circumcircle of the triangle $A H C$ intersects the line $A B$ at $M$ different from $A$, and that the circumcircle of the triangle $A H B$ intersects the line $A C$ at $N$ different from $A$. Prove that the circumcenter of the triangle $M N H$ lies on the line $O H$.
|
In the sequel, we denote $\angle B A C=\alpha, \angle C B A=\beta, \angle A C B=\gamma$. Let $O^{\prime}$ be the circumcenter of the triangle $M N H$. The lengths of line segments starting from the point $H$ will be treated as signed quantities.
Let us denote by $M^{\prime}, N^{\prime}$ the point of intersection of $C H, B H$, respectively, with the circumcircle of the triangle $A B C$ (distinct from $C, B$, respectively.) From the fact that 4 points $A, M, H, C$ lie on the same circle, we see that $\angle M H M^{\prime}=\alpha$ holds. Furthermore, $\angle B M^{\prime} C, \angle B N^{\prime} C$ and $\alpha$ are all subtended by the same arc $\widehat{B C}$ of the circumcircle of the triangle $A B C$ at points on the circle, and therefore, we have $\angle B M^{\prime} C=\alpha$, and $\angle B N^{\prime} C=\alpha$ as well. We also have $\angle A B H=\angle A C N^{\prime}$ as they are subtended by the same $\operatorname{arc} A N^{\prime}$ of the circumcircle of the triangle $A B C$ at points on the circle. Since $H M^{\prime} \perp B M, H N^{\prime} \perp A C$, we conclude that
$$
\angle M^{\prime} H B=90^{\circ}-\angle A B H=90^{\circ}-\angle A C N^{\prime}=\alpha
$$
is valid as well. Putting these facts together, we obtain the fact that the quadrilateral $H B M^{\prime} M$ is a rhombus. In a similar manner, we can conclude that the quadrilateral $H C N^{\prime} N$ is also a rhombus. Since both of these rhombuses are made up of 4 right triangles with an angle of magnitude $\alpha$, we also see that these rhombuses are similar.
Let us denote by $P, Q$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O^{\prime}$. Since $O^{\prime}$ is the circumcenter of the triangle $M N H, P, Q$ are respectively, the midpoints of the line segments $H M, H N$. Furthermore, if we denote by $R, S$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O$, then since $O$ is the circumcenter of both the triangle $M^{\prime} B C$ and the triangle $N^{\prime} B C$, we see that $R$ is the intersection point of $H M$ and the perpendicular bisector of $B M^{\prime}$, and $S$ is the intersection point of $H N$ and the perpendicular bisector of $C N^{\prime}$.
We note that the similarity map $\phi$ between the rhombuses $H B M^{\prime} M$ and $H C N^{\prime} N$ carries the perpendicular bisector of $B M^{\prime}$ onto the perpendicular bisector of $C N^{\prime}$, and straight line $H M$ onto the straight line $H N$, and hence $\phi$ maps $R$ onto $S$, and $P$ onto $Q$. Therefore, we get $H P: H R=H Q: H S$. If we now denote by $X, Y$ the intersection points of the line $H O^{\prime}$ with the line through $R$ and perpendicular to $H P$, and with the line through $S$ and perpendicular to $H Q$, respectively, then we get
$$
H O^{\prime}: H X=H P: H R=H Q: H S=H O^{\prime}: H Y
$$
so that we must have $H X=H Y$, and therefore, $X=Y$. But it is obvious that the point of intersection of the line through $R$ and perpendicular to $H P$ with the line through $S$ and perpendicular to $H Q$ must be $O$, and therefore, we conclude that $X=Y=O$ and that the points $H, O^{\prime}, O$ are collinear.
Alternate Solution: Deduction of the fact that both of the quadrilaterals $H B M^{\prime} M$ and $H C N^{\prime} N$ are rhombuses is carried out in the same way as in the preceding proof.
We then see that the point $M$ is located in a symmetric position with the point $B$ with respect to the line $C H$, we conclude that we have $\angle C M B=\beta$. Similarly, we have $\angle C N B=\gamma$. If we now put $x=\angle A H O^{\prime}$, then we get
$$
\angle O^{\prime}=\beta-\alpha-x, \angle M N H=90^{\circ}-\beta-\alpha+x
$$
from which it follows that
$$
\angle A N M=180^{\circ}-\angle M N H-\left(90^{\circ}-\alpha\right)=\beta-x
$$
Similarly, we get
$$
\angle N M A=\gamma+x
$$
Using the laws of sines, we then get
$$
\begin{aligned}
\frac{\sin (\gamma+x)}{\sin (\beta-x)} & =\frac{A N}{A M}=\frac{A C}{A M} \cdot \frac{A B}{A C} \cdot \frac{A N}{A B} \\
& =\frac{\sin \beta}{\sin (\beta-\alpha)} \cdot \frac{\sin \gamma}{\sin \beta} \cdot \frac{\sin (\gamma-\alpha)}{\sin \gamma}=\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}
\end{aligned}
$$
On the other hand, if we let $y=\angle A H O$, we then get
$$
\angle O H B=180^{\circ}-\gamma-y, \angle C H O=180^{\circ}-\beta+y,
$$
and since
$$
\angle H B O=\gamma-\alpha, \angle O C H=\beta-\alpha,
$$
using the laws of sines and observing that $O B=O C$, we get
$$
\begin{aligned}
\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}=\frac{\sin \angle H B O}{\sin \angle O C H} & =\frac{\sin \left(180^{\circ}-\gamma-y\right) \cdot \frac{O H}{O B}}{\sin \left(180^{\circ}-\beta+y\right) \cdot \frac{O H}{O C}} \\
& =\frac{\sin \left(180^{\circ}-\gamma-y\right)}{\sin \left(180^{\circ}-\beta+y\right)}=\frac{\sin (\gamma+y)}{\sin (\beta-y)}
\end{aligned}
$$
We then get $\sin (\gamma+x) \sin (\beta-y)=\sin (\beta-x) \sin (\gamma+y)$. Expanding both sides of the last identity by using the addition formula for the sine function and after factoring and using again the addition formula we obtain that $\sin (x-y) \sin (\beta+\gamma)=0$. This implies that $x-y$ must be an integral multiple of $180^{\circ}$, and hence we conclude that $H, O, O^{\prime}$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle satisfying the condition $A B>B C$ and $A C>B C$. Denote by $O$ and $H$ the circumcenter and the orthocenter, respectively, of the triangle $A B C$. Suppose that the circumcircle of the triangle $A H C$ intersects the line $A B$ at $M$ different from $A$, and that the circumcircle of the triangle $A H B$ intersects the line $A C$ at $N$ different from $A$. Prove that the circumcenter of the triangle $M N H$ lies on the line $O H$.
|
In the sequel, we denote $\angle B A C=\alpha, \angle C B A=\beta, \angle A C B=\gamma$. Let $O^{\prime}$ be the circumcenter of the triangle $M N H$. The lengths of line segments starting from the point $H$ will be treated as signed quantities.
Let us denote by $M^{\prime}, N^{\prime}$ the point of intersection of $C H, B H$, respectively, with the circumcircle of the triangle $A B C$ (distinct from $C, B$, respectively.) From the fact that 4 points $A, M, H, C$ lie on the same circle, we see that $\angle M H M^{\prime}=\alpha$ holds. Furthermore, $\angle B M^{\prime} C, \angle B N^{\prime} C$ and $\alpha$ are all subtended by the same arc $\widehat{B C}$ of the circumcircle of the triangle $A B C$ at points on the circle, and therefore, we have $\angle B M^{\prime} C=\alpha$, and $\angle B N^{\prime} C=\alpha$ as well. We also have $\angle A B H=\angle A C N^{\prime}$ as they are subtended by the same $\operatorname{arc} A N^{\prime}$ of the circumcircle of the triangle $A B C$ at points on the circle. Since $H M^{\prime} \perp B M, H N^{\prime} \perp A C$, we conclude that
$$
\angle M^{\prime} H B=90^{\circ}-\angle A B H=90^{\circ}-\angle A C N^{\prime}=\alpha
$$
is valid as well. Putting these facts together, we obtain the fact that the quadrilateral $H B M^{\prime} M$ is a rhombus. In a similar manner, we can conclude that the quadrilateral $H C N^{\prime} N$ is also a rhombus. Since both of these rhombuses are made up of 4 right triangles with an angle of magnitude $\alpha$, we also see that these rhombuses are similar.
Let us denote by $P, Q$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O^{\prime}$. Since $O^{\prime}$ is the circumcenter of the triangle $M N H, P, Q$ are respectively, the midpoints of the line segments $H M, H N$. Furthermore, if we denote by $R, S$ the feet of the perpendicular lines on $H M$ and $H N$, respectively, drawn from the point $O$, then since $O$ is the circumcenter of both the triangle $M^{\prime} B C$ and the triangle $N^{\prime} B C$, we see that $R$ is the intersection point of $H M$ and the perpendicular bisector of $B M^{\prime}$, and $S$ is the intersection point of $H N$ and the perpendicular bisector of $C N^{\prime}$.
We note that the similarity map $\phi$ between the rhombuses $H B M^{\prime} M$ and $H C N^{\prime} N$ carries the perpendicular bisector of $B M^{\prime}$ onto the perpendicular bisector of $C N^{\prime}$, and straight line $H M$ onto the straight line $H N$, and hence $\phi$ maps $R$ onto $S$, and $P$ onto $Q$. Therefore, we get $H P: H R=H Q: H S$. If we now denote by $X, Y$ the intersection points of the line $H O^{\prime}$ with the line through $R$ and perpendicular to $H P$, and with the line through $S$ and perpendicular to $H Q$, respectively, then we get
$$
H O^{\prime}: H X=H P: H R=H Q: H S=H O^{\prime}: H Y
$$
so that we must have $H X=H Y$, and therefore, $X=Y$. But it is obvious that the point of intersection of the line through $R$ and perpendicular to $H P$ with the line through $S$ and perpendicular to $H Q$ must be $O$, and therefore, we conclude that $X=Y=O$ and that the points $H, O^{\prime}, O$ are collinear.
Alternate Solution: Deduction of the fact that both of the quadrilaterals $H B M^{\prime} M$ and $H C N^{\prime} N$ are rhombuses is carried out in the same way as in the preceding proof.
We then see that the point $M$ is located in a symmetric position with the point $B$ with respect to the line $C H$, we conclude that we have $\angle C M B=\beta$. Similarly, we have $\angle C N B=\gamma$. If we now put $x=\angle A H O^{\prime}$, then we get
$$
\angle O^{\prime}=\beta-\alpha-x, \angle M N H=90^{\circ}-\beta-\alpha+x
$$
from which it follows that
$$
\angle A N M=180^{\circ}-\angle M N H-\left(90^{\circ}-\alpha\right)=\beta-x
$$
Similarly, we get
$$
\angle N M A=\gamma+x
$$
Using the laws of sines, we then get
$$
\begin{aligned}
\frac{\sin (\gamma+x)}{\sin (\beta-x)} & =\frac{A N}{A M}=\frac{A C}{A M} \cdot \frac{A B}{A C} \cdot \frac{A N}{A B} \\
& =\frac{\sin \beta}{\sin (\beta-\alpha)} \cdot \frac{\sin \gamma}{\sin \beta} \cdot \frac{\sin (\gamma-\alpha)}{\sin \gamma}=\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}
\end{aligned}
$$
On the other hand, if we let $y=\angle A H O$, we then get
$$
\angle O H B=180^{\circ}-\gamma-y, \angle C H O=180^{\circ}-\beta+y,
$$
and since
$$
\angle H B O=\gamma-\alpha, \angle O C H=\beta-\alpha,
$$
using the laws of sines and observing that $O B=O C$, we get
$$
\begin{aligned}
\frac{\sin (\gamma-\alpha)}{\sin (\beta-\alpha)}=\frac{\sin \angle H B O}{\sin \angle O C H} & =\frac{\sin \left(180^{\circ}-\gamma-y\right) \cdot \frac{O H}{O B}}{\sin \left(180^{\circ}-\beta+y\right) \cdot \frac{O H}{O C}} \\
& =\frac{\sin \left(180^{\circ}-\gamma-y\right)}{\sin \left(180^{\circ}-\beta+y\right)}=\frac{\sin (\gamma+y)}{\sin (\beta-y)}
\end{aligned}
$$
We then get $\sin (\gamma+x) \sin (\beta-y)=\sin (\beta-x) \sin (\gamma+y)$. Expanding both sides of the last identity by using the addition formula for the sine function and after factoring and using again the addition formula we obtain that $\sin (x-y) \sin (\beta+\gamma)=0$. This implies that $x-y$ must be an integral multiple of $180^{\circ}$, and hence we conclude that $H, O, O^{\prime}$ are collinear.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution:"
}
|
0a291d96-de84-5662-9c32-37cc21e9831c
| 605,417
|
Find all functions $f$ from the set $\mathbf{R}$ of real numbers into $\mathbf{R}$ which satisfy for all $x, y, z \in \mathbf{R}$ the identity
$$
f(f(x)+f(y)+f(z))=f(f(x)-f(y))+f(2 x y+f(z))+2 f(x z-y z) .
$$
|
It is clear that if $f$ is a constant function which satisfies the given equation, then the constant must be 0 . Conversely, $f(x)=0$ clearly satisfies the given equation, so, the identically 0 function is a solution. In the sequel, we consider the case where $f$ is not a constant function.
Let $t \in \mathbf{R}$ and substitute $(x, y, z)=(t, 0,0)$ and $(x, y, z)=(0, t, 0)$ into the given functional equation. Then, we obtain, respectively,
$$
\begin{aligned}
& f(f(t)+2 f(0))=f(f(t)-f(0))+f(f(0))+2 f(0), \\
& f(f(t)+2 f(0))=f(f(0)-f(t))+f(f(0))+2 f(0)
\end{aligned}
$$
from which we conclude that $f(f(t)-f(0))=f(f(0)-f(t))$ holds for all $t \in \mathbf{R}$. Now, suppose for some pair $u_{1}, u_{2}, f\left(u_{1}\right)=f\left(u_{2}\right)$ is satisfied. Then by substituting $(x, y, z)=\left(s, 0, u_{1}\right)$ and $(x, y, z)=\left(s, 0, u_{2}\right)$ into the functional equation and comparing the resulting identities, we can easily conclude that
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)
$$
holds for all $s \in \mathbf{R}$. Since $f$ is not a constant function there exists an $s_{0}$ such that $f\left(s_{0}\right)-f(0) \neq$ 0 . If we put $u_{1}=f\left(s_{0}\right)-f(0), u_{2}=-u_{1}$, then $f\left(u_{1}\right)=f\left(u_{2}\right)$, so we have by $(*)$
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)=f\left(-s u_{1}\right)
$$
for all $s \in \mathbf{R}$. Since $u_{1} \neq 0$, we conclude that
$$
f(x)=f(-x)
$$
holds for all $x \in \mathbf{R}$.
Next, if $f(u)=f(0)$ for some $u \neq 0$, then by $(*)$, we have $f(s u)=f(s 0)=f(0)$ for all $s$, which implies that $f$ is a constant function, contradicting our assumption. Therefore, we must have $f(s) \neq f(0)$ whenever $s \neq 0$.
We will now show that if $f(x)=f(y)$ holds, then either $x=y$ or $x=-y$ must hold. Suppose on the contrary that $f\left(x_{0}\right)=f\left(y_{0}\right)$ holds for some pair of non-zero numbers $x_{0}, y_{0}$ for which $x_{0} \neq y_{0}, x_{0} \neq-y_{0}$. Since $f\left(-y_{0}\right)=f\left(y_{0}\right)$, we may assume, by replacing $y_{0}$ by $-y_{0}$ if necessary, that $x_{0}$ and $y_{0}$ have the same sign. In view of $(*)$, we see that $f\left(s x_{0}\right)=f\left(s y_{0}\right)$ holds for all $s$, and therefore, there exists some $r>0, r \neq 1$ such that
$$
f(x)=f(r x)
$$
holds for all $x$. Replacing $x$ by $r x$ and $y$ by $r y$ in the given functional equation, we obtain
$$
f(f(r x)+f(r y)+f(z))=f(f(r x)-f(r y))+f\left(2 r^{2} x y+f(z)\right)+2 f(r(x-y) z)
$$
and replacing $x$ by $r^{2} x$ in the functional equation, we get
$$
f\left(f\left(r^{2} x\right)+f(y)+f(z)\right)=f\left(f\left(r^{2} x\right)-f(y)\right)+f\left(2 r^{2} x y+f(z)\right)+2 f\left(\left(r^{2} x-y\right) z\right)
$$
Since $f(r x)=f(x)$ holds for all $x \in \mathbf{R}$, we see that except for the last term on the right-hand side, all the corresponding terms appearing in the identities (i) and (ii) above are equal, and hence we conclude that
$$
\left.f(r(x-y) z)=f\left(\left(r^{2} x-y\right) z\right)\right)
$$
must hold for arbitrary choice of $x, y, z \in \mathbf{R}$. For arbitrarily fixed pair $u, v \in \mathbf{R}$, substitute $(x, y, z)=\left(\frac{v-u}{r^{2}-1}, \frac{v-r^{2} u}{r^{2}-1}, 1\right)$ into the identity (iii). Then we obtain $f(v)=f(r u)=f(u)$, since $x-y=u, r^{2} x-y=v, z=1$. But this implies that the function $f$ is a constant, contradicting our assumption. Thus we conclude that if $f(x)=f(y)$ then either $x=y$ or $x=-y$ must hold.
By substituting $z=0$ in the functional equation, we get
$$
f(f(x)+f(y)+f(0))=f(f(x)-f(y)+f(0))=f((f(x)-f(y))+f(2 x y+f(0))+2 f(0)
$$
Changing $y$ to $-y$ in the identity above and using the fact that $f(y)=f(-y)$, we see that all the terms except the second term on the right-hand side in the identity above remain the same. Thus we conclude that $f(2 x y+f(0))=f(-2 x y+f(0))$, from which we get either $2 x y+f(0)=-2 x y+f(0)$ or $2 x y+f(0)=2 x y-f(0)$ for all $x, y \in \mathbf{R}$. The first of these alternatives says that $4 x y=0$, which is impossible if $x y \neq 0$. Therefore the second alternative must be valid and we get that $f(0)=0$.
Finally, let us show that if $f$ satisfies the given functional equation and is not a constant function, then $f(x)=x^{2}$. Let $x=y$ in the functional equation, then since $f(0)=0$, we get
$$
f(2 f(x)+f(z))=f\left(2 x^{2}+f(z)\right)
$$
from which we conclude that either $2 f(x)+f(z)=2 x^{2}+f(z)$ or $2 f(x)+f(z)=-2 x^{2}-f(z)$ must hold. Suppose there exists $x_{0}$ for which $f\left(x_{0}\right) \neq x_{0}^{2}$, then from the second alternative, we see that $f(z)=-f\left(x_{0}\right)-x_{0}^{2}$ must hold for all $z$, which means that $f$ must be a constant function, contrary to our assumption. Therefore, the first alternative above must hold, and we have $f(x)=x^{2}$ for all $x$, establishing our claim.
It is easy to check that $f(x)=x^{2}$ does satisfy the given functional equation, so we conclude that $f(x)=0$ and $f(x)=x^{2}$ are the only functions that satisfy the requirement.
|
f(x)=0 \text{ and } f(x)=x^{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f$ from the set $\mathbf{R}$ of real numbers into $\mathbf{R}$ which satisfy for all $x, y, z \in \mathbf{R}$ the identity
$$
f(f(x)+f(y)+f(z))=f(f(x)-f(y))+f(2 x y+f(z))+2 f(x z-y z) .
$$
|
It is clear that if $f$ is a constant function which satisfies the given equation, then the constant must be 0 . Conversely, $f(x)=0$ clearly satisfies the given equation, so, the identically 0 function is a solution. In the sequel, we consider the case where $f$ is not a constant function.
Let $t \in \mathbf{R}$ and substitute $(x, y, z)=(t, 0,0)$ and $(x, y, z)=(0, t, 0)$ into the given functional equation. Then, we obtain, respectively,
$$
\begin{aligned}
& f(f(t)+2 f(0))=f(f(t)-f(0))+f(f(0))+2 f(0), \\
& f(f(t)+2 f(0))=f(f(0)-f(t))+f(f(0))+2 f(0)
\end{aligned}
$$
from which we conclude that $f(f(t)-f(0))=f(f(0)-f(t))$ holds for all $t \in \mathbf{R}$. Now, suppose for some pair $u_{1}, u_{2}, f\left(u_{1}\right)=f\left(u_{2}\right)$ is satisfied. Then by substituting $(x, y, z)=\left(s, 0, u_{1}\right)$ and $(x, y, z)=\left(s, 0, u_{2}\right)$ into the functional equation and comparing the resulting identities, we can easily conclude that
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)
$$
holds for all $s \in \mathbf{R}$. Since $f$ is not a constant function there exists an $s_{0}$ such that $f\left(s_{0}\right)-f(0) \neq$ 0 . If we put $u_{1}=f\left(s_{0}\right)-f(0), u_{2}=-u_{1}$, then $f\left(u_{1}\right)=f\left(u_{2}\right)$, so we have by $(*)$
$$
f\left(s u_{1}\right)=f\left(s u_{2}\right)=f\left(-s u_{1}\right)
$$
for all $s \in \mathbf{R}$. Since $u_{1} \neq 0$, we conclude that
$$
f(x)=f(-x)
$$
holds for all $x \in \mathbf{R}$.
Next, if $f(u)=f(0)$ for some $u \neq 0$, then by $(*)$, we have $f(s u)=f(s 0)=f(0)$ for all $s$, which implies that $f$ is a constant function, contradicting our assumption. Therefore, we must have $f(s) \neq f(0)$ whenever $s \neq 0$.
We will now show that if $f(x)=f(y)$ holds, then either $x=y$ or $x=-y$ must hold. Suppose on the contrary that $f\left(x_{0}\right)=f\left(y_{0}\right)$ holds for some pair of non-zero numbers $x_{0}, y_{0}$ for which $x_{0} \neq y_{0}, x_{0} \neq-y_{0}$. Since $f\left(-y_{0}\right)=f\left(y_{0}\right)$, we may assume, by replacing $y_{0}$ by $-y_{0}$ if necessary, that $x_{0}$ and $y_{0}$ have the same sign. In view of $(*)$, we see that $f\left(s x_{0}\right)=f\left(s y_{0}\right)$ holds for all $s$, and therefore, there exists some $r>0, r \neq 1$ such that
$$
f(x)=f(r x)
$$
holds for all $x$. Replacing $x$ by $r x$ and $y$ by $r y$ in the given functional equation, we obtain
$$
f(f(r x)+f(r y)+f(z))=f(f(r x)-f(r y))+f\left(2 r^{2} x y+f(z)\right)+2 f(r(x-y) z)
$$
and replacing $x$ by $r^{2} x$ in the functional equation, we get
$$
f\left(f\left(r^{2} x\right)+f(y)+f(z)\right)=f\left(f\left(r^{2} x\right)-f(y)\right)+f\left(2 r^{2} x y+f(z)\right)+2 f\left(\left(r^{2} x-y\right) z\right)
$$
Since $f(r x)=f(x)$ holds for all $x \in \mathbf{R}$, we see that except for the last term on the right-hand side, all the corresponding terms appearing in the identities (i) and (ii) above are equal, and hence we conclude that
$$
\left.f(r(x-y) z)=f\left(\left(r^{2} x-y\right) z\right)\right)
$$
must hold for arbitrary choice of $x, y, z \in \mathbf{R}$. For arbitrarily fixed pair $u, v \in \mathbf{R}$, substitute $(x, y, z)=\left(\frac{v-u}{r^{2}-1}, \frac{v-r^{2} u}{r^{2}-1}, 1\right)$ into the identity (iii). Then we obtain $f(v)=f(r u)=f(u)$, since $x-y=u, r^{2} x-y=v, z=1$. But this implies that the function $f$ is a constant, contradicting our assumption. Thus we conclude that if $f(x)=f(y)$ then either $x=y$ or $x=-y$ must hold.
By substituting $z=0$ in the functional equation, we get
$$
f(f(x)+f(y)+f(0))=f(f(x)-f(y)+f(0))=f((f(x)-f(y))+f(2 x y+f(0))+2 f(0)
$$
Changing $y$ to $-y$ in the identity above and using the fact that $f(y)=f(-y)$, we see that all the terms except the second term on the right-hand side in the identity above remain the same. Thus we conclude that $f(2 x y+f(0))=f(-2 x y+f(0))$, from which we get either $2 x y+f(0)=-2 x y+f(0)$ or $2 x y+f(0)=2 x y-f(0)$ for all $x, y \in \mathbf{R}$. The first of these alternatives says that $4 x y=0$, which is impossible if $x y \neq 0$. Therefore the second alternative must be valid and we get that $f(0)=0$.
Finally, let us show that if $f$ satisfies the given functional equation and is not a constant function, then $f(x)=x^{2}$. Let $x=y$ in the functional equation, then since $f(0)=0$, we get
$$
f(2 f(x)+f(z))=f\left(2 x^{2}+f(z)\right)
$$
from which we conclude that either $2 f(x)+f(z)=2 x^{2}+f(z)$ or $2 f(x)+f(z)=-2 x^{2}-f(z)$ must hold. Suppose there exists $x_{0}$ for which $f\left(x_{0}\right) \neq x_{0}^{2}$, then from the second alternative, we see that $f(z)=-f\left(x_{0}\right)-x_{0}^{2}$ must hold for all $z$, which means that $f$ must be a constant function, contrary to our assumption. Therefore, the first alternative above must hold, and we have $f(x)=x^{2}$ for all $x$, establishing our claim.
It is easy to check that $f(x)=x^{2}$ does satisfy the given functional equation, so we conclude that $f(x)=0$ and $f(x)=x^{2}$ are the only functions that satisfy the requirement.
|
{
"resource_path": "APMO/segmented/en-apmo2010_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution:"
}
|
536cdc0e-c8cf-5464-ae38-5327852cf390
| 260,846
|
Let $A B C$ be an acute triangle with altitudes $A D, B E$ and $C F$, and let $O$ be the center of its circumcircle. Show that the segments $O A, O F, O B, O D, O C, O E$ dissect the triangle $A B C$ into three pairs of triangles that have equal areas.
|
Let $M$ and $N$ be midpoints of sides $B C$ and $A C$, respectively. Notice that $\angle M O C=\frac{1}{2} \angle B O C=\angle E A B, \angle O M C=90^{\circ}=\angle A E B$, so triangles $O M C$ and $A E B$ are similar and we get $\frac{O M}{A E}=\frac{O C}{A B}$. For triangles $O N A$ and $B D A$ we also have $\frac{O N}{B D}=\frac{O A}{B A}$. Then $\frac{O M}{A E}=\frac{O N}{B D}$ or $B D \cdot O M=A E \cdot O N$.
Denote by $S(\Phi)$ the area of the figure $\Phi$. So, we see that $S(O B D)=\frac{1}{2} B D \cdot O M=$ $\frac{1}{2} A E \cdot O N=S(O A E)$. Analogously, $S(O C D)=S(O A F)$ and $S(O C E)=S(O B F)$.
Alternative solution. Let $R$ be the circumradius of triangle $A B C$, and as usual write $A, B, C$ for angles $\angle C A B, \angle A B C, \angle B C A$ respectively, and $a, b, c$ for sides $B C, C A, A B$ respectively. Then the area of triangle $O C D$ is
$$
S(O C D)=\frac{1}{2} \cdot O C \cdot C D \cdot \sin (\angle O C D)=\frac{1}{2} R \cdot C D \cdot \sin (\angle O C D)
$$
Now $C D=b \cos C$, and
$$
\angle O C D=\frac{180^{\circ}-2 A}{2}=90^{\circ}-A
$$
(since triangle $O B C$ is isosceles, and $\angle B O C=2 A$ ). So
$$
S(O C D)=\frac{1}{2} R b \cos C \sin \left(90^{\circ}-A\right)=\frac{1}{2} R b \cos C \cos A
$$
A similar calculation gives
$$
\begin{aligned}
S(O A F) & =\frac{1}{2} O A \cdot A F \cdot \sin (\angle O A F) \\
& =\frac{1}{2} R \cdot(b \cos A) \sin \left(90^{\circ}-C\right) \\
& =\frac{1}{2} R b \cos A \cos C
\end{aligned}
$$
so $O C D$ and $O A F$ have the same area. In the same way we find that $O B D$ and $O A E$ have the same area, as do $O C E$ and $O B F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with altitudes $A D, B E$ and $C F$, and let $O$ be the center of its circumcircle. Show that the segments $O A, O F, O B, O D, O C, O E$ dissect the triangle $A B C$ into three pairs of triangles that have equal areas.
|
Let $M$ and $N$ be midpoints of sides $B C$ and $A C$, respectively. Notice that $\angle M O C=\frac{1}{2} \angle B O C=\angle E A B, \angle O M C=90^{\circ}=\angle A E B$, so triangles $O M C$ and $A E B$ are similar and we get $\frac{O M}{A E}=\frac{O C}{A B}$. For triangles $O N A$ and $B D A$ we also have $\frac{O N}{B D}=\frac{O A}{B A}$. Then $\frac{O M}{A E}=\frac{O N}{B D}$ or $B D \cdot O M=A E \cdot O N$.
Denote by $S(\Phi)$ the area of the figure $\Phi$. So, we see that $S(O B D)=\frac{1}{2} B D \cdot O M=$ $\frac{1}{2} A E \cdot O N=S(O A E)$. Analogously, $S(O C D)=S(O A F)$ and $S(O C E)=S(O B F)$.
Alternative solution. Let $R$ be the circumradius of triangle $A B C$, and as usual write $A, B, C$ for angles $\angle C A B, \angle A B C, \angle B C A$ respectively, and $a, b, c$ for sides $B C, C A, A B$ respectively. Then the area of triangle $O C D$ is
$$
S(O C D)=\frac{1}{2} \cdot O C \cdot C D \cdot \sin (\angle O C D)=\frac{1}{2} R \cdot C D \cdot \sin (\angle O C D)
$$
Now $C D=b \cos C$, and
$$
\angle O C D=\frac{180^{\circ}-2 A}{2}=90^{\circ}-A
$$
(since triangle $O B C$ is isosceles, and $\angle B O C=2 A$ ). So
$$
S(O C D)=\frac{1}{2} R b \cos C \sin \left(90^{\circ}-A\right)=\frac{1}{2} R b \cos C \cos A
$$
A similar calculation gives
$$
\begin{aligned}
S(O A F) & =\frac{1}{2} O A \cdot A F \cdot \sin (\angle O A F) \\
& =\frac{1}{2} R \cdot(b \cos A) \sin \left(90^{\circ}-C\right) \\
& =\frac{1}{2} R b \cos A \cos C
\end{aligned}
$$
so $O C D$ and $O A F$ have the same area. In the same way we find that $O B D$ and $O A E$ have the same area, as do $O C E$ and $O B F$.
|
{
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
bde58b6c-5e7d-500f-a39d-4e26409f0c00
| 261,160
|
Determine all positive integers $n$ for which $\frac{n^{2}+1}{[\sqrt{n}]^{2}+2}$ is an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.
|
We will show that there are no positive integers $n$ satisfying the condition of the problem.
Let $m=[\sqrt{n}]$ and $a=n-m^{2}$. We have $m \geq 1$ since $n \geq 1$. From $n^{2}+1=\left(m^{2}+a\right)^{2}+1 \equiv$ $(a-2)^{2}+1\left(\bmod \left(m^{2}+2\right)\right)$, it follows that the condition of the problem is equivalent to the fact that $(a-2)^{2}+1$ is divisible by $m^{2}+2$. Since we have
$$
0<(a-2)^{2}+1 \leq \max \left\{2^{2},(2 m-2)^{2}\right\}+1 \leq 4 m^{2}+1<4\left(m^{2}+2\right)
$$
we see that $(a-2)^{2}+1=k\left(m^{2}+2\right)$ must hold with $k=1,2$ or 3 . We will show that none of these can occur.
Case 1. When $k=1$. We get $(a-2)^{2}-m^{2}=1$, and this implies that $a-2= \pm 1, m=0$ must hold, but this contradicts with fact $m \geq 1$.
Case 2. When $k=2$. We have $(a-2)^{2}+1=2\left(m^{2}+2\right)$ in this case, but any perfect square is congruent to $0,1,4 \bmod 8$, and therefore, we have $(a-2)^{2}+1 \equiv 1,2,5(\bmod 8)$, while $2\left(m^{2}+2\right) \equiv 4,6(\bmod 8)$. Thus, this case cannot occur either.
Case 3. When $k=3$. We have $(a-2)^{2}+1=3\left(m^{2}+2\right)$ in this case. Since any perfect square is congruent to 0 or $1 \bmod 3$, we have $(a-2)^{2}+1 \equiv 1,2(\bmod 3)$, while $3\left(m^{2}+2\right) \equiv 0$ $(\bmod 3)$, which shows that this case cannot occur either.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $n$ for which $\frac{n^{2}+1}{[\sqrt{n}]^{2}+2}$ is an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.
|
We will show that there are no positive integers $n$ satisfying the condition of the problem.
Let $m=[\sqrt{n}]$ and $a=n-m^{2}$. We have $m \geq 1$ since $n \geq 1$. From $n^{2}+1=\left(m^{2}+a\right)^{2}+1 \equiv$ $(a-2)^{2}+1\left(\bmod \left(m^{2}+2\right)\right)$, it follows that the condition of the problem is equivalent to the fact that $(a-2)^{2}+1$ is divisible by $m^{2}+2$. Since we have
$$
0<(a-2)^{2}+1 \leq \max \left\{2^{2},(2 m-2)^{2}\right\}+1 \leq 4 m^{2}+1<4\left(m^{2}+2\right)
$$
we see that $(a-2)^{2}+1=k\left(m^{2}+2\right)$ must hold with $k=1,2$ or 3 . We will show that none of these can occur.
Case 1. When $k=1$. We get $(a-2)^{2}-m^{2}=1$, and this implies that $a-2= \pm 1, m=0$ must hold, but this contradicts with fact $m \geq 1$.
Case 2. When $k=2$. We have $(a-2)^{2}+1=2\left(m^{2}+2\right)$ in this case, but any perfect square is congruent to $0,1,4 \bmod 8$, and therefore, we have $(a-2)^{2}+1 \equiv 1,2,5(\bmod 8)$, while $2\left(m^{2}+2\right) \equiv 4,6(\bmod 8)$. Thus, this case cannot occur either.
Case 3. When $k=3$. We have $(a-2)^{2}+1=3\left(m^{2}+2\right)$ in this case. Since any perfect square is congruent to 0 or $1 \bmod 3$, we have $(a-2)^{2}+1 \equiv 1,2(\bmod 3)$, while $3\left(m^{2}+2\right) \equiv 0$ $(\bmod 3)$, which shows that this case cannot occur either.
|
{
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
df30d942-b14f-5cd4-a5e3-dba02e74ca21
| 261,170
|
For $2 k$ real numbers $a_{1}, a_{2}, \ldots, a_{k}, b_{1}, b_{2}, \ldots, b_{k}$ define the sequence of numbers $X_{n}$ by
$$
X_{n}=\sum_{i=1}^{k}\left[a_{i} n+b_{i}\right] \quad(n=1,2, \ldots)
$$
If the sequence $X_{n}$ forms an arithmetic progression, show that $\sum_{i=1}^{k} a_{i}$ must be an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.
|
Let us write $A=\sum_{i=1}^{k} a_{i}$ and $B=\sum_{i=1}^{k} b_{i}$. Summing the corresponding terms of the following inequalities over $i$,
$$
a_{i} n+b_{i}-1<\left[a_{i} n+b_{i}\right] \leq a_{i} n+b_{i}
$$
we obtain $A n+B-k<X_{n}<A n+B$. Now suppose that $\left\{X_{n}\right\}$ is an arithmetic progression with the common difference $d$, then we have $n d=X_{n+1}-X_{1}$ and $A+B-k<X_{1} \leq A+B$ Combining with the inequalities obtained above, we get
$$
A(n+1)+B-k<n d+X_{1}<A(n+1)+B,
$$
or
$$
A n-k \leq A n+\left(A+B-X_{1}\right)-k<n d<A n+\left(A+B-X_{1}\right)<A n+k,
$$
from which we conclude that $|A-d|<\frac{k}{n}$ must hold. Since this inequality holds for any positive integer $n$, we must have $A=d$. Since $\left\{X_{n}\right\}$ is a sequence of integers, $d$ must be an integer also, and thus we conclude that $A$ is also an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
For $2 k$ real numbers $a_{1}, a_{2}, \ldots, a_{k}, b_{1}, b_{2}, \ldots, b_{k}$ define the sequence of numbers $X_{n}$ by
$$
X_{n}=\sum_{i=1}^{k}\left[a_{i} n+b_{i}\right] \quad(n=1,2, \ldots)
$$
If the sequence $X_{n}$ forms an arithmetic progression, show that $\sum_{i=1}^{k} a_{i}$ must be an integer. Here $[r]$ denotes the greatest integer less than or equal to $r$.
|
Let us write $A=\sum_{i=1}^{k} a_{i}$ and $B=\sum_{i=1}^{k} b_{i}$. Summing the corresponding terms of the following inequalities over $i$,
$$
a_{i} n+b_{i}-1<\left[a_{i} n+b_{i}\right] \leq a_{i} n+b_{i}
$$
we obtain $A n+B-k<X_{n}<A n+B$. Now suppose that $\left\{X_{n}\right\}$ is an arithmetic progression with the common difference $d$, then we have $n d=X_{n+1}-X_{1}$ and $A+B-k<X_{1} \leq A+B$ Combining with the inequalities obtained above, we get
$$
A(n+1)+B-k<n d+X_{1}<A(n+1)+B,
$$
or
$$
A n-k \leq A n+\left(A+B-X_{1}\right)-k<n d<A n+\left(A+B-X_{1}\right)<A n+k,
$$
from which we conclude that $|A-d|<\frac{k}{n}$ must hold. Since this inequality holds for any positive integer $n$, we must have $A=d$. Since $\left\{X_{n}\right\}$ is a sequence of integers, $d$ must be an integer also, and thus we conclude that $A$ is also an integer.
|
{
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
47f9799b-15a3-5677-a00a-5c4e96c7ffcd
| 605,479
|
Let $a$ and $b$ be positive integers, and let $A$ and $B$ be finite sets of integers satisfying:
(i) $A$ and $B$ are disjoint;
(ii) if an integer $i$ belongs either to $A$ or to $B$, then $i+a$ belongs to $A$ or $i-b$ belongs to $B$.
Prove that $a|A|=b|B|$. (Here $|X|$ denotes the number of elements in the set $X$.)
|
Let $A^{*}=\{n-a: n \in A\}$ and $B^{*}=\{n+b: n \in B\}$. Then, by (ii), $A \cup B \subseteq A^{*} \cup B^{*}$ and by (i),
$$
|A \cup B| \leq\left|A^{*} \cup B^{*}\right| \leq\left|A^{*}\right|+\left|B^{*}\right|=|A|+|B|=|A \cup B|
$$
Thus, $A \cup B=A^{*} \cup B^{*}$ and $A^{*}$ and $B^{*}$ have no element in common. For each finite set $X$ of integers, let $\sum(X)=\sum_{x \in X} x$. Then
$$
\begin{aligned}
\sum(A)+\sum(B) & =\sum(A \cup B) \\
& =\sum\left(A^{*} \cup B^{*}\right)=\sum\left(A^{*}\right)+\sum\left(B^{*}\right) \\
& =\sum(A)-a|A|+\sum(B)+b|B|
\end{aligned}
$$
which implies $a|A|=b|B|$.
Alternative solution. Let us construct a directed graph whose vertices are labelled by the members of $A \cup B$ and such that there is an edge from $i$ to $j$ iff $j \in A$ and $j=i+a$ or $j \in B$ and $j=i-b$. From (ii), each vertex has out-degree $\geq 1$ and, from (i), each vertex has in-degree $\leq 1$. Since the sum of the out-degrees equals the sum of the in-degrees, each vertex has in-degree and out-degree equal to 1. This is only possible if the graph is the union of disjoint cycles, say $G_{1}, G_{2}, \ldots, G_{n}$. Let $\left|A_{k}\right|$ be the number of elements of $A$ in $G_{k}$ and $\left|B_{k}\right|$ be the number of elements of $B$ in $G_{k}$. The cycle $G_{k}$ will involve increasing vertex labels by $a$ a total of $\left|A_{k}\right|$ times and decreasing them by $b$ a total of $\left|B_{k}\right|$ times. Since it is a cycle, we have $a\left|A_{k}\right|=b\left|B_{k}\right|$. Summing over all cycles gives the result.
|
a|A|=b|B|
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $a$ and $b$ be positive integers, and let $A$ and $B$ be finite sets of integers satisfying:
(i) $A$ and $B$ are disjoint;
(ii) if an integer $i$ belongs either to $A$ or to $B$, then $i+a$ belongs to $A$ or $i-b$ belongs to $B$.
Prove that $a|A|=b|B|$. (Here $|X|$ denotes the number of elements in the set $X$.)
|
Let $A^{*}=\{n-a: n \in A\}$ and $B^{*}=\{n+b: n \in B\}$. Then, by (ii), $A \cup B \subseteq A^{*} \cup B^{*}$ and by (i),
$$
|A \cup B| \leq\left|A^{*} \cup B^{*}\right| \leq\left|A^{*}\right|+\left|B^{*}\right|=|A|+|B|=|A \cup B|
$$
Thus, $A \cup B=A^{*} \cup B^{*}$ and $A^{*}$ and $B^{*}$ have no element in common. For each finite set $X$ of integers, let $\sum(X)=\sum_{x \in X} x$. Then
$$
\begin{aligned}
\sum(A)+\sum(B) & =\sum(A \cup B) \\
& =\sum\left(A^{*} \cup B^{*}\right)=\sum\left(A^{*}\right)+\sum\left(B^{*}\right) \\
& =\sum(A)-a|A|+\sum(B)+b|B|
\end{aligned}
$$
which implies $a|A|=b|B|$.
Alternative solution. Let us construct a directed graph whose vertices are labelled by the members of $A \cup B$ and such that there is an edge from $i$ to $j$ iff $j \in A$ and $j=i+a$ or $j \in B$ and $j=i-b$. From (ii), each vertex has out-degree $\geq 1$ and, from (i), each vertex has in-degree $\leq 1$. Since the sum of the out-degrees equals the sum of the in-degrees, each vertex has in-degree and out-degree equal to 1. This is only possible if the graph is the union of disjoint cycles, say $G_{1}, G_{2}, \ldots, G_{n}$. Let $\left|A_{k}\right|$ be the number of elements of $A$ in $G_{k}$ and $\left|B_{k}\right|$ be the number of elements of $B$ in $G_{k}$. The cycle $G_{k}$ will involve increasing vertex labels by $a$ a total of $\left|A_{k}\right|$ times and decreasing them by $b$ a total of $\left|B_{k}\right|$ times. Since it is a cycle, we have $a\left|A_{k}\right|=b\left|B_{k}\right|$. Summing over all cycles gives the result.
|
{
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
3a4c3513-24bf-5cee-b1b4-fdc9f8815d47
| 605,490
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$, and let $P$ be a point on the extension of $A C$ such that $P B$ and $P D$ are tangent to $\omega$. The tangent at $C$ intersects $P D$ at $Q$ and the line $A D$ at $R$. Let $E$ be the second point of intersection between $A Q$ and $\omega$. Prove that $B, E, R$ are collinear.
|
To show $B, E, R$ are collinear, it is equivalent to show the lines $A D, B E, C Q$ are concurrent. Let $C Q$ intersect $A D$ at $R$ and $B E$ intersect $A D$ at $R^{\prime}$. We shall show $R D / R A=R^{\prime} D / R^{\prime} A$ so that $R=R^{\prime}$.
Since $\triangle P A D$ is similar to $\triangle P D C$ and $\triangle P A B$ is similar to $\triangle P B C$, we have $A D / D C=$ $P A / P D=P A / P B=A B / B C$. Hence, $A B \cdot D C=B C \cdot A D$. By Ptolemy's theorem, $A B \cdot D C=B C \cdot A D=\frac{1}{2} C A \cdot D B$. Similarly $C A \cdot E D=C E \cdot A D=\frac{1}{2} A E \cdot D C$.
Thus
$$
\frac{D B}{A B}=\frac{2 D C}{C A}
$$
and
$$
\frac{D C}{C A}=\frac{2 E D}{A E}
$$
Since the triangles $R D C$ and $R C A$ are similar, we have $\frac{R D}{R C}=\frac{D C}{C A}=\frac{R C}{R A}$. Thus using (4)
$$
\frac{R D}{R A}=\frac{R D \cdot R A}{R A^{2}}=\left(\frac{R C}{R A}\right)^{2}=\left(\frac{D C}{C A}\right)^{2}=\left(\frac{2 E D}{A E}\right)^{2}
$$
Using the similar triangles $A B R^{\prime}$ and $E D R^{\prime}$, we have $R^{\prime} D / R^{\prime} B=E D / A B$. Using the similar triangles $D B R^{\prime}$ and $E A R^{\prime}$ we have $R^{\prime} A / R^{\prime} B=E A / D B$. Thus using (3) and (4),
$$
\frac{R^{\prime} D}{R^{\prime} A}=\frac{E D \cdot D B}{E A \cdot A B}=\left(\frac{2 E D}{A E}\right)^{2}
$$
It follows from (5) and (6) that $R=R^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\omega$, and let $P$ be a point on the extension of $A C$ such that $P B$ and $P D$ are tangent to $\omega$. The tangent at $C$ intersects $P D$ at $Q$ and the line $A D$ at $R$. Let $E$ be the second point of intersection between $A Q$ and $\omega$. Prove that $B, E, R$ are collinear.
|
To show $B, E, R$ are collinear, it is equivalent to show the lines $A D, B E, C Q$ are concurrent. Let $C Q$ intersect $A D$ at $R$ and $B E$ intersect $A D$ at $R^{\prime}$. We shall show $R D / R A=R^{\prime} D / R^{\prime} A$ so that $R=R^{\prime}$.
Since $\triangle P A D$ is similar to $\triangle P D C$ and $\triangle P A B$ is similar to $\triangle P B C$, we have $A D / D C=$ $P A / P D=P A / P B=A B / B C$. Hence, $A B \cdot D C=B C \cdot A D$. By Ptolemy's theorem, $A B \cdot D C=B C \cdot A D=\frac{1}{2} C A \cdot D B$. Similarly $C A \cdot E D=C E \cdot A D=\frac{1}{2} A E \cdot D C$.
Thus
$$
\frac{D B}{A B}=\frac{2 D C}{C A}
$$
and
$$
\frac{D C}{C A}=\frac{2 E D}{A E}
$$

Since the triangles $R D C$ and $R C A$ are similar, we have $\frac{R D}{R C}=\frac{D C}{C A}=\frac{R C}{R A}$. Thus using (4)
$$
\frac{R D}{R A}=\frac{R D \cdot R A}{R A^{2}}=\left(\frac{R C}{R A}\right)^{2}=\left(\frac{D C}{C A}\right)^{2}=\left(\frac{2 E D}{A E}\right)^{2}
$$
Using the similar triangles $A B R^{\prime}$ and $E D R^{\prime}$, we have $R^{\prime} D / R^{\prime} B=E D / A B$. Using the similar triangles $D B R^{\prime}$ and $E A R^{\prime}$ we have $R^{\prime} A / R^{\prime} B=E A / D B$. Thus using (3) and (4),
$$
\frac{R^{\prime} D}{R^{\prime} A}=\frac{E D \cdot D B}{E A \cdot A B}=\left(\frac{2 E D}{A E}\right)^{2}
$$
It follows from (5) and (6) that $R=R^{\prime}$.
|
{
"resource_path": "APMO/segmented/en-apmo2013_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
fbec6dda-212e-5638-8659-c762b5b6e97f
| 261,186
|
For a positive integer $m$ denote by $S(m)$ and $P(m)$ the sum and product, respectively, of the digits of $m$. Show that for each positive integer $n$, there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ satisfying the following conditions:
$$
S\left(a_{1}\right)<S\left(a_{2}\right)<\cdots<S\left(a_{n}\right) \text { and } S\left(a_{i}\right)=P\left(a_{i+1}\right) \quad(i=1,2, \ldots, n)
$$
(We let $\left.a_{n+1}=a_{1}.\right)$ (Problem Committee of the Japan Mathematical Olympiad Foundation)
|
Let $k$ be a sufficiently large positive integer. Choose for each $i=2,3, \ldots, n$, $a_{i}$ to be a positive integer among whose digits the number 2 appears exactly $k+i-2$ times and the number 1 appears exactly $2^{k+i-1}-2(k+i-2)$ times, and nothing else. Then, we have $S\left(a_{i}\right)=2^{k+i-1}$ and $P\left(a_{i}\right)=2^{k+i-2}$ for each $i, 2 \leq i \leq n$. Then, we let $a_{1}$ be a positive integer among whose digits the number 2 appears exactly $k+n-1$ times and the number 1 appears exactly $2^{k}-2(k+n-1)$ times, and nothing else. Then, we see that $a_{1}$ satisfies $S\left(a_{1}\right)=2^{k}$ and $P\left(a_{1}\right)=2^{k+n-1}$. Such a choice of $a_{1}$ is possible if we take $k$ to be large enough to satisfy $2^{k}>2(k+n-1)$ and we see that the numbers $a_{1}, \ldots, a_{n}$ chosen this way satisfy the given requirements.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $m$ denote by $S(m)$ and $P(m)$ the sum and product, respectively, of the digits of $m$. Show that for each positive integer $n$, there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ satisfying the following conditions:
$$
S\left(a_{1}\right)<S\left(a_{2}\right)<\cdots<S\left(a_{n}\right) \text { and } S\left(a_{i}\right)=P\left(a_{i+1}\right) \quad(i=1,2, \ldots, n)
$$
(We let $\left.a_{n+1}=a_{1}.\right)$ (Problem Committee of the Japan Mathematical Olympiad Foundation)
|
Let $k$ be a sufficiently large positive integer. Choose for each $i=2,3, \ldots, n$, $a_{i}$ to be a positive integer among whose digits the number 2 appears exactly $k+i-2$ times and the number 1 appears exactly $2^{k+i-1}-2(k+i-2)$ times, and nothing else. Then, we have $S\left(a_{i}\right)=2^{k+i-1}$ and $P\left(a_{i}\right)=2^{k+i-2}$ for each $i, 2 \leq i \leq n$. Then, we let $a_{1}$ be a positive integer among whose digits the number 2 appears exactly $k+n-1$ times and the number 1 appears exactly $2^{k}-2(k+n-1)$ times, and nothing else. Then, we see that $a_{1}$ satisfies $S\left(a_{1}\right)=2^{k}$ and $P\left(a_{1}\right)=2^{k+n-1}$. Such a choice of $a_{1}$ is possible if we take $k$ to be large enough to satisfy $2^{k}>2(k+n-1)$ and we see that the numbers $a_{1}, \ldots, a_{n}$ chosen this way satisfy the given requirements.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
926b6029-7a9d-56f1-9d99-850851b2b42f
| 605,529
|
Let $S=\{1,2, \ldots, 2014\}$. For each non-empty subset $T \subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \subseteq S$ is a disjoint union of non-empty subsets $A, B, C \subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)
|
Answer: 108 - 2014!.
For any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:
$$
\text { If } x_{1} \in X \text { and } X \subseteq S \text {, then } x_{1}=r(X) \text {. }
$$
If $|X| \leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \in X$ and $y \neq x_{1}$. We can write $X$ as a disjoint union of $\left\{x_{1}, y\right\}$ and two other subsets. We already proved that $r\left(\left\{x_{1}, y\right\}\right)=x_{1}$ (since $\left|\left\{x_{1}, y\right\}\right|=2<2012$ ) and it follows that $y \neq r(X)$ for every $y \in X$ except $x_{1}$. We have proved the fact.
Note that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.
There are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \in X \subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \backslash\left\{x_{1}\right\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\left(S_{1}\right)$ and for $x_{2} \in X \subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \cdot 2013 \cdots 5$ ways to choose $x_{1}, x_{2}, \ldots, x_{2010} \in S$ so that for all $i=1,2 \ldots, 2010$, $x_{i}=r(X)$ for each $X \subseteq S \backslash\left\{x_{1}, \ldots, x_{i-1}\right\}$ and $x_{i} \in X$.
We are now left with four elements $Y=\left\{y_{1}, y_{2}, y_{3}, y_{4}\right\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\left(\left\{y_{1}, y_{2}\right\}\right)=r\left(\left\{y_{1}, y_{3}\right\}\right)=r\left(\left\{y_{1}, y_{4}\right\}\right)$. The only subsets whose representative has not been assigned yet are $\left\{y_{1}, y_{2}, y_{3}\right\},\left\{y_{1}, y_{2}, y_{4}\right\}$, $\left\{y_{1}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}\right\},\left\{y_{2}, y_{4}\right\},\left\{y_{3}, y_{4}\right\}$. These subsets can be assigned in any way, hence giving $3^{4} \cdot 2^{3}$ more choices.
In conclusion, the total number of assignments is $2014 \cdot 2013 \cdots 4 \cdot 3^{4} \cdot 2^{3}=108 \cdot 2014$ !.
|
108 \cdot 2014!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S=\{1,2, \ldots, 2014\}$. For each non-empty subset $T \subseteq S$, one of its members is chosen as its representative. Find the number of ways to assign representatives to all non-empty subsets of $S$ so that if a subset $D \subseteq S$ is a disjoint union of non-empty subsets $A, B, C \subseteq S$, then the representative of $D$ is also the representative of at least one of $A, B, C$. (Warut Suksompong, Thailand)
|
Answer: 108 - 2014!.
For any subset $X$ let $r(X)$ denotes the representative of $X$. Suppose that $x_{1}=r(S)$. First, we prove the following fact:
$$
\text { If } x_{1} \in X \text { and } X \subseteq S \text {, then } x_{1}=r(X) \text {. }
$$
If $|X| \leq 2012$, then we can write $S$ as a disjoint union of $X$ and two other subsets of $S$, which gives that $x_{1}=r(X)$. If $|X|=2013$, then let $y \in X$ and $y \neq x_{1}$. We can write $X$ as a disjoint union of $\left\{x_{1}, y\right\}$ and two other subsets. We already proved that $r\left(\left\{x_{1}, y\right\}\right)=x_{1}$ (since $\left|\left\{x_{1}, y\right\}\right|=2<2012$ ) and it follows that $y \neq r(X)$ for every $y \in X$ except $x_{1}$. We have proved the fact.
Note that this fact is true and can be proved similarly, if the ground set $S$ would contain at least 5 elements.
There are 2014 ways to choose $x_{1}=r(S)$ and for $x_{1} \in X \subseteq S$ we have $r(X)=x_{1}$. Let $S_{1}=S \backslash\left\{x_{1}\right\}$. Analogously, we can state that there are 2013 ways to choose $x_{2}=r\left(S_{1}\right)$ and for $x_{2} \in X \subseteq S_{1}$ we have $r(X)=x_{2}$. Proceeding similarly (or by induction), there are $2014 \cdot 2013 \cdots 5$ ways to choose $x_{1}, x_{2}, \ldots, x_{2010} \in S$ so that for all $i=1,2 \ldots, 2010$, $x_{i}=r(X)$ for each $X \subseteq S \backslash\left\{x_{1}, \ldots, x_{i-1}\right\}$ and $x_{i} \in X$.
We are now left with four elements $Y=\left\{y_{1}, y_{2}, y_{3}, y_{4}\right\}$. There are 4 ways to choose $r(Y)$. Suppose that $y_{1}=r(Y)$. Then we clearly have $y_{1}=r\left(\left\{y_{1}, y_{2}\right\}\right)=r\left(\left\{y_{1}, y_{3}\right\}\right)=r\left(\left\{y_{1}, y_{4}\right\}\right)$. The only subsets whose representative has not been assigned yet are $\left\{y_{1}, y_{2}, y_{3}\right\},\left\{y_{1}, y_{2}, y_{4}\right\}$, $\left\{y_{1}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}, y_{4}\right\},\left\{y_{2}, y_{3}\right\},\left\{y_{2}, y_{4}\right\},\left\{y_{3}, y_{4}\right\}$. These subsets can be assigned in any way, hence giving $3^{4} \cdot 2^{3}$ more choices.
In conclusion, the total number of assignments is $2014 \cdot 2013 \cdots 4 \cdot 3^{4} \cdot 2^{3}=108 \cdot 2014$ !.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
541b1cb1-d6a3-5fee-aff1-899a319fd3fc
| 261,240
|
Find all positive integers $n$ such that for any integer $k$ there exists an integer $a$ for which $a^{3}+a-k$ is divisible by $n$. (Warut Suksompong, Thailand)
|
Answer: All integers $n=3^{b}$, where $b$ is a nonnegative integer.
We are looking for integers $n$ such that the set $A=\left\{a^{3}+a \mid a \in \mathbf{Z}\right\}$ is a complete residue system by modulo $n$. Let us call this property by $\left(^{*}\right)$. It is not hard to see that $n=1$ satisfies $\left({ }^{*}\right)$ and $n=2$ does not.
If $a \equiv b(\bmod n)$, then $a^{3}+a \equiv b^{3}+b(\bmod n)$. So $n$ satisfies $\left(^{*}\right)$ iff there are no $a, b \in\{0, \ldots, n-1\}$ with $a \neq b$ and $a^{3}+a \equiv b^{3}+b(\bmod n)$.
First, let us prove that $3^{j}$ satisfies $\left(^{*}\right)$ for all $j \geq 1$. Suppose that $a^{3}+a \equiv b^{3}+b\left(\bmod 3^{j}\right)$ for $a \neq b$. Then $(a-b)\left(a^{2}+a b+b^{2}+1\right) \equiv 0\left(\bmod 3^{j}\right)$. We can easily check mod 3 that $a^{2}+a b+b^{2}+1$ is not divisible by 3 .
Next note that if $A$ is not a complete residue system modulo integer $r$, then it is also not a complete residue system modulo any multiple of $r$. Hence it remains to prove that any prime $p>3$ does not satisfy (*).
If $p \equiv 1(\bmod 4)$, there exists $b$ such that $b^{2} \equiv-1(\bmod p)$. We then take $a=0$ to obtain the congruence $a^{3}+a \equiv b^{3}+b(\bmod p)$.
Suppose now that $p \equiv 3(\bmod 4)$. We will prove that there are integers $a, b \not \equiv 0(\bmod p)$ such that $a^{2}+a b+b^{2} \equiv-1(\bmod p)$. Note that we may suppose that $a \not \equiv b(\bmod p)$, since otherwise if $a \equiv b(\bmod p)$ satisfies $a^{2}+a b+b^{2}+1 \equiv 0(\bmod p)$, then $(2 a)^{2}+(2 a)(-a)+$ $a^{2}+1 \equiv 0(\bmod p)$ and $2 a \not \equiv-a(\bmod p)$. Letting $c$ be the inverse of $b$ modulo $p$ (i.e. $b c \equiv 1(\bmod p)$ ), the relation is equivalent to $(a c)^{2}+a c+1 \equiv-c^{2}(\bmod p)$. Note that $-c^{2}$ can take on the values of all non-quadratic residues modulo $p$. If we can find an integer $x$ such that $x^{2}+x+1$ is a non-quadratic residue modulo $p$, the values of $a$ and $c$ will follow immediately. Hence we focus on this latter task.
Note that if $x, y \in\{0, \ldots, p-1\}=B$, then $x^{2}+x+1 \equiv y^{2}+y+1(\bmod p)$ iff $p$ divides $x+y+1$. We can deduce that $x^{2}+x+1$ takes on $(p+1) / 2$ values as $x$ varies in $B$. Since there are $(p-1) / 2$ non-quadratic residues modulo $p$, the $(p+1) / 2$ values that $x^{2}+x+1$ take on must be 0 and all the quadratic residues.
Let $C$ be the set of quadratic residues modulo $p$ and 0 , and let $y \in C$. Suppose that $y \equiv z^{2}(\bmod p)$ and let $z \equiv 2 w+1(\bmod p)$ (we can always choose such $\left.w\right)$. Then $y+3 \equiv$ $4\left(w^{2}+w+1\right)(\bmod p)$. From the previous paragraph, we know that $4\left(w^{2}+w+1\right) \in C$. This means that $y \in C \Longrightarrow y+3 \in C$. Unless $p=3$, the relation implies that all elements of $B$ are in $C$, a contradiction. This concludes the proof.
|
All integers $n=3^{b}$, where $b$ is a nonnegative integer.
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that for any integer $k$ there exists an integer $a$ for which $a^{3}+a-k$ is divisible by $n$. (Warut Suksompong, Thailand)
|
Answer: All integers $n=3^{b}$, where $b$ is a nonnegative integer.
We are looking for integers $n$ such that the set $A=\left\{a^{3}+a \mid a \in \mathbf{Z}\right\}$ is a complete residue system by modulo $n$. Let us call this property by $\left(^{*}\right)$. It is not hard to see that $n=1$ satisfies $\left({ }^{*}\right)$ and $n=2$ does not.
If $a \equiv b(\bmod n)$, then $a^{3}+a \equiv b^{3}+b(\bmod n)$. So $n$ satisfies $\left(^{*}\right)$ iff there are no $a, b \in\{0, \ldots, n-1\}$ with $a \neq b$ and $a^{3}+a \equiv b^{3}+b(\bmod n)$.
First, let us prove that $3^{j}$ satisfies $\left(^{*}\right)$ for all $j \geq 1$. Suppose that $a^{3}+a \equiv b^{3}+b\left(\bmod 3^{j}\right)$ for $a \neq b$. Then $(a-b)\left(a^{2}+a b+b^{2}+1\right) \equiv 0\left(\bmod 3^{j}\right)$. We can easily check mod 3 that $a^{2}+a b+b^{2}+1$ is not divisible by 3 .
Next note that if $A$ is not a complete residue system modulo integer $r$, then it is also not a complete residue system modulo any multiple of $r$. Hence it remains to prove that any prime $p>3$ does not satisfy (*).
If $p \equiv 1(\bmod 4)$, there exists $b$ such that $b^{2} \equiv-1(\bmod p)$. We then take $a=0$ to obtain the congruence $a^{3}+a \equiv b^{3}+b(\bmod p)$.
Suppose now that $p \equiv 3(\bmod 4)$. We will prove that there are integers $a, b \not \equiv 0(\bmod p)$ such that $a^{2}+a b+b^{2} \equiv-1(\bmod p)$. Note that we may suppose that $a \not \equiv b(\bmod p)$, since otherwise if $a \equiv b(\bmod p)$ satisfies $a^{2}+a b+b^{2}+1 \equiv 0(\bmod p)$, then $(2 a)^{2}+(2 a)(-a)+$ $a^{2}+1 \equiv 0(\bmod p)$ and $2 a \not \equiv-a(\bmod p)$. Letting $c$ be the inverse of $b$ modulo $p$ (i.e. $b c \equiv 1(\bmod p)$ ), the relation is equivalent to $(a c)^{2}+a c+1 \equiv-c^{2}(\bmod p)$. Note that $-c^{2}$ can take on the values of all non-quadratic residues modulo $p$. If we can find an integer $x$ such that $x^{2}+x+1$ is a non-quadratic residue modulo $p$, the values of $a$ and $c$ will follow immediately. Hence we focus on this latter task.
Note that if $x, y \in\{0, \ldots, p-1\}=B$, then $x^{2}+x+1 \equiv y^{2}+y+1(\bmod p)$ iff $p$ divides $x+y+1$. We can deduce that $x^{2}+x+1$ takes on $(p+1) / 2$ values as $x$ varies in $B$. Since there are $(p-1) / 2$ non-quadratic residues modulo $p$, the $(p+1) / 2$ values that $x^{2}+x+1$ take on must be 0 and all the quadratic residues.
Let $C$ be the set of quadratic residues modulo $p$ and 0 , and let $y \in C$. Suppose that $y \equiv z^{2}(\bmod p)$ and let $z \equiv 2 w+1(\bmod p)$ (we can always choose such $\left.w\right)$. Then $y+3 \equiv$ $4\left(w^{2}+w+1\right)(\bmod p)$. From the previous paragraph, we know that $4\left(w^{2}+w+1\right) \in C$. This means that $y \in C \Longrightarrow y+3 \in C$. Unless $p=3$, the relation implies that all elements of $B$ are in $C$, a contradiction. This concludes the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
8b09d69e-d589-5acd-92b6-7275eb54e80f
| 261,249
|
Let $n$ and $b$ be positive integers. We say $n$ is $b$-discerning if there exists a set consisting of $n$ different positive integers less than $b$ that has no two different subsets $U$ and $V$ such that the sum of all elements in $U$ equals the sum of all elements in $V$.
(a) Prove that 8 is a 100 -discerning.
(b) Prove that 9 is not 100-discerning.
(Senior Problems Committee of the Australian Mathematical Olympiad Committee)
|
(a) Take $S=\{3,6,12,24,48,95,96,97\}$, i.e.
$$
S=\left\{3 \cdot 2^{k}: 0 \leq k \leq 5\right\} \cup\left\{3 \cdot 2^{5}-1,3 \cdot 2^{5}+1\right\}
$$
As $k$ ranges between 0 to 5 , the sums obtained from the numbers $3 \cdot 2^{k}$ are $3 t$, where $1 \leq t \leq 63$. These are 63 numbers that are divisible by 3 and are at most $3 \cdot 63=189$.
Sums of elements of $S$ are also the numbers $95+97=192$ and all the numbers that are sums of 192 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all divisible by 3 and at least equal to 192. In addition, sums of elements of $S$ are the numbers 95 and all the numbers that are sums of 95 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $-1 \bmod$ 3.
Finally, sums of elements of $S$ are the numbers 97 and all the numbers that are sums of 97 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $1 \bmod 3$.
Hence there are at least $63+64+64+64=255$ different sums from elements of $S$. On the other hand, $S$ has $2^{8}-1=255$ non-empty subsets. Therefore $S$ has no two different subsets with equal sums of elements. Therefore, 8 is 100 -discerning.
(b) Suppose that 9 is 100 -discerning. Then there is a set $S=\left\{s_{1}, \ldots, s_{9}\right\}, s_{i}<100$ that has no two different subsets with equal sums of elements. Assume that $0<s_{1}<\cdots<s_{9}<$ 100.
Let $X$ be the set of all subsets of $S$ having at least 3 and at most 6 elements and let $Y$ be the set of all subsets of $S$ having exactly 2 or 3 or 4 elements greater than $s_{3}$.
The set $X$ consists of
$$
\binom{9}{3}+\binom{9}{4}+\binom{9}{5}+\binom{9}{6}=84+126+126+84=420
$$
subsets of $S$. The set in $X$ with the largest sums of elements is $\left\{s_{4}, \ldots, s_{9}\right\}$ and the smallest sums is in $\left\{s_{1}, s_{2}, s_{3}\right\}$. Thus the sum of the elements of each of the 420 sets in $X$ is at least $s_{1}+s_{2}+s_{3}$ and at most $s_{4}+\cdots+s_{9}$, which is one of $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1$ integers. From the pigeonhole principle it follows that $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1 \geq 420$, i.e.,
$$
\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right) \geq 419
$$
Now let us calculate the number of subsets in $Y$. Observe that $\left\{s_{4}, \ldots, s_{9}\right\}$ has $\binom{6}{2}$ 2-element subsets, $\binom{6}{3}$ 3-element subsets and $\binom{6}{4}$ 4-element subsets, while $\left\{s_{1}, s_{2}, s_{3}\right\}$ has exactly 8 subsets. Hence the number of subsets of $S$ in $Y$ equals
$$
8\left(\binom{6}{2}+\binom{6}{3}+\binom{6}{4}\right)=8(15+20+15)=400
$$
The set in $Y$ with the largest sum of elements is $\left\{s_{1}, s_{2}, s_{3}, s_{6}, s_{7}, s_{8}, s_{9}\right\}$ and the smallest sum is in $\left\{s_{4}, s_{5}\right\}$. Again, by the pigeonhole principle it follows that $\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+\right.$ $\left.s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right)+1 \geq 400$, i.e.,
$$
\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right) \geq 399
$$
Adding (1) and (2) yields $2\left(s_{6}+s_{7}+s_{8}+s_{9}\right) \geq 818$, so that $s_{9}+98+97+96 \geq$ $s_{9}+s_{8}+s_{7}+s_{6} \geq 409$, i.e. $s_{9} \geq 118$, a contradiction with $s_{9}<100$. Therefore, 9 is not 100-discerning.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ and $b$ be positive integers. We say $n$ is $b$-discerning if there exists a set consisting of $n$ different positive integers less than $b$ that has no two different subsets $U$ and $V$ such that the sum of all elements in $U$ equals the sum of all elements in $V$.
(a) Prove that 8 is a 100 -discerning.
(b) Prove that 9 is not 100-discerning.
(Senior Problems Committee of the Australian Mathematical Olympiad Committee)
|
(a) Take $S=\{3,6,12,24,48,95,96,97\}$, i.e.
$$
S=\left\{3 \cdot 2^{k}: 0 \leq k \leq 5\right\} \cup\left\{3 \cdot 2^{5}-1,3 \cdot 2^{5}+1\right\}
$$
As $k$ ranges between 0 to 5 , the sums obtained from the numbers $3 \cdot 2^{k}$ are $3 t$, where $1 \leq t \leq 63$. These are 63 numbers that are divisible by 3 and are at most $3 \cdot 63=189$.
Sums of elements of $S$ are also the numbers $95+97=192$ and all the numbers that are sums of 192 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all divisible by 3 and at least equal to 192. In addition, sums of elements of $S$ are the numbers 95 and all the numbers that are sums of 95 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $-1 \bmod$ 3.
Finally, sums of elements of $S$ are the numbers 97 and all the numbers that are sums of 97 and sums obtained from the numbers $3 \cdot 2^{k}$ with $0 \leq k \leq 5$. These are 64 numbers that are all congruent to $1 \bmod 3$.
Hence there are at least $63+64+64+64=255$ different sums from elements of $S$. On the other hand, $S$ has $2^{8}-1=255$ non-empty subsets. Therefore $S$ has no two different subsets with equal sums of elements. Therefore, 8 is 100 -discerning.
(b) Suppose that 9 is 100 -discerning. Then there is a set $S=\left\{s_{1}, \ldots, s_{9}\right\}, s_{i}<100$ that has no two different subsets with equal sums of elements. Assume that $0<s_{1}<\cdots<s_{9}<$ 100.
Let $X$ be the set of all subsets of $S$ having at least 3 and at most 6 elements and let $Y$ be the set of all subsets of $S$ having exactly 2 or 3 or 4 elements greater than $s_{3}$.
The set $X$ consists of
$$
\binom{9}{3}+\binom{9}{4}+\binom{9}{5}+\binom{9}{6}=84+126+126+84=420
$$
subsets of $S$. The set in $X$ with the largest sums of elements is $\left\{s_{4}, \ldots, s_{9}\right\}$ and the smallest sums is in $\left\{s_{1}, s_{2}, s_{3}\right\}$. Thus the sum of the elements of each of the 420 sets in $X$ is at least $s_{1}+s_{2}+s_{3}$ and at most $s_{4}+\cdots+s_{9}$, which is one of $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1$ integers. From the pigeonhole principle it follows that $\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right)+1 \geq 420$, i.e.,
$$
\left(s_{4}+\cdots+s_{9}\right)-\left(s_{1}+s_{2}+s_{3}\right) \geq 419
$$
Now let us calculate the number of subsets in $Y$. Observe that $\left\{s_{4}, \ldots, s_{9}\right\}$ has $\binom{6}{2}$ 2-element subsets, $\binom{6}{3}$ 3-element subsets and $\binom{6}{4}$ 4-element subsets, while $\left\{s_{1}, s_{2}, s_{3}\right\}$ has exactly 8 subsets. Hence the number of subsets of $S$ in $Y$ equals
$$
8\left(\binom{6}{2}+\binom{6}{3}+\binom{6}{4}\right)=8(15+20+15)=400
$$
The set in $Y$ with the largest sum of elements is $\left\{s_{1}, s_{2}, s_{3}, s_{6}, s_{7}, s_{8}, s_{9}\right\}$ and the smallest sum is in $\left\{s_{4}, s_{5}\right\}$. Again, by the pigeonhole principle it follows that $\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+\right.$ $\left.s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right)+1 \geq 400$, i.e.,
$$
\left(s_{1}+s_{2}+s_{3}+s_{6}+s_{7}+s_{8}+s_{9}\right)-\left(s_{4}+s_{5}\right) \geq 399
$$
Adding (1) and (2) yields $2\left(s_{6}+s_{7}+s_{8}+s_{9}\right) \geq 818$, so that $s_{9}+98+97+96 \geq$ $s_{9}+s_{8}+s_{7}+s_{6} \geq 409$, i.e. $s_{9} \geq 118$, a contradiction with $s_{9}<100$. Therefore, 9 is not 100-discerning.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# Solution."
}
|
d80210e6-a097-5993-aa27-92adb8bca0bf
| 605,580
|
Circles $\omega$ and $\Omega$ meet at points $A$ and $B$. Let $M$ be the midpoint of the $\operatorname{arc} A B$ of circle $\omega$ ( $M$ lies inside $\Omega$ ). A chord $M P$ of circle $\omega$ intersects $\Omega$ at $Q(Q$ lies inside $\omega)$. Let $\ell_{P}$ be the tangent line to $\omega$ at $P$, and let $\ell_{Q}$ be the tangent line to $\Omega$ at $Q$. Prove that the circumcircle of the triangle formed by the lines $\ell_{P}, \ell_{Q}$, and $A B$ is tangent to $\Omega$. (Ilya Bogdanov, Russia and Medeubek Kungozhin, Kazakhstan)
|
Denote $X=A B \cap \ell_{P}, Y=A B \cap \ell_{Q}$, and $Z=\ell_{P} \cap \ell_{Q}$. Without loss of generality we have $A X<B X$. Let $F=M P \cap A B$.
Denote by $R$ the second point of intersection of $P Q$ and $\Omega$; by $S$ the point of $\Omega$ such that $S R \| A B$; and by $T$ the point of $\Omega$ such that $R T \| \ell_{P}$. Since $M$ is the midpoint of arc $A B$, the tangent $\ell_{M}$ at $M$ to $\omega$ is parallel to $A B$, so $\angle(A B, P M)=\angle\left(P M, \ell_{P}\right)$. Therefore we have $\angle P R T=\angle M P X=\angle P F X=\angle P R S$. Thus the point $Q$ is the midpoint of the $\operatorname{arc} T Q S$ of $\Omega$, hence $S T \| \ell_{Q}$. So the corresponding sides of the triangles $R S T$ and $X Y Z$ are parallel, and there exist a homothety $h$ mapping $R S T$ to $X Y Z$.
Let $D$ be the second point of intersection of $X R$ and $\Omega$. We claim that $D$ is the center of the homothety $h$; since $D \in \Omega$, this implies that the circumcircles of triangles $R S T$ and $X Y Z$ are tangent, as required. So, it remains to prove this claim. In order to do this, it suffices to show that $D \in S Y$.
By $\angle P F X=\angle X P F$ we have $X F^{2}=X P^{2}=X A \cdot X B=X D \cdot X R$. Therefore, $\frac{X F}{X D}=\frac{X R}{X F}$, so the triangles $X D F$ and $X F R$ are similar, hence $\angle D F X=\angle X R F=\angle D R Q=$ $\angle D Q Y$; thus the points $D, Y, Q$, and $F$ are concyclic. It follows that $\angle Y D Q=\angle Y F Q=$ $\angle S R Q=180^{\circ}-\angle S D Q$ which means exactly that the points $Y, D$, and $S$ are collinear, with $D$ between $S$ and $Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Circles $\omega$ and $\Omega$ meet at points $A$ and $B$. Let $M$ be the midpoint of the $\operatorname{arc} A B$ of circle $\omega$ ( $M$ lies inside $\Omega$ ). A chord $M P$ of circle $\omega$ intersects $\Omega$ at $Q(Q$ lies inside $\omega)$. Let $\ell_{P}$ be the tangent line to $\omega$ at $P$, and let $\ell_{Q}$ be the tangent line to $\Omega$ at $Q$. Prove that the circumcircle of the triangle formed by the lines $\ell_{P}, \ell_{Q}$, and $A B$ is tangent to $\Omega$. (Ilya Bogdanov, Russia and Medeubek Kungozhin, Kazakhstan)
|
Denote $X=A B \cap \ell_{P}, Y=A B \cap \ell_{Q}$, and $Z=\ell_{P} \cap \ell_{Q}$. Without loss of generality we have $A X<B X$. Let $F=M P \cap A B$.

Denote by $R$ the second point of intersection of $P Q$ and $\Omega$; by $S$ the point of $\Omega$ such that $S R \| A B$; and by $T$ the point of $\Omega$ such that $R T \| \ell_{P}$. Since $M$ is the midpoint of arc $A B$, the tangent $\ell_{M}$ at $M$ to $\omega$ is parallel to $A B$, so $\angle(A B, P M)=\angle\left(P M, \ell_{P}\right)$. Therefore we have $\angle P R T=\angle M P X=\angle P F X=\angle P R S$. Thus the point $Q$ is the midpoint of the $\operatorname{arc} T Q S$ of $\Omega$, hence $S T \| \ell_{Q}$. So the corresponding sides of the triangles $R S T$ and $X Y Z$ are parallel, and there exist a homothety $h$ mapping $R S T$ to $X Y Z$.
Let $D$ be the second point of intersection of $X R$ and $\Omega$. We claim that $D$ is the center of the homothety $h$; since $D \in \Omega$, this implies that the circumcircles of triangles $R S T$ and $X Y Z$ are tangent, as required. So, it remains to prove this claim. In order to do this, it suffices to show that $D \in S Y$.
By $\angle P F X=\angle X P F$ we have $X F^{2}=X P^{2}=X A \cdot X B=X D \cdot X R$. Therefore, $\frac{X F}{X D}=\frac{X R}{X F}$, so the triangles $X D F$ and $X F R$ are similar, hence $\angle D F X=\angle X R F=\angle D R Q=$ $\angle D Q Y$; thus the points $D, Y, Q$, and $F$ are concyclic. It follows that $\angle Y D Q=\angle Y F Q=$ $\angle S R Q=180^{\circ}-\angle S D Q$ which means exactly that the points $Y, D$, and $S$ are collinear, with $D$ between $S$ and $Y$.
|
{
"resource_path": "APMO/segmented/en-apmo2014_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
4cd3c0ca-6b01-5351-8e48-0a03b74760c3
| 605,596
|
Let $A B C$ be a triangle, and let $D$ be a point on side $B C$. A line through $D$ intersects side $A B$ at $X$ and ray $A C$ at $Y$. The circumcircle of triangle $B X D$ intersects the circumcircle $\omega$ of triangle $A B C$ again at point $Z \neq B$. The lines $Z D$ and $Z Y$ intersect $\omega$ again at $V$ and $W$, respectively. Prove that $A B=V W$.
|
Suppose $X Y$ intersects $\omega$ at points $P$ and $Q$, where $Q$ lies between $X$ and $Y$. We will show that $V$ and $W$ are the reflections of $A$ and $B$ with respect to the perpendicular bisector of $P Q$. From this, it follows that $A V W B$ is an isosceles trapezoid and hence $A B=V W$.
First, note that
$$
\angle B Z D=\angle A X Y=\angle A P Q+\angle B A P=\angle A P Q+\angle B Z P,
$$
so $\angle A P Q=\angle P Z V=\angle P Q V$, and hence $V$ is the reflection of $A$ with respect to the perpendicular bisector of $P Q$.
Now, suppose $W^{\prime}$ is the reflection of $B$ with respect to the perpendicular bisector of $P Q$, and let $Z^{\prime}$ be the intersection of $Y W^{\prime}$ and $\omega$. It suffices to show that $B, X, D, Z^{\prime}$ are concyclic. Note that
$$
\angle Y D C=\angle P D B=\angle P C B+\angle Q P C=\angle W^{\prime} P Q+\angle Q P C=\angle W^{\prime} P C=\angle Y Z^{\prime} C .
$$
So $D, C, Y, Z^{\prime}$ are concyclic. Next, $\angle B Z^{\prime} D=\angle C Z^{\prime} B-\angle C Z^{\prime} D=180^{\circ}-\angle B X D$ and due to the previous concyclicity we are done.
Alternative solution 1. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $A B Z C$ and $Z D C Y$ in turn, we have $\angle A Z B=\angle A C B=\angle W Z V$ (or $180^{\circ}-\angle W Z V$ if $Z$ lies between $W$ and $C$ ).
So $A B=V W$ because they subtend equal (or supplementary) angles in $\omega$.
Alternative solution 2. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle D X A=\angle V Z B=$ $180^{\circ}-B A V$. So $X D \| A V$.
Using cyclic quadrilaterals $Z D C Y$ and $B C W Z$ in turn, we have $\angle Y D C=\angle Y Z C=$ $\angle W B C$. So $X D \| B W$.
Hence $B W \| A V$ which implies that $A V W B$ is an isosceles trapezium with $A B=V W$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, and let $D$ be a point on side $B C$. A line through $D$ intersects side $A B$ at $X$ and ray $A C$ at $Y$. The circumcircle of triangle $B X D$ intersects the circumcircle $\omega$ of triangle $A B C$ again at point $Z \neq B$. The lines $Z D$ and $Z Y$ intersect $\omega$ again at $V$ and $W$, respectively. Prove that $A B=V W$.
|
Suppose $X Y$ intersects $\omega$ at points $P$ and $Q$, where $Q$ lies between $X$ and $Y$. We will show that $V$ and $W$ are the reflections of $A$ and $B$ with respect to the perpendicular bisector of $P Q$. From this, it follows that $A V W B$ is an isosceles trapezoid and hence $A B=V W$.
First, note that
$$
\angle B Z D=\angle A X Y=\angle A P Q+\angle B A P=\angle A P Q+\angle B Z P,
$$
so $\angle A P Q=\angle P Z V=\angle P Q V$, and hence $V$ is the reflection of $A$ with respect to the perpendicular bisector of $P Q$.
Now, suppose $W^{\prime}$ is the reflection of $B$ with respect to the perpendicular bisector of $P Q$, and let $Z^{\prime}$ be the intersection of $Y W^{\prime}$ and $\omega$. It suffices to show that $B, X, D, Z^{\prime}$ are concyclic. Note that
$$
\angle Y D C=\angle P D B=\angle P C B+\angle Q P C=\angle W^{\prime} P Q+\angle Q P C=\angle W^{\prime} P C=\angle Y Z^{\prime} C .
$$
So $D, C, Y, Z^{\prime}$ are concyclic. Next, $\angle B Z^{\prime} D=\angle C Z^{\prime} B-\angle C Z^{\prime} D=180^{\circ}-\angle B X D$ and due to the previous concyclicity we are done.
Alternative solution 1. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $A B Z C$ and $Z D C Y$ in turn, we have $\angle A Z B=\angle A C B=\angle W Z V$ (or $180^{\circ}-\angle W Z V$ if $Z$ lies between $W$ and $C$ ).
So $A B=V W$ because they subtend equal (or supplementary) angles in $\omega$.
Alternative solution 2. Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle Z D Y=\angle Z B A=\angle Z C Y$. So $Z D C Y$ is cyclic.
Using cyclic quadrilaterals $B X D Z$ and $A B Z V$ in turn, we have $\angle D X A=\angle V Z B=$ $180^{\circ}-B A V$. So $X D \| A V$.
Using cyclic quadrilaterals $Z D C Y$ and $B C W Z$ in turn, we have $\angle Y D C=\angle Y Z C=$ $\angle W B C$. So $X D \| B W$.
Hence $B W \| A V$ which implies that $A V W B$ is an isosceles trapezium with $A B=V W$.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
372115e8-55ec-5e65-a7c6-4e677231b56e
| 261,024
|
Let $S=\{2,3,4, \ldots\}$ denote the set of integers that are greater than or equal to 2 . Does there exist a function $f: S \rightarrow S$ such that
$$
f(a) f(b)=f\left(a^{2} b^{2}\right) \text { for all } a, b \in S \text { with } a \neq b ?
$$
|
We prove that there is no such function. For arbitrary elements $a$ and $b$ of $S$, choose an integer $c$ that is greater than both of them. Since $b c>a$ and $c>b$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(a^{2}\right) f\left(b^{2} c^{2}\right)=f\left(a^{2}\right) f(b) f(c)
$$
Furthermore, since $a c>b$ and $c>a$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(b^{2}\right) f\left(a^{2} c^{2}\right)=f\left(b^{2}\right) f(a) f(c)
$$
Comparing these two equations, we find that for all elements $a$ and $b$ of $S$,
$$
f\left(a^{2}\right) f(b)=f\left(b^{2}\right) f(a) \quad \Longrightarrow \quad \frac{f\left(a^{2}\right)}{f(a)}=\frac{f\left(b^{2}\right)}{f(b)} .
$$
It follows that there exists a positive rational number $k$ such that
$$
f\left(a^{2}\right)=k f(a), \quad \text { for all } a \in S
$$
Substituting this into the functional equation yields
$$
f(a b)=\frac{f(a) f(b)}{k}, \quad \text { for all } a, b \in S \text { with } a \neq b .
$$
Now combine the functional equation with equations (1) and (2) to obtain
$$
f(a) f\left(a^{2}\right)=f\left(a^{6}\right)=\frac{f(a) f\left(a^{5}\right)}{k}=\frac{f(a) f(a) f\left(a^{4}\right)}{k^{2}}=\frac{f(a) f(a) f\left(a^{2}\right)}{k}, \quad \text { for all } a \in S .
$$
It follows that $f(a)=k$ for all $a \in S$. Substituting $a=2$ and $b=3$ into the functional equation yields $k=1$, however $1 \notin S$ and hence we have no solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S=\{2,3,4, \ldots\}$ denote the set of integers that are greater than or equal to 2 . Does there exist a function $f: S \rightarrow S$ such that
$$
f(a) f(b)=f\left(a^{2} b^{2}\right) \text { for all } a, b \in S \text { with } a \neq b ?
$$
|
We prove that there is no such function. For arbitrary elements $a$ and $b$ of $S$, choose an integer $c$ that is greater than both of them. Since $b c>a$ and $c>b$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(a^{2}\right) f\left(b^{2} c^{2}\right)=f\left(a^{2}\right) f(b) f(c)
$$
Furthermore, since $a c>b$ and $c>a$, we have
$$
f\left(a^{4} b^{4} c^{4}\right)=f\left(b^{2}\right) f\left(a^{2} c^{2}\right)=f\left(b^{2}\right) f(a) f(c)
$$
Comparing these two equations, we find that for all elements $a$ and $b$ of $S$,
$$
f\left(a^{2}\right) f(b)=f\left(b^{2}\right) f(a) \quad \Longrightarrow \quad \frac{f\left(a^{2}\right)}{f(a)}=\frac{f\left(b^{2}\right)}{f(b)} .
$$
It follows that there exists a positive rational number $k$ such that
$$
f\left(a^{2}\right)=k f(a), \quad \text { for all } a \in S
$$
Substituting this into the functional equation yields
$$
f(a b)=\frac{f(a) f(b)}{k}, \quad \text { for all } a, b \in S \text { with } a \neq b .
$$
Now combine the functional equation with equations (1) and (2) to obtain
$$
f(a) f\left(a^{2}\right)=f\left(a^{6}\right)=\frac{f(a) f\left(a^{5}\right)}{k}=\frac{f(a) f(a) f\left(a^{4}\right)}{k^{2}}=\frac{f(a) f(a) f\left(a^{2}\right)}{k}, \quad \text { for all } a \in S .
$$
It follows that $f(a)=k$ for all $a \in S$. Substituting $a=2$ and $b=3$ into the functional equation yields $k=1$, however $1 \notin S$ and hence we have no solutions.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
28499edb-ddd1-5c48-83f2-a5d0cd555339
| 605,623
|
A sequence of real numbers $a_{0}, a_{1}, \ldots$ is said to be good if the following three conditions hold.
(i) The value of $a_{0}$ is a positive integer.
(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\frac{a_{i}}{a_{i}+2}$.
(iii) There exists a positive integer $k$ such that $a_{k}=2014$.
Find the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \ldots$ of real numbers with the property that $a_{n}=2014$.
Answer: 60.
|
Note that
$$
a_{i+1}+1=2\left(a_{i}+1\right) \text { or } a_{i+1}+1=\frac{a_{i}+a_{i}+2}{a_{i}+2}=\frac{2\left(a_{i}+1\right)}{a_{i}+2} .
$$
Hence
$$
\frac{1}{a_{i+1}+1}=\frac{1}{2} \cdot \frac{1}{a_{i}+1} \text { or } \frac{1}{a_{i+1}+1}=\frac{a_{i}+2}{2\left(a_{i}+1\right)}=\frac{1}{2} \cdot \frac{1}{a_{i}+1}+\frac{1}{2} .
$$
Therefore,
$$
\frac{1}{a_{k}+1}=\frac{1}{2^{k}} \cdot \frac{1}{a_{0}+1}+\sum_{i=1}^{k} \frac{\varepsilon_{i}}{2^{k-i+1}}
$$
where $\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\left(a_{k}+1\right)$ and putting $a_{k}=2014$, we get
$$
2^{k}=\frac{2015}{a_{0}+1}+2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . Since $\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,
$$
2^{k}-1=2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \mid 2^{k}-1$. Since $2015=$ $5 \cdot 13 \cdot 31$, from the Fermat little theorem we obtain $5\left|2^{4}-1,13\right| 2^{12}-1$ and $31 \mid 2^{30}-1$. We also have $\operatorname{lcm}[4,12,30]=60$, hence $5\left|2^{60}-1,13\right| 2^{60}-1$ and $31 \mid 2^{60}-1$, which gives $2015 \mid 2^{60}-1$.
But $5 \nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.
Alternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\frac{a_{i+1}-1}{2}$ or $a_{i}=\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that
$$
a_{i}=\left\{\begin{array}{cl}
\frac{a_{i+1}-1}{2} & \text { if } a_{i+1}>1 \\
\frac{2 a_{i+1}}{1-a_{i+1}} & \text { if } a_{i+1}<1
\end{array}\right.
$$
Thus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.
$$
\begin{aligned}
& \frac{2014}{1}, \frac{2013}{2}, \frac{2011}{4}, \frac{2007}{8}, \frac{1999}{16}, \frac{1983}{32}, \frac{1951}{64}, \frac{1887}{128}, \frac{1759}{256}, \frac{1503}{512}, \frac{991}{1024}, \frac{1982}{33}, \frac{1949}{66}, \frac{1883}{132}, \frac{1751}{264}, \frac{1487}{528}, \frac{959}{1056}, \frac{1918}{97}, \frac{1821}{194}, \frac{1627}{388}, \\
& \frac{1239}{776}, \frac{463}{1552}, \frac{926}{1089}, \frac{1852}{163}, \frac{1689}{326}, \frac{1363}{652}, \frac{711}{1304}, \frac{1422}{593}, \frac{829}{1186}, \frac{1658}{357}, \frac{1301}{714}, \frac{587}{1428}, \frac{1174}{841}, \frac{333}{1682}, \frac{666}{1349}, \frac{1332}{683}, \frac{649}{1366}, \frac{1298}{717}, \frac{581}{1434}, \frac{1162}{853}, \\
& \frac{309}{1706}, \frac{618}{1397}, \frac{1236}{779}, \frac{457}{1558}, \frac{914}{1101}, \frac{1828}{187}, \frac{1641}{374}, \frac{1267}{748}, \frac{519}{1496}, \frac{1038}{977}, \frac{61}{1954}, \frac{122}{1893}, \frac{244}{1771}, \frac{488}{1527}, \frac{976}{1039}, \frac{1952}{63}, \frac{1889}{126}, \frac{1763}{252}, \frac{1511}{504}, \frac{1007}{1008}, \frac{2014}{1}
\end{aligned}
$$
There are 61 terms in the above list. Thus $k=60$.
Alternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.
Alternative solution 2. Start with $a_{k}=\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\frac{m_{i}}{n_{i}}$ for $i \geq 0$ where
$$
\left(m_{i+1}, n_{i+1}\right)= \begin{cases}\left(m_{i}-n_{i}, 2 n_{i}\right) & \text { if } m_{i}>n_{i} \\ \left(2 m_{i}, n_{i}-m_{i}\right) & \text { if } m_{i}<n_{i}\end{cases}
$$
Easy inductions show that $m_{i}+n_{i}=2015,1 \leq m_{i}, n_{i} \leq 2014$ and $\operatorname{gcd}\left(m_{i}, n_{i}\right)=1$ for $i \geq 0$. Since $a_{0} \in \mathbb{N}^{+}$and $\operatorname{gcd}\left(m_{k}, n_{k}\right)=1$, we require $n_{k}=1$. An easy induction shows that $\left(m_{i}, n_{i}\right) \equiv\left(-2^{i}, 2^{i}\right)(\bmod 2015)$ for $i=0,1, \ldots, k$.
Thus $2^{k} \equiv 1(\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \equiv 1(\bmod 2015)$. But since $1 \leq n_{k}, m_{k} \leq 2014$, it follows that $a_{0}$ is an integer.
|
60
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of real numbers $a_{0}, a_{1}, \ldots$ is said to be good if the following three conditions hold.
(i) The value of $a_{0}$ is a positive integer.
(ii) For each non-negative integer $i$ we have $a_{i+1}=2 a_{i}+1$ or $a_{i+1}=\frac{a_{i}}{a_{i}+2}$.
(iii) There exists a positive integer $k$ such that $a_{k}=2014$.
Find the smallest positive integer $n$ such that there exists a good sequence $a_{0}, a_{1}, \ldots$ of real numbers with the property that $a_{n}=2014$.
Answer: 60.
|
Note that
$$
a_{i+1}+1=2\left(a_{i}+1\right) \text { or } a_{i+1}+1=\frac{a_{i}+a_{i}+2}{a_{i}+2}=\frac{2\left(a_{i}+1\right)}{a_{i}+2} .
$$
Hence
$$
\frac{1}{a_{i+1}+1}=\frac{1}{2} \cdot \frac{1}{a_{i}+1} \text { or } \frac{1}{a_{i+1}+1}=\frac{a_{i}+2}{2\left(a_{i}+1\right)}=\frac{1}{2} \cdot \frac{1}{a_{i}+1}+\frac{1}{2} .
$$
Therefore,
$$
\frac{1}{a_{k}+1}=\frac{1}{2^{k}} \cdot \frac{1}{a_{0}+1}+\sum_{i=1}^{k} \frac{\varepsilon_{i}}{2^{k-i+1}}
$$
where $\varepsilon_{i}=0$ or 1 . Multiplying both sides by $2^{k}\left(a_{k}+1\right)$ and putting $a_{k}=2014$, we get
$$
2^{k}=\frac{2015}{a_{0}+1}+2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . Since $\operatorname{gcd}(2,2015)=1$, we have $a_{0}+1=2015$ and $a_{0}=2014$. Therefore,
$$
2^{k}-1=2015 \cdot\left(\sum_{i=1}^{k} \varepsilon_{i} \cdot 2^{i-1}\right)
$$
where $\varepsilon_{i}=0$ or 1 . We now need to find the smallest $k$ such that $2015 \mid 2^{k}-1$. Since $2015=$ $5 \cdot 13 \cdot 31$, from the Fermat little theorem we obtain $5\left|2^{4}-1,13\right| 2^{12}-1$ and $31 \mid 2^{30}-1$. We also have $\operatorname{lcm}[4,12,30]=60$, hence $5\left|2^{60}-1,13\right| 2^{60}-1$ and $31 \mid 2^{60}-1$, which gives $2015 \mid 2^{60}-1$.
But $5 \nmid 2^{30}-1$ and so $k=60$ is the smallest positive integer such that $2015 \mid 2^{k}-1$. To conclude, the smallest positive integer $k$ such that $a_{k}=2014$ is when $k=60$.
Alternative solution 1. Clearly all members of the sequence are positive rational numbers. For each positive integer $i$, we have $a_{i}=\frac{a_{i+1}-1}{2}$ or $a_{i}=\frac{2 a_{i+1}}{1-a_{i+1}}$. Since $a_{i}>0$ we deduce that
$$
a_{i}=\left\{\begin{array}{cl}
\frac{a_{i+1}-1}{2} & \text { if } a_{i+1}>1 \\
\frac{2 a_{i+1}}{1-a_{i+1}} & \text { if } a_{i+1}<1
\end{array}\right.
$$
Thus $a_{i}$ is uniquely determined from $a_{i+1}$. Hence starting from $a_{k}=2014$, we simply run the sequence backwards until we reach a positive integer. We compute as follows.
$$
\begin{aligned}
& \frac{2014}{1}, \frac{2013}{2}, \frac{2011}{4}, \frac{2007}{8}, \frac{1999}{16}, \frac{1983}{32}, \frac{1951}{64}, \frac{1887}{128}, \frac{1759}{256}, \frac{1503}{512}, \frac{991}{1024}, \frac{1982}{33}, \frac{1949}{66}, \frac{1883}{132}, \frac{1751}{264}, \frac{1487}{528}, \frac{959}{1056}, \frac{1918}{97}, \frac{1821}{194}, \frac{1627}{388}, \\
& \frac{1239}{776}, \frac{463}{1552}, \frac{926}{1089}, \frac{1852}{163}, \frac{1689}{326}, \frac{1363}{652}, \frac{711}{1304}, \frac{1422}{593}, \frac{829}{1186}, \frac{1658}{357}, \frac{1301}{714}, \frac{587}{1428}, \frac{1174}{841}, \frac{333}{1682}, \frac{666}{1349}, \frac{1332}{683}, \frac{649}{1366}, \frac{1298}{717}, \frac{581}{1434}, \frac{1162}{853}, \\
& \frac{309}{1706}, \frac{618}{1397}, \frac{1236}{779}, \frac{457}{1558}, \frac{914}{1101}, \frac{1828}{187}, \frac{1641}{374}, \frac{1267}{748}, \frac{519}{1496}, \frac{1038}{977}, \frac{61}{1954}, \frac{122}{1893}, \frac{244}{1771}, \frac{488}{1527}, \frac{976}{1039}, \frac{1952}{63}, \frac{1889}{126}, \frac{1763}{252}, \frac{1511}{504}, \frac{1007}{1008}, \frac{2014}{1}
\end{aligned}
$$
There are 61 terms in the above list. Thus $k=60$.
Alternative solution 1 is quite computationally intensive. Calculating the first few terms indicates some patterns that are easy to prove. This is shown in the next solution.
Alternative solution 2. Start with $a_{k}=\frac{m_{0}}{n_{0}}$ where $m_{0}=2014$ and $n_{0}=1$ as in alternative solution 1. By inverting the sequence as in alternative solution 1, we have $a_{k-i}=\frac{m_{i}}{n_{i}}$ for $i \geq 0$ where
$$
\left(m_{i+1}, n_{i+1}\right)= \begin{cases}\left(m_{i}-n_{i}, 2 n_{i}\right) & \text { if } m_{i}>n_{i} \\ \left(2 m_{i}, n_{i}-m_{i}\right) & \text { if } m_{i}<n_{i}\end{cases}
$$
Easy inductions show that $m_{i}+n_{i}=2015,1 \leq m_{i}, n_{i} \leq 2014$ and $\operatorname{gcd}\left(m_{i}, n_{i}\right)=1$ for $i \geq 0$. Since $a_{0} \in \mathbb{N}^{+}$and $\operatorname{gcd}\left(m_{k}, n_{k}\right)=1$, we require $n_{k}=1$. An easy induction shows that $\left(m_{i}, n_{i}\right) \equiv\left(-2^{i}, 2^{i}\right)(\bmod 2015)$ for $i=0,1, \ldots, k$.
Thus $2^{k} \equiv 1(\bmod 2015)$. As in the official solution, the smallest such $k$ is $k=60$. This yields $n_{k} \equiv 1(\bmod 2015)$. But since $1 \leq n_{k}, m_{k} \leq 2014$, it follows that $a_{0}$ is an integer.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
35b4378f-60b8-52b6-81e4-64686cfb86f6
| 605,633
|
Let $n$ be a positive integer. Consider $2 n$ distinct lines on the plane, no two of which are parallel. Of the $2 n$ lines, $n$ are colored blue, the other $n$ are colored red. Let $\mathcal{B}$ be the set of all points on the plane that lie on at least one blue line, and $\mathcal{R}$ the set of all points on the plane that lie on at least one red line. Prove that there exists a circle that intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points.
|
Consider a line $\ell$ on the plane and a point $P$ on it such that $\ell$ is not parallel to any of the $2 n$ lines. Rotate $\ell$ about $P$ counterclockwise until it is parallel to one of the $2 n$ lines. Take note of that line and keep rotating until all the $2 n$ lines are met. The $2 n$ lines are now ordered according to which line is met before or after. Say the lines are in order $\ell_{1}, \ldots, \ell_{2 n}$. Clearly there must be $k \in\{1, \ldots, 2 n-1\}$ such that $\ell_{k}$ and $\ell_{k+1}$ are of different colors.
Now we set up a system of $X-$ and $Y$ - axes on the plane. Consider the two angular bisectors of $\ell_{k}$ and $\ell_{k+1}$. If we rotate $\ell_{k+1}$ counterclockwise, the line will be parallel to one of the bisectors before the other. Let the bisector that is parallel to the rotation of $\ell_{k+1}$ first be the $X$-axis, and the other the $Y$-axis. From now on, we will be using the directed angle notation: for lines $s$ and $s^{\prime}$, we define $\angle\left(s, s^{\prime}\right)$ to be a real number in $[0, \pi)$ denoting the angle in radians such that when $s$ is rotated counterclockwise by $\angle\left(s, s^{\prime}\right)$ radian, it becomes parallel to $s^{\prime}$. Using this
notation, we notice that there is no $i=1, \ldots, 2 n$ such that $\angle\left(X, l_{i}\right)$ is between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$.
Because the $2 n$ lines are distinct, the set $S$ of all the intersections between $\ell_{i}$ and $\ell_{j}(i \neq j)$ is a finite set of points. Consider a rectangle with two opposite vertices lying on $\ell_{k}$ and the other two lying on $\ell_{k+1}$. With respect to the origin (the intersection of $\ell_{k}$ and $\ell_{k+1}$ ), we can enlarge the rectangle as much as we want, while all the vertices remain on the lines. Thus, there is one of these rectangles $R$ which contains all the points in $S$ in its interior. Since each side of $R$ is parallel to either $X$ - or $Y$ - axis, $R$ is a part of the four lines $x= \pm a, y= \pm b$. where $a, b>0$.
Consider the circle $\mathcal{C}$ tangent to the right of the $x=a$ side of the rectangle, and to both $\ell_{k}$ and $\ell_{k+1}$. We claim that this circle intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points. Since $\mathcal{C}$ is tangent to both $\ell_{k}$ and $\ell_{k+1}$ and the two lines have different colors, it is enough to show that $\mathcal{C}$ intersects with each of the other $2 n-2$ lines in exactly 2 points. Note that no two lines intersect on the circle because all the intersections between lines are in $S$ which is in the interior of $R$.
Consider any line $L$ among these $2 n-2$ lines. Let $L$ intersect with $\ell_{k}$ and $\ell_{k+1}$ at the points $M$ and $N$, respectively ( $M$ and $N$ are not necessarily distinct). Notice that both $M$ and $N$ must be inside $R$. There are two cases:
(i) $L$ intersects $R$ on the $x=-a$ side once and another time on $x=a$ side;
(ii) $L$ intersects $y=-b$ and $y=b$ sides.
However, if (ii) happens, $\angle\left(\ell_{k}, L\right)$ and $\angle\left(L, \ell_{k+1}\right)$ would be both positive, and then $\angle(X, L)$ would be between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$, a contradiction. Thus, only (i) can happen. Then $L$ intersects $\mathcal{C}$ in exactly two points, and we are done.
Alternative solution. By rotating the diagram we can ensure that no line is vertical. Let $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ be the lines listed in order of increasing gradient. Then there is a $k$ such that lines $\ell_{k}$ and $\ell_{k+1}$ are oppositely coloured. By rotating our coordinate system and cyclicly relabelling our lines we can ensure that $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ are listed in order of increasing gradient, $\ell_{1}$ and $\ell_{2 n}$ are oppositely coloured, and no line is vertical.
Let $\mathcal{D}$ be a circle centred at the origin and of sufficiently large radius so that
- All intersection points of all pairs of lines lie strictly inside $\mathcal{D}$; and
- Each line $\ell_{i}$ intersects $\mathcal{D}$ in two points $A_{i}$ and $B_{i}$ say, such that $A_{i}$ is on the right semicircle (the part of the circle in the positive $x$ half plane) and $B_{i}$ is on the left semicircle.
Note that the anticlockwise order of the points $A_{i}, B_{i}$ around $\mathcal{D}$ is $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$.
(If $A_{i+1}$ occurred before $A_{i}$ then rays $r_{i}$ and $r_{i+1}$ (as defined below) would intersect outside $\mathcal{D}$.)
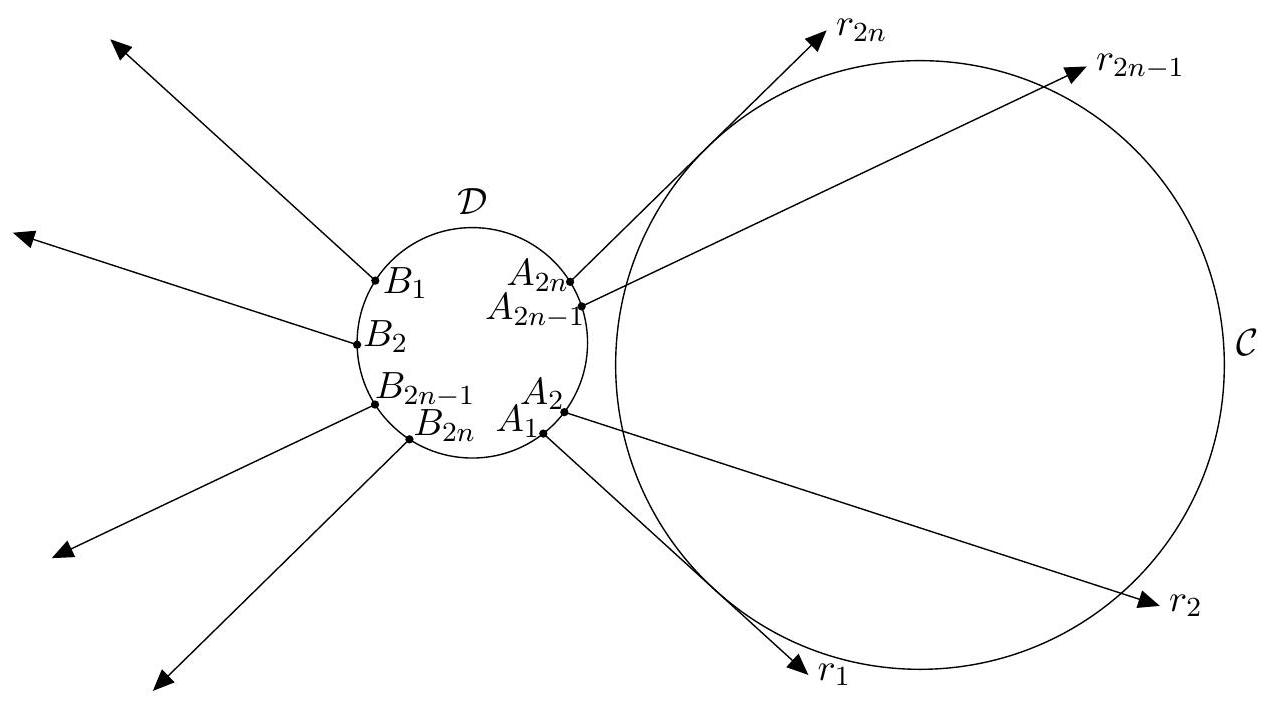
For each $i$, let $r_{i}$ be the ray that is the part of the line $\ell_{i}$ starting from point $A_{i}$ and that extends to the right. Let $\mathcal{C}$ be any circle tangent to $r_{1}$ and $r_{2 n}$, that lies entirely to the right of $\mathcal{D}$. Then $\mathcal{C}$ intersects each of $r_{2}, r_{3}, \ldots, r_{2 n-1}$ twice and is tangent to $r_{1}$ and $r_{2 n}$. Thus $\mathcal{C}$ has the required properties.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $n$ be a positive integer. Consider $2 n$ distinct lines on the plane, no two of which are parallel. Of the $2 n$ lines, $n$ are colored blue, the other $n$ are colored red. Let $\mathcal{B}$ be the set of all points on the plane that lie on at least one blue line, and $\mathcal{R}$ the set of all points on the plane that lie on at least one red line. Prove that there exists a circle that intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points.
|
Consider a line $\ell$ on the plane and a point $P$ on it such that $\ell$ is not parallel to any of the $2 n$ lines. Rotate $\ell$ about $P$ counterclockwise until it is parallel to one of the $2 n$ lines. Take note of that line and keep rotating until all the $2 n$ lines are met. The $2 n$ lines are now ordered according to which line is met before or after. Say the lines are in order $\ell_{1}, \ldots, \ell_{2 n}$. Clearly there must be $k \in\{1, \ldots, 2 n-1\}$ such that $\ell_{k}$ and $\ell_{k+1}$ are of different colors.
Now we set up a system of $X-$ and $Y$ - axes on the plane. Consider the two angular bisectors of $\ell_{k}$ and $\ell_{k+1}$. If we rotate $\ell_{k+1}$ counterclockwise, the line will be parallel to one of the bisectors before the other. Let the bisector that is parallel to the rotation of $\ell_{k+1}$ first be the $X$-axis, and the other the $Y$-axis. From now on, we will be using the directed angle notation: for lines $s$ and $s^{\prime}$, we define $\angle\left(s, s^{\prime}\right)$ to be a real number in $[0, \pi)$ denoting the angle in radians such that when $s$ is rotated counterclockwise by $\angle\left(s, s^{\prime}\right)$ radian, it becomes parallel to $s^{\prime}$. Using this
notation, we notice that there is no $i=1, \ldots, 2 n$ such that $\angle\left(X, l_{i}\right)$ is between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$.
Because the $2 n$ lines are distinct, the set $S$ of all the intersections between $\ell_{i}$ and $\ell_{j}(i \neq j)$ is a finite set of points. Consider a rectangle with two opposite vertices lying on $\ell_{k}$ and the other two lying on $\ell_{k+1}$. With respect to the origin (the intersection of $\ell_{k}$ and $\ell_{k+1}$ ), we can enlarge the rectangle as much as we want, while all the vertices remain on the lines. Thus, there is one of these rectangles $R$ which contains all the points in $S$ in its interior. Since each side of $R$ is parallel to either $X$ - or $Y$ - axis, $R$ is a part of the four lines $x= \pm a, y= \pm b$. where $a, b>0$.

Consider the circle $\mathcal{C}$ tangent to the right of the $x=a$ side of the rectangle, and to both $\ell_{k}$ and $\ell_{k+1}$. We claim that this circle intersects $\mathcal{B}$ in exactly $2 n-1$ points, and also intersects $\mathcal{R}$ in exactly $2 n-1$ points. Since $\mathcal{C}$ is tangent to both $\ell_{k}$ and $\ell_{k+1}$ and the two lines have different colors, it is enough to show that $\mathcal{C}$ intersects with each of the other $2 n-2$ lines in exactly 2 points. Note that no two lines intersect on the circle because all the intersections between lines are in $S$ which is in the interior of $R$.
Consider any line $L$ among these $2 n-2$ lines. Let $L$ intersect with $\ell_{k}$ and $\ell_{k+1}$ at the points $M$ and $N$, respectively ( $M$ and $N$ are not necessarily distinct). Notice that both $M$ and $N$ must be inside $R$. There are two cases:
(i) $L$ intersects $R$ on the $x=-a$ side once and another time on $x=a$ side;
(ii) $L$ intersects $y=-b$ and $y=b$ sides.
However, if (ii) happens, $\angle\left(\ell_{k}, L\right)$ and $\angle\left(L, \ell_{k+1}\right)$ would be both positive, and then $\angle(X, L)$ would be between $\angle\left(X, \ell_{k}\right)$ and $\angle\left(X, \ell_{k+1}\right)$, a contradiction. Thus, only (i) can happen. Then $L$ intersects $\mathcal{C}$ in exactly two points, and we are done.
Alternative solution. By rotating the diagram we can ensure that no line is vertical. Let $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ be the lines listed in order of increasing gradient. Then there is a $k$ such that lines $\ell_{k}$ and $\ell_{k+1}$ are oppositely coloured. By rotating our coordinate system and cyclicly relabelling our lines we can ensure that $\ell_{1}, \ell_{2}, \ldots, \ell_{2 n}$ are listed in order of increasing gradient, $\ell_{1}$ and $\ell_{2 n}$ are oppositely coloured, and no line is vertical.
Let $\mathcal{D}$ be a circle centred at the origin and of sufficiently large radius so that
- All intersection points of all pairs of lines lie strictly inside $\mathcal{D}$; and
- Each line $\ell_{i}$ intersects $\mathcal{D}$ in two points $A_{i}$ and $B_{i}$ say, such that $A_{i}$ is on the right semicircle (the part of the circle in the positive $x$ half plane) and $B_{i}$ is on the left semicircle.
Note that the anticlockwise order of the points $A_{i}, B_{i}$ around $\mathcal{D}$ is $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$.
(If $A_{i+1}$ occurred before $A_{i}$ then rays $r_{i}$ and $r_{i+1}$ (as defined below) would intersect outside $\mathcal{D}$.)

For each $i$, let $r_{i}$ be the ray that is the part of the line $\ell_{i}$ starting from point $A_{i}$ and that extends to the right. Let $\mathcal{C}$ be any circle tangent to $r_{1}$ and $r_{2 n}$, that lies entirely to the right of $\mathcal{D}$. Then $\mathcal{C}$ intersects each of $r_{2}, r_{3}, \ldots, r_{2 n-1}$ twice and is tangent to $r_{1}$ and $r_{2 n}$. Thus $\mathcal{C}$ has the required properties.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
73d35a90-ea20-5e0d-a185-baa0a5765d98
| 261,046
|
Determine all sequences $a_{0}, a_{1}, a_{2}, \ldots$ of positive integers with $a_{0} \geq 2015$ such that for all integers $n \geq 1$ :
(i) $a_{n+2}$ is divisible by $a_{n}$;
(ii) $\left|s_{n+1}-(n+1) a_{n}\right|=1$, where $s_{n+1}=a_{n+1}-a_{n}+a_{n-1}-\cdots+(-1)^{n+1} a_{0}$.
Answer: There are two families of answers:
(a) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c+1$ for some integer $c \geq 2014$, and
(b) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c-1$ for some integer $c \geq 2016$.
|
Let $\left\{a_{n}\right\}_{n=0}^{\infty}$ be a sequence of positive integers satisfying the given conditions. We can rewrite (ii) as $s_{n+1}=(n+1) a_{n}+h_{n}$, where $h_{n} \in\{-1,1\}$. Substituting $n$ with $n-1$ yields $s_{n}=n a_{n-1}+h_{n-1}$, where $h_{n-1} \in\{-1,1\}$. Note that $a_{n+1}=s_{n+1}+s_{n}$, therefore there exists $\delta_{n} \in\{-2,0,2\}$ such that
$$
a_{n+1}=(n+1) a_{n}+n a_{n-1}+\delta_{n}
$$
We also have $\left|s_{2}-2 a_{1}\right|=1$, which yields $a_{0}=3 a_{1}-a_{2} \pm 1 \leq 3 a_{1}$, and therefore $a_{1} \geq \frac{a_{0}}{3} \geq 671$. Substituting $n=2$ in (1), we find that $a_{3}=3 a_{2}+2 a_{1}+\delta_{2}$. Since $a_{1} \mid a_{3}$, we have $a_{1} \mid 3 a_{2}+\delta_{2}$, and therefore $a_{2} \geq 223$. Using (1), we obtain that $a_{n} \geq 223$ for all $n \geq 0$.
Lemma 1: For $n \geq 4$, we have $a_{n+2}=(n+1)(n+4) a_{n}$.
Proof. For $n \geq 3$ we have
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}>n a_{n-1}+3 .
$$
By applying (2) with $n$ substituted by $n-1$ we have for $n \geq 4$,
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}<n a_{n-1}+\left(a_{n-1}-3\right)+\delta_{n-1}<(n+1) a_{n-1}
$$
Using (1) to write $a_{n+2}$ in terms of $a_{n}$ and $a_{n-1}$ along with (2), we obtain that for $n \geq 3$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& <(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+3(n+2) \\
& <\left(n^{2}+5 n+5\right) a_{n} .
\end{aligned}
$$
Also for $n \geq 4$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& >(n+3)(n+1) a_{n}+n a_{n} \\
& =\left(n^{2}+5 n+3\right) a_{n} .
\end{aligned}
$$
Since $a_{n} \mid a_{n+2}$, we obtain that $a_{n+2}=\left(n^{2}+5 n+4\right) a_{n}=(n+1)(n+4) a_{n}$, as desired.
Lemma 2: For $n \geq 4$, we have $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$.
Proof. Using the recurrence $a_{n+3}=(n+3) a_{n+2}+(n+2) a_{n+1}+\delta_{n+2}$ and writing $a_{n+3}$, $a_{n+2}$ in terms of $a_{n+1}, a_{n}$ according to Lemma 1 we obtain
$$
(n+2)(n+4) a_{n+1}=(n+3)(n+1)(n+4) a_{n}+\delta_{n+2} .
$$
Hence $n+4 \mid \delta_{n+2}$, which yields $\delta_{n+2}=0$ and $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$, as desired.
Suppose there exists $n \geq 1$ such that $a_{n+1} \neq \frac{(n+1)(n+3)}{n+2} a_{n}$. By Lemma 2, there exist a greatest integer $1 \leq m \leq 3$ with this property. Then $a_{m+2}=\frac{(m+2)(m+4)}{m+3} a_{m+1}$. If $\delta_{m+1}=0$, we have $a_{m+1}=\frac{(m+1)(m+3)}{m+2} a_{m}$, which contradicts our choice of $m$. Thus $\delta_{m+1} \neq 0$.
Clearly $m+3 \mid a_{m+1}$. Write $a_{m+1}=(m+3) k$ and $a_{m+2}=(m+2)(m+4) k$. Then $(m+$ 1) $a_{m}+\delta_{m+1}=a_{m+2}-(m+2) a_{m+1}=(m+2) k$. So, $a_{m} \mid(m+2) k-\delta_{m+1}$. But $a_{m}$ also divides $a_{m+2}=(m+2)(m+4) k$. Combining the two divisibility conditions, we obtain $a_{m} \mid(m+4) \delta_{m+1}$. Since $\delta_{m+1} \neq 0$, we have $a_{m} \mid 2 m+8 \leq 14$, which contradicts the previous result that $a_{n} \geq 223$ for all nonnegative integers $n$.
So, $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$ for $n \geq 1$. Substituting $n=1$ yields $3 \mid a_{1}$. Letting $a_{1}=3 c$, we have by induction that $a_{n}=n!(n+2) c$ for $n \geq 1$. Since $\left|s_{2}-2 a_{1}\right|=1$, we then get $a_{0}=c \pm 1$, yielding the two families of solutions. By noting that $(n+2) n!=n!+(n+1)!$, we have $s_{n+1}=c(n+2)!+(-1)^{n}\left(c-a_{0}\right)$. Hence both families of solutions satisfy the given conditions.
|
a_{n}=c(n+2) n! \text{ for all } n \geq 1 \text{ and } a_{0}=c \pm 1 \text{ for some integer } c \geq 2014
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all sequences $a_{0}, a_{1}, a_{2}, \ldots$ of positive integers with $a_{0} \geq 2015$ such that for all integers $n \geq 1$ :
(i) $a_{n+2}$ is divisible by $a_{n}$;
(ii) $\left|s_{n+1}-(n+1) a_{n}\right|=1$, where $s_{n+1}=a_{n+1}-a_{n}+a_{n-1}-\cdots+(-1)^{n+1} a_{0}$.
Answer: There are two families of answers:
(a) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c+1$ for some integer $c \geq 2014$, and
(b) $a_{n}=c(n+2) n$ ! for all $n \geq 1$ and $a_{0}=c-1$ for some integer $c \geq 2016$.
|
Let $\left\{a_{n}\right\}_{n=0}^{\infty}$ be a sequence of positive integers satisfying the given conditions. We can rewrite (ii) as $s_{n+1}=(n+1) a_{n}+h_{n}$, where $h_{n} \in\{-1,1\}$. Substituting $n$ with $n-1$ yields $s_{n}=n a_{n-1}+h_{n-1}$, where $h_{n-1} \in\{-1,1\}$. Note that $a_{n+1}=s_{n+1}+s_{n}$, therefore there exists $\delta_{n} \in\{-2,0,2\}$ such that
$$
a_{n+1}=(n+1) a_{n}+n a_{n-1}+\delta_{n}
$$
We also have $\left|s_{2}-2 a_{1}\right|=1$, which yields $a_{0}=3 a_{1}-a_{2} \pm 1 \leq 3 a_{1}$, and therefore $a_{1} \geq \frac{a_{0}}{3} \geq 671$. Substituting $n=2$ in (1), we find that $a_{3}=3 a_{2}+2 a_{1}+\delta_{2}$. Since $a_{1} \mid a_{3}$, we have $a_{1} \mid 3 a_{2}+\delta_{2}$, and therefore $a_{2} \geq 223$. Using (1), we obtain that $a_{n} \geq 223$ for all $n \geq 0$.
Lemma 1: For $n \geq 4$, we have $a_{n+2}=(n+1)(n+4) a_{n}$.
Proof. For $n \geq 3$ we have
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}>n a_{n-1}+3 .
$$
By applying (2) with $n$ substituted by $n-1$ we have for $n \geq 4$,
$$
a_{n}=n a_{n-1}+(n-1) a_{n-2}+\delta_{n-1}<n a_{n-1}+\left(a_{n-1}-3\right)+\delta_{n-1}<(n+1) a_{n-1}
$$
Using (1) to write $a_{n+2}$ in terms of $a_{n}$ and $a_{n-1}$ along with (2), we obtain that for $n \geq 3$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& <(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+3(n+2) \\
& <\left(n^{2}+5 n+5\right) a_{n} .
\end{aligned}
$$
Also for $n \geq 4$,
$$
\begin{aligned}
a_{n+2} & =(n+3)(n+1) a_{n}+(n+2) n a_{n-1}+(n+2) \delta_{n}+\delta_{n+1} \\
& >(n+3)(n+1) a_{n}+n a_{n} \\
& =\left(n^{2}+5 n+3\right) a_{n} .
\end{aligned}
$$
Since $a_{n} \mid a_{n+2}$, we obtain that $a_{n+2}=\left(n^{2}+5 n+4\right) a_{n}=(n+1)(n+4) a_{n}$, as desired.
Lemma 2: For $n \geq 4$, we have $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$.
Proof. Using the recurrence $a_{n+3}=(n+3) a_{n+2}+(n+2) a_{n+1}+\delta_{n+2}$ and writing $a_{n+3}$, $a_{n+2}$ in terms of $a_{n+1}, a_{n}$ according to Lemma 1 we obtain
$$
(n+2)(n+4) a_{n+1}=(n+3)(n+1)(n+4) a_{n}+\delta_{n+2} .
$$
Hence $n+4 \mid \delta_{n+2}$, which yields $\delta_{n+2}=0$ and $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$, as desired.
Suppose there exists $n \geq 1$ such that $a_{n+1} \neq \frac{(n+1)(n+3)}{n+2} a_{n}$. By Lemma 2, there exist a greatest integer $1 \leq m \leq 3$ with this property. Then $a_{m+2}=\frac{(m+2)(m+4)}{m+3} a_{m+1}$. If $\delta_{m+1}=0$, we have $a_{m+1}=\frac{(m+1)(m+3)}{m+2} a_{m}$, which contradicts our choice of $m$. Thus $\delta_{m+1} \neq 0$.
Clearly $m+3 \mid a_{m+1}$. Write $a_{m+1}=(m+3) k$ and $a_{m+2}=(m+2)(m+4) k$. Then $(m+$ 1) $a_{m}+\delta_{m+1}=a_{m+2}-(m+2) a_{m+1}=(m+2) k$. So, $a_{m} \mid(m+2) k-\delta_{m+1}$. But $a_{m}$ also divides $a_{m+2}=(m+2)(m+4) k$. Combining the two divisibility conditions, we obtain $a_{m} \mid(m+4) \delta_{m+1}$. Since $\delta_{m+1} \neq 0$, we have $a_{m} \mid 2 m+8 \leq 14$, which contradicts the previous result that $a_{n} \geq 223$ for all nonnegative integers $n$.
So, $a_{n+1}=\frac{(n+1)(n+3)}{n+2} a_{n}$ for $n \geq 1$. Substituting $n=1$ yields $3 \mid a_{1}$. Letting $a_{1}=3 c$, we have by induction that $a_{n}=n!(n+2) c$ for $n \geq 1$. Since $\left|s_{2}-2 a_{1}\right|=1$, we then get $a_{0}=c \pm 1$, yielding the two families of solutions. By noting that $(n+2) n!=n!+(n+1)!$, we have $s_{n+1}=c(n+2)!+(-1)^{n}\left(c-a_{0}\right)$. Hence both families of solutions satisfy the given conditions.
|
{
"resource_path": "APMO/segmented/en-apmo2015_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
71c9b35e-6606-5f4b-b991-ba54992574de
| 605,658
|
We say that a triangle $A B C$ is great if the following holds: for any point $D$ on the side $B C$, if $P$ and $Q$ are the feet of the perpendiculars from $D$ to the lines $A B$ and $A C$, respectively, then the reflection of $D$ in the line $P Q$ lies on the circumcircle of the triangle $A B C$.
Prove that triangle $A B C$ is great if and only if $\angle A=90^{\circ}$ and $A B=A C$.
|
For every point $D$ on the side $B C$, let $D^{\prime}$ be the reflection of $D$ in the line $P Q$. We will first prove that if the triangle satisfies the condition then it is isosceles and right-angled at $A$.
Choose $D$ to be the point where the angle bisector from $A$ meets $B C$. Note that $P$ and $Q$ lie on the rays $A B$ and $A C$ respectively. Furthermore, $P$ and $Q$ are reflections of each other in the line $A D$, from which it follows that $P Q \perp A D$. Therefore, $D^{\prime}$ lies on the line $A D$ and we may deduce that either $D^{\prime}=A$ or $D^{\prime}$ is the second point of the angle bisector at $A$ and the circumcircle of $A B C$. However, since $A P D Q$ is a cyclic quadrilateral, the segment $P Q$ intersects the segment $A D$. Therefore, $D^{\prime}$ lies on the ray $D A$ and therefore $D^{\prime}=A$. By angle chasing we obtain
$$
\angle P D^{\prime} Q=\angle P D Q=180^{\circ}-\angle B A C
$$
and since $D^{\prime}=A$ we also know $\angle P D^{\prime} Q=\angle B A C$. This implies that $\angle B A C=90^{\circ}$.
Now we choose $D$ to be the midpoint of $B C$. Since $\angle B A C=90^{\circ}$, we can deduce that $D Q P$ is the medial triangle of triangle $A B C$. Therefore, $P Q \| B C$ from which it follows that $D D^{\prime} \perp B C$. But the distance from $D^{\prime}$ to $B C$ is equal to both the circumradius of triangle $A B C$ and to the distance from $A$ to $B C$. This can only happen if $A=D^{\prime}$. This implies that $A B C$ is isosceles and right-angled at $A$.
We will now prove that if $A B C$ is isosceles and right-angled at $A$ then the required property in the problem holds. Let $D$ be any point on side $B C$. Then $D^{\prime} P=D P$ and we also have $D P=B P$. Hence, $D^{\prime} P=B P$ and similarly $D^{\prime} Q=C Q$. Note that $A P D Q D^{\prime}$ is cyclic with diameter $P Q$. Therefore, $\angle A P D^{\prime}=\angle A Q D^{\prime}$, from which we obtain $\angle B P D^{\prime}=\angle C Q D^{\prime}$. So triangles $D^{\prime} P B$ and $D^{\prime} Q C$ are similar. It follows that $\angle P D^{\prime} Q=\angle P D^{\prime} C+\angle C D^{\prime} Q=$ $\angle P D^{\prime} C+\angle B D^{\prime} P=\angle B D^{\prime} C$ and $\frac{D^{\prime} P}{D^{\prime} Q}=\frac{D^{\prime} B}{D^{\prime} C}$. So we also obtain that triangles $D^{\prime} P Q$ and $D^{\prime} B C$ are similar. But since $D P Q$ and $D^{\prime} P Q$ are congruent, we may deduce that $\angle B D^{\prime} C=$ $\angle P D^{\prime} Q=\angle P D Q=90^{\circ}$. Therefore, $D^{\prime}$ lies on the circle with diameter $B C$, which is the circumcircle of triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We say that a triangle $A B C$ is great if the following holds: for any point $D$ on the side $B C$, if $P$ and $Q$ are the feet of the perpendiculars from $D$ to the lines $A B$ and $A C$, respectively, then the reflection of $D$ in the line $P Q$ lies on the circumcircle of the triangle $A B C$.
Prove that triangle $A B C$ is great if and only if $\angle A=90^{\circ}$ and $A B=A C$.
|
For every point $D$ on the side $B C$, let $D^{\prime}$ be the reflection of $D$ in the line $P Q$. We will first prove that if the triangle satisfies the condition then it is isosceles and right-angled at $A$.
Choose $D$ to be the point where the angle bisector from $A$ meets $B C$. Note that $P$ and $Q$ lie on the rays $A B$ and $A C$ respectively. Furthermore, $P$ and $Q$ are reflections of each other in the line $A D$, from which it follows that $P Q \perp A D$. Therefore, $D^{\prime}$ lies on the line $A D$ and we may deduce that either $D^{\prime}=A$ or $D^{\prime}$ is the second point of the angle bisector at $A$ and the circumcircle of $A B C$. However, since $A P D Q$ is a cyclic quadrilateral, the segment $P Q$ intersects the segment $A D$. Therefore, $D^{\prime}$ lies on the ray $D A$ and therefore $D^{\prime}=A$. By angle chasing we obtain
$$
\angle P D^{\prime} Q=\angle P D Q=180^{\circ}-\angle B A C
$$
and since $D^{\prime}=A$ we also know $\angle P D^{\prime} Q=\angle B A C$. This implies that $\angle B A C=90^{\circ}$.
Now we choose $D$ to be the midpoint of $B C$. Since $\angle B A C=90^{\circ}$, we can deduce that $D Q P$ is the medial triangle of triangle $A B C$. Therefore, $P Q \| B C$ from which it follows that $D D^{\prime} \perp B C$. But the distance from $D^{\prime}$ to $B C$ is equal to both the circumradius of triangle $A B C$ and to the distance from $A$ to $B C$. This can only happen if $A=D^{\prime}$. This implies that $A B C$ is isosceles and right-angled at $A$.

We will now prove that if $A B C$ is isosceles and right-angled at $A$ then the required property in the problem holds. Let $D$ be any point on side $B C$. Then $D^{\prime} P=D P$ and we also have $D P=B P$. Hence, $D^{\prime} P=B P$ and similarly $D^{\prime} Q=C Q$. Note that $A P D Q D^{\prime}$ is cyclic with diameter $P Q$. Therefore, $\angle A P D^{\prime}=\angle A Q D^{\prime}$, from which we obtain $\angle B P D^{\prime}=\angle C Q D^{\prime}$. So triangles $D^{\prime} P B$ and $D^{\prime} Q C$ are similar. It follows that $\angle P D^{\prime} Q=\angle P D^{\prime} C+\angle C D^{\prime} Q=$ $\angle P D^{\prime} C+\angle B D^{\prime} P=\angle B D^{\prime} C$ and $\frac{D^{\prime} P}{D^{\prime} Q}=\frac{D^{\prime} B}{D^{\prime} C}$. So we also obtain that triangles $D^{\prime} P Q$ and $D^{\prime} B C$ are similar. But since $D P Q$ and $D^{\prime} P Q$ are congruent, we may deduce that $\angle B D^{\prime} C=$ $\angle P D^{\prime} Q=\angle P D Q=90^{\circ}$. Therefore, $D^{\prime}$ lies on the circle with diameter $B C$, which is the circumcircle of triangle $A B C$.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
81c2b023-cfa5-5fa3-b87d-f6b983a0117d
| 260,693
|
A positive integer is called fancy if it can be expressed in the form
$$
2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{100}}
$$
where $a_{1}, a_{2}, \ldots, a_{100}$ are non-negative integers that are not necessarily distinct.
Find the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.
Answer: The answer is $n=2^{101}-1$.
|
Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \ldots, a_{r}$ such that $r \leq 100$ and $k=2^{a_{1}}+\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:
$$
\begin{aligned}
2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+\left(1+1+2+\cdots+2^{s-1}\right) 2^{a_{r}} \\
& =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\cdots+2^{a_{r}+s-1} .
\end{aligned}
$$
This shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \geq 0$, which shows that $k$ has a multiple that is a fancy number.
We will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .
For the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that
$$
c n=2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}
$$
where $r \leq 100$ and $a_{1}<a_{2}<\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:
- If $a_{r} \geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.
- If $a_{r} \leq 100$, then $\left\{a_{1}, \ldots, a_{r}\right\}$ is a proper subset of $\{0,1, \ldots, 100\}$. Then
$$
n \leq c n<2^{0}+2^{1}+\cdots+2^{100}=n
$$
This is also a contradiction.
From these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.
|
2^{101}-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is called fancy if it can be expressed in the form
$$
2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{100}}
$$
where $a_{1}, a_{2}, \ldots, a_{100}$ are non-negative integers that are not necessarily distinct.
Find the smallest positive integer $n$ such that no multiple of $n$ is a fancy number.
Answer: The answer is $n=2^{101}-1$.
|
Let $k$ be any positive integer less than $2^{101}-1$. Then $k$ can be expressed in binary notation using at most 100 ones, and therefore there exists a positive integer $r$ and non-negative integers $a_{1}, a_{2}, \ldots, a_{r}$ such that $r \leq 100$ and $k=2^{a_{1}}+\cdots+2^{a_{r}}$. Notice that for a positive integer $s$ we have:
$$
\begin{aligned}
2^{s} k & =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+\left(1+1+2+\cdots+2^{s-1}\right) 2^{a_{r}} \\
& =2^{a_{1}+s}+2^{a_{2}+s}+\cdots+2^{a_{r-1}+s}+2^{a_{r}}+2^{a_{r}}+\cdots+2^{a_{r}+s-1} .
\end{aligned}
$$
This shows that $k$ has a multiple that is a sum of $r+s$ powers of two. In particular, we may take $s=100-r \geq 0$, which shows that $k$ has a multiple that is a fancy number.
We will now prove that no multiple of $n=2^{101}-1$ is a fancy number. In fact we will prove a stronger statement, namely, that no multiple of $n$ can be expressed as the sum of at most 100 powers of 2 .
For the sake of contradiction, suppose that there exists a positive integer $c$ such that $c n$ is the sum of at most 100 powers of 2 . We may assume that $c$ is the smallest such integer. By repeatedly merging equal powers of two in the representation of $c n$ we may assume that
$$
c n=2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}}
$$
where $r \leq 100$ and $a_{1}<a_{2}<\ldots<a_{r}$ are distinct non-negative integers. Consider the following two cases:
- If $a_{r} \geq 101$, then $2^{a_{r}}-2^{a_{r}-101}=2^{a_{r}-101} n$. It follows that $2^{a_{1}}+2^{a_{2}}+\cdots+2^{a_{r}-1}+2^{a_{r}-101}$ would be a multiple of $n$ that is smaller than $c n$. This contradicts the minimality of $c$.
- If $a_{r} \leq 100$, then $\left\{a_{1}, \ldots, a_{r}\right\}$ is a proper subset of $\{0,1, \ldots, 100\}$. Then
$$
n \leq c n<2^{0}+2^{1}+\cdots+2^{100}=n
$$
This is also a contradiction.
From these contradictions we conclude that it is impossible for cn to be the sum of at most 100 powers of 2 . In particular, no multiple of $n$ is a fancy number.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
3b0e7405-eba8-5a35-9ddf-4a27ed786d7b
| 605,693
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
We present two approaches. The first one introduces an auxiliary point and studies similarities in the figure. The second one reduces the problem to computations involving a particular exradius of a triangle. The second approach has two variants.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
We present two approaches. The first one introduces an auxiliary point and studies similarities in the figure. The second one reduces the problem to computations involving a particular exradius of a triangle. The second approach has two variants.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
8817de03-1ca7-53cd-bcd6-18d6c28edfed
| 260,709
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
.
Let the line through $N$ tangent to $\omega$ at point $X \neq E$ intersect $A B$ at point $M^{\prime}$. It suffices to show that $M^{\prime} R \| A C$, since this would yield $M^{\prime}=M$.
Suppose that the line $P O$ intersects $A C$ at $Q$ and the circumcircle of $A M^{\prime} O$ at $Y$, respectively. Then
$$
\angle A Y M^{\prime}=\angle A O M^{\prime}=90^{\circ}-\angle M^{\prime} O P
$$
By angle chasing we have $\angle E O Q=\angle F O P=90^{\circ}-\angle A O F=\angle M^{\prime} A O=\angle M^{\prime} Y P$ and by symmetry $\angle E Q O=\angle M^{\prime} P Y$. Therefore $\triangle M^{\prime} Y P \sim \triangle E O Q$.
On the other hand, we have
$$
\begin{aligned}
\angle M^{\prime} O P & =\angle M^{\prime} O F+\angle F O P=\frac{1}{2}(\angle F O X+\angle F O P+\angle E O Q)= \\
& =\frac{1}{2}\left(\frac{180^{\circ}-\angle X O E}{2}\right)=90^{\circ}-\frac{\angle X O E}{2} .
\end{aligned}
$$
Since we know that $\angle A Y M^{\prime}$ and $\angle M^{\prime} O P$ are complementary this implies
$$
\angle A Y M^{\prime}=\frac{\angle X O E}{2}=\angle N O E
$$
Therefore, $\angle A Y M^{\prime}$ and $\angle N O E$ are congruent angles, and this means that $A$ and $N$ are corresponding points in the similarity of triangles $\triangle M^{\prime} Y P$ and $\triangle E O Q$. It follows that
$$
\frac{A M^{\prime}}{M^{\prime} P}=\frac{N E}{E Q}=\frac{N R}{R P}
$$
We conclude that $M^{\prime} R \| A C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
.

Let the line through $N$ tangent to $\omega$ at point $X \neq E$ intersect $A B$ at point $M^{\prime}$. It suffices to show that $M^{\prime} R \| A C$, since this would yield $M^{\prime}=M$.
Suppose that the line $P O$ intersects $A C$ at $Q$ and the circumcircle of $A M^{\prime} O$ at $Y$, respectively. Then
$$
\angle A Y M^{\prime}=\angle A O M^{\prime}=90^{\circ}-\angle M^{\prime} O P
$$
By angle chasing we have $\angle E O Q=\angle F O P=90^{\circ}-\angle A O F=\angle M^{\prime} A O=\angle M^{\prime} Y P$ and by symmetry $\angle E Q O=\angle M^{\prime} P Y$. Therefore $\triangle M^{\prime} Y P \sim \triangle E O Q$.
On the other hand, we have
$$
\begin{aligned}
\angle M^{\prime} O P & =\angle M^{\prime} O F+\angle F O P=\frac{1}{2}(\angle F O X+\angle F O P+\angle E O Q)= \\
& =\frac{1}{2}\left(\frac{180^{\circ}-\angle X O E}{2}\right)=90^{\circ}-\frac{\angle X O E}{2} .
\end{aligned}
$$
Since we know that $\angle A Y M^{\prime}$ and $\angle M^{\prime} O P$ are complementary this implies
$$
\angle A Y M^{\prime}=\frac{\angle X O E}{2}=\angle N O E
$$
Therefore, $\angle A Y M^{\prime}$ and $\angle N O E$ are congruent angles, and this means that $A$ and $N$ are corresponding points in the similarity of triangles $\triangle M^{\prime} Y P$ and $\triangle E O Q$. It follows that
$$
\frac{A M^{\prime}}{M^{\prime} P}=\frac{N E}{E Q}=\frac{N R}{R P}
$$
We conclude that $M^{\prime} R \| A C$, as desired.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution 1"
}
|
8817de03-1ca7-53cd-bcd6-18d6c28edfed
| 260,709
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
a.
As in Solution 1, we introduce point $M^{\prime}$ and reduce the problem to proving $\frac{P R}{R N}=\frac{P M^{\prime}}{M^{\prime} A}$. Menelaus theorem in triangle $A N P$ with transversal line $F R E$ yields
$$
\frac{P R}{R N} \cdot \frac{N E}{E A} \cdot \frac{A F}{F P}=1
$$
Since $A F=E A$, we have $\frac{F P}{N E}=\frac{P R}{R N}$, so that it suffices to prove
$$
\frac{F P}{N E}=\frac{P M^{\prime}}{M^{\prime} A}
$$
This is a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$. Indeed, setting $a=M^{\prime} N, b=N A, c=M^{\prime} A, s=\frac{a+b+c}{2}, x=s-a, y=s-b$ and $z=s-c$, then $A E=A F=s, M^{\prime} F=z$ and $N E=y$. From $\triangle O F P \sim \triangle A F O$ we have $F P=\frac{r_{a}^{2}}{s}$, where $r_{a}=O F$ is the exradius opposite $A$. Combining the following two standard formulas for the area of a triangle
$$
\left|A M^{\prime} N\right|^{2}=x y z s \quad \text { (Heron's formula) and } \quad\left|A M^{\prime} N\right|=r_{a}(s-a),
$$
we have $r_{a}^{2}=\frac{y z s}{x}$. Therefore, $F P=\frac{y z}{x}$. We can now write everything in (1) in terms of $x, y, z$. We conclude that we have to verify
$$
\frac{\frac{y z}{x}}{y}=\frac{z+\frac{y z}{x}}{x+y}
$$
which is easily seen to be true.
Note: Antoher approach using Menalaus theorem is to construct the tangent from $M$ to create a point $N^{\prime}$ in $A C$ and then prove, using the theorem, that $P, R$ and $N^{\prime}$ are collinear. This also reduces to an algebraic identity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
a.
As in Solution 1, we introduce point $M^{\prime}$ and reduce the problem to proving $\frac{P R}{R N}=\frac{P M^{\prime}}{M^{\prime} A}$. Menelaus theorem in triangle $A N P$ with transversal line $F R E$ yields
$$
\frac{P R}{R N} \cdot \frac{N E}{E A} \cdot \frac{A F}{F P}=1
$$
Since $A F=E A$, we have $\frac{F P}{N E}=\frac{P R}{R N}$, so that it suffices to prove
$$
\frac{F P}{N E}=\frac{P M^{\prime}}{M^{\prime} A}
$$
This is a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$. Indeed, setting $a=M^{\prime} N, b=N A, c=M^{\prime} A, s=\frac{a+b+c}{2}, x=s-a, y=s-b$ and $z=s-c$, then $A E=A F=s, M^{\prime} F=z$ and $N E=y$. From $\triangle O F P \sim \triangle A F O$ we have $F P=\frac{r_{a}^{2}}{s}$, where $r_{a}=O F$ is the exradius opposite $A$. Combining the following two standard formulas for the area of a triangle
$$
\left|A M^{\prime} N\right|^{2}=x y z s \quad \text { (Heron's formula) and } \quad\left|A M^{\prime} N\right|=r_{a}(s-a),
$$
we have $r_{a}^{2}=\frac{y z s}{x}$. Therefore, $F P=\frac{y z}{x}$. We can now write everything in (1) in terms of $x, y, z$. We conclude that we have to verify
$$
\frac{\frac{y z}{x}}{y}=\frac{z+\frac{y z}{x}}{x+y}
$$
which is easily seen to be true.
Note: Antoher approach using Menalaus theorem is to construct the tangent from $M$ to create a point $N^{\prime}$ in $A C$ and then prove, using the theorem, that $P, R$ and $N^{\prime}$ are collinear. This also reduces to an algebraic identity.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution 2"
}
|
8817de03-1ca7-53cd-bcd6-18d6c28edfed
| 260,709
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
b.
As in Solution 1, we introduce point $M^{\prime}$. Let the line through $M^{\prime}$ and parallel to $A N$ intersect $E F$ at $R^{\prime}$. Let $P^{\prime}$ be the intersection of lines $N R^{\prime}$ and $A M$. It suffices to show that $P^{\prime} O \| F E$, since this would yield $P=P^{\prime}$, and then $R=R^{\prime}$ and $M=M^{\prime}$. Hence it is enough to prove that
$$
\frac{A F}{F P^{\prime}}=\frac{A D}{D O}
$$
where $D$ is the intersection of $A O$ and $E F$. Once again, this reduces to a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$.
Let $u=P^{\prime} F$ and $x, y, z, s$ as in Solution 2a. Note that since $A E=A F$ and $M^{\prime} R^{\prime} \| A E$, we have $M^{\prime} R^{\prime}=M^{\prime} F=z$. Since $M^{\prime} R^{\prime} \| A N$, we have $\frac{P^{\prime} M^{\prime}}{P^{\prime} A}=\frac{M^{\prime} R^{\prime}}{N A}$, that is,
$$
\frac{u+z}{u+x+y+z}=\frac{z}{x+z}
$$
From this last equation we obtain $u=\frac{y z}{x}$. Hence $\frac{A F}{F P^{\prime}}=\frac{x s}{y z}$. Also, as in Solution 2a, we have $r_{a}^{2}=\frac{y z s}{x}$.
Finally, using similar triangles $O D F, F D A$ and $O F A$, and the above equalities, we have
$$
\frac{A D}{D O}=\frac{A D}{D F} \cdot \frac{D F}{D O}=\frac{A F}{O F} \cdot \frac{A F}{O F}=\frac{s^{2}}{r_{a}^{2}}=\frac{s^{2}}{\frac{y z s}{x}}=\frac{x s}{y z}=\frac{A F}{F P^{\prime}}
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ and $A C$ be two distinct rays not lying on the same line, and let $\omega$ be a circle with center $O$ that is tangent to ray $A C$ at $E$ and ray $A B$ at $F$. Let $R$ be a point on segment $E F$. The line through $O$ parallel to $E F$ intersects line $A B$ at $P$. Let $N$ be the intersection of lines $P R$ and $A C$, and let $M$ be the intersection of line $A B$ and the line through $R$ parallel to $A C$. Prove that line $M N$ is tangent to $\omega$.
|
b.
As in Solution 1, we introduce point $M^{\prime}$. Let the line through $M^{\prime}$ and parallel to $A N$ intersect $E F$ at $R^{\prime}$. Let $P^{\prime}$ be the intersection of lines $N R^{\prime}$ and $A M$. It suffices to show that $P^{\prime} O \| F E$, since this would yield $P=P^{\prime}$, and then $R=R^{\prime}$ and $M=M^{\prime}$. Hence it is enough to prove that
$$
\frac{A F}{F P^{\prime}}=\frac{A D}{D O}
$$
where $D$ is the intersection of $A O$ and $E F$. Once again, this reduces to a computation regarding the triangle $A M^{\prime} N$ and its excircle opposite $A$.
Let $u=P^{\prime} F$ and $x, y, z, s$ as in Solution 2a. Note that since $A E=A F$ and $M^{\prime} R^{\prime} \| A E$, we have $M^{\prime} R^{\prime}=M^{\prime} F=z$. Since $M^{\prime} R^{\prime} \| A N$, we have $\frac{P^{\prime} M^{\prime}}{P^{\prime} A}=\frac{M^{\prime} R^{\prime}}{N A}$, that is,
$$
\frac{u+z}{u+x+y+z}=\frac{z}{x+z}
$$
From this last equation we obtain $u=\frac{y z}{x}$. Hence $\frac{A F}{F P^{\prime}}=\frac{x s}{y z}$. Also, as in Solution 2a, we have $r_{a}^{2}=\frac{y z s}{x}$.
Finally, using similar triangles $O D F, F D A$ and $O F A$, and the above equalities, we have
$$
\frac{A D}{D O}=\frac{A D}{D F} \cdot \frac{D F}{D O}=\frac{A F}{O F} \cdot \frac{A F}{O F}=\frac{s^{2}}{r_{a}^{2}}=\frac{s^{2}}{\frac{y z s}{x}}=\frac{x s}{y z}=\frac{A F}{F P^{\prime}}
$$
as required.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution 2"
}
|
8817de03-1ca7-53cd-bcd6-18d6c28edfed
| 260,709
|
The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.
## Answer: 57
|
The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.
We first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.
We will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.
Lemma: Suppose we have a directed graph on $n \geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.
Proof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.
|
57
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The country Dreamland consists of 2016 cities. The airline Starways wants to establish some one-way flights between pairs of cities in such a way that each city has exactly one flight out of it. Find the smallest positive integer $k$ such that no matter how Starways establishes its flights, the cities can always be partitioned into $k$ groups so that from any city it is not possible to reach another city in the same group by using at most 28 flights.
## Answer: 57
|
The flights established by Starways yield a directed graph $G$ on 2016 vertices in which each vertex has out-degree equal to 1.
We first show that we need at least 57 groups. For this, suppose that $G$ has a directed cycle of length 57. Then, for any two cities in the cycle, one is reachable from the other using at most 28 flights. So no two cities in the cycle can belong to the same group. Hence, we need at least 57 groups.
We will now show that 57 groups are enough. Consider another auxiliary directed graph $H$ in which the vertices are the cities of Dreamland and there is an arrow from city $u$ to city $v$ if $u$ can be reached from $v$ using at most 28 flights. Each city has out-degree at most 28 . We will be done if we can split the cities of $H$ in at most 57 groups such that there are no arrows between vertices of the same group. We prove the following stronger statement.
Lemma: Suppose we have a directed graph on $n \geq 1$ vertices such that each vertex has out-degree at most 28. Then the vertices can be partitioned into 57 groups in such a way that no vertices in the same group are connected by an arrow.
Proof: We apply induction. The result is clear for 1 vertex. Now suppose we have more than one vertex. Since the out-degree of each vertex is at most 28 , there is a vertex, say $v$, with in-degree at most 28. If we remove the vertex $v$ we obtain a graph with fewer vertices which still satifies the conditions, so by inductive hypothesis we may split it into at most 57 groups with no adjacent vertices in the same group. Since $v$ has in-degree and out-degree at most 28 , it has at most 56 neighboors in the original directed graph. Therefore, we may add $v$ back and place it in a group in which it has no neighbors. This completes the inductive step.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
842fab19-0a9e-5f76-b92c-64771e2a0233
| 260,724
|
Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
$$
(z+1) f(x+y)=f(x f(z)+y)+f(y f(z)+x)
$$
for all positive real numbers $x, y, z$.
Answer: The only solution is $f(x)=x$ for all positive real numbers $x$.
|
The identity function $f(x)=x$ clearly satisfies the functional equation. Now, let $f$ be a function satisfying the functional equation. Plugging $x=y=1$ into (3) we get $2 f(f(z)+1)=(z+1)(f(2))$ for all $z \in \mathbb{R}^{+}$. Hence, $f$ is not bounded above.
Lemma. Let $a, b, c$ be positive real numbers. If $c$ is greater than $1, a / b$ and $b / a$, then the system of linear equations
$$
c u+v=a \quad u+c v=b
$$
has a positive real solution $u, v$.
Proof. The solution is
$$
u=\frac{c a-b}{c^{2}-1} \quad v=\frac{c b-a}{c^{2}-1} .
$$
The numbers $u$ and $v$ are positive if the conditions on $c$ above are satisfied.
We will now prove that
$$
f(a)+f(b)=f(c)+f(d) \quad \text { for all } a, b, c, d \in \mathbb{R}^{+} \text {with } a+b=c+d
$$
Consider $a, b, c, d \in \mathbb{R}^{+}$such that $a+b=c+d$. Since $f$ is not bounded above, we can choose a positive number $e$ such that $f(e)$ is greater than $1, a / b, b / a, c / d$ and $d / c$. Using the above lemma, we can find $u, v, w, t \in \mathbb{R}^{+}$satisfying
$$
\begin{array}{ll}
f(e) u+v=a, & u+f(e) v=b \\
f(e) w+t=c, & w+f(e) t=d .
\end{array}
$$
Note that $u+v=w+t$ since $(u+v)(f(e)+1)=a+b$ and $(w+t)(f(e)+1)=c+d$. Plugging $x=u, y=v$ and $z=e$ into (3) yields $f(a)+f(b)=(e+1) f(u+v)$. Similarly, we have $f(c)+f(d)=(e+1) f(w+t)$. The claim follows immediately.
We then have
$$
y f(x)=f(x f(y)) \quad \text { for all } x, y \in \mathbb{R}^{+}
$$
since by (3) and (4),
$$
(y+1) f(x)=f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)+f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)=f(x f(y))+f(x) .
$$
Now, let $a=f(1 / f(1))$. Plugging $x=1$ and $y=1 / f(1)$ into (5) yields $f(a)=1$. Hence $a=a f(a)$ and $f(a f(a))=f(a)=1$. Since $a f(a)=f(a f(a))$ by (5), we have $f(1)=a=1$. It follows from (5) that
$$
f(f(y))=y \quad \text { for all } y \in \mathbb{R}^{+} .
$$
Using (4) we have for all $x, y \in \mathbb{R}^{+}$that
$$
\begin{aligned}
& f(x+y)+f(1)=f(x)+f(y+1), \quad \text { and } \\
& f(y+1)+f(1)=f(y)+f(2)
\end{aligned}
$$
Therefore
$$
f(x+y)=f(x)+f(y)+b \quad \text { for all } x, y \in \mathbb{R}^{+},
$$
where $b=f(2)-2 f(1)=f(2)-2$. Using (5), (7) and (6), we get
$$
4+2 b=2 f(2)=f(2 f(2))=f(f(2)+f(2))=f(f(2))+f(f(2))+b=4+b
$$
This shows that $b=0$ and thus
$$
f(x+y)=f(x)+f(y) \quad \text { for all } x, y \in \mathbb{R}^{+} .
$$
In particular, $f$ is strictly increasing.
We conclude as follows. Take any positive real number $x$. If $f(x)>x$, then $f(f(x))>$ $f(x)>x=f(f(x))$, a contradiction. Similarly, it is not possible that $f(x)<x$. This shows that $f(x)=x$ for all positive real numbers $x$.
|
f(x)=x
|
Yes
|
Yes
|
proof
|
Algebra
|
Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
$$
(z+1) f(x+y)=f(x f(z)+y)+f(y f(z)+x)
$$
for all positive real numbers $x, y, z$.
Answer: The only solution is $f(x)=x$ for all positive real numbers $x$.
|
The identity function $f(x)=x$ clearly satisfies the functional equation. Now, let $f$ be a function satisfying the functional equation. Plugging $x=y=1$ into (3) we get $2 f(f(z)+1)=(z+1)(f(2))$ for all $z \in \mathbb{R}^{+}$. Hence, $f$ is not bounded above.
Lemma. Let $a, b, c$ be positive real numbers. If $c$ is greater than $1, a / b$ and $b / a$, then the system of linear equations
$$
c u+v=a \quad u+c v=b
$$
has a positive real solution $u, v$.
Proof. The solution is
$$
u=\frac{c a-b}{c^{2}-1} \quad v=\frac{c b-a}{c^{2}-1} .
$$
The numbers $u$ and $v$ are positive if the conditions on $c$ above are satisfied.
We will now prove that
$$
f(a)+f(b)=f(c)+f(d) \quad \text { for all } a, b, c, d \in \mathbb{R}^{+} \text {with } a+b=c+d
$$
Consider $a, b, c, d \in \mathbb{R}^{+}$such that $a+b=c+d$. Since $f$ is not bounded above, we can choose a positive number $e$ such that $f(e)$ is greater than $1, a / b, b / a, c / d$ and $d / c$. Using the above lemma, we can find $u, v, w, t \in \mathbb{R}^{+}$satisfying
$$
\begin{array}{ll}
f(e) u+v=a, & u+f(e) v=b \\
f(e) w+t=c, & w+f(e) t=d .
\end{array}
$$
Note that $u+v=w+t$ since $(u+v)(f(e)+1)=a+b$ and $(w+t)(f(e)+1)=c+d$. Plugging $x=u, y=v$ and $z=e$ into (3) yields $f(a)+f(b)=(e+1) f(u+v)$. Similarly, we have $f(c)+f(d)=(e+1) f(w+t)$. The claim follows immediately.
We then have
$$
y f(x)=f(x f(y)) \quad \text { for all } x, y \in \mathbb{R}^{+}
$$
since by (3) and (4),
$$
(y+1) f(x)=f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)+f\left(\frac{x}{2} f(y)+\frac{x}{2}\right)=f(x f(y))+f(x) .
$$
Now, let $a=f(1 / f(1))$. Plugging $x=1$ and $y=1 / f(1)$ into (5) yields $f(a)=1$. Hence $a=a f(a)$ and $f(a f(a))=f(a)=1$. Since $a f(a)=f(a f(a))$ by (5), we have $f(1)=a=1$. It follows from (5) that
$$
f(f(y))=y \quad \text { for all } y \in \mathbb{R}^{+} .
$$
Using (4) we have for all $x, y \in \mathbb{R}^{+}$that
$$
\begin{aligned}
& f(x+y)+f(1)=f(x)+f(y+1), \quad \text { and } \\
& f(y+1)+f(1)=f(y)+f(2)
\end{aligned}
$$
Therefore
$$
f(x+y)=f(x)+f(y)+b \quad \text { for all } x, y \in \mathbb{R}^{+},
$$
where $b=f(2)-2 f(1)=f(2)-2$. Using (5), (7) and (6), we get
$$
4+2 b=2 f(2)=f(2 f(2))=f(f(2)+f(2))=f(f(2))+f(f(2))+b=4+b
$$
This shows that $b=0$ and thus
$$
f(x+y)=f(x)+f(y) \quad \text { for all } x, y \in \mathbb{R}^{+} .
$$
In particular, $f$ is strictly increasing.
We conclude as follows. Take any positive real number $x$. If $f(x)>x$, then $f(f(x))>$ $f(x)>x=f(f(x))$, a contradiction. Similarly, it is not possible that $f(x)<x$. This shows that $f(x)=x$ for all positive real numbers $x$.
|
{
"resource_path": "APMO/segmented/en-apmo2016_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
fbcdcc19-eb52-5c0c-8362-4140868a0ad3
| 605,761
|
We call a 5-tuple of integers arrangeable if its elements can be labeled $a$, $b, c, d, e$ in some order so that $a-b+c-d+e=29$. Determine all 2017-tuples of integers $n_{1}, n_{2}, \ldots, n_{2017}$ such that if we place them in a circle in clockwise order, then any 5 -tuple of numbers in consecutive positions on the circle is arrangeable.
Answer: $n_{1}=\cdots=n_{2017}=29$.
|
A valid 2017-tuple is $n_{1}=\cdots=n_{2017}=29$. We will show that it is the only solution.
We first replace each number $n_{i}$ in the circle by $m_{i}:=n_{i}-29$. Since the condition $a-b+$ $c-d+e=29$ can be rewritten as $(a-29)-(b-29)+(c-29)-(d-29)+(e-29)=0$, we have that any five consecutive replaced integers in the circle can be labeled $a, b, c, d, e$ in such a way that $a-b+c-d+e=0$. We claim that this is possible only when all of the $m_{i}$ 's are 0 (and thus all of the original $n_{i}$ 's are 29).
We work with indexes modulo 2017. Notice that for every $i, m_{i}$ and $m_{i+5}$ have the same parity. Indeed, this follows from $m_{i} \equiv m_{i+1}+m_{i+2}+m_{i+3}+m_{i+4} \equiv m_{i+5}(\bmod 2)$. Since $\operatorname{gcd}(5,2017)=1$, this implies that all $m_{i}$ 's are of the same parity. Since $m_{1}+m_{2}+m_{3}+m_{4}+m_{5}$ is even, all $m_{i}$ 's must be even as well.
Suppose for the sake of contradiction that not all $m_{i}$ 's are zero. Then our condition still holds when we divide each number in the circle by 2 . However, by performing repeated divisions, we eventually reach a point where some $m_{i}$ is odd. This is a contradiction.
|
n_{1}=\cdots=n_{2017}=29
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We call a 5-tuple of integers arrangeable if its elements can be labeled $a$, $b, c, d, e$ in some order so that $a-b+c-d+e=29$. Determine all 2017-tuples of integers $n_{1}, n_{2}, \ldots, n_{2017}$ such that if we place them in a circle in clockwise order, then any 5 -tuple of numbers in consecutive positions on the circle is arrangeable.
Answer: $n_{1}=\cdots=n_{2017}=29$.
|
A valid 2017-tuple is $n_{1}=\cdots=n_{2017}=29$. We will show that it is the only solution.
We first replace each number $n_{i}$ in the circle by $m_{i}:=n_{i}-29$. Since the condition $a-b+$ $c-d+e=29$ can be rewritten as $(a-29)-(b-29)+(c-29)-(d-29)+(e-29)=0$, we have that any five consecutive replaced integers in the circle can be labeled $a, b, c, d, e$ in such a way that $a-b+c-d+e=0$. We claim that this is possible only when all of the $m_{i}$ 's are 0 (and thus all of the original $n_{i}$ 's are 29).
We work with indexes modulo 2017. Notice that for every $i, m_{i}$ and $m_{i+5}$ have the same parity. Indeed, this follows from $m_{i} \equiv m_{i+1}+m_{i+2}+m_{i+3}+m_{i+4} \equiv m_{i+5}(\bmod 2)$. Since $\operatorname{gcd}(5,2017)=1$, this implies that all $m_{i}$ 's are of the same parity. Since $m_{1}+m_{2}+m_{3}+m_{4}+m_{5}$ is even, all $m_{i}$ 's must be even as well.
Suppose for the sake of contradiction that not all $m_{i}$ 's are zero. Then our condition still holds when we divide each number in the circle by 2 . However, by performing repeated divisions, we eventually reach a point where some $m_{i}$ is odd. This is a contradiction.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
a9b03a01-c330-50d9-b298-8cf63e8e60ca
| 605,770
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. Let $N$ be the midpoint of $A C$. Let $M$ be the intersection point of the circumcircle of triangle $A D Z$ and the segment $A B$. We will show that $M$ is the midpoint of $A B$. To do this, let $D^{\prime}$ the reflection of $D$ with respect to $M$. It suffices to show that $A D B D^{\prime}$ is a parallelogram.
The internal and external bisectors of an angle in a triangle are perpendicular. This implies that $Z D$ is a diameter of the circumcircle of $A Z D$ and thus $\angle Z M D=90^{\circ}$. This means that $Z M$ is the perpendicular bisector of $D^{\prime} D$ and thus $Z D^{\prime}=Z D$. By construction, $Z$ is in the perpendicular bisector of $A C$ and thus $Z A=Z C$.
Now, let $\alpha$ be the angle $\angle B A D=\angle D A C$. In the cyclic quadrilateral $A Z D M$ we get $\angle M Z D=\angle M A D=\alpha$, and thus $\angle D^{\prime} Z D=2 \alpha$. By angle chasing we get
$$
\angle A Z N=90^{\circ}-\angle Z A N=\angle D A C=\alpha,
$$
which implies that $\angle A Z C=2 \alpha$. Therefore,
$$
\angle D^{\prime} Z A=\angle D^{\prime} Z D-\angle A Z D=2 \alpha-\angle A Z D=\angle A Z C-\angle A Z D=\angle D Z C .
$$
Combining $\angle D^{\prime} Z A=\angle D Z C, Z D^{\prime}=Z D$ and $Z A=Z C$, we obtain by the $S A S$ criterion that the triangles $D^{\prime} Z A$ and $D Z C$ are congruent. In particular, $D^{\prime} A=D C$ and $\angle D^{\prime} A Z=$ $\angle D C Z$. From here $D B=D C=D^{\prime} A$.
Finally, let $\beta=\angle A B C=\angle A D C$. We get the first of the following equalities by the sum of angles around point $A$ and the second one by the sum of internal angles of quadrilateral $A Z C D$
$$
\begin{aligned}
& 360^{\circ}=\angle D^{\prime} A Z+\angle Z A D+\angle D A B+\angle B A D^{\prime}=\angle D^{\prime} A Z+90^{\circ}+\alpha+\angle B A D^{\prime} \\
& 360^{\circ}=\angle D C Z+\angle Z A D+\angle C Z A+\angle A D C=\angle D C Z+90^{\circ}+2 \alpha+\beta
\end{aligned}
$$
By canceling equal terms we conclude that $\angle B A D^{\prime}=\alpha+\beta$. Also, $\angle A B D=\alpha+\beta$. Therefore, the segments $D^{\prime} A$ and $D B$ are parallel and have the same length. We conclude that $A D B D^{\prime}$ is a parallelogram. As the diagonals of a parallelogram intersect at their midpoints, we obtain that $M$ is the midpoint of $A B$ as desired.
Variant of solution. The solution above is indirect in the sense that it assumes that $M$ is in the circumcircle of $A Z D$ and then shows that $M$ is the midpoint of $A B$. We point out that the same ideas in the solution can be used to give a direct solution. Here we present a sketch on how to proceed in this manner.
Now we know that $M$ is the midpoint of the side $A B$. We construct the point $D^{\prime}$ in the same way. Now we have directly that $A D B D^{\prime}$ is a parallelogram and thus $D^{\prime} A=D B=D C$. By construction $Z A=Z C$. Also, the two sums of angles equal to $360^{\circ}$ in the previous solution let us conclude that $\angle D^{\prime} A Z=\angle D C Z$. Once again, we use (differently) the $S A S$ criterion and obtain that the triangles $D^{\prime} A Z$ and $D C Z$ are congruent. Thus, $D^{\prime} Z=D Z$.
We finish the problem by noting that $Z M$ is a median of the isosceles triangle $D^{\prime} Z D$, so it is also a perpendicular bisector. This shows that $\angle D M Z=90^{\circ}=\angle D A Z$, and therefore $M$ lies in the circumcircle of $D A Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. Let $N$ be the midpoint of $A C$. Let $M$ be the intersection point of the circumcircle of triangle $A D Z$ and the segment $A B$. We will show that $M$ is the midpoint of $A B$. To do this, let $D^{\prime}$ the reflection of $D$ with respect to $M$. It suffices to show that $A D B D^{\prime}$ is a parallelogram.
The internal and external bisectors of an angle in a triangle are perpendicular. This implies that $Z D$ is a diameter of the circumcircle of $A Z D$ and thus $\angle Z M D=90^{\circ}$. This means that $Z M$ is the perpendicular bisector of $D^{\prime} D$ and thus $Z D^{\prime}=Z D$. By construction, $Z$ is in the perpendicular bisector of $A C$ and thus $Z A=Z C$.
Now, let $\alpha$ be the angle $\angle B A D=\angle D A C$. In the cyclic quadrilateral $A Z D M$ we get $\angle M Z D=\angle M A D=\alpha$, and thus $\angle D^{\prime} Z D=2 \alpha$. By angle chasing we get
$$
\angle A Z N=90^{\circ}-\angle Z A N=\angle D A C=\alpha,
$$
which implies that $\angle A Z C=2 \alpha$. Therefore,
$$
\angle D^{\prime} Z A=\angle D^{\prime} Z D-\angle A Z D=2 \alpha-\angle A Z D=\angle A Z C-\angle A Z D=\angle D Z C .
$$
Combining $\angle D^{\prime} Z A=\angle D Z C, Z D^{\prime}=Z D$ and $Z A=Z C$, we obtain by the $S A S$ criterion that the triangles $D^{\prime} Z A$ and $D Z C$ are congruent. In particular, $D^{\prime} A=D C$ and $\angle D^{\prime} A Z=$ $\angle D C Z$. From here $D B=D C=D^{\prime} A$.
Finally, let $\beta=\angle A B C=\angle A D C$. We get the first of the following equalities by the sum of angles around point $A$ and the second one by the sum of internal angles of quadrilateral $A Z C D$
$$
\begin{aligned}
& 360^{\circ}=\angle D^{\prime} A Z+\angle Z A D+\angle D A B+\angle B A D^{\prime}=\angle D^{\prime} A Z+90^{\circ}+\alpha+\angle B A D^{\prime} \\
& 360^{\circ}=\angle D C Z+\angle Z A D+\angle C Z A+\angle A D C=\angle D C Z+90^{\circ}+2 \alpha+\beta
\end{aligned}
$$
By canceling equal terms we conclude that $\angle B A D^{\prime}=\alpha+\beta$. Also, $\angle A B D=\alpha+\beta$. Therefore, the segments $D^{\prime} A$ and $D B$ are parallel and have the same length. We conclude that $A D B D^{\prime}$ is a parallelogram. As the diagonals of a parallelogram intersect at their midpoints, we obtain that $M$ is the midpoint of $A B$ as desired.

Variant of solution. The solution above is indirect in the sense that it assumes that $M$ is in the circumcircle of $A Z D$ and then shows that $M$ is the midpoint of $A B$. We point out that the same ideas in the solution can be used to give a direct solution. Here we present a sketch on how to proceed in this manner.
Now we know that $M$ is the midpoint of the side $A B$. We construct the point $D^{\prime}$ in the same way. Now we have directly that $A D B D^{\prime}$ is a parallelogram and thus $D^{\prime} A=D B=D C$. By construction $Z A=Z C$. Also, the two sums of angles equal to $360^{\circ}$ in the previous solution let us conclude that $\angle D^{\prime} A Z=\angle D C Z$. Once again, we use (differently) the $S A S$ criterion and obtain that the triangles $D^{\prime} A Z$ and $D C Z$ are congruent. Thus, $D^{\prime} Z=D Z$.
We finish the problem by noting that $Z M$ is a median of the isosceles triangle $D^{\prime} Z D$, so it is also a perpendicular bisector. This shows that $\angle D M Z=90^{\circ}=\angle D A Z$, and therefore $M$ lies in the circumcircle of $D A Z$.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
62bc85d1-87c1-5509-a2b1-505f944e2474
| 605,781
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. We proceed directly. As above, we name
$$
\alpha=\angle D A C=\angle A Z N=\angle C Z N=\angle D C B .
$$
Let $L$ be the midpoint of the segment $B C$. Since $M$ and $N$ are midpoints of $A B$ and $A C$, we have that $M N=C L$ and that the segment $M N$ is parallel to $B C$. Thus, $\angle A N M=\angle A C B$.
Therefore, $\angle Z N M=\angle A C B+90^{\circ}$. Also, $\angle D C Z=\angle D C B+\angle A C B+\angle Z C A=\angle A C B+90^{\circ}$. We conclude that $\angle Z N M=\angle D C Z$.
Now, the triangles $Z N C$ and $C L D$ are similar since $\angle D C L=90^{\circ}=\angle C N Z$ and $\angle D C L=$ $\alpha=\angle C Z N$. We use this fact to obtain the following chain of equalities
$$
\frac{C D}{M N}=\frac{C D}{C L}=\frac{C Z}{Z N}
$$
We combine the equality above with $\angle Z N M=\angle D C Z$ to conclude that the triangles $Z N M$ and $Z C D$ are similar. In particular, $\angle M Z N=\angle D Z C$ and $\frac{Z M}{Z N}=\frac{Z D}{Z C}$. Since we also have $\angle M Z D=\angle M Z N+\angle N Z D=\angle D Z C+\angle N Z D=\angle N Z C$, we conclude that the triangles $M Z D$ and $N Z C$ are similar. This yields that $\angle Z M D=90^{\circ}$ and therefore $M$ is in the circumcircle of triangle $D A Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. We proceed directly. As above, we name
$$
\alpha=\angle D A C=\angle A Z N=\angle C Z N=\angle D C B .
$$
Let $L$ be the midpoint of the segment $B C$. Since $M$ and $N$ are midpoints of $A B$ and $A C$, we have that $M N=C L$ and that the segment $M N$ is parallel to $B C$. Thus, $\angle A N M=\angle A C B$.
Therefore, $\angle Z N M=\angle A C B+90^{\circ}$. Also, $\angle D C Z=\angle D C B+\angle A C B+\angle Z C A=\angle A C B+90^{\circ}$. We conclude that $\angle Z N M=\angle D C Z$.
Now, the triangles $Z N C$ and $C L D$ are similar since $\angle D C L=90^{\circ}=\angle C N Z$ and $\angle D C L=$ $\alpha=\angle C Z N$. We use this fact to obtain the following chain of equalities
$$
\frac{C D}{M N}=\frac{C D}{C L}=\frac{C Z}{Z N}
$$
We combine the equality above with $\angle Z N M=\angle D C Z$ to conclude that the triangles $Z N M$ and $Z C D$ are similar. In particular, $\angle M Z N=\angle D Z C$ and $\frac{Z M}{Z N}=\frac{Z D}{Z C}$. Since we also have $\angle M Z D=\angle M Z N+\angle N Z D=\angle D Z C+\angle N Z D=\angle N Z C$, we conclude that the triangles $M Z D$ and $N Z C$ are similar. This yields that $\angle Z M D=90^{\circ}$ and therefore $M$ is in the circumcircle of triangle $D A Z$.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
62bc85d1-87c1-5509-a2b1-505f944e2474
| 605,781
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. Let $m$ be the perpendicular bisector of $A D$; thus $m$ passes through the center $O$ of the circumcircle of triangle $A B C$. Since $A D$ is the internal angle bisector of $A$ and $O M$ and $O N$ are perpendicular to $A B$ and $A C$ respectively, we obtain that $O M$ and $O N$ form equal angles with $A D$. This implies that they are symmetric with respect to $M$.
Therefore, the line $M O$ passes through the point $Z^{\prime}$ symmetrical to $Z$ with respect to $m$. Since $\angle D A Z=90^{\circ}$, then also $\angle A D Z^{\prime}=90^{\circ}$. Moreover, since $A Z=D Z^{\prime}$, we have that $\angle A Z Z^{\prime}=\angle D Z^{\prime} Z=90^{\circ}$, so $A Z Z^{\prime} D$ is a rectangle. Since $\angle A M Z^{\prime}=\angle A M O=90^{\circ}$, we conclude that $M$ is in the circle with diameter $A Z^{\prime}$, which is the circumcircle of the rectangle. Thus $M$ lies on the circumcircle of the triangle $A D Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $D$ be the intersection point of the internal bisector of angle $B A C$ and the circumcircle of $A B C$. Let $Z$ be the intersection point of the perpendicular bisector of $A C$ with the external bisector of angle $\angle B A C$. Prove that the midpoint of the segment $A B$ lies on the circumcircle of triangle $A D Z$.
|
. Let $m$ be the perpendicular bisector of $A D$; thus $m$ passes through the center $O$ of the circumcircle of triangle $A B C$. Since $A D$ is the internal angle bisector of $A$ and $O M$ and $O N$ are perpendicular to $A B$ and $A C$ respectively, we obtain that $O M$ and $O N$ form equal angles with $A D$. This implies that they are symmetric with respect to $M$.
Therefore, the line $M O$ passes through the point $Z^{\prime}$ symmetrical to $Z$ with respect to $m$. Since $\angle D A Z=90^{\circ}$, then also $\angle A D Z^{\prime}=90^{\circ}$. Moreover, since $A Z=D Z^{\prime}$, we have that $\angle A Z Z^{\prime}=\angle D Z^{\prime} Z=90^{\circ}$, so $A Z Z^{\prime} D$ is a rectangle. Since $\angle A M Z^{\prime}=\angle A M O=90^{\circ}$, we conclude that $M$ is in the circle with diameter $A Z^{\prime}$, which is the circumcircle of the rectangle. Thus $M$ lies on the circumcircle of the triangle $A D Z$.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3"
}
|
62bc85d1-87c1-5509-a2b1-505f944e2474
| 605,781
|
Let $A(n)$ denote the number of sequences $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers for which $a_{1}+\cdots+a_{k}=n$ and each $a_{i}+1$ is a power of two $(i=1,2, \ldots, k)$. Let $B(n)$ denote the number of sequences $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integers for which $b_{1}+\cdots+b_{m}=n$ and each inequality $b_{j} \geq 2 b_{j+1}$ holds $(j=1,2, \ldots, m-1)$.
Prove that $A(n)=B(n)$ for every positive integer $n$.
|
We say that a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers has type $A$ if $a_{i}+1$ is a power of two for $i=1,2, \ldots, k$. We say that a sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integer has type $B$ if $b_{j} \geq 2 b_{j+1}$ for $j=1,2, \ldots, m-1$.
Recall that the binary representation of a positive integer expresses it as a sum of distinct powers of two in a unique way. Furthermore, we have the following formula for every positive integer $N$
$$
2^{N}-1=2^{N-1}+2^{N-2}+\cdots+2^{1}+2^{0}
$$
Given a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of type $A$, use the preceding formula to express each term as a sum of powers of two. Write these powers of two in left-aligned rows, in decreasing order of size. By construction, $a_{i}$ is the sum of the numbers in the $i$ th row. For example, we obtain the following array when we start with the type A sequence $15,15,7,3,3,3,1$.
| 8 | 4 | 2 | 1 |
| :--- | :--- | :--- | :--- |
| 8 | 4 | 2 | 1 |
| 4 | 2 | 1 | |
| 2 | 1 | | |
| 2 | 1 | | |
| 2 | 1 | | |
| 1 | | | |
| 27 | 13 | 5 | 2 |
Define the sequence $b_{1}, b_{2}, \ldots, b_{n}$ by setting $b_{j}$ to be the sum of the numbers in the $j$ th column of the array. For example, we obtain the sequence $27,13,5,2$ from the array above. We now show that this new sequence has type B. This is clear from the fact that each column in the array contains at least as many entries as the column to the right of it and that each number larger than 1 in the array is twice the number to the right of it. Furthermore, it is clear that $a_{1}+a_{2}+\cdots+a_{k}=b_{1}+b_{2}+\cdots+b_{m}$, since both are equal to the sum of all the entries in the array.
We now show that we can do this operation backwards. Suppose that we are given a type B sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$. We construct an array inductively as follows:
- We fill $b_{m}$ left-aligned rows with the numbers $2^{m-1}, 2^{m-2}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-1}-2 b_{m}$ left aligned rows with the numbers $2^{m-2}, 2^{m-3}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-2}-2 b_{m-1}$ left aligned rows with the numbers $2^{m-3}, 2^{m-4}, \ldots, 2^{1}, 2^{0}$, and so on.
- In the last step we fill $b_{1}-2 b_{2}$ left-aligned rows with the number 1 .
For example, if we start with the type B sequence $27,13,5,2$, we obtain once again the array above. We define the sequence $a_{1}, a_{2}, \ldots, a_{k}$ by setting $a_{i}$ to be the sum of the numbers in the $i$ th row of the array. By construction, this sequence has type A. Furthermore, it is clear that $a_{1}+\cdots+a_{k}=b_{1}+\cdots+b_{m}$, since once again both sums are equal to the sum of all the entries in the array.
We have defined an operation that starts with a sequence of type A , produces an array whose row sums are given by the sequence, and outputs a sequence of type B corresponding to the column sums. We have also defined an operation that starts with a sequence of type B, produces an array whose column sums are given by the sequence, and outputs a sequence of type A corresponding to the row sums. The arrays produced in both cases comprise leftaligned rows of the form $2^{N-1}, 2^{N-2}, \ldots, 2^{1}, 2^{0}$, with non-increasing lengths. Let us refer to arrays obeying these properties as marvelous.
To show that these two operations are inverses of each other, it then suffices to prove that marvelous arrays are uniquely defined by either their row sums or their column sums. The former is obviously true and the latter arises from the observation that each step in the above inductive algorithm was forced in order to create a marvelous array with the prescribed column sums.
Thus, we have produced a bijection between the sequences of type A with sum $n$ and the sequences of type B with sum $n$. So we can conclude that $A(n)=B(n)$ for every positive integer $n$.
Remark The solution above provides a bijection between type A and type B sequences via an algorithm. There are alternative ways to provide such a bijection. For example, given the numbers $a_{1} \geq \ldots \geq a_{k}$ we may define the $b_{i}$ 's as
$$
b_{j}=\sum_{i}\left\lfloor\frac{a_{i}+1}{2^{j}}\right\rfloor .
$$
Conversely, given the numbers $b_{1} \geq \ldots \geq b_{m}$, one may define the $a_{i}$ 's by taking, as in the solution, $b_{m}$ numbers equal to $2^{m}-1, b_{m-1}-2 b_{m}$ numbers equal to $2^{m-1}-1, \ldots$, and $b_{1}-2 b_{2}$ numbers equal to $2^{1}-1$. One now needs to verify that these maps are mutually inverse.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A(n)$ denote the number of sequences $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers for which $a_{1}+\cdots+a_{k}=n$ and each $a_{i}+1$ is a power of two $(i=1,2, \ldots, k)$. Let $B(n)$ denote the number of sequences $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integers for which $b_{1}+\cdots+b_{m}=n$ and each inequality $b_{j} \geq 2 b_{j+1}$ holds $(j=1,2, \ldots, m-1)$.
Prove that $A(n)=B(n)$ for every positive integer $n$.
|
We say that a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of positive integers has type $A$ if $a_{i}+1$ is a power of two for $i=1,2, \ldots, k$. We say that a sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$ of positive integer has type $B$ if $b_{j} \geq 2 b_{j+1}$ for $j=1,2, \ldots, m-1$.
Recall that the binary representation of a positive integer expresses it as a sum of distinct powers of two in a unique way. Furthermore, we have the following formula for every positive integer $N$
$$
2^{N}-1=2^{N-1}+2^{N-2}+\cdots+2^{1}+2^{0}
$$
Given a sequence $a_{1} \geq a_{2} \geq \ldots \geq a_{k}$ of type $A$, use the preceding formula to express each term as a sum of powers of two. Write these powers of two in left-aligned rows, in decreasing order of size. By construction, $a_{i}$ is the sum of the numbers in the $i$ th row. For example, we obtain the following array when we start with the type A sequence $15,15,7,3,3,3,1$.
| 8 | 4 | 2 | 1 |
| :--- | :--- | :--- | :--- |
| 8 | 4 | 2 | 1 |
| 4 | 2 | 1 | |
| 2 | 1 | | |
| 2 | 1 | | |
| 2 | 1 | | |
| 1 | | | |
| 27 | 13 | 5 | 2 |
Define the sequence $b_{1}, b_{2}, \ldots, b_{n}$ by setting $b_{j}$ to be the sum of the numbers in the $j$ th column of the array. For example, we obtain the sequence $27,13,5,2$ from the array above. We now show that this new sequence has type B. This is clear from the fact that each column in the array contains at least as many entries as the column to the right of it and that each number larger than 1 in the array is twice the number to the right of it. Furthermore, it is clear that $a_{1}+a_{2}+\cdots+a_{k}=b_{1}+b_{2}+\cdots+b_{m}$, since both are equal to the sum of all the entries in the array.
We now show that we can do this operation backwards. Suppose that we are given a type B sequence $b_{1} \geq b_{2} \geq \ldots \geq b_{m}$. We construct an array inductively as follows:
- We fill $b_{m}$ left-aligned rows with the numbers $2^{m-1}, 2^{m-2}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-1}-2 b_{m}$ left aligned rows with the numbers $2^{m-2}, 2^{m-3}, \ldots, 2^{1}, 2^{0}$.
- Then we fill $b_{m-2}-2 b_{m-1}$ left aligned rows with the numbers $2^{m-3}, 2^{m-4}, \ldots, 2^{1}, 2^{0}$, and so on.
- In the last step we fill $b_{1}-2 b_{2}$ left-aligned rows with the number 1 .
For example, if we start with the type B sequence $27,13,5,2$, we obtain once again the array above. We define the sequence $a_{1}, a_{2}, \ldots, a_{k}$ by setting $a_{i}$ to be the sum of the numbers in the $i$ th row of the array. By construction, this sequence has type A. Furthermore, it is clear that $a_{1}+\cdots+a_{k}=b_{1}+\cdots+b_{m}$, since once again both sums are equal to the sum of all the entries in the array.
We have defined an operation that starts with a sequence of type A , produces an array whose row sums are given by the sequence, and outputs a sequence of type B corresponding to the column sums. We have also defined an operation that starts with a sequence of type B, produces an array whose column sums are given by the sequence, and outputs a sequence of type A corresponding to the row sums. The arrays produced in both cases comprise leftaligned rows of the form $2^{N-1}, 2^{N-2}, \ldots, 2^{1}, 2^{0}$, with non-increasing lengths. Let us refer to arrays obeying these properties as marvelous.
To show that these two operations are inverses of each other, it then suffices to prove that marvelous arrays are uniquely defined by either their row sums or their column sums. The former is obviously true and the latter arises from the observation that each step in the above inductive algorithm was forced in order to create a marvelous array with the prescribed column sums.
Thus, we have produced a bijection between the sequences of type A with sum $n$ and the sequences of type B with sum $n$. So we can conclude that $A(n)=B(n)$ for every positive integer $n$.
Remark The solution above provides a bijection between type A and type B sequences via an algorithm. There are alternative ways to provide such a bijection. For example, given the numbers $a_{1} \geq \ldots \geq a_{k}$ we may define the $b_{i}$ 's as
$$
b_{j}=\sum_{i}\left\lfloor\frac{a_{i}+1}{2^{j}}\right\rfloor .
$$
Conversely, given the numbers $b_{1} \geq \ldots \geq b_{m}$, one may define the $a_{i}$ 's by taking, as in the solution, $b_{m}$ numbers equal to $2^{m}-1, b_{m-1}-2 b_{m}$ numbers equal to $2^{m-1}-1, \ldots$, and $b_{1}-2 b_{2}$ numbers equal to $2^{1}-1$. One now needs to verify that these maps are mutually inverse.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
af37d72c-51b6-59d4-84ab-161c2b46f22e
| 260,410
|
Call a rational number $r$ powerful if $r$ can be expressed in the form $\frac{p^{k}}{q}$ for some relatively prime positive integers $p, q$ and some integer $k>1$. Let $a, b, c$ be positive
rational numbers such that $a b c=1$. Suppose there exist positive integers $x, y, z$ such that $a^{x}+b^{y}+c^{z}$ is an integer. Prove that $a, b, c$ are all powerful.
|
Let $a=\frac{a_{1}}{b_{1}}, b=\frac{a_{2}}{b_{2}}$, where $\operatorname{gcd}\left(a_{1}, b_{1}\right)=\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$. Then $c=\frac{b_{1} b_{2}}{a_{1} a_{2}}$. The condition that $a^{x}+b^{y}+c^{z}$ is an integer becomes
$$
\frac{a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}}{a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y}} \in \mathbb{Z}
$$
which can be restated as
$$
a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y} \mid a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
In particular, $a_{1}^{z}$ divides the right-hand side. Since it divides the first and second terms in the sum, we conclude that $a_{1}^{z} \mid b_{1}^{x+z} b_{2}^{y+z}$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=1$, we have $a_{1}^{z} \mid b_{2}^{y+z}$.
Let $p$ be a prime that divides $a_{1}$. Let $m, n \geq 1$ be integers such that $p^{n} \| a_{1}$ (i.e. $p^{n} \mid a_{1}$ but $\left.p^{n+1} \nmid a_{1}\right)$ and $p^{m} \| b_{2}$. The fact that $a_{1}^{z} \mid b_{2}^{y+z}$ implies $n z \leq m(y+z)$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=$ $\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$, we have $p$ does not divide $b_{1}$ and does not divide $a_{2}$. Thus
$$
p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x} \text { and } p^{m(y+z)} \| b_{1}^{x+z} b_{2}^{y+z}
$$
On the other hand, (1) implies that
$$
p^{n z+m y} \mid a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
If $n z<m(y+z)$, then (2) gives $p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}$, which contradicts (3). Thus $n z=m(y+z)$ so $n$ is divisible by $k:=\frac{y+z}{\operatorname{gcd}(z, y+z)}>1$. Thus each exponent in the prime decomposition of $a_{1}$ must be divisible by $k$. Hence $a_{1}$ is a perfect $k$-power which means $a$ is powerful. Similarly, $b$ and $c$ are also powerful.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Call a rational number $r$ powerful if $r$ can be expressed in the form $\frac{p^{k}}{q}$ for some relatively prime positive integers $p, q$ and some integer $k>1$. Let $a, b, c$ be positive
rational numbers such that $a b c=1$. Suppose there exist positive integers $x, y, z$ such that $a^{x}+b^{y}+c^{z}$ is an integer. Prove that $a, b, c$ are all powerful.
|
Let $a=\frac{a_{1}}{b_{1}}, b=\frac{a_{2}}{b_{2}}$, where $\operatorname{gcd}\left(a_{1}, b_{1}\right)=\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$. Then $c=\frac{b_{1} b_{2}}{a_{1} a_{2}}$. The condition that $a^{x}+b^{y}+c^{z}$ is an integer becomes
$$
\frac{a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}}{a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y}} \in \mathbb{Z}
$$
which can be restated as
$$
a_{1}^{z} a_{2}^{z} b_{1}^{x} b_{2}^{y} \mid a_{1}^{x+z} a_{2}^{z} b_{2}^{y}+a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
In particular, $a_{1}^{z}$ divides the right-hand side. Since it divides the first and second terms in the sum, we conclude that $a_{1}^{z} \mid b_{1}^{x+z} b_{2}^{y+z}$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=1$, we have $a_{1}^{z} \mid b_{2}^{y+z}$.
Let $p$ be a prime that divides $a_{1}$. Let $m, n \geq 1$ be integers such that $p^{n} \| a_{1}$ (i.e. $p^{n} \mid a_{1}$ but $\left.p^{n+1} \nmid a_{1}\right)$ and $p^{m} \| b_{2}$. The fact that $a_{1}^{z} \mid b_{2}^{y+z}$ implies $n z \leq m(y+z)$. Since $\operatorname{gcd}\left(a_{1}, b_{1}\right)=$ $\operatorname{gcd}\left(a_{2}, b_{2}\right)=1$, we have $p$ does not divide $b_{1}$ and does not divide $a_{2}$. Thus
$$
p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x} \text { and } p^{m(y+z)} \| b_{1}^{x+z} b_{2}^{y+z}
$$
On the other hand, (1) implies that
$$
p^{n z+m y} \mid a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z} .
$$
If $n z<m(y+z)$, then (2) gives $p^{n z} \| a_{1}^{z} a_{2}^{y+z} b_{1}^{x}+b_{1}^{x+z} b_{2}^{y+z}$, which contradicts (3). Thus $n z=m(y+z)$ so $n$ is divisible by $k:=\frac{y+z}{\operatorname{gcd}(z, y+z)}>1$. Thus each exponent in the prime decomposition of $a_{1}$ must be divisible by $k$. Hence $a_{1}$ is a perfect $k$-power which means $a$ is powerful. Similarly, $b$ and $c$ are also powerful.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
38e76064-44d1-57d3-9c7e-f0a4c4f83e4c
| 260,417
|
Let $n$ be a positive integer. A pair of $n$-tuples $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ with integer entries is called an exquisite pair if
$$
\left|a_{1} b_{1}+\cdots+a_{n} b_{n}\right| \leq 1
$$
Determine the maximum number of distinct $n$-tuples with integer entries such that any two of them form an exquisite pair.
Answer: The maximum is $n^{2}+n+1$.
|
First, we construct an example with $n^{2}+n+1 n$-tuples, each two of them forming an exquisite pair. In the following list, $*$ represents any number of zeros as long as the total number of entries is $n$.
- (*)
- $(*, 1, *)$
- $(*,-1, *)$
- $(*, 1, *, 1, *)$
- $(*, 1, *,-1, *)$
For example, for $n=2$ we have the tuples $(0,0),(0,1),(1,0),(0,-1),(-1,0),(1,1),(1,-1)$. The total number of such tuples is $1+n+n+\binom{n}{2}+\binom{n}{2}=n^{2}+n+1$. For any two of them, at most two of the products $a_{i} b_{i}$ are non-zero. The only case in which two of them are non-zero is when we take a sequence $(*, 1, *, 1, *)$ and a sequence $(*, 1, *,-1, *)$ with zero entries in the same places. But in this case one $a_{i} b_{i}$ is 1 and the other -1 . This shows that any two of these sequences form an exquisite pair.
Next, we claim that among any $n^{2}+n+2$ tuples, some two of them do not form an exquisite pair. We begin with lemma.
Lemma. Given $2 n+1$ distinct non-zero $n$-tuples of real numbers, some two of them $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ satisfy $a_{1} b_{1}+\cdots+a_{n} b_{n}>0$.
Proof of Lemma. We proceed by induction. The statement is easy for $n=1$ since for every three non-zero numbers there are two of them with the same sign. Assume that the statement is true for $n-1$ and consider $2 n+1$ tuples with $n$ entries. Since we are working with tuples of real numbers, we claim that we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Let us postpone the proof of this claim for the moment.
If one of the remaining tuples $b$ has a negative last entry, then $a$ and $b$ satisfy the desired condition. So we may assume all the remaining tuples has a non-negative last entry. Now, from each tuple remove the last number. If two $n$-tuples $b$ and $c$ yield the same $(n-1)$-tuple, then
$$
b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}+b_{n} c_{n}=b_{1}^{2}+\cdots+b_{n-1}^{2}+b_{n} c_{n}>0
$$
and we are done. The remaining case is that all the $n$-tuples yield distinct ( $n-1$ )-tuples. Then at most one of them is the zero $(n-1)$-tuple, and thus we can use the inductive hypothesis on $2 n-1$ of them. So we find $b$ and $c$ for which
$$
\left(b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}\right)+b_{n} c_{n}>0+b_{n} c_{n}>0
$$
The only thing that we are left to prove is that in the inductive step we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Fix one of the tuples $x=\left(x_{1}, \ldots, x_{n}\right)$. Set a real number $\varphi$ for which $\tan \varphi=\frac{x_{1}}{x_{2}}$. Change each tuple $a=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ (including $x$ ), to the tuple
$$
\left(a_{1} \cos \varphi-a_{2} \sin \varphi, a_{1} \sin \varphi+a_{2} \cos \varphi, a_{3}, a_{4}, \ldots, a_{n}\right)
$$
A straightforward calculation shows that the first coordinate of the tuple $x$ becomes 0 , and that all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$ are preserved. We may iterate this process until all the entries of $x$ except for the last one are equal to 0 . We finish by multiplying all the entries in all the tuples by a suitable constant that makes the last entry of $x$ equal to -1 . This preserves the sign of all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$.
We proceed to the proof of our claim. Let $A$ be a set of non-zero tuples among which any two form an exquisite pair. It suffices to prove that $|A| \leq n^{2}+n$. We can write $A$ as a disjoint union of subsets $A_{1} \cup A_{2} \cup \ldots \cup A_{n}$, where $A_{i}$ is the set of tuples in $A$ whose last non-zero entry appears in the $i$ th position. We will show that $\left|A_{i}\right| \leq 2 i$, which will finish our proof since $2+4+\cdots+2 n=n^{2}+n$.
Proceeding by contradiction, suppose that $\left|A_{i}\right| \geq 2 i+1$. If $A_{i}$ has three or more tuples whose only non-zero entry is in the $i$ th position, then for two of them this entry has the same sign. Since the tuples are different and their entries are integers, this yields two tuples for which $\left|\sum a_{i} b_{i}\right| \geq 2$, a contradiction. So there are at most two such tuples. We remove them from $A_{i}$.
Now, for each of the remaining tuples $a$, if it has a positive $i$ th coordinate, we keep $a$ as it is. If it has a negative $i$ th coordinate, we replace it with the opposite tuple $-a$ with entries with opposite signs. This does not changes the exquisite pairs condition.
After making the necessary changes, we have two cases. The first case is that there are two tuples $a$ and $b$ that have the same first $i-1$ coordinates and thus
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}=a_{1}^{2}+\cdots+a_{i-1}^{2}>0
$$
and thus is at least 1 (the entries are integers). The second case is that no two tuples have the same first $i-1$ coordinates, but then by the Lemma we find two tuples $a$ and $b$ for which
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1} \geq 1
$$
In any case, we obtain
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}+a_{i} b_{i} \geq 2
$$
This yields a final contradiction to the exquisite pair hypothesis.
|
n^{2}+n+1
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. A pair of $n$-tuples $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ with integer entries is called an exquisite pair if
$$
\left|a_{1} b_{1}+\cdots+a_{n} b_{n}\right| \leq 1
$$
Determine the maximum number of distinct $n$-tuples with integer entries such that any two of them form an exquisite pair.
Answer: The maximum is $n^{2}+n+1$.
|
First, we construct an example with $n^{2}+n+1 n$-tuples, each two of them forming an exquisite pair. In the following list, $*$ represents any number of zeros as long as the total number of entries is $n$.
- (*)
- $(*, 1, *)$
- $(*,-1, *)$
- $(*, 1, *, 1, *)$
- $(*, 1, *,-1, *)$
For example, for $n=2$ we have the tuples $(0,0),(0,1),(1,0),(0,-1),(-1,0),(1,1),(1,-1)$. The total number of such tuples is $1+n+n+\binom{n}{2}+\binom{n}{2}=n^{2}+n+1$. For any two of them, at most two of the products $a_{i} b_{i}$ are non-zero. The only case in which two of them are non-zero is when we take a sequence $(*, 1, *, 1, *)$ and a sequence $(*, 1, *,-1, *)$ with zero entries in the same places. But in this case one $a_{i} b_{i}$ is 1 and the other -1 . This shows that any two of these sequences form an exquisite pair.
Next, we claim that among any $n^{2}+n+2$ tuples, some two of them do not form an exquisite pair. We begin with lemma.
Lemma. Given $2 n+1$ distinct non-zero $n$-tuples of real numbers, some two of them $\left(a_{1}, \ldots, a_{n}\right)$ and $\left(b_{1}, \ldots, b_{n}\right)$ satisfy $a_{1} b_{1}+\cdots+a_{n} b_{n}>0$.
Proof of Lemma. We proceed by induction. The statement is easy for $n=1$ since for every three non-zero numbers there are two of them with the same sign. Assume that the statement is true for $n-1$ and consider $2 n+1$ tuples with $n$ entries. Since we are working with tuples of real numbers, we claim that we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Let us postpone the proof of this claim for the moment.
If one of the remaining tuples $b$ has a negative last entry, then $a$ and $b$ satisfy the desired condition. So we may assume all the remaining tuples has a non-negative last entry. Now, from each tuple remove the last number. If two $n$-tuples $b$ and $c$ yield the same $(n-1)$-tuple, then
$$
b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}+b_{n} c_{n}=b_{1}^{2}+\cdots+b_{n-1}^{2}+b_{n} c_{n}>0
$$
and we are done. The remaining case is that all the $n$-tuples yield distinct ( $n-1$ )-tuples. Then at most one of them is the zero $(n-1)$-tuple, and thus we can use the inductive hypothesis on $2 n-1$ of them. So we find $b$ and $c$ for which
$$
\left(b_{1} c_{1}+\cdots+b_{n-1} c_{n-1}\right)+b_{n} c_{n}>0+b_{n} c_{n}>0
$$
The only thing that we are left to prove is that in the inductive step we may assume that one of the tuples is $a=(0,0, \ldots, 0,-1)$. Fix one of the tuples $x=\left(x_{1}, \ldots, x_{n}\right)$. Set a real number $\varphi$ for which $\tan \varphi=\frac{x_{1}}{x_{2}}$. Change each tuple $a=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ (including $x$ ), to the tuple
$$
\left(a_{1} \cos \varphi-a_{2} \sin \varphi, a_{1} \sin \varphi+a_{2} \cos \varphi, a_{3}, a_{4}, \ldots, a_{n}\right)
$$
A straightforward calculation shows that the first coordinate of the tuple $x$ becomes 0 , and that all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$ are preserved. We may iterate this process until all the entries of $x$ except for the last one are equal to 0 . We finish by multiplying all the entries in all the tuples by a suitable constant that makes the last entry of $x$ equal to -1 . This preserves the sign of all the expressions of the form $a_{1} b_{1}+\cdots+a_{n} b_{n}$.
We proceed to the proof of our claim. Let $A$ be a set of non-zero tuples among which any two form an exquisite pair. It suffices to prove that $|A| \leq n^{2}+n$. We can write $A$ as a disjoint union of subsets $A_{1} \cup A_{2} \cup \ldots \cup A_{n}$, where $A_{i}$ is the set of tuples in $A$ whose last non-zero entry appears in the $i$ th position. We will show that $\left|A_{i}\right| \leq 2 i$, which will finish our proof since $2+4+\cdots+2 n=n^{2}+n$.
Proceeding by contradiction, suppose that $\left|A_{i}\right| \geq 2 i+1$. If $A_{i}$ has three or more tuples whose only non-zero entry is in the $i$ th position, then for two of them this entry has the same sign. Since the tuples are different and their entries are integers, this yields two tuples for which $\left|\sum a_{i} b_{i}\right| \geq 2$, a contradiction. So there are at most two such tuples. We remove them from $A_{i}$.
Now, for each of the remaining tuples $a$, if it has a positive $i$ th coordinate, we keep $a$ as it is. If it has a negative $i$ th coordinate, we replace it with the opposite tuple $-a$ with entries with opposite signs. This does not changes the exquisite pairs condition.
After making the necessary changes, we have two cases. The first case is that there are two tuples $a$ and $b$ that have the same first $i-1$ coordinates and thus
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}=a_{1}^{2}+\cdots+a_{i-1}^{2}>0
$$
and thus is at least 1 (the entries are integers). The second case is that no two tuples have the same first $i-1$ coordinates, but then by the Lemma we find two tuples $a$ and $b$ for which
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1} \geq 1
$$
In any case, we obtain
$$
a_{1} b_{1}+\cdots+a_{i-1} b_{i-1}+a_{i} b_{i} \geq 2
$$
This yields a final contradiction to the exquisite pair hypothesis.
|
{
"resource_path": "APMO/segmented/en-apmo2017_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
2a220212-df66-5ade-90bc-624bb4afc978
| 605,852
|
Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.
|
Lemma 1. In a triangle $A B C$, let $D$ be the intersection of the interior angle bisector at $A$ with the circumcircle of $A B C$, and let $I$ be the incenter of $\triangle A B C$. Then
$$
D I=D B=D C
$$
Proof.
$$
\angle D B I=\frac{\angle B A C}{2}+\frac{\widehat{B}}{2}=\angle D I B \quad \Rightarrow \quad D I=D B
$$
Analogously $D I=D C$.
We start solving the problem. First we state some position considerations. Since there is an arc of the circumcircle of $B H M$ outside the triangle $A B C$, it must happen that $K$ and $N$ lie on opposite sides of $A M$. Similarly, $L$ and $M$ lie on opposite sides of $A N$. Also, $K$ and $L$ lie on the same side of $M N$, and opposite to $A$. Therefore, $F$ lies inside the triangle $A M N$.
Now, since $H$ is the orthocenter of $\triangle A B C$ and the circumcircles of $B M H$ and $C N H$ are tangent we have
$$
\angle A B H=90^{\circ}-\angle B A C=\angle A C H \quad \Rightarrow \quad \angle M H N=\angle M B H+\angle N C H=180^{\circ}-2 \angle B A C .
$$
So $\angle M B H=\angle M K H=\angle N C H=\angle N L H=90^{\circ}-\angle B A C$ and, since $M N \| K L$, we have
$$
\angle F M N=\angle F N M=90^{\circ}-\angle B A C \Rightarrow \angle M F N=2 \angle B A C .
$$
The relations (1) and (2) yield that the quadrilateral $M F N H$ is cyclic, with the vertices in this order around the circumference. Since $F M=F N, \angle M F N=2 \angle B A C$ and $F$ is the correct side of $M N$ we have that the point $F$ is the circumcenter of triangle $A M N$, and thus $F A=F M=F N$.
Since the quadrilateral $M F N H$ is cyclic, $F M=F N$ and $H$ lies on the correct side of $M N$, we have that $H, J$ and $F$ are collinear. According to Lemma $1, F J=F M=F N$. So $F J=F A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.
|
Lemma 1. In a triangle $A B C$, let $D$ be the intersection of the interior angle bisector at $A$ with the circumcircle of $A B C$, and let $I$ be the incenter of $\triangle A B C$. Then
$$
D I=D B=D C
$$

Proof.
$$
\angle D B I=\frac{\angle B A C}{2}+\frac{\widehat{B}}{2}=\angle D I B \quad \Rightarrow \quad D I=D B
$$
Analogously $D I=D C$.
We start solving the problem. First we state some position considerations. Since there is an arc of the circumcircle of $B H M$ outside the triangle $A B C$, it must happen that $K$ and $N$ lie on opposite sides of $A M$. Similarly, $L$ and $M$ lie on opposite sides of $A N$. Also, $K$ and $L$ lie on the same side of $M N$, and opposite to $A$. Therefore, $F$ lies inside the triangle $A M N$.
Now, since $H$ is the orthocenter of $\triangle A B C$ and the circumcircles of $B M H$ and $C N H$ are tangent we have
$$
\angle A B H=90^{\circ}-\angle B A C=\angle A C H \quad \Rightarrow \quad \angle M H N=\angle M B H+\angle N C H=180^{\circ}-2 \angle B A C .
$$
So $\angle M B H=\angle M K H=\angle N C H=\angle N L H=90^{\circ}-\angle B A C$ and, since $M N \| K L$, we have
$$
\angle F M N=\angle F N M=90^{\circ}-\angle B A C \Rightarrow \angle M F N=2 \angle B A C .
$$
The relations (1) and (2) yield that the quadrilateral $M F N H$ is cyclic, with the vertices in this order around the circumference. Since $F M=F N, \angle M F N=2 \angle B A C$ and $F$ is the correct side of $M N$ we have that the point $F$ is the circumcenter of triangle $A M N$, and thus $F A=F M=F N$.

Since the quadrilateral $M F N H$ is cyclic, $F M=F N$ and $H$ lies on the correct side of $M N$, we have that $H, J$ and $F$ are collinear. According to Lemma $1, F J=F M=F N$. So $F J=F A$.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "# Solution."
}
|
85a4a617-2773-5189-93bd-57b19ded3478
| 605,867
|
Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.
|
: According to Solution 1, we have $\angle M H N=180^{\circ}-2 \angle B A C$ and since the point $J$ is the incenter of $\triangle M H N$, we have $\angle M J N=90^{\circ}+\frac{1}{2} \angle M H N=180^{\circ}-\angle B A C$. So the quadrilateral $A M J N$ is cyclic.
According to Solution 1, the point $F$ is the circumcenter of $\triangle A M N$. So $F J=F A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocenter of the triangle $A B C$. Let $M$ and $N$ be the midpoints of the sides $A B$ and $A C$, respectively. Assume that $H$ lies inside the quadrilateral $B M N C$ and that the circumcircles of triangles $B M H$ and $C N H$ are tangent to each other. The line through $H$ parallel to $B C$ intersects the circumcircles of the triangles $B M H$ and $C N H$ in the points $K$ and $L$, respectively. Let $F$ be the intersection point of $M K$ and $N L$ and let $J$ be the incenter of triangle $M H N$. Prove that $F J=F A$.
|
: According to Solution 1, we have $\angle M H N=180^{\circ}-2 \angle B A C$ and since the point $J$ is the incenter of $\triangle M H N$, we have $\angle M J N=90^{\circ}+\frac{1}{2} \angle M H N=180^{\circ}-\angle B A C$. So the quadrilateral $A M J N$ is cyclic.
According to Solution 1, the point $F$ is the circumcenter of $\triangle A M N$. So $F J=F A$.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
85a4a617-2773-5189-93bd-57b19ded3478
| 605,867
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
There are two cases: $2 n-1<x<2 n$ and $2 n<x<2 n+1$. Note that $f(2018-x)=-f(x)$ and $g(2018-x)=-g(x)$, that is, a half turn about the point $(1009,0)$ preserves the graphs of $f$ and $g$. So it suffices to consider only the case $2 n-1<x<2 n$.
Let $d(x)=g(x)-f(x)$. We will show that $d(x)>2$ whenever $2 n-1<x<2 n$ and $n \in\{1,2, \ldots, 1009\}$.
For any non-integer $x$ with $0<x<2018$, we have
$$
d(x+2)-d(x)=\left(\frac{1}{x+1}-\frac{1}{x+2}\right)+\left(\frac{1}{x-2018}-\frac{1}{x-2017}\right)>0+0=0
$$
Hence it suffices to prove $d(x)>2$ for $1<x<2$. Since $x<2$, it follows that $\frac{1}{x-2 i-1}>$ $\frac{1}{x-2 i}$ for $i=2,3, \ldots, 1008$. We also have $\frac{1}{x-2018}<0$. Hence it suffices to prove the following
for $1<x<2$.
$$
\begin{aligned}
& \frac{1}{x-1}+\frac{1}{x-3}-\frac{1}{x}-\frac{1}{x-2}>2 \\
\Leftrightarrow & \left(\frac{1}{x-1}+\frac{1}{2-x}\right)+\left(\frac{1}{x-3}-\frac{1}{x}\right)>2 \\
\Leftrightarrow & \frac{1}{(x-1)(2-x)}+\frac{3}{x(x-3)}>2 .
\end{aligned}
$$
By the $G M-H M$ inequality (alternatively, by considering the maximum of the quadratic $(x-1)(2-x))$ we have
$$
\frac{1}{x-1} \cdot \frac{1}{2-x}>\left(\frac{2}{(x-1)+(2-x)}\right)^{2}=4
$$
To find a lower bound for $\frac{3}{x(x-3)}$, note that $x(x-3)<0$ for $1<x<2$. So we seek an upper bound for $x(x-3)$. From the shape of the quadratic, this occurs at $x=1$ or $x=2$, both of which yield $\frac{3}{x(x-3)}>-\frac{3}{2}$.
It follows that $d(x)>4-\frac{3}{2}>2$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
There are two cases: $2 n-1<x<2 n$ and $2 n<x<2 n+1$. Note that $f(2018-x)=-f(x)$ and $g(2018-x)=-g(x)$, that is, a half turn about the point $(1009,0)$ preserves the graphs of $f$ and $g$. So it suffices to consider only the case $2 n-1<x<2 n$.
Let $d(x)=g(x)-f(x)$. We will show that $d(x)>2$ whenever $2 n-1<x<2 n$ and $n \in\{1,2, \ldots, 1009\}$.
For any non-integer $x$ with $0<x<2018$, we have
$$
d(x+2)-d(x)=\left(\frac{1}{x+1}-\frac{1}{x+2}\right)+\left(\frac{1}{x-2018}-\frac{1}{x-2017}\right)>0+0=0
$$
Hence it suffices to prove $d(x)>2$ for $1<x<2$. Since $x<2$, it follows that $\frac{1}{x-2 i-1}>$ $\frac{1}{x-2 i}$ for $i=2,3, \ldots, 1008$. We also have $\frac{1}{x-2018}<0$. Hence it suffices to prove the following
for $1<x<2$.
$$
\begin{aligned}
& \frac{1}{x-1}+\frac{1}{x-3}-\frac{1}{x}-\frac{1}{x-2}>2 \\
\Leftrightarrow & \left(\frac{1}{x-1}+\frac{1}{2-x}\right)+\left(\frac{1}{x-3}-\frac{1}{x}\right)>2 \\
\Leftrightarrow & \frac{1}{(x-1)(2-x)}+\frac{3}{x(x-3)}>2 .
\end{aligned}
$$
By the $G M-H M$ inequality (alternatively, by considering the maximum of the quadratic $(x-1)(2-x))$ we have
$$
\frac{1}{x-1} \cdot \frac{1}{2-x}>\left(\frac{2}{(x-1)+(2-x)}\right)^{2}=4
$$
To find a lower bound for $\frac{3}{x(x-3)}$, note that $x(x-3)<0$ for $1<x<2$. So we seek an upper bound for $x(x-3)$. From the shape of the quadratic, this occurs at $x=1$ or $x=2$, both of which yield $\frac{3}{x(x-3)}>-\frac{3}{2}$.
It follows that $d(x)>4-\frac{3}{2}>2$, as desired.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
e9416f41-7b24-51c7-8d9d-4e9f3fd5dc23
| 605,885
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
As in Solution 1, we may assume $2 n-1<x<2 n$ for some $1 \leq n \leq 1009$. Let $d(x)=$ $f(x)-g(x)$, and note that
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}
$$
We split the sum into three parts: the terms before $m=n$, after $m=n$, and the term $m=n$. The first two are
$$
\begin{aligned}
0 & \leq \sum_{m=1}^{n-1} \frac{1}{(x-2 m)(x-2 m+1)} \\
& \leq \sum_{m=1}^{n-1} \frac{1}{(2 n-1-2 m)(2 n-2 m)}=\sum_{i=1}^{n-1} \frac{1}{(2 i)(2 i-1)} \leq \sum_{i=1}^{1008} \frac{1}{2 i-1}-\frac{1}{2 i} \\
0 & \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-x)(2 m-1-x)} \\
& \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-2 n+1)(2 m-2 n)}=\sum_{i=1}^{1009-n} \frac{1}{(2 i+1)(2 i)} \leq \sum_{i=1}^{1008} \frac{1}{2 i}-\frac{1}{2 i+1} .
\end{aligned}
$$
When we add the two sums the terms telescope and we are left with
$$
0 \leq \sum_{1 \leq m \leq 1009, m \neq n} \frac{1}{(x-2 m)(x-2 m+1)} \leq 1-\frac{1}{2017}<1
$$
For the term $m=n$, we write
$$
0<-(x-2 n)(x-2 n+1)=0.25-(x-2 n+0.5)^{2} \leq 0.25
$$
whence
$$
-4 \geq \frac{1}{(x-2 n)(x-2 n+1)}
$$
Finally, $\frac{1}{x}<1$ since $x>2 n-1 \geq 1$. Combining these we get
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}<1+1-4<-2 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
As in Solution 1, we may assume $2 n-1<x<2 n$ for some $1 \leq n \leq 1009$. Let $d(x)=$ $f(x)-g(x)$, and note that
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}
$$
We split the sum into three parts: the terms before $m=n$, after $m=n$, and the term $m=n$. The first two are
$$
\begin{aligned}
0 & \leq \sum_{m=1}^{n-1} \frac{1}{(x-2 m)(x-2 m+1)} \\
& \leq \sum_{m=1}^{n-1} \frac{1}{(2 n-1-2 m)(2 n-2 m)}=\sum_{i=1}^{n-1} \frac{1}{(2 i)(2 i-1)} \leq \sum_{i=1}^{1008} \frac{1}{2 i-1}-\frac{1}{2 i} \\
0 & \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-x)(2 m-1-x)} \\
& \leq \sum_{m=n+1}^{1009} \frac{1}{(2 m-2 n+1)(2 m-2 n)}=\sum_{i=1}^{1009-n} \frac{1}{(2 i+1)(2 i)} \leq \sum_{i=1}^{1008} \frac{1}{2 i}-\frac{1}{2 i+1} .
\end{aligned}
$$
When we add the two sums the terms telescope and we are left with
$$
0 \leq \sum_{1 \leq m \leq 1009, m \neq n} \frac{1}{(x-2 m)(x-2 m+1)} \leq 1-\frac{1}{2017}<1
$$
For the term $m=n$, we write
$$
0<-(x-2 n)(x-2 n+1)=0.25-(x-2 n+0.5)^{2} \leq 0.25
$$
whence
$$
-4 \geq \frac{1}{(x-2 n)(x-2 n+1)}
$$
Finally, $\frac{1}{x}<1$ since $x>2 n-1 \geq 1$. Combining these we get
$$
d(x)=\frac{1}{x}+\sum_{m=1}^{1009} \frac{1}{(x-2 m)(x-2 m+1)}<1+1-4<-2 .
$$
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2"
}
|
e9416f41-7b24-51c7-8d9d-4e9f3fd5dc23
| 605,885
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
First notice that
$$
f(x)-g(x)=\frac{1}{x}-\frac{1}{x-1}+\frac{1}{x-2}-\cdots-\frac{1}{x-2017}+\frac{1}{x-2018} .
$$
As in Solution 1, we may deal only with the case $2 n<x<2 n+1$. Then $x-2 k+1$ and $x-2 k$ never differ in sign for any integer $k$. Then
$$
\begin{aligned}
-\frac{1}{x-2 k+1}+\frac{1}{x-2 k} & =\frac{1}{(x-2 k+1)(x-2 k)}>0 \quad \text { for } k=1,2, \ldots, n-1, n+2, \ldots, 1009 \\
\frac{1}{x-2 n}-\frac{1}{x-2 n-1} & =\frac{1}{(x-2 n)(2 n+1-x)} \geq\left(\frac{2}{x-2 n+2 n+1-x}\right)^{2}=4
\end{aligned}
$$
Therefore, summing all inequalities and collecting the remaining terms we find $f(x)-g(x)>$ $4+\frac{1}{x-2}>4-1=3$ for $0<x<1$ and, for $n>0$,
$$
\begin{aligned}
f(x)-g(x) & >\frac{1}{x}-\frac{1}{x-2 n+1}+4+\frac{1}{x-2 n-2} \\
& =\frac{1}{x}-\frac{1}{x-2 n+1}+4-\frac{1}{2 n+2-x} \\
& >\frac{1}{x}-\frac{1}{2 n-2 n+1}+4-\frac{1}{2 n+2-2 n-1} \\
& =2+\frac{1}{x}>2 .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f(x)$ and $g(x)$ be given by
$$
f(x)=\frac{1}{x}+\frac{1}{x-2}+\frac{1}{x-4}+\cdots+\frac{1}{x-2018}
$$
and
$$
g(x)=\frac{1}{x-1}+\frac{1}{x-3}+\frac{1}{x-5}+\cdots+\frac{1}{x-2017} .
$$
Prove that
$$
|f(x)-g(x)|>2
$$
for any non-integer real number $x$ satisfying $0<x<2018$.
|
First notice that
$$
f(x)-g(x)=\frac{1}{x}-\frac{1}{x-1}+\frac{1}{x-2}-\cdots-\frac{1}{x-2017}+\frac{1}{x-2018} .
$$
As in Solution 1, we may deal only with the case $2 n<x<2 n+1$. Then $x-2 k+1$ and $x-2 k$ never differ in sign for any integer $k$. Then
$$
\begin{aligned}
-\frac{1}{x-2 k+1}+\frac{1}{x-2 k} & =\frac{1}{(x-2 k+1)(x-2 k)}>0 \quad \text { for } k=1,2, \ldots, n-1, n+2, \ldots, 1009 \\
\frac{1}{x-2 n}-\frac{1}{x-2 n-1} & =\frac{1}{(x-2 n)(2 n+1-x)} \geq\left(\frac{2}{x-2 n+2 n+1-x}\right)^{2}=4
\end{aligned}
$$
Therefore, summing all inequalities and collecting the remaining terms we find $f(x)-g(x)>$ $4+\frac{1}{x-2}>4-1=3$ for $0<x<1$ and, for $n>0$,
$$
\begin{aligned}
f(x)-g(x) & >\frac{1}{x}-\frac{1}{x-2 n+1}+4+\frac{1}{x-2 n-2} \\
& =\frac{1}{x}-\frac{1}{x-2 n+1}+4-\frac{1}{2 n+2-x} \\
& >\frac{1}{x}-\frac{1}{2 n-2 n+1}+4-\frac{1}{2 n+2-2 n-1} \\
& =2+\frac{1}{x}>2 .
\end{aligned}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 3"
}
|
e9416f41-7b24-51c7-8d9d-4e9f3fd5dc23
| 605,885
|
A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:
(i) All the squares are congruent.
(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.
(iii) Each square touches exactly three other squares.
How many positive integers $n$ are there with $2018 \leq n \leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?
Answer: 501
|
We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.
For any two different squares $A$ and $B$, let us write $A \sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \sim B$ is $3 n$. But $A \sim B$ if and only if $B \sim A$. Hence the total number of instances of $A \sim B$ is even. Thus $3 n$ and hence also $n$ is even.
We now construct tri-connected collections for each even $n$ in the range. We show two
Construction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.

Putting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \geq 38$.
Construction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \leq m \leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \geq 4$, this will be true. The picture for $n=24$ is as follows:
To treat the other cases, consider the following gadget

Two squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.
This gives us a valid configuration for $6 n+8$ squares, $n \geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \geq 4$, which finishes the proof for all even numbers at least 36 .
|
501
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A collection of $n$ squares on the plane is called tri-connected if the following criteria are satisfied:
(i) All the squares are congruent.
(ii) If two squares have a point $P$ in common, then $P$ is a vertex of each of the squares.
(iii) Each square touches exactly three other squares.
How many positive integers $n$ are there with $2018 \leq n \leq 3018$, such that there exists a collection of $n$ squares that is tri-connected?
Answer: 501
|
We will prove that there is no tri-connected collection if $n$ is odd, and that tri-connected collections exist for all even $n \geq 38$. Since there are 501 even numbers in the range from 2018 to 3018, this yields 501 as the answer.
For any two different squares $A$ and $B$, let us write $A \sim B$ to mean that square $A$ touches square $B$. Since each square touches exactly three other squares, and there are $n$ squares in total, the total number of instances of $A \sim B$ is $3 n$. But $A \sim B$ if and only if $B \sim A$. Hence the total number of instances of $A \sim B$ is even. Thus $3 n$ and hence also $n$ is even.
We now construct tri-connected collections for each even $n$ in the range. We show two
Construction 1 The idea is to use the following two configurations. Observe that in each configuration every square is related to three squares except for the leftmost and rightmost squares which are related to two squares. Note that the configuration on the left is of variable length. Also observe that multiple copies of the configuration on the right can be chained together to end around corners.

Putting the above two types of configurations together as in the following figure yields a tri-connected collection for every even $n \geq 38$.

Construction 2 Consider a regular $4 n$-gon $A_{1} A_{2} \cdots A_{4 n}$, and make $4 n$ squares on the outside of the $4 n$-gon with one side being on the $4 n$-gon. Reflect squares sharing sides $A_{4 m+2} A_{4 m+3}, A_{4 m+3} A_{4 m+4}$ across line $A_{4 m+2} A_{4 m+4}$, for $0 \leq m \leq n-1$. This will produce a tri-connected set of $6 n$ squares, as long as the squares inside the $4 n$-gon do not intersect. When $n \geq 4$, this will be true. The picture for $n=24$ is as follows:

To treat the other cases, consider the following gadget

Two squares touch 3 other squares, and the squares containing $X, Y$ touch 2 other squares. Take the $4 n$-gon from above, and break it into two along the line $A_{1} A_{2 n}$, moving the two parts away from that line. Do so until the gaps can be exactly filled by inserting two copies of the above figure, so that the vertices $X, Y$ touch the two vertices which used to be $A_{1}$ in one instance, and the two vertices which used to be $A_{2 n}$ in the other.
This gives us a valid configuration for $6 n+8$ squares, $n \geq 4$. Finally, if we had instead spread the two parts out more and inserted two copies of the above figure into each gap, we would get $6 n+16$ for $n \geq 4$, which finishes the proof for all even numbers at least 36 .
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
99df8265-842c-5db0-8573-bcaa6c1c8dd8
| 605,916
|
Let $A B C$ be an equilateral triangle. From the vertex $A$ we draw a ray towards the interior of the triangle such that the ray reaches one of the sides of the triangle. When the ray reaches a side, it then bounces off following the law of reflection, that is, if it arrives with a directed angle $\alpha$, it leaves with a directed angle $180^{\circ}-\alpha$. After $n$ bounces, the ray returns to $A$ without ever landing on any of the other two vertices. Find all possible values of $n$.
Answer: All $n \equiv 1,5 \bmod 6$ with the exception of 5 and 17
|
Consider an equilateral triangle $A A_{1} A_{2}$ of side length $m$ and triangulate it with unitary triangles. See the figure. To each of the vertices that remain after the triangulation we can assign a pair of coordinates $(a, b)$ where $a, b$ are non-negative integers, $a$ is the number of edges we travel in the $A A_{1}$ direction and $b$ is the number of edges we travel in the $A A_{2}$ direction to arrive to the vertex, (we have $A=(0,0), A_{1}=(m, 0)$ and $A_{2}=(0, m)$ ). The unitary triangle with vertex $A$ will be our triangle $A B C,(B=(1,0), C=(0,1))$. We can obtain every unitary triangle by starting with $A B C$ and performing reflections with respect to a side (the vertex $(1,1)$ is the reflection of $A$ with respect to $B C$, the vertex $(0,2)$ is the reflection of $B=(1,0)$ with respect to the side formed by $C=(1,0)$ and $(1,1)$, and so on).
When we reflect a vertex $(a, b)$ with respect to a side of one of the triangles, the congruence of $a-b$ is preserved modulo 3. Furthermore, an induction argument shows that any two vertices $(a, b)$ and $\left(a^{\prime}, b^{\prime}\right)$ with $a-b \equiv a^{\prime}-b^{\prime}$ mod 3 can be obtained from each other by a series of such reflections. Therefore, the set of vertices $V$ that result from the reflections of $A$ will be those of the form $(a, b)$ satisfying $a \equiv b \bmod 3$. See the green vertices in the figure.
Now, let $U$ be the set of vertices $u$ that satisfy that the line segment between $u$ and $A$ does not pass through any other vertex. A pair $(a, b)$ is in $U$ if and only if $\operatorname{gcd}(a, b)=1$, since otherwise for $d=\operatorname{gcd}(a, b)$ we have that the vertex $(a / d, b / d)$ also lies on the line segment between $u$ and $A$.
Observe that the rays that come out from $A$ and eventually return to $A$ are those that come out towards a vertex in $V \cap U$ (they would be in $V$ to be able to come back to $A$ and in $U$ so that they do not reach a vertex beforehand). In the diagram, a ray toward one such vertex $(a, b)$ will intersect exactly $(a-1)+(b-1)+(a+b-1)=2(a+b)-3$ lines: $a-1$ of them parallel to $A B, b-1$ parallel to $A C$ and $a+b-1$ parallel to $B C$. Therefore, in the triangle $A B C$ the ray will bounce $2(a+b)-3$ times before returning to $A$. So we want to find all
$n=2(a+b)-3$ where $a \equiv b \bmod 3$ and $\operatorname{gcd}(a, b)=1$.
If $a+b$ is a multiple of 3 then we cannot satisfy both conditions simultaneously, therefore $n$ is not a multiple of 3 . We also know that $n$ is odd. Therefore $n \equiv 1,5,7,11 \bmod 12$. Note that the pair $(1,3 k+1)$ satisfies the conditions and we can create $n=2(3 k+2)-3=6 k+1$ for all $k \geq 0$ (this settles the question for $n \equiv 1,7 \bmod 12$ ). For $n \equiv 5 \bmod 12$ consider the pair $(3 k-1,3 k+5)$ when $k$ is even or $(3 k-4,3 k+8)$ when $k$ is odd. This gives us all the integers of the form $12 k+5$ for $k \geq 2$. For $11 \bmod 12$, take the pairs $(3 k-1,3 k+2)($ with $k \geq 1)$, which yield all positive integers of the form $12 k-1$.
Finally, to discard 5 and 17 note that the only pairs $(a, b)$ that are solutions to $2(a+b)-3=5$ or $2(a+b)-3=17$ with the same residue $\bmod 3$ in this range are the non-relatively prime pairs $(2,2),(2,8)$ and $(5,5)$.
|
n \equiv 1,5 \bmod 6 \text{ with the exception of 5 and 17}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an equilateral triangle. From the vertex $A$ we draw a ray towards the interior of the triangle such that the ray reaches one of the sides of the triangle. When the ray reaches a side, it then bounces off following the law of reflection, that is, if it arrives with a directed angle $\alpha$, it leaves with a directed angle $180^{\circ}-\alpha$. After $n$ bounces, the ray returns to $A$ without ever landing on any of the other two vertices. Find all possible values of $n$.
Answer: All $n \equiv 1,5 \bmod 6$ with the exception of 5 and 17
|
Consider an equilateral triangle $A A_{1} A_{2}$ of side length $m$ and triangulate it with unitary triangles. See the figure. To each of the vertices that remain after the triangulation we can assign a pair of coordinates $(a, b)$ where $a, b$ are non-negative integers, $a$ is the number of edges we travel in the $A A_{1}$ direction and $b$ is the number of edges we travel in the $A A_{2}$ direction to arrive to the vertex, (we have $A=(0,0), A_{1}=(m, 0)$ and $A_{2}=(0, m)$ ). The unitary triangle with vertex $A$ will be our triangle $A B C,(B=(1,0), C=(0,1))$. We can obtain every unitary triangle by starting with $A B C$ and performing reflections with respect to a side (the vertex $(1,1)$ is the reflection of $A$ with respect to $B C$, the vertex $(0,2)$ is the reflection of $B=(1,0)$ with respect to the side formed by $C=(1,0)$ and $(1,1)$, and so on).
When we reflect a vertex $(a, b)$ with respect to a side of one of the triangles, the congruence of $a-b$ is preserved modulo 3. Furthermore, an induction argument shows that any two vertices $(a, b)$ and $\left(a^{\prime}, b^{\prime}\right)$ with $a-b \equiv a^{\prime}-b^{\prime}$ mod 3 can be obtained from each other by a series of such reflections. Therefore, the set of vertices $V$ that result from the reflections of $A$ will be those of the form $(a, b)$ satisfying $a \equiv b \bmod 3$. See the green vertices in the figure.
Now, let $U$ be the set of vertices $u$ that satisfy that the line segment between $u$ and $A$ does not pass through any other vertex. A pair $(a, b)$ is in $U$ if and only if $\operatorname{gcd}(a, b)=1$, since otherwise for $d=\operatorname{gcd}(a, b)$ we have that the vertex $(a / d, b / d)$ also lies on the line segment between $u$ and $A$.
Observe that the rays that come out from $A$ and eventually return to $A$ are those that come out towards a vertex in $V \cap U$ (they would be in $V$ to be able to come back to $A$ and in $U$ so that they do not reach a vertex beforehand). In the diagram, a ray toward one such vertex $(a, b)$ will intersect exactly $(a-1)+(b-1)+(a+b-1)=2(a+b)-3$ lines: $a-1$ of them parallel to $A B, b-1$ parallel to $A C$ and $a+b-1$ parallel to $B C$. Therefore, in the triangle $A B C$ the ray will bounce $2(a+b)-3$ times before returning to $A$. So we want to find all

$n=2(a+b)-3$ where $a \equiv b \bmod 3$ and $\operatorname{gcd}(a, b)=1$.
If $a+b$ is a multiple of 3 then we cannot satisfy both conditions simultaneously, therefore $n$ is not a multiple of 3 . We also know that $n$ is odd. Therefore $n \equiv 1,5,7,11 \bmod 12$. Note that the pair $(1,3 k+1)$ satisfies the conditions and we can create $n=2(3 k+2)-3=6 k+1$ for all $k \geq 0$ (this settles the question for $n \equiv 1,7 \bmod 12$ ). For $n \equiv 5 \bmod 12$ consider the pair $(3 k-1,3 k+5)$ when $k$ is even or $(3 k-4,3 k+8)$ when $k$ is odd. This gives us all the integers of the form $12 k+5$ for $k \geq 2$. For $11 \bmod 12$, take the pairs $(3 k-1,3 k+2)($ with $k \geq 1)$, which yield all positive integers of the form $12 k-1$.
Finally, to discard 5 and 17 note that the only pairs $(a, b)$ that are solutions to $2(a+b)-3=5$ or $2(a+b)-3=17$ with the same residue $\bmod 3$ in this range are the non-relatively prime pairs $(2,2),(2,8)$ and $(5,5)$.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
79b79dc5-cac5-57c1-8175-4d52b9cb9207
| 261,105
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
Notice that if $P(x)$ is a solution, then so is $P(x)+k$ and $-P(x)+k$ for any integer $k$, so we may assume that the leading coefficient of $P(x)$ is positive and that $P(0)=0$, i.e., we can assume that $P(x)=\sum_{i=1}^{n} a_{i} x^{i}$ with $a_{n}>0$. We are going to prove that $P(x)=x^{n}$ in this case.
Let $p$ be a large prime such that $p>\sum_{i=1}^{n}\left|a_{i}\right|$. Because $P$ has a positive leading coefficient and $p$ is large enough, we can find $t \in \mathbb{R}$ such that $P(t)=p$. Denote the greatest common divisor of the polynomial $P(x)-p$ and $P(2 x)-P(2 t)$ as $f(x)$, and $t$ is a root of it, so $f$ is a non-constant polynomial. Notice that $P(2 t)$ is an integer by using the hypothesis for $s=2$ and $t$. Since $P(x)-p$ and $P(2 x)-P(2 t)$ are polynomials with integer coefficients, $f$ can be chosen as a polynomial with rational coefficients.
In the following, we will prove that $f$ is the same as $P(x)-p$ up to a constant multiplier. Say $P(x)-p=f(x) g(x)$, where $f$ and $g$ are non-constant polynomials. By Gauss's lemma, we can get $f_{1}, g_{1}$ with $P(x)-p=f_{1}(x) g_{1}(x)$ where $f_{1}$ is a scalar multiple of $f$ and $g_{1}$ is a scalar multiple of $g$ and one of $f_{1}, g_{1}$ has constant term $\pm 1$ (this is because $-p=P(0)-p=f(0) g(0)$ with $p$ prime). So $P(x)-p$ has at least one root $r$ with absolute value not greater than 1 (using
Vieta, the product of the roots of the polynomial with constant term $\pm 1$ is $\pm 1$ ), but
$$
|P(r)-p|=\left|\sum_{i=1}^{n} a_{i} r^{i}-p\right|>p-\sum_{i=1}^{n}\left|a_{i}\right|>0
$$
hence we get a contradiction!
Therefore $f$ is a constant multiple of $P(x)-p$, so $P(2 x)-P(2 t)$ is a constant multiple of $P(x)-p$ because they both have the same degree. By comparing leading coefficients we get that $P(2 x)-P(2 t)=2^{n}(P(x)-p)$. Comparing the rest of the coefficients we get that $P(x)=a_{n} x^{n}$. If we let $a=b=\left(1 / a_{n}\right)^{1 / n}$, then $P(a)=P(b)=1$, so $P(a b)$ must also be an integer. But $P(a b)=\frac{1}{a_{n}}$. Therefore $a_{n}=1$ and the proof is complete.
|
P(x)=x^{n}+k,-x^{n}+k
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
Notice that if $P(x)$ is a solution, then so is $P(x)+k$ and $-P(x)+k$ for any integer $k$, so we may assume that the leading coefficient of $P(x)$ is positive and that $P(0)=0$, i.e., we can assume that $P(x)=\sum_{i=1}^{n} a_{i} x^{i}$ with $a_{n}>0$. We are going to prove that $P(x)=x^{n}$ in this case.
Let $p$ be a large prime such that $p>\sum_{i=1}^{n}\left|a_{i}\right|$. Because $P$ has a positive leading coefficient and $p$ is large enough, we can find $t \in \mathbb{R}$ such that $P(t)=p$. Denote the greatest common divisor of the polynomial $P(x)-p$ and $P(2 x)-P(2 t)$ as $f(x)$, and $t$ is a root of it, so $f$ is a non-constant polynomial. Notice that $P(2 t)$ is an integer by using the hypothesis for $s=2$ and $t$. Since $P(x)-p$ and $P(2 x)-P(2 t)$ are polynomials with integer coefficients, $f$ can be chosen as a polynomial with rational coefficients.
In the following, we will prove that $f$ is the same as $P(x)-p$ up to a constant multiplier. Say $P(x)-p=f(x) g(x)$, where $f$ and $g$ are non-constant polynomials. By Gauss's lemma, we can get $f_{1}, g_{1}$ with $P(x)-p=f_{1}(x) g_{1}(x)$ where $f_{1}$ is a scalar multiple of $f$ and $g_{1}$ is a scalar multiple of $g$ and one of $f_{1}, g_{1}$ has constant term $\pm 1$ (this is because $-p=P(0)-p=f(0) g(0)$ with $p$ prime). So $P(x)-p$ has at least one root $r$ with absolute value not greater than 1 (using
Vieta, the product of the roots of the polynomial with constant term $\pm 1$ is $\pm 1$ ), but
$$
|P(r)-p|=\left|\sum_{i=1}^{n} a_{i} r^{i}-p\right|>p-\sum_{i=1}^{n}\left|a_{i}\right|>0
$$
hence we get a contradiction!
Therefore $f$ is a constant multiple of $P(x)-p$, so $P(2 x)-P(2 t)$ is a constant multiple of $P(x)-p$ because they both have the same degree. By comparing leading coefficients we get that $P(2 x)-P(2 t)=2^{n}(P(x)-p)$. Comparing the rest of the coefficients we get that $P(x)=a_{n} x^{n}$. If we let $a=b=\left(1 / a_{n}\right)^{1 / n}$, then $P(a)=P(b)=1$, so $P(a b)$ must also be an integer. But $P(a b)=\frac{1}{a_{n}}$. Therefore $a_{n}=1$ and the proof is complete.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1"
}
|
c6176993-dc8d-5b38-9f4f-afccb089548d
| 261,113
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: Assume $P(x)=\sum_{i=0}^{n} a_{i} x^{i}$. Consider the following system of equations
$$
\begin{aligned}
& a_{0}=P(0) \\
& a_{n} t^{n}+a_{n-1} t^{n-1}+\cdots+a_{0}=P(t) \\
& 2^{n} a_{n} t^{n}+2^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(2 t) \\
& \vdots \\
& n^{n} a_{n} t^{n}+n^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(n t)
\end{aligned}
$$
viewing $a_{k} t^{k}$ as variables. Note that if $P(t)$ is an integer, then by the hypothesis all the terms on the right hand side of the equations are integers as well. By using Cramer's rule, we can get that $a_{k} t^{k}=D / M$, where $D$ is an integer and $M$ is the following determinant
$$
\left|\begin{array}{ccccc}
1 & 0 & 0 & \cdots & 0 \\
1 & 1 & 1 & \cdots & 1 \\
1 & 2 & 4 & \cdots & 2^{n} \\
\vdots & \vdots & \vdots & & \vdots \\
1 & n & n^{2} & \cdots & n^{n}
\end{array}\right| \neq 0
$$
Thus, if we let $r$ be the smallest positive index such that $a_{r} \neq 0$, we can express each $t \in \mathbb{R}$ with $P(t) \in \mathbb{Z}$ in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ for some integer $m$, and where $M^{\prime}=M \times a_{r}$ is a constant.
We can choose $L$ large enough such that $\left.P\right|_{\mathbb{R}_{\geq L}}$ is injective, and for any larger $N$, the growth order of the number of values in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ is $N^{r}$, while the growth order of the number of integers in $[P(L), P(N)]$ is $N^{n}$, so $r=n$. Therefore $P(x)$ is of the form $a_{n} x^{n}+k$. The problem can be finished as in Solution 1.
|
P(x)=x^{n}+k,-x^{n}+k
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all polynomials $P(x)$ with integer coefficients such that for all real numbers $s$ and $t$, if $P(s)$ and $P(t)$ are both integers, then $P(s t)$ is also an integer.
Answer: $P(x)=x^{n}+k,-x^{n}+k$ for $n$ a non-negative integer and $k$ an integer.
|
: Assume $P(x)=\sum_{i=0}^{n} a_{i} x^{i}$. Consider the following system of equations
$$
\begin{aligned}
& a_{0}=P(0) \\
& a_{n} t^{n}+a_{n-1} t^{n-1}+\cdots+a_{0}=P(t) \\
& 2^{n} a_{n} t^{n}+2^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(2 t) \\
& \vdots \\
& n^{n} a_{n} t^{n}+n^{n-1} a_{n-1} t^{n-1}+\cdots+a_{0}=P(n t)
\end{aligned}
$$
viewing $a_{k} t^{k}$ as variables. Note that if $P(t)$ is an integer, then by the hypothesis all the terms on the right hand side of the equations are integers as well. By using Cramer's rule, we can get that $a_{k} t^{k}=D / M$, where $D$ is an integer and $M$ is the following determinant
$$
\left|\begin{array}{ccccc}
1 & 0 & 0 & \cdots & 0 \\
1 & 1 & 1 & \cdots & 1 \\
1 & 2 & 4 & \cdots & 2^{n} \\
\vdots & \vdots & \vdots & & \vdots \\
1 & n & n^{2} & \cdots & n^{n}
\end{array}\right| \neq 0
$$
Thus, if we let $r$ be the smallest positive index such that $a_{r} \neq 0$, we can express each $t \in \mathbb{R}$ with $P(t) \in \mathbb{Z}$ in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ for some integer $m$, and where $M^{\prime}=M \times a_{r}$ is a constant.
We can choose $L$ large enough such that $\left.P\right|_{\mathbb{R}_{\geq L}}$ is injective, and for any larger $N$, the growth order of the number of values in the form $\left(\frac{m}{M^{\prime}}\right)^{1 / r}$ is $N^{r}$, while the growth order of the number of integers in $[P(L), P(N)]$ is $N^{n}$, so $r=n$. Therefore $P(x)$ is of the form $a_{n} x^{n}+k$. The problem can be finished as in Solution 1.
|
{
"resource_path": "APMO/segmented/en-apmo2018_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 2"
}
|
c6176993-dc8d-5b38-9f4f-afccb089548d
| 261,113
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
First we perform the following substitutions on the original relation:
1. With $a=b=1$, we find that $f(1)+1 \mid f(1)^{2}+1$, which implies $f(1)=1$.
2. With $a=1$, we find that $b+1 \mid f(b)+1$. In particular, $b \leq f(b)$ for all $b \in \mathbb{Z}^{+}$.
3. With $b=1$, we find that $f(a)+1 \mid a^{2}+f(a)$, and thus $f(a)+1 \mid a^{2}-1$. In particular, $f(a) \leq a^{2}-2$ for all $a \geq 2$.
Now, let $p$ be any odd prime. Substituting $a=p$ and $b=f(p)$ in the original relation, we find that $2 f(p) \mid p^{2}+f(p) f(f(p))$. Therefore, $f(p) \mid p^{2}$. Hence the possible values of $f(p)$ are $1, p$ and $p^{2}$. By (2) above, $f(p) \geq p$ and by (3) above $f(p) \leq p^{2}-2$. So $f(p)=p$ for all primes $p$.
Substituting $a=p$ into the original relation, we find that $b+p \mid p^{2}+p f(b)$. However, since $(b+p)(f(b)+p-b)=p^{2}-b^{2}+b f(b)+p f(b)$, we have $b+p \mid b f(b)-b^{2}$. Thus, for any fixed $b$ this holds for arbitrarily large primes $p$ and therefore we must have $b f(b)-b^{2}=0$, or $f(b)=b$, as desired.
|
f(n)=n
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
First we perform the following substitutions on the original relation:
1. With $a=b=1$, we find that $f(1)+1 \mid f(1)^{2}+1$, which implies $f(1)=1$.
2. With $a=1$, we find that $b+1 \mid f(b)+1$. In particular, $b \leq f(b)$ for all $b \in \mathbb{Z}^{+}$.
3. With $b=1$, we find that $f(a)+1 \mid a^{2}+f(a)$, and thus $f(a)+1 \mid a^{2}-1$. In particular, $f(a) \leq a^{2}-2$ for all $a \geq 2$.
Now, let $p$ be any odd prime. Substituting $a=p$ and $b=f(p)$ in the original relation, we find that $2 f(p) \mid p^{2}+f(p) f(f(p))$. Therefore, $f(p) \mid p^{2}$. Hence the possible values of $f(p)$ are $1, p$ and $p^{2}$. By (2) above, $f(p) \geq p$ and by (3) above $f(p) \leq p^{2}-2$. So $f(p)=p$ for all primes $p$.
Substituting $a=p$ into the original relation, we find that $b+p \mid p^{2}+p f(b)$. However, since $(b+p)(f(b)+p-b)=p^{2}-b^{2}+b f(b)+p f(b)$, we have $b+p \mid b f(b)-b^{2}$. Thus, for any fixed $b$ this holds for arbitrarily large primes $p$ and therefore we must have $b f(b)-b^{2}=0$, or $f(b)=b$, as desired.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
e4279abb-f097-5750-9f9d-b74b221dac8c
| 605,968
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
: As above, we have relations (1)-(3). In (2) and (3), for $b=2$ we have $3 \mid f(2)+1$ and $f(2)+1 \mid 3$. These imply $f(2)=2$.
Now, using $a=2$ we get $2+b \mid 4+2 f(b)$. Let $f(b)=x$. We have
$$
\begin{aligned}
1+x & \equiv 0 \quad(\bmod b+1) \\
4+2 x & \equiv 0 \quad(\bmod b+2)
\end{aligned}
$$
From the first equation $x \equiv b(\bmod b+1)$ so $x=b+(b+1) t$ for some integer $t \geq 0$. Then
$$
0 \equiv 4+2 x \equiv 4+2(b+(b+1) t) \equiv 4+2(-2-t) \equiv-2 t \quad(\bmod b+2)
$$
Also $t \leq b-2$ because $1+x \mid b^{2}-1$ by (3).
If $b+2$ is odd, then $t \equiv 0(\bmod b+2)$. Then $t=0$, which implies $f(b)=b$.
If $b+2$ is even, then $t \equiv 0(\bmod (b+2) / 2)$. Then $t=0$ or $t=(b+2) / 2$. But if $t \neq 0$, then by definition $(b+4) / 2=(1+t)=(x+1) /(b+1)$ and since $x+1 \mid b^{2}-1$, then $(b+4) / 2$ divides $b-1$. Therefore $b+4 \mid 10$ and the only possibility is $b=6$. So for even $b, b \neq 6$ we have $f(b)=b$.
Finally, by (2) and (3), for $b=6$ we have $7 \mid f(6)+1$ and $f(6)+1 \mid 35$. This means $f(6)=6$ or $f(6)=34$. The later is discarded as, for $a=5, b=6$, we have by the original equation that $11 \mid 5(5+f(6))$. Therefore $f(n)=n$ for every positive integer $n$.
|
f(n)=n
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
: As above, we have relations (1)-(3). In (2) and (3), for $b=2$ we have $3 \mid f(2)+1$ and $f(2)+1 \mid 3$. These imply $f(2)=2$.
Now, using $a=2$ we get $2+b \mid 4+2 f(b)$. Let $f(b)=x$. We have
$$
\begin{aligned}
1+x & \equiv 0 \quad(\bmod b+1) \\
4+2 x & \equiv 0 \quad(\bmod b+2)
\end{aligned}
$$
From the first equation $x \equiv b(\bmod b+1)$ so $x=b+(b+1) t$ for some integer $t \geq 0$. Then
$$
0 \equiv 4+2 x \equiv 4+2(b+(b+1) t) \equiv 4+2(-2-t) \equiv-2 t \quad(\bmod b+2)
$$
Also $t \leq b-2$ because $1+x \mid b^{2}-1$ by (3).
If $b+2$ is odd, then $t \equiv 0(\bmod b+2)$. Then $t=0$, which implies $f(b)=b$.
If $b+2$ is even, then $t \equiv 0(\bmod (b+2) / 2)$. Then $t=0$ or $t=(b+2) / 2$. But if $t \neq 0$, then by definition $(b+4) / 2=(1+t)=(x+1) /(b+1)$ and since $x+1 \mid b^{2}-1$, then $(b+4) / 2$ divides $b-1$. Therefore $b+4 \mid 10$ and the only possibility is $b=6$. So for even $b, b \neq 6$ we have $f(b)=b$.
Finally, by (2) and (3), for $b=6$ we have $7 \mid f(6)+1$ and $f(6)+1 \mid 35$. This means $f(6)=6$ or $f(6)=34$. The later is discarded as, for $a=5, b=6$, we have by the original equation that $11 \mid 5(5+f(6))$. Therefore $f(n)=n$ for every positive integer $n$.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
e4279abb-f097-5750-9f9d-b74b221dac8c
| 605,968
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
: We proceed by induction. As in Solution 1, we have $f(1)=1$. Suppose that $f(n-1)=n-1$ for some integer $n \geq 2$.
With the substitution $a=n$ and $b=n-1$ in the original relation we obtain that $f(n)+$ $n-1 \mid n^{2}+f(n)(n-1)$. Since $f(n)+n-1 \mid(n-1)(f(n)+n-1)$, then $f(n)+n-1 \mid 2 n-1$.
With the substitution $a=n-1$ and $b=n$ in the original relation we obtain that $2 n-$ $1 \mid(n-1)^{2}+(n-1) f(n)=(n-1)(n-1+f(n))$. Since $(2 n-1, n-1)=1$, we deduce that $2 n-1 \mid f(n)+n-1$.
Therefore, $f(n)+n-1=2 n-1$, which implies the desired $f(n)=n$.
|
f(n)=n
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{Z}^{+}$be the set of positive integers. Determine all functions $f: \mathbb{Z}^{+} \rightarrow \mathbb{Z}^{+}$ such that $a^{2}+f(a) f(b)$ is divisible by $f(a)+b$ for all positive integers $a$ and $b$.
Answer: The answer is $f(n)=n$ for all positive integers $n$.
Clearly, $f(n)=n$ for all $n \in \mathbb{Z}^{+}$satisfies the original relation. We show some possible approaches to prove that this is the only possible function.
|
: We proceed by induction. As in Solution 1, we have $f(1)=1$. Suppose that $f(n-1)=n-1$ for some integer $n \geq 2$.
With the substitution $a=n$ and $b=n-1$ in the original relation we obtain that $f(n)+$ $n-1 \mid n^{2}+f(n)(n-1)$. Since $f(n)+n-1 \mid(n-1)(f(n)+n-1)$, then $f(n)+n-1 \mid 2 n-1$.
With the substitution $a=n-1$ and $b=n$ in the original relation we obtain that $2 n-$ $1 \mid(n-1)^{2}+(n-1) f(n)=(n-1)(n-1+f(n))$. Since $(2 n-1, n-1)=1$, we deduce that $2 n-1 \mid f(n)+n-1$.
Therefore, $f(n)+n-1=2 n-1$, which implies the desired $f(n)=n$.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 3"
}
|
e4279abb-f097-5750-9f9d-b74b221dac8c
| 605,968
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
Suppose that for integers $m$ and $a_{1}$ all the terms of the sequence are integers. For each $i \geq 1$, write the $i$ th term of the sequence as $a_{i}=b_{i} 2^{c_{i}}$ where $b_{i}$ is the largest odd divisor of $a_{i}$ (the "odd part" of $a_{i}$ ) and $c_{i}$ is a nonnegative integer.
Lemma 1. The sequence $b_{1}, b_{2}, \ldots$ is bounded above by $2^{m}$.
Proof. Suppose this is not the case and take an index $i$ for which $b_{i}>2^{m}$ and for which $c_{i}$ is minimal. Since $a_{i} \geq b_{i}>2^{m}$, we are in the second case of the recursion. Therefore, $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}>2^{m}$ and $c_{i+1}=c_{i}-1<c_{i}$. This contradicts the minimality of $c_{i}$.
Lemma 2. The sequence $b_{1}, b_{2}, \ldots$ is nondecreasing.
Proof. If $a_{i} \geq 2^{m}$, then $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}$. On the other hand, if $a_{i}<2^{m}$, then
$$
a_{i+1}=a_{i}^{2}+2^{m}=b_{i}^{2} 2^{2 c_{i}}+2^{m}
$$
and we have the following cases:
- If $2 c_{i}>m$, then $a_{i+1}=2^{m}\left(b_{i}^{2} 2^{2 c_{i}-m}+1\right)$, so $b_{i+1}=b_{i}^{2} 2^{2 c_{i}-m}+1>b_{i}$.
- If $2 c_{i}<m$, then $a_{i+1}=2^{2 c_{i}}\left(b_{i}^{2}+2^{m-2 c_{i}}\right)$, so $b_{i+1}=b_{i}^{2}+2^{m-2 c_{i}}>b_{i}$.
- If $2 c_{i}=m$, then $a_{i+1}=2^{m+1} \cdot \frac{b_{i}^{2}+1}{2}$, so $b_{i+1}=\left(b_{i}^{2}+1\right) / 2 \geq b_{i}$ since $b_{i}^{2}+1 \equiv 2(\bmod 4)$.
By combining these two lemmas we obtain that the sequence $b_{1}, b_{2}, \ldots$ is eventually constant. Fix an index $j$ such that $b_{k}=b_{j}$ for all $k \geq j$. Since $a_{n}$ descends to $a_{n} / 2$ whenever $a_{n} \geq 2^{m}$, there are infinitely many terms which are smaller than $2^{m}$. Thus, we can choose an $i>j$ such that $a_{i}<2^{m}$. From the proof of Lemma $2, a_{i}<2^{m}$ and $b_{i+1}=b_{i}$ can happen simultaneously only when $2 c_{i}=m$ and $b_{i+1}=b_{i}=1$. By Lemma 2 , the sequence $b_{1}, b_{2}, \ldots$ is constantly 1 and thus $a_{1}, a_{2}, \ldots$ are all powers of two. Tracing the sequence starting from $a_{i}=2^{c_{i}}=2^{m / 2}<2^{m}$,
$$
2^{m / 2} \rightarrow 2^{m+1} \rightarrow 2^{m} \rightarrow 2^{m-1} \rightarrow 2^{2 m-2}+2^{m}
$$
Note that this last term is a power of two if and only if $2 m-2=m$. This implies that $m$ must be equal to 2 . When $m=2$ and $a_{1}=2^{\ell}$ for $\ell \geq 1$ the sequence eventually cycles through $2,8,4,2, \ldots$. When $m=2$ and $a_{1}=1$ the sequence fails as the first terms are $1,5,5 / 2$.
|
m=2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
Suppose that for integers $m$ and $a_{1}$ all the terms of the sequence are integers. For each $i \geq 1$, write the $i$ th term of the sequence as $a_{i}=b_{i} 2^{c_{i}}$ where $b_{i}$ is the largest odd divisor of $a_{i}$ (the "odd part" of $a_{i}$ ) and $c_{i}$ is a nonnegative integer.
Lemma 1. The sequence $b_{1}, b_{2}, \ldots$ is bounded above by $2^{m}$.
Proof. Suppose this is not the case and take an index $i$ for which $b_{i}>2^{m}$ and for which $c_{i}$ is minimal. Since $a_{i} \geq b_{i}>2^{m}$, we are in the second case of the recursion. Therefore, $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}>2^{m}$ and $c_{i+1}=c_{i}-1<c_{i}$. This contradicts the minimality of $c_{i}$.
Lemma 2. The sequence $b_{1}, b_{2}, \ldots$ is nondecreasing.
Proof. If $a_{i} \geq 2^{m}$, then $a_{i+1}=a_{i} / 2$ and thus $b_{i+1}=b_{i}$. On the other hand, if $a_{i}<2^{m}$, then
$$
a_{i+1}=a_{i}^{2}+2^{m}=b_{i}^{2} 2^{2 c_{i}}+2^{m}
$$
and we have the following cases:
- If $2 c_{i}>m$, then $a_{i+1}=2^{m}\left(b_{i}^{2} 2^{2 c_{i}-m}+1\right)$, so $b_{i+1}=b_{i}^{2} 2^{2 c_{i}-m}+1>b_{i}$.
- If $2 c_{i}<m$, then $a_{i+1}=2^{2 c_{i}}\left(b_{i}^{2}+2^{m-2 c_{i}}\right)$, so $b_{i+1}=b_{i}^{2}+2^{m-2 c_{i}}>b_{i}$.
- If $2 c_{i}=m$, then $a_{i+1}=2^{m+1} \cdot \frac{b_{i}^{2}+1}{2}$, so $b_{i+1}=\left(b_{i}^{2}+1\right) / 2 \geq b_{i}$ since $b_{i}^{2}+1 \equiv 2(\bmod 4)$.
By combining these two lemmas we obtain that the sequence $b_{1}, b_{2}, \ldots$ is eventually constant. Fix an index $j$ such that $b_{k}=b_{j}$ for all $k \geq j$. Since $a_{n}$ descends to $a_{n} / 2$ whenever $a_{n} \geq 2^{m}$, there are infinitely many terms which are smaller than $2^{m}$. Thus, we can choose an $i>j$ such that $a_{i}<2^{m}$. From the proof of Lemma $2, a_{i}<2^{m}$ and $b_{i+1}=b_{i}$ can happen simultaneously only when $2 c_{i}=m$ and $b_{i+1}=b_{i}=1$. By Lemma 2 , the sequence $b_{1}, b_{2}, \ldots$ is constantly 1 and thus $a_{1}, a_{2}, \ldots$ are all powers of two. Tracing the sequence starting from $a_{i}=2^{c_{i}}=2^{m / 2}<2^{m}$,
$$
2^{m / 2} \rightarrow 2^{m+1} \rightarrow 2^{m} \rightarrow 2^{m-1} \rightarrow 2^{2 m-2}+2^{m}
$$
Note that this last term is a power of two if and only if $2 m-2=m$. This implies that $m$ must be equal to 2 . When $m=2$ and $a_{1}=2^{\ell}$ for $\ell \geq 1$ the sequence eventually cycles through $2,8,4,2, \ldots$. When $m=2$ and $a_{1}=1$ the sequence fails as the first terms are $1,5,5 / 2$.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution."
}
|
3a221d29-c277-5b6e-bbb7-647e39d7c41b
| 261,386
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
: Let $m$ be a positive integer and suppose that $\left\{a_{n}\right\}$ consists only of positive integers. Call a number small if it is smaller than $2^{m}$ and large otherwise. By the recursion,
after a small number we have a large one and after a large one we successively divide by 2 until we get a small one.
First, we note that $\left\{a_{n}\right\}$ is bounded. Indeed, $a_{1}$ turns into a small number after a finite number of steps. After this point, each small number is smaller than $2^{m}$, so each large number is smaller than $2^{2 m}+2^{m}$. Now, since $\left\{a_{n}\right\}$ is bounded and consists only of positive integers, it is eventually periodic. We focus only on the cycle.
Any small number $a_{n}$ in the cycle can be writen as $a / 2$ for $a$ large, so $a_{n} \geq 2^{m-1}$, then $a_{n+1} \geq 2^{2 m-2}+2^{m}=2^{m-2}\left(4+2^{m}\right)$, so we have to divide $a_{n+1}$ at least $m-1$ times by 2 until we get a small number. This means that $a_{n+m}=\left(a_{n}^{2}+2^{m}\right) / 2^{m-1}$, so $2^{m-1} \mid a_{n}^{2}$, and therefore $2^{\lceil(m-1) / 2\rceil} \mid a_{n}$ for any small number $a_{n}$ in the cycle. On the other hand, $a_{n} \leq 2^{m}-1$, so $a_{n+1} \leq 2^{2 m}-2^{m+1}+1+2^{m} \leq 2^{m}\left(2^{m}-1\right)$, so we have to divide $a_{n+1}$ at most $m$ times by two until we get a small number. This means that after $a_{n}$, the next small number is either $N=a_{m+n}=\left(a_{n}^{2} / 2^{m-1}\right)+2$ or $a_{m+n+1}=N / 2$. In any case, $2^{\lceil(m-1) / 2\rceil}$ divides $N$.
If $m$ is odd, then $x^{2} \equiv-2\left(\bmod 2^{\lceil(m-1) / 2\rceil}\right)$ has a solution $x=a_{n} / 2^{(m-1) / 2}$. If $(m-1) / 2 \geq$ $2 \Longleftrightarrow m \geq 5$ then $x^{2} \equiv-2(\bmod 4)$, which has no solution. So if $m$ is odd, then $m \leq 3$.
If $m$ is even, then $2^{m-1}\left|a_{n}^{2} \Longrightarrow 2^{\lceil(m-1) / 2\rceil}\right| a_{n} \Longleftrightarrow 2^{m / 2} \mid a_{n}$. Then if $a_{n}=2^{m / 2} x$, $2 x^{2} \equiv-2\left(\bmod 2^{m / 2}\right) \Longleftrightarrow x^{2} \equiv-1\left(\bmod 2^{(m / 2)-1}\right)$, which is not possible for $m \geq 6$. So if $m$ is even, then $m \leq 4$.
The cases $m=1,2,3,4$ are handed manually, checking the possible small numbers in the cycle, which have to be in the interval $\left[2^{m-1}, 2^{m}\right)$ and be divisible by $2^{\lceil(m-1) / 2\rceil}$ :
- For $m=1$, the only small number is 1 , which leads to 5 , then $5 / 2$.
- For $m=2$, the only eligible small number is 2 , which gives the cycle $(2,8,4)$. The only way to get to 2 is by dividing 4 by 2 , so the starting numbers greater than 2 are all numbers that lead to 4 , which are the powers of 2 .
- For $m=3$, the eligible small numbers are 4 and 6 ; we then obtain $4,24,12,6,44,22,11,11 / 2$.
- For $m=4$, the eligible small numbers are 8 and 12 ; we then obtain $8,80,40,20,10, \ldots$ or $12,160,80,40,20,10, \ldots$, but in either case 10 is not an elegible small number.
|
m=2, a_{1}=2^{\ell} \text{ for } \ell \geq 1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m$ be a fixed positive integer. The infinite sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined in the following way: $a_{1}$ is a positive integer, and for every integer $n \geq 1$ we have
$$
a_{n+1}= \begin{cases}a_{n}^{2}+2^{m} & \text { if } a_{n}<2^{m} \\ a_{n} / 2 & \text { if } a_{n} \geq 2^{m}\end{cases}
$$
For each $m$, determine all possible values of $a_{1}$ such that every term in the sequence is an integer.
Answer: The only value of $m$ for which valid values of $a_{1}$ exist is $m=2$. In that case, the only solutions are $a_{1}=2^{\ell}$ for $\ell \geq 1$.
|
: Let $m$ be a positive integer and suppose that $\left\{a_{n}\right\}$ consists only of positive integers. Call a number small if it is smaller than $2^{m}$ and large otherwise. By the recursion,
after a small number we have a large one and after a large one we successively divide by 2 until we get a small one.
First, we note that $\left\{a_{n}\right\}$ is bounded. Indeed, $a_{1}$ turns into a small number after a finite number of steps. After this point, each small number is smaller than $2^{m}$, so each large number is smaller than $2^{2 m}+2^{m}$. Now, since $\left\{a_{n}\right\}$ is bounded and consists only of positive integers, it is eventually periodic. We focus only on the cycle.
Any small number $a_{n}$ in the cycle can be writen as $a / 2$ for $a$ large, so $a_{n} \geq 2^{m-1}$, then $a_{n+1} \geq 2^{2 m-2}+2^{m}=2^{m-2}\left(4+2^{m}\right)$, so we have to divide $a_{n+1}$ at least $m-1$ times by 2 until we get a small number. This means that $a_{n+m}=\left(a_{n}^{2}+2^{m}\right) / 2^{m-1}$, so $2^{m-1} \mid a_{n}^{2}$, and therefore $2^{\lceil(m-1) / 2\rceil} \mid a_{n}$ for any small number $a_{n}$ in the cycle. On the other hand, $a_{n} \leq 2^{m}-1$, so $a_{n+1} \leq 2^{2 m}-2^{m+1}+1+2^{m} \leq 2^{m}\left(2^{m}-1\right)$, so we have to divide $a_{n+1}$ at most $m$ times by two until we get a small number. This means that after $a_{n}$, the next small number is either $N=a_{m+n}=\left(a_{n}^{2} / 2^{m-1}\right)+2$ or $a_{m+n+1}=N / 2$. In any case, $2^{\lceil(m-1) / 2\rceil}$ divides $N$.
If $m$ is odd, then $x^{2} \equiv-2\left(\bmod 2^{\lceil(m-1) / 2\rceil}\right)$ has a solution $x=a_{n} / 2^{(m-1) / 2}$. If $(m-1) / 2 \geq$ $2 \Longleftrightarrow m \geq 5$ then $x^{2} \equiv-2(\bmod 4)$, which has no solution. So if $m$ is odd, then $m \leq 3$.
If $m$ is even, then $2^{m-1}\left|a_{n}^{2} \Longrightarrow 2^{\lceil(m-1) / 2\rceil}\right| a_{n} \Longleftrightarrow 2^{m / 2} \mid a_{n}$. Then if $a_{n}=2^{m / 2} x$, $2 x^{2} \equiv-2\left(\bmod 2^{m / 2}\right) \Longleftrightarrow x^{2} \equiv-1\left(\bmod 2^{(m / 2)-1}\right)$, which is not possible for $m \geq 6$. So if $m$ is even, then $m \leq 4$.
The cases $m=1,2,3,4$ are handed manually, checking the possible small numbers in the cycle, which have to be in the interval $\left[2^{m-1}, 2^{m}\right)$ and be divisible by $2^{\lceil(m-1) / 2\rceil}$ :
- For $m=1$, the only small number is 1 , which leads to 5 , then $5 / 2$.
- For $m=2$, the only eligible small number is 2 , which gives the cycle $(2,8,4)$. The only way to get to 2 is by dividing 4 by 2 , so the starting numbers greater than 2 are all numbers that lead to 4 , which are the powers of 2 .
- For $m=3$, the eligible small numbers are 4 and 6 ; we then obtain $4,24,12,6,44,22,11,11 / 2$.
- For $m=4$, the eligible small numbers are 8 and 12 ; we then obtain $8,80,40,20,10, \ldots$ or $12,160,80,40,20,10, \ldots$, but in either case 10 is not an elegible small number.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
3a221d29-c277-5b6e-bbb7-647e39d7c41b
| 261,386
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
Let $N$ be the radical center of the circumcircles of triangles $A B C, B M P$ and $C M P$. The pairwise radical axes of these circles are $B D, C E$ and $P M$, and hence they concur at $N$. Now, note that in directed angles:
$$
\angle M C E=\angle M P E=\angle M P Y=\angle M B Y .
$$
It follows that $B Y$ is parallel to $C E$, and analogously that $C X$ is parallel to $B D$. Then, if $L$ is the intersection of $B Y$ and $C X$, it follows that $B N C L$ is a parallelogram. Since $B M=M C$ we deduce that $L$ is the reflection of $N$ with respect to $M$, and therefore $L \in A M$. Using power of a point from $L$ to the circumcircles of triangles $B P M$ and $C P M$, we have
$$
L Y \cdot L B=L P \cdot L M=L X \cdot L C
$$
Hence, $B Y X C$ is cyclic. Using the cyclic quadrilateral we find in directed angles:
$$
\angle L X Y=\angle L B C=\angle B C N=\angle N D E .
$$
Since $C X \| B N$, it follows that $X Y \| D E$.
Let $Q$ and $R$ be two points in $\Gamma$ such that $C Q, B R$, and $A M$ are all parallel. Then in directed angles:
$$
\angle Q D B=\angle Q C B=\angle A M B=\angle P M B=\angle P D B .
$$
Then $D, P, Q$ are collinear. Analogously $E, P, R$ are collinear. From here we get $\angle P R Q=$ $\angle P D E=\angle P X Y$, since $X Y$ and $D E$ are parallel. Therefore $Q R Y X$ is cyclic. Let $S$ be the radical center of the circumcircle of triangle $A B C$ and the circles $B C Y X$ and $Q R Y X$. This point lies in the lines $B C, Q R$ and $X Y$ because these are the radical axes of the circles. Let $T$ be the second intersection of $A S$ with $\Gamma$. By power of a point from $S$ to the circumcircle of $A B C$ and the circle $B C X Y$ we have
$$
S X \cdot S Y=S B \cdot S C=S T \cdot S A
$$
Therefore $T$ is in the circumcircle of triangle $A X Y$. Since $Q$ and $R$ are fixed regardless of the choice of $P$, then $S$ is also fixed, since it is the intersection of $Q R$ and $B C$. This implies $T$ is also fixed, and therefore, the circumcircle of triangle $A X Y$ goes through $T \neq A$ for any choice of $P$.
Now we show an alternative way to prove that $B C X Y$ and $Q R X T$ are cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
Let $N$ be the radical center of the circumcircles of triangles $A B C, B M P$ and $C M P$. The pairwise radical axes of these circles are $B D, C E$ and $P M$, and hence they concur at $N$. Now, note that in directed angles:
$$
\angle M C E=\angle M P E=\angle M P Y=\angle M B Y .
$$

It follows that $B Y$ is parallel to $C E$, and analogously that $C X$ is parallel to $B D$. Then, if $L$ is the intersection of $B Y$ and $C X$, it follows that $B N C L$ is a parallelogram. Since $B M=M C$ we deduce that $L$ is the reflection of $N$ with respect to $M$, and therefore $L \in A M$. Using power of a point from $L$ to the circumcircles of triangles $B P M$ and $C P M$, we have
$$
L Y \cdot L B=L P \cdot L M=L X \cdot L C
$$
Hence, $B Y X C$ is cyclic. Using the cyclic quadrilateral we find in directed angles:
$$
\angle L X Y=\angle L B C=\angle B C N=\angle N D E .
$$
Since $C X \| B N$, it follows that $X Y \| D E$.
Let $Q$ and $R$ be two points in $\Gamma$ such that $C Q, B R$, and $A M$ are all parallel. Then in directed angles:
$$
\angle Q D B=\angle Q C B=\angle A M B=\angle P M B=\angle P D B .
$$
Then $D, P, Q$ are collinear. Analogously $E, P, R$ are collinear. From here we get $\angle P R Q=$ $\angle P D E=\angle P X Y$, since $X Y$ and $D E$ are parallel. Therefore $Q R Y X$ is cyclic. Let $S$ be the radical center of the circumcircle of triangle $A B C$ and the circles $B C Y X$ and $Q R Y X$. This point lies in the lines $B C, Q R$ and $X Y$ because these are the radical axes of the circles. Let $T$ be the second intersection of $A S$ with $\Gamma$. By power of a point from $S$ to the circumcircle of $A B C$ and the circle $B C X Y$ we have
$$
S X \cdot S Y=S B \cdot S C=S T \cdot S A
$$
Therefore $T$ is in the circumcircle of triangle $A X Y$. Since $Q$ and $R$ are fixed regardless of the choice of $P$, then $S$ is also fixed, since it is the intersection of $Q R$ and $B C$. This implies $T$ is also fixed, and therefore, the circumcircle of triangle $A X Y$ goes through $T \neq A$ for any choice of $P$.
Now we show an alternative way to prove that $B C X Y$ and $Q R X T$ are cyclic.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "# Problem 3.",
"solution_match": "\nSolution."
}
|
936de2fe-2844-5df4-aa45-a257faed6359
| 606,018
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
. Let the lines $D P$ and $E P$ meet the circumcircle of $A B C$ again at $Q$ and $R$, respectively. Then $\angle D Q C \angle D B C=\angle D P M$, so $Q C \| P M$. Similarly, $R B \| P M$.
Now, $\angle Q C B=\angle P M B=\angle P X C=\angle(Q X, C X)$, which is half of the arc $Q C$ in the circumcircle $\omega_{C}$ of $Q X C$. So $\omega_{C}$ is tangent to $B S$; analogously, $\omega_{B}$, the circumcicle of $R Y B$, is also tangent to $B C$. Since $B R \| C Q$, the inscribed trapezoid $B R Q C$ is isosceles, and by symmetry $Q R$ is also tangent to both circles, and the common perpendicular bisector of $B R$ and $C Q$ passes through the centers of $\omega_{B}$ and $\omega_{C}$. Since $M B=M C$ and $P M\|B R\| C Q$, the line $P M$ is the radical axis of $\omega_{B}$ and $\omega_{C}$.
However, $P M$ is also the radical axis of the circumcircles $\gamma_{B}$ of $P M B$ and $\gamma_{C}$ of $P M C$. Let $C X$ and $P M$ meet at $Z$. Let $p(K, \omega)$ denote the power of a point $K$ with respect to a circumference $\omega$. We have
$$
p\left(Z, \gamma_{B}\right)=p\left(Z, \gamma_{C}\right)=Z X \cdot Z C=p\left(Z, \omega_{B}\right)=p\left(Z, \omega_{C}\right)
$$
Point $Z$ is thus the radical center of $\gamma_{B}, \gamma_{C}, \omega_{B}, \omega_{C}$. Thus, the radical axes $B Y, C X, P M$ meet at $Z$. From here,
$$
\begin{aligned}
& Z Y \cdot Z B=Z C \cdot Z X \Rightarrow B C X Y \text { cyclic } \\
& P Y \cdot P R=P X \cdot P Q \Rightarrow Q R X T \text { cyclic. }
\end{aligned}
$$
We may now finish as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$
be a scalene triangle with circumcircle $\Gamma$. Let $M$ be the midpoint of $B C$. A variable point $P$ is selected in the line segment $A M$. The circumcircles of triangles $B P M$ and $C P M$ intersect $\Gamma$ again at points $D$ and $E$, respectively. The lines $D P$ and $E P$ intersect (a second time) the circumcircles to triangles $C P M$ and $B P M$ at $X$ and $Y$, respectively. Prove that as $P$ varies, the circumcircle of $\triangle A X Y$ passes through a fixed point $T$ distinct from $A$.
|
. Let the lines $D P$ and $E P$ meet the circumcircle of $A B C$ again at $Q$ and $R$, respectively. Then $\angle D Q C \angle D B C=\angle D P M$, so $Q C \| P M$. Similarly, $R B \| P M$.

Now, $\angle Q C B=\angle P M B=\angle P X C=\angle(Q X, C X)$, which is half of the arc $Q C$ in the circumcircle $\omega_{C}$ of $Q X C$. So $\omega_{C}$ is tangent to $B S$; analogously, $\omega_{B}$, the circumcicle of $R Y B$, is also tangent to $B C$. Since $B R \| C Q$, the inscribed trapezoid $B R Q C$ is isosceles, and by symmetry $Q R$ is also tangent to both circles, and the common perpendicular bisector of $B R$ and $C Q$ passes through the centers of $\omega_{B}$ and $\omega_{C}$. Since $M B=M C$ and $P M\|B R\| C Q$, the line $P M$ is the radical axis of $\omega_{B}$ and $\omega_{C}$.
However, $P M$ is also the radical axis of the circumcircles $\gamma_{B}$ of $P M B$ and $\gamma_{C}$ of $P M C$. Let $C X$ and $P M$ meet at $Z$. Let $p(K, \omega)$ denote the power of a point $K$ with respect to a circumference $\omega$. We have
$$
p\left(Z, \gamma_{B}\right)=p\left(Z, \gamma_{C}\right)=Z X \cdot Z C=p\left(Z, \omega_{B}\right)=p\left(Z, \omega_{C}\right)
$$
Point $Z$ is thus the radical center of $\gamma_{B}, \gamma_{C}, \omega_{B}, \omega_{C}$. Thus, the radical axes $B Y, C X, P M$ meet at $Z$. From here,
$$
\begin{aligned}
& Z Y \cdot Z B=Z C \cdot Z X \Rightarrow B C X Y \text { cyclic } \\
& P Y \cdot P R=P X \cdot P Q \Rightarrow Q R X T \text { cyclic. }
\end{aligned}
$$
We may now finish as in Solution 1.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "# Problem 3.",
"solution_match": "\nSolution 2"
}
|
936de2fe-2844-5df4-aa45-a257faed6359
| 606,018
|
Consider a $2018 \times 2019$ board with integers in each unit square. Two unit squares are said to be neighbours if they share a common edge. In each turn, you choose some unit squares. Then for each chosen unit square the average of all its neighbours is calculated. Finally, after these calculations are done, the number in each chosen unit square is replaced by the corresponding average. Is it always possible to make the numbers in all squares become the same after finitely many turns?
Answer: No
|
Let $n$ be a positive integer relatively prime to 2 and 3 . We may study the whole process modulo $n$ by replacing divisions by $2,3,4$ with multiplications by the corresponding inverses modulo $n$. If at some point the original process makes all the numbers equal, then the process modulo $n$ will also have all the numbers equal. Our aim is to choose $n$ and an initial configuration modulo $n$ for which no process modulo $n$ reaches a board with all numbers equal modulo $n$. We split this goal into two lemmas.
Lemma 1. There is a $2 \times 3$ board that stays constant modulo 5 and whose entries are not all equal.
Proof. Here is one such a board:
The fact that the board remains constant regardless of the choice of squares can be checked square by square.
Lemma 2. If there is an $r \times s$ board with $r \geq 2, s \geq 2$, that stays constant modulo 5 , then there is also a $k r \times l s$ board with the same property.
Proof. We prove by a case by case analysis that repeateadly reflecting the $r \times s$ with respect to an edge preserves the property:
- If a cell had 4 neighbors, after reflections it still has the same neighbors.
- If a cell with $a$ had 3 neighbors $b, c, d$, we have by hypothesis that $a \equiv 3^{-1}(b+c+d) \equiv$ $2(b+c+d)(\bmod 5)$. A reflection may add $a$ as a neighbor of the cell and now
$$
4^{-1}(a+b+c+d) \equiv 4(a+b+c+d) \equiv 4 a+2 a \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c) \equiv 3(b+c)$ $(\bmod 5)$. If the reflections add one $a$ as neighbor, now
$$
3^{-1}(a+b+c) \equiv 2(3(b+c)+b+c) \equiv 8(b+c) \equiv 3(b+c) \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c)(\bmod 5)$. If the reflections add two $a$ 's as neighbors, now
$$
4^{-1}(2 a+b+c) \equiv\left(2^{-1} a+2^{-1} a\right) \equiv a \quad(\bmod 5)
$$
In the three cases, any cell is still preserved modulo 5 after an operation. Hence we can fill in the $k r \times l s$ board by $k \times l$ copies by reflection.
Since 2|2018 and 3|2019, we can get through reflections the following board:
By the lemmas above, the board is invariant modulo 5, so the answer is no.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider a $2018 \times 2019$ board with integers in each unit square. Two unit squares are said to be neighbours if they share a common edge. In each turn, you choose some unit squares. Then for each chosen unit square the average of all its neighbours is calculated. Finally, after these calculations are done, the number in each chosen unit square is replaced by the corresponding average. Is it always possible to make the numbers in all squares become the same after finitely many turns?
Answer: No
|
Let $n$ be a positive integer relatively prime to 2 and 3 . We may study the whole process modulo $n$ by replacing divisions by $2,3,4$ with multiplications by the corresponding inverses modulo $n$. If at some point the original process makes all the numbers equal, then the process modulo $n$ will also have all the numbers equal. Our aim is to choose $n$ and an initial configuration modulo $n$ for which no process modulo $n$ reaches a board with all numbers equal modulo $n$. We split this goal into two lemmas.
Lemma 1. There is a $2 \times 3$ board that stays constant modulo 5 and whose entries are not all equal.
Proof. Here is one such a board:

The fact that the board remains constant regardless of the choice of squares can be checked square by square.
Lemma 2. If there is an $r \times s$ board with $r \geq 2, s \geq 2$, that stays constant modulo 5 , then there is also a $k r \times l s$ board with the same property.
Proof. We prove by a case by case analysis that repeateadly reflecting the $r \times s$ with respect to an edge preserves the property:
- If a cell had 4 neighbors, after reflections it still has the same neighbors.
- If a cell with $a$ had 3 neighbors $b, c, d$, we have by hypothesis that $a \equiv 3^{-1}(b+c+d) \equiv$ $2(b+c+d)(\bmod 5)$. A reflection may add $a$ as a neighbor of the cell and now
$$
4^{-1}(a+b+c+d) \equiv 4(a+b+c+d) \equiv 4 a+2 a \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c) \equiv 3(b+c)$ $(\bmod 5)$. If the reflections add one $a$ as neighbor, now
$$
3^{-1}(a+b+c) \equiv 2(3(b+c)+b+c) \equiv 8(b+c) \equiv 3(b+c) \equiv a \quad(\bmod 5)
$$
- If a cell with $a$ had 2 neighbors $b, c$, we have by hypothesis that $a \equiv 2^{-1}(b+c)(\bmod 5)$. If the reflections add two $a$ 's as neighbors, now
$$
4^{-1}(2 a+b+c) \equiv\left(2^{-1} a+2^{-1} a\right) \equiv a \quad(\bmod 5)
$$
In the three cases, any cell is still preserved modulo 5 after an operation. Hence we can fill in the $k r \times l s$ board by $k \times l$ copies by reflection.
Since 2|2018 and 3|2019, we can get through reflections the following board:

By the lemmas above, the board is invariant modulo 5, so the answer is no.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
5cc1ae6c-1b53-5f93-935e-a9744bfa473a
| 261,423
|
Determine all the functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}+f(y)\right)=f(f(x))+f\left(y^{2}\right)+2 f(x y)
$$
for all real number $x$ and $y$.
Answer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.
|
By substituting $x=y=0$ in the given equation of the problem, we obtain that $f(0)=0$. Also, by substituting $y=0$, we get $f\left(x^{2}\right)=f(f(x))$ for any $x$.
Furthermore, by letting $y=1$ and simplifying, we get
$$
2 f(x)=f\left(x^{2}+f(1)\right)-f\left(x^{2}\right)-f(1)
$$
from which it follows that $f(-x)=f(x)$ must hold for every $x$.
Suppose now that $f(a)=f(b)$ holds for some pair of numbers $a, b$. Then, by letting $y=a$ and $y=b$ in the given equation, comparing the two resulting identities and using the fact that $f\left(a^{2}\right)=f(f(a))=f(f(b))=f\left(b^{2}\right)$ also holds under the assumption, we get the fact that
$$
f(a)=f(b) \Rightarrow f(a x)=f(b x) \quad \text { for any real number } x
$$
Consequently, if for some $a \neq 0, f(a)=0$, then we see that, for any $x, f(x)=f\left(a \cdot \frac{x}{a}\right)=$ $f\left(0 \cdot \frac{x}{a}\right)=f(0)=0$, which gives a trivial solution to the problem.
In the sequel, we shall try to find a non-trivial solution for the problem. So, let us assume from now on that if $a \neq 0$ then $f(a) \neq 0$ must hold. We first note that since $f(f(x))=f\left(x^{2}\right)$ for all $x$, the right-hand side of the given equation equals $f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)$, which is invariant if we interchange $x$ and $y$. Therefore, we have
$$
f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)=f\left(x^{2}+f(y)\right)=f\left(y^{2}+f(x)\right) \quad \text { for every pair } x, y
$$
Next, let us show that for any $x, f(x) \geq 0$ must hold. Suppose, on the contrary, $f(s)=-t^{2}$ holds for some pair $s, t$ of non-zero real numbers. By setting $x=s, y=t$ in the right hand side of (2), we get $f\left(s^{2}+f(t)\right)=f\left(t^{2}+f(s)\right)=f(0)=0$, so $f(t)=-s^{2}$. We also have $f\left(t^{2}\right)=f\left(-t^{2}\right)=f(f(s))=f\left(s^{2}\right)$. By applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=s$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
and similarly, by applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=t$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
Consequently, we obtain
$$
f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)
$$
By applying (1) with $a=s \sqrt{s^{2}+t^{2}}, b=t \sqrt{s^{2}+t^{2}}$ and $x=1 / \sqrt{s^{2}+t^{2}}$, we obtain $f(s)=$ $f(t)=-s^{2}$, from which it follows that
$$
0=f\left(s^{2}+f(s)\right)=f\left(s^{2}\right)+f\left(s^{2}\right)+2 f\left(s^{2}\right)=4 f\left(s^{2}\right)
$$
a contradiction to the fact $s^{2}>0$. Thus we conclude that for all $x \neq 0, f(x)>0$ must be satisfied.
Now, we show the following fact
$$
k>0, f(k)=1 \Leftrightarrow k=1
$$
Let $k>0$ for which $f(k)=1$. We have $f\left(k^{2}\right)=f(f(k))=f(1)$, so by $(1), f(1 / k)=f(k)=$ 1 , so we may assume $k \geq 1$. By applying (2) with $x=\sqrt{k^{2}-1}$ and $y=k$, and using $f(x) \geq 0$, we get
$$
f\left(k^{2}-1+f(k)\right)=f\left(k^{2}-1\right)+f\left(k^{2}\right)+2 f\left(k \sqrt{k^{2}-1}\right) \geq f\left(k^{2}-1\right)+f\left(k^{2}\right) .
$$
This simplifies to $0 \geq f\left(k^{2}-1\right) \geq 0$, so $k^{2}-1=0$ and thus $k=1$.
Next we focus on showing $f(1)=1$. If $f(1)=m \leq 1$, then we may proceed as above by setting $x=\sqrt{1-m}$ and $y=1$ to get $m=1$. If $f(1)=m \geq 1$, now we note that $f(m)=f(f(1))=f\left(1^{2}\right)=f(1)=m \leq m^{2}$. We may then proceed as above with $x=\sqrt{m^{2}-m}$ and $y=1$ to show $m^{2}=m$ and thus $m=1$.
We are now ready to finish. Let $x>0$ and $m=f(x)$. Since $f(f(x))=f\left(x^{2}\right)$, then $f\left(x^{2}\right)=$ $f(m)$. But by (1), $f\left(m / x^{2}\right)=1$. Therefore $m=x^{2}$. For $x<0$, we have $f(x)=f(-x)=f\left(x^{2}\right)$ as well. Therefore, for all $x, f(x)=x^{2}$.
|
f(x)=0 \text{ or } f(x)=x^2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all the functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}+f(y)\right)=f(f(x))+f\left(y^{2}\right)+2 f(x y)
$$
for all real number $x$ and $y$.
Answer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.
|
By substituting $x=y=0$ in the given equation of the problem, we obtain that $f(0)=0$. Also, by substituting $y=0$, we get $f\left(x^{2}\right)=f(f(x))$ for any $x$.
Furthermore, by letting $y=1$ and simplifying, we get
$$
2 f(x)=f\left(x^{2}+f(1)\right)-f\left(x^{2}\right)-f(1)
$$
from which it follows that $f(-x)=f(x)$ must hold for every $x$.
Suppose now that $f(a)=f(b)$ holds for some pair of numbers $a, b$. Then, by letting $y=a$ and $y=b$ in the given equation, comparing the two resulting identities and using the fact that $f\left(a^{2}\right)=f(f(a))=f(f(b))=f\left(b^{2}\right)$ also holds under the assumption, we get the fact that
$$
f(a)=f(b) \Rightarrow f(a x)=f(b x) \quad \text { for any real number } x
$$
Consequently, if for some $a \neq 0, f(a)=0$, then we see that, for any $x, f(x)=f\left(a \cdot \frac{x}{a}\right)=$ $f\left(0 \cdot \frac{x}{a}\right)=f(0)=0$, which gives a trivial solution to the problem.
In the sequel, we shall try to find a non-trivial solution for the problem. So, let us assume from now on that if $a \neq 0$ then $f(a) \neq 0$ must hold. We first note that since $f(f(x))=f\left(x^{2}\right)$ for all $x$, the right-hand side of the given equation equals $f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)$, which is invariant if we interchange $x$ and $y$. Therefore, we have
$$
f\left(x^{2}\right)+f\left(y^{2}\right)+2 f(x y)=f\left(x^{2}+f(y)\right)=f\left(y^{2}+f(x)\right) \quad \text { for every pair } x, y
$$
Next, let us show that for any $x, f(x) \geq 0$ must hold. Suppose, on the contrary, $f(s)=-t^{2}$ holds for some pair $s, t$ of non-zero real numbers. By setting $x=s, y=t$ in the right hand side of (2), we get $f\left(s^{2}+f(t)\right)=f\left(t^{2}+f(s)\right)=f(0)=0$, so $f(t)=-s^{2}$. We also have $f\left(t^{2}\right)=f\left(-t^{2}\right)=f(f(s))=f\left(s^{2}\right)$. By applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=s$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
and similarly, by applying (2) with $x=\sqrt{s^{2}+t^{2}}$ and $y=t$, we obtain
$$
f\left(s^{2}+t^{2}\right)+2 f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)=0
$$
Consequently, we obtain
$$
f\left(s \cdot \sqrt{s^{2}+t^{2}}\right)=f\left(t \cdot \sqrt{s^{2}+t^{2}}\right)
$$
By applying (1) with $a=s \sqrt{s^{2}+t^{2}}, b=t \sqrt{s^{2}+t^{2}}$ and $x=1 / \sqrt{s^{2}+t^{2}}$, we obtain $f(s)=$ $f(t)=-s^{2}$, from which it follows that
$$
0=f\left(s^{2}+f(s)\right)=f\left(s^{2}\right)+f\left(s^{2}\right)+2 f\left(s^{2}\right)=4 f\left(s^{2}\right)
$$
a contradiction to the fact $s^{2}>0$. Thus we conclude that for all $x \neq 0, f(x)>0$ must be satisfied.
Now, we show the following fact
$$
k>0, f(k)=1 \Leftrightarrow k=1
$$
Let $k>0$ for which $f(k)=1$. We have $f\left(k^{2}\right)=f(f(k))=f(1)$, so by $(1), f(1 / k)=f(k)=$ 1 , so we may assume $k \geq 1$. By applying (2) with $x=\sqrt{k^{2}-1}$ and $y=k$, and using $f(x) \geq 0$, we get
$$
f\left(k^{2}-1+f(k)\right)=f\left(k^{2}-1\right)+f\left(k^{2}\right)+2 f\left(k \sqrt{k^{2}-1}\right) \geq f\left(k^{2}-1\right)+f\left(k^{2}\right) .
$$
This simplifies to $0 \geq f\left(k^{2}-1\right) \geq 0$, so $k^{2}-1=0$ and thus $k=1$.
Next we focus on showing $f(1)=1$. If $f(1)=m \leq 1$, then we may proceed as above by setting $x=\sqrt{1-m}$ and $y=1$ to get $m=1$. If $f(1)=m \geq 1$, now we note that $f(m)=f(f(1))=f\left(1^{2}\right)=f(1)=m \leq m^{2}$. We may then proceed as above with $x=\sqrt{m^{2}-m}$ and $y=1$ to show $m^{2}=m$ and thus $m=1$.
We are now ready to finish. Let $x>0$ and $m=f(x)$. Since $f(f(x))=f\left(x^{2}\right)$, then $f\left(x^{2}\right)=$ $f(m)$. But by (1), $f\left(m / x^{2}\right)=1$. Therefore $m=x^{2}$. For $x<0$, we have $f(x)=f(-x)=f\left(x^{2}\right)$ as well. Therefore, for all $x, f(x)=x^{2}$.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution."
}
|
f811246b-d256-505e-90f8-f33b85e54a03
| 606,051
|
Determine all the functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}+f(y)\right)=f(f(x))+f\left(y^{2}\right)+2 f(x y)
$$
for all real number $x$ and $y$.
Answer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.
|
After proving that $f(x)>0$ for $x \neq 0$ as in the previous solution, we may also proceed as follows. We claim that $f$ is injective on the positive real numbers. Suppose that $a>b>0$ satisfy $f(a)=f(b)$. Then by setting $x=1 / b$ in (1) we have $f(a / b)=f(1)$. Now, by induction on $n$ and iteratively setting $x=a / b$ in (1) we get $f\left((a / b)^{n}\right)=1$ for any positive integer $n$.
Now, let $m=f(1)$ and $n$ be a positive integer such that $(a / b)^{n}>m$. By setting $x=$ $\sqrt{(a / b)^{n}-m}$ and $y=1$ in (2) we obtain that
$f\left((a / b)^{n}-m+f(1)\right)=f\left((a / b)^{n}-m\right)+f\left(1^{2}\right)+2 f\left(\sqrt{\left.(a / b)^{n}-m\right)}\right) \geq f\left((a / b)^{n}-m\right)+f(1)$.
Since $f\left((a / b)^{n}\right)=f(1)$, this last equation simplifies to $f\left((a / b)^{n}-m\right) \leq 0$ and thus $m=$ $(a / b)^{n}$. But this is impossible since $m$ is constant and $a / b>1$. Thus, $f$ is injective on the positive real numbers. Since $f(f(x))=f\left(x^{2}\right)$, we obtain that $f(x)=x^{2}$ for any real value $x$.
|
f(x)=0 \text{ for all } x \text{ and } f(x)=x^{2} \text{ for all } x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all the functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}+f(y)\right)=f(f(x))+f\left(y^{2}\right)+2 f(x y)
$$
for all real number $x$ and $y$.
Answer: The possible functions are $f(x)=0$ for all $x$ and $f(x)=x^{2}$ for all $x$.
|
After proving that $f(x)>0$ for $x \neq 0$ as in the previous solution, we may also proceed as follows. We claim that $f$ is injective on the positive real numbers. Suppose that $a>b>0$ satisfy $f(a)=f(b)$. Then by setting $x=1 / b$ in (1) we have $f(a / b)=f(1)$. Now, by induction on $n$ and iteratively setting $x=a / b$ in (1) we get $f\left((a / b)^{n}\right)=1$ for any positive integer $n$.
Now, let $m=f(1)$ and $n$ be a positive integer such that $(a / b)^{n}>m$. By setting $x=$ $\sqrt{(a / b)^{n}-m}$ and $y=1$ in (2) we obtain that
$f\left((a / b)^{n}-m+f(1)\right)=f\left((a / b)^{n}-m\right)+f\left(1^{2}\right)+2 f\left(\sqrt{\left.(a / b)^{n}-m\right)}\right) \geq f\left((a / b)^{n}-m\right)+f(1)$.
Since $f\left((a / b)^{n}\right)=f(1)$, this last equation simplifies to $f\left((a / b)^{n}-m\right) \leq 0$ and thus $m=$ $(a / b)^{n}$. But this is impossible since $m$ is constant and $a / b>1$. Thus, $f$ is injective on the positive real numbers. Since $f(f(x))=f\left(x^{2}\right)$, we obtain that $f(x)=x^{2}$ for any real value $x$.
|
{
"resource_path": "APMO/segmented/en-apmo2019_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 2"
}
|
f811246b-d256-505e-90f8-f33b85e54a03
| 606,051
|
Let $\Gamma$ be the circumcircle of $\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.
|
From the conditions, we have
Let $P$ be the intersection of $A C$ and $B F$. Then we have
$$
\angle P A E=\angle C B A=\angle B A C=\angle B F C .
$$
This implies $A, P, F, E$ are concyclic. It follows that
$$
\angle F P E=\angle F A E=\angle F B A,
$$
and hence $A B$ and $E P$ are parallel. So $E, P, D$ are collinear, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be the circumcircle of $\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.
|
From the conditions, we have

Let $P$ be the intersection of $A C$ and $B F$. Then we have
$$
\angle P A E=\angle C B A=\angle B A C=\angle B F C .
$$
This implies $A, P, F, E$ are concyclic. It follows that
$$
\angle F P E=\angle F A E=\angle F B A,
$$
and hence $A B$ and $E P$ are parallel. So $E, P, D$ are collinear, and the result follows.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1"
}
|
bfe99559-b2a2-5e18-958e-8e267a77beb3
| 260,974
|
Let $\Gamma$ be the circumcircle of $\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.
|
Let $E^{\prime}$ be any point on the extension of $E A$. From $\angle A E D=\angle E^{\prime} A B=\angle A C D$, points $A, D, C, E$ are concyclic.

Let $P$ be the intersection of $B F$ and $D E$. From $\angle A F P=\angle A C B=\angle A E P$, the points $A, P, F, E$ are concyclic. In addition, from $\angle E P A=\angle E F A=\angle D B A$, points $A, B, D, P$ are concyclic.
By considering the radical centre of $(B D F E),(A P F E)$ and $(B D P A)$, we find that the lines $B D, A P, E F$ are concurrent at $C$. The result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be the circumcircle of $\triangle A B C$. Let $D$ be a point on the side $B C$. The tangent to $\Gamma$ at $A$ intersects the parallel line to $B A$ through $D$ at point $E$. The segment $C E$ intersects $\Gamma$ again at $F$. Suppose $B, D, F, E$ are concyclic. Prove that $A C, B F, D E$ are concurrent.
|
Let $E^{\prime}$ be any point on the extension of $E A$. From $\angle A E D=\angle E^{\prime} A B=\angle A C D$, points $A, D, C, E$ are concyclic.

Let $P$ be the intersection of $B F$ and $D E$. From $\angle A F P=\angle A C B=\angle A E P$, the points $A, P, F, E$ are concyclic. In addition, from $\angle E P A=\angle E F A=\angle D B A$, points $A, B, D, P$ are concyclic.
By considering the radical centre of $(B D F E),(A P F E)$ and $(B D P A)$, we find that the lines $B D, A P, E F$ are concurrent at $C$. The result follows.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2"
}
|
bfe99559-b2a2-5e18-958e-8e267a77beb3
| 260,974
|
Show that $r=2$ is the largest real number $r$ which satisfies the following condition:
If a sequence $a_{1}, a_{2}, \ldots$ of positive integers fulfills the inequalities
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+r a_{n+1}}
$$
for every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \geq M$.
|
. First, let us assume that $r>2$, and take a positive integer $a \geq 1 /(r-2)$.
Then, if we let $a_{n}=a+\lfloor n / 2\rfloor$ for $n=1,2, \ldots$, the sequence $a_{n}$ satisfies the inequalities
$$
\sqrt{a_{n}^{2}+r a_{n+1}} \geq \sqrt{a_{n}^{2}+r a_{n}} \geq \sqrt{a_{n}^{2}+\left(2+\frac{1}{a}\right) a_{n}} \geq a_{n}+1=a_{n+2}
$$
but since $a_{n+2}>a_{n}$ for any $n$, we see that $r$ does not satisfy the condition given in the problem.
Now we show that $r=2$ does satisfy the condition of the problem. Suppose $a_{1}, a_{2}, \ldots$ is a sequence of positive integers satisfying the inequalities given in the problem, and there exists a positive integer $m$ for which $a_{m+2}>a_{m}$ is satisfied.
By induction we prove the following assertion:
$$
a_{m+2 k} \leq a_{m+2 k-1}=a_{m+1} \text { holds for every positive integer } k
$$
The truth of $(\dagger)$ for $k=1$ follows from the inequalities below
$$
2 a_{m+2}-1=a_{m+2}^{2}-\left(a_{m+2}-1\right)^{2} \leq a_{m}^{2}+2 a_{m+1}-\left(a_{m+2}-1\right)^{2} \leq 2 a_{m+1}
$$
Let us assume that $(\dagger)$ holds for some positive integer $k$. From
$$
a_{m+1}^{2} \leq a_{m+2 k+1}^{2} \leq a_{m+2 k-1}^{2}+2 a_{m+2 k} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
it follows that $a_{m+2 k+1}=a_{m+1}$ must hold. Furthermore, since $a_{m+2 k} \leq a_{m+1}$, we have
$$
a_{m+2 k+2}^{2} \leq a_{m+2 k}^{2}+2 a_{m+2 k+1} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
from which it follows that $a_{m+2 k+2} \leq a_{m+1}$, which proves the assertion $(\dagger)$.
We can conclude that for the value of $m$ with which we started our argument above, $a_{m+2 k+1}=a_{m+1}$ holds for every positive integer $k$. Therefore, in order to finish the proof, it is enough to show that $a_{m+2 k}$ becomes constant after some value of $k$. Since every $a_{m+2 k}$ is a positive integer less than or equal to $a_{m+1}$, there exists $k=K$ for which $a_{m+2 K}$ takes the maximum value. By the monotonicity of $a_{m+2 k}$, it then follows that $a_{m+2 k}=a_{m+2 K}$ for all $k \geq K$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that $r=2$ is the largest real number $r$ which satisfies the following condition:
If a sequence $a_{1}, a_{2}, \ldots$ of positive integers fulfills the inequalities
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+r a_{n+1}}
$$
for every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \geq M$.
|
. First, let us assume that $r>2$, and take a positive integer $a \geq 1 /(r-2)$.
Then, if we let $a_{n}=a+\lfloor n / 2\rfloor$ for $n=1,2, \ldots$, the sequence $a_{n}$ satisfies the inequalities
$$
\sqrt{a_{n}^{2}+r a_{n+1}} \geq \sqrt{a_{n}^{2}+r a_{n}} \geq \sqrt{a_{n}^{2}+\left(2+\frac{1}{a}\right) a_{n}} \geq a_{n}+1=a_{n+2}
$$
but since $a_{n+2}>a_{n}$ for any $n$, we see that $r$ does not satisfy the condition given in the problem.
Now we show that $r=2$ does satisfy the condition of the problem. Suppose $a_{1}, a_{2}, \ldots$ is a sequence of positive integers satisfying the inequalities given in the problem, and there exists a positive integer $m$ for which $a_{m+2}>a_{m}$ is satisfied.
By induction we prove the following assertion:
$$
a_{m+2 k} \leq a_{m+2 k-1}=a_{m+1} \text { holds for every positive integer } k
$$
The truth of $(\dagger)$ for $k=1$ follows from the inequalities below
$$
2 a_{m+2}-1=a_{m+2}^{2}-\left(a_{m+2}-1\right)^{2} \leq a_{m}^{2}+2 a_{m+1}-\left(a_{m+2}-1\right)^{2} \leq 2 a_{m+1}
$$
Let us assume that $(\dagger)$ holds for some positive integer $k$. From
$$
a_{m+1}^{2} \leq a_{m+2 k+1}^{2} \leq a_{m+2 k-1}^{2}+2 a_{m+2 k} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
it follows that $a_{m+2 k+1}=a_{m+1}$ must hold. Furthermore, since $a_{m+2 k} \leq a_{m+1}$, we have
$$
a_{m+2 k+2}^{2} \leq a_{m+2 k}^{2}+2 a_{m+2 k+1} \leq a_{m+1}^{2}+2 a_{m+1}<\left(a_{m+1}+1\right)^{2}
$$
from which it follows that $a_{m+2 k+2} \leq a_{m+1}$, which proves the assertion $(\dagger)$.
We can conclude that for the value of $m$ with which we started our argument above, $a_{m+2 k+1}=a_{m+1}$ holds for every positive integer $k$. Therefore, in order to finish the proof, it is enough to show that $a_{m+2 k}$ becomes constant after some value of $k$. Since every $a_{m+2 k}$ is a positive integer less than or equal to $a_{m+1}$, there exists $k=K$ for which $a_{m+2 K}$ takes the maximum value. By the monotonicity of $a_{m+2 k}$, it then follows that $a_{m+2 k}=a_{m+2 K}$ for all $k \geq K$.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
6153a381-e07e-53b5-80de-558f60948be5
| 606,096
|
Show that $r=2$ is the largest real number $r$ which satisfies the following condition:
If a sequence $a_{1}, a_{2}, \ldots$ of positive integers fulfills the inequalities
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+r a_{n+1}}
$$
for every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \geq M$.
|
We only give an alternative proof of the assertion $(\dagger)$ in solution 1 . Let $\left\{a_{n}\right\}$ be a sequence satisfying the inequalities given in the problem. We will use the following key observations:
(a) If $a_{n+1} \leq a_{n}$ for some $n \geq 1$, then
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+2 a_{n+1}}<\sqrt{a_{n}^{2}+2 a_{n}+1}=a_{n}+1,
$$
hence $a_{n}=a_{n+2}$.
(b) If $a_{n} \leq a_{n+1}$ for some $n \geq 1$, then
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+2 a_{n+1}}<\sqrt{a_{n+1}^{2}+2 a_{n+1}+1}=a_{n+1}+1
$$
hence $a_{n} \leq a_{n+2} \leq a_{n+1}$.
Now let $m$ be a positive integer such that $a_{m+2}>a_{m}$. By the observations above, we must have $a_{m}<a_{m+2} \leq a_{m+1}$. Thus the assertion ( $\dagger$ ) is true for $k=1$. Assume that the assertion holds for some positive integer $k$. Using observation (a), we get $a_{m+2 k+1}=a_{m+2 k-1}=a_{m+1}$. Thus $a_{m+2 k} \leq a_{m+2 k+1}$, and then using observation (b), we get $a_{m+2 k+2} \leq a_{m+2 k+1}=a_{m+1}$, which proves the assertion ( $\dagger$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Show that $r=2$ is the largest real number $r$ which satisfies the following condition:
If a sequence $a_{1}, a_{2}, \ldots$ of positive integers fulfills the inequalities
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+r a_{n+1}}
$$
for every positive integer $n$, then there exists a positive integer $M$ such that $a_{n+2}=a_{n}$ for every $n \geq M$.
|
We only give an alternative proof of the assertion $(\dagger)$ in solution 1 . Let $\left\{a_{n}\right\}$ be a sequence satisfying the inequalities given in the problem. We will use the following key observations:
(a) If $a_{n+1} \leq a_{n}$ for some $n \geq 1$, then
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+2 a_{n+1}}<\sqrt{a_{n}^{2}+2 a_{n}+1}=a_{n}+1,
$$
hence $a_{n}=a_{n+2}$.
(b) If $a_{n} \leq a_{n+1}$ for some $n \geq 1$, then
$$
a_{n} \leq a_{n+2} \leq \sqrt{a_{n}^{2}+2 a_{n+1}}<\sqrt{a_{n+1}^{2}+2 a_{n+1}+1}=a_{n+1}+1
$$
hence $a_{n} \leq a_{n+2} \leq a_{n+1}$.
Now let $m$ be a positive integer such that $a_{m+2}>a_{m}$. By the observations above, we must have $a_{m}<a_{m+2} \leq a_{m+1}$. Thus the assertion ( $\dagger$ ) is true for $k=1$. Assume that the assertion holds for some positive integer $k$. Using observation (a), we get $a_{m+2 k+1}=a_{m+2 k-1}=a_{m+1}$. Thus $a_{m+2 k} \leq a_{m+2 k+1}$, and then using observation (b), we get $a_{m+2 k+2} \leq a_{m+2 k+1}=a_{m+1}$, which proves the assertion ( $\dagger$ ).
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2"
}
|
6153a381-e07e-53b5-80de-558f60948be5
| 606,096
|
Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.
|
We claim that $k=2^{a}$ for all $a \geq 0$.
Let $A=\{1,2,4,8, \ldots\}$ and $B=\mathbb{N} \backslash A$. For any set $T$, let $s(T)$ denote the sum of the elements of $T$. (If $T$ is empty, we let $s(T)=0$.)
We first show that any positive integer $k=2^{a}$ satisfies the desired property. Let $B^{\prime}$ be a subset of $B$ with $a$ elements, and let $S=A \cup B^{\prime}$. Recall that any nonnegative integer has a unique binary representation. Hence, for any integer $t>s\left(B^{\prime}\right)$ and any subset $B^{\prime \prime} \subseteq B^{\prime}$, the number $t-s\left(B^{\prime \prime}\right)$ can be written as a sum of distinct elements of $A$ in a unique way. This means that $t$ can be written as a sum of distinct elements of $B^{\prime}$ in exactly $2^{a}$ ways.
Next, assume that some positive integer $k$ satisfies the desired property for a positive integer $m \geq 2$ and a set $S$. Clearly, $S$ is infinite.
Lemma: For all sufficiently large $x \in S$, the smallest element of $S$ larger than $x$ is $2 x$.
Proof of Lemma: Let $x \in S$ with $x>3 m$, and let $x<y<2 x$. We will show that $y \notin S$. Suppose first that $y>x+m$. Then $y-x$ can be written as a sum of distinct elements of $S$ not including $x$ in $k$ ways. If $y \in S$, then $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Suppose now that $y \leq x+m$. We consider $z \in(2 x-m, 2 x)$. Similarly as before, $z-x$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$ in $k$ ways. If $y \in S$, then since $m<z-y<x, z-y$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$. This means that $z$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction.
We now show that $2 x \in S$; assume for contradiction that this is not the case. Observe that $2 x$ can be written as a sum of distinct elements of $S$ including $x$ in exactly $k-1$ ways. This means that $2 x$ can also be written as a sum of distinct elements of $S$ not including $x$. If this sum includes any number less than $x-m$, then removing this number, we can write some number $y \in(x+m, 2 x)$ as a sum of distinct elements of $S$ not including $x$. Now if $y=y^{\prime}+x$ where $y^{\prime} \in(m, x)$ then $y^{\prime}$ can be written as
a sum of distinct elements of $S$ including $x$ in exactly $k$ ways. Therefore $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Hence the sum only includes numbers in the range $[x-m, x)$. Clearly two numbers do not suffice. On the other hand, three such numbers sum to at least $3(x-m)>2 x$, a contradiction.
From the Lemma, we have that $S=T \cup U$, where $T$ is finite and $U=\{x, 2 x, 4 x, 8 x, \ldots\}$ for some positive integer $x$. Let $y$ be any positive integer greater than $s(T)$. For any subset $T^{\prime} \subseteq T$, if $y-s\left(T^{\prime}\right) \equiv 0(\bmod x)$, then $y-s\left(T^{\prime}\right)$ can be written as a sum of distinct elements of $U$ in a unique way; otherwise $y-s\left(T^{\prime}\right)$ cannot be written as a sum of distinct elements of $U$. Hence the number of ways to write $y$ as a sum of distinct elements of $S$ is equal to the number of subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv y(\bmod x)$. Since this holds for all $y$, for any $0 \leq a \leq x-1$ there are exactly $k$ subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv a(\bmod x)$. This means that there are $k x$ subsets of $T$ in total. But the number of subsets of $T$ is a power of 2 , and therefore $k$ is a power of 2 , as claimed.
|
k=2^{a}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.
|
We claim that $k=2^{a}$ for all $a \geq 0$.
Let $A=\{1,2,4,8, \ldots\}$ and $B=\mathbb{N} \backslash A$. For any set $T$, let $s(T)$ denote the sum of the elements of $T$. (If $T$ is empty, we let $s(T)=0$.)
We first show that any positive integer $k=2^{a}$ satisfies the desired property. Let $B^{\prime}$ be a subset of $B$ with $a$ elements, and let $S=A \cup B^{\prime}$. Recall that any nonnegative integer has a unique binary representation. Hence, for any integer $t>s\left(B^{\prime}\right)$ and any subset $B^{\prime \prime} \subseteq B^{\prime}$, the number $t-s\left(B^{\prime \prime}\right)$ can be written as a sum of distinct elements of $A$ in a unique way. This means that $t$ can be written as a sum of distinct elements of $B^{\prime}$ in exactly $2^{a}$ ways.
Next, assume that some positive integer $k$ satisfies the desired property for a positive integer $m \geq 2$ and a set $S$. Clearly, $S$ is infinite.
Lemma: For all sufficiently large $x \in S$, the smallest element of $S$ larger than $x$ is $2 x$.
Proof of Lemma: Let $x \in S$ with $x>3 m$, and let $x<y<2 x$. We will show that $y \notin S$. Suppose first that $y>x+m$. Then $y-x$ can be written as a sum of distinct elements of $S$ not including $x$ in $k$ ways. If $y \in S$, then $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Suppose now that $y \leq x+m$. We consider $z \in(2 x-m, 2 x)$. Similarly as before, $z-x$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$ in $k$ ways. If $y \in S$, then since $m<z-y<x, z-y$ can be written as a sum of distinct elements of $S$ not including $x$ or $y$. This means that $z$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction.
We now show that $2 x \in S$; assume for contradiction that this is not the case. Observe that $2 x$ can be written as a sum of distinct elements of $S$ including $x$ in exactly $k-1$ ways. This means that $2 x$ can also be written as a sum of distinct elements of $S$ not including $x$. If this sum includes any number less than $x-m$, then removing this number, we can write some number $y \in(x+m, 2 x)$ as a sum of distinct elements of $S$ not including $x$. Now if $y=y^{\prime}+x$ where $y^{\prime} \in(m, x)$ then $y^{\prime}$ can be written as
a sum of distinct elements of $S$ including $x$ in exactly $k$ ways. Therefore $y$ can be written as a sum of distinct elements of $S$ in at least $k+1$ ways, a contradiction. Hence the sum only includes numbers in the range $[x-m, x)$. Clearly two numbers do not suffice. On the other hand, three such numbers sum to at least $3(x-m)>2 x$, a contradiction.
From the Lemma, we have that $S=T \cup U$, where $T$ is finite and $U=\{x, 2 x, 4 x, 8 x, \ldots\}$ for some positive integer $x$. Let $y$ be any positive integer greater than $s(T)$. For any subset $T^{\prime} \subseteq T$, if $y-s\left(T^{\prime}\right) \equiv 0(\bmod x)$, then $y-s\left(T^{\prime}\right)$ can be written as a sum of distinct elements of $U$ in a unique way; otherwise $y-s\left(T^{\prime}\right)$ cannot be written as a sum of distinct elements of $U$. Hence the number of ways to write $y$ as a sum of distinct elements of $S$ is equal to the number of subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv y(\bmod x)$. Since this holds for all $y$, for any $0 \leq a \leq x-1$ there are exactly $k$ subsets $T^{\prime} \subseteq T$ such that $s\left(T^{\prime}\right) \equiv a(\bmod x)$. This means that there are $k x$ subsets of $T$ in total. But the number of subsets of $T$ is a power of 2 , and therefore $k$ is a power of 2 , as claimed.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution:"
}
|
951f719b-cab5-5b40-9f46-333e91c9b568
| 606,114
|
Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.
|
. We give an alternative proof of the first half of the lemma in the Solution 1 above.
Let $s_{1}<s_{2}<\cdots$ be the elements of $S$. For any positive integer $r$, define $A_{r}(x)=\prod_{n=1}^{r}\left(1+x^{s_{n}}\right)$. For each $n$ such that $m \leq n<s_{r+1}$, all $k$ ways of writing $n$ as a sum of elements of $S$ must only use $s_{1}, \ldots, s_{r}$, so the coefficient of $x^{n}$ in $A_{r}(x)$ is $k$. Similarly the number of ways of writing $s_{r+1}$ as a sum of elements of $S$ without using $s_{r+1}$ is exactly $k-1$. Hence the coefficient of $x^{s_{r+1}}$ in $A_{r}(x)$ is $k-1$.
Fix a $t$ such that $s_{t}>2(m+1)$. Write
$$
A_{t-1}(x)=u(x)+k\left(x^{m+1}+\cdots+x^{s_{t}-1}\right)+x^{s_{t}} v(x)
$$
for some $u(x), v(x)$ where $u(x)$ is of degree at most $m$.
Note that
$$
A_{t+1}(x)=A_{t-1}(x)+x^{s_{t}} A_{t-1}(x)+x^{s_{t+1}} A_{t-1}(x)+x^{s_{t}+s_{t+1}} A_{t-1}(x)
$$
If $s_{t+1}+m+1<2 s_{t}$, we can find the term $x^{s_{t+1}+m+1}$ in $x^{s_{t}} A_{t-1}(x)$ and in $x^{s_{t+1}} A_{t-1}(x)$. Hence the coefficient of $x^{s_{t+1}+m+1}$ in $A_{t+1}(x)$ is at least $2 k$, which is impossible. So $s_{t+1} \geq 2 s_{t}-(m+1)>$ $s_{t}+m+1$.
Now
$$
A_{t}(x)=A_{t-1}(x)+x^{s_{t}} u(x)+k\left(x^{s_{t}+m+1}+\cdots x^{2 s_{t}-1}\right)+x^{2 s_{t}} v(x)
$$
Recall that the coefficent of $x^{s_{t+1}}$ in $A_{t}(x)$ is $k-1$. But if $s_{t}+m+1<s_{t+1}<s_{2 t}$, then the coefficient of $x^{s_{t+1}}$ in $A_{t}(x)$ is at least $k$, which is a contradiction. Therefore $s_{t+1} \geq 2 s_{t}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine all positive integers $k$ for which there exist a positive integer $m$ and a set $S$ of positive integers such that any integer $n>m$ can be written as a sum of distinct elements of $S$ in exactly $k$ ways.
|
. We give an alternative proof of the first half of the lemma in the Solution 1 above.
Let $s_{1}<s_{2}<\cdots$ be the elements of $S$. For any positive integer $r$, define $A_{r}(x)=\prod_{n=1}^{r}\left(1+x^{s_{n}}\right)$. For each $n$ such that $m \leq n<s_{r+1}$, all $k$ ways of writing $n$ as a sum of elements of $S$ must only use $s_{1}, \ldots, s_{r}$, so the coefficient of $x^{n}$ in $A_{r}(x)$ is $k$. Similarly the number of ways of writing $s_{r+1}$ as a sum of elements of $S$ without using $s_{r+1}$ is exactly $k-1$. Hence the coefficient of $x^{s_{r+1}}$ in $A_{r}(x)$ is $k-1$.
Fix a $t$ such that $s_{t}>2(m+1)$. Write
$$
A_{t-1}(x)=u(x)+k\left(x^{m+1}+\cdots+x^{s_{t}-1}\right)+x^{s_{t}} v(x)
$$
for some $u(x), v(x)$ where $u(x)$ is of degree at most $m$.
Note that
$$
A_{t+1}(x)=A_{t-1}(x)+x^{s_{t}} A_{t-1}(x)+x^{s_{t+1}} A_{t-1}(x)+x^{s_{t}+s_{t+1}} A_{t-1}(x)
$$
If $s_{t+1}+m+1<2 s_{t}$, we can find the term $x^{s_{t+1}+m+1}$ in $x^{s_{t}} A_{t-1}(x)$ and in $x^{s_{t+1}} A_{t-1}(x)$. Hence the coefficient of $x^{s_{t+1}+m+1}$ in $A_{t+1}(x)$ is at least $2 k$, which is impossible. So $s_{t+1} \geq 2 s_{t}-(m+1)>$ $s_{t}+m+1$.
Now
$$
A_{t}(x)=A_{t-1}(x)+x^{s_{t}} u(x)+k\left(x^{s_{t}+m+1}+\cdots x^{2 s_{t}-1}\right)+x^{2 s_{t}} v(x)
$$
Recall that the coefficent of $x^{s_{t+1}}$ in $A_{t}(x)$ is $k-1$. But if $s_{t}+m+1<s_{t+1}<s_{2 t}$, then the coefficient of $x^{s_{t+1}}$ in $A_{t}(x)$ is at least $k$, which is a contradiction. Therefore $s_{t+1} \geq 2 s_{t}$.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 2"
}
|
951f719b-cab5-5b40-9f46-333e91c9b568
| 606,114
|
Let $\mathbb{Z}$ denote the set of all integers. Find all polynomials $P(x)$ with integer coefficients that satisfy the following property:
For any infinite sequence $a_{1}, a_{2}, \ldots$ of integers in which each integer in $\mathbb{Z}$ appears exactly once, there exist indices $i<j$ and an integer $k$ such that $a_{i}+a_{i+1}+\cdots+a_{j}=P(k)$.
|
Part 1: All polynomials with $\operatorname{deg} P=1$ satisfy the given property.
Suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \geq 0$. Denote $s_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}(\bmod c)$. It suffices to show that there exist indices $i$ and $j$ such that $j-i \geq 2$ and $s_{j}-s_{i} \equiv d$ $(\bmod c)$.
Consider $c+1$ indices $e_{1}, e_{2}, \ldots, e_{c+1}>1$ such that $a_{e_{l}} \equiv d(\bmod c)$. By the pigeonhole principle, among the $n+1$ pairs $\left(s_{e_{1}-1}, s_{e_{1}}\right),\left(s_{e_{2}-1}, s_{e_{2}}\right), \ldots,\left(s_{e_{n+1}-1}, s_{e_{n+1}}\right)$, some two are equal, say $\left(s_{m-1}, s_{m}\right)$ and $\left(s_{n-1}, s_{n}\right)$. We can then take $i=m-1$ and $j=n$.
Part 2: All polynomials with $\operatorname{deg} P \neq 1$ do not satisfy the given property.
Lemma: If $\operatorname{deg} P \neq 1$, then for any positive integers $A, B$, and $C$, there exists an integer $y$ with $|y|>C$ such that no value in the range of $P$ falls within the interval $[y-A, y+B]$.
Proof of Lemma: The claim is immediate when $P$ is constant or when $\operatorname{deg} P$ is even since $P$ is bounded from below. Let $P(x)=a_{n} x^{n}+\cdots+a_{1} x+a_{0}$ be of odd degree greater than 1 , and assume without
loss of generality that $a_{n}>0$. Since $P(x+1)-P(x)=a_{n} n x^{n-1}+\ldots$, and $n-1>0$, the gap between $P(x)$ and $P(x+1)$ grows arbitrarily for large $x$. The claim follows.
Suppose $\operatorname{deg} P \neq 1$. We will inductively construct a sequence $\left\{a_{i}\right\}$ such that for any indices $i<j$ and any integer $k$ it holds that $a_{i}+a_{i+1}+\cdots+a_{j} \neq P(k)$. Suppose that we have constructed the sequence up to $a_{i}$, and $m$ is an integer with smallest magnitude yet to appear in the sequence. We will add two more terms to the sequence. Take $a_{i+2}=m$. Consider all the new sums of at least two consecutive terms; each of them contains $a_{i+1}$. Hence all such sums are in the interval $\left[a_{i+1}-A, a_{i+1}+B\right]$ for fixed constants $A, B$. The lemma allows us to choose $a_{i+1}$ so that all such sums avoid the range of $P$.
Alternate Solution for Part 1: Again, suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \geq 0$. Let $S_{i}=\left\{a_{j}+a_{j+1}+\cdots+a_{i}(\bmod c) \mid j=1,2, \ldots, i\right\}$. Then $S_{i+1}=\left\{s_{i}+a_{i+1}\right.$ $\left.(\bmod c) \mid s_{i} \in S_{i}\right\} \cup\left\{a_{i+1}(\bmod c)\right\}$. Hence $\left|S_{i+1}\right|=\left|S_{i}\right|$ or $S_{i+1}=\left|S_{i}\right|+1$, with the former occuring exactly when $0 \in S_{i}$. Since $\left|S_{i}\right| \leq c$, the latter can only occur finitely many times, so there exists $I$ such that $0 \in S_{i}$ for all $i \geq I$. Let $t>I$ be an index with $a_{t} \equiv d(\bmod c)$. Then we can find a sum of at least two consecutive terms ending at $a_{t}$ and congruent to $d(\bmod c)$.
Alternate Construction when $P(x)$ is constant or of even degree
If $P(x)$ is of even degree, then $P$ is bounded from below or from above. In case of $P$ is constant or bounded from above, then there exists a positive integer $c$ such that $P(x)<c$. Let $\left\{a_{i}\right\}$ be the sequence
$$
0,1,-1,2,3,-2,4,5,-3, \cdots
$$
which is given by $a_{3 n+1}=2 n, a_{3 n+2}=2 n+1, a_{3 n+3}=-(n+1)$ for all $n \geq 0$. Notice that for any $i<j$ we have $a_{i}+\cdots+a_{j} \geq 0$. Then for the sequence $\left\{b_{n}\right\}$ defined by $b_{n}=a_{n}+c$, clearly $b_{i}+\cdots+b_{j} \geq\left(a_{i}+\cdots+a_{j}\right)+2 c>c$ which is out side the range of $P(x)$.
Now if $P$ is bounded from below, there exist a positive integer $c$ such that $P(x)>-c$. In this case, take $b_{n}$ to be $b_{n}=-a_{n}-c$. Then for all $i<j$ we have $b_{i}+\cdots+b_{j} \leq-\left(a_{1}+\cdots a_{n}\right)-2 c<-c$ which is again out side the range of $P(x)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\mathbb{Z}$ denote the set of all integers. Find all polynomials $P(x)$ with integer coefficients that satisfy the following property:
For any infinite sequence $a_{1}, a_{2}, \ldots$ of integers in which each integer in $\mathbb{Z}$ appears exactly once, there exist indices $i<j$ and an integer $k$ such that $a_{i}+a_{i+1}+\cdots+a_{j}=P(k)$.
|
Part 1: All polynomials with $\operatorname{deg} P=1$ satisfy the given property.
Suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \geq 0$. Denote $s_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}(\bmod c)$. It suffices to show that there exist indices $i$ and $j$ such that $j-i \geq 2$ and $s_{j}-s_{i} \equiv d$ $(\bmod c)$.
Consider $c+1$ indices $e_{1}, e_{2}, \ldots, e_{c+1}>1$ such that $a_{e_{l}} \equiv d(\bmod c)$. By the pigeonhole principle, among the $n+1$ pairs $\left(s_{e_{1}-1}, s_{e_{1}}\right),\left(s_{e_{2}-1}, s_{e_{2}}\right), \ldots,\left(s_{e_{n+1}-1}, s_{e_{n+1}}\right)$, some two are equal, say $\left(s_{m-1}, s_{m}\right)$ and $\left(s_{n-1}, s_{n}\right)$. We can then take $i=m-1$ and $j=n$.
Part 2: All polynomials with $\operatorname{deg} P \neq 1$ do not satisfy the given property.
Lemma: If $\operatorname{deg} P \neq 1$, then for any positive integers $A, B$, and $C$, there exists an integer $y$ with $|y|>C$ such that no value in the range of $P$ falls within the interval $[y-A, y+B]$.
Proof of Lemma: The claim is immediate when $P$ is constant or when $\operatorname{deg} P$ is even since $P$ is bounded from below. Let $P(x)=a_{n} x^{n}+\cdots+a_{1} x+a_{0}$ be of odd degree greater than 1 , and assume without
loss of generality that $a_{n}>0$. Since $P(x+1)-P(x)=a_{n} n x^{n-1}+\ldots$, and $n-1>0$, the gap between $P(x)$ and $P(x+1)$ grows arbitrarily for large $x$. The claim follows.
Suppose $\operatorname{deg} P \neq 1$. We will inductively construct a sequence $\left\{a_{i}\right\}$ such that for any indices $i<j$ and any integer $k$ it holds that $a_{i}+a_{i+1}+\cdots+a_{j} \neq P(k)$. Suppose that we have constructed the sequence up to $a_{i}$, and $m$ is an integer with smallest magnitude yet to appear in the sequence. We will add two more terms to the sequence. Take $a_{i+2}=m$. Consider all the new sums of at least two consecutive terms; each of them contains $a_{i+1}$. Hence all such sums are in the interval $\left[a_{i+1}-A, a_{i+1}+B\right]$ for fixed constants $A, B$. The lemma allows us to choose $a_{i+1}$ so that all such sums avoid the range of $P$.
Alternate Solution for Part 1: Again, suppose $P(x)=c x+d$, and assume without loss of generality that $c>d \geq 0$. Let $S_{i}=\left\{a_{j}+a_{j+1}+\cdots+a_{i}(\bmod c) \mid j=1,2, \ldots, i\right\}$. Then $S_{i+1}=\left\{s_{i}+a_{i+1}\right.$ $\left.(\bmod c) \mid s_{i} \in S_{i}\right\} \cup\left\{a_{i+1}(\bmod c)\right\}$. Hence $\left|S_{i+1}\right|=\left|S_{i}\right|$ or $S_{i+1}=\left|S_{i}\right|+1$, with the former occuring exactly when $0 \in S_{i}$. Since $\left|S_{i}\right| \leq c$, the latter can only occur finitely many times, so there exists $I$ such that $0 \in S_{i}$ for all $i \geq I$. Let $t>I$ be an index with $a_{t} \equiv d(\bmod c)$. Then we can find a sum of at least two consecutive terms ending at $a_{t}$ and congruent to $d(\bmod c)$.
Alternate Construction when $P(x)$ is constant or of even degree
If $P(x)$ is of even degree, then $P$ is bounded from below or from above. In case of $P$ is constant or bounded from above, then there exists a positive integer $c$ such that $P(x)<c$. Let $\left\{a_{i}\right\}$ be the sequence
$$
0,1,-1,2,3,-2,4,5,-3, \cdots
$$
which is given by $a_{3 n+1}=2 n, a_{3 n+2}=2 n+1, a_{3 n+3}=-(n+1)$ for all $n \geq 0$. Notice that for any $i<j$ we have $a_{i}+\cdots+a_{j} \geq 0$. Then for the sequence $\left\{b_{n}\right\}$ defined by $b_{n}=a_{n}+c$, clearly $b_{i}+\cdots+b_{j} \geq\left(a_{i}+\cdots+a_{j}\right)+2 c>c$ which is out side the range of $P(x)$.
Now if $P$ is bounded from below, there exist a positive integer $c$ such that $P(x)>-c$. In this case, take $b_{n}$ to be $b_{n}=-a_{n}-c$. Then for all $i<j$ we have $b_{i}+\cdots+b_{j} \leq-\left(a_{1}+\cdots a_{n}\right)-2 c<-c$ which is again out side the range of $P(x)$.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# Solution:"
}
|
9da51615-88b2-5097-a788-7bb706eea4af
| 606,135
|
Let $n \geq 3$ be a fixed integer. The number 1 is written $n$ times on a blackboard. Below the blackboard, there are two buckets that are initially empty. A move consists of erasing two of the numbers $a$ and $b$, replacing them with the numbers 1 and $a+b$, then adding one stone to the first bucket and $\operatorname{gcd}(a, b)$ stones to the second bucket. After some finite number of moves, there are $s$ stones in the first bucket and $t$ stones in the second bucket, where $s$ and $t$ are positive integers. Find all possible values of the ratio $\frac{t}{s}$.
|
The answer is the set of all rational numbers in the interval $[1, n-1)$. First, we show that no other numbers are possible. Clearly the ratio is at least 1, since for every move, at least one stone is added to the second bucket. Note that the number $s$ of stones in the first bucket is always equal to $p-n$, where $p$ is the sum of the numbers on the blackboard. We will assume that the numbers are written in a row, and whenever two numbers $a$ and $b$ are erased, $a+b$ is written in the place of the number on the right. Let $a_{1}, a_{2}, \ldots, a_{n}$ be the numbers on the blackboard from left to right, and let
$$
q=0 \cdot a_{1}+1 \cdot a_{2}+\cdots+(n-1) a_{n}
$$
Since each number $a_{i}$ is at least 1 , we always have
$$
q \leq(n-1) p-(1+\cdots+(n-1))=(n-1) p-\frac{n(n-1)}{2}=(n-1) s+\frac{n(n-1)}{2}
$$
Also, if a move changes $a_{i}$ and $a_{j}$ with $i<j$, then $t$ changes by $\operatorname{gcd}\left(a_{i}, a_{j}\right) \leq a_{i}$ and $q$ increases by
$$
(j-1) a_{i}-(i-1)\left(a_{i}-1\right) \geq i a_{i}-(i-1)\left(a_{i}-1\right) \geq a_{i}
$$
Hence $q-t$ never decreases. We may assume without loss of generality that the first move involves the rightmost 1. Then immediately after this move, $q=0+1+\cdots+(n-2)+(n-1) \cdot 2=\frac{(n+2)(n-1)}{2}$ and
$t=1$. So after that move, we always have
$$
\begin{aligned}
t & \leq q+1-\frac{(n+2)(n-1)}{2} \\
& \leq(n-1) s+\frac{n(n-1)}{2}-\frac{(n+2)(n-1)}{2}+1 \\
& =(n-1) s-(n-2)<(n-1) s
\end{aligned}
$$
Hence, $\frac{t}{s}<n-1$. So $\frac{t}{s}$ must be a rational number in $[1, n-1)$.
After a single move, we have $\frac{t}{s}=1$, so it remains to prove that $\frac{t}{s}$ can be any rational number in $(1, n-1)$. We will now show by induction on $n$ that for any positive integer $a$, it is possible to reach a situation where there are $n-1$ occurrences of 1 on the board and the number $a^{n-1}$, with $t$ and $s$ equal to $a^{n-2}(a-1)(n-1)$ and $a^{n-1}-1$, respectively. For $n=2$, this is clear as there is only one possible move at each step, so after $a-1$ moves $s$ and $t$ will both be equal to $a-1$. Now assume that the claim is true for $n-1$, where $n>2$. Call the algorithm which creates this situation using $n-1$ numbers algorithm $A$. Then to reach the situation for size $n$, we apply algorithm $A$, to create the number $a^{n-2}$. Next, apply algorithm $A$ again and then add the two large numbers, repeat until we get the number $a^{n-1}$. Then algorithm $A$ was applied $a$ times and the two larger numbers were added $a-1$ times. Each time the two larger numbers are added, $t$ increases by $a^{n-2}$ and each time algorithm $A$ is applied, $t$ increases by $a^{n-3}(a-1)(n-2)$. Hence, the final value of $t$ is
$$
t=(a-1) a^{n-2}+a \cdot a^{n-3}(a-1)(n-2)=a^{n-2}(a-1)(n-1)
$$
This completes the induction.
Now we can choose 1 and the large number $b$ times for any positive integer $b$, and this will add $b$ stones to each bucket. At this point we have
$$
\frac{t}{s}=\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}
$$
So we just need to show that for any rational number $\frac{p}{q} \in(1, n-1)$, there exist positive integers $a$ and $b$ such that
$$
\frac{p}{q}=\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}
$$
Rearranging, we see that this happens if and only if
$$
b=\frac{q a^{n-2}(a-1)(n-1)-p\left(a^{n-1}-1\right)}{p-q} .
$$
If we choose $a \equiv 1(\bmod p-q)$, then this will be an integer, so we just need to check that the numerator is positive for sufficiently large $a$.
$$
\begin{aligned}
q a^{n-2}(a-1)(n-1)-p\left(a^{n-1}-1\right) & >q a^{n-2}(a-1)(n-1)-p a^{n-1} \\
& =a^{n-2}(a(q(n-1)-p)-(n-1))
\end{aligned}
$$
which is positive for sufficiently large $a$ since $q(n-1)-p>0$.
Alternative solution for the upper bound. Rather than starting with $n$ occurrences of 1 , we may start with infinitely many 1 s , but we are restricted to having at most $n-1$ numbers which are not equal to 1 on the board at any time. It is easy to see that this does not change the problem. Note also that we can ignore the 1 we write on the board each move, so the allowed move is to rub off two numbers and write their sum. We define the width and score of a number on the board as follows. Colour that number red, then reverse every move up to that point all the way back to the situation when the numbers are all 1 s . Whenever a red number is split, colour the two replacement numbers
red. The width of the original number is equal to the maximum number of red integers greater than 1 which appear on the board at the same time. The score of the number is the number of stones which were removed from the second bucket during these splits. Then clearly the width of any number is at most $n-1$. Also, $t$ is equal to the sum of the scores of the final numbers. We claim that if a number $p>1$ has a width of at most $w$, then its score is at most $(p-1) w$. We will prove this by strong induction on $p$. If $p=1$, then clearly $p$ has a score of 0 , so the claim is true. If $p>1$, then $p$ was formed by adding two smaller numbers $a$ and $b$. Clearly $a$ and $b$ both have widths of at most $w$. Moreover, if $a$ has a width of $w$, then at some point in the reversed process there will be $w$ numbers in the set $\{2,3,4, \ldots\}$ that have split from $a$, and hence there can be no such numbers at this point which have split from $b$. Between this point and the final situation, there must always be at least one number in the set $\{2,3,4, \ldots\}$ that split from $a$, so the width of $b$ is at most $w-1$. Therefore, $a$ and $b$ cannot both have widths of $w$, so without loss of generality, $a$ has width at most $w$ and $b$ has width at most $w-1$. Then by the inductive hypothesis, $a$ has score at most $(a-1) w$ and $b$ has score at most $(b-1)(w-1)$. Hence, the score of $p$ is at most
$$
\begin{aligned}
(a-1) w+(b-1)(w-1)+\operatorname{gcd}(a, b) & \leq(a-1) w+(b-1)(w-1)+b \\
& =(p-1) w+1-w \\
& \leq(p-1) w .
\end{aligned}
$$
This completes the induction.
Now, since each number $p$ in the final configuration has width at most $(n-1)$, it has score less than $(n-1)(p-1)$. Hence the number $t$ of stones in the second bucket is less than the sum over the values of $(n-1)(p-1)$, and $s$ is equal to the sum of the the values of $(p-1)$. Therefore, $\frac{t}{s}<n-1$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n \geq 3$ be a fixed integer. The number 1 is written $n$ times on a blackboard. Below the blackboard, there are two buckets that are initially empty. A move consists of erasing two of the numbers $a$ and $b$, replacing them with the numbers 1 and $a+b$, then adding one stone to the first bucket and $\operatorname{gcd}(a, b)$ stones to the second bucket. After some finite number of moves, there are $s$ stones in the first bucket and $t$ stones in the second bucket, where $s$ and $t$ are positive integers. Find all possible values of the ratio $\frac{t}{s}$.
|
The answer is the set of all rational numbers in the interval $[1, n-1)$. First, we show that no other numbers are possible. Clearly the ratio is at least 1, since for every move, at least one stone is added to the second bucket. Note that the number $s$ of stones in the first bucket is always equal to $p-n$, where $p$ is the sum of the numbers on the blackboard. We will assume that the numbers are written in a row, and whenever two numbers $a$ and $b$ are erased, $a+b$ is written in the place of the number on the right. Let $a_{1}, a_{2}, \ldots, a_{n}$ be the numbers on the blackboard from left to right, and let
$$
q=0 \cdot a_{1}+1 \cdot a_{2}+\cdots+(n-1) a_{n}
$$
Since each number $a_{i}$ is at least 1 , we always have
$$
q \leq(n-1) p-(1+\cdots+(n-1))=(n-1) p-\frac{n(n-1)}{2}=(n-1) s+\frac{n(n-1)}{2}
$$
Also, if a move changes $a_{i}$ and $a_{j}$ with $i<j$, then $t$ changes by $\operatorname{gcd}\left(a_{i}, a_{j}\right) \leq a_{i}$ and $q$ increases by
$$
(j-1) a_{i}-(i-1)\left(a_{i}-1\right) \geq i a_{i}-(i-1)\left(a_{i}-1\right) \geq a_{i}
$$
Hence $q-t$ never decreases. We may assume without loss of generality that the first move involves the rightmost 1. Then immediately after this move, $q=0+1+\cdots+(n-2)+(n-1) \cdot 2=\frac{(n+2)(n-1)}{2}$ and
$t=1$. So after that move, we always have
$$
\begin{aligned}
t & \leq q+1-\frac{(n+2)(n-1)}{2} \\
& \leq(n-1) s+\frac{n(n-1)}{2}-\frac{(n+2)(n-1)}{2}+1 \\
& =(n-1) s-(n-2)<(n-1) s
\end{aligned}
$$
Hence, $\frac{t}{s}<n-1$. So $\frac{t}{s}$ must be a rational number in $[1, n-1)$.
After a single move, we have $\frac{t}{s}=1$, so it remains to prove that $\frac{t}{s}$ can be any rational number in $(1, n-1)$. We will now show by induction on $n$ that for any positive integer $a$, it is possible to reach a situation where there are $n-1$ occurrences of 1 on the board and the number $a^{n-1}$, with $t$ and $s$ equal to $a^{n-2}(a-1)(n-1)$ and $a^{n-1}-1$, respectively. For $n=2$, this is clear as there is only one possible move at each step, so after $a-1$ moves $s$ and $t$ will both be equal to $a-1$. Now assume that the claim is true for $n-1$, where $n>2$. Call the algorithm which creates this situation using $n-1$ numbers algorithm $A$. Then to reach the situation for size $n$, we apply algorithm $A$, to create the number $a^{n-2}$. Next, apply algorithm $A$ again and then add the two large numbers, repeat until we get the number $a^{n-1}$. Then algorithm $A$ was applied $a$ times and the two larger numbers were added $a-1$ times. Each time the two larger numbers are added, $t$ increases by $a^{n-2}$ and each time algorithm $A$ is applied, $t$ increases by $a^{n-3}(a-1)(n-2)$. Hence, the final value of $t$ is
$$
t=(a-1) a^{n-2}+a \cdot a^{n-3}(a-1)(n-2)=a^{n-2}(a-1)(n-1)
$$
This completes the induction.
Now we can choose 1 and the large number $b$ times for any positive integer $b$, and this will add $b$ stones to each bucket. At this point we have
$$
\frac{t}{s}=\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}
$$
So we just need to show that for any rational number $\frac{p}{q} \in(1, n-1)$, there exist positive integers $a$ and $b$ such that
$$
\frac{p}{q}=\frac{a^{n-2}(a-1)(n-1)+b}{a^{n-1}-1+b}
$$
Rearranging, we see that this happens if and only if
$$
b=\frac{q a^{n-2}(a-1)(n-1)-p\left(a^{n-1}-1\right)}{p-q} .
$$
If we choose $a \equiv 1(\bmod p-q)$, then this will be an integer, so we just need to check that the numerator is positive for sufficiently large $a$.
$$
\begin{aligned}
q a^{n-2}(a-1)(n-1)-p\left(a^{n-1}-1\right) & >q a^{n-2}(a-1)(n-1)-p a^{n-1} \\
& =a^{n-2}(a(q(n-1)-p)-(n-1))
\end{aligned}
$$
which is positive for sufficiently large $a$ since $q(n-1)-p>0$.
Alternative solution for the upper bound. Rather than starting with $n$ occurrences of 1 , we may start with infinitely many 1 s , but we are restricted to having at most $n-1$ numbers which are not equal to 1 on the board at any time. It is easy to see that this does not change the problem. Note also that we can ignore the 1 we write on the board each move, so the allowed move is to rub off two numbers and write their sum. We define the width and score of a number on the board as follows. Colour that number red, then reverse every move up to that point all the way back to the situation when the numbers are all 1 s . Whenever a red number is split, colour the two replacement numbers
red. The width of the original number is equal to the maximum number of red integers greater than 1 which appear on the board at the same time. The score of the number is the number of stones which were removed from the second bucket during these splits. Then clearly the width of any number is at most $n-1$. Also, $t$ is equal to the sum of the scores of the final numbers. We claim that if a number $p>1$ has a width of at most $w$, then its score is at most $(p-1) w$. We will prove this by strong induction on $p$. If $p=1$, then clearly $p$ has a score of 0 , so the claim is true. If $p>1$, then $p$ was formed by adding two smaller numbers $a$ and $b$. Clearly $a$ and $b$ both have widths of at most $w$. Moreover, if $a$ has a width of $w$, then at some point in the reversed process there will be $w$ numbers in the set $\{2,3,4, \ldots\}$ that have split from $a$, and hence there can be no such numbers at this point which have split from $b$. Between this point and the final situation, there must always be at least one number in the set $\{2,3,4, \ldots\}$ that split from $a$, so the width of $b$ is at most $w-1$. Therefore, $a$ and $b$ cannot both have widths of $w$, so without loss of generality, $a$ has width at most $w$ and $b$ has width at most $w-1$. Then by the inductive hypothesis, $a$ has score at most $(a-1) w$ and $b$ has score at most $(b-1)(w-1)$. Hence, the score of $p$ is at most
$$
\begin{aligned}
(a-1) w+(b-1)(w-1)+\operatorname{gcd}(a, b) & \leq(a-1) w+(b-1)(w-1)+b \\
& =(p-1) w+1-w \\
& \leq(p-1) w .
\end{aligned}
$$
This completes the induction.
Now, since each number $p$ in the final configuration has width at most $(n-1)$, it has score less than $(n-1)(p-1)$. Hence the number $t$ of stones in the second bucket is less than the sum over the values of $(n-1)(p-1)$, and $s$ is equal to the sum of the the values of $(p-1)$. Therefore, $\frac{t}{s}<n-1$.
|
{
"resource_path": "APMO/segmented/en-apmo2020_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution:"
}
|
7f8f1632-ce51-5e24-9db0-47b26446bd10
| 606,148
|
Prove that for each real number $r>2$, there are exactly two or three positive real numbers $x$ satisfying the equation $x^{2}=r\lfloor x\rfloor$.
Note: $\lfloor x\rfloor$ denotes the largest integer less than or equal to $x$
|
Let $r>2$ be a real number. Let $x$ be a positive real number such that $x^{2}=r\lfloor x\rfloor$ with $\lfloor x\rfloor=k$. Since $x>0$ and $x^{2}=r k$, we also have $k>0$. From $k \leq x<k+1$, we get $k^{2} \leq x^{2}=r k<$ $k^{2}+2 k+1 \leq k^{2}+3 k$, hence $k \leq r<k+3$, or $r-3<k \leq r$. There are at most three positive integers in the interval $(r-3, r]$. Thus there are at most three possible values for $k$. Consequently, there are at most three positive solutions to the given equation.
Now suppose that $k$ is a positive integer in the interval $[r-2, r]$. There are at least two such positive integer. Observe that $k \leq \sqrt{r k} \leq \sqrt{(k+2) k}<k+1$ and so $r k=r\lfloor\sqrt{r k}\rfloor$. We conclude that the equation $x^{2}=r\lfloor x\rfloor$ has at least two positive solutions, namely $x=\sqrt{r k}$ with $k \in[r-2, r]$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for each real number $r>2$, there are exactly two or three positive real numbers $x$ satisfying the equation $x^{2}=r\lfloor x\rfloor$.
Note: $\lfloor x\rfloor$ denotes the largest integer less than or equal to $x$
|
Let $r>2$ be a real number. Let $x$ be a positive real number such that $x^{2}=r\lfloor x\rfloor$ with $\lfloor x\rfloor=k$. Since $x>0$ and $x^{2}=r k$, we also have $k>0$. From $k \leq x<k+1$, we get $k^{2} \leq x^{2}=r k<$ $k^{2}+2 k+1 \leq k^{2}+3 k$, hence $k \leq r<k+3$, or $r-3<k \leq r$. There are at most three positive integers in the interval $(r-3, r]$. Thus there are at most three possible values for $k$. Consequently, there are at most three positive solutions to the given equation.
Now suppose that $k$ is a positive integer in the interval $[r-2, r]$. There are at least two such positive integer. Observe that $k \leq \sqrt{r k} \leq \sqrt{(k+2) k}<k+1$ and so $r k=r\lfloor\sqrt{r k}\rfloor$. We conclude that the equation $x^{2}=r\lfloor x\rfloor$ has at least two positive solutions, namely $x=\sqrt{r k}$ with $k \in[r-2, r]$.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution "
}
|
6c726acd-7c5f-56e3-8c41-96274f3501a1
| 606,157
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
There are two possible families of solutions:
- $P(x)=x+d$, for some integer $d \geq-2022$.
- $P(x)=-x+d$, for some integer $d \leq 2022$.
Suppose $P$ satisfies the problem conditions. Clearly $P$ cannot be a constant polynomial. Notice that a polynomial $P$ satifies the conditions if and only if $-P$ also satisfies them. Hence, we may assume the leading coefficient of $P$ is positive. Then, there exists positive integer $M$ such that $P(x)>0$ for $x \geq M$.
Lemma 1. For any positive integer $n$, the integers $P(1), P(2), \ldots, P(n)$ leave pairwise distinct remainders upon division by $n$.
Proof. Assume for contradiction that this is not the case. Then, for some $1 \leq y<z \leq n$, there exists $0 \leq r \leq n-1$ such that $P(y) \equiv P(z) \equiv r(\bmod n)$. Since $P(a n+b) \equiv P(b)(\bmod n)$ for all $a, b$ integers, we have $P(a n+y) \equiv P(a n+z) \equiv r(\bmod n)$ for any integer $a$. Let $A$ be a positive integer such that $A n \geq M$, and let $k$ be a positive integer such that $k>2 A+2021$. Each of the $2(k-A)$ integers $P(A n+y), P(A n+z), P((A+1) n+y), P((A+1) n+z), \ldots, P((k-1) n+y), P((k-1) n+z)$ leaves one of the $k$ remainders
$$
r, n+r, 2 n+r, \ldots,(k-1) n+r
$$
upon division by $k n$. This implies that at least $2(k-A)-k=k-2 A$ (possibly overlapping) pairs leave the same remainder upon division by $k n$. Since $k-2 A>2021$ and all of the $2(k-A)$ integers are positive, we find more than 2021 pairs $a, b$ with $a<b \leq k n$ for which $|P(b)|-|P(a)|$ is divisible by $k n$-hence, $P_{k n}>2021$, a contradiction.
Next, we show that $P$ is linear. Assume that this is not the case, i.e., $\operatorname{deg} P \geq 2$. Then we can find a positive integer $k$ such that $P(k)-P(1) \geq k$. This means that among the integers $P(1), P(2), \ldots, P(P(k)-P(1))$, two of them, namely $P(k)$ and $P(1)$, leave the same remainder upon division by $P(k)-P(1)$ - contradicting the lemma (by taking $n=P(k)-P(1)$ ). Hence, $P$ must be linear.
We can now write $P(x)=c x+d$ with $c>0$. We prove that $c=1$ by two ways.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
There are two possible families of solutions:
- $P(x)=x+d$, for some integer $d \geq-2022$.
- $P(x)=-x+d$, for some integer $d \leq 2022$.
Suppose $P$ satisfies the problem conditions. Clearly $P$ cannot be a constant polynomial. Notice that a polynomial $P$ satifies the conditions if and only if $-P$ also satisfies them. Hence, we may assume the leading coefficient of $P$ is positive. Then, there exists positive integer $M$ such that $P(x)>0$ for $x \geq M$.
Lemma 1. For any positive integer $n$, the integers $P(1), P(2), \ldots, P(n)$ leave pairwise distinct remainders upon division by $n$.
Proof. Assume for contradiction that this is not the case. Then, for some $1 \leq y<z \leq n$, there exists $0 \leq r \leq n-1$ such that $P(y) \equiv P(z) \equiv r(\bmod n)$. Since $P(a n+b) \equiv P(b)(\bmod n)$ for all $a, b$ integers, we have $P(a n+y) \equiv P(a n+z) \equiv r(\bmod n)$ for any integer $a$. Let $A$ be a positive integer such that $A n \geq M$, and let $k$ be a positive integer such that $k>2 A+2021$. Each of the $2(k-A)$ integers $P(A n+y), P(A n+z), P((A+1) n+y), P((A+1) n+z), \ldots, P((k-1) n+y), P((k-1) n+z)$ leaves one of the $k$ remainders
$$
r, n+r, 2 n+r, \ldots,(k-1) n+r
$$
upon division by $k n$. This implies that at least $2(k-A)-k=k-2 A$ (possibly overlapping) pairs leave the same remainder upon division by $k n$. Since $k-2 A>2021$ and all of the $2(k-A)$ integers are positive, we find more than 2021 pairs $a, b$ with $a<b \leq k n$ for which $|P(b)|-|P(a)|$ is divisible by $k n$-hence, $P_{k n}>2021$, a contradiction.
Next, we show that $P$ is linear. Assume that this is not the case, i.e., $\operatorname{deg} P \geq 2$. Then we can find a positive integer $k$ such that $P(k)-P(1) \geq k$. This means that among the integers $P(1), P(2), \ldots, P(P(k)-P(1))$, two of them, namely $P(k)$ and $P(1)$, leave the same remainder upon division by $P(k)-P(1)$ - contradicting the lemma (by taking $n=P(k)-P(1)$ ). Hence, $P$ must be linear.
We can now write $P(x)=c x+d$ with $c>0$. We prove that $c=1$ by two ways.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution "
}
|
e382d9eb-3e12-5e5b-8bf5-28bca614e37a
| 606,171
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
If $c \geq 2$, then $P(1)$ and $P(2)$ leave the same remainder upon division by $c$, contradicting the Lemma. Hence $c=1$.
|
c=1
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
If $c \geq 2$, then $P(1)$ and $P(2)$ leave the same remainder upon division by $c$, contradicting the Lemma. Hence $c=1$.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1"
}
|
e382d9eb-3e12-5e5b-8bf5-28bca614e37a
| 606,171
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
Suppose $c \geq 2$. Let $n$ be a positive integer such that $n>2 c M, n\left(1-\frac{3}{2 c}\right)>2022$ and $2 c \mid n$. Notice that for any positive integers $i$ such that $\frac{3 n}{2 c}+i<n, P\left(\frac{3 n}{2 c}+i\right)-P\left(\frac{n}{2 c}+i\right)=n$. Hence, $\left(\frac{n}{2 c}+i, \frac{3 n}{2 c}+i\right)$ satifies the condition in the question for all positive integers $i$ such that $\frac{3 n}{2 c}+i<n$. Hence, $P_{n}>2021$, a contradiction. Then, $c=1$.
If $d \leq-2023$, then there are at least 2022 pairs $a<b$ such that $P(a)=P(b)$, namely $(a, b)=$ $(1,-2 d-1),(2,-2 d-2), \ldots,(-d-1,-d+1)$. This implies that $d \geq-2022$.
Finally, we verify that $P(x)=x+d$ satisfies the condition for any $d \geq-2022$. Fix a positive integer $n$. Note that $\| P(b)|-|P(a)||<n$ for all positive integers $a<b \leq n$, so the only pairs $a, b$ for which $|P(b)|-|P(a)|$ could be divisible by $n$ are those for which $|P(a)|=|P(b)|$. When $d \geq-2022$, there are indeed at most 2021 such pairs.
|
P(x)=x+d \text{ for any } d \geq -2022
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a polynomial $P$ and a positive integer $n$, define $P_{n}$ as the number of positive integer pairs $(a, b)$ such that $a<b \leq n$ and $|P(a)|-|P(b)|$ is divisible by $n$.
Determine all polynomial $P$ with integer coefficients such that for all positive integers $n, P_{n} \leq 2021$.
|
Suppose $c \geq 2$. Let $n$ be a positive integer such that $n>2 c M, n\left(1-\frac{3}{2 c}\right)>2022$ and $2 c \mid n$. Notice that for any positive integers $i$ such that $\frac{3 n}{2 c}+i<n, P\left(\frac{3 n}{2 c}+i\right)-P\left(\frac{n}{2 c}+i\right)=n$. Hence, $\left(\frac{n}{2 c}+i, \frac{3 n}{2 c}+i\right)$ satifies the condition in the question for all positive integers $i$ such that $\frac{3 n}{2 c}+i<n$. Hence, $P_{n}>2021$, a contradiction. Then, $c=1$.
If $d \leq-2023$, then there are at least 2022 pairs $a<b$ such that $P(a)=P(b)$, namely $(a, b)=$ $(1,-2 d-1),(2,-2 d-2), \ldots,(-d-1,-d+1)$. This implies that $d \geq-2022$.
Finally, we verify that $P(x)=x+d$ satisfies the condition for any $d \geq-2022$. Fix a positive integer $n$. Note that $\| P(b)|-|P(a)||<n$ for all positive integers $a<b \leq n$, so the only pairs $a, b$ for which $|P(b)|-|P(a)|$ could be divisible by $n$ are those for which $|P(a)|=|P(b)|$. When $d \geq-2022$, there are indeed at most 2021 such pairs.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2"
}
|
e382d9eb-3e12-5e5b-8bf5-28bca614e37a
| 606,171
|
Let $A B C D$ be a cyclic convex quadrilateral and $\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.
|
Let $L$ be the intersection of the bisectors of $\angle A B C$ and $\angle B C D$. Let $N$ be the $E$-excenter of $\triangle B C E$. Let $\angle B A C=\angle B D C=\alpha, \angle D B C=\beta$ and $\angle A C B=\gamma$.
We have the following:
$$
\begin{array}{r}
\angle C B L=\frac{1}{2} \angle A B C=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \gamma \text { and } \angle B C L=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta, \\
\angle C B N=90^{\circ}-\frac{1}{2} \beta \text { and } \angle B C N=90^{\circ}-\frac{1}{2} \gamma, \\
\angle M B L=\angle M B C+\angle C B L=90^{\circ}-\frac{1}{2} \gamma \text { and } \angle M C L=90^{\circ}-\frac{1}{2} \beta, \\
\angle L C N=\angle L B N=180^{\circ}-\frac{1}{2}(\alpha+\beta+\gamma) .
\end{array}
$$
Applying the sine rule to $\triangle M B L$ and $\triangle M C L$ we obtain
$$
\frac{M B}{M L}=\frac{M C}{M L}=\frac{\sin \angle B L M}{\sin \angle M B L}=\frac{\sin \angle C L M}{\sin \angle M C L}
$$
It follows that
$$
\frac{\sin \angle B L M}{\sin \angle C L M}=\frac{\sin \angle M B L}{\sin \angle M C L}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)}
$$
Now
$$
\frac{\sin \angle B L M}{\sin \angle M L C} \cdot \frac{\sin \angle L C N}{\sin \angle N C B} \cdot \frac{\sin \angle N B C}{\sin \angle N B L}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)} \cdot \frac{\sin \left(90^{\circ}-\frac{1}{2} \beta\right)}{\sin \left(90^{\circ}-\frac{1}{2} \gamma\right)}=1
$$
Hence $L M, B N, C N$ are concurrent and therefore $L, M, N$ are collinear.
## Alternative proof
We proceed similarly as above until the equation (1).
We use the following lemma.
Lemma: If $\pi>\alpha, \beta, \gamma, \delta>0, \alpha+\beta=\gamma+\delta<\pi$, and $\frac{\sin \alpha}{\sin \beta}=\frac{\sin \gamma}{\sin \delta}$, then $\alpha=\gamma$ and $\beta=\delta$.
Proof of Lemma: Let $\theta=\alpha+\beta=\gamma+\delta$. Then $\frac{\sin (\theta-\beta)}{\sin \beta}=\frac{\sin (\theta-\delta)}{\sin \delta}$.
$$
\begin{gathered}
\Longleftrightarrow \sin (\theta-\beta) \sin \delta=\sin (\theta-\delta) \sin \beta \\
\Longleftrightarrow(\sin \theta \cos \beta-\sin \beta \cos \theta) \sin \delta=(\sin \theta \cos \delta-\sin \delta \cos \theta) \sin \beta \\
\Longleftrightarrow \sin \theta \cos \beta \sin \delta=\sin \theta \cos \delta \sin \beta \\
\Longleftrightarrow \sin \theta \sin (\beta-\delta)=0
\end{gathered}
$$
Since $0<\theta<\pi$, then $\sin \theta \neq 0$. Therefore, $\sin (\beta-\delta)=0$, and we must have $\beta=\delta$.
Applying the sine rule to $\triangle N B L$ and $\triangle N C L$ we obtain
$$
\begin{aligned}
& \frac{N B}{N L}=\frac{\sin \angle B L N}{\sin \angle L B N} \\
& \frac{N C}{N L}=\frac{\sin \angle C L N}{\sin \angle L C N}
\end{aligned}
$$
Since $\angle L B N=\angle L C N$, it follows that
$$
\frac{\sin \angle B L N}{\sin \angle C L N}=\frac{N B}{N C}=\frac{\sin \angle B C N}{\sin \angle C B N}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)}=\frac{\sin \angle B L M}{\sin \angle C L M}
$$
By the lemma, it is concluded that $\angle B L M=\angle B L N$ and $\angle C L M=\angle C L N$. Therefore, $L, M, N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic convex quadrilateral and $\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.
|
Let $L$ be the intersection of the bisectors of $\angle A B C$ and $\angle B C D$. Let $N$ be the $E$-excenter of $\triangle B C E$. Let $\angle B A C=\angle B D C=\alpha, \angle D B C=\beta$ and $\angle A C B=\gamma$.
We have the following:
$$
\begin{array}{r}
\angle C B L=\frac{1}{2} \angle A B C=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \gamma \text { and } \angle B C L=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta, \\
\angle C B N=90^{\circ}-\frac{1}{2} \beta \text { and } \angle B C N=90^{\circ}-\frac{1}{2} \gamma, \\
\angle M B L=\angle M B C+\angle C B L=90^{\circ}-\frac{1}{2} \gamma \text { and } \angle M C L=90^{\circ}-\frac{1}{2} \beta, \\
\angle L C N=\angle L B N=180^{\circ}-\frac{1}{2}(\alpha+\beta+\gamma) .
\end{array}
$$
Applying the sine rule to $\triangle M B L$ and $\triangle M C L$ we obtain
$$
\frac{M B}{M L}=\frac{M C}{M L}=\frac{\sin \angle B L M}{\sin \angle M B L}=\frac{\sin \angle C L M}{\sin \angle M C L}
$$
It follows that
$$
\frac{\sin \angle B L M}{\sin \angle C L M}=\frac{\sin \angle M B L}{\sin \angle M C L}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)}
$$
Now
$$
\frac{\sin \angle B L M}{\sin \angle M L C} \cdot \frac{\sin \angle L C N}{\sin \angle N C B} \cdot \frac{\sin \angle N B C}{\sin \angle N B L}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)} \cdot \frac{\sin \left(90^{\circ}-\frac{1}{2} \beta\right)}{\sin \left(90^{\circ}-\frac{1}{2} \gamma\right)}=1
$$
Hence $L M, B N, C N$ are concurrent and therefore $L, M, N$ are collinear.
## Alternative proof
We proceed similarly as above until the equation (1).
We use the following lemma.
Lemma: If $\pi>\alpha, \beta, \gamma, \delta>0, \alpha+\beta=\gamma+\delta<\pi$, and $\frac{\sin \alpha}{\sin \beta}=\frac{\sin \gamma}{\sin \delta}$, then $\alpha=\gamma$ and $\beta=\delta$.
Proof of Lemma: Let $\theta=\alpha+\beta=\gamma+\delta$. Then $\frac{\sin (\theta-\beta)}{\sin \beta}=\frac{\sin (\theta-\delta)}{\sin \delta}$.
$$
\begin{gathered}
\Longleftrightarrow \sin (\theta-\beta) \sin \delta=\sin (\theta-\delta) \sin \beta \\
\Longleftrightarrow(\sin \theta \cos \beta-\sin \beta \cos \theta) \sin \delta=(\sin \theta \cos \delta-\sin \delta \cos \theta) \sin \beta \\
\Longleftrightarrow \sin \theta \cos \beta \sin \delta=\sin \theta \cos \delta \sin \beta \\
\Longleftrightarrow \sin \theta \sin (\beta-\delta)=0
\end{gathered}
$$
Since $0<\theta<\pi$, then $\sin \theta \neq 0$. Therefore, $\sin (\beta-\delta)=0$, and we must have $\beta=\delta$.
Applying the sine rule to $\triangle N B L$ and $\triangle N C L$ we obtain
$$
\begin{aligned}
& \frac{N B}{N L}=\frac{\sin \angle B L N}{\sin \angle L B N} \\
& \frac{N C}{N L}=\frac{\sin \angle C L N}{\sin \angle L C N}
\end{aligned}
$$
Since $\angle L B N=\angle L C N$, it follows that
$$
\frac{\sin \angle B L N}{\sin \angle C L N}=\frac{N B}{N C}=\frac{\sin \angle B C N}{\sin \angle C B N}=\frac{\cos (\gamma / 2)}{\cos (\beta / 2)}=\frac{\sin \angle B L M}{\sin \angle C L M}
$$
By the lemma, it is concluded that $\angle B L M=\angle B L N$ and $\angle C L M=\angle C L N$. Therefore, $L, M, N$ are collinear.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution 1"
}
|
1df0f04f-7786-5944-8c9d-b08d52c547dd
| 606,205
|
Let $A B C D$ be a cyclic convex quadrilateral and $\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.
|
Denote by $N$ the excenter of triangle $B C E$ opposite $E$. Since $B L$ bisects $\angle A B C$, we have $\angle C B L=$ $\frac{\angle A B C}{2}$. Since $M$ is the midpoint of arc $B C$, we have $\angle M B C=\frac{1}{2}(\angle M B C+\angle M C B)$ It follows by angle chasing that
$$
\begin{aligned}
\angle M B L & =\angle M B C+\angle C B L=\frac{1}{2}(\angle M B C+\angle M C B+\angle A B C) \\
& =\frac{1}{2}(\angle M B A+\angle M C B)=90^{\circ}-\frac{\angle B C E}{2}=\angle B C N .
\end{aligned}
$$
Denote by $X$ and $Y$ the second intersections of lines $B M$ and $C M$ with the circumcircle of $B C L$, respectively. Since $\angle M B C=\angle M C B$, we have $B C \| X Y$. It suffices to show that $B N \| X L$ and $C N \| Y L$. Indeed, from this it follows that $\triangle B C N \sim \triangle X Y L$, and therefore a homothety with center $M$ that maps $B$ to $X$ and $C$ to $Y$ also maps $N$ to $L$, implying that $N$ lies on the line $L M$.
By symmetry, it suffices to show that $C N \| Y L$, which is equivalent to showing that $\angle B C N=\angle X Y L$. But we have $\angle B C N=\angle M B L=\angle X B L=\angle X Y L$, completing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic convex quadrilateral and $\Gamma$ be its circumcircle. Let $E$ be the intersection of the diagonals $A C$ and $B D$, let $L$ be the center of the circle tangent to sides $A B, B C$, and $C D$, and let $M$ be the midpoint of the arc $B C$ of $\Gamma$ not containing $A$ and $D$. Prove that the excenter of triangle $B C E$ opposite $E$ lies on the line $L M$.
|
Denote by $N$ the excenter of triangle $B C E$ opposite $E$. Since $B L$ bisects $\angle A B C$, we have $\angle C B L=$ $\frac{\angle A B C}{2}$. Since $M$ is the midpoint of arc $B C$, we have $\angle M B C=\frac{1}{2}(\angle M B C+\angle M C B)$ It follows by angle chasing that
$$
\begin{aligned}
\angle M B L & =\angle M B C+\angle C B L=\frac{1}{2}(\angle M B C+\angle M C B+\angle A B C) \\
& =\frac{1}{2}(\angle M B A+\angle M C B)=90^{\circ}-\frac{\angle B C E}{2}=\angle B C N .
\end{aligned}
$$
Denote by $X$ and $Y$ the second intersections of lines $B M$ and $C M$ with the circumcircle of $B C L$, respectively. Since $\angle M B C=\angle M C B$, we have $B C \| X Y$. It suffices to show that $B N \| X L$ and $C N \| Y L$. Indeed, from this it follows that $\triangle B C N \sim \triangle X Y L$, and therefore a homothety with center $M$ that maps $B$ to $X$ and $C$ to $Y$ also maps $N$ to $L$, implying that $N$ lies on the line $L M$.
By symmetry, it suffices to show that $C N \| Y L$, which is equivalent to showing that $\angle B C N=\angle X Y L$. But we have $\angle B C N=\angle M B L=\angle X B L=\angle X Y L$, completing the proof.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution 2"
}
|
1df0f04f-7786-5944-8c9d-b08d52c547dd
| 606,205
|
Given a $32 \times 32$ table, we put a mouse (facing up) at the bottom left cell and a piece of cheese at several other cells. The mouse then starts moving. It moves forward except that when it reaches a piece of cheese, it eats a part of it, turns right, and continues moving forward. We say that a subset of cells containing cheese is good if, during this process, the mouse tastes each piece of cheese exactly once and then falls off the table. Show that:
(a) No good subset consists of 888 cells.
(b) There exists a good subset consisting of at least 666 cells.
|
(a) For the sake of contradiction, assume a good subset consisting of 888 cells exists. We call those cheese-cells and the other ones gap-cells. Observe that since each cheese-cell is visited once, each gap-cell is visited at most twice (once vertically and once horizontally). Define a finite sequence $s$ whose $i$-th element is $C$ if the $i$-th step of the mouse was onto a cheese-cell, and $G$ if it was onto a gap-cell. By assumption, $s$ contains $888 C$ 's. Note that $s$ does not contain a contiguous block of 4 (or more) $C$ 's. Hence $s$ contains at least $888 / 3=296$ such $C$-blocks and thus at least $295 G^{\prime}$ 's. But since each gap-cell is traversed at most twice, this implies there are at least $\lceil 295 / 2\rceil=148$ gap-cells, for a total of $888+148=1036>32^{2}$ cells, a contradiction.
(b) Let $L_{i}, X_{i}$ be two $2^{i} \times 2^{i}$ tiles that allow the mouse to "turn left" and "cross", respectively. In detail, the "turn left" tiles allow the mouse to enter at its bottom left cell facing up and to leave at its bottom left cell facing left. The "cross" tiles allow the mouse to enter at its top right facing down and leave at its bottom left facing left, while also to enter at its bottom left facing up and leave at its top right facing right.
(a) Basic tiles
(b) Inductive construction
(c) $16 \times 16$
Note that given two $2^{i} \times 2^{i}$ tiles $L_{i}, X_{i}$ we can construct larger $2^{i+1} \times 2^{i+1}$ tiles $L_{i+1}, X_{i+1}$ inductively as shown on in (b). The construction works because the path intersects itself (or the other path) only inside the smaller $X$-tiles where it works by induction.
For a tile $T$, let $|T|$ be the number of pieces of cheese in it. By straightforward induction, $\left|L_{i}\right|=\left|X_{i}\right|+1$ and $\left|L_{i+1}\right|=4 \cdot\left|L_{i}\right|-1$. From the initial condition $\left|L_{1}\right|=3$. We now easily compute $\left|L_{2}\right|=11,\left|L_{3}\right|=43,\left|L_{4}\right|=171$, and $\left|L_{5}\right|=683$. Hence we get the desired subset.
## Another proof of (a).
Let $X_{N}$ be the largest possible density of cheese-cells in a good subset on an $N \times N$ table. We will show that $X_{N} \leq 4 / 5+o(1)$. Specifically, this gives $X_{32} \leq 817 / 1024$. We look at the (discrete analogue) of the winding number of the trajectory of the mouse. Since the mouse enters and leaves the table, for every 4 right turns in its trajectory there has to be a self-crossing. But each self-crossing requires a different empty square, hence $X_{N} \leq 4 / 5$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Given a $32 \times 32$ table, we put a mouse (facing up) at the bottom left cell and a piece of cheese at several other cells. The mouse then starts moving. It moves forward except that when it reaches a piece of cheese, it eats a part of it, turns right, and continues moving forward. We say that a subset of cells containing cheese is good if, during this process, the mouse tastes each piece of cheese exactly once and then falls off the table. Show that:
(a) No good subset consists of 888 cells.
(b) There exists a good subset consisting of at least 666 cells.
|
(a) For the sake of contradiction, assume a good subset consisting of 888 cells exists. We call those cheese-cells and the other ones gap-cells. Observe that since each cheese-cell is visited once, each gap-cell is visited at most twice (once vertically and once horizontally). Define a finite sequence $s$ whose $i$-th element is $C$ if the $i$-th step of the mouse was onto a cheese-cell, and $G$ if it was onto a gap-cell. By assumption, $s$ contains $888 C$ 's. Note that $s$ does not contain a contiguous block of 4 (or more) $C$ 's. Hence $s$ contains at least $888 / 3=296$ such $C$-blocks and thus at least $295 G^{\prime}$ 's. But since each gap-cell is traversed at most twice, this implies there are at least $\lceil 295 / 2\rceil=148$ gap-cells, for a total of $888+148=1036>32^{2}$ cells, a contradiction.
(b) Let $L_{i}, X_{i}$ be two $2^{i} \times 2^{i}$ tiles that allow the mouse to "turn left" and "cross", respectively. In detail, the "turn left" tiles allow the mouse to enter at its bottom left cell facing up and to leave at its bottom left cell facing left. The "cross" tiles allow the mouse to enter at its top right facing down and leave at its bottom left facing left, while also to enter at its bottom left facing up and leave at its top right facing right.
(a) Basic tiles
(b) Inductive construction
(c) $16 \times 16$

Note that given two $2^{i} \times 2^{i}$ tiles $L_{i}, X_{i}$ we can construct larger $2^{i+1} \times 2^{i+1}$ tiles $L_{i+1}, X_{i+1}$ inductively as shown on in (b). The construction works because the path intersects itself (or the other path) only inside the smaller $X$-tiles where it works by induction.
For a tile $T$, let $|T|$ be the number of pieces of cheese in it. By straightforward induction, $\left|L_{i}\right|=\left|X_{i}\right|+1$ and $\left|L_{i+1}\right|=4 \cdot\left|L_{i}\right|-1$. From the initial condition $\left|L_{1}\right|=3$. We now easily compute $\left|L_{2}\right|=11,\left|L_{3}\right|=43,\left|L_{4}\right|=171$, and $\left|L_{5}\right|=683$. Hence we get the desired subset.
## Another proof of (a).
Let $X_{N}$ be the largest possible density of cheese-cells in a good subset on an $N \times N$ table. We will show that $X_{N} \leq 4 / 5+o(1)$. Specifically, this gives $X_{32} \leq 817 / 1024$. We look at the (discrete analogue) of the winding number of the trajectory of the mouse. Since the mouse enters and leaves the table, for every 4 right turns in its trajectory there has to be a self-crossing. But each self-crossing requires a different empty square, hence $X_{N} \leq 4 / 5$.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# Solution."
}
|
57846a27-b487-59b0-aea9-f0c09db3dc6f
| 606,226
|
Determine all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ such that $f(f(a)-b)+b f(2 a)$ is a perfect square for all integers $a$ and $b$.
|
.
There are two families of functions which satisfy the condition:
(1) $f(n)= \begin{cases}0 & \text { if } n \text { is even, and } \\ \text { any perfect square } & \text { if } n \text { is odd }\end{cases}$
(2) $f(n)=n^{2}$, for every integer $n$.
It is straightforward to verify that the two families of functions are indeed solutions. Now, suppose that f is any function which satisfies the condition that $f(f(a)-b)+b f(2 a)$ is a perfect square for every pair $(a, b)$ of integers. We denote this condition by $\left(^{*}\right)$. We will show that $f$ must belong to either Family (1) or Family (2).
Claim 1. $f(0)=0$ and $f(n)$ is a perfect square for every integer $n$.
Proof. Plugging $(a, b) \rightarrow(0, f(0))$ in $\left(^{*}\right)$ shows that $f(0)(f(0)+1)=z^{2}$ for some integer $z$. Thus, $(2 f(0)+1-2 z)(2 f(0)+1+2 z)=1$. Therefore, $f(0)$ is either -1 or 0.
Suppose, for sake of contradiction, that $f(0)=-1$. For any integer $a$, plugging $(a, b) \rightarrow(a, f(a))$ implies that $f(a) f(2 a)-1$ is a square. Thus, for each $a \in \mathbb{Z}$, there exists $x \in \mathbb{Z}$ such that $f(a) f(2 a)=x^{2}+1$ This implies that any prime divisor of $f(a)$ is either 2 or is congruent to $1(\bmod 4)$, and that $4 \nmid f(a)$, for every $a \in \mathbb{Z}$.
Plugging $(a, b) \rightarrow(0,3)$ in $\left(^{*}\right)$ shows that $f(-4)-3$ is a square. Thus, there is $y \in \mathbb{Z}$ such that $f(-4)=y^{2}+3$. Since $4 \nmid f(-4)$, we note that $f(-4)$ is a positive integer congruent to $3(\bmod 4)$, but any prime dividing $f(-4)$ is either 2 or is congruent to $1(\bmod 4)$. This gives a contradiction. Therefore, $f(0)$ must be 0 .
For every integer $n$, plugging $(a, b) \rightarrow(0,-n)$ in $\left(^{*}\right)$ shows that $f(n)$ is a square.
Replacing $b$ with $f(a)-b$, we find that for all integers $a$ and $b$,
$$
f(b)+(f(a)-b) f(2 a) \text { is a square. }
$$
Now, let $S$ be the set of all integers $n$ such that $f(n)=0$. We have two cases:
- Case 1: $S$ is unbounded from above.
We claim that $f(2 n)=0$ for any integer $n$. Fix some integer $n$, and let $k \in S$ with $k>f(n)$. Then, plugging $(a, b) \mapsto(n, k)$ in $\left({ }^{* *}\right)$ gives us that $f(k)+(f(n)-k) f(2 n)=(f(n)-k) f(2 n)$ is a square. But $f(n)-k<0$ and $f(2 n)$ is a square by Claim 1. This is possible only if $f(2 n)=0$. In summary, $f(n)=0$ whenever $n$ is even and Claim 1 shows that $f(n)$ is a square whenever $n$ is odd.
- Case 2: $S$ is bounded from above.
Let $T$ be the set of all integers $n$ such that $f(n)=n^{2}$. We show that $T$ is unbounded from above. In fact, we show that $\frac{p+1}{2} \in T$ for all primes $p$ big enough.
Fix a prime number $p$ big enough, and let $n=\frac{p+1}{2}$. Plugging $(a, b) \mapsto(n, 2 n)$ in ( $\left.{ }^{* *}\right)$ shows us that $f(2 n)(f(n)-2 n+1)$ is a square for any integer $n$. For $p$ big enough, we have $2 n \notin S$, so $f(2 n)$ is a non-zero square. As a result, when $p$ is big enough, $f(n)$ and $f(n)-2 n+1=f(n)-p$ are both squares. Writing $f(n)=k^{2}$ and $f(n)-p=m^{2}$ for some $k, m \geq 0$, we have
$$
(k+m)(k-m)=k^{2}-m^{2}=p \Longrightarrow k+m=p, k-m=1 \Longrightarrow k=n, m=n-1
$$
Thus, $f(n)=k^{2}=n^{2}$, giving us $n=\frac{p+1}{2} \in T$.
Next, for all $k \in T$ and $n \in \mathbb{Z}$, plugging $(a, b) \mapsto(n, k)$ in $(* *)$ shows us that $k^{2}+(f(n)-k) f(2 n)$ is a square. But that means $(2 k-f(2 n))^{2}-\left(f(2 n)^{2}-4 f(n) f(2 n)\right)=4\left(k^{2}+(f(n)-k) f(2 n)\right)$ is also a square. When $k$ is large enough, we have $\left|f(2 n)^{2}-4 f(n) f(2 n)\right|+1<|2 k-f(2 n)|$. As a result, we must have $f(2 n)^{2}=4 f(n) f(2 n)$ and thus $f(2 n) \in\{0,4 f(n)\}$ for all integers $n$.
Finally, we prove that $f(n)=n^{2}$ for all integers $n$. Fix $n$, and take $k \in T$ big enough such that $2 k \notin S$. Then, we have $f(k)=k^{2}$ and $f(2 k)=4 f(k)=4 k^{2}$. Plugging $(a, b) \mapsto(k, n)$ to $(* *)$ shows us that $f(n)+\left(k^{2}-n\right) 4 k^{2}=\left(2 k^{2}-n\right)^{2}+\left(f(n)-n^{2}\right)$ is a square. Since $T$ is unbounded from above, we can take $k \in T$ such that $2 k \notin S$ and also $\left|2 k^{2}-n\right|>\left|f(n)-n^{2}\right|$. This forces $f(n)=n^{2}$, giving us the second family of solution.
## Another approach of Case 1.
Claim 2. One of the following is true.
(i) For every integer $n, f(2 n)=0$.
(ii) There exists an integer $K>0$ such that for every integer $n \geq K, f(n)>0$.
Proof. Suppose that there exists an integer $\alpha \neq 0$ such that $f(2 \alpha)>0$. We claim that for every integer $n \geq f(\alpha)+1$, we have $f(n)>0$.
For every $n \geq f(\alpha)+1$, plugging $(a, b) \rightarrow(\alpha, f(\alpha)-n)$ in $\left(^{*}\right)$ shows that $f(n)+(f(\alpha)-n) f(2 \alpha)$ is a square, and in particular, is non-negative. Hence, $f(n) \geq(n-f(\alpha)) f(2 \alpha)>0$, as desired.
If $f$ belongs to Case (i), Claim 1 shows that $f$ belongs to Family (1).
If $f$ belongs to Case (ii), then $S$ is bounded from above. From Case 2 we get $f(n)=n^{2}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ such that $f(f(a)-b)+b f(2 a)$ is a perfect square for all integers $a$ and $b$.
|
.
There are two families of functions which satisfy the condition:
(1) $f(n)= \begin{cases}0 & \text { if } n \text { is even, and } \\ \text { any perfect square } & \text { if } n \text { is odd }\end{cases}$
(2) $f(n)=n^{2}$, for every integer $n$.
It is straightforward to verify that the two families of functions are indeed solutions. Now, suppose that f is any function which satisfies the condition that $f(f(a)-b)+b f(2 a)$ is a perfect square for every pair $(a, b)$ of integers. We denote this condition by $\left(^{*}\right)$. We will show that $f$ must belong to either Family (1) or Family (2).
Claim 1. $f(0)=0$ and $f(n)$ is a perfect square for every integer $n$.
Proof. Plugging $(a, b) \rightarrow(0, f(0))$ in $\left(^{*}\right)$ shows that $f(0)(f(0)+1)=z^{2}$ for some integer $z$. Thus, $(2 f(0)+1-2 z)(2 f(0)+1+2 z)=1$. Therefore, $f(0)$ is either -1 or 0.
Suppose, for sake of contradiction, that $f(0)=-1$. For any integer $a$, plugging $(a, b) \rightarrow(a, f(a))$ implies that $f(a) f(2 a)-1$ is a square. Thus, for each $a \in \mathbb{Z}$, there exists $x \in \mathbb{Z}$ such that $f(a) f(2 a)=x^{2}+1$ This implies that any prime divisor of $f(a)$ is either 2 or is congruent to $1(\bmod 4)$, and that $4 \nmid f(a)$, for every $a \in \mathbb{Z}$.
Plugging $(a, b) \rightarrow(0,3)$ in $\left(^{*}\right)$ shows that $f(-4)-3$ is a square. Thus, there is $y \in \mathbb{Z}$ such that $f(-4)=y^{2}+3$. Since $4 \nmid f(-4)$, we note that $f(-4)$ is a positive integer congruent to $3(\bmod 4)$, but any prime dividing $f(-4)$ is either 2 or is congruent to $1(\bmod 4)$. This gives a contradiction. Therefore, $f(0)$ must be 0 .
For every integer $n$, plugging $(a, b) \rightarrow(0,-n)$ in $\left(^{*}\right)$ shows that $f(n)$ is a square.
Replacing $b$ with $f(a)-b$, we find that for all integers $a$ and $b$,
$$
f(b)+(f(a)-b) f(2 a) \text { is a square. }
$$
Now, let $S$ be the set of all integers $n$ such that $f(n)=0$. We have two cases:
- Case 1: $S$ is unbounded from above.
We claim that $f(2 n)=0$ for any integer $n$. Fix some integer $n$, and let $k \in S$ with $k>f(n)$. Then, plugging $(a, b) \mapsto(n, k)$ in $\left({ }^{* *}\right)$ gives us that $f(k)+(f(n)-k) f(2 n)=(f(n)-k) f(2 n)$ is a square. But $f(n)-k<0$ and $f(2 n)$ is a square by Claim 1. This is possible only if $f(2 n)=0$. In summary, $f(n)=0$ whenever $n$ is even and Claim 1 shows that $f(n)$ is a square whenever $n$ is odd.
- Case 2: $S$ is bounded from above.
Let $T$ be the set of all integers $n$ such that $f(n)=n^{2}$. We show that $T$ is unbounded from above. In fact, we show that $\frac{p+1}{2} \in T$ for all primes $p$ big enough.
Fix a prime number $p$ big enough, and let $n=\frac{p+1}{2}$. Plugging $(a, b) \mapsto(n, 2 n)$ in ( $\left.{ }^{* *}\right)$ shows us that $f(2 n)(f(n)-2 n+1)$ is a square for any integer $n$. For $p$ big enough, we have $2 n \notin S$, so $f(2 n)$ is a non-zero square. As a result, when $p$ is big enough, $f(n)$ and $f(n)-2 n+1=f(n)-p$ are both squares. Writing $f(n)=k^{2}$ and $f(n)-p=m^{2}$ for some $k, m \geq 0$, we have
$$
(k+m)(k-m)=k^{2}-m^{2}=p \Longrightarrow k+m=p, k-m=1 \Longrightarrow k=n, m=n-1
$$
Thus, $f(n)=k^{2}=n^{2}$, giving us $n=\frac{p+1}{2} \in T$.
Next, for all $k \in T$ and $n \in \mathbb{Z}$, plugging $(a, b) \mapsto(n, k)$ in $(* *)$ shows us that $k^{2}+(f(n)-k) f(2 n)$ is a square. But that means $(2 k-f(2 n))^{2}-\left(f(2 n)^{2}-4 f(n) f(2 n)\right)=4\left(k^{2}+(f(n)-k) f(2 n)\right)$ is also a square. When $k$ is large enough, we have $\left|f(2 n)^{2}-4 f(n) f(2 n)\right|+1<|2 k-f(2 n)|$. As a result, we must have $f(2 n)^{2}=4 f(n) f(2 n)$ and thus $f(2 n) \in\{0,4 f(n)\}$ for all integers $n$.
Finally, we prove that $f(n)=n^{2}$ for all integers $n$. Fix $n$, and take $k \in T$ big enough such that $2 k \notin S$. Then, we have $f(k)=k^{2}$ and $f(2 k)=4 f(k)=4 k^{2}$. Plugging $(a, b) \mapsto(k, n)$ to $(* *)$ shows us that $f(n)+\left(k^{2}-n\right) 4 k^{2}=\left(2 k^{2}-n\right)^{2}+\left(f(n)-n^{2}\right)$ is a square. Since $T$ is unbounded from above, we can take $k \in T$ such that $2 k \notin S$ and also $\left|2 k^{2}-n\right|>\left|f(n)-n^{2}\right|$. This forces $f(n)=n^{2}$, giving us the second family of solution.
## Another approach of Case 1.
Claim 2. One of the following is true.
(i) For every integer $n, f(2 n)=0$.
(ii) There exists an integer $K>0$ such that for every integer $n \geq K, f(n)>0$.
Proof. Suppose that there exists an integer $\alpha \neq 0$ such that $f(2 \alpha)>0$. We claim that for every integer $n \geq f(\alpha)+1$, we have $f(n)>0$.
For every $n \geq f(\alpha)+1$, plugging $(a, b) \rightarrow(\alpha, f(\alpha)-n)$ in $\left(^{*}\right)$ shows that $f(n)+(f(\alpha)-n) f(2 \alpha)$ is a square, and in particular, is non-negative. Hence, $f(n) \geq(n-f(\alpha)) f(2 \alpha)>0$, as desired.
If $f$ belongs to Case (i), Claim 1 shows that $f$ belongs to Family (1).
If $f$ belongs to Case (ii), then $S$ is bounded from above. From Case 2 we get $f(n)=n^{2}$.
|
{
"resource_path": "APMO/segmented/en-apmo2021_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution 1"
}
|
408a70f4-0624-5077-907e-bc33b4c129c8
| 261,228
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.1
By inspection, we see that the pairs $(a, b)$ with $a=b$ are solutions, and so too are the pairs $(a, 1)$. We will see that these are the only solutions.
- Case 1. Consider the case $b<a$. Since $b-1$ is a multiple of $a-1$, it follows that $b=1$. This yields the second set of solutions described above.
- Case 2. This leaves the case $b \geq a$. Since the positive integer $a^{3}$ is a multiple of $b^{2}$, there is a positive integer $c$ such that $a^{3}=b^{2} c$.
Note that $a \equiv b \equiv 1$ modulo $a-1$. So we have
$$
1 \equiv a^{3}=b^{2} c \equiv c \quad(\bmod a-1) .
$$
If $c<a$, then we must have $c=1$, hence, $a^{3}=b^{2}$. So there is a positive integer $d$ such that $a=d^{2}$ and $b=d^{3}$. Now $a-1 \mid b-1$ yields $d^{2}-1 \mid d^{3}-1$. This implies that $d+1 \mid d(d+1)+1$, which is impossible.
If $c \geq a$, then $b^{2} c \geq b^{2} a \geq a^{3}=b^{2} c$. So there's equality throughout, implying $a=c=b$. This yields the first set of solutions described above.
Therefore, the solutions described above are the only solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.1
By inspection, we see that the pairs $(a, b)$ with $a=b$ are solutions, and so too are the pairs $(a, 1)$. We will see that these are the only solutions.
- Case 1. Consider the case $b<a$. Since $b-1$ is a multiple of $a-1$, it follows that $b=1$. This yields the second set of solutions described above.
- Case 2. This leaves the case $b \geq a$. Since the positive integer $a^{3}$ is a multiple of $b^{2}$, there is a positive integer $c$ such that $a^{3}=b^{2} c$.
Note that $a \equiv b \equiv 1$ modulo $a-1$. So we have
$$
1 \equiv a^{3}=b^{2} c \equiv c \quad(\bmod a-1) .
$$
If $c<a$, then we must have $c=1$, hence, $a^{3}=b^{2}$. So there is a positive integer $d$ such that $a=d^{2}$ and $b=d^{3}$. Now $a-1 \mid b-1$ yields $d^{2}-1 \mid d^{3}-1$. This implies that $d+1 \mid d(d+1)+1$, which is impossible.
If $c \geq a$, then $b^{2} c \geq b^{2} a \geq a^{3}=b^{2} c$. So there's equality throughout, implying $a=c=b$. This yields the first set of solutions described above.
Therefore, the solutions described above are the only solutions.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "# Solution 1"
}
|
1fd82075-3560-5477-8609-b10bd8415ebf
| 606,253
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.2
We will start by showing that there are positive integers $x, c, d$ such that $a=x^{2} c d$ and $b=x^{3} c$. Let $g=\operatorname{gcd}(a, b)$ so that $a=g d$ and $b=g x$ for some coprime $d$ and $x$. Then, $b^{2} \mid a^{3}$ is equivalent to $g^{2} x^{2} \mid g^{3} d^{3}$, which is equivalent to $x^{2} \mid g d^{3}$. Since $x$ and $d$ are coprime, this implies $x^{2} \mid g$. Hence, $g=x^{2} c$ for some $c$, giving $a=x^{2} c d$ and $b=x^{3} c$ as required.
Now, it remains to find all positive integers $x, c, d$ satisfying
$$
x^{2} c d-1 \mid x^{3} c-1
$$
That is, $x^{3} c \equiv 1\left(\bmod x^{2} c d-1\right)$. Assuming that this congruence holds, it follows that $d \equiv x^{3} c d \equiv x$ $\left(\bmod x^{2} c d-1\right)$. Then, either $x=d$ or $x-d \geq x^{2} c d-1$ or $d-x \geq x^{2} c d-1$.
- If $x=d$ then $b=a$.
- If $x-d \geq x^{2} c d-1$, then $x-d \geq x^{2} c d-1 \geq x-1 \geq x-d$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=d=1$, which implies that $a=b=1$.
- If $d-x \geq x^{2} c d-1$, then $d-x \geq x^{2} c d-1 \geq d-1 \geq d-x$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=1$, which implies that $b=1$.
Hence the only solutions are the pairs $(a, b)$ such that $a=b$ or $b=1$. These pairs can be checked to satisfy the given conditions.
|
a=b \text{ or } b=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.2
We will start by showing that there are positive integers $x, c, d$ such that $a=x^{2} c d$ and $b=x^{3} c$. Let $g=\operatorname{gcd}(a, b)$ so that $a=g d$ and $b=g x$ for some coprime $d$ and $x$. Then, $b^{2} \mid a^{3}$ is equivalent to $g^{2} x^{2} \mid g^{3} d^{3}$, which is equivalent to $x^{2} \mid g d^{3}$. Since $x$ and $d$ are coprime, this implies $x^{2} \mid g$. Hence, $g=x^{2} c$ for some $c$, giving $a=x^{2} c d$ and $b=x^{3} c$ as required.
Now, it remains to find all positive integers $x, c, d$ satisfying
$$
x^{2} c d-1 \mid x^{3} c-1
$$
That is, $x^{3} c \equiv 1\left(\bmod x^{2} c d-1\right)$. Assuming that this congruence holds, it follows that $d \equiv x^{3} c d \equiv x$ $\left(\bmod x^{2} c d-1\right)$. Then, either $x=d$ or $x-d \geq x^{2} c d-1$ or $d-x \geq x^{2} c d-1$.
- If $x=d$ then $b=a$.
- If $x-d \geq x^{2} c d-1$, then $x-d \geq x^{2} c d-1 \geq x-1 \geq x-d$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=d=1$, which implies that $a=b=1$.
- If $d-x \geq x^{2} c d-1$, then $d-x \geq x^{2} c d-1 \geq d-1 \geq d-x$. Hence, each of these inequalities must in fact be an equality. This implies that $x=c=1$, which implies that $b=1$.
Hence the only solutions are the pairs $(a, b)$ such that $a=b$ or $b=1$. These pairs can be checked to satisfy the given conditions.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "# Solution 1"
}
|
1fd82075-3560-5477-8609-b10bd8415ebf
| 606,253
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.3
All answers are $(n, n)$ and $(n, 1)$ where $n$ is any positive integer. They all clearly work.
To show that these are all solutions, note that we can easily eliminate the case $a=1$ or $b=1$. Thus, assume that $a, b \neq 1$ and $a \neq b$. By the second divisibility, we see that $a-1 \mid b-a$. However, $\operatorname{gcd}(a, b) \mid b-a$ and $a-1$ is relatively prime to $\operatorname{gcd}(a, b)$. This implies that $(a-1) \operatorname{gcd}(a, b) \mid b-a$, which implies $\operatorname{gcd}(a, b) \left\lvert\, \frac{b-1}{a-1}-1\right.$.
The last relation implies that $\operatorname{gcd}(a, b)<\frac{b-1}{a-1}$, since the right-hand side are positive. However, due to the first divisibility,
$$
\operatorname{gcd}(a, b)^{3}=\operatorname{gcd}\left(a^{3}, b^{3}\right) \geq \operatorname{gcd}\left(b^{2}, b^{3}\right)=b^{2} .
$$
Combining these two inequalities, we get that
$$
b^{\frac{2}{3}}<\frac{b-1}{a-1}<2 \frac{b}{a}
$$
This implies $a<2 b^{\frac{1}{3}}$. However, $b^{2} \mid a^{3}$ gives $b \leq a^{\frac{3}{2}}$. This forces
$$
a<2\left(a^{\frac{3}{2}}\right)^{\frac{1}{3}}=2 \sqrt{a} \Longrightarrow a<4 .
$$
Extracting $a=2,3$ by hand yields no additional solution.
|
(n, n) \text{ and } (n, 1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs $(a, b)$ of positive integers such that $a^{3}$ is a multiple of $b^{2}$ and $b-1$ is a multiple of $a-1$. Note: An integer $n$ is said to be a multiple of an integer $m$ if there is an integer $k$ such that $n=k m$.
|
.3
All answers are $(n, n)$ and $(n, 1)$ where $n$ is any positive integer. They all clearly work.
To show that these are all solutions, note that we can easily eliminate the case $a=1$ or $b=1$. Thus, assume that $a, b \neq 1$ and $a \neq b$. By the second divisibility, we see that $a-1 \mid b-a$. However, $\operatorname{gcd}(a, b) \mid b-a$ and $a-1$ is relatively prime to $\operatorname{gcd}(a, b)$. This implies that $(a-1) \operatorname{gcd}(a, b) \mid b-a$, which implies $\operatorname{gcd}(a, b) \left\lvert\, \frac{b-1}{a-1}-1\right.$.
The last relation implies that $\operatorname{gcd}(a, b)<\frac{b-1}{a-1}$, since the right-hand side are positive. However, due to the first divisibility,
$$
\operatorname{gcd}(a, b)^{3}=\operatorname{gcd}\left(a^{3}, b^{3}\right) \geq \operatorname{gcd}\left(b^{2}, b^{3}\right)=b^{2} .
$$
Combining these two inequalities, we get that
$$
b^{\frac{2}{3}}<\frac{b-1}{a-1}<2 \frac{b}{a}
$$
This implies $a<2 b^{\frac{1}{3}}$. However, $b^{2} \mid a^{3}$ gives $b \leq a^{\frac{3}{2}}$. This forces
$$
a<2\left(a^{\frac{3}{2}}\right)^{\frac{1}{3}}=2 \sqrt{a} \Longrightarrow a<4 .
$$
Extracting $a=2,3$ by hand yields no additional solution.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "# Solution 1"
}
|
1fd82075-3560-5477-8609-b10bd8415ebf
| 606,253
|
Let $A B C$ be a right triangle with $\angle B=90^{\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\triangle A C D$ and the circumcircle of $\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.
|
.1
Let the line $E F$ intersect the line $B C$ at $P$ and the circumcircle of $\triangle A C D$ at $G$ distinct from $F$. We will prove that $P$ is the fixed point.
First, notice that $\triangle B E D$ is isosceles with $E B=E D$. This implies $\angle E B C=\angle E D P$.
Then, $\angle D A G=\angle D F G=\angle E B C=\angle E D P$ which implies $A G \| D C$. Hence, $A G C D$ is an isosceles trapezoid.
Also, $A G \| D C$ and $A E=E D$. This implies $\triangle A E G \cong \triangle D E P$ and $A G=D P$.
Since $B$ is the foot of the perpendicular from $A$ onto the side $C D$ of the isosceles trapezoid $A G C D$, we have $P B=P D+D B=A G+D B=B C$, which does not depend on the choice of $D$. Hence, the initial statement is proven.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right triangle with $\angle B=90^{\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\triangle A C D$ and the circumcircle of $\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.

|
.1
Let the line $E F$ intersect the line $B C$ at $P$ and the circumcircle of $\triangle A C D$ at $G$ distinct from $F$. We will prove that $P$ is the fixed point.
First, notice that $\triangle B E D$ is isosceles with $E B=E D$. This implies $\angle E B C=\angle E D P$.
Then, $\angle D A G=\angle D F G=\angle E B C=\angle E D P$ which implies $A G \| D C$. Hence, $A G C D$ is an isosceles trapezoid.
Also, $A G \| D C$ and $A E=E D$. This implies $\triangle A E G \cong \triangle D E P$ and $A G=D P$.
Since $B$ is the foot of the perpendicular from $A$ onto the side $C D$ of the isosceles trapezoid $A G C D$, we have $P B=P D+D B=A G+D B=B C$, which does not depend on the choice of $D$. Hence, the initial statement is proven.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2"
}
|
f0000b7c-a3e2-50a5-a918-f70d20c0d7f2
| 606,272
|
Let $A B C$ be a right triangle with $\angle B=90^{\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\triangle A C D$ and the circumcircle of $\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.

|
.2
Set up a coordinate system where $B C$ is along the positive $x$-axis, $B A$ is along the positive $y$-axis, and $B$ is the origin. Take $A=(0, a), B=(0,0), C=(c, 0), D=(-d, 0)$ where $a, b, c, d>0$. Then $E=\left(-\frac{d}{2}, \frac{a}{2}\right)$. The general equation of a circle is
$$
x^{2}+y^{2}+2 f x+2 g y+h=0
$$
Substituting the coordinates of $A, D, C$ into (1) and solving for $f, g, h$, we find that the equation of the circumcircle of $\triangle A D C$ is
$$
x^{2}+y^{2}+(d-c) x+\left(\frac{c d}{a}-a\right) y-c d=0
$$
Similarly, the equation of the circumcircle of $\triangle B D E$ is
$$
x^{2}+y^{2}+d x+\left(\frac{d^{2}}{2 a}-\frac{a}{2}\right) y=0
$$
Then (3)-(2) gives the equation of the line $D F$ which is
$$
c x+\frac{a^{2}+d^{2}-2 c d}{2 a} y+c d=0
$$
Solving (3) and (4) simultaneously, we get
$$
F=\left(\frac{c\left(d^{2}-a^{2}-2 c d\right)}{a^{2}+(d-2 c)^{2}}, \frac{2 a c(c-d)}{a^{2}+(d-2 c)^{2}}\right)
$$
and the other solution $D=(-d, 0)$.
From this we obtain the equation of the line $E F$ which is $a x+(d-2 c) y+a c=0$. It passes through $P(-c, 0)$ which is independent of $d$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right triangle with $\angle B=90^{\circ}$. Point $D$ lies on the line $C B$ such that $B$ is between $D$ and $C$. Let $E$ be the midpoint of $A D$ and let $F$ be the second intersection point of the circumcircle of $\triangle A C D$ and the circumcircle of $\triangle B D E$. Prove that as $D$ varies, the line $E F$ passes through a fixed point.

|
.2
Set up a coordinate system where $B C$ is along the positive $x$-axis, $B A$ is along the positive $y$-axis, and $B$ is the origin. Take $A=(0, a), B=(0,0), C=(c, 0), D=(-d, 0)$ where $a, b, c, d>0$. Then $E=\left(-\frac{d}{2}, \frac{a}{2}\right)$. The general equation of a circle is
$$
x^{2}+y^{2}+2 f x+2 g y+h=0
$$
Substituting the coordinates of $A, D, C$ into (1) and solving for $f, g, h$, we find that the equation of the circumcircle of $\triangle A D C$ is
$$
x^{2}+y^{2}+(d-c) x+\left(\frac{c d}{a}-a\right) y-c d=0
$$
Similarly, the equation of the circumcircle of $\triangle B D E$ is
$$
x^{2}+y^{2}+d x+\left(\frac{d^{2}}{2 a}-\frac{a}{2}\right) y=0
$$
Then (3)-(2) gives the equation of the line $D F$ which is
$$
c x+\frac{a^{2}+d^{2}-2 c d}{2 a} y+c d=0
$$
Solving (3) and (4) simultaneously, we get
$$
F=\left(\frac{c\left(d^{2}-a^{2}-2 c d\right)}{a^{2}+(d-2 c)^{2}}, \frac{2 a c(c-d)}{a^{2}+(d-2 c)^{2}}\right)
$$
and the other solution $D=(-d, 0)$.
From this we obtain the equation of the line $E F$ which is $a x+(d-2 c) y+a c=0$. It passes through $P(-c, 0)$ which is independent of $d$.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "# Solution 2"
}
|
f0000b7c-a3e2-50a5-a918-f70d20c0d7f2
| 606,272
|
Find all positive integers $k<202$ for which there exists a positive integer $n$ such that
$$
\left\{\frac{n}{202}\right\}+\left\{\frac{2 n}{202}\right\}+\cdots+\left\{\frac{k n}{202}\right\}=\frac{k}{2}
$$
where $\{x\}$ denote the fractional part of $x$.
Note: $\{x\}$ denotes the real number $k$ with $0 \leq k<1$ such that $x-k$ is an integer.
|
Denote the equation in the problem statement as $\left(^{*}\right)$, and note that it is equivalent to the condition that the average of the remainders when dividing $n, 2 n, \ldots, k n$ by 202 is 101 . Since $\left\{\frac{i n}{202}\right\}$ is invariant in each residue class modulo 202 for each $1 \leq i \leq k$, it suffices to consider $0 \leq n<202$.
If $n=0$, so is $\left\{\frac{i n}{202}\right\}$, meaning that $(*)$ does not hold for any $k$. If $n=101$, then it can be checked that $\left(^{*}\right)$ is satisfied if and only if $k=1$. From now on, we will assume that $101 \nmid n$.
For each $1 \leq i \leq k$, let $a_{i}=\left\lfloor\frac{i n}{202}\right\rfloor=\frac{i n}{202}-\left\{\frac{i n}{202}\right\}$. Rewriting $\left(^{*}\right)$ and multiplying the equation by 202, we find that
$$
n(1+2+\ldots+k)-202\left(a_{1}+a_{2}+\ldots+a_{k}\right)=101 k
$$
Equivalently, letting $z=a_{1}+a_{2}+\ldots+a_{k}$,
$$
n k(k+1)-404 z=202 k
$$
Since $n$ is not divisible by 101 , which is prime, it follows that $101 \mid k(k+1)$. In particular, $101 \mid k$ or $101 \mid k+1$. This means that $k \in\{100,101,201\}$. We claim that all these values of $k$ work.
- If $k=201$, we may choose $n=1$. The remainders when dividing $n, 2 n, \ldots, k n$ by 202 are 1,2 , ..., 201, which have an average of 101 .
- If $k=100$, we may choose $n=2$. The remainders when dividing $n, 2 n, \ldots, k n$ by 202 are 2,4 , ..., 200, which have an average of 101.
- If $k=101$, we may choose $n=51$. To see this, note that the first four remainders are $51,102,153$, 2 , which have an average of 77 . The next four remainders $(53,104,155,4)$ are shifted upwards from the first four remainders by 2 each, and so on, until the 25 th set of the remainders ( 99 , $150,201,50)$ which have an average of 125 . Hence, the first 100 remainders have an average of $\frac{77+125}{2}=101$. The 101th remainder is also 101 , meaning that the average of all 101 remainders is 101 .
In conclusion, all values $k \in\{1,100,101,201\}$ satisfy the initial condition.
|
k \in\{1,100,101,201\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $k<202$ for which there exists a positive integer $n$ such that
$$
\left\{\frac{n}{202}\right\}+\left\{\frac{2 n}{202}\right\}+\cdots+\left\{\frac{k n}{202}\right\}=\frac{k}{2}
$$
where $\{x\}$ denote the fractional part of $x$.
Note: $\{x\}$ denotes the real number $k$ with $0 \leq k<1$ such that $x-k$ is an integer.
|
Denote the equation in the problem statement as $\left(^{*}\right)$, and note that it is equivalent to the condition that the average of the remainders when dividing $n, 2 n, \ldots, k n$ by 202 is 101 . Since $\left\{\frac{i n}{202}\right\}$ is invariant in each residue class modulo 202 for each $1 \leq i \leq k$, it suffices to consider $0 \leq n<202$.
If $n=0$, so is $\left\{\frac{i n}{202}\right\}$, meaning that $(*)$ does not hold for any $k$. If $n=101$, then it can be checked that $\left(^{*}\right)$ is satisfied if and only if $k=1$. From now on, we will assume that $101 \nmid n$.
For each $1 \leq i \leq k$, let $a_{i}=\left\lfloor\frac{i n}{202}\right\rfloor=\frac{i n}{202}-\left\{\frac{i n}{202}\right\}$. Rewriting $\left(^{*}\right)$ and multiplying the equation by 202, we find that
$$
n(1+2+\ldots+k)-202\left(a_{1}+a_{2}+\ldots+a_{k}\right)=101 k
$$
Equivalently, letting $z=a_{1}+a_{2}+\ldots+a_{k}$,
$$
n k(k+1)-404 z=202 k
$$
Since $n$ is not divisible by 101 , which is prime, it follows that $101 \mid k(k+1)$. In particular, $101 \mid k$ or $101 \mid k+1$. This means that $k \in\{100,101,201\}$. We claim that all these values of $k$ work.
- If $k=201$, we may choose $n=1$. The remainders when dividing $n, 2 n, \ldots, k n$ by 202 are 1,2 , ..., 201, which have an average of 101 .
- If $k=100$, we may choose $n=2$. The remainders when dividing $n, 2 n, \ldots, k n$ by 202 are 2,4 , ..., 200, which have an average of 101.
- If $k=101$, we may choose $n=51$. To see this, note that the first four remainders are $51,102,153$, 2 , which have an average of 77 . The next four remainders $(53,104,155,4)$ are shifted upwards from the first four remainders by 2 each, and so on, until the 25 th set of the remainders ( 99 , $150,201,50)$ which have an average of 125 . Hence, the first 100 remainders have an average of $\frac{77+125}{2}=101$. The 101th remainder is also 101 , meaning that the average of all 101 remainders is 101 .
In conclusion, all values $k \in\{1,100,101,201\}$ satisfy the initial condition.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "# Solution\n\n"
}
|
513f66a1-fd29-55f9-851f-5961803af774
| 606,286
|
Let $n$ and $k$ be positive integers. Cathy is playing the following game. There are $n$ marbles and $k$ boxes, with the marbles labelled 1 to $n$. Initially, all marbles are placed inside one box. Each turn, Cathy chooses a box and then moves the marbles with the smallest label, say $i$, to either any empty box or the box containing marble $i+1$. Cathy wins if at any point there is a box containing only marble $n$.
Determine all pairs of integers $(n, k)$ such that Cathy can win this game.
|
We claim Cathy can win if and only if $n \leq 2^{k-1}$.
First, note that each non-empty box always contains a consecutive sequence of labeled marbles. This is true since Cathy is always either removing from or placing in the lowest marble in a box. As a consequence, every move made is reversible.
Next, we prove by induction that Cathy can win if $n=2^{k-1}$. The base case of $n=k=1$ is trivial. Assume a victory can be obtained for $m$ boxes and $2^{m-1}$ marbles. Consider the case of $m+1$ boxes and $2^{m}$ marbles. Cathy can first perform a sequence of moves so that only marbles $2^{m-1}, \ldots, 2^{m}$ are left in the starting box, while keeping one box, say $B$, empty. Now move the marble $2^{m-1}$ to box $B$, then reverse all of the initial moves while treating $B$ as the starting box. At the end of that, we will have marbles $2^{m-1}+1, \ldots, 2^{m}$ in the starting box, marbles $1,2, \ldots, 2^{m-1}$ in box $B$, and $m-1$ empty boxes. By repeating the original sequence of moves on marbles $2^{m-1}+1, \ldots, 2^{m}$, using the $m$ boxes that are not box $B$, we can reach a state where only marble $2^{m}$ remains in the starting box. Therefore
a victory is possible if $n=2^{k-1}$ or smaller.
We now prove by induction that Cathy loses if $n=2^{k-1}+1$. The base case of $n=2$ and $k=1$ is trivial. Assume a victory is impossible for $m$ boxes and $2^{m-1}+1$ marbles. For the sake of contradiction, suppose that victory is possible for $m+1$ boxes and $2^{m}+1$ marbles. In a winning sequence of moves, consider the last time a marble $2^{m-1}+1$ leaves the starting box, call this move $X$. After $X$, there cannot be a time when marbles $1, \ldots, 2^{m-1}+1$ are all in the same box. Otherwise, by reversing these moves after $X$ and deleting marbles greater than $2^{m-1}+1$, it gives us a winning sequence of moves for $2^{m-1}+1$ marbles and $m$ boxes (as the original starting box is not used here), contradicting the inductive hypothesis. Hence starting from $X$, marbles 1 will never be in the same box as any marbles greater than or equal to $2^{m-1}+1$.
Now delete marbles $2, \ldots, 2^{m-1}$ and consider the winning moves starting from $X$. Marble 1 would only move from one empty box to another, while blocking other marbles from entering its box. Thus we effectively have a sequence of moves for $2^{m-1}+1$ marbles, while only able to use $m$ boxes. This again contradicts the inductive hypothesis. Therefore, a victory is not possible if $n=2^{k-1}+1$ or greater.
|
n \leq 2^{k-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ and $k$ be positive integers. Cathy is playing the following game. There are $n$ marbles and $k$ boxes, with the marbles labelled 1 to $n$. Initially, all marbles are placed inside one box. Each turn, Cathy chooses a box and then moves the marbles with the smallest label, say $i$, to either any empty box or the box containing marble $i+1$. Cathy wins if at any point there is a box containing only marble $n$.
Determine all pairs of integers $(n, k)$ such that Cathy can win this game.
|
We claim Cathy can win if and only if $n \leq 2^{k-1}$.
First, note that each non-empty box always contains a consecutive sequence of labeled marbles. This is true since Cathy is always either removing from or placing in the lowest marble in a box. As a consequence, every move made is reversible.
Next, we prove by induction that Cathy can win if $n=2^{k-1}$. The base case of $n=k=1$ is trivial. Assume a victory can be obtained for $m$ boxes and $2^{m-1}$ marbles. Consider the case of $m+1$ boxes and $2^{m}$ marbles. Cathy can first perform a sequence of moves so that only marbles $2^{m-1}, \ldots, 2^{m}$ are left in the starting box, while keeping one box, say $B$, empty. Now move the marble $2^{m-1}$ to box $B$, then reverse all of the initial moves while treating $B$ as the starting box. At the end of that, we will have marbles $2^{m-1}+1, \ldots, 2^{m}$ in the starting box, marbles $1,2, \ldots, 2^{m-1}$ in box $B$, and $m-1$ empty boxes. By repeating the original sequence of moves on marbles $2^{m-1}+1, \ldots, 2^{m}$, using the $m$ boxes that are not box $B$, we can reach a state where only marble $2^{m}$ remains in the starting box. Therefore
a victory is possible if $n=2^{k-1}$ or smaller.
We now prove by induction that Cathy loses if $n=2^{k-1}+1$. The base case of $n=2$ and $k=1$ is trivial. Assume a victory is impossible for $m$ boxes and $2^{m-1}+1$ marbles. For the sake of contradiction, suppose that victory is possible for $m+1$ boxes and $2^{m}+1$ marbles. In a winning sequence of moves, consider the last time a marble $2^{m-1}+1$ leaves the starting box, call this move $X$. After $X$, there cannot be a time when marbles $1, \ldots, 2^{m-1}+1$ are all in the same box. Otherwise, by reversing these moves after $X$ and deleting marbles greater than $2^{m-1}+1$, it gives us a winning sequence of moves for $2^{m-1}+1$ marbles and $m$ boxes (as the original starting box is not used here), contradicting the inductive hypothesis. Hence starting from $X$, marbles 1 will never be in the same box as any marbles greater than or equal to $2^{m-1}+1$.
Now delete marbles $2, \ldots, 2^{m-1}$ and consider the winning moves starting from $X$. Marble 1 would only move from one empty box to another, while blocking other marbles from entering its box. Thus we effectively have a sequence of moves for $2^{m-1}+1$ marbles, while only able to use $m$ boxes. This again contradicts the inductive hypothesis. Therefore, a victory is not possible if $n=2^{k-1}+1$ or greater.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "# Solution\n\n"
}
|
df23b3a2-8ce7-5128-8009-201b6601e22f
| 606,292
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
The minimum value is $-\frac{1}{8}$. There are eight equality cases in total. The first one is
$$
\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right) .
$$
Cyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \rightarrow$ $(-a,-b,-c,-d))$ all four entries in each of the four quadruples give four more equality cases.
|
-\frac{1}{8}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
The minimum value is $-\frac{1}{8}$. There are eight equality cases in total. The first one is
$$
\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right) .
$$
Cyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \rightarrow$ $(-a,-b,-c,-d))$ all four entries in each of the four quadruples give four more equality cases.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution\n\n"
}
|
71effd28-d619-58ef-a8ba-b1ab23a743e5
| 606,301
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
.1
Since the expression is cyclic, we could WLOG $a=\max \{a, b, c, d\}$. Let
$$
S(a, b, c, d)=(a-b)(b-c)(c-d)(d-a)
$$
Note that we have given $(a, b, c, d)$ such that $S(a, b, c, d)=-\frac{1}{8}$. Therefore, to prove that $S(a, b, c, d) \geq$ $-\frac{1}{8}$, we just need to consider the case where $S(a, b, c, d)<0$.
- Exactly 1 of $a-b, b-c, c-d, d-a$ is negative.
Since $a=\max \{a, b, c, d\}$, then we must have $d-a<0$. This forces $a>b>c>d$. Now, let us write
$$
S(a, b, c, d)=-(a-b)(b-c)(c-d)(a-d)
$$
Write $a-b=y, b-c=x, c-d=w$ for some positive reals $w, x, y>0$. Plugging to the original condition, we have
$$
(d+w+x+y)^{2}+(d+w+x)^{2}+(d+w)^{2}+d^{2}-1=0(*)
$$
and we want to prove that $w x y(w+x+y) \leq \frac{1}{8}$. Consider the expression $(*)$ as a quadratic in $d$ :
$$
4 d^{2}+d(6 w+4 x+2 y)+\left((w+x+y)^{2}+(w+x)^{2}+w^{2}-1\right)=0
$$
Since $d$ is a real number, then the discriminant of the given equation has to be non-negative, i.e. we must have
$$
\begin{aligned}
4 & \geq 4\left((w+x+y)^{2}+(w+x)^{2}+w^{2}\right)-(3 w+2 x+y)^{2} \\
& =\left(3 w^{2}+2 w y+3 y^{2}\right)+4 x(w+x+y) \\
& \geq 8 w y+4 x(w+x+y) \\
& =4(x(w+x+y)+2 w y)
\end{aligned}
$$
However, AM-GM gives us
$$
w x y(w+x+y) \leq \frac{1}{2}\left(\frac{x(w+x+y)+2 w y}{2}\right)^{2} \leq \frac{1}{8}
$$
This proves $S(a, b, c, d) \geq-\frac{1}{8}$ for any $a, b, c, d \in \mathbb{R}$ such that $a>b>c>d$. Equality holds if and only if $w=y, x(w+x+y)=2 w y$ and $w x y(w+x+y)=\frac{1}{8}$. Solving these equations gives us $w^{4}=\frac{1}{16}$ which forces $w=\frac{1}{2}$ since $w>0$. Solving for $x$ gives us $x(x+1)=\frac{1}{2}$, and we will get $x=-\frac{1}{2}+\frac{\sqrt{3}}{2}$ as $x>0$. Plugging back gives us $d=-\frac{1}{4}-\frac{\sqrt{3}}{4}$, and this gives us
$$
(a, b, c, d)=\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}\right)
$$
Thus, any cyclic permutation of the above solution will achieve the minimum equality.
- Exactly 3 of $a-b, b-c, c-d, d-a$ are negative Since $a=\max \{a, b, c, d\}$, then $a-b$ has to be positive. So we must have $b<c<d<a$. Now, note that
$$
\begin{aligned}
S(a, b, c, d) & =(a-b)(b-c)(c-d)(d-a) \\
& =(a-d)(d-c)(c-b)(b-a) \\
& =S(a, d, c, b)
\end{aligned}
$$
Now, note that $a>d>c>b$. By the previous case, $S(a, d, c, b) \geq-\frac{1}{8}$, which implies that
$$
S(a, b, c, d)=S(a, d, c, b) \geq-\frac{1}{8}
$$
as well. Equality holds if and only if
$$
(a, b, c, d)=\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right)
$$
and its cyclic permutation.
|
\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
.1
Since the expression is cyclic, we could WLOG $a=\max \{a, b, c, d\}$. Let
$$
S(a, b, c, d)=(a-b)(b-c)(c-d)(d-a)
$$
Note that we have given $(a, b, c, d)$ such that $S(a, b, c, d)=-\frac{1}{8}$. Therefore, to prove that $S(a, b, c, d) \geq$ $-\frac{1}{8}$, we just need to consider the case where $S(a, b, c, d)<0$.
- Exactly 1 of $a-b, b-c, c-d, d-a$ is negative.
Since $a=\max \{a, b, c, d\}$, then we must have $d-a<0$. This forces $a>b>c>d$. Now, let us write
$$
S(a, b, c, d)=-(a-b)(b-c)(c-d)(a-d)
$$
Write $a-b=y, b-c=x, c-d=w$ for some positive reals $w, x, y>0$. Plugging to the original condition, we have
$$
(d+w+x+y)^{2}+(d+w+x)^{2}+(d+w)^{2}+d^{2}-1=0(*)
$$
and we want to prove that $w x y(w+x+y) \leq \frac{1}{8}$. Consider the expression $(*)$ as a quadratic in $d$ :
$$
4 d^{2}+d(6 w+4 x+2 y)+\left((w+x+y)^{2}+(w+x)^{2}+w^{2}-1\right)=0
$$
Since $d$ is a real number, then the discriminant of the given equation has to be non-negative, i.e. we must have
$$
\begin{aligned}
4 & \geq 4\left((w+x+y)^{2}+(w+x)^{2}+w^{2}\right)-(3 w+2 x+y)^{2} \\
& =\left(3 w^{2}+2 w y+3 y^{2}\right)+4 x(w+x+y) \\
& \geq 8 w y+4 x(w+x+y) \\
& =4(x(w+x+y)+2 w y)
\end{aligned}
$$
However, AM-GM gives us
$$
w x y(w+x+y) \leq \frac{1}{2}\left(\frac{x(w+x+y)+2 w y}{2}\right)^{2} \leq \frac{1}{8}
$$
This proves $S(a, b, c, d) \geq-\frac{1}{8}$ for any $a, b, c, d \in \mathbb{R}$ such that $a>b>c>d$. Equality holds if and only if $w=y, x(w+x+y)=2 w y$ and $w x y(w+x+y)=\frac{1}{8}$. Solving these equations gives us $w^{4}=\frac{1}{16}$ which forces $w=\frac{1}{2}$ since $w>0$. Solving for $x$ gives us $x(x+1)=\frac{1}{2}$, and we will get $x=-\frac{1}{2}+\frac{\sqrt{3}}{2}$ as $x>0$. Plugging back gives us $d=-\frac{1}{4}-\frac{\sqrt{3}}{4}$, and this gives us
$$
(a, b, c, d)=\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}\right)
$$
Thus, any cyclic permutation of the above solution will achieve the minimum equality.
- Exactly 3 of $a-b, b-c, c-d, d-a$ are negative Since $a=\max \{a, b, c, d\}$, then $a-b$ has to be positive. So we must have $b<c<d<a$. Now, note that
$$
\begin{aligned}
S(a, b, c, d) & =(a-b)(b-c)(c-d)(d-a) \\
& =(a-d)(d-c)(c-b)(b-a) \\
& =S(a, d, c, b)
\end{aligned}
$$
Now, note that $a>d>c>b$. By the previous case, $S(a, d, c, b) \geq-\frac{1}{8}$, which implies that
$$
S(a, b, c, d)=S(a, d, c, b) \geq-\frac{1}{8}
$$
as well. Equality holds if and only if
$$
(a, b, c, d)=\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right)
$$
and its cyclic permutation.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution 5"
}
|
71effd28-d619-58ef-a8ba-b1ab23a743e5
| 606,301
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
.2
The minimum value is $-\frac{1}{8}$. There are eight equality cases in total. The first one is
$$
\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right) .
$$
Cyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \rightarrow$ $(-a,-b,-c,-d)$ ) all four entries in each of the four quadruples give four more equality cases. We then begin the proof by the following optimization:
Claim 1. In order to get the minimum value, we must have $a+b+c+d=0$.
Proof. Assume not, let $\delta=\frac{a+b+c+d}{4}$ and note that
$$
(a-\delta)^{2}+(b-\delta)^{2}+(c-\delta)^{2}+(d-\delta)^{2}<a^{2}+b^{2}+c^{2}+d^{2}
$$
so by shifting by $\delta$ and scaling, we get an even smaller value of $(a-b)(b-c)(c-d)(d-a)$.
The key idea is to substitute the variables
$$
\begin{aligned}
& x=a c+b d \\
& y=a b+c d \\
& z=a d+b c
\end{aligned}
$$
so that the original expression is just $(x-y)(x-z)$. We also have the conditions $x, y, z \geq-0.5$ because of:
$$
2 x+\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=(a+c)^{2}+(b+d)^{2} \geq 0
$$
Moreover, notice that
$$
0=(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(x+y+z) \Longrightarrow x+y+z=\frac{-1}{2}
$$
Now, we reduce to the following optimization problem.
Claim 2. Let $x, y, z \geq-0.5$ such that $x+y+z=-0.5$. Then, the minimum value of
$$
(x-y)(x-z)
$$
is $-1 / 8$. Moreover, the equality case occurs when $x=-1 / 4$ and $\{y, z\}=\{1 / 4,-1 / 2\}$.
Proof. We notice that
$$
\begin{aligned}
(x-y)(x-z)+\frac{1}{8} & =\left(2 y+z+\frac{1}{2}\right)\left(2 z+y+\frac{1}{2}\right)+\frac{1}{8} \\
& =\frac{1}{8}(4 y+4 z+1)^{2}+\left(y+\frac{1}{2}\right)\left(z+\frac{1}{2}\right) \geq 0
\end{aligned}
$$
The last inequality is true since both $y+\frac{1}{2}$ and $z+\frac{1}{2}$ are not less than zero.
The equality in the last inequality is attained when either $y+\frac{1}{2}=0$ or $z+\frac{1}{2}=0$, and $4 y+4 z+1=0$. This system of equations give $(y, z)=(1 / 4,-1 / 2)$ or $(y, z)=(-1 / 2,1 / 4)$ as the desired equality cases.
Note: We can also prove (the weakened) Claim 2 by using Lagrange Multiplier, as follows. We first prove that, in fact, $x, y, z \in[-0.5,0.5]$. This can be proved by considering that
$$
-2 x+\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=(a-c)^{2}+(b-d)^{2} \geq 0
$$
We will prove the Claim 2, only that in this case, $x, y, z \in[-0.5,0.5]$. This is already sufficient to prove the original question. We already have the bounded domain $[-0.5,0.5]^{3}$, so the global minimum must occur somewhere. Thus, it suffices to consider two cases:
- If the global minimum lies on the boundary of $[-0.5,0.5]^{3}$. Then, one of $x, y, z$ must be -0.5 or 0.5 . By symmetry between $y$ and $z$, we split to a few more cases.
- If $x=0.5$, then $y=z=-0.5$, so $(x-y)(x-z)=1$, not the minimum.
- If $x=-0.5$, then both $y$ and $z$ must be greater or equal to $x$, so $(x-y)(x-z) \geq 0$, not the minimum.
- If $y=0.5$, then $x=z=-0.5$, so $(x-y)(x-z)=0$, not the minimum.
- If $y=-0.5$, then $z=-x$, so
$$
(x-y)(x-z)=2 x(x+0.5)
$$
which obtain the minimum at $x=-1 / 4$. This gives the desired equality case.
- If the global minimum lies in the interior $(-0.5,0.5)^{3}$, then we apply Lagrange multiplier:
$$
\begin{aligned}
& \frac{\partial}{\partial x}(x-y)(x-z)=\lambda \frac{\partial}{\partial x}(x+y+z) \\
& \frac{\partial}{\partial y}(x-y)(x-z)=\lambda \frac{\partial}{\partial y}(x+y+z) \\
& \frac{\partial}{\partial z}(x-y)(x-z) \Longrightarrow z-x=\lambda \frac{\partial}{\partial z}(x+y+z) \\
& \Longrightarrow y-x=\lambda .
\end{aligned}
$$
Adding the last two equations gives $\lambda=0$, or $x=y=z$. This gives $(x-y)(x-z)=0$, not the minimum.
Having exhausted all cases, we are done.
|
-\frac{1}{8}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b, c, d$ be real numbers such that $a^{2}+b^{2}+c^{2}+d^{2}=1$. Determine the minimum value of $(a-b)(b-c)(c-d)(d-a)$ and determine all values of $(a, b, c, d)$ such that the minimum value is achieved.
|
.2
The minimum value is $-\frac{1}{8}$. There are eight equality cases in total. The first one is
$$
\left(\frac{1}{4}+\frac{\sqrt{3}}{4},-\frac{1}{4}-\frac{\sqrt{3}}{4}, \frac{1}{4}-\frac{\sqrt{3}}{4},-\frac{1}{4}+\frac{\sqrt{3}}{4}\right) .
$$
Cyclic shifting all the entries give three more quadruples. Moreover, flipping the sign $((a, b, c, d) \rightarrow$ $(-a,-b,-c,-d)$ ) all four entries in each of the four quadruples give four more equality cases. We then begin the proof by the following optimization:
Claim 1. In order to get the minimum value, we must have $a+b+c+d=0$.
Proof. Assume not, let $\delta=\frac{a+b+c+d}{4}$ and note that
$$
(a-\delta)^{2}+(b-\delta)^{2}+(c-\delta)^{2}+(d-\delta)^{2}<a^{2}+b^{2}+c^{2}+d^{2}
$$
so by shifting by $\delta$ and scaling, we get an even smaller value of $(a-b)(b-c)(c-d)(d-a)$.
The key idea is to substitute the variables
$$
\begin{aligned}
& x=a c+b d \\
& y=a b+c d \\
& z=a d+b c
\end{aligned}
$$
so that the original expression is just $(x-y)(x-z)$. We also have the conditions $x, y, z \geq-0.5$ because of:
$$
2 x+\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=(a+c)^{2}+(b+d)^{2} \geq 0
$$
Moreover, notice that
$$
0=(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(x+y+z) \Longrightarrow x+y+z=\frac{-1}{2}
$$
Now, we reduce to the following optimization problem.
Claim 2. Let $x, y, z \geq-0.5$ such that $x+y+z=-0.5$. Then, the minimum value of
$$
(x-y)(x-z)
$$
is $-1 / 8$. Moreover, the equality case occurs when $x=-1 / 4$ and $\{y, z\}=\{1 / 4,-1 / 2\}$.
Proof. We notice that
$$
\begin{aligned}
(x-y)(x-z)+\frac{1}{8} & =\left(2 y+z+\frac{1}{2}\right)\left(2 z+y+\frac{1}{2}\right)+\frac{1}{8} \\
& =\frac{1}{8}(4 y+4 z+1)^{2}+\left(y+\frac{1}{2}\right)\left(z+\frac{1}{2}\right) \geq 0
\end{aligned}
$$
The last inequality is true since both $y+\frac{1}{2}$ and $z+\frac{1}{2}$ are not less than zero.
The equality in the last inequality is attained when either $y+\frac{1}{2}=0$ or $z+\frac{1}{2}=0$, and $4 y+4 z+1=0$. This system of equations give $(y, z)=(1 / 4,-1 / 2)$ or $(y, z)=(-1 / 2,1 / 4)$ as the desired equality cases.
Note: We can also prove (the weakened) Claim 2 by using Lagrange Multiplier, as follows. We first prove that, in fact, $x, y, z \in[-0.5,0.5]$. This can be proved by considering that
$$
-2 x+\left(a^{2}+b^{2}+c^{2}+d^{2}\right)=(a-c)^{2}+(b-d)^{2} \geq 0
$$
We will prove the Claim 2, only that in this case, $x, y, z \in[-0.5,0.5]$. This is already sufficient to prove the original question. We already have the bounded domain $[-0.5,0.5]^{3}$, so the global minimum must occur somewhere. Thus, it suffices to consider two cases:
- If the global minimum lies on the boundary of $[-0.5,0.5]^{3}$. Then, one of $x, y, z$ must be -0.5 or 0.5 . By symmetry between $y$ and $z$, we split to a few more cases.
- If $x=0.5$, then $y=z=-0.5$, so $(x-y)(x-z)=1$, not the minimum.
- If $x=-0.5$, then both $y$ and $z$ must be greater or equal to $x$, so $(x-y)(x-z) \geq 0$, not the minimum.
- If $y=0.5$, then $x=z=-0.5$, so $(x-y)(x-z)=0$, not the minimum.
- If $y=-0.5$, then $z=-x$, so
$$
(x-y)(x-z)=2 x(x+0.5)
$$
which obtain the minimum at $x=-1 / 4$. This gives the desired equality case.
- If the global minimum lies in the interior $(-0.5,0.5)^{3}$, then we apply Lagrange multiplier:
$$
\begin{aligned}
& \frac{\partial}{\partial x}(x-y)(x-z)=\lambda \frac{\partial}{\partial x}(x+y+z) \\
& \frac{\partial}{\partial y}(x-y)(x-z)=\lambda \frac{\partial}{\partial y}(x+y+z) \\
& \frac{\partial}{\partial z}(x-y)(x-z) \Longrightarrow z-x=\lambda \frac{\partial}{\partial z}(x+y+z) \\
& \Longrightarrow y-x=\lambda .
\end{aligned}
$$
Adding the last two equations gives $\lambda=0$, or $x=y=z$. This gives $(x-y)(x-z)=0$, not the minimum.
Having exhausted all cases, we are done.
|
{
"resource_path": "APMO/segmented/en-apmo2022_sol.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "# Solution 5"
}
|
71effd28-d619-58ef-a8ba-b1ab23a743e5
| 606,301
|
Let $n \geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.
Show that it is possible to arrange these squares in a way such that every square touches exactly two other squares.
|
Set aside the squares with sidelengths $n-3, n-2, n-1$, and $n$ and suppose we can split the remaining squares into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$.
String the squares of each set $A, B$ along two parallel diagonals, one for each diagonal. Now use the four largest squares along two perpendicular diagonals to finish the construction: one will have sidelengths $n$ and $n-3$, and the other, sidelengths $n-1$ and $n-2$. If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-1$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration, in which the $A$ and $B$-diagonals are represented by unit squares, and the sidelengths $a_{i}$ of squares from $A$ and $b_{j}$ of squares from $B$ are indicated within each square, follows:
Since $\left(a_{1}+a_{2}+\cdots+a_{k}\right) \sqrt{2}+\frac{((n-3)+(n-2)) \sqrt{2}}{2}=\left(b_{1}+b_{2}+\cdots+b_{\ell}+2\right) \sqrt{2}+\frac{(n+(n-1)) \sqrt{2}}{2}$, this case is done.
If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-2$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration follows:
Since $\left(a_{1}+a_{2}+\cdots+a_{k}\right) \sqrt{2}+\frac{((n-3)+(n-1)) \sqrt{2}}{2}=\left(b_{1}+b_{2}+\cdots+b_{\ell}+1\right) \sqrt{2}+\frac{(n+(n-2)) \sqrt{2}}{2}$, this case is also done.
In both cases, the distance between the $A$-diagonal and the $B$-diagonal is $\frac{((n-3)+n) \sqrt{2}}{2}=\frac{(2 n-3) \sqrt{2}}{2}$. Since $a_{i}, b_{j} \leq n-4, \frac{\left(a_{i}+b_{j}\right) \sqrt{2}}{2}<\frac{(2 n-4) \sqrt{2}}{2}<\frac{(2 n-3) \sqrt{2}}{2}$, and therefore the $A$ - and $B$-diagonals do not overlap.
Finally, we prove that it is possible to split the squares of sidelengths 1 to $n-4$ into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$. One can do that in several ways; we present two possibilities:
- Direct construction: Split the numbers from 1 to $n-4$ into several sets of four consecutive numbers $\{t, t+1, t+2, t+3\}$, beginning with the largest numbers; put squares of sidelengths $t$ and $t+3$ in $A$ and squares of sidelengths $t+1$ and $t+2$ in $B$. Notice that $t+(t+3)=$ $(t+1)+(t+2)$. In the end, at most four numbers remain.
- If only 1 remains, put the corresponding square in $A$, so the sum of the sidelengths of the squares in $A$ is one unit larger that those in $B$;
- If 1 and 2 remains, put the square of sidelength 2 in $A$ and the square of sidelength 1 in $B$ (the difference is 1 );
- If 1,2 , and 3 remains, put the squares of sidelengths 1 and 3 in $A$, and the square of sidelength 2 in $B$ (the difference is 2 );
- If $1,2,3$, and 4 remains, put the squares of sidelengths 2 and 4 in $A$, and the squares of sidelengths 1 and 3 in $B$ (the difference is 2 ).
- Indirect construction: Starting with $A$ and $B$ as empty sets, add the squares of sidelengths $n-4, n-3, \ldots, 2$ to either $A$ or $B$ in that order such that at each stage the difference between the sum of the sidelengths in $A$ and the sum of the sidelengths of B is minimized. By induction it is clear that after adding an integer $j$ to one of the sets, this difference is at most $j$. In particular, the difference is 0,1 or 2 at the end. Finally adding the final 1 to one of the sets can ensure that the final difference is 1 or 2 . If necessary, flip $A$ and $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.
Show that it is possible to arrange these squares in a way such that every square touches exactly two other squares.
|
Set aside the squares with sidelengths $n-3, n-2, n-1$, and $n$ and suppose we can split the remaining squares into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$.
String the squares of each set $A, B$ along two parallel diagonals, one for each diagonal. Now use the four largest squares along two perpendicular diagonals to finish the construction: one will have sidelengths $n$ and $n-3$, and the other, sidelengths $n-1$ and $n-2$. If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-1$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration, in which the $A$ and $B$-diagonals are represented by unit squares, and the sidelengths $a_{i}$ of squares from $A$ and $b_{j}$ of squares from $B$ are indicated within each square, follows:

Since $\left(a_{1}+a_{2}+\cdots+a_{k}\right) \sqrt{2}+\frac{((n-3)+(n-2)) \sqrt{2}}{2}=\left(b_{1}+b_{2}+\cdots+b_{\ell}+2\right) \sqrt{2}+\frac{(n+(n-1)) \sqrt{2}}{2}$, this case is done.
If the sum of the sidelengths of the squares in $A$ is 1 unit larger than the sum of the sidelengths of the squares in $B$, attach the squares with sidelengths $n-3$ and $n-2$ to the $A$-diagonal, and the other two squares to the $B$-diagonal. The resulting configuration follows:

Since $\left(a_{1}+a_{2}+\cdots+a_{k}\right) \sqrt{2}+\frac{((n-3)+(n-1)) \sqrt{2}}{2}=\left(b_{1}+b_{2}+\cdots+b_{\ell}+1\right) \sqrt{2}+\frac{(n+(n-2)) \sqrt{2}}{2}$, this case is also done.
In both cases, the distance between the $A$-diagonal and the $B$-diagonal is $\frac{((n-3)+n) \sqrt{2}}{2}=\frac{(2 n-3) \sqrt{2}}{2}$. Since $a_{i}, b_{j} \leq n-4, \frac{\left(a_{i}+b_{j}\right) \sqrt{2}}{2}<\frac{(2 n-4) \sqrt{2}}{2}<\frac{(2 n-3) \sqrt{2}}{2}$, and therefore the $A$ - and $B$-diagonals do not overlap.
Finally, we prove that it is possible to split the squares of sidelengths 1 to $n-4$ into two sets $A$ and $B$ such that the sum of the sidelengths of the squares in $A$ is 1 or 2 units larger than the sum of the sidelengths of the squares in $B$. One can do that in several ways; we present two possibilities:
- Direct construction: Split the numbers from 1 to $n-4$ into several sets of four consecutive numbers $\{t, t+1, t+2, t+3\}$, beginning with the largest numbers; put squares of sidelengths $t$ and $t+3$ in $A$ and squares of sidelengths $t+1$ and $t+2$ in $B$. Notice that $t+(t+3)=$ $(t+1)+(t+2)$. In the end, at most four numbers remain.
- If only 1 remains, put the corresponding square in $A$, so the sum of the sidelengths of the squares in $A$ is one unit larger that those in $B$;
- If 1 and 2 remains, put the square of sidelength 2 in $A$ and the square of sidelength 1 in $B$ (the difference is 1 );
- If 1,2 , and 3 remains, put the squares of sidelengths 1 and 3 in $A$, and the square of sidelength 2 in $B$ (the difference is 2 );
- If $1,2,3$, and 4 remains, put the squares of sidelengths 2 and 4 in $A$, and the squares of sidelengths 1 and 3 in $B$ (the difference is 2 ).
- Indirect construction: Starting with $A$ and $B$ as empty sets, add the squares of sidelengths $n-4, n-3, \ldots, 2$ to either $A$ or $B$ in that order such that at each stage the difference between the sum of the sidelengths in $A$ and the sum of the sidelengths of B is minimized. By induction it is clear that after adding an integer $j$ to one of the sets, this difference is at most $j$. In particular, the difference is 0,1 or 2 at the end. Finally adding the final 1 to one of the sets can ensure that the final difference is 1 or 2 . If necessary, flip $A$ and $B$.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 1"
}
|
771f559a-5e7e-5f34-b318-cd602a03c47f
| 606,314
|
Let $n \geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.
Show that it is possible to arrange these squares in a way such that every square touches exactly two other squares.
|
Solve the problem by induction in $n$. Construct examples for $n=5,6,7,8,9,10$ (one can use the constructions from the previous solution, for instance). For $n>10$, set aside the six larger squares and arrange them in the following fashion:
By the induction hypothesis, one can arrange the remaining $n-6$ squares away from the six larger squares, so we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 5$ be an integer. Consider $n$ squares with side lengths $1,2, \ldots, n$, respectively. The squares are arranged in the plane with their sides parallel to the $x$ and $y$ axes. Suppose that no two squares touch, except possibly at their vertices.
Show that it is possible to arrange these squares in a way such that every square touches exactly two other squares.
|
Solve the problem by induction in $n$. Construct examples for $n=5,6,7,8,9,10$ (one can use the constructions from the previous solution, for instance). For $n>10$, set aside the six larger squares and arrange them in the following fashion:

By the induction hypothesis, one can arrange the remaining $n-6$ squares away from the six larger squares, so we are done.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 2"
}
|
771f559a-5e7e-5f34-b318-cd602a03c47f
| 606,314
|
Find all integers $n$ satisfying $n \geq 2$ and $\frac{\sigma(n)}{p(n)-1}=n$, in which $\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.
Answer: $n=6$.
|
Let $n=p_{1}^{\alpha_{1}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\sigma(n)=\left(1+p_{1}+\cdots+p_{1}^{\alpha_{1}}\right) \ldots\left(1+p_{k}+\cdots+p_{k}^{\alpha_{k}}\right)$. Hence
$p_{k}-1=\frac{\sigma(n)}{n}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}}+\cdots+\frac{1}{p_{i}^{\alpha_{i}}}\right)<\prod_{i=1}^{k} \frac{1}{1-\frac{1}{p_{i}}}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}-1}\right) \leq \prod_{i=1}^{k}\left(1+\frac{1}{i}\right)=k+1$,
that is, $p_{k}-1<k+1$, which is impossible for $k \geq 3$, because in this case $p_{k}-1 \geq 2 k-2 \geq k+1$. Then $k \leq 2$ and $p_{k}<k+2 \leq 4$, which implies $p_{k} \leq 3$.
If $k=1$ then $n=p^{\alpha}$ and $\sigma(n)=1+p+\cdots+p^{\alpha}$, and in this case $n \nmid \sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\alpha} 3^{\beta}$ with $\alpha, \beta>0$. If $\alpha>1$ or $\beta>1$,
$$
\frac{\sigma(n)}{n}>\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)=2 .
$$
Therefore $\alpha=\beta=1$ and the only answer is $n=6$.
Comment: There are other ways to deal with the case $n=2^{\alpha} 3^{\beta}$. For instance, we have $2^{\alpha+2} 3^{\beta}=\left(2^{\alpha+1}-1\right)\left(3^{\beta+1}-1\right)$. Since $2^{\alpha+1}-1$ is not divisible by 2 , and $3^{\beta+1}-1$ is not divisible by 3 , we have
$$
\left\{\begin{array} { l }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 ^ { \beta + 1 } - 1 = 2 ^ { \alpha + 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array} { c }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 \cdot ( 2 ^ { \alpha + 1 } - 1 ) - 1 = 2 \cdot 2 ^ { \alpha + 1 } }
\end{array} \Longleftrightarrow \left\{\begin{array}{r}
2^{\alpha+1}=4 \\
3^{\beta}=3
\end{array}\right.\right.\right.
$$
and $n=2^{\alpha} 3^{\beta}=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all integers $n$ satisfying $n \geq 2$ and $\frac{\sigma(n)}{p(n)-1}=n$, in which $\sigma(n)$ denotes the sum of all positive divisors of $n$, and $p(n)$ denotes the largest prime divisor of $n$.
Answer: $n=6$.
|
Let $n=p_{1}^{\alpha_{1}} \cdot \ldots \cdot p_{k}^{\alpha_{k}}$ be the prime factorization of $n$ with $p_{1}<\ldots<p_{k}$, so that $p(n)=p_{k}$ and $\sigma(n)=\left(1+p_{1}+\cdots+p_{1}^{\alpha_{1}}\right) \ldots\left(1+p_{k}+\cdots+p_{k}^{\alpha_{k}}\right)$. Hence
$p_{k}-1=\frac{\sigma(n)}{n}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}}+\cdots+\frac{1}{p_{i}^{\alpha_{i}}}\right)<\prod_{i=1}^{k} \frac{1}{1-\frac{1}{p_{i}}}=\prod_{i=1}^{k}\left(1+\frac{1}{p_{i}-1}\right) \leq \prod_{i=1}^{k}\left(1+\frac{1}{i}\right)=k+1$,
that is, $p_{k}-1<k+1$, which is impossible for $k \geq 3$, because in this case $p_{k}-1 \geq 2 k-2 \geq k+1$. Then $k \leq 2$ and $p_{k}<k+2 \leq 4$, which implies $p_{k} \leq 3$.
If $k=1$ then $n=p^{\alpha}$ and $\sigma(n)=1+p+\cdots+p^{\alpha}$, and in this case $n \nmid \sigma(n)$, which is not possible. Thus $k=2$, and $n=2^{\alpha} 3^{\beta}$ with $\alpha, \beta>0$. If $\alpha>1$ or $\beta>1$,
$$
\frac{\sigma(n)}{n}>\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)=2 .
$$
Therefore $\alpha=\beta=1$ and the only answer is $n=6$.
Comment: There are other ways to deal with the case $n=2^{\alpha} 3^{\beta}$. For instance, we have $2^{\alpha+2} 3^{\beta}=\left(2^{\alpha+1}-1\right)\left(3^{\beta+1}-1\right)$. Since $2^{\alpha+1}-1$ is not divisible by 2 , and $3^{\beta+1}-1$ is not divisible by 3 , we have
$$
\left\{\begin{array} { l }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 ^ { \beta + 1 } - 1 = 2 ^ { \alpha + 2 } }
\end{array} \Longleftrightarrow \left\{\begin{array} { c }
{ 2 ^ { \alpha + 1 } - 1 = 3 ^ { \beta } } \\
{ 3 \cdot ( 2 ^ { \alpha + 1 } - 1 ) - 1 = 2 \cdot 2 ^ { \alpha + 1 } }
\end{array} \Longleftrightarrow \left\{\begin{array}{r}
2^{\alpha+1}=4 \\
3^{\beta}=3
\end{array}\right.\right.\right.
$$
and $n=2^{\alpha} 3^{\beta}=6$.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
8ef1d7ed-6915-53dc-ba6b-a82e5c8b3aae
| 606,316
|
Let $A B C D$ be a parallelogram. Let $W, X, Y$, and $Z$ be points on sides $A B, B C, C D$, and $D A$, respectively, such that the incenters of triangles $A W Z, B X W, C Y X$ and $D Z Y$ form a parallelogram. Prove that $W X Y Z$ is a parallelogram.
|
Let the four incenters be $I_{1}, I_{2}, I_{3}$, and $I_{4}$ with inradii $r_{1}, r_{2}, r_{3}$, and $r_{4}$ respectively (in the order given in the question). Without loss of generality, let $I_{1}$ be closer to $A B$ than $I_{2}$. Let the acute angle between $I_{1} I_{2}$ and $A B$ (and hence also the angle between $I_{3} I_{4}$ and $C D$ ) be $\theta$. Then
$$
r_{2}-r_{1}=I_{1} I_{2} \sin \theta=I_{3} I_{4} \sin \theta=r_{4}-r_{3}
$$
which implies $r_{1}+r_{4}=r_{2}+r_{3}$. Similar arguments show that $r_{1}+r_{2}=r_{3}+r_{4}$. Thus we obtain $r_{1}=r_{3}$ and $r_{2}=r_{4}$.
Now let's consider the possible positions of $W, X, Y, Z$. Suppose $A Z \neq C X$. Without loss of generality assume $A Z>C X$. Since the incircles of $A W Z$ and $C Y X$ are symmetric about the centre of the parallelogram $A B C D$, this implies $C Y>A W$. Using similar arguments, we have
$$
C Y>A W \Longrightarrow B W>D Y \Longrightarrow D Z>B X \Longrightarrow C X>A Z
$$
which is a contradiction. Therefore $A Z=C X \Longrightarrow A W=C Y$ and $W X Y Z$ is a parallelogram.
Comment: There are several ways to prove that $r_{1}=r_{3}$ and $r_{2}=r_{4}$. The proposer shows the following three alternative approaches:
Using parallel lines: Let $O$ be the centre of parallelogram $A B C D$ and $P$ be the centre of parallelogram $I_{1} I_{2} I_{3} I_{4}$. Since $A I_{1}$ and $C I_{3}$ are angle bisectors, we must have $A I_{1} \| C I_{3}$. Let $\ell_{1}$ be the line through $O$ parallel to $A I_{1}$. Since $A O=O C, \ell_{1}$ is halfway between $A I_{1}$ and $C I_{3}$. Hence $P$ must lie on $\ell_{1}$.
Similarly, $P$ must also lie on $\ell_{2}$, the line through $O$ parallel to $B I_{2}$. Thus $P$ is the intersection of $\ell_{1}$ and $\ell_{2}$, which must be $O$. So the four incentres and hence the four incircles must be symmetric about $O$, which implies $r_{1}=r_{3}$ and $r_{2}=r_{4}$.
Using a rotation: Let the bisectors of $\angle D A B$ and $\angle A B C$ meet at $X$ and the bisectors of $\angle B C D$ and $\angle C D A$ meet at $Y$. Then $I_{1}$ is on $A X, I_{2}$ is on $B X, I_{3}$ is on $C Y$, and $I_{4}$ is on $D Y$. Let $O$ be the centre of $A B C D$. Then a 180 degree rotation about $O$ takes $\triangle A X B$ to $\triangle C Y D$. Under the same transformation $I_{1} I_{2}$ is mapped to a parallel segment $I_{1}^{\prime} I_{2}^{\prime}$ with $I_{1}^{\prime}$ on $C Y$ and $I_{2}^{\prime}$ on $D Y$. Since $I_{1} I_{2} I_{3} I_{4}$ is a parallelogram, $I_{3} I_{4}=I_{1} I_{2}$ and $I_{3} I_{4} \| I_{1} I_{2}$. Hence $I_{1}^{\prime} I_{2}^{\prime}$ and $I_{3} I_{4}$ are parallel, equal length segments on sides $C Y, D Y$ and we conclude that $I_{1}^{\prime}=I_{3}, I_{2}^{\prime}=I_{4}$. Hence the centre of $I_{1} I_{2} I_{3} I_{4}$ is also $O$ and we establish that by rotational symmetry that $r_{1}=r_{3}$ and $r_{2}=r_{4}$.
Using congruent triangles: Let $A I_{1}$ and $B I_{2}$ intersect at $E$ and let $C I_{3}$ and $D I_{4}$ intersect at $F$. Note that $\triangle A B E$ and $\triangle C D F$ are congruent, since $A B=C D$ and corresponding pairs of angles are equal (equal opposite angles parallelogram $A B C D$ are each bisected).
Since $A I_{1} \| C I_{3}$ and $I_{1} I_{2} \| I_{4} I_{3}, \angle I_{2} I_{1} E=\angle I_{4} I_{3} F$. Similarly $\angle I_{1} I_{2} E=\angle I_{3} I_{4} F$. Furthermore $I_{1} I_{2}=I_{3} I_{4}$. Hence triangles $I_{2} I_{1} E$ and $I 4 I_{3} F$ are also congruent.
Hence $A B E I_{1} I_{2}$ and $D C F I_{3} I_{4}$ are congruent. Therefore, the perpendicular distance from $I_{1}$ to $A B$ equals the perpendicular distance from $I_{3}$ to $C D$, that is, $r_{1}=r_{3}$. Similarly $r_{2}=r_{4}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. Let $W, X, Y$, and $Z$ be points on sides $A B, B C, C D$, and $D A$, respectively, such that the incenters of triangles $A W Z, B X W, C Y X$ and $D Z Y$ form a parallelogram. Prove that $W X Y Z$ is a parallelogram.
|
Let the four incenters be $I_{1}, I_{2}, I_{3}$, and $I_{4}$ with inradii $r_{1}, r_{2}, r_{3}$, and $r_{4}$ respectively (in the order given in the question). Without loss of generality, let $I_{1}$ be closer to $A B$ than $I_{2}$. Let the acute angle between $I_{1} I_{2}$ and $A B$ (and hence also the angle between $I_{3} I_{4}$ and $C D$ ) be $\theta$. Then
$$
r_{2}-r_{1}=I_{1} I_{2} \sin \theta=I_{3} I_{4} \sin \theta=r_{4}-r_{3}
$$
which implies $r_{1}+r_{4}=r_{2}+r_{3}$. Similar arguments show that $r_{1}+r_{2}=r_{3}+r_{4}$. Thus we obtain $r_{1}=r_{3}$ and $r_{2}=r_{4}$.

Now let's consider the possible positions of $W, X, Y, Z$. Suppose $A Z \neq C X$. Without loss of generality assume $A Z>C X$. Since the incircles of $A W Z$ and $C Y X$ are symmetric about the centre of the parallelogram $A B C D$, this implies $C Y>A W$. Using similar arguments, we have
$$
C Y>A W \Longrightarrow B W>D Y \Longrightarrow D Z>B X \Longrightarrow C X>A Z
$$
which is a contradiction. Therefore $A Z=C X \Longrightarrow A W=C Y$ and $W X Y Z$ is a parallelogram.
Comment: There are several ways to prove that $r_{1}=r_{3}$ and $r_{2}=r_{4}$. The proposer shows the following three alternative approaches:
Using parallel lines: Let $O$ be the centre of parallelogram $A B C D$ and $P$ be the centre of parallelogram $I_{1} I_{2} I_{3} I_{4}$. Since $A I_{1}$ and $C I_{3}$ are angle bisectors, we must have $A I_{1} \| C I_{3}$. Let $\ell_{1}$ be the line through $O$ parallel to $A I_{1}$. Since $A O=O C, \ell_{1}$ is halfway between $A I_{1}$ and $C I_{3}$. Hence $P$ must lie on $\ell_{1}$.
Similarly, $P$ must also lie on $\ell_{2}$, the line through $O$ parallel to $B I_{2}$. Thus $P$ is the intersection of $\ell_{1}$ and $\ell_{2}$, which must be $O$. So the four incentres and hence the four incircles must be symmetric about $O$, which implies $r_{1}=r_{3}$ and $r_{2}=r_{4}$.
Using a rotation: Let the bisectors of $\angle D A B$ and $\angle A B C$ meet at $X$ and the bisectors of $\angle B C D$ and $\angle C D A$ meet at $Y$. Then $I_{1}$ is on $A X, I_{2}$ is on $B X, I_{3}$ is on $C Y$, and $I_{4}$ is on $D Y$. Let $O$ be the centre of $A B C D$. Then a 180 degree rotation about $O$ takes $\triangle A X B$ to $\triangle C Y D$. Under the same transformation $I_{1} I_{2}$ is mapped to a parallel segment $I_{1}^{\prime} I_{2}^{\prime}$ with $I_{1}^{\prime}$ on $C Y$ and $I_{2}^{\prime}$ on $D Y$. Since $I_{1} I_{2} I_{3} I_{4}$ is a parallelogram, $I_{3} I_{4}=I_{1} I_{2}$ and $I_{3} I_{4} \| I_{1} I_{2}$. Hence $I_{1}^{\prime} I_{2}^{\prime}$ and $I_{3} I_{4}$ are parallel, equal length segments on sides $C Y, D Y$ and we conclude that $I_{1}^{\prime}=I_{3}, I_{2}^{\prime}=I_{4}$. Hence the centre of $I_{1} I_{2} I_{3} I_{4}$ is also $O$ and we establish that by rotational symmetry that $r_{1}=r_{3}$ and $r_{2}=r_{4}$.
Using congruent triangles: Let $A I_{1}$ and $B I_{2}$ intersect at $E$ and let $C I_{3}$ and $D I_{4}$ intersect at $F$. Note that $\triangle A B E$ and $\triangle C D F$ are congruent, since $A B=C D$ and corresponding pairs of angles are equal (equal opposite angles parallelogram $A B C D$ are each bisected).
Since $A I_{1} \| C I_{3}$ and $I_{1} I_{2} \| I_{4} I_{3}, \angle I_{2} I_{1} E=\angle I_{4} I_{3} F$. Similarly $\angle I_{1} I_{2} E=\angle I_{3} I_{4} F$. Furthermore $I_{1} I_{2}=I_{3} I_{4}$. Hence triangles $I_{2} I_{1} E$ and $I 4 I_{3} F$ are also congruent.
Hence $A B E I_{1} I_{2}$ and $D C F I_{3} I_{4}$ are congruent. Therefore, the perpendicular distance from $I_{1}$ to $A B$ equals the perpendicular distance from $I_{3}$ to $C D$, that is, $r_{1}=r_{3}$. Similarly $r_{2}=r_{4}$.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
5f56a53f-2cd7-5611-aa33-44b1c7c296f2
| 606,319
|
Let $c>0$ be a given positive real and $\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that
$$
f((c+1) x+f(y))=f(x+2 y)+2 c x \quad \text { for all } x, y \in \mathbb{R}_{>0}
$$
Answer: $f(x)=2 x$ for all $x>0$.
|
We first prove that $f(x) \geq 2 x$ for all $x>0$. Suppose, for the sake of contradiction, that $f(y)<2 y$ for some positive $y$. Choose $x$ such that $f((c+1) x+f(y))$ and $f(x+2 y)$ cancel out, that is,
$$
(c+1) x+f(y)=x+2 y \Longleftrightarrow x=\frac{2 y-f(y)}{c}
$$
Notice that $x>0$ because $2 y-f(y)>0$. Then $2 c x=0$, which is not possible. This contradiction yields $f(y) \geq 2 y$ for all $y>0$.
Now suppose, again for the sake of contradiction, that $f(y)>2 y$ for some $y>0$. Define the following sequence: $a_{0}$ is an arbitrary real greater than $2 y$, and $f\left(a_{n}\right)=f\left(a_{n-1}\right)+2 c x$, so that
$$
\left\{\begin{array}{r}
(c+1) x+f(y)=a_{n} \\
x+2 y=a_{n-1}
\end{array} \Longleftrightarrow x=a_{n-1}-2 y \quad \text { and } \quad a_{n}=(c+1)\left(a_{n-1}-2 y\right)+f(y) .\right.
$$
If $x=a_{n-1}-2 y>0$ then $a_{n}>f(y)>2 y$, so inductively all the substitutions make sense.
For the sake of simplicity, let $b_{n}=a_{n}-2 y$, so $b_{n}=(c+1) b_{n-1}+f(y)-2 y \quad(*)$. Notice that $x=b_{n-1}$ in the former equation, so $f\left(a_{n}\right)=f\left(a_{n-1}\right)+2 c b_{n-1}$. Telescoping yields
$$
f\left(a_{n}\right)=f\left(a_{0}\right)+2 c \sum_{i=0}^{n-1} b_{i} .
$$
One can find $b_{n}$ from the recurrence equation $(*): b_{n}=\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{n}-\frac{f(y)-2 y}{c}$, and then
$$
\begin{aligned}
f\left(a_{n}\right) & =f\left(a_{0}\right)+2 c \sum_{i=0}^{n-1}\left(\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{i}-\frac{f(y)-2 y}{c}\right) \\
& =f\left(a_{0}\right)+2\left(b_{0}+\frac{f(y)-2 y}{c}\right)\left((c+1)^{n}-1\right)-2 n(f(y)-2 y)
\end{aligned}
$$
Since $f\left(a_{n}\right) \geq 2 a_{n}=2 b_{n}+4 y$,
$$
\begin{aligned}
& f\left(a_{0}\right)+2\left(b_{0}+\frac{f(y)-2 y}{c}\right)\left((c+1)^{n}-1\right)-2 n(f(y)-2 y) \geq 2 b_{n}+4 y \\
= & 2\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{n}-2 \frac{f(y)-2 y}{c}
\end{aligned}
$$
which implies
$$
f\left(a_{0}\right)+2 \frac{f(y)-2 y}{c} \geq 2\left(b_{0}+\frac{f(y)-2 y}{c}\right)+2 n(f(y)-2 y)
$$
which is not true for sufficiently large $n$.
A contradiction is reached, and thus $f(y)=2 y$ for all $y>0$. It is immediate that this function satisfies the functional equation.
|
f(x)=2x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $c>0$ be a given positive real and $\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that
$$
f((c+1) x+f(y))=f(x+2 y)+2 c x \quad \text { for all } x, y \in \mathbb{R}_{>0}
$$
Answer: $f(x)=2 x$ for all $x>0$.
|
We first prove that $f(x) \geq 2 x$ for all $x>0$. Suppose, for the sake of contradiction, that $f(y)<2 y$ for some positive $y$. Choose $x$ such that $f((c+1) x+f(y))$ and $f(x+2 y)$ cancel out, that is,
$$
(c+1) x+f(y)=x+2 y \Longleftrightarrow x=\frac{2 y-f(y)}{c}
$$
Notice that $x>0$ because $2 y-f(y)>0$. Then $2 c x=0$, which is not possible. This contradiction yields $f(y) \geq 2 y$ for all $y>0$.
Now suppose, again for the sake of contradiction, that $f(y)>2 y$ for some $y>0$. Define the following sequence: $a_{0}$ is an arbitrary real greater than $2 y$, and $f\left(a_{n}\right)=f\left(a_{n-1}\right)+2 c x$, so that
$$
\left\{\begin{array}{r}
(c+1) x+f(y)=a_{n} \\
x+2 y=a_{n-1}
\end{array} \Longleftrightarrow x=a_{n-1}-2 y \quad \text { and } \quad a_{n}=(c+1)\left(a_{n-1}-2 y\right)+f(y) .\right.
$$
If $x=a_{n-1}-2 y>0$ then $a_{n}>f(y)>2 y$, so inductively all the substitutions make sense.
For the sake of simplicity, let $b_{n}=a_{n}-2 y$, so $b_{n}=(c+1) b_{n-1}+f(y)-2 y \quad(*)$. Notice that $x=b_{n-1}$ in the former equation, so $f\left(a_{n}\right)=f\left(a_{n-1}\right)+2 c b_{n-1}$. Telescoping yields
$$
f\left(a_{n}\right)=f\left(a_{0}\right)+2 c \sum_{i=0}^{n-1} b_{i} .
$$
One can find $b_{n}$ from the recurrence equation $(*): b_{n}=\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{n}-\frac{f(y)-2 y}{c}$, and then
$$
\begin{aligned}
f\left(a_{n}\right) & =f\left(a_{0}\right)+2 c \sum_{i=0}^{n-1}\left(\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{i}-\frac{f(y)-2 y}{c}\right) \\
& =f\left(a_{0}\right)+2\left(b_{0}+\frac{f(y)-2 y}{c}\right)\left((c+1)^{n}-1\right)-2 n(f(y)-2 y)
\end{aligned}
$$
Since $f\left(a_{n}\right) \geq 2 a_{n}=2 b_{n}+4 y$,
$$
\begin{aligned}
& f\left(a_{0}\right)+2\left(b_{0}+\frac{f(y)-2 y}{c}\right)\left((c+1)^{n}-1\right)-2 n(f(y)-2 y) \geq 2 b_{n}+4 y \\
= & 2\left(b_{0}+\frac{f(y)-2 y}{c}\right)(c+1)^{n}-2 \frac{f(y)-2 y}{c}
\end{aligned}
$$
which implies
$$
f\left(a_{0}\right)+2 \frac{f(y)-2 y}{c} \geq 2\left(b_{0}+\frac{f(y)-2 y}{c}\right)+2 n(f(y)-2 y)
$$
which is not true for sufficiently large $n$.
A contradiction is reached, and thus $f(y)=2 y$ for all $y>0$. It is immediate that this function satisfies the functional equation.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 1"
}
|
dd411c39-5b48-5da3-bcb5-63a2b9f6ed98
| 606,322
|
Let $c>0$ be a given positive real and $\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that
$$
f((c+1) x+f(y))=f(x+2 y)+2 c x \quad \text { for all } x, y \in \mathbb{R}_{>0}
$$
Answer: $f(x)=2 x$ for all $x>0$.
|
After proving that $f(y) \geq 2 y$ for all $y>0$, one can define $g(x)=f(x)-2 x, g: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{\geq 0}$, and our goal is proving that $g(x)=0$ for all $x>0$. The problem is now rewritten as
$$
\begin{aligned}
& g((c+1) x+g(y)+2 y)+2((c+1) x+g(y)+2 y)=g(x+2 y)+2(x+2 y)+2 c x \\
\Longleftrightarrow & g((c+1) x+g(y)+2 y)+2 g(y)=g(x+2 y) .
\end{aligned}
$$
This readily implies that $g(x+2 y) \geq 2 g(y)$, which can be interpreted as $z>2 y \Longrightarrow g(z) \geq$ $2 g(y)$, by plugging $z=x+2 y$.
Now we prove by induction that $z>2 y \Longrightarrow g(z) \geq 2 m \cdot g(y)$ for any positive integer $2 m$. In fact, since $(c+1) x+g(y)+2 y>2 y, g((c+1) x+g(y)+2 y) \geq 2 m \cdot g(y)$, and by (??),
$$
g(x+2 y) \geq 2 m \cdot g(y)+2 g(y)=2(m+1) g(y)
$$
and we are done by plugging $z=x+2 y$ again.
The problem now is done: if $g(y)>0$ for some $y>0$, choose a fixed $z>2 y$ arbitrarily and and integer $m$ such that $m>\frac{g(z)}{2 g(y)}$. Then $g(z)<2 m \cdot g(y)$, contradiction.
|
f(x)=2x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $c>0$ be a given positive real and $\mathbb{R}_{>0}$ be the set of all positive reals. Find all functions $f: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{>0}$ such that
$$
f((c+1) x+f(y))=f(x+2 y)+2 c x \quad \text { for all } x, y \in \mathbb{R}_{>0}
$$
Answer: $f(x)=2 x$ for all $x>0$.
|
After proving that $f(y) \geq 2 y$ for all $y>0$, one can define $g(x)=f(x)-2 x, g: \mathbb{R}_{>0} \rightarrow \mathbb{R}_{\geq 0}$, and our goal is proving that $g(x)=0$ for all $x>0$. The problem is now rewritten as
$$
\begin{aligned}
& g((c+1) x+g(y)+2 y)+2((c+1) x+g(y)+2 y)=g(x+2 y)+2(x+2 y)+2 c x \\
\Longleftrightarrow & g((c+1) x+g(y)+2 y)+2 g(y)=g(x+2 y) .
\end{aligned}
$$
This readily implies that $g(x+2 y) \geq 2 g(y)$, which can be interpreted as $z>2 y \Longrightarrow g(z) \geq$ $2 g(y)$, by plugging $z=x+2 y$.
Now we prove by induction that $z>2 y \Longrightarrow g(z) \geq 2 m \cdot g(y)$ for any positive integer $2 m$. In fact, since $(c+1) x+g(y)+2 y>2 y, g((c+1) x+g(y)+2 y) \geq 2 m \cdot g(y)$, and by (??),
$$
g(x+2 y) \geq 2 m \cdot g(y)+2 g(y)=2(m+1) g(y)
$$
and we are done by plugging $z=x+2 y$ again.
The problem now is done: if $g(y)>0$ for some $y>0$, choose a fixed $z>2 y$ arbitrarily and and integer $m$ such that $m>\frac{g(z)}{2 g(y)}$. Then $g(z)<2 m \cdot g(y)$, contradiction.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution 2"
}
|
dd411c39-5b48-5da3-bcb5-63a2b9f6ed98
| 606,322
|
There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:
First, he chooses an endpoint of each segment as a "sink". Then he places the present at the endpoint of the segment he is at. The present moves as follows:
- If it is on a line segment, it moves towards the sink.
- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.
If the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.
|
Draw a circle that encloses all the intersection points between line segments and extend all line segments until they meet the circle, and then move Tony and all his friends to the circle. Number the intersection points with the circle from 1 to $2 n$ anticlockwise, starting from Tony (Tony has number 1). We will prove that the friends eligible to receive presents are the ones on even-numbered intersection points.
First part: at most $n$ friends can receive a present.
The solution relies on a well-known result: the $n$ lines determine regions inside the circle; then it is possible to paint the regions with two colors such that no regions with a common (line) boundary have the same color. The proof is an induction on $n$ : the fact immediately holds for $n=0$, and the induction step consists on taking away one line $\ell$, painting the regions obtained with $n-1$ lines, drawing $\ell$ again and flipping all colors on exactly one half plane determined by $\ell$.
Now consider the line starting on point 1. Color the regions in red and blue such that neighboring regions have different colors, and such that the two regions that have point 1 as a vertex are red on the right and blue on the left, from Tony's point of view. Finally, assign to each red region the clockwise direction and to each blue region the anticlockwise direction. Because of the coloring, every boundary will have two directions assigned, but the directions are the same since every boundary divides regions of different colors. Then the present will follow the directions assigned to the regions: it certainly does for both regions in the beginning, and when the present reaches an intersection it will keep bordering one of the two regions it was dividing. To finish this part of the problem, consider the regions that share a boundary with the circle. The directions alternate between outcoming and incoming, starting from 1 (outcoming), so all even-numbered vertices are directed as incoming and are the only ones able to receive presents. Second part: all even-numbered vertices can receive a present.
First notice that, since every two chords intersect, every chord separates the endpoints of each of the other $n-1$ chords. Therefore, there are $n-1$ vertices on each side of every chord, and each chord connects vertices $k$ and $k+n, 1 \leq k \leq n$.
We prove a stronger result by induction in $n$ : let $k$ be an integer, $1 \leq k \leq n$. Direct each chord from $i$ to $i+n$ if $1 \leq i \leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \ldots, k+n$. Now suppose that each chord sends a present, starting from the vertex opposite to each sink, and all presents move with the same rules. Then $k-i$ sends a present to $k+i+1, i=0,1, \ldots, n-1$ (indices taken modulo $2 n$ ). In particular, for $i=k-1$, Tony, in vertex 1 , send a present to vertex $2 k$. Also, the $n$ paths the presents make do not cross (but they may touch.) More formally, for all $i, 1 \leq i \leq n$, if one path takes a present from $k-i$ to $k+i+1$, separating the circle into two regions, all paths taking a present from $k-j$ to $k+j+1, j<i$, are completely contained in one region, and all paths taking a present from
$k-j$ to $k+j+1, j>i$, are completely contained in the other region. For instance, possible ${ }^{1}$ paths for $k=3$ and $n=5$ follow:
The result is true for $n=1$. Let $n>1$ and assume the result is true for less chords. Consider the chord that takes $k$ to $k+n$ and remove it. Apply the induction hypothesis to the remaining $n-1$ lines: after relabeling, presents would go from $k-i$ to $k+i+2,1 \leq i \leq n-1$ if the chord were not there.
Reintroduce the chord that takes $k$ to $k+n$. From the induction hypothesis, the chord intersects the paths of the presents in the following order: the $i$-th path the chord intersects is the the one that takes $k-i$ to $k+i, i=1,2, \ldots, n-1$.
Paths without chord $k \rightarrow k+n$
Corrected paths with chord $k \rightarrow k+n$
Then the presents cover the following new paths: the present from $k$ will leave its chord and take the path towards $k+1$; then, for $i=1,2, \ldots, n-1$, the present from $k-i$ will meet the chord from $k$ to $k+n$, move towards the intersection with the path towards $k+i+1$ and go to $k+i+1$, as desired. Notice that the paths still do not cross. The induction (and the solution) is now complete.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:
First, he chooses an endpoint of each segment as a "sink". Then he places the present at the endpoint of the segment he is at. The present moves as follows:
- If it is on a line segment, it moves towards the sink.
- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.
If the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.
|
Draw a circle that encloses all the intersection points between line segments and extend all line segments until they meet the circle, and then move Tony and all his friends to the circle. Number the intersection points with the circle from 1 to $2 n$ anticlockwise, starting from Tony (Tony has number 1). We will prove that the friends eligible to receive presents are the ones on even-numbered intersection points.
First part: at most $n$ friends can receive a present.
The solution relies on a well-known result: the $n$ lines determine regions inside the circle; then it is possible to paint the regions with two colors such that no regions with a common (line) boundary have the same color. The proof is an induction on $n$ : the fact immediately holds for $n=0$, and the induction step consists on taking away one line $\ell$, painting the regions obtained with $n-1$ lines, drawing $\ell$ again and flipping all colors on exactly one half plane determined by $\ell$.
Now consider the line starting on point 1. Color the regions in red and blue such that neighboring regions have different colors, and such that the two regions that have point 1 as a vertex are red on the right and blue on the left, from Tony's point of view. Finally, assign to each red region the clockwise direction and to each blue region the anticlockwise direction. Because of the coloring, every boundary will have two directions assigned, but the directions are the same since every boundary divides regions of different colors. Then the present will follow the directions assigned to the regions: it certainly does for both regions in the beginning, and when the present reaches an intersection it will keep bordering one of the two regions it was dividing. To finish this part of the problem, consider the regions that share a boundary with the circle. The directions alternate between outcoming and incoming, starting from 1 (outcoming), so all even-numbered vertices are directed as incoming and are the only ones able to receive presents. Second part: all even-numbered vertices can receive a present.
First notice that, since every two chords intersect, every chord separates the endpoints of each of the other $n-1$ chords. Therefore, there are $n-1$ vertices on each side of every chord, and each chord connects vertices $k$ and $k+n, 1 \leq k \leq n$.
We prove a stronger result by induction in $n$ : let $k$ be an integer, $1 \leq k \leq n$. Direct each chord from $i$ to $i+n$ if $1 \leq i \leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \ldots, k+n$. Now suppose that each chord sends a present, starting from the vertex opposite to each sink, and all presents move with the same rules. Then $k-i$ sends a present to $k+i+1, i=0,1, \ldots, n-1$ (indices taken modulo $2 n$ ). In particular, for $i=k-1$, Tony, in vertex 1 , send a present to vertex $2 k$. Also, the $n$ paths the presents make do not cross (but they may touch.) More formally, for all $i, 1 \leq i \leq n$, if one path takes a present from $k-i$ to $k+i+1$, separating the circle into two regions, all paths taking a present from $k-j$ to $k+j+1, j<i$, are completely contained in one region, and all paths taking a present from
$k-j$ to $k+j+1, j>i$, are completely contained in the other region. For instance, possible ${ }^{1}$ paths for $k=3$ and $n=5$ follow:

The result is true for $n=1$. Let $n>1$ and assume the result is true for less chords. Consider the chord that takes $k$ to $k+n$ and remove it. Apply the induction hypothesis to the remaining $n-1$ lines: after relabeling, presents would go from $k-i$ to $k+i+2,1 \leq i \leq n-1$ if the chord were not there.
Reintroduce the chord that takes $k$ to $k+n$. From the induction hypothesis, the chord intersects the paths of the presents in the following order: the $i$-th path the chord intersects is the the one that takes $k-i$ to $k+i, i=1,2, \ldots, n-1$.

Paths without chord $k \rightarrow k+n$

Corrected paths with chord $k \rightarrow k+n$
Then the presents cover the following new paths: the present from $k$ will leave its chord and take the path towards $k+1$; then, for $i=1,2, \ldots, n-1$, the present from $k-i$ will meet the chord from $k$ to $k+n$, move towards the intersection with the path towards $k+i+1$ and go to $k+i+1$, as desired. Notice that the paths still do not cross. The induction (and the solution) is now complete.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 1"
}
|
86f2f1e7-71d9-54b7-9207-e735b0c224a2
| 606,325
|
There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:
First, he chooses an endpoint of each segment as a "sink". Then he places the present at the endpoint of the segment he is at. The present moves as follows:
- If it is on a line segment, it moves towards the sink.
- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.
If the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.
|
First part: at most n friends can receive a present.
Similarly to the first solution, consider a circle that encompasses all line segments, extend the lines, and use the endpoints of the chords instead of the line segments, and prove that each chord connects vertices $k$ and $k+n$. We also consider, even in the first part, $n$ presents leaving from $n$ outcoming vertices.
First we prove that a present always goes to a sink. If it does not, then it loops; let it first enter the loop at point $P$ after turning from chord $a$ to chord $b$. Therefore after it loops once,
[^0]it must turn to chord $b$ at $P$. But $P$ is the intersection of $a$ and $b$, so the present should turn from chord $a$ to chord $b$, which can only be done in one way - the same way it came in first. This means that some part of chord $a$ before the present enters the loop at $P$ is part of the loop, which contradicts the fact that $P$ is the first point in the loop. So no present enters a loop, and every present goes to a sink.
There are no loops
No two paths cross
The present paths also do not cross: in fact, every time two paths share a point $P$, intersection of chords $a$ and $b$, one path comes from $a$ to $b$ and the other path comes from $b$ to $a$, and they touch at $P$. This implies the following sequence of facts:
- Every path divides the circle into two regions with paths connecting vertices within each region.
- All $n$ presents will be delivered to $n$ different persons; that is, all sinks receive a present. This implies that every vertex is an endpoint of a path.
- The number of chord endpoints inside each region is even, because they are connected within their own region.
Now consider the path starting at vertex 1 , with Tony. It divides the circle into two regions with an even number of vertices in their interior. Then there is an even number of vertices between Tony and the recipient of his present, that is, their vertex is an even numbered one. Second part: all even-numbered vertices can receive a present.
The construction is the same as the in the previous solution: direct each chord from $i$ to $i+n$ if $1 \leq i \leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \ldots, k+n$. Then, since the paths do not cross, $k$ will send a present to $k+1, k-1$ will send a present to $k+2$, and so on, until 1 sends a present to $(k+1)+(k-1)=2 k$.
[^0]: ${ }^{1}$ The paths do not depend uniquely on $k$ and $n$; different chord configurations and vertex labelings may change the paths.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $n$ line segments on the plane, no three intersecting at a point, and each pair intersecting once in their respective interiors. Tony and his $2 n-1$ friends each stand at a distinct endpoint of a line segment. Tony wishes to send Christmas presents to each of his friends as follows:
First, he chooses an endpoint of each segment as a "sink". Then he places the present at the endpoint of the segment he is at. The present moves as follows:
- If it is on a line segment, it moves towards the sink.
- When it reaches an intersection of two segments, it changes the line segment it travels on and starts moving towards the new sink.
If the present reaches an endpoint, the friend on that endpoint can receive their present. Prove Tony can send presents to exactly $n$ of his $2 n-1$ friends.
|
First part: at most n friends can receive a present.
Similarly to the first solution, consider a circle that encompasses all line segments, extend the lines, and use the endpoints of the chords instead of the line segments, and prove that each chord connects vertices $k$ and $k+n$. We also consider, even in the first part, $n$ presents leaving from $n$ outcoming vertices.
First we prove that a present always goes to a sink. If it does not, then it loops; let it first enter the loop at point $P$ after turning from chord $a$ to chord $b$. Therefore after it loops once,
[^0]it must turn to chord $b$ at $P$. But $P$ is the intersection of $a$ and $b$, so the present should turn from chord $a$ to chord $b$, which can only be done in one way - the same way it came in first. This means that some part of chord $a$ before the present enters the loop at $P$ is part of the loop, which contradicts the fact that $P$ is the first point in the loop. So no present enters a loop, and every present goes to a sink.

There are no loops

No two paths cross
The present paths also do not cross: in fact, every time two paths share a point $P$, intersection of chords $a$ and $b$, one path comes from $a$ to $b$ and the other path comes from $b$ to $a$, and they touch at $P$. This implies the following sequence of facts:
- Every path divides the circle into two regions with paths connecting vertices within each region.
- All $n$ presents will be delivered to $n$ different persons; that is, all sinks receive a present. This implies that every vertex is an endpoint of a path.
- The number of chord endpoints inside each region is even, because they are connected within their own region.
Now consider the path starting at vertex 1 , with Tony. It divides the circle into two regions with an even number of vertices in their interior. Then there is an even number of vertices between Tony and the recipient of his present, that is, their vertex is an even numbered one. Second part: all even-numbered vertices can receive a present.
The construction is the same as the in the previous solution: direct each chord from $i$ to $i+n$ if $1 \leq i \leq k$ and from $i+n$ to $i$ otherwise; in other words, the sinks are $k+1, k+2, \ldots, k+n$. Then, since the paths do not cross, $k$ will send a present to $k+1, k-1$ will send a present to $k+2$, and so on, until 1 sends a present to $(k+1)+(k-1)=2 k$.
[^0]: ${ }^{1}$ The paths do not depend uniquely on $k$ and $n$; different chord configurations and vertex labelings may change the paths.
|
{
"resource_path": "APMO/segmented/en-apmo2023_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 2"
}
|
86f2f1e7-71d9-54b7-9207-e735b0c224a2
| 606,325
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Let $\ell$ be the radical axis of circles $B Q X$ and $C P X$. Since $X$ and $Y$ are on $\ell$, it is sufficient to show that $A$ is on $\ell$. Let line $A X$ intersect segments $B C$ and $D E$ at $Z$ and $Z^{\prime}$, respectively. Then it is sufficient to show that $Z$ is on $\ell$. By $B C \| D E$, we obtain
$$
\frac{B Z}{Z C}=\frac{D Z^{\prime}}{Z^{\prime} E}=\frac{P Z}{Z Q},
$$
thus $B Z \cdot Q Z=C Z \cdot P Z$, which implies that $Z$ is on $\ell$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|

Let $\ell$ be the radical axis of circles $B Q X$ and $C P X$. Since $X$ and $Y$ are on $\ell$, it is sufficient to show that $A$ is on $\ell$. Let line $A X$ intersect segments $B C$ and $D E$ at $Z$ and $Z^{\prime}$, respectively. Then it is sufficient to show that $Z$ is on $\ell$. By $B C \| D E$, we obtain
$$
\frac{B Z}{Z C}=\frac{D Z^{\prime}}{Z^{\prime} E}=\frac{P Z}{Z Q},
$$
thus $B Z \cdot Q Z=C Z \cdot P Z$, which implies that $Z$ is on $\ell$.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 1"
}
|
c2662896-d3ab-5e68-bb60-20bb487f6879
| 606,331
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Let circle $B Q X$ intersect line $A B$ at a point $S$ which is different from $B$. Then $\angle D E X=$ $\angle X Q C=\angle B S X$, thus $S$ is on circle $D E X$. Similarly, let circle $C P X$ intersect line $A C$ at a point $T$ which is different from $C$. Then $T$ is on circle $D E X$. The power of $A$ with respect to the circle $D E X$ is $A S \cdot A D=A T \cdot A E$. Since $\frac{A D}{A B}=\frac{A E}{A C}, A S \cdot A B=A T \cdot A C$. Then $A$ is in the radical axis of circles $B Q X$ and $C P X$, which implies that three points $A, X$ and $Y$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|

Let circle $B Q X$ intersect line $A B$ at a point $S$ which is different from $B$. Then $\angle D E X=$ $\angle X Q C=\angle B S X$, thus $S$ is on circle $D E X$. Similarly, let circle $C P X$ intersect line $A C$ at a point $T$ which is different from $C$. Then $T$ is on circle $D E X$. The power of $A$ with respect to the circle $D E X$ is $A S \cdot A D=A T \cdot A E$. Since $\frac{A D}{A B}=\frac{A E}{A C}, A S \cdot A B=A T \cdot A C$. Then $A$ is in the radical axis of circles $B Q X$ and $C P X$, which implies that three points $A, X$ and $Y$ are collinear.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 2"
}
|
c2662896-d3ab-5e68-bb60-20bb487f6879
| 606,331
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.
The homothety implies that $A, Y$, and $Y^{\prime}$ are collinear, and that $\angle D Y^{\prime} E=\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,
$\angle D Y^{\prime} E=\angle B Y C=\angle B Y X+\angle X Y C=\angle X Q P+\angle X P Q=180^{\circ}-\angle P X Q=180^{\circ}-\angle D X E$,
which implies that $D Y^{\prime} E X$ is cyclic. Therefore
$$
\angle D Y^{\prime} X=\angle D E X=\angle P Q X=\angle B Y X
$$
which, combined with $D Y^{\prime} \| B Y$, implies $Y^{\prime} X \| Y X$. This proves that $X, Y$, and $Y^{\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle. Let $D$ be a point on side $A B$ and $E$ be a point on side $A C$ such that lines $B C$ and $D E$ are parallel. Let $X$ be an interior point of $B C E D$. Suppose rays $D X$ and $E X$ meet side $B C$ at points $P$ and $Q$, respectively such that both $P$ and $Q$ lie between $B$ and $C$. Suppose that the circumcircles of triangles $B Q X$ and $C P X$ intersect at a point $Y \neq X$. Prove that points $A, X$, and $Y$ are collinear.
|
Consider the (direct) homothety that takes triangle $A D E$ to triangle $A B C$, and let $Y^{\prime}$ be the image of $Y$ under this homothety; in other words, let $Y^{\prime}$ be the intersection of the line parallel to $B Y$ through $D$ and the line parallel to $C Y$ through $E$.

The homothety implies that $A, Y$, and $Y^{\prime}$ are collinear, and that $\angle D Y^{\prime} E=\angle B Y C$. Since $B Q X Y$ and $C P X Y$ are cyclic,
$\angle D Y^{\prime} E=\angle B Y C=\angle B Y X+\angle X Y C=\angle X Q P+\angle X P Q=180^{\circ}-\angle P X Q=180^{\circ}-\angle D X E$,
which implies that $D Y^{\prime} E X$ is cyclic. Therefore
$$
\angle D Y^{\prime} X=\angle D E X=\angle P Q X=\angle B Y X
$$
which, combined with $D Y^{\prime} \| B Y$, implies $Y^{\prime} X \| Y X$. This proves that $X, Y$, and $Y^{\prime}$ are collinear, which in turn shows that $A, X$, and $Y$ are collinear.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 1",
"solution_match": "# Solution 3"
}
|
c2662896-d3ab-5e68-bb60-20bb487f6879
| 606,331
|
Consider a $100 \times 100$ table, and identify the cell in row $a$ and column $b, 1 \leq a, b \leq 100$, with the ordered pair $(a, b)$. Let $k$ be an integer such that $51 \leq k \leq 99$. A $k$-knight is a piece that moves one cell vertically or horizontally and $k$ cells to the other direction; that is, it moves from $(a, b)$ to $(c, d)$ such that $(|a-c|,|b-d|)$ is either $(1, k)$ or $(k, 1)$. The $k$-knight starts at cell $(1,1)$, and performs several moves. A sequence of moves is a sequence of cells $\left(x_{0}, y_{0}\right)=(1,1)$, $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{n}, y_{n}\right)$ such that, for all $i=1,2, \ldots, n, 1 \leq x_{i}, y_{i} \leq 100$ and the $k$-knight can move from $\left(x_{i-1}, y_{i-1}\right)$ to $\left(x_{i}, y_{i}\right)$. In this case, each cell $\left(x_{i}, y_{i}\right)$ is said to be reachable. For each $k$, find $L(k)$, the number of reachable cells.
Answer: $L(k)=\left\{\begin{array}{ll}100^{2}-(2 k-100)^{2} & \text { if } k \text { is even } \\ \frac{100^{2}-(2 k-100)^{2}}{2} & \text { if } k \text { is odd }\end{array}\right.$.
|
Cell $(x, y)$ is directly reachable from another cell if and only if $x-k \geq 1$ or $x+k \leq 100$ or $y-k \geq 1$ or $y+k \leq 100$, that is, $x \geq k+1$ or $x \leq 100-k$ or $y \geq k+1$ or $y \leq 100-k(*)$. Therefore the cells $(x, y)$ for which $101-k \leq x \leq k$ and $101-k \leq y \leq k$ are unreachable. Let $S$ be this set of unreachable cells in this square, namely the square of cells $(x, y), 101-k \leq x, y \leq k$. If condition $(*)$ is valid for both $(x, y)$ and $(x \pm 2, y \pm 2)$ then one can move from $(x, y)$ to $(x \pm 2, y \pm 2)$, if they are both in the table, with two moves: either $x \leq 50$ or $x \geq 51$; the same is true for $y$. In the first case, move $(x, y) \rightarrow(x+k, y \pm 1) \rightarrow(x, y \pm 2)$ or $(x, y) \rightarrow$ $(x \pm 1, y+k) \rightarrow(x \pm 2, y)$. In the second case, move $(x, y) \rightarrow(x-k, y \pm 1) \rightarrow(x, y \pm 2)$ or $(x, y) \rightarrow(x \pm 1, y-k) \rightarrow(x \pm 2, y)$.
Hence if the table is colored in two colors like a chessboard, if $k \leq 50$, cells with the same color as $(1,1)$ are reachable. Moreover, if $k$ is even, every other move changes the color of the occupied cell, and all cells are potentially reachable; otherwise, only cells with the same color as $(1,1)$ can be visited. Therefore, if $k$ is even then the reachable cells consists of all cells except the center square defined by $101-k \leq x \leq k$ and $101-k \leq y \leq k$, that is, $L(k)=100^{2}-(2 k-100)^{2}$; if $k$ is odd, then only half of the cells are reachable: the ones with the same color as $(1,1)$, and $L(k)=\frac{1}{2}\left(100^{2}-(2 k-100)^{2}\right)$.
|
L(k)=\left\{\begin{array}{ll}100^{2}-(2 k-100)^{2} & \text { if } k \text { is even } \\ \frac{100^{2}-(2 k-100)^{2}}{2} & \text { if } k \text { is odd }\end{array}\right.}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider a $100 \times 100$ table, and identify the cell in row $a$ and column $b, 1 \leq a, b \leq 100$, with the ordered pair $(a, b)$. Let $k$ be an integer such that $51 \leq k \leq 99$. A $k$-knight is a piece that moves one cell vertically or horizontally and $k$ cells to the other direction; that is, it moves from $(a, b)$ to $(c, d)$ such that $(|a-c|,|b-d|)$ is either $(1, k)$ or $(k, 1)$. The $k$-knight starts at cell $(1,1)$, and performs several moves. A sequence of moves is a sequence of cells $\left(x_{0}, y_{0}\right)=(1,1)$, $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{n}, y_{n}\right)$ such that, for all $i=1,2, \ldots, n, 1 \leq x_{i}, y_{i} \leq 100$ and the $k$-knight can move from $\left(x_{i-1}, y_{i-1}\right)$ to $\left(x_{i}, y_{i}\right)$. In this case, each cell $\left(x_{i}, y_{i}\right)$ is said to be reachable. For each $k$, find $L(k)$, the number of reachable cells.
Answer: $L(k)=\left\{\begin{array}{ll}100^{2}-(2 k-100)^{2} & \text { if } k \text { is even } \\ \frac{100^{2}-(2 k-100)^{2}}{2} & \text { if } k \text { is odd }\end{array}\right.$.
|
Cell $(x, y)$ is directly reachable from another cell if and only if $x-k \geq 1$ or $x+k \leq 100$ or $y-k \geq 1$ or $y+k \leq 100$, that is, $x \geq k+1$ or $x \leq 100-k$ or $y \geq k+1$ or $y \leq 100-k(*)$. Therefore the cells $(x, y)$ for which $101-k \leq x \leq k$ and $101-k \leq y \leq k$ are unreachable. Let $S$ be this set of unreachable cells in this square, namely the square of cells $(x, y), 101-k \leq x, y \leq k$. If condition $(*)$ is valid for both $(x, y)$ and $(x \pm 2, y \pm 2)$ then one can move from $(x, y)$ to $(x \pm 2, y \pm 2)$, if they are both in the table, with two moves: either $x \leq 50$ or $x \geq 51$; the same is true for $y$. In the first case, move $(x, y) \rightarrow(x+k, y \pm 1) \rightarrow(x, y \pm 2)$ or $(x, y) \rightarrow$ $(x \pm 1, y+k) \rightarrow(x \pm 2, y)$. In the second case, move $(x, y) \rightarrow(x-k, y \pm 1) \rightarrow(x, y \pm 2)$ or $(x, y) \rightarrow(x \pm 1, y-k) \rightarrow(x \pm 2, y)$.
Hence if the table is colored in two colors like a chessboard, if $k \leq 50$, cells with the same color as $(1,1)$ are reachable. Moreover, if $k$ is even, every other move changes the color of the occupied cell, and all cells are potentially reachable; otherwise, only cells with the same color as $(1,1)$ can be visited. Therefore, if $k$ is even then the reachable cells consists of all cells except the center square defined by $101-k \leq x \leq k$ and $101-k \leq y \leq k$, that is, $L(k)=100^{2}-(2 k-100)^{2}$; if $k$ is odd, then only half of the cells are reachable: the ones with the same color as $(1,1)$, and $L(k)=\frac{1}{2}\left(100^{2}-(2 k-100)^{2}\right)$.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 2",
"solution_match": "# Solution\n\n"
}
|
2ffa4ba7-344e-58dd-9d2e-da6dde452a8e
| 606,344
|
Let $n$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers. Prove that
$$
\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}} \geq \frac{2}{1+a_{1} a_{2} \ldots a_{n}}-\frac{1}{2^{n}}
$$
|
We first prove the following lemma:
Lemma 1. For $k$ positive integer and $x, y>0$,
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
The proof goes by induction. For $k=1$, we have
$$
\left(\frac{2}{1+x}\right)^{2}+\left(\frac{2}{1+y}\right)^{2} \geq 2\left(\frac{2}{1+x y}\right)
$$
which reduces to
$$
x y(x-y)^{2}+(x y-1)^{2} \geq 0 .
$$
For $k>1$, by the inequality $2\left(A^{2}+B^{2}\right) \geq(A+B)^{2}$ applied at $A=\left(\frac{2}{1+x}\right)^{2^{k-1}}$ and $B=\left(\frac{2}{1+y}\right)^{2^{k-1}}$ followed by the induction hypothesis
$$
\begin{aligned}
2\left(\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}}\right) & \geq\left(\left(\frac{2}{1+x}\right)^{2^{k-1}}+\left(\frac{2}{1+y}\right)^{2^{k-1}}\right)^{2} \\
& \geq\left(2\left(\frac{2}{1+x y}\right)^{2^{k-2}}\right)^{2}=4\left(\frac{2}{1+x y}\right)^{2^{k-1}}
\end{aligned}
$$
from which the lemma follows.
The problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:
$$
\begin{aligned}
\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}} & \geq \frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n} \cdot 1}\right)^{2^{n-1}} \\
\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n}}\right)^{2^{n-1}} & \geq \frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} \\
\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-2}}\right)^{2^{n-2}}+\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} & \geq \frac{1}{2^{n-3}}\left(\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\right)^{2^{n-3}} \\
\ldots & )^{2^{k}} \\
\frac{1}{2^{k}}\left(\frac{2}{1+a_{k}}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+a_{k+1} \ldots a_{n-1} a_{n}}\right)^{2^{k-1}} & \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+a_{k} \ldots a_{n-2} a_{n-1} a_{n}}\right)^{2} \\
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\frac{1}{2}\left(\frac{2}{1+a_{2} \ldots a_{n-1} a_{n}}\right)^{2} & \geq \frac{2}{1+a_{1} \ldots a_{n-2} a_{n-1} a_{n}}
\end{aligned}
$$
Comment: Equality occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}=1$.
Comment: The main motivation for the lemma is trying to "telescope" the sum
$$
\frac{1}{2^{n}}+\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}}
$$
that is,
$$
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\cdots+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}}
$$
to obtain an expression larger than or equal to
$$
\frac{2}{1+a_{1} a_{2} \ldots a_{n}}
$$
It seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:
$$
\frac{1}{2^{k}}\left(\frac{2}{1+x}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+y}\right)^{2^{k}} \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+x y}\right)^{2^{i-1}}
$$
or
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer and $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers. Prove that
$$
\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}} \geq \frac{2}{1+a_{1} a_{2} \ldots a_{n}}-\frac{1}{2^{n}}
$$
|
We first prove the following lemma:
Lemma 1. For $k$ positive integer and $x, y>0$,
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
The proof goes by induction. For $k=1$, we have
$$
\left(\frac{2}{1+x}\right)^{2}+\left(\frac{2}{1+y}\right)^{2} \geq 2\left(\frac{2}{1+x y}\right)
$$
which reduces to
$$
x y(x-y)^{2}+(x y-1)^{2} \geq 0 .
$$
For $k>1$, by the inequality $2\left(A^{2}+B^{2}\right) \geq(A+B)^{2}$ applied at $A=\left(\frac{2}{1+x}\right)^{2^{k-1}}$ and $B=\left(\frac{2}{1+y}\right)^{2^{k-1}}$ followed by the induction hypothesis
$$
\begin{aligned}
2\left(\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}}\right) & \geq\left(\left(\frac{2}{1+x}\right)^{2^{k-1}}+\left(\frac{2}{1+y}\right)^{2^{k-1}}\right)^{2} \\
& \geq\left(2\left(\frac{2}{1+x y}\right)^{2^{k-2}}\right)^{2}=4\left(\frac{2}{1+x y}\right)^{2^{k-1}}
\end{aligned}
$$
from which the lemma follows.
The problem now can be deduced from summing the following applications of the lemma, multiplied by the appropriate factor:
$$
\begin{aligned}
\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}} & \geq \frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n} \cdot 1}\right)^{2^{n-1}} \\
\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n}}\right)^{2^{n-1}} & \geq \frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} \\
\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-2}}\right)^{2^{n-2}}+\frac{1}{2^{n-2}}\left(\frac{2}{1+a_{n-1} a_{n}}\right)^{2^{n-2}} & \geq \frac{1}{2^{n-3}}\left(\frac{2}{1+a_{n-2} a_{n-1} a_{n}}\right)^{2^{n-3}} \\
\ldots & )^{2^{k}} \\
\frac{1}{2^{k}}\left(\frac{2}{1+a_{k}}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+a_{k+1} \ldots a_{n-1} a_{n}}\right)^{2^{k-1}} & \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+a_{k} \ldots a_{n-2} a_{n-1} a_{n}}\right)^{2} \\
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\frac{1}{2}\left(\frac{2}{1+a_{2} \ldots a_{n-1} a_{n}}\right)^{2} & \geq \frac{2}{1+a_{1} \ldots a_{n-2} a_{n-1} a_{n}}
\end{aligned}
$$
Comment: Equality occurs if and only if $a_{1}=a_{2}=\cdots=a_{n}=1$.
Comment: The main motivation for the lemma is trying to "telescope" the sum
$$
\frac{1}{2^{n}}+\sum_{i=1}^{n} \frac{1}{2^{i}}\left(\frac{2}{1+a_{i}}\right)^{2^{i}}
$$
that is,
$$
\frac{1}{2}\left(\frac{2}{1+a_{1}}\right)^{2}+\cdots+\frac{1}{2^{n-1}}\left(\frac{2}{1+a_{n-1}}\right)^{2^{n-1}}+\frac{1}{2^{n}}\left(\frac{2}{1+a_{n}}\right)^{2^{n}}+\frac{1}{2^{n}}\left(\frac{2}{1+1}\right)^{2^{n}}
$$
to obtain an expression larger than or equal to
$$
\frac{2}{1+a_{1} a_{2} \ldots a_{n}}
$$
It seems reasonable to obtain a inequality that can be applied from right to left, decreases the exponent of the factor $1 / 2^{k}$ by 1 , and multiplies the variables in the denominator. Given that, the lemma is quite natural:
$$
\frac{1}{2^{k}}\left(\frac{2}{1+x}\right)^{2^{k}}+\frac{1}{2^{k}}\left(\frac{2}{1+y}\right)^{2^{k}} \geq \frac{1}{2^{k-1}}\left(\frac{2}{1+x y}\right)^{2^{i-1}}
$$
or
$$
\left(\frac{2}{1+x}\right)^{2^{k}}+\left(\frac{2}{1+y}\right)^{2^{k}} \geq 2\left(\frac{2}{1+x y}\right)^{2^{k-1}}
$$
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 3",
"solution_match": "# Solution\n\n"
}
|
633aac9c-db10-5818-8461-399e1809ac3d
| 606,346
|
Prove that for every positive integer $t$ there is a unique permutation $a_{0}, a_{1}, \ldots, a_{t-1}$ of $0,1, \ldots, t-$ 1 such that, for every $0 \leq i \leq t-1$, the binomial coefficient $\binom{t+i}{2 a_{i}}$ is odd and $2 a_{i} \neq t+i$.
|
We constantly make use of Kummer's theorem which, in particular, implies that $\binom{n}{k}$ is odd if and only if $k$ and $n-k$ have ones in different positions in binary. In other words, if $S(x)$ is the set of positions of the digits 1 of $x$ in binary (in which the digit multiplied by $2^{i}$ is in position $i),\binom{n}{k}$ is odd if and only if $S(k) \subseteq S(n)$. Moreover, if we set $k<n, S(k)$ is a proper subset of $S(n)$, that is, $|S(k)|<|S(n)|$.
We start with a lemma that guides us how the permutation should be set.
## Lemma 1.
$$
\sum_{i=0}^{t-1}|S(t+i)|=t+\sum_{i=0}^{t-1}|S(2 i)|
$$
The proof is just realizing that $S(2 i)=\{1+x, x \in S(i)\}$ and $S(2 i+1)=\{0\} \cup\{1+x, x \in S(i)\}$, because $2 i$ in binary is $i$ followed by a zero and $2 i+1$ in binary is $i$ followed by a one. Therefore
$$
\begin{aligned}
\sum_{i=0}^{t-1}|S(t+i)| & =\sum_{i=0}^{2 t-1}|S(i)|-\sum_{i=0}^{t-1}|S(i)|=\sum_{i=0}^{t-1}|S(2 i)|+\sum_{i=0}^{t-1}|S(2 i+1)|-\sum_{i=0}^{t-1}|S(i)| \\
& =\sum_{i=0}^{t-1}|S(i)|+\sum_{i=0}^{t-1}(1+|S(i)|)-\sum_{i=0}^{t-1}|S(i)|=t+\sum_{i=0}^{t-1}|S(i)|=t+\sum_{i=0}^{t-1}|S(2 i)|
\end{aligned}
$$
The lemma has an immediate corollary: since $t+i>2 a_{i}$ and $\binom{t+i}{2 a_{i}}$ is odd for all $i, 0 \leq i \leq t-1$, $S\left(2 a_{i}\right) \subset S(t+i)$ with $\left|S\left(2 a_{i}\right)\right| \leq|S(t+i)|-1$. Since the sum of $\left|S\left(2 a_{i}\right)\right|$ is $t$ less than the sum of $|S(t+i)|$, and there are $t$ values of $i$, equality must occur, that is, $\left|S\left(2 a_{i}\right)\right|=|S(t+i)|-1$, which in conjunction with $S\left(2 a_{i}\right) \subset S(t+i)$ means that $t+i-2 a_{i}=2^{k_{i}}$ for every $i, 0 \leq i \leq t-1$, $k_{i} \in S(t+i)$ (more precisely, $\left\{k_{i}\right\}=S(t+i) \backslash S\left(2 a_{i}\right)$.)
In particular, for $t+i$ odd, this means that $t+i-2 a_{i}=1$, because the only odd power of 2 is 1. Then $a_{i}=\frac{t+i-1}{2}$ for $t+i$ odd, which takes up all the numbers greater than or equal to $\frac{t-1}{2}$. Now we need to distribute the numbers that are smaller than $\frac{t-1}{2}$ (call these numbers small). If $t+i$ is even then by Lucas' Theorem $\binom{t+i}{2 a_{i}} \equiv\binom{\frac{t+i}{2}}{a_{i}}(\bmod 2)$, so we pair numbers from $\lceil t / 2\rceil$ to $t-1$ (call these numbers big) with the small numbers.
Say that a set $A$ is paired with another set $B$ whenever $|A|=|B|$ and there exists a bijection $\pi: A \rightarrow B$ such that $S(a) \subset S(\pi(a))$ and $|S(a)|=|S(\pi(a))|-1$; we also say that $a$ and $\pi(a)$ are paired. We prove by induction in $t$ that $A_{t}=\{0,1,2, \ldots,\lfloor t / 2\rfloor-1\}$ (the set of small numbers) and $B_{t}=\{\lceil t / 2\rceil, \ldots, t-2, t-1\}$ (the set of big numbers) can be uniquely paired.
The claim is immediate for $t=1$ and $t=2$. For $t>2$, there is exactly one power of two in $B_{t}$, since $t / 2 \leq 2^{a}<t \Longleftrightarrow a=\left\lceil\log _{2}(t / 2)\right\rceil$. Let $2^{a}$ be this power of two. Then, since $2^{a} \geq t / 2$, no number in $A_{t}$ has a one in position $a$ in binary. Since for every number $x, 2^{a} \leq x<t, a \in S(x)$ and $a \notin S(y)$ for all $y \in A_{t}, x$ can only be paired with $x-2^{a}$, since $S(x)$ needs to be stripped of exactly one position. This takes cares of $x \in B_{t}, 2^{a} \leq x<t$, and $y \in A_{t}, 0 \leq y<t-2^{a}$.
Now we need to pair the numbers from $A^{\prime}=\left\{t-2^{a}, t-2^{a}+1, \ldots,\lfloor t / 2\rfloor-1\right\} \subset A$ with the numbers from $B^{\prime}=\left\{\lceil t / 2\rceil,\lceil t / 2\rceil+1, \ldots, 2^{a}-1\right\} \subset B$. In order to pair these $t-2\left(t-2^{a}\right)=$ $2^{a+1}-t<t$ numbers, we use the induction hypothesis and a bijection between $A^{\prime} \cup B^{\prime}$ and $B_{2^{a+1}-t} \cup A_{2^{a+1}-t}$. Let $S=S\left(2^{a}-1\right)=\{0,1,2, \ldots, a-1\}$. Then take a pair $x, y, x \in A_{2^{a+1}-t}$ and $y \in B_{2^{a+1}-t}$ and biject it with $2^{a}-1-x \in B^{\prime}$ and $2^{a}-1-y \in A^{\prime}$. In fact,
$$
0 \leq x \leq\left\lfloor\frac{2^{a+1}-t}{2}\right\rfloor-1=2^{a}-\left\lceil\frac{t}{2}\right\rceil-1 \Longleftrightarrow\left\lceil\frac{t}{2}\right\rceil \leq 2^{a}-1-x \leq 2^{a}-1
$$
and
$$
\left\lceil\frac{2^{a+1}-t}{2}\right\rceil=2^{a}-\left\lfloor\frac{t}{2}\right\rfloor \leq y \leq 2^{a+1}-t-1 \Longleftrightarrow t-2^{a} \leq 2^{a}-1-y \leq\left\lfloor\frac{t}{2}\right\rfloor-1
$$
Moreover, $S\left(2^{a}-1-x\right)=S \backslash S(x)$ and $S\left(2^{a}-1-y\right)=S \backslash S(y)$ are complements with respect to $S$, and $S(x) \subset S(y)$ and $|S(x)|=|S(y)|-1$ implies $S\left(2^{a}-1-y\right) \subset S\left(2^{a}-1-x\right)$ and $\left|S\left(2^{a}-1-y\right)\right|=\left|S\left(2^{a}-1-x\right)\right|-1$. Therefore a pairing between $A^{\prime}$ and $B^{\prime}$ corresponds to a pairing between $A_{2^{a+1}-t}$ and $B_{2^{a+1}-t}$. Since the latter pairing is unique, the former pairing is also unique, and the result follows.
We illustrate the bijection by showing the case $t=23$ :
$$
A_{23}=\{0,1,2, \ldots, 10\}, \quad B_{23}=\{12,13,14, \ldots, 22\}
$$
The pairing is
$$
\left(\begin{array}{ccccccccccc}
12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\
8 & 9 & 10 & 7 & 0 & 1 & 2 & 3 & 4 & 5 & 6
\end{array}\right)
$$
in which the bijection is between
$$
\left(\begin{array}{cccc}
12 & 13 & 14 & 15 \\
8 & 9 & 10 & 7
\end{array}\right) \quad \text { and } \quad\left(\begin{array}{llll}
3 & 2 & 1 & 0 \\
7 & 6 & 5 & 8
\end{array}\right) \rightarrow\left(\begin{array}{llll}
5 & 6 & 7 & 8 \\
1 & 2 & 3 & 0
\end{array}\right) .
$$
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Prove that for every positive integer $t$ there is a unique permutation $a_{0}, a_{1}, \ldots, a_{t-1}$ of $0,1, \ldots, t-$ 1 such that, for every $0 \leq i \leq t-1$, the binomial coefficient $\binom{t+i}{2 a_{i}}$ is odd and $2 a_{i} \neq t+i$.
|
We constantly make use of Kummer's theorem which, in particular, implies that $\binom{n}{k}$ is odd if and only if $k$ and $n-k$ have ones in different positions in binary. In other words, if $S(x)$ is the set of positions of the digits 1 of $x$ in binary (in which the digit multiplied by $2^{i}$ is in position $i),\binom{n}{k}$ is odd if and only if $S(k) \subseteq S(n)$. Moreover, if we set $k<n, S(k)$ is a proper subset of $S(n)$, that is, $|S(k)|<|S(n)|$.
We start with a lemma that guides us how the permutation should be set.
## Lemma 1.
$$
\sum_{i=0}^{t-1}|S(t+i)|=t+\sum_{i=0}^{t-1}|S(2 i)|
$$
The proof is just realizing that $S(2 i)=\{1+x, x \in S(i)\}$ and $S(2 i+1)=\{0\} \cup\{1+x, x \in S(i)\}$, because $2 i$ in binary is $i$ followed by a zero and $2 i+1$ in binary is $i$ followed by a one. Therefore
$$
\begin{aligned}
\sum_{i=0}^{t-1}|S(t+i)| & =\sum_{i=0}^{2 t-1}|S(i)|-\sum_{i=0}^{t-1}|S(i)|=\sum_{i=0}^{t-1}|S(2 i)|+\sum_{i=0}^{t-1}|S(2 i+1)|-\sum_{i=0}^{t-1}|S(i)| \\
& =\sum_{i=0}^{t-1}|S(i)|+\sum_{i=0}^{t-1}(1+|S(i)|)-\sum_{i=0}^{t-1}|S(i)|=t+\sum_{i=0}^{t-1}|S(i)|=t+\sum_{i=0}^{t-1}|S(2 i)|
\end{aligned}
$$
The lemma has an immediate corollary: since $t+i>2 a_{i}$ and $\binom{t+i}{2 a_{i}}$ is odd for all $i, 0 \leq i \leq t-1$, $S\left(2 a_{i}\right) \subset S(t+i)$ with $\left|S\left(2 a_{i}\right)\right| \leq|S(t+i)|-1$. Since the sum of $\left|S\left(2 a_{i}\right)\right|$ is $t$ less than the sum of $|S(t+i)|$, and there are $t$ values of $i$, equality must occur, that is, $\left|S\left(2 a_{i}\right)\right|=|S(t+i)|-1$, which in conjunction with $S\left(2 a_{i}\right) \subset S(t+i)$ means that $t+i-2 a_{i}=2^{k_{i}}$ for every $i, 0 \leq i \leq t-1$, $k_{i} \in S(t+i)$ (more precisely, $\left\{k_{i}\right\}=S(t+i) \backslash S\left(2 a_{i}\right)$.)
In particular, for $t+i$ odd, this means that $t+i-2 a_{i}=1$, because the only odd power of 2 is 1. Then $a_{i}=\frac{t+i-1}{2}$ for $t+i$ odd, which takes up all the numbers greater than or equal to $\frac{t-1}{2}$. Now we need to distribute the numbers that are smaller than $\frac{t-1}{2}$ (call these numbers small). If $t+i$ is even then by Lucas' Theorem $\binom{t+i}{2 a_{i}} \equiv\binom{\frac{t+i}{2}}{a_{i}}(\bmod 2)$, so we pair numbers from $\lceil t / 2\rceil$ to $t-1$ (call these numbers big) with the small numbers.
Say that a set $A$ is paired with another set $B$ whenever $|A|=|B|$ and there exists a bijection $\pi: A \rightarrow B$ such that $S(a) \subset S(\pi(a))$ and $|S(a)|=|S(\pi(a))|-1$; we also say that $a$ and $\pi(a)$ are paired. We prove by induction in $t$ that $A_{t}=\{0,1,2, \ldots,\lfloor t / 2\rfloor-1\}$ (the set of small numbers) and $B_{t}=\{\lceil t / 2\rceil, \ldots, t-2, t-1\}$ (the set of big numbers) can be uniquely paired.
The claim is immediate for $t=1$ and $t=2$. For $t>2$, there is exactly one power of two in $B_{t}$, since $t / 2 \leq 2^{a}<t \Longleftrightarrow a=\left\lceil\log _{2}(t / 2)\right\rceil$. Let $2^{a}$ be this power of two. Then, since $2^{a} \geq t / 2$, no number in $A_{t}$ has a one in position $a$ in binary. Since for every number $x, 2^{a} \leq x<t, a \in S(x)$ and $a \notin S(y)$ for all $y \in A_{t}, x$ can only be paired with $x-2^{a}$, since $S(x)$ needs to be stripped of exactly one position. This takes cares of $x \in B_{t}, 2^{a} \leq x<t$, and $y \in A_{t}, 0 \leq y<t-2^{a}$.
Now we need to pair the numbers from $A^{\prime}=\left\{t-2^{a}, t-2^{a}+1, \ldots,\lfloor t / 2\rfloor-1\right\} \subset A$ with the numbers from $B^{\prime}=\left\{\lceil t / 2\rceil,\lceil t / 2\rceil+1, \ldots, 2^{a}-1\right\} \subset B$. In order to pair these $t-2\left(t-2^{a}\right)=$ $2^{a+1}-t<t$ numbers, we use the induction hypothesis and a bijection between $A^{\prime} \cup B^{\prime}$ and $B_{2^{a+1}-t} \cup A_{2^{a+1}-t}$. Let $S=S\left(2^{a}-1\right)=\{0,1,2, \ldots, a-1\}$. Then take a pair $x, y, x \in A_{2^{a+1}-t}$ and $y \in B_{2^{a+1}-t}$ and biject it with $2^{a}-1-x \in B^{\prime}$ and $2^{a}-1-y \in A^{\prime}$. In fact,
$$
0 \leq x \leq\left\lfloor\frac{2^{a+1}-t}{2}\right\rfloor-1=2^{a}-\left\lceil\frac{t}{2}\right\rceil-1 \Longleftrightarrow\left\lceil\frac{t}{2}\right\rceil \leq 2^{a}-1-x \leq 2^{a}-1
$$
and
$$
\left\lceil\frac{2^{a+1}-t}{2}\right\rceil=2^{a}-\left\lfloor\frac{t}{2}\right\rfloor \leq y \leq 2^{a+1}-t-1 \Longleftrightarrow t-2^{a} \leq 2^{a}-1-y \leq\left\lfloor\frac{t}{2}\right\rfloor-1
$$
Moreover, $S\left(2^{a}-1-x\right)=S \backslash S(x)$ and $S\left(2^{a}-1-y\right)=S \backslash S(y)$ are complements with respect to $S$, and $S(x) \subset S(y)$ and $|S(x)|=|S(y)|-1$ implies $S\left(2^{a}-1-y\right) \subset S\left(2^{a}-1-x\right)$ and $\left|S\left(2^{a}-1-y\right)\right|=\left|S\left(2^{a}-1-x\right)\right|-1$. Therefore a pairing between $A^{\prime}$ and $B^{\prime}$ corresponds to a pairing between $A_{2^{a+1}-t}$ and $B_{2^{a+1}-t}$. Since the latter pairing is unique, the former pairing is also unique, and the result follows.
We illustrate the bijection by showing the case $t=23$ :
$$
A_{23}=\{0,1,2, \ldots, 10\}, \quad B_{23}=\{12,13,14, \ldots, 22\}
$$
The pairing is
$$
\left(\begin{array}{ccccccccccc}
12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 \\
8 & 9 & 10 & 7 & 0 & 1 & 2 & 3 & 4 & 5 & 6
\end{array}\right)
$$
in which the bijection is between
$$
\left(\begin{array}{cccc}
12 & 13 & 14 & 15 \\
8 & 9 & 10 & 7
\end{array}\right) \quad \text { and } \quad\left(\begin{array}{llll}
3 & 2 & 1 & 0 \\
7 & 6 & 5 & 8
\end{array}\right) \rightarrow\left(\begin{array}{llll}
5 & 6 & 7 & 8 \\
1 & 2 & 3 & 0
\end{array}\right) .
$$
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 4",
"solution_match": "# Solution\n\n"
}
|
52f0ff97-cac7-5dcb-a7bd-27d483c7c644
| 606,347
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
We start with the following lemma.
Lemma 1. Points $M, N, P, Q$ are concyclic.
Point $M$ is the Miquel point of lines $A P=A B, P S=\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \ell$, and $B C$, which is $L R S$.
Then, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\circ}$ )
$$
\begin{aligned}
\measuredangle N M P & =\measuredangle N M S+\measuredangle S M P=\measuredangle N R S+\measuredangle S A P=\measuredangle N R Q+\measuredangle D A B=\measuredangle N R Q+\measuredangle D C B \\
& =\measuredangle N R Q+\measuredangle Q C R=\measuredangle N R Q+\measuredangle Q N R=\measuredangle N Q R=\measuredangle N Q P,
\end{aligned}
$$
which implies that $M N Q P$ is a cyclic quadrilateral.
Let $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,
$$
\measuredangle T E M=\measuredangle L E M=\measuredangle L A M=\measuredangle S A M=\measuredangle S P M=\measuredangle Q P M=\measuredangle Q N M=\measuredangle T N M,
$$
that is, $T$ lies in the circumcircle $\omega$ of $E M N$. If $T=E$, the same computation shows that $\measuredangle L E M=\measuredangle E N M$, which means that $t$ is tangent to $\omega$.
Now let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\omega$ as well, and that if $V=E$ then $t$ is tangent to $\omega$.
Therefore, since $\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \neq E$ and $V \neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
We start with the following lemma.
Lemma 1. Points $M, N, P, Q$ are concyclic.
Point $M$ is the Miquel point of lines $A P=A B, P S=\ell, A S=A D$, and $B R=B C$, and point $N$ is the Miquel point of lines $C Q=C D, R C=B C, Q R=\ell$, and $D S=A D$. Both points $M$ and $N$ are on the circumcircle of the triangle determined by the common lines $A D, \ell$, and $B C$, which is $L R S$.
Then, since quadrilaterals $Q N R C, P M A S$, and $A B C D$ are all cyclic, using directed angles (modulo $180^{\circ}$ )
$$
\begin{aligned}
\measuredangle N M P & =\measuredangle N M S+\measuredangle S M P=\measuredangle N R S+\measuredangle S A P=\measuredangle N R Q+\measuredangle D A B=\measuredangle N R Q+\measuredangle D C B \\
& =\measuredangle N R Q+\measuredangle Q C R=\measuredangle N R Q+\measuredangle Q N R=\measuredangle N Q R=\measuredangle N Q P,
\end{aligned}
$$
which implies that $M N Q P$ is a cyclic quadrilateral.

Let $E$ be the Miquel point of $A B C D$ (that is, of lines $A B, B C, C D, D A$ ). It is well known that $E$ lies in the line $t$ connecting the intersections of the opposite lines of $A B C D$. Let lines $N Q$ and $t$ meet at $T$. If $T \neq E$, using directed angles, looking at the circumcircles of $L A B$ (which contains, by definition, $E$ and $M$ ), $A P S$ (which also contains $M$ ), and $M N Q P$,
$$
\measuredangle T E M=\measuredangle L E M=\measuredangle L A M=\measuredangle S A M=\measuredangle S P M=\measuredangle Q P M=\measuredangle Q N M=\measuredangle T N M,
$$
that is, $T$ lies in the circumcircle $\omega$ of $E M N$. If $T=E$, the same computation shows that $\measuredangle L E M=\measuredangle E N M$, which means that $t$ is tangent to $\omega$.
Now let lines $M P$ and $t$ meet at $V$. An analogous computation shows, by looking at the circumcircles of $L C D$ (which contains $E$ and $N$ ), $C Q R$, and $M N Q P$, that $V$ lies in $\omega$ as well, and that if $V=E$ then $t$ is tangent to $\omega$.
Therefore, since $\omega$ meet $t$ at $T, V$, and $E$, either $T=V$ if both $T \neq E$ and $V \neq E$ or $T=V=E$. At any rate, the intersection of lines $M P$ and $N Q$ lies in $t$.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 1"
}
|
848a0115-7f58-5c49-91e2-d109890bfbd5
| 606,351
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.
Lemma 2. Denote by $\operatorname{pow}_{\omega} X$ the power of point $X$ with respect to circle $\omega$. Let $\Gamma_{1}$ and $\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\Gamma_{1}$ and $\Gamma_{2}$ is given by
$$
\left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0
$$
Proof: Let $\Gamma_{i}$ have the equation $\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(r_{i} x+s_{i} y+t_{i} z\right)$. Then $\operatorname{pow}_{\Gamma_{i}} P=\Gamma_{i}(P)$. In particular, $\operatorname{pow}_{\Gamma_{i}} A=\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\operatorname{pow}_{\Gamma_{i}} B=s_{i}$ and $\operatorname{pow}_{\Gamma_{i}} C=t_{i}$.
Finally, the radical axis is
$$
\begin{aligned}
& \operatorname{pow}_{\Gamma_{1}} P=\operatorname{pow}_{\Gamma_{2}} P \\
\Longleftrightarrow & \Gamma_{1}(x, y, z)=\Gamma_{2}(x, y, z) \\
\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\
\Longleftrightarrow & \left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0 .
\end{aligned}
$$
We still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :
- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;
- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;
- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.
Looking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.
Associate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are
- MP: $(K A \cdot K P-K B \cdot K P) x+(Q S \cdot Q P-Q R \cdot Q P) y=0$
- $N Q:(K C \cdot K Q-K D \cdot K Q) x+(P R \cdot P Q-P S \cdot P Q) z=0$
- MP: $(-Q C \cdot Q K+Q D \cdot Q K) y+(P B \cdot P K-P A \cdot P K) z=0$
These equations simplify to
- $M P:(A B \cdot K P) x+(P Q \cdot R S) y=0$
- $N Q:(-C D \cdot K Q) x+(P Q \cdot R S) z=0$
- $M P:(C D \cdot K Q) y+(A B \cdot K P) z=0$
Now, if $u=A B \cdot K P, v=P Q \cdot R S$, and $w=C D \cdot K Q$, it suffices to show that
$$
\left|\begin{array}{ccc}
u & v & 0 \\
-w & 0 & v \\
0 & w & u
\end{array}\right|=0
$$
which is a straightforward computation.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Line $\ell$ intersects sides $B C$ and $A D$ of cyclic quadrilateral $A B C D$ in its interior points $R$ and $S$ respectively, and intersects ray $D C$ beyond point $C$ at $Q$, and ray $B A$ beyond point $A$ at $P$. Circumcircles of the triangles $Q C R$ and $Q D S$ intersect at $N \neq Q$, while circumcircles of the triangles $P A S$ and $P B R$ intersect at $M \neq P$. Let lines $M P$ and $N Q$ meet at point $X$, lines $A B$ and $C D$ meet at point $K$ and lines $B C$ and $A D$ meet at point $L$. Prove that point $X$ lies on line $K L$.
|
Barycentric coordinates are a viable way to solve the problem, but even the solution we have found had some clever computations. Here is an outline of this solution.
Lemma 2. Denote by $\operatorname{pow}_{\omega} X$ the power of point $X$ with respect to circle $\omega$. Let $\Gamma_{1}$ and $\Gamma_{2}$ be circles with different centers. Considering $A B C$ as the reference triangle in barycentric coordinates, the radical axis of $\Gamma_{1}$ and $\Gamma_{2}$ is given by
$$
\left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0
$$
Proof: Let $\Gamma_{i}$ have the equation $\Gamma_{i}(x, y, z)=-a^{2} y z-b^{2} z x-c^{2} x y+(x+y+z)\left(r_{i} x+s_{i} y+t_{i} z\right)$. Then $\operatorname{pow}_{\Gamma_{i}} P=\Gamma_{i}(P)$. In particular, $\operatorname{pow}_{\Gamma_{i}} A=\Gamma_{i}(1,0,0)=r_{i}$ and, similarly, $\operatorname{pow}_{\Gamma_{i}} B=s_{i}$ and $\operatorname{pow}_{\Gamma_{i}} C=t_{i}$.
Finally, the radical axis is
$$
\begin{aligned}
& \operatorname{pow}_{\Gamma_{1}} P=\operatorname{pow}_{\Gamma_{2}} P \\
\Longleftrightarrow & \Gamma_{1}(x, y, z)=\Gamma_{2}(x, y, z) \\
\Longleftrightarrow & r_{1} x+s_{1} y+t_{1} z=r_{2} x+s_{2} y+t_{2} z \\
\Longleftrightarrow & \left(\operatorname{pow}_{\Gamma_{1}} A-\operatorname{pow}_{\Gamma_{2}} A\right) x+\left(\operatorname{pow}_{\Gamma_{1}} B-\operatorname{pow}_{\Gamma_{2}} B\right) y+\left(\operatorname{pow}_{\Gamma_{1}} C-\operatorname{pow}_{\Gamma_{2}} C\right) z=0 .
\end{aligned}
$$
We still use the Miquel point $E$ of $A B C D$. Notice that the problem is equivalent to proving that lines $M P, N Q$, and $E K$ are concurrent. The main idea is writing these three lines as radical axes. In fact, by definition of points $M, N$, and $E$ :
- $M P$ is the radical axis of the circumcircles of $P A S$ and $P B R$;
- $N Q$ is the radical axis of the circumcircles of $Q C R$ and $Q D S$;
- $E K$ is the radical axis of the circumcircles of $K B C$ and $K A D$.
Looking at these facts and the diagram, it makes sense to take triangle $K Q P$ the reference triangle. Because of that, we do not really need to draw circles nor even points $M$ and $N$, as all powers can be computed directly from points in lines $K P, K Q$, and $P Q$.

Associate $P$ with the $x$-coordinate, $Q$ with the $y$-coordinate, and $K$ with the $z$-coordinate. Applying the lemma, the equations of lines $P M, Q N$, and $E K$ are
- MP: $(K A \cdot K P-K B \cdot K P) x+(Q S \cdot Q P-Q R \cdot Q P) y=0$
- $N Q:(K C \cdot K Q-K D \cdot K Q) x+(P R \cdot P Q-P S \cdot P Q) z=0$
- MP: $(-Q C \cdot Q K+Q D \cdot Q K) y+(P B \cdot P K-P A \cdot P K) z=0$
These equations simplify to
- $M P:(A B \cdot K P) x+(P Q \cdot R S) y=0$
- $N Q:(-C D \cdot K Q) x+(P Q \cdot R S) z=0$
- $M P:(C D \cdot K Q) y+(A B \cdot K P) z=0$
Now, if $u=A B \cdot K P, v=P Q \cdot R S$, and $w=C D \cdot K Q$, it suffices to show that
$$
\left|\begin{array}{ccc}
u & v & 0 \\
-w & 0 & v \\
0 & w & u
\end{array}\right|=0
$$
which is a straightforward computation.
|
{
"resource_path": "APMO/segmented/en-apmo2024_sol.jsonl",
"problem_match": "# Problem 5",
"solution_match": "# Solution 2"
}
|
848a0115-7f58-5c49-91e2-d109890bfbd5
| 606,351
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.