problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Some $1 \times 2$ dominoes, each covering two adjacent unit squares, are placed on a board of size $n \times n$ so that no two of them touch (not even at a corner). Given that the total area covered by the dominoes is 2008 , find the least possible value of $n$.
Answer: 77
|
Following the pattern from the figure, we have space for
$$
6+18+30+\ldots+150=\frac{156 \cdot 13}{2}=1014
$$
dominoes, giving the area $2028>2008$.
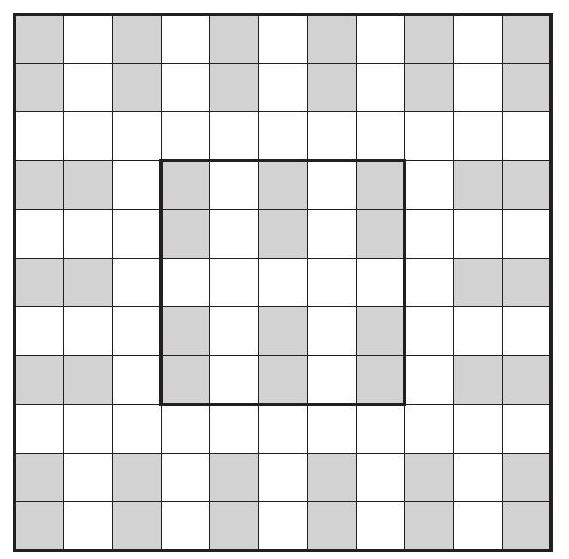
The square $76 \times 76$ is not enough. If it was, consider the "circumferences" of the 1004 dominoes of size $2 \times 3$, see figure; they should fit inside $77 \times 77$ square without overlapping. But $6 \cdot 1004=6024>5929=77 \cdot 77$.
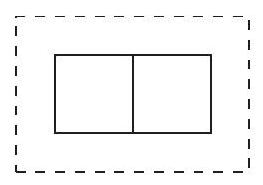
|
77
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Some $1 \times 2$ dominoes, each covering two adjacent unit squares, are placed on a board of size $n \times n$ so that no two of them touch (not even at a corner). Given that the total area covered by the dominoes is 2008 , find the least possible value of $n$.
Answer: 77
|
Following the pattern from the figure, we have space for
$$
6+18+30+\ldots+150=\frac{156 \cdot 13}{2}=1014
$$
dominoes, giving the area $2028>2008$.

The square $76 \times 76$ is not enough. If it was, consider the "circumferences" of the 1004 dominoes of size $2 \times 3$, see figure; they should fit inside $77 \times 77$ square without overlapping. But $6 \cdot 1004=6024>5929=77 \cdot 77$.

|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Let $A B C D$ be a parallelogram. The circle with diameter $A C$ intersects the line $B D$ at points $P$ and $Q$. The perpendicular to the line $A C$ passing through the point $C$ intersects the lines $A B$ and $A D$ at points $X$ and $Y$, respectively. Prove that the points $P, Q, X$ and $Y$ lie on the same circle.
|
If the lines $B D$ and $X Y$ are parallel the statement is trivial. Let $M$ be the intersection point of $B D$ and $X Y$.
By Intercept Theorem $M B / M D=M C / M Y$ and $M B / M D=M X / M C$, hence $M C^{2}=M X \cdot M Y$. By the circle property $M C^{2}=M P \cdot M Q$ (line $M C$ is tangent and line $M P$ is secant to the circle). Therefore we have $M X \cdot M Y=M P \cdot M Q$ and the quadrilateral $P Q Y X$ is inscribed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a parallelogram. The circle with diameter $A C$ intersects the line $B D$ at points $P$ and $Q$. The perpendicular to the line $A C$ passing through the point $C$ intersects the lines $A B$ and $A D$ at points $X$ and $Y$, respectively. Prove that the points $P, Q, X$ and $Y$ lie on the same circle.
|
If the lines $B D$ and $X Y$ are parallel the statement is trivial. Let $M$ be the intersection point of $B D$ and $X Y$.
By Intercept Theorem $M B / M D=M C / M Y$ and $M B / M D=M X / M C$, hence $M C^{2}=M X \cdot M Y$. By the circle property $M C^{2}=M P \cdot M Q$ (line $M C$ is tangent and line $M P$ is secant to the circle). Therefore we have $M X \cdot M Y=M P \cdot M Q$ and the quadrilateral $P Q Y X$ is inscribed.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Assume that $a, b, c$ and $d$ are the sides of a quadrilateral inscribed in a given circle. Prove that the product $(a b+c d)(a c+b d)(a d+b c)$ acquires its maximum when the quadrilateral is a square.
|
Let $A B C D$ be the quadrilateral, and let $A B=a, B C=b, C D=c, A D=d, A C=e, B D=f$. Ptolemy's Theorem gives $a c+b d=e f$. Since the area of triangle $A B C$ is $a b e / 4 R$, where $R$ is the circumradius, and similarly the area of triangle $A C D$, the product $(a b+c d) e$ equals $4 R$ times the area of quadrilateral $A B C D$. Similarly, this is also the value of the product $f(a d+b c)$, so $(a b+c d)(a c+b d)(a d+b c)$ is maximal when the quadrilateral has maximal area. Since the area of the quadrilateral is equal to $\frac{1}{2} e f \sin u$, where $u$ is one of the angles between the diagonals $A C$ and $B D$, it is maximal when all the factors of the product $d e \sin u$ are maximal. The diagonals $d$ and $e$ are maximal when they are diagonals of the circle, and $\sin u$ is maximal when $u=90^{\circ}$. Thus, $(a b+c d)(a c+b d)(a d+b c)$ is maximal when $A B C D$ is a square.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Assume that $a, b, c$ and $d$ are the sides of a quadrilateral inscribed in a given circle. Prove that the product $(a b+c d)(a c+b d)(a d+b c)$ acquires its maximum when the quadrilateral is a square.
|
Let $A B C D$ be the quadrilateral, and let $A B=a, B C=b, C D=c, A D=d, A C=e, B D=f$. Ptolemy's Theorem gives $a c+b d=e f$. Since the area of triangle $A B C$ is $a b e / 4 R$, where $R$ is the circumradius, and similarly the area of triangle $A C D$, the product $(a b+c d) e$ equals $4 R$ times the area of quadrilateral $A B C D$. Similarly, this is also the value of the product $f(a d+b c)$, so $(a b+c d)(a c+b d)(a d+b c)$ is maximal when the quadrilateral has maximal area. Since the area of the quadrilateral is equal to $\frac{1}{2} e f \sin u$, where $u$ is one of the angles between the diagonals $A C$ and $B D$, it is maximal when all the factors of the product $d e \sin u$ are maximal. The diagonals $d$ and $e$ are maximal when they are diagonals of the circle, and $\sin u$ is maximal when $u=90^{\circ}$. Thus, $(a b+c d)(a c+b d)(a d+b c)$ is maximal when $A B C D$ is a square.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Let $A B$ be a diameter of a circle $S$, and let $L$ be the tangent at $A$. Furthermore, let $c$ be a fixed, positive real, and consider all pairs of points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that $|A X| \cdot|A Y|=c$. The lines $B X$ and $B Y$ intersect $S$ at points $P$ and $Q$, respectively. Show that all the lines $P Q$ pass through a common point.
|
Let $S$ be the unit circle in the $x y$-plane with origin $O$, put $A=(1,0), B=(-1,0)$, take $L$ as the line $x=1$, and suppose $X=(1,2 p)$ and $Y=(1,-2 q)$, where $p$ and $q$ are positive real numbers with $p q=\frac{c}{4}$. If $\alpha=\angle A B P$ and $\beta=\angle A B Q$, then $\tan \alpha=p$ and $\tan \beta=q$.
Let $P Q$ intersect the $x$-axis in the point $R$. By the Inscribed Angle Theorem, $\angle R O P=2 \alpha$ and $\angle R O Q=2 \beta$. The triangle $O P Q$ is isosceles, from which $\angle O P Q=\angle O Q P=90^{\circ}-\alpha-\beta$, and $\angle O R P=90^{\circ}-\alpha+\beta$. The Law of Sines gives
$$
\frac{O R}{\sin \angle O P R}=\frac{O P}{\sin \angle O R P}
$$
which implies
$$
\begin{aligned}
O R & =\frac{\sin \angle O P R}{\sin \angle O R P}=\frac{\sin \left(90^{\circ}-\alpha-\beta\right)}{\sin \left(90^{\circ}-\alpha+\beta\right)}=\frac{\cos (\alpha+\beta)}{\cos (\alpha-\beta)} \\
& =\frac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta+\sin \alpha \sin \beta}=\frac{1-\tan \alpha \tan \beta}{1+\tan \alpha \tan \beta} \\
& =\frac{1-p q}{1+p q}=\frac{1-\frac{c}{4}}{1+\frac{c}{4}}=\frac{4-c}{4+c} .
\end{aligned}
$$
Hence the point $R$ lies on all lines $P Q$.
|
\frac{4-c}{4+c}
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle $S$, and let $L$ be the tangent at $A$. Furthermore, let $c$ be a fixed, positive real, and consider all pairs of points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that $|A X| \cdot|A Y|=c$. The lines $B X$ and $B Y$ intersect $S$ at points $P$ and $Q$, respectively. Show that all the lines $P Q$ pass through a common point.
|
Let $S$ be the unit circle in the $x y$-plane with origin $O$, put $A=(1,0), B=(-1,0)$, take $L$ as the line $x=1$, and suppose $X=(1,2 p)$ and $Y=(1,-2 q)$, where $p$ and $q$ are positive real numbers with $p q=\frac{c}{4}$. If $\alpha=\angle A B P$ and $\beta=\angle A B Q$, then $\tan \alpha=p$ and $\tan \beta=q$.
Let $P Q$ intersect the $x$-axis in the point $R$. By the Inscribed Angle Theorem, $\angle R O P=2 \alpha$ and $\angle R O Q=2 \beta$. The triangle $O P Q$ is isosceles, from which $\angle O P Q=\angle O Q P=90^{\circ}-\alpha-\beta$, and $\angle O R P=90^{\circ}-\alpha+\beta$. The Law of Sines gives
$$
\frac{O R}{\sin \angle O P R}=\frac{O P}{\sin \angle O R P}
$$
which implies
$$
\begin{aligned}
O R & =\frac{\sin \angle O P R}{\sin \angle O R P}=\frac{\sin \left(90^{\circ}-\alpha-\beta\right)}{\sin \left(90^{\circ}-\alpha+\beta\right)}=\frac{\cos (\alpha+\beta)}{\cos (\alpha-\beta)} \\
& =\frac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta+\sin \alpha \sin \beta}=\frac{1-\tan \alpha \tan \beta}{1+\tan \alpha \tan \beta} \\
& =\frac{1-p q}{1+p q}=\frac{1-\frac{c}{4}}{1+\frac{c}{4}}=\frac{4-c}{4+c} .
\end{aligned}
$$
Hence the point $R$ lies on all lines $P Q$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Let $A B$ be a diameter of a circle $S$, and let $L$ be the tangent at $A$. Furthermore, let $c$ be a fixed, positive real, and consider all pairs of points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that $|A X| \cdot|A Y|=c$. The lines $B X$ and $B Y$ intersect $S$ at points $P$ and $Q$, respectively. Show that all the lines $P Q$ pass through a common point.
|
Perform an inversion in the point $B$. Since angles are preserved under inversion, the problem transforms into the following: Let $S$ be a line, let the circle $L$ be tangent to it at point $A$, with $\infty$ as the diametrically opposite point. Consider all points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that if $\alpha=\angle A B X$ and $\beta=\angle A B Y$, then $\tan \alpha \tan \beta=\frac{c}{4}$. The lines $X \infty$ and $Y \infty$ will intersect $S$ in points $P$ and $Q$, respectively. Show that all the circles $P Q \infty$ will pass through a common point.
To prove this, draw the line through $A$ and $\infty$, and define $R$ as the point lying on this line, opposite to $\infty$, and at distance $\frac{c r}{2}$ from $A$, where $r$ is the radius of $L$. Since
$$
\tan \alpha=\frac{|A P|}{2 r}, \quad \tan \beta=\frac{|A Q|}{2 r},
$$
we have
$$
\frac{c}{4}=\tan \alpha \tan \beta=\frac{|A P||A Q|}{4 r^{2}}
$$
so that $|A P|=\frac{c r^{2}}{|A Q|}$, whence
$$
\tan \angle \infty R P=\frac{|A P|}{|A R|}=\frac{\frac{c r^{2}}{|A Q|}}{\frac{c r}{2}}=\frac{2 r}{|A Q|}=\tan \angle \infty Q P
$$
Consequently, $\infty, P, Q$, and $R$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle $S$, and let $L$ be the tangent at $A$. Furthermore, let $c$ be a fixed, positive real, and consider all pairs of points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that $|A X| \cdot|A Y|=c$. The lines $B X$ and $B Y$ intersect $S$ at points $P$ and $Q$, respectively. Show that all the lines $P Q$ pass through a common point.
|
Perform an inversion in the point $B$. Since angles are preserved under inversion, the problem transforms into the following: Let $S$ be a line, let the circle $L$ be tangent to it at point $A$, with $\infty$ as the diametrically opposite point. Consider all points $X$ and $Y$ lying on $L$, on opposite sides of $A$, such that if $\alpha=\angle A B X$ and $\beta=\angle A B Y$, then $\tan \alpha \tan \beta=\frac{c}{4}$. The lines $X \infty$ and $Y \infty$ will intersect $S$ in points $P$ and $Q$, respectively. Show that all the circles $P Q \infty$ will pass through a common point.
To prove this, draw the line through $A$ and $\infty$, and define $R$ as the point lying on this line, opposite to $\infty$, and at distance $\frac{c r}{2}$ from $A$, where $r$ is the radius of $L$. Since
$$
\tan \alpha=\frac{|A P|}{2 r}, \quad \tan \beta=\frac{|A Q|}{2 r},
$$
we have
$$
\frac{c}{4}=\tan \alpha \tan \beta=\frac{|A P||A Q|}{4 r^{2}}
$$
so that $|A P|=\frac{c r^{2}}{|A Q|}$, whence
$$
\tan \angle \infty R P=\frac{|A P|}{|A R|}=\frac{\frac{c r^{2}}{|A Q|}}{\frac{c r}{2}}=\frac{2 r}{|A Q|}=\tan \angle \infty Q P
$$
Consequently, $\infty, P, Q$, and $R$ are concyclic.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2008"
}
|
In a circle of diameter 1, some chords are drawn. The sum of their lengths is greater than 19. Prove that there is a diameter intersecting at least 7 chords.
|
For each hord consider the smallest arc subtended by it and the symmetric image of this arc accordingly to the center. The sum of lengths of all these arcs is more than $19 \cdot 2=38$. As $\frac{38}{\pi \cdot 1}>12$, there is a point on the circumference belonging to $>\frac{12}{2}$ original arcs, so it belongs to $\geq 7$ original arcs. We can take a diameter containing this point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a circle of diameter 1, some chords are drawn. The sum of their lengths is greater than 19. Prove that there is a diameter intersecting at least 7 chords.
|
For each hord consider the smallest arc subtended by it and the symmetric image of this arc accordingly to the center. The sum of lengths of all these arcs is more than $19 \cdot 2=38$. As $\frac{38}{\pi \cdot 1}>12$, there is a point on the circumference belonging to $>\frac{12}{2}$ original arcs, so it belongs to $\geq 7$ original arcs. We can take a diameter containing this point.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Let $M$ be a point on $B C$ and $N$ be a point on $A B$ such that $A M$ and $C N$ are angle bisectors of the triangle $A B C$. Given that
$$
\frac{\angle B N M}{\angle M N C}=\frac{\angle B M N}{\angle N M A}
$$
prove that the triangle $A B C$ is isosceles.
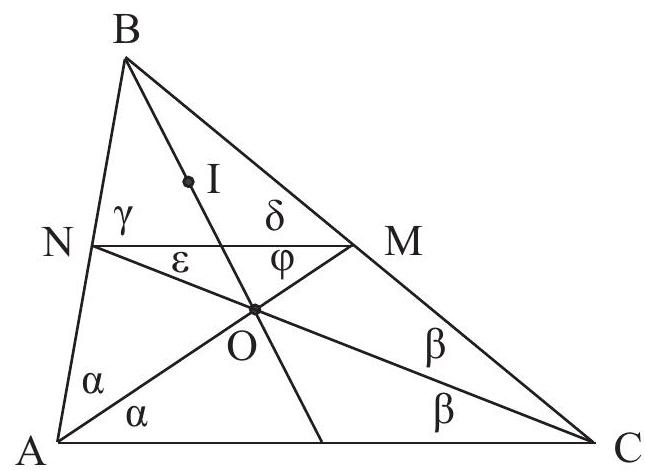
|
Let $O$ and $I$ be the incentres of $A B C$ and $N B M$, respectively; denote angles as in the figure. We get
$$
\alpha+\beta=\varepsilon+\varphi, \quad \gamma+\delta=2 \alpha+2 \beta, \quad \gamma=k \cdot \varepsilon, \quad \delta=k \cdot \varphi
$$
From here we get $k=2$. Therefore $\triangle N I M=\triangle N O M$, so $I O \perp N M$. In the triangle $N B M$ the bisector coincides with the altitude, so $B N=B M$. So we get
$$
\frac{A B \cdot B C}{A C+B C}=\frac{B C \cdot A B}{A B+A C}
$$
and $A B=B C$.
|
A B=B C
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $M$ be a point on $B C$ and $N$ be a point on $A B$ such that $A M$ and $C N$ are angle bisectors of the triangle $A B C$. Given that
$$
\frac{\angle B N M}{\angle M N C}=\frac{\angle B M N}{\angle N M A}
$$
prove that the triangle $A B C$ is isosceles.

|
Let $O$ and $I$ be the incentres of $A B C$ and $N B M$, respectively; denote angles as in the figure. We get
$$
\alpha+\beta=\varepsilon+\varphi, \quad \gamma+\delta=2 \alpha+2 \beta, \quad \gamma=k \cdot \varepsilon, \quad \delta=k \cdot \varphi
$$
From here we get $k=2$. Therefore $\triangle N I M=\triangle N O M$, so $I O \perp N M$. In the triangle $N B M$ the bisector coincides with the altitude, so $B N=B M$. So we get
$$
\frac{A B \cdot B C}{A C+B C}=\frac{B C \cdot A B}{A B+A C}
$$
and $A B=B C$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Find all quadruples of real numbers $(a, b, c, d)$ satisfying the system of equations
$$
\left\{\begin{array}{l}
(b+c+d)^{2010}=3 a \\
(a+c+d)^{2010}=3 b \\
(a+b+d)^{2010}=3 c \\
(a+b+c)^{2010}=3 d
\end{array}\right.
$$
|
There are two solutions: $(0,0,0,0)$ and $\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$.
If $(a, b, c, d)$ satisfies the equations, then we may as well assume $a \leq b \leq c \leq d$. These are non-negative because an even power of a real number is always non-negative. It follows that
$$
b+c+d \geq a+c+d \geq a+b+d \geq a+b+c
$$
and since $x \mapsto x^{2010}$ is increasing for $x \geq 0$ we have that
$$
3 a=(b+c+d)^{2010} \geq(a+c+d)^{2010} \geq(a+b+d)^{2010} \geq(a+b+c)^{2010}=3 d
$$
We conclude that $a=b=c=d$ and all the equations take the form $(3 a)^{2010}=3 a$, so $a=0$ or $3 a=1$. Finally, it is clear that $a=b=c=d=0$ and $a=b=c=d=\frac{1}{3}$ solve the system.
|
(0,0,0,0) \text{ and } \left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all quadruples of real numbers $(a, b, c, d)$ satisfying the system of equations
$$
\left\{\begin{array}{l}
(b+c+d)^{2010}=3 a \\
(a+c+d)^{2010}=3 b \\
(a+b+d)^{2010}=3 c \\
(a+b+c)^{2010}=3 d
\end{array}\right.
$$
|
There are two solutions: $(0,0,0,0)$ and $\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$.
If $(a, b, c, d)$ satisfies the equations, then we may as well assume $a \leq b \leq c \leq d$. These are non-negative because an even power of a real number is always non-negative. It follows that
$$
b+c+d \geq a+c+d \geq a+b+d \geq a+b+c
$$
and since $x \mapsto x^{2010}$ is increasing for $x \geq 0$ we have that
$$
3 a=(b+c+d)^{2010} \geq(a+c+d)^{2010} \geq(a+b+d)^{2010} \geq(a+b+c)^{2010}=3 d
$$
We conclude that $a=b=c=d$ and all the equations take the form $(3 a)^{2010}=3 a$, so $a=0$ or $3 a=1$. Finally, it is clear that $a=b=c=d=0$ and $a=b=c=d=\frac{1}{3}$ solve the system.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $x$ be a real number such that $0<x<\frac{\pi}{2}$. Prove that
$$
\cos ^{2}(x) \cot (x)+\sin ^{2}(x) \tan (x) \geq 1 \text {. }
$$
|
The geometric-arithmetic inequality gives
$$
\cos x \sin x \leq \frac{\cos ^{2} x+\sin ^{2} x}{2}=\frac{1}{2} .
$$
It follows that
$$
1=\left(\cos ^{2} x+\sin ^{2} x\right)^{2}=\cos ^{4} x+\sin ^{4} x+2 \cos ^{2} x \sin ^{2} x \leq \cos ^{4} x+\sin ^{4} x+\frac{1}{2}
$$
so
$$
\cos ^{4} x+\sin ^{4} x \geq \frac{1}{2} \geq \cos x \sin x .
$$
The required inequality follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x$ be a real number such that $0<x<\frac{\pi}{2}$. Prove that
$$
\cos ^{2}(x) \cot (x)+\sin ^{2}(x) \tan (x) \geq 1 \text {. }
$$
|
The geometric-arithmetic inequality gives
$$
\cos x \sin x \leq \frac{\cos ^{2} x+\sin ^{2} x}{2}=\frac{1}{2} .
$$
It follows that
$$
1=\left(\cos ^{2} x+\sin ^{2} x\right)^{2}=\cos ^{4} x+\sin ^{4} x+2 \cos ^{2} x \sin ^{2} x \leq \cos ^{4} x+\sin ^{4} x+\frac{1}{2}
$$
so
$$
\cos ^{4} x+\sin ^{4} x \geq \frac{1}{2} \geq \cos x \sin x .
$$
The required inequality follows.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $x_{1}, x_{2}, \ldots, x_{n}(n \geq 2)$ be real numbers greater than 1 . Suppose that $\left|x_{i}-x_{i+1}\right|<1$ for $i=1,2, \ldots, n-1$. Prove that
$$
\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{1}}<2 n-1
$$
|
The proof is by induction on $n$.
We establish first the base case $n=2$. Suppose that $x_{1}>1, x_{2}>1,\left|x_{1}-x_{2}\right|<1$ and moreover $x_{1} \leq x_{2}$. Then
$$
\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{1}} \leq 1+\frac{x_{2}}{x_{1}}<1+\frac{x_{1}+1}{x_{1}}=2+\frac{1}{x_{1}}<2+1=2 \cdot 2-1 .
$$
Now we proceed to the inductive step, and assume that the numbers $x_{1}, x_{2}, \ldots, x_{n}, x_{n+1}>1$ are given such that $\left|x_{i}-x_{i+1}\right|<1$ for $i=1,2, \ldots, n-1, n$. Let
$$
S=\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{1}}, \quad S^{\prime}=\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}}{x_{1}}
$$
The inductive assumption is that $S<2 n-1$ and the goal is that $S^{\prime}<2 n+1$. From the above relations involving $S$ and $S^{\prime}$ we see that it suffices to prove the inequality
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}} \leq 2
$$
We consider two cases. If $x_{n} \leq x_{n+1}$, then using the conditions $x_{1}>1$ and $x_{n+1}-x_{n}<1$ we obtain
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}} \leq 1+\frac{x_{n+1}-x_{n}}{x_{1}}<1+\frac{1}{x_{1}}<2,
$$
and if $x_{n}>x_{n+1}$, then using the conditions $x_{n}<x_{n+1}+1$ and $x_{n+1}>1$ we get
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}}<\frac{x_{n}}{x_{n+1}}<\frac{x_{n+1}+1}{x_{n+1}}=1+\frac{1}{x_{n+1}}<1+1=2 .
$$
The induction is now complete.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x_{1}, x_{2}, \ldots, x_{n}(n \geq 2)$ be real numbers greater than 1 . Suppose that $\left|x_{i}-x_{i+1}\right|<1$ for $i=1,2, \ldots, n-1$. Prove that
$$
\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{1}}<2 n-1
$$
|
The proof is by induction on $n$.
We establish first the base case $n=2$. Suppose that $x_{1}>1, x_{2}>1,\left|x_{1}-x_{2}\right|<1$ and moreover $x_{1} \leq x_{2}$. Then
$$
\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{1}} \leq 1+\frac{x_{2}}{x_{1}}<1+\frac{x_{1}+1}{x_{1}}=2+\frac{1}{x_{1}}<2+1=2 \cdot 2-1 .
$$
Now we proceed to the inductive step, and assume that the numbers $x_{1}, x_{2}, \ldots, x_{n}, x_{n+1}>1$ are given such that $\left|x_{i}-x_{i+1}\right|<1$ for $i=1,2, \ldots, n-1, n$. Let
$$
S=\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{1}}, \quad S^{\prime}=\frac{x_{1}}{x_{2}}+\frac{x_{2}}{x_{3}}+\ldots+\frac{x_{n-1}}{x_{n}}+\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}}{x_{1}}
$$
The inductive assumption is that $S<2 n-1$ and the goal is that $S^{\prime}<2 n+1$. From the above relations involving $S$ and $S^{\prime}$ we see that it suffices to prove the inequality
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}} \leq 2
$$
We consider two cases. If $x_{n} \leq x_{n+1}$, then using the conditions $x_{1}>1$ and $x_{n+1}-x_{n}<1$ we obtain
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}} \leq 1+\frac{x_{n+1}-x_{n}}{x_{1}}<1+\frac{1}{x_{1}}<2,
$$
and if $x_{n}>x_{n+1}$, then using the conditions $x_{n}<x_{n+1}+1$ and $x_{n+1}>1$ we get
$$
\frac{x_{n}}{x_{n+1}}+\frac{x_{n+1}-x_{n}}{x_{1}}<\frac{x_{n}}{x_{n+1}}<\frac{x_{n+1}+1}{x_{n+1}}=1+\frac{1}{x_{n+1}}<1+1=2 .
$$
The induction is now complete.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Find all polynomials $P(x)$ with real coefficients such that
$$
(x-2010) P(x+67)=x P(x)
$$
for every integer $x$.
|
Taking $x=0$ in the given equality leads to $-2010 P(67)=0$, implying $P(67)=0$. Whenever $i$ is an integer such that $1 \leq i<30$ and $P(i \cdot 67)=0$, taking $x=i \cdot 67$ leads to $(i \cdot 67-2010) P((i+1) \cdot 67)=0$; as $i \cdot 67<2010$ for $i<30$, this implies $P((i+1) \cdot 67)=0$. Thus, by induction, $P(i \cdot 67)=0$ for all $i=1,2, \ldots, 30$. Hence
$$
P(x) \equiv(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67) Q(x)
$$
where $Q(x)$ is another polynomial.
Substituting this expression for $P$ in the original equality, one obtains
$$
(x-2010) \cdot x(x-67) \ldots(x-29 \cdot 67) Q(x+67)=x(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67) Q(x)
$$
which is equivalent to
$$
x(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67)(Q(x+67)-Q(x))=0 .
$$
By conditions of the problem, this holds for every integer $x$. Hence there are infinitely many roots of polynomial $Q(x+67)-Q(x)$, implying that $Q(x+67)-Q(x) \equiv 0$. Let $c=Q(0)$; then $Q(i \cdot 67)=c$ for every integer $i$ by easy induction. Thus polynomial $Q(x)-c$ has infinitely many roots whence $Q(x) \equiv c$.
Consequently, $P(x)=c(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67)$ for some real number $c$. As equation (1) shows, all such polynomials fit.
|
P(x)=c(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all polynomials $P(x)$ with real coefficients such that
$$
(x-2010) P(x+67)=x P(x)
$$
for every integer $x$.
|
Taking $x=0$ in the given equality leads to $-2010 P(67)=0$, implying $P(67)=0$. Whenever $i$ is an integer such that $1 \leq i<30$ and $P(i \cdot 67)=0$, taking $x=i \cdot 67$ leads to $(i \cdot 67-2010) P((i+1) \cdot 67)=0$; as $i \cdot 67<2010$ for $i<30$, this implies $P((i+1) \cdot 67)=0$. Thus, by induction, $P(i \cdot 67)=0$ for all $i=1,2, \ldots, 30$. Hence
$$
P(x) \equiv(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67) Q(x)
$$
where $Q(x)$ is another polynomial.
Substituting this expression for $P$ in the original equality, one obtains
$$
(x-2010) \cdot x(x-67) \ldots(x-29 \cdot 67) Q(x+67)=x(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67) Q(x)
$$
which is equivalent to
$$
x(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67)(Q(x+67)-Q(x))=0 .
$$
By conditions of the problem, this holds for every integer $x$. Hence there are infinitely many roots of polynomial $Q(x+67)-Q(x)$, implying that $Q(x+67)-Q(x) \equiv 0$. Let $c=Q(0)$; then $Q(i \cdot 67)=c$ for every integer $i$ by easy induction. Thus polynomial $Q(x)-c$ has infinitely many roots whence $Q(x) \equiv c$.
Consequently, $P(x)=c(x-67)(x-2 \cdot 67) \ldots(x-30 \cdot 67)$ for some real number $c$. As equation (1) shows, all such polynomials fit.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $\mathbb{R}$ denote the set of real numbers. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}\right)+f(x y)=f(x) f(y)+y f(x)+x f(x+y)
$$
for all $x, y \in \mathbb{R}$.
|
Setting $x=0$ in the equation we get $f(0) f(y)=(2-y) f(0)$. If $f(0) \neq 0$, then $f(y)=2-y$ and it is easy to verify that this is a solution to the equation.
Now assume $f(0)=0$. Setting $y=0$ in the equation we get $f\left(x^{2}\right)=x f(x)$. Interchanging $x$ and $y$ and subtracting from the original equation we get
$$
x f(x)-y f(y)=y f(x)-x f(y)+(x-y) f(x+y)
$$
or equivalently
$$
(x-y)(f(x)+f(y))=(x-y) f(x+y) \text {. }
$$
For $x \neq y$ we therefore have $f(x+y)=f(x)+f(y)$. Since $f(0)=0$ this clearly also holds for $x=0$, and for $x=y \neq 0$ we have
$$
f(2 x)=f\left(\frac{x}{3}\right)+f\left(\frac{5 x}{3}\right)=f\left(\frac{x}{3}\right)+f\left(\frac{2 x}{3}\right)+f(x)=f(x)+f(x) .
$$
Setting $x=y$ in the original equation, using $f\left(x^{2}\right)=x f(x)$ and $f(2 x)=2 f(x)$ we get
$$
0=f(x)^{2}+x f(x)=f(x)(f(x)+x) .
$$
So for each $x$, either $f(x)=0$ or $f(x)=-x$. But then
$$
f(x)+f(y)=f(x+y)= \begin{cases}0 & \text { or } \\ -(x+y)\end{cases}
$$
and we conclude that $f(x)=-x$ if and only if $f(y)=-y$ when $x, y \neq 0$. We therefore have either $f(x)=-x$ for all $x$ or $f(x)=0$ for all $x$. It is easy to verify that both are solutions to the original equation.
|
f(x)=-x \text{ or } f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{R}$ denote the set of real numbers. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2}\right)+f(x y)=f(x) f(y)+y f(x)+x f(x+y)
$$
for all $x, y \in \mathbb{R}$.
|
Setting $x=0$ in the equation we get $f(0) f(y)=(2-y) f(0)$. If $f(0) \neq 0$, then $f(y)=2-y$ and it is easy to verify that this is a solution to the equation.
Now assume $f(0)=0$. Setting $y=0$ in the equation we get $f\left(x^{2}\right)=x f(x)$. Interchanging $x$ and $y$ and subtracting from the original equation we get
$$
x f(x)-y f(y)=y f(x)-x f(y)+(x-y) f(x+y)
$$
or equivalently
$$
(x-y)(f(x)+f(y))=(x-y) f(x+y) \text {. }
$$
For $x \neq y$ we therefore have $f(x+y)=f(x)+f(y)$. Since $f(0)=0$ this clearly also holds for $x=0$, and for $x=y \neq 0$ we have
$$
f(2 x)=f\left(\frac{x}{3}\right)+f\left(\frac{5 x}{3}\right)=f\left(\frac{x}{3}\right)+f\left(\frac{2 x}{3}\right)+f(x)=f(x)+f(x) .
$$
Setting $x=y$ in the original equation, using $f\left(x^{2}\right)=x f(x)$ and $f(2 x)=2 f(x)$ we get
$$
0=f(x)^{2}+x f(x)=f(x)(f(x)+x) .
$$
So for each $x$, either $f(x)=0$ or $f(x)=-x$. But then
$$
f(x)+f(y)=f(x+y)= \begin{cases}0 & \text { or } \\ -(x+y)\end{cases}
$$
and we conclude that $f(x)=-x$ if and only if $f(y)=-y$ when $x, y \neq 0$. We therefore have either $f(x)=-x$ for all $x$ or $f(x)=0$ for all $x$. It is easy to verify that both are solutions to the original equation.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
An $n \times n$ board is coloured in $n$ colours such that the main diagonal (from top-left to bottom-right) is coloured in the first colour; the two adjacent diagonals are coloured in the second colour; the two next diagonals (one from above and one from below) are coloured in the third colour, etc.; the two corners (top-right and bottom-left) are coloured in the $n$-th colour. It happens that it is possible to place on the board $n$ rooks, no two attacking each other and such that no two rooks stand on cells of the same colour. Prove that $n \equiv 0(\bmod 4)$ or $n \equiv 1$ $(\bmod 4)$.
|
Use the usual coordinate system for which the cells of the main diagonal have coordinates $(k, k)$, where $k=1, \ldots, n$. Let $(k, f(k))$ be the coordinates of the $k$-th rook. Then by color restrictions for rooks we have
$$
\sum_{k=1}^{n}(f(k)-k)^{2}=\sum_{i=0}^{n-1} i^{2}=\frac{n(n-1)(2 n-1)}{6} .
$$
Since the rooks are non-attacking we have
$$
\sum_{k=1}^{n}(f(k))^{2}=\sum_{i=1}^{n} i^{2}=\frac{n(n+1)(2 n+1)}{6} .
$$
By subtracting these equalities we obtain
$$
\sum_{k=1}^{n} k f(k)=\frac{n\left(2 n^{2}+9 n+1\right)}{12}
$$
Now it is trivial to check that the last number is integer if and only if $n \equiv 0$ or $1(\bmod 4)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An $n \times n$ board is coloured in $n$ colours such that the main diagonal (from top-left to bottom-right) is coloured in the first colour; the two adjacent diagonals are coloured in the second colour; the two next diagonals (one from above and one from below) are coloured in the third colour, etc.; the two corners (top-right and bottom-left) are coloured in the $n$-th colour. It happens that it is possible to place on the board $n$ rooks, no two attacking each other and such that no two rooks stand on cells of the same colour. Prove that $n \equiv 0(\bmod 4)$ or $n \equiv 1$ $(\bmod 4)$.
|
Use the usual coordinate system for which the cells of the main diagonal have coordinates $(k, k)$, where $k=1, \ldots, n$. Let $(k, f(k))$ be the coordinates of the $k$-th rook. Then by color restrictions for rooks we have
$$
\sum_{k=1}^{n}(f(k)-k)^{2}=\sum_{i=0}^{n-1} i^{2}=\frac{n(n-1)(2 n-1)}{6} .
$$
Since the rooks are non-attacking we have
$$
\sum_{k=1}^{n}(f(k))^{2}=\sum_{i=1}^{n} i^{2}=\frac{n(n+1)(2 n+1)}{6} .
$$
By subtracting these equalities we obtain
$$
\sum_{k=1}^{n} k f(k)=\frac{n\left(2 n^{2}+9 n+1\right)}{12}
$$
Now it is trivial to check that the last number is integer if and only if $n \equiv 0$ or $1(\bmod 4)$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
There are some cities in a country; one of them is the capital. For any two cities $A$ and $B$ there is a direct flight from $A$ to $B$ and a direct flight from $B$ to $A$, both having the same price. Suppose that all round trips with exactly one landing in every city have the same total cost. Prove that all round trips that miss the capital and with exactly one landing in every remaining city cost the same.
|
Let $C$ be the capital and $C_{1}, C_{2}, \ldots, C_{n}$ be the remaining cities. Denote by $d(x, y)$ the price of the connection between the cities $x$ and $y$, and let $\sigma$ be the total price of a round trip going exactly once through each city.
Now consider a round trip missing the capital and visiting every other city exactly once; let $s$ be the total price of that trip. Suppose $C_{i}$ and $C_{j}$ are two consecutive cities on the route. Replacing the flight $C_{i} \rightarrow C_{j}$ by two flights: from $C_{i}$ to the capital and from the capital to $C_{j}$, we get a round trip through all cities, with total price $\sigma$. It follows that $\sigma=s+d\left(C, C_{i}\right)+d\left(C, C_{j}\right)-$ $d\left(C_{i}, C_{j}\right)$, so it remains to show that the quantity $\alpha(i, j)=d\left(C, C_{i}\right)+d\left(C, C_{j}\right)-d\left(C_{i}, C_{j}\right)$ is the same for all 2-element subsets $\{i, j\} \subset\{1,2, \ldots, n\}$.
For this purpose, note that $\alpha(i, j)=\alpha(i, k)$ whenever $i, j, k$ are three distinct indices; indeed, this equality is equivalent to $d\left(C_{j}, C\right)+d\left(C, C_{i}\right)+d\left(C_{i}, C_{k}\right)=d\left(C_{j}, C_{i}\right)+d\left(C_{i}, C\right)+d\left(C, C_{k}\right)$, which is true by considering any trip from $C_{k}$ to $C_{j}$ going through all cities except $C$ and $C_{i}$ exactly once and completing this trip to a round trip in two ways: $C_{j} \rightarrow C \rightarrow C_{i} \rightarrow C_{k}$ and $C_{j} \rightarrow C_{i} \rightarrow C \rightarrow C_{k}$. Therefore the values of $\alpha$ coincide on any pair of 2-element sets sharing a common element. But then clearly $\alpha(i, j)=\alpha\left(i, j^{\prime}\right)=\alpha\left(i^{\prime}, j^{\prime}\right)$ for all indices $i, j, i^{\prime}, j^{\prime}$ with $i \neq j, i^{\prime} \neq j^{\prime}$, and the solution is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are some cities in a country; one of them is the capital. For any two cities $A$ and $B$ there is a direct flight from $A$ to $B$ and a direct flight from $B$ to $A$, both having the same price. Suppose that all round trips with exactly one landing in every city have the same total cost. Prove that all round trips that miss the capital and with exactly one landing in every remaining city cost the same.
|
Let $C$ be the capital and $C_{1}, C_{2}, \ldots, C_{n}$ be the remaining cities. Denote by $d(x, y)$ the price of the connection between the cities $x$ and $y$, and let $\sigma$ be the total price of a round trip going exactly once through each city.
Now consider a round trip missing the capital and visiting every other city exactly once; let $s$ be the total price of that trip. Suppose $C_{i}$ and $C_{j}$ are two consecutive cities on the route. Replacing the flight $C_{i} \rightarrow C_{j}$ by two flights: from $C_{i}$ to the capital and from the capital to $C_{j}$, we get a round trip through all cities, with total price $\sigma$. It follows that $\sigma=s+d\left(C, C_{i}\right)+d\left(C, C_{j}\right)-$ $d\left(C_{i}, C_{j}\right)$, so it remains to show that the quantity $\alpha(i, j)=d\left(C, C_{i}\right)+d\left(C, C_{j}\right)-d\left(C_{i}, C_{j}\right)$ is the same for all 2-element subsets $\{i, j\} \subset\{1,2, \ldots, n\}$.
For this purpose, note that $\alpha(i, j)=\alpha(i, k)$ whenever $i, j, k$ are three distinct indices; indeed, this equality is equivalent to $d\left(C_{j}, C\right)+d\left(C, C_{i}\right)+d\left(C_{i}, C_{k}\right)=d\left(C_{j}, C_{i}\right)+d\left(C_{i}, C\right)+d\left(C, C_{k}\right)$, which is true by considering any trip from $C_{k}$ to $C_{j}$ going through all cities except $C$ and $C_{i}$ exactly once and completing this trip to a round trip in two ways: $C_{j} \rightarrow C \rightarrow C_{i} \rightarrow C_{k}$ and $C_{j} \rightarrow C_{i} \rightarrow C \rightarrow C_{k}$. Therefore the values of $\alpha$ coincide on any pair of 2-element sets sharing a common element. But then clearly $\alpha(i, j)=\alpha\left(i, j^{\prime}\right)=\alpha\left(i^{\prime}, j^{\prime}\right)$ for all indices $i, j, i^{\prime}, j^{\prime}$ with $i \neq j, i^{\prime} \neq j^{\prime}$, and the solution is complete.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
In a club with 30 members, every member initially had a hat. One day each member sent his hat to a different member (a member could have received more than one hat). Prove that there exists a group of 10 members such that no one in the group has received a hat from another one in the group.
|
Let $S$ be the given group of 30 people. Consider all subsets $A \subset S$ such that no member of $A$ received a hat from a member of $A$. Among such subsets, let $T$ be a subset of maximal cardinality. The assertion of the problem is that $|T| \geq 10$.
Let $U \subset S$ consist of all people that have received a hat from a person belonging to $T$. Now consider any member $x \in S \backslash(T \cup U)$. Since $x \notin U$, no member of $T$ sent his hat to $x$. It follows that no member of $T$ sent a hat to a person from $T \cup\{x\}$. But the maximality of $T$ implies that some person from $T \cup\{x\}$ sent his hat to a person from the same subset. This means that $x$ sent his hat to a person from $T$. Consequently, all members of the subset $S \backslash(T \cup U)$ sent their hats to people in $T$. In particular, $S \backslash(T \cup U)$ has the property described in the beginning. The maximality of $T$ gives $|S \backslash(T \cup U)| \leq|T|$. Finally, we obviously have $|U| \leq|T|$, so
$$
|T| \geq|S \backslash(T \cup U)|=|S|-|T|-|U| \geq|S|-2|T|,
$$
or $|T| \geq \frac{1}{3}|S|=10$, as desired.
|
10
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a club with 30 members, every member initially had a hat. One day each member sent his hat to a different member (a member could have received more than one hat). Prove that there exists a group of 10 members such that no one in the group has received a hat from another one in the group.
|
Let $S$ be the given group of 30 people. Consider all subsets $A \subset S$ such that no member of $A$ received a hat from a member of $A$. Among such subsets, let $T$ be a subset of maximal cardinality. The assertion of the problem is that $|T| \geq 10$.
Let $U \subset S$ consist of all people that have received a hat from a person belonging to $T$. Now consider any member $x \in S \backslash(T \cup U)$. Since $x \notin U$, no member of $T$ sent his hat to $x$. It follows that no member of $T$ sent a hat to a person from $T \cup\{x\}$. But the maximality of $T$ implies that some person from $T \cup\{x\}$ sent his hat to a person from the same subset. This means that $x$ sent his hat to a person from $T$. Consequently, all members of the subset $S \backslash(T \cup U)$ sent their hats to people in $T$. In particular, $S \backslash(T \cup U)$ has the property described in the beginning. The maximality of $T$ gives $|S \backslash(T \cup U)| \leq|T|$. Finally, we obviously have $|U| \leq|T|$, so
$$
|T| \geq|S \backslash(T \cup U)|=|S|-|T|-|U| \geq|S|-2|T|,
$$
or $|T| \geq \frac{1}{3}|S|=10$, as desired.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
There is a pile of 1000 matches. Two players each take turns and can take 1 to 5 matches. It is also allowed at most 10 times during the whole game to take 6 matches, for example 7 exceptional moves can be done by the first player and 3 moves by the second and then no more exceptional moves are allowed. Whoever takes the last match wins. Determine which player has a winning strategy.
|
The second player wins.
Let $r$ be the number of the remaining exceptional moves in the current position (at the beginning of the game $r=10$ and $r$ decreases during the game). The winning strategy of the
second player is the following. After his move the number of matches in the pile must have the form $6 n+r$, where $n>r$, or $7 n$, where $n \leq r$ (observe that $6 n+r=7 n$ for $n=r$ ).
At the beginning of the game the initial number of matches $1000=6 \cdot 165+10$ agrees with this strategy.
What happens during two consecutive moves?
Consider the case $n>r$ first. If the first player takes $k=1,2, \ldots 5$ matches (and hence $r$ is not changing during his move) then the second player takes $6-k$ matches. So players take 6 matches together and the pile contains now $6(n-1)+r$ matches.
If the first player takes 6 matches, then $r$ decreases by 1 . The second player takes 1 match. After his turn the pile contains $6(n-1)+(r-1)$ matches as he wish.
Now consider the case $n \leq r$. In this situation we have much enough exceptional moves, and we may assume that now each move the players can take up to 6 matches. Then if the first player takes $k$ matches, the second player takes $7-k$ matches.
|
The\ second\ player\ wins.
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There is a pile of 1000 matches. Two players each take turns and can take 1 to 5 matches. It is also allowed at most 10 times during the whole game to take 6 matches, for example 7 exceptional moves can be done by the first player and 3 moves by the second and then no more exceptional moves are allowed. Whoever takes the last match wins. Determine which player has a winning strategy.
|
The second player wins.
Let $r$ be the number of the remaining exceptional moves in the current position (at the beginning of the game $r=10$ and $r$ decreases during the game). The winning strategy of the
second player is the following. After his move the number of matches in the pile must have the form $6 n+r$, where $n>r$, or $7 n$, where $n \leq r$ (observe that $6 n+r=7 n$ for $n=r$ ).
At the beginning of the game the initial number of matches $1000=6 \cdot 165+10$ agrees with this strategy.
What happens during two consecutive moves?
Consider the case $n>r$ first. If the first player takes $k=1,2, \ldots 5$ matches (and hence $r$ is not changing during his move) then the second player takes $6-k$ matches. So players take 6 matches together and the pile contains now $6(n-1)+r$ matches.
If the first player takes 6 matches, then $r$ decreases by 1 . The second player takes 1 match. After his turn the pile contains $6(n-1)+(r-1)$ matches as he wish.
Now consider the case $n \leq r$. In this situation we have much enough exceptional moves, and we may assume that now each move the players can take up to 6 matches. Then if the first player takes $k$ matches, the second player takes $7-k$ matches.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $n$ be an integer with $n \geq 3$. Consider all dissections of a convex $n$-gon into triangles by $n-3$ non-intersecting diagonals, and all colourings of the triangles with black and white so that triangles with a common side are always of a different colour. Find the least possible number of black triangles.
|
. The answer is $\left\lfloor\frac{n-1}{3}\right\rfloor$.
Let $f(n)$ denote the minimum number of black triangles in an $n$-gon. It is clear that $f(3)=0$ and that $f(n)$ is at least 1 for $n=4,5,6$. It is easy to see that for $n=4,5,6$ there is a coloring with only one black triangle, so $f(n)=1$ for $n=4,5,6$.
First we prove by induction that $f(n) \leq\left\lfloor\frac{n-1}{3}\right\rfloor$. The case for $n=3,4,5$ has already been established. Given an $(n+3)$-gon, draw a diagonal that splits it into an $n$-gon and a 5 -gon. Color the $n$-gon with at most $\left\lfloor\frac{n-1}{3}\right\rfloor$ black triangles. We can then color the 5 -gon compatibly with only one black triangle so $f(n+3) \leq\left\lfloor\frac{n-1}{3}\right\rfloor+1=\left\lfloor\frac{n+3-1}{3}\right\rfloor$.
Now we prove by induction that $f(n) \geq\left\lfloor\frac{n-1}{3}\right\rfloor$. The case for $n=3,4,5$ has already been established. Given an $(n+3)$-gon, we color it with $f(n+3)$ black triangles and pick one of the black triangles. It separates theree polygons from the $(n+3)$-gon, say an $(a+1)$-gon, $(b+1)$-gon and a $(c+1)$-gon such that $n+3=a+b+c$. We write $r_{m}$ for the remainder of the integer $m$ when divided by 3 . Then
$$
\begin{aligned}
f(n+3) & \geq f(a+1)+f(b+1)+f(c+1)+1 \\
& \geq\left\lfloor\frac{a}{3}\right\rfloor+\left\lfloor\frac{b}{3}\right\rfloor+\left\lfloor\frac{c}{3}\right\rfloor+1 \\
& =\frac{a-r_{a}}{3}+\frac{b-r_{b}}{3}+\frac{c-r_{c}}{3}+1 \\
& =\frac{n+3-1-r_{n}}{3}+\frac{4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right)}{3} \\
& =\left\lfloor\frac{n+3-1}{3}\right\rfloor+\frac{4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right)}{3} .
\end{aligned}
$$
Since $0 \leq r_{n}, r_{a}, r_{b}, r_{c} \leq 2$, we have that $4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right) \geq 4+0-6=-2$. But since this number is divisible by 3 , it is in fact $\geq 0$. This completes the induction.
|
\left\lfloor\frac{n-1}{3}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be an integer with $n \geq 3$. Consider all dissections of a convex $n$-gon into triangles by $n-3$ non-intersecting diagonals, and all colourings of the triangles with black and white so that triangles with a common side are always of a different colour. Find the least possible number of black triangles.
|
. The answer is $\left\lfloor\frac{n-1}{3}\right\rfloor$.
Let $f(n)$ denote the minimum number of black triangles in an $n$-gon. It is clear that $f(3)=0$ and that $f(n)$ is at least 1 for $n=4,5,6$. It is easy to see that for $n=4,5,6$ there is a coloring with only one black triangle, so $f(n)=1$ for $n=4,5,6$.
First we prove by induction that $f(n) \leq\left\lfloor\frac{n-1}{3}\right\rfloor$. The case for $n=3,4,5$ has already been established. Given an $(n+3)$-gon, draw a diagonal that splits it into an $n$-gon and a 5 -gon. Color the $n$-gon with at most $\left\lfloor\frac{n-1}{3}\right\rfloor$ black triangles. We can then color the 5 -gon compatibly with only one black triangle so $f(n+3) \leq\left\lfloor\frac{n-1}{3}\right\rfloor+1=\left\lfloor\frac{n+3-1}{3}\right\rfloor$.
Now we prove by induction that $f(n) \geq\left\lfloor\frac{n-1}{3}\right\rfloor$. The case for $n=3,4,5$ has already been established. Given an $(n+3)$-gon, we color it with $f(n+3)$ black triangles and pick one of the black triangles. It separates theree polygons from the $(n+3)$-gon, say an $(a+1)$-gon, $(b+1)$-gon and a $(c+1)$-gon such that $n+3=a+b+c$. We write $r_{m}$ for the remainder of the integer $m$ when divided by 3 . Then
$$
\begin{aligned}
f(n+3) & \geq f(a+1)+f(b+1)+f(c+1)+1 \\
& \geq\left\lfloor\frac{a}{3}\right\rfloor+\left\lfloor\frac{b}{3}\right\rfloor+\left\lfloor\frac{c}{3}\right\rfloor+1 \\
& =\frac{a-r_{a}}{3}+\frac{b-r_{b}}{3}+\frac{c-r_{c}}{3}+1 \\
& =\frac{n+3-1-r_{n}}{3}+\frac{4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right)}{3} \\
& =\left\lfloor\frac{n+3-1}{3}\right\rfloor+\frac{4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right)}{3} .
\end{aligned}
$$
Since $0 \leq r_{n}, r_{a}, r_{b}, r_{c} \leq 2$, we have that $4+r_{n}-\left(r_{a}+r_{b}+r_{c}\right) \geq 4+0-6=-2$. But since this number is divisible by 3 , it is in fact $\geq 0$. This completes the induction.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2010"
}
|
Let $n$ be an integer with $n \geq 3$. Consider all dissections of a convex $n$-gon into triangles by $n-3$ non-intersecting diagonals, and all colourings of the triangles with black and white so that triangles with a common side are always of a different colour. Find the least possible number of black triangles.
|
. Call two triangles neighbours if they have a common side. Let the dissections of convex $n$-gons together with appropriate colourings be called $n$-colourings.
Observe that all triangles of an arbitrary $n$-colouring can be listed, starting with an arbitrary triangle and always continuing the list by a triangle that is a neighbour to some triangle already
in the list. Indeed, suppose that some triangle $\Delta$ is missing from the list. Choose a point $A$ inside a triangle in the list, as well as a point $D$ inside $\Delta$. By convexity, the line segment $A D$ is entirely inside the polygon. As the vertices of the triangles are vertices of the polygon, $A D$ crosses the sides of the triangles only outside their vertices. Hence any consecutive triangles that $A D$ passes through are neighbours. The first triangle that ray $A D$ visits and that is not in the list is one that the list can be continued with.
Consider such a list of all triangles that starts with a white triangle. Each triangle has at most three neighbours and each black triangle has at least one neighbour occurring in the list before it. Thus at most two neighbours of any black triangle are following it in the list. Each white triangle except for the first one is a neighbour of some triangle preceding it in the list, and according to the construction, that triangle is black. Hence among all triangles except for the first one, there are at most twice as many white triangles as there are black triangles. Altogether, this means $w \leq 2 b+1$ where $b$ and $w$ are the numbers of black and white triangles in the construction, respectively. Observe that this formula holds also if there are no white triangles.
Hence there are at most $3 b+1$ triangles altogether, i.e., $n-2 \leq 3 b+1$. In integers, this implies $b \geq\left\lceil\frac{n}{3}\right\rceil-1$ which is equivalent to $b \geq\left\lfloor\frac{n-1}{3}\right\rfloor$.
This number of black triangles can be achieved as follows. Number all vertices of the polygon by 0 through $n-1$.
If $n=3 k, k \in \mathbb{N}^{+}$, then draw diagonals $(0,3 i-1),(3 i-1,3 i+1),(3 i+1,0)$ for all $i=1, \ldots, k-1$. Colour black every triangle whose vertices are $0,3 i-1$ and $3 i+1$ for some $i=1, \ldots, k-1$.
If $n=3 k-1$ or $n=3 k-2$ then take a described $3 k$-colouring and cut out 1 or 2 white triangles, respectively (e.g., triangles with vertices $0,1,2$ and $0, n-1, n-2$ ).
|
\left\lfloor\frac{n-1}{3}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be an integer with $n \geq 3$. Consider all dissections of a convex $n$-gon into triangles by $n-3$ non-intersecting diagonals, and all colourings of the triangles with black and white so that triangles with a common side are always of a different colour. Find the least possible number of black triangles.
|
. Call two triangles neighbours if they have a common side. Let the dissections of convex $n$-gons together with appropriate colourings be called $n$-colourings.
Observe that all triangles of an arbitrary $n$-colouring can be listed, starting with an arbitrary triangle and always continuing the list by a triangle that is a neighbour to some triangle already
in the list. Indeed, suppose that some triangle $\Delta$ is missing from the list. Choose a point $A$ inside a triangle in the list, as well as a point $D$ inside $\Delta$. By convexity, the line segment $A D$ is entirely inside the polygon. As the vertices of the triangles are vertices of the polygon, $A D$ crosses the sides of the triangles only outside their vertices. Hence any consecutive triangles that $A D$ passes through are neighbours. The first triangle that ray $A D$ visits and that is not in the list is one that the list can be continued with.
Consider such a list of all triangles that starts with a white triangle. Each triangle has at most three neighbours and each black triangle has at least one neighbour occurring in the list before it. Thus at most two neighbours of any black triangle are following it in the list. Each white triangle except for the first one is a neighbour of some triangle preceding it in the list, and according to the construction, that triangle is black. Hence among all triangles except for the first one, there are at most twice as many white triangles as there are black triangles. Altogether, this means $w \leq 2 b+1$ where $b$ and $w$ are the numbers of black and white triangles in the construction, respectively. Observe that this formula holds also if there are no white triangles.
Hence there are at most $3 b+1$ triangles altogether, i.e., $n-2 \leq 3 b+1$. In integers, this implies $b \geq\left\lceil\frac{n}{3}\right\rceil-1$ which is equivalent to $b \geq\left\lfloor\frac{n-1}{3}\right\rfloor$.
This number of black triangles can be achieved as follows. Number all vertices of the polygon by 0 through $n-1$.
If $n=3 k, k \in \mathbb{N}^{+}$, then draw diagonals $(0,3 i-1),(3 i-1,3 i+1),(3 i+1,0)$ for all $i=1, \ldots, k-1$. Colour black every triangle whose vertices are $0,3 i-1$ and $3 i+1$ for some $i=1, \ldots, k-1$.
If $n=3 k-1$ or $n=3 k-2$ then take a described $3 k$-colouring and cut out 1 or 2 white triangles, respectively (e.g., triangles with vertices $0,1,2$ and $0, n-1, n-2$ ).
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2010"
}
|
Let $A B C D$ be a square and let $S$ be the point of intersection of its diagonals $A C$ and $B D$. Two circles $k, k^{\prime}$ go through $A, C$ and $B, D$; respectively. Furthermore, $k$ and $k^{\prime}$ intersect in exactly two different points $P$ and $Q$. Prove that $S$ lies on $P Q$.
|
It is clear that $P Q$ is the radical axis of $k$ and $k^{\prime}$. The power of $S$ with respect to $k$ is $-|A S| \cdot|C S|$ and the power of $S$ with respect to $k^{\prime}$ is $-|B S| \cdot|D S|$. Because $A B C D$ is a square, these two numbers are clearly the same. Thus, $S$ has the same power with respect to $k$ and $k^{\prime}$ and lies on the radical axis $P Q$ of $k$ and $k^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square and let $S$ be the point of intersection of its diagonals $A C$ and $B D$. Two circles $k, k^{\prime}$ go through $A, C$ and $B, D$; respectively. Furthermore, $k$ and $k^{\prime}$ intersect in exactly two different points $P$ and $Q$. Prove that $S$ lies on $P Q$.
|
It is clear that $P Q$ is the radical axis of $k$ and $k^{\prime}$. The power of $S$ with respect to $k$ is $-|A S| \cdot|C S|$ and the power of $S$ with respect to $k^{\prime}$ is $-|B S| \cdot|D S|$. Because $A B C D$ is a square, these two numbers are clearly the same. Thus, $S$ has the same power with respect to $k$ and $k^{\prime}$ and lies on the radical axis $P Q$ of $k$ and $k^{\prime}$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $A B C D$ be a convex quadrilateral with precisely one pair of parallel sides.
a) Show that the lengths of its sides $A B, B C, C D, D A$ (in this order) do not form an arithmetic progression.
b) Show that there is such a quadrilateral for which the lengths of its sides $A B, B C, C D$, $D A$ form an arithmetic progression after the order of the lengths is changed.
|
Assume that the lengths of the sides form an arithmetic progression with the first term $a$ and the difference $d$. Suppose that sides $A B$ and $C D$ are parallel, $|A B|>|C D|$ and let $E$ be a point on $A B$ such that $|B E|=|C D|$. Then $|D E|=|C B|$ as opposite sides of a parallelogram, so $|A D|$ and $|D E|$ are two non-consequent terms of the arithmetic progression and $|A D|-|D E|= \pm 2 d$. Further, $|A E|=|A B|-|D C|=2 d$. We get a contradiction to the triangle inequality $|A E|>|| A D|-| D E \mid$.
We take a triangle with sides $3,3,2$ and add a parallelogram with sides 1 and 2 on the side of length 2 to obtain a trapezoid. Then the lengths of the sides are 1, 2, 4, 3 .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with precisely one pair of parallel sides.
a) Show that the lengths of its sides $A B, B C, C D, D A$ (in this order) do not form an arithmetic progression.
b) Show that there is such a quadrilateral for which the lengths of its sides $A B, B C, C D$, $D A$ form an arithmetic progression after the order of the lengths is changed.
|
Assume that the lengths of the sides form an arithmetic progression with the first term $a$ and the difference $d$. Suppose that sides $A B$ and $C D$ are parallel, $|A B|>|C D|$ and let $E$ be a point on $A B$ such that $|B E|=|C D|$. Then $|D E|=|C B|$ as opposite sides of a parallelogram, so $|A D|$ and $|D E|$ are two non-consequent terms of the arithmetic progression and $|A D|-|D E|= \pm 2 d$. Further, $|A E|=|A B|-|D C|=2 d$. We get a contradiction to the triangle inequality $|A E|>|| A D|-| D E \mid$.
We take a triangle with sides $3,3,2$ and add a parallelogram with sides 1 and 2 on the side of length 2 to obtain a trapezoid. Then the lengths of the sides are 1, 2, 4, 3 .
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
In an acute triangle $A B C$, the segment $C D$ is an altitude and $H$ is the orthocentre. Given that the circumcentre of the triangle lies on the line containing the bisector of the angle $D H B$, determine all possible values of $\angle C A B$.
|
The value is $\angle C A B=60^{\circ}$.
Denote by $\ell$ the line containing the angle bisector of $D H B$, and let $E$ be the point where the ray $C D \rightarrow$ intersects the circumcircle of the triangle $A B C$ again. The rays $H D \rightarrow$ and $H B \rightarrow$ are symmetric with respect to $\ell$ by the definition of $\ell$. On the other hand, if the circumcenter of $A B C$ lies on $\ell$, then the circumcircle is symmetric with respect to $\ell$. It follows that the intersections of the rays $H D^{\rightarrow}$ and $H B^{\rightarrow}$ with the circle, which are $E$ and $B$, are symmetric with respect to $\ell$. Moreover, since $H \in \ell$, we conclude that $H E=H B$.
However, as $E$ lies on the circumcircle of $A B C$, we have
$$
\angle A B E=\angle A C E=90^{\circ}-\angle C A B=\angle H B A .
$$
This proves that the points $H$ and $E$ are symmetric with respect to the line $A B$. Thus $H B=E B$ and the triangle $B H E$ is equilateral. Finally, $\angle C A B=\angle C E B=60^{\circ}$.
Obviously the value $\angle C A B=60^{\circ}$ is attained for an equilateral triangle $A B C$.
|
60^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In an acute triangle $A B C$, the segment $C D$ is an altitude and $H$ is the orthocentre. Given that the circumcentre of the triangle lies on the line containing the bisector of the angle $D H B$, determine all possible values of $\angle C A B$.
|
The value is $\angle C A B=60^{\circ}$.
Denote by $\ell$ the line containing the angle bisector of $D H B$, and let $E$ be the point where the ray $C D \rightarrow$ intersects the circumcircle of the triangle $A B C$ again. The rays $H D \rightarrow$ and $H B \rightarrow$ are symmetric with respect to $\ell$ by the definition of $\ell$. On the other hand, if the circumcenter of $A B C$ lies on $\ell$, then the circumcircle is symmetric with respect to $\ell$. It follows that the intersections of the rays $H D^{\rightarrow}$ and $H B^{\rightarrow}$ with the circle, which are $E$ and $B$, are symmetric with respect to $\ell$. Moreover, since $H \in \ell$, we conclude that $H E=H B$.
However, as $E$ lies on the circumcircle of $A B C$, we have
$$
\angle A B E=\angle A C E=90^{\circ}-\angle C A B=\angle H B A .
$$
This proves that the points $H$ and $E$ are symmetric with respect to the line $A B$. Thus $H B=E B$ and the triangle $B H E$ is equilateral. Finally, $\angle C A B=\angle C E B=60^{\circ}$.
Obviously the value $\angle C A B=60^{\circ}$ is attained for an equilateral triangle $A B C$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Assume that all angles of a triangle $A B C$ are acute. Let $D$ and $E$ be points on the sides $A C$ and $B C$ of the triangle such that $A, B, D$, and $E$ lie on the same circle. Further suppose the circle through $D, E$, and $C$ intersects the side $A B$ in two points $X$ and $Y$. Show that the midpoint of $X Y$ is the foot of the altitude from $C$ to $A B$.
|
We write the power of the point $A$ with respect to the circle $\gamma$ trough $D, E$, and $C$ :
$$
|A X||A Y|=|A D \| A C|=|A C|^{2}-|A C||C D| .
$$
Similarly, if we calculate the power of $B$ with respect to $\gamma$ we get
$$
|B X||B Y|=|B C|^{2}-|B C||C E| \text {. }
$$
We have also that $|A C||C D|=|B C||C E|$, the power of the point $C$ with respect to the circle through $A, B, D$, and $E$. Further if $M$ is the middle point of $X Y$ then
$$
|A X||A Y|=|A M|^{2}-|X M|^{2} \quad \text { and } \quad|B X||B Y|=|B M|^{2}-|X M|^{2} \text {. }
$$
Combining the four displayed identities we get
$$
|A M|^{2}-|B M|^{2}=|A C|^{2}-|B C|^{2} .
$$
By the theorem of Pythagoras the same holds for the point $H$ on $A B$ such that $C H$ is the altitude of the triangle $A B C$. Then since $H$ lies on the side $A B$ we get
$|A B|(|A M|-|B M|)=|A M|^{2}-|B M|^{2}=|A C|^{2}-|B C|^{2}=|A H|^{2}-|B H|^{2}=|A B|(|A H|-|B H|)$.
We conclude that $M=H$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Assume that all angles of a triangle $A B C$ are acute. Let $D$ and $E$ be points on the sides $A C$ and $B C$ of the triangle such that $A, B, D$, and $E$ lie on the same circle. Further suppose the circle through $D, E$, and $C$ intersects the side $A B$ in two points $X$ and $Y$. Show that the midpoint of $X Y$ is the foot of the altitude from $C$ to $A B$.
|
We write the power of the point $A$ with respect to the circle $\gamma$ trough $D, E$, and $C$ :
$$
|A X||A Y|=|A D \| A C|=|A C|^{2}-|A C||C D| .
$$
Similarly, if we calculate the power of $B$ with respect to $\gamma$ we get
$$
|B X||B Y|=|B C|^{2}-|B C||C E| \text {. }
$$
We have also that $|A C||C D|=|B C||C E|$, the power of the point $C$ with respect to the circle through $A, B, D$, and $E$. Further if $M$ is the middle point of $X Y$ then
$$
|A X||A Y|=|A M|^{2}-|X M|^{2} \quad \text { and } \quad|B X||B Y|=|B M|^{2}-|X M|^{2} \text {. }
$$
Combining the four displayed identities we get
$$
|A M|^{2}-|B M|^{2}=|A C|^{2}-|B C|^{2} .
$$
By the theorem of Pythagoras the same holds for the point $H$ on $A B$ such that $C H$ is the altitude of the triangle $A B C$. Then since $H$ lies on the side $A B$ we get
$|A B|(|A M|-|B M|)=|A M|^{2}-|B M|^{2}=|A C|^{2}-|B C|^{2}=|A H|^{2}-|B H|^{2}=|A B|(|A H|-|B H|)$.
We conclude that $M=H$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
The points $M$ and $N$ are chosen on the angle bisector $A L$ of a triangle $A B C$ such that $\angle A B M=\angle A C N=23^{\circ} . X$ is a point inside the triangle such that $B X=C X$ and $\angle B X C=2 \angle B M L$. Find $\angle M X N$.
|
Answer: $\angle M X N=2 \angle A B M=46^{\circ}$.
Let $\angle B A C=2 \alpha$. The triangles $A B M$ and $A C N$ are similar, therefore $\angle C N L=\angle B M L=$ $\alpha+23^{\circ}$. Let $K$ be the midpoint of the arc $B C$ of the circumcircle of the triangle $A B C$. Then $K$ belongs to the the line $A L$ and $\angle K B C=\alpha$. Both $X$ and $K$ belong to the perpendicular bisector of the segment $B C$, hence $\angle B X K=\frac{1}{2} \angle B X C=\angle B M L$, so the quadrilateral $B M X K$ is inscribed. Then
$$
\angle X M N=\angle X B K=\angle X B C+\angle K B C=\left(90^{\circ}-\angle B M L\right)+\alpha=90^{\circ}-(\angle B M L-\alpha)=67^{\circ} .
$$
Analogously we have $\angle C X K=\frac{1}{2} \angle B X C=\angle C N L$, therefore the quadrilateral $C X N K$ is inscribed also and $\angle X N M=\angle X C K=67^{\circ}$. Thus, the triangle $M X N$ is equilateral and
$\angle M X N=180^{\circ}-2 \cdot 67^{\circ}=46^{\circ}$.
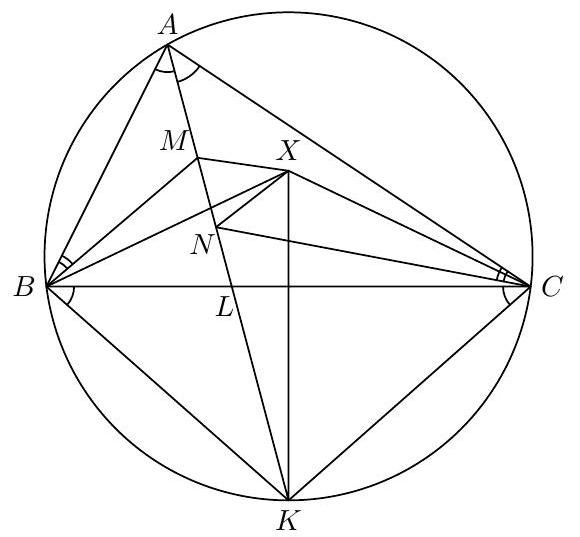
|
46^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The points $M$ and $N$ are chosen on the angle bisector $A L$ of a triangle $A B C$ such that $\angle A B M=\angle A C N=23^{\circ} . X$ is a point inside the triangle such that $B X=C X$ and $\angle B X C=2 \angle B M L$. Find $\angle M X N$.
|
Answer: $\angle M X N=2 \angle A B M=46^{\circ}$.
Let $\angle B A C=2 \alpha$. The triangles $A B M$ and $A C N$ are similar, therefore $\angle C N L=\angle B M L=$ $\alpha+23^{\circ}$. Let $K$ be the midpoint of the arc $B C$ of the circumcircle of the triangle $A B C$. Then $K$ belongs to the the line $A L$ and $\angle K B C=\alpha$. Both $X$ and $K$ belong to the perpendicular bisector of the segment $B C$, hence $\angle B X K=\frac{1}{2} \angle B X C=\angle B M L$, so the quadrilateral $B M X K$ is inscribed. Then
$$
\angle X M N=\angle X B K=\angle X B C+\angle K B C=\left(90^{\circ}-\angle B M L\right)+\alpha=90^{\circ}-(\angle B M L-\alpha)=67^{\circ} .
$$
Analogously we have $\angle C X K=\frac{1}{2} \angle B X C=\angle C N L$, therefore the quadrilateral $C X N K$ is inscribed also and $\angle X N M=\angle X C K=67^{\circ}$. Thus, the triangle $M X N$ is equilateral and
$\angle M X N=180^{\circ}-2 \cdot 67^{\circ}=46^{\circ}$.

|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
For a positive integer $k$, let $d(k)$ denote the number of divisors of $k$ (e.g. $d(12)=6$ ) and let $s(k)$ denote the digit sum of $k$ (e.g. $s(12)=3$ ). A positive integer $n$ is said to be amusing if there exists a positive integer $k$ such that $d(k)=s(k)=n$. What is the smallest amusing odd integer greater than 1 ?
|
The answer is 9 . For every $k$ we have $s(k) \equiv k(\bmod 9)$. Calculating remainders modulo 9 we have the following table
| $m$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $m^{2}$ | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 4 | 1 |
| $m^{6}$ | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
If $d(k)=3$, then $k=p^{2}$ with $p$ a prime, but $p^{2} \equiv 3(\bmod 9)$ is impossible. This shows that 3 is not an amusing number. If $d(k)=5$, then $k=p^{4}$ with $p$ a prime, but $p^{4} \equiv 5(\bmod 9)$ is impossible. This shows that 5 is not an amusing number. If $d(k)=7$, then $k=p^{6}$ with $p$ a prime, but $p^{6} \equiv 7(\bmod 9)$ is impossible. This shows that 7 is not an amusing number. To see that 9 is amusing, note that $d(36)=s(36)=9$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer $k$, let $d(k)$ denote the number of divisors of $k$ (e.g. $d(12)=6$ ) and let $s(k)$ denote the digit sum of $k$ (e.g. $s(12)=3$ ). A positive integer $n$ is said to be amusing if there exists a positive integer $k$ such that $d(k)=s(k)=n$. What is the smallest amusing odd integer greater than 1 ?
|
The answer is 9 . For every $k$ we have $s(k) \equiv k(\bmod 9)$. Calculating remainders modulo 9 we have the following table
| $m$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $m^{2}$ | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 4 | 1 |
| $m^{6}$ | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
If $d(k)=3$, then $k=p^{2}$ with $p$ a prime, but $p^{2} \equiv 3(\bmod 9)$ is impossible. This shows that 3 is not an amusing number. If $d(k)=5$, then $k=p^{4}$ with $p$ a prime, but $p^{4} \equiv 5(\bmod 9)$ is impossible. This shows that 5 is not an amusing number. If $d(k)=7$, then $k=p^{6}$ with $p$ a prime, but $p^{6} \equiv 7(\bmod 9)$ is impossible. This shows that 7 is not an amusing number. To see that 9 is amusing, note that $d(36)=s(36)=9$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Find all positive integers $n$ such that the decimal representation of $n^{2}$ consists of odd digits only.
|
The only such numbers are $n=1$ and $n=3$.
If $n$ is even, then so is the last digit of $n^{2}$. If $n$ is odd and divisible by 5 , then $n=10 k+5$ for some integer $k \geq 0$ and the second-to-last digit of $n^{2}=(10 k+5)^{2}=100 k^{2}+100 k+25$ equals 2 .
Thus we may restrict ourselves to numbers of the form $n=10 k \pm m$, where $m \in\{1,3\}$. Then
$$
n^{2}=(10 k \pm m)^{2}=100 k^{2} \pm 20 k m+m^{2}=20 k(5 k \pm m)+m^{2}
$$
and since $m^{2} \in\{1,9\}$, the second-to-last digit of $n^{2}$ is even unless the number $20 k(5 k-m)$ is equal to zero. We therefore have $n^{2}=m^{2}$ so $n=1$ or $n=3$. These numbers indeed satisfy the required condition.
|
n=1 \text{ and } n=3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that the decimal representation of $n^{2}$ consists of odd digits only.
|
The only such numbers are $n=1$ and $n=3$.
If $n$ is even, then so is the last digit of $n^{2}$. If $n$ is odd and divisible by 5 , then $n=10 k+5$ for some integer $k \geq 0$ and the second-to-last digit of $n^{2}=(10 k+5)^{2}=100 k^{2}+100 k+25$ equals 2 .
Thus we may restrict ourselves to numbers of the form $n=10 k \pm m$, where $m \in\{1,3\}$. Then
$$
n^{2}=(10 k \pm m)^{2}=100 k^{2} \pm 20 k m+m^{2}=20 k(5 k \pm m)+m^{2}
$$
and since $m^{2} \in\{1,9\}$, the second-to-last digit of $n^{2}$ is even unless the number $20 k(5 k-m)$ is equal to zero. We therefore have $n^{2}=m^{2}$ so $n=1$ or $n=3$. These numbers indeed satisfy the required condition.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Let $p$ be a prime number. For each $k, 1 \leq k \leq p-1$, there exists a unique integer denoted by $k^{-1}$ such that $1 \leq k^{-1} \leq p-1$ and $k^{-1} \cdot k \equiv 1(\bmod p)$. Prove that the sequence
$$
1^{-1}, \quad 1^{-1}+2^{-1}, \quad 1^{-1}+2^{-1}+3^{-1}, \quad \ldots, \quad 1^{-1}+2^{-1}+\cdots+(p-1)^{-1}
$$
(addition modulo $p$ ) contains at most $(p+1) / 2$ distinct elements.
|
Calculating modulo $p$ we have that $(p-k) k^{-1}=-1$ so $(p-k)^{-1}=-k^{-1}$. If $p$ is odd, we set $m=\frac{p-1}{2}$ and it follows that
$$
\sum_{k=1}^{p-1} k^{-1}=\sum_{k=1}^{m}\left(k^{-1}+(p-k)^{-1}\right)=0
$$
For $\ell$ such that $m<\ell<p-1$ we calculate the $\ell$-th term in the sequence
$$
\sum_{k=1}^{\ell} k^{-1}=\sum_{k=1}^{\ell} k^{-1}-\sum_{k=1}^{p-1} k^{-1}=-\sum_{k=\ell+1}^{p-1} k^{-1}=-\sum_{k=1}^{p-\ell-1}(p-k)^{-1}=\sum_{k=1}^{p-\ell-1} k^{-1}
$$
and see that it is equal to one of the first $m-1$ terms in the sequence. We conclude that there are at most $m+1=\frac{p+1}{2}$ distinct terms in the sequence (the first $m$ and the last one).
If $p$ is the even prime 2 , then the sequence contains only one term 1 , and $1<(2+1) / 2$.
|
\frac{p+1}{2}
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number. For each $k, 1 \leq k \leq p-1$, there exists a unique integer denoted by $k^{-1}$ such that $1 \leq k^{-1} \leq p-1$ and $k^{-1} \cdot k \equiv 1(\bmod p)$. Prove that the sequence
$$
1^{-1}, \quad 1^{-1}+2^{-1}, \quad 1^{-1}+2^{-1}+3^{-1}, \quad \ldots, \quad 1^{-1}+2^{-1}+\cdots+(p-1)^{-1}
$$
(addition modulo $p$ ) contains at most $(p+1) / 2$ distinct elements.
|
Calculating modulo $p$ we have that $(p-k) k^{-1}=-1$ so $(p-k)^{-1}=-k^{-1}$. If $p$ is odd, we set $m=\frac{p-1}{2}$ and it follows that
$$
\sum_{k=1}^{p-1} k^{-1}=\sum_{k=1}^{m}\left(k^{-1}+(p-k)^{-1}\right)=0
$$
For $\ell$ such that $m<\ell<p-1$ we calculate the $\ell$-th term in the sequence
$$
\sum_{k=1}^{\ell} k^{-1}=\sum_{k=1}^{\ell} k^{-1}-\sum_{k=1}^{p-1} k^{-1}=-\sum_{k=\ell+1}^{p-1} k^{-1}=-\sum_{k=1}^{p-\ell-1}(p-k)^{-1}=\sum_{k=1}^{p-\ell-1} k^{-1}
$$
and see that it is equal to one of the first $m-1$ terms in the sequence. We conclude that there are at most $m+1=\frac{p+1}{2}$ distinct terms in the sequence (the first $m$ and the last one).
If $p$ is the even prime 2 , then the sequence contains only one term 1 , and $1<(2+1) / 2$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
For which $k$ do there exist $k$ pairwise distinct primes $p_{1}, p_{2}, \ldots, p_{k}$ such that
$$
p_{1}^{2}+p_{2}^{2}+\cdots+p_{k}^{2}=2010 ?
$$
|
We show that it is possible only if $k=7$.
The 15 smallest prime squares are:
$$
4,9,25,49,121,169,289,361,529,841,961,1369,1681,1849,2209
$$
Since $2209>2010$ we see that $k \leq 14$.
Now we note that $p^{2} \equiv 1 \bmod 8$ if $p$ is an odd prime. We also have that $2010 \equiv 2 \bmod 8$. If all the primes are odd, then writing the original equation modulo 8 we get
$$
k \cdot 1 \equiv 2 \bmod 8
$$
so either $k=2$ or $k=10$.
$k=2:$ As $2010 \equiv 0 \bmod 3$ and $x^{2} \equiv 0$ or $x^{2} \equiv 1 \bmod 3$ we conclude that $p_{1} \equiv p_{2} \equiv 0$ mod 3. But that is impossible.
$k=10$ : The sum of first 10 odd prime squares is already greater than $2010(961+841+$ $529+\cdots>2010)$ so this is impossible.
Now we consider the case when one of the primes is 2 . Then the original equation modulo 8 takes the form
$$
4+(k-1) \cdot 1 \equiv 2 \quad \bmod 8
$$
so $k \equiv 7 \bmod 8$ and therefore $k=7$.
For $k=7$ there are 4 possible solutions:
$$
\begin{aligned}
4+9+49+169+289+529+961 & =2010 \\
4+9+25+121+361+529+961 & =2010 \\
4+9+25+49+121+841+961 & =2010 \\
4+9+49+121+169+289+1369 & =2010
\end{aligned}
$$
Finding them should not be too hard. We are already asuming that 4 is included. Considerations modulo 3 show that 9 must also be included. The square 1681 together with the 6 smallest prime squares gives a sum already greater than 2010 , so only prime squares up to $37^{2}=1369$ can be considered. If 25 is included, then for the remaining 4 prime squares considerations modulo 10 one can see that 3 out of 4 prime squares from $\{121,361,841,961\}$ have to be used and two of four cases are successful. If 25 is not included, then for the remaining 5 places again from considerations modulo 10 one can see, that 4 of them will be from the set $\{49,169,289,529,1369\}$ and two out of five cases are successful.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For which $k$ do there exist $k$ pairwise distinct primes $p_{1}, p_{2}, \ldots, p_{k}$ such that
$$
p_{1}^{2}+p_{2}^{2}+\cdots+p_{k}^{2}=2010 ?
$$
|
We show that it is possible only if $k=7$.
The 15 smallest prime squares are:
$$
4,9,25,49,121,169,289,361,529,841,961,1369,1681,1849,2209
$$
Since $2209>2010$ we see that $k \leq 14$.
Now we note that $p^{2} \equiv 1 \bmod 8$ if $p$ is an odd prime. We also have that $2010 \equiv 2 \bmod 8$. If all the primes are odd, then writing the original equation modulo 8 we get
$$
k \cdot 1 \equiv 2 \bmod 8
$$
so either $k=2$ or $k=10$.
$k=2:$ As $2010 \equiv 0 \bmod 3$ and $x^{2} \equiv 0$ or $x^{2} \equiv 1 \bmod 3$ we conclude that $p_{1} \equiv p_{2} \equiv 0$ mod 3. But that is impossible.
$k=10$ : The sum of first 10 odd prime squares is already greater than $2010(961+841+$ $529+\cdots>2010)$ so this is impossible.
Now we consider the case when one of the primes is 2 . Then the original equation modulo 8 takes the form
$$
4+(k-1) \cdot 1 \equiv 2 \quad \bmod 8
$$
so $k \equiv 7 \bmod 8$ and therefore $k=7$.
For $k=7$ there are 4 possible solutions:
$$
\begin{aligned}
4+9+49+169+289+529+961 & =2010 \\
4+9+25+121+361+529+961 & =2010 \\
4+9+25+49+121+841+961 & =2010 \\
4+9+49+121+169+289+1369 & =2010
\end{aligned}
$$
Finding them should not be too hard. We are already asuming that 4 is included. Considerations modulo 3 show that 9 must also be included. The square 1681 together with the 6 smallest prime squares gives a sum already greater than 2010 , so only prime squares up to $37^{2}=1369$ can be considered. If 25 is included, then for the remaining 4 prime squares considerations modulo 10 one can see that 3 out of 4 prime squares from $\{121,361,841,961\}$ have to be used and two of four cases are successful. If 25 is not included, then for the remaining 5 places again from considerations modulo 10 one can see, that 4 of them will be from the set $\{49,169,289,529,1369\}$ and two out of five cases are successful.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
Determine all positive integers $n$ for which there exists an infinite subset $A$ of the set $\mathbb{N}$ of positive integers such that for all pairwise distinct $a_{1}, \ldots, a_{n} \in A$ the numbers $a_{1}+\cdots+a_{n}$ and $a_{1} \cdots a_{n}$ are coprime.
|
For $n=1$ the statement is obviously false. We assert that it is true for all $n>1$.
We first consider the sequence $x_{0}, x_{1}, \ldots$ of positive integers which is recursively defined by $x_{0}=n$ and $x_{k+1}=\left(x_{0}+\cdots+x_{k}\right) !+1$ for $k \geq 0$. We claim that the set $A:=\left\{x_{k} \mid k \geq 1\right\}$ satisfies the condition.
Suppose the contrary that there exist $1 \leq i_{1}<\cdots<i_{n}$ such that $x_{i_{1}}+\cdots+x_{i_{n}}$ and $x_{i_{1}} \cdots x_{i_{n}}$ have a common prime factor $p$. Then there exist a $j \in\{1, \ldots, n\}$ such that $p \mid x_{i_{j}}$. From the definition of the sequence $\left(x_{1}, x_{2}, \ldots\right)$ we get $x_{k} \equiv 1(\bmod p)$ for every integer $k>i_{j}$. This implies $p \mid x_{i_{1}}+\ldots x_{i_{j-1}}+n-j=: S$. Because of $S>0$ and $S \leq x_{0}+\cdots+x_{i_{j}-1}$ we have $p \mid\left(x_{0}+\cdots+x_{i_{j}-1}\right) !=x_{i_{j}}-1$ which contradicts $p \mid x_{i_{j}}$.
Thus, for every pairwise distinct $a_{1}, \ldots, a_{n} \in A$ the numbers $a_{1}+\cdots+a_{n}$ and $a_{1} \cdots a_{n}$ are indeed coprime.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $n$ for which there exists an infinite subset $A$ of the set $\mathbb{N}$ of positive integers such that for all pairwise distinct $a_{1}, \ldots, a_{n} \in A$ the numbers $a_{1}+\cdots+a_{n}$ and $a_{1} \cdots a_{n}$ are coprime.
|
For $n=1$ the statement is obviously false. We assert that it is true for all $n>1$.
We first consider the sequence $x_{0}, x_{1}, \ldots$ of positive integers which is recursively defined by $x_{0}=n$ and $x_{k+1}=\left(x_{0}+\cdots+x_{k}\right) !+1$ for $k \geq 0$. We claim that the set $A:=\left\{x_{k} \mid k \geq 1\right\}$ satisfies the condition.
Suppose the contrary that there exist $1 \leq i_{1}<\cdots<i_{n}$ such that $x_{i_{1}}+\cdots+x_{i_{n}}$ and $x_{i_{1}} \cdots x_{i_{n}}$ have a common prime factor $p$. Then there exist a $j \in\{1, \ldots, n\}$ such that $p \mid x_{i_{j}}$. From the definition of the sequence $\left(x_{1}, x_{2}, \ldots\right)$ we get $x_{k} \equiv 1(\bmod p)$ for every integer $k>i_{j}$. This implies $p \mid x_{i_{1}}+\ldots x_{i_{j-1}}+n-j=: S$. Because of $S>0$ and $S \leq x_{0}+\cdots+x_{i_{j}-1}$ we have $p \mid\left(x_{0}+\cdots+x_{i_{j}-1}\right) !=x_{i_{j}}-1$ which contradicts $p \mid x_{i_{j}}$.
Thus, for every pairwise distinct $a_{1}, \ldots, a_{n} \in A$ the numbers $a_{1}+\cdots+a_{n}$ and $a_{1} \cdots a_{n}$ are indeed coprime.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw10sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2010"
}
|
The real numbers $x_{1}, \ldots, x_{2011}$ satisfy
$$
x_{1}+x_{2}=2 x_{1}^{\prime}, \quad x_{2}+x_{3}=2 x_{2}^{\prime}, \quad \ldots, \quad x_{2011}+x_{1}=2 x_{2011}^{\prime}
$$
where $x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{2011}^{\prime}$ is a permutation of $x_{1}, x_{2}, \ldots, x_{2011}$. Prove that $x_{1}=x_{2}=\cdots=x_{2011}$.
|
For convenience we call $x_{2011}$ also $x_{0}$. Let $k$ be the largest of the numbers $x_{1}, \ldots, x_{2011}$, and consider an equation $x_{n-1}+x_{n}=2 k$, where $1 \leq n \leq 2011$. Hence we get $2 \max \left(x_{n-1}, x_{n}\right) \geq x_{n-1}+x_{n}=2 k$, so either $x_{n-1}$ or $x_{n}$, say $x_{n-1}$, satisfies $x_{n-1} \geq k$. Since also $x_{n-1} \leq k$, we then have $x_{n-1}=k$, and then also $x_{n}=2 k-x_{n-1}=2 k-k=k$. That is, in such an equation both variables on the left equal $k$. Now let $\mathcal{E}$ be the set of such equations, and let $\mathcal{S}$ be the set of subscripts on the left of these equations. From $x_{n}=k \forall n \in \mathcal{S}$ we get $|\mathcal{S}| \leq|\mathcal{E}|$. On the other hand, since the total number of appearances of these subscripts is $2|\mathcal{E}|$ and each subscript appears on the left in no more than two equations, we have $2|\mathcal{E}| \leq 2|\mathcal{S}|$. Thus $2|\mathcal{E}|=2|\mathcal{S}|$, so for each $n \in \mathcal{S}$ the set $\mathcal{E}$ contains both equations with the subscript $n$ on the left. Now assume $1 \in \mathcal{S}$ without loss of generality. Then the equation $x_{1}+x_{2}=2 k$ belongs to $\mathcal{E}$, so $2 \in \mathcal{S}$. Continuing in this way we find that all subscripts belong to $\mathcal{S}$, so $x_{1}=x_{2}=\cdots=x_{2011}=k$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The real numbers $x_{1}, \ldots, x_{2011}$ satisfy
$$
x_{1}+x_{2}=2 x_{1}^{\prime}, \quad x_{2}+x_{3}=2 x_{2}^{\prime}, \quad \ldots, \quad x_{2011}+x_{1}=2 x_{2011}^{\prime}
$$
where $x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{2011}^{\prime}$ is a permutation of $x_{1}, x_{2}, \ldots, x_{2011}$. Prove that $x_{1}=x_{2}=\cdots=x_{2011}$.
|
For convenience we call $x_{2011}$ also $x_{0}$. Let $k$ be the largest of the numbers $x_{1}, \ldots, x_{2011}$, and consider an equation $x_{n-1}+x_{n}=2 k$, where $1 \leq n \leq 2011$. Hence we get $2 \max \left(x_{n-1}, x_{n}\right) \geq x_{n-1}+x_{n}=2 k$, so either $x_{n-1}$ or $x_{n}$, say $x_{n-1}$, satisfies $x_{n-1} \geq k$. Since also $x_{n-1} \leq k$, we then have $x_{n-1}=k$, and then also $x_{n}=2 k-x_{n-1}=2 k-k=k$. That is, in such an equation both variables on the left equal $k$. Now let $\mathcal{E}$ be the set of such equations, and let $\mathcal{S}$ be the set of subscripts on the left of these equations. From $x_{n}=k \forall n \in \mathcal{S}$ we get $|\mathcal{S}| \leq|\mathcal{E}|$. On the other hand, since the total number of appearances of these subscripts is $2|\mathcal{E}|$ and each subscript appears on the left in no more than two equations, we have $2|\mathcal{E}| \leq 2|\mathcal{S}|$. Thus $2|\mathcal{E}|=2|\mathcal{S}|$, so for each $n \in \mathcal{S}$ the set $\mathcal{E}$ contains both equations with the subscript $n$ on the left. Now assume $1 \in \mathcal{S}$ without loss of generality. Then the equation $x_{1}+x_{2}=2 k$ belongs to $\mathcal{E}$, so $2 \in \mathcal{S}$. Continuing in this way we find that all subscripts belong to $\mathcal{S}$, so $x_{1}=x_{2}=\cdots=x_{2011}=k$.
|
{
"exam": "BalticWay",
"problem_label": "A-1",
"problem_match": "\n## A-1 DEN\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2011"
}
|
The real numbers $x_{1}, \ldots, x_{2011}$ satisfy
$$
x_{1}+x_{2}=2 x_{1}^{\prime}, \quad x_{2}+x_{3}=2 x_{2}^{\prime}, \quad \ldots, \quad x_{2011}+x_{1}=2 x_{2011}^{\prime}
$$
where $x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{2011}^{\prime}$ is a permutation of $x_{1}, x_{2}, \ldots, x_{2011}$. Prove that $x_{1}=x_{2}=\cdots=x_{2011}$.
|
Again we call $x_{2011}$ also $x_{0}$. Taking the square on both sides of all the equations and adding the results, we get
$$
\sum_{n=1}^{2011}\left(x_{n-1}+x_{n}\right)^{2}=4 \sum_{n=1}^{2011} x_{n}^{\prime 2}=4 \sum_{n=1}^{2011} x_{n}^{2}
$$
which can be transformed with some algebra into
$$
\sum_{n=1}^{2011}\left(x_{n-1}-x_{n}\right)^{2}=0
$$
Hence the assertion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The real numbers $x_{1}, \ldots, x_{2011}$ satisfy
$$
x_{1}+x_{2}=2 x_{1}^{\prime}, \quad x_{2}+x_{3}=2 x_{2}^{\prime}, \quad \ldots, \quad x_{2011}+x_{1}=2 x_{2011}^{\prime}
$$
where $x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{2011}^{\prime}$ is a permutation of $x_{1}, x_{2}, \ldots, x_{2011}$. Prove that $x_{1}=x_{2}=\cdots=x_{2011}$.
|
Again we call $x_{2011}$ also $x_{0}$. Taking the square on both sides of all the equations and adding the results, we get
$$
\sum_{n=1}^{2011}\left(x_{n-1}+x_{n}\right)^{2}=4 \sum_{n=1}^{2011} x_{n}^{\prime 2}=4 \sum_{n=1}^{2011} x_{n}^{2}
$$
which can be transformed with some algebra into
$$
\sum_{n=1}^{2011}\left(x_{n-1}-x_{n}\right)^{2}=0
$$
Hence the assertion follows.
|
{
"exam": "BalticWay",
"problem_label": "A-1",
"problem_match": "\n## A-1 DEN\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2011"
}
|
Geometry
Let $A B$ and $C D$ be two diameters of the circle $\mathcal{C}$. For an arbitrary point $P$ on $\mathcal{C}$, let $R$ and $S$ be the feet of the perpendiculars from $P$ to $A B$ and $C D$, respectively. Show that the length of $R S$ is independent of the choice of $P$.
|
Let $O$ be the centre of $\mathcal{C}$. Then $P, R, S$, and $O$ are points on a circle $\mathcal{C}^{\prime}$ with diameter $O P$, equal to the radius of $\mathcal{C}$. The segment $R S$ is a chord in this circle subtending the angle $B O D$ or a supplementary angle. Since the angle as well as radius of $\mathcal{C}^{\prime}$ are independent of $P$, so is $R S$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Geometry
Let $A B$ and $C D$ be two diameters of the circle $\mathcal{C}$. For an arbitrary point $P$ on $\mathcal{C}$, let $R$ and $S$ be the feet of the perpendiculars from $P$ to $A B$ and $C D$, respectively. Show that the length of $R S$ is independent of the choice of $P$.
|
Let $O$ be the centre of $\mathcal{C}$. Then $P, R, S$, and $O$ are points on a circle $\mathcal{C}^{\prime}$ with diameter $O P$, equal to the radius of $\mathcal{C}$. The segment $R S$ is a chord in this circle subtending the angle $B O D$ or a supplementary angle. Since the angle as well as radius of $\mathcal{C}^{\prime}$ are independent of $P$, so is $R S$.

|
{
"exam": "BalticWay",
"problem_label": "G-1",
"problem_match": "\n## G-1 FIN\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2011"
}
|
Let $E$ be an interior point of the convex quadrilateral $A B C D$. Construct triangles $\triangle A B F$, $\triangle B C G, \triangle C D H$ and $\triangle D A I$ on the outside of the quadrilateral such that the similarities $\triangle A B F \sim \triangle D C E, \triangle B C G \sim \triangle A D E, \triangle C D H \sim \triangle B A E$ and $\triangle D A I \sim \triangle C B E$ hold. Let $P$, $Q, R$ and $S$ be the projections of $E$ on the lines $A B, B C, C D$ and $D A$, respectively. Prove that if the quadrilateral $P Q R S$ is cyclic, then
$$
E F \cdot C D=E G \cdot D A=E H \cdot A B=E I \cdot B C .
$$
|
We consider oriented angles modulo $180^{\circ}$. From the cyclic quadrilaterals $A P E S$, $B Q E P, P Q R S, C R E Q, D S E R$ and $\triangle D C E \sim \triangle A B F$ we get
$$
\begin{aligned}
\angle A E B & =\angle E A B+\angle A B E=\angle E S P+\angle P Q E \\
& =\angle E S R+\angle R S P+\angle P Q R+\angle R Q E \\
& =\angle E S R+\angle R Q E=\angle E D C+\angle D C E \\
& =\angle D E C=\angle A F B,
\end{aligned}
$$
so the quadrilateral $A E B F$ is cyclic. By Ptolemy we then have
$$
E F \cdot A B=A E \cdot B F+B E \cdot A F .
$$
This transforms by $A B: B F: A F=D C: C E: D E$ into
Since the expression on the right of this equation is invariant under cyclic permutation of the vertices of the quadrilateral $A B C D$, the asserted equation follows immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $E$ be an interior point of the convex quadrilateral $A B C D$. Construct triangles $\triangle A B F$, $\triangle B C G, \triangle C D H$ and $\triangle D A I$ on the outside of the quadrilateral such that the similarities $\triangle A B F \sim \triangle D C E, \triangle B C G \sim \triangle A D E, \triangle C D H \sim \triangle B A E$ and $\triangle D A I \sim \triangle C B E$ hold. Let $P$, $Q, R$ and $S$ be the projections of $E$ on the lines $A B, B C, C D$ and $D A$, respectively. Prove that if the quadrilateral $P Q R S$ is cyclic, then
$$
E F \cdot C D=E G \cdot D A=E H \cdot A B=E I \cdot B C .
$$
|
We consider oriented angles modulo $180^{\circ}$. From the cyclic quadrilaterals $A P E S$, $B Q E P, P Q R S, C R E Q, D S E R$ and $\triangle D C E \sim \triangle A B F$ we get
$$
\begin{aligned}
\angle A E B & =\angle E A B+\angle A B E=\angle E S P+\angle P Q E \\
& =\angle E S R+\angle R S P+\angle P Q R+\angle R Q E \\
& =\angle E S R+\angle R Q E=\angle E D C+\angle D C E \\
& =\angle D E C=\angle A F B,
\end{aligned}
$$
so the quadrilateral $A E B F$ is cyclic. By Ptolemy we then have
$$
E F \cdot A B=A E \cdot B F+B E \cdot A F .
$$
This transforms by $A B: B F: A F=D C: C E: D E$ into

Since the expression on the right of this equation is invariant under cyclic permutation of the vertices of the quadrilateral $A B C D$, the asserted equation follows immediately.
|
{
"exam": "BalticWay",
"problem_label": "G-3",
"problem_match": "\n## G-3 DEN\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2011"
}
|
The incircle of a triangle $A B C$ touches the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be a point on the incircle such that $F G$ is a diameter. The lines $E G$ and $F D$ intersect at $H$. Prove that $C H \| A B$.
|
We work in the opposite direction. Suppose that $H^{\prime}$ is the point where $D F$ intersect the line through $C$ parallel to $A B$. We need to show that $H^{\prime}=H$. For this purpose it suffices to prove that $E, G, H^{\prime}$ are collinear, which reduces to showing that if $G^{\prime} \neq E$ is the common point of $E H^{\prime}$ and the incircle, then $G^{\prime}=G$.
Note that $H^{\prime}$ and $B$ lie on the same side of $A C$. Hence $C H^{\prime} \| A B$ gives $\angle A C H^{\prime}=180^{\circ}-\angle B A C$. Also, some homothety with center $D$ maps the segment $B F$ to the segment $C H^{\prime}$. Thus the equality $B D=B F$ implies that $C H^{\prime}=C D=C E$, i.e. the triangle $E C H^{\prime}$ is isosceles and
$$
\angle H^{\prime} E C=\frac{1}{2}\left(180^{\circ}-\angle E C H^{\prime}\right)=\frac{1}{2} \angle B A C .
$$
But $G^{\prime}$ and $H^{\prime}$ lie on the same side of $A C$, so $\angle G^{\prime} E C=\angle H^{\prime} E C$ and consequently
$$
\angle G^{\prime} F E=\angle G^{\prime} E C=\angle H^{\prime} E C=\frac{1}{2} \angle B A C
$$
so that
$$
\angle G^{\prime} F A=\angle G^{\prime} F E+\angle E F A=\frac{1}{2} \angle B A C+\frac{1}{2}\left(180^{\circ}-\angle F A E\right)=90^{\circ} .
$$
Hence $F G^{\prime}$ is a diameter of the incircle and the desired equality $G^{\prime}=G$ follows.
Remark. A similar proof also works in the forward direction: one may compute $\angle E H D=$ $\frac{1}{2} \angle A C B$. Hence $H$ lies on the circle centred at $C$ that passes through $D$ and $E$. Consequently the triangle $E H C$ is isosceles, wherefore
$$
\angle E C H=180^{\circ}-2 \angle G E C=180^{\circ}-\angle B A C .
$$
Thus the lines $A B$ and $C H$ are indeed parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The incircle of a triangle $A B C$ touches the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be a point on the incircle such that $F G$ is a diameter. The lines $E G$ and $F D$ intersect at $H$. Prove that $C H \| A B$.
|
We work in the opposite direction. Suppose that $H^{\prime}$ is the point where $D F$ intersect the line through $C$ parallel to $A B$. We need to show that $H^{\prime}=H$. For this purpose it suffices to prove that $E, G, H^{\prime}$ are collinear, which reduces to showing that if $G^{\prime} \neq E$ is the common point of $E H^{\prime}$ and the incircle, then $G^{\prime}=G$.

Note that $H^{\prime}$ and $B$ lie on the same side of $A C$. Hence $C H^{\prime} \| A B$ gives $\angle A C H^{\prime}=180^{\circ}-\angle B A C$. Also, some homothety with center $D$ maps the segment $B F$ to the segment $C H^{\prime}$. Thus the equality $B D=B F$ implies that $C H^{\prime}=C D=C E$, i.e. the triangle $E C H^{\prime}$ is isosceles and
$$
\angle H^{\prime} E C=\frac{1}{2}\left(180^{\circ}-\angle E C H^{\prime}\right)=\frac{1}{2} \angle B A C .
$$
But $G^{\prime}$ and $H^{\prime}$ lie on the same side of $A C$, so $\angle G^{\prime} E C=\angle H^{\prime} E C$ and consequently
$$
\angle G^{\prime} F E=\angle G^{\prime} E C=\angle H^{\prime} E C=\frac{1}{2} \angle B A C
$$
so that
$$
\angle G^{\prime} F A=\angle G^{\prime} F E+\angle E F A=\frac{1}{2} \angle B A C+\frac{1}{2}\left(180^{\circ}-\angle F A E\right)=90^{\circ} .
$$
Hence $F G^{\prime}$ is a diameter of the incircle and the desired equality $G^{\prime}=G$ follows.
Remark. A similar proof also works in the forward direction: one may compute $\angle E H D=$ $\frac{1}{2} \angle A C B$. Hence $H$ lies on the circle centred at $C$ that passes through $D$ and $E$. Consequently the triangle $E H C$ is isosceles, wherefore
$$
\angle E C H=180^{\circ}-2 \angle G E C=180^{\circ}-\angle B A C .
$$
Thus the lines $A B$ and $C H$ are indeed parallel.
|
{
"exam": "BalticWay",
"problem_label": "G-4",
"problem_match": "\n## G-4 POL\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2011"
}
|
Let $A B C D$ be a convex quadrilateral such that $\angle A D B=\angle B D C$. Suppose that a point $E$ on the side $A D$ satisfies the equality
$$
A E \cdot E D+B E^{2}=C D \cdot A E .
$$
Show that $\angle E B A=\angle D C B$.
|
Let $F$ be the point symmetric to $E$ with respect to the line $D B$. Then the equality $\angle A D B=\angle B D C$ shows that $F$ lies on the line $D C$, on the same side of $D$ as $C$. Moreover, we have $A E \cdot E D<C D \cdot A E$, or $F D=E D<C D$, so in fact $F$ lies on the segment $D C$.
Note now that triangles $D E B$ and $D F B$ are congruent (symmetric with respect to the line $D B)$, so $\angle A E B=\angle B F C$. Also, we have
$$
B E^{2}=C D \cdot A E-A E \cdot E D=A E \cdot(C D-E D)=A E \cdot(C D-F D)=A E \cdot C F
$$
Therefore
$$
\frac{B E}{A E}=\frac{C F}{B E}=\frac{C F}{B F}
$$
This shows that the triangles $B E A$ and $C F B$ are similar, which gives $\angle E B A=\angle F C B=$ $\angle D C B$, as desired.
## Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $\angle A D B=\angle B D C$. Suppose that a point $E$ on the side $A D$ satisfies the equality
$$
A E \cdot E D+B E^{2}=C D \cdot A E .
$$
Show that $\angle E B A=\angle D C B$.
|
Let $F$ be the point symmetric to $E$ with respect to the line $D B$. Then the equality $\angle A D B=\angle B D C$ shows that $F$ lies on the line $D C$, on the same side of $D$ as $C$. Moreover, we have $A E \cdot E D<C D \cdot A E$, or $F D=E D<C D$, so in fact $F$ lies on the segment $D C$.

Note now that triangles $D E B$ and $D F B$ are congruent (symmetric with respect to the line $D B)$, so $\angle A E B=\angle B F C$. Also, we have
$$
B E^{2}=C D \cdot A E-A E \cdot E D=A E \cdot(C D-E D)=A E \cdot(C D-F D)=A E \cdot C F
$$
Therefore
$$
\frac{B E}{A E}=\frac{C F}{B E}=\frac{C F}{B F}
$$
This shows that the triangles $B E A$ and $C F B$ are similar, which gives $\angle E B A=\angle F C B=$ $\angle D C B$, as desired.
## Number Theory
|
{
"exam": "BalticWay",
"problem_label": "G-5",
"problem_match": "\n## G-5 POL\n",
"resource_path": "BalticWay/segmented/en-bw11sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2011"
}
|
The numbers from 1 to 360 are partitioned into 9 subsets of consecutive integers and the sums of the numbers in each subset are arranged in the cells of a $3 \times 3$ square. Is it possible that the square turns out to be a magic square?
Remark: A magic square is a square in which the sums of the numbers in each row, in each column and in both diagonals are all equal.
Answer: Yes.
|
. If the numbers $a_{1}, a_{2}, \ldots, a_{9}$ form a $3 \times 3$ magic square, then the numbers $a_{1}+d, a_{2}+d, \ldots, a_{9}+d$ form a $3 \times 3$ magic square, too. Hence it is sufficient to divide all the numbers into parts with equal numbers of elements: i.e. from $40 k+1$ to $40(k+1), k=0,1, \ldots, 8$. Then we need to arrange the least numbers of these parts (i.e. the numbers $1,41,81, \ldots, 321$ ) in the form of a magic square (we omit here an example, it is similar to the magic square with numbers 1 , $2, \ldots, 9)$. After that all other numbers $1+s, 41+s, \ldots, 321+s$ will also form a magic square $(s=1, \ldots, 39)$, and so do the whole sums.
|
Yes
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The numbers from 1 to 360 are partitioned into 9 subsets of consecutive integers and the sums of the numbers in each subset are arranged in the cells of a $3 \times 3$ square. Is it possible that the square turns out to be a magic square?
Remark: A magic square is a square in which the sums of the numbers in each row, in each column and in both diagonals are all equal.
Answer: Yes.
|
. If the numbers $a_{1}, a_{2}, \ldots, a_{9}$ form a $3 \times 3$ magic square, then the numbers $a_{1}+d, a_{2}+d, \ldots, a_{9}+d$ form a $3 \times 3$ magic square, too. Hence it is sufficient to divide all the numbers into parts with equal numbers of elements: i.e. from $40 k+1$ to $40(k+1), k=0,1, \ldots, 8$. Then we need to arrange the least numbers of these parts (i.e. the numbers $1,41,81, \ldots, 321$ ) in the form of a magic square (we omit here an example, it is similar to the magic square with numbers 1 , $2, \ldots, 9)$. After that all other numbers $1+s, 41+s, \ldots, 321+s$ will also form a magic square $(s=1, \ldots, 39)$, and so do the whole sums.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
The numbers from 1 to 360 are partitioned into 9 subsets of consecutive integers and the sums of the numbers in each subset are arranged in the cells of a $3 \times 3$ square. Is it possible that the square turns out to be a magic square?
Remark: A magic square is a square in which the sums of the numbers in each row, in each column and in both diagonals are all equal.
Answer: Yes.
|
. Distribute the numbers into nine parts $40 k+1,40 k+2, \ldots, 40 k+40$, $k=0,2, \ldots, 8$. Note that the sums of these parts form an arithmetic progression: the sums are $(40 k+1+40 k+40) \cdot 20=1600 k+820, k=0,1, \ldots, 8$. It remains to construct a magic square of the numbers of the progression $820,2420, \ldots, 13620$ as follows. Start from an initial magic square with $0,1, \ldots, 8$ (or similar), multiply all members by 1600 (this is again a magic square) and add 820 to every member (again a magic square).
|
Yes
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The numbers from 1 to 360 are partitioned into 9 subsets of consecutive integers and the sums of the numbers in each subset are arranged in the cells of a $3 \times 3$ square. Is it possible that the square turns out to be a magic square?
Remark: A magic square is a square in which the sums of the numbers in each row, in each column and in both diagonals are all equal.
Answer: Yes.
|
. Distribute the numbers into nine parts $40 k+1,40 k+2, \ldots, 40 k+40$, $k=0,2, \ldots, 8$. Note that the sums of these parts form an arithmetic progression: the sums are $(40 k+1+40 k+40) \cdot 20=1600 k+820, k=0,1, \ldots, 8$. It remains to construct a magic square of the numbers of the progression $820,2420, \ldots, 13620$ as follows. Start from an initial magic square with $0,1, \ldots, 8$ (or similar), multiply all members by 1600 (this is again a magic square) and add 820 to every member (again a magic square).
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. We may assume $a \leq b \leq c$, whence $\max \{|a-b|,|b-c|,|c-a|\}=c-a$. The initial inequality is equivalent to
$$
c-a \leq 1+\frac{1}{3}\left(a^{2}+b^{2}+c^{2}-a b-b c-a c\right)
$$
which in turn is equivalent to
$$
c-a \leq 1+\frac{1}{6}\left((a-c)^{2}+(b-c)^{2}+(a-b)^{2}\right) .
$$
Since $\sqrt{\frac{(c-b)^{2}+(b-a)^{2}}{2}} \geq \frac{c-a}{2}$, we have
$$
(a-c)^{2}+(b-c)^{2}+(a-b)^{2} \geq \frac{3}{2}(c-a)^{2}
$$
and hence
$$
1+\frac{1}{6}\left((a-c)^{2}+(b-c)^{2}+(a-b)^{2}\right) \geq 1+\frac{1}{4}(c-a)^{2} \geq c-a
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. We may assume $a \leq b \leq c$, whence $\max \{|a-b|,|b-c|,|c-a|\}=c-a$. The initial inequality is equivalent to
$$
c-a \leq 1+\frac{1}{3}\left(a^{2}+b^{2}+c^{2}-a b-b c-a c\right)
$$
which in turn is equivalent to
$$
c-a \leq 1+\frac{1}{6}\left((a-c)^{2}+(b-c)^{2}+(a-b)^{2}\right) .
$$
Since $\sqrt{\frac{(c-b)^{2}+(b-a)^{2}}{2}} \geq \frac{c-a}{2}$, we have
$$
(a-c)^{2}+(b-c)^{2}+(a-b)^{2} \geq \frac{3}{2}(c-a)^{2}
$$
and hence
$$
1+\frac{1}{6}\left((a-c)^{2}+(b-c)^{2}+(a-b)^{2}\right) \geq 1+\frac{1}{4}(c-a)^{2} \geq c-a
$$
as desired.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$. By the well-known inequality $x y+y z+z x \leq$ $x^{2}+y^{2}+z^{2}$ (it can be shown by $2 x y \leq x^{2}+y^{2}$, etc., and adding all three such inequalities) we have
$$
\begin{gathered}
a b+b c+c a-a+c-1=(a+1) b+b(c-1)+(a+1)(c-1) \leq(a+1)^{2}+b^{2}+(c-1)^{2} \\
\quad=a^{2}+b^{2}+c^{2}+2(a-c+1)=(a+b+c)^{2}-2(a b+b c+c a+c-a-1)
\end{gathered}
$$
or
$$
a b+b c+c a+c-a \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
proof
|
Yes
|
Incomplete
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$. By the well-known inequality $x y+y z+z x \leq$ $x^{2}+y^{2}+z^{2}$ (it can be shown by $2 x y \leq x^{2}+y^{2}$, etc., and adding all three such inequalities) we have
$$
\begin{gathered}
a b+b c+c a-a+c-1=(a+1) b+b(c-1)+(a+1)(c-1) \leq(a+1)^{2}+b^{2}+(c-1)^{2} \\
\quad=a^{2}+b^{2}+c^{2}+2(a-c+1)=(a+b+c)^{2}-2(a b+b c+c a+c-a-1)
\end{gathered}
$$
or
$$
a b+b c+c a+c-a \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$ and take $c=a+x, b=a+y$, where $x \geq y \geq 0$. The inequality $3(a b+b c+c a+c-a-1) \leq(a+b+c)^{2}$ then reduces to
$$
x^{2}-x y+y^{2}+3 \geq 3 x \text {. }
$$
The latter inequality is equivalent to the inequality
$$
\left(\frac{x}{2}-y\right)^{2}+\frac{3}{4} x^{2}-3 x+3 \geq 0
$$
which in turn is equivalent to the inequality
$$
\frac{4}{3}\left(\frac{x}{2}-y\right)^{2}+(x-2)^{2} \geq 0
$$
Remark 1. The inequality $x^{2}-3 x-x y+y^{2}+3 \geq 0$ can also be proven by noticing that the discriminant of the LHS, $(y+3)^{2}-4\left(y^{2}+3\right)=-3(y-1)^{2}$, is non-positive. Since the quadratic polynomial in $x$ has positive leading coefficient, its all values are non-negative.
Remark 2. Another way to prove the inequality $x^{2}-3 x-x y+y^{2}+3 \geq 0$ is, by AM-GM, the following:
$$
\begin{aligned}
& 3 x+x y=\sqrt{(\sqrt{2} x)^{2}\left(\frac{3}{\sqrt{2}}+\frac{y}{\sqrt{2}}\right)^{2}} \leq \frac{(\sqrt{2} x)^{2}+\left(\frac{3}{\sqrt{2}}+\frac{y}{\sqrt{2}}\right)^{2}}{2} \\
&= x^{2}+\frac{9}{4}+\frac{3}{2} y+\frac{y^{2}}{4}=3+x^{2}+y^{2}-\frac{3}{4}(y-1)^{2} \leq 3+x^{2}+y^{2} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$ and take $c=a+x, b=a+y$, where $x \geq y \geq 0$. The inequality $3(a b+b c+c a+c-a-1) \leq(a+b+c)^{2}$ then reduces to
$$
x^{2}-x y+y^{2}+3 \geq 3 x \text {. }
$$
The latter inequality is equivalent to the inequality
$$
\left(\frac{x}{2}-y\right)^{2}+\frac{3}{4} x^{2}-3 x+3 \geq 0
$$
which in turn is equivalent to the inequality
$$
\frac{4}{3}\left(\frac{x}{2}-y\right)^{2}+(x-2)^{2} \geq 0
$$
Remark 1. The inequality $x^{2}-3 x-x y+y^{2}+3 \geq 0$ can also be proven by noticing that the discriminant of the LHS, $(y+3)^{2}-4\left(y^{2}+3\right)=-3(y-1)^{2}$, is non-positive. Since the quadratic polynomial in $x$ has positive leading coefficient, its all values are non-negative.
Remark 2. Another way to prove the inequality $x^{2}-3 x-x y+y^{2}+3 \geq 0$ is, by AM-GM, the following:
$$
\begin{aligned}
& 3 x+x y=\sqrt{(\sqrt{2} x)^{2}\left(\frac{3}{\sqrt{2}}+\frac{y}{\sqrt{2}}\right)^{2}} \leq \frac{(\sqrt{2} x)^{2}+\left(\frac{3}{\sqrt{2}}+\frac{y}{\sqrt{2}}\right)^{2}}{2} \\
&= x^{2}+\frac{9}{4}+\frac{3}{2} y+\frac{y^{2}}{4}=3+x^{2}+y^{2}-\frac{3}{4}(y-1)^{2} \leq 3+x^{2}+y^{2} .
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$ and take $a=b-k, c=b+l$, where $k, l \geq 0$. The inequality $3(a b+b c+c a+c-a-1) \leq(a+b+c)^{2}$ then reduces to
$$
k^{2}+l^{2}+k l-3 l-3 k+3 \geq 0 .
$$
This is equivalent to
$$
(k-1)^{2}+(l-1)^{2}+(k-1)(l-1) \geq 0,
$$
which holds, since $x^{2}+y^{2}+x y \geq 0$ for all real numbers $x, y$.
Remark. The inequality $k^{2}+l^{2}+k l-3 l-3 k+3 \geq 0$ can also be proven by separating perfect squares as
$$
\frac{1}{4}(k-l)^{2}+\frac{3}{4}(k+l)^{2}-3 \cdot(k+l)+3 \geq 0
$$
which is in turn similar to
$$
(k-l)^{2}+3(k+l-2)^{2} \geq 0 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$ and take $a=b-k, c=b+l$, where $k, l \geq 0$. The inequality $3(a b+b c+c a+c-a-1) \leq(a+b+c)^{2}$ then reduces to
$$
k^{2}+l^{2}+k l-3 l-3 k+3 \geq 0 .
$$
This is equivalent to
$$
(k-1)^{2}+(l-1)^{2}+(k-1)(l-1) \geq 0,
$$
which holds, since $x^{2}+y^{2}+x y \geq 0$ for all real numbers $x, y$.
Remark. The inequality $k^{2}+l^{2}+k l-3 l-3 k+3 \geq 0$ can also be proven by separating perfect squares as
$$
\frac{1}{4}(k-l)^{2}+\frac{3}{4}(k+l)^{2}-3 \cdot(k+l)+3 \geq 0
$$
which is in turn similar to
$$
(k-l)^{2}+3(k+l-2)^{2} \geq 0 .
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 4",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$. Expand the inequality $3(a b+b c+c a+c-a-1) \leq$ $(a+b+c)^{2}$ fully to obtain $a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3 \geq 0$. Now fix $\alpha \in \mathbb{R}$ and consider the set
$$
\gamma=\left\{(a, b, c): a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0\right\} .
$$
Note that $\gamma$ is a quadric. Its invariants are
$\delta=\left|\begin{array}{ccc}1 & -\frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & 1\end{array}\right|=0, \quad \Delta=\left|\begin{array}{cccc}1 & -\frac{1}{2} & -\frac{1}{2} & \frac{3}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} & 0 \\ -\frac{1}{2} & -\frac{1}{2} & 1 & -\frac{3}{2} \\ \frac{3}{2} & 0 & -\frac{3}{2} & 3+\alpha\end{array}\right|=0, \quad S=3 \cdot\left|\begin{array}{cc}1 & -\frac{1}{2} \\ -\frac{1}{2} & 1\end{array}\right|=\frac{9}{4}$,
and
$$
K=\left|\begin{array}{ccc}
1 & -\frac{1}{2} & \frac{3}{2} \\
-\frac{1}{2} & 1 & 0 \\
\frac{3}{2} & 0 & 3+\alpha
\end{array}\right|+\left|\begin{array}{ccc}
1 & -\frac{1}{2} & \frac{3}{2} \\
-\frac{1}{2} & 1 & -\frac{3}{2} \\
\frac{3}{2} & -\frac{3}{2} & 3+\alpha
\end{array}\right|+\left|\begin{array}{ccc}
1 & -\frac{1}{2} & 0 \\
-\frac{1}{2} & 1 & -\frac{3}{2} \\
0 & -\frac{3}{2} & 3+\alpha
\end{array}\right|=\frac{9 \alpha}{4} .
$$
In the case $\alpha>0$, it is known from the theory of quadrics that the surface $\gamma$ is an imaginary elliptic cylinder $(\delta=\Delta=0, S>0$, and $K>0)$ and therefore contains no real points. Hence the condition $a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0$ implies that $\alpha \leq 0$, therefore
$$
a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3=-\alpha \geq 0
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. Assume $a \leq b \leq c$. Expand the inequality $3(a b+b c+c a+c-a-1) \leq$ $(a+b+c)^{2}$ fully to obtain $a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3 \geq 0$. Now fix $\alpha \in \mathbb{R}$ and consider the set
$$
\gamma=\left\{(a, b, c): a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0\right\} .
$$
Note that $\gamma$ is a quadric. Its invariants are
$\delta=\left|\begin{array}{ccc}1 & -\frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & 1\end{array}\right|=0, \quad \Delta=\left|\begin{array}{cccc}1 & -\frac{1}{2} & -\frac{1}{2} & \frac{3}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} & 0 \\ -\frac{1}{2} & -\frac{1}{2} & 1 & -\frac{3}{2} \\ \frac{3}{2} & 0 & -\frac{3}{2} & 3+\alpha\end{array}\right|=0, \quad S=3 \cdot\left|\begin{array}{cc}1 & -\frac{1}{2} \\ -\frac{1}{2} & 1\end{array}\right|=\frac{9}{4}$,
and
$$
K=\left|\begin{array}{ccc}
1 & -\frac{1}{2} & \frac{3}{2} \\
-\frac{1}{2} & 1 & 0 \\
\frac{3}{2} & 0 & 3+\alpha
\end{array}\right|+\left|\begin{array}{ccc}
1 & -\frac{1}{2} & \frac{3}{2} \\
-\frac{1}{2} & 1 & -\frac{3}{2} \\
\frac{3}{2} & -\frac{3}{2} & 3+\alpha
\end{array}\right|+\left|\begin{array}{ccc}
1 & -\frac{1}{2} & 0 \\
-\frac{1}{2} & 1 & -\frac{3}{2} \\
0 & -\frac{3}{2} & 3+\alpha
\end{array}\right|=\frac{9 \alpha}{4} .
$$
In the case $\alpha>0$, it is known from the theory of quadrics that the surface $\gamma$ is an imaginary elliptic cylinder $(\delta=\Delta=0, S>0$, and $K>0)$ and therefore contains no real points. Hence the condition $a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0$ implies that $\alpha \leq 0$, therefore
$$
a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3=-\alpha \geq 0
$$
as desired.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 5",
"tier": "T3",
"year": "2012"
}
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. We start as in Solution 5: construct the quadric
$$
\gamma=\left\{(a, b, c): a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0\right\} .
$$
Now note that the substitution
$$
\left\{\begin{array}{l}
a=2 x-y+2 z \\
b=2 y+2 z \\
c=-2 x-y+2 z
\end{array}\right.
$$
gives (in the new coordinate system)
$$
\gamma=\left\{(x, y, z): 12 x^{2}+9 y^{2}+12 x+3+\alpha=0\right\} .
$$
(The columns of the coefficient matrix $C=\left(\begin{array}{ccc}2 & -1 & 2 \\ 0 & 2 & 2 \\ -2 & -1 & 2\end{array}\right)$ of the substitution are in fact the orthogonalized eigenvectors of $\left(\begin{array}{ccc}1 & -\frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & 1\end{array}\right)$.) Since
$$
12 x^{2}+9 y^{2}+12 x+3+\alpha=3(2 x+1)^{2}+9 y^{2}+\alpha
$$
it is clear that in the case $\alpha>0$, the set $\gamma$ is void.
Remark 1. Solutions 5 and 6 are presented here for instructive purposes only.
Remark 2. Solutions 3, 4, and 6 suggest also general substitutions in the initial equation that directly leave the inequality in the form of sum of squares. Let these substitutions be mentioned here.
- Solution 3 suggests $T=\frac{a-2 b+c}{2}, U=c-a-2$, and reduces the original inequality to $\frac{4}{3} T^{2}+U^{2} \geq 0$;
- solution 4 together with its remark suggests $T=2 b-a-c, U=c-a-2$, and reduces the original inequality to $T^{2}+3 U^{2} \geq 0$;
- solution 6 suggests $U=\frac{a-c}{2}+1, T=\frac{-a+2 b-c}{6}$, and reduces the original inequality to $3 U^{2}+9 T^{2} \geq 0$.
Hence, up to scaling, all these three solutions are essentially the same.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be real numbers. Prove that
$$
a b+b c+c a+\max \{|a-b|,|b-c|,|c-a|\} \leq 1+\frac{1}{3}(a+b+c)^{2} .
$$
|
. We start as in Solution 5: construct the quadric
$$
\gamma=\left\{(a, b, c): a^{2}+b^{2}+c^{2}-a b-a c-b c+3 a-3 c+3+\alpha=0\right\} .
$$
Now note that the substitution
$$
\left\{\begin{array}{l}
a=2 x-y+2 z \\
b=2 y+2 z \\
c=-2 x-y+2 z
\end{array}\right.
$$
gives (in the new coordinate system)
$$
\gamma=\left\{(x, y, z): 12 x^{2}+9 y^{2}+12 x+3+\alpha=0\right\} .
$$
(The columns of the coefficient matrix $C=\left(\begin{array}{ccc}2 & -1 & 2 \\ 0 & 2 & 2 \\ -2 & -1 & 2\end{array}\right)$ of the substitution are in fact the orthogonalized eigenvectors of $\left(\begin{array}{ccc}1 & -\frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & 1\end{array}\right)$.) Since
$$
12 x^{2}+9 y^{2}+12 x+3+\alpha=3(2 x+1)^{2}+9 y^{2}+\alpha
$$
it is clear that in the case $\alpha>0$, the set $\gamma$ is void.
Remark 1. Solutions 5 and 6 are presented here for instructive purposes only.
Remark 2. Solutions 3, 4, and 6 suggest also general substitutions in the initial equation that directly leave the inequality in the form of sum of squares. Let these substitutions be mentioned here.
- Solution 3 suggests $T=\frac{a-2 b+c}{2}, U=c-a-2$, and reduces the original inequality to $\frac{4}{3} T^{2}+U^{2} \geq 0$;
- solution 4 together with its remark suggests $T=2 b-a-c, U=c-a-2$, and reduces the original inequality to $T^{2}+3 U^{2} \geq 0$;
- solution 6 suggests $U=\frac{a-c}{2}+1, T=\frac{-a+2 b-c}{6}$, and reduces the original inequality to $3 U^{2}+9 T^{2} \geq 0$.
Hence, up to scaling, all these three solutions are essentially the same.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 6",
"tier": "T3",
"year": "2012"
}
|
a) Show that the equation
$$
\lfloor x\rfloor\left(x^{2}+1\right)=x^{3},
$$
where $\lfloor x\rfloor$ denotes the largest integer not larger than $x$, has exactly one real solution in each interval between consecutive positive integers.
b) Show that none of the positive real solutions of this equation is rational.
|
a) Let $k=\lfloor x\rfloor$ and $y=x-k$. Then the equation becomes
$$
k\left((k+y)^{2}+1\right)=(k+y)^{3},
$$
which reduces to
$$
y(k+y)^{2}=k \text {. }
$$
The function $f(y)=y(k+y)^{2}$ is strictly increasing in $[0,1]$ and continuous in the same interval. As $f(0)=0<k$ and $f(1)=(k+1)^{2}>k$, there exists exactly one $y_{0} \in(0,1)$ such that $f\left(y_{0}\right)=k$.
b) The equation (1) has no positive integral solutions. Assume that $x=k+y$ is rational and let $x=n / d$, where $n$ and $d$ are relatively prime positive integers. The given equation then becomes
$$
\frac{k\left(n^{2}+d^{2}\right)}{d^{2}}=\frac{n^{3}}{d^{3}}
$$
or
$$
d k\left(n^{2}+d^{2}\right)=n^{3} .
$$
Since $x$ is not an integer, $d$ has at least one prime divisor. It follows from the last equation that this prime divisor also divides $n$, a contradiction.
Remark. In a), one can also consider the function $g(y)=y(k+y)^{2}-k$, perhaps expand it, and, using its derivative in $(0,1)$, prove that $g$ is strictly increasing in $[0,1]$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
a) Show that the equation
$$
\lfloor x\rfloor\left(x^{2}+1\right)=x^{3},
$$
where $\lfloor x\rfloor$ denotes the largest integer not larger than $x$, has exactly one real solution in each interval between consecutive positive integers.
b) Show that none of the positive real solutions of this equation is rational.
|
a) Let $k=\lfloor x\rfloor$ and $y=x-k$. Then the equation becomes
$$
k\left((k+y)^{2}+1\right)=(k+y)^{3},
$$
which reduces to
$$
y(k+y)^{2}=k \text {. }
$$
The function $f(y)=y(k+y)^{2}$ is strictly increasing in $[0,1]$ and continuous in the same interval. As $f(0)=0<k$ and $f(1)=(k+1)^{2}>k$, there exists exactly one $y_{0} \in(0,1)$ such that $f\left(y_{0}\right)=k$.
b) The equation (1) has no positive integral solutions. Assume that $x=k+y$ is rational and let $x=n / d$, where $n$ and $d$ are relatively prime positive integers. The given equation then becomes
$$
\frac{k\left(n^{2}+d^{2}\right)}{d^{2}}=\frac{n^{3}}{d^{3}}
$$
or
$$
d k\left(n^{2}+d^{2}\right)=n^{3} .
$$
Since $x$ is not an integer, $d$ has at least one prime divisor. It follows from the last equation that this prime divisor also divides $n$, a contradiction.
Remark. In a), one can also consider the function $g(y)=y(k+y)^{2}-k$, perhaps expand it, and, using its derivative in $(0,1)$, prove that $g$ is strictly increasing in $[0,1]$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Observe first that for any integer $m>2$ the quadratic polynomial $x^{2}-m x+1$ has two distinct positive roots whose product equals 1 .
Moreover, for any integer $m>2$ there exists a pair of integers $\left(a_{m}, b_{m}\right)$ such that the polynomial $x^{2012}-a_{m} x-b_{m}$ is divisible by the polynomial $x^{2}-m x+1$. Indeed, dividing the monomial $x^{2012}$ by the monic polynomial $x^{2}-m x+1$ we get a remainder $R_{m}(x)$ which is a polynomial with integer coefficients and degree at most 1. Thus $R_{m}(x)=a_{m} x+b_{m}$ for some integers $a_{m}$ and $b_{m}$, which clearly meet our demand.
Now, for a fixed $m>2$, any root of the polynomial $x^{2}-m x+1$ is also a root of the polynomial $x^{2012}-a_{m} x-b_{m}$. Therefore the set of solutions of the equation $x^{2012}=a_{m} x+b_{m}$ contains the two distinct roots of the polynomial $x^{2}-m x+1$, whose product is equal to 1 . This means that the pair $(a, b)=\left(a_{m}, b_{m}\right)$ has the required property.
It remains to show that when $m$ ranges over all integers greater than 2 , we get infinitely many distinct pairs $\left(a_{m}, b_{m}\right)$. To this end, note that for $m_{1} \neq m_{2}$ the roots of the polynomial $x^{2}-m_{1} x+1$ are distinct from the roots of the polynomial $x^{2}-m_{2} x+1$, since a common root of them would be a root of their difference $\left(m_{2}-m_{1}\right) x$, and so it would be equal to zero, which is not a root of any $x^{2}-m x+1$. As the polynomial $x^{2012}-a x-b$ has at most 2012 distinct roots, it is divisible by $x^{2}-m x+1$ for at most 1006 values of $m$. Hence the same pair $\left(a_{m}, b_{m}\right)$ can be obtained for at most 1006 values of $m$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Observe first that for any integer $m>2$ the quadratic polynomial $x^{2}-m x+1$ has two distinct positive roots whose product equals 1 .
Moreover, for any integer $m>2$ there exists a pair of integers $\left(a_{m}, b_{m}\right)$ such that the polynomial $x^{2012}-a_{m} x-b_{m}$ is divisible by the polynomial $x^{2}-m x+1$. Indeed, dividing the monomial $x^{2012}$ by the monic polynomial $x^{2}-m x+1$ we get a remainder $R_{m}(x)$ which is a polynomial with integer coefficients and degree at most 1. Thus $R_{m}(x)=a_{m} x+b_{m}$ for some integers $a_{m}$ and $b_{m}$, which clearly meet our demand.
Now, for a fixed $m>2$, any root of the polynomial $x^{2}-m x+1$ is also a root of the polynomial $x^{2012}-a_{m} x-b_{m}$. Therefore the set of solutions of the equation $x^{2012}=a_{m} x+b_{m}$ contains the two distinct roots of the polynomial $x^{2}-m x+1$, whose product is equal to 1 . This means that the pair $(a, b)=\left(a_{m}, b_{m}\right)$ has the required property.
It remains to show that when $m$ ranges over all integers greater than 2 , we get infinitely many distinct pairs $\left(a_{m}, b_{m}\right)$. To this end, note that for $m_{1} \neq m_{2}$ the roots of the polynomial $x^{2}-m_{1} x+1$ are distinct from the roots of the polynomial $x^{2}-m_{2} x+1$, since a common root of them would be a root of their difference $\left(m_{2}-m_{1}\right) x$, and so it would be equal to zero, which is not a root of any $x^{2}-m x+1$. As the polynomial $x^{2012}-a x-b$ has at most 2012 distinct roots, it is divisible by $x^{2}-m x+1$ for at most 1006 values of $m$. Hence the same pair $\left(a_{m}, b_{m}\right)$ can be obtained for at most 1006 values of $m$, which concludes the proof.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Observe first that for any integer $c>2$ the equations $x=x-0$ and $x^{2}=c x-1$ have two common distinct positive solutions whose product equals 1 . Let those solutions be $x_{1}$ and $x_{2}$.
Define a sequence $\left(f_{n}\right)$ by $f_{0}=0, f_{1}=1$, and $f_{n+2}=c f_{n+1}-f_{n}, n \geq 0$. Suppose that $x_{1}$ and $x_{2}$ are also common solutions of the equations $x^{n}=f_{n} x-f_{n-1}$ and $x^{n+1}=f_{n+1} x-f_{n}$, then the following equalities hold for $x=x_{1}$ and $x=x_{2}$ :
$$
\begin{aligned}
& x^{n+2}-f_{n+2} x+f_{n+1}=x^{n+2}-\left(c f_{n+1}-f_{n}\right) x+\left(c f_{n}-f_{n-1}\right) \\
= & x^{n+2}-c\left(f_{n+1} x-f_{n}\right)+\left(f_{n} x-f_{n-1}\right)=x^{n+2}-c x^{n+1}+x^{n}=x^{n}\left(x^{2}-c x+1\right)=0,
\end{aligned}
$$
which shows that $x_{1}$ and $x_{2}$ are solutions of $x^{n+2}=f_{n+2} x-f_{n+1}$ as well.
Now note that for different integers $c$, all corresponding members of the sequences $\left(f_{n}\right)$ are different. At first note that these sequences $\left(f_{n}\right)$ are strictly increasing: by inductive argument we have
$$
f_{n+2}-f_{n+1}=(c-1) f_{n+1}-f_{n}>f_{n+1}-f_{n}>0 .
$$
This also shows that all members are positive.
Now, let us have integers $c$ and $c^{\prime}$ with $c^{\prime} \geq c+1>3$ and let the corresponding sequences be $\left(f_{n}\right)$ and $\left(f_{n}^{\prime}\right)$. Then again by induction
$f_{n+2}^{\prime} \geq(c+1) f_{n+1}^{\prime}-f_{n}^{\prime}=c f_{n+1}^{\prime}+\left(f_{n+1}^{\prime}-f_{n}^{\prime}\right)>c f_{n+1}^{\prime}>c f_{n+1}>c f_{n+1}-f_{n}=f_{n+2}$.
We have shown that for all integers $c>2$, the respective pairs $\left(f_{2012},-f_{2011}\right)$ are different, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Observe first that for any integer $c>2$ the equations $x=x-0$ and $x^{2}=c x-1$ have two common distinct positive solutions whose product equals 1 . Let those solutions be $x_{1}$ and $x_{2}$.
Define a sequence $\left(f_{n}\right)$ by $f_{0}=0, f_{1}=1$, and $f_{n+2}=c f_{n+1}-f_{n}, n \geq 0$. Suppose that $x_{1}$ and $x_{2}$ are also common solutions of the equations $x^{n}=f_{n} x-f_{n-1}$ and $x^{n+1}=f_{n+1} x-f_{n}$, then the following equalities hold for $x=x_{1}$ and $x=x_{2}$ :
$$
\begin{aligned}
& x^{n+2}-f_{n+2} x+f_{n+1}=x^{n+2}-\left(c f_{n+1}-f_{n}\right) x+\left(c f_{n}-f_{n-1}\right) \\
= & x^{n+2}-c\left(f_{n+1} x-f_{n}\right)+\left(f_{n} x-f_{n-1}\right)=x^{n+2}-c x^{n+1}+x^{n}=x^{n}\left(x^{2}-c x+1\right)=0,
\end{aligned}
$$
which shows that $x_{1}$ and $x_{2}$ are solutions of $x^{n+2}=f_{n+2} x-f_{n+1}$ as well.
Now note that for different integers $c$, all corresponding members of the sequences $\left(f_{n}\right)$ are different. At first note that these sequences $\left(f_{n}\right)$ are strictly increasing: by inductive argument we have
$$
f_{n+2}-f_{n+1}=(c-1) f_{n+1}-f_{n}>f_{n+1}-f_{n}>0 .
$$
This also shows that all members are positive.
Now, let us have integers $c$ and $c^{\prime}$ with $c^{\prime} \geq c+1>3$ and let the corresponding sequences be $\left(f_{n}\right)$ and $\left(f_{n}^{\prime}\right)$. Then again by induction
$f_{n+2}^{\prime} \geq(c+1) f_{n+1}^{\prime}-f_{n}^{\prime}=c f_{n+1}^{\prime}+\left(f_{n+1}^{\prime}-f_{n}^{\prime}\right)>c f_{n+1}^{\prime}>c f_{n+1}>c f_{n+1}-f_{n}=f_{n+2}$.
We have shown that for all integers $c>2$, the respective pairs $\left(f_{2012},-f_{2011}\right)$ are different, as desired.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Consider any even integer $2 c>2$. The roots of $x^{2}-2 c x+1$ are $c \pm \sqrt{c^{2}-1}$ and their product is 1 . Now consider the expansion
$$
\left(c+\sqrt{c^{2}-1}\right)^{2012}=\alpha+\beta \sqrt{c^{2}-1}=\beta\left(c+\sqrt{c^{2}-1}\right)+(\alpha-\beta c)
$$
where $\alpha$ and $\beta$ are some integers. Denote $a=\beta$ and $b=\alpha-\beta c$, then $c+\sqrt{c^{2}-1}$ is a solution of $x^{2012}=a x+b$.
Simple calculation shows that
$$
\left(c-\sqrt{c^{2}-1}\right)^{2012}=\alpha-\beta \sqrt{c^{2}-1}=\beta\left(c-\sqrt{c^{2}-1}\right)+(\alpha-\beta c),
$$
yielding that also $c-\sqrt{c^{2}-1}$ is a solution of $x^{2012}=a x+b$.
To complete the proof, it remains to point out that $a=\beta \geq 2012 \cdot c^{2011}$ which means that the number $a$ can be chosen arbitrarily large.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Consider any even integer $2 c>2$. The roots of $x^{2}-2 c x+1$ are $c \pm \sqrt{c^{2}-1}$ and their product is 1 . Now consider the expansion
$$
\left(c+\sqrt{c^{2}-1}\right)^{2012}=\alpha+\beta \sqrt{c^{2}-1}=\beta\left(c+\sqrt{c^{2}-1}\right)+(\alpha-\beta c)
$$
where $\alpha$ and $\beta$ are some integers. Denote $a=\beta$ and $b=\alpha-\beta c$, then $c+\sqrt{c^{2}-1}$ is a solution of $x^{2012}=a x+b$.
Simple calculation shows that
$$
\left(c-\sqrt{c^{2}-1}\right)^{2012}=\alpha-\beta \sqrt{c^{2}-1}=\beta\left(c-\sqrt{c^{2}-1}\right)+(\alpha-\beta c),
$$
yielding that also $c-\sqrt{c^{2}-1}$ is a solution of $x^{2012}=a x+b$.
To complete the proof, it remains to point out that $a=\beta \geq 2012 \cdot c^{2011}$ which means that the number $a$ can be chosen arbitrarily large.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2012"
}
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Note that the function $f:(1, \infty) \rightarrow \mathbb{R}, f(x)=x+x^{-1}$, is strictly increasing (it can be easily shown by derivative) and achieves all values of $(2, \infty)$. Hence let us have an arbitrary integer $c>2$ where $c=\lambda+\lambda^{-1}$ for some real $\lambda>1$.
Define
$$
a=\frac{\lambda^{2012}-\lambda^{-2012}}{\lambda-\lambda^{-1}}, \quad b=\frac{-\lambda^{2011}+\lambda^{-2011}}{\lambda-\lambda^{-1}} .
$$
Then it is easy to verify that $\lambda$ and $\lambda^{-1}$ are solutions of $x^{2012}=a x+b$.
Note that $a$ and $b$ are integers. Indeed: for any positive integer $k$, we have
$$
\lambda^{k}-\left(\lambda^{-1}\right)^{k}=\left(\lambda-\lambda^{-1}\right) \cdot\left(\lambda^{k-1}+\lambda^{k-2} \cdot \lambda^{-1}+\ldots+\lambda \cdot\left(\lambda^{-1}\right)^{k-2}+\left(\lambda^{-1}\right)^{k-1}\right),
$$
where the rightmost factor is a symmetric polynomial with integral coefficients in two variables and therefore can be expressed as a polynomial with integral coefficients in symmetric fundamental polynomials $\lambda+\lambda^{-1}$ and $\lambda \cdot \lambda^{-1}=1$, hence is an integer.
If there were only a finite number of integer pairs $(a, b)$ for which $x^{2012}-a x-b$ has two distinct roots whose product is 1 , the number of all such roots would also be finite. This would be a contradiction since by the construction above, there are infinitely many such numbers $\lambda$ for which $\lambda+\lambda^{-1} \in\{3,4, \ldots\}$ and that $\lambda, \lambda^{-1}$ are roots of some $x^{2012}-a x-b$ where $a, b$ are integers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for infinitely many pairs $(a, b)$ of integers the equation
$$
x^{2012}=a x+b
$$
has among its solutions two distinct real numbers whose product is 1 .
|
. Note that the function $f:(1, \infty) \rightarrow \mathbb{R}, f(x)=x+x^{-1}$, is strictly increasing (it can be easily shown by derivative) and achieves all values of $(2, \infty)$. Hence let us have an arbitrary integer $c>2$ where $c=\lambda+\lambda^{-1}$ for some real $\lambda>1$.
Define
$$
a=\frac{\lambda^{2012}-\lambda^{-2012}}{\lambda-\lambda^{-1}}, \quad b=\frac{-\lambda^{2011}+\lambda^{-2011}}{\lambda-\lambda^{-1}} .
$$
Then it is easy to verify that $\lambda$ and $\lambda^{-1}$ are solutions of $x^{2012}=a x+b$.
Note that $a$ and $b$ are integers. Indeed: for any positive integer $k$, we have
$$
\lambda^{k}-\left(\lambda^{-1}\right)^{k}=\left(\lambda-\lambda^{-1}\right) \cdot\left(\lambda^{k-1}+\lambda^{k-2} \cdot \lambda^{-1}+\ldots+\lambda \cdot\left(\lambda^{-1}\right)^{k-2}+\left(\lambda^{-1}\right)^{k-1}\right),
$$
where the rightmost factor is a symmetric polynomial with integral coefficients in two variables and therefore can be expressed as a polynomial with integral coefficients in symmetric fundamental polynomials $\lambda+\lambda^{-1}$ and $\lambda \cdot \lambda^{-1}=1$, hence is an integer.
If there were only a finite number of integer pairs $(a, b)$ for which $x^{2012}-a x-b$ has two distinct roots whose product is 1 , the number of all such roots would also be finite. This would be a contradiction since by the construction above, there are infinitely many such numbers $\lambda$ for which $\lambda+\lambda^{-1} \in\{3,4, \ldots\}$ and that $\lambda, \lambda^{-1}$ are roots of some $x^{2012}-a x-b$ where $a, b$ are integers.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 4",
"tier": "T3",
"year": "2012"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ for which
$$
f(x+y)=f(x-y)+f(f(1-x y))
$$
holds for all real numbers $x$ and $y$.
Answer: $f(x) \equiv 0$.
|
Substituting $y=0$ gives $f(x)=f(x)+f(f(1))$, hence $f(f(1))=0$. Using this after substituting $x=0$ into the original equation gives $f(y)=f(-y)$ for all $y$, i.e., $f$ is even.
Substituting $x=1$ into the original equation gives $f(1+y)=f(1-y)+$ $f(f(1-y))$. By $f$ being even, also $f(-1-y)=f(1-y)+f(f(1-y))$. Hence $f(f(1-y))=f(1-y-2)-f(1-y)$. As $1-y$ covers all real values, one can conclude that
$$
f(f(z))=f(z-2)-f(z)
$$
for all real numbers $z$.
Substituting $-z$ for $z$ into (4) and simplifying the terms by using that $f$ is even, one obtains $f(f(z))=f(z+2)-f(z)$. Together with (4), this implies
$$
f(z+2)=f(z-2)
$$
for all real numbers $z$.
Now taking $y=2$ in the original equation followed by applying (5) leads to $f(f(1-2 x))=0$ for all real $x$. As $1-2 x$ covers all real values, one can conclude that
$$
f(f(z))=0
$$
for all real numbers $z$. Thus the original equation reduces to
$$
f(x+y)=f(x-y) .
$$
Taking $x=y$ here gives $f(2 x)=f(0)$, i.e., $f$ is constant, as $2 x$ covers all real numbers. As 0 must be among the values of $f$ by (6), $f(x) \equiv 0$ is the only possibility.
|
f(x) \equiv 0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ for which
$$
f(x+y)=f(x-y)+f(f(1-x y))
$$
holds for all real numbers $x$ and $y$.
Answer: $f(x) \equiv 0$.
|
Substituting $y=0$ gives $f(x)=f(x)+f(f(1))$, hence $f(f(1))=0$. Using this after substituting $x=0$ into the original equation gives $f(y)=f(-y)$ for all $y$, i.e., $f$ is even.
Substituting $x=1$ into the original equation gives $f(1+y)=f(1-y)+$ $f(f(1-y))$. By $f$ being even, also $f(-1-y)=f(1-y)+f(f(1-y))$. Hence $f(f(1-y))=f(1-y-2)-f(1-y)$. As $1-y$ covers all real values, one can conclude that
$$
f(f(z))=f(z-2)-f(z)
$$
for all real numbers $z$.
Substituting $-z$ for $z$ into (4) and simplifying the terms by using that $f$ is even, one obtains $f(f(z))=f(z+2)-f(z)$. Together with (4), this implies
$$
f(z+2)=f(z-2)
$$
for all real numbers $z$.
Now taking $y=2$ in the original equation followed by applying (5) leads to $f(f(1-2 x))=0$ for all real $x$. As $1-2 x$ covers all real values, one can conclude that
$$
f(f(z))=0
$$
for all real numbers $z$. Thus the original equation reduces to
$$
f(x+y)=f(x-y) .
$$
Taking $x=y$ here gives $f(2 x)=f(0)$, i.e., $f$ is constant, as $2 x$ covers all real numbers. As 0 must be among the values of $f$ by (6), $f(x) \equiv 0$ is the only possibility.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
There are 2012 lamps arranged on a table. Two persons play the following game. In each move the player flips the switch of one lamp, but he must never get back an arrangement of the lit lamps that has already been on the table. A player who cannot move loses. Which player has a winning strategy?
Answer: the first player has a winning strategy.
|
. The first player can pick one lamp and keep switching it on and off during the whole game. The second player cannot switch this particular lamp, he always has to switch some other lamp so that the arrangement of the other lamps becomes different from any that has already been on the table. So the first player always has a move, and the second player eventually runs out of the possible moves.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 2012 lamps arranged on a table. Two persons play the following game. In each move the player flips the switch of one lamp, but he must never get back an arrangement of the lit lamps that has already been on the table. A player who cannot move loses. Which player has a winning strategy?
Answer: the first player has a winning strategy.
|
. The first player can pick one lamp and keep switching it on and off during the whole game. The second player cannot switch this particular lamp, he always has to switch some other lamp so that the arrangement of the other lamps becomes different from any that has already been on the table. So the first player always has a move, and the second player eventually runs out of the possible moves.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "# Problem 6",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
There are 2012 lamps arranged on a table. Two persons play the following game. In each move the player flips the switch of one lamp, but he must never get back an arrangement of the lit lamps that has already been on the table. A player who cannot move loses. Which player has a winning strategy?
Answer: the first player has a winning strategy.
|
. Note that the parity of the lit lamps changes with each move. So all the possible states can be divided into two disjoint sets, one with odd number of of the lamps lit and the other with even number of the lamps lit. We get a bipartite graph where the vertices are the states and two states are connected with an edge if it is possible to get from one state to another by switching one lamp off or on.
We want to use Hall's marriage theorem to get a perfect matching of the states. The assumption of the theorem is the following: for every subset A of the states in one set there is at least as many neighboring states in the second set. Let the number of states in $A$ be $n$, and let $B$ be the set of neighboring states of $A$, containing $m$ states. Since each state in $A$ has exactly 2012 neighbors and all these neighbors belong to the set $B$, there are exactly $2012 n$ edges between $A$ and $B$. Since each state in $B$ has exactly 2012 neighbors (some of them may not belong to $A$ ), there is at most $2012 m$ edges between $A$ and $B$. Hence $2012 n \leq 2012 m$, or $n \leq m$, i.e. the assumption of the theorem is satisfied.
Now the Hall's theorem states that there is a perfect matching. On every move the first player has to switch the lamp which changes the state into it's partner in the perfect matching. Any lamp the second player can switch results in a state whose partner has not been used yet, so the first player always has a move, and the secod player eventually loses.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 2012 lamps arranged on a table. Two persons play the following game. In each move the player flips the switch of one lamp, but he must never get back an arrangement of the lit lamps that has already been on the table. A player who cannot move loses. Which player has a winning strategy?
Answer: the first player has a winning strategy.
|
. Note that the parity of the lit lamps changes with each move. So all the possible states can be divided into two disjoint sets, one with odd number of of the lamps lit and the other with even number of the lamps lit. We get a bipartite graph where the vertices are the states and two states are connected with an edge if it is possible to get from one state to another by switching one lamp off or on.
We want to use Hall's marriage theorem to get a perfect matching of the states. The assumption of the theorem is the following: for every subset A of the states in one set there is at least as many neighboring states in the second set. Let the number of states in $A$ be $n$, and let $B$ be the set of neighboring states of $A$, containing $m$ states. Since each state in $A$ has exactly 2012 neighbors and all these neighbors belong to the set $B$, there are exactly $2012 n$ edges between $A$ and $B$. Since each state in $B$ has exactly 2012 neighbors (some of them may not belong to $A$ ), there is at most $2012 m$ edges between $A$ and $B$. Hence $2012 n \leq 2012 m$, or $n \leq m$, i.e. the assumption of the theorem is satisfied.
Now the Hall's theorem states that there is a perfect matching. On every move the first player has to switch the lamp which changes the state into it's partner in the perfect matching. Any lamp the second player can switch results in a state whose partner has not been used yet, so the first player always has a move, and the secod player eventually loses.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "# Problem 6",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
On a $2012 \times 2012$ board, some cells on the top-right to bottom-left diagonal are marked. None of the marked cells is in a corner. Integers are written in each cell of this board in the following way. All the numbers in the cells along the upper and the left sides of the board are 1's. All the numbers in the marked cells are 0's. Each of the other cells contains a number that is equal to the sum of its upper neighbour and its left neighbour. Prove that the number in the bottom right corner is not divisible by 2011 .
|
. Let a peg go on the board, stepping from a cell to the neighbor cell right or below. Then the number in the bottom right corner of the board is equal to the number of paths of the peg from the top left corner to the bottom right corner, which do not visit the marked cells.
The total number of paths (including those that pass through the marked cells) equals $\left(\begin{array}{l}4022 \\ 2011\end{array}\right)$; this number is not divisible by 2011, because 2011 is a prime number. The number of paths that pass through the $k$-th cell of the diagonal equals $\left(\begin{array}{c}2011 \\ k\end{array}\right)^{2}$, because in order to visit this cell starting from the corner the peg should make 2011 steps, $k$ of which are horizontal, and others are vertical; and after the visit it also should make 2011 steps, $k$ of which is vertical. Since $k \neq 0,2011$ (because the marked cells are not in the corner) this number is divisible by 2011.
So the number in the low right corner equals the difference of the number that is not divisible by 2011 and several numbers that are divisible by 2011 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On a $2012 \times 2012$ board, some cells on the top-right to bottom-left diagonal are marked. None of the marked cells is in a corner. Integers are written in each cell of this board in the following way. All the numbers in the cells along the upper and the left sides of the board are 1's. All the numbers in the marked cells are 0's. Each of the other cells contains a number that is equal to the sum of its upper neighbour and its left neighbour. Prove that the number in the bottom right corner is not divisible by 2011 .
|
. Let a peg go on the board, stepping from a cell to the neighbor cell right or below. Then the number in the bottom right corner of the board is equal to the number of paths of the peg from the top left corner to the bottom right corner, which do not visit the marked cells.
The total number of paths (including those that pass through the marked cells) equals $\left(\begin{array}{l}4022 \\ 2011\end{array}\right)$; this number is not divisible by 2011, because 2011 is a prime number. The number of paths that pass through the $k$-th cell of the diagonal equals $\left(\begin{array}{c}2011 \\ k\end{array}\right)^{2}$, because in order to visit this cell starting from the corner the peg should make 2011 steps, $k$ of which are horizontal, and others are vertical; and after the visit it also should make 2011 steps, $k$ of which is vertical. Since $k \neq 0,2011$ (because the marked cells are not in the corner) this number is divisible by 2011.
So the number in the low right corner equals the difference of the number that is not divisible by 2011 and several numbers that are divisible by 2011 .
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "# Problem 7",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
On a $2012 \times 2012$ board, some cells on the top-right to bottom-left diagonal are marked. None of the marked cells is in a corner. Integers are written in each cell of this board in the following way. All the numbers in the cells along the upper and the left sides of the board are 1's. All the numbers in the marked cells are 0's. Each of the other cells contains a number that is equal to the sum of its upper neighbour and its left neighbour. Prove that the number in the bottom right corner is not divisible by 2011 .
|
. Turning the board $45^{\circ}$ so that the upper left corner is on the top we notice that the numbers written on the board constitute the Pascal's triangle. If there were no marked cells on the board, then the number on the bottom cell
would be $\left(\begin{array}{l}4022 \\ 2011\end{array}\right)$, which is not divisible by 2011. All the cells on the diagonal that is
now horizontal, would be of the form $\left(\begin{array}{c}2011 \\ k\end{array}\right)$; all of them, except the numbers in the corners, would be divisible by 2011. If we substitute the numbers on the diagonal with their remainders modulo 2011, then all the numbers on the diagonal are 0's, independent of whether they were marked or not, except in the corners there are 1 's. After this change all numbers below the diagonal get substituted with their remainders modulo 2011. All the numbers below the diagonal are now 0's, except along the sides are 1's and in the bottom corner there is 2 . Hence the remainder of the number written in the bottom corner modulo 2012 is 2 .
|
2
|
Yes
|
Yes
|
proof
|
Number Theory
|
On a $2012 \times 2012$ board, some cells on the top-right to bottom-left diagonal are marked. None of the marked cells is in a corner. Integers are written in each cell of this board in the following way. All the numbers in the cells along the upper and the left sides of the board are 1's. All the numbers in the marked cells are 0's. Each of the other cells contains a number that is equal to the sum of its upper neighbour and its left neighbour. Prove that the number in the bottom right corner is not divisible by 2011 .
|
. Turning the board $45^{\circ}$ so that the upper left corner is on the top we notice that the numbers written on the board constitute the Pascal's triangle. If there were no marked cells on the board, then the number on the bottom cell
would be $\left(\begin{array}{l}4022 \\ 2011\end{array}\right)$, which is not divisible by 2011. All the cells on the diagonal that is
now horizontal, would be of the form $\left(\begin{array}{c}2011 \\ k\end{array}\right)$; all of them, except the numbers in the corners, would be divisible by 2011. If we substitute the numbers on the diagonal with their remainders modulo 2011, then all the numbers on the diagonal are 0's, independent of whether they were marked or not, except in the corners there are 1 's. After this change all numbers below the diagonal get substituted with their remainders modulo 2011. All the numbers below the diagonal are now 0's, except along the sides are 1's and in the bottom corner there is 2 . Hence the remainder of the number written in the bottom corner modulo 2012 is 2 .
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "# Problem 7",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
A directed graph does not contain directed cycles. The number of edges in any directed path does not exceed 99. Prove that it is possible to colour the edges of the graph in 2 colours so that the number of edges in any single-coloured directed path in the graph will not exceed 9 .
|
Label each vertex by the number from 0 to 99 , that is equal to the length of the longest directed path that ends in this vertex. Then every edge goes from a vertex with a smaller label to a vertex with a larger label. Now colour this edge in red if the digit of tens in the larger label is greater than the digit of tens in the smaller label. Otherwise colour this edge in blue. Since the number of tens is the same in all vertices on a blue path, the length of the path cannot exceed 9 . Since the number of tens is different in all vertices on a red path, the length of the path also cannot exceed 9 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A directed graph does not contain directed cycles. The number of edges in any directed path does not exceed 99. Prove that it is possible to colour the edges of the graph in 2 colours so that the number of edges in any single-coloured directed path in the graph will not exceed 9 .
|
Label each vertex by the number from 0 to 99 , that is equal to the length of the longest directed path that ends in this vertex. Then every edge goes from a vertex with a smaller label to a vertex with a larger label. Now colour this edge in red if the digit of tens in the larger label is greater than the digit of tens in the smaller label. Otherwise colour this edge in blue. Since the number of tens is the same in all vertices on a blue path, the length of the path cannot exceed 9 . Since the number of tens is different in all vertices on a red path, the length of the path also cannot exceed 9 .
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "# Problem 8",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Zeroes are written in all cells of a $5 \times 5$ board. We can take an arbitrary cell and increase by 1 the number in this cell and all cells having a common side with it. Is it possible to obtain the number 2012 in all cells simultaneously?
Answer: No.
|
. Let $a_{(i, j)}$ be the number written in the cell in the row $i$ and column $j$. To prove that it is not possible to get 2012 written in each cell, we choose a factor $c_{(i, j)}$ for each cell, such that
$$
S=\sum_{1 \leq i, j \leq 5} c_{(i, j)} \cdot a_{(i, j)}
$$
increases by the same number each time a cell is chosen. If we choose the factors $c_{(i, j)}$ as shown in Figure 1, then $S$ increases by 22 each time a cell is chosen. Hence $S$ is divisible by 22 at all times. The sum of all the $c_{(i, j)}$ is 138 , hence if 2012 is written in each cell, then
$$
S=138 \cdot 2012=2^{3} \cdot 3 \cdot 23 \cdot 503
$$
which cannot be reached, since it is not divisible by 22 .
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Zeroes are written in all cells of a $5 \times 5$ board. We can take an arbitrary cell and increase by 1 the number in this cell and all cells having a common side with it. Is it possible to obtain the number 2012 in all cells simultaneously?
Answer: No.
|
. Let $a_{(i, j)}$ be the number written in the cell in the row $i$ and column $j$. To prove that it is not possible to get 2012 written in each cell, we choose a factor $c_{(i, j)}$ for each cell, such that
$$
S=\sum_{1 \leq i, j \leq 5} c_{(i, j)} \cdot a_{(i, j)}
$$
increases by the same number each time a cell is chosen. If we choose the factors $c_{(i, j)}$ as shown in Figure 1, then $S$ increases by 22 each time a cell is chosen. Hence $S$ is divisible by 22 at all times. The sum of all the $c_{(i, j)}$ is 138 , hence if 2012 is written in each cell, then
$$
S=138 \cdot 2012=2^{3} \cdot 3 \cdot 23 \cdot 503
$$
which cannot be reached, since it is not divisible by 22 .
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Zeroes are written in all cells of a $5 \times 5$ board. We can take an arbitrary cell and increase by 1 the number in this cell and all cells having a common side with it. Is it possible to obtain the number 2012 in all cells simultaneously?
Answer: No.
|
. Divide all cells into six disjoint sets as follows: the set $A$ consists of all corner cells, the set $B$ consists of all cells, having a common side with the corner cells, the set $C$ consists of all diagonal neighbors of the corner cells, the set $D$ consists of all middle cells of the sides of the board, the set $E$ consists of all cells having a common side with the center cell, and the set $F$ has only the center cell in it. Suppose we choose $a$ times a cell from the set $A, b$ times from the set $B$ etc. Suppose that after a number of steps we get the number $s$ written in each cell. Since only the cells from the sets $A$ and $B$ contribute to the numbers written in the cells of the set $A$ and each choice from these sets contributes exactly 1 to the sum of the numbers written in the cells of the set $A$, we have $a+b=4 s$. Similarly, considering the sum of the numbers written in the cells of the set $B$, we see that choosing a cell from the set $A$ contributes 2 to the sum, choosing a cell from the set $B$ contributes 1, a cell from $C$ contributes 2 and a cell from $D$ contributes 2, hence $2 a+b+2 c+2 d=8 s$. Continuing, we get $b+c+2 e=4 s, b+d+e=4 s$, $2 c+d+e+4 f=4 s$, and $e+f=s$. Eliminating $a, b, d, e$, and $f$ from these equations we get $11 c=4 s$. This is only possible if $s$ is divisible by 11 . Since 2012 is not divisible by 11, it is not possible to get 2012 written in each cell.
Remark. For every positive $s$ divisible by 11 it is possible to get $s$ written in each cell. For $s=11$ Figure 2 shows how many times one has to choose each cell. If $s$ is larger than 11 , we can simply repeat these steps as many times as needed. The same figure can also be used for choosing factors as in Solution 1.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Zeroes are written in all cells of a $5 \times 5$ board. We can take an arbitrary cell and increase by 1 the number in this cell and all cells having a common side with it. Is it possible to obtain the number 2012 in all cells simultaneously?
Answer: No.
|
. Divide all cells into six disjoint sets as follows: the set $A$ consists of all corner cells, the set $B$ consists of all cells, having a common side with the corner cells, the set $C$ consists of all diagonal neighbors of the corner cells, the set $D$ consists of all middle cells of the sides of the board, the set $E$ consists of all cells having a common side with the center cell, and the set $F$ has only the center cell in it. Suppose we choose $a$ times a cell from the set $A, b$ times from the set $B$ etc. Suppose that after a number of steps we get the number $s$ written in each cell. Since only the cells from the sets $A$ and $B$ contribute to the numbers written in the cells of the set $A$ and each choice from these sets contributes exactly 1 to the sum of the numbers written in the cells of the set $A$, we have $a+b=4 s$. Similarly, considering the sum of the numbers written in the cells of the set $B$, we see that choosing a cell from the set $A$ contributes 2 to the sum, choosing a cell from the set $B$ contributes 1, a cell from $C$ contributes 2 and a cell from $D$ contributes 2, hence $2 a+b+2 c+2 d=8 s$. Continuing, we get $b+c+2 e=4 s, b+d+e=4 s$, $2 c+d+e+4 f=4 s$, and $e+f=s$. Eliminating $a, b, d, e$, and $f$ from these equations we get $11 c=4 s$. This is only possible if $s$ is divisible by 11 . Since 2012 is not divisible by 11, it is not possible to get 2012 written in each cell.
Remark. For every positive $s$ divisible by 11 it is possible to get $s$ written in each cell. For $s=11$ Figure 2 shows how many times one has to choose each cell. If $s$ is larger than 11 , we can simply repeat these steps as many times as needed. The same figure can also be used for choosing factors as in Solution 1.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Two players $A$ and $B$ play the following game. Before the game starts, $A$ chooses 1000 not necessarily different odd primes, and then $B$ chooses half of them and writes them on a blackboard. In each turn a player chooses a positive integer $n$, erases some primes $p_{1}, p_{2}, \ldots, p_{n}$ from the blackboard and writes all the prime factors of $p_{1} p_{2} \ldots p_{n}-2$ instead (if a prime occurs several times in the prime factorization of $p_{1} p_{2} \ldots p_{n}-2$, it is written as many times as it occurs). Player $A$ starts, and the player whose move leaves the blackboard empty loses the game. Prove that one of the two players has a winning strategy and determine who.
Remark: Since 1 has no prime factors, erasing a single 3 is a legal move.
|
Player $A$ has a winning strategy.

Figure 1

Figure 2
Let player $A$ choose 1000 primes all congruent to 1 modulo 4 . Then there are 500 primes congruent to 1 modulo 4 when the game begins. Let $P$ denote the parity of the number of primes congruent to 3 modulo 4 on the blackboard. When the game starts, $P$ is even. Remember that the number of primes congruent to 3 modulo 4 in the prime factorization of a number is even if the number is congruent to 1 modulo 4, and odd if the number is congruent to 3 modulo 4 . In each turn the parity of $P$ changes, because the number of primes congruent to 3 modulo 4 among $p_{1}, p_{2}, \ldots$, $p_{n}$ and in the prime factorization of $p_{1} p_{2} \ldots p_{n}-2$ is of different parity. Hence $P$ is odd after each of $A$ 's turns and even after each of $B$ 's turns, so $A$ cannot lose. Since the product of all the primes on the blackboard decreases with each turn, the game eventually ends, hence $A$ wins.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Two players $A$ and $B$ play the following game. Before the game starts, $A$ chooses 1000 not necessarily different odd primes, and then $B$ chooses half of them and writes them on a blackboard. In each turn a player chooses a positive integer $n$, erases some primes $p_{1}, p_{2}, \ldots, p_{n}$ from the blackboard and writes all the prime factors of $p_{1} p_{2} \ldots p_{n}-2$ instead (if a prime occurs several times in the prime factorization of $p_{1} p_{2} \ldots p_{n}-2$, it is written as many times as it occurs). Player $A$ starts, and the player whose move leaves the blackboard empty loses the game. Prove that one of the two players has a winning strategy and determine who.
Remark: Since 1 has no prime factors, erasing a single 3 is a legal move.
|
Player $A$ has a winning strategy.

Figure 1

Figure 2
Let player $A$ choose 1000 primes all congruent to 1 modulo 4 . Then there are 500 primes congruent to 1 modulo 4 when the game begins. Let $P$ denote the parity of the number of primes congruent to 3 modulo 4 on the blackboard. When the game starts, $P$ is even. Remember that the number of primes congruent to 3 modulo 4 in the prime factorization of a number is even if the number is congruent to 1 modulo 4, and odd if the number is congruent to 3 modulo 4 . In each turn the parity of $P$ changes, because the number of primes congruent to 3 modulo 4 among $p_{1}, p_{2}, \ldots$, $p_{n}$ and in the prime factorization of $p_{1} p_{2} \ldots p_{n}-2$ is of different parity. Hence $P$ is odd after each of $A$ 's turns and even after each of $B$ 's turns, so $A$ cannot lose. Since the product of all the primes on the blackboard decreases with each turn, the game eventually ends, hence $A$ wins.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Rotate the triangle $A B C$ by $60^{\circ}$ around the point $A$ (Figure 3). Let $T^{\prime}$ and $C^{\prime}$ be the images of $T$ and $C$, respectively. Then the triangle $A T T^{\prime}$ is equilateral and $\angle A T^{\prime} C^{\prime}=120^{\circ}$, meaning that $B, T, T^{\prime}, C^{\prime}$ are collinear and $T A+T B+T C=B C^{\prime}$. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram. Then $2 A M=A A^{\prime}$. It remains to observe that the triangles $B A C^{\prime}$ and $A B A^{\prime}$ are equal, since $B A$ is common, $\angle B A C^{\prime}=120^{\circ}=\angle A^{\prime} B A$, and $A C^{\prime}=B A^{\prime}$.
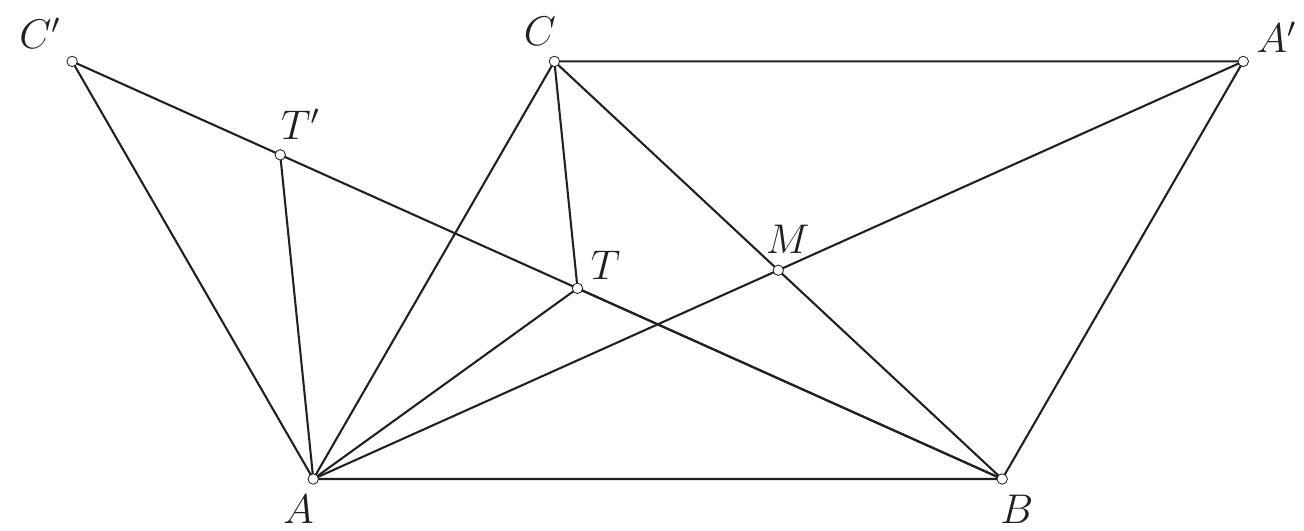
Figure 3
Remark. The rotation used here is the same as that used in finding a point $P$ in the triangle such that the total distance from the three vertices of the triangle to $P$ is the minimum possible (Fermat point); this is exactly the point $T$ in the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Rotate the triangle $A B C$ by $60^{\circ}$ around the point $A$ (Figure 3). Let $T^{\prime}$ and $C^{\prime}$ be the images of $T$ and $C$, respectively. Then the triangle $A T T^{\prime}$ is equilateral and $\angle A T^{\prime} C^{\prime}=120^{\circ}$, meaning that $B, T, T^{\prime}, C^{\prime}$ are collinear and $T A+T B+T C=B C^{\prime}$. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram. Then $2 A M=A A^{\prime}$. It remains to observe that the triangles $B A C^{\prime}$ and $A B A^{\prime}$ are equal, since $B A$ is common, $\angle B A C^{\prime}=120^{\circ}=\angle A^{\prime} B A$, and $A C^{\prime}=B A^{\prime}$.

Figure 3
Remark. The rotation used here is the same as that used in finding a point $P$ in the triangle such that the total distance from the three vertices of the triangle to $P$ is the minimum possible (Fermat point); this is exactly the point $T$ in the problem.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram. Since $\angle B A^{\prime} C=60^{\circ}$ and $\angle B T C=120^{\circ}$, the point $T$ lies on the circumcircle of $A^{\prime} B C$. Let $X$ be the second intersection point of $A T$ with this circumcircle and let $Y$ be the midpoint of $A^{\prime} X$. The triangle $B C X$ is equilateral, since $\angle B X C=\angle B A^{\prime} C=60^{\circ}$ and $\angle B C X=\angle B T X=180^{\circ}-\angle B T A=60^{\circ}$. Therefore $T B+T C=T X$. So it is sufficient to show that $A X=A A^{\prime}$.
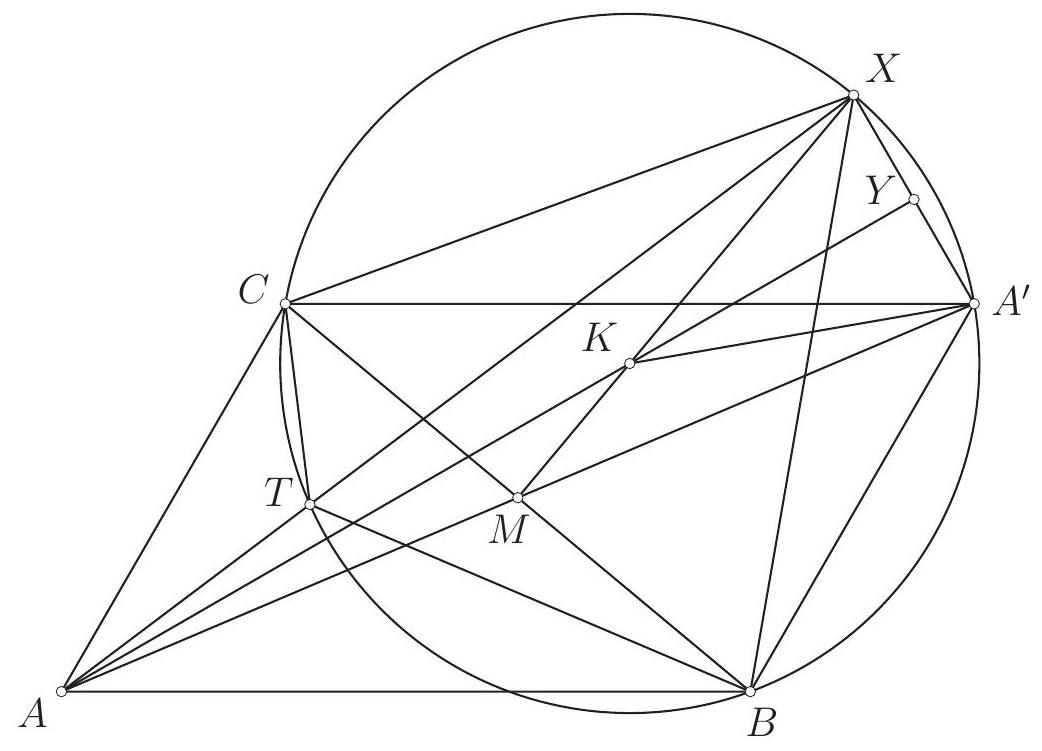
Figure 4
Let $K$ be the intersection point of the medians of $B C X$. Since $X M$ is a median for both $B C X$ and $A A^{\prime} X$, it follows that $K$ is also the intersection point of the medians of $A A^{\prime} X$. Thus $K$ lies on the median $A Y$. Since the triangle $K A^{\prime} X$ is equilateral, we have $K Y \perp A^{\prime} X$, so $A Y$ is both the height and the median of $A A^{\prime} X$.
Consequently, $T A+T B+T C=A X=A A^{\prime}=2 A M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram. Since $\angle B A^{\prime} C=60^{\circ}$ and $\angle B T C=120^{\circ}$, the point $T$ lies on the circumcircle of $A^{\prime} B C$. Let $X$ be the second intersection point of $A T$ with this circumcircle and let $Y$ be the midpoint of $A^{\prime} X$. The triangle $B C X$ is equilateral, since $\angle B X C=\angle B A^{\prime} C=60^{\circ}$ and $\angle B C X=\angle B T X=180^{\circ}-\angle B T A=60^{\circ}$. Therefore $T B+T C=T X$. So it is sufficient to show that $A X=A A^{\prime}$.

Figure 4
Let $K$ be the intersection point of the medians of $B C X$. Since $X M$ is a median for both $B C X$ and $A A^{\prime} X$, it follows that $K$ is also the intersection point of the medians of $A A^{\prime} X$. Thus $K$ lies on the median $A Y$. Since the triangle $K A^{\prime} X$ is equilateral, we have $K Y \perp A^{\prime} X$, so $A Y$ is both the height and the median of $A A^{\prime} X$.
Consequently, $T A+T B+T C=A X=A A^{\prime}=2 A M$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram (Figure 5). Use notations $A B=c, A C=b, 2 A M=A A^{\prime}=d, T A=x, T B=y, T C=z$. From $\angle A B T=60^{\circ}-\angle B A T=\angle C A T=60^{\circ}-\angle A C T$ one gets $\triangle A B T \sim \triangle C A T$. So $y: x=c: b$, and we have totally $\triangle A B T \sim \triangle C A T \sim \triangle A^{\prime} A B$, giving $x=b \cdot \frac{c}{d}=c \cdot \frac{b}{d}$, $y=c \cdot \frac{c}{d}, z=b \cdot \frac{b}{d}$. By applying the law of cosines in triangle $A^{\prime} A B$, we finally get
$$
x+y+z=\frac{b c+c^{2}+b^{2}}{d}=\frac{d^{2}}{d}=d .
$$
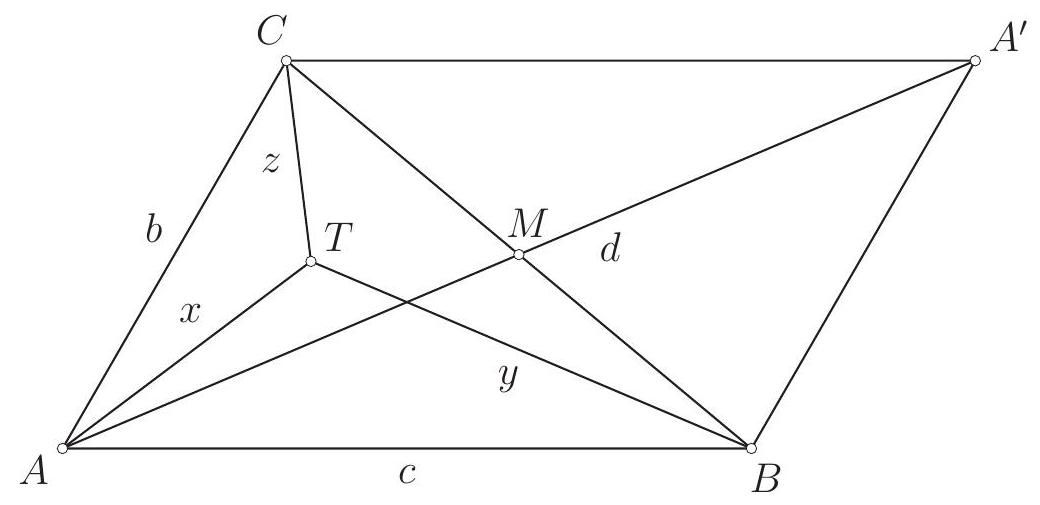
Figure 5
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $\angle A=60^{\circ}$. The point $T$ lies inside the triangle in such a way that $\angle A T B=\angle B T C=\angle C T A=120^{\circ}$. Let $M$ be the midpoint of $B C$. Prove that $T A+T B+T C=2 A M$.
|
. Let $A^{\prime}$ be a point such that $A B A^{\prime} C$ is a parallelogram (Figure 5). Use notations $A B=c, A C=b, 2 A M=A A^{\prime}=d, T A=x, T B=y, T C=z$. From $\angle A B T=60^{\circ}-\angle B A T=\angle C A T=60^{\circ}-\angle A C T$ one gets $\triangle A B T \sim \triangle C A T$. So $y: x=c: b$, and we have totally $\triangle A B T \sim \triangle C A T \sim \triangle A^{\prime} A B$, giving $x=b \cdot \frac{c}{d}=c \cdot \frac{b}{d}$, $y=c \cdot \frac{c}{d}, z=b \cdot \frac{b}{d}$. By applying the law of cosines in triangle $A^{\prime} A B$, we finally get
$$
x+y+z=\frac{b c+c^{2}+b^{2}}{d}=\frac{d^{2}}{d}=d .
$$

Figure 5
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2012"
}
|
Let $P_{0}, P_{1}, \ldots, P_{8}=P_{0}$ be successive points on a circle and $Q$ be a point inside the polygon $P_{0} P_{1} \ldots P_{7}$ such that $\angle P_{i-1} Q P_{i}=45^{\circ}$ for $i=1, \ldots, 8$. Prove that the sum
$$
\sum_{i=1}^{8} P_{i-1} P_{i}{ }^{2}
$$
is minimal if and only if $Q$ is the centre of the circle.
|
By the cosine law we have (Figure 6)
$$
P_{i-1} P_{i}^{2}=Q P_{i-1}^{2}+Q P_{i}^{2}-\sqrt{2} \cdot Q P_{i-1} \cdot Q P_{i} .
$$
Hence, using the AM-GM inequality,
$$
\sum_{i=1}^{8} P_{i-1} P_{i}^{2}=\sum_{i=1}^{8}\left(2 \cdot Q P_{i}^{2}-\sqrt{2} \cdot Q P_{i-1} \cdot Q P_{i}\right) \geq(2-\sqrt{2}) \sum_{i=1}^{8} Q P_{i}^{2}
$$
The equality holds if and only if all distances $Q P_{i}$ are equally large, i.e. $Q$ is the centre of the circle. So it remains to show that the sum in the last expression is independent of $Q$. Indeed, by the Pythagorean theorem,
$$
\sum_{i=1}^{8} Q P_{i}^{2}=\left(P_{0} P_{2}^{2}+P_{4} P_{6}^{2}\right)+\left(P_{1} P_{3}^{2}+P_{5} P_{7}^{2}\right)=2 d^{2}
$$
where $d$ is the diameter of the circle. The last equality follows form the fact that $P_{0} P_{2} P_{4} P_{6}$ is a cyclic quadrilateral with perpendicular diagonals, so $P_{0} P_{2}{ }^{2}+P_{4} P_{6}{ }^{2}=$ $d^{2}$.
Remark. The sum $\sum_{i=1}^{8} Q P_{i}{ }^{2}=\sum_{i=1}^{4} Q P_{2 i-1}{ }^{2}+\sum_{i=1}^{4} Q P_{2 i}{ }^{2}$ can also be computed easily using coordinates, e.g. expressing each term by the coordinates of $Q$.
Figure 6
Figure 7
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P_{0}, P_{1}, \ldots, P_{8}=P_{0}$ be successive points on a circle and $Q$ be a point inside the polygon $P_{0} P_{1} \ldots P_{7}$ such that $\angle P_{i-1} Q P_{i}=45^{\circ}$ for $i=1, \ldots, 8$. Prove that the sum
$$
\sum_{i=1}^{8} P_{i-1} P_{i}{ }^{2}
$$
is minimal if and only if $Q$ is the centre of the circle.
|
By the cosine law we have (Figure 6)
$$
P_{i-1} P_{i}^{2}=Q P_{i-1}^{2}+Q P_{i}^{2}-\sqrt{2} \cdot Q P_{i-1} \cdot Q P_{i} .
$$
Hence, using the AM-GM inequality,
$$
\sum_{i=1}^{8} P_{i-1} P_{i}^{2}=\sum_{i=1}^{8}\left(2 \cdot Q P_{i}^{2}-\sqrt{2} \cdot Q P_{i-1} \cdot Q P_{i}\right) \geq(2-\sqrt{2}) \sum_{i=1}^{8} Q P_{i}^{2}
$$
The equality holds if and only if all distances $Q P_{i}$ are equally large, i.e. $Q$ is the centre of the circle. So it remains to show that the sum in the last expression is independent of $Q$. Indeed, by the Pythagorean theorem,
$$
\sum_{i=1}^{8} Q P_{i}^{2}=\left(P_{0} P_{2}^{2}+P_{4} P_{6}^{2}\right)+\left(P_{1} P_{3}^{2}+P_{5} P_{7}^{2}\right)=2 d^{2}
$$
where $d$ is the diameter of the circle. The last equality follows form the fact that $P_{0} P_{2} P_{4} P_{6}$ is a cyclic quadrilateral with perpendicular diagonals, so $P_{0} P_{2}{ }^{2}+P_{4} P_{6}{ }^{2}=$ $d^{2}$.
Remark. The sum $\sum_{i=1}^{8} Q P_{i}{ }^{2}=\sum_{i=1}^{4} Q P_{2 i-1}{ }^{2}+\sum_{i=1}^{4} Q P_{2 i}{ }^{2}$ can also be computed easily using coordinates, e.g. expressing each term by the coordinates of $Q$.

Figure 6

Figure 7
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "# Problem 12",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Let $A B C$ be an acute triangle, and let $H$ be its orthocentre. Denote by $H_{A}, H_{B}$ and $H_{C}$ the second intersection of the circumcircle with the altitudes from $A, B$ and $C$ respectively. Prove that the area of $\triangle H_{A} H_{B} H_{C}$ does not exceed the area of $\triangle A B C$.
|
. We know that the points $H_{A}, H_{B}$ and $H_{C}$ are in fact the reflection of $H$ on the sides (Figure 7). Since $A B C$ is acute (i.e. $H$ lies in the interior of $A B C$ ), we have $S_{A H_{C} B H_{A} C H_{B}}=2 S_{A B C}$. We thus have to show that $2 S_{H_{A} H_{B} H_{C}} \leq S_{A H_{C} B H_{A} C H_{B}}$, which is equivalent to
$$
S_{H_{A} H_{B} H_{C}} \leq S_{H_{A} C H_{B}}+S_{H_{B} A H_{C}}+S_{H_{C} B H_{A}}
$$
Notice that the triangles on the RHS are isosceles (e.g. $H_{A} C=H C=H_{B} C$ ). If now for example $\angle H_{A} H_{B} H_{C} \geq 90^{\circ}$, then obviously already $S_{H_{A} H_{B} H_{C}} \leq S_{H_{A} B H_{C}}$. It may therefore be supposed that $H_{A} H_{B} H_{C}$ is acute-angled. Denote by $M$ its orthocentre, which then lies inside the triangle. Denote by $M_{A}, M_{B}$ and $M_{C}$ the reflections of the orthocentre on the sides $H_{B} H_{C}, H_{C} H_{A}$ and $H_{A} H_{B}$, respectively. These lie on the circumcircle, and therefore we have $S_{H_{B} M_{A} H_{C}} \leq S_{H_{B} A H_{C}}, S_{H_{C} M_{B} H_{A}} \leq S_{H_{C} B H_{A}}$ and $S_{H_{A} M_{C} H_{B}} \leq S_{H_{A} C H_{B}}$. Since
$$
S_{H_{A} H_{B} H_{C}}=S_{H_{B} M_{A} H_{C}}+S_{H_{C} M_{B} H_{A}}+S_{H_{A} M_{C} H_{B}},
$$
we arrive to the required result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle, and let $H$ be its orthocentre. Denote by $H_{A}, H_{B}$ and $H_{C}$ the second intersection of the circumcircle with the altitudes from $A, B$ and $C$ respectively. Prove that the area of $\triangle H_{A} H_{B} H_{C}$ does not exceed the area of $\triangle A B C$.
|
. We know that the points $H_{A}, H_{B}$ and $H_{C}$ are in fact the reflection of $H$ on the sides (Figure 7). Since $A B C$ is acute (i.e. $H$ lies in the interior of $A B C$ ), we have $S_{A H_{C} B H_{A} C H_{B}}=2 S_{A B C}$. We thus have to show that $2 S_{H_{A} H_{B} H_{C}} \leq S_{A H_{C} B H_{A} C H_{B}}$, which is equivalent to
$$
S_{H_{A} H_{B} H_{C}} \leq S_{H_{A} C H_{B}}+S_{H_{B} A H_{C}}+S_{H_{C} B H_{A}}
$$
Notice that the triangles on the RHS are isosceles (e.g. $H_{A} C=H C=H_{B} C$ ). If now for example $\angle H_{A} H_{B} H_{C} \geq 90^{\circ}$, then obviously already $S_{H_{A} H_{B} H_{C}} \leq S_{H_{A} B H_{C}}$. It may therefore be supposed that $H_{A} H_{B} H_{C}$ is acute-angled. Denote by $M$ its orthocentre, which then lies inside the triangle. Denote by $M_{A}, M_{B}$ and $M_{C}$ the reflections of the orthocentre on the sides $H_{B} H_{C}, H_{C} H_{A}$ and $H_{A} H_{B}$, respectively. These lie on the circumcircle, and therefore we have $S_{H_{B} M_{A} H_{C}} \leq S_{H_{B} A H_{C}}, S_{H_{C} M_{B} H_{A}} \leq S_{H_{C} B H_{A}}$ and $S_{H_{A} M_{C} H_{B}} \leq S_{H_{A} C H_{B}}$. Since
$$
S_{H_{A} H_{B} H_{C}}=S_{H_{B} M_{A} H_{C}}+S_{H_{C} M_{B} H_{A}}+S_{H_{A} M_{C} H_{B}},
$$
we arrive to the required result.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "# Problem 13",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Let $A B C$ be an acute triangle, and let $H$ be its orthocentre. Denote by $H_{A}, H_{B}$ and $H_{C}$ the second intersection of the circumcircle with the altitudes from $A, B$ and $C$ respectively. Prove that the area of $\triangle H_{A} H_{B} H_{C}$ does not exceed the area of $\triangle A B C$.
|
. Let the angles of $A B C$ be denoted by $\alpha, \beta$ and $\gamma$, the radius of the circumcircle by $R$. Then
$$
S_{A B C}=2 R^{2} \sin \alpha \sin \beta \sin \gamma
$$
By peripheric angles we get
$$
\angle H_{A} H_{B} H_{C}=\angle H_{A} H_{B} B+\angle B H_{B} H_{C}=\angle H_{A} A B+\angle B C H_{C}=180^{\circ}-2 \beta,
$$
Figure 8
and correspondingly $\angle H_{B} H_{C} H_{A}=180^{\circ}-2 \gamma$ and $\angle H_{C} H_{A} H_{B}=180^{\circ}-2 \alpha$. Thus
$$
\begin{aligned}
& S_{H_{A} H_{B} H_{C}}=2 R^{2} \sin \left(180^{\circ}-2 \beta\right) \sin (\left.180^{\circ}-2 \gamma\right) \sin \left(180^{\circ}-2 \alpha\right) \\
&=2 R^{2} \sin (2 \beta) \sin (2 \gamma) \sin (2 \alpha)=8 S_{A B C} \cos \alpha \cos \beta \cos \gamma \\
& \leq 8 S_{A B C}\left(\frac{\cos \alpha+\cos \beta+\cos \gamma}{3}\right)^{3} \leq S_{A B C}
\end{aligned}
$$
where the last inequality follows from Jensen's inequality for the cosine function.
Remark. There are also other solutions that combine the ideas appearing in Solutions 1 and 2 in different way.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle, and let $H$ be its orthocentre. Denote by $H_{A}, H_{B}$ and $H_{C}$ the second intersection of the circumcircle with the altitudes from $A, B$ and $C$ respectively. Prove that the area of $\triangle H_{A} H_{B} H_{C}$ does not exceed the area of $\triangle A B C$.
|
. Let the angles of $A B C$ be denoted by $\alpha, \beta$ and $\gamma$, the radius of the circumcircle by $R$. Then
$$
S_{A B C}=2 R^{2} \sin \alpha \sin \beta \sin \gamma
$$
By peripheric angles we get
$$
\angle H_{A} H_{B} H_{C}=\angle H_{A} H_{B} B+\angle B H_{B} H_{C}=\angle H_{A} A B+\angle B C H_{C}=180^{\circ}-2 \beta,
$$

Figure 8
and correspondingly $\angle H_{B} H_{C} H_{A}=180^{\circ}-2 \gamma$ and $\angle H_{C} H_{A} H_{B}=180^{\circ}-2 \alpha$. Thus
$$
\begin{aligned}
& S_{H_{A} H_{B} H_{C}}=2 R^{2} \sin \left(180^{\circ}-2 \beta\right) \sin (\left.180^{\circ}-2 \gamma\right) \sin \left(180^{\circ}-2 \alpha\right) \\
&=2 R^{2} \sin (2 \beta) \sin (2 \gamma) \sin (2 \alpha)=8 S_{A B C} \cos \alpha \cos \beta \cos \gamma \\
& \leq 8 S_{A B C}\left(\frac{\cos \alpha+\cos \beta+\cos \gamma}{3}\right)^{3} \leq S_{A B C}
\end{aligned}
$$
where the last inequality follows from Jensen's inequality for the cosine function.
Remark. There are also other solutions that combine the ideas appearing in Solutions 1 and 2 in different way.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "# Problem 13",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
Given a triangle $A B C$, let its incircle touch the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be the midpoint of the segment $D E$. Prove that $\angle E F C=$ $\angle G F D$.
|
. Let $\omega$ be the circumcircle of the triangle $C E F$ and let $H$ be the second point of intersection of the circle $\omega$ with the line $C G$ (Figure 8). Assume also, without loss of generality, that $A C<B C$. (If $A C=B C$, the whole problem becomes trivial due to symmetry.) Then the points $G, H, B$ lie on the same side of the line $C F$ and the vertex $A$ lies on the opposite side. The points $E, F, H, C$ lie on the circle $\omega$ while the points $E$ and $D$ are symmetric with respect to the line $\mathrm{CH}$. Hence
$$
\angle E F C=\angle E H C=\angle C H D .
$$
The line $A C$ is tangent to the incircle of $A B C$ at $E$, so we have $\angle G D F=$ $\angle E D F=\angle A E F=180^{\circ}-\angle C E F$. Now, using the circle $\omega$, we see that $\angle C E F=$
Figure 9
$180^{\circ}-\angle C H F=180^{\circ}-\angle G H F$. Combining the above relations we conclude that $\angle G D F=\angle G H F$, so that the points $G, F, H, D$ lie on a circle. Therefore $\angle C H D=$ $\angle G H D=\angle G F D$, which together with $(*)$ proves the assertion of the problem.
Remark. This problem is trivial for those who rely on the following known result: a symmedian through one of the vertices of a triangle passes through the point of intersection of the tangents to the circumcircle at the other two vertices (http://www. cut-the-knot.org/Curriculum/Geometry/Symmedian.shtml\#explanation). Applying this result to triangle $D E F$ and the symmedian through $F$ gives that the symmedian coincides with $F C$. Now use the definition of symmedian.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let its incircle touch the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be the midpoint of the segment $D E$. Prove that $\angle E F C=$ $\angle G F D$.
|
. Let $\omega$ be the circumcircle of the triangle $C E F$ and let $H$ be the second point of intersection of the circle $\omega$ with the line $C G$ (Figure 8). Assume also, without loss of generality, that $A C<B C$. (If $A C=B C$, the whole problem becomes trivial due to symmetry.) Then the points $G, H, B$ lie on the same side of the line $C F$ and the vertex $A$ lies on the opposite side. The points $E, F, H, C$ lie on the circle $\omega$ while the points $E$ and $D$ are symmetric with respect to the line $\mathrm{CH}$. Hence
$$
\angle E F C=\angle E H C=\angle C H D .
$$
The line $A C$ is tangent to the incircle of $A B C$ at $E$, so we have $\angle G D F=$ $\angle E D F=\angle A E F=180^{\circ}-\angle C E F$. Now, using the circle $\omega$, we see that $\angle C E F=$

Figure 9
$180^{\circ}-\angle C H F=180^{\circ}-\angle G H F$. Combining the above relations we conclude that $\angle G D F=\angle G H F$, so that the points $G, F, H, D$ lie on a circle. Therefore $\angle C H D=$ $\angle G H D=\angle G F D$, which together with $(*)$ proves the assertion of the problem.
Remark. This problem is trivial for those who rely on the following known result: a symmedian through one of the vertices of a triangle passes through the point of intersection of the tangents to the circumcircle at the other two vertices (http://www. cut-the-knot.org/Curriculum/Geometry/Symmedian.shtml\#explanation). Applying this result to triangle $D E F$ and the symmedian through $F$ gives that the symmedian coincides with $F C$. Now use the definition of symmedian.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2012"
}
|
Given a triangle $A B C$, let its incircle touch the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be the midpoint of the segment $D E$. Prove that $\angle E F C=$ $\angle G F D$.
|
. We show that the ray from a triangle vertex $F$ though the intersection $C$ of the tangents to the circumcircle at the two other vertices $D$ and $E$ is the symmedian of triangle $D F E$ : Let the circle with centre $C$ and radius $C D=C E$ meet the rays $F D$ and $F E$ again in $P$ and $Q$ (Figure 9$)$. Then
$$
\angle D P C=\angle P D C=\angle F D B=\angle F E D=180^{\circ}-\angle Q E D=\angle Q P D,
$$
whence $P, C, Q$ are collinear. Thus $P Q$ is a diameter of circle $D E Q P$. Triangles $F D E$ and $F Q P$ are similar and have a common angle at $F$. Consequently, the desired result follows since $G$ is the midpoint of $D E$ and $C$ is the midpoint of $Q P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$, let its incircle touch the sides $B C, C A, A B$ at $D, E, F$, respectively. Let $G$ be the midpoint of the segment $D E$. Prove that $\angle E F C=$ $\angle G F D$.
|
. We show that the ray from a triangle vertex $F$ though the intersection $C$ of the tangents to the circumcircle at the two other vertices $D$ and $E$ is the symmedian of triangle $D F E$ : Let the circle with centre $C$ and radius $C D=C E$ meet the rays $F D$ and $F E$ again in $P$ and $Q$ (Figure 9$)$. Then
$$
\angle D P C=\angle P D C=\angle F D B=\angle F E D=180^{\circ}-\angle Q E D=\angle Q P D,
$$
whence $P, C, Q$ are collinear. Thus $P Q$ is a diameter of circle $D E Q P$. Triangles $F D E$ and $F Q P$ are similar and have a common angle at $F$. Consequently, the desired result follows since $G$ is the midpoint of $D E$ and $C$ is the midpoint of $Q P$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2012"
}
|
The circumcentre $O$ of a given cyclic quadrilateral $A B C D$ lies inside the quadrilateral but not on the diagonal $A C$. The diagonals of the quadrilateral intersect at $I$.
The circumcircle of the triangle $A O I$ meets the sides $A D$ and $A B$ at points $P$ and $Q$, respectively; the circumcircle of the triangle $C O I$ meets the sides $C B$ and $C D$ at points $R$ and $S$, respectively. Prove that $P Q R S$ is a parallelogram.
|
Assume w.l.o.g. that angle $A B C$ is obtuse (otherwise switch $B$ and $D$, Figure 10). As $A, I, O$ and $P$ are concyclic, we get $\angle Q A I=\angle Q O I$; similarly $\angle R C I=\angle R O I$. Hence
$$
\begin{aligned}
\angle Q O R=\angle Q O I+\angle R O I=\angle Q A I+\angle R C I & =\angle B A C+\angle B C A \\
& =180^{\circ}-\angle A B C=180^{\circ}-\angle Q B R .
\end{aligned}
$$
It follows that points $Q, O, R$ and $B$ are concyclic.
Furthermore, $\angle P A I=180^{\circ}-\angle P O I$ and $\angle S C I=180^{\circ}-\angle S O I$ imply
$$
\begin{aligned}
\angle P O S=360^{\circ}-\angle P O I-\angle S O I=\angle P A I+\angle S C I & =\angle D A C+\angle D C A \\
& =180^{\circ}-\angle A D C=180^{\circ}-\angle P D S .
\end{aligned}
$$
Hence also points $P, O, S$ and $D$ are concyclic.
As $O$ is the circumcentre of $A B C D$, we have $A O=O B$ and $\angle B A O=\angle O B A$. These are inscribed angles in circumcircles of $A P Q$ and $B Q R$, respectively, and both of them are based on the same chord $O Q$. Therefore the radii of these two circumcircles are equal. Similarly, the radii of circumcircles of $B Q R, C R S$ and $D S P$ are also equal.
As $\angle Q A P=\angle B A D=180^{\circ}-\angle B C D=180^{\circ}-\angle R C S$ and radii of the circumcircles of $A Q O P$ and $O R C S$ are equal, the chords $Q P$ and $R S$ have equal lengths; similarly also $Q R$ and $P S$ have equal lengths. Thus $P Q R S$ is a parallelogram.
Remark. In the case of $O$ lying in the diagonal $A C$, the necessary triangles $A O I$ and $C O I$ are degenerate and have no circumcircle. The statement of the problem still holds if the circumcentre of $A B C D$ does not lie inside the quadrilateral (Figure 11) and even if the circumcircles of $A O I$ and $C O I$ meet prolongations of sides.
Figure 10
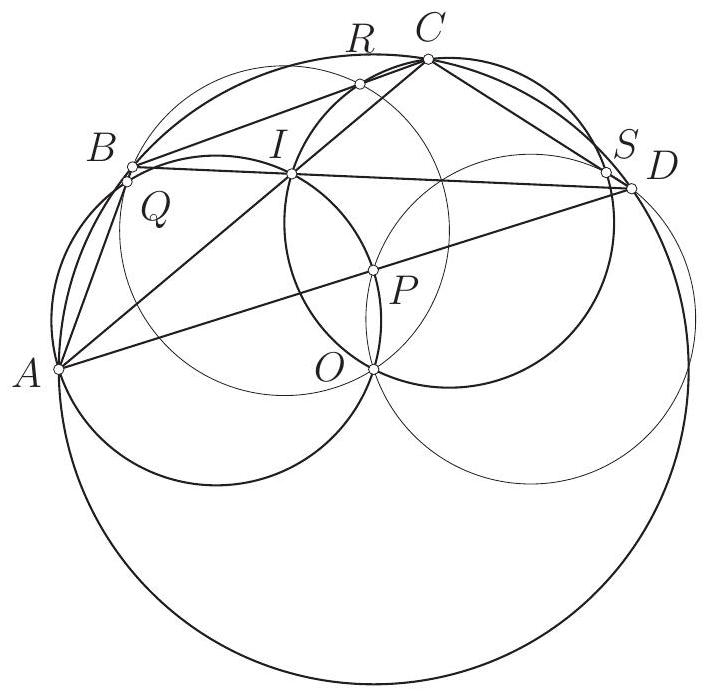
Figure 11
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The circumcentre $O$ of a given cyclic quadrilateral $A B C D$ lies inside the quadrilateral but not on the diagonal $A C$. The diagonals of the quadrilateral intersect at $I$.
The circumcircle of the triangle $A O I$ meets the sides $A D$ and $A B$ at points $P$ and $Q$, respectively; the circumcircle of the triangle $C O I$ meets the sides $C B$ and $C D$ at points $R$ and $S$, respectively. Prove that $P Q R S$ is a parallelogram.
|
Assume w.l.o.g. that angle $A B C$ is obtuse (otherwise switch $B$ and $D$, Figure 10). As $A, I, O$ and $P$ are concyclic, we get $\angle Q A I=\angle Q O I$; similarly $\angle R C I=\angle R O I$. Hence
$$
\begin{aligned}
\angle Q O R=\angle Q O I+\angle R O I=\angle Q A I+\angle R C I & =\angle B A C+\angle B C A \\
& =180^{\circ}-\angle A B C=180^{\circ}-\angle Q B R .
\end{aligned}
$$
It follows that points $Q, O, R$ and $B$ are concyclic.
Furthermore, $\angle P A I=180^{\circ}-\angle P O I$ and $\angle S C I=180^{\circ}-\angle S O I$ imply
$$
\begin{aligned}
\angle P O S=360^{\circ}-\angle P O I-\angle S O I=\angle P A I+\angle S C I & =\angle D A C+\angle D C A \\
& =180^{\circ}-\angle A D C=180^{\circ}-\angle P D S .
\end{aligned}
$$
Hence also points $P, O, S$ and $D$ are concyclic.
As $O$ is the circumcentre of $A B C D$, we have $A O=O B$ and $\angle B A O=\angle O B A$. These are inscribed angles in circumcircles of $A P Q$ and $B Q R$, respectively, and both of them are based on the same chord $O Q$. Therefore the radii of these two circumcircles are equal. Similarly, the radii of circumcircles of $B Q R, C R S$ and $D S P$ are also equal.
As $\angle Q A P=\angle B A D=180^{\circ}-\angle B C D=180^{\circ}-\angle R C S$ and radii of the circumcircles of $A Q O P$ and $O R C S$ are equal, the chords $Q P$ and $R S$ have equal lengths; similarly also $Q R$ and $P S$ have equal lengths. Thus $P Q R S$ is a parallelogram.
Remark. In the case of $O$ lying in the diagonal $A C$, the necessary triangles $A O I$ and $C O I$ are degenerate and have no circumcircle. The statement of the problem still holds if the circumcentre of $A B C D$ does not lie inside the quadrilateral (Figure 11) and even if the circumcircles of $A O I$ and $C O I$ meet prolongations of sides.

Figure 10

Figure 11
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Let $n, m$ and $k$ be positive integers satisfying $(n-1) n(n+1)=m^{k}$. Prove that $k=1$.
|
Since $\operatorname{gcd}(n,(n-1)(n+1))=1$, if $(n-1) n(n+1)$ is a $k$-th power for $k \geq 1$, then $n$ and $(n-1)(n+1)=n^{2}-1$ must be $k$-th powers as well. Then $n=m_{1}^{k}$ and $n^{2}-1=m_{2}^{k}=\left(m_{1}^{2}\right)^{k}-1$. But the difference of two positive $k$-th powers can never be 1 , if $k>1$. So $k=1$.
|
k=1
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n, m$ and $k$ be positive integers satisfying $(n-1) n(n+1)=m^{k}$. Prove that $k=1$.
|
Since $\operatorname{gcd}(n,(n-1)(n+1))=1$, if $(n-1) n(n+1)$ is a $k$-th power for $k \geq 1$, then $n$ and $(n-1)(n+1)=n^{2}-1$ must be $k$-th powers as well. Then $n=m_{1}^{k}$ and $n^{2}-1=m_{2}^{k}=\left(m_{1}^{2}\right)^{k}-1$. But the difference of two positive $k$-th powers can never be 1 , if $k>1$. So $k=1$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "# Problem 16",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Let $d(n)$ denote the number of positive divisors of $n$. Find all triples $(n, k, p)$, where $n$ and $k$ are positive integers and $p$ is a prime number, such that
$$
n^{d(n)}-1=p^{k} .
$$
|
Note first that $n^{d(n)}$ is always a square: if $d(n)$ is an even number this is clear; but $d(n)$ is odd exactly if $n$ is a square, and then its power $n^{d(n)}$ is also a square.
Let $n^{d(n)}=m^{2}, m>0$. Then
$$
(m+1)(m-1)=m^{2}-1=n^{d(n)}-1=p^{k} .
$$
There is no solution for $m=1$. If $m=2$, we get $(n, k, p)=(2,1,3)$. If $m>2$, we have $m-1, m+1>1$ and because both factors divide $p^{k}$, they are both powers of $p$. The only possibility is $m-1=2, m+1=4$. Hence $m=3$ and $n^{d(n)}=m^{2}=9$. This leads to the solution $(n, k, p)=(3,3,2)$. So the only solutions are $(n, k, p)=(2,1,3)$ and $(n, k, p)=(3,3,2)$.
|
(2,1,3) \text{ and } (3,3,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $d(n)$ denote the number of positive divisors of $n$. Find all triples $(n, k, p)$, where $n$ and $k$ are positive integers and $p$ is a prime number, such that
$$
n^{d(n)}-1=p^{k} .
$$
|
Note first that $n^{d(n)}$ is always a square: if $d(n)$ is an even number this is clear; but $d(n)$ is odd exactly if $n$ is a square, and then its power $n^{d(n)}$ is also a square.
Let $n^{d(n)}=m^{2}, m>0$. Then
$$
(m+1)(m-1)=m^{2}-1=n^{d(n)}-1=p^{k} .
$$
There is no solution for $m=1$. If $m=2$, we get $(n, k, p)=(2,1,3)$. If $m>2$, we have $m-1, m+1>1$ and because both factors divide $p^{k}$, they are both powers of $p$. The only possibility is $m-1=2, m+1=4$. Hence $m=3$ and $n^{d(n)}=m^{2}=9$. This leads to the solution $(n, k, p)=(3,3,2)$. So the only solutions are $(n, k, p)=(2,1,3)$ and $(n, k, p)=(3,3,2)$.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "# Problem 17",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Find all triples $(a, b, c)$ of integers satisfying $a^{2}+b^{2}+c^{2}=20122012$.
|
First consider the equation modulo 4. Since a square can only be congruent to 0 or 1 modulo 4, and 20122012 is divisible by 4, we can conclude that all of $a, b$ and $c$ have to be even. Substituting $a=2 a_{1}, b=2 b_{1}, c=2 c_{1}$ the equation turns into $a_{1}^{2}+b_{1}^{2}+c_{1}^{2}=5030503$.
If we now consider the remaining equation modulo 8 , we can see that the right side is congruent to 7, whilst the only quadratic residues modulo 8 are 0,1 and 4 , and hence the left hand side can never be congruent to 7 .
We therefore conclude that the original equation has no integer solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all triples $(a, b, c)$ of integers satisfying $a^{2}+b^{2}+c^{2}=20122012$.
|
First consider the equation modulo 4. Since a square can only be congruent to 0 or 1 modulo 4, and 20122012 is divisible by 4, we can conclude that all of $a, b$ and $c$ have to be even. Substituting $a=2 a_{1}, b=2 b_{1}, c=2 c_{1}$ the equation turns into $a_{1}^{2}+b_{1}^{2}+c_{1}^{2}=5030503$.
If we now consider the remaining equation modulo 8 , we can see that the right side is congruent to 7, whilst the only quadratic residues modulo 8 are 0,1 and 4 , and hence the left hand side can never be congruent to 7 .
We therefore conclude that the original equation has no integer solutions.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "# Problem 18",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Show that $n^{n}+(n+1)^{n+1}$ is composite for infinitely many positive integers $n$.
|
We will show that for any positive integer $n \equiv 4(\bmod 6)$ the number $n^{n}+(n+1)^{n+1}$ is divisible by 3 and hence composite. Indeed, for any such $n$ we have $n \equiv 1(\bmod 3)$ and hence $n^{n}+(n+1)^{n+1} \equiv 1^{n}+2^{n+1}=1+2^{n+1}(\bmod 3)$. Moreover, the exponent $n+1$ is odd, which implies that $2^{n+1} \equiv 2(\bmod 3)$. It follows that $n^{n}+(n+1)^{n+1} \equiv 1+2 \equiv 0(\bmod 3)$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that $n^{n}+(n+1)^{n+1}$ is composite for infinitely many positive integers $n$.
|
We will show that for any positive integer $n \equiv 4(\bmod 6)$ the number $n^{n}+(n+1)^{n+1}$ is divisible by 3 and hence composite. Indeed, for any such $n$ we have $n \equiv 1(\bmod 3)$ and hence $n^{n}+(n+1)^{n+1} \equiv 1^{n}+2^{n+1}=1+2^{n+1}(\bmod 3)$. Moreover, the exponent $n+1$ is odd, which implies that $2^{n+1} \equiv 2(\bmod 3)$. It follows that $n^{n}+(n+1)^{n+1} \equiv 1+2 \equiv 0(\bmod 3)$, as claimed.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "# Problem 19",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Find all integer solutions of the equation $2 x^{6}+y^{7}=11$.
|
There are no solutions. The hardest part of the problem is to determine a modulus $m$ that would yield a contradiction. There should be few sixth and seventh powers modulo $m$, hence, a natural choice is $6 \cdot 7+1=43$. Luckily, it is a prime.
Now, just write out sixth powers $(0,1,4,11,16,21,35,41)$ and seventh powers $(0,1,6,7,36,37,42)$ modulo 43 , and see that they can't be combined to give 11. Indeed,
$$
\begin{aligned}
2 x^{6} \bmod 43 & \in\{0,2,8,22,27,32,39,42\}, \\
11-y^{7} \bmod 43 & \in\{4,5,10,11,12,17,18\},
\end{aligned}
$$
and these sets do not intersect.
Remark. To find the sixth and seventh powers modulo 43, we can note that 3 is a primitive root modulo 43. So the nonzero sixth powers are exactly the powers of $3^{6} \equiv 41 \equiv-2$ and the nonzero seventh powers are the powers of $3^{7} \equiv 37 \equiv-6$ $(\bmod 43)$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all integer solutions of the equation $2 x^{6}+y^{7}=11$.
|
There are no solutions. The hardest part of the problem is to determine a modulus $m$ that would yield a contradiction. There should be few sixth and seventh powers modulo $m$, hence, a natural choice is $6 \cdot 7+1=43$. Luckily, it is a prime.
Now, just write out sixth powers $(0,1,4,11,16,21,35,41)$ and seventh powers $(0,1,6,7,36,37,42)$ modulo 43 , and see that they can't be combined to give 11. Indeed,
$$
\begin{aligned}
2 x^{6} \bmod 43 & \in\{0,2,8,22,27,32,39,42\}, \\
11-y^{7} \bmod 43 & \in\{4,5,10,11,12,17,18\},
\end{aligned}
$$
and these sets do not intersect.
Remark. To find the sixth and seventh powers modulo 43, we can note that 3 is a primitive root modulo 43. So the nonzero sixth powers are exactly the powers of $3^{6} \equiv 41 \equiv-2$ and the nonzero seventh powers are the powers of $3^{7} \equiv 37 \equiv-6$ $(\bmod 43)$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "# Problem 20",
"resource_path": "BalticWay/segmented/en-bw12sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2012"
}
|
Let $n$ be a positive integer. Assume that $n$ numbers are to be chosen from the table
$$
\begin{array}{cccc}
0 & 1 & \cdots & n-1 \\
n & n+1 & \cdots & 2 n-1 \\
\vdots & \vdots & \ddots & \vdots \\
(n-1) n & (n-1) n+1 & \cdots & n^{2}-1
\end{array}
$$
with no two of them from the same row or the same column. Find the maximal value of the product of these $n$ numbers.
|
The product is $R(\sigma)=\prod_{i=0}^{n-1}(n i+\sigma(i))$, for some permutation $\sigma:\{0,1, \ldots, n-1\} \rightarrow\{0,1, \ldots, n-1\}$. Let $\sigma$ be such that $R(\sigma)$ is maximal. We may assume that all the multipliers $n i+\sigma(i)$ are positive, because otherwise the product is zero, that is the smallest possible.
Assume further that $\sigma(a)>\sigma(b)$ for some $a>b$. Let a permutation $\tau$ be defined by
$$
\tau(i)= \begin{cases}\sigma(b), & i=a \\ \sigma(a), & i=b \\ \sigma(i), & \text { otherwise }\end{cases}
$$
We have
$$
\frac{R(\tau)}{R(\sigma)}=\frac{(n a+\tau(a))(n b+\tau(b))}{(n a+\sigma(a))(n b+\sigma(b))}=\frac{(n a+\sigma(b))(n b+\sigma(a))}{(n a+\sigma(a))(n b+\sigma(b))}>1
$$
as
$(n a+\sigma(b))(n b+\sigma(a))-(n a+\sigma(a))(n b+\sigma(b))=n(a \sigma(a)+b \sigma(b)-a \sigma(b)-b \sigma(a))=n(a-b)(\sigma(a)-\sigma(b))>0$.
This is a contradiction with the maximality of $R(\sigma)$, hence, $\sigma$ has to satisfy $\sigma(a)<\sigma(b)$ for all $a>b$. Thus, $\sigma(i)=n-1-i$ for all $i$, and
$$
R(\sigma)=\prod_{i=0}^{n-1}(n i+n-1-i)=\prod_{i=0}^{n-1}(i+1)(n-1)=(n-1)^{n} n!
$$
|
(n-1)^{n} n!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Assume that $n$ numbers are to be chosen from the table
$$
\begin{array}{cccc}
0 & 1 & \cdots & n-1 \\
n & n+1 & \cdots & 2 n-1 \\
\vdots & \vdots & \ddots & \vdots \\
(n-1) n & (n-1) n+1 & \cdots & n^{2}-1
\end{array}
$$
with no two of them from the same row or the same column. Find the maximal value of the product of these $n$ numbers.
|
The product is $R(\sigma)=\prod_{i=0}^{n-1}(n i+\sigma(i))$, for some permutation $\sigma:\{0,1, \ldots, n-1\} \rightarrow\{0,1, \ldots, n-1\}$. Let $\sigma$ be such that $R(\sigma)$ is maximal. We may assume that all the multipliers $n i+\sigma(i)$ are positive, because otherwise the product is zero, that is the smallest possible.
Assume further that $\sigma(a)>\sigma(b)$ for some $a>b$. Let a permutation $\tau$ be defined by
$$
\tau(i)= \begin{cases}\sigma(b), & i=a \\ \sigma(a), & i=b \\ \sigma(i), & \text { otherwise }\end{cases}
$$
We have
$$
\frac{R(\tau)}{R(\sigma)}=\frac{(n a+\tau(a))(n b+\tau(b))}{(n a+\sigma(a))(n b+\sigma(b))}=\frac{(n a+\sigma(b))(n b+\sigma(a))}{(n a+\sigma(a))(n b+\sigma(b))}>1
$$
as
$(n a+\sigma(b))(n b+\sigma(a))-(n a+\sigma(a))(n b+\sigma(b))=n(a \sigma(a)+b \sigma(b)-a \sigma(b)-b \sigma(a))=n(a-b)(\sigma(a)-\sigma(b))>0$.
This is a contradiction with the maximality of $R(\sigma)$, hence, $\sigma$ has to satisfy $\sigma(a)<\sigma(b)$ for all $a>b$. Thus, $\sigma(i)=n-1-i$ for all $i$, and
$$
R(\sigma)=\prod_{i=0}^{n-1}(n i+n-1-i)=\prod_{i=0}^{n-1}(i+1)(n-1)=(n-1)^{n} n!
$$
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Let $k$ and $n$ be positive integers and let $x_{1}, x_{2}, \ldots, x_{k}, y_{1}, y_{2}, \ldots, y_{n}$ be distinct integers. A polynomial $P$ with integer coefficients satisfies
$$
P\left(x_{1}\right)=P\left(x_{2}\right)=\ldots=P\left(x_{k}\right)=54
$$
and
$$
P\left(y_{1}\right)=P\left(y_{2}\right)=\ldots=P\left(y_{n}\right)=2013 .
$$
Determine the maximal value of $k n$.
|
Letting $Q(x)=P(x)-54$, we see that $Q$ has $k$ zeroes at $x_{1}, \ldots, x_{k}$, while $Q\left(y_{i}\right)=1959$ for $i=1, \ldots, n$. We notice that $1959=3 \cdot 653$, and an easy check shows that 653 is a prime number. As
$$
Q(x)=\prod_{j=1}^{k}\left(x-x_{j}\right) S(x)
$$
and $S(x)$ is a polynomial with integer coefficients, we have
$$
Q\left(y_{i}\right)=\prod_{j=1}^{k}\left(y_{i}-x_{j}\right) S\left(x_{j}\right)=1959 .
$$
Now all numbers $a_{i}=y_{i}-x_{1}$ have to be in the set $\{ \pm 1, \pm 3, \pm 653, \pm 1959\}$. Clearly, $n$ can be at most 4 , and if $n=4$, then two of the $a_{i}$ 's are $\pm 1$, one has absolute value 3 and the fourth one has absolute value 653 . Assuming $a_{1}=1, a_{2}=-1, x_{1}$ has to be the average of $y_{1}$ and $y_{2}$. Let $\left|y_{3}-x_{1}\right|=3$. If $k \geq 2$, then $x_{2} \neq x_{1}$, and the set of numbers $b_{i}=y_{i}-x_{2}$ has the same properties as the $a_{i}$ 's. Then $x_{2}$ is the average of, say $y_{2}$ and $y_{3}$ or $y_{3}$ and $y_{1}$. In either case $\left|y_{4}-x_{2}\right| \neq 653$. So if $k \geq 2$, then $n \leq 3$. In a quite similar fashion one shows that $k \geq 3$ implies $n \leq 2$.
The polynomial $P(x)=653 x^{2}\left(x^{2}-4\right)+2013$ shows the $n k=6$ indeed is possible.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $k$ and $n$ be positive integers and let $x_{1}, x_{2}, \ldots, x_{k}, y_{1}, y_{2}, \ldots, y_{n}$ be distinct integers. A polynomial $P$ with integer coefficients satisfies
$$
P\left(x_{1}\right)=P\left(x_{2}\right)=\ldots=P\left(x_{k}\right)=54
$$
and
$$
P\left(y_{1}\right)=P\left(y_{2}\right)=\ldots=P\left(y_{n}\right)=2013 .
$$
Determine the maximal value of $k n$.
|
Letting $Q(x)=P(x)-54$, we see that $Q$ has $k$ zeroes at $x_{1}, \ldots, x_{k}$, while $Q\left(y_{i}\right)=1959$ for $i=1, \ldots, n$. We notice that $1959=3 \cdot 653$, and an easy check shows that 653 is a prime number. As
$$
Q(x)=\prod_{j=1}^{k}\left(x-x_{j}\right) S(x)
$$
and $S(x)$ is a polynomial with integer coefficients, we have
$$
Q\left(y_{i}\right)=\prod_{j=1}^{k}\left(y_{i}-x_{j}\right) S\left(x_{j}\right)=1959 .
$$
Now all numbers $a_{i}=y_{i}-x_{1}$ have to be in the set $\{ \pm 1, \pm 3, \pm 653, \pm 1959\}$. Clearly, $n$ can be at most 4 , and if $n=4$, then two of the $a_{i}$ 's are $\pm 1$, one has absolute value 3 and the fourth one has absolute value 653 . Assuming $a_{1}=1, a_{2}=-1, x_{1}$ has to be the average of $y_{1}$ and $y_{2}$. Let $\left|y_{3}-x_{1}\right|=3$. If $k \geq 2$, then $x_{2} \neq x_{1}$, and the set of numbers $b_{i}=y_{i}-x_{2}$ has the same properties as the $a_{i}$ 's. Then $x_{2}$ is the average of, say $y_{2}$ and $y_{3}$ or $y_{3}$ and $y_{1}$. In either case $\left|y_{4}-x_{2}\right| \neq 653$. So if $k \geq 2$, then $n \leq 3$. In a quite similar fashion one shows that $k \geq 3$ implies $n \leq 2$.
The polynomial $P(x)=653 x^{2}\left(x^{2}-4\right)+2013$ shows the $n k=6$ indeed is possible.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Let $\mathbb{R}$ denote the set of real numbers. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x f(y)+y)+f(-f(x))=f(y f(x)-y)+y \quad \text { for all } x, y \in \mathbb{R}
$$
|
Let $f(0)=c$. We make the following substitutions in the initial equation:
1) $x=0, y=0 \Longrightarrow f(0)+f(-c)=f(0) \Longrightarrow f(-c)=0$.
2) $x=0, y=-c \Longrightarrow f(-c)+f(-c)=f\left(c-c^{2}\right)-c \Longrightarrow f\left(c-c^{2}\right)=c$.
3) $x=-c, y=-c \Longrightarrow f(-c)+f(0)=f(c)-c \Longrightarrow f(c)=2 c$.
4) $x=0, y=c \Longrightarrow f(c)+f(-c)=f\left(c^{2}-c\right)+c \Longrightarrow f\left(c^{2}-c\right)=c$.
5) $x=-c, y=c^{2}-c \Longrightarrow f(-c)+f(0)=f\left(c-c^{2}\right)+c^{2}-c \Longrightarrow c=c^{2} \Longrightarrow c=0$ or 1 .
Suppose that $c=0$. Let $f(-1)=d+1$. We make the following substitutions in the initial equation:
1) $x=0 \Longrightarrow f(y)+f(0)=f(-y)+y \Longrightarrow y-f(y)=-f(-y)$ for any $y \in \mathbb{R}$.
2) $y=0 \Longrightarrow f(0)+f(-f(x))=f(0) \Longrightarrow f(-f(x))=0$ for any $x \in \mathbb{R}$.
3) $x=-1 \Longrightarrow f(y-f(y))+0=f(d y)+y \Longrightarrow f(d y)=-y+f(-f(-y))=-y$ for any $y \in \mathbb{R}$.
Thus, for any $x \in \mathbb{R}$ we have $f(x)=f(-f(d x))=0$. However, this function does not satisfy the initial equation. Suppose that $c=1$. We take $x=0$ in the initial equation:
$$
f(y)+f(-c)=f(0)+y \Longrightarrow f(y)=y+1
$$
for any $y \in \mathbb{R}$. The function satisfies the initial equation.
Answer: $\quad f(x) \equiv x+1$.
|
f(x) \equiv x+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{R}$ denote the set of real numbers. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x f(y)+y)+f(-f(x))=f(y f(x)-y)+y \quad \text { for all } x, y \in \mathbb{R}
$$
|
Let $f(0)=c$. We make the following substitutions in the initial equation:
1) $x=0, y=0 \Longrightarrow f(0)+f(-c)=f(0) \Longrightarrow f(-c)=0$.
2) $x=0, y=-c \Longrightarrow f(-c)+f(-c)=f\left(c-c^{2}\right)-c \Longrightarrow f\left(c-c^{2}\right)=c$.
3) $x=-c, y=-c \Longrightarrow f(-c)+f(0)=f(c)-c \Longrightarrow f(c)=2 c$.
4) $x=0, y=c \Longrightarrow f(c)+f(-c)=f\left(c^{2}-c\right)+c \Longrightarrow f\left(c^{2}-c\right)=c$.
5) $x=-c, y=c^{2}-c \Longrightarrow f(-c)+f(0)=f\left(c-c^{2}\right)+c^{2}-c \Longrightarrow c=c^{2} \Longrightarrow c=0$ or 1 .
Suppose that $c=0$. Let $f(-1)=d+1$. We make the following substitutions in the initial equation:
1) $x=0 \Longrightarrow f(y)+f(0)=f(-y)+y \Longrightarrow y-f(y)=-f(-y)$ for any $y \in \mathbb{R}$.
2) $y=0 \Longrightarrow f(0)+f(-f(x))=f(0) \Longrightarrow f(-f(x))=0$ for any $x \in \mathbb{R}$.
3) $x=-1 \Longrightarrow f(y-f(y))+0=f(d y)+y \Longrightarrow f(d y)=-y+f(-f(-y))=-y$ for any $y \in \mathbb{R}$.
Thus, for any $x \in \mathbb{R}$ we have $f(x)=f(-f(d x))=0$. However, this function does not satisfy the initial equation. Suppose that $c=1$. We take $x=0$ in the initial equation:
$$
f(y)+f(-c)=f(0)+y \Longrightarrow f(y)=y+1
$$
for any $y \in \mathbb{R}$. The function satisfies the initial equation.
Answer: $\quad f(x) \equiv x+1$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Prove that the following inequality holds for all positive real numbers $x, y, z$ :
$$
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{z^{2}+x^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{x+y+z}{2}
$$
|
The inequality is symmetric, so we may assume $x \leq y \leq z$. Then we have
$$
x^{3} \leq y^{3} \leq z^{3} \quad \text { and } \quad \frac{1}{y^{2}+z^{2}} \leq \frac{1}{x^{2}+z^{2}} \leq \frac{1}{x^{2}+y^{2}}
$$
Therefore, by the rearrangement inequality we have:
$$
\begin{gathered}
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{y^{3}}{y^{2}+z^{2}}+\frac{z^{3}}{x^{2}+z^{2}}+\frac{x^{3}}{x^{2}+y^{2}} \\
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{z^{3}}{y^{2}+z^{2}}+\frac{x^{3}}{x^{2}+z^{2}}+\frac{y^{3}}{x^{2}+y^{2}} \\
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{1}{2}\left(\frac{y^{3}+z^{3}}{y^{2}+z^{2}}+\frac{x^{3}+z^{3}}{x^{2}+z^{2}}+\frac{x^{3}+y^{3}}{x^{2}+y^{2}}\right)
\end{gathered}
$$
What's more, by the rearrangement inequality we have:
$$
\begin{gathered}
x^{3}+y^{3} \geq x y^{2}+x^{2} y \\
2 x^{3}+2 y^{3} \geq\left(x^{2}+y^{2}\right)(x+y) \\
\frac{x^{3}+y^{3}}{x^{2}+y^{2}} \geq \frac{x+y}{2}
\end{gathered}
$$
Applying it to the previous inequality we obtain:
$$
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{1}{2}\left(\frac{y+z}{2}+\frac{x+z}{2}+\frac{x+y}{2}\right)
$$
Which is the thesis.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that the following inequality holds for all positive real numbers $x, y, z$ :
$$
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{z^{2}+x^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{x+y+z}{2}
$$
|
The inequality is symmetric, so we may assume $x \leq y \leq z$. Then we have
$$
x^{3} \leq y^{3} \leq z^{3} \quad \text { and } \quad \frac{1}{y^{2}+z^{2}} \leq \frac{1}{x^{2}+z^{2}} \leq \frac{1}{x^{2}+y^{2}}
$$
Therefore, by the rearrangement inequality we have:
$$
\begin{gathered}
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{y^{3}}{y^{2}+z^{2}}+\frac{z^{3}}{x^{2}+z^{2}}+\frac{x^{3}}{x^{2}+y^{2}} \\
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{z^{3}}{y^{2}+z^{2}}+\frac{x^{3}}{x^{2}+z^{2}}+\frac{y^{3}}{x^{2}+y^{2}} \\
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{1}{2}\left(\frac{y^{3}+z^{3}}{y^{2}+z^{2}}+\frac{x^{3}+z^{3}}{x^{2}+z^{2}}+\frac{x^{3}+y^{3}}{x^{2}+y^{2}}\right)
\end{gathered}
$$
What's more, by the rearrangement inequality we have:
$$
\begin{gathered}
x^{3}+y^{3} \geq x y^{2}+x^{2} y \\
2 x^{3}+2 y^{3} \geq\left(x^{2}+y^{2}\right)(x+y) \\
\frac{x^{3}+y^{3}}{x^{2}+y^{2}} \geq \frac{x+y}{2}
\end{gathered}
$$
Applying it to the previous inequality we obtain:
$$
\frac{x^{3}}{y^{2}+z^{2}}+\frac{y^{3}}{x^{2}+z^{2}}+\frac{z^{3}}{x^{2}+y^{2}} \geq \frac{1}{2}\left(\frac{y+z}{2}+\frac{x+z}{2}+\frac{x+y}{2}\right)
$$
Which is the thesis.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Numbers 0 and 2013 are written at two opposite vertices of a cube. Some real numbers are to be written at the remaining 6 vertices of the cube. On each edge of the cube the difference between the numbers at its endpoints is written. When is the sum of squares of the numbers written on the edges minimal?
|
Answer:
$$
\left\{x_{1}, \ldots, x_{6}\right\}=\left\{\frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}\right\}
$$
The function
$$
(x-a)^{2}+(x-b)^{2}+(x-c)^{2}
$$
attains its minimum when $x=\frac{a+b+c}{3}$. Let's call the vertices of the cube adjacent, if they are connected with an edge. If $S$ is minimal then numbers $x_{1} \ldots, x_{6}$ are such that any of them is the arithmetic mean of the numbers written on adjacent vertices (otherwise, S can be made smaller). This gives us 6 equalities:
$$
\left\{\begin{array}{l}
x_{1}=\frac{x_{4}+x_{5}}{3} \\
x_{2}=\frac{x_{4}+x_{6}}{3} \\
x_{3}=\frac{x_{5}+x_{6}}{3} \\
x_{4}=\frac{x_{1}+x_{2}+2013}{3} \\
x_{5}=\frac{x_{1}+x_{3}+2013}{3} \\
x_{6}=\frac{x_{2}+x_{3}+2013}{3}
\end{array}\right.
$$
Here $x_{1}, x_{2}, x_{3}$ are written on vertices that are adjacent to the vertex that contains 0 . By solving this system we get the answer.
|
\left\{\frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}\right\}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Numbers 0 and 2013 are written at two opposite vertices of a cube. Some real numbers are to be written at the remaining 6 vertices of the cube. On each edge of the cube the difference between the numbers at its endpoints is written. When is the sum of squares of the numbers written on the edges minimal?
|
Answer:
$$
\left\{x_{1}, \ldots, x_{6}\right\}=\left\{\frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{2 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}, \frac{3 \cdot 2013}{5}\right\}
$$
The function
$$
(x-a)^{2}+(x-b)^{2}+(x-c)^{2}
$$
attains its minimum when $x=\frac{a+b+c}{3}$. Let's call the vertices of the cube adjacent, if they are connected with an edge. If $S$ is minimal then numbers $x_{1} \ldots, x_{6}$ are such that any of them is the arithmetic mean of the numbers written on adjacent vertices (otherwise, S can be made smaller). This gives us 6 equalities:
$$
\left\{\begin{array}{l}
x_{1}=\frac{x_{4}+x_{5}}{3} \\
x_{2}=\frac{x_{4}+x_{6}}{3} \\
x_{3}=\frac{x_{5}+x_{6}}{3} \\
x_{4}=\frac{x_{1}+x_{2}+2013}{3} \\
x_{5}=\frac{x_{1}+x_{3}+2013}{3} \\
x_{6}=\frac{x_{2}+x_{3}+2013}{3}
\end{array}\right.
$$
Here $x_{1}, x_{2}, x_{3}$ are written on vertices that are adjacent to the vertex that contains 0 . By solving this system we get the answer.

|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2013"
}
|
Numbers 0 and 2013 are written at two opposite vertices of a cube. Some real numbers are to be written at the remaining 6 vertices of the cube. On each edge of the cube the difference between the numbers at its endpoints is written. When is the sum of squares of the numbers written on the edges minimal?
|
$$
\begin{gathered}
S=\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+\left(x_{4}-x_{1}\right)^{2}+\left(x_{4}-x_{2}\right)^{2}+\left(x_{5}-x_{1}\right)^{2}+\left(x_{5}-x_{3}\right)^{2}+\right. \\
\left(x_{6}-x_{2}\right)^{2}+\left(x_{6}-x_{3}\right)^{2}+\left(2013-x_{4}\right)^{2}+\left(2013-x_{5}\right)^{2}+\left(2013-x_{6}\right)^{2}= \\
=\left(\frac{1}{2} x_{1}^{2}+\left(x_{4}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)+\left(\frac{1}{2} x_{1}^{2}+\left(x_{5}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{5}\right)^{2}\right)+ \\
+\left(\frac{1}{2} x_{2}^{2}+\left(x_{4}-x_{2}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)+\left(\frac{1}{2} x_{2}^{2}+\left(x_{6}-x_{2}\right)^{2}+\frac{1}{2}\left(2013-x_{6}\right)^{2}\right)+ \\
+\left(\frac{1}{2} x_{3}^{2}+\left(x_{5}-x_{3}\right)^{2}+\frac{1}{2}\left(2013-x_{5}\right)^{2}\right)+\left(\frac{1}{2} x_{3}^{2}+\left(x_{6}-x_{3}\right)^{2}+\frac{1}{2}\left(2013-x_{6}\right)^{2}\right)
\end{gathered}
$$
Consider the expression
$$
\begin{aligned}
S_{1} & =\left(\frac{1}{2} x_{1}^{2}+\left(x_{4}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)= \\
& =\left(\frac{x_{1}}{2}\right)^{2}+\left(\frac{x_{1}}{2}\right)^{2}+\left(x_{4}-x_{1}\right)^{2}+\left(\frac{2013-x_{4}}{2}\right)^{2}+\left(\frac{2013-x_{4}}{2}\right)^{2}
\end{aligned}
$$
and note that
$$
\left(\frac{x_{1}}{2}\right)+\left(\frac{x_{1}}{2}\right)+\left(x_{4}-x_{1}\right)+\left(\frac{2013-x_{4}}{2}\right)+\left(\frac{2013-x_{4}}{2}\right)=2013
$$
If the sum of 5 numbers is fixed, then the sum of their squares is minimal if all of them are equal. It follows that:
$$
\frac{x_{1}}{2}=x_{4}-x_{1}=\frac{2013-x_{4}}{2}
$$
from where we get $x_{1}=2 \cdot 2013 / 5$ and $x_{4}=3 \cdot 2013 / 5$. Values for $x_{2}, x_{3}, x_{5}, x_{6}$ can be obtained similarly.
|
x_{1}=\frac{2 \cdot 2013}{5}, \, x_{4}=\frac{3 \cdot 2013}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Numbers 0 and 2013 are written at two opposite vertices of a cube. Some real numbers are to be written at the remaining 6 vertices of the cube. On each edge of the cube the difference between the numbers at its endpoints is written. When is the sum of squares of the numbers written on the edges minimal?
|
$$
\begin{gathered}
S=\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+\left(x_{4}-x_{1}\right)^{2}+\left(x_{4}-x_{2}\right)^{2}+\left(x_{5}-x_{1}\right)^{2}+\left(x_{5}-x_{3}\right)^{2}+\right. \\
\left(x_{6}-x_{2}\right)^{2}+\left(x_{6}-x_{3}\right)^{2}+\left(2013-x_{4}\right)^{2}+\left(2013-x_{5}\right)^{2}+\left(2013-x_{6}\right)^{2}= \\
=\left(\frac{1}{2} x_{1}^{2}+\left(x_{4}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)+\left(\frac{1}{2} x_{1}^{2}+\left(x_{5}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{5}\right)^{2}\right)+ \\
+\left(\frac{1}{2} x_{2}^{2}+\left(x_{4}-x_{2}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)+\left(\frac{1}{2} x_{2}^{2}+\left(x_{6}-x_{2}\right)^{2}+\frac{1}{2}\left(2013-x_{6}\right)^{2}\right)+ \\
+\left(\frac{1}{2} x_{3}^{2}+\left(x_{5}-x_{3}\right)^{2}+\frac{1}{2}\left(2013-x_{5}\right)^{2}\right)+\left(\frac{1}{2} x_{3}^{2}+\left(x_{6}-x_{3}\right)^{2}+\frac{1}{2}\left(2013-x_{6}\right)^{2}\right)
\end{gathered}
$$
Consider the expression
$$
\begin{aligned}
S_{1} & =\left(\frac{1}{2} x_{1}^{2}+\left(x_{4}-x_{1}\right)^{2}+\frac{1}{2}\left(2013-x_{4}\right)^{2}\right)= \\
& =\left(\frac{x_{1}}{2}\right)^{2}+\left(\frac{x_{1}}{2}\right)^{2}+\left(x_{4}-x_{1}\right)^{2}+\left(\frac{2013-x_{4}}{2}\right)^{2}+\left(\frac{2013-x_{4}}{2}\right)^{2}
\end{aligned}
$$
and note that
$$
\left(\frac{x_{1}}{2}\right)+\left(\frac{x_{1}}{2}\right)+\left(x_{4}-x_{1}\right)+\left(\frac{2013-x_{4}}{2}\right)+\left(\frac{2013-x_{4}}{2}\right)=2013
$$
If the sum of 5 numbers is fixed, then the sum of their squares is minimal if all of them are equal. It follows that:
$$
\frac{x_{1}}{2}=x_{4}-x_{1}=\frac{2013-x_{4}}{2}
$$
from where we get $x_{1}=2 \cdot 2013 / 5$ and $x_{4}=3 \cdot 2013 / 5$. Values for $x_{2}, x_{3}, x_{5}, x_{6}$ can be obtained similarly.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2013"
}
|
Santa Claus has at least $n$ gifts for $n$ children. For $i \in\{1,2, \ldots, n\}$, the $i$-th child considers $x_{i}>0$ of these items to be desirable. Assume that
$$
\frac{1}{x_{1}}+\ldots+\frac{1}{x_{n}} \leq 1
$$
Prove that Santa Claus can give each child a gift that this child likes.
|
Evidently the age of the children is immaterial, so we may suppose
$$
1 \leq x_{1} \leq x_{2} \leq \ldots \leq x_{n}
$$
Let us now consider the following procedure. First the oldest child chooses its favourite present and keeps it, then the second oldest child chooses its favourite remaining present, and so it goes on until either the presents are distributed in the expected way or some unlucky child is forced to take a present it does not like.
Let us assume, for the sake of a contradiction, that the latter happens, say to the $k$-th oldest child, where $1 \leq k \leq n$. Since the oldest child likes at least one of the items Santa Claus has, we must have $k \geq 2$. Moreover, at the moment the $k$-th child is to make its decision, only $k-1$ items are gone so far, which means that $x_{k} \leq k-1$.
For this reason, we have
$$
\frac{1}{x_{1}}+\ldots+\frac{1}{x_{k}} \geq \underbrace{\frac{1}{k-1}+\ldots+\frac{1}{k-1}}_{k}=\frac{k}{k-1}>1
$$
contrary to our assumption. This proves that the procedure considered above always leads to a distribution of the presents to the children of the desired kind, whereby the problem is solved.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Santa Claus has at least $n$ gifts for $n$ children. For $i \in\{1,2, \ldots, n\}$, the $i$-th child considers $x_{i}>0$ of these items to be desirable. Assume that
$$
\frac{1}{x_{1}}+\ldots+\frac{1}{x_{n}} \leq 1
$$
Prove that Santa Claus can give each child a gift that this child likes.
|
Evidently the age of the children is immaterial, so we may suppose
$$
1 \leq x_{1} \leq x_{2} \leq \ldots \leq x_{n}
$$
Let us now consider the following procedure. First the oldest child chooses its favourite present and keeps it, then the second oldest child chooses its favourite remaining present, and so it goes on until either the presents are distributed in the expected way or some unlucky child is forced to take a present it does not like.
Let us assume, for the sake of a contradiction, that the latter happens, say to the $k$-th oldest child, where $1 \leq k \leq n$. Since the oldest child likes at least one of the items Santa Claus has, we must have $k \geq 2$. Moreover, at the moment the $k$-th child is to make its decision, only $k-1$ items are gone so far, which means that $x_{k} \leq k-1$.
For this reason, we have
$$
\frac{1}{x_{1}}+\ldots+\frac{1}{x_{k}} \geq \underbrace{\frac{1}{k-1}+\ldots+\frac{1}{k-1}}_{k}=\frac{k}{k-1}>1
$$
contrary to our assumption. This proves that the procedure considered above always leads to a distribution of the presents to the children of the desired kind, whereby the problem is solved.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "# Problem 6",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
A positive integer is written on a blackboard. Players $A$ and $B$ play the following game: in each move one has to choose a divisor $m$ of the number $n$ written on the blackboard for which $1<m<n$ and replace $n$ with $n-m$. Player $A$ makes the first move, players move alternately. The player who can't make a move loses the game. For which starting numbers is there a winning strategy for player $B$ ?
|
Firstly note that for a given $n$ exactly one player has a winning strategy. We'll show by induction that $B$ has a winning strategy if $n$ is odd.
First step of the induction is clear. Assume $n$ is odd and $B$ has a winning strategy for all odd integers smaller than $n$. If player $A$ can't make a move, $B$ wins. In other case, $A$ chooses a divisor $m$. Note that $m \mid n-m$ and $m<n-m$, because $m \leq \frac{n}{3}$ as $n$ is odd. Therefore $B$ may choose $m$ (in particular can make a move) and pass a number $n-2 m$ to player $A$. The number is odd and smaller than $n$, so the thesis is correct by induction.
Now, let $n$ be even, but not a power of 2 . In that case $n$ has an odd divisor greater than one. Player $A$ may choose an odd divisor and pass an odd integer to player $B$. Then we have a situation where $B$ starts with an odd integer, so $A$ has a winning strategy.
Consider now $n=2^{k}$ for positive integer $k$. Once again we'll prove it by induction. Thesis: for odd $k$ player $B$ has a winning strategy and for even $k$ player $A$ has a winning strategy. Base: for $k=1$ player $B$ has a winning strategy as $A$ can't make the first move. For $k=2$ player $A$ may win, passing 2 to player $B$. The step of the induction is split to two parts:
- Assume $A$ has a winning strategy for $2^{k}$, then player $B$ has one for $2^{k+1}$. Let $n=2^{k+1}$. Player $A$ has to choose a divisor $2^{l}$ for $1 \leq l \leq k$. If he chooses $2^{k}$, he passes $n-2^{k}=2^{k}$ to player $B$. By induction player $B$ has a winning strategy. If $A$ chooses a smaller divisor, passes an even integer, which is not a power of 2 as $2^{k}<n-2^{l}<n=2^{k+1}$. We have already proved that the starting player (in that case $B$ ) has a winning strategy for such number.
- Assume $B$ has a winning strategy for $2^{k}$, then player $A$ has one for $2^{k+1}$. Let $n=2^{k+1}$. It is sufficient for player $A$ to choose a divisor $2^{k}$, then he passes number $2^{k}$ to $B$. By induction second player (in this case $A$ ) has a winning strategy.
To sum up: player $B$ has a winning strategy for odd $n$ and for $n=2 \cdot 4^{k}$ for non-negative integer $k$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is written on a blackboard. Players $A$ and $B$ play the following game: in each move one has to choose a divisor $m$ of the number $n$ written on the blackboard for which $1<m<n$ and replace $n$ with $n-m$. Player $A$ makes the first move, players move alternately. The player who can't make a move loses the game. For which starting numbers is there a winning strategy for player $B$ ?
|
Firstly note that for a given $n$ exactly one player has a winning strategy. We'll show by induction that $B$ has a winning strategy if $n$ is odd.
First step of the induction is clear. Assume $n$ is odd and $B$ has a winning strategy for all odd integers smaller than $n$. If player $A$ can't make a move, $B$ wins. In other case, $A$ chooses a divisor $m$. Note that $m \mid n-m$ and $m<n-m$, because $m \leq \frac{n}{3}$ as $n$ is odd. Therefore $B$ may choose $m$ (in particular can make a move) and pass a number $n-2 m$ to player $A$. The number is odd and smaller than $n$, so the thesis is correct by induction.
Now, let $n$ be even, but not a power of 2 . In that case $n$ has an odd divisor greater than one. Player $A$ may choose an odd divisor and pass an odd integer to player $B$. Then we have a situation where $B$ starts with an odd integer, so $A$ has a winning strategy.
Consider now $n=2^{k}$ for positive integer $k$. Once again we'll prove it by induction. Thesis: for odd $k$ player $B$ has a winning strategy and for even $k$ player $A$ has a winning strategy. Base: for $k=1$ player $B$ has a winning strategy as $A$ can't make the first move. For $k=2$ player $A$ may win, passing 2 to player $B$. The step of the induction is split to two parts:
- Assume $A$ has a winning strategy for $2^{k}$, then player $B$ has one for $2^{k+1}$. Let $n=2^{k+1}$. Player $A$ has to choose a divisor $2^{l}$ for $1 \leq l \leq k$. If he chooses $2^{k}$, he passes $n-2^{k}=2^{k}$ to player $B$. By induction player $B$ has a winning strategy. If $A$ chooses a smaller divisor, passes an even integer, which is not a power of 2 as $2^{k}<n-2^{l}<n=2^{k+1}$. We have already proved that the starting player (in that case $B$ ) has a winning strategy for such number.
- Assume $B$ has a winning strategy for $2^{k}$, then player $A$ has one for $2^{k+1}$. Let $n=2^{k+1}$. It is sufficient for player $A$ to choose a divisor $2^{k}$, then he passes number $2^{k}$ to $B$. By induction second player (in this case $A$ ) has a winning strategy.
To sum up: player $B$ has a winning strategy for odd $n$ and for $n=2 \cdot 4^{k}$ for non-negative integer $k$.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "# Problem 7",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
There are $n$ rooms in a sauna, each has unlimited capacity. No room may be attended by a female and a male simultaneously. Moreover, males want to share a room only with males that they don't know and females want to share a room only with females that they know. Find the biggest number $k$ such that any $k$ couples can visit the sauna at the same time, given that two males know each other if and only if their wives know each other.
|
First we'll show it by induction that it is possible for $n-1$ couples to visit the sauna at the same time. The base of induction is clear.
Assume that $n-2$ couples may be placed in $n-1$ rooms. Take an additional couple. Let $k$ be the number of couples that they know and $m$ be the number of rooms taken by males.
If $m>k$, there is a room with males that aren't known by the additional guy. Then he may enter the room and his wife may enter an empty room ( $n$-th room).
If $m \leq k$ we have $n-2-k<n-1-m$. There are $n-2-k$ females that the additional woman doesn't know and $n-1-m$ rooms taken by females (or empty). It means, that there is a room taken only by females (maybe $0)$ that the additional woman know, so she may join them. The additional man may enter the $n$-th room.
Now we only have to show that it is the biggest number. For $n$ couples that don't know each other, men need to be placed in different rooms, so they need $n$ rooms. Then there is no place for women.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are $n$ rooms in a sauna, each has unlimited capacity. No room may be attended by a female and a male simultaneously. Moreover, males want to share a room only with males that they don't know and females want to share a room only with females that they know. Find the biggest number $k$ such that any $k$ couples can visit the sauna at the same time, given that two males know each other if and only if their wives know each other.
|
First we'll show it by induction that it is possible for $n-1$ couples to visit the sauna at the same time. The base of induction is clear.
Assume that $n-2$ couples may be placed in $n-1$ rooms. Take an additional couple. Let $k$ be the number of couples that they know and $m$ be the number of rooms taken by males.
If $m>k$, there is a room with males that aren't known by the additional guy. Then he may enter the room and his wife may enter an empty room ( $n$-th room).
If $m \leq k$ we have $n-2-k<n-1-m$. There are $n-2-k$ females that the additional woman doesn't know and $n-1-m$ rooms taken by females (or empty). It means, that there is a room taken only by females (maybe $0)$ that the additional woman know, so she may join them. The additional man may enter the $n$-th room.
Now we only have to show that it is the biggest number. For $n$ couples that don't know each other, men need to be placed in different rooms, so they need $n$ rooms. Then there is no place for women.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "# Problem 8",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
In a country there are 2014 airports, no three of them lying on a line. Two airports are connected by a direct flight if and only if the line passing through them divides the country in two parts, each with 1006 airports in it. Show that there are no two airports such that one can travel from the first to the second, visiting each of the 2014 airports exactly once.
|
Denote airports as points on the plane. Each airport that is a vertex of the convex hull of these points has only one direct flight. (When we rotate the line that passes through such point the numbers of other points in the half-planes change monotonically.) If an airport has only one direct flight then it can be only the starting point or the endpoint of the journey that visits all 2014 airports. The convex hull contains at least 3 vertices, so there are at least three airports that has only one direct flight. It means that such a journey is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a country there are 2014 airports, no three of them lying on a line. Two airports are connected by a direct flight if and only if the line passing through them divides the country in two parts, each with 1006 airports in it. Show that there are no two airports such that one can travel from the first to the second, visiting each of the 2014 airports exactly once.
|
Denote airports as points on the plane. Each airport that is a vertex of the convex hull of these points has only one direct flight. (When we rotate the line that passes through such point the numbers of other points in the half-planes change monotonically.) If an airport has only one direct flight then it can be only the starting point or the endpoint of the journey that visits all 2014 airports. The convex hull contains at least 3 vertices, so there are at least three airports that has only one direct flight. It means that such a journey is impossible.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
A white equilateral triangle is split into $n^{2}$ equal smaller triangles by lines that are parallel to the sides of the triangle. Denote a line of triangles to be all triangles that are placed between two adjacent parallel lines that form the grid. In particular, a triangle in a corner is also considered to be a line of triangles.
We are to paint all triangles black by a sequence of operations of the following kind: choose a line of triangles that contains at least one white triangle and paint this line black (a possible situation with $n=6$ after four operations is shown in Figure 1; arrows show possible next operations in this situation). Find the smallest and largest possible number of operations.
|
Answer: The smallest possible number of operations is $n$ and the largest possible number of operations is $3 n-2$.
If all the operations are done with lines parallel to one side of the triangle, then the game will end after $n$ operations. Let's show by induction that the number of operations cannot be smaller. The basis for the induction, $n=1$, is evident, assume that for $n=k$ at least $k$ operations are necessary. For $n=k+1$ there will be an operation that colors the bottom right corner triangle, we can assume that it is done, coloring all the
Figure 1
bottom line of the triangle (it can only increase the number of black squares). Order of operations is irrelevant, if we do this operation as the first one then a white triangle with $n=k$ remains for which at least $k$ operations are needed.
Now let's show that it is possible to do $3 n-2$ operations. If $n=1$ then it is evident. Assume that we have proved it for $n=k$. For $n=k+1$ we start with three operations $\mathrm{A}, \mathrm{B}$ and C coloring two rightmost corners and the rightmost line. We have used 3 operations and reduced the field to the situation when $n=k$ (Fig. 2).
Figure 2
At last we show that there cannot be more than $3 n-2$ operations. If all $n$ lines parallel to one side of the triangle are colored then the whole triangle is colored black. Therefore the number of operations made before the last operation cannot be greater than $3(n-1)$, which gives the total number of operations not greater than $3 n-2$.
|
n \text{ and } 3n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A white equilateral triangle is split into $n^{2}$ equal smaller triangles by lines that are parallel to the sides of the triangle. Denote a line of triangles to be all triangles that are placed between two adjacent parallel lines that form the grid. In particular, a triangle in a corner is also considered to be a line of triangles.
We are to paint all triangles black by a sequence of operations of the following kind: choose a line of triangles that contains at least one white triangle and paint this line black (a possible situation with $n=6$ after four operations is shown in Figure 1; arrows show possible next operations in this situation). Find the smallest and largest possible number of operations.
|
Answer: The smallest possible number of operations is $n$ and the largest possible number of operations is $3 n-2$.
If all the operations are done with lines parallel to one side of the triangle, then the game will end after $n$ operations. Let's show by induction that the number of operations cannot be smaller. The basis for the induction, $n=1$, is evident, assume that for $n=k$ at least $k$ operations are necessary. For $n=k+1$ there will be an operation that colors the bottom right corner triangle, we can assume that it is done, coloring all the

Figure 1
bottom line of the triangle (it can only increase the number of black squares). Order of operations is irrelevant, if we do this operation as the first one then a white triangle with $n=k$ remains for which at least $k$ operations are needed.
Now let's show that it is possible to do $3 n-2$ operations. If $n=1$ then it is evident. Assume that we have proved it for $n=k$. For $n=k+1$ we start with three operations $\mathrm{A}, \mathrm{B}$ and C coloring two rightmost corners and the rightmost line. We have used 3 operations and reduced the field to the situation when $n=k$ (Fig. 2).

Figure 2
At last we show that there cannot be more than $3 n-2$ operations. If all $n$ lines parallel to one side of the triangle are colored then the whole triangle is colored black. Therefore the number of operations made before the last operation cannot be greater than $3(n-1)$, which gives the total number of operations not greater than $3 n-2$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|

From similar right triangles we get
$$
\frac{B E}{A E}=\frac{\frac{B D}{A D} E D}{\frac{A D}{B D} E D}=\left(\frac{B D}{A D}\right)^{2}
$$
and analogously
$$
\frac{C F}{A F}=\left(\frac{C D}{A D}\right)^{2}
$$
Now, because $A C>A B$, the lines $B C$ and $E F$ intersect in a point $X$ on the extension of segment $B C$ beyond $B$. Menelaus' theorem gives
$$
B X \frac{C F}{A F}=C X \frac{B E}{A E}, \quad C X \frac{D G}{A G}=D X \frac{C F}{A F}, \quad D X \frac{B E}{A E}=B X \frac{D G}{A G}
$$
Adding these relations and rerranging terms we arrive at
$$
B C \frac{D G}{A G}=B D \frac{C F}{A F}+C D \frac{B E}{A E}=B C \frac{B D \cdot C D}{A D^{2}}=B C \frac{A D \cdot H D}{A D^{2}}=B C \frac{H D}{A D}
$$
whence
$$
\frac{D G}{A G}=\frac{H D}{A D}
$$
Hence follows
$$
\frac{A D}{A G}=\frac{A G+D G}{A G}=\frac{A D+H D}{A D}=\frac{A H}{A D}
$$
which is equivalent to the problem's assertion.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|

From similar right triangles we get
$$
\frac{B E}{A E}=\frac{\frac{B D}{A D} E D}{\frac{A D}{B D} E D}=\left(\frac{B D}{A D}\right)^{2}
$$
and analogously
$$
\frac{C F}{A F}=\left(\frac{C D}{A D}\right)^{2}
$$
Now, because $A C>A B$, the lines $B C$ and $E F$ intersect in a point $X$ on the extension of segment $B C$ beyond $B$. Menelaus' theorem gives
$$
B X \frac{C F}{A F}=C X \frac{B E}{A E}, \quad C X \frac{D G}{A G}=D X \frac{C F}{A F}, \quad D X \frac{B E}{A E}=B X \frac{D G}{A G}
$$
Adding these relations and rerranging terms we arrive at
$$
B C \frac{D G}{A G}=B D \frac{C F}{A F}+C D \frac{B E}{A E}=B C \frac{B D \cdot C D}{A D^{2}}=B C \frac{A D \cdot H D}{A D^{2}}=B C \frac{H D}{A D}
$$
whence
$$
\frac{D G}{A G}=\frac{H D}{A D}
$$
Hence follows
$$
\frac{A D}{A G}=\frac{A G+D G}{A G}=\frac{A D+H D}{A D}=\frac{A H}{A D}
$$
which is equivalent to the problem's assertion.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2013"
}
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|
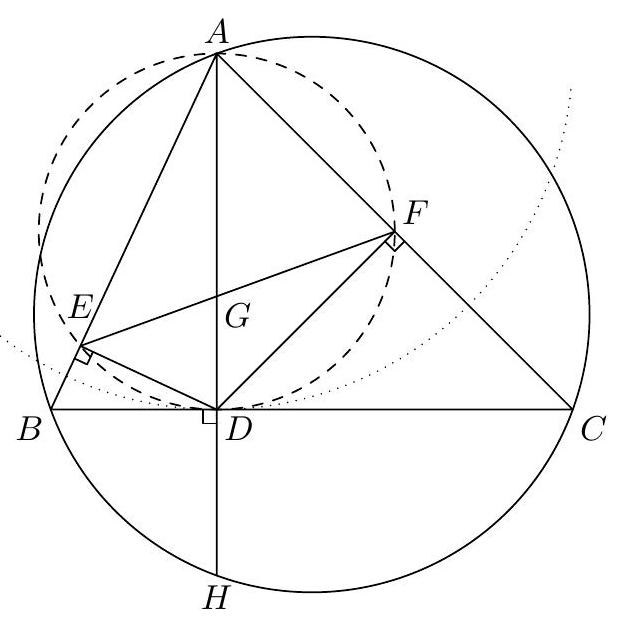
Inversion in the circle with centre $A$ and radius $A D$ maps the line $B C$ and the circle with diameter $A D$, passing through $E$ and $F$, therefore $B$ and $E$ and $C$ and $F$, therefore the circumcircle and the line $E F$ and therefore $H$ and $G$ onto one another. Hence the assertion follows.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|

Inversion in the circle with centre $A$ and radius $A D$ maps the line $B C$ and the circle with diameter $A D$, passing through $E$ and $F$, therefore $B$ and $E$ and $C$ and $F$, therefore the circumcircle and the line $E F$ and therefore $H$ and $G$ onto one another. Hence the assertion follows.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2013"
}
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|
Since $\angle A E D$ and $\angle A F D$ are right angles, $A F D E$ is cyclic. Then
$$
\angle A E F=\angle A D F
$$
Segment $D F$ is an altitude in a right triangle $A D C$, so
$$
\angle A D F=\angle A C D
$$
and
$$
\angle A C D=\angle A H B
$$
as angles inscribed in the circumcircle of $\triangle A B C$. Thus $\angle A E F=\angle A H B$, and $B E G H$ is cyclic. Then by the power of the point
$$
A E \cdot A B=A G \cdot A H
$$
On the other hand, since $D E$ is an altitude in a right triangle $A D B$,
$$
A E \cdot A B=A D^{2}
$$
It follows that $A G \cdot A H=A D^{2}$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute triangle $A B C$ with $A C>A B$, let $D$ be the projection of $A$ on $B C$, and let $E$ and $F$ be the projections of $D$ on $A B$ and $A C$, respectively. Let $G$ be the intersection point of the lines $A D$ and $E F$. Let $H$ be the second intersection point of the line $A D$ and the circumcircle of triangle $A B C$. Prove that
$$
A G \cdot A H=A D^{2}
$$
|
Since $\angle A E D$ and $\angle A F D$ are right angles, $A F D E$ is cyclic. Then
$$
\angle A E F=\angle A D F
$$
Segment $D F$ is an altitude in a right triangle $A D C$, so
$$
\angle A D F=\angle A C D
$$
and
$$
\angle A C D=\angle A H B
$$
as angles inscribed in the circumcircle of $\triangle A B C$. Thus $\angle A E F=\angle A H B$, and $B E G H$ is cyclic. Then by the power of the point
$$
A E \cdot A B=A G \cdot A H
$$
On the other hand, since $D E$ is an altitude in a right triangle $A D B$,
$$
A E \cdot A B=A D^{2}
$$
It follows that $A G \cdot A H=A D^{2}$, and the result follows.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2013"
}
|
A trapezoid $A B C D$ with bases $A B$ and $C D$ is such that the circumcircle of the triangle $B C D$ intersects the line $A D$ in a point $E$, distinct from $A$ and $D$. Prove that the circumcircle of the triangle $A B E$ is tangent to the line $B C$.
|

If point $E$ lies on the segment $A D$ it is sufficient to prove $\angle C B E=\angle B A E$. It is true, since both angles are equal to $180^{\circ}-\angle A D C$. If point $D$ lies on the segment $A E$ we have $\angle C B E=\angle C D E=\angle B A E$, which proves the thesis. In the end, if point $A$ lies on the segment $D E$ we have $180^{\circ}-\angle C B E=\angle C D E=\angle B A E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A trapezoid $A B C D$ with bases $A B$ and $C D$ is such that the circumcircle of the triangle $B C D$ intersects the line $A D$ in a point $E$, distinct from $A$ and $D$. Prove that the circumcircle of the triangle $A B E$ is tangent to the line $B C$.
|

If point $E$ lies on the segment $A D$ it is sufficient to prove $\angle C B E=\angle B A E$. It is true, since both angles are equal to $180^{\circ}-\angle A D C$. If point $D$ lies on the segment $A E$ we have $\angle C B E=\angle C D E=\angle B A E$, which proves the thesis. In the end, if point $A$ lies on the segment $D E$ we have $180^{\circ}-\angle C B E=\angle C D E=\angle B A E$.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "# Problem 12",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2013"
}
|
A trapezoid $A B C D$ with bases $A B$ and $C D$ is such that the circumcircle of the triangle $B C D$ intersects the line $A D$ in a point $E$, distinct from $A$ and $D$. Prove that the circumcircle of the triangle $A B E$ is tangent to the line $B C$.
|
By $\measuredangle$ denote a directed angle modulo $\pi$. Since $A B C D$ is a trapezoid, $\measuredangle B A E=\measuredangle C D E$, and since $B C D E$ is cyclic, $\measuredangle C D E=\measuredangle C B E$. Hence $\measuredangle B A E=\measuredangle C B E$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A trapezoid $A B C D$ with bases $A B$ and $C D$ is such that the circumcircle of the triangle $B C D$ intersects the line $A D$ in a point $E$, distinct from $A$ and $D$. Prove that the circumcircle of the triangle $A B E$ is tangent to the line $B C$.
|
By $\measuredangle$ denote a directed angle modulo $\pi$. Since $A B C D$ is a trapezoid, $\measuredangle B A E=\measuredangle C D E$, and since $B C D E$ is cyclic, $\measuredangle C D E=\measuredangle C B E$. Hence $\measuredangle B A E=\measuredangle C B E$, and the result follows.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "# Problem 12",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2013"
}
|
All faces of a tetrahedron are right-angled triangles. It is known that three of its edges have the same length $s$. Find the volume of the tetrahedron.
|
The three equal edges clearly cannot bound a face by themselves, for then this triangle would be equilateral and not right-angled. Nor can they be incident to the same vertex, for then the opposite face would again be equilateral.
Hence we may name the tetrahedron $A B C D$ in such a way that $A B=B C=C D=s$. The angles $\angle A B C$ and $\angle B C D$ must then be right, and $A C=B D=s \sqrt{2}$. Suppose that $\angle A D C$ is right. Then by the Pythagorean theorem applied to $A C D$, we find $A D=s$. The reverse of the Pythagorean theorem applied to $A B D$, we see that $\angle D A B$ is right too. The quadrilateral $A B C D$ then has four right angles, and so must be a square.
From this contradiction, we conclude that $\angle A D C$ is not right. Since we already know that $A C>C D, \angle C A D$ cannot be right either, and the right angle of $A C D$ must be $\angle A C D$. The Pythagorean theorem gives $A D=s \sqrt{3}$. From the reverse of the Pythagorean theorem, we may now conclude that $\angle A B D$ is right. Consequently, $A B$ is perpendicular to $B C D$, and the volume of the tetrahedron may be simply calculated as
$$
\frac{A B \cdot B C \cdot C D}{6}=\frac{s^{3}}{6}
$$
|
\frac{s^3}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
All faces of a tetrahedron are right-angled triangles. It is known that three of its edges have the same length $s$. Find the volume of the tetrahedron.
|

The three equal edges clearly cannot bound a face by themselves, for then this triangle would be equilateral and not right-angled. Nor can they be incident to the same vertex, for then the opposite face would again be equilateral.
Hence we may name the tetrahedron $A B C D$ in such a way that $A B=B C=C D=s$. The angles $\angle A B C$ and $\angle B C D$ must then be right, and $A C=B D=s \sqrt{2}$. Suppose that $\angle A D C$ is right. Then by the Pythagorean theorem applied to $A C D$, we find $A D=s$. The reverse of the Pythagorean theorem applied to $A B D$, we see that $\angle D A B$ is right too. The quadrilateral $A B C D$ then has four right angles, and so must be a square.
From this contradiction, we conclude that $\angle A D C$ is not right. Since we already know that $A C>C D, \angle C A D$ cannot be right either, and the right angle of $A C D$ must be $\angle A C D$. The Pythagorean theorem gives $A D=s \sqrt{3}$. From the reverse of the Pythagorean theorem, we may now conclude that $\angle A B D$ is right. Consequently, $A B$ is perpendicular to $B C D$, and the volume of the tetrahedron may be simply calculated as
$$
\frac{A B \cdot B C \cdot C D}{6}=\frac{s^{3}}{6}
$$
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "# Problem 13",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Circles $\alpha$ and $\beta$ of the same radius intersect in two points, one of which is $P$. Denote by $A$ and $B$, respectively, the points diametrically opposite to $P$ on each of $\alpha$ and $\beta$. A third circle of the same radius passes through $P$ and intersects $\alpha$ and $\beta$ in the points $X$ and $Y$, respectively.
Show that the line $X Y$ is parallel to the line $A B$.
|
Let $M$ be the third circle, and denote by $Z$ the point on $M$ diametrically opposite to $P$.
Since $\angle A X P=\angle P X Z=90^{\circ}$, the three points $A, X, Z$ are collinear. Likewise, the three points $B, Y, Z$ are collinear. Point $P$ is equidistant to the three vertices of triangle $A B Z$, for $P A=P B=P Z$ is the common diameter of the circles. Therefore $P$ is the circumcentre of $A B Z$, which means the perpendiculars $P X$ and $P Y$ bisect the sides $A Z$ and $B Z$. Ergo, $X$ and $Y$ are midpoints on $A Z$ and $B Z$, which leads to the desired conclusion $X Y \| A B$.
Remark. Note that $A$ and $Z$ are symmetric with respect to $P X$, thus we immediately obtain $A X=X Z$, and similarly $B Y=Y Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Circles $\alpha$ and $\beta$ of the same radius intersect in two points, one of which is $P$. Denote by $A$ and $B$, respectively, the points diametrically opposite to $P$ on each of $\alpha$ and $\beta$. A third circle of the same radius passes through $P$ and intersects $\alpha$ and $\beta$ in the points $X$ and $Y$, respectively.
Show that the line $X Y$ is parallel to the line $A B$.
|
Let $M$ be the third circle, and denote by $Z$ the point on $M$ diametrically opposite to $P$.
Since $\angle A X P=\angle P X Z=90^{\circ}$, the three points $A, X, Z$ are collinear. Likewise, the three points $B, Y, Z$ are collinear. Point $P$ is equidistant to the three vertices of triangle $A B Z$, for $P A=P B=P Z$ is the common diameter of the circles. Therefore $P$ is the circumcentre of $A B Z$, which means the perpendiculars $P X$ and $P Y$ bisect the sides $A Z$ and $B Z$. Ergo, $X$ and $Y$ are midpoints on $A Z$ and $B Z$, which leads to the desired conclusion $X Y \| A B$.
Remark. Note that $A$ and $Z$ are symmetric with respect to $P X$, thus we immediately obtain $A X=X Z$, and similarly $B Y=Y Z$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Four circles in a plane have a common center. Their radii form a strictly increasing arithmetic progression. Prove that there is no square with each vertex lying on a different circle.
|
First we prove the following lemma:
Lemma 1. If $A B C D$ is a square then for arbitrary point $E$
$$
E A^{2}+E C^{2}=E B^{2}+E D^{2}
$$
Proof. Let $A^{\prime}, C^{\prime}$ be projections of $E$ on sides $A B$, and $C D$ respectively. Then
$$
\begin{aligned}
& E A^{2}+E C^{2}=\left(E A^{\prime 2}+A A^{\prime 2}\right)+\left(E C^{\prime 2}+C C^{\prime 2}\right) \\
& E B^{2}+E D^{2}=\left(E A^{\prime 2}+A^{\prime} B^{2}\right)+\left(E C^{\prime 2}+C^{\prime} D^{2}\right)
\end{aligned}
$$
As $A^{\prime} B=C C^{\prime}$ and $A A^{\prime}=C^{\prime} D$ then $E A^{2}+E C^{2}=E B^{2}+E D^{2}$. Note that $E$ does not have to be inside the square, it is true for arbitrary point.
Now let $O$ be the common center of circles and $A B C D$ be a square with each vertex lying on a different circle, assume that $A$ lies on the largest circle. If $a$ is the radius of the smallest circle and $p$ is the difference of the arithmetic progression then the radii of the circles are $a, a+p, a+2 p$ and $a+3 p$, these are also distances from $O$ to the vertices of the square $A B C D, O A=a+3 p$. Consider the expression $O A^{2}+O C^{2}-O B^{2}-O D^{2}$. Its smallest possible value is attained when $O C=a$, therefore
$$
O A^{2}+O C^{2}-O B^{2}-O D^{2} \geq(a+3 p)^{2}+a^{2}-(a+p)^{2}-(a+2 p)^{2}=4 p^{2}>0
$$
what contradicts the lemma.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Four circles in a plane have a common center. Their radii form a strictly increasing arithmetic progression. Prove that there is no square with each vertex lying on a different circle.
|

First we prove the following lemma:
Lemma 1. If $A B C D$ is a square then for arbitrary point $E$
$$
E A^{2}+E C^{2}=E B^{2}+E D^{2}
$$
Proof. Let $A^{\prime}, C^{\prime}$ be projections of $E$ on sides $A B$, and $C D$ respectively. Then
$$
\begin{aligned}
& E A^{2}+E C^{2}=\left(E A^{\prime 2}+A A^{\prime 2}\right)+\left(E C^{\prime 2}+C C^{\prime 2}\right) \\
& E B^{2}+E D^{2}=\left(E A^{\prime 2}+A^{\prime} B^{2}\right)+\left(E C^{\prime 2}+C^{\prime} D^{2}\right)
\end{aligned}
$$
As $A^{\prime} B=C C^{\prime}$ and $A A^{\prime}=C^{\prime} D$ then $E A^{2}+E C^{2}=E B^{2}+E D^{2}$. Note that $E$ does not have to be inside the square, it is true for arbitrary point.
Now let $O$ be the common center of circles and $A B C D$ be a square with each vertex lying on a different circle, assume that $A$ lies on the largest circle. If $a$ is the radius of the smallest circle and $p$ is the difference of the arithmetic progression then the radii of the circles are $a, a+p, a+2 p$ and $a+3 p$, these are also distances from $O$ to the vertices of the square $A B C D, O A=a+3 p$. Consider the expression $O A^{2}+O C^{2}-O B^{2}-O D^{2}$. Its smallest possible value is attained when $O C=a$, therefore
$$
O A^{2}+O C^{2}-O B^{2}-O D^{2} \geq(a+3 p)^{2}+a^{2}-(a+p)^{2}-(a+2 p)^{2}=4 p^{2}>0
$$
what contradicts the lemma.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
We call a positive integer $n$ delightful if there exists an integer $k, 1<k<n$, such that
$$
1+2+\cdots+(k-1)=(k+1)+(k+2)+\cdots+n
$$
Does there exist a delightful number $N$ satisfying the inequalities
$$
2013^{2013}<\frac{N}{2013^{2013}}<2013^{2013}+4 ?
$$
|
Consider a delightful number $n$. Then there exists an integer $x, 1<x<n$ satisfying
$$
\begin{gathered}
\sum_{i=1}^{x-1} i=\sum_{i=x+1}^{n} i=\sum_{i=1}^{n} i-\sum_{i=1}^{x} i \\
x^{2}=x+2 \cdot \frac{(x-1) x}{2}=x+2 \sum_{i=1}^{x-1} i=\sum_{i=1}^{x-1} i+\sum_{i=1}^{x} i=\sum_{i=1}^{n} i=\frac{n(n+1)}{2} .
\end{gathered}
$$
Now $n$ and $n+1$ are relatively prime so one of them is divisible by 2 and the other one must then be a perfect, odd square, as $x^{2}$ is on the LHS. Now consider the inequality
$$
\left(2013^{2013}\right)^{2}<n<\left(2013^{2013}\right)^{2}+4 \cdot 2013^{2013}=\left(2013^{2013}+2\right)^{2}-4
$$
The only perfect square in this interval is clearly $\left(2013^{2013}+1\right)^{2}$ which is even. Therefore neither $n$ nor $n+1$ can be an odd, perfect square. Hence no delightful number $N$ satisfy the condition.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
We call a positive integer $n$ delightful if there exists an integer $k, 1<k<n$, such that
$$
1+2+\cdots+(k-1)=(k+1)+(k+2)+\cdots+n
$$
Does there exist a delightful number $N$ satisfying the inequalities
$$
2013^{2013}<\frac{N}{2013^{2013}}<2013^{2013}+4 ?
$$
|
Consider a delightful number $n$. Then there exists an integer $x, 1<x<n$ satisfying
$$
\begin{gathered}
\sum_{i=1}^{x-1} i=\sum_{i=x+1}^{n} i=\sum_{i=1}^{n} i-\sum_{i=1}^{x} i \\
x^{2}=x+2 \cdot \frac{(x-1) x}{2}=x+2 \sum_{i=1}^{x-1} i=\sum_{i=1}^{x-1} i+\sum_{i=1}^{x} i=\sum_{i=1}^{n} i=\frac{n(n+1)}{2} .
\end{gathered}
$$
Now $n$ and $n+1$ are relatively prime so one of them is divisible by 2 and the other one must then be a perfect, odd square, as $x^{2}$ is on the LHS. Now consider the inequality
$$
\left(2013^{2013}\right)^{2}<n<\left(2013^{2013}\right)^{2}+4 \cdot 2013^{2013}=\left(2013^{2013}+2\right)^{2}-4
$$
The only perfect square in this interval is clearly $\left(2013^{2013}+1\right)^{2}$ which is even. Therefore neither $n$ nor $n+1$ can be an odd, perfect square. Hence no delightful number $N$ satisfy the condition.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "# Problem 16",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Let $c$ and $n>c$ be positive integers. Mary's teacher writes $n$ positive integers on a blackboard. Is it true that for all $n$ and $c$ Mary can always label the numbers written by the teacher by $a_{1}, \ldots, a_{n}$ in such an order that the cyclic product $\left(a_{1}-a_{2}\right) \cdot\left(a_{2}-a_{3}\right) \cdot \ldots \cdot\left(a_{n-1}-a_{n}\right) \cdot\left(a_{n}-a_{1}\right)$ would be congruent to either 0 or $c$ modulo $n$ ?
|
Answer: Yes.
|
proof
|
Yes
|
Problem not solved
|
proof
|
Number Theory
|
Let $c$ and $n>c$ be positive integers. Mary's teacher writes $n$ positive integers on a blackboard. Is it true that for all $n$ and $c$ Mary can always label the numbers written by the teacher by $a_{1}, \ldots, a_{n}$ in such an order that the cyclic product $\left(a_{1}-a_{2}\right) \cdot\left(a_{2}-a_{3}\right) \cdot \ldots \cdot\left(a_{n-1}-a_{n}\right) \cdot\left(a_{n}-a_{1}\right)$ would be congruent to either 0 or $c$ modulo $n$ ?
|
Answer: Yes.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "# Problem 17",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Let $c$ and $n>c$ be positive integers. Mary's teacher writes $n$ positive integers on a blackboard. Is it true that for all $n$ and $c$ Mary can always label the numbers written by the teacher by $a_{1}, \ldots, a_{n}$ in such an order that the cyclic product $\left(a_{1}-a_{2}\right) \cdot\left(a_{2}-a_{3}\right) \cdot \ldots \cdot\left(a_{n-1}-a_{n}\right) \cdot\left(a_{n}-a_{1}\right)$ would be congruent to either 0 or $c$ modulo $n$ ?
|
If some two of these $n$ integers are congruent modulo $n$ then Mary can choose them consecutively and obtain a product divisible by $n$. Hence we may assume in the rest that these $n$ integers written by the teacher are pairwise incongruent modulo $n$. This means that they cover all residues modulo $n$. If $n$ is composite then Mary can find integers $k$ and $l$ such that $n=k l$ and $2 \leq k \leq l \leq n-2$. Let Mary denote $a_{1}, a_{2}, a_{3}, a_{4}$ such that $a_{1} \equiv k, a_{2} \equiv 0, a_{3} \equiv l+1$ and $a_{4} \equiv 1$. The remaining numbers can be denoted in arbitrary order. The product is divisible by $n$ as the product of the first and the third factor is $(k-0) \cdot((l+1)-1)=k l=n$. If $n$ is prime then the numbers $c i$, where $i=0,1, \ldots, n-1$, cover all residues modulo $n$. Let Mary denote the numbers in such a way that $a_{i} \equiv c(n-i)$ for every $i=1, \ldots, n$. Then every factor in the product is congruent to $c$ modulo $n$, meaning that the product is congruent to $c^{n}$ modulo $n$. But $c^{n} \equiv c$ by Fermat's theorem, and Mary has done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $c$ and $n>c$ be positive integers. Mary's teacher writes $n$ positive integers on a blackboard. Is it true that for all $n$ and $c$ Mary can always label the numbers written by the teacher by $a_{1}, \ldots, a_{n}$ in such an order that the cyclic product $\left(a_{1}-a_{2}\right) \cdot\left(a_{2}-a_{3}\right) \cdot \ldots \cdot\left(a_{n-1}-a_{n}\right) \cdot\left(a_{n}-a_{1}\right)$ would be congruent to either 0 or $c$ modulo $n$ ?
|
If some two of these $n$ integers are congruent modulo $n$ then Mary can choose them consecutively and obtain a product divisible by $n$. Hence we may assume in the rest that these $n$ integers written by the teacher are pairwise incongruent modulo $n$. This means that they cover all residues modulo $n$. If $n$ is composite then Mary can find integers $k$ and $l$ such that $n=k l$ and $2 \leq k \leq l \leq n-2$. Let Mary denote $a_{1}, a_{2}, a_{3}, a_{4}$ such that $a_{1} \equiv k, a_{2} \equiv 0, a_{3} \equiv l+1$ and $a_{4} \equiv 1$. The remaining numbers can be denoted in arbitrary order. The product is divisible by $n$ as the product of the first and the third factor is $(k-0) \cdot((l+1)-1)=k l=n$. If $n$ is prime then the numbers $c i$, where $i=0,1, \ldots, n-1$, cover all residues modulo $n$. Let Mary denote the numbers in such a way that $a_{i} \equiv c(n-i)$ for every $i=1, \ldots, n$. Then every factor in the product is congruent to $c$ modulo $n$, meaning that the product is congruent to $c^{n}$ modulo $n$. But $c^{n} \equiv c$ by Fermat's theorem, and Mary has done.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "# Problem 17",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2013"
}
|
Find all pairs $(x, y)$ of integers such that $y^{3}-1=x^{4}+x^{2}$.
|
If $x=0$, we get a solution $(x, y)=(0,1)$. This solution will turn out to be the only one. If $(x, y)$ is a solution then $(-x, y)$ also is a solution therefore we can assume that $x \geq 1$. We add 1 to both sides and factor: $y^{3}=x^{4}+x^{2}+1=\left(x^{2}+x+1\right)\left(x^{2}-x+1\right)$. We show that the factors $x^{2}+x+1$ and $x^{2}-x+1$ are co-prime. Assume that a prime $p$ divides both of them. Then $p \mid x^{2}+x+1-\left(x^{2}-x+1\right)=2 x$. Since $x^{2}+x+1$ is always odd, $p \mid x$. But then $p$ does not divide $x^{2}+x+1$, a contradiction. Since $x^{2}+x+1$ and $x^{2}-x+1$ have no prime factors in common and their product is a cube, both of them are cubes by a consequence of the fundamental theorem of arithmetic. Therefore, $x^{2}+x+1=a^{3}$ and $x^{2}-x+1=b^{3}$ for some non-negative integers $a$ and $b$.
As $x \geq 1$ the first equation implies that $a>x^{\frac{2}{3}}$. But since clearly $b<a$ we get
$$
x^{2}-x+1=b^{3} \leq(a-1)^{3}=a^{3}-3 a^{2}+3 a-1 \leq a^{3}-3 a^{2}+3 a \leq a^{3}-2 a^{2}=x^{2}+x+1-2 a^{2}<x^{2}+x+1-2 x^{\frac{4}{3}}
$$
when $2 a^{2} \leq 3 a^{2}-3 a$, i.e. $a^{2} \geq 3 a$ which holds for $a \geq 3$. Clearly $a=2$ is impossible and $a=1$ means $x=0$. We got $x^{2}-x+1<x^{2}+x+1-2 x^{\frac{4}{3}}$ which means $0 \leq 2 x-2 x^{\frac{4}{3}}$. Hence $x=1$, but then 3 would be a cube, a contradiction.
Remark. There are many ways to guess the factorization $x^{4}+x^{2}+1=\left(x^{2}+x+1\right)\left(x^{2}-x+1\right)$. Writing $x^{4}+x+1=\left(x^{2}+1\right)^{2}-x^{2}$ we immediately obtain it. Another way to see it is to write $p(x)=x^{4}+x^{2}+1$ and notice that $p(0)=1 \cdot 1, p(1)=3 \cdot 1, p(2)=7 \cdot 3$, so there probably is a quadratic factor $q(x)$ for which $q(0)=1, q(1)=3, q(2)=7$ (clearly, there cannot be linear factors). It is easy to see then that $q(x)=x^{2}+x+1$ and the factorization can be completed with the long division. One more way is to write $x^{4}+x^{2}+1=$ $\left(x^{2}+a x+b\right)\left(x^{2}+c x+d\right)$ and compare the coefficients.
It is well-known that if $s$ and $t$ are co-prime integers whose product is a perfect $k$ th power, then $s$ and $t$ both are perfect $k$ th powers. The proof goes like this. Let $a=p_{1}^{\alpha_{1}} \ldots p_{h}^{\alpha_{h}}, b=q_{1}^{\beta_{1}} \ldots q_{\ell}^{\beta_{\ell}}$ and $x=r_{1}^{\gamma_{1}} \ldots r_{m}^{\gamma_{m}}$ be the prime factorizations of $a, b$ and $x$. In the prime factorization of $x^{k}$, every exponent is divisible by $k$, so the same must hold for the factorization of $s t$. But $s$ and $t$ are co-prime, so the exponents of primes in $s$ and $t$ must be divisible by $k$. Therefore $s$ and $t$ are perfect $k$ th powers.
|
(0,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs $(x, y)$ of integers such that $y^{3}-1=x^{4}+x^{2}$.
|
If $x=0$, we get a solution $(x, y)=(0,1)$. This solution will turn out to be the only one. If $(x, y)$ is a solution then $(-x, y)$ also is a solution therefore we can assume that $x \geq 1$. We add 1 to both sides and factor: $y^{3}=x^{4}+x^{2}+1=\left(x^{2}+x+1\right)\left(x^{2}-x+1\right)$. We show that the factors $x^{2}+x+1$ and $x^{2}-x+1$ are co-prime. Assume that a prime $p$ divides both of them. Then $p \mid x^{2}+x+1-\left(x^{2}-x+1\right)=2 x$. Since $x^{2}+x+1$ is always odd, $p \mid x$. But then $p$ does not divide $x^{2}+x+1$, a contradiction. Since $x^{2}+x+1$ and $x^{2}-x+1$ have no prime factors in common and their product is a cube, both of them are cubes by a consequence of the fundamental theorem of arithmetic. Therefore, $x^{2}+x+1=a^{3}$ and $x^{2}-x+1=b^{3}$ for some non-negative integers $a$ and $b$.
As $x \geq 1$ the first equation implies that $a>x^{\frac{2}{3}}$. But since clearly $b<a$ we get
$$
x^{2}-x+1=b^{3} \leq(a-1)^{3}=a^{3}-3 a^{2}+3 a-1 \leq a^{3}-3 a^{2}+3 a \leq a^{3}-2 a^{2}=x^{2}+x+1-2 a^{2}<x^{2}+x+1-2 x^{\frac{4}{3}}
$$
when $2 a^{2} \leq 3 a^{2}-3 a$, i.e. $a^{2} \geq 3 a$ which holds for $a \geq 3$. Clearly $a=2$ is impossible and $a=1$ means $x=0$. We got $x^{2}-x+1<x^{2}+x+1-2 x^{\frac{4}{3}}$ which means $0 \leq 2 x-2 x^{\frac{4}{3}}$. Hence $x=1$, but then 3 would be a cube, a contradiction.
Remark. There are many ways to guess the factorization $x^{4}+x^{2}+1=\left(x^{2}+x+1\right)\left(x^{2}-x+1\right)$. Writing $x^{4}+x+1=\left(x^{2}+1\right)^{2}-x^{2}$ we immediately obtain it. Another way to see it is to write $p(x)=x^{4}+x^{2}+1$ and notice that $p(0)=1 \cdot 1, p(1)=3 \cdot 1, p(2)=7 \cdot 3$, so there probably is a quadratic factor $q(x)$ for which $q(0)=1, q(1)=3, q(2)=7$ (clearly, there cannot be linear factors). It is easy to see then that $q(x)=x^{2}+x+1$ and the factorization can be completed with the long division. One more way is to write $x^{4}+x^{2}+1=$ $\left(x^{2}+a x+b\right)\left(x^{2}+c x+d\right)$ and compare the coefficients.
It is well-known that if $s$ and $t$ are co-prime integers whose product is a perfect $k$ th power, then $s$ and $t$ both are perfect $k$ th powers. The proof goes like this. Let $a=p_{1}^{\alpha_{1}} \ldots p_{h}^{\alpha_{h}}, b=q_{1}^{\beta_{1}} \ldots q_{\ell}^{\beta_{\ell}}$ and $x=r_{1}^{\gamma_{1}} \ldots r_{m}^{\gamma_{m}}$ be the prime factorizations of $a, b$ and $x$. In the prime factorization of $x^{k}$, every exponent is divisible by $k$, so the same must hold for the factorization of $s t$. But $s$ and $t$ are co-prime, so the exponents of primes in $s$ and $t$ must be divisible by $k$. Therefore $s$ and $t$ are perfect $k$ th powers.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "# Problem 18",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Let $a_{0}$ be a positive integer and $a_{n}=5 a_{n-1}+4$, for all $n \geq 1$. Can $a_{0}$ be chosen so that $a_{54}$ is a multiple of 2013?
|
Let $x_{n}=\frac{a_{n}}{5^{n}}$. Then $x_{0}=a$ and $5^{n} x_{n}=a_{n}=5 a_{n-1}+4=5^{n} x_{n-1}+4$. So $x_{n}=x_{n-1}+\frac{4}{5^{n}}$. By induction,
$$
x_{n}=x_{0}+\left(\frac{4}{5}+\frac{4}{5^{2}}+\cdots+\frac{4}{5^{n}}\right)=a+\frac{4}{5}\left(1+\frac{1}{5}+\cdots+\frac{1}{5^{n-1}}\right)=a+\frac{4}{5} \cdot \frac{1-\frac{1}{5^{n}}}{1-\frac{1}{5}}=a+1-\frac{1}{5^{n}}
$$
So $a_{n}=5^{n} x_{n}=5^{n}(a+1)-1$. Now 2013 and $5^{n}$ are relatively prime. So there is a $b, 0<b<2013$, also relatively prime to 2013 , such that $5^{54}=2013 c+b$. To have 2013 as a factor of $a_{54}$, it suffices to find an integer $y$ such that $(a+1) b-1=2013 y$. But this is a linear Diophantine equation in $a+1$ and $y$; it has an infinite family of solutions, among them such that $a+1 \geq 2$.
|
a+1 \geq 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a_{0}$ be a positive integer and $a_{n}=5 a_{n-1}+4$, for all $n \geq 1$. Can $a_{0}$ be chosen so that $a_{54}$ is a multiple of 2013?
|
Let $x_{n}=\frac{a_{n}}{5^{n}}$. Then $x_{0}=a$ and $5^{n} x_{n}=a_{n}=5 a_{n-1}+4=5^{n} x_{n-1}+4$. So $x_{n}=x_{n-1}+\frac{4}{5^{n}}$. By induction,
$$
x_{n}=x_{0}+\left(\frac{4}{5}+\frac{4}{5^{2}}+\cdots+\frac{4}{5^{n}}\right)=a+\frac{4}{5}\left(1+\frac{1}{5}+\cdots+\frac{1}{5^{n-1}}\right)=a+\frac{4}{5} \cdot \frac{1-\frac{1}{5^{n}}}{1-\frac{1}{5}}=a+1-\frac{1}{5^{n}}
$$
So $a_{n}=5^{n} x_{n}=5^{n}(a+1)-1$. Now 2013 and $5^{n}$ are relatively prime. So there is a $b, 0<b<2013$, also relatively prime to 2013 , such that $5^{54}=2013 c+b$. To have 2013 as a factor of $a_{54}$, it suffices to find an integer $y$ such that $(a+1) b-1=2013 y$. But this is a linear Diophantine equation in $a+1$ and $y$; it has an infinite family of solutions, among them such that $a+1 \geq 2$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "# Problem 19",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2013"
}
|
Let $a_{0}$ be a positive integer and $a_{n}=5 a_{n-1}+4$, for all $n \geq 1$. Can $a_{0}$ be chosen so that $a_{54}$ is a multiple of 2013?
|
Denote $f(x)=5 x+4$, this function is a bijection for residues modulo 2013, and it has an inverse $g(x)=$ $1208 x+1207$. One can easily check that $f(g(x)) \equiv g(f(x)) \equiv x(\bmod 2013)$.
Denote $f^{0}(x)=x$ and $f^{n+1}(x)=f\left(f^{n}(x)\right)$, in other words $f^{n}(x)$ is an $n$-fold application of $f$ to $x$. Take $a_{0}=g^{54}(0)$, clearly $a_{0}>0$ and
$$
a_{54}=f^{54}\left(a_{0}\right)=f^{54}\left(g^{54}(0)\right) \equiv 0 \quad(\bmod 2013)
$$
|
a_{0}=g^{54}(0)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $a_{0}$ be a positive integer and $a_{n}=5 a_{n-1}+4$, for all $n \geq 1$. Can $a_{0}$ be chosen so that $a_{54}$ is a multiple of 2013?
|
Denote $f(x)=5 x+4$, this function is a bijection for residues modulo 2013, and it has an inverse $g(x)=$ $1208 x+1207$. One can easily check that $f(g(x)) \equiv g(f(x)) \equiv x(\bmod 2013)$.
Denote $f^{0}(x)=x$ and $f^{n+1}(x)=f\left(f^{n}(x)\right)$, in other words $f^{n}(x)$ is an $n$-fold application of $f$ to $x$. Take $a_{0}=g^{54}(0)$, clearly $a_{0}>0$ and
$$
a_{54}=f^{54}\left(a_{0}\right)=f^{54}\left(g^{54}(0)\right) \equiv 0 \quad(\bmod 2013)
$$
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "# Problem 19",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2013"
}
|
Find all polynomials $f$ with non-negative integer coefficients such that for all primes $p$ and positive integers $n$ there exist a prime $q$ and a positive integer $m$ such that $f\left(p^{n}\right)=q^{m}$.
|
Notice that among the constant polynomials the only solutions are $P(t)=q^{m}$ where $q$ is a prime and $m$ a positive integer. Assume that
$$
P(t)=a_{k} t^{k}+\cdots a_{0}
$$
where $a_{k} \neq 0$ and $a_{0}, a_{1}, \ldots, a_{k}$ are non-negative integers, is a polynomial that fullfills the conditions.
First consider the case $a_{0} \neq 1$. Since $a_{0}$ is a non-negative integer different from 1 , there exists a prime $p$ such that $p$ divides $a_{0}$, and hence $p$ divides $P\left(p^{n}\right)$ for all $n$. Thus $P\left(p^{n}\right)$ is a power of $p$ for all positive integers $n$. If there exists a $k^{\prime}<k$ such that $a_{k^{\prime}} \neq 0$, then for sufficiently large $n$ we have
$$
\left(p^{n}\right)^{k}>a_{k-1}\left(p^{n}\right)^{k-1}+\cdots+a_{0}>0
$$
and hence $P\left(p^{n}\right) \not \equiv 0\left(\bmod p^{n k}\right)$, but this contradicts $P\left(p^{n}\right)=p^{m}$ for some integer $m$ since obviously $P\left(p^{n}\right)>$ $p^{n k}$ and therefore $m$ must be greater than $n k$. We conclude that in this case $P(t)=a_{k} t^{k}$, and it is easy to see that only $a_{k}=1$ is a possibility.
Now consider the case $a_{0}=1$. Let $Q(t)=P(P(t))$. Now $Q$ must as well as $P$ satisfy the conditions. Since $Q(0)=P(P(0))=P(1)>1$ and $Q$ is not constant, we know from the previous that $Q(t)=t^{k}$, which contradicts that $Q(0)>1$. Hence there are no solutions in this case.
Thus all polynomials that satisfy the conditions are $P(t)=t^{m}$ where $m$ is a positive integer, and $P(t)=q^{m}$ where $q$ is a prime and $m$ is a positive integer.
## The 20 contest problems were submitted by 9 countries:
| Country | | Proposed problems | | |
| :--- | :--- | :---: | :--- | :--- |
| Denmark | 1 | 11 | 16 | 20 |
| Estonia | 17 | | | |
| Finland | 2 | 18 | 19 | |
| Germany | 6 | | | |
| Lithuania | 3 | | | |
| Latvia | 5 | 10 | 15 | |
| Poland | 4 | 7 | 8 | |
| St. Petersburg | 9 | | | |
| Sweden | 13 | 14 | | |
The solution 2 of the problem 19 originate from the contest paper of the Germany team. Some solutions have been added by coordinators.
|
P(t)=t^{m} \text{ where } m \text{ is a positive integer, and } P(t)=q^{m} \text{ where } q \text{ is a prime and } m \text{ is a positive integer}
|
Yes
|
Yes
|
proof
|
Number Theory
|
Find all polynomials $f$ with non-negative integer coefficients such that for all primes $p$ and positive integers $n$ there exist a prime $q$ and a positive integer $m$ such that $f\left(p^{n}\right)=q^{m}$.
|
Notice that among the constant polynomials the only solutions are $P(t)=q^{m}$ where $q$ is a prime and $m$ a positive integer. Assume that
$$
P(t)=a_{k} t^{k}+\cdots a_{0}
$$
where $a_{k} \neq 0$ and $a_{0}, a_{1}, \ldots, a_{k}$ are non-negative integers, is a polynomial that fullfills the conditions.
First consider the case $a_{0} \neq 1$. Since $a_{0}$ is a non-negative integer different from 1 , there exists a prime $p$ such that $p$ divides $a_{0}$, and hence $p$ divides $P\left(p^{n}\right)$ for all $n$. Thus $P\left(p^{n}\right)$ is a power of $p$ for all positive integers $n$. If there exists a $k^{\prime}<k$ such that $a_{k^{\prime}} \neq 0$, then for sufficiently large $n$ we have
$$
\left(p^{n}\right)^{k}>a_{k-1}\left(p^{n}\right)^{k-1}+\cdots+a_{0}>0
$$
and hence $P\left(p^{n}\right) \not \equiv 0\left(\bmod p^{n k}\right)$, but this contradicts $P\left(p^{n}\right)=p^{m}$ for some integer $m$ since obviously $P\left(p^{n}\right)>$ $p^{n k}$ and therefore $m$ must be greater than $n k$. We conclude that in this case $P(t)=a_{k} t^{k}$, and it is easy to see that only $a_{k}=1$ is a possibility.
Now consider the case $a_{0}=1$. Let $Q(t)=P(P(t))$. Now $Q$ must as well as $P$ satisfy the conditions. Since $Q(0)=P(P(0))=P(1)>1$ and $Q$ is not constant, we know from the previous that $Q(t)=t^{k}$, which contradicts that $Q(0)>1$. Hence there are no solutions in this case.
Thus all polynomials that satisfy the conditions are $P(t)=t^{m}$ where $m$ is a positive integer, and $P(t)=q^{m}$ where $q$ is a prime and $m$ is a positive integer.
## The 20 contest problems were submitted by 9 countries:
| Country | | Proposed problems | | |
| :--- | :--- | :---: | :--- | :--- |
| Denmark | 1 | 11 | 16 | 20 |
| Estonia | 17 | | | |
| Finland | 2 | 18 | 19 | |
| Germany | 6 | | | |
| Lithuania | 3 | | | |
| Latvia | 5 | 10 | 15 | |
| Poland | 4 | 7 | 8 | |
| St. Petersburg | 9 | | | |
| Sweden | 13 | 14 | | |
The solution 2 of the problem 19 originate from the contest paper of the Germany team. Some solutions have been added by coordinators.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "# Problem 20",
"resource_path": "BalticWay/segmented/en-bw13sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2013"
}
|
Show that
$$
\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \cos \left(2^{2} \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{1}{2^{24}}
$$
|
We start by rewriting the expression as follows:
$\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{\sin \left(56^{\circ}\right) \cdot \cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{\sin \left(56^{\circ}\right)}$
Now, by applying the double-angle formula $\sin (x) \cos (x)=\sin (2 x) / 2$ to $x=56^{\circ}$, we obtain
$$
\begin{gathered}
\frac{\sin \left(56^{\circ}\right) \cdot \cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{\sin \left(56^{\circ}\right)} \\
=\frac{\sin \left(2 \cdot 56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{2 \cdot \sin \left(56^{\circ}\right)} .
\end{gathered}
$$
Similarly, by applying the double-angle formula 24 times, we get
$$
\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{\sin \left(2^{24} \cdot 56^{\circ}\right)}{2^{24} \cdot \sin \left(56^{\circ}\right)}
$$
It remains to prove that $\sin \left(2^{24} \cdot 56^{\circ}\right)=\sin \left(56^{\circ}\right)$. If we can show that
$$
2^{24} \cdot 56=360 \cdot k+56
$$
for some integer $k$, then the desired equality follows by the periodicity of the sine function. Note that
$$
k=\frac{2^{24} \cdot 56-56}{360}=7 \cdot \frac{2^{24}-1}{45} .
$$
Since $\varphi(45)=24$, the Euler theorem implies that $k$ is indeed an integer, as claimed.
|
\frac{1}{2^{24}}
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that
$$
\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \cos \left(2^{2} \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{1}{2^{24}}
$$
|
We start by rewriting the expression as follows:
$\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{\sin \left(56^{\circ}\right) \cdot \cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{\sin \left(56^{\circ}\right)}$
Now, by applying the double-angle formula $\sin (x) \cos (x)=\sin (2 x) / 2$ to $x=56^{\circ}$, we obtain
$$
\begin{gathered}
\frac{\sin \left(56^{\circ}\right) \cdot \cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{\sin \left(56^{\circ}\right)} \\
=\frac{\sin \left(2 \cdot 56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)}{2 \cdot \sin \left(56^{\circ}\right)} .
\end{gathered}
$$
Similarly, by applying the double-angle formula 24 times, we get
$$
\cos \left(56^{\circ}\right) \cdot \cos \left(2 \cdot 56^{\circ}\right) \cdot \ldots \cdot \cos \left(2^{23} \cdot 56^{\circ}\right)=\frac{\sin \left(2^{24} \cdot 56^{\circ}\right)}{2^{24} \cdot \sin \left(56^{\circ}\right)}
$$
It remains to prove that $\sin \left(2^{24} \cdot 56^{\circ}\right)=\sin \left(56^{\circ}\right)$. If we can show that
$$
2^{24} \cdot 56=360 \cdot k+56
$$
for some integer $k$, then the desired equality follows by the periodicity of the sine function. Note that
$$
k=\frac{2^{24} \cdot 56-56}{360}=7 \cdot \frac{2^{24}-1}{45} .
$$
Since $\varphi(45)=24$, the Euler theorem implies that $k$ is indeed an integer, as claimed.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $a_{0}, a_{1}, \ldots, a_{N}$ be real numbers satisfying $a_{0}=a_{N}=0$ and
$$
a_{i+1}-2 a_{i}+a_{i-1}=a_{i}^{2}
$$
for $i=1,2, \ldots, N-1$. Prove that $a_{i} \leqslant 0$ for $i=1,2, \ldots, N-1$.
|
Assume the contrary. Then, there is an index $i$ for which $a_{i}=\max _{0 \leqslant j \leqslant N} a_{j}$ and $a_{i}>0$. This $i$ cannot be equal to 0 or $N$, since $a_{0}=a_{N}=0$. Thus, from $a_{i} \geqslant a_{i-1}$ and $a_{i} \geqslant a_{i+1}$ we obtain $0<a_{i}^{2}=\left(a_{i+1}-a_{i}\right)+\left(a_{i-1}-a_{i}\right) \leqslant 0$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{0}, a_{1}, \ldots, a_{N}$ be real numbers satisfying $a_{0}=a_{N}=0$ and
$$
a_{i+1}-2 a_{i}+a_{i-1}=a_{i}^{2}
$$
for $i=1,2, \ldots, N-1$. Prove that $a_{i} \leqslant 0$ for $i=1,2, \ldots, N-1$.
|
Assume the contrary. Then, there is an index $i$ for which $a_{i}=\max _{0 \leqslant j \leqslant N} a_{j}$ and $a_{i}>0$. This $i$ cannot be equal to 0 or $N$, since $a_{0}=a_{N}=0$. Thus, from $a_{i} \geqslant a_{i-1}$ and $a_{i} \geqslant a_{i+1}$ we obtain $0<a_{i}^{2}=\left(a_{i+1}-a_{i}\right)+\left(a_{i-1}-a_{i}\right) \leqslant 0$, which is a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Positive real numbers $a, b, c$ satisfy $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3$. Prove the inequality
$$
\frac{1}{\sqrt{a^{3}+b}}+\frac{1}{\sqrt{b^{3}+c}}+\frac{1}{\sqrt{c^{3}+a}} \leqslant \frac{3}{\sqrt{2}} .
$$
|
Applying several AM-GM inequalities (and using $1 / a+1 / b+1 / c=3$ ) we obtain
$$
\begin{aligned}
\frac{1}{\sqrt{a^{3}+b}}+\frac{1}{\sqrt{b^{3}+c}}+\frac{1}{\sqrt{c^{3}+a}} & \leqslant \frac{1}{\sqrt{2 a \sqrt{a b}}}+\frac{1}{\sqrt{2 b \sqrt{b c}}}+\frac{1}{\sqrt{2 c \sqrt{c a}}} \\
& =\frac{1}{\sqrt{2}}\left(\frac{\sqrt{a \sqrt{a b}}}{a \sqrt{a b}}+\frac{\sqrt{b \sqrt{b c}}}{b \sqrt{b c}}+\frac{\sqrt{c \sqrt{c a}}}{c \sqrt{c a}}\right) \\
& \leqslant \frac{1}{2 \sqrt{2}}\left(\frac{a+\sqrt{a b}}{a \sqrt{a b}}+\frac{b+\sqrt{b c}}{b \sqrt{b c}}+\frac{c+\sqrt{c a}}{c \sqrt{c a}}\right) \\
& =\frac{1}{2 \sqrt{2}}\left(3+\frac{1}{\sqrt{a b}}+\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{c a}}\right) \\
& =\frac{1}{2 \sqrt{2}}\left(3+\frac{\sqrt{a b}}{a b}+\frac{\sqrt{b c}}{b c}+\frac{\sqrt{c a}}{c a}\right) \\
& \leqslant \frac{1}{2 \sqrt{2}}\left(3+\frac{a+b}{2 a b}+\frac{b+c}{2 b c}+\frac{c+a}{2 a c}\right) \\
& =\frac{1}{2 \sqrt{2}}(3+3)=\frac{3}{\sqrt{2}} .
\end{aligned}
$$
|
\frac{3}{\sqrt{2}}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Positive real numbers $a, b, c$ satisfy $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3$. Prove the inequality
$$
\frac{1}{\sqrt{a^{3}+b}}+\frac{1}{\sqrt{b^{3}+c}}+\frac{1}{\sqrt{c^{3}+a}} \leqslant \frac{3}{\sqrt{2}} .
$$
|
Applying several AM-GM inequalities (and using $1 / a+1 / b+1 / c=3$ ) we obtain
$$
\begin{aligned}
\frac{1}{\sqrt{a^{3}+b}}+\frac{1}{\sqrt{b^{3}+c}}+\frac{1}{\sqrt{c^{3}+a}} & \leqslant \frac{1}{\sqrt{2 a \sqrt{a b}}}+\frac{1}{\sqrt{2 b \sqrt{b c}}}+\frac{1}{\sqrt{2 c \sqrt{c a}}} \\
& =\frac{1}{\sqrt{2}}\left(\frac{\sqrt{a \sqrt{a b}}}{a \sqrt{a b}}+\frac{\sqrt{b \sqrt{b c}}}{b \sqrt{b c}}+\frac{\sqrt{c \sqrt{c a}}}{c \sqrt{c a}}\right) \\
& \leqslant \frac{1}{2 \sqrt{2}}\left(\frac{a+\sqrt{a b}}{a \sqrt{a b}}+\frac{b+\sqrt{b c}}{b \sqrt{b c}}+\frac{c+\sqrt{c a}}{c \sqrt{c a}}\right) \\
& =\frac{1}{2 \sqrt{2}}\left(3+\frac{1}{\sqrt{a b}}+\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{c a}}\right) \\
& =\frac{1}{2 \sqrt{2}}\left(3+\frac{\sqrt{a b}}{a b}+\frac{\sqrt{b c}}{b c}+\frac{\sqrt{c a}}{c a}\right) \\
& \leqslant \frac{1}{2 \sqrt{2}}\left(3+\frac{a+b}{2 a b}+\frac{b+c}{2 b c}+\frac{c+a}{2 a c}\right) \\
& =\frac{1}{2 \sqrt{2}}(3+3)=\frac{3}{\sqrt{2}} .
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Find all functions $f$ defined on all real numbers and taking real values such that
$$
f(f(y))+f(x-y)=f(x f(y)-x)
$$
for all real numbers $x, y$.
Answer: $f(x)=0$.
|
Substituting $x=y=0$ into the original equality gives $f(f(0))+f(0)=f(0)$, implying
$$
f(f(0))=0
$$
Selecting $x=\frac{f(0)}{2}$ and $y=f(0)$ in the original equality gives
$$
f(f(f(0)))+f\left(-\frac{f(0)}{2}\right)=f\left(\frac{f(0)}{2} \cdot f(f(0))-\frac{f(0)}{2}\right) .
$$
Applying (1) here leads to $f(0)+f\left(-\frac{f(0)}{2}\right)=f\left(-\frac{f(0)}{2}\right)$ which yields
$$
f(0)=0
$$
Substituting $y=0$ into the original equation we obtain $f(f(0))+f(x)=f(x f(0)-x)$, which in the light of (2) reduces to
$$
f(x)=f(-x)
$$
for all $x$. Finally, let us substitute $x=0$ into the original equation. In the light of (2) and (3), we obtain $f(f(y))+f(y)=0$, i. e.,
$$
f(f(y))=-f(y)
$$
for all real numbers $y$. Now, for each real $y$, we have
$$
\begin{aligned}
& f(y)=-f(f(y)) \quad(\text { by }(4)) \\
& =f(f(f(y))) \quad(\text { by (4)) } \\
& =f(-f(y)) \quad(\text { by }(4)) \\
& =f(f(y)) \quad \text { (by (3)) } \\
& =-f(y), \quad(\text { by (4)) }
\end{aligned}
$$
so that $f(y)=0$.
|
f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f$ defined on all real numbers and taking real values such that
$$
f(f(y))+f(x-y)=f(x f(y)-x)
$$
for all real numbers $x, y$.
Answer: $f(x)=0$.
|
Substituting $x=y=0$ into the original equality gives $f(f(0))+f(0)=f(0)$, implying
$$
f(f(0))=0
$$
Selecting $x=\frac{f(0)}{2}$ and $y=f(0)$ in the original equality gives
$$
f(f(f(0)))+f\left(-\frac{f(0)}{2}\right)=f\left(\frac{f(0)}{2} \cdot f(f(0))-\frac{f(0)}{2}\right) .
$$
Applying (1) here leads to $f(0)+f\left(-\frac{f(0)}{2}\right)=f\left(-\frac{f(0)}{2}\right)$ which yields
$$
f(0)=0
$$
Substituting $y=0$ into the original equation we obtain $f(f(0))+f(x)=f(x f(0)-x)$, which in the light of (2) reduces to
$$
f(x)=f(-x)
$$
for all $x$. Finally, let us substitute $x=0$ into the original equation. In the light of (2) and (3), we obtain $f(f(y))+f(y)=0$, i. e.,
$$
f(f(y))=-f(y)
$$
for all real numbers $y$. Now, for each real $y$, we have
$$
\begin{aligned}
& f(y)=-f(f(y)) \quad(\text { by }(4)) \\
& =f(f(f(y))) \quad(\text { by (4)) } \\
& =f(-f(y)) \quad(\text { by }(4)) \\
& =f(f(y)) \quad \text { (by (3)) } \\
& =-f(y), \quad(\text { by (4)) }
\end{aligned}
$$
so that $f(y)=0$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.