id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
58,559 | The snail Leona fell into the middle of a square grid. She decided to crawl "in a spiral" as indicated in the picture; she will not visit any square twice and will not skip any square.
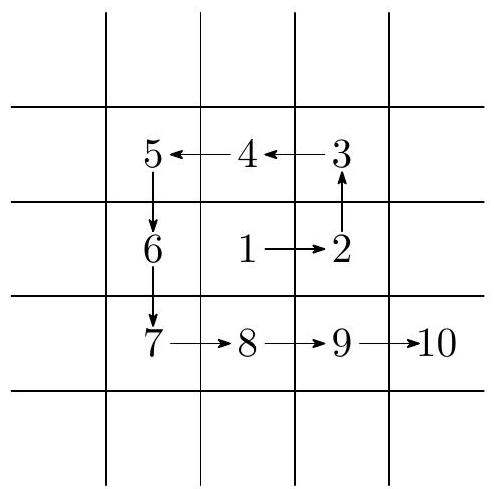
From the first square to the second, she crawled east, from the second to the third, north, from the third to the fourth, west, from the fourth to the fifth, also west, from the fifth to the sixth, south... In which direction did she crawl from the 81st to the 82nd square?
(M. Petrová) | east |
5,522 | If the interior angles \( A, B, C \) of triangle \( \triangle ABC \) satisfy \(\sin A = \cos B = \tan C\), find the value of \(\cos^3 A + \cos^2 A - \cos A\). | \dfrac{1}{2} |
60,985 | 8. Let the sequence $a_{n}=\left[(\sqrt{2}+1)^{n}+\left(\frac{1}{2}\right)^{n}\right], n \geq 0$, where $[x]$ denotes the greatest integer less than or equal to $x$. Then
$$
\sum_{n=1}^{\infty} \frac{1}{a_{n-1} a_{n+1}}=
$$ | \frac{1}{8} |
68,973 | ## Task A-4.4.
Determine the number of complex solutions to the equation
$$
z^{2019}=z+\bar{z}
$$ | 2019 |
25,282 | [Ratio of areas of triangles with a common angle] Auxiliary similar triangles $\quad]$
In triangle $A B C$, angle $C$ is $30^{\circ}$, and angle $A$ is acute. A line perpendicular to side $B C$ is drawn, cutting off triangle $C N M$ from triangle $A B C$ (point $N$ lies between vertices $B$ and $C$). The areas of triangles $C N M$ and $A B C$ are in the ratio $3: 16$. Segment $M N$ is half the height $B H$ of triangle $A B C$. Find the ratio $A H: H C$. | \frac{1}{3} |
25,799 | 42nd Putnam 1981 Problem A4 A particle moves in a straight line inside a square side 1. It is reflected from the sides, but absorbed by the four corners. It starts from an arbitrary point P inside the square. Let c(k) be the number of possible starting directions from which it reaches a corner after traveling a distance k or less. Find the smallest constant a 2 , such that from some constants a 1 and a 0 , c(k) ≤ a 2 k 2 + a 1 k + a 0 for all P and all k. Solution | \pi |
62,937 | What is the maximum number of sides a convex polygon can have if it can be divided into right-angled triangles with acute angles of 30 and 60 degrees? | 12 |
54,029 | 4. If $z_{1}, z_{2}, z_{3} \in \mathbb{C}$ such that $\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|=1, z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=0$ and $z_{1}+z_{2}+z_{3} \neq 0$, calculate $\left|z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right|$. R.M.T. $4 / 2015$ | 2 |
22,034 | Let \( a_{1}, a_{2}, \cdots, a_{21} \) be a permutation of \( 1, 2, \cdots, 21 \) such that
$$
\left|a_{20}-a_{21}\right| \geqslant\left|a_{19}-a_{21}\right| \geqslant\left|a_{18}-a_{21}\right| \geqslant \cdots \geqslant\left|a_{1}-a_{21}\right|.
$$
The number of such permutations is \[\qquad\]. | 3070 |
1,104 | Prove that \((1 + \frac{x}{y})(1 + \frac{y}{z})(1 + \frac{z}{x}) \geq 2 + 2\frac{x + y + z}{w}\) for all positive reals \(x\), \(y\), \(z\), where \(w\) is the cube root of \(xyz\). | (1 + \frac{x}{y})(1 + \frac{y}{z})(1 + \frac{z}{x}) \geq 2 + 2\frac{x + y + z}{w} |
58,672 | 9.1. Petya wrote ten natural numbers on the board, none of which are equal. It is known that among these ten numbers, three can be chosen that are divisible by 5. It is also known that among the ten numbers written, four can be chosen that are divisible by 4. Can the sum of all the numbers written on the board be less than $75$?
(P. Kozhevnikov) | 71 |
32,484 | [Example 1.4.5] On the plane, there are finitely many polygons. If any two of these polygons are intersected by a line passing through the origin, then these polygons are said to be properly placed. Find the smallest natural number $m$, such that for any set of properly placed polygons, one can draw $m$ lines passing through the origin, so that each of these polygons intersects at least one of these $m$ lines. | 2 |
16,898 | The "Hua Luogeng" Golden Cup Junior Math Invitational Contest was first held in 1986, the second in 1988, and the third in 1991, and has subsequently been held every 2 years. The sum of the digits of the year of the first "Hua Cup" is: \( A_1 = 1 + 9 + 8 + 6 = 24 \). The sum of the digits of the years of the first two "Hua Cup" contests is: \( A_2 = 1 + 9 + 8 + 6 + 1 + 9 + 8 + 8 = 50 \). Find the sum of the digits of the years of the first 50 "Hua Cup" contests, \( A_{50} \). | 629 |
59,948 | 209. "Fibonacci Tetrahedron". Find the volume of the tetrahedron whose vertices are located at the points with coordinates $\left(F_{n}, F_{n+1}, F_{n+2}\right), \quad\left(F_{n+3}, F_{n+4}, F_{n+5}\right), \quad\left(F_{n+6}, F_{n+7}, F_{n+8}\right)$ and $\left(F_{n+9}, F_{n+10}, F_{n+11}\right)$, where $F_{i}$ is the $i$-th term of the Fibonacci sequence: $1,1,2,3,5,8 \ldots$. | 0 |
63,699 | 4. Masha has 2 kg of "Swallow" candies, 3 kg of "Truffle" candies, 4 kg of "Bird's Milk" candies, and 5 kg of "Citron" candies. What is the maximum number of New Year's gifts she can make if each gift must contain 3 different types of candies, 100 grams of each? | 45 |
30,520 | Question 234: In the interval $[1,1000]$, take $\mathrm{n}$ different numbers $\mathrm{a}_{1}, \mathrm{a}_{2}, \ldots, \mathrm{a}_{\mathrm{n}}$. There always exist two numbers $\mathrm{a}_{\mathrm{i}},$ $a_{j}$, such that $0<\left|a_{i}-a_{j}\right|<1+3 \sqrt[3]{a_{i} a_{j}}$. Find the minimum possible value of $n$. | 11 |
54,498 | ## Task A-1.4.
Determine the smallest natural number whose sum of digits is divisible by 7 and has the property that the sum of the digits of its successor is also divisible by 7. | 69999 |
63,688 | 7. For four different integers, all their pairwise sums and pairwise products were calculated and written on the board. What is the smallest number of different numbers that could have appeared on the board? (I. Rubanov) | 6 |
4,352 | Let \( ABC \) be a triangle, and let \( D, E \), and \( F \) be the midpoints of sides \( BC, CA \), and \( AB \), respectively. Let the angle bisectors of \( \angle FDE \) and \( \angle FBD \) meet at \( P \). Given that \( \angle BAC = 37^\circ \) and \( \angle CBA = 85^\circ \), determine the degree measure of \( \angle BPD \). | 61 |
9,465 | 2. (8 points) Dad's birthday is on May 1st, and Chunchun's birthday is on July 1st. Starting from December 26, 2012 (Day 1), until Day 2013, Dad and Chunchun have had $\qquad$ birthdays in total. | 11 |
50,322 | A unit side regular hexagonal lattice point is reflected to the midpoint of the six sides. Calculate the area of the resulting hexagon.
Consider an arbitrary internal point of a regular hexagon with a side length of one unit. This point is reflected to the midpoint of each of the six sides. Calculate the area of the resulting hexagon. | \frac{9\sqrt{3}}{2} |
56,731 | In the triangle $ABC$ below, there is a point $D$ on its side $AB$, such that $AB=CD$, $\widehat{ABC}=100^{\circ}$, and $\widehat{DCB}=40^{\circ}$.
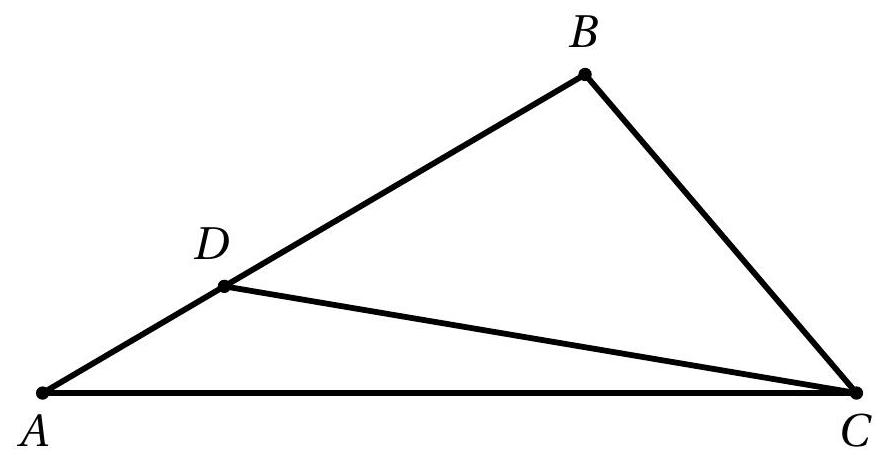
a) What is the measure of the angle $\widehat{BDC}$?
b) What is the measure of the angle $\widehat{ACD}$?
# | 10 |
7,220 | Let the function \( f(x) \) (for \( x \in \mathbf{R}, x \neq 0 \)) satisfy the condition \( f(x_{1} x_{2}) = f(x_{1}) + f(x_{2}) \) for any nonzero real numbers \( x_{1} \) and \( x_{2} \), and \( f(x) \) is an increasing function over \( (0, +\infty) \). Then the solution to the inequality \( f(x) + f\left(x - \frac{1}{2}\right) \leqslant 0 \) is ______. | \left[ \frac{1 - \sqrt{17}}{4}, 0 \right) \cup \left( 0, \frac{1}{2} \right) \cup \left( \frac{1}{2}, \frac{1 + \sqrt{17}}{4} \right] |
57,051 | 4. Let the set $M=\{1,2, \cdots, 2020\}, A \subseteq M$, and for any element $x$ in set $A$, $4x \notin A$. Then the maximum number of elements in set $A$ is $\qquad$ . | 1616 |
26,630 | Consider 2022 lines in the plane, no two of which are parallel and no three of which are concurrent. Let $E$ be the set of their intersection points. We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors. How many colors are needed at a minimum to achieve such a coloring? | 3 |
52,513 | ## Task Condition
Calculate the areas of figures bounded by lines given in polar coordinates.
$$
r=2 \cos 6 \phi
$$ | 2\pi |
53,268 | Exercise 10. Count the number of rearrangements $a_{1}, a_{2}, \ldots, a_{2023}$ of the sequence $1,2, \ldots, 2023$ such that $a_{k}>k$ for exactly one value of $k$. | 2^{2023}-2024 |
18,863 | Given an equilateral triangle $\triangle ABC$. Points $D$ and $E$ are taken on side $BC$ such that $BC = 3DE$. Construct an equilateral triangle $\triangle DEF$ and connect point $A$ to point $F$. Draw $DG$ parallel to $AF$ intersecting side $AB$ at point $G$, and draw $EH$ parallel to $AF$ intersecting side $AC$ at point $H$. Draw perpendiculars $GI \perp AF$ and $HJ \perp AF$. Given that the area of $\triangle BDF$ is $45$ and the area of $\triangle DEF$ is $30$, find the ratio $GI \div HJ$. | 3 |
15,895 | Let $\alpha = \left(\alpha_{1}, \ldots, \alpha_{n}\right)$ and $\beta = \left(\beta_{1}, \ldots, \beta_{n}\right)$ be two sets of exponents with an equal sum.
Prove that if $\alpha \neq \beta$, then for all non-negative $x_{1}, \ldots, x_{n}$ the inequality $T_{\alpha}\left(x_{1}, \ldots, x_{n}\right) \geq T_{\beta}\left(x_{1}, \ldots, x_{n}\right)$ holds.
Definitions of the polynomials $T_{\alpha}$ can be found in problem $\underline{61417}$, and the definition of comparison for the exponents can be found in the reference book. | T_{\alpha}\left(x_{1}, \ldots, x_{n}\right) \geq T_{\beta}\left(x_{1}, \ldots, x_{n}\right) |
53,218 | A rhombus has diagonal lengths of 6 and 8 units. A regular triangle is inscribed in the rhombus, with one vertex at one endpoint of the shorter diagonal, and one side parallel to the longer diagonal of the rhombus. What is the height of this triangle? | \frac{96-24\sqrt{3}}{13} |
7,043 | Let \( x_0 > x_1 > \cdots > x_n \) be real numbers. Show that \( x_0 + \frac{1}{x_0 - x_1} + \frac{1}{x_1 - x_2} + \cdots + \frac{1}{x_{n-1} - x_n} \geq x_n + 2n \). | x_0 + \frac{1}{x_0 - x_1} + \frac{1}{x_1 - x_2} + \cdots + \frac{1}{x_{n-1} - x_n} \geq x_n + 2n |
68,642 | \section*{Exercise 1 - 011011}
For an isosceles triangle, the following are given: \(A B=c=87.51 \text{ m}, \angle C A B=\alpha=93.42^{\circ}\). Calculate the remaining angles and sides! | 127.40\, |
62,866 | 8. (10 points) In the inscribed quadrilateral $A B C D$, the degree measures of the angles are in the ratio $\angle A: \angle B: \angle C=2: 3: 4$. Find the length of $A C$, if $C D=5, B C=6 \sqrt{3}-2.5$. | 13 |
58,641 | ## 239. Math Puzzle $4 / 85$
A round steel rod is to withstand a tensile force of 150000 N. The permissible stress of the steel grade used is $12000 \mathrm{~N} / \mathrm{cm}^{2}$.
How large must the diameter of the rod be? $(\pi=3.14)$ | 3.99 |
17,882 | Given \( \triangle ABC \), let \( I \) be its incenter and the angle bisectors of \(\angle A\), \(\angle B\), and \(\angle C\) intersect the opposite sides at \( A' \), \( B' \), and \( C' \) respectively. Prove that \(\frac{1}{4} < \frac{AI \cdot BI \cdot CI}{AA' \cdot BB' \cdot CC'} \leq \frac{8}{27}\). | \frac{1}{4} < \frac{AI \cdot BI \cdot CI}{AA' \cdot BB' \cdot CC'} \leq \frac{8}{27} |
23,926 | Given a function \( f: \mathbf{R} \rightarrow \mathbf{R} \) such that for any real numbers \( x \) and \( y \), \( f(2x) + f(2y) = f(x+y) f(x-y) \). Additionally, \( f(\pi) = 0 \) and \( f(x) \) is not identically zero. What is the period of \( f(x) \)? | 4\pi |
54,608 | How many prime numbers are there among the four-digit numbers whose digits are $1,2,3$ and $4$ in some order?
$^{1}$ Let's prove and use the fact that to determine the divisibility of a number, it is sufficient to test its divisibility only by prime numbers whose squares are not greater than the number in question. | 4 |
56,689 | 7. Builders need to tile the floor in a small house with small square tiles. The client says that the variant with more red tiles is preferable. For variants with the same number of red tiles, the one with more orange tiles is preferable; and generally, the client's preferences for colors are: red, orange, yellow, green, blue, indigo. His wife, however, wants the opposite:
- the number of indigo tiles should be at least as many as the total number of red, orange, yellow, green, and blue tiles;
- the number of blue tiles should be at least as many as the total number of red, orange, yellow, and green tiles;
- the number of green tiles should be at least as many as the total number of red, orange, and yellow tiles;
- the number of yellow tiles should be at least as many as the total number of red and orange tiles;
- the number of orange tiles should be at least as many as the number of red tiles.
The floor requires 100 tiles.
How many green tiles will be needed if the most preferable variant for the client is chosen, which also meets the conditions set by his wife? | 13 |
14,096 | Given 155 birds perched on a circle \( C \). If \(\overparen{P_{i} P_{j}} \leqslant 10^{\circ}\), then birds \( P_{i} \) and \( P_{j} \) are considered mutually visible. Find the minimum number of pairs of mutually visible birds (assuming multiple birds can occupy the same position). | 270 |
1,835 | B3. In a red box, there are twelve balls numbered from 1 to 12. Jan moved some of these balls to a green box. He found that for any two balls in the green box, if the numbers on these balls are $a$ and $b$, then the ball with the number $|a-b|$ is in the red box. What is the maximum number of balls Jan could have moved to the green box?
## 55th Mathematical Competition for High School Students in Slovenia
Regional Competition, March 30, 2011
## Solutions for 1st Year
In section A, a correct answer will be awarded two points, while an incorrect answer will result in a deduction of half a point. To avoid a potential negative final score, each contestant is given an initial 2 points.
| A1 | A2 | A3 |
| :---: | :---: | :---: |
| C | C | D |
Explanations: | 6 |
26,949 | 2. For $x, y \in[1,3]$ find the minimum value of the expression
$$
A=\frac{\left(3 x y+x^{2}\right) \sqrt{3 x y+x-3 y}+\left(3 x y+y^{2}\right) \sqrt{3 x y+y-3 x}}{x^{2} y+y^{2} x}
$$ | 4 |
66,361 | 1. Given the function $y=\frac{\left|x^{2}-1\right|}{x-1}$, its graph intersects with the graph of the function $y=k x-2$ at two points. Then the range of the real number $k$ is $\qquad$ . | (0,1)\cup(1,4) |
16,446 | Given the hyperbola \( C: \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 \) with \( a > 0 \) and \( b > 0 \), the eccentricity is \( \frac{\sqrt{17}}{3} \). Let \( F \) be the right focus, and points \( A \) and \( B \) lie on the right branch of the hyperbola. Let \( D \) be the point symmetric to \( A \) with respect to the origin \( O \), with \( D F \perp A B \). If \( \overrightarrow{A F} = \lambda \overrightarrow{F B} \), find \( \lambda \). | \dfrac{1}{2} |
30,444 | $15 \cdot 26$ Let the natural number $n(n>3)$ have the following property: when the set $S_{n}=\{3,4, \cdots, n\}$ is arbitrarily divided into two groups, there is always a group containing three numbers $a, b, c$ (allowing $a=b$), such that $a b=c$. Find the smallest value of such $n$.
(China National Training Team Test Question, 1988) | 243 |
17,286 | Let the following system of equations be satisfied for positive numbers \(x, y, z\):
\[
\left\{
\begin{array}{l}
x^{2}+x y+y^{2}=147 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=163
\end{array}\right.
\]
Find the value of the expression \( x y+y z+x z \). | 56 |
61,714 | 1. (Easy) Among all victims of zombie bites, $10 \%$ are prescribed the experimental drug Undetenin to treat them. Overall, $4 \%$ of the human population suffer an adverse reaction to Undetenin. Out of all the patients being treated with Undetenin, $2 \%$ suffer an adverse reaction to the drug. What is the probability that a patient allergic to Undetenin is prescribed the drug? | 5 |
27,400 | 3. Given $0 \leq a_{k} \leq 1(k=1,2, \ldots, 2020)$, let $a_{2021}=a_{1}, a_{2022}=a_{2}$, then the maximum value of $\sum_{k=1}^{2020}\left(a_{k}-\right.$ $\left.a_{k+1} a_{k+2}\right)$ is $\qquad$ . | 1010 |
9,921 | A heap of stones has a total weight of 100 kg, where the weight of each stone does not exceed 2 kg. Choose some stones from this heap in any combination and find the difference between the sum of these chosen stones' weights and 10 kg. Denote by $d$ the minimum value of the absolute value of these differences. Find the maximum value of $d$ among all heaps of stones satisfying the above conditions. | \dfrac{10}{11} |
23,184 | Jack has a large number of tiles, each of which is in the shape of a right-angled triangle with side lengths \(3 \text{ cm}, 4 \text{ cm}\) and \(5 \text{ cm}\). Is it possible for Jack to combine a number of these tiles, without gaps or overlap, to form a rectangle of size \(2016 \text{ cm} \times 2021 \text{ cm}\)? | \text{Yes} |
34,279 | In a corner stand, there are three shelves measuring $30 \mathrm{~cm} \times 40 \mathrm{~cm}$, and the distance between adjacent shelves is equal. Where the two walls and the middle shelf meet, three spiders have made their nests. Once, one of them climbed diagonally up one wall to the corner of the top shelf, another crawled diagonally down the other wall to the corner of the bottom shelf. The third spider remained in place and observed that its companions appeared at an angle of $120^{\circ}$. What is the distance between the shelves? (The adjacent shelves are the same distance apart.) | 35 |
57,360 | 13. Among the thirteen natural numbers from $1 \sim 13$, select twelve natural numbers to fill in the 12 empty cells in the figure, so that the sum of the four numbers in each row is equal, and the sum of the three numbers in each column is equal. What is the number that is not filled in the cells? And please fill in the other numbers in the cells.
---
The translation preserves the original format and line breaks. | 7 |
11,798 | A circle touches the sides of an angle at points $A$ and $B$. The distance from point $C$, which lies on the circle, to the line segment $AB$ is 8. Find the sum of the distances from point $C$ to the sides of the angle, given that one of these distances is 30 less than the other. | 34 |
23,276 | Find the number of subsets of $\{1,2,3,\ldots,10\}$ that contain exactly one pair of consecutive integers. Examples of such subsets are $\{\mathbf{1},\mathbf{2},5\}$ and $\{1,3,\mathbf{6},\mathbf{7},10\}.$
Please give the answer directly without any intermediate steps. | 235 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.