Dataset Viewer
question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-operations-to-reduce-x-to-zero | Change Your Perspective | JAVA Explanation | change-your-perspective-java-explanation-5phd | Logic\nInitially, this question might look like a DP problem: pick either left or right recursively and collect the number of operations along the way. A brute | ciote | NORMAL | 2022-06-11T01:26:17.092317+00:00 | 2022-06-11T08:18:42.701216+00:00 | 18,240 | false | ### Logic\nInitially, this question might look like a DP problem: pick either left or right recursively and collect the number of operations along the way. A brute force approach would result in an `O(2^n)` complexity which isn\'t great. Memoization would improve this but we\'ll exceed the memory limit as I\'ve tested. Besides, we can do better.\n\nBy simply reframing the question, we can come up with an `O(n)` complexity solution. The difficulty in this question arises from deciding whether to choose the left or the right element to remove at any given point. However, while we\'re removing elements from the array, we\'re definitely going to be letting some elements remain as well. In particular, the middle elements. \n\n**Key observation:**\n> The number of elements removed equals <ins>n minus the number of elements that *aren\'t* removed</ins>.\n>> Therefore, to find the minimum number of elements to remove, we can find the maximum number of elements to not remove!\n\n\n\nSo, instead of trying to find the minimum number of operations, why don\'t we focus on finding the longest subarray in the middle. One main thing to note is that our subarray should sum to **`sum - x`** (where `sum` is the sum of all elements in our array).\nWhy? because the middle elements are technically the ones we don\'t want. If the sum of the outer elements equals `x`, then we\'re looking for a middle sum of `sum - x`. If this doesn\'t quite make sense, pay attention to the below diagram with `nums = [1,5,3,9,1,7,1,3], x = 12`:\n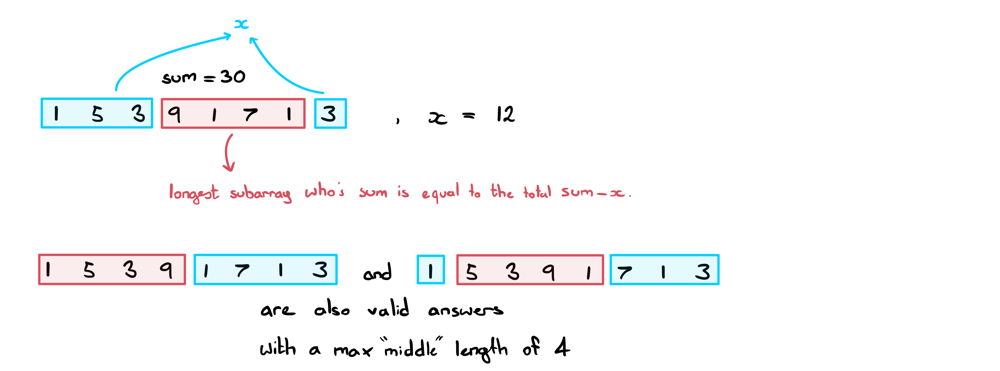\n(Keep in mind that this approach only works due to the absence of negative numbers!)\n___\n### Finding our max middle subarray length:\nWe can find this using a two-pointer / sliding window approach. Start left and right both at index 0.\n* Increment right until the current window sum is `> sum - x`\n* Update our `maxLength` if and only if our current window sum `== sum - x`\n* Repeat the above steps until we reach the end of the array.\n\n\n\nAwesome! Now we have everything we need to start coding.\n___\n### How should I approach this question in an interview?\nWhen you\'re presented this question, it might not be obvious that there exists a solution other than DP (at least, it wasn\'t obvious for me!). So, how would you know to approach the question through any other means? What saved me when doing this question was the simple realisation that removing edge values is the same as shrinking the array. Hence, there will always remain a middle subarray of length >= 0.\n\nA habit that I\'ve developed over time whenever I run into trouble coming up with a solution is to <ins>reframe the question</ins>. Often times when you\'re given a question in an interview, it\'s riddled with questionable requirements or red herrings. The interviewer is likely expecting you to *extract out* the core requirements from the question and truncate it down to as simple a question as you can manage.\n\nIt does take time and practice to spot the owl from the trees. That being said, here are some effective ways to ease yourself into the right mindset: \n* If a question is implicitly asking for A when the question is actually solved using B, draw examples and look for alternate patterns.\n* Pay attention to the constraints of the inputs/outputs (in this question, the values being strictly positive was a hint!)\n* Be creative! Even try rewording the question to something as different as you can think of while still maintaining the requirements of the question. \n\nIf all else fails, pay attention to the subtle hints your interviewer might be throwing your way. (By the way, the best way to get hints from your interviewer is to explain all your thoughts to them as you go. If they don\'t know where you\'re stuck, they can\'t help you). \n\n___\n### Code:\nIf you have any questions, suggestions or improvements, feel free to let me know. Thanks for reading!\n```java\npublic int minOperations(int[] nums, int x) {\n\tint sum = 0;\n\tfor (int num: nums) sum += num;\n\n\tint maxLength = -1, currSum = 0;\n\tfor (int l=0, r=0; r<nums.length; r++) {\n\t\tcurrSum += nums[r];\n\t\twhile (l <= r && currSum > sum - x) currSum -= nums[l++];\n\t\tif (currSum == sum - x) maxLength = Math.max(maxLength, r-l+1);\n\t}\n\n\treturn maxLength == -1 ? -1 : nums.length - maxLength;\n}\n```\n\n**Time complexity:** `O(n)`\n**Space complexity:** `O(1)` | 687 | 2 | ['Two Pointers', 'Java'] | 53 |
minimum-operations-to-reduce-x-to-zero | [Java] Detailed Explanation - O(N) Prefix Sum/Map - Longest Target Sub-Array | java-detailed-explanation-on-prefix-summ-hdew | Key Notes:\n- We could use dfs+memo or BFS, but they are too slow and will TLE (?)\n- If it exists an answer, then it means we have a subarray in the middle of | frankkkkk | NORMAL | 2020-11-15T04:01:47.274207+00:00 | 2020-11-15T04:57:20.483673+00:00 | 24,339 | false | **Key Notes:**\n- We could use dfs+memo or BFS, but they are too slow and will TLE (?)\n- If it exists an answer, then it means we have **a subarray in the middle of original array whose sum is == totalSum - x**\n- If we want to minimize our operations, then we should **maximize the length of the middle subarray.**\n\t- Then the qeustion becomes: *Find the Longest Subarray with Sum Equals to TotalSum - X*\n\t- We could simply use Map + Prefix Sum to get it!\n\n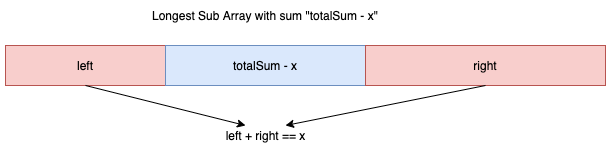\n\n**Similar Idea:** \n- [918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/)\n- [1423. Maximum Points You Can Obtain from Cards](https://leetcode.com/problems/maximum-points-you-can-obtain-from-cards/)\n\n```java\nint target = -x;\nfor (int num : nums) target += num;\n\nif (target == 0) return nums.length; // since all elements are positive, we have to take all of them\n\nMap<Integer, Integer> map = new HashMap<>();\nmap.put(0, -1);\nint sum = 0;\nint res = Integer.MIN_VALUE;\n\nfor (int i = 0; i < nums.length; ++i) {\n\n\tsum += nums[i];\n\tif (map.containsKey(sum - target)) {\n\t\tres = Math.max(res, i - map.get(sum - target));\n\t}\n\n // no need to check containsKey since sum is unique\n\tmap.put(sum, i);\n}\n\nreturn res == Integer.MIN_VALUE ? -1 : nums.length - res;\n``` | 492 | 5 | [] | 32 |
minimum-operations-to-reduce-x-to-zero | Are you stuck ? once read this . logic explained clearly | easy-to-understand | are-you-stuck-once-read-this-logic-expla-ugx7 | so , the problem is saying that we can remove either leftmost or rightmost element and we have to remove them in such a way that \n1.remove minimum number of el | kevaljoshi2312 | NORMAL | 2021-02-24T14:04:21.056506+00:00 | 2021-02-24T14:04:21.056548+00:00 | 13,070 | false | so , the problem is saying that we can remove either leftmost or rightmost element and we have to remove them in such a way that \n1.remove minimum number of elements and\n2. sum of all removed element is X \n\nNow main point is that if successfully remove elements such that sum of removed elements is X , then \n1. sum of remaining array elements will be (sum-X) \n2. remaing array will be subarray of original array.\n\n\n.\n\nSo , now our task is find subaarray whose sum is (sum - X) and its length is maximum ( because we want to remove minimum number of elements , so we will have to maximise remianing element ) .\n\ntime - O(N)\nspace - O(1)\n\n```\nint minOperations(vector<int>& v, int x) \n {\n int i,len=0,sum1=0,sum2=0;\n for(i=0;i<v.size();i++)\n sum2+=v[i]; // calculating sum of whole array \n\t\t\t\n sum2-=x; // this is sum of remiaing elements . after removing X \n\t\t\n if(sum2==0) // sum of array is equal to X . means we\'ll have to remove all elements\n return v.size();\n\t\t\t\n// sliding window technique \n// i points to begining of subarray and j points to end of subarray \n\n\t\t// sum2 is desired sum while sum1 is current sum\n int j;i=0;\n for(j=0;j<v.size();j++)\n {\n sum1+=v[j];\n\t\t\t\n while(i<v.size()&&sum1>sum) // if sum of current subaaray is greater than desired sum\n sum1-=v[i++];\n\t\t\t\t\n if(sum1==sum2) // if sum of current subarray is equal to desired sum then update length\n len=max(len,j-i+1); // we want subarray with maximum length \n }\n if(!len) // No subarray found with desired sum .\n return -1;\n return v.size()-len;\n }\n\n | 326 | 1 | ['C', 'C++'] | 34 |
minimum-operations-to-reduce-x-to-zero | ✅ [C++/Python] Simple Solution w/ Explanation | Sliding Window | cpython-simple-solution-w-explanation-sl-q7ra | Sometimes, converting a problem into some other familiar one helps a lot. This question is one of them.\nLet me state a different problem, and your task is to r | r0gue_shinobi | NORMAL | 2022-06-11T01:11:30.684302+00:00 | 2022-06-11T02:56:41.180591+00:00 | 15,310 | false | Sometimes, converting a problem into some other familiar one helps a lot. This question is one of them.\nLet me state a different problem, and your task is to relate how solving this problem will help in solving the actual one.\n> Given an array containing integers, your task is to find the length of the longest subarray with a given sum.\n\nIf you were able to relate, congratulations! \uD83C\uDF89\nAnd if not, don\'t worry; it happens with all of us (or maybe use hints \uD83D\uDE09).\nContinue reading below to find the solution.\n___\n___\n\u2705 **Solution I - Sliding Window [Accepted]**\n\nWe need to make `prefix_sum + suffix_sum = x`. But instead of this, finding a subarray whose sum is `sum(nums) - x` will do the job. Now we only need to maximize the length of this subarray to minimize the length of `prefix + suffix`, which can be done greedily. By doing this, we can get the minimum length, i.e., the minimum number of operations to reduce `x` to exactly `0` (if possible).\n\nIf you haven\'t heard the term "sliding window" before, visit [this link](https://stackoverflow.com/questions/8269916/what-is-sliding-window-algorithm-examples).\n\n1. Let us take a sliding window whose ends are defined by `start_idx` and `end_idx`.\n2. If the sum of this sliding window (subarray) exceeds the target, keep reducing the window size (by increasing `start_idx`) until its sum becomes `<= target`.\n3. If the sum becomes equal to the target, compare the length, and store if it exceeds the previous length.\n4. Return `-1` if the sum of the sliding window never becomes equal to `target`.\n\n<iframe src="https://leetcode.com/playground/PoeSGL3x/shared" frameBorder="0" width="1080" height="450"></iframe>\n\n- **Time Complexity:** `O(n)`\n- **Space Complexity:** `O(1)`\n\n___\n___\nIf you like the solution, please **upvote**! \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F\n | 207 | 1 | ['Greedy', 'C', 'Sliding Window', 'Python', 'Python3'] | 15 |
minimum-operations-to-reduce-x-to-zero | ✅ 96.51% Sliding Window | 9651-sliding-window-by-vanamsen-3lh5 | Comprehensive Guide to Solving "Minimum Operations to Reduce X to Zero"\n\n## Introduction & Problem Statement\n\nGiven an integer array nums and an integer x, | vanAmsen | NORMAL | 2023-09-20T00:12:02.046844+00:00 | 2023-09-20T02:02:46.884474+00:00 | 24,536 | false | # Comprehensive Guide to Solving "Minimum Operations to Reduce X to Zero"\n\n## Introduction & Problem Statement\n\nGiven an integer array `nums` and an integer `x`, the task is to find the minimum number of operations to reduce `x` to exactly 0 by removing either the leftmost or rightmost element from the array `nums` in each operation. What makes this problem intriguing is that it\'s not a straightforward minimization problem; it involves searching for subarrays, working with prefix sums, and applying two-pointer techniques.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Array Constraints**: \n - $$1 \\leq \\text{nums.length} \\leq 10^5$$\n - $$1 \\leq \\text{nums}[i] \\leq 10^4$$\n \n2. **Target Number `x`**:\n - $$1 \\leq x \\leq 10^9$$\n\n3. **Operations**: \n You can either remove the leftmost or the rightmost element from the array `nums` and subtract its value from $$ x $$.\n\n4. **Minimization Objective**: \n The goal is to minimize the number of operations to reduce $$ x $$ to zero.\n\n---\n\n## One Primary Strategy to Solve the Problem:\n\n## Live Coding & Explain\nhttps://youtu.be/3dhzAV81hBI?si=QgcosgkvdbMBBKtq\n\n# Approach: Sliding Window with Prefix Sum\n\nTo solve this problem, we apply the Sliding Window technique with a twist involving Prefix Sum. We use two pointers, `left` and `right`, to traverse the array `nums` and find the longest subarray whose sum equals the total sum of elements in `nums` minus `x`.\n\n## Key Data Structures:\n\n- **max_len**: An integer to store the length of the longest subarray that can be excluded to make the sum equal to `x`.\n- **cur_sum**: An integer to store the sum of elements in the current subarray.\n\n## Enhanced Breakdown:\n\n1. **Initialize and Calculate the Target**:\n - Compute `target = sum(nums) - x`, as we\'re interested in finding a subarray with this sum.\n - Initialize `max_len`, `cur_sum`, and `left` to 0.\n \n2. **Check for Edge Cases**:\n - If `target` is zero, it means we need to remove all elements to make the sum equal to `x`. In this case, return the total number of elements, `n`.\n\n3. **Traverse the Array with Two Pointers**:\n - Iterate through `nums` using a `right` pointer.\n - Update `cur_sum` by adding the current element `nums[right]`.\n \n4. **Sliding Window Adjustment**:\n - If `cur_sum` exceeds `target`, slide the `left` pointer to the right by one position and decrease `cur_sum` by `nums[left]`.\n\n5. **Update Max Length**:\n - If `cur_sum` matches `target`, update `max_len` with the length of the current subarray, which is `right - left + 1`.\n\n6. **Conclude and Return**:\n - After the loop, if `max_len` is non-zero, return `n - max_len`. Otherwise, return -1, indicating it\'s not possible to reduce `x` to zero.\n\n## Complexity Analysis:\n\n**Time Complexity**: \n- Since we traverse the array only once, the time complexity is $$ O(n) $$.\n\n**Space Complexity**: \n- The algorithm uses only a constant amount of extra space, thus having a space complexity of $$ O(1) $$.\n\n---\n\n# Code\n``` Python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target, n = sum(nums) - x, len(nums)\n \n if target == 0:\n return n\n \n max_len = cur_sum = left = 0\n \n for right, val in enumerate(nums):\n cur_sum += val\n while left <= right and cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n if cur_sum == target:\n max_len = max(max_len, right - left + 1)\n \n return n - max_len if max_len else -1\n```\n``` Go []\nfunc minOperations(nums []int, x int) int {\n target, n := -x, len(nums)\n for _, num := range nums {\n target += num\n }\n \n if target == 0 {\n return n\n }\n \n maxLen, curSum, left := 0, 0, 0\n \n for right, val := range nums {\n curSum += val\n for left <= right && curSum > target {\n curSum -= nums[left]\n left++\n }\n if curSum == target {\n if right - left + 1 > maxLen {\n maxLen = right - left + 1\n }\n }\n }\n \n if maxLen != 0 {\n return n - maxLen\n }\n return -1\n}\n```\n``` Rust []\nimpl Solution {\n pub fn min_operations(nums: Vec<i32>, x: i32) -> i32 {\n let mut target: i32 = -x;\n let n = nums.len() as i32;\n \n for &num in &nums {\n target += num;\n }\n \n if target == 0 {\n return n;\n }\n \n let (mut max_len, mut cur_sum, mut left) = (0, 0, 0);\n \n for right in 0..n as usize {\n cur_sum += nums[right];\n while left <= right as i32 && cur_sum > target {\n cur_sum -= nums[left as usize];\n left += 1;\n }\n if cur_sum == target {\n max_len = std::cmp::max(max_len, right as i32 - left + 1);\n }\n }\n \n if max_len != 0 { n - max_len } else { -1 }\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0, n = nums.size();\n for (int num : nums) target += num;\n target -= x;\n \n if (target == 0) return n;\n \n int max_len = 0, cur_sum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n cur_sum += nums[right];\n while (left <= right && cur_sum > target) {\n cur_sum -= nums[left];\n left++;\n }\n if (cur_sum == target) {\n max_len = max(max_len, right - left + 1);\n }\n }\n \n return max_len ? n - max_len : -1;\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int target = -x, n = nums.length;\n for (int num : nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n``` PHP []\nclass Solution {\n function minOperations($nums, $x) {\n $target = 0;\n $n = count($nums);\n foreach ($nums as $num) $target += $num;\n $target -= $x;\n \n if ($target === 0) return $n;\n \n $maxLen = $curSum = $left = 0;\n \n for ($right = 0; $right < $n; ++$right) {\n $curSum += $nums[$right];\n while ($left <= $right && $curSum > $target) {\n $curSum -= $nums[$left];\n $left++;\n }\n if ($curSum === $target) {\n $maxLen = max($maxLen, $right - $left + 1);\n }\n }\n \n return $maxLen ? $n - $maxLen : -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n let target = -x, n = nums.length;\n for (let num of nums) target += num;\n \n if (target === 0) return n;\n \n let maxLen = 0, curSum = 0, left = 0;\n \n for (let right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum === target) {\n maxLen = Math.max(maxLen, right - left + 1);\n }\n }\n \n return maxLen ? n - maxLen : -1;\n};\n```\n``` C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int target = -x, n = nums.Length;\n foreach (int num in nums) target += num;\n \n if (target == 0) return n;\n \n int maxLen = 0, curSum = 0, left = 0;\n \n for (int right = 0; right < n; ++right) {\n curSum += nums[right];\n while (left <= right && curSum > target) {\n curSum -= nums[left];\n left++;\n }\n if (curSum == target) {\n maxLen = Math.Max(maxLen, right - left + 1);\n }\n }\n \n return maxLen != 0 ? n - maxLen : -1;\n }\n}\n```\n\n## Performance\n\n| Language | Fastest Runtime (ms) | Memory Usage (MB) |\n|-----------|----------------------|-------------------|\n| Java | 4 | 56 |\n| Rust | 15 | 3 |\n| JavaScript| 76 | 52.8 |\n| C++ | 110 | 99 |\n| Go | 137 | 8.6 |\n| C# | 236 | 54.6 |\n| PHP | 340 | 31.8 |\n| Python3 | 913 | 30.2 |\n\n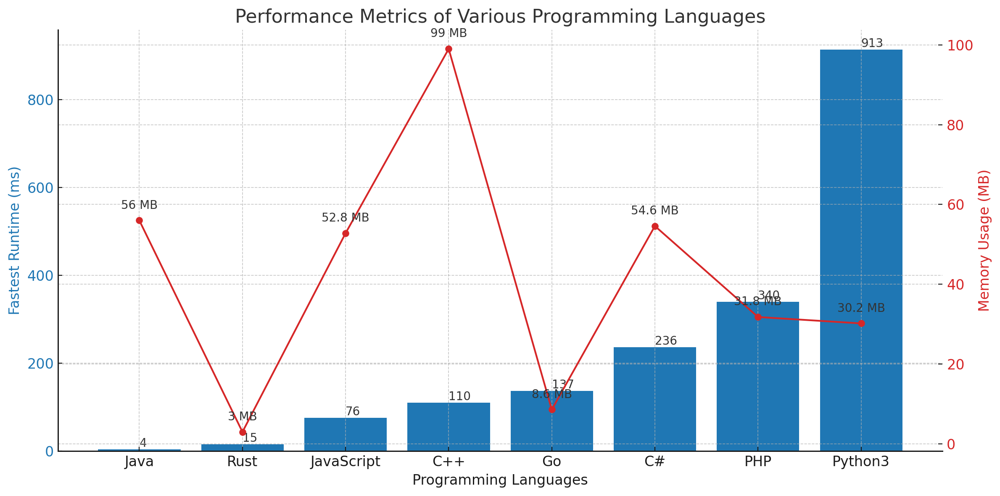\n\n\n## Live Coding in Rust\nhttps://youtu.be/CU93rMboS7w?si=r2ryBueD4fCiKZ7w\n\n## Conclusion\n\nThe problem "Minimum Operations to Reduce X to Zero" may look complicated initially due to its minimization objective. However, understanding the underlying logic of subarray sums and applying a sliding window approach can simplify it. This not only solves the problem efficiently but also enhances one\'s understanding of array manipulation techniques. Happy coding! | 159 | 12 | ['Sliding Window', 'PHP', 'Prefix Sum', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript', 'C#'] | 21 |
minimum-operations-to-reduce-x-to-zero | C# Sliding window O(n) Time O(1) Space | c-sliding-window-on-time-o1-space-by-leo-y5zf | This problem is equivalent to finding the longest subarray whose sum is == totalSum - x\n\n\npublic class Solution\n{\n public int MinOperations(int[] nums, | leoooooo | NORMAL | 2020-11-15T04:07:14.553530+00:00 | 2020-11-15T04:36:47.527931+00:00 | 7,352 | false | **This problem is equivalent to finding the longest subarray whose sum is == totalSum - x**\n\n```\npublic class Solution\n{\n public int MinOperations(int[] nums, int x)\n {\n int sum = nums.Sum() - x;\n if(sum < 0) return -1;\n if(sum == 0) return nums.Length;\n int start = 0, cur = 0, len = -1;\n for(int end = 0; end < nums.Length; end++)\n {\n if (cur < sum)\n cur += nums[end];\n while (cur >= sum)\n {\n if (cur == sum)\n len = Math.Max(len, end - start + 1);\n cur -= nums[start++];\n }\n }\n\n return len == -1 ? -1 : nums.Length - len;\n }\n}\n``` | 137 | 1 | [] | 17 |
minimum-operations-to-reduce-x-to-zero | Two Sum vs. Hash Map | two-sum-vs-hash-map-by-votrubac-z7hf | Started solving this problem using DP, but then realized that the constraints are too large.\n\nThen, I realized that, to reach x, we will take l numbers from t | votrubac | NORMAL | 2020-11-15T04:04:47.654907+00:00 | 2022-06-11T21:51:33.324811+00:00 | 13,154 | false | Started solving this problem using DP, but then realized that the constraints are too large.\n\nThen, I realized that, to reach `x`, we will take `l` numbers from the left, and `r` numbers from the right. We just need to find `min(l + r)`.\n\n#### Approach 1: Hash Map\nAs you count the sum of the first `l` numbers, you need to find a complement `(x - sum)` number formed by numbers on the right. To do so, we can use a hashmap where we will store the rolling sum.\n**C++**\n```cpp\nint minOperations(vector<int>& nums, int x) {\n unordered_map<int, int> left;\n int res = INT_MAX;\n for (auto l = 0, sum = 0; l <= nums.size() && sum <= x; ++l) {\n left[sum] = l;\n if (l < nums.size())\n sum += nums[l];\n }\n for (int r = nums.size() - 1, sum = 0; r >= 0 && sum <= x; --r) {\n auto it = left.find(x - sum);\n if (it != end(left) && r + 1 >= it->second) {\n res = min(res, (int)nums.size() - r - 1 + it->second);\n }\n sum += nums[r];\n }\n return res == INT_MAX ? -1 : res;\n}\n```\n#### Approach 2: Two Sum\n> Note that this only works because we do not have negative values in the input array.\n\nI got a feeling that this problem is a twisted variation of [Two Sum](https://leetcode.com/problems/two-sum/). The rolling sum always increases, so we can use two pointers - both starting from one side - to find portions of the array that sum to `x`. \n**C++**\n```cpp\nint minOperations(vector<int>& nums, int x) {\n int sum = accumulate(begin(nums), end(nums), 0);\n int l = 0, r = 0, res = INT_MAX, sz = nums.size();\n while (l <= r)\n if (sum >= x) {\n if (sum == x)\n res = min(res, l + sz - r);\n if (r < sz)\n sum -= nums[r++];\n else\n break;\n }\n else\n sum += nums[l++];\n return res == INT_MAX ? -1 : res;\n}\n``` | 121 | 4 | ['C'] | 21 |
minimum-operations-to-reduce-x-to-zero | [Python] O(n) solution, using cumulative sums | python-on-solution-using-cumulative-sums-1lfl | We can reformulate this problem: we need to choose several values from the beginning and several values from end, such that sum of this numbers is equal to x. I | dbabichev | NORMAL | 2021-01-14T08:47:21.066085+00:00 | 2021-02-26T12:46:17.645169+00:00 | 5,850 | false | We can reformulate this problem: we need to choose several values from the beginning and several values from end, such that sum of this numbers is equal to `x`. It is equivalent to finding some contiguous subarray, such that it has sum of elements equal to `sum(nums) - x`, which has the biggest length. In this way problem becomes quite classical and I prefer to solve it using cumulative sums.\n\nImagine, that we have `nums = [1,1,4,2,3], x = 5`. Then we need to find contiguous subarray, such that its sum is equal to `sum(nums) - x = 6`. It means, that we need to find two cumulative sums, one of them equal to `goal` plus another one. Note also, that all `nums` are **positive**, so all cumulative sums will be different.\n\nWe keep in `dic` indexes for each cumulative sum, so, when we iterate `num in dic` and check if `num + goal in dic`, then we can get length of window: `dic[num + goal] - dic[num]` and update `ans`.\n\n**Complexity**: time complexity is `O(n)`, space complexity as well.\n\n**Remark**: this idea will work also if we can have **negative** numbers in our `nums`. We need to keep in `dic` smallest and biggest indexes for each value of cumulative sum and then find maximum between ends of two segments. If we asked to find window of minimum length, and we have negative numbers, it is also possible, but we need to keep defaultdict of all indexes and then use idea of merge sort to find closest pair. Complexities will be also `O(n)`. I think I saw these problems on leetcode, but I do not remember they numbers, if you recognize them, please let me know!\n\n```\nclass Solution:\n def minOperations(self, nums, x) :\n cumsum = [0] + list(accumulate(nums))\n dic = {c:i for i,c in enumerate(cumsum)}\n goal = cumsum[-1] - x\n ans = -float("inf")\n\n if goal < 0: return -1\n\n for num in dic:\n if num + goal in dic:\n ans = max(ans, dic[num + goal] - dic[num])\n\n return len(nums) - ans if ans != -float("inf") else -1\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 103 | 17 | [] | 6 |
minimum-operations-to-reduce-x-to-zero | C++ | Sliding Window | Easy Solution | c-sliding-window-easy-solution-by-_panka-yitw | If helpful do upvote\nThanks\n\n\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total=0, n=nums.size();\n for | _pankajMahtolia | NORMAL | 2020-11-17T09:13:35.809490+00:00 | 2020-11-17T09:13:35.809522+00:00 | 5,522 | false | **If helpful do upvote\nThanks**\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total=0, n=nums.size();\n for(auto i:nums) total+=i;\n if(x>total) return -1;\n int left=0,right=0, curr=0, ans=-1;\n for(; right<n;right++){\n curr+=nums[right];\n while(curr>total-x&&left<=right){\n curr-=nums[left];\n left++;\n }\n if(curr==total-x) ans=max(ans, right-left+1);\n }\n if(ans==-1) return ans;\n return n-ans;\n \n }\n};\n``` | 70 | 8 | [] | 4 |
minimum-operations-to-reduce-x-to-zero | 🚀95.97% || Two Pointers - Sliding Window || Commented Code🚀 | 9597-two-pointers-sliding-window-comment-nkkz | Porblem Description\nGiven an array of integers, nums, and an integer x. Each element in nums can be subtracted from x. The goal is to reduce x to exactly 0 usi | MohamedMamdouh20 | NORMAL | 2023-09-20T00:55:43.092683+00:00 | 2023-09-20T01:23:51.483831+00:00 | 8,033 | false | # Porblem Description\nGiven an array of integers, `nums`, and an integer `x`. Each element in `nums` can be subtracted from x. The **goal** is to reduce `x` to exactly `0` using a **minimum** number of operations.\n\nIn each **operation**, you can choose to **remove** either the `leftmost` or the `rightmost` element from the array `nums` and subtract its value from `x`.\n\n- **Constraints:**\n- `1 <= nums.length <= 10e5`\n- `1 <= nums[i] <= 10e4`\n- `1 <= x <= 10e9`\n\n---\n\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s interesting problem\uD83D\uDE80\n\nToday we have **two things**, **array** of intergers and **number** `x`.\nWe can do **one** operation **each** time select `rightmost` or `leftmost` item from the array and **subtract** it from `x`.\nThe goal is to make `x` equal to `zero`.\n\nLook interesting \uD83E\uDD2F\nLet\'s **simplify** our problem a little ?\nWe only need to know **sum** of numbers from `right` and `left` that equal to `x`.\nBut how we get this number ?\uD83E\uDD14\nLet\'s see this example:\n```\nnums = (3, 4, 7, 1, 3, 8, 2, 4), x = 9\n```\nwe can see here that the answer of minimum elements from `left` and `right` (operations) is `3` which are `(3, 2, 4)`\nThere is also something interesting.\uD83E\uDD29\nWe can see that there is a subarray that we **didn\'t touch** which is `(4, 7, 1, 3, 8)`\n\nLet\'s make a **relation** between them\uD83D\uDE80\n```\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + sum(3, 2, 4)\nsum(3, 4, 7, 1, 3, 8, 2, 4) = sum(4, 7, 1, 3, 8) + x\nsum(3, 4, 7, 1, 3, 8, 2, 4) - x = sum(4, 7, 1, 3, 8) \n23 = sum(4, 7, 1, 3, 8) \n```\nWe can see something here.\uD83D\uDE00\nThat the `sum subarray` that I talked about before is the `sum of the whole array - x`\n\nOk we made a **relation** between them but **why** I walked through all of this ?\n\nThe reason is that we can **utilize** an efficient technique that is called **Two Pointers**.\uD83D\uDE80\uD83D\uDE80\n\nThats it, instead of finding the **minimum** number of operations from `leftmost` and `rightmost` elements. We can find the **continous subarray** that **anyother** element in the array is the **answer** to our **minimum** operations.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n# Approach\n1. Calculate the total sum of elements.\n2. Compute the target value as the difference between the total sum and the provided target `x`.\n3. Check if the target value is `negative`; if so, return `-1` as the target sum is not achievable.\n4. Check if the target value is `zero`; if so, **return** the **size** of nums since we need to subtract **all** of the elements from x.\n5. Initialize pointers `leftIndex` and `rightIndex` to track a sliding window.\n6. Within the loop, check if `currentSum` exceeds the target value. If it does, increment `leftIndex` and update `currentSum`.\n7. Whenever `currentSum` equals the target value, calculate the **minimum** number of operations required and update `minOperations`.\n8. **Return** the **minimum** number of operations.\n\n---\n\n\n\n# Complexity\n- **Time complexity:**$$O(N)$$\nIn this method we have two pointers, each of them can iterate over the array at most once. So the complexity is `2 * N` which is `O(N)`.\n- **Space complexity:**$$O(1)$$\nWe are storing couple of variables and not storing arrays or other data structure so the complexity is `O(1)`.\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int targetSum) {\n int totalSum = accumulate(nums.begin(), nums.end(), 0);\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.size(); // Return the number of elements if target sum is 0\n\n int n = nums.size(); // Number of elements in the vector\n int minOperations = INT_MAX; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == INT_MAX) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n};\n```\n```Java []\nclass Solution {\n public int minOperations(int[] nums, int targetSum) {\n int totalSum = Arrays.stream(nums).sum();\n int target = totalSum - targetSum; // Calculate the target sum difference\n\n if (target < 0)\n return -1; // Return -1 if target sum is not achievable\n\n if (target == 0)\n return nums.length; // Return the number of elements if target sum is 0\n\n int n = nums.length; // Number of elements in the array\n int minOperations = Integer.MAX_VALUE; // Minimum operations to achieve the target sum\n int currentSum = 0; // Current sum of elements\n int leftIndex = 0, rightIndex = 0; // Pointers for the sliding window\n\n while (rightIndex < n) {\n currentSum += nums[rightIndex];\n rightIndex++;\n\n while (currentSum > target && leftIndex < n) {\n currentSum -= nums[leftIndex];\n leftIndex++;\n }\n\n if (currentSum == target)\n minOperations = Math.min(minOperations, n - (rightIndex - leftIndex));\n }\n\n return (minOperations == Integer.MAX_VALUE) ? -1 : minOperations; // Return the minimum operations or -1 if not possible\n }\n}\n```\n```Python []\nclass Solution:\n def minOperations(self, nums, targetSum) -> int:\n totalSum = sum(nums)\n target = totalSum - targetSum # Calculate the target sum difference\n\n if target < 0:\n return -1 # Return -1 if target sum is not achievable\n\n if target == 0:\n return len(nums) # Return the number of elements if target sum is 0\n\n n = len(nums) # Number of elements in the list\n minOperations = float(\'inf\') # Minimum operations to achieve the target sum\n currentSum = 0 # Current sum of elements\n leftIndex = 0\n rightIndex = 0 # Pointers for the sliding window\n\n while rightIndex < n:\n currentSum += nums[rightIndex]\n rightIndex += 1\n\n while currentSum > target and leftIndex < n:\n currentSum -= nums[leftIndex]\n leftIndex += 1\n\n if currentSum == target:\n minOperations = min(minOperations, n - (rightIndex - leftIndex))\n\n return -1 if minOperations == float(\'inf\') else minOperations # Return the minimum operations or -1 if not possible\n```\n\n\n\n | 67 | 4 | ['Array', 'Two Pointers', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3'] | 14 |
minimum-operations-to-reduce-x-to-zero | How we think about a solution - O(n) time, O(1) space - Python, JavaScript, Java, C++ | how-we-think-about-a-solution-on-time-o1-ymou | Welcome to my article. Before starting the article, why do I have to get multiple downvotes for a miniute every day? That is obviously deliberate downvotes. I c | niits | NORMAL | 2023-09-20T01:58:22.412434+00:00 | 2023-09-23T16:39:56.080961+00:00 | 2,847 | false | Welcome to my article. Before starting the article, why do I have to get multiple downvotes for a miniute every day? That is obviously deliberate downvotes. I can tell who is doing it. Please show your respect to others! Thanks.\n\n# Intuition\nTry to find target number with sum(nums) - x which is `unnecessary numbers`\n\n---\n\n# Solution Video\n\nIn the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n\nhttps://youtu.be/RUF-4_3fzew\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Minimum Operations to Reduce X to Zero \n`1:13` How we think about a solution\n`3:47` Explain how to solve Minimum Operations to Reduce X to Zero\n`13:00` Coding\n`15:26` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,382\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nWe have two choices to take numbers from left or right side. But problem is we don\'t know what numbers are coming next, next next or next next next...so it\'s tough to manage left and right numbers at the same time.\n\nThat\'s why I changed my idea to this. We have to subtract some numbers from `x`. In other words, If we can calculate numbers which don\'t need for `x` and subtract the `unnecessary numbers` from `total number` of input array, we can get `x`. That formula is\n\n```\ntotal numbers in array - unnecessary numbers = x\n```\n\nAnd an important point is that as I told you, we have two choices to take numbers from left side or right side. That\'s why `position of unnecessary numbers` is around middle of input array for the most cases and `it is consecutive places`.\n\nLet\'s see concrete expamle.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n```\n\ncalculation of `unnecessary numbers` is\n```\ntotal numbers in array - unnecessary numbers = x\n\u2193\ntotal numbers in array - x = unnecessary numbers\n\n30 - 10 = 20\n\n30: total number of input array\n10: x\n20: unnecessary numbers \n```\n\n\nAt first, we have to find `20` from `input array`. Let\'s break the numbers into small pieces.\n\n```\n[3,2] = 5\n[20] = 20\n[1,1,3] = 5\n\n[3,2] is an case where we take 3 and 2 from left side.\n[1,1,3] is an case where we take 3, 1 and 1 from right side.\nThe total of [3,2] and [1,1,3] is 10 (3+2+1+1+3) which is x.\n```\nIn this case, if we can find `[20]`, all we have to do is to calculate this.\n```\n6 - 1 = 5\n\n6: total length of input array\n1: length of [20]\n5: length of [3,2] + [1,1,3]\n```\n```\nOutput : 5 (minimum number of operations to make x zero)\n```\n\n`position of unnecessary numbers` is around middle of input array and it is `consective places`, so looks like we can use `sliding window` technique to find `length of array for unnecessary numbers`.\n\n\n### Overview Algorithm\n1. Calculate the target sum as the sum of `nums` minus `x`.\n2. Check if the target sum is negative, return -1 if it is.\n3. Initialize variables `left`, `cur_sum`, and `max_sub_length`.\n4. Iterate through the `nums` array using a sliding window approach to find the longest subarray with the sum equal to the target.\n\n### Detailed Explanation\n1. Calculate the target sum:\n - Calculate the `target` as the sum of `nums` minus `x`. This is the sum we want to achieve by finding a subarray in the given array.\n\n2. Check if the target sum is negative:\n - If `target` is less than 0, it means it\'s not possible to achieve the target sum by removing elements from the array. Return -1.\n\n3. Initialize variables:\n - `left`: Initialize a pointer to the left end of the window.\n - `cur_sum`: Initialize a variable to keep track of the current sum in the window.\n - `max_sub_length`: Initialize a variable to keep track of the maximum subarray length with the sum equal to the target.\n\n4. Iterate through the array using a sliding window:\n - Start a loop over the array using the right pointer.\n - Update the current sum by adding the current element at the right pointer.\n - Check if the current sum is greater than the target:\n - If the current sum exceeds the target, move the left pointer to the right until the current sum is less than or equal to the target.\n - Check if the current sum is equal to the target:\n - If the current sum equals the target, update the maximum subarray length if needed.\n - At each iteration, keep track of the maximum subarray length found so far.\n\n5. Return the result:\n - After the loop, return -1 if no valid subarray was found (max_sub_length remains as initialized), or return the difference between the total length of the array and the maximum subarray length.\n\nThis algorithm efficiently finds the longest subarray with a sum equal to the target sum using a sliding window approach.\n\n# How it works\nLet\'s think about this input.\n```\nInput: nums = [3,2,20,1,1,3], x = 10\n\ntarget(unnecessary numbers) = 20 (fixed)\ncur_sum = 0\nleft = 0\nright = 0\nmax_sub_length = 0\nn = 6 (fixed)\n```\niteration thorugh input array one by one\n```\nwhen right = 0, add 3 to cur_sum\n\ncur_sum = 3\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 1, add 2 to cur_sum\n\ncur_sum = 5\nleft = 0\nmax_sub_length = 0\n```\n\n```\nwhen right = 2, add 20 to cur_sum\n\ncur_sum = 25 \u2192 20(while loop, 25 - 3 - 2)\nleft = 0 \u2192 2 (while loop, 0 + 1 + 1)\nmax_sub_length = 1 (if statement, max(-inf, 2 - 2 + 1))\n```\n\n```\nwhen right = 3, add 1 to cur_sum\n\ncur_sum = 21 \u2192 1(while loop, 21 - 20)\nleft = 2 \u2192 3 (while loop, 2 + 1)\nmax_sub_length = 1\n```\n\n```\nwhen right = 4, add 1 to cur_sum\n\ncur_sum = 2\nleft = 3\nmax_sub_length = 1\n```\n\n```\nwhen right = 5, add 3 to cur_sum\n\ncur_sum = 5\nleft = 3\nmax_sub_length = 1\n```\n\n```\nreturn 6(n) - 1(max_sub_length)\n```\n\n```\nOutput: 5 (operations)\n```\n\n\n\n\n# Complexity\n- Time complexity: O(n)\n`n` is the length of the input nums array. This is because there is a single loop that iterates through the elements of the array once.\n\n\n- Space complexity: O(1)\nbecause the code uses a constant amount of additional memory regardless of the size of the input nums array. The space used for variables like `target`, `left`, `cur_sum`, `max_sub_length`, and `n` does not depend on the size of the input array and remains constant.\n\n\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums) - x\n \n if target < 0:\n return -1\n \n left = 0\n cur_sum = 0\n max_sub_length = float(\'-inf\')\n n = len(nums)\n \n for right in range(n):\n cur_sum += nums[right]\n \n while cur_sum > target:\n cur_sum -= nums[left]\n left += 1\n \n if cur_sum == target:\n max_sub_length = max(max_sub_length, right - left + 1)\n \n return -1 if max_sub_length == float(\'-inf\') else n - max_sub_length\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @param {number} x\n * @return {number}\n */\nvar minOperations = function(nums, x) {\n const target = nums.reduce((acc, num) => acc + num, 0) - x;\n \n if (target < 0) {\n return -1;\n }\n \n let left = 0;\n let curSum = 0;\n let maxSubLength = Number.NEGATIVE_INFINITY;\n const n = nums.length;\n \n for (let right = 0; right < n; right++) {\n curSum += nums[right];\n \n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n \n if (curSum === target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n \n return maxSubLength === Number.NEGATIVE_INFINITY ? -1 : n - maxSubLength; \n};\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int target = 0;\n for (int num : nums) {\n target += num;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = Integer.MIN_VALUE;\n int n = nums.length;\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = Math.max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == Integer.MIN_VALUE ? -1 : n - maxSubLength; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int target = 0;\n for (int i : nums) {\n target += i;\n }\n target -= x;\n\n if (target < 0) {\n return -1;\n }\n\n int left = 0;\n int curSum = 0;\n int maxSubLength = INT_MIN;\n int n = nums.size();\n\n for (int right = 0; right < n; right++) {\n curSum += nums[right];\n\n while (curSum > target) {\n curSum -= nums[left];\n left++;\n }\n\n if (curSum == target) {\n maxSubLength = std::max(maxSubLength, right - left + 1);\n }\n }\n\n return maxSubLength == INT_MIN ? -1 : n - maxSubLength; \n }\n};\n```\n\n\n---\n\nThank you for reading such a long article. \n\n\u2B50\uFE0F Please upvote it if you understand how we think about a solution and don\'t forget to subscribe to my youtube channel!\n\n\nMy next post for daily coding challenge on Sep 21, 2023\nhttps://leetcode.com/problems/median-of-two-sorted-arrays/solutions/4070884/my-thought-process-ologminn-m-time-o1-space-python-javascript-java-c/\n\nHave a nice day!\n\n\n | 48 | 6 | ['C++', 'Java', 'Python3', 'JavaScript'] | 5 |
minimum-operations-to-reduce-x-to-zero | C++ | 2 Approaches | c-2-approaches-by-datnguyen2k3-ei91 | Approach 1: Hash map, prefix sum, two sum\n\t- Idea: + create hash map satisfy mapLeft[prefix sum] = i, i is last index in prefix sum\n\t\t\t+ brute force from | datnguyen2k3 | NORMAL | 2022-06-11T01:18:16.295147+00:00 | 2022-10-28T05:46:54.158741+00:00 | 6,989 | false | Approach 1: Hash map, prefix sum, two sum\n\t- Idea: + create hash map satisfy mapLeft[prefix sum] = i, i is last index in prefix sum\n\t\t\t+ brute force from last index in array to first index and create suffix sum, find i satisfy mapLeft[x - suffix sum] > 0 \n\t\t\t => that\'s mean prefix sum + suffix sum = x, and min operation = min (min operation, size(prefix sum) + size(suffix sum) );\n\t+ Time: O(n)\n\t+ Space: O(n)\n\t\t\t \n\tclass Solution {\n\tpublic:\n\t\tint minOperations(vector<int>& nums, int x) {\n\t\t\tunordered_map<int, int> mapLeft;\n\t\t\tint n = nums.size();\n\t\t\tint ans = INT_MAX;\n\n\t\t\tfor(int i = 0, prefixSum = 0; i < n; i++) {\n\t\t\t\tprefixSum += nums[i];\n\t\t\t\tmapLeft[prefixSum] = i + 1;\n\t\t\t\tif (prefixSum == x)\n\t\t\t\t\tans = min(ans, i + 1);\n\t\t\t}\n\n\t\t\tfor(int i = n - 1, suffixSum = 0; i >= 0; i--) {\n\t\t\t\tsuffixSum += nums[i];\n\t\t\t\tif(suffixSum == x)\n\t\t\t\t\tans = min(ans, n - i);\n\t\t\t\tif(mapLeft[x - suffixSum] > 0 && i + 1 > mapLeft[x - suffixSum]) // if i + 1 <= mapLeft => both prefix sum and suffix sum have same elements\n\t\t\t\t\tans = min(ans, n - i + mapLeft[x - suffixSum]); // n - i is size suffix sum, mapLeft[x - suffixSum] is size prefix sum\n\t\t\t}\n\n\t\t\treturn ans == INT_MAX ? -1 : ans;\n\t\t}\n\t};\n\t\nApproach 2: longest subarray have sum == sum(nums) - x\n\t- Idea: If u find longest subarray have sum == sum(nums) - x \n\t\t\t=> minimun operation = nums.size() - size(longest subarray)\n\nTime: O(n)\nSpace: O(1)\n\n\tclass Solution {\n\tpublic:\n\t\tint minOperations(vector<int>& nums, int x) {\n\t\t\tint sum = accumulate(nums.begin(), nums.end(), 0);\n\n\t\t\tif(sum < x) return -1;\n\t\t\tif(sum == x) return nums.size();\n\n\t\t\tint target = sum - x, currentSum = 0, start = 0, maxSize = 0;\n\t\t\tfor(int i = 0; i < nums.size(); i++) {\n\t\t\t\tcurrentSum += nums[i];\n\n\t\t\t\twhile(currentSum > target)\n\t\t\t\t\tcurrentSum -= nums[start++];\n\n\t\t\t\tif(currentSum == target)\n\t\t\t\t\tmaxSize = max(maxSize, i - start + 1);\n\t\t\t}\n\n\t\t\treturn (maxSize == 0) ? - 1 : nums.size() - maxSize;\n\t\t}\n\t};\n\t | 44 | 1 | ['C', 'Sliding Window', 'Prefix Sum'] | 3 |
minimum-operations-to-reduce-x-to-zero | [Python3] O(n) Time O(1) space solution | python3-on-time-o1-space-solution-by-red-19ve | The idea is to find the length of the maximum length subarray that has a sum equal to sum(nums) - x. This makes sense because after removing the optimal element | redsand | NORMAL | 2021-01-14T14:43:00.556612+00:00 | 2021-01-15T14:28:43.900817+00:00 | 2,055 | false | The idea is to find the length of the maximum length subarray that has a sum equal to ```sum(nums) - x```. This makes sense because after removing the optimal elements from the ends, this is what we will be left with. So instead of removing elements, add elements to this subarray in a sliding window fashion and optimize for the largest length of this subarray.\n\nExample:\n```nums = [1,1,4,2,3], x = 5```\n\nsum = 11\nreq_subarray_sum = 11 - 5 = 6\nThe longest subarray with this sum is from index 0 to index 2 (1 + 1 + 4). This has length 3.\nresult = len(nums) - max_subarray_size = 5 - 3 = 2\n\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n arr_sum = sum(nums)\n if arr_sum < x:\n return -1\n if arr_sum == x:\n return len(nums)\n \n required_subarray_sum = arr_sum - x\n left = curr_sum = max_subarray_size = 0\n for right, num in enumerate(nums):\n curr_sum += num\n while curr_sum > required_subarray_sum:\n curr_sum -= nums[left]\n left += 1\n if curr_sum == required_subarray_sum:\n max_subarray_size = max(max_subarray_size, right - left + 1)\n \n return len(nums) - max_subarray_size if max_subarray_size > 0 else -1\n``` | 37 | 0 | [] | 6 |
minimum-operations-to-reduce-x-to-zero | Minimum Operations to Reduce X to Zero | JS | Explanation | beats 100% | minimum-operations-to-reduce-x-to-zero-j-5bfv | Idea:\n\nThis problem is tasking us to essentially find when the sum of the starting and ending subarrays of nums is equal to x. Put another way, it\'s asking u | sgallivan | NORMAL | 2021-01-15T00:26:36.699248+00:00 | 2021-01-15T00:26:36.699277+00:00 | 1,276 | false | ***Idea:***\n\nThis problem is tasking us to essentially find when the sum of the starting and ending subarrays of **nums** is equal to **x**. Put another way, it\'s asking us to find when any subarray of consecutive elements in **nums** is equal to the sum of all elements in **nums** minus **x**.\n```\n <-A-> <------ B ------> <-C->\n nums = [1, 1, 1, 1, 1, 1, 1, 1, 1]\n\t \n\t if sum(A) + sum(C) = x\n\t then x = sum(nums) - sum(B)\n```\nSo now we need to find any consecutive subarray of **nums** whose sum is equal to a specific value. Any time you\'re talking about checking the sum of a consecutive subarray, it should naturally bring to mind the use of a **prefix sum array**.\n\nThe sum of any consecutive subarray, **i** to **j**, of **nums** can be defined as the sum of all elements of **nums** up to **j** minus the sum of all the elements of **nums** *before* **i**. This is aided by creating a prefix sum array containing the running sum of elements in **nums**.\n```\n\t\t\t <------ A ------>\n <-B->\n\t\t\t <-- C -->\n nums = [1, 1, 1, 1, 1, 1, 1, 1, 1]\n\t\t\t\t\t i j\n prefixSum = [1, 2, 3, 4, 5, 6, 7, 8, 9]\n\t \n\t if prefixSum[n] = sum(nums[0] to nums[n])\n\t and sum(A) = prefixSum[j]\n\t and sum(B) = prefixSum[i-1]\n\t then sum(C) = prefixSum[j] - prefixSum[i-1]\n```\n\nUsing a prefix sum array, we can then use a **2-pointer** **sliding window** to evaluate which subarrays have the specified value and keep track of which one has the largest subarray size. The answer, if possible, will be its difference from **nums.length**.\n\nThe best result for the code below is **92ms / 50.2MB**.\n\n` `\n***Implementation:***\n\nThe prefix sum array is simple to achieve; we just iterate through **nums** and make each **i**th element of the prefix sum array the sum of **nums[0]** through **nums[i]** by taking the previous value (**nums[i-1]**) and adding **nums[i]** to it. Since we don\'t need the individual elements of **nums** after this, we can run the conversion in place.\n\n(***Note**: Normally in a prefix sum array you will want to add a leading **0** to the array as the equation for a subarray starting with **i = 0** will lead to an **nums[i-1]** value outside the range of **nums**. In this instance, however, we can handle the issue more efficiently later.*)\n\nOnce **nums** has been updated, the last element **nums[len-1]** will equal the total sum of **nums**. This means that we\'ll be looking for a subarray of nums that sums to **nums[len-1] - x**, or **y**. If **y** is negative, then there exists no possibility for a solution, since all elements of **nums** are positive integers, so we can **return -1**. If **y** is **0**, then the only possible solution is the entire **nums** array, so we can **return len**.\n\nOtherwise, we can use **i** and **j** as two pointers to form a sliding window of **nums**. While we iterate, we should keep track of the size (**best**) of the largest successful subarray. If at any time during the iteration, **i** moves far enough that no remaining subarray can beat **best**, or if **nums[i]** is already larger than **x**, then we should force an end. Starting with **best = 0** means that **i** should move all the way to **len** if no matches are found.\n\nSince we\'ll be using **nums[i]** a number of times, we can store it in **l**, representing the left endpoint value sum. Setting the initial value of **l** to **0** and only updating it to be based off **nums[i]** *after* the first iteration will allow us to avoid needing to **unshift()** a **0** onto the prefix sum array beforehand.\n\nThen, during each iteration, we\'ll move **j** up as long as the subarray sum (**nums[j] - l**) is less than **y**. If the sliding window has stopped on a subarray that equals **y**, then we update **best** if necessary.\n\nSince **best** represents the largest subarray length, we actually want to **return len - best**, but if no match was ever found (**best > 0**), then we should **return -1** instead.\n\n` `\n***Code:***\n```\nvar minOperations = function(nums, x) {\n let len = nums.length, best = 0\n for (let i = 1; i < len; i++) nums[i] += nums[i-1]\n let y = nums[len-1] - x\n if (y < 0) return -1\n if (y === 0) return len\n for (let i = -1, j = l = 0; i < len - best && l <= x; l = nums[++i]) {\n while (nums[j] - l < y) j++\n if (nums[j] - l === y) best = Math.max(best, j - i)\n }\n return best > 0 ? len - best : -1\n};\n``` | 33 | 0 | ['JavaScript'] | 1 |
minimum-operations-to-reduce-x-to-zero | C++| Simple | O(N) | Sliding Window | | c-simple-on-sliding-window-by-persistent-z3iz | Goal is to find a window of longest length which has sum equal to s - x, where s is sum of all the elements of the array.\n When such a window is found all the | persistentBeast | NORMAL | 2022-06-11T07:26:47.147091+00:00 | 2022-06-12T10:27:29.518002+00:00 | 3,589 | false | * Goal is to **find a window of longest length** which has sum equal to `s - x`, where `s` is sum of all the elements of the array.\n* When such a window is found all the elements outside this window will sum to `x` and no of operations will be equal to their count. \n* **TC : O(N) | SC : O(1)**\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n \n int n = nums.size(), s = 0, ans = 1000000;\n \n for(int i = 0; i < n ; i++) s += nums[i];\n \n if(s < x) return -1;\n \n int st = 0, end = 0, windowSum = 0;\n \n while(end < n){ \n windowSum += nums[end]; \n while(windowSum > (s - x)){\n windowSum -= nums[st]; //Reducing window size\n st++;\n } \n if(windowSum == s - x){\n ans = min(ans, n - (end - st + 1));\n } \n end++; \n }\n\t\t\n return (ans == 1000000 ? -1 : ans);\n \n }\n};\n``` | 29 | 0 | ['C', 'Sliding Window'] | 5 |
minimum-operations-to-reduce-x-to-zero | [Java/Python 3] Sliding window: Longest subarray sum to the target = sum(nums) - x. | javapython-3-sliding-window-longest-suba-uev4 | Using sliding window to find the longest subarry that sums to sum(nums) - x.\njava\n public int minOperations(int[] nums, int x) {\n int target = Arra | rock | NORMAL | 2020-11-15T04:42:40.768272+00:00 | 2022-12-03T16:31:11.169729+00:00 | 3,290 | false | Using sliding window to find the longest subarry that sums to `sum(nums) - x`.\n```java\n public int minOperations(int[] nums, int x) {\n int target = Arrays.stream(nums).sum() - x, size = -1, n = nums.length;\n for (int lo = -1, hi = 0, winSum = 0; hi < n; ++hi) {\n winSum += nums[hi];\n while (lo + 1 < nums.length && winSum > target) {\n winSum -= nums[++lo];\n }\n if (winSum == target) {\n size = Math.max(size, hi - lo);\n }\n }\n return size < 0 ? -1 : n - size;\n }\n```\n\n```python\n def minOperations(self, nums: List[int], x: int) -> int:\n target, size, win_sum, lo, n = sum(nums) - x, -1, 0, -1, len(nums)\n for hi, num in enumerate(nums):\n win_sum += num\n while lo + 1 < n and win_sum > target:\n lo += 1\n win_sum -= nums[lo]\n if win_sum == target:\n size = max(size, hi - lo)\n return -1 if size < 0 else n - size\n```\n\n**Analysis:**\n\nTime: O(n), space: O(1), where n = nums.length.\n\n----\n\nSimilar problems:\n[918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/description/)\n[1423. Maximum Points You Can Obtain from Cards](https://leetcode.com/problems/maximum-points-you-can-obtain-from-cards/discuss/597777/JavaPython-3-Sliding-window-O(k)-short-codes-w-brief-comments-and-analysis.) | 28 | 0 | ['Java', 'Python3'] | 7 |
minimum-operations-to-reduce-x-to-zero | ✅97.65%🔥Sum of Subarray Reduction🔥 | 9765sum-of-subarray-reduction-by-mrake-26e8 | Problem\n\n### This problem involves finding the minimum number of operations to reduce the sum of elements in the array nums to exactly zero, given that you ca | MrAke | NORMAL | 2023-09-20T00:49:33.147774+00:00 | 2023-09-20T00:49:33.147800+00:00 | 2,406 | false | # Problem\n\n### This problem involves finding the minimum number of operations to reduce the sum of elements in the array nums to exactly zero, given that you can perform operations to remove elements from either the left or right end of the array.\n---\n# Solution\n\n##### **1.** Calculate the total sum of all elements in the nums array and store it in the variable total.\n\n##### **2.** Calculate the target value that we want to reach, which is target = total - x. Essentially, we want to find a subarray whose sum is equal to target.\n\n##### **3.** Initialize two pointers, left and right, both starting at index 0, and a variable running_sum to keep track of the sum of elements within the sliding window.\n\n##### **4.** Initialize a variable max_length to -1. This variable will be used to keep track of the maximum length of a subarray with a sum equal to target.\n\n#### **5.** Iterate through the nums array using the right pointer. At each step, add the value at nums[right] to running_sum.\n\n#### **6.** Check if running_sum is greater than target. If it is, this means the current subarray sum is too large. In this case, we need to shrink the sliding window by incrementing the left pointer and subtracting the value at nums[left] from running_sum until running_sum is less than or equal to target.\n\n#### **7.** Once the sliding window is valid (i.e., running_sum is equal to target), calculate its length (right - left + 1) and update max_length if this length is greater than the current maximum length.\n\n#### **8.** Continue this process until you\'ve iterated through the entire nums array.\n\n#### **9.** After the loop, check if max_length has been updated. If it has, it means we found a subarray with the sum equal to target. The minimum number of operations required to reduce x to zero is equal to n - max_length, where n is the length of the original array nums. If max_length is still -1, return -1 to indicate that it\'s not possible to reduce x to zero.\n---\n# Summary\n\n#### In summary, the algorithm uses a sliding window approach to find the subarray with the sum equal to the target, and then calculates the minimum number of operations required based on the length of that subarray. If no such subarray exists, it returns -1.\n\n---\n# Code\n```Python3 []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```python []\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n total = sum(nums)\n target = total - x\n left = 0\n n = len(nums)\n max_length = -1\n running_sum = 0\n\n for right in range(n):\n running_sum += nums[right]\n\n #shrink sliding window to make sure running_sum is not greater than target\n while running_sum > target and left <= right:\n running_sum -= nums[left]\n left += 1\n\n #now we have a avalid sliding window\n if running_sum == target:\n max_length = max(max_length, right - left + 1)\n \n return n - max_length if max_length != -1 else -1\n```\n```C# []\npublic class Solution {\n public int MinOperations(int[] nums, int x) {\n int total = nums.Sum();\n int target = total - x;\n int left = 0;\n int n = nums.Length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.Max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(std::vector<int>& nums, int x) {\n int total = std::accumulate(nums.begin(), nums.end(), 0);\n int target = total - x;\n int left = 0;\n int n = nums.size();\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = std::max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n};\n\n```\n```C []\nint minOperations(int* nums, int numsSize, int x) {\n int total = 0;\n for (int i = 0; i < numsSize; i++) {\n total += nums[i];\n }\n\n int target = total - x;\n int left = 0;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < numsSize; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n int currentLength = right - left + 1;\n maxLength = (maxLength == -1) ? currentLength : (currentLength > maxLength ? currentLength : maxLength);\n }\n }\n\n return (maxLength != -1) ? numsSize - maxLength : -1;\n}\n\n```\n```Java []\npublic class Solution {\n public int minOperations(int[] nums, int x) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n\n int target = total - x;\n int left = 0;\n int n = nums.length;\n int maxLength = -1;\n int runningSum = 0;\n\n for (int right = 0; right < n; right++) {\n runningSum += nums[right];\n\n while (runningSum > target && left <= right) {\n runningSum -= nums[left];\n left++;\n }\n\n if (runningSum == target) {\n maxLength = Math.max(maxLength, right - left + 1);\n }\n }\n\n return maxLength != -1 ? n - maxLength : -1;\n }\n}\n\n```\n```Go []\nfunc minOperations(nums []int, x int) int {\n total := 0\n for _, num := range nums {\n total += num\n }\n\n target := total - x\n left := 0\n n := len(nums)\n maxLength := -1\n runningSum := 0\n\n for right := 0; right < n; right++ {\n runningSum += nums[right]\n\n for runningSum > target && left <= right {\n runningSum -= nums[left]\n left++\n }\n\n if runningSum == target {\n currentLength := right - left + 1\n if maxLength == -1 || currentLength > maxLength {\n maxLength = currentLength\n }\n }\n }\n\n if maxLength != -1 {\n return n - maxLength\n }\n\n return -1\n}\n\n```\n\n\n | 26 | 14 | ['Array', 'Hash Table', 'C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'C#'] | 5 |
minimum-operations-to-reduce-x-to-zero | [Python3] O(N) hash table of prefix | python3-on-hash-table-of-prefix-by-ye15-ljid | Algo \nHere, we maintain a mapping of prefix sum to index mapping. Then, we go over nums inversely to compute suffix sum, and check if a complement exists in th | ye15 | NORMAL | 2020-11-15T04:08:15.092260+00:00 | 2021-01-15T05:11:33.425344+00:00 | 2,109 | false | Algo \nHere, we maintain a mapping of prefix sum to index mapping. Then, we go over `nums` inversely to compute suffix sum, and check if a complement exists in the prefix sum (via hash table). If so, check the length and update `ans`. \n\nImplementation \n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n mp = {0: 0}\n prefix = 0\n for i, num in enumerate(nums, 1): \n prefix += num\n mp[prefix] = i \n \n ans = mp.get(x, inf)\n for i, num in enumerate(reversed(nums), 1): \n x -= num\n if x in mp and mp[x] + i <= len(nums): ans = min(ans, i + mp[x])\n return ans if ans < inf else -1 \n```\n\nAnalysis\nTime complexity `O(N)`\nSpace complexity `O(N)`\n\nEdited on 1/14/2021\nAdding implementation to use complement\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n x = sum(nums) - x\n if not x: return len(nums) # edge case \n \n seen = {0: -1}\n ans = prefix = 0\n for i, num in enumerate(nums): \n prefix += num\n if prefix - x in seen: ans = max(ans, i - seen[prefix - x])\n seen.setdefault(prefix, i)\n return len(nums) - ans if ans else -1\n``` | 25 | 2 | ['Python3'] | 9 |
minimum-operations-to-reduce-x-to-zero | sliding window [c++] | sliding-window-c-by-vishwasgajawada-vscp | \nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total=0,n=nums.size();\n for(int num : nums)total+=num;\n | vishwasgajawada | NORMAL | 2021-01-14T09:34:52.724598+00:00 | 2021-10-04T17:38:44.204258+00:00 | 1,706 | false | ```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total=0,n=nums.size();\n for(int num : nums)total+=num;\n int need=total-x,cur=0,longest=0;\n if(need==0)return n;\n int l=0,r=0;\n while(l<=r){\n if(cur<need){\n if(r<n)cur+=nums[r++];\n else break;\n }else if(cur>need){\n cur-=nums[l++];\n }else{\n longest=max(longest,r-l);\n cur-=nums[l++];\n }\n }\n if(cur==need)longest=max(longest,r-l);\n if(longest==0)return -1;\n return n-longest;\n }\n};\n\n``` | 19 | 3 | ['C'] | 3 |
minimum-operations-to-reduce-x-to-zero | [Python 3] Two sum problem using HashMap - O(N) - Clean & Concise | python-3-two-sum-problem-using-hashmap-o-b2vb | python\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n n = len(nums)\n\n leftMap = dict()\n leftMap[0] = - | hiepit | NORMAL | 2021-05-18T11:43:51.327696+00:00 | 2021-05-18T11:45:14.912315+00:00 | 776 | false | ```python\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n n = len(nums)\n\n leftMap = dict()\n leftMap[0] = -1\n left = 0\n for i in range(n):\n left += nums[i]\n if left not in leftMap:\n leftMap[left] = i\n\n right = 0\n ans = n + 1\n for i in range(n, -1, -1):\n if i < n: right += nums[i]\n left = x - right\n if left in leftMap: # left + right = x -> left = x - right\n ans = min(ans, leftMap[left] + 1 + n - i)\n if ans == n + 1: return -1\n return ans\n```\nComplexity:\n- Time & Space: `O(N)`, where `N` is number of elements in the array `nums`.\n\n**Simillar problems**\n1. [1. Two Sum](https://leetcode.com/problems/two-sum/)\n2. [1865. Finding Pairs With a Certain Sum](https://leetcode.com/problems/finding-pairs-with-a-certain-sum/) | 17 | 0 | [] | 0 |
minimum-operations-to-reduce-x-to-zero | C++ || Explained Solution || Best Time and Space Complexity | c-explained-solution-best-time-and-space-4ohc | Please Upvote the solution if helpful --> else comment down the problem and I will try to improve upon that! Thanks for reading .\n```\nclass Solution {\npublic | code-to-learn | NORMAL | 2022-06-11T10:09:08.019965+00:00 | 2022-06-11T10:50:12.255671+00:00 | 1,106 | false | **Please Upvote the solution if helpful --> else comment down the problem and I will try to improve upon that! Thanks for reading .**\n```\nclass Solution {\npublic:\n // O(n) time complexity solution and O(1) space complexity\n // Given Problem (equivalent) => Finding longest subarray with sum=totalSum(nums) - x \n // The above problem will minimize the target(x) using minimum elements from extreme left and right \n\t// Not clear ???? \n\t// Okay , let me explain it !\n // Assume array to be divided into 3 portions : ----- [-----] ----- \n // Observe we can take elements from left and right portion to form x and our goal is to use least elements possible\n // So , we alternatively need to maximize the size of the middle portion and its sum = total sum-x\n \n int minOperations(vector<int>& nums, int x) {\n // Finding total sum of the array\n int sum=0;\n for(auto it:nums){\n sum+=it;\n }\n // Finding required sum of the middle portion\n sum-=x; \n // Edge Case --> If middle portion Sum =0 --> we need to take all elements (Since all elements >=1)\n if(sum==0){\n return nums.size();\n }\n // Edge Case --> If middle portion Sum < 0 --> Not possible because this implies that total sum of array< x\n if(sum<0) return -1;\n int curr=nums[0];\n int ans=-1; // number of elements taken in middle portion \n // start --> starting index of middle portion taken into account currently , end--> last index taken into account\n int start=0,end=0;\n // we will traverse the array till end <= last index\n while(end<nums.size()){\n // case 1 --> current sum is less than required sum --> move end to next pointer \n if(curr<sum){\n end++;\n if(end==nums.size()) break;\n curr+=nums[end];\n }\n // case 2 --> current sum is greater than required sum --> move start pointer to next index \n else if(curr>sum){\n curr-=nums[start];\n start++;\n }\n \n // case 3 --> current sum is equal to required Sum --> move start pointer to next index to explore better answer\n // alternatively we could have taken end pointer to next index , but to avoid edge cases of end pointer (out of bound), we have taken former case\n else if(curr==sum){\n int val=end-start+1;\n ans=max(ans,val);\n curr-=nums[start];\n start++;\n }\n }\n if(ans==-1) return -1; // if after whole traversal , ans==-1 (initialized value) --> we didn\'t find any valid answer --> hence return -1\n else return nums.size()-ans; // else return ( total array length) - (maximum length of middle portion )\n }\n // Time Complexity : Linear O(n)\n // Space Complexity : O(1) since we only used constant number of variable and hence fixed memory \n\t\n}; | 16 | 0 | [] | 3 |
minimum-operations-to-reduce-x-to-zero | ✅Easiest Solution with explanation and annotations! | easiest-solution-with-explanation-and-an-5r1s | Intuition\nWe can use prefix sum and suffix sum here. \nFor every number in prefix sum we\'ll check if its complement is present in suffix. If it is it means we | parthdharmale008 | NORMAL | 2023-09-20T05:42:48.418526+00:00 | 2023-09-20T05:48:46.071246+00:00 | 2,336 | false | # Intuition\nWe can use prefix sum and suffix sum here. \nFor every number in prefix sum we\'ll check if its complement is present in suffix. If it is it means we can make our `x` if it is not it means we can\'t make `x` with that particular prefix, so move on to the next one.\n\n# Approach\n- Firstly we find our `n` which is size of the array.\n- Write base cases for `n = 1, sum < x and sum == x.`\n- Now we find our prefix sum using a for loop and sotre it in an array `prefix`.\n- Now create a map for suffix sum `suff`, we are creating map so we get the index of the suffix sum which we will require later for finding the number of operations.\n- Our last prefixSum `sum` will be equal to total sum of the array. So we use it to find suffix sum and store it in `suff`. We also store the index here in the map so our `key` is `sum` and `value` is `index`.\n- We do `suff[0] = n` because the sum 0 will be at last so its index will be last.\n\nNow, starts the main logic - \n- Iterate over the `prefix` array and find our `target`.\n- If target is present in the map `suff` as a key, we find minimum noOfOps by taking `minimum of noOfOps and current number of ops`.\n- We find current `no of ops` by following- we have our index of prefix sum as `i` it means we need to pop `i` numbers from start. \n- We have our suffix Sum index as `suff[target]` but this is from start. So we need to pop `n - suff[target]` to get that suffix sum.\n- hence ` i + n - suff[target]`\n- Note how we are updating noOfOps only if we have our target, so at last if `noOfOps` is still `INT_MAX` it means we have no answer hence return `-1 ` else return `noOfOps`.\n\n# I\'ve explained test case 3 below for better understanding.\n\n\n\n# Note- This code doesnt\'t beat 100% because i\'ve kept it simple for better understanding. You can use the same for loop used for prefixsum to calculate suffixsum and you\'ll save a lot of time there. Also a lot of times runtime isn\'t accurate because of slow network so try resubmitting for better runtime.\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n if(n == 1 && nums[0] != x) return -1;\n vector<int> prefix;\n prefix.push_back(0);\n\n int sum = 0;\n for(int i =0;i < n ;i++){\n sum += nums[i];\n prefix.push_back(sum);\n }\n if(sum < x) return -1;\n if(sum == x) return n;\n unordered_map<int,int> suff;\n\n for(int i = 0;i < n; i++){\n suff[sum] = i;\n sum -= nums[i];\n\n }\n suff[0] = n;\n\n // Main Logic\n\n int noOfOps = INT_MAX;\n\n int i = 0;\n while(prefix[i] <= x){\n int target = x - prefix[i];\n\n if(suff[target]){\n noOfOps = min(noOfOps, i + n - suff[target]);\n }\n i++;\n }\n if(noOfOps == INT_MAX) return -1;\n return noOfOps;\n \n }\n};\n``` | 15 | 0 | ['Array', 'Prefix Sum', 'C++', 'Java'] | 4 |
minimum-operations-to-reduce-x-to-zero | Very Easy C++ Solution with Explanation (Sliding Window) - beats 88.2% submissions | very-easy-c-solution-with-explanation-sl-twpo | Explanation\nThis is a slighty tricky variant of Sliding Window problem.\n\nTrick to make this question easy :\n Total = Sum of all elements of the nums array.\ | vatsalkesarwani | NORMAL | 2021-06-12T22:21:41.261778+00:00 | 2021-06-12T22:21:41.261804+00:00 | 1,271 | false | **Explanation**\nThis is a slighty tricky variant of Sliding Window problem.\n\nTrick to make this question easy :\n* Total = Sum of all elements of the nums array.\n* Now find max operation to find (total-x) in the array\n\nCheck result :\n* If the result comes to 0 then return -1\n* else return size-result\n\nTime Complexity : O(n)\nSpace Complexity: O(1)\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& n, int x) {\n int size = n.size();\n int total = 0;\n int len = 0;\n for(int i : n) total += i;\n if(total == x) return size;\n int need = total - x;\n int i = 0 , j = 0;\n int sum = 0;\n while( j < size ) {\n sum += n[j]; \n while(i < j && sum > need){\n sum -= n[i++];\n }\n if(sum == need){\n \n len = max(len, j-i+1);\n }\n j++;\n } \n if(len == 0) return -1; \n return size-len;\n }\n};\n``` | 15 | 1 | ['Two Pointers', 'Greedy', 'C', 'Sliding Window'] | 0 |
minimum-operations-to-reduce-x-to-zero | 💯🔥 1 Method || C++ | Java || Python || JavaScript 💯🔥 | 1-method-c-java-python-javascript-by-use-7c2v | Read Whole article : https://www.nileshblog.tech/minimum-operations-to-reduce-x-to-zero/\n\nExplanation of Problem with Example (HandWritten).\nTime Complexity: | user6845R | NORMAL | 2023-09-20T06:15:23.243780+00:00 | 2023-09-20T06:15:23.243809+00:00 | 1,105 | false | Read Whole article : https://www.nileshblog.tech/minimum-operations-to-reduce-x-to-zero/\n\nExplanation of Problem with Example (HandWritten).\nTime Complexity:\n\n**Prefix Sum + Hashmap (Longest Subarry )Approach : O(N)**\n\nPython :\nJava:\nc++:\nJavaScript:\n\nRead Whole article :https://www.nileshblog.tech/minimum-operations-to-reduce-x-to-zero/\n\n\n | 14 | 1 | ['C', 'Prefix Sum', 'Python', 'Java', 'JavaScript'] | 3 |
minimum-operations-to-reduce-x-to-zero | Java || Greedy + DP + HashMap + BinarySearch + Prefix Sum + Sliding Window || 5 approaches | java-greedy-dp-hashmap-binarysearch-pref-4a1j | \n\t// O(2^n) O(n)\n\t// Recursion\n\t// TLE\n\tpublic int minOperationsRec(int[] nums, int x) {\n\n\t\tint len = nums.length;\n\t\tint count = minOperationsHel | LegendaryCoder | NORMAL | 2021-06-08T02:38:36.745067+00:00 | 2021-06-08T02:39:07.496763+00:00 | 517 | false | \n\t// O(2^n) O(n)\n\t// Recursion\n\t// TLE\n\tpublic int minOperationsRec(int[] nums, int x) {\n\n\t\tint len = nums.length;\n\t\tint count = minOperationsHelper(nums, x, 0, len - 1);\n\t\treturn (count == Integer.MAX_VALUE) ? -1 : count;\n\t}\n\n\t// O(2^n) O(n)\n\t// Recursion\n\tpublic int minOperationsHelper(int[] nums, int x, int si, int ei) {\n\n\t\tif (x == 0)\n\t\t\treturn 0;\n\n\t\tif (x < 0 || si > ei)\n\t\t\treturn Integer.MAX_VALUE;\n\n\t\tint front = minOperationsHelper(nums, x - nums[si], si + 1, ei);\n\t\tint rear = minOperationsHelper(nums, x - nums[ei], si, ei - 1);\n\n\t\tint min = Math.min(front, rear);\n\t\treturn min == Integer.MAX_VALUE ? min : min + 1;\n\t}\n\n\t// O(n^2) O(n^2)\n\t// Memoization\n\t// TLE\n\tpublic int minOperationsMemo(int[] nums, int x) {\n\n\t\tint len = nums.length;\n\t\tint[][] memo = new int[len][len];\n\t\tint count = minOperationsHelper(nums, x, 0, len - 1, memo);\n\t\treturn (count == Integer.MAX_VALUE) ? -1 : count;\n\t}\n\n\t// O(n^2) O(n^2)\n\t// Memoization\n\tpublic int minOperationsHelper(int[] nums, int x, int si, int ei, int[][] memo) {\n\n\t\tif (x == 0)\n\t\t\treturn 0;\n\n\t\tif (x < 0 || si > ei)\n\t\t\treturn Integer.MAX_VALUE;\n\n\t\tif (memo[si][ei] != 0)\n\t\t\treturn memo[si][ei];\n\n\t\tint front = minOperationsHelper(nums, x - nums[si], si + 1, ei, memo);\n\t\tint rear = minOperationsHelper(nums, x - nums[ei], si, ei - 1, memo);\n\n\t\tint min = Math.min(front, rear);\n\t\tint ans = (min == Integer.MAX_VALUE) ? min : min + 1;\n\t\tmemo[si][ei] = ans;\n\t\treturn ans;\n\t}\n\n\t// O(n) O(n)\n\t// HashMap\n\tpublic int minOperations1(int[] nums, int x) {\n\n\t\tint len = nums.length, total = 0;\n\t\tfor (int i = 0; i < len; i++)\n\t\t\ttotal += nums[i];\n\n\t\tint target = total - x;\n\t\tint ans = subArraySumK1(nums, target);\n\t\treturn (ans == -1) ? -1 : len - ans;\n\t}\n\n\t// O(n) O(n)\n\t// HashMap\n\tpublic int subArraySumK1(int[] arr, int K) {\n\n\t\tif (K == 0)\n\t\t\treturn 0;\n\n\t\tint len = arr.length, sum = 0, ans = -1;\n\t\tHashMap<Integer, Integer> map = new HashMap<>();\n\t\tmap.put(sum, -1);\n\n\t\tfor (int i = 0; i < len; i++) {\n\n\t\t\tsum += arr[i];\n\t\t\tif (map.containsKey(sum - K)) {\n\t\t\t\tint idx = map.get(sum - K);\n\t\t\t\tif (i - idx > ans)\n\t\t\t\t\tans = i - idx;\n\t\t\t}\n\t\t\tmap.put(sum, i);\n\t\t}\n\n\t\treturn ans;\n\t}\n\n\t// O(n^2) O(n)\n\t// Brute Force\n\t// TLE\n\tpublic int minOperations2(int[] nums, int x) {\n\n\t\tint len = nums.length, total = 0;\n\t\tfor (int i = 0; i < len; i++)\n\t\t\ttotal += nums[i];\n\n\t\tint target = total - x;\n\t\tint ans = subArraySum2(nums, target);\n\t\treturn (ans == -1) ? -1 : len - ans;\n\t}\n\n\t// O(n^2) O(n)\n\t// Brute Force\n\tpublic int subArraySum2(int[] nums, int target) {\n\n\t\tint len = nums.length, ans = -1;\n\n\t\tint[] prefix = new int[len];\n\t\tprefix[0] = nums[0];\n\t\tfor (int i = 1; i < len; i++)\n\t\t\tprefix[i] = prefix[i - 1] + nums[i];\n\n\t\tfor (int i = 0; i < len; i++) {\n\t\t\tfor (int j = i; j < len; j++) {\n\t\t\t\tint sum = prefix[j] - prefix[i] + nums[i];\n\t\t\t\tif (sum == target) {\n\t\t\t\t\tif (j - i + 1 > ans)\n\t\t\t\t\t\tans = j - i + 1;\n\t\t\t\t} else if (sum > target)\n\t\t\t\t\tbreak;\n\t\t\t}\n\t\t}\n\n\t\treturn ans;\n\t}\n\n\t// O(nlogn) O(n)\n\t// Binary Search\n\tpublic int minOperations3(int[] nums, int x) {\n\n\t\tint len = nums.length, total = 0;\n\t\tfor (int i = 0; i < len; i++)\n\t\t\ttotal += nums[i];\n\n\t\tint target = total - x;\n\t\tint ans = subArraySum3(nums, target);\n\t\treturn (ans == -1) ? -1 : len - ans;\n\t}\n\n\t// O(nlogn) O(n)\n\t// Binary Search\n\tpublic int subArraySum3(int[] nums, int target) {\n\n\t\tint len = nums.length, ans = -1;\n\t\tint[] prefix = new int[len];\n\n\t\tprefix[0] = nums[0];\n\t\tfor (int i = 1; i < len; i++)\n\t\t\tprefix[i] = prefix[i - 1] + nums[i];\n\n\t\tfor (int i = 0; i < len; i++) {\n\t\t\tint sum = target + prefix[i] - nums[i];\n\t\t\tint j = binarySearch(prefix, i, len - 1, sum);\n\t\t\tif (j != -1 && j - i + 1 > ans)\n\t\t\t\tans = j - i + 1;\n\t\t}\n\n\t\treturn ans;\n\t}\n\n\t// O(nlogn) O(n)\n\t// Binary Search\n\tpublic int binarySearch(int[] prefix, int lo, int hi, int key) {\n\n\t\twhile (lo <= hi) {\n\n\t\t\tint mid = (lo + hi) / 2;\n\t\t\tif (prefix[mid] == key)\n\t\t\t\treturn mid;\n\t\t\telse if (prefix[mid] > key)\n\t\t\t\thi = mid - 1;\n\t\t\telse\n\t\t\t\tlo = mid + 1;\n\t\t}\n\n\t\treturn -1;\n\t}\n\n\t// O(n) O(1)\n\t// Sliding Window\n\tpublic int minOperations4(int[] nums, int x) {\n\n\t\tint len = nums.length, total = 0;\n\t\tfor (int i = 0; i < len; i++)\n\t\t\ttotal += nums[i];\n\n\t\tint target = total - x;\n\t\tint ans = subArraySumK4(nums, target);\n\t\treturn (ans == -1) ? -1 : len - ans;\n\t}\n\n\t// O(n) O(1)\n\t// Sliding Window\n\tpublic int subArraySumK4(int[] arr, int K) {\n\n\t\tint len = arr.length, ptr1 = 0, ptr2 = -1, sum = 0, ans = -1;\n\n\t\twhile (ptr1 < len) {\n\n\t\t\twhile (ptr1 < len) {\n\t\t\t\tsum += arr[ptr1];\n\t\t\t\tif (sum == K) {\n\t\t\t\t\tif (ptr1 - ptr2 > ans)\n\t\t\t\t\t\tans = ptr1 - ptr2;\n\t\t\t\t}\n\t\t\t\tif (sum > K) {\n\t\t\t\t\tptr1++;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t\tptr1++;\n\t\t\t}\n\n\t\t\twhile (ptr2 < ptr1 - 1) {\n\t\t\t\tptr2++;\n\t\t\t\tsum -= arr[ptr2];\n\t\t\t\tif (sum == K) {\n\t\t\t\t\tif (ptr1 - ptr2 - 1 > ans)\n\t\t\t\t\t\tans = ptr1 - ptr2 - 1;\n\t\t\t\t}\n\t\t\t\tif (sum < K)\n\t\t\t\t\tbreak;\n\t\t\t}\n\n\t\t}\n\n\t\treturn ans;\n\t} | 14 | 2 | [] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ | Easy Solution w/ Explanation | Sliding Window ✅ | c-easy-solution-w-explanation-sliding-wi-hfyo | Please upvote the post if you like it :)\n\nIntuition:\nwe can basically think this problem as finding the longest subarray with sum sum - x, since we are delet | prantik0128 | NORMAL | 2022-06-11T04:33:00.684634+00:00 | 2022-06-11T04:36:04.386795+00:00 | 1,095 | false | **Please upvote the post if you like it :)**\n\n**Intuition:**\nwe can basically think this problem as `finding the longest subarray` with **sum** `sum - x`, since we are deleting only from the ends so we will be left out with sum `sum-x` left if we are able to remove elements with sum `x` \nThis is how we come to down to the approach of using `sliding window` with variable size using `2 pointers` \n\n* Here we are taking **2 pointers** -> `start_ind, end_ind`\n* If the `sum` of the `subarray` exceeds the `target` then we simply reduce the `window size` i.e increasing `start_ind` until it is `<=target`\n* If the sum==target we simply mark the found as true and compare the length(`end_ind-start_ind+1`) if it is more than `max_len` then we store it.\n* Return `-1` if the **sum** of the sliding window never becomes equal to **target**\n****\n**Code(C++):**\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int sum=0;\n for(int i:nums) sum+=i;\n int target = sum-x;\n int cur_sum=0,max_len=0;\n int start_ind=0;\n bool found = false;\n for(int end_ind=0;end_ind<n;end_ind++){\n cur_sum+=nums[end_ind];\n while(start_ind<=end_ind && cur_sum>target){\n cur_sum -=nums[start_ind];\n start_ind+=1;\n }\n if(cur_sum==target){\n found = true;\n max_len = max(max_len,end_ind-start_ind+1);\n }\n }\n return found?n-max_len:-1;\n }\n};\n```\n\n**Time Complexity : O(N)**\n**Space Complexity : O(1)** | 13 | 0 | ['C', 'Sliding Window'] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ ☄️ | SLIDING WINDOW | O(1) Space / O(n) Time | c-sliding-window-o1-space-on-time-by-meg-cjud | The problem can be thought of as finding the longest subarray with sum total - x ,because we are deleting elements from the ends only .So there will be a subarr | megamind_ | NORMAL | 2022-06-11T02:01:54.187973+00:00 | 2022-06-11T06:28:29.418926+00:00 | 1,747 | false | The problem can be thought of as finding the longest subarray with sum `total - x` ,because we are deleting elements from the ends only .So there will be a subarray left of sum `total-x` left if we were able to remove elements with sum `x`. \n The approach is to use the concept of the variable-size sliding window using 2 pointers. Initialize i, j and sum = k .If the sum is less than k just increment j, if the sum is equal to k compute the max and if the sum is greater than k subtract ith element while the sum is less than k.\n# Time Complexity : O(n)\n# Space Complexity : O(1)\n```\n int total = 0;\n for(int i : nums)total+=i;\n \n int target = total -x;\n \n if(target<0)return -1;\n if(target ==0)return nums.size();\n \n int i = 0, j = 0, sum = 0;\n int maxLen = -1;\n \n while (j < nums.size()) {\n sum += nums[j];\n if (sum < target) {\n j++;\n }\n else if (sum == target) {\n maxLen = max(maxLen, j-i+1);\n j++;\n }\n else if (sum > target) {\n while (sum > target) {\n sum -= nums[i];\n i++;\n }\n if(sum == target){\n maxLen = max(maxLen, j-i+1);\n }\n j++;\n }\n }\n \n if(maxLen==-1)return -1;\n \n return nums.size()-maxLen;\n```\n\n | 10 | 1 | [] | 1 |
minimum-operations-to-reduce-x-to-zero | [C++] Cumulative Sums Solution Explained, ~100% Time, ~70% Space | c-cumulative-sums-solution-explained-100-vsqh | Okay, I tried a number of approaches, including a 2d matrix for DP and a double-ended BFS, before realising that there was a much easier and performant solution | ajna | NORMAL | 2021-01-14T23:58:00.439707+00:00 | 2021-01-15T00:03:28.978472+00:00 | 1,268 | false | Okay, I tried a number of approaches, including a 2d matrix for DP and a double-ended BFS, before realising that there was a much easier and performant solution; the tips for the problem definitely did not help.\n\nThe core idea is to compute and store all the partial sums from the left together with the indexes in which we can achieve them, then look for matches computing cumulative sums from the right, but I guess it will become clearer with some explanations.\n\nFirst of all we declare a few support variables:\n* `res`, our accumulator variable, initialised to `-1` (which will flag no valid solution was found);\n* `len` will store the length of the vector;\n* `tot` will store the partial sums;\n* `m` is an `unordered_map` that we will use with partial sums as keys and indexes at which they were obtained as values.\n\nWe will then proceed and populate `m`; first of all we will have `0` obtained at the fictitious position of `-1`, that is to say: before even starting the sum, that is our initial value for it.\n\nLooping from the left, we will compute the cumulative sum, store it in `tot` and store the matching index in `m[tot]`, as announced; we will loop as long as `i` is within the margins of our vector and `tot` is less than `x` (no point in proceeding further).\n\nOnce done, we have to deal with 2 edge cases:\n* we run through the whole vector (`m[tot] == len - 1)`, so we return `len` if `tot == x` (ie: we need each single element to reach that value) or `-1` otherwise (ie: even summing them all, we cannot reach `x`);\n* alternatively, if `tot == x`, it means that potentially we might proceed only removing from the left, but we do not return it yet, since removing from the right or a mix of the two might be even more convenient, so we just store `m[tot] + 1` (because we were storing `0`-based indexes) into `res` and move on with the second loop to check that.\n\nWe can now reset `tot == 0` and start computing a cumulative sum from the right. As soon as we find a matching key of `x - tot`, we update `res`, since it means that we might achieve `x` summing `tot` and, of course `x - tot`.\n\nTo update `res`, we check if a value of `res` was previously found (ie: `res > -1`), otherwise we take the top value `len` and then compute the minimum between it and the current one, found moving `m[tot] + 1` steps from the left (as explained above) and `len - j` steps from the right.\n\nOnce done, we can return `res` :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n // support variables\n int res = -1, len = nums.size(), tot = 0;\n unordered_map<int, int> m;\n // storing the position of all the partial sums from left up to x\n // and relative indexes\n m[0] = -1;\n for (int i = 0; i < len && tot < x; i++) {\n m[tot += nums[i]] = i;\n }\n // edge case: x >= the sum of all the elements in the vector\n if (m[tot] == len - 1) return tot == x ? m[tot] + 1 : -1;\n // edge case: x found just summing left numbers\n if (tot == x) res = m[tot] + 1;\n // resetting tot\n tot = 0;\n // moving on from the right\n for (int j = len - 1; j >= 0 && tot < x; j--) {\n // updating res if there is a match\n if (m.find(x - (tot += nums[j])) != end(m)) {\n res = min(res > -1 ? res : len, m[x - tot] + 1 + len - j);\n }\n }\n return res;\n }\n};\n```\n\nMicro-optimisation, you might find even more efficient to limit the second loop in some edge cases, when a viable `res` was already found and it does not make sense to parse from the right a long list of values relatively small compared to `x`:\n\n```cpp\n\n // moving on from the right\n for (int j = len - 1, lmt = res > -1 ? len - res : 0; j >= lmt && tot < x; j--) {\n // updating res if there is a match\n if (m.find(x - (tot += nums[j])) != end(m)) {\n res = min(res > -1 ? res : len, m[x - tot] + 1 + len - j);\n }\n }\n``` | 10 | 0 | ['C', 'C++'] | 3 |
minimum-operations-to-reduce-x-to-zero | JAVA | Recursion | Sliding Window | 2 Solutions | java-recursion-sliding-window-2-solution-9yu0 | Recursive Solution: (Please note that it will give time limit exceeded (TLE) if submitted )\n\nclass Solution {\n int ans;\n public int minOperations(int[ | deepmehta | NORMAL | 2021-01-14T14:11:48.554505+00:00 | 2021-01-14T14:11:48.554542+00:00 | 1,432 | false | **Recursive Solution:** (Please note that it will give time limit exceeded (TLE) if submitted )\n```\nclass Solution {\n int ans;\n public int minOperations(int[] nums, int x) {\n ans = Integer.MAX_VALUE;\n recur(nums,0,nums.length-1,x,0);\n return ans==Integer.MAX_VALUE?-1:ans;\n }\n public void recur(int nums[],int start, int end,int target,int steps){\n if(target==0){\n ans = Math.min(ans,steps);\n return;\n }\n if(start>end || target<0){\n return;\n }\n \n recur(nums,start+1,end,target-nums[start],steps+1);\n recur(nums,start,end-1,target-nums[end],steps+1); \n }\n}\n```\n\n**Sliding Window Approach:**\n```\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int sum = 0;\n for(int num: nums){\n sum+=num;\n }\n sum -= x; // ****totalsum-target to find maxSubArray \n int left = 0,right = 0,ans = -1;\n int subArraySum = 0;\n while(right<nums.length){\n subArraySum+=nums[right];\n if(subArraySum>sum){\n while(subArraySum>sum && left<=right){\n subArraySum-=nums[left++];\n }\n }\n if(subArraySum==sum){\n ans = Math.max(ans,right-left+1);\n }\n right++;\n }\n return ans==-1?ans:nums.length-ans;\n }\n}\n``` | 10 | 1 | ['Recursion', 'Sliding Window', 'Java'] | 3 |
minimum-operations-to-reduce-x-to-zero | C++ prefix sums O(n) | c-prefix-sums-on-by-radheshsarma2299-ahp2 | We can observe that we are deleting some part of prefix(possibly none) and some part of suffix(possibly none) from the given array such that sum of prefix and s | radheshsarma2299 | NORMAL | 2020-11-15T11:58:42.393942+00:00 | 2020-11-15T11:58:42.393971+00:00 | 792 | false | We can observe that we are deleting some part of prefix(possibly none) and some part of suffix(possibly none) from the given array such that sum of prefix and suffix deleted is x\nSo we create a map between the suffix sum and the length of suffix\nNow we iterate from left to right,\nlet say we are at index i, then let say prefix[i] denotes the prefix sum till i.\nThen we have prefix[i] value for the current prefix , we need x - prefix[i] from the suffix to get a sum of x. So we can use the map created to check and update the answer.\nWe check all prefix and report the minimum answer.Since this algorithm checks all prefixes , it would include the optimal solution\nWe need to handle base case where x > sum , return -1 since the array sum is less than x , so no prefix or suffix could reduce x to zero\n\nTime Complexity : O(n)\nSpace Complexity : O(n)\n\n\tclass Solution \n\t{\n\t\tpublic:\n\t\t\tint minOperations(vector<int>& nums, int x) {\n\t\t\t\tint sum = 0;\n\t\t\t\tfor(int i = 0; i < nums.size(); i++)sum += nums[i];\n\t\t\t\tif(x > sum)return -1;\n\n\t\t\t\tunordered_map<int,int> mp;\n\n\t\t\t\t sum = 0;\n\t\t\t\tint ans = 1000000000;\n\t\t\t\tfor(int i = 0; i < nums.size(); i++)\n\t\t\t\t{\n\t\t\t\t\tsum += nums[i];\n\t\t\t\t\tif(sum == x)ans = min(ans,i+1);\n\t\t\t\t}\n\t\t\t\tsum = 0;\n\t\t\t\tfor(int i = nums.size()-1; i >=0 ; i--)\n\t\t\t\t{ \n\t\t\t\t\tsum += nums[i];\n\t\t\t\t\tmp[sum] = nums.size()-i;\n\t\t\t\t}\n\n\t\t\t\tif(mp.find(x) != mp.end())ans = min(ans,mp[x]);\n\n\t\t\t\tsum = 0;\n\n\t\t\t\tfor(int i = 0; i < nums.size(); i++)\n\t\t\t\t{\n\t\t\t\t\tsum += nums[i];\n\t\t\t\t\tif(mp.find(x-sum) != mp.end())ans = min(ans, i + 1 + mp[x-sum]);\n\n\t\t\t\t}\n\n\t\t\t\tif(ans ==1000000000)ans = -1;\n\n\t\t\t\treturn ans;\n\n\n\t\t\t}\n\t}; | 10 | 1 | [] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ Prefix Sum & Binary Search/Unordered map/Sliding Window||w Explanation | c-prefix-sum-binary-searchunordered-maps-0v0g | Intuition\n Describe your first thoughts on how to solve this problem. \nThis code efficiently finds the minimum length of a subarray that sums up to x using pr | anwendeng | NORMAL | 2023-09-20T02:24:44.063519+00:00 | 2023-09-20T08:15:24.233524+00:00 | 1,615 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis code efficiently finds the minimum length of a subarray that sums up to x using prefix sums and binary search techniques.\n\nSecond approach does not use binary search. Insteadly the hash table unordered_map plays the role! The TC is reduced to linear $O(n)$.\n\n3rd approach uses sliding window method. TC=O(n) SC=O(1).\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The code begins by initializing a prefix vector with the first element of the nums array. This prefix vector is used to store prefix sums of the nums array.\n2. It then enters a loop to calculate the prefix sums for the remaining elements of the nums array. If at any point the sum exceeds the target x, the loop breaks. This loop accumulates the prefix sums and stores them in the prefix vector.\n3. After calculating the prefix sums, the code performs a binary search using lower_bound to find the index of x in the prefix vector. This binary search is crucial for efficiently searching for a subarray that sums up to x\n4. f the binary search finds an exact match for x in the prefix vector, the code updates the answer (ans) with the index (idx + 1). If no match is found, ans remains at its initial value of INT_MAX.\n5. The code then enters a backward loop, starting from the end of the nums array and decrementing x by the value of the current element. If x becomes negative, the loop breaks, as no subarray can sum to a negative value.\n6. If x becomes zero, it means the current subarray from the end of the nums array to the current position has a sum equal to x. The code updates ans with the length of this subarray (n - j).\n7. In this loop, a second binary search is performed to find the index of x in the prefix vector, but this time it\'s done in reverse. The condition idx < j ensures that we\'re not considering prefixes that include the current element itself.\n8. f the binary search in the reverse loop finds an exact match for x, the code updates ans with the minimum of its current value and the length of the subarray from the reverse binary search (idx + 1 + (n - j)).\n9. Finally, the code checks if ans remains at its initial value of INT_MAX. If so, it returns -1, indicating that no subarray was found. Otherwise, it returns the calculated ans.\n\nLet\'s consider the testcase\n```[3,2,20,1,1,3], x=10 ```\nThe process\n```\nsz=3, prefix=25\nx=10 ans=2147483647\nprefix=5\nj=5 suffix=3 prefix=5 idx=2\nj=4 suffix=4 prefix=5 idx=2\nupdate ans=5\nj=3 suffix=5 prefix=5 idx=2\nj=2 suffix=25 prefix=0 idx=0\n```\nThe testcase ```[1,1,4,2,3] x=5 ```Process\nsz=3, prefix=6\nx=5 ans=2147483647\nprefix=2\nupdate ans=3\nj=4 suffix=3 prefix=2 idx=2\nupdate ans=2\nj=3 suffix=5 prefix=0 idx=0\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$ O(n * \\log n)$ vs $O(n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n)$\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n vector<int> prefix={nums[0]};\n for(int i=1; i<n; i++){\n // cout<<prefix[i-1]<<endl;\n if (prefix[i-1]>=x) break;\n prefix.push_back(prefix[i-1]+nums[i]);\n }\n int sz=prefix.size();\n // cout<<"sz="<<sz<<endl;\n int idx=lower_bound(prefix.begin(), prefix.end(), x)-prefix.begin();\n int ans=INT_MAX;\n if (idx!=sz && prefix[idx]==x){\n ans=idx+1;\n // cout<<"x="<<x<<" idx="<<idx<<" ans="<<ans<<endl;\n }\n for(int j=n-1; j>=0; j--){\n x-=nums[j];\n if (x<0) break;\n if (x==0) ans=min(ans, (n-j));\n idx=lower_bound(prefix.begin(), prefix.end(), x)-prefix.begin();\n if (idx<j && prefix[idx]==x){//idx<j very important\n // cout<<"x="<<x<<" idx="<<idx<<" ans="<<idx+(n-j)+1<<endl;\n ans=min(ans, idx+1+(n-j));\n } \n }\n return ans==INT_MAX?-1:ans;\n }\n};\n```\n# code with Explaination in comments\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n vector<int> prefix = {nums[0]}; // Initialize a prefix sum array with the first element of nums.\n\n for (int i = 1; i < n; i++) {\n // Calculate the prefix sum for each element in nums.\n if (prefix[i - 1] >= x) break; // If the sum exceeds x, exit the loop.\n prefix.push_back(prefix[i - 1] + nums[i]);\n }\n\n int sz = prefix.size(); // Get the size of the prefix sum array.\n\n int idx = lower_bound(prefix.begin(), prefix.end(), x) - prefix.begin(); // Find the index of x in the prefix sum array.\n\n int ans = INT_MAX; // Initialize ans to a large value.\n\n if (idx != sz && prefix[idx] == x) {\n ans = idx + 1; // If x is found in the prefix sum array, update ans.\n }\n\n for (int j = n - 1; j >= 0; j--) {\n x -= nums[j]; // Subtract the current element from x.\n\n if (x < 0) break; // If x becomes negative, exit the loop.\n\n if (x == 0) ans = min(ans, (n - j)); // If x becomes zero, update ans with the length of the subarray.\n\n idx = lower_bound(prefix.begin(), prefix.end(), x) - prefix.begin(); // Find the index of x in the prefix sum array.\n\n if (idx < j && prefix[idx] == x) {\n // If x is found before the current element in the prefix sum array, update ans.\n ans = min(ans, idx + 1 + (n - j));\n }\n }\n\n return ans == INT_MAX ? -1 : ans; // If ans is still the initial large value, return -1; otherwise, return ans.\n }\n};\n\n```\n# Code without binary searching using unordered_map\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int prefix=nums[0]; // Initialize the prefix sum with the first element.\n unordered_map<int, int> mp={{prefix, 0}};\n int ans = INT_MAX;\n\n for (int i=1; i < n; i++) {\n prefix+=nums[i];\n if (prefix>x) break;\n mp[prefix]=i; \n }\n // for (auto [k, v]: mp)\n // cout<<k<<"->"<<v<<endl;\n\n if (mp.count(x)) ans=mp[x]+1;\n // cout<<"x="<<x<<" idx="<<ans-1<<" ans="<<ans<<endl;\n\n for (int j=n-1; j >= 0; j--) {\n x-=nums[j];\n if (x<0) break;\n if (x==0) ans=min(ans, (n-j));\n int idx=-1;\n if (mp.count(x) && (idx=mp[x])<j) {\n // cout<<"x="<<x<<" idx="<<idx<<" ans="<<idx+(n-j)+1<<endl;\n ans=min(ans, idx+1+(n-j));\n }\n }\n return ans==INT_MAX?-1:ans;\n }\n};\n\n\n```\n# Code with sliding windows\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n int prefix=nums[0];\n int sz=n;\n for(int i=1; i<n; i++){\n// cout<<prefix<<endl;\n if (prefix>x) {\n sz=i;\n break;\n }\n prefix+=nums[i];\n }\n // cout<<"sz="<<sz<<", prefix="<<prefix<<endl;\n \n if (sz==n && prefix<x) //impossible\n return -1;\n\n prefix-=nums[sz-1];// let prefix<=x\n int idx=sz-1;\n int ans=INT_MAX;\n if (idx>=0 && prefix==x) ans=sz-1;\n\n int suffix=0;\n\n for (int j=n-1; j >= 0; j--) {\n suffix+=nums[j];\n while (suffix+prefix>x && prefix>0){\n idx--;\n prefix-=nums[idx];\n if (suffix+prefix <= x) break;\n }\n if (suffix+prefix==x){\n ans=min(ans, (n-j)+idx);\n // cout<<(n-j)<<" idx="<<idx<<" ,"<<(n-j)+idx<<endl;\n }\n if (suffix>=x) break;\n }\n\n return ans==INT_MAX ? -1 : ans;\n }\n};\n\n\n\n``` | 9 | 0 | ['Hash Table', 'Binary Search', 'Sliding Window', 'Prefix Sum', 'C++'] | 2 |
minimum-operations-to-reduce-x-to-zero | ✅✅JAVA || Beats 99% || 🔥🔥 DP ||🔥🔥 Sliding Window | java-beats-99-dp-sliding-window-by-sumit-8yme | Intuition\n Describe your first thoughts on how to solve this problem. \nDp will give memory limit exceeded.\nso we need to do it by sliding window\n# Approach\ | sumitdarshanala | NORMAL | 2023-09-20T08:52:15.334562+00:00 | 2023-09-20T08:52:15.334581+00:00 | 764 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDp will give memory limit exceeded.\nso we need to do it by sliding window\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe need a { subarray of sum } as \ntarget = total sum - x\nthen max subarray sum of target \nto get min operation on x\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n- Dp\n```\n class Solution {\n public int minOperations(int[] nums, int x) {\n int n = nums.length;\n int dp[][] = new int [n+1][n+1];\n\n for(int [] arr : dp)Arrays.fill(arr,-1);\n\n int temp = helper(nums,x,0,n-1,n,dp);\n\n return temp == 1000000 ? -1:temp;\n }\n public int helper(int[] nums,int x,int i,int j,int n,int dp[][]){\n if(x == 0)return 0;\n if(i > j || i >= n || j < 0 || x < 0){\n return 1000000;\n }\n if(dp[i][j] != -1)return dp[i][j];\n\n int ans = 1000000;\n ans = Math.min(ans,1+helper(nums,x-nums[i],i+1,j,n,dp));\n ans = Math.min(ans,1+helper(nums,x-nums[j],i,j-1,n,dp));\n return dp[i][j] = ans;\n }\n }\n```\n# Code\n- Sliding Window\n```\nclass Solution {\n public int minOperations(int [] nums,int x){\n int n = nums.length;\n int sum = 0;\n for(int i : nums)sum += i;\n int target = sum - x;\n int j = 0;\n int min = Integer.MIN_VALUE;\n sum = 0;\n for(int i = 0;i < n; i++){\n sum += nums[i];\n while(j <= i && sum > target){\n sum -= nums[j];\n j++;\n }\n if(sum == target){\n min = Math.max(min,i-j+1);\n }\n }\n if(min == Integer.MIN_VALUE)return -1;\n return n-min;\n }\n}\n``` | 8 | 0 | ['Dynamic Programming', 'Sliding Window', 'Java'] | 3 |
minimum-operations-to-reduce-x-to-zero | [C++/Full Explanation] Simple Sliding Window || Why DP won't work here explanation | cfull-explanation-simple-sliding-window-198pn | class Solution {\npublic:\n \n\t// We can do this question with the help of DP concept of take from front and back and return minimum of the operation but in | Sameer_111 | NORMAL | 2022-06-11T04:56:18.515188+00:00 | 2022-06-11T04:58:21.424655+00:00 | 940 | false | class Solution {\npublic:\n \n\t// We can do this question with the help of DP concept of take from front and back and return minimum of the operation but in that case it will give TLE \n\t// and here we are not able to optimize due to high constraints 1<=x<=10^9.\n\t// That is why sliding window works here, So we find total sum and subtract x from it now we have to find the maximum window in which (totalSum-x) come \n\t// and satisfy so totalLength-maxWindow of (TotalSum-x) will give minimum operation in which we get x to become zero.\n\t// So this is the the approach i do here.\n\t//PLZ UPVOTE IF YOU LIKE THE POST :)\n\t\n\tint minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int t = 0;\n for(auto x:nums) t+=x;\n t-=x;\n if(t==0) return n;\n if(t<0) return -1;\n int i = 0,j = 0,sum = 0,c = -1;\n while(j<n){\n sum+=nums[j];\n while(sum>t){\n sum-=nums[i];\n i++;\n }\n if(sum==t){\n c = max(c,j-i+1);\n }\n j++;\n }\n return (c==-1)?-1:n-c;\n }\n}; | 8 | 0 | ['Two Pointers', 'C', 'Sliding Window', 'Prefix Sum', 'C++'] | 1 |
minimum-operations-to-reduce-x-to-zero | Python Sliding Window Using maxLen of continuous subarray concept | python-sliding-window-using-maxlen-of-co-tbjs | Idea is to do using continous subarray with max length size which return continous subarray length. The elements that are not included in the subarray (exterior | aayuskh | NORMAL | 2021-01-14T23:52:47.652390+00:00 | 2021-01-14T23:52:47.652433+00:00 | 459 | false | Idea is to do using continous subarray with max length size which return continous subarray length. The elements that are not included in the subarray (exterior to it) is the ans. So, in this case len(nums) - maxLen of continous subarray.\nNow x is actually sum of exterior, to do continous subarray we need total sum - x (exclude x sum)\n\n```\nclass Solution(object):\n def minOperations(self, nums, x):\n """\n :type nums: List[int]\n :type x: int\n :rtype: int\n """\n maxLen = total = windowStart = 0\n targetSum = sum(nums)\n \n # edge cases\n if targetSum < x: return -1\n if targetSum == x: return len(nums)\n \n # opposite of sliding window but still do sliding window\n # so instead of find continous subarray,\n # we need to find outer points that is not included in continous subarray\n k = targetSum - x # this is for continous subarray\n \n for windowEnd in range(len(nums)):\n total += nums[windowEnd]\n \n while total > k:\n total -= nums[windowStart]\n windowStart += 1\n \n if total == k:\n maxLen = max(maxLen, windowEnd - windowStart + 1)\n \n \n return len(nums) - maxLen if maxLen != 0 else -1\n``` | 8 | 0 | ['Sliding Window', 'Python'] | 1 |
minimum-operations-to-reduce-x-to-zero | Simple solution by finding the longest array with a target in Java | simple-solution-by-finding-the-longest-a-4trx | Essentially, we need to find the longest array with a sum of - (sum(array) - x). If we do find this, this might either be - \n1. Starting from the left end: In | amoghrajesh1999 | NORMAL | 2021-01-14T11:11:30.273381+00:00 | 2021-01-14T11:11:30.273406+00:00 | 870 | false | Essentially, we need to find the longest array with a sum of - (sum(array) - x). If we do find this, this might either be - \n1. Starting from the left end: In this case, We will have found the answer which has minimum length from right\n2. Somewhere in the middle: Will be a valid answer since we can pick elements from either sides\n3. Starting from right end: Similar to 1\n\nWe find such a longest array and the answer will be length(array) - length of longest array as found earlier\n\nCode in Java - \n```\nclass Solution {\n public int minOperations(int[] nums, int k) {\n int target = -1 * k;\n for(int e: nums){\n target += e;\n }\n \n if(target == 0){\n return nums.length;\n }\n if(target < 0){\n return -1;\n }\n \n HashMap<Integer, Integer> map = new HashMap<>();\n int sum = 0;\n int m = -1;\n \n for(int i = 0; i < nums.length; i++){\n sum += nums[i];\n if(sum == target){\n m = i + 1;\n }\n if(!map.containsKey(sum)){\n map.put(sum, i);\n }\n if(map.containsKey(sum - target)){\n if(m < (i - map.get(sum - target))){\n m = i - map.get(sum - target);\n }\n }\n }\n return m != -1 ? nums.length - m : m;\n \n }\n}\n```\n | 8 | 2 | ['Java'] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ | PREFIX SUM | HASHMAP | O(n) TIME COMPLEXITY | c-prefix-sum-hashmap-on-time-complexity-m3k5i | \nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n const int n = nums.size();\n int ans = INT_MAX, sum = 0;\n | UnknownOffline | NORMAL | 2022-06-11T03:01:52.357807+00:00 | 2022-06-11T03:01:52.357837+00:00 | 473 | false | ```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n const int n = nums.size();\n int ans = INT_MAX, sum = 0;\n unordered_map<int,int> m;\n for(int i = n - 1;i >=0;i--) {\n sum += nums[i];\n m[sum] = i + 1;\n if(sum == x) ans = min(ans,n - i);\n }\n sum = 0;\n for(int i = 0;i<n;i++){\n sum += nums[i];\n if(sum == x) ans = min(ans,i + 1);\n if(m[x-sum] != 0 && m[x-sum] - 1> i) ans = min(ans,i + n - m[x - sum] + 2);\n }\n return ans == INT_MAX?-1:ans;\n }\n};\n```\n### UPVOTE IF YOU LIKE | 7 | 0 | ['C', 'Prefix Sum'] | 1 |
minimum-operations-to-reduce-x-to-zero | Python | Prefix Sum & Sliding Window | With Explanation | python-prefix-sum-sliding-window-with-ex-on9w | Detailed Explanation:\n1. Idea: the aim of this question is to find the minimum operations to reduce x to 0, i.e. find the minimum number of elements from the s | Mikey98 | NORMAL | 2022-06-11T01:19:09.316490+00:00 | 2022-06-11T23:25:13.186463+00:00 | 1,545 | false | Detailed Explanation:\n1. Idea: the aim of this question is to find the minimum operations to reduce `x` to 0, i.e. find the minimum number of elements from the start and end that can sum up to `x`. We can transform this problem to: **find the longest subarray in `nums` that sum to `goal`**, where `goal = sum(nums) - x`.\n\n2. Solution: use a silding window, both `left` and `right` edge start from index `0`. Store the `current_sum` in the current window. If the `current_sum > goal` we move the `left` edge one step to right. If the `current_sum = goal`, update the `max_length`.\n\n3. Note: this solution works because **in this problem all the numbers are positive** !\n\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n # find the longest subarray that sum to \'goal\'\n s = sum(nums)\n n = len(nums)\n goal = s - x\n max_length = -1\n left = 0\n current_sum = 0\n\n for right, num in enumerate(nums):\n current_sum += num\n # if larger, move `left` to right\n while current_sum > goal and left <= right:\n current_sum -= nums[left]\n left += 1\n # check if equal\n if current_sum == goal:\n max_length = max(max_length, right-left+1)\n\n return n - max_length if max_length != -1 else -1 | 7 | 0 | ['Sliding Window', 'Python', 'Python3'] | 3 |
minimum-operations-to-reduce-x-to-zero | Javascript | Simple Prefix Sum Sliding Window Solution w/ Explanation| beats 100% / 94% | javascript-simple-prefix-sum-sliding-win-avtg | Idea:\n\nThis problem is tasking us to essentially find when the sum of the starting and ending subarrays of nums is equal to x. Put another way, it\'s asking u | sgallivan | NORMAL | 2021-01-14T23:19:15.114947+00:00 | 2021-01-14T23:56:51.173970+00:00 | 418 | false | ***Idea:***\n\nThis problem is tasking us to essentially find when the sum of the starting and ending subarrays of **nums** is equal to **x**. Put another way, it\'s asking us to find when any subarray of consecutive elements in **nums** is equal to the sum of all elements in **nums** minus **x**.\n```\n <-A-> <------ B ------> <-C->\n nums = [1, 1, 1, 1, 1, 1, 1, 1, 1]\n\t \n\t if sum(A) + sum(C) = x\n\t then x = sum(nums) - sum(B)\n```\nSo now we need to find any consecutive subarray of **nums** whose sum is equal to a specific value. Any time you\'re talking about checking the sum of a consecutive subarray, it should naturally bring to mind the use of a **prefix sum array**.\n\nThe sum of any consecutive subarray, **i** to **j**, of **nums** can be defined as the sum of all elements of **nums** up to **j** minus the sum of all the elements of **nums** *before* **i**. This is aided by creating a prefix sum array containing the running sum of elements in **nums**.\n```\n\t\t\t <------ A ------>\n <-B->\n\t\t\t <-- C -->\n nums = [1, 1, 1, 1, 1, 1, 1, 1, 1]\n\t\t\t\t\t i j\n prefixSum = [1, 2, 3, 4, 5, 6, 7, 8, 9]\n\t \n\t if prefixSum[n] = sum(nums[0] to nums[n])\n\t and sum(A) = prefixSum[j]\n\t and sum(B) = prefixSum[i-1]\n\t then sum(C) = prefixSum[j] - prefixSum[i-1]\n```\n\nUsing a prefix sum array, we can then use a **2-pointer** **sliding window** to evaluate which subarrays have the specified value and keep track of which one has the largest subarray size. The answer, if possible, will be its difference from **nums.length**.\n\nThe best result for the code below is **92ms / 50.2MB**.\n\n` `\n***Implementation:***\n\nThe prefix sum array is simple to achieve; we just iterate through **nums** and make each **i**th element of the prefix sum array the sum of **nums[0]** through **nums[i]** by taking the previous value (**nums[i-1]**) and adding **nums[i]** to it. Since we don\'t need the individual elements of **nums** after this, we can run the conversion in place.\n\n(***Note**: Normally in a prefix sum array you will want to add a leading **0** to the array as the equation for a subarray starting with **i = 0** will lead to an **nums[i-1]** value outside the range of **nums**. In this instance, however, we can handle the issue more efficiently later.*)\n\nOnce **nums** has been updated, the last element **nums[len-1]** will equal the total sum of **nums**. This means that we\'ll be looking for a subarray of nums that sums to **nums[len-1] - x**, or **y**. If **y** is negative, then there exists no possibility for a solution, since all elements of **nums** are positive integers, so we can **return -1**. If **y** is **0**, then the only possible solution is the entire **nums** array, so we can **return len**.\n\nOtherwise, we can use **i** and **j** as two pointers to form a sliding window of **nums**. While we iterate, we should keep track of the size (**best**) of the largest successful subarray. If at any time during the iteration, **i** moves far enough that no remaining subarray can beat **best**, or if **nums[i]** is already larger than **x**, then we should force an end. Starting with **best = 0** means that **i** should move all the way to **len** if no matches are found.\n\nSince we\'ll be using **nums[i]** a number of times, we can store it in **l**, representing the left endpoint value sum. Setting the initial value of **l** to **0** and only updating it to be based off **nums[i]** *after* the first iteration will allow us to avoid needing to **unshift()** a **0** onto the prefix sum array beforehand.\n\nThen, during each iteration, we\'ll move **j** up as long as the subarray sum (**nums[j] - l**) is less than **y**. If the sliding window has stopped on a subarray that equals **y**, then we update **best** if necessary.\n\nSince **best** represents the largest subarray length, we actually want to **return len - best**, but if no match was ever found (**best > 0**), then we should **return -1** instead.\n\n` `\n***Code:***\n```\nvar minOperations = function(nums, x) {\n let len = nums.length, best = 0\n for (let i = 1; i < len; i++) nums[i] += nums[i-1]\n let y = nums[len-1] - x\n if (y < 0) return -1\n if (y === 0) return len\n for (let i = -1, j = l = 0; i < len - best && l <= x; l = nums[++i]) {\n while (nums[j] - l < y) j++\n if (nums[j] - l === y) best = Math.max(best, j - i)\n }\n return best > 0 ? len - best : -1\n};\n``` | 7 | 0 | ['JavaScript'] | 0 |
minimum-operations-to-reduce-x-to-zero | Python, find the longest window | python-find-the-longest-window-by-warmr0-n5u8 | Essentially we\'re looking to remove the longest sequence of numbers so that what\'s left is equal to x. \nReformulating the problem this way it becomes a class | warmr0bot | NORMAL | 2021-01-14T10:18:27.317899+00:00 | 2021-01-14T10:18:27.317938+00:00 | 1,046 | false | Essentially we\'re looking to remove the longest sequence of numbers so that what\'s left is equal to `x`. \nReformulating the problem this way it becomes a classic window sliding problem. \nComplexity Time: O(N), Memory: O(1) \n```\ndef minOperations(self, nums: List[int], x: int) -> int:\n\tN = len(nums)\n\ttoremove = sum(nums) - x\n\tif toremove < 0: return -1\n\n\tlongest_removal = -1\n\tleft = 0\n\tfor right in range(N):\n\t\ttoremove -= nums[right]\n\t\twhile toremove < 0:\n\t\t\ttoremove += nums[left]\n\t\t\tleft += 1\n\t\tif toremove == 0:\n\t\t\tlongest_removal = max(longest_removal, right - left + 1)\n\n\treturn N - longest_removal if longest_removal != -1 else -1\n``` | 7 | 0 | ['Sliding Window', 'Python', 'Python3'] | 0 |
minimum-operations-to-reduce-x-to-zero | [Python] Clear Two Pointers Solution with Video Explanation | python-clear-two-pointers-solution-with-t1nu6 | Video with clear visualization and explanation:\nhttps://youtu.be/kRHZdzYYn50\n\n\nIntuition: Two Pointers\n\n\nCode\n\nclass Solution:\n def minOperations(s | iverson52000 | NORMAL | 2020-11-15T23:26:11.418370+00:00 | 2020-11-15T23:26:11.418407+00:00 | 787 | false | Video with clear visualization and explanation:\nhttps://youtu.be/kRHZdzYYn50\n\n\nIntuition: Two Pointers\n\n\n**Code**\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n target = sum(nums)-x\n n = len(nums)\n\n if target < 0: return -1\n if target == 0: return n\n \n left = 0; cur_sum = 0; n_target = -1\n \n for i in range(n):\n if cur_sum < target:\n cur_sum += nums[i]\n while cur_sum >= target:\n if cur_sum == target:\n n_target = max(n_target, i-left+1)\n cur_sum -= nums[left]\n left += 1\n \n return n-n_target if n_target != -1 else -1\n```\n\nTime: O(n)\nSpace: O(1)\n\nFeel free to subscribe to my channel. More LeetCoding videos coming up! | 7 | 1 | ['Python'] | 2 |
minimum-operations-to-reduce-x-to-zero | [C++/Java] 2-Pointer O(n) Solutions! | cjava-2-pointer-on-solutions-by-admin007-fzcx | It is easy to observe that in order to find the shortest required operations that sum up to x is finding the longest subarray that sums up to total - x. \n\nApp | admin007 | NORMAL | 2020-11-15T05:15:52.314317+00:00 | 2020-11-15T05:32:20.637861+00:00 | 1,223 | false | It is easy to observe that in order to find the shortest required operations that sum up to *x* is finding the longest subarray that sums up to *total - x*. \n\n**Approach 1 Find the longest subarray sum equals to a target value:**\n\n**C++**\n```\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n int n = nums.size();\n int maxi = -1;\n int left = 0;\n int current = 0;\n\n for (int right = 0; right < n; right++) {\n current += nums[right]; // sum([left ,..., right]) = total - x\n while (current > total - x && left <= right) {\n current -= nums[left];\n left += 1; / if larger, move to left\n }\n if (current == total - x) { // check if they are equal\n maxi = max(maxi, right - left + 1);\n }\n }\n return maxi != -1 ? n - maxi : -1;\n }\n```\n\n**Java**\n```\n public int minOperations(int[] nums, int x) {\n int total = 0;\n for (int num : nums) {\n total += num;\n }\n int n = nums.length;\n int maxi = -1;\n int left = 0;\n int current = 0;\n\n for (int right = 0; right < n; right++) {\n current += nums[right]; // sum([left ,..., right]) = total - x\n while (current > total - x && left <= right) { \n current -= nums[left];\n left += 1; // if larger, move to left\n }\n if (current == total - x) { // check they are equal\n maxi = Math.max(maxi, right - left + 1);\n }\n }\n return maxi != -1 ? n - maxi : -1;\n }\n```\n\n**Approach 2 Use 2-pointer technique directly:**\n\nWe can also solve this problem directly without a transition by \n1. Sum up the *nums* array\n2. Set 2 pointers *left* and *right* to 0. Initialize an int *cur* to represent the sum from nums[0] to nums[left-1] and from nums[right+1] to nums[last]. Initialize an int *min* to record the minimum length that sums up to x\n3. While (right < nums.length) \n\t- Calculate *cur*.\n\t- If *cur* is smaller than *x*, move left to left.\n\t- If *cur* is equal to *x*, update the *min*.\n\n**C++**\n```\npublic:\n int minOperations(vector<int>& nums, int x) {\n int current = 0;\n for (int num : nums) {\n current += num;\n }\n int n = nums.size();\n int mini = INT_MAX;\n int left = 0;\n for (int right = 0; right < n; right++) {\n current -= nums[right];\n while (current < x && left <= right) {\n current += nums[left];\n left += 1;\n }\n if (current == x) {\n mini = min(mini, (n - 1 - right) + left);\n }\n }\n return mini != INT_MAX ? mini : -1;\n }\n```\n\n**Java**\n```\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int current = 0;\n for (int num : nums) {\n current += num;\n }\n int n = nums.length;\n int mini = Integer.MAX_VALUE;\n int left = 0;\n\n for (int right = 0; right < n; right++) {\n current -= nums[right];\n while (current < x && left <= right) {\n current += nums[left];\n left += 1;\n }\n if (current == x) {\n mini = Math.min(mini, (n-1-right)+left);\n }\n }\n return mini != Integer.MAX_VALUE ? mini : -1;\n }\n}\n```\n | 7 | 0 | ['C', 'Java'] | 1 |
minimum-operations-to-reduce-x-to-zero | Convert to calculate longest subarray with fixed target sum | convert-to-calculate-longest-subarray-wi-para | Just convert to another question:\nThe longest subarray with sum = (sum of nums - x);\n\nThen the question is much easier. Just play the trick of calculating p | nadabao | NORMAL | 2020-11-15T04:07:18.892713+00:00 | 2020-11-15T05:06:00.559015+00:00 | 442 | false | Just convert to another question:\nThe longest subarray with sum = (sum of nums - x);\n\nThen the question is much easier. Just play the trick of calculating presum and store in map. \nFor this type of question, please refer to leetcode 560:\nhttps://leetcode.com/problems/subarray-sum-equals-k/\n\n```\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int sum = 0;\n for (int num : nums) sum += num;\n int target = sum - x;\n\t\t\n // find the longest subarray that sums = target\n int presum = 0;\n int res = Integer.MIN_VALUE;\n Map<Integer, Integer> map = new HashMap<>();\n map.put(0, -1); // For the special case presum == target\n\t\t\n for (int i = 0; i < nums.length; i++) {\n presum += nums[i];\n if (!map.containsKey(presum)) map.put(presum, i); // Always store smallest index\n if (map.containsKey(presum - target)) {\n res = Math.max(res, i - map.get(presum - target));\n }\n }\n \n if (res == Integer.MIN_VALUE) return -1;\n return nums.length - res;\n }\n}\n``` | 7 | 1 | [] | 0 |
minimum-operations-to-reduce-x-to-zero | [Javascript] Two pointers O(n) | javascript-two-pointers-on-by-alanchangh-vyv6 | ```\nvar minOperations = function(nums, x) {\n let l = 0,\n r = nums.length-1,\n res = nums.length+1;\n \n let n = x;\n \n while (l | alanchanghsnu | NORMAL | 2020-11-15T04:01:49.122473+00:00 | 2020-11-15T04:13:04.925451+00:00 | 999 | false | ```\nvar minOperations = function(nums, x) {\n let l = 0,\n r = nums.length-1,\n res = nums.length+1;\n \n let n = x;\n \n while (l <= r && n-nums[l] >= 0)\n n -= nums[l++];\n \n if (n === 0)\n res = l;\n \n while (l < r && l >= 0) {\n while (n-nums[r] >= 0)\n n -= nums[r--];\n \n if (n === 0)\n res = Math.min(res, l+nums.length-1-r);\n \n n += nums[--l];\n }\n \n return res === nums.length+1 ? -1 : res;\n}; | 7 | 1 | ['Two Pointers', 'JavaScript'] | 0 |
minimum-operations-to-reduce-x-to-zero | Best O(N) Solution | best-on-solution-by-kumar21ayush03-sj57 | Approach\nSliding Window Technique\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int minOpe | kumar21ayush03 | NORMAL | 2023-09-21T10:32:50.500211+00:00 | 2023-09-21T10:32:50.500238+00:00 | 638 | false | # Approach\nSliding Window Technique\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int sum = 0;\n for (int i = 0; i < n; i++)\n sum += nums[i];\n sum -= x;\n if (sum == 0)\n return n;\n int start = 0, curSum = 0, len = 0;\n for (int end = 0; end < n; end++) {\n curSum += nums[end];\n while (start < n && curSum > sum) {\n curSum -= nums[start];\n start++;\n }\n if (curSum == sum)\n len = max (len, end - start + 1);\n } \n if (!len) \n return -1;\n return n - len; \n }\n};\n``` | 6 | 0 | ['C++'] | 0 |
minimum-operations-to-reduce-x-to-zero | Simple Java Solution | faster than 95.37% | simple-java-solution-faster-than-9537-by-slbr | Finding the minimum number of removing is equal to finding the maximum number of remaining.\nSliding window can help us find the maximum number of remaining eas | angzhanh | NORMAL | 2022-06-11T01:32:21.614252+00:00 | 2022-06-11T01:32:35.768773+00:00 | 1,279 | false | Finding the minimum number of removing is equal to finding the maximum number of remaining.\nSliding window can help us find the maximum number of remaining easily!\n```\nclass Solution {\n public int minOperations(int[] nums, int x) {\n int n = nums.length;\n \n int sum = 0;\n for (int i = 0; i < n; i++) \n sum += nums[i];\n int target = sum - x;\n \n if (target < 0)\n return -1;\n if (target == 0)\n return n;\n \n int left = 0, right = 0;\n int maximum = 0;\n while (right < n) {\n target -= nums[right++];\n \n while (target < 0)\n target += nums[left++];\n \n if (target == 0)\n maximum = Math.max(maximum, right - left);\n }\n \n return maximum == 0 ? -1 : nums.length - maximum;\n }\n}\n```\n\nHowever, when I first meet this question, I come up with a solution which use greedy and backtrack.\nWhen remove the number (assume you have [a, ..., b]), choose the bigger one (assume a is bigger than b, so we choose a), if it doesn\'t work, backtrack, choose the other one (b).\nI think it\'s a nice idea but it meets TLE, I also post this code below\n```\nclass Solution {\n public int minOperations(int[] nums, int x) {\n LinkedList<Integer> removed = new LinkedList<>();\n return helper(nums, 0, nums.length - 1, x, removed) ? removed.size() : -1;\n }\n \n private boolean helper(int[] nums, int left, int right, int x, LinkedList<Integer> removed) {\n if (x == 0)\n return true;\n \n if (x < 0)\n return false;\n \n if (left > right)\n return false;\n \n if (nums[left] > x && nums[right] > x)\n return false;\n \n if (nums[left] >= nums[right]) { // greedy\n removed.add(nums[left]);\n if (helper(nums, left + 1, right, x - nums[left], removed))\n return true;\n removed.removeLast(); // backtrack\n\n removed.add(nums[right]);\n if (helper(nums, left, right - 1, x - nums[right], removed))\n return true;\n removed.removeLast();\n } else {\n removed.add(nums[right]);\n if (helper(nums, left, right - 1, x - nums[right], removed))\n return true;\n removed.removeLast();\n\n removed.add(nums[left]);\n if (helper(nums, left + 1, right, x - nums[left], removed))\n return true;\n removed.removeLast();\n }\n return false;\n }\n}\n``` | 6 | 0 | ['Sliding Window', 'Java'] | 0 |
minimum-operations-to-reduce-x-to-zero | C++ | O(1) Space | Faster than 97% | Contiguous subarray sum | Unique Approach | c-o1-space-faster-than-97-contiguous-sub-mcip | Explanantion\n Step 1 - Find the SUM of whole array. \n Step 2 - Then, Subtract the given element from the total SUM.\n Step 3 - Now, All we have to do is take | nishsolvesalgo | NORMAL | 2021-09-05T09:35:19.470407+00:00 | 2021-09-05T09:36:30.204806+00:00 | 424 | false | **Explanantion**\n* **Step 1** - Find the ***SUM*** of whole array. \n* **Step 2** - Then, Subtract the given element from the total ***SUM***.\n* **Step 3** - Now, All we have to do is take a left and right pointer traverse through the array and find Contiguous subarrays sum (i.e include all elements from left to right pointer in the sum ) that equal to our previous ***SUM*** that we calculated this can be easily done using if and else blocks. If curr_sum is less than ***SUM*** then add right element and increment right. if curr_sum is greater than the ***SUM*** then decrese left element and increment left. And if curr_sum == ***SUM*** then update ans = min(ans, n - (right - left)).\n* **Step 4** - If there is no Contiguous subarray whose sum equal to ***SUM*** that means it is not possible to make X from this subarray by picking element from left and right. So, return -1. else return ans\n\n**Complexity - O(N) Time | O(1) Space**\n\n**Code - C++**\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int sum = 0;\n for(int a:nums)\n sum += a; // Adding all elements from array \n sum -= x; // Basically we have to find Contiguous elements which sum to this\n\t\t\n int left = 0, right = 0;\n int curr_sum = 0, ans = INT_MAX;\n while(right <= n && left <= right){\n if(curr_sum == sum){\n ans = min(ans, n - (right - left));\n curr_sum -= nums[left];\n left++;\n continue;\n }\n if(curr_sum < sum){\n curr_sum += nums[right];\n right++;\n }else if(curr_sum > sum){\n curr_sum -= nums[left];\n left++;\n }\n }\n return ans == INT_MAX ? -1 : ans;\n }\n};\n```\n\n***Thanks for Reading, Upvote if you like it :)*** | 6 | 0 | ['C', 'Sliding Window'] | 1 |
minimum-operations-to-reduce-x-to-zero | Minimum Operations to Reduce X to Zero || C++ || Easy || 99%beat || Hash map | minimum-operations-to-reduce-x-to-zero-c-mki6 | \nAs we count the sum of the first l numbers, you need to find a complement (x - sum) number formed by numbers on the right. To do so, we can use a hashmap wher | thekalyan001 | NORMAL | 2021-01-14T10:30:01.559669+00:00 | 2021-01-14T10:30:13.194170+00:00 | 520 | false | \nAs we count the sum of the first l numbers, you need to find a complement (x - sum) number formed by numbers on the right. To do so, we can use a hashmap where we will store the rolling sum.\nUpvote if you liked :)\n```\nint minOperations(vector<int>& nums, int x) {\n unordered_map<int, int> left;\n int res = INT_MAX;\n for (auto l = 0, sum = 0; l < nums.size() && sum <= x; ++l) {\n left[sum] = l;\n sum += nums[l];\n }\n for (int r = nums.size() - 1, sum = 0; r >= 0 && sum <= x; --r) {\n auto it = left.find(x - sum);\n if (it != end(left) && r + 1 >= it->second) {\n res = min(res, (int)nums.size() - r - 1 + it->second);\n }\n sum += nums[r];\n }\n return res == INT_MAX ? -1 : res;\n}\n``` | 6 | 1 | ['C'] | 0 |
minimum-operations-to-reduce-x-to-zero | C++ Prefix Sum Solution + Binary Search | c-prefix-sum-solution-binary-search-by-p-2vgx | \nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n \n if(nums.size() == 1){\n if(x == nums[0])\n | pikabu | NORMAL | 2020-11-15T04:32:35.604408+00:00 | 2020-11-15T04:32:35.604439+00:00 | 408 | false | ```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n \n if(nums.size() == 1){\n if(x == nums[0])\n return 1;\n return -1;\n }\n if(nums[0] > x && nums[nums.size() -1] > x)\n return -1;\n \n vector<long long> presum(nums.size()+1,0);\n \n presum[0] = 0;\n for(int i=1;i<=nums.size();i++){\n presum[i] = presum[i-1] + nums[i-1];\n }\n int ans = nums.size()+1;\n \n long long end_sum = 0;\n int end_elements = 0;\n int j = nums.size()-1;\n while(j>=0){\n if(binary_search(presum.begin(),presum.end(),x-end_sum)){\n int id = lower_bound(presum.begin(),presum.end(),x-end_sum) - presum.begin();\n if(id+end_elements <= nums.size()){\n ans = min(ans,id+end_elements);\n }\n }\n end_elements++;\n \n end_sum += nums[j--];\n \n }\n \n if(ans == nums.size()+1)\n return -1;\n else return ans;\n \n }\n};\n``` | 6 | 0 | [] | 0 |
minimum-operations-to-reduce-x-to-zero | JAVA TC: 100% beats , MC: 95% beat, sliding window | java-tc-100-beats-mc-95-beat-sliding-win-e2j1 | sum_total : totla sum of array.\nwe need to find longest lenghted subarray which sums to (sum_total -x)\n\nwe can find the the largest lengthhed subarray using | jerryjohnthomastvm | NORMAL | 2022-06-11T17:06:16.748288+00:00 | 2022-06-11T18:03:38.642017+00:00 | 735 | false | sum_total : totla sum of array.\nwe need to find longest lenghted subarray which sums to (sum_total -x)\n\nwe can find the the largest lengthhed subarray using sliding window,\nmove left pointer when the sum>=(required) otherwise keep on increasing right pointer\n\nAns. total_length - length of largest sub_array with sum as (sum_total -x)\n\n```\nclass Solution {\n public int minOperations(int[] nums, int xx) {\n \n \n int x=0;\n for(int t:nums)\n x+=t;\n \n if(x==xx)\n return nums.length;\n \n x-=xx;\n \n int l=0;\n int sum=0;\n int ans=-1;\n \n \n // System.out.println(x);\n for(int r=0; r<nums.length;r++)\n {\n sum+=nums[r];\n // System.out.println(l+" "+r+" "+sum);\n \n while(sum>=x && l<=r)\n {\n if(sum==x)\n ans=Math.max(ans, r-l+1);\n // System.out.println("in"+ ans);\n sum-=nums[l++];\n }\n }\n \n if(ans==-1)\n return -1;\n return nums.length-ans;\n \n }\n}\n```\nKindly upvote me if found helpful | 5 | 0 | ['Sliding Window', 'Java'] | 0 |
minimum-operations-to-reduce-x-to-zero | C++ || EASY TO UNDERSTAND || Prefix Sum + Suffix Sum + Binary Search || 2 Approaches | c-easy-to-understand-prefix-sum-suffix-s-5vmi | Time Complexity O(NlogN)\n\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n vector<int> pre(n, | aarindey | NORMAL | 2022-06-11T10:29:04.317277+00:00 | 2022-06-11T13:18:41.454643+00:00 | 252 | false | **Time Complexity O(NlogN)**\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n vector<int> pre(n,0);\n vector<int> suff(n,0);\n pre[0]=nums[0];\n suff[n-1]=nums[n-1];\n for(int i=1;i<n;i++)\n {\n pre[i]=pre[i-1]+nums[i];\n }\n for(int i=n-2;i>=0;i--)\n {\n suff[i]=suff[i+1]+nums[i];\n }\n int count=INT_MAX;\n for(int i=n-1;i>=0;i--)\n {\n if(suff[i]>x)\n {\n break;\n }\n if(suff[i]==x)\n {\n count=min(count,n-i);\n }\n else\n {\n int idx=lower_bound(pre.begin(),pre.end(),x-suff[i])-pre.begin();\n if(idx<i&&pre[idx]+suff[i]==x)\n {\n count=min(count,idx+1+n-i);\n }\n }\n }\n for(int i=0;i<n;i++)\n {\n if(pre[i]>x)\n {\n break;\n }\n if(pre[i]==x)\n {\n count=min(count,i+1);\n }\n }\n return count==INT_MAX?-1:count;\n }\n};\n```\n**Optimized Approach \nTime Complexity O(N)**\n```\n#define ll long long int\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n int total=accumulate(nums.begin(),nums.end(),0);\n if(total==x)\n return n;\n if(x>total)\n return -1;\n unordered_map<int,int> mp;\n mp[0]=0;\n int target=total-x;\n int ans=INT_MIN;\n int curr=0;\n for(int i=0;i<n;i++)\n {\n curr+=nums[i];\n mp[curr]=i;\n \n if(curr==target)\n {\n ans=max(ans,i+1);\n }\n if(curr==(total-target))\n {\n ans=max(ans,n-i-1);\n }\n if(curr>target)\n {\n if(mp.find(curr-target)!=mp.end())\n {\n ans=max(ans,i-mp[curr-target]);\n }\n }\n }\n return (ans==INT_MIN)?-1:(n-ans);\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 5 | 0 | [] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ Solution Using Two Pointer | c-solution-using-two-pointer-by-conquist-fnyp | C++ Solution Using Two Pointer\n\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n int left=0,r | Conquistador17 | NORMAL | 2022-06-11T05:28:57.893469+00:00 | 2022-06-11T05:28:57.893503+00:00 | 1,363 | false | # **C++ Solution Using Two Pointer**\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n=nums.size();\n int left=0,right=0;\n int sum=0;\n int ans=-1;\n for(int i=0;i<n;i++){\n sum+=nums[i];\n }\n \n cout<<sum;\n int cur=nums[0];\n while(left<n&&right<n){\n if(cur<sum-x){\n \n right++;\n if(right==n)break;\n cur+=nums[right];\n }\n if(cur>sum-x){\n \n cur-=nums[left];\n \n left++;\n }\n if(cur==sum-x){\n ans=max(ans,right-left+1);\n right++;\n if(right==n)break;\n cur+=nums[right];\n }\n // cout<<cur<<endl;\n }\n return ans==-1?-1:n-ans;\n }\n};\n```\n# **Please Share and Upvote** | 5 | 0 | ['Two Pointers', 'C', 'C++'] | 1 |
minimum-operations-to-reduce-x-to-zero | ✅ C++ | O(N) | Easy to understand | c-on-easy-to-understand-by-kjs_27-ibj1 | To solve this problem first we need to calculate the maximum length of subarray with sum which is equal to difference of total sum and x. \n\nExample:\nnums = [ | kjs_27 | NORMAL | 2022-06-11T05:20:39.458647+00:00 | 2022-06-18T20:08:29.139476+00:00 | 774 | false | To solve this problem first we need to calculate the maximum length of subarray with sum which is equal to difference of total sum and x. \n\n**Example:**\n**nums** = [3,2,5,4,11,5]\n**x** = 10\n\nTotal sum = 3 + 2 + 5 + 4 + 11 + 5 = 30\nSum - x = 20\n\nLength of maximum subarray with sum = 20 is 3 as shown;\n\n\n\nClearly we can say that the sum of remaining elements other than subarray is x. So we need to return the remaining length other than subarray.\n\nThat is we need to return 6 - 3 which is equal to 3.\nSo the **output** for the above test case is 3.\n\n**C++ code**\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int l = 0;\n int sum = 0, res = 0, maxi = -1,n = nums.size();\n for(int i = 0;i<n;i++) // To calculate total sum\n {\n sum = sum + nums[i];\n }\n for(int i = 0;i<n;i++) // To calculate length of maximum subarray with \'sum = total sum - x\'\n {\n res = res + nums[i];\n while((l<n) && (sum - x < res))\n {\n res = res - nums[l];\n l++;\n }\n if(sum - res == x)\n {\n maxi = max(i - l + 1, maxi);\n }\n }\n if(maxi == -1)\n {\n return -1;\n }\n return n - maxi;\n \n }\n};\n```\n\n**Time complexity -** O(N)\n**Space complexity -** O(1)\n\n**Please upvote if you liked it :)**\n\n\n\n | 5 | 0 | ['C'] | 0 |
minimum-operations-to-reduce-x-to-zero | [CPP] ✔Easy 🔥Intuition 🟢Full explanations 🚀 2 approaches | cpp-easy-intuition-full-explanations-2-a-2uqa | Approach 1 :- DP\nUsed the classic Top Down DP(Knapsack 0/1) along with memoization\nBut it gives TLE . The constraints are large for test cases.\n\nTime Comple | nitin23rathod | NORMAL | 2022-06-11T03:47:25.012048+00:00 | 2022-06-11T03:47:25.012085+00:00 | 288 | false | # **Approach 1 :- DP**\nUsed the classic Top Down DP(Knapsack 0/1) along with memoization\n***But it gives TLE*** . The constraints are large for test cases.\n\n**Time Complexity O(N^2).\nSpace Complexity O(N^2).**\n\n```\nclass Solution {\npublic:\n vector<vector<int>>dp;\n int solve(vector<int>&nums,int s,int e,int x,int count=0){\n if(x==0)return count;\n if(s>e){\n return INT_MAX; \n }\n if(dp[s][e]!=-1)return dp[s][e];\n int leftSide=solve(nums,s+1,e,x-nums[s] ,count+1);\n int rightSide=solve(nums,s,e-1,x-nums[e],count+1);\n \n return dp[s][e]=min(leftSide,rightSide);\n \n }\n int minOperations(vector<int>& nums, int x) {\n dp.resize(nums.size(),vector<int>(nums.size(),-1));\n int res=solve(nums,0,nums.size()-1,x);\n return res==INT_MAX?-1:res;\n }\n}; \n```\n\n# Approah 2 :- Sliding window\nWhen we look at the question, it says we need the numbers from either left or right which should meet our target in minimum elements .\nBut its kinda tough to keep a check on left and right sides. But what if we keep a check on the middle block which is.\n(Sum of entire array ) - target = new_target\n\nnow we need to find the maximum elements which can make this new Target 0 . and return total number - this maximum number.\n\n**Time Complexity O(KN) where k is the maximum size of the sliding window\nSpace Complexity O(1)**\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x){ \n int res=-1,n=nums.size(), new_target=-x, left=0;\n \n for(auto i:nums)\n new_target+=i;\n \n if(new_target<0)return -1;\n \n for(int right=0;right<n;right++){\n new_target-=nums[right];\n while(new_target<0){\n new_target+=nums[left++];\n }\n if(new_target==0){\n res=max(res,right-left+1);\n }\n }\n\n return n-res>n?-1:n-res;\n }\n\t//**If you find helpfull click upvote button **\n};\n```\n | 5 | 0 | ['C'] | 0 |
minimum-operations-to-reduce-x-to-zero | DP Top Down and Sliding window Solutions in C++ | dp-top-down-and-sliding-window-solutions-dja0 | Approach 1 DP\nUsed the classic Top Down DP(Knapsack 0/1) along with memoization\nBut it gives TLE . The constraints are large for test cases.\n\nTime Complexit | ManthanJoshi | NORMAL | 2021-09-04T11:17:27.573445+00:00 | 2021-09-04T11:19:26.376837+00:00 | 699 | false | **Approach 1** **DP**\nUsed the classic Top Down DP(**Knapsack 0/1**) along with memoization\nBut it gives **TLE** . The constraints are large for test cases.\n\n**Time Complexity O(N^2)\nSpace Complexity O(N^2)**\n```\n// Classic Knapsack 0/1 problem\nclass Solution {\npublic:\n vector<vector<int>>dp;\n int solve(vector<int>&nums,int s,int e,int x,int count=0){\n if(x==0)return count;\n if(s>e){\n return INT_MAX; \n }\n if(dp[s][e]!=-1)return dp[s][e];\n int leftSide=solve(nums,s+1,e,x-nums[s] ,count+1);\n int rightSide=solve(nums,s,e-1,x-nums[e],count+1);\n \n return dp[s][e]=min(leftSide,rightSide);\n \n }\n int minOperations(vector<int>& nums, int x) {\n dp.resize(nums.size(),vector<int>(nums.size(),-1));\n int res=solve(nums,0,nums.size()-1,x);\n return res==INT_MAX?-1:res;\n }\n}; \n```\n\n**Approah 2** **Sliding window**\n\nWhen we look at the question, it says we need the numbers from either left or right which should meet our target in minimum elements .\nBut its kinda tough to keep a check on left and right sides. But what if we keep a check on the middle block which is.\n**(Sum of entire array ) - target = new_target**\n \n now we need to find the maximum elements which can make this new Target 0 . and return total number - this maximum number.\n\n**Time Complexity O(KN) where k is the maximum size of the sliding window \nSpace Complexity O(1)** \n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x){ \n int res=-1,n=nums.size(), new_target=-x, left=0;\n \n for(auto i:nums)\n new_target+=i;\n \n if(new_target<0)return -1;\n \n for(int right=0;right<n;right++){\n new_target-=nums[right];\n while(new_target<0){\n new_target+=nums[left++];\n }\n if(new_target==0){\n res=max(res,right-left+1);\n }\n }\n\n return n-res>n?-1:n-res;\n }\n};\n```\n | 5 | 0 | ['Dynamic Programming', 'Sliding Window'] | 0 |
minimum-operations-to-reduce-x-to-zero | Minimum Operations to Reduce X to Zero | C++ | Finding Maximum Sub-Array | 99% beat | minimum-operations-to-reduce-x-to-zero-c-afk4 | As stated by the first hint: "Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray." \n\nThis code uses a sliding window | yongweic | NORMAL | 2021-01-15T02:08:24.505841+00:00 | 2021-01-15T02:08:24.505872+00:00 | 186 | false | As stated by the first hint: "Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray." \n\nThis code uses a sliding window to find the maximum subarray.\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int l = 0;\n int r = 0;\n \n int total = 0; // total sum of array\n for (int n : nums) {\n total += n;\n }\n \n int goal = total - x; // sub-array sum that corresponds to solving the problem (prefix + suffix = x)\n \n int arrSum = 0; // sum of sub-array\n \n int minOps = INT_MAX;\n bool exists = false;\n \n while (l != nums.size() - 1) {\n if (arrSum == goal) {\n exists = true;\n if (nums.size() - (r - l) < minOps) minOps = nums.size() - (r - l);\n \n if (r < nums.size()) arrSum += nums[r++];\n else break; \n }\n else if (arrSum < goal && r < nums.size()) arrSum += nums[r++];\n else if (arrSum > goal && l < nums.size()) arrSum -= nums[l++];\n else break;\n }\n \n if (exists) return minOps;\n return -1;\n }\n};\n``` | 5 | 2 | [] | 1 |
minimum-operations-to-reduce-x-to-zero | C++ Simple and Easy Solution | c-simple-and-easy-solution-by-yehudisk-bzwu | \nclass Solution {\npublic:\n int findMaxSub(vector<int>& nums, int k) {\n int sum = 0, maxi = 0;\n unordered_map<int, int> m;\n \n | yehudisk | NORMAL | 2021-01-14T12:48:50.437026+00:00 | 2021-01-14T12:48:50.437063+00:00 | 601 | false | ```\nclass Solution {\npublic:\n int findMaxSub(vector<int>& nums, int k) {\n int sum = 0, maxi = 0;\n unordered_map<int, int> m;\n \n for (int i=0; i<nums.size(); i++) {\n sum += nums[i];\n \n if (sum == k)\n maxi = i+1;\n \n if (m.find(sum) == m.end())\n m[sum] = i;\n \n if (m.find(sum - k) != m.end())\n maxi = max(maxi, i - m[sum-k]);\n }\n return maxi;\n }\n \n int minOperations(vector<int>& nums, int x) {\n if ((nums[0] > x) && (nums[nums.size()-1] > x))\n return -1;\n \n int sum = 0;\n for (auto a : nums)\n sum += a;\n \n if (sum == x) return nums.size();\n \n int res = findMaxSub(nums, sum-x);\n return res <= 0 ? -1 : nums.size() - res;\n }\n};\n```\n**Like it? please upvote...** | 5 | 1 | ['C'] | 0 |
minimum-operations-to-reduce-x-to-zero | 🔥2 Approaches💯 || 🌟O(1) SC || 💯Clean & Best Code✅ | 2-approaches-o1-sc-clean-best-code-by-ad-16ug | Connect with me on LinkedIN : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Complexity\n\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n) | aDish_21 | NORMAL | 2023-09-20T06:34:59.105751+00:00 | 2023-09-20T14:21:37.252110+00:00 | 411 | false | ### Connect with me on LinkedIN : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Complexity\n```\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n) for Approach 1\nO(1) for Approach 2\n```\n\n# Code\n## Please Upvote if u found it useful\uD83E\uDD17\n# 1st Approach(Using PrefixSum + HashMap):-\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size(), minOper = n + 1, prefixSum = 0;\n unordered_map<int, int> mp;\n for(int i = 0 ; i < n ; i++){\n prefixSum += nums[i];\n if(prefixSum == x)\n minOper = i + 1;\n if(prefixSum > x)\n break;\n mp[prefixSum] = i + 1;\n }\n int suffixSum = 0;\n for(int i = n - 1 ; i >= 0 ; i--){\n suffixSum += nums[i];\n if(suffixSum == x)\n minOper = min(minOper, n - i);\n else if(suffixSum < x){\n if(mp.find(x - suffixSum) != mp.end())\n minOper = min(minOper, n - i + mp[x - suffixSum]);\n }\n else\n break;\n }\n return (minOper != n + 1) ? minOper : -1;\n }\n};\n```\n# 2nd Approach(Using Sliding Window):-\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size(), i = 0, j = 0, maxi = 0, total_sum = 0;\n for(auto it : nums)\n total_sum += it;\n if(total_sum < x)\n return -1;\n if(total_sum == x)\n return n;\n int req_sum = total_sum - x, curr_sum = 0;\n while(j < n){\n curr_sum += nums[j];\n while(curr_sum > req_sum)\n curr_sum -= nums[i++];\n if(curr_sum == req_sum)\n maxi = max(maxi, j - i + 1);\n j++;\n }\n return (maxi != 0) ? n - maxi : -1;\n }\n};\n``` | 4 | 0 | ['Array', 'Hash Table', 'Sliding Window', 'Prefix Sum', 'C++'] | 1 |
minimum-operations-to-reduce-x-to-zero | EASY SOLUTION || EXPLANATION || C++ || Beat 98.9 % || | easy-solution-explanation-c-beat-989-by-oxs8m | \n# Approach\n Describe your approach to solving the problem. \n##### Try to find maximum subarray that have the sum == total_sum of array - x\n\n# Code\n\nclas | amol_2004 | NORMAL | 2023-09-20T05:08:43.772745+00:00 | 2023-09-20T05:08:43.772774+00:00 | 327 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n##### Try to find maximum subarray that have the `sum == total_sum of array - x`\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int total_sum = 0;\n int n = nums.size();\n for(int i = 0; i < n; i++)\n total_sum += nums[i];\n total_sum -= x;\n\n int ans = INT_MAX;\n int sum = 0;\n int i = 0, j = 0;\n while(j < n){\n sum += nums[j];\n if(sum > total_sum)\n while(i <= j && sum > total_sum)\n sum -= nums[i++];\n\n if(sum == total_sum)\n ans = min(ans, n - (j - i) - 1);\n j++;\n }\n\n return ans == INT_MAX ? -1 : ans;\n\n }\n};\n```\n\n | 4 | 0 | ['Two Pointers', 'Sliding Window', 'C++'] | 1 |
minimum-operations-to-reduce-x-to-zero | 🔥98.80% Acceptance📈 rate | Using Sliding Window🧭 | Explained in details✅ | 9880-acceptance-rate-using-sliding-windo-3jwg | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this code is to find a subarray with the maximum possible sum (equ | nikkipriya_78 | NORMAL | 2023-09-20T04:00:01.834799+00:00 | 2023-10-07T13:55:41.988135+00:00 | 292 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to find a subarray with the maximum possible sum (equal to targetSum) within the given nums array. The goal is to minimize the number of operations to reduce x to 0. By calculating the maximum subarray length, we can determine the minimum number of operations required.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate the targetSum by iterating through the nums array and subtract x from the sum of all elements. If targetSum is negative, it means there is no solution, so return -1.\n\n2. Initialize two pointers, left and right, both initially at the beginning of the array. Also, initialize currentSum and maxLength to 0 and -1, respectively.\n\n3. Iterate through the nums array using the right pointer. At each step, add the current element to currentSum.\n\n4. Check if currentSum is greater than targetSum. If it is, it means the current subarray sum is too large. In this case, move the left pointer to the right to reduce the subarray size until currentSum is less than or equal to targetSum.\n\n5. If currentSum becomes equal to targetSum, update maxLength to be the maximum of its current value and the length of the current subarray (right - left + 1).\n\n6. Repeat steps 3-5 until the right pointer reaches the end of the array.\n\n7. Finally, return n - maxLength as the minimum number of operations needed. If maxLength remains -1, return -1, indicating that n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the nums array twice: once to calculate targetSum and once to find the maximum subarray length. Each iteration takes O(n) time.\nTherefore, the overall time complexity is O(n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because the code uses a constant amount of extra space, regardless of the size of the input array nums.\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n int targetSum = 0;\n for (int num : nums) {\n targetSum += num;\n }\n targetSum -= x;\n if (targetSum < 0) return -1; // If x is greater than the sum of all elements, no solution exists.\n\n int left = 0;\n int currentSum = 0;\n int maxLength = -1;\n\n for (int right = 0; right < n; right++) {\n currentSum += nums[right];\n\n while (currentSum > targetSum) {\n currentSum -= nums[left];\n left++;\n }\n\n if (currentSum == targetSum) {\n maxLength = max(maxLength, right - left + 1);\n }\n }\n\n return (maxLength == -1) ? -1 : n - maxLength;\n }\n};\n\n``` | 4 | 0 | ['Array', 'Hash Table', 'Binary Search', 'Sliding Window', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
minimum-operations-to-reduce-x-to-zero | very easy to understand solution O(N) time, O(1) SPACE | very-easy-to-understand-solution-on-time-9o1g | Intuition\nwe can take only elements which are present at corner i.e in starting and in last so we try to find window of (total sum of array - k) \nso , n-k win | abhinav_raj531 | NORMAL | 2023-09-20T02:39:31.367671+00:00 | 2023-09-20T02:47:53.560308+00:00 | 134 | false | # Intuition\nwe can take only elements which are present at corner i.e in starting and in last so we try to find window of (total sum of array - k) \nso , n-k window, will contain sum == k. \n\n# Approach\nhere, we are using sliding window approch to find the largest window of elments that contains (total sum of array - k) so the remaining corner parts will have the sum == k.\n\n# Complexity\n- Time complexity:\n<O(n)>\n\n- Space complexity:\n<O(1)>\n\n# Code\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n // PLEASE UPVOTE\n int n = nums.size();\n int sum = accumulate(nums.begin(),nums.end(),0);\n int req = sum-x; \n if(req<0) return -1;\n int j = 0 ;\n int k = 0;\n int ans = -1e9;\n for(int i = 0 ;i< n ;i++){\n k+=nums[i];\n while(k>req){\n k-=nums[j];\n j++;\n }\n if(k==req){\n ans= max(ans,i-j+1);\n }\n }\n if(ans==-1e9) return -1;\n else return n- ans;\n }\n};\n``` | 4 | 0 | ['Sliding Window', 'C++'] | 0 |
minimum-operations-to-reduce-x-to-zero | C++ | Minimum Operations to Reduce X to Zero | 2 Approaches with Explanation | c-minimum-operations-to-reduce-x-to-zero-o2a2 | Approach 1\n\t1. Maintain two cumulative sum left and right . Also check the edge cases (if x is present in the left or right)\n\t2. Go from start to end of lef | badhansen | NORMAL | 2022-06-11T09:59:41.682010+00:00 | 2022-06-11T10:53:53.392667+00:00 | 189 | false | **Approach 1**\n\t1. Maintain two cumulative sum `left` and `right` . Also check the edge cases (if x is present in the `left` or `right`)\n\t2. Go from start to end of `left` and check if remaining is present or not in the `right` one.\n\t3. `ans` will be sum of two indices.\n\n**Time:** `O(N log N)`\n**Space:** `O(N)`\n**N** = Length of the array\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int n = nums.size();\n vector<int> left(n), right(n);\n left[0] = nums[0], right[0] = nums[n - 1];\n for(int i = 1, j = n - 2; i < n; i++, j--){\n left[i] = left[i - 1] + nums[i];\n right[i] = right[i - 1] + nums[j];\n }\n \n int pos = lower_bound(left.begin(), left.end(), x) - left.begin();\n int ans = INT_MAX;\n \n if(pos == 0){\n if(x == left[0]) ans = 1;\n else ans = INT_MAX;\n }\n else{\n if(pos < n && left[pos] == x) ans = pos + 1;\n else ans = INT_MAX;\n }\n \n pos = lower_bound(right.begin(), right.end(), x) - right.begin();\n \n if(pos == 0){\n if(x == right[0]) ans = 1;\n }\n else{\n if(pos < n && right[pos] == x) ans = min(ans, pos + 1);\n }\n\n for(int i = 1; i <= n; i++){\n int rem = x - left[i - 1];\n if(rem <= 0) break;\n pos = lower_bound(right.begin(), right.end(), rem) - right.begin();\n if(pos == n) continue;\n if(left[i - 1] + right[pos] == x) ans = min(ans, i + pos + 1);\n }\n \n return ans > n ? -1 : ans;\n }\n};\n```\nAfter some observations if the array is circular then this problem will be converted as **Find the maximum length subarray whose sum is** `x`. But the array is not circular and we need to find sum of `x`. If the sum is present then `totalsum - x` will be present also. And if we found this sum then the anser will be `length - max found length`. \n\n**Time:** `O(N)`\n**Space:** `O(1)`\n\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n int sum = 0, n = nums.size();\n for(int i = 0; i < n; i++){\n sum += nums[i];\n }\n \n if(x > sum) return -1;\n \n int target = sum - x, left = 0;\n int ans = INT_MIN, currsum = 0;\n \n for(int right = 0; right < n; right++){\n currsum += nums[right];\n while(left < n && currsum - nums[left] >= target){ \n currsum -= nums[left++];\n }\n if(currsum == target) ans = max(ans, right - left + 1);\n }\n\n if(ans < 0) return -1;\n return n - ans;\n }\n};\n```\n\n | 4 | 0 | ['Binary Search', 'Sliding Window', 'Binary Tree'] | 1 |
minimum-operations-to-reduce-x-to-zero | Kotlin || O(n) time || O(1) space | kotlin-on-time-o1-space-by-yezhizhen-9w5q | \n fun minOperations(nums: IntArray, x: Int): Int {\n //find longest subarray sum to total_sum - x\n var target = nums.sum() - x; var sum = 0\n | yezhizhen | NORMAL | 2022-06-11T07:31:04.772806+00:00 | 2022-06-11T07:31:04.772869+00:00 | 99 | false | ```\n fun minOperations(nums: IntArray, x: Int): Int {\n //find longest subarray sum to total_sum - x\n var target = nums.sum() - x; var sum = 0\n var l = 0; var ans = -1;\n for(r in 0 until nums.size)\n {\n sum += nums[r]\n while(l <= r && sum > target) //move left pointer\n sum -= nums[l++];\n if(target == sum)\n ans = max(ans, r - l + 1)\n }\n return if(ans == - 1) -1 else nums.size - ans\n }\n``` | 4 | 0 | ['Kotlin'] | 1 |
minimum-operations-to-reduce-x-to-zero | Binary Search | c++ | O(nlogn) | binary-search-c-onlogn-by-vivek_9680-f3s2 | First, I thought it\'s dp but when I saw the constraint then i came to know that it\'s not dp.\nWhen we see closely, see the prefix[i] + suffix[j]==x then i + ( | vivek_9680 | NORMAL | 2022-06-11T07:01:44.353174+00:00 | 2022-06-11T07:45:41.794587+00:00 | 198 | false | First, I thought it\'s dp but when I saw the constraint then i came to know that it\'s not dp.\nWhen we see closely, see the prefix[i] + suffix[j]==x then i + (n-j) is our answer.\nI am giving the example:\n[1,1,4,2,3] and x = 5\npre = [0,1,2,6,8,11] //add 0 for simplicity\nsuff = [11,10,9,5,3,0] \n\nIn this scenario there are two cases:\npre[2] + suff[4] = 2 + 3 = 5 so, noOfOperation = 2 + (5-4) = 2 + 1 = 3\npre[0] + suff[3] = 0 + 5 = 5 so, noOfOperation = 0 + (5-3) = 0 + 2 = 2\n\nNo other cases, which gives you pre[i] + suff[j] == x.\ntherefore, minimum number of operation = min(3,2) = 2.\n\nIf you check in linear order it will give you **O(n^2)** time complexity.\n\nAssume we pick the jth suffix element and binary seach on prefix then we find out the index in log n time.\nfor every suffix element, we do log n operation so, the time complexity is **O(n log n).**\n\nHere is my code:\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums, int x) {\n \n int n = nums.size();\n \n vector<long> pre(n+1,0);\n \n int noOfOperation = n+1;\n \n //calculate the prefixsum\n for(int i=0;i<n;i++){\n pre[i+1] = pre[i] + nums[i];\n }\n \n \n int suff = 0;\n \n for(int i=n;i>=0;i--){\n \n int s = 0, e = i;\n \n //apply binary search and find the x-suff index\n while(s<=e){\n \n int m = (s+e)>>1;\n \n if(pre[m]==x-suff){\n noOfOperation = min(noOfOperation,m+(n-i));\n break;\n }else if(pre[m]>x-suff){\n e = m-1;\n }else\n s = m+1;\n } \n \n if(i-1>=0) suff += nums[i-1];\n }\n \n return noOfOperation==n+1?-1:noOfOperation;\n }\n};\n```\n\n | 4 | 0 | ['C', 'Binary Tree'] | 3 |
minimum-operations-to-reduce-x-to-zero | C++ || Sliding window || 1658. Minimum Operations to Reduce X to Zero || Easy | c-sliding-window-1658-minimum-operations-llf8 | \t// Here ans is the window size we have to maximize the window size\n\t// because more we maximize window size lesser the elements willl be remainig in nums\n\ | anubhavsingh11 | NORMAL | 2022-06-11T06:40:26.363171+00:00 | 2022-06-11T06:41:00.556899+00:00 | 193 | false | \t// Here ans is the window size we have to maximize the window size\n\t// because more we maximize window size lesser the elements willl be remainig in nums\n\t// ans hence our no of operation will be reduced\n\t// Here we are checking for window of max size for sum=totalsum-x \n\t//so that sum of remainig elements becomes x \n\t\n\t\n\tclass Solution {\n\tpublic:\n\t\tint minOperations(vector<int>& nums, int x) {\n\t\t\tint ans=0;\n\t\t\tint sum=0;\n\t\t\tfor(int i=0;i<nums.size();i++){\n\t\t\t\tsum+=nums[i];\n\t\t\t}\n\t\t\tsum-=x;\n\t\t\tif(sum==0) return nums.size();\n\n\t\t\tint i=0,j=0,s1=0;\n\t\t\twhile(j<nums.size())\n\t\t\t{\n\t\t\t\ts1+=nums[j];\n\t\t\t\twhile(i<nums.size()&&s1>sum)\n\t\t\t\t{\n\t\t\t\t\ts1-=nums[i];\n\t\t\t\t\ti++;\n\t\t\t\t}\n\t\t\t\tif(s1==sum){\n\t\t\t\t\tans=max(ans,j-i+1);\n\t\t\t\t} \n\t\t\t\tj++;\n\t\t\t}\n\t\t\treturn ans==0?-1:nums.size()-ans;\n\t\t}\n\t}; | 4 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 0 |
minimum-operations-to-reduce-x-to-zero | Python | reverse thinking | prefix sum + hash map | with comments | python-reverse-thinking-prefix-sum-hash-j7wd3 | When I first read this problem, I think I have seen it elsewhere. Then I realize that it\'s pretty similar to Leetcode 325 Maximum Size Subarray Sum Equals k. \ | BoluoUp | NORMAL | 2022-06-11T05:09:37.422625+00:00 | 2022-06-11T05:09:37.422667+00:00 | 633 | false | When I first read this problem, I think I have seen it elsewhere. Then I realize that it\'s pretty similar to *Leetcode 325 Maximum Size Subarray Sum Equals k*. \n\nTo get the minimum operations to reduce x to 0, we can get the longest length of subarray sum equals "new" target ```sum(nums) - x```. The answer will be ```len(nums)``` - ```longest```. Also, don\'t forget to deal with the corner cases. \n\nI use prefix sum and hashmap to solve 325. Below is my code with comments. Feel free to ask if you have any questions!\n```\nclass Solution:\n def minOperations(self, nums: List[int], x: int) -> int:\n # corner cases\n if x > sum(nums):\n return -1\n elif x == sum(nums):\n return len(nums)\n \n target = sum(nums) - x # "new" target\n longest = 0 # track the longest subarray sum equals target\n preSum = 0 # prefix sum\n hashMap = {} # hash map (prefix sum: index) \n \n for i, n in enumerate(nums):\n preSum += n\n \n # generate a hash map preSum -> i\n if preSum not in hashMap:\n hashMap[preSum] = i\n \n # when subarray sum equals target\n if preSum == target:\n longest = max(longest, i + 1)\n \n # when the difference between prefix sum and target is another prefix sum\n diff = preSum - target\n if diff in hashMap:\n longest = max(longest, i - hashMap.get(diff))\n \n if longest == 0: # corner case: NO subarray sum equals target\n return -1\n else:\n return len(nums) - longest\n``` | 4 | 0 | ['Prefix Sum', 'Python'] | 0 |
End of preview. Expand
in Data Studio
LeetCode Solution Dataset
This dataset contains community-contributed LeetCode solutions scraped from public discussions and solution pages, enriched with metadata such as vote counts, author info, tags, and full code content. The goal is to make high-quality, peer-reviewed coding solutions programmatically accessible for research, analysis, educational use, or developer tooling.
Column Descriptions
| Column Name | Type | Description |
|---|---|---|
question_slug |
string |
The unique slug of the LeetCode question |
title |
string |
Title of the submitted solution |
slug |
string |
URL-safe identifier for the solution (can be used to reconstruct URL) |
summary |
string |
Short description or intro snippet of the solution |
author |
string |
Username of the contributor |
certification |
string |
LeetCode’s certification level for the author |
created_at |
timestamp |
When the solution was originally posted |
updated_at |
timestamp |
When the solution was last modified |
hit_count |
int |
Number of views the solution has received |
has_video |
boolean |
Whether the solution includes a video explanation |
content |
string |
The full markdown content including code blocks |
upvotes |
int |
Total number of upvotes |
downvotes |
int |
Total number of downvotes |
tags |
list[str] |
List of tags (e.g. algorithm type, difficulty, company, etc.) |
comments |
int |
Number of top-level comments on the solution |
question_slug: Construct the link this way: "https://leetcode.com/problems/{question_slug}/description/"
This dataset is part of a broader collection of LeetCode-related resources. It complements:
- LeetCode Problem Detailed – includes full problem descriptions, metadata, and statistics for each LeetCode question.
- LeetCode Problem Set – a lightweight list of problems with slugs, titles, difficulty levels, and basic stats (without descriptions or solutions). Note: New questions and solutions are added weekly. If you'd like updates or more in-depth coverage for specific problems, feel free to reach out!
The scraper used to collect this dataset is available here: timetooth/leetcode_scraper. Drop a ⭐ if you find it useful!
- Downloads last month
- 36