problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
XXXIX OM - I - Problem 1
For each positive number $ a $, determine the number of roots of the polynomial $ x^3+(a+2)x^2-x-3a $.
|
Let's denote the considered polynomial by $ F(x) $. A polynomial of the third degree has at most three real roots. We will show that the polynomial $ F $ has at least three real roots - and thus has exactly three real roots (for any value of the parameter $ a > 0 $).
It is enough to notice that
If a continuous function with real values takes values of different signs at two points, then at some point in the interval bounded by these points, it takes the value zero (Darboux property).
Hence, in each of the intervals $ (-a-3; -2) $, $ (-2; 0) $, $ (0; 2) $, there is a root of the polynomial $ F $.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XX OM - II - Task 2
Find all four-digit numbers in which the thousands digit is equal to the hundreds digit, and the tens digit is equal to the units digit, and which are squares of integers.
|
Suppose the number $ x $ satisfies the conditions of the problem and denote its consecutive digits by the letters $ a, a, b, b $. Then
The number $ x $ is divisible by $ 11 $, so as a square of an integer, it is divisible by $ 11^2 $, i.e., $ x = 11^2 \cdot k^2 $ ($ k $ - an integer), hence
Therefore,
The number $ a+b $ is thus divisible by $ 11 $. Since $ 0 < a \leq 9 $, $ 0 \leq b \leq 9 $, then $ 0 < a+b \leq 18 $, hence
Therefore, we conclude that $ b \ne 0 $, $ b \ne 1 $; since $ b $ is the last digit of the square of an integer, it cannot be any of the digits $ 2, 3, 7, 8 $. Thus, $ b $ is one of the digits $ 4, 5, 6, 9 $. The corresponding values of $ a $ are $ 7, 6, 5, 2 $, so the possible values of $ x $ are only the numbers $ 7744 $, $ 6655 $, $ 5566 $, $ 2299 $. Only the first one is a square of an integer.
The problem has one solution, which is the number $ 7744 $.
|
7744
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
V OM - I - Task 2
Investigate when the sum of the cubes of three consecutive natural numbers is divisible by $18$.
|
Let $ a - 1 $, $ a $, $ a + 1 $, be three consecutive natural numbers; the sum of their cubes
can be transformed in the following way:
Since one of the numbers $ a - 1 $, $ a $, $ a + 1 $ is divisible by $ 3 $, then one of the numbers $ a $ and $ (a + 1) (a - 1) + 3 $ is also divisible by $ 3 $. Therefore, the sum $ S $ of the cubes of three consecutive natural numbers is always divisible by $ 9 $.
The sum $ S $ is thus divisible by $ 18 = 9 \cdot 2 $ if and only if it is divisible by $ 2 $. Since $ S = 3a^3 + 6a $, $ S $ is even if and only if $ a $ is even, i.e., when $ a - 1 $ is odd. Hence, the conclusion:
The sum of the cubes of three consecutive natural numbers is divisible by $ 18 $ if and only if the first of these numbers is odd.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LIX OM - II - Task 1
Determine the maximum possible length of a sequence of consecutive integers, each of which can be expressed in the form $ x^3 + 2y^2 $ for some integers $ x, y $.
|
A sequence of five consecutive integers -1, 0, 1, 2, 3 satisfies the conditions of the problem: indeed, we have
On the other hand, among any six consecutive integers, there exists a number, say
$ m $, which gives a remainder of 4 or 6 when divided by 8. The number $ m $ is even; if there were a representation
in the form $ m = x^3 +2y^2 $ for some integers $ x, y $, then the number $ x $ would be even. In this case, however,
we would obtain the divisibility $ 8|x^3 $ and as a result, the numbers $ m $ and $ 2y^2 $ would give the same remainder (4 or 6) when divided by 8.
Therefore, the number $ y^2 $ would give a remainder of 2 or 3 when divided by 4. This is impossible: the equalities
prove that the square of an integer can give a remainder of only 0 or 1 when divided by 4.
We have thus shown that among any six consecutive integers, there exists a number that cannot be represented
in the form $ x^3 +2y^2 $.
Answer: The maximum possible length of such a sequence is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XV OM - I - Problem 11
In triangle $ ABC $, angle $ A $ is $ 20^\circ $, $ AB = AC $. On sides $ AB $ and $ AC $, points $ D $ and $ E $ are chosen such that $ \measuredangle DCB = 60^\circ $ and $ \measuredangle EBC = 50^\circ $. Calculate the angle $ EDC $.
|
Let $ \measuredangle EDC = x $ (Fig. 9). Notice that $ \measuredangle ACB = \measuredangle $ABC$ = 80^\circ $, $ \measuredangle CDB = 180^\circ-80^\circ-60^\circ = 40^\circ $, $ \measuredangle CEB = 180^\circ - 80^\circ-50^\circ = \measuredangle EBC $, hence $ EC = CB $. The ratio $ \frac{DC}{CE} $ of the sides of triangle $ EDC $ equals the ratio of the sides $ \frac{DC}{CB} $ of triangle $ BDC $, so the ratios of the sines of the angles opposite the corresponding sides in these triangles are equal:
The right side of the obtained equation can be transformed:
We need to find the convex angle $ x $ that satisfies the equation
or the equation
By transforming the products of sines into differences of cosines, we obtain an equivalent equation
Considering the condition $ 0 < x < 180^\circ $, we get $ x = 30^\circ $.
Note. The last part of the solution can be slightly shortened. Specifically, from the form of equation (1), it is immediately clear that it has a root $ x = 30^\circ $. No other convex angle satisfies this equation; if
then
so
thus, if $ 0 < x < 180^\circ $ and $ 0 < y < 180^\circ $, then $ x = y $.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXVIII - II - Task 3
In a hat, there are 7 slips of paper. On the $ n $-th slip, the number $ 2^n-1 $ is written ($ n = 1, 2, \ldots, 7 $). We draw slips randomly until the sum exceeds 124. What is the most likely value of this sum?
|
The sum of the numbers $2^0, 2^1, \ldots, 2^6$ is $127$. The sum of any five of these numbers does not exceed $2^2 + 2^3 + 2^4 + 2^5 + 2^6 = 124$. Therefore, we must draw at least six slips from the hat.
Each of the events where we draw six slips from the hat, and the seventh slip with the number $2^{n-1}$ ($n = 1, 2, \ldots, 7$) remains in the hat, is equally likely. The probability of such an event is thus $\displaystyle \frac{1}{7}$.
The sum of the numbers on the drawn slips is equal to $127 - 2^{n-1}$. If $n = 1$, this sum is $126$; if $n = 2$, it is $125$; if $n = 3, 4, 5, 6$ or $7$, the sum is less than $124$ and we must draw a seventh slip. In this last case, the sum of the numbers on all the drawn slips will be $127$. Therefore, the probability that the sum of the numbers on all the slips drawn according to the conditions of the problem is $125$, $126$, or $127$, is $\displaystyle \frac{1}{7}$, $\displaystyle \frac{1}{7}$, $\displaystyle \frac{5}{7}$, respectively.
Thus, the most probable value of the sum is $127$.
|
127
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XLII OM - I - Problem 8
Determine the largest natural number $ n $ for which there exist in space $ n+1 $ polyhedra $ W_0, W_1, \ldots, W_n $ with the following properties:
(1) $ W_0 $ is a convex polyhedron with a center of symmetry,
(2) each of the polyhedra $ W_i $ ($ i = 1,\ldots, n $) is obtained from $ W_0 $ by a translation,
(3) each of the polyhedra $ W_i $ ($ i = 1,\ldots, n $) has a point in common with $ W_0 $,
(4) the polyhedra $ W_0, W_1, \ldots, W_n $ have pairwise disjoint interiors.
|
Suppose that polyhedra $W_0, W_1, \ldots, W_n$ satisfy the given conditions. Polyhedron $W_1$ is the image of $W_0$ under a translation by a certain vector $\overrightarrow{\mathbf{v}}$ (condition (2)). Let $O_0$ be the center of symmetry of polyhedron $W_0$ (condition (1)); the point $O_1$, which is the image of $O_0$ under the translation by $\overrightarrow{\mathbf{v}}$, is the center of symmetry of $W_1$. Figure 3 illustrates a planar variant of the considered problem (a representation of the spatial configuration would obscure this illustration); polyhedra $W_0$ and $W_1$ are depicted as centrally symmetric polygons.
om42_1r_img_3.jpg
By condition (3), polyhedra $W_0$ and $W_1$ have common points (possibly many). Let $K$ be a common point of $W_0$ and $W_1$ (arbitrarily chosen). Denote by $L$ the image of point $K$ under the central symmetry with respect to $O_1$; thus, $L \in W_1$. Let $N$ be a point such that $\overrightarrow{NL} = \overrightarrow{\mathbf{v}}$ and let $M$ be the midpoint of segment $NK$ (Figure 4). Therefore, $N \in W_0$. According to condition (1), the set $W_0$ is convex; this means that with any two points belonging to $W_0$, the entire segment connecting these points is contained in $W_0$. Since $K \in W_0$ and $N \in W_0$, it follows that $M \in W_0$. Segment $MO_1$ connects the midpoints of segments $KN$ and $KL$, and thus $\overrightarrow{MO_1} = \frac{1}{2} \overrightarrow{NL} = \frac{1}{2} \overrightarrow{\mathbf{v}}$, which means $M$ is the midpoint of segment $O_0O_1$.
Let $U$ be the image of polyhedron $W_0$ under a homothety with center $O_0$ and scale factor 3. We will show that $W_1 \subset U$. Take any point $P \in W_1$: let $Q \in W_0$ be a point such that $\overrightarrow{QP} = \overrightarrow{\mathbf{v}}$ and let $S$ be the center of symmetry of parallelogram $O_0O_1PQ$. The medians $O_0S$ and $QM$ of triangle $O_0O_1Q$ intersect at a point $G$ such that $\overrightarrow{O_0G} = \frac{2}{3}\overrightarrow{O_0S} = \frac{1}{3}\overrightarrow{O_0P}$ (Figure 5). This means that $P$ is the image of point $G$ under the considered homothety. Since $G$ is a point on segment $QM$ with endpoints in the set (convex) $W_0$, it follows that $G \in W_0$. Therefore, $P \in U$ and from the arbitrariness of the choice of point $P \in W_1$ we conclude that $W_1 \subset U$.
om42_1r_img_4.jpg
om42_1r_img_5.jpg
In the same way, we prove that each of the sets $W_i (i=1, \ldots, n)$ is contained in $U$. Of course, also $W_0 \subset U$. Thus, the set $W_0 \cup W_1 \cup \ldots \cup W_n$ is a polyhedron contained in $U$. By conditions (2) and (4), its volume equals the volume of $W_0$ multiplied by $n+1$. On the other hand, the volume of $U$ equals the volume of $W_0$ multiplied by 27. Therefore, $n \leq 26$.
It remains to note that the value $n = 26$ can be achieved (example realization: 27 cubes $W_0, \ldots, W_{26}$ arranged like a Rubik's cube). Thus, the sought number is $26$.
Note. We obtain the same result assuming that $W_0, \ldots, W_n$ are any bounded, closed convex bodies (not necessarily polyhedra), with non-empty interiors, satisfying conditions (1)-(4); the reasoning carries over without any changes. Moreover, condition (4) turns out to be unnecessary. This was proven by Marcin Kasperski in the work 27 convex sets without a center of symmetry, awarded a gold medal at the Student Mathematical Paper Competition in 1991; a summary of the work is presented in Delta, issue 3 (1992).
|
26
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXIV OM - III - Task 2
Let $ p_n $ be the probability that a series of 100 consecutive heads will appear in $ n $ coin tosses. Prove that the sequence of numbers $ p_n $ is convergent and calculate its limit.
|
The number of elementary events is equal to the number of $n$-element sequences with two values: heads and tails, i.e., the number $2^n$. A favorable event is a sequence containing 100 consecutive heads. We estimate the number of unfavorable events from above, i.e., the number of sequences not containing 100 consecutive heads.
Let $n = 100k + r$, where $k \geq 0$ and $0 \leq r < 100$. Each $n$-element sequence thus consists of $k$ 100-element sequences and one $r$-element sequence. The total number of 100-element sequences with two values is $2^{100}$; therefore, after excluding the sequence composed of 100 heads, there remain $2^{100} - 1$ 100-element sequences. Each $n$-element sequence not containing 100 consecutive heads thus consists of $k$ such 100-element sequences and some $r$-element sequence. Hence, the number of unfavorable events is not greater than $(2^{100} - 1)^k \cdot 2^r$. Therefore,
If $n$ tends to infinity, then of course $k$ also tends to infinity. Since for $0 < q < 1$ we have $\displaystyle \lim_{k \to \infty} q^k = 0$, then $\displaystyle \lim_{k \to \infty} \left( 1 - \frac{1}{2^{100}} \right)^k = 0$. Therefore, from (1) by the squeeze theorem, we have $\displaystyle \lim_{k \to \infty} q^k = 0$, so $\displaystyle \lim_{n \to \infty} p_n = 1$.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
XXII OM - III - Problem 5
Find the largest integer $ A $ such that for every permutation of the set of natural numbers not greater than 100, the sum of some 10 consecutive terms is at least $ A $.
|
The sum of all natural numbers not greater than $100$ is equal to $1 + 2 + \ldots + 100 = \frac{1 + 100}{2} \cdot 100 = 5050$. If $a_1, a_2, \ldots, a_{100}$ is some permutation of the set of natural numbers not greater than $100$ and the sum of any $10$ terms of this permutation is less than some number $B$, then in particular
By adding these inequalities side by side, we get that $a_1 + a_2 + \ldots + a_{100} = 1 + 2 + \ldots + 100 < 10B$, which means $505 < B$.
Thus, the number $A$ defined in the problem satisfies the inequality
On the other hand, consider the following permutation $a_1, a_2, \ldots, a_{100}$ of the set of natural numbers not greater than $100$
This permutation can be defined by the formulas:
We will prove that the sum of any $10$ consecutive terms of this permutation is not greater than $505$.
Indeed, if the first of the considered $10$ terms has an even number $2k$, then
If, however, the first of the considered terms has an odd number $2k + 1$, then
Thus, the sum of any $10$ consecutive terms of this permutation is not greater than $505$. Therefore, the number $A$ defined in the problem satisfies the inequality
From (1) and (2), it follows that $A = 505$.
Note 1. The problem can be generalized as follows: Find the largest integer $A$ such that for any permutation of the set of natural numbers not greater than an even number $n = 2t$, the sum of some $m = 2r$ (where $r$ is a divisor of $t$) consecutive terms is at least $A$.
By making minor changes in the solution provided above, consisting in replacing the number $100$ with $2t$ and the number $10$ with $2r$, it can be proved that $A = \frac{1}{2} m(n + 1)$.
Note 2. In the case where $m \leq n$ are any natural numbers, it is generally not true that every permutation of the set of natural numbers not greater than $n$ contains $m$ consecutive terms with a sum not less than $\frac{1}{2} m(n + 1)$. For example, for $n = 6$, $m = 4$, the permutation $6, 4, 1, 2, 3, 5$ does not contain four consecutive terms with a sum not less than $14$.
|
505
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XV OM - II - Task 3
Prove that if three prime numbers form an arithmetic progression with a difference not divisible by 6, then the smallest of these numbers is $3$.
|
Suppose that the prime numbers $ p_1 $, $ p_2 $, $ p_3 $ form an arithmetic progression with a difference $ r > 0 $ not divisible by $ 6 $, and the smallest of them is $ p_1 $. Then
Therefore, $ p_1 \geq 3 $, for if $ p_1 = 2 $, the number $ p_3 $ would be an even number greater than $ 2 $, and thus would not be a prime number. Hence, the numbers $ p_1 $ and $ p_2 $ are odd, and the number $ r $ equal to the difference $ p_2 - p_1 $ is even and one of the cases holds: $ r = 6k + 2 $ or $ r = 6k + 4 $, where $ k $ is an integer $ \geq 0 $.
We will prove that $ p_1 $ is divisible by $ 3 $. Indeed, if $ p_1 = 3m + 1 $ ($ m $ - an integer) and $ r = 6k + 2 $, it would follow that $ p_2 = 3m + 6k + 3 $ is divisible by $ 3 $, and since $ p_2 > 3 $, $ p_2 $ would not be a prime number. If, on the other hand, $ p_1 = 3m + 1 $ and $ r = 6k + 4 $, then $ p_3 = 3m + 12k + 9 $ would not be a prime number. Similarly, from the assumption that $ p_1 = 3m + 2 $ and $ r = 6k + 2 $, it would follow that $ p_3 = 3m + 12k + 6 $ is not a prime number, and from the assumption that $ p_1 = 3m + 2 $ and $ r = 6k + 4 $, we would get $ p_2 = 3m + 6k + 6 $, and thus $ p_2 $ would not be a prime number.
Therefore, $ p_1 $ is a prime number divisible by $ 3 $, i.e., $ p_1 = 3 $.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
XLIII OM - I - Problem 2
In square $ABCD$ with side length $1$, point $E$ lies on side $BC$, point $F$ lies on side $CD$, the measures of angles $EAB$ and $EAF$ are $20^{\circ}$ and $45^{\circ}$, respectively. Calculate the height of triangle $AEF$ drawn from vertex $A$.
|
The measure of angle $ FAD $ is $ 90^\circ - (20^\circ + 45^\circ) = 25^\circ $. From point $ A $, we draw a ray forming angles of $ 20^\circ $ and $ 25^\circ $ with rays $ AE $ and $ AF $, respectively, and we place a segment $ AG $ of length $ 1 $ on it (figure 2).
From the equality $ |AG| =|AB| = 1 $, $ | \measuredangle EAG| = | \measuredangle EAB| = 20^\circ $, it follows that triangle $ EAG $ is congruent to $ EAB $.
Similarly, from the equality $ |AG| = |AD| = 1 $, $ | \measuredangle FAG| = | \measuredangle FAD| = 25^\circ $, it follows that triangle $ FAG $ is congruent to $ FAD $.
This means that
point $ G $ lies on segment $ EF $ and is the foot of the altitude of triangle $ AEF $ drawn from vertex $ A $. Its length $ |AG| = 1 $.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
L OM - I - Problem 11
In an urn, there are two balls: a white one and a black one. Additionally, we have 50 white balls and 50 black balls at our disposal. We perform the following action 50 times: we draw a ball from the urn, and then return it to the urn along with one more ball of the same color as the drawn ball. After completing these actions, we have 52 balls in the urn. What is the most probable number of white balls in the urn?
|
Let $ P(k,n) $, where $ 1 \leq k\leq n-1 $, denote the probability of the event that when there are $ n $ balls in the urn, exactly $ k $ of them are white. Then
Using the above relationships, we prove by induction (with respect to $ n $) that $ P(k,n) = 1/(n-1) $ for $ k = 1,2,\ldots,n-1 $. In particular
Therefore, each possible number of white balls after $ 50 $ draws (from $ 1 $ to $ 51 $) is equally likely.
|
51
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XLVI OM - III - Problem 2
The diagonals of a convex pentagon divide this pentagon into a pentagon and ten triangles. What is the maximum possible number of triangles with equal areas?
|
om46_3r_img_12.jpg
Let's denote the considered pentagon by $ABCDE$, and the pentagon formed by the intersection points of the diagonals by $KLMNP$ so that the following triangles are those mentioned in the problem:
$\Delta_0$: triangle $LEM$; $\quad \Delta_1$: triangle $EMA$;
$\Delta_2$: triangle $MAN$; $\quad \Delta_3$: triangle $ANB$;
$\Delta_4$: triangle $NBP$; $\quad \Delta_5$: triangle $BPC$;
$\Delta_6$: triangle $PCK$; $\quad \Delta_7$: triangle $CKD$;
$\Delta_8$: triangle $KDL$; $\quad \Delta_9$: triangle $DLE$
(figure 12). We will start by proving the implication:
We assume that the numbering of the triangles is cyclic (that is, we assume: $\Delta_{-1} = \Delta_9$; $\Delta_{10} = \Delta_0$).
Suppose, for example, that triangles $\Delta_4$, $\Delta_5$, and $\Delta_6$ have equal areas. From the equality of the areas of triangles $NBP$ and $BPC$, it follows that segment $BP$ is a median in triangle $BCN$; from the equality of the areas of triangles $BPC$ and $PCK$, it follows that segment $CP$ is a median in triangle $BCK$. Point $P$ would then be the common midpoint of diagonals $BK$ and $CN$ of quadrilateral $BCKN$, which should therefore be a parallelogram - but the lines $BN$ and $CK$ intersect at point $E$. This is a contradiction; implication (1) is proven.
We proceed to the main solution. The example of a regular pentagon shows that it is possible to obtain five triangles $\Delta_i$ with equal areas. We will prove that it is not possible to obtain seven such triangles.
Suppose, therefore, that there exists a seven-element set $Z$, contained in the set $\{0,1,\ldots,9\}$, such that triangles $\Delta_i$ with indices $i \in Z$ have equal areas. Let $k$, $l$, $m$ be three numbers from the set $\{0,1,\ldots,9\}$, not belonging to $Z$. Consider all triples of consecutive indices:
where, as before, the addition $i \pm 1$ should be understood modulo $10$. Each number from the set $\{0,1,\ldots,9\}$ belongs to exactly three triples $T_i$. This applies, in particular, to each of the numbers $k$, $l$, $m$. Therefore, the three-element set $\{k,l,m\}$ has a non-empty intersection with at most nine triples $T_i$. At least one triple $T_j$ remains that does not contain any of the numbers $k$, $l$, $m$, and is therefore contained in the set $Z$. The number $j$ must be even, according to observation (1).
Without loss of generality, assume that $j = 2$. This means that the numbers $1$, $2$, $3$ belong to the set $Z$. Therefore, the numbers $0$ and $4$ cannot belong to it (since, again by observation (1), the triples $\{0,1,2\}$ and $\{2,3,4\}$ are excluded); thus, one of the numbers $k$, $l$, $m$ equals $0$, and another equals $4$. The third of these numbers must be part of the triple $\{6,7,8\}$ (which otherwise would be contained in the set $Z$, contrary to implication (1)). The roles of the numbers $6$ and $8$ are symmetric in this context. We therefore have to consider two essentially different cases:
The set $Z$, respectively, has one of the following forms:
Let $S_i$ be the area of triangle $\Delta_i$ (for $i = 0,1,\ldots,9$). We will show that the implications hold:
This will be a proof that none of the seven-element sets $Z$ listed above can be the set of indices of triangles with equal areas. According to earlier statements, this will also justify the conclusion that among the ten triangles $\Delta_i$, there are never seven triangles with the same area.
Proof of implication (2). From the given equalities of areas:
and
it follows (respectively) that points $N$ and $P$ are the midpoints of segments $BM$ and $BK$, and points $M$ and $L$ are the midpoints of segments $EN$ and $EK$ (figure 13).
Thus, segment $NP$ connects the midpoints of two sides of triangle $BMK$, and segment $ML$ connects the midpoints of two sides of triangle $ENK$, and therefore
- and
The obtained parallelism relations show that quadrilateral $AMKN$ is a parallelogram; hence $|MK| = |AN|$. Line $MK$ is parallel to $NC$, so triangles $ENC$ and $EMK$ are similar in the ratio $|EN| : |EM| = 2$. Therefore, $|NC| = 2 \cdot |MK|$, and consequently
The segments $PC$ and $AN$, lying on the same line, are the bases of triangles $ANB$ and $BPC$ with a common vertex $B$. The ratio of the lengths of these bases is therefore also the ratio of the areas of the triangles: area($BPC$) : area($ANB$) = $3 : 2$, i.e., $S_5 : S_3 = 3 : 2$. The conclusion of implication (2) is thus proven.
om46_3r_img_13.jpg
om46_3r_img_14.jpg
Proof of implication (3). The given equalities of the areas of triangles:
and
show that points $M$ and $N$ divide segment $EB$ into three equal parts, and similarly, points $L$ and $K$ divide segment $EC$ into three equal parts. Therefore, line $BC$ is parallel to $ML$ (i.e., to $AM$). Since $N$ is the midpoint of segment $BM$, triangles $AMN$ and $CBN$ are similar in the ratio $-1$ (figure 14). Hence, area($AMN$) = area($CBN$) $> $ area($CBP$), i.e., $S_2 > S_5$. This completes the proof of implication (3), and thus also the proof of the general theorem: it is not possible to have seven triangles $\Delta_i$ with equal areas.
The reasoning conducted in the last case (proof of (3)) also provides a hint on how to obtain six triangles $\Delta_i$ with equal areas. We take any isosceles triangle $BCE$ where $|EB| = |EC|$. On the sides $EB$ and $EC$, we find points $M$ and $N$ and $L$ and $K$, dividing these sides into three equal parts:
The intersection points of line $ML$ with lines $CN$ and $BK$ are denoted by $A$ and $D$, respectively (figure 14 can still serve as an illustration; one only needs to imagine moving point $E$ to the perpendicular bisector of side $BC$ and appropriately repositioning the other points). The equalities (4) and (5) then hold; and thanks to the assumption that triangle $BCE$ is isosceles (and the resulting symmetry of the entire configuration), all areas appearing in relations (4) and (5) are equal.
Conclusion: six of the triangles $\Delta_i$ can have equal areas, and this number cannot be increased.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LIX OM - I - Task 9
Determine the smallest real number a with the following property:
For any real numbers $ x, y, z \geqslant a $ satisfying the condition $ x + y + z = 3 $
the inequality holds
|
Answer: $ a = -5 $.
In the solution, we will use the following identity:
Suppose that the number $ a \leqslant 1 $ has the property given in the problem statement. The numbers
$ x = a, y = z = 2\cdot (\frac{3-a}{2}) $ satisfy the conditions $ x, y, z \geqslant a $ and $ x+y+z = 3 $, thus
by virtue of (1), from which the inequality $ a \geqslant -5 $ follows.
We will now show that the number $ a = -5 $ satisfies the conditions of the problem. For this purpose, consider numbers
$ x, y, z \geqslant-5 $ such that $ x + y + z = 3 $. Without loss of generality, assume that
$ x \leqslant y \leqslant z $. The sum $ y + z $ is a positive number, because otherwise, given
$ y\leqslant z $, we would have $ x \leqslant y \leqslant 0 $, which would imply that $ x +y + z \leqslant y + z \leqslant 0 $,
contradicting the condition $ x+y+z = 3 $. Since $ y + z > 0 $, the inequality
holds, and from the identity (1) we finally obtain
(Note: The last part of the text seems to be incomplete or missing in the original Polish text, so the translation reflects that.)
|
-5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XLIV OM - I - Problem 11
In six different cells of an $ n \times n $ table, we place a cross; all arrangements of crosses are equally probable. Let $ p_n $ be the probability that in some row or column there will be at least two crosses. Calculate the limit of the sequence $ (np_n) $ as $ n \to \infty $.
|
Elementary events are determined by six-element subsets of the set of $n^2$ cells of the table; there are $\binom{n^2}{6}$ of them. Let $\mathcal{Z}$ be the complementary event to the event considered in the problem. The configurations favorable to event $\mathcal{Z}$ are obtained as follows: we place the first cross in any arbitrarily chosen cell: here we have $n^2$ possibilities. We then "cross out" the entire horizontal row and the entire vertical row intersecting at the cell where we placed the first cross, and place the second cross in any of the remaining cells: thus, we now have $(n-1)^2$ possibilities. We repeat this scheme four more times and obtain the number of possibilities equal to $n^2 (n -1 )^2 (n - 2)^2 (n - 3)^2 (n - 4 )^2 (n - 5)^2$. This number must still be divided by $6!$ (the number of permutations of a six-element set) to make the reasoning independent of the order of placing the crosses.
Thus, the probability of event $\mathcal{Z}$ (equal to $1 - p_n$) is
One should not multiply all these factors! Let us denote the numerator of the obtained fraction by $L_n$, and the denominator by $M_n$. It is enough to notice that
where $\phi(n)$ and $f(n)$ are polynomials (in the variable $n$), of degree (at most) 4 and 10, respectively; similarly,
where $\psi(n)$ and $g(n)$ are polynomials (in the variable $n$), of degree (at most) 8 and 10, respectively. Therefore,
Since the polynomials $f(n)$ and $g(n)$ are of degree (at most) tenth, then
and consequently, $\displaystyle \lim_{n\to \infty} np_n = 30$.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XV OM - I - Problem 7
Given a circle and points $ A $ and $ B $ inside it. Find a point $ P $ on this circle such that the angle $ APB $ is subtended by a chord $ MN $ equal to $ AB $. Does the problem have a solution if the given points, or only one of them, lie outside the circle?
|
Suppose that point $ P $ of a given circle $ C $ with radius $ r $ is a solution to the problem (Fig. 7).
Since points $ A $ and $ B $ lie inside the circle $ C $, points $ M $ and $ N $ lie on the rays $ PA $ and $ PB $ respectively, and angle $ APB $ coincides with angle $ MPN $. Triangles $ APB $ and $ MPN $ have equal bases $ AB = MN = a $ and a common angle at the vertex $ \measuredangle APB = \measuredangle MPN = \alpha $; hence, the circles circumscribed around these triangles have the same radius $ r = \frac{a}{2 \sin \alpha} $, and point $ P $ lies on the circle with radius $ r $ passing through points $ A $ and $ B $. Therefore, the construction of the desired point is as follows (Fig. 7a). We construct circles with radius $ r $ passing through points $ A $ and $ B $. Since $ AB < 2r $, there are 2 such circles: $ K_1 $ and $ K_2 $. If $ P $ is a common point of circles $ K_1 $ and $ C $, or circles $ K_2 $ and $ C $, then $ P $ is a solution to the problem. Indeed, the rays $ PA $ and $ PB $ intersect the given circle $ C $ at points $ M $ and $ N $; from triangle $ MPN $ we have $ MN = 2r \sin \measuredangle MPN = 2r \sin \measuredangle APB $; but in triangle $ APB $ we have $ \sin \measuredangle APB = AB \colon 2r $, so $ MN = AB $.
Each of the circles $ K_1 $ and $ K_2 $ intersects the circle $ C $ at two points; if $ O_1 $ and $ O_2 $ are the centers of circles $ K_1 $ and $ K_2 $, then
since $ OA < r $, $ AO_1 = r $; similarly $ 0 < OO_2 < 2r $.
The problem thus has 4 solutions.
Let us examine whether the above reasoning remains valid for any position of points $ A $ and $ B $. If point $ P $ is a solution to the problem, then points $ M $ and $ N $ lie on the lines $ PA $ and $ PB $, but not necessarily on the rays $ PA $ and $ PB $, so angle $ MPN $ coincides either with angle $ APB $ or with the adjacent angle to angle $ APB $. The conclusion that triangles $ APB $ and $ MPN $ have the same circumradius remains valid, hence point $ P $ lies, as before, on the circle with radius $ r $ passing through $ A $ and $ B $. Conversely, if point $ P $ is a common point of the given circle and a circle $ K $ with radius $ r $ passing through $ A $ and $ B $, then this point, provided it is different from $ A $ and $ B $, is a solution to the problem, as we conclude in the same way as before.
For such a point $ P $ to exist, the following conditions must be met:
1. There must exist a circle with radius $ r $ passing through points $ A $ and $ B $; this is the case when $ AB \leq 2r $. If $ AB < 2r $, there are two such circles $ K_1 $ and $ K_2 $ with centers $ O_1 $ and $ O_2 $. If $ AB = 2r $, there is one such circle: $ K_1 = K_2 $, $ O_1 = O_2 $.
2. There must exist a common point of circle $ K_1 $ or $ K_2 $ with the given circle $ C $, different from $ A $ and $ B $.
The table below gives the number of solutions for different cases of the position of points $ A $ and $ B $.
We propose to the Reader to provide a detailed justification of the above data for each of the cases 2-6 and to make the appropriate drawings.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXVI - I - Task 1
At the ball, there were 42 people. Lady $ A_1 $ danced with 7 gentlemen, Lady $ A_2 $ danced with 8 gentlemen, ..., Lady $ A_n $ danced with all the gentlemen. How many gentlemen were at the ball?
|
The number of ladies at the ball is $ n $, so the number of gentlemen is $ 42-n $. The lady with number $ k $, where $ 1 \leq k \leq n $, danced with $ k+6 $ gentlemen. Therefore, the lady with number $ n $ danced with $ n+ 6 $ gentlemen. These were all the gentlemen present at the ball. Thus, $ 42-n = n + 6 $. Solving this equation, we get $ n = 18 $. The number of gentlemen at the ball is therefore $ 42-18 = 24 $.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
L OM - II - Task 5
Let $ S = \{1, 2,3,4, 5\} $. Determine the number of functions $ f: S \to S $ satisfying the equation $ f^{50} (x) = x $ for all $ x \in S $.
Note: $ f^{50}(x) = \underbrace{f \circ f \circ \ldots \circ f}_{50} (x) $.
|
Let $ f $ be a function satisfying the conditions of the problem. For numbers $ x \neq y $, we get $ f^{49}(f(x)) = x \neq y = f^{49}(f(y)) $, hence $ f(x) \neq f(y) $. Therefore, $ f $ is a permutation of the set $ S $. Denote by $ r(x) $ ($ x \in S $) the smallest positive integer such that $ f^{r(x)}(x) = x $. Then $ r(x) \leq 5 $ and $ r(x) \mid 50 $, so $ r(x) \in \{1, 2, 5\} $.
If there exists a number $ a \in S $ such that $ r(a) = 5 $, then the numbers $ a $, $ f(a) $, $ f^2(a) $, $ f^3(a) $, $ f^4(a) $ are distinct; they thus exhaust the set $ S $. Then for any number $ x \in S $, $ r(x) = 5 $. The function $ f $ is thus uniquely determined by the permutation $ (f(1), f^2(1), f^3(1), f^4(1)) $ of the set $ \{2, 3, 4, 5\} $; hence it can be defined in $ 4! = 24 $ ways.
If for all $ x \in S $, $ r(x) = 1 $, then $ f $ is the identity function. Such a function is unique.
The remaining case to consider is when the maximum value attained by the function $ r $ is $ 2 $. Let $ a $ be an element of the set $ S $ such that $ r(a) = 2 $. Then also $ r(b) = 2 $, where $ b = f(a) $.
If $ r(x) = 1 $ for all $ x \in S \setminus \{a, b\} $, then $ f $ is determined by the choice of a two-element subset $ \{a, b\} $ of the set $ S $, which can be done in $ {5 \choose 2} = 10 $ ways.
If, however, there exists a number $ c \in S \setminus \{a, b\} $ such that $ r(c) = 2 $, then by setting $ d = f(c) $ and denoting by $ e $ the unique element of the set $ S \setminus \{a, b, c, d\} $, we have
Such a function $ f $ is determined by the choice of the number $ e $ (which can be done in $ 5 $ ways) and the partition of the set $ S \setminus \{e\} $ into two two-element subsets $ \{a, b\} $ and $ \{c, d\} $ (there are $ 3 $ such partitions). We thus get $ 15 $ functions of the form (1).
In total, there are $ 50 $ functions satisfying the conditions of the problem.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXII OM - III - Task 3
How many locks at least need to be placed on the treasury so that with a certain distribution of keys among the 11-member committee authorized to open the treasury, any 6 members can open it, but no 5 can? Determine the distribution of keys among the committee members with the minimum number of locks.
|
Suppose that for some natural number $ n $ there exists a key distribution to $ n $ locks among an 11-member committee such that the conditions of the problem are satisfied. Let $ A_i $ denote the set of locks that the $ i $-th member of the committee can open, where $ i = 1, 2, \ldots, 11 $, and let $ A $ denote the set of all locks. Then from the conditions of the problem, we have
for any five-element subset $ \{ i_1, \ldots, i_5\} $ of the set $ \{1, 2, \ldots, 11\} $ and
for any six-element subset $ \{j_1, \ldots, j_6\} $ of the set $ \{1,2,\ldots, 11\} $.
From (1), it follows that the set $ A - (A_{i_1} \cup \ldots \cup A_{i_5}) $ is non-empty. Let $ x_{i_1}, \ldots, x_{i_5} $ be one of its elements, i.e., a lock that the group of committee members numbered $ i_1, \ldots, i_5 $ cannot open. From (2), it follows that for every $ j \not \in \{i_1, \ldots, i_5 \} $ we have $ x_{i_1 , \ldots, i_5} \in A_j $.
Suppose that $ x_{i_1,\ldots,i_5} = x_{k_1, \ldots, k_5} $ for some subsets $ \{i_1, \ldots, i_5\} $ and $ \{k_1, \ldots, k_5\} $. If these subsets were different, then, for example, $ i_t \not \in \{ k_1, \ldots, k_5 \} $. Therefore, $ x_{k_1, \ldots, k_5} \in A_{i_t} $; but on the other hand, this leads to a contradiction. The obtained contradiction proves that $ \{i_1, \ldots,i_5\} = \{ k_1, \ldots, k_5 \} $.
In other words, different five-element subsets $ \{i_1, \ldots, i_5\} $ correspond to different locks. Therefore, the number of locks is not less than the number of five-element subsets of an 11-element set, i.e., $ n \geq \binom{11}{5} = 462 $.
We will now prove that if we install $ \binom{11}{5} $ locks on the treasury, then we can distribute the keys to them among the members of the 11-member committee in such a way that the conditions of the problem are satisfied.
Let us associate each of the $ \binom{11}{5} $ locks with a five-element subset of the set $ \{1, 2, \ldots, 11\} $ in a one-to-one manner. If a lock corresponds to the subset $ \{i_1, \ldots, i_5\} $, then the keys to it are given to all members of the committee whose numbers are different from $ i_1, \ldots, i_5 $.
We will show that no five members of the committee can open a certain lock, and therefore the treasury. Indeed, the members of the committee numbered $ i_1, \ldots, i_5 $ do not have the key to the lock corresponding to the subset $ \{i_1, \ldots, i_5\} $.
We will show that any six members of the committee can open any lock, and therefore the treasury. If the members of the committee have numbers $ j_1, \ldots, j_6 $ and want to open a lock corresponding to the subset $ \{i_1, \ldots, i_5\} $, then one of the six numbers $ j_1, \ldots, j_6 $ does not belong to this five-element subset, say $ j_t \not \in \{i_1, \ldots, i_5 \} $. Therefore, the member of the committee numbered $ j_t $ has the key to the lock corresponding to the subset $ \{i_1, \ldots, i_5\} $.
Thus, the smallest number satisfying the conditions of the problem is $ \binom{11}{5} = 462 $.
|
462
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Consider the set $M$ of integers $n \in[-100 ; 500]$, for which the expression $A=n^{3}+2 n^{2}-5 n-6$ is divisible by 11. How many integers are contained in $M$? Find the largest and smallest of them?
|
Answer: 1) 164 numbers; 2) $n_{\text {min }}=-100, n_{\text {max }}=497$.
|
164
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solution. According to the problem, the sum of the original numbers is represented by the expression:
$$
\begin{aligned}
& \left(a_{1}+2\right)^{2}+\left(a_{2}+2\right)^{2}+\ldots+\left(a_{50}+2\right)^{2}=a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2} \rightarrow \\
& {\left[\left(a_{1}+2\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+2\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+2\right)^{2}-a_{50}^{2}\right]=0 \rightarrow} \\
& \rightarrow 4\left(a_{1}+1\right)+4\left(a_{2}+1\right)+\ldots+4\left(a_{50}+1\right)=0 \rightarrow a_{1}+a_{2}+\ldots+a_{50}=-50
\end{aligned}
$$
Then, if we add 3, we get:
$$
\begin{aligned}
& \left(a_{1}+3\right)^{2}+\left(a_{2}+3\right)^{2}+\ldots+\left(a_{50}+3\right)^{2}-\left(a_{1}^{2}+a_{2}^{2}+\ldots+a_{50}^{2}\right)= \\
& =\left[\left(a_{1}+3\right)^{2}-a_{1}^{2}\right]+\left[\left(a_{2}+3\right)^{2}-a_{2}^{2}\right]+\ldots\left[\left(a_{50}+3\right)^{2}-a_{50}^{2}\right]= \\
& =3\left(2 a_{1}+3\right)+3\left(2 a_{2}+3\right)+\ldots+3\left(2 a_{50}+3\right)=6\left(a_{1}+a_{2}+\ldots+a_{50}\right)+9 \cdot 50= \\
& =-300+450=150
\end{aligned}
$$
|
Answer: will increase by 150.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A set of 60 numbers is such that adding 3 to each of them does not change the value of the sum of their squares. By how much will the sum of the squares of these numbers change if 4 is added to each number?
|
Answer: will increase by 240.
|
240
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A set of 70 numbers is such that adding 4 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 5 is added to each number?
|
Answer: will increase by 350.
|
350
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A set of 80 numbers is such that adding 5 to each of them does not change the magnitude of the sum of their squares. By how much will the sum of the squares of these numbers change if 6 is added to each number?
|
Answer: will increase by 480.
|
480
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the fraction $\frac{p}{q}$ with the smallest possible natural denominator, for which $\frac{1}{2014}<\frac{p}{q}<\frac{1}{2013}$. Enter the denominator of this fraction in the provided field
|
5. Find the fraction $\frac{p}{q}$ with the smallest possible natural denominator, for which
$\frac{1}{2014}<\frac{p}{q}<\frac{1}{2013}$. Enter the denominator of this fraction in the provided field
Answer: 4027
|
4027
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. If $\quad a=\overline{a_{1} a_{2} a_{3} a_{4} a_{5} a_{6}}, \quad$ then $\quad P(a)=\overline{a_{6} a_{1} a_{2} a_{3} a_{4} a_{5}}$, $P(P(a))=\overline{a_{5} a_{6} a_{1} a_{2} a_{3} a_{4}} \quad$ with $\quad a_{5} \neq 0, a_{6} \neq 0, a_{1} \neq 0 . \quad$ From the equality $P(P(a))=a$ it follows that $a_{1}=a_{5}, a_{2}=a_{6}, a_{3}=a_{1}$, $a_{4}=a_{2}, a_{5}=a_{3}, a_{6}=a_{4}$, that is, $a_{1}=a_{3}=a_{5}=t, t=1,2, \ldots, 9$ and $a_{2}=a_{4}=a_{6}=u, u=1,2, \ldots, 9$. Thus, the sought $a=\overline{\text { tututu }}$ and there are 81 such different numbers ( $t$ and $u$ can take any values of the decimal system digits from 1 to 9).
Let $n>2-$ be a prime number, $a=\overline{a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2} a_{n-1} a_{n}}$. Then
$$
\begin{gathered}
P(a)=\overline{a_{n} a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2} a_{n-1}} \\
P(P(a))=\overline{a_{n-1} a_{n} a_{1} a_{2} a_{3} a_{4} \ldots a_{n-3} a_{n-2}}
\end{gathered}
$$
The property $P(P(a))=a$ gives the relations $a_{1}=a_{n-1}=a_{n-3}=\ldots=a_{1}$. For a prime $n>2$, all the digits of the number $a$ are involved in the chain, so they are all equal to each other.
|
Answer: 1) 81 is the number; 2) $a=\overline{t u t u t u}, t, u$, where $t, u$ - are any digits, not equal to zero.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Square the numbers $a=10001, b=100010001$. Extract the square root of the number $c=1000200030004000300020001$.
|
1) $a^{2}=100020001$; 2) $b^{2}=10002000300020001$; 3) $\sqrt{c}=1000100010001$.
|
1000100010001
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{5 n+3}{7 n+8}$ be reduced? For which integers $n$ can this occur?
|
Answer: it can be reduced by 19 when $n=19k+7, k \in Z$.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{4 n+3}{5 n+2}$ be reduced? For which integers $n$ can this occur?
|
Answer: can be reduced by 7 when $n=7 k+1, k \in Z$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The angle at vertex $B$ of triangle $A B C$ is $130^{\circ}$. Through points $A$ and $C$, lines perpendicular to line $A C$ are drawn and intersect the circumcircle of triangle $A B C$ at points $E$ and $D$. Find the acute angle between the diagonals of the quadrilateral with vertices at points $A, C, D$ and $E$.
Problem 1 Answer: 12 students.
|
Solution. Let $a$ be the number of students in the first category, $c$ be the number of students in the third category, and $b$ be the part of students from the second category who will definitely lie in response to the first question (and say "YES" to all three questions), while the rest of the students from this category will answer "NO" to all three questions. Then, "YES" to the first question will be given by $a+b+c=25$ students. "YES" to the second question will be given by $b+c=21$ students. "YES" to the third question will be given by $b=6$ students. Solving the system, we get: $a=4, b=6, c=15$. Then, to the second category, we should assign $31-a-c=12$ students.
Problem 2 Answer: $a= \pm 5-2 \sqrt{6}$.
Solution. By Vieta's theorem, the roots of the equation are $m=(a+2 \sqrt{6})$ and $n=\left(\frac{1}{a}-2 \sqrt{6}\right)$.
Then we have:
$$
\left[\begin{array}{l}
a=m-2 \sqrt{6} \\
\frac{1}{a}=n+2 \sqrt{6}
\end{array} \rightarrow 1=m n+2 \sqrt{6}(m-n)-24 \rightarrow 2 \sqrt{6}(m-n)=25-m n\right.
$$
If $m, n \in Z, m \neq n$, then $2 \sqrt{6}=\frac{25-m n}{m-n}$ is a rational number, which is incorrect. Therefore, $m=n$ and then $m^{2}=25 \rightarrow m= \pm 5 \rightarrow a= \pm 5-2 \sqrt{6}$.
Problem 3 Answer: 5400 numbers.
Solution. Write $496125=3^{4} \cdot 5^{3} \cdot 7^{2}$. There are a total of $3^{4} \cdot 5^{3}=10125$ multiples of 49. Among them, $3^{3} \cdot 5^{3}=3375$ numbers are divisible by 3, $3^{4} \cdot 5^{2}=2025$ numbers are divisible by 5, and $3^{3} \cdot 5^{2}=675$ numbers are divisible by 15. Then, among the numbers that are multiples of 49, there are $3375+2025-675=4725$ numbers that are divisible by either 3 or 5. Therefore, the numbers that are not divisible by either 3 or 5 will be $10125-4775=$ 5400 desired numbers.
Problem 4 Answer: $n=210$.
Solution. According to the problem, $n=7 k$ and the expression
$$
n^{2}+25 n+100=(n+5)(n+20)=(7 k+5)(7 k+20)
$$
must be divisible by 5 and 23. Note that if one of the factors is divisible by 5, then the other is also divisible by 5 and vice versa, so:
$$
7 k+5=5 m \rightarrow 7 k=5(m-1) \rightarrow\left\{\begin{array}{c}
k=5 t \\
m=7 t+1
\end{array} \rightarrow n=35 t, t \in Z\right.
$$
Case 1. $7 k+5$ is divisible by 23:
$$
35 t+5=23 u \rightarrow\left\{\begin{array}{l}
t=23 v-10 \\
u=35 v-15
\end{array} \rightarrow n=35 t=35(23 v-10) \rightarrow n_{\min }=455\right.
$$
Case 2. $7 k+20$ is divisible by 23:
$$
35 t+20=23 u \rightarrow\left\{\begin{array}{c}
t=23 v+6 \\
u=35 v+10
\end{array} \rightarrow n=35 t=35(23 v+6) \rightarrow n_{\min }=210\right.
$$
Choosing the smallest of the found $n_{\min }$, we get $n_{\min }=210$.
Problem 5 Answer: $80^{\circ}$.
Solution. Figures 1 and 2 show the possible geometric configurations.
Fig 1
Fig 2
In the figures, point $O$ is the center of the circle $K$ circumscribed around triangle $A B C$.
Case 1. $\alpha>90^{\circ}$ (Fig. 1). Quadrilateral $A B C D$ is inscribed in circle $K$ by construction, so point $O$ is equidistant from points $C$ and $D$ at a distance equal to the radius of circle $K$. Similarly, point $O$ is equidistant from points $A$ and $E$ at the same distance. Therefore, point $O$ is the intersection point of the diagonals of rectangle $A C D E$. The angle $C D O$, as the opposite angle to $\alpha$ in the inscribed quadrilateral $A B C D$, is equal to $180^{\circ}-\alpha$. The desired angle between the diagonals of rectangle $A C D E$ is: $180^{\circ}-2\left(180^{\circ}-\alpha\right)=2\left(\alpha-90^{\circ}\right)$.
Case 2. $\alpha<90^{\circ}$ (Fig. 2). Point $O$ is equidistant from points $A, C, D$ and $E$, so it is the intersection point of the diagonals of rectangle $A C D E$ with these vertices. The angle $A D C$ is equal to $\alpha$, as it is inscribed and subtends the same arc of circle $K$ as angle $A B C$. Then the desired angle $D O C$ is: $180^{\circ}-2 \alpha=2\left(90^{\circ}-\alpha\right)$.
In case 1, $\alpha=130^{\circ}$, so case 1 applies, and $2\left(\alpha-90^{\circ}\right)=80^{\circ}$.
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a convex quadrilateral $A B C D$, the lengths of sides $B C$ and $A D$ are 2 and $2 \sqrt{2}$ respectively. The distance between the midpoints of diagonals $B D$ and $A C$ is 1. Find the angle between the lines $B C$ and $A D$.
|
Answer: $\alpha=45^{\circ}$.
|
45
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let's introduce the notation: $A B=2 c, A C=2 b, \measuredangle B A C=\alpha$. The feet of the perpendicular bisectors are denoted by points $P$ and $Q$. Then, in the right triangle $\triangle A M Q$, the hypotenuse $A M=\frac{b}{\cos \alpha}$. And in the right triangle $\triangle A N P$, the hypotenuse $A N=\frac{c}{\cos \alpha}$. By the cosine theorem for triangles $A M N$ and $A B C$ respectively, we have
$$
\begin{aligned}
& N M^{2}=A M^{2}+A N^{2}-2 A M \cdot A N \cdot \cos \alpha=\frac{c^{2}+b^{2}-2 b c \cos \alpha}{\cos ^{2} \alpha} \\
& B C^{2}=A B^{2}+A C^{2}-2 A B \cdot A C \cdot \cos \alpha=4\left(c^{2}+b^{2}-2 b c \cos \alpha\right)
\end{aligned}
$$
By the condition, $M N=B C$, therefore $\cos ^{2} \alpha=\frac{1}{4} \Leftrightarrow \cos \alpha= \pm \frac{1}{2}$, from which $\alpha=60^{\circ}$ or $\alpha=120^{\circ}$. We will show that both cases are possible, that is, if $\alpha=60^{\circ}$ or $\alpha=120^{\circ}$, then $M N=B C$.
Case 1. If $\alpha=60^{\circ}$, then $\measuredangle P N A=30^{\circ}$, so $A N=2 c=A B$, and $\measuredangle A M Q=30^{\circ}$, so $A M=2 b=A C$. Therefore, $\triangle A N M=\triangle A B C$ by two sides and the angle $\alpha$ between them. Consequently, $M N=B C$.
Case 2. If $\alpha=120^{\circ}$, then $\measuredangle B A N=60^{\circ}$. Further, $A N=N B$, so $\triangle N A B$ is isosceles, hence $\measuredangle A B N=60^{\circ}$, thus $\triangle N A B$ is equilateral. Therefore, $A N=A B$. Similarly, $\triangle M A C$ is equilateral. Therefore, $A M=A C$. Hence,
$\triangle A N M=\triangle A B C$ by two sides and the angle $\alpha$ between them. Consequently, $M N=B C$.
|
Answer: $60^{\circ}$ or $120^{\circ}$.
|
60
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5. In triangle $A B C$, the perpendicular bisectors of sides $A B$ and $A C$ intersect lines $A C$ and $A B$ at points $N$ and $M$ respectively. The length of segment $N M$ is equal to the length of side $B C$ of the triangle. The angle at vertex $C$ of the triangle is $40^{\circ}$. Find the angle at vertex $B$ of the triangle.
|
Answer: $80^{\circ}$ or $20^{\circ}$.
## Final round of the "Rosatom" Olympiad, 9th grade, CIS, February 2020
#
|
80
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The sum $b_{6}+b_{7}+\ldots+b_{2018}$ of the terms of the geometric progression $\left\{b_{n}\right\}, b_{n}>0$ is 6. The sum of the same terms taken with alternating signs $b_{6}-b_{7}+b_{8}-\ldots-b_{2017}+b_{2018}$ is 3. Find the sum of the squares of the same terms $b_{6}^{2}+b_{7}^{2}+\ldots+b_{2018}^{2}$.
|
Answer: $b_{6}^{2}+b_{7}^{2}+\ldots+b_{2018}^{2}=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $A=\overline{a b c b a}$ be a five-digit symmetric number, $a \neq 0$. If $1 \leq a \leq 8$, then the last digit of the number $A+11$ will be $a+1$, and therefore the first digit in the representation of $A+11$ should also be $a+1$. This is possible only with a carry-over from the digit, i.e., when $b=c=9$. Then $A+11=(a+1) 999(a+1)$ is a symmetric number for any $a=1,2, \ldots, 8$. The case $a=9$ is impossible, since $A+11$ ends in zero, and thus, due to symmetry, it should start with zero. But a number cannot start with zero.
The total number of solutions is equal to the number of possible choices for the number $a$, which is eight.
|
Answer: eight numbers of the form $\overline{a 999 a}$, where $a=1,2, \ldots, 8$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Integers, the decimal representation of which reads the same from left to right and from right to left, we will call symmetric. For example, the number 513315 is symmetric, while 513325 is not. How many six-digit symmetric numbers exist such that adding 110 to them leaves them symmetric?
|
Answer: 81 numbers of the form $\overline{a b 99 b a}$, where $a=1,2, \ldots, 9, b=0,1,2, \ldots, 8$.
|
81
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In city "N", there are 12 horizontal and 16 vertical streets, of which a pair of horizontal and a pair of vertical streets form the rectangular boundary of the city, while the rest divide it into blocks that are squares with a side length of 100m. Each block has an address consisting of two integers $(i ; j), i=1,2, . ., 11, j=1,2, \ldots, 15-$ the numbers of the streets that bound it from below and from the left. Taxis transport passengers from one block to another, adhering to the following rules: 1) pick-up and drop-off can be made at any point on the boundary of the block at the passenger's request; 2) it is forbidden to enter inside the block; 3) transportation is carried out along the shortest path; 4) a fee of 1 coin is charged for every 100m traveled (rounding the distance to the nearest 100m in favor of the driver). How many blocks are there in the city? What is the maximum and minimum fare that a driver can charge a passenger for a ride from block $(7,2)$ to block $(2 ; 1)$ without violating the rules?
|
Answer: 165 blocks; $c_{\min }=4$ coins, $c_{\max }=8$ coins.
|
165
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Integers, the decimal representation of which reads the same from left to right and from right to left, we will call symmetric. For example, the number 5134315 is symmetric, while 5134415 is not. How many seven-digit symmetric numbers exist such that adding 1100 to them leaves them symmetric?
|
Answer: 810 numbers of the form $\overline{a b c 9 c b a}$, where $a=1,2, \ldots, 9$, $b=0,1,2, \ldots, 9, c=0,1,2, \ldots, 8$.
|
810
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In city "N", there are 7 horizontal and 13 vertical streets, of which a pair of horizontal and a pair of vertical streets form the rectangular boundary of the city, while the rest divide it into blocks that are squares with a side length of 100 m. Each block has an address consisting of two integers $(i ; j), i=1,2, . ., 6, j=1,2, \ldots, 12$ - the numbers of the streets that bound it from below and from the left. Taxis transport passengers from one block to another, adhering to the following rules: 1) pick-up and drop-off can be made at any point on the boundary of the block at the passenger's request; 2) it is forbidden to enter inside the block; 3) transportation is carried out along the shortest path; 4) a fee of 1 coin is charged for every 100 m traveled (rounding the distance to the nearest 100 m in favor of the driver). How many blocks are there in the city? What is the maximum and minimum fare that the driver can charge the passenger for a ride from block $(4,2)$ to block $(1 ; 9)$ without violating the rules.
|
# Answer: 72 blocks; $c_{\min }=8$ coins, $c_{\max }=12$ coins.
|
72
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Integers, whose decimal notation reads the same from left to right and from right to left, we will call symmetric. For example, the number 513151315 is symmetric, while 513152315 is not. How many nine-digit symmetric numbers exist such that adding 11000 to them leaves them symmetric?
|
Answer: 8100 numbers of the form $\overline{a b c d 9 d c b a}$, where $a=1,2, \ldots, 9$, $b=0,1,2, \ldots, 9, c=0,1,2, \ldots, 9, d=0,1,2, \ldots, 8$.
|
8100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In city "N", there are 10 horizontal and 12 vertical streets, of which a pair of horizontal and a pair of vertical streets form the rectangular boundary of the city, while the rest divide it into blocks that are squares with a side length of 100 meters. Each block has an address consisting of two integers $(i ; j), i=1,2, . ., 9, j=1,2, \ldots, 11-$ the numbers of the streets that bound it from below and from the left. Taxis transport passengers from one block to another, adhering to the following rules: 1) pick-up and drop-off can be made at any point on the boundary of the block at the passenger's request; 2) it is forbidden to enter inside the block; 3) transportation is carried out along the shortest path; 4) a fee of 1 coin is charged for every 100 meters traveled (rounding the distance to the nearest 100 meters in favor of the driver). How many blocks are there in the city? What is the maximum and minimum fare that the driver can charge the passenger for a ride from block $(7,1)$ to block $(2 ; 10)$ without violating the rules?
|
Answer: 99 blocks; $c_{\min }=10$ coins, $c_{\max }=14$ coins.
|
99
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Kuzya the flea can make a jump in any direction on a plane for exactly 19 mm. Her task is to get from point $A$ to point $B$ on the plane, the distance between which is 1812 cm. What is the minimum number of jumps she must make to do this?
|
Answer: $n_{\min }=954$ jumps.
|
954
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A plot of land in the form of a right-angled triangle with legs of 4 and 3 needs to be divided by a line $L$ into two plots such that 1) the plots have equal area; 2) the length of the common boundary (fence) of the plots is minimized. Indicate the points on the sides of the triangle through which the desired line $L$ passes and find the length of the fence.
|
Problem 6. Answer: 1) The line intersects the larger leg $B C$ (angle $\measuredangle C=90^{\circ}$) at point $M: B M=\sqrt{10}$ and the hypotenuse $B A$ at point $N: B N=\sqrt{10}$.
2) $L_{\text {min }}=2$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. When purchasing goods for an amount of no less than 1000 rubles, the store provides a discount on subsequent purchases of $50 \%$. Having 1200 rubles in her pocket, Dasha wanted to buy 4 kg of strawberries and 6 kg of sugar. In the store, strawberries were sold at a price of 300 rubles per kg, and sugar - at a price of 30 rubles per kg. Realizing that she didn't have enough money for the purchase, Dasha still managed to buy what she intended. How did she do it?
|
First purchase: 3 kg of strawberries, 4 kg of sugar. Its cost is $300 \times 3 + 4 \times 30 = 1020$ rubles. Second purchase: 1 kg of strawberries, 2 kg of sugar. With a $50\%$ discount, its price is $(300 + 60) \cdot 0.5 = 180$ rubles. The total amount of both purchases is $1200$ rubles.
|
1200
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. According to the properties of logarithms, after transformations we get
$$
\begin{aligned}
& \log _{2}\left(b_{2} b_{3} \ldots b_{n}\right)=\log _{2} b_{1}^{2} \\
& b_{2} b_{3} \ldots b_{n}=b_{1}^{2}
\end{aligned}
$$
Using the formula for the general term of a geometric progression, we get
$$
b_{2}=b_{1} q, b_{3}=b_{1} q^{2}, \ldots, b_{n}=b_{1} q^{n-1}
$$
and using these relations and the formula for the sum of an arithmetic progression
$$
1+2+\ldots+(n-1)=\frac{n(n-1)}{2}
$$
we transform the obtained equation to
$$
b_{1}^{n-1} q^{1+2+\ldots+(n-1)}=b_{1}^{2} \Rightarrow b_{1}^{n-3} q^{n(n-1) / 2}=1
$$
Taking the logarithm with base $q$, we find
$$
\begin{aligned}
& (n-3) \log _{q} b_{1}+\frac{n(n-1)}{2}=0 \\
& \frac{n-3}{2} \log _{q} b_{1}^{2}+\frac{n(n-1)}{2}=0 \\
& \log _{q} b_{1}^{2}=-\frac{n(n-1)}{n-3}
\end{aligned}
$$
Since
$$
\frac{n(n-1)}{n-3}=\frac{n(n-3)+2(n-3)+6}{n-3}=n+2+\frac{6}{n-3}
$$
then
$$
\log _{q} b_{1}^{2}=-n-2-\frac{6}{n-3} .
$$
According to the problem's condition, the quantity
$$
\frac{6}{n-3}
$$
must be an integer. This is possible only for
$$
n \in\{2 ; 4 ; 5 ; 6 ; 9\}
$$
Substituting the specified values into the formula obtained above, we find all possible values of the desired quantity
$$
\begin{aligned}
& n=2 \Rightarrow \log _{q} b_{1}^{2}=2 \\
& n=4 \Rightarrow \log _{q} b_{1}^{2}=-12 \\
& n=5 \Rightarrow \log _{q} b_{1}^{2}=-10 \\
& n=6 \Rightarrow \log _{q} b_{1}^{2}=-10 \\
& n=9 \Rightarrow \log _{q} b_{1}^{2}=-12
\end{aligned}
$$
From this, it is clear that the smallest value of the desired quantity is -12 and it is achieved for two values: $n=4$ and $n=9$.
|
Answer: -12 when $n=4$ and $n=9$.
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The polynomial $p_{1}=x-a$ can have a root $x=a$ coinciding with one of the roots of the product $p(x)=p_{1}(x) \cdot p_{2}(x)$.
Case $1 \quad a=1$
Then the polynomial $p_{2}(x)=(x-1)^{r}(x-2)^{s}(x+3)^{t}$, where $r \geq 1, s \geq 1, t \geq 1-$ are integers, $r+s+t=4$, satisfies the condition of the problem. The polynomial sum $p_{1}(x)+p_{2}(x)$ has a constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}-1=(-1)^{t} \cdot 2^{s} \cdot 3^{t}-1$ which has a maximum value $u_{\max }=17$ when $r=1, s=1, t=2$.
Case $2 \quad a=2$
Then the polynomial $p_{2}(x)=(x-1)^{r}(x-2)^{s}(x+3)^{t}$ and the polynomial $p_{1}(x)+p_{2}(x)$ has a constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}-2=(-1)^{t} \cdot 2^{s} \cdot 3^{t}-2$, taking the maximum value $u_{\max }=16$ when $r=1, s=1, t=2$.
Case $3 \quad a=-3$
The constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}+3$ takes the maximum value $u_{\max }=21$ when $s=r=1, t=2$
The required polynomials: $p_{2}(x)=(x-1)(x-2)(x+3)^{2}, p_{1}(x)=x+3$
|
Answer: $p_{1}(x)=x+3, p_{2}(x)=(x-1)(x-2)(x+3)^{2} ; a_{0}=21$
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A natural number $a$ is divisible by 21 and has 105 different divisors, including 1 and $a$. Find the smallest such $a$.
|
Answer: $a_{\min }=2^{6} \cdot 3^{4} \cdot 7^{2}=254016$
|
254016
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A natural number $a$ is divisible by 35 and has 75 different divisors, including 1 and $a$. Find the smallest such $a$.
|
Answer: $a_{\text {min }}=2^{4} \cdot 5^{4} \cdot 7^{2}=490000$.
|
490000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A natural number $a$ is divisible by 55 and has 117 distinct divisors, including 1 and $a$. Find the smallest such $a$.
|
Answer: $a_{\min }=2^{12} \cdot 5^{2} \cdot 11^{2}=12390400$.
|
12390400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The border of a square with a side of 9, cut out of white cardboard, is painted red. It is necessary to cut the square into 6 equal-area parts, the boundaries of which contain segments painted red with the same total length.
## Solutions
Option 1
Problem 1
|
Answer: 2 km.
Solution
$S-$ the length of the path, $S_{1}$ - the length of the path on descents, $S_{2}$ - the length of the path on ascents, $S / 2=S_{1}+S_{2}$
$t=15-8-6=1-$ the time of the journey there and back. Then
$1=\frac{S_{1}}{6}+\frac{S_{2}}{3}+\frac{S}{2 \cdot 4}+\frac{S_{1}}{3}+\frac{S_{2}}{6}+\frac{S}{2 \cdot 4}=\left(\frac{1}{6}+\frac{1}{3}\right)\left(S_{1}+S_{2}\right)+\frac{S}{4}=\left(\frac{1}{6}+\frac{1}{3}\right) \frac{S}{2}+\frac{S}{4}=\frac{S}{2} \rightarrow S=2$
Problem 2 Answer: $\frac{1}{6}$
Solution.
By the condition $\frac{p}{q}5 p$. Considering the naturality of $p$ and $q$, and the condition $p+q<8$ we have
$6 p<p+q<8 \rightarrow p=1 \rightarrow q=6$
Problem 3 Answer: $a_{\min }=15876$
Solution
Among the divisors of an even number divisible by 21 and being a square of an integer, there are $7^{2}, 3^{2}, 2^{2}$, i.e.
$a=7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2}$. Considering the five-digit nature, the inequality holds:
$10000 \leq 7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2} \leq 99998 \rightarrow 6 \leq k^{2} \leq 57 \rightarrow k_{\min }^{2}=9 \rightarrow a_{\min }=7^{2} \cdot 3^{2} \cdot 4 \cdot 9=15876$
Problem 4 Answer: $x=\frac{3}{2}$
Solution
$x=\frac{4-[x]}{2} \rightarrow\{x\}=x-[x]=\frac{4-[x]}{2}-[x]=\frac{4-3[x]}{2}$
Since $0 \leq\{x\}<1 \rightarrow 0 \leq \frac{4-3[x]}{2}<1 \rightarrow \frac{2}{3}<[x] \leq \frac{4}{3}$ and the number $[x]-$ is an integer, the only valid value is $[x]=1$. Then $x=\frac{3}{2}$
Problem 5
Solution
O - the center of the square, the polygon $O B C D$ - one of the six desired pieces, $B C=x, C D=y, a=9$.
$S_{\text {OBCD }}=\frac{a^{2}}{6}=\frac{a}{4} \cdot(x+y) \rightarrow x+y=\frac{2 a}{3}=6$ - the length of the red part of the boundary of the polygon.
A way of cutting (one of ...)
Variant 2
Problem 1 Answer: 3 km.
Problem 2 Answer: $\frac{1}{4}$
Problem 3 Answer: $a_{\max }=5625$
Problem 4 Answer: $x=\frac{5}{2}$
Problem 5 Answer:
Variant 3
Problem 1 Answer: 1.5 km.
Problem 2 Answer: $\frac{1}{4}, \frac{1}{5}$
Problem 3 Answer: $a_{\text {min }}=327184$
Problem 4 Answer: $x=-\frac{7}{2}$
Problem 5 Answer:
Variant 4
Problem 1 Answer: 1.4 km.
Problem 2 Answer: $\frac{1}{6}, \frac{1}{7}$
Problem 3 Answer: $a_{\max }=74529$
Problem 4 Answer: $x=-\frac{3}{2}$
Problem 5 Answer:
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.17. Final round of the "Rosatom" Olympiad, 7th grade
# Answers and solutions
Problem 1 Answer: 9
There exists a set of 8 buttons in which there are no three buttons of the same color: each color has two buttons. In any set of 9 buttons, there will be at least one triplet of buttons of the same color.
If we assume the opposite, that there are no more than 2 buttons of the same color, then there can be no more than 8 such buttons in total, which contradicts the condition.
|
Answer: 9 buttons.
Problem 2 Answer: 1261
\[
\left\{\begin{array}{l}
a=35 n+1 \\
a=45 m+1
\end{array} \rightarrow 35 n=45 m \rightarrow 7 n=9 m \rightarrow\left\{\begin{array}{c}
n=9 t \\
m=7 t, t \in Z
\end{array} \rightarrow\right.\right.
\]
\[
a=315 t+1 \geq 1000 \rightarrow t \geq 4 \rightarrow a_{\text {min }}=1261
\]
## Problem 3 Answer: 1) 4026 2) Sasha
At each step of the game, the sum of the numbers written on the cards in the bag does not change.
At the beginning of the game, it was \(2013 \times 2=4026\). Each step of the game changes the parity of the number of cards in the bag, as it reduces their number by one. Initially, the total number of cards in the bag is odd, so Sasha will make his move when the number of cards in the bag is odd, and Dasha when it is even. The last move occurs when there is one card in the bag, i.e., their number is odd, and Sasha will notice this.
Problem 4 Answer: 1) \(17 \quad\) 2) 90
\((12,18,21,24,27,30,36,42,45,48,54,60,63,72,81,84,90)\)
\(x, y\) - digits of the desired number
\[
a=10 x+y=3 k, \quad a=10 x+y=(x+y) m \rightarrow\left\{\begin{array}{c}
x+y=\frac{3 k}{m}, 2 \leq m \leq 10, \\
10 x+y=3 k, 4 \leq k \leq 33
\end{array}\right.
\]
\[
\left\{\begin{array}{l}
x=\frac{k}{3} \cdot \frac{m-1}{m} \\
y=\frac{k}{3} \cdot \frac{10-m}{m}
\end{array}\right.
\]
Case \(m=2 \rightarrow\left\{\begin{array}{l}
x=k / 6 \\
y=4 k / 3
\end{array} \rightarrow k=6 t \rightarrow\left\{\begin{array}{l}
x=t \\
y=8 t
\end{array} \rightarrow t=1 \rightarrow a=18\right.\right.
\]
Case \(m=3 \rightarrow\left\{\begin{array}{l}
x=2 k / 9 \\
y=7 k / 9
\end{array} \rightarrow k=9 t \rightarrow\left\{\begin{array}{l}
x=2 t \\
y=7 t
\end{array} \rightarrow a=27\right.\right.
\]
Case \(m=4 \rightarrow\left\{\begin{array}{l}
x=k / 4 \\
y=k / 2
\end{array} \rightarrow k=4 t \rightarrow\left\{\begin{array}{l}
x=t \\
y=2 t
\end{array} \rightarrow a=12,24,36,48\right.\right.
\]
Case \(m=5 \rightarrow\left\{\begin{array}{c}
x=4 k / 15 \\
y=k / 3
\end{array} \rightarrow k=15 t \rightarrow\left\{\begin{array}{l}
x=4 t \\
y=5 t
\end{array} \rightarrow a=45\right.\right.
\]
Case \(m=6 \rightarrow\left\{\begin{array}{l}
x=5 k / 18 \\
y=2 k / 9
\end{array} \rightarrow k=18 t \rightarrow\left\{\begin{array}{l}
x=5 t \\
y=4 t
\end{array} \rightarrow a=54\right.\right.
\]
Case \(m=7 \rightarrow\left\{\begin{array}{l}
x=2 k / 7 \\
y=k / 7
\end{array} \rightarrow k=7 t \rightarrow\left\{\begin{array}{l}
x=2 t \\
y=t
\end{array} \rightarrow a=21,42,63,84\right.\right.
\]
Case \(m=8 \rightarrow\left\{\begin{array}{c}
x=7 k / 24 \\
y=k / 12
\end{array} \rightarrow k=24 t \rightarrow\left\{\begin{array}{l}
x=7 t \\
y=2 t
\end{array} \rightarrow a=72\right.\right.
\]
Case \(m=9 \rightarrow\left\{\begin{array}{c}
x=8 k / 27 \\
y=k / 27
\end{array} \rightarrow k=27 t \rightarrow\left\{\begin{array}{c}
x=8 t \\
y=t
\end{array} \rightarrow a=81\right.\right.
\]
Case \(m=10 \rightarrow\left\{\begin{array}{c}
x=3 k / 10 \\
y=0
\end{array} \rightarrow k=10 t \rightarrow\left\{\begin{array}{l}
x=3 t \\
y=0
\end{array} \rightarrow a=30,60,90\right.\right.
\]
\[
a_{\max }=90, \text{ number of numbers } 17
\]
Problem 5 Answer: 2 weights
Indicate the minimum number of 3 kg weights needed to weigh loads of 1, 2, 3, and 4 kg.
Load of 1 kg - 2 weights of 3 kg are needed
Load of 2 kg or 3 kg - 1 weight of 3 kg is needed
Load of 4 kg - 2 weights of 3 kg are needed
The weight of any load when divided by 5 has a remainder of 0, 1, 2, 3, or 4. If the remainder is 0, the load can be weighed using only 5 kg weights. If the weight of the load is \(5 n+1\), the weighing picture is obtained from the picture of weighing 1 kg:
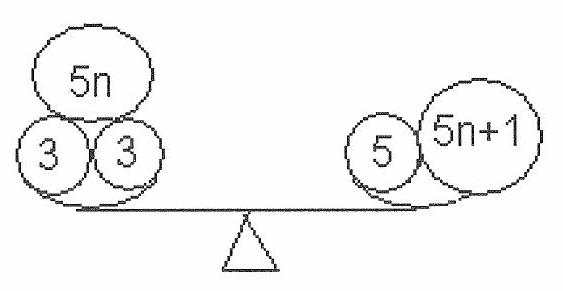
If the weight of the load is \(5 n+2\), the weighing picture can be used for a 2 kg load:
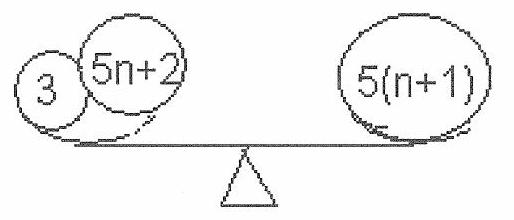
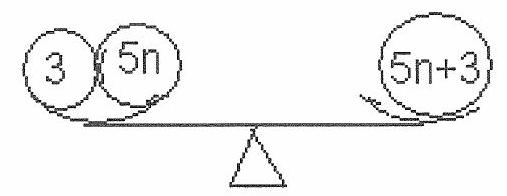
If the weight of the load is \(5 n+3\), the weighing picture can be used for a 3 kg load:
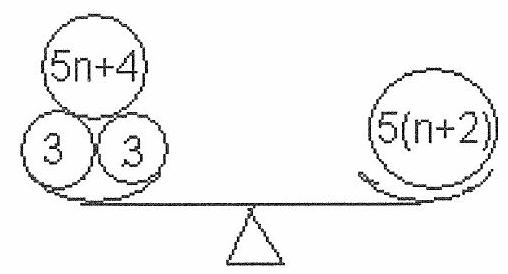
Finally, a load of \(5 n+4\) kg is weighed similarly to a 4 kg load:
|
1261
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the decimal representation of a six-digit number $a$, there are no zeros and the sum of its digits is 18. Find the sum of all different numbers obtained from the number $a$ by cyclic permutations of its digits. In a cyclic permutation, all digits of the number, except the last one, are shifted one place to the right, and the last one is moved to the first place.
|
3. Solution. Case 1. The number $a=333333$. This number does not change under cyclic permutations, so it is the only one and the sum of the numbers is the number itself, that is, 333333.
Case 2. The number $a$ consists of three identical cycles of two digits each, for example, $a=242424$. Such numbers have two different cyclic permutations: 242424 and 424242, the sum of which is $666666=2 \cdot 333333$. For any other such number, we will get the same sum of its cyclic permutations: $151515+515151=666666$ and so on.
Case 3. The number $a$ consists of two identical cycles of three digits each, for example, $a=423423$. Such numbers have three different cyclic permutations: 423423, 342342, and 234234, the sum of which is $999999=3 \cdot 333333$. For any other such number, we will get the same sum of its cyclic permutations: $513513+351351+135135=999999$ and so on.
Case 4. All six cyclic permutations are different. Let $a=a_{5} \cdot 10^{5}+a_{4} \cdot 10^{4}+a_{3} \cdot 10^{3}+a_{2} \cdot 10^{2}+a_{1} \cdot 10+a_{0}$.
If we write out all its cyclic permutations in the same form, add the results, and regroup the terms, we get
$a_{5}\left(10^{5}+10^{4}+\ldots+1\right)+a_{4}\left(10^{5}+10^{4}+\ldots+1\right)+\ldots+a_{0}\left(10^{5}+10^{4}+\ldots+1\right)=$ $=\left(a_{5}+a_{4}+a_{3}+a_{2}+a_{1}+a_{0}\right)\left(10^{5}+10^{4}+\ldots+1\right)=18 \cdot 111111=1999998$
|
1999998
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On a sheet of paper, 14 parallel lines $L$ and 15 lines $P$ perpendicular to them are drawn. The distances between adjacent lines from $L$ from the first to the last are given: 2;4;6;2;4;6;2;4;6;2;4;6;2. The distances between adjacent lines from $P$ are also known: 3;1;2;6;3;1;2;6;3;1;2;6;3;1. Find the greatest length of the side of a square whose boundaries lie on the lines $L$ and $P$.
|
5. Solution. We will prove that the maximum length of the side of the square is 40. Calculate the distance from the first to the last line in $P: 3+1+2+6+3+1+2+6+3+1+2+6+3+1=40$. Therefore, the side length of the square cannot be more than 40. On the other hand, in $L$ the distance from the second line to the third line from the end is $4+6+2+4+6+2+4+6+2+4=40$. This means that a square with a side length of 40 exists.
|
40
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(29)=P(37)=2022$. Find the smallest possible value of $P(0)>0$ under these conditions.
|
Answer: $P(0)_{\min }=949$.
|
949
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(11)=P(13)=2021$. Find the smallest possible value of $P(0)>0$ under these conditions.
|
Answer: $P(0)_{\text {min }}=19$.
|
19
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(19)=P(21)=2020$. Find the smallest possible value of $P(0)>0$ under these conditions.
|
Answer: $P(0)_{\min }=25$.
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The number $A$ in decimal form is represented as $A=\overline{7 a 631 b}$, where $a, b$ are non-zero digits. The number $B$ is obtained by summing all distinct six-digit numbers, including $A$, that are formed by cyclic permutations of the digits of $A$ (the first digit moves to the second position, the second to the third, and so on, with the last digit moving to the first position). How many numbers $A$ exist such that $B$ is divisible by 121? Find the largest such $A$.
|
2. Solution. The sum of the digits of number $A$ and the numbers obtained from $A$ by cyclic permutations of its digits is $a+b+17$. After summing these numbers (there are 6 of them), in each digit place of number $B$ we get
$a+b+17$, so $B=(a+b+17)\left(10^{5}+10^{4}+10^{3}+10^{2}+10+1\right)=(a+b+17) \cdot 111111$. Since
$111111=3 \cdot 7 \cdot 11 \cdot 13 \cdot 37$, $B$ is divisible by 121 if and only if $a+b+17$ is divisible by 11. Since $a$ and $b$ are digits, there are only two possible cases: $a+b=5$ and $a+b=16$. From this, we find the possible pairs of $a$ and $b$: $a=1, b=4 ; a=2, b=3 ; a=3, b=2 ; a=4, b=1 ; a=7, b=9 ; a=8, b=8 ; a=9, b=7$. Thus, 7 numbers satisfy the condition of the problem. The largest number is obtained when $a=9, b=7$. It is 796317.
|
796317
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The real numbers $x_{1}, x_{2}$, and $x_{3}$ are the three roots of the equation $x^{3}-3 x^{2}+2(1-p) x+4=0$, considering their possible multiplicities. Find the smallest value of the expression $\left(x_{1}-1\right)^{2}+\left(x_{2}-1\right)^{2}+\left(x_{3}-1\right)^{2}$ under these conditions. For which $p$ is it realized?
|
The smallest value 6 is achieved when $p=1$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many different pairs of integers $a$ and $b$ exist such that the equation $a x^{2}+b x+1944=0$ has positive integer roots?
|
Answer: $\quad 108+24=132$ pairs.
|
132
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. How many different pairs of integers $a$ and $b$ exist such that the equation $a x^{2}+b x+432=0$ has positive integer roots
|
Answer: $\quad 78+20=98$ pairs.
|
98
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. By the condition
$$
T(t)=\frac{270-s(t)}{s(t) / t}=\frac{t(270-s(t))}{s(t)}=C>1, t \in[0.5 ; 1]
$$
Then $s(t)=\frac{270 t}{t+C}$ on this interval. The speed of movement
$$
\begin{aligned}
& v(t)=s^{\prime}(t)=\frac{270 C}{(t+C)^{2}}=60 \text { when } t=1 \text {, i.e. } \\
& \qquad 2 c^{2}-5 c+2=0 \rightarrow C_{1}=2, C_{2}=\frac{1}{2}
\end{aligned}
$$
The second value of the constant is not allowed by the condition. Thus, $s(t)=\frac{270 t}{t+2}$ and $s(1)=90$.
$$
v(t)=\left.\frac{540}{(t+2)^{2}}\right|_{t=\frac{1}{2}}=\frac{432}{5}=86.4 \text { km } / \text { hour }
$$
|
Answer: 1) 90 km; 2) 86.4 km/hour
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. If $m+2019 n$ and $n+2019 m$ are divisible by $d$, then the number
$$
2019(m+2019 n)-(n+2019 m)=(2019^2-1) n
$$
is also divisible by $d$. If $n$ is divisible by $d$, and $m+2019 n$ is divisible by $d$, then $m$ is divisible by $d$ and the numbers $m$ and $n$ are not coprime. Therefore, $d$ divides the number
$$
2019^2-1=2018 \cdot 2020=2^3 \cdot 5 \cdot 101 \cdot 1009
$$
Thus, the smallest possible prime number is $d=101$. It remains to find coprime $m$ and $n$ for which it is realized. For example, $m=102, n=1$. Then
$$
\begin{gathered}
m+2019 n=102+2019=2121=21 \cdot 101 \text { and } \\
n+2019 m=1+2019 \cdot 102=205939=2039 \cdot 101 .
\end{gathered}
$$
|
Answer: $d_{\text {min }}=101$.
|
101
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Kostya is making a car trip from point A to point B, which are 320 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Kostya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. One hour after the start of the trip, he looked at the speedometer - 60 km/h. On the time interval $[1 ; 2]$, Kostya noticed that $T>1$ and does not change. How far from point $A$ was the car two hours after the start of the trip? What was the speed of the car 2 hours after the start of the trip?
|
Answer: 1) 128 km; 2) 38.4 km/h.
|
128
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+2024 n$ and $n+2024 m$ have a common prime divisor $d>7$. Find the smallest possible value of the number $d$ under these conditions.
|
Answer: $d_{\min }=17$.
For example,
$$
\begin{aligned}
& m=16, n=1 \rightarrow 2024 m+n=2024 \cdot 16+1=32385=17 \cdot 1905 \\
& m+2024 n=16+2024=17 \cdot 120
\end{aligned}
$$
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1941 n$ and $n+1941 m$ have a common prime divisor $d>8$. Find the smallest possible value of the number $d$ under these conditions.
|
Answer: $d_{\min }=97$.
For example,
$$
\begin{aligned}
& m=96, n=1 \rightarrow 1941 m+n=1941 \cdot 96+1=97 \cdot 1921 \\
& m+1941 n=96+1941=97 \cdot 21
\end{aligned}
$$
|
97
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Danya is making a car trip from point A to point B, which are 300 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Danya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. One hour after the start of the trip, he looked at the speedometer - 75 km/h. On the time interval $[1 ; 1.5]$, Danya noticed that $T$ did not change. How far from point $A$ was the car 90 minutes after the start of the trip, and what was its speed?
|
Answer: 1) 180 km; 2) 48 km/h.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1947 n$ and $n+1947 m$ have a common prime divisor $d>9$. Find the smallest possible value of the number $d$ under these conditions.
|
Answer: $d_{\min }=139$.
For example,
$$
\begin{aligned}
& m=138, n=1 \rightarrow 1947 m+n=1947 \cdot 138+1=139 \cdot 1933 \\
& m+1947 n=138+1947=139 \cdot 15
\end{aligned}
$$
|
139
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3. Find the sum of such divisors.
|
1. Solution. Among the divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3, the number 2 can be chosen with exponents $0,1,2,3$ (4 options), the number 3 - with exponents 1,2 (2 options), and the number 5 - with exponents $0,1,2$ (3 options). Therefore, the total number of divisors is $4 \cdot 2 \cdot 3=24$. The sum of the divisors of the number $b=2^{3} \cdot 5^{2}$ is $(1+2+4+8)(1+5+25)=465$. Then the sum of the divisors of the number $a$, which are divisible by 3, is $\left(3+3^{2}\right) \cdot 465=12 \cdot 465=5580$.
|
5580
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many integers $b$ exist such that the equation $x^{2}+b x-9600=0$ has an integer solution that is a multiple of both 10 and 12? Specify the largest possible $b$.
|
2. Solution. Since the desired integer solution $x$ is divisible by 10 and 12, it is divisible by 60, hence it can be written in the form $x=60 t, t \in Z$. Substitute $x=60 t$ into the original equation:
$3600 t^{2}+60 b t-9600=0$. Express $b: b=\frac{160}{t}-60 t$. For $b$ to be an integer, $t$ must be a divisor of the number 160. $160=2^{5} \cdot 5$. The number $160=2^{5} \cdot 5$ has 12 positive divisors: $1,2,2^{2}, 2^{3}, 2^{4}, 2^{5}, 5,2 \cdot 5,2^{2} \cdot 5,2^{3} \cdot 5,2^{4} \cdot 5,2^{5} \cdot 5$. Taking the sign into account, we get 24 divisors. Each of them corresponds to a solution $x=60 t$ and an integer $b=\frac{160}{t}-60 t$. Therefore, the number of integers $b$ that satisfy the condition of the problem is 24. Since $b$ decreases as $t$ increases, the maximum $b$ corresponds to the smallest $t=-160$, so $b_{\max }=-1+60 \cdot 160=9599$.
|
9599
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many three-digit positive numbers $x$ exist that are divisible by 3 and satisfy the equation $GCD(15, GCD(x, 20))=5$? Find the largest one.
|
3. Solution. Since 20 is not divisible by 3, $NOD(x, 20)$ is also not divisible by 3. Therefore, the equation $NOD(15, NOD(x, 20))=5$ is equivalent to the condition that $NOD(x, 20)$ is divisible by 5, which is possible if and only if $x$ is divisible by 5. Thus, the condition of the problem is equivalent to $x$ being divisible by 5 and by 3, that is, $x$ is divisible by 15. Therefore, $x$ can be written as $x=15m, m=1,2 \ldots$. The smallest three-digit $x=105$ is obtained when $m=7$, and the largest three-digit $x=990$ is obtained when $m=66$, making a total of 60 numbers.
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The quadratic trinomial $p(x)=a x^{2}+b x+c, a>0$ when divided by ( $x-1$ ) gives a remainder of 4, and when divided by ( $x-2$ ) - a remainder of 15. Find the maximum possible value of the ordinate of the vertex of the parabola $y=p(x)$ under these conditions. For what value of $x$ is it achieved?
|
4. Solution. By the Remainder Theorem, the remainder of the division of a polynomial $p(x)$ by $x-a$ is $p(a)$.
Therefore, the conditions of the problem are equivalent to the system:
$\left\{\begin{array}{l}4 a+2 b+c=15 \\ a+b+c=4\end{array} \Rightarrow\left\{\begin{array}{l}b=11-3 a \\ c=2 a-7\end{array}\right.\right.$.
Thus, $p(x)=a x^{2}+(11-3 a) x+2 a-7$. The minimum value of the quadratic trinomial $p(x)$ (the ordinate of the vertex of the parabola) is achieved at its vertex $x_{s}=\frac{3 a-11}{2 a}$. It is equal to $p_{\text {min }}(x)=p\left(x_{k}\right)=p\left(\frac{3 a-11}{2 a}\right)=-\frac{a^{2}-38 a+121}{4 a}=\frac{19}{2}-\frac{1}{4}\left(a+\frac{121}{a}\right)=4-\left(\sqrt{a}-\frac{11}{\sqrt{a}}\right)^{2}$.
This value is maximal if and only if $\sqrt{a}-\frac{11}{\sqrt{a}}=0$, that is, $a=11$. When $a=11$, $x_{s}=1$,
and $p\left(x_{s}\right)=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the sides of triangle $A B C$ with side lengths 2, 3, and 4, external squares $A B B_{1} A_{1}, B C C_{2} B_{2}, C A A_{3} C_{3}$ are constructed. Find the sum of the squares of the side lengths of the hexagon $A_{1} B_{1} B_{2} C_{2} C_{3} A_{3}$.
## Answers and Solutions
Problem 1 Answer: 165 m.
|
Solution
$m$ - the number of steps Petya takes, $n$ - the number of steps Vova takes
$0.75 m=0.55 n=L-$ path length
$k$ - the step number of Petya leading to the coincidence of the footprint,
$i$ - the step number of Vova leading to the coincidence of the footprint,
$0.75 k=0.55 i \rightarrow 15 k=11 i \rightarrow\left\{\begin{array}{l}k=11 t \\ i=15 t\end{array}, t=0,1, \ldots T\right.$
Total number of footprints: $(m+1)+(n+1)-(T+1)=15 T+11 T-T+1=25 t+1=501 \rightarrow T=20$ $m=11 \cdot T=220 \rightarrow L=0.75 \cdot 220=165$
Problem 2 Answer: $x=6, y=55$ or $x=55, y=6$
Solution
$y(x-5)=5(x+5) \rightarrow y=5+\frac{50}{x-5} \rightarrow x-5= \pm 1 ; \pm 2 ; \pm 5 ; \pm 10 ; \pm 25 ; \pm 50$
$y-5= \pm 50 ; \pm 25 ; \pm 10 ; \pm 5 ; \pm 2 ; \pm 1 \rightarrow x+y-10= \pm 51 ; \pm 27 ; \pm 15 ;$
The maximum value of $x+y$ is 61 and is achieved at $x=6, y=55$ or $x=55, y=6$
Problem 3 Answer: $a=-\frac{9}{8}, b=-6$
## Solution
When dividing the polynomial $P(x)=a x^{4}+3 x^{3}+b$ by $x-2$, we have the remainder $16 a+b+24=0$. Then
$P(x)=(x-2)\left(a x^{3}+(2 a+3) x^{2}+(4 a+6) x+(8 a+12)\right)=(x-2) P_{1}(x)$
When dividing the polynomial $P_{1}(x)$ by $x-2$, we have the remainder $32 a+36=0 \rightarrow a=-\frac{9}{8} \rightarrow b=-6$.
Problem 4 Answer: $a=2$
Solution
Condition for the existence of roots:
$\frac{D}{4}=16(a-1)^{2}+8(a-4) \geq 0 \rightarrow 2 a^{2}-3 a-2 \geq 0 \rightarrow a \in(-\infty ;-0.5] \cup[2 ;+\infty)$.
$x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(a-1)^{2}-\frac{4-a}{4}=a^{2}-\frac{7 a}{4}$
We need to find the minimum of this quadratic trinomial on the set $(-\infty ;-0.5] \cup[2 ;+\infty)$.
The abscissa of its vertex $a=\frac{7}{8}$ is closer to 2 than to $-0.5$, since $2-\frac{7}{8}=\frac{9}{8}<\frac{7}{8}+\frac{1}{2}=\frac{11}{8}$.
Therefore, the minimum possible value of the sum of the squares of the roots of the equation is achieved at $a=2$.
Problem 5 Answer: 116
Solution
Additional construction: $B C=C K=a, M$ - midpoint of side $A B$.
$\square A C K=\square C_{2} C B_{3}=\square K C B_{3}=180^{\circ}-\square B C A$
$\square A C K={ }_{B_{3} C C_{2} \rightarrow C_{2} B_{3}=A K=2 C M}$
$C M^{2}=\frac{2 a^{2}+2 b^{2}-c^{2}}{4} \rightarrow C_{2} B_{3}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}$
Similarly,
$$
B_{1} B_{2}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}, \quad A_{1} A_{3}{ }^{2}=2 b^{2}+2 c^{2}-a^{2}
$$
$A_{1} A_{2}{ }^{2}=c^{2}, B_{2} C_{2}{ }^{2}=a^{2}, A_{3} B_{3}{ }^{2}=b^{2}$
Combining, we arrive at the sum $\sigma^{2}$ of the squares of the sides of the hexagon being $4\left(a^{2}+b^{2}+c^{2}\right) \cdot$ In the conditions of the variant $1 a=2, b=3, c=4$, therefore $\sigma^{2}=4(4+9+16)=116$
|
116
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dima drew a parallelogram $A B C D$ and points $M$ and $N$ on sides $B C$ and $C D$ respectively such that $B M: M C=D N: N C=2: 3$. After that, he erased everything except points $A, M$ and $N$ using a cloth. Vova restored the drawing using a ruler and a compass. How did he do it?
|
4. Points $B$ and $D$ are the intersection points of lines $C M$ and $C N$ with the line passing through point $O$ and parallel to line $M N$.
## Problem 5
Numbers $A$, when divided by $n$, have a remainder of $r$, when divided by $n+1$ - a remainder of $r+1$, and when divided by $n+2$ - a remainder of $r+2$, have the form: $A=n(n+1)(n+2) t-n+r, A_{\min }$ corresponds to $t=1$
In the variant $1 n=11, r=5 \rightarrow A_{\min }=1710$
|
1710
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Pasha, Masha, Tolya, and Olya ate 88 candies, and each of them ate at least one candy. Masha and Tolya ate 57 candies, but Pasha ate the most candies. How many candies did Olya eat?
|
Solution. Either Masha or Tolya ate no less than 29 candies, then Pasha ate no less than 30 candies. Then the number of candies eaten by Pasha, Masha, and Tolya is no less than $57+30=87$. Since there are a total of 88 candies, and Olya did not refuse any candies, she gets one candy.
Answer: 1 candy.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Pete is trying to lay out a square on a table using identical cardboard rectangles measuring $14 \times 10$. Will he be able to do this? Propose your version of constructing such a square. What is the minimum number of rectangles he will need?
|
Solution. Let $n$ be the number of rectangles that form the square. Then the area of the square is $S=14 \cdot 10 \cdot n$. If the side of the square is formed by $m$ sides of length 14 and $k$ sides of length 10, then the length of the side of the square is $14 m + 10 k$, and its area is $S=(14 m + 10 k)^{2}$. Equating the expressions for the areas, we get
$$
14 \cdot 10 \cdot n = (14 m + 10 k)^{2} \rightarrow 7 \cdot 5 \cdot n = (7 m + 5 k)^{2}
$$
We can assume that the numbers $m$ and $k$ are coprime. Otherwise, the side of the square can be reduced by a factor of $p > 1$, where $p$ is a common divisor of $m$ and $k$.
The left-hand side of the equation (*) is divisible by 7, so the number $7 m + 5 k$ is divisible by 7, and $(7 m + 5 k)^{2}$ is divisible by 49. Therefore, the left-hand side of (*) is divisible by 49, which is possible only if $n$ is divisible by 7. Similarly, it can be shown that $n$ is divisible by 5. Thus, $n = 35 \cdot s, s \in \mathbb{Z}$, and the smallest possible number of rectangles is $n = 35$. The figure below shows a square assembled from 35 rectangles.
Answer: 35 rectangles.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a rectangular table, the letters of the word "олимпиада" (olympiada) are arranged in a certain order.
| $\mathrm{O}$ | Л | И | M | П | И | A | Д | A |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Л | И | M | П | И | A | Д | A | O |
| И | M | П | И | A | Д | A | O | Л |
| M | П | И | A | Д | A | O | Л | И |
You need to read the word "олимпиада" (olympiada), starting from the letter "O" located in the top-left corner of the table and ending with the letter "A". You are allowed to move from one letter to another if they are in adjacent cells of the table. Find the number of different ways to read the word "олимпиада" (olympiada) according to the given table.
|
Solution. In each cell of the table shown below
| $\mathrm{O}$ | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 | | |
| 1 | 4 | 10 | 20 | 35 | 56 | | | |
the number of different paths leading to the letter in that cell when reading the word "олимпиада" (Olympiada) is recorded. For example, in the cell in the third column and second row, i.e., to the letter $M$, there are three different ways to read "олим" (Olim): two paths from the cell in the second column and second row, and one path from the cell in the second column and first row. In general, to obtain the number in the cell at the intersection of row $i$ and column $j$, you need to add the number in the $(j-1)$-th cell of row $i$ and the number in the $j$-th cell of row $(i-1)$. In each of the shaded cells, where the last letter "A" of the word "олимпиада" (Olympiada) is located, the number of different ways to read this word, provided that the reading ends in this cell, is indicated. To get the answer, you need to add all the numbers in the highlighted cells: $n=56+28+8+1=93$.
Answer: $n=93$.
## Answers for other variants.
## Variant 2
|
93
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let point $M$ divide edge $A B$ in the ratio $A M: M B=\lambda$, point $N$ divide edge $D C$ in the ratio $D N: N C=\mu$, and point $P$ divide edge $D B$ in the ratio $D P: P B=\theta$. We need to find the ratio $A Q: Q C$.
Let $T$ be the intersection point of line $P N$ with line $B C$, then point $Q$ is the intersection point of line $M T$ with line $A C$. Let $B M=a$, $C N=b$, and $B P=c$. Then $M A=\lambda a$, $N D=\mu b$, and $P D=\theta c$.
Applying Menelaus' theorem to triangle $C B D$ and the transversal $P T$:
$$
\frac{C T}{T B} \cdot \frac{B P}{P D} \cdot \frac{D N}{N C}=1 \quad \text{or} \quad \frac{C T}{T B} \cdot \frac{1}{\theta} \cdot \mu=1.
$$
From this, we find $\frac{C T}{T B}=\frac{\theta}{\mu}$.
Now, applying Menelaus' theorem to triangle $A C B$ and the transversal $M T$:
$$
\frac{A Q}{Q C} \cdot \frac{C T}{T B} \cdot \frac{B M}{M A}=1 \quad \text{or} \quad \frac{A Q}{Q C} \cdot \frac{\theta}{\mu} \cdot \frac{1}{\lambda}=1.
$$
From this, we get
$$
\frac{A Q}{Q C}=\frac{\lambda \mu}{\theta}
$$
According to the problem, $\lambda=2$, $\mu=3$, and $\theta=\frac{1}{2}$, then $\frac{A Q}{Q C}=12$.
|
Answer: $A Q: Q C=12$.
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Represent the number 80 as the sum of two prime numbers. In how many ways can this be done? Let's remind you that one is not considered a prime number.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
Solution. We organize the enumeration of all prime numbers from 2 to 73 in the form of a table.
| 1 | 7 | 13 | 19 | 25 | 31 | 37 | 43 | 49 | 55 | 61 | 67 | 73 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 8 | 14 | 20 | 26 | 32 | 38 | 44 | 50 | 56 | 62 | 68 | 74 |
| 3 | 9 | 15 | 21 | 27 | 33 | 39 | 45 | 51 | 57 | 63 | 69 | 75 |
| 4 | 10 | 16 | 22 | 28 | 34 | 40 | 46 | 52 | 58 | 64 | 70 | 76 |
| 5 | 11 | 17 | 23 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 71 | 77 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 |
In the table, composite numbers from 4 to 78 are marked in dark color (1 is neither prime nor composite), and there are 21 prime numbers. In the following two tables, pairs of numbers $(a ; b)$ are listed for which $a+b=80$ and $a$ is a prime number.
| a | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| b | 78 | 77 | 75 | 73 | 69 | 67 | 63 | 61 | 57 |
| a | 29 | 31 | 37 | 41 | 47 | 53 | 59 | 71 | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| b | 51 | 49 | 43 | 39 | 33 | 27 | 21 | 9 | |
In the second row of the table (b), composite numbers are marked in dark color. Thus, the number 80 can be represented as the sum of two prime numbers in four ways: $80=7+73, 80=13+67, 80=19+61, 80=37+43$.
Answer: $80=7+73, 80=13+67, 80=19+61, 80=37+43$; four ways.
|
4
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. On a sheet of paper, 12 consecutive integers are written. After one of them is crossed out, the sum of the remaining numbers equals 325. Which number was crossed out?
|
Solution. Let $n, n+1, \ldots, n+k-1, n+k, n+k+1, \ldots, n+11$ be 12 consecutive integers, and the number $n+k, k=0,1,2, \ldots, 11$ is crossed out. The sum of the numbers after crossing out is
$$
\frac{2 n+11}{2} \cdot 12-(n+k)=325 \rightarrow 11 n+66-k=325 \rightarrow k=11 n-259
$$
Considering the condition $k \in[0 ; 11]$, we get $0 \leq 11 n-259 \leq 11 \rightarrow \frac{259}{11} \leq n \leq \frac{270}{11}$. In this interval, there is only one integer $n=24$ and $k=5$. Therefore, the crossed-out number is $n+k=29$.
Answer: 29.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A football is sewn from 256 pieces of leather: white ones in the shape of hexagons and black ones in the shape of pentagons. Black pentagons only border white hexagons, and any white hexagon borders three black pentagons and three white hexagons. Find the number of white hexagons on the football.
|
Answer: 160.
Criteria for checking works, 7th grade
Preliminary round of the sectoral physics and mathematics olympiad for schoolchildren "Rosatom", mathematics
#
|
160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. For what least integer $n$ are all solutions of the equation
$$
x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6(n-8)(n+2)=0 \text { greater than }-1 \text { ? }
$$
|
Solution. Rewrite the equation as
$$
x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6 n^{2}+36 n+96=0 .
$$
Notice that $x_{1}=1>-1$ is a solution for all $n$ (the sum of the coefficients of the polynomial on the left side of the equation is zero for all $n$). Divide the equation by $x-1$:
$$
x^{2}-5(n-2) x+6\left(n^{2}-6 n-16\right)=0
$$
The roots of this equation are: $x_{2}=3(n+2), x_{3}=2(n-8)$. We seek when these solutions are greater than -1:
$$
\left\{\begin{array} { l }
{ 3 ( n + 2 ) > - 1 } \\
{ 2 ( n - 8 ) > - 1 }
\end{array} \rightarrow \left\{\begin{array}{l}
n>-\frac{7}{3}, n \in Z \\
n>\frac{15}{2}, n \in Z
\end{array} \rightarrow n \geq 8\right.\right.
$$
Since $n$ is an integer, then $n \geq 8, n \in Z$.
Answer: $n_{\min }=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The midline of a trapezoid is 4. A line parallel to the bases of the trapezoid and dividing its area in half intersects the lateral sides at points $M$ and $N$. Find the smallest possible length of the segment $M N$.
|
# Solution.
Notations: $A D=a, B C=b, C K=H, N E=h$ - heights of triangles $N C P$ and $D N Q$, $M N=x$
$$
S_{\text {AMND }}=S_{\text {MBCN }} \rightarrow \frac{x+b}{2} H=\frac{a+x}{2} h \rightarrow \frac{H}{h}=\frac{a+x}{x+b}
$$
$\square N C P \quad \square D N Q \rightarrow \frac{H}{h}=\frac{x-b}{a-x} \rightarrow \frac{a+x}{x+b}=\frac{x-b}{a-x} \rightarrow a^{2}-x^{2}=x^{2}-b^{2} \rightarrow x=\sqrt{\frac{a^{2}+b^{2}}{2}}$.
Since $a+b=8$, then $x=\sqrt{\frac{a^{2}+(8-a)^{2}}{2}}=\sqrt{a^{2}-16 a+32}=\sqrt{(a-4)^{2}+16}$.
Answer: $M N_{\text {min }}=4$.
## Answers for other variants.
## Variant 2
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all $x$ that satisfy the inequality $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6 \leq 0$ for any natural $n$.
|
Solution. The roots of the quadratic trinomial $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6$ are
$$
x_{1}=1-\frac{2}{n}, x_{2}=1+\frac{3}{n}
$$
Factorize the left side of the inequality
$$
n^{2}\left(x-\left(1-\frac{2}{n}\right)\right)\left(x-\left(1+\frac{3}{n}\right)\right) \leq 0
$$
Solving the inequality using the interval method, we get $x \in\left[1-\frac{2}{n} ; 1+\frac{3}{n}\right]$. Only $x=1$ belongs to this interval for any $n$.
Answer: $x=1$
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the edges of a trihedral angle with vertex at point $S$, there are points $M, N$, and $K$ such that $S M^{2}+S N^{2}+S K^{2} \leq 12$. Find the area of triangle $S M N$, given that the angle $M S N$ is $30^{\circ}$, and the volume of the pyramid $S M N K$ is maximally possible.
|
Solution. Let's introduce the notations: $S M=m, S N=n, S K=k$.
The volume of the pyramid $S M N K$ is
$$
V=\frac{1}{3} S_{S M N} \cdot h=\frac{1}{6} m n \sin \alpha \cdot h=\frac{1}{6} m n \sin \alpha \cdot k \sin \beta=\frac{\sin \alpha \sin \beta}{6} m n k .
$$
The values of the angles $\alpha, \beta$ depend on the trihedral angle but not on the positions of the points $M, N, K$ on its edges. Therefore, the maximum volume of the pyramid $S M N K$ corresponds to the maximum value of the product $m \cdot n \cdot k$, given the condition $m^{2}+n^{2}+k^{2} \leq p$. From the inequality of the geometric mean and the arithmetic mean of three numbers, it follows that $\sqrt[3]{m^{2} n^{2} k^{2}} \leq \frac{m^{2}+n^{2}+k^{2}}{3} \leq \frac{p}{3}$
Equality is achieved when $m=n=k$. Then, when $m=n=k=\sqrt{\frac{p}{3}}$, the volume of the pyramid is maximized, and the area of the triangle $S M N$ takes the value $\frac{p \sin \alpha}{6}$. In our case, $p=12, \alpha=30^{\circ}$, so $S_{S M N}=1$.
Answer: $S_{S M N}=1$.
## Answers for other variants.
## Variant 2
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Quadrilateral $ABCD$ is inscribed in a circle, and its diagonals intersect at point $P$. Points $K, L$, and $M$ are the midpoints of sides $AB, BC$, and $CD$ respectively. The radius of the circle circumscribed around triangle $KLP$ is 1. Find the radius of the circle circumscribed around triangle $LMP$.
Problem 1 Answer: 18 passengers.
|
Solution. Let $y_{k}$ be the number of passengers in the car with number $k, k=1,2,3, \ldots, 10$. According to the problem, $\sum_{k=1}^{10} y_{k}=270$. Additionally, it is stated that $y_{2} \geq y_{1}+2, y_{3} \geq y_{1}+4, \ldots, y_{9} \geq y_{1}+16, \quad y_{10} \geq y_{1}+18$. Adding these inequalities,
$$
y_{2}+y_{3}+\ldots+y_{9}+y_{10} \geq y_{1}+2+y_{1}+4+\ldots+y_{1}+16+y_{1}+18
$$
or
$$
270-y_{1} \geq 9 y_{1}+90
$$
From this, we get $y_{1} \leq 18$. From the conditions $y_{10} \geq y_{1}+18$ and $y_{10} \leq 2 y_{1}$, it follows that $2 y_{1} \geq y_{1}+18$ or $y_{1} \geq 18$. Comparing the obtained inequalities, we conclude that $y_{1}=18$. The set $y_{1}=18, y_{2}=20$, $\ldots, y_{10}=36$ satisfies the conditions of the problem.
Problem 2 Answer: $x=\frac{8 \pi}{5}$.
Solution. Introduce the notations: $u=\sin x, v=\sin 2 x, w=\sin 3 x$. Then the equation becomes
$$
(u+v+w)^{3}=u^{3}+v^{3}+w^{3}
$$
Rewrite the equation as
$$
(u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=0
$$
Using the formulas for the difference and sum of cubes, as well as the difference of squares, factorize the left-hand side of the equation
$$
\begin{aligned}
& (u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=(v+w)\left((u+v+w)^{2}+u(u+v+w)+u^{2}\right)- \\
& -(v+w)\left(v^{2}-v w+w^{2}\right)=(v+w)\left[\left((u+v+w)^{2}-v^{2}\right)+\left(u^{2}-w^{2}\right)+u(u+w)+v(u+w)\right]= \\
& =(v+w)(u+w)(u+2 v+w+u-w+u+v))=3(v+w)(u+w)(u+v)
\end{aligned}
$$
As a result, the equation takes the form
$$
3(v+w)(u+w)(u+v)=0
$$
Returning to the original variables, we get the equation:
Case $1 . \sin x+\sin 2 x=0$.
$\left[\begin{array}{c}2 x=-x+2 \pi k \\ 2 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{3}, \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$ The largest solution on the interval $(0 ; 2 \pi)$ is $x=\frac{4 \pi}{3}$
Case $2 . \sin x+\sin 3 x=0$.
$\left[\begin{array}{c}3 x=-x+2 \pi k \\ 3 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{\pi k}{2}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{3 \pi}{2} \\ x=\frac{\pi}{2}+\pi m, m, k \in Z .\end{array} \quad\right.\right.$.
Case $3 . \sin 3 x+\sin 2 x=0$.
$\left[\begin{array}{c}3 x=-2 x+2 \pi k \\ 3 x=\pi+2 x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{5}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{8 \pi}{5} \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$.
The largest solution among $\frac{4 \pi}{3}, \frac{3 \pi}{2}, \frac{8 \pi}{5}$ is $x=\frac{8 \pi}{5}$.
Problem 3 Answer: all 100 digits after the decimal point are nines.
Solution. Consider $(7+4 \sqrt{3})^{2023}$. Use the binomial formula
$$
(7+4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(4 \sqrt{3})^{k}=a+b \sqrt{3}
$$
where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$.
Now consider $(7-4 \sqrt{3})^{2023}:$
$$
(7-4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(-4 \sqrt{3})^{k}=a-b \sqrt{3}
$$
where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$.
Adding the obtained equalities, we get
$$
(7+4 \sqrt{3})^{2023}+(7-4 \sqrt{3})^{2023}=a+b \sqrt{3}+a-b \sqrt{3}=2 a \in N
$$
From this, we have
$$
\begin{aligned}
& (7+4 \sqrt{3})^{2023}=2 a-(7-4 \sqrt{3})^{2023}=2 a-\frac{(7-4 \sqrt{3})^{2023} \cdot(7+4 \sqrt{3})^{2023}}{(7+4 \sqrt{3})^{2023}}=2 a-\frac{1}{(7+4 \sqrt{3})^{2023}}= \\
& =2 a-1+1-\frac{1}{(7+4 \sqrt{3})^{2023}}, \quad 2 a-1 \in N .
\end{aligned}
$$
Notice that $\frac{1}{(7+4 \sqrt{3})^{2023}}0
$$
Then, considering the non-negativity of $x$, we find $x=\frac{\sqrt{2 \pm \sqrt{3}}}{4}$. It remains to check the condition $x \leq \frac{1}{2}$ :
$$
\frac{\sqrt{2 \pm \sqrt{3}}}{4} \vee \frac{1}{2} \leftrightarrow \sqrt{2 \pm \sqrt{3}} \vee 2 \leftrightarrow 2 \pm \sqrt{3} \vee 4 \leftrightarrow \pm \sqrt{3} \vee 2 \rightarrow \pm \sqrt{3}<2
$$
Therefore, both roots $x=\frac{\sqrt{2+\sqrt{3}}}{2}$ and $x=\frac{\sqrt{2-\sqrt{3}}}{2}$ satisfy the condition $x \leq \frac{1}{2}$.
Problem 5 Answer: $R=1$.
Solution. Consider triangles $A B P$ and $D C P$. They are similar by two equal angles ( $\angle B A C=\angle B D C, . \angle A B D=\angle A D C$ as angles inscribed in a circle and subtending the same arc). Therefore, the sides of these triangles are proportional:
$$
\frac{A B}{D C}=\frac{A P}{D P}=\frac{B P}{P C}
$$
Now consider triangles $A K P$ and $D C P$. By the condition $A K=\frac{A B}{2}, D M=\frac{D C}{2}$, so $\frac{A K}{D M}=\frac{A B}{D C}$. As a result, we have $\frac{A K}{D M}=\frac{A P}{D B}$. Therefore, triangle $A P K$ is similar to triangle $D P M$ by an equal angle and proportional sides. Then the angle $A P K$ is equal to the angle $D P M$ as angles in similar triangles, lying opposite proportional sides.
By the problem's condition, $K L$ and
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
0.35 \cdot 160+0.1 x=0.2 \cdot 160+0.2 x, 0.15 \cdot 160=0.1 x, x=240 \text {. }
$$
In total, it results in $160+240=400$ g of solution.
|
Answer: 400.
## Problem 9
Points $B_{1}$ and $C_{1}$ are the feet of the altitudes of triangle $ABC$, drawn from vertices $B$ and $C$ respectively. It is known that $AB=7, \quad AC=6, \sin \angle BAC=\frac{2 \sqrt{110}}{21}$. Find the length of the segment $B_{1}C_{1}$.
## Solution:
Let the angle $\angle BAC$ be denoted by $\alpha$. There are two possible cases: 1) $00$.
$$
\begin{aligned}
& \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{(2 x+2)^{2}-(x+4)^{2}}=a x^{2}, \\
& \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{3\left(x^{2}-4\right)}=a x^{2}, \\
& |2 x+2|+|x+4|=3 a x^{2} .
\end{aligned}
$$
If $a \leq 0$, then the left side $>0$, and the right side $\leq 0$; equation ( ${ }^{*}$ ) has no solutions.
If $a>0$, equation (*) has at least 2 solutions.
The original equation can have fewer solutions only if at least one of the numbers $\pm 2$ is a solution ( ي $\left.^{2}\right)$.
2 is a solution of (*), if $12=12 a, a=1 ;(-2)$ is a solution of (*), if $4=12 a, a=1 / 3$.
When $a=1$, equation (*) becomes $|2 x+2|+|x+4|=3 x^{2}$ and has roots $x_{1}=-1, x_{2}=2$. The original equation has a single root $x=-1$.
When $a=1 / 3$, equation (*) becomes $|2 x+2|+|x+4|=x^{2}$ and has roots $x_{1}=-2, x_{2}=\frac{3+\sqrt{33}}{2}$. The original equation has a single root $x=\frac{3+\sqrt{33}}{2}$.
Answer: the equation has no more than one root when $a \leq 0$, when $a=1 / 3$, and when $a=1$.
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points). Tourist Nikolai Petrovich was late by $\Delta t=5$ minutes for the departure of his riverboat, which had set off downstream. Fortunately, the owner of a fast motorboat agreed to help Nikolai Petrovich. Catching up with the riverboat and disembarking the unlucky tourist, the motorboat immediately set off on its return journey. How much time passed from the departure of the motorboat until its return? Assume that the speed of the riverboat relative to the water is $k=3$ times the speed of the river current, and the speed of the motorboat is $n=5$ times the speed of the river current.
|
1. $s=\left(3 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot\left(t_{1}+\Delta t\right)=\left(5 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot t_{1} \rightarrow 4 \Delta t=2 t_{1} \rightarrow t_{1}=2 \Delta t=10$ min $t_{2}=\frac{s}{5 v_{\mathrm{T}}-v_{\mathrm{T}}}=\frac{6 v_{\mathrm{T}} \cdot t_{1}}{4 v_{\mathrm{T}}}=\frac{3}{2} t_{1}=3 \Delta t=15$ min $\rightarrow$ $T=t_{1}+t_{2}=5 \Delta t=25$ min
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) A satellite is launched vertically from the pole of the Earth at the first cosmic speed. To what maximum distance from the Earth's surface will the satellite travel? (The acceleration due to gravity at the Earth's surface $g=10 \mathrm{m} / \mathrm{c}^{2}$, radius of the Earth $R=6400$ km).
|
2.
According to the law of conservation of energy: $\frac{m v_{I}^{2}}{2}-\frac{\gamma m M}{R}=-\frac{\gamma m M}{R+H}$
The first cosmic speed $v_{I}=\sqrt{g R}$
The acceleration due to gravity at the surface $g=\frac{\gamma M}{R^{2}}$
Then $\frac{m g R}{2}-m g R=-\frac{m g R^{2}}{R+H}$
Finally, $H=R=6400$ km.
(15 points)
|
6400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (15 points) Looking down from the edge of the stream bank, Vovochka decided that the height of his rubber boots would be enough to cross the stream. However, after crossing, Vovochka got his legs wet up to his knees ($H=52$ cm). Estimate the height $h$ of Vovochka's boots. Assume the depth of the stream is constant, and the refractive index of water $n=1.33$.
Rector of SPbPU

A.I. Rudskoy S.A. Staroytov
## Instructions for Evaluating Final Round Solutions of the Polytechnic Physics Olympiad
The version given to the participant contains 6 problems of varying difficulty.
The evaluation of the work is based on the points received for each individual problem.
The score for solving each problem in the version is one of the following coefficients:
1.0 - the problem is solved correctly;
0.8 - the problem is solved correctly and the answer is given in a general form; there is an error in the unit of measurement of the obtained physical quantity or an arithmetic error;
0.6 - the problem is not fully solved; all necessary physical relationships for solving the problem are present; there is an error in algebraic transformations;
0.4 - the problem is not fully solved; some physical relationships necessary for solving the problem are missing;
0.2 - the problem is not solved; the work contains only some notes related to solving the problem or describing the phenomenon considered in the problem;
0.0 - the solution to the problem or any notes related to it are absent in the work.
The coefficient is entered in the first column "For the Teacher" of the "Answer Sheet". In the second column of the section, the score is entered, which is the product of the coefficient received for the solution and the maximum score for the given problem.
The obtained scores are summed and entered in the "Total" row.
Table for converting coefficients to points.
| \multirow{coefficient}{max points}{} | 10 | 15 | 20 | 25 |
| :---: | :---: | :---: | :---: | :---: |
| 1 | 10 | 15 | 20 | 25 |
| 0.8 | 8 | 12 | 16 | 20 |
| 0.6 | 6 | 9 | 12 | 15 |
| 0.4 | 4 | 6 | 8 | 10 |
| 0.2 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 |
|
6. From the figure
$\frac{d}{h}=\operatorname{tg} \alpha ; \quad \frac{d}{H}=\operatorname{tg} \beta ; \quad \frac{H}{h}=\frac{\operatorname{tg} \alpha}{\operatorname{tg} \beta}$
Since all the information about the bottom of the stream falls into the space limited by the eye's pupil, all angles are small: $\operatorname{tg} \alpha \approx \sin \alpha ; \operatorname{tg} \beta \approx \sin \beta$
Then $\frac{H}{h}=\frac{\sin \alpha}{\sin \beta}=n$
$h=\frac{H}{n}=39 \mathrm{~cm}$.
(15 points)
|
39
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Dmitry is three times as old as Grigory was when Dmitry was as old as Grigory is now. When Grigory becomes as old as Dmitry is now, the sum of their ages will be 49 years. How old is Grigory?
|
Solution: Let Gregory be $y$ years old in the past, and Dmitry be $x$ years old. Then currently, Gregory is $x$ years old, and Dmitry is $3 y$ years old. In the future, Gregory will be $3 y$ years old, and Dmitry will be $z$ years old, and according to the condition, $z+3 y=49$. Since $z-3 y=3 y-x ; 3 y-x=x-y$, then $9 y-x=49$ and $x=2 y$. From this, we get that $x=14, y=7$. Currently, Gregory is 14 years old. Answer: 14.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\frac{4}{\sqrt{\log _{3}(81 x)}+\sqrt{\log _{3} x}}+\sqrt{\log _{3} x}=3$.
|
Solution: Using the properties of logarithms, our equation can be rewritten as $\frac{4}{\sqrt{4+\log _{3} x}+\sqrt{\log _{3} x}}+\sqrt{\log _{3} x}=3$. Let $t=\log _{3} x$. Then $\frac{4}{\sqrt{4+t}+\sqrt{t}}+\sqrt{t}=3$. Multiplying the numerator and denominator of the first fraction by $\sqrt{t+4}-\sqrt{t}$, we arrive at the equation $\sqrt{t+4}=3$. From this, we get that $t=5$ and $x=3^{5}=243$. Answer: 243.
|
243
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. On the sides $B C, C A, A B$ of an equilateral triangle $A B C$ with side length 7, points $A_{1}, B_{1}, C_{1}$ are taken respectively. It is known that $A C_{1}=B A_{1}=C B_{1}=3$. Find the ratio of the area of triangle $A B C$ to the area of the triangle formed by the lines $A A_{1}, B B_{1}, C C_{1}$.
|
Solution:
Triangles $A B A_{1}, B C B_{1}, C A C_{1}$ are equal by sides and the angle between them, triangles $A D C_{1}, B E A_{1}, C F B_{1}$ are equal by side and angles. Triangle $A D C_{1}$ is similar to $A B A_{1}$ by two angles, triangle $A B C$ is similar to $D E F$. Let $S=S_{A B C}, S_{1}=S_{A B A_{1}}, S_{2}=S_{A C_{1} D}, S_{0}=S_{D E F} \cdot$ Then
$$
\begin{aligned}
& \qquad A A_{1}=\sqrt{A B^{2}+B A_{1}^{2}-2 A B \cdot B C_{1} \cos 60^{\circ}}=\sqrt{49+9-21}=\sqrt{37} \\
& \frac{S_{2}}{S_{1}}=\left(\frac{A C_{1}}{A A_{1}}\right)^{2}=\frac{9}{37}, \frac{S_{1}}{S}=\frac{B A_{1}}{B C}=\frac{3}{7} \\
& S_{0}=S-3 S_{1}+3 S_{2}=S-3 \cdot \frac{3}{7} S+3 \cdot \frac{9}{37} \cdot \frac{3}{7} S=\frac{S}{37}, \frac{S}{S_{0}}=37 \\
& \text { answer: } 37 \text {. }
\end{aligned}
$$
|
37
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Ivan is twice as old as Peter was when Ivan was as old as Peter is now. When Peter becomes as old as Ivan is now, the sum of their ages will be 54 years. How old is Peter?
|
Solution: Let Peter's age in the past be $y$ years, and Ivan's age be $x$ years. Then currently, Peter is $x$ years old, and Ivan is $2 y$ years old. In the future, Peter will be $2 y$ years old, and Ivan will be $z$ years old, and according to the condition, $z+2 y=54$. Since $z-2 y=2 y-x ; 2 y-x=x-y$, then $6 y-x=54$ and $2 x=3 y$. From this, we get that $x=18$. Currently, Peter is 18 years old. Answer: 18.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\frac{1}{\sqrt{\log _{5}(5 x)}+\sqrt{\log _{5} x}}+\sqrt{\log _{5} x}=2$.
|
Solution: Using the properties of logarithms, our equation can be rewritten as $\frac{1}{\sqrt{1+\log _{5} x}+\sqrt{\log _{5} x}}+\sqrt{\log _{5} x}=2$. Let $t=\log _{5} x$. Then $\frac{1}{\sqrt{1+t}+\sqrt{t}}+\sqrt{t}=2$. By multiplying the numerator and denominator of the first fraction by $\sqrt{t+1}-\sqrt{t}$, we arrive at the equation $\sqrt{t+1}=2$. From this, we get that $t=3$, so $x=5^{3}=125$. Answer: 125.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. On the sides $B C, C A, A B$ of an equilateral triangle $A B C$ with side length 11, points $A_{1}, B_{1}, C_{1}$ are taken respectively. It is known that $A C_{1}=B A_{1}=C B_{1}=5$. Find the ratio of the area of triangle $A B C$ to the area of the triangle formed by the lines $A A_{1}, B B_{1}, C C_{1}$.
|
Solution:
Triangles $A B A_{1}, B C B_{1}, C A C_{1}$ are equal by sides and the angle between them, triangles $A D C_{1}, B E A_{1}, C F B_{1}$ are equal by side and angles. Triangle $A D C_{1}$ is similar to $A B A_{1}$ by two angles, triangle $A B C$ is similar to $D E F$. Let $S=S_{A B C}, S_{1}=S_{A B A_{1}}, S_{2}=S_{A C_{1} D}$,
$S_{0}=S_{\text {DEF }} \cdot$ Then
$A A_{1}=\sqrt{A B^{2}+B A_{1}^{2}-2 A B \cdot B C_{1} \cos 60^{\circ}}=\sqrt{91}$,
$$
\frac{S_{2}}{S_{1}}=\left(\frac{A C_{1}}{A A_{1}}\right)^{2}=\frac{25}{91}, \frac{S_{1}}{S}=\frac{B A_{1}}{B C}=\frac{5}{11}
$$
$S_{0}=S-3 S_{1}+3 S_{2}=S-3 \cdot \frac{5}{11} S+3 \cdot \frac{25}{91} \cdot \frac{5}{11} S=\frac{S}{91}, \frac{S}{S_{0}}=91$.
Answer: 91.
|
91
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. For what values of the parameter $a$ does the equation $x^{4}-40 x^{2}+144=a\left(x^{2}+4 x-12\right)$ have exactly three distinct solutions?
|
Solution: Factorize the right and left sides of the equation:
$(x-2)(x+2)(x-6)(x+6)=a(x-2)(x+6)$. The equation can be written as
$(x-2)(x+6)\left(x^{2}-4 x-12-a\right)=0$. It is obvious that 2 and -6 are roots of this equation. We are satisfied with the situation where exactly one of the roots of the equation $x^{2}-4 x-12-a=0$ does not coincide with 2 and -6. The total number of solutions will be three if the last equation has one root $x_{3}$, such that $x_{3} \neq x_{1}, x_{3} \neq x_{2}$, or if this equation has two roots $x_{3}, x_{4}$, one of which coincides with $x_{1}$ or $x_{2}$.
The equation $x^{2}-4 x-12-a=0$ has one root when $a=-16$ and this root coincides with 2. This case does not suit us. The number 2 is a root of this equation when $a=-16$. This case has already been considered. The number -6 is a root of this equation when $a=48$, and in this case, the second root is different from 2 and -6 - Answer: $a=48$.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
From channel A to the Wiki site, $850 * 0.06=51$ people will transition
From channel B to the Wiki site, $1500 * 0.042=63$ people will transition
From channel C to the Wiki site, $4536 / 72=63$ people will transition
|
Answer: The most people will transition from channels B and V - 63 people each
## 2
Cost of transition from advertising on channel A: $-3417 / 51 = 67$ rubles
Cost of transition from advertising on channel B: $4914 / 63 = 78$ rubles
Answer: The lowest cost of transition to the site from advertising on channel A - 67 rubles
## 3
Number of sales after advertising on channel A: $51 * 0.05 = 2.55$ - round to 2 sales (by number of people)
Revenue from sales minus advertising expenses: $(2 * 2500) - 3417 = 1583$ rubles
Number of sales after advertising on channel B: $63 * 0.05 = 3.15$ - round to 3 sales (by number of people)
Revenue from sales minus advertising expenses: $(3 * 2500) - 4914 = 2586$ rubles
Number of sales after advertising on channel B: $63 * 0.05 = 3.15$ - round to 3 sales (by number of people)
Revenue from sales minus advertising expenses: $(3 * 2500) - 4536 = 2964$ rubles
Answer: Advertising on channel B will bring Vika the most profit.
|
2964
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
Expenses for medical services provided to a child (under 18 years old) of the taxpayer by medical organizations
Correct answers: Pension contributions under a non-state pension agreement concluded by the taxpayer with a non-state pension fund in their own favor, Expenses for medical services provided to a child (under 18 years old) of the taxpayer by medical organizations, Expenses for their own education
Question 11
Score: 6.00
An investor has a brokerage account with an investment company. In 2021, the investor received the following income from securities:
- dividends on shares of JSC “Winning” amounted to 50,000 rubles;
- coupon income from government bonds OFZ amounted to 40,000 rubles;
- coupon income from corporate bonds of JSC “Reliable” amounted to 30,000 rubles.
In addition, the investor received a capital gain from selling 100 shares of JSC “Risky” at 200 rubles per share. The purchase price of 1 share was 150 rubles. The investor held the shares for 4 months.
The investor's salary for 2021 before taxation amounted to 1,000,000 rubles.
2022 Higher Trial - qualifying stage
rubles.
Calculate the amount of personal income tax (NDFL) on income from securities.
|
Answer and write it in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 16250
Question 12
Score: 5.00
Insert the missing terms from the drop-down list.
Under the insurance contract, one party
insured; insurance premium; beneficiary; insurer; insurance amount
undertakes to pay the other party
insured; insurance premium; beneficiary; insurer; insurance amount
in the event of an occurrence of an event provided for in the contract (insurance event) to compensate the other party
insured; insurance premium; beneficiary; insurer; insurance amount
or any other person in whose favor the contract is concluded
insured; insurance premium; beneficiary; insurer; insurance amount
, for losses caused by this event (pay insurance compensation) within the amount determined by the contract insured; insurance premium; beneficiary; insurer; insurance amount
Correct answer:
Insert the missing terms from the drop-down list.
Under the insurance contract, one party [insurer] undertakes to pay the other party [insurance premium] in the event of an occurrence of an event provided for in the contract (insurance event) to compensate the other party [insured] or any other person in whose favor the contract is concluded [beneficiary], for losses caused by this event (pay insurance compensation) within the amount determined by the contract [insurance amount].
Question 13
Score: 3.00
Mark all correct statements.
Owners of a voluntary life insurance policy are entitled to a tax deduction
Select one or more answers:
|
16250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the higher the risk of a financial instrument, the higher its return
Correct answers: the higher the reliability of a financial instrument, the higher its return, a financial instrument can be reliable, profitable, and liquid at the same time, risk is not related to the return of a financial instrument
Question 15
Score: 6.00
Agnia's monthly salary in 2021 is 60,000 rubles (before taxation). It is known that on 01.01.2021, Agnia opened the following deposits in banks (she had no deposits before):
| Bank | Deposit amount, rub. | Interest rate, % per annum |
| :---: | :---: | :---: |
| A | 500,000 | 4.5 |
| B | 400,000 | 3.9 |
| C | 300,000 | 5.0 |
| C | 100,000 | 0.75 |
Interest on all these deposits is accrued and paid once at the end of the year. The key rate of the Bank of Russia on 01.01.21 was 4.25%. It is known that Agnia's total income for 2021 did not exceed 5,000,000 rubles. Calculate the amount of personal income tax (NDFL) Agnia should pay on the interest received in 2021.
|
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 1378
Question 16
Score: 5.00
Establish the correspondence between specific taxes and their types.
| personal income tax | federal tax; local tax; regional tax; |
| :---: | :---: |
| land tax | federal tax; local tax; regional tax; |
| profit tax | federal tax; local tax; regional tax; |
| property tax of individuals | federal tax; local tax; regional tax; |
| transport tax | federal tax; local tax; regional tax; |
Correct answer:
personal income tax $\rightarrow$ federal tax,
land tax $\rightarrow$ local tax,
profit tax $\rightarrow$ federal tax,
property tax of individuals $\rightarrow$ local tax,
transport tax $\rightarrow$ regional tax
Question 17
Score: 6.00
Kirill wants to buy a TV costing 30000 rubles on credit. The bank offers him the necessary amount on loan with the condition that the borrowed amount must be repaid in three equal monthly installments. At the end of each month, interest must also be paid on the remaining debt, calculated at an annual rate of $18 \%$. Calculate the percentage of overpayment by Kirill from the loan amount.
Answer write in percentages as an integer without spaces and units of measurement.
Answer:
Correct answer: 3
Question 18
Score: 6.00
An investor has accumulated 400000 rubles and deposited them in a bank for 7 months at an annual interest rate of $6 \%$. Interest is compounded monthly. Calculate the amount of interest the investor will receive upon closing the deposit.
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 14212
Question 19
Score: 3.00
Mark all correct statements.
If a bank, which is your counterparty, has its license revoked, then
Select one or more answers:
|
1378
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 15. Problem 15
What amount of mortgage credit in rubles will a bank client receive if their initial payment of 1800000 rubles amounted to $30 \%$ of the cost of the purchased property?
|
Answer in the form of a number should bewrittenwithoutspaces,withoutunitsofmeasurementandanycharacters.
## Answer: 4200000
#
|
4200000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.