problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
5.
reducing transaction time
## Correct answers:
using licensed software, using a personal computer instead of a public one, using antivirus programs
Question 3
Balya: 7.00
Mr. Vshokoladov earned X rubles per month throughout 2021. In addition, during this year, he won 2000000 rubles in a lottery. What is $X$ if the total amount of personal income tax paid by Mr. Vshokoladov for this year was 1239480 rubles.
|
Answer in rubles, without spaces and units of measurement.
Answer:
Correct answer: 600000
Question 4
Score: 3.00
Select all correct continuations of the statement.
2022 Higher Trial - qualifying stage
To file a petition to recognize a citizen as bankrupt...
## Select one or more answers:
\ulcorner
|
600000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
A custodian stores securities, clients' money, and other material assets
Correct answers: A paid investment advisor consults and provides recommendations to the client on investment management, A trustee manages the client's property in their own name
Find the correspondence between the term and the statement so that all 5 pairs are correct. All 5 terms must be used.
The service may involve changing the terms of an existing loan
According to federal law, this service is available only once during the entire loan period
The service provides options for reducing the term or the amount of loan payments
During the term of this service, the bank does not charge the borrower penalties and cannot demand early repayment of the loan
This service may include
refinancing; consolidation of debts; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
Correct answer:
The service may involve changing the terms of an existing loan $\rightarrow$ restructuring,
According to federal law, this service is available only once during the entire loan period $\rightarrow$ mortgage holidays,
The service provides options for reducing the term or the amount of loan payments $\rightarrow$ early repayment,
During the term of this service, the bank does not charge the borrower penalties and cannot demand early repayment of the loan $\rightarrow$ loan holidays, This service may include consolidation of debts $\rightarrow$ refinancing
Question 8
Score: 7.00
The Ivanov family carefully plans their budget. Lidia Nikolaevna works as a doctor and earns 1,000,000 rubles per year (before income tax). Arkady Petrovich is an entrepreneur, and his annual profit from the business is 2,000,000 rubles, which is taxed at a rate of $15 \%$ under the simplified taxation system (USN).
On average, the family's expenses amount to 205,000 rubles per month, excluding vacation expenses.
The Ivanovs had been saving money for a trip to Paris for a year, but due to the pandemic, they decided to postpone the trip for a year and temporarily place the accumulated savings in a bank deposit at an annual interest rate of $12 \%$ with interest paid at the end of each quarter. The deposit term is 12 months, and interest income is reinvested. Calculate the Ivanov family's income from the deposit.
|
Answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number according to rounding rules.
Answer:
Correct answer: 13806
question 9
Score: 3.00
Select all possible features of an authentic ruble banknote.
Select one or more answers:
$\Gamma$
|
13806
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
watermark
Correct answers: raised relief of certain text fragments, watermark, inscriptions and ornaments
Question 10
Score: 7.00
Vladimir has saved 16,500 rubles to buy a gaming console as a birthday gift for his brother, which amounts to 220 US dollars at the current exchange rate. The birthday is not until a month from now, and Vladimir is comparing three
Financial Literacy 11th Grade Day 1
alternatives: 1) buy the console now; 2) buy US dollars with the saved amount now, and convert them back to rubles in a month to buy the console; or 3) deposit 16,500 rubles in the bank now, with the condition that he will receive 16,665 rubles in a month, and then buy the chosen console.
Calculate the minimum exchange rate of US dollars at the end of the month for the second alternative to be economically beneficial for Vladimir. Assume that there are no bank fees or currency conversion fees.
|
Answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number according to rounding rules.
Answer: $\qquad$
Correct answer: 76
Question 11
Score: 3.00
What services can currently be provided remotely? Select all appropriate options.
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the driver's marital status
Correct answers: bonus-malus coefficient, engine power, driver's age
Question 14
Score: 7.00
Maria Ivanovna has retired. She did not have a funded pension, only a social insurance pension, and her individual pension coefficient amount is 120. In addition, Maria Ivanovna has a bank deposit of 600,000 rubles, placed at an annual interest rate of $4 \%$ with monthly interest payments, which she does not reinvest but withdraws from the account monthly. How much money does Maria Ivanovna have available each month if the fixed part of her pension is 6050 rubles per month, and the cost of the pension coefficient is 99 rubles?
|
Provide the answer in rubles, without spaces and units of measurement.
Answer:
The correct answer is: 19930
Question 15
Score: 7.00
Insert the missing words from the list below (not all provided words will be needed!):
Paying
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
with a card, you spend the bank's funds, which you will have to return later.
If you do this before the end of the
credit; preferential; higher; cash withdrawal; service; blocking;
bonus; debit; freeze; lower; transfer;
period, the fee for using these funds is not charged, if you do not manage to, you will have to pay interest, which is usually significantly
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
than the interest on a regular loan. In addition, the bank usually
charges interest for
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
money from an ATM and an annual fee for
credit; preferential; higher; cash withdrawal; service; blocking;
bonus; debit; freeze; lower; transfer;
card.
Correct answer:
Insert the missing words from the list below (not all provided words will be needed!):
Paying [credit] card, you spend the bank's funds, which you will have to return later. If you do this before the end of the [preferential] period, the fee for using these funds is not charged, if you do not manage to - you will have to pay interest, which is usually significantly [higher] than the interest on a regular loan. In addition, the bank usually charges interest for [cash withdrawal] money from an ATM and an annual fee for
[service] card.
Question 16
Score: 3.00
In what cases is no commission charged for a transfer between individuals in Russia? Select all applicable answers.
Select one or more answers:
|
19930
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.
when transferring money abroad
Correct answers: when using the Fast Payment System for amounts up to 100 thousand rubles per month, when transferring funds between one's own accounts in the same bank
Question 17
Score: 7.00
Last year, a beauty salon offered a $20 \%$ discount on facial massage when purchasing a membership for 30000 rubles. This year, it was decided to change the loyalty program and, when purchasing a membership for 30000 rubles, an additional $20 \%$ of this amount would be credited to the client's account. How will the number of facial massages that a client can now attend with a membership for 30000 rubles change, if the cost of a massage is 1500 rubles?
In the answer, write a non-negative integer without units of measurement. If the number of massages has not changed, put 0.
|
Answer:
The correct answer: 1
Question 18
Score: 3.00
Select all true statements regarding digital financial assets $(DFA)$.
Select one or more answers:
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
The Bank of Russia will ensure the conversion of the "digital ruble" into another form of money (rubles) at a one-to-one ratio.
Correct answers: Stablecoins, backed by cash or gold, are an example of a CBDC., The Bank of Russia will ensure the conversion of the "digital ruble" into another form of money (rubles) at a one-to-one ratio.
Question 19
Score: 7.00
Angelika owns a commercial space of 30 sq. m. She wanted to organize a music club there and give piano lessons. But a friend offered Angelika a job as a manager in his company, and she decided to calculate which option would be more economically beneficial for her. If she opens the club, Angelika plans to choose a simplified tax system with a rate of $15 \%$ of the profit received, while her salary, which she spends entirely on monthly expenses, after paying personal income tax, will be 60,900 rubles per month.
Additional information:
rent rate: 12,000 rubles per 1 sq m per year, paid at the beginning of the year.
interest rate on a loan: $12 \%$ per year, with interest accrued at the end of the year interest rate on a deposit: $9 \%$ per year, with interest accrued at the end of the year Determine the minimum annual profit Angelika needs to achieve from the music club (before taxation) for this alternative to be economically beneficial for her.
|
Provide the answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number.
Answer: $\qquad$
Correct answer: 1321412
Question 20
Score: 7.00
Financial Literacy 11th Grade Day 1
Ivan and Petr, twin brothers, went on a vacation by the sea together and purchased two different travel insurance policies, which also cover medical expenses during the trip. Ivan bought insurance for 450 rubles with a deductible of $25. Petr bought insurance for 500 rubles with no deductible. During the trip, the brothers fell ill and had to see a doctor, which cost $100 for each of them. Calculate how much more the brother who bought the less advantageous insurance policy paid compared to the other brother? Conduct calculations in rubles, using the exchange rate of 75 rubles per $. Provide the answer in rubles, without spaces and units of measurement.
Answer:
Correct answer: 1825
|
1321412
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the higher the risk of a financial instrument, the higher its return
Correct answers: the higher the reliability of a financial instrument, the higher its return, a financial instrument can be reliable, profitable, and liquid at the same time, risk is not related to the return of a financial instrument
Question 15
Score: 6.00
Agnia's monthly salary in 2021 is 60,000 rubles (before taxation). It is known that on 01.01.2021, Agnia opened the following deposits in banks (she had no deposits before):
| Bank | Deposit amount, rub. | Interest rate, % per annum |
| :---: | :---: | :---: |
| A | 500000 | 4.5 |
| B | 400000 | 3.9 |
| C | 300000 | 5.0 |
| C | 100000 | 0.75 |
Interest on all these deposits is accrued and paid once at the end of the year. The key rate of the Bank of Russia on 01.01.21 was 4.25%. It is known that Agnia's total income for 2021 did not exceed 5,000,000 rubles. Calculate the amount of personal income tax (NDFL) Agnia should pay on the interest received in 2021.
|
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 1378
Question 16
Score: 5.00
Establish the correspondence between specific taxes and their types.
| personal income tax | federal tax; local tax; regional tax; |
| :---: | :---: |
| land tax | federal tax; local tax; regional tax; |
| profit tax | federal tax; local tax; regional tax; |
| property tax of individuals | federal tax; local tax; regional tax; |
| transport tax | federal tax; local tax; regional tax; |
Correct answer:
personal income tax $\rightarrow$ federal tax,
land tax $\rightarrow$ local tax,
profit tax $\rightarrow$ federal tax,
property tax of individuals $\rightarrow$ local tax,
transport tax $\rightarrow$ regional tax
Question 17
Score: 6.00
Kirill wants to buy a TV costing 30000 rubles on credit. The bank offers him the necessary amount on loan with the condition that the borrowed amount must be repaid in three equal monthly installments. At the end of each month, interest must also be paid on the remaining debt, calculated at an annual rate of $18 \%$. Calculate the percentage of overpayment by Kirill from the loan amount.
Answer write in percentages as an integer without spaces and units of measurement.
Answer:
Correct answer: 3
Question 18
Score: 6.00
An investor has accumulated 400000 rubles and deposited them in a bank for 7 months at an annual interest rate of $6 \%$. Interest is compounded monthly. Calculate the amount of interest the investor will receive upon closing the deposit.
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 14212
Question 19
Score: 3.00
Mark all correct statements.
If a bank, which is your counterparty, has its license revoked, then
Select one or more answers:
|
1378
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a square of grid paper containing an integer number of cells, a hole in the shape of a square, also consisting of an integer number of cells, was cut out. How many cells did the large square contain if 209 cells remained after the cutout?
|
Answer: 225 cells
Solution. The side of the larger square contains $n$ sides of a cell, and the side of the smaller square contains $m$ sides of a cell. Then $n^{2}-m^{2}=209 \rightarrow(n-m)(n+m)=209=11 \cdot 19$.
Case 1. $\left\{\begin{array}{c}n+m=209 \\ n-m=1\end{array} \rightarrow\left\{\begin{array}{c}n=105 \\ m=104\end{array}\right.\right.$ case does not occur due to the absence of a hole
Case 2. $\left\{\begin{array}{l}n+m=19 \\ n-m=11\end{array} \rightarrow\left\{\begin{array}{l}n=15 \\ m=4\end{array}\right.\right.$
|
225
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (mathematics) There are scales with two pans, 4 weights of 2 kg each, 3 weights of 3 kg each, and two weights of 5 kg each. In how many different ways can a 12 kg load be balanced on the scales, if the weights are allowed to be placed on both pans?
|
Answer: 7 ways
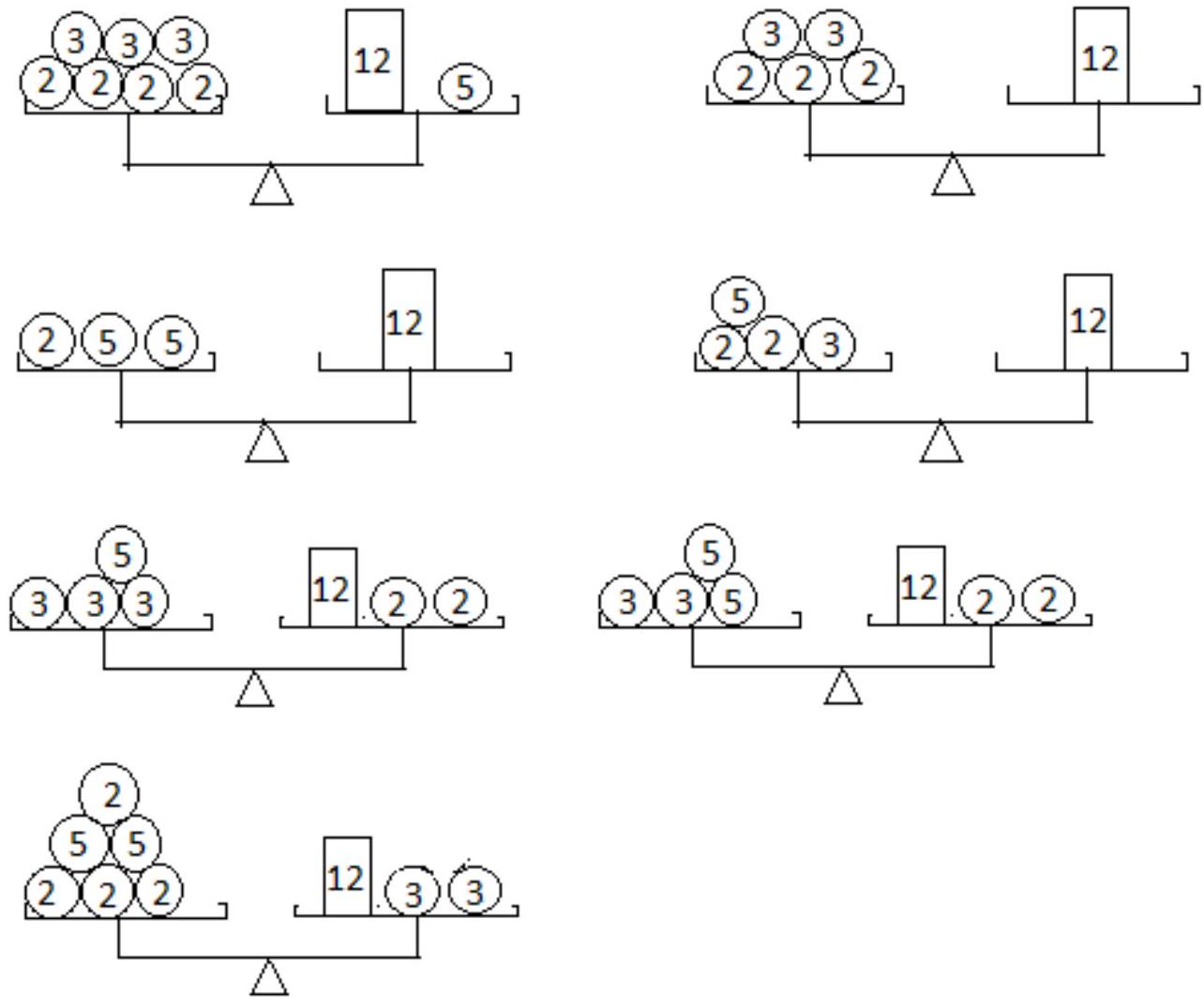
Solution: Let $x$ be the number of 2 kg weights used in weighing, $y$ be the number of 3 kg weights, and $z$ be the number of 5 kg weights. Then the equilibrium condition is given by
$$
\pm 2 x \pm 3 y \pm 5 z=12
$$
The plus sign before an unknown, for example $x$, means that the 2 kg weights are placed on the opposite pan from the 12 kg load. Otherwise, a minus sign is used. Keeping the same notation, we assume that $x, y$, and $z$ are integers that can take negative values, with $|x| \leq 4,|y| \leq 3,|z| \leq 2$. In this case, the equilibrium condition takes the form of the equation
$$
2 x+3 y+5 z=12
$$
Let $z=t \in[-2 ; 2]$. Then, solving the Diophantine equation,
$2 x+3 y=12-5 t \rightarrow\left\{\begin{array}{c}x=5 t-12-3 s \\ y=12-5 t+2 s, s \in Z\end{array}\right.$
Case 1. $t=-2$
$\left\{\begin{array}{c}x=-22-3 s \\ y=22+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|22+3 s| \leq 4 \rightarrow s=-8,-7,-6 \\ |22+2 s| \leq 3 \rightarrow s=-13,-12,-11,-10\end{array} \rightarrow s \in \varnothing\right.\right.$
Case 2. $t=-1$
$\left\{\begin{array}{c}x=-17-3 s \\ y=17+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|17+3 s| \leq 4 \rightarrow s=-5,-6,-7 \\ |17+2 s| \leq 3 \rightarrow s=-7,-8,-9,-10\end{array} \rightarrow s_{1}=-7 \rightarrow\left\{\begin{array}{c}x=4 \\ y=3 \\ z=-1\end{array}\right.\right.\right.$
Case 3. $t=0$
$\left\{\begin{array}{c}x=-12-3 s \\ y=12+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|12+3 s| \leq 4 \rightarrow s=-5,-4,-3 \\ |12+2 s| \leq 3 \rightarrow s=-7,-6,-5\end{array} \rightarrow s_{2}=-5 \rightarrow\left\{\begin{array}{l}x=3 \\ y=2 \\ z=0\end{array}\right.\right.\right.$
Case 4. $t=1$
$\left\{\begin{array}{c}x=-7-3 s \\ y=7+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|7+3 s| \leq 4 \rightarrow s=-1,-2,-3 \\ |7+2 s| \leq 3 \rightarrow s=-2,-3,-4,-5\end{array} \rightarrow s_{3}=-2 \rightarrow\left\{\begin{array}{l}x=-1 \\ y=3, s_{4}=-3 \\ z=1\end{array} \rightarrow\left\{\begin{array}{l}x=2 \\ y=1 \\ z=1\end{array}\right.\right.\right.\right.$
Case 5. $t=2$
$\left\{\begin{array}{c}x=-2-3 s \\ y=2+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{l}|2+3 s| \leq 4 \rightarrow s=0,-1,-2 \\ |2+2 s| \leq 3 \rightarrow s=0,-1,-2\end{array} \rightarrow s_{5}=0 \rightarrow\left\{\begin{array}{l}x=-2 \\ y=2,2 \\ z=2\end{array},-1 \rightarrow\left\{\begin{array}{l}x=1 \\ y=0 \\ z=2\end{array}\right.\right.\right.\right.$
$s_{7}=-2 \rightarrow\left\{\begin{array}{c}x=4 \\ y=-2 \\ z=2\end{array}\right.$
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Subtract the second equation from the first:
$x^{2}-2 x+y^{4}-8 y^{3}+24 y^{2}-32 y=-17 \rightarrow(x-1)^{2}+(y-2)^{4}=0 \rightarrow\left\{\begin{array}{l}x=1 \\ y=2\end{array}\right.$
Then $z=x^{2}+y^{4}-8 y^{3}=1+16-64=-47$
|
Answer: the only solution is $x=1, y=2, z=-47$.
|
-47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Express z from the first equation and substitute into the second:
$x^{2}-2 x+y^{2}-2 \sqrt{3} y=-4 \rightarrow(x-1)^{2}+(y-\sqrt{3})^{2}=0 \rightarrow\left\{\begin{array}{c}x=1 \\ y=\sqrt{3}\end{array} \rightarrow z=x^{2}+y^{2}+2 x=6\right.$
|
Answer: $x=1, y=\sqrt{3}, z=6$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. The administration divided the region into several districts based on the principle: the population of a large district exceeds $8 \%$ of the region's population and for any large district, there are two non-large districts with a combined population that is larger. Into what minimum number of districts was the region divided?
|
Answer: 8 districts.
Solution. The number of "small" districts is no less than 2 according to the condition, and their population does not exceed $8 \%$ of the total population of the region. We will show that the number of districts in the region is no less than 8. If the number of districts in the region is no more than 7, but there are no more than 5 "large" districts with a population of less than $16 \%$ each. Then the total population of the region cannot amount to $100 \%$. Indeed, $2 \cdot 8 \%+5 \cdot 16 \%=96 \%<100 \%$. Thus, the number of districts in the region is no less than 8. A division into 8 districts is possible, for example, $8 \%+8 \%+14 \%+14 \%+14 \%+14 \%+14 \%+14 \%=100 \%$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Point $M$ is located on side $CD$ of a square such that $CM: MD=1: 3$. Line $AM$ intersects the circumcircle of the square at point $E$. The area of triangle $ACE$ is 14. Find the side length of the square.
|
Answer: 10.
Solution.
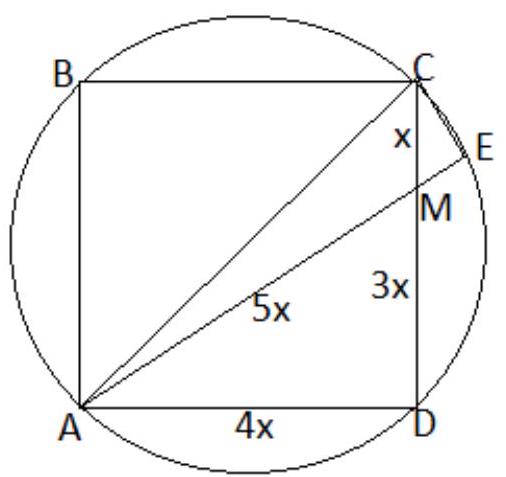
Triangles $A M D$ and $C M E$ are similar with a similarity coefficient $k=5$. Then
$$
C E=\frac{4 x}{5}, M E=\frac{3 x}{5} \rightarrow A E=5 x+\frac{3 x}{5}=\frac{28}{5} x
$$
Triangle $A C E$ is a right triangle, therefore:
$$
S_{A C E}=\frac{1}{2} A E \cdot C E=\frac{1}{2} \cdot \frac{28}{5} \cdot \frac{4}{5} x^{2}=14 \rightarrow x^{2}=\frac{25}{4} \rightarrow x=\frac{5}{2} \rightarrow A D=4 x=10
$$
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Seven students in the class receive one two every two days of study, and nine other students receive one two every three days each. The rest of the students in the class never receive twos. From Monday to Friday, 30 new twos appeared in the journal. How many new twos will appear in the class journal on Saturday?
|
Answer: 9
Solution. Over the period from Monday to Saturday (six days), in the journal, there will be 3 new twos from each student of the first group (seven people) and 2 new twos from each of the 9 students of the second group. The total number of new twos for the school week is $7 \cdot 3 + 9 \cdot 2 = 39$. Then, on Saturday, the journal will have $39 - 30 = 9$ new twos.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Through the vertex $B$ of an equilateral triangle $ABC$, a line $L$ is drawn, intersecting the extension of side $AC$ beyond point $C$. On line $L$, segments $BM$ and $BN$ are laid out, each equal in length to the side of triangle $ABC$. The lines $MC$ and $NA$ intersect at a common point $D$ and intersect the sides $AB$ and $BC$ of the triangle at points $P$ and $Q$ respectively. Prove that a circle can be circumscribed around quadrilateral $PBQD$. Find the radius of this circle if the length of segment $PQ$ is $\sqrt{3}$.
|
# Answer: 1.
Solution. Triangles $M B C$ and $A B N$ are isosceles, therefore
$$
\begin{gathered}
\angle B M C = \angle B C M = \alpha \rightarrow \angle N B C = 2 \alpha, \angle B A N = \angle B N A = \beta \rightarrow \angle A B M = 2 \beta \\
2 \alpha + 2 \beta + 60^{\circ} = 180^{\circ} \rightarrow \alpha + \beta = 60^{\circ}
\end{gathered}
$$
In triangle $M D N$, angle $P D Q$ is $180^{\circ} - \alpha - \beta = 120^{\circ}$, and the sum of the opposite angles of quadrilateral $P B Q D$ is $180^{\circ}$, so a circle can be circumscribed around it.
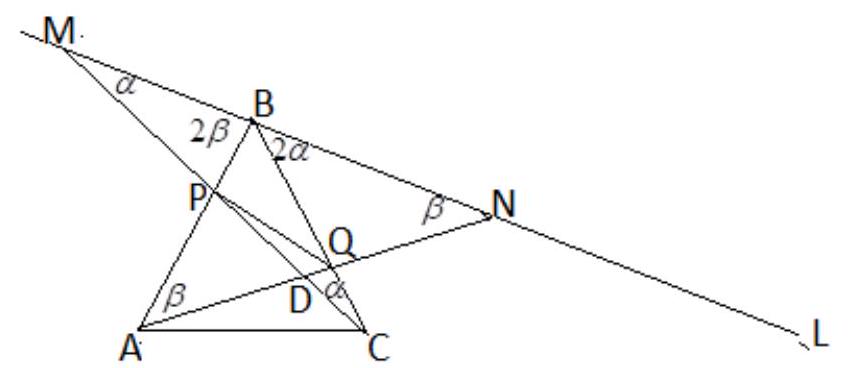
By the Law of Sines, $P Q = 2 R \sin 120^{\circ} = \sqrt{3} \rightarrow R = 1$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
16. The last digit of a six-digit number was moved to the beginning (for example, $456789 \rightarrow$ 945678), and the resulting six-digit number was added to the original number. Which numbers from the interval param 1 could have resulted from the addition? In the answer, write the sum of the obtained numbers.
| param1 | Answer |
| :---: | :---: |
| $[891870 ; 891899]$ | |
| $[375355 ; 375380]$ | |
| $[427411 ; 427434]$ | |
| $[639619 ; 639647]$ | |
|
16. The last digit of a six-digit number was moved to the beginning (for example, $456789 \rightarrow$ 945678), and the resulting six-digit number was added to the original number. Which numbers from the interval param 1 could have resulted from the addition? In the answer, write the sum of the obtained numbers.
| param1 | Answer |
| :---: | :---: |
| $[891870 ; 891899]$ | 1783771 |
| $[375355 ; 375380]$ | 750739 |
| $[427411 ; 427434]$ | 854843 |
| $[639619 ; 639647]$ | 1279267 |
|
1279267
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+11 x+23$.
|
Answer: 22.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+11 x+23>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-46)>0$, from which $-2<x<46$. On this interval, there are 45 natural values of $x: x=1, x=2, \ldots, x=45$. In this interval, $y$ takes integer values only for even $x$ - a total of 22 possibilities. Thus, we get 22 points belonging to the parabola, both of whose coordinates are natural numbers.
|
22
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can be repeated) so that the resulting 12-digit number is divisible by 45. In how many ways can this be done?
|
Answer: 13122.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We will choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $2 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=13122$.
|
13122
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{4}+3 x+\frac{253}{4}$.
|
Answer: 11.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+3 x+\frac{253}{4}>0 \Leftrightarrow-\frac{1}{4}(x+11)(x-23)>0$, from which $-11<x<23$. On this interval, there are 22 natural values of $x: x=1, x=2, \ldots, x=22$. During this interval, $y$ takes integer values only for even $x$ - a total of 11 possibilities. Therefore, we get 11 points belonging to the parabola, both of whose coordinates are natural numbers.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 18. In how many ways can this be done?
|
Answer: 3645.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6$ or 8 (5 ways).
To ensure divisibility by nine, we proceed as follows. Choose three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0, 1, 2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $5 \cdot 9 \cdot 9 \cdot 9 \cdot 1 = 3645$.
|
3645
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+9 x+19$.
|
Answer: 18.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+9 x+19>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-38)>0$, from which $-2<x<38$. On this interval, there are 37 natural values of $x: x=1, x=2, \ldots, x=37$. In this interval, $y$ takes integer values only for even $x$ - a total of 18 possibilities. Thus, we get 18 points belonging to the parabola, both of whose coordinates are natural numbers.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 45. In how many ways can this be done?
|
Answer: 1458.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We select three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $2 \cdot 9 \cdot 9 \cdot 9 \cdot 1=1458$ ways.
|
1458
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+5 x+39$.
|
Answer: 12.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+5 x+39>0 \Leftrightarrow-\frac{1}{4}(x+6)(x-26)>0$, from which $-6<x<26$. On this interval, there are 25 natural values of $x: x=1, x=2, \ldots, x=25$. In this interval, $y$ takes integer values only for even $x$ - a total of 12 possibilities. Therefore, we get 12 points belonging to the parabola, both of whose coordinates are natural numbers.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done?
|
Answer: 26244.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $2, 4, 6$ or 8 (4 ways).
To ensure divisibility by nine, we proceed as follows. Choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $4 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=26244$.
|
26244
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+13 x+42$.
|
Answer: 13.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+13 x+42>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-42)>0$, from which $-3<x<42$. On this interval, there are 41 natural values of $x: x=1, x=2, \ldots, x=41$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 13 possibilities. Thus, we get 13 points belonging to the parabola, both of whose coordinates are natural numbers.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-7 x^{2}+7 x=1$, respectively.
|
Answer: 34.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-7\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-7 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-6 x+1\right)=0,
$$
from which $x=1$ or $x=3 \pm \sqrt{8}$. The largest root is $a=3+\sqrt{8}$, and the smallest is $-b=3-\sqrt{8}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{3+\sqrt{8}}{3-\sqrt{8}}+\frac{3-\sqrt{8}}{3+\sqrt{8}}=\frac{(3+\sqrt{8})^{2}+(3-\sqrt{8})^{2}}{(3+\sqrt{8})(3-\sqrt{8})}=\frac{2(9+8)}{1}=34
$$
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 * *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. Choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+7 x+54$.
|
Answer: 8.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+7 x+54>0 \Leftrightarrow-\frac{1}{3}(x+6)(x-27)>0$, from which $-6<x<27$. On this interval, there are 26 natural values of $x: x=1, x=2, \ldots, x=26$. In this interval, $y$ takes integer values only when $x$ is divisible by 3 - a total of 8 possibilities. Therefore, we get 8 points on the parabola, both of whose coordinates are natural numbers.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{p}{q}+\frac{q}{p}$, where $p$ and $q$ are the largest and smallest roots of the equation $x^{3}+6 x^{2}+6 x=-1$, respectively.
|
Answer: 23.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}+1\right)+6\left(x^{2}+x\right)=0 \Leftrightarrow(x+1)\left(x^{2}-x+1\right)+6 x(x+1)=0 \Leftrightarrow(x+1)\left(x^{2}+5 x+1\right)=0 \text {, }
$$
from which $x=-1$ or $x=\frac{-5 \pm \sqrt{21}}{2}$. The largest root is $p=\frac{-5+\sqrt{21}}{2}$, and the smallest is $-q=\frac{-5-\sqrt{21}}{2}$. Then
$$
\frac{p}{q}+\frac{q}{p}=\frac{-5+\sqrt{21}}{-5-\sqrt{21}}+\frac{-5-\sqrt{21}}{-5+\sqrt{21}}=\frac{(-5+\sqrt{21})^{2}+(-5-\sqrt{21})^{2}}{(-5-\sqrt{21})(-5+\sqrt{21})}=\frac{2(25+21)}{4}=23 .
$$
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,6,7,8$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 2160.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6, 8$ (5 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $5 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2160$ ways.
|
2160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+5 x+72$.
|
Answer: 7.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+5 x+72>0 \Leftrightarrow-\frac{1}{3}(x+9)(x-24)>0$, from which $-9<x<24$. On this interval, there are 23 natural values of $x: x=1, x=2, \ldots, x=23$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-9 x^{2}+9 x=1$, respectively.
|
Answer: 62.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-9\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-9 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-8 x+1\right)=0
$$
from which $x=1$ or $x=4 \pm \sqrt{15}$. The largest root is $a=4+\sqrt{15}$, the smallest is $-b=4-\sqrt{15}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{4+\sqrt{15}}{4-\sqrt{15}}+\frac{4-\sqrt{15}}{4+\sqrt{15}}=\frac{(4+\sqrt{15})^{2}+(4-\sqrt{15})^{2}}{(4+\sqrt{15})(4-\sqrt{15})}=\frac{2(16+15)}{1}=62
$$
|
62
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 15. In how many ways can this be done?
|
# Answer: 864.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 2=864$ ways.
|
864
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+20 x+63$.
|
Answer: 20.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+20 x+63>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-63)>0$, from which $-3<x<63$. On this interval, there are 62 natural values of $x: x=1, x=2, \ldots, x=62$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 20 possibilities. Thus, we get 20 points belonging to the parabola, both of whose coordinates are natural numbers.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{p}{q}+\frac{q}{p}$, where $p$ and $q$ are the largest and smallest roots of the equation $x^{3}-8 x^{2}+8 x=1$, respectively.
|
# Answer: 47.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-8\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-8 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-7 x+1\right)=0 \text {, }
$$
from which $x=1$ or $x=\frac{7 \pm \sqrt{45}}{2}$. The largest root is $p=\frac{7+\sqrt{45}}{2}$, and the smallest is $-q=\frac{7-\sqrt{45}}{2}$. Then
$$
\frac{p}{q}+\frac{q}{p}=\frac{7+\sqrt{45}}{7-\sqrt{45}}+\frac{7-\sqrt{45}}{7+\sqrt{45}}=\frac{(7+\sqrt{45})^{2}+(7-\sqrt{45})^{2}}{(7+\sqrt{45})(7-\sqrt{45})}=\frac{2(49+45)}{4}=47
$$
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 1728.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 8$ (4 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $4 \cdot 6 \cdot 6 \cdot 6 \cdot 2=1728$ ways.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+50$.
|
Answer: 7.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+50>0 \Leftrightarrow x^{2}<450$, from which $-\sqrt{450}<x<\sqrt{450}$. On this interval, there are 21 natural values of $x: x=1, x=2, \ldots, x=21$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 75. In how many ways can this be done?
|
Answer: 2592.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit from the available options (1 way).
To ensure divisibility by three, we proceed as follows. Select four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and choose the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $1 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=2592$ ways.
|
2592
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Plot on the plane $(x ; y)$ the set of points satisfying the equation $|15 x|+|8 y|+|120-15 x-8 y|=120$, and find the area of the resulting figure.
|
Answer: 60.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 1 5 x \geq 0 , } \\
{ 8 y \geq 0 , } \\
{ 1 2 0 - 1 5 x - 8 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
15 x+8 y \leq 120
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(8 ; 0), G(0 ; 15), N(0 ; 0)$, the area of which is equal to 60.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+70$.
|
Answer: 4.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+70>0 \Leftrightarrow x^{2}<210$, from which $-\sqrt{210}<x<\sqrt{210}$. On this interval, there are 14 natural values of $x: x=1, x=2, \ldots, x=14$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 4 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can repeat) so that the resulting 11-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 1296.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0, 4, or 8 as the last digit (3 ways).
To ensure divisibility by 3, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $3 \cdot 6 \cdot 6 \cdot 6 \cdot 2=1296$ ways.
|
1296
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|3 x|+|4 y|+|48-3 x-4 y|=48$, and find the area of the resulting figure.
|
Answer: 96.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 3 x \geq 0 , } \\
{ 4 y \geq 0 , } \\
{ 4 8 - 3 x - 4 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
3 x+4 y \leq 48
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(16 ; 0), G(0 ; 12), N(0 ; 0)$, the area of which is equal to 96.
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+33$.
|
Answer: 5.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+33>0 \Leftrightarrow x^{2}<297$, from which $-\sqrt{297}<x<\sqrt{297}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 07 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,6,7$ (digits can repeat) so that the resulting 11-digit number is divisible by 75. In how many ways can this be done?
|
# Answer: 432.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit (1 way) from the available options.
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fifth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get that in total $1 \cdot 6 \cdot 6 \cdot 6 \cdot 2=432$ ways.
|
432
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Plot on the plane $(x ; y)$ the set of points satisfying the equation $|5 x|+|12 y|+|60-5 x-12 y|=60$, and find the area of the resulting figure.
|
Answer: 30.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 5 x \geq 0 } \\
{ 1 2 y \geq 0 , } \\
{ 6 0 - 5 x - 1 2 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
5 x+12 y \leq 60
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(12 ; 0), G(0 ; 5), N(0 ; 0)$, the area of which is 30.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the plane $x O y$ that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+98$
|
Answer: 5.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+98>0 \Leftrightarrow x^{2}<294$, from which $-\sqrt{294}<x<\sqrt{294}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0 or 4 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|4 x|+|3 y|+|24-4 x-3 y|=24$, and find the area of the resulting figure.
#
|
# Answer: 24.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 4 x \geq 0 , } \\
{ 3 y \geq 0 , } \\
{ 2 4 - 4 x - 3 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
4 x+3 y \leq 24
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(6 ; 0), G(0 ; 8), N(0 ; 0)$, the area of which is 24.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 20-gon $M$. Find the number of quadruples of vertices of this 20-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 765.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{20}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{20}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 9 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 10 parallel chords. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{10} K_{11}$, a total of 10 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 8 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 9 parallel chords. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments. There are also 10 such sets.
In total, we get $10 \cdot 45 + 10 \cdot 36 = 810$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 10 diameters with vertices at the given points, thus we get $C_{10}^{2}=45$ rectangles. Therefore, we have $810 - 45 = 765$ quadrilaterals with at least one pair of parallel sides.
|
765
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 291000, such that $k^{2}-1$ is divisible by 291.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 97)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 97. Let's consider two cases.
a) $(k+1): 97$, i.e., $k=97 p+96, p \in \mathrm{Z}$. Then we get $(97 p+95)(97 p+97):(3 \cdot 97) \Leftrightarrow(97 p+95)(p+1): 3$. The first factor is divisible by 3 when $p=3 q+1, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=291 q+193, k=291 q+290, q \in \mathrm{Z}$.
b) $(k-1): 97$, i.e., $k=97 p+1, p \in \mathrm{Z}$. Then we get $97 p(97 p+2):(3 \cdot 97) \Leftrightarrow(97 p+2) p ; 3$. The first factor is divisible by 3 when $p=3 q+1, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=291 q+98$, $k=291 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders of $193, 290, 98, 1$ when divided by 291, meaning that every 4 out of 291 consecutive numbers fit. Since $291000=291 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 16-gon $M$. Find the number of quadruples of vertices of this 16-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 364.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{16}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{16}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 7 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 8 parallel chords. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{8} K_{9}$ - a total of 8 such sets.
Now, let's take a chord connecting vertices that are one apart, for example, $K_{6} K_{8}$. There are 6 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 7 parallel chords. From these, we can form $C_{7}^{2}=21$ pairs of parallel segments. There are also 8 such sets.
In the end, we get $8 \cdot 28 + 8 \cdot 21 = 392$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{8}^{2}=28$ rectangles. Therefore, we have $392 - 28 = 364$ quadrilaterals with at least one pair of parallel sides.
|
364
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 445000, such that $k^{2}-1$ is divisible by 445. Answer: 4000.
|
Solution. Factoring the dividend and divisor, we get the condition $(k-1)(k+1):(5 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathrm{Z}$. Then we get $(89 p+87)(89 p+89):(5 \cdot 89) \Leftrightarrow(89 p+87)(p+1): 5$. The first factor is divisible by 5 when $p=5 q+2, q \in \mathrm{Z}$, and the second when $p=5 q+4, q \in \mathrm{Z}$, from which we obtain that $k=445 q+276, k=445 q+444, q \in Z$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathrm{Z}$. Then we get $89 p(89 p+2):(5 \cdot 89) \Leftrightarrow(89 p+2) p: 5$. The first factor is divisible by 5 when $p=5 q+2, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=445 q+179$, $k=445 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $276, 444, 179, 1$ when divided by 445, meaning that every 4 out of 445 consecutive numbers fit. Since $445000=445 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 22-gon $M$. Find the number of quadruples of vertices of this 22-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 1045.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{22}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{22}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 10 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 11 chords parallel to each other. From these, we can form $C_{11}^{2}=55$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{11} K_{12}$ - a total of 11 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 9 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments. There are also 11 such sets.
In the end, we get $11 \cdot 55 + 11 \cdot 45 = 1100$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 11 diameters with vertices at the given points, thus we get $C_{11}^{2}=55$ rectangles. Therefore, we have $1100 - 55 = 1045$ quadrilaterals with at least one pair of parallel sides.
|
1045
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 485000, such that $k^{2}-1$ is divisible by 485.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(5 \cdot 97)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 97. Let's consider two cases.
a) $(k+1): 97$, i.e., $k=97 p+96, p \in \mathrm{Z}$. Then we get $(97 p+95)(97 p+97):(5 \cdot 97) \Leftrightarrow(97 p+95)(p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathrm{Z}$, and the second when $p=5 q+4, q \in \mathrm{Z}$, from which we obtain that $k=485 q+96, k=485 q+484, q \in \mathrm{Z}$.
b) $(k-1): 97$, i.e., $k=97 p+1, p \in \mathrm{Z}$. Then we get $97 p(97 p+2):(5 \cdot 97) \Leftrightarrow(97 p+2) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=485 q+389$, $k=485 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $96,484,389,1$ when divided by 485, meaning that every 4 out of 485 consecutive numbers fit. Since $485000=485 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 18-gon $M$. Find the number of quadruples of vertices of this 18-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 540.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{18}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{18}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 8 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{9} K_{10}$ - a total of 9 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 7 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 8 chords parallel to each other. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments. There are also 9 such sets.
In the end, we get $9 \cdot 36 + 9 \cdot 28 = 576$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{9}^{2}=36$ rectangles. Therefore, we have $576 - 36 = 540$ quadrilaterals with at least one pair of parallel sides.
|
540
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 267000, such that $k^{2}-1$ is divisible by 267.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathbb{Z}$. Then we get $(89 p+87)(89 p+89):(3 \cdot 89) \Leftrightarrow (89 p+87)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second factor is divisible by 3 when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=267 q+88, k=267 q+266, q \in \mathbb{Z}$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathbb{Z}$. Then we get $89 p(89 p+2):(3 \cdot 89) \Leftrightarrow (89 p+2) p \vdots 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathbb{Z}$, and the second factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, from which we obtain that $k=267 q+179$, $k=267 q+1, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $88, 266, 179, 1$ when divided by 267, meaning that every 4 out of 267 consecutive numbers fit. Since $267000=267 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $5 x^{2}-6 x y+y^{2}=6^{100}$.
|
Answer: 19594.
Solution: By factoring the left and right sides of the equation, we get $(5 x-y)(x-y)=2^{100} \cdot 3^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
5 x - y = 2 ^ { k } \cdot 3 ^ { l }, \\
x - y = 2 ^ { 1 0 0 - k } \cdot 3 ^ { 1 0 0 - l }
\end{array} \text { or } \left\{\begin{array}{l}
5 x-y=-2^{k} \cdot 3^{l}, \\
x-y=-2^{100-k} \cdot 3^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=2^{k-2} \cdot 3^{l}-2^{98-k} \cdot 3^{100-l} \\
y=2^{k-2} \cdot 3^{l}-5 \cdot 2^{98-k} \cdot 3^{100-l}
\end{array}\right.
$$
Consider the first equation. The exponents in the powers of three are non-negative. The sum of the exponents in the powers of two is 96, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $2 \leq k \leq 98,0 \leq l \leq 100-$ a total of $97 \cdot 101=9797$ options.
The second system also has 9797 solutions; thus, there are 19594 solutions in total.
|
19594
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $6 x^{2}-7 x y+y^{2}=10^{100}$.
|
Answer: 19998.
Solution: By factoring the left and right sides of the equation, we get $(6 x-y)(x-y)=2^{100} \cdot 5^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
6 x - y = 2 ^ { k } \cdot 5 ^ { l } , \\
x - y = 2 ^ { 1 0 0 - k } \cdot 5 ^ { 1 0 0 - l }
\end{array} \text { or } \left\{\begin{array}{l}
6 x-y=-2^{k} \cdot 5^{l} \\
x-y=-2^{100-k} \cdot 5^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=2^{k} \cdot 5^{l-1}-2^{100-k} \cdot 5^{99-l} \\
y=2^{k} \cdot 5^{l-1}-6 \cdot 2^{100-k} \cdot 5^{99-l}
\end{array}\right.
$$
Consider the first equation. The exponents of the powers of two are non-negative. The sum of the exponents of the powers of five is 98, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $0 \leq k \leq 100,1 \leq l \leq 99$ - a total of $99 \cdot 101=9999$ options.
The second system also has 9999 solutions; thus, there are 19998 solutions in total.
|
19998
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $x^{2}+6 x y+5 y^{2}=10^{100}$.
|
Answer: 19594.
Solution: By factoring the left and right sides of the equation, we get $(x+5 y)(x+y)=2^{100} \cdot 5^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
x+5 y=2^{k} \cdot 5^{l}, \\
x+y=2^{100-k} \cdot 5^{100-l}
\end{array} \text { or } \left\{\begin{array}{l}
x+5 y=-2^{k} \cdot 5^{l}, \\
x+y=-2^{100-k} \cdot 5^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
y=2^{k-2} \cdot 5^{l}-2^{98-k} \cdot 5^{100-l} \\
x=5 \cdot 2^{98-k} \cdot 5^{100-l}-2^{k-2} \cdot 5^{l}
\end{array}\right.
$$
Consider the first equation. The exponents of the powers of five are non-negative. The sum of the exponents of the powers of two is 96, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $2 \leq k \leq 98,0 \leq l \leq 100-$ a total of $97 \cdot 101=9797$ options.
The second system also has 9797 solutions; thus, there are 19594 solutions in total.
|
19594
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $x^{2}+7 x y+6 y^{2}=15^{50}$.
|
Answer: 4998.
Solution: Factoring the left and right sides of the equation, we get $(x+6 y)(x+y)=5^{50} \cdot 3^{50}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
x+6 y=5^{k} \cdot 3^{l}, \\
x+y=5^{50-k} \cdot 3^{50-l}
\end{array} \text { or } \left\{\begin{array}{l}
x+6 y=-5^{k} \cdot 3^{l}, \\
x+y=-5^{50-k} \cdot 3^{50-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 50]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=6 \cdot 5^{49-k} \cdot 3^{50-l}-5^{k-1} \cdot 3^{l} \\
y=5^{k-1} \cdot 3^{l}-5^{49-k} \cdot 3^{50-l}
\end{array}\right.
$$
Consider the first equation. The exponents in the powers of three are non-negative. The sum of the exponents in the powers of five is 48, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $1 \leq k \leq 49, 0 \leq l \leq 50$ - a total of $49 \cdot 51=2499$ options.
"Phystech-2015", 10th grade, solutions to ticket 8
The second system also has 2499 solutions; thus, there are 4998 solutions in total.
|
4998
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 242400, such that $k^{2}+2 k$ is divisible by 303. Answer: 3200.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k+2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k+2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p+2):(3 \cdot 101) \Leftrightarrow p(101 p+2): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+202, q \in \mathrm{Z}$.
b) $(k+2): 101$, i.e., $k=101 p+99, p \in Z$. Then we get $(101 p+99)(101 p+101):(3 \cdot 101) \Leftrightarrow(101 p+99)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=303 q+99, k=303 q+301, q \in Z$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 202, 99, 301$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $242400=303 \cdot 800$, we get $4 \cdot 800=3200$ numbers.
|
3200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 20-gon $M$. Find the number of quadruples of vertices of this 20-gon that are the vertices of trapezoids.
|
Answer: 720.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{20}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{20}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 9 more chords parallel to it ( $K_{5} K_{8}$ and so on), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{10} K_{11}$, a total of 10 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 8 more chords parallel to it ( $K_{5} K_{9}$ and so on), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments. There are also 10 such sets.
In total, we get $10 \cdot 45 + 10 \cdot 36 = 810$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle are diameters, and there are 10 diameters with vertices at the given points, thus we have $C_{10}^{2}=45$ rectangles. Subtracting twice the number of rectangles, we get $810 - 90 = 720$ quadrilaterals that have at least one pair of parallel sides.
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 16-gon $M$. Find the number of quadruples of vertices of this 16-gon that are the vertices of trapezoids.
|
Answer: 336.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{16}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{16}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 7 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 8 parallel chords. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{8} K_{9}$, a total of 8 such sets.
Now, let's take a chord connecting vertices that are one apart, for example, $K_{6} K_{8}$. There are 6 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 7 parallel chords. From these, we can form $C_{7}^{2}=21$ pairs of parallel segments. There are also 8 such sets.
In the end, we get $8 \cdot 28 + 8 \cdot 21 = 392$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus yielding $C_{8}^{2}=28$ rectangles. Subtracting twice the number of rectangles, we get $392 - 56 = 336$ quadrilaterals that have at least one pair of parallel sides.
|
336
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 333300, such that $k^{2}-2 k$ is divisible by 303. Answer: 4400.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k-2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-2):(3 \cdot 101) \Leftrightarrow p(101 p-2): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+1, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+101, q \in \mathrm{Z}$.
b) $(k-2): 101$, i.e., $k=101 p+2, p \in \mathrm{Z}$. Then we get $(101 p+2) 101 p:(3 \cdot 101) \Leftrightarrow(101 p+2) p: 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=303 q+204$, $k=303 q+2, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 204, 2$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $333300=303 \cdot 1100$, we get $4 \cdot 1100=4400$ numbers.
|
4400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 22-gon $M$. Find the number of quadruples of vertices of this 22-gon that are the vertices of trapezoids.
|
Answer: 990.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{22}$ in a circle. Each trapezoid side is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{22}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 10 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 11 chords parallel to each other. From these, we can form $C_{11}^{2}=55$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{11} K_{12}$ - a total of 11 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 9 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments. There are also 11 such sets.
In total, we get $11 \cdot 55 + 11 \cdot 45 = 1100$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle are diameters, and there are 11 diameters with vertices at the given points, thus there are $C_{11}^{2}=55$ rectangles. Subtracting twice the number of rectangles, we get $1100 - 110 = 990$ quadrilaterals with at least one pair of parallel sides.
|
990
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 454500, such that $k^{2}-k$ is divisible by 505. Answer: 3600.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k-1)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-1):(5 \cdot 101) \Leftrightarrow p(101 p-1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathrm{Z}$, and the second when $p=5 q+1, q \in \mathrm{Z}$, from which we obtain that $k=505 q, k=505 q+101, q \in \mathrm{Z}$.
b) $(k-1): 101$, i.e., $k=101 p+1, p \in \mathrm{Z}$. Then we get $(101 p+1) 101 p:(5 \cdot 101) \Leftrightarrow(101 p+1) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=505 q+405$, $k=505 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 405, 1$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $454500=505 \cdot 900$, we get $4 \cdot 900=3600$ numbers.
|
3600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 18-gon $M$. Find the number of quadruples of vertices of this 18-gon that are the vertices of trapezoids.
|
Answer: 504.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{18}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{18}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 8 more chords parallel to it ( $K_{5} K_{8}$ and so on), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{9} K_{10}$ - a total of 9 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 7 more chords parallel to it ( $K_{5} K_{9}$ and so on), i.e., we get a set of 8 chords parallel to each other. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments. There are also 9 such sets.
In the end, we get $9 \cdot 36 + 9 \cdot 28 = 576$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{9}^{2}=36$ rectangles. Subtracting twice the number of rectangles, we get $576 - 72 = 504$ quadrilaterals that have at least one pair of parallel sides.
|
504
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find the number of integer solutions ( $x ; y ; z$ ) of the equation param 1 , satisfying the condition param 2.
| param1 | param2 | |
| :---: | :---: | :---: |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=2160$ | $\|x+y+z\| \leq 60$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=12960$ | $\|x+y+z\|<71$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=6000$ | $\|x+y+z\| \leq 102$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=36000$ | $\|x+y+z\|<87$ | |

|
12. Find the number of integer solutions ( $x ; y ; z$ ) of the equation param 1 , satisfying the condition param 2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=2160$ | $\|x+y+z\| \leq 60$ | 60 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=12960$ | $\|x+y+z\|<71$ | 70 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=6000$ | $\|x+y+z\| \leq 102$ | 102 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=36000$ | $\|x+y+z\|<87$ | 86 |
|
86
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | |
|
17. It is known that the number $a$ satisfies the equation param 1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param 1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | 2 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | -2 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | 4 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | -4 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. In a football tournament held in a single round-robin format (each team must play each other exactly once), $N$ teams are participating. At some point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | |
| :---: | :---: |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 15 | |
| | |

|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | Answer |
| :---: | :---: |
| 10 | 63 |
| 11 | 69 |
| 12 | 75 |
| 13 | 81 |
| 15 | 93 |
| | |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "Yes" answer?
| param1 | param2 | |
| :---: | :---: | :---: |
| 105 | 53 | |
| 129 | 65 | |
| :---: | :---: | :---: |
| 167 | 84 | |
| 125 | 63 | |
| 207 | 104 | |
|
20. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "True" answer?
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 105 | 53 | 54 |
| 129 | 65 | 66 |
| :---: | :---: | :---: |
| 167 | 84 | 85 |
| 125 | 63 | 64 |
| 207 | 104 | 105 |
|
54
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | |
| 20 | 210 | |
| 22 | 250 | |
| 24 | 300 | |
| 26 | 330 | |
|
18. For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | 108 |
| 20 | 210 | 99 |
| 22 | 250 | 117 |
| 24 | 300 | 143 |
| 26 | 330 | 148 |
|
108
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Find param 1 given param 2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| maximum $2 x+y$ | $\|4 x-3 y\|+5 \sqrt{x^{2}+y^{2}-20 y+100}=30$ | |
| maximum $x+2 y$ | $\|4 y-3 x\|+5 \sqrt{x^{2}+y^{2}+20 y+100}=40$ | |
| maximum $2 y-x$ | $\|4 y+3 x\|+5 \sqrt{x^{2}+y^{2}+10 x+25}=15$ | |
| maximum $x-5 y$ | $\|5 x-12 y\|+13 \sqrt{x^{2}+y^{2}-26 y+169}=156$ | |
| minimum $y-5 x$ | $\|5 y-12 x\|+13 \sqrt{x^{2}+y^{2}+26 x+169}=156$ | |
|
20. Find param 1 given param2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| maximum $2 x+y$ | $\|4 x-3 y\|+5 \sqrt{x^{2}+y^{2}-20 y+100}=30$ | 16 |
| maximum $x+2 y$ | $\|4 y-3 x\|+5 \sqrt{x^{2}+y^{2}+20 y+100}=40$ | -12 |
| maximum $2 y-x$ | $\|4 y+3 x\|+5 \sqrt{x^{2}+y^{2}+10 x+25}=15$ | 8 |
| maximum $x-5 y$ | $\|5 x-12 y\|+13 \sqrt{x^{2}+y^{2}-26 y+169}=156$ | -5 |
| minimum $y-5 x$ | $\|5 y-12 x\|+13 \sqrt{x^{2}+y^{2}+26 x+169}=156$ | 5 |
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the table, there are 140 different cards with numbers $3,6,9, \ldots 417,420$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $7?$
|
Answer: 1390.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a common difference of 3. Therefore, the remainders when these numbers are divided by 7 alternate. Indeed, if one of these numbers is divisible by 7, i.e., has the form $7k$, where $k \in \mathbb{N}$, then the numbers following it are $7k+3, 7k+6, 7k+9=7(k+1)+2, 7k+12=7(k+1)+5, 7k+15=7(k+2)+1, 7k+18=7(k+2)+4$, which give remainders $2, 4, 6, 1, 3, 5$ respectively when divided by 7. Next comes the number $7k+21$, which is divisible by 7, and then the remainders repeat. Thus, the remainders when the given numbers are divided by 7 go in the order $\ldots 0; 3; 6; 2; 5; 1; 4; 0 \ldots$
Among the 140 given numbers, there are 20 numbers that give remainders $0, 1, 2, 3, 4, 5, 6$ when divided by 7.
The sum of two numbers can be divisible by 7 in the following cases.
1) Both numbers are divisible by 7. There are 20 cards with such numbers, and we need to choose 2 of them - there are $C_{20}^{2} = \frac{1}{2} \cdot 20 \cdot 19 = 190$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 7 - then the other must give a remainder of 6 when divided by 7. This pair of numbers can be chosen in $20 \cdot 20 = 400$ ways.
3) One of the numbers gives a remainder of 2 when divided by 7 - then the other gives a remainder of 5, and, similarly to the second case, there are 400 ways to choose 2 numbers.
4) One of the numbers gives a remainder of 3 when divided by 7 - then the other gives a remainder of 4 - also 400 ways.
In total, there are 1390 ways.
|
1390
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|x-1|+|5-x| \leqslant 4 \\
\frac{x^{2}-6 x+2 y+7}{y+x-4} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 4.
Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $x<1$. Then $1-x+5-x \leqslant 4 \Leftrightarrow x \geqslant 1$, i.e., there are no solutions.
2) $1 \leqslant x \leqslant 5$. Then $x-1+5-x \leqslant 4 \Leftrightarrow 4 \leqslant 4$, which is always true, so the solution is $x \in [1; 5]$.
3) $x>5$. Then $x-1+x-5 \leqslant 4 \Leftrightarrow x \leqslant 5$, i.e., there are no solutions.
Combining the results, we get that $x \in [1; 5]$.
Now let's move to the second inequality. The denominator of the fraction in its left part is zero at points belonging to the line $\ell$ with the equation $y=4-x$ (in this case, the inequality is not satisfied, as the fraction is undefined). The numerator of the fraction is zero when $x^{2}-6 x+2 y+7=0 \Leftrightarrow y=\frac{1}{2}(x-2)^{2}-1$. This set of points is a parabola with branches upwards and the vertex at point $C(2; -1)$. The points of intersection of the line and the parabola can be determined from the system of equations $\left\{\begin{array}{l}y=4-x, \\ x^{2}-6 x+2 y+7=0\end{array} \Leftrightarrow\left\{\begin{array}{l}y=4-x, \\ x^{2}-8 x+15=0 .\end{array}\right.\right.$ From this, we get two points $-A(5; -1)$ and $C(3; 1)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points below the parabola and above the line (in this case, the numerator is negative, and the denominator is positive);
- at points above the parabola and below the line (the numerator is positive, and the denominator is negative).
Considering also the restriction $x \in [1; 5]$ from the first inequality, we get that the set $M$ is the union of two sets $M_{1}$ and $M_{2}$; the first of which is a curvilinear triangle $B C D$, where $B(1; -1)$ and $D(1; 3)$ are the points of intersection of the line $x=1$ with the parabola and the line $\ell$ respectively (its sides are segments $C D, B D$ and the arc of the parabola $B C$), and the second is the region bounded by the segment $A C$ and the arc of the parabola $A C$ (all points of the line $A C$ do not belong to the set, while the other boundary points do belong).
From the symmetry of the parabola relative to its axis (i.e., the line $x=3$), it follows that the area of the figure $M_{3}$, bounded by the segment $B C$ and the arc of the parabola $B C$, is equal to the area of $M_{2}$. But $M_{1} \cup M_{3}=\triangle B C D$, and the area of this triangle is easy to find: $S_{\triangle B C D}=\frac{1}{2} \cdot 4 \cdot 2=4$.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the table, there are 210 different cards with numbers $2,4,6, \ldots 418,420$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $7?$
|
Answer: 3135.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 7 alternate. Indeed, if one of these numbers is divisible by 7, i.e., has the form $7k$, where $k \in \mathbb{N}$, then the following numbers are $7k+2, 7k+4, 7k+6, 7k+8=7(k+1)+1, 7k+10=7(k+1)+3, 7k+12=7(k+1)+5$, giving remainders $2, 4, 6, 1, 3, 5$ respectively when divided by 7. Next comes the number $7k+14$, which is divisible by 7, and then the remainders repeat. Thus, the remainders of the given numbers when divided by 7 go in the order $\ldots 0; 2; 4; 6; 1; 3; 5; 0 \ldots$
Among the 210 given numbers, there are 30 numbers each that give remainders $0, 1, 2, 3, 4, 5, 6$ when divided by 7.
The sum of two numbers can be divisible by 7 in the following cases.
1) Both numbers are divisible by 7. There are 30 cards with such numbers, and we need to choose 2 of them - there are $C_{30}^{2} = \frac{1}{2} \cdot 30 \cdot 29 = 435$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 7 - then the other must give a remainder of 6 when divided by 7. This pair of numbers can be chosen in $30 \cdot 30 = 900$ ways.
3) One of the numbers gives a remainder of 2 when divided by 7 - then the other gives a remainder of 5, and, similarly to the second case, we get 900 ways to choose 2 numbers.
4) One of the numbers gives a remainder of 3 when divided by 7 - then the other gives a remainder of 4 - also 900 ways.
In total, there are 3135 ways.
|
3135
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|y|+|4-y| \leqslant 4 \\
\frac{y^{2}+x-4 y+1}{2 y+x-7} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $y < 0$. Then $-y-4+y \leqslant 4 \Leftrightarrow -4 \leqslant 4$, which is always true, so $y \in (-\infty, 0)$.
2) $0 \leqslant y \leqslant 4$. Then $y-4+y \leqslant 4 \Leftrightarrow 2y \leqslant 8 \Leftrightarrow y \leqslant 4$, so $y \in [0, 4]$.
3) $y > 4$. Then $y-4+y \leqslant 4 \Leftrightarrow y \leqslant 4$, which means there are no solutions.
Combining the results, we get that $y \in [0, 4]$.
Now, let's move to the second inequality. The denominator of the fraction on its left side is zero at points belonging to the line $x=7-2y$ (let's call it $\ell$; the inequality is not satisfied here because the fraction is undefined). The numerator of the fraction is zero when $x+y^2-4y+1=0 \Leftrightarrow x=-(y-2)^2+3$. This set of points is a parabola with branches to the left and a vertex at point $C(3, 2)$. Note that the parabola and the line intersect the x-axis at points $B(-1, 0)$ and $D(7, 0)$, respectively. The points of intersection of the line $\ell$ and the parabola can be determined from the system of equations $\left\{\begin{array}{l}x=7-2y, \\ x=-y^2+4y-1\end{array} \Leftrightarrow \Leftrightarrow\left\{\begin{array}{l}x=7-2y, \\ y^2-6y+8=0 .\end{array}\right.\right.$
From this, we get two points $-A(-1, 4)$ and $C(3, 2)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points to the right of the parabola and above the line (where both the numerator and the denominator of the fraction are positive);
- at points to the left of the parabola and below the line (where both the numerator and the denominator of the fraction are negative).
Considering also the restriction $y \in [0, 4]$ from the first inequality, we get that the set $M$ is the union of two sets $M_1$ and $M_2$; the first is a curvilinear triangle $BCD$ (its sides are segments $CD$, $BD$, and the arc of the parabola $BC$), and the second is the region bounded by the segment $AC$ and the arc of the parabola $AC$ (all points of the line $AC$ do not belong to the set, while all other boundary points do).
From the symmetry of the parabola relative to its axis (i.e., the line $y=2$), it follows that the area of the figure $M_3$, bounded by the segment $BC$ and the arc of the parabola $BC$, is equal to the area of $M_2$. But $M_1 \cup M_3 = \triangle BCD$, and the area of this triangle is easy to find: $S_{\triangle BCD} = \frac{1}{2} \cdot 8 \cdot 2 = 8$.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 200 different cards with numbers $2,3,2^{2}, 3^{2}, \ldots, 2^{100}, 3^{100}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a cube of an integer?
|
Answer: 4389.
Solution. To obtain the cube of a natural number, it is necessary and sufficient for each factor to enter the prime factorization of the number in a power that is a multiple of 3.
Suppose two cards with powers of two are chosen. We have 33 exponents divisible by 3 $(3,6,9, \ldots, 99)$, 34 exponents giving a remainder of 1 when divided by 3 $(1,4,7, \ldots, 100)$, and 33 exponents giving a remainder of 2 when divided by 3 $(2,5,8, \ldots, 98)$. We need the sum of the exponents to be a multiple of 3. For the sum of two natural numbers to be divisible by 3, we can either choose two numbers divisible by 3 $\left(C_{33}^{2}=\frac{33 \cdot 32}{2}=528\right.$ ways $)$, or take one number giving a remainder of 1 when divided by 3 and one number giving a remainder of 2 when divided by 3 $(34 \cdot 33=1122$ ways). We get $528+1122=1650$ ways.
The number of ways when the exponents on both chosen cards are powers of three is exactly the same, i.e., 1650.
If one card with a power of two and one card with a power of three are taken, then both exponents must be divisible by 3 - we get $33 \cdot 33=1089$ ways.
In total: $1650+1650+1089=4389$ ways.
|
4389
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
y-x \geqslant|x+y| \\
\frac{x^{2}+8 x+y^{2}+6 y}{2 y-x-8} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. The first inequality is equivalent to the system ${ }^{1}$ $\left\{\begin{array}{l}x+y \leqslant y-x, \\ x+y \geqslant x-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x \leqslant 0, \\ y \geqslant 0 .\end{array}\right.\right.$
Consider the second inequality. It can be written as $\frac{(x+4)^{2}+(y+3)^{2}-25}{2 y-x-8} \leqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at the point $Q(-4 ;-3)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=4+\frac{x}{2}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array}{l}
x = 2 y - 8 \\
x ^ { 2 } + 8 x + y ^ { 2 } + 6 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x = 2 y - 8 \\
( 2 y - 8 ) ^ { 2 } + 8 ( 2 y - 8 ) + y ^ { 2 } + 6 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=2 y-8 \\
y^{2}-2 y=0
\end{array}\right.\right.\right.
$$
from which we get two points $A(-4 ; 2)$ and $B(-8 ; 0)$. Also denote the origin by $O$, and the intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ; 4)$).
The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located above the line $\ell$ (the numerator is negative, and the denominator is positive);
- outside the circle $\omega$ at points located below the line $\ell$ (the numerator is positive, and the denominator is negative).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located above this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located above the chord $A B$ is equal to the segment of the circle located above the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 4 \cdot 4=8$.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 100 different cards with numbers $2,5,2^{2}, 5^{2}, \ldots, 2^{50}, 5^{50}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a cube of an integer?
|
Answer: 1074.
Solution. To obtain the cube of a natural number, it is necessary and sufficient for each factor to enter the prime factorization of the number in a power that is a multiple of 3.
Suppose two cards with powers of two are chosen. We have 16 exponents that are divisible by 3 $(3,6,9, \ldots, 48)$, 17 exponents that give a remainder of 1 when divided by $3(1,4,7, \ldots, 49)$, and 17 exponents that give a remainder of 2 when divided by $3(2,5,8, \ldots, 50)$. We need the sum of the exponents to be a multiple of 3. For the sum of two natural numbers to be divisible by 3, we can either choose two numbers that are divisible by $3\left(C_{16}^{2}=\frac{16 \cdot 15}{2}=120\right)$, or take one number that gives a remainder of 1 when divided by 3 and one number that gives a remainder of 2 when divided by $3(17 \cdot 17=289$ ways). We get $120+289=409$ ways.
The number of ways when the powers of five are written on both chosen cards is exactly the same, i.e., 409.
If one card with a power of two and one card with a power of five are taken, then both exponents must be divisible by 3 - we get $16 \cdot 16=256$ ways.
In total: $409+409+256=1074$ ways.
|
1074
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
x+y+|x-y| \leqslant 0 \\
\frac{x^{2}+6 x+y^{2}-8 y}{x+3 y+6} \geqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 3.
Solution. The first inequality is equivalent to the system $\left\{\begin{array}{l}x-y \leqslant-x-, \\ x-y \geqslant x+y\end{array} \Leftrightarrow\left\{\begin{array}{l}x \leqslant 0, \\ y \leqslant 0 .\end{array}\right.\right.$
Consider the second inequality. It can be written as $\frac{(x+3)^{2}+(y-4)^{2}-25}{x+3 y+6} \geqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at the point $Q(-3 ; 4)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=-2-\frac{x}{3}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array} { l }
{ x = - 3 y - 6 , } \\
{ x ^ { 2 } + 6 x + y ^ { 2 } - 8 y = 0 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x = - 3 y - 6 } \\
{ ( 3 y + 6 ) ^ { 2 } - 6 ( 3 y + 6 ) + y ^ { 2 } - 8 y = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=-3 y-6 \\
y^{2}+y=0
\end{array}\right.\right.\right.
$$
from which we obtain two points $A(-3 ;-1)$ and $B(-6 ; 0)$. Also denote the origin by $O$, and the intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ;-2)$).
The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located below the line $\ell$ (the numerator and denominator are negative);
- outside the circle $\omega$ at points located above the line $\ell$ (the numerator and denominator are positive).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located below this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located below the chord $A B$ is equal to the segment of the circle located below the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 3 \cdot 2=3$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two parabolas param 1 and param 2 touch at a point lying on the $O x$ axis. Through point $D$, the second intersection point of the first parabola with the $O x$ axis, a vertical line is drawn, intersecting the second parabola at point $A$ and the common tangent to the parabolas at point $B$. Find the ratio $D A: D B$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $y=x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | |
| $y=2 x^{2}+a x+b$ | $y=-5 x^{2}+c x+d$ | |
| $y=x^{2}+a x+b$ | $y=-6 x^{2}+c x+d$ | |
| $y=2 x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | |
|
1. Two parabolas param 1 and param 2 touch at a point lying on the $O x$ axis. Through point $D$, the second intersection point of the first parabola with the $O x$ axis, a vertical line is drawn, intersecting the second parabola at point $A$ and the common tangent to the parabolas at point $B$. Find the ratio $D A: D B$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $y=x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | 4 |
| $y=2 x^{2}+a x+b$ | $y=-5 x^{2}+c x+d$ | 3.5 |
| $y=x^{2}+a x+b$ | $y=-6 x^{2}+c x+d$ | 7 |
| $y=2 x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | 2.5 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the smallest possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :--- |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-6 x^{2}+14 x+2=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+6 x^{2}+15 x+27=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}+3 x^{2}+7 x+17=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}-3 x^{2}+8 x+5=0$ | |
|
7. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the smallest possible value of the sum $a+b$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-6 x^{2}+14 x+2=0$ | 3 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+6 x^{2}+15 x+27=0$ | -3 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}+3 x^{2}+7 x+17=0$ | 1 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}-3 x^{2}+8 x+5=0$ | -1 |
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "Yes" answer?
| param1 | param2 | |
| :---: | :---: | :---: |
| 120 | 60 | |
|
9. On the table, there are param 1 visually identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee that you will get at least one "Yes" answer?
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 120 | 60 | 63 |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the maximum possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | |
|
17. It is known that the number $a$ satisfies the equation param 1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param 1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | 2 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | -2 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | 4 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | -4 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | |
| :---: | :---: |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 15 | |
|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | Answer |
| :---: | :---: |
| 10 | 63 |
| 11 | 69 |
| 12 | 75 |
| 13 | 81 |
| 15 | 93 |
| | |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point $(60 ; 45)$. Find the number of such squares.
|
Answer: 2070.
Solution. Draw through the given point $(60 ; 45)$ vertical and horizontal lines $(x=60$ and $y=45)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 45 ways: $(60 ; 0),(60 ; 1), \ldots,(60 ; 44)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=60$ and $y=45$ divide the plane. Consider the “lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $15 \leqslant x \leqslant 59,0 \leqslant y \leqslant 44$. We get $45^{2}$ ways.
The total number of ways is $45^{2}+45=46 \cdot 45=2070$.
|
2070
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the coordinate plane, consider squares all of whose vertices have natural coordinates, and the center is located at the point $(55 ; 40)$. Find the number of such squares.
|
Answer: 1560.
Solution. Draw through the given point $(55 ; 40)$ vertical and horizontal lines $(x=55$ and $y=40)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 39 ways: $(55 ; 1),(55 ; 1), \ldots,(55 ; 39)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=55$ and $y=40$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be natural, it is necessary and sufficient for this vertex to fall into the square $16 \leqslant x \leqslant 54,1 \leqslant y \leqslant 39$. We get $39^{2}$ ways.
The total number of ways is $39^{2}+39=39 \cdot 40=1560$.
|
1560
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $x^{2}+x y=30000000$.
|
Answer: 256.
Solution. By factoring the left and right sides of the equation, we get $x(x+y)=$ $3 \cdot 2^{7} \cdot 5^{7}$. Then, if $x>0$, $x$ is one of the divisors of the right side. The right side has a total of $2 \cdot 8 \cdot 8=128$ divisors (since any divisor can be represented as $3^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 7, and 7, respectively, i.e., there are 2 ways to choose $a$, 8 ways to choose $b$, and 8 ways to choose $c$). Note that if the right side is divisible by $x$, then it automatically follows that $y \in \mathbb{Z}$, and $y$ is uniquely determined. Therefore, there are a total of $2 \cdot 128=256$ pairs of numbers.
|
256
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 70, 1 \leqslant b \leqslant 50$, and at the same time,
the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 1260.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b \vdots 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 14 values of $a$ and 10 values of $b$ that are multiples of 5. Therefore, there are $14 \cdot 50=700$ pairs $(a ; b)$ such that $a \vdots 5$ and $10 \cdot 70=700$ pairs such that $b \vdots 5$. Additionally, there are $14 \cdot 10=140$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $700+700-140=1260$.
|
1260
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that for three consecutive natural values of the argument, the quadratic function $f(x)$ takes the values 6, 14, and 14, respectively. Find the greatest possible value of $f(x)$.
|
Answer: 15.
Solution. Let $n, n+1, n+2$ be the three given consecutive values of the argument. Since a quadratic function takes the same values at points symmetric with respect to the x-coordinate of the vertex of the parabola $x_{\text{v}}$, then $x_{\text{v}}=n+1.5$, and thus $f(x)$ can be represented as $f(x)=a(x-n-1.5)^{2}+c$. Since $f(n)=6, f(n+1)=14$, we get $\frac{9}{4} a+c=6, \frac{a}{4}+c=14$, from which $a=-4, c=15$. But $c=f\left(x_{\text{v}}\right)$ and is the maximum value of the function.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two equal rectangles $P Q R S$ and $P_{1} Q_{1} R_{1} S_{1}$ are inscribed in triangle $A B C$ (with points $P$ and $P_{1}$ lying on side $A B$, points $Q$ and $Q_{1}$ lying on side $B C$, and points $R, S, R_{1}$ and $S_{1}$ lying on side $A C$). It is known that $P S=3, P_{1} S_{1}=9$. Find the area of triangle $A B C$.
|
Answer: 72.
Solution. Draw the height $B F$ of triangle $A B C$. Let it intersect segments $P Q$ and $P_{1} Q_{1}$ at points $H$ and $M$ respectively. Note that $H M=6$. From the similarity of triangles $B P Q$ and $B P_{1} Q_{1}$, it follows that $\frac{B H}{P Q}=\frac{B M}{P_{1} Q_{1}}$ (the ratio of the height to the base is written), from which $\frac{B H}{3}=\frac{6+B H}{9}, B H=3$. Therefore, the area of triangle $B P Q$ is $\frac{1}{2} \cdot 3 \cdot 3=\frac{9}{2}$. But triangles $A B C$ and $B P Q$ are similar (the similarity coefficient is $B F: B H=12: 3=4$), hence the area of triangle $A B C$ is $16 \cdot \frac{9}{2}=72$.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $y^{2}-x y=700000000$.
|
Answer: 324.
Solution. Factoring the left and right sides of the equation, we get $y(y-x)=$ $7 \cdot 2^{8} \cdot 5^{8}$. Then if $y>0$, $y$ is one of the divisors of the right side. The right side has a total of $2 \cdot 9 \cdot 9=162$ divisors (since any divisor can be represented as $7^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 8, and 8, respectively, i.e., there are 2 ways to choose $a$, 9 ways to choose $b$, and 9 ways to choose $c$). Note that if the right side is divisible by $y$, then it automatically follows that $x \in \mathbb{Z}$, and in this case, $x$ is uniquely determined. Therefore, there are a total of $2 \cdot 162=324$ pairs of numbers.
|
324
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 80,1 \leqslant b \leqslant 30$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 864.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 16 values of $a$ and 6 values of $b$ that are multiples of 5. Therefore, there are $16 \cdot 30=480$ pairs $(a ; b)$ such that $a: 5$ and $6 \cdot 80=480$ pairs such that $b: 5$. Additionally, there are $16 \cdot 6=96$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $480+480-96=864$.
|
864
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 267000, such that $k^{2}-1$ is divisible by 267. Answer: 4000.
|
Solution. Factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathrm{Z}$. Then we get $(89 p+87)(89 p+89):(3 \cdot 89) \Leftrightarrow(89 p+87)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=267 q+88, k=267 q+266, q \in \mathrm{Z}$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathrm{Z}$. Then we get $89 p(89 p+2):(3 \cdot 89) \Leftrightarrow(89 p+2) p: 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=267 q+179$, $k=267 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $88,266,179,1$ when divided by 267, meaning that every 4 out of 267 consecutive numbers fit. Since $267000=267 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 242400, such that $k^{2}+2 k$ is divisible by 303.
|
Answer: 3200.
Solution. By factoring the dividend and divisor, we get the condition $k(k+2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k+2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p+2):(3 \cdot 101) \Leftrightarrow p(101 p+2) \vdots 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=303 q, k=303 q+202, q \in \mathbb{Z}$.
b) $(k+2): 101$, i.e., $k=101 p+99, p \in \mathbb{Z}$. Then we get $(101 p+99)(101 p+101):(3 \cdot 101) \Leftrightarrow (101 p+99)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=303 q+99, k=303 q+301, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders 0, 202, 99, 301 when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $242400=303 \cdot 800$, we get $4 \cdot 800=3200$ numbers.
|
3200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 353500, such that $k^{2}+k$ is divisible by 505.
|
Answer: 2800.
Solution: By factoring the dividend and divisor, we get the condition $k(k+1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k+1)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p+1):(5 \cdot 101) \Leftrightarrow p(101 p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, from which we get $k=505 q, k=505 q+404, q \in \mathbb{Z}$.
b) $(k+1): 101$, i.e., $k=101 p+100, p \in \mathbb{Z}$. Then we get $(101 p+100)(101 p+101):(5 \cdot 101) \Leftrightarrow (101 p+100)(p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, from which we get $k=505 q+100, k=505 q+504, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 404, 100, 504$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $353500=505 \cdot 700$, we get $4 \cdot 700=2800$ numbers.

Answer: $(8 ; 2)$.
Solution: Transform the equation of the system (add $64 x^{2}+64 y^{2}$ to both sides):
$$
\begin{gathered}
\left(x^{2}+y^{2}\right)^{2}+144+24 x^{2}+24 y^{2}=64 x^{2}+64 y^{2}+128 x y \Leftrightarrow\left(x^{2}+y^{2}+12\right)^{2}=(8 x+8 y)^{2} \Leftrightarrow \\
\Leftrightarrow\left[\begin{array}{l}
x^{2} + y^{2} + 12 = 8 x + 8 y, \\
x^{2} + y^{2} + 12 = -8 x - 8 y
\end{array} \Leftrightarrow \left[\begin{array}{l}
(x-4)^{2}+(y-4)^{2}=20, \\
(x+4)^{2}+(y+4)^{2}=20 .
\end{array}\right.\right.
\end{gathered}
$$
We get two circles of radius $2 \sqrt{5}$ with centers at points $(4 ; 4)$ and $(-4 ;-4)$.
The inequality in the system defines a half-plane. Consider the relative positions of each circle with the line $y=2 x-14$, which is the boundary of this half-plane.
a) $\left\{\begin{array}{l}(x-4)^{2}+(y-4)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}(x-4)^{2}+(2 x-18)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}5 x^{2}-80 x+320=0, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}x=8, \\ y=2 .\end{array}\right.\right.\right.\right.$
b) $\left\{\begin{array}{l}(x+4)^{2}+(y+4)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}(x+4)^{2}+(2 x-10)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}5 x^{2}-32 x+96=0, \\ y=2 x-14\end{array} \Leftrightarrow \varnothing\right.\right.\right.$.
In this case, the centers of the considered circles, the points $(4 ; 4)$ and $(-4 ;-4)$, do not lie in the half-plane, as their coordinates do not satisfy the inequality. Therefore, the second circle has no common points with the half-plane, while the first circle has a unique common point $(8 ; 2)$.
|
2800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 333300, such that $k^{2}-2 k$ is divisible by 303. Answer: 4400.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k-2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-2):(3 \cdot 101) \Leftrightarrow p(101 p-2) \vdots 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+1, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+101, q \in \mathrm{Z}$.
b) $(k-2): 101$, i.e., $k=101 p+2, p \in \mathrm{Z}$. Then we get $(101 p+2) 101 p:(3 \cdot 101) \Leftrightarrow(101 p+2) p \vdots 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=303 q+204$, $k=303 q+2, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 204, 2$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $333300=303 \cdot 1100$, we get $4 \cdot 1100=4400$ numbers.
|
4400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 454500, such that $k^{2}-k$ is divisible by 505.
|
Answer: 3600.
Solution. By factoring the dividend and divisor, we get the condition $k(k-1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k-1)$ is divisible by 101. Let's consider two cases.
a) $k \vdots: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p-1):(5 \cdot 101) \Leftrightarrow p(101 p-1) \vdots 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second when $p=5 q+1, q \in \mathbb{Z}$, from which we obtain that $k=505 q, k=505 q+101, q \in \mathbb{Z}$.
b) $(k-1): 101$, i.e., $k=101 p+1, p \in \mathbb{Z}$. Then we get $(101 p+1) 101 p:(5 \cdot 101) \Leftrightarrow (101 p+1) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, and the second when $p=5 q, q \in \mathbb{Z}$, from which we obtain that $k=505 q+405$, $k=505 q+1, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 405, 1$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $454500=505 \cdot 900$, we get $4 \cdot 900=3600$ numbers.
|
3600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 700. The answer should be presented as an integer.
|
Answer: 2520.
Solution. Since $700=7 \cdot 2^{2} \cdot 5^{2}$, the sought numbers can consist of the following digits: (a) two twos, two fives, one seven, and three ones, or (b) one four, two fives, one seven, and four ones. We will calculate the number of variants in each case.
(a) First, we choose two places out of eight for the twos ( $C_{8}^{2}=\frac{8!}{2!6!}$ ways), then two places out of the remaining six for the fives ( $C_{6}^{2}=\frac{6!}{4!2!}$ ways), and then one place out of the remaining four for the seven ( $C_{4}^{1}=4$ ways). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{2} \cdot C_{6}^{2} \cdot 4=\frac{8!}{3!2!2!}=1680$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!4!}=840$.
Finally, we get $840+1680=2520$ ways.
|
2520
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.