problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
28. Circles $\Omega_{1}$ and $\Omega_{2}$ of equal radii intersect at points $B$ and $C$. A point $A$ is chosen on circle $\Omega_{1}$. Ray $A B$ intersects circle $\Omega_{2}$ at point $D$ (point $B$ lies between points $A$ and $D$). On ray $D C$, a point $E$ is chosen such that $D C = C E$. Find $A E$, if param1.
| param1 | Answer |
| :---: | :---: |
| $A C=5, A D=6$ | |
| $A C=5, A D=8$ | |
| $A C=13, A D=10$ | |
| $A C=13, A D=24$ | |
|
28. Circles $\Omega_{1}$ and $\Omega_{2}$ of equal radii intersect at points $B$ and $C$. A point $A$ is chosen on circle $\Omega_{1}$. Ray $A B$ intersects circle $\Omega_{2}$ at point $D$ (point $B$ lies between points $A$ and $D$). On ray $D C$, a point $E$ is chosen such that $D C = C E$. Find $A E$, if param1.
| param1 | Answer |
| :---: | :---: |
| $A C=5, A D=6$ | 8 |
| $A C=5, A D=8$ | 6 |
| $A C=13, A D=10$ | 24 |
| $A C=13, A D=24$ | 10 |
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. On the board, there are param1 natural numbers. It is known that the sum of any five of them is not less than param2. Find the smallest possible value of the sum of all the numbers written on the board.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 20 | 117 | |
| 18 | 97 | |
| 19 | 107 | |
| 26 | 153 | |
| 17 | 123 | |
|
30. On the board, ragat1 natural numbers are written. It is known that the sum of any five of them is not less than param2. Find the smallest possible value of the sum of all numbers written on the board.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 20 | 117 | 477 |
| 18 | 97 | 357 |
| 19 | 107 | 415 |
| 26 | 153 | 804 |
| 17 | 123 | 423 |
|
477
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given quadratic trinomials $f_{1}(x)=x^{2}-a x-3, f_{2}(x)=x^{2}+2 x-b, f_{3}(x)=3 x^{2}+(2-2 a) x-6-b$ and $f_{4}(x)=3 x^{2}+(4-a) x-3-2 b$. Let the differences of their roots be $A, B, C$ and $D$ respectively. It is known that $|C| \neq|D|$. Find the ratio $\frac{A^{2}-B^{2}}{C^{2}-D^{2}}$. The values of $A, B, C, D, a, b$ are not given.
|
Answer: 3.
Solution. Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=\frac{\sqrt{T}}{|a|}$. Applying this formula four times, we get
$$
A=\sqrt{a^{2}+12}, B=\sqrt{4+4 b}, C=\frac{1}{3} \sqrt{(2-2 a)^{2}+12(6+b)}, D=\frac{1}{3} \sqrt{(4-a)^{2}+12(3+2 b)}
$$
From this, it follows that $C^{2}-D^{2}=\frac{1}{9}\left(\left(4 a^{2}-8 a+12 b+76\right)-\left(a^{2}-8 a+24 b+52\right)\right)=\frac{1}{3}\left(a^{2}-4 b+8\right), A^{2}-$ $B^{2}=a^{2}-4 b+8$. Therefore, the desired ratio is 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the table, there are 100 different cards with numbers $3, 6, 9, \ldots 297, 300$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $5?$
|
Answer: 990.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a common difference of 3. Therefore, the remainders of these numbers when divided by 5 alternate. Indeed, if one of these numbers is divisible by 5, i.e., has the form $5k$, where $k \in \mathbb{N}$, then the next number is $5k+3$ - and it gives a remainder of 3 when divided by 5; then $-5k+6=5(k+1)+1$, giving a remainder of 1 when divided by 5; then $-5k+9=5(k+1)+4$, giving a remainder of 4 when divided by 5; then $5k+12=5(k+2)+2$, giving a remainder of 2 when divided by 5; finally, the next one is $5k+15=5(k+3)$, which is again divisible by 5, after which the order of remainders repeats. Thus, the remainders of the given numbers when divided by 5 go in the order $\ldots 0 ; 3 ; 1 ; 4 ; 2 ; 0 \ldots$
Among the 100 given numbers, there are 20 numbers that give remainders of $0, 1, 2, 3, 4$ when divided by 5.
The sum of two numbers can be divisible by 5 in the following cases.
1) Both numbers are divisible by 5. There are 20 cards with such numbers, and we need to choose 2 of them - there are $C_{20}^{2}=$ $\frac{1}{2} \cdot 20 \cdot 19=190$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 5 - then the other must give a remainder of 4 when divided by 5. This pair of numbers can be chosen in $20 \cdot 20=400$ ways.
3) One of the numbers gives a remainder of 2 when divided by 5 - then the other gives a remainder of 3, and, similarly to the second case, we get 400 ways to choose 2 numbers.
In total, there are 990 ways.
|
990
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|y|+|4+y| \leqslant 4 \\
\frac{x-y^{2}-4 y-3}{2 y-x+3} \geqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $y<0$. Then $y+4-y \leqslant 4 \Leftrightarrow 4 \leqslant 4$, i.e., the solution is $y \in \mathbb{R}$, but since $y<0$, we have $y \in (-\infty; 0)$.
2) $y=0$. Then $y+4-y \leqslant 4 \Leftrightarrow 4 \leqslant 4$, i.e., the solution is $y=0$.
3) $y>0$. Then $y+4+y \leqslant 4 \Leftrightarrow y \leqslant 0$, i.e., there are no solutions.
Combining the results, we get that $y \in[-4 ; 0]$.
Now, let's move to the second inequality. The denominator of the fraction in its left part is zero at points belonging to the line $x=2 y+3$ (let's call it $\ell$; in this case, the inequality is not satisfied, as the fraction is undefined). The numerator of the fraction is zero when $x-y^{2}-4 y-3=0 \Leftrightarrow x=(y+2)^{2}-1$. This set of points is a parabola with branches to the right and the vertex at point $C(-1 ;-2)$. The points of intersection of the line and the parabola can be determined from the system of equations $\left\{\begin{array}{l}x=2 y+3, \\ x=y^{2}+4 y+3\end{array} \Leftrightarrow\left\{\begin{array}{l}x=2 y+3, \\ y^{2}+2 y=0 .\end{array}\right.\right.$ From this, we get two points - $A(3 ; 0)$ and $C(-1 ;-2)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points to the right of the parabola and above the line (in this case, both the numerator and the denominator of the fraction are positive);
- at points to the left of the parabola and below the line (both the numerator and the denominator of the fraction are negative).
Considering also the restriction $y \in[-4 ; 0]$ from the first inequality, we get that the set $M$ is the union of two sets $M_{1}$ and $M_{2}$; the first of them is a curvilinear triangle $B C D$, where $B(3 ;-4)$ and $D(-5 ;-4)$ are the points of intersection of the parabola and the line $\ell$ with the line $y=-4$ (its sides are segments $C D, B D$ and the arc of the parabola $B C$), and the second is the region bounded by the segment $A C$ and the arc of the parabola $A C$ (in this case, all points of the line $A C$ do not belong to the set, and all other boundary points do belong).
From the symmetry of the parabola relative to its axis (i.e., the line $y=-2$), it follows that the area of the figure $M_{3}$, bounded by the segment $B C$ and the arc of the parabola $B C$, is equal to the area of $M_{2}$. But $M_{1} \cup M_{3}=\triangle B C D$, and the area of this triangle is easy to find: $S_{\triangle B C D}=\frac{1}{2} \cdot 8 \cdot 2=8$.
## Ticket 2
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given quadratic trinomials $f_{1}(x)=x^{2}-2 x+a, f_{2}(x)=x^{2}+b x-2, f_{3}(x)=4 x^{2}+(b-6) x+3 a-2$ and $f_{4}(x)=4 x^{2}+(3 b-2) x-6+a$. Let the differences of their roots be $A, B, C$ and $D$ respectively. It is known that $|C| \neq|D|$. Find the ratio $\frac{A^{2}-B^{2}}{C^{2}-D^{2}}$. The values of $A, B, C, D, a, b$ are not given.
|
Answer: 2.
Solution. Let $\alpha x^{2}+\beta x+\gamma$ be a quadratic trinomial with a positive discriminant $T$. Then its roots are determined by the formula $x_{1,2}=\frac{-b \pm \sqrt{T}}{2 a}$, so $\left|x_{2}-x_{1}\right|=\left|\frac{-b+\sqrt{T}-(-b-\sqrt{T})}{2 a}\right|=\frac{\sqrt{T}}{|a|}$. Applying this formula four times, we get
$$
A=\sqrt{4-4 a}, B=\sqrt{b^{2}+8}, C=\frac{1}{4} \sqrt{(b-6)^{2}-16(3 a-2)}, D=\frac{1}{4} \sqrt{(3 b-2)^{2}-16(a-6)}
$$
From this, it follows that $C^{2}-D^{2}=\frac{1}{16}\left(\left(b^{2}-48 a-12 b+68\right)-\left(9 b^{2}-16 a-12 b+100\right)\right)=\frac{1}{2}\left(-b^{2}-4 a-4\right)$, $A^{2}-B^{2}=-b^{2}-4 a-4$. Therefore, the desired ratio is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a right triangle $ABC (\angle B=90^{\circ})$, a circle $\Gamma$ with center $I$ is inscribed, touching sides $AB$ and $BC$ at points $K$ and $L$ respectively. A line passing through point $I$ intersects sides $AB$ and $BC$ at points $M$ and $N$ respectively. Find the radius of the circle $\Gamma$ if $MK=225$, $NL=64$. Find $AC$ if it is additionally known that line $MN$ is parallel to $AC$.
|
Answer: $R=120, AC=680$.
Solution. Angles $KIM$ and $LNI$ are equal as corresponding angles when lines $BC$ and $KI$ are parallel, so right triangles $KIM$ and $LNI$ are similar. Therefore, $\frac{MK}{KI}=\frac{IL}{LN}$, or (if we denote the radius of the circle by $r$) $\frac{225}{r}=\frac{r}{64}$, from which $r=120$.
Then $BM=BK+KM=r+KM=345, BN=BL+LN=r+LN=184$, hence $MN^2=$ $345^2+184^2=23^2\left(15^2+8^2\right)=23^2 \cdot 17^2, MN=23 \cdot 17$. Let $h$ be the height of triangle $BMN$, drawn from the vertex of the right angle $B$. Then the area of triangle $BMN$ can be expressed in two ways: $2S_{\triangle BMN}=BN \cdot BM=MN \cdot h$, so $184 \cdot 345=17 \cdot 23 \cdot h, h=\frac{2760}{17}$.
If $MN \| AC$, then triangles $BAC$ and $BMN$ are similar, and the coefficient of their similarity $k$ is the ratio of the heights of these triangles, drawn from vertex $B$. It remains to note that the height of triangle $ABC$, drawn from $B$, is equal to $r+h=120+\frac{2760}{17}=\frac{4800}{17}$. Therefore, $k=\frac{h+r}{h}=\frac{4800}{17}: \frac{2760}{17}=\frac{40}{23}$ and $AC=k \cdot MN=\frac{40}{23} \cdot 23 \cdot 17=680$.
|
680
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the table, there are 150 different cards with numbers $2, 4, 6, \ldots 298, 300$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $5?$
|
Answer: 2235.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 5 alternate. Indeed, if one of these numbers is divisible by 5, i.e., has the form $5k$, where $k \in \mathbb{N}$, then the next number is $5k+2$ - and it gives a remainder of 2 when divided by 5, then $-5k+4$, giving a remainder of 4 when divided by 5, then $5k+6=5(k+1)+1$, giving a remainder of 1 when divided by 5, then $5k+8=5(k+1)+3$, giving a remainder of 3 when divided by 5; finally, the next one is $5k+10=5(k+2)$, which is again divisible by 5, after which the order of remainders repeats. Thus, the remainders of the given numbers when divided by 5 go in the order $\ldots 0 ; 2 ; 4 ; 1 ; 3 ; 0 \ldots$
Among the 150 given numbers, there are 30 numbers that give remainders of $0, 1, 2, 3, 4$ when divided by 5.
The sum of two numbers can be divisible by 5 in the following cases.
1) Both numbers are divisible by 5. There are 30 cards with such numbers, and we need to choose 2 of them - there are $C_{30}^{2}=$ $\frac{1}{2} \cdot 30 \cdot 29=435$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 5 - then the second number must give a remainder of 4 when divided by 5. This pair of numbers can be chosen in $30 \cdot 30=900$ ways.
3) One of the numbers gives a remainder of 2 when divided by 5 - then the second number gives a remainder of 3, and, similarly to the second case, we get 900 ways to choose 2 numbers.
In total, there are 2235 ways.
|
2235
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|x|+|4-x| \leqslant 4 \\
\frac{x^{2}-4 x-2 y+2}{y-x+3} \geqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 4.
Solution. Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $x<0$. Then $-x-x+4 \leqslant 4 \Leftrightarrow -2x \leqslant 0 \Leftrightarrow x \geqslant 0$, i.e., there are no solutions in this case.
2) $0 \leqslant x \leqslant 4$. Then $x-x+4 \leqslant 4 \Leftrightarrow 4 \leqslant 4$, which is always true, so all $x \in [0; 4]$ are solutions.
3) $x>4$. Then $x+x-4 \leqslant 4 \Leftrightarrow x \leqslant 4$, i.e., there are no solutions in this case either.
Combining the results, we get that $x \in [0; 4]$.
Now let's move to the second inequality. The denominator of the fraction in its left part is zero at points belonging to the line $y=x-3$ (in this case, the inequality is not satisfied, as the fraction is undefined). The numerator of the fraction is zero when $x^{2}-4 x-2 y+2=0 \Leftrightarrow y=\frac{1}{2}(x-2)^{2}-1$. This set of points is a parabola with branches upwards and vertex at point $C(2; -1)$. Note also that the parabola intersects the y-axis at point $B(0; 1)$, and the line intersects the y-axis at point $D(0; -3)$. The points of intersection of the line and the parabola can be determined from the system of equations $\left\{\begin{array}{l}y=x-3, \\ x^{2}-4 x-2 y+2=0\end{array} \Leftrightarrow\left\{\begin{array}{l}y=x-3, \\ x^{2}-6 x+8=0 .\end{array}\right.\right.$
From this, we get two points - $A(4; 1)$ and $C(2; -1)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points below the parabola and above the line (in this case, both the numerator and the denominator of the fraction are positive);
- at points above the parabola and below the line (both the numerator and the denominator of the fraction are negative).
Considering also the restriction $x \in [0; 4]$ from the first inequality, we get that the set $M$ is the union of two sets $M_{1}$ and $M_{2}$; the first of which is a curvilinear triangle $B C D$ (its sides are segments $C D, B D$ and the arc of the parabola $B C$), and the second is the region bounded by segment $A C$ and the arc of the parabola $A C$ (in this case, all points of the line $A C$ do not belong to the set, while all other boundary points do belong).
From the symmetry of the parabola relative to its axis (i.e., the line $x=2$), it follows that the area of the figure $M_{3}$, bounded by segment $B C$ and the arc of the parabola $B C$, is equal to the area of $M_{2}$. But $M_{1} \cup M_{3}=\triangle B C D$, and the area of this triangle is easy to find: $S_{\triangle B C D}=\frac{1}{2} \cdot 4 \cdot 2=4$.
The problem is considered fully solved (and the maximum number of points is awarded), only if all necessary transformations are provided in the solution text and all logical steps are fully explained; the obtained answers are also reduced to a simplified form.
The presence of a correct answer does not guarantee a positive score for the problem. A correct answer without justification does not add points.
A full and justified solution to the problem is awarded the full number of points (indicated in parentheses after the problem number). Some partial progress is evaluated according to the instructions. In other cases, the score is set at the discretion of the checker.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are 306 different cards with numbers $3,19,3^{2}, 19^{2}, \ldots, 3^{153}, 19^{153}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer?
|
Answer: 17328.
Solution. To obtain the square of a natural number, it is necessary and sufficient that each factor enters the prime factorization of the number in an even power.
Suppose two cards with powers of three are chosen. We have 76 even exponents $(2,4,6, \ldots, 152)$ and 77 odd exponents $(1,3,5, \ldots, 153)$. We need the sum of the exponents to be even. For the sum of two natural numbers to be even, we can either choose two even numbers $\left(C_{76}^{2}=\frac{76 \cdot 75}{2}=2850\right)$, or two odd numbers ( $C_{77}^{2}=\frac{77 \cdot 76}{2}=2926$ ways). We get $2850+2926=5776$ ways.
The number of ways when both chosen cards have powers of the number 19 is exactly the same, i.e., 5776.
If one card with a power of three and one card with a power of the number 19 are taken, then both exponents must be even - we get $76 \cdot 76=5776$ ways.
In total: $5776 \cdot 3=17328$ ways.
|
17328
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
x-y \geqslant|x+y| \\
\frac{x^{2}-6 x+y^{2}-8 y}{3 y-x+6} \geqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 3.
Solution. The first inequality is equivalent to the system ${ }^{1}$ $\left\{\begin{array}{l}x+y \leqslant x-y, \\ x+y \geqslant y-x\end{array} \Leftrightarrow\left\{\begin{array}{l}y \leqslant 0, \\ x \geqslant 0 .\end{array}\right.\right.$
Consider the second inequality. It can be written as $\frac{(x-3)^{2}+(y-4)^{2}-25}{3 y-x+6} \geqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at point $Q(3 ; 4)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=-2+\frac{x}{3}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array}{l}
x = 3 y + 6, \\
x ^ { 2 } - 6 x + y ^ { 2 } - 8 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x = 3 y + 6 \\
( 3 y + 6 ) ^ { 2 } - 6 ( 3 y + 6 ) + y ^ { 2 } - 8 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=3 y+6 \\
y^{2}+y=0
\end{array}\right.\right.\right.
$$
from which we obtain two points $A(3 ;-1)$ and $B(6 ; 0)$. Also, denote the origin by $O$, and the point of intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ;-2)$).
The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located below the line $\ell$ (the numerator and denominator are negative)
- outside the circle $\omega$ at points located above the line $\ell$ (the numerator and denominator are positive).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located below this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located below the chord $A B$ is equal to the segment of the circle located below the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 3 \cdot 2=3$.[^0]
## Ticket 10
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. There are 294 different cards with numbers $7, 11, 7^{2}, 11^{2}, \ldots, 7^{147}, 11^{147}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer?
|
Answer: 15987.
Solution. To obtain the square of a natural number, it is necessary and sufficient that each factor enters the prime factorization of the number in an even power.
Suppose two cards with powers of seven are chosen. We have 73 even exponents $(2,4,6, \ldots, 146)$ and 74 odd exponents $(1,3,5, \ldots, 147)$. We need the sum of the exponents to be even. For the sum of two natural numbers to be even, we can either choose two even numbers $\left(C_{73}^{2}=\frac{73 \cdot 72}{2}=2628\right.$ ways $)$, or two odd numbers $\left(C_{74}^{2}=\frac{74 \cdot 73}{2}=2701\right.$ ways $)$. We get $2628+$ $2701=5329$ ways.
The number of ways when the powers of 11 are written on both chosen cards is exactly the same, i.e., 5329.
If one card with a power of seven and one card with a power of 11 are taken, then both exponents must be even - we get $73 \cdot 73=5329$ ways.
In total: $5329 \cdot 3=15987$ ways.
|
15987
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
y+x \geqslant|x-y| \\
\frac{x^{2}-8 x+y^{2}+6 y}{x+2 y-8} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. The first inequality is equivalent to the system $\left\{\begin{array}{l}x-y \leqslant x+y, \\ x-y \geqslant-x-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geqslant 0, \\ y \geqslant 0 .\end{array}\right.\right.$.
Consider the second inequality. It can be written as $\frac{(x-4)^{2}+(y+3)^{2}-25}{x+2 y-8} \leqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at the point $Q(4 ;-3)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=4-\frac{x}{2}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array}{l}
x=8-2 y, \\
x^{2}-8 x+y^{2}+6 y=0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=8-2 y \\
(8-2 y)^{2}-8(8-2 y)+y^{2}+6 y=0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=8-2 y \\
y^{2}-2 y=0
\end{array}\right.\right.\right.
$$
from which we obtain two points $A(4 ; 2)$ and $B(8 ; 0)$. Also, denote the origin by $O$, and the intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ; 4)$). The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located above the line $\ell$ (the numerator is negative, and the denominator is positive)
- outside the circle $\omega$ at points located below the line $\ell$ (the numerator is positive, and the denominator is negative).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located above this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located above the chord $A B$ is equal to the segment of the circle located above the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 4 \cdot 4=8$.[^1]
The problem is considered fully solved (and the maximum number of points is awarded), only if all necessary transformations are provided in the solution text and all logical steps are fully explained; the answers obtained are reduced to a simplified form.
The presence of a correct answer does not guarantee a positive score for the problem. A correct answer without justification does not add points.
A full and justified solution to the problem is awarded the full number of points (indicated in parentheses after the problem number). Some partial progress is evaluated according to the instructions. In other cases, the score is set at the discretion of the checker.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $p$, for each of which the numbers $p-2$, $2 \cdot \sqrt{p}$, and $-3-p$ are respectively the first, second, and third terms of some geometric progression.
|
Answer: $p=1$.
Solution. For the given numbers to be consecutive terms of a geometric progression, it is necessary and sufficient that they are non-zero and $(2 \sqrt{p})^{2}=(p-2)(-p-3)$, from which
$$
\left\{\begin{array}{l}
p>0 \\
p^{2}+5 p-6=0
\end{array} \Leftrightarrow p=1\right.
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the number $2016 * * * * 02 * *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and the fifth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $p$, for each of which the numbers $-p-12, 2 \cdot \sqrt{p}$, and $p-5$ are respectively the first, second, and third terms of some geometric progression.
|
Answer: $p=4$.
Solution. For the specified numbers to be consecutive terms of a geometric progression, it is necessary and sufficient that they are non-zero and $(2 \sqrt{p})^{2}=(-p-12)(p-5)$, from which
$$
\left\{\begin{array}{l}
p>0, \\
p^{2}+11 p-60=0
\end{array} \Leftrightarrow p=4\right.
$$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the number $2016^{* * * *} 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,6,7,8$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done
|
Answer: 2160.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6, 8$ (5 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get a total of $5 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2160$ ways.
|
2160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $p$, for each of which the numbers $p-2$, $3 \cdot \sqrt{p}$, and $-8-p$ are respectively the first, second, and third terms of some geometric progression.
|
Answer: $p=1$.
Solution. For the given numbers to be consecutive terms of a geometric progression, it is necessary and sufficient that they are non-zero and $(3 \sqrt{p})^{2}=(p-2)(-8-p)$, from which
$$
\left\{\begin{array}{l}
p>0 \\
p^{2}+15 p-16=0
\end{array} \Leftrightarrow p=1\right.
$$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 15. In how many ways can this be done?
|
# Answer: 864.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 2=864$ ways.
|
864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all values of $p$, for each of which the numbers $-p-8$, $3 \cdot \sqrt{p}$, and $p-7$ are the first, second, and third terms, respectively, of some geometric progression.
|
Answer: $p=4$.
Solution. For the specified numbers to be consecutive terms of a geometric progression, it is necessary and sufficient that they are non-zero and $(3 \sqrt{p})^{2}=(-p-8)(p-7)$, from which
$$
\left\{\begin{array}{l}
p>0, \\
p^{2}+10 p-56=0
\end{array} \Leftrightarrow p=4\right.
$$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 1728.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 8$ (4 ways).
To ensure divisibility by 3, we proceed as follows. Select three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $4 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 1728$ ways.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|3 x|+|4 y|+|48-3 x-4 y|=48$, and find the area of the resulting figure.
#
|
# Answer: 96.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 3 x \geq 0 , } \\
{ 4 y \geq 0 , } \\
{ 4 8 - 3 x - 4 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
3 x+4 y \leq 48
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(16 ; 0), G(0 ; 12), N(0 ; 0)$, the area of which is 96.
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that $\operatorname{tg}(\alpha+2 \gamma)+2 \operatorname{tg} \alpha-4 \operatorname{tg}(2 \gamma)=0, \operatorname{tg} \gamma=\frac{1}{3}$. Find $\operatorname{ctg} \alpha$.
|
Answer: 2 or $\frac{1}{3}$.
Solution. $\operatorname{tg} 2 \gamma=\frac{2 \operatorname{tg} \gamma}{1-\operatorname{tg}^{2} \gamma}=\frac{2 / 3}{1-1 / 9}=\frac{3}{4}$. Then the given equality can be transformed as follows:
$$
\frac{\operatorname{tg} \alpha+\operatorname{tg} 2 \gamma}{1-\operatorname{tg} \alpha \operatorname{tg} 2 \gamma}+2 \operatorname{tg} \alpha-3=0 \Leftrightarrow \frac{\operatorname{tg} \alpha+\frac{3}{4}}{1-\frac{3}{4} \operatorname{tg} \alpha}+2 \operatorname{tg} \alpha-3=0
$$
By bringing to a common denominator and simplifying, we obtain the equivalent equation on the domain of definition $2 \operatorname{tg}^{2} \alpha-7 \operatorname{tg} \alpha+3=0$, from which $\operatorname{tg} \alpha=3$ or $\operatorname{tg} \alpha=\frac{1}{2}$. Both options are valid (since the denominators do not become zero). Therefore, $\operatorname{ctg} \alpha=\frac{1}{3}$ or $\operatorname{ctg} \alpha=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|5 x|+|12 y|+|60-5 x-12 y|=60$, and find the area of the resulting figure.
#
|
# Answer: 30.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 5 x \geq 0 , } \\
{ 1 2 y \geq 0 , } \\
{ 6 0 - 5 x - 1 2 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
5 x+12 y \leq 60
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(12 ; 0), G(0 ; 5), N(0 ; 0)$, the area of which is 30.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that $\operatorname{tg}(2 \alpha-\beta)-4 \operatorname{tg} 2 \alpha+4 \operatorname{tg} \beta=0, \operatorname{tg} \alpha=-3$. Find $\operatorname{ctg} \beta$.
|
Answer: -1 or $\frac{4}{3}$.
Solution. $\operatorname{tg} 2 \alpha=\frac{2 \operatorname{tg} \alpha}{1-\operatorname{tg}^{2} \alpha}=\frac{-6}{1-9}=\frac{3}{4}$. Then the given equality can be transformed as follows:
$$
\frac{\operatorname{tg} 2 \alpha-\operatorname{tg} \beta}{1+\operatorname{tg} 2 \alpha \operatorname{tg} \beta}-4 \operatorname{tg} 2 \alpha+4 \operatorname{tg} \beta=0 \Leftrightarrow \frac{\frac{3}{4}-\operatorname{tg} \beta}{1+\frac{3}{4} \operatorname{tg} \beta}-3+4 \operatorname{tg} \beta=0
$$
By bringing to a common denominator and simplifying, we obtain the equivalent equation on the domain of definition $4 \operatorname{tg}^{2} \beta+\operatorname{tg} \beta-3=0$, from which $\operatorname{tg} \beta=\frac{3}{4}$ or $\operatorname{tg} \beta=-1$. Both options are valid (since the denominators do not become zero). Therefore, $\operatorname{ctg} \beta=\frac{4}{3}$ or $\operatorname{ctg} \beta=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 1400. The answer should be presented as an integer.
|
Answer: 5880.
Solution. Since $1400=7 \cdot 2^{3} \cdot 5^{2}$, the sought numbers can consist of the following digits: (a) three twos, two fives, one seven, and two ones, (b) one four, one two, two fives, one seven, and three ones, or (c) one eight, two fives, one seven, and four ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the twos ( $C_{8}^{3}=\frac{8!}{3!5!}$ ways), then two places out of the remaining five for the fives ( $C_{5}^{2}=\frac{5!}{3!2!}$ ways), and then one place out of the remaining three for the seven ( $C_{3}^{1}=1$ way). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{3} \cdot C_{5}^{2} \cdot 3=\frac{8!}{3!2!2!}=1680$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!3!}=3360$.
(c) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!4!}=840$. Finally, we get $1680+3360+840=5880$ ways.
|
5880
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
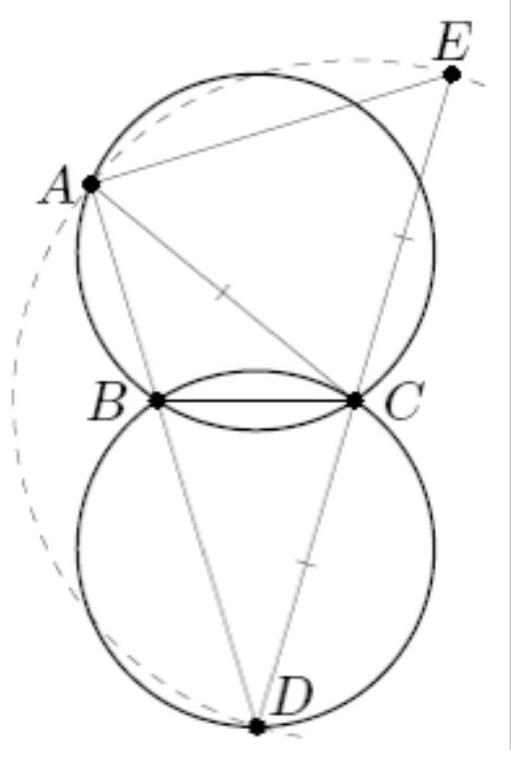
6. [5 points] Two circles of the same radius 9 intersect at points $A$ and $B$. On the first circle, a point $C$ is chosen, and on the second circle, a point $D$ is chosen. It turns out that point $B$ lies on the segment $C D$, and $\angle C A D=90^{\circ}$. On the perpendicular to $C D$ passing through point $B$, a point $F$ is chosen such that $B F=B D$ (points $A$ and $F$ are on opposite sides of the line $C D$). Find the length of the segment $C F$.
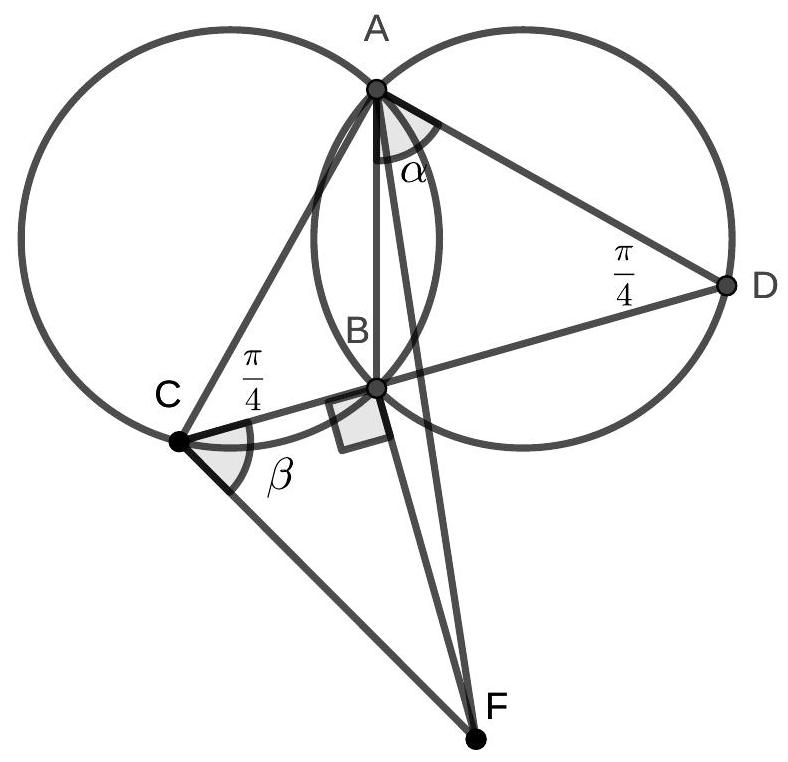
Fig. 1: variant 1, problem 6
|
Answer: 18.
Solution. Let $R=9$ be the radii of the circles given in the condition, $\angle B A D=\alpha, \angle B C F=\beta$. Then $\angle B A C=\frac{\pi}{2}-\alpha$, and by the sine rule $B D=2 R \sin \alpha, B C=2 R \sin \left(\frac{\pi}{2}-\alpha\right)=2 R \cos \alpha$. Therefore, $C F^{2}=B C^{2}+B D^{2}=4 R^{2} \cos ^{2} \alpha+4 R^{2} \sin ^{2} \alpha=4 R^{2}$, from which $C F=2 R=18$.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 7000. The answer should be presented as an integer.
|
Answer: 5600.
Solution. Since $7000=7 \cdot 2^{3} \cdot 5^{3}$, the sought numbers can consist of the following digits: (a) three twos, three fives, one seven, and one one, (b) four, two, three fives, one seven, and two ones, or (c) eight, three fives, one seven, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the twos ( $C_{8}^{3}=\frac{8!}{3!5!}$ ways), then three places out of the remaining five for the fives ( $C_{5}^{3}=\frac{5!}{3!2!}$ ways), and then one place out of the remaining two for the seven ( $C_{2}^{1}=2$ ways). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{3} \cdot C_{5}^{3} \cdot 2=\frac{8!}{3!3!}=1120$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!3!}=3360$.
(c) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$. Finally, we get $1120+3360+1120=5600$ ways.
|
5600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
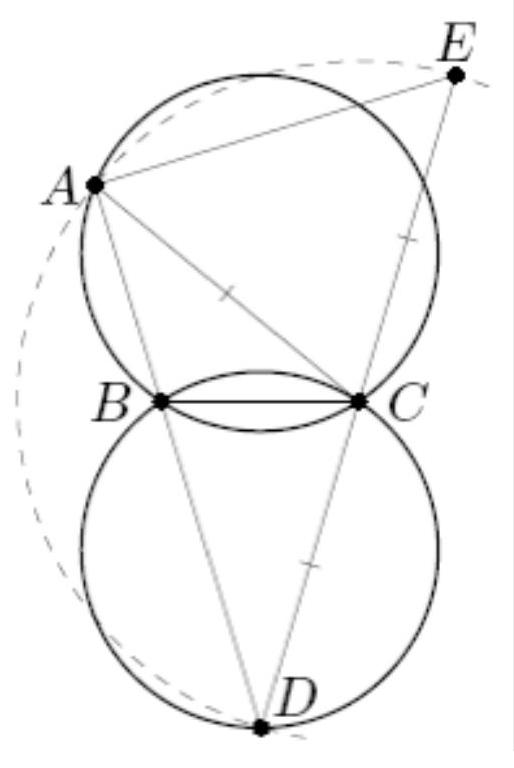
6. [5 points] Two circles of the same radius 7 intersect at points $A$ and $B$. On the first circle, a point $C$ is chosen, and on the second circle, a point $D$ is chosen. It turns out that point $B$ lies on the segment $C D$, and $\angle C A D=90^{\circ}$. On the perpendicular to $C D$ passing through point $B$, a point $F$ is chosen such that $B F=B D$ (points $A$ and $F$ are on opposite sides of the line $C D$). Find the length of the segment $C F$.
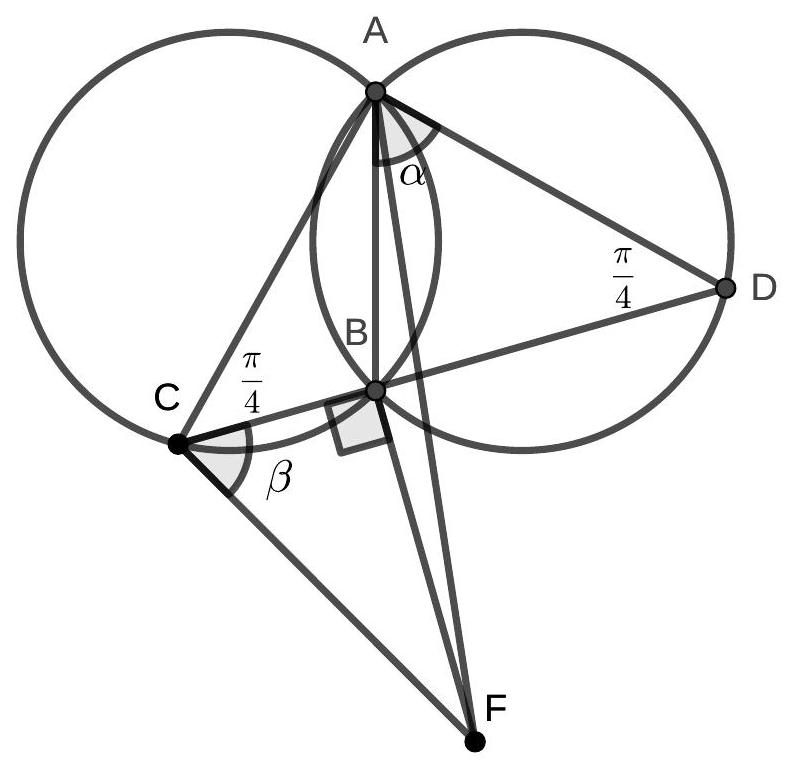
Fig. 3: variant 2, problem 6
|
Answer: 14.
Solution. Let $R=7$ be the radii of the circles given in the condition, $\angle B A D=\alpha, \angle B C F=\beta$. Then $\angle B A C=\frac{\pi}{2}-\alpha$, and by the sine rule $B D=2 R \sin \alpha, B C=2 R \sin \left(\frac{\pi}{2}-\alpha\right)=2 R \cos \alpha$. Therefore, $C F^{2}=B C^{2}+B D^{2}=4 R^{2} \cos ^{2} \alpha+4 R^{2} \sin ^{2} \alpha=4 R^{2}$, from which $C F=2 R=14$.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 59),(59 ; 59)$, and $(59 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=59-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 370330
Solution. There are two possible cases.
1) Both selected nodes lie on the lines specified in the condition. Each of them contains 58 points inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 116 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line with the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{116 \cdot 113}{2}=6554$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (116 ways). Now, let's count how many ways there are to choose the second node. In total, there are $58^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (116 nodes), as well as the nodes that lie on the same horizontal (56 nodes, considering the previously excluded diagonal nodes) or vertical (56 nodes) line with the chosen one. Therefore, the second node can be chosen in $58^{2}-116-112=$ 3136 ways, and the number of ways to choose a pair of nodes is $116 \cdot 3136=363776$.
Summarizing, we have $6554+363776=370330$ ways.
|
370330
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. [5 points] Point $D$ lies on side $A C$ of triangle $A B C$. The circle with diameter $B D$ intersects sides $A B$ and $B C$ at points $P$ and $T$ respectively. Points $M$ and $N$ are the midpoints of segments $A D$ and $C D$ respectively. It is known that $P M \| T N$.
a) Find the angle $A B C$.
b) Suppose additionally that $M P=1, N T=\frac{3}{2}, B D=\sqrt{5}$. Find the area of triangle $A B C$.
|
Answer: (a) $90^{\circ} ;$ ( $\mathbf{\text { ( ) }} 5$.
Solution. (a) Points $P$ and $T$ lie on the circle with diameter $B D$, therefore $\angle B P D=\angle B T D=90^{\circ}$. Consequently, triangles $A D P$ and $D C T$ are right-angled; $P M$ and $T N$ are their medians. Since the median of a right-angled triangle, drawn to the hypotenuse, is equal to half of it, $T N=C N=D N, P M=$ $A M=D M$. Let $\angle T C D=\gamma$. Since triangle $C T N$ is isosceles, and $\angle C T N=\gamma, \angle T N D=$ $2 \gamma$ (as the external angle of $\triangle C T N$ ). Angles $P M A$ and $T N D$ are equal due to the parallelism of lines $P M$ and $T N$. And since triangle $A M P$ is also isosceles, $\angle P A M=90^{\circ}-\frac{1}{2} \angle P M A=90^{\circ}-\frac{1}{2} \angle T N D=$ $90^{\circ}-\gamma$. Therefore, the sum of angles $A$ and $C$ of triangle $A B C$ is $90^{\circ}$, and its third angle $\angle A B C$ is also $90^{\circ}$.
(b) As stated above, $C D=2 N T=3, A D=2 M P=2$. Let $\angle A D B=\psi$. Then $\angle B D C=$ $180^{\circ}-\psi$. By the cosine theorem for triangles $A B D$ and $A C D$, we get that $A B^{2}=4+5-4 \sqrt{5} \cos \psi$, $B C^{2}=9+5-6 \sqrt{5} \cos \left(180^{\circ}-\psi\right)$. But by the Pythagorean theorem $A B^{2}+B C^{2}=A C^{2}=25$, from which it follows that $9-4 \sqrt{5} \cos \psi+14+6 \sqrt{5} \cos \psi=25, \cos \psi=\frac{1}{\sqrt{5}}$. Further, we find: $\sin \psi=\sqrt{1-\cos ^{2} \psi}=\frac{2}{\sqrt{5}}, S_{\triangle A B C}=$ $S_{\triangle A B D}+S_{\triangle B C D}=\frac{1}{2} D A \cdot D B \sin \psi+\frac{1}{2} D C \cdot D B \sin \left(180^{\circ}-\psi\right)=\frac{1}{2} A C \cdot B D \sin \psi=\frac{1}{2} \cdot 5 \cdot \sqrt{5} \cdot \frac{2}{\sqrt{5}}=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 69),(69 ; 69)$, and ( $69 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=69-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 601460.
Solution. There are two possible cases.
1) Both selected nodes lie on the specified lines. There are 68 points on each of them inside the square, and there are no duplicates among them (the intersection point of the lines has non-integer coordinates). There are 136 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). Since we counted ordered pairs of points, each pair of points was counted twice. Thus, in this case, we get $\frac{136 \cdot 133}{2}=9044$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (136 ways). Now, let's count how many ways there are to choose the second node. There are a total of $68^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (136 in total), as well as the nodes that lie on the same horizontal line as the chosen one (66 in total, considering the previously excluded diagonal nodes) or on the same vertical line (66 in total). Therefore, the second node can be chosen in $68^{2}-136-132=$ 4356 ways, and the number of ways to choose a pair of nodes is $136 \cdot 4356=592416$.
Summarizing, we have $9044+592416=601460$ ways.
|
601460
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 65),(65 ; 65)$ and ( $65 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=65-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
# Answer: 500032.
Solution. There are two possible cases.
1) Both selected nodes lie on the lines specified in the condition. There are 64 points on each of them inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 128 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{128 \cdot 125}{2}=8000$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (128 ways). Now, let's count how many ways there are to choose the second node. There are a total of $64^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (128 nodes), as well as the nodes that lie on the same horizontal (62 nodes, considering the previously excluded diagonal nodes) or vertical (62 nodes) as the chosen one. Therefore, the second node can be chosen in $64^{2}-128-124=3844$ ways, and the number of ways to choose a pair of nodes is $128 \cdot 3844=492032$.
Summarizing, we have $8000+492032=500032$ ways.
|
500032
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. [6 points] Solve the equation $\sqrt{x+1}-\sqrt{4-x}+3=2 \sqrt{4+3 x-x^{2}}$.
|
Answer: $3, \frac{3-2 \sqrt{6}}{2}$.
Solution. Let $\sqrt{x+1}-\sqrt{4-x}=t$. Squaring both sides of this equation, we get $(x+1)-2 \sqrt{(x+1)(4-x)}+(4-x)=t^{2}$, from which $2 \sqrt{4+3 x-x^{2}}=5-t^{2}$. The equation becomes $t+3=5-t^{2}$; hence $t^{2}+t-2=0$, i.e., $t=1$ or $t=-2$. We consider each case separately.
$$
\begin{aligned}
& \sqrt{x+1}-\sqrt{4-x}=1 \Leftrightarrow \sqrt{x+1}=1+\sqrt{4-x} \Leftrightarrow\left\{\begin{array}{l}
x+1=1+4-x+2 \sqrt{4-x} \\
-1 \leqslant x \leqslant 4
\end{array}\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ \sqrt { 4 - x } = x - 2 , } \\
{ - 1 \leqslant x \leqslant 4 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
4-x=x^{2}-4 x+4 \\
2 \leqslant x \leqslant 4
\end{array}\right.\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ x ^ { 2 } - 3 x = 0 , } \\
{ 2 \leqslant x \leqslant 4 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=0 \text { or } x=3, \\
2 \leqslant x \leqslant 4
\end{array} \quad \Leftrightarrow x=3 ;\right.\right. \\
& \sqrt{x+1}-\sqrt{4-x}=-2 \Leftrightarrow \sqrt{x+1}+2=\sqrt{4-x} \Leftrightarrow\left\{\begin{array}{l}
x+1+4 \sqrt{x+1}+4=4-x \\
-1 \leqslant x \leqslant 4
\end{array}\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ 4 \sqrt { x + 1 } = - 1 - 2 x , } \\
{ - 1 \leqslant x \leqslant 4 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
16 x+16=1+4 x+4 x^{2}, \\
-1 \leqslant x \leqslant-0.5
\end{array}\right.\right. \\
& \Leftrightarrow\left\{\begin{array} { l }
{ 4 x ^ { 2 } - 1 2 x - 1 5 = 0 , } \\
{ - 1 \leqslant x \leqslant - 0 . 5 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=\frac{3 \pm 2 \sqrt{6}}{2}, \\
-1 \leqslant x \leqslant-0.5
\end{array} \quad \Leftrightarrow x=\frac{3-2 \sqrt{6}}{2} .\right.\right.
\end{aligned}
$$
Thus, the equation has two roots: $x=\frac{3-2 \sqrt{6}}{2}$ and $x=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 63),(63 ; 63)$, and $(63 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=63-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 453902.
Solution. There are two possible cases.
1) Both selected nodes lie on the specified lines. There are 62 points on each of them inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 124 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{124 \cdot 121}{2}=7502$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (124 ways). Now, let's count how many ways there are to choose the second node. In total, there are $62^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (124 nodes), as well as the nodes that lie on the same horizontal (60 nodes, considering the previously excluded diagonal nodes) or vertical (60 nodes) line as the chosen one. Therefore, the second node can be chosen in $62^{2}-124-120=3600$ ways, and the number of ways to choose a pair of nodes is $124 \cdot 3600=446400$.
Summarizing, we have $7502+446400=453902$ ways.
|
453902
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. On the sides of triangle $A B C$, points were marked: 10 - on side $A B$, 11 - on side $B C$, 12 - on side $A C$. At the same time, none of the vertices of the triangle were marked. How many triangles exist with vertices at the marked points?
|
Answer: 4951.
Solution. Three points out of the 33 given can be chosen in $C_{33}^{3}=5456$ ways. In this case, a triangle is formed in all cases except when all three points lie on one side of the triangle. Thus, $C_{12}^{3}+C_{11}^{3}+C_{10}^{3}=220+165+120=505$ ways do not work. Therefore, there are $5456-505=4951$ triangles.
|
4951
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point $(50 ; 30)$. Find the number of such squares.
|
Answer: 930.
Solution. Draw through the given point $(50 ; 30)$ vertical and horizontal lines $(x=50$ and $y=30)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 30 ways: $(50 ; 0),(50 ; 1), \ldots,(50 ; 29)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four regions into which the lines $x=50$ and $y=30$ divide the plane. Consider the “lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $20 \leqslant x \leqslant 49,0 \leqslant y \leqslant 29$. We get $30^{2}$ ways.
The total number of ways is $30^{2}+30=31 \cdot 30=930$.
|
930
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the coordinate plane, squares are considered, all vertices of which have natural coordinates, and the center is located at the point $(55 ; 25)$. Find the number of such squares.
|
Answer: 600.
Solution. Draw through the given point $(55 ; 25)$ vertical and horizontal lines $(x=55$ and $y=25)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 24 ways: $(55 ; 1),(55 ; 2), \ldots,(55 ; 24)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four regions into which the lines $x=55$ and $y=25$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $31 \leqslant x \leqslant 54,1 \leqslant y \leqslant 24$. We get $24^{2}$ ways.
The total number of ways is $24^{2}+24=24 \cdot 25=600$.
|
600
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 70, 1 \leqslant b \leqslant 50$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 1260.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 14 values of $a$ and 10 values of $b$ that are multiples of 5. Therefore, there are $14 \cdot 50=$ 700 pairs $(a ; b)$ such that $a \vdots 5$ and $10 \cdot 70=700$ pairs such that $b \vdots 5$. Additionally, there are $14 \cdot 10=140$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $700+700-140=1260$.
|
1260
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Plot the figure $\Phi$ on the plane, consisting of points $(x ; y)$ of the coordinate plane such that the system of inequalities is satisfied
$$
\left\{\begin{array}{l}
\sqrt{x^{2}-3 y^{2}+4 x+4} \leqslant 2 x+1 \\
x^{2}+y^{2} \leqslant 4
\end{array}\right.
$$
Determine how many parts the figure $\Phi$ consists of.
|
Solution. The first inequality is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ x ^ { 2 } - 3 y ^ { 2 } + 4 x + 4 \leqslant 4 x ^ { 2 } + 4 x + 1 , } \\
{ ( x + 2 ) ^ { 2 } - 3 y ^ { 2 } \geqslant 0 , } \\
{ 2 x + 1 \geqslant 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x^{2}+y^{2} \geqslant 1 \\
(x+2-y \sqrt{3})(x+2+y \sqrt{3}) \geqslant 0 \\
x \geqslant-0.5
\end{array}\right.\right.
$$
The first of these inequalities, together with the second inequality of the original system, defines the set of points located between two concentric circles centered at ( $0 ; 0$ ) with radii 1 and 2. The third inequality defines the half-plane to the right of the line $x=-0.5$. The second inequality defines two vertical angles, the boundaries of which are the lines $\ell_{1}$ and $\ell_{2}$ with equations $y= \pm \frac{x+2}{\sqrt{3}}$ (such that the point $(0 ; 0)$ lies inside one of these angles). The lines $\ell_{1}$ and $\ell_{2}$ both pass through the point ( $-2 ; 0$ ), which lies on the larger circle, and are tangent to the smaller circle at the points $\left(-\frac{1}{2} ; \pm \frac{\sqrt{3}}{2}\right)$ (the coordinates of the points of tangency can be found by solving the corresponding systems of equations).
By intersecting all the specified sets, we obtain the figure $\Phi$, which, as can be easily seen, consists of one part.
## TICKET 14
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 80,1 \leqslant b \leqslant 30$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 864.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 16 values of $a$ and 6 values of $b$ that are multiples of 5. Therefore, there are $16 \cdot 30 = 480$ pairs $(a ; b)$ such that $a \vdots \cdot 5$ and $6 \cdot 80 = 480$ pairs such that $b \vdots 5$. Additionally, there are $16 \cdot 6 = 96$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $480 + 480 - 96 = 864$.
|
864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Plot the figure $\Phi$ on the plane, consisting of points $(x ; y)$ of the coordinate plane such that the system of inequalities is satisfied
$$
\left\{\begin{array}{l}
\sqrt{y^{2}-8 x^{2}-6 y+9} \leqslant 3 y-1 \\
x^{2}+y^{2} \leqslant 9
\end{array}\right.
$$
Determine how many parts the figure $\Phi$ consists of.
|
Solution. The first inequality is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ y ^ { 2 } - 8 x ^ { 2 } - 6 y + 9 \leqslant 9 y ^ { 2 } - 6 y + 1 , } \\
{ ( y - 3 ) ^ { 2 } - 8 x ^ { 2 } \geqslant 0 , } \\
{ 3 y - 1 \geqslant 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x^{2}+y^{2} \geqslant 1 \\
(y-3-2 x \sqrt{2})(y-3+2 x \sqrt{2}) \geqslant 0 \\
y \geqslant \frac{1}{3}
\end{array}\right.\right.
$$
The first of these inequalities, together with the second inequality of the original system, defines the set of points lying between two concentric circles centered at ( $0 ; 0$ ) with radii 1 and 2. The third inequality defines the half-plane above the line $y=\frac{1}{3}$. The second inequality defines two vertical angles, the boundaries of which are the lines $\ell_{1}$ and $\ell_{2}$ with equations $y=3 \pm 2 x \sqrt{2}$ (such that the point $(0 ; 0)$ lies inside one of these angles). The lines $\ell_{1}$ and $\ell_{2}$ both pass through the point $(3 ; 0)$ and are tangent to the smaller circle at the points $\left( \pm \frac{2 \sqrt{2}}{3} ; \frac{1}{3}\right)$ (the coordinates of the points of tangency can be found by solving the corresponding systems of equations).
By intersecting all the specified sets, we obtain the figure $\Phi$, which, as can be easily seen, consists of one part.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2. There are 90 cards - 10 with the digit 1, 10 with the digit $2, \ldots, 10$ with the digit 9. From all these cards, two numbers were formed, one of which is three times the other. Prove that one of these numbers can be factored into four not necessarily distinct natural factors, greater than one.
|
Solution. Let these numbers be $A$ and $B=3A$. Then the sum of the digits of the number $B$ is divisible by 3. But the sum of the digits on all cards is divisible by 9 (and therefore by 3), so the sum of the digits of the number $A$ is divisible by 3. This means that the number $A$ is divisible by 3. But then the number $B=3A$ is divisible by 9 and the sum of its digits is divisible by 9. Since the sum of the digits on all cards is divisible by 9, then the sum of the digits of the number $A$ is also divisible by 9. This means that the number $A$ is divisible by 9. Therefore, the number $B=3A$ is divisible by 27. Thus, the number $B$ is divisible by 27 and is greater than 27, so it can be factored into 4 multipliers $3,3,3$ and $\frac{B}{27}>1$.
Comment. It has been proven that the larger of the numbers is divisible by 9 - 3 points.
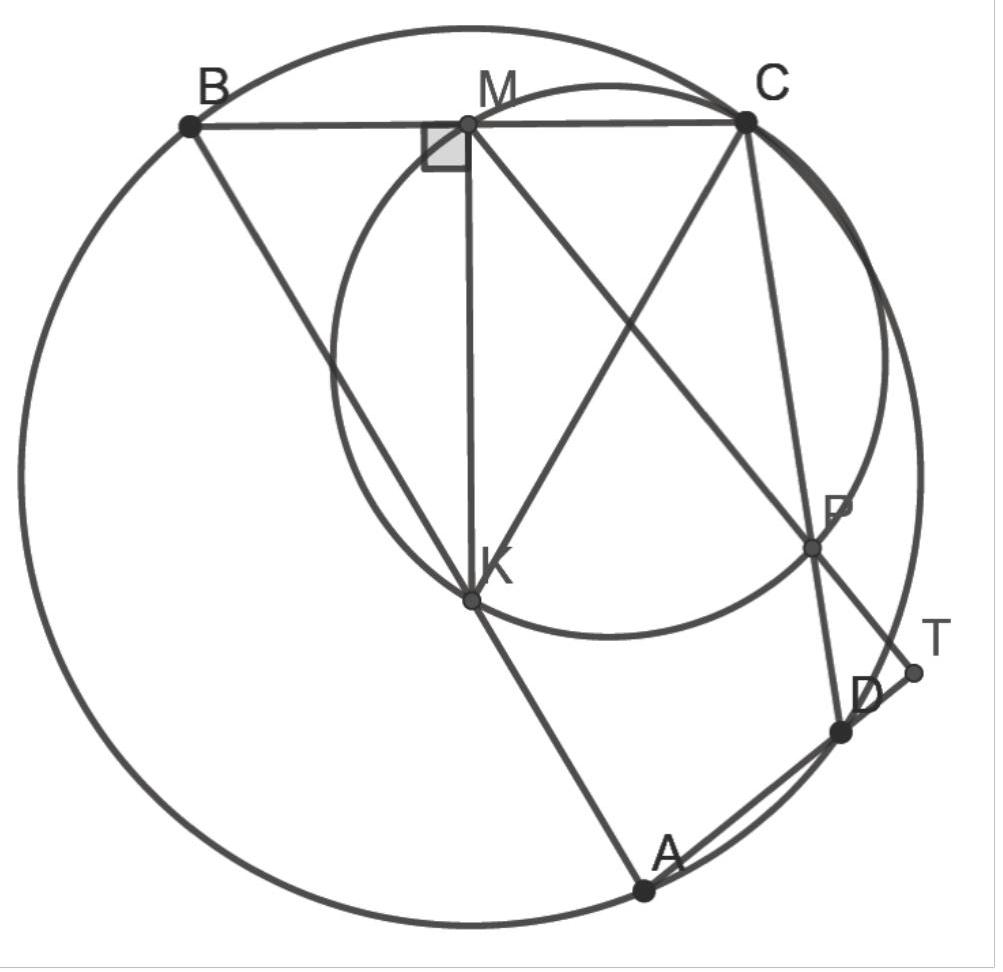
10.3-1. Let $B$ and $C$ be the points of intersection of two circles of equal radii. On the first circle, a point $A$ is chosen. The ray $AB$ intersects the second circle at point $D$ $(D \neq B)$. On the ray $DC$, a point $E$ is chosen such that $DC = CE$. Find the angle $CEA$ if the angle $CDB$ is $50^{\circ}$.
Answer. $40^{\circ}$.
Solution. First, we will prove that the angle $DAE$ is a right angle. Connect points $A$ and $C$. The common chord $BC$ of the two equal circles subtends equal arcs of these circles, so the inscribed angles $BAC$ and $BDC$ that subtend these arcs are equal. Therefore, triangle $ACD$ is isosceles, from which it follows that $AC = CD = CE$ (the last equality is due to the problem's condition). Thus, point $C$ is the center of the circle circumscribed around triangle $DAE$. Segment $DE$ is the diameter of this circle, which implies that angle $DAE$ is a right angle.
$$
\text{Then } \angle CEA = \angle DEA = 90^{\circ} - \angle ADE = 90^{\circ} - \angle CDB = 40^{\circ} \text{.}
$$
Comment. The correct answer without justification - 0 points.
10.3-2. Let $B$ and $C$ be the points of intersection of two circles of equal radii. On the first circle, a point $A$ is chosen. The ray $AB$ intersects the second circle at point $D$ $(D \neq B)$. On the ray $DC$, a point $E$ is chosen such that $DC = CE$. Find the angle $CEA$ if the angle $CDB$ is $40^{\circ}$.
Answer. $50^{\circ}$.
Solution. First, we will prove that the angle $DAE$ is a right angle. Connect points $A$ and $C$. The common chord $BC$ of the two equal circles subtends equal arcs of these circles, so the inscribed angles $BAC$ and $BDC$ that subtend these arcs are equal. Therefore, triangle $ACD$ is isosceles, from which it follows that $AC = CD = CE$ (the last equality is due to the problem's condition). Thus, point $C$ is the center of the circle circumscribed around triangle $DAE$. Segment $DE$ is the diameter of this circle, which implies that angle $DAE$ is a right angle.
Then $\angle CEA = \angle DEA = 90^{\circ} - \angle ADE = 90^{\circ} - \angle CDB = 50^{\circ}$.
Comment. The correct answer without justification - 0 points.
|
40
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
10.4. Quadrilateral $A B C D$ is inscribed in a circle. The perpendicular to side $B C$, drawn through its midpoint - point $M$, intersects side $A B$ at point $K$. The circle with diameter $K C$ intersects segment $C D$ at point $P(P \neq C)$. Find the angle between the lines $M P$ and $A D$.
|
Answer: $90^{\circ}$.
Solution. We will prove that the lines $M P$ and $A D$ are perpendicular. Let $\omega$ be the circle constructed with $K C$ as its diameter, then point $M$ lies on $\omega$, since angle $C M K$ is a right angle. Therefore, $\angle C P M = \angle C K M = \alpha$ (they subtend the arc $C M$ of circle $\omega$). Let $T$ be the point of intersection of lines $A D$ and $M P$. We will assume that point $D$ lies on segment $A T$. The other case is considered similarly. Then $\angle T P D = \alpha$ (angles $T P D$ and $C P M$ are vertical). Therefore, to prove that lines $A D$ and $M P$ are perpendicular, we need to prove that $\angle P D T + \alpha = \frac{\pi}{2}$.
If $\angle P D T = \beta$, then $\angle P D A = \pi - \beta \Rightarrow \angle A B C = \beta$, since quadrilateral $A B C D$ is cyclic. Finally, $B K = C K$, because $M K$ is the perpendicular bisector of $B C$. Therefore, $\angle K C M = \angle K B M = \beta$. From the right triangle $K M C$, we get $\alpha + \beta = \frac{\pi}{2}$. The statement is proved.
Comment. Only one case of the position of point $D$ is considered - no points are deducted.
It is proved that point $M$ lies on $\omega-1$ point.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. It is known that for pairwise distinct numbers $a, b, c$, the equality param1 holds. What is the smallest value that the expression $a+b+c$ can take?
| param1 | Answer |
| :---: | :---: |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+2\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -2 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+4\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -4 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+6\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -6 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+8\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -8 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+10\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -10 |
|
30. It is known that for pairwise distinct numbers $a, b, c$, the equality param1 holds. What is the smallest value that the expression $a+b+c$ can take?
| param1 | Answer |
| :---: | :---: |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+2\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -2 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+4\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -4 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+6\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -6 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+8\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -8 |
| $a^{3}(b-c)+b^{3}(c-a)+c^{3}(a-b)+10\left(a^{2}(b-c)+b^{2}(c-a)+c^{2}(a-b)\right)=0$ | -10 |
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | |
| 1372 | |
| 1228 | |
| 1092 | |
| 964 | |
|
8. For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | 39 |
| 1372 | 33 |
| 1228 | 35 |
| 1092 | 27 |
| 964 | 29 |
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A regular param 1 -sided polygon is inscribed in a circle, with different natural numbers written at its vertices. A pair of non-adjacent vertices of the polygon $A$ and $B$ is called interesting if, on at least one of the two arcs $A B$, all the numbers written at the vertices of the arc are greater than the numbers written at the vertices $A$ and $B$. What is the minimum number of interesting pairs of vertices that this polygon can have?
| param1 | Answer |
| :---: | :---: |
| 55 | |
| 60 | |
| 70 | |
| 85 | |
| 95 | |
|
9. A regular param 1-gon is inscribed in a circle, with different natural numbers written at its vertices. A pair of non-adjacent vertices of the polygon $A$ and $B$ is called interesting if, on at least one of the two arcs $A B$, all the numbers written at the vertices of the arc are greater than the numbers written at the vertices $A$ and $B$. What is the smallest number of interesting pairs of vertices that this polygon can have?
| param1 | Answer |
| :---: | :---: |
| 55 | 52 |
| 60 | 57 |
| 70 | 67 |
| 85 | 82 |
| 95 | 92 |
|
92
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (12 points) The sequence of functions is defined by the formulas:
$$
f_{0}(x)=2 \sqrt{x}, f_{n+1}(x)=\frac{4}{2-f_{n}(x)}, n=0,1,2 \ldots, x \in[4 ; 9]
$$
Find $f_{2023}(4)$.
|
Answer: -2.
Solution. It is easy to calculate that $f_{3}(x)=f_{0}(x)$, therefore
$$
f_{2023}(x)=f_{1}(x)=\frac{2}{1-\sqrt{x}}
$$
Then $f_{2023}(4)=-2$.
Remark. One can immediately compute the values of the functions at the given point. The sequence will be $f_{0}(4)=4, f_{1}(4)=-2, f_{2}(4)=1, f_{3}(4)=4 \ldots$
Evaluation criteria. A fully justified solution - 12 points. Calculation errors - minus 1 point. The relation $f_{3}(x)=f_{0}(x)$ found - 7 points, the equality $f_{2023}(x)=f_{1}(x)$ found - another 4 points.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (15 points) The vertices of the broken line $A B C D E F G$ have coordinates $A(-1 ; -7), B(2 ; 5), C(3 ; -8), D(-3 ; 4), E(5 ; -1), F(-4 ; -2), G(6 ; 4)$.
Find the sum of the angles with vertices at points $B, E, C, F, D$.
|
Answer: $135^{\circ}$.
Solution. The closed broken line $B C D E F B$ forms a five-pointed "star". The sum of the angles at the rays of this star is $180^{\circ}$.
We will prove that the sum of the angles at the rays of any five-pointed star $B C D E F B$ is $180^{\circ}$. Let $O$ be the point of intersection of the lines $B F$ and $E D$, and the angle between them is $B O D=\alpha$. Denote the angle at the ray by the same letter as the vertex of the ray.
$$
\angle E+\angle F=180^{\circ}-\alpha=\angle O B D+\angle O D B
$$
We have:
$$
\begin{aligned}
180^{\circ} & =\angle C+\angle C B D+\angle C D B=\angle C+(\angle B+\angle O B D)+(\angle D+\angle O D B)= \\
& =\angle C+\angle B+\angle D+(\angle O B D+\angle O D B)=\angle C+\angle B+\angle D+\angle E+\angle F
\end{aligned}
$$
Another proof. Let the ray $\bar{a}$ coincide with the ray $B C$. Rotate the ray $\bar{a}$ until it coincides with the ray $B F$. The ray $\bar{a}$ will rotate by the angle $\angle B$. Then rotate the ray $\bar{a}$ (in its new position) until it coincides with the ray $E F$. The ray $\bar{a}$ will rotate by another angle $\angle F$, and from the start of the movement, by the angle $\angle B+\angle F$. Then rotate the ray $\bar{a}$ again until it coincides with the ray $E D$. The ray $\bar{a}$ will rotate by another angle $\angle D$, and from the start of the movement, by the angle $\angle B+\angle F+\angle E$. After performing two more similar rotations, the ray $\bar{a}$ will coincide with the ray $C B$, i.e., it will have rotated by $180^{\circ}$ from the start of the movement and, at the same time, by the sum of the angles $\angle B+\angle F+\angle E+\angle D+\angle C$.
The point of intersection of the segments $A B$ and $F G$ is the point $K(1 ; 1)$.
We will prove this. Let $L(1 ;-2), M(6 ;-2)$. Then $\triangle K F L \sim \triangle G F M$, since their legs are proportional. Therefore, $\angle K F L=\angle G F M$, so $K \in F G$. Similarly, $K \in A B$.
Another way. The equation of the line $A B: y=4 x-3$. The equation of the line $F G: y=\frac{3}{5} x+\frac{2}{5}$. Solving the system of these two equations, we get the coordinates of the intersection point of these lines: $(1 ; 1)$.
Find the lengths of the sides of $\triangle B K G: B K=\sqrt{1^{2}+4^{2}}=\sqrt{17}, B G=\sqrt{4^{2}+(-1)^{2}}=\sqrt{17}, G K=\sqrt{5^{2}+3^{2}}=\sqrt{34}$. The triangle $B K G$ is isosceles and, by the converse of the Pythagorean theorem, it is a right triangle.
Therefore, the angle $\angle B K G=45^{\circ}$. It is an exterior angle for $\triangle F K B$ and $\angle K F B+\angle K B F=45^{\circ}$. Since $\angle A B C=\angle F B C-\angle F B A$, $\angle E F G=\angle E F B-\angle G F B$, the required sum of the angles
$$
\begin{gathered}
\angle A B C+\angle E F G+\angle B C D+\angle C D E+\angle D E F= \\
=\angle F B C+\angle E F B-(\angle F B A+\angle G F B)+\angle B C D+\angle C D E+\angle D E F= \\
=180^{\circ}-45^{\circ}=135^{\circ}
\end{gathered}
$$
Remark. A similar solution can be obtained based on the fact that the sum of the angles at the rays of any seven-pointed "star" is also $180^{\circ}$ (the proof is essentially the same as the second proof for the five-pointed star). Since the angle $\angle B K G=45^{\circ}$, the sum of the two angles of the seven-pointed star with vertices at points $A$ and $G$ is $45^{\circ}$.
Grading criteria. Full solution 15 points. If the coordinates of point $K$ are found from the drawing or guessed - minus 2 points. If the fact that $\angle B K G=45^{\circ}$ is found from the drawing or guessed - minus 3 points. If the problem is not solved, but it is shown that the sum of all angles at the rays of a five- or seven-pointed star is $180^{\circ}$, then 8 points.
|
135
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (12 points) The sequence of functions is defined by the formulas:
$$
f_{0}(x)=2 \sqrt{x}, f_{n+1}(x)=\frac{4}{2-f_{n}(x)}, n=0,1,2 \ldots, x \in[4 ; 9]
$$
Find $f_{2023}(9)$.
|
Answer: -1.
Solution. It is easy to calculate that $f_{3}(x)=f_{0}(x)$, therefore,
$$
f_{2023}(x)=f_{1}(x)=\frac{2}{1-\sqrt{x}}
$$
Then $f_{2023}(9)=-1$.
Remark. One can immediately compute the values of the functions at the given point. The sequence will be $f_{0}(9)=6, f_{1}(9)=-1, f_{2}(9)=\frac{4}{3}, f_{3}(9)=6 \ldots$
Evaluation Criteria. A fully justified solution - 12 points. Calculation errors - minus 1 point. The relation $f_{3}(x)=f_{0}(x)$ found - 7 points, the equality $f_{2023}(x)=f_{1}(x)$ found - another 4 points.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (15 points) The vertices of the broken line $A B C D E F G$ have coordinates $A(0 ; -5), B(3 ; 7), C(4 ; -6), D(-2 ; 6), E(6 ; 1), F(-3 ; 0), G(7 ; 6)$.
Find the sum of the angles with vertices at points $B, E, C, F, D$.
|
Answer: $135^{\circ}$.
Solution. The closed broken line $B C D E F B$ forms a five-pointed "star". The sum of the angles at the rays of this star is $180^{\circ}$.
We will prove that the sum of the angles at the rays of any five-pointed star $B C D E F B$ is $180^{\circ}$. Let $O$ be the point of intersection of the lines $B F$ and $E D$, and the angle between them is $B O D=\alpha$. Denote the angle at the ray by the same letter as the vertex of the ray.
$$
\angle E+\angle F=180^{\circ}-\alpha=\angle O B D+\angle O D B .
$$
Therefore,
$$
\begin{array}{r}
180^{\circ}=\angle C+\angle C B D+\angle C D B=\angle C+(\angle B+\angle O B D)+(\angle D+\angle O D B)= \\
\quad=\angle C+\angle B+\angle D+(\angle O B D+\angle O D B)=\angle C+\angle B+\angle D+\angle E+\angle F
\end{array}
$$
Another proof. Let the ray $\bar{a}$ coincide with the ray $В C$. Rotate the ray $\bar{a}$ until it coincides with the ray $B F$. The ray $\bar{a}$ will rotate by the angle $\angle B$. Then rotate the ray $\bar{a}$ (in its new position) until it coincides with the ray $E F$. The ray $\bar{a}$ will rotate by another angle $\angle F$, and from the start of the movement, by the angle $\angle B+\angle F$. Then rotate the ray $\bar{a}$ again, this time until it coincides with the ray $E D$. The ray $\bar{a}$ will rotate by another angle $\angle D$, and from the start of the movement, by the angle $\angle B+\angle F+\angle E$. After performing two more similar rotations, the ray $\bar{a}$ will coincide with the ray $C B$, i.e., it will have rotated by $180^{\circ}$ from the start of the movement and, at the same time, by the sum of the angles $\angle B+\angle F+\angle E+\angle D+\angle C$.
The point of intersection of the segments $A B$ and $F G$ is the point $K(2 ; 3)$.
We will prove this. Let $L(2 ; 0), M(7 ; 0)$. Then $\triangle K F L \sim \triangle G F M$, since their legs are proportional. Therefore, $\angle K F L=\angle G F M$, so $K \in F G$. Similarly, $K \in A B$.
Another way. The equation of the line $A B: y=4 x-5$. The equation of the line $F G: y=\frac{3}{5} x+\frac{9}{5}$. Solving the system of these two equations, we get the coordinates of the intersection point of these lines: $(2 ; 3)$.
Find the lengths of the sides of $\triangle B K G: B K=\sqrt{1^{2}+4^{2}}=\sqrt{17}, B G=$ $\sqrt{4^{2}+(-1)^{2}}=\sqrt{17}, G K=\sqrt{5^{2}+3^{2}}=\sqrt{34}$. The triangle $\triangle B K G$ is isosceles and, by the converse of the Pythagorean theorem, it is a right triangle.
Therefore, the angle $\angle B K G=45^{\circ}$. It is an exterior angle for $\triangle F K B$ and $\angle K F B+\angle K B F=45^{\circ}$. Since $\angle A B C=\angle F B C-\angle F B A$, $\angle E F G=\angle E F B-\angle G F B$, the required sum of the angles
$$
\begin{gathered}
\angle A B C+\angle E F G+\angle B C D+\angle C D E+\angle D E F= \\
=\angle F B C+\angle E F B-(\angle F B A+\angle G F B)+\angle B C D+\angle C D E+\angle D E F= \\
=180^{\circ}-45^{\circ}=135^{\circ}
\end{gathered}
$$
Remark. A similar solution can be obtained based on the fact that the sum of the angles at the rays of any seven-pointed "star" is also $180^{\circ}$ (the proof, in essence, does not differ from the second proof for a five-pointed star). Since the angle $\angle B K G=45^{\circ}$, the sum of the two angles of the seven-pointed star with vertices at points $A$ and $G$ is $45^{\circ}$.
Grading criteria. Full solution 15 points. If the coordinates of point $K$ are found from the drawing or guessed - minus 2 points. If the fact that $\angle B K G=45^{\circ}$ is found from the drawing or guessed - minus 3 points. If the problem is not solved, but it is shown that the sum of all angles at the rays of a five- or seven-pointed star is $180^{\circ}$, then 8 points.
|
135
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation
$$
2 x+2+\operatorname{arctg} x \cdot \sqrt{x^{2}+1}+\operatorname{arctg}(x+2) \cdot \sqrt{x^{2}+4 x+5}=0
$$
|
Answer: -1.
Solution. Let $f(x)=x+\operatorname{arctg} x \cdot \sqrt{x^{2}+1}$. The original equation can be rewritten as $f(x)+f(x+2)=0$. Note that the function $f(x)$ is odd. It is increasing on the positive half-axis (as the sum of increasing functions). Due to its oddness, it is increasing on the entire real line. Further, we have
$$
f(x)=-f(x+2) ; \quad f(x)=f(-x-2)
$$
Since an increasing function takes each of its values exactly once, it follows that $x=-x-2$, from which $x=-1$.
Remark. The monotonicity of the left side of the original equation could also have been established using the derivative.
Evaluation. 12 points for a correct solution. If the answer is guessed but not proven that there are no other solutions, 3 points.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem No. 6 (10 points)
The density of a body is defined as the ratio of its mass to the volume it occupies. A homogeneous cube with a volume of \( V = 8 \, \text{m}^3 \) is given. As a result of heating, each of its edges increased by 4 mm. By what percentage did the density of this cube change?
Answer: decreased by \( 6 \% \)
|
# Solution and evaluation criteria:
Volume of the cube: $v=a^{3}$, where $a$ is the length of the edge, therefore:
$a=2 \partial m=200 mm$.
Final edge length: $a_{\kappa}=204$ mm.
Thus, the final volume: $V_{\kappa}=a_{K}^{3}=2.04^{3}=8.489664 \partial \mu^{3} \approx 1.06 V$.
Therefore, the density:
$\rho_{K}=\frac{m}{V_{K}}=\frac{m}{1.06 V}=0.94 \frac{m}{V} \approx 0.94 \rho$. The density has decreased by approximately $6 \%$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 7 (10 points)
A person and his faithful dog started moving along the perimeter of a block from point A at the same time $t_{0}=0$ min. The person moved with a constant speed clockwise, while the dog ran with a constant speed counterclockwise (see fig.). It is known that they met for the first time after $t_{1}=1$ min from the start of the movement. This meeting occurred at point $B$. Given that they continued to move in the same direction and at the same speed after this, determine at what moment in time they will next be at point $B$ simultaneously. Note that $A B=C D=100$ m, $B C=A D=300$ m.
|
# Answer: in 9 min
## Solution and evaluation criteria:
In $t_{1}=1$ min, the person and the dog together covered a distance equal to the perimeter of the block, with the person moving 100 meters from the starting point of the journey.
That is, during each subsequent meeting, the person will be 100 meters away from the location of the previous meeting.
Perimeter of the block: $A B+B C+C D+D A=100+300+100+300=800$ meters.
So, it will take another 8 minutes.
And the next time the person and the dog will be at the point at the moment: $t_{\kappa}=9$ min.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem No. 6 (10 points)
The density of a body is defined as the ratio of its mass to the volume it occupies. A homogeneous cube with a volume of \( V = 27 \partial \mu^{3} \) is given. As a result of heating, each of its edges increased by 9 mm. By what percentage did the density of this cube change?
|
# Answer: decreased by $8 \%$
## Solution and evaluation criteria:
Volume of a cube: $v=a^{3}$, where $a$ is the length of the edge, therefore:
$a=3 dm=300 mm$.
Final edge length: $a_{K}=309 mm$.
Thus, the final volume: $V_{K}=a_{K}^{3}=3.09^{3}=29.503629 dm^{3} \approx 1.09 V$.
Therefore, the density:
$\rho_{K}=\frac{m}{V_{K}}=\frac{m}{1.09 V}=0.92 \frac{m}{V} \approx 0.92 \rho$. The density has decreased by approximately $8 \%$. (4 points)
#
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 7 (10 points)
A person and his faithful dog started moving along the perimeter of a block from point $A$ simultaneously at time $t_{0}=0$ min. The person moved with a constant speed clockwise, while the dog ran with a constant speed counterclockwise (see figure). It is known that they met for the first time after $t_{1}=2$ min from the start of the movement. This meeting occurred at point $B$. Given that they continued to move in their respective directions and at the same constant speeds, determine the moment of time when they will next be at point $B$ simultaneously. Note that $A B=C D=100$ m, $B C=A D=200$ m.
|
# Answer: in 14 min
## Solution and evaluation criteria:
In $t_{1}=2$ min, the person and the dog together covered a distance equal to the perimeter of the block, with the person moving 100 meters from the starting point of the journey.
That is, during each subsequent meeting, the person will be 100 meters away from the location of the previous meeting.
(
The perimeter of the block: $A B+B C+C D+D A=100+200+100+200=600$ meters.
That is, it will take another 12 minutes
And the next time the person and the dog will be at the same point at the moment:
$t_{\kappa}=14$ min.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 8 (15 points)
In some English-speaking countries, temperature is measured in degrees Fahrenheit. An English schoolboy, observing a thermometer in a glass of cooling water, noticed that it cooled by $30^{\circ} \mathrm{F}$. He became curious about how much heat was released. In books, he found the following formula that allows calculating the answer to his question: $Q=4200 \cdot V \cdot \Delta T$, where $V$ is the volume of water in liters, $\Delta T$ is the change in its temperature. However, the change in temperature in this formula must be substituted in degrees Celsius. Degrees Fahrenheit are related to degrees Celsius by the following relationship: ${ }^{\circ} F={ }^{\circ} C \cdot \frac{9}{5}+32$. What result should he get if he had 2 liters of water at his disposal?
|
# Answer: 140 kJ
## Solution and grading criteria:
The change in temperature in degrees Fahrenheit is related to the change in temperature in degrees Celsius:
That is, in degrees Celsius, the water cooled by: $\Delta^{\circ} \mathrm{C}=\frac{5}{9} \cdot \Delta^{\circ} F=\frac{5}{9} \cdot 30 \approx 16.67^{\circ} \mathrm{C}$.
Therefore, the amount of heat released is:
$Q=4200 \cdot V \cdot \Delta T=4200 \cdot 2 \cdot 16.67 \approx 140$ kJ
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. 20 balls of the same mass are moving along a chute towards a metal wall with the same speed. Coming towards them at the same speed are 16 balls of the same mass. When two balls collide, they fly apart with the same speed. After colliding with the wall, a ball bounces off it with the same speed. (The balls move only along the chute). How many collisions will there be between the balls?
|
# Answer: 510.
Solution. We will assume that initially, each ball moving towards the wall has a red flag, and the rest of the balls have blue flags. Imagine that when the balls collide, they exchange flags. Then each blue flag moves at a constant speed in one direction (away from the wall), and each red flag reaches the wall and then moves in the opposite direction. The number of collisions between the balls is equal to the number of flag exchanges. Each red flag will exchange once with each blue flag. Any two red flags will also exchange places once. Therefore, the total number of exchanges is $20 \cdot 16 + \frac{20 \cdot 19}{2} = 510$.
Evaluation. 14 points for a correct solution.
## $2015 / 16$ academic year
#
|
510
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Andrei was driving to the airport of a neighboring city. After an hour of driving at a speed of 60 km/h, he realized that if he did not change his speed, he would be 20 minutes late. Then he sharply increased his speed, as a result of which he covered the remaining part of the journey at an average speed of 90 km/h and arrived at the airport 20 minutes earlier than originally planned. What is the distance from Andrei's home to the airport?
|
Answer: 180 km.
Solution. Let the distance from Andrey's house to the airport be $s$ km, and the time he intended to spend on the road be $1+t$ hours. Then
$$
s=60+60\left(t+\frac{1}{3}\right)=60+90\left(t-\frac{1}{3}\right)
$$
From this,
$$
60 t+20=90 t-30, \quad t=\frac{5}{3}, \quad s=180
$$
Evaluation. Full score for the solution is 12 points.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A natural number $n$ is such that the number $36 n^{2}$ has exactly 51 different natural divisors. How many natural divisors does the number $5 n$ have?
|
Answer: 16.
Solution. Let $m=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{l}^{k_{l}}$, where $p_{1}, p_{2}, \ldots, p_{l}$ are pairwise distinct prime numbers. Then the number of natural divisors of the number $m$ is
$$
\tau(m)=\left(k_{1}+1\right)\left(k_{2}+1\right) \ldots\left(k_{l}+1\right)
$$
Indeed, a common divisor of the number $m$ has the form
$$
d=p_{1}^{a_{1}} \cdot p_{2}^{a_{2}} \cdot \ldots \cdot p_{l}^{a_{l}}
$$
where for each $i$ the exponent $a_{i}$ takes values from 0 to $k_{i}-$ a total of $k_{i}+1$ values. By the multiplication rule, we obtain the formula (*).
The number $m=36 n^{2}$ has at least two prime divisors (2 and 3).
Considering the equality $\tau(m)=3 \cdot 17$, we get two factors in the formula (*). Therefore, the number $m$ has the form $m=2^{2} 3^{16}$ or $m=2^{16} 3^{2}$. In this case, $n=p^{7}$, where $p$ is equal to 2 or 3. Then
$$
5 n=5 p^{7}, \quad \tau(5 n)=2 \cdot 8=16
$$
Evaluation. 13 points for a complete solution. Participants in the Olympiad can use the formula (*) without proof.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Viktor was driving to the airport of a neighboring city. After half an hour of driving at a speed of 60 km/h, he realized that if he did not change his speed, he would be 15 minutes late. Then he increased his speed, as a result of which he covered the remaining part of the journey at an average speed of 80 km/h and arrived at the airport 15 minutes earlier than originally planned. What is the distance from Viktor's home to the airport?
|
Answer: 150 km.
Solution. Let the distance from Viktor's house to the airport be $s$ km, and the time he intended to spend on the road $\frac{1}{2}+t$ hours. Then
$$
s=30+60\left(t+\frac{1}{4}\right)=30+80\left(t-\frac{1}{4}\right)
$$
From this,
$$
60 t+15=80 t-20, \quad t=\frac{7}{4}, \quad s=150
$$
Evaluation. Full solution: 12 points.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A natural number $n$ is such that the number $100 n^{2}$ has exactly 55 different natural divisors. How many natural divisors does the number 10n have?
|
Answer: 18.
Solution. Let $m=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{l}^{k_{l}}$, where $p_{1}, p_{2}, \ldots, p_{l}$ are pairwise distinct prime numbers. Then the number of natural divisors of the number $m$ is
$$
\tau(m)=\left(k_{1}+1\right)\left(k_{2}+1\right) \ldots\left(k_{l}+1\right)
$$
Indeed, a common divisor of the number $m$ has the form
$$
d=p_{1}^{a_{1}} \cdot p_{2}^{a_{2}} \cdot \ldots \cdot p_{l}^{a_{l}}
$$
where for each $i$ the exponent $a_{i}$ takes values from 0 to $k_{i}-$ a total of $k_{i}+1$ values. By the multiplication rule, we obtain the formula (*).
The number $m=100 n^{2}$ has at least two prime divisors (2 and 5).
Considering the equality $\tau(m)=5 \cdot 11$, we get two factors in the formula (*). Therefore, the number $m$ has the form $m=2^{4} 5^{10}$ or $m=2^{10} 5^{4}$. In this case, $n=p q^{4}$, where $p=2, q=5$ or $p=5, q=2$. Then
$$
10 n=p^{2} q^{5}, \quad \tau(10 n)=3 \cdot 6=18
$$
Evaluation. 13 points for a complete solution. Participants in the Olympiad can use the formula (*) without proof.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) The medians drawn from vertices $A$ and $B$ of triangle $ABC$ are perpendicular to each other. Find the area of the square with side $AB$, if $BC=28, AC=44$.
#
|
# Answer: 544
Solution. Let $D$ be the midpoint of $B C$, $E$ be the midpoint of $A C$, and $M$ be the point of intersection of the medians. Let $M D=a$, $M E=b$. Then $A M=2 a$, $B M=2 b$. From the right triangles $B M D$ and $A M E$, we have $a^{2}+4 b^{2}=B D^{2}=14^{2}$ and $4 a^{2}+b^{2}=A E^{2}=22^{2}$. Adding these equations and dividing by 5, we get $a^{2}+b^{2}=136$. Therefore, $A B^{2}=A M^{2}+B M^{2}=4\left(a^{2}+b^{2}\right)=544$.
|
544
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) In a $4 \times 5$ grid, 5 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 240
Solution. From the condition, it follows that in some row, two cells are marked (while in the others, only one each). This row can be chosen in 4 ways, and the two crosses in it can be chosen in $5 \cdot 4 / 2=10$ ways. The remaining three crosses can be chosen in $3 \cdot 2 \cdot 1=6$ ways. By the rule of product, the total number of ways is $4 \cdot 10 \cdot 6=240$.
|
240
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) Fresh mushrooms contain $80 \%$ water by mass, while dried mushrooms contain $20 \%$ water. How many kg of dried mushrooms can be obtained from 20 kg of fresh mushrooms?
|
# Answer: 5 kg
Solution. The dry matter in fresh mushrooms is 4 kg, which constitutes $80 \%$ of the weight in dried mushrooms. By setting up the corresponding proportion, we will find the weight of the dried mushrooms.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) The medians drawn from vertices $A$ and $B$ of triangle $ABC$ are perpendicular to each other. Find the area of the square with side $AB$, if $BC=36, AC=48$.
#
|
# Answer: 720
Solution. Let $D$ be the midpoint of $B C$, $E$ be the midpoint of $A C$, and $M$ be the point of intersection of the medians. Let $M D=a$, $M E=b$. Then $A M=2 a$, $B M=2 b$. From the right triangles $B M D$ and $A M E$, we have $a^{2}+4 b^{2}=B D^{2}=18^{2}$ and $4 a^{2}+b^{2}=A E^{2}=24^{2}$. Adding these equations and dividing by 5, we get $a^{2}+b^{2}=180$. Therefore, $A B^{2}=A M^{2}+B M^{2}=4\left(a^{2}+b^{2}\right)=720$.
|
720
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) In a $3 \times 4$ grid, 4 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 36
Solution. From the condition, it follows that in some row, two cells are marked (while in the others, only one each). This row can be chosen in 3 ways, and the two crosses in it can be placed in $4 \cdot 3 / 2=6$ ways. The remaining two crosses can be chosen in 2 ways. By the multiplication rule, the total will be $3 \cdot 6 \cdot 2=36$ variants.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) A ball was thrown from the surface of the Earth at an angle of $30^{\circ}$ with a speed of $v_{0}=20 \mathrm{M} / \mathrm{c}$. How long will it take for the velocity vector of the ball to turn by an angle of $60^{\circ}$? Neglect air resistance. The acceleration due to gravity is $g=10 \mathrm{M} / \mathrm{c}^{2}$.
|
Answer: $t=2 s$
Solution. In fact, the problem requires finding the total flight time of the ball. The $y$-coordinate of the ball changes according to the law: $y=v_{0 y} t-\frac{g t^{2}}{2}=v_{0} \sin 30^{\circ} t-\frac{g t^{2}}{2}=10 \cdot t-5 t^{2}=0$
From this, we obtain that: $t=2 s$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a row, the numbers $1,2,3, \ldots, 2014,2015$ are written. We will call a number from this row good if, after its removal, the sum of all the remaining 2014 numbers is divisible by 2016. Find all the good numbers.
|
Answer: The only good number is 1008.
Solution. The remainder of the division of the sum of all 2015 numbers by 2016 is 1008:
$(1+2015)+(2+2014)+\ldots+(1007+1009)+1008=2016 \cdot 1007+1008$.
Therefore, only 1008 can be crossed out.
Scoring. 12 points for a correct solution. If it is shown that 1008 is a good number, but it is not proven that there are no other good numbers, 6 points.
|
1008
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let
$$
\sqrt{49-a^{2}}-\sqrt{25-a^{2}}=3
$$
Calculate the value of the expression
$$
\sqrt{49-a^{2}}+\sqrt{25-a^{2}} .
$$
|
Answer: 8.
Solution. Let
$$
\sqrt{49-a^{2}}+\sqrt{25-a^{2}}=x
$$
Multiplying this equality by the original one, we get $24=3x$.
Evaluation. Full solution: 11 points.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (10 points) Five identical non-ideal ammeters are connected as shown in the figure. Ideal power supply is connected to points $A$ and $B$. Determine the sum of the readings of all ammeters, given that the reading of the first ammeter $I_{1}=2 \mathrm{MA}$.
|
Answer: $24$ mA
Solution. As a result of analyzing the proposed electrical circuit, it can be concluded that: $I_{2}=I_{1}=2$ mA.
\[
\begin{aligned}
& I_{3}=2 I_{1}=4 \mathrm{mA} \\
& I_{5}=I_{3}+I_{1}=6 \mathrm{mA} \\
& I_{4}=\frac{5}{3} I_{5}=10 \mathrm{mA}
\end{aligned}
\]
The sum of the readings of all ammeters: $I=I_{1}+I_{2}+I_{3}+I_{4}+I_{5}=24$ mA. (2 points)
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=2, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{2019}$.
|
Answer: 2020.
Solution. Let's list the first terms of the sequence:
$$
1,2,4,6,7,7,7,8,10,12,13,13,13,14,16,18,19,19,19,20,21,23, \ldots
$$
We can observe a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{2019}=a_{3+6 \cdot 336}=a_{3}+6 \cdot 636=4+6 \cdot 636=2020
$$
Evaluation. 12 points for a complete solution. If the pattern is noticed but not proven, then (with the correct answer) 6 points.
|
2020
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The infantry column stretched out over 1 km. Sergeant Kim, riding out on a gyro-scooter from the end of the column, reached its beginning and returned to the end. The infantrymen walked 2 km 400 m during this time. How far did the sergeant travel during this time?
|
Answer: 3 km $600 \mathrm{~m}$
Solution. Let the speed of the column be $x$ km/h, and the sergeant travels $k$ times faster, i.e., at a speed of $k x$ km/h. To reach the end of the column, Kim traveled $t_{1}=\frac{1}{k x-x}$ hours (catching up), and in the opposite direction, $t_{2}=\frac{1}{k x+x}$ hours (meeting head-on). During this time, the column covered 2.4 km, i.e., $x\left(t_{1}+t_{2}\right)=2.4$. Substituting the expressions for $t_{1}$ and $t_{2}$, we get
$$
\frac{x}{k x-x}+\frac{x}{k x+x}=2.4 ; \quad \frac{1}{k-1}+\frac{1}{k+1}=2.4 ; \quad 2 k=2.4\left(k^{2}-1\right) .
$$
The obtained quadratic equation has a single positive root $k=\frac{3}{2}$. The sergeant travels 1.5 times faster than the column. Therefore, the distance he covers will also be 1.5 times greater.
Evaluation. Full solution: 12 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=3, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{1000}$.
|
Answer: 1002.
Solution. Let's list the first terms of the sequence:
$$
1,3,5,6,6,6,7,9,11,12,12,12,13,15,17,18,18,18,19,21, \ldots
$$
We can see a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{1000}=a_{4+6 \cdot 166}=a_{4}+6 \cdot 166=6+6 \cdot 166=1002
$$
Evaluation. Full solution is worth 12 points. If the pattern is noticed but not proven, then (with the correct answer) 6 points.
|
1002
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) The price of an entry ticket to the stadium is 400 p. After reducing the entry fee, the number of spectators increased by $25 \%$, and the revenue increased by $12.5 \%$. What is the new price of the entry ticket after the price reduction?
|
Answer: 360
Solution. Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 1.25 = 400 - 1.125$. From which $x = 360$.
|
360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) A tourist travels from point $A$ to point $B$ in 1 hour 56 minutes. The route from $A$ to $B$ goes uphill first, then on flat ground, and finally downhill. What is the length of the road on flat ground if the tourist's speed downhill is 6 km/h, uphill is 4 km/h, and on flat ground is 5 km/h, and the total distance between $A$ and $B$ is $x$ km? Additionally, the distances uphill and on flat ground are whole numbers of kilometers.
|
# Answer: 3
Solution. Let $x$ km be the distance the tourist walks uphill, $y$ km - on flat ground, then $9-x-y$ km - downhill. We get $\frac{x}{4}+\frac{y}{5}+\frac{9-x-y}{6}=\frac{29}{15}$. After transformations, $5 x+2 y=26$. It is obvious that $x$ must be even and $x+y \leq 9$. The only solution is $x=4, y=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) A chess player played 40 chess games and scored 25 points (1 point for each win, -0.5 points for a draw, 0 points for a loss). Find the difference between the number of his wins and the number of his losses.
#
|
# Answer: 10
Solution. Let the chess player have $n$ wins and $m$ losses. Then we get $n+0.5 \cdot(40-n-m)=25$. In the end, $n-m=10$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) The price of an entry ticket to the stadium is 400 p. After increasing the entry fee, the number of spectators decreased by $20 \%$, but the revenue increased by $5 \%$. What is the new price of the entry ticket after the price increase?
|
Answer: 525
Solution. Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 0.8 = 400 \cdot 1.05$. From which $x=525$.
|
525
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) A tourist travels from point $A$ to point $B$ in 2 hours and 14 minutes. The route from $A$ to $B$ goes uphill first, then on flat terrain, and finally downhill. What is the length of the uphill road if the tourist's speed downhill is 6 km/h, uphill is 4 km/h, and on flat terrain is 5 km/h, and the total distance between $A$ and $B$ is 10 km? Additionally, the distances uphill and on flat terrain are whole numbers of kilometers.
|
Answer: 6
Solution. Let $x$ km be the distance the tourist walks uphill, $y$ km - on flat ground, then $10-x-y$ km - downhill. We get $\frac{x}{4}+\frac{y}{5}+\frac{10-x-y}{6}=\frac{67}{30}$. After transformations, $5 x+2 y=34$. It is obvious that $x$ must be even and $x+y \leq 10$. The only solution is $x=6, y=2$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) A chess player played 42 games and scored 30 points (1 point for each win, -0.5 points for each draw, 0 points for each loss). Find the difference between the number of his wins and the number of his losses.
|
Answer: 18
Solution. Let the chess player have $n$ wins and $m$ losses. Then we get $n+0.5 \cdot(42-n-m)=30$. In the end, $n-m=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) An aluminum and a copper part have the same volume. The density of aluminum $\rho_{A}=2700 \mathrm{kg} / \mathrm{m}^{3}$, the density of copper $\rho_{M}=8900 \mathrm{kg} / \mathrm{m}^{3}$. Find the mass of copper, if it is known that the masses of the parts differ by $\Delta m=60 \mathrm{g}$.
|
Answer: 862
Solution. Volume of aluminum: $V=\frac{m_{M}-\Delta m}{\rho_{A}}$, volume of copper: $V=\frac{m_{M}}{\rho_{M}}$. We get: $\frac{m_{M}}{\rho_{M}}=\frac{m_{M}-\Delta m}{\rho_{A}} . \quad$ From this, the mass of aluminum: $m_{A}=\frac{\Delta m \cdot \rho_{M}}{\rho_{M}-\rho_{A}}=\frac{0.06 \cdot 8900}{8900-2700} \approx 0.086 \kappa 2 \approx 86 g$.
|
862
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A mowing crew mowed the entire meadow in two days. On the first day, half of the meadow and another 3 hectares were mowed, and on the second day, a third of the remaining area and another 6 hectares were mowed. What is the area of the meadow?
|
Answer: 24 hectares.
Solution. 6 hectares made up two-thirds of the remainder. Therefore, 9 hectares were mowed on the second day. Together with the 3 hectares from the first day, this totals 12 hectares, which constitute half of the meadow's area. Therefore, the total area of the meadow is 24 hectares.
Evaluation. 12 points for the correct solution.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) After walking one-fifth of the way from home to school, Olya realized she had forgotten her notebook. If she does not go back for it, she will arrive at school 6 minutes before the bell, but if she returns, she will be 2 minutes late. How much time (in minutes) does the journey to school take?
|
# Answer: 20 min
Solution. The extra $2 / 5$ of the journey takes 8 min. Therefore, the entire journey to school will take 20 min.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the smallest root of the equation
$$
\sqrt{x+2}+2 \sqrt{x-1}+3 \sqrt{3 x-2}=10
$$
|
Answer: 2
Solution. It is clear that 2 is a root of the equation. The function on the left side of the equation is increasing (as the sum of increasing functions). Therefore, there are no other roots.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) In a $5 \times 5$ grid, 6 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 4200
Solution. From the condition, it follows that in some row $a$ and some column $b$ there are two crosses (and in all other rows and columns - one each). Both row $a$ and column $b$ can be chosen in 5 ways. There are two possible cases.
First. At the intersection of $a$ and $b$, there is a cross. We choose one more cross from each line in 4 ways. Now, three rows and three columns remain unoccupied. The remaining crosses are placed at their intersections in $3 \cdot 2 \cdot 1=6$ ways. Thus, there are $5 \cdot 5 \cdot 4 \cdot 4 \cdot 6=2400$ arrangements of the first type.
Second. At the intersection of $a$ and $b$, there is no cross. Then, we choose two crosses from each of these two lines in $4 \cdot 3 / 2=6$ ways. Now, two rows and two columns remain unoccupied. The remaining crosses are placed at their intersections in two ways. Thus, there are $5 \cdot 5 \cdot 6 \cdot 6 \cdot 2=1800$ arrangements of the second type.
In total, there are $2400+1800=4200$ ways to arrange 6 crosses.
|
4200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) A bullet with a mass of $m=10$ g, flying horizontally at a speed of $v_{1}=500 \mathrm{M} / \mathrm{c}$, penetrates a massive board and exits with a speed of $v_{2}=200 \mathrm{M} / \mathrm{c}$. Find the magnitude of the work done on the bullet by the resistance force of the board.
|
Answer: 1050 J
Solution. From the law of conservation of energy, it follows that
$$
A=\frac{m v_{1}^{2}}{2}-\frac{m v_{2}^{2}}{2}=\frac{0.01 \cdot 500^{2}}{2}-\frac{0.01 \cdot 200^{2}}{2}=1050 \text { J. }
$$
|
1050
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (15 points) A light ray falls at an angle $\alpha=30^{\circ}$ on the front surface of a parallel glass plate. The refractive index of the glass is $n=1.5$. By what angle is the ray, reflected from the back surface of the plate and exiting back through the front surface, deflected from the direction of the incident ray?
|
Answer: $120^{\circ}$
Solution. The described situation is illustrated in the figure.
We need to find the angle between rays 1 and 2. It is clear that the required angle is $180^{\circ}-2 \alpha=120^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) Kolya, after walking a quarter of the way from home to school, realized he had forgotten his workbook. If he does not go back for it, he will arrive at school 5 minutes before the bell, but if he does go back, he will be one minute late. How much time (in minutes) does the journey to school take?
|
# Answer: 12 min
Solution. The extra $2 / 4$ of the journey takes 6 min. Therefore, the entire journey to school will take 12 min.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the largest root of the equation
$$
3 \sqrt{x-2}+2 \sqrt{2 x+3}+\sqrt{x+1}=11
$$
|
Answer: 3
Solution. It is clear that 3 is a root of the equation. The function on the left side of the equation is increasing (as the sum of increasing functions). Therefore, there are no other roots.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) In a $4 \times 4$ grid, 5 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 432
Solution. From the condition, it follows that in some row $a$ and some column $b$ there are two crosses (and in all other rows and columns - one each). Both row $a$ and column $b$ can be chosen in 4 ways. There are two possible cases.
First. At the intersection of $a$ and $b$, there is a cross. We choose one more cross from each line in 3 ways. Now, two rows and two columns remain unoccupied. The remaining crosses are placed at their intersections in 2 ways. Thus, there are 4.4$\cdot$3$\cdot$3$\cdot$2=288 arrangements of the first type.
Second. At the intersection of $a$ and $b$, there is no cross. Then, we choose two crosses from each of these two lines in 3 ways. Now, only one row and one column remain unoccupied, at the intersection of which a cross needs to be placed. Thus, there are 4$\cdot$4$\cdot$3$\cdot$3=144 arrangements of the second type. In total, there are $288+144=432$ ways to arrange 5 crosses.
|
432
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (20 points) A bullet with a mass of $m=10$ g, flying horizontally at a speed of $v_{1}=400 \mathrm{m} / \mathrm{s}$, penetrates a massive board and exits with a speed of $v_{2}=100 \mathrm{m} / \mathrm{s}$. Find the magnitude of the work done on the bullet by the resistance force of the board.
|
Answer: 750 J
Solution. From the law of conservation of energy, it follows that
$$
A=\frac{m v_{1}^{2}}{2}-\frac{m v_{2}^{2}}{2}=\frac{0.01 \cdot 400^{2}}{2}-\frac{0.01 \cdot 100^{2}}{2}=750 \text { J. }
$$
|
750
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (15 points) A light ray falls at an angle $\alpha=60^{\circ}$ on the front surface of a parallel glass plate. The refractive index of the glass is $n=1.6$. By what angle is the ray, reflected from the back surface of the plate and exiting back through the front surface, deflected from the direction of the incident ray?
|
Answer: $60^{\circ}$
Solution. The described situation is illustrated in the figure.
We need to find the angle between rays 1 and 2. It is clear that the required angle is $180^{\circ}-2 \alpha=60^{\circ}$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem №4 (10 points)
A parallel beam of light falls on the base of a glass cone (refractive index $n=1.5$) along its axis (see fig.). The cross-section of the beam coincides with the base of the cone, the radius
of which is $R=1 \mathrm{~cm}$. The height of the cone is $h=1.73 \mathrm{~cm}$. Determine the area of the bright spot on the screen, perpendicular to the axis of the cone and located at a distance $a=1$ cm from the vertex of the cone.
#
|
# Solution:
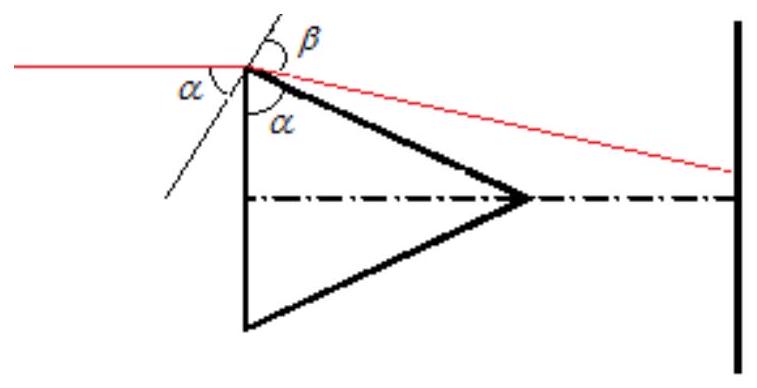
$\operatorname{tg} \alpha=\frac{h}{R}=1.73$, i.e., $\alpha=60^{\circ}$
The law of refraction for rays passing through the cone:
$\frac{\sin \alpha}{\sin \beta}=\frac{1}{1.5}$
As a result: $\sin \beta=\frac{3 \sqrt{3}}{4} \geq 1$
We obtain that the rays passing through the cone experience total internal reflection.
From geometric considerations, it is found that they fall on the other side of the cone at the normal.
(2 points)
Therefore, the light spot on the screen is bounded by two circles with radii:
$R_{1}=a \cdot \operatorname{tg} 60^{\circ}=0.01 \sqrt{3}=0.0173 \text{ m}$
$R_{2}=\left((h+a) \cdot \operatorname{tg} 60^{\circ}\right)-R=0.0273 \sqrt{3}-0.01=0.0373 \text{ m}$
We obtain:
$S=\pi R_{2}^{2}-\pi R_{1}^{2}=0.0034 \text{ m}^{2}=34 \text{ cm}^{2}$
# Multidisciplinary Engineering Olympiad "Star" NATURAL SCIENCES 2016
March 29, 2016
PROTOCOL № 1 of the meeting of the jury
PRESENT: Keller A.V., Zalyapin V.I., Zamishlyayeva A.A., Vorontsov A.G., Kuts D.A., Gusev A.V.
HEARD: on the distribution of points among the winners and prizewinners of the olympiad
## 11th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 45 points.
## 10th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 95 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 94 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 9th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 8th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 75 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 74 - 65 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 64 - 40 points.
## 7th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 6th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 80 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 79 - 40 points.
## Chairmen of the jury:

Keller A.V.
Vorontsov A.G.
|
34
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (16 points) A truck left the village of Mirny at a speed of 40 km/h. At the same time, a car left the city of Tikhaya in the same direction as the truck. In the first hour of the journey, the car traveled 50 km, and in each subsequent hour, it traveled 5 km more than in the previous hour. How many hours will it take for the car to catch up with the truck if the distance between the village and the city is 135 km?
|
# Answer: 6.
Solution. In the first hour of travel, the pursuit speed of the car relative to the truck was $50-40=10$ km/h. In each subsequent hour, the pursuit speed increases by 5 km/h. Thus, the pursuit speeds form an arithmetic progression $10,15,20 \ldots$ km/h. Let's find the number of hours $n$ until the cars meet. The sum of this progression is equal to the total distance the car will travel until it meets the truck $\frac{20+5(n-1)}{2} \cdot n=135$. After transformation, we get the equation $n^{2}+3 n-54=0$, the roots of which are $6,-9$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (16 points) A truck left the village of Mirny at a speed of 40 km/h. At the same time, a car left the city of Tikhaya in the same direction as the truck. In the first hour of the journey, the car traveled 50 km, and in each subsequent hour, it traveled 5 km more than in the previous hour. How many hours will it take for the car to catch up with the truck if the distance between the village and the city is 175 km?
|
# Answer: 7.
Solution. In the first hour of travel, the pursuit speed of the car relative to the truck was $50-40=10$ km/h. In each subsequent hour, the pursuit speed increases by 5 km/h. Thus, the pursuit speeds form an arithmetic progression $10,15,20 \ldots$ km/h. Let's find the number of hours $n$ until the cars meet. The sum of this progression is equal to the total distance the car will travel until it meets the truck $\frac{20+5(n-1)}{2} \cdot n=175$. After transformation, we get the equation $n^{2}+3 n-70=0$, the roots of which are $7,-10$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (15 points) Two heaters are connected sequentially to the same DC power source. The water in the pot boiled after $t_{1}=3$ minutes from the first heater. The same water, taken at the same initial temperature, boiled after $t_{2}=6$ minutes from the second heater. How long would it take for the water to boil if the heaters were connected in parallel? Neglect heat dissipation to the surroundings.
|
Answer: 2 min.
Solution. The amount of heat required for heating in the first case $Q=I^{2} R_{1} t_{1}$. The amount of heat required for heating in the second case $Q=$ $I^{2} R_{2} t_{2}$. The amount of heat required for heating in the case of parallel connection $Q=I^{2} \frac{R_{1} \cdot R_{2}}{R_{1}+R_{2}} t$. As a result, we get:
$$
t=\frac{t_{1} t_{2}}{t_{1}+t_{2}}=\frac{3 \cdot 6}{3+6}=2 \text { min. }
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.