problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
2. The cold water tap fills the bathtub in 19 minutes, while the hot water tap fills it in 23 minutes. The hot water tap was opened. After how many minutes should the cold water tap be opened so that by the time the bathtub is completely filled, there is an equal amount of cold and hot water in it?
|
Answer: in 2 minutes.
Solution. Half of the bathtub is filled with hot water in 11.5 minutes, and with cold water in 9.5 minutes. Therefore, the hot water tap should be open for 2 minutes longer.
Evaluation. 12 points for the correct solution.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. A certain mechanism consists of 25 parts, some of which are large, and some are small. It is known that among any 12 parts taken, there will be at least one small part, and among any 15 parts, there will be at least one large part. How many of each type of part does the mechanism contain?
|
Answer: 11 large parts and 14 small parts.
Solution. Since among any 12 parts there is a small one, there are no more than 11 large parts. Since among any 15 parts there is a large one, there are no more than 14 small parts. If there were fewer than 11 large parts or fewer than 14 small parts, the total number of parts would be less than 25, but according to the condition, there are 25. Therefore, there are 11 large parts and 14 small parts.
Grading. 13 points for a correct solution. 2 points for a correct answer (without justification). If the correctness of the answer is shown but its uniqueness is not justified, 6 points.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Masha's tablet, which she needed for a presentation at school, was completely drained. Using additional equipment, the tablet can be fully charged in 2 hours and 40 minutes, without it in 8 hours. Masha first put the discharged tablet on regular charging, and when she found the equipment, she switched to fast charging and fully charged the tablet. It is known that the tablet charges uniformly both with fast and regular charging. Find the total charging time of the tablet, if it was on fast charging for a third of the total charging time. Give your answer in minutes.
|
Answer: 288.
Solution. The tablet charges in 160 minutes on fast charging, and in 480 minutes on regular charging. Therefore, on fast charging, $\frac{1}{160}$ of the full charge is completed in 1 minute, and on regular charging, $\frac{1}{480}$ of the full charge is completed in 1 minute. Let $t-$ be the total charging time, then $\frac{t}{3} \cdot \frac{1}{160}+\frac{2 t}{3} \cdot \frac{1}{480}=1$ or $t \cdot \frac{5}{3 \cdot 480}=1$.
We get that $t=\frac{1440}{5}=288$.
|
288
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) There are ten weights of different weights, each weighing an integer number of grams. It is known that the weight of the lightest and heaviest weight differs by 9 grams. One weight is lost. Find its weight if the total weight of the remaining weights is 2022 grams.
|
Answer: 223.
Solution. Let $x$ be the weight of the lightest weight. Denote the weight of the lost weight as $(x+y)$ $(0<y<9)$. Then $x+(x+1)+(x+2)+\cdots+(x+$ $9)-(x+y)=2022$. Combine like terms: $10 x+45-x-y=$ 2022 or $9 x=1977+y$. From this, $1977+y$ is divisible by 9. Considering the condition $0<y<9$, we get that $y=3$. Therefore, $x=1980: 9=220$, $x+y=223$.
|
223
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) In a garden plot, it was decided to create a rectangular flower bed. Due to a lack of space, the length of the flower bed was reduced by $10 \%$, and the width was reduced by $20 \%$. As a result, the perimeter of the flower bed decreased by $12 \%$. However, this was not enough, so it was decided to reduce the length by $20 \%$ and the width by $10 \%$. By what percentage did the perimeter of the rectangular flower bed decrease from the original version?
|
Answer: 18.
Solution. Let $x$ be the length of the flower bed, $y$ be the width of the flower bed. After the reduction: $0.9 x$ - length of the flower bed, $0.8 y$ - width of the flower bed, $2(0.9 x + 0.8 y)$ - perimeter. We get the equation: $2(0.9 x + 0.8 y) = 0.88 \cdot 2(x + y)$ or $x = 4 y$. The original perimeter: $10 y$. After the second reduction: $0.8 x = 3.2 y$ - length of the flower bed, $0.9 y$ - width of the flower bed, $2(3.2 y + 0.9 y) = 8.2 y$ - perimeter. The perimeter decreased by $1.8 y$ or by $18\%$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (15 points) A one-and-a-half kilogram model of a sports car body was made from carbon fiber for aerodynamic studies at a scale of 1:10. What is the mass of the actual body if it is also entirely made of carbon fiber?
|
Answer: 1500 kg.
Solution. All dimensions of the body are 10 times larger compared to the model. Therefore, the volume of the body is larger by $10 \cdot 10 \cdot 10=1000$ times. Mass is directly proportional to volume, therefore, the mass of the body:
$$
m_{\text {body }}=1000 \cdot m_{\text {model }}=1500 \text { kg. }
$$
|
1500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A car traveled half of the distance at a speed 20 km/h faster than the average speed, and the second half of the distance at a speed 20% lower than the average. Determine the average speed of the car.
|
Answer: 60 km/h.
Solution. The average speed $v=\frac{s+s}{t_{1}+t_{2}}=\frac{s+s}{\frac{s}{v+20}+\frac{s}{0.8 v}}=\frac{2}{\frac{1}{v+20}+\frac{1}{0.8 v}}$. Solving this equation, we get $v=60$ km/h.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (15 points) A pedestrian is moving towards a crosswalk along a straight path at a constant speed of 3.6 km/h. At the initial moment, the distance from the pedestrian to the crosswalk is 20 m. The length of the crosswalk is $5 \mathrm{~m}$. At what distance from the crosswalk will the pedestrian be after half a minute?
|
Answer: 5 m.
Solution. The pedestrian's speed is 3.6 km/h = 1 m/s. In half a minute, he walked $s = v t = 1 \cdot 30 s = 30$ m. From the crossing, he is at a distance of $l = s - 20 - 5 = 5$ m.
## Tasks, answers, and evaluation criteria
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Masha's tablet, which she needed for a presentation at school, was completely drained. Using additional equipment, the tablet can be fully charged in 3 hours, without it in 9 hours. Masha first put the discharged tablet on regular charging, and when she found the equipment, she switched to fast charging and fully charged the tablet. It is known that the tablet charges uniformly both with fast and regular charging. Find the total charging time of the tablet if it was on fast charging for one third of the total charging time. Give your answer in minutes.
|
Answer: 324.
Solution. The tablet charges in 180 minutes on fast charging, and in 540 minutes on regular charging. Therefore, on fast charging, $\frac{1}{180}$ of the full charge is completed in 1 minute, and on regular charging, $\frac{1}{540}$ of the full charge is completed in 1 minute. Let $t$ be the total charging time, then $\frac{t}{3} \cdot \frac{1}{180}+\frac{2 t}{3} \cdot \frac{1}{540}=1$ or $t \cdot \frac{5}{3 \cdot 540}=1$. We get that $t=\frac{1620}{5}=324$.
|
324
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) There are ten weights of different weights, each weighing an integer number of grams. It is known that the weight of the lightest weight and the heaviest differs by 9 grams. One weight is lost. Find the weight of the lightest weight if the total weight of the remaining weights is 2022 grams.
#
|
# Answer: 220.
Solution. Let $x$ be the weight of the lightest weight. Denote the weight of the lost weight as $(x+y)$ $(0<y<9)$. Then $x+(x+1)+(x+2)+\cdots+(x+$ 9) - $(x+y)=2022$. Combine like terms: $10 x+45-x-y=$ 2022 or $9 x=1977+y$. From this, $1977+y$ is divisible by 9. Considering the condition $0<y<9$, we get that $y=3$. Therefore, $x=1980: 9=220$.
|
220
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) In a garden plot, it was decided to create a rectangular flower bed. Due to a lack of space, the length of the flower bed was reduced by $10 \%$, and the width was reduced by $20 \%$. As a result, the perimeter of the flower bed decreased by $12.5 \%$. However, this was not enough, so it was decided to reduce the length by $20 \%$ and the width by $10 \%$. By what percentage did the perimeter of the rectangular flower bed decrease from the original version?
|
Answer: 14.
Solution. Let $x$ be the length of the flower bed, $y$ be the width of the flower bed. After the reduction: $0.9 x$ - length of the flower bed, $0.8 y$ - width of the flower bed, $2(0.9 x + 0.8 y)$ - perimeter. We get the equation: $\quad 2(0.9 x + 0.8 y) = 0.875 \cdot 2(x + y) \quad$ or $\quad x = 3 y$. The original perimeter: $8 y$. After the second reduction:
$0.8 x = 2.4 y$ - length of the flower bed, $0.9 y$ - width of the flower bed, $2(2.4 y + 0.9 y) = 6.6 y$ - perimeter. The perimeter decreased by $1.4 y$ or by $14\%$.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (15 points) A one-kilogram model of a sports car body was made from carbon fiber for aerodynamic studies at a scale of 1:11. What is the mass of the actual body if it is also entirely made of carbon fiber?
|
Answer: 1331 kg.
Solution. All dimensions of the body are 11 times larger compared to the model. Therefore, the volume of the body is larger by $11 \cdot 11 \cdot 11=1331$ times. The mass is directly proportional to the volume, therefore, the mass of the body:
$$
m_{\text {body }}=1331 \cdot m_{\text {model }}=1331 \text { kg. }
$$
|
1331
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A car traveled half of the distance at a speed 30 km/h faster than the average speed, and the second half of the distance at a speed 30% lower than the average. Determine the average speed of the car.
|
Answer: 40 km/h.
Solution. The average speed $v=\frac{s+s}{t_{1}+t_{2}}=\frac{s+s}{\frac{s}{v+30}+\frac{s}{0.7 v}}=\frac{2}{\frac{1}{v+30}+\frac{1}{0.7 v}}$. Solving this equation, we get $v=40$ km/h.
|
40
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem No. 5 (10 points)
When constructing this structure, a homogeneous wire of constant cross-section was used. It is known that points $B, D, F$ and $H$ are located equally at the midpoints of the corresponding sides of the square ACEG. The resistance of segment $A B$ is $R_{0}=1 \Omega$. Determine the resistance of the entire structure if it is connected to the electrical circuit at points C and $G$.
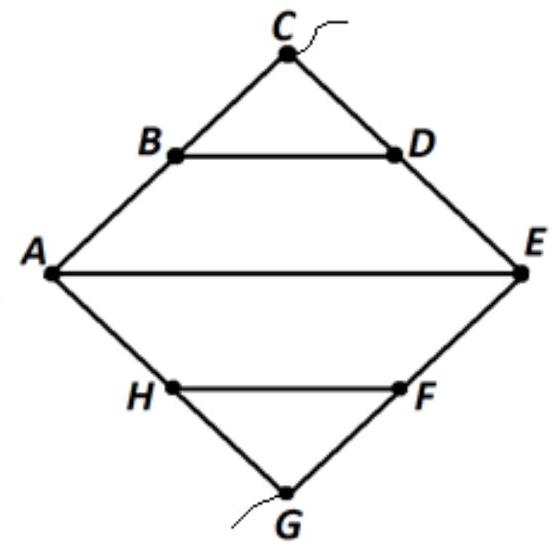
|
Answer: 2 Ohms
## Solution and grading criteria:
The resistance of a resistor is proportional to its length.
Taking this into account, the proposed circuit can be replaced by an equivalent one:
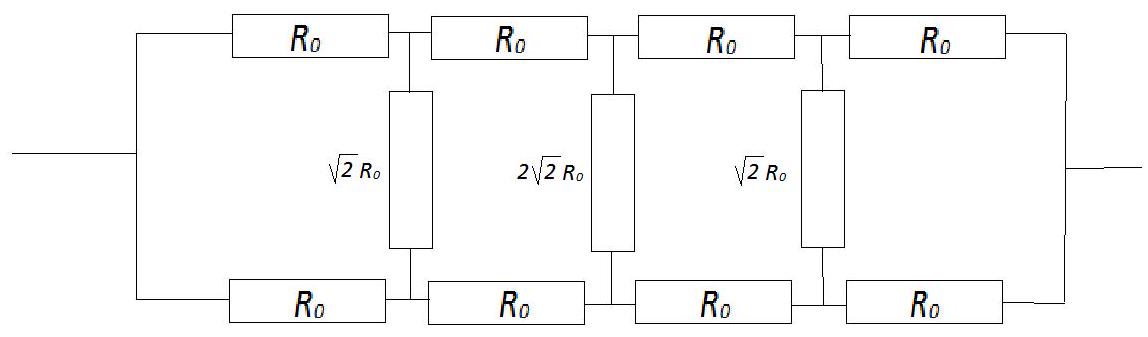
Its resistance: $\quad R=2 R_{0} \approx 2$ Ohms
#
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) When walking uphill, the tourist walks 2 km/h slower, and downhill 2 km/h faster, than when walking on flat ground. Climbing the mountain takes the tourist 10 hours, while descending the mountain takes 6 hours. What is the tourist's speed on flat ground?
|
# Answer: 8
Solution. Let $x$ km/h be the tourist's speed on flat terrain. According to the problem, we get the equation $10(x-2)=6(x+2)$. From this, we find $x=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) Mitya, Anton, Gosha, and Boris bought a lottery ticket for 20 rubles. Mitya paid $24\%$ of the ticket's cost, Anton - 3 rubles 70 kopecks, Gosha - 0.21 of the ticket's cost, and Boris contributed the remaining amount. The boys agreed to divide the winnings in proportion to their contributions. The ticket won 1000 rubles. What amount (in rubles) is due to Boris?
|
Answer: 365
Solution. The ticket costs 2000 kop. Mitya paid 480 kop, Anton - 370 kop, Gosha - 420 kop, therefore, Boris had to pay an additional 730 kop. Since the prize is 50 times the cost of the ticket, Boris is entitled to 365 rubles.
|
365
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) When walking uphill, the tourist walks 3 km/h slower, and downhill 3 km/h faster, than when walking on flat ground. Climbing the mountain takes the tourist 8 hours, while descending the mountain takes 4 hours. What is the tourist's speed on flat ground?
|
# Answer: 9
Solution. Let $x$ km/h be the tourist's speed on flat terrain. According to the problem, we get the equation $8(x-3)=4(x+3)$. From this, we find $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (16 points) Mitya, Anton, Gosha, and Boris bought a lottery ticket for 20 rubles. Mitya paid $24\%$ of the ticket's cost, Anton - 3 rubles 70 kopecks, Gosha - $0.21$ of the ticket's cost, and Boris contributed the remaining amount. The boys agreed to divide the winnings in proportion to their contributions. The ticket won 800 rubles. What amount (in rubles) is due to Boris?
|
Answer: 292
Solution. The ticket costs 2000 kop. Mitya paid 480 kop, Anton - 370 kop, Gosha - 420 kop, therefore, Boris had to pay an additional 730 kop. Since the prize is 40 times the cost of the ticket, Boris is entitled to 292 rubles.
|
292
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) The dividend is six times larger than the divisor, and the divisor is four times larger than the quotient. Find the dividend.
|
# Answer: 144
Solution. From the condition of the problem, it follows that the quotient is 6. Then the divisor is 24, and the dividend is 144.
|
144
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Hooligan Vasily tore out a whole chapter from a book, the first page of which was numbered 231, and the number of the last page consisted of the same digits. How many sheets did Vasily tear out of the book?
#
|
# Answer: 41
Solution. The number of the last page starts with the digit 3 and must be even, so the last page has the number 312. Vasily tore out $312-231+1=82$ pages or 41 sheets.
|
41
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) Divide the number 90 into two parts such that $40\%$ of one part is 15 more than $30\%$ of the other part. Write the larger of the two parts in your answer.
|
Answer: 60
Solution. Let one part of the number be $x$, then the other part will be $90-x$. We get the equation $0.4 \cdot x = 0.3 \cdot (90 - x) + 15$, solving it we get $x = 60$, and the other part of the number is 30.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) A one-kilogram model of a sports car body was made from aluminum at a scale of 1:10. What is the mass of the actual body if it is also entirely made of aluminum?
|
Answer: 1000 kg
Solution. All dimensions of the body are 10 times larger compared to the model. Therefore, the volume of the body is larger by $10 \cdot 10 \cdot 10=1000$ times. Mass is directly proportional to volume, therefore, the mass of the body:
$$
m_{\text {body }}=1000 m_{\text {model }}=1000 \text { kg. }
$$
Preliminary Stage
6th grade
2018-2019
Variant 2
Tasks, answers, and evaluation criteria
|
1000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) The dividend is five times larger than the divisor, and the divisor is four times larger than the quotient. Find the dividend.
#
|
# Answer: 100
Solution. From the condition of the problem, it follows that the quotient is 5. Then the divisor is 20, and the dividend is 100.
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Hooligan Vasily tore out a whole chapter from a book, the first page of which was numbered 241, and the number of the last page consisted of the same digits. How many sheets did Vasily tear out of the book?
#
|
# Answer: 86
Solution. The number of the last page starts with the digit 4 and must be even, so the last page has the number 412. Vasily tore out $412-241+1=172$ pages or 86 sheets.
|
86
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) Divide the number 80 into two parts such that $30\%$ of one part is 10 more than $20\%$ of the other part. Write the smaller of the two parts in your answer.
|
Answer: 28
Solution. Let one part of the number be $x$, then the other part will be $80-x$. We get the equation $0.3 \cdot x = 0.2 \cdot (80 - x) + 10$, solving it we get $x = 52$, and the other part of the number is 28.
|
28
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (20 points) A two-kilogram model of a sports car body was made from aluminum at a scale of $1: 8$. What is the mass of the actual body if it is also entirely made of aluminum?
|
Answer: 1024 kg
Solution. All dimensions of the body are 8 times larger compared to the model. Therefore, the volume of the body is larger by $8 \cdot 8 \cdot 8=512$ times. The mass is directly proportional to the volume, therefore, the mass of the body:
$m_{\text {body }}=512 m_{\text {model }}=1024$ kg
|
1024
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Find the area of the triangle cut off by the line $y=3 x+1$ from the figure defined by the inequality $|x-1|+|y-2| \leq 2$.
|
Answer: 2.
Solution. The figure defined by the given inequality is a square.
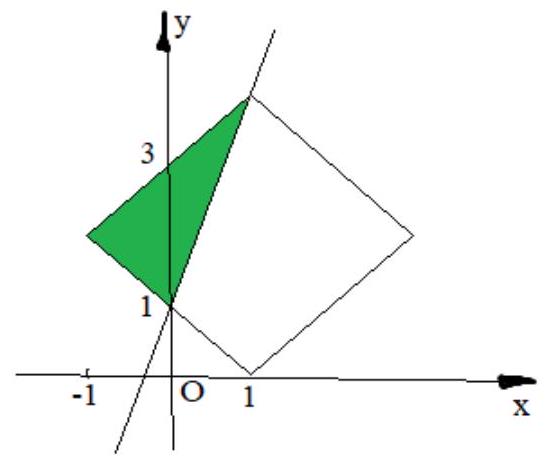
The side of the square is $2 \sqrt{2}$ (this can be found using the Pythagorean theorem). The given line passes through the vertex of the square and cuts off a triangle with the smaller leg equal to $\sqrt{2}$, and the larger leg - the side of the square. Therefore, the area of the cut-off right triangle is $S=\frac{1}{2} \cdot \sqrt{2} \cdot 2 \sqrt{2}=2$ square units.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) A section of a regular triangular pyramid passes through the midline of the base and is perpendicular to the base. Find the area of the section if the side of the base is 6 and the height of the pyramid is 8.
|
Answer: 9.
Solution. The section MNP passes through the midline of the base of the pyramid $MN$ and is perpendicular to the base. Therefore, the height $PH$ of the triangle $MNP$ is parallel to the height of the pyramid $DO$.
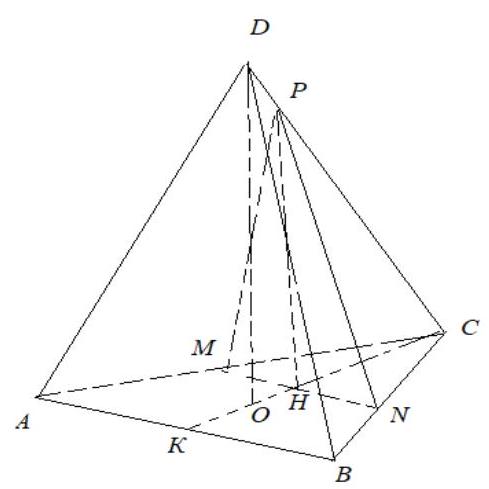
We have $OC: OK=2: 1, CH=HK$, therefore, $CH: CO=3: 4$. Using the similarity of triangles $DOC$ and $PHC$, we get that $PH=\frac{3}{4} DO=\frac{3}{4} \cdot 8=6$. Then the area of the section is $S=\frac{1}{2} \cdot PH \cdot MN=\frac{1}{2} \cdot 6 \cdot 3=9$ sq.units.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Find the area of the triangle cut off by the line $y=2x+2$ from the figure defined by the inequality $|x-2|+|y-3| \leq 3$.
|
Answer: 3.
Solution. The figure defined by the given inequality is a square.
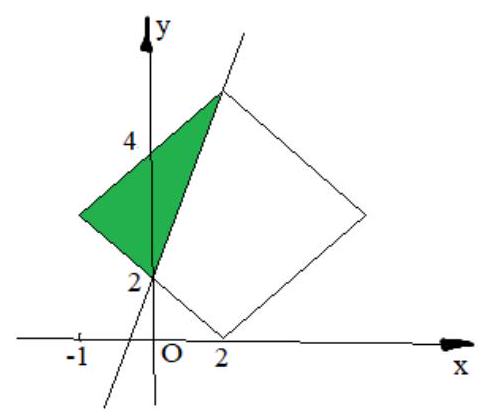
The side of the square is $3 \sqrt{2}$ (this value can be found using the Pythagorean theorem). The given line passes through the vertex of the square and cuts off a triangle with the smaller leg equal to $\sqrt{2}$, and the larger leg - the side of the square. Therefore, the area of the cut-off right triangle is $S=\frac{1}{2} \cdot \sqrt{2} \cdot 3 \sqrt{2}=3$ square units.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) The cross-section of a regular triangular pyramid passes through the midline of the base and is perpendicular to the base. Find the area of the cross-section if the side of the base is 8 and the height of the pyramid is 12.
|
Answer: 18.
Solution. The section MNP passes through the midline of the base of the pyramid $MN$ and is perpendicular to the base. Therefore, the height $PH$ of the triangle $MNP$ is parallel to the height of the pyramid $DO$.
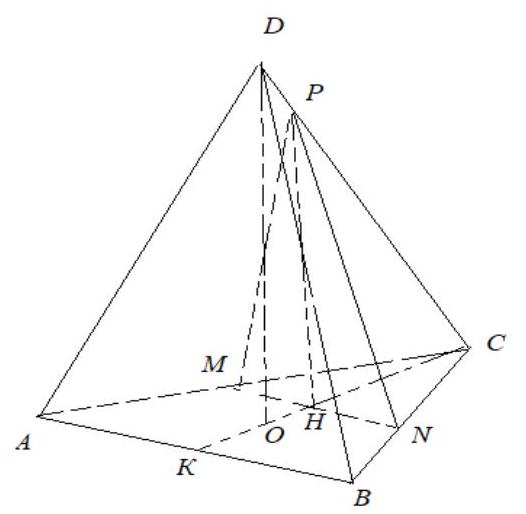
We have $OC: OK=2: 1, \quad CH=HK$, therefore, $CH: CO=3: 4$. Using the similarity of triangles $DOC$ and $PHC$, we get that $PH=\frac{3}{4} DO=\frac{3}{4} \cdot 12=9$. Then the area of the section is $S=\frac{1}{2} \cdot PH \cdot MN=\frac{1}{2} \cdot 9 \cdot 4=18$ sq.units.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) There are two circles: one with center at point $A$ and radius 6, and another with center at point $B$ and radius 3. Their common internal tangent touches the circles at points $C$ and $D$, respectively. Lines $A B$ and $C D$ intersect at point $E$. Find $C D$, if $A E=10$.
|
Answer: 12
Solution. Triangles $A C E$ and $B D E$ are similar (they have vertical angles and a right angle each) with a similarity coefficient of 2. From triangle $A C E$, using the Pythagorean theorem, we find $C E=8$. Therefore, $D E=4$, and $C D=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the largest root of the equation
$$
\left|\cos (\pi x)+x^{3}-3 x^{2}+3 x\right|=3-x^{2}-2 x^{3}
$$
|
# Answer: 1
Solution. It is obvious that 1 is a root of the equation (when $x=1$, both sides of the equation are equal to zero). If $x>1$, the right side of the equation is negative, while the left side of the equation is always non-negative.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) Find the smallest natural number that is simultaneously twice a perfect square and three times a perfect cube.
#
|
# Answer: 648
Solution. We have $k=3 n^{3}=2 m^{2}$. From this, the numbers $m$ and $n$ can be represented as $n=2 a, m=3 b$. After substitution, we get $4 a^{3}=3 b^{2}$. Further, we have $a=3 c, b=2 d, 9 c^{3}=d^{2}$. Here, the smallest solution is $c=1, d=3$. Then $a=3$, $b=6, n=6, m=18, k=648$.
|
648
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (15 points) The efficiency of an ideal heat engine is $40 \%$. What will it become if the temperature of the heater is increased by $40 \%$, and the temperature of the cooler is decreased by $40 \%$?
|
Answer: $\approx 74 \%$.
Solution. The efficiency of an ideal heat engine: $\eta=1-\frac{T_{X}}{T_{H}}$. That is, initially the ratio of the temperatures of the refrigerator and the heater: $\frac{T_{X}}{T_{H}}=1-0.4=0.6$. After the changes:
$$
\eta_{2}=1-\frac{0.6 T_{X}}{1.4 T_{H}}=1-\frac{0.6 \cdot 0.6}{1.4} \approx 0.74 \approx 74 \% .
$$
|
74
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A point light source is located at an equal distance $x=10 \mathrm{~cm}$ from the lens and its principal optical axis. Its direct image is located at a distance $y=5 \mathrm{~cm}$ from the principal optical axis. Determine the optical power of the lens and the distance between the light source and its image.
|
Answer: -10 Dptr $u \approx 7.1$ cm
Solution. The image is upright, therefore, it is virtual. Magnification: $\Gamma=\frac{y}{x}=\frac{f}{d}$. We obtain that the distance from the lens to the image: $f=d \cdot \frac{y}{x}=10 \cdot \frac{5}{10}=5 \mathrm{~cm} . \quad$ The power of the lens: $D=\frac{1}{d}-\frac{1}{f}=\frac{1}{0.1}-\frac{1}{0.05}=-10$ Dptr. The distance between the source and its image: $s=\sqrt{(x-y)^{2}+(d-f)^{2}}=\sqrt{50} \approx 7.1 \mathrm{~cm}$.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) There are two circles: one with center at point $A$ and radius 5, and another with center at point $B$ and radius 15. Their common internal tangent touches the circles at points $C$ and $D$ respectively. Lines $A B$ and $C D$ intersect at point $E$. Find $C D$, if $B E=39$.
|
# Answer: 48
Solution. Triangles $A C E$ and $B D E$ are similar (they have vertical angles and a right angle each) with a similarity coefficient of $1 / 3$. Therefore, $A E=13$. From triangle $A C E$, using the Pythagorean theorem, we find $C E=12$. Hence, $D E=36$, and $C D=48$.
|
48
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the smallest root of the equation
$$
\sin (\pi x)+\tan x=x+x^{3}
$$
|
Answer: 0
Solution. Obviously, 0 is a root of the equation (when $x=0$, both sides of the equation are equal to zero). If $x<0$, the right side of the equation is negative, while the left side of the equation is always non-negative.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) Find the smallest natural number that is simultaneously twice a perfect cube and three times a perfect square.
#
|
# Answer: 432
Solution. We have $k=2 n^{3}=3 m^{2}$. From this, the numbers $m$ and $n$ can be represented as $n=3 a, m=2 b$. After substitution, we get $9 a^{3}=2 b^{2}$. Further, we have $a=2 c, b=3 d, 4 c^{3}=d^{2}$. Here, the smallest solution is $c=1, d=2$. Then $a=2$, $b=6, n=6, m=12, k=432$.
|
432
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. (15 points) The efficiency of an ideal heat engine is $50 \%$. What will it become if the temperature of the heater is increased by $50 \%$, and the temperature of the cooler is decreased by $50 \%$?
|
Answer: $\approx 83 \%$
Solution. The efficiency of an ideal heat engine: $\eta=1-\frac{T_{X}}{T_{H}}$. That is, at the beginning, the ratio of the temperatures of the refrigerator and the heater: $\frac{T_{X}}{T_{H}}=1-0.5=0.5$. After the changes:
$$
\eta_{2}=1-\frac{0.5 T_{X}}{1.5 T_{H}}=1-\frac{0.5 \cdot 0.5}{1.5} \approx 0.83=83 \% .
$$
|
83
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A point light source is located at an equal distance $x=10 \mathrm{~cm}$ from the lens and its principal optical axis. Its direct image is located at a distance $y=20 \mathrm{~cm}$ from the principal optical axis. Determine the optical power of the lens and the distance between the light source and its image.
|
Answer: 5 Dpt $i \approx 14.1$ cm
Solution. The image is upright, therefore, it is virtual. Magnification: $\Gamma=\frac{y}{x}=\frac{f}{d}$. We obtain the distance from the lens to the image: $f=d \cdot \frac{y}{x}=10 \cdot \frac{20}{10}=20 \mathrm{~cm} . \quad$ The optical power of the lens: $D=\frac{1}{d}-\frac{1}{f}=\frac{1}{0.1}-\frac{1}{0.2}=5$ Dpt. The distance between the source and its image: $s=\sqrt{(x-y)^{2}+(d-f)^{2}}=\sqrt{200} \approx 14.1 \mathrm{~cm}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many times in a day does the angle between the hour and minute hands equal exactly $17^{\circ}$?
|
Answer: 44.
Solution. Over the time interval from 0:00 to 12:00, the hour hand will make one complete revolution, while the minute hand will make 12 such revolutions. Therefore, during this time, the minute hand will catch up with the hour hand 11 times. Between two consecutive meetings of the hands, the angle between them will be exactly $17^{\circ}$ twice. Thus, between midnight and noon, the required angle between the hands will occur $11 \cdot 2=22$ times, and over a full day, such moments will be twice as many.
Grading. 12 points for a correct solution.
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation
$$
\sqrt{\frac{x-2}{11}}+\sqrt{\frac{x-3}{10}}=\sqrt{\frac{x-11}{2}}+\sqrt{\frac{x-10}{3}}
$$
|
Answer: 13.
Solution. If we perform the variable substitution $x=t+13$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t \leqslant 0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=13$.
Estimation. 12 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
$$
\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right) \text{ for } (m>0) \Rightarrow\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right)
$$
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let in triangle $A B C$
$$
\cos (2 \angle A-\angle B)+\sin (\angle A+\angle B)=2 \text {. }
$$
Find the side $B C$, if $A B=4$.
|
Answer: 2.
Solution. Each term in the left part of the equation does not exceed 1. Therefore, the equality will hold only if each of them equals 1. We solve the corresponding equations, denoting $\alpha=\angle A, \beta=\angle B:$
$$
2 \alpha-\beta=2 \pi n, n \in \mathbb{Z} ; \quad \alpha+\beta=\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z}
$$
Considering that $0<\alpha<\pi, 0<\beta<\pi$, we get
$$
2 \alpha-\beta=0 ; \quad \alpha+\beta=\frac{\pi}{2} .
$$
From this,
$$
\beta=2 \alpha, \quad 3 \alpha=\frac{\pi}{2}, \quad \alpha=\frac{\pi}{6}, \quad \beta=\frac{\pi}{3} .
$$
Thus, $A B C$ is a right triangle with hypotenuse $A B$ and an angle of $30^{\circ}$ opposite side $B C$. Therefore, $B C=A B / 2=2$.
Evaluation. 12 points for a correct solution.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many times in a day does the angle between the hour and minute hands equal exactly $19^{\circ}$?
|
Answer: 44.
Solution. Over the time interval from 0:00 to 12:00, the hour hand will make one complete revolution, while the minute hand will make 12 such revolutions. Therefore, during this time, the minute hand will catch up with the hour hand 11 times. Between two consecutive meetings of the hands, the angle between them will be exactly $17^{\circ}$ twice. Thus, between midnight and noon, the required angle between the hands will occur $11 \cdot 2=22$ times, and over a full day, such moments will be twice as many.
Grading. 12 points for a correct solution.
|
44
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Solve the equation
$$
\sqrt{\frac{x-3}{11}}+\sqrt{\frac{x-4}{10}}=\sqrt{\frac{x-11}{3}}+\sqrt{\frac{x-10}{4}}
$$
|
Answer: 14.
Solution. If we perform the variable substitution $x=t+14$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t<0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=14$.
Estimation. 12 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
$$
\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right) \text{ for } (m>0) \Rightarrow\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right)
$$
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A circle is inscribed with 2019 numbers. For any two adjacent numbers $x$ and $y$, the inequalities $|x-y| \geqslant 2, x+y \geqslant 6$ are satisfied. Find the smallest possible sum of the recorded numbers.
|
Answer: 6060.
Solution. Due to the odd number of total numbers, there will be three consecutive numbers $x, y$, and $z$ such that $x>y>z$. Adding the inequalities $y-z \geqslant 2$ and $y+z \geqslant 6$, we get $y \geqslant 4$. Then $x \geqslant y+2 \geqslant 6$. A number not less than 6 has been found. The remaining numbers can be divided into 1009 pairs of adjacent numbers. Therefore, the sum of all numbers $S \geqslant 6+1009 \cdot 6=6060$.
The lower bound for $S$ obtained can be achieved if one of the numbers is 6, and then, in a circle, the numbers 4 and 2 alternate.
Evaluation. 14 points for a complete solution. 5 points for an example without estimation, 7 points for estimation without an example.
|
6060
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The infantry column stretched out over 1 km. Sergeant Kim, riding out on a gyro-scooter from the end of the column, reached its beginning and returned to the end. The infantrymen walked 2 km $400 \mathrm{m}$ during this time. How far did the sergeant travel during this time?
|
Answer: 3 km $600 \mathrm{~m}$
Solution. Let the speed of the column be $x$ km/h, and the sergeant travels $k$ times faster, i.e., at a speed of $k x$ km/h. To reach the end of the column, Kim traveled $t_{1}=\frac{1}{k x-x}$ hours (catching up), and in the opposite direction, $t_{2}=\frac{1}{k x+x}$ hours (meeting head-on). During this time, the column covered 2.4 km, i.e., $x\left(t_{1}+t_{2}\right)=2.4$. Substituting the expressions for $t_{1}$ and $t_{2}$, we get
$$
\frac{x}{k x-x}+\frac{x}{k x+x}=2.4 ; \quad \frac{1}{k-1}+\frac{1}{k+1}=2.4 ; \quad 2 k=2.4\left(k^{2}-1\right) .
$$
The obtained quadratic equation has a single positive root $k=\frac{3}{2}$. The sergeant travels 1.5 times faster than the column. Therefore, the distance he covers will also be 1.5 times greater.
Evaluation. Full solution: 12 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A circle is inscribed with 1001 numbers. For any two adjacent numbers $x$ and $y$, the inequalities $|x-y| \geqslant 4, x+y \geqslant 6$ are satisfied. Find the smallest possible sum of the recorded numbers.
|
Answer: 3009.
Solution. Due to the odd number of total numbers, there will be three consecutive numbers $x, y$, and $z$ such that $x>y>z$. Adding the inequalities $y-z \geqslant 4$ and $y+z \geqslant 6$, we get $y \geqslant 5$. Then $x \geqslant y+4 \geqslant 9$. A number not less than 9 has been found. The remaining numbers can be divided into 500 pairs of adjacent numbers. Therefore, the sum of all numbers $S \geqslant 9+500 \cdot 6=3009$.
The lower bound for $S$ obtained can be achieved if one of the numbers is 9, and then, in a circle, alternating numbers 5 and 1 are placed.
Evaluation. 14 points for a complete solution. 5 points for an example without estimation, 7 points for estimation without an example.
|
3009
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (10 points) A beam of light with a diameter of $d_{1}=5 \mathrm{~cm}$ falls on a thin diverging lens with an optical power of $D_{p}=-6$ Diopters. On a screen positioned parallel to the lens, a bright spot with a diameter of $d_{2}=20 \mathrm{~cm}$ is observed. After replacing the thin diverging lens with a thin converging lens, the size of the spot on the screen remains unchanged. Determine the optical power $D_{c}$ of the converging lens.
|
# Answer: 10 Dptr
Solution. The optical scheme corresponding to the condition:
(3 points)
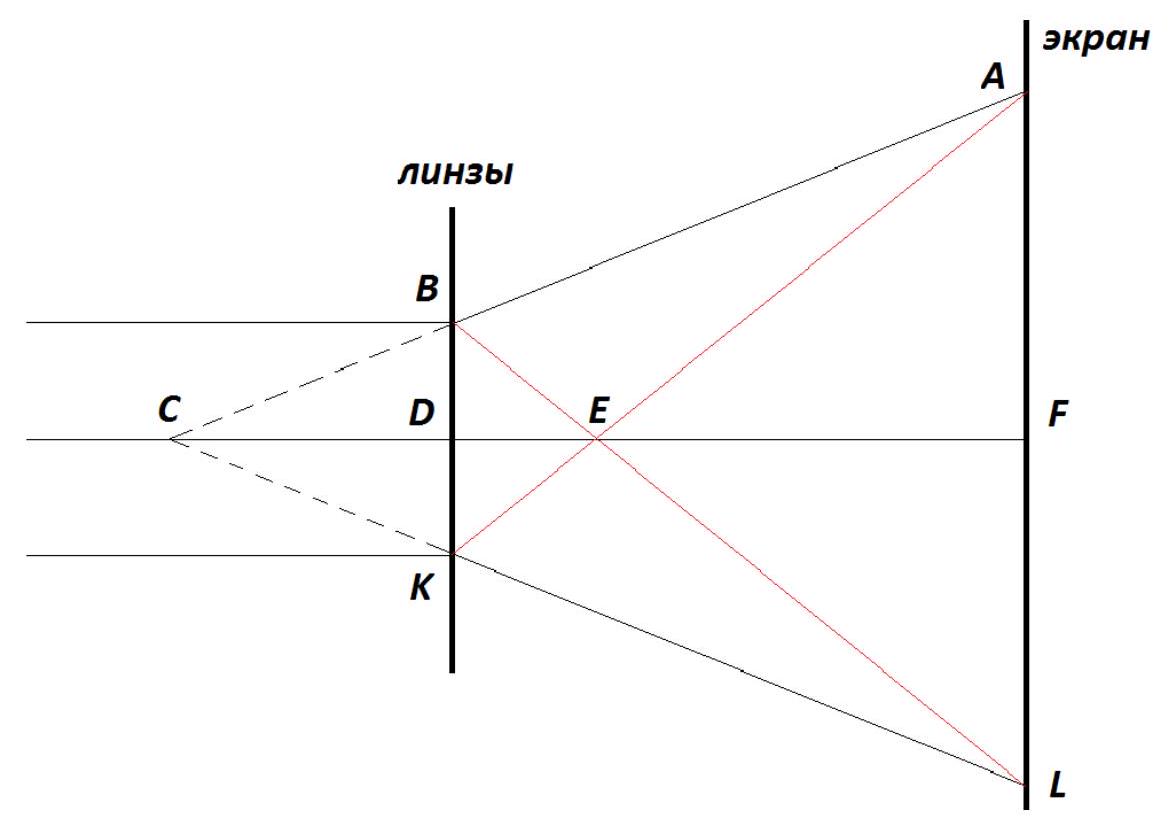
The path of the rays after the diverging lens is shown in black, and after the converging lens in red. We have $C D=\left|\frac{1}{D_{p}}\right|=\frac{1}{6}$.
From the similarity of triangles, it follows that: $\frac{C D}{C F}=\frac{B K}{A L}=\frac{1}{4}$,
then $D F=C F-C D=4 C D-C D=3 C D=\frac{1}{2}$.
From the similarity of triangles, it follows that: $\frac{D E}{F E}=\frac{B K}{A L}$.
We get that: $D E=\frac{1}{5} D F=\frac{1}{10}$.
As a result, the optical power of the converging lens: $D_{c}=\frac{1}{D E}=10$ Dptr.
(2 points)
|
10
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 6 (10 points)
A cylinder with a mass of $M=1$ kg was placed on rails inclined at an angle $\alpha=30^{\circ}$ to the horizontal (the side view is shown in the figure). What is the minimum mass $m$ of the load that needs to be attached to the thread wound around the cylinder so that it starts rolling upwards? Slippage is absent.
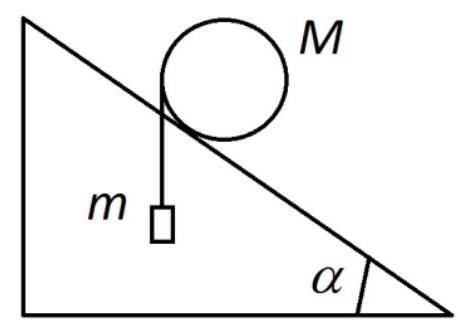
Answer: 1 kg
#
|
# Solution and evaluation criteria:
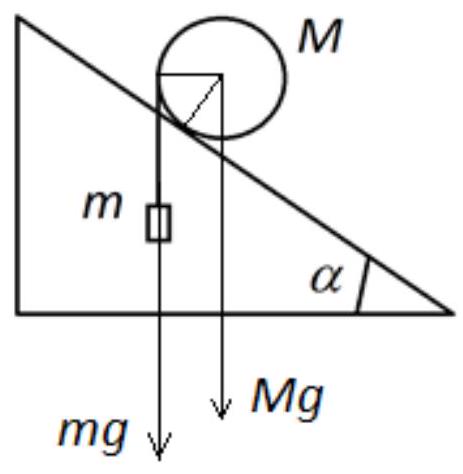
The moment of forces relative to the point of contact of the cylinder with the plane: $m g($ ( $-R \sin \alpha)=M g R \sin \alpha$ (5 points) $m\left(1-\frac{1}{2}\right)=M \frac{1}{2}$
$m=M=1 \kappa 2$
(5 points)
#
|
1
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 7 (10 points)
In the electrical circuit shown in the diagram, the resistances of the resistors are $R_{1}=10$ Ohms and $R_{2}=30$ Ohms. An ammeter is connected to points A and B in the circuit. When the polarity of the current source is reversed, the ammeter readings change by one and a half times. Determine the internal resistance of the source. Consider the ammeter to be ideal. Assume that the resistance of the diodes in the forward direction is negligible, and in the reverse direction, it is infinitely large.
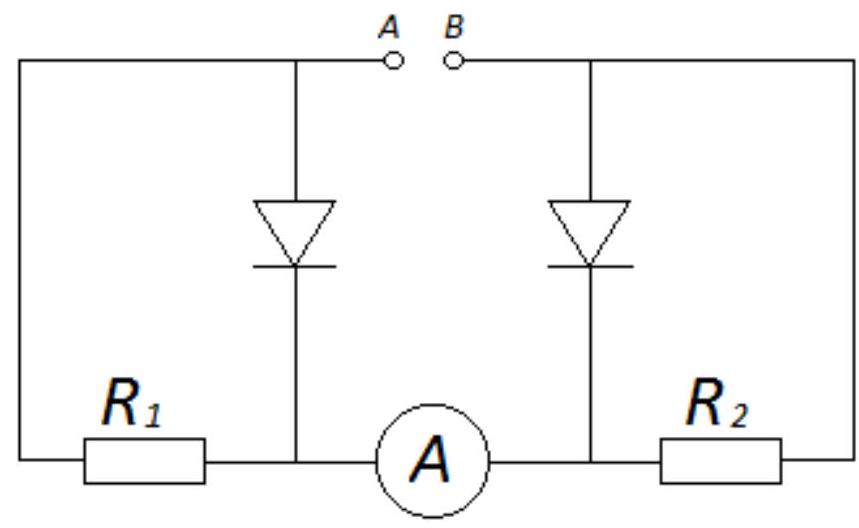
## Answer: 30 Ohms
#
|
# Solution and Evaluation Criteria:
When the positive terminal of the power supply is connected to point $A$, the current flows only through resistor $R_{2}$, and in this case: $I_{1}=\frac{\varepsilon}{R_{2}+r}$.
## (3 points)
When the polarity is reversed, the current flows only through resistance $R_{1}$, and:
$I_{2}=\frac{\varepsilon}{R_{1}+r}$
According to the condition: $I_{2}=1.5 I_{1}$
We get:
$$
\begin{aligned}
& 1.5 I_{1}\left(R_{1}+r\right)=I_{1}\left(R_{2}+r\right) \\
& 1.5(10+r)=30+r \\
& r=30 \text { Ohms. }
\end{aligned}
$$
|
30
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The area of triangle $A B C$ is 1. On the rays $A B, B C$, $C A$, points $B^{\prime}, C^{\prime}, A^{\prime}$ are laid out respectively, such that
$$
B B^{\prime}=2 A B, \quad C C^{\{\prime}=3 B C, \quad A A^{\prime}=4 C A .
$$
Calculate the area of triangle $A^{\prime} B^{\prime} C^{\prime}$.
|
Answer: 36.
Solution. We will solve the problem in a general form, assuming that
$$
B B^{\prime}=q A B, \quad C C^{\{\prime}=r B C, \quad A A^{\prime}=p C A .
$$
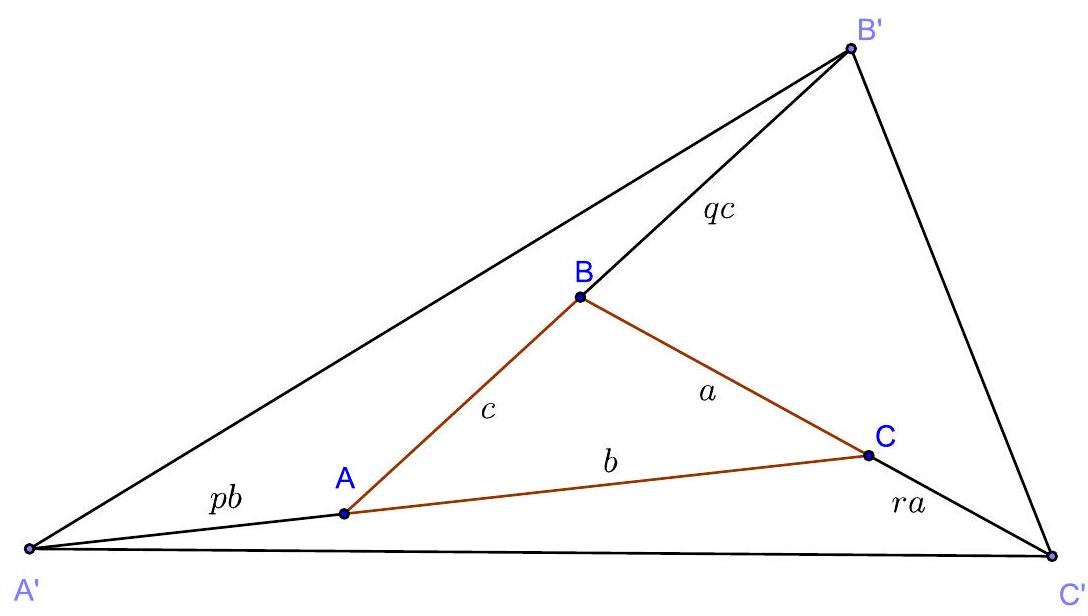
We will calculate the area of triangle \( A^{\prime} B^{\prime} A \):
$$
S_{A^{\prime} B^{\prime} A}=\frac{1}{2} A^{\prime} A \cdot A B^{\prime} \cdot \sin \angle A^{\prime} A B^{\prime}=\frac{1}{2} p b(c+q c) \sin \angle B A C=
$$
$$
=p(1+q) \cdot \frac{1}{2} b c \sin \angle B A C=p(1+q) \cdot S_{A B C}=p(1+q)
$$
(We used the equality of the sines of adjacent angles). Similarly, we find that \( S_{B^{\prime} B C^{\prime}}=q(1+r) \), \( S_{C C^{\prime} A^{\prime}}=r(1+p) \). Adding the areas of the specified three triangles and the original triangle \( A B C \), we find the desired area:
$$
S_{A^{\prime} B^{\prime} C^{\prime}}=1+p+q+r+p q+q r+r p
$$
Evaluation. 13 points for a correct solution.
|
36
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation
$$
\sqrt{\frac{x-2}{11}}+\sqrt{\frac{x-3}{10}}+\sqrt{\frac{x-4}{9}}=\sqrt{\frac{x-11}{2}}+\sqrt{\frac{x-10}{3}}+\sqrt{\frac{x-9}{4}}
$$
|
Solution. If we perform the variable substitution $x=t+13$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}+\sqrt{\frac{t}{9}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}+\sqrt{\frac{t}{4}+1}
$$
Now it is clear that for $t>0$ the right-hand side of the equation is greater, and for $-2 \leqslant t \leqslant 0$ the left-hand side is greater. Therefore, the only solution is $t=0$, which implies $x=13$.
Estimation. For a correct solution, 13 points. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The engine of a car traveling at a speed of $v_{0}=72 \mathrm{km} / \mathbf{h}$ operates with a power of $P=50$ kW. Determine the distance from the point of engine shutdown at which the car will stop, if the resistance force is proportional to the car's speed. The mass of the car is m=1500 kg. (15
## points)
|
Answer: $240 m$
Solution. The power of the engine: $P=F v=F_{\text {conp }} v_{0}=\alpha v_{0}^{2}$, that is, the coefficient of resistance to the car's movement: $\alpha=\frac{P}{v_{0}^{2}}$ (3 points). The projection of the second law of Newton, for a small time interval, when moving with the engine off: $m \frac{\Delta v}{\Delta t}=-F_{\text {conp }}=-\alpha v$ (3 points). Considering that: $v \Delta t=\Delta s$, we get $m \Delta v=-\alpha \Delta s$ (3 points). Transitioning to final increments, we get: $m\left(0-v_{0}\right)=-\alpha s=-\frac{P}{v_{0}} s(3$ points $)$.
Final answer: $s=\frac{m v_{0}^{3}}{P}=\frac{1500 \cdot 20^{3}}{50000}=240$ meters (3 points).
|
240
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. The area of triangle $A B C$ is 1. On the rays $A B, B C$, $C A$, points $B^{\prime}, C^{\prime}, A^{\prime}$ are laid out respectively, such that
$$
B B^{\prime}=A B, \quad C C^{\prime}=2 B C, \quad A A^{\prime}=3 C A
$$
Calculate the area of triangle $A^{\prime} B^{\prime} C^{\prime}$.
|
Answer: 18.
Solution. We will solve the problem in a general form, assuming that
$$
B B^{\prime}=q A B, \quad C C^{\prime}=r B C, \quad A A^{\prime}=p C A .
$$
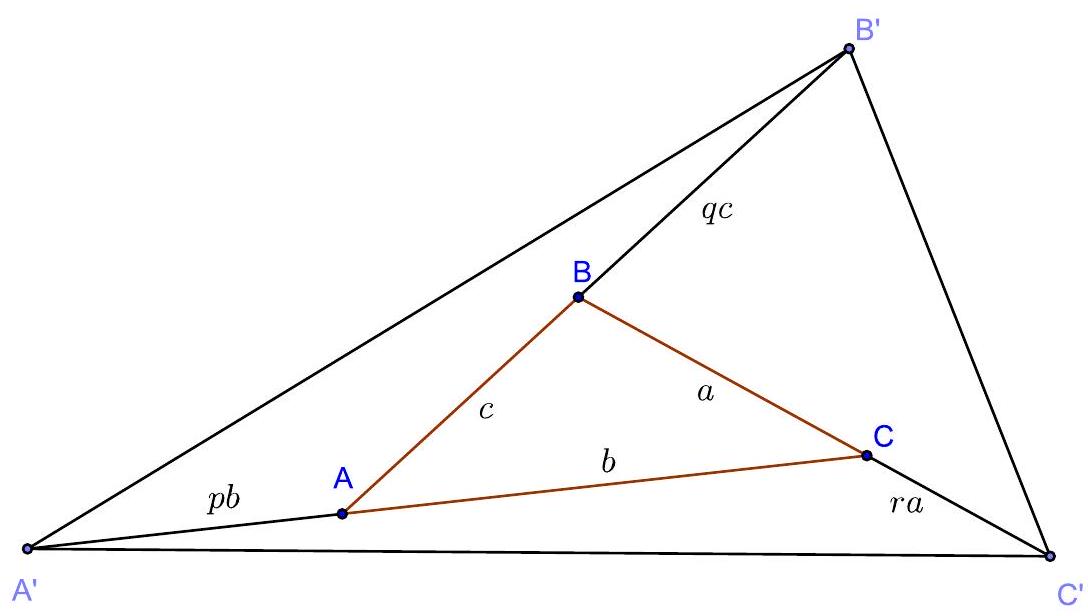
We will calculate the area of triangle \( A^{\prime} B^{\prime} A \):
$$
S_{A^{\prime} B^{\prime} A}=\frac{1}{2} A^{\prime} A \cdot A B^{\prime} \cdot \sin \angle A^{\prime} A B^{\prime}=\frac{1}{2} p b(c+q c) \sin \angle B A C=
$$
$$
=p(1+q) \cdot \frac{1}{2} b c \sin \angle B A C=p(1+q) \cdot S_{A B C}=p(1+q)
$$
(We used the equality of the sines of adjacent angles). Similarly, we find that \( S_{B^{\prime} B C^{\prime}}=q(1+r) \), \( S_{C C^{\prime} A^{\prime}}=r(1+p) \). Adding the areas of the specified three triangles and the original triangle \( A B C \), we find the desired area:
$$
S_{A^{\prime} B^{\prime} C^{\prime}}=1+p+q+r+p q+q r+r p
$$
Evaluation. 13 points for a correct solution.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation
$$
\sqrt{\frac{x-3}{11}}+\sqrt{\frac{x-4}{10}}+\sqrt{\frac{x-5}{9}}=\sqrt{\frac{x-11}{3}}+\sqrt{\frac{x-10}{4}}+\sqrt{\frac{x-9}{5}}
$$
|
Answer: 14.
Solution. If we perform the variable substitution $x=t+14$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}+\sqrt{\frac{t}{9}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}+\sqrt{\frac{t}{4}+1} .(*)
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t<0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=14$.
Estimation. 13 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. An ideal gas was expanded in such a way that during the process, the pressure of the gas turned out to be directly proportional to its volume. As a result, the gas heated up by $\Delta T=100^{\circ} \mathrm{C}$, and the work done by the gas was $A=831$ J. Determine the amount of substance that participated in this process. The gas constant $R=8.31$ J/mol$\cdot$K. (15 points)
|
Answer: 2 moles
Solution. From the condition $p=\alpha V$ (3 points). The work of the gas is equal to the area under the graph of the given process, constructed in coordinates $p-V$:
$A=\frac{p_{1}+p_{2}}{2} \cdot\left(V_{2}-V_{1}\right)=\frac{\alpha V_{1}+\alpha V_{2}}{2} \cdot\left(V_{2}-V_{1}\right)=\frac{\alpha}{2} \cdot\left(V_{2}^{2}-V_{1}^{2}\right) \quad(4$ points). From the equation of state of an ideal gas: $p V=\alpha V V=\alpha V^{2}=\nu R T \quad(4$ points). As a result, we get: $A=\frac{\alpha}{2} \cdot\left(V_{2}^{2}-V_{1}^{2}\right)=\frac{1}{2} v R \Delta T \quad(2$ points $) . \quad$ Final answer: $\quad v=\frac{2 A}{R \Delta T}=\frac{2 \cdot 831}{8.31 \cdot 100}=2$ moles (2 points).
|
2
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two small balls with charges $Q=-20 \cdot 10^{-6}$ C and $q=50 \cdot 10^{-6}$ C are located at the vertices $A$ and $B$ of a mountain slope (see figure). It is known that $AB=2$ m, $AC=3$ m. The masses of the balls are the same and equal to $m=200$ g each. At the initial moment of time, the ball with charge $q$ is released with zero initial velocity. Determine its speed at the moment when it reaches point $C$. The surface of the mountain slope is considered smooth. The acceleration due to gravity $g=10$ m/s², and the proportionality constant in Coulomb's law $k=9 \cdot 10^{9}$ N·m²/C². (10 points)
|
Answer: $5 \mathrm{M} / \mathrm{c}$
Solution. The law of conservation of energy for this situation:
$k \frac{Q q}{A B}+m g \cdot A B=\frac{m v^{2}}{2}+k \frac{Q q}{B C}(5$ points $)$.
As a result, we get: $v=\sqrt{\frac{2 k Q q}{m \cdot A B}+2 \cdot g \cdot A B-\frac{2 k Q q}{m \cdot B C}}=\sqrt{\frac{2 \cdot 9 \cdot 10^{9} \cdot\left(-20 \cdot 10^{-6}\right) \cdot 50 \cdot 10^{-6}}{0.2 \cdot 2}+2 \cdot 10 \cdot 2-\frac{2 \cdot 9 \cdot 10^{9} \cdot\left(-20 \cdot 10^{-6}\right) \cdot 50 \cdot 10^{-6}}{0.2 \cdot 3}}=5 \cdot \mathrm{m} / \mathrm{c}$ $(2$ points $)$.
|
5
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
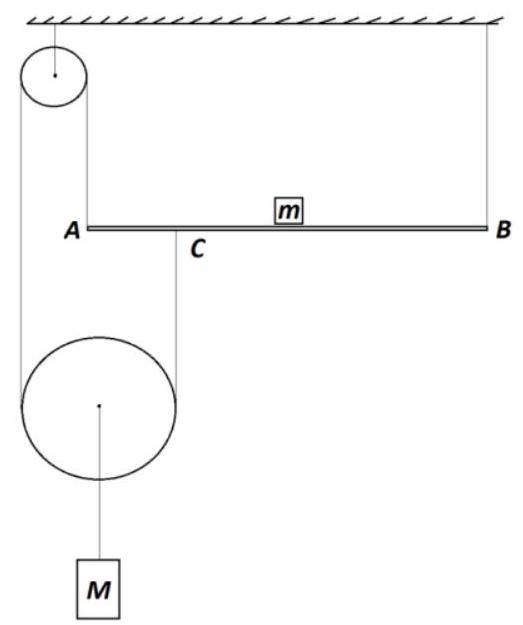
Problem No. 5 (15 points)
The system shown in the figure is in equilibrium. It is known that the uniform rod $AB$ and the load lying on it have the same mass $m=10$ kg, and the load is located at a distance of one quarter of the length of the rod from its left end. Determine the mass $m$ of the second load suspended from the center of one of the pulleys. The threads and pulleys are weightless, and there is no friction in the pulley axes.
|
Answer: 100 kg
# Solution and grading criteria:
Diagram with forces correctly placed.
Tension force in the thread: $T=\frac{M g}{2}$
The lever rule, written relative to point v:
$m g \cdot \frac{1}{2} A B+m g \cdot \frac{3}{4} A B+T \cdot \frac{3}{4} A B=T \cdot A B$
As a result, we get: $M=10 m=100$ kg.
A person walked slowly in a straight line at a speed of $v_{1}=1$ m/s. At time $t_{1}$, he turned strictly to the right and walked at a speed twice as fast. After another time interval $t_{1}$, he turned strictly to the right again, and his speed became three times the initial speed. After the last right turn, he ran at a speed of $4 v_{1}$ and returned to the starting point of his trajectory. Determine his average speed over the entire path.
## Answer: $2.1 \mathrm{~m} / \mathrm{s}$
## Solution and grading criteria:
From the condition, we can conclude that the person's trajectory is a rectangle.
(2 points)
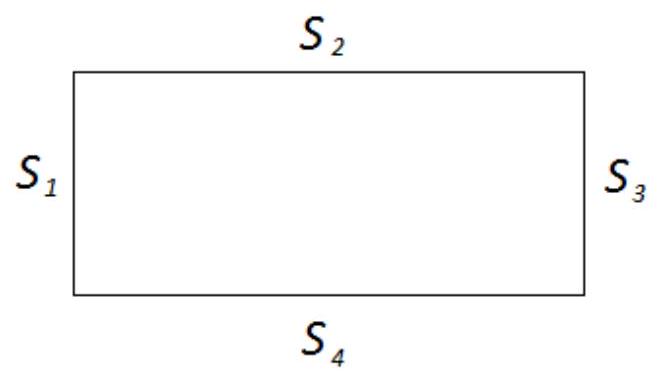
Moreover, $S_{2}=2 S_{1}$
Average speed:
$v_{\text{avg}}=\frac{S_{1}+S_{2}+S_{3}+S_{4}}{t_{1}+t_{2}+t_{3}+t_{4}}=\frac{6 S_{1}}{t_{1}+t_{1}+\frac{S_{1}}{3 v_{1}}+\frac{2 S_{1}}{4 v_{1}}}=\frac{6 S_{1}}{t_{1}+t_{1}+\frac{t_{1}}{3}+\frac{t_{1}}{2}}=\frac{6 S_{1}}{\frac{17}{6} t_{1}}=\frac{36}{17} v_{1} \approx 2.1 \mathrm{~m} / \mathrm{s}$
## Problem 7 (10 points)
A person holds one end of a light board, and the other end of the board rests on a cylinder lying on the ground. The length of the board is $L=10$ m. How far will the person walk before meeting the cylinder? The radius of the wheel is much smaller than the length of the board. There is no slipping.

Answer: $20 \mathrm{~m}$
Solution and grading criteria:
The speed of the person is equal to the speed of the top point of the cylinder, which is twice the speed of the center of the cylinder.
Thus, the distance the person will walk is twice the distance the cylinder has rolled.
Obviously, $S_{\text {person }}-S_{\text {cylinder }}=L=10 \mathrm{~m}$ (3 points)
We get: $S_{\text {person }}=20$ meters
|
100
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
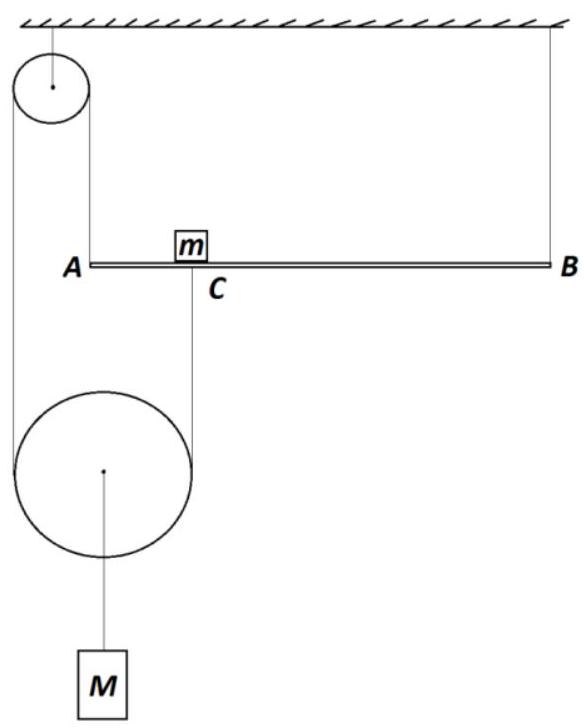
Problem No. 5 (15 points)
The system shown in the figure is in equilibrium. It is known that the uniform rod $AB$ and the load lying on it have the same mass $m=10$ kg. The load is located exactly in the middle of the rod. The thread, passing over the pulleys, is attached to one end of the rod and at a distance of one quarter of the rod's length from its left end. Determine the mass $m_2$ of the second load, suspended from the center of one of the pulleys. The threads and pulleys are weightless, and there is no friction in the pulley axes.
Answer: 80 kg
#
|
# Solution and Evaluation Criteria:
Diagram with forces correctly placed.
Tension force in the string: $T=\frac{M g}{2}$
The lever rule, written relative to point v:
$m g \cdot \frac{1}{2} A B+m g \cdot \frac{1}{2} A B+T \cdot \frac{3}{4} A B=T \cdot A B$
As a result, we get: $M=8 m=80$ kg.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $A B C$, the median $B K$ is twice as small as side $A B$ and forms an angle of $32^{\circ}$ with it. Find the angle $A B C$.
|
Answer: $106^{\circ}$.
Solution. Let $K$ be the midpoint of segment $B D$. Then $A B C D$ is a parallelogram. In triangle $A B D$, we have the equality of sides $A B$ and $B D$. Therefore,
$$
\angle B D A=\frac{1}{2}\left(180^{\circ}-32^{\circ}\right)=74^{\circ}
$$
Angles $A D B$ and $C B D$ are equal as alternate interior angles. Thus,
$$
\angle A B C=\angle A B D+\angle D B C=32^{\circ}+74^{\circ}=106^{\circ} .
$$
Evaluation. 13 points for a correct solution.
|
106
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $A B C$, the median $B N$ is twice as short as side $A B$ and forms an angle of $20^{\circ}$ with it. Find the angle $A B C$.
|
Answer: $100^{\circ}$.
Solution. Let $N$ be the midpoint of segment $B D$. Then $A B C D-$ is a parallelogram. In triangle $A B D$, we have the equality of sides $A B$ and $B D$. Therefore,
$$
\angle B D A=\frac{1}{2}\left(180^{\circ}-20^{\circ}\right)=80^{\circ} \text {. }
$$
Angles $A D B$ and $C B D$ are equal as alternate interior angles. Thus,
$$
\angle A B C=\angle A B D+\angle D B C=20^{\circ}+80^{\circ}=100^{\circ} .
$$
Evaluation. 13 points for a correct solution.
|
100
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. What is the greatest length that a closed, non-self-intersecting broken line can have, which runs along the grid lines of a $6 \times 10$ cell field?
#
|
# Answer: 76.
Solution. We will color the nodes of the grid in a checkerboard pattern, with black and white colors. The length of a closed non-self-intersecting broken line is equal to the number of nodes it passes through. Each segment of the broken line connects a black and a white node. When traversing the broken line, the colors of the nodes alternate, so the length of the closed broken line is an even number. Since there are 77 nodes in total in the grid, the length of the broken line is at most 76. A corresponding example is easily constructed (Fig. 2).
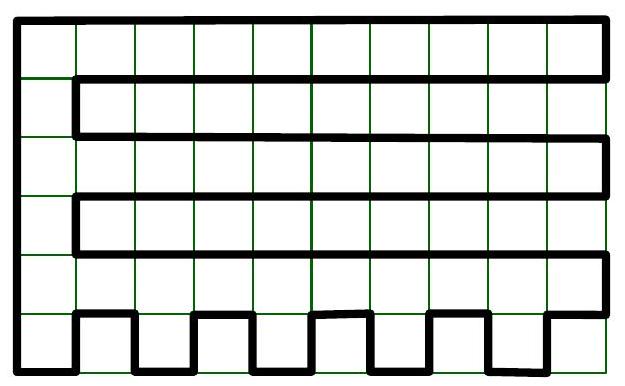
Fig. 2
Remark. Another reasoning is possible. Let's start constructing a closed broken line from some node. Since we need to return to it, the number of horizontal steps to the right is the same as the number of steps to the left. Therefore, the number of horizontal steps is even. The same is true for vertical steps. Hence, we again obtain that the length of the closed broken line (whose segments follow the grid lines) is an even number.
Evaluation. 13 points for a correct solution. 1 point for only the answer. 4 points if an example of a broken line of length 76 is provided, but there is no estimation of the length of the broken line.
|
76
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. 100 balls of the same mass move along a trough towards a metal wall with the same speed. After colliding with the wall, a ball bounces off it with the same speed. Upon collision of two balls, they scatter with the same speed. (The balls move only along the trough). Find the total number of collisions between the balls.
|
Answer: 4950.
Solution. We will assume that each ball has a flag. Imagine that upon collision, the balls exchange flags. Then each flag flies to the wall at a constant speed, and after hitting the wall, it flies in the opposite direction. The number of collisions between the balls is equal to the number of flag exchanges. Any two flags will swap places exactly once. Therefore, the total number of exchanges is $\frac{100 \cdot 99}{2}=4950$.
Evaluation. 14 points for a correct solution.
#
|
4950
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Let's call a number small if it is a 10-digit number and there does not exist a smaller 10-digit number with the same sum of digits. How many small numbers exist
|
Solution. Answer: 90.
It is clear that the sum of the digits of a 10-digit number can take any value from 1 to 90 inclusive. For each of the 90 possible sums of the digits, there is a unique smallest 10-digit number with such a sum of digits. Therefore, there are 90 small numbers.
## Criteria
One of the largest suitable criteria is used:
7 p. Any complete solution to the problem.
1 p. There is only the correct answer.
|
90
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. On the board, there are $N$ natural numbers, where $N \geqslant 5$. It is known that the sum of all the numbers is 80, and the sum of any five of them is no more than 19. What is the smallest value that $N$ can take?
|
Solution. Answer: 26.
The condition of the problem is equivalent to the sum of the five largest numbers not exceeding 19, and the sum of all numbers being 80. Note that among the five largest numbers, there must be a number not greater than 3 (otherwise, if all of them are not less than 4, their sum is not less than $4 \cdot 5=20$, but it should not exceed 19).
Let the total number of numbers be $x$. Since among the five largest numbers there is a number not greater than 3, then all the other $x-5$ numbers are not greater than 3. Therefore, the sum of all numbers does not exceed $3(x-5)+19$, and on the other hand, it is equal to 80. Thus, we get the inequality $3(x-5)+19 \geqslant 80$. Solving this inequality and considering that $x$ is an integer, we get that $x \geqslant 26$.
It remains to provide an example of such 26 numbers. Let's take 24 threes and 2 fours, then the total sum is $24 \cdot 3 + 2 \cdot 4 = 80$, and the sum of any five is not greater than $3 \cdot 3 + 2 \cdot 4 = 17 \leqslant 19$.
## Criteria
The most appropriate criterion is used:
7 points. Any complete solution of the problem.
3 points. 26 numbers satisfying the condition of the problem are explicitly provided.
|
26
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1010 of them such that the sum of any two does not equal 2021 or 2022. How many
ways are there to do this
|
Solution. Answer: $\frac{1011 \cdot 1012}{2}=511566$.
Let's write our numbers in the following order: $2021,1,2020,2,2019,3, \ldots, 1012,1010,1011$.
Notice that if two numbers sum to 2021 or 2022, they stand next to each other in this sequence. Our task is reduced to the following: 2021 objects (for convenience, let's consider them as 2021 balls) are lined up, and we need to count the number of ways to choose 1010 of them, such that no two chosen balls are adjacent.
Let's paint the unchosen balls red and the chosen ones blue. Place all 1011 red balls in a row. We need to place 1010 blue balls in the gaps between them (or at the ends) such that no two blue balls are adjacent. There are exactly 1012 such gaps: 1010 gaps between two red balls, and 2 gaps at the ends; in each of these gaps, we can place no more than one blue ball. Therefore, we need to count the number of ways to choose 1010 gaps out of 1012 available. As is known, this value is equal to $C_{1012}^{1010}=C_{1012}^{2}=\frac{1012 \cdot 1011}{2}=511566$.
Another solution.
We will divide the numbers from 1 to 2021 into 1011 groups - 1010 non-overlapping groups of pairs of numbers that sum to 2022 (specifically: $(1,2021),(2,2020), \ldots,(1009,1013)$, $(1010,1012))$ and a group consisting of the remaining number 1011.
In each group, by the condition, we can choose no more than one number. Therefore, to choose 1010 numbers, we need to choose a group from which no numbers will be taken, and from all other groups, we need to choose exactly one number each.
Suppose we do not take any number from the group $(a, 2022-a)$ (here and below we will assume that in such notation $a \leqslant 2022-a$). From all other groups, we need to choose exactly one number each, in particular, we need to take 1011 (if $a=1011$, then this step is skipped). Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this way, we get that from the pair $(a+1,2022-(a+1))$ we choose the number $2022-(a+1)$. Thus, in all pairs where the smallest number is greater than $a$, the chosen numbers are uniquely determined (specifically, the largest numbers in these pairs must be chosen).
Now consider all pairs where the smallest number is less than $a$. Consider among them the pair $(b, 2022-b)$ in which the largest number, i.e., $2022-b$, is chosen (the case where such pairs do not exist will be considered separately), and if there are several such pairs, consider the one where $b$ is maximal. From all pairs from $(b+1,2022-(b+1))$ to $(a-1,2022-(a-1))$, the smallest number was always chosen (due to the maximality of $b$). In the pair $(b-1,2022-(b-1))$, the number $2022-(b-1)$ was chosen (otherwise $(b-1)+(2022-b)=2021$). Similarly, in the pair $(b-2,2022-(b-2))$, the number $2022-(b-2)$ was chosen, and so on, in the pair $(1,2021)$, the number 2021 was chosen.
Now let's understand how the set of numbers satisfying the condition is determined. First, a group $(a, 2022-a)$ (i.e., a number $1 \leqslant a \leqslant 1011$) is chosen, in which no number is chosen. Then, in all groups where the smallest number is greater than $a$, the choice is uniquely determined (from the group, the largest number is chosen). Second, a pair $(b, 2022-b)$ (i.e., a number $1 \leqslant b \leqslant a-1$) is chosen, and in all other pairs, the choice is uniquely determined (in pairs with the smallest number from $b+1$ to $a-1$, the smallest number is chosen, and in pairs where it is less than $b$, the largest number is chosen).
It remains to count the number of options. Fix some $a$, then the number of ways to choose $b$ will be exactly $a-1$, plus one more option, where in all pairs with the smallest number less than $a$, the smallest number was chosen (i.e., the number $b$ simply does not exist). In total, there are $a$ options for the number $b$. Summing over all $a \leqslant 1011$, we get $1+2+3+\ldots+1010+1011=\frac{1011 \cdot 1012}{2}=511566$ options for our set. Clearly, all these options are distinct and satisfy the condition (the set is uniquely determined by the chosen numbers $a$ and $b$).
## Criteria
The highest appropriate criterion is used:
7 p. Any complete solution to the problem.
7 6. Any complete solution to the problem, but the answer is given in the form of a formula or expression (e.g., $\frac{1011 \cdot 1012}{2}$ or $C_{1012}^{2}$).
6 6. Any complete solution to the problem, but the answer is given in the form of a formula with an ellipsis (e.g., $1+2+3+\ldots+1010+1011$).
2 6. The numbers are divided into pairs, but there is no further progress.
16 . The correct answer is given.
|
511566
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Petya was given several physics problems and several math problems for homework. All the problems solved by Petya constitute $5 \%$ of the total number of physics problems and $20 \%$ of the total number of math problems. What percentage of the total number of problems did Petya solve?
|
Solution. Answer: $4 \%$.
Let Pete solve $N$ problems. This constitutes $5 \%$ ( $\frac{1}{20}$ of) the physics problems, so the total number of physics problems was $20 \mathrm{~N}$. Similarly, the number of math problems was $5 N$, so the total number of problems assigned was $20 N + 5 N = 25 N$. The problems solved by Pete constitute $\frac{N}{25 N} \cdot 100 \% = 4 \%$.
## Criteria
The largest suitable criterion is used:
7 points. Any complete solution to the problem.
7 points. Any complete solution to the problem, but the answer is given not in percentages, but as a fraction $\frac{1}{25}$ or 0.04.
3 points. Only the correct answer is given.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a two-digit number, each digit was increased by 2 or by 4 (different digits could be increased by different numbers), as a result of which the number increased fourfold. What could the original number have been? Find all possible options and prove that there are no others.
|
Solution. Answer: 14.
Let $x$ be the original number, then the resulting number equals $4 x$. In this case, after increasing two digits, the number itself was increased by 22, 24, 42, or 44. This results in four cases:
- $4 x-x=22$
- $4 x-x=24$
- $4 x-x=42$
- $4 x-x=44$.
Among them, only the third one fits, corresponding to the value $x=14$.
One highest suitable criterion is used:
7 points. Any complete solution to the problem.
3 points. Only the correct answer.
If the problem is reduced to considering the four cases mentioned in the solution, then 1 point is deducted for each case not correctly analyzed.
|
14
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. We will call a natural number odd-powered if all its prime divisors enter its factorization with an odd exponent. What is the maximum number of odd-powered numbers that can occur consecutively?
## Answer: 7.
|
Solution. Note that among any eight consecutive natural numbers, there will definitely be a number that is divisible by 4 but not by 8. Then the number 2 will appear in its factorization to the second power.
Example of seven odd-power numbers: $37,38,39,40,41,42,43$.
Problem 4/1. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=14$.
Answer: 7.
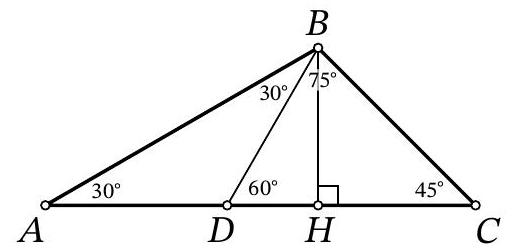
Fig. 1: to the solution of problem $4 / 1$
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.
Draw the height $B H$ in triangle $A B C$ (Fig. 1). Triangle $B H C$ is a right isosceles triangle, so $C H=B H$. Triangles $A B H$ and $B D H$ are right triangles with an angle of $30^{\circ}$, so in them the legs opposite the angle of $30^{\circ}$ are half the hypotenuse. It turns out that $2 B H=A B, 2 H D=B D$.
Then
$$
C D=C H+H D=B H+H D=\frac{A B}{2}+\frac{B D}{2}=\frac{A B+A D}{2}=7
$$
Problem 4/2. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=16$.
Answer: 8.
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.

Fig. 2: to the solution of problem $4 / 2$
Draw the height $B H$ in triangle $A B C$ (Fig. 2). Triangle $B H C$ is a right isosceles triangle, so $C H=B H$. Triangles $A B H$ and $B D H$ are right triangles with an angle of $30^{\circ}$, so in them the legs opposite the angle of $30^{\circ}$ are half the hypotenuse. It turns out that $2 B H=A B, 2 H D=B D$.
Then
$$
C D=C H+H D=B H+H D=\frac{A B}{2}+\frac{B D}{2}=\frac{A B+A D}{2}=8
$$
Problem 4/3. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=18$.
Answer: 9.
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.
=200-x$. Solving this, we get $x=80$.
## Criteria
One of the largest suitable criteria is used:
## 7 points. Any complete solution of the problem.
2 6. The correct answer is given with a check that it fits, but it is not proven that there are no other answers.
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. On an island, there live knights who always tell the truth, and liars who always lie. One day, 30 inhabitants of this island sat around a round table. Each of them said one of two phrases: "My left neighbor is a liar" or "My right neighbor is a liar." What is the smallest number of knights that can be at the table?
|
# Answer: 10.
Solution. Next to each liar, there must be at least one knight (otherwise, if liars sit on both sides of a liar, the statement made by the liar would definitely be true). Therefore, among any three consecutive residents, there is at least one knight. If we divide all the people sitting at the table into groups of three consecutive residents, we get that there is at least one knight in each group, so there are at least 10 knights in total.
Let's provide an example where there are exactly 10 knights. Suppose the residents sit as follows: knight, two liars, knight, two liars, and so on. Each knight says any of the given phrases—it will be true in any case. A liar says, "My left neighbor is a liar" if the person on the left is a knight, and vice versa, he says, "My right neighbor is a liar" if the person on the right is a knight. It is clear that all the conditions of the problem are satisfied.
## Criteria
## The following criteria are cumulative:
5 p. It is proven that there are at least 10 knights.
2 6. It is proven that there can be exactly 10 knights.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Five different natural numbers are written in a circle on the board. Each of them, Petya divided by the next one in the clockwise direction, and then wrote down the 5 resulting numbers (not necessarily integers) on a piece of paper. Can the sum of the 5 numbers on the paper be an integer?
|
Answer: Yes, it can.
Solution. For example, for the numbers $1,2,4,8,16$, after division, the sum is $1 / 2+1 / 2+1 / 2+1 / 2+16=18$.
## Criteria
One suitable criterion is used:
7 p. Any complete solution to the problem.
0 p. There is only the correct answer, but the correct example is not provided.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Carlson has three boxes, each containing 10 candies. One box is labeled with the number 4, another with 7, and the third with 10. In one operation, Carlson sequentially performs the following two actions:
- he takes from any box a number of candies equal to the number written on it;
- he eats 3 of the taken candies, and puts the rest in any other box.
What is the maximum number of candies Carlson can eat as a result of several such operations?
|
Answer: 27.
Solution. Since at each step, Karlson eats 3 candies, the total number of candies eaten is divisible by 3. We will prove that it does not exceed 27; for this, it is sufficient to show that it cannot equal 30, that is, Karlson cannot eat all the candies. Indeed, if this were possible, then before the last operation, there would be exactly 3 candies left, meaning that each box would contain no more than 3 candies. However, each of the numbers $4, 7, 10$ is greater than 3, so the last operation would be impossible, leading to a contradiction.
The example below shows how Karlson could act to eat exactly 27 candies. In the $k$-th line, it is written how many candies remain in each box after the $(k-1)$-th operation. The three numbers in each line are the number of candies remaining in the boxes at the corresponding step. The notation $(a, b, c)$ means that in the box with number 4, there were $a$ candies left, in the box with number $7-b$ candies, and in the box with number $10-c$ candies.
|
27
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The incircle of triangle $ABC$ touches sides $AB$ and $AC$ at points $D$ and $E$ respectively. Point $I_{A}$ is the excenter of the excircle opposite side $BC$ of triangle $ABC$, and points $K$ and $L$ are the midpoints of segments $DI_{A}$ and $EI_{A}$ respectively. Lines $BK$ and $CL$ intersect at point $F$, which lies inside angle $BAC$. Find $\angle BFC$, if $\angle BAC=50^{\circ}$. (The excircle touches side $C$ and the extensions of sides $AB$ and $AC$ beyond points $B$ and $C$ respectively.)
|
5. The circle inscribed in triangle $ABC$ touches sides $AB$ and $AC$ at points $D$ and $E$ respectively. Point $I_{A}$ is the center of the excircle opposite side $BC$ of triangle $ABC$, and points $K$ and $L$ are the midpoints of segments $DI_{A}$ and $EI_{A}$ respectively. Lines $BK$ and $CL$ intersect at point $F$, which lies inside angle $BAC$. Find $\angle BFC$ if $\angle BAC = 50^{\circ}$. (The excircle touches side $BC$ and the extensions of sides $AB$ and $AC$ beyond points $B$ and $C$ respectively.)
Answer: $130^{\circ}$.
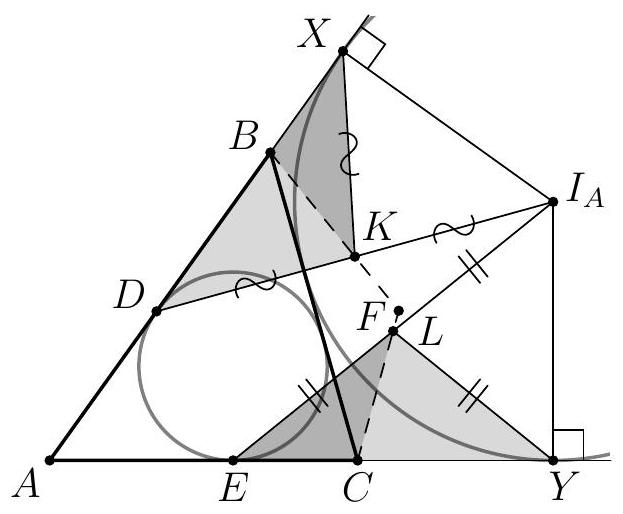
Fig. 7: for the solution of problem 5.
Let $X$ and $Y$ be the points of tangency of the excircle opposite side $BC$ with the extensions of sides $AB$ and $AC$ respectively (Fig. 7). Right triangles $DXI_{A}$ and $EYI_{A}$ are symmetric with respect to the angle bisector of angle $A$, hence they are equal and isosceles triangles $DKX$ and $YLE$. In these triangles, points $B$ and $C$ are marked on the bases such that $BD = CY = p - b$, where $p$ is the semiperimeter of triangle $ABC$, and $b$ is the length of side $AC$. Consequently, we conclude that $\angle KBD = \angle LCY$ and, thus, quadrilateral $ABFC$ is cyclic. This leads to the relation $\angle BFC = 180^{\circ} - \angle BAC = 130^{\circ}$.
## Criteria
+ Correct solution - 7 points.
|
130
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. Masha and the Bear ate a basket of raspberries and 40 pies, starting and finishing at the same time. At first, Masha was eating raspberries, and the Bear was eating pies, then (at some point) they switched. The Bear ate both raspberries and pies 3 times faster than Masha. How many pies did Masha eat, if they ate the raspberries equally?
|
Answer: 4 pies. Solution: The bear ate his half of the raspberries three times faster than Masha. This means Masha ate pies for three times less time than the bear. Since she eats three times slower, she ate 9 times fewer pies than the bear. Dividing the pies in the ratio of $9: 1$, we see that Masha got the 10th part, that is, 4 pies.
Criterion: Correct answer - no less than 2 points, with full justification - 7 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. At a round table sit 10 elves, each with a basket of nuts in front of them. Each was asked, "How many nuts do your two neighbors have together?" and, going around the circle, the answers received were 110, 120, 130, 140, 150, 160, 170, 180, 190, and 200. How many nuts does the elf who answered 160 have?
|
Answer: 55. Solution. We will call the elves 1-m, 2-m, etc., in the order of receiving answers. The odd-numbered ones sit every other. In their answers, the number of nuts of each even number is counted twice, so the sum $110+130+150+170+190=750$ is equal to twice the number of nuts of all even numbers. Therefore, the even-numbered ones have 375 nuts in total. The 8th and 10th together have 190 nuts, and the 2nd and 4th together have 130 nuts. Therefore, the 6th has 375-190-130=55 nuts.
Criterion. 1 point for the correct answer without justification. 3 points for the answer and a correct example for all.
|
55
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.2. At a party, 24 people gathered. A guest is considered an introvert if they have no more than three acquaintances among the other guests. It turned out that each guest has at least three acquaintances who are introverts. How many introverts could there have been at the party? Provide all possible answers and prove that there are no others.
#
|
# Answer: 24.
Solution. Let $a$ be the number of pairs of introverts who know each other, and $b$ be the number of pairs of acquaintances where one of the pair is an introvert. Each person who came to the party is included in at least three pairs, since they know at least three other introverts, and pairs of introvert-introvert are counted twice. Therefore, $2a + b \geq 3 \cdot 24$.
On the other hand, each introvert can be included in no more than three pairs, so $2a + b$ is no more than three times the number of introverts. As a result, we conclude that three times the number of introverts is not less than three times the number of guests, which is only possible if all those who came to the party are introverts.
Another solution. From the condition, it follows that each introvert knows three other introverts and no one else; that is, there can be no acquaintances between introverts and extroverts (let's call the rest of the people extroverts). But then an extrovert cannot know three introverts, as required by the condition. Therefore, there are no extroverts at this party.
## Criteria
## Kurchatov School Olympiad in Mathematics - 2019 Final Stage.
Any correct solution to the problem is worth 7 points.
Solutions that unjustifiably use the fact that some cases are "optimal" ("best", "worst", etc.) are not credited.
In the absence of a correct solution, the following criterion is used:
## 16. There is a correct answer.
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9.4. It is known that the number 400000001 is the product of two prime numbers $p$ and $q$. Find the sum of the natural divisors of the number $p+q-1$.
---
The text has been translated while preserving the original formatting and line breaks.
|
Answer: 45864.
Solution. The number $n=400000001$ can be written in the following form
\[
\begin{aligned}
n & =4 \cdot 10^{8}+1=4 \cdot 10^{8}+4 \cdot 10^{4}+1-4 \cdot 10^{4}= \\
& =\left(2 \cdot 10^{4}+1\right)^{2}-\left(2 \cdot 10^{2}\right)^{2}=\left(2 \cdot 10^{4}+2 \cdot 10^{2}+1\right)\left(2 \cdot 10^{4}-2 \cdot 10^{2}+1\right)
\end{aligned}
\]
Since $n$ is the product of two prime numbers $p$ and $q$, the factorization obtained above is exactly this. Therefore,
\[
p+q-1=2 \cdot 10^{4}+2 \cdot 10^{2}+1+2 \cdot 10^{4}-2 \cdot 10^{2}+1-1=4 \cdot 10^{4}+1
\]
To factorize the last number, we can use the same trick.
\[
\begin{aligned}
4 \cdot 10^{4}+1 & =4 \cdot 10^{4}+4 \cdot 10^{2}+1-4 \cdot 10^{2}=\left(2 \cdot 10^{2}+1\right)^{2}-(2 \cdot 10)^{2}= \\
& =(201-20)(201+20)=181 \cdot 221=13 \cdot 17 \cdot 181
\end{aligned}
\]
The sum of the natural divisors of the obtained number can be found, for example, using the formula
\[
(13+1)(17+1)(181+1)=45864
\]
## Criteria
The highest appropriate criterion is used:
76. Any correct solution to the problem.
5 6. The correct prime factorization of the number $p+q-1$ is obtained, but due to an error, an incorrect answer is given.
4 6. The answer is given under the assumption that $p+q-1=181 \cdot 221$ is the prime factorization.
3 6. The value of $p+q-1$ is correctly calculated.
In any of the above cases, points are deducted for the following deficiency:
-2 6. The correct factorization of the given number in the problem is provided, but it is not shown where this factorization comes from, nor that it indeed gives the required number when multiplied.
|
45864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Alexei wrote several consecutive natural numbers on the board. It turned out that only two of the written numbers have a digit sum divisible by 8: the smallest and the largest. What is the maximum number of numbers that could have been written on the board?
|
Answer: 16.
Example: numbers from 9999991 to 10000007.
Evaluation. We will prove that there cannot be more than 16 numbers. Let's call a number $x$ good if the sum of its digits is divisible by 8. Among the listed numbers, there must be a number $x$ ending in 0, otherwise there are too few numbers. The number $x$ is not the first one, since then both $x$ and $x+8$ are good, and there are no more than 9 numbers. Among the numbers $x, x+1, \ldots, x+7$ there must be a good one - the largest with the specified property. The number $x-1$ ends in 9, so among the numbers $x-1, x-2, \ldots, x-8$ there must be a good one - the smallest with the specified property. Thus, all selected numbers fit into the interval from $x-8$ to $x+7$ inclusive. Therefore, the number of numbers written on the board does not exceed 16.
$\pm$ The evaluation is correct, the example has a minor error. 5-6 points
$\mp$ The evaluation without an example. 3 points
$\mp$ The example without an evaluation. 3 points
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. For positive numbers $x$ and $y$, it is known that
$$
\frac{1}{1+x+x^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+x+y}=1
$$
What values can the product $x y$ take? List all possible options and prove that there are no others.
|
Answer: 1.
Solution. Note that for each positive $y$ the function
$$
f_{y}(x)=\frac{1}{1+x+x^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+x+y}
$$
strictly decreases on the ray $(0 ;+\infty)$, since the denominators of all three fractions increase. Therefore, the function $f_{y}$ takes each value no more than once. Moreover, it is not difficult to see that
$$
\begin{aligned}
f_{y}(1 / y) & =\frac{1}{1+1 / y+1 / y^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+1 / y+y}= \\
& =\frac{y^{2}}{1+y+y^{2}}+\frac{1}{1+y+y^{2}}+\frac{y}{1+y+y^{2}}=1
\end{aligned}
$$
from which we conclude that $x=1 / y$.
## Criteria
One of the largest suitable criteria is used:
7 6. Any correct solution to the problem.
3 6. The monotonicity of the left side with respect to $x$ or $y$ is noted.
3 6. It is proven that for any $y$ there is no more than one $x$ satisfying the equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Through the point with coordinates $(9,9)$, lines (including those parallel to the coordinate axes) are drawn, dividing the plane into angles of $9^{\circ}$. Find the sum of the x-coordinates of the points of intersection of these lines with the line $y=10-x$.
|
Answer: 190. Solution. The picture is symmetric with respect to the line $y=x$, so the sum of the abscissas is equal to the sum of the ordinates. Through the point $(9,9)$, 20 lines are drawn, the line $y=20-x$ intersects 19 of them. For each point on the line $y=20-x$, the sum of the coordinates is 20, so the total sum of the abscissas and ordinates is 380, and the sum of the abscissas is half of that.
Criterion. 2 points for the correct answer without a correct justification. 4 points if all ideas are found, but the answer is incorrect due to a wrong count of the number of intersection points (for example, the student counts them as 20 or 40).
|
190
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. Jerry has nine cards with digits from 1 to 9. He lays them out in a row, forming a nine-digit number. Tom writes down all 8 two-digit numbers formed by adjacent digits (for example, for the number 789456123, these numbers are $78, 89, 94, 45$, $56, 61, 12, 23$). For each two-digit number divisible by 9, Tom gives Jerry a piece of cheese. What is the maximum number of pieces of cheese Jerry can get?
|
Answer: 4.
Solution. Note that among two-digit numbers, only 18, 27, 36, 45, and numbers obtained by swapping their digits are divisible by 9 (there are also 90 and 99, but we do not have the digit 0 and only one digit 9). Thus, only four pairs of digits from the available ones can form a number divisible by 9. To get an example, we need to arrange all these pairs in any order:
$$
182736459 .
$$
## Criteria
The highest applicable criterion is used:
## 7 6. Any correct solution to the problem.
3 6. It is proven that it is impossible to get 5 two-digit numbers divisible by 9.
3 6. An example with 4 two-digit numbers divisible by 9 is provided.
16 . The correct answer is given.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. The miserly knight has 5 chests of gold: the first chest contains 1001 gold coins, the second - 2002, the third - 3003, the fourth - 4004, the fifth - 5005. Every day, the miserly knight chooses 4 chests, takes 1 coin from each, and places them in the remaining chest. After some time, there were no coins left in the first chest, and there were exactly 2019 coins in another chest. Which one?
|
Answer: in the fifth.
Solution. Let's look at the remainders of the number of coins in the chests when divided by 5. Each day, the number of coins in each chest either decreases by 1 or increases by 4, which means the remainder when divided by 5 always decreases by 1 (if it was 0, it will become 4). Since after some time there were no coins left in the first chest, the number of days that have passed is $5k+1$ for some natural number $k$, and in each chest, the remainder has decreased by 1. Since 2019 gives a remainder of 4 when divided by 5, such a number of coins could only remain in the fifth chest.
## Criteria
The largest suitable criterion is used:
76. Any correct solution to the problem.
## 3 6. The idea of considering remainders when divided by 5 is present.
## 16. The correct answer is given.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.4. On the sides $AB$ and $AC$ of triangle $ABC$, points $X$ and $Y$ are chosen such that $\angle A Y B = \angle A X C = 134^{\circ}$. On the ray $YB$ beyond point $B$, point $M$ is marked, and on the ray $XC$ beyond point $C$, point $N$ is marked. It turns out that $MB = AC$ and $AB = CN$. Find $\angle MAN$.
Answer: $46^{\circ}$.
|
Solution. Note that $\angle A C N=\angle C A X+\angle A X C=\angle B A Y+\angle A Y B=\angle A B M$. Adding
Fig. 1: to the solution of problem $?$ ?
## Kurchatov School Olympiad in Mathematics - 2019 Final Round.
to the obtained equality of angles, and given the equalities of segments $A C=B M$ and $A B=C N$, we conclude that by the first criterion, triangles $A C N$ and $M B A$ are equal (Fig. ??), which means $\angle N A C = \angle A M B$. Then the following chain of equalities holds: $\angle M A N=\angle N A C+\angle C A B+\angle B A M=\angle A M B + \angle Y A B + \angle B A M = \angle Y A M + \angle A M Y = 180^{\circ} - \angle A Y B = 180^{\circ} - 134^{\circ} = 46^{\circ}$.
## Criteria
The largest suitable criterion is used:
76 . Any correct solution to the problem.
5 6. A correct solution with an incorrect answer due to an arithmetic error.
3 6. It is proven that triangles $A C N$ and $M B A$ are equal.
16 . The correct answer is provided.
|
46
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.5. A lame rook makes moves alternating between one and two squares, with the direction of the move being freely chosen (in any of the four directions). What is the maximum number of cells on a $6 \times 6$ board it can visit, if visiting the same cell twice is prohibited, but the starting cell and the first move can be chosen freely?
|
Answer: 34.
Solution. An example for 34 cells is shown in Fig. ??. The visited cells are numbered from 1 to 34.
| 5 | 2 | 4 | 3 | 13 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 6 | 1 | 7 | 8 | 14 | 9 |
| 28 | 31 | | 34 | 12 | 11 |
| 27 | 32 | | 33 | 15 | 16 |
| 29 | 30 | 20 | 19 | 21 | 18 |
| 26 | 25 | 23 | 24 | 22 | 17 |
Fig. 2: to the solution of problem $? ?$
We will show that it is impossible to visit 35 or more cells. For this, we divide the $6 \times 6$ square into nine $2 \times 2$ squares and color them in a checkerboard pattern (Fig. ??). This results in 20 black cells and 16 white cells. Each move of length 2 connects two cells of different colors, and the pairs of cells for different "long" moves do not overlap. Since there are 16 white cells, the number of long moves does not exceed 16. Due to the alternation, this guarantees that the total number of moves does not exceed 33, and thus the number of visited cells does not exceed 34.
## Kurchatov School Olympiad in Mathematics - 2019 Final Round.
## Criteria
One of the largest suitable criteria is used:
7 6. Any correct solution to the problem.
3 6. An example of traversing 34 cells is constructed.
3 6. It is proven that it is impossible to visit 35 cells.
|
34
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. In a five-digit number, each digit was increased by 2 or by 4 (different digits could be increased by different numbers), as a result of which the number increased fourfold. What could the original number have been? Find all possible options and prove that there are no others.
|
Solution. Answer: 14074.
Let the original five-digit number be denoted by $N$, then the resulting number is equal to $4N$. Their difference is $3N$ and is a five-digit number consisting of 2 and 4. This difference $3N$ is not less than $3 \cdot 10000$, so it starts with a four.
By the divisibility rule for 3, the sum of the digits of the number $3N$ is divisible by 3, so it cannot consist of two fours and three twos, three fours and two twos, or five fours. Therefore, the number $3N$ consists either of one four and four twos, or of four fours and one two. Then the number $N$ can be one of the numbers $\frac{42222}{3}=14074, \frac{44442}{3}=14814, \frac{44424}{3}=14808, \frac{44244}{3}=14748$, $\frac{42444}{3}=14148$.
It is also clear that the number $N$ could not contain an eight in its decimal representation, so only the number 14074 remains to be checked. And it fits: $14074 \cdot 4 = 56296$, all the digits of the quadrupled number are greater than the corresponding original digits by 2 or 4.
## Criteria
The highest applicable criterion is used:
7 points. Any complete solution of the problem.
6 points. A generally correct solution, but an arithmetic error is made that does not affect its course.
5 points. The numbers $14074, 14814, 14808, 14748, 14148$ are obtained justifiably.
4 points. It is proven that the number is increased by either one four and four twos, or four fours and one two.
1 point. There is only the answer.
|
14074
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1010 of them such that the sum of any two does not equal 2021 or 2022. How many ways are there to do this?
|
Solution. Answer: $\frac{1011 \cdot 1012}{2}=511566$.
Let's write our numbers in the following order: $2021,1,2020,2,2019,3, \ldots, 1012,1010,1011$. Notice that if two numbers sum to 2021 or 2022, they stand next to each other in this sequence. Our task is reduced to the following: 2021 objects (for convenience, let's consider them as 2021 balls) are lined up, and we need to count the number of ways to choose 1010 of them, such that no two chosen balls are adjacent.
Let's paint the unchosen balls red and the chosen ones blue. Place all 1011 red balls in a row. We need to place 1010 blue balls in the gaps between them (or at the ends) such that no two blue balls are adjacent. There are exactly 1012 such gaps: 1010 gaps between two red balls, and 2 gaps at the ends; in each of these gaps, we can place no more than one blue ball. Therefore, we need to count the number of ways to choose 1010 gaps out of 1012 available. As is known, this value is $C_{1012}^{1010}=C_{1012}^{2}=\frac{1012 \cdot 1011}{2}=511566$.
Another solution.
We will divide the numbers from 1 to 2021 into 1011 groups - 1010 non-overlapping groups of pairs of numbers that sum to 2022 (specifically: $(1,2021),(2,2020), \ldots,(1009,1013)$, $(1010,1012))$ and a group consisting of the remaining number 1011.
In each group, by the condition, we can choose no more than one number. Therefore, to choose 1010 numbers, we need to choose a group from which no numbers will be taken, and from all other groups, we need to choose exactly one number each.
Suppose we do not take any number from the group $(a, 2022-a)$ (here and below we will assume that in such notation $a \leqslant 2022-a$). From all other groups, we need to choose exactly one number each, in particular, we need to take 1011 (if $a=1011$, then this step is skipped). Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this way, we get that from the pair $(a+1,2022-(a+1))$ we take the number $2022-(a+1)$. Thus, in all pairs where the smallest number is greater than $a$, the chosen numbers are uniquely determined (specifically, the largest numbers in these pairs must be chosen).
Now consider all pairs where the smallest number is less than $a$. Consider among them the pair $(b, 2022-b)$ in which the largest number, i.e., $2022-b$, is chosen (the case where such pairs do not exist will be considered separately), and if there are several such pairs, consider the one where $b$ is maximal. From all pairs from $(b+1,2022-(b+1))$ to $(a-1,2022-(a-1))$, the smallest number was always chosen (due to the maximality of $b$). In the pair $(b-1,2022-(b-1))$, the number $2022-(b-1)$ was chosen (otherwise $(b-1)+(2022-b)=2021$). Similarly, in the pair $(b-2,2022-(b-2))$, the number $2022-(b-2)$ was chosen, and so on, in the pair $(1,2021)$, the number 2021 was chosen.
Now let's understand how the set of numbers satisfying the condition is determined. First, a group $(a, 2022-a)$ (i.e., a number $1 \leqslant a \leqslant 1011$) is chosen, in which no number is chosen. Then, in all groups where the smallest number is greater than $a$, the choice is uniquely determined (from the group, the largest number is chosen). Second, a pair $(b, 2022-b)$ (i.e., a number $1 \leqslant b \leqslant a-1$) is chosen, and in all other pairs, the choice is uniquely determined (in pairs with the smallest number from $b+1$ to $a-1$, the smallest number is chosen, and in pairs where it is less than $b$, the largest number is chosen).
It remains to count the number of options. Fix some $a$, then the number of ways to choose $b$ will be exactly $a-1$, plus one more option, where in all pairs with the smallest number less than $a$, the smallest number was chosen (i.e., the number $b$ simply does not exist). In total, there are $a$ options for the number $b$. Summing over all $a \leqslant 1011$, we get $1+2+3+\ldots+1010+1011=\frac{1011 \cdot 1012}{2}=511566$ options for our set. Clearly, all these options are distinct and satisfy the condition (the set is uniquely determined by the chosen numbers $a$ and $b$).
## Criteria
The highest appropriate criterion is used:
7 points. Any complete solution to the problem.
7 points. Any complete solution to the problem, but the answer is given in the form of a formula or expression (e.g., $\frac{1011 \cdot 1012}{2}$ or $C_{1012}^{2}$).
6 points. Any complete solution to the problem, but the answer is given in the form of a formula with an ellipsis (e.g., $1+2+3+\ldots+1010+1011$).
2 points. The numbers are divided into pairs, but there is no further progress.
16. The correct answer is given.
|
511566
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Petya has a $3 \times$ 3 table. He places chips in its cells according to the following rules:
- no more than one chip can be placed in each cell;
- a chip can be placed in an empty cell if the corresponding row and column already contain an even number of chips (0 is considered an even number).
What is the maximum number of chips Petya can place?
|
Solution. Answer: 9.
Let $a, b, c$ denote the left, middle, and right columns of the table, and $1, 2, 3$ denote the bottom, middle, and top rows of the table. Petya can fill all 9 cells of the table with chips, for example, in the following order: $a 1, b 2, c 3, a 2, b 3, c 1, a 3, b 1, c 2$. Obviously, it is not possible to place more than 9 chips.
## Criteria
The largest suitable criterion is used:
7 6. Any complete solution to the problem.
2 p. There is only the correct answer (the algorithm for placing the chips is missing).
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1011 of them such that the sum of any two does not equal 2021 or 2022. How many ways are there to do this?
|
Solution. Answer: 1.
Among the numbers from 1 to 2021, we can select 1010 non-overlapping pairs of numbers that sum to 2022. Specifically: $(1,2021),(2,2020), \ldots,(1009,1013),(1010,1012)$; only the number 1011 remains unpaired.
According to the condition, from each pair, we can choose no more than one number. Therefore, to choose 1011 numbers, we must select exactly one number from each pair, and also select the number 1011. Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this process, we find that from each pair, the largest number must be chosen.
If the numbers $1011,1012,1013, \ldots, 2021$ are chosen, the condition of the problem is satisfied (since the sum of any two is at least 2023) and this method of selection is the only one.
## Criteria
The following is the only suitable criterion used:
7 p. Any complete solution to the problem.
3 p. The numbers are divided into pairs, but there is no further progress.
0 6. Only the answer is present.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In the Kurchatov School, exactly 2 people sit at each desk. It is known that exactly $70 \%$ of the boys have a boy as a desk partner, and exactly $40 \%$ of the girls have a girl as a desk partner. How many times more boys are there than girls?
|
Answer: 2 times.
Solution. Let the number of boys be $x$, and the number of girls be $y$. Note that $30\%$ of the boys sit at desks with girls and $60\%$ of the girls sit at desks with boys. Since exactly 2 people sit at each desk, then $0.3 x = 0.6 y$, from which $x = 2 y$. Thus, there are 2 times more boys than girls.
## Criteria
## 7 p. Any complete solution of the problem.
## 2 p. A particular case is provided.
1 p. Only the correct answer.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 2. Find the number of ways to color all natural numbers from 1 to 20 in blue and red such that both colors are used and the product of all red numbers is coprime with the product of all blue numbers.
|
Answer: $2^{6}-2=62$ ways.
Solution. Note that all even numbers must be of the same color. Since among them are the numbers 6, 10, and 14, the numbers divisible by 3, 5, and 7 must be of the same color. The remaining numbers are $1, 11, 13, 17$, and 19. Note that they can be distributed in any way among the two colors. Thus, we have 6 groups, each of which can be of any color, i.e., a total of $2^{6}$ ways of coloring.
Note that 2 of these do not fit, where all numbers are of the same color. In total, we get $2^{6}-2=62$ ways.
## Criteria
The most suitable criterion is used:
7 points. Any complete solution to the problem.
3 points. Noted that even numbers, as well as numbers divisible by 3, 5, and 7, must be of the same color.
1 point. The correct answer is given.
The following errors in an otherwise correct solution result in point deductions:
-1 point. Not considered that both colors must be present.
-2 points. Not considered that both colors must be present, and not considered that "1" is not a coprime number.
-2 points. Not considered the alternative coloring, i.e., there are two pairs of groups: 1 group - red, 2 group - blue and 1 group - blue, 2 group - red.
-1 point. When considering monochromatic groups, the number 1 or one of the prime numbers greater than 10 is omitted. If more than one monochromatic group is omitted, the solution is not considered correct overall.
-3 points. Not considered that both colors must be present, and not considered the alternative coloring.
|
62
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. On the board, the numbers $2,3,5, \ldots, 2003,2011,2017$ are written, i.e., all prime numbers not exceeding 2020. In one operation, two numbers $a, b$ can be replaced by the largest prime number not exceeding $\sqrt{a^{2}-a b+b^{2}}$. After several operations, only one number remains on the board. What is the maximum value it can take?
|
Answer: The maximum value is 2011.
Solution. Note that if $a$ $2011^{2}$, therefore, as a result of this operation, the number 2011 will appear on the board.
Remark. The inequality $a<\sqrt{a^{2}-a b+b^{2}}<b$ for $a<b$ can be proven geometrically. The matter is that in a triangle with sides $a$ and $b$ and an angle of $60^{\circ}$ between them, the length of the third side is exactly $\sqrt{a^{2}-a b+b^{2}}$. Since the angle $60^{\circ}$ is always the middle in size in its triangle, the side opposite to it is also the middle in size.
## Criteria
Any complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed up:
3 p. It is shown how to get 2011, but it is not proven that a larger number cannot be obtained.
4 p. It is proven that a number larger than 2011 cannot be obtained.
|
2011
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a plane, an overlapping square and a circle are drawn. Together they occupy an area of 2018 cm². The area of intersection is 137 cm². The area of the circle is 1371 cm². What is the perimeter of the square?
|
Answer: 112 cm.
The area of the part of the circle outside the square is $1371-137=1234$ cm $^{2}$, therefore, the area of the square can be expressed by the formula $2018-1234=784 \mathrm{~cm}^{2}$. In conclusion, the length of the side of the square is $\sqrt{784}=28$ cm, and its perimeter is 112 cm.
## Criteria
+ Correct solution - 7 points.
$\pm$ Arithmetic error with correct reasoning - 5 points.
|
112
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Gosha entered a natural number into the calculator. Then he performed the following operation, consisting of two actions, three times: first, he extracted the square root, and then took the integer part of the obtained number. In the end, he got the number 1. What is the largest number that Gosha could have initially entered?
Let's recall, the integer part of a number is the largest integer not exceeding the given number.
|
Answer: 255.
Solution. Suppose he entered a number not less than 256. Then after the first operation, he would get a number not less than $[\sqrt{256}]=16$, after the second - not less than $[\sqrt{16}]=4$, after the third - not less than $[\sqrt{4}]=2$, which is a contradiction.
Let's assume Gosha entered the number 255. Then after the first operation, he would get $[\sqrt{255}]=15$, after the second $-[\sqrt{15}]=3$, after the third $-[\sqrt{3}]=1$. Therefore, the answer to the problem is the number 255.
## Criteria
## The following criteria are cumulative:
4 p. It is proven that the number entered by Gosha is not greater than 255.
3 p. It is proven that the number 255 satisfies the condition of the problem.
|
255
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. Lёnya has cards with digits from 1 to 7. How many ways are there to glue them into two three-digit numbers (one card will not be used) so that each of them is divisible by 9?
|
Answer: 36.
Solution. The sum of the digits in each number is divisible by 9, which means the overall sum of the used digits is also divisible by 9. The sum of all given digits $1+2+\ldots+7$ is 28. If we remove the digit 1, the remaining sum is 27, which is divisible by 9; removing any other digit cannot result in a sum divisible by 9. Therefore, the digits used are $2,3,4,5,6,7$.
Notice that the smallest possible sum of three of these digits is $2+3+4=9$, and the largest is $5+6+7=18$. No other sums divisible by 9 can be obtained; 9 and 18 can only be obtained in one way. Thus, one number consists of the digits $2,3,4$, and the other consists of $5,6,7$.
There are six numbers that can be formed from the digits 2,3,4, and six numbers that can be formed from the digits $5,6,7$. We need all possible pairs of these numbers.
## Criteria
A complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
2 p. It is proven that the digit 1 is not used.
3 p. Assuming (possibly unjustified) that the digit 1 is not used, it is proven that one number consists of the digits $2,3,4$, and the other of $5,6,7$.
1 6. The above is not proven but stated.
2 p. The correct answer is provided.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. Five numbers $2,0,1,9,0$ are written in a circle on the board in the given order clockwise (the last zero is written next to the first two). In one move, the sum of each pair of adjacent numbers is written between them. For example, such an arrangement of numbers (on the right) will be after the first move:
After 5 moves, Polina calculated the sum of all numbers from the first zero (the one initially between 2 and 1) to the second zero (the one initially between 9 and 2) when moving around the circle clockwise, while Alina calculated the sum of all other numbers. What is the difference between Alina's and Polina's numbers?
|
Answer: $8 \cdot 3^{5}=1944$.
Solution. Let's see how the numbers between the first and second zero (which Polina will count at the end) change. On each move, each "old" number is included as an addend in two "new" numbers. This means that if all the "new" numbers are added together, each "old" number will be summed twice, so the sum of the "new" numbers is twice the sum of the "old" numbers. Therefore, the total sum of the numbers between the first and second zero triples on each move.
The same thing happens with the other numbers. It remains to note that their difference is initially 8, and it triples with each move. After five moves, it will reach the value $8 \cdot 3^{5}=1944$.
## Criteria
## The largest suitable criterion is used:
7 p. Any complete solution to the problem.
## 4 p. It is proven that the sum of the numbers on the segment between two zeros triples on each move.
## 3 p. The correct answer is given.
|
1944
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Dodson, Williams, and their horse Bolivar want to get from city A to city B as quickly as possible. Along the road, there are 27 telegraph poles that divide the entire journey into 28 equal segments. Dodson takes 9 minutes to walk one segment, Williams takes 11 minutes, and either of them can ride Bolivar to cover the distance in 3 minutes (Bolivar cannot carry both). They set out from city A simultaneously; the journey is considered complete when all of them arrive in city B.
They agreed that part of the way Dodson will ride, then tie Bolivar to one of the telegraph poles and continue on foot, while Williams will initially walk and then ride Bolivar. At which pole should Dodson tie Bolivar to minimize the travel time to city B?
Answer: at the 12th, counting from A.
|
Solution. Let the distance from A to B be taken as a unit, and time will be measured in minutes. Then Dodson's speed is $1 / 9$, Williams' speed is $1 / 11$, and Bolivar's speed is $-1 / 3$.
Let the desired post have the number $k$ (i.e., the distance from city A is $k / 28$). Then Dodson will arrive in time
$$
\frac{k}{28}: \frac{1}{3}+\frac{28-k}{28}: \frac{1}{9}=9-\frac{6 k}{28}
$$
and Williams in
$$
\frac{k}{28}: \frac{1}{11}+\frac{28-k}{28}: \frac{1}{3}=3+\frac{8 k}{28}
$$
We need to find $k$ for which these values coincide:
$$
9-\frac{6 k}{28}=3+\frac{8 k}{28} \quad \Leftrightarrow \quad 6 \cdot 28=14 k \quad \Leftrightarrow \quad k=12
$$
It remains to understand why $k=12$ gives the best time. Indeed, for smaller $k$, Dodson's time will increase, and for larger $k$, Williams' time will increase. Thus, for all other $k$, the time of at least one of the characters will be greater than when $k=12$.
## Criteria
The highest suitable criterion is used:
7 p. Any complete solution to the problem.
4 p. The position of the post where the characters' times coincide is found, but it is not proven that this is the best time.
2 p. The idea of equating the characters' times is present, but an error was made in formulating or solving the equation.
1 p. The correct answer is given.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. In the cells of an $8 \times 8$ chessboard, there are 8 white and 8 black chips such that no two chips are in the same cell. Additionally, no column or row contains chips of the same color. For each white chip, the distance to the black chip in the same column is calculated. What is the maximum value that the sum of these distances can take? The distance between chips is the distance between the centers of the cells they occupy.
|
Answer: 32
Solution. An example of chip placement where the sum of distances is 32 is shown in the figure:
We will prove that the sum of distances cannot be greater than 32. For this, consider an arbitrary placement of chips that satisfies the condition. Let \( S \) be the sum of the distances specified in the condition.
Let the white and black chips in the \( i \)-th column be in rows \( a_i \) and \( b_i \), respectively. We estimate the distance between them:
\[
|a_i - b_i| = |(a_i - 4.5) - (b_i - 4.5)| \leq |a_i - 4.5| + |b_i - 4.5|
\]
(essentially, this is the triangle inequality for points \( a_i, b_i \), and 4.5 on a line). Summing this estimate for all differences \( |a_i - b_i| \), we get:
\[
S \leq |a_1 - 4.5| + |a_2 - 4.5| + \ldots + |a_8 - 4.5| + |b_1 - 4.5| + |b_2 - 4.5| + \ldots + |b_8 - 4.5|
\]
Notice that the right-hand side does not depend on the placement of the chips, as the numbers \( a_i, 0 \leq i \leq 8 \), are some permutation of the numbers from 1 to 8. Similarly for \( b_i \). We have:
\[
\begin{aligned}
S & \leq |1 - 4.5| + |2 - 4.5| + \ldots + |8 - 4.5| + |1 - 4.5| + |2 - 4.5| + \ldots + |8 - 4.5| = \\
& = 2 \cdot (3.5 + 2.5 + 1.5 + 0.5 + 0.5 + 1.5 + 2.5 + 3.5) = 32
\end{aligned}
\]
Remark. From the proof of the estimate, it is not difficult to understand how any example with the required sum of distances is constructed: in each column, a chip of one color is in the upper half, and a chip of the other color is in the lower half. In any other case, equality in the triangle inequality will not be achieved.
## Criteria
A complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
6 points. It is proven that the sum of distances cannot exceed 32.
If the solution is unjustifiably reduced to some "optimal" case or class of cases (for example, it is claimed without proof that in each column, the black and white chips must be in different halves of the column), then points for this part are not given.
1 point. An example of chip placement is provided where the sum of distances is 32.
|
32
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In each cell of a $15 \times 15$ table, a number $-1, 0$, or $+1$ is written such that the sum of the numbers in any row is non-positive, and the sum of the numbers in any column is non-negative. What is the smallest number of zeros that can be written in the cells of the table?
|
Answer: 15.
Evaluation. Since the sum of the numbers in all rows is non-positive, the sum of all numbers in the table is also non-positive. On the other hand, if the sum of the numbers in any column is non-negative, then the sum of all numbers in the table is non-negative. Therefore, the sum of all numbers in the table is actually zero, and the sums of the numbers in each column and each row are also zero.
In each row, there must be at least one zero, because otherwise the sum of all fifteen +1 and -1 would be odd, while it should be zero.
Thus, there must be at least 15 zeros in the table.

Fig. 2: Solution to problem 5.
Example. One possible example with 15 zeros is shown in Fig. 2. The symbols “+” and “-” correspond to the placement of numbers +1 and -1, and the shaded cells represent the placement of zeros.
## Criteria
+ Correct solution - 7 points.
-. Correct answer given without explanations (or with incorrect explanations) - 1 point.
The solution naturally divides into two parts: an example of number placement with 15 zeros and a proof that there are at least 15 zeros. Points for these parts are summed.
干 Correct example with 15 zeros provided - 3 points.
$\pm$ It is justified that there cannot be fewer than 15 zeros (or that there is at least one zero in each row/column) - 4 points.
- It is noted that the sum of the numbers in each row and each column must be zero, but the conclusion about the presence of a zero in any row/column did not follow - 1 point out of 4 possible for the estimate.
|
15
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.