problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 1
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
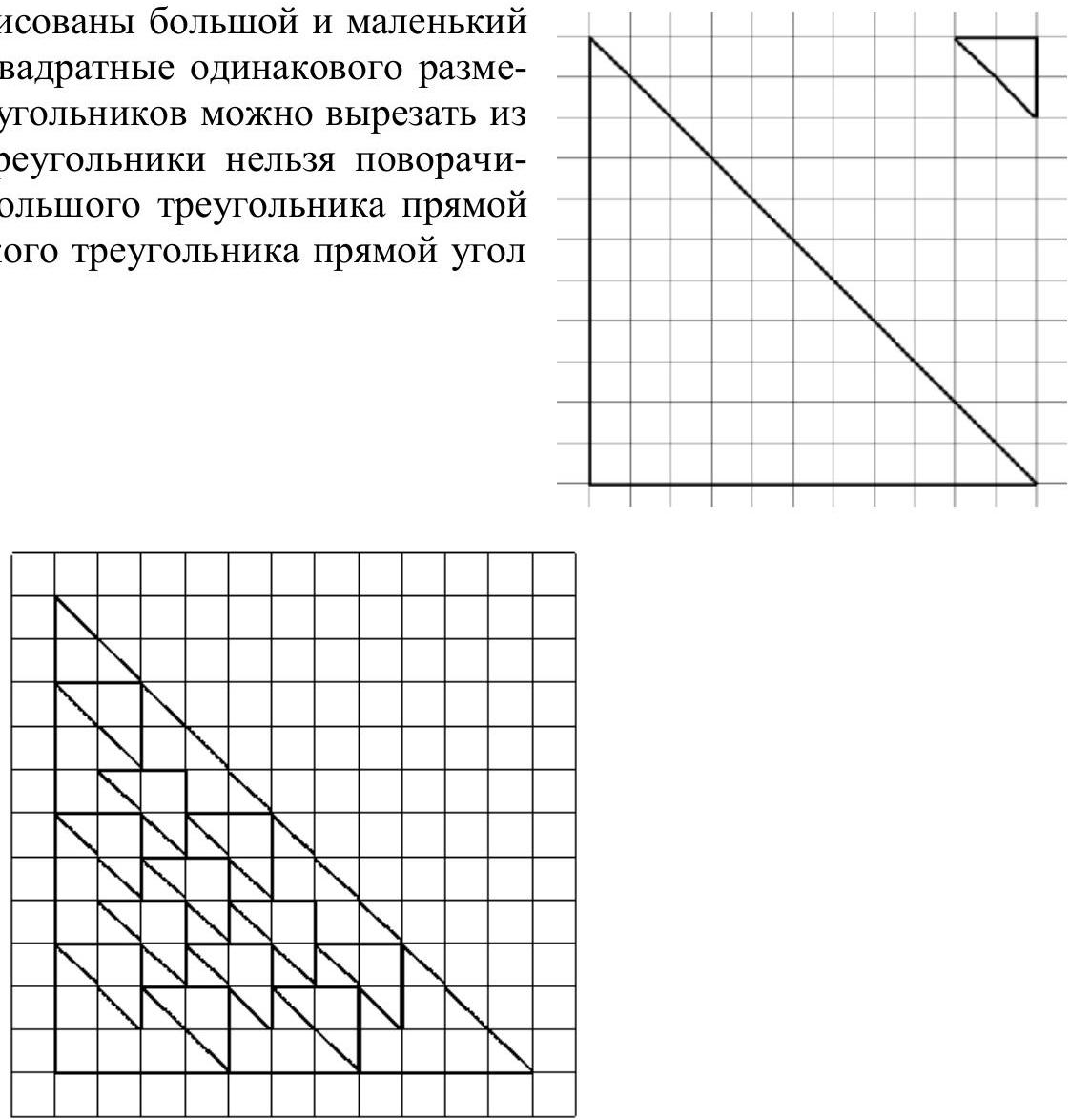
4. On graph paper, large and small triangles are drawn (all cells are square and of the same size). How many small triangles can be cut out from the large triangle? The triangles cannot be rotated or flipped (the large triangle has a right angle at the bottom left, the small triangle has a right angle at the top right).
|
Answer: 12.
Solution. See the figure.
Comment. Correct drawing with 12 triangles - 20 points. Incorrect answer with drawing - 1 point. Any answer without drawing - 0 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a row, all natural numbers from 1 to 100 inclusive are written in ascending order. Under each number in this row, the product of its digits is written. The same procedure is applied to the resulting row, and so on. How many odd numbers will be in the fifth row?
|
Answer: 19.
Solution: Note that if a number contains an even digit in its notation, then the product of the digits will be even. However, then in all subsequent rows, the product will also be even. Let's find all the products of two digits in the multiplication table that are written using only odd digits:
$$
\begin{array}{rr}
1=1 \cdot 1 ; \quad 3=1 \cdot 3 ; & 5=1 \cdot 5 ; \quad 7=1 \cdot 7 \\
9=1 \cdot 9 ; \quad 9=3 \cdot 3 ; \quad 15=3 \cdot 5 ; \quad 35=5 \cdot 7
\end{array}
$$
All other products contain even digits. Therefore, products consisting of odd digits will only be under numbers that consist of the specified digits. The list of numbers: $1,3,5,7,9,11,13,15,17,19,31,33,35,51,53,57,71,75,91$ - a total of 19 numbers.
Comment: Correct solution - 20 points. If the correct approach is followed but one extra number is written or one number is missing - 18 points. The solution is started, and there is some progress - 5 points. The solution is started, but the progress is insignificant - 1 point. The solution is incorrect or missing - 0 points.
|
19
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a certain day, there were several nuts in the bag. The next day, as many nuts were added to the bag as there already were, but eight nuts were taken away. On the third day, again as many nuts were added as there already were, but eight were taken away. The same thing happened on the fourth day, and after that, there were no nuts left in the bag. How many nuts were there in the bag at the beginning?
|
Answer: 7 nuts.
Solution. At the beginning of the fourth day, there were $(0+8): 2=4$ nuts in the bag. Therefore, at the beginning of the third day, there were $(4+8): 2=6$, and at the very beginning $-(6+8): 2=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Sixth-graders were discussing how old their principal is. Anya said: "He is older than 38 years." Borya said: "He is younger than 35 years." Vova: "He is younger than 40 years." Galya: "He is older than 40 years." Dima: "Borya and Vova are right." Sasha: "You are all wrong." It turned out that the boys and girls made the same number of mistakes. Can we find out how old the principal is?
|
Solution. Note that Anya and Vova cannot be wrong at the same time, so Sasha is wrong. Also, at least one of the pair "Anya-Borya" and at least one of the pair "Vova-Galya" is wrong. Thus, there are no fewer than three wrong answers, and due to the evenness, there are exactly four: two boys and two girls. This means that no more than one girl and no more than two boys are correct. Dima essentially confirms Borya's words. However, Borya, Dima, and Vova cannot be correct at the same time, so Borya and Dima are wrong, and among the boys, only Vova is right, and among the girls, only Anya is right. Therefore, the principal is 39 years old.
|
39
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Natural numbers divisible by 3 were painted in two colors: red and blue, such that the sum of a blue and a red number is red, and the product of a blue and a red number is blue. In how many ways can the numbers be colored so that the number 546 is blue?
|
Answer: 7.
Solution: We will prove that all blue numbers are divisible by the same number. First, we will prove that the product of two blue numbers is blue. Assume the statement is false. Let $a$ and $b$ be two such blue numbers that their product is a red number. Let $d$ be some red number (we can take $d = ab$). Then $a + d$ is red. From this, it follows that $a \cdot b + b \cdot d = b(a + d)$ is blue, since the blue number $b$ is multiplied by the red number $a + d$. The number $b \cdot d$ is also blue, and the number $a \cdot b$ is red by assumption. We have obtained that the sum of a blue and a red number is blue, which contradicts the condition. Therefore, the assumption is false, and the product of any two blue numbers is a blue number. Together with the condition, this means that the product of a blue number and any number is a blue number.
Let $a_0$ be the smallest blue number, and $a$ be any blue number. It can be represented as $a = k \cdot a_0 + r$, where $0 \leq r < a_0$. The remainder $r$ cannot be a blue number, since $a_0$ is the smallest blue number. The product $k \cdot a_0$, by the proven fact, is a blue number. The sum on the right, of a blue and a red number, is a red number by the condition, but the number on the left side of the equation is blue; a contradiction. Therefore, the remainder $r = 0$, and any blue number is divisible by the smallest blue number. The number $546 = 2 \cdot 3 \cdot 7 \cdot 13$. Only numbers divisible by 3 are considered, and among them, blue can be all numbers divisible by 6, or by 21, or by 39, or by 42, or by 78, or by 273, or by 546, a total of 7 ways.
Comment: 20 points for finding all ways. 15 points for establishing that blue numbers are divisible by divisors of the number 546, but the correct answer is not obtained. 5 points for finding at least one way in the absence of a general solution. 15 points for gaps in the justification. 2 points for starting the solution and making some progress.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the smallest natural $n>1$, for which the sum of no two natural powers is a perfect square of a natural number.
#
|
# Answer.4.
Solution. For $n=2: 2^{1}+2^{1}=2^{2}$. For $n=3: 3^{3}+3^{2}=6^{2}$. Let $n=4$. Suppose there exist such $m, k$ that $4^{m}+4^{k}=a^{2}$.
Any power of 4 gives a remainder of 1 when divided by 3 (since $\left.4^{m}=(3+1)^{m}\right)$. Therefore, $4^{m}+4^{k}$ will give a remainder of 2 when divided by 3. But the square of an integer gives a remainder of 0 or 1 when divided by 3.
Comment. Correct solution - 20 points. Proven that $n \geq 4-12$ points. Proven that $n \geq 3-3$ points. Proven that $n \leq 5-3$ points. Solution not completed, but there is progress - 5 points. Solution started, but progress is minimal - 1 point.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. How many irreducible fractions exist where the sum of the numerator and denominator is 100?
|
Answer: 20.
Solution: Consider the equation $a+b=100$. If $a$ and $b$ have a common divisor, then this divisor also divides 100, meaning that the only possible prime common divisors of $a$ and $b$ satisfying the equation can be 2 and 5. We will pair all numbers as ( $a, 100-a$ ). Since the fraction $\frac{a}{b}$ is irreducible, we exclude even numbers from 1 to 100 (leaving 50 numbers), and numbers divisible by 5 (leaving 40 numbers). Among these 40 numbers, each number $a$ corresponds to the number $100-a$, because if $a$ is odd and not divisible by 5, then $100-a$ also has these properties. We will write the smaller of the numbers $a, 100-a$ in the numerator of the fraction. This results in 20 pairs.
Comment: Correct solution - 20 points. Incomplete justification - 15 points. Correct solution with one calculation error - 18 points. Solution not completed or incorrect, but with good progress - 10 points. Solution started, with some progress - 5 points. Solution started, but with insignificant progress - 1 point. Only the correct answer without a solution - 1 point.
|
20
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Two squirrels had the same number of pine cones and the same number of cedar cones. In total, each squirrel had fewer than 25 cones. The first squirrel gathered as many pine cones as it already had and 26 cedar cones. It ended up with more pine cones than cedar cones. The second squirrel gathered as many cedar cones as it already had and ate 4 pine cones. It ended up with more cedar cones than pine cones. How many pine and cedar cones did each squirrel have initially?
|
Answer: 17 pine cones, 7 cedar cones.
Solution. Let the number of pine cones be $x$ and the number of cedar cones be $y$. We can write the conditions as: $\left\{\begin{array}{l}x+y=26 \\ 2 y>x-4\end{array}\right.$
Add the second and third inequalities: $2(x+y)>x+y+22$, or $x+y>22$. But $x+y=26$, so $x+y>22$ is always true. Now, we need to solve the system: $\left\{\begin{array}{l}x+y=26 \\ 2 y>x-4\end{array}\right.$
From the first equation, we have $y=26-x$. Substitute this into the second inequality: $2(26-x)>x-4$, or $52-2x>x-4$, which simplifies to $56>3x$, or $x<\frac{56}{3}$. Since $x$ and $y$ are integers, we need to find integer solutions for $x$ and $y$.
We also have $2y>x-4$, or $2(26-x)>x-4$, which simplifies to $52-2x>x-4$, or $56>3x$, or $x<\frac{56}{3}$. This gives us the inequality $\left\{\begin{array}{l}x>\frac{49}{3} \\ x<\frac{56}{3}\end{array}\right.$
In the interval $\left(\frac{49}{3} ; \frac{56}{3}\right)$, the only integer is 17. Therefore, $x=17, y=7$.
Comment. Correct solution - 20 points. Correct solution with one calculation error - 18 points. Total number of cones found, but solution not completed - 15 points. Solution started, some progress made - 5 points. Solution started, but progress insignificant - 1 point. Only correct answer without solution - 1 point.
|
17
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
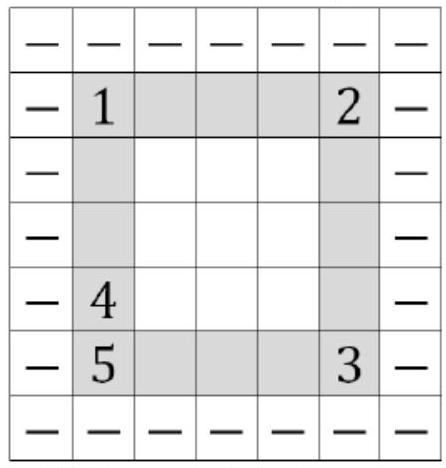
5. A $7 \times 7$ table is filled with non-zero integers. First, the border of the table is filled with negative numbers. Then, the cells are filled in any order, and the next number is equal to the product of the previously placed numbers that are closest to it in the same row or column. What is the maximum number of positive numbers that can be in the table?
|
# Answer. 24.
Solution. Evaluation. We will prove that there must be at least one negative number in the shaded area. Suppose this is not the case. Consider the corner cell of the shaded area where the number was placed last among the four corners (it is shaded black). By assumption, if some other numbers are placed in the cells of its row and column, they are positive. Therefore, a negative number must be placed in the black cell. There are at least \(4 \cdot 6 + 1 = 25\) negative numbers, so there are at most 24 positive numbers.
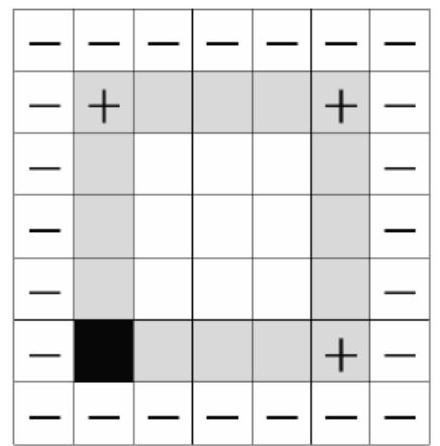
Example. We will place numbers in the shaded area in the order indicated by the numbers. In cells 1 and 2, we will choose factors by column, in cells 3 and 4, we will choose factors by row, resulting in positive numbers. In cell 5, there will be a negative number. All other cells can be filled with positive numbers, totaling 24.
Comment. Correct solution - 20 points. A filling method that is not optimal is proposed - 5 points. If the sequence of filling the cells is not indicated - 1 point.
## Variant 4
|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. A circle passing through the vertices $L$ and $M$ of trapezoid $K L M N$ intersects the lateral sides $K L$ and $M N$ at points $P$ and $Q$ respectively and touches the base $K N$ at point $S$. It turns out that $\angle L S M=50^{\circ}$, and $\angle K L S=\angle S N M$. Find $\angle P S Q$.
|
Answer: $65^{\circ}$.
Solution. Since $K S$ is a tangent to the circle, then
$$
\angle K S P=\angle S Q P=\angle S L P=\angle K L S=\angle S N M .
$$
But $\angle K S P$ and $\angle S N M$ are corresponding angles for the lines $P S$ and $M N$, so $P S \| M N$ and the inscribed quadrilateral $S Q M P$ is a trapezoid. Therefore, it is an isosceles trapezoid and, hence, $\angle P S Q=\angle S P M=\angle S L M$, the latter by the inscribed quadrilateral $S P L M$. From the parallelism of the lines $K N$ and $L M$ we have
$$
\angle S L M=\angle K S L=\angle K S P+\angle P S L=\angle S M P+\angle P M L=\angle L M S .
$$
Thus
$$
2 \angle P S Q=2 \angle S L M=\angle S L M+L M S=180^{\circ}-\angle L S M=130^{\circ}
$$
Comment. Correct solution - 20 points. Solution not completed, but with good progress - 10 points. Solution started, with some progress - 2 points. Incorrect or no solution - 0 points.
|
65
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A little squirrel collected 15 nuts in the forest weighing $50, 51, \ldots, 64$ grams. He knows the weight of each nut. Using a balance scale, the little squirrel tries to prove to his friends that the first nut weighs 50 g, the second 51 g, the third 52 g, and so on (initially, the friends know nothing about the weights of the nuts). What is the minimum number of weights the little squirrel will need, if both the weights and the nuts can be placed on either pan of the balance, and the number of weighings is unlimited? (The weights of the weights are known to both the little squirrel and his friends. There is an unlimited supply of weights weighing $1, 2, \ldots, 1000$ g.)
|
Answer. One weight.
Solution. Note that it is impossible to do without weights altogether, since if the weight of each nut is halved, the results of all weighings will not change. We will show that the baby squirrel can manage with the help of one 1 g weight. First, he will convince his friends that the nuts weigh $n, (n+1), \ldots, (n+14)$ g. For this, he will place a nut weighing 51 g on one pan of the scales, and a nut weighing 50 g and the weight on the other pan. The scales will show equality, and his friends will learn that the weighed nuts differ by exactly one gram. Then the same needs to be done with nuts weighing 52 and 51 g, and so on. Finally, with the last weighing, the baby squirrel will show his friends what $n$ is. For this, he will place nuts weighing from 50 to 57 g on one pan of the scales, and the remaining nuts and the weight on the other pan. The scales will again show equality. Thus, the friends will know that
$$
n+(n+1)+\cdots+(n+7)=(n+8)+(n+9)+\cdots+(n+14)+1
$$
Therefore, $8 n+28=7 n+78$, i.e., $n=50$.
Comment. Correct solution - 20 points. A solution with 2 weights - 2 points. A solution with more than 2 weights - 1 point. Incorrect or no solution - 0 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On 8 balls, numbers are written: $2,3,4,5,6,7,8,9$. In how many ways can the balls be placed into three boxes so that no box contains a number and its divisor?
|
Answer: 432.
Solution. The numbers 5 and 7 can be placed in any box, the number of ways is $3 \cdot 3=9$. The numbers $2, 4, 8$ must be in different boxes, the number of ways is $3 \cdot 2 \cdot 1=6$. Thus, the numbers $2, 4, 5, 7, 8$ can be arranged in 54 ways. Suppose the numbers 2 and 3 are placed in the same box (this box is already chosen for the number 2). Then there are two choices left for the number 9, and 2 choices for the number 6, in total $54 \cdot 2 \cdot 2=216$ ways. Suppose the numbers 2 and 3 are placed in different boxes, the number of choices for the box for 3 is 2. Then the box for the number 6 is chosen in a unique way, and the box for the number 9 is any of the two where there is no number 3, in total $54 \cdot 2 \cdot 2=216$ ways, thus $216+216=432$.
|
432
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. What is the maximum number of cells in an $8 \times 8$ square that can be colored so that the centers of any four colored cells do not form the vertices of a rectangle with sides parallel to the edges of the square?
|
Answer: 24 cells.
Solution: Suppose that no less than 25 cells are marked. We will say that a pair of marked cells in the same row covers a pair of columns in which these cells are located. A prohibited quartet arises when a pair of columns is covered twice. If in one row there are $m$ marked cells, and in another $n>m+1$ marked cells, then by moving one marked cell from the second row to the first, the number of covered pairs in the first row will increase by $m$, and in the second row it will decrease by $n-1>m$, i.e., the total number of pairs will decrease. Thus, the minimum number of pairs for a given number of marked cells is achieved when the maximum number of cells in a row differs from the minimum by no more than 1. Let's consider two cases.
1) There is a column in which no more than two cells are marked. Let's strike it out, in which case seven columns will remain, i.e., 21 pairs. One of the possible distributions of 23 cells is seven rows with three cells and one row with two cells, which gives $7 \cdot 3+1=22$ marked pairs. By the pigeonhole principle, there will be a pair of columns covered twice. As shown above, with a different distribution of marked pairs, there will be more.
2) In each column, no fewer than three cells are marked. Since $8 \cdot 3<25$, there will be a row in which no fewer than four cells are marked. Let these be the first four cells in the bottom row. Above them, in each of the first four columns, there are at least two more cells - a total of at least eight. They are located in seven rows, therefore, two of them are in the same row. Together with the corresponding cells in the bottom row, they form a prohibited quartet. An example for 24 cells is shown in the figure.

|
24
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $5 \times 5$ square, color as many cells black as possible, so that the following condition is met: any segment connecting two black cells must necessarily pass through a white cell.
|
Answer. We will prove that it is impossible to color more than 9 cells. Divide the square into 9 parts:

In each part, no more than one cell can be colored.
9 cells can be colored as follows:

Comment. A correct solution, including justification that the number of colored cells is maximal, and a diagram - 20 points. An incomplete justification that the number of colored cells is maximal - 15 points. Only an answer in the form of a diagram - 10 points. The solution is started but progress is insignificant - 1 point.
2. A baby squirrel had a reserve of pine and spruce cones, with pine cones making up 60%. In August, it collected more spruce cones, and now the pine cones made up 20%. In September, the baby squirrel collected more pine cones, and now the pine cones made up 80%. By what factor did the total number of cones increase over the two months?
## Answer. 12.
Solution. In August, the percentage of pine cones decreased by 3 times, meaning the total number of cones increased by 3 times. In September, the percentage of spruce cones decreased from 80% to 20%, meaning the total number of cones increased by 4 times. In total, over the two months, the total number of cones increased by \(3 \cdot 4 = 12\) times.
Comment. A correct solution - 20 points. There is a gap in the justification - 15 points. A correct equation is set up, but not brought to a correct solution - 10 points. The solution is started, with some progress - 5 points. The solution is started, but progress is insignificant - 1 point.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a rectangle of size $7 \times 9$ cells, some cells contain one baby squirrel each, such that in every rectangle of size $2 \times 3$ (or $3 \times 2$) there are exactly 2 baby squirrels. Draw how they can be seated.
|
Answer. For example, like this (21 squirrels sit in the shaded cells).
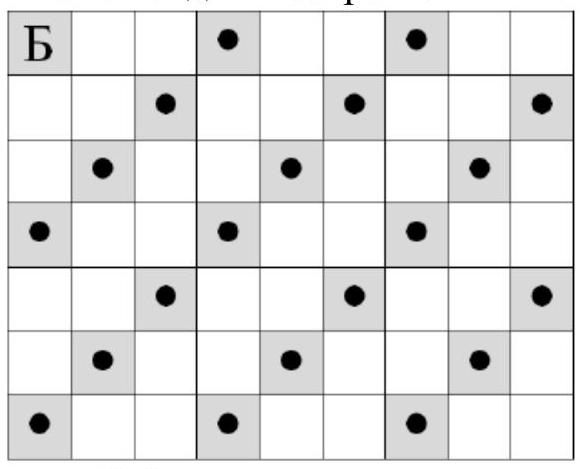
Comment. A correct example - 20 points.
|
21
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Diana wrote a two-digit number, and appended to it a two-digit number that was a permutation of the digits of the first number. It turned out that the difference between the first and second numbers is equal to the sum of the digits of the first number. What four-digit number was written?
|
# Answer: 5445.
Solution. The difference between such numbers is always divisible by 9, since $10a + b - (10b + a) = 9(a - b)$. This difference equals the sum of two digits, so it is no more than 18. However, it cannot be 18, because then both the first and second numbers would be 99. Therefore, the difference between the two numbers is 9, and the tens digits of the two numbers differ by no more than 1. But the sum of the tens digits of the two numbers is the sum of the digits of the first number, and it equals 9. Clearly, only the digits 4 and 5 fit.
Comment. Correct solution - 20 points. Incomplete proof - 10 points. Solution by trial and error, without proving that there are no other options - 5 points. The answer includes the number 4554 - 1 point is deducted. Some progress in the solution - 5 points. The solution is started, but there is no noticeable progress - 1 point. The correct answer is given without explanation - 0 points.
|
5445
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. For a children's party, pastries were prepared: 10 eclairs, 20 mini tarts, 30 chocolate brownies, 40 cream puffs. What is the maximum number of children who can each take three different pastries?
|
Answer: 30.
Solution: From eclairs, baskets, and brownies, at least 2 pastries must be taken, and there are 60 of them in total, meaning no more than 30 children can take three different pastries. They can do this as follows: 10 children will take an eclair, a brownie, and a roll, and 20 children will take a basket, a brownie, and a roll.
Comment: Correct solution - 20 points. Proof that 30 is the maximum value - 10 points, example - 10 points. If the proof is insufficiently justified, 5 points are deducted. Solution started, with some progress - 5 points. Solution started, but no significant progress - 1 point. Correct answer given without explanation - 0 points.
|
30
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On 900 cards, all natural numbers from 1 to 900 are written. Cards with squares of integers are removed, and the remaining cards are renumbered, starting from 1.
Then the operation of removing squares is repeated. How many times will this operation have to be repeated to remove all the cards
|
Answer: 59.
Solution: During the first operation, 30 cards will be removed, leaving $900-30=30 \cdot 29$ cards. Since $30 \cdot 29 > 29^2$, all squares except $30^2$ remain. During the second operation, 29 cards will be removed. There will be $30 \cdot 29 - 29 = 29^2$ cards left. Thus, in two operations, we transition from the number $30^2$ to the number $29^2$. Let's write this in a general form: during the first operation, $n$ cards will be removed, leaving $n^2 - n = n(n-1) > (n-1)^2$ cards. During the second operation, $n-1$ cards will be removed. There will be $n^2 - n - (n-1) = (n-1)^2$ cards left, meaning that in two operations, we always transition from the number $n^2$ to the number $(n-1)^2$. In total, there are 30 squares among the numbers from 1 to 900, and 29 transitions between them. To reach a single card, it will take $2 \cdot 29$ operations, and one more to remove the last card with the number 1.
Comment: Correct solution - 20 points. There is a gap in the justification - 15 points. Errors in the calculation of the number of options with a correct idea - 5 points are deducted. The solution is started, with some progress - 5 points. The solution is started, but there is no noticeable progress - 1 point. The correct answer is given without explanation - 0 points.
## Variant 4
|
59
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Squirrel Pusistik and Lohmatik ate a basket of berries and a bag of seeds, which contained more than 50 but less than 65 seeds, starting and finishing at the same time. At first, Pusistik ate berries, and Lohmatik ate seeds, then (at some point) they switched. Lohmatik ate berries six times faster than Pusistik, and seeds only three times faster. How many seeds did Lohmatik eat if Lohmatik ate twice as many berries as Pusistik?
|
# Answer: 54.
Solution. Divide the berries into 3 equal parts. Each part, Lomhatic ate 6 times faster than Pushistik, but there are two parts, so he spent only 3 times less time on the berries than Pushistik. Therefore, Pushistik ate the seeds in one-third the time of Lomhatic. Since Pushistik eats three times slower, he ate 9 times fewer seeds than Lomhatic. Dividing the seeds in the ratio of 9:1, we see that Pushistik got one-tenth of the seeds, from which it is not difficult to understand that there were 60 seeds in the bag. Therefore, Pushistik ate 6 seeds, and Lomhatic - 54.
Comment. Correct solution - 20 points. Solution started, with some progress - 5 points. Solution started, but no significant progress - 1 point. Incorrect or no solution - 0 points.
|
54
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all natural numbers $a$ for which the number
$$
\frac{a+1+\sqrt{a^{5}+2 a^{2}+1}}{a^{2}+1}
$$
is also a natural number.
|
Answer. $a=1$.
Solution. Let $a+1=b, \sqrt{a^{5}+2 a^{2}+1}=c$. Write the polynomial $c^{2}-b^{2}=$ $a^{5}+2 a^{2}+1-(a+1)^{2}=a^{5}+a^{2}-2 a$, and divide it by $a^{2}+1$ using long division, we get a remainder of $-(a+1)$. For $a>1$, the absolute value of the remainder is less than $a^{2}+1$, so the remainder cannot be divisible by $a^{2}+1$ for any $a>1$. If $c^{2}-b^{2}$ is not divisible by the denominator $a^{2}+1$, then $b+c$ is also not divisible. The equation is satisfied by the unique value $a=1$.
Comment. Correct solution - 20 points. There is a gap in the justification - 15 points. The value $a=1$ is found, but it is not proven that there are no other solutions - 1 point. The proof is started - another 1 point. The proof is started, and there is some progress - 5 points. The proof is partially conducted - 10 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Three squirrels usually eat porridge for breakfast: semolina (M), buckwheat (B), oatmeal (O), and millet (R). No porridge is liked by all three squirrels, but for each pair of squirrels, there is at least one porridge that they both like. How many different tables can be made where each cell contains a plus (if it is liked) or a minus (if it is not liked)?
| | M | B | O | R |
| :--- | :--- | :--- | :--- | :--- |
| Squirrel 1 | | | | |
| Squirrel 2 | | | | |
| Squirrel 3 | | | | |
|
Answer: 132.
Solution: If two different pairs like the same porridge, then the porridge is liked by three squirrels, violating the first condition. From three squirrels, three different pairs can be formed, and these three pairs like different porridges. There are 4 ways to choose these 3 porridges, and $3!=6$ ways to distribute 3 porridges among the three pairs. In total, there are 24 ways to distribute the porridges that the pairs like. The fourth porridge can have the following scenarios: 1) it is not liked by anyone, 2) it is liked by only one squirrel, 3) it is liked by only one pair.
In case 1), the total number of options remains 24. In case 2), the number 24 is multiplied by the number of ways to choose the squirrel who likes the fourth porridge, which is 3, resulting in 72. In case 3), the situation is as follows: there is a pair that likes two porridges, and two pairs that like two other porridges. The first two porridges can be chosen in $\frac{4 \cdot 3}{2}=6$ ways. The pair that likes the first two porridges can be chosen in three ways (since we choose one out of three). The two remaining porridges can be distributed among the two remaining pairs in two ways. In total, there are $6 \cdot 3 \cdot 2=36$ options in this case. Therefore, the total number of different tables can be $24+72+36=132$.
Comment: Correct solution - 20 points. Correct solution with computational errors - 15 points. Partial case considered - 5 points. Solution started but progress is insignificant - 1 point. Only the correct answer without a solution - 0 points.
## Variant 3
|
132
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the border of a circular glade, points $A, B, C, D$ are marked clockwise. At point $A$ is a squirrel named An, at point $B$ is a squirrel named Bim, at point $C$ stands a pine tree, and at point $D$ stands an oak tree. The squirrels started running simultaneously, An towards the pine tree, and Bim towards the oak tree. They collided at point $M$, which is closer to the pine tree than to the oak tree. Is it true that if An had run from point $A$ to the oak tree, and Bim from point $B$ to the pine tree, An would have arrived first? Each squirrel runs in a straight line and at a constant speed.
|
Answer: No.
Solution: Let the speed of Ana be $-v$, and the speed of Bim be $-u$. They both reached point $M$ at the same time, so $\frac{A M}{v}=\frac{B M}{u}$. Triangles $D A M$ and $C B M$ are similar (by three angles).
Therefore, $\frac{A D}{B C}=\frac{A M}{B M}$. But $\frac{A M}{B M}=\frac{v}{u}$, so $\frac{A D}{B C}=\frac{v}{u}$, which means $\frac{A D}{v}=\frac{B C}{u}$. Thus, the squirrels will arrive at the same time.
Comment: Correct solution - 20 points. Correct solution not fully completed - 15 points. Solution with inaccuracies - 15 points. Solution based on an example - 10 points. Some progress - 5 points. Incorrect or no solution - 0 points.
3. In how many ways can 30 apples be distributed into 3 baskets such that the first basket has fewer apples than the second, the second has fewer apples than the third, and no basket is empty?
## Answer: 61.
Solution: Consider the equation $a+b+c=30$. Arrange 30 units in a row, choose two gaps between the units, and place a dash in each. The number of units to the left of the first dash is $a$ (the number of apples in the first basket), and the number to the right of the second dash is $c$ (the number of apples in the third basket). The number of ways to choose two gaps is $\frac{29 \cdot 28}{2}=406$. We need to subtract the number of cases where among the numbers $a, b, c$ there are equal numbers. Let $a=b$. Then $2 a+c=30$, this equation has 14 non-zero solutions ( $c$ is even and can vary from 2 to 28). Similarly, there will be 14 cases when $a=c$ or $b=c$. Thus, $406-3 \cdot 14=364$. The case $a=b=c$ is counted once in the total number of ways and subtracted three times, but it should be excluded only once, so we need to add 2. The number $364+2=366$ is the number of ordered triples of distinct $a, b, c$. But we need the order $a<b<c$, so we divide by the number of permutations of three elements: $\frac{366}{6}=61$.
Comment: Correct solution - 20 points. Correct solution not fully completed - 15 points. Significant progress in the solution - 10 points. Only the correct answer without a solution - 0 points.
|
61
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (7-8 grade) Maria Ivanovna is a strict algebra teacher. She only puts twos, threes, and fours in the grade book, and she never gives the same student two twos in a row. It is known that she gave Vovochka 6 grades for the quarter. In how many different ways could she have done this? Answer: 448 ways.
|
Solution. Let $a_{n}$ be the number of ways to assign $n$ grades. It is easy to notice that $a_{1}=3$, $a_{2}=8$. Note that 3 or 4 can be placed after any grade, while 2 can only be placed if a 3 or 4 preceded it. Thus, a sequence of length $n$ can be obtained by appending 3 or 4 to a sequence of length $n-1$ or by appending 32 or 42 to a sequence of length $n-2$, from which we get the recurrence relation $a_{n}=2 a_{n-1}+2 a_{n-2}$. From this, it is easy to find that $a_{3}=22, a_{4}=60, a_{5}=164, a_{6}=448$.
|
448
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. 7-8 grade Excellent student Kolya found the sum of the digits of all numbers from 0 to 2012 and added them all together. What number did he get? Answer: 28077.
|
Solution. Note that the numbers 0 and 999, 1 and 998, ..., 499 and 500 complement each other to 999, i.e., the sum of their digit sums is 27. Adding their digit sums, we get $27 \times 500 = 13500$. The sum of the digits of the numbers from 1000 to 1999, by similar reasoning, is 14500 (here we account for the fact that each number has an additional one, so the sum increases by a thousand). The numbers 2000, 2001, ... 2012 remain, and their digit sum is 77. In total, we get $13500 + 14500 + 77 = 28077$.
|
28077
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (9th grade) In how many ways can the numbers $1,2,3,4,5,6$ be written in a row so that for any three consecutive numbers $a, b, c$, the quantity $a c-b^{2}$ is divisible by 7? Answer: 12.
|
Solution. Each subsequent member will be obtained from the previous one by multiplying by a certain fixed value (modulo 7). This value can only be 3 or 5. And the first term can be any, so there are 12 options in total.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A line parallel to the selected side of a triangle with an area of 16 cuts off a smaller triangle with an area of 9. Find the area of the quadrilateral, three vertices of which coincide with the vertices of the smaller triangle, and the fourth lies on the selected side. Choose the answer option with the number closest to the one you found.
|
Answer: 12. (C)
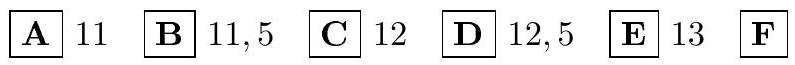
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A line parallel to the selected side of a triangle with an area of 27 cuts off a smaller triangle with an area of 3. Find the area of the quadrilateral, three vertices of which coincide with the vertices of the smaller triangle, and the fourth lies on the selected side. Choose the answer option with the number closest to the one you found.
Choose the answer option with the number closest to the one you found.
|
Answer: 9. (B)
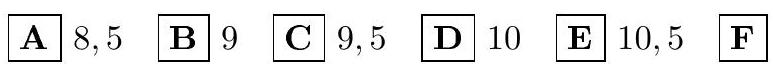
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A line parallel to the selected side of a triangle with an area of 27 cuts off a smaller triangle with an area of 12. Find the area of the quadrilateral, three vertices of which coincide with the vertices of the smaller triangle, and the fourth lies on the selected side. Choose the answer option with the number closest to the one you found.
|
Answer: 18. (E)
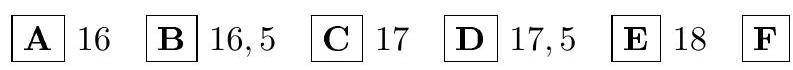
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
\frac{y^{2}+x y-\sqrt[4]{x^{5} y^{3}}-\sqrt[4]{x y^{7}}}{\sqrt[4]{y^{5}}-\sqrt[4]{x^{2} y^{3}}} \cdot(\sqrt[4]{x}+\sqrt[4]{y})
$$
where $x=3, \underbrace{22 \ldots 2}_{2013} 3, y=4, \underbrace{77 \ldots .7}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 8. (D)
Options.
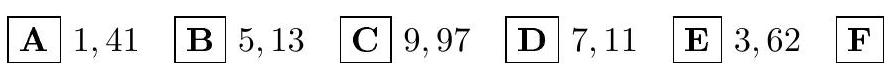
|
8
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
(\sqrt[4]{x}+\sqrt[4]{y}) \cdot \frac{x^{2}+x y-\sqrt[4]{x^{7} y}-\sqrt[4]{x^{3} y^{5}}}{\sqrt[4]{x^{5}}-\sqrt[4]{x^{3} y^{2}}}
$$
where $x=1, \underbrace{11 \ldots 1}_{2013} 2, y=3, \underbrace{88 \ldots 8}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 5. (B)
Options.
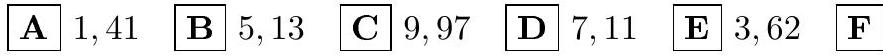
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
\frac{\sqrt[4]{x^{5} y^{3}}+\sqrt[4]{x y^{7}}-x y-y^{2}}{\sqrt[4]{x^{2} y^{3}}-\sqrt[4]{y^{5}}} \cdot(\sqrt[4]{x}+\sqrt[4]{y})
$$
where $x=2, \underbrace{44 \ldots .4}_{2013} 5, y=1, \underbrace{55 \ldots .5}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 4. (E)
Options.
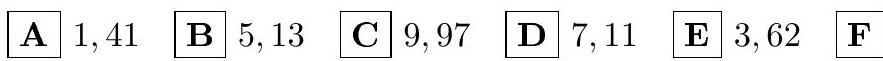
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In how many ways can a coach form a hockey team consisting of one goalkeeper, two defenders, and three forwards if he has 2 goalkeepers, 5 defenders, and 8 forwards at his disposal? Among the proposed answer options, choose the one closest to the correct one.
|
Answer: 1120. (B)
$$
\begin{array}{|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 915 & \mathbf{B} & 1120 & \mathbf{C} & 1400 & \mathbf{D} \\
1960 & \mathbf{E} & 2475 & \mathbf{F} \\
\hline
\end{array}
$$
|
1120
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In how many ways can a team be selected from a group consisting of 7 boys and 8 girls, so that the team has 4 boys and 3 girls? Among the proposed answer options, choose the one closest to the correct one.
|
Answer: 1960. (D)
$$
\begin{array}{|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} 915 & \mathbf{B} & 1120 & \mathbf{C} & 1400 & \mathbf{D} & 1960 & \mathbf{E} \\
\hline
\end{array}
$$
|
1960
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In how many ways can a coach form a basketball team consisting of two guards and three forwards if he has 6 guards and 11 forwards at his disposal? Among the options provided, choose the one closest to the correct answer.
|
Answer: 2475. (E)
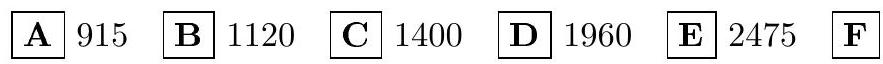
|
2475
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
3. In how many ways can a team be assembled consisting of 3 painters and 4 plasterers, if there are 6 painters and 8 plasterers? Among the options provided, choose the one closest to the correct answer.
|
Answer: $1400 .(\mathrm{C})$
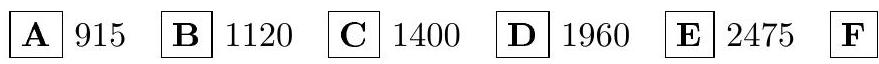
|
1400
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the number of different values of $a$ for which the equation
$$
\left(3-a^{2}\right) x^{2}-3 a x-1=0
$$
has a unique solution
|
Answer: 2. (C)
Options.
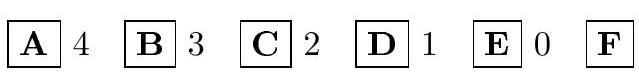
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine how many different values of $a$ exist for which the equation
$$
\left(a^{2}-5\right) x^{2}-2 a x+1=0
$$
has a unique solution
|
Answer: 2. (C)
Options.
$$
\begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 0 & \mathbf{B} & 1 & \mathbf{C} & 2 & \mathbf{D} & 3 & \mathbf{E} \\
\hline
\end{array}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Ivan Semenovich leaves for work at the same time every day, drives at the same speed, and arrives exactly at 9:00. One day he overslept and left 40 minutes later than usual. To avoid being late, Ivan Semenovich drove at a speed 60% faster than usual and arrived at 8:35. By what percentage should he have increased his usual speed to arrive exactly at 9:00?
|
Answer: By $30 \%$.
Solution: By increasing the speed by $60 \%$, i.e., by 1.6 times, Ivan Semenovich reduced the time by 1.6 times and gained 40+25=65 minutes. Denoting the usual travel time as $T$, we get $\frac{T}{1.6}=T-65$, from which $T=\frac{520}{3}$. To arrive in $T-40=\frac{400}{3}$, the speed needed to be increased by $\frac{520}{3} \div \frac{400}{3}=1.3$ times, i.e., by $30 \%$.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The English club is attended by 20 gentlemen. Some of them are acquainted (acquaintances are mutual, i.e., if A knows B, then B knows A). It is known that there are no three gentlemen in the club who are pairwise acquainted.
One day, the gentlemen came to the club, and each pair of acquaintances shook hands with each other (once). What is the maximum number of handshakes that could have been made?
|
Answer: 100 handshakes.
Solution: Choose a gentleman with the maximum number of acquaintances (if there are several, choose any one). Suppose he has $n$ acquaintances. These acquaintances cannot be pairwise acquainted with each other. Consider the remaining $(20-n-1)$ gentlemen, each of whom has no more than $n$ acquaintances, so the number of handshakes they make does not exceed $(20-n-1) \cdot n$. Therefore, the total number does not exceed $(20-n) \cdot n$. This number is maximal when $n=10$. It can be shown that 100 handshakes are possible - by dividing the gentlemen into 2 groups of 10 people each and ensuring that each person in the first group is acquainted with each person in the second (while there are no acquaintances within the groups).
|
100
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the inequality $\frac{\sqrt{\frac{x}{\gamma}+(\alpha+2)}-\frac{x}{\gamma}-\alpha}{x^{2}+a x+b} \geqslant 0$.
In your answer, specify the number equal to the number of integer roots of this inequality. If there are no integer roots, or if there are infinitely many roots, enter the digit 0 in the answer sheet.
$$
\alpha=3, \gamma=1, a=-15, b=54 .
$$
|
# Answer: 7.
Solution. Given the numerical values, we solve the inequality:
$$
\frac{\sqrt{x+5}-x-3}{x^{2}-15 x+54} \geqslant 0 \Leftrightarrow \frac{\sqrt{x+5}-x-3}{(x-6)(x-9)} \geqslant 0
$$
Since $\sqrt{x+5} \geqslant x+3 \Leftrightarrow\left[\begin{array}{c}-5 \leqslant x \leqslant-3, \\ x+5 \geqslant(x+3)^{2}\end{array}\right.$, the expression in the numerator is non-negative for $x \in[-5 ;-1]$, and negative for $x>-1$.
It is also true that $x^{2}-15 x+54<0$ for $x \in(6 ; 9)$, otherwise this expression is non-negative.
Therefore, $x \in[-5 ;-1] \bigcup(6 ; 9)$, and the number of integer solutions is $5+2=7$.
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. From point $M$, lying inside triangle $A B C$, perpendiculars are drawn to the sides $B C, A C, A B$, with lengths $k, l$, and $m$ respectively. Find the area of triangle $A B C$, if $\angle C A B=\alpha$ and $\angle A B C=\beta$. If the answer is not an integer, round it to the nearest integer.
$$
\alpha=\frac{\pi}{6}, \beta=\frac{\pi}{4}, k=3, l=2, m=4
$$
|
Answer: 67.
Solution. Denoting the sides of the triangle by $a, b, c$, using the sine theorem we get $S=\frac{k a+l b+m c}{2}=R(k \sin \alpha+l \sin \beta+m \sin \gamma)$.
Since, in addition, $S=2 R^{2} \sin \alpha \sin \beta \sin \gamma$, we can express $R=\frac{k \sin \alpha+l \sin \beta+m \sin \gamma}{2 \sin \alpha \sin \beta \sin \gamma}$.
Therefore, $S=\frac{(k \sin \alpha+l \sin \beta+m \sin \gamma)^{2}}{2 \sin \alpha \sin \beta \sin \gamma}$.
After substituting the numerical values of $k, l, m, \alpha, \beta, \gamma$ we get
$$
S=\frac{(3 \sin \alpha+2 \sin \beta+4 \sin \gamma)^{2}}{2 \sin \alpha \sin \beta \sin \gamma}=\frac{(3+4 \sqrt{2}+2 \sqrt{6})^{2}}{\sqrt{3}+1} \approx 67
$$
|
67
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all integer values of $a$, not exceeding 15 in absolute value, for each of which the inequality
$$
\frac{4 x-a-4}{6 x+a-12} \leqslant 0
$$
is satisfied for all $x$ in the interval $[2 ; 3]$. In your answer, specify the sum of all such $a$.
|
Answer: -7.
Solution. Solving the inequality using the interval method, we find that its left side equals 0 at $x=1+\frac{a}{4}$ and is undefined at $x=2-\frac{a}{6}$. These two values coincide when $a=\frac{12}{5}$. In this case, the inequality has no solutions.
For $a>\frac{12}{5}$, the solution to the inequality is the interval $\left(2-\frac{a}{6} ; 1+\frac{a}{4}\right]$, and the inequality holds for all $x \in[2 ; 3]$ if $\left\{\begin{array}{c}2-\frac{a}{6}<2, \\ 3 \leqslant 1+\frac{a}{4}\end{array} \Leftrightarrow a \geqslant 8\right.$.
For $a<\frac{12}{5}$, the solution to the inequality is the interval $\left[1+\frac{a}{4} ; 2-\frac{a}{6}\right)$, and the inequality holds for all $x \in[2 ; 3]$ if $\left\{\begin{array}{l}1+\frac{a}{4} \leqslant 2, \\ 3<2-\frac{a}{6}\end{array} \Leftrightarrow a<-6\right.$.
Therefore, $a \in(-\infty ;-6) \bigcup[8 ;+\infty)$, and the required values are: $a \in[-15 ;-6) \bigcup[8 ; 15]$. The sum of the integer values:
$$
-15-14-13-\ldots-8-7+8+9+\ldots+14+15=-7
$$
## Set of Creative Problems.
I. Find all natural values of $n$ not exceeding 100 for which the sum $1^{2}+2^{2}+3^{2}+\ldots+n^{2}$ is divisible by 50. Arrange these values of $n$ in ascending order: $n_{1}<n_{2}<\ldots<n_{k}$. In the answer, specify $n_{4}$.
Solution. Since $1^{2}+2^{2}+3^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}$, then $n(n+1)(2 n+1)$ must be divisible by $300=2^{2} \cdot 3 \cdot 5^{2}$. Since the numbers $n, n+1$, and $2 n+1$ are pairwise coprime, one of them must be divisible by 25.
- If $n$ is divisible by 25, then $n=25,50,75$ or 100. Substituting these values into the expression, we find that divisibility holds for $n=75$ and $n=100$.
- If $n+1$ is divisible by 25, then $n=24,49,74$ or 99. Substituting these values into the expression, we find that divisibility holds for $n=24$ and $n=99$.
- If $2 n+1$ is divisible by 25 and is odd, then $n=12,37,62$ or 87. Substituting these values into the expression, we find that divisibility holds for $n=12$ and $n=87$.
Thus, the values that work are $12,24,75,87,99,100$. The fourth of these is 87.
Answer: 87.
|
-7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. The master's day shift lasts $10 \%$ longer than the apprentice's shift. If the apprentice worked as long as the master, and the master worked as long as the apprentice, they would produce the same number of parts. By what percentage does the master produce more parts per day than the apprentice?
|
Solution. Let $p=10 \%$. Suppose the productivity of the apprentice is $a$ parts per hour, the master's productivity is $b$ parts per hour, the apprentice's workday is $n$ hours, and the master's workday is $m$ hours. Then from the condition it follows:
$$
m=n\left(1+\frac{p}{100}\right), \quad \text { and } \quad m a=n b \Rightarrow n\left(1+\frac{p}{100}\right) a=n b \Rightarrow b=\left(1+\frac{p}{100}\right) a .
$$
In a day, the master makes $b m-a n=\frac{p}{100}\left(2+\frac{p}{100}\right)$ an more parts than the apprentice, which as a percentage of the apprentice's daily output is
$$
\frac{p}{100}\left(2+\frac{p}{100}\right) a n \cdot \frac{100}{a n}=p\left(2+\frac{p}{100}\right)
$$
If $p=10 \%$, then $p\left(2+\frac{p}{100}\right)=21$.
Answer: 21. (C)
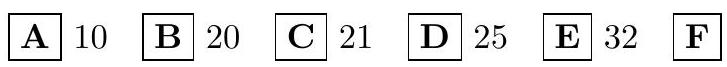
|
21
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. Find the sum of all two-digit numbers for each of which the sum of the squares of the digits is 37 more than the product of the same digits.
|
Solution. 1st method. For a two-digit number $\overline{a b}$, the condition means that
$$
a^{2}+b^{2}-a b=37
$$
Since the equation is symmetric, i.e., with each solution $(a, b)$, the pair $(b, a)$ is also a solution, we can assume without loss of generality that $a \geqslant b$.
- Suppose $a \leqslant 6$. Then the equation (1) has no solutions, because $b \leqslant a$ and $37=a^{2}+b^{2}-a b=a^{2}+b(b-a) \leqslant a^{2} \leqslant 36$.
- For $a=7$, the equation (1) becomes $b^{2}-7 b+12=0 \Longleftrightarrow b=3, b=4$. This gives us the solutions 73, 74, and considering the symmetry, 37, 47.
- For $a=8$ and $a=9$, the equation (1) becomes $b^{2}-8 b-27=0$ and $b^{2}-9 b-44=0$ respectively. Both equations have no integer solutions.
It remains to sum all the obtained numbers: $73+74+37+47=231$.
2nd method. Another solution to this problem. For a two-digit number $\overline{a b}$, the condition means that
$$
a^{2}+b^{2}-a b=37 \Longleftrightarrow(2 a-b)^{2}+3 b^{2}=148
$$
Then $b \leqslant 7$ and a complete enumeration of the cases
| $b$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $3 b^{2}$ | 0 | 3 | 12 | 27 | 48 | 75 | 108 | 147 |
| $(2 a-b)^{2}$ | 37 | 145 | 126 | 121 | 100 | 73 | 40 | 1 |
leaves only three options:
$$
\left[\begin{array}{l}
b=3 \\
2 a-b= \pm 11
\end{array} \Rightarrow a=7 ; \quad\left[\begin{array}{l}
b=4 \\
2 a-b= \pm 10
\end{array} \Rightarrow a=7 ; \quad\left[\begin{array}{l}
b=7 \\
2 a-b= \pm 1
\end{array} \Rightarrow a=3, a=4\right.\right.\right.
$$
Thus, these are the numbers $37, 47, 73, 74$. Their sum is 231.
Answer: 231. (C)
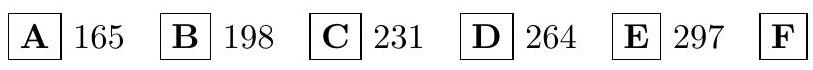
|
231
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.2. Find the sum of all two-digit numbers for each of which the sum of the squares of the digits is 57 more than the product of the same digits.
|
Solution. Such two-digit numbers are $18, 78, 81, 87$. Their sum is 264.
Answer: 264. (D)
\section*{| A | 165 | $\mathbf{B}$ | 198 | $\mathbf{C}$ | 231 | $\mathbf{D}$ | 264 | $\mathbf{E}$ | 297 | $\mathbf{F}$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
|
264
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3. Find the sum of all two-digit numbers for each of which the sum of the squares of the digits is 73 more than the product of the same digits.
|
Solution. Such two-digit numbers are $19, 89, 91, 98$. Their sum is 297.
Answer: 297. ( ( )
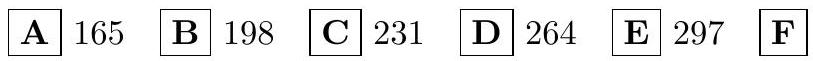
|
297
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.4. Find the sum of all two-digit numbers for each of which the sum of the squares of the digits is 31 more than the product of the same digits.
|
Solution. Such two-digit numbers are $16, 56, 61, 65$. Their sum is 198.
Answer: 198. (B)

|
198
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. The segment connecting the lateral sides of the trapezoid and parallel to its bases, which are 3 and 21, divides the trapezoid into two parts of equal area. Find the length of this segment.
|
Solution. 1st method. Let $a=3$ and $b=21$ be the lengths of the bases of the trapezoid. If $c$ is the length of the segment parallel to the bases, and $h_{1}$ and $h_{2}$ are the parts of the height of the trapezoid adjacent to the bases $a$ and $b$ respectively, then, by equating the areas, we get:
$$
\frac{a+c}{2} h_{1}=\frac{c+b}{2} h_{2}=\frac{1}{2} \cdot \frac{a+b}{2}\left(h_{1}+h_{2}\right) \Longleftrightarrow\left\{\begin{array}{l}
\frac{b+c}{a+c}=\frac{h_{1}}{h_{2}} \\
\frac{2(b+c)}{a+b}=1+\frac{h_{1}}{h_{2}}
\end{array}\right.
$$
From which
$$
\frac{2(b+c)}{a+b}=\frac{a+b+2 c}{a+c}
$$
Finally, we get $2 c^{2}=a^{2}+b^{2}$. Therefore
$$
c=\sqrt{\frac{a^{2}+b^{2}}{2}}=\sqrt{\frac{9+441}{2}}=15
$$
2nd method. Let $A B C D$ be a trapezoid with bases $A D=a=3, B C=b=21$ (see Fig. 1). Let $M N$ be the segment parallel to the bases. Let $F$ be the intersection point of the lines $A B$ and $C D$, the area of triangle $B C F$ is $a^{2} S$ and $M N=x$. Then
- from the similarity $M N F \sim B C F$ with the coefficient $k_{1}=x / a$ it follows: $S_{M N F}=k_{1}^{2} S_{B C F}=x^{2} S$;
- from the similarity $A D F \sim B C F$ with the coefficient $k_{2}=b / a$ it follows: $S_{A D F}=k_{2}^{2} S_{B C F}=b^{2} S$.
It remains to note that
$$
S_{A M N D}=S_{M B C N} \Longrightarrow\left(x^{2}-a^{2}\right) S=\left(b^{2}-x^{2}\right) S \Longrightarrow 2 x^{2}=a^{2}+b^{2}
$$
From which $x=\sqrt{\left(a^{2}+b^{2}\right) / 2}=15$.
Answer: 15. (C)
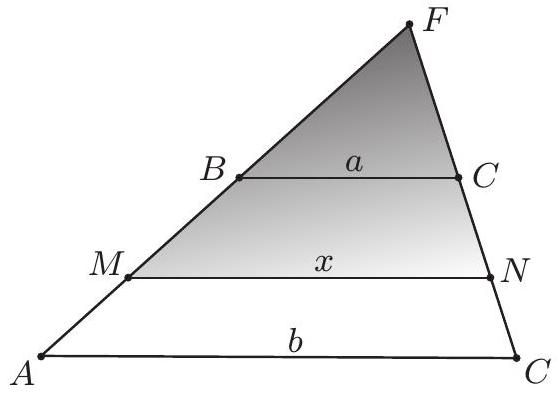
Fig. 1:
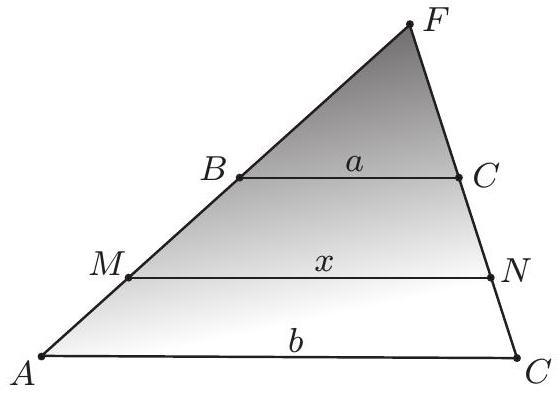
Fig. 2:
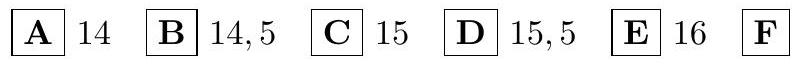
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. The segment connecting the lateral sides of the trapezoid and parallel to its bases, which are 7 and 17, divides the trapezoid into two parts of equal area. Find the length of this segment.
|
Solution. $c=\sqrt{\left(a^{2}+b^{2}\right) / 2}=\sqrt{(49+289) / 2}=13$.
Answer: 13. (E)
$$
\begin{array}{|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 11 & \mathbf{B} & 11.5 & \mathbf{C} & 12 & \mathbf{D} \\
12.5 & \mathbf{E} & 13 & \mathbf{F} \\
\hline
\end{array}
$$
|
13
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{2} 18-\log _{3} 12\right)-\log _{3} 16-4 \log _{2} 3
$$
do not exceed 8.
|
Solution. Let $a=\log _{2} 3$. Then the condition of the problem will turn into the inequality
$$
x^{2}+2\left(a-\frac{1}{a}\right) x-4\left(a+\frac{1}{a}+2\right) \leqslant 0
$$
Considering that $a \in\left(\frac{3}{2}, 2\right)$, we get $x \in\left[-2 a-2, \frac{2}{a}+2\right]$. Since $-6<-2 a-2<-5.3<\frac{2}{a}+2<4$, the integer solutions will be the numbers $-5,-4,-3,-2,-1,0,1,2,3$.
Answer: -9 . (A)
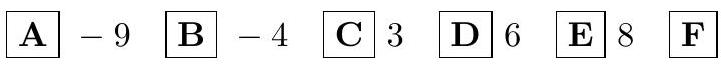
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{2} 20-\log _{5} 8\right)-\log _{2} 5-9 \log _{5} 2
$$
do not exceed 6.
|
Solution. Let $a=\log _{2} 5$. Then the condition of the problem will turn into the inequality
$$
x^{2}+\left(a-\frac{3}{a}+2\right) x-\left(a+\frac{9}{a}+6\right) \leqslant 0
$$
Considering that $a \in(2,3)$, we get $x \in\left[-a-3, \frac{3}{a}+1\right]$. Since $-6<-a-3<-5,2<\frac{3}{a}+1<3$, the integer solutions will be the numbers $-5,-4,-3,-2,-1,0,1,2$.
Answer: $-12 .(\mathrm{C})$
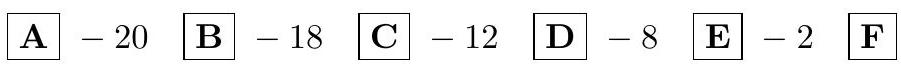
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{2} 36-\log _{3} 16\right)-\log _{2} 9-4 \log _{3} 8
$$
do not exceed 11.
|
Solution. Let $a=\log _{2} 3$. Then the condition of the problem will turn into the inequality
$$
x^{2}+2\left(a-\frac{2}{a}+1\right) x-\left(2 a+\frac{12}{a}+11\right) \leqslant 0
$$
Considering that $a \in\left(\frac{3}{2}, 2\right)$, we get $x \in\left[-2 a-3, \frac{4}{a}+1\right]$. Since $-7<-2 a-3<-6,3<\frac{4}{a}+1<4$, the integer solutions will be the numbers $-6,-5,-4,-3,-2,-1,0,1,2,3$.
Answer: $-15 .(\mathrm{B})$
$$
\begin{array}{|l|l|l|l|l|l|l|l|}
\hline \mathbf{A}-20 & \mathbf{B}-15 & \mathbf{C} & -10 & \mathbf{D} & -5 & \mathbf{E} 0 & \mathbf{F} \\
\hline
\end{array}
$$
|
-15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{5} 2-\log _{2} 10\right)-\log _{2} 25-3 \log _{5} 2
$$
do not exceed 7.
|
Solution. Let $a=\log _{2} 5$. Then the condition of the problem will turn into the inequality
$$
x^{2}-\left(a-\frac{1}{a}+1\right) x-\left(2 a+\frac{3}{a}+7\right) \leqslant 0 .
$$
Considering that $a \in(2,3)$, we get $x \in\left[-\frac{1}{a}-2, a+3\right]$. Since $-3<-\frac{1}{a}-2<-2,5<a+3<6$, the integer solutions will be the numbers $-2,-1,0,1,2,3,4,5$.
Answer: 12. (D)
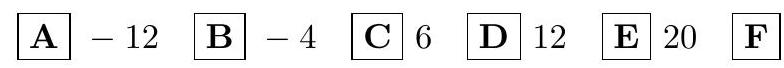
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Three pirates, Joe, Bill, and Tom, found a treasure containing 70 identical gold coins, and they want to divide them so that each of them gets at least 10 coins. How many ways are there to do this?
|
Solution. Let the treasure consist of $n=70$ coins and each pirate should receive no less than $k=10$ coins.
Give each pirate $k-1$ coins, and lay out the remaining $n-3 k+3$ coins in a row. To divide the remaining coins among the pirates, it is sufficient to place two dividers in the $n-3 k+2$ spaces between the coins. Thus, Joe will receive the coins to the left of the first divider, Bill the coins between the two dividers, and Tom the coins to the right of the second divider. The number of ways to place these two dividers is $C_{n-3 k+2}^{2}=\frac{(n-3 k+2)(n-3 k+1)}{2}$.
If $n=70, k=10$, then we get $C_{42}^{2}=861$ ways.
Answer: 861.
|
861
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. Three pirates, Joe, Bill, and Tom, found a treasure containing 80 identical gold coins, and they want to divide them so that each of them gets at least 15 coins. How many ways are there to do this?
|
Solution. Since $n=80, k=15$, it results in $C_{37}^{2}=666$ ways.
Answer: 666.
|
666
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.3. Three pirates, Joe, Bill, and Tom, found a treasure containing 100 identical gold coins, and they want to divide them so that each of them gets at least 25 coins. How many ways are there to do this?
|
Solution. Since $n=100, k=25$, it results in $C_{27}^{2}=351$ ways.
Answer: 351.
|
351
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Three pirates, Joe, Bill, and Tom, found a treasure containing 110 identical gold coins, and they want to divide them so that each of them gets at least 30 coins. How many ways are there to do this?
|
Solution. Since $n=110, k=30$, we get $C_{22}^{2}=231$ ways.
Answer: 231.
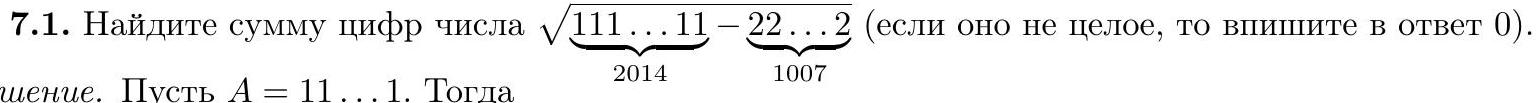
Solution. Let $A=\underbrace{11 \ldots 1}_{1007}$. Then
$$
\sqrt{\underbrace{111 \ldots 11}_{2014}-\underbrace{22 \ldots 2}_{1007}}=\sqrt{A \cdot 10^{1007}+A-2 A}=\sqrt{A(9 A+1)-A}=3 A=\underbrace{33 \ldots 3}_{1007} .
$$
Answer: 3021

Solution. The number is $\underbrace{66 \ldots 6}_{1007}$.
Answer: 6042.
|
231
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Specify the integer closest to the larger root of the equation
$$
\operatorname{arctg}\left(\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. Let $y=\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}$, then $\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}=y+1$ and the equation will take the form
$$
\operatorname{arctg}(y+1)-\operatorname{arctg} y=\frac{\pi}{4}
$$
Since $0 \leqslant \operatorname{arctg} y<\operatorname{arctg}(y+1)<\frac{\pi}{2}$, the last equation is equivalent to
$$
\operatorname{tg}(\operatorname{arctg}(y+1)-\operatorname{arctg} y)=1 \Longleftrightarrow \frac{1}{1+(y+1) y}=1 \Longleftrightarrow y=0 \Longleftrightarrow \frac{2 x}{7}=\frac{7}{8 x} \Longleftrightarrow|x|=\frac{7}{4}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Specify the integer closest to the smaller root of the equation
$$
\operatorname{arctg}\left(\left(\frac{5 x}{26}+\frac{13}{10 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{5 x}{26}-\frac{13}{10 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{5 x}{26}=\frac{13}{10 x} \Longleftrightarrow|x|=\frac{13}{5}$.
Answer: -3 .
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Specify the integer closest to the smaller root of the equation
$$
\operatorname{arctg}\left(\left(\frac{7 x}{10}-\frac{5}{14 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{7 x}{10}+\frac{5}{14 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{7 x}{10}=\frac{5}{14 x} \Longleftrightarrow |x|=\frac{5}{7}$.
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arctg}\left(\left(\frac{3 x}{22}-\frac{11}{6 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{3 x}{22}+\frac{11}{6 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{3 x}{22}=\frac{11}{6 x} \Longleftrightarrow |x|=\frac{11}{3}$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Indicate the integer closest to the smaller root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{2 x}{7}=\frac{7}{8 x} \Longleftrightarrow |x|=\frac{7}{4}$.
Answer: -2.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{5 x}{26}+\frac{13}{10 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{5 x}{26}-\frac{13}{10 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{5 x}{26}=\frac{13}{10 x} \Longleftrightarrow|x|=\frac{13}{5}$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.7. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{7 x}{10}-\frac{5}{14 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{7 x}{10}+\frac{5}{14 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{7 x}{10}=\frac{5}{14 x} \Longleftrightarrow |x|=\frac{5}{7}$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.8. Provide the integer closest to the smaller root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{3 x}{22}-\frac{11}{6 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{3 x}{22}+\frac{11}{6 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{3 x}{22}=\frac{11}{6 x} \Longleftrightarrow |x|=\frac{11}{3}$.
Answer: -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. In the triangular pyramid $S A B C$, the edges $S B, A B$ are perpendicular and $\angle A B C=120^{\circ}$. Point $D$ on edge $A C$ is such that segment $S D$ is perpendicular to at least two medians of triangle $A B C$ and $C D=A B=44 \sqrt[3]{4}$. Find $A D$ (if the answer is not an integer, round it to the nearest hundredth).
|
Solution. Since segment $SD$ is perpendicular to two medians of triangle $ABC$, it is perpendicular to the plane $(ABC)$ (see Fig. 3). By the theorem of three perpendiculars, it follows that $DB \perp AB$.
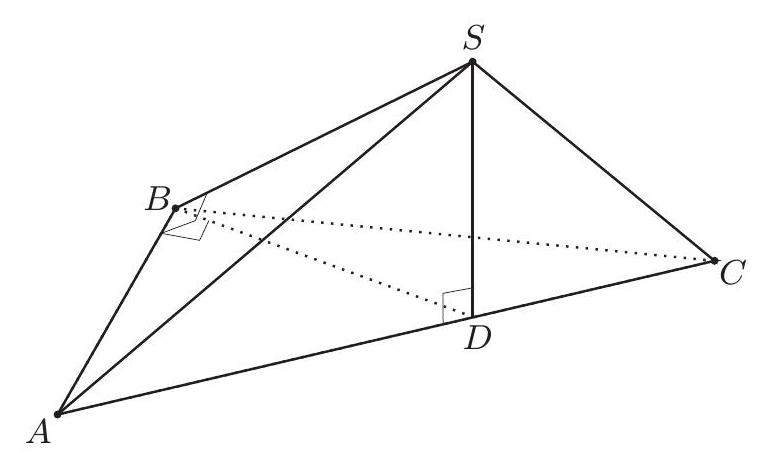
Fig. 3:
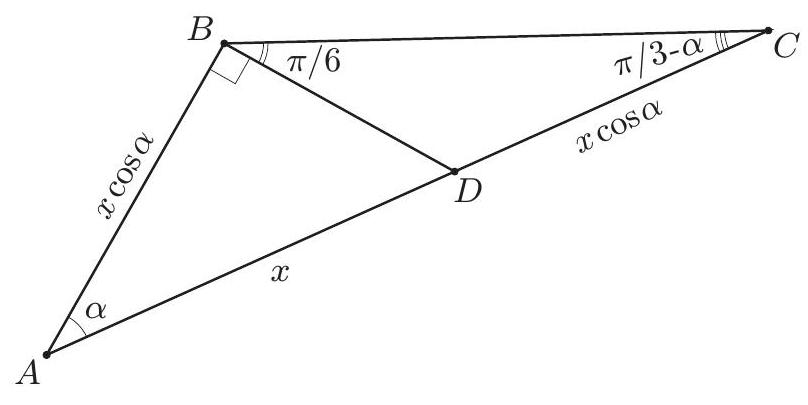
Fig. 4:
Let $\alpha = \angle BAC, x = AD$. Then, applying the Law of Sines in triangle $ABC$ (see Fig. 4), we have:
$$
\begin{aligned}
\frac{x \cos \alpha}{\sin (\pi / 3 - \alpha)} & = \frac{x + x \cos \alpha}{\sin (2 \pi / 3)} \Longleftrightarrow \sin \alpha = \frac{\sqrt{3} \cos^2 \alpha}{1 + \cos \alpha} \Longleftrightarrow (1 - \cos^2 \alpha)(1 + \cos \alpha)^2 = 3 \cos^4 \alpha \Longleftrightarrow \\
\Longleftrightarrow 4 \cos^4 \alpha + 2 \cos^3 \alpha - 2 \cos \alpha - 1 = 0 & \Longleftrightarrow (\cos 2\alpha + 1)(2 \cos^3 \alpha - 1) = 0
\end{aligned}
$$
Since $\alpha < \pi / 2$, from the last equation: $\cos \alpha = 1 / \sqrt[3]{2}$. Therefore, $AD = AB / \cos \alpha = 88$.
## Answer: 88.
|
88
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. For the function $f(x)=2013-8 x^{3}+12 x^{2}-14 x-a-\sin 2 \pi x$ find the number of integer values of $a$, for each of which the equation
$$
\underbrace{f(f(\ldots f}_{2013 \text { times }}(x) \ldots))=2 x-1
$$
on the interval $[50 ; 51]$ has a unique solution.
|
Solution. Since
$$
2013-8 x^{3}+12 x^{2}-14 x-a-\sin 2 \pi x=2008-(2 x-1)^{3}-4(2 x-1)-a+\sin \pi(2 x-1)
$$
then after the substitution of the variable $t=2 x-1$, we get a new problem: "For the function $F(t)=2008-t^{3}-4 t- a+\sin \pi t$, find the number of integer values of $a$, for each of which the equation
$$
\underbrace{F(F(\ldots F}_{2013 \text { times }}(t) \ldots))=t
$$
on the interval $[99 ; 101]$ has a unique solution."
The function $F(t)=2008-t^{3}-4 t-a+\sin \pi t$ is monotonically decreasing over the entire number line (which can be verified either by calculating $F^{\prime}(t)$ or by directly using the definition of a monotonically decreasing function). Therefore,
$$
\underbrace{F(F(\ldots F}_{2013 \text { times }}(t) \ldots))=t \Longleftrightarrow F(t)=t .
$$
The function $g(t)=t-F(t)$ is monotonically increasing. Consequently, the equation $g(t)=0$ has a unique solution on $[99 ; 101]$ if and only if
$$
\left\{\begin{array} { l }
{ g ( 1 0 1 ) \geqslant 0 , } \\
{ g ( 9 9 ) \leqslant 0 , }
\end{array} \Longleftrightarrow \left\{\begin{array}{l}
101-2008+101^{3}+404+a \geqslant 0 \\
99-2008+99^{3}+396+a \leqslant 0
\end{array}\right.\right.
$$
From the obtained two-sided estimates for $a$, it follows that the number of integer values of $a$ is
$$
g(101)-g(99)+1=2+101^{3}-99^{3}+404-396+1=60013
$$
## Answer 60013 .
|
60013
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2 For the function $f(x)=2013-a+12 x^{2}-\cos 2 \pi x-8 x^{3}-16 x$ find the number of integer values of $a$, for each of which the equation
$$
\underbrace{f(f(\ldots f}_{2013 \text { times }}(x) \ldots))=2 x-1
$$
on the interval $[50 ; 51]$ has a unique solution.
|
Solution. After substituting $t=2 x-1$, we obtain a new problem for the function $F(t)=2007-t^{3}-5 t-a+\cos \pi t$. The number of integer values of $a$ is
$$
g(101)-g(99)+1=2+101^{3}-99^{3}+505-495+1=60015, \quad \text { where } g(t)=t-F(t) .
$$
## Answer 60015 .
|
60015
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3 For the function $f(x)=2013+\sin 2 \pi x-8 x^{3}-12 x^{2}-18 x-a$, find the number of integer values of $a$ for each of which the equation
$$
\underbrace{f(f(\ldots f}_{2013 \text { times }}(x) \ldots))=2 x+1
$$
has a unique solution on the interval $[49,50]$.
|
Solution. After substituting $t=2 x+1$, we obtain a new problem for the function $F(t)=2020-t^{3}-6 t-a-\sin \pi t$. The number of integer values of $a$ is
$$
g(101)-g(99)+1=2+101^{3}-99^{3}+606-594+1=60017, \quad \text { where } g(t)=t-F(t)
$$
Answer 60017.
|
60017
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4 For the function $f(x)=2013-a+\cos 2 \pi x-12 x^{2}-8 x^{3}-20 x$ find the number of integer values of $a$, for each of which the equation
$$
\underbrace{f(f(\ldots f}_{2013 \text { times }}(x) \ldots))=2 x+1
$$
has a unique solution on the interval $[49,50]$.
|
Solution. After substituting $t=2 x+1$, we obtain a new problem for the function $F(t)=2021-t^{3}-7 t-a-\cos \pi t$. The number of integer values of $a$ is
$$
g(101)-g(99)+1=2+101^{3}-99^{3}+707-693+1=60019, \quad \text { where } g(t)=t-F(t)
$$
Answer 60019.
|
60019
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. An apple, a pear, an orange, and a banana were placed in four boxes (one fruit per box). Inscriptions were made on the boxes:
On the 1st: Here lies an orange.
On the 2nd: Here lies a pear.
On the 3rd: If in the first box lies a banana, then here lies an apple or a pear.
On the 4th: Here lies an apple.
It is known that none of the inscriptions correspond to reality.
Determine which fruit lies in which box. In your answer, write down sequentially, without spaces, the numbers of the boxes in which the apple, pear, orange, and banana lie, respectively (you should get a 4-digit number).
|
Answer: 2431
Solution: The inscription on the 3rd box is incorrect, so in the first box lies a banana, and in the third - not an apple and not a pear, therefore, an orange. From the inscription on the 4th box, it follows that there is no apple there, so since the banana is in the 1st, and the orange is in the 2nd, then in the 4th lies a pear. The apple remains, which lies in the second box.
|
2431
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Beginner millionaire Bill buys a bouquet of 7 roses for $20 for the entire bouquet. Then he can sell a bouquet of 5 roses for $20 per bouquet. How many bouquets does he need to buy to earn a difference of $1000?
|
Answer: 125
Solution. Let's call "operation" the purchase of 5 bouquets (= 35 roses) and the subsequent sale of 7 bouquets (= 35 roses). The purchase cost is $5 \cdot 20=\$ 100$, and the selling price is $7 \cdot 20=\$ 140$. The profit from one operation is $\$ 40$.
Since $\frac{1000}{40}=25$, 25 such operations are needed. Therefore, Bill needs to buy $5 \cdot 25=125$ bouquets.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 3. Find a natural number $N(N>1)$, if the numbers 1743, 2019, and 3008 give the same remainder when divided by $N$.
|
Answer: 23.
Solution. From the condition, it follows that the numbers $2019-1743=276$ and $3008-2019=989$ are divisible by $N$. Since $276=2^{2} \cdot 3 \cdot 23$, and $989=23 \cdot 43$, then $N=23$.
|
23
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 4. Find the smallest natural number $n$ such that $n^{2}$ and $(n+1)^{2}$ contain the digit 7.
|
Answer: 26.
Solution. There are no squares ending in the digit 7. There are no two-digit squares starting with 7. Therefore, $n \geq 10$. The first square containing 7 is $576=24^{2}$. Since $25^{2}=625,26^{2}=676,27^{2}=729$, the answer is $n=26$.
Problem 4a. Find the smallest natural number $n$ such that $n^{2}$ and $(n+1)^{2}$ contain the digit 7, but $(n+2)^{2}$ does not.
Answer: 27.
Solution. There are no squares ending in the digit 7. There are no two-digit squares starting with 7. Therefore, $n \geq 10$. The first square containing 7 is $576=24^{2}$. Since $25^{2}=625,26^{2}=676,27^{2}=729,28^{2}=784,29^{2}=841$, the answer is $n=27$.
|
26
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. A square with an integer side length was cut into 2020 squares. It is known that the areas of 2019 squares are 1, and the area of the 2020th square is not equal to 1. Find all possible values that the area of the 2020th square can take. In your answer, provide the smallest of the obtained area values.
|
Answer: 112225.
|
112225
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. Master Li Si Qing makes fans. Each fan consists of 6 sectors, painted on both sides in red and blue (see fig.). Moreover, if one side of a sector is painted red, the opposite side is painted blue and vice versa. Any two fans made by the master differ in coloring (if one coloring can be transformed into another by flipping the fan, they are considered the same). What is the maximum number of fans the master can make?
|
Answer: 36.
## Solution:
The coloring of one side can be chosen in $2^{6}=64$ ways. It uniquely determines the coloring of the opposite side. However, some fans - those that transform into each other when flipped, we have counted twice. To find their number, let's see how many fans transform into themselves when flipped. There are 8 such fans in total. So, we need to divide the remaining 64 $8=56$ by two - which gives us 28. We need to add those 8 that transform into themselves.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. How many solutions in integers does the equation
$6 y^{2}+3 x y+x+2 y-72=0$ have?
|
Answer: 4.
## Solution:
Factorize:
$(3 y+1)(2 y+x)=72$.
The first factor must give a remainder of 1 when divided by 3. The number 72 has only 4 divisors that give such a remainder: $-8,-2,1,4$. They provide 4 solutions.
Problem 7a. How many solutions in integers does the equation
$6 y^{2}+3 x y+x+2 y+180=0$ have?
Answer: 6.
## Solution:
Factorize:
$(3 y+1)(2 y+x)=180$.
The first factor must give a remainder of 1 when divided by 3. The number 180 has only 6 divisors that give such a remainder: $-20,-5,-2,1,4,10$. They provide 6 solutions.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 9. In a convex quadrilateral $A B C D$, side $A B$ is equal to diagonal $B D, \angle A=65^{\circ}$, $\angle B=80^{\circ}, \angle C=75^{\circ}$. What is $\angle C A D$ (in degrees $) ?$
|
Answer: 15.
Solution. Since triangle $ABD$ is isosceles, then $\angle BDA = \angle BAD = 65^{\circ}$. Therefore, $\angle DBA = 180^{\circ} - 130^{\circ} = 50^{\circ}$. Hence, $\angle CBD = 80^{\circ} - 50^{\circ} = 30^{\circ}$, $\angle CDB = 180^{\circ} - 75^{\circ} - 30^{\circ} = 75^{\circ}$. This means that triangle $DBC$ is isosceles, so $BC = BD = AB$. Therefore, $\angle BCA = \angle BAC = \frac{1}{2}(180^{\circ} - 80^{\circ}) = 50^{\circ}$. Hence, $\angle CAD = 65^{\circ} - 50^{\circ} = 15^{\circ}$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A trip to St. Petersburg is being organized for 30 schoolchildren along with their parents, some of whom will be driving cars. Each car can accommodate 5 people, including the driver. What is the minimum number of parents that need to be invited on the trip?
ANSWER: 10
|
Solution: No more than 4 students can fit in a car, so 8 cars will be needed, i.e., 10 drivers.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.
In the test, there are 4 sections, each containing the same number of questions. Andrey answered 20 questions correctly. The percentage of his correct answers was more than 60 but less than 70. How many questions were in the test?
|
Answer: 32.
Solution. According to the condition $\frac{60}{100}<\frac{20}{x}<\frac{70}{100}$, hence $28 \frac{4}{7}=\frac{200}{7}<x<\frac{100}{3}=33 \frac{1}{3}$, that is $29 \leq x \leq 33$. From the first condition of the problem, it follows that the number of questions must be divisible by 4.
|
32
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A trip to Nizhny Novgorod is being organized for 50 schoolchildren along with their parents, some of whom will be driving cars. Each car can accommodate 6 people, including the driver. What is the minimum number of parents that need to be invited on the trip?
ANSWER: 10
|
Solution: No more than 5 students can fit in a car, so 10 cars will be needed, i.e., 10 drivers.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The test consists of 5 sections, each containing the same number of questions. Pavel answered 32 questions correctly. The percentage of his correct answers turned out to be more than 70 but less than 77. How many questions were in the test?
ANSWER: 45.
|
Solution: from the condition $0.7<32 / x<0.77$ it follows that $41<x<46$, but $x$ is a multiple of 5, so $x=45$.
|
45
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the largest natural number that cannot be represented as the sum of two composite numbers.
ANSWER: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. Odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we can see that 11 cannot be represented in such a way.
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final stage tasks for the 2015/2016 academic year for grades 5-6
The solutions are similar to those of variant v2a, so only the answers are provided.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest natural N such that N+2 is divisible (without remainder) by 2, N+3 by 3, ..., N+10 by 10.
ANSWER: 2520.
|
Solution: Note that $N$ must be divisible by $2,3,4, \ldots, 10$, therefore, $N=$ LCM $(2,3,4, . ., 10)=2^{3} \times 3^{2} \times 5 \times 7=2520$.
|
2520
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Five runners ran a relay. If the first runner ran twice as fast, they would have spent $5 \%$ less time. If the second runner ran twice as fast, they would have spent $10 \%$ less time. If the third runner ran twice as fast, they would have spent $12 \%$ less time. If the fourth runner ran twice as fast, they would have spent $15 \%$ less time. By what percentage less time would they have spent if the fifth runner ran twice as fast?
OTBET: by $8 \%$
|
Solution: If each ran twice as fast, they would run 50% faster. This means that if the 5th ran faster, the time would decrease by $50-5-10-12-15=8 \%$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation
$$
\log _{3}(x+2) \cdot \log _{3}(2 x+1) \cdot\left(3-\log _{3}\left(2 x^{2}+5 x+2\right)\right)=1
$$
|
Problem 4.
Answer: $x=1$.
Solution. For admissible values $x>-\frac{1}{2}$ we have: $\log _{3}(x+2)>0$.
If $\log _{3}(2 x+1)0$ and the left side of the equation is negative.
Thus, all three factors on the left side of the equation are positive, and the roots should be sought only among those $x$ for which
$$
\left\{x>0,2 x^{2}+5 x+20$ and the discriminant of this equation as a quadratic in $t$ is $D(p)=p(p-1)^{2}(p-4)$, then
$$
\{D(p) \geqslant 0, p>0\} \Longleftrightarrow p \in\{1\} \cup[4 ;+\infty)
$$
But for $p \geqslant 4: x \geqslant 40$, so $p=1$ and $t=1$, which is satisfied only if $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Petrov lists the odd numbers: $1,3,5, \ldots, 2013$, while Vasechkin lists the even numbers: $2,4, \ldots, 2012$. Each of them calculated the sum of all digits of all their numbers and told the excellent student Masha. Masha subtracted Vasechkin's result from Petrov's result. What did she get?
|
Answer: 1007.
Solution: Let's break down the numbers of Petrov and Vasechkin into pairs as follows: $(2,3),(4,5), \ldots,(98,99),(100,101), \ldots$ (2012,2013), with 1 left unpaired for Petrov. Notice that in each pair, the sum of the digits of the second number is 1 greater than that of the first (since they differ only in the last digit). There will be a total of $\frac{2012}{2}=1006$ such pairs. Therefore, the difference in the sums of the digits will be 1006, and considering the 1 left unpaired for Petrov, it will be -1007.
|
1007
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. There are no fewer than 150 boys studying at the school, and there are $15 \%$ more girls than boys. When the boys went on a trip, 6 buses were needed, and each bus had the same number of students. How many people in total study at the school, given that the total number of students is no more than 400?
|
Answer: 387.
Solution: The number of boys is a multiple of 6, let's denote it as $6n$, obviously, $n \geqslant 25$. Then the number of girls is $6n \times 1.15 = 6.9n$. The total number of students is $12.9n \leqslant 400$, so $n \leqslant 31$. Considering that $6.9n$ must be an integer, and therefore $n$ must be a multiple of 10, we get that $n=30$, i.e., a total of 387 students.
|
387
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In the school Spartakiad, teams from classes $8^{\mathrm{A}}$, $8^{\text {Б }}$, and $8^{\mathrm{B}}$ participated. In each of the competitions, one of these teams took 1st place, another took 2nd place, and another took 3rd place. After the Spartakiad, points were tallied: $x$ points were awarded for 1st place, $y$ for 2nd place, and $z$ for 3rd place $\left(x>y>z>0-\right.$ integers). In the end, team $8^{\mathrm{A}}$ received 22 points, and teams $8^{\text {Б }}$ and $8^{\text {В }}$ each received 9 points. How many competitions were there in total, and which team took 2nd place in the grenade throwing competition, given that the team $8^{\text {B }}$ took 1st place in the vault over the "goat"?
|
Answer: 5 competitions, $8^{\text {B }}$.
Solution: Let $n \geqslant 2$ be the number of competitions in the Spartakiad, then the total number of points scored by all teams is $n(x+y+z)=22+9+9=40$. But $z \geqslant 1, y \geqslant 2, x \geqslant 3$, so $x+y+z \geqslant 6$. Consider the possible cases: $x+y+z=8, n=5$; $x+y+z=10, n=4$ and $x+y+z=20, n=2$.
(a) Case $x+y+z=10, n=4$. Clearly, $x \leqslant 6$ (otherwise $8^{\mathrm{B}}$ would score more than 9 points). Consider the possible cases:
- $x=6$. Then $y=3, z=1$, but then $8^{\mathrm{A}}$ would not score 22 points.
- $x=5$. Then $8^{\mathrm{A}}$ would score less than 20 points.
- $x \leqslant 4$. Then $x+y+z \leqslant 9$.
Thus, the specified case is impossible.
(b) Case $x+y+z=20, n=2$. If we assume that $x<11$, then team $8^{\mathrm{A}}$ would not be able to score 22 points. If $x \geqslant 11$, then team $8^{\text {B }}$ would end up with more than 11 points, which is incorrect. Thus, the specified case is impossible.
(c) Case $x+y+z=8, n=5$. Clearly, in this case $z=1$, $x+y=7$. Consider the cases:
- Suppose $x=4, y=3$. Then $y+z=4$, so teams $8^{\text {B }}$ and $8^{\text {B }}$ scored at least 4 points in each competition. Then over 5 competitions, they should have scored at least 20 points (while in fact they scored $9+9=18$ ).
- Suppose $x=5, y=2$. Then team $8^{\text {B }}$ once took 1st place and 4 times last. Team $8^{\mathrm{A}}$ did not take first place in the vault. The only way to score 22 points: 2nd place and victory in the remaining 4 competitions. This means that team $8^{\text {B }}$ in these four competitions consistently took 2nd place (and in the vault $-3-\mathrm{rd})$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Famous skater Tony Hawk is riding a skateboard (segment $A B$) in a ramp, which is a semicircle with diameter $P Q$. Point $M$ is the midpoint of the skateboard, $C$ is the foot of the perpendicular dropped from point $A$ to the diameter $P Q$. What values can the angle $\angle A C M$ take if it is known that the angular measure of the arc $A B$ is $24^{\circ} ?$
|
Answer: $12^{\circ}$.
Solution: Extend the line $A C$ to intersect the circle at point $D$ (see figure). The chord $A D$ is perpendicular to the diameter $P Q$, therefore, it is bisected by it. Thus, $C M$ is the midline of triangle $A B D$, so $C M \| B D$ and, therefore, $\angle A C M=\angle A D B$. The angle $\angle A D B$ is an inscribed angle, subtending the arc $A B$, hence it is equal to half of the arc.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the number of natural numbers from 1 to 100 that have exactly four natural divisors, at least three of which do not exceed 10.
|
Answer: 8.
Solution: A number has exactly 4 natural divisors if it is either the cube of a prime number or the product of two prime numbers. The cubes of prime numbers (satisfying the conditions) are: 8 and 27. Prime numbers not greater than 10 are - 2, 3, 5, and 7. All their pairwise products satisfy the conditions, and their number is 6.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Karlson filled a conical glass with lemonade and drank half of it by height (measuring from the surface of the liquid to the apex of the cone), and Little Man drank the second half. How many times more lemonade did Karlson drink compared to Little Man?
|
# Answer: 7 times.
Solution. Let $r$ and $h$ be the radius of the base and the height of the conical glass, respectively. Then the volume of lemonade in the entire glass is $V_{\text {glass}}=\frac{1}{3} \pi r^{2} h$. The volume of lemonade drunk by Little One is $V_{\text {Little}}=\frac{1}{3} \pi(r / 2)^{2}(h / 2)=\frac{V_{\text {glass}}}{8}$. Therefore, Carlsson drank $\frac{7}{8} V_{\text {glass}}$, i.e., 7 times more than Little One.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Malvina and Buratino play according to the following rules: Malvina writes six different numbers in a row on the board, and Buratino comes up with his own four numbers $x_{1}, x_{2}, x_{3}, x_{4}$ and writes under each of Malvina's numbers one of the sums $x_{1}+x_{2}, x_{1}+x_{3}, x_{1}+x_{4}$, $x_{2}+x_{3}, x_{2}+x_{4}, x_{3}+x_{4}$ (each one exactly once). For each sum that equals the number above it, Buratino gets 3 apples, and for each sum that is greater, he gets 1 apple. What is the maximum number of apples that Buratino can guarantee to get?
|
# Answer: 14.
## Solution.
Solution. Let Malvina write the numbers $a_{1}>a_{2}>a_{3}>a_{4}>a_{5}>a_{6}$. If Buratino comes up with the numbers $x_{1}=\left(a_{1}+a_{2}-a_{3}\right) / 2, x_{2}=\left(a_{1}+a_{3}-a_{2}\right) / 2, x_{3}=\left(a_{2}+a_{3}-a_{1}\right) / 2, x_{4}=a_{4}-x_{3}$, then by writing $x_{1}+x_{2}=a_{1}$ under $a_{1}, x_{1}+x_{3}=a_{2}$ under $a_{2}, x_{2}+x_{3}=a_{3}$ under $a_{1}, x_{3}+x_{4}=a_{4}$ under $a_{4}$, $x_{1}+x_{4} \geqslant a_{4} \geqslant a_{5}$ under $a_{5}$ and $x_{2}+x_{4} \geqslant a_{4} \geqslant a_{6}$ under $a_{6}$, he will get 14 apples.
To get more than 14 apples, Buratino must ensure at least 5 equalities, which is not always possible: among any 5 sums composed by Buratino, there are such 4 that the sum of two of them equals the sum of the other two. Therefore, if Malvina writes such 6 numbers that the sum of no two of them equals the sum of any other two (for example, $1,10,100,1000,10000,100000$), then Buratino will not be able to get 15 or more apples.
|
14
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all four-digit numbers $\overline{a b c d}$ (where $a, b, c, d$ are the digits of the decimal representation), each of which is a divisor of at least one of the three four-digit numbers $\overline{b c d a}, \overline{c d a b}, \overline{d a b c}$ formed from it.
|
Answer: All numbers of the form $\overline{a b a b}$, where $a$ and $b$ are any digits except zero (there are 81 such numbers).
## Solution.
From the problem statement, it follows that there exists $k \in \mathbb{N}$ such that at least one of the following equalities holds:
(I) $k \cdot \overline{a b c d}=\overline{b c d a}$
(II) $k \cdot \overline{a b c d}=\overline{c d a b}$
(III) $k \cdot \overline{a b c d}=\overline{d a b c}$.
Since all numbers $\overline{a b c d}, \overline{b c d a}, \overline{a b c d}, \overline{d a b c}$ are four-digit numbers, we have $1 \leqslant k \leqslant 9$ and $a, b, c, d \neq 0$.
We will sequentially analyze all cases. By subtracting the left and right sides of equation (I) from the left and right sides of the equality $10 \cdot \overline{a b c d}=\overline{a b c d 0}$, we get
$$
(10-k) \overline{a b c d}=9999 a
$$
Since $9999=3^{2} \cdot 11 \cdot 101$, both sides of equation (2) are divisible by the prime number 101, and due to the constraints $1 \leqslant 10-k \leqslant 9$, we get $\overline{a b c d}: 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (2) by 101, we get
$$
(10-k) \overline{a b}=99 a
$$
Now, considering that both sides of the obtained equation are divisible by 11, and again due to the inequalities $1 \leqslant 10-k \leqslant 9$, we get $\overline{a b}: 11 \Leftrightarrow a=b$. Thus, the solutions to equation (I) are exactly all numbers of the form $\overline{\text { aaaa }}$ (for $k=1$).
Subtract equation (II) from the equality $100 \cdot \overline{a b c d}=\overline{a b c d 00}$. We get
$$
(100-k) \overline{a b c d}=\overline{a b} \cdot 9999
$$
Similarly to case (I), we have $\overline{a b c d}: 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (3) by 101, we get
$$
(100-k) \overline{a b}=\overline{a b} \cdot 99
$$
Therefore, the solutions to equation (II) are exactly all numbers of the form $\overline{a b a b}$ (for $k=1$). Subtract equation (III) from the equality $1000 \cdot \overline{a b c d}=\overline{a b c d 000}$. We get
$$
(1000-k) \overline{a b c d}=\overline{a b c} \cdot 9999
$$
For $1 \leqslant k \leqslant 9$, we have $\text{GCD}(101, (1000-k))=1 \Rightarrow \overline{a b c d} \vdots 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (4) by 101, we get
$$
(1000-k) \overline{a b}=\overline{a b a} \cdot 99
$$
Further, for $1 \leqslant k \leqslant 9$, we have $\text{GCD}(11, (1000-k))=1 \Rightarrow \overline{a b} \vdots 11 \Leftrightarrow a=b$. Therefore, the solutions to equation (III) are exactly all numbers of the form $\overline{\text { aaaa }}$ (for $k=1$).
Obviously, all solutions to equations (I) and (III) are contained among the solutions to equation (II).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. For what values of $a$ does the equation
$$
[x]^{2}+2012 x+a=0
$$
(where $[x]$ is the integer part of $x$, i.e., the greatest integer not exceeding $x$) have the maximum number of solutions? What is this number?
|
Answer: 89 solutions at $1006^{2}-20120
\end{array}\right.
$
has the maximum number of integer solutions.
The solution to the first inequality is the interval $\left[-1006-\sqrt{1006^{2}-a} ;-1006+\sqrt{1006^{2}-a}\right]$ under the condition $a \leqslant 1006^{2}$.
The solution to the second inequality for $a>1006^{2}-2012$ is the entire real line, and for $a \leqslant 1006^{2}-2012-$ the set is
$\left(-\infty ;-1006-\sqrt{1006^{2}-2012-a}\right) \cup\left(-1006-\sqrt{1006^{2}-2012-a} ;+\infty\right)$.
Thus, the solutions to the system form:
for $1006^{2}-20121006^{2}$ - 2012. The parameter can be represented as $a=1006^{2}-2012+b, b>0$. The solutions form the interval $[-1006-\sqrt{2012-b} ;-1006+\sqrt{2012-b}]$ and the smaller $b$ is, the larger this interval is.
Since $44^{2}=19360)$. Therefore, for $1006^{2}-2012<a \leqslant$ $1006^{2}-1936$ the number of integer solutions is equal to the number of integer points on the interval $[-1006-44 ;-1006+44]$, i.e., 89.
For $a=1006^{2}-2012$, the point $k=-1006$ disappears from the solution. As $a$ further decreases, new integer points $-1006 \pm 45$ will first appear in the set
$\left[-1006-\sqrt{1006^{2}-a} ;-1006-\sqrt{1006^{2}-2012-a}\right) \cup\left(-1006-\sqrt{1006^{2}-2012-a} ;-1006+\sqrt{1006^{2}-a}\right]$ at $a=1006^{2}-45^{2}=1006^{2}-2025$. However, at this point, integer points lying on the interval $\left[-1006-\sqrt{1006^{2}-2012-a} ;-1006+\sqrt{1006^{2}-2012-a}\right]=$ $[-1006-\sqrt{13} ;-1006+\sqrt{13}]$, i.e., 7 points: $-1006 ;-1006 \pm 1 ;-1006 \pm 2 ;-1006 \pm 3$, must be excluded from the solution. Since further decreasing $a$ reduces the total length of the solution set, the number of integer points will also decrease.
|
89
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Determine how many zeros the number $N!$ ends with!
|
Solution. Let $N=2014$. Among the first 2014 natural numbers, 402 numbers are divisible by 5, of which 80 numbers are divisible by 25. Among these 80 numbers, 16 numbers are divisible by 125, of which 3 numbers are divisible by 625. There are more even numbers among the first 2014 natural numbers than those divisible by 5. Therefore, the number of zeros at the end of the number 2014! is determined by the number of "fives" as divisors in this number. In total: $402+80+16+3=501$ zeros.
## Answer:
|
501
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. By how much is the sum of the squares of the first hundred even numbers greater than the sum of the squares of the first hundred odd numbers
|
Answer: 20100.
Solution: Group the terms as $\left(2^{2}-1^{2}\right)+\left(4^{2}-3^{2}\right)+\cdots+\left(200^{2}-199^{2}\right)=$ $(2-1) \cdot(2+1)+(4-3) \cdot(4+3)+\ldots+(200-199) \cdot(200+199)=1+2+\cdots+$ $199+200$. Divide the terms into pairs that give the same sum: $1+200=2+199=\ldots=100+101=201$. There will be exactly 100 such pairs, so the sum is 20100.
|
20100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Petrov and Vasechkin were repairing a fence. Each had to nail a certain number of boards (the same amount). Petrov nailed two nails into some boards, and three nails into the rest. Vasechkin nailed three nails into some boards, and five nails into the rest. Find out how many boards each of them nailed, if it is known that Petrov nailed 87 nails, and Vasechkin nailed 94 nails.
|
Answer: 30.
Solution: If Petrov had nailed 2 nails into each board, he would have nailed 43 boards and had one extra nail. If he had nailed 3 nails into each board, he would have nailed 29 boards. Therefore, the desired number lies between 29 and 43 (inclusive). Similarly, if Vasechkin had nailed 3 nails into each board, he would have nailed 31 boards and had 1 extra nail, and if he had nailed 5 nails into each board, he would have nailed 18 boards and had 4 extra nails. This means there were 29, 30, or 31 boards. Note that Vasechkin nailed an odd number of nails into each board, so the number of boards must be even - 30.
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Six natural numbers (possibly repeating) are written on the faces of a cube, such that the numbers on adjacent faces differ by more than 1. What is the smallest possible value of the sum of these six numbers?
|
Answer: 18.
Solution: Consider three faces that share a common vertex. The numbers on them differ pairwise by 2, so the smallest possible sum would be for $1+3+5=9$. The same can be said about the remaining three faces.
Thus, the sum cannot be less than 18. We will show that 18 can be achieved - place the number 1 on the top and bottom faces of the cube, 3 on the right and left faces, and 5 on the front and back faces.
|
18
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the smallest three-digit number with the property that if a number, which is 1 greater, is appended to it on the right, then the result (a six-digit number) will be a perfect square.
|
Answer: 183
Solution: Let the required number be a, then $1000a + a + 1 = n^2$. We can rewrite this as: $1001a = (n - 1)(n + 1)$. Factorize $1001 = 7 \times 11 \times 13$, meaning the product (n-1)(n+1) must be divisible by 7, 11, and 13. Additionally, for the square to be a six-digit number, $n$ must be in the interval $[317; 999]$.
Consider the following cases:
a) $n-1$ is divisible by $143, n+1$ is divisible by 7, then we find $n=573$;
b) $n-1$ is divisible by $7, n+1$ is divisible by 143, then $n=428$;
c) $n-1$ is divisible by $77, n+1$ is divisible by 13, then $n=155$ - does not fit;
d) $n-1$ is divisible by $13, n+1$ is divisible by 77, then $n=846$;
e) $n-1$ is divisible by 91, $n+1$ is divisible by 11, then $n=274$ - does not fit;
f) $n-1$ is divisible by $11, n+1$ is divisible by 91, then $n=727$.
The smallest $n=428, n^2=428^2=183184$.
|
183
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.