problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. The robotics club accepts only those who know mathematics, physics, or programming. It is known that 8 members of the club know physics, 7 know mathematics, and 11 know programming. Additionally, it is known that at least two know both physics and mathematics, at least three know both mathematics and programming, and at least four know both physics and programming. What is the maximum number of club members possible under these conditions? | Answer 19.
2. From the sequence of natural numbers $1,2,3, \ldots$, all perfect squares (squares of integers) have been removed. What number will be in the 2018th position among the remaining numbers?
Answer: 2063. | 19 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6. The sequence $a_{n}$ is defined as follows:
$$
a_{1}=1, a_{n+1}=a_{n}+\frac{2 a_{n}}{n}, \text { for } n \geq 1 . \text { Find } a_{200}
$$ | Answer: 20100.
## Variant 3a (Chelyabinsk) | 20100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
6. The sequence $a_{n}$ is defined as follows:
$a_{1}=1, a_{n+1}=a_{n}+\frac{2 a_{n}}{n}$, for $n \geq 1$. Find $a_{999}$. | Answer: 499500.
## School Olympiad "Conquer Sparrow Hills"
## Tasks for 7-8 Grades
## Variant 1b (Zheleznovodsk) | 499500 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. Thirteen millionaires arrived at the economic forum and settled in the "Super Luxury+" hotel. The hotel has rooms of 3 different types: 6-star, 7-star, and 8-star. The millionaires need to be accommodated in such a way that all three types of rooms are used (i.e., at least one person must be placed in a 6-star room, at least one in a 7-star room, and at least one in an 8-star room). Additionally, a richer millionaire cannot be placed in a room with fewer stars than a less wealthy one.
In how many ways can they be accommodated (all millionaires have different wealth levels)? | Answer: $C_{12}^{2}=66$. | 66 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6. The sequence $a_{n}$ is defined as follows:
$a_{1}=2, a_{n+1}=a_{n}+\frac{2 a_{n}}{n}$, for $n \geq 1$. Find $a_{100}$. | Answer: 10100.
## Variant 2b (Saratov) | 10100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. A school coach decided to reward 12 students who ran the distance in the best time. Each of them should be awarded a "gold", "silver", or "bronze" medal. All three types of medals must be used (at least once), and the one who finished earlier cannot be awarded a less valuable medal than the one who finished later.
In how many ways can the coach distribute the medals (all runners have different times)? | Answer: $C_{11}^{2}=55$. | 55 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
3. Petrov lists the odd numbers: $1,3,5, \ldots, 2013$, while Vasechkin lists the even numbers $2,4, \ldots, 2012$. Each of them calculated the sum of all digits of all their numbers and told the result to the excellent student Masha. Masha subtracted the result of Vasechkin from the result of Petrov. What did she get? | Answer: 1007.
Solution: Let's break down the numbers of Petrov and Vasechkin into pairs as follows: $(2,3),(4,5), \ldots,(98,99),(100,101), \ldots$ (2012,2013), with 1 left unpaired for Petrov. Notice that in each pair, the sum of the digits of the second number is 1 greater than that of the first (since they differ only in the last digit). There will be a total of $\frac{2012}{2}=1006$ such pairs. Therefore, the difference in the sums of the digits will be 1006, and with the 1 left unpaired for Petrov, it becomes -1007. | 1007 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. The board for playing "Battleship" is $10 \times 10$. What is the maximum number of ships of size $1 \times 4$ that can be placed on it? | Answer: 24.
Solution: It is easy to show by trial that 24 ships can be placed. Let's color the board in 4 colors as shown in the figure. Note that each ship of size $1 \times 4$ contains one cell of each color, and there will be 24 yellow cells.
 | 24 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Find the number of pairs of natural numbers $(x, y), 1 \leqslant x, y \leqslant 1000$, such that $x^{2}+y^{2}$ is divisible by 5. | Answer: 360000.
Solution: We have 200 numbers for each of the remainders $0,1,2,3,5$ when divided by 5. There are two cases: a) the numbers $x, y$ are both divisible by 5; b) or one number gives a remainder of 1 or 4, and the other gives a remainder of 2 or 3 when divided by 5. In the first case, we get $200 \times 200=40000$ options, in the second case $2 \times 400 \times 400=320000$, in total $40000+320000=$ 360000. | 360000 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. Let $\Sigma(n)$ denote the sum of the digits of the number $n$. Find the smallest three-digit $n$ such that $\Sigma(n)=\Sigma(2 n)=\Sigma(3 n)=\ldots=\Sigma\left(n^{2}\right)$ | Answer: 999.
Solution: Let the desired number be $\overline{a b c}$. Note that this number is not less than 101 (since 100 does not work). Therefore, $101 \cdot \overline{a b c}=\overline{a b c 00}+\overline{a b c}$
also has the same sum of digits. But the last digits of this number are obviously $b$ and $c$, so the sum of the remaining digits must be equal to $a$. Therefore, $\Sigma(\overline{a b c}+a)=a$. If $a<9$, then $\overline{a b c}+a-$ is a three-digit number, the first digit of which is not less than $a$, which leads to a contradiction, since the second and third digits cannot be zeros. Thus, $a=9$ and $\overline{a b c}+a \leqslant 999+9=1008$. Therefore, $\overline{a b c}+a=\overline{100 d}$. But $\Sigma(\overline{100 d})=a=9$, so $d=8$, from which $\overline{a b c}=999$. | 999 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. Solution. From the formulas for the sum of a geometric progression, we know
$$
\begin{aligned}
& \frac{b_{1}}{1-q}=60 \\
& \frac{b_{1}^{2}}{1-q^{2}}=1200
\end{aligned}
$$
By dividing the second equation by the first, we get $\frac{b_{1}}{1+q}=20$, which is the answer.
Remark. We could also find $b_{1}=30, q=1 / 2$. | Answer: 20 (option $1-2:-30)$.
Translate the text above into English, please retain the original text's line breaks and format, and output the translation result directly.
Note: The provided text is already in English, so no translation is needed. However, if the task is to restate it as a translation, here it is:
Answer: 20 (option $1-2:-30)$.
| 20 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. Thirteen millionaires arrived at the economic forum and settled in the "Super Luxury+" hotel. The hotel has rooms of 3 different types: 6-star, 7-star, and 8-star. The millionaires need to be accommodated in such a way that all three types of rooms are used (i.e., at least one person must be placed in a 6-star room, at least one in a 7-star room, and at least one in an 8-star room). Additionally, a richer millionaire cannot be placed in a room with fewer stars than a less wealthy one.
In how many ways can they be accommodated (all millionaires have different wealth levels)? | Answer: $C_{12}^{2}=66$. | 66 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
2. A school coach decided to reward 12 students who ran the distance in the best time. Each of them must be awarded a "gold", "silver", or "bronze" medal. All three types of medals must be used, and the one who finished earlier cannot be awarded a less valuable medal than the one who finished later.
In how many ways can the coach distribute the medals (all runners have different times)? | Answer: $C_{11}^{2}=55$. | 55 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Petrov and Vasechkin were repairing a fence. Each had to nail a certain number of boards (the same amount). Petrov nailed two nails into some boards and three nails into others. Vasechkin nailed three nails into some boards and five nails into the rest. Find out how many boards each of them nailed, given that Petrov nailed 87 nails, and Vasechkin nailed 94. | Answer: 30.
Solution: If Petrov had nailed 2 nails into each board, he would have nailed 43 boards and had one extra nail. If he had nailed 3 nails into each board, he would have nailed 29 boards. Therefore, the desired number lies between 29 and 43 (inclusive). Similarly, if Vasechkin had nailed 3 nails into each board, he would have nailed 31 boards and had 1 extra nail, and if he had nailed 5 nails into each board, he would have nailed 18 boards and had 4 extra nails. This means there were 29, 30, or 31 boards. Note that Vasechkin nailed an odd number of nails into each board, so the number of boards must be even - 30. | 30 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2. Six natural numbers (possibly repeating) are written on the faces of a cube, such that the numbers on adjacent faces differ by more than 1. What is the smallest possible value of the sum of these six numbers? | Answer: 18.
Solution: Consider three faces that share a common vertex. The numbers on them differ pairwise by 2, so the smallest possible sum would be for $1+3+5=9$. The same can be said about the remaining three faces.
Thus, the sum cannot be less than 18. We will show that 18 can be achieved - place the number 1 on the top and bottom faces of the cube, 3 on the right and left faces, and 5 on the front and back faces. | 18 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
3. In the Slytherin faculty at Hogwarts, there are 30 students. Some are friends (friendship is mutual, i.e., if A is friends with B, then B is also friends with A), but there are no 3 people who are pairwise friends with each other. On New Year's, each student sent cards to all their friends. What is the maximum number of cards that could have been sent? | Answer: 450.
Solution: Let's find the person with the most friends. Suppose there are no fewer than 15, and denote their number as $15+a$. We will divide the students into two groups: the first group will consist of these $15+a$ students. According to the condition, they cannot be friends with each other, so each of them has no more than 15-a friends. The second group will consist of the remaining 15-a, each of whom has no more than $15+a$ friends. Thus, each group will send no more than 225- $a^{2}$ cards. Therefore, in total, no more than 450-2 $a^{2}$ cards will be sent, which does not exceed 450.
Note that this value is achievable. Divide the students into two groups of 15 people each, and let each representative of one group be friends with all representatives of the other group. | 450 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. Points $A_{1}, \ldots, A_{12}$ are the vertices of a regular 12-gon. How many different 11-segment open broken lines without self-intersections with vertices at these points exist? Broken lines that can be transformed into each other by rotation are considered the same. | Answer: 1024.
Solution: The first vertex of the broken line can be chosen in 12 ways. Each subsequent vertex (except the last one) can be chosen in two ways - it must be adjacent to the already marked vertices to avoid self-intersections. The last vertex is chosen uniquely. We get $12 * 2^{10}$ ways. Considering 12 possible rotations, we get that each broken line will be counted 12 times, so this number must be divided by 12.
Remark: Here, it was implied in the condition that the broken line has a starting and ending point. If, however, we consider broken lines as geometric objects, i.e., without a distinguished "head" and "tail," this significantly complicates the problem. | 1024 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Find the smallest three-digit number with the property that if a number, which is 1 greater, is appended to it on the right, then the result (a six-digit number) will be a perfect square. Answer: 183 | Solution: Let the required number be \(a\), then \(1000a + a + 1 = n^2\). We can write it as: \(1001a = (n - 1)(n + 1)\). Factorize \(1001 = 7 \times 11 \times 13\), so the product \((n - 1)(n + 1)\) must be divisible by 7, 11, and 13. Moreover, for the square to be a six-digit number, \(n\) must be in the interval \([317; 999]\).
Consider the following cases:
a) \(n - 1\) is divisible by 143, \(n + 1\) is divisible by 7, then we find \(n = 573\);
b) \(n - 1\) is divisible by 7, \(n + 1\) is divisible by 143, then \(n = 428\);
c) \(n - 1\) is divisible by 77, \(n + 1\) is divisible by 13, then \(n = 155\) - does not fit;
d) \(n - 1\) is divisible by 13, \(n + 1\) is divisible by 77, then \(n = 846\);
e) \(n - 1\) is divisible by 91, \(n + 1\) is divisible by 11, then \(n = 274\) - does not fit;
f) \(n - 1\) is divisible by 11, \(n + 1\) is divisible by 91, then \(n = 727\).
The smallest \(n = 428, n^2 = 428^2 = 183184\). | 183 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. Pete came up with all the numbers that can be formed using the digits 2, 0, 1, 8 (each digit can be used no more than once). Find their sum. | Answer: 78331
Solution: First, consider the units place. Each of the digits 1, 2, 8 appears once in this place for single-digit numbers, twice for two-digit numbers, four times for three-digit numbers, and four times for four-digit numbers - a total of 11 times.
In the tens place, each of them appears 3 times for two-digit numbers, 4 times for three-digit numbers, and 4 times for four-digit numbers - also 11 times.
In the hundreds place, each appears 6 times in three-digit numbers and 4 times in single-digit numbers.
In the thousands place, each appears 6 times.
In total, we get $11 \times 11 + 11 \times 11 \times 10 + 11 \times 10 \times 100 + 11 \times 1000 \times 6 = 78331$. | 78331 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
7. Given a sequence of natural numbers $a_{n}$, the terms of which satisfy
the relations $a_{n+1}=k \cdot \frac{a_{n}}{a_{n-1}}$ (for $n \geq 2$). All terms of the sequence are integers. It is known that $a_{1}=1$, and $a_{2018}=2020$. Find the smallest natural $k$ for which this is possible. | Answer: 2020
Solution: Let $a_2=x$. Then all terms of the sequence will have the form $x^{m} k^{n}$.
The powers of $k$ will repeat with a period of 6: $0,0,1,2,2,1,0,0, \ldots$
The powers of $x$ will also repeat with a period of 6: 0,1,1,0,-1,-1,0,1,...
Since 2018 gives a remainder of 2 when divided by 6, then $a_{2018}=a_{2}=x=2020$. For all terms of the sequence to be integers, $k$ must be a multiple of $x$, the smallest such $k$ is 2020. | 2020 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. Solve the inequality
$$
(2+\sqrt{3})^{x}+2<3(\sqrt{2-\sqrt{3}})^{2 x}
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the given inequality and belong to the interval $(-20 ; 53)$. | Answer: The solution to the inequality is $(-\infty ; 0)$. The desired sum $-19-18-\cdots-2-1=-190$. We write -190 as the answer. | -190 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
3. The area of triangle $\triangle A B C$ is 10 cm $^{2}$. What is the smallest value in centimeters that the circumference of the circle circumscribed around triangle $\triangle A B C$ can take, given that the midpoints of the heights of this triangle lie on the same line? If the answer is not an integer, round it to the nearest integer. | Answer: The smallest value is $2 \pi \sqrt{10}$ cm. In the answer, we write 20, since $2 \pi \sqrt{10} \approx 19.8691 \ldots$ | 20 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. First method: Since $x_{1}^{3}-2015 x_{1}+2016=0$ and $x_{2}^{3}-2015 x_{2}+2016=0$, then $x_{1}^{3}-x_{2}^{3}=2015 \cdot\left(x_{1}-x_{2}\right)$. Therefore, $x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}=2015$.
Second method: By Vieta's theorem (but then it needs to be justified that there are three distinct roots): $x_{1}+x_{2}+x_{3}=0, x_{1} x_{2} x_{3}=-2016$. Therefore,
$$
\begin{aligned}
x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-x_{1} x_{2}=\left(-x_{3}\right)^{2}+\frac{2016}{x_{3}} & \\
=\frac{x_{3}^{3}+2016}{x_{3}} & =\frac{2015 x_{3}}{x_{3}}=2015
\end{aligned}
$$ | Answer: 2015.
Answer to option: 4-2: 2016. | 2015 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. Let $\alpha=\pi x$.
$$
\begin{aligned}
& \cos (8 \alpha)+2 \cos (4 \alpha)-\cos (2 \alpha)+2 \sin (\alpha)+3=0 \Longleftrightarrow \\
& 2 \cos ^{2} 4 \alpha-1+2 \cos 4 \alpha-1+2 \sin ^{2} \alpha+2 \sin \alpha+3=0 \Longleftrightarrow \\
& 2\left(\cos 4 \alpha+\frac{1}{2}\right)^{2}+2\left(\sin \alpha+\frac{1}{2}\right)^{2}=0
\end{aligned}
$$
From which
$$
\left\{\begin{array} { l }
{ \operatorname { cos } 4 \alpha = - 1 / 2 } \\
{ \operatorname { sin } \alpha = - 1 / 2 }
\end{array} \Longleftrightarrow \left[\begin{array}{l}
\alpha=-\frac{\pi}{6}+2 \pi m, m \in \mathbb{Z} \\
\alpha=-\frac{5 \pi}{6}+2 \pi n, n \in \mathbb{Z}
\end{array}\right.\right.
$$
Thus $x=-1 / 6+2 m, x=-5 / 6+2 n, m, n \in \mathbb{Z}$. The sum of the first two positive roots: $1 \frac{1}{6}+1 \frac{5}{6}=3$. The next two positive roots are 4 greater, i.e., equal to 7, and so on. The desired sum is
$$
3+7+11+\cdots+(3+4 \cdot 49)=\frac{6+4 \cdot 49}{2} \cdot 50=5050
$$ | Answer: 5050
Answer to option: 7-2: 4950.
Solutions for option 17-1 and answers to all options | 5050 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. Drop perpendiculars $D D_{1}, D D_{2}, D D_{3}$ from point $D$ to the planes $S B C$, $S A C$, and $S A B$ respectively. Let $D D_{1}=x, D D_{2}=y, D D_{3}=z$. According to the condition, we form the system of equations
$$
\left\{\begin{array}{l}
y^{2}+z^{2}=5 \\
x^{2}+z^{2}=13 \\
x^{2}+y^{2}=10
\end{array}\right.
$$
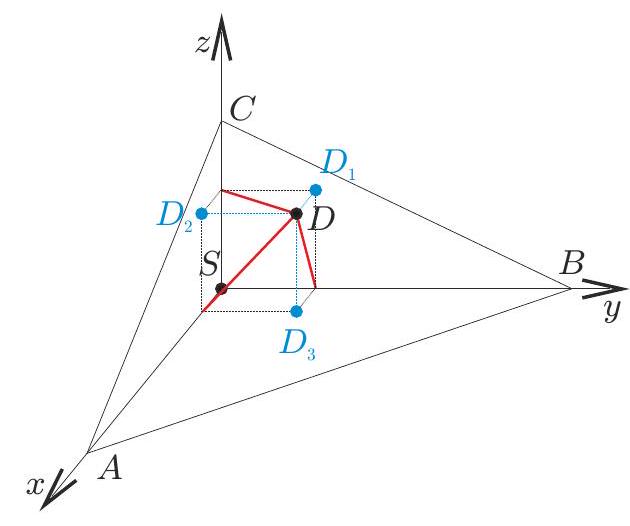
Fig. 6:
From here, we find $x=3, y=1, z=2$. Let the lengths of the edges $S A, S B$, and $S C$ be $a, b$, and $c$ respectively. Since points $A, B, C$, and $D$ lie in the same plane, the relation $\frac{3}{a}+\frac{1}{b}+\frac{2}{c}=1$ holds.
Using the inequality between the arithmetic mean and the geometric mean for three variables, we get:
$$
\begin{aligned}
& \frac{\frac{3}{a}+\frac{1}{b}+\frac{2}{c}}{3} \geqslant \sqrt[3]{\frac{3}{a} \cdot \frac{1}{b} \cdot \frac{2}{c}}=\sqrt[3]{\frac{6}{a b c}} \Longleftrightarrow \\
& \Longleftrightarrow 1=\left(\frac{3}{a}+\frac{1}{b}+\frac{2}{c}\right)^{3} \geqslant \frac{6 \cdot 27}{a b c} \Longleftrightarrow a b c \geqslant 6 \cdot 27
\end{aligned}
$$
with equality holding when $\frac{3}{a}=\frac{1}{b}=\frac{2}{c}=\frac{1}{3}$. The volume of the pyramid $V=\frac{a b c}{6}$, so $V \geqslant 27$. Equality holds when $a=9, b=3, c=6$. | Answer: 27.
Answer to option 17-2: 108.
Answer to option $17-3: 27$.
Answer to option $17-4: 108$.
[^0]: ${ }^{1}$ This equality can be proven by expressing $B C^{2}$ from two triangles $B A C$ and $B D C$ using the planimetric cosine theorem. | 27 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
7. A natural number $N$ ends in ...70, and it has exactly 72 natural divisors (including 1 and itself). How many natural divisors does the number 80N have? ANSWER: 324. | Solution: Each divisor of the number $\mathrm{N}$ can be represented in the form $2^{a} \cdot 5^{b} \cdot q$, where q is not divisible by 2 and 5, and the numbers $a, b$ are 0 or 1. Therefore, there are only 4 different combinations for the pair a and b, which means there are $72 / 4=18$ possible values for q. These correspond to divisors of the number $80 \mathrm{~N}$ in the form $2^{c} \cdot 5^{d} \cdot q$, where c=0,...,5 and $d=0,1,2$. There are 18 for each q, i.e., a total of $18 * 18=324$. | 324 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. Solve the inequality
$$
\frac{4+\sqrt{-3-x}}{3-|x+4|} \leqslant 1
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the given inequality and do not exceed 12 in absolute value. | Solution. Transferring 1 to the left side and bringing to a common denominator:
$$
\frac{1+\sqrt{-3-x}+|x+4|}{3-|x+4|} \leqslant 0
$$
For $x>-3$, the expression under the square root is negative, meaning there are no solutions. For $x \leqslant-3$, the numerator is positive, and thus,
$$
3-|x+4|3 \Longleftrightarrow x>-1
$$
or $x<-7$.
Therefore, the solution to the inequality is: $x<-7$. The required integer roots according to the condition are: $-12, -11, \ldots$, -8. Their sum is -50.
Answer: -50. | -50 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
4. The number 2015 can be represented as the sum of consecutive integers in various ways, for example, $2015=1007+1008$ or $2015=$ $401+402+403+404+405$. In how many ways can this be done? | Answer: 16.
Solution: The sum of $k$ numbers starting from $n$ is $S(k, n)=\frac{1}{2}(2 n+k-1) \cdot k$. That is, we need to solve the equation $(2 n+k-1) \cdot k=4030$ in integers. Obviously, $k$ can be any divisor of $4030=2 \times 5 \times 13 \times 31$. Note that each of the prime factors $(2,5,13$ and 31$)$ can be in the power of 0 or 1 - in total 16 options. | 16 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
9. Given triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$, the areas of which are 1 and 2025, respectively. It is known that rays $A B$ and $A^{\prime} B^{\prime}$ are parallel and point in opposite directions (see figure). The same is true for pairs $B C$ and $B^{\prime} C^{\prime}, C A$ and $C^{\prime} A^{\prime} . A^{\prime \prime}, B^{\prime \prime}$ and $C^{\prime \prime}$ are the midpoints of segments $A A^{\prime}, B B^{\prime}$ and $C C^{\prime}$. Find the area of triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. | Answer: 484.
Solution: Obviously, triangles $A B C A^{\prime} B^{\prime} C^{\prime}$ are similar with a coefficient of 45.
Three trapezoids are formed, in which $A^{\prime \prime} B^{\prime \prime}, B^{\prime \prime} C^{\prime \prime}$ and $C^{\prime \prime} A^{\prime \prime}$ are segments connecting the midpoints of the diagonals (i.e., equal to half the difference of the bases). Therefore, triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ is also similar to $\triangle A B C$ and its coefficient is $(45-1) / 2=22$. Consequently, its area is $22^{2}=484$ times larger than the area of the small triangle. | 484 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4. A school coach decided to reward 12 students who ran the distance in the best time. Each of them must be awarded a "gold", "silver", or "bronze" medal. All three types of medals must be used, and the one who finished earlier cannot be awarded a less valuable medal than the one who finished later.
How many ways can the coach distribute the medals (all runners have different times)? | Answer: $C_{11}^{2}=55$.
Solution: see 9th grade. | 55 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. On a line, there are 16 points $A_{1}, \ldots A_{16}$, spaced 1 cm apart. Misha constructs circles according to the following rules:
a) The circles do not intersect or touch.
b) Inside each circle, there is at least one of the specified points $\mathrm{A}_{1}, \ldots \mathrm{A}_{16}$.
c) None of these points lie on the circle.
d) Different circles contain different sets of points. For example, if one circle contains points $A_{1}$ and $A_{2}$ inside and the rest outside, then it is not possible to construct another circle that contains only $A_{1}$ and $A_{2}$ inside.
What is the maximum number of circles Misha can construct according to these rules? | Answer: 31.
Solution: see 9th grade.
## Tasks for 7-8 grades
## Option 3b (Moscow) | 31 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Each worker on the construction site has at least one construction specialty. 10 people have the specialty of a mason, 9 - the specialty of a painter, 8 - the specialty of a plasterer. It is known that at least four people have the specialties of a mason and a plasterer simultaneously, at least five people - the specialties of a mason and a painter, and at least three people - the specialties of a painter and a plasterer. What is the maximum number of workers that can be on the construction site under these conditions? | # Answer 18.
Solution: According to the principle of inclusion-exclusion, the total number of workers is K+M+S - KM-KS-MS + KMS = 10+9+8-4-5-3 + KMS = 15 + KMS. Note that the number of workers proficient in all three specialties cannot exceed 3. | 18 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. Natural numbers, for which the sum of the digits equals 5, were arranged in ascending order. What number is in the $122-$nd position? | Answer: 40001.
Solution: Let's calculate the number of such numbers for different digit counts.
Let $n$ be the number of digits. Subtract 1 from the most significant digit, we get a number (which can now start with zero), the sum of whose digits is 4. Represent this as follows - there are 4 balls, between which $n-1$ partitions are placed. This can be chosen in $C_{n+3}^{4}$ ways.
Let's construct a table:
| Number of digits | Number of ways |
| :--- | :---: |
| 1 | $C_{4}^{4}=1$ |
| 2 | $C_{5}^{4}=5$ |
| 3 | $C_{6}^{4}=15$ |
| 4 | $C_{7}^{4}=35$ |
| 5 | $C_{8}^{4}=70$ |
| TOTAL | $\mathbf{1 2 6}$ |
Obviously, the 126th number - the largest 5-digit number - will be 50000.
Thus, the 125th number is 41000.
the 124th is 40100
the 123rd is 40010
the 122nd is 40001 | 40001 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. On a line, there are 16 points $A_{1}, \ldots A_{16}$, spaced $1 \mathrm{~cm}$ apart. Misha constructs circles according to the following rules:
a) The circles do not intersect or touch.
b) Inside each circle, there is at least one of the specified points $\mathrm{A}_{1}, \ldots \mathrm{A}_{16}$.
c) None of these points lie on the circle.
d) Different circles contain different sets of points. For example, if one circle contains points $\mathrm{A}_{1}$ and $\mathrm{A}_{2}$ inside and the rest outside, then it is not possible to construct another circle that contains only $\mathrm{A}_{1}$ and $\mathrm{A}_{2}$ inside.
What is the maximum number of circles Misha can construct according to these rules?
Answer: 31. | Solution: We can represent such a system of circles as a tree with 16 leaves.
In such a tree, there cannot be more than 31 nodes. It is easy to construct a binary tree in which there are exactly 31 nodes. | 31 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. The sequence $a_{n}$ is defined as follows:
$a_{1}=2, a_{n+1}=a_{n}+\frac{2 a_{n}}{n}$, for $n \geq 1$. Find $a_{999}$. | Answer: 999000.
Solution: Consider the beginning of the sequence: $a_{1}=2, a_{2}=6, a_{3}=12, a_{4}=20, \ldots$
We can notice a pattern - the difference between consecutive terms forms an arithmetic progression: $4,6,8, \ldots$.
From this, we get the formula for the $\mathrm{n}$-th term $a_{n}=n \cdot(n+1)$, which can be proven by induction.
Thus, $a_{999}=999 \cdot 1000=999000$. | 999000 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. The robotics club accepts only those who know mathematics, physics, or programming. It is known that 8 members of the club know physics, 7 know mathematics, and 11 know programming. Additionally, it is known that at least two know both physics and mathematics, at least three know both mathematics and programming, and at least four know both physics and programming. What is the maximum number of club members possible under these conditions? | Answer 19.
3 Natural numbers, the sum of whose digits is 5, were arranged in ascending order. What number is in the $111-$th place?
Answer: 23000. | 23000 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. On a line, there are 15 points $A_{1}, \ldots A_{15}$, spaced 1 cm apart. Petya constructs circles according to the following rules:
a) The circles do not intersect or touch.
b) Inside each circle, there is at least one of the specified points $\mathrm{A}_{1}, \ldots \mathrm{A}_{15}$.
c) None of these points lie on the circle.
d) Different circles contain different sets of points. For example, if one circle contains points $\mathrm{A}_{1}$ and $\mathrm{A}_{2}$ inside and the rest outside, then it is not possible to construct another circle that contains only $\mathrm{A}_{1}$ and $\mathrm{A}_{2}$ inside.
What is the maximum number of circles Petya can construct according to these rules? | Answer: 29.
## Option 2b (Saratov) | 29 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
2. Let there be $n$ voters, and $k$ votes were cast for a given candidate. Then $0.50332 \leqslant$ $\frac{k}{n} \leqslant 0.50333$, and $1.00664 \leqslant \frac{2 k}{n} \leqslant 1.00666$. If we denote $m=2 k-n$, then $0.00664 \leqslant \frac{m}{n} \leqslant$ 0.00666.
- If $m=1$, then $150.1<\frac{1}{0.00666} \leqslant n \leqslant \frac{1}{0.00664}<150.7$ - no integer solutions.
- If $m=2$, then $300<\frac{2}{0.00666} \leqslant n \leqslant \frac{2}{0.00664}<302$. But if $n=301$ and $m=2$, then the corresponding value of $k$ does not exist.
- If $m=3$, then $450<\frac{3}{0.00666} \leqslant n \leqslant \frac{3}{0.00664}<452$. Therefore, $n=451, k=227$, and all inequalities are satisfied. | Answer: 451. Answer to the option: $5-2: 341$.
# | 451 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Let $\Sigma(n)$ denote the sum of the digits of the number $n$. Find the smallest three-digit $n$ such that $\Sigma(n)=\Sigma(2 n)=\Sigma(3 n)=\ldots=\Sigma\left(n^{2}\right)$ | Answer: 999
Solution: Let the desired number be $\overline{a b c}$. Note that this number is not less than 101 (since 100 does not work). Therefore, $101 \cdot \overline{a b c}=\overline{a b c 00}+\overline{a b c}$ also has the same sum of digits. But the last digits of this number are obviously $b$ and $c$, so the sum of the remaining digits must be equal to $a$. Therefore, $\Sigma(\overline{a b c}+a)=a$. If $a<9$, then $\overline{a b c}+a-$ is a three-digit number, the first digit of which is not less than $a$, which leads to a contradiction, since the second and third digits cannot be zeros. Thus, $a=9$ and $\overline{a b c}+a \leqslant 999+9=1008$. Therefore, $\overline{a b c}+a=\overline{100 d}$. But $\Sigma(\overline{100 d})=a=9$, so $d=8$, from which $\overline{a b c}=999$. | 999 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Igor Gorshkov has all seven books about Harry Potter. In how many ways can Igor arrange these seven volumes on three different bookshelves, so that each shelf has at least one book? (Arrangements that differ by the order of books on the shelf are considered different). | Answer: $C_{6}^{2} \times 7!=75600$.
Solution: First, we can arrange the books in any order, which gives 7! options. Place two dividers into 6 gaps between the books - this can be done in $C_{6}^{2}$ ways. The dividers will divide the books into three parts, which need to be placed on the 1st, 2nd, and 3rd shelves. In total, we get $C_{6}^{2} \times 7!=75600$ options. | 75600 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Find the sum of all natural numbers that have exactly four natural divisors, three of which (of the divisors) are less than 15, and the fourth is not less than 15. | Answer: $\left((2+3+5+7+11+13)^{2}-\left(2^{2}+3^{2}+5^{2}+7^{2}+11^{2}+13^{2}\right)\right) / 2-$ $6-10-14+27=649$.
Solution: The numbers $N$ specified have exactly 4 divisors either if $N=$ $p^{3}$, or if $N=p q$, where $p$ and $q$ are primes. In the first case, only 27 fits. In the second case, we need to consider the pairwise products of all prime numbers less than 15. These numbers are $p_{i}=2,3,5,7,11,13$. The sum of their pairwise products can be calculated as $S_{p q}=2 \cdot(3+5+7+$ $11+13)+3 \cdot(5+7+11+13)+5 \cdot(7+11+13)+7 \cdot(11+13)+11 \cdot 13=652$. From the pairwise products, we need to exclude 6, 10, and 14, as they are less than 15. In the end, $S=27+S_{p q}-6-10-14=649$. | 649 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. A right-angled triangle is called Pythagorean if the lengths of all its sides are natural numbers. Find the greatest integer that divides the product of the lengths of the sides of any Pythagorean triangle. | # Problem 5.
Answer: 60.
Solution. Since a triangle with sides $3,4,5$ is a right triangle, the desired number cannot be greater than 60. We will show that the product of the lengths of the sides of any Pythagorean triangle is divisible by 60, i.e., by 3, by 4, and by 5.
The remainders when the square of an integer is divided by 3 and 4 can only be 0 and 1. Therefore, if $a$ and $b$ are not divisible by 3 and 4, then $a^{2}+b^{2}$, when divided by 3 and 4, gives a remainder of 2, and thus cannot be a perfect square.
The remainders when an integer is divided by 5 can only be 0, 1, and 4. Therefore, if $a$ and $b$ are not divisible by 5 and $a^{2}+b^{2}$ is a perfect square, then one of the numbers - $a^{2}$ or $b^{2}$ - has a remainder of 1, and the other has a remainder of 4. Consequently, $a^{2}+b^{2}$ is divisible by 5. | 60 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
8. Let's call a number "remarkable" if it has exactly 4 distinct natural divisors, and among them, there are two such that neither is a multiple of the other. How many "remarkable" two-digit numbers exist?
# | # Answer 36.
Solution: Such numbers must have the form $p_{1} \cdot p_{2}$, where $p_{1}, p_{2}$ are prime numbers. Note that the smaller of these prime numbers cannot be greater than 7, because otherwise the product will be at least 121. It is sufficient to check $p_{1}=2,3,5,7$. For 2, we get the second factor: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, or 47 - 14 options, for 3 we get: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 - 10 options, for 5: 3, 5, 7, 11, 13, 17, 19 - 7 options, and for 7: 3, 5, 7, 11, 13 - 5 options. In total, $14+10+7+5=36$ options. | 36 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
9. Assemble a square of the smallest area from squares of size $1 \times 1$, $2 \times 2$, and $3 \times 3$, such that the number of squares of each size is the same. | Answer:

Solution. Let $n$ be the number of squares of each type. Then $n + 4n + 9n = 14n$ must be a perfect square. The smallest $n$ for which this is possible is 14. The figure shows an example of how to construct a 14x14 square (other arrangements are possible, as long as there are 14 squares of each type). | 14 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
10. The company conducted a survey among its employees - which social networks they use: VKontakte or Odnoklassniki. Some employees said they use VKontakte, some - Odnoklassniki, some said they use both social networks, and 40 employees said they do not use social networks. Among all those who use social networks, 75% use VKontakte, and 65% use both networks. The proportion of employees who use Odnoklassniki from the total number of all employees is 5/6. How many employees work in the company? | Answer: 540
Solution: Since 75% of social media users use VKontakte, it follows that only 25% use Odnoklassniki. Additionally, 65% use both networks, so the total percentage of users of Odnoklassniki is $65 + 25 = 90\%$ of social media users. These $90\%$ constitute $5 / 6$ of the company's employees, so $100\%$ constitutes $10 / 9 * 5 / 6 = 50 / 54$ of all employees. Therefore, those who do not use social media constitute 1 - 50/54 = 4/54, and there are 40 such people. Thus, the total number of employees is 540. | 540 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
11. In a regular 2017-gon, all diagonals are drawn. Petya randomly selects some $\mathrm{N}$ diagonals. What is the smallest $N$ such that among the selected diagonals, there are guaranteed to be two of the same length? | Answer: 1008.
Solution: Let's choose an arbitrary vertex and consider all the diagonals emanating from it. There are 2014 of them, and by length, they are divided into 1007 pairs. Clearly, by rotating the polygon, any of its diagonals can be aligned with one of these. Therefore, there are only 1007 different sizes of diagonals. Thus, by choosing 1008, Petya is guaranteed to get at least two of the same. | 1008 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. A pirate schooner has taken a merchant ship by boarding. Ten pirates did not participate in the fight, while the rest lost either a hand, a leg, or both a hand and a leg in the battle. $54\%$ of the participants in the battle lost a hand, and $34\%$ lost both a hand and a leg. It is known that $2/3$ of all the pirates on the schooner lost a leg. How many pirates were on the schooner? | Answer: 60 pirates.
Solution - similar to option v3a. | 60 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
5. In a regular 1000-gon, all diagonals are drawn. What is the maximum number of diagonals that can be selected such that among any three of the selected diagonals, at least two have the same length? | Answer: 2000
Solution: For the condition of the problem to be met, it is necessary that the lengths of the diagonals take no more than two different values. The diagonals connecting diametrically opposite vertices are 500. Any other diagonal can be rotated to coincide with a diagonal of the corresponding length, i.e., there are 1000 of them. Therefore, 2000 can be chosen while satisfying the condition. | 2000 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6. In how many ways can the number 1024 be factored into three natural factors such that the first factor is divisible by the second, and the second is divisible by the third? | Answer: 14
Solution: Note that the factors have the form $2^{a} \times 2^{b} \times 2^{c}$, where $\mathrm{a}+\mathrm{b}+\mathrm{c}=10$ and $a \geq b \geq c$. Obviously, c is less than 4, otherwise the sum would be greater than 10. Let's consider the cases:
$c=0)$ Then $b=0, \ldots, 5, a=10-b-6$ options
c=1) Then $b=1, . .4, a=9-b-4$ options
$c=2) b=2,3,4, a=8-b-3$ options.
$c=3) b=3, a=4-1$ option.
In total $6+4+3+1=14$ options. | 14 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. A rectangle $A D E C$ is described around a right triangle $A B C$ with legs $A B=5$ and $B C=6$, as shown in the figure. What is the area of $A D E C$? | # Answer 30.
Solution: The area of the rectangle is twice the area of the triangle. | 30 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. In the Empire of Westeros, there were 1000 cities and 2017 roads (each road connected some two cities). From any city, you could travel to any other. One day, an evil wizard enchanted $N$ roads, making it impossible to travel on them. As a result, 7 kingdoms formed, such that within each kingdom, you could travel from any city to any other by roads, but you could not travel from one kingdom to another by roads. What is the largest $N$ for which this is possible? | Answer: 1024.
Solution: Suppose the evil wizard enchanted all 2017 roads. This would result in 1000 kingdoms (each consisting of one city). Now, imagine that the good wizard disenchants the roads so that there are 7 kingdoms. He must disenchant at least 993 roads, as each road can reduce the number of kingdoms by no more than 1. Therefore, the evil wizard could not have enchanted more than 2017-993=1024 roads.
For graders: Partial credit can be given for a correct answer obtained for some specific case - without a general proof. | 1024 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6. Jack Sparrow needed to distribute 150 piastres into 10 purses. After placing a certain number of piastres in the first purse, he put more in each subsequent purse than in the previous one. As a result, it turned out that the number of piastres in the first purse was not less than half the number of piastres in the last purse. How many piastres are in the 6th purse? | # Answer: 16
Solution: Let there be $x$ piastres in the first purse. Then in the second there are no less than $\mathrm{x}+1$, in the third - no less than $\mathrm{x}+2$... in the 10th - no less than $\mathrm{x}+9$. Thus, on one side $x+$ $x+1+\cdots+x+9=10 x+45 \leq 150$, From which $x \leq 10$. On the other side $x \geq(x+$ 9 )/2, from which $x \geq 9$. Therefore, in the first there are 9 or 10 piastres. But 9 cannot be, because then in the last one there will be no more than 18 and the sum will not be 150.
So in the 1st there are 10, in the second - no less than 11, in the 3rd - no less than 12, in the 4th - no less than 13, in the 5th no less than 14 and in the $6-$th - no less than 15. But with 15 the sum is less than 150. So it must be 16. And it cannot be more because then in the last purse there will be 21.
For graders: Partial credit can be given for a correct example of distribution (trial and error) without proof of uniqueness. | 16 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
7. Find the smallest natural number $N$, such that the decimal representation of the number $N \times 999$ consists entirely of sevens. | Answer 778556334111889667445223
Solution: $N \times 999=77 \ldots 7$, then $N$ is a multiple of 7, denote $n=N / 7$. We get $999 n=$ $1000 n-n=11 \ldots 1$, so $1000 n-111 \ldots 1=n$. Write it as a column subtraction and repeat the found digits of $\mathrm{N}$ with a shift of 3 to the left $* * * * * * * 000$
1111111111
$* * * * * * 889$
$* * * * 889000$
1111111111
$* * * 777889$
777889000
111111111
6667778889
Notice that the digits repeat every 3, so we get
$n=111222333444555666777889$.
Therefore, $\mathrm{N}=7 \mathrm{n}=778556334111889667445223$.
For graders: an alternative approach is to take the number 111... 1 and start dividing it by 999 in a column, until it divides evenly. I think you shouldn't deduct points if at the very end the number n was incorrectly multiplied by 7.
## Variant $2-\mathrm{b}$ | 778556334111889667445223 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. How many natural numbers from 1 to 2017 have exactly three distinct natural divisors? | Answer: 14.
Solution: Only squares of prime numbers have exactly three divisors. Note that $47^{2}>2017$, so it is sufficient to consider the squares of prime numbers from 2 to 43. There are 14 of them. | 14 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Petya is coming up with a password for his smartphone. The password consists of 4 decimal digits. Petya wants the password not to contain the digit 7, and at the same time, the password should have at least two (or more) identical digits. In how many ways can Petya do this? | # Answer 3537.
Solution: The total number of passwords not containing the digit 7 will be $9^{4}=6561$. Among these, 9x8x7x6=3024 consist of different digits. Therefore, the number of passwords containing identical digits is 6561-3024=3537 passwords. | 3537 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. In the computer center, there are 200 computers, some of which (in pairs) are connected by cables, a total of 345 cables are used. We will call a "cluster" a set of computers such that a signal from any computer in this set can reach all other computers via cables (possibly through intermediate computers). Initially, all computers formed one cluster. But one night, a malicious hacker cut several cables, resulting in 8 clusters. Find the maximum possible number of cables that were cut. | Answer: 153.
Solution: Let's try to imagine the problem this way: an evil hacker has cut all the wires. What is the minimum number of wires the admin needs to restore to end up with 8 clusters? Obviously, by adding a wire, the admin can reduce the number of clusters by one. This means that from 200 clusters, 8 can be obtained by restoring 192 wires. Therefore, the hacker could have cut a maximum of 153 wires. | 153 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. In trapezoid $A B C D$ with bases $A D / / B C$, the diagonals intersect at point $E$. It is known that the areas $S(\triangle A D E)=12$ and $S(\triangle B C E)=3$. Find the area of the trapezoid. | Answer: 27
Solution: Triangle ADE and CBE are similar, their areas are in the ratio of the square of the similarity coefficient. Therefore, this coefficient is
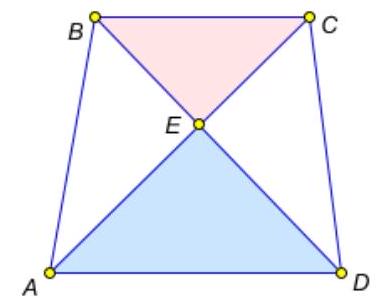 | 27 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
7. Find the smallest natural number ending in the digit 2 that doubles when this digit is moved to the beginning. | Answer: 105263157894736842
Solution: Let's write the number in the form ***...** 2 and gradually restore the "asterisks" by multiplying by 2:
```
\(* * \ldots * * 2 \times 2=* * * . . . * * 4\)
\(* * * . . * 42 \times 2=* * * \ldots * 84\)
\(* * * . . .842 \times 2=* * * \ldots * 684\)
***... \(* 6842 \times 2=* * * \ldots * 3684\)
\(* * * . . * 36842 \times 2=* * * \ldots * 73684\)
\(* * * . . * 736842 \times 2=* * * . . . * 473684\)
\(* * * . . * 4736842 \times 2=* * * \ldots * 9473684\)
\(\cdots\)
\(105263157894736842 \times 2=210526315789473684\)
``` | 105263157894736842 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2. At the international StarCraft championship, 100 participants gathered. The game is played in a knockout format, meaning in each match, two players compete, the loser is eliminated from the tournament, and the winner remains. Find the maximum possible number of participants who won exactly two games? | # Answer: 49
Solution: Each participant (except the winner) lost one game to someone. There are 99 such participants, so no more than 49 participants could have won 2 games (someone must lose 2 games to them).
We can show that there could be 49 such participants. Let's say №3 won against №1 and №2, №5 won against №3 and №4, ... №99 won against №97 and №98, and №100 won against №99. Then all participants with odd numbers (except the first) won exactly 2 games. | 49 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. A box of sugar has the shape of a rectangular parallelepiped. It contains 280 sugar cubes, each of which is a $1 \times 1 \times 1$ cm cube. Find the surface area of the box, given that the length of each of its sides is less than 10 cm. | # Answer: 262
Solution: $\mathbf{2 8 0}=\mathbf{2}^{3} \mathbf{x} \mathbf{x} \mathbf{x}$. From the condition that the lengths of the sides are integers less than 10, it follows that its edges are equal to 5, 7, and 8. The surface area is $2 *\left(5^{*} 7+5 * 8+7 * 8\right)=262$ | 262 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. We will call a number "remarkable" if it has exactly 4 distinct natural divisors, and among them, there are two such that neither is a multiple of the other. How many "remarkable" two-digit numbers exist? | Answer 36.
Solution: Such numbers must have the form $p_{1} \cdot p_{2}$, where $p_{1}, p_{2}$ are prime numbers. Note that the smaller of these prime numbers cannot be greater than 7, otherwise the product will be no less than 121. It is sufficient to check $p_{1}=2,3,5,7$. For 2, we get the second factor: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, or 47 - 14 options, for 3 we get: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 - 10 options, for $5: 3, \quad 5,7,11,13,17,19, \quad-7$ options and for $7: 3,5,7,11,13,-5$ options. In total $14+10+7+5=36$ options. | 36 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
7. Find all three-digit numbers $\overline{\Pi B \Gamma}$, consisting of different digits $\Pi, B$, and $\Gamma$, for which the equality $\overline{\Pi B \Gamma}=(\Pi+B+\Gamma) \times(\Pi+B+\Gamma+1)$ holds. | Answer: 156.
Solution: Note that П+В $\Gamma \geq 3$ and $\leq 24$ (since the digits are different). Moreover, the numbers
$\overline{\Pi В \Gamma}$ and $(П+B+\Gamma)$ must give the same remainder when divided by 9. This is only possible when П+В $\Gamma) \times(П+B+\Gamma+1)=90$-a two-digit number. By trying $12,15,18,21,24$, we get $\overline{\Pi В \Gamma}=$ $156=12 \times 13$.
## Variant 1-b | 156 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
2. At the international table tennis championship, 200 participants gathered. The game is played in a knockout format, i.e., in each match, two players participate, the loser is eliminated from the championship, and the winner remains. Find the maximum possible number of participants who won at least three matches. | Answer: 66.
Solution: Each participant (except the winner) lost one game to someone. There are 199 such participants, so no more than 66 participants could have won 3 games (someone must lose 3 games to them).
We will show that there could be 66 such participants. Let №4 win against №1,2,3; №7 - against №4,5,6,... №199 - against №196,197,198, and №200 win against №199. Then all participants with numbers giving a remainder of 1 when divided by 3 (except the first) won exactly 3 games. | 66 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. Kolya has 440 identical cubes with a side length of 1 cm. Kolya assembled a rectangular parallelepiped from them, with all edges having a length of at least 5 cm. Find the total length of all the edges of this parallelepiped | Answer: 96.
Solution: $440=2^{3} \times 5 \times 11$. Since all edges have a length of at least 5, their lengths are 8, 5, and 11. Each edge is included 4 times, so the total length is ( $8+5+11)^{*} 4=96$. | 96 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
1. Solve the inequality
$$
\frac{2^{2+\sqrt{x-1}}-24}{2^{1+\sqrt{x-1}}-8}>1 .
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the given inequality and belong to the interval $(-70 ; 34)$. | Solution. Let $t=2^{1+\sqrt{x-1}}$, we get
$$
\frac{2 t-24}{t-8} \geqslant 1 \Longleftrightarrow \frac{t-16}{t-8} \geqslant 0 \Longleftrightarrow t \in(-\infty ; 8) \cup[16 ;+\infty)
$$
From this, either $2^{1+\sqrt{x-1}}<2^{3}, \sqrt{x-1}<2, x \in[1 ; 5)$, or $2^{1+\sqrt{x-1}} \geqslant 2^{4}, \sqrt{x-1} \geqslant 3, x \in[10 ;+\infty)$. Therefore, the solution to the inequality is $x \in[1 ; 5) \cup(10 ;+\infty)$. The desired sum is
$$
1+2+3+4+(10+11+12+\ldots+33)=10+\frac{10+33}{2} \cdot 24=526
$$
Answer: 526. | 526 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
3. Inside a right triangle $ABC$ with hypotenuse $AC$, a point $M$ is taken such that the areas of triangles $ABM$ and $BCM$ are one-third and one-fourth of the area of triangle $ABC$, respectively. Find $BM$, if $AM=60$ and $CM=70$. If the answer is not an integer, round it to the nearest integer. | Solution. Denoting $A B=c, B C=a$, we get
$$
\left\{\begin{array}{l}
\left(c-\frac{c}{4}\right)^{2}+\left(\frac{a}{3}\right)^{2}=60^{2} \\
\left(\frac{c}{4}\right)^{2}+\left(a-\frac{a}{3}\right)^{2}=70^{2}
\end{array}\right.
$$
We solve the system and find $B M=\left(\frac{a}{3}\right)^{2}+\left(\frac{c}{4}\right)^{2}=\frac{100^{2}}{7}$. Therefore, $B M=\frac{100}{\sqrt{7}}$. We write the nearest integer in the answer.
Answer: 38. | 38 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. Find all $a$ for which the system
$$
\left\{\begin{array}{l}
x^{2}+4 y^{2}=1 \\
x+2 y=a
\end{array}\right.
$$
has a unique solution. If necessary, round it to two decimal places. If there are no solutions, put 0 in the answer. | Solution. Since $2 y=a-x$, from the first equation we get:
$$
x^{2}+(a-x)^{2}=1 \Longleftrightarrow 2 x^{2}-2 a x+a^{2}-1=0
$$
This equation has a unique solution when $\frac{D}{4}=2-a^{2}=0$. Therefore, $a= \pm \sqrt{2}$, and the smallest value is $-\sqrt{2} \approx-1.414214 \ldots$
Answer: $-1.41$.
I-A. The sum of 28218 natural numbers is $2016 \cdot 15$, and their product is $-\left(2016^{2}+15\right)$. Find all possible sets of such numbers. In the answer, indicate the sum of the largest and smallest numbers from all the found sets. If such numbers do not exist, then in the answer, indicate the number 0.
Solution. From the factorization $2016^{2}+15=3 \cdot 19 \cdot 113 \cdot 631$, we conclude that in the problem
$$
\left\{\begin{array}{l}
a_{1}+\ldots+a_{28218}=2016 \cdot 15 \\
a_{1} \cdot \ldots \cdot a_{28218}=2016^{2}+15=3 \cdot 19 \cdot 113 \cdot 631
\end{array}\right.
$$
the numbers $a_{k}$ not equal to 1 can be no more than 4 (i.e., no more than the number of prime factors), so the problem is equivalent to the following
$$
\left\{\begin{array}{l}
a_{1}+a_{2}+a_{3}+a_{4}=2026 \\
a_{1} \cdot a_{2} \cdot a_{3} \cdot a_{4}=3 \cdot 19 \cdot 113 \cdot 631 \\
a_{5}=a_{6}=\ldots=a_{28218}=1
\end{array}\right.
$$
We solve the last problem: The set $a_{1}, a_{2}, a_{3}, a_{4}$ consists of the numbers $1,19,113,3 \cdot 631$.
It remains to calculate $(3 \cdot 631)+1=1894$.
Answer: 1894. | 1894 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
9. The sum of 1265 natural numbers is $2016+33$, and their product is $-\left(2016^{2}+33\right)$. Find all possible sets of such numbers. In your answer, indicate the sum of the largest and smallest numbers from all the found sets. If such numbers do not exist, then in your answer, indicate the number 0.
Hint: $2016^{2}+33=3 \cdot 41 \cdot 173 \cdot 191$. | Answer 574.
II-A. Solve the equation
$$
(1+\cos x+\cos 2 x+\cos 3 x+\cos 4 x)^{4}+(\sin x+\sin 2 x+\sin 3 x+\sin 4 x)^{4}=\frac{3}{4}+\frac{\cos 8 x}{4}
$$
Find the sum of all roots on the interval $A$, rounding to the nearest integer if necessary. If there are no roots or infinitely many roots on this interval, write the digit 0 in the answer.
Solution. 1st method of solving. The following is true:
$$
\begin{aligned}
& (1+\cos 4 x)+(\cos x+\cos 3 x)+\cos 2 x=\cos 2 x(2 \cos 2 x+2 \cos 2 x+1) \\
& \sin 2 x+\sin 4 x+(\sin x+\sin 3 x)=\sin 2 x(1+2 \cos 2 x+2 \cos x)
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
& (2 \cos 2 x+2 \cos 2 x+1)^{4}\left(\cos ^{4} 2 x+\sin ^{4} 2 x\right)=\frac{3}{4}+\frac{1-2 \sin ^{2} 4 x}{4} \Longleftrightarrow \\
& \left(4 \cos ^{2} x+2 \cos x-1\right)^{4}\left(\cos ^{4} 2 x+\sin ^{4} 2 x\right)=1-\frac{\sin ^{2} 4 x}{2} \Longleftrightarrow \\
& \left(4 \cos ^{2} x+2 \cos x-1\right)^{4}\left(1-\frac{\sin ^{2} 4 x}{2}\right)=1-\frac{\sin ^{2} 4 x}{2} \Longleftrightarrow \\
& \left(4 \cos ^{2} x+2 \cos x-1\right)^{4}=1 \Longleftrightarrow \\
& 4 \cos ^{2} x+2 \cos x-1= \pm 1
\end{aligned}
$$
Solving the quadratic equations (in terms of the variable $\cos x$) $4 \cos ^{2} x+2 \cos x-2=0$ and $4 \cos ^{2} x+2 \cos x=0$, we arrive at $\cos x=1 / 2 ;-1 ; 0 ;-1 / 2$.
Answer: $x= \pm \frac{\pi}{3}+2 \pi n, x= \pm \frac{2 \pi}{3}+2 \pi n, x=\frac{\pi}{2}+\pi n, x=\pi+2 \pi n, n \in \mathbb{Z}$.
2nd method of solving. It is easy to see that there are no solutions on the set $x=2 \pi n, n \in \mathbb{Z}$. Consider all other values $x \in \mathbb{R}$. The equation is equivalent to:
$$
\begin{aligned}
& \left(\frac{\sin \frac{5 x}{2} \cos 2 x}{\sin \frac{x}{2}}\right)^{4}+\left(\frac{\sin \frac{5 x}{2} \sin 2 x}{\sin \frac{x}{2}}\right)^{4}=1-\frac{\sin ^{2} 4 x}{2} \Longleftrightarrow \\
& \left(\frac{\sin \frac{5 x}{2}}{\sin \frac{x}{2}}\right)^{4}\left(\cos ^{4} 2 x+\sin ^{4} 2 x\right)=1-\frac{\sin ^{2} 4 x}{2} \Longleftrightarrow \\
& \left(\frac{\sin \frac{5 x}{2}}{\sin \frac{x}{2}}\right)^{4}\left(1-\frac{\sin ^{2} 4 x}{2}\right)=1-\frac{\sin ^{2} 4 x}{2} \Longleftrightarrow \\
& \left(\frac{\sin \frac{5 x}{2}}{\sin \frac{x}{2}}\right)^{4}=1
\end{aligned}
$$
Solve the equation
$\sin \frac{5 x}{2}= \pm \sin \frac{x}{2} \Longleftrightarrow\left[\begin{array}{l}\frac{5 x}{2}= \pm \frac{x}{2}+2 \pi n, \\ \frac{5 x}{2}=\pi \pm \frac{x}{2}+2 \pi m,\end{array} \Longleftrightarrow\right.$
$$
\left[\begin{array} { l }
{ 3 x = 2 \pi n , } \\
{ 2 x = 2 \pi n , } \\
{ 3 x = \pi + 2 \pi n , } \\
{ 2 x = \pi + 2 \pi n }
\end{array} \Leftrightarrow \left[\begin{array}{l}
x=\frac{2 \pi n}{3} \\
x=\pi n \\
x=\frac{\pi}{3}+\frac{2 \pi n}{3} \\
x=\frac{\pi}{2}+\pi n
\end{array}\right.\right.
$$
The original equation on the set $x \neq 2 \pi n, n \in \mathbb{Z}$ is equivalent to
$$
\left[\begin{array}{l}
x=\frac{2 \pi m}{3}, m \in \mathbb{Z}, m \neq 3 s, s \in \mathbb{Z} \\
x=\frac{\pi}{3}+\frac{2 \pi n}{3}, n \in \mathbb{Z} \\
x=\frac{\pi}{2}+\pi n, n \in \mathbb{Z}
\end{array}\right.
$$
Answer: On the set $A=[2 \pi m ; 2 \pi m+\pi]$. Answer $\frac{5 \pi}{2}+8 \pi m, m \in \mathbb{Z}$. | 574 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
8. Equation:
$$
\cos \frac{a \pi x}{x^{2}+4}-\cos \frac{\pi\left(x^{2}-4 a x+4\right)}{4 x^{2}+16}=-\sqrt{2-\sqrt{2}}
$$
inequality $f(a) \leqslant 5$. Answer: $a \in\left[-\frac{21}{2} ; \frac{21}{2}\right]$, the length of the interval is 21.
V-A. Let $a_{n}$ be the number of permutations $\left(k_{1}, k_{2}, \ldots, k_{n}\right)$ of the numbers $(1,2, \ldots, n)$ such that the following two conditions are satisfied:
- $k_{1}=1 ;$
- For any index $i=1,2, \ldots, n-1$, the inequality $\left|k_{i}-k_{i+1}\right| \leqslant 2$ holds.
What is the number $a_{N}$? | Solution. We will prove in several steps:
Step 1. Prove that there is a recurrence relation: $a_{n}=a_{n-1}+a_{n-3}+1$. The following are the possible beginnings of permutations:
- In the sequence $(1,2, \ldots, n)$. Discard the first one, and decrease the remaining numbers by 1. What remains satisfies the conditions for permutations at $n-1$. Therefore, there are $a_{n-1}$ such permutations.
- In the sequence $(1,3,2,4, \ldots, n)$. Discard the first three terms of the permutation $(1,3,2)$. Decrease the remaining numbers by three. What remains satisfies the conditions for permutations at $n-3$. Therefore, there are $a_{n-3}$ such permutations.
- There is also one permutation of the form $(1,3,5,7, \ldots, 6,4,2)$. In the middle, there is a transition from the last odd number not exceeding $n$ to the last even number not exceeding $n$. Thus, we have
$$
a_{n}=a_{n-1}+a_{n-3}+1
$$
Step 2. Calculate the initial elements of the sequence
$$
\begin{aligned}
& a_{1}=1, \quad a_{2}=1, \quad a_{3}=2, \quad a_{4}=4, \quad a_{5}=6, \quad a_{6}=9, \quad a_{7}=14, \quad a_{8}=21, \quad a_{9}=31, \\
& a_{10}=46, \quad a_{11}=68, \quad a_{12}=100, \quad a_{13}=147, \quad a_{14}=216, \quad a_{15}=317, \\
& a_{16}=465, \quad a_{17}=682, \quad a_{18}=1000, \quad a_{19}=1466, \quad a_{20}=2149, \quad a_{21}=3150, \\
& a_{22}=4617, \quad a_{23}=6767, \quad a_{24}=9918, \quad a_{25}=14536, \quad a_{26}=21304, \quad a_{27}=31223, \\
& a_{28}=45760, \quad a_{29}=67065, \quad a_{30}=98289, \quad a_{31}=144050, \quad a_{32}=211116, \quad a_{33}=309406, \\
& a_{34}=453457, \quad a_{35}=664574, \quad a_{36}=973981, \quad a_{37}=1427439, \quad a_{38}=2092014, \\
& a_{39}=3065996, \quad a_{40}=4493436, \quad a_{41}=6585451, \quad a_{42}=9651448, \quad a_{43}=14144885, \\
& a_{44}=20730337, \quad a_{45}=30381786, \quad a_{46}=44526672, \quad a_{47}=65257010
\end{aligned}
$$
Answer: $a_{41}=6585451$. | 6585451 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
2. Ivan Semenovich leaves for work at the same time every day, drives at the same speed, and arrives exactly at 9:00. One day he overslept and left 40 minutes later than usual. To avoid being late, Ivan Semenovich drove at a speed 60% faster than usual and arrived at 8:35. By what percentage should he have increased his usual speed to arrive exactly at 9:00? | Answer: By $30 \%$.
Solution: By increasing the speed by $60 \%$, i.e., by 1.6 times, Ivan Semenovich reduced the time by 1.6 times and gained 40+25=65 minutes. Denoting the usual travel time as $T$, we get $\frac{T}{1.6}=T-65$, from which $T=\frac{520}{3}$. To arrive in $T-40=\frac{400}{3}$, the speed needed to be increased by $\frac{520}{3} \div \frac{400}{3}=1.3$ times, i.e., by $30 \%$. | 30 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. The English club is attended by 20 gentlemen. Some of them are acquainted (acquaintances are mutual, i.e., if A knows B, then B knows A). It is known that there are no three gentlemen in the club who are pairwise acquainted.
One day, the gentlemen came to the club, and each pair of acquaintances shook hands with each other (once). What is the maximum number of handshakes that could have been made? | Answer: 100 handshakes.
Solution: Choose a gentleman with the maximum number of acquaintances (if there are several, choose any one). Suppose he has $n$ acquaintances. These acquaintances cannot be pairwise acquainted with each other. Consider the remaining $(20-n-1)$ gentlemen, each of whom has no more than $n$ acquaintances, so the number of handshakes they make does not exceed $(20-n-1) \cdot n$. Therefore, the total number does not exceed $(20-n) \cdot n$. This number is maximal when $n=10$. It can be shown that 100 handshakes are possible - by dividing the gentlemen into 2 groups of 10 people each and ensuring that each person in the first group is acquainted with each person in the second (while there are no acquaintances within the groups). | 100 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Ms. Olga Ivanovna, the class teacher of 5B, is staging a "Mathematical Ballet." She wants to arrange the boys and girls so that there are exactly 2 boys 5 meters away from each girl. What is the maximum number of girls that can participate in the ballet, given that 5 boys are participating? | Answer: 20 girls.
Solution: Let's select and fix two arbitrary boys - $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$. Suppose they are 5 m away from some girl - G. Then $\mathrm{M}_{1}, \mathrm{M}_{2}$, and G form an isosceles triangle with the legs being 5 m. Given the fixed positions of $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$, there can be no more than two such triangles (a diagram would be helpful here!). Therefore, for any pair of boys, there can be no more than two girls. The total number of pairs of boys is $C_{5}^{2}=10$, from which we obtain the upper bound.
It is not difficult to show that this bound is achievable - simply by placing the boys in a row with an interval of 1 m and constructing all possible isosceles triangles (their vertices will obviously be different). | 20 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
7. Given a polynomial $P(x)$, not identically zero. It is known that for all $x$ the identity $(x-2020) \cdot P(x+1)=(x+2021) \cdot P(x)$ holds. How many roots does the equation $P(x)=0$ have? Answer: 4042 | Solution:
First, we prove two auxiliary lemmas:
Lemma 1. If $x_{0} \neq 2020$ is a root of $P(x)$, then $x_{0}+1$ is also a root.
Proof: Substitute $\left(x_{0}-2020\right) \cdot P\left(x_{0}+1\right)=\left(x_{0}+2021\right) \cdot P\left(x_{0}\right)=0$ but $\left(x_{0}-2020\right) \neq 0$.
Lemma 2. If $x_{0} \neq -2021$ is a root of $P(x)$, then $x_{0}-1$ is also a root.
Proof: Substitute $0=\left(x_{0}-2020\right) \cdot P\left(x_{0}+1\right)=\left(x_{0}+2021\right) \cdot P\left(x_{0}\right)$ but $\left(x_{0}+2021\right) \neq 0$.
Substitute $x=2020$ into the identity, we get $0=4041 P(2020)$, hence 2020 is a root.
By sequentially applying Lemma 2, we obtain that $x=2019, 2018, \ldots, -2021$ are roots.
We will now prove that there are no other roots.
1) Suppose that the root $x_{0}$ is not an integer, then by Lemma 1, $x_{0}+1, x_{0}+2, \ldots, x_{0}+n, \ldots$ are also roots. But a polynomial (not identically zero) cannot have infinitely many roots - contradiction.
2) Suppose that $x_{0}$ is an integer and does not belong to the interval $[-2021 ; 2020]$. If $x_{0}>2020$, then (by Lemma 1) $x_{0}+1, x_{0}+2, \ldots, x_{0}+n, \ldots$ are also roots. If $x_{0}<-2021$, then (by Lemma 2) $x_{0}-1, x_{0}-2, \ldots, x_{0}-n, \ldots$ are also roots. In either case, a non-zero polynomial cannot have infinitely many roots - contradiction.
Thus, the roots are the integers from -2021 to 2020 inclusive, their number is 4042. | 4042 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. 2-1. Find the minimum value of the function
$$
f(x)=x^{2}+(x-2)^{2}+(x-4)^{2}+\ldots+(x-100)^{2}
$$
If the result is a non-integer, round it to the nearest integer and write it as the answer. | Solution. Knowledge of arithmetic progression is required. It turns out to be a quadratic function
$f(x)=51 x^{2}-2(2+4+6+\ldots+100) x+(2^{2}+4^{2}+6^{2}+\ldots+100^{2})=51 x^{2}-2 \cdot 50 \cdot 51 x+4 \cdot(1^{2}+2^{2}+3^{2}+\ldots+50^{2})$.
The minimum is achieved at the point $x_{0}=50$. In this case,
$f(50)=50^{2}+48^{2}+46^{2}+\ldots+2^{2}+0^{2}+2^{2}+4^{2}+\ldots+50^{2}=2 \cdot(2^{2}+4^{2}+\ldots+50^{2})=8 \cdot(1^{2}+2^{2}+3^{2}+\ldots+25^{2})$.
Now we need the formula
$$
1^{2}+2^{2}+3^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}
$$
(it is known, but in principle, it can be derived). Then $f(50)=8 \cdot \frac{25 \cdot 26 \cdot 51}{6}=17 \cdot 26 \cdot 100=44200$.
Answer: $44'200$. | 44200 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2-2. Find the minimum value of the function
$$
f(x)=x^{2}+(x-2)^{2}+(x-4)^{2}+\ldots+(x-102)^{2}
$$
If the result is a non-integer, round it to the nearest integer and write it as the answer. | Solution. $f(x)=52 x^{2}-2(2+4+\ldots+102) x+2^{2}+4^{2}+\ldots+102^{2}=52 x^{2}-2 \cdot 51 \cdot 52 x+4\left(1^{2}+2^{2}+3^{2}+\ldots+51^{2}\right)$.
The minimum of the function $f$ is achieved at the point $x_{0}=51 . f(51)=51^{2}+49^{2}+\ldots 1^{2}+1^{2}+3^{2}+\ldots+49^{2}+51^{2}=$ $2\left(1^{2}+3^{2}+\ldots 51^{2}\right)$. Since $1^{2}+3^{2}+\ldots+(2 n-1)^{2}=\frac{n\left(4 n^{2}-1\right)}{3}$ (a less well-known formula, but it can also be derived), then $f(51)=\frac{26\left(52^{2}-1\right)}{3}=46852$.
Answer: 46852 . | 46852 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2-3. Find the minimum value of the function
$$
f(x)=(x-1)^{2}+(x-3)^{2}+\ldots+(x-101)^{2}
$$
If the result is a non-integer, round it to the nearest integer and write it in the answer. | Solution. $f(x)=51 x^{2}-2(1+3+\ldots+101) x+\left(1^{2}+3^{2}+\ldots+101^{2}\right)=51 x^{2}-2 \cdot 51^{2} x+\left(1^{2}+3^{2}+\ldots+101^{2}\right)$.
The minimum of the function $f$ is achieved at the point $x_{0}=51$. Since $1^{2}+3^{2}+\ldots+(2 n-1)^{2}=\frac{n\left(4 n^{2}-1\right)}{3}$, then $f(51)=51^{3}-2 \cdot 51^{3}+51^{3}+\frac{51^{3}}{3}-\frac{51}{3}=\frac{51^{3}}{3}-\frac{51}{3}=44200$.
Answer: 44200. | 44200 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2-4. Find the minimum value of the function
$$
f(x)=x^{2}+(x-2)^{2}+(x-4)^{2}+\ldots+(x-104)^{2}
$$
If the result is a non-integer, round it to the nearest integer and write it in the answer. | Solution. $f(x)=53 x^{2}-2(2+4+\ldots 104) x+4\left(1^{2}+2^{2}+\ldots+52^{2}\right)=53 x^{2}-2 \cdot 52 \cdot 53 x+4 \cdot \frac{52 \cdot 53 \cdot 105}{6}$ (since $\left.1^{2}+2^{2}+3^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}\right)$.
The minimum of the function $f$ is achieved at the point $x_{0}=52 . f(52)=53 \cdot 52^{2}-2 \cdot 53 \cdot 52^{2}+2 \cdot 52 \cdot 53 \cdot 35=$ $52 \cdot 53(70-52)=49608$.
Answer: 49608 | 49608 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. Determine how many roots of the equation
$$
4 \sin 2 x + 3 \cos 2 x - 2 \sin x - 4 \cos x + 1 = 0
$$
are located on the interval $\left[10^{2014!} \pi ; 10^{2014!+2015} \pi\right]$. In your answer, write the sum of all digits of the found number. | Solution. Let $t=\sin x+2 \cos x$. Then $t^{2}=\sin ^{2} x+2 \sin 2 x+4 \cos ^{2} x=2 \sin 2 x+\frac{3}{2} \cos 2 x+\frac{5}{2}$. The original equation is equivalent to $t^{2}-t-2=0$. From which
$$
\left[\begin{array}{c}
\operatorname{sin} x + 2 \operatorname{cos} x = -1, \\
\operatorname{sin} x + 2 \operatorname{cos} x = 2
\end{array} \Longleftrightarrow \left[\begin{array}{c}
\sin (x+\varphi)=-\frac{1}{\sqrt{5}} \\
\sin (x+\varphi)=\frac{2}{\sqrt{5}}
\end{array}\right.\right.
$$
where $\varphi=\operatorname{arctg} 2$. Therefore, the original equation has exactly four roots on any interval of the form $[2 k \pi ; 2(k+1) \pi], k \in \mathbb{Z}$. Let the number of roots be denoted by $N$. Since there are four different roots in one period (the minimum period of the functions involved in the equation is $2 \pi$), then
$$
\begin{aligned}
& N=4 \cdot \frac{10^{2014!+2015} \pi-10^{2014!} \pi}{2 \pi}=2 \cdot 10^{2014!}\left(10^{2015}-1\right)= \\
&=2 \cdot 10^{2014!} \cdot \underbrace{9 \ldots 9}_{2015}=1 \underbrace{9 \ldots 9}_{2014} 8 \cdot 10^{2014!}=1 \underbrace{9 \ldots 9}_{2014} 8 \underbrace{0 \ldots 0}_{2014!}
\end{aligned}
$$
The sum of all digits of this number is $1+8+9 \cdot 2014=9 \cdot 2015=18135$.
## Answer: 18135 | 18135 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Task 4. Find the smallest natural $m$, for which there exists such a natural $n$ that the sets of the last 2014 digits in the decimal representation of the numbers $a=2015^{3 m+1}$ and $b=2015^{6 n+2}$ are the same, and $a<b$. | Solution. The coincidence of the last 2014 digits of the two specified powers means divisibility by \(10^{2014}\) of the difference
\[
2015^{6 n+2}-2015^{3 m+1}=2015^{3 m+1} \cdot\left(2015^{6 n-3 m+1}-1\right)
\]
since the first factor in the obtained decomposition is not divisible by 2, and the second is not divisible by 5, the divisibility of the obtained product by \(10^{2014}\) means two divisibilities at once
\[
2015^{3 m+1} \vdots 5^{2014}, \quad 2015^{6 n-3 m+1}-1 \vdots 2^{2014}
\]
The first divisibility means the inequality \(3 m+1 \geqslant 2014\), or \(m \geqslant m_{0}=671\). Let's check that the number \(m=m_{0}\) is realizable, i.e., for it, for some \(n=n_{0}\), the second divisibility also holds.
Indeed, let \(N=2^{2014}\) and note that for the odd \(K=2015\), the number
\[
K^{N}-1=\left(K^{N / 2}+1\right)\left(K^{N / 2}-1\right)=\ldots=\left(K^{N / 2}+1\right)\left(K^{N / 4}+1\right) \ldots\left(K^{1}+1\right)\left(K^{1}-1\right)
\]
is divisible by \(N\) (in the last representation of this number, all expressions in parentheses are even, and the number of parentheses is 2014). Therefore, \(\left(2015^{N}-1\right) \vdots 2^{2014}\), and the equality \(6 n_{0}-3 m_{0}+1=N\) holds for
\[
n_{0}=\left(\frac{N-1}{3}+m_{0}\right) / 2
\]
where \(n_{0} \in \mathbb{N}\), since the number
\[
N-1=2^{2014}-1=(3-1)^{2014}-1
\]
is divisible by three, and the quotient \((N-1) / 3\) is odd.
Answer: \(m=671\). | 671 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
8. In a trapezoid, the diagonals intersect at a right angle, and one of them is equal to the midline. Determine the angle this diagonal forms with the bases of the trapezoid. | Answer: $60^{\circ}$.
Solution: We perform a parallel translation of the diagonal - we will get a right triangle, in which the leg is half the hypotenuse. | 60 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. In the wallet of the merchant Hans, there are 20 silver coins worth 2 crowns each, 15 silver coins worth 3 crowns each, and 3 gold ducats (1 ducat equals 5 crowns). In how many ways can Hans pay a sum of 10 ducats? Coins of the same denomination are indistinguishable. | Answer: 26
Solution. If the merchant paid $x$ coins at 2 crowns each, $y$ coins at 3 crowns each, and $z$ ducats (i.e., $z$ times 5 crowns), we get the system: $2 x+3 y+5 z=50, x \in[0 ; 20], y \in[0 ; 15], z \in[0 ; 3]$.
a) When $z=0$, we get the equation $2 x+3 y=50$, which has suitable solutions under the condition for $y=4,6,8,10,12,14$ - a total of 6 solutions.
b) When $z=1$, we get the equation $2 x+3 y=45$, which has suitable solutions under the condition for $x=0,3,6,9,12,15,18$ - a total of 7 solutions.
When $z=2$, there are 7 solutions, and when $z=3$, there are 6 solutions. These two cases could be analyzed similarly to the previous one. However, this is not necessary, using the fact that the amount to be paid is exactly half of all the merchant's money. Therefore, the number of ways using 2 ducats is equal to the number of ways using 1 ducat (since 2 ducats will remain in the wallet); similarly, the number of ways using 3 ducats is equal to the number of ways without ducats.
Thus, the total number of ways: $6+7+7+6=26$.
Answer to variant 172: 17 ways.
Answer to variant 173: 26 ways.
Answer to variant 174: 22 ways. | 26 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
1. According to the condition, these numbers are written only with the digits $0,1,2,6,8$. Then, three-digit numbers that are multiples of 4 can end with exactly 10 variants: $00,08,12,16,20,28,60,68,80,88$. In each of these 10 variants, the first place can be occupied by any of the 4 digits $1,2,6,8$. Additionally, the last 8 variants give two-digit numbers, and the second one gives a single-digit number. Therefore, the total number of such numbers is: $10 \cdot 4+8+1=49$. | # Answer: 49.
Answer to option: 1-2: 53.
## Solutions for option 1-2.
According to the condition, these numbers are written only with the digits $0,2,3,4,5,7$. Then, three-digit numbers that are multiples of 4 can end with exactly 9 variants: $00,04,20,24,32,40,44,52,72$. In this case, the first place in each of these 9 variants can be occupied by any of the 5 digits $2,3,4,5,7$. Additionally, the last 7 variants give two-digit numbers, and the second one gives a single-digit number. Therefore, the total number of such numbers is: $9 \cdot 5 + 7 + 1 = 53$. | 49 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
3. A parallelepiped is inscribed in a sphere of radius $\sqrt{3}$, and the volume of the parallelepiped is 8. Find the surface area of the parallelepiped. | 3. $S_{\text {full }}=24$
The translation is provided while maintaining the original text's formatting and structure. | 24 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
6. Ms. Olga Ivanovna, the class teacher of 5B, is staging a "Mathematical Ballet." She wants to arrange the boys and girls so that exactly 2 boys are 5 meters away from each girl. What is the maximum number of girls that can participate in the ballet if it is known that 5 boys are participating? | Answer: 20 girls.
Solution: Let's select and fix two arbitrary boys - $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$. Suppose they are 5 m away from some girl - G. Then $\mathrm{M}_{1}, \mathrm{M}_{2}$, and G form an isosceles triangle with the legs being 5 m. Given the fixed positions of $\mathrm{M}_{1}$ and $\mathrm{M}_{2}$, there can be no more than two such triangles (a diagram would be helpful here!). Therefore, for any pair of boys, there can be no more than two girls. The total number of pairs of boys is $C_{5}^{2}=10$, from which we obtain the upper bound.
It is not difficult to show that this bound is achievable - simply by placing the boys in a row with an interval of 1 m and constructing all possible isosceles triangles (their vertices will obviously be different). | 20 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
1.2 Mishа noticed that the tram passed by him in 4 seconds, and a tunnel 64 meters long in 12 seconds. Find the length of the tram (in meters), assuming that its speed remains constant throughout the entire observation period. | Answer: 32. (E)
 | 32 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2.1 Find $f(2013)$, if for any real $x$ and $y$ the equality holds
$$
f(x-y)=f(x)+f(y)-2xy
$$ | Solution. Substitute $x=y=0$. We get $f(0)=2 f(0)+0$, from which we obtain that $f(0)=0$. Substitute $x=y$. We get $0=f(0)=f(x)+f(x)-2 x^{2}$. Hence, $f(x)=x^{2}$.
Answer: 4052169. (C)
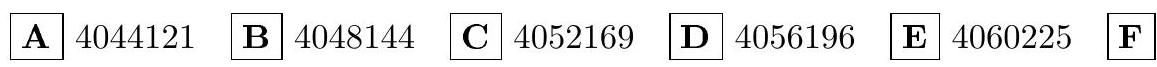 | 4052169 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3-1. Calculate the sum
$$
S=\frac{2014}{2 \cdot 5}+\frac{2014}{5 \cdot 8}+\frac{2014}{8 \cdot 11}+\ldots+\frac{2014}{2012 \cdot 2015}
$$
In your answer, specify the remainder from dividing by 5 the even number closest to the obtained value of $S$. | Solution. Since
$$
\begin{aligned}
& \frac{1}{2 \cdot 5}+\frac{1}{5 \cdot 8}+\frac{1}{8 \cdot 11}+\ldots+\frac{1}{2012 \cdot 2015}= \\
& =\frac{1}{3} \cdot\left(\left(\frac{1}{2}-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{8}\right)+\left(\frac{1}{8}-\frac{1}{11}\right)+\ldots\left(\frac{1}{2012}-\frac{1}{2015}\right)\right)= \\
& \quad=\frac{1}{3} \cdot\left(\frac{1}{2}-\frac{1}{2015}\right)=\frac{1}{6} \cdot \frac{2013}{2015}
\end{aligned}
$$
the desired sum is
$$
\frac{2014 \cdot 2013}{6 \cdot 2015}=335.33 \ldots
$$
The desired natural number is 336.
Answer: 1. (V)
Options.
 | 336 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4-2. A circle touches the sides of an angle at points $A$ and $B$. The distance from a point $C$ lying on the circle to the line $A B$ is 6. Find the sum of the distances from point $C$ to the sides of the angle, given that one of these distances is 5 more than the other. | Answer: 13. (C)
Options.
 | 13 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4-3. A circle touches the sides of an angle at points $A$ and $B$. The distance from a point $C$ lying on the circle to the line $A B$ is 6. Find the sum of the distances from point $C$ to the sides of the angle, given that one of these distances is nine times smaller than the other. | Answer: 20. (E)
Answer options.
 | 20 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4-4. A circle touches the sides of an angle at points $A$ and $B$. The distance from a point $C$ lying on the circle to the line $A B$ is 8. Find the sum of the distances from point $C$ to the sides of the angle, given that one of these distances is 30 less than the other. | Answer: 34. (B)
Answer options.
 | 34 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
6-2. From three mathematicians and ten economists, a committee of seven people needs to be formed. At the same time, the committee must include at least one mathematician. In how many ways can the committee be formed? | Solution. Direct calculation gives: $C_{13}^{7}-C_{10}^{7}=1596$.
Answer: 1596. | 1596 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6-3. From twelve students and three teachers, a school committee consisting of nine people needs to be formed. At the same time, at least one teacher must be included in it. In how many ways can the committee be formed? | Solution. Direct calculation gives: $C_{15}^{9}-C_{12}^{9}=4785$.
Answer: 4785. | 4785 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
6-4. From eleven students and three teachers, a school committee consisting of eight people needs to be formed. At the same time, at least one teacher must be included in it. In how many ways can the committee be formed? | Solution. Direct calculation gives: $C_{14}^{8}-C_{11}^{8}=2838$.
Answer: 2838. | 2838 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
10-1. At the base of the pyramid $S A B C D$ lies a trapezoid $A B C D$ with bases $B C$ and $A D$. Points $P_{1}$, $P_{2}, P_{3}$ belong to the side $B C$, such that $B P_{1}<B P_{2}<B P_{3}<B C$. Points $Q_{1}, Q_{2}, Q_{3}$ belong to the side $A D$, such that $A Q_{1}<A Q_{2}<A Q_{3}<A D$. Denote the points of intersection of $B Q_{1}$ with $A P_{1}$, $P_{2} Q_{1}$ with $P_{1} Q_{2}$, $P_{3} Q_{2}$ with $P_{2} Q_{3}$, and $C Q_{3}$ with $P_{3} D$ as $R_{1}, R_{2}, R_{3}$, and $R_{4}$, respectively. It is known that the sum of the volumes of the pyramids $S R_{1} P_{1} R_{2} Q_{1}$ and $S R_{3} P_{3} R_{4} Q_{3}$ is 78. Find the minimum value of the quantity
$$
V_{S A B R_{1}}^{2}+V_{S R_{2} P_{2} R_{3} Q_{2}}^{2}+V_{S C D R_{4}}^{2}
$$
In your answer, specify the integer closest to the found value. | Solution. From the properties of the trapezoid, it follows that the triangles (see Fig. 2), shaded with the same color, have the same area. From this, the equality of the sums of the areas marked
Fig. 2:
with the same color on Fig. 3 follows. The equality of the sums of the areas takes the form
$$
S_{A B R_{1}}+S_{R_{2} P_{2} R_{3} Q_{2}}+S_{C D R_{4}}=S_{R_{1} P_{1} R_{2} Q_{1}}+S_{R_{3} P_{3} R_{4} Q_{3}}
$$
Fig. 3:
From which
$$
V_{S A B R_{1}}+V_{S R_{2} P_{2} R_{3} Q_{2}}+V_{S C D R_{4}}=V_{S R_{1} P_{1} R_{2} Q_{1}}+V_{S R_{3} P_{3} R_{4} Q_{3}}=78
$$
Let $a_{1}=V_{S A B R_{1}}, a_{2}=V_{S R_{2} P_{2} R_{3} Q_{2}}, a_{3}=V_{S C D R_{4}}$. From the problem statement: $a_{1}+a_{2}+a_{3}=78$, and we need to find $a_{1}^{2}+a_{2}^{2}+a_{3}^{2} \rightarrow \min$, under the condition that $a_{1}, a_{2}, a_{3}$ are non-negative. The inequality holds
$$
\left(\frac{a_{1}}{3}+\frac{a_{2}}{3}+\frac{a_{3}}{3}\right)^{2} \leqslant \frac{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}{3}
$$
For school students, this inequality is justified by applying the inequality $2 a b \leqslant a^{2}+b^{2}$ three times. We obtain
$$
a_{1}^{2}+a_{2}^{2}+a_{3}^{2} \geqslant \frac{\left(a_{1}+a_{2}+a_{3}\right)^{2}}{3}=2028
$$
Equality is achieved when $a_{1}=a_{2}=a_{3}=26$.
Answer: 2028. | 2028 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. Let $\Sigma(n)$ denote the sum of the digits of the number $n$. Find the smallest three-digit $n$ such that $\Sigma(n)=\Sigma(2 n)=\Sigma(3 n)=\ldots=\Sigma\left(n^{2}\right)$ | Answer: 999.
Solution: Let the desired number be $\overline{a b c}$. Note that this number is not less than 101 (since 100 does not work). Therefore, $101 \cdot \overline{a b c}=\overline{a b c 00}+\overline{a b c}$ also has the same sum of digits. But the last digits of this number are obviously $b$ and $c$, so the sum of the remaining digits must be equal to $a$. Therefore, $\Sigma(\overline{a b c}+a)=a$. If $a<9$, then $\overline{a b c}+a-$ is a three-digit number, the first digit of which is not less than $a$, which leads to a contradiction, since the second and third digits cannot be zeros. Thus, $a=9$ and $\overline{a b c}+a \leqslant 999+9=1008$. Therefore, $\overline{a b c}+a=\overline{100 d}$. But $\Sigma(\overline{100 d})=a=9$, so $d=8$, from which $\overline{a b c}=999$. | 999 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. The test consists of 5 sections, each containing the same number of questions. Pavel answered 32 questions correctly. The percentage of his correct answers turned out to be more than 70 but less than 77. How many questions were in the test?
ANSWER: 45. | Solution: from the condition $0.7<32 / x<0.77$ it follows that $41<x<46$, but $x$ is a multiple of 5, so $x=45$. | 45 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. How many five-digit numbers of the form $\overline{a b 16 c}$ are divisible by 16? ( $a, b, c-$ are arbitrary digits, not necessarily different).
ANSWER: 90. | Solution: Note that the first digit does not affect divisibility, hence $a=1, \ldots, 9$. On the other hand, divisibility by 8 implies that $c=0$ or 8. If $c=0$, then $\mathrm{b}$ must be even, and if $\mathrm{c}=8$ - odd. In both cases, we get 5 options, from which the total number is $9 *(5+5)=90$.
Lomonosov Moscow State University
## School Olympiad "Conquer Vorobyovy Gory" in Mathematics
Final stage tasks for the 2015/2016 academic year for 7-8 grades | 90 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Philatelist Andrey decided to distribute all his stamps equally into 3 envelopes, but it turned out that one stamp was extra. When he distributed them equally into 5 envelopes, 3 stamps were extra; finally, when he distributed them equally into 7 envelopes, 5 stamps remained. How many stamps does Andrey have in total, if it is known that recently he bought an additional album for them, which can hold 150 stamps, as such an old album was no longer sufficient?
ANSWER 208. | Solution. If the desired number is $x$, then the number $x+2$ must be divisible by 3, 5, and 7, i.e., it has the form $3 \cdot 5 \cdot 7 \cdot p$. Therefore, $x=105 p-2$. Since by the condition $150<x \leq 300$, then $p=2$. Therefore, $x=208$. | 208 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. Find the smallest natural number $N$ such that the number $99 N$ consists only of threes.
ANSWER: 3367. | Solution. The number 33N must consist of all ones. A number is divisible by 33 if it is divisible by 3 and by 11. A number consisting of all ones is divisible by 3 if the number of ones is a multiple of 3, and it is divisible by 11 if the number of ones is a multiple of 2. The smallest such number is 111111, so 33N = 111111, from which \( N=3367 \).
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final Round Tasks for 2015/2016 Academic Year for 7-8 Grades | 3367 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
12. (9) On a plane, there are 9 points arranged in a $3 \times 3$ grid, as shown in the figure.

a) Lines are drawn through all possible pairs of points. How many different lines are obtained?
b) How many different triangles exist with vertices at these points? | Answer: a) 20 ; b) 76.
Solution: a) The number of pairs of points will be $C_{9}^{2}=36$, but lines coincide when three points lie on the same line. There are $8=3$ horizontals +3 verticals +2 diagonals such cases. Therefore, subtract $36-8 \times 2=20$.
b) The number of triplets of points is $C_{9}^{3}=84$, but not all form a triangle, i.e., we need to subtract 8 triplets lying on the same line. $84-8=76$. | 20 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Subsets and Splits
No saved queries yet
Save your SQL queries to embed, download, and access them later. Queries will appear here once saved.