problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. (17 points) In triangle $A B C$, a point $N$ is taken on side $A C$ such that $A N=N C$. Side $A B$ is twice as long as $B N$, and the angle between $A B$ and $B N$ is $50^{\circ}$. Find the angle $A B C$. | Answer: 115.
Solution. Complete triangle $A B C$ to parallelogram $A B C D$.
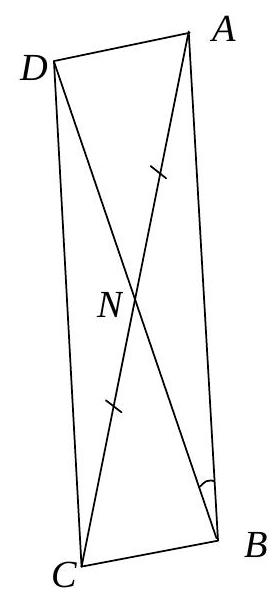
Then, $D B=2 N B=A B$. Therefore, triangle $A B D$ is isosceles and $\angle A D B=\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$. $\angle A D B=\angle D B A$ (alternate interior angles when lines are parallel). In the end, we get $\angle A B C=\angle A B D+\angle D B C=50^{\circ}+65^{\circ}=115^{\circ}$. | 115 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. (20 points) Determine the angle between the hour and minute hands at the moment when they show 13 hours and 20 minutes. | Answer: $80^{\circ}$.
Solution. The minute hand has moved away from twelve by $\frac{20}{60} \cdot 360=120^{0}$. The hour hand has moved away from twelve by $\frac{1}{12} \cdot 360+\frac{20}{60} \cdot \frac{1}{12} \cdot 360=40^{\circ}$. The angle between the hands $120^{\circ}-40^{\circ}=80^{\circ}$. | 80 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. (17 points) Given a rectangle $A B C D$. On two sides of the rectangle, different points are chosen, six points on $A B$ and seven - on $B C$. How many different triangles exist with vertices at the chosen points? | Answer: 231.
Solution. To form a triangle, one needs to choose two points on one side and one point on another. There are 6 ways to choose the first point on $AB$, 5 ways to choose the second, and since the triangle does not change with the permutation of its vertices, we divide $6 \cdot 5$ by 2. Thus, $\frac{6 \cdot 5}{2}=15$ ways to choose two points on side $AB$, and 7 ways on side $BC$. In total, $15 \cdot 7=105$ ways. Similarly, $\frac{7 \cdot 6}{2}=21$ ways to choose two points on side $BC$ and 6 ways to choose one point on side $AB$. In total, $21 \cdot 6=126$ ways. Therefore, there are 231 different triangles with vertices in the chosen points. | 231 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) In triangle $A B C$, a point $N$ is taken on side $A C$ such that $A N=N C$. Side $A B$ is twice as long as $B N$, and the angle between $A B$ and $B N$ is $40^{\circ}$. Find the angle $A B C$. | Answer: 110.
## Solution.
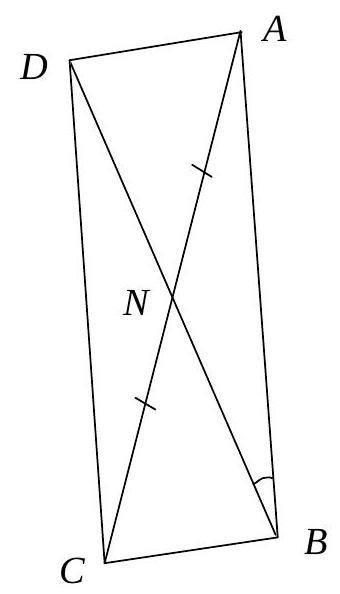
Extend triangle $ABC$ to parallelogram $ABCD$. Then, $DB=2NB=AB$. Therefore, triangle $ABD$ is isosceles and $\angle ADB=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$. $\angle ADB=\angle DBA$ (alternate interior angles when lines are parallel). In the end, we get $\angle ABC=\angle ABD+\angle DBC=40^{\circ}+70^{\circ}=110^{\circ}$. | 110 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. (20 points) Determine the angle between the hour and minute hands at the moment when they show 15 hours and 40 minutes. | Answer: $130^{\circ}$.
Solution. The minute hand has moved away from twelve by $\frac{40}{60} \cdot 360=240^{\circ}$. The hour hand has moved away from twelve by $\frac{3}{12} \cdot 360+\frac{40}{60} \cdot \frac{1}{12} \cdot 360=110^{\circ}$. The angle between the hands: $240^{\circ}-110^{\circ}=130^{\circ}$. | 130 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
1. (17 points) Masha's tablet, which she needed for a presentation at school, was completely drained. Using additional equipment, the tablet can be fully charged in 2 hours and 40 minutes, without it in 8 hours. Masha first put the discharged tablet on regular charging, and when she found the equipment, she switched to fast charging and fully charged the tablet. It is known that the tablet charges uniformly both with fast and regular charging. Find the total charging time of the tablet, if it was on fast charging for a third of the total charging time. Give your answer in minutes. | Answer: 288.
Solution. The tablet charges in 160 minutes on fast charging, and in 480 minutes on regular charging. Therefore, on fast charging, $\frac{1}{160}$ of the full charge is completed in 1 minute, and on regular charging, $\frac{1}{480}$ of the full charge is completed in 1 minute. Let $t-$ be the total charging time, then $\frac{t}{3} \cdot \frac{1}{160}+\frac{2 t}{3} \cdot \frac{1}{480}=1$ or $t \cdot \frac{5}{3 \cdot 480}=1$.
We get that $t=\frac{1440}{5}=288$. | 288 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. (17 points) There are ten weights of different weights, each weighing an integer number of grams. It is known that the weight of the lightest and heaviest weight differs by 9 grams. One weight is lost. Find its weight if the total weight of the remaining weights is 2022 grams. | Answer: 223.
Solution. Let $x$ be the weight of the lightest weight. Denote the weight of the lost weight as $(x+y)$ $(0<y<9)$. Then $x+(x+1)+(x+2)+\cdots+(x+$ $9)-(x+y)=2022$. Combine like terms: $10 x+45-x-y=$ 2022 or $9 x=1977+y$. From this, $1977+y$ is divisible by 9. Considering the condition $0<y<9$, we get that $y=3$. Therefore, $x=1980: 9=220$, $x+y=223$. | 223 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. (16 points) In a garden plot, it was decided to create a rectangular flower bed. Due to a lack of space, the length of the flower bed was reduced by $10 \%$, and the width was reduced by $20 \%$. As a result, the perimeter of the flower bed decreased by $12 \%$. However, this was not enough, so it was decided to reduce the length by $20 \%$ and the width by $10 \%$. By what percentage did the perimeter of the rectangular flower bed decrease from the original version? | Answer: 18.
Solution. Let $x$ be the length of the flower bed, $y$ be the width of the flower bed. After the reduction: $0.9 x$ - length of the flower bed, $0.8 y$ - width of the flower bed, $2(0.9 x + 0.8 y)$ - perimeter. We get the equation: $2(0.9 x + 0.8 y) = 0.88 \cdot 2(x + y)$ or $x = 4 y$. The original perimeter: $10 y$. After the second reduction: $0.8 x = 3.2 y$ - length of the flower bed, $0.9 y$ - width of the flower bed, $2(3.2 y + 0.9 y) = 8.2 y$ - perimeter. The perimeter decreased by $1.8 y$ or by $18\%$. | 18 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. (15 points) A one-and-a-half kilogram model of a sports car body was made from carbon fiber for aerodynamic studies at a scale of 1:10. What is the mass of the actual body if it is also entirely made of carbon fiber? | Answer: 1500 kg.
Solution. All dimensions of the body are 10 times larger compared to the model. Therefore, the volume of the body is larger by $10 \cdot 10 \cdot 10=1000$ times. Mass is directly proportional to volume, therefore, the mass of the body:
$$
m_{\text {body }}=1000 \cdot m_{\text {model }}=1500 \text { kg. }
$$ | 1500 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. (20 points) A car traveled half of the distance at a speed 20 km/h faster than the average speed, and the second half of the distance at a speed 20% lower than the average. Determine the average speed of the car. | Answer: 60 km/h.
Solution. The average speed $v=\frac{s+s}{t_{1}+t_{2}}=\frac{s+s}{\frac{s}{v+20}+\frac{s}{0.8 v}}=\frac{2}{\frac{1}{v+20}+\frac{1}{0.8 v}}$. Solving this equation, we get $v=60$ km/h. | 60 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. (17 points) Masha's tablet, which she needed for a presentation at school, was completely drained. Using additional equipment, the tablet can be fully charged in 3 hours, without it in 9 hours. Masha first put the discharged tablet on regular charging, and when she found the equipment, she switched to fast charging and fully charged the tablet. It is known that the tablet charges uniformly both with fast and regular charging. Find the total charging time of the tablet if it was on fast charging for one third of the total charging time. Give your answer in minutes. | Answer: 324.
Solution. The tablet charges in 180 minutes on fast charging, and in 540 minutes on regular charging. Therefore, on fast charging, $\frac{1}{180}$ of the full charge is completed in 1 minute, and on regular charging, $\frac{1}{540}$ of the full charge is completed in 1 minute. Let $t$ be the total charging time, then $\frac{t}{3} \cdot \frac{1}{180}+\frac{2 t}{3} \cdot \frac{1}{540}=1$ or $t \cdot \frac{5}{3 \cdot 540}=1$. We get that $t=\frac{1620}{5}=324$. | 324 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. (17 points) There are ten weights of different weights, each weighing an integer number of grams. It is known that the weight of the lightest weight and the heaviest differs by 9 grams. One weight is lost. Find the weight of the lightest weight if the total weight of the remaining weights is 2022 grams.
# | # Answer: 220.
Solution. Let $x$ be the weight of the lightest weight. Denote the weight of the lost weight as $(x+y)$ $(0<y<9)$. Then $x+(x+1)+(x+2)+\cdots+(x+$ 9) - $(x+y)=2022$. Combine like terms: $10 x+45-x-y=$ 2022 or $9 x=1977+y$. From this, $1977+y$ is divisible by 9. Considering the condition $0<y<9$, we get that $y=3$. Therefore, $x=1980: 9=220$. | 220 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. (16 points) In a garden plot, it was decided to create a rectangular flower bed. Due to a lack of space, the length of the flower bed was reduced by $10 \%$, and the width was reduced by $20 \%$. As a result, the perimeter of the flower bed decreased by $12.5 \%$. However, this was not enough, so it was decided to reduce the length by $20 \%$ and the width by $10 \%$. By what percentage did the perimeter of the rectangular flower bed decrease from the original version? | Answer: 14.
Solution. Let $x$ be the length of the flower bed, $y$ be the width of the flower bed. After the reduction: $0.9 x$ - length of the flower bed, $0.8 y$ - width of the flower bed, $2(0.9 x + 0.8 y)$ - perimeter. We get the equation: $\quad 2(0.9 x + 0.8 y) = 0.875 \cdot 2(x + y) \quad$ or $\quad x = 3 y$. The original perimeter: $8 y$. After the second reduction:
$0.8 x = 2.4 y$ - length of the flower bed, $0.9 y$ - width of the flower bed, $2(2.4 y + 0.9 y) = 6.6 y$ - perimeter. The perimeter decreased by $1.4 y$ or by $14\%$. | 14 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. (15 points) A one-kilogram model of a sports car body was made from carbon fiber for aerodynamic studies at a scale of 1:11. What is the mass of the actual body if it is also entirely made of carbon fiber? | Answer: 1331 kg.
Solution. All dimensions of the body are 11 times larger compared to the model. Therefore, the volume of the body is larger by $11 \cdot 11 \cdot 11=1331$ times. The mass is directly proportional to the volume, therefore, the mass of the body:
$$
m_{\text {body }}=1331 \cdot m_{\text {model }}=1331 \text { kg. }
$$ | 1331 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
5. (20 points) A car traveled half of the distance at a speed 30 km/h faster than the average speed, and the second half of the distance at a speed 30% lower than the average. Determine the average speed of the car. | Answer: 40 km/h.
Solution. The average speed $v=\frac{s+s}{t_{1}+t_{2}}=\frac{s+s}{\frac{s}{v+30}+\frac{s}{0.7 v}}=\frac{2}{\frac{1}{v+30}+\frac{1}{0.7 v}}$. Solving this equation, we get $v=40$ km/h. | 40 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. (16 points) Mitya, Anton, Gosha, and Boris bought a lottery ticket for 20 rubles. Mitya paid $24\%$ of the ticket's cost, Anton - 3 rubles 70 kopecks, Gosha - 0.21 of the ticket's cost, and Boris contributed the remaining amount. The boys agreed to divide the winnings in proportion to their contributions. The ticket won 1000 rubles. What amount (in rubles) is due to Boris? | Answer: 365
Solution. The ticket costs 2000 kop. Mitya paid 480 kop, Anton - 370 kop, Gosha - 420 kop, therefore, Boris had to pay an additional 730 kop. Since the prize is 50 times the cost of the ticket, Boris is entitled to 365 rubles. | 365 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. (16 points) Mitya, Anton, Gosha, and Boris bought a lottery ticket for 20 rubles. Mitya paid $24\%$ of the ticket's cost, Anton - 3 rubles 70 kopecks, Gosha - $0.21$ of the ticket's cost, and Boris contributed the remaining amount. The boys agreed to divide the winnings in proportion to their contributions. The ticket won 800 rubles. What amount (in rubles) is due to Boris? | Answer: 292
Solution. The ticket costs 2000 kop. Mitya paid 480 kop, Anton - 370 kop, Gosha - 420 kop, therefore, Boris had to pay an additional 730 kop. Since the prize is 40 times the cost of the ticket, Boris is entitled to 292 rubles. | 292 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. (16 points) The dividend is six times larger than the divisor, and the divisor is four times larger than the quotient. Find the dividend. | # Answer: 144
Solution. From the condition of the problem, it follows that the quotient is 6. Then the divisor is 24, and the dividend is 144. | 144 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. (17 points) Hooligan Vasily tore out a whole chapter from a book, the first page of which was numbered 231, and the number of the last page consisted of the same digits. How many sheets did Vasily tear out of the book?
# | # Answer: 41
Solution. The number of the last page starts with the digit 3 and must be even, so the last page has the number 312. Vasily tore out $312-231+1=82$ pages or 41 sheets. | 41 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) Divide the number 90 into two parts such that $40\%$ of one part is 15 more than $30\%$ of the other part. Write the larger of the two parts in your answer. | Answer: 60
Solution. Let one part of the number be $x$, then the other part will be $90-x$. We get the equation $0.4 \cdot x = 0.3 \cdot (90 - x) + 15$, solving it we get $x = 60$, and the other part of the number is 30. | 60 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
6. (20 points) A one-kilogram model of a sports car body was made from aluminum at a scale of 1:10. What is the mass of the actual body if it is also entirely made of aluminum? | Answer: 1000 kg
Solution. All dimensions of the body are 10 times larger compared to the model. Therefore, the volume of the body is larger by $10 \cdot 10 \cdot 10=1000$ times. Mass is directly proportional to volume, therefore, the mass of the body:
$$
m_{\text {body }}=1000 m_{\text {model }}=1000 \text { kg. }
$$
Preliminary Stage
6th grade
2018-2019
Variant 2
Tasks, answers, and evaluation criteria | 1000 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. (16 points) The dividend is five times larger than the divisor, and the divisor is four times larger than the quotient. Find the dividend.
# | # Answer: 100
Solution. From the condition of the problem, it follows that the quotient is 5. Then the divisor is 20, and the dividend is 100. | 100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. (17 points) Hooligan Vasily tore out a whole chapter from a book, the first page of which was numbered 241, and the number of the last page consisted of the same digits. How many sheets did Vasily tear out of the book?
# | # Answer: 86
Solution. The number of the last page starts with the digit 4 and must be even, so the last page has the number 412. Vasily tore out $412-241+1=172$ pages or 86 sheets. | 86 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) Divide the number 80 into two parts such that $30\%$ of one part is 10 more than $20\%$ of the other part. Write the smaller of the two parts in your answer. | Answer: 28
Solution. Let one part of the number be $x$, then the other part will be $80-x$. We get the equation $0.3 \cdot x = 0.2 \cdot (80 - x) + 10$, solving it we get $x = 52$, and the other part of the number is 28. | 28 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
6. (20 points) A two-kilogram model of a sports car body was made from aluminum at a scale of $1: 8$. What is the mass of the actual body if it is also entirely made of aluminum? | Answer: 1024 kg
Solution. All dimensions of the body are 8 times larger compared to the model. Therefore, the volume of the body is larger by $8 \cdot 8 \cdot 8=512$ times. The mass is directly proportional to the volume, therefore, the mass of the body:
$m_{\text {body }}=512 m_{\text {model }}=1024$ kg | 1024 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) The cross-section of a regular triangular pyramid passes through the midline of the base and is perpendicular to the base. Find the area of the cross-section if the side of the base is 8 and the height of the pyramid is 12. | Answer: 18.
Solution. The section MNP passes through the midline of the base of the pyramid $MN$ and is perpendicular to the base. Therefore, the height $PH$ of the triangle $MNP$ is parallel to the height of the pyramid $DO$.
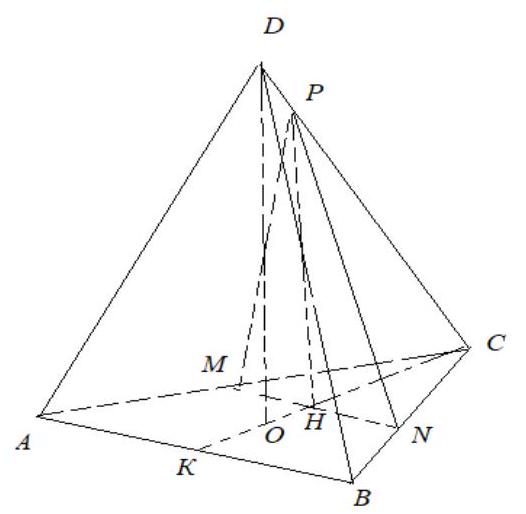
We have $OC: OK=2: 1, \quad CH=HK$, therefore, $CH: CO=3: 4$. Using the similarity of triangles $DOC$ and $PHC$, we get that $PH=\frac{3}{4} DO=\frac{3}{4} \cdot 12=9$. Then the area of the section is $S=\frac{1}{2} \cdot PH \cdot MN=\frac{1}{2} \cdot 9 \cdot 4=18$ sq.units. | 18 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) Find the smallest natural number that is simultaneously twice a perfect square and three times a perfect cube.
# | # Answer: 648
Solution. We have $k=3 n^{3}=2 m^{2}$. From this, the numbers $m$ and $n$ can be represented as $n=2 a, m=3 b$. After substitution, we get $4 a^{3}=3 b^{2}$. Further, we have $a=3 c, b=2 d, 9 c^{3}=d^{2}$. Here, the smallest solution is $c=1, d=3$. Then $a=3$, $b=6, n=6, m=18, k=648$. | 648 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. (15 points) The efficiency of an ideal heat engine is $40 \%$. What will it become if the temperature of the heater is increased by $40 \%$, and the temperature of the cooler is decreased by $40 \%$? | Answer: $\approx 74 \%$.
Solution. The efficiency of an ideal heat engine: $\eta=1-\frac{T_{X}}{T_{H}}$. That is, initially the ratio of the temperatures of the refrigerator and the heater: $\frac{T_{X}}{T_{H}}=1-0.4=0.6$. After the changes:
$$
\eta_{2}=1-\frac{0.6 T_{X}}{1.4 T_{H}}=1-\frac{0.6 \cdot 0.6}{1.4} \approx 0.74 \approx 74 \% .
$$ | 74 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. (16 points) There are two circles: one with center at point $A$ and radius 5, and another with center at point $B$ and radius 15. Their common internal tangent touches the circles at points $C$ and $D$ respectively. Lines $A B$ and $C D$ intersect at point $E$. Find $C D$, if $B E=39$. | # Answer: 48
Solution. Triangles $A C E$ and $B D E$ are similar (they have vertical angles and a right angle each) with a similarity coefficient of $1 / 3$. Therefore, $A E=13$. From triangle $A C E$, using the Pythagorean theorem, we find $C E=12$. Hence, $D E=36$, and $C D=48$. | 48 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. (17 points) Find the smallest natural number that is simultaneously twice a perfect cube and three times a perfect square.
# | # Answer: 432
Solution. We have $k=2 n^{3}=3 m^{2}$. From this, the numbers $m$ and $n$ can be represented as $n=3 a, m=2 b$. After substitution, we get $9 a^{3}=2 b^{2}$. Further, we have $a=2 c, b=3 d, 4 c^{3}=d^{2}$. Here, the smallest solution is $c=1, d=2$. Then $a=2$, $b=6, n=6, m=12, k=432$. | 432 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. (15 points) The efficiency of an ideal heat engine is $50 \%$. What will it become if the temperature of the heater is increased by $50 \%$, and the temperature of the cooler is decreased by $50 \%$? | Answer: $\approx 83 \%$
Solution. The efficiency of an ideal heat engine: $\eta=1-\frac{T_{X}}{T_{H}}$. That is, at the beginning, the ratio of the temperatures of the refrigerator and the heater: $\frac{T_{X}}{T_{H}}=1-0.5=0.5$. After the changes:
$$
\eta_{2}=1-\frac{0.5 T_{X}}{1.5 T_{H}}=1-\frac{0.5 \cdot 0.5}{1.5} \approx 0.83=83 \% .
$$ | 83 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. How many times in a day does the angle between the hour and minute hands equal exactly $17^{\circ}$? | Answer: 44.
Solution. Over the time interval from 0:00 to 12:00, the hour hand will make one complete revolution, while the minute hand will make 12 such revolutions. Therefore, during this time, the minute hand will catch up with the hour hand 11 times. Between two consecutive meetings of the hands, the angle between them will be exactly $17^{\circ}$ twice. Thus, between midnight and noon, the required angle between the hands will occur $11 \cdot 2=22$ times, and over a full day, such moments will be twice as many.
Grading. 12 points for a correct solution. | 44 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. Solve the equation
$$
\sqrt{\frac{x-2}{11}}+\sqrt{\frac{x-3}{10}}=\sqrt{\frac{x-11}{2}}+\sqrt{\frac{x-10}{3}}
$$ | Answer: 13.
Solution. If we perform the variable substitution $x=t+13$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t \leqslant 0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=13$.
Estimation. 12 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
$$
\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right) \text{ for } (m>0) \Rightarrow\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right)
$$ | 13 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
1. How many times in a day does the angle between the hour and minute hands equal exactly $19^{\circ}$? | Answer: 44.
Solution. Over the time interval from 0:00 to 12:00, the hour hand will make one complete revolution, while the minute hand will make 12 such revolutions. Therefore, during this time, the minute hand will catch up with the hour hand 11 times. Between two consecutive meetings of the hands, the angle between them will be exactly $17^{\circ}$ twice. Thus, between midnight and noon, the required angle between the hands will occur $11 \cdot 2=22$ times, and over a full day, such moments will be twice as many.
Grading. 12 points for a correct solution. | 44 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. Solve the equation
$$
\sqrt{\frac{x-3}{11}}+\sqrt{\frac{x-4}{10}}=\sqrt{\frac{x-11}{3}}+\sqrt{\frac{x-10}{4}}
$$ | Answer: 14.
Solution. If we perform the variable substitution $x=t+14$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t<0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=14$.
Estimation. 12 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points.
$$
\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right) \text{ for } (m>0) \Rightarrow\left(\frac{x-k}{m}>\frac{x-m}{k} \Longleftrightarrow x>k+m\right)
$$ | 14 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
4. A circle is inscribed with 2019 numbers. For any two adjacent numbers $x$ and $y$, the inequalities $|x-y| \geqslant 2, x+y \geqslant 6$ are satisfied. Find the smallest possible sum of the recorded numbers. | Answer: 6060.
Solution. Due to the odd number of total numbers, there will be three consecutive numbers $x, y$, and $z$ such that $x>y>z$. Adding the inequalities $y-z \geqslant 2$ and $y+z \geqslant 6$, we get $y \geqslant 4$. Then $x \geqslant y+2 \geqslant 6$. A number not less than 6 has been found. The remaining numbers can be divided into 1009 pairs of adjacent numbers. Therefore, the sum of all numbers $S \geqslant 6+1009 \cdot 6=6060$.
The lower bound for $S$ obtained can be achieved if one of the numbers is 6, and then, in a circle, the numbers 4 and 2 alternate.
Evaluation. 14 points for a complete solution. 5 points for an example without estimation, 7 points for estimation without an example. | 6060 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
4. A circle is inscribed with 1001 numbers. For any two adjacent numbers $x$ and $y$, the inequalities $|x-y| \geqslant 4, x+y \geqslant 6$ are satisfied. Find the smallest possible sum of the recorded numbers. | Answer: 3009.
Solution. Due to the odd number of total numbers, there will be three consecutive numbers $x, y$, and $z$ such that $x>y>z$. Adding the inequalities $y-z \geqslant 4$ and $y+z \geqslant 6$, we get $y \geqslant 5$. Then $x \geqslant y+4 \geqslant 9$. A number not less than 9 has been found. The remaining numbers can be divided into 500 pairs of adjacent numbers. Therefore, the sum of all numbers $S \geqslant 9+500 \cdot 6=3009$.
The lower bound for $S$ obtained can be achieved if one of the numbers is 9, and then, in a circle, alternating numbers 5 and 1 are placed.
Evaluation. 14 points for a complete solution. 5 points for an example without estimation, 7 points for estimation without an example. | 3009 | Inequalities | math-word-problem | Yes | Yes | olympiads | false |
# Problem № 7 (10 points)
In the electrical circuit shown in the diagram, the resistances of the resistors are $R_{1}=10$ Ohms and $R_{2}=30$ Ohms. An ammeter is connected to points A and B in the circuit. When the polarity of the current source is reversed, the ammeter readings change by one and a half times. Determine the internal resistance of the source. Consider the ammeter to be ideal. Assume that the resistance of the diodes in the forward direction is negligible, and in the reverse direction, it is infinitely large.
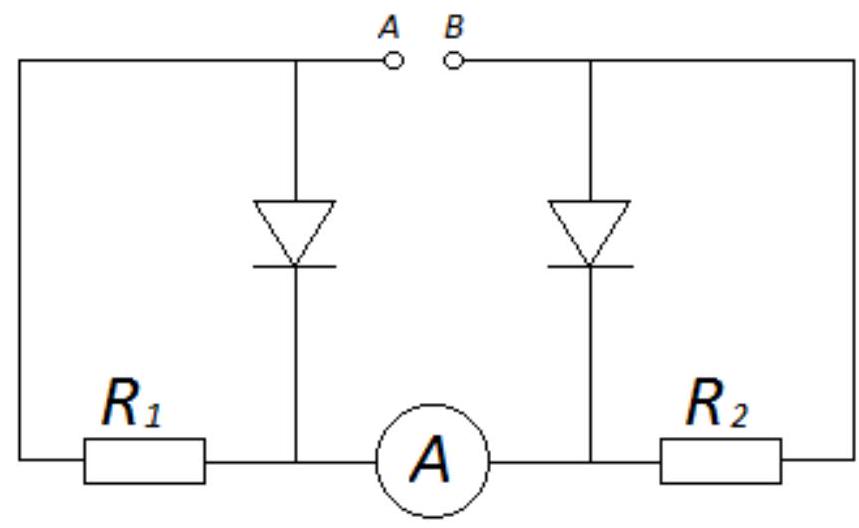
## Answer: 30 Ohms
# | # Solution and Evaluation Criteria:
When the positive terminal of the power supply is connected to point $A$, the current flows only through resistor $R_{2}$, and in this case: $I_{1}=\frac{\varepsilon}{R_{2}+r}$.
## (3 points)
When the polarity is reversed, the current flows only through resistance $R_{1}$, and:
$I_{2}=\frac{\varepsilon}{R_{1}+r}$
According to the condition: $I_{2}=1.5 I_{1}$
We get:
$$
\begin{aligned}
& 1.5 I_{1}\left(R_{1}+r\right)=I_{1}\left(R_{2}+r\right) \\
& 1.5(10+r)=30+r \\
& r=30 \text { Ohms. }
\end{aligned}
$$ | 30 | Other | math-word-problem | Yes | Yes | olympiads | false |
2. The area of triangle $A B C$ is 1. On the rays $A B, B C$, $C A$, points $B^{\prime}, C^{\prime}, A^{\prime}$ are laid out respectively, such that
$$
B B^{\prime}=2 A B, \quad C C^{\{\prime}=3 B C, \quad A A^{\prime}=4 C A .
$$
Calculate the area of triangle $A^{\prime} B^{\prime} C^{\prime}$. | Answer: 36.
Solution. We will solve the problem in a general form, assuming that
$$
B B^{\prime}=q A B, \quad C C^{\{\prime}=r B C, \quad A A^{\prime}=p C A .
$$
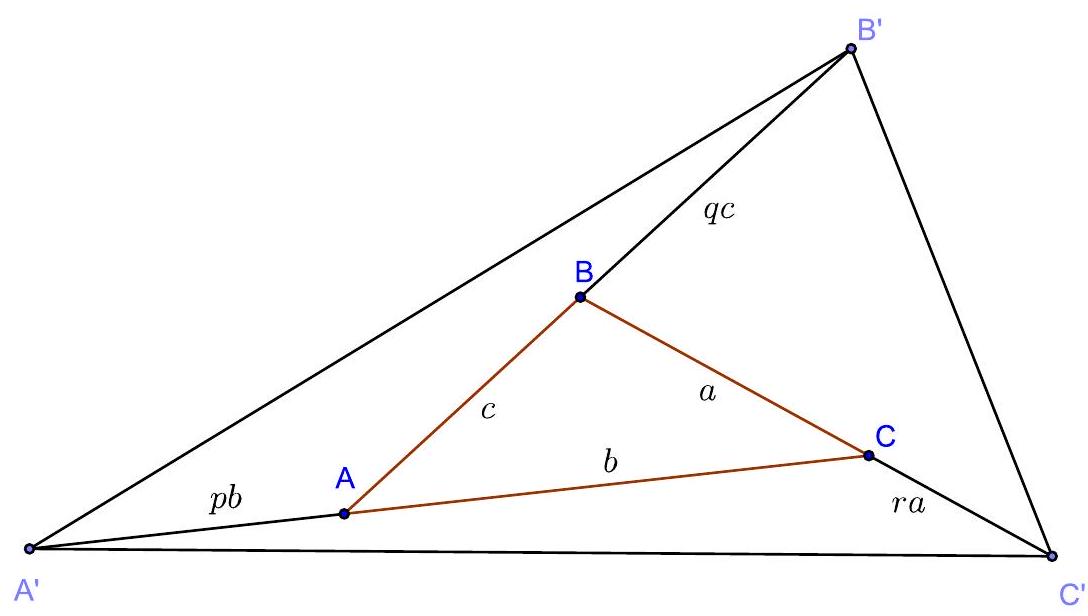
We will calculate the area of triangle \( A^{\prime} B^{\prime} A \):
$$
S_{A^{\prime} B^{\prime} A}=\frac{1}{2} A^{\prime} A \cdot A B^{\prime} \cdot \sin \angle A^{\prime} A B^{\prime}=\frac{1}{2} p b(c+q c) \sin \angle B A C=
$$
$$
=p(1+q) \cdot \frac{1}{2} b c \sin \angle B A C=p(1+q) \cdot S_{A B C}=p(1+q)
$$
(We used the equality of the sines of adjacent angles). Similarly, we find that \( S_{B^{\prime} B C^{\prime}}=q(1+r) \), \( S_{C C^{\prime} A^{\prime}}=r(1+p) \). Adding the areas of the specified three triangles and the original triangle \( A B C \), we find the desired area:
$$
S_{A^{\prime} B^{\prime} C^{\prime}}=1+p+q+r+p q+q r+r p
$$
Evaluation. 13 points for a correct solution. | 36 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. Solve the equation
$$
\sqrt{\frac{x-2}{11}}+\sqrt{\frac{x-3}{10}}+\sqrt{\frac{x-4}{9}}=\sqrt{\frac{x-11}{2}}+\sqrt{\frac{x-10}{3}}+\sqrt{\frac{x-9}{4}}
$$ | Solution. If we perform the variable substitution $x=t+13$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}+\sqrt{\frac{t}{9}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}+\sqrt{\frac{t}{4}+1}
$$
Now it is clear that for $t>0$ the right-hand side of the equation is greater, and for $-2 \leqslant t \leqslant 0$ the left-hand side is greater. Therefore, the only solution is $t=0$, which implies $x=13$.
Estimation. For a correct solution, 13 points. If the answer is guessed but the uniqueness of the solution is not proven, 3 points. | 13 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. The engine of a car traveling at a speed of $v_{0}=72 \mathrm{km} / \mathbf{h}$ operates with a power of $P=50$ kW. Determine the distance from the point of engine shutdown at which the car will stop, if the resistance force is proportional to the car's speed. The mass of the car is m=1500 kg. (15
## points) | Answer: $240 m$
Solution. The power of the engine: $P=F v=F_{\text {conp }} v_{0}=\alpha v_{0}^{2}$, that is, the coefficient of resistance to the car's movement: $\alpha=\frac{P}{v_{0}^{2}}$ (3 points). The projection of the second law of Newton, for a small time interval, when moving with the engine off: $m \frac{\Delta v}{\Delta t}=-F_{\text {conp }}=-\alpha v$ (3 points). Considering that: $v \Delta t=\Delta s$, we get $m \Delta v=-\alpha \Delta s$ (3 points). Transitioning to final increments, we get: $m\left(0-v_{0}\right)=-\alpha s=-\frac{P}{v_{0}} s(3$ points $)$.
Final answer: $s=\frac{m v_{0}^{3}}{P}=\frac{1500 \cdot 20^{3}}{50000}=240$ meters (3 points). | 240 | Calculus | math-word-problem | Yes | Yes | olympiads | false |
2. The area of triangle $A B C$ is 1. On the rays $A B, B C$, $C A$, points $B^{\prime}, C^{\prime}, A^{\prime}$ are laid out respectively, such that
$$
B B^{\prime}=A B, \quad C C^{\prime}=2 B C, \quad A A^{\prime}=3 C A
$$
Calculate the area of triangle $A^{\prime} B^{\prime} C^{\prime}$. | Answer: 18.
Solution. We will solve the problem in a general form, assuming that
$$
B B^{\prime}=q A B, \quad C C^{\prime}=r B C, \quad A A^{\prime}=p C A .
$$
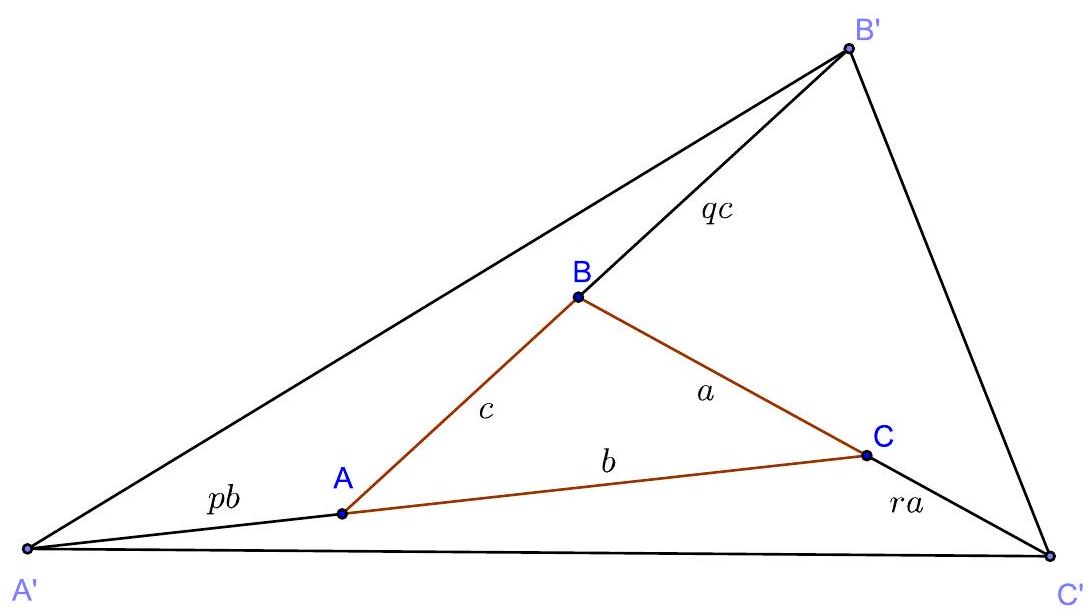
We will calculate the area of triangle \( A^{\prime} B^{\prime} A \):
$$
S_{A^{\prime} B^{\prime} A}=\frac{1}{2} A^{\prime} A \cdot A B^{\prime} \cdot \sin \angle A^{\prime} A B^{\prime}=\frac{1}{2} p b(c+q c) \sin \angle B A C=
$$
$$
=p(1+q) \cdot \frac{1}{2} b c \sin \angle B A C=p(1+q) \cdot S_{A B C}=p(1+q)
$$
(We used the equality of the sines of adjacent angles). Similarly, we find that \( S_{B^{\prime} B C^{\prime}}=q(1+r) \), \( S_{C C^{\prime} A^{\prime}}=r(1+p) \). Adding the areas of the specified three triangles and the original triangle \( A B C \), we find the desired area:
$$
S_{A^{\prime} B^{\prime} C^{\prime}}=1+p+q+r+p q+q r+r p
$$
Evaluation. 13 points for a correct solution. | 18 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
3. Solve the equation
$$
\sqrt{\frac{x-3}{11}}+\sqrt{\frac{x-4}{10}}+\sqrt{\frac{x-5}{9}}=\sqrt{\frac{x-11}{3}}+\sqrt{\frac{x-10}{4}}+\sqrt{\frac{x-9}{5}}
$$ | Answer: 14.
Solution. If we perform the variable substitution $x=t+14$, then in all the expressions under the square roots, 1 will be factored out:
$$
\sqrt{\frac{t}{11}+1}+\sqrt{\frac{t}{10}+1}+\sqrt{\frac{t}{9}+1}=\sqrt{\frac{t}{2}+1}+\sqrt{\frac{t}{3}+1}+\sqrt{\frac{t}{4}+1} .(*)
$$
Now it is clear that for $t>0$ the right side of the equation is greater, and for $-2 \leqslant t<0$ the left side is greater. Therefore, the only solution is $t=0$, which implies $x=14$.
Estimation. 13 points for a correct solution. If the answer is guessed but the uniqueness of the solution is not proven, 3 points. | 14 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem No. 5 (15 points)
The system shown in the figure is in equilibrium. It is known that the uniform rod $AB$ and the load lying on it have the same mass $m=10$ kg, and the load is located at a distance of one quarter of the length of the rod from its left end. Determine the mass $m$ of the second load suspended from the center of one of the pulleys. The threads and pulleys are weightless, and there is no friction in the pulley axes.
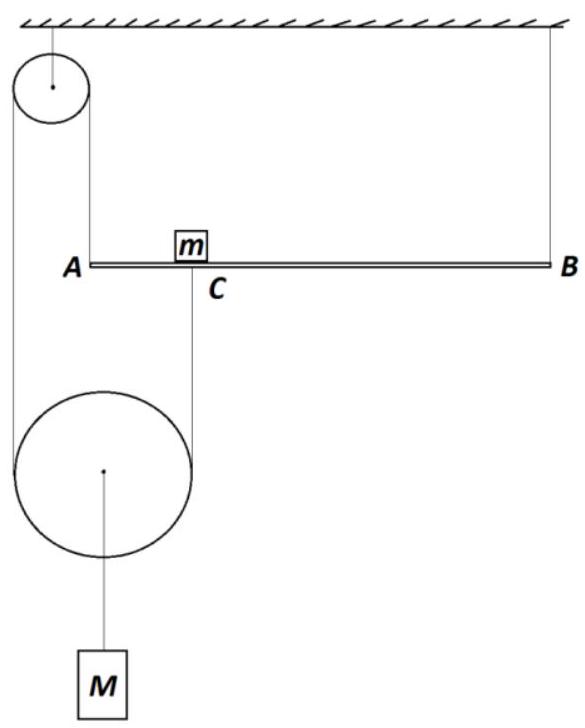 | Answer: 100 kg
# Solution and grading criteria:
Diagram with forces correctly placed.
Tension force in the thread: $T=\frac{M g}{2}$
The lever rule, written relative to point v:
$m g \cdot \frac{1}{2} A B+m g \cdot \frac{3}{4} A B+T \cdot \frac{3}{4} A B=T \cdot A B$
As a result, we get: $M=10 m=100$ kg.
A person walked slowly in a straight line at a speed of $v_{1}=1$ m/s. At time $t_{1}$, he turned strictly to the right and walked at a speed twice as fast. After another time interval $t_{1}$, he turned strictly to the right again, and his speed became three times the initial speed. After the last right turn, he ran at a speed of $4 v_{1}$ and returned to the starting point of his trajectory. Determine his average speed over the entire path.
## Answer: $2.1 \mathrm{~m} / \mathrm{s}$
## Solution and grading criteria:
From the condition, we can conclude that the person's trajectory is a rectangle.
(2 points)
Moreover, $S_{2}=2 S_{1}$
Average speed:
$v_{\text{avg}}=\frac{S_{1}+S_{2}+S_{3}+S_{4}}{t_{1}+t_{2}+t_{3}+t_{4}}=\frac{6 S_{1}}{t_{1}+t_{1}+\frac{S_{1}}{3 v_{1}}+\frac{2 S_{1}}{4 v_{1}}}=\frac{6 S_{1}}{t_{1}+t_{1}+\frac{t_{1}}{3}+\frac{t_{1}}{2}}=\frac{6 S_{1}}{\frac{17}{6} t_{1}}=\frac{36}{17} v_{1} \approx 2.1 \mathrm{~m} / \mathrm{s}$
## Problem 7 (10 points)
A person holds one end of a light board, and the other end of the board rests on a cylinder lying on the ground. The length of the board is $L=10$ m. How far will the person walk before meeting the cylinder? The radius of the wheel is much smaller than the length of the board. There is no slipping.

Answer: $20 \mathrm{~m}$
Solution and grading criteria:
The speed of the person is equal to the speed of the top point of the cylinder, which is twice the speed of the center of the cylinder.
Thus, the distance the person will walk is twice the distance the cylinder has rolled.
Obviously, $S_{\text {person }}-S_{\text {cylinder }}=L=10 \mathrm{~m}$ (3 points)
We get: $S_{\text {person }}=20$ meters | 100 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem No. 5 (15 points)
The system shown in the figure is in equilibrium. It is known that the uniform rod $AB$ and the load lying on it have the same mass $m=10$ kg. The load is located exactly in the middle of the rod. The thread, passing over the pulleys, is attached to one end of the rod and at a distance of one quarter of the rod's length from its left end. Determine the mass $m_2$ of the second load, suspended from the center of one of the pulleys. The threads and pulleys are weightless, and there is no friction in the pulley axes.
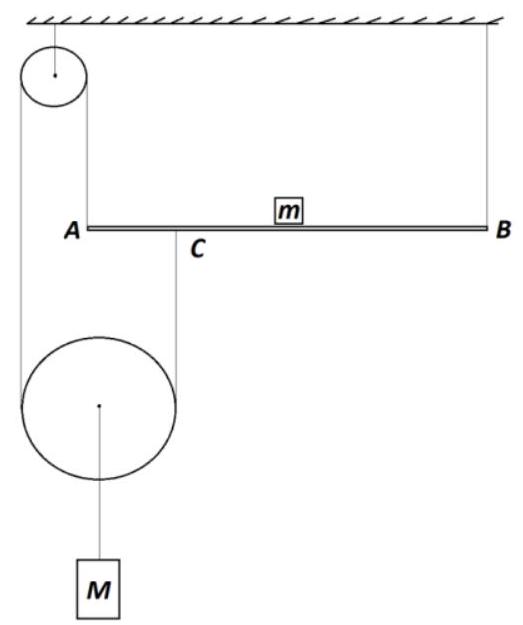
Answer: 80 kg
# | # Solution and Evaluation Criteria:
Diagram with forces correctly placed.
Tension force in the string: $T=\frac{M g}{2}$
The lever rule, written relative to point v:
$m g \cdot \frac{1}{2} A B+m g \cdot \frac{1}{2} A B+T \cdot \frac{3}{4} A B=T \cdot A B$
As a result, we get: $M=8 m=80$ kg. | 80 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
2. In triangle $A B C$, the median $B K$ is twice as small as side $A B$ and forms an angle of $32^{\circ}$ with it. Find the angle $A B C$. | Answer: $106^{\circ}$.
Solution. Let $K$ be the midpoint of segment $B D$. Then $A B C D$ is a parallelogram. In triangle $A B D$, we have the equality of sides $A B$ and $B D$. Therefore,
$$
\angle B D A=\frac{1}{2}\left(180^{\circ}-32^{\circ}\right)=74^{\circ}
$$
Angles $A D B$ and $C B D$ are equal as alternate interior angles. Thus,
$$
\angle A B C=\angle A B D+\angle D B C=32^{\circ}+74^{\circ}=106^{\circ} .
$$
Evaluation. 13 points for a correct solution. | 106 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
2. In triangle $A B C$, the median $B N$ is twice as short as side $A B$ and forms an angle of $20^{\circ}$ with it. Find the angle $A B C$. | Answer: $100^{\circ}$.
Solution. Let $N$ be the midpoint of segment $B D$. Then $A B C D-$ is a parallelogram. In triangle $A B D$, we have the equality of sides $A B$ and $B D$. Therefore,
$$
\angle B D A=\frac{1}{2}\left(180^{\circ}-20^{\circ}\right)=80^{\circ} \text {. }
$$
Angles $A D B$ and $C B D$ are equal as alternate interior angles. Thus,
$$
\angle A B C=\angle A B D+\angle D B C=20^{\circ}+80^{\circ}=100^{\circ} .
$$
Evaluation. 13 points for a correct solution. | 100 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4. What is the greatest length that a closed, non-self-intersecting broken line can have, which runs along the grid lines of a $6 \times 10$ cell field?
# | # Answer: 76.
Solution. We will color the nodes of the grid in a checkerboard pattern, with black and white colors. The length of a closed non-self-intersecting broken line is equal to the number of nodes it passes through. Each segment of the broken line connects a black and a white node. When traversing the broken line, the colors of the nodes alternate, so the length of the closed broken line is an even number. Since there are 77 nodes in total in the grid, the length of the broken line is at most 76. A corresponding example is easily constructed (Fig. 2).
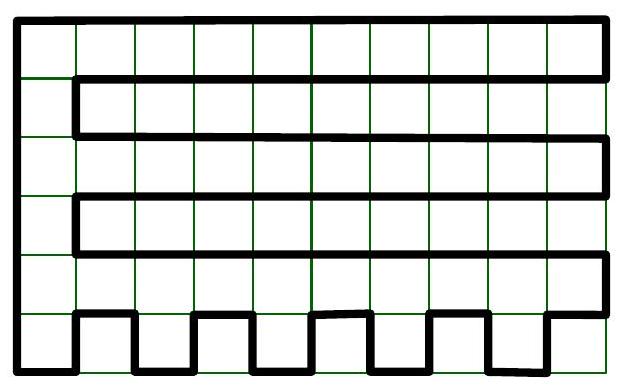
Fig. 2
Remark. Another reasoning is possible. Let's start constructing a closed broken line from some node. Since we need to return to it, the number of horizontal steps to the right is the same as the number of steps to the left. Therefore, the number of horizontal steps is even. The same is true for vertical steps. Hence, we again obtain that the length of the closed broken line (whose segments follow the grid lines) is an even number.
Evaluation. 13 points for a correct solution. 1 point for only the answer. 4 points if an example of a broken line of length 76 is provided, but there is no estimation of the length of the broken line. | 76 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
4. 100 balls of the same mass move along a trough towards a metal wall with the same speed. After colliding with the wall, a ball bounces off it with the same speed. Upon collision of two balls, they scatter with the same speed. (The balls move only along the trough). Find the total number of collisions between the balls. | Answer: 4950.
Solution. We will assume that each ball has a flag. Imagine that upon collision, the balls exchange flags. Then each flag flies to the wall at a constant speed, and after hitting the wall, it flies in the opposite direction. The number of collisions between the balls is equal to the number of flag exchanges. Any two flags will swap places exactly once. Therefore, the total number of exchanges is $\frac{100 \cdot 99}{2}=4950$.
Evaluation. 14 points for a correct solution.
# | 4950 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 1. Let's call a number small if it is a 10-digit number and there does not exist a smaller 10-digit number with the same sum of digits. How many small numbers exist | Solution. Answer: 90.
It is clear that the sum of the digits of a 10-digit number can take any value from 1 to 90 inclusive. For each of the 90 possible sums of the digits, there is a unique smallest 10-digit number with such a sum of digits. Therefore, there are 90 small numbers.
## Criteria
One of the largest suitable criteria is used:
7 p. Any complete solution to the problem.
1 p. There is only the correct answer. | 90 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. On the board, there are $N$ natural numbers, where $N \geqslant 5$. It is known that the sum of all the numbers is 80, and the sum of any five of them is no more than 19. What is the smallest value that $N$ can take? | Solution. Answer: 26.
The condition of the problem is equivalent to the sum of the five largest numbers not exceeding 19, and the sum of all numbers being 80. Note that among the five largest numbers, there must be a number not greater than 3 (otherwise, if all of them are not less than 4, their sum is not less than $4 \cdot 5=20$, but it should not exceed 19).
Let the total number of numbers be $x$. Since among the five largest numbers there is a number not greater than 3, then all the other $x-5$ numbers are not greater than 3. Therefore, the sum of all numbers does not exceed $3(x-5)+19$, and on the other hand, it is equal to 80. Thus, we get the inequality $3(x-5)+19 \geqslant 80$. Solving this inequality and considering that $x$ is an integer, we get that $x \geqslant 26$.
It remains to provide an example of such 26 numbers. Let's take 24 threes and 2 fours, then the total sum is $24 \cdot 3 + 2 \cdot 4 = 80$, and the sum of any five is not greater than $3 \cdot 3 + 2 \cdot 4 = 17 \leqslant 19$.
## Criteria
The most appropriate criterion is used:
7 points. Any complete solution of the problem.
3 points. 26 numbers satisfying the condition of the problem are explicitly provided. | 26 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1010 of them such that the sum of any two does not equal 2021 or 2022. How many
ways are there to do this | Solution. Answer: $\frac{1011 \cdot 1012}{2}=511566$.
Let's write our numbers in the following order: $2021,1,2020,2,2019,3, \ldots, 1012,1010,1011$.
Notice that if two numbers sum to 2021 or 2022, they stand next to each other in this sequence. Our task is reduced to the following: 2021 objects (for convenience, let's consider them as 2021 balls) are lined up, and we need to count the number of ways to choose 1010 of them, such that no two chosen balls are adjacent.
Let's paint the unchosen balls red and the chosen ones blue. Place all 1011 red balls in a row. We need to place 1010 blue balls in the gaps between them (or at the ends) such that no two blue balls are adjacent. There are exactly 1012 such gaps: 1010 gaps between two red balls, and 2 gaps at the ends; in each of these gaps, we can place no more than one blue ball. Therefore, we need to count the number of ways to choose 1010 gaps out of 1012 available. As is known, this value is equal to $C_{1012}^{1010}=C_{1012}^{2}=\frac{1012 \cdot 1011}{2}=511566$.
Another solution.
We will divide the numbers from 1 to 2021 into 1011 groups - 1010 non-overlapping groups of pairs of numbers that sum to 2022 (specifically: $(1,2021),(2,2020), \ldots,(1009,1013)$, $(1010,1012))$ and a group consisting of the remaining number 1011.
In each group, by the condition, we can choose no more than one number. Therefore, to choose 1010 numbers, we need to choose a group from which no numbers will be taken, and from all other groups, we need to choose exactly one number each.
Suppose we do not take any number from the group $(a, 2022-a)$ (here and below we will assume that in such notation $a \leqslant 2022-a$). From all other groups, we need to choose exactly one number each, in particular, we need to take 1011 (if $a=1011$, then this step is skipped). Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this way, we get that from the pair $(a+1,2022-(a+1))$ we choose the number $2022-(a+1)$. Thus, in all pairs where the smallest number is greater than $a$, the chosen numbers are uniquely determined (specifically, the largest numbers in these pairs must be chosen).
Now consider all pairs where the smallest number is less than $a$. Consider among them the pair $(b, 2022-b)$ in which the largest number, i.e., $2022-b$, is chosen (the case where such pairs do not exist will be considered separately), and if there are several such pairs, consider the one where $b$ is maximal. From all pairs from $(b+1,2022-(b+1))$ to $(a-1,2022-(a-1))$, the smallest number was always chosen (due to the maximality of $b$). In the pair $(b-1,2022-(b-1))$, the number $2022-(b-1)$ was chosen (otherwise $(b-1)+(2022-b)=2021$). Similarly, in the pair $(b-2,2022-(b-2))$, the number $2022-(b-2)$ was chosen, and so on, in the pair $(1,2021)$, the number 2021 was chosen.
Now let's understand how the set of numbers satisfying the condition is determined. First, a group $(a, 2022-a)$ (i.e., a number $1 \leqslant a \leqslant 1011$) is chosen, in which no number is chosen. Then, in all groups where the smallest number is greater than $a$, the choice is uniquely determined (from the group, the largest number is chosen). Second, a pair $(b, 2022-b)$ (i.e., a number $1 \leqslant b \leqslant a-1$) is chosen, and in all other pairs, the choice is uniquely determined (in pairs with the smallest number from $b+1$ to $a-1$, the smallest number is chosen, and in pairs where it is less than $b$, the largest number is chosen).
It remains to count the number of options. Fix some $a$, then the number of ways to choose $b$ will be exactly $a-1$, plus one more option, where in all pairs with the smallest number less than $a$, the smallest number was chosen (i.e., the number $b$ simply does not exist). In total, there are $a$ options for the number $b$. Summing over all $a \leqslant 1011$, we get $1+2+3+\ldots+1010+1011=\frac{1011 \cdot 1012}{2}=511566$ options for our set. Clearly, all these options are distinct and satisfy the condition (the set is uniquely determined by the chosen numbers $a$ and $b$).
## Criteria
The highest appropriate criterion is used:
7 p. Any complete solution to the problem.
7 6. Any complete solution to the problem, but the answer is given in the form of a formula or expression (e.g., $\frac{1011 \cdot 1012}{2}$ or $C_{1012}^{2}$).
6 6. Any complete solution to the problem, but the answer is given in the form of a formula with an ellipsis (e.g., $1+2+3+\ldots+1010+1011$).
2 6. The numbers are divided into pairs, but there is no further progress.
16 . The correct answer is given. | 511566 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. In a two-digit number, each digit was increased by 2 or by 4 (different digits could be increased by different numbers), as a result of which the number increased fourfold. What could the original number have been? Find all possible options and prove that there are no others. | Solution. Answer: 14.
Let $x$ be the original number, then the resulting number equals $4 x$. In this case, after increasing two digits, the number itself was increased by 22, 24, 42, or 44. This results in four cases:
- $4 x-x=22$
- $4 x-x=24$
- $4 x-x=42$
- $4 x-x=44$.
Among them, only the third one fits, corresponding to the value $x=14$.
One highest suitable criterion is used:
7 points. Any complete solution to the problem.
3 points. Only the correct answer.
If the problem is reduced to considering the four cases mentioned in the solution, then 1 point is deducted for each case not correctly analyzed. | 14 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 1. Grandfather Frost had 120 chocolate candies and 200 jelly candies. At the morning performance, he gave candies to the children: each child received one chocolate candy and one jelly candy. Counting the candies after the performance, Grandfather Frost found that there were three times as many jelly candies left as chocolate candies. How many children were at the performance? | Answer: 80.
Solution. Let the total number of children be $x$, then after the morning party, Grandfather Frost had $120-x$ chocolate candies and $200-x$ jelly candies left. Since there were three times as many jelly candies left as chocolate candies, we get the equation $3 \cdot(120-x)=200-x$. Solving this, we get $x=80$.
## Criteria
One of the largest suitable criteria is used:
## 7 points. Any complete solution of the problem.
2 6. The correct answer is given with a check that it fits, but it is not proven that there are no other answers. | 80 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. Five different natural numbers are written in a circle on the board. Each of them, Petya divided by the next one in the clockwise direction, and then wrote down the 5 resulting numbers (not necessarily integers) on a piece of paper. Can the sum of the 5 numbers on the paper be an integer? | Answer: Yes, it can.
Solution. For example, for the numbers $1,2,4,8,16$, after division, the sum is $1 / 2+1 / 2+1 / 2+1 / 2+16=18$.
## Criteria
One suitable criterion is used:
7 p. Any complete solution to the problem.
0 p. There is only the correct answer, but the correct example is not provided. | 18 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. Carlson has three boxes, each containing 10 candies. One box is labeled with the number 4, another with 7, and the third with 10. In one operation, Carlson sequentially performs the following two actions:
- he takes from any box a number of candies equal to the number written on it;
- he eats 3 of the taken candies, and puts the rest in any other box.
What is the maximum number of candies Carlson can eat as a result of several such operations? | Answer: 27.
Solution. Since at each step, Karlson eats 3 candies, the total number of candies eaten is divisible by 3. We will prove that it does not exceed 27; for this, it is sufficient to show that it cannot equal 30, that is, Karlson cannot eat all the candies. Indeed, if this were possible, then before the last operation, there would be exactly 3 candies left, meaning that each box would contain no more than 3 candies. However, each of the numbers $4, 7, 10$ is greater than 3, so the last operation would be impossible, leading to a contradiction.
The example below shows how Karlson could act to eat exactly 27 candies. In the $k$-th line, it is written how many candies remain in each box after the $(k-1)$-th operation. The three numbers in each line are the number of candies remaining in the boxes at the corresponding step. The notation $(a, b, c)$ means that in the box with number 4, there were $a$ candies left, in the box with number $7-b$ candies, and in the box with number $10-c$ candies. | 27 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
5. The incircle of triangle $ABC$ touches sides $AB$ and $AC$ at points $D$ and $E$ respectively. Point $I_{A}$ is the excenter of the excircle opposite side $BC$ of triangle $ABC$, and points $K$ and $L$ are the midpoints of segments $DI_{A}$ and $EI_{A}$ respectively. Lines $BK$ and $CL$ intersect at point $F$, which lies inside angle $BAC$. Find $\angle BFC$, if $\angle BAC=50^{\circ}$. (The excircle touches side $C$ and the extensions of sides $AB$ and $AC$ beyond points $B$ and $C$ respectively.) | 5. The circle inscribed in triangle $ABC$ touches sides $AB$ and $AC$ at points $D$ and $E$ respectively. Point $I_{A}$ is the center of the excircle opposite side $BC$ of triangle $ABC$, and points $K$ and $L$ are the midpoints of segments $DI_{A}$ and $EI_{A}$ respectively. Lines $BK$ and $CL$ intersect at point $F$, which lies inside angle $BAC$. Find $\angle BFC$ if $\angle BAC = 50^{\circ}$. (The excircle touches side $BC$ and the extensions of sides $AB$ and $AC$ beyond points $B$ and $C$ respectively.)
Answer: $130^{\circ}$.
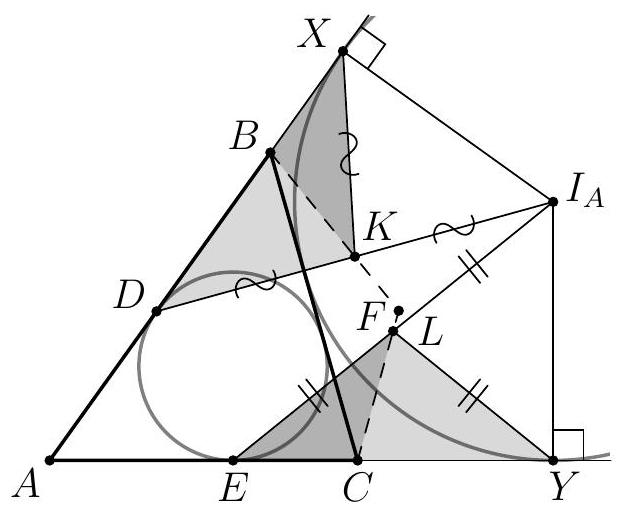
Fig. 7: for the solution of problem 5.
Let $X$ and $Y$ be the points of tangency of the excircle opposite side $BC$ with the extensions of sides $AB$ and $AC$ respectively (Fig. 7). Right triangles $DXI_{A}$ and $EYI_{A}$ are symmetric with respect to the angle bisector of angle $A$, hence they are equal and isosceles triangles $DKX$ and $YLE$. In these triangles, points $B$ and $C$ are marked on the bases such that $BD = CY = p - b$, where $p$ is the semiperimeter of triangle $ABC$, and $b$ is the length of side $AC$. Consequently, we conclude that $\angle KBD = \angle LCY$ and, thus, quadrilateral $ABFC$ is cyclic. This leads to the relation $\angle BFC = 180^{\circ} - \angle BAC = 130^{\circ}$.
## Criteria
+ Correct solution - 7 points. | 130 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
6.3. At a round table sit 10 elves, each with a basket of nuts in front of them. Each was asked, "How many nuts do your two neighbors have together?" and, going around the circle, the answers received were 110, 120, 130, 140, 150, 160, 170, 180, 190, and 200. How many nuts does the elf who answered 160 have? | Answer: 55. Solution. We will call the elves 1-m, 2-m, etc., in the order of receiving answers. The odd-numbered ones sit every other. In their answers, the number of nuts of each even number is counted twice, so the sum $110+130+150+170+190=750$ is equal to twice the number of nuts of all even numbers. Therefore, the even-numbered ones have 375 nuts in total. The 8th and 10th together have 190 nuts, and the 2nd and 4th together have 130 nuts. Therefore, the 6th has 375-190-130=55 nuts.
Criterion. 1 point for the correct answer without justification. 3 points for the answer and a correct example for all. | 55 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
Problem 9.2. At a party, 24 people gathered. A guest is considered an introvert if they have no more than three acquaintances among the other guests. It turned out that each guest has at least three acquaintances who are introverts. How many introverts could there have been at the party? Provide all possible answers and prove that there are no others.
# | # Answer: 24.
Solution. Let $a$ be the number of pairs of introverts who know each other, and $b$ be the number of pairs of acquaintances where one of the pair is an introvert. Each person who came to the party is included in at least three pairs, since they know at least three other introverts, and pairs of introvert-introvert are counted twice. Therefore, $2a + b \geq 3 \cdot 24$.
On the other hand, each introvert can be included in no more than three pairs, so $2a + b$ is no more than three times the number of introverts. As a result, we conclude that three times the number of introverts is not less than three times the number of guests, which is only possible if all those who came to the party are introverts.
Another solution. From the condition, it follows that each introvert knows three other introverts and no one else; that is, there can be no acquaintances between introverts and extroverts (let's call the rest of the people extroverts). But then an extrovert cannot know three introverts, as required by the condition. Therefore, there are no extroverts at this party.
## Criteria
## Kurchatov School Olympiad in Mathematics - 2019 Final Stage.
Any correct solution to the problem is worth 7 points.
Solutions that unjustifiably use the fact that some cases are "optimal" ("best", "worst", etc.) are not credited.
In the absence of a correct solution, the following criterion is used:
## 16. There is a correct answer. | 24 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 9.4. It is known that the number 400000001 is the product of two prime numbers $p$ and $q$. Find the sum of the natural divisors of the number $p+q-1$.
---
The text has been translated while preserving the original formatting and line breaks. | Answer: 45864.
Solution. The number $n=400000001$ can be written in the following form
\[
\begin{aligned}
n & =4 \cdot 10^{8}+1=4 \cdot 10^{8}+4 \cdot 10^{4}+1-4 \cdot 10^{4}= \\
& =\left(2 \cdot 10^{4}+1\right)^{2}-\left(2 \cdot 10^{2}\right)^{2}=\left(2 \cdot 10^{4}+2 \cdot 10^{2}+1\right)\left(2 \cdot 10^{4}-2 \cdot 10^{2}+1\right)
\end{aligned}
\]
Since $n$ is the product of two prime numbers $p$ and $q$, the factorization obtained above is exactly this. Therefore,
\[
p+q-1=2 \cdot 10^{4}+2 \cdot 10^{2}+1+2 \cdot 10^{4}-2 \cdot 10^{2}+1-1=4 \cdot 10^{4}+1
\]
To factorize the last number, we can use the same trick.
\[
\begin{aligned}
4 \cdot 10^{4}+1 & =4 \cdot 10^{4}+4 \cdot 10^{2}+1-4 \cdot 10^{2}=\left(2 \cdot 10^{2}+1\right)^{2}-(2 \cdot 10)^{2}= \\
& =(201-20)(201+20)=181 \cdot 221=13 \cdot 17 \cdot 181
\end{aligned}
\]
The sum of the natural divisors of the obtained number can be found, for example, using the formula
\[
(13+1)(17+1)(181+1)=45864
\]
## Criteria
The highest appropriate criterion is used:
76. Any correct solution to the problem.
5 6. The correct prime factorization of the number $p+q-1$ is obtained, but due to an error, an incorrect answer is given.
4 6. The answer is given under the assumption that $p+q-1=181 \cdot 221$ is the prime factorization.
3 6. The value of $p+q-1$ is correctly calculated.
In any of the above cases, points are deducted for the following deficiency:
-2 6. The correct factorization of the given number in the problem is provided, but it is not shown where this factorization comes from, nor that it indeed gives the required number when multiplied. | 45864 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
4. Alexei wrote several consecutive natural numbers on the board. It turned out that only two of the written numbers have a digit sum divisible by 8: the smallest and the largest. What is the maximum number of numbers that could have been written on the board? | Answer: 16.
Example: numbers from 9999991 to 10000007.
Evaluation. We will prove that there cannot be more than 16 numbers. Let's call a number $x$ good if the sum of its digits is divisible by 8. Among the listed numbers, there must be a number $x$ ending in 0, otherwise there are too few numbers. The number $x$ is not the first one, since then both $x$ and $x+8$ are good, and there are no more than 9 numbers. Among the numbers $x, x+1, \ldots, x+7$ there must be a good one - the largest with the specified property. The number $x-1$ ends in 9, so among the numbers $x-1, x-2, \ldots, x-8$ there must be a good one - the smallest with the specified property. Thus, all selected numbers fit into the interval from $x-8$ to $x+7$ inclusive. Therefore, the number of numbers written on the board does not exceed 16.
$\pm$ The evaluation is correct, the example has a minor error. 5-6 points
$\mp$ The evaluation without an example. 3 points
$\mp$ The example without an evaluation. 3 points | 16 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
9.4. Through the point with coordinates $(9,9)$, lines (including those parallel to the coordinate axes) are drawn, dividing the plane into angles of $9^{\circ}$. Find the sum of the x-coordinates of the points of intersection of these lines with the line $y=10-x$. | Answer: 190. Solution. The picture is symmetric with respect to the line $y=x$, so the sum of the abscissas is equal to the sum of the ordinates. Through the point $(9,9)$, 20 lines are drawn, the line $y=20-x$ intersects 19 of them. For each point on the line $y=20-x$, the sum of the coordinates is 20, so the total sum of the abscissas and ordinates is 380, and the sum of the abscissas is half of that.
Criterion. 2 points for the correct answer without a correct justification. 4 points if all ideas are found, but the answer is incorrect due to a wrong count of the number of intersection points (for example, the student counts them as 20 or 40). | 190 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Problem 7.4. On the sides $AB$ and $AC$ of triangle $ABC$, points $X$ and $Y$ are chosen such that $\angle A Y B = \angle A X C = 134^{\circ}$. On the ray $YB$ beyond point $B$, point $M$ is marked, and on the ray $XC$ beyond point $C$, point $N$ is marked. It turns out that $MB = AC$ and $AB = CN$. Find $\angle MAN$.
Answer: $46^{\circ}$. | Solution. Note that $\angle A C N=\angle C A X+\angle A X C=\angle B A Y+\angle A Y B=\angle A B M$. Adding
Fig. 1: to the solution of problem $?$ ?
## Kurchatov School Olympiad in Mathematics - 2019 Final Round.
to the obtained equality of angles, and given the equalities of segments $A C=B M$ and $A B=C N$, we conclude that by the first criterion, triangles $A C N$ and $M B A$ are equal (Fig. ??), which means $\angle N A C = \angle A M B$. Then the following chain of equalities holds: $\angle M A N=\angle N A C+\angle C A B+\angle B A M=\angle A M B + \angle Y A B + \angle B A M = \angle Y A M + \angle A M Y = 180^{\circ} - \angle A Y B = 180^{\circ} - 134^{\circ} = 46^{\circ}$.
## Criteria
The largest suitable criterion is used:
76 . Any correct solution to the problem.
5 6. A correct solution with an incorrect answer due to an arithmetic error.
3 6. It is proven that triangles $A C N$ and $M B A$ are equal.
16 . The correct answer is provided. | 46 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Problem 7.5. A lame rook makes moves alternating between one and two squares, with the direction of the move being freely chosen (in any of the four directions). What is the maximum number of cells on a $6 \times 6$ board it can visit, if visiting the same cell twice is prohibited, but the starting cell and the first move can be chosen freely? | Answer: 34.
Solution. An example for 34 cells is shown in Fig. ??. The visited cells are numbered from 1 to 34.
| 5 | 2 | 4 | 3 | 13 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 6 | 1 | 7 | 8 | 14 | 9 |
| 28 | 31 | | 34 | 12 | 11 |
| 27 | 32 | | 33 | 15 | 16 |
| 29 | 30 | 20 | 19 | 21 | 18 |
| 26 | 25 | 23 | 24 | 22 | 17 |
Fig. 2: to the solution of problem $? ?$
We will show that it is impossible to visit 35 or more cells. For this, we divide the $6 \times 6$ square into nine $2 \times 2$ squares and color them in a checkerboard pattern (Fig. ??). This results in 20 black cells and 16 white cells. Each move of length 2 connects two cells of different colors, and the pairs of cells for different "long" moves do not overlap. Since there are 16 white cells, the number of long moves does not exceed 16. Due to the alternation, this guarantees that the total number of moves does not exceed 33, and thus the number of visited cells does not exceed 34.
## Kurchatov School Olympiad in Mathematics - 2019 Final Round.
## Criteria
One of the largest suitable criteria is used:
7 6. Any correct solution to the problem.
3 6. An example of traversing 34 cells is constructed.
3 6. It is proven that it is impossible to visit 35 cells. | 34 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. In a five-digit number, each digit was increased by 2 or by 4 (different digits could be increased by different numbers), as a result of which the number increased fourfold. What could the original number have been? Find all possible options and prove that there are no others. | Solution. Answer: 14074.
Let the original five-digit number be denoted by $N$, then the resulting number is equal to $4N$. Their difference is $3N$ and is a five-digit number consisting of 2 and 4. This difference $3N$ is not less than $3 \cdot 10000$, so it starts with a four.
By the divisibility rule for 3, the sum of the digits of the number $3N$ is divisible by 3, so it cannot consist of two fours and three twos, three fours and two twos, or five fours. Therefore, the number $3N$ consists either of one four and four twos, or of four fours and one two. Then the number $N$ can be one of the numbers $\frac{42222}{3}=14074, \frac{44442}{3}=14814, \frac{44424}{3}=14808, \frac{44244}{3}=14748$, $\frac{42444}{3}=14148$.
It is also clear that the number $N$ could not contain an eight in its decimal representation, so only the number 14074 remains to be checked. And it fits: $14074 \cdot 4 = 56296$, all the digits of the quadrupled number are greater than the corresponding original digits by 2 or 4.
## Criteria
The highest applicable criterion is used:
7 points. Any complete solution of the problem.
6 points. A generally correct solution, but an arithmetic error is made that does not affect its course.
5 points. The numbers $14074, 14814, 14808, 14748, 14148$ are obtained justifiably.
4 points. It is proven that the number is increased by either one four and four twos, or four fours and one two.
1 point. There is only the answer. | 14074 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1010 of them such that the sum of any two does not equal 2021 or 2022. How many ways are there to do this? | Solution. Answer: $\frac{1011 \cdot 1012}{2}=511566$.
Let's write our numbers in the following order: $2021,1,2020,2,2019,3, \ldots, 1012,1010,1011$. Notice that if two numbers sum to 2021 or 2022, they stand next to each other in this sequence. Our task is reduced to the following: 2021 objects (for convenience, let's consider them as 2021 balls) are lined up, and we need to count the number of ways to choose 1010 of them, such that no two chosen balls are adjacent.
Let's paint the unchosen balls red and the chosen ones blue. Place all 1011 red balls in a row. We need to place 1010 blue balls in the gaps between them (or at the ends) such that no two blue balls are adjacent. There are exactly 1012 such gaps: 1010 gaps between two red balls, and 2 gaps at the ends; in each of these gaps, we can place no more than one blue ball. Therefore, we need to count the number of ways to choose 1010 gaps out of 1012 available. As is known, this value is $C_{1012}^{1010}=C_{1012}^{2}=\frac{1012 \cdot 1011}{2}=511566$.
Another solution.
We will divide the numbers from 1 to 2021 into 1011 groups - 1010 non-overlapping groups of pairs of numbers that sum to 2022 (specifically: $(1,2021),(2,2020), \ldots,(1009,1013)$, $(1010,1012))$ and a group consisting of the remaining number 1011.
In each group, by the condition, we can choose no more than one number. Therefore, to choose 1010 numbers, we need to choose a group from which no numbers will be taken, and from all other groups, we need to choose exactly one number each.
Suppose we do not take any number from the group $(a, 2022-a)$ (here and below we will assume that in such notation $a \leqslant 2022-a$). From all other groups, we need to choose exactly one number each, in particular, we need to take 1011 (if $a=1011$, then this step is skipped). Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this way, we get that from the pair $(a+1,2022-(a+1))$ we take the number $2022-(a+1)$. Thus, in all pairs where the smallest number is greater than $a$, the chosen numbers are uniquely determined (specifically, the largest numbers in these pairs must be chosen).
Now consider all pairs where the smallest number is less than $a$. Consider among them the pair $(b, 2022-b)$ in which the largest number, i.e., $2022-b$, is chosen (the case where such pairs do not exist will be considered separately), and if there are several such pairs, consider the one where $b$ is maximal. From all pairs from $(b+1,2022-(b+1))$ to $(a-1,2022-(a-1))$, the smallest number was always chosen (due to the maximality of $b$). In the pair $(b-1,2022-(b-1))$, the number $2022-(b-1)$ was chosen (otherwise $(b-1)+(2022-b)=2021$). Similarly, in the pair $(b-2,2022-(b-2))$, the number $2022-(b-2)$ was chosen, and so on, in the pair $(1,2021)$, the number 2021 was chosen.
Now let's understand how the set of numbers satisfying the condition is determined. First, a group $(a, 2022-a)$ (i.e., a number $1 \leqslant a \leqslant 1011$) is chosen, in which no number is chosen. Then, in all groups where the smallest number is greater than $a$, the choice is uniquely determined (from the group, the largest number is chosen). Second, a pair $(b, 2022-b)$ (i.e., a number $1 \leqslant b \leqslant a-1$) is chosen, and in all other pairs, the choice is uniquely determined (in pairs with the smallest number from $b+1$ to $a-1$, the smallest number is chosen, and in pairs where it is less than $b$, the largest number is chosen).
It remains to count the number of options. Fix some $a$, then the number of ways to choose $b$ will be exactly $a-1$, plus one more option, where in all pairs with the smallest number less than $a$, the smallest number was chosen (i.e., the number $b$ simply does not exist). In total, there are $a$ options for the number $b$. Summing over all $a \leqslant 1011$, we get $1+2+3+\ldots+1010+1011=\frac{1011 \cdot 1012}{2}=511566$ options for our set. Clearly, all these options are distinct and satisfy the condition (the set is uniquely determined by the chosen numbers $a$ and $b$).
## Criteria
The highest appropriate criterion is used:
7 points. Any complete solution to the problem.
7 points. Any complete solution to the problem, but the answer is given in the form of a formula or expression (e.g., $\frac{1011 \cdot 1012}{2}$ or $C_{1012}^{2}$).
6 points. Any complete solution to the problem, but the answer is given in the form of a formula with an ellipsis (e.g., $1+2+3+\ldots+1010+1011$).
2 points. The numbers are divided into pairs, but there is no further progress.
16. The correct answer is given. | 511566 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Task 2. Find the number of ways to color all natural numbers from 1 to 20 in blue and red such that both colors are used and the product of all red numbers is coprime with the product of all blue numbers. | Answer: $2^{6}-2=62$ ways.
Solution. Note that all even numbers must be of the same color. Since among them are the numbers 6, 10, and 14, the numbers divisible by 3, 5, and 7 must be of the same color. The remaining numbers are $1, 11, 13, 17$, and 19. Note that they can be distributed in any way among the two colors. Thus, we have 6 groups, each of which can be of any color, i.e., a total of $2^{6}$ ways of coloring.
Note that 2 of these do not fit, where all numbers are of the same color. In total, we get $2^{6}-2=62$ ways.
## Criteria
The most suitable criterion is used:
7 points. Any complete solution to the problem.
3 points. Noted that even numbers, as well as numbers divisible by 3, 5, and 7, must be of the same color.
1 point. The correct answer is given.
The following errors in an otherwise correct solution result in point deductions:
-1 point. Not considered that both colors must be present.
-2 points. Not considered that both colors must be present, and not considered that "1" is not a coprime number.
-2 points. Not considered the alternative coloring, i.e., there are two pairs of groups: 1 group - red, 2 group - blue and 1 group - blue, 2 group - red.
-1 point. When considering monochromatic groups, the number 1 or one of the prime numbers greater than 10 is omitted. If more than one monochromatic group is omitted, the solution is not considered correct overall.
-3 points. Not considered that both colors must be present, and not considered the alternative coloring. | 62 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. On the board, the numbers $2,3,5, \ldots, 2003,2011,2017$ are written, i.e., all prime numbers not exceeding 2020. In one operation, two numbers $a, b$ can be replaced by the largest prime number not exceeding $\sqrt{a^{2}-a b+b^{2}}$. After several operations, only one number remains on the board. What is the maximum value it can take? | Answer: The maximum value is 2011.
Solution. Note that if $a$ $2011^{2}$, therefore, as a result of this operation, the number 2011 will appear on the board.
Remark. The inequality $a<\sqrt{a^{2}-a b+b^{2}}<b$ for $a<b$ can be proven geometrically. The matter is that in a triangle with sides $a$ and $b$ and an angle of $60^{\circ}$ between them, the length of the third side is exactly $\sqrt{a^{2}-a b+b^{2}}$. Since the angle $60^{\circ}$ is always the middle in size in its triangle, the side opposite to it is also the middle in size.
## Criteria
Any complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed up:
3 p. It is shown how to get 2011, but it is not proven that a larger number cannot be obtained.
4 p. It is proven that a number larger than 2011 cannot be obtained. | 2011 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
1. On a plane, an overlapping square and a circle are drawn. Together they occupy an area of 2018 cm². The area of intersection is 137 cm². The area of the circle is 1371 cm². What is the perimeter of the square? | Answer: 112 cm.
The area of the part of the circle outside the square is $1371-137=1234$ cm $^{2}$, therefore, the area of the square can be expressed by the formula $2018-1234=784 \mathrm{~cm}^{2}$. In conclusion, the length of the side of the square is $\sqrt{784}=28$ cm, and its perimeter is 112 cm.
## Criteria
+ Correct solution - 7 points.
$\pm$ Arithmetic error with correct reasoning - 5 points. | 112 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. Gosha entered a natural number into the calculator. Then he performed the following operation, consisting of two actions, three times: first, he extracted the square root, and then took the integer part of the obtained number. In the end, he got the number 1. What is the largest number that Gosha could have initially entered?
Let's recall, the integer part of a number is the largest integer not exceeding the given number. | Answer: 255.
Solution. Suppose he entered a number not less than 256. Then after the first operation, he would get a number not less than $[\sqrt{256}]=16$, after the second - not less than $[\sqrt{16}]=4$, after the third - not less than $[\sqrt{4}]=2$, which is a contradiction.
Let's assume Gosha entered the number 255. Then after the first operation, he would get $[\sqrt{255}]=15$, after the second $-[\sqrt{15}]=3$, after the third $-[\sqrt{3}]=1$. Therefore, the answer to the problem is the number 255.
## Criteria
## The following criteria are cumulative:
4 p. It is proven that the number entered by Gosha is not greater than 255.
3 p. It is proven that the number 255 satisfies the condition of the problem. | 255 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Task 3. Lёnya has cards with digits from 1 to 7. How many ways are there to glue them into two three-digit numbers (one card will not be used) so that each of them is divisible by 9? | Answer: 36.
Solution. The sum of the digits in each number is divisible by 9, which means the overall sum of the used digits is also divisible by 9. The sum of all given digits $1+2+\ldots+7$ is 28. If we remove the digit 1, the remaining sum is 27, which is divisible by 9; removing any other digit cannot result in a sum divisible by 9. Therefore, the digits used are $2,3,4,5,6,7$.
Notice that the smallest possible sum of three of these digits is $2+3+4=9$, and the largest is $5+6+7=18$. No other sums divisible by 9 can be obtained; 9 and 18 can only be obtained in one way. Thus, one number consists of the digits $2,3,4$, and the other consists of $5,6,7$.
There are six numbers that can be formed from the digits 2,3,4, and six numbers that can be formed from the digits $5,6,7$. We need all possible pairs of these numbers.
## Criteria
A complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
2 p. It is proven that the digit 1 is not used.
3 p. Assuming (possibly unjustified) that the digit 1 is not used, it is proven that one number consists of the digits $2,3,4$, and the other of $5,6,7$.
1 6. The above is not proven but stated.
2 p. The correct answer is provided. | 36 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. Five numbers $2,0,1,9,0$ are written in a circle on the board in the given order clockwise (the last zero is written next to the first two). In one move, the sum of each pair of adjacent numbers is written between them. For example, such an arrangement of numbers (on the right) will be after the first move:
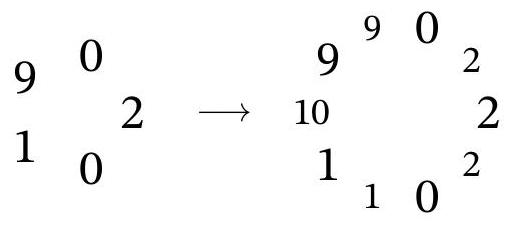
After 5 moves, Polina calculated the sum of all numbers from the first zero (the one initially between 2 and 1) to the second zero (the one initially between 9 and 2) when moving around the circle clockwise, while Alina calculated the sum of all other numbers. What is the difference between Alina's and Polina's numbers? | Answer: $8 \cdot 3^{5}=1944$.
Solution. Let's see how the numbers between the first and second zero (which Polina will count at the end) change. On each move, each "old" number is included as an addend in two "new" numbers. This means that if all the "new" numbers are added together, each "old" number will be summed twice, so the sum of the "new" numbers is twice the sum of the "old" numbers. Therefore, the total sum of the numbers between the first and second zero triples on each move.
The same thing happens with the other numbers. It remains to note that their difference is initially 8, and it triples with each move. After five moves, it will reach the value $8 \cdot 3^{5}=1944$.
## Criteria
## The largest suitable criterion is used:
7 p. Any complete solution to the problem.
## 4 p. It is proven that the sum of the numbers on the segment between two zeros triples on each move.
## 3 p. The correct answer is given. | 1944 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. In the cells of an $8 \times 8$ chessboard, there are 8 white and 8 black chips such that no two chips are in the same cell. Additionally, no column or row contains chips of the same color. For each white chip, the distance to the black chip in the same column is calculated. What is the maximum value that the sum of these distances can take? The distance between chips is the distance between the centers of the cells they occupy. | Answer: 32
Solution. An example of chip placement where the sum of distances is 32 is shown in the figure:
We will prove that the sum of distances cannot be greater than 32. For this, consider an arbitrary placement of chips that satisfies the condition. Let \( S \) be the sum of the distances specified in the condition.
Let the white and black chips in the \( i \)-th column be in rows \( a_i \) and \( b_i \), respectively. We estimate the distance between them:
\[
|a_i - b_i| = |(a_i - 4.5) - (b_i - 4.5)| \leq |a_i - 4.5| + |b_i - 4.5|
\]
(essentially, this is the triangle inequality for points \( a_i, b_i \), and 4.5 on a line). Summing this estimate for all differences \( |a_i - b_i| \), we get:
\[
S \leq |a_1 - 4.5| + |a_2 - 4.5| + \ldots + |a_8 - 4.5| + |b_1 - 4.5| + |b_2 - 4.5| + \ldots + |b_8 - 4.5|
\]
Notice that the right-hand side does not depend on the placement of the chips, as the numbers \( a_i, 0 \leq i \leq 8 \), are some permutation of the numbers from 1 to 8. Similarly for \( b_i \). We have:
\[
\begin{aligned}
S & \leq |1 - 4.5| + |2 - 4.5| + \ldots + |8 - 4.5| + |1 - 4.5| + |2 - 4.5| + \ldots + |8 - 4.5| = \\
& = 2 \cdot (3.5 + 2.5 + 1.5 + 0.5 + 0.5 + 1.5 + 2.5 + 3.5) = 32
\end{aligned}
\]
Remark. From the proof of the estimate, it is not difficult to understand how any example with the required sum of distances is constructed: in each column, a chip of one color is in the upper half, and a chip of the other color is in the lower half. In any other case, equality in the triangle inequality will not be achieved.
## Criteria
A complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
6 points. It is proven that the sum of distances cannot exceed 32.
If the solution is unjustifiably reduced to some "optimal" case or class of cases (for example, it is claimed without proof that in each column, the black and white chips must be in different halves of the column), then points for this part are not given.
1 point. An example of chip placement is provided where the sum of distances is 32. | 32 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. In each cell of a $15 \times 15$ table, a number $-1, 0$, or $+1$ is written such that the sum of the numbers in any row is non-positive, and the sum of the numbers in any column is non-negative. What is the smallest number of zeros that can be written in the cells of the table? | Answer: 15.
Evaluation. Since the sum of the numbers in all rows is non-positive, the sum of all numbers in the table is also non-positive. On the other hand, if the sum of the numbers in any column is non-negative, then the sum of all numbers in the table is non-negative. Therefore, the sum of all numbers in the table is actually zero, and the sums of the numbers in each column and each row are also zero.
In each row, there must be at least one zero, because otherwise the sum of all fifteen +1 and -1 would be odd, while it should be zero.
Thus, there must be at least 15 zeros in the table.

Fig. 2: Solution to problem 5.
Example. One possible example with 15 zeros is shown in Fig. 2. The symbols “+” and “-” correspond to the placement of numbers +1 and -1, and the shaded cells represent the placement of zeros.
## Criteria
+ Correct solution - 7 points.
-. Correct answer given without explanations (or with incorrect explanations) - 1 point.
The solution naturally divides into two parts: an example of number placement with 15 zeros and a proof that there are at least 15 zeros. Points for these parts are summed.
干 Correct example with 15 zeros provided - 3 points.
$\pm$ It is justified that there cannot be fewer than 15 zeros (or that there is at least one zero in each row/column) - 4 points.
- It is noted that the sum of the numbers in each row and each column must be zero, but the conclusion about the presence of a zero in any row/column did not follow - 1 point out of 4 possible for the estimate. | 15 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. There is a deck of 1024 cards, each with a different set of digits from 0 to 9, and all sets are distinct (including an empty card). We will call a set of cards complete if each digit from 0 to 9 appears exactly once on them.
Find all natural $k$ for which there exists a set of $k$ cards with the following condition: among them, no complete set can be selected, but adding any card from the deck violates this condition. | Solution. Answer: 512.
For each card, consider another card that complements it to a complete set (for example, for the card 3679, such a card would be 012458). It is clear that all 1024 cards can be divided into 512 non-overlapping pairs of cards that complement each other to a complete set. Next, we will prove that in any desired set, there must be exactly one card from each such pair, i.e., \( k = 512 \).
From the condition, it follows that at most one card from each pair can be among the selected ones. Now we will show that at least one card from each pair must be included.
Consider a pair of complementary cards, denoted as \( A \) and \( B \). Suppose neither of them is in the selected set. According to the condition, adding any card from the deck will result in a complete set. Adding card \( A \) to the set, we will find several cards that complement \( A \) to a complete set, i.e., all the digits on these cards simply match the set of digits on card \( B \). Similarly, adding card \( B \), we will find several cards from the set whose digits match the set of digits on card \( A \). Then, combining all these cards (which match the sets on cards \( A \) and \( B \)), we will get a complete set, which is a contradiction.
Now let's provide an example of a possible set for \( k = 512 \). Choose all cards that do not have the digit 9; there are exactly 512 such cards. It is clear that there is no complete set among them (the digit 9 is not present anywhere), and for each unselected card, its complement is among the selected ones, i.e., adding it will result in a complete set from these two cards.
## Criteria
## Points for the following achievements are summed up:
4 6. Proved that \( k \geqslant 512 \) (or that in each pair of cards that complement each other to a complete set, at least one card must be selected).
1 6. Proved that \( k \leqslant 512 \) (or that in each pair of cards that complement each other to a complete set, no more than one card should be selected).
1 6. Provided a correct example of a set of 512 cards.
1 6. Provided justification that the example set of 512 cards meets the conditions of the problem.
0 6. Only the correct answer. | 512 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. In a certain company, there are 100 shareholders, and any 66 of them collectively own at least $50\%$ of the company's shares. What is the largest percentage of all shares that one shareholder can own? (The percentage of shares in the company owned by a shareholder can be non-integer.) | Answer: $25 \%$.
Solution. Consider any shareholder $A$. Divide the other 99 shareholders into three groups $B, C, D$ of 33 shareholders each. By the condition, $B$ and $C$ together have at least $50 \%$ of the company's shares, similarly for $C$ and $D$, and for $B$ and $D$. Adding all this up and dividing by two, we get that $B, C, D$ together have at least $((50+50+50) : 2) \% = 75 \%$ of the shares, so $A$ has no more than the remaining $25 \%$ of the shares.
Moreover, $A$ can have exactly $25 \%$ of the shares if all other shareholders have an equal number of shares, each with $\frac{75}{99} \% = \frac{25}{33} \%$. Clearly, in this case, any 66 shareholders of the company together have at least $66 \cdot \frac{25}{33} \% = 50 \%$ of the shares.
## Criteria
The largest applicable criterion is used:
The following criteria are summed:
5 p. It is proven that any shareholder has no more than $25 \%$ of the shares.
2 p. It is proven that some shareholder can have exactly $25 \%$ of the shares. | 25 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 5. In triangle $A B C$, the angle at vertex $B$ is $120^{\circ}$, point $M$ is the midpoint of side $A C$. Points $E$ and $F$ are chosen on sides $A B$ and $B C$ respectively such that $A E=E F=F C$. Find $\angle E M F$. | Answer: $90^{\circ}$.
Solution. Note that the sum of angles $A$ and $C$ is $60^{\circ}$. Let $A E=E F=F C=u$.
On the line $E M$, place a point $G$ such that point $M$ is the midpoint of segment $E G$. Triangles $A M E$ and $C M G$ are equal by two sides and the angle between them, so $\angle M C G=\angle M A E=\angle A$ and $C G=A E=u$.
Note that $\angle F C G=\angle F C M+\angle M C G=\angle C+\angle A=60^{\circ}$.
Since $F C=u=C G$, triangle $F C G$ is equilateral, and $F G=u$. Therefore, triangle $E F G$ is isosceles, $E F=F G=u$. Its median $F M$ is also an altitude, so $\angle E M F=90^{\circ}$.
## Criteria
One of the largest suitable criteria is used:
7 p. Any complete solution to the problem.
1 p. A point symmetric to $E$ or $G$ relative to $M$ is considered, but there is no further progress.
0 p. Only the correct answer is given. | 90 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
5. A cube with a side of 5 is made up of 125 smaller cubes with a side of 1. How many small cubes does a plane perpendicular to one of the cube's diagonals and passing through its midpoint intersect? | Answer: 55.
Let's introduce a coordinate system such that the cube is located in the first octant (the set of points with non-negative coordinates) and the mentioned diagonal extends from the origin $O$. The midpoint of the cube's diagonal has coordinates $(5 / 2, 5 / 2, 5 / 2)$, so the specified plane is given by the equation $x + y + z = 15 / 2$. Consider one of the 125 small cubes. Let the vertex closest to point $O$ have coordinates $(k, m, n)$, where the integers $k, m, n$ satisfy the inequalities $0 \leqslant k, m, n \leqslant 4$. The vertex farthest from point $O$ has coordinates $(k+1, m+1, n+1)$. Thus, the small cube intersects the plane if and only if $k + m + n \leqslant 15 / 2 \leqslant k + 1 + m + 1 + n + 1$, which is equivalent to the condition $k + m + n \in (9 / 2 ; 15 / 2)$. Considering the integer nature of the sum $k + m + n$, we get only three cases: $k + m + n = 5$, $k + m + n = 6$, or $k + m + n = 7$. Let's calculate the number of small cubes for each of the three cases.
(i) $k + m + n = 5$. List the ways to split 5 into three summands and indicate the number of different permutations of these summands: $0 + 1 + 4$ (6 solutions), $0 + 2 + 3$ (6 solutions), $1 + 1 + 3$ (3 solutions), $1 + 2 + 2$ (3 solutions) - a total of 18.
(ii) $k + m + n = 6. 0 + 2 + 4$ (6 solutions), $0 + 3 + 3$ (3 solutions), $1 + 1 + 4$ (3 solutions), $1 + 2 + 3$ (6 solutions), $2 + 2 + 2$ (1 solution) - a total of 19.
(iii) $k + m + n = 7$. All such small cubes are symmetric to those with the condition $k + m + n = 5$ relative to the center of the cube - a total of 18.
In total: $18 + 19 + 18 = 55$.
t The intersected small cubes are divided into three layers, and the number of small cubes in at least two layers is correctly calculated with justification. 6 points
± The intersected small cubes are divided into three layers, and the number of small cubes in at least one layer is correctly calculated with justification. 5 points
± The intersected small cubes are divided into three layers, and the number of small cubes in at least one layer is correctly calculated, but the justification is not strict or is missing. 4 points
Ғ The intersected small cubes are divided into three layers, but there is no further progress. 3 points
- The correct answer is given without justification. 2 points
- The equation of the plane is written. 1 point | 55 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Problem 1. At a round table, 60 people are sitting. Each of them is either a knight, who always tells the truth, or a liar, who always lies. Each person at the table said: "Among the next 3 people sitting to my right, there is no more than one knight." How many knights could have been sitting at the table? List all possible options and prove that there are no others. | Answer: 30.
Solution. Consider any arbitrary quartet of consecutive people. If there were at least 3 knights in it, the leftmost of them would definitely lie, which is impossible. If there were at least 3 liars, the leftmost of them would definitely tell the truth, which is also impossible. Therefore, in every quartet of consecutive people, there are exactly 2 knights and 2 liars. Dividing all the people into 15 such quartets, we get that there are $15 \cdot 2=30$ knights.
Another solution. Notice that at the table, there cannot be only knights or only liars. Then there will be a pair of knight-liar sitting next to each other in this exact order. Consider 4 cases of who can sit to the right of this pair.
Case 1. Two knights sit to the right.
Then we get the sequence
$$
\text { knight-liar-knight-knight, }
$$
which contradicts the condition, as the first knight lied.
Case 2. Two liars sit to the right.
Then we get the sequence
knight-liar-liar-liar.
Whoever sits immediately after this sequence, the first liar will tell the truth, which contradicts the condition.
Case 3. A knight-liar pair sits to the right in this exact order.
Then we get the sequence
$$
\text { knight-liar-knight-liar. }
$$
Consider the first liar. He lies, so among the next three, there must be at least two knights. From this, we uniquely get
$$
\text { knight-liar-knight-liar-knight. }
$$
Now consider the second knight. He tells the truth, so the sixth person in the sequence will be a liar:
$$
\text { knight-liar-knight-liar-knight-liar. }
$$
Continuing these considerations, we get an alternating arrangement where there are an equal number of knights and liars.
Case 4. A liar-knight pair sits to the right in this exact order.
Then we get the sequence
$$
\text { knight-liar-liar-knight. }
$$
Consider the first liar. He lies, so among the next three, there must be at least two knights. From this, we uniquely get
$$
\text { knight-liar-liar-knight-knight. }
$$
Now consider the second knight. He tells the truth, so the sixth and seventh people in the sequence will be liars
knight-liar-liar-knight-knight-liar-liar.
Continuing these considerations, we get an arrangement where there are an equal number of knights and liars.
## Criteria
The highest applicable criterion is used:
7 p. Any complete solution to the problem.
7 6. The problem is correctly solved for the case where both knights and liars are present at the table.
4 p. Both possible cases of arranging knights and liars are considered in the solution, but there is no justification for why there are no other arrangements.
2 p. One of the two possible cases of arranging knights and liars is considered in the solution, but there is no justification for why there are no other arrangements.
1 6. Only the correct answer is present. | 30 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
1. On an island, there live knights who always tell the truth and liars who always lie. The population of the island is 1000 people, distributed across 10 villages (with no fewer than two people in each village). One day, every islander claimed that all their fellow villagers are liars. How many liars live on the island? (Two residents are fellow villagers if they live in the same village.) | Answer: 990.
In one village, at least two knights cannot live, because otherwise the knights would lie. Also, in the village, they cannot all be liars, since then these liars would tell the truth. Therefore, in each village there is exactly one knight, and there are 10 knights in total, and 990 liars. | 990 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
2. Petya climbed up a moving upward escalator, counting 75 steps, and then descended the same escalator (i.e., moving against the direction of the escalator), counting 150 steps. During the descent, Petya walked three times faster than during the ascent. How many steps are there on the stopped escalator? | Answer: 120.
For convenience, let's introduce a unit of time during which Petya took one step while ascending the escalator. We will measure all speeds in steps per unit of time. Petya's speed while ascending is 1 step per unit of time, and his speed while descending is 3 steps per unit of time. Let the speed of the escalator be $x$. The absolute speed of Petya was $1+x$ while ascending and $3-x$ while descending. Petya spent 75 units of time ascending and 50 units of time descending (he took steps three times faster while descending). The distance covered while ascending and descending was the same - the length of the escalator. Therefore, $75 \cdot(1+x)=50 \cdot(3-x)$, from which $125 x=75, x=0.6$.
The length of the escalator is $75 \cdot(1+0.6)=120$ steps. This is the number of steps on the stopped escalator. | 120 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
3. For a convex quadrilateral $A B C D$, it is known that $A B=B C=C A=$ $C D, \angle A C D=10^{\circ}$. A circle $\omega$ is circumscribed around triangle $B C D$ with center $O$. Line $D A$ intersects circle $\omega$ at points $D$ and $E$. Find the measure of angle $E O A$, express your answer in degrees. | Answer: 65.
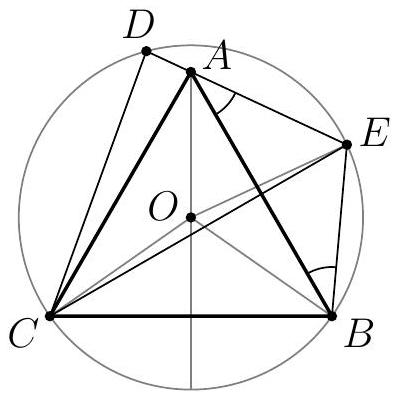
Fig. 2: to the solution of problem 3.
Fig. 2. Since triangle $A D C$ is isosceles, and we know the angle at its vertex, the angles at its base are $\angle D A C = \angle C D A = 85^{\circ}$. Therefore, $\angle B A E = 180^{\circ} - \angle D A C - \angle C A B = 35^{\circ}$. Angle $E B C$ complements angle $E D C$ to $180^{\circ}$ and is thus $95^{\circ}$, from which $\angle E B A = 35^{\circ}$. Consequently, triangle $A E B$ is isosceles, and line $C E$ is the perpendicular bisector of $A B$. But then $C B$ is the angle bisector of $\angle B C A$, so $\angle B C E = 30^{\circ}$, and the corresponding central angle $\angle B O E = 60^{\circ}$.
On the other hand, $\angle C O E = 2 \angle C D E = 170^{\circ}$, from which $\angle C O B = 110^{\circ}$.
Finally, from the symmetry of triangle $A B C$ with respect to $A O$, it is easy to see that the desired angle $\angle E O A$ complements to $180^{\circ}$ the sum of angle $\angle B O E$ and half of angle $\angle C O B$, i.e., $\angle E O A = 180^{\circ} - \angle B O E - \frac{1}{2} \angle C O B = 65^{\circ}$. | 65 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
4. Anya writes a natural number, and Boris replaces one of its digits with a digit differing by 1. What is the smallest number Anya should write to ensure that the resulting number is guaranteed to be divisible by 11? | Answer: 909090909.
According to the divisibility rule for 11, the remainder of a number when divided by 11 is the same as the remainder of the alternating sum of its digits when divided by 11. Therefore, changing a digit by 1 also changes the remainder by 1 when divided by 11. This means the original number gives a remainder of 10 or 1 when divided by 11.
If the original number gives a remainder of 10 when divided by 11, then any change in its digits should increase the remainder of the alternating sum of its digits by 1 when divided by 11. Thus, the digits in odd positions (counting from the end) can only be increased by 1, and the digits in even positions can only be decreased by 1, i.e., the number has the form ...909090. The smallest number of this form that gives a remainder of 10 when divided by 11 is 9090909090.
If the original number gives a remainder of 1 when divided by 11, then, similarly, it has the form ...90909, and the smallest number that fits the condition is 909090909. | 909090909 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
5. The bottom of the box is an $8 \times 8$ table. What is the smallest non-zero number of $2 \times 1$ or $1 \times 2$ tiles that can be placed on the bottom of the box so that no tile can be moved either horizontally or vertically? Each tile must occupy exactly two cells, not occupied by other tiles. | Answer: 28.

Fig. 3: Solution to problem 5.
Example: The arrangement of 28 tiles can be seen in Fig. 3.
Estimation. Cells not covered by tiles will be called empty. First, let's prove that no two empty cells can be adjacent by side.
Assume the opposite: some two empty cells are adjacent. Consider the figure formed by the adjacent empty cells. Note that the figure cannot have concave angles (see the figure), because the tile covering the cell marked with a cross can be moved vertically if it is vertical, or horizontally if it is horizontal.
If the figure has no concave angles, then it is a rectangle. Denote its dimensions as $a \times b$, where $a \geqslant b$. The situation $a \geqslant 3$ is impossible, because at least one side of the rectangle of length $a$ must be adjacent to tiles (not the edge of the box), but then the tile adjacent to a non-edge cell of the considered side can be pushed into the rectangle. A short enumeration can prove that rectangles $2 \times 2$ and $2 \times 1$ of empty cells are also impossible.
Thus, all empty cells are isolated. No empty cell can be at the edge of the board, otherwise one of the tiles adjacent to this empty cell can be pushed onto this empty cell. Tiles adjacent to an empty cell can be placed in only two ways, as shown in the figure.
From this, it follows, in particular, that two empty cells cannot be in the same row or column at a distance of two, and they also cannot be adjacent diagonally.
Now we are ready to complete the estimation. Suppose that it is possible to use fewer than 28 tiles. Then more than 8 empty cells will remain. Since empty cells cannot be adjacent to the edge of the box, they will be concentrated in the central $6 \times 6$ square. Divide the $6 \times 6$ square into four $3 \times 3$ squares. One of the squares must contain at least three empty cells. However, a short enumeration of their potential placements shows that this is impossible. Contradiction. | 28 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
6. On the parade ground, 2018 soldiers are lined up in one row. The commander can order either all soldiers standing in even positions or all soldiers standing in odd positions to leave the formation. After this order, the remaining soldiers close up into one row. In how many ways can the commander issue a series of 8 orders so that exactly 7 soldiers remain in the formation? | Answer: 30.
Let's add 30 imaginary people to the end of the line. We will number all the people in the line from 0 to 2047. We will write all these numbers in binary using 11 digits. This will result in sequences from 00000000000 to 11111111111. The imaginary soldiers correspond to numbers from 11111100010 to 11111111111 (from 2018 to 2047 in binary notation).
Notice that soldiers in even positions have 1 as the last digit in their binary representation, while soldiers in odd positions have 0. This means that after the order is executed, only soldiers with a fixed last digit remain in the line. After the next order, only soldiers with a fixed second-to-last digit remain, and so on.
After a series of 8 orders, the soldiers remaining in the line will have binary numbers of the form $\overline{x x a b c d e f g h}$, where the symbols $x$ represent digits that can take any value; $a, b, c, d, e, f, g, h$ are the digits fixed in the first eight orders. Clearly, soldiers with $\overline{x x x}=000,001,010,011,100,101,110$ were indeed present in the initial line, as the minimum number of an imaginary soldier starts with 111. We are interested in situations where the soldier with the number $\overline{111 a b c d e f g h}$ is imaginary (otherwise, 8 people remain). This happens exactly in 30 cases: from 11111100010 to 11111111111. In total, there are 30 possible groups of 7 people. | 30 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
2. When a five-digit number is multiplied by 9, the result is a number composed of the same digits but in reverse order. Find the original number. | Answer: 10989.
Let $\overline{a b c d e}$ be the original number. The condition is written as the equation $9 \cdot \overline{a b c d e}=\overline{e d c b a}$. Note that $a=1$, because if $a \geqslant 2$, then $9 \cdot \overline{a b c d e} \geqslant 9 \cdot 20000>100000>\overline{e d c b a}$.
We have $9 \cdot \overline{1 b c d e}=\overline{e d c b 1}$. From this, the last digit $e=9$ is uniquely determined.
Working with $9 \cdot \overline{1 b c d 9}=\overline{9 d c b 1}$. Note that if $b \geqslant 2$, then $9 \cdot \overline{1 b c d 9}>$ $9 \cdot 12000>100000>\overline{e d c b a}$. Therefore, $b=0$ or $b=1$. Let's consider these two cases:
If $b=0$, the equation reduces to $9 \cdot \overline{10 c d 9}=\overline{9 d c 01}$. Considering the second-to-last digit, we conclude that $d=8$. By trying the possible values of the digit $c$, we find the unique solution $\overline{a b c d e}=10989$.
If $b=1$, the equation is rewritten as $9 \cdot \overline{11 c d 9}=\overline{9 d c 11}$. Analyzing the second-to-last digit, we get $d=7$. But $9 \cdot \overline{11 c 79}>9 \cdot 11000=99000>\overline{97 c 11}$, which is a contradiction. Therefore, there are no solutions in the case $b=1$.
The only number that satisfies the condition of the problem is 10989. | 10989 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. We will call a pair of numbers magical if the numbers in the pair add up to a multiple of 7. What is the maximum number of magical pairs of adjacent numbers that can be obtained by writing down all the numbers from 1 to 30 in a row in some order? | Answer: 26.
Example: $1,6,8,13,15,20,22,27,29,2,5,9,12,16,19,23,26,30,3,4$, $10,11,17,18,24,25,7,14,21,28$. It is not hard to see that in this sequence, only the pairs $(29,2),(30,3),(25,7)$ are not magical.
Evaluation: Suppose it is possible to make no less than 27 pairs magical. Then there would be no more than two non-magical pairs. Let's color all numbers from 1 to 30 in four colors depending on the remainder when divided by 7: numbers with remainders 1 or 6 - in red; with remainders 2 or 5 - in blue; with remainders 3 or 4 - in purple; with remainder 0 - in orange.
Note that numbers in a magical pair must be of the same color. Therefore, if there were no more than two non-magical pairs, the color would have changed no more than twice when moving along the row from left to right, i.e., there would be no more than three colors. But there are four, a contradiction. | 26 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
5. Dima has 25 identical bricks of size $5 \times 14 \times 17$. Dima wants to build a tower from all his bricks, each time adding one more brick on top (each new brick adds 5, 14, or 17 to the current height of the tower). We will call a number $n$ constructible if Dima can build a tower of height exactly $n$. How many constructible numbers exist? | Answer: 98.
In essence, we need to find the number of different towers by height that can be built from the given set of bricks.
Mentally reduce the length, width, and height of each brick by 5: from $5 \times 14 \times 17$ to $0 \times 9 \times 12$. Then the total height of a potential tower will decrease by $25 \cdot 5$, and the number of different towers by height, composed of the new bricks, will coincide with the number of different towers by height from the old ones. Now reduce the dimensions of the bricks by three times: from $0 \times 9 \times 12$ to $0 \times 3 \times 4$. The sizes of potential towers will also decrease by three times, and the number of different towers by height will remain unchanged.
Thus, the original problem is equivalent to the following: how many different values can be obtained by adding the numbers $0,3,4$ in a quantity of 25? Note that if the number 3 appears at least four times in the sum, then the set $3,3,3,3$ can be replaced by the set $4,4,4,0$; with this replacement, both the sum and the number of numbers remain the same. Therefore, we can consider only those sums where the number 3 appears no more than three times.
If the number 3 appears 0 times, then there are 26 different values of the sum: $0,4,8, \ldots, 4 \cdot 25$.
If the number 3 appears 1 time, then there are 25 different values of the sum: $3,3+4,3+8, \ldots, 3+4 \cdot 24$.
If the number 3 appears 2 times, then there are 24 different values of the sum: $6,6+4,6+8, \ldots, 6+4 \cdot 23$.
If the number 3 appears 3 times, then there are 23 different values of the sum: $9,9+4,9+8, \ldots, 9+4 \cdot 22$.
The values in the first, second, third, and fourth lists give remainders when divided by 4 of $0,3,2,1$, respectively, and therefore the values in different lists are different.
In total, $26+25+24+23=98$ possible values of the tower height. | 98 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
6. The bottom of the box is an $8 \times 8$ table. What is the smallest non-zero number of $2 \times 1$ or $1 \times 2$ tiles that can be placed on the bottom of the box so that no tile can be moved either horizontally or vertically? Each tile must occupy exactly two cells, not occupied by other tiles. | Answer: 28.

Fig. 1: to the solution of problem 6.
Example: the arrangement of 28 tiles can be seen in Fig. 1.
Estimate. Cells not covered by tiles will be called empty. To begin with, let's prove that no two empty cells can be adjacent by side.
Assume the opposite: some two empty cells are adjacent. Consider the figure formed by the adjacent empty cells. Note that the figure cannot have concave angles (see the figure), because the tile covering the cell marked with a cross can be moved vertically if it is vertical, or horizontally if it is horizontal.
If the figure has no concave angles, then it is a rectangle. Let its dimensions be $a \times b$, where $a \geqslant b$. The situation $a \geqslant 3$ is impossible, because at least one side of the rectangle of length $a$ must be adjacent to tiles (not the edge of the box), but then the tile adjacent to a non-edge cell of the considered side can be pushed into the rectangle. A short enumeration can prove that rectangles $2 \times 2$ and $2 \times 1$ of empty cells are also impossible.
Thus, all empty cells are isolated. No empty cell can be at the edge of the board, otherwise one of the tiles adjacent to this empty cell can be pushed onto this empty cell. Tiles adjacent to an empty cell can be placed in only two ways, as shown in the figure.
From this, in particular, it follows that two empty cells cannot be in the same row or column at a distance of two, and they also cannot be adjacent diagonally.
Now we are ready to complete the estimate. Suppose that it is possible to manage with fewer than 28 tiles. Then more than 8 empty cells will remain. Since empty cells cannot be adjacent to the edge of the box, they will be concentrated in the central $6 \times 6$ square. Divide the $6 \times 6$ square into four $3 \times 3$ squares. One of the squares must contain at least three empty cells. But a short enumeration of their potential placements shows that this is impossible. Contradiction. | 28 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
10.4. Through the point with coordinates $(10,9)$, lines (including those parallel to the coordinate axes) have been drawn, dividing the plane into angles of $10^{\circ}$. Find the sum of the x-coordinates of the points of intersection of these lines with the line $y=101-x$. | Answer: 867. Solution: Shift the entire picture to the left by 1. We get a set of lines passing through the point $(9,9)$ and intersecting the line $y=100-x$. The picture will become symmetric with respect to the line $y=x$, so the sum of the abscissas on it is equal to the sum of the ordinates. Through the point $(9,9)$, 18 lines are drawn, and the line $y=100-x$ intersects 17 of them. For each point on the line $y=100-x$, the sum of the coordinates is 100, so the total sum of the abscissas and ordinates is 1700, and the sum of the abscissas is half of that, which is 850. However, on the symmetric picture, each abscissa is 1 less than the original, so the desired sum is $850+17=867$.
Criterion: No less than 1 point for the correct answer without a correct justification. 1 point for the idea of shifting the picture so that it becomes symmetric with respect to the axes. 5 points if all ideas are found, but the answer is incorrect due to an incorrect count of the number of intersection points (for example, the student counts 18 or 36 points). | 867 | Geometry | math-word-problem | Yes | Yes | olympiads | false |
Task 4. A pair of natural numbers is called good if one of the numbers is divisible by the other. Numbers from 1 to 30 were divided into 15 pairs. What is the maximum number of good pairs that could result? | Solution. Answer: 13.
First, let's prove that more than 13 good pairs could not have been formed. We will call a number bad if it is prime and not less than 15. There are only four bad numbers: \(17, 19, 23, 29\). None of the other numbers from 1 to 30 can be divisible by any bad number, and the bad numbers themselves can only be divisible by one (among the others). Consequently, at most one of the bad numbers can form a good pair with one, and the remaining at least three bad numbers will "ruin" at least 2 pairs.
Now let's consider the following 13 good pairs: \((1,27), (2,4), (3,6), (5,25), (7,21)\), \((8,16), (9,18), (10,20), (11,22), (12,24), (13,26), (14,28), (15,30)\). The remaining 4 numbers can be paired, for example, as follows: \((17,19), (23,29)\). In total, we have exactly 13 good pairs.
## Criteria
One of the largest suitable criteria is used:
7 points. Any complete solution to the problem.
4 points. An example consisting of 13 good pairs is constructed.
3 points. It is proven that there are no more than 13 good pairs.
1 point. The idea of considering "large" prime numbers (17, 19, 23, 29) is present, but there is no further progress. | 13 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. In a $3 \times 3$ table, natural numbers (not necessarily distinct) are placed such that the sums in all rows and columns are different. What is the minimum value that the sum of the numbers in the table can take? | Answer: 17.
Solution. Note that in each row and column, the sum of the numbers is no less than 3. Then, the doubled sum of all numbers in the table, which is equal to the sum of the sums of the numbers in the rows and columns, is no less than \(3+4+\ldots+8=33\), so the simple sum of the numbers in the table is no less than 17.
Example of a table with a sum of 17:
| 1 | 1 | 1 |
| :--- | :--- | :--- |
| 1 | 2 | 2 |
| 2 | 3 | 4 |
## Criteria
The largest suitable criterion is used:
7 p. Any complete solution to the problem.
4 p. It is proven that the sum of the numbers in the table is no less than 17.
3 p. An example of a table with a sum of 17 is provided. | 17 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 3. In the vertices of a regular 2019-gon, numbers are placed such that the sum of the numbers in any nine consecutive vertices is 300. It is known that the 19th vertex has the number 19, and the 20th vertex has the number 20. What number is in the 2019th vertex? | Answer: 61.
Solution. Let the numbers at the vertices be denoted as $x_{1}, x_{2}, \ldots, x_{2019}$. Since the sum of any nine consecutive numbers is the same, the numbers that are 8 apart are equal. Therefore, $x_{1}=x_{10}=x_{19}=\ldots=x_{1+9 k}=\ldots$. Since 2019 is not divisible by 9 but is divisible by 3, continuing this sequence in a cycle will include all numbers of the form $x_{3 k+1}$. Similar sequences can be constructed starting from the numbers $x_{2}$ and $x_{3}$. Thus, the numbers at the vertices that have the same remainder when divided by 3 are equal.
Since each set of nine consecutive numbers contains three sets of vertices with different remainders when divided by 3, the sum of the numbers in each such set is 100. Note that 19 gives a remainder of 1 when divided by 3, 20 gives a remainder of 2, and 2019 gives a remainder of 0, so the number at vertex 2019 is $100 - 19 - 20 = 61$.
## Criteria
## The largest suitable criterion is used:
## 7 p. Any complete solution to the problem.
4 p. It is proven that numbers that are 2 apart are equal.
1 p. It is noted that numbers that are 8 apart are equal. | 61 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
Problem 4. Polycarp has 2 boxes, the first of which contains $n$ coins, and the second is empty. In one move, he can either transfer one coin from the first box to the second, or remove exactly $k$ coins from the first box, where $k$ is the number of coins in the second box. For which $n$ can Polycarp make the first box empty in no more than 10 moves?
Answer: for $n$ from 0 to 30 inclusive. | Solution. Let's call a move where one coin is moved from the first box to the second box a move of the first type, and a move where coins are removed from the first box a move of the second type. Suppose a total of $x$ moves of the first type and $y$ moves of the second type were made. Then, the second box contains no more than $x$ coins. Therefore, when performing moves of the second type, we will remove no more than $x y$ coins from the first box, meaning we will remove no more than $x + x y$ coins in total. Since $x + y \leqslant 10$, then
$$
x + x y \leqslant x + x(10 - x) = -x^2 + 11x
$$
For integer values of $x$, the maximum of this expression is achieved at points $x = 5$ and $x = 6$ and is equal to $5 \cdot 6 = 30$. Thus, $n \leqslant 30$. We will prove that any $n \leqslant 30$ works.
If we make 5 moves of the first type and then 5 moves of the second type, we will remove exactly 30 coins from the first box. Write down the sequence of 1s and 2s, where 1 represents a move of the first type and 2 represents a move of the second type. Notice that if in this sequence we swap a neighboring pair 12 to a pair 21, the total number of coins removed from the first box will decrease by 1. We can do this until all 2s are on the left and all 1s are on the right. Then we will replace 1 with 2, and on each step, the number of coins removed using such a sequence of operations will also decrease by 1. Thus, for any $n$ from 0 to 30, we can provide the required sequence of operations.
## Criteria
The following single most appropriate criterion is used:
7 6. Any complete solution to the problem.
If in the solution $n$ is considered a natural number, and the number 0 is not mentioned in the answer, the score is not reduced.
4 b. It is proven that $n$ does not exceed 30, but it is not explained why all smaller $n$ also work.
3 6. All examples for $n$ from 1 to 30 are described.
For the following error in a solution that otherwise fits one of the criteria above, the score is reduced:
-1 6. The maximum value of the expression $-x^2 + 11x$ for integer $x$ is found incorrectly due to an arithmetic error. | 30 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
Task 2. Lёnya has cards with digits from 1 to 7. How many ways are there to glue them into two three-digit numbers (one card will not be used) so that their product is divisible by 81, and their sum is divisible by 9? | Answer: 36.
Solution. If one of the numbers is not divisible by 9, then the other is not either, since their sum is divisible by 9. But then the product cannot be divisible by 81, a contradiction. Therefore, both numbers are divisible by 9.
Then the sum of the digits in each number is divisible by 9, and thus the total sum of the used digits is also divisible by 9. The sum of all given digits $1+2+\ldots+7$ is 28. If we discard the digit 1, the remaining sum is 27, which is divisible by 9; discarding any other digit cannot result in a sum divisible by 9. Therefore, the digits used are 2, $3,4,5,6,7$.
Note that the smallest possible sum of three of these digits is $2+3+4=9$, and the largest is $5+6+7=18$. Other sums divisible by 9 cannot be obtained; 9 and 18 can only be obtained in one way. Thus, one number consists of the digits $2,3,4$, and the other of $5,6,7$.
There are six numbers that can be formed from the digits $2,3,4$, and six numbers that can be formed from the digits $5,6,7$. We need all possible pairs of these numbers.
## Criteria
Any complete solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
1 point. It is proven that both numbers must be divisible by 9.
2 points. Assuming (possibly unjustified) that both numbers are divisible by 9, it is proven that the digit 1 is not used.
3 points. Assuming (possibly unjustified) that both numbers are divisible by 9 and the digit 1 is not used, it is proven that one number consists of the digits 2,3,4, and the other of $5,6,7$.
1 point. The previous is not proven but stated. | 36 | Number Theory | math-word-problem | Yes | Yes | olympiads | false |
3. Calculate the value of the expression
$$
\frac{\left(3^{4}+4\right) \cdot\left(7^{4}+4\right) \cdot\left(11^{4}+4\right) \cdot \ldots \cdot\left(2015^{4}+4\right) \cdot\left(2019^{4}+4\right)}{\left(1^{4}+4\right) \cdot\left(5^{4}+4\right) \cdot\left(9^{4}+4\right) \cdot \ldots \cdot\left(2013^{4}+4\right) \cdot\left(2017^{4}+4\right)}
$$ | 3. Calculate the value of the expression
$$
\frac{\left(3^{4}+4\right) \cdot\left(7^{4}+4\right) \cdot\left(11^{4}+4\right) \cdot \ldots \cdot\left(2015^{4}+4\right) \cdot\left(2019^{4}+4\right)}{\left(1^{4}+4\right) \cdot\left(5^{4}+4\right) \cdot\left(9^{4}+4\right) \cdot \ldots \cdot\left(2013^{4}+4\right) \cdot\left(2017^{4}+4\right)}
$$
Answer: $2020^{2}+1=4080401$.
Let's use the formula
$$
\begin{aligned}
a^{4}+4 & =a^{4}+4 a^{2}+4-4 a^{2}=\left(a^{2}+2\right)^{2}-(2 a)^{2}= \\
& =\left(a^{2}-2 a+2\right)\left(a^{2}+2 a+2\right)=\left((a-1)^{2}+1\right)\left((a+1)^{2}+1\right)
\end{aligned}
$$
Now the expression in the numerator of the desired fraction can be written as the product
$$
\left(2^{2}+1\right) \cdot\left(4^{2}+1\right) \cdot\left(6^{2}+1\right) \cdot \ldots \cdot\left(2018^{2}+1\right) \cdot\left(2020^{2}+1\right),
$$
while the expression in the denominator is written as
$$
\left(0^{2}+1\right) \cdot\left(2^{2}+1\right) \cdot\left(4^{2}+1\right) \cdot \ldots \cdot\left(2016^{2}+1\right) \cdot\left(2018^{2}+1\right)
$$
By canceling the common factors in the numerator and the denominator, we arrive at the answer.
## Criteria
+ Correct solution - 7 points.
+ Arithmetic error with the correct idea of the solution - 6 points.
+ The solution contains the idea of factoring $a^{4}+4$, but there is no further progress - 2 points.
- The problem is reduced to some infinite product or sum - this is not considered progress (0 points). | 4080401 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. The natural numbers $1,2, \ldots, 64$ are written in the cells of an $8 \times 8$ table such that for all $k=1,2,3, \ldots, 63$ the numbers $k$ and $k+1$ are in adjacent cells. What is the maximum possible value of the sum of the numbers on the main diagonal? | 5. The natural numbers $1,2, \ldots, 64$ are written in the cells of an $8 \times 8$ table such that for all $k=1,2,3, \ldots, 63$ the numbers $k$ and $k+1$ are in adjacent cells. What is the maximum possible value of the sum of the numbers on the main diagonal?
Answer: 432.
Estimate. We color the cells of the table in a checkerboard pattern so that the cells on the chosen main diagonal are white. Without loss of generality, we can assume that the number 1 is not above the diagonal. We find the maximum value of the smallest number that falls on the diagonal. Since adjacent numbers are in cells of different colors, and there are only 12 white cells below the diagonal, one of the numbers from 1 to 26 must fall on the diagonal. The remaining numbers on the diagonal are guaranteed to have the same parity, so their sum does not exceed the sum of the even numbers from 52 to 64. Therefore, we conclude that the sum of the numbers on the diagonal has an upper bound:
$$
26+52+54+56+58+60+62+64=432
$$
An example of a suitable arrangement of numbers is shown in Fig. 6.
| 52 | 51 | 50 | 49 | 44 | 43 | 34 | 33 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 53 | 54 | 55 | 48 | 45 | 42 | 35 | 32 |
| 6 | 7 | 56 | 47 | 46 | 41 | 36 | 31 |
| 5 | 8 | 57 | 58 | 59 | 40 | 37 | 30 |
| 4 | 9 | 16 | 17 | 60 | 39 | 38 | 29 |
| 3 | 10 | 15 | 18 | 61 | 62 | 63 | 28 |
| 2 | 11 | 14 | 19 | 22 | 23 | 64 | 27 |
| 1 | 12 | 13 | 20 | 21 | 24 | 25 | 26 |
Fig. 6: to the solution of problem 5.
## Criteria
+ Correct solution - 7 points.
$\pm$ Correct upper bound on the sum of the numbers on the diagonal is proven - 4 points.
干 A correct example of an arrangement with the maximum sum of numbers on the diagonal is provided - 3 points.
- Correct answer without further progress - 1 point. | 432 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Problem 2. At a round table, 60 people are sitting. Each of them is either a knight, who always tells the truth, or a liar, who always lies. Each person at the table said: "Among the next 3 people sitting to my right, there is no more than one knight." How many knights could have been sitting at the table? List all possible options and prove that there are no others. | Answer: 30.
Solution. Consider any four consecutive people. If there were at least 3 knights among them, the leftmost knight would definitely lie, which is impossible. If there were at least 3 liars, the leftmost liar would definitely tell the truth, which is also impossible. Therefore, in every group of four consecutive people, there are exactly 2 knights and 2 liars. By dividing all the people into 15 such groups, we get that there are $15 \cdot 2 = 30$ knights.
Another solution. Notice that there cannot be only knights or only liars sitting at the table. Then there must be a pair of knight-liar sitting next to each other in that exact order. Consider the 4 cases of who can sit to the right of this pair.
Case 1. Two knights sit to the right.
Then we get the sequence
$$
\text { knight-liar-knight-knight, }
$$
which contradicts the condition, as the first knight lied.
Case 2. Two liars sit to the right.
Then we get the sequence
$$
\text { knight-liar-liar-liar. }
$$
Whoever sits immediately after this sequence, the first liar will tell the truth, which contradicts the condition.
Case 3. A knight and a liar sit to the right in that exact order.
Then we get the sequence
$$
\text { knight-liar-knight-liar. }
$$
Consider the first liar. He lies, so among the next three, there must be at least two knights. From this, we uniquely get
knight-liar-knight-liar-knight
Now consider the second knight. He tells the truth, so the sixth person in the sequence will be a liar:
knight-liar-knight-liar-knight-liar.
Continuing this reasoning, we get an alternating arrangement where there are an equal number of knights and liars.
Case 4. A liar and a knight sit to the right in that exact order. Then we get the sequence
$$
\text { knight-liar-liar-knight. }
$$
Consider the first liar. He lies, so among the next three, there must be at least two knights. From this, we uniquely get
knight-liar-liar-knight-knight
Now consider the second knight. He tells the truth, so the sixth and seventh people in the sequence will be liars
knight-liar-liar-knight-knight-liar-liar.
Continuing this reasoning, we get an arrangement where there are an equal number of knights and liars.
## Criteria
The highest applicable criterion is used:
7 6. Any complete solution to the problem.
7 6. The problem is correctly solved for the case where both knights and liars are present at the table.
4 6. Both possible cases of arranging knights and liars are considered in the solution, but there is no justification for why there are no other arrangements.
2 6. One of the two possible cases of arranging knights and liars is considered in the solution, but there is no justification for why there are no other arrangements.
1 6. Only the correct answer is present. | 30 | Logic and Puzzles | math-word-problem | Yes | Yes | olympiads | false |
7.1. Masha and the Bear ate a basket of raspberries and 60 pies, starting and finishing at the same time. At first, Masha was eating raspberries, and the Bear was eating pies, then (at some point) they switched. The Bear ate raspberries 6 times faster than Masha, and pies only 3 times faster. How many pies did the Bear eat, if he ate twice as many raspberries as Masha? | Answer: 54 pies. Solution: Divide the raspberries into 3 equal parts. The bear ate each part 6 times faster than Masha, but there are two parts, so he spent only 3 times less time on the raspberries than Masha. This means Masha ate pies in one-third of the time the bear did. Since she eats three times slower, she ate 9 times fewer pies than the bear. Dividing the pies in the ratio of 9:1, we see that Masha got the 10th part, which is 6 pies. The remaining 54 pies went to the bear.
Criterion: Correct answer - no less than 2 points, with full justification - 7 points. | 54 | Algebra | math-word-problem | Yes | Yes | olympiads | false |
5. On the table, there are 2018 playing cards (2018 stacks, each with one card). Petya wants to combine them into one deck of 2018 cards in 2017 operations. Each operation consists of merging two stacks. When Petya merges stacks of $a$ and $b$ cards, Vasily Ivanovich pays Petya $a \cdot b$ rubles. What is the maximum amount of money Petya can earn by performing all 2017 operations? | Answer: $\frac{2017 \cdot 2018}{2}=2035153$
Let's mentally connect the cards in one stack with invisible threads, each with each. Then the operation of combining two stacks with $a$ and $b$ cards adds exactly $a \cdot b$ threads. In the end, each card will be connected by a thread to each other, and the number of threads will not depend on the way the operations are performed and will be equal to $\frac{2017 \cdot 2018}{2}$. This is exactly how many rubles Petya will earn.
Another solution. Notice that when combining stacks of $a$ and $b$ cards, we earn exactly $\frac{1}{2}\left((a+b)^{2}-a^{2}-b^{2}\right)$ rubles; therefore, the final amount we will earn is exactly
$$
\frac{1}{2}(2018^{2} \underbrace{-1^{2}-1^{2}-\ldots-1^{2}}_{2018 \text { times }})=\frac{1}{2}\left(2018^{2}-2018\right)
$$
## Criteria
+ Correct solution - 7 points.
+. In a logically correct solution, the answer is presented as a sum with an ellipsis - at least 1 point is deducted. For example, an answer in the form of $1+2+\ldots+2017$ - 6 points.
$\pm$ It is proven that the answer does not depend on the way the operations are performed - at least 5 points.
-. Correct answer without justification or with incorrect reasoning - 1 point.
Example of incorrect reasoning: in the work, the sum is calculated for a specific way of acting, but it is not proven that the maximum sum is achieved precisely with this method (and it is not proven that the sum does not actually depend on the order of operations).
| 2035153 | Combinatorics | math-word-problem | Yes | Yes | olympiads | false |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.