problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. Find the number of natural numbers $k$, not exceeding 333300, such that $k^{2}-2 k$ is divisible by 303. Answer: 4400.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k-2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-2):(3 \cdot 101) \Leftrightarrow p(101 p-2) \vdots 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+1, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+101, q \in \mathrm{Z}$.
b) $(k-2): 101$, i.e., $k=101 p+2, p \in \mathrm{Z}$. Then we get $(101 p+2) 101 p:(3 \cdot 101) \Leftrightarrow(101 p+2) p \vdots 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=303 q+204$, $k=303 q+2, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 204, 2$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $333300=303 \cdot 1100$, we get $4 \cdot 1100=4400$ numbers.
|
4400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of natural numbers $k$, not exceeding 454500, such that $k^{2}-k$ is divisible by 505.
|
Answer: 3600.
Solution. By factoring the dividend and divisor, we get the condition $k(k-1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k-1)$ is divisible by 101. Let's consider two cases.
a) $k \vdots: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p-1):(5 \cdot 101) \Leftrightarrow p(101 p-1) \vdots 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second when $p=5 q+1, q \in \mathbb{Z}$, from which we obtain that $k=505 q, k=505 q+101, q \in \mathbb{Z}$.
b) $(k-1): 101$, i.e., $k=101 p+1, p \in \mathbb{Z}$. Then we get $(101 p+1) 101 p:(5 \cdot 101) \Leftrightarrow (101 p+1) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, and the second when $p=5 q, q \in \mathbb{Z}$, from which we obtain that $k=505 q+405$, $k=505 q+1, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 405, 1$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $454500=505 \cdot 900$, we get $4 \cdot 900=3600$ numbers.
|
3600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 700. The answer should be presented as an integer.
|
Answer: 2520.
Solution. Since $700=7 \cdot 2^{2} \cdot 5^{2}$, the sought numbers can consist of the following digits: (a) two twos, two fives, one seven, and three ones, or (b) one four, two fives, one seven, and four ones. We will calculate the number of variants in each case.
(a) First, we choose two places out of eight for the twos ( $C_{8}^{2}=\frac{8!}{2!6!}$ ways), then two places out of the remaining six for the fives ( $C_{6}^{2}=\frac{6!}{4!2!}$ ways), and then one place out of the remaining four for the seven ( $C_{4}^{1}=4$ ways). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{2} \cdot C_{6}^{2} \cdot 4=\frac{8!}{3!2!2!}=1680$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!4!}=840$.
Finally, we get $840+1680=2520$ ways.
|
2520
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 4900. The answer should be presented as an integer.
|
Answer: 4200.
Solution. Since $4900=7^{2} \cdot 2^{2} \cdot 5^{2}$, the sought numbers can consist of the following digits: (a) two twos, two fives, two sevens, and two ones, or (b) a four, two fives, two sevens, and three ones. We will calculate the number of variants in each case.
(a) First, we choose two places out of eight for the twos ( $C_{8}^{2}=\frac{8!}{2!6!}$ ways), then two places out of the remaining six for the fives ( $C_{6}^{2}=\frac{6!}{4!2!}$ ways), and then two places out of the remaining four for the sevens ( $C_{4}^{2}=\frac{4!}{2!2!}$ ways). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{2} \cdot C_{6}^{2} \cdot C_{4}^{2}=\frac{8!}{2!2!2!2!} \cdot 4=2520$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!2!3!}=1680$. Finally, we get $2520+1680=4200$ ways.
|
4200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] A magician has a set of $12^{2}$ different cards. Each card has one side red and the other side blue; on each card, there is a natural number from 1 to 12 written on both sides. We will call a card a duplicate if the numbers on both sides of the card are the same. The magician wants to draw two cards such that at least one of them is a duplicate, and no number appears on both drawn cards simultaneously. In how many ways can he do this?
|
Answer: 1386.
Solution. Since the magician has a set of $12^{2}$ cards, all possible card variants exist (for each pair of numbers $(i ; j)$, where $1 \leqslant i \leqslant 12,1 \leqslant j \leqslant 12$, there is a card with the number $i$ written on the red side and $j$ on the blue side). Let's consider two types of card sets.
1) Both cards are duplicates. The number of ways to choose a pair of cards is
$$
C_{12}^{2}=\frac{12(12-1)}{2}=66
$$
2) Only one of the cards is a duplicate. Then it can be chosen in 12 ways, after which the second card can be chosen in any way except: (a) all duplicates (12 in total, including the already chosen card), (b) all cards with the same number on the red side as the chosen duplicate (11 in total, excluding the chosen card), (c) all cards with the same number on the blue side as the chosen duplicate (also 11). Thus, the second card can be chosen in $12^{2}-12-11-11=110$ ways. Therefore, in this case, there are $12 \cdot 110=1320$ ways to choose a pair of cards.
Thus, there are a total of $66+1320=1386$ ways.
|
1386
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] A magician has a set of $15^{2}$ different cards. Each card has one side red and the other side blue; on each card, there is a natural number from 1 to 15 written on both sides. We will call a card a duplicate if the numbers on both sides of the card are the same. The magician wants to draw two cards such that at least one of them is a duplicate, and no number appears on both drawn cards simultaneously. In how many ways can he do this?
|
Answer: 2835.
Solution. Since the magician has a set of $15^{2}$ cards, all possible card variants exist (for each pair of numbers $(i ; j)$, where $1 \leqslant i \leqslant 15,1 \leqslant j \leqslant 15$, there is a card with the number $i$ written on the red side and $j$ on the blue side). Let's consider two types of card sets.
1) Both cards are duplicates. The number of ways to choose a pair of cards is
$$
C_{15}^{2}=\frac{15(15-1)}{2}=105
$$
2) Only one of the cards is a duplicate. Then it can be chosen in 15 ways, after which the second card can be chosen in any way except for: (a) all duplicates (15 in total, including the already chosen card), (b) all cards with the same number on the red side as the chosen duplicate (14 in total, excluding the chosen card), (c) all cards with the same number on the blue side as the chosen duplicate (also 14). Thus, the second card can be chosen in $15^{2}-15-14-14=182$ ways. Therefore, in this case, there are $15 \cdot 182=2730$ ways to choose a pair of cards.
Thus, there are $105+2730=2835$ ways in total.
|
2835
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] A magician has a set of $20^{2}$ different cards. Each card has one side red and the other side blue; on each card, there is a natural number from 1 to 20 written on both sides. We will call a card a duplicate if the numbers on both sides of the card are the same. The magician wants to draw two cards such that at least one of them is a duplicate, and no number appears on both drawn cards simultaneously. In how many ways can he do this?
|
Answer: 7030.
Solution. Since the set contains $20^{2}$ cards, the magician has all possible card variants (for each pair of numbers $(i ; j)$, where $1 \leqslant i \leqslant 20,1 \leqslant j \leqslant 20$, there will be a card with the number $i$ written on the red side and $j$ on the blue side). Let's consider two types of card sets.
1) Both cards are duplicates. The number of ways to choose a pair of cards is
$$
C_{20}^{2}=\frac{20(20-1)}{2}=190
$$
2) Only one of the cards is a duplicate. Then it can be chosen in 20 ways, after which the second card can be chosen in any way except for: (a) all duplicates (20 in total, including the already chosen card), (b) all cards that have the same number on the red side as the chosen duplicate (19 in total, excluding the chosen card), (c) all cards that have the same number on the blue side as the chosen duplicate (also 19). Thus, the second card can be chosen in $20^{2}-20-19-19=342$ ways. Therefore, in this case, there are $20 \cdot 342=6840$ ways to choose a pair of cards.
Thus, there are a total of $190+6840=7030$ ways.
|
7030
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] A magician has a set of $16^{2}$ different cards. Each card has one side red and the other side blue; on each card, there is a natural number from 1 to 16 written on both sides. We will call a card a duplicate if the numbers on both sides of the card are the same. The magician wants to draw two cards such that at least one of them is a duplicate, and no number appears on both drawn cards simultaneously. In how many ways can he do this?
|
Answer: 3480.
Solution. Since the magician has a set of $16^{2}$ cards, there are all possible card variants (for each pair of numbers $(i ; j)$, where $1 \leqslant i \leqslant 16,1 \leqslant j \leqslant 16$ there will be a card with the number $i$ written on the red side and $j$ on the blue side). Let's consider two types of card sets.
1) Both cards are duplicates. The number of ways to choose a pair of cards is
$$
C_{16}^{2}=\frac{16(16-1)}{2}=120
$$
2) Only one of the cards is a duplicate. Then it can be chosen in 16 ways, after which the second card can be chosen in any way except for: (a) all duplicates (16 in total, including the already chosen card), (b) all cards that have the same number on the red side as the chosen duplicate (15 in addition to the chosen card), (c) all cards that have the same number on the blue side as the chosen duplicate (also 15). Thus, the second card can be chosen in $16^{2}-16-15-15=210$ ways. Therefore, in this case, there are $16 \cdot 210=3360$ ways to choose a pair of cards.
Thus, there are a total of $120+3360=3480$ ways.
|
3480
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point ( $60 ; 45$ ). Find the number of such squares.
|
Answer: 2070.
Solution. Draw through the given point $(60 ; 45)$ vertical and horizontal lines $(x=60$ and $y=45)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "bottom" vertex of the square can be located in 45 ways: $(60 ; 0),(60 ; 1), \ldots,(60 ; 44)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=60$ and $y=45$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $15 \leqslant x \leqslant 59,0 \leqslant y \leqslant 44$. We get $45^{2}$ ways.
The total number of ways is $45^{2}+45=46 \cdot 45=2070$.
|
2070
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have natural coordinates, and the center is located at the point $(55 ; 40)$. Find the number of such squares.
|
Answer: 1560.
Solution. Draw through the given point $(55 ; 40)$ vertical and horizontal lines $(x=55$ and $y=40)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 39 ways: $(55 ; 1),(55 ; 1), \ldots,(55 ; 39)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=55$ and $y=40$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be natural, it is necessary and sufficient for this vertex to fall into the square $16 \leqslant x \leqslant 54,1 \leqslant y \leqslant 39$. We get $39^{2}$ ways.
The total number of ways is $39^{2}+39=39 \cdot 40=1560$.
|
1560
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point ( $25 ; 60$ ). Find the number of such squares.
|
Answer: 650.
Solution. Draw through the given point $(25 ; 60)$ vertical and horizontal lines $(x=25$ and $y=60)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "left" vertex of the square can be located in 25 ways: $(0 ; 60),(1 ; 60), \ldots,(24 ; 60)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four regions into which the lines $x=25$ and $y=60$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $0 \leqslant x \leqslant 24,35 \leqslant y \leqslant 59$. We get $25^{2}$ ways.
The total number of ways is $25^{2}+25=26 \cdot 25=650$.
|
650
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have natural coordinates, and the center is located at the point $(35 ; 65)$. Find the number of such squares.
|
Answer: 1190.
Solution. Draw through the given point $(35 ; 65)$ vertical and horizontal lines $(x=35$ and $y=65)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "left" vertex of the square can be located in 34 ways: $(1 ; 65),(2 ; 65), \ldots(34 ; 65)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=35$ and $y=65$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be natural, it is necessary and sufficient for this vertex to fall into the square $1 \leqslant x \leqslant 34,31 \leqslant y \leqslant 64$. We get $34^{2}$ ways.
The total number of ways is $34^{2}+34=34 \cdot 35=1190$.
|
1190
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. Given the number $5300 \ldots 0035$ (100 zeros). It is required to replace some two zeros with non-zero digits so that after the replacement, the resulting number is divisible by 495. In how many ways can this be done?
|
Answer: 22100.
Solution. $495=5 \cdot 9 \cdot 11$. Divisibility by 5 is always satisfied since the number ends in five. For investigating divisibility by 11, it is significant which positions the replaceable digits occupy.
First case. We replace two zeros in positions of the same parity (both even or both odd). For divisibility by 11, the sum of the two new digits must be divisible by 11, and since each digit is within [1;9], the sum must be 11. Note that divisibility by 9 is automatically satisfied in this case (the sum of the digits of the number is $16+11=27$). The following pairs of digits fit: $2--9,3--8,4--7$, $5--6$. Let's count the number of ways to perform the replacement. First, we choose one of these four pairs of digits (4 ways), then place the smaller digit in the position of any zero (100 ways); finally, place the larger digit in a position of the same parity (49 ways) - in total, we get $4 \cdot 100 \cdot 49=19600$ ways.
Second case. We replace two zeros in positions of different parity. Then, for divisibility by 11, these digits must be the same (denote each by $k$), and for divisibility by 9, $16+2 k ; 9$ must hold. This condition is satisfied only by $k=1$. Such a replacement can be made in $50 \cdot 50=2500$ ways (choose one of fifty even positions and one of fifty odd positions).
In total, we get $19600+2500=22100$ ways.
|
22100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. Given the number $800 \ldots 008$ (80 zeros). It is required to replace some two zeros with non-zero digits so that after the replacement, the resulting number is divisible by 198. In how many ways can this be done?
|
Answer: 14080.
Solution. $198=2 \cdot 9 \cdot 11$. Divisibility by 2 is always satisfied since the number ends in eight. For investigating divisibility by 11, it is significant on which positions the replaceable digits stand.
First case. We replace two zeros in positions of the same parity (both even or both odd). For divisibility by 11, the sum of the two new digits must be divisible by 11, and since each digit is within the range $[1 ; 9]$, the sum must be 11. Note that divisibility by 9 is automatically satisfied in this case (the sum of the digits of the number is $16+11=27$). The following pairs of digits fit: $2--9,3--8,4--7$, $5--6$. Let's count the number of ways to perform the replacement. First, we choose one of these four pairs of digits (4 ways), then place the smaller digit in the position of any of the zeros (80 ways); finally, place the larger digit in the same parity position (39 ways) - in total, we get $4 \cdot 80 \cdot 39=12480$ ways.
Second case. We replace two zeros in positions of different parity. Then, for divisibility by 11, these digits must be the same (denote each by $k$), and for divisibility by 9, $16+2 k: 9$ must hold. This condition is satisfied only by $k=1$. Such a replacement can be made in $40 \cdot 40=1600$ ways (choose one of fifty even positions and one of fifty odd positions).
In total, we get $12480+1600=14080$ ways.
|
14080
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. Given the number $500 \ldots 005$ (80 zeros). It is required to replace some two zeros with non-zero digits so that after the replacement, the resulting number is divisible by 165. In how many ways can this be done?
|
Answer: 17280.
Solution. $165=3 \cdot 5 \cdot 11$. Divisibility by 5 is always satisfied since the number ends in a five. For divisibility by 11, it is significant on which positions the replaceable digits stand.
First case. We replace two zeros in positions of the same parity (both even or both odd). For divisibility by 11, the sum of the two new digits must be divisible by 11, and since each digit is within [1;9], the sum must be 11. Note that divisibility by 3 is automatically satisfied (the sum of the digits of the number is $10+11=21$). The following pairs of digits fit: $2--9,3--8,4--7$, 5 - -6. Let's count the number of ways to perform the replacement. First, we choose one of these four pairs of digits (4 ways), then place the smaller digit in the place of any zero (80 ways); finally, place the larger digit in the same parity position (39 ways) - in total, we get $4 \cdot 80 \cdot 39=12480$ ways.
Second case. We replace two zeros in positions of different parity. Then, for divisibility by 11, these digits must be the same (denote each by $k$), and for divisibility by 3, $10+2 k \vdots 3$ must hold. This condition is satisfied by $k=1, k=4$, and $k=7$. Such a replacement can be made in $3 \cdot 40 \cdot 40=4800$ ways (choose one of the three digits, and then one of fifty even positions and one of fifty odd positions).
In total, we get $12480+4800=17280$ ways.
|
17280
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. Given the number $200 \ldots 002$ (100 zeros). It is required to replace some two zeros with non-zero digits so that after the replacement, the resulting number is divisible by 66. In how many ways can this be done?
|
Answer: 27100.
Solution. $66=3 \cdot 2 \cdot 11$. Divisibility by 2 is always satisfied since the number ends in two. To investigate divisibility by 11, it is significant which positions the replaceable digits occupy.
First case. We replace two zeros in positions of the same parity (both even or both odd). For divisibility by 11, the sum of the two new digits must be divisible by 11, and since each digit is within the range $[1 ; 9]$, the sum must be 11. Note that divisibility by 3 is automatically satisfied (the sum of the digits of the number is $4+11=15$). The following pairs of digits fit: $2--9,3--8,4--7$, $5--6$. Let's count the number of ways to perform the replacement. First, we choose one of these four pairs of digits (4 ways), then place the smaller digit in the position of any zero (100 ways); finally, place the larger digit in the same parity position (49 ways) - in total, this gives $4 \cdot 100 \cdot 49=19600$ ways.
Second case. We replace two zeros in positions of different parity. Then, for divisibility by 11, these digits must be the same (denote each by $k$), and for divisibility by 3, $4+2 k \vdots 3$ must hold. This condition is satisfied by $k=1, k=4$, and $k=7$. Such a replacement can be made in $3 \cdot 50 \cdot 50=7500$ ways (choose one of the three digits, then one of fifty even positions and one of fifty odd positions).
In total, we get $19600+7500=27100$ ways.
|
27100
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On each of the lines $x=0$ and $x=2$, there are 62 points with ordinates $1, 2, 3, \ldots, 62$. In how many ways can three points be chosen from the marked 124 points so that they form the vertices of a right triangle?
|
Answer: 7908.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 4$. Since $AH$ and $BH$ are integers, the following cases are possible: $AH = BH = 2$, $AH = 4$ and $BH = 1$, $AH = 1$ and $BH = 4$.
In the first of these cases, the hypotenuse $AB$, equal to 4, can be placed in $58 \cdot 2 = 116$ ways (62 - 4 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 5, and it can be placed in $2(62 - 5) = 114$ ways. For each position of the hypotenuse, there are two ways to place the vertex - this gives $2 \cdot 114 = 228$ ways.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the second leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 62 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 122 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $62 \cdot 122 = 7564$ ways.
In total, we get $116 + 228 + 7564 = 7908$ ways.
|
7908
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On each of the lines $y=0$ and $y=2$, there are 64 points with abscissas $1,2,3, \ldots, 64$. In how many ways can three points be chosen from the marked 128 points so that they form the vertices of a right triangle?
|
Answer: 8420.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 4$. Since $AH$ and $BH$ are integers, the following cases are possible: $AH = BH = 2$, $AH = 4$ and $BH = 1$, $AH = 1$ and $BH = 4$.
In the first of these cases, the hypotenuse $AB$, equal to 4, can be placed in $60 \cdot 2 = 120$ ways (64 - 4 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 5, and it can be placed in $2(64 - 5) = 118$ ways. For each position of the hypotenuse, there are two ways to place the vertex - this gives $2 \cdot 118 = 236$ ways.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the second leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 64 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 126 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $64 \cdot 126 = 8064$ ways.
In total, we get $120 + 236 + 8064 = 8420$ ways.
|
8420
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given 2117 cards, on which natural numbers from 1 to 2117 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done?
|
Answer: 22386.
Solution. We will take the cards in turn. There are several cases depending on the number written on the first card.
1) The number on the card ends in 00 (there are 21 such cards). For the sum to be divisible by 100, the second card must also end in 00. We get $C_{2} 1^{2}=\frac{21 \cdot 20}{2}=210$ options.
2) Similarly, if the number on the card ends in 50 (there are also 21 such cards), then for the sum to be divisible by 100, the second card must also end in 50, i.e., here we also have 210 options.
3) The number on the card ends in a number from 1 to 17 (there are $17 \cdot 22=374$ such cards). For each of them, a pair can be chosen in 21 ways (if the number ends in 1, then any card with a number ending in 99 will do; if the number ends in 2, any card with a number ending in 98, and so on). Thus, we get $374 \cdot 21=7854$ options.
4) The number on the card ends in a number from 18 to 49 (there are $32 \cdot 21=672$ such cards). For each of them, a pair can be chosen in 21 ways (similarly to the previous case). Thus, we get $672 \cdot 21=14112$ options.
5) The number on the card ends in a number from 51 to 99. All such options were considered when examining the third and fourth cases (these cards formed pairs with the cards initially chosen).
In total, we get $210+210+7854+14112=22386$ ways.
|
22386
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Find the number of distinct quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have two distinct roots, which are powers of the number 7 with integer non-negative exponents, and at the same time, their coefficients in absolute value do not exceed $343^{36}$.
|
Answer: 2969.
Solution. Such quadratic trinomials can be represented in the form $\left(x-7^{a}\right)\left(x-7^{b}\right)$, where $a \geqslant 0$, $b \geqslant 0$ are integers. To avoid repetitions, we assume that $a>b$. Expanding the brackets, we get $x^{2}-\left(7^{a}+7^{b}\right) x+7^{a+b}$. By the condition
$$
\left\{\begin{array} { l }
{ 7 ^ { a } + 7 ^ { b } \leqslant 3 4 3 ^ { 3 6 } , } \\
{ 7 ^ { a + b } \leqslant 3 4 3 ^ { 3 6 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
7^{a}+7^{b} \leqslant 7^{108} \\
a+b \leqslant 108
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=108, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=108 \Rightarrow 0 \text { values of } b \text {; } \\
& a=107 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=106 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& \text {. } \\
& a=55 \Rightarrow 54 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 53\}) \text {; } \\
& a=54 \Rightarrow 54 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 53\}) \text {; } \\
& a=53 \Rightarrow 53 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 52\}) \text {; } \\
& a=52 \Rightarrow 52 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 51\}) \text {; } \\
& a=1 \Rightarrow 1 \text { value of } b(b=0) \text {; } \\
& a=0 \Rightarrow 0 \text { values of } b \text {. }
\end{aligned}
$$
Summing up, we get $(2+3+4+\ldots 54)+(54+53+52+\ldots+1)=2969$ options.
|
2969
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given 2414 cards, on which natural numbers from 1 to 2414 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done?
|
Answer: 29112.
Solution. We will take cards in turn. There are several cases depending on the number written on the first card.
1) The number on the card ends in 00 (there are 24 such cards). For the sum to be divisible by 100, the second card must also end in 00. We get a total of $C_{2} 4^{2}=\frac{24 \cdot 23}{2}=276$ options.
2) Similarly, if the number on the card ends in 50 (there are also 24 such cards), then for the sum to be divisible by 100, the second card must also end in 50, i.e., here we also have 276 options.
3) The number on the card ends in a number from 1 to 14 (there are $14 \cdot 25=350$ such cards). For each of them, a pair can be chosen in 24 ways (if the number ends in 1, then any card with a number ending in 99 will do; if the number ends in 2, any card with a number ending in 98, and so on). Thus, we get $350 \cdot 24=8400$ options.
4) The number on the card ends in a number from 15 to 49 (there are $35 \cdot 24=840$ such cards). For each of them, a pair can be chosen in 24 ways (similarly to the previous case). Thus, we get $840 \cdot 24=20160$ options.
5) The number on the card ends in a number from 51 to 99. All such options were considered when examining the third and fourth cases (these cards formed pairs with the cards initially chosen).
In total, we get $276+276+8400+20160=29112$ ways.
|
29112
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Find the number of distinct quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have two distinct roots, which are powers of the number 5 with integer non-negative exponents, and at the same time, their coefficients in absolute value do not exceed $122^{20}$.
|
Answer: 5699.
Solution. Such quadratic trinomials can be represented in the form $\left(x-5^{a}\right)\left(x-5^{b}\right)$, where $a \geqslant 0$, $b \geqslant 0$ are integers. To avoid repetitions, we assume that $a>b$. Expanding the brackets, we get $x^{2}-\left(5^{a}+5^{b}\right) x+5^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 5 ^ { a } + 5 ^ { b } \leqslant 1 2 5 ^ { 5 0 } , } \\
{ 5 ^ { a + b } \leqslant 1 2 5 ^ { 5 0 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
5^{a}+5^{b} \leqslant 5^{150} \\
a+b \leqslant 150
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=150, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=150 \Rightarrow 0 \text { values of } b \text {; } \\
& a=149 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=148 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& a=76 \Rightarrow 75 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 74\}) \text {; } \\
& a=75 \Rightarrow 75 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 74\}) \text {; } \\
& a=74 \Rightarrow 74 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 73\}) \text {; } \\
& a=73 \Rightarrow 73 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 72\}) \text {; } \\
& a=1 \Rightarrow 1 \text { value of } b(b=0) \text {; } \\
& a=0 \Rightarrow 0 \text { values of } b \text {. }
\end{aligned}
$$
Summing up, we get $(2+3+4+\ldots 75)+(75+74+73+\ldots+1)=5699$ options.
|
5699
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. The numbers $x$ and $y$ are solutions to the system of equations param 1, where $a$ is a parameter. What param 2 value does the expression param 3 take?
| param1 | param2 | param3 | |
| :---: | :---: | :---: | :---: |
| $\left\{\begin{array}{l}a x+y=a+1 \\ x+4 a y=3\end{array}\right.$ | maximum | $x^{2}-6 y^{2}$ | |
| $\left\{\begin{array}{l}-x+a y=2 a \\ a x-y=3 a-5\end{array}\right.$ | minimum | $x^{2}+y^{2}$ | |
| $\left\{\begin{array}{l}a x+9 y=a+3 \\ x+a y=2\end{array}\right.$ | maximum | $3 y^{2}-x^{2}$ | |
| $\left\{\begin{array}{l}x+a y=3 a \\ a x+y=a+4\end{array}\right.$ | minimum | $2 x^{2}+y^{2}$ | |
|
5. The numbers $x$ and $y$ are solutions to the system of equations param 1, where $a$ is a parameter. What param 2 value does the expression param 3 take?
| param1 | param2 | param3 | Answer |
| :---: | :---: | :---: | :---: |
| $\left\{\begin{array}{l}a x+y=a+1 \\ x+4 a y=3\end{array}\right.$ | maximum | $x^{2}-6 y^{2}$ | 27 |
| $\left\{\begin{array}{l}-x+a y=2 a \\ a x-y=3 a-5\end{array}\right.$ | minimum | $x^{2}+y^{2}$ | 2 |
| $\left\{\begin{array}{l}a x+9 y=a+3 \\ x+a y=2\end{array}\right.$ | maximum | $3 y^{2}-x^{2}$ | 2 |
| $\left\{\begin{array}{l}x+a y=3 a \\ a x+y=a+4\end{array}\right.$ | minimum | $2 x^{2}+y^{2}$ | 6 |
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
9. Given a regular param1. Find the number of its vertex quadruples that are vertices of a convex quadrilateral with exactly two angles equal to $90^{\circ}$. (Two quadruples of vertices that differ in the order of vertices are considered the same.)
| param1 | |
| :---: | :---: |
| 16-gon | |
| 18-gon | |
| 20-gon | |
| 14-gon | |
|
9. Given a regular param1. Find the number of its vertex quadruples that are vertices of a convex quadrilateral with exactly two angles equal to $90^{\circ}$. (Two quadruples of vertices that differ in the order of vertices are considered the same.)
| param1 | Answer |
| :---: | :---: |
| 16-gon | 336 |
| 18-gon | 504 |
| 20-gon | 720 |
| 14-gon | 210 |
|
504
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
10. Find the sum of the roots of the equation param1 that lie in the interval param2. Write the answer in degrees.
| param 1 | param2 | |
| :---: | :---: | :---: |
| $\sin x+\sin ^{2} x+\cos ^{3} x=0$ | $\left[360^{\circ} ; 720^{\circ}\right]$ | |
| $\cos x-\cos ^{2} x-\sin ^{3} x=0$ | $\left[180^{\circ} ; 540^{\circ}\right]$ | |
| $\sin x+\sin ^{2} x+\cos ^{3} x=0$ | $\left[-360^{\circ} ; 0^{\circ}\right]$ | |
| $\cos x-\cos ^{2} x-\sin ^{3} x=0$ | $\left[-540^{\circ} ;-180^{\circ}\right]$ | |
|
10. Find the sum of the roots of the equation param1 lying in the interval param2. Write the answer in degrees.
| param 1 | param2 | Answer |
| :---: | :---: | :---: |
| $\sin x+\sin ^{2} x+\cos ^{3} x=0$ | $\left[360^{\circ} ; 720^{\circ}\right]$ | 1800 |
| $\cos x-\cos ^{2} x-\sin ^{3} x=0$ | $\left[180^{\circ} ; 540^{\circ}\right]$ | 990 |
| $\sin x+\sin ^{2} x+\cos ^{3} x=0$ | $\left[-360^{\circ} ; 0^{\circ}\right]$ | -360 |
| $\cos x-\cos ^{2} x-\sin ^{3} x=0$ | $\left[-540^{\circ} ;-180^{\circ}\right]$ | -1170 |
|
-360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=6 \\
\operatorname{LCM}(a ; b ; c)=2^{15} \cdot 3^{16}
\end{array}\right.
$$
|
Answer: 7560.
Solution. Let $a=2^{\alpha_{1}} \cdot 3^{\alpha_{2}}, b=2^{\beta_{1}} \cdot 3^{\beta_{2}}, c=2^{\gamma_{1}} \cdot 3^{\gamma_{2}}$ (the numbers $a$, $b$, $c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=2^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 3^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=2^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 3^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 5 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=16 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (2). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 15)$ - 3 sets (due to different permutations of these numbers);
$(1 ; 15 ; 15)$ - also three sets
$(1 ; k ; 15)$, where $2 \leqslant k \leqslant 14$ - there are 13 different values of $k$, and for each of them 6 permutations - a total of 78 options.
Thus, there are $3+3+6 \cdot 13=84$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 14=90$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is made independently of the other, the total number of ways is $84 \cdot 90=7560$.
|
7560
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=15 \\
\operatorname{LCM}(a ; b ; c)=3^{15} \cdot 5^{18}
\end{array}\right.
$$
|
Answer: 8568.
Solution. Let $a=3^{\alpha_{1}} \cdot 5^{\alpha_{2}}, b=3^{\beta_{1}} \cdot 5^{\beta_{2}}, c=3^{\gamma_{1}} \cdot 5^{\gamma_{2}}$ (the numbers $a$, $b$, $c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=3^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 5^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=3^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 5^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 5 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=18 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (7). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 15)$ - 3 sets (due to different permutations of these numbers);
$(1 ; 15 ; 15)$ - also three sets
$(1 ; k ; 15)$, where $2 \leqslant k \leqslant 14$ - there are 13 different values of $k$, and for each of them 6 permutations - a total of 78 options.
Thus, there are $3+3+6 \cdot 13=84$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 16=102$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is independent of the other, the total number of ways is $84 \cdot 102=8568$.
|
8568
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=21 \\
\operatorname{LCM}(a ; b ; c)=3^{17} \cdot 7^{15}
\end{array}\right.
$$
|
Answer: 8064.
Solution. Let $a=3^{\alpha_{1}} \cdot 7^{\alpha_{2}}, b=3^{\beta_{1}} \cdot 7^{\beta_{2}}, c=3^{\gamma_{1}} \cdot 7^{\gamma_{2}}$ (the numbers $a$, $b, c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=3^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=3^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 7 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=15 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (12). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 17)-3$ sets (due to different permutations of these numbers);
$(1 ; 17 ; 17)$ - also three sets
$(1 ; k ; 17)$, where $2 \leqslant k \leqslant 16$ - there are 15 different values of $k$,
and for each of them 6 permutations - a total of 90 options.
Thus, there are $3+3+6 \cdot 15=96$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 13=84$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is made independently of the other, the total number of ways is $96 \cdot 84=8064$.
|
8064
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=10 \\
\operatorname{LCM}(a ; b ; c)=2^{17} \cdot 5^{16}
\end{array}\right.
$$
|
Answer: 8640.
Solution. Let $a=2^{\alpha_{1}} \cdot 5^{\alpha_{2}}, b=2^{\beta_{1}} \cdot 5^{\beta_{2}}, c=2^{\gamma_{1}} \cdot 5^{\gamma_{2}}$ (the numbers $a$, $b$, $c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=2^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 5^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=2^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 5^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 7 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=16 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (17). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 17)$ - 3 sets (due to different permutations of these numbers);
$(1 ; 17 ; 17)$ - also three sets
$(1 ; k ; 17)$, where $2 \leqslant k \leqslant 16$ - there are 15 different values of $k$, and for each of them 6 permutations - a total of 90 options.
Thus, there are $3+3+6 \cdot 15=96$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 14=90$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is made independently of the other, the total number of ways is $96 \cdot 90=8640$.
|
8640
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=35 \\
\operatorname{LCM}(a ; b ; c)=5^{18} \cdot 7^{16}
\end{array}\right.
$$
|
Answer: 9180.
Solution. Let $a=5^{\alpha_{1}} \cdot 7^{\alpha_{2}}, b=5^{\beta_{1}} \cdot 7^{\beta_{2}}, c=5^{\gamma_{1}} \cdot 7^{\gamma_{2}}$ (the numbers $a$, $b, c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=5^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=5^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 8 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=16 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (22). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 18)-3$ sets (due to different permutations of these numbers);
$(1 ; 18 ; 18)$ - also three sets
$(1 ; k ; 18)$, where $2 \leqslant k \leqslant 17$ - there are 16 different values of $k$, and for each of them 6 permutations - a total of 96 options.
Thus, there are $3+3+6 \cdot 16=102$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 14=90$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is independent of the other, the total number of ways is $102 \cdot 90=9180$.
|
9180
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$, satisfying the system of equations
$$
\left\{\begin{array}{l}
\text { GCD }(a ; b ; c)=14 \\
\text { LCM }(a ; b ; c)=2^{17} \cdot 7^{18}
\end{array}\right.
$$
|
Answer: 9792.
Solution. Let $a=2^{\alpha_{1}} \cdot 7^{\alpha_{2}}, b=2^{\beta_{1}} \cdot 7^{\beta_{2}}, c=2^{\gamma_{1}} \cdot 7^{\gamma_{2}}$ (the numbers $a$, $b, c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=2^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=2^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 7^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 7 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=18 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (27). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 17)-3$ sets (due to different permutations of these numbers);
$(1 ; 17 ; 17)$ - also three sets
$(1 ; k ; 17)$, where $2 \leqslant k \leqslant 16$ - there are 15 different values of $k$,
and for each of them 6 permutations - a total of 90 options.
Thus, there are $3+3+6 \cdot 15=96$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 16=102$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is independent of the other, the total number of ways is $96 \cdot 102=9792$.
|
9792
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\operatorname{GCD}(a ; b ; c)=22 \\
\operatorname{LCM}(a ; b ; c)=2^{16} \cdot 11^{19}
\end{array}\right.
$$
|
Answer: 9720.
Solution. Let $a=2^{\alpha_{1}} \cdot 11^{\alpha_{2}}, b=2^{\beta_{1}} \cdot 11^{\beta_{2}}, c=2^{\gamma_{1}} \cdot 11^{\gamma_{2}}$ (the numbers $a, b, c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=2^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 11^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=2^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 11^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 6 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=19 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (32). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 16)$ - 3 sets (due to different permutations of these numbers);
$(1 ; 16 ; 16)$ - also three sets;
$(1 ; k ; 16)$, where $2 \leqslant k \leqslant 15-$ there are 14 different values of $k$,
and for each of them 6 permutations - a total of 84 options.
Thus, there are $3+3+6 \cdot 14=90$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 17=108$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is made independently of the other, the total number of ways is $90 \cdot 108=9720$.
|
9720
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. [5 points] Find the number of triples of natural numbers $(a ; b ; c)$ that satisfy the system of equations
$$
\left\{\begin{array}{l}
\text { GCD }(a ; b ; c)=33, \\
\text { LCM }(a ; b ; c)=3^{19} \cdot 11^{15} .
\end{array}\right.
$$
|
Answer: 9072.
Solution. Let $a=3^{\alpha_{1}} \cdot 11^{\alpha_{2}}, b=3^{\beta_{1}} \cdot 11^{\beta_{2}}, c=3^{\gamma_{1}} \cdot 11^{\gamma_{2}}$ (the numbers $a, b, c$ cannot contain any other prime factors - otherwise the second condition of the system is violated). From this,
$$
\operatorname{LCM}(a ; b ; c)=3^{\max \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 11^{\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}, \quad \text { GCD }(a ; b ; c)=3^{\min \left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)} \cdot 11^{\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)}
$$
Considering the system given in the condition, we obtain the relations
$$
\left\{\begin{array} { l }
{ \operatorname { max } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 9 , } \\
{ \operatorname { min } ( \alpha _ { 1 } ; \beta _ { 1 } ; \gamma _ { 1 } ) = 1 }
\end{array} \quad \text { and } \quad \left\{\begin{array}{l}
\max \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=15 \\
\min \left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)=1
\end{array}\right.\right.
$$
Consider the first system (37). The following sets of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$ are possible:
$(1 ; 1 ; 19)$ - 3 sets (due to different permutations of these numbers);
$(1 ; 19 ; 19)$ - also three sets
$(1 ; k ; 19)$, where $2 \leqslant k \leqslant 18-$ there are 17 different values of $k$, and for each of them 6 permutations - a total of 102 options.
Thus, there are $3+3+6 \cdot 17=108$ ways to choose the triplet of numbers $\left(\alpha_{1} ; \beta_{1} ; \gamma_{1}\right)$. Similarly, we establish that there are $3+3+6 \cdot 13=84$ ways to choose $\left(\alpha_{2} ; \beta_{2} ; \gamma_{2}\right)$, and since one choice is made independently of the other, the total number of ways is $108 \cdot 84=9072$.
|
9072
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Which whole numbers from 1 to 60000 (inclusive) are there more of, and by how many: those containing only even digits or those containing only odd digits?
|
Answer: There are 780 more numbers containing only odd digits.
Solution. Consider $k$-digit numbers ( $1 \leqslant k \leqslant 4$ ). The number of numbers consisting only of odd digits is $5^{k}$ (for each of the $k$ positions, any of the digits $1,3,5,7$, 9 can be chosen); the number of numbers consisting only of even digits is $4 \cdot 5^{k-1}$ (for the first position, any of the digits $2,4,6,8$ can be chosen, and for the remaining positions - any of the digits $0,2,4,6$, 8). Therefore, there are $5^{k}-4 \cdot 5^{k-1}=5^{k-1}$ more $k$-digit numbers containing only odd digits in their notation than numbers containing only even digits.
Consider 5-digit numbers not exceeding 60000. Among them, the number of numbers written only with odd digits is $3 \cdot 5^{4}$, and the number of numbers written only with even digits is $2 \cdot 5^{4}+1$ (do not forget to account for the number 60000 itself).
Thus, there are $1+5+5^{2}+5^{3}+5^{4}-1=780$ more numbers written only with odd digits.
|
780
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On each of the lines $y=3$ and $y=4$, there are 73 points with abscissas $1,2,3, \ldots, 73$. In how many ways can three points be chosen from the marked 146 so that they form the vertices of a right triangle?
|
Answer: 10654.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 1$. Since $AH$ and $BH$ are integers, then $AH = BH = 1$.
The hypotenuse $AB$, equal to 2, can be placed in $71 \cdot 2 = 142$ ways (with $73 - 2$ ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the other leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 73 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 144 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, this gives $73 \cdot 144 = 10512$ ways.
In total, we get $142 + 10512 = 10654$ ways.
|
10654
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the extension of side $A C$ of triangle $A B C$ beyond point $A$, point $T$ is marked such that $\angle B A C=2 \angle B T C$. Find the area of triangle $A B C$, given that $A B=A C, B T=70$, $A T=37$.
|
Answer: 420.
Solution. Let $\angle B T A=\alpha$, then by the condition $\angle B A C=2 \alpha$. Triangle $A B C$ is isosceles with base $B C$, so $\angle A B C=\angle A C B=\frac{1}{2}\left(180^{\circ}-2 \alpha\right)=90^{\circ}-\alpha$. By the sum of angles in triangle $T B C$, we get that $\angle T B C=180^{\circ}-\angle T C B-\angle B T C=90^{\circ}$. Moreover, $\angle T B A=\angle T B C-\angle A B C=\alpha$. From the equality of angles, it follows that triangles $A B T$ and $A B C$ are isosceles, $A C=A B=A T$.
Then we get $C T=2 A T=74, B C=\sqrt{C T^{2}-B T^{2}}=24, S_{\triangle B T C}=\frac{1}{2} \cdot B C \cdot B T=840$, $S_{\triangle A B C}=\frac{1}{2} S_{\triangle B C T}=420$.
|
420
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Which whole numbers from 1 to 80000 (inclusive) are there more of, and by how many: those containing only even digits or those containing only odd digits?
|
Answer: There are 780 more numbers containing only odd digits.
Solution. Consider $k$-digit numbers ( $1 \leqslant k \leqslant 4$ ). The number of numbers consisting only of odd digits is $5^{k}$ (for each of the $k$ positions, any of the digits $1,3,5,7$, 9 can be chosen); the number of numbers consisting only of even digits is $4 \cdot 5^{k-1}$ (for the first position, any of the digits $2,4,6,8$ can be chosen, and for the remaining positions - any of the digits $0,2,4,6$, 8). Therefore, there are $5^{k}-4 \cdot 5^{k-1}=5^{k-1}$ more $k$-digit numbers containing only odd digits in their notation than numbers containing only even digits.
Consider 5-digit numbers not exceeding 80,000. Among them, the number of numbers written only with odd digits is $4 \cdot 5^{4}$, and the number of numbers written only with even digits is $3 \cdot 5^{4}+1$ (do not forget to account for the number 80000 itself).
Thus, there are $1+5+5^{2}+5^{3}+5^{4}-1=780$ more numbers written only with odd digits.
|
780
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On each of the lines $x=5$ and $x=6$, there are 58 points with ordinates $1, 2, 3, \ldots, 58$. In how many ways can three points be chosen from the marked 116 so that they form the vertices of a right triangle?
|
Answer: 6724.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 1$. Since $AH$ and $BH$ are integers, then $AH = BH = 1$.
The hypotenuse $AB$, equal to 2, can be placed in $56 \cdot 2 = 112$ ways (with $58 - 2$ ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the other leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 58 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 114 ways (all points except the already chosen $B$ and $C$) - in total, this gives $58 \cdot 114 = 6612$ ways.
In total, we get $112 + 6612 = 6724$ ways.
|
6724
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the extension of side $A C$ of triangle $A B C$ beyond point $A$, point $T$ is marked such that $\angle B A C=2 \angle B T C$. Find the area of triangle $A B C$, given that $A B=A C, B T=42$, $A T=29$.
|
Answer: 420.
Solution. Let $\angle B T A=\alpha$, then by the condition $\angle B A C=2 \alpha$. Triangle $A B C$ is isosceles with base $B C$, so $\angle A B C=\angle A C B=\frac{1}{2}\left(180^{\circ}-2 \alpha\right)=90^{\circ}-\alpha$. By the sum of angles in triangle $T B C$, we get that $\angle T B C=180^{\circ}-\angle T C B-\angle B T C=90^{\circ}$. Moreover, $\angle T B A=\angle T B C-\angle A B C=\alpha$. From the equality of angles, it follows that triangles $A B T$ and $A B C$ are isosceles, $A C=A B=A T$.
Then we get $C T=2 A T=58, B C=\sqrt{C T^{2}-B T^{2}}=40, S_{\triangle B T C}=\frac{1}{2} \cdot B C \cdot B T=840$, $S_{\triangle A B C}=\frac{1}{2} S_{\triangle B C T}=420$.
|
420
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given 6000 cards, on which natural numbers from 1 to 6000 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done?
|
Answer: 179940.
Solution. We will take the cards in turn. There are several cases depending on the number written on the first card.
1) The number on the card ends in 00 (there are 60 such cards). For the sum to be divisible by 100, the second card must also have a number ending in 00. We get a total of $C_{60}^{2}=\frac{60 \cdot 59}{2}=1770$ options.
2) Similarly, if the number on the card ends in 50 (there are also 60 such cards), then for the sum to be divisible by 100, the second card must also have a number ending in 50, i.e., here we also have 1770 options.
3) The number on the card ends in a number from 1 to 49 (there are $49 \cdot 60=2940$ such cards). For each of them, a pair can be chosen in 60 ways (if the number ends in 1, then any card with a number ending in 99 will do; if the number ends in 2, any card with a number ending in 98, and so on). Thus, we get $2940 \cdot 60=176400$ options.
4) The number on the card ends in a number from 51 to 99. All such options were accounted for when considering the third case (these cards formed pairs with the cards initially chosen).
In total, we get $1770+1770+176400=179940$ ways.
|
179940
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Find the number of distinct quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have two distinct roots, which are powers of the number 3 with natural exponents, and at the same time, their coefficients in absolute value do not exceed \(27^{45}\).
|
Answer: 4489.
Solution. Such quadratic trinomials can be represented as $\left(x-3^{a}\right)\left(x-3^{b}\right)$, where $a, b$ are natural numbers. To avoid repetitions, we assume that $a>b$. Expanding the brackets, we get $x^{2}-\left(3^{a}+3^{b}\right) x+3^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 3 ^ { a } + 3 ^ { b } \leqslant 2 7 ^ { 4 5 } , } \\
{ 3 ^ { a + b } \leqslant 2 7 ^ { 4 5 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
3^{a}+3^{b} \leqslant 3^{135} \\
a+b \leqslant 135
\end{array}\right.\right.
$$
Note that if for some natural numbers $a$ and $b$ the second inequality holds, then the first inequality is also true. For each value of $a$, we list the number of suitable values of $b:$
$$
\begin{aligned}
& a=135 \Rightarrow 0 \text { values of } b \text {; } \\
& a=134 \Rightarrow 1 \text { value of } b(b=1) \text {; } \\
& a=133 \Rightarrow 2 \text { values of } b(b \in\{1 ; 2\}) \text {; }
\end{aligned}
$$

$$
\begin{aligned}
& a=69 \Rightarrow 66 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 66\}) \text {; } \\
& a=68 \Rightarrow 67 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 67\}) \text {; } \\
& a=67 \Rightarrow 66 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 66\}) \text {; } \\
& a=66 \Rightarrow 65 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 65\}) \text {; } \\
& a=2 \Rightarrow 1 \text { value of } b(b=1) \text {; } \\
& a=1 \Rightarrow 0 \text { values of } b \text {. }
\end{aligned}
$$
Summing up, we get $(1+2+3+\ldots 67)+(66+65+64+\ldots+1)=4489$ options.
|
4489
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given 5000 cards, on which natural numbers from 1 to 5000 are written (each card has exactly one number, and the numbers do not repeat). It is required to choose two cards such that the sum of the numbers written on them is divisible by 100. In how many ways can this be done?
|
Answer: 124950.
Solution. We will take the cards in turn. There are several cases depending on the number written on the first card.
1) The number on the card ends in 00 (there are 50 such cards). For the sum to be divisible by 100, the second card must be chosen so that the number on it also ends in 00. We get a total of $C_{50}^{2}=\frac{50 \cdot 49}{2}=1225$ options.
2) Similarly, if the number on the card ends in 50 (there are also 50 such cards), then for the sum to be divisible by 100, the second card must be chosen so that the number on it ends in 50, i.e., here we also have 1225 options.
3) The number on the card ends in a number from 1 to 49 (there are $49 \cdot 50=2450$ such cards). For each of them, a pair can be chosen in 50 ways (if the number ends in 1, then any card with a number ending in 99 will do; if the number ends in 2, any card with a number ending in 98, and so on). Thus, we get $2450 \cdot 50=122500$ options.
4) The number on the card ends in a number from 51 to 99. All such options were accounted for when considering the third case (these cards formed pairs with the cards initially chosen).
In total, we get $1225+1225+122500=124950$ ways.
|
124950
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Find the number of distinct quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have two distinct roots, which are powers of the number 5 with natural exponents, and at the same time, their coefficients in absolute value do not exceed $125^{48}$.
|
Answer: 5112.
Solution. Such quadratic trinomials can be represented in the form $\left(x-5^{a}\right)\left(x-5^{b}\right)$, where $a, b$ are natural numbers. To avoid repetitions, we assume that $a>b$. Expanding the brackets, we get $x^{2}-\left(5^{a}+5^{b}\right) x+5^{a+b}$. By the condition
$$
\left\{\begin{array} { l }
{ 5 ^ { a } + 5 ^ { b } \leqslant 1 2 5 ^ { 4 8 } } \\
{ 5 ^ { a + b } \leqslant 1 2 5 ^ { 4 8 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
5^{a}+5^{b} \leqslant 5^{144} \\
a+b \leqslant 144
\end{array}\right.\right.
$$
Note that if for some natural numbers $a$ and $b$ the second inequality holds, then the first inequality is also true. For each value of $a$, we list the number of suitable values of $b:$
$$
\begin{aligned}
& a=144 \Rightarrow 0 \text { values of } b \text {; } \\
& a=143 \Rightarrow 1 \text { value of } b(b=1) \text {; } \\
& a=142 \Rightarrow 2 \text { values of } b(b \in\{1 ; 2\}) \text {; } \\
& a=73 \Rightarrow 66 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 71\}) \text {; } \\
& a=72 \Rightarrow 67 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 71\}) \text {; } \\
& a=71 \Rightarrow 66 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 70\}) \text {; } \\
& a=70 \Rightarrow 65 \text { values of } b(b \in\{1 ; 2 ; \ldots ; 69\}) \text {; } \\
& a=2 \Rightarrow 1 \text { value of } b(b=1) \text {; } \\
& a=1 \Rightarrow 0 \text { values of } b \text {. }
\end{aligned}
$$
Summing up, we get $(1+2+3+\ldots 71)+(71+70+69+\ldots+1)=5112$ options.
|
5112
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On the table, there are 130 different cards with numbers $502, 504, 506, \ldots, 758, 760$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the sum of the numbers on the selected cards is divisible by 3?
|
Answer: 119282
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 3 alternate. Indeed, if one of these numbers is divisible by 3, i.e., has the form $3k$, where $k \in \mathbb{N}$, then the next number is $3k+2$ - and it gives a remainder of 2 when divided by 3, followed by $3k+4$, which gives a remainder of 1 when divided by 3, and then $3k+6$, which is again divisible by 3. Thus, the remainders of the given numbers when divided by 3 follow the pattern $\ldots 0 ; 2 ; 1 ; 0 ; 2 ; 1 ; 0 \ldots$.
Among the given numbers, there are 44 that give a remainder of 1 when divided by 3 (they form the set $A=\{502 ; 508 ; 514 ; \ldots ; 760\}$), 43 numbers that are divisible by 3 ($B=\{504 ; 510 ; 516 ; \ldots ; 756\}$), and 43 numbers that give a remainder of 2 when divided by 3 ($C=\{506 ; 512 ; 518 ; \ldots ; 758\}$).
The sum of three numbers can be divisible by 3 in the following cases.
1) All three numbers give the same remainder when divided by 3. There are $C_{44}^{3}$ ways to choose 3 numbers from set $A$ and $C_{43}^{3}$ ways to choose 3 numbers from sets $B$ and $C$. In total, we get $\frac{44 \cdot 43 \cdot 42}{6} + 2 \cdot \frac{43 \cdot 42 \cdot 41}{6} = 13244 + 2 \cdot 12341 = 37926$ ways.
2) If not all remainders are the same, the only suitable case is when all three remainders are different, i.e., we must choose one number from each of the sets $A, B, C$. We get $44 \cdot 43 \cdot 43 = 81356$ ways.
In total, we get 119282 ways.
|
119282
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On the table, there are 140 different cards with numbers $4, 8, 12, \ldots, 556, 560$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the sum of the numbers on the selected cards is divisible by 3?
|
Answer: 149224.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 4. Therefore, the remainders of these numbers when divided by 3 alternate. Indeed, if one of these numbers is divisible by 3, i.e., has the form $3k$, where $k \in \mathbb{N}$, then the next number is $3k+4=3(k+1)+1$ - and it gives a remainder of 1 when divided by 3, followed by $3k+8=3(k+2)+2$, which gives a remainder of 2 when divided by 3, and then $-3k+12$, which is again divisible by 3. Thus, the remainders of the given numbers when divided by 3 go in the order $\ldots 0 ; 1 ; 2 ; 0 ; 1 ; 2 ; 0 \ldots$
Among the given numbers, there are 47 that give a remainder of 1 when divided by 3 (they form the set $A=\{4 ; 16 ; 28 ; \ldots ; 556\}$), 46 numbers that are divisible by 3 ($B=\{12 ; 24 ; 36 ; \ldots ; 552\}$), and 47 numbers that give a remainder of 2 when divided by 3 ($C=\{8 ; 20 ; 32 ; \ldots ; 560\}$).
The sum of three numbers can be divisible by 3 in the following cases.
1) All three numbers give the same remainder when divided by 3. There are $C_{46}^{3}$ ways to choose 3 numbers from set $B$ and $C_{47}^{3}$ ways to choose 3 numbers from sets $A$ and $C$. In total, we get $\frac{46 \cdot 45 \cdot 44}{6}+2 \cdot \frac{47 \cdot 46 \cdot 45}{6}=15180+2 \cdot 16215=47610$ ways.
2) If not all remainders are the same, then only the case where all three remainders are different fits, i.e., we must choose one number from each of the sets $A, B, C$. We get $47 \cdot 47 \cdot 46=$ 101614 ways.
In total, we get 149224 ways.
|
149224
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On the table, there are 200 different cards with numbers $201, 203, 205, \ldots, 597, 599$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the sum of the numbers on the selected cards is divisible by 3?
|
Answer: 437844.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 3 alternate. Indeed, if one of these numbers is divisible by 3, i.e., has the form $3k$, where $k \in \mathbb{N}$, then the next number is $3k+2$ - and it gives a remainder of 2 when divided by 3, followed by $3k+4 = 3(k+1)+1$, which gives a remainder of 1 when divided by 3, and then $3k+6$, which is again divisible by 3. Thus, the remainders of the given numbers when divided by 3 go in the order ... $0 ; 2 ; 1 ; 0 ; 2 ; 1 ; 0 \ldots$.
Among the given numbers, there are 66 that give a remainder of 1 when divided by 3 (they form the set $A=\{205 ; 211 ; 217 ; \ldots ; 595\}$), 67 numbers that are divisible by 3 ($B=\{201 ; 207 ; 213 ; \ldots ; 597\}$), and 67 numbers that give a remainder of 2 when divided by 3 ($C=\{203 ; 209 ; 215 ; \ldots ; 599\}$).
The sum of three numbers can be divisible by 3 in the following cases.
1) All three numbers give the same remainder when divided by 3. There are $C_{66}^{3}$ ways to choose 3 numbers from set $A$ and $C_{67}^{3}$ ways to choose 3 numbers from sets $B$ and $C$. In total, we get $\frac{66 \cdot 65 \cdot 64}{6} + 2 \cdot \frac{67 \cdot 66 \cdot 65}{6} = 45760 + 2 \cdot 47905 = 141570$ ways.
2) If not all remainders are the same, then only the case where all three remainders are different fits, i.e., we must choose one number from each of the sets $A, B, C$. We get $66 \cdot 67 \cdot 67 = 296274$ ways.
In total, we get 437844 ways.
|
437844
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On the table, there are 160 different cards with numbers $5, 10, 15, \ldots, 795, 800$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the sum of the numbers on the selected cards is divisible by 3?
|
Answer: 223342.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a common difference of 5. Therefore, the remainders when these numbers are divided by 3 alternate. Indeed, if one of these numbers is divisible by 3, i.e., has the form $3k$, where $k \in \mathbb{N}$, then the next number is $3k+5=3(k+1)+2$ - and it gives a remainder of 2 when divided by 3, followed by $3k+10=3(k+3)+1$, which gives a remainder of 1 when divided by 3, and then $-3k+15$, which is again divisible by 3. Thus, the remainders when these numbers are divided by 3 follow the pattern $\ldots 0 ; 2 ; 1 ; 0 ; 2 ; 1 ; 0 \ldots$
Among the given numbers, there are 53 numbers that give a remainder of 1 when divided by 3 (they form the set $A=\{10 ; 25 ; 40 ; \ldots ; 790\}$), 53 numbers that are divisible by 3 ($B=\{15 ; 30 ; 45 ; \ldots ; 795\}$), and 54 numbers that give a remainder of 2 when divided by 3 ($C=\{5 ; 20 ; 35 ; \ldots ; 800\}$).
The sum of three numbers can be divisible by 3 in the following cases.
1) All three numbers give the same remainder when divided by 3. There are $C_{54}^{3}$ ways to choose 3 numbers from set $C$ and $C_{53}^{3}$ ways to choose 3 numbers from sets $A$ and $B$. In total, we get $\frac{54 \cdot 53 \cdot 52}{6}+2 \cdot \frac{53 \cdot 52 \cdot 51}{6}=24804+2 \cdot 23426=71656$ ways.
2) If not all remainders are the same, the only suitable case is when all three remainders are different, i.e., we must choose one number from each of the sets $A, B, C$. We get $53 \cdot 54 \cdot 54=$ 151686 ways.
In total, we get 223342 ways.
|
223342
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. There are 207 different cards with numbers $1,2,3,2^{2}, 3^{2}, \ldots, 2^{103}, 3^{103}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer divisible by 6?
|
Answer: 267903.
Solution. Consider the case when one of the selected cards has a one written on it. Then, on the other two cards, even powers of two and three must be recorded. There are 51 ways to choose an even power of two and 51 ways to choose an even power of three, and since this choice is made independently, the total number of ways in this case is $51^{2}=2601$.
Now let's move on to the case when the card with one is not used. There are two possibilities: take two cards with powers of three and one with a power of two, or vice versa.
Suppose we take two cards with powers of two. Since the power of two in the product of the selected numbers must be even, the powers of two on the selected cards must have the same parity. We have a total of 52 cards with odd powers and 51 cards with even powers. Thus, there are $C_{52}^{2}=\frac{52 \cdot 51}{2}=1326$ ways to choose cards with odd powers and $C_{51}^{2}=\frac{51 \cdot 50}{2}=1275$ ways to choose two cards with even powers, totaling 2601 ways. After selecting the cards with powers of two, we can choose any card with an even power of three (51 ways). Since the choice of the card with the power of three is independent of the previous choice, in total, we get $2601 \cdot 51=132651$ ways.
It is easy to see that if we take two cards with powers of three and one with a power of two, the number of ways will be the same as in the previous case. Therefore, we get $2601 + 132651 \cdot 2 = 267903$ ways.
|
267903
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. There are 183 different cards with numbers $1,2,11,2^{2}, 11^{2}, \ldots, 2^{91}, 11^{91}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the product of the numbers on the selected cards is a square of an integer divisible by 22?
|
Answer: 184275.
Solution. Consider the case when one of the selected cards has the number one written on it. Then, on the other two cards, even powers of the numbers two and eleven must be recorded. There are 45 ways to choose an even power of two and 45 ways to choose an even power of eleven, and since this choice is made independently, the total number of ways in this case is $45^{2}=2025$.
Now let's move on to the case when the card with the number one is not used. There are two possibilities: take two cards with powers of two and one with a power of eleven, or vice versa.
Suppose we take two cards with powers of two. Since the number two must be present in an even power in the product of the selected numbers, the powers of two on the selected cards must have the same parity. We have a total of 46 cards with odd powers and 45 cards with even powers. Thus, there are $C_{46}^{2}=\frac{46 \cdot 45}{2}=1035$ ways to choose cards with odd powers and $C_{45}^{2}=\frac{45 \cdot 44}{2}=990$ ways to choose two cards with even powers - in total, we get 2025 ways. After selecting the cards with powers of two, we can choose any card with an even power of eleven (45 ways). Since the choice of the card with the power of eleven is independent of the previous choice, in total, we get $2025 \cdot 45=91125$ ways.
It is easy to see that if we take two cards with powers of eleven and one with a power of two, the number of ways will be the same as in the previous case. Therefore, we get $2025+91125 \cdot 2=184275$ ways.
|
184275
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. There are 195 different cards with numbers $1, 5, 7, 5^{2}, 7^{2}, \ldots, 5^{97}, 7^{97}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer divisible by 35?
|
Answer: 223488.
Solution. Consider the case when one of the selected cards has a one written on it. Then, on the other two cards, even powers of fives and sevens must be recorded. There are 48 ways to choose an even power of five and 48 ways to choose an even power of seven, and since this choice is made independently, the total number of ways in this case is $48^{2}=2304$.
Now let's move on to the case when the card with one is not used. There are two possibilities: to take two cards with powers of five and one with a power of seven, or vice versa.
Suppose we take two cards with powers of seven. Since the product of the selected numbers must contain seven in an even power, the powers of seven on the selected cards must have the same parity. We have a total of 49 cards with odd powers and 48 cards with even powers. Thus, there are $C_{49}^{2}=\frac{49 \cdot 48}{2}=1176$ ways to choose cards with odd powers and $C_{48}^{2}=\frac{48 \cdot 47}{2}=1128$ ways to choose two cards with even powers, totaling 2304 ways. After selecting the cards with powers of seven, we can choose any card with an even power of five (48 ways). Since the choice of the card with the power of five is independent of the previous choice, in total, we get $2304 \cdot 48=110592$ ways.
It is easy to see that if we take two cards with powers of five and one with a power of seven, the number of ways will be the same as in the previous case. Therefore, we get $2304+110592 \cdot 2=223488$ ways.
|
223488
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. There are 167 different cards with numbers $1, 3, 11, 3^{2}, 11^{2}, \ldots, 3^{83}, 11^{83}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 3 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer divisible by 33?
|
Answer: 139523.
Solution. Consider the case when one of the selected cards has the number one written on it. Then, on the other two cards, even powers of the numbers three and eleven must be recorded. There are 41 ways to choose an even power of three and 41 ways to choose an even power of eleven, and since this choice is made independently, the total number of ways in this case is $41^{2}=1681$.
Now let's move on to the case when the card with the number one is not used. There are two possibilities: to take two cards with powers of three and one with a power of eleven, or vice versa. Suppose we take two cards with powers of three. Since the number three must be present in an even power in the product of the selected numbers, the powers of three on the selected cards must have the same parity. We have a total of 42 cards with odd powers and 41 cards with even powers. Thus, there are $C_{42}^{2}=\frac{42 \cdot 41}{2}=861$ ways to choose cards with odd powers and $C_{41}^{2}=\frac{41 \cdot 40}{2}=820$ ways to choose two cards with even powers - in total, we get 1681 ways. After selecting the cards with powers of three, we can choose any card with an even power of eleven (41 ways). Since the choice of the card with the power of eleven is independent of the previous choice, in total, we get $1681 \cdot 41=68921$ ways.
It is easy to see that if we take two cards with powers of eleven and one with a power of three, the number of ways will be the same as in the previous case. Therefore, we get $1681+68921 \cdot 2=139523$ ways.
|
139523
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On each of the lines $y=1$ and $y=6$, there are 200 points with abscissas $1,2,3, \ldots, 200$. In how many ways can three points be chosen from the 400 marked points so that they form the vertices of a right triangle?
|
Answer: $C_{200}^{2} \cdot 4 + 190 \cdot 2 + 174 \cdot 4 = 80676$.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle lies on the other line. Let $A B C$ be the given triangle with a right angle at vertex $C$, and $C H$ be its height dropped to the hypotenuse. From the proportionality of segments of a right triangle, we get that $C H^{2} = A H \cdot B H$, i.e., $A H \cdot B H = 25$. Since $A H$ and $B H$ are integers, the following cases are possible: $A H = B H = 5, A H = 25$ and $B H = 1, A H = 1$ and $B H = 25$.
In the first of these cases, the hypotenuse $A B$, equal to 10, can be placed in $190 \cdot 2 = 380$ ways (200 - 10 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 26, and it can be placed in $2(200 - 26) = 348$ ways. For each position of the hypotenuse, there are two ways to place the vertex - resulting in $2 \cdot 348 = 696$ ways.
2) One of the legs of the triangle (let's call it $B C$) is perpendicular to the given lines, and the other leg ($A C$) lies on one of the given lines. Then the position of leg $B C$ can be chosen in 200 ways. For each variant of the placement of leg $B C$, vertex $A$ can be placed in 398 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $200 \cdot 398 = 79600$ ways.
In total, we get $380 + 696 + 79600 = 80676$ ways.
|
80676
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On each of the lines $x=2$ and $x=9$, there are 400 points with ordinates $1,2,3, \ldots, 400$. In how many ways can three points be chosen from the 800 marked points so that they form the vertices of a right triangle?
|
Answer: 321372.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 49$. Since $AH$ and $BH$ are integers, the following cases are possible: $AH = BH = 7$, $AH = 49$ and $BH = 1$, $AH = 1$ and $BH = 49$.
In the first of these cases, the hypotenuse $AB$, equal to 14, can be placed in $386 \cdot 2 = 772$ ways (400 - 14 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 50, and it can be placed in $2(400 - 50) = 700$ ways. For each position of the hypotenuse, there are two ways to place the vertex - resulting in $2 \cdot 700 = 1400$ ways.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the second leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 400 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 798 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $400 \cdot 798 = 319200$ ways.
In total, we get $772 + 1400 + 319200 = 321372$ ways.
|
321372
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On each of the lines $y=1$ and $y=12$, there are 200 points with abscissas $1,2,3, \ldots, 200$. In how many ways can three points be chosen from the 400 marked points so that they form the vertices of a right triangle?
|
Answer: 80268.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of the segments of the right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 121$. Since $AH$ and $BH$ are integers, the following cases are possible: $AH = BH = 11$, $AH = 121$ and $BH = 1$, $AH = 1$ and $BH = 121$.
In the first of these cases, the hypotenuse $AB$, equal to 22, can be placed in $178 \cdot 2 = 356$ ways (200 - 22 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 122, and it can be placed in $2(200 - 122) = 156$ ways. For each position of the hypotenuse, there are two ways to place the vertex - resulting in $2 \cdot 156 = 312$ ways.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the second leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 200 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 398 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $200 \cdot 398 = 79600$ ways.
In total, we get $356 + 312 + 79600 = 80268$ ways.
|
80268
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On each of the lines $x=2$ and $x=15$, there are 400 points with ordinates $1,2,3, \ldots, 400$. In how many ways can three points be chosen from the 800 marked points so that they form the vertices of a right triangle?
|
Answer: 320868.
Solution. There are two possibilities.
1) The hypotenuse of the triangle lies on one of the lines, and the vertex of the right angle is on the second line. Let $ABC$ be the given triangle with a right angle at vertex $C$, and $CH$ be its height dropped to the hypotenuse. From the proportionality of segments of a right triangle, we get that $CH^2 = AH \cdot BH$, i.e., $AH \cdot BH = 169$. Since $AH$ and $BH$ are integers, the following cases are possible: $AH = BH = 13$, $AH = 169$ and $BH = 1$, $AH = 1$ and $BH = 169$.
In the first of these cases, the hypotenuse $AB$, equal to 26, can be placed in $374 \cdot 2 = 748$ ways (400 - 26 ways of placement on each of the two given lines), and the position of vertex $C$ is uniquely determined.
In the second and third cases, the length of the hypotenuse is 170, and it can be placed in $2(400 - 170) = 460$ ways. For each position of the hypotenuse, there are two ways to place the vertex - resulting in $2 \cdot 460 = 920$ ways.
2) One of the legs of the triangle (let's call it $BC$) is perpendicular to the given lines, and the second leg ($AC$) lies on one of the given lines. Then the position of the leg $BC$ can be chosen in 400 ways. For each variant of the placement of the leg $BC$, the vertex $A$ can be placed in 798 ways (all points except the already chosen $B$ and $C$ are suitable) - in total, we get $400 \cdot 798 = 319200$ ways.
In total, we get $748 + 920 + 319200 = 320868$ ways.
|
320868
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of distinct reduced quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have at least one root, all their roots are powers of the number 3 with integer non-negative exponents, and their coefficients in absolute value do not exceed \(27^{47}\).
|
Answer: 5111.
Solution. Such quadratic trinomials can be represented in the form $\left(x-3^{a}\right)\left(x-3^{b}\right)$, where $a \geqslant 0$, $b \geqslant 0$ are integers. To avoid repetitions, we assume that $a \geqslant b$. Expanding the brackets, we get $x^{2}-\left(3^{a}+3^{b}\right) x+3^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 3 ^ { a } + 3 ^ { b } \leqslant 2 7 ^ { 4 7 } , } \\
{ 3 ^ { a + b } \leqslant 2 7 ^ { 4 7 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
3^{a}+3^{b} \leqslant 3^{141} \\
a+b \leqslant 141
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=141, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=141 \Rightarrow 0 \text { values of } b \text {; } \\
& a=140 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=139 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& a=71 \Rightarrow 71 \text { value of } b(b \in\{0 ; 1 ; \ldots ; 70\}) \text {; } \\
& a=70 \Rightarrow 71 \text { value of } b(b \in\{0 ; 1 ; \ldots ; 70\}) \text {; } \\
& a=69 \Rightarrow 70 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 69\}) \text {; } \\
& a=68 \Rightarrow 69 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 68\}) \text {; } \\
& a=1 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=0 \Rightarrow 1 \text { value of } b(b=0) \text {. }
\end{aligned}
$$
Summing up, we get $(2+3+4+\ldots 71)+(71+70+69+\ldots+1)=5111$ options.
|
5111
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of distinct reduced quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have at least one root, all their roots are powers of the number 5 with integer non-negative exponents, and their coefficients in absolute value do not exceed $122^{85}$.
|
Answer: 16511.
Solution. Such quadratic trinomials can be represented in the form $\left(x-5^{a}\right)\left(x-5^{b}\right)$, where $a \geqslant 0$, $b \geqslant 0$ are integers. To avoid repetitions, we assume that $a \geqslant b$. Expanding the brackets, we get $x^{2}-\left(5^{a}+5^{b}\right) x+5^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 5 ^ { a } + 5 ^ { b } \leqslant 1 2 5 ^ { 8 5 } , } \\
{ 5 ^ { a + b } \leqslant 1 2 5 ^ { 8 5 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
5^{a}+5^{b} \leqslant 5^{255} \\
a+b \leqslant 255
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=255, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=255 \Rightarrow 0 \text { values of } b \text {; } \\
& a=254 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=253 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& a=128 \Rightarrow 128 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 127\}) \text {; } \\
& a=127 \Rightarrow 128 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 127\}) \text {; } \\
& a=126 \Rightarrow 127 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 126\}) \text {; } \\
& a=125 \Rightarrow 126 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 125\}) \text {; }
\end{aligned}
$$
$$
\begin{gathered}
a=1 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \\
a=0 \Rightarrow 1 \text { value of } b(b=0) .
\end{gathered}
$$
Summing up, we get $(2+3+4+\ldots 128)+(128+127+126+\ldots+1)=16511$ options.
|
16511
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of distinct reduced quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have at least one root, all their roots are powers of the number 7 with integer non-negative exponents, and their coefficients in absolute value do not exceed \(49^{68}\).
|
Answer: 4760.
Solution. Such quadratic trinomials can be represented in the form $\left(x-7^{a}\right)\left(x-7^{b}\right)$, where $a \geqslant 0$, $b \geqslant 0$ are integers. To avoid repetitions, we assume that $a \geqslant b$. Expanding the brackets, we get $x^{2}-\left(7^{a}+7^{b}\right) x+7^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 7 ^ { a } + 7 ^ { b } \leqslant 4 9 ^ { 6 8 } , } \\
{ 7 ^ { a + b } \leqslant 4 9 ^ { 6 8 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
7^{a}+7^{b} \leqslant 7^{136} \\
a+b \leqslant 136
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=136, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=136 \Rightarrow 0 \text { values of } b \text {; } \\
& a=135 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=134 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& a=69 \Rightarrow 68 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 67\}) \text {; } \\
& a=68 \Rightarrow 69 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 68\}) \text {; } \\
& a=67 \Rightarrow 68 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 67\}) \text {; } \\
& a=66 \Rightarrow 67 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 66\}) \text {; } \\
& a=1 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=0 \Rightarrow 1 \text { value of } b(b=0) \text {. }
\end{aligned}
$$
Summing up, we get $(2+3+4+\ldots 69)+(68+67+66+\ldots+1)=4760$ options.
|
4760
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of distinct reduced quadratic trinomials (i.e., with the leading coefficient equal to 1) with integer coefficients such that they have at least one root,
all their roots are powers of the number 11 with integer non-negative exponents, and their coefficients in absolute value do not exceed $1331^{38}$.
|
Answer: 3363.
Solution. Such quadratic trinomials can be represented in the form $\left(x-11^{a}\right)\left(x-11^{b}\right)$, where $a \geqslant 0, b \geqslant 0$ are integers. To avoid repetitions, we assume that $a \geqslant b$. Expanding the brackets, we get $x^{2}-\left(11^{a}+11^{b}\right) x+11^{a+b}$. According to the condition
$$
\left\{\begin{array} { l }
{ 1 1 ^ { a } + 1 1 ^ { b } \leqslant 1 3 3 1 ^ { 3 8 } , } \\
{ 1 1 ^ { a + b } \leqslant 1 3 3 1 ^ { 3 8 } }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
11^{a}+11^{b} \leqslant 11^{114} \\
a+b \leqslant 114
\end{array}\right.\right.
$$
Note that if the second inequality holds, then the first inequality is true except for one case $a=114, b=0$. For each value of $a$, we list the number of suitable values of $b$:
$$
\begin{aligned}
& a=114 \Rightarrow 0 \text { values of } b \text {; } \\
& a=113 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=112 \Rightarrow 3 \text { values of } b(b \in\{0 ; 1 ; 2\}) \text {; } \\
& a=58 \Rightarrow 57 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 56\}) \text {; } \\
& a=57 \Rightarrow 58 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 57\}) \text {; } \\
& a=56 \Rightarrow 57 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 56\}) \text {; } \\
& a=55 \Rightarrow 56 \text { values of } b(b \in\{0 ; 1 ; \ldots ; 55\}) \text {; } \\
& a=1 \Rightarrow 2 \text { values of } b(b \in\{0 ; 1\}) \text {; } \\
& a=0 \Rightarrow 1 \text { value of } b(b=0) \text {. }
\end{aligned}
$$
Summing up, we get $(2+3+4+\ldots 58)+(57+56+55+\ldots+1)=3363$ options.
|
3363
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
9.5. Does there exist thirteen consecutive natural numbers such that their sum is a 2021st power of a natural number?
|
Answer. They exist.
Solution. Let's denote 13 consecutive numbers as $N-6, N-5$, ..., $N+5, N+6$. Then their sum is $13N$. If $N=13^{2020}$, then the sum will be $13N = 13 \cdot 13^{2020} = 13^{2021}$.
Comment. A correct answer without justification - 0 points.
9.6-1. On a given circle $\omega$, points $A, B$, and $C$ are chosen such that angle $ABC$ is $70^{\circ}$. Let $D$ be the point of intersection of the angle bisector of $ABC$ with the circle $\omega$, and let point $K$ be symmetric to point $A$ with respect to point $D$. The line $KC$ intersects the circle again at point $P (P \neq C$, point $C$ lies on the segment $KP)$. Find the angle $ADP$.
Answer. $90^{\circ}$.
Solution. We will prove that $PD$ is perpendicular to $AK. AD = DK$, so we need to prove that $\alpha = \angle APD = \beta = \angle KPD$. But $\alpha = \angle APD = \angle ABD$ (inscribed, subtend arc $AD$), $\beta = \angle CPD = \angle CBD$ (inscribed, subtend arc $CD$). Finally, $\angle ABD = \angle CBD$, since $BD$ is the bisector of $\angle ABC$. The statement is proved.
Comment. A correct answer without justification - 0 points.
9.6-2. On a given circle $\omega$, points $A, B$, and $C$ are chosen such that angle $ABC$ is $65^{\circ}$. Let $D$ be the point of intersection of the angle bisector of $ABC$ with the circle $\omega$, and let point $K$ be symmetric to point $A$ with respect to point $D$. The line $KC$ intersects the circle again at point $P (P \neq C$, point $C$ lies on the segment $KP)$. Find the angle $ADP$.
Answer. $90^{\circ}$.
Solution. We will prove that $PD$ is perpendicular to $AK. AD = DK$, so we need to prove that $\alpha = \angle APD = \beta = \angle KPD$. But $\alpha = \angle APD = \angle ABD$ (inscribed, subtend arc $AD$), $\beta = \angle CPD = \angle CBD$ (inscribed, subtend arc $CD$). Finally, $\angle ABD = \angle CBD$, since $BD$ is the bisector of $\angle ABC$. The statement is proved.
Comment. A correct answer without justification - 0 points.
|
90
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 3375. The answer should be presented as an integer.
|
Answer: 1680.
Solution. Since $3375=3^{3} \cdot 5^{3}$, the sought numbers can consist of the following digits: (a) three threes, three fives, and two ones, or (b) one three, one nine, three fives, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then three places out of the remaining five for the fives ( $C_{5}^{3}=\frac{5!}{3!2!}$ ways). Finally, the remaining places are occupied by ones. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{3}=\frac{8!}{3!3!2!}=560$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$.
Finally, we get $560+1120=1680$ ways.
|
1680
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 16875. The answer should be presented as an integer.
|
Answer: 1120.
Solution. Since $16875=3^{3} \cdot 5^{4}$, the sought numbers can consist of the following digits: (a) three threes, four fives, and one one, or (b) one three, one nine, four fives, and two ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then one place out of the remaining five for the one ( $C_{5}^{1}=5$ ways). Finally, the remaining places are occupied by fives. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{1}=\frac{8!}{3!5!} \cdot 5=280$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{4!2!}=840$. Finally, we get $280+840=1120$ ways.
|
1120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 9261. The answer should be presented as an integer.
|
Answer: 1680.
Solution. Since $9261=3^{3} \cdot 7^{3}$, the sought numbers can consist of the following digits: (a) three threes, three sevens, and two ones, or (b) one three, one nine, three sevens, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then three places out of the remaining five for the sevens $\left(C_{5}^{3}=\frac{5!}{3!2!}\right.$ ways). Finally, the remaining places are occupied by ones. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{3}=\frac{8!}{3!3!2!}=560$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$. Finally, we get $560+1120=1680$ ways.
|
1680
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. [3 points] Find the number of eight-digit numbers, the product of the digits of each of which is equal to 64827. The answer should be presented as an integer.
|
Answer: 1120.
Solution. Since $64827=3^{3} \cdot 7^{4}$, the sought numbers can consist of the following digits: (a) three threes, four sevens, and one one, or (b) one three, one nine, four sevens, and two ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the threes $\left(C_{8}^{3}=\frac{8!}{3!5!}\right.$ ways), then one place out of the remaining five for the one ( $C_{5}^{1}=5$ ways). Finally, the remaining places are occupied by sevens. By the multiplication rule, we get $C_{8}^{3} \cdot C_{5}^{1}=\frac{8!}{3!5!} \cdot 5=280$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{4!2!}=840$.
Finally, we get $280+840=1120$ ways.
|
1120
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can be repeated) so that the resulting 12-digit number is divisible by 45. In how many ways can this be done
|
Answer: 13122.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by nine, we proceed as follows. We will choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $2 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=13122$.
|
13122
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 18. In how many ways can this be done?
|
Answer: 3645.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6$ or 8 (5 ways).
To ensure divisibility by nine, we proceed as follows. Choose three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0, 1, 2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $5 \cdot 9 \cdot 9 \cdot 9 \cdot 1 = 3645$ ways.
|
3645
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 45. In how many ways can this be done?
|
Answer: 1458.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We select three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $2 \cdot 9 \cdot 9 \cdot 9 \cdot 1=1458$ ways.
|
1458
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done
|
Answer: 26244.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $2, 4, 6$ or 8 (4 ways).
To ensure divisibility by nine, we proceed as follows. We select four digits arbitrarily (this can be done in 9.9 .9 .9 ways), and then choose the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $4 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=26244$.
|
26244
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2016^{* * * *} 02 * *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by three, we proceed as follows. Choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. Given a right triangular prism $A B C A_{1} B_{1} C_{1}$. A sphere with diameter $B C$ intersects the edges $A C$ and $A B$ at points $P$ and $Q$, respectively, different from the vertices of the prism. Segments $B_{1} P$ and $C_{1} Q$ intersect at point $T$, and $B_{1} P=5, T Q=2$.
a) Find the angle $T P A$.
b) Find the ratio $A P: C P$.
c) Suppose it is additionally known that $A C=3$. Find the volume of the prism.
|
Answer: a) $90^{\circ}$, b) $2: 1$, c) $V=15$.
Solution. a) Points $P$ and $Q$ lie on the circle with diameter $BC$; therefore, $\angle BPC=90^{\circ}, \angle BQC=90^{\circ}$ (i.e., $BP$ and $CQ$ are altitudes of triangle $ABC$). The line $BP$ is the projection of the line $TP$ onto the base plane, and since $BP \perp PA$, by the theorem of three perpendiculars, $TP \perp PA$, i.e., $\angle TPA=90^{\circ}$.
b) Since the lines $B_1P$ and $C_1Q$ intersect, all four points $B_1, C_1, P$, and $Q$ lie in the same plane (let's call it $\alpha$). Therefore, the lines $PQ$ and $B_1C_1$ lie in the same plane $\alpha$, and since they do not intersect (as they lie in the parallel bases of the prism), $PQ \parallel B_1C_1$. Hence, $PQ \parallel BC$. The trapezoid $PQBC$ is inscribed in a circle, so it is isosceles, and the angles at its base $BC$ are equal, which means triangle $ABC$ is isosceles ($AB=AC$).
Triangles $B_1C_1T$ and $PQT$ are similar by two angles. From the equality of triangles $CC_1Q$ and $BB_1P$, it follows that $B_1P = C_1Q$, so both triangles $B_1C_1T$ and $PQT$ are isosceles with bases $B_1C_1$ and $PQ$ respectively. Therefore, $PQ: BC = PQ: B_1C_1 = TQ: TC_1 = TQ: (QC_1 - TQ) = TQ: (B_1P - TQ) = 2: 3$, from which $\frac{CP}{AP} = \frac{AC - AP}{AP} = \frac{AC}{AP} - 1 = \frac{BC}{PQ} - 1 = \frac{3}{2} - 1 = \frac{1}{2}$.
c) If $AC = 3$, then $CP = 1, AP = 2, AB = 3; BP = \sqrt{AB^2 - AP^2} = \sqrt{5}; BB_1 = \sqrt{B_1P^2 - BP^2} = 2\sqrt{5}$. Therefore, the area of the base of the prism is $S_{ABC} = \frac{1}{2} \cdot 3 \cdot \sqrt{5}$, and the volume of the prism is $V = S_{ABC} \cdot BB_1 = 15$.
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,6,7,8$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 2160.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6, 8$ (5 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get a total of $5 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2160$ ways.
|
2160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 864.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 2=864$ ways.
|
864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 1728.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 8$ (4 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this choice can be made in two ways.
Applying the rule of product, we get that in total $4 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 1728$ ways.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 75. In how many ways can this be done?
|
Answer: 2592.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit (1 way).
To ensure divisibility by three, we proceed as follows. Select four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and choose the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $1 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2592$ ways.
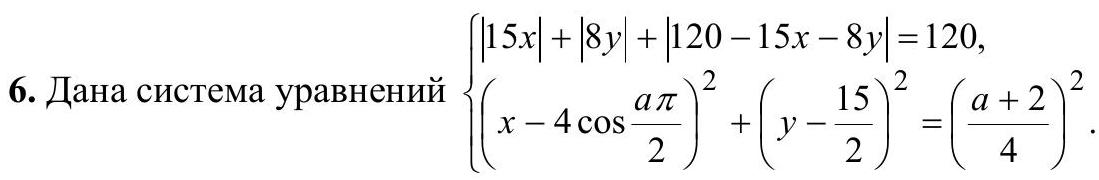
a) Plot on the plane $(x ; y)$ the set of points satisfying the first equation of the system, and find the area of the resulting figure.
b) Find all values of the parameter $a$ for which the system has exactly three solutions.
Answer: a) 60, b) $a=-36, a=32$.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right side). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array}{l}
85 x \geq 0, \\
8 y \geq 0, \\
120 - 15 x - 8 y \geq 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
15 x + 8 y \leq 120
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(8 ; 0), G(0 ; 15), N(0 ; 0)$, the area of which is 60.
The second equation of the original system defines a circle (or a point when $a=-2$). The system can have exactly three solutions only in one case: when the circle defined by the second equation is circumscribed around the triangle $E G N$. The center of the circle circumscribed around a right triangle is the midpoint of the hypotenuse, and its radius is half the hypotenuse, from which we obtain the conditions
$$
4 \cos \frac{a \pi}{2}=4,\left(\frac{a+2}{4}\right)^{2}=\left(\frac{17}{2}\right)^{2}
$$
The second equation gives two values of the parameter: $a=-36$ and $a=32$. By substitution, we verify that both satisfy the first equation.
|
2592
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can repeat) so that the resulting 11-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 1296.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0, 4, or 8 as the last digit (3 ways).
To ensure divisibility by 3, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get a total of $3 \cdot 6 \cdot 6 \cdot 6 \cdot 2=1296$ ways.
|
1296
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 07 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,6,7$ (digits can repeat) so that the resulting 11-digit number is divisible by 75. In how many ways can this be done?
|
Answer: 432.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit (1 way).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get that there are $1 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 432$ ways in total.
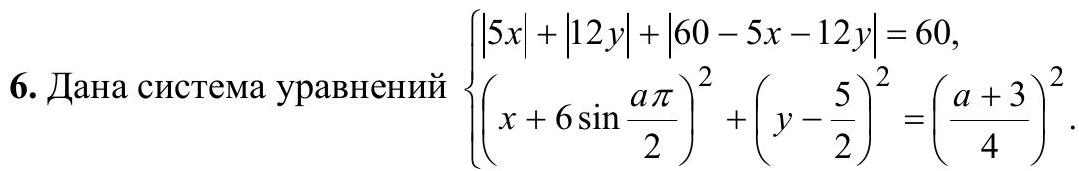
a) Plot on the plane $(x ; y)$ the set of points satisfying the first equation of the system, and find the area of the resulting figure.
b) Find all values of the parameter $a$ for which the system has exactly three solutions.
Answer: a) 30, b) $a=-29, a=23$.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right side). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array}{l}
5 x \geq 0, \\
12 y \geq 0, \\
60 - 5 x - 12 y \geq 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
5 x + 12 y \leq 60
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(12 ; 0), G(0 ; 5), N(0 ; 0)$, the area of which is 30.
The second equation of the original system defines a circle (or a point when $a=-3$). The system can have exactly three solutions only in one case: when the circle defined by the second equation is circumscribed around the triangle $E G N$. The center of the circle circumscribed around a right triangle is the midpoint of the hypotenuse, and its radius is half the hypotenuse, from which we obtain the conditions
$$
-6 \sin \frac{a \pi}{2} = 6, \left(\frac{a+3}{4}\right)^{2} = \left(\frac{13}{2}\right)^{2}
$$
The second equation gives two values of the parameter: $a=-29$ and $a=23$. By substitution, we verify that both values satisfy the first equation.
|
432
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0 or 4 as the last digit (2 ways).
To ensure divisibility by 3, we proceed as follows. Choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 5184$ ways.
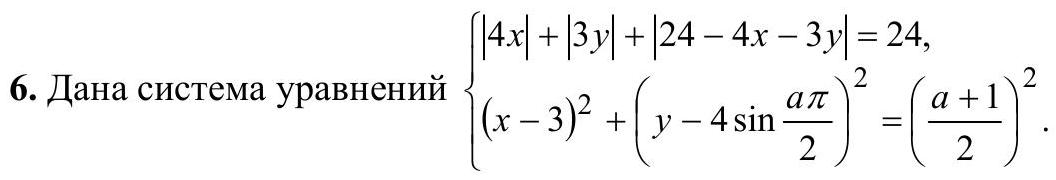
a) Plot on the plane $(x ; y)$ the set of points satisfying the first equation of the system, and find the area of the resulting figure.
b) Find all values of the parameter $a$ for which the system has exactly three solutions.
Answer: a) 24 ; b) $a=-11, a=9$.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right side). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array}{l}
4 x \geq 0, \\
3 y \geq 0, \\
24 - 4 x - 3 y \geq 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
4 x + 3 y \leq 24
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(6 ; 0), G(0 ; 8), N(0 ; 0)$, the area of which is 24.
The second equation of the original system defines a circle (or a point when $a=-1$). The system can have exactly three solutions only in one case: when the circle defined by the second equation is circumscribed around the triangle $E G N$. The center of the circle circumscribed around a right triangle is the midpoint of the hypotenuse, and its radius is half the hypotenuse, from which we obtain the conditions
$$
4 \sin \frac{a \pi}{2} = 4, \left(\frac{a+1}{2}\right)^{2} = (5)^{2}
$$
The second equation gives two values of the parameter: $a=-11$ and $a=9$. By substitution, we verify that both satisfy the first equation.
|
5184
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
30. On the board, there are param1 natural numbers. It is known that the sum of any five of them is not less than param2. Find the smallest possible value of the sum of all the numbers written on the board.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 20 | 117 | |
| 18 | 97 | |
| 19 | 107 | |
| 26 | 153 | |
| 17 | 123 | |
|
30. On the board, ragat1 natural numbers are written. It is known that the sum of any five of them is not less than param2. Find the smallest possible value of the sum of all numbers written on the board.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 20 | 117 | 477 |
| 18 | 97 | 357 |
| 19 | 107 | 415 |
| 26 | 153 | 804 |
| 17 | 123 | 423 |
|
477
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On the table, there are 100 different cards with numbers $3, 6, 9, \ldots 297, 300$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $5?$
|
Answer: 990.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a common difference of 3. Therefore, the remainders of these numbers when divided by 5 alternate. Indeed, if one of these numbers is divisible by 5, i.e., has the form $5k$, where $k \in \mathbb{N}$, then the next number is $5k+3$ - and it gives a remainder of 3 when divided by 5; then $-5k+6=5(k+1)+1$, giving a remainder of 1 when divided by 5; then $-5k+9=5(k+1)+4$, giving a remainder of 4 when divided by 5; then $5k+12=5(k+2)+2$, giving a remainder of 2 when divided by 5; finally, the next one is $5k+15=5(k+3)$, which is again divisible by 5, after which the order of remainders repeats. Thus, the remainders of the given numbers when divided by 5 go in the order $\ldots 0 ; 3 ; 1 ; 4 ; 2 ; 0 \ldots$
Among the 100 given numbers, there are 20 numbers that give remainders of $0, 1, 2, 3, 4$ when divided by 5.
The sum of two numbers can be divisible by 5 in the following cases.
1) Both numbers are divisible by 5. There are 20 cards with such numbers, and we need to choose 2 of them - there are $C_{20}^{2}=$ $\frac{1}{2} \cdot 20 \cdot 19=190$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 5 - then the other must give a remainder of 4 when divided by 5. This pair of numbers can be chosen in $20 \cdot 20=400$ ways.
3) One of the numbers gives a remainder of 2 when divided by 5 - then the other gives a remainder of 3, and, similarly to the second case, we get 400 ways to choose 2 numbers.
In total, there are 990 ways.
|
990
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. In a right triangle $ABC (\angle B=90^{\circ})$, a circle $\Gamma$ with center $I$ is inscribed, touching sides $AB$ and $BC$ at points $K$ and $L$ respectively. A line passing through point $I$ intersects sides $AB$ and $BC$ at points $M$ and $N$ respectively. Find the radius of the circle $\Gamma$ if $MK=225$, $NL=64$. Find $AC$ if it is additionally known that line $MN$ is parallel to $AC$.
|
Answer: $R=120, AC=680$.
Solution. Angles $KIM$ and $LNI$ are equal as corresponding angles when lines $BC$ and $KI$ are parallel, so right triangles $KIM$ and $LNI$ are similar. Therefore, $\frac{MK}{KI}=\frac{IL}{LN}$, or (if we denote the radius of the circle by $r$) $\frac{225}{r}=\frac{r}{64}$, from which $r=120$.
Then $BM=BK+KM=r+KM=345, BN=BL+LN=r+LN=184$, hence $MN^2=$ $345^2+184^2=23^2\left(15^2+8^2\right)=23^2 \cdot 17^2, MN=23 \cdot 17$. Let $h$ be the height of triangle $BMN$, drawn from the vertex of the right angle $B$. Then the area of triangle $BMN$ can be expressed in two ways: $2S_{\triangle BMN}=BN \cdot BM=MN \cdot h$, so $184 \cdot 345=17 \cdot 23 \cdot h, h=\frac{2760}{17}$.
If $MN \| AC$, then triangles $BAC$ and $BMN$ are similar, and the coefficient of their similarity $k$ is the ratio of the heights of these triangles, drawn from vertex $B$. It remains to note that the height of triangle $ABC$, drawn from $B$, is equal to $r+h=120+\frac{2760}{17}=\frac{4800}{17}$. Therefore, $k=\frac{h+r}{h}=\frac{4800}{17}: \frac{2760}{17}=\frac{40}{23}$ and $AC=k \cdot MN=\frac{40}{23} \cdot 23 \cdot 17=680$.
|
680
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On the table, there are 150 different cards with numbers $2, 4, 6, \ldots 298, 300$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $5?$
|
Answer: 2235.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 5 alternate. Indeed, if one of these numbers is divisible by 5, i.e., has the form $5k$, where $k \in \mathbb{N}$, then the next number is $5k+2$ - and it gives a remainder of 2 when divided by 5, then $-5k+4$, giving a remainder of 4 when divided by 5, then $5k+6=5(k+1)+1$, giving a remainder of 1 when divided by 5, then $5k+8=5(k+1)+3$, giving a remainder of 3 when divided by 5; finally, the next one is $5k+10=5(k+2)$, which is again divisible by 5, after which the order of remainders repeats. Thus, the remainders of the given numbers when divided by 5 go in the order $\ldots 0 ; 2 ; 4 ; 1 ; 3 ; 0 \ldots$
Among the 150 given numbers, there are 30 numbers that give remainders of $0, 1, 2, 3, 4$ when divided by 5.
The sum of two numbers can be divisible by 5 in the following cases.
1) Both numbers are divisible by 5. There are 30 cards with such numbers, and we need to choose 2 of them - there are $C_{30}^{2}=$ $\frac{1}{2} \cdot 30 \cdot 29=435$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 5 - then the second number must give a remainder of 4 when divided by 5. This pair of numbers can be chosen in $30 \cdot 30=900$ ways.
3) One of the numbers gives a remainder of 2 when divided by 5 - then the second number gives a remainder of 3, and, similarly to the second case, we get 900 ways to choose 2 numbers.
In total, there are 2235 ways.
|
2235
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. There are 306 different cards with numbers $3,19,3^{2}, 19^{2}, \ldots, 3^{153}, 19^{153}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer?
|
Answer: 17328.
Solution. To obtain the square of a natural number, it is necessary and sufficient that each factor enters the prime factorization of the number in an even power.
Suppose two cards with powers of three are chosen. We have 76 even exponents $(2,4,6, \ldots, 152)$ and 77 odd exponents $(1,3,5, \ldots, 153)$. We need the sum of the exponents to be even. For the sum of two natural numbers to be even, we can either choose two even numbers $\left(C_{76}^{2}=\frac{76 \cdot 75}{2}=2850\right)$, or two odd numbers ( $C_{77}^{2}=\frac{77 \cdot 76}{2}=2926$ ways). We get $2850+2926=5776$ ways.
The number of ways when both chosen cards have powers of the number 19 is exactly the same, i.e., 5776.
If one card with a power of three and one card with a power of the number 19 are taken, then both exponents must be even - we get $76 \cdot 76=5776$ ways.
In total: $5776 \cdot 3=17328$ ways.
|
17328
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. There are 294 different cards with numbers $7, 11, 7^{2}, 11^{2}, \ldots, 7^{147}, 11^{147}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a square of an integer?
|
Answer: 15987.
Solution. To obtain the square of a natural number, it is necessary and sufficient that each factor enters the prime factorization of the number in an even power.
Suppose two cards with powers of seven are chosen. We have 73 even exponents $(2,4,6, \ldots, 146)$ and 74 odd exponents $(1,3,5, \ldots, 147)$. We need the sum of the exponents to be even. For the sum of two natural numbers to be even, we can either choose two even numbers $\left(C_{73}^{2}=\frac{73 \cdot 72}{2}=2628\right.$ ways $)$, or two odd numbers $\left(C_{74}^{2}=\frac{74 \cdot 73}{2}=2701\right.$ ways $)$. We get $2628+$ $2701=5329$ ways.
The number of ways when the powers of 11 are written on both chosen cards is exactly the same, i.e., 5329.
If one card with a power of seven and one card with a power of 11 are taken, then both exponents must be even - we get $73 \cdot 73=5329$ ways.
In total: $5329 \cdot 3=15987$ ways.
|
15987
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. In the number $2016 * * * * 02 * *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and the fifth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. In the number $2016^{* * * *} 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,6,7,8$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done
|
Answer: 2160.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6, 8$ (5 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get a total of $5 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2160$ ways.
|
2160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 15. In how many ways can this be done?
|
# Answer: 864.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 2=864$ ways.
|
864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 1728.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 8$ (4 ways).
To ensure divisibility by 3, we proceed as follows. Select three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $4 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 1728$ ways.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|3 x|+|4 y|+|48-3 x-4 y|=48$, and find the area of the resulting figure.
#
|
# Answer: 96.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 3 x \geq 0 , } \\
{ 4 y \geq 0 , } \\
{ 4 8 - 3 x - 4 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
3 x+4 y \leq 48
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(16 ; 0), G(0 ; 12), N(0 ; 0)$, the area of which is 96.
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|5 x|+|12 y|+|60-5 x-12 y|=60$, and find the area of the resulting figure.
#
|
# Answer: 30.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 5 x \geq 0 , } \\
{ 1 2 y \geq 0 , } \\
{ 6 0 - 5 x - 1 2 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
5 x+12 y \leq 60
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(12 ; 0), G(0 ; 5), N(0 ; 0)$, the area of which is 30.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 1400. The answer should be presented as an integer.
|
Answer: 5880.
Solution. Since $1400=7 \cdot 2^{3} \cdot 5^{2}$, the sought numbers can consist of the following digits: (a) three twos, two fives, one seven, and two ones, (b) one four, one two, two fives, one seven, and three ones, or (c) one eight, two fives, one seven, and four ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the twos ( $C_{8}^{3}=\frac{8!}{3!5!}$ ways), then two places out of the remaining five for the fives ( $C_{5}^{2}=\frac{5!}{3!2!}$ ways), and then one place out of the remaining three for the seven ( $C_{3}^{1}=1$ way). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{3} \cdot C_{5}^{2} \cdot 3=\frac{8!}{3!2!2!}=1680$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!3!}=3360$.
(c) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!4!}=840$. Finally, we get $1680+3360+840=5880$ ways.
|
5880
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. [5 points] Two circles of the same radius 9 intersect at points $A$ and $B$. On the first circle, a point $C$ is chosen, and on the second circle, a point $D$ is chosen. It turns out that point $B$ lies on the segment $C D$, and $\angle C A D=90^{\circ}$. On the perpendicular to $C D$ passing through point $B$, a point $F$ is chosen such that $B F=B D$ (points $A$ and $F$ are on opposite sides of the line $C D$). Find the length of the segment $C F$.
Fig. 1: variant 1, problem 6
|
Answer: 18.
Solution. Let $R=9$ be the radii of the circles given in the condition, $\angle B A D=\alpha, \angle B C F=\beta$. Then $\angle B A C=\frac{\pi}{2}-\alpha$, and by the sine rule $B D=2 R \sin \alpha, B C=2 R \sin \left(\frac{\pi}{2}-\alpha\right)=2 R \cos \alpha$. Therefore, $C F^{2}=B C^{2}+B D^{2}=4 R^{2} \cos ^{2} \alpha+4 R^{2} \sin ^{2} \alpha=4 R^{2}$, from which $C F=2 R=18$.
|
18
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [4 points] Find the number of eight-digit numbers, the product of whose digits equals 7000. The answer should be presented as an integer.
|
Answer: 5600.
Solution. Since $7000=7 \cdot 2^{3} \cdot 5^{3}$, the sought numbers can consist of the following digits: (a) three twos, three fives, one seven, and one one, (b) four, two, three fives, one seven, and two ones, or (c) eight, three fives, one seven, and three ones. We will calculate the number of variants in each case.
(a) First, we choose three places out of eight for the twos ( $C_{8}^{3}=\frac{8!}{3!5!}$ ways), then three places out of the remaining five for the fives ( $C_{5}^{3}=\frac{5!}{3!2!}$ ways), and then one place out of the remaining two for the seven ( $C_{2}^{1}=2$ ways). Finally, the remaining places are occupied by ones. By the rule of product, we get $C_{8}^{3} \cdot C_{5}^{3} \cdot 2=\frac{8!}{3!3!}=1120$ ways.
(b) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{2!3!}=3360$.
(c) Reasoning similarly, we find that the number of ways in this case is $\frac{8!}{3!3!}=1120$. Finally, we get $1120+3360+1120=5600$ ways.
|
5600
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. [5 points] Two circles of the same radius 7 intersect at points $A$ and $B$. On the first circle, a point $C$ is chosen, and on the second circle, a point $D$ is chosen. It turns out that point $B$ lies on the segment $C D$, and $\angle C A D=90^{\circ}$. On the perpendicular to $C D$ passing through point $B$, a point $F$ is chosen such that $B F=B D$ (points $A$ and $F$ are on opposite sides of the line $C D$). Find the length of the segment $C F$.
Fig. 3: variant 2, problem 6
|
Answer: 14.
Solution. Let $R=7$ be the radii of the circles given in the condition, $\angle B A D=\alpha, \angle B C F=\beta$. Then $\angle B A C=\frac{\pi}{2}-\alpha$, and by the sine rule $B D=2 R \sin \alpha, B C=2 R \sin \left(\frac{\pi}{2}-\alpha\right)=2 R \cos \alpha$. Therefore, $C F^{2}=B C^{2}+B D^{2}=4 R^{2} \cos ^{2} \alpha+4 R^{2} \sin ^{2} \alpha=4 R^{2}$, from which $C F=2 R=14$.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 59),(59 ; 59)$, and $(59 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=59-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 370330
Solution. There are two possible cases.
1) Both selected nodes lie on the lines specified in the condition. Each of them contains 58 points inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 116 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line with the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{116 \cdot 113}{2}=6554$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (116 ways). Now, let's count how many ways there are to choose the second node. In total, there are $58^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (116 nodes), as well as the nodes that lie on the same horizontal (56 nodes, considering the previously excluded diagonal nodes) or vertical (56 nodes) line with the chosen one. Therefore, the second node can be chosen in $58^{2}-116-112=$ 3136 ways, and the number of ways to choose a pair of nodes is $116 \cdot 3136=363776$.
Summarizing, we have $6554+363776=370330$ ways.
|
370330
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 69),(69 ; 69)$, and ( $69 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=69-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 601460.
Solution. There are two possible cases.
1) Both selected nodes lie on the specified lines. There are 68 points on each of them inside the square, and there are no duplicates among them (the intersection point of the lines has non-integer coordinates). There are 136 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). Since we counted ordered pairs of points, each pair of points was counted twice. Thus, in this case, we get $\frac{136 \cdot 133}{2}=9044$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (136 ways). Now, let's count how many ways there are to choose the second node. There are a total of $68^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (136 in total), as well as the nodes that lie on the same horizontal line as the chosen one (66 in total, considering the previously excluded diagonal nodes) or on the same vertical line (66 in total). Therefore, the second node can be chosen in $68^{2}-136-132=$ 4356 ways, and the number of ways to choose a pair of nodes is $136 \cdot 4356=592416$.
Summarizing, we have $9044+592416=601460$ ways.
|
601460
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 65),(65 ; 65)$ and ( $65 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=65-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
# Answer: 500032.
Solution. There are two possible cases.
1) Both selected nodes lie on the lines specified in the condition. There are 64 points on each of them inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 128 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{128 \cdot 125}{2}=8000$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (128 ways). Now, let's count how many ways there are to choose the second node. There are a total of $64^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (128 nodes), as well as the nodes that lie on the same horizontal (62 nodes, considering the previously excluded diagonal nodes) or vertical (62 nodes) as the chosen one. Therefore, the second node can be chosen in $64^{2}-128-124=3844$ ways, and the number of ways to choose a pair of nodes is $128 \cdot 3844=492032$.
Summarizing, we have $8000+492032=500032$ ways.
|
500032
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. [5 points] On a plane with a given rectangular Cartesian coordinate system, a square is drawn with vertices at points $(0 ; 0),(0 ; 63),(63 ; 63)$, and $(63 ; 0)$. Find the number of ways to choose two grid nodes inside this square (not including its boundary) such that at least one of these nodes lies on one of the lines $y=x$ or $y=63-x$, but neither of the chosen nodes lies on any line parallel to any of the coordinate axes.
|
Answer: 453902.
Solution. There are two possible cases.
1) Both selected nodes lie on the specified lines. There are 62 points on each of them inside the square, and there are no repetitions among them (the intersection point of the lines has non-integer coordinates). There are 124 ways to choose the first point, and 3 fewer ways to choose the second (all points are suitable except the first and the two points lying on the same horizontal or vertical line as the first). In this case, we counted each pair of points twice since we considered ordered pairs of points. Therefore, in this case, we get $\frac{124 \cdot 121}{2}=7502$ ways.
2) Exactly one of the selected nodes lies on the lines given in the condition. First, choose the node lying on one of the lines (124 ways). Now, let's count how many ways there are to choose the second node. In total, there are $62^{2}$ nodes marked in the square; from this, we need to exclude the nodes on the diagonals (124 nodes), as well as the nodes that lie on the same horizontal (60 nodes, considering the previously excluded diagonal nodes) or vertical (60 nodes) line as the chosen one. Therefore, the second node can be chosen in $62^{2}-124-120=3600$ ways, and the number of ways to choose a pair of nodes is $124 \cdot 3600=446400$.
Summarizing, we have $7502+446400=453902$ ways.
|
453902
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. On the sides of triangle $A B C$, points were marked: 10 - on side $A B$, 11 - on side $B C$, 12 - on side $A C$. At the same time, none of the vertices of the triangle were marked. How many triangles exist with vertices at the marked points?
|
Answer: 4951.
Solution. Three points out of the 33 given can be chosen in $C_{33}^{3}=5456$ ways. In this case, a triangle is formed in all cases except when all three points lie on one side of the triangle. Thus, $C_{12}^{3}+C_{11}^{3}+C_{10}^{3}=220+165+120=505$ ways do not work. Therefore, there are $5456-505=4951$ triangles.
|
4951
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point $(50 ; 30)$. Find the number of such squares.
|
Answer: 930.
Solution. Draw through the given point $(50 ; 30)$ vertical and horizontal lines $(x=50$ and $y=30)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 30 ways: $(50 ; 0),(50 ; 1), \ldots,(50 ; 29)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four regions into which the lines $x=50$ and $y=30$ divide the plane. Consider the “lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $20 \leqslant x \leqslant 49,0 \leqslant y \leqslant 29$. We get $30^{2}$ ways.
The total number of ways is $30^{2}+30=31 \cdot 30=930$.
|
930
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. On the coordinate plane, squares are considered, all vertices of which have natural coordinates, and the center is located at the point $(55 ; 25)$. Find the number of such squares.
|
Answer: 600.
Solution. Draw through the given point $(55 ; 25)$ vertical and horizontal lines $(x=55$ and $y=25)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 24 ways: $(55 ; 1),(55 ; 2), \ldots,(55 ; 24)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four regions into which the lines $x=55$ and $y=25$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $31 \leqslant x \leqslant 54,1 \leqslant y \leqslant 24$. We get $24^{2}$ ways.
The total number of ways is $24^{2}+24=24 \cdot 25=600$.
|
600
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.