problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1941 n$ and $n+1941 m$ have a common prime divisor $d>8$. Find the smallest possible value of the number $d$ under these conditions.
|
Answer: $d_{\min }=97$.
For example,
$$
\begin{aligned}
& m=96, n=1 \rightarrow 1941 m+n=1941 \cdot 96+1=97 \cdot 1921 \\
& m+1941 n=96+1941=97 \cdot 21
\end{aligned}
$$
|
97
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Danya is making a car trip from point A to point B, which are 300 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Danya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. One hour after the start of the trip, he looked at the speedometer - 75 km/h. On the time interval $[1 ; 1.5]$, Danya noticed that $T$ did not change. How far from point $A$ was the car 90 minutes after the start of the trip, and what was its speed?
|
Answer: 1) 180 km; 2) 48 km/h.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1947 n$ and $n+1947 m$ have a common prime divisor $d>9$. Find the smallest possible value of the number $d$ under these conditions.
|
Answer: $d_{\min }=139$.
For example,
$$
\begin{aligned}
& m=138, n=1 \rightarrow 1947 m+n=1947 \cdot 138+1=139 \cdot 1933 \\
& m+1947 n=138+1947=139 \cdot 15
\end{aligned}
$$
|
139
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3. Find the sum of such divisors.
|
1. Solution. Among the divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3, the number 2 can be chosen with exponents $0,1,2,3$ (4 options), the number 3 - with exponents 1,2 (2 options), and the number 5 - with exponents $0,1,2$ (3 options). Therefore, the total number of divisors is $4 \cdot 2 \cdot 3=24$. The sum of the divisors of the number $b=2^{3} \cdot 5^{2}$ is $(1+2+4+8)(1+5+25)=465$. Then the sum of the divisors of the number $a$, which are divisible by 3, is $\left(3+3^{2}\right) \cdot 465=12 \cdot 465=5580$.
|
5580
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. How many integers $b$ exist such that the equation $x^{2}+b x-9600=0$ has an integer solution that is a multiple of both 10 and 12? Specify the largest possible $b$.
|
2. Solution. Since the desired integer solution $x$ is divisible by 10 and 12, it is divisible by 60, hence it can be written in the form $x=60 t, t \in Z$. Substitute $x=60 t$ into the original equation:
$3600 t^{2}+60 b t-9600=0$. Express $b: b=\frac{160}{t}-60 t$. For $b$ to be an integer, $t$ must be a divisor of the number 160. $160=2^{5} \cdot 5$. The number $160=2^{5} \cdot 5$ has 12 positive divisors: $1,2,2^{2}, 2^{3}, 2^{4}, 2^{5}, 5,2 \cdot 5,2^{2} \cdot 5,2^{3} \cdot 5,2^{4} \cdot 5,2^{5} \cdot 5$. Taking the sign into account, we get 24 divisors. Each of them corresponds to a solution $x=60 t$ and an integer $b=\frac{160}{t}-60 t$. Therefore, the number of integers $b$ that satisfy the condition of the problem is 24. Since $b$ decreases as $t$ increases, the maximum $b$ corresponds to the smallest $t=-160$, so $b_{\max }=-1+60 \cdot 160=9599$.
|
9599
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many three-digit positive numbers $x$ exist that are divisible by 3 and satisfy the equation $GCD(15, GCD(x, 20))=5$? Find the largest one.
|
3. Solution. Since 20 is not divisible by 3, $NOD(x, 20)$ is also not divisible by 3. Therefore, the equation $NOD(15, NOD(x, 20))=5$ is equivalent to the condition that $NOD(x, 20)$ is divisible by 5, which is possible if and only if $x$ is divisible by 5. Thus, the condition of the problem is equivalent to $x$ being divisible by 5 and by 3, that is, $x$ is divisible by 15. Therefore, $x$ can be written as $x=15m, m=1,2 \ldots$. The smallest three-digit $x=105$ is obtained when $m=7$, and the largest three-digit $x=990$ is obtained when $m=66$, making a total of 60 numbers.
|
60
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the sides of triangle $A B C$ with side lengths 2, 3, and 4, external squares $A B B_{1} A_{1}, B C C_{2} B_{2}, C A A_{3} C_{3}$ are constructed. Find the sum of the squares of the side lengths of the hexagon $A_{1} B_{1} B_{2} C_{2} C_{3} A_{3}$.
## Answers and Solutions
Problem 1 Answer: 165 m.
|
Solution
$m$ - the number of steps Petya takes, $n$ - the number of steps Vova takes
$0.75 m=0.55 n=L-$ path length
$k$ - the step number of Petya leading to the coincidence of the footprint,
$i$ - the step number of Vova leading to the coincidence of the footprint,
$0.75 k=0.55 i \rightarrow 15 k=11 i \rightarrow\left\{\begin{array}{l}k=11 t \\ i=15 t\end{array}, t=0,1, \ldots T\right.$
Total number of footprints: $(m+1)+(n+1)-(T+1)=15 T+11 T-T+1=25 t+1=501 \rightarrow T=20$ $m=11 \cdot T=220 \rightarrow L=0.75 \cdot 220=165$
Problem 2 Answer: $x=6, y=55$ or $x=55, y=6$
Solution
$y(x-5)=5(x+5) \rightarrow y=5+\frac{50}{x-5} \rightarrow x-5= \pm 1 ; \pm 2 ; \pm 5 ; \pm 10 ; \pm 25 ; \pm 50$
$y-5= \pm 50 ; \pm 25 ; \pm 10 ; \pm 5 ; \pm 2 ; \pm 1 \rightarrow x+y-10= \pm 51 ; \pm 27 ; \pm 15 ;$
The maximum value of $x+y$ is 61 and is achieved at $x=6, y=55$ or $x=55, y=6$
Problem 3 Answer: $a=-\frac{9}{8}, b=-6$
## Solution
When dividing the polynomial $P(x)=a x^{4}+3 x^{3}+b$ by $x-2$, we have the remainder $16 a+b+24=0$. Then
$P(x)=(x-2)\left(a x^{3}+(2 a+3) x^{2}+(4 a+6) x+(8 a+12)\right)=(x-2) P_{1}(x)$
When dividing the polynomial $P_{1}(x)$ by $x-2$, we have the remainder $32 a+36=0 \rightarrow a=-\frac{9}{8} \rightarrow b=-6$.
Problem 4 Answer: $a=2$
Solution
Condition for the existence of roots:
$\frac{D}{4}=16(a-1)^{2}+8(a-4) \geq 0 \rightarrow 2 a^{2}-3 a-2 \geq 0 \rightarrow a \in(-\infty ;-0.5] \cup[2 ;+\infty)$.
$x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(a-1)^{2}-\frac{4-a}{4}=a^{2}-\frac{7 a}{4}$
We need to find the minimum of this quadratic trinomial on the set $(-\infty ;-0.5] \cup[2 ;+\infty)$.
The abscissa of its vertex $a=\frac{7}{8}$ is closer to 2 than to $-0.5$, since $2-\frac{7}{8}=\frac{9}{8}<\frac{7}{8}+\frac{1}{2}=\frac{11}{8}$.
Therefore, the minimum possible value of the sum of the squares of the roots of the equation is achieved at $a=2$.
Problem 5 Answer: 116
Solution
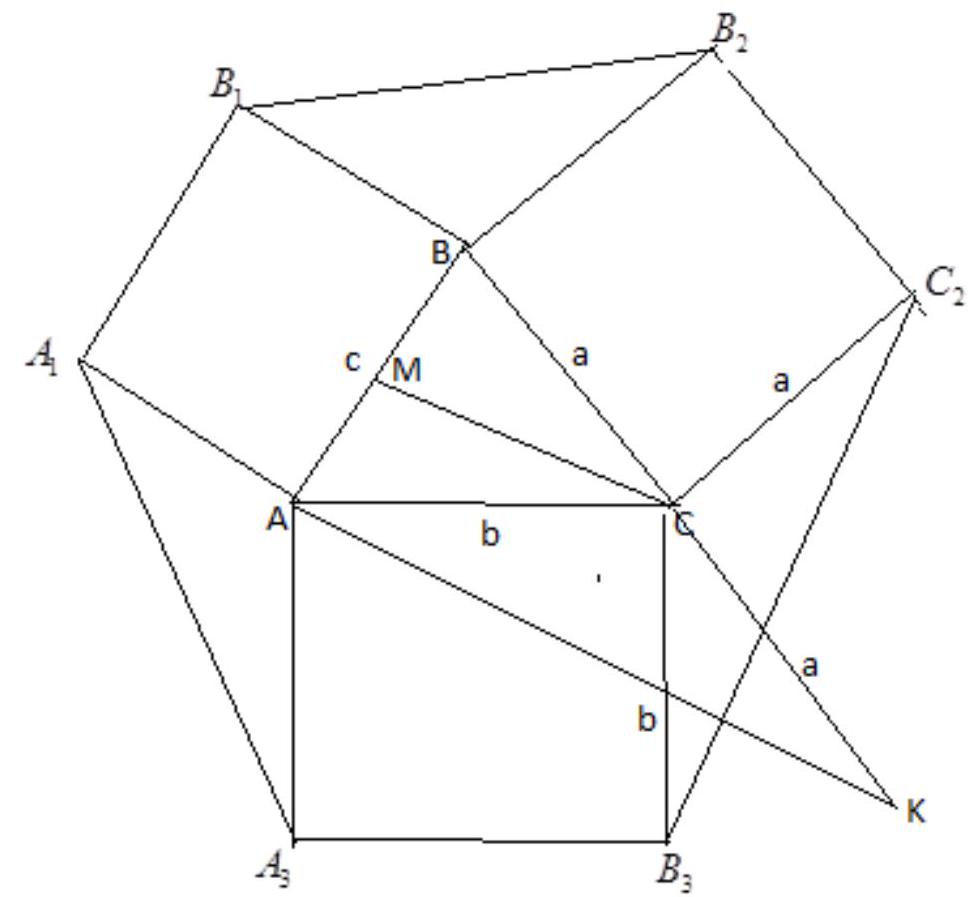
Additional construction: $B C=C K=a, M$ - midpoint of side $A B$.
$\square A C K=\square C_{2} C B_{3}=\square K C B_{3}=180^{\circ}-\square B C A$
$\square A C K={ }_{B_{3} C C_{2} \rightarrow C_{2} B_{3}=A K=2 C M}$
$C M^{2}=\frac{2 a^{2}+2 b^{2}-c^{2}}{4} \rightarrow C_{2} B_{3}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}$
Similarly,
$$
B_{1} B_{2}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}, \quad A_{1} A_{3}{ }^{2}=2 b^{2}+2 c^{2}-a^{2}
$$
$A_{1} A_{2}{ }^{2}=c^{2}, B_{2} C_{2}{ }^{2}=a^{2}, A_{3} B_{3}{ }^{2}=b^{2}$
Combining, we arrive at the sum $\sigma^{2}$ of the squares of the sides of the hexagon being $4\left(a^{2}+b^{2}+c^{2}\right) \cdot$ In the conditions of the variant $1 a=2, b=3, c=4$, therefore $\sigma^{2}=4(4+9+16)=116$
|
116
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Dima drew a parallelogram $A B C D$ and points $M$ and $N$ on sides $B C$ and $C D$ respectively such that $B M: M C=D N: N C=2: 3$. After that, he erased everything except points $A, M$ and $N$ using a cloth. Vova restored the drawing using a ruler and a compass. How did he do it?
|
4. Points $B$ and $D$ are the intersection points of lines $C M$ and $C N$ with the line passing through point $O$ and parallel to line $M N$.
## Problem 5
Numbers $A$, when divided by $n$, have a remainder of $r$, when divided by $n+1$ - a remainder of $r+1$, and when divided by $n+2$ - a remainder of $r+2$, have the form: $A=n(n+1)(n+2) t-n+r, A_{\min }$ corresponds to $t=1$
In the variant $1 n=11, r=5 \rightarrow A_{\min }=1710$
|
1710
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Pete is trying to lay out a square on a table using identical cardboard rectangles measuring $14 \times 10$. Will he be able to do this? Propose your version of constructing such a square. What is the minimum number of rectangles he will need?
|
Solution. Let $n$ be the number of rectangles that form the square. Then the area of the square is $S=14 \cdot 10 \cdot n$. If the side of the square is formed by $m$ sides of length 14 and $k$ sides of length 10, then the length of the side of the square is $14 m + 10 k$, and its area is $S=(14 m + 10 k)^{2}$. Equating the expressions for the areas, we get
$$
14 \cdot 10 \cdot n = (14 m + 10 k)^{2} \rightarrow 7 \cdot 5 \cdot n = (7 m + 5 k)^{2}
$$
We can assume that the numbers $m$ and $k$ are coprime. Otherwise, the side of the square can be reduced by a factor of $p > 1$, where $p$ is a common divisor of $m$ and $k$.
The left-hand side of the equation (*) is divisible by 7, so the number $7 m + 5 k$ is divisible by 7, and $(7 m + 5 k)^{2}$ is divisible by 49. Therefore, the left-hand side of (*) is divisible by 49, which is possible only if $n$ is divisible by 7. Similarly, it can be shown that $n$ is divisible by 5. Thus, $n = 35 \cdot s, s \in \mathbb{Z}$, and the smallest possible number of rectangles is $n = 35$. The figure below shows a square assembled from 35 rectangles.
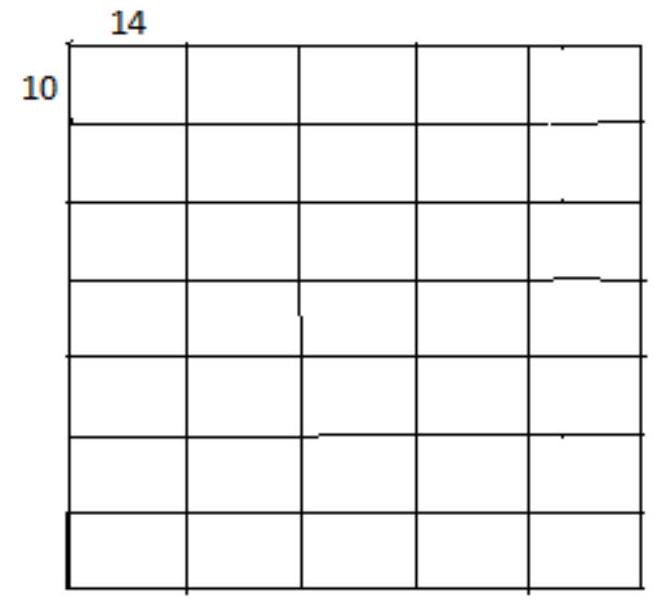
Answer: 35 rectangles.
|
35
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a rectangular table, the letters of the word "олимпиада" (olympiada) are arranged in a certain order.
| $\mathrm{O}$ | Л | И | M | П | И | A | Д | A |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Л | И | M | П | И | A | Д | A | O |
| И | M | П | И | A | Д | A | O | Л |
| M | П | И | A | Д | A | O | Л | И |
You need to read the word "олимпиада" (olympiada), starting from the letter "O" located in the top-left corner of the table and ending with the letter "A". You are allowed to move from one letter to another if they are in adjacent cells of the table. Find the number of different ways to read the word "олимпиада" (olympiada) according to the given table.
|
Solution. In each cell of the table shown below
| $\mathrm{O}$ | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 3 | 6 | 10 | 15 | 21 | 28 | | |
| 1 | 4 | 10 | 20 | 35 | 56 | | | |
the number of different paths leading to the letter in that cell when reading the word "олимпиада" (Olympiada) is recorded. For example, in the cell in the third column and second row, i.e., to the letter $M$, there are three different ways to read "олим" (Olim): two paths from the cell in the second column and second row, and one path from the cell in the second column and first row. In general, to obtain the number in the cell at the intersection of row $i$ and column $j$, you need to add the number in the $(j-1)$-th cell of row $i$ and the number in the $j$-th cell of row $(i-1)$. In each of the shaded cells, where the last letter "A" of the word "олимпиада" (Olympiada) is located, the number of different ways to read this word, provided that the reading ends in this cell, is indicated. To get the answer, you need to add all the numbers in the highlighted cells: $n=56+28+8+1=93$.
Answer: $n=93$.
## Answers for other variants.
## Variant 2
|
93
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a sheet of paper, 12 consecutive integers are written. After one of them is crossed out, the sum of the remaining numbers equals 325. Which number was crossed out?
|
Solution. Let $n, n+1, \ldots, n+k-1, n+k, n+k+1, \ldots, n+11$ be 12 consecutive integers, and the number $n+k, k=0,1,2, \ldots, 11$ is crossed out. The sum of the numbers after crossing out is
$$
\frac{2 n+11}{2} \cdot 12-(n+k)=325 \rightarrow 11 n+66-k=325 \rightarrow k=11 n-259
$$
Considering the condition $k \in[0 ; 11]$, we get $0 \leq 11 n-259 \leq 11 \rightarrow \frac{259}{11} \leq n \leq \frac{270}{11}$. In this interval, there is only one integer $n=24$ and $k=5$. Therefore, the crossed-out number is $n+k=29$.
Answer: 29.
|
29
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A football is sewn from 256 pieces of leather: white ones in the shape of hexagons and black ones in the shape of pentagons. Black pentagons only border white hexagons, and any white hexagon borders three black pentagons and three white hexagons. Find the number of white hexagons on the football.
|
Answer: 160.
Criteria for checking works, 7th grade
Preliminary round of the sectoral physics and mathematics olympiad for schoolchildren "Rosatom", mathematics
#
|
160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
0.35 \cdot 160+0.1 x=0.2 \cdot 160+0.2 x, 0.15 \cdot 160=0.1 x, x=240 \text {. }
$$
In total, it results in $160+240=400$ g of solution.
|
Answer: 400.
## Problem 9
Points $B_{1}$ and $C_{1}$ are the feet of the altitudes of triangle $ABC$, drawn from vertices $B$ and $C$ respectively. It is known that $AB=7, \quad AC=6, \sin \angle BAC=\frac{2 \sqrt{110}}{21}$. Find the length of the segment $B_{1}C_{1}$.
## Solution:
Let the angle $\angle BAC$ be denoted by $\alpha$. There are two possible cases: 1) $00$.
$$
\begin{aligned}
& \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{(2 x+2)^{2}-(x+4)^{2}}=a x^{2}, \\
& \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{3\left(x^{2}-4\right)}=a x^{2}, \\
& |2 x+2|+|x+4|=3 a x^{2} .
\end{aligned}
$$
If $a \leq 0$, then the left side $>0$, and the right side $\leq 0$; equation ( ${ }^{*}$ ) has no solutions.
If $a>0$, equation (*) has at least 2 solutions.
The original equation can have fewer solutions only if at least one of the numbers $\pm 2$ is a solution ( ي $\left.^{2}\right)$.
2 is a solution of (*), if $12=12 a, a=1 ;(-2)$ is a solution of (*), if $4=12 a, a=1 / 3$.
When $a=1$, equation (*) becomes $|2 x+2|+|x+4|=3 x^{2}$ and has roots $x_{1}=-1, x_{2}=2$. The original equation has a single root $x=-1$.
When $a=1 / 3$, equation (*) becomes $|2 x+2|+|x+4|=x^{2}$ and has roots $x_{1}=-2, x_{2}=\frac{3+\sqrt{33}}{2}$. The original equation has a single root $x=\frac{3+\sqrt{33}}{2}$.
Answer: the equation has no more than one root when $a \leq 0$, when $a=1 / 3$, and when $a=1$.
|
400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (10 points). Tourist Nikolai Petrovich was late by $\Delta t=5$ minutes for the departure of his riverboat, which had set off downstream. Fortunately, the owner of a fast motorboat agreed to help Nikolai Petrovich. Catching up with the riverboat and disembarking the unlucky tourist, the motorboat immediately set off on its return journey. How much time passed from the departure of the motorboat until its return? Assume that the speed of the riverboat relative to the water is $k=3$ times the speed of the river current, and the speed of the motorboat is $n=5$ times the speed of the river current.
|
1. $s=\left(3 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot\left(t_{1}+\Delta t\right)=\left(5 v_{\mathrm{T}}+v_{\mathrm{T}}\right) \cdot t_{1} \rightarrow 4 \Delta t=2 t_{1} \rightarrow t_{1}=2 \Delta t=10$ min $t_{2}=\frac{s}{5 v_{\mathrm{T}}-v_{\mathrm{T}}}=\frac{6 v_{\mathrm{T}} \cdot t_{1}}{4 v_{\mathrm{T}}}=\frac{3}{2} t_{1}=3 \Delta t=15$ min $\rightarrow$ $T=t_{1}+t_{2}=5 \Delta t=25$ min
|
25
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (15 points) A satellite is launched vertically from the pole of the Earth at the first cosmic speed. To what maximum distance from the Earth's surface will the satellite travel? (The acceleration due to gravity at the Earth's surface $g=10 \mathrm{m} / \mathrm{c}^{2}$, radius of the Earth $R=6400$ km).
|
2.
According to the law of conservation of energy: $\frac{m v_{I}^{2}}{2}-\frac{\gamma m M}{R}=-\frac{\gamma m M}{R+H}$
The first cosmic speed $v_{I}=\sqrt{g R}$
The acceleration due to gravity at the surface $g=\frac{\gamma M}{R^{2}}$
Then $\frac{m g R}{2}-m g R=-\frac{m g R^{2}}{R+H}$
Finally, $H=R=6400$ km.
(15 points)
|
6400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (15 points) Looking down from the edge of the stream bank, Vovochka decided that the height of his rubber boots would be enough to cross the stream. However, after crossing, Vovochka got his legs wet up to his knees ($H=52$ cm). Estimate the height $h$ of Vovochka's boots. Assume the depth of the stream is constant, and the refractive index of water $n=1.33$.
Rector of SPbPU

A.I. Rudskoy S.A. Staroytov
## Instructions for Evaluating Final Round Solutions of the Polytechnic Physics Olympiad
The version given to the participant contains 6 problems of varying difficulty.
The evaluation of the work is based on the points received for each individual problem.
The score for solving each problem in the version is one of the following coefficients:
1.0 - the problem is solved correctly;
0.8 - the problem is solved correctly and the answer is given in a general form; there is an error in the unit of measurement of the obtained physical quantity or an arithmetic error;
0.6 - the problem is not fully solved; all necessary physical relationships for solving the problem are present; there is an error in algebraic transformations;
0.4 - the problem is not fully solved; some physical relationships necessary for solving the problem are missing;
0.2 - the problem is not solved; the work contains only some notes related to solving the problem or describing the phenomenon considered in the problem;
0.0 - the solution to the problem or any notes related to it are absent in the work.
The coefficient is entered in the first column "For the Teacher" of the "Answer Sheet". In the second column of the section, the score is entered, which is the product of the coefficient received for the solution and the maximum score for the given problem.
The obtained scores are summed and entered in the "Total" row.
Table for converting coefficients to points.
| \multirow{coefficient}{max points}{} | 10 | 15 | 20 | 25 |
| :---: | :---: | :---: | :---: | :---: |
| 1 | 10 | 15 | 20 | 25 |
| 0.8 | 8 | 12 | 16 | 20 |
| 0.6 | 6 | 9 | 12 | 15 |
| 0.4 | 4 | 6 | 8 | 10 |
| 0.2 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 |
|
6. From the figure
$\frac{d}{h}=\operatorname{tg} \alpha ; \quad \frac{d}{H}=\operatorname{tg} \beta ; \quad \frac{H}{h}=\frac{\operatorname{tg} \alpha}{\operatorname{tg} \beta}$
Since all the information about the bottom of the stream falls into the space limited by the eye's pupil, all angles are small: $\operatorname{tg} \alpha \approx \sin \alpha ; \operatorname{tg} \beta \approx \sin \beta$
Then $\frac{H}{h}=\frac{\sin \alpha}{\sin \beta}=n$
$h=\frac{H}{n}=39 \mathrm{~cm}$.
(15 points)
|
39
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Dmitry is three times as old as Grigory was when Dmitry was as old as Grigory is now. When Grigory becomes as old as Dmitry is now, the sum of their ages will be 49 years. How old is Grigory?
|
Solution: Let Gregory be $y$ years old in the past, and Dmitry be $x$ years old. Then currently, Gregory is $x$ years old, and Dmitry is $3 y$ years old. In the future, Gregory will be $3 y$ years old, and Dmitry will be $z$ years old, and according to the condition, $z+3 y=49$. Since $z-3 y=3 y-x ; 3 y-x=x-y$, then $9 y-x=49$ and $x=2 y$. From this, we get that $x=14, y=7$. Currently, Gregory is 14 years old. Answer: 14.
|
14
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\frac{4}{\sqrt{\log _{3}(81 x)}+\sqrt{\log _{3} x}}+\sqrt{\log _{3} x}=3$.
|
Solution: Using the properties of logarithms, our equation can be rewritten as $\frac{4}{\sqrt{4+\log _{3} x}+\sqrt{\log _{3} x}}+\sqrt{\log _{3} x}=3$. Let $t=\log _{3} x$. Then $\frac{4}{\sqrt{4+t}+\sqrt{t}}+\sqrt{t}=3$. Multiplying the numerator and denominator of the first fraction by $\sqrt{t+4}-\sqrt{t}$, we arrive at the equation $\sqrt{t+4}=3$. From this, we get that $t=5$ and $x=3^{5}=243$. Answer: 243.
|
243
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. On the sides $B C, C A, A B$ of an equilateral triangle $A B C$ with side length 7, points $A_{1}, B_{1}, C_{1}$ are taken respectively. It is known that $A C_{1}=B A_{1}=C B_{1}=3$. Find the ratio of the area of triangle $A B C$ to the area of the triangle formed by the lines $A A_{1}, B B_{1}, C C_{1}$.
|
Solution:
Triangles $A B A_{1}, B C B_{1}, C A C_{1}$ are equal by sides and the angle between them, triangles $A D C_{1}, B E A_{1}, C F B_{1}$ are equal by side and angles. Triangle $A D C_{1}$ is similar to $A B A_{1}$ by two angles, triangle $A B C$ is similar to $D E F$. Let $S=S_{A B C}, S_{1}=S_{A B A_{1}}, S_{2}=S_{A C_{1} D}, S_{0}=S_{D E F} \cdot$ Then
$$
\begin{aligned}
& \qquad A A_{1}=\sqrt{A B^{2}+B A_{1}^{2}-2 A B \cdot B C_{1} \cos 60^{\circ}}=\sqrt{49+9-21}=\sqrt{37} \\
& \frac{S_{2}}{S_{1}}=\left(\frac{A C_{1}}{A A_{1}}\right)^{2}=\frac{9}{37}, \frac{S_{1}}{S}=\frac{B A_{1}}{B C}=\frac{3}{7} \\
& S_{0}=S-3 S_{1}+3 S_{2}=S-3 \cdot \frac{3}{7} S+3 \cdot \frac{9}{37} \cdot \frac{3}{7} S=\frac{S}{37}, \frac{S}{S_{0}}=37 \\
& \text { answer: } 37 \text {. }
\end{aligned}
$$
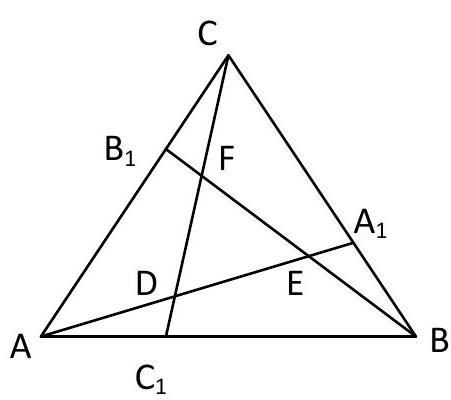
|
37
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Ivan is twice as old as Peter was when Ivan was as old as Peter is now. When Peter becomes as old as Ivan is now, the sum of their ages will be 54 years. How old is Peter?
|
Solution: Let Peter's age in the past be $y$ years, and Ivan's age be $x$ years. Then currently, Peter is $x$ years old, and Ivan is $2 y$ years old. In the future, Peter will be $2 y$ years old, and Ivan will be $z$ years old, and according to the condition, $z+2 y=54$. Since $z-2 y=2 y-x ; 2 y-x=x-y$, then $6 y-x=54$ and $2 x=3 y$. From this, we get that $x=18$. Currently, Peter is 18 years old. Answer: 18.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation $\frac{1}{\sqrt{\log _{5}(5 x)}+\sqrt{\log _{5} x}}+\sqrt{\log _{5} x}=2$.
|
Solution: Using the properties of logarithms, our equation can be rewritten as $\frac{1}{\sqrt{1+\log _{5} x}+\sqrt{\log _{5} x}}+\sqrt{\log _{5} x}=2$. Let $t=\log _{5} x$. Then $\frac{1}{\sqrt{1+t}+\sqrt{t}}+\sqrt{t}=2$. By multiplying the numerator and denominator of the first fraction by $\sqrt{t+1}-\sqrt{t}$, we arrive at the equation $\sqrt{t+1}=2$. From this, we get that $t=3$, so $x=5^{3}=125$. Answer: 125.
|
125
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. On the sides $B C, C A, A B$ of an equilateral triangle $A B C$ with side length 11, points $A_{1}, B_{1}, C_{1}$ are taken respectively. It is known that $A C_{1}=B A_{1}=C B_{1}=5$. Find the ratio of the area of triangle $A B C$ to the area of the triangle formed by the lines $A A_{1}, B B_{1}, C C_{1}$.
|
Solution:
Triangles $A B A_{1}, B C B_{1}, C A C_{1}$ are equal by sides and the angle between them, triangles $A D C_{1}, B E A_{1}, C F B_{1}$ are equal by side and angles. Triangle $A D C_{1}$ is similar to $A B A_{1}$ by two angles, triangle $A B C$ is similar to $D E F$. Let $S=S_{A B C}, S_{1}=S_{A B A_{1}}, S_{2}=S_{A C_{1} D}$,
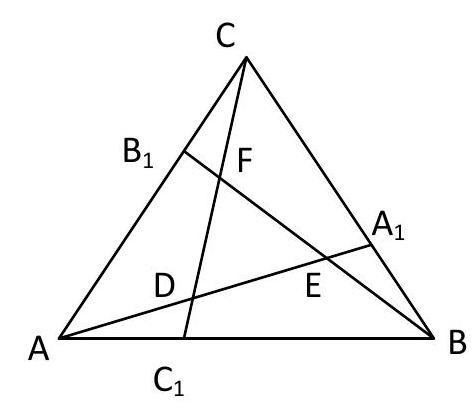
$S_{0}=S_{\text {DEF }} \cdot$ Then
$A A_{1}=\sqrt{A B^{2}+B A_{1}^{2}-2 A B \cdot B C_{1} \cos 60^{\circ}}=\sqrt{91}$,
$$
\frac{S_{2}}{S_{1}}=\left(\frac{A C_{1}}{A A_{1}}\right)^{2}=\frac{25}{91}, \frac{S_{1}}{S}=\frac{B A_{1}}{B C}=\frac{5}{11}
$$
$S_{0}=S-3 S_{1}+3 S_{2}=S-3 \cdot \frac{5}{11} S+3 \cdot \frac{25}{91} \cdot \frac{5}{11} S=\frac{S}{91}, \frac{S}{S_{0}}=91$.
Answer: 91.
|
91
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. For what values of the parameter $a$ does the equation $x^{4}-40 x^{2}+144=a\left(x^{2}+4 x-12\right)$ have exactly three distinct solutions?
|
Solution: Factorize the right and left sides of the equation:
$(x-2)(x+2)(x-6)(x+6)=a(x-2)(x+6)$. The equation can be written as
$(x-2)(x+6)\left(x^{2}-4 x-12-a\right)=0$. It is obvious that 2 and -6 are roots of this equation. We are satisfied with the situation where exactly one of the roots of the equation $x^{2}-4 x-12-a=0$ does not coincide with 2 and -6. The total number of solutions will be three if the last equation has one root $x_{3}$, such that $x_{3} \neq x_{1}, x_{3} \neq x_{2}$, or if this equation has two roots $x_{3}, x_{4}$, one of which coincides with $x_{1}$ or $x_{2}$.
The equation $x^{2}-4 x-12-a=0$ has one root when $a=-16$ and this root coincides with 2. This case does not suit us. The number 2 is a root of this equation when $a=-16$. This case has already been considered. The number -6 is a root of this equation when $a=48$, and in this case, the second root is different from 2 and -6 - Answer: $a=48$.
|
48
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
From channel A to the Wiki site, $850 * 0.06=51$ people will transition
From channel B to the Wiki site, $1500 * 0.042=63$ people will transition
From channel C to the Wiki site, $4536 / 72=63$ people will transition
|
Answer: The most people will transition from channels B and V - 63 people each
## 2
Cost of transition from advertising on channel A: $-3417 / 51 = 67$ rubles
Cost of transition from advertising on channel B: $4914 / 63 = 78$ rubles
Answer: The lowest cost of transition to the site from advertising on channel A - 67 rubles
## 3
Number of sales after advertising on channel A: $51 * 0.05 = 2.55$ - round to 2 sales (by number of people)
Revenue from sales minus advertising expenses: $(2 * 2500) - 3417 = 1583$ rubles
Number of sales after advertising on channel B: $63 * 0.05 = 3.15$ - round to 3 sales (by number of people)
Revenue from sales minus advertising expenses: $(3 * 2500) - 4914 = 2586$ rubles
Number of sales after advertising on channel B: $63 * 0.05 = 3.15$ - round to 3 sales (by number of people)
Revenue from sales minus advertising expenses: $(3 * 2500) - 4536 = 2964$ rubles
Answer: Advertising on channel B will bring Vika the most profit.
|
2964
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
Expenses for medical services provided to a child (under 18 years old) of the taxpayer by medical organizations
Correct answers: Pension contributions under a non-state pension agreement concluded by the taxpayer with a non-state pension fund in their own favor, Expenses for medical services provided to a child (under 18 years old) of the taxpayer by medical organizations, Expenses for their own education
Question 11
Score: 6.00
An investor has a brokerage account with an investment company. In 2021, the investor received the following income from securities:
- dividends on shares of JSC “Winning” amounted to 50,000 rubles;
- coupon income from government bonds OFZ amounted to 40,000 rubles;
- coupon income from corporate bonds of JSC “Reliable” amounted to 30,000 rubles.
In addition, the investor received a capital gain from selling 100 shares of JSC “Risky” at 200 rubles per share. The purchase price of 1 share was 150 rubles. The investor held the shares for 4 months.
The investor's salary for 2021 before taxation amounted to 1,000,000 rubles.
2022 Higher Trial - qualifying stage
rubles.
Calculate the amount of personal income tax (NDFL) on income from securities.
|
Answer and write it in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 16250
Question 12
Score: 5.00
Insert the missing terms from the drop-down list.
Under the insurance contract, one party
insured; insurance premium; beneficiary; insurer; insurance amount
undertakes to pay the other party
insured; insurance premium; beneficiary; insurer; insurance amount
in the event of an occurrence of an event provided for in the contract (insurance event) to compensate the other party
insured; insurance premium; beneficiary; insurer; insurance amount
or any other person in whose favor the contract is concluded
insured; insurance premium; beneficiary; insurer; insurance amount
, for losses caused by this event (pay insurance compensation) within the amount determined by the contract insured; insurance premium; beneficiary; insurer; insurance amount
Correct answer:
Insert the missing terms from the drop-down list.
Under the insurance contract, one party [insurer] undertakes to pay the other party [insurance premium] in the event of an occurrence of an event provided for in the contract (insurance event) to compensate the other party [insured] or any other person in whose favor the contract is concluded [beneficiary], for losses caused by this event (pay insurance compensation) within the amount determined by the contract [insurance amount].
Question 13
Score: 3.00
Mark all correct statements.
Owners of a voluntary life insurance policy are entitled to a tax deduction
Select one or more answers:
|
16250
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the higher the risk of a financial instrument, the higher its return
Correct answers: the higher the reliability of a financial instrument, the higher its return, a financial instrument can be reliable, profitable, and liquid at the same time, risk is not related to the return of a financial instrument
Question 15
Score: 6.00
Agnia's monthly salary in 2021 is 60,000 rubles (before taxation). It is known that on 01.01.2021, Agnia opened the following deposits in banks (she had no deposits before):
| Bank | Deposit amount, rub. | Interest rate, % per annum |
| :---: | :---: | :---: |
| A | 500,000 | 4.5 |
| B | 400,000 | 3.9 |
| C | 300,000 | 5.0 |
| C | 100,000 | 0.75 |
Interest on all these deposits is accrued and paid once at the end of the year. The key rate of the Bank of Russia on 01.01.21 was 4.25%. It is known that Agnia's total income for 2021 did not exceed 5,000,000 rubles. Calculate the amount of personal income tax (NDFL) Agnia should pay on the interest received in 2021.
|
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 1378
Question 16
Score: 5.00
Establish the correspondence between specific taxes and their types.
| personal income tax | federal tax; local tax; regional tax; |
| :---: | :---: |
| land tax | federal tax; local tax; regional tax; |
| profit tax | federal tax; local tax; regional tax; |
| property tax of individuals | federal tax; local tax; regional tax; |
| transport tax | federal tax; local tax; regional tax; |
Correct answer:
personal income tax $\rightarrow$ federal tax,
land tax $\rightarrow$ local tax,
profit tax $\rightarrow$ federal tax,
property tax of individuals $\rightarrow$ local tax,
transport tax $\rightarrow$ regional tax
Question 17
Score: 6.00
Kirill wants to buy a TV costing 30000 rubles on credit. The bank offers him the necessary amount on loan with the condition that the borrowed amount must be repaid in three equal monthly installments. At the end of each month, interest must also be paid on the remaining debt, calculated at an annual rate of $18 \%$. Calculate the percentage of overpayment by Kirill from the loan amount.
Answer write in percentages as an integer without spaces and units of measurement.
Answer:
Correct answer: 3
Question 18
Score: 6.00
An investor has accumulated 400000 rubles and deposited them in a bank for 7 months at an annual interest rate of $6 \%$. Interest is compounded monthly. Calculate the amount of interest the investor will receive upon closing the deposit.
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 14212
Question 19
Score: 3.00
Mark all correct statements.
If a bank, which is your counterparty, has its license revoked, then
Select one or more answers:
|
1378
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 15. Problem 15
What amount of mortgage credit in rubles will a bank client receive if their initial payment of 1800000 rubles amounted to $30 \%$ of the cost of the purchased property?
|
Answer in the form of a number should bewrittenwithoutspaces,withoutunitsofmeasurementandanycharacters.
## Answer: 4200000
#
|
4200000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
reducing transaction time
## Correct answers:
using licensed software, using a personal computer instead of a public one, using antivirus programs
Question 3
Balya: 7.00
Mr. Vshokoladov earned X rubles per month throughout 2021. In addition, during this year, he won 2000000 rubles in a lottery. What is $X$ if the total amount of personal income tax paid by Mr. Vshokoladov for this year was 1239480 rubles.
|
Answer in rubles, without spaces and units of measurement.
Answer:
Correct answer: 600000
Question 4
Score: 3.00
Select all correct continuations of the statement.
2022 Higher Trial - qualifying stage
To file a petition to recognize a citizen as bankrupt...
## Select one or more answers:
\ulcorner
|
600000
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
A custodian stores securities, clients' money, and other material assets
Correct answers: A paid investment advisor consults and provides recommendations to the client on investment management, A trustee manages the client's property in their own name
Find the correspondence between the term and the statement so that all 5 pairs are correct. All 5 terms must be used.
The service may involve changing the terms of an existing loan
According to federal law, this service is available only once during the entire loan period
The service provides options for reducing the term or the amount of loan payments
During the term of this service, the bank does not charge the borrower penalties and cannot demand early repayment of the loan
This service may include
refinancing; consolidation of debts; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
refinancing; loan holidays; mortgage holidays; early repayment; restructuring;
Correct answer:
The service may involve changing the terms of an existing loan $\rightarrow$ restructuring,
According to federal law, this service is available only once during the entire loan period $\rightarrow$ mortgage holidays,
The service provides options for reducing the term or the amount of loan payments $\rightarrow$ early repayment,
During the term of this service, the bank does not charge the borrower penalties and cannot demand early repayment of the loan $\rightarrow$ loan holidays, This service may include consolidation of debts $\rightarrow$ refinancing
Question 8
Score: 7.00
The Ivanov family carefully plans their budget. Lidia Nikolaevna works as a doctor and earns 1,000,000 rubles per year (before income tax). Arkady Petrovich is an entrepreneur, and his annual profit from the business is 2,000,000 rubles, which is taxed at a rate of $15 \%$ under the simplified taxation system (USN).
On average, the family's expenses amount to 205,000 rubles per month, excluding vacation expenses.
The Ivanovs had been saving money for a trip to Paris for a year, but due to the pandemic, they decided to postpone the trip for a year and temporarily place the accumulated savings in a bank deposit at an annual interest rate of $12 \%$ with interest paid at the end of each quarter. The deposit term is 12 months, and interest income is reinvested. Calculate the Ivanov family's income from the deposit.
|
Answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number according to rounding rules.
Answer:
Correct answer: 13806
question 9
Score: 3.00
Select all possible features of an authentic ruble banknote.
Select one or more answers:
$\Gamma$
|
13806
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
watermark
Correct answers: raised relief of certain text fragments, watermark, inscriptions and ornaments
Question 10
Score: 7.00
Vladimir has saved 16,500 rubles to buy a gaming console as a birthday gift for his brother, which amounts to 220 US dollars at the current exchange rate. The birthday is not until a month from now, and Vladimir is comparing three
Financial Literacy 11th Grade Day 1
alternatives: 1) buy the console now; 2) buy US dollars with the saved amount now, and convert them back to rubles in a month to buy the console; or 3) deposit 16,500 rubles in the bank now, with the condition that he will receive 16,665 rubles in a month, and then buy the chosen console.
Calculate the minimum exchange rate of US dollars at the end of the month for the second alternative to be economically beneficial for Vladimir. Assume that there are no bank fees or currency conversion fees.
|
Answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number according to rounding rules.
Answer: $\qquad$
Correct answer: 76
Question 11
Score: 3.00
What services can currently be provided remotely? Select all appropriate options.
|
76
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the driver's marital status
Correct answers: bonus-malus coefficient, engine power, driver's age
Question 14
Score: 7.00
Maria Ivanovna has retired. She did not have a funded pension, only a social insurance pension, and her individual pension coefficient amount is 120. In addition, Maria Ivanovna has a bank deposit of 600,000 rubles, placed at an annual interest rate of $4 \%$ with monthly interest payments, which she does not reinvest but withdraws from the account monthly. How much money does Maria Ivanovna have available each month if the fixed part of her pension is 6050 rubles per month, and the cost of the pension coefficient is 99 rubles?
|
Provide the answer in rubles, without spaces and units of measurement.
Answer:
The correct answer is: 19930
Question 15
Score: 7.00
Insert the missing words from the list below (not all provided words will be needed!):
Paying
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
with a card, you spend the bank's funds, which you will have to return later.
If you do this before the end of the
credit; preferential; higher; cash withdrawal; service; blocking;
bonus; debit; freeze; lower; transfer;
period, the fee for using these funds is not charged, if you do not manage to, you will have to pay interest, which is usually significantly
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
than the interest on a regular loan. In addition, the bank usually
charges interest for
credit; preferential; higher; cash withdrawal; service; blocking; bonus; debit; freeze; lower; transfer;
money from an ATM and an annual fee for
credit; preferential; higher; cash withdrawal; service; blocking;
bonus; debit; freeze; lower; transfer;
card.
Correct answer:
Insert the missing words from the list below (not all provided words will be needed!):
Paying [credit] card, you spend the bank's funds, which you will have to return later. If you do this before the end of the [preferential] period, the fee for using these funds is not charged, if you do not manage to - you will have to pay interest, which is usually significantly [higher] than the interest on a regular loan. In addition, the bank usually charges interest for [cash withdrawal] money from an ATM and an annual fee for
[service] card.
Question 16
Score: 3.00
In what cases is no commission charged for a transfer between individuals in Russia? Select all applicable answers.
Select one or more answers:
|
19930
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
The Bank of Russia will ensure the conversion of the "digital ruble" into another form of money (rubles) at a one-to-one ratio.
Correct answers: Stablecoins, backed by cash or gold, are an example of a CBDC., The Bank of Russia will ensure the conversion of the "digital ruble" into another form of money (rubles) at a one-to-one ratio.
Question 19
Score: 7.00
Angelika owns a commercial space of 30 sq. m. She wanted to organize a music club there and give piano lessons. But a friend offered Angelika a job as a manager in his company, and she decided to calculate which option would be more economically beneficial for her. If she opens the club, Angelika plans to choose a simplified tax system with a rate of $15 \%$ of the profit received, while her salary, which she spends entirely on monthly expenses, after paying personal income tax, will be 60,900 rubles per month.
Additional information:
rent rate: 12,000 rubles per 1 sq m per year, paid at the beginning of the year.
interest rate on a loan: $12 \%$ per year, with interest accrued at the end of the year interest rate on a deposit: $9 \%$ per year, with interest accrued at the end of the year Determine the minimum annual profit Angelika needs to achieve from the music club (before taxation) for this alternative to be economically beneficial for her.
|
Provide the answer in rubles, without spaces and units of measurement. Round the answer to the nearest whole number.
Answer: $\qquad$
Correct answer: 1321412
Question 20
Score: 7.00
Financial Literacy 11th Grade Day 1
Ivan and Petr, twin brothers, went on a vacation by the sea together and purchased two different travel insurance policies, which also cover medical expenses during the trip. Ivan bought insurance for 450 rubles with a deductible of $25. Petr bought insurance for 500 rubles with no deductible. During the trip, the brothers fell ill and had to see a doctor, which cost $100 for each of them. Calculate how much more the brother who bought the less advantageous insurance policy paid compared to the other brother? Conduct calculations in rubles, using the exchange rate of 75 rubles per $. Provide the answer in rubles, without spaces and units of measurement.
Answer:
Correct answer: 1825
|
1321412
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.
the higher the risk of a financial instrument, the higher its return
Correct answers: the higher the reliability of a financial instrument, the higher its return, a financial instrument can be reliable, profitable, and liquid at the same time, risk is not related to the return of a financial instrument
Question 15
Score: 6.00
Agnia's monthly salary in 2021 is 60,000 rubles (before taxation). It is known that on 01.01.2021, Agnia opened the following deposits in banks (she had no deposits before):
| Bank | Deposit amount, rub. | Interest rate, % per annum |
| :---: | :---: | :---: |
| A | 500000 | 4.5 |
| B | 400000 | 3.9 |
| C | 300000 | 5.0 |
| C | 100000 | 0.75 |
Interest on all these deposits is accrued and paid once at the end of the year. The key rate of the Bank of Russia on 01.01.21 was 4.25%. It is known that Agnia's total income for 2021 did not exceed 5,000,000 rubles. Calculate the amount of personal income tax (NDFL) Agnia should pay on the interest received in 2021.
|
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 1378
Question 16
Score: 5.00
Establish the correspondence between specific taxes and their types.
| personal income tax | federal tax; local tax; regional tax; |
| :---: | :---: |
| land tax | federal tax; local tax; regional tax; |
| profit tax | federal tax; local tax; regional tax; |
| property tax of individuals | federal tax; local tax; regional tax; |
| transport tax | federal tax; local tax; regional tax; |
Correct answer:
personal income tax $\rightarrow$ federal tax,
land tax $\rightarrow$ local tax,
profit tax $\rightarrow$ federal tax,
property tax of individuals $\rightarrow$ local tax,
transport tax $\rightarrow$ regional tax
Question 17
Score: 6.00
Kirill wants to buy a TV costing 30000 rubles on credit. The bank offers him the necessary amount on loan with the condition that the borrowed amount must be repaid in three equal monthly installments. At the end of each month, interest must also be paid on the remaining debt, calculated at an annual rate of $18 \%$. Calculate the percentage of overpayment by Kirill from the loan amount.
Answer write in percentages as an integer without spaces and units of measurement.
Answer:
Correct answer: 3
Question 18
Score: 6.00
An investor has accumulated 400000 rubles and deposited them in a bank for 7 months at an annual interest rate of $6 \%$. Interest is compounded monthly. Calculate the amount of interest the investor will receive upon closing the deposit.
Answer write in rubles as an integer without spaces and units of measurement.
Answer: $\qquad$
Correct answer: 14212
Question 19
Score: 3.00
Mark all correct statements.
If a bank, which is your counterparty, has its license revoked, then
Select one or more answers:
|
1378
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a square of grid paper containing an integer number of cells, a hole in the shape of a square, also consisting of an integer number of cells, was cut out. How many cells did the large square contain if 209 cells remained after the cutout?
|
Answer: 225 cells
Solution. The side of the larger square contains $n$ sides of a cell, and the side of the smaller square contains $m$ sides of a cell. Then $n^{2}-m^{2}=209 \rightarrow(n-m)(n+m)=209=11 \cdot 19$.
Case 1. $\left\{\begin{array}{c}n+m=209 \\ n-m=1\end{array} \rightarrow\left\{\begin{array}{c}n=105 \\ m=104\end{array}\right.\right.$ case does not occur due to the absence of a hole
Case 2. $\left\{\begin{array}{l}n+m=19 \\ n-m=11\end{array} \rightarrow\left\{\begin{array}{l}n=15 \\ m=4\end{array}\right.\right.$
|
225
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Subtract the second equation from the first:
$x^{2}-2 x+y^{4}-8 y^{3}+24 y^{2}-32 y=-17 \rightarrow(x-1)^{2}+(y-2)^{4}=0 \rightarrow\left\{\begin{array}{l}x=1 \\ y=2\end{array}\right.$
Then $z=x^{2}+y^{4}-8 y^{3}=1+16-64=-47$
|
Answer: the only solution is $x=1, y=2, z=-47$.
|
-47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
16. The last digit of a six-digit number was moved to the beginning (for example, $456789 \rightarrow$ 945678), and the resulting six-digit number was added to the original number. Which numbers from the interval param 1 could have resulted from the addition? In the answer, write the sum of the obtained numbers.
| param1 | Answer |
| :---: | :---: |
| $[891870 ; 891899]$ | |
| $[375355 ; 375380]$ | |
| $[427411 ; 427434]$ | |
| $[639619 ; 639647]$ | |
|
16. The last digit of a six-digit number was moved to the beginning (for example, $456789 \rightarrow$ 945678), and the resulting six-digit number was added to the original number. Which numbers from the interval param 1 could have resulted from the addition? In the answer, write the sum of the obtained numbers.
| param1 | Answer |
| :---: | :---: |
| $[891870 ; 891899]$ | 1783771 |
| $[375355 ; 375380]$ | 750739 |
| $[427411 ; 427434]$ | 854843 |
| $[639619 ; 639647]$ | 1279267 |
|
1279267
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+11 x+23$.
|
Answer: 22.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+11 x+23>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-46)>0$, from which $-2<x<46$. On this interval, there are 45 natural values of $x: x=1, x=2, \ldots, x=45$. In this interval, $y$ takes integer values only for even $x$ - a total of 22 possibilities. Thus, we get 22 points belonging to the parabola, both of whose coordinates are natural numbers.
|
22
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can be repeated) so that the resulting 12-digit number is divisible by 45. In how many ways can this be done?
|
Answer: 13122.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We will choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $2 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=13122$.
|
13122
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 18. In how many ways can this be done?
|
Answer: 3645.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6$ or 8 (5 ways).
To ensure divisibility by nine, we proceed as follows. Choose three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0, 1, 2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $5 \cdot 9 \cdot 9 \cdot 9 \cdot 1 = 3645$.
|
3645
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+9 x+19$.
|
Answer: 18.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+9 x+19>0 \Leftrightarrow-\frac{1}{4}(x+2)(x-38)>0$, from which $-2<x<38$. On this interval, there are 37 natural values of $x: x=1, x=2, \ldots, x=37$. In this interval, $y$ takes integer values only for even $x$ - a total of 18 possibilities. Thus, we get 18 points belonging to the parabola, both of whose coordinates are natural numbers.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,1,2,3,4,5,6,7,8$ (digits can repeat) so that the resulting 10-digit number is divisible by 45. In how many ways can this be done?
|
Answer: 1458.
Solution. For a number to be divisible by 45, it is necessary and sufficient that it is divisible by 5 and by 9. To ensure divisibility by 5, we can choose 0 or 5 as the last digit (2 ways).
To ensure divisibility by nine, we proceed as follows. We select three digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9$ ways), and choose the fourth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that there are $2 \cdot 9 \cdot 9 \cdot 9 \cdot 1=1458$ ways.
|
1458
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $1,2,3,4,5,6,7,8,9$ (digits can repeat) so that the resulting 12-digit number is divisible by 18. In how many ways can this be done?
|
Answer: 26244.
Solution. For a number to be divisible by 18, it is necessary and sufficient that it is divisible by 2 and by 9. To ensure divisibility by 2, we can choose the last digit from the available options as $2, 4, 6$ or 8 (4 ways).
To ensure divisibility by nine, we proceed as follows. Choose four digits arbitrarily (this can be done in $9 \cdot 9 \cdot 9 \cdot 9$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 9. Since these digits give all possible remainders when divided by $9 (0,1,2, \ldots, 8)$, and each remainder occurs exactly once, the last digit can be chosen in one way.
Applying the rule of product, we get that the total number of ways is $4 \cdot 9 \cdot 9 \cdot 9 \cdot 9 \cdot 1=26244$.
|
26244
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+13 x+42$.
|
Answer: 13.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+13 x+42>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-42)>0$, from which $-3<x<42$. On this interval, there are 41 natural values of $x: x=1, x=2, \ldots, x=41$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 13 possibilities. Thus, we get 13 points belonging to the parabola, both of whose coordinates are natural numbers.
|
13
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-7 x^{2}+7 x=1$, respectively.
|
Answer: 34.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-7\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-7 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-6 x+1\right)=0,
$$
from which $x=1$ or $x=3 \pm \sqrt{8}$. The largest root is $a=3+\sqrt{8}$, and the smallest is $-b=3-\sqrt{8}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{3+\sqrt{8}}{3-\sqrt{8}}+\frac{3-\sqrt{8}}{3+\sqrt{8}}=\frac{(3+\sqrt{8})^{2}+(3-\sqrt{8})^{2}}{(3+\sqrt{8})(3-\sqrt{8})}=\frac{2(9+8)}{1}=34
$$
|
34
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 * *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 15. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. Choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{p}{q}+\frac{q}{p}$, where $p$ and $q$ are the largest and smallest roots of the equation $x^{3}+6 x^{2}+6 x=-1$, respectively.
|
Answer: 23.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}+1\right)+6\left(x^{2}+x\right)=0 \Leftrightarrow(x+1)\left(x^{2}-x+1\right)+6 x(x+1)=0 \Leftrightarrow(x+1)\left(x^{2}+5 x+1\right)=0 \text {, }
$$
from which $x=-1$ or $x=\frac{-5 \pm \sqrt{21}}{2}$. The largest root is $p=\frac{-5+\sqrt{21}}{2}$, and the smallest is $-q=\frac{-5-\sqrt{21}}{2}$. Then
$$
\frac{p}{q}+\frac{q}{p}=\frac{-5+\sqrt{21}}{-5-\sqrt{21}}+\frac{-5-\sqrt{21}}{-5+\sqrt{21}}=\frac{(-5+\sqrt{21})^{2}+(-5-\sqrt{21})^{2}}{(-5-\sqrt{21})(-5+\sqrt{21})}=\frac{2(25+21)}{4}=23 .
$$
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,6,7,8$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 2160.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 6, 8$ (5 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $5 \cdot 6 \cdot 6 \cdot 6 \cdot 2 = 2160$ ways.
|
2160
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{a}{b}+\frac{b}{a}$, where $a$ and $b$ are the largest and smallest roots of the equation $x^{3}-9 x^{2}+9 x=1$, respectively.
|
Answer: 62.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-9\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-9 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-8 x+1\right)=0
$$
from which $x=1$ or $x=4 \pm \sqrt{15}$. The largest root is $a=4+\sqrt{15}$, the smallest is $-b=4-\sqrt{15}$. Then
$$
\frac{a}{b}+\frac{b}{a}=\frac{4+\sqrt{15}}{4-\sqrt{15}}+\frac{4-\sqrt{15}}{4+\sqrt{15}}=\frac{(4+\sqrt{15})^{2}+(4-\sqrt{15})^{2}}{(4+\sqrt{15})(4-\sqrt{15})}=\frac{2(16+15)}{1}=62
$$
|
62
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 15. In how many ways can this be done?
|
# Answer: 864.
Solution. For a number to be divisible by 15, it is necessary and sufficient that it is divisible by 5 and by 3. To ensure divisibility by 5, we can choose 0 or 5 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fourth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this choice can be made in two ways.
Applying the rule of product, we get that in total $2 \cdot 6 \cdot 6 \cdot 6 \cdot 2=864$ ways.
|
864
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+20 x+63$.
|
Answer: 20.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+20 x+63>0 \Leftrightarrow-\frac{1}{3}(x+3)(x-63)>0$, from which $-3<x<63$. On this interval, there are 62 natural values of $x: x=1, x=2, \ldots, x=62$. In this case, $y$ takes integer values only when $x$ is divisible by 3 - a total of 20 possibilities. Thus, we get 20 points belonging to the parabola, both of whose coordinates are natural numbers.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the value of the expression $\frac{p}{q}+\frac{q}{p}$, where $p$ and $q$ are the largest and smallest roots of the equation $x^{3}-8 x^{2}+8 x=1$, respectively.
|
# Answer: 47.
Solution. The given equation is equivalent to the following
$$
\left(x^{3}-1\right)-8\left(x^{2}-x\right)=0 \Leftrightarrow(x-1)\left(x^{2}+x+1\right)-8 x(x-1)=0 \Leftrightarrow(x-1)\left(x^{2}-7 x+1\right)=0 \text {, }
$$
from which $x=1$ or $x=\frac{7 \pm \sqrt{45}}{2}$. The largest root is $p=\frac{7+\sqrt{45}}{2}$, and the smallest is $-q=\frac{7-\sqrt{45}}{2}$. Then
$$
\frac{p}{q}+\frac{q}{p}=\frac{7+\sqrt{45}}{7-\sqrt{45}}+\frac{7-\sqrt{45}}{7+\sqrt{45}}=\frac{(7+\sqrt{45})^{2}+(7-\sqrt{45})^{2}}{(7+\sqrt{45})(7-\sqrt{45})}=\frac{2(49+45)}{4}=47
$$
|
47
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2016 * * * * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can be repeated) so that the resulting 11-digit number is divisible by 6. In how many ways can this be done?
|
Answer: 1728.
Solution. For a number to be divisible by 6, it is necessary and sufficient that it is divisible by 2 and by 3. To ensure divisibility by 2, we can choose the last digit from the available options as $0, 2, 4, 8$ (4 ways).
To ensure divisibility by three, we proceed as follows. Choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $4 \cdot 6 \cdot 6 \cdot 6 \cdot 2=1728$ ways.
|
1728
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 75. In how many ways can this be done?
|
Answer: 2592.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit from the available options (1 way).
To ensure divisibility by three, we proceed as follows. Select four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and choose the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $1 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=2592$ ways.
|
2592
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Plot on the plane $(x ; y)$ the set of points satisfying the equation $|15 x|+|8 y|+|120-15 x-8 y|=120$, and find the area of the resulting figure.
|
Answer: 60.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 1 5 x \geq 0 , } \\
{ 8 y \geq 0 , } \\
{ 1 2 0 - 1 5 x - 8 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
15 x+8 y \leq 120
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(8 ; 0), G(0 ; 15), N(0 ; 0)$, the area of which is equal to 60.
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 02 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,7,8,9$ (digits can repeat) so that the resulting 11-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 1296.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0, 4, or 8 as the last digit (3 ways).
To ensure divisibility by 3, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and select the fourth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 8), this selection can be made in two ways.
Applying the rule of product, we get that in total $3 \cdot 6 \cdot 6 \cdot 6 \cdot 2=1296$ ways.
|
1296
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|3 x|+|4 y|+|48-3 x-4 y|=48$, and find the area of the resulting figure.
|
Answer: 96.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 3 x \geq 0 , } \\
{ 4 y \geq 0 , } \\
{ 4 8 - 3 x - 4 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
3 x+4 y \leq 48
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(16 ; 0), G(0 ; 12), N(0 ; 0)$, the area of which is equal to 96.
|
96
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 07 *$, each of the 5 asterisks needs to be replaced with any of the digits $0,2,4,5,6,7$ (digits can repeat) so that the resulting 11-digit number is divisible by 75. In how many ways can this be done?
|
# Answer: 432.
Solution. For a number to be divisible by 75, it is necessary and sufficient that it is divisible by 25 and by 3. To ensure divisibility by 25, we can choose 5 as the last digit (1 way) from the available options.
To ensure divisibility by three, we proceed as follows. We will choose three digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6$ ways), and the fifth digit will be chosen so that the sum of all the digits of the number is divisible by 3. Since among the given digits, there are two digits divisible by 3 (0 and 6), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get that in total $1 \cdot 6 \cdot 6 \cdot 6 \cdot 2=432$ ways.
|
432
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Plot on the plane $(x ; y)$ the set of points satisfying the equation $|5 x|+|12 y|+|60-5 x-12 y|=60$, and find the area of the resulting figure.
|
Answer: 30.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 5 x \geq 0 } \\
{ 1 2 y \geq 0 , } \\
{ 6 0 - 5 x - 1 2 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
5 x+12 y \leq 60
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(12 ; 0), G(0 ; 5), N(0 ; 0)$, the area of which is 30.
|
30
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In the number $2 * 0 * 1 * 6 * 0 * 2 *$, each of the 6 asterisks needs to be replaced with any of the digits $0,2,4,5,7,9$ (digits can be repeated) so that the resulting 12-digit number is divisible by 12. In how many ways can this be done?
|
Answer: 5184.
Solution. For a number to be divisible by 12, it is necessary and sufficient that it is divisible by 4 and by 3. To ensure divisibility by 4, we can choose 0 or 4 as the last digit from the available options (2 ways).
To ensure divisibility by three, we proceed as follows. We will choose four digits arbitrarily (this can be done in $6 \cdot 6 \cdot 6 \cdot 6$ ways), and then select the fifth digit so that the sum of all the digits of the number is divisible by 3. Since among the given digits there are two digits that are divisible by 3 (0 and 9), two digits that give a remainder of 1 when divided by 3 (4 and 7), and two digits that give a remainder of 2 when divided by 3 (2 and 5), this selection can be made in two ways.
Applying the rule of product, we get a total of $2 \cdot 6 \cdot 6 \cdot 6 \cdot 6 \cdot 2=5184$ ways.
|
5184
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the plane $(x ; y)$, plot the set of points satisfying the equation $|4 x|+|3 y|+|24-4 x-3 y|=24$, and find the area of the resulting figure.
#
|
# Answer: 24.
Solution. Note that the equality $|a|+|b|+|c|=a+b+c$ holds if and only if the numbers $a, b$, and $c$ are non-negative (since if at least one of them is negative, the left side is greater than the right). Therefore, the first equation is equivalent to the system of inequalities
$$
\left\{\begin{array} { l }
{ 4 x \geq 0 , } \\
{ 3 y \geq 0 , } \\
{ 2 4 - 4 x - 3 y \geq 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x \geq 0 \\
y \geq 0 \\
4 x+3 y \leq 24
\end{array}\right.\right.
$$
This system defines a triangle on the plane with vertices $E(6 ; 0), G(0 ; 8), N(0 ; 0)$, the area of which is 24.
|
24
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 20-gon $M$. Find the number of quadruples of vertices of this 20-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 765.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{20}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{20}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 9 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 10 parallel chords. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{10} K_{11}$, a total of 10 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 8 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 9 parallel chords. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments. There are also 10 such sets.
In total, we get $10 \cdot 45 + 10 \cdot 36 = 810$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 10 diameters with vertices at the given points, thus we get $C_{10}^{2}=45$ rectangles. Therefore, we have $810 - 45 = 765$ quadrilaterals with at least one pair of parallel sides.
|
765
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 291000, such that $k^{2}-1$ is divisible by 291.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 97)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 97. Let's consider two cases.
a) $(k+1): 97$, i.e., $k=97 p+96, p \in \mathrm{Z}$. Then we get $(97 p+95)(97 p+97):(3 \cdot 97) \Leftrightarrow(97 p+95)(p+1): 3$. The first factor is divisible by 3 when $p=3 q+1, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=291 q+193, k=291 q+290, q \in \mathrm{Z}$.
b) $(k-1): 97$, i.e., $k=97 p+1, p \in \mathrm{Z}$. Then we get $97 p(97 p+2):(3 \cdot 97) \Leftrightarrow(97 p+2) p ; 3$. The first factor is divisible by 3 when $p=3 q+1, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=291 q+98$, $k=291 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders of $193, 290, 98, 1$ when divided by 291, meaning that every 4 out of 291 consecutive numbers fit. Since $291000=291 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 16-gon $M$. Find the number of quadruples of vertices of this 16-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 364.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{16}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{16}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 7 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 8 parallel chords. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{8} K_{9}$ - a total of 8 such sets.
Now, let's take a chord connecting vertices that are one apart, for example, $K_{6} K_{8}$. There are 6 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 7 parallel chords. From these, we can form $C_{7}^{2}=21$ pairs of parallel segments. There are also 8 such sets.
In the end, we get $8 \cdot 28 + 8 \cdot 21 = 392$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{8}^{2}=28$ rectangles. Therefore, we have $392 - 28 = 364$ quadrilaterals with at least one pair of parallel sides.
|
364
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 445000, such that $k^{2}-1$ is divisible by 445. Answer: 4000.
|
Solution. Factoring the dividend and divisor, we get the condition $(k-1)(k+1):(5 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathrm{Z}$. Then we get $(89 p+87)(89 p+89):(5 \cdot 89) \Leftrightarrow(89 p+87)(p+1): 5$. The first factor is divisible by 5 when $p=5 q+2, q \in \mathrm{Z}$, and the second when $p=5 q+4, q \in \mathrm{Z}$, from which we obtain that $k=445 q+276, k=445 q+444, q \in Z$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathrm{Z}$. Then we get $89 p(89 p+2):(5 \cdot 89) \Leftrightarrow(89 p+2) p: 5$. The first factor is divisible by 5 when $p=5 q+2, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=445 q+179$, $k=445 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $276, 444, 179, 1$ when divided by 445, meaning that every 4 out of 445 consecutive numbers fit. Since $445000=445 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 22-gon $M$. Find the number of quadruples of vertices of this 22-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 1045.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{22}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{22}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 10 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 11 chords parallel to each other. From these, we can form $C_{11}^{2}=55$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{11} K_{12}$ - a total of 11 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 9 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments. There are also 11 such sets.
In the end, we get $11 \cdot 55 + 11 \cdot 45 = 1100$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 11 diameters with vertices at the given points, thus we get $C_{11}^{2}=55$ rectangles. Therefore, we have $1100 - 55 = 1045$ quadrilaterals with at least one pair of parallel sides.
|
1045
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 485000, such that $k^{2}-1$ is divisible by 485.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(5 \cdot 97)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 97. Let's consider two cases.
a) $(k+1): 97$, i.e., $k=97 p+96, p \in \mathrm{Z}$. Then we get $(97 p+95)(97 p+97):(5 \cdot 97) \Leftrightarrow(97 p+95)(p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathrm{Z}$, and the second when $p=5 q+4, q \in \mathrm{Z}$, from which we obtain that $k=485 q+96, k=485 q+484, q \in \mathrm{Z}$.
b) $(k-1): 97$, i.e., $k=97 p+1, p \in \mathrm{Z}$. Then we get $97 p(97 p+2):(5 \cdot 97) \Leftrightarrow(97 p+2) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=485 q+389$, $k=485 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $96,484,389,1$ when divided by 485, meaning that every 4 out of 485 consecutive numbers fit. Since $485000=485 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given a regular 18-gon $M$. Find the number of quadruples of vertices of this 18-gon that are the vertices of convex quadrilaterals, which have at least one pair of parallel sides.
|
Answer: 540.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{18}$ in a circle. Each quadrilateral with a pair of parallel sides is determined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{18}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 8 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{9} K_{10}$ - a total of 9 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 7 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 8 chords parallel to each other. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments. There are also 9 such sets.
In the end, we get $9 \cdot 36 + 9 \cdot 28 = 576$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{9}^{2}=36$ rectangles. Therefore, we have $576 - 36 = 540$ quadrilaterals with at least one pair of parallel sides.
|
540
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 267000, such that $k^{2}-1$ is divisible by 267.
|
Answer: 4000.
Solution. By factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathbb{Z}$. Then we get $(89 p+87)(89 p+89):(3 \cdot 89) \Leftrightarrow (89 p+87)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second factor is divisible by 3 when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=267 q+88, k=267 q+266, q \in \mathbb{Z}$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathbb{Z}$. Then we get $89 p(89 p+2):(3 \cdot 89) \Leftrightarrow (89 p+2) p \vdots 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathbb{Z}$, and the second factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, from which we obtain that $k=267 q+179$, $k=267 q+1, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $88, 266, 179, 1$ when divided by 267, meaning that every 4 out of 267 consecutive numbers fit. Since $267000=267 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $5 x^{2}-6 x y+y^{2}=6^{100}$.
|
Answer: 19594.
Solution: By factoring the left and right sides of the equation, we get $(5 x-y)(x-y)=2^{100} \cdot 3^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
5 x - y = 2 ^ { k } \cdot 3 ^ { l }, \\
x - y = 2 ^ { 1 0 0 - k } \cdot 3 ^ { 1 0 0 - l }
\end{array} \text { or } \left\{\begin{array}{l}
5 x-y=-2^{k} \cdot 3^{l}, \\
x-y=-2^{100-k} \cdot 3^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=2^{k-2} \cdot 3^{l}-2^{98-k} \cdot 3^{100-l} \\
y=2^{k-2} \cdot 3^{l}-5 \cdot 2^{98-k} \cdot 3^{100-l}
\end{array}\right.
$$
Consider the first equation. The exponents in the powers of three are non-negative. The sum of the exponents in the powers of two is 96, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $2 \leq k \leq 98,0 \leq l \leq 100-$ a total of $97 \cdot 101=9797$ options.
The second system also has 9797 solutions; thus, there are 19594 solutions in total.
|
19594
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $6 x^{2}-7 x y+y^{2}=10^{100}$.
|
Answer: 19998.
Solution: By factoring the left and right sides of the equation, we get $(6 x-y)(x-y)=2^{100} \cdot 5^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
6 x - y = 2 ^ { k } \cdot 5 ^ { l } , \\
x - y = 2 ^ { 1 0 0 - k } \cdot 5 ^ { 1 0 0 - l }
\end{array} \text { or } \left\{\begin{array}{l}
6 x-y=-2^{k} \cdot 5^{l} \\
x-y=-2^{100-k} \cdot 5^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=2^{k} \cdot 5^{l-1}-2^{100-k} \cdot 5^{99-l} \\
y=2^{k} \cdot 5^{l-1}-6 \cdot 2^{100-k} \cdot 5^{99-l}
\end{array}\right.
$$
Consider the first equation. The exponents of the powers of two are non-negative. The sum of the exponents of the powers of five is 98, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $0 \leq k \leq 100,1 \leq l \leq 99$ - a total of $99 \cdot 101=9999$ options.
The second system also has 9999 solutions; thus, there are 19998 solutions in total.
|
19998
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $x^{2}+6 x y+5 y^{2}=10^{100}$.
|
Answer: 19594.
Solution: By factoring the left and right sides of the equation, we get $(x+5 y)(x+y)=2^{100} \cdot 5^{100}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
x+5 y=2^{k} \cdot 5^{l}, \\
x+y=2^{100-k} \cdot 5^{100-l}
\end{array} \text { or } \left\{\begin{array}{l}
x+5 y=-2^{k} \cdot 5^{l}, \\
x+y=-2^{100-k} \cdot 5^{100-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 100]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
y=2^{k-2} \cdot 5^{l}-2^{98-k} \cdot 5^{100-l} \\
x=5 \cdot 2^{98-k} \cdot 5^{100-l}-2^{k-2} \cdot 5^{l}
\end{array}\right.
$$
Consider the first equation. The exponents of the powers of five are non-negative. The sum of the exponents of the powers of two is 96, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $2 \leq k \leq 98,0 \leq l \leq 100-$ a total of $97 \cdot 101=9797$ options.
The second system also has 9797 solutions; thus, there are 19594 solutions in total.
|
19594
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(x ; y)$ that satisfy the condition $x^{2}+7 x y+6 y^{2}=15^{50}$.
|
Answer: 4998.
Solution: Factoring the left and right sides of the equation, we get $(x+6 y)(x+y)=5^{50} \cdot 3^{50}$. Since each factor on the left side is an integer, it follows that
$$
\left\{\begin{array}{l}
x+6 y=5^{k} \cdot 3^{l}, \\
x+y=5^{50-k} \cdot 3^{50-l}
\end{array} \text { or } \left\{\begin{array}{l}
x+6 y=-5^{k} \cdot 3^{l}, \\
x+y=-5^{50-k} \cdot 3^{50-l}
\end{array}\right.\right.
$$
where $k$ and $l$ are integers from the interval $[0 ; 50]$.
Let's find the number of solutions to the first system. Expressing $x$ and $y$ from it, we get
$$
\left\{\begin{array}{l}
x=6 \cdot 5^{49-k} \cdot 3^{50-l}-5^{k-1} \cdot 3^{l} \\
y=5^{k-1} \cdot 3^{l}-5^{49-k} \cdot 3^{50-l}
\end{array}\right.
$$
Consider the first equation. The exponents in the powers of three are non-negative. The sum of the exponents in the powers of five is 48, so at least one of them is positive, i.e., the corresponding term is an integer. Since the left side of the equation is also an integer, the second term on the right side of the equation must also be an integer. Therefore, for the existence of integer solutions, it is necessary and sufficient that $1 \leq k \leq 49, 0 \leq l \leq 50$ - a total of $49 \cdot 51=2499$ options.
"Phystech-2015", 10th grade, solutions to ticket 8
The second system also has 2499 solutions; thus, there are 4998 solutions in total.
|
4998
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 242400, such that $k^{2}+2 k$ is divisible by 303. Answer: 3200.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k+2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k+2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p+2):(3 \cdot 101) \Leftrightarrow p(101 p+2): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+202, q \in \mathrm{Z}$.
b) $(k+2): 101$, i.e., $k=101 p+99, p \in Z$. Then we get $(101 p+99)(101 p+101):(3 \cdot 101) \Leftrightarrow(101 p+99)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=303 q+99, k=303 q+301, q \in Z$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 202, 99, 301$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $242400=303 \cdot 800$, we get $4 \cdot 800=3200$ numbers.
|
3200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 20-gon $M$. Find the number of quadruples of vertices of this 20-gon that are the vertices of trapezoids.
|
Answer: 720.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{20}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{20}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 9 more chords parallel to it ( $K_{5} K_{8}$ and so on), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{10} K_{11}$, a total of 10 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 8 more chords parallel to it ( $K_{5} K_{9}$ and so on), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments. There are also 10 such sets.
In total, we get $10 \cdot 45 + 10 \cdot 36 = 810$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle are diameters, and there are 10 diameters with vertices at the given points, thus we have $C_{10}^{2}=45$ rectangles. Subtracting twice the number of rectangles, we get $810 - 90 = 720$ quadrilaterals that have at least one pair of parallel sides.
|
720
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 16-gon $M$. Find the number of quadruples of vertices of this 16-gon that are the vertices of trapezoids.
|
Answer: 336.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{16}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{16}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 7 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 8 parallel chords. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{8} K_{9}$, a total of 8 such sets.
Now, let's take a chord connecting vertices that are one apart, for example, $K_{6} K_{8}$. There are 6 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 7 parallel chords. From these, we can form $C_{7}^{2}=21$ pairs of parallel segments. There are also 8 such sets.
In the end, we get $8 \cdot 28 + 8 \cdot 21 = 392$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus yielding $C_{8}^{2}=28$ rectangles. Subtracting twice the number of rectangles, we get $392 - 56 = 336$ quadrilaterals that have at least one pair of parallel sides.
|
336
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 333300, such that $k^{2}-2 k$ is divisible by 303. Answer: 4400.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k-2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-2):(3 \cdot 101) \Leftrightarrow p(101 p-2): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+1, q \in \mathrm{Z}$, from which we obtain that $k=303 q, k=303 q+101, q \in \mathrm{Z}$.
b) $(k-2): 101$, i.e., $k=101 p+2, p \in \mathrm{Z}$. Then we get $(101 p+2) 101 p:(3 \cdot 101) \Leftrightarrow(101 p+2) p: 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=303 q+204$, $k=303 q+2, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 204, 2$ when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $333300=303 \cdot 1100$, we get $4 \cdot 1100=4400$ numbers.
|
4400
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 22-gon $M$. Find the number of quadruples of vertices of this 22-gon that are the vertices of trapezoids.
|
Answer: 990.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{22}$ in a circle. Each trapezoid side is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{22}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 10 more chords parallel to it ( $K_{5} K_{8}$, etc.), i.e., we get a set of 11 chords parallel to each other. From these, we can form $C_{11}^{2}=55$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{11} K_{12}$ - a total of 11 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 9 more chords parallel to it ( $K_{5} K_{9}$, etc.), i.e., we get a set of 10 chords parallel to each other. From these, we can form $C_{10}^{2}=45$ pairs of parallel segments. There are also 11 such sets.
In total, we get $11 \cdot 55 + 11 \cdot 45 = 1100$ quadrilaterals. With this method of counting, rectangles have been counted twice. Note that both diagonals of an inscribed rectangle are diameters, and there are 11 diameters with vertices at the given points, thus there are $C_{11}^{2}=55$ rectangles. Subtracting twice the number of rectangles, we get $1100 - 110 = 990$ quadrilaterals with at least one pair of parallel sides.
|
990
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the number of natural numbers $k$, not exceeding 454500, such that $k^{2}-k$ is divisible by 505. Answer: 3600.
|
Solution. Factoring the dividend and divisor, we get the condition $k(k-1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k-1)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathrm{Z}$. Then we get $101 p(101 p-1):(5 \cdot 101) \Leftrightarrow p(101 p-1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathrm{Z}$, and the second when $p=5 q+1, q \in \mathrm{Z}$, from which we obtain that $k=505 q, k=505 q+101, q \in \mathrm{Z}$.
b) $(k-1): 101$, i.e., $k=101 p+1, p \in \mathrm{Z}$. Then we get $(101 p+1) 101 p:(5 \cdot 101) \Leftrightarrow(101 p+1) p: 5$. The first factor is divisible by 5 when $p=5 q+4, q \in \mathrm{Z}$, and the second when $p=5 q, q \in \mathrm{Z}$, from which we obtain that $k=505 q+405$, $k=505 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 101, 405, 1$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $454500=505 \cdot 900$, we get $4 \cdot 900=3600$ numbers.
|
3600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Given a regular 18-gon $M$. Find the number of quadruples of vertices of this 18-gon that are the vertices of trapezoids.
|
Answer: 504.
Solution. Let's inscribe the given polygon $K_{1} K_{2} \ldots K_{18}$ in a circle. Each trapezoid is defined by a pair of parallel chords with endpoints at points $K_{1}, \ldots, K_{18}$.
Consider a chord connecting two adjacent vertices of the polygon, for example, $K_{6} K_{7}$. There are 8 more chords parallel to it ( $K_{5} K_{8}$ and so on), i.e., we get a set of 9 chords parallel to each other. From these, we can form $C_{9}^{2}=36$ pairs of parallel segments.
We will get similar sets if we consider all chords parallel to $K_{1} K_{2}, \ldots, K_{9} K_{10}$ - a total of 9 such sets.
Now, let's take a chord connecting vertices that are one apart from each other, for example, $K_{6} K_{8}$. There are 7 more chords parallel to it ( $K_{5} K_{9}$ and so on), i.e., we get a set of 8 chords parallel to each other. From these, we can form $C_{8}^{2}=28$ pairs of parallel segments. There are also 9 such sets.
In the end, we get $9 \cdot 36 + 9 \cdot 28 = 576$ quadrilaterals. With this method of counting, rectangles were counted twice. Note that both diagonals of an inscribed rectangle in a circle are diameters, and there are 8 diameters with vertices at the given points, thus we get $C_{9}^{2}=36$ rectangles. Subtracting twice the number of rectangles, we get $576 - 72 = 504$ quadrilaterals that have at least one pair of parallel sides.
|
504
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. Find the number of integer solutions ( $x ; y ; z$ ) of the equation param 1 , satisfying the condition param 2.
| param1 | param2 | |
| :---: | :---: | :---: |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=2160$ | $\|x+y+z\| \leq 60$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=12960$ | $\|x+y+z\|<71$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=6000$ | $\|x+y+z\| \leq 102$ | |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=36000$ | $\|x+y+z\|<87$ | |

|
12. Find the number of integer solutions ( $x ; y ; z$ ) of the equation param 1 , satisfying the condition param 2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=2160$ | $\|x+y+z\| \leq 60$ | 60 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=12960$ | $\|x+y+z\|<71$ | 70 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=6000$ | $\|x+y+z\| \leq 102$ | 102 |
| $60^{x} \cdot\left(\frac{500}{3}\right)^{y} \cdot 360^{z}=36000$ | $\|x+y+z\|<87$ | 86 |
|
86
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. In a football tournament held in a single round-robin format (each team must play each other exactly once), $N$ teams are participating. At some point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | |
| :---: | :---: |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 15 | |
| | |

|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | Answer |
| :---: | :---: |
| 10 | 63 |
| 11 | 69 |
| 12 | 75 |
| 13 | 81 |
| 15 | 93 |
| | |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "Yes" answer?
| param1 | param2 | |
| :---: | :---: | :---: |
| 105 | 53 | |
| 129 | 65 | |
| :---: | :---: | :---: |
| 167 | 84 | |
| 125 | 63 | |
| 207 | 104 | |
|
20. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "True" answer?
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 105 | 53 | 54 |
| 129 | 65 | 66 |
| :---: | :---: | :---: |
| 167 | 84 | 85 |
| 125 | 63 | 64 |
| 207 | 104 | 105 |
|
54
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
18. For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | |
| 20 | 210 | |
| 22 | 250 | |
| 24 | 300 | |
| 26 | 330 | |
|
18. For each natural $n$, which is not a perfect square, the number of values of the variable $x$ is calculated, for which both numbers $x+\sqrt{n}$ and $x^{2}+param1 \cdot \sqrt{n}$ are natural numbers less than param2. Find the total number of such values of $x$.
| param1 | param2 | answer |
| :---: | :---: | :---: |
| 18 | 200 | 108 |
| 20 | 210 | 99 |
| 22 | 250 | 117 |
| 24 | 300 | 143 |
| 26 | 330 | 148 |
|
108
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the table, there are 140 different cards with numbers $3,6,9, \ldots 417,420$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $7?$
|
Answer: 1390.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a common difference of 3. Therefore, the remainders when these numbers are divided by 7 alternate. Indeed, if one of these numbers is divisible by 7, i.e., has the form $7k$, where $k \in \mathbb{N}$, then the numbers following it are $7k+3, 7k+6, 7k+9=7(k+1)+2, 7k+12=7(k+1)+5, 7k+15=7(k+2)+1, 7k+18=7(k+2)+4$, which give remainders $2, 4, 6, 1, 3, 5$ respectively when divided by 7. Next comes the number $7k+21$, which is divisible by 7, and then the remainders repeat. Thus, the remainders when the given numbers are divided by 7 go in the order $\ldots 0; 3; 6; 2; 5; 1; 4; 0 \ldots$
Among the 140 given numbers, there are 20 numbers that give remainders $0, 1, 2, 3, 4, 5, 6$ when divided by 7.
The sum of two numbers can be divisible by 7 in the following cases.
1) Both numbers are divisible by 7. There are 20 cards with such numbers, and we need to choose 2 of them - there are $C_{20}^{2} = \frac{1}{2} \cdot 20 \cdot 19 = 190$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 7 - then the other must give a remainder of 6 when divided by 7. This pair of numbers can be chosen in $20 \cdot 20 = 400$ ways.
3) One of the numbers gives a remainder of 2 when divided by 7 - then the other gives a remainder of 5, and, similarly to the second case, there are 400 ways to choose 2 numbers.
4) One of the numbers gives a remainder of 3 when divided by 7 - then the other gives a remainder of 4 - also 400 ways.
In total, there are 1390 ways.
|
1390
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the table, there are 210 different cards with numbers $2,4,6, \ldots 418,420$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the sum of the numbers on the selected cards is divisible by $7?$
|
Answer: 3135.
Solution. The given numbers, arranged in ascending order, form an arithmetic progression with a difference of 2. Therefore, the remainders of these numbers when divided by 7 alternate. Indeed, if one of these numbers is divisible by 7, i.e., has the form $7k$, where $k \in \mathbb{N}$, then the following numbers are $7k+2, 7k+4, 7k+6, 7k+8=7(k+1)+1, 7k+10=7(k+1)+3, 7k+12=7(k+1)+5$, giving remainders $2, 4, 6, 1, 3, 5$ respectively when divided by 7. Next comes the number $7k+14$, which is divisible by 7, and then the remainders repeat. Thus, the remainders of the given numbers when divided by 7 go in the order $\ldots 0; 2; 4; 6; 1; 3; 5; 0 \ldots$
Among the 210 given numbers, there are 30 numbers each that give remainders $0, 1, 2, 3, 4, 5, 6$ when divided by 7.
The sum of two numbers can be divisible by 7 in the following cases.
1) Both numbers are divisible by 7. There are 30 cards with such numbers, and we need to choose 2 of them - there are $C_{30}^{2} = \frac{1}{2} \cdot 30 \cdot 29 = 435$ ways to do this.
2) One of the numbers gives a remainder of 1 when divided by 7 - then the other must give a remainder of 6 when divided by 7. This pair of numbers can be chosen in $30 \cdot 30 = 900$ ways.
3) One of the numbers gives a remainder of 2 when divided by 7 - then the other gives a remainder of 5, and, similarly to the second case, we get 900 ways to choose 2 numbers.
4) One of the numbers gives a remainder of 3 when divided by 7 - then the other gives a remainder of 4 - also 900 ways.
In total, there are 3135 ways.
|
3135
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 200 different cards with numbers $2,3,2^{2}, 3^{2}, \ldots, 2^{100}, 3^{100}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a cube of an integer?
|
Answer: 4389.
Solution. To obtain the cube of a natural number, it is necessary and sufficient for each factor to enter the prime factorization of the number in a power that is a multiple of 3.
Suppose two cards with powers of two are chosen. We have 33 exponents divisible by 3 $(3,6,9, \ldots, 99)$, 34 exponents giving a remainder of 1 when divided by 3 $(1,4,7, \ldots, 100)$, and 33 exponents giving a remainder of 2 when divided by 3 $(2,5,8, \ldots, 98)$. We need the sum of the exponents to be a multiple of 3. For the sum of two natural numbers to be divisible by 3, we can either choose two numbers divisible by 3 $\left(C_{33}^{2}=\frac{33 \cdot 32}{2}=528\right.$ ways $)$, or take one number giving a remainder of 1 when divided by 3 and one number giving a remainder of 2 when divided by 3 $(34 \cdot 33=1122$ ways). We get $528+1122=1650$ ways.
The number of ways when the exponents on both chosen cards are powers of three is exactly the same, i.e., 1650.
If one card with a power of two and one card with a power of three are taken, then both exponents must be divisible by 3 - we get $33 \cdot 33=1089$ ways.
In total: $1650+1650+1089=4389$ ways.
|
4389
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. There are 100 different cards with numbers $2,5,2^{2}, 5^{2}, \ldots, 2^{50}, 5^{50}$ (each card has exactly one number, and each number appears exactly once). In how many ways can 2 cards be chosen so that the product of the numbers on the chosen cards is a cube of an integer?
|
Answer: 1074.
Solution. To obtain the cube of a natural number, it is necessary and sufficient for each factor to enter the prime factorization of the number in a power that is a multiple of 3.
Suppose two cards with powers of two are chosen. We have 16 exponents that are divisible by 3 $(3,6,9, \ldots, 48)$, 17 exponents that give a remainder of 1 when divided by $3(1,4,7, \ldots, 49)$, and 17 exponents that give a remainder of 2 when divided by $3(2,5,8, \ldots, 50)$. We need the sum of the exponents to be a multiple of 3. For the sum of two natural numbers to be divisible by 3, we can either choose two numbers that are divisible by $3\left(C_{16}^{2}=\frac{16 \cdot 15}{2}=120\right)$, or take one number that gives a remainder of 1 when divided by 3 and one number that gives a remainder of 2 when divided by $3(17 \cdot 17=289$ ways). We get $120+289=409$ ways.
The number of ways when the powers of five are written on both chosen cards is exactly the same, i.e., 409.
If one card with a power of two and one card with a power of five are taken, then both exponents must be divisible by 3 - we get $16 \cdot 16=256$ ways.
In total: $409+409+256=1074$ ways.
|
1074
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "Yes" answer?
| param1 | param2 | |
| :---: | :---: | :---: |
| 120 | 60 | |
|
9. On the table, there are param 1 visually identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee that you will get at least one "Yes" answer?
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| 120 | 60 | 63 |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | |
| :---: | :---: |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 15 | |
|
19. In a football tournament held in a single round-robin format (each team must play every other team exactly once), $N$ teams are participating. At a certain point in the tournament, the coach of team $A$ noticed that any two teams, different from $A$, have played a different number of games. It is also known that by this point, team $A$ has played more than 1 game. How many teams $N$ could have participated in this tournament? Write the sum of all possible values of $N$ in the answer.
| param1 | Answer |
| :---: | :---: |
| 10 | 63 |
| 11 | 69 |
| 12 | 75 |
| 13 | 81 |
| 15 | 93 |
| | |
|
63
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the coordinate plane, squares are considered, all vertices of which have integer non-negative coordinates, and the center is located at the point $(60 ; 45)$. Find the number of such squares.
|
Answer: 2070.
Solution. Draw through the given point $(60 ; 45)$ vertical and horizontal lines $(x=60$ and $y=45)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 45 ways: $(60 ; 0),(60 ; 1), \ldots,(60 ; 44)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=60$ and $y=45$ divide the plane. Consider the “lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be non-negative, it is necessary and sufficient for this vertex to fall into the square $15 \leqslant x \leqslant 59,0 \leqslant y \leqslant 44$. We get $45^{2}$ ways.
The total number of ways is $45^{2}+45=46 \cdot 45=2070$.
|
2070
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On the coordinate plane, consider squares all of whose vertices have natural coordinates, and the center is located at the point $(55 ; 40)$. Find the number of such squares.
|
Answer: 1560.
Solution. Draw through the given point $(55 ; 40)$ vertical and horizontal lines $(x=55$ and $y=40)$. There are two possible cases.
a) The vertices of the square lie on these lines (and its diagonals are parallel to the coordinate axes). Then the "lower" vertex of the square can be located in 39 ways: $(55 ; 1),(55 ; 1), \ldots,(55 ; 39)$ (the position of the other vertices is uniquely determined in this case).
b) The vertices of the square do not lie on the specified lines. This means that the vertices lie one in each of the four parts into which the lines $x=55$ and $y=40$ divide the plane. Consider the "lower left" vertex (its location uniquely determines the other vertices). For the coordinates of all vertices of the square to be natural, it is necessary and sufficient for this vertex to fall into the square $16 \leqslant x \leqslant 54,1 \leqslant y \leqslant 39$. We get $39^{2}$ ways.
The total number of ways is $39^{2}+39=39 \cdot 40=1560$.
|
1560
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $x^{2}+x y=30000000$.
|
Answer: 256.
Solution. By factoring the left and right sides of the equation, we get $x(x+y)=$ $3 \cdot 2^{7} \cdot 5^{7}$. Then, if $x>0$, $x$ is one of the divisors of the right side. The right side has a total of $2 \cdot 8 \cdot 8=128$ divisors (since any divisor can be represented as $3^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 7, and 7, respectively, i.e., there are 2 ways to choose $a$, 8 ways to choose $b$, and 8 ways to choose $c$). Note that if the right side is divisible by $x$, then it automatically follows that $y \in \mathbb{Z}$, and $y$ is uniquely determined. Therefore, there are a total of $2 \cdot 128=256$ pairs of numbers.
|
256
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 70, 1 \leqslant b \leqslant 50$, and at the same time,
the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 1260.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b \vdots 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 14 values of $a$ and 10 values of $b$ that are multiples of 5. Therefore, there are $14 \cdot 50=700$ pairs $(a ; b)$ such that $a \vdots 5$ and $10 \cdot 70=700$ pairs such that $b \vdots 5$. Additionally, there are $14 \cdot 10=140$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $700+700-140=1260$.
|
1260
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. It is known that for three consecutive natural values of the argument, the quadratic function $f(x)$ takes the values 6, 14, and 14, respectively. Find the greatest possible value of $f(x)$.
|
Answer: 15.
Solution. Let $n, n+1, n+2$ be the three given consecutive values of the argument. Since a quadratic function takes the same values at points symmetric with respect to the x-coordinate of the vertex of the parabola $x_{\text{v}}$, then $x_{\text{v}}=n+1.5$, and thus $f(x)$ can be represented as $f(x)=a(x-n-1.5)^{2}+c$. Since $f(n)=6, f(n+1)=14$, we get $\frac{9}{4} a+c=6, \frac{a}{4}+c=14$, from which $a=-4, c=15$. But $c=f\left(x_{\text{v}}\right)$ and is the maximum value of the function.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two equal rectangles $P Q R S$ and $P_{1} Q_{1} R_{1} S_{1}$ are inscribed in triangle $A B C$ (with points $P$ and $P_{1}$ lying on side $A B$, points $Q$ and $Q_{1}$ lying on side $B C$, and points $R, S, R_{1}$ and $S_{1}$ lying on side $A C$). It is known that $P S=3, P_{1} S_{1}=9$. Find the area of triangle $A B C$.
|
Answer: 72.
Solution. Draw the height $B F$ of triangle $A B C$. Let it intersect segments $P Q$ and $P_{1} Q_{1}$ at points $H$ and $M$ respectively. Note that $H M=6$. From the similarity of triangles $B P Q$ and $B P_{1} Q_{1}$, it follows that $\frac{B H}{P Q}=\frac{B M}{P_{1} Q_{1}}$ (the ratio of the height to the base is written), from which $\frac{B H}{3}=\frac{6+B H}{9}, B H=3$. Therefore, the area of triangle $B P Q$ is $\frac{1}{2} \cdot 3 \cdot 3=\frac{9}{2}$. But triangles $A B C$ and $B P Q$ are similar (the similarity coefficient is $B F: B H=12: 3=4$), hence the area of triangle $A B C$ is $16 \cdot \frac{9}{2}=72$.
|
72
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the number of pairs of integers $(x ; y)$ that satisfy the equation $y^{2}-x y=700000000$.
|
Answer: 324.
Solution. Factoring the left and right sides of the equation, we get $y(y-x)=$ $7 \cdot 2^{8} \cdot 5^{8}$. Then if $y>0$, $y$ is one of the divisors of the right side. The right side has a total of $2 \cdot 9 \cdot 9=162$ divisors (since any divisor can be represented as $7^{a} \cdot 2^{b} \cdot 5^{c}$, where $a, b$, and $c$ are non-negative integers not exceeding 1, 8, and 8, respectively, i.e., there are 2 ways to choose $a$, 9 ways to choose $b$, and 9 ways to choose $c$). Note that if the right side is divisible by $y$, then it automatically follows that $x \in \mathbb{Z}$, and in this case, $x$ is uniquely determined. Therefore, there are a total of $2 \cdot 162=324$ pairs of numbers.
|
324
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 80,1 \leqslant b \leqslant 30$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 864.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 16 values of $a$ and 6 values of $b$ that are multiples of 5. Therefore, there are $16 \cdot 30=480$ pairs $(a ; b)$ such that $a: 5$ and $6 \cdot 80=480$ pairs such that $b: 5$. Additionally, there are $16 \cdot 6=96$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $480+480-96=864$.
|
864
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 267000, such that $k^{2}-1$ is divisible by 267. Answer: 4000.
|
Solution. Factoring the dividend and divisor, we get the condition $(k-1)(k+1):(3 \cdot 89)$. This means that one of the numbers $(k+1)$ or $(k-1)$ is divisible by 89. Let's consider two cases.
a) $(k+1): 89$, i.e., $k=89 p+88, p \in \mathrm{Z}$. Then we get $(89 p+87)(89 p+89):(3 \cdot 89) \Leftrightarrow(89 p+87)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathrm{Z}$, and the second when $p=3 q+2, q \in \mathrm{Z}$, from which we obtain that $k=267 q+88, k=267 q+266, q \in \mathrm{Z}$.
b) $(k-1): 89$, i.e., $k=89 p+1, p \in \mathrm{Z}$. Then we get $89 p(89 p+2):(3 \cdot 89) \Leftrightarrow(89 p+2) p: 3$. The first factor is divisible by 3 when $p=3 q+2, q \in \mathrm{Z}$, and the second when $p=3 q, q \in \mathrm{Z}$, from which we obtain that $k=267 q+179$, $k=267 q+1, q \in \mathrm{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $88,266,179,1$ when divided by 267, meaning that every 4 out of 267 consecutive numbers fit. Since $267000=267 \cdot 1000$, we get $4 \cdot 1000=4000$ numbers.
|
4000
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 242400, such that $k^{2}+2 k$ is divisible by 303.
|
Answer: 3200.
Solution. By factoring the dividend and divisor, we get the condition $k(k+2):(3 \cdot 101)$. This means that one of the numbers $k$ or $(k+2)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p+2):(3 \cdot 101) \Leftrightarrow p(101 p+2) \vdots 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=303 q, k=303 q+202, q \in \mathbb{Z}$.
b) $(k+2): 101$, i.e., $k=101 p+99, p \in \mathbb{Z}$. Then we get $(101 p+99)(101 p+101):(3 \cdot 101) \Leftrightarrow (101 p+99)(p+1): 3$. The first factor is divisible by 3 when $p=3 q, q \in \mathbb{Z}$, and the second when $p=3 q+2, q \in \mathbb{Z}$, from which we obtain that $k=303 q+99, k=303 q+301, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders 0, 202, 99, 301 when divided by 303, meaning that every 4 out of 303 consecutive numbers fit. Since $242400=303 \cdot 800$, we get $4 \cdot 800=3200$ numbers.
|
3200
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of natural numbers $k$, not exceeding 353500, such that $k^{2}+k$ is divisible by 505.
|
Answer: 2800.
Solution: By factoring the dividend and divisor, we get the condition $k(k+1):(5 \cdot 101)$. This means that one of the numbers $k$ or $(k+1)$ is divisible by 101. Let's consider two cases.
a) $k: 101$, i.e., $k=101 p, p \in \mathbb{Z}$. Then we get $101 p(101 p+1):(5 \cdot 101) \Leftrightarrow p(101 p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, from which we get $k=505 q, k=505 q+404, q \in \mathbb{Z}$.
b) $(k+1): 101$, i.e., $k=101 p+100, p \in \mathbb{Z}$. Then we get $(101 p+100)(101 p+101):(5 \cdot 101) \Leftrightarrow (101 p+100)(p+1): 5$. The first factor is divisible by 5 when $p=5 q, q \in \mathbb{Z}$, and the second factor is divisible by 5 when $p=5 q+4, q \in \mathbb{Z}$, from which we get $k=505 q+100, k=505 q+504, q \in \mathbb{Z}$.
Thus, the numbers that satisfy the condition of the problem are those that give remainders $0, 404, 100, 504$ when divided by 505, meaning that every 4 out of 505 consecutive numbers fit. Since $353500=505 \cdot 700$, we get $4 \cdot 700=2800$ numbers.

Answer: $(8 ; 2)$.
Solution: Transform the equation of the system (add $64 x^{2}+64 y^{2}$ to both sides):
$$
\begin{gathered}
\left(x^{2}+y^{2}\right)^{2}+144+24 x^{2}+24 y^{2}=64 x^{2}+64 y^{2}+128 x y \Leftrightarrow\left(x^{2}+y^{2}+12\right)^{2}=(8 x+8 y)^{2} \Leftrightarrow \\
\Leftrightarrow\left[\begin{array}{l}
x^{2} + y^{2} + 12 = 8 x + 8 y, \\
x^{2} + y^{2} + 12 = -8 x - 8 y
\end{array} \Leftrightarrow \left[\begin{array}{l}
(x-4)^{2}+(y-4)^{2}=20, \\
(x+4)^{2}+(y+4)^{2}=20 .
\end{array}\right.\right.
\end{gathered}
$$
We get two circles of radius $2 \sqrt{5}$ with centers at points $(4 ; 4)$ and $(-4 ;-4)$.
The inequality in the system defines a half-plane. Consider the relative positions of each circle with the line $y=2 x-14$, which is the boundary of this half-plane.
a) $\left\{\begin{array}{l}(x-4)^{2}+(y-4)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}(x-4)^{2}+(2 x-18)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}5 x^{2}-80 x+320=0, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}x=8, \\ y=2 .\end{array}\right.\right.\right.\right.$
b) $\left\{\begin{array}{l}(x+4)^{2}+(y+4)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}(x+4)^{2}+(2 x-10)^{2}=20, \\ y=2 x-14\end{array} \Leftrightarrow\left\{\begin{array}{l}5 x^{2}-32 x+96=0, \\ y=2 x-14\end{array} \Leftrightarrow \varnothing\right.\right.\right.$.
In this case, the centers of the considered circles, the points $(4 ; 4)$ and $(-4 ;-4)$, do not lie in the half-plane, as their coordinates do not satisfy the inequality. Therefore, the second circle has no common points with the half-plane, while the first circle has a unique common point $(8 ; 2)$.
|
2800
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.