problem
stringlengths 2
5.64k
| solution
stringlengths 2
13.5k
| answer
stringlengths 2
43
| problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 70, 1 \leqslant b \leqslant 50$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 1260.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 14 values of $a$ and 10 values of $b$ that are multiples of 5. Therefore, there are $14 \cdot 50=$ 700 pairs $(a ; b)$ such that $a \vdots 5$ and $10 \cdot 70=700$ pairs such that $b \vdots 5$. Additionally, there are $14 \cdot 10=140$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $700+700-140=1260$.
|
1260
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the number of pairs of integers $(a ; b)$ such that $1 \leqslant a \leqslant 80,1 \leqslant b \leqslant 30$, and the area $S$ of the figure defined by the system of inequalities
$$
\left\{\begin{array}{l}
\frac{x}{a}+\frac{y}{b} \geqslant 1 \\
x \leqslant a \\
y \leqslant b
\end{array}\right.
$$
is such that the number $2 S$ is divisible by 5.
|
Answer: 864.
Solution. The given system of inequalities defines a triangle on the plane with vertices $(a ; 0),(0 ; b)$, and $(a ; b)$. This triangle is right-angled, and its doubled area is equal to the product of the legs, i.e., $a b$. According to the condition, $a b: 5$, so one of the numbers $a$ or $b$ must be divisible by 5.
Under the given constraints, there are 16 values of $a$ and 6 values of $b$ that are multiples of 5. Therefore, there are $16 \cdot 30 = 480$ pairs $(a ; b)$ such that $a \vdots \cdot 5$ and $6 \cdot 80 = 480$ pairs such that $b \vdots 5$. Additionally, there are $16 \cdot 6 = 96$ pairs such that both numbers $a$ and $b$ are divisible by 5. Thus, the total number of desired pairs is $480 + 480 - 96 = 864$.
|
864
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
10.2. There are 90 cards - 10 with the digit 1, 10 with the digit $2, \ldots, 10$ with the digit 9. From all these cards, two numbers were formed, one of which is three times the other. Prove that one of these numbers can be factored into four not necessarily distinct natural factors, greater than one.
|
Solution. Let these numbers be $A$ and $B=3A$. Then the sum of the digits of the number $B$ is divisible by 3. But the sum of the digits on all cards is divisible by 9 (and therefore by 3), so the sum of the digits of the number $A$ is divisible by 3. This means that the number $A$ is divisible by 3. But then the number $B=3A$ is divisible by 9 and the sum of its digits is divisible by 9. Since the sum of the digits on all cards is divisible by 9, then the sum of the digits of the number $A$ is also divisible by 9. This means that the number $A$ is divisible by 9. Therefore, the number $B=3A$ is divisible by 27. Thus, the number $B$ is divisible by 27 and is greater than 27, so it can be factored into 4 multipliers $3,3,3$ and $\frac{B}{27}>1$.
Comment. It has been proven that the larger of the numbers is divisible by 9 - 3 points.
10.3-1. Let $B$ and $C$ be the points of intersection of two circles of equal radii. On the first circle, a point $A$ is chosen. The ray $AB$ intersects the second circle at point $D$ $(D \neq B)$. On the ray $DC$, a point $E$ is chosen such that $DC = CE$. Find the angle $CEA$ if the angle $CDB$ is $50^{\circ}$.
Answer. $40^{\circ}$.
Solution. First, we will prove that the angle $DAE$ is a right angle. Connect points $A$ and $C$. The common chord $BC$ of the two equal circles subtends equal arcs of these circles, so the inscribed angles $BAC$ and $BDC$ that subtend these arcs are equal. Therefore, triangle $ACD$ is isosceles, from which it follows that $AC = CD = CE$ (the last equality is due to the problem's condition). Thus, point $C$ is the center of the circle circumscribed around triangle $DAE$. Segment $DE$ is the diameter of this circle, which implies that angle $DAE$ is a right angle.
$$
\text{Then } \angle CEA = \angle DEA = 90^{\circ} - \angle ADE = 90^{\circ} - \angle CDB = 40^{\circ} \text{.}
$$
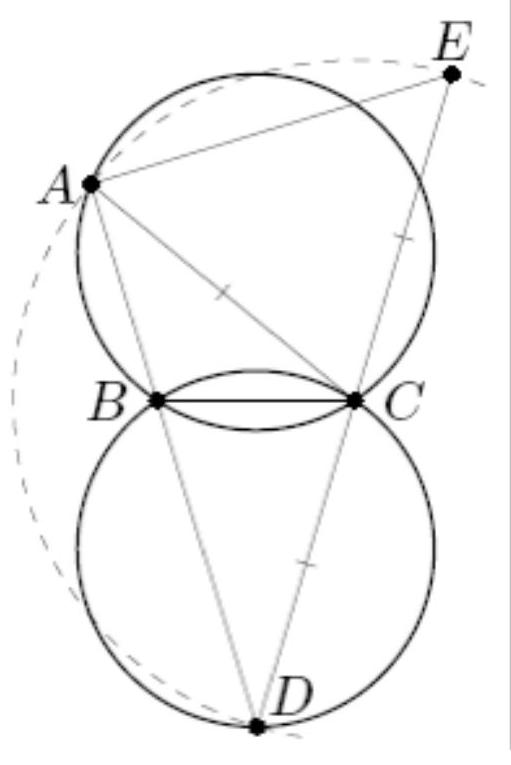
Comment. The correct answer without justification - 0 points.
10.3-2. Let $B$ and $C$ be the points of intersection of two circles of equal radii. On the first circle, a point $A$ is chosen. The ray $AB$ intersects the second circle at point $D$ $(D \neq B)$. On the ray $DC$, a point $E$ is chosen such that $DC = CE$. Find the angle $CEA$ if the angle $CDB$ is $40^{\circ}$.
Answer. $50^{\circ}$.
Solution. First, we will prove that the angle $DAE$ is a right angle. Connect points $A$ and $C$. The common chord $BC$ of the two equal circles subtends equal arcs of these circles, so the inscribed angles $BAC$ and $BDC$ that subtend these arcs are equal. Therefore, triangle $ACD$ is isosceles, from which it follows that $AC = CD = CE$ (the last equality is due to the problem's condition). Thus, point $C$ is the center of the circle circumscribed around triangle $DAE$. Segment $DE$ is the diameter of this circle, which implies that angle $DAE$ is a right angle.
Then $\angle CEA = \angle DEA = 90^{\circ} - \angle ADE = 90^{\circ} - \angle CDB = 50^{\circ}$.
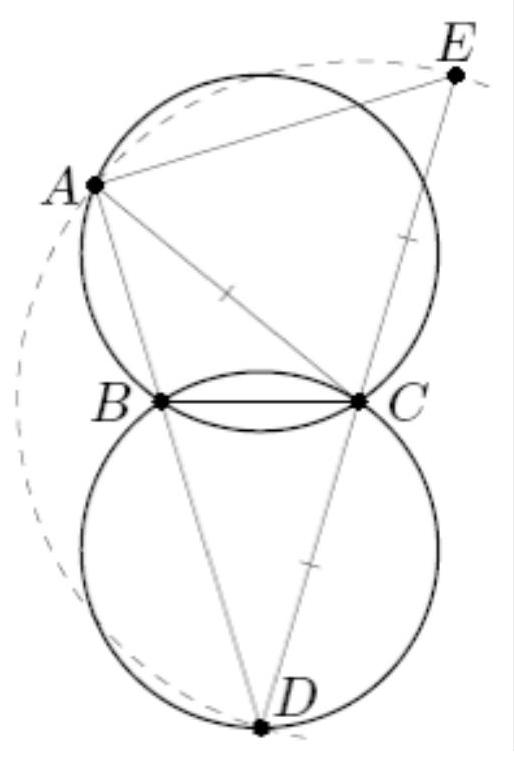
Comment. The correct answer without justification - 0 points.
|
40
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false |
10.4. Quadrilateral $A B C D$ is inscribed in a circle. The perpendicular to side $B C$, drawn through its midpoint - point $M$, intersects side $A B$ at point $K$. The circle with diameter $K C$ intersects segment $C D$ at point $P(P \neq C)$. Find the angle between the lines $M P$ and $A D$.
|
Answer: $90^{\circ}$.
Solution. We will prove that the lines $M P$ and $A D$ are perpendicular. Let $\omega$ be the circle constructed with $K C$ as its diameter, then point $M$ lies on $\omega$, since angle $C M K$ is a right angle. Therefore, $\angle C P M = \angle C K M = \alpha$ (they subtend the arc $C M$ of circle $\omega$). Let $T$ be the point of intersection of lines $A D$ and $M P$. We will assume that point $D$ lies on segment $A T$. The other case is considered similarly. Then $\angle T P D = \alpha$ (angles $T P D$ and $C P M$ are vertical). Therefore, to prove that lines $A D$ and $M P$ are perpendicular, we need to prove that $\angle P D T + \alpha = \frac{\pi}{2}$.
If $\angle P D T = \beta$, then $\angle P D A = \pi - \beta \Rightarrow \angle A B C = \beta$, since quadrilateral $A B C D$ is cyclic. Finally, $B K = C K$, because $M K$ is the perpendicular bisector of $B C$. Therefore, $\angle K C M = \angle K B M = \beta$. From the right triangle $K M C$, we get $\alpha + \beta = \frac{\pi}{2}$. The statement is proved.
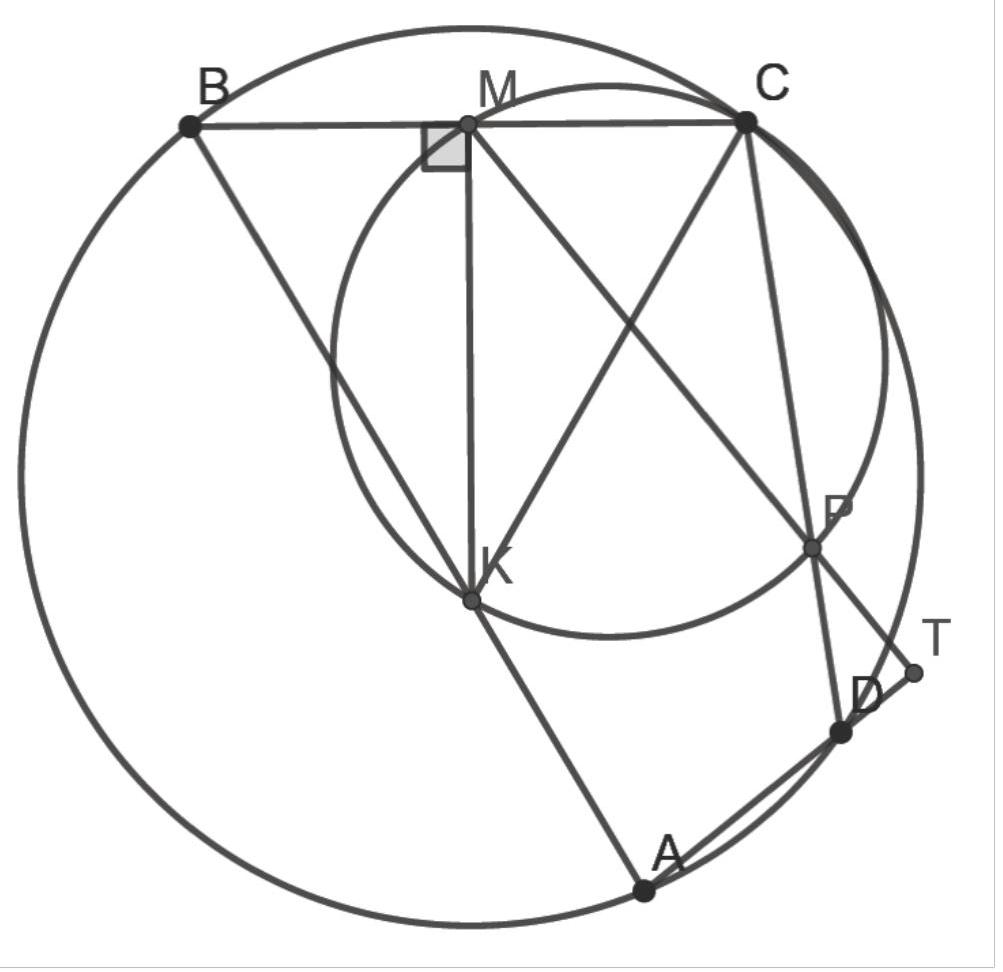
Comment. Only one case of the position of point $D$ is considered - no points are deducted.
It is proved that point $M$ lies on $\omega-1$ point.
|
90
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | |
| 1372 | |
| 1228 | |
| 1092 | |
| 964 | |
|
8. For each natural $n$, which is not a perfect square, all values of the variable $x$ are calculated for which both numbers $x+\sqrt{n}$ and $x^{3}+$ param1 $\sqrt{n}$ are integers. Find the total number of such values of $x$.
| param1 | answer |
| :---: | :---: |
| 1524 | 39 |
| 1372 | 33 |
| 1228 | 35 |
| 1092 | 27 |
| 964 | 29 |
|
33
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
9. A regular param 1 -sided polygon is inscribed in a circle, with different natural numbers written at its vertices. A pair of non-adjacent vertices of the polygon $A$ and $B$ is called interesting if, on at least one of the two arcs $A B$, all the numbers written at the vertices of the arc are greater than the numbers written at the vertices $A$ and $B$. What is the minimum number of interesting pairs of vertices that this polygon can have?
| param1 | Answer |
| :---: | :---: |
| 55 | |
| 60 | |
| 70 | |
| 85 | |
| 95 | |
|
9. A regular param 1-gon is inscribed in a circle, with different natural numbers written at its vertices. A pair of non-adjacent vertices of the polygon $A$ and $B$ is called interesting if, on at least one of the two arcs $A B$, all the numbers written at the vertices of the arc are greater than the numbers written at the vertices $A$ and $B$. What is the smallest number of interesting pairs of vertices that this polygon can have?
| param1 | Answer |
| :---: | :---: |
| 55 | 52 |
| 60 | 57 |
| 70 | 67 |
| 85 | 82 |
| 95 | 92 |
|
92
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (15 points) The vertices of the broken line $A B C D E F G$ have coordinates $A(-1 ; -7), B(2 ; 5), C(3 ; -8), D(-3 ; 4), E(5 ; -1), F(-4 ; -2), G(6 ; 4)$.
Find the sum of the angles with vertices at points $B, E, C, F, D$.
|
Answer: $135^{\circ}$.
Solution. The closed broken line $B C D E F B$ forms a five-pointed "star". The sum of the angles at the rays of this star is $180^{\circ}$.
We will prove that the sum of the angles at the rays of any five-pointed star $B C D E F B$ is $180^{\circ}$. Let $O$ be the point of intersection of the lines $B F$ and $E D$, and the angle between them is $B O D=\alpha$. Denote the angle at the ray by the same letter as the vertex of the ray.
$$
\angle E+\angle F=180^{\circ}-\alpha=\angle O B D+\angle O D B
$$
We have:
$$
\begin{aligned}
180^{\circ} & =\angle C+\angle C B D+\angle C D B=\angle C+(\angle B+\angle O B D)+(\angle D+\angle O D B)= \\
& =\angle C+\angle B+\angle D+(\angle O B D+\angle O D B)=\angle C+\angle B+\angle D+\angle E+\angle F
\end{aligned}
$$
Another proof. Let the ray $\bar{a}$ coincide with the ray $B C$. Rotate the ray $\bar{a}$ until it coincides with the ray $B F$. The ray $\bar{a}$ will rotate by the angle $\angle B$. Then rotate the ray $\bar{a}$ (in its new position) until it coincides with the ray $E F$. The ray $\bar{a}$ will rotate by another angle $\angle F$, and from the start of the movement, by the angle $\angle B+\angle F$. Then rotate the ray $\bar{a}$ again until it coincides with the ray $E D$. The ray $\bar{a}$ will rotate by another angle $\angle D$, and from the start of the movement, by the angle $\angle B+\angle F+\angle E$. After performing two more similar rotations, the ray $\bar{a}$ will coincide with the ray $C B$, i.e., it will have rotated by $180^{\circ}$ from the start of the movement and, at the same time, by the sum of the angles $\angle B+\angle F+\angle E+\angle D+\angle C$.
The point of intersection of the segments $A B$ and $F G$ is the point $K(1 ; 1)$.
We will prove this. Let $L(1 ;-2), M(6 ;-2)$. Then $\triangle K F L \sim \triangle G F M$, since their legs are proportional. Therefore, $\angle K F L=\angle G F M$, so $K \in F G$. Similarly, $K \in A B$.
Another way. The equation of the line $A B: y=4 x-3$. The equation of the line $F G: y=\frac{3}{5} x+\frac{2}{5}$. Solving the system of these two equations, we get the coordinates of the intersection point of these lines: $(1 ; 1)$.
Find the lengths of the sides of $\triangle B K G: B K=\sqrt{1^{2}+4^{2}}=\sqrt{17}, B G=\sqrt{4^{2}+(-1)^{2}}=\sqrt{17}, G K=\sqrt{5^{2}+3^{2}}=\sqrt{34}$. The triangle $B K G$ is isosceles and, by the converse of the Pythagorean theorem, it is a right triangle.
Therefore, the angle $\angle B K G=45^{\circ}$. It is an exterior angle for $\triangle F K B$ and $\angle K F B+\angle K B F=45^{\circ}$. Since $\angle A B C=\angle F B C-\angle F B A$, $\angle E F G=\angle E F B-\angle G F B$, the required sum of the angles
$$
\begin{gathered}
\angle A B C+\angle E F G+\angle B C D+\angle C D E+\angle D E F= \\
=\angle F B C+\angle E F B-(\angle F B A+\angle G F B)+\angle B C D+\angle C D E+\angle D E F= \\
=180^{\circ}-45^{\circ}=135^{\circ}
\end{gathered}
$$
Remark. A similar solution can be obtained based on the fact that the sum of the angles at the rays of any seven-pointed "star" is also $180^{\circ}$ (the proof is essentially the same as the second proof for the five-pointed star). Since the angle $\angle B K G=45^{\circ}$, the sum of the two angles of the seven-pointed star with vertices at points $A$ and $G$ is $45^{\circ}$.
Grading criteria. Full solution 15 points. If the coordinates of point $K$ are found from the drawing or guessed - minus 2 points. If the fact that $\angle B K G=45^{\circ}$ is found from the drawing or guessed - minus 3 points. If the problem is not solved, but it is shown that the sum of all angles at the rays of a five- or seven-pointed star is $180^{\circ}$, then 8 points.
|
135
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (15 points) The vertices of the broken line $A B C D E F G$ have coordinates $A(0 ; -5), B(3 ; 7), C(4 ; -6), D(-2 ; 6), E(6 ; 1), F(-3 ; 0), G(7 ; 6)$.
Find the sum of the angles with vertices at points $B, E, C, F, D$.
|
Answer: $135^{\circ}$.
Solution. The closed broken line $B C D E F B$ forms a five-pointed "star". The sum of the angles at the rays of this star is $180^{\circ}$.
We will prove that the sum of the angles at the rays of any five-pointed star $B C D E F B$ is $180^{\circ}$. Let $O$ be the point of intersection of the lines $B F$ and $E D$, and the angle between them is $B O D=\alpha$. Denote the angle at the ray by the same letter as the vertex of the ray.
$$
\angle E+\angle F=180^{\circ}-\alpha=\angle O B D+\angle O D B .
$$
Therefore,
$$
\begin{array}{r}
180^{\circ}=\angle C+\angle C B D+\angle C D B=\angle C+(\angle B+\angle O B D)+(\angle D+\angle O D B)= \\
\quad=\angle C+\angle B+\angle D+(\angle O B D+\angle O D B)=\angle C+\angle B+\angle D+\angle E+\angle F
\end{array}
$$
Another proof. Let the ray $\bar{a}$ coincide with the ray $В C$. Rotate the ray $\bar{a}$ until it coincides with the ray $B F$. The ray $\bar{a}$ will rotate by the angle $\angle B$. Then rotate the ray $\bar{a}$ (in its new position) until it coincides with the ray $E F$. The ray $\bar{a}$ will rotate by another angle $\angle F$, and from the start of the movement, by the angle $\angle B+\angle F$. Then rotate the ray $\bar{a}$ again, this time until it coincides with the ray $E D$. The ray $\bar{a}$ will rotate by another angle $\angle D$, and from the start of the movement, by the angle $\angle B+\angle F+\angle E$. After performing two more similar rotations, the ray $\bar{a}$ will coincide with the ray $C B$, i.e., it will have rotated by $180^{\circ}$ from the start of the movement and, at the same time, by the sum of the angles $\angle B+\angle F+\angle E+\angle D+\angle C$.
The point of intersection of the segments $A B$ and $F G$ is the point $K(2 ; 3)$.
We will prove this. Let $L(2 ; 0), M(7 ; 0)$. Then $\triangle K F L \sim \triangle G F M$, since their legs are proportional. Therefore, $\angle K F L=\angle G F M$, so $K \in F G$. Similarly, $K \in A B$.
Another way. The equation of the line $A B: y=4 x-5$. The equation of the line $F G: y=\frac{3}{5} x+\frac{9}{5}$. Solving the system of these two equations, we get the coordinates of the intersection point of these lines: $(2 ; 3)$.
Find the lengths of the sides of $\triangle B K G: B K=\sqrt{1^{2}+4^{2}}=\sqrt{17}, B G=$ $\sqrt{4^{2}+(-1)^{2}}=\sqrt{17}, G K=\sqrt{5^{2}+3^{2}}=\sqrt{34}$. The triangle $\triangle B K G$ is isosceles and, by the converse of the Pythagorean theorem, it is a right triangle.
Therefore, the angle $\angle B K G=45^{\circ}$. It is an exterior angle for $\triangle F K B$ and $\angle K F B+\angle K B F=45^{\circ}$. Since $\angle A B C=\angle F B C-\angle F B A$, $\angle E F G=\angle E F B-\angle G F B$, the required sum of the angles
$$
\begin{gathered}
\angle A B C+\angle E F G+\angle B C D+\angle C D E+\angle D E F= \\
=\angle F B C+\angle E F B-(\angle F B A+\angle G F B)+\angle B C D+\angle C D E+\angle D E F= \\
=180^{\circ}-45^{\circ}=135^{\circ}
\end{gathered}
$$
Remark. A similar solution can be obtained based on the fact that the sum of the angles at the rays of any seven-pointed "star" is also $180^{\circ}$ (the proof, in essence, does not differ from the second proof for a five-pointed star). Since the angle $\angle B K G=45^{\circ}$, the sum of the two angles of the seven-pointed star with vertices at points $A$ and $G$ is $45^{\circ}$.
Grading criteria. Full solution 15 points. If the coordinates of point $K$ are found from the drawing or guessed - minus 2 points. If the fact that $\angle B K G=45^{\circ}$ is found from the drawing or guessed - minus 3 points. If the problem is not solved, but it is shown that the sum of all angles at the rays of a five- or seven-pointed star is $180^{\circ}$, then 8 points.
|
135
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
# Problem № 7 (10 points)
A person and his faithful dog started moving along the perimeter of a block from point $A$ simultaneously at time $t_{0}=0$ min. The person moved with a constant speed clockwise, while the dog ran with a constant speed counterclockwise (see figure). It is known that they met for the first time after $t_{1}=2$ min from the start of the movement. This meeting occurred at point $B$. Given that they continued to move in their respective directions and at the same constant speeds, determine the moment of time when they will next be at point $B$ simultaneously. Note that $A B=C D=100$ m, $B C=A D=200$ m.
|
# Answer: in 14 min
## Solution and evaluation criteria:
In $t_{1}=2$ min, the person and the dog together covered a distance equal to the perimeter of the block, with the person moving 100 meters from the starting point of the journey.
That is, during each subsequent meeting, the person will be 100 meters away from the location of the previous meeting.
(
The perimeter of the block: $A B+B C+C D+D A=100+200+100+200=600$ meters.
That is, it will take another 12 minutes
And the next time the person and the dog will be at the same point at the moment:
$t_{\kappa}=14$ min.
|
14
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
# Problem № 8 (15 points)
In some English-speaking countries, temperature is measured in degrees Fahrenheit. An English schoolboy, observing a thermometer in a glass of cooling water, noticed that it cooled by $30^{\circ} \mathrm{F}$. He became curious about how much heat was released. In books, he found the following formula that allows calculating the answer to his question: $Q=4200 \cdot V \cdot \Delta T$, where $V$ is the volume of water in liters, $\Delta T$ is the change in its temperature. However, the change in temperature in this formula must be substituted in degrees Celsius. Degrees Fahrenheit are related to degrees Celsius by the following relationship: ${ }^{\circ} F={ }^{\circ} C \cdot \frac{9}{5}+32$. What result should he get if he had 2 liters of water at his disposal?
|
# Answer: 140 kJ
## Solution and grading criteria:
The change in temperature in degrees Fahrenheit is related to the change in temperature in degrees Celsius:
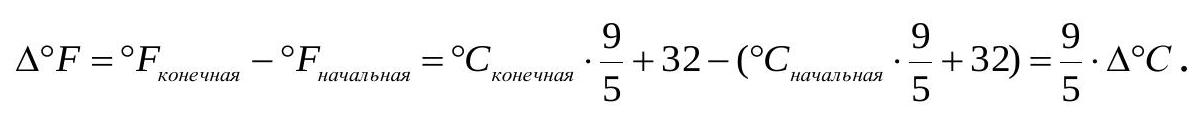
That is, in degrees Celsius, the water cooled by: $\Delta^{\circ} \mathrm{C}=\frac{5}{9} \cdot \Delta^{\circ} F=\frac{5}{9} \cdot 30 \approx 16.67^{\circ} \mathrm{C}$.
Therefore, the amount of heat released is:
$Q=4200 \cdot V \cdot \Delta T=4200 \cdot 2 \cdot 16.67 \approx 140$ kJ
|
140
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. 20 balls of the same mass are moving along a chute towards a metal wall with the same speed. Coming towards them at the same speed are 16 balls of the same mass. When two balls collide, they fly apart with the same speed. After colliding with the wall, a ball bounces off it with the same speed. (The balls move only along the chute). How many collisions will there be between the balls?
|
# Answer: 510.
Solution. We will assume that initially, each ball moving towards the wall has a red flag, and the rest of the balls have blue flags. Imagine that when the balls collide, they exchange flags. Then each blue flag moves at a constant speed in one direction (away from the wall), and each red flag reaches the wall and then moves in the opposite direction. The number of collisions between the balls is equal to the number of flag exchanges. Each red flag will exchange once with each blue flag. Any two red flags will also exchange places once. Therefore, the total number of exchanges is $20 \cdot 16 + \frac{20 \cdot 19}{2} = 510$.
Evaluation. 14 points for a correct solution.
## $2015 / 16$ academic year
#
|
510
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Andrei was driving to the airport of a neighboring city. After an hour of driving at a speed of 60 km/h, he realized that if he did not change his speed, he would be 20 minutes late. Then he sharply increased his speed, as a result of which he covered the remaining part of the journey at an average speed of 90 km/h and arrived at the airport 20 minutes earlier than originally planned. What is the distance from Andrei's home to the airport?
|
Answer: 180 km.
Solution. Let the distance from Andrey's house to the airport be $s$ km, and the time he intended to spend on the road be $1+t$ hours. Then
$$
s=60+60\left(t+\frac{1}{3}\right)=60+90\left(t-\frac{1}{3}\right)
$$
From this,
$$
60 t+20=90 t-30, \quad t=\frac{5}{3}, \quad s=180
$$
Evaluation. Full score for the solution is 12 points.
|
180
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. A natural number $n$ is such that the number $36 n^{2}$ has exactly 51 different natural divisors. How many natural divisors does the number $5 n$ have?
|
Answer: 16.
Solution. Let $m=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{l}^{k_{l}}$, where $p_{1}, p_{2}, \ldots, p_{l}$ are pairwise distinct prime numbers. Then the number of natural divisors of the number $m$ is
$$
\tau(m)=\left(k_{1}+1\right)\left(k_{2}+1\right) \ldots\left(k_{l}+1\right)
$$
Indeed, a common divisor of the number $m$ has the form
$$
d=p_{1}^{a_{1}} \cdot p_{2}^{a_{2}} \cdot \ldots \cdot p_{l}^{a_{l}}
$$
where for each $i$ the exponent $a_{i}$ takes values from 0 to $k_{i}-$ a total of $k_{i}+1$ values. By the multiplication rule, we obtain the formula (*).
The number $m=36 n^{2}$ has at least two prime divisors (2 and 3).
Considering the equality $\tau(m)=3 \cdot 17$, we get two factors in the formula (*). Therefore, the number $m$ has the form $m=2^{2} 3^{16}$ or $m=2^{16} 3^{2}$. In this case, $n=p^{7}$, where $p$ is equal to 2 or 3. Then
$$
5 n=5 p^{7}, \quad \tau(5 n)=2 \cdot 8=16
$$
Evaluation. 13 points for a complete solution. Participants in the Olympiad can use the formula (*) without proof.
|
16
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Viktor was driving to the airport of a neighboring city. After half an hour of driving at a speed of 60 km/h, he realized that if he did not change his speed, he would be 15 minutes late. Then he increased his speed, as a result of which he covered the remaining part of the journey at an average speed of 80 km/h and arrived at the airport 15 minutes earlier than originally planned. What is the distance from Viktor's home to the airport?
|
Answer: 150 km.
Solution. Let the distance from Viktor's house to the airport be $s$ km, and the time he intended to spend on the road $\frac{1}{2}+t$ hours. Then
$$
s=30+60\left(t+\frac{1}{4}\right)=30+80\left(t-\frac{1}{4}\right)
$$
From this,
$$
60 t+15=80 t-20, \quad t=\frac{7}{4}, \quad s=150
$$
Evaluation. Full solution: 12 points.
|
150
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. A natural number $n$ is such that the number $100 n^{2}$ has exactly 55 different natural divisors. How many natural divisors does the number 10n have?
|
Answer: 18.
Solution. Let $m=p_{1}^{k_{1}} \cdot p_{2}^{k_{2}} \cdot \ldots \cdot p_{l}^{k_{l}}$, where $p_{1}, p_{2}, \ldots, p_{l}$ are pairwise distinct prime numbers. Then the number of natural divisors of the number $m$ is
$$
\tau(m)=\left(k_{1}+1\right)\left(k_{2}+1\right) \ldots\left(k_{l}+1\right)
$$
Indeed, a common divisor of the number $m$ has the form
$$
d=p_{1}^{a_{1}} \cdot p_{2}^{a_{2}} \cdot \ldots \cdot p_{l}^{a_{l}}
$$
where for each $i$ the exponent $a_{i}$ takes values from 0 to $k_{i}-$ a total of $k_{i}+1$ values. By the multiplication rule, we obtain the formula (*).
The number $m=100 n^{2}$ has at least two prime divisors (2 and 5).
Considering the equality $\tau(m)=5 \cdot 11$, we get two factors in the formula (*). Therefore, the number $m$ has the form $m=2^{4} 5^{10}$ or $m=2^{10} 5^{4}$. In this case, $n=p q^{4}$, where $p=2, q=5$ or $p=5, q=2$. Then
$$
10 n=p^{2} q^{5}, \quad \tau(10 n)=3 \cdot 6=18
$$
Evaluation. 13 points for a complete solution. Participants in the Olympiad can use the formula (*) without proof.
|
18
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (17 points) The medians drawn from vertices $A$ and $B$ of triangle $ABC$ are perpendicular to each other. Find the area of the square with side $AB$, if $BC=28, AC=44$.
#
|
# Answer: 544
Solution. Let $D$ be the midpoint of $B C$, $E$ be the midpoint of $A C$, and $M$ be the point of intersection of the medians. Let $M D=a$, $M E=b$. Then $A M=2 a$, $B M=2 b$. From the right triangles $B M D$ and $A M E$, we have $a^{2}+4 b^{2}=B D^{2}=14^{2}$ and $4 a^{2}+b^{2}=A E^{2}=22^{2}$. Adding these equations and dividing by 5, we get $a^{2}+b^{2}=136$. Therefore, $A B^{2}=A M^{2}+B M^{2}=4\left(a^{2}+b^{2}\right)=544$.
|
544
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (17 points) In a $4 \times 5$ grid, 5 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 240
Solution. From the condition, it follows that in some row, two cells are marked (while in the others, only one each). This row can be chosen in 4 ways, and the two crosses in it can be chosen in $5 \cdot 4 / 2=10$ ways. The remaining three crosses can be chosen in $3 \cdot 2 \cdot 1=6$ ways. By the rule of product, the total number of ways is $4 \cdot 10 \cdot 6=240$.
|
240
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (17 points) The medians drawn from vertices $A$ and $B$ of triangle $ABC$ are perpendicular to each other. Find the area of the square with side $AB$, if $BC=36, AC=48$.
#
|
# Answer: 720
Solution. Let $D$ be the midpoint of $B C$, $E$ be the midpoint of $A C$, and $M$ be the point of intersection of the medians. Let $M D=a$, $M E=b$. Then $A M=2 a$, $B M=2 b$. From the right triangles $B M D$ and $A M E$, we have $a^{2}+4 b^{2}=B D^{2}=18^{2}$ and $4 a^{2}+b^{2}=A E^{2}=24^{2}$. Adding these equations and dividing by 5, we get $a^{2}+b^{2}=180$. Therefore, $A B^{2}=A M^{2}+B M^{2}=4\left(a^{2}+b^{2}\right)=720$.
|
720
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (17 points) In a $3 \times 4$ grid, 4 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 36
Solution. From the condition, it follows that in some row, two cells are marked (while in the others, only one each). This row can be chosen in 3 ways, and the two crosses in it can be placed in $4 \cdot 3 / 2=6$ ways. The remaining two crosses can be chosen in 2 ways. By the multiplication rule, the total will be $3 \cdot 6 \cdot 2=36$ variants.
|
36
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. In a row, the numbers $1,2,3, \ldots, 2014,2015$ are written. We will call a number from this row good if, after its removal, the sum of all the remaining 2014 numbers is divisible by 2016. Find all the good numbers.
|
Answer: The only good number is 1008.
Solution. The remainder of the division of the sum of all 2015 numbers by 2016 is 1008:
$(1+2015)+(2+2014)+\ldots+(1007+1009)+1008=2016 \cdot 1007+1008$.
Therefore, only 1008 can be crossed out.
Scoring. 12 points for a correct solution. If it is shown that 1008 is a good number, but it is not proven that there are no other good numbers, 6 points.
|
1008
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Nils has a goose farm. Nils calculated that if he sells 75 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 15 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-75)=(k-15) x(n+100) \\
k n=(k+20)(n-75)=(k-15)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=60, n=300$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Nils has a goose farm. Nils calculated that if he sells 50 geese, the feed will last 20 days longer than if he doesn't sell any. If he buys an additional 100 geese, the feed will run out 10 days earlier than if he doesn't make such a purchase. How many geese does Nils have?
|
Answer: 300.
Solution. Let $A$ be the total amount of feed (in kg), $x$ be the amount of feed per goose per day (in kg), $n$ be the number of geese, and $k$ be the number of days the feed will last. Then
$$
\begin{gathered}
A=k x n=(k+20) x(n-50)=(k-10) x(n+100) \\
k n=(k+20)(n-50)=(k-10)(n+100)
\end{gathered}
$$
Solving the obtained system of two equations with two variables, we find that $k=20, n=100$.
Evaluation. 12 points for a correct solution. If the system is set up but not solved, 4 points.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
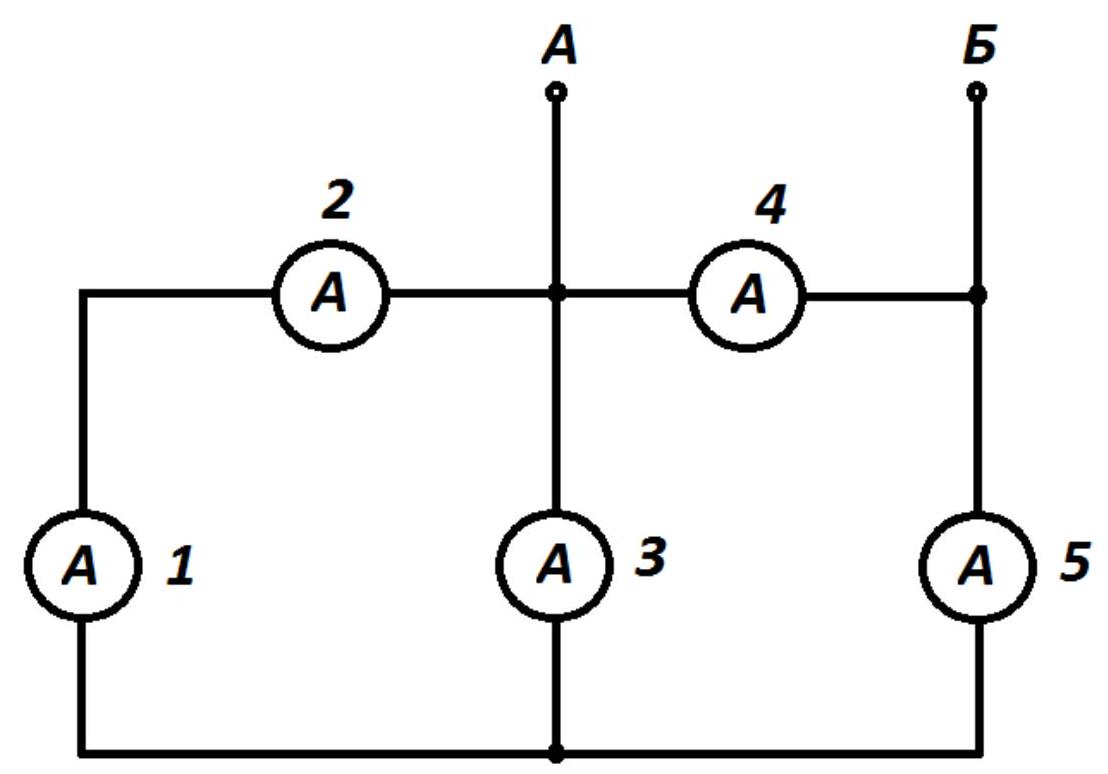
5. (10 points) Five identical non-ideal ammeters are connected as shown in the figure. Ideal power supply is connected to points $A$ and $B$. Determine the sum of the readings of all ammeters, given that the reading of the first ammeter $I_{1}=2 \mathrm{MA}$.
|
Answer: $24$ mA
Solution. As a result of analyzing the proposed electrical circuit, it can be concluded that: $I_{2}=I_{1}=2$ mA.
\[
\begin{aligned}
& I_{3}=2 I_{1}=4 \mathrm{mA} \\
& I_{5}=I_{3}+I_{1}=6 \mathrm{mA} \\
& I_{4}=\frac{5}{3} I_{5}=10 \mathrm{mA}
\end{aligned}
\]
The sum of the readings of all ammeters: $I=I_{1}+I_{2}+I_{3}+I_{4}+I_{5}=24$ mA. (2 points)
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=2, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{2019}$.
|
Answer: 2020.
Solution. Let's list the first terms of the sequence:
$$
1,2,4,6,7,7,7,8,10,12,13,13,13,14,16,18,19,19,19,20,21,23, \ldots
$$
We can observe a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{2019}=a_{3+6 \cdot 336}=a_{3}+6 \cdot 636=4+6 \cdot 636=2020
$$
Evaluation. 12 points for a complete solution. If the pattern is noticed but not proven, then (with the correct answer) 6 points.
|
2020
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. The sequence $\left(a_{n}\right)$ is defined by the following relations: $a_{1}=1, a_{2}=3, a_{n}=a_{n-1}-a_{n-2}+n$ (for $n \geqslant 3$). Find $a_{1000}$.
|
Answer: 1002.
Solution. Let's list the first terms of the sequence:
$$
1,3,5,6,6,6,7,9,11,12,12,12,13,15,17,18,18,18,19,21, \ldots
$$
We can see a pattern: $a_{n+6}=a_{n}+6$. Let's prove it. We have
$a_{n+1}=a_{n}-a_{n-1}+n+1=\left(a_{n-1}-a_{n-2}+n\right)-a_{n-1}+n+1=-a_{n-2}+2 n+1$.
By substituting $n$ with $n+2$ in the obtained equation, we get
$$
a_{n+3}=-a_{n}+2(n+2)+1=-a_{n}+2 n+5 .
$$
Now, let's substitute $n$ with $n+3$:
$$
a_{n+6}=-a_{n+3}+2(n+3)+5=a_{n}-2 n-5+2(n+3)+5=a_{n}+6
$$
Now it's easy to find the answer:
$$
a_{1000}=a_{4+6 \cdot 166}=a_{4}+6 \cdot 166=6+6 \cdot 166=1002
$$
Evaluation. Full solution is worth 12 points. If the pattern is noticed but not proven, then (with the correct answer) 6 points.
|
1002
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. (17 points) The price of an entry ticket to the stadium is 400 p. After reducing the entry fee, the number of spectators increased by $25 \%$, and the revenue increased by $12.5 \%$. What is the new price of the entry ticket after the price reduction?
|
Answer: 360
Solution. Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 1.25 = 400 - 1.125$. From which $x = 360$.
|
360
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. (17 points) The price of an entry ticket to the stadium is 400 p. After increasing the entry fee, the number of spectators decreased by $20 \%$, but the revenue increased by $5 \%$. What is the new price of the entry ticket after the price increase?
|
Answer: 525
Solution. Let the number of viewers before the ticket price reduction be 1 person. Then the revenue was 400 rubles. Let $x$ rubles be the new ticket price. We get the equation $x \cdot 0.8 = 400 \cdot 1.05$. From which $x=525$.
|
525
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (16 points) A chess player played 42 games and scored 30 points (1 point for each win, -0.5 points for each draw, 0 points for each loss). Find the difference between the number of his wins and the number of his losses.
|
Answer: 18
Solution. Let the chess player have $n$ wins and $m$ losses. Then we get $n+0.5 \cdot(42-n-m)=30$. In the end, $n-m=18$.
|
18
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (20 points) An aluminum and a copper part have the same volume. The density of aluminum $\rho_{A}=2700 \mathrm{kg} / \mathrm{m}^{3}$, the density of copper $\rho_{M}=8900 \mathrm{kg} / \mathrm{m}^{3}$. Find the mass of copper, if it is known that the masses of the parts differ by $\Delta m=60 \mathrm{g}$.
|
Answer: 862
Solution. Volume of aluminum: $V=\frac{m_{M}-\Delta m}{\rho_{A}}$, volume of copper: $V=\frac{m_{M}}{\rho_{M}}$. We get: $\frac{m_{M}}{\rho_{M}}=\frac{m_{M}-\Delta m}{\rho_{A}} . \quad$ From this, the mass of aluminum: $m_{A}=\frac{\Delta m \cdot \rho_{M}}{\rho_{M}-\rho_{A}}=\frac{0.06 \cdot 8900}{8900-2700} \approx 0.086 \kappa 2 \approx 86 g$.
|
862
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. A mowing crew mowed the entire meadow in two days. On the first day, half of the meadow and another 3 hectares were mowed, and on the second day, a third of the remaining area and another 6 hectares were mowed. What is the area of the meadow?
|
Answer: 24 hectares.
Solution. 6 hectares made up two-thirds of the remainder. Therefore, 9 hectares were mowed on the second day. Together with the 3 hectares from the first day, this totals 12 hectares, which constitute half of the meadow's area. Therefore, the total area of the meadow is 24 hectares.
Evaluation. 12 points for the correct solution.
|
24
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. (16 points) After walking one-fifth of the way from home to school, Olya realized she had forgotten her notebook. If she does not go back for it, she will arrive at school 6 minutes before the bell, but if she returns, she will be 2 minutes late. How much time (in minutes) does the journey to school take?
|
# Answer: 20 min
Solution. The extra $2 / 5$ of the journey takes 8 min. Therefore, the entire journey to school will take 20 min.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (17 points) In a $5 \times 5$ grid, 6 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 4200
Solution. From the condition, it follows that in some row $a$ and some column $b$ there are two crosses (and in all other rows and columns - one each). Both row $a$ and column $b$ can be chosen in 5 ways. There are two possible cases.
First. At the intersection of $a$ and $b$, there is a cross. We choose one more cross from each line in 4 ways. Now, three rows and three columns remain unoccupied. The remaining crosses are placed at their intersections in $3 \cdot 2 \cdot 1=6$ ways. Thus, there are $5 \cdot 5 \cdot 4 \cdot 4 \cdot 6=2400$ arrangements of the first type.
Second. At the intersection of $a$ and $b$, there is no cross. Then, we choose two crosses from each of these two lines in $4 \cdot 3 / 2=6$ ways. Now, two rows and two columns remain unoccupied. The remaining crosses are placed at their intersections in two ways. Thus, there are $5 \cdot 5 \cdot 6 \cdot 6 \cdot 2=1800$ arrangements of the second type.
In total, there are $2400+1800=4200$ ways to arrange 6 crosses.
|
4200
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (20 points) A bullet with a mass of $m=10$ g, flying horizontally at a speed of $v_{1}=500 \mathrm{M} / \mathrm{c}$, penetrates a massive board and exits with a speed of $v_{2}=200 \mathrm{M} / \mathrm{c}$. Find the magnitude of the work done on the bullet by the resistance force of the board.
|
Answer: 1050 J
Solution. From the law of conservation of energy, it follows that
$$
A=\frac{m v_{1}^{2}}{2}-\frac{m v_{2}^{2}}{2}=\frac{0.01 \cdot 500^{2}}{2}-\frac{0.01 \cdot 200^{2}}{2}=1050 \text { J. }
$$
|
1050
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (15 points) A light ray falls at an angle $\alpha=30^{\circ}$ on the front surface of a parallel glass plate. The refractive index of the glass is $n=1.5$. By what angle is the ray, reflected from the back surface of the plate and exiting back through the front surface, deflected from the direction of the incident ray?
|
Answer: $120^{\circ}$
Solution. The described situation is illustrated in the figure.
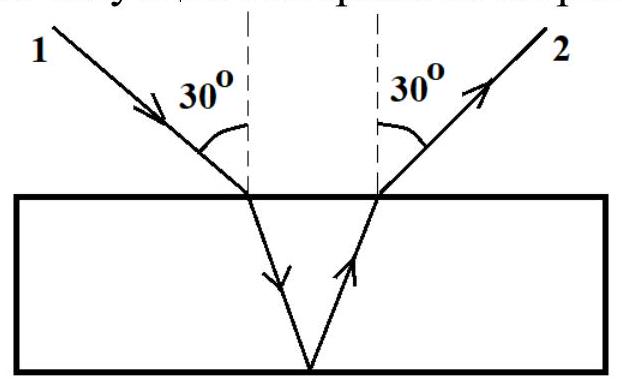
We need to find the angle between rays 1 and 2. It is clear that the required angle is $180^{\circ}-2 \alpha=120^{\circ}$.
|
120
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (17 points) In a $4 \times 4$ grid, 5 crosses need to be placed such that each row and each column contains at least one cross. How many ways can this be done?
|
# Answer: 432
Solution. From the condition, it follows that in some row $a$ and some column $b$ there are two crosses (and in all other rows and columns - one each). Both row $a$ and column $b$ can be chosen in 4 ways. There are two possible cases.
First. At the intersection of $a$ and $b$, there is a cross. We choose one more cross from each line in 3 ways. Now, two rows and two columns remain unoccupied. The remaining crosses are placed at their intersections in 2 ways. Thus, there are 4.4$\cdot$3$\cdot$3$\cdot$2=288 arrangements of the first type.
Second. At the intersection of $a$ and $b$, there is no cross. Then, we choose two crosses from each of these two lines in 3 ways. Now, only one row and one column remain unoccupied, at the intersection of which a cross needs to be placed. Thus, there are 4$\cdot$4$\cdot$3$\cdot$3=144 arrangements of the second type. In total, there are $288+144=432$ ways to arrange 5 crosses.
|
432
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (20 points) A bullet with a mass of $m=10$ g, flying horizontally at a speed of $v_{1}=400 \mathrm{m} / \mathrm{s}$, penetrates a massive board and exits with a speed of $v_{2}=100 \mathrm{m} / \mathrm{s}$. Find the magnitude of the work done on the bullet by the resistance force of the board.
|
Answer: 750 J
Solution. From the law of conservation of energy, it follows that
$$
A=\frac{m v_{1}^{2}}{2}-\frac{m v_{2}^{2}}{2}=\frac{0.01 \cdot 400^{2}}{2}-\frac{0.01 \cdot 100^{2}}{2}=750 \text { J. }
$$
|
750
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (15 points) A light ray falls at an angle $\alpha=60^{\circ}$ on the front surface of a parallel glass plate. The refractive index of the glass is $n=1.6$. By what angle is the ray, reflected from the back surface of the plate and exiting back through the front surface, deflected from the direction of the incident ray?
|
Answer: $60^{\circ}$
Solution. The described situation is illustrated in the figure.
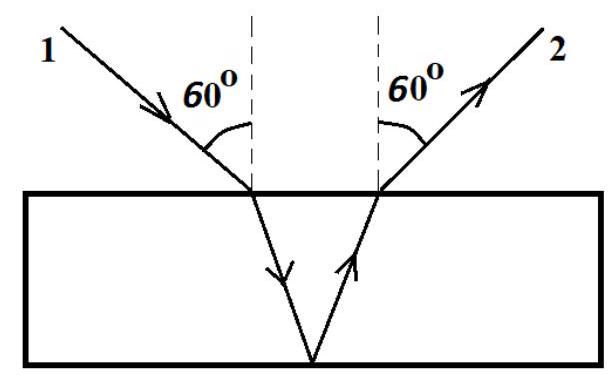
We need to find the angle between rays 1 and 2. It is clear that the required angle is $180^{\circ}-2 \alpha=60^{\circ}$
|
60
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
# Problem №4 (10 points)
A parallel beam of light falls on the base of a glass cone (refractive index $n=1.5$) along its axis (see fig.). The cross-section of the beam coincides with the base of the cone, the radius
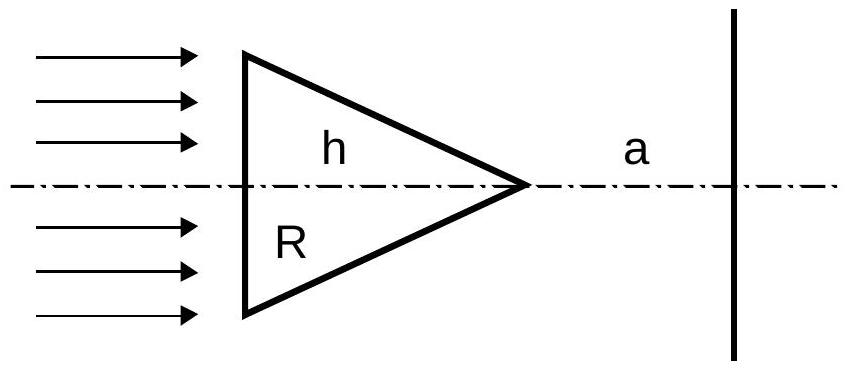
of which is $R=1 \mathrm{~cm}$. The height of the cone is $h=1.73 \mathrm{~cm}$. Determine the area of the bright spot on the screen, perpendicular to the axis of the cone and located at a distance $a=1$ cm from the vertex of the cone.
#
|
# Solution:
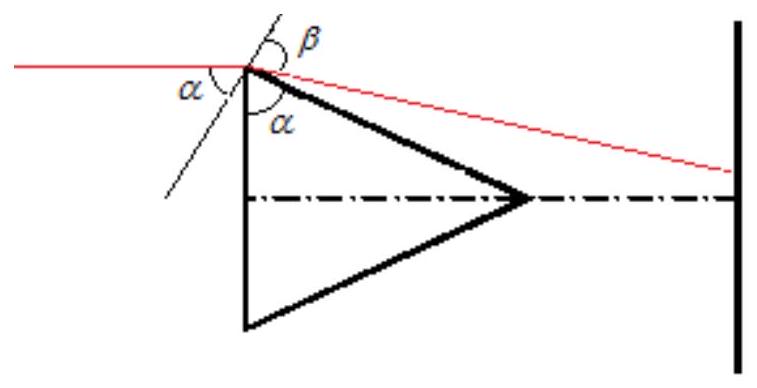
$\operatorname{tg} \alpha=\frac{h}{R}=1.73$, i.e., $\alpha=60^{\circ}$
The law of refraction for rays passing through the cone:
$\frac{\sin \alpha}{\sin \beta}=\frac{1}{1.5}$
As a result: $\sin \beta=\frac{3 \sqrt{3}}{4} \geq 1$
We obtain that the rays passing through the cone experience total internal reflection.
From geometric considerations, it is found that they fall on the other side of the cone at the normal.
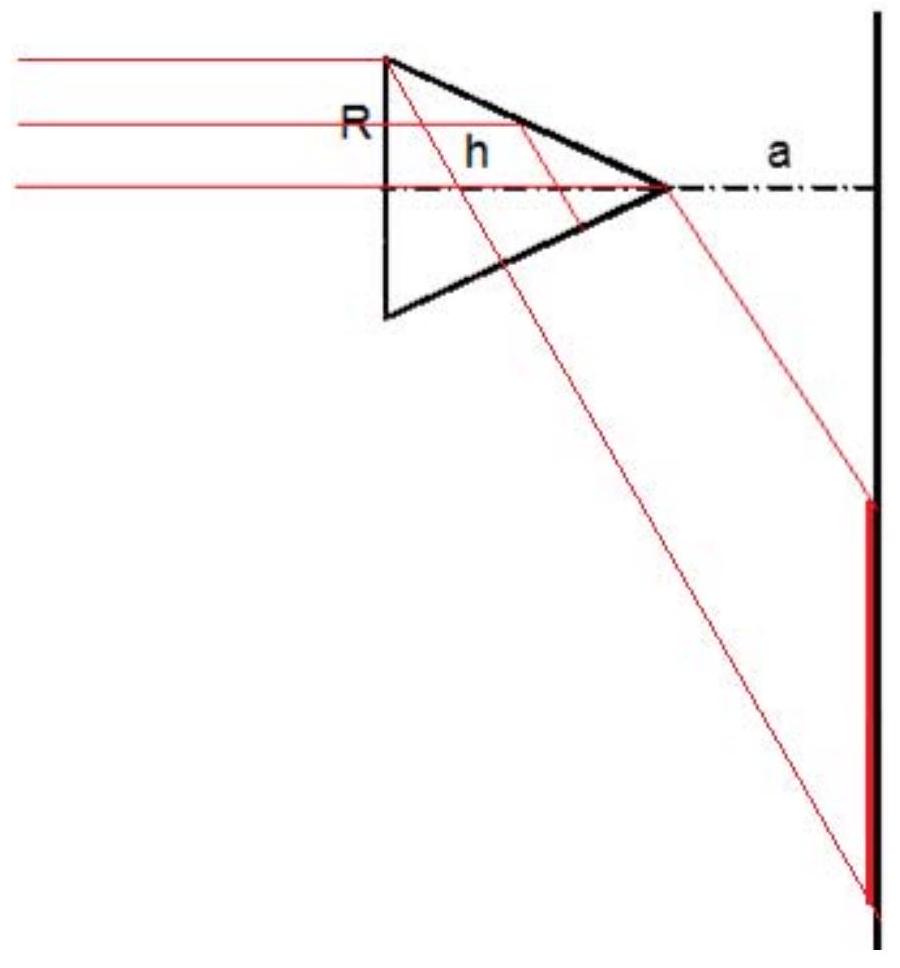
(2 points)
Therefore, the light spot on the screen is bounded by two circles with radii:
$R_{1}=a \cdot \operatorname{tg} 60^{\circ}=0.01 \sqrt{3}=0.0173 \text{ m}$
$R_{2}=\left((h+a) \cdot \operatorname{tg} 60^{\circ}\right)-R=0.0273 \sqrt{3}-0.01=0.0373 \text{ m}$
We obtain:
$S=\pi R_{2}^{2}-\pi R_{1}^{2}=0.0034 \text{ m}^{2}=34 \text{ cm}^{2}$
# Multidisciplinary Engineering Olympiad "Star" NATURAL SCIENCES 2016
March 29, 2016
PROTOCOL № 1 of the meeting of the jury
PRESENT: Keller A.V., Zalyapin V.I., Zamishlyayeva A.A., Vorontsov A.G., Kuts D.A., Gusev A.V.
HEARD: on the distribution of points among the winners and prizewinners of the olympiad
## 11th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 45 points.
## 10th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 95 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 94 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 9th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 8th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 75 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 74 - 65 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 64 - 40 points.
## 7th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 70 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 69 - 40 points.
## 6th Grade
- to consider the winners of the olympiad and award diplomas of the 1st degree to participants who scored 100 - 90 points;
- to consider the prizewinners of the olympiad and award diplomas of the 2nd degree to participants who scored 89 - 80 points;
- to consider the prizewinners of the olympiad and award diplomas of the 3rd degree to participants who scored 79 - 40 points.
## Chairmen of the jury:

Keller A.V.
Vorontsov A.G.
|
34
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Andrei, Boris, and Valentin participated in a 1 km race. (We assume that each of them ran at a constant speed). Andrei was 50 m ahead of Boris at the finish line. And Boris was 40 m ahead of Valentin at the finish line. What was the distance between Andrei and Valentin at the moment Andrei finished?
|
Answer: 88 m.
Solution. Let the speeds of Andrey, Boris, and Valentin be $a, b$, and $c$ m/s, respectively. From the condition, it follows that $b=0.95 a, c=0.96 b$. Therefore, $c=0.96 \cdot 0.95 a=0.912 a$. This means that when Andrey runs 1000 m, Valentin will cover 912 m. The lag will be 88 m.
Evaluation. 12 points for a correct solution.
|
88
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. A palindrome is a number that reads the same from left to right and from right to left. For example, the numbers 353 and $4884-$ are palindromes. It is known that a three-digit number $x$ is a palindrome. To it, 32 was added and a four-digit number was obtained, which is also a palindrome. Find $x$.
|
# Answer: 969.
Solution. Since $x+32$ is a four-digit number, the inequality $x+32 \geqslant 1000$ holds, from which $x \geqslant 968$. From the fact that $x$ is a three-digit palindrome, we get that this number starts and ends with the digit 9, and its middle digit is not less than 6. By checking the four possible options, we find the only answer.
Evaluation. If the answer is found but its uniqueness is not proven, 6 points. For a complete solution, 12 points.
|
969
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. An aquarium in the shape of a rectangular parallelepiped has dimensions: length $1.5 m$, width - $400 mm$, height - 80 cm. It is filled with water at a rate of 2 liters/minute. How many seconds after the start of filling will the aquarium be completely filled? (10 points)
|
Answer: 14400 s
Solution. Volume of the aquarium $\quad V=1.5 \cdot 0.4 \cdot 0.8=0.48 \mathrm{~m}^{3}$.
Filling rate $v=\frac{0.002 \mu^{3}}{60 s}$ (3 points). The aquarium will be completely filled in time $\quad t=\frac{V}{v}=\frac{0.48 \cdot 60}{0.002}=14400 ~ s \quad(4$ points $)$.
|
14400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. Two people are walking towards each other from points $A$ and $B$ with speeds $v_{1}=6 \mathrm{~m} / \mathrm{s}$ and $v_{2}=4 \mathrm{~m} / \mathrm{s}$. At the moment of their meeting, one of them turned around and walked in the opposite direction, while the other continued in the same direction. The person who turned around, upon returning to their starting point, waited for the second person. They waited for $t_{2}=10 \mathrm{min}$. Determine how much time $t_{1}$ passed from the start of the journey until the meeting. (15 points)
|
Answer: 20 min
Solution. Let $S$ be the distance between points A and B. We get $S=v_{1} t_{1}+v_{2} t_{1}$ (5 points). In addition, the same distance can be expressed as follows: $S=v_{2} t_{1}+v_{2} t_{1}+v_{2} t_{2}$ (5 points). As a result, we get $t_{1}=\frac{v_{2} t_{2}}{v_{1}-v_{2}}=\frac{4 \cdot 10}{6-4}=20 \text{min}$ (5 points).
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. A snail is crawling from one tree to another. In half a day, it crawled $l_{1}=4$ m. It realized it was all too much and turned back. It crawled $l_{2}=3$ m. It got tired. It fell asleep. The next day, everything repeated. And so every day. The distance between the trees is $s=40$ m. On which day of its journey will the snail reach the tree? (10 points)
|
Answer: on the 37th day
Solution. In one day, the snail advances towards the other tree by:
$\Delta l=l_{1}-l_{2}=1$ m (3 points). At a distance of $l_{1}=4$ m (i.e., one transition) from its goal, it will be after 36 days of travel (4 points). Therefore, the goal will be reached on the 37th day of travel (3 points).
## Tasks, answers, and evaluation criteria
6th grade
|
37
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. A palindrome is a number that reads the same from left to right and from right to left. For example, the numbers 333 and $4884-$ are palindromes. It is known that a three-digit number $x$ is a palindrome. To it, 22 was added and a four-digit number was obtained, which is also a palindrome. Find $x$.
|
# Answer: 979.
Solution. Since $x+22$ is a four-digit number, the inequality $x+22 \geqslant 1000$ holds, from which $x \geqslant 978$. From the fact that $x$ is a three-digit palindrome, we get that this number starts and ends with the digit 9, and its middle digit is not less than 7. By checking the four possible options, we find the only answer.
Evaluation. If the answer is found but its uniqueness is not proven, 6 points. For a complete solution, 12 points.
|
979
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. An aquarium in the shape of a rectangular parallelepiped has dimensions: length $2 m$, width - 600 mm, height - 60 cm. It is filled with water at a rate of 3 liters/minute. How many seconds after the start of filling will the aquarium be completely filled? (10 points)
|
Answer: 14400 s
Solution. Volume of the aquarium: $V=2 \cdot 0.6 \cdot 0.6=0.72 m^{3}$ (3 points). Filling rate: $v=\frac{0.003 m^{3}}{60 s}$ (3 points). The aquarium will be completely filled in: $t=\frac{V}{v}=\frac{0.72 \cdot 60}{0.003}=14400 s$ (4 points).
|
14400
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. Two people are walking towards each other from points $A$ and $B$ with speeds $v_{1}=6 \mathrm{~m} / \mathrm{c}$ and $v_{2}=4 \mathrm{~m} / \mathrm{c}$. At the moment of their meeting, one of them turned around and walked in the opposite direction, while the other continued in the same direction. The person who did not change direction arrived at the final point of their journey $t_{2}=10$ minutes earlier than the person who turned around. Determine how much time $t_{1}$ passed from the start of the journey until the meeting. (15 points)
|
Answer: 30 min
Solution. The distance from point $B$ to the meeting place $S=v_{2} t_{1}$ (5 points). In addition, the same distance can be expressed as follows: $S=v_{1}\left(t_{1}-t_{2}\right)$ (5 points). As a result, we get: $t_{1}=\frac{v_{1} t_{2}}{v_{1}-v_{2}}=\frac{6 \cdot 10}{6-4}=30$ min (5 points).
|
30
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. A snail is crawling from one tree to another. In half a day, it crawled $l_{1}=5$ m. It realized it was all too much and turned back. It crawled $l_{2}=4$ m. It got tired. It fell asleep. The next day, everything repeated. And so every day. The distance between the trees is $s=30$ m. On which day of its journey will the snail reach the tree? (10 points)
|
Answer: on the 26th day
Solution. In one day, the snail advances towards the other tree by:
$\Delta l=l_{1}-l_{2}=1$ m (3 points). At a distance of $l_{1}=5$ m (i.e., one transition) from its goal, it will be after 25 days of travel (4 points). Therefore, the goal will be reached on the 26th day of travel. (3 points).
|
26
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Let $a, b, c, d, e$ be positive integers. Their sum is 2018. Let $M=\max (a+b, b+c, c+d, d+e)$. Find the smallest possible value of $M$.
|
Answer: 673.
Solution. Estimation. We have the inequalities
$$
a+b \leqslant M ; \quad b+c \leqslant M ; \quad c+d \leqslant M ; \quad d+e \leqslant M
$$
Multiply the first and last inequalities by 2 and add the other two. We get:
$$
2(a+b+c+d+e)+b+d \leqslant 6 M ; \quad 6 M \geqslant 4036+b+d \geqslant 4038 ; \quad M \geqslant 673 .
$$
Example. The equality $M=673$ is achieved when $a=c=e=672$, $b=d=1$.
Evaluation. 14 points for a correct solution. If there is only a correct example, 7 points.
## Multidisciplinary Engineering Olympiad "Star" in Natural Sciences Final Stage 2017-2018 academic year Problems, answers, and evaluation criteria 9th grade Variant 1 physics
|
673
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. The specific heat capacity of a body with a mass of $m=2$ kg depends on the temperature as follows: $c=c_{0}(1+\alpha t)$, where $c_{0}=150$ J/kg ${ }^{\circ} \mathrm{C}-$ specific heat capacity at $0^{\circ} \mathrm{C}, \alpha=0.05^{\circ} \mathrm{C}^{-1}$ - temperature coefficient, $t$ - temperature in degrees Celsius. Determine the amount of heat that must be transferred to this body to heat it from $20^{\circ} \mathrm{C}$ to $100^{\circ} \mathrm{C}$. (10 points)
|
Answer: 96 kJ
Solution. Given that the specific heat capacity depends linearly on temperature, we can calculate its average value: $c_{c p}=\frac{c_{0}\left(1+\alpha t_{h}\right)+c_{0}\left(1+\alpha_{\kappa}\right)}{2}=600 \frac{\text { J }}{\text { kg } \cdot{ }^{\circ} \mathrm{C}} \quad(5$ points). The required amount of heat: $Q=c_{\varphi} m \Delta t=600 \cdot 2 \cdot 80=96000$ J = 96 kJ (5 points $)$.
|
96
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. A parallel beam of light falls normally on a thin lens. Behind the lens, at a distance of $80 \mathrm{~cm}$ from it, there is a screen on which a circular spot of a certain diameter is visible. If the screen is moved 40 cm, a spot of the same diameter will again be visible on the screen. Determine the focal length of the lens.
## (15 points)
|
Answer: 100 cm or 60 cm
Solution. A diagram explaining the situation described in the problem (5 points):
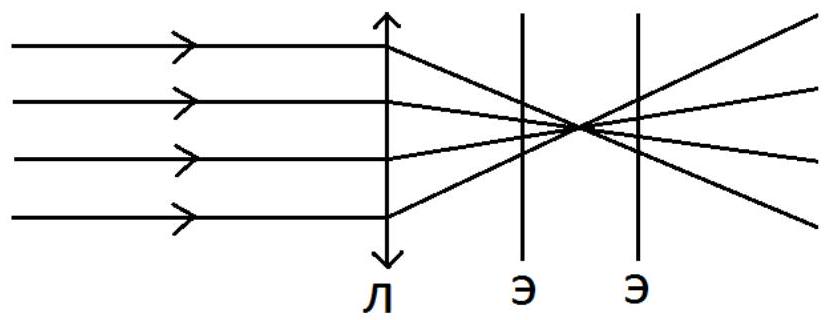
From this, it is clear that there are two possible scenarios: the screen can be moved away from the lens or moved closer to it. As a result, the focal length of the lens $F_{1}=80+20=100$ cm (5 points). Or $F_{2}=80-20=60$ cm (5 points).
## Final Stage
2017-2018 academic year
## Tasks, answers, and evaluation criteria
9th grade
Variant II
hatf Ћвtgr
r
|
100
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. Let $a, b, c, d, e$ be positive integers. Their sum is 2345. Let $M=\max (a+b, b+c, c+d, d+e)$. Find the smallest possible value of $M$.
|
Answer: 782.
Solution. Estimation. We have the inequalities
$$
a+b \leqslant M ; \quad b+c \leqslant M ; \quad c+d \leqslant M ; \quad d+e \leqslant M
$$
Multiply the first and last inequalities by 2 and add the other two. We get:
$2(a+b+c+d+e)+b+d \leqslant 6 M ; \quad 6 M \geqslant 4690+b+d \geqslant 4692 ; \quad M \geqslant 782$.
Example. The equality $M=782$ is achieved when $a=c=e=781$, $b=d=1$.
Evaluation. 14 points for a correct solution. If there is only a correct example, 7 points.
## Multidisciplinary Engineering Olympiad "Star" in Natural Sciences Final Stage 2017-2018 academic year Problems, answers, and evaluation criteria 9th grade Variant 2 physics
|
782
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. A parallel beam of light falls normally on a thin lens with a focal length of $F=150$ cm. Behind the lens, there is a screen on which a circular spot of a certain diameter is visible. If the screen is moved 40 cm, a spot of the same diameter will again be visible on the screen. Determine the initial distance from the lens to the screen. (15 points)
|
Answer: 170 cm or 130 cm
Solution. A diagram explaining the situation described in the problem (5 points):
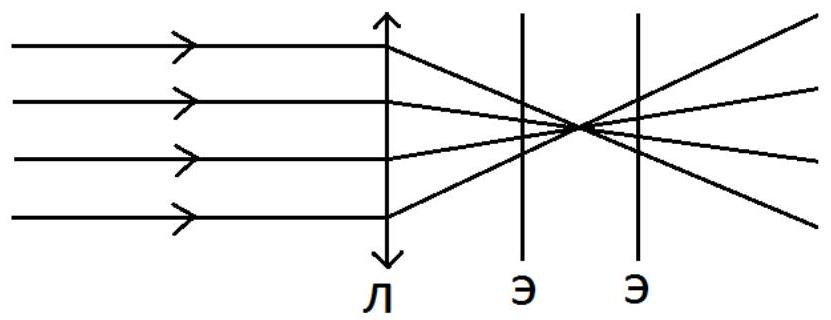
From this, we can see that there are two possible scenarios: the screen can be moved away from the lens or moved closer to it. As a result, the initial distance from the lens to the screen:
$S_{1}=150+20=170 \mathrm{~cm} \quad\left(5\right.$ points) or $S_{2}=150-20=130 \mathrm{~cm}$ (5 points).
|
170
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On a circle, 40 red points and one blue point are marked. All possible polygons with vertices at the marked points are considered. Which type of polygons is more numerous, and by how many: those with a blue vertex, or those without it?
|
Answer: The number of polygons with a blue vertex is 780 more than the number of polygons without a blue vertex.
Solution. Let's call polygons with a blue vertex blue, and those without a blue vertex red. Take an arbitrary red polygon. Adding a blue vertex to it gives exactly one blue polygon. Thus, any blue polygon with at least four vertices can be obtained this way. Therefore, the difference between the number of blue polygons and the number of red polygons is equal to the number of blue triangles. The number of blue triangles is the same as the number of ways to choose two red points (two red vertices of a blue triangle), i.e., $\frac{40 \cdot 39}{2} = 780$.
Evaluation. 14 points for a correct solution.
## Tasks, answers, and evaluation criteria
7th grade
Variant 1 physics
|
780
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. At the ends of a vertically positioned homogeneous spring, two small loads are fixed. Above is a load with mass $m_{1}$, and below is $-m_{2}$. A person grabbed the middle of the spring and held it vertically in the air. In this case, the upper half of the spring was deformed by $x_{1}=8 \mathrm{~cm}$, and the lower half by $x_{2}=15 \mathrm{~cm}$. After that, he placed the spring on a horizontal surface without flipping it and released it. Determine the magnitude of the spring's deformation in this case. Neglect the size of the person's hand compared to the length of the spring.
## $(15$ points)
|
Answer: 16 cm
Solution. If the stiffness of the spring is $k$, then the stiffness of half the spring is $2 k$ (4 points). For the situation where the spring is held by a person: $m_{1} g=2 k x_{1}$ (4 points).
For the situation where the spring stands on a surface: $m_{1} g=k x$ (4 points). We obtain that $x=2 x_{1}=16$ cm (3 points).
|
16
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. On a circle, 60 red points and one blue point are marked. All possible polygons with vertices at the marked points are considered. Which type of polygons is more numerous, and by how many: those with a blue vertex, or those without it?
|
Answer: The number of polygons with a blue vertex is 1770 more than the number of polygons without a blue vertex.
Solution. Let's call polygons with a blue vertex blue, and those without a blue vertex red. Take an arbitrary red polygon. Adding a blue vertex to it gives exactly one blue polygon. Thus, any blue polygon with at least four vertices can be obtained this way. Therefore, the difference between the number of blue polygons and the number of red polygons is equal to the number of blue triangles. The number of blue triangles is the same as the number of ways to choose two red points (two red vertices of a blue triangle), i.e., $\frac{60 \cdot 59}{2}=1770$.
Evaluation. 14 points for a correct solution.
## Multidisciplinary Engineering Olympiad "Star" in Natural Sciences
## Final Stage 2017-2018 academic year
## Problems, Answers, and Evaluation Criteria
## 7th Grade Variant 2
physics5. A person is walking parallel to a railway track at a constant speed. A train also passes by at a constant speed. The person noticed that depending on the direction of the train's movement, it passes by in either $t_{1}=2 \text{ min}$ or $t_{2}=4$ min. Determine how long it would take the person to walk from one end of the train to the other.
## (15 points)
Answer: 8 min
Solution. When the train and the person are moving towards each other, $l=\left(v_{n}+v_{4}\right) \cdot t_{1} \quad$ (3 points), where $l$ is the length of the train, $v_{n}$ is its speed, and $v_{4}$ is the person's speed. If the directions of the train and the person are the same, then $l=\left(v_{n}-v_{4}\right) \cdot t_{2} \quad$ (3 points). In the situation where the person is walking along the train: $l=v_{u} \cdot t_{3}$ (3 points). Solving this system of equations, we get the final answer: $t_{3}=\frac{2 t_{1} t_{2}}{t_{2}-t_{1}}=\frac{2 \cdot 2 \cdot 4}{4-2}=8$ minutes (6 points).
|
1770
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the sum of all four-digit numbers in which the digits $0,3,6,9$ do not appear.
|
Answer: $9999 \cdot 6^{4} / 2=6479352$.
Solution. All four-digit numbers that meet the condition of the problem are divided into pairs of numbers of the form (1111,8888), (1112,8887), (1113,8886), ..., (4555,5444). In each pair, the sum of the numbers is 9999. Let's count the number of pairs. In total, there are $6^{4}$ four-digit numbers of the specified type (since each digit can be chosen in 4 ways). Therefore, there are half as many pairs. The sum of all numbers is $9999 \cdot 6^{4} / 2=6479352$.
Grading. 12 points for a correct solution. The answer can also be presented as the formula $9999 \cdot 6^{4} / 2$. If the formula is correct but there are arithmetic errors in the calculation using this formula, 10 points.
|
6479352
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. What is the greatest length that a closed, non-self-intersecting broken line can have, which runs along the grid lines of a square grid of size $8 \times 8$?
#
|
# Answer: 80.
Solution. We will color the nodes of the grid in a checkerboard pattern, with black and white colors. The length of a closed non-self-intersecting broken line is equal to the number of nodes it passes through. Each segment of the broken line connects a black and a white node. When traversing the broken line, the colors of the nodes alternate, so the length of the closed broken line is an even number. Since there are 81 nodes in total in the grid, the length of the broken line is at most 80. A corresponding example is easily constructed (Fig. 1).
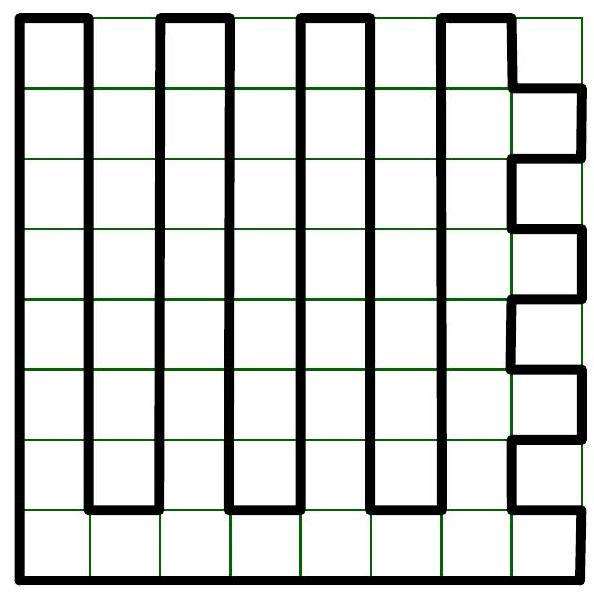
Fig. 1
Remark. Another reasoning is possible. Let's start constructing a closed broken line starting from some node. Since we need to return to it, the number of horizontal steps to the right is the same as the number of steps to the left. Therefore, the number of horizontal steps is even. The same is true for vertical steps. Hence, we again obtain that the length of the closed broken line (whose segments follow the grid lines) is an even number.
Evaluation. 14 points for a correct solution. 1 point if only the answer is given. 4 points if an example of a broken line of length 80 is provided, but there is no estimation of the length of the broken line.
2016-2017 academic year
\section*{Tasks, answers, and evaluation criteria for 7th grade
|
80
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Find the sum of all four-digit numbers in which the digits $0,4,5,9$ do not appear.
|
Answer: $9999 \cdot 6^{4} / 2=6479352$.
Solution. All four-digit numbers that meet the condition of the problem are divided into pairs of numbers of the form (1111,8888$),(1112,8887),(1113,8886)$, $\ldots$... (4555,5444$)$. In each pair, the sum of the numbers is 9999. Let's count the number of pairs. In total, there are $6^{4}$ four-digit numbers of the specified type (since each digit can be chosen in 4 ways). Therefore, there are half as many pairs. The sum of all numbers is $9999 \cdot 6^{4} / 2=6479352$.
Grading. 12 points for a correct solution. The answer can also be presented as the formula $9999 \cdot 6^{4} / 2$. If the formula is correct but there are arithmetic errors in the calculation using this formula, 10 points.
|
6479352
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. What is the greatest length that a closed, non-self-intersecting broken line can have, which runs along the grid lines of a $6 \times 10$ cell field?
|
Answer: 76.
Solution. We will color the nodes of the grid in a checkerboard pattern, with black and white colors. The length of a closed non-self-intersecting broken line is equal to the number of nodes it passes through. Each segment of the broken line connects a black and a white node. When traversing the broken line, the colors of the nodes alternate, so the length of the closed broken line is an even number. Since there are 77 nodes in total in the grid, the length of the broken line is at most 76. A corresponding example is easily constructed (Fig. 2).
Fig. 2
Remark. Another reasoning is possible. Let's start constructing a closed broken line from some node. Since we need to return to it, the number of horizontal steps to the right is the same as the number of steps to the left. Therefore, the number of horizontal steps is even. The same is true for vertical steps. Hence, we again obtain that the length of the closed broken line (whose segments follow the grid lines) is an even number.
Evaluation. 14 points for a correct solution. 1 point if only the answer is given. 4 points if an example of a broken line of length 76 is provided, but there is no estimation of the length of the broken line.
|
76
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given a parallelogram $A B C D$. It is known that the centers of the circles circumscribed around triangles $A B C$ and $C D A$ lie on the diagonal $B D$. Find the angle $D B C$, if $\angle A B D=40^{\circ}$.
|
Answer: $50^{\circ}$ or $40^{\circ}$.
Solution. The center of the circle circumscribed around triangle $A B C$ lies on the perpendicular bisector of segment $A C$. Therefore, either this center is the midpoint of $A C$ (and then $A B C D$ is a rectangle), or $D B \perp A C$ (and then $A B C D$ is a rhombus). In the first case, angle $D B C$ complements angle $A B D$ to a right angle, and in the second case, these angles are equal to each other.
Evaluation. 10 points for a correct solution. If only the case of the rhombus is considered, 6 points. If only the case of the rectangle is considered, 4 points.
|
50
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. Given a parallelogram $A B C D$. It is known that the centers of the circles circumscribed around triangles $A B C$ and $C D A$ lie on the diagonal $B D$. Find the angle $D B C$, if $\angle A B D=35^{\circ}$.
|
Answer: $55^{\circ}$ or $35^{\circ}$.
Solution. The center of the circle circumscribed around triangle $A B C$ lies on the perpendicular bisector of segment $A C$. Therefore, either this center is the midpoint of $A C$ (and then $A B C D$ is a rectangle), or $D B \perp A C$ (and then $A B C D$ is a rhombus). In the first case, angle $D B C$ complements angle $A B D$ to a right angle, and in the second case, these angles are equal to each other.
Evaluation. 10 points for a correct solution. If only the case of the rhombus is considered, 6 points. If only the case of the rectangle is considered, 4 points.
|
55
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. (17 points) Three cyclists, Dima, Misha, and Petya, started a 1 km race simultaneously. At the moment Misha finished, Dima still had to cover one tenth of the distance, and at the moment Dima finished, Petya still had to cover one tenth of the distance. How far apart (in meters) were Petya and Dima when Misha finished? (The cyclists are riding at constant speeds).
|
Answer: 90.
Solution. Let $v_{1}$ be the speed of Misha, $v_{2}$ be the speed of Dima, and $v_{3}$ be the speed of Petya. Then $v_{2}=0.9 v_{1}$, since in the same amount of time Misha traveled 1000 m, while Dima traveled 900 m, and $v_{3}=0.9 v_{2}$, since in the same amount of time Dima traveled 1000 m, while Petya traveled 900 m. Since $v_{3}=$ $0.9 \cdot 0.9 v_{1}=0.81 v_{1}$, at the moment Misha finished, Petya had traveled 810 meters. The distance between Petya and Dima: $900-810=90$.
|
90
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (16 points) In a class, some students study only English, some study only German, and some study both languages. What percentage of the class studies both languages if 90% of all students study English and 80% study German?
|
Answer: 70.
Solution. From the condition, it follows that $10 \%$ do not study English and $20 \%$ do not study German. Therefore, $10 \%+20 \%=30 \%$ study only one language, and the remaining $70 \%$ study both languages.
|
70
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
1. (17 points) Three cyclists, Dima, Misha, and Petya, started a 1 km race simultaneously. At the moment Misha finished, Dima still had to cover one tenth of the distance, and at the moment Dima finished, Petya still had to cover one tenth of the distance. How far apart (in meters) were Petya and Misha when Misha finished? (The cyclists are riding at constant speeds).
|
Answer: 190.
Solution. Let $v_{1}$ be the speed of Misha, $v_{2}$ be the speed of Dima, and $v_{3}$ be the speed of Petya. Then $v_{2}=0.9 v_{1}$, since in the same time Misha traveled $1000 \mathrm{m}$, while Dima traveled $900 \mathrm{m}$, and $v_{3}=0.9 v_{2}$, since in the same time Dima traveled 1000 m, while Petya traveled 900 m. Since $v_{3}=$ $0.9 \cdot 0.9 v_{1}=0.81 v_{1}$, at the moment Misha finished, Petya had traveled 810 meters. The distance between Petya and Misha:
$1000-810=190$
|
190
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (17 points) Point $M$ lies inside segment $A B$, the length of which is 60 cm. Points are chosen: $N$ at the midpoint of $A M, P$ at the midpoint of $M B, C$ at the midpoint of $N M, D$ at the midpoint of $M P$. Find the length of segment $C D$.
|
Answer: 15 cm.
## Solution.
$$
\begin{aligned}
& \quad \dot{N} \quad \dot{C} \quad \dot{M} \dot{D} \cdot B \\
& N P=N M+M P=\frac{1}{2} A M+\frac{1}{2} M B=\frac{1}{2} A B=30 \\
& C D=C M+M D=\frac{1}{2} N M+\frac{1}{2} M P=\frac{1}{2} N P=15
\end{aligned}
$$
|
15
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (16 points) In a class, some students study only English, some study only German, and some study both languages. What percentage of the class studies both languages if 80% of all students study English and 70% study German?
|
Answer: 50.
Solution. From the condition, it follows that $20 \%$ do not study English and $30 \%$ do not study German. Therefore, $20 \%+30 \%=50 \%$ study only one language, and the remaining $50 \%$ study both languages.
|
50
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (16 points) Aunt Masha decided to bake a cake. She kneaded the dough, which according to the recipe contains flour, butter, and sugar in the weight ratio of $3: 2: 1$, and mixed butter with sugar for the cream in the ratio of 2:3. Changing her mind about baking the cake, she combined both mixtures, added 200 g of flour, and prepared dough for cookies, in which flour, butter, and sugar are in the ratio of 5:3:2. How much butter did Aunt Masha use? Write the answer in grams.
|
Answer: 480.
Solution. Let the cake dough contain flour, butter, and sugar in the amounts of $3 x$, $2 x$, and $x$ respectively, and the cream contain butter and sugar in the amounts of $2 y$ and $3 y$ respectively. Using the ratios for the cookies, we get the system of equations $\left\{\begin{array}{l}\frac{3 x+200}{2 x+2 y}=\frac{5}{3}, \\ \frac{2 x+2 y}{x+3 y}=\frac{3}{2} .\end{array}\right.$ After transformations, we get the system $\left\{\begin{array}{c}x+10 y=600, \\ x-5 y=0 .\end{array}\right.$ From which we find that $x=200, y=40$. Therefore, Aunt Masha spent $2 x+2 y=400+80=480$ grams of butter.
|
480
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (15 points) A ball was thrown vertically upwards from a balcony. It is known that it hit the ground after 6 seconds. Given that the initial speed of the ball is 20 m/s, determine the height of the balcony. The acceleration due to gravity is 10 m/s².
|
Answer: 60 m.
Solution. The equation of motion of the ball:
$$
y=0=h_{0}+v_{0} t-\frac{g t^{2}}{2}=h_{0}+20 \cdot 6-\frac{10 \cdot 6^{2}}{2}
$$
We get $h_{0}=60 m$ m.
|
60
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (20 points) Two mutually perpendicular rays, propagating in the same vertical plane, fall from air onto a horizontal glass surface.
The refractive index of the glass $n=1.5$. The angle of refraction for the first ray $\beta=25^{\circ}$. Determine the angle between the refracted rays.
|
Answer: $56^{\circ}$.
Solution. The law of refraction for the first ray $\frac{\sin \alpha}{\sin 25^{\circ}}=1.5$. Therefore, the angle of incidence of the first ray $\alpha=39.34^{\circ}$. The angle of incidence of the second ray $\beta=90^{\circ}-39.34^{\circ}=$ $50.66^{\circ}$. The law of refraction for the second ray $\frac{\sin 50.66^{\circ}}{\sin \gamma}=1.5$. The angle of refraction of the second ray $\gamma=31^{\circ}$. The angle between the refracted rays: $\beta+\gamma=56^{\circ}$.
|
56
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (16 points) Aunt Masha decided to bake a cake. She mixed the dough, which according to the recipe includes flour, butter, and sugar in the weight ratio of $3: 2: 1$, and mixed butter with sugar for the cream in the ratio of $2: 3$. Changing her mind about baking the cake, she combined both mixtures, added 300 g of flour, and prepared dough for cookies, in which flour, butter, and sugar are in the ratio of 5:3:2. How much flour did Aunt Masha use? Write the answer in grams.
|
Answer: 1200.
Solution. Let the dough for the cake contain flour, butter, and sugar in the amounts of $3x$, $2x$, and $x$ respectively, and the cream contain butter and sugar in the amounts of $2y$ and $3y$ respectively. Using the ratios for the cookies, we get the system of equations $\left\{\begin{array}{l}\frac{3x+300}{2x+2y}=\frac{5}{3}, \\ \frac{2x+2y}{x+3y}=\frac{3}{2} .\end{array}\right.$
We find that $x=300, y=60$. Thus, Aunt Masha spent $3x+300=900+300=1200$ grams of flour.
3. (17 points) In a right triangle, the legs are 5 and 12. Find the distance between the centers of the inscribed and circumscribed circles. Write the square of this distance in the answer.
Answer: 16.25.
Solution. By the Pythagorean theorem, the hypotenuse is 13, and the area of the triangle is $S=\frac{1}{2} \cdot 5 \cdot 12=30$. The semiperimeter $p=\frac{5+12+13}{2}=15$, so the radius of the inscribed circle $r=\frac{s}{p}=2$. Let $O_{1}$ be the center of the inscribed circle, $O_{1}P$ and $O_{1}K$ be the radii of the inscribed circle, drawn to the leg and the hypotenuse at the points of tangency of the circle, with legs $BC=12, AC=5$ by the problem statement. We have $BP=BC-r=12-2=10$. By the property of tangents drawn from one point to a circle, $BK=BP=10$. The center of the circumscribed circle $O_{2}$ around the right triangle lies at the midpoint of the hypotenuse and $BO_{2}=6.5$.
In the right triangle $KO_{1}O_{2}$, we have $KO_{2}=10-6.5=3.5, KO_{1}=r=2, O_{1}O_{2}$ is the desired distance. By the Pythagorean theorem, $O_{1}O_{2}^2=4+12.25=16.25$.
|
1200
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (20 points) Two mutually perpendicular rays, propagating in the same vertical plane, fall from air onto a horizontal glass surface. The refractive index of the glass $n=1.6$. The angle of refraction for the first ray $\beta=30^{\circ}$. Determine the angle between the refracted rays.
|
Answer: $52^{\circ}$.
Solution. The law of refraction for the first ray $\frac{\sin \alpha}{\sin 30^{\circ}}=1.6$. Therefore, the angle of incidence of the first ray $\alpha=53.13^{0}$. The angle of incidence of the second ray $\beta=90^{0}-53.13^{0}=$ $36.87^{\circ}$. The law of refraction for the second ray $\frac{\sin 36.87^{\circ}}{\sin \gamma}=1.6$. The angle of refraction of the second ray $\gamma=22^{0}$. In the end, we get the angle between the refracted rays $\beta+$ $\gamma=52^{0}$.
|
52
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (15 points) Two springs with stiffnesses of $6 \mathrm{kH} / \mathrm{m}$ and $12 \mathrm{kH} / \mathrm{m}$ are connected in series. How much work is required to stretch this system by 10 cm.
|
Answer: 20 J.
Solution. Total stiffness: $k=\frac{k_{1} k_{2}}{k_{1}+k_{2}}=\frac{6 \cdot 12}{6+12}=4 \mathrm{kH} / \mathrm{m}$. Work:
$$
A=\Delta W=\frac{k x^{2}}{2}=\frac{4000 \cdot \cdot 0.1^{2}}{2}=20 \text { J. }
$$
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (12 points) During the break, a fly flew into the math classroom and started crawling on a poster, on which the graph of a quadratic function $y=f(x)$ was depicted in the coordinate plane, with the leading coefficient equal to 1. Initially, the fly moved exactly along the parabola up to the point with an abscissa equal to 2, but then it started moving along a straight line until it hit the parabola again at the point with an abscissa equal to 4. Find $f(3)$, given that the line $y=2023 x$ intersects the fly's path along the straight line segment at its midpoint.
|
Answer: 6068.
Solution. Let the quadratic function be of the form $y=x^{2}+b x+c$. The midpoint of the line segment has coordinates $\left(\frac{2+4}{2} ; \frac{f(2)+f(4)}{2}\right)$, on the other hand, $\left(3 ; 6069\right)$. Since $f(2)=4+2 b+c, f(4)=16+4 b+c$, then $20+6 b+2 c=12138$ or $3 b+c=6059$. Therefore, $f(3)=9+3 b+c=9+6059=6068$.
Grading criteria. Full points for a complete and justified solution - 12 points. For a correct approach with arithmetic errors, minus 3 points.
|
6068
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (13 points) In a dance ensemble, there are 8 boys and 16 girls. Some of them form mixed (boy and girl) dance pairs. It is known that in each pair, at least one of the partners does not belong to any other pair. What is the maximum number of dance pairs that can be formed in this ensemble?
|
Answer: 22.
Solution. Example. Let Yana and Maxim be the best dancers in the ensemble. If Maxim dances with all the girls except Yana, and Yana dances with all the boys except Maxim, then the condition of the problem is satisfied and the number of pairs will be $15+7=22$.
Estimate. Let's call a pair in which the partner does not participate in other pairs - male, and a pair in which the partner does not participate in other pairs - female. (A pair can be both male and female). If there are 8 male pairs, then there are no other pairs. Therefore, if we want the total number of pairs to be more than 8, the number of male pairs should not exceed 7. If there are 16 female pairs, then there are also no other pairs. And if we want the total number of pairs to be more than 16, the number of female pairs should not exceed 15. Thus, the total number of pairs (each of which is either male or female) is no more than $7+15=22$.
Grading criteria. Full solution - 13 points. Only the example is worth 6 points; only the estimate - 7 points.
|
22
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (12 points) During the break, a fly flew into the math classroom and started crawling on a poster, on which the graph of a quadratic function $y=f(x)$ was depicted in the coordinate plane, with the leading coefficient equal to -1. Initially, the fly moved exactly along the parabola up to the point with an abscissa of 2, but then it started moving along a straight line until it hit the parabola again at the point with an abscissa of 4. Find $f(3)$, given that the line $y=2023 x$ intersects the fly's path along the straight line segment at its midpoint.
|
Answer: 6070.
Solution. Let the quadratic function be of the form $y=-x^{2}+b x+c$. The midpoint of the line segment has coordinates $\left(\frac{2+4}{2} ; \frac{f(2)+f(4)}{2}\right)$, and on the other hand, $(3 ; 6069)$. Since $f(2)=-4+2 b+c, f(4)=-16+4 b+c$, then $-20+6 b+2 c=12138$ or $3 b+c=6079$. Therefore, $f(3)=-9+3 b+c=-9+6079=6070$.
Grading criteria. Full points for a complete and justified solution - 12 points. For a correct approach with arithmetic errors, minus 3 points.
|
6070
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
4. (13 points) In a dance ensemble, there are 8 boys and 20 girls. Some of them form mixed (boy and girl) dance pairs. It is known that in each pair, at least one of the partners does not belong to any other pair. What is the maximum number of dance pairs that can be formed in this ensemble?
|
Answer: 26.
Solution. Example. Let Yana and Maxim be the best dancers in the ensemble. If Maxim dances with all the girls except Yana, and Yana dances with all the boys except Maxim, then the condition of the problem is satisfied and the number of pairs will be $19+7=26$.
Estimate. Let's call a pair in which the partner does not participate in other pairs - male, and a pair in which the partner does not participate in other pairs - female. (A pair can be both male and female). If there are 8 male pairs, then there are no other pairs. Therefore, if we want the total number of pairs to be more than 8, the number of male pairs should not exceed 7. If there are 20 female pairs, then there are also no other pairs. And if we want the total number of pairs to be more than 20, the number of female pairs should not exceed 19. Thus, the total number of pairs (each of which is either male or female) is no more than $7+19=26$.
Grading criteria. Full solution - 13 points. Only the example is worth 6 points; only the estimate - 7 points.
|
26
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (15 points) The density of a body $\rho$ is defined as the ratio of the body's mass $m$ to its volume $V$. A unit of mass used in jewelry is the carat (1 carat equals 0.2 grams). A unit of length used in many countries is the inch (1 inch equals 2.54 centimeters). It is known that the density of diamond is $\rho=3.5 \mathrm{r} / \mathrm{c}^{3}$. Convert this value to carats per cubic inch.
|
Answer: $\approx 287$ carats/inch ${ }^{3}$.
Solution. 1 gram $=\frac{1}{0.2}$ carat $=5$ carats,
1 cm $=\frac{1}{2.54}$ inch.
We get: $\rho=3.5 \frac{\mathrm{r}}{\mathrm{cm}^{3}}=3.5 \frac{5 \text { carats }}{\left(\frac{1}{2.54} \text { inch }\right)^{3}}=3.5 \cdot 5 \cdot 2.54^{3} \frac{\text { carats }}{\text { inch }{ }^{3}} \approx 287 \frac{\text { carats }}{\text { inch }{ }^{3}}$.
(5 points)
|
287
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
5. (15 points) The density of a body $\rho$ is defined as the ratio of the body's mass $m$ to its volume $V$. A unit of mass used in jewelry is the carat (1 carat equals 0.2 grams). A unit of length used in many countries is the inch (1 inch equals 2.54 centimeters). It is known that the density of emerald is $\rho=2.7 \text{ g} / \mathrm{cm}^{3}$. Convert this value to carats per cubic inch.
|
Answer: $\approx 221$ carats/inch ${ }^{3}$.
Solution. 1 gram $=\frac{1}{0.2}$ carat $=5$ carats,
1 cm $=\frac{1}{2.54}$ inch.
(2 points)
|
221
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (12 points) Find a natural number $n$ such that the numbers $n+30$ and $n-17$ are squares of other numbers.
|
Answer: 546.
Solution. From the condition of the problem, it follows that $\left\{\begin{array}{l}n+30=k^{2} \\ n-17=m^{2}\end{array}\right.$. Subtracting the second equation from the first, we get $k^{2}-m^{2}=47(*)$ or $(k-m)(k+m)=47$. Since 47 is a prime number, the possible cases are $\left\{\begin{array}{l}k-m= \pm 1, \\ k+m= \pm 47\end{array}\right.$ or conversely $\left\{\begin{array}{l}k-m= \pm 47, \\ k+m= \pm 1,\end{array}\right.$ but for any case $k= \pm 24$. Then $n=24^{2}-30=546$. Verification: $n-17=546-17=529=23^{2}$.
Grading criteria. Full solution 12 points. If equation (*) is obtained, 6 points, if all possible cases for the factors are obtained, plus 3 points. If the solution process is correct but there are arithmetic errors, minus 2 points.
|
546
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (15 points) Every day, Ivan Ivanovich is taken to work by a company car. One day, Ivan Ivanovich decided to walk and left the house an hour earlier than usual. On the way, he met the company car and finished the journey in it. As a result, he arrived at work 10 minutes earlier than the usual time. How long did Ivan Ivanovich walk?
|
Answer: 55 minutes.
Solution. Since Ivan Ivanovich saved the driver 10 minutes by walking, the car travels from Ivan Ivanovich's house to the meeting point in 5 minutes.
We get: $u T=5 v$,
(2 points)
where $u$ is Ivan Ivanovich's walking speed, $v$ is the car's speed, and $T$ is the time Ivan Ivanovich walked. The distance from Ivan Ivanovich's house to his workplace: $s=v t$,
and on the other hand: $s=u T+v(t-T+50)$.
Solving the system of equations (1), (2), and (3), we get: $T=55$ minutes.
|
55
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (12 points) Find a natural number $n$ such that the numbers $n+15$ and $n-14$ are squares of other numbers.
|
Answer: 210.
Solution. From the condition of the problem, it follows that $\left\{\begin{array}{l}n+15=k^{2} \\ n-14=m^{2}\end{array}\right.$ Subtracting the second equation from the first, we get $k^{2}-m^{2}=29(*)$ or $(k-m)(k+m)=29$. Since 29 is a prime number, the possible cases are $\left\{\begin{array}{l}k-m= \pm 1 \\ k+m= \pm 29,\end{array}\right.$ or conversely $\left\{\begin{array}{l}k-m= \pm 29, \\ k+m= \pm 1,\end{array}\right.$ but for any case $k= \pm 15$. Then $n=15^{2}-15=210$. Verification: $n-14=210-14=196=14^{2}$.
Grading criteria. Full solution 12 points. If equation (*) is obtained, 6 points, if all possible cases for the factors are obtained, plus 3 points. If the solution process is correct but there are arithmetic errors, minus 2 points.
|
210
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (15 points) Every day, Ivan Ivanovich is taken to work by a company car. One day, Ivan Ivanovich decided to walk and left home one and a half hours earlier than usual. On the way, he met the company car and finished the journey in it. As a result, he arrived at work 20 minutes earlier than the usual time. How long did Ivan Ivanovich walk?
|
Answer: 80 minutes.
Solution. Since Ivan Ivanovich saved the driver 20 minutes by walking, the car takes 10 minutes to drive from Ivan Ivanovich's house to the meeting point.
We get: $u T=10 v$,
(2 points)
where $u$ is Ivan Ivanovich's walking speed, $v$ is the car's speed, and $T$ is the time Ivan Ivanovich walked. The distance from Ivan Ivanovich's house to his workplace: $s=v t$,
and on the other hand: $s=u T+v(t-T+70)$.
(4 points)
Solving the system of equations (1), (2), and (3), we get $T=80$ minutes.
(4 points)
|
80
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Let $d$ - the greatest common divisor of eight natural numbers, the sum of which is equal to 595. What is the largest value that $d$ can take?
|
Answer: 35.
Solution. If each of the numbers is divisible by $d$, then their sum is also a multiple of $d$. Therefore, $d$ is a divisor of the number 595. Let's factorize the latter into prime factors: $595=5 \cdot 7 \cdot 17$ and list all its divisors:
$$
1,5,7,17,35,85,119,595
$$
Each of the eight numbers (from the problem statement) is not less than $d$. Therefore, their sum, which is 595, is not less than $8 d$. From the inequality $595 \geqslant 8 d$ we get $d \leqslant 74$. From the list $(*)$ the largest possible value is 35.
It is not difficult to come up with a corresponding example (which is far from unique): let seven numbers be 70, and one more be 105.
Evaluation. 13 points for a complete solution. 7 points for an estimate without an example. 6 points for an example without an estimate.
|
35
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (10 points) A rigid board of mass $m$ and length $l=20 m$ is partially lying on the edge of a horizontal surface, hanging off it by three quarters of its length. To prevent the board from falling, a stone of mass $2 m$ is placed at the very edge of the board. How far from the stone can a person of mass $m / 2$ walk along the board? Neglect the sizes of the stone and the person compared to the size of the board.
|
Answer: $15 m$
Solution. The moment rule: $2 m g \cdot \frac{l}{4}=m g \cdot \frac{l}{4}+\frac{m}{2} g \cdot\left(x-\frac{l}{4}\right)$.
As a result, we get $x=\frac{3}{4} l=15$ m.
|
15
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. (15 points) The mass of a vessel completely filled with kerosene is 31 kg. If this vessel is completely filled with water, its mass will be 33 kg. Determine the mass of the empty vessel. The density of water $\rho_{W}=1000 \kappa g / \mathrm{m}^{3}$, the density of kerosene $\rho_{K}=800$ kg $/ \mathrm{m}^{3}$.
|
Answer: 23 kg
Solution. The mass of the vessel filled with kerosene $m_{1}=m_{c}+\rho_{K} V$,
where $m_{c}$ is the mass of the empty vessel, $V$ is the volume occupied by the kerosene. The mass of the vessel filled with water: $m_{2}=m_{c}+\rho_{b} V$. (4 points)
We get that $V=\frac{m_{2}-m_{1}}{\rho_{B}-\rho_{K}}=\frac{33-31}{1000-800}=0.01 \mathrm{~m}^{3}$.
The mass of the empty vessel: $m_{c}=m_{1}-\rho_{K} V=31-800 \cdot 0.01=23$ kg.
## Multidisciplinary Engineering Olympiad "Star"
in natural sciences 7th grade
## Final Stage Variant 2 Problems, answers, and evaluation criteria
$2018-2019$
|
23
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. Let $d$ be the greatest common divisor of ten natural numbers whose sum is 1001. What is the largest value that $d$ can take?
|
Answer: 91.
Solution. If each of the numbers is divisible by $d$, then their sum is also divisible by $d$. Therefore, $d$ is a divisor of the number 1001. Let's factorize the latter into prime factors: $1001=7 \cdot 11 \cdot 13$ and list all its divisors:
$$
1,7,11,13,77,91,143,1001
$$
Each of the ten numbers (from the problem statement) is not less than $d$. Therefore, their sum, which is 1001, is not less than $10d$. From the inequality $1001 \geqslant 10d$ we get $d \leqslant 101$. From the list $(*)$ the largest possible value is 91.
It is not difficult to come up with a corresponding example (it is unique): nine numbers are equal to 91, and one more is 182.
Scoring. 13 points for a complete solution. 7 points for an estimate without an example. 6 points for an example without an estimate.
|
91
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (10 points) A rigid board of mass $m$ and length $l=24$ m is partially lying on the edge of a horizontal surface, hanging off it by two-thirds of its length. To prevent the board from falling, a stone of mass $2 m$ is placed at the very edge of the board. How far from the stone can a person of mass $m$ walk along the board? Neglect the sizes of the stone and the person compared to the size of the board.
|
Answer: $20 m$
Solution. The moment rule: $2 m g \cdot \frac{l}{3}=m g \cdot \frac{l}{6}+m g \cdot\left(x-\frac{l}{3}\right)$.
As a result, we get $x=\frac{5}{6} l=20 m$.
|
20
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (12 points) There are four weights of different masses. Katya weighs the weights in pairs. As a result, she got 1800, 1970, 2110, 2330, and 2500 grams. How many grams does the sixth weighing variant weigh?
|
Answer: 2190.
Solution. Let $x, y, z, t$ be the weight of each weight. Then the pairwise weighings will be $x+y, x+z, x+t, y+z, y+t, z+t$ grams. There are three pairs of given numbers: 1) $x+y$ and $z+t$, 2) $x+z$ and $y+t$, 3) $x+t$ and $y+z$, with the same total weight $x+y+z+t$. Let's find pairs with the same sum: $1800+$ $2500=1970+2330=4300$. Notice that there are no other pairs of given numbers with the same sum. Then the sixth weighing option: $4300-2110=$ 2190.
Grading criteria. Full solution - 12 points. If the participant noticed that three pairs out of six numbers - the total weights of two weights, when summed, give the weight of all weights, and therefore must be the same, give 7 points. The total weight of all weights is found - another 2 points. Noted that there are no other pairs of given numbers with the same sum, except for the found ones - another 2 points. Arithmetic errors in the correct solution process - minus 2 points.
|
2190
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. (12 points) There are four weights of different masses. Katya weighs the weights in pairs. As a result, she got 1700, 1870, 2110, 2330, and 2500 grams. How many grams does the sixth weighing variant weigh?
|
Answer: 2090.
Solution. Let $x, y, z, t$ be the weight of each weight. Then the pairwise weighings will be $x+y, x+z, x+t, y+z, y+t, z+t$ grams. There are three pairs: 1) $x+$ y and $z+t, 2) x+z$ and 3) $y+t, x+t$ and $y+z$ with the same weight $x+y+z+t$. Let's find pairs with the same sum: $1700+2500=$
$1870+2330$. Notice that there are no other pairs of these numbers with the same sum. Then the sixth weighing option: $4200-2110=2090$.
Grading criteria. Full solution - 12 points. If the participant noticed that three pairs out of six numbers - the total weights of two weights, when summed, give the weight of all weights, and therefore must be the same, give 7 points. The total weight of all weights is found - another 2 points. Noted that there are no other pairs of these numbers with the same sum, except for the found ones - another 2 points. Arithmetic errors in the correct solution process - minus 2 points.
|
2090
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. The sofa cost 62500 rubles. Once a month, its price changed by $20 \%$ either increasing or decreasing. It is known that over the course of six months, the price increased three times and decreased three times (the order in which this happened is unknown). Can the final price of the sofa after six months be determined uniquely? If so, what did it become?
|
Answer: Yes; the sofa will cost 55296 rubles.
Solution. An increase in price by $20 \%$ means the current price is multiplied by $6 / 5$, and a decrease in price by $20 \%$ means the current price is multiplied by $4 / 5$. Therefore, regardless of the order in which the price increased or decreased, the price of the sofa after six months will be $62500 \cdot(6 / 5)^{3} \cdot(4 / 5)^{3}=$ 55296 rubles.
Evaluation. If only some specific cases are considered and the correct numerical answer is obtained, 4 points. For a complete solution, 12 points.
|
55296
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. How many five-digit numbers exist where the sum of the first two digits is half the sum of the last two digits?
|
Answer: 2250.
Solution. Let the first two digits of the number be $a$ and $b$, and the last two digits be $c$ and $d$. We need to find the number of combinations of these digits for which $2(a+b)=c+d$. Since $c+d \leqslant 18$, then $a+b \leqslant 9$.
Let $x_{i}(i=1,2, \ldots, 9)$ denote the number of pairs of the first two digits whose sum is $i$. The first digit can take values from 1 to $i$, after which the second digit is uniquely determined. Thus, $x_{i}=i$.
Let $y_{i}(i=1,2, \ldots, 9)$ denote the number of pairs of the last two digits whose sum is $2i$. Each time, the digit $d$ is uniquely determined by the digit $c$: $d=2i-c$. Therefore, we need to count the number of possible values for the digit $c$. If $i \leqslant 4$, i.e., $2i \leqslant 8$, then the digit $c$ can take values from 0 to $2i-$ a total of $2i+1$ values. In other words, in this case, $y_{i}=2i+1$. If $5 \leqslant i \leqslant 9$, i.e., $10 \leqslant 2i \leqslant 18$, then the digit $c$ can take values from $2i-9$ to $9-$ a total of $19-2i$ values, and $y_{i}=19-2i$.
Let's compile the found values of $x_{i}$ and $y_{i}$ into one table.
| $i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $x_{i}$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| $y_{i}$ | 3 | 5 | 7 | 9 | 9 | 7 | 5 | 3 | 1 |
The number of five-digit numbers in which $a+b=i$ and $c+d=2i$ is $10 x_{i} y_{i}$ (the middle digit can be chosen in 10 ways). Therefore, the total number of the desired numbers is $10\left(x_{1} y_{1}+x_{2} y_{2}+\ldots+x_{9} y_{9}\right)$. Substituting the found values gives the answer 2250.
Evaluation. 13 points for a complete solution. If all $x_{i}$ and $y_{i}$ are correctly found but there is an arithmetic error in the final calculation, 11 points. If the solution approach is correct but some $x_{i}$ or $y_{i}$ are incorrectly determined, 4-5 points.
|
2250
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. (15 points) Density is defined as the ratio of the mass of a body to its volume. There are two cubes. The second cube is made of a material with twice the density of the first, and the side length of the second cube is 100% greater than the side length of the first. By what percentage is the mass of the second cube greater than the mass of the first?
|
Answer: by $1500 \%$
Solution. From the condition, we get $\rho_{2}=2 \rho_{1}$, i.e., $\frac{m_{2}}{V_{2}}=2 \cdot \frac{m_{1}}{V_{1}}$.
Also, from the condition, it follows that the side length of the second cube $a_{2}=2 a_{1}$.
(2 points)
Therefore, their volumes are related by the ratio $V_{2}=a_{2}^{3}=\left(2 a_{1}\right)^{3}=8 V_{1}$.
(3 points)
We obtain $\frac{m_{2}}{8 V_{1}}=2 \cdot \frac{m_{1}}{V_{1}}$. (2 points) From which it follows that $m_{2}=16 m_{1}$.
That is, the mass of the second cube is greater by $1500 \%$.

Multidisciplinary Engineering Olympiad "Star" in Natural Sciences
6th grade
Final Stage
$2018-2019$
Variant 2
Tasks, answers, and evaluation criteria
|
1500
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. The item cost 64 rubles. Once a month, its price changed by $50\%$ either increasing or decreasing. It is known that over the course of six months, the price increased three times and decreased three times (the order in which this happened is unknown). Can the final price of the item after six months be determined uniquely? If so, what did it become?
|
Answer: Yes; the item will cost 27 rubles.
Solution. An increase of $50\%$ means that the current price is multiplied by $3/2$, and a decrease of $50\%$ means that the current price is multiplied by $1/2$. Therefore, regardless of the order in which the price increased or decreased, the price of the sofa after six months will be $64 \cdot (3/2)^3 \cdot (1/2)^3 = 27$ rubles.
Evaluation. If only some specific cases are considered and the correct numerical answer is obtained, 4 points. For a complete solution, 12 points.
|
27
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
3. How many five-digit numbers exist where the sum of the first two digits is twice the sum of the last two digits?
|
Answer: 2600.
Solution. Let the first two digits of the number be $a$ and $b$, and the last two digits be $c$ and $d$. We need to find the number of combinations of these digits for which $a+b=2(c+d)$. Since $a+b \leqslant 18$, then $c+d \leqslant 9$.
Let $x_{i}(i=1,2, \ldots, 9)$ denote the number of pairs of the last two digits whose sum is $i$. The first digit can take values from 0 to $i$, after which the second digit is uniquely determined. Thus, $x_{i}=i+1$.
Let $y_{i}(i=1,2, \ldots, 9)$ denote the number of pairs of the first two digits whose sum is $2i$. Each time, the digit $b$ is uniquely determined by the digit $a$: $b=2i-a$. Therefore, we need to count the number of possible values for the digit $a$. If $i \leqslant 4$, i.e., $2i \leqslant 8$, then the digit $a$ can take values from 1 to $2i$ - a total of $2i$ values. In other words, in this case, $y_{i}=2i$. If $5 \leqslant i \leqslant 9$, i.e., $10 \leqslant 2i \leqslant 18$, then the digit $a$ can take values from $2i-9$ to $9$ - a total of $19-2i$ values, and $y_{i}=19-2i$.
Let's compile the found values of $x_{i}$ and $y_{i}$ into one table.
| $i$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $x_{i}$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $y_{i}$ | 2 | 4 | 6 | 8 | 9 | 7 | 5 | 3 | 1 |
The number of five-digit numbers in which $c+d=i$ and $a+b=2i$ is $10 x_{i} y_{i}$ (the middle digit can be chosen in 10 ways). Therefore, the total number of the desired numbers is $10\left(x_{1} y_{1}+x_{2} y_{2}+\ldots+x_{9} y_{9}\right)$. Substituting the found values gives the answer 2600.
Evaluation. 13 points for a complete solution. If all $x_{i}$ and $y_{i}$ are correctly found but there is an arithmetic error in the final calculation, 11 points. If the solution approach is correct but some $x_{i}$ or $y_{i}$ are incorrectly determined, 4-5 points.
|
2600
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
6. (10 points) An Englishman was the owner of a plot of land in Russia. He knows that, in the units familiar to him, the size of his plot is three acres. The cost of the land is 250000 rubles per hectare. It is known that 1 acre $=4840$ square yards, 1 yard $=0.9144$ meters, 1 hectare $=10000 m^{2}$. Calculate how much the Englishman will receive as a result of the sale.
|
Answer: approximately 303514 rubles
Solution. 1 square yard $=0.9144 \cdot 0.9144=0.83612736 \mu^{2}$,
3 acres $=3 \cdot 4840=14520$ square yards $a=14520 \cdot 0.83612739=12140.57 \mu^{2}$ (2 points), 12140.57 $\mu^{2}=\frac{12140.57 \mu^{2}}{10000} \approx 1.214057 ~ 2 a$,
$$
1.214057 \cdot 250000=303514.25 \text { rubles }
$$
|
303514
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
8. (15 points) Density is defined as the ratio of the mass of a body to its volume. There are two cubes. The second cube is made of a material with half the density of the first, and the side length of the second cube is 100% greater than the side length of the first. By what percentage is the mass of the second cube greater than the mass of the first?
|
Answer: by $300 \%$
Solution. From the condition, it follows that $\rho_{2}=\frac{1}{2} \rho_{1}$, i.e., $\frac{m_{2}}{V_{2}}=\frac{1}{2} \cdot \frac{m_{1}}{V_{1}}$.
It also follows from the condition that the side length of the second cube $a_{2}=2 a_{1}$.
(2 points)
Therefore, their volumes are related by the ratio $V_{2}=a_{2}^{3}=\left(2 a_{1}\right)^{3}=8 V_{1}$.
(3 points)
We obtain $\frac{m_{2}}{8 V_{1}}=\frac{1}{2} \cdot \frac{m_{1}}{V_{1}}$. (2 points) From which it follows that $m_{2}=4 m_{1}$.
That is, the mass of the second cube is greater by $300 \%$.
|
300
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
7. $\left(10\right.$ points) An arc, with a central angle of $\alpha=60^{\circ}$, is cut from a circle with radius $R=40 \mathrm{~cm}$. A charge $q=5$ μC is uniformly distributed along the arc. Determine the electric field strength $E$ at the center of curvature of this arc.
|
Answer: 269 kV/m.
Solution. Consider a small element of the arc of length $d l$, on which charge $d q$ is located. It creates a field strength at the point of interest:
$d E=k \frac{d q}{R^{2}}$.
The projection of this field strength onto the horizontal direction is:
$d E \cos \beta=k \frac{d q}{R^{2}} \cos \beta$.
The charge of this element is: $d q=\frac{q}{R \cdot \frac{\pi}{3}} \cdot d l$.
We obtain: $d E \cos \beta=k \frac{\frac{q}{R \cdot \frac{\pi}{3}} \cdot d l}{R^{2}} \cos \beta=k \frac{3 q \cdot d l \cdot \cos \beta}{\pi R^{3}}$.
Note that: $d l \cdot \cos \beta=d y$.
Summing over all such elements, we get:
$E=k \frac{3 q \cdot 2 R \sin 30^{\circ}}{\pi R^{3}}=6 k \frac{q \sin 30^{\circ}}{\pi R^{2}}=6 \cdot 9 \cdot 10^{9} \frac{5 \cdot 10^{-6} \sin 30^{\circ}}{\pi \cdot 0.4^{2}}=268574 \frac{\mathrm{V}}{\mathrm{m}}$.
|
269
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
2. (17 points) Given a rectangle $A B C D$. On two sides of the rectangle, different points are chosen, five points on $A B$ and six on $B C$. How many different triangles exist with vertices at the chosen points?
|
Answer: 135.
Solution. To form a triangle, one needs to choose two points on one side and one point on another. We have: 5 ways to choose the first point on $AB$, 4 ways - the second, and since the triangle does not change with the permutation of its vertices, we divide $5 \cdot 4$ by 2. Thus, $\frac{5 \cdot 4}{2}=10$ ways to choose two points on side $AB$, and 6 ways on side $BC$. In total, $10 \cdot 6=60$ ways. Similarly, $\frac{6 \cdot 5}{2}=15$ ways to choose two points on side $BC$ and 5 ways to choose one point on side $AB$. In total, $15 \cdot 5=75$ ways. Therefore, there are 135 different triangles with vertices at the chosen points.
|
135
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.