problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
Problem 2. Let $n$ three-digit numbers satisfy the following properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Solution. Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of 6 A's (which means that we add 1 to the current digit) and $2 G$ 's (which means go to the next digit). Then for example 324 can be obtained from 111 by the string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case, we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the form $\overline{* c}$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. For any set $A=\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ of five distinct positive integers denote by $S_{A}$ the sum of its elements, and denote by $T_{A}$ the number of triples $(i, j, k)$ with $1 \leqslant i<j<k \leqslant 5$ for which $x_{i}+x_{j}+x_{k}$ divides $S_{A}$.
Find the largest possible value of $T_{A}$.
|
Solution. We will prove that the maximum value that $T_{A}$ can attain is 4 . Let $A=$ $\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right\}$ be a set of five positive integers such that $x_{1}x_{4}$ and $x_{3}>x_{2}$. Analogously we can show that any triple of form $(x, y, 5)$ where $y>2$ isn't good.
By above, the number of good triples can be at most 5 and only triples $(1,2,5),(2,3,4)$, $(1,3,4),(1,2,4),(1,2,3)$ can be good. But if triples $(1,2,5)$ and $(2,3,4)$ are simultaneously good we have that:
$$
x_{1}+x_{2}+x_{5} \mid x_{3}+x_{4} \Rightarrow x_{5}<x_{3}+x_{4}
$$
and
$$
x_{2}+x_{3}+x_{4} \mid x_{1}+x_{5} \Rightarrow x_{2}+x_{3}+x_{4} \leqslant x_{1}+x_{5} \stackrel{(1)}{<} x_{1}+x_{3}+x_{4}<x_{2}+x_{3}+x_{4},
$$
which is impossible. Therefore, $T_{A} \leqslant 4$.
Alternatively, one can prove the statement above by adding up the two inequalities $x_{1}+x_{2}+x_{4}<x_{3}+x_{4}$ and $x_{2}+x_{3}+x_{4}<x_{1}+x_{5}$ that are derived from the divisibilities.
To show that $T_{A}=4$ is possible, consider the numbers $1,2,3,4,494$. This works because $6|498,7| 497,8 \mid 496$, and $9 \mid 495$.
Remark. The motivation for construction is to realize that if we choose $x_{1}, x_{2}, x_{3}, x_{4}$ we can get all the conditions $x_{5}$ must satisfy. Let $S=x_{1}+x_{2}+x_{3}+x_{4}$. Now we have to choose $x_{5}$ such that
$$
S-x_{i} \mid x_{i}+x_{5} \text {, i.e. } x_{5} \equiv-x_{i} \quad \bmod \left(S-x_{i}\right) \forall i \in\{1,2,3,4\}
$$
By the Chinese Remainder Theorem it is obvious that if $S-x_{1}, S-x_{2}, S-x_{3}, S-x_{4}$ are pairwise coprime, such $x_{5}$ must exist. To make all these numbers pairwise coprime it's natural to take $x_{1}, x_{2}, x_{3}, x_{4}$ to be all odd and then solve mod 3 issues. Fortunately it can be seen that $1,5,7,11$ easily works because $13,17,19,23$ are pairwise coprime.
However, even without the knowledge of this theorem it makes sense intuitively that this system must have a solution for some $x_{1}, x_{2}, x_{3}, x_{4}$. By taking $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=$ $(1,2,3,4)$ we get pretty simple system which can be solved by hand rather easily.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of the expression
$$
A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}
$$

$19^{\text {th }}$ Junior Balkan Mathematical Olympiad June 24-29, 2015, Belgrade, Serbia
|
## Solution:
We can rewrite $A$ as follows:
$$
\begin{aligned}
& A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)-a^{2}-b^{2}-c^{2}= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-\left(a^{2}+b^{2}+c^{2}\right)=2\left(\frac{a b+b c+c a}{a b c}\right)-\left((a+b+c)^{2}-2(a b+b c+c a)\right)= \\
& 2\left(\frac{a b+b c+c a}{a b c}\right)-(9-2(a b+b c+c a))=2\left(\frac{a b+b c+c a}{a b c}\right)+2(a b+b c+c a)-9= \\
& 2(a b+b c+c a)\left(\frac{1}{a b c}+1\right)-9
\end{aligned}
$$
Recall now the well-known inequality $(x+y+z)^{2} \geq 3(x y+y z+z x)$ and set $x=a b, y=b c, z=c a$, to obtain $(a b+b c+c a)^{2} \geq 3 a b c(a+b+c)=9 a b c$, where we have used $a+b+c=3$. By taking the square roots on both sides of the last one we obtain:
$$
a b+b c+c a \geq 3 \sqrt{a b c}
$$
Also by using AM-GM inequality we get that
$$
\frac{1}{a b c}+1 \geq 2 \sqrt{\frac{1}{a b c}}
$$
Multiplication of (1) and (2) gives:
$$
(a b+b c+c a)\left(\frac{1}{a b c}+1\right) \geq 3 \sqrt{a b c} \cdot 2 \sqrt{\frac{1}{a b c}}=6
$$
So $A \geq 2 \cdot 6-9=3$ and the equality holds if and only if $a=b=c=1$, so the minimum value is 3.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
C1. Consider a regular $2 n+1$-gon $P$ in the plane, where $n$ is a positive integer. We say that a point $S$ on one of the sides of $P$ can be seen from a point $E$ that is external to $P$, if the line segment $S E$ contains no other points that lie on the sides of $P$ except $S$. We want to color the sides of $P$ in 3 colors, such that every side is colored in exactly one color, and each color must be used at least once. Moreover, from every point in the plane external to $P$, at most 2 different colors on $P$ can be seen (ignore the vertices of $P$, we consider them colorless). Find the largest positive integer for which such a coloring is possible.
|
Solution. Answer: $n=1$ is clearly a solution, we can just color each side of the equilateral triangle in a different color, and the conditions are satisfied. We prove there is no larger $n$ that fulfills the requirements.
Lemma 1. Given a regular $2 n+1$-gon in the plane, and a sequence of $n+1$ consecutive sides $s_{1}, s_{2}, \ldots, s_{n+1}$ there is an external point $Q$ in the plane, such that the color of each $s_{i}$ can be seen from $Q$, for $i=1,2, \ldots, n+1$.
Proof. It is obvious that for a semi-circle $S$, there is a point $R$ in the plane far enough on the perpendicular bisector of the diameter of $S$ such that almost the entire semi-circle can be seen from $R$.
Now, it is clear that looking at the circumscribed circle around the $2 n+1$-gon, there is a semi-circle $S$ such that each $s_{i}$ either has both endpoints on it, or has an endpoint that is on the semi-circle, and is not on the semicircle's end. So, take $Q$ to be a point in the plane from which almost all of $S$ can be seen, clearly, the color of each $s_{i}$ can be seen from $Q$. $\diamond$ Take $n \geq 2$, denote the sides $a_{1}, a_{2}, \ldots, a_{2 n+1}$ in that order, and suppose we have a coloring that satisfies the condition of the problem. Let's call the 3 colors red, green and blue. We must have 2 adjacent sides of different colors, say $a_{1}$ is red and $a_{2}$ is green. Then, by Lemma 1 :
(i) We cannot have a blue side among $a_{1}, a_{2}, \ldots, a_{n+1}$.
(ii) We cannot have a blue side among $a_{2}, a_{1}, a_{2 n+1}, \ldots, a_{n+3}$.
We are required to have at least one blue side, and according to 1 ) and 2), that can only be $a_{n+2}$, so $a_{n+2}$ is blue. Now, applying Lemma 1 on the sequence of sides $a_{2}, a_{3}, \ldots, a_{n+2}$ we get that $a_{2}, a_{3}, \ldots, a_{n+1}$ are all green. Applying Lemma 1 on the sequence of sides $a_{1}, a_{2 n+1}, a_{2 n}, \ldots, a_{n+2}$ we get that $a_{2 n+1}, a_{2 n}, \ldots, a_{n+3}$ are all red.
Therefore $a_{n+1}, a_{n+2}$ and $a_{n+3}$ are all of different colors, and for $n \geq 2$ they can all be seen from the same point according to Lemma 1 , so we have a contradiction.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
NT5. Find all positive integers $n$ such that there exists a prime number $p$, such that
$$
p^{n}-(p-1)^{n}
$$
is a power of 3 .
Note. A power of 3 is a number of the form $3^{a}$ where $a$ is a positive integer.
|
Solution. Suppose that the positive integer $n$ is such that
$$
p^{n}-(p-1)^{n}=3^{a}
$$
for some prime $p$ and positive integer $a$.
If $p=2$, then $2^{n}-1=3^{a}$ by $(1)$, whence $(-1)^{n}-1 \equiv 0(\bmod 3)$, so $n$ should be even. Setting $n=2 s$ we obtain $\left(2^{s}-1\right)\left(2^{s}+1\right)=3^{a}$. It follows that $2^{s}-1$ and $2^{s}+1$ are both powers of 3 , but since they are both odd, they are co-prime, and we have $2^{s}-1=1$, i.e. $s=1$ and $n=2$. If $p=3$, then (1) gives $3 \mid 2^{n}$, which is impossible.
Let $p \geq 5$. Then it follows from (1) that we can not have $3 \mid p-1$. This means that $2^{n}-1 \equiv 0$ $(\bmod 3)$, so $n$ should be even, and let $n=2 k$. Then
$$
p^{2 k}-(p-1)^{2 k}=3^{a} \Longleftrightarrow\left(p^{k}-(p-1)^{k}\right)\left(p^{k}+(p-1)^{k}\right)=3^{a}
$$
If $d=\left(p^{k}-(p-1)^{k}, p^{k}+(p-1)^{k}\right)$, then $d \mid 2 p^{k}$. However, both numbers are powers of 3 , so $d=1$ and $p^{k}-(p-1)^{k}=1, p^{k}+(p-1)^{k}=3^{a}$.
If $k=1$, then $n=2$ and we can take $p=5$. For $k \geq 2$ we have $1=p^{k}-(p-1)^{k} \geq p^{2}-(p-1)^{2}$ (this inequality is equivalent to $p^{2}\left(p^{k-2}-1\right) \geq(p-1)^{2}\left((p-1)^{k-2}-1\right)$, which is obviously true). Then $1 \geq p^{2}-(p-1)^{2}=2 p-1 \geq 9$, which is absurd.
It follows that the only solution is $n=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A5. Find the largest positive integer $n$ for which the inequality
$$
\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c} \leq \frac{5}{2}
$$
holds for all $a, b, c \in[0,1]$. Here $\sqrt[1]{a b c}=a b c$.
|
Solution. Let $n_{\max }$ be the sought largest value of $n$, and let $E_{a, b, c}(n)=\frac{a+b+c}{a b c+1}+\sqrt[n]{a b c}$. Then $E_{a, b, c}(m)-E_{a, b, c}(n)=\sqrt[m]{a b c}-\sqrt[n]{a b c}$ and since $a . b c \leq 1$ we clearly have $E_{a, b, c}(m) \geq$ $E_{a, b, c}(n)$ for $m \geq n$. So if $E_{a, b, c}(n) \geq \frac{5}{2}$ for some choice of $a, b, c \in[0,1]$, it must be $n_{\max } \leq n$. We use this remark to determine the upper bound $n_{\max } \leq 3$ by plugging some particular values of $a, b, c$ into the given inequality as follow's:
$$
\text { For }(a, b, c)=(1,1, c), c \in[0,1] \text {, inequality (1) implies } \frac{c+2}{c+1}+\sqrt[n]{c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{c+1}+\sqrt[n]{c} \leq
$$
$\frac{3}{2}$. Obviously, every $x \in[0 ; 1]$ is written as $\sqrt[n]{c}$ for some $c \in[0 ; 1]$. So the last inequality is equivalent to:
$$
\begin{aligned}
& \frac{1}{x^{n}+1}+x \leq \frac{3}{2} \Leftrightarrow 2+2 x^{n+1}+2 x \leq 3 x^{n}+3 \Leftrightarrow 3 x^{n}+1 \geq 2 x^{n+1}+2 x \\
\Leftrightarrow & 2 x^{n}(1-x)+(1-x)+(x-1)\left(x^{n-1}+\cdots+x\right) \geq 0 \\
\Leftrightarrow & (1-x)\left[2 x^{n}+1-\left(x^{n-1}+x^{n-2}+\ldots+x\right)\right] \geq 0, \forall x \in[0,1]
\end{aligned}
$$
For $n=4$, the left hand side of the above becomes $(1-x)\left(2 x^{4}+1-x^{3}-x^{2}-x\right)=$ $(1-x)(x-1)\left(2 x^{3}+x^{2}-1\right)=-(1-x)^{2}\left(2 x^{3}+x^{2}-1\right)$ which for $x=0.9$ is negative. Thus. $n_{\max } \leq 3$ as claimed.
Now, we shall prove that for $n=3$ inequality (1) holds for all $a, b, c \in[0,1]$, and this would mean $n_{\max }=3$. We shall use the following Lemma:
Lemma. For all $a, b, c \in[0 ; 1]: a+b+c \leq a b c+2$.
Proof of the Lemma: The required result comes by adding the following two inequalities side by side
$$
\begin{aligned}
& 0 \leq(a-1)(b-1) \Leftrightarrow a+b \leq a b+1 \Leftrightarrow a+b-a b \leq 1 \\
& 0 \leq(a b-1)(c-1) \Leftrightarrow a b+c \leq a b c+1
\end{aligned}
$$
Because of the Lemma, our inequality (1) for $n=3$ wrill be proved if the following weaker inequality is proved for all $a, b, c \in[0,1]$ :
$$
\frac{a b c+2}{a b c+1}+\sqrt[3]{a b c} \leq \frac{5}{2} \Leftrightarrow \frac{1}{a b c+1}+\sqrt[3]{a b c} \leq \frac{3}{2}
$$
Denoting $\sqrt[3]{a b c}=y \in[0 ; 1]$, this inequality becomes:
$$
\begin{aligned}
& \frac{1}{y^{3}+1}+y \leq \frac{3}{2} \Leftrightarrow 2+2 y^{4}+2 y \leq 3 y^{3}+3 \Leftrightarrow-2 y^{4}+3 y^{3}-2 y+1 \geq 0 \\
\Leftrightarrow & 2 y^{3}(1-y)+(y-1) y(y+1)+(1-y) \geq 0 \Leftrightarrow(1-y)\left(2 y^{3}+1-y^{2}-y\right) \geq 0
\end{aligned}
$$
The last inequality is obvious because $1-y \geq 0$ and $2 y^{3}+1-y^{2}-y=y^{3}+(y-1)^{2}(y+1) \geq 0$.
## Geometry
2
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
## A3 MNE
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt[3]{\frac{c}{a}}>2
$$
|
## Solution:
Starting from the double expression on the left-hand side of given inequality, and applying twice the Arithmetic-Geometric mean inequality, we find that
$$
\begin{aligned}
2 \frac{a}{b}+2 \sqrt{\frac{b}{c}}+2 \sqrt[3]{\frac{c}{a}} & =\frac{a}{b}+\left(\frac{a}{b}+\sqrt{\frac{b}{c}}+\sqrt{\frac{b}{c}}\right)+2 \sqrt[3]{\frac{c}{a}} \\
& \geq \frac{a}{b}+3 \sqrt[3]{\frac{a}{b}} \sqrt{\frac{b}{c}} \sqrt{\frac{b}{c}}+2 \sqrt[3]{\frac{c}{a}} \\
& =\frac{a}{b}+3 \sqrt[3]{\frac{a}{c}}+2 \sqrt[3]{\frac{c}{a}} \\
& \left.=\frac{a}{b}+\sqrt[3]{\frac{a}{c}}+2 \sqrt[3]{\frac{a}{c}}+\sqrt[3]{\frac{c}{a}}\right) \\
& \geq \frac{a}{b}+\sqrt[3]{\frac{a}{c}}+2 \cdot 2 \sqrt{\sqrt[3]{\frac{a}{c}} \sqrt[3]{\frac{c}{a}}} \\
& =\frac{a}{b}+\sqrt[3]{\frac{a}{c}}+4 \\
& >4
\end{aligned}
$$
which yields the given inequality.
(A4) GRE
Let $a, b, c$ be positive real numbers such that $a+b+c=3$. Find the minimum value of
$$
A=\frac{2-a^{3}}{a}+\frac{2-b^{3}}{b}+\frac{2-c^{3}}{c}
$$
|
4
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
## C4
Let $A=1 \cdot 4 \cdot 7 \cdot \ldots \cdot 2014$ be the product of the numbers less or equal to 2014 that give remainder 1 when divided by 3 . Find the last non-zero digit of $A$.
|
Solution. Grouping the elements of the product by ten we get:
$$
\begin{aligned}
& (30 k+1)(30 k+4)(30 k+7)(30 k+10)(30 k+13)(30 k+16) \\
& (30 k+19)(30 k+22)(30 k+25)(30 k+28)= \\
& =(30 k+1)(15 k+2)(30 k+7)(120 k+40)(30 k+13)(15 k+8) \\
& (30 k+19)(15 k+11)(120 k+100)(15 k+14)
\end{aligned}
$$
(We divide all even numbers not divisible by five, by two and multiply all numbers divisible by five with four.)
We denote $P_{k}=(30 k+1)(15 k+2)(30 k+7)(30 k+13)(15 k+8)(30 k+19)(15 k+11)(15 k+14)$. For all the numbers not divisible by five, only the last digit affects the solution, since the power of two in the numbers divisible by five is greater than the power of five. Considering this, for even $k, P_{k}$ ends with the same digit as $1 \cdot 2 \cdot 7 \cdot 3 \cdot 8 \cdot 9 \cdot 1 \cdot 4$, i.e. six and for odd $k, P_{k}$ ends with the same digit as $1 \cdot 7 \cdot 7 \cdot 3 \cdot 3 \cdot 9 \cdot 6 \cdot 9$, i.e. six. Thus $P_{0} P_{1} \ldots P_{66}$ ends with six. If we remove one zero from the end of all numbers divisible with five, we get that the last nonzero digit of the given product is the same as the one from $6 \cdot 2011 \cdot 2014 \cdot 4 \cdot 10 \cdot 16 \cdot \ldots .796 \cdot 802$. Considering that $4 \cdot 6 \cdot 2 \cdot 8$ ends with four and removing one zero from every fifth number we get that the last nonzero digit is the same as in $4 \cdot 4^{26} \cdot 784 \cdot 796 \cdot 802 \cdot 1 \cdot 4 \cdot \ldots \cdot 76 \cdot 79$. Repeating the process we did for the starting sequence we conclude that the last nonzero number will be the same as in $2 \cdot 6 \cdot 6 \cdot 40 \cdot 100 \cdot 160 \cdot 220 \cdot 280 \cdot 61 \cdot 32 \cdot 67 \cdot 73 \cdot 38 \cdot 79$, which is two.
Let $A B C$ be a triangle with $\measuredangle B=\measuredangle C=40^{\circ}$. The bisector of the $\measuredangle B$ meets $A C$ at the point $D$ . Prove that $\overline{B D}+\overline{D A}=\overline{B C}$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem N2. Find all positive integers $n$ such that $36^{n}-6$ is a product of two or more consecutive positive integers.
|
Solution. Answer: $n=1$.
Among each four consecutive integers there is a multiple of 4 . As $36^{n}-6$ is not a multiple of 4 , it must be the product of two or three consecutive positive integers.
Case I. If $36^{n}-6=x(x+1)$ (all letters here and below denote positive integers), then $4 \cdot 36^{n}-23=(2 x+1)^{2}$, whence $\left(2 \cdot 6^{n}+2 x+1\right)\left(2 \cdot 6^{n}-2 x-1\right)=23$. As 23 is prime, this leads to $2 \cdot 6^{n}+2 x+1=23,2 \cdot 6^{n}-2 x-1=1$. Subtracting these yields $4 x+2=22, x=5, n=1$, which is a solution to the problem.
Case II. If $36^{n}-6=(y-1) y(y+1)$, then
$$
36^{n}=y^{3}-y+6=\left(y^{3}+8\right)-(y+2)=(y+2)\left(y^{2}-2 y+3\right)
$$
Thus each of $y+2$ and $y^{2}-2 y+3$ can have only 2 and 3 as prime factors, so the same is true for their GCD. This, combined with the identity $y^{2}-2 y+3=$ $(y+2)(y-4)+11$ yields $\operatorname{GCD}\left(y+2 ; y^{2}-2 y+3\right)=1$. Now $y+2<y^{2}-2 y+3$ and the latter number is odd, so $y+2=4^{n}, y^{2}-2 y+3=9^{n}$. The former identity implies $y$ is even and now by the latter one $9^{n} \equiv 3(\bmod 4)$, while in fact $9^{n} \equiv 1(\bmod 4)$ - a contradiction. So, in this case there is no such $n$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A1. Let $a, b, c$ be positive real numbers such that $a b c=8$. Prove that
$$
\frac{a b+4}{a+2}+\frac{b c+4}{b+2}+\frac{c a+4}{c+2} \geq 6
$$
|
Solution. We have $a b+4=\frac{8}{c}+4=\frac{4(c+2)}{c}$ and similarly $b c+4=\frac{4(a+2)}{a}$ and $c a+4=\frac{4(b+2)}{b}$. It follows that
$$
(a b+4)(b c+4)(c a+4)=\frac{64}{a b c}(a+2)(b+2)(c+2)=8(a+2)(b+2)(c+2)
$$
so that
$$
\frac{(a b+4)(b c+4)(c a+4)}{(a+2)(b+2)(c+2)}=8
$$
Applying AM-GM, we conclude:
$$
\frac{a b+4}{a+2}+\frac{b c+4}{b+2}+\frac{c a+4}{c+2} \geq 3 \cdot \sqrt[3]{\frac{(a b+4)(b c+4)(c a+4)}{(a+2)(b+2)(c+2)}}=6
$$
Alternatively, we can write LHS as
$$
\frac{b c(a b+4)}{2(b c+4)}+\frac{a c(b c+4)}{2(a c+4)}+\frac{a b(c a+4)}{2(a b+4)}
$$
and then apply AM-GM.
|
6
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
A3. Determine the number of pairs of integers $(m, n)$ such that
$$
\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}} \in \mathbb{Q}
$$
|
Solution. Let $r=\sqrt{n+\sqrt{2016}}+\sqrt{m-\sqrt{2016}}$. Then
$$
n+m+2 \sqrt{n+\sqrt{2016}} \cdot \sqrt{m-\sqrt{2016}}=r^{2}
$$
and
$$
(m-n) \sqrt{2106}=\frac{1}{4}\left(r^{2}-m-n\right)^{2}-m n+2016 \in \mathbb{Q}
$$
Since $\sqrt{2016} \notin \mathbb{Q}$, it follows that $m=n$. Then
$$
\sqrt{n^{2}-2016}=\frac{1}{2}\left(r^{2}-2 n\right) \in \mathbb{Q}
$$
Hence, there is some nonnegative integer $p$ such that $n^{2}-2016=p^{2}$ and (1) becomes $2 n+2 p=r^{2}$.
It follows that $2(n+p)=r^{2}$ is the square of a rational and also an integer, hence a perfect square. On the other hand, $2016=(n-p)(n+p)$ and $n+p$ is a divisor of 2016, larger than $\sqrt{2016}$. Since $n+p$ is even, so is also $n-p$, and $r^{2}=2(n+p)$ is a divisor of $2016=2^{5} \cdot 3^{2} \cdot 7$, larger than $2 \sqrt{2016}>88$. The only possibility is $r^{2}=2^{4} \cdot 3^{2}=12^{2}$. Hence, $n+p=72$ and $n-p=28$, and we conclude that $n=m=50$. Thus, there is only one such pair.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
C1. Let $S_{n}$ be the sum of reciprocal values of non-zero digits of all positive integers up to (and including) $n$. For instance, $S_{13}=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{2}+\frac{1}{1}+\frac{1}{3}$. Find the least positive integer $k$ making the number $k!\cdot S_{2016}$ an integer.
|
## Solution.
We will first calculate $S_{999}$, then $S_{1999}-S_{999}$, and then $S_{2016}-S_{1999}$.
Writing the integers from 1 to 999 as 001 to 999, adding eventually also 000 (since 0 digits actually do not matter), each digit appears exactly 100 times in each position(as unit, ten, or hundred). Hence
$$
S_{999}=300 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
For the numbers in the interval $1000 \rightarrow 1999$, compared to $0 \rightarrow 999$, there are precisely 1000 more digits 1 . We get
$$
S_{1999}-S_{999}=1000+S_{999} \Longrightarrow S_{1999}=1000+600 \cdot\left(\frac{1}{1}+\frac{1}{2}+\cdots+\frac{1}{9}\right)
$$
Finally, in the interval $2000 \rightarrow 2016$, the digit 1 appears twice as unit and seven times as a ten, the digit 2 twice as a unit and 17 times as a thousand, the digits $3,4,5$, and 6 each appear exactly twice as units, and the digits 7,8 , and 9 each appear exactly once as a unit. Hence
$$
S_{2016}-S_{1999}=9 \cdot 1+19 \cdot \frac{1}{2}+2 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+1 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right)
$$
In the end, we get
$$
\begin{aligned}
S_{2016} & =1609 \cdot 1+619 \cdot \frac{1}{2}+602 \cdot\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)+601 \cdot\left(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}\right) \\
& =m+\frac{1}{2}+\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\frac{2}{6}+\frac{6}{7}+\frac{1}{8}+\frac{7}{9}=n+\frac{p}{2^{3} \cdot 3^{2} \cdot 5 \cdot 7}
\end{aligned}
$$
where $m, n$, and $p$ are positive integers, $p$ coprime to $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Then $k!\cdot S_{2016}$ is an integer precisely when $k$ ! is a multiple of $2^{3} \cdot 3^{2} \cdot 5 \cdot 7$. Since $7 \mid k!$, it follows that $k \geq 7$. Also, $7!=2^{4} \cdot 3^{2} \cdot 5 \cdot 7$, implying that the least $k$ satisfying $k!\cdot S_{2016} \in \mathbb{Z}$ is $k=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
N2. Find the maximum number of natural numbers $x_{1}, x_{2}, \ldots, x_{m}$ satisfying the conditions:
a) No $x_{i}-x_{j}, 1 \leq i<j \leq m$ is divisible by 11 ; and
b) The sum $x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1}$ is divisible by 11 .
|
Solution. The required maximum is 10 .
According to a), the numbers $x_{i}, 1 \leq i \leq m$, are all different $(\bmod 11)$ (1)
Hence, the number of natural numbers satisfying the conditions is at most 11.
If $x_{j} \equiv 0(\bmod 11)$ for some $j$, then
$$
x_{2} x_{3} \ldots x_{m}+x_{1} x_{3} \ldots x_{m}+\cdots+x_{1} x_{2} \ldots x_{m-1} \equiv x_{1} \ldots x_{j-1} x_{j+1} \ldots x_{m} \quad(\bmod 11)
$$
which would lead to $x_{i} \equiv 0(\bmod 11)$ for some $i \neq j$, contradicting (1).
We now prove that 10 is indeed the required maximum.
Consider $x_{i}=i$, for all $i \in\{1,2, \ldots, 10\}$. The products $2 \cdot 3 \cdots \cdot 10,1 \cdot 3 \cdots \cdots 10, \ldots$, $1 \cdot 2 \cdots \cdot 9$ are all different $(\bmod 11)$, and so
$$
2 \cdot 3 \cdots \cdots 10+1 \cdot 3 \cdots \cdots 10+\cdots+1 \cdot 2 \cdots \cdot 9 \equiv 1+2+\cdots+10 \quad(\bmod 11)
$$
and condition b) is satisfied, since $1+2+\cdots+10=55=5 \cdot 11$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A 2. Find the maximum positive integer $k$ such that for any positive integers $m, n$ such that $m^{3}+n^{3}>$ $(m+n)^{2}$, we have
$$
m^{3}+n^{3} \geq(m+n)^{2}+k
$$
|
Solution. We see that for $m=3$ and $n=2$ we have $m^{3}+n^{3}>(m+n)^{2}$, thus
$$
3^{3}+2^{3} \geq(3+2)^{2}+k \Rightarrow k \leq 10
$$
We will show that $k=10$ is the desired maximum. In other words, we have to prove that
$$
m^{3}+n^{3} \geq(m+n)^{2}+10
$$
The last inequality is equivalent to
$$
(m+n)\left(m^{2}+n^{2}-m n-m-n\right) \geq 10
$$
If $m+n=2$ or $m+n=3$, then $(m, n)=(1,1),(1,2),(2,1)$ and we can check that none of them satisfies the condition $m^{3}+n^{3}>(m+n)^{2}$.
If $m+n=4$, then $(m, n)=(1,3),(2,2),(3,1)$. The pair $(m, n)=(2,2)$ doesn't satisfy the condition. The pairs $(m, n)=(1,3),(3,1)$ satisfy the condition and we can readily check that $m^{3}+n^{3} \geq(m+$ $n)^{2}+10$.
If $m+n \geq 5$ then we will show that
$$
m^{2}+n^{2}-m n-m-n \geq 2
$$
which is equivalent to
$$
(m-n)^{2}+(m-1)^{2}+(n-1)^{2} \geq 6
$$
If at least one of the numbers $m, n$ is greater or equal to 4 then $(m-1)^{2} \geq 9$ or $(n-1)^{2} \geq 9$ hence the desired result holds. As a result, it remains to check what happens if $m \leq 3$ and $n \leq 3$. Using the condition $m+n \geq 5$ we have that all such pairs are $(m, n)=(2,3),(3,2),(3,3)$.
All of them satisfy the condition and also the inequality $m^{2}+n^{2}-m n-m-n \geq 2$, thus we have the desired result.
|
10
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A 4. Let $k>1, n>2018$ be positive integers, and let $n$ be odd. The nonzero rational numbers $x_{1}$, $x_{2}, \ldots, x_{n}$ are not all equal and satisfy
$$
x_{1}+\frac{k}{x_{2}}=x_{2}+\frac{k}{x_{3}}=x_{3}+\frac{k}{x_{4}}=\cdots=x_{n-1}+\frac{k}{x_{n}}=x_{n}+\frac{k}{x_{1}}
$$
Find:
a) the product $x_{1} x_{2} \ldots x_{n}$ as a function of $k$ and $n$
b) the least value of $k$, such that there exist $n, x_{1}, x_{2}, \ldots, x_{n}$ satisfying the given conditions.
|
Solution. a) If $x_{i}=x_{i+1}$ for some $i$ (assuming $x_{n+1}=x_{1}$ ), then by the given identity all $x_{i}$ will be equal, a contradiction. Thus $x_{1} \neq x_{2}$ and
$$
x_{1}-x_{2}=k \frac{x_{2}-x_{3}}{x_{2} x_{3}}
$$
Analogously
$$
x_{1}-x_{2}=k \frac{x_{2}-x_{3}}{x_{2} x_{3}}=k^{2} \frac{x_{3}-x_{4}}{\left(x_{2} x_{3}\right)\left(x_{3} x_{4}\right)}=\cdots=k^{n} \frac{x_{1}-x_{2}}{\left(x_{2} x_{3}\right)\left(x_{3} x_{4}\right) \ldots\left(x_{1} x_{2}\right)}
$$
Since $x_{1} \neq x_{2}$ we get
$$
x_{1} x_{2} \ldots x_{n}= \pm \sqrt{k^{n}}= \pm k^{\frac{n-1}{2}} \sqrt{k}
$$
If one among these two values, positive or negative, is obtained, then the other one will be also obtained by changing the sign of all $x_{i}$ since $n$ is odd.
b) From the above result, as $n$ is odd, we conclude that $k$ is a perfect square, so $k \geq 4$. For $k=4$ let $n=2019$ and $x_{3 j}=4, x_{3 j-1}=1, x_{3 j-2}=-2$ for $j=1,2, \ldots, 673$. So the required least value is $k=4$.
Comment by PSC. There are many ways to construct the example when $k=4$ and $n=2019$. Since $3 \mid 2019$, the idea is to find three numbers $x_{1}, x_{2}, x_{3}$ satisfying the given equations, not all equal, and repeat them as values for the rest of the $x_{i}$ 's. So, we want to find $x_{1}, x_{2}, x_{3}$ such that
$$
x_{1}+\frac{4}{x_{2}}=x_{2}+\frac{4}{x_{3}}=x_{3}+\frac{4}{x_{1}}
$$
As above, $x_{1} x_{2} x_{3}= \pm 8$. Suppose without loss of generality that $x_{1} x_{2} x_{3}=-8$. Then, solving the above system we see that if $x_{1} \neq 2$, then
$$
x_{2}=-\frac{4}{x_{1}-2} \text { and } x_{3}=2-\frac{4}{x_{1}}
$$
leading to infinitely many solutions. The example in the official solution is obtained by choosing $x_{1}=-2$.
Comment by PSC. An alternative formulation of the problem's statement could be the following: Let $k>1$ be a positive integer. Suppose that there exists an odd positive integer $n>2018$ and nonzero rational numbers $x_{1}, x_{2}, \ldots, x_{n}$, not all of them equal, that satisfy
$$
x_{1}+\frac{k}{x_{2}}=x_{2}+\frac{k}{x_{3}}=x_{3}+\frac{k}{x_{4}}=\cdots=x_{n-1}+\frac{k}{x_{n}}=x_{n}+\frac{k}{x_{1}}
$$
Find the minimum value of $k$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
C 2. A set $T$ of $n$ three-digit numbers has the following five properties:
(1) No number contains the digit 0 .
(2) The sum of the digits of each number is 9 .
(3) The units digits of any two numbers are different.
(4) The tens digits of any two numbers are different.
(5) The hundreds digits of any two numbers are different.
Find the largest possible value of $n$.
|
Solution. Let $S$ denote the set of three-digit numbers that have digit sum equal to 9 and no digit equal to 0 . We will first find the cardinality of $S$. We start from the number 111 and each element of $S$ can be obtained from 111 by a string of $6 A$ 's (which means that we add 1 to the current digit) and 2 G's (which means go to the next digit). Then for example 324 can be obtained from 111 by the
string AAGAGAAA. There are in total
$$
\frac{8!}{6!\cdot 2!}=28
$$
such words, so $S$ contains 28 numbers. Now, from the conditions (3), (4), (5), if $\overline{a b c}$ is in $T$ then each of the other numbers of the form $\overline{* c}$ cannot be in $T$, neither $\overline{* * *}$ can be, nor $\overline{a * *}$. Since there are $a+b-2$ numbers of the first category, $a+c-2$ from the second and $b+c-2$ from the third one. In
these three categories there are
$$
(a+b-2)+(b+c-2)+(c+a-2)=2(a+b+c)-6=2 \cdot 9-6=12
$$
distinct numbers that cannot be in $T$ if $\overline{a b c}$ is in $T$. So, if $T$ has $n$ numbers, then $12 n$ are the forbidden ones that are in $S$, but each number from $S$ can be a forbidden number no more than three times, once for each of its digits, so
$$
n+\frac{12 n}{3} \leq 28 \Longleftrightarrow n \leq \frac{28}{5}
$$
and since $n$ is an integer, we get $n \leq 5$. A possible example for $n=5$ is
$$
T=\{144,252,315,423,531\}
$$
Comment by PSC. It is classical to compute the cardinality of $S$ and this can be done in many ways. In general, the number of solutions of the equation
$$
x_{1}+x_{2}+\cdots+x_{k}=n
$$
in positive integers, where the order of $x_{i}$ matters, is well known that equals to $\binom{n-1}{k-1}$. In our case,
we want to count the number of positive solutions to we want to count the number of positive solutions to $a+b+c=9$. By the above, this equals to $\binom{9-1}{3-1}=28$. Using the general result above, we can also find that there are $a+b-2$ numbers of the
form $\overline{* * c}$.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
C2 Five players $(A, B, C, D, E)$ take part in a bridge tournament. Every two players must play (as partners) against every other two players. Any two given players can be partners not more than once per day. What is the least number of days needed for this tournament?
|
Solution: A given pair must play with three other pairs and these plays must be in different days, so at three days are needed. Suppose that three days suffice. Let the pair $A B$ play against $C D$ on day $x$. Then $A B-D E$ and $C D-B E$ cannot play on day $x$. Then one of the other two plays of $D E$ (with $A C$ and $B C$ ) must be on day $x$. Similarly, one of the plays of $B E$ with $A C$ or $A D$ must be on day $x$. Thus, two of the plays in the chain $B C-D E-A C-B E-A D$ are on day $x$ (more than two among these cannot be on one day).
Consider the chain $A B-C D-E A-B D-C E-A B$. At least three days are needed for playing all the matches within it. For each of these days we conclude (as above) that there are exactly two of the plays in the chain $B C-D E-A C-B E-A D-B C$ on that day. This is impossible, as this chain consists of five plays.
It remains to show that four days will suffice:
Day 1: $A B-C D, A C-D E, A D-C E, A E-B C$
Day 2: $A B-D E, A C-B D, A D-B C, B E-C D$
Day 3: $A B-C E, A D-B E, A E-B D, B C-D E$
Day 4: $A C-B E, A E-C D, B D-C E$.
Remark: It is possible to have 5 games in one day (but not on each day).
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
G2 In a right trapezoid $A B C D(A B \| C D)$ the angle at vertex $B$ measures $75^{\circ}$. Point $H$ is the foot of the perpendicular from point $A$ to the line $B C$. If $B H=D C$ and $A D+A H=8$, find the area of $A B C D$.
|
Solution: Produce the legs of the trapezoid until they intersect at point $E$. The triangles $A B H$ and $E C D$ are congruent (ASA). The area of $A B C D$ is equal to area of triangle $E A H$ of hypotenuse
$$
A E=A D+D E=A D+A H=8
$$
Let $M$ be the midpoint of $A E$. Then
$$
M E=M A=M H=4
$$
and $\angle A M H=30^{\circ}$. Now, the altitude from $H$ to AM equals one half of $M H$, namely 2. Finally, the area is 8 .
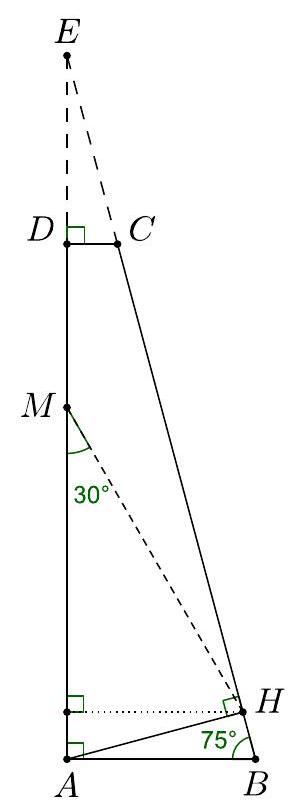
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
G6. A point $O$ and the circles $k_{1}$ with center $O$ and radius $3, k_{2}$ with center $O$ and radius 5, are given. Let $A$ be a point on $k_{1}$ and $B$ be a point on $k_{2}$. If $A B C$ is equilateral triangle, find the maximum value of the distance $O C$.
|
## Solution
It is easy to see that the points $O$ and $C$ must be in different semi-planes with respect to the line $A B$.
Let $O P B$ be an equilateral triangle ( $P$ and $C$ on the same side of $O B$ ). Since $\angle P B C$ $=60^{\circ}-\angle A B P$ and $\angle O B A=60^{\circ}-\angle A B P$, then $\angle P B C=\angle O B A$. Hence the triangles $A O B$ and $C P B$ are equal and $P C=O A$. From the triangle $O P C$ we have
$$
O C \leq O P+P C=O B+O A=8
$$
Hence, the maximum yalue of the distance $O C$ is 8 (when the point $P$ lies on $O C$ )
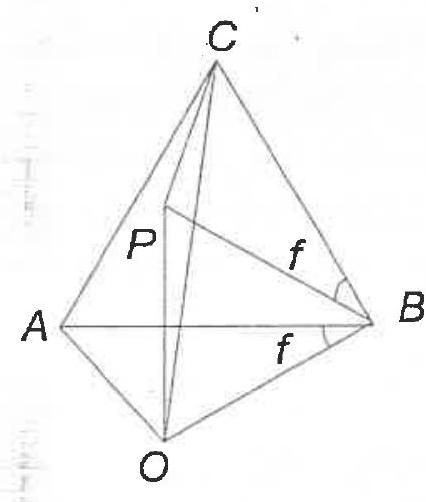
Figure 8
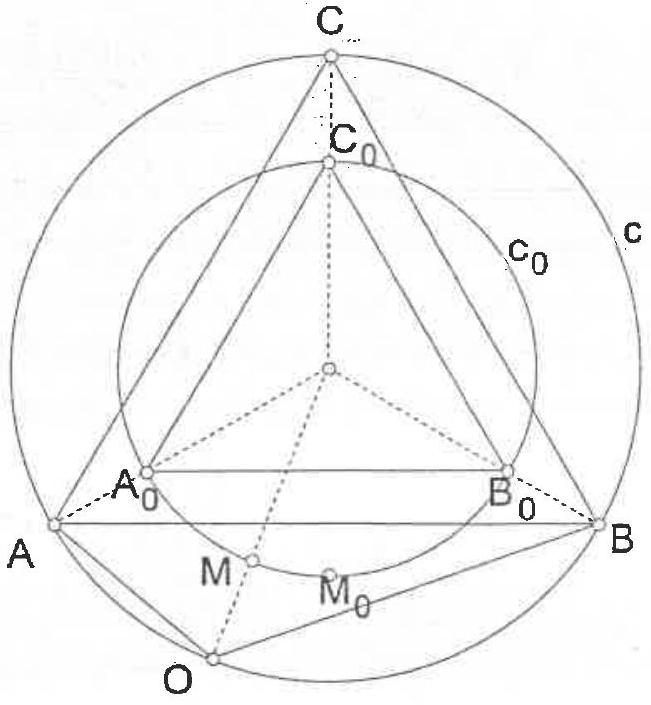
Figure 9
## Complement to the solution
Indeed there exists a triangle $\mathrm{OAB}$ with $\mathrm{OA}=3, \mathrm{OB}=5$ and $\mathrm{OC}=8$.
To construct such a triangle, let's first consider a point $M$ on the minor arc $\widehat{A_{0} B_{0}}$ of the circumference $\left(c_{0}\right)$ of an arbitrary equilateral triangle $A_{0} B_{0} C_{0}$. As $\mathrm{M}$ moves along $\widehat{\mathrm{A}_{0} \mathrm{~B}_{0}}$ from the midpoint position $\mathrm{M}_{0}$ towards $\mathrm{A}_{0}$, the ratio $\frac{\mathrm{MA}_{0}}{\mathrm{MB}_{0}}$ takes on all the decreasing values from 1 to 0 . Thus there exists a position of $\mathrm{M}$ such that $\frac{\mathrm{MA}_{0}}{\mathrm{MB}_{0}}=\frac{3}{5}$. Now a homothesy centered at the center of $\left(\mathrm{c}_{0}\right)$ can take $\mathrm{A}_{0}, \mathrm{~B}_{0}, \mathrm{C}_{0}, \mathrm{M}$ to the new positions $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{O}$ so that $\mathrm{OA}=3$ and $\mathrm{OB}=5$. Then, since $\mathrm{C}$ lies on the minor arc $\overparen{\mathrm{AB}}$ of the circumference (c) of the equilateral triangle $\mathrm{ABC}$ we get $\mathrm{OC}=\mathrm{OA}+\mathrm{OB}=3+5=8$ as wanted, (figure 9).
|
8
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
NT2. Find all natural numbers $n$ such that $5^{n}+12^{n}$ is perfect square.
|
## Solution
By checking the cases $n=1,2,3$ we get the solution $n=2$ and $13^{2}=5^{2}+12^{2}$.
If $n=2 k+1$ is odd, we consider the equation modulo 5 and we obtain
$$
\begin{aligned}
x^{2} & \equiv 5^{2 k+1}+12^{2 k+1}(\bmod 5) \equiv 2^{2 k} \cdot 2(\bmod 5) \\
& \equiv(-1)^{k} \cdot 2(\bmod 5) \equiv \pm 2(\bmod 5)
\end{aligned}
$$
This is not possible, because the square residue of any natural number module 5 is 0,1 or 4. Therefore $n$ is even and $x^{2}=5^{2 k}+12^{2 k}$. Rearrange this equation in the form
$$
5^{2 k}=\left(x-12^{k}\right)\left(x+12^{k}\right)
$$
If 5 divides both factors on the right, it must also divide their difference, that is
$$
5 \mid\left(x+12^{k}\right)-\left(x-12^{k}\right)=2 \cdot 12^{k}
$$
which is not possible. Therefore we must have
$$
x-12^{k}=1 \text { and } x+12^{k}=5^{2 k}
$$
By adding the above equalities we get
$$
5^{2 k}-1=2 \cdot 12^{k}
$$
For $k \geq 2$, we have the inequality
$$
25^{k}-1>24^{k}=2^{k} \cdot 12^{k}>2 \cdot 12^{k}
$$
Thus we conclude that there exists a unique solution to our problem, namely $n=2$.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A4 Let $x, y$ be positive real numbers such that $x^{3}+y^{3} \leq x^{2}+y^{2}$. Find the greatest possible value of the product $x y$.
|
## Solution 1
We have $(x+y)\left(x^{2}+y^{2}\right) \geq(x+y)\left(x^{3}+y^{3}\right) \geq\left(x^{2}+y^{2}\right)^{2}$, hence $x+y \geq x^{2}+y^{2}$. Now $2(x+y) \geq(1+1)\left(x^{2}+y^{2}\right) \geq(x+y)^{2}$, thus $2 \geq x+y$. Because $x+y \geq 2 \sqrt{x y}$, we will obtain $1 \geq x y$. Equality holds when $x=y=1$.
So the greatest possible value of the product $x y$ is 1 .
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
A7 Let $a, b, c$ be positive real numbers with $a b c=1$. Prove the inequality:
$$
\frac{2 a^{2}+\frac{1}{a}}{b+\frac{1}{a}+1}+\frac{2 b^{2}+\frac{1}{b}}{c+\frac{1}{b}+1}+\frac{2 c^{2}+\frac{1}{c}}{a+\frac{1}{c}+1} \geq 3
$$
|
## Solution 1
By $A M-G M$ we have $2 x^{2}+\frac{1}{x}=x^{2}+x^{2}+\frac{1}{x} \geq 3 \sqrt[3]{\frac{x^{4}}{x}}=3 x$ for all $x>0$, so we have:
$\sum_{\text {cyc }} \frac{2 a^{2}+\frac{1}{a}}{b+\frac{1}{a}+1} \geq \sum_{c y c} \frac{3 a}{1+b+b c}=3\left(\sum_{c y c} \frac{a^{2}}{1+a+a b}\right) \geq \frac{3(a+b+c)^{2}}{3+a+b+c+a b+b c+c a}$.
By $A M-G M$ we have $a b+b c+c a \geq 3$ and $a+b+c \geq 3$. But $3\left(a^{2}+b^{2}+c^{2}\right) \geq(a+b+c)^{2} \geq$ $3(a+b+c)$. So $(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a \geq 3+a+b+c+a b+b c+c a$. Hence $\sum_{c y c} \frac{2 a^{2}+\frac{1}{a}}{b+\frac{1}{a}+1} \geq \frac{3(a+b+c)^{2}}{3+a+b+c+a b+b c+c a} \geq \frac{3(a+b+c)^{2}}{(a+b+c)^{2}}=3$.
|
3
|
Inequalities
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
G3 The vertices $A$ and $B$ of an equilateral $\triangle A B C$ lie on a circle $k$ of radius 1 , and the vertex $C$ is inside $k$. The point $D \neq B$ lies on $k, A D=A B$ and the line $D C$ intersects $k$ for the second time in point $E$. Find the length of the segment $C E$.
|
## Solution
As $A D=A C, \triangle C D A$ is isosceles. If $\varangle A D C=\varangle A C D=\alpha$ and $\varangle B C E=\beta$, then $\beta=120^{\circ}-\alpha$. The quadrilateral $A B E D$ is cyclic, so $\varangle A B E=180^{\circ}-\alpha$. Then $\varangle C B E=$ $120^{\circ}-\alpha$ so $\varangle C B E=\beta$. Thus $\triangle C B E$ is isosceles, so $A E$ is the perpendicular bisector of $B C$, so it bisects $\varangle B A C$. Now the arc $B E$ is intercepted by a $30^{\circ}$ inscribed angle, so it measures $60^{\circ}$. Then $B E$ equals the radius of $k$, namely 1 . Hence $C E=B E=1$.
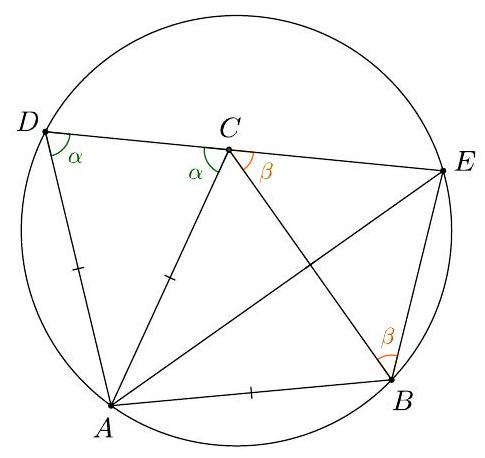
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
NT3 Let $s(a)$ denote the sum of digits of a given positive integer $a$. The sequence $a_{1}, a_{2}, \ldots a_{n}, \ldots$ of positive integers is such that $a_{n+1}=a_{n}+s\left(a_{n}\right)$ for each positive integer $n$. Find the greatest possible $n$ for which it is possible to have $a_{n}=2008$.
|
## Solution
Since $a_{n-1} \equiv s\left(a_{n-1}\right)$ (all congruences are modulo 9 ), we have $2 a_{n-1} \equiv a_{n} \equiv 2008 \equiv 10$, so $a_{n-1} \equiv 5$. But $a_{n-1}<2008$, so $s\left(a_{n-1}\right) \leq 28$ and thus $s\left(a_{n-1}\right)$ can equal 5,14 or 23 . We check $s(2008-5)=s(2003)=5, s(2008-14)=s(1994)=23, s(2008-23)=s(1985)=$ 23. Thus $a_{n-1}$ can equal 1985 or 2003 . As above $2 a_{n-2} \equiv a_{n-1} \equiv 5 \equiv 14$, so $a_{n-2} \equiv 7$. But $a_{n-2}<2003$, so $s\left(a_{n-2}\right) \leq 28$ and thus $s\left(a_{n-2}\right)$ can equal 16 or 25 . Checking as above we see that the only possibility is $s(2003-25)=s(1978)=25$. Thus $a_{n-2}$ can be only 1978. Now $2 a_{n-3} \equiv a_{n-2} \equiv 7 \equiv 16$ and $a_{n-3} \equiv 8$. But $s\left(a_{n-3}\right) \leq 27$ and thus $s\left(a_{n-3}\right)$ can equal 17 or 26 . The check works only for $s(1978-17)=s(1961)=17$. Thus $a_{n-3}=1961$ and similarly $a_{n-4}=1939 \equiv 4, a_{n-5}=1919 \equiv 2$ (if they exist). The search for $a_{n-6}$ requires a residue of 1 . But $a_{n-6}<1919$, so $s\left(a_{n-6}\right) \leq 27$ and thus $s\left(a_{n-6}\right)$ can be equal only to 10 or 19 . The check fails for both $s(1919-10)=s(1909)=19$ and $s(1919-19)=s(1900)=10$. Thus $n \leq 6$ and the case $n=6$ is constructed above (1919, 1939, 1961, 1978, 2003, 2008).
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
NT4 Find all integers $n$ such that $n^{4}+8 n+11$ is a product of two or more consecutive integers.
|
Solution
We will prove that $n^{4}+8 n+11$ is never a multiple of 3 . This is clear if $n$ is a multiple of 3 . If
$n$ is not a multiple of 3 , then $n^{4}+8 n+11=\left(n^{4}-1\right)+12+8 n=(n-1)(n+1)\left(n^{2}+1\right)+12+8 n$, where $8 n$ is the only term not divisible by 3 . Thus $n^{4}+8 n+11$ is never the product of three or more integers.
It remains to discuss the case when $n^{4}+8 n+11=y(y+1)$ for some integer $y$. We write this as $4\left(n^{4}+8 n+11\right)=4 y(y+1)$ or $4 n^{4}+32 n+45=(2 y+1)^{2}$. A check shows that among $n= \pm 1$ and $n=0$ only $n=1$ satisfies the requirement, as $1^{4}+8 \cdot 1+11=20=4 \cdot 5$. Now let $|n| \geq 2$. The identities $4 n^{2}+32 n+45=\left(2 n^{2}-2\right)^{2}+8(n+2)^{2}+9$ and $4 n^{4}+32 n+45=$ $\left(2 n^{2}+8\right)^{2}-32 n(n-1)-19$ indicate that for $|n| \geq 2,2 n^{2}-2<2 y+1<2 n^{2}+8$. But $2 y+1$ is odd, so it can equal $2 n^{2} \pm 1 ; 2 n^{2}+3 ; 2 n^{2}+5$ or $2 n^{2}+7$. We investigate them one by one.
If $4 n^{4}+32 n+45=\left(2 n^{2}-1\right)^{2} \Rightarrow n^{2}+8 n+11=0 \Rightarrow(n+4)^{2}=5$, which is impossible, as 5 is not a perfect square.
If $4 n^{4}+32 n+45=\left(2 n^{2}+1\right)^{2} \Rightarrow n^{2}-8 n-11=0 \Rightarrow(n-4)^{2}=27$ which also fails.
Also $4 n^{4}+32 n+45=\left(2 n^{2}+3\right)^{2} \Rightarrow 3 n^{2}-8 n-9=0 \Rightarrow 9 n^{2}-24 n-27=0 \Rightarrow(3 n-4)^{2}=43$ fails.
If $4 n^{4}+32 n+45=\left(2 n^{2}+5\right)^{2} \Rightarrow 5 n^{2}-8 n=5 \Rightarrow 25 n^{2}-40 n=25 \Rightarrow(5 n-4)^{2}=41$ which also fails.
Finally, if $4 n^{4}+32 n+45=\left(2 n^{2}+7\right)^{2}$, then $28 n^{2}-32 n+4=0 \Rightarrow 4(n-1)(7 n-1)=0$, whence $n=1$ that we already found. Thus the only solution is $n=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
NT6 Let $f: \mathbb{N} \rightarrow \mathbb{R}$ be a function, satisfying the following condition:
for every integer $n>1$, there exists a prime divisor $p$ of $n$ such that $f(n)=f\left(\frac{n}{p}\right)-f(p)$. If
$$
f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006
$$
determine the value of
$$
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right)
$$
|
## Solution
If $n=p$ is prime number, we have
$$
f(p)=f\left(\frac{p}{p}\right)-f(p)=f(1)-f(p)
$$
i.e.
$$
f(p)=\frac{f(1)}{2}
$$
If $n=p q$, where $p$ and $q$ are prime numbers, then
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f(q)-f(p)=\frac{f(1)}{2}-\frac{f(1)}{2}=0
$$
If $n$ is a product of three prime numbers, we have
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=0-f(p)=-f(p)=-\frac{f(1)}{2}
$$
With mathematical induction by a number of prime multipliers we shell prove that: if $n$ is a product of $k$ prime numbers then
$$
f(n)=(2-k) \frac{f(1)}{2}
$$
For $k=1$, clearly the statement (2), holds.
Let statement (2) holds for all integers $n$, where $n$ is a product of $k$ prime numbers.
Now let $n$ be a product of $k+1$ prime numbers. Then we have $n=n_{1} p$, where $n_{1}$ is a product of $k$ prime numbers.
So
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=f\left(n_{1}\right)-f(p)=(2-k) \frac{f(1)}{2}-\frac{f(1)}{2}=(2-(k+1)) \frac{f(1)}{2}
$$
So (2) holds for every integer $n>1$.
Now from $f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right)=2006$ and because of (2) we have
$$
\begin{aligned}
2006 & =f\left(2^{2007}\right)+f\left(3^{2008}\right)+f\left(5^{2009}\right) \\
& =\frac{2-2007}{2} f(1)+\frac{2-2008}{2} f(1)+\frac{2-2009}{2} f(1)=-\frac{3 \cdot 2006}{2} f(1)
\end{aligned}
$$
i.e.
$$
f(1)=-\frac{2}{3}
$$
Since
$$
2007=3^{2} \cdot 223,2008=2^{3} \cdot 251,2009=7^{2} \cdot 41
$$
and because of (2) and (3), we get
$$
\begin{aligned}
f\left(2007^{2}\right)+f\left(2008^{3}\right)+f\left(2009^{5}\right) & =\frac{2-6}{2} f(1)+\frac{2-12}{2} f(1)+\frac{2-15}{2} f(1) \\
& =-\frac{27}{2} f(1)=-\frac{27}{2} \cdot\left(-\frac{2}{3}\right)=9
\end{aligned}
$$
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
ALG 5. Let $A B C$ be a scalene triangle with $B C=a, A C=b$ and $A B=c$, where $a_{r} b, c$ are positive integers. Prove that
$$
\left|a b^{2}+b c^{2}+c a^{2}-a^{2} b-b^{2} c-c^{2} a\right| \geq 2
$$
|
Solution. Denote $E=a b^{2}+b c^{2}+c a^{2}-a^{2} b-b^{2} c-c^{2} a$. We have
$$
\begin{aligned}
E= & \left(a b c-c^{2} a\right)+\left(c a^{2}-a^{2} b\right)+\left(b c^{2}-b^{2} c\right)+\left(a b^{2}-a b c\right)= \\
& (b-c)\left(a c-a^{2}-b c+a b\right)=(b-c)\left(a a^{2}-b\right)(c-a)
\end{aligned}
$$
So, $|E|=|a-b| \cdot|b-c| \cdot|c-a|$. By hypothesis each factor from $|E|$ is a positive integer. We shall prove that at least one factor from $|E|$ is greater than 1. Suppose that $|a-b|=|b-c|=|c-a|=1$. It follows that the numbers $a-b, b-c, c-a$ are odd. So, the number $0=(a-b)+(b-c) \div(c-a)$ is olso odd, a contradiction. Hence, $|E| \geq 1 \cdot 1 \cdot 2=2$.
|
2
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
87.3. Let $f$ be a strictly increasing function defined in the set of natural numbers satisfying the conditions $f(2)=a>2$ and $f(m n)=f(m) f(n)$ for all natural numbers $m$ and $n$. Determine the smallest possible value of $a$.
|
Solution. Since $f(n)=n^{2}$ is a function satisfying the conditions of the problem, the smallest posiible $a$ is at most 4. Assume $a=3$. It is easy to prove by induction that $f\left(n^{k}\right)=f(n)^{k}$ for all $k \geq 1$. So, taking into account that $f$ is strictly increasing, we get
$$
\begin{gathered}
f(3)^{4}=f\left(3^{4}\right)=f(81)>f(64)=f\left(2^{6}\right)=f(2)^{6} \\
=3^{6}=27^{2}>25^{2}=5^{4}
\end{gathered}
$$
as well as
$$
\begin{aligned}
& f(3)^{8}=f\left(3^{8}\right)=f(6561)<f(8192) \\
& \quad=f\left(2^{13}\right)=f(2)^{13}=3^{13}<6^{8}
\end{aligned}
$$
So we arrive at $5<f(3)<6$. But this is not possible, since $f(3)$ is an integer. So $a=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
91.1. Determine the last two digits of the number
$$
2^{5}+2^{5^{2}}+2^{5^{3}}+\cdots+2^{5^{1991}}
$$
written in decimal notation.
|
Solution. We first show that all numbers $2^{5^{k}}$ are of the form $100 p+32$. This can be shown by induction. The case $k=1$ is clear $\left(2^{5}=32\right)$. Assume $2^{5^{k}}=100 p+32$. Then, by the binomial formula,
$$
2^{5^{k+1}}=\left(2^{5^{k}}\right)^{5}=(100 p+32)^{5}=100 q+32^{5}
$$
and
$$
\begin{gathered}
(30+2)^{5}=30^{5}+5 \cdot 30^{4} \cdot 2+10 \cdot 30^{3} \cdot 4+10 \cdot 30^{2} \cdot 8+5 \cdot 30 \cdot 16+32 \\
=100 r+32
\end{gathered}
$$
So the last two digits of the sum in the problem are the same as the last digits of the number $1991 \cdot 32$, or 12 .
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
92.4. Peter has many squares of equal side. Some of the squares are black, some are white. Peter wants to assemble a big square, with side equal to $n$ sides of the small squares, so that the big square has no rectangle formed by the small squares such that all the squares in the vertices of the rectangle are of equal colour. How big a square is Peter able to assemble?
|
Solution. We show that Peter only can make a $4 \times 4$ square. The construction is possible, if $n=4$ :

Now consider the case $n=5$. We may assume that at least 13 of the 25 squares are black. If five black squares are on one horizontal row, the remaining eight ones are distributed on the other four rows. At least one row has two black squres. A rectangle with all corners black is created. Next assume that one row has four black squares. Of the remaing 9 squares, at least three are one row. At least two of these three have to be columns having the assumed four black squares. If no row has more than four black squares, there have to be at least three rows with exactly three black squares. Denote these rows by $A, B$, and $C$. Let us call the columns in which the black squares on row $A$ lie black columns, and the other two columns white columns. If either row $B$ or row $C$ has at least two black squares which are on black columns, a rectancle with black corners arises. If both rows $B$ and $C$ have only one black square on the black columns, then both of them have two black squares on the two white columns, and they make the black corners of a rectangle. So Peter cannot make a $5 \times 5$ square in the way he wishes.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
96.4. The real-valued function $f$ is defined for positive integers, and the positive integer a satisfies
$$
\begin{gathered}
f(a)=f(1995), \quad f(a+1)=f(1996), \quad f(a+2)=f(1997) \\
f(n+a)=\frac{f(n)-1}{f(n)+1} \quad \text { for all positive integers } n
\end{gathered}
$$
(i) Show that $f(n+4 a)=f(n)$ for all positive integers $n$.
(ii) Determine the smallest possible $a$.
|
Solution. To prove (i), we the formula $f(n+a)=\frac{f(n)-1}{f(n)+1}$ repeatedly:
$$
\begin{gathered}
f(n+2 a)=f((n+a)+a)=\frac{\frac{f(n)-1}{f(n)+1}-1}{\frac{f(n)-1}{f(n)+1}+1}=-\frac{1}{f(n)} \\
f(n+4 a)=f((n+2 a)+2 a)=-\frac{1}{-\frac{1}{f(n)}}=f(n)
\end{gathered}
$$
(ii) If $a=1$, then $f(1)=f(a)=f(1995)=f(3+498 \cdot 4 a)=f(3)=f(1+2 a)=-\frac{1}{f(1)}$. This clearly is not possible, since $f(1)$ and $\frac{1}{f(1)}$ have equal sign. So $a \neq 1$.
If $a=2$, we obtain $f(2)=f(a)=f(1995)=f(3+249 \cdot 4 a)=f(3)=f(a+1)=f(1996)=$ $f(4+249 \cdot 4 a)=f(4)=f(2+a)=\frac{f(2)-1}{f(2)+1}$, or $f(2)^{2}+f(2)=f(2)-1$. This quadratic equation in $f(2)$ has no real solutions. So $a \neq 2$.
If $a=3$, we try to construct $f$ by choosing $f(1), f(2)$, and $f(3)$ arbitrarily and by computing the other values of $f$ by the recursion formula $f(n+3)=\frac{f(n)-1}{f(n)+1}$. We have to check that $f$ defined in this way satisfies the conditions of the problem.
The condition
$$
f(n+a)=f(n+3)=\frac{f(n)-1}{f(n)+1}
$$
is valid because of the construction. Further, by (i),
$$
f(n+12)=f(n+4 a)=f(n)
$$
which implies
$$
\begin{gathered}
f(a)=f(3)=f(3+166 \cdot 12)=f(1995) \\
f(a+1)=f(4)=f(4+166 \cdot 12)=f(1996) \\
f(a+2)=f(5)=f(5+166 \cdot 12)=f(1997)
\end{gathered}
$$
as required.
We remark that the choice $f(n)=-1$ makes $f(n+3)$ undefined, the choice $f(n)=0$ makes $f(n+3)=-1$ and $f(n+6)$ is undefined, and $f(n)=1$ makes $f(n+3)=0$ so $f(n+9)$ is undefined. In the choice of $f(1), f(2)$, and $f(3)$ we have to avoid $-1,0,1$.
In conclusion, we see that $a=3$ is the smallest possible value for $a$.
|
3
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
97.1. Let A be a set of seven positive numbers. Determine the maximal number of triples $(x, y, z)$ of elements of A satisfying $x<y$ and $x+y=z$.
|
Solution. Let $0<a_{1}<a_{2}<\ldots<a_{7}$ be the elements of the set $A$. If $\left(a_{i}, a_{j}, a_{k}\right)$ is a triple of the kind required in the problem, then $a_{i}<a_{j}<a_{i}+a_{j}=a_{k}$. There are at most $k-1$ pairs $\left(a_{i}, a_{j}\right)$ such that $a_{i}+a_{j}=a_{k}$. The number of pairs satisfying $a_{i}<a_{j}$ is at most $\left\lfloor\frac{k-1}{2}\right\rfloor$. The total number of pairs is at most
$$
\sum_{k=3}^{7}\left\lfloor\frac{k-1}{2}\right\rfloor=1+1+2+2+3=9
$$
The value 9 can be reached, if $A=\{1,2, \ldots, 7\}$. In this case the triples $(1,2,3),(1,3,4)$, $(1,4,5),(1,5,6),(1,6,7),(2,3,5),(2,4,6),(2,5,7)$, and $(3,4,7)$ satisfy the conditions of the problem.
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
99.2. Consider 7-gons inscribed in a circle such that all sides of the 7-gon are of different length. Determine the maximal number of $120^{\circ}$ angles in this kind of a 7-gon.
|
Solution. It is easy to give examples of heptagons $A B C D E F G$ inscribed in a circle with all sides unequal and two angles equal to $120^{\circ}$. These angles cannot lie on adjacent vertices of the heptagon. In fact, if $\angle A B C=\angle B C D=120^{\circ}$, and arc $B C$ equals $b^{\circ}$, then arcs $A B$ and $C D$ both are $120^{\circ}-b^{\circ}$ (compute angles in isosceles triangles with center of the circle as the to vertex), and $A B=C D$, contrary to the assumption. So if the heptagon has three angles of $120^{\circ}$, their vertices are, say $A, C$, and $E$. Then each of the arcs $G A B, B C D$, $D E F$ are $360^{\circ}-240^{\circ}=120^{\circ}$. The arcs are disjoint, so they cover the whole circumference. The $F$ has to coincide with $G$, and the heptagon degenerates to a hexagon. There can be at most two $120^{\circ}$ angles.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
01.3. Determine the number of real roots of the equation
$$
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2}=0
$$
|
Solution. Write
$$
\begin{gathered}
x^{8}-x^{7}+2 x^{6}-2 x^{5}+3 x^{4}-3 x^{3}+4 x^{2}-4 x+\frac{5}{2} \\
=x(x-1)\left(x^{6}+2 x^{4}+3 x^{2}+4\right)+\frac{5}{2}
\end{gathered}
$$
If $x(x-1) \geq 0$, i.e. $x \leq 0$ or $x \geq 1$, the equation has no roots. If $0x(x-1)=\left(x-\frac{1}{2}\right)^{2}-\frac{1}{4} \geq-\frac{1}{4}$ and $x^{6}+2 x^{4}+3 x+4<1+2+3+4=10$. The value of the left-hand side of the equation now is larger than $-\frac{1}{4} \cdot 10+\frac{5}{2}=0$. The equation has no roots in the interval $(0,1)$ either.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
06.3. A sequence of positive integers $\left\{a_{n}\right\}$ is given by
$$
a_{0}=m \quad \text { and } \quad a_{n+1}=a_{n}^{5}+487
$$
for all $n \geq 0$. Determine all values of $m$ for which the sequence contains as many square numbers as possible.
|
Solution. Consider the expression $x^{5}+487$ modulo 4. Clearly $x \equiv 0 \Rightarrow x^{5}+487 \equiv 3$, $x \equiv 1 \Rightarrow x^{5}+487 \equiv 0 ; x \equiv 2 \Rightarrow x^{5}+487 \equiv 3$, and $x \equiv 3 \Rightarrow x^{5}+487 \equiv 2$. Square numbers are always $\equiv 0$ or $\equiv 1 \bmod 4$. If there is an even square in the sequence, then all subsequent numbers of the sequence are either $\equiv 2$ or $\equiv 3 \bmod 4$, and hence not squares. If there is an odd square in the sequence, then the following number in the sequence can be an even square, but then none of the other numbers are squares. So the maximal number of squares in the sequence is two. In this case the first number of the sequence has to be the first square, since no number of the sequence following another one satisfies $x \equiv 1 \bmod 4$. We have to find numbers $k^{2}$ such that $k^{10}+487=n^{2}$. We factorize $n^{2}-k^{10}$. Because 487 is a prime, $n-k^{5}=1$ and $n+k^{5}=487$ or $n=244$ and $k=3$. The only solution of the problem thus is $m=3^{2}=9$.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
09.2. On a faded piece of paper it is possible, with some effort, to discern the following:
$$
\left(x^{2}+x+a\right)\left(x^{15}-\ldots\right)=x^{17}+x^{13}+x^{5}-90 x^{4}+x-90
$$
Some parts have got lost, partly the constant term of the first factor of the left side, partly the main part of the other factor. It would be possible to restore the polynomial forming the other factor, but we restrict ourselves to asking the question: What is the value of the constant term a? We assume that all polynomials in the statement above have only integer coefficients.
|
Solution. We denote the polynomial $x^{2}+x+a$ by $P_{a}(x)$, the polynomial forming the other factor of the left side by $Q(x)$ and the polynomial on the right side by $R(x)$. The polynomials are integer valued for every integer $x$. For $x=0$ we get $P_{a}(0)=a$ and $R(0)=-90$, so $a$ is a divisor of $90=2 \cdot 3 \cdot 3 \cdot 5$. For $x=-1$ we get $P_{a}(-1)=-184$, so $a$ is also a divisor of $184=2 \cdot 2 \cdot 2 \cdot 23$. But the only prime factor in common is 2 . So the only possibilities for $a$ are $\pm 2$ and $\pm 1$. If $a=1$, we get for $x=1$ that $P_{1}(1)=3$, while $R(1)=4-180=-176$, which cannot be divided by 3 . If $a=-2$ we get for $x=1$ that $P_{2}(1)=0$, i.e. the left side is equal to 0 , while the right side is equal to $R(1)=-176$, which is different from 0 . Neither $a=1$ nor $a=-2$ will thus work. It remains to check $a=2$ and $a=-1$. Before we use the procedure above again, we need a factorization of $R(x)$. We observe that $x^{4}+1$ is a divisor of $R(x)$, since the right side may be written as $\left(x^{4}+1\right)\left(x^{13}+x-90\right)$. If $a=-1$ we get for $x=2$ that $P_{1}(2)=5$, while $x^{4}+1=17$ and $x^{13}+x-90=8104$. So the right hand side is not divisible by 5 . Now, the only remaining possibility is $a=2$, i.e. $x^{2}+x+2$ is a divisor of $R(x)$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3. Laura has 2010 lamps connected with 2010 buttons in front of her. For each button, she wants to know the corresponding lamp. In order to do this, she observes which lamps are lit when Richard presses a selection of buttons. (Not pressing anything is also a possible selection.) Richard always presses the buttons simultaneously, so the lamps are lit simultaneously, too.
a) If Richard chooses the buttons to be pressed, what is the maximum number of different combinations of buttons he can press until Laura can assign the buttons to the lamps correctly?
b) Supposing that Laura will choose the combinations of buttons to be pressed, what is the minimum number of attempts she has to do until she is able to associate the buttons with the lamps in a correct way?
|
Solution. a) Let us say that two lamps are separated, if one of the lamps is turned on while the other lamp remains off. Laura can find out which lamps belong to the buttons if every two lamps are separated. Let Richard choose two arbitrary lamps. To begin with, he turns both lamps on and then varies all the other lamps in all possible ways. There are $2^{2008}$ different combinations for the remaining $2010-2=2008$ lamps. Then Richard turns
the two chosen lamps off. Also, at this time there are $2^{2008}$ combinations for the remaining lamps. Consequently, for the $2^{2009}$ combinations in all, it is not possible to separate the two lamps of the first pair. However, we cannot avoid the separation if we add one more combination. Indeed, for every pair of lamps, we see that if we turn on a combination of lamps $2^{2009}+1$ times, there must be at least one setup where exactly one of the lamps is turned on and the other is turned off. Thus, the answer is $2^{2009}+1$.
b) For every new step with a combination of lamps turned on, we get a partition of the set of lamps into smaller and smaller subsets where elements belonging to the same subset cannot be separated. In each step every subset is either unchanged or divided into two smaller parts, i.e. the total number of subsets after $\mathrm{k}$ steps will be at most $2^{k}$. We are finished when the number of subsets is equal to 2010 , so the answer is at least $\left\lceil\log _{2} 2010\right\rceil=11$. But it is easy to see that Laura certainly can choose buttons in every step in such a way that there are at most $2^{11-k}$ lamps in every part of the partition after $k$ steps. Thus, the answer is 11 .
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4. A positive integer is called simple if its ordinary decimal representation consists entirely of zeroes and ones. Find the least positive integer $k$ such that each positive integer $n$ can be written as $n=a_{1} \pm a_{2} \pm a_{3} \pm \cdots \pm a_{k}$, where $a_{1}, \ldots, a_{k}$ are simple.
|
Solution. We can always write $n=a_{l}+a_{2}+\cdots+a_{9}$ where $a_{j}$ has 1 's in the places where $n$ has digits greater or equal to $j$ and 0 's in the other places. So $k \leq 9$. To show that $k \geq 9$, consider $n=10203040506070809$. Suppose $n=a_{l}+a_{2}+\cdots+a_{j}-a_{j+l}-a_{j+2}-\cdots-a_{k}$, where $a_{l}, \ldots, a_{k}$ are simple, and $k<9$. Then all digits of $b_{l}=a_{l}+\cdots+a_{j}$ are not greater than $j$ and all digits of $b_{2}=a_{j+l}+\cdots+a_{k}$ are not greater than $k-j$. We have $n+b_{2}=b_{l}$. We perform column addition of $n$ and $b_{2}$ and consider digit $j+1$ in the number $n$. There will be no carry digit coming from lower decimal places, since the sum there is less that $10 \ldots 0+88 \ldots 8=98 \ldots 8$. So in the column of $j+1$ we get the sum of $j+1$ and the corresponding digit in $b_{2}$. The resulting digit should be less than $j+1$. Thus in the corresponding place in $b_{2}$ we have at least $9-j$. But $9-j \leq k-j$, implying $k \geq 9$. Hence, we have proved that the maximal $k$ is 9 .
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
PROBLEM 1. The real numbers $a, b, c$ are such that $a^{2}+b^{2}=2 c^{2}$, and also such that $a \neq b, c \neq-a, c \neq-b$. Show that
$$
\frac{(a+b+2 c)\left(2 a^{2}-b^{2}-c^{2}\right)}{(a-b)(a+c)(b+c)}
$$
is an integer.
|
SolUTiON. Let us first note that
$$
\frac{a+b+2 c}{(a+c)(b+c)}=\frac{(a+c)+(b+c)}{(a+c)(b+c)}=\frac{1}{a+c}+\frac{1}{b+c}
$$
Further we have
$$
2 a^{2}-b^{2}-c^{2}=2 a^{2}-\left(2 c^{2}-a^{2}\right)-c^{2}=3 a^{2}-3 c^{2}=3(a+c)(a-c)
$$
and
$$
2 a^{2}-b^{2}-c^{2}=2\left(2 c^{2}-b^{2}\right)-b^{2}-c^{2}=3 c^{2}-3 b^{2}=3(b+c)(c-b)
$$
so that
$$
\frac{(a+b+2 c)\left(2 a^{2}-b^{2}-c^{2}\right)}{(a-b)(a+c)(b+c)}=\frac{3(a-c)+3(c-b)}{a-b}=\frac{3(a-b)}{a-b}=3
$$
an integer.
|
3
|
Algebra
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Find the smallest positive integer $n$, such that there exist $n$ integers $x_{1}, x_{2}, \ldots, x_{n}$ (not necessarily different), with $1 \leq x_{k} \leq n, 1 \leq k \leq n$, and such that
$$
x_{1}+x_{2}+\cdots+x_{n}=\frac{n(n+1)}{2}, \quad \text { and } \quad x_{1} x_{2} \cdots x_{n}=n!
$$
but $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\} \neq\{1,2, \ldots, n\}$.
|
Solution. If it is possible to find a set of numbers as required for some $n=k$, then it will also be possible for $n=k+1$ (choose $x_{1}, \ldots, x_{k}$ as for $n=k$, and
let $x_{k+1}=k+1$ ). Thus we have to find a positive integer $n$ such that a set as required exists, and prove that such a set does not exist for $n-1$.
For $n=9$ we have $8+6+3=9+4+4$, and $8 \cdot 6 \cdot 3=9 \cdot 4 \cdot 4$, so that a set of numbers as required will exist for all $n \geq 9$. It remains to eliminate $n=8$.
Assume $x_{1}, \ldots, x_{8}$ are numbers that satisfy the conditions of the problem. Since 5 and 7 are primes, and since $2 \cdot 5>8$ and $2 \cdot 7>8$, two of the $x$-numbers have to be equal to 5 and 7 ; without loss of generality we can assume that $x_{1}=5, x_{2}=7$. For the remaining numbers we have $x_{3} x_{4} \cdots x_{8}=2^{7} \cdot 3^{2}$, and $x_{3}+x_{4}+\cdots+x_{8}=36-12=24$. Since $3^{2}=9>8$, it follows that exactly two of the numbers $x_{3}, \ldots, x_{8}$ are divisible by 3 , and the rest of the numbers are powers of 2. There are three possible cases to consider: two of the numbers are equal to 3 ; two of the numbers are equal to 6 ; one number is equal to 3 and another one is equal to 6 .
Case 1. $x_{3}=x_{4}=3$
We then have $x_{5}+x_{6}+x_{7}+x_{8}=18$, and $x_{5} x_{6} x_{7} x_{8}=2^{7}$. The possible powers of 2 with sum 18 are $(1,1,8,8)$ and $(2,4,4,8)$, none of them gives the product $2^{7}$.
Case 2. $x_{3}=3, x_{4}=6$
We have $x_{5}+x_{6}+x_{7}+x_{8}=15$, and $x_{5} x_{6} x_{7} x_{8}=2^{6}$. It is immediate to check that the only possibility for the remaining numbers is $(1,2,4,8)$, which is not allowed, since it gives $\left\{x_{1}, x_{2}, \ldots, x_{8}\right\}=\{1,2, \ldots, 8\}$.
Case 3. $x_{3}=x_{4}=6$
Now we have $x_{5}+x_{6}+x_{7}+x_{8}=12$, and $x_{5} x_{6} x_{7} x_{8}=2^{5}$. The possible powers of 2 which give the correct sum are $(1,1,2,8)$ and $(2,2,4,4)$, but again, they do not give the desired product.
Thus the smallest positive integer with the required property is 9 .
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXIV OM - I - Problem 10
Find the smallest natural number $ n > 1 $ with the following property: there exists a set $ Z $ consisting of $ n $ points in the plane such that every line $ AB $ ($ A, B \in Z $) is parallel to some other line $ CD $ ($ C, D \in Z $).
|
We will first prove that the set $ Z $ of vertices of a regular pentagon has the property given in the problem, that is, $ n \leq 5 $. We will show that each side of the regular pentagon is parallel to a certain diagonal and vice versa, each diagonal is parallel to a corresponding side.
It suffices to prove that $ AB \parallel CE $ (Fig. 11). Since a circle can be circumscribed around quadrilateral $ ABCE $ (namely, it is the circle circumscribed around the given regular pentagon), we have $ \measuredangle A + \measuredangle BCE = \pi $. Since $ \measuredangle A = \measuredangle B $, it follows that $ \measuredangle BCE = \pi - \measuredangle B $, which proves that $ AB \parallel CE $.
On the other hand, from the conditions of the problem, it follows that $ n \geq 4 $, since there are at least two different parallel lines, each containing at least two points of the set $ Z $. If $ n = 4 $ and points $ A, B, C, D $ satisfied the conditions of the problem, they would be the vertices of a trapezoid. However, none of the diagonals of a trapezoid is parallel to another line determined by its vertices. Therefore, $ n > 4 $, and from the previously proven inequality $ n \leq 5 $, it follows that $ n = 5 $.
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LVII OM - III - Problem 2
Determine all positive integers $ k $ for which the number $ 3^k+5^k $ is a power of an integer with an exponent greater than 1.
|
If $ k $ is an even number, then the numbers $ 3^k $ and $ 5^k $ are squares of odd numbers, giving a remainder of 1 when divided by 4. Hence, the number $ 3^k + 5^k $ gives a remainder of 2 when divided by 4, and thus is divisible by 2 but not by $ 2^2 $. Such a number cannot be a power of an integer with an exponent greater than 1.
If $ k $ is an odd number, then
The second factor on the right side of the above relationship contains an odd (equal to $ k $) number of odd summands.
Hence, the number $ 3^k + 5^k $ is divisible by 8 and not by 16. If this number is a power of an integer with an exponent greater than 1, then it must be a cube of an integer.
If $ k = 1 $, then the considered number is a cube of an integer: $ 3^1 + 5^1 = 2^3 $. Let us assume in the further part of the reasoning that $ k \geq 3 $. From the relationship
it follows that cubes of integers give remainders of 0, 1, 8 when divided by 9. For $ k \geq 3 $ we have $ 9 | 3^k $, so $ 3^k + 5^k \equiv 5^k (\mod 9) $.
The remainders of the numbers $ 5, 5^2, 5^3, 5^4, 5^5, 5^6 $ when divided by 9 are 5, 7, 8, 4, 2, 1, respectively. Therefore, if $ 3^k + 5^k $ is a cube of an integer for $ k \geq 3 $, then $ 3 | k $. We have previously shown that $ k $ cannot be an even number.
Thus, the number $ k $ is of the form $ 6l + 3 $, where $ l $ is a non-negative integer.
From the relationship $ 3^3 \equiv 5^3 \equiv 6 (\mod 7) $ and $ 3^6 \equiv 5^6 \equiv 1 (\mod 7) $, it follows that
However, from direct verification, we obtain that the cube of an integer gives a remainder of 0, 1, or 6 when divided by 7:
Therefore, the considered number for $ k \geq 3 $ cannot be a cube of an integer, which concludes the solution of the problem.
Answer: $ k = 1 $.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXXIV OM - II - Problem 6
For a given number $ n $, let $ p_n $ denote the probability that when a pair of integers $ k, m $ satisfying the conditions $ 0 \leq k \leq m \leq 2^n $ is chosen at random (each pair is equally likely), the number $ \binom{m}{k} $ is even. Calculate $ \lim_{n\to \infty} p_n $.
|
om34_2r_img_10.jpg
The diagram in Figure 10 shows Pascal's triangle written modulo $2$, meaning it has zeros and ones in the places where the usual Pascal's triangle has even and odd numbers, respectively. Just like in the usual Pascal's triangle, each element here is the sum of the elements directly above it, according to the addition table modulo 2: $0+0=0$, $0+1=1$, $1+0=1$, $1+1 = 0$. The drawn horizontal lines divide this triangle into layers:
- layer $W_0$ consisting of row number $0$,
- layer $W_1$ consisting of row number $1$,
- layer $W_2$ consisting of rows number $2$ and $3$,
- layer $W_3$ consisting of rows number $4$, $5$, $6$, $7$,
- $\ldots$
- layer $W_j$ consisting of rows with numbers from $2^{j-1}$ to $2^j-1$
- $\ldots$
We will prove by induction that in any layer $W_j$ there are two disjoint triangles, each identical to the triangle formed by the layers $W_0, W_1, \ldots, W_{j-1}$, and that these two triangles are separated by an inverted triangle composed entirely of zeros; the top row of the layer consists of extreme ones and zeros, and the bottom row of the layer consists of all ones.
For $j = 1, 2, 3$, this is visible from the diagrams (the diagonal lines define the division into the triangles mentioned). Assume the above relationships are true for some $j$ and consider the layer $W_{j+1}$. By the induction hypothesis, the last row of layer $W_j$ has the form $111\ldots 111$, and thus, according to the addition rule given above, the first row of layer $W_{j+1}$ has the form $100\ldots 001$. The extreme ones of this row give rise to two new copies of Pascal's triangle, and between them are zeros. Layer $W_{j+1}$ has as many rows as the layers $W_0, W_1, \ldots, W_j$ taken together, so at the base of each of these two triangles at the bottom of layer $W_{j+1}$ will be the same pattern of digits as in the last row of layer $W_j$, i.e., a row of ones. They will fill the last row of layer $W_{j+1}$. This completes the proof of the inductive thesis.
The number $p_n$ defined in the problem is the ratio of the number of zeros in the rows numbered from $0$ to $2^n$ to the number of all elements in these rows. These rows cover the layers $W_0, W_1, \ldots, W_n$ and the first row of layer $W_{n+1}$. From the relationship proved above, it follows that in the sum of layers $W_0, \ldots, W_j$ there are three times as many ones as in the sum of layers $W_0, \ldots, W_{j-1}\ (j = 1, 2, 3, \ldots)$, and since there is one one in layer $W_0$, there are $3^n$ ones in the sum of layers $W_0, \ldots, W_n$. Adding to this the two extreme ones of the next row, we see that there are $a_n = 3^n + 2$ ones in the considered fragment of Pascal's triangle. The total number of elements in this fragment is $b_n = 1 + 2 + 3 + \ldots + (2^n + 1) = (2^n + 1)(2^n + 2) / 2$, and thus there are $b_n - a_n$ zeros. The probability in question is
\[
\frac{b_n - a_n}{b_n} = \frac{(2^n + 1)(2^n + 2) / 2 - (3^n + 2)}{(2^n + 1)(2^n + 2) / 2}
\]
Hence,
\[
\lim_{n \to \infty} p_n = 1
\]
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
IX OM - II - Task 2
Six equal disks are placed on a plane in such a way that their centers lie at the vertices of a regular hexagon with a side equal to the diameter of the disks. How many rotations will a seventh disk of the same size make while rolling externally on the same plane along the disks until it returns to its initial position?
|
Let circle $K$ with center $O$ and radius $r$ roll without slipping on a circle with center $S$ and radius $R$ (Fig. 16). The rolling without slipping means that different points of one circle successively coincide with different points of the other circle, and in this correspondence, the length of the arc between two points of one circle equals the length of the arc between the corresponding points of the other circle.
Consider two positions $K$ and $K_1$ of the moving circle, corresponding to centers $O$ and $O_1$ and points of tangency with the fixed circle $A$ and $B_1$; let $B$ be the point on the circumference of circle $K$ that, in the new position, passes to the point of tangency $B_1$, and let $\alpha$ and $\beta$ denote the radian measures of angles $ASB_1$ and $AOB$. Since the length of arc $AB_1$ of the fixed circle equals the length of arc $AB$ of the moving circle, we have $R \alpha = r \beta$. The radius $OA$ of the moving circle will take the new position $O_1A_1$, with $\measuredangle A_1O_1B_1 = \measuredangle AOB = \beta$. Draw the radius $O_1A_0$ parallel to $OA$; we get $\measuredangle A_0O_1B_1 = \measuredangle ASB_1 = \alpha$. The angle $A_0O_1A_1 = \alpha + \beta$ is equal to the angle through which circle $K$ has rotated when moving from position $K$ to position $K_1$. If $R = r$, then $\beta = \alpha$, and the angle of rotation is then $2 \alpha$.
Once the above is established, it is easy to answer the posed question.
The moving disk $K$ rolls successively on six given disks; the transition from one to another occurs at positions where disk $K$ is simultaneously tangent to two adjacent fixed disks. Let $K_1$ and $K_2$ be the positions where disk $K$ is tangent to fixed disk $N$ and to one of the adjacent disks (Fig. 17). Then $\measuredangle O_1SO_2 = 120^\circ$, so when moving from position $K_1$ to position $K_2$, the disk rotates by $240^\circ$. The disk will return to its initial position after $6$ such rotations, having rotated a total of $6 \cdot 240^\circ = 4 \cdot 360^\circ$, i.e., it will complete $4$ full rotations.
Note. We can more generally consider the rolling of a disk with radius $r$ on any curve $C$ (Fig. 18). When the point of tangency $A$ traverses an arc $AB_1$ of length $l$ on the curve, the angle through which the disk rotates is $\alpha + \beta$, where $\alpha$ is the angle between the lines $OA$ and $O_1B_1$, i.e., the angle between the normals to the curve $C$ at points $A$ and $B$, and $\beta = \frac{l}{r}$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXXVI OM - III - Problem 1
Determine the largest number $ k $ such that for every natural number $ n $ there are at least $ k $ natural numbers greater than $ n $, less than $ n+17 $, and coprime with the product $ n(n+17) $.
|
We will first prove that for every natural number $n$, there exists at least one natural number between $n$ and $n+17$ that is coprime with $n(n+17)$.
In the case where $n$ is an even number, the required property is satisfied by the number $n+1$. Of course, the numbers $n$ and $n+1$ are coprime. If a number $d > 1$ were a common divisor of $n+1$ and $n+17$, then it would divide the difference $(n+17)-(n+1) = 16$, and thus would be an even number. However, since $n+1$ is an odd number, such a $d$ does not exist. Therefore, the numbers $n+1$ and $n(n+17)$ are coprime.
In the case where $n$ is an odd number, the required property is satisfied by the number $n + 16$. Indeed, the numbers $n+16$ and $n+17$ are coprime. Similarly, as above, we conclude that $n$ and $n+16$ are also coprime. Therefore, $n+16$ and $n(n+17)$ are coprime.
In this way, we have shown that $k \geq 1$.
Consider the number $n = 16!$. The numbers $n+2, n+3, \ldots, n+16$ are not coprime with $n(n+17)$, because for $j = 2, 3, \ldots, 16$, the numbers $n+j$ and $n$ are divisible by $j$. Only the number $n+1$ is coprime with $n(n+17)$. From this example, it follows that $k \leq 1$. Therefore, $k = 1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
III OM - I - Task 4
a) Given points $ A $, $ B $, $ C $ not lying on a straight line. Determine three mutually parallel lines passing through points $ A $, $ B $, $ C $, respectively, so that the distances between adjacent parallel lines are equal.
b) Given points $ A $, $ B $, $ C $, $ D $ not lying on a plane. Determine four mutually parallel planes passing through points $ A $, $ B $, $ C $, $ D $, respectively, so that the distances between adjacent parallel planes are equal.
|
a) Suppose that the lines $a$, $b$, $c$ passing through points $A$, $B$, $C$ respectively and being mutually parallel satisfy the condition of the problem, that is, the distances between adjacent parallel lines are equal. Then the line among $a$, $b$, $c$ that lies between the other two is equidistant from them. Let this line be, for example, line $b$. In this case, points $A$ and $C$ are equidistant from line $b$ and lie on opposite sides of it; therefore, line $b$ intersects segment $AC$ at its midpoint $M$. From the fact that points $A$, $B$, $C$ do not lie on a straight line, it follows that point $M$ is different from point $B$.
Hence the construction: we draw line $b$ through point $B$ and through the midpoint $M$ of segment $AC$, and then we draw through points $A$ and $C$ lines $a$ and $c$ parallel to line $b$ (Fig. 12). The parallel lines $a$, $b$, $c$ determined in this way solve the problem, since points $A$ and $C$, and thus lines $a$ and $c$, are equidistant from line $b$ and lie on opposite sides of this line.
We found the above solution assuming that among the sought lines $a$, $b$, $c$, the line $b$ lies between lines $a$ and $c$; since the "inner" line can equally well be $a$ or $c$, the problem has three solutions.
b) Suppose that the planes $\alpha$, $\beta$, $\gamma$, $\delta$, passing through points $A$, $B$, $C$, $D$ respectively and being mutually parallel, satisfy the condition of the problem, that is, the distances between adjacent planes are equal. Let these planes be in the order $\alpha$, $\beta$, $\gamma$, $\delta$. We mean by this that plane $\beta$ is equidistant from planes $\alpha$ and $\gamma$, and plane $\gamma$ is equidistant from planes $\beta$ and $\delta$.
In this case, points $A$ and $C$ are equidistant from plane $\beta$ and lie on opposite sides of it, so plane $\beta$ passes through the midpoint $M$ of segment $AC$. Similarly, plane $\gamma$ passes through the midpoint $N$ of segment $BD$. From the fact that points $A$, $B$, $C$, $D$ do not lie in a plane, it follows that point $M$ is different from point $B$, and point $N$ is different from point $C$.
From this, we derive the following construction. We connect point $B$ with the midpoint $M$ of segment $AC$, and point $C$ with the midpoint $N$ of segment $BD$ (Figure 13 shows a parallel projection of the figure). Lines $BM$ and $CN$ are skew; if they lay in the same plane, then points $A$, $B$, $C$, $D$ would lie in the same plane, contrary to the assumption. We know from stereometry that through two skew lines $BM$ and $CN$ one can draw two and only two parallel planes $\beta$ and $\gamma$.
To do this, we draw through point $M$ a line $m$ parallel to line $CN$, and through point $N$ a line $n$ parallel to line $BM$; plane $\beta$ is then determined by lines $m$ and $BM$, and plane $\gamma$ by lines $n$ and $CN$.
Finally, we draw through points $A$ and $D$ planes $\alpha$ and $\delta$ parallel to planes $\beta$ and $\gamma$; we can determine them, as indicated in Figure 13, by drawing through each of points $A$ and $D$ lines parallel to lines $BM$ and $CN$.
The planes $\alpha$, $\beta$, $\gamma$, $\delta$ determined in this way solve the problem, since points $A$ and $C$, and thus planes $\alpha$ and $\gamma$, are equidistant from plane $\beta$ and lie on opposite sides of this plane - and similarly, planes $\beta$ and $\delta$ are equidistant from plane $\gamma$ and lie on opposite sides of this plane.
We found the above solution assuming that the sought planes are in the order $\alpha$, $\beta$, $\gamma$, $\delta$. For other orders of the sought planes, we will find other solutions in the same way. The number of all possible orders, or permutations of the letters $\alpha$, $\beta$, $\gamma$, $\delta$, is $4!$, i.e., $24$. However, note that two "reverse" permutations, such as $\alpha$, $\beta$, $\gamma$, $\delta$ and $\delta$, $\gamma$, $\beta$, $\alpha$, give the same solution. Therefore, the problem has $\frac{24}{2} = 12$ solutions corresponding to the permutations.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LV OM - III - Task 5
Determine the maximum number of lines in space passing through a fixed point and such that any two intersect at the same angle.
|
Let $ \ell_1,\ldots,\ell_n $ be lines passing through a common point $ O $. A pair of intersecting lines determines four angles on the plane containing them: two vertical angles with measure $ \alpha \leq 90^\circ $ and the other two angles with measure $ 180^\circ - \alpha $. According to the assumption, the value of $ \alpha $ is the same for every pair $ \ell_i, \ell_j $.
Consider a sphere $ S $ centered at $ O $ with an arbitrary radius, and denote by $ A_i $, $ B_i $ the points of intersection of the line $ \ell_i $ with this sphere. Each of the segments $ A_iA_j $, $ A_iB_j $, $ B_iB_j $ (for $ i \neq j $) is a chord of the sphere $ S $, determined by a central angle of measure $ \alpha $ or $ 180^\circ - \alpha $. Therefore, these segments have at most two different lengths $ a $ and $ b $.
Fix the notation so that $ \measuredangle A_iOA_n = \alpha $ for $ i = 1,\ldots,n-1 $. Then the points $ A_1, \ldots, A_{n-1} $ lie on a single circle (lying in a plane perpendicular to the line $ \ell_n $). Let $ A_1C $ be the diameter of this circle. Each of the points $ A_2,\ldots,A_{n-1} $ is at a distance $ a $ or $ b $ from the point $ A_1 $; hence, on each of the two semicircles with endpoints $ A_1 $ and $ C $, there are at most two points from the set $ \{A_2,\ldots ,A_{n-1}\} $. Therefore, this set has at most four elements; which means that $ n \leq 6 $.
On the other hand, if $ n = 6 $, we can place the points $ A_1,A_2,\ldots,A_5 $ at the vertices of a regular pentagon, and the plane of this pentagon at such a distance from the point $ A_6 $ that these six points, together with their antipodal points $ B_1,\ldots,B_6 $, are the vertices of a regular icosahedron. The segments $ A_iB_i $ (diameters of the sphere $ S $) connect opposite vertices of this icosahedron and any two of them form the same angle. Therefore, $ n = 6 $ is the largest possible number of lines $ \ell_i $.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XVI OM - II - Task 4
Find all prime numbers $ p $ such that $ 4p^2 +1 $ and $ 6p^2 + 1 $ are also prime numbers.
|
To solve the problem, we will investigate the divisibility of the numbers \( u = 4p^2 + 1 \) and \( v = 6p^2 + 1 \) by \( 5 \). It is known that the remainder of the division of the product of two integers by a natural number is equal to the remainder of the division of the product of their remainders by that number. Based on this, we can easily find the following:
\begin{center}
When \( p \equiv 0 \pmod{5} \), then \( u \equiv 1 \pmod{5} \), \( v \equiv 1 \pmod{5} \);\\
When \( p \equiv 1 \pmod{5} \), then \( u \equiv 0 \pmod{5} \), \( v \equiv 2 \pmod{5} \);\\
When \( p \equiv 2 \pmod{5} \), then \( u \equiv 2 \pmod{5} \), \( v \equiv 0 \pmod{5} \);\\
When \( p \equiv 3 \pmod{5} \), then \( u \equiv 2 \pmod{5} \), \( v \equiv 0 \pmod{5} \);\\
When \( p \equiv 4 \pmod{5} \), then \( u \equiv 0 \pmod{5} \), \( v \equiv 2 \pmod{5} \).\\
\end{center}
From the above, it follows that the numbers \( u \) and \( v \) can both be prime numbers only when \( p \equiv 0 \pmod{5} \), i.e., when \( p = 5 \), since \( p \) must be a prime number. In this case, \( u = 4 \cdot 5^2 + 1 = 101 \), \( v = 6 \cdot 5^2 + 1 = 151 \), so they are indeed prime numbers.
Therefore, the only solution to the problem is \( p = 5 \).
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
L OM - I - Task 5
Find all pairs of positive integers $ x $, $ y $ satisfying the equation $ y^x = x^{50} $.
|
We write the given equation in the form $ y = x^{50/x} $. Since for every $ x $ being a divisor of $ 50 $, the number on the right side is an integer, we obtain solutions of the equation for $ x \in \{1,2,5,10,25,50\} $. Other solutions of this equation will only be obtained when $ x \geq 2 $ and for some $ k \geq 2 $, the number $ x $ is simultaneously the $ k $-th power of some natural number and a divisor of the number $ 50k $. If $ p $ is a prime divisor of such a number $ x $, then $ p^k|50^k $. Since $ p^k > k $, it cannot be that $ p^k|k $, so $ p \in \{2,5\} $. If $ p = 2 $, then $ 2^k|2k $, from which $ k = 2 $. If, however, $ p = 5 $, then $ 5^k|25k $, from which again $ k = 2 $. Therefore, $ x $ must simultaneously be the square of some natural number and a divisor of the number $ 100 $.
We obtain two new values of $ x $ in this case: $ x = 4 $ and $ x = 100 $. Thus, the given equation has 8 solutions:
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXXIX OM - I - Problem 1
For each positive number $ a $, determine the number of roots of the polynomial $ x^3+(a+2)x^2-x-3a $.
|
Let's denote the considered polynomial by $ F(x) $. A polynomial of the third degree has at most three real roots. We will show that the polynomial $ F $ has at least three real roots - and thus has exactly three real roots (for any value of the parameter $ a > 0 $).
It is enough to notice that
If a continuous function with real values takes values of different signs at two points, then at some point in the interval bounded by these points, it takes the value zero (Darboux property).
Hence, in each of the intervals $ (-a-3; -2) $, $ (-2; 0) $, $ (0; 2) $, there is a root of the polynomial $ F $.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
V OM - I - Task 2
Investigate when the sum of the cubes of three consecutive natural numbers is divisible by $18$.
|
Let $ a - 1 $, $ a $, $ a + 1 $, be three consecutive natural numbers; the sum of their cubes
can be transformed in the following way:
Since one of the numbers $ a - 1 $, $ a $, $ a + 1 $ is divisible by $ 3 $, then one of the numbers $ a $ and $ (a + 1) (a - 1) + 3 $ is also divisible by $ 3 $. Therefore, the sum $ S $ of the cubes of three consecutive natural numbers is always divisible by $ 9 $.
The sum $ S $ is thus divisible by $ 18 = 9 \cdot 2 $ if and only if it is divisible by $ 2 $. Since $ S = 3a^3 + 6a $, $ S $ is even if and only if $ a $ is even, i.e., when $ a - 1 $ is odd. Hence, the conclusion:
The sum of the cubes of three consecutive natural numbers is divisible by $ 18 $ if and only if the first of these numbers is odd.
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LIX OM - II - Task 1
Determine the maximum possible length of a sequence of consecutive integers, each of which can be expressed in the form $ x^3 + 2y^2 $ for some integers $ x, y $.
|
A sequence of five consecutive integers -1, 0, 1, 2, 3 satisfies the conditions of the problem: indeed, we have
On the other hand, among any six consecutive integers, there exists a number, say
$ m $, which gives a remainder of 4 or 6 when divided by 8. The number $ m $ is even; if there were a representation
in the form $ m = x^3 +2y^2 $ for some integers $ x, y $, then the number $ x $ would be even. In this case, however,
we would obtain the divisibility $ 8|x^3 $ and as a result, the numbers $ m $ and $ 2y^2 $ would give the same remainder (4 or 6) when divided by 8.
Therefore, the number $ y^2 $ would give a remainder of 2 or 3 when divided by 4. This is impossible: the equalities
prove that the square of an integer can give a remainder of only 0 or 1 when divided by 4.
We have thus shown that among any six consecutive integers, there exists a number that cannot be represented
in the form $ x^3 +2y^2 $.
Answer: The maximum possible length of such a sequence is 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XXIV OM - III - Task 2
Let $ p_n $ be the probability that a series of 100 consecutive heads will appear in $ n $ coin tosses. Prove that the sequence of numbers $ p_n $ is convergent and calculate its limit.
|
The number of elementary events is equal to the number of $n$-element sequences with two values: heads and tails, i.e., the number $2^n$. A favorable event is a sequence containing 100 consecutive heads. We estimate the number of unfavorable events from above, i.e., the number of sequences not containing 100 consecutive heads.
Let $n = 100k + r$, where $k \geq 0$ and $0 \leq r < 100$. Each $n$-element sequence thus consists of $k$ 100-element sequences and one $r$-element sequence. The total number of 100-element sequences with two values is $2^{100}$; therefore, after excluding the sequence composed of 100 heads, there remain $2^{100} - 1$ 100-element sequences. Each $n$-element sequence not containing 100 consecutive heads thus consists of $k$ such 100-element sequences and some $r$-element sequence. Hence, the number of unfavorable events is not greater than $(2^{100} - 1)^k \cdot 2^r$. Therefore,
If $n$ tends to infinity, then of course $k$ also tends to infinity. Since for $0 < q < 1$ we have $\displaystyle \lim_{k \to \infty} q^k = 0$, then $\displaystyle \lim_{k \to \infty} \left( 1 - \frac{1}{2^{100}} \right)^k = 0$. Therefore, from (1) by the squeeze theorem, we have $\displaystyle \lim_{k \to \infty} q^k = 0$, so $\displaystyle \lim_{n \to \infty} p_n = 1$.
|
1
|
Combinatorics
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
XV OM - II - Task 3
Prove that if three prime numbers form an arithmetic progression with a difference not divisible by 6, then the smallest of these numbers is $3$.
|
Suppose that the prime numbers $ p_1 $, $ p_2 $, $ p_3 $ form an arithmetic progression with a difference $ r > 0 $ not divisible by $ 6 $, and the smallest of them is $ p_1 $. Then
Therefore, $ p_1 \geq 3 $, for if $ p_1 = 2 $, the number $ p_3 $ would be an even number greater than $ 2 $, and thus would not be a prime number. Hence, the numbers $ p_1 $ and $ p_2 $ are odd, and the number $ r $ equal to the difference $ p_2 - p_1 $ is even and one of the cases holds: $ r = 6k + 2 $ or $ r = 6k + 4 $, where $ k $ is an integer $ \geq 0 $.
We will prove that $ p_1 $ is divisible by $ 3 $. Indeed, if $ p_1 = 3m + 1 $ ($ m $ - an integer) and $ r = 6k + 2 $, it would follow that $ p_2 = 3m + 6k + 3 $ is divisible by $ 3 $, and since $ p_2 > 3 $, $ p_2 $ would not be a prime number. If, on the other hand, $ p_1 = 3m + 1 $ and $ r = 6k + 4 $, then $ p_3 = 3m + 12k + 9 $ would not be a prime number. Similarly, from the assumption that $ p_1 = 3m + 2 $ and $ r = 6k + 2 $, it would follow that $ p_3 = 3m + 12k + 6 $ is not a prime number, and from the assumption that $ p_1 = 3m + 2 $ and $ r = 6k + 4 $, we would get $ p_2 = 3m + 6k + 6 $, and thus $ p_2 $ would not be a prime number.
Therefore, $ p_1 $ is a prime number divisible by $ 3 $, i.e., $ p_1 = 3 $.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
XLIII OM - I - Problem 2
In square $ABCD$ with side length $1$, point $E$ lies on side $BC$, point $F$ lies on side $CD$, the measures of angles $EAB$ and $EAF$ are $20^{\circ}$ and $45^{\circ}$, respectively. Calculate the height of triangle $AEF$ drawn from vertex $A$.
|
The measure of angle $ FAD $ is $ 90^\circ - (20^\circ + 45^\circ) = 25^\circ $. From point $ A $, we draw a ray forming angles of $ 20^\circ $ and $ 25^\circ $ with rays $ AE $ and $ AF $, respectively, and we place a segment $ AG $ of length $ 1 $ on it (figure 2).
From the equality $ |AG| =|AB| = 1 $, $ | \measuredangle EAG| = | \measuredangle EAB| = 20^\circ $, it follows that triangle $ EAG $ is congruent to $ EAB $.
Similarly, from the equality $ |AG| = |AD| = 1 $, $ | \measuredangle FAG| = | \measuredangle FAD| = 25^\circ $, it follows that triangle $ FAG $ is congruent to $ FAD $.
This means that
point $ G $ lies on segment $ EF $ and is the foot of the altitude of triangle $ AEF $ drawn from vertex $ A $. Its length $ |AG| = 1 $.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XLVI OM - III - Problem 2
The diagonals of a convex pentagon divide this pentagon into a pentagon and ten triangles. What is the maximum possible number of triangles with equal areas?
|
om46_3r_img_12.jpg
Let's denote the considered pentagon by $ABCDE$, and the pentagon formed by the intersection points of the diagonals by $KLMNP$ so that the following triangles are those mentioned in the problem:
$\Delta_0$: triangle $LEM$; $\quad \Delta_1$: triangle $EMA$;
$\Delta_2$: triangle $MAN$; $\quad \Delta_3$: triangle $ANB$;
$\Delta_4$: triangle $NBP$; $\quad \Delta_5$: triangle $BPC$;
$\Delta_6$: triangle $PCK$; $\quad \Delta_7$: triangle $CKD$;
$\Delta_8$: triangle $KDL$; $\quad \Delta_9$: triangle $DLE$
(figure 12). We will start by proving the implication:
We assume that the numbering of the triangles is cyclic (that is, we assume: $\Delta_{-1} = \Delta_9$; $\Delta_{10} = \Delta_0$).
Suppose, for example, that triangles $\Delta_4$, $\Delta_5$, and $\Delta_6$ have equal areas. From the equality of the areas of triangles $NBP$ and $BPC$, it follows that segment $BP$ is a median in triangle $BCN$; from the equality of the areas of triangles $BPC$ and $PCK$, it follows that segment $CP$ is a median in triangle $BCK$. Point $P$ would then be the common midpoint of diagonals $BK$ and $CN$ of quadrilateral $BCKN$, which should therefore be a parallelogram - but the lines $BN$ and $CK$ intersect at point $E$. This is a contradiction; implication (1) is proven.
We proceed to the main solution. The example of a regular pentagon shows that it is possible to obtain five triangles $\Delta_i$ with equal areas. We will prove that it is not possible to obtain seven such triangles.
Suppose, therefore, that there exists a seven-element set $Z$, contained in the set $\{0,1,\ldots,9\}$, such that triangles $\Delta_i$ with indices $i \in Z$ have equal areas. Let $k$, $l$, $m$ be three numbers from the set $\{0,1,\ldots,9\}$, not belonging to $Z$. Consider all triples of consecutive indices:
where, as before, the addition $i \pm 1$ should be understood modulo $10$. Each number from the set $\{0,1,\ldots,9\}$ belongs to exactly three triples $T_i$. This applies, in particular, to each of the numbers $k$, $l$, $m$. Therefore, the three-element set $\{k,l,m\}$ has a non-empty intersection with at most nine triples $T_i$. At least one triple $T_j$ remains that does not contain any of the numbers $k$, $l$, $m$, and is therefore contained in the set $Z$. The number $j$ must be even, according to observation (1).
Without loss of generality, assume that $j = 2$. This means that the numbers $1$, $2$, $3$ belong to the set $Z$. Therefore, the numbers $0$ and $4$ cannot belong to it (since, again by observation (1), the triples $\{0,1,2\}$ and $\{2,3,4\}$ are excluded); thus, one of the numbers $k$, $l$, $m$ equals $0$, and another equals $4$. The third of these numbers must be part of the triple $\{6,7,8\}$ (which otherwise would be contained in the set $Z$, contrary to implication (1)). The roles of the numbers $6$ and $8$ are symmetric in this context. We therefore have to consider two essentially different cases:
The set $Z$, respectively, has one of the following forms:
Let $S_i$ be the area of triangle $\Delta_i$ (for $i = 0,1,\ldots,9$). We will show that the implications hold:
This will be a proof that none of the seven-element sets $Z$ listed above can be the set of indices of triangles with equal areas. According to earlier statements, this will also justify the conclusion that among the ten triangles $\Delta_i$, there are never seven triangles with the same area.
Proof of implication (2). From the given equalities of areas:
and
it follows (respectively) that points $N$ and $P$ are the midpoints of segments $BM$ and $BK$, and points $M$ and $L$ are the midpoints of segments $EN$ and $EK$ (figure 13).
Thus, segment $NP$ connects the midpoints of two sides of triangle $BMK$, and segment $ML$ connects the midpoints of two sides of triangle $ENK$, and therefore
- and
The obtained parallelism relations show that quadrilateral $AMKN$ is a parallelogram; hence $|MK| = |AN|$. Line $MK$ is parallel to $NC$, so triangles $ENC$ and $EMK$ are similar in the ratio $|EN| : |EM| = 2$. Therefore, $|NC| = 2 \cdot |MK|$, and consequently
The segments $PC$ and $AN$, lying on the same line, are the bases of triangles $ANB$ and $BPC$ with a common vertex $B$. The ratio of the lengths of these bases is therefore also the ratio of the areas of the triangles: area($BPC$) : area($ANB$) = $3 : 2$, i.e., $S_5 : S_3 = 3 : 2$. The conclusion of implication (2) is thus proven.
om46_3r_img_13.jpg
om46_3r_img_14.jpg
Proof of implication (3). The given equalities of the areas of triangles:
and
show that points $M$ and $N$ divide segment $EB$ into three equal parts, and similarly, points $L$ and $K$ divide segment $EC$ into three equal parts. Therefore, line $BC$ is parallel to $ML$ (i.e., to $AM$). Since $N$ is the midpoint of segment $BM$, triangles $AMN$ and $CBN$ are similar in the ratio $-1$ (figure 14). Hence, area($AMN$) = area($CBN$) $> $ area($CBP$), i.e., $S_2 > S_5$. This completes the proof of implication (3), and thus also the proof of the general theorem: it is not possible to have seven triangles $\Delta_i$ with equal areas.
The reasoning conducted in the last case (proof of (3)) also provides a hint on how to obtain six triangles $\Delta_i$ with equal areas. We take any isosceles triangle $BCE$ where $|EB| = |EC|$. On the sides $EB$ and $EC$, we find points $M$ and $N$ and $L$ and $K$, dividing these sides into three equal parts:
The intersection points of line $ML$ with lines $CN$ and $BK$ are denoted by $A$ and $D$, respectively (figure 14 can still serve as an illustration; one only needs to imagine moving point $E$ to the perpendicular bisector of side $BC$ and appropriately repositioning the other points). The equalities (4) and (5) then hold; and thanks to the assumption that triangle $BCE$ is isosceles (and the resulting symmetry of the entire configuration), all areas appearing in relations (4) and (5) are equal.
Conclusion: six of the triangles $\Delta_i$ can have equal areas, and this number cannot be increased.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
LIX OM - I - Task 9
Determine the smallest real number a with the following property:
For any real numbers $ x, y, z \geqslant a $ satisfying the condition $ x + y + z = 3 $
the inequality holds
|
Answer: $ a = -5 $.
In the solution, we will use the following identity:
Suppose that the number $ a \leqslant 1 $ has the property given in the problem statement. The numbers
$ x = a, y = z = 2\cdot (\frac{3-a}{2}) $ satisfy the conditions $ x, y, z \geqslant a $ and $ x+y+z = 3 $, thus
by virtue of (1), from which the inequality $ a \geqslant -5 $ follows.
We will now show that the number $ a = -5 $ satisfies the conditions of the problem. For this purpose, consider numbers
$ x, y, z \geqslant-5 $ such that $ x + y + z = 3 $. Without loss of generality, assume that
$ x \leqslant y \leqslant z $. The sum $ y + z $ is a positive number, because otherwise, given
$ y\leqslant z $, we would have $ x \leqslant y \leqslant 0 $, which would imply that $ x +y + z \leqslant y + z \leqslant 0 $,
contradicting the condition $ x+y+z = 3 $. Since $ y + z > 0 $, the inequality
holds, and from the identity (1) we finally obtain
(Note: The last part of the text seems to be incomplete or missing in the original Polish text, so the translation reflects that.)
|
-5
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
XV OM - I - Problem 7
Given a circle and points $ A $ and $ B $ inside it. Find a point $ P $ on this circle such that the angle $ APB $ is subtended by a chord $ MN $ equal to $ AB $. Does the problem have a solution if the given points, or only one of them, lie outside the circle?
|
Suppose that point $ P $ of a given circle $ C $ with radius $ r $ is a solution to the problem (Fig. 7).
Since points $ A $ and $ B $ lie inside the circle $ C $, points $ M $ and $ N $ lie on the rays $ PA $ and $ PB $ respectively, and angle $ APB $ coincides with angle $ MPN $. Triangles $ APB $ and $ MPN $ have equal bases $ AB = MN = a $ and a common angle at the vertex $ \measuredangle APB = \measuredangle MPN = \alpha $; hence, the circles circumscribed around these triangles have the same radius $ r = \frac{a}{2 \sin \alpha} $, and point $ P $ lies on the circle with radius $ r $ passing through points $ A $ and $ B $. Therefore, the construction of the desired point is as follows (Fig. 7a). We construct circles with radius $ r $ passing through points $ A $ and $ B $. Since $ AB < 2r $, there are 2 such circles: $ K_1 $ and $ K_2 $. If $ P $ is a common point of circles $ K_1 $ and $ C $, or circles $ K_2 $ and $ C $, then $ P $ is a solution to the problem. Indeed, the rays $ PA $ and $ PB $ intersect the given circle $ C $ at points $ M $ and $ N $; from triangle $ MPN $ we have $ MN = 2r \sin \measuredangle MPN = 2r \sin \measuredangle APB $; but in triangle $ APB $ we have $ \sin \measuredangle APB = AB \colon 2r $, so $ MN = AB $.
Each of the circles $ K_1 $ and $ K_2 $ intersects the circle $ C $ at two points; if $ O_1 $ and $ O_2 $ are the centers of circles $ K_1 $ and $ K_2 $, then
since $ OA < r $, $ AO_1 = r $; similarly $ 0 < OO_2 < 2r $.
The problem thus has 4 solutions.
Let us examine whether the above reasoning remains valid for any position of points $ A $ and $ B $. If point $ P $ is a solution to the problem, then points $ M $ and $ N $ lie on the lines $ PA $ and $ PB $, but not necessarily on the rays $ PA $ and $ PB $, so angle $ MPN $ coincides either with angle $ APB $ or with the adjacent angle to angle $ APB $. The conclusion that triangles $ APB $ and $ MPN $ have the same circumradius remains valid, hence point $ P $ lies, as before, on the circle with radius $ r $ passing through $ A $ and $ B $. Conversely, if point $ P $ is a common point of the given circle and a circle $ K $ with radius $ r $ passing through $ A $ and $ B $, then this point, provided it is different from $ A $ and $ B $, is a solution to the problem, as we conclude in the same way as before.
For such a point $ P $ to exist, the following conditions must be met:
1. There must exist a circle with radius $ r $ passing through points $ A $ and $ B $; this is the case when $ AB \leq 2r $. If $ AB < 2r $, there are two such circles $ K_1 $ and $ K_2 $ with centers $ O_1 $ and $ O_2 $. If $ AB = 2r $, there is one such circle: $ K_1 = K_2 $, $ O_1 = O_2 $.
2. There must exist a common point of circle $ K_1 $ or $ K_2 $ with the given circle $ C $, different from $ A $ and $ B $.
The table below gives the number of solutions for different cases of the position of points $ A $ and $ B $.
We propose to the Reader to provide a detailed justification of the above data for each of the cases 2-6 and to make the appropriate drawings.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. By what natural number can the numerator and denominator of the ordinary fraction of the form $\frac{4 n+3}{5 n+2}$ be reduced? For which integers $n$ can this occur?
|
Answer: can be reduced by 7 when $n=7 k+1, k \in Z$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $A=\overline{a b c b a}$ be a five-digit symmetric number, $a \neq 0$. If $1 \leq a \leq 8$, then the last digit of the number $A+11$ will be $a+1$, and therefore the first digit in the representation of $A+11$ should also be $a+1$. This is possible only with a carry-over from the digit, i.e., when $b=c=9$. Then $A+11=(a+1) 999(a+1)$ is a symmetric number for any $a=1,2, \ldots, 8$. The case $a=9$ is impossible, since $A+11$ ends in zero, and thus, due to symmetry, it should start with zero. But a number cannot start with zero.
The total number of solutions is equal to the number of possible choices for the number $a$, which is eight.
|
Answer: eight numbers of the form $\overline{a 999 a}$, where $a=1,2, \ldots, 8$.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. A plot of land in the form of a right-angled triangle with legs of 4 and 3 needs to be divided by a line $L$ into two plots such that 1) the plots have equal area; 2) the length of the common boundary (fence) of the plots is minimized. Indicate the points on the sides of the triangle through which the desired line $L$ passes and find the length of the fence.
|
Problem 6. Answer: 1) The line intersects the larger leg $B C$ (angle $\measuredangle C=90^{\circ}$) at point $M: B M=\sqrt{10}$ and the hypotenuse $B A$ at point $N: B N=\sqrt{10}$.
2) $L_{\text {min }}=2$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. According to the properties of logarithms, after transformations we get
$$
\begin{aligned}
& \log _{2}\left(b_{2} b_{3} \ldots b_{n}\right)=\log _{2} b_{1}^{2} \\
& b_{2} b_{3} \ldots b_{n}=b_{1}^{2}
\end{aligned}
$$
Using the formula for the general term of a geometric progression, we get
$$
b_{2}=b_{1} q, b_{3}=b_{1} q^{2}, \ldots, b_{n}=b_{1} q^{n-1}
$$
and using these relations and the formula for the sum of an arithmetic progression
$$
1+2+\ldots+(n-1)=\frac{n(n-1)}{2}
$$
we transform the obtained equation to
$$
b_{1}^{n-1} q^{1+2+\ldots+(n-1)}=b_{1}^{2} \Rightarrow b_{1}^{n-3} q^{n(n-1) / 2}=1
$$
Taking the logarithm with base $q$, we find
$$
\begin{aligned}
& (n-3) \log _{q} b_{1}+\frac{n(n-1)}{2}=0 \\
& \frac{n-3}{2} \log _{q} b_{1}^{2}+\frac{n(n-1)}{2}=0 \\
& \log _{q} b_{1}^{2}=-\frac{n(n-1)}{n-3}
\end{aligned}
$$
Since
$$
\frac{n(n-1)}{n-3}=\frac{n(n-3)+2(n-3)+6}{n-3}=n+2+\frac{6}{n-3}
$$
then
$$
\log _{q} b_{1}^{2}=-n-2-\frac{6}{n-3} .
$$
According to the problem's condition, the quantity
$$
\frac{6}{n-3}
$$
must be an integer. This is possible only for
$$
n \in\{2 ; 4 ; 5 ; 6 ; 9\}
$$
Substituting the specified values into the formula obtained above, we find all possible values of the desired quantity
$$
\begin{aligned}
& n=2 \Rightarrow \log _{q} b_{1}^{2}=2 \\
& n=4 \Rightarrow \log _{q} b_{1}^{2}=-12 \\
& n=5 \Rightarrow \log _{q} b_{1}^{2}=-10 \\
& n=6 \Rightarrow \log _{q} b_{1}^{2}=-10 \\
& n=9 \Rightarrow \log _{q} b_{1}^{2}=-12
\end{aligned}
$$
From this, it is clear that the smallest value of the desired quantity is -12 and it is achieved for two values: $n=4$ and $n=9$.
|
Answer: -12 when $n=4$ and $n=9$.
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The border of a square with a side of 9, cut out of white cardboard, is painted red. It is necessary to cut the square into 6 equal-area parts, the boundaries of which contain segments painted red with the same total length.
## Solutions
Option 1
Problem 1
|
Answer: 2 km.
Solution
$S-$ the length of the path, $S_{1}$ - the length of the path on descents, $S_{2}$ - the length of the path on ascents, $S / 2=S_{1}+S_{2}$
$t=15-8-6=1-$ the time of the journey there and back. Then
$1=\frac{S_{1}}{6}+\frac{S_{2}}{3}+\frac{S}{2 \cdot 4}+\frac{S_{1}}{3}+\frac{S_{2}}{6}+\frac{S}{2 \cdot 4}=\left(\frac{1}{6}+\frac{1}{3}\right)\left(S_{1}+S_{2}\right)+\frac{S}{4}=\left(\frac{1}{6}+\frac{1}{3}\right) \frac{S}{2}+\frac{S}{4}=\frac{S}{2} \rightarrow S=2$
Problem 2 Answer: $\frac{1}{6}$
Solution.
By the condition $\frac{p}{q}5 p$. Considering the naturality of $p$ and $q$, and the condition $p+q<8$ we have
$6 p<p+q<8 \rightarrow p=1 \rightarrow q=6$
Problem 3 Answer: $a_{\min }=15876$
Solution
Among the divisors of an even number divisible by 21 and being a square of an integer, there are $7^{2}, 3^{2}, 2^{2}$, i.e.
$a=7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2}$. Considering the five-digit nature, the inequality holds:
$10000 \leq 7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2} \leq 99998 \rightarrow 6 \leq k^{2} \leq 57 \rightarrow k_{\min }^{2}=9 \rightarrow a_{\min }=7^{2} \cdot 3^{2} \cdot 4 \cdot 9=15876$
Problem 4 Answer: $x=\frac{3}{2}$
Solution
$x=\frac{4-[x]}{2} \rightarrow\{x\}=x-[x]=\frac{4-[x]}{2}-[x]=\frac{4-3[x]}{2}$
Since $0 \leq\{x\}<1 \rightarrow 0 \leq \frac{4-3[x]}{2}<1 \rightarrow \frac{2}{3}<[x] \leq \frac{4}{3}$ and the number $[x]-$ is an integer, the only valid value is $[x]=1$. Then $x=\frac{3}{2}$
Problem 5
Solution
O - the center of the square, the polygon $O B C D$ - one of the six desired pieces, $B C=x, C D=y, a=9$.
$S_{\text {OBCD }}=\frac{a^{2}}{6}=\frac{a}{4} \cdot(x+y) \rightarrow x+y=\frac{2 a}{3}=6$ - the length of the red part of the boundary of the polygon.
A way of cutting (one of ...)
Variant 2
Problem 1 Answer: 3 km.
Problem 2 Answer: $\frac{1}{4}$
Problem 3 Answer: $a_{\max }=5625$
Problem 4 Answer: $x=\frac{5}{2}$
Problem 5 Answer:
Variant 3
Problem 1 Answer: 1.5 km.
Problem 2 Answer: $\frac{1}{4}, \frac{1}{5}$
Problem 3 Answer: $a_{\text {min }}=327184$
Problem 4 Answer: $x=-\frac{7}{2}$
Problem 5 Answer:
Variant 4
Problem 1 Answer: 1.4 km.
Problem 2 Answer: $\frac{1}{6}, \frac{1}{7}$
Problem 3 Answer: $a_{\max }=74529$
Problem 4 Answer: $x=-\frac{3}{2}$
Problem 5 Answer:
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The real numbers $x_{1}, x_{2}$, and $x_{3}$ are the three roots of the equation $x^{3}-3 x^{2}+2(1-p) x+4=0$, considering their possible multiplicities. Find the smallest value of the expression $\left(x_{1}-1\right)^{2}+\left(x_{2}-1\right)^{2}+\left(x_{3}-1\right)^{2}$ under these conditions. For which $p$ is it realized?
|
The smallest value 6 is achieved when $p=1$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The quadratic trinomial $p(x)=a x^{2}+b x+c, a>0$ when divided by ( $x-1$ ) gives a remainder of 4, and when divided by ( $x-2$ ) - a remainder of 15. Find the maximum possible value of the ordinate of the vertex of the parabola $y=p(x)$ under these conditions. For what value of $x$ is it achieved?
|
4. Solution. By the Remainder Theorem, the remainder of the division of a polynomial $p(x)$ by $x-a$ is $p(a)$.
Therefore, the conditions of the problem are equivalent to the system:
$\left\{\begin{array}{l}4 a+2 b+c=15 \\ a+b+c=4\end{array} \Rightarrow\left\{\begin{array}{l}b=11-3 a \\ c=2 a-7\end{array}\right.\right.$.
Thus, $p(x)=a x^{2}+(11-3 a) x+2 a-7$. The minimum value of the quadratic trinomial $p(x)$ (the ordinate of the vertex of the parabola) is achieved at its vertex $x_{s}=\frac{3 a-11}{2 a}$. It is equal to $p_{\text {min }}(x)=p\left(x_{k}\right)=p\left(\frac{3 a-11}{2 a}\right)=-\frac{a^{2}-38 a+121}{4 a}=\frac{19}{2}-\frac{1}{4}\left(a+\frac{121}{a}\right)=4-\left(\sqrt{a}-\frac{11}{\sqrt{a}}\right)^{2}$.
This value is maximal if and only if $\sqrt{a}-\frac{11}{\sqrt{a}}=0$, that is, $a=11$. When $a=11$, $x_{s}=1$,
and $p\left(x_{s}\right)=4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Pasha, Masha, Tolya, and Olya ate 88 candies, and each of them ate at least one candy. Masha and Tolya ate 57 candies, but Pasha ate the most candies. How many candies did Olya eat?
|
Solution. Either Masha or Tolya ate no less than 29 candies, then Pasha ate no less than 30 candies. Then the number of candies eaten by Pasha, Masha, and Tolya is no less than $57+30=87$. Since there are a total of 88 candies, and Olya did not refuse any candies, she gets one candy.
Answer: 1 candy.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let point $M$ divide edge $A B$ in the ratio $A M: M B=\lambda$, point $N$ divide edge $D C$ in the ratio $D N: N C=\mu$, and point $P$ divide edge $D B$ in the ratio $D P: P B=\theta$. We need to find the ratio $A Q: Q C$.
Let $T$ be the intersection point of line $P N$ with line $B C$, then point $Q$ is the intersection point of line $M T$ with line $A C$. Let $B M=a$, $C N=b$, and $B P=c$. Then $M A=\lambda a$, $N D=\mu b$, and $P D=\theta c$.
Applying Menelaus' theorem to triangle $C B D$ and the transversal $P T$:
$$
\frac{C T}{T B} \cdot \frac{B P}{P D} \cdot \frac{D N}{N C}=1 \quad \text{or} \quad \frac{C T}{T B} \cdot \frac{1}{\theta} \cdot \mu=1.
$$
From this, we find $\frac{C T}{T B}=\frac{\theta}{\mu}$.
Now, applying Menelaus' theorem to triangle $A C B$ and the transversal $M T$:
$$
\frac{A Q}{Q C} \cdot \frac{C T}{T B} \cdot \frac{B M}{M A}=1 \quad \text{or} \quad \frac{A Q}{Q C} \cdot \frac{\theta}{\mu} \cdot \frac{1}{\lambda}=1.
$$
From this, we get
$$
\frac{A Q}{Q C}=\frac{\lambda \mu}{\theta}
$$
According to the problem, $\lambda=2$, $\mu=3$, and $\theta=\frac{1}{2}$, then $\frac{A Q}{Q C}=12$.
|
Answer: $A Q: Q C=12$.
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Represent the number 80 as the sum of two prime numbers. In how many ways can this be done? Let's remind you that one is not considered a prime number.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
Solution. We organize the enumeration of all prime numbers from 2 to 73 in the form of a table.
| 1 | 7 | 13 | 19 | 25 | 31 | 37 | 43 | 49 | 55 | 61 | 67 | 73 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 8 | 14 | 20 | 26 | 32 | 38 | 44 | 50 | 56 | 62 | 68 | 74 |
| 3 | 9 | 15 | 21 | 27 | 33 | 39 | 45 | 51 | 57 | 63 | 69 | 75 |
| 4 | 10 | 16 | 22 | 28 | 34 | 40 | 46 | 52 | 58 | 64 | 70 | 76 |
| 5 | 11 | 17 | 23 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 71 | 77 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 |
In the table, composite numbers from 4 to 78 are marked in dark color (1 is neither prime nor composite), and there are 21 prime numbers. In the following two tables, pairs of numbers $(a ; b)$ are listed for which $a+b=80$ and $a$ is a prime number.
| a | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| b | 78 | 77 | 75 | 73 | 69 | 67 | 63 | 61 | 57 |
| a | 29 | 31 | 37 | 41 | 47 | 53 | 59 | 71 | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| b | 51 | 49 | 43 | 39 | 33 | 27 | 21 | 9 | |
In the second row of the table (b), composite numbers are marked in dark color. Thus, the number 80 can be represented as the sum of two prime numbers in four ways: $80=7+73, 80=13+67, 80=19+61, 80=37+43$.
Answer: $80=7+73, 80=13+67, 80=19+61, 80=37+43$; four ways.
|
4
|
Combinatorics
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. For what least integer $n$ are all solutions of the equation
$$
x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6(n-8)(n+2)=0 \text { greater than }-1 \text { ? }
$$
|
Solution. Rewrite the equation as
$$
x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6 n^{2}+36 n+96=0 .
$$
Notice that $x_{1}=1>-1$ is a solution for all $n$ (the sum of the coefficients of the polynomial on the left side of the equation is zero for all $n$). Divide the equation by $x-1$:
$$
x^{2}-5(n-2) x+6\left(n^{2}-6 n-16\right)=0
$$
The roots of this equation are: $x_{2}=3(n+2), x_{3}=2(n-8)$. We seek when these solutions are greater than -1:
$$
\left\{\begin{array} { l }
{ 3 ( n + 2 ) > - 1 } \\
{ 2 ( n - 8 ) > - 1 }
\end{array} \rightarrow \left\{\begin{array}{l}
n>-\frac{7}{3}, n \in Z \\
n>\frac{15}{2}, n \in Z
\end{array} \rightarrow n \geq 8\right.\right.
$$
Since $n$ is an integer, then $n \geq 8, n \in Z$.
Answer: $n_{\min }=8$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The midline of a trapezoid is 4. A line parallel to the bases of the trapezoid and dividing its area in half intersects the lateral sides at points $M$ and $N$. Find the smallest possible length of the segment $M N$.
|
# Solution.
Notations: $A D=a, B C=b, C K=H, N E=h$ - heights of triangles $N C P$ and $D N Q$, $M N=x$
$$
S_{\text {AMND }}=S_{\text {MBCN }} \rightarrow \frac{x+b}{2} H=\frac{a+x}{2} h \rightarrow \frac{H}{h}=\frac{a+x}{x+b}
$$
$\square N C P \quad \square D N Q \rightarrow \frac{H}{h}=\frac{x-b}{a-x} \rightarrow \frac{a+x}{x+b}=\frac{x-b}{a-x} \rightarrow a^{2}-x^{2}=x^{2}-b^{2} \rightarrow x=\sqrt{\frac{a^{2}+b^{2}}{2}}$.
Since $a+b=8$, then $x=\sqrt{\frac{a^{2}+(8-a)^{2}}{2}}=\sqrt{a^{2}-16 a+32}=\sqrt{(a-4)^{2}+16}$.
Answer: $M N_{\text {min }}=4$.
## Answers for other variants.
## Variant 2
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find all $x$ that satisfy the inequality $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6 \leq 0$ for any natural $n$.
|
Solution. The roots of the quadratic trinomial $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6$ are
$$
x_{1}=1-\frac{2}{n}, x_{2}=1+\frac{3}{n}
$$
Factorize the left side of the inequality
$$
n^{2}\left(x-\left(1-\frac{2}{n}\right)\right)\left(x-\left(1+\frac{3}{n}\right)\right) \leq 0
$$
Solving the inequality using the interval method, we get $x \in\left[1-\frac{2}{n} ; 1+\frac{3}{n}\right]$. Only $x=1$ belongs to this interval for any $n$.
Answer: $x=1$
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the edges of a trihedral angle with vertex at point $S$, there are points $M, N$, and $K$ such that $S M^{2}+S N^{2}+S K^{2} \leq 12$. Find the area of triangle $S M N$, given that the angle $M S N$ is $30^{\circ}$, and the volume of the pyramid $S M N K$ is maximally possible.
|
Solution. Let's introduce the notations: $S M=m, S N=n, S K=k$.
The volume of the pyramid $S M N K$ is
$$
V=\frac{1}{3} S_{S M N} \cdot h=\frac{1}{6} m n \sin \alpha \cdot h=\frac{1}{6} m n \sin \alpha \cdot k \sin \beta=\frac{\sin \alpha \sin \beta}{6} m n k .
$$
The values of the angles $\alpha, \beta$ depend on the trihedral angle but not on the positions of the points $M, N, K$ on its edges. Therefore, the maximum volume of the pyramid $S M N K$ corresponds to the maximum value of the product $m \cdot n \cdot k$, given the condition $m^{2}+n^{2}+k^{2} \leq p$. From the inequality of the geometric mean and the arithmetic mean of three numbers, it follows that $\sqrt[3]{m^{2} n^{2} k^{2}} \leq \frac{m^{2}+n^{2}+k^{2}}{3} \leq \frac{p}{3}$
Equality is achieved when $m=n=k$. Then, when $m=n=k=\sqrt{\frac{p}{3}}$, the volume of the pyramid is maximized, and the area of the triangle $S M N$ takes the value $\frac{p \sin \alpha}{6}$. In our case, $p=12, \alpha=30^{\circ}$, so $S_{S M N}=1$.
Answer: $S_{S M N}=1$.
## Answers for other variants.
## Variant 2
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Quadrilateral $ABCD$ is inscribed in a circle, and its diagonals intersect at point $P$. Points $K, L$, and $M$ are the midpoints of sides $AB, BC$, and $CD$ respectively. The radius of the circle circumscribed around triangle $KLP$ is 1. Find the radius of the circle circumscribed around triangle $LMP$.
Problem 1 Answer: 18 passengers.
|
Solution. Let $y_{k}$ be the number of passengers in the car with number $k, k=1,2,3, \ldots, 10$. According to the problem, $\sum_{k=1}^{10} y_{k}=270$. Additionally, it is stated that $y_{2} \geq y_{1}+2, y_{3} \geq y_{1}+4, \ldots, y_{9} \geq y_{1}+16, \quad y_{10} \geq y_{1}+18$. Adding these inequalities,
$$
y_{2}+y_{3}+\ldots+y_{9}+y_{10} \geq y_{1}+2+y_{1}+4+\ldots+y_{1}+16+y_{1}+18
$$
or
$$
270-y_{1} \geq 9 y_{1}+90
$$
From this, we get $y_{1} \leq 18$. From the conditions $y_{10} \geq y_{1}+18$ and $y_{10} \leq 2 y_{1}$, it follows that $2 y_{1} \geq y_{1}+18$ or $y_{1} \geq 18$. Comparing the obtained inequalities, we conclude that $y_{1}=18$. The set $y_{1}=18, y_{2}=20$, $\ldots, y_{10}=36$ satisfies the conditions of the problem.
Problem 2 Answer: $x=\frac{8 \pi}{5}$.
Solution. Introduce the notations: $u=\sin x, v=\sin 2 x, w=\sin 3 x$. Then the equation becomes
$$
(u+v+w)^{3}=u^{3}+v^{3}+w^{3}
$$
Rewrite the equation as
$$
(u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=0
$$
Using the formulas for the difference and sum of cubes, as well as the difference of squares, factorize the left-hand side of the equation
$$
\begin{aligned}
& (u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=(v+w)\left((u+v+w)^{2}+u(u+v+w)+u^{2}\right)- \\
& -(v+w)\left(v^{2}-v w+w^{2}\right)=(v+w)\left[\left((u+v+w)^{2}-v^{2}\right)+\left(u^{2}-w^{2}\right)+u(u+w)+v(u+w)\right]= \\
& =(v+w)(u+w)(u+2 v+w+u-w+u+v))=3(v+w)(u+w)(u+v)
\end{aligned}
$$
As a result, the equation takes the form
$$
3(v+w)(u+w)(u+v)=0
$$
Returning to the original variables, we get the equation:
Case $1 . \sin x+\sin 2 x=0$.
$\left[\begin{array}{c}2 x=-x+2 \pi k \\ 2 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{3}, \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$ The largest solution on the interval $(0 ; 2 \pi)$ is $x=\frac{4 \pi}{3}$
Case $2 . \sin x+\sin 3 x=0$.
$\left[\begin{array}{c}3 x=-x+2 \pi k \\ 3 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{\pi k}{2}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{3 \pi}{2} \\ x=\frac{\pi}{2}+\pi m, m, k \in Z .\end{array} \quad\right.\right.$.
Case $3 . \sin 3 x+\sin 2 x=0$.
$\left[\begin{array}{c}3 x=-2 x+2 \pi k \\ 3 x=\pi+2 x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{5}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{8 \pi}{5} \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$.
The largest solution among $\frac{4 \pi}{3}, \frac{3 \pi}{2}, \frac{8 \pi}{5}$ is $x=\frac{8 \pi}{5}$.
Problem 3 Answer: all 100 digits after the decimal point are nines.
Solution. Consider $(7+4 \sqrt{3})^{2023}$. Use the binomial formula
$$
(7+4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(4 \sqrt{3})^{k}=a+b \sqrt{3}
$$
where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$.
Now consider $(7-4 \sqrt{3})^{2023}:$
$$
(7-4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(-4 \sqrt{3})^{k}=a-b \sqrt{3}
$$
where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$.
Adding the obtained equalities, we get
$$
(7+4 \sqrt{3})^{2023}+(7-4 \sqrt{3})^{2023}=a+b \sqrt{3}+a-b \sqrt{3}=2 a \in N
$$
From this, we have
$$
\begin{aligned}
& (7+4 \sqrt{3})^{2023}=2 a-(7-4 \sqrt{3})^{2023}=2 a-\frac{(7-4 \sqrt{3})^{2023} \cdot(7+4 \sqrt{3})^{2023}}{(7+4 \sqrt{3})^{2023}}=2 a-\frac{1}{(7+4 \sqrt{3})^{2023}}= \\
& =2 a-1+1-\frac{1}{(7+4 \sqrt{3})^{2023}}, \quad 2 a-1 \in N .
\end{aligned}
$$
Notice that $\frac{1}{(7+4 \sqrt{3})^{2023}}0
$$
Then, considering the non-negativity of $x$, we find $x=\frac{\sqrt{2 \pm \sqrt{3}}}{4}$. It remains to check the condition $x \leq \frac{1}{2}$ :
$$
\frac{\sqrt{2 \pm \sqrt{3}}}{4} \vee \frac{1}{2} \leftrightarrow \sqrt{2 \pm \sqrt{3}} \vee 2 \leftrightarrow 2 \pm \sqrt{3} \vee 4 \leftrightarrow \pm \sqrt{3} \vee 2 \rightarrow \pm \sqrt{3}<2
$$
Therefore, both roots $x=\frac{\sqrt{2+\sqrt{3}}}{2}$ and $x=\frac{\sqrt{2-\sqrt{3}}}{2}$ satisfy the condition $x \leq \frac{1}{2}$.
Problem 5 Answer: $R=1$.
Solution. Consider triangles $A B P$ and $D C P$. They are similar by two equal angles ( $\angle B A C=\angle B D C, . \angle A B D=\angle A D C$ as angles inscribed in a circle and subtending the same arc). Therefore, the sides of these triangles are proportional:
$$
\frac{A B}{D C}=\frac{A P}{D P}=\frac{B P}{P C}
$$
Now consider triangles $A K P$ and $D C P$. By the condition $A K=\frac{A B}{2}, D M=\frac{D C}{2}$, so $\frac{A K}{D M}=\frac{A B}{D C}$. As a result, we have $\frac{A K}{D M}=\frac{A P}{D B}$. Therefore, triangle $A P K$ is similar to triangle $D P M$ by an equal angle and proportional sides. Then the angle $A P K$ is equal to the angle $D P M$ as angles in similar triangles, lying opposite proportional sides.
By the problem's condition, $K L$ and
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.
when transferring money abroad
Correct answers: when using the Fast Payment System for amounts up to 100 thousand rubles per month, when transferring funds between one's own accounts in the same bank
Question 17
Score: 7.00
Last year, a beauty salon offered a $20 \%$ discount on facial massage when purchasing a membership for 30000 rubles. This year, it was decided to change the loyalty program and, when purchasing a membership for 30000 rubles, an additional $20 \%$ of this amount would be credited to the client's account. How will the number of facial massages that a client can now attend with a membership for 30000 rubles change, if the cost of a massage is 1500 rubles?
In the answer, write a non-negative integer without units of measurement. If the number of massages has not changed, put 0.
|
Answer:
The correct answer: 1
Question 18
Score: 3.00
Select all true statements regarding digital financial assets $(DFA)$.
Select one or more answers:
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (mathematics) There are scales with two pans, 4 weights of 2 kg each, 3 weights of 3 kg each, and two weights of 5 kg each. In how many different ways can a 12 kg load be balanced on the scales, if the weights are allowed to be placed on both pans?
|
Answer: 7 ways
Solution: Let $x$ be the number of 2 kg weights used in weighing, $y$ be the number of 3 kg weights, and $z$ be the number of 5 kg weights. Then the equilibrium condition is given by
$$
\pm 2 x \pm 3 y \pm 5 z=12
$$
The plus sign before an unknown, for example $x$, means that the 2 kg weights are placed on the opposite pan from the 12 kg load. Otherwise, a minus sign is used. Keeping the same notation, we assume that $x, y$, and $z$ are integers that can take negative values, with $|x| \leq 4,|y| \leq 3,|z| \leq 2$. In this case, the equilibrium condition takes the form of the equation
$$
2 x+3 y+5 z=12
$$
Let $z=t \in[-2 ; 2]$. Then, solving the Diophantine equation,
$2 x+3 y=12-5 t \rightarrow\left\{\begin{array}{c}x=5 t-12-3 s \\ y=12-5 t+2 s, s \in Z\end{array}\right.$
Case 1. $t=-2$
$\left\{\begin{array}{c}x=-22-3 s \\ y=22+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|22+3 s| \leq 4 \rightarrow s=-8,-7,-6 \\ |22+2 s| \leq 3 \rightarrow s=-13,-12,-11,-10\end{array} \rightarrow s \in \varnothing\right.\right.$
Case 2. $t=-1$
$\left\{\begin{array}{c}x=-17-3 s \\ y=17+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|17+3 s| \leq 4 \rightarrow s=-5,-6,-7 \\ |17+2 s| \leq 3 \rightarrow s=-7,-8,-9,-10\end{array} \rightarrow s_{1}=-7 \rightarrow\left\{\begin{array}{c}x=4 \\ y=3 \\ z=-1\end{array}\right.\right.\right.$
Case 3. $t=0$
$\left\{\begin{array}{c}x=-12-3 s \\ y=12+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|12+3 s| \leq 4 \rightarrow s=-5,-4,-3 \\ |12+2 s| \leq 3 \rightarrow s=-7,-6,-5\end{array} \rightarrow s_{2}=-5 \rightarrow\left\{\begin{array}{l}x=3 \\ y=2 \\ z=0\end{array}\right.\right.\right.$
Case 4. $t=1$
$\left\{\begin{array}{c}x=-7-3 s \\ y=7+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{c}|7+3 s| \leq 4 \rightarrow s=-1,-2,-3 \\ |7+2 s| \leq 3 \rightarrow s=-2,-3,-4,-5\end{array} \rightarrow s_{3}=-2 \rightarrow\left\{\begin{array}{l}x=-1 \\ y=3, s_{4}=-3 \\ z=1\end{array} \rightarrow\left\{\begin{array}{l}x=2 \\ y=1 \\ z=1\end{array}\right.\right.\right.\right.$
Case 5. $t=2$
$\left\{\begin{array}{c}x=-2-3 s \\ y=2+2 s, s \in Z\end{array} \rightarrow\left\{\begin{array}{l}|2+3 s| \leq 4 \rightarrow s=0,-1,-2 \\ |2+2 s| \leq 3 \rightarrow s=0,-1,-2\end{array} \rightarrow s_{5}=0 \rightarrow\left\{\begin{array}{l}x=-2 \\ y=2,2 \\ z=2\end{array},-1 \rightarrow\left\{\begin{array}{l}x=1 \\ y=0 \\ z=2\end{array}\right.\right.\right.\right.$
$s_{7}=-2 \rightarrow\left\{\begin{array}{c}x=4 \\ y=-2 \\ z=2\end{array}\right.$
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Express z from the first equation and substitute into the second:
$x^{2}-2 x+y^{2}-2 \sqrt{3} y=-4 \rightarrow(x-1)^{2}+(y-\sqrt{3})^{2}=0 \rightarrow\left\{\begin{array}{c}x=1 \\ y=\sqrt{3}\end{array} \rightarrow z=x^{2}+y^{2}+2 x=6\right.$
|
Answer: $x=1, y=\sqrt{3}, z=6$
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. The administration divided the region into several districts based on the principle: the population of a large district exceeds $8 \%$ of the region's population and for any large district, there are two non-large districts with a combined population that is larger. Into what minimum number of districts was the region divided?
|
Answer: 8 districts.
Solution. The number of "small" districts is no less than 2 according to the condition, and their population does not exceed $8 \%$ of the total population of the region. We will show that the number of districts in the region is no less than 8. If the number of districts in the region is no more than 7, but there are no more than 5 "large" districts with a population of less than $16 \%$ each. Then the total population of the region cannot amount to $100 \%$. Indeed, $2 \cdot 8 \%+5 \cdot 16 \%=96 \%<100 \%$. Thus, the number of districts in the region is no less than 8. A division into 8 districts is possible, for example, $8 \%+8 \%+14 \%+14 \%+14 \%+14 \%+14 \%+14 \%=100 \%$.
|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Point $M$ is located on side $CD$ of a square such that $CM: MD=1: 3$. Line $AM$ intersects the circumcircle of the square at point $E$. The area of triangle $ACE$ is 14. Find the side length of the square.
|
Answer: 10.
Solution.
Triangles $A M D$ and $C M E$ are similar with a similarity coefficient $k=5$. Then
$$
C E=\frac{4 x}{5}, M E=\frac{3 x}{5} \rightarrow A E=5 x+\frac{3 x}{5}=\frac{28}{5} x
$$
Triangle $A C E$ is a right triangle, therefore:
$$
S_{A C E}=\frac{1}{2} A E \cdot C E=\frac{1}{2} \cdot \frac{28}{5} \cdot \frac{4}{5} x^{2}=14 \rightarrow x^{2}=\frac{25}{4} \rightarrow x=\frac{5}{2} \rightarrow A D=4 x=10
$$
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Seven students in the class receive one two every two days of study, and nine other students receive one two every three days each. The rest of the students in the class never receive twos. From Monday to Friday, 30 new twos appeared in the journal. How many new twos will appear in the class journal on Saturday?
|
Answer: 9
Solution. Over the period from Monday to Saturday (six days), in the journal, there will be 3 new twos from each student of the first group (seven people) and 2 new twos from each of the 9 students of the second group. The total number of new twos for the school week is $7 \cdot 3 + 9 \cdot 2 = 39$. Then, on Saturday, the journal will have $39 - 30 = 9$ new twos.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Through the vertex $B$ of an equilateral triangle $ABC$, a line $L$ is drawn, intersecting the extension of side $AC$ beyond point $C$. On line $L$, segments $BM$ and $BN$ are laid out, each equal in length to the side of triangle $ABC$. The lines $MC$ and $NA$ intersect at a common point $D$ and intersect the sides $AB$ and $BC$ of the triangle at points $P$ and $Q$ respectively. Prove that a circle can be circumscribed around quadrilateral $PBQD$. Find the radius of this circle if the length of segment $PQ$ is $\sqrt{3}$.
|
# Answer: 1.
Solution. Triangles $M B C$ and $A B N$ are isosceles, therefore
$$
\begin{gathered}
\angle B M C = \angle B C M = \alpha \rightarrow \angle N B C = 2 \alpha, \angle B A N = \angle B N A = \beta \rightarrow \angle A B M = 2 \beta \\
2 \alpha + 2 \beta + 60^{\circ} = 180^{\circ} \rightarrow \alpha + \beta = 60^{\circ}
\end{gathered}
$$
In triangle $M D N$, angle $P D Q$ is $180^{\circ} - \alpha - \beta = 120^{\circ}$, and the sum of the opposite angles of quadrilateral $P B Q D$ is $180^{\circ}$, so a circle can be circumscribed around it.
By the Law of Sines, $P Q = 2 R \sin 120^{\circ} = \sqrt{3} \rightarrow R = 1$.
|
1
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{4}+3 x+\frac{253}{4}$.
|
Answer: 11.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+3 x+\frac{253}{4}>0 \Leftrightarrow-\frac{1}{4}(x+11)(x-23)>0$, from which $-11<x<23$. On this interval, there are 22 natural values of $x: x=1, x=2, \ldots, x=22$. During this interval, $y$ takes integer values only for even $x$ - a total of 11 possibilities. Therefore, we get 11 points belonging to the parabola, both of whose coordinates are natural numbers.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{4}+5 x+39$.
|
Answer: 12.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{4}+5 x+39>0 \Leftrightarrow-\frac{1}{4}(x+6)(x-26)>0$, from which $-6<x<26$. On this interval, there are 25 natural values of $x: x=1, x=2, \ldots, x=25$. In this interval, $y$ takes integer values only for even $x$ - a total of 12 possibilities. Therefore, we get 12 points belonging to the parabola, both of whose coordinates are natural numbers.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+7 x+54$.
|
Answer: 8.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+7 x+54>0 \Leftrightarrow-\frac{1}{3}(x+6)(x-27)>0$, from which $-6<x<27$. On this interval, there are 26 natural values of $x: x=1, x=2, \ldots, x=26$. In this interval, $y$ takes integer values only when $x$ is divisible by 3 - a total of 8 possibilities. Therefore, we get 8 points on the parabola, both of whose coordinates are natural numbers.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{3}+5 x+72$.
|
Answer: 7.
Solution. Let's find those values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+5 x+72>0 \Leftrightarrow-\frac{1}{3}(x+9)(x-24)>0$, from which $-9<x<24$. On this interval, there are 23 natural values of $x: x=1, x=2, \ldots, x=23$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+50$.
|
Answer: 7.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+50>0 \Leftrightarrow x^{2}<450$, from which $-\sqrt{450}<x<\sqrt{450}$. On this interval, there are 21 natural values of $x: x=1, x=2, \ldots, x=21$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 7 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+70$.
|
Answer: 4.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+70>0 \Leftrightarrow x^{2}<210$, from which $-\sqrt{210}<x<\sqrt{210}$. On this interval, there are 14 natural values of $x: x=1, x=2, \ldots, x=14$. During this time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 4 possibilities. Therefore, we get 7 points belonging to the parabola, both of whose coordinates are natural numbers.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the $x O y$ plane having natural coordinates $(x, y)$ and lying on the parabola $y=-\frac{x^{2}}{9}+33$.
|
Answer: 5.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{9}+33>0 \Leftrightarrow x^{2}<297$, from which $-\sqrt{297}<x<\sqrt{297}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Find the number of points in the plane $x O y$ that have natural coordinates $(x, y)$ and lie on the parabola $y=-\frac{x^{2}}{3}+98$
|
Answer: 5.
Solution. Let's find the values of $x$ for which $y$ is positive: $-\frac{x^{2}}{3}+98>0 \Leftrightarrow x^{2}<294$, from which $-\sqrt{294}<x<\sqrt{294}$. On this interval, there are 17 natural values of $x: x=1, x=2, \ldots, x=17$. At the same time, $y$ takes integer values only when $x$ is divisible by 3 - a total of 5 possibilities. Thus, we get 5 points belonging to the parabola, both coordinates of which are natural numbers.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | |
|
17. It is known that the number $a$ satisfies the equation param 1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param 1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | 2 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | -2 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | 4 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | -4 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
20. Find param 1 given param 2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| maximum $2 x+y$ | $\|4 x-3 y\|+5 \sqrt{x^{2}+y^{2}-20 y+100}=30$ | |
| maximum $x+2 y$ | $\|4 y-3 x\|+5 \sqrt{x^{2}+y^{2}+20 y+100}=40$ | |
| maximum $2 y-x$ | $\|4 y+3 x\|+5 \sqrt{x^{2}+y^{2}+10 x+25}=15$ | |
| maximum $x-5 y$ | $\|5 x-12 y\|+13 \sqrt{x^{2}+y^{2}-26 y+169}=156$ | |
| minimum $y-5 x$ | $\|5 y-12 x\|+13 \sqrt{x^{2}+y^{2}+26 x+169}=156$ | |
|
20. Find param 1 given param2.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| maximum $2 x+y$ | $\|4 x-3 y\|+5 \sqrt{x^{2}+y^{2}-20 y+100}=30$ | 16 |
| maximum $x+2 y$ | $\|4 y-3 x\|+5 \sqrt{x^{2}+y^{2}+20 y+100}=40$ | -12 |
| maximum $2 y-x$ | $\|4 y+3 x\|+5 \sqrt{x^{2}+y^{2}+10 x+25}=15$ | 8 |
| maximum $x-5 y$ | $\|5 x-12 y\|+13 \sqrt{x^{2}+y^{2}-26 y+169}=156$ | -5 |
| minimum $y-5 x$ | $\|5 y-12 x\|+13 \sqrt{x^{2}+y^{2}+26 x+169}=156$ | 5 |
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|x-1|+|5-x| \leqslant 4 \\
\frac{x^{2}-6 x+2 y+7}{y+x-4} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 4.
Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $x<1$. Then $1-x+5-x \leqslant 4 \Leftrightarrow x \geqslant 1$, i.e., there are no solutions.
2) $1 \leqslant x \leqslant 5$. Then $x-1+5-x \leqslant 4 \Leftrightarrow 4 \leqslant 4$, which is always true, so the solution is $x \in [1; 5]$.
3) $x>5$. Then $x-1+x-5 \leqslant 4 \Leftrightarrow x \leqslant 5$, i.e., there are no solutions.
Combining the results, we get that $x \in [1; 5]$.
Now let's move to the second inequality. The denominator of the fraction in its left part is zero at points belonging to the line $\ell$ with the equation $y=4-x$ (in this case, the inequality is not satisfied, as the fraction is undefined). The numerator of the fraction is zero when $x^{2}-6 x+2 y+7=0 \Leftrightarrow y=\frac{1}{2}(x-2)^{2}-1$. This set of points is a parabola with branches upwards and the vertex at point $C(2; -1)$. The points of intersection of the line and the parabola can be determined from the system of equations $\left\{\begin{array}{l}y=4-x, \\ x^{2}-6 x+2 y+7=0\end{array} \Leftrightarrow\left\{\begin{array}{l}y=4-x, \\ x^{2}-8 x+15=0 .\end{array}\right.\right.$ From this, we get two points $-A(5; -1)$ and $C(3; 1)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points below the parabola and above the line (in this case, the numerator is negative, and the denominator is positive);
- at points above the parabola and below the line (the numerator is positive, and the denominator is negative).
Considering also the restriction $x \in [1; 5]$ from the first inequality, we get that the set $M$ is the union of two sets $M_{1}$ and $M_{2}$; the first of which is a curvilinear triangle $B C D$, where $B(1; -1)$ and $D(1; 3)$ are the points of intersection of the line $x=1$ with the parabola and the line $\ell$ respectively (its sides are segments $C D, B D$ and the arc of the parabola $B C$), and the second is the region bounded by the segment $A C$ and the arc of the parabola $A C$ (all points of the line $A C$ do not belong to the set, while the other boundary points do belong).
From the symmetry of the parabola relative to its axis (i.e., the line $x=3$), it follows that the area of the figure $M_{3}$, bounded by the segment $B C$ and the arc of the parabola $B C$, is equal to the area of $M_{2}$. But $M_{1} \cup M_{3}=\triangle B C D$, and the area of this triangle is easy to find: $S_{\triangle B C D}=\frac{1}{2} \cdot 4 \cdot 2=4$.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
|y|+|4-y| \leqslant 4 \\
\frac{y^{2}+x-4 y+1}{2 y+x-7} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. Consider the first inequality. To open the absolute values, we consider three possible cases.
1) $y < 0$. Then $-y-4+y \leqslant 4 \Leftrightarrow -4 \leqslant 4$, which is always true, so $y \in (-\infty, 0)$.
2) $0 \leqslant y \leqslant 4$. Then $y-4+y \leqslant 4 \Leftrightarrow 2y \leqslant 8 \Leftrightarrow y \leqslant 4$, so $y \in [0, 4]$.
3) $y > 4$. Then $y-4+y \leqslant 4 \Leftrightarrow y \leqslant 4$, which means there are no solutions.
Combining the results, we get that $y \in [0, 4]$.
Now, let's move to the second inequality. The denominator of the fraction on its left side is zero at points belonging to the line $x=7-2y$ (let's call it $\ell$; the inequality is not satisfied here because the fraction is undefined). The numerator of the fraction is zero when $x+y^2-4y+1=0 \Leftrightarrow x=-(y-2)^2+3$. This set of points is a parabola with branches to the left and a vertex at point $C(3, 2)$. Note that the parabola and the line intersect the x-axis at points $B(-1, 0)$ and $D(7, 0)$, respectively. The points of intersection of the line $\ell$ and the parabola can be determined from the system of equations $\left\{\begin{array}{l}x=7-2y, \\ x=-y^2+4y-1\end{array} \Leftrightarrow \Leftrightarrow\left\{\begin{array}{l}x=7-2y, \\ y^2-6y+8=0 .\end{array}\right.\right.$
From this, we get two points $-A(-1, 4)$ and $C(3, 2)$.
The second inequality is satisfied:
- at points on the parabola (except points $A$ and $C$);
- at points to the right of the parabola and above the line (where both the numerator and the denominator of the fraction are positive);
- at points to the left of the parabola and below the line (where both the numerator and the denominator of the fraction are negative).
Considering also the restriction $y \in [0, 4]$ from the first inequality, we get that the set $M$ is the union of two sets $M_1$ and $M_2$; the first is a curvilinear triangle $BCD$ (its sides are segments $CD$, $BD$, and the arc of the parabola $BC$), and the second is the region bounded by the segment $AC$ and the arc of the parabola $AC$ (all points of the line $AC$ do not belong to the set, while all other boundary points do).
From the symmetry of the parabola relative to its axis (i.e., the line $y=2$), it follows that the area of the figure $M_3$, bounded by the segment $BC$ and the arc of the parabola $BC$, is equal to the area of $M_2$. But $M_1 \cup M_3 = \triangle BCD$, and the area of this triangle is easy to find: $S_{\triangle BCD} = \frac{1}{2} \cdot 8 \cdot 2 = 8$.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
y-x \geqslant|x+y| \\
\frac{x^{2}+8 x+y^{2}+6 y}{2 y-x-8} \leqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 8.
Solution. The first inequality is equivalent to the system ${ }^{1}$ $\left\{\begin{array}{l}x+y \leqslant y-x, \\ x+y \geqslant x-y\end{array} \Leftrightarrow\left\{\begin{array}{l}x \leqslant 0, \\ y \geqslant 0 .\end{array}\right.\right.$
Consider the second inequality. It can be written as $\frac{(x+4)^{2}+(y+3)^{2}-25}{2 y-x-8} \leqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at the point $Q(-4 ;-3)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=4+\frac{x}{2}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array}{l}
x = 2 y - 8 \\
x ^ { 2 } + 8 x + y ^ { 2 } + 6 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x = 2 y - 8 \\
( 2 y - 8 ) ^ { 2 } + 8 ( 2 y - 8 ) + y ^ { 2 } + 6 y = 0
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=2 y-8 \\
y^{2}-2 y=0
\end{array}\right.\right.\right.
$$
from which we get two points $A(-4 ; 2)$ and $B(-8 ; 0)$. Also denote the origin by $O$, and the intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ; 4)$).
The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located above the line $\ell$ (the numerator is negative, and the denominator is positive);
- outside the circle $\omega$ at points located below the line $\ell$ (the numerator is positive, and the denominator is negative).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located above this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located above the chord $A B$ is equal to the segment of the circle located above the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 4 \cdot 4=8$.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On the coordinate plane, consider a figure $M$ consisting of all points with coordinates $(x ; y)$ that satisfy the system of inequalities
$$
\left\{\begin{array}{l}
x+y+|x-y| \leqslant 0 \\
\frac{x^{2}+6 x+y^{2}-8 y}{x+3 y+6} \geqslant 0
\end{array}\right.
$$
Sketch the figure $M$ and find its area.
|
Answer: 3.
Solution. The first inequality is equivalent to the system $\left\{\begin{array}{l}x-y \leqslant-x-, \\ x-y \geqslant x+y\end{array} \Leftrightarrow\left\{\begin{array}{l}x \leqslant 0, \\ y \leqslant 0 .\end{array}\right.\right.$
Consider the second inequality. It can be written as $\frac{(x+3)^{2}+(y-4)^{2}-25}{x+3 y+6} \geqslant 0$. The numerator of the fraction on the left side of the inequality is zero on the circle of radius 5 centered at the point $Q(-3 ; 4)$ (let's call it $\omega$). The denominator of the fraction is zero on the line $y=-2-\frac{x}{3}$ (let's call it $\ell$). The points of intersection of the circle and the line are determined from the system of equations
$$
\left\{\begin{array} { l }
{ x = - 3 y - 6 , } \\
{ x ^ { 2 } + 6 x + y ^ { 2 } - 8 y = 0 }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ x = - 3 y - 6 } \\
{ ( 3 y + 6 ) ^ { 2 } - 6 ( 3 y + 6 ) + y ^ { 2 } - 8 y = 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=-3 y-6 \\
y^{2}+y=0
\end{array}\right.\right.\right.
$$
from which we obtain two points $A(-3 ;-1)$ and $B(-6 ; 0)$. Also denote the origin by $O$, and the intersection of the line $\ell$ with the $O y$ axis by $C$ (it is not difficult to determine that the coordinates of point $C$ are $(0 ;-2)$).
The inequality is satisfied:
- at all points of the circle $\omega$ except points $A$ and $B$ (then the numerator of the fraction is zero);
- inside the circle $\omega$ at points located below the line $\ell$ (the numerator and denominator are negative);
- outside the circle $\omega$ at points located above the line $\ell$ (the numerator and denominator are positive).
Describe the set of points $M$ that satisfy the original system of inequalities. It consists of the segment of the circle bounded by the chord $A B$ and located below this chord, as well as the curvilinear triangle $A O C$, the boundaries of which are the arc $A O$ of the circle $\omega$ and the segments $A C$ and $C O$ (while the points of the line $\ell$ do not belong to the set, and the other boundary points do belong).
Note that due to symmetry, the segment of the circle located below the chord $A B$ is equal to the segment of the circle located below the chord $A O$. Therefore, the area of the figure $M$ is equal to the area of the triangle $A C O$, i.e., $\frac{1}{2} \cdot 3 \cdot 2=3$.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two parabolas param 1 and param 2 touch at a point lying on the $O x$ axis. Through point $D$, the second intersection point of the first parabola with the $O x$ axis, a vertical line is drawn, intersecting the second parabola at point $A$ and the common tangent to the parabolas at point $B$. Find the ratio $D A: D B$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $y=x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | |
| $y=2 x^{2}+a x+b$ | $y=-5 x^{2}+c x+d$ | |
| $y=x^{2}+a x+b$ | $y=-6 x^{2}+c x+d$ | |
| $y=2 x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | |
|
1. Two parabolas param 1 and param 2 touch at a point lying on the $O x$ axis. Through point $D$, the second intersection point of the first parabola with the $O x$ axis, a vertical line is drawn, intersecting the second parabola at point $A$ and the common tangent to the parabolas at point $B$. Find the ratio $D A: D B$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $y=x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | 4 |
| $y=2 x^{2}+a x+b$ | $y=-5 x^{2}+c x+d$ | 3.5 |
| $y=x^{2}+a x+b$ | $y=-6 x^{2}+c x+d$ | 7 |
| $y=2 x^{2}+a x+b$ | $y=-3 x^{2}+c x+d$ | 2.5 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the smallest possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :--- |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-6 x^{2}+14 x+2=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+6 x^{2}+15 x+27=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}+3 x^{2}+7 x+17=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}-3 x^{2}+8 x+5=0$ | |
|
7. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the smallest possible value of the sum $a+b$.
| param1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-6 x^{2}+14 x+2=0$ | 3 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+6 x^{2}+15 x+27=0$ | -3 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}+3 x^{2}+7 x+17=0$ | 1 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}-3 x^{2}+8 x+5=0$ | -1 |
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
17. It is known that the number $a$ satisfies the equation param1, and the number $b$ satisfies the equation param2. Find the maximum possible value of the sum $a+b$.
| param1 | param2 | |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | |
|
17. It is known that the number $a$ satisfies the equation param 1, and the number $b$ satisfies the equation param2. Find the greatest possible value of the sum $a+b$.
| param 1 | param2 | Answer |
| :---: | :---: | :---: |
| $x^{3}-3 x^{2}+5 x-17=0$ | $x^{3}-3 x^{2}+5 x+11=0$ | 2 |
| $x^{3}+3 x^{2}+6 x-9=0$ | $x^{3}+3 x^{2}+6 x+17=0$ | -2 |
| $x^{3}-6 x^{2}+16 x-28=0$ | $x^{3}-6 x^{2}+16 x-4=0$ | 4 |
| $x^{3}+6 x^{2}+17 x+7=0$ | $x^{3}+6 x^{2}+17 x+29=0$ | -4 |
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given two linear functions $f(x)$ and $g(x)$ such that the graphs $y=f(x)$ and $y=g(x)$ are parallel lines, not parallel to the coordinate axes. Find the minimum value of the function $(g(x))^{2}+$ $2 f(x)$, if the minimum value of the function $(f(x))^{2}+2 g(x)$ is 5.
|
Answer: -7.
Solution. Let $f(x)=a x+b, g(x)=a x+c$, where $a \neq 0$. Consider $h(x)=(f(x))^{2}+2 g(x)$. Expanding the brackets, we get $h(x)=(a x+b)^{2}+2(a x+c)=a^{2} x^{2}+2 a(b+1) x+b^{2}+2 c$. The graph of $y=$ $h(x)$ is a parabola opening upwards, and the minimum value is attained at the vertex. The x-coordinate of the vertex is $x_{\mathrm{v}}=-\frac{b+1}{a}$; the y-coordinate of the vertex is $h\left(x_{\text {v }}\right)=-2 b-1+2 c$.
Similarly, we obtain that the minimum value of the expression $(g(x))^{2}+2 f(x)$ is $-2 c-1+2 b$. Note that the sum of these two minimum values is -2, therefore, if one of these minimum values is 5, then the other is $-2-5=-7$.
|
-7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The equation $x^{2}+a x+5=0$ has two distinct roots $x_{1}$ and $x_{2}$; in this case,
$$
x_{1}^{2}+\frac{250}{19 x_{2}^{3}}=x_{2}^{2}+\frac{250}{19 x_{1}^{3}}
$$
Find all possible values of $a$.
|
Answer: $a=10$.
Solution. For the equation to have roots, its discriminant must be positive, hence $a^{2}-20>0$. Under this condition, by Vieta's theorem, $x_{1}+x_{2}=-a, x_{1} x_{2}=5$. Then $x_{1}^{2}+$ $x_{1} x_{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-x_{1} x_{2}=a^{2}-5$.
Transform the given equality:
$$
x_{1}^{2}-x_{2}^{2}+\frac{250}{19} \cdot \frac{x_{1}^{3}-x_{2}^{3}}{x_{1}^{3} x_{2}^{3}}=0 \Leftrightarrow\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)+\frac{250\left(x_{1}-x_{2}\right)\left(x_{1}^{2}+x_{1} x_{2}+x_{2}^{2}\right)}{19\left(x_{1} x_{2}\right)^{3}}=0
$$
Since the roots are distinct, $x_{1}-x_{2} \neq 0$. Dividing both sides by $x_{1}-x_{2}$ and substituting the values given above, we get $-a+\frac{250}{19} \cdot \frac{a^{2}-5}{125}=0 \Leftrightarrow 2 a^{2}-19 a-10=0$, from which $a=10$ or $a=-0.5$. Only $a=10$ satisfies the inequality $a^{2}-20>0$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Given two linear functions $f(x)$ and $g(x)$ such that the graphs $y=f(x)$ and $y=g(x)$ are parallel lines, not parallel to the coordinate axes. Find the minimum value of the function $(g(x))^{2}+$ $8 f(x)$, if the minimum value of the function $(f(x))^{2}+8 g(x)$ is -29.
|
Answer: -3.
Solution. Let $f(x)=a x+b, g(x)=a x+c$, where $a \neq 0$. Consider $h(x)=(f(x))^{2}+8 g(x)$. Expanding the brackets, we get $h(x)=(a x+b)^{2}+8(a x+c)=a^{2} x^{2}+2 a(b+4) x+b^{2}+8 c$. The graph of $y=$ $h(x)$ is a parabola opening upwards, and the minimum value is attained at the vertex. The x-coordinate of the vertex is $x_{\text {v }}=-\frac{b+4}{a}$; the y-coordinate of the vertex is $h\left(x_{\text {v }}\right)=-8 b-16+8 c$.
Similarly, we find that the minimum value of the expression $(g(x))^{2}+2 f(x)$ is $-8 c-16+8 b$. Note that the sum of these two minimum values is -32, therefore, if one of these minimum values is -29, then the other is $-32+29=-3$.
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 9