problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1. (17 points) When walking uphill, the tourist walks 3 km/h slower, and downhill 3 km/h faster, than when walking on flat ground. Climbing the mountain takes the tourist 8 hours, while descending the mountain takes 4 hours. What is the tourist's speed on flat ground?
|
# Answer: 9
Solution. Let $x$ km/h be the tourist's speed on flat terrain. According to the problem, we get the equation $8(x-3)=4(x+3)$. From this, we find $x=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Find the area of the triangle cut off by the line $y=3 x+1$ from the figure defined by the inequality $|x-1|+|y-2| \leq 2$.
|
Answer: 2.
Solution. The figure defined by the given inequality is a square.
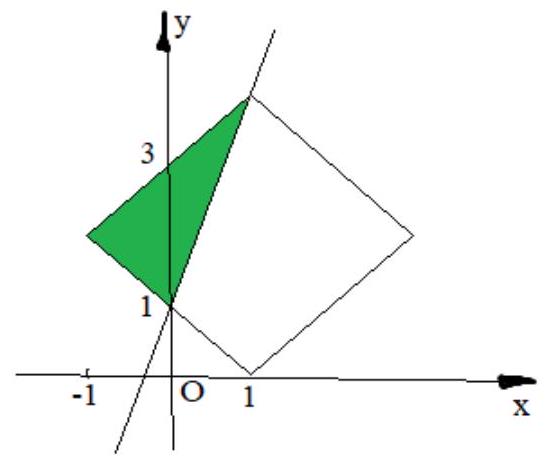
The side of the square is $2 \sqrt{2}$ (this can be found using the Pythagorean theorem). The given line passes through the vertex of the square and cuts off a triangle with the smaller leg equal to $\sqrt{2}$, and the larger leg - the side of the square. Therefore, the area of the cut-off right triangle is $S=\frac{1}{2} \cdot \sqrt{2} \cdot 2 \sqrt{2}=2$ square units.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. (17 points) A section of a regular triangular pyramid passes through the midline of the base and is perpendicular to the base. Find the area of the section if the side of the base is 6 and the height of the pyramid is 8.
|
Answer: 9.
Solution. The section MNP passes through the midline of the base of the pyramid $MN$ and is perpendicular to the base. Therefore, the height $PH$ of the triangle $MNP$ is parallel to the height of the pyramid $DO$.
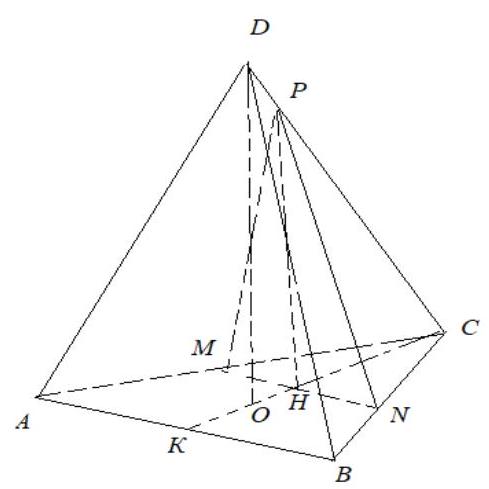
We have $OC: OK=2: 1, CH=HK$, therefore, $CH: CO=3: 4$. Using the similarity of triangles $DOC$ and $PHC$, we get that $PH=\frac{3}{4} DO=\frac{3}{4} \cdot 8=6$. Then the area of the section is $S=\frac{1}{2} \cdot PH \cdot MN=\frac{1}{2} \cdot 6 \cdot 3=9$ sq.units.
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (17 points) Find the area of the triangle cut off by the line $y=2x+2$ from the figure defined by the inequality $|x-2|+|y-3| \leq 3$.
|
Answer: 3.
Solution. The figure defined by the given inequality is a square.
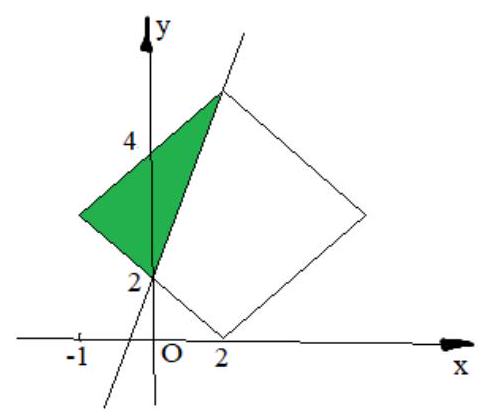
The side of the square is $3 \sqrt{2}$ (this value can be found using the Pythagorean theorem). The given line passes through the vertex of the square and cuts off a triangle with the smaller leg equal to $\sqrt{2}$, and the larger leg - the side of the square. Therefore, the area of the cut-off right triangle is $S=\frac{1}{2} \cdot \sqrt{2} \cdot 3 \sqrt{2}=3$ square units.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. (16 points) There are two circles: one with center at point $A$ and radius 6, and another with center at point $B$ and radius 3. Their common internal tangent touches the circles at points $C$ and $D$, respectively. Lines $A B$ and $C D$ intersect at point $E$. Find $C D$, if $A E=10$.
|
Answer: 12
Solution. Triangles $A C E$ and $B D E$ are similar (they have vertical angles and a right angle each) with a similarity coefficient of 2. From triangle $A C E$, using the Pythagorean theorem, we find $C E=8$. Therefore, $D E=4$, and $C D=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the largest root of the equation
$$
\left|\cos (\pi x)+x^{3}-3 x^{2}+3 x\right|=3-x^{2}-2 x^{3}
$$
|
# Answer: 1
Solution. It is obvious that 1 is a root of the equation (when $x=1$, both sides of the equation are equal to zero). If $x>1$, the right side of the equation is negative, while the left side of the equation is always non-negative.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A point light source is located at an equal distance $x=10 \mathrm{~cm}$ from the lens and its principal optical axis. Its direct image is located at a distance $y=5 \mathrm{~cm}$ from the principal optical axis. Determine the optical power of the lens and the distance between the light source and its image.
|
Answer: -10 Dptr $u \approx 7.1$ cm
Solution. The image is upright, therefore, it is virtual. Magnification: $\Gamma=\frac{y}{x}=\frac{f}{d}$. We obtain that the distance from the lens to the image: $f=d \cdot \frac{y}{x}=10 \cdot \frac{5}{10}=5 \mathrm{~cm} . \quad$ The power of the lens: $D=\frac{1}{d}-\frac{1}{f}=\frac{1}{0.1}-\frac{1}{0.05}=-10$ Dptr. The distance between the source and its image: $s=\sqrt{(x-y)^{2}+(d-f)^{2}}=\sqrt{50} \approx 7.1 \mathrm{~cm}$.
|
-10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (17 points) Find the smallest root of the equation
$$
\sin (\pi x)+\tan x=x+x^{3}
$$
|
Answer: 0
Solution. Obviously, 0 is a root of the equation (when $x=0$, both sides of the equation are equal to zero). If $x<0$, the right side of the equation is negative, while the left side of the equation is always non-negative.
|
0
|
Calculus
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. (20 points) A point light source is located at an equal distance $x=10 \mathrm{~cm}$ from the lens and its principal optical axis. Its direct image is located at a distance $y=20 \mathrm{~cm}$ from the principal optical axis. Determine the optical power of the lens and the distance between the light source and its image.
|
Answer: 5 Dpt $i \approx 14.1$ cm
Solution. The image is upright, therefore, it is virtual. Magnification: $\Gamma=\frac{y}{x}=\frac{f}{d}$. We obtain the distance from the lens to the image: $f=d \cdot \frac{y}{x}=10 \cdot \frac{20}{10}=20 \mathrm{~cm} . \quad$ The optical power of the lens: $D=\frac{1}{d}-\frac{1}{f}=\frac{1}{0.1}-\frac{1}{0.2}=5$ Dpt. The distance between the source and its image: $s=\sqrt{(x-y)^{2}+(d-f)^{2}}=\sqrt{200} \approx 14.1 \mathrm{~cm}$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Let in triangle $A B C$
$$
\cos (2 \angle A-\angle B)+\sin (\angle A+\angle B)=2 \text {. }
$$
Find the side $B C$, if $A B=4$.
|
Answer: 2.
Solution. Each term in the left part of the equation does not exceed 1. Therefore, the equality will hold only if each of them equals 1. We solve the corresponding equations, denoting $\alpha=\angle A, \beta=\angle B:$
$$
2 \alpha-\beta=2 \pi n, n \in \mathbb{Z} ; \quad \alpha+\beta=\frac{\pi}{2}+2 \pi k, k \in \mathbb{Z}
$$
Considering that $0<\alpha<\pi, 0<\beta<\pi$, we get
$$
2 \alpha-\beta=0 ; \quad \alpha+\beta=\frac{\pi}{2} .
$$
From this,
$$
\beta=2 \alpha, \quad 3 \alpha=\frac{\pi}{2}, \quad \alpha=\frac{\pi}{6}, \quad \beta=\frac{\pi}{3} .
$$
Thus, $A B C$ is a right triangle with hypotenuse $A B$ and an angle of $30^{\circ}$ opposite side $B C$. Therefore, $B C=A B / 2=2$.
Evaluation. 12 points for a correct solution.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The infantry column stretched out over 1 km. Sergeant Kim, riding out on a gyro-scooter from the end of the column, reached its beginning and returned to the end. The infantrymen walked 2 km $400 \mathrm{m}$ during this time. How far did the sergeant travel during this time?
|
Answer: 3 km $600 \mathrm{~m}$
Solution. Let the speed of the column be $x$ km/h, and the sergeant travels $k$ times faster, i.e., at a speed of $k x$ km/h. To reach the end of the column, Kim traveled $t_{1}=\frac{1}{k x-x}$ hours (catching up), and in the opposite direction, $t_{2}=\frac{1}{k x+x}$ hours (meeting head-on). During this time, the column covered 2.4 km, i.e., $x\left(t_{1}+t_{2}\right)=2.4$. Substituting the expressions for $t_{1}$ and $t_{2}$, we get
$$
\frac{x}{k x-x}+\frac{x}{k x+x}=2.4 ; \quad \frac{1}{k-1}+\frac{1}{k+1}=2.4 ; \quad 2 k=2.4\left(k^{2}-1\right) .
$$
The obtained quadratic equation has a single positive root $k=\frac{3}{2}$. The sergeant travels 1.5 times faster than the column. Therefore, the distance he covers will also be 1.5 times greater.
Evaluation. Full solution: 12 points.
|
3
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. (10 points) A beam of light with a diameter of $d_{1}=5 \mathrm{~cm}$ falls on a thin diverging lens with an optical power of $D_{p}=-6$ Diopters. On a screen positioned parallel to the lens, a bright spot with a diameter of $d_{2}=20 \mathrm{~cm}$ is observed. After replacing the thin diverging lens with a thin converging lens, the size of the spot on the screen remains unchanged. Determine the optical power $D_{c}$ of the converging lens.
|
# Answer: 10 Dptr
Solution. The optical scheme corresponding to the condition:
(3 points)
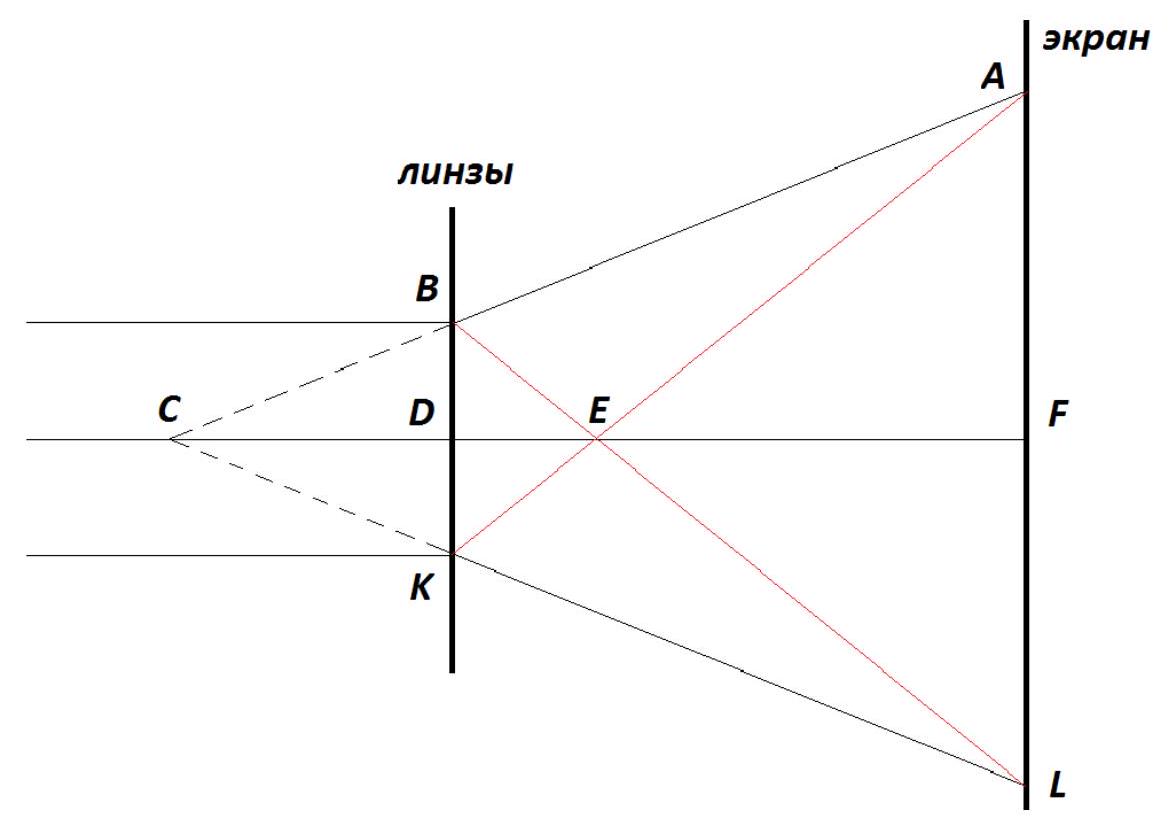
The path of the rays after the diverging lens is shown in black, and after the converging lens in red. We have $C D=\left|\frac{1}{D_{p}}\right|=\frac{1}{6}$.
From the similarity of triangles, it follows that: $\frac{C D}{C F}=\frac{B K}{A L}=\frac{1}{4}$,
then $D F=C F-C D=4 C D-C D=3 C D=\frac{1}{2}$.
From the similarity of triangles, it follows that: $\frac{D E}{F E}=\frac{B K}{A L}$.
We get that: $D E=\frac{1}{5} D F=\frac{1}{10}$.
As a result, the optical power of the converging lens: $D_{c}=\frac{1}{D E}=10$ Dptr.
(2 points)
|
10
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem № 6 (10 points)
A cylinder with a mass of $M=1$ kg was placed on rails inclined at an angle $\alpha=30^{\circ}$ to the horizontal (the side view is shown in the figure). What is the minimum mass $m$ of the load that needs to be attached to the thread wound around the cylinder so that it starts rolling upwards? Slippage is absent.
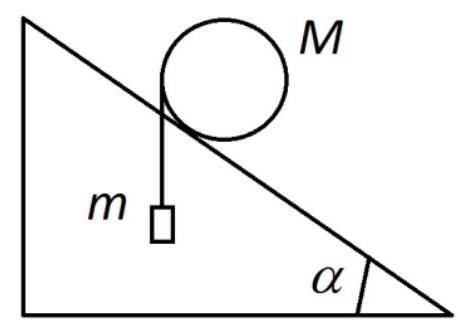
Answer: 1 kg
#
|
# Solution and evaluation criteria:
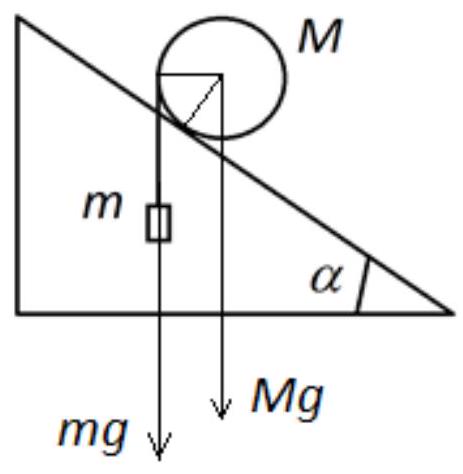
The moment of forces relative to the point of contact of the cylinder with the plane: $m g($ ( $-R \sin \alpha)=M g R \sin \alpha$ (5 points) $m\left(1-\frac{1}{2}\right)=M \frac{1}{2}$
$m=M=1 \kappa 2$
(5 points)
#
|
1
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. An ideal gas was expanded in such a way that during the process, the pressure of the gas turned out to be directly proportional to its volume. As a result, the gas heated up by $\Delta T=100^{\circ} \mathrm{C}$, and the work done by the gas was $A=831$ J. Determine the amount of substance that participated in this process. The gas constant $R=8.31$ J/mol$\cdot$K. (15 points)
|
Answer: 2 moles
Solution. From the condition $p=\alpha V$ (3 points). The work of the gas is equal to the area under the graph of the given process, constructed in coordinates $p-V$:
$A=\frac{p_{1}+p_{2}}{2} \cdot\left(V_{2}-V_{1}\right)=\frac{\alpha V_{1}+\alpha V_{2}}{2} \cdot\left(V_{2}-V_{1}\right)=\frac{\alpha}{2} \cdot\left(V_{2}^{2}-V_{1}^{2}\right) \quad(4$ points). From the equation of state of an ideal gas: $p V=\alpha V V=\alpha V^{2}=\nu R T \quad(4$ points). As a result, we get: $A=\frac{\alpha}{2} \cdot\left(V_{2}^{2}-V_{1}^{2}\right)=\frac{1}{2} v R \Delta T \quad(2$ points $) . \quad$ Final answer: $\quad v=\frac{2 A}{R \Delta T}=\frac{2 \cdot 831}{8.31 \cdot 100}=2$ moles (2 points).
|
2
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Two small balls with charges $Q=-20 \cdot 10^{-6}$ C and $q=50 \cdot 10^{-6}$ C are located at the vertices $A$ and $B$ of a mountain slope (see figure). It is known that $AB=2$ m, $AC=3$ m. The masses of the balls are the same and equal to $m=200$ g each. At the initial moment of time, the ball with charge $q$ is released with zero initial velocity. Determine its speed at the moment when it reaches point $C$. The surface of the mountain slope is considered smooth. The acceleration due to gravity $g=10$ m/s², and the proportionality constant in Coulomb's law $k=9 \cdot 10^{9}$ N·m²/C². (10 points)
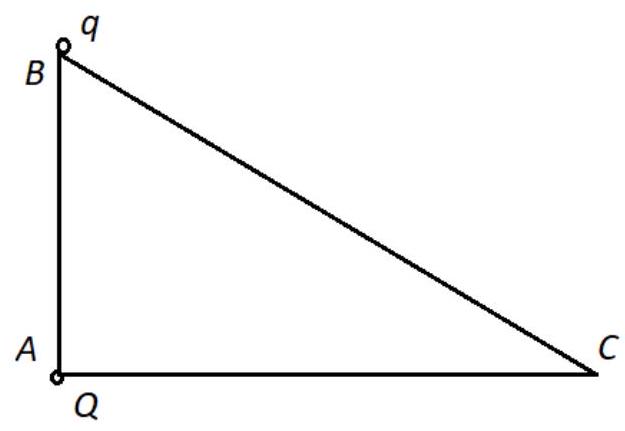
|
Answer: $5 \mathrm{M} / \mathrm{c}$
Solution. The law of conservation of energy for this situation:
$k \frac{Q q}{A B}+m g \cdot A B=\frac{m v^{2}}{2}+k \frac{Q q}{B C}(5$ points $)$.
As a result, we get: $v=\sqrt{\frac{2 k Q q}{m \cdot A B}+2 \cdot g \cdot A B-\frac{2 k Q q}{m \cdot B C}}=\sqrt{\frac{2 \cdot 9 \cdot 10^{9} \cdot\left(-20 \cdot 10^{-6}\right) \cdot 50 \cdot 10^{-6}}{0.2 \cdot 2}+2 \cdot 10 \cdot 2-\frac{2 \cdot 9 \cdot 10^{9} \cdot\left(-20 \cdot 10^{-6}\right) \cdot 50 \cdot 10^{-6}}{0.2 \cdot 3}}=5 \cdot \mathrm{m} / \mathrm{c}$ $(2$ points $)$.
|
5
|
Other
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Petya was given several physics problems and several math problems for homework. All the problems solved by Petya constitute $5 \%$ of the total number of physics problems and $20 \%$ of the total number of math problems. What percentage of the total number of problems did Petya solve?
|
Solution. Answer: $4 \%$.
Let Pete solve $N$ problems. This constitutes $5 \%$ ( $\frac{1}{20}$ of) the physics problems, so the total number of physics problems was $20 \mathrm{~N}$. Similarly, the number of math problems was $5 N$, so the total number of problems assigned was $20 N + 5 N = 25 N$. The problems solved by Pete constitute $\frac{N}{25 N} \cdot 100 \% = 4 \%$.
## Criteria
The largest suitable criterion is used:
7 points. Any complete solution to the problem.
7 points. Any complete solution to the problem, but the answer is given not in percentages, but as a fraction $\frac{1}{25}$ or 0.04.
3 points. Only the correct answer is given.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. We will call a natural number odd-powered if all its prime divisors enter its factorization with an odd exponent. What is the maximum number of odd-powered numbers that can occur consecutively?
## Answer: 7.
|
Solution. Note that among any eight consecutive natural numbers, there will definitely be a number that is divisible by 4 but not by 8. Then the number 2 will appear in its factorization to the second power.
Example of seven odd-power numbers: $37,38,39,40,41,42,43$.
Problem 4/1. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=14$.
Answer: 7.
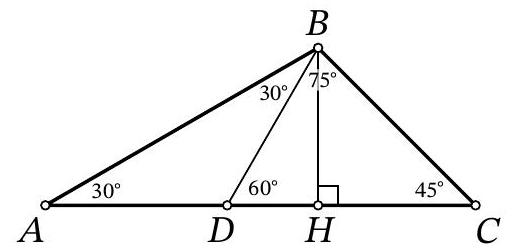
Fig. 1: to the solution of problem $4 / 1$
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.
Draw the height $B H$ in triangle $A B C$ (Fig. 1). Triangle $B H C$ is a right isosceles triangle, so $C H=B H$. Triangles $A B H$ and $B D H$ are right triangles with an angle of $30^{\circ}$, so in them the legs opposite the angle of $30^{\circ}$ are half the hypotenuse. It turns out that $2 B H=A B, 2 H D=B D$.
Then
$$
C D=C H+H D=B H+H D=\frac{A B}{2}+\frac{B D}{2}=\frac{A B+A D}{2}=7
$$
Problem 4/2. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=16$.
Answer: 8.
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.

Fig. 2: to the solution of problem $4 / 2$
Draw the height $B H$ in triangle $A B C$ (Fig. 2). Triangle $B H C$ is a right isosceles triangle, so $C H=B H$. Triangles $A B H$ and $B D H$ are right triangles with an angle of $30^{\circ}$, so in them the legs opposite the angle of $30^{\circ}$ are half the hypotenuse. It turns out that $2 B H=A B, 2 H D=B D$.
Then
$$
C D=C H+H D=B H+H D=\frac{A B}{2}+\frac{B D}{2}=\frac{A B+A D}{2}=8
$$
Problem 4/3. On side $A C$ of triangle $A B C$, a point $D$ is chosen. It is known that $\angle B A C=30^{\circ}, \angle D B C=75^{\circ}, \angle B C A=45^{\circ}$. Find $C D$, if it is known that $B A+A D=18$.
Answer: 9.
Solution. From the sum of the angles of triangle $A B C$, it follows that $\angle A B D=30^{\circ}$. Therefore, $A D=B D$.
. Therefore, among any three consecutive residents, there is at least one knight. If we divide all the people sitting at the table into groups of three consecutive residents, we get that there is at least one knight in each group, so there are at least 10 knights in total.
Let's provide an example where there are exactly 10 knights. Suppose the residents sit as follows: knight, two liars, knight, two liars, and so on. Each knight says any of the given phrases—it will be true in any case. A liar says, "My left neighbor is a liar" if the person on the left is a knight, and vice versa, he says, "My right neighbor is a liar" if the person on the right is a knight. It is clear that all the conditions of the problem are satisfied.
## Criteria
## The following criteria are cumulative:
5 p. It is proven that there are at least 10 knights.
2 6. It is proven that there can be exactly 10 knights.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.2. Masha and the Bear ate a basket of raspberries and 40 pies, starting and finishing at the same time. At first, Masha was eating raspberries, and the Bear was eating pies, then (at some point) they switched. The Bear ate both raspberries and pies 3 times faster than Masha. How many pies did Masha eat, if they ate the raspberries equally?
|
Answer: 4 pies. Solution: The bear ate his half of the raspberries three times faster than Masha. This means Masha ate pies for three times less time than the bear. Since she eats three times slower, she ate 9 times fewer pies than the bear. Dividing the pies in the ratio of $9: 1$, we see that Masha got the 10th part, that is, 4 pies.
Criterion: Correct answer - no less than 2 points, with full justification - 7 points.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 11.4. For positive numbers $x$ and $y$, it is known that
$$
\frac{1}{1+x+x^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+x+y}=1
$$
What values can the product $x y$ take? List all possible options and prove that there are no others.
|
Answer: 1.
Solution. Note that for each positive $y$ the function
$$
f_{y}(x)=\frac{1}{1+x+x^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+x+y}
$$
strictly decreases on the ray $(0 ;+\infty)$, since the denominators of all three fractions increase. Therefore, the function $f_{y}$ takes each value no more than once. Moreover, it is not difficult to see that
$$
\begin{aligned}
f_{y}(1 / y) & =\frac{1}{1+1 / y+1 / y^{2}}+\frac{1}{1+y+y^{2}}+\frac{1}{1+1 / y+y}= \\
& =\frac{y^{2}}{1+y+y^{2}}+\frac{1}{1+y+y^{2}}+\frac{y}{1+y+y^{2}}=1
\end{aligned}
$$
from which we conclude that $x=1 / y$.
## Criteria
One of the largest suitable criteria is used:
7 6. Any correct solution to the problem.
3 6. The monotonicity of the left side with respect to $x$ or $y$ is noted.
3 6. It is proven that for any $y$ there is no more than one $x$ satisfying the equation.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.1. Jerry has nine cards with digits from 1 to 9. He lays them out in a row, forming a nine-digit number. Tom writes down all 8 two-digit numbers formed by adjacent digits (for example, for the number 789456123, these numbers are $78, 89, 94, 45$, $56, 61, 12, 23$). For each two-digit number divisible by 9, Tom gives Jerry a piece of cheese. What is the maximum number of pieces of cheese Jerry can get?
|
Answer: 4.
Solution. Note that among two-digit numbers, only 18, 27, 36, 45, and numbers obtained by swapping their digits are divisible by 9 (there are also 90 and 99, but we do not have the digit 0 and only one digit 9). Thus, only four pairs of digits from the available ones can form a number divisible by 9. To get an example, we need to arrange all these pairs in any order:
$$
182736459 .
$$
## Criteria
The highest applicable criterion is used:
## 7 6. Any correct solution to the problem.
3 6. It is proven that it is impossible to get 5 two-digit numbers divisible by 9.
3 6. An example with 4 two-digit numbers divisible by 9 is provided.
16 . The correct answer is given.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7.3. The miserly knight has 5 chests of gold: the first chest contains 1001 gold coins, the second - 2002, the third - 3003, the fourth - 4004, the fifth - 5005. Every day, the miserly knight chooses 4 chests, takes 1 coin from each, and places them in the remaining chest. After some time, there were no coins left in the first chest, and there were exactly 2019 coins in another chest. Which one?
|
Answer: in the fifth.
Solution. Let's look at the remainders of the number of coins in the chests when divided by 5. Each day, the number of coins in each chest either decreases by 1 or increases by 4, which means the remainder when divided by 5 always decreases by 1 (if it was 0, it will become 4). Since after some time there were no coins left in the first chest, the number of days that have passed is $5k+1$ for some natural number $k$, and in each chest, the remainder has decreased by 1. Since 2019 gives a remainder of 4 when divided by 5, such a number of coins could only remain in the fifth chest.
## Criteria
The largest suitable criterion is used:
76. Any correct solution to the problem.
## 3 6. The idea of considering remainders when divided by 5 is present.
## 16. The correct answer is given.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. Petya has a $3 \times$ 3 table. He places chips in its cells according to the following rules:
- no more than one chip can be placed in each cell;
- a chip can be placed in an empty cell if the corresponding row and column already contain an even number of chips (0 is considered an even number).
What is the maximum number of chips Petya can place?
|
Solution. Answer: 9.
Let $a, b, c$ denote the left, middle, and right columns of the table, and $1, 2, 3$ denote the bottom, middle, and top rows of the table. Petya can fill all 9 cells of the table with chips, for example, in the following order: $a 1, b 2, c 3, a 2, b 3, c 1, a 3, b 1, c 2$. Obviously, it is not possible to place more than 9 chips.
## Criteria
The largest suitable criterion is used:
7 6. Any complete solution to the problem.
2 p. There is only the correct answer (the algorithm for placing the chips is missing).
|
9
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 5. The numbers from 1 to 2021 are written on a board. Denis wants to choose 1011 of them such that the sum of any two does not equal 2021 or 2022. How many ways are there to do this?
|
Solution. Answer: 1.
Among the numbers from 1 to 2021, we can select 1010 non-overlapping pairs of numbers that sum to 2022. Specifically: $(1,2021),(2,2020), \ldots,(1009,1013),(1010,1012)$; only the number 1011 remains unpaired.
According to the condition, from each pair, we can choose no more than one number. Therefore, to choose 1011 numbers, we must select exactly one number from each pair, and also select the number 1011. Then we cannot choose 1010 (otherwise $1011+1010=2021$), but then we must choose 1012 (otherwise nothing is chosen from the last pair). Then we cannot choose 1009 (otherwise $1012+1009=2021$), but then we must choose 1013 (otherwise nothing is chosen from the second-to-last pair). Continuing this process, we find that from each pair, the largest number must be chosen.
If the numbers $1011,1012,1013, \ldots, 2021$ are chosen, the condition of the problem is satisfied (since the sum of any two is at least 2023) and this method of selection is the only one.
## Criteria
The following is the only suitable criterion used:
7 p. Any complete solution to the problem.
3 p. The numbers are divided into pairs, but there is no further progress.
0 6. Only the answer is present.
|
1
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 1. In the Kurchatov School, exactly 2 people sit at each desk. It is known that exactly $70 \%$ of the boys have a boy as a desk partner, and exactly $40 \%$ of the girls have a girl as a desk partner. How many times more boys are there than girls?
|
Answer: 2 times.
Solution. Let the number of boys be $x$, and the number of girls be $y$. Note that $30\%$ of the boys sit at desks with girls and $60\%$ of the girls sit at desks with boys. Since exactly 2 people sit at each desk, then $0.3 x = 0.6 y$, from which $x = 2 y$. Thus, there are 2 times more boys than girls.
## Criteria
## 7 p. Any complete solution of the problem.
## 2 p. A particular case is provided.
1 p. Only the correct answer.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 3. Dodson, Williams, and their horse Bolivar want to get from city A to city B as quickly as possible. Along the road, there are 27 telegraph poles that divide the entire journey into 28 equal segments. Dodson takes 9 minutes to walk one segment, Williams takes 11 minutes, and either of them can ride Bolivar to cover the distance in 3 minutes (Bolivar cannot carry both). They set out from city A simultaneously; the journey is considered complete when all of them arrive in city B.
They agreed that part of the way Dodson will ride, then tie Bolivar to one of the telegraph poles and continue on foot, while Williams will initially walk and then ride Bolivar. At which pole should Dodson tie Bolivar to minimize the travel time to city B?
Answer: at the 12th, counting from A.
|
Solution. Let the distance from A to B be taken as a unit, and time will be measured in minutes. Then Dodson's speed is $1 / 9$, Williams' speed is $1 / 11$, and Bolivar's speed is $-1 / 3$.
Let the desired post have the number $k$ (i.e., the distance from city A is $k / 28$). Then Dodson will arrive in time
$$
\frac{k}{28}: \frac{1}{3}+\frac{28-k}{28}: \frac{1}{9}=9-\frac{6 k}{28}
$$
and Williams in
$$
\frac{k}{28}: \frac{1}{11}+\frac{28-k}{28}: \frac{1}{3}=3+\frac{8 k}{28}
$$
We need to find $k$ for which these values coincide:
$$
9-\frac{6 k}{28}=3+\frac{8 k}{28} \quad \Leftrightarrow \quad 6 \cdot 28=14 k \quad \Leftrightarrow \quad k=12
$$
It remains to understand why $k=12$ gives the best time. Indeed, for smaller $k$, Dodson's time will increase, and for larger $k$, Williams' time will increase. Thus, for all other $k$, the time of at least one of the characters will be greater than when $k=12$.
## Criteria
The highest suitable criterion is used:
7 p. Any complete solution to the problem.
4 p. The position of the post where the characters' times coincide is found, but it is not proven that this is the best time.
2 p. The idea of equating the characters' times is present, but an error was made in formulating or solving the equation.
1 p. The correct answer is given.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 8.3. How many lines exist that pass through the point $(0,2019)$ and intersect the parabola $y=x^{2}$ at two points with integer coordinates on the $y$-axis?
Answer: 9.
|
Solution. A vertical line obviously does not fit. All lines, different from the vertical one and passing through the point $(0,2019)$, are given by the equation $y=k x+2019$ for some $k$. Let such a line intersect the parabola at points $\left(a, a^{2}\right)$ and $\left(b, b^{2}\right)$, where $a^{2}$ and $b^{2}$ are integers. Without loss of generality, we will assume $a<b$. We write the system of equations
$$
\left\{\begin{array}{l}
a^{2}=k a+2019 \\
b^{2}=k b+2019
\end{array}\right.
$$
Subtracting one equation from the other, we get $a^{2}-b^{2}=k(a-b)$, and since $a \neq b$, we conclude that $k=a+b$. Substituting the obtained $k$ into any of the equations of the system, we arrive at the relation $-a b=2019$.
Note that this equality is equivalent to the fact that the points $\left(a, a^{2}\right)$ and $\left(b, b^{2}\right)$ lie on the same line. This can be verified by substituting $k=a+b$ and $2019=-a b$ into the system above.
Squaring the equation, we get $a^{2} b^{2}=2019^{2}$, where $a^{2}$ and $b^{2}$ are non-negative integers (but $a$ and $b$ are not necessarily integers!). Considering the prime factorization $2019^{2}=3^{2} \cdot 673^{2}$, we have 9 options for decomposing the number $2019^{2}$ into the product $a^{2} \cdot b^{2}$ (taking into account the order of the factors). Since $a$ and $b$ have different signs, and $a<b$, each such option corresponds to a unique solution $a=-\sqrt{a^{2}}, b=\sqrt{b^{2}}$ and, accordingly, one sought line.
Remark. A similar idea underlies the well-known geometric construction - the Matiyasevich-Steckin sieve.
## Criteria
The highest suitable criterion is used:
76 . Any correct solution to the problem.
3 6. The equation equivalent to the equality $-a b=2019$ from the solution is obtained, but the further calculation of the number of lines is done incorrectly for some reason.
2 6. The equation equivalent to the equality $k=a+b$ from the solution is obtained.
## 16 . The correct answer is given.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.1. Jerry has nine cards with digits from 1 to 9. He lays them out in a row, forming a nine-digit number. Tom writes down all 8 two-digit numbers formed by adjacent digits (for example, for the number 789456123, these numbers are $78, 89, 94, 45$, $56, 61, 12, 23$). For each two-digit number divisible by 9, Tom gives Jerry a piece of cheese. What is the maximum number of pieces of cheese Jerry can get?
|
Answer: 4.
Solution. Note that among two-digit numbers, only 18, 27, 36, 45, and numbers obtained by swapping their digits are divisible by 9 (there are also 90 and 99, but we do not have the digit 0 and only one digit 9). Thus, only four pairs of digits from the available ones can form a number divisible by 9. To get an example, we need to arrange all these pairs in any order:
$$
182736459
$$
## Criteria
The highest applicable criterion is used:
## 76 . Any correct solution to the problem.
3 6. It is proven that it is impossible to get 5 two-digit numbers divisible by 9.
## 3 6. An example with 4 two-digit numbers divisible by 9 is provided.
## 16 . The correct answer is given.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6.3. A country has the shape of a square and is divided into 25 identical square counties. In each county, either a knight-count, who always tells the truth, or a liar-count, who always lies, rules. One day, each count said: "Among my neighbors, there are an equal number of knights and liars." What is the maximum number of knights that could have been? (Counts are neighbors if their counties share a common side.)
|
Answer: 8.
Solution. First, note that counties with exactly three neighboring counties must be governed by lying counts (Fig. ??). Therefore, the corner counties are also governed by liars, since both of their neighbors are liars.
| | $L$ | $L$ | $L$ | |
| :--- | :--- | :--- | :--- | :--- |
| $L$ | | | | $L$ |
| $L$ | | | | $L$ |
| $L$ | | | | $L$ |
| | $L$ | $L$ | $L$ | |
Fig. 1: to the solution of problem $? ?$
It remains to figure out the central $3 \times 3$ square. All cells cannot be occupied by knights, since then the central knight would have all neighbors as knights. Therefore, there are no more than 8 knights. An example with eight knights is shown in Fig. ??.
| | | | | |
| :--- | :--- | :--- | :--- | :--- |
| | $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ | |
| | $\mathrm{P}$ | | $\mathrm{P}$ | |
| | $\mathrm{P}$ | $\mathrm{P}$ | $\mathrm{P}$ | |
| | | | | |
Fig. 2: to the solution of problem $?$ ?
## Criteria
Any correct solution to the problem is worth 7 points. In the absence of such a solution, the following criteria are summed:
4 6. It is proven that knights can only be in the central $3 \times 3$ square.
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Buses from Moscow to Oryol depart at the beginning of each hour (at 00 minutes). Buses from Oryol to Moscow depart in the middle of each hour (at 30 minutes). The journey between the cities takes 5 hours. How many buses from Oryol will the bus that left from Moscow meet on its way?
|
Answer: 10.
It is clear that all buses from Moscow will meet the same number of buses from Orel, and we can assume that a bus from Moscow departed at 12:00. It is easy to understand that it will meet buses that left Orel at $7:30, 8:30, \ldots, 15:30, 16:30$ and only them. There are 10 such buses.
$\pm$ Correct reasoning with an arithmetic error leading to an incorrect answer. 4-5 points
Ғ Frequency of encounters (every half hour) has been calculated, but the answer is incorrect. 3 points
- Correct answer without explanation. 1 point
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Nезнayka, Doctor Pilulkin, Knopochka, Vintik, and Znayka participated in a math competition. Each problem in the competition was solved by exactly four of them. Znayka solved strictly more than each of the others - 10 problems, while Nезнayka solved strictly fewer than each of the others - 6 problems. How many problems were there in the math competition?
|
Answer: 10.
Each of Dr. Pill, Knopochka, and Vintik, according to the condition, solved from 7 to 9 problems. Therefore, the total number of solved problems ranges from $10+6+3 \cdot 7=37$ to $10+6+3 \cdot 9=43$. Note that this number should be equal to four times the number of problems. Among the numbers from 37 to 43, only one is divisible by 4 - this number is 40. Therefore, the total number of solved problems is 40, and the total number of problems was 10.
## Criteria
+ Correct solution - 7 points.
$\mp$ Correct answer without explanations (or with incorrect explanations) - 2 points.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. If the width of a rectangle is increased by $30 \%$, and the height is decreased by $20 \%$, its perimeter will not change. Will the perimeter decrease or increase, and by what percentage, if instead the width of the original rectangle is decreased by $20 \%$, and the height is increased by $30 \%$?
|
Answer. It will increase by $10 \%$. Solution. Let the width of the original rectangle be $s$, and the height be $h$. In the first case, the modified width and height will be 1.3 and 0.8 $s$ respectively. According to the condition, $2(s+h)=2(1.3 s+0.8 h)$, from which $h=1.5 s$. This means that the original perimeter is $2(s+1.5 s)=5 s$. In the second case, the perimeter will be $2(0.8 s+1.3 h)=2(0.8 s+1.3 \cdot 1.5 s)=5.5$ s. This number is greater than $5 s$ by $0.5 s$, that is, by $10 \%$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. In a school tic-tac-toe tournament, 16 students participated, each playing one game against every other student. A win was worth 5 points, a draw -2 points, and a loss -0 points. After the tournament, it was found that the participants collectively scored 550 points. What is the maximum number of participants who could have never played a draw in this tournament?
## Answer:
|
Solution. A total of $\frac{16 \cdot 15}{2}=120$ games were played in the tournament. In each game, either 5 points were awarded (in case of a win-loss) or 4 points (in case of a draw). If all games had ended in a draw, the total number of points for all participants would have been $120 \cdot 4=480$, which is 70 points less than the actual total points of all participants. In a non-draw game, the two participants collectively receive 1 point more than in a draw game. This means that exactly 70 games ended with one participant winning, and the remaining 50 games ended in a draw.
Suppose that at least 6 participants never played a draw. Then the draw games could only have been played between the remaining 10 participants, and they played a total of $\frac{10 \cdot 9}{2}=45$ games, which is less than 50. This is a contradiction. Therefore, no more than 5 participants never played a draw.
It is not difficult to describe an example for 5 participants. Fix 11 participants, they played $\frac{11 \cdot 10}{2}=55$ games among themselves. Choose any 50 of these games, let them be draws (it is clear then that each of the fixed 11 participants will play at least one draw), and all other games in the tournament ended with one participant winning. Therefore, $16-11=5$ people never played a draw. It is clear that all conditions of the problem are satisfied.
## Criteria
## The following criteria are cumulative:
2 6. A correct example is described where exactly 5 people never played a draw.
5 p. It is proven that no more than 5 people never played a draw.
If the proof that no more than 5 people never played a draw is missing:
2 p. It is proven that there were exactly 50 draws (or that there were exactly 70 decisive games).
|
5
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Several numbers were written on the board, their arithmetic mean was equal to $M$. They added the number 15, after which the arithmetic mean increased to $M+2$. After that, they added the number 1, and the arithmetic mean decreased to $M+1$. How many numbers were on the board initially? (Find all options and prove that there are no others.)
|
Answer: 4.
Let there be $k$ numbers in the original list with a sum of $S$. Then, by the condition,
$$
\frac{S+15}{k+1}-\frac{S}{k}=2, \quad \frac{S+15}{k+1}-\frac{S+16}{k+2}=1.
$$
By bringing to a common denominator and transforming in an obvious way, we get that these equations are equivalent to the following two:
$$
15 k-S=2 k(k+1), \quad S-k+14=(k+1)(k+2)
$$
Adding them, we arrive at the equation for $k$:
$$
14(k+1)=(k+1)(2 k+k+2),
$$
from which $k=4$.
GHz The correct system of equations is written, but solved incorrectly. 3 points
- One of the equations is obtained correctly, the second one incorrectly. 2 points
- The correct answer without justification. (An example of a list of four numbers satisfying the condition is not considered a justification.) 1 point
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. How many solutions in natural numbers does the equation
$$
(2 x+y)(2 y+x)=2017^{2017} ?
$$
|
Answer: 0.
Note that the sum of the numbers $A=2x+y$ and $B=2y+x$ is divisible by 3. Since the number on the right side is not divisible by 3, neither $A$ nor $B$ are divisible by 3. Therefore, one of these two numbers gives a remainder of 2 when divided by 3, and the other gives a remainder of 1. Thus, their product gives a remainder of 2. However, the number 2017 gives a remainder of 1, and therefore $2017^{2017}$ also gives a remainder of 1.
$\pm$ It is established that the system of equations cannot be solved in integers due to divisibility by 3, but there is no strict justification for why this will happen in all cases. 5 points
Ғ In the solution, several different factorizations are analyzed, and for each, it is established that the corresponding system of equations has no solutions. 3 points
- Correct answer without justification. 1 point
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 2. Dodson, Williams, and their horse Bolivar want to get from city A to city B as quickly as possible. Along the road, there are 27 telegraph poles that divide the entire journey into 28 equal segments. Dodson takes 9 minutes to walk one segment, Williams takes 11 minutes, and either of them can ride Bolivar to cover the distance in 3 minutes (Bolivar cannot carry both). They set out from city A simultaneously; the journey is considered complete when all of them arrive in city B.
They agreed that part of the way Dodson will ride, then tie Bolivar to one of the telegraph poles and continue on foot, while Williams will initially walk and then ride Bolivar. At which pole should Dodson tie Bolivar to minimize the travel time to city B?
Answer: at the 12th, counting from A.
|
Solution. Let the distance from A to B be taken as a unit, and time will be measured in minutes. Then Dodson's speed is $1 / 9$, Williams' speed is $1 / 11$, and Bolivar's speed is $-1 / 3$.
Let the desired post have the number $k$ (i.e., the distance from city A is $k / 28$). Then Dodson will arrive in time
$$
\frac{k}{28}: \frac{1}{3}+\frac{28-k}{28}: \frac{1}{9}=9-\frac{6 k}{28}
$$
while Williams will take
$$
\frac{k}{28}: \frac{1}{11}+\frac{28-k}{28}: \frac{1}{3}=3+\frac{8 k}{28}
$$
We need to find $k$ for which these values coincide:
$$
9-\frac{6 k}{28}=3+\frac{8 k}{28} \quad \Leftrightarrow \quad 6 \cdot 28=14 k \quad \Leftrightarrow \quad k=12
$$
It remains to understand why $k=12$ gives the best time. Indeed, for smaller $k$, Dodson's time will increase, and for larger $k$, Williams' time will increase. Thus, for all other $k$, the time of at least one of the characters will be greater than when $k=12$.
## Criteria
The highest suitable criterion is used:
7 p. Any complete solution to the problem.
4 p. The position of the post is found where the time of the characters coincides, but it is not proven that this is the best time.
2 p. The idea of equating the time of the characters is present, but an error was made in the formulation or solution of the equation.
1 p. The correct answer is given.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a toy store, 125 plush bears are sold in $k$ different colors and six different sizes. For what largest $k$ can we assert that there will be at least three identical bears? (i.e., matching both in color and size) (20 points)
|
Solution: If $k=10$, then there are 60 varieties of teddy bears in the store. If there are no more than two of each type, then there are no more than 120 teddy bears in the store - a contradiction. Therefore, there will be at least three identical teddy bears among them.
If $k=11$, then there may not be three identical teddy bears. Indeed, there will be at least 66 varieties of teddy bears, among which 59 types can be sold with 2 copies each, and another 7 types - with one copy each. For $k \geq 11$, there will be more varieties of teddy bears, so as a counterexample, one can remove the second copies of the existing types and add one new copy of each added type.
Answer: 10
|
10
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find four real numbers $x_{1}, x_{2}, x_{3}, x_{4}$, such that each, when added to the product of the others, equals two.
|
Solution. Let $x_{1} x_{2} x_{3} x_{4}=p$. Then our system of equations will take the form:
$$
x_{i}+\frac{p}{x_{i}}=2, \quad i=1,2,3,4
$$
The case when one of the sought numbers is zero leads to a contradiction. Indeed, substituting zero for $x_{1}$, we get
$$
x_{2} x_{3} x_{4}=2, x+2=x+3=x+4=2 \text {. }
$$
Thus, all $x_{i}$ are roots of the same quadratic equation $x_{i}^{2}-2 x_{i}+p=0$. Therefore, among them, there can only be two different ones. Let's consider three cases.
(a) $x_{1}=x_{2}=x_{3}=x_{4}=m, m+m^{2}=2$. Due to the monotonicity of the function $m+m^{2}$, we have only one real solution $m=1$.
(b) Three of the sought numbers are equal, and the fourth is not equal to them. Let $x_{1}=x_{2}=x_{3}=m$, $x_{4}=n, m \neq n$
$$
\left\{\begin{array}{l}
m+m^{2} n=2 \\
n+m^{3}=2
\end{array}\right.
$$
From this, $(m-n)\left(1-m^{2}\right)=0$. Since $m \neq n$, we get that $1-m^{2}=0$. Note that $m \neq 1$, because otherwise, from the system of relations, it immediately follows that $n=1$, which contradicts $m \neq n$. Therefore, $m=-1$, from which it follows that $n=3$. This gives us four more solutions.
(c) $x_{1}=x_{2}=m, x_{3}=x_{4}=n, m \neq n$,
$$
\left\{\begin{array}{l}
m+m n^{2}=2 \\
n+n m^{2}=2
\end{array}\right.
$$
From this, $(m-n)(1-m n)=0 \Rightarrow m n=1$. Then $m+n=2, m=n=1$. Contradiction.
Thus, either $x_{1}=x_{2}=x_{3}=x_{4}=1$, or one of the $x_{i}=3$, and the rest are equal to $-1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On a piece of paper, 25 points are marked - the centers of the cells of a $5 \times 5$ square. The points are colored with several colors. It is known that no three points of the same color lie on any straight line (vertical, horizontal, or at any angle). What is the minimum number of colors that could have been used? (20 points)
|
Solution: If no more than two colors are used, then, in particular, in the first row there will be at least three points of the same color - they lie on the same straight line. An example of using three colors (identical numbers denote points painted in the same color):
## Answer: 3 colors
| 1 | 2 | 2 | 3 | 3 |
| :--- | :--- | :--- | :--- | :--- |
| 2 | 3 | 1 | 3 | 2 |
| 3 | 3 | 2 | 1 | 2 |
| 1 | 1 | 3 | 2 | 3 |
| 2 | 2 | 3 | 1 | 1 |
|
3
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Daria Dmitrievna is preparing a test on number theory. She promised to give each student as many problems as the number of addends they create in the numerical example
$$
a_{1}+a_{2}+\ldots+a_{n}=2021
$$
where all numbers $a_{i}$ are natural numbers, greater than 10, and are palindromes (do not change if their digits are written in reverse order). If a student does not find any such example, they will receive 2021 problems on the test. What is the minimum number of problems a student can receive? (20 points)
|
Solution: A student cannot receive one problem since 2021 is not a palindrome. Suppose he can receive two problems, then at least one of the numbers $a_{1}, a_{2}$ is a four-digit number. If it starts with 2, then the second digit is 0 and the number itself is 2002. In this case, the second number is 19, which is not a palindrome. If the number starts with 1, then its last digit is also 1, and the last digit of the second number must be zero, which is incorrect for palindromes. Therefore, the student could not have received two problems. An example of three problems exists, for instance, $1111+888+22=2021$.
Answer: 3
|
3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. for $a<0.5$
## Correct answer: for $a<1$
## Question 3
Correct
Points: 1.00 out of a maximum of 1.00
Question 4
Correct
Points: 1.00 out of a maximum of 1.00
## Question 5
Correct
Points: 1.00 out of a maximum of 1.00
Worker $A$ and worker $B$ can complete the work in 7.2 days, worker $A$ and worker $C$ in 9 days, worker $B$ and worker $C$ in 12 days. How many days will they take to complete the work if they all work together?
|
Answer: 6
Correct answer: 6
A piece of copper-tin alloy has a total mass of 12 kg and contains 45% copper. How much pure tin should be added to this piece of alloy to obtain a new alloy containing 40% copper?
Answer: 1.5
Correct answer: 1.5
Find a two-digit number that is three times the product of its digits. If the digits of this number are reversed, the ratio of the resulting number to the given number is $\frac{7}{4}$.
Answer: 24
Correct answer: 24
## Question 7
Correct
Points: 1.00 out of a maximum of 1.00
## Question 8
Correct
Points: 1.00 out of a maximum of 1.00
Question 9
Correct
Points: 1.00 out of a maximum of 1.00
Answer: 8
Correct answer: 8
Three edges emanating from one vertex of a rectangular parallelepiped are equal to $a, b$, c. Find the length of the diagonal of this parallelepiped.
Choose one answer:
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let $x$ be a natural number. Solve the equation
$$
\frac{x-1}{x}+\frac{x-2}{x}+\frac{x-3}{x} \cdots+\frac{1}{x}=3
$$
|
Solution. Multiply both sides of the equation by $x$. We get
$$
(x-1)+(x-2)+(x-3)+\ldots+1=3 x
$$
The left side of this equation is the sum of the terms of an arithmetic progression, where $a_{1}=x-1, d=-1$, and $a_{n}=1$. The progression has $(x-1)$ terms.
Since $S_{n}=\frac{a_{1}+a_{n}}{2} \cdot n$, the equation can be rewritten as
$$
\frac{x-1+1}{2} \cdot(x-1)=3 x \quad \Rightarrow \quad x^{2}=7 x \quad \Rightarrow \quad x=7(x \neq 0)
$$
Answer. $x=7$
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Solve the equation $\sqrt{6-x}+\sqrt{x-4}=x^{2}-10 x+27$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
3. Given $4 \leq x \leq 6$. Find the maximum of the function $f(x)=\sqrt{6-x}+\sqrt{x-4}$
$f^{\prime}(x)=-\frac{1}{\sqrt{6-x}}+\frac{1}{\sqrt{x-4}} \Rightarrow f^{\prime}(x)=0 ; \sqrt{4-x}=\sqrt{6-x} \Rightarrow x=5$. When $x=5$, $f(x)$ has a maximum value of 2. On the other hand, $x^{2}-10 x+27=(x-5)^{2}+2 \Rightarrow \min \varphi(x)=x^{2}-10 x+27=2$ when $x=5$. Therefore, equality is possible only when $x=5$. Answer: $\{5\}$.
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the inequality $\frac{\left|x^{2}-3 x\right|-\left|x^{2}-2\right|}{\left|x^{2}-x-2\right|-\left|x^{2}-2 x\right|} \geq 0$. In the answer, indicate the sum of all natural numbers that are solutions to the inequality.
|
4. $\frac{\left|x^{2}-3 x\right|-\left|x^{2}-2\right|}{\left|x^{2}-x-2\right|-\left|x^{2}-2 x\right|} * \frac{\left|x^{2}-3 x\right|+\left|x^{2}-2\right|}{\left|x^{2}-x-2\right|+\left|x^{2}-2 x\right|} \geq 0 \Leftrightarrow \frac{\left(x^{2}-3 x\right)^{2}-\left(x^{2}-2\right)^{2}}{\left(x^{2}-x-2\right)^{2}-\left(x^{2}-2 x\right)^{2}} \geq 0 \Leftrightarrow$ $\Leftrightarrow \frac{\left(x^{2}-3 x-x^{2}+2\right)\left(x^{2}-3 x+x^{2}-2\right)}{\left(x^{2}-x-2-x^{2}+2 x\right)\left(x^{2}-x-2+x^{2}-2 x\right)} \geq 0 \Leftrightarrow \frac{(2-3 x)\left(2 x^{2}-3 x-2\right)}{(x-2)\left(2 x^{2}-3 x-2\right)} \geq 0 \Leftrightarrow$ $\frac{x-\frac{2}{3}}{x-2} \leq 0 \Rightarrow \frac{2}{3} \leq x<2$
. Answer: $\{1\}$
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find all solutions to the equation $2017^{x}-2016^{x}=1$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
5. It is obvious that $x=1$ will be a solution to the given equation. Let's show that there are no others. We have: $\left(\frac{2017}{2016}\right)^{x}=1+\frac{1}{2016^{x}} ;\left(\frac{2017}{2016}\right)^{x}-1=\frac{1}{2016^{x}}$ From this, it is clear that the function on the left side is increasing, while the function on the right side is decreasing. Therefore, the equation has no more than one solution. Answer: $\{1\}$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Three circles with radii $1,2,3$ touch each other externally. Find the radius of the circle passing through the three points of tangency of these circles.
|
6. Let the centers of the given circles be denoted as $O_{1}, O_{2}, O_{3}$. Let $K, M, N$ be the points of tangency of the given circles. Then $O_{1} K=O_{1} N=1, O_{2} K=O_{2} M=2, O_{3} M=O_{3} N=3$.
We will show that the desired circle coincides with the incircle of the triangle $O_{1}, O_{2}, O_{3}$. Indeed, if we inscribe a circle in the triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$, then the segments connecting its vertices to the points of tangency will be the radii of the corresponding circles. Let $r$ be the radius of this circle. We will write the area of the triangle $O_{1}, O_{2}, O_{3}$ in terms of the perimeter and $r$, and using Heron's formula.
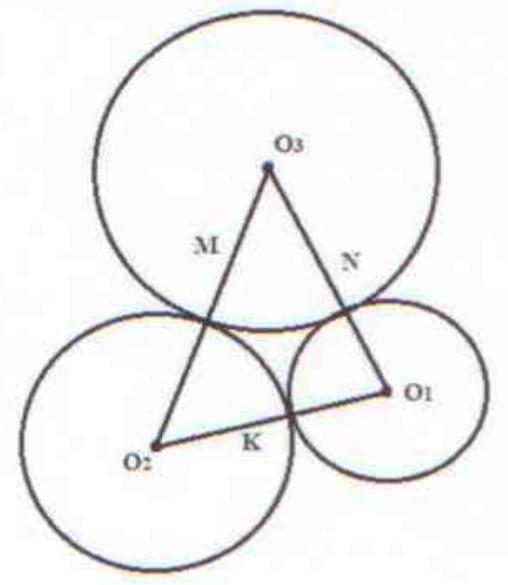
By equating these expressions for the area, we get: $\frac{1}{2} \operatorname{Pr}=\sqrt{p(p-a)(p-b)(p-c)}$, where $\mathrm{P}$ is the perimeter, and $p=\frac{\mathrm{P}}{2} ; a, b, c$ are the sides of the triangle $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$. We obtain: $\frac{1}{2} r(2+4+6)=\sqrt{6(6-3)(6-4)(6-5)} \Rightarrow 6 r=6 ; r=1$. Answer: $\{1\}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. A raft departed from point $A$ to point $B$ downstream the river. After 2.4 hours, a motorboat (with its own speed of 20 km/h) set off in pursuit of the raft. The motorboat caught up with the raft and immediately turned back to point $A$. After 3.6 hours, the motorboat arrived at point $A$, while the raft reached point $B$. Determine the speed of the river current.
|
7. Let the speed of the river current be $x$ km/h, $t$-the time elapsed from the moment the boat left until the moment of the meeting. Then, by the condition: 1) the distance traveled by the raft until the meeting, 2) the distance traveled by the motorboat until the meeting, 3) the distance traveled by the motorboat after the meeting, are equal to each other. From this we get:
$(2.4+t) x=t(20+x)=(3.6-2.4-t)(20-x)$. From this we find: $t=\frac{2.4}{20} x \Rightarrow x=4$. Answer: 4 km/h.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
the sum: $\cos 20^{\circ}+\cos 40^{\circ}+\cos 60^{\circ}+\cdots+\cos 160^{\circ}+\cos 180^{\circ}$
|
2.
$\cos 20^{\circ}+\cos 40^{\circ}+\cos 60^{\circ}+\cos 80^{\circ}+\cos 100^{\circ}+\cos 120^{\circ}+\cos 140^{\circ}+\cos 160^{\circ}+$ $\cos 180^{\circ}=\cos 20+\cos 40+\frac{1}{2}+\sin 10^{\circ}-\sin 10^{\circ}-\frac{1}{2}-\cos 40^{\circ}-1-\cos 20=-1$ Answer: $\{-1\}$
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Two pedestrians set out simultaneously from $A$ to $B$ and from $B$ to $A$. When the first had walked half the distance, the second had 24 km left to walk, and when the second had walked half the distance, the first had 15 km left to walk. How many kilometers will the second pedestrian have left to walk after the first finishes his walk?
|
3. Let $v_{1}, v_{2}$ be the speeds of the first and second pedestrians, $S$ be the distance from $A$ to $B$, and $x$ be the distance the second pedestrian still needs to walk when the first pedestrian finishes the crossing. From the problem statement, we get the system $\frac{S}{2} \frac{v_{2}}{v_{1}}+24=S, \frac{S}{2} \frac{v_{1}}{v_{2}}+15=S$. Denoting $\frac{v_{1}}{v_{2}}=u$ and dividing the second equation by the first, we get $8 u^{2}-6 u-5=0 \Rightarrow u=\frac{5}{4} \Rightarrow S=40 \text{ km}$. Since $S \frac{v_{2}}{v_{1}}+x=S$, then $x=8 \text{ km}$. Answer: 8 km.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Solve the inequality: $\frac{\left(\left|x^{2}-2\right|-7\right)(|x+3|-5)}{|x-3|-|x-1|}>0$. Write the largest integer that is a solution to the inequality in your answer.
|
5. $\frac{\left(\left|x^{2}-2\right|-7\right)\left(\left|x^{2}-2\right|+7\right)(|x+3|-5)(|x+3|+5)}{(|x-3|-|x-1|)(|x-3|+|x-1|)}>0 \Leftrightarrow \frac{\left(\left(x^{2}-2\right)^{2}-49\right)\left((x+3)^{2}-25\right)}{(x-3)^{2}-(x-1)^{2}}>0$ $\Leftrightarrow \frac{\left(x^{2}-2-7\right)\left(x^{2}-2+7\right)(x+3-5)(x+3+5)}{(x-3-x+1)(x-3+x-1)}>0 \Leftrightarrow \frac{(x-3)(x+3)(x-2)(x+8)}{(-2)(2 x-4)}>0$, $x \neq 2 \Leftrightarrow(x-3)(x+3)(x+8)<0$
, Solve using the interval method:

From here, the solution is: $x<-8 ;-3<x<3 ; x \neq 2$. Therefore, the answer is: $\{1\}$
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let the cost of a pound of rice be x coins, a pound of brown sugar be y coins, and a pound of refined sugar be z coins. We obtain the system:
$$
\left\{\begin{array}{l}
4 x+\frac{9}{2} y+12 z=6 ; \\
12 x+6 y+6 z=8
\end{array}\right. \text { Subtract the first equation from twice the second equation and }
$$
express y in terms of x. We get $y=\frac{4}{3}-\frac{8}{3} x$. Substitute into the second equation and express $\mathrm{z}$ in terms of $\mathrm{x} z=\frac{2}{3} x$. Find the cost of the purchase:
$$
4 x+3 y+6 z=4 x+4-8 x+4 x=4
$$
|
Answer: 4 pounds sterling.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the inequality: $\log _{|x-1|}\left(\frac{x-2}{x}\right)>1$. In the answer, indicate the largest negative integer that is a solution to this inequality.
|
1. Find the domain: $(x-2) x>0$. From this, $x<0$ or $x>2$. If $|x-1|<1$, then $0<x<2$. But if $|x-1|>1$, then $x<0$ or $x>2$. Therefore, the inequality is equivalent to the system:
$\left\{\begin{array}{c}|x-1|>1 \\ \frac{x-2}{x}>|x-1|\end{array} \Leftrightarrow\right.$ a) $\left\{\begin{array}{c}x<0 \\ \frac{x-2}{x}>1-x\end{array}\right.$ or b) $\left\{\begin{array}{c}x>2 \\ \frac{x-2}{x}>x-1\end{array}\right.$
From this, the solution to the first system a) is $-\sqrt{2}<x<0$, and the second system b) has no solutions. Answer: $\{-1\}$
|
-1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Solve the equation in integers: $5 x^{2}-2 x y+2 y^{2}-2 x-2 y=3$. In the answer, write the sum of all solutions $(x, y)$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
5. Transforming the equation, we get: $(x+y)^{2}-2(x+y)+1+y^{2}-4 x y+4 x^{2}=4 \Leftrightarrow(x+y-1)^{2}+(y-2 x)^{2}=4$. Since $x$ and $y$ are integers, this equality is possible only in four cases:
$\left\{\begin{array}{c}x+y-1=0 \\ y-2 x=2\end{array}, \quad\left\{\begin{array}{c}x+y-1=2 \\ y-2 x=0\end{array}, \quad\left\{\begin{array}{c}x+y-1=0 \\ y-2 x=-2\end{array}, \quad\left\{\begin{array}{c}x+y-1=-2 \\ y-2 x=0\end{array}\right.\right.\right.\right.$
The first and fourth systems do not have integer solutions. The second system has the integer solution $x=1, y=2$, the third system has the solution $x=1, y=0$. $\underline{\text { Answer: }}\{4\}$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Determine which of the numbers is greater: (1000!) $)^{2}$ or $1000^{1000}$. Write 1 in the answer if the first is greater or equal, 2 if the second is greater.
|
8. Let's show that the left number is greater than the right one. For this, we will write the first number as follows: $(1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot \ldots \cdot 1000)(1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot \ldots \cdot 1000)=(1 \cdot 1000)(2 \cdot 999)(3 \cdot 998)(4 \cdot 997) \ldots(k(1000-k+1)) \ldots$ In this product, in each pair in parentheses, the product of the numbers is obviously not less than 1000, and since there are exactly a thousand such pairs, the product of these pairs will be strictly
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. What is the maximum area that a triangle with sides $a, b, c$ can have, given that the sides are within the ranges: $0 < a \leq 1, 1 \leq b \leq 2, 2 \leq c \leq 3$?
|
9. Among the triangles with two sides $a, b$, which satisfy the conditions $0<a \leq 1, 1 \leq b \leq 2$. The right triangle with legs $a=1, b=2$ has the largest area. Its area $S=1$. On the other hand, the third side $c=\sqrt{5}$ as the hypotenuse of the right triangle satisfies the condition that $2 \leq c \leq 3$ and therefore among all the considered triangles, the right triangle with legs 1 and 2 has the largest area. Answer: $\{1\}$
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Given a triangle $\mathrm{PEF}$ with sides $\mathrm{PE}=3, \mathrm{PF}=5, \mathrm{EF}=7$. On the extension of side $\mathrm{FP}$ beyond point $\mathrm{P}$, a segment $\mathrm{PA}=1.5$ is laid out. Find the distance $d$ between the centers of the circumcircles of triangles $\mathrm{EPA}$ and $\mathrm{EAF}$. In the answer, specify the number equal to $2d$.
|
3. By the cosine theorem for angle EPF, we find that $\operatorname{Cos} E P F=-\frac{1}{2}$. Therefore, the angle $\mathrm{EPF}=120^{\circ}$; hence the adjacent angle will be $60^{\circ}$. Draw a perpendicular from point E to PF, meeting at point D. Since angle EPF is obtuse, point D will lie outside triangle EPF. In the right triangle PED, PD lies opposite the angle $30^{\circ}$, so $\mathrm{PD}=\frac{1}{2} \mathrm{EP}=1.5$. Therefore, point D coincides with point A. Thus, we have two right triangles: EAP and EAF. The centers of the circumcircles of these triangles lie on the midpoints of the corresponding hypotenuses. Therefore, the desired distance is equal to the midline of triangle EPF, i.e., $d=2.5$. Hence, the answer is: $\{5\}$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find all integers $n$ for which the equality $\frac{n^{2}+3 n+5}{n+2}=1+\sqrt{6-2 n}$ holds.
|
5. We have: $\frac{n^{2}+3 n+5}{n+2}-1=\sqrt{6-2 n} ; \frac{n^{2}+2 n+3}{n+2}=\sqrt{6-2 n} ; n+\frac{3}{n+2}=\sqrt{6-2 n}$. Since for integer $n$, the right-hand side can be either an integer or irrational, while the left-hand side is either an integer or rational, the given equality is possible only if $\frac{3}{n+2}$ is an integer. Then $n+2=\{-1 ; 1 ;-3 ; 3\} \rightarrow n=\{-3 ;-1 ;-5 ; 1\}$. Then we find that $6-2 n$ will be the square of an integer only for $n=-5$ and $n=1$. Upon verification, we find that only $n=1$ is a solution to the original equation. Answer $\{1\}$
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Solve the system
$$
\left\{\begin{array}{l}
\operatorname{tg}^{3} x+\operatorname{tg}^{3} y+\operatorname{tg}^{3} z=36 \\
\operatorname{tg}^{2} x+\operatorname{tg}^{2} y+\operatorname{tg}^{2} z=14 \\
\left(\operatorname{tg}^{2} x+\operatorname{tg} y\right)(\operatorname{tg} x+\operatorname{tg} z)(\operatorname{tg} y+\operatorname{tg} z)=60
\end{array}\right.
$$
In the answer, indicate the sum of the minimum and maximum $\operatorname{tgx}$, which are solutions to the system.
|
6. Let $\operatorname{tg} x=x_{1}, \operatorname{tg} y=x_{2}, \operatorname{tg} z=x_{3}$.
Then $\left\{\begin{array}{l}x_{1}^{3}+x_{2}^{3}+x_{3}^{3}=36 \\ x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=14 \\ \left(x_{1}+x_{2}\right)\left(x_{1}+x_{3}\right)\left(x_{2}+x_{3}\right)=60\end{array}\right.$. Further, let $\left\{\begin{array}{l}x_{1}+x_{2}+x_{3}=a \\ x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3}=b \text {. } \\ x_{1} x_{2} x_{3}=c\end{array}\right.$.
We will use the identities: $(x+y+z)^{3}-3(x+y+z)(x y+x z+y z)=x^{3}+y^{3}+z^{3}-3 x y z$
$$
x^{2}+y^{2}+z^{2}=(x+y+z)^{2}-2(x y+x z+y z)
$$
Then the system can be written as
$\left\{\begin{array}{l}a^{3}-3(a b-c)=36 \\ a^{2}-2 b=14 \\ a b-c=60\end{array} \Rightarrow\left\{\begin{array}{l}a^{3}-3 \cdot 60=36 \\ a^{2}-2 b=14 \\ a b-c=60\end{array} \Rightarrow a^{3}=216, a=6 \Rightarrow\right.\right.$
Then $2 b=36-14=22, b=11$. And finally $c=66-60=6$.
Thus, we have the system: $\left\{\begin{array}{l}x_{1}+x_{2}+x_{3}=6 \\ x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3}=11 \\ x_{1} x_{2} x_{3}=6\end{array}\right.$.
Consider the cubic equation in $x$ with roots $x_{1}, x_{2}, x_{3}$. Then by Vieta's theorem, we have $x^{3}-x^{2}\left(x_{1}+x_{2}+x_{3}\right)+x\left(x_{1} x_{2}+x_{1} x_{3}+x_{2} x_{3}\right)-x_{1} x_{2} x_{3}=0$.
Further, we have: $x^{3}-6 x^{2}+11 x-6=0$. Let's find the roots of this equation. The first root will be obviously $x=1$, the other roots $x=2, x=3$.
Since the system is symmetric with respect to the cyclic permutation of the variables $x_{1}, x_{2}, x_{3}$, the system has six solutions, which are obtained by cyclic permutation of the numbers $1,2,3$. Therefore, the minimum value of $\operatorname{tgx}$ is 1, and the maximum is 3.
Thus, the answer is: $\{4\}$
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the integer part of the number $\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6}}}}}$
|
9. Let $a=\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6}}}}}$. It is easy to see that $a>\sqrt{6}>2 \Rightarrow$ $a>2$. Let's find an upper bound for this number. At the end of the expression for $a$, replace $\sqrt{6}$ with $\sqrt{9}$. Then we get that $a<\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{6+\sqrt{9}}}}}=\sqrt{6+\sqrt{6+\sqrt{6+3}}}=\sqrt{6+\sqrt{6+3}}=\sqrt{6+3}=3$. Thus, $2<a<3$. From this, it follows that $[a]=2$. Answer: $\{2\}$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1.
The pedestrian's speed is 5 km/h. There are more oncoming trams than overtaking ones, because the speed of the former relative to the pedestrian is greater than that of the latter. If we assume that the pedestrian is standing still, the speed of the oncoming trams is the sum of the tram's own speed $V+$ the pedestrian's speed. Therefore, the relative speed of the oncoming trams is $V+5$, and the relative speed of the overtaking trams is $V-5$. It is clear that the number of trams passing a given point in a certain time is proportional to their speed, from which we have the equation:
$$
\frac{V+5}{V-5}=\frac{600}{225} \rightarrow V=11 \text { km } / \text { hour. }
$$
|
Answer: $11 \mathrm{km} /$ hour.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A professor from the Department of Mathematical Modeling at FEFU last academic year gave 6480 twos, thereby overachieving the commitments taken at the beginning of the year. In the next academic year, the number of professors increased by 3, and each of them started giving more twos. As a result, a new record was set for enclosed spaces: 11200 twos in a year. How many professors were there initially, if each professor gives the same number of twos as the others during the session?
|
1. The professors of the Department of Mathematical Modeling at DVFU in the previous academic year gave 6480 twos, thereby over-fulfilling the obligations they had taken on at the beginning of the year. In the next academic year, the number of professors increased by 3, and each of them started giving more twos. As a result, a new record for enclosed spaces was set: 11200 twos in a year. How many professors were there initially, if each professor gives the same number of twos in a session as the others?
Let the number of professors be $p$. Then the number of twos given by each of them is $6480 / p$. This number is less than the number of twos given in the next academic year $-11200 /(p+3)$. Therefore, $p \geq 5$. Each professor gives an integer number of twos, so $6480=2^{4} 3^{4} 5$ is divisible by $p$ and $11200=2^{6} 5^{2} 7$ is divisible by $p+3$. The number $p$ cannot be divisible by 3, since 11200 is not divisible by 3. Therefore, $p=5^{m} 2^{n} \geq 5$, where either $m=0 ; n=3,4$, or $m=1 ; n=0,1,2,3,4$. In the first case, we get values $p+3=11$ or $p+3=19$, which are not divisors of 11200. If $m=1$, then $p+3=13,23,43,83$ for $n=1,2,3,4$ and therefore the only option that satisfies the conditions is $m=1, n=0, p=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find natural numbers $n$ such that for all positive numbers $a, b, c$, satisfying the inequality
$$
n(a b+b c+c a)>5\left(a^{2}+b^{2}+c^{2}\right)
$$
there exists a triangle with sides $a, b, c$.
|
2. Find natural numbers $n$ such that for all positive numbers $a, b, c$ satisfying the inequality
$$
n(a b+b c+c a)>5\left(a^{2}+b^{2}+c^{2}\right)
$$
there exists a triangle with sides $a, b, c$.
$\square$ Since $(a b+b c+c a) \leq\left(a^{2}+b^{2}+c^{2}\right)$, then $n>5$. If $n \geq 7$, then the numbers $a=1, b=1, c=2$ satisfy the inequality $n(a b+b c+c a)>5\left(a^{2}+b^{2}+c^{2}\right)$, but cannot be the lengths of the sides of a triangle. Therefore, it remains to check the value $n=6$. We will show that from the condition $6(a b+b c+c a)>5\left(a^{2}+b^{2}+c^{2}\right)$, where $0<a \leq b \leq c$, it follows that $c<a+b$ and therefore the numbers $a, b, c$ are the lengths of the sides of some triangle.
Indeed, considering the condition as a quadratic inequality in terms of $c$, we get
$$
5 c^{2}+6(a+b) c+\left[5\left(a^{2}+b^{2}\right)-6 a b\right]<0 ; \quad D / 4=16\left(a b-(a-b)^{2}\right) \leq 16 a b
$$
Therefore, taking into account that $2 \sqrt{a b} \leq a+b$, we conclude
$$
c<\frac{3(a+b)+4 \sqrt{a b}}{5} \leq a+b
$$
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A rectangle is drawn on the board. It is known that if its width is increased by $30 \%$, and its length is decreased by $20 \%$, then its perimeter remains unchanged. How would the perimeter of the original rectangle change if its width were decreased by $20 \%$, and its length were increased by $30 \%$?
|
Answer. It will increase by $10 \%$.
Solution. Let's denote the width of the original rectangle as $a$, and the height as $b$. In the first case, the modified width and length will be $1.3a$ and $0.8b$ respectively. According to the condition, $2(a+b) = 2(1.3a + 0.8b)$, from which we get $b = 1.5a$. This means the original perimeter is $2(a + 1.5a) = 5a$. In the second case, the perimeter will be $2(0.8a + 1.3b) = 2(0.8a + 1.3 \cdot 1.5a) = 5.5a$. This number is greater than $5a$ by $0.5a$, which is $10 \%$.
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Several teams held a hockey tournament - each team played against each other once. 2 points were awarded for a win, 1 point for a draw, and no points for a loss. The team "Squirrels" won the most games and scored the fewest points. What is the minimum number of teams that could have participated in the tournament
|
Answer: 6 teams.
Solution. In a tournament with $n$ teams, the "Squirrels" scored less than the average number, i.e., no more than $n-2$ points. Therefore, some team must have scored more than the average, i.e., no less than $n$ points. For this, they had to win at least one match. Consequently, the "Squirrels" must have won at least two matches, i.e., scored no less than 4 points. Therefore, $n \geq 6$. An example for six teams is shown in the table.
| Team | $\mathbf{1}$ | $\mathbf{2}$ | $\mathbf{3}$ | $\mathbf{4}$ | $\mathbf{5}$ | Squirrels | Total |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $\mathbf{1}$ | | 1 | 1 | 1 | 1 | 2 | 6 |
| $\mathbf{2}$ | 1 | | 1 | 2 | 1 | 0 | 5 |
| $\mathbf{3}$ | 1 | 1 | | 1 | 2 | 0 | 5 |
| $\mathbf{4}$ | 1 | 0 | 1 | | 1 | 2 | 5 |
| $\mathbf{5}$ | 1 | 1 | 0 | 1 | | 2 | 5 |
| Squirrels | 0 | 2 | 2 | 0 | 0 | | 4 |
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On the glade, there are 6 fewer bushes than trees. Birds flew in and sat both on the bushes and on the trees. They sat so that there were an equal number of birds on all the trees and an equal number of birds on all the bushes, but there were at least 10 more birds on a tree than on a bush. There were a total of 128 birds on the trees. How many bushes were there?
|
Answer: 2.
Solution: There are no fewer than 7 trees, as there are 6 more trees than shrubs. There are no fewer than 11 birds on one tree, as there are at least 10 more birds on one tree than on one shrub. There cannot be 12 or more trees, as then there would be $12 \cdot 11=$ 132 or more birds on the trees. Therefore, the number of trees can be 7 or 8 or 9 or 10 or 11. However, among these, only the number 8 is a divisor of the number 128. Therefore, there are 8 trees, and 6 fewer shrubs, which means 2 shrubs.
Comment: Correct solution - 20 points. There are gaps in the justification - 15 points. The problem is solved by trial and error, and it is not shown that there are no other options - 10 points. The solution is started, and there is some progress - 5 points. The solution is started, but the progress is insignificant - 1 point. The correct answer is given without explanation - 1 point.
## Variant 2
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. There are 28 students in the class. 17 have a cat at home, and 10 have a dog. 5 students have neither a cat nor a dog. How many students have both a cat and a dog?
|
Answer: 4.
Solution: The number of students with cats or dogs is $28-5=23$. If we add $17+10=27$, it exceeds 23 due to those who have both a cat and a dog, who were counted twice. The number of such students is $27-23=4$.
Comment: Correct solution - 20 points. Solution started, with some progress - 5 points. Solution started, but progress is insignificant - 1 point. Correct answer given without explanation - 1 point.
|
4
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On graph paper, large and small triangles are drawn (all cells are square and of the same size). How many small triangles can be cut out from the large triangle? The triangles cannot be rotated or flipped (the large triangle has a right angle at the bottom left, the small triangle has a right angle at the top right).
|
Answer: 12.
Solution. See the figure.
Comment. Correct drawing with 12 triangles - 20 points. Incorrect answer with drawing - 1 point. Any answer without drawing - 0 points.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On a certain day, there were several nuts in the bag. The next day, as many nuts were added to the bag as there already were, but eight nuts were taken away. On the third day, again as many nuts were added as there already were, but eight were taken away. The same thing happened on the fourth day, and after that, there were no nuts left in the bag. How many nuts were there in the bag at the beginning?
|
Answer: 7 nuts.
Solution. At the beginning of the fourth day, there were $(0+8): 2=4$ nuts in the bag. Therefore, at the beginning of the third day, there were $(4+8): 2=6$, and at the very beginning $-(6+8): 2=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Natural numbers divisible by 3 were painted in two colors: red and blue, such that the sum of a blue and a red number is red, and the product of a blue and a red number is blue. In how many ways can the numbers be colored so that the number 546 is blue?
|
Answer: 7.
Solution: We will prove that all blue numbers are divisible by the same number. First, we will prove that the product of two blue numbers is blue. Assume the statement is false. Let $a$ and $b$ be two such blue numbers that their product is a red number. Let $d$ be some red number (we can take $d = ab$). Then $a + d$ is red. From this, it follows that $a \cdot b + b \cdot d = b(a + d)$ is blue, since the blue number $b$ is multiplied by the red number $a + d$. The number $b \cdot d$ is also blue, and the number $a \cdot b$ is red by assumption. We have obtained that the sum of a blue and a red number is blue, which contradicts the condition. Therefore, the assumption is false, and the product of any two blue numbers is a blue number. Together with the condition, this means that the product of a blue number and any number is a blue number.
Let $a_0$ be the smallest blue number, and $a$ be any blue number. It can be represented as $a = k \cdot a_0 + r$, where $0 \leq r < a_0$. The remainder $r$ cannot be a blue number, since $a_0$ is the smallest blue number. The product $k \cdot a_0$, by the proven fact, is a blue number. The sum on the right, of a blue and a red number, is a red number by the condition, but the number on the left side of the equation is blue; a contradiction. Therefore, the remainder $r = 0$, and any blue number is divisible by the smallest blue number. The number $546 = 2 \cdot 3 \cdot 7 \cdot 13$. Only numbers divisible by 3 are considered, and among them, blue can be all numbers divisible by 6, or by 21, or by 39, or by 42, or by 78, or by 273, or by 546, a total of 7 ways.
Comment: 20 points for finding all ways. 15 points for establishing that blue numbers are divisible by divisors of the number 546, but the correct answer is not obtained. 5 points for finding at least one way in the absence of a general solution. 15 points for gaps in the justification. 2 points for starting the solution and making some progress.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the smallest natural $n>1$, for which the sum of no two natural powers is a perfect square of a natural number.
#
|
# Answer.4.
Solution. For $n=2: 2^{1}+2^{1}=2^{2}$. For $n=3: 3^{3}+3^{2}=6^{2}$. Let $n=4$. Suppose there exist such $m, k$ that $4^{m}+4^{k}=a^{2}$.
Any power of 4 gives a remainder of 1 when divided by 3 (since $\left.4^{m}=(3+1)^{m}\right)$. Therefore, $4^{m}+4^{k}$ will give a remainder of 2 when divided by 3. But the square of an integer gives a remainder of 0 or 1 when divided by 3.
Comment. Correct solution - 20 points. Proven that $n \geq 4-12$ points. Proven that $n \geq 3-3$ points. Proven that $n \leq 5-3$ points. Solution not completed, but there is progress - 5 points. Solution started, but progress is minimal - 1 point.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. A little squirrel collected 15 nuts in the forest weighing $50, 51, \ldots, 64$ grams. He knows the weight of each nut. Using a balance scale, the little squirrel tries to prove to his friends that the first nut weighs 50 g, the second 51 g, the third 52 g, and so on (initially, the friends know nothing about the weights of the nuts). What is the minimum number of weights the little squirrel will need, if both the weights and the nuts can be placed on either pan of the balance, and the number of weighings is unlimited? (The weights of the weights are known to both the little squirrel and his friends. There is an unlimited supply of weights weighing $1, 2, \ldots, 1000$ g.)
|
Answer. One weight.
Solution. Note that it is impossible to do without weights altogether, since if the weight of each nut is halved, the results of all weighings will not change. We will show that the baby squirrel can manage with the help of one 1 g weight. First, he will convince his friends that the nuts weigh $n, (n+1), \ldots, (n+14)$ g. For this, he will place a nut weighing 51 g on one pan of the scales, and a nut weighing 50 g and the weight on the other pan. The scales will show equality, and his friends will learn that the weighed nuts differ by exactly one gram. Then the same needs to be done with nuts weighing 52 and 51 g, and so on. Finally, with the last weighing, the baby squirrel will show his friends what $n$ is. For this, he will place nuts weighing from 50 to 57 g on one pan of the scales, and the remaining nuts and the weight on the other pan. The scales will again show equality. Thus, the friends will know that
$$
n+(n+1)+\cdots+(n+7)=(n+8)+(n+9)+\cdots+(n+14)+1
$$
Therefore, $8 n+28=7 n+78$, i.e., $n=50$.
Comment. Correct solution - 20 points. A solution with 2 weights - 2 points. A solution with more than 2 weights - 1 point. Incorrect or no solution - 0 points.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. In a $5 \times 5$ square, color as many cells black as possible, so that the following condition is met: any segment connecting two black cells must necessarily pass through a white cell.
|
Answer. We will prove that it is impossible to color more than 9 cells. Divide the square into 9 parts:

In each part, no more than one cell can be colored.
9 cells can be colored as follows:

Comment. A correct solution, including justification that the number of colored cells is maximal, and a diagram - 20 points. An incomplete justification that the number of colored cells is maximal - 15 points. Only an answer in the form of a diagram - 10 points. The solution is started but progress is insignificant - 1 point.
2. A baby squirrel had a reserve of pine and spruce cones, with pine cones making up 60%. In August, it collected more spruce cones, and now the pine cones made up 20%. In September, the baby squirrel collected more pine cones, and now the pine cones made up 80%. By what factor did the total number of cones increase over the two months?
## Answer. 12.
Solution. In August, the percentage of pine cones decreased by 3 times, meaning the total number of cones increased by 3 times. In September, the percentage of spruce cones decreased from 80% to 20%, meaning the total number of cones increased by 4 times. In total, over the two months, the total number of cones increased by \(3 \cdot 4 = 12\) times.
Comment. A correct solution - 20 points. There is a gap in the justification - 15 points. A correct equation is set up, but not brought to a correct solution - 10 points. The solution is started, with some progress - 5 points. The solution is started, but progress is insignificant - 1 point.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find all natural numbers $a$ for which the number
$$
\frac{a+1+\sqrt{a^{5}+2 a^{2}+1}}{a^{2}+1}
$$
is also a natural number.
|
Answer. $a=1$.
Solution. Let $a+1=b, \sqrt{a^{5}+2 a^{2}+1}=c$. Write the polynomial $c^{2}-b^{2}=$ $a^{5}+2 a^{2}+1-(a+1)^{2}=a^{5}+a^{2}-2 a$, and divide it by $a^{2}+1$ using long division, we get a remainder of $-(a+1)$. For $a>1$, the absolute value of the remainder is less than $a^{2}+1$, so the remainder cannot be divisible by $a^{2}+1$ for any $a>1$. If $c^{2}-b^{2}$ is not divisible by the denominator $a^{2}+1$, then $b+c$ is also not divisible. The equation is satisfied by the unique value $a=1$.
Comment. Correct solution - 20 points. There is a gap in the justification - 15 points. The value $a=1$ is found, but it is not proven that there are no other solutions - 1 point. The proof is started - another 1 point. The proof is started, and there is some progress - 5 points. The proof is partially conducted - 10 points.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (9th grade) In how many ways can the numbers $1,2,3,4,5,6$ be written in a row so that for any three consecutive numbers $a, b, c$, the quantity $a c-b^{2}$ is divisible by 7? Answer: 12.
|
Solution. Each subsequent member will be obtained from the previous one by multiplying by a certain fixed value (modulo 7). This value can only be 3 or 5. And the first term can be any, so there are 12 options in total.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A line parallel to the selected side of a triangle with an area of 16 cuts off a smaller triangle with an area of 9. Find the area of the quadrilateral, three vertices of which coincide with the vertices of the smaller triangle, and the fourth lies on the selected side. Choose the answer option with the number closest to the one you found.
|
Answer: 12. (C)
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A line parallel to the selected side of a triangle with an area of 27 cuts off a smaller triangle with an area of 3. Find the area of the quadrilateral, three vertices of which coincide with the vertices of the smaller triangle, and the fourth lies on the selected side. Choose the answer option with the number closest to the one you found.
Choose the answer option with the number closest to the one you found.
|
Answer: 9. (B)
|
9
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
\frac{y^{2}+x y-\sqrt[4]{x^{5} y^{3}}-\sqrt[4]{x y^{7}}}{\sqrt[4]{y^{5}}-\sqrt[4]{x^{2} y^{3}}} \cdot(\sqrt[4]{x}+\sqrt[4]{y})
$$
where $x=3, \underbrace{22 \ldots 2}_{2013} 3, y=4, \underbrace{77 \ldots .7}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 8. (D)
Options.
|
8
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
(\sqrt[4]{x}+\sqrt[4]{y}) \cdot \frac{x^{2}+x y-\sqrt[4]{x^{7} y}-\sqrt[4]{x^{3} y^{5}}}{\sqrt[4]{x^{5}}-\sqrt[4]{x^{3} y^{2}}}
$$
where $x=1, \underbrace{11 \ldots 1}_{2013} 2, y=3, \underbrace{88 \ldots 8}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 5. (B)
Options.
|
5
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
2. Calculate
$$
\frac{\sqrt[4]{x^{5} y^{3}}+\sqrt[4]{x y^{7}}-x y-y^{2}}{\sqrt[4]{x^{2} y^{3}}-\sqrt[4]{y^{5}}} \cdot(\sqrt[4]{x}+\sqrt[4]{y})
$$
where $x=2, \underbrace{44 \ldots .4}_{2013} 5, y=1, \underbrace{55 \ldots .5}_{2014}$. Choose the answer option with the number closest to the one you found.
|
Answer: 4. (E)
Options.
|
4
|
Algebra
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine the number of different values of $a$ for which the equation
$$
\left(3-a^{2}\right) x^{2}-3 a x-1=0
$$
has a unique solution
|
Answer: 2. (C)
Options.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Determine how many different values of $a$ exist for which the equation
$$
\left(a^{2}-5\right) x^{2}-2 a x+1=0
$$
has a unique solution
|
Answer: 2. (C)
Options.
$$
\begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 0 & \mathbf{B} & 1 & \mathbf{C} & 2 & \mathbf{D} & 3 & \mathbf{E} \\
\hline
\end{array}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Solve the inequality $\frac{\sqrt{\frac{x}{\gamma}+(\alpha+2)}-\frac{x}{\gamma}-\alpha}{x^{2}+a x+b} \geqslant 0$.
In your answer, specify the number equal to the number of integer roots of this inequality. If there are no integer roots, or if there are infinitely many roots, enter the digit 0 in the answer sheet.
$$
\alpha=3, \gamma=1, a=-15, b=54 .
$$
|
# Answer: 7.
Solution. Given the numerical values, we solve the inequality:
$$
\frac{\sqrt{x+5}-x-3}{x^{2}-15 x+54} \geqslant 0 \Leftrightarrow \frac{\sqrt{x+5}-x-3}{(x-6)(x-9)} \geqslant 0
$$
Since $\sqrt{x+5} \geqslant x+3 \Leftrightarrow\left[\begin{array}{c}-5 \leqslant x \leqslant-3, \\ x+5 \geqslant(x+3)^{2}\end{array}\right.$, the expression in the numerator is non-negative for $x \in[-5 ;-1]$, and negative for $x>-1$.
It is also true that $x^{2}-15 x+54<0$ for $x \in(6 ; 9)$, otherwise this expression is non-negative.
Therefore, $x \in[-5 ;-1] \bigcup(6 ; 9)$, and the number of integer solutions is $5+2=7$.
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all integer values of $a$, not exceeding 15 in absolute value, for each of which the inequality
$$
\frac{4 x-a-4}{6 x+a-12} \leqslant 0
$$
is satisfied for all $x$ in the interval $[2 ; 3]$. In your answer, specify the sum of all such $a$.
|
Answer: -7.
Solution. Solving the inequality using the interval method, we find that its left side equals 0 at $x=1+\frac{a}{4}$ and is undefined at $x=2-\frac{a}{6}$. These two values coincide when $a=\frac{12}{5}$. In this case, the inequality has no solutions.
For $a>\frac{12}{5}$, the solution to the inequality is the interval $\left(2-\frac{a}{6} ; 1+\frac{a}{4}\right]$, and the inequality holds for all $x \in[2 ; 3]$ if $\left\{\begin{array}{c}2-\frac{a}{6}<2, \\ 3 \leqslant 1+\frac{a}{4}\end{array} \Leftrightarrow a \geqslant 8\right.$.
For $a<\frac{12}{5}$, the solution to the inequality is the interval $\left[1+\frac{a}{4} ; 2-\frac{a}{6}\right)$, and the inequality holds for all $x \in[2 ; 3]$ if $\left\{\begin{array}{l}1+\frac{a}{4} \leqslant 2, \\ 3<2-\frac{a}{6}\end{array} \Leftrightarrow a<-6\right.$.
Therefore, $a \in(-\infty ;-6) \bigcup[8 ;+\infty)$, and the required values are: $a \in[-15 ;-6) \bigcup[8 ; 15]$. The sum of the integer values:
$$
-15-14-13-\ldots-8-7+8+9+\ldots+14+15=-7
$$
## Set of Creative Problems.
I. Find all natural values of $n$ not exceeding 100 for which the sum $1^{2}+2^{2}+3^{2}+\ldots+n^{2}$ is divisible by 50. Arrange these values of $n$ in ascending order: $n_{1}<n_{2}<\ldots<n_{k}$. In the answer, specify $n_{4}$.
Solution. Since $1^{2}+2^{2}+3^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}$, then $n(n+1)(2 n+1)$ must be divisible by $300=2^{2} \cdot 3 \cdot 5^{2}$. Since the numbers $n, n+1$, and $2 n+1$ are pairwise coprime, one of them must be divisible by 25.
- If $n$ is divisible by 25, then $n=25,50,75$ or 100. Substituting these values into the expression, we find that divisibility holds for $n=75$ and $n=100$.
- If $n+1$ is divisible by 25, then $n=24,49,74$ or 99. Substituting these values into the expression, we find that divisibility holds for $n=24$ and $n=99$.
- If $2 n+1$ is divisible by 25 and is odd, then $n=12,37,62$ or 87. Substituting these values into the expression, we find that divisibility holds for $n=12$ and $n=87$.
Thus, the values that work are $12,24,75,87,99,100$. The fourth of these is 87.
Answer: 87.
|
-7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{2} 18-\log _{3} 12\right)-\log _{3} 16-4 \log _{2} 3
$$
do not exceed 8.
|
Solution. Let $a=\log _{2} 3$. Then the condition of the problem will turn into the inequality
$$
x^{2}+2\left(a-\frac{1}{a}\right) x-4\left(a+\frac{1}{a}+2\right) \leqslant 0
$$
Considering that $a \in\left(\frac{3}{2}, 2\right)$, we get $x \in\left[-2 a-2, \frac{2}{a}+2\right]$. Since $-6<-2 a-2<-5.3<\frac{2}{a}+2<4$, the integer solutions will be the numbers $-5,-4,-3,-2,-1,0,1,2,3$.
Answer: -9 . (A)
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.2. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{2} 20-\log _{5} 8\right)-\log _{2} 5-9 \log _{5} 2
$$
do not exceed 6.
|
Solution. Let $a=\log _{2} 5$. Then the condition of the problem will turn into the inequality
$$
x^{2}+\left(a-\frac{3}{a}+2\right) x-\left(a+\frac{9}{a}+6\right) \leqslant 0
$$
Considering that $a \in(2,3)$, we get $x \in\left[-a-3, \frac{3}{a}+1\right]$. Since $-6<-a-3<-5,2<\frac{3}{a}+1<3$, the integer solutions will be the numbers $-5,-4,-3,-2,-1,0,1,2$.
Answer: $-12 .(\mathrm{C})$
|
-12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Find the sum of all integer values of the argument $x$ for which the corresponding values of the function
$$
y=x^{2}+x\left(\log _{5} 2-\log _{2} 10\right)-\log _{2} 25-3 \log _{5} 2
$$
do not exceed 7.
|
Solution. Let $a=\log _{2} 5$. Then the condition of the problem will turn into the inequality
$$
x^{2}-\left(a-\frac{1}{a}+1\right) x-\left(2 a+\frac{3}{a}+7\right) \leqslant 0 .
$$
Considering that $a \in(2,3)$, we get $x \in\left[-\frac{1}{a}-2, a+3\right]$. Since $-3<-\frac{1}{a}-2<-2,5<a+3<6$, the integer solutions will be the numbers $-2,-1,0,1,2,3,4,5$.
Answer: 12. (D)
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. Specify the integer closest to the larger root of the equation
$$
\operatorname{arctg}\left(\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. Let $y=\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}$, then $\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}=y+1$ and the equation will take the form
$$
\operatorname{arctg}(y+1)-\operatorname{arctg} y=\frac{\pi}{4}
$$
Since $0 \leqslant \operatorname{arctg} y<\operatorname{arctg}(y+1)<\frac{\pi}{2}$, the last equation is equivalent to
$$
\operatorname{tg}(\operatorname{arctg}(y+1)-\operatorname{arctg} y)=1 \Longleftrightarrow \frac{1}{1+(y+1) y}=1 \Longleftrightarrow y=0 \Longleftrightarrow \frac{2 x}{7}=\frac{7}{8 x} \Longleftrightarrow|x|=\frac{7}{4}
$$
Answer: 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. Specify the integer closest to the smaller root of the equation
$$
\operatorname{arctg}\left(\left(\frac{5 x}{26}+\frac{13}{10 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{5 x}{26}-\frac{13}{10 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{5 x}{26}=\frac{13}{10 x} \Longleftrightarrow|x|=\frac{13}{5}$.
Answer: -3 .
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.3. Specify the integer closest to the smaller root of the equation
$$
\operatorname{arctg}\left(\left(\frac{7 x}{10}-\frac{5}{14 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{7 x}{10}+\frac{5}{14 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{7 x}{10}=\frac{5}{14 x} \Longleftrightarrow |x|=\frac{5}{7}$.
Answer: -1.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.4. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arctg}\left(\left(\frac{3 x}{22}-\frac{11}{6 x}\right)^{2}\right)-\operatorname{arctg}\left(\left(\frac{3 x}{22}+\frac{11}{6 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{3 x}{22}=\frac{11}{6 x} \Longleftrightarrow |x|=\frac{11}{3}$.
Answer: 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. Indicate the integer closest to the smaller root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{2 x}{7}+\frac{7}{8 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{2 x}{7}-\frac{7}{8 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{2 x}{7}=\frac{7}{8 x} \Longleftrightarrow |x|=\frac{7}{4}$.
Answer: -2.
|
-2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.6. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{5 x}{26}+\frac{13}{10 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{5 x}{26}-\frac{13}{10 x}\right)^{2}\right)=-\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{5 x}{26}=\frac{13}{10 x} \Longleftrightarrow|x|=\frac{13}{5}$.
Answer: 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.7. Indicate the integer closest to the larger root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{7 x}{10}-\frac{5}{14 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{7 x}{10}+\frac{5}{14 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{7 x}{10}=\frac{5}{14 x} \Longleftrightarrow |x|=\frac{5}{7}$.
Answer: 1.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.8. Provide the integer closest to the smaller root of the equation
$$
\operatorname{arcctg}\left(\left(\frac{3 x}{22}-\frac{11}{6 x}\right)^{2}\right)-\operatorname{arcctg}\left(\left(\frac{3 x}{22}+\frac{11}{6 x}\right)^{2}\right)=\frac{\pi}{4}
$$
|
Solution. The equation is equivalent to $\frac{3 x}{22}=\frac{11}{6 x} \Longleftrightarrow |x|=\frac{11}{3}$.
Answer: -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 7. How many solutions in integers does the equation
$6 y^{2}+3 x y+x+2 y-72=0$ have?
|
Answer: 4.
## Solution:
Factorize:
$(3 y+1)(2 y+x)=72$.
The first factor must give a remainder of 1 when divided by 3. The number 72 has only 4 divisors that give such a remainder: $-8,-2,1,4$. They provide 4 solutions.
Problem 7a. How many solutions in integers does the equation
$6 y^{2}+3 x y+x+2 y+180=0$ have?
Answer: 6.
## Solution:
Factorize:
$(3 y+1)(2 y+x)=180$.
The first factor must give a remainder of 1 when divided by 3. The number 180 has only 6 divisors that give such a remainder: $-20,-5,-2,1,4,10$. They provide 6 solutions.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A trip to St. Petersburg is being organized for 30 schoolchildren along with their parents, some of whom will be driving cars. Each car can accommodate 5 people, including the driver. What is the minimum number of parents that need to be invited on the trip?
ANSWER: 10
|
Solution: No more than 4 students can fit in a car, so 8 cars will be needed, i.e., 10 drivers.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. A trip to Nizhny Novgorod is being organized for 50 schoolchildren along with their parents, some of whom will be driving cars. Each car can accommodate 6 people, including the driver. What is the minimum number of parents that need to be invited on the trip?
ANSWER: 10
|
Solution: No more than 5 students can fit in a car, so 10 cars will be needed, i.e., 10 drivers.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the largest natural number that cannot be represented as the sum of two composite numbers.
ANSWER: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. Odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we can see that 11 cannot be represented in such a way.
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final stage tasks for the 2015/2016 academic year for grades 5-6
The solutions are similar to those of variant v2a, so only the answers are provided.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Five runners ran a relay. If the first runner ran twice as fast, they would have spent $5 \%$ less time. If the second runner ran twice as fast, they would have spent $10 \%$ less time. If the third runner ran twice as fast, they would have spent $12 \%$ less time. If the fourth runner ran twice as fast, they would have spent $15 \%$ less time. By what percentage less time would they have spent if the fifth runner ran twice as fast?
OTBET: by $8 \%$
|
Solution: If each ran twice as fast, they would run 50% faster. This means that if the 5th ran faster, the time would decrease by $50-5-10-12-15=8 \%$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Solve the equation
$$
\log _{3}(x+2) \cdot \log _{3}(2 x+1) \cdot\left(3-\log _{3}\left(2 x^{2}+5 x+2\right)\right)=1
$$
|
Problem 4.
Answer: $x=1$.
Solution. For admissible values $x>-\frac{1}{2}$ we have: $\log _{3}(x+2)>0$.
If $\log _{3}(2 x+1)0$ and the left side of the equation is negative.
Thus, all three factors on the left side of the equation are positive, and the roots should be sought only among those $x$ for which
$$
\left\{x>0,2 x^{2}+5 x+20$ and the discriminant of this equation as a quadratic in $t$ is $D(p)=p(p-1)^{2}(p-4)$, then
$$
\{D(p) \geqslant 0, p>0\} \Longleftrightarrow p \in\{1\} \cup[4 ;+\infty)
$$
But for $p \geqslant 4: x \geqslant 40$, so $p=1$ and $t=1$, which is satisfied only if $x=1$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.