problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
1.3. A ballpoint pen costs 10 rubles, a fountain pen costs 60 rubles, and a gel pen costs 70 rubles. What is the maximum number of fountain pens that can be bought if you need to buy exactly 25 pens in total and among them there must be pens of all three types, and you need to spend exactly 1000 rubles on them?
|
Answer: 9. Comments. The solutions are two triples of integers $(11,9,5)$ and $(12,3,10)$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.4. A ballpoint pen costs 10 rubles, a gel pen costs 30 rubles, and a fountain pen costs 60 rubles. What is the maximum number of ballpoint pens that can be bought if you need to buy exactly 20 pens in total and among them there must be pens of all three types, and you need to spend exactly 500 rubles on them?
|
Answer: 11. Comments. The solutions are two triples of integers $(11,5,4)$ and $(8,10,2)$.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. A plane parallel to the base of a quadrilateral pyramid with a volume of 81 cuts off a smaller pyramid with a volume of 3. Find the volume of the pyramid whose four vertices coincide with the vertices of the section, and the fifth vertex lies in the base plane of the larger pyramid.
|
Answer: 6. Solution. If we denote the first given volume as $V$, and the second as $v$ (in this case $V=81, v=3$), then the larger pyramid and the smaller pyramid are similar with a similarity coefficient of $\sqrt[3]{\frac{V}{v}}$. Therefore, the height $H$ of the larger pyramid relates to the height $h$ of the smaller pyramid as $\sqrt[3]{\frac{V}{v}}$. Since the height of the pyramid whose volume we need to find is $H-h$, then $\frac{H-h}{h}=\sqrt[3]{\frac{V}{v}}-1$. Therefore, the volume of the pyramid we are looking for is $v\left(\sqrt[3]{\frac{V}{v}}-1\right)$.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Find the number of all integer solutions of the inequality $\sqrt{1-\sin \frac{\pi x}{4}-3 \cos \frac{\pi x}{2}}-\sqrt{6} \cdot \sin \frac{\pi x}{4} \geq 0$, belonging to the interval [1991; 2013].
|
Answer: 8. Solution. Denoting $\sin \frac{\pi x}{4}=t$, we get $\sqrt{1-t-3\left(1-2 t^{2}\right)} \geq \sqrt{6} \cdot t$, or $\sqrt{6 t^{2}-t-2} \geq \sqrt{6} \cdot t$. For non-negative $t$, we obtain $6 t^{2}-t-2 \geq 6 t^{2}$, or $t \leq-2$, which means there are no solutions. For $t<0$, the condition $6 t^{2}-t-2 \geq 0$ gives $t \leq-\frac{1}{2}$. Thus, we get the solution $\sin \frac{\pi x}{4} \leq-\frac{1}{2}$, from which $-\frac{5 \pi}{6}+2 \pi k \leq \frac{\pi x}{4} \leq-\frac{\pi}{6}+2 \pi k$, or $-\frac{10}{3}+8 k \leq x \leq-\frac{2}{3}+8 k$.
Integer solutions: $5+8 k, 6+8 k, 7+8 k$. From the given interval, the solutions will be: 1991, $1997,1998,1999,2005,2006,2007,2013$ - 8 numbers.
|
8
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2. Find the number of all integer solutions of the inequality $\sqrt{3 \cos \frac{\pi x}{2}-\cos \frac{\pi x}{4}+1}-\sqrt{6} \cdot \cos \frac{\pi x}{4} \geq 0$, belonging to the interval [1991; 2013].
|
Answer: 9. Comments. Solution of the inequality: $\frac{8}{3}+8 k \leq x \leq \frac{16}{3}+8 k$. From the given interval, the following numbers will be included in the answer: 1995, 1996, 1997, 2003, 2004, 2005, 2011, 2012, 2013 - 9 numbers.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.3. Find the number of all integer solutions of the inequality $\sqrt{1+\sin \frac{\pi x}{4}-3 \cos \frac{\pi x}{2}}+\sqrt{6} \cdot \sin \frac{\pi x}{4} \geq 0$, belonging to the interval [1991; 2013].
|
Answer: 9. Comments. Solution of the inequality: $\frac{2}{3}+8 k \leq x \leq \frac{10}{3}+8 k$. From the given interval, the following numbers will be included in the answer: 1993, 1994, 1995, 2001, 2002, 2003, 2009, 2010, 2011 - 9 numbers.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4. Find the number of all integer solutions of the inequality $\sqrt{3 \cos \frac{\pi x}{2}+\cos \frac{\pi x}{4}+1}+\sqrt{6} \cdot \cos \frac{\pi x}{4} \geq 0$, belonging to the interval $[1991 ; 2013]$.
|
Answer: 9. Comments. Solution of the inequality: $-\frac{4}{3}+8 k \leq x \leq \frac{4}{3}+8 k$. From the given interval, the following will be included in the answer: 1991, 1992, 1993, 1999, 2000, 2001, 2007, 2008, 2009 - 9 numbers.
|
9
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. From one point on a circular track, a pedestrian and a cyclist started simultaneously in the same direction. The cyclist's speed is $55\%$ greater than the pedestrian's speed, and therefore the cyclist overtakes the pedestrian from time to time. At how many different points on the track will the overtakes occur?
|
Answer: 11.
Solution: Let's assume the length of the path is 55 (in some units), and the speeds of the pedestrian and the cyclist are $100 x$ and $155 x$. Then, the overtakes will occur every $1 / x$ units of time. During this time, the pedestrian covers 100 units, which means he will be 10 units away in the opposite direction from the start. This will happen at each overtake. At the 11th overtake, the pedestrian will have covered 1100 units and will be back at the starting point, after which the overtake points will start repeating.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. Solve the equation $\frac{n!}{2}=k!+l!$ in natural numbers, where $n!=1 \cdot 2 \cdot \ldots n$. If there are no solutions, write 0; if there is one solution, write $n$; if there are multiple solutions, write the sum of the values of $n$ for all solutions. Recall that a solution is a triplet $(n, k, l)$; if solutions differ in at least one component, they are considered different.
|
Answer: 10 (all triples of solutions $(n, k, l):(3,1,2),(3,2,1),(4,3,3)$).
Solution. Note that if $k4$, then $n!>4 \cdot(n-1)!\geqslant 2 \cdot(k!+l!)$, so there are no such solutions. If $n=2$, we get $1=k!+l!$ - no solutions; if $n=3$, the equation $3=k!+l!$ has two solutions: $k=1, l=2$ and $k=2, l=1$; if $n=4$, the equation $12=k!+l!$ gives one more solution $k=l=3$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given a parallelogram $A B C D$ and points $A_{1}, B_{1}, C_{1}$, and $D_{1}$ are chosen such that point $A$ is the midpoint of segment $D D_{1}$, point $B$ is the midpoint of $A A_{1}$, point $C$ is the midpoint of $B B_{1}$, and point $D$ is the midpoint of $C C_{1}$. Find the area of $A_{1} B_{1} C_{1} D_{1}$, given that $S(A B C D)=1$.
|
# Answer: 5
## Solution:
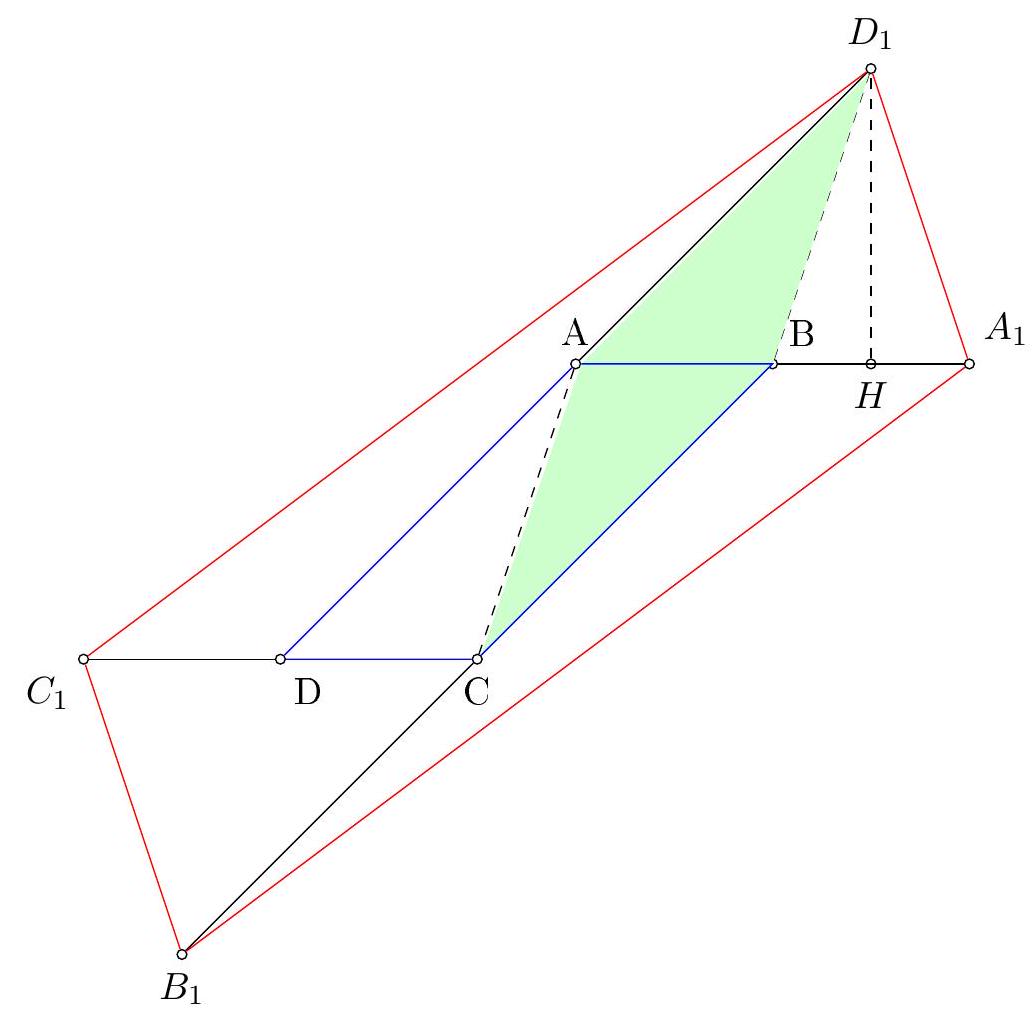
Notice that triangles $\triangle A B C$ and $\triangle A B D_{1}$ are congruent, hence their areas are equal. Triangles $\triangle A B D_{1}$ and $\triangle A_{1} B D_{1}$ share the same height $D_{1} H$ and have equal bases, thus they are equal in area. Therefore, $S\left(\triangle A A_{1} D_{1}\right)=1$. It can be shown that $S\left(\triangle B B_{1} A_{1}\right)=S\left(\triangle C C_{1} B_{1}\right)=S\left(\triangle D D_{1} C_{1}\right)=1$. Adding these up, we get $S\left(A_{1} B_{1} C_{1} D_{1}\right)=5$.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Kolya started playing $W o W$ at the moment when the hour and minute hands were opposite. He finished playing after an integer number of minutes, and at the end, the minute hand coincided with the hour hand. How long did he play (if it is known that he played for less than 12 hours)
|
Solution: The minute hand catches up with the hour hand at a speed of $\frac{11^{\circ}}{2}$ /min. For them to coincide, the difference in their angles of rotation should be $180+360 k$. This value is a multiple of 11 when $k=5,16, \ldots$. According to the problem, only $k=5$ fits, which gives us 6 o'clock.
|
6
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A stack of A4 sheets was folded in half and folded in two (resulting in an A5 booklet). After that, the pages of the resulting booklet were renumbered: $1,2,3, \ldots$ It turned out that the sum of the numbers on one of the sheets was 74. How many sheets were in the stack?
|
Answer: 9. Solution. Note that the sum of the numbers on each leaf is the same. If the last page has the number $n$, then on the first leaf, the numbers will be $1,2, n-1$ and $n$. Therefore, $2n + 2 = 74$, from which we get that the number of pages $n=36$. Four pages are placed on each leaf, so there were 9 leaves.
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a $3 \times 3$ table, the following numbers are written:
| 10 | 20 | 40 |
| :---: | :---: | :---: |
| 32 | 61 | 91 |
| 100 | 1000 | 2000 |
It is allowed to swap any two numbers in one move. What is the minimum number of moves required to achieve that the sum of the numbers in each column is divisible by $3 ?$
|
Answer: 2. Solution.
| 1 | 2 | 1 |
| :--- | :--- | :--- |
| 2 | 1 | 1 |
| 1 | 1 | 2 |
Let's write down the remainders of these numbers when divided by 3. It is not hard to notice that the sum of the numbers is divisible by 3 if and only if the sum of the corresponding remainders is divisible by 3. The remainders equal to 2 need to be gathered in one column, which will require no less than 2 moves. It is clear that this can be done in 2 moves.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the number of integers from 1 to 3400 that are divisible by 34 and have exactly 2 odd natural divisors. For example, the number 34 has divisors $1,2,17$ and 34, exactly two of which are odd.
|
Answer: 7. Solution. It is obvious that if a number is divisible by 34, then its divisors will always be 1 and 17. According to the condition, there should be no other odd divisors, so these must be numbers of the form $17 \cdot 2^{k}$, $k \geqslant 1$ (and only they). These numbers fall within the specified range for $k=1,2, \ldots, 7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Find all values of $a$ for which the quadratic function $f(x)=a x^{2}-2 a x+1$ takes values, the modulus of which does not exceed 2, at all points of the interval $[0 ; 2]$. In your answer, specify the total length of the intervals to which the found values of $a$ belong.
|
Answer: 4 (the desired set of values for $a:[-1 ; 0) \cup(0 ; 3]$).
Solution. For the function $f(x)$ to be quadratic, it is necessary that $a \neq 0$. The vertex of the parabola, which is the graph of the given function, is located at the point $(1 ; 1-a)$. Since $f(0)=f(2)=1$, the condition of the problem is satisfied if $|1-a| \leqslant 2$, i.e., $-1 \leqslant a \leqslant 3$. Therefore, the desired set of values for $a$ is the union $[-1 ; 0) \cup(0 ; 3]$, and the total length of these intervals is 4.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.3. Find all values of $a$ for which the quadratic function $f(x)=a x^{2}+2 a x-1$ takes values, the modulus of which does not exceed 3, at all points of the interval $[-2 ; 0]$. In your answer, specify the total length of the intervals to which the found values of $a$ belong.
|
Answer: 6 (the set of desired values of $a$: $[-4 ; 0) \cup(0 ; 2]$).
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.4. Find all values of $a$ for which the quadratic function $f(x)=a x^{2}+4 a x-1$ takes values, the modulus of which does not exceed 4, at all points of the interval $[-4 ; 0]$. In your answer, specify the total length of the intervals to which the found values of $a$ belong.
|
Answer. 2 (the set of desired values of $a: \left[-\frac{5}{4} ; 0\right) \cup\left(0 ; \frac{3}{4}\right]$).
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. Solve the equation $\frac{n!}{2}=k!+l!$ in natural numbers, where $n!=1 \cdot 2 \ldots n$. If there are no solutions, indicate 0; if there is one solution, indicate $n$; if there are multiple solutions, indicate the sum of the values of $n$ for all solutions. Recall that a solution is a triplet ( $n, k, l$); if solutions differ in at least one component, they are considered different.
|
Answer: 10 (all triples of solutions $(n, k, l):(3,1,2),(3,2,1),(4,3,3)$).
Solution. Note that if $k4$, then $n!>4 \cdot(n-1)!\geqslant 2 \cdot(k!+l!)$, so there are no such solutions. If $n=2$, we get $1=k!+l!$ - no solutions; if $n=3$, the equation $3=k!+l!$ has two solutions: $k=1, l=2$ and $k=2, l=1$; if $n=4$, the equation $12=k!+l!$ gives one more solution $k=l=3$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. In an acute-angled triangle $A B C$, the median $B M$ and the altitude $C H$ were drawn. It turned out that $B M=C H=\sqrt{3}$, and $\angle M B C=\angle A C H$. Find the perimeter of triangle $A B C$.
|
Answer: 6.
Solution. We will prove that triangle $ABC$ is equilateral, with all sides equal to 2. Drop a perpendicular $MK$ from point $M$ to side $AB$. In triangle $BMK$, the leg $KM$ is half the hypotenuse $MB$, so $\angle KBM = 30^{\circ}$. Let $O$ be the intersection of $MB$ and $CH$, then $\angle MOC = 60^{\circ}$. Denote $\angle MBC = \angle ACH = \alpha$, then $\angle HCB = 60^{\circ} - \alpha$, so $\angle BCA = 60^{\circ}$. Therefore, triangles $MOC$ and $MCB$ are similar by two angles. From the similarity, we get $MC^2 = BM \cdot OM = CH \cdot OM$. By the Law of Sines, $OM = MC \cdot \sin \alpha / \sin 60^{\circ}$. From triangle $AHC$, we find $HC = 2MC \cdot \cos \alpha$. Substituting this into the formula $MC^2 = CH \cdot OM$ and canceling $MC^2$, we get $\sin 2\alpha = \sqrt{3} / 2$, from which $\alpha = 30^{\circ}$. Therefore, triangle $ABC$ is equilateral.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. For an infinite sequence of numbers $x_{1}, x_{2}, x_{3}, \ldots$, for all natural $n \geq 4$, the relation $x_{n}=x_{n-1} \cdot x_{n-3}$ holds. It is known that $x_{1}=1, x_{2}=1, x_{3}=-1$. Find $x_{2022}$.
|
# Answer: 1.
Solution. All members of the sequence have a modulus of 1. Mark the positive ones with a plus and the negative ones with a minus. Write out the beginning of the sequence:
$$
[++---+-]++---+-++\ldots
$$
It is clear that three consecutive members completely determine how the sequence will look further. Thus, if we see ++- again, as at the beginning, the sequence will start to repeat. Therefore, the period is seven, so the 2022nd position holds the same value as the sixth $(2022=6(\bmod 7))$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 6. In a square room, there is a light bulb on each wall that can shine in one of the seven colors of the rainbow. There are no light bulbs in the room that shine the same color. In one move, a person can change the color of one of the light bulbs to a color that is not used by any light bulb in the room at the moment of the move, which will also change the colors to the two remaining unused colors. (After this, there are still no two light bulbs with the same color in the room). What is the minimum number of moves needed to ensure that each light bulb has shone in each of the seven colors?
|
Answer: 8 moves.
Solution. Each light bulb on the walls of the room must change color 6 times, and there are four walls, so the total number of color changes is at least 24. On the other hand, in one move, the color of three light bulbs changes, so the number of moves is at least 8. An example for 8 moves can be provided (see the figure).

|
8
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Detective Podberezyakov is pursuing Maksim Detochkin (each driving their own car). At the beginning, both were driving on the highway at a speed of 60 km/h, with Podberezyakov lagging behind Detochkin by 2 km. Upon entering the city, each of them reduced their speed to 40 km/h, and upon exiting the city, finding themselves on a good highway, each increased their speed to 70 km/h. When the highway ended, at the border with a dirt road, each had to reduce their speed to 30 km/h again. What was the distance between them on the dirt road?
|
Answer: 1 km.
Solution: At the moment Detochkin entered the city, Podberezyakov was 2 km behind him. Podberezyakov covered this distance in 2/60 hours, during which time Detochkin traveled $\frac{2}{60} \cdot 40$ km. That is, the distance was multiplied by 40/60. Similarly, when exiting the city and transitioning to the dirt road, the distance is multiplied by 70/40 and then by 30/70. In the end, $2 \times \frac{40}{60} \times \frac{70}{40} \times \frac{30}{70}=1$ km.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. And our cat gave birth to kittens yesterday! It is known that the two lightest kittens weigh a total of 80 g, the four heaviest weigh 200 g, and the total weight of all the kittens is 500 g. How many kittens did the cat give birth to?
|
Answer: 11.
Solution: The two lightest weigh 80 g, so the others weigh no less than 40 g each. Similarly, we find that all except the 4 heaviest weigh no more than 50 g. Consider the kittens that are not among the 2 lightest and the 4 heaviest. Their total weight is 500-200-80=220g. There must be 5 of them, because if there were 4, the weight could not be more than $4 \times 50=200$ g, and if there were 6, their weight would be no less than $6 \times 40=240$ g. Therefore, there are 11 kittens in total.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the sum
$$
\begin{aligned}
& \frac{1}{(\sqrt[4]{1}+\sqrt[4]{2})(\sqrt{1}+\sqrt{2})}+\frac{1}{(\sqrt[4]{2}+\sqrt[4]{3})(\sqrt{2}+\sqrt{3})}+ \\
& +\ldots+\frac{1}{(\sqrt[4]{9999}+\sqrt[4]{10000})(\sqrt{9999}+\sqrt{10000})}
\end{aligned}
$$
|
Answer: 9. Solution. If we multiply the numerator and denominator of the fraction $\frac{1}{(\sqrt{n}+\sqrt{n}+1)(\sqrt{n}+\sqrt{n+1})}$ by $\sqrt[4]{n}-\sqrt[4]{n+1}$, we get $\sqrt[4]{n+1}-\sqrt[4]{n}$. The specified
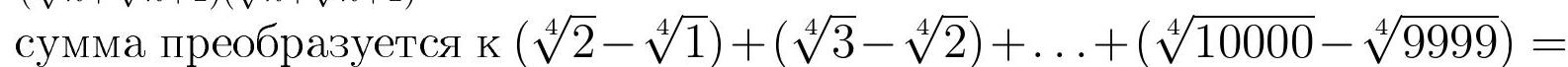
$\sqrt[4]{10000}-\sqrt[4]{1}=9$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Given a parallelogram $A B C D$ and points $A_{1}, B_{1}, C_{1}$, and $D_{1}$ are chosen such that point $A$ is the midpoint of segment $D D_{1}$, point $B$ is the midpoint of $A A_{1}$, point $C$ is the midpoint of $B B_{1}$, and point $D$ is the midpoint of $C C_{1}$. a) Prove that $A_{1} B_{1} C_{1} D_{1}$ is also a parallelogram. b) Find its area if it is known that $S(A B C D)=1$.
|
# Answer: b) 5
## Solution:
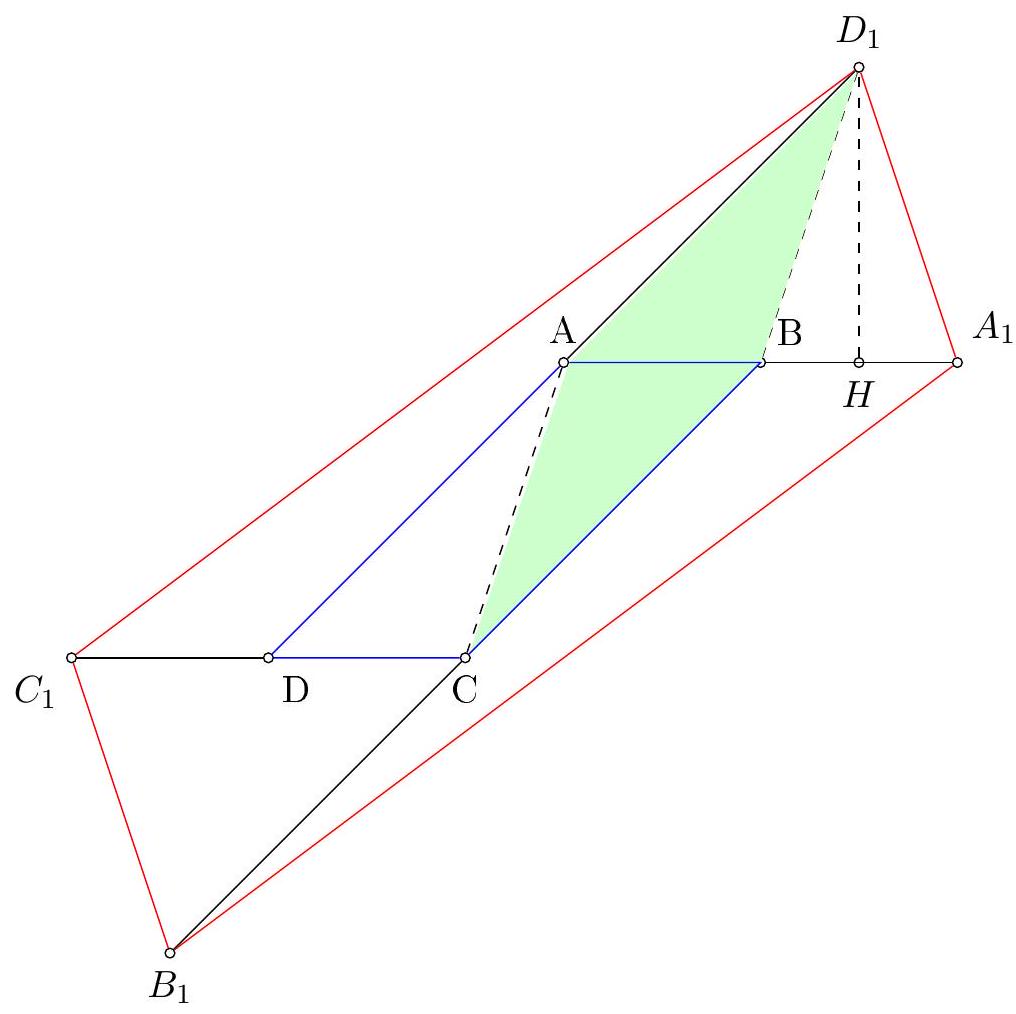
a) From the properties of a parallelogram, it follows that $A B = C D, \angle B A D_{1} = 180^{\circ} - \angle B A D = 180^{\circ} - \angle B C D = \angle D C B_{1}, A D_{1} = A D = B C = C B_{1}$. Therefore, triangles $\triangle A B D_{1}$ and $\triangle C B D_{1}$ are congruent. Since $C C_{1} = 2 C D = 2 A B = A A_{1}$, triangles $\triangle C C_{1} B_{1}$ and $\triangle A A_{1} D_{1}$ are also congruent. Therefore, $A_{1} D_{1} = B_{1} C_{1}$, and similarly, it can be shown that $A_{1} B_{1} = C_{1} D_{1}$. If the opposite sides of a quadrilateral are equal, then it is a parallelogram.
b) Note that triangles $\triangle A B C$ and $\triangle A B D_{1}$ are congruent, so their areas are equal. Triangles $\triangle A B D_{1}$ and $\triangle A_{1} B D_{1}$ have the same height $D_{1} H$ and equal bases, so they are equal in area. Thus, $S\left(\triangle A A_{1} D_{1}\right) = 1$. It can be shown that $S\left(\triangle B B_{1} A_{1}\right) = S\left(\triangle C C_{1} B_{1}\right) = S\left(\triangle D D_{1} C_{1}\right) = 1$. Adding these, we get $S\left(A_{1} B_{1} C_{1} D_{1}\right) = 5$
|
5
|
Geometry
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
1. The sum of positive integers is 11. In the first part of this equation, identical numbers are hidden behind cards with the same letters, and different numbers - behind cards with different letters.
Consider the equation: $\quad \mathbf{C}+\mathbf{y}+\mathbf{M}+\mathbf{M}+\mathbf{A}=11$.
Can you tell which number is hidden behind the letter M?
|
Answer: 1. Solution. If $M=1$, then the sum $C+y+A=9$, which is only possible with the set of numbers 2, 3, 4 (in any order). If $M=2$, then the sum $C+y+A=7$, which is impossible, as this sum is not less than $1+3+4=8$. If $M>2$, this is even more impossible.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Having walked $2 / 5$ of the length of a narrow bridge, a pedestrian noticed that a car was approaching the bridge from behind. Then he walked back and met the car at the beginning of the bridge. If the pedestrian had continued walking forward, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the pedestrian's speed.
|
Answer: 5.
Solution. In the time $t$ that the pedestrian walked towards the car until they met at the beginning of the bridge, he covered $2 / 5$ of the bridge's length. Therefore, if the pedestrian continued walking forward, in time $t$ he would have covered another $2 / 5$ of the bridge's length, and he would have $1 / 5$ of the bridge's length left to walk. According to the problem, in time $t$, the car would have reached the beginning of the bridge and would have the entire bridge left to travel before meeting the pedestrian. Thus, the ratio of the car's speed to the pedestrian's speed is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many solutions does the equation
$$
\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}=\frac{2}{x^{2}} ?
$$
|
Answer: 1.
Solution. Let us consider the functions
$$
f(x)=\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}} \quad \text { and } \quad g(x)=\frac{2}{x^{2}}.
$$
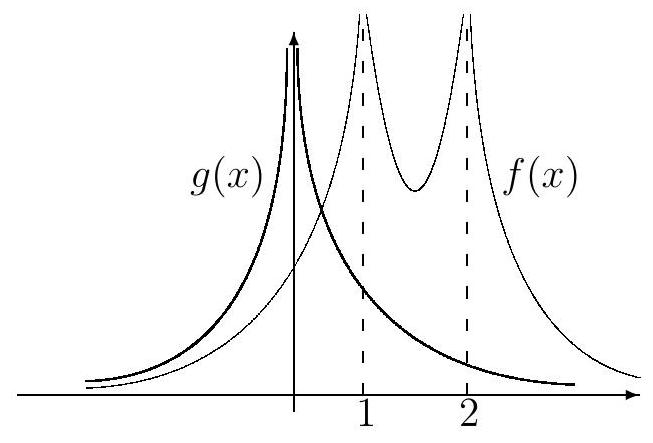
For $x < 0$, both functions $f$ and $g$ are positive, and for $x \in (0 ; 1)$, the function $f$ is decreasing from $+\infty$ to 2 (not including), since $f^{\prime}(x) = -\frac{2}{(x-1)^{3}} - \frac{2}{(x-2)^{3}} < 0$ for $x \in (0 ; 1)$, while the function $g$ is decreasing from $+\infty$ to 2 (not including), since $g^{\prime}(x) = \frac{-4}{x^{3}} < 0$ for $x > 0$. Therefore, for $x \in (0 ; 1)$, the inequality $f(x) > g(x)$ holds, and for $x > 2$, the inequalities $0 < \frac{1}{(x-1)^{2}} < \frac{1}{x^{2}}$ and $\frac{1}{(x-2)^{2}} > \frac{1}{x^{2}}$ hold, so $f(x) > g(x)$, meaning that the equation has no solutions for $x > 2$.
## Second Solution.
The original equation, under the conditions $x \neq 0, x \neq 1, x \neq 2$, is equivalent to the equation $6 x^{3} - 21 x^{2} + 24 x - 8 = 0$. Consider the function $f(x) = 6 x^{3} - 21 x^{2} + 24 x - 8$. Since $f^{\prime}(x) = 18 x^{2} - 42 x + 24$, then $x = 1$ is a point of maximum, and $x = \frac{4}{3}$ is a point of minimum. The function $f$ is increasing on the domain $(-\infty, 1) \cup \left(\frac{4}{3} ; +\infty\right)$ and decreasing on the interval $\left(1 ; \frac{4}{3}\right)$. Since $f(0) = -8, f(1) = 1, f\left(\frac{4}{3}\right) = \frac{8}{9}$, the equation $f(x) = 0$ has a unique root, which lies in the interval $(0 ; 1)$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given three points, the distances between which are 4, 6, and 7. How many pairwise distinct triangles exist for which each of these points is either a vertex or the midpoint of a side?
|
Answer: 11.
Solution. Let's list all the constructions of triangles that satisfy the condition of the problem, indicating the lengths of the sides.
| | Description of the Triangle | | Lengths of Sides |
| :---: | :---: | :---: | :---: |
| №1 | All points are vertices | | $4,6,7$ |
| | One point is a vertex, two are midpoints of sides | | |
| №2 | | The vertex is at the extension of both sides of lengths 4 and 6 | $8,12,14$ |
| №3 | | The extension of the side of length 4 | $8,14,2 \sqrt{94}$ |
| №4 | | The extension of the side of length 6 | $12,14,2 \sqrt{154}$ |
| №5 | | The vertex is at the extension of both sides of lengths 4 and 7 | $8,12,14$ |
| №6 | | The extension of the side of length 4 | $8,12,2 \sqrt{55}$ |
| №7 | | The extension of the side of length 7 | $12,14,2 \sqrt{154}$ |
| №8 | | The vertex is at the extension of both sides of lengths 6 and 7 | $8,12,14$ |
| №9 | | The extension of the side of length 6 | $8,12,2 \sqrt{55}$ |
| №10 | | The extension of the side of length 7 | $8,14,2 \sqrt{94}$ |
| | Two points are vertices, one is the midpoint of a side | | |
| №11 | | The vertices are on the side of length 4, the side of length 7 is extended | $4,14, \sqrt{154}$ |
| №12 | | The side of length 6 is extended | $4,12, \sqrt{154}$ |
| №13 | | The vertices are on the side of length 6, the side of length 4 is extended | $6,8, \sqrt{94}$ |
| №14 | | The side of length 7 is extended | $6,14, \sqrt{94}$ |
| №15 | | The vertices are on the side of length 7, the side of length 4 is extended | $7,8, \sqrt{55}$ |
| №16 | | The side of length 6 is extended | $7,12, \sqrt{55}$ |
| №17 | All points are midpoints of sides | | $8,12,14$ |
Thus, there are 17 ways of construction, leading to 11 different triangles.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In a commercial football tournament, five teams participated. Each was supposed to play exactly one match against each other. Due to financial difficulties, the organizers canceled some games. In the end, it turned out that all teams had scored a different number of points, and no team had a zero in the points scored column. What is the minimum number of games that could have been played in the tournament, if three points were awarded for a win, one for a draw, and zero for a loss?
|
Answer: 6.
Solution. The minimum possible total score: $1+2+3+4+5=15$. In one game, a maximum of 3 points (in total) can be scored. Therefore, there were at least 5 games. However, if there were exactly 5 games, then all games would have to end with one of the teams winning, and then no team would have scored exactly 1 point.
Thus, there were at least 6 games. An example of the tournament results can be given by the table.
| $*$ | 1 | 2 | 3 | 4 | 5 | $\sum$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | $*$ | $*$ | $*$ | 3 | 3 | 6 |
| 2 | $*$ | $*$ | $*$ | $*$ | 3 | 3 |
| 3 | $*$ | $*$ | $*$ | 1 | 3 | 4 |
| 4 | 0 | $*$ | 1 | $*$ | 1 | 2 |
| 5 | 0 | 0 | 0 | 1 | $*$ | 1 |
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. How many triples of numbers $a, b, c$ exist, each of which is a root of the corresponding equation $a x^{2}+b x+c=0$?
|
Answer: 5.
Solution. If $a=0$ or $a=b=c$, then $a=b=c=0$. Otherwise: if $a=b \neq c$, then either $a=b=-1, c=0$, or $a=b=1, c=-2$; if $a \neq b=c$, then either $a=1, b=c=-0.5$; if $a=c \neq b$, then $a=c=c_{0}, b=1 / c_{0}$, where the number $c_{0}<0$ is the unique root of the equation $c^{3}+c=-1$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Task 1. Every time my brother tells the truth, our grandmother sneezes. One day, my brother said he got a "5" in math, but grandmother didn't sneeze. Then, slightly doubting his first words, he said he got a "4," and grandmother sneezed. Encouraged by grandmother's sneeze, he confirmed that he definitely got no less than 3, but grandmother didn't sneeze again. So, what grade did my brother actually get in math?
|
Answer: $« 2 »$.
Solution. If the grandmother did not sneeze, then the brother definitely lied, so he did not get a "5" and even more than that, less than 3. If the grandmother did sneeze, then it is not certain that he told the truth at that moment, as the condition does not prohibit the grandmother from sneezing when the brother is lying.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) In a nine-story building, there are 4 apartments on each floor. How many entrances are there in this building if there are a total of 180 apartments?
|
Answer: 5.
Solution. The number of entrances is $180:(4 \cdot 9)=5$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. (14 points) The old man was pulling the turnip, and one by one, the old woman, the granddaughter, the dog, and the cat joined him. They pulled and pulled, but couldn't pull out the turnip! The cat called the mouse. They pulled and pulled, and finally pulled out the turnip! It is known that each subsequent participant pulls with a quarter of the strength of the previous one. How many men from the village, pulling with the same strength as the old man, should have been called to help the old man and the cat pull out the turnip?
|
Answer: 2.
Solution. The old woman, the granddaughter, Zhuchka, and the mouse pull with a combined force of
$$
\frac{3}{4}+\left(\frac{3}{4}\right)^{2}+\left(\frac{3}{4}\right)^{3}+\left(\frac{3}{4}\right)^{5}=\frac{2019}{1024}=1 \frac{995}{1024}
$$
of the force of the old man. Therefore, two men need to be called.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. (14 points) Misha drew a triangle with a perimeter of 11 and cut it into parts with three straight cuts parallel to the sides, as shown in the figure. The perimeters of the three shaded figures (trapezoids) turned out to be 5, 7, and 9. Find the perimeter of the small triangle that resulted from the cutting.
#
|
# Answer: 10.
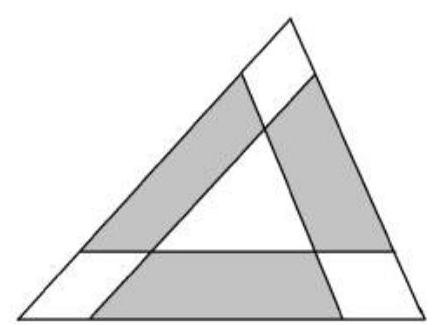
Solution. Since opposite sides of parallelograms are equal, the lateral sides of each resulting trapezoid are equal to the corresponding segments on the sides of the original triangle. Therefore, the sum of the perimeters of the three trapezoids is equal to the sum of the perimeter of the original triangle (the sum of the larger bases and lateral sides of the three trapezoids) and the perimeter of the new triangle (the sum of the smaller bases of the trapezoids). Thus, the perimeter of the new triangle is equal to the sum of the perimeters of the trapezoids minus the perimeter of the original triangle: \(a + b + c - P\).
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. (14 points) Two people spend time playing a game: they take turns naming prime numbers not exceeding 100 such that the last digit of the number named by one player is equal to the first digit of the number named by the next player (except for the first prime number named in the game). Repeating numbers that have already been named is not allowed. The player who cannot name the next prime number according to these rules loses. Prove that one of the players can act in such a way as to guarantee a win, and find the smallest possible number of prime numbers that will be used by both players in such a game.
#
|
# Answer: 3.
Solution. We will describe a winning strategy for the first player. First, the first player names a prime number ending in 9 and different from 79 (for example, 19). Since among the numbers $90, \ldots, 99$ the only prime is 97, the second player must name this number on their next move. Then, on the third move, the first player names 79, and the second player loses. The first player cannot win in fewer moves, as for any digit from 1 to 9, there exists a prime number in the first hundred that starts with this digit.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
# Task 1.
Mom told Dima that he should eat 13 spoons of porridge. Dima told his friend that he had eaten 26 spoons of porridge. Each child, telling about Dima's feat, increased the amount of porridge Dima had eaten by 2 or 3 times. As a result, one of the children told Dima's mom about 33696 spoons of porridge. How many times in total did the children, including Dima, tell about the feat?
|
Answer: 9
Solution. $33696=2^{5} \cdot 3^{4} \cdot 13$. From this, it follows that the story of the feat was retold 5 times with the amount of porridge doubling and 4 times with it tripling, totaling 9 times.
## B-2
Dad persuaded Natasha to eat 11 spoons of porridge. Natasha told her friend that she had eaten 22 spoons of porridge. Then each child, retelling the story of Natasha's feat, increased the amount of porridge she had eaten by 2 or 3 times. As a result, one of the children told Natasha's dad about 21384 spoons of porridge. How many times in total did the children, including Natasha, retell the story?
## Answer: 8
## B-3
Mom told Grisha that he had to eat 3 spoons of porridge. Grisha told his friend that he had eaten 9 spoons of porridge. Then each child, retelling the story of Grisha's feat, increased the amount of porridge he had eaten by 3 or 5 times. As a result, one of the children told Grisha's mom about 18225 spoons of porridge. How many times in total did the children, including Grisha, retell the story?
Answer: 7
## B-4
Dad persuaded Tanya to eat 7 spoons of porridge. Tanya told her friend that she had eaten 21 spoons of porridge. Then each child, retelling the story of Tanya's feat, increased the amount of porridge she had eaten by 2 or 3 times. As a result, one of the children told Tanya's dad about 27216 spoons of porridge. How many times in total did the children, including Tanya, retell the story?
Answer: 9
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary Stage 2020/21 academic year for 5-6 grades
#
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On graph paper (the side of a cell is 1 cm) a rectangle is drawn, the sides of which lie on the grid lines, with one side being 7 cm shorter than the other. It turned out that it can be cut into several pieces along the grid lines and form a square from them. What can the side of this square be? Find all possible values.
|
Answer: 6 cm.
Solution. Let the larger side of the rectangle be $k$ cm, where $k>7$, and the side of the resulting square be $n$ cm. Then, from the equality of the areas, we get $k(k-7)=n^{2}$. Since $n<k$, let $n=k-m$, where $m \geqslant 1$. Then $k^{2}-7 k=(k-m)^{2}, k^{2}-7 k=k^{2}-2 m k+m^{2}$, from which $m(2 k-m)=7 k$. Therefore, one of the numbers $m$ or $2 k-m$ is divisible by 7.
If $m=7 s$, then we get $s(2 k-7 s)=k$, from which
$$
k=\frac{7 s^{2}}{2 s-1}=7\left(\frac{s}{2}+\frac{1}{4}+\frac{1}{4(2 s-1)}\right) \quad \Rightarrow \quad 4 k=14 s+7+\frac{7}{2 s-1}
$$
This means that 7 is divisible by $2 s-1$, which is possible only when $s=1$ or $s=4$. In the first case, $m=7, k=7$ and $n=0$, which is impossible. In the second case, we get $m=28, k=16$ and $n=12$.
The case where $2 k-m$ is divisible by 7 reduces to the previous one by substituting $m_{1}=2 k-m, m=$ $2 k-m_{1}$.
Thus, the only possible value of $n$ is 12, with $k=16$. The rectangle $16 \times 9$ can be cut along the grid lines and assembled into a square $12 \times 12$ in many ways.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. On a vast meadow, a lamb is grazing, tied with two ropes to two stakes (each stake with its own rope).
a) What shape will the area on the meadow be, where the lamb can eat the grass?
b) In the middle between the stakes, a rose grows, and the distance between the stakes is 20 meters. What should the lengths of the ropes be so that the lamb cannot eat the rose?
|
Answer: b) Exactly one of the ropes is shorter than 10 m.
Solution. a) The desired figure is the intersection of two circles with centers at the stakes and radii equal to the lengths $l_{1}$ and $l_{2}$ of the first and second ropes, respectively. Therefore, it can be either the figure shaded in Fig. 3, or a complete circle. The latter case occurs if $\left|l_{1}-l_{2}\right| \geqslant r$, where $r$ is the distance between the stakes, since then one of the circles is completely inside the other, and the desired figure coincides with the circle of the smaller radius.
b) For the rose not to fall within the area on the meadow where the lamb can eat grass, it must lie outside one of the circles bounding this figure. The distance from it to each of the stakes is $r / 2=20 / 2=10 \mathrm{m}$, so the length of one of the ropes must be less than $10 \mathrm{m}$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the number of numbers from 1 to 3400 that are divisible by 34 and have exactly 2 odd natural divisors. For example, the number 34 has divisors $1,2,17$ and 34, exactly two of which are odd.
|
Answer: 7. Solution. It is obvious that if a number is divisible by 34, then its divisors will always include 1 and 17. According to the condition, there should be no other odd divisors, so these must be numbers of the form $17 \cdot 2^{k}$, $k \geqslant 1$ (and only they). These numbers fall within the specified range for $k=1,2, \ldots, 7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find the sum
$$
\begin{aligned}
& \frac{1}{(\sqrt[4]{1}+\sqrt[4]{2})(\sqrt{1}+\sqrt{2})}+\frac{1}{(\sqrt[4]{2}+\sqrt[4]{3})(\sqrt{2}+\sqrt{3})}+ \\
& +\ldots+\frac{1}{(\sqrt[4]{9999}+\sqrt[4]{10000})(\sqrt{9999}+\sqrt{10000})}
\end{aligned}
$$
|
Answer: 9. Solution. If we multiply the numerator and denominator of the fraction $\frac{1}{(\sqrt[4]{n}+\sqrt[4]{n+1})(\sqrt{n}+\sqrt{n+1})}$ by $\sqrt[4]{n}-\sqrt[4]{n+1}$, we get $\sqrt[4]{n+1}-\sqrt[4]{n}$. The specified sum transforms to $(\sqrt[4]{2}-\sqrt[4]{1})+(\sqrt[4]{3}-\sqrt[4]{2})+\ldots+(\sqrt[4]{10000}-\sqrt[4]{9999})=$ $\sqrt[4]{10000}-\sqrt[4]{1}=9$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Trapezoid $A B C D$ with base $A D=6$ is inscribed in a circle. The tangent to the circle at point $A$ intersects lines $B D$ and $C D$ at points $M$ and $N$ respectively. Find $A N$, if $A B \perp M D$ and $A M=3$.
|
Answer: 12. Solution. The condition $A B \perp M D$ means that $\angle A B D=90^{\circ}$, that is, the base $A D$ is the diameter of the circle. Since the trapezoid is inscribed, it is isosceles. $\triangle D N A$ and $\triangle D A C$ are similar as right triangles with a common angle. From the equality of angles $\angle C A D$ and $\angle B D A$, the similarity of $\triangle D A C$ and $\triangle M D A$ follows. Therefore, $\triangle D N A \square \triangle M D A$, that is, $\frac{A N}{A D}=\frac{A D}{A M}=2$, hence $A N=12$.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. The parabola $y=x^{2}$ intersects with the line $y=25$. A circle is constructed on the segment between the intersection points of the parabola and the line as its diameter. Find the area of the convex polygon whose vertices are the intersection points of the given circle and the parabola. Provide the nearest integer to the value of this area.
|
Answer: 10. Solution. The parabola $y=x^{2}$ intersects the line $y=a$ at points with coordinates $( \pm \sqrt{a} ; a)$. Each of the intersection points of the circle and the parabola mentioned in the problem has coordinates $\left(x ; x^{2}\right)$. For such a point, the distance to the line $y=a$ is $\left|a-x^{2}\right|$, the distance to the y-axis is $|x|$, and the distance to the intersection point of these lines (the center of the circle) is $\sqrt{a}$. By the Pythagorean theorem, $x^{2}+\left(a-x^{2}\right)^{2}=a$, which simplifies to $\left(a-x^{2}\right)\left(a-x^{2}-1\right)=0$. Besides the two points with coordinates $( \pm \sqrt{a} ; a)$, the circle and the parabola also intersect at two points $( \pm \sqrt{a-1} ; a-1)$, which lie on the line $y=a-1$.
Thus, the polygon mentioned in the problem is a trapezoid with height 1 and bases $2 \sqrt{a}$ and $2 \sqrt{a-1}$. Its area is $\sqrt{a}+\sqrt{a-1}$. For $a=25$, we get $5+\sqrt{24} \approx 9.898979 \ldots$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Solve the equation $\left(x^{2}-2 x+4\right)^{x^{2}-2 x+3}=625$. In the answer, specify the sum of the squares of all its roots. If there are no roots, put 0.
|
Answer: 6. Solution. Since $x^{2}-2 x+3>0$, then $x^{2}-2 x+4>1$. The function $f(z)=z^{z-1}$ is increasing for $z>1$ (if $1<z_{1}<z_{2}$, then $f\left(z_{1}\right)=z_{1}^{z_{1}-1}<z_{1}^{z_{2}-1}<z_{2}^{z_{2}-1}=f\left(z_{2}\right)$. Therefore, the original equation, which is of the form $f\left(x^{2}-2 x+4\right)=f(5)$, is equivalent to the equation $x^{2}-2 x+4=5$. From this, $x=1 \pm \sqrt{2}$. The sum of the squares of the roots of the equation is $(1+\sqrt{2})^{2}+(1-\sqrt{2})^{2}=6$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. A team of athletes, one third of whom are snowboarders, descended from the mountain. Some of them got into a cable car carriage, which can accommodate no more than 10 people, while all the others descended on their own, and their number turned out to be more than $45 \%$, but less than $50 \%$ of the total number. Determine the number of snowboarders (if it is determined from the condition of the problem ambiguously, then write in the answer the sum of all possible its values).
|
Answer: 5. Solution. If there were $x$ snowboarders and $y$ people descended on the cable car, then there were a total of $3 x$ athletes and $\left\{\begin{array}{l}\frac{9}{20}=\frac{45}{100}<\frac{3 x-y}{3 x}<\frac{50}{100}=\frac{10}{20}, \\ y \leq 10\end{array} \Rightarrow\right.$ $\left\{\begin{array}{l}x<\frac{20}{30} y \leq \frac{20}{3}<7, \\ y \in\left(\frac{30}{20} x ; \frac{33}{20} x\right) .\end{array}\right.$
By trying the values $x=1,2, \ldots, 6$, we find that only when $x=5$ the obtained interval $y \in\left(\frac{30}{20} x ; \frac{33}{20} x\right)$ contains an integer $(y=8)$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.1. Find the number of roots of the equation
$$
\operatorname{arctg}\left(\operatorname{tg}\left(\sqrt{13 \pi^{2}+12 \pi x-12 x^{2}}\right)\right)=\arcsin \left(\sin \sqrt{\frac{13 \pi^{2}}{4}+3 \pi x-3 x^{2}}\right)
$$
|
Answer: 9. Solution. Let's make the substitution $t=\sqrt{\frac{13 \pi^{2}}{4}+3 \pi x-3 x^{2}}$. Since $\frac{13 \pi^{2}}{4}+3 \pi x-3 x^{2}=4 \pi^{2}-3\left(x-\frac{\pi}{2}\right)^{2}$, then $0 \leq t \leq 2 \pi$. The original equation, after the specified substitution, transforms into the equation $\operatorname{arctg}(\operatorname{tg} 2 t)=\arcsin (\sin t)$.
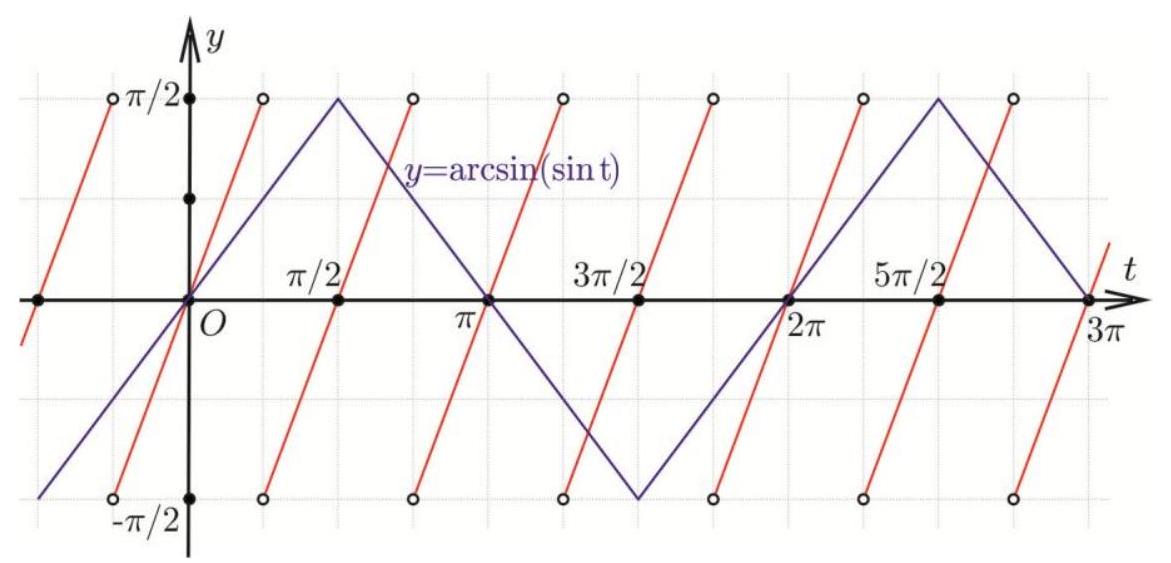
The graphs of the functions $f(t)=\operatorname{arctg}(\operatorname{tg} 2 t)$ and $g(t)=\arcsin (\sin t)$ on the interval $[0 ; 2 \pi]$ have five points of intersection: $t_{1}=0, t_{2} \in\left(\frac{\pi}{2} ; \pi\right), t_{3}=\pi, t_{4} \in\left(\pi ; \frac{3 \pi}{2}\right)$, and $t_{5}=2 \pi$.
The value of $t_{2}$ is found from the system: $\left\{\begin{array}{c}y=\pi-t, \\ y=2\left(t-\frac{\pi}{2}\right)\end{array} \Leftrightarrow t_{2}=\frac{2 \pi}{3}\right.$.
Similarly, we find $t_{4}:\left\{\begin{array}{c}y=\pi-t, \\ y=2\left(t-\frac{3 \pi}{2}\right)\end{array} \Leftrightarrow t_{4}=\frac{4 \pi}{3}\right.$.
The equations $\sqrt{4 \pi^{2}-3\left(x-\frac{\pi}{2}\right)^{2}}=t_{k}$ have two distinct solutions for $k=1,2,3,4$. The equation $\sqrt{4 \pi^{2}-3\left(x-\frac{\pi}{2}\right)^{2}}=t_{6}$ has a unique solution. In total, we get 9 solutions.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) In a large family, one of the children has 3 brothers and 6 sisters, while another has 4 brothers and 5 sisters. How many boys are there in this family
|
Answer: 4.
Solution. In the family, boys have fewer brothers than girls have, and girls have fewer sisters than boys have. Therefore, there are 4 boys and 6 girls in the family.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Let $S(n)$ be the sum of the digits in the decimal representation of the number $n$. Find $S\left(S\left(S\left(S\left(2017^{2017}\right)\right)\right)\right)$. Answer. 1.
|
Solution. Since $2017^{2017}<10000^{2017}$, the number of digits in the representation of $2017^{2017}$ does not exceed $4 \cdot 2017=$ 8068, and their sum $S\left(2017^{2017}\right)$ does not exceed $9 \cdot 8068=72612$. Then we sequentially obtain $S\left(S\left(2017^{2017}\right)\right) \leqslant 6+9 \cdot 4=42, S\left(S\left(S\left(2017^{2017}\right)\right)\right) \leqslant 3+9=12, S\left(S\left(S\left(S\left(2017^{2017}\right)\right)\right)\right) \leqslant 9$. Note also that the sum of the digits of a number gives the same remainder when divided by 9 as the number itself. Since 2016 is divisible by 9, the number $2017^{2017}=(2016+1)^{2017}$ gives a remainder of 1 when divided by 9. Therefore, $\left.S\left(S\left(S\left(2017^{2017}\right)\right)\right)\right)=1$.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Two trains, each containing 15 identical cars, were moving towards each other at constant speeds. Exactly 28 seconds after the first cars of the trains met, passenger Sasha, sitting in the third car, passed passenger Valera from the oncoming train, and another 32 seconds later, the last cars of these trains had completely passed each other. In which car, by count, was Valera traveling?
Answer: 12.
|
Solution. Since 60 seconds have passed from the moment the "zero" cars parted ways (which is also the moment the first cars met) to the moment the 15th cars parted ways, the next cars parted ways every $60: 15=4$ seconds. Therefore, after 28 seconds, the 7th cars of the trains had just parted ways, meaning the 7th car of one train had just aligned with the 8th car of the other. At this moment, Sasha's 3rd car aligned with Valery's car, which has the number $8+(7-3)=12$.
|
12
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the area of the figure defined on the coordinate plane by the system
$$
\left\{\begin{array}{l}
\sqrt{1-x}+2 x \geqslant 0 \\
-1-x^{2} \leqslant y \leqslant 2+\sqrt{x}
\end{array}\right.
$$
|
Answer: 4.
Solution. The system is defined under the condition $x \in[0,1]$, under which the first inequality of the system is satisfied. Since the functions $y=x^{2}$ and $y=\sqrt{x}$ are inverses of each other for $x \in[0,1]$, the area of the figure defined by the conditions $x \in[0,1],-1-x^{2} \leqslant y \leqslant 2+\sqrt{x}$, consists of the same parts as the area of the rectangle defined by the conditions $x \in[0,1], y \in[-2,2]$, i.e., it is equal to 4.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 3.
In triangle $A B C$, the bisector $B E$ and the median $A D$ are equal and perpendicular. Find the area of triangle $A B C$, if $A B=\sqrt{13}$.
|
Answer: 12
Solution. Let $A B=c, B E=A D=2 a$. Since triangle $A B D$ is isosceles (the bisector is perpendicular to the base, $A B=B D=c, B C=2 c$), then by the formula for the length of the bisector (where $\angle A B C=\beta$) $2 a=\frac{4 c^{2}}{3 c} \cos \frac{\beta}{2} \Leftrightarrow \frac{3 a}{2}=c \cos \frac{\beta}{2}$. Consider triangle $A B F$ (where $F$ is the midpoint of segment AD and the intersection point of the bisector and the median). We have $a=c \sin \frac{\beta}{2}$, $c=\frac{a}{\sin \frac{\beta}{2}}$. Therefore, $\operatorname{tg} \frac{\beta}{2}=\frac{2}{3}$ and $\cos \frac{\beta}{2}=\frac{3}{\sqrt{13}}, \sin \frac{\beta}{2}=\frac{2}{\sqrt{13}}, \sin \beta=\frac{12}{13}$. The area of triangle $A B C$ is $S_{A B C}=c^{2} \sin \beta=\frac{12}{13} c^{2}$.
## B-2
In triangle $A B C$, the bisector $B E$ and the median $A D$ are equal and perpendicular. Find the area of triangle $A B C$ if $A B=\sqrt{26}$.
Answer: 24
## B-3
In triangle $A B C$, the bisector $B E$ and the median $A D$ are equal and perpendicular. Find the area of triangle $A B C$ if $B E=A D=4$.
Answer: 12
## B-4
In triangle $A B C$, the bisector $B E$ and the median $A D$ are equal and perpendicular. Find the area of triangle $A B C$ if $B E=A D=6$.
Answer: 27
## Lomonosov High School Mathematics Olympiad
Preliminary stage 2020/21 academic year for 9th grade
## B-1
#
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Points $A$ and $B$ lie on a circle with center $O$ and radius 6, and point $C$ is equidistant from points $A, B$, and $O$. Another circle with center $Q$ and radius 8 is circumscribed around triangle $A C O$. Find $B Q$. Answer: 10
|
Solution. Since $A Q=O Q=8$ and $A C=O C$, triangles $\triangle A C Q$ and $\triangle O C Q$ are equal. Therefore, points $A$ and $O$ are symmetric with respect to the line $C Q$, so $A O \perp C Q$.
Next, $\angle B O Q=\angle B O C+\angle C O Q=\angle A O C+\angle O C Q=\pi / 2$. Therefore, $B Q=\sqrt{B O^{2}+O Q^{2}}=\sqrt{6^{2}+8^{2}}=10$.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A motorcycle and a quad bike are driving on a circular road, a quarter of which passes through a forest, and the remaining part - through a field. The motorcycle's speed when driving through the forest is 20 km/h, and through the field - 60 km/h. The quad bike's speed when driving through the forest is 40 km/h, and through the field - 45 km/h. The quad bike and the motorcycle enter the forest at the same time. Which of the vehicles will overtake the other first, and on which lap will this happen?
|
Answer: The quad will overtake the motorcycle on its $10-\mathrm{th}$ lap while the quad is on its 11-th lap.
|
10
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. In a convex quadrilateral $A B C D$, diagonals $A C$ and $D B$ are perpendicular to sides $D C$ and $A B$ respectively. A perpendicular is drawn from point $B$ to side $A D$, intersecting $A C$ at point $O$. Find $A O$, if $A B=4, O C=6$.
|
Answer: 2. Solution. Since $\angle A B D=\angle A C D=90^{\circ}$, the quadrilateral is inscribed in a circle with diameter $A D$. Therefore, $\angle A C B=\angle A D B$ - as angles subtending the same arc. Since $B H$ is the altitude in the right $\triangle A B D$, then $\angle A D B=\angle A B H$. Then triangles $A B O$ and $A C B$ are similar by two angles, and the following ratios hold: $\frac{A B}{A O}=\frac{A C}{A B} \Leftrightarrow \frac{4}{A O}=\frac{A O+6}{4}$ $\Leftrightarrow A O^{2}+6 A O-16=0 \Leftrightarrow A O=-8$ or $A O=2$. Answer: $A O=2$.
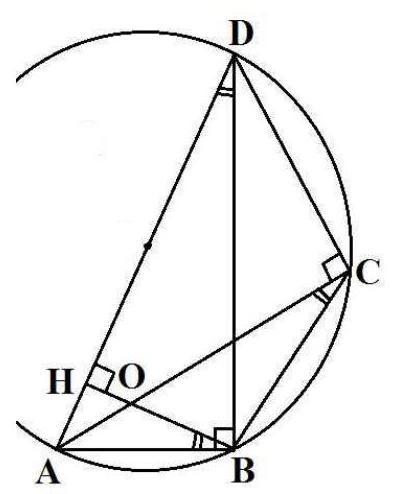
## Answer for variant 152: 9.
Answer for variant 153: 1.
Answer for variant 154: 12.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Masha, bored during a math lesson, performed the following operation on a certain 2015-digit natural number: she discarded the last digit of its decimal representation and added twice the discarded digit to the number obtained by multiplying the remaining number by 3. She then performed the same operation on the resulting number, and so on. After applying this operation multiple times, the numbers Masha obtained stopped changing, and she stopped.
a) What number did Masha end up with?
b) What is the smallest number Masha could have started with (indicate its last two digits)
|
Answer: a) 17; b) 09 (the number $100 \ldots 0009$).
Solution. a) Let this number be $n$, ending in the digit $y$. Then $n=10 x+y$ after the next operation will become $3 x+2 y$. The equation $10 x+y=3 x+2 y$ is equivalent to $7 x=y$ and, since $y$ is a digit, then $y=7, x=1$. Therefore, $n=17$.
b) Note that if the initial number is not equal to 17, then it must decrease: $10 x+y>3 x+2 y \Leftrightarrow 7 x>y$ (which for $x \neq 0$ and $x \neq 1$ is always true). From the relation $2(10 x+y)=17 x+3 x+2 y$ it follows that the number $10 x+y$ is divisible by 17 if and only if $3 x+2 y$ is divisible by 17. Since the stabilization of the operation occurs at the number 17, the initial number must also be divisible by 17.
Let's find the smallest 2015-digit number that is divisible by 17. For convenience, let's list the remainders of the powers of 10 when divided by 17 (see table):
| Power | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| Remainder | 10 | 15 | 14 | 4 | 6 | 9 | 5 | 16 | 7 | 2 | 3 | 13 | 11 | 8 | 12 | 1 | 10 |
Since the remainders repeat every 17 powers, and $10^{16} \equiv 1(\bmod 17)$ (this notation means that $10^{16}$ and 1 give the same remainder when divided by 17), and $2014=16 \cdot 125+14$, then $10^{2014} \equiv 10^{14} \equiv 8(\bmod 17)$, so $10^{2014}+9$ is divisible by 17. This will be the smallest 2015-digit number that is divisible by 17. It ends in 09.
Answer for variant 152: a) 17; b) 99 (the number 999...9999).
Answer for variant 153: a) 17; b) 05 (the number 100...0005).
Answer for variant 154: a) 17; b) 88 (the number 999...9988).
|
9
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. Solve the inequality
$$
8 \cdot \frac{|x+1|-|x-7|}{|2 x-3|-|2 x-9|}+3 \cdot \frac{|x+1|+|x-7|}{|2 x-3|+|2 x-9|} \leqslant 8
$$
In the answer, write the sum of its integer solutions that satisfy the condition $|x|<120$.
|
Answer: 6 (solution of the inequality: $\left.\left[\frac{3}{2} ; 3\right) \cup\left(3 ; \frac{9}{2}\right]\right)$.
Solution. Let $a$ and $b$ be the first and second terms in the left part of the inequality, respectively. Then $b>0$ and
$$
a b=24 \cdot \frac{(x+1)^{2}-(x-7)^{2}}{(2 x-3)^{2}-(2 x-9)^{2}}=24 \cdot \frac{8 \cdot(2 x-6)}{6 \cdot(4 x-12)}=16
$$
for $x \neq 3$, from which $a=\frac{16}{b}$. The inequality $\frac{16}{b}+b \leqslant 8\left(\Leftrightarrow\left(\frac{4}{\sqrt{b}}-\sqrt{b}\right)^{2} \leqslant 0\right)$ is satisfied only when $b=4$. It remains to solve the equation
$$
3 \cdot \frac{|x+1|+|x-7|}{|2 x-3|+|2 x-9|}=4
$$
If $x \geqslant 7$ or $x \leqslant-1$, the expression on the left side equals $\frac{3}{2}$. If $-1<x<\frac{3}{2}$ or $\frac{9}{2}<x<7$, it equals $\frac{6}{|3-x|}<4$. For all $\frac{3}{2} \leqslant x \leqslant \frac{9}{2}$, the equation turns into a true equality. Thus, taking into account the condition $x \neq 3$, we obtain the solution of the original inequality: $\left[\frac{3}{2} ; 3\right) \cup\left(3 ; \frac{9}{2}\right]$. The integer solutions are 2 and 4, both of which satisfy the condition $|x|<120$, their sum is 6.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3. Solve the inequality
$$
12 \cdot \frac{|x+10|-|x-20|}{|4 x-25|-|4 x-15|}-\frac{|x+10|+|x-20|}{|4 x-25|+|4 x-15|} \geqslant-6
$$
In the answer, write the sum of its integer solutions that satisfy the condition $|x|<100$.
|
Answer: 10 (solution of the inequality: $\left.\left[\frac{15}{4} ; 5\right) \cup\left(5 ; \frac{25}{4}\right]\right)$.)
|
10
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.4. Solve the inequality
$$
9 \cdot \frac{|x+4|-|x-2|}{|3 x+14|-|3 x-8|}+11 \cdot \frac{|x+4|+|x-2|}{|3 x+14|+|3 x-8|} \leqslant 6
$$
In the answer, write the sum of its integer solutions that satisfy the condition $|x|<110$.
|
Answer: -6 (solution of the inequality: $[-4 ;-1) \cup(-1 ; 2]$ ).
|
-6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Propose a word problem that reduces to solving the inequality
$$
\frac{11}{x+1.5}+\frac{8}{x} \geqslant \frac{12}{x+2}+2
$$
Write the problem statement, its solution, and the answer.
Example of the required problem. Points A and B are connected by two roads: one is 19 km long, and the other is 12 km long. At 12:00, a pedestrian left point A on the longer road and walked the first 11 km at a constant speed, and then, getting tired, walked the remaining distance to point B at an average speed 1.5 km/h slower. At 14:00, a second pedestrian left point A on the shorter road and walked the entire distance at an average speed 0.5 km/h faster than the first pedestrian initially walked. What was the average speed at which the first pedestrian walked the last 8 km of the journey, if it is known that he arrived at point B no earlier than the second pedestrian?
Brief solution. If \( x \) is the required average speed of the first pedestrian (in km/h) on the second part of the journey, then \( x+1.5 \) is his speed on the first part, and \( (x+1.5)+0.5=x+2 \) is the average speed of the second pedestrian. Then, by calculating the time each pedestrian spent on the journey, we obtain the required inequality. Since by the problem's condition \( x > 0 \), both sides of the inequality can be multiplied by the quantity \( x(x+1.5)(x+2) > 0 \), then we get \( 11x(x+2) + 8(x+1.5)(x+2) \geqslant 12x(x+1.5) + 2x(x+1.5)(x+2) \), or, after transformations, \( (x-4)(x+1)(x+3) \leqslant 0 \). Therefore, \( 0 < x \leqslant 4 \), and all found values of \( x \) satisfy the problem's condition.
|
Answer: no more than 4 km/h.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. (14 points) Find the greatest integer value of $a$ for which the equation
$$
(x-a)(x-7)+3=0
$$
has at least one integer root.
|
Answer: 11.
Solution. For the desired values of $a$, the numbers $x-a$ and $x-7$ are integers, and their product is -3, so there are 4 possible cases:
$$
\left\{\begin{array} { l }
{ x - a = 1 , } \\
{ x - 7 = - 3 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = 3 , } \\
{ x - 7 = - 1 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = - 1 , } \\
{ x - 7 = 3 ; }
\end{array} \quad \left\{\begin{array}{l}
x-a=-3 \\
x-7=1,
\end{array}\right.\right.\right.\right.
$$
from which we find respectively
$$
\left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 4 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 6 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 1 1 , } \\
{ x = 1 0 ; }
\end{array} \quad \left\{\begin{array}{l}
a=11 \\
x=8
\end{array}\right.\right.\right.\right.
$$
Thus, the desired values are $a=3$ and $a=11$, of which the largest is 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. Find the sum of all roots of the equation $x^{2}-31 x+220=2^{x}\left(31-2 x-2^{x}\right)$.
|
Answer: 7. Solution. The original equation is equivalent to the equation $\left(x+2^{x}\right)^{2}-31\left(x+2^{x}\right)+220=0 \Leftrightarrow\left[\begin{array}{l}x+2^{x}=11, \\ x+2^{x}=20 .\end{array}\right.$
Each of the equations in this system has no more than one root, as the function $f(x)=x+2^{x}$ is monotonically increasing. The first equation has a root $x=3$, and the second has a root $x=4$. The sum of the roots is 7.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2. Find the sum of all roots of the equation $x^{2}-41 x+330=3^{x}\left(41-2 x-3^{x}\right)$.
|
Answer: 5. Instructions. Roots of the equation: 2 and 3.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. In an isosceles triangle \(ABC\), one of the angles is equal to the difference of the other two, and one of the angles is twice another. The angle bisectors of angles \(A\), \(B\), and \(C\) intersect the circumcircle of the triangle at points \(L\), \(O\), and \(M\) respectively. Find the area of triangle \(LOM\), if the area of triangle \(ABC\) is 8. If the answer is not an integer, round it to the nearest integer.
|
Answer: 11. Solution. Let in triangle $ABC$ the angle $\alpha$ be equal to the difference of angles $\beta-\gamma$. Since $\alpha+\beta+\gamma=180^{\circ}$, then $\beta-\gamma+\beta+\gamma=180^{\circ}$ and therefore $\beta=90^{\circ}$. If $\beta=90^{\circ}$ is twice one of the angles $\alpha$ or $\gamma$, then the triangle will be isosceles, which contradicts the condition. Let for definiteness $\alpha>\gamma$. Then $\beta=90^{\circ}, \alpha=60^{\circ}, \gamma=30^{\circ}$.
By the inscribed angle theorem:
$\angle MLC = \angle MBC = 45^{\circ}, \angle CLO = \angle CAO = 30^{\circ}$. Therefore, $\angle MLO = 75^{\circ}$. Similarly,
$\angle LOM = \angle LOA + \angle AOM = \angle LCA + \angle ABM = 15^{\circ} + 45^{\circ} = 60^{\circ}$,
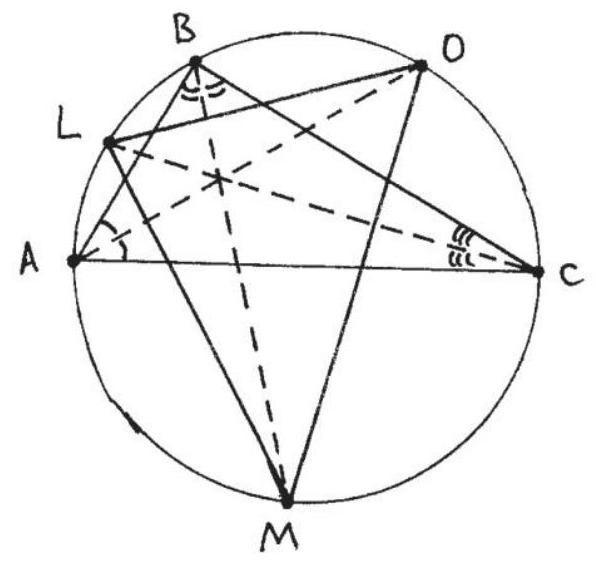
$\angle OML = \angle OMB + \angle BML = \angle OAB + \angle BCL = 30^{\circ} + 15^{\circ} = 45^{\circ}$.
Thus, the angles of triangle $LOM$ are $\alpha_{1}=75^{\circ}, \beta_{1}=60^{\circ}, \gamma_{1}=45^{\circ}$.
Using the sine rule, we get the formula for the area of a triangle inscribed in a circle of radius $R: S=\frac{1}{2} a b \sin \gamma=\frac{1}{2} \cdot 2 R \sin \alpha \cdot 2 R \sin \beta \cdot \sin \gamma=2 R^{2} \sin \alpha \sin \beta \sin \gamma$.
Therefore, $\frac{S_{LOM}}{S_{ABC}}=\frac{2 R \cdot \sin \alpha_{1} \sin \beta_{1} \sin \gamma_{1}}{2 R \cdot \sin \alpha \sin \beta \sin \gamma}=\frac{\sin 75^{\circ} \sin 60^{\circ} \sin 45^{\circ}}{\sin 90^{\circ} \sin 60^{\circ} \sin 30^{\circ}}=\sqrt{2} \cdot \sin 75^{\circ}$. Since $\sin 75^{\circ}=\sin \left(45^{\circ}+30^{\circ}\right)=\frac{\sqrt{6}+\sqrt{2}}{4}$, we get: $\frac{S_{LOM}}{S_{ABC}}=\frac{\sqrt{3}+1}{2}$.
Therefore, $S_{LOM}=4 \sqrt{3}+4 \approx 11$.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.4. Find the minimum value of the expression $(\sqrt{2(1+\cos 2 x)}-\sqrt{3-\sqrt{2}} \sin x+1) \cdot(3+2 \sqrt{7-\sqrt{2}} \cos y-\cos 2 y)$. If the answer is not an integer, round it to the nearest integer.
|
Answer: -9 . Instructions. Exact answer: $2 \sqrt{2}-12$.
|
-9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Find the largest integer $k$ such that for at least one natural number $n>1000$, the number $n!=1 \cdot 2 \cdot \ldots \cdot n$ is divisible by $2^{n+k+2}$.
|
Answer: -3. Solution. The highest power of two that divides $n!$ is the finite sum $\left[\frac{n}{2^{1}}\right]+\left[\frac{n}{2^{2}}\right]+\ldots \leq \frac{n}{2^{1}}+\frac{n}{2^{2}}+\ldots<n$, so it does not exceed $n-1$. At the same time, the equality of this power to the value $n-1$ is achieved at powers of two (for example, when $n=2^{10}=1024$). Therefore, $(k+2)_{\max }=-1, k_{\max }=-3$.
|
-3
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. A set of natural numbers is called bad if it is possible to select several numbers from it such that their sum equals 2012. Find the smallest such $n$ that the numbers $503, 504, \ldots, 2011$ can be partitioned into $n$ sets such that none of these sets are bad.
|
Answer: $n=2$.
Solution: We will show that the given set can be divided into two subsets, neither of which are bad. Consider the sets $M_{1}=\{503,504, \ldots, 671\}$, $M_{2}=\{672,673, \ldots, 1006\}$, $M_{3}=\{1007,1008, \ldots, 1340\}$, $M_{4}=\{1341,1342, \ldots, 2011\}$, and show that $M_{1} \cup M_{3}$ and $M_{2} \cup M_{4}$ are not bad.
We will prove that $M_{1} \cup M_{3}$ is not bad. Consider the cases:
- Four numbers from the set $M_{1}$ give a sum $S \geqslant 503+504+505+506=$ $2018>2012$
- Three numbers from the set $M_{1}$ give a sum $S \leqslant 669+670+671=2010<2012$
- One number from the set $M_{1}$ and one from $M_{3}$ give a sum $S \leqslant 671+1340=$ $2011<2012$;
Similarly, it can be proven for $M_{2} \cup M_{4}$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1.1. (2 points) Find the greatest value of $x$ that satisfies the inequality
$$
\left(6+5 x+x^{2}\right) \sqrt{2 x^{2}-x^{3}-x} \leqslant 0
$$
|
Answer: 1.
Solution.
$$
\left[\begin{array} { c }
{ 2 x ^ { 2 } - x ^ { 3 } - x = 0 ; } \\
{ \{ \begin{array} { c }
{ 2 x ^ { 2 } - x ^ { 3 } - x > 0 ; } \\
{ 6 + 5 x + x ^ { 2 } \leqslant 0 ; }
\end{array} }
\end{array} \Longleftrightarrow \left[\begin{array} { l }
{ - x ( x - 1 ) ^ { 2 } = 0 ; } \\
{ \{ \begin{array} { c }
{ - x ( x - 1 ) ^ { 2 } > 0 ; } \\
{ ( x + 2 ) ( x + 3 ) \leqslant 0 ; }
\end{array} }
\end{array} \Longleftrightarrow \left[\begin{array}{l}
x=0 \\
x=1 ; \\
\left\{\begin{array}{l}
x<0 ; \\
-3 \leqslant x \leqslant-2
\end{array}\right.
\end{array}\right.\right.\right.
$$
All solutions of the last system are negative. Therefore, the greatest solution of the original inequality will be 1.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.3.1. (12 points) Simplify the expression
$$
\left(\frac{2}{\sqrt[3]{3}}+3\right)-\left(\frac{\sqrt[3]{3}+1}{2}-\frac{1}{\sqrt[3]{9}+\sqrt[3]{3}+1}-\frac{2}{1-\sqrt[3]{3}}\right): \frac{3+\sqrt[3]{9}+2 \sqrt[3]{3}}{2}
$$
Answer: 3.
|
Solution. Let's introduce the notation $a=\sqrt[3]{3}$. Then the expression transforms to
$$
\left(\frac{2}{a}+3\right)-\left(\frac{a+1}{a^{3}-1}-\frac{1}{a^{2}+a+1}-\frac{2}{1-a}\right): \frac{a^{3}+a^{2}+2 a}{a^{3}-1}
$$
and after simplifications and performing the division, it transforms to $\left(\frac{2}{a}+3\right)-\frac{2}{a}$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.2.1. (12 points) Every morning, each member of the Ivanov family drinks an 180-gram cup of coffee with milk. The amount of milk and coffee in their cups varies. Masha Ivanova found out that she drank $\frac{2}{9}$ of all the milk consumed that morning and $\frac{1}{6}$ of all the coffee consumed that morning. How many people are in this family?
|
Answer: 5.
Solution. Let there be $x$ (for example, grams) of milk and $y$ grams of coffee, and $n$ people in the family. Since each family member drank the same amount of coffee with milk, then $\left(\frac{2 x}{9}+\frac{y}{6}\right) n=$ $=x+y \Leftrightarrow(4 x+3 y) n=18 x+18 y \Leftrightarrow 2 x(2 n-9)=3 y(6-n)$. From this, it follows that $2 n-9$ and $6-n$ have the same sign, that is, $4.5<n<6$. Since $n$ is an integer, then $n=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.3.1. (12 points) Among all possible triangles $ABC$ such that $BC=2 \sqrt[4]{3}, \angle BAC=\frac{\pi}{3}$, find the one with the maximum area. What is this area?
|
Answer: 3.
Solution. The locus of points from which the segment $B C$ is "seen" at an angle $\alpha$ consists of arcs of two circles, from the centers of which the segment $B C$ is "seen" at an angle $2 \pi-2 \alpha$. The points on these arcs that are farthest from the segment are their midpoints. Therefore, the desired triangle is isosceles, and its area is $\frac{a^{2}}{4 \operatorname{tg} \frac{\alpha}{2}}$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.2.1. (12 points) Calculate the value of the expression $\arccos \frac{\sqrt{6}+1}{2 \sqrt{3}}-\arccos \sqrt{\frac{2}{3}}$. Write the obtained expression in the form $\frac{a \pi}{b}$, where $a$ and $b$ are integers, and are coprime, and specify the value of $|a-b|$.
#
|
# Answer: 7.
Solution. Since $\alpha=\arccos \frac{\sqrt{6}+1}{2 \sqrt{3}} \in\left(0 ; \frac{\pi}{2}\right)$ and $\beta=\arccos \sqrt{\frac{2}{3}} \in\left(0 ; \frac{\pi}{2}\right)$, then $A=\alpha-\beta \in\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)$. Therefore, $\sin A=\sin \alpha \cos \beta-\cos \alpha \sin \beta$. After calculations, we get $\sin A=-\frac{1}{2}$, from which it follows that $A=-\frac{\pi}{6}$. Thus, $a=-1, b=6$, and $|a-b|=7$. Note that the answer can also be written as $a=1, b=-6$, but the absolute value of the difference remains the same.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.4.1. (12 points) How many integer roots of the equation
$$
\cos 2 \pi x + \cos \pi x = \sin 3 \pi x + \sin \pi x
$$
lie between the roots of the equation $x^{2} + 10 x - 17 = 0$?
|
# Answer: 7.
Solution. If $x=2 k, k \in \mathbb{Z}$, then $\cos 2 \pi x+\cos \pi x=\cos 4 \pi k+\cos 2 \pi k=2, \sin 3 \pi x+\sin \pi x=$ $\sin 6 \pi k+\sin 2 \pi k=0$, so there are no even numbers among the roots of the first equation.
If, however, $x=2 k+1, k \in \mathbb{Z}$, then $\cos 2 \pi x+\cos \pi x=\cos (4 \pi k+2 \pi)+\cos (2 \pi k+\pi)=0, \sin 3 \pi x+\sin \pi x=$ $\sin (6 \pi k+3 \pi)+\sin (2 \pi k+\pi)=0$, so all odd numbers are roots of the first equation.
The roots of the second equation are $-5 \pm \sqrt{42}$; the smaller one lies between -12 and -11, and the larger one lies between 1 and 2. Thus, between the roots of the second equation lie 7 odd numbers $-11,-9,-7,-5,-3,-1,1$, which are 7 integer roots of the first equation.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.2.1. (12 points) Find the greatest integer value of $a$ for which the equation
$$
\sqrt[3]{x^{2}-(a+7) x+7 a}+\sqrt[3]{3}=0
$$
has at least one integer root.
|
Answer: 11.
Solution. For the desired values of $a$, the numbers $x-a$ and $x-7$ are integers, and their product is -3, so there are 4 possible cases:
$$
\left\{\begin{array} { l }
{ x - a = 1 , } \\
{ x - 7 = - 3 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = 3 , } \\
{ x - 7 = - 1 ; }
\end{array} \quad \left\{\begin{array} { l }
{ x - a = - 1 , } \\
{ x - 7 = 3 ; }
\end{array} \quad \left\{\begin{array}{l}
x-a=-3 \\
x-7=1
\end{array}\right.\right.\right.\right.
$$
from which we find respectively
$$
\left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 4 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 3 , } \\
{ x = 6 ; }
\end{array} \quad \left\{\begin{array} { l }
{ a = 1 1 , } \\
{ x = 1 0 ; }
\end{array} \quad \left\{\begin{array}{l}
a=11 \\
x=8
\end{array}\right.\right.\right.\right.
$$
Thus, the desired values are $a=3$ and $a=11$, of which the largest is 11.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.3.1. (12 points) The curve given by the equation $y=2^{p} x^{2}+5 p x-2^{p^{2}}$ intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. Find the sum of all values of the parameter $p$ for which the center of the circle circumscribed around triangle $A B C$ lies on the $O x$ axis.
|
Answer: -1.
Solution. Let $x_{1}$ and $x_{2}$ be the roots of the quadratic trinomial $a x^{2}+b x+c (c \neq 0)$, the graph of which intersects the $O x$ axis at points $A$ and $B$, and the $O y$ axis at point $C$. Then $A\left(x_{1} ; 0\right), B\left(x_{2} ; 0\right), C(0 ; c)$. The fact that the center of the circle circumscribed around triangle $A B C$ lies on the $O x$ axis is equivalent to the angle $A C B$ being a right angle. It is not difficult to find that the slope of the line $A C$ is $k_{1}=-\frac{c}{x_{1}}$, and the slope of the line $B C$ is $k_{2}=-\frac{c}{x_{2}}$. The perpendicularity of these lines is equivalent to the condition $k_{1} \cdot k_{2}=-1$, that is, $x_{1} x_{2}=-c^{2}$, which, taking into account Vieta's theorem, can be rewritten as $a c=-1$.
For the trinomial from the problem statement, the condition $a c=-1$ becomes $2^{p+p^{2}}=1$, from which $p=0$, $p=-1$.
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.4.1. (12 points) Find all pairs of integers $(x, y)$ that are solutions to the equation
$$
7 x y-13 x+15 y-37=0 \text {. }
$$
In your answer, indicate the sum of the found values of $x$.
|
Answer: 4.
Solution. Multiplying both sides of the equation by 7, we get
$$
7 \cdot 7 x y - 13 \cdot 7 x + 15 \cdot 7 y - 37 \cdot 7 = 0
$$
Rewriting this equation, we have
$$
(7 x + 15)(7 y - 13) = 64
$$
If $x$ and $y$ are integers, then the numbers $7 x + 15$ and $7 y - 13$ are also integers and leave a remainder of 1 when divided by 7. All possible factorizations of the number 64 into the product of two integers are as follows:
$$
64 = 1 \cdot 64 = 2 \cdot 32 = 4 \cdot 16 = 8 \cdot 8 = -1 \cdot (-64) = -2 \cdot (-32) = -4 \cdot (-16) = -8 \cdot (-8)
$$
Among these factors, the numbers that leave a remainder of 1 when divided by 7 are 1, 8, and 64. Therefore, the possible cases are
$$
\begin{gathered}
7 x + 15 = 1, 7 y - 13 = 64 \Rightarrow (x, y) = (-2, 11) \\
7 x + 15 = 8, 7 y - 13 = 8 \Rightarrow (x, y) = (-1, 3) \\
7 x + 15 = 64, 7 y - 13 = 1 \Rightarrow (x, y) = (7, 2)
\end{gathered}
$$
Thus, the sum of the possible values of $x$ is $-2 - 1 + 7 = 4$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Find the minimum value of the discriminant of a quadratic trinomial, the graph of which has no common points with the regions located below the x-axis and above the graph of the function $y=\frac{1}{\sqrt{1-x^{2}}}$.
|
Answer: -4.
Solution. Since the discriminant of a quadratic trinomial
$$
D=b^{2}-4 a c
$$
we will find the maximum value of the product $a c$. Since for all $x$ the inequality $a x^{2}+b x+c \geqslant 0$ holds, then $a \geqslant 0, c \geqslant 0$. Let
$$
f(x)=\frac{1}{\sqrt{1-x^{2}}}-\left(a x^{2}+b x+c\right)
$$
Since for all $|x|<1$ it is true that $f(x) \geqslant 0$, then
$$
0 \leqslant f\left(\frac{1}{\sqrt{2}}\right)+f\left(-\frac{1}{\sqrt{2}}\right)=2 \sqrt{2}-(a+2 c)
$$
Thus, $a+2 c \leqslant 2 \sqrt{2}$, so from the inequality between the arithmetic mean and the geometric mean, we get:
$$
2 \sqrt{2} \geqslant a+2 c \geqslant 2 \cdot \sqrt{a \cdot 2 c}=2 \sqrt{2} \sqrt{a c}
$$
Therefore, $a c \leqslant 1$.
We will prove that 1 is the maximum of $a c$. Indeed, let $a=2 c=\sqrt{2}, b=0$, then the original inequality takes the form:
$$
\sqrt{2} x^{2}+\frac{1}{\sqrt{2}} \leqslant \frac{1}{\sqrt{1-x^{2}}} \Leftrightarrow\left\{\begin{array}{l}
\left(2 x^{2}-1\right)^{2}\left(x^{2}+1\right) \geqslant 0 \\
|x|<1
\end{array}\right.
$$
Therefore, for the discriminant of the quadratic trinomial, the following inequalities hold:
$$
D=b^{2}-4 a c \geqslant-4 a c \geqslant-4
$$
and its minimum value is -4.
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. In triangle $ABC$, the bisectors $AL, BM$, and $CN$ are drawn, and $\angle ANM = \angle ALC$. Find the radius of the circumcircle of triangle $LMN$, two sides of which are equal to 3 and 4.
|
Answer: 2
Solution.
The following statement is true:
Let $A L, B M$ and $C N$ be the bisectors of the internal angles of a triangle. If $\angle A N M = \angle A L C$, then $\angle B C A = 120^{\circ}$.
Proof. Draw $M D \| A L$, then $\angle C M D = \frac{\alpha}{2}$. The angle $\angle A L C$ is an external angle of triangle $A L B$, so $\angle A N M = \angle A L C = \frac{\alpha}{2} + \beta$. The angle $\angle B M C$ is an internal angle of triangle $B M C$, so $\angle B M C = \pi - \frac{\beta}{2} - \gamma = \alpha + \frac{\beta}{2}$. Therefore, $\angle B M D = \alpha + \frac{\beta}{2} - \frac{\alpha}{2} = \frac{\alpha + \beta}{2}$. The angle $\angle N M C$ is an external angle of triangle $A N M$, so $\angle N M C = \frac{3 \alpha}{2} + \beta$. Therefore, $\angle B M N = \frac{3 \alpha}{2} + \beta - \frac{\alpha + \beta}{2} - \frac{\alpha}{2} = \frac{\alpha + \beta}{2}$. This means triangles $B M N$ and $B M D$ are congruent, so $N M = M D$ and $\angle M D N = \frac{\pi - (\alpha + \beta)}{2} = \frac{\gamma}{2}$. Therefore, points $N, M, C$ and $D$ lie on the same circle, and since $N M$ and $N D$ are chords subtending equal arcs, $N M = N D$, i.e., triangle $N M D$ is equilateral, so $\frac{\gamma}{2} = \frac{\pi}{3}$. Therefore, $\angle B C A = 120^{\circ}$ (see Fig. 4).
Fig. 4
Remark. The converse statement is also true: if $\angle B C A = 120^{\circ}$ and $A L, B M$ and $C N$ are the bisectors of the internal angles of the triangle, then $\angle A N M = \angle A L C$.
The line $C B$ is the bisector of angle $N C F$ ( $\Rightarrow$ point $L$ is equidistant from lines $C N$ and $C F$ ), and the line $A L$ is the bisector of angle $B A F$ ( $\Rightarrow$ point $L$ is equidistant from lines $A N = N B$ and $A F = C F$). Therefore, point $L$ is equidistant from lines $N C$ and $N B$, i.e., line $N L$ is the bisector of angle $B N C$. Similarly, the line $C A$ is the bisector of angle $E C N$ ( $\Rightarrow$ point $M$ is equidistant from lines $C N$ and $C E$ ), and the line $B M$ is the bisector of angle $A B C$ ( $\Rightarrow$ point $M$ is equidistant from lines $B A = N A$ and $B E = C E$). Therefore, point $M$ is equidistant from lines $N A$ and $N C$, i.e., line $N M$ is the bisector of angle $A N C$. Therefore, $\angle M N L = 90^{\circ}$ (see Fig. 5).
Let's estimate the values that the tangents of the acute angles of $\triangle L M N$ can take.
From $\triangle A N C$ we get that $\angle A N C = 120^{\circ} - \alpha \Rightarrow \angle M N C = 60^{\circ} - \frac{\alpha}{2} \Rightarrow \angle N M C = 60^{\circ} + \frac{\alpha}{2}$.
From $\triangle B N C$ we get that $\angle B N C = 120^{\circ} - \beta \Rightarrow \angle L N C = 60^{\circ} - \frac{\beta}{2} \Rightarrow \angle N L C = 60^{\circ} + \frac{\beta}{2}$.
By the Law of Sines for $\triangle N M C$ we get: $\frac{N C}{\sin \angle N M C} = \frac{N M}{\sin \angle N C M} \Rightarrow N C = \frac{2 N M \sin \left(60^{\circ} + \frac{\alpha}{2}\right)}{\sqrt{3}}$.
By the Law of Sines for $\triangle N L C$ we get: $\frac{N C}{\sin \angle N L C} = \frac{N L}{\sin \angle N C L} \Rightarrow N C = \frac{2 N L \sin \left(60^{\circ} + \frac{\beta}{2}\right)}{\sqrt{3}}$.
Considering the equality $\frac{\alpha}{2} + \frac{\beta}{2} = 30^{\circ}$ from the last two relations, we get that
$$
\operatorname{tg} \angle N L M = \frac{N M}{N L} = \frac{\sin \left(90^{\circ} - \frac{\alpha}{2}\right)}{\sin \left(60^{\circ} + \frac{\alpha}{2}\right)}
$$
Since $\frac{\alpha}{2} \in (0^{\circ}, 30^{\circ})$ and the function $y = \sin t$ is increasing in the first quadrant, then $\operatorname{tg} \angle N L M \in \left(\frac{\sqrt{3}}{2} ; \frac{2}{\sqrt{3}}\right)$. If 3 and 4 are the lengths of the legs of $\triangle N L M$, then either $\operatorname{tg} \angle N L M = \frac{3}{4}$ or $\operatorname{tg} \angle N L M = \frac{4}{3}$. But since $\frac{3}{4} < \frac{\sqrt{3}}{2} = \sqrt{\frac{3}{4}}$, this case is impossible. Therefore, only the case where $M L = 4$ (hypotenuse) and 3 is the length of one of the legs is possible. The length of the other leg by the Pythagorean theorem is $\sqrt{7}$. Since the inequalities $\frac{\sqrt{3}}{2} < \frac{\sqrt{7}}{3} < \frac{2}{\sqrt{3}} \Leftrightarrow \frac{3}{4} < \frac{7}{9} < \frac{4}{3}$ hold, this case is realized. Since in a right triangle the radius of the circumscribed circle is half the hypotenuse, then
$$
R = \frac{M L}{2} = 2
$$
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Problem 4. The Dursleys are hiding Harry Potter on an island that is 9 km from the shore. The shore is straight. On the shore, 15 kilometers from the point on the shore closest to the island, Hagrid is on a magical motorcycle and wants to reach Harry as quickly as possible. The motorcycle travels along the shore at a speed of $50 \mathrm{km} /$ hour, and over the sea at a speed of 40 km/hour. Hagrid's plan is: first travel $X$ kilometers along the shore, and then head straight for the island. What value of $X$ is best suited for Hagrid's purposes?
|
# Answer: 3.
Solution. Let $A$ be the point from which Hagrid starts, $B$ be the island, and $C$ be the point where the motorcycle crashes into the sea. The travel time is $t=\frac{A C}{50}+\frac{B C}{40}=p A C+q B C=q\left(\frac{p}{q} A C+B C\right)$, where $p=\frac{1}{50}, q=\frac{1}{40}$. Thus, we aim to minimize $\frac{p}{q} A C+B C$. Mark an arbitrary point $D$ on the shore, construct a circle with $A D$ as the diameter and radius $q \cdot s: 2$ (where $s$ is arbitrary). Draw a circle centered at $D$ with radius $p \cdot s$, and let this circle intersect the first on land at point $E$. Drop a perpendicular $B F$ from $A E$, and it will intersect the shoreline at the optimal point $C$.
We will prove that $\frac{p}{q} A C+B C$ is minimal. From the similarity of triangles $A F C$ and $A E D$, it follows that $C F / A C=D E / A D=\frac{p}{q}, C F=\frac{p}{q} A C$, which means $\frac{p}{q} A C+B C=B F$. If we take any other point $M$ on the shore and calculate $\frac{p}{q} A M+B M$, we get the following: $\frac{p}{q} A M+B M=K M+M B$, where $K M$ is the perpendicular from $K$ to $A E$. And in turn, $K M+M B>B K>B F$.
Let $L$ be the point on the shore closest to the island. Triangles $B C L$ and $A C F$ are similar, from which $C L=\frac{B L \cdot C F}{A F}$. Therefore, $C L=12$ and $A C=X=3$.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10.1. Propose a word problem that reduces to solving the inequality
$$
\frac{11}{x+1.5}+\frac{8}{x} \geqslant \frac{12}{x+2}+2
$$
Write the problem statement, its solution, and the answer.
Example of the required problem. Points A and B are connected by two roads: one is 19 km long, and the other is 12 km long. At 12:00, a pedestrian left point A on the longer road and walked the first 11 km at a constant speed, and then, getting tired, walked the remaining distance to point B at an average speed 1.5 km/h slower. At 14:00, a second pedestrian left point A on the shorter road and walked the entire distance at an average speed 0.5 km/h faster than the first pedestrian initially. What was the average speed of the first pedestrian for the last 8 km of the journey, if it is known that he arrived at point B no earlier than the second pedestrian?
Brief solution. If \( x \) is the required average speed of the first pedestrian (in km/h) on the second part of the journey, then \( x+1.5 \) is his speed on the first part, and \( (x+1.5)+0.5 = x+2 \) is the average speed of the second pedestrian. Then, by calculating the time each pedestrian spent on the journey, we obtain the required inequality. Since by the problem's condition \( x > 0 \), both sides of the inequality can be multiplied by the quantity \( x(x+1.5)(x+2) > 0 \), then we get \( 11x(x+2) + 8(x+1.5)(x+2) \geqslant 12x(x+1.5) + 2x(x+1.5)(x+2) \), or, after transformations, \( (x-4)(x+1)(x+3) \leqslant 0 \). Therefore, \( 0 < x \leqslant 4 \), and all found values of \( x \) satisfy the problem's condition.
|
Answer: no more than 4 km/h.
|
4
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. (2 points) How many roots does the equation $x^{2}-x \sqrt{5}+\sqrt{2}=0$ have?
|
Answer: 0.
Solution. Since $D=5-4 \sqrt{2}<0$, the equation has no roots.
|
0
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4.1. (12 points) In trapezoid $A B C D$ with bases $A D=17$ and $B C=9$, points $E$ and $F$ are marked on the bases respectively such that $M E N F$ is a rectangle, where $M$ and $N$ are the midpoints of the diagonals of the trapezoid. Find the length of segment $E F$.
|
Answer: 4.
Solution. The segment connecting the midpoints of the diagonals of a trapezoid is equal to half the difference of the bases, so $M N=\frac{A D-B C}{2}=4$. Since $M E N F$ is a rectangle, its diagonals are equal. Therefore, $E F=M N=4$.
|
4
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the minimum value of the expression $\frac{1}{1-x^{2}}+\frac{4}{4-y^{2}}$ under the conditions $|x|<1,|y|<2$ and $x y=1$.
Answer: 4.
|
Solution. Using the inequality between the arithmetic mean and the geometric mean, under the given conditions on $x$ and $y$, we obtain
$$
\frac{1}{1-x^{2}}+\frac{4}{4-y^{2}} \geqslant 2 \sqrt{\frac{1}{1-x^{2}} \cdot \frac{4}{4-y^{2}}}=\frac{4}{\sqrt{5-4 x^{2}-y^{2}}}=\frac{4}{\sqrt{1-(2 x-y)^{2}}} \geqslant 4
$$
and all inequalities become equalities if $2 x=y$ and $x y=1$, i.e., $x=\frac{1}{\sqrt{2}}, y=\sqrt{2}$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Having walked $2 / 5$ of the length of a narrow bridge, a pedestrian noticed that a car was approaching the bridge from behind. Then he walked back and met the car at the beginning of the bridge. If the pedestrian had continued walking forward, the car would have caught up with him at the end of the bridge. Find the ratio of the car's speed to the pedestrian's speed.
|
Answer: 5.
Solution. In the time $t$ that the pedestrian walked towards the car until they met at the beginning of the bridge, he covered $2 / 5$ of the bridge's length. Therefore, if the pedestrian continued walking forward, in time $t$ he would have covered another $2 / 5$ of the bridge's length, and he would have $1 / 5$ of the bridge's length left to walk, while according to the problem, the car would have reached the beginning of the bridge in time $t$ and would have the entire bridge left to travel before meeting the pedestrian. Thus, the ratio of the car's speed to the pedestrian's speed is 5.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. How many solutions does the equation
\[
\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}=\frac{2}{x^{2}} ?
\]
|
Answer: 1.
Solution. Let's introduce the functions $f(x)=\frac{1}{(x-1)^{2}}+\frac{1}{(x-2)^{2}}$ and $g(x)=\frac{2}{x^{2}}$.
For $x<0$, both functions $f$ and $g$ are positive, but $f(x)$ increases from $+\infty$ to 2 (not inclusive), since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}<0 \quad \text { for } \quad x \in(-\infty ; 0)$, while $g(x)$ decreases from $+\infty$ to 2 (not inclusive), since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(-\infty ; 0)$. Therefore, for $x<0$, the equation $f(x)=g(x)$ has no solutions.
For $0<x<1$, the function $f$ decreases from $+\infty$ to 2 (not inclusive), since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}<0 \quad \text { for } \quad x \in(0 ; 1)$, while the function $g$ decreases from $+\infty$ to 2 (not inclusive), since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(0 ; 1)$. However, for $0<x<1$, the inequality $f(x)>g(x)$ holds, because $\frac{1}{(x-1)^{2}}>\frac{1}{x^{2}}$ and $\frac{1}{(x-2)^{2}}>\frac{1}{x^{2}}$, so $f(x)>g(x)$. Therefore, for $0<x<1$, the equation has no solutions.
For $x>2$, the function $f$ increases from 2 (not inclusive) to $+\infty$, since $f^{\prime}(x)=\frac{-2}{(x-1)^{3}}-\frac{2}{(x-2)^{3}}>0 \quad \text { for } \quad x \in(2 ; +\infty)$, while the function $g$ decreases from 2 (not inclusive) to 0, since $g^{\prime}(x)=\frac{-4}{x^{3}}<0 \quad \text { for } \quad x \in(2 ; +\infty)$. For $x>2$, the inequalities $0<\frac{1}{(x-1)^{2}}<\frac{1}{x^{2}}$ and $\frac{1}{(x-2)^{2}}<\frac{1}{x^{2}}$ hold, so $f(x)<g(x)$. Therefore, for $x>2$, the equation has no solutions.
## Second Solution.
The original equation, under the conditions $x \neq 0, x \neq 1, x \neq 2$, is equivalent to the equation $6 x^{3}-21 x^{2}+24 x-8=0$. Consider the function $f(x)=6 x^{3}-21 x^{2}+24 x-8$. Since $f^{\prime}(x)=18 x^{2}-42 x+24$, $x=1$ is a point of maximum, and $x=\frac{4}{3}$ is a point of minimum. The function $f$ is increasing on the domain $(-\infty, 1) \cup\left(\frac{4}{3} ;+\infty\right)$ and decreasing on the interval $\left(1 ; \frac{4}{3}\right)$. Since $f(0)=-8, f(1)=1, f\left(\frac{4}{3}\right)=\frac{8}{9}$, the equation $f(x)=0$ has a unique root, which lies in the interval $(0 ; 1)$.
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Given three points, the distances between which are 4, 6, and 7. How many pairwise distinct triangles exist for which each of these points is either a vertex or the midpoint of a side?
|
Answer: 11.
Solution. Let's list all the constructions of triangles that satisfy the condition of the problem, with
| | Description of the triangle | | Side lengths |
| :---: | :---: | :---: | :---: |
| №1 | All points are vertices | | $4,6,7$ |
| | One point is a vertex, two are midpoints of sides | | |
| №2 | | The vertex is at the extension of both sides of lengths 4 and 6 | $8,12,14$ |
| №3 | | The extension of the side of length 4 | $8,14,2 \sqrt{94}$ |
| №4 | | The extension of the side of length 6 | $12,14,2 \sqrt{154}$ |
| №5 | | The vertex is at the extension of both sides of lengths 4 and 7 | $8,12,14$ |
| №6 | | The extension of the side of length 4 | $8,12,2 \sqrt{55}$ |
| №7 | | The extension of the side of length 7 | $12,14,2 \sqrt{154}$ |
indicating the lengths of the sides.
| №8 | | The vertex is at the extension of both sides of lengths 6 and 7 | $8,12,14$ |
| :---: | :---: | :---: | :---: |
| №9 | | The extension of the side of length 6 | $8,12,2 \sqrt{55}$ |
| $\overline{№ 10}$ | | The extension of the side of length 7 | $8,14,2 \sqrt{94}$ |
| | Two points are vertices, one is the midpoint of a side | | |
| №11 | | The vertices are on the side of length 4, the side of length 7 is extended | $4,14, \sqrt{154}$ |
| $\overline{№ 12}$ | | The side of length 6 is extended | $4,12, \sqrt{154}$ |
| №13 | | The vertices are on the side of length 6, the side of length 4 is extended | $6,8, \sqrt{94}$ |
| №14 | | The side of length 7 is extended | $6,14, \sqrt{94}$ |
| №15 | | The vertices are on the side of length 7, the side of length 4 is extended | $7,8, \sqrt{55}$ |
| №16 | | The side of length 6 is extended | $7,12, \sqrt{55}$ |
| №17 | All points are midpoints of sides | | $8,12,14$ |
Thus, there are 17 ways of construction, leading to 11 different triangles.
|
11
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. The divisors of a natural number $n$ (including $n$ and 1), which has more than three divisors, were listed in ascending order: $1=d_{1}<d_{2} \ldots<d_{k}=n$. The differences $u_{1}=d_{2}-d_{1}, u_{2}=d_{3}-d_{2}, \ldots, u_{k-1}=d_{k}-d_{k-1}$ turned out to be such that $u_{2}-u_{1}=u_{3}-u_{2}=\ldots=u_{k-1}-u_{k-2}$. Find all such $n$. (S. Berlov)
|
Answer: 10. Solution: Let $n$ be odd. Then $u_{k-1}=d_{k}-d_{k-1} \geq n-n / 3=2 n / 3$. In this case, $u_{k-2}=d_{k-1}-d_{k-2}n / 3$, but $u_{k-1}-u_{k-2}=u_{k-2}-u_{k-3}<u_{k-2}<n / 3$ - a contradiction. In the case of even $n$, we get $u_{k-1}=d_{k}-d_{k-1}=n / 2, u_{k-2}=d_{k-1}-d_{k-2}=n / 2-d_{k-2}$, so $u_{k-1}-u_{k-2}=d_{k-2}$. But $u_{2}-u_{1}=d_{3}-2 d_{2}+d_{1}=d_{3}-3$, which can only equal $d_{k-2}$ when $k=4$. Then $d_{k-2}=d_{2}=2, d_{3}=n / 2=d_{2}+3=5$ and $n=10$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. From the odd natural numbers from 1 to 47, 12 fractions less than 1 were formed, using each number exactly once. The resulting fractions were divided into groups of equal values. What is the smallest number of groups that could have been obtained? (I. Rubanov)
|
Answer: 7. Solution: Evaluation. A fraction containing at least one of the prime numbers 17, 19, 23, 29, 31, 37, 41, 43, 47 cannot equal any of our other fractions, because already $17 \cdot 3 > 47$. Since there are no more than nine such "lonely" fractions, among the constructed fractions there are some that are not equal to them. Therefore, if there are at least six "lonely" fractions, there are no fewer than seven groups of equal fractions. Suppose there are five "lonely" fractions (obviously, there cannot be fewer). Replace one of the remaining fractions with an equivalent irreducible fraction $\mathrm{m} / \mathrm{n}$. Since all fractions are less than 1, then $n \geq 3$. The denominators of fractions equal to $m / n$ are odd, multiples of $n$, and do not exceed 47. If $n \geq 5$, then there are no more than five such denominators, and among the seven remaining fractions, there will be two that are not equal; the evaluation is proven. For $n=3$, there are eight odd numbers that are multiples of 3 and do not exceed 47: $3, 9, 15, 21, 27, 33, 39, 45$. But all the remaining fractions after reduction should give $1 / 3$, and in one set, fractions $1 / 3$ and $3 / 9$, as well as fractions $5 / 15$ and $15 / 45$, cannot coexist, so there are no more than six fractions equal to $1 / 3$. Thus, in this case, among the seven remaining fractions, there will be two that are not equal. Example when there are exactly 7 classes: $\{1 / 3, 5 / 15, 7 / 21, 9 / 27, 11 / 33, 13 / 39\}, \{25 / 41\}, \{35 / 43\}, \{45 / 47\}, \{17 / 19\}, \{23 / 29\}, \{31 / 37\}$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. For what largest $n$ can the numbers $1,2, \ldots, 14$ be colored red and blue so that for any number $k=1,2, \ldots, n$ there exist a pair of blue numbers whose difference is $k$, and a pair of red numbers whose difference is also $k$? (D. Khramtsov)
|
Answer: $n=11$. Solution. Obviously, $\mathrm{n} \leq 12$, since there is only one pair of numbers with a difference of 13. Suppose the required is possible for $n=12$. The number 12 can be represented as the difference of numbers from 1 to 14 in exactly two ways: 13-1 and 14-2. Let the number 1 be red for definiteness. Then the number 13 is also red, and the numbers 2 and 14 are blue. Next, there are three pairs with a difference of 11: 12-1, 13-2, 14-3. The pair 13 and 2 is bicolored, so the other two pairs are monochromatic, which means the number 12 is red (like 1), and the number 3 is blue. Continuing in this way to consider differences of $10, 9, 8$, and 7, at each step we will find that all possible pairs, except for two, are already bicolored, and therefore the colors of two more numbers are uniquely determined. In the end, we will find that the numbers from 2 to 7 inclusive are blue, and the numbers from 8 to 13 are red. But in this case, the number 6 cannot be represented as the difference of either red or blue numbers - a contradiction. Therefore, $n \leq 11$. It remains to show that $n$ can equal 11. One example looks like this: the numbers $1,2,4,6,8,10,12$ are red, and the numbers 14, 13, 11, 9, 7, 5, 3 are blue (the arrangement of blue and red numbers is symmetric relative to the midpoint of the segment [1, 14]). There are other examples as well.
|
11
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. For four different integers, all their pairwise sums and pairwise products were calculated and written on the board. What is the smallest number of different numbers that could have appeared on the board? (I. Rubanov)
|
Answer: 6. Solution: If we take the numbers $-1,0,1,2$, it is easy to verify that each of the numbers written on the board will be equal to -2, -1, 0, 1, 2, or 3 - a total of 6 different values. We will show that fewer than six different numbers could not appear on the board. Let the taken numbers be $ac+d$. If $ac+d$. Variant for completing the solution. Let $u$ and $v$ be the two largest numbers in absolute value, with $|u| \leq|v|$. If $|u| \geq 2$, then $|uv| \geq 2|v|$, which is greater than any sum. If $|u| \leq 1$, then among the original numbers there must be $-1,0$, 1. If $v>0$, at least 6 different numbers are written on the board: $-1,0,1, v,-v, v+1$. The case $v<0$ is handled similarly.
Criteria. Only the answer - 0 points.
A correct example for 6 - 2 points.
Proved that there are no fewer than five values, with no further substantial progress - 1 point.
Proved that there are no fewer than 6 different numbers, but no example - 3 points.
A correct example for 6 and proof that there are no fewer than five values, without further substantial progress - 3 points.
The same plus substantial, but incomplete progress in proving the existence of a sixth value - 4 points.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $ABC$, $AC=1$, $AB=2$, $O$ is the point of intersection of the angle bisectors. A segment passing through point $O$ parallel to side $BC$ intersects sides $AC$ and $AB$ at points $K$ and $M$ respectively. Find the perimeter of triangle $AKM$.
|
Answer: 3. Solution. Note that $\angle K C O=\angle B C O=\angle K O C$ (alternate interior angles). Therefore, $O K=K C$. Similarly, $B M=O M$. Therefore, $A K+A M+K M=A K+K C+A M+B M=3$.
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Viewers rate a movie with an integer number of points from 0 to 10. At any given time, the movie's rating is calculated as the sum of all the given ratings divided by their number. At some point in time $T$, the rating was an integer, and then with each new voting viewer, it decreased by one. What is the maximum number of viewers who could have voted after moment $T$? (O. Dmitriev, R. Zhenodarov)
|
Answer: 5. Solution: Consider a moment when the rating has decreased by 1. Suppose that before this, $n$ people had voted, and the rating was an integer $x$. This means the sum of the scores was $n x$. Let the next viewer give a score of $y$. Then the sum of the scores becomes $n x + y = (n + 1)(x - 1)$, from which we get $y = x - n - 1$. The maximum possible value of $x$ is 10, and the minimum possible value of $n$ is 1; therefore, the maximum value of $y$ (on the first such step) is 8. With each subsequent step, the value of $x$ decreases by 1, and the value of $n$ increases by 1. Thus, on the second step, the value of $y$ does not exceed 6, on the third step - 4, and so on. Since any rating is not less than 0, the number of steps does not exceed 5.
It remains to show that five steps are possible. Suppose the rating at moment $T$ is 10 (with one voter), then the second viewer gives 8 points, the third - 6, the fourth - 4, the fifth - 2, and the sixth - 0. Then the rating sequentially takes the values $9, 8, 7, 6$, and 5.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Given two numbers (not necessarily integers), not equal to 0. If each of them is increased by one, their product will double. By what factor will their product increase if each of the original numbers is squared and then decreased by one? (D. Shiryayev, I. Rubanov)
|
Answer. 4 times. Solution. Let the numbers be denoted by $a$ and $b$. According to the condition, $(a+1)(b+1)=a b+a+b+1=2 a b$. By combining like terms in the last equality, we get $a b-a-b-1=0$, from which $(a-1)(b-1)=a b-a-b+1=2$ and $\left(a^{2}-1\right)\left(b^{2}-1\right)=(a-1)(b-1)(a+1)(b+1)=2 \cdot 2 a b=4 a b$.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In a football tournament where each team played against each other once, teams $A$, B, V, G, D, and E participated. Teams received 3 points for a win, 1 point for a draw, and 0 points for a loss. In the end, it turned out that teams $A$, B, V, G, and D each scored 7 points. What is the maximum number of points that team E could have scored?
|
Answer: 7 points. Solution: In a match where one of the teams won, the teams together score 3 points, in a match that ended in a draw - 2 points. Since 7 is not divisible by 3, the team that scored 7 points must have at least one draw. Since there are five such teams, there were at least three draws in the tournament. In total, as is easy to check, 15 matches were played. Therefore, all teams together scored no more than $2 \times 3 + 3 \times 12 = 42$ points. Of these, 35 points were scored by teams A, B, V, G, and D. Therefore, team $\mathrm{E}$ scored no more than 42-35 = 7 points. How it could-
| | $A$ | $B$ | $B$ | $\Gamma$ | $D$ | $E$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $A$ | $\mathrm{x}$ | 3 | 3 | 1 | 0 | 0 |
| $B$ | 0 | $\mathrm{x}$ | 3 | 3 | 1 | 0 |
| $B$ | 0 | 0 | $\mathrm{x}$ | 3 | 3 | 1 |
| $\Gamma$ | 1 | 0 | 0 | $\mathrm{x}$ | 3 | 3 |
| $D$ | 3 | 1 | 0 | 0 | $\mathrm{x}$ | 3 |
| $E$ | 3 | 3 | 1 | 0 | 0 | $\mathrm{x}$ |
have scored exactly 7 points is shown in the table on the right.
|
7
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Before starting to solve the problem, Kolya looked at the clock. It was two o'clock. Spending exactly an hour on solving it, Kolya looked at the clock again and noticed that the angle between the hour and minute hands remained the same. When did Kolya start solving the problem?
|
Answer. At 1 hour $8^{2} /{ }_{11}$ min or at 1 hour $40^{10} / 11$ min. Solution. Let it be $x$ minutes past two when Petya looked at the clock. Since the minute hand moves $6^{\circ}$ per minute, and the hour hand $-0,5^{\circ}$, the hour hand at this moment formed an angle of $30^{\circ}+0,5 x^{\circ}$ with the 12 o'clock direction, and the minute hand - an angle of $6 x^{\circ}$. In one hour, the minute hand made a full revolution and returned to its original position, while the hour hand turned $30^{\circ}$. Clearly, the minute hand will be directed along the line bisecting the angle between the two positions of the hour hand. Thus, $6 x^{\circ}=\left(\left(30^{\circ}+0,5 x^{\circ}\right)+\left(60^{\circ}+0,5 x^{\circ}\right)\right) / 2$, if the minute hand lies inside the angle formed by the two positions of the hour hand, or $6 x^{\circ}-180^{\circ}=\left(\left(30^{\circ}+0,5 x^{\circ}\right)+\left(60^{\circ}+0,5 x^{\circ}\right)\right) / 2$, if not. Solving these two equations, we get the two answers given above.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. For what largest $p$ does there exist a convex $n$-gon in which the lengths of the diagonals take on no more than two distinct values? (I. Rubanov)
|
Answer. For $n=7$. Solution. Example. A regular heptagon. It has diagonals of exactly two types: connecting vertices one apart and two apart. Evaluation. Let $A B$ be a side of a convex polygon $M$, which has diagonals of only two possible lengths $x$ and $y$. Then for any vertex $C$, not adjacent to $A$ and $B$, the sides $C A$ and $C B$ of triangle $A C B$ can only equal $x$ and $y$. The choice of these side lengths uniquely determines the vertex $C$, as it must lie on the same side of the line $A B$ as the entire polygon $M$. However, there are only four such combinations of sides: $C A=C B=x ; C A=C B=y ; C A=x, C B=y$; $C A=y, C B=y$. Of these, only one of the first two combinations is possible: otherwise, the corresponding vertices $C_{1}$ and $C_{2}$ of the polygon $M$ would lie on the perpendicular bisector of the side $A B$, and the one closer to $A B$ would be inside the triangle with vertices at $A, B$, and the other of these vertices, which contradicts the convexity of $M$. Thus, the polygon $M$ has no more than three vertices not adjacent to vertices $A$ and $B$, meaning it has no more than 7 vertices.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Vintik and Shpuntik built a machine called "Tug-Push," which moves forward on syrup with a fuel consumption of Zl/km, and backward on orange juice with a fuel consumption of 5l/km. Leaving home, they drove the machine in turns. Vintik drove 12 km in both directions. Shpuntik drove forward half as much as Vintik, and backward twice as much, after which the 75 liters of fuel they had ran out. How many kilometers will Vintik and Shpuntik have to walk back home?
|
Answer: 9 km. Solution: Let Vintik travel $2 x$ km forward and $y$ km back, then $2 x+y=12$ and $9 x+15 y=75$ (since together they traveled $3 x$ km forward and $3 y$ km back). Solving the system, we get $x=5, y=2$. It remains to calculate $3 x-3 y=9$.
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. A rectangular grid with sides 629 and 630 is cut into several squares (all cuts follow the grid lines). What is the smallest number of squares with an odd side that can be in such a partition? Don't forget to explain why there cannot be a smaller number of squares with an odd side in the partition.
|
Answer: Two. Solution. An example when there are exactly two squares: two squares with a side of 315 adjoin the side of the rectangle with a length of 630, and the remaining rectangle $630 \times 314$ is cut into squares $2 \times 2$. A smaller number of squares with an odd side cannot be: to each of the sides of length 629, at least one square with an odd side adjoins, and this cannot be the same square, as then its side would be at least 630, which is impossible. Note. One square with an odd side cannot exist also because the area of the rectangle is even, while the total area of all squares in this case would be odd.
|
2
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. We will call two numbers almost equal to each other if they are equal to each other or differ from each other by no more than one. A rectangular grid with sides of natural numbers a and b is such that it is impossible to cut out a rectangle along the grid lines, the area of which is almost equal to half the area of the original rectangle. What is the smallest value that the number $|a-b|$ can take? (E. Molchanov, S. Berlov)
|
Answer: 4. Solution: If one of the sides of the rectangle is even, a rectangle of half the area can be cut from it along the midline. Therefore, it is sufficient to consider the case where both sides are odd. In this case, $|b-a|$ is even. If $|b-a|=0$, then $a=b=2n+1$, half the area of the rectangle is $2n^2+2n+0.5$, and we can cut from it a rectangle of almost this area, $2n \times (n+1)$, with an area of $2n(n+1)$, and when $a=1$ - the square $1 \times 1$ with an area almost equal to $1/2$. If $|b-a|=2$, then $a=2n+1$, $b=2n-1$, half the area of the rectangle is $2n^2-0.5$, and we can cut from it a rectangle $2n \times n$ with an area almost equal to this number, $2n^2$. Thus, $|a-b| \geq 4$. Assuming $a=2n+3, b=2n-1$, we get a rectangle whose half area is $2n^2+2n-1.5$. Almost equal to it are the integer areas $2n^2+2n-1$ and $2n^2+2n-2$. For $n=3$, $2n^2+2n-1=23$ and $2n^2+2n-2=22=2 \cdot 11$. The prime numbers 23 and 11 are greater than the sides of the resulting rectangle $9 \times 5$ when $n=3$, so it is impossible to cut from it a rectangle along the grid lines with an area almost equal to half its area. Thus, the minimum possible value of $|a-b|$ is 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. On each of five cards, a number is written. The cards lie on the table numbers down. We can, by paying a ruble, point to any three cards, and we will be told the sum of the numbers written on them. For what minimum price can we surely find out the sum of all five numbers? (I. Rubanov)
|
Answer: For 4 rubles. Solution: Let the numbers written be $a, b, c, d, e$. We ask about the sums $a+b+c, a+b+d$, $a+b+e, c+d+e$. Then, by adding the first three sums and subtracting the fourth from the result, we get $3(a+b)$, then $a+b$ and, by adding $c+d+e$ to the result, the sum of all five numbers.
Suppose we managed to get by with three questions. Let's call the presence of a card in a question an occurrence. If there is a card with three occurrences, then we increase the number on it by 2, and decrease all other numbers by 1. Then the answers to all three questions will not change, but the sum of all numbers will decrease by 2. Therefore, it is impossible to determine this sum with such three questions. This means that each card has no more than two occurrences, and this is only possible if four cards have two occurrences each, and one has one. By changing the notation if necessary, we can assume that the single occurrence is on card $e$, and one of the questions is $-a+b+c$. Then in another question without card $e$, two of the three cards $a, b, c$ must be present. By changing the notation if necessary, we can assume that this is the question $a+b+d$. Then in the third question, neither of the cards $a$ and $b$ can be present, so this is the question $c+d+e$. But then, by increasing each of the numbers $a$ and $e$ by 2 and simultaneously decreasing each of the numbers $b, c$, and $d$ by 1, the answers to all three questions will not change, but the sum of all five numbers will increase by 1. Therefore, in this case, it is also impossible to determine the sum of all five numbers.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. On the side AC of triangle ABC with an angle of 120 degrees at vertex B, points D and E are marked such that $AD = AB$ and $CE = CB$. A perpendicular $DF$ is dropped from point D to the line BE. Find the ratio $BD / DF$.
|
Answer. 2. Solution. Let $\angle C A B=\alpha, \angle A C B=\beta$. Since $A D=A B$ and $C E=C B$, we have
$\angle D B E=\angle D B A+\angle E B C-\angle A B C=\left(180^{\circ}-\alpha\right) / 2+\left(180^{\circ}-\beta\right) / 2-120^{\circ}=60^{\circ}-(\alpha+\beta) / 2=30^{\circ}$.
Thus, in the right triangle $B F D$, the angle at vertex $B$ is $30^{\circ}$, from which $B D / D F=2$.
|
2
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.