problem
stringlengths 15
4.7k
| solution
stringlengths 2
11.9k
| answer
stringclasses 51
values | problem_type
stringclasses 8
values | question_type
stringclasses 4
values | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | source
stringclasses 6
values | synthetic
bool 1
class |
|---|---|---|---|---|---|---|---|---|
7. In the school Spartakiad, teams from classes $8^{\mathrm{A}}$, $8^{\text {Б }}$, and $8^{\mathrm{B}}$ participated. In each of the competitions, one of these teams took 1st place, another took 2nd place, and another took 3rd place. After the Spartakiad, points were tallied: $x$ points were awarded for 1st place, $y$ for 2nd place, and $z$ for 3rd place $\left(x>y>z>0-\right.$ integers). In the end, team $8^{\mathrm{A}}$ received 22 points, and teams $8^{\text {Б }}$ and $8^{\text {В }}$ each received 9 points. How many competitions were there in total, and which team took 2nd place in the grenade throwing competition, given that the team $8^{\text {B }}$ took 1st place in the vault over the "goat"?
|
Answer: 5 competitions, $8^{\text {B }}$.
Solution: Let $n \geqslant 2$ be the number of competitions in the Spartakiad, then the total number of points scored by all teams is $n(x+y+z)=22+9+9=40$. But $z \geqslant 1, y \geqslant 2, x \geqslant 3$, so $x+y+z \geqslant 6$. Consider the possible cases: $x+y+z=8, n=5$; $x+y+z=10, n=4$ and $x+y+z=20, n=2$.
(a) Case $x+y+z=10, n=4$. Clearly, $x \leqslant 6$ (otherwise $8^{\mathrm{B}}$ would score more than 9 points). Consider the possible cases:
- $x=6$. Then $y=3, z=1$, but then $8^{\mathrm{A}}$ would not score 22 points.
- $x=5$. Then $8^{\mathrm{A}}$ would score less than 20 points.
- $x \leqslant 4$. Then $x+y+z \leqslant 9$.
Thus, the specified case is impossible.
(b) Case $x+y+z=20, n=2$. If we assume that $x<11$, then team $8^{\mathrm{A}}$ would not be able to score 22 points. If $x \geqslant 11$, then team $8^{\text {B }}$ would end up with more than 11 points, which is incorrect. Thus, the specified case is impossible.
(c) Case $x+y+z=8, n=5$. Clearly, in this case $z=1$, $x+y=7$. Consider the cases:
- Suppose $x=4, y=3$. Then $y+z=4$, so teams $8^{\text {B }}$ and $8^{\text {B }}$ scored at least 4 points in each competition. Then over 5 competitions, they should have scored at least 20 points (while in fact they scored $9+9=18$ ).
- Suppose $x=5, y=2$. Then team $8^{\text {B }}$ once took 1st place and 4 times last. Team $8^{\mathrm{A}}$ did not take first place in the vault. The only way to score 22 points: 2nd place and victory in the remaining 4 competitions. This means that team $8^{\text {B }}$ in these four competitions consistently took 2nd place (and in the vault $-3-\mathrm{rd})$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. Famous skater Tony Hawk is riding a skateboard (segment $A B$) in a ramp, which is a semicircle with diameter $P Q$. Point $M$ is the midpoint of the skateboard, $C$ is the foot of the perpendicular dropped from point $A$ to the diameter $P Q$. What values can the angle $\angle A C M$ take if it is known that the angular measure of the arc $A B$ is $24^{\circ} ?$
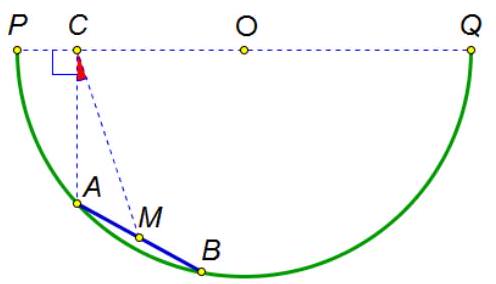
|
Answer: $12^{\circ}$.
Solution: Extend the line $A C$ to intersect the circle at point $D$ (see figure). The chord $A D$ is perpendicular to the diameter $P Q$, therefore, it is bisected by it. Thus, $C M$ is the midline of triangle $A B D$, so $C M \| B D$ and, therefore, $\angle A C M=\angle A D B$. The angle $\angle A D B$ is an inscribed angle, subtending the arc $A B$, hence it is equal to half of the arc.
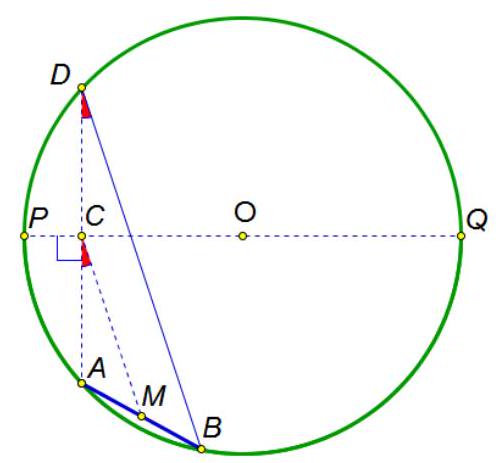
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Find the number of natural numbers from 1 to 100 that have exactly four natural divisors, at least three of which do not exceed 10.
|
Answer: 8.
Solution: A number has exactly 4 natural divisors if it is either the cube of a prime number or the product of two prime numbers. The cubes of prime numbers (satisfying the conditions) are: 8 and 27. Prime numbers not greater than 10 are - 2, 3, 5, and 7. All their pairwise products satisfy the conditions, and their number is 6.
|
8
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Karlson filled a conical glass with lemonade and drank half of it by height (measuring from the surface of the liquid to the apex of the cone), and Little Man drank the second half. How many times more lemonade did Karlson drink compared to Little Man?
|
# Answer: 7 times.
Solution. Let $r$ and $h$ be the radius of the base and the height of the conical glass, respectively. Then the volume of lemonade in the entire glass is $V_{\text {glass}}=\frac{1}{3} \pi r^{2} h$. The volume of lemonade drunk by Little One is $V_{\text {Little}}=\frac{1}{3} \pi(r / 2)^{2}(h / 2)=\frac{V_{\text {glass}}}{8}$. Therefore, Carlsson drank $\frac{7}{8} V_{\text {glass}}$, i.e., 7 times more than Little One.
|
7
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Find all four-digit numbers $\overline{a b c d}$ (where $a, b, c, d$ are the digits of the decimal representation), each of which is a divisor of at least one of the three four-digit numbers $\overline{b c d a}, \overline{c d a b}, \overline{d a b c}$ formed from it.
|
Answer: All numbers of the form $\overline{a b a b}$, where $a$ and $b$ are any digits except zero (there are 81 such numbers).
## Solution.
From the problem statement, it follows that there exists $k \in \mathbb{N}$ such that at least one of the following equalities holds:
(I) $k \cdot \overline{a b c d}=\overline{b c d a}$
(II) $k \cdot \overline{a b c d}=\overline{c d a b}$
(III) $k \cdot \overline{a b c d}=\overline{d a b c}$.
Since all numbers $\overline{a b c d}, \overline{b c d a}, \overline{a b c d}, \overline{d a b c}$ are four-digit numbers, we have $1 \leqslant k \leqslant 9$ and $a, b, c, d \neq 0$.
We will sequentially analyze all cases. By subtracting the left and right sides of equation (I) from the left and right sides of the equality $10 \cdot \overline{a b c d}=\overline{a b c d 0}$, we get
$$
(10-k) \overline{a b c d}=9999 a
$$
Since $9999=3^{2} \cdot 11 \cdot 101$, both sides of equation (2) are divisible by the prime number 101, and due to the constraints $1 \leqslant 10-k \leqslant 9$, we get $\overline{a b c d}: 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (2) by 101, we get
$$
(10-k) \overline{a b}=99 a
$$
Now, considering that both sides of the obtained equation are divisible by 11, and again due to the inequalities $1 \leqslant 10-k \leqslant 9$, we get $\overline{a b}: 11 \Leftrightarrow a=b$. Thus, the solutions to equation (I) are exactly all numbers of the form $\overline{\text { aaaa }}$ (for $k=1$).
Subtract equation (II) from the equality $100 \cdot \overline{a b c d}=\overline{a b c d 00}$. We get
$$
(100-k) \overline{a b c d}=\overline{a b} \cdot 9999
$$
Similarly to case (I), we have $\overline{a b c d}: 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (3) by 101, we get
$$
(100-k) \overline{a b}=\overline{a b} \cdot 99
$$
Therefore, the solutions to equation (II) are exactly all numbers of the form $\overline{a b a b}$ (for $k=1$). Subtract equation (III) from the equality $1000 \cdot \overline{a b c d}=\overline{a b c d 000}$. We get
$$
(1000-k) \overline{a b c d}=\overline{a b c} \cdot 9999
$$
For $1 \leqslant k \leqslant 9$, we have $\text{GCD}(101, (1000-k))=1 \Rightarrow \overline{a b c d} \vdots 101 \Leftrightarrow \overline{a b}=\overline{c d}$. Dividing equation (4) by 101, we get
$$
(1000-k) \overline{a b}=\overline{a b a} \cdot 99
$$
Further, for $1 \leqslant k \leqslant 9$, we have $\text{GCD}(11, (1000-k))=1 \Rightarrow \overline{a b} \vdots 11 \Leftrightarrow a=b$. Therefore, the solutions to equation (III) are exactly all numbers of the form $\overline{\text { aaaa }}$ (for $k=1$).
Obviously, all solutions to equations (I) and (III) are contained among the solutions to equation (II).
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. (5-7) Sergei collects toy trains. He has several sets, each with a different number of cars. If all the sets are combined into one train, there will be 112 cars. If you take the three smallest sets, there will be 25 cars in them, and in the three largest - 50 cars. How many sets does Sergei have? How many cars are in the largest set?
|
Answer: 9 sets. 18 or 19 cars.
Solution: Let $a_{1}, a_{2}, \ldots, a_{n}$ be the number of cars in the sets, ordered in ascending order. Note that $a_{3} \geqslant 9$, otherwise the total length of the three smallest sets would be less than $a_{1}+a_{2}+a_{3} \leqslant 7+8+9=2450$.
Thus, the remaining $112-50-25=37$ cars form sets whose lengths are in the range from 10 to 15. If we assume that the number of these sets is 1 or 2, then their total length is no more than 30. And if we assume that there are 4 or more, then their total length will be more than 40. Therefore, the number of such sets is 3, and thus the total number of sets is 9.
Since $a_{7} \leqslant 16$, then $a_{8}+a_{9} \geqslant 50-16=34$. This is only possible when $a_{9} \geqslant 18$. The case $a_{9}>19$ is impossible, because then $a_{7}+a_{8}<50-19=31$, so $a_{7} \leqslant 14$, therefore, $a_{4}+a_{5}+a_{6} \leqslant 11+12+13=36<37$. It can be shown that both cases are possible by explicitly indicating the lengths: $\{7,8,10,11,12,14,15,17,18\}$ and $\{7,8,10,11,12,14,15,16,19\}$.
|
9
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. $(5-7,8)$ Nезнayka and Ponchik have the same amounts of money, composed of coins worth $1, 3, 5$, and 7 ferthings.
Nезнayka has as many 1-ferthing coins as Ponchik has 3-ferthing coins;
3-ferthing coins - as many as Ponchik has 5-ferthing coins; 5-ferthing coins - as many as Ponchik has 7-ferthing coins; and 7-ferthing coins - as many as Ponchik has 1-ferthing coins;
Determine how many 7-ferthing coins Nезнayka has, given that each has 20 coins.
|
Answer: 5 coins.
Solution: Let $x, y, z, t$ be the number of 1, 3, 5, and 7-ferting coins that Nезнайка has. It is known that $x+y+z+t=20$ and $x+$ $3 y+5 z+7 t=3 x+5 y+7 z+t$. From the last equation, it follows that $6 t=2(x+y+z)$. Substituting $x+y+z=20-t$, we get the equation $6 t=2(20-t)$, the solution of which is $t=5$.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
10. $(8,9)$ Find the smallest possible value of $\left|2015 m^{5}-2014 n^{4}\right|$, where $m$ and $n$ are natural numbers.
|
Answer: 0.
Solution: Consider numbers of the form $m=2014^{a} \cdot 2015^{b}$ and $n=2014^{c} \cdot 2015^{d}$. Then $\left|2015 m^{5}-2014 n^{4}\right|=\left|2014^{5 a} \cdot 2015^{5 b+1}-2014^{4 c+1} \cdot 2015^{4 d}\right|$. This value equals 0 in the case $5 a=4 c+1,5 b+1=4 d$. It is not difficult to find such numbers, for example, $a=c=1, b=3, d=4$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11. (9) Integers $a, b$ and $c$ are such that $a \cdot\left(1-\frac{\sqrt{7}}{2}\right)^{2}+b \cdot\left(1-\frac{\sqrt{7}}{2}\right)+c=5$. What is the minimum value of $|a+b+c|$ under this condition?
|
Answer: 2.
Solution: If $a=0$, then $b=0$ and $c=5$, hence $|a+b+c|=5$. If $a \neq 0$, then consider the quadratic function $f(x)=a x^{2}+b x+c$. Notice that $f(x)-5$ has roots $1 \pm \frac{\sqrt{7}}{2}$. Therefore, $f(x)=$ $5+k \cdot\left(4 x^{2}-8 x-3\right), k \neq 0$, i.e., $|a+b+c|=|5-7 k|$, The minimum value of 2 is achieved when $k=1$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
15. (9) Find $q$, for which $x^{2}+x+q=0$ has two distinct real roots satisfying the relation $x_{1}^{4}+2 x_{1} x_{2}^{2}-x_{2}=19$.
|
Answer: $q=-3$.
Solution: If $x$ is a root, then $x^{2}=-x-q$, hence $x^{4}=x^{2}+$ $2 q x+q^{2}=(2 q-1) x+q^{2}-q$. Then $x_{1}^{4}+2 x_{1} x_{2}^{2}-x_{2}=(2 q-1) x_{1}+q^{2}-q+$ $2 q x_{2}-x_{2}=(2 q-1)\left(x_{1}+x_{2}\right)+q^{2}-q$. Using Vieta's theorem
$x_{1}+x_{2}=-1$, we get $q^{2}-3 q+1=19$. Solving, we obtain $q_{1}=-3$, $q_{2}=6$, but for $q=6$ the original equation has no roots.
## Lomonosov Moscow State University
## "Conquer Sparrow Hills" Olympiad Variant 3-1
|
-3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. From the condition about 15 kg, it follows that the container can contain either only items weighing 5 and 10 kg, or only items weighing 2, 3, and 10 kg. Let $x, y, z, u$ denote the number of items weighing $2, 3, 5$, and 10 kg, respectively.
In the first case, the conditions of the problem give the system $\left\{\begin{array}{l}u=z+5, \\ 5 z+10 u=100,\end{array}\right.$ which has no solutions in natural numbers.
In the second case, for natural numbers $x, y, u$, we obtain the system of equations
$$
\left\{\begin{array} { l }
{ u = x + y + 5 , } \\
{ 2 x + 3 y + 1 0 u = 1 0 0 , }
\end{array} \Leftrightarrow \left\{\begin{array} { l }
{ u = x + y + 5 , } \\
{ 1 2 x = 5 0 - 1 3 y , }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
x=y=2 \\
u=9
\end{array}\right.\right.\right.
$$
|
Answer: 2 items weighing 2 and 3 kg, 9 items weighing 10 kg.
Answer to variant 4-2: 2 weighing 3 and 5 kg, 12 weighing 7 kg.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Dima went to school in the morning, but after walking exactly half the distance, he realized he had forgotten his mobile phone at home. Dima estimated (he had an A in mental arithmetic) that if he continued walking at the same speed, he would arrive at school 3 minutes before the first bell, but if he ran home for the phone and then ran to school, he would arrive 3 minutes after the bell. Dima decided to run home, but he got out of breath while running (he had a C in physical education), and walked from home to school at his usual speed. As a result, he was 15 minutes late for the first class! How many times faster is the speed at which he runs compared to the speed at which he walks?
|
Answer: 2.
Solution: Let $x$ be the time it takes for Dima to walk from home to school, $y$ be the time it takes for Dima to run from home to school, and $T$ be the remaining time until the bell rings (at the moment Dima noticed the loss). Then the conditions of the problem can be written as $\left\{\begin{array}{l}\frac{x}{2}=T-3 \\ \frac{y}{2}+y=T+3 \\ \frac{y}{2}+x=T+15\end{array}\right.$ Solving this, we get that $x=24, y=12, T=15$, from which it follows that he runs twice as fast as he walks.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Famous skater Tony Hawk is riding a skateboard (segment $A B$) in a ramp, which is a semicircle with diameter $P Q$. Point $M$ is the midpoint of the skateboard, $C$ is the foot of the perpendicular dropped from point $A$ to the diameter $P Q$. What values can the angle $\angle A C M$ take if it is known that the angular measure of the arc $A B$ is $24^{\circ}$?
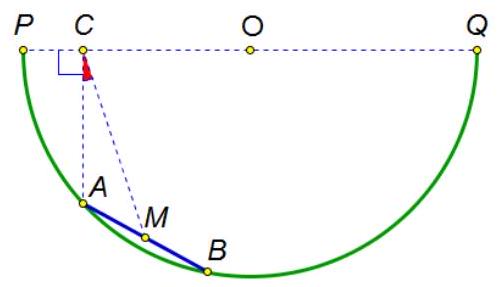
|
Answer: $12^{\circ}$.
Solution: Extend the line $A C$ to intersect the circle at point $D$ (see figure). The chord $A D$ is perpendicular to the diameter $P Q$, therefore, it is bisected by it. Thus, $C M$ is the midline of triangle $A B D$, so $C M \| B D$ and, therefore, $\angle A C M=\angle A D B$. The angle $\angle A D B$ is inscribed, subtends the arc $A B$, and thus is equal to half of it.

|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
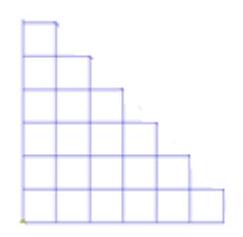
1. Place the numbers $1,2,3,4,5,6,7,8$ and 9 in the nine cells of the figure shown in the diagram, so that the sum of the numbers in each column, starting from the second, is 1 more than in the previous one. It is sufficient to find at least one such arrangement. In your answer, indicate the number in the first column.
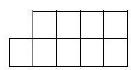
|
Answer: 7.
Solution: For now, we will not pay attention to the order of numbers in one column.
The sum of the given numbers is 45. Let $x$ be the number in the bottom-left cell. Then $5x + 10 = 45$, from which $x = 7$. Therefore, the sum of the numbers in the second column is $8 = 5 + 3 = 6 + 2$. If the second column contains 3 and 5, then the third column must contain 1 and 8, the fourth column must contain 6 and 4, and the last column must contain 2 and 9. If the second column contains 6 and 2, then the third column can contain 1 and 8 or 4 and 5. It can be shown that if the third column contains 1 and 8, it is impossible to select numbers for the fourth column. Therefore, the third column must contain 4 and 5, then the fourth column must contain 1 and 9, and the last column must contain 3 and 8. This results in 2 arrangements without considering the order of the numbers.
Notice that in each column (except the first), the numbers can be swapped, which gives 16 options for each arrangement. In the end, we get 32 options considering the order of the numbers in the columns.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Answer: 1 (in all options).
|
Solution. (Option 6-1). Let's represent $k$ as $k=10 a+b$, where $a, b$ are integers and $1 \leqslant b \leqslant 9$. Then $k^{2}+6 k=10\left(10 a^{2}+2 a b+6 a\right)+b^{2}+6 b$. The expression $b^{2}+6 b$ ends in 6 only if $b=2$. But in this case $k^{2}+6 k=$ $100\left(a^{2}+a\right)+16$, which means the second-to-last digit is 1.
In option $6-2$, we need to consider that $k^{2}+2 k-8=(k-2)^{2}+6(k-2)$.
|
1
|
Other
|
MCQ
|
Yes
|
Yes
|
olympiads
| false
|
5. Find the set of pairs of real numbers $(x, y)$ satisfying the conditions:
$$
\left\{\begin{array}{l}
3^{-x} y^{4}-2 y^{2}+3^{x} \leq 0 \\
27^{x}+y^{4}-3^{x}-1=0
\end{array}\right.
$$
Calculate the values of the expression $x_{k}^{3}+y_{k}^{3}$ for each solution $\left(x_{k}, y_{k}\right)$ of the system and find the minimum among them. In the answer, specify the found minimum value, rounding it to two decimal places if necessary. If the original system has no solutions, then put the digit 0 in the answer field.
|
Answer: The solution to the system is $(x, y)=(0, \pm 1)$. Answer -1.
## 1 Creative problems (7 items)
|
-1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $n$ be the time in minutes it takes for the slower boy to complete a lap. Then $n>5, n \in \mathbb{N}$. The speed at which the faster boy catches up to the slower one is
$$
\frac{1}{5}-\frac{1}{n}=\frac{n-5}{5 n}\left(\frac{\text { lap }}{\text { min }}\right)
$$
therefore, the time between meetings is
$$
\frac{5 n}{n-5}=\frac{5(n-5)+25}{n-5}=5+\frac{25}{n-5}(\text { min })
$$
and since this is an integer, $(n-5)$ must divide 25. The natural divisors of $25$ are $1, 5,$ and $25$. Thus, $n=6$ or $n=10$ or $n=30$, which correspond to meeting times of 30 minutes, 10 minutes, and 6 minutes, respectively. Since the time between meetings is at least 12 minutes, the only value that satisfies the given condition is $n=6$.
|
Answer: 6 min.
Answer to option 172: 12 min.
Answer to option $173: 56$ min.
Answer to option $174: 4$ min.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The total number of students in the school must be divisible by 7 and 4, which means it must be divisible by 28. Since the number is no more than 40, there were 28 students in total. The number of prize winners is $(1 / 7 + 1 / 4 + 1 / 4) \cdot 28 = 18$ people. Therefore, 10 students did not receive any medals.
|
Answer: $x=10$.
Answer to the variant: $4-2: x=18$.
|
10
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The right side of the inequality is zero when $|x| \leqslant 10$ (for other $x$ it is undefined). Denoting $\alpha=\frac{\pi x}{4}$, we get:
$$
\begin{aligned}
& \frac{\sin 2 \alpha-\cos 2 \alpha+1}{\sin 2 \alpha+\cos 2 \alpha-1} \geqslant 0 \Longleftrightarrow \frac{2 \sin \alpha \cos \alpha+2 \sin ^{2} \alpha}{2 \sin \alpha \cos \alpha-2 \sin ^{2} \alpha} \geqslant 0 \Longleftrightarrow \\
& \Longleftrightarrow\left\{\begin{array} { l }
{ \frac { \cos \alpha + \sin \alpha } { \cos \alpha - \sin \alpha } \geqslant 0 , } \\
{ \sin \alpha \neq 0 }
\end{array} \Longleftrightarrow \left\{\begin{array}{l}
\frac{1+\operatorname{tg} \alpha}{1-\operatorname{tg} \alpha} \geqslant 0 \\
\operatorname{tg} \alpha \neq 0
\end{array}\right.\right.
\end{aligned}
$$
Therefore, $x \in[-1+4 k ; 4 k) \cup(4 k ; 4 k+1)$. On the interval $[-10,10]$, the integers are $-9,-5,-1,3,7$, of which the numbers $-9,-5,-1,3$ are within the specified interval, and their sum is -12.
|
Answer: -12.
Answer to the option: $4-2: 12$.
|
-12
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. If there are $x$ black pieces, then there are $32-x$ white pieces. Since each black piece (pentagonal) borders only white pieces, the number of black and white piece borders will be $5 x$. On the other hand, such borders are $3 \cdot(32-x)$. From the equation $5 x=3 \cdot(32-x)$ we get $x=12$.
|
Answer: 12.
Answer to option: 5-2: 20.
|
12
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. After substituting $x=\cos \alpha, y=\sin \alpha$, the second equation is satisfied, and the first equation can be written as $\cos ^{15} 3 \alpha+\sin ^{16} 3 \alpha=1$. From the chain
$$
1=\cos ^{15} 3 \alpha+\sin ^{16} 3 \alpha \leqslant \cos ^{2} 3 \alpha+\sin ^{2} 3 \alpha=1
$$
it follows that $\cos ^{15} 3 \alpha=\cos ^{2} 3 \alpha$ and $\sin ^{16} 3 \alpha=\sin ^{2} 3 \alpha$. Therefore, either $3 \alpha=\pi / 2+\pi k$ or $3 \alpha=2 \pi k$, which means $\alpha=\frac{\pi}{6}+\frac{\pi k}{3}$ or $\alpha=\frac{2 \pi n}{3}$. This results in 9 pairs of solutions $(x, y)$:
$$
\left(\frac{\sqrt{3}}{2} ; \pm \frac{1}{2}\right) ;\left(-\frac{\sqrt{3}}{2} ; \pm \frac{1}{2}\right) ;\left(-\frac{1}{2} ; \pm \frac{\sqrt{3}}{2}\right) ;(0 ; \pm 1) ;(1 ; 0)
$$
|
Answer: 9.
Answer to option: $6-2$ : 9.
The equation $\cos 3 x=0$ is equivalent to
$$
3 x=\pi / 2+2 \pi k, k \in \mathbb{Z}, \quad 3 x=-\pi / 2+2 \pi n, n \in \mathbb{Z}
$$
Answers and solutions to option $\mathbf{7}-1$
|
9
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let $n$ be the time in minutes it takes for the slower boy to complete a lap. Then $n>5, n \in \mathbb{N}$. The speed at which the faster boy catches up to the slower one is
$$
\frac{1}{5}-\frac{1}{n}=\frac{n-5}{5 n}\left(\frac{\text { lap }}{\text { min }}\right)
$$
therefore, the time between meetings is
$$
\left.\frac{5 n}{n-5}=\frac{5(n-5)+25}{n-5}=5+\frac{25}{n-5} \text { (min }\right)
$$
and since this is an integer, $(n-5)$ must divide 25. The natural divisors of $25$ are $1, 5,$ and $25$. Thus, $n=6$ or $n=10$ or $n=30$, which correspond to meeting times of 30 minutes, 10 minutes, and 6 minutes, respectively. Since the time between meetings is at least 12 minutes, the only value that satisfies the given condition is $n=6$.
|
Answer: 6 min.
Answer to option 17 - $2: 12$ min.
Answer to option 17 - $\mathbf{\text { : }}$ : 56 min.
Answer to option $17-4: 4$ min.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. Find the side $B C$ of the quadrilateral $A B C D$, if $\angle B A C=\alpha, \angle A C D=\beta, \angle B C A+\angle C A D=\frac{\pi}{2}$ and $A D=a$. In the answer, write the result rounded to two decimal places.
$$
\alpha=\arcsin \frac{5}{13}, \beta=\arcsin \frac{12}{13}, a=24
$$
|
Solution. Since the sum of angles $\angle B A C+\angle A C D=\arcsin \frac{5}{13}+\arcsin \frac{12}{13}=\frac{\pi}{2}$, then $\angle B A D+\angle B C D=$ $\pi$. Therefore, a circle can be circumscribed around quadrilateral $A B C D$. Next, by the Law of Sines $\frac{A D}{\sin \beta}=\frac{B C}{\sin \alpha} \Rightarrow B C=\frac{24 \cdot 5}{12}=10$.
Answer: 10.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The digits of numbers from 20 to 99 occupy the first $80 \cdot 2=160$ places in this sequence. There are $2021-160=1861$ places left. The digits of numbers from 100 to 719 occupy the next $(719-99) \cdot 3=1860$ places. Therefore, the 2021st place is the first digit of the number 720, which is 7.
|
Answer: 7. Answer to option: $1-2: 0$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The equation is transformed into the form
$$
t^{\alpha}=\alpha(t+1), \quad \alpha=\lg 2 \in(0,1), \quad t=x^{2}-3>0
$$
where:
1) the left side of the equation is a concave up function (since $\alpha \in(0 ; 1)$), defined for $t \geqslant 0$
2) the right side of the equation is a linear function with a positive slope
3) at $t=0$, the value of the left side is less than the value of the right side; at $t=1$, the value of the left side is, on the contrary, greater than the value of the right side, since
$$
1^{\alpha}=\lg 10>\lg 4=\alpha \cdot(1+1)
$$
Therefore, the graphs intersect at two points (one between 0 and 1, the other to the right of 1), each of which generates two roots of the original equation.
|
Answer: 4. Answer to option: $1-2: 4$.
保留源文本的换行和格式,直接输出翻译结果。
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# 3. We have
$$
\begin{aligned}
& 42=\frac{1}{\sqrt{x+2}+\sqrt{x+3}}+\frac{1}{\sqrt{x+3}+\sqrt{x+4}}+\ldots+\frac{1}{\sqrt{x+2017}+\sqrt{x+2018}} \equiv \\
& \equiv(\sqrt{x+3}-\sqrt{x+2})+(\sqrt{x+4}-\sqrt{x+3})+\ldots(\sqrt{x+2018}-\sqrt{x+2017}) \equiv \\
& \equiv \sqrt{x+2018}-\sqrt{x+2} \Leftrightarrow \\
& \Leftrightarrow 42(\sqrt{x+2018}+\sqrt{x+2})=2018-2 \Leftrightarrow x=7
\end{aligned}
$$
|
Answer: $x=7$. Answer to option $5-2: x=6$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Compare the numbers
$$
\left(1+\frac{1}{1755}\right)\left(1+\frac{1}{1756}\right) \ldots\left(1+\frac{1}{2015}\right) \text { and } \sqrt{\frac{8}{7}} .
$$
Indicate in the answer "1" if the first number is greater; "2", if the second number is greater; "0", if the numbers are equal.
|
Answer: The first is greater
Solution: (Solution: on the left, bring each parenthesis to a common denominator, use the inequality $\frac{n \cdot n}{(n-1)(n+1)}>1$ and we get that the square of the first number is greater than $\frac{2015}{1755}=\frac{31}{27}>\frac{8}{7$.)
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9. Calculate (without using a calculator) $\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}$, given that this number is an integer.
|
Answer: 3.
Solution: Note that $2<\sqrt[3]{9+4 \sqrt{5}}<3$ and $0<\sqrt[3]{9-4 \sqrt{5}}<1$. Therefore, $2<\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}<4$, hence this number is 3.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
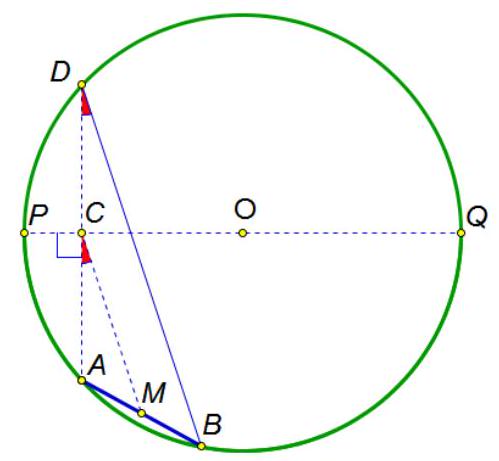
6. Famous skater Tony Hawk is riding a skateboard (segment $A B$) in a ramp, which is a semicircle with diameter $P Q$. Point $M$ is the midpoint of the skateboard, $C$ is the foot of the perpendicular dropped from point $A$ to the diameter $P Q$. What values can the angle $\angle A C M$ take if it is known that the angular measure of the arc $A B$ is $24^{\circ}$?
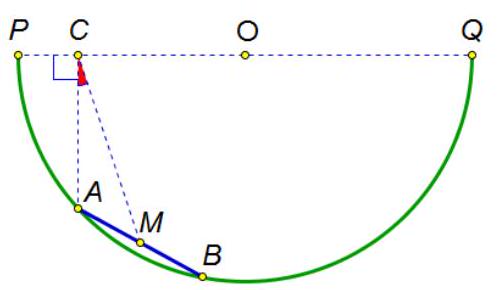
|
Answer: $12^{\circ}$.
Solution: Extend the line $A C$ to intersect the circle at point $D$ (see figure). The chord $A D$ is perpendicular to the diameter $P Q$, therefore, it is bisected by it. Thus, $C M$ is the midline of triangle $A B D$, so $C M \| B D$ and, therefore, $\angle A C M=\angle A D B$. The angle $\angle A D B$ is an inscribed angle, subtending the arc $A B$, hence it is equal to half of the arc.
|
12
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. In the school Spartakiad, teams from classes $8^{\mathrm{A}}$, $8^{\mathrm{E}}$, and $8^{\mathrm{B}}$ participated. In each of the competitions, one of these teams took 1st place, another took 2nd place, and another took 3rd place. After the Spartakiad, points were tallied: $x$ points were awarded for 1st place, $y$ for 2nd place, and $z$ for 3rd place $\left(x>y>z>0\right.$ - integers). In the end, team $8^{\mathrm{A}}$ received 22 points, and teams $8^{\text {B }}$ and $8^{\text {E }}$ each received 9 points. How many competitions were there in total, and which team took 2nd place in the grenade throwing competition, given that the team $8^{\mathrm{B}}$ took 1st place in the vault over the "buck"?
|
Answer: 5 competitions, $8^{\text{B}}$.
Solution: See the solution to problem 7 for 8th grade.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Given three numbers $a, b, c$. It is known that the arithmetic mean of the numbers $a$ and $b$ is 5 more than the arithmetic mean of all three numbers. And the arithmetic mean of the numbers $a$ and $c$ is 8 less than the arithmetic mean of all three numbers. By how much does the arithmetic mean of the numbers $b$ and $c$ differ from the arithmetic mean of all three numbers?
|
Answer: 3 more.
Solution: The arithmetic mean of the numbers $\frac{a+b}{2}, \frac{b+c}{2}, \frac{a+c}{2}$, obviously, coincides with the arithmetic mean of the numbers $a, b, c$. Therefore, if one $\frac{a+b}{2}$ is 5 more, and $\frac{a+c}{2}$ is 8 less, then, to get the same result, $\frac{b+c}{2}$ must be 3 more.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
12. In how many ways can the number 10000 be factored into three natural factors, none of which is divisible by 10? Factorizations that differ only in the order of the factors are considered the same.
#
|
# Answer: 6.
Solution: Each of the factors should only include powers of 2 and 5 (they cannot be included simultaneously, as it would be a multiple of 10). There can be two factors that are powers of two, in which case the third factor is 625. Or conversely, two factors are powers of five, and the third factor is 16. In each case, there are 3 variants.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Let's call an integer "extraordinary" if it has exactly one even divisor other than 2. How many extraordinary numbers exist in the interval $[1 ; 75]$?
|
Answer: 12
Solution: This number should be equal to a prime multiplied by 2. There are 12 such numbers:
$\begin{array}{llllllllllll}2 & 3 & 5 & 7 & 11 & 13 & 17 & 19 & 23 & 29 & 31 & 37\end{array}$
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. In a trapezoid, the diagonals of which intersect at a right angle, it is known that the midline is 6.5 and one of the diagonals is 12. Find the second diagonal
#
|
# Answer 5
Solution: Let's parallel translate one of the diagonals so that it forms a right-angled triangle with the other. Then, in this triangle, one leg is 12, and the hypotenuse is 13, so the remaining leg is 5.
## Option $2-$ -
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The Mad Hatter's clock is fast by 15 minutes per hour, while the March Hare's clock is slow by 10 minutes per hour. One day, they set their clocks by the Dormouse's clock (which is stopped and always shows 12:00) and agreed to meet at 5 o'clock in the evening for their traditional
five-o'clock tea. How long will the Mad Hatter wait for the March Hare if each arrives exactly at 5:00 PM by their own clocks?
|
# Answer: 2 hours.
Solution: The Mad Hatter's clock runs at a speed of 5/4 of normal, so it will take 4 hours of normal time to pass 5 hours. Similarly, the March Hare's clock runs at a speed of 5/6 of normal, so it will take 6 hours of normal time to pass 5 hours.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The robot moves along straight segments, making turns of 90 degrees to the right or left every minute (neglect the time for turning). The robot travels 10 meters per minute. What is the minimum distance from the starting position that the robot can be after 9 minutes, if it did not turn during the first minute?
#
|
# Answer: $10 \text{~m}$
Solution: We can consider a coordinate grid with nodes spaced 10m apart. Clearly, the robot travels along the nodes of this grid. It cannot return to the initial position in 9 minutes. However, it can be at a distance of 10 m - it is easy to construct an example.
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The turtle crawled out of its house and moved in a straight line at a constant speed of 5 m/hour. After an hour, it turned $90^{\circ}$ (right or left) and continued moving, then crawled for another hour, then turned $90^{\circ}$ (right or left) again... and so on. It crawled for 11 hours, turning $90^{\circ}$ at the end of each hour. What is the shortest distance from the house it could have been?
|
Answer 5 m.
Solution: We can consider a coordinate grid with nodes spaced 5 m apart. It is clear that the turtle crawls along the nodes of this grid. In 11 hours, it cannot return to the initial position. However, it can be 5 m away - it is easy to construct an example.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Let's call a number "marvelous" if it has exactly 3 different odd natural divisors (and an arbitrary number of even divisors). How many "marvelous" two-digit numbers exist?
|
Answer: 7.
Solution: Such numbers have the form $2^{k} \times p^{2}$, where $p-$ is an odd prime number. Clearly, $p$ does not exceed 7, since the result must be a two-digit number. If $p=3$, then $k=0,1,2,3$; If $p=5$, then $k=0,1$; if $p=7$, then $k=0$. In total, there are 7 options.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. It is known that for some natural numbers $a, b$, the number $N=\frac{a^{2}+b^{2}}{a b-1}$ is also natural. Find all possible values of $N$.
---
The provided text has been translated into English while preserving the original formatting and structure.
|
Answer: 5.
Solution: It is not difficult to find the solution $a=2, b=1, N=5$. Let's prove that no other $N$ is possible.
Let $\left(a_{0}, b_{0}\right)$ be a solution corresponding to the smallest value of $a^{2}+b^{2}$. Without loss of generality, we can assume that $a_{0}>b_{0}$. If $b_{0}=1$, then $N=\frac{a^{2}+1}{a-1}$, from which $a=2$ or $a=3$, and in both cases $N=5$.
Now let $b_{0}>1$. Consider the quadratic equation $x^{2}-b_{0} N x+\left(b_{0}^{2}+N\right)=0$, then $a_{0}$ is its root. By Vieta's theorem, the second root is $a_{1}=b_{0} N-a_{0}$ and it is also positive and integer. From the minimality of $a^{2}+b^{2}$, it follows that $a_{1}>a_{0}$ (they cannot be equal). Then $\left(a_{1}-1\right)\left(a_{0}-1\right) \geqslant b_{0}\left(b_{0}+1\right)$, but on the other hand, $\left(a_{1}-1\right)\left(a_{0}-1\right)=a_{1} a_{0}-\left(a_{1}+a_{0}\right)+1=b_{0}^{2}+N-b_{0} N+1$. Therefore, $b_{0}^{2}+N-b_{0} N+1 \geqslant b_{0}^{2}+b$, which is impossible for $b_{0}>1$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1 Misha noticed that a tram passed by him in 3 seconds, and a tunnel 100 meters long in 13 seconds. Find the speed of the tram (in meters per second), assuming that it remains the same throughout the entire observation period.
|
Solution. Let the speed of the tram (in meters per second) be $v$, and the length of the tram (in meters) be $l$. If $t_{1}$ and $t_{2}$ are the times it takes for the tram to pass by Mishka and through a tunnel of length $a$ respectively, then
$$
\left\{\begin{array} { l }
{ l = v \cdot t _ { 1 } } \\
{ a + l = v \cdot t _ { 2 } }
\end{array} \Longrightarrow \left\{\begin{array}{l}
v=\frac{a}{t_{2}-t_{1}} \\
l=\frac{a t_{1}}{t_{2}-t_{1}}
\end{array}\right.\right.
$$
Since $t_{1}=3, t_{2}=13$ and $a=100$, then $v=10$.
Answer: 10. (A)
|
10
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.3 Mishа noticed that the tram passed by him in 2 seconds, and a tunnel 96 meters long - in 10 seconds. Find the speed of the tram (in meters per second), assuming that it remains the same throughout the entire observation period.
|
Answer: 12. (B)
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-2. Calculate the sum
$$
S=\frac{2013}{2 \cdot 6}+\frac{2013}{6 \cdot 10}+\frac{2013}{10 \cdot 14}+\ldots+\frac{2013}{2010 \cdot 2014}
$$
In your answer, specify the remainder when the nearest even number to the obtained value of $S$ is divided by 5.
|
Answer: 2. (C)
Options.
$$
\begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 0 & \mathbf{B} & 1 & \mathbf{C} & 2 & \mathbf{D} & 3 & \mathbf{E} \\
4 & \mathbf{F} \\
\hline
\end{array}
$$
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3-4. Calculate the sum
$$
S=\frac{2015}{3 \cdot 8}+\frac{2015}{8 \cdot 13}+\frac{2015}{13 \cdot 18}+\ldots+\frac{2015}{2008 \cdot 2013}
$$
In your answer, specify the remainder when dividing by 5 the natural number closest to the obtained value of $S$.
|
Answer: 4. ( ( $\mathbf{2}$ )
Options.
|
4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-1. Solve the inequality
$$
\sqrt{3 x-7}-\sqrt{3 x^{2}-13 x+13} \geqslant 3 x^{2}-16 x+20
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the inequality.
|
Solution. As a result of the substitution $v=\sqrt{3 x-7}, u=\sqrt{3 x^{2}-13 x+13}$, we obtain the equivalent inequality $u \leqslant v$. Therefore, $x$ satisfies the inequality $3 x^{2}-13 x+13 \leqslant 3 x-7 \Longleftrightarrow 2 \leqslant x \leqslant 10 / 3$. Out of the two integer values $x=2$ and $x=3$, only $x=3$ falls within the domain of valid values.
Answer: (B) 3.
Answer options.
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-2. Solve the inequality
$$
\sqrt{6 x-13}-\sqrt{3 x^{2}-13 x+13} \geqslant 3 x^{2}-19 x+26
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the inequality.
|
Solution. The inequality is satisfied only by the following integer values: $x=3, x=4$.
Answer: (D) 7.
Answer choices.
$$
\begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 2 & \mathbf{B} & 3 & \mathbf{C} & 5 & \mathbf{D} & 7 & \mathbf{E} \\
\hline
\end{array}
$$
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-3. Solve the inequality
$$
\sqrt{5 x-11}-\sqrt{5 x^{2}-21 x+21} \geqslant 5 x^{2}-26 x+32
$$
In your answer, specify the sum of all integer values of $x$ that satisfy the inequality.
|
Solution. The inequality is satisfied by only one integer value: $x=3$.
Answer: (B) 3.
Answer choices.
$$
\begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline \mathbf{A} & 2 & \mathbf{B} & 3 & \mathbf{C} & 5 & \mathbf{D} & 7 & \mathbf{E} \\
\hline
\end{array}
$$
|
3
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5-4. Solve the inequality
$$
\sqrt{10 x-21}-\sqrt{5 x^{2}-21 x+21} \geqslant 5 x^{2}-31 x+42
$$
In your answer, indicate the sum of all integer values of $x$ that satisfy the inequality.
|
Solution. The inequality is satisfied only by the following integer values: $x=3, x=4$.
Answer: (D) 7.
Answer choices.
|
7
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8-2. Find all common points of the graphs
$$
y=8 \cos ^{2} \pi x \cdot \cos 2 \pi x \cdot \cos 4 \pi x \quad \text { and } \quad y=\cos 6 \pi x
$$
with abscissas belonging to the interval $[-1 ; 0]$. In your answer, specify the sum of the abscissas of the found points.
|
Solution. This is equivalent to $\sin 9 \pi x=\sin (-5 \pi x), x \neq n, n \in \mathbb{Z}$. From this, $x=k / 7$ or $x=1 / 4+l / 2, k, l \in \mathbb{Z}$.
The roots of the equation in the interval $[-1 ; 0]$ are: $-1 / 7,-2 / 7,-3 / 7,-4 / 7,-5 / 7,-6 / 7$ and $-1 / 4,-3 / 4$.
Answer: -4 .
|
-4
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. Compare the numbers
$$
\left(1+\frac{1}{1755}\right)\left(1+\frac{1}{1756}\right) \ldots\left(1+\frac{1}{2015}\right) \text { and } \sqrt{\frac{8}{7}}
$$
Indicate in the answer «1» if the first number is greater; «2», if the second number is greater; «0», if the numbers are equal.
|
Answer: The first one is greater.
Solution: Convert each parenthesis on the left to a common denominator, then use the inequality $\frac{n \cdot n}{(n-1)(n+1)}>1$. Then we get that the square of the first number is greater than $\frac{2015}{1755}=\frac{31}{27}>\frac{8}{7}$.
|
1
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. How many different right-angled triangles exist, one of the legs of which is equal to $\sqrt{1001}$, and the other leg and the hypotenuse are expressed as natural numbers?
ANSWER: 4.
|
Solution: Let's write down the Pythagorean theorem: $a^{2}+1001=b^{2}$. From this, we get $(b-a)(b+a)=1001=7 \times 11 \times 13$. We can represent 1001 as the product of two factors $1 \times 1001=7 \times 143=11 \times 91=13 \times 77$ - the first factor must be smaller - there are only 4 options
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final Round Tasks for 2015/2016 Academic Year for 7-8 Grades
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the largest natural number that cannot be represented as the sum of two composite numbers.
OTBET: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. And odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we are convinced that 11 cannot be represented in this way.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Five runners ran a relay. If the first runner ran twice as fast, they would have spent $5 \%$ less time. If the second runner ran twice as fast, they would have spent $10 \%$ less time. If the third runner ran twice as fast, they would have spent $12 \%$ less time. If the fourth runner ran twice as fast, they would have spent $15 \%$ less time. By what percentage less time would they have spent if the fifth runner ran twice as fast?
OTBET: by $8 \%$
|
Solution: If each ran twice as fast, they would run 50% faster. This means that if the 5th runner ran faster, the time would decrease by $50-5-10-12-15=8 \%$.
|
8
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. Find all values of $a$, for each of which the system
$$
\left\{\begin{array}{l}
|y|+|y-x| \leqslant a-|x-1| \\
(y-4)(y+3) \geqslant(4-x)(3+x)
\end{array}\right.
$$
has exactly two solutions.
|
# Problem 5.
Answer: when $a=7$.
Solution. By the triangle inequality:
$$
|y|+|y-x|+|x-1| \geqslant|y-(y-x)-(x-1)|=1
$$
therefore, the first inequality can have solutions only when $a \geqslant 1$. In this case, it is equivalent to the system of inequalities
$$
-\frac{a-1}{2} \leqslant y \leqslant \frac{a+1}{2}, \quad-\frac{a-1}{2} \leqslant x \leqslant \frac{a+1}{2}, \quad x-\frac{a+1}{2} \leqslant y \leqslant x+\frac{a-1}{2}
$$
which defines a hexagon on the coordinate plane if $a>1$, and a triangle if $a=1$.
The second inequality of the system is equivalent to the inequality $(x-0.5)^{2}+(y-0.5)^{2} \geqslant 49 / 2$ and thus defines the complement to the entire plane of the interior of a circle with center $(1 / 2,1 / 2)$ and radius $7 / \sqrt{2}$.
If $a=1$, the system has no solutions.
Since for $a>1$ the vertices $\left(-\frac{a-1}{2},-\frac{a-1}{2}\right)$ and $\left(\frac{a+1}{2}, \frac{a+1}{2}\right)$ of the larger diagonal of the hexagon are the farthest from the point $(1 / 2,1 / 2)$ among all points of the hexagon, the intersection of the considered sets will consist of exactly two points if and only if the circle of the second set passes through these vertices. The point $(1 / 2,1 / 2)$ is the midpoint of the larger diagonal, and the length of this diagonal is $a \sqrt{2}$. Therefore, $a \sqrt{2}=14 / \sqrt{2}$, i.e., $a=7$.
|
7
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. In a school on this island, both knights and liars study in the same class. One day, the teacher asked four children: Anu, Banu, Vanu, and Danu, who among them had completed their homework. They answered:
- Anu: Banu, Vanu, and Danu completed the homework.
- Banu: Anu, Vanu, and Danu did not complete the homework.
- Vanu: Don't believe them, sir! Anu and Banu are liars!
- Danu: No, sir, Anu, Banu, and Vanu are knights!
How many knights are among these children?
|
Answer: 1.
Solution: If Vanu is a knight, then all the others are liars.
Let Vanu be a liar. Then Danu is also a liar (since he says Vanu is a knight). And at least one of Anu and Banu must be a knight. Both of them cannot be knights, as they contradict each other. In any case, only one of the children is a knight.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. In triangle $\triangle A B C$, the sides $A B=5$ and $A C=6$ are known. What should the side $B C$ be so that the angle $\angle A C B$ is as large as possible? Provide the length of side $B C$, rounded to the nearest integer.
|
Answer: 3
Solution: Construct $AC=6$. Then the geometric locus of points $B$ will be a circle of radius 5 centered at point $A$. The angle $\angle ACB$ will be the largest when $CB$ is tangent to the circle (see figure). Then $CB \perp AB$ and by the Pythagorean theorem we get $BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{11} \approx 3$.
## 2013/2014 Academic Year CRITERIA FOR DETERMINING WINNERS AND PRIZE WINNERS ${ }^{1}$
## of the school students' competition "CONQUER SPARROW MOUNTAINS!" IN MATHEMATICS
ELIMINATION STAGE
WINNER:
From 95 points inclusive and above.
PRIZE WINNER:
From
91 points to
94
points inclusive.
FINAL STAGE
WINNER (Diploma I degree):
From 90 points inclusive and above.
PRIZE WINNER (Diploma II degree):
From 75 points to 89 points inclusive.
PRIZE WINNER (Diploma III degree):
from 60 points to 74 points inclusive.[^0]
[^0]: ${ }^{1}$ Approved at the meeting of the jury of the school students' competition "Conquer Sparrow Mountains!" in mathematics
|
3
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Natural numbers $m, n$ are such that the fraction $\frac{m}{n}$ is irreducible, while the fraction $\frac{4 m+3 n}{5 m+2 n}$ is reducible. By which natural numbers can it be reduced?
|
# Answer: 7
Let the numbers $4 m+3 n$ and $5 m+2 n$ have a common divisor $d>1$. Then there exist natural numbers $a$ and $b$ such that the system holds:
$$
\left\{\begin{array}{l}
4 m+3 n=a d \\
5 m+2 n=b d
\end{array}\right.
$$
From this system, we can express $m$ and $n$: $7 n=d(5 a-4 b), 7 m=d(3 b-2 a)$. If 7 does not divide $d$, then $m$ and $n$ are divisible by $d>1$, which contradicts the irreducibility of the fraction $\frac{m}{n}$. Therefore, $d=7$.
|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14. Let's call an integer "extraordinary" if it has exactly one even divisor other than 2. How many extraordinary numbers exist in the interval $[1 ; 75]$?
|
Answer: 12
Solution: This number should be equal to a prime multiplied by 2. There are 12 such numbers:
$\begin{array}{llllllllllll}2 & 3 & 5 & 7 & 11 & 13 & 17 & 19 & 23 & 29 & 31 & 37\end{array}$
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
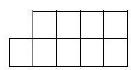
15. A right-angled triangle was cut along a straight line into two parts and these parts were assembled into a square (see fig). What is the length of the shorter leg if the longer leg is 10?
#
|
# Answer 5.
Solution: The short leg is equal to the side of the square, and the long leg is twice the side of the square.
|
5
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5. In how many ways can the number 10000 be factored into three natural factors, none of which is divisible by 10? Factorizations that differ only in the order of the factors are considered the same.
|
Answer: 6.
Solution: Each of the factors should only include powers of 2 and 5 (they cannot be included simultaneously, as it would be a multiple of 10). There can be two factors that are powers of two, in which case the third factor is 625. Or conversely, two factors are powers of five, and the third factor is 16. In each case, there are 3 variants.
|
6
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Vovochka approached a slot machine, on the screen of which the number 0 was lit. The game rules stated: «The screen shows the number of points. If you throw a 1 ruble coin, the number of points will increase by 1. If you throw a 2 ruble coin, the number of points will double. If you score 50 points, the machine will give a prize. If you get a number greater than 50, all the points will be lost.» What is the minimum amount of rubles Vovochka can spend to get the prize?
|
# Answer: 11 rubles.
Solution: Let's try to solve it from the end - how to get from 50 to 1 with the least amount of rubles, if you can only divide by 2 and subtract 1. We get: 50 >25->24->12->6->3->2->1. That is, it will take 4 two-ruble and 3 one-ruble coins. Obviously, if you use 3 two-ruble coins and fewer than 5 one-ruble coins (which corresponds to multiplying by 8), you cannot get a number greater than 40. Fewer one-ruble coins will also not suffice - this can be shown by enumeration.
|
11
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. The Mad Hatter's clock is fast by 15 minutes per hour, while the March Hare's clock is slow by 10 minutes per hour. One day, they set their clocks by the Dormouse's clock (which is stopped and always shows 12:00) and agreed to meet at 5 o'clock in the evening for their traditional five o'clock tea. How long will the Mad Hatter wait for the March Hare if each arrives exactly at 17:00 by their own clocks?
|
Answer: 2 hours.
Solution: The Mad Hatter's clock runs at a speed of $5 / 4$ of normal, so it will take 4 hours of normal time to pass 5 hours. Similarly, the March Hare's clock runs at a speed of $5 / 6$ of normal, so it will take 6 hours of normal time to pass 5 hours.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. We will call a number "marvelous" if it has exactly 3 different odd natural divisors (and an arbitrary number of even divisors). How many "marvelous" two-digit numbers exist?
|
Answer: 7.
Solution: Such numbers have the form $2^{k} \times p^{2}$, where $p-$ is an odd prime number. Clearly, $p$ does not exceed 7, since the result must be a two-digit number. If $p=3$, then $k=0,1,2,3$; If $p=5$, then $\mathrm{k}=0,1$; if $\mathrm{p}=7$, then $k=0$. In total, there are 7 options.

|
7
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Six numbers are given, the arithmetic mean of which is equal to some number A. Petrov calculated the arithmetic mean of the first four numbers - it turned out to be A+10. Vasechkin calculated the arithmetic mean of the last four numbers - it is A - 7. In which direction and by how much does the arithmetic mean of the first, second, fifth, and sixth of these numbers differ from A?
|
Answer: 3 less.
Solution - similar to option v3a.
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. If you open the cold water tap, the bathtub will fill up in 10 minutes, if you open the hot water tap, it will take 15 minutes. If you pull the plug, the bathtub will completely drain in 12 minutes. How long will it take to fill the bathtub if you open both taps and pull the plug?
#
|
# Answer: 12 min.
Solution: Let's take one bathtub as a unit of volume. The cold water tap flows at a rate of $1 / 10$ of a bathtub per minute, and the hot water tap flows at a rate of $1 / 15$ of a bathtub per minute. Water drains from the drain hole at a rate of $1 / 12$ of a bathtub per minute. Therefore, the total rate is $1 / 10 + 1 / 15 - 1 / 12 = 1 / 12$, so the bathtub will be filled in 12 minutes.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. The turtle crawled out of its house and moved in a straight line at a constant speed of 5 m/hour. After an hour, it turned $90^{\circ}$ (right or left) and continued moving, then crawled for another hour, then turned $90^{\circ}$ (right or left) again... and so on. It crawled for 11 hours, turning $90^{\circ}$ at the end of each hour. What is the shortest distance from the house it could have been?
|
Answer 5 m.
Solution: We can consider a coordinate grid with nodes spaced 5 m apart. It is clear that the turtle crawls along

the nodes of this grid. The turtle cannot return to the initial position in 11 hours. However, it can be at a distance of 5 m - it is easy to construct an example.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many different right-angled triangles exist, one of the legs of which is equal to $\sqrt{2016}$, and the other leg and the hypotenuse are expressed as natural numbers
ANSWER: 12.
|
Solution. According to the condition $c^{2}-b^{2}=a^{2}=2016$, that is, $(c-b)(c+b)=2^{5} \cdot 3^{2} \cdot 7$. The system $\left\{\begin{array}{l}c-b=n, \\ c+b=k\end{array}\right.$ (here $n-$ is one of the divisors of the number 2016, and $k=\frac{2016}{n}$) has natural solutions $c=\frac{n+k}{2}, b=\frac{k-n}{2}$, if $n<k$ (that is, $n \leq 44$) and $n$ and $k$ are even.
Possible values of $n$: $2,2^{2}=4,2^{3}=8,2^{4}=16,2 \cdot 3=6,2^{2} \cdot 3=12,2^{3} \cdot 3=24$, $2 \cdot 7=14,2^{2} \cdot 7=28,2 \cdot 3^{2}=18,2^{2} \cdot 3^{2}=36,2 \cdot 3 \cdot 7=21$ - a total of 12 options.
|
12
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. How many different right-angled triangles exist, one of the legs of which is equal to $\sqrt{1001}$, and the other leg and the hypotenuse are expressed as natural numbers
ANSWER: 4.
|
Solution: Let's write down the Pythagorean theorem: $a^{2}+1001=b^{2}$. From this, we get $(b-a)(b+a)=1001=7 \times 11 \times 13$. We can represent 1001 as the product of two factors $1 \times 1001=7 \times 143=11 \times 91=13 \times 77$ - the first factor must be smaller - there are 4 options in total.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the largest natural number that cannot be represented as the sum of two composite numbers.
OTBET: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. And odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we find that 11 cannot be represented in this way.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Let $f(x)=x^{2}+p x+q$ where $p, q$ are some coefficients. By how much can the maximum value of the function $g(x)=|f(x)|$ differ from the minimum value of this function on the interval $[2 ; 6]$?
ANSWER: by 2.
|
Solution: For $f(x)=x^{2}+p x+q$ the difference between the maximum and the minimum value is at least 4 (this can be shown graphically). By choosing $q$,
we find that the maximum value of the modulus of the minimum differs by no more than 2. Example: $f(x)=(x-4)^{2}-2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7. Solve the equation in natural numbers $2 n-\frac{1}{n^{5}}=3-\frac{2}{n}$
ANSWER: $n=1$.
|
Solution: $2 n=3-\frac{2}{n}+\frac{1}{n^{5}} \leq 3$, only $\mathrm{n}=1$ fits
Lomonosov Moscow State University
## School Olympiad "Conquer Sparrow Hills" in Mathematics
Final Stage Tasks for the 2015/2016 Academic Year for 9th Grade
|
1
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Captain Jack Sparrow found a cave with a pirate treasure. In it, there are 6 chests, and the treasure is only in one of them, while the other chests are home to venomous snakes, ready to attack anyone who disturbs their peace.
On the first chest, it says “The treasure is in the third chest.”
On the second, “The treasure is in me or in the first chest.”
On the third, “There is no treasure in me.”
On the fourth, “The treasure lies in a chest with an odd number.”
On the fifth, “There is no treasure in the second and sixth chests.”
On the sixth, “There is no treasure in the fourth chest.”
Help Jack find the treasure, knowing that exactly half of the inscriptions are true. In your answer, indicate the number of the chest with the treasure.
ANSWER: 2.
|
Solution: Let's create a $6 \times 6$ table. In the і-th row and ј-th column, we will place a cross if the і-th statement is true when the treasure is in the ј-th chest:
| | 1 | 2 | 3 | 4 | 5 | 6 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | | | X | | | |
| 2 | X | X | | | | |
| 3 | X | X | | X | X | X |
| 4 | X | | X | | X | |
| 5 | X | | X | X | X | |
| 6 | X | X | X | | X | X |
According to the problem, the column that fits is the one with exactly 3 crosses - i.e., the second.
|
2
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
4. Find the largest natural number that cannot be represented as the sum of two composite numbers.
ANSWER: 11
|
Solution: Even numbers greater than 8 can be represented as the sum of two even numbers greater than 2. And odd numbers greater than 12 can be represented as the sum of 9 and an even composite number. By direct verification, we are convinced that 11 cannot be represented in this way.
|
11
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
30. Find the number of natural numbers $n$, not exceeding 3134, for which the equation $x^{[x]}=n$ has a solution. Here $[x]$ is the greatest integer not exceeding $x$.
|
Answer: 422.
III. Solve the inequality
$$
\frac{4^{-|x-2|}}{\sqrt{x^{2}-x-2}+2} \leqslant \frac{2^{1-|x|}}{\sqrt{x^{2}+6 x}+4}.
$$
In the answer, write the smallest root by absolute value, rounding it to two decimal places if necessary. If there are no solutions, then write the number 0.
Solution. Rewrite the inequality as
$$
\frac{4^{-|x-2|}}{\sqrt{(x+1)(x-2)}+2} \leqslant \frac{2^{-|x|}}{\sqrt{\left(\frac{x}{2}+3\right)\left(\frac{x}{2}\right)}+2}
$$
If we denote the left side by $f(x)$, then the right side is $f\left(\frac{x}{2}+2\right)$, and we get the inequality
$$
f(x) \leqslant f\left(\frac{x}{2}+2\right)
$$
Let's analyze the monotonicity. The domain of the original inequality is the set $(-\infty ;-6] \cup[2 ; \infty)$
On the set $x \leqslant-6$, both the left and right sides of the inequality are increasing, so we get $x \leqslant \frac{x}{2}+2$.
On the set $x \geqslant 2$, both the left and right sides of the inequality are decreasing, so we get $x \geqslant \frac{x}{2}+2$.
Since the solution to the inequality will be $x \in(-\infty ;-6] \cup[4 ; \infty)$, then $x=4$.
Answer: 4.
|
4
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1. Place the numbers $1,2,3,4,5,6,7,8$ and 9 in the nine cells of the figure shown in the diagram, so that the sum of the numbers in each column, starting from the second, is 1 more than in the previous one. It is sufficient to find at least one such arrangement. In your answer, indicate the number in the first column.
|
Answer: 7.
Solution: For now, we will not pay attention to the order of numbers in one column.
The sum of the given numbers is 45. Let $x$ be the number in the bottom-left cell. Then $5x + 10 = 45$, from which $x = 7$. Therefore, the sum of the numbers in the second column is $8 = 5 + 3 = 6 + 2$. If the second column contains 3 and 5, then the third column must contain 1 and 8, the fourth column must contain 6 and 4, and the last column must contain 2 and 9. If the second column contains 6 and 2, then the third column can contain 1 and 8 or 4 and 5. It can be shown that if the third column contains 1 and 8, it is impossible to select numbers for the fourth column. Therefore, the third column must contain 4 and 5, then the fourth column must contain 1 and 9, and the last column must contain 3 and 8. This results in 2 arrangements without considering the order of the numbers.
Notice that in each column (except the first), the numbers can be swapped, which gives 16 options for each arrangement. In the end, we get 32 options considering the order of the numbers in the columns.
|
7
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2. Find the smallest possible value of $\left|2015 m^{5}-2014 n^{4}\right|$, given that $m, n$ are natural numbers.
|
Answer: 0.
Solution: Let's find $N=2014^{x} \cdot 2015^{y}$ such that $m^{5}=2014^{x-1} \cdot 2015^{y}$ and $n^{4}=2014^{x} \cdot 2015^{y-1}$. For this, $x$ and $y-1$ must be multiples of 4, and $x-1$ and $y-5$ must be multiples of 5. For example, $x=16$ and $y=5$ work. Then, if we take $m=2014^{3} \cdot 2015$ and $n=2014^{4} \cdot 2015$, we get $\left|2015 m^{5}-2014 n^{4}\right|=0$.
|
0
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
9.2. On the board in the laboratory, two numbers are written. Every day, the senior researcher Pyotr Ivanovich erases both numbers from the board and writes down their arithmetic mean and harmonic mean ${ }^{2}$. In the morning of the first day, the numbers 1 and 2 were written on the board.
Find the product of the numbers written on the board in the evening of the 2016th day.
|
# Solution:
The product of the numbers on the board does not change.
Indeed, $\frac{a+b}{2} \times \frac{2}{\frac{1}{a}+\frac{1}{b}}=a b$. Therefore, the desired product is 2.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.4. Is it possible to measure out exactly 4 liters of water into the larger of the two containers, using only a 3-liter and a 5-liter container, from a tap? If so, provide an example of how to do it.
|
Solution. You can, fill up 5 liters, pour 3 liters into the second container, then pour out this water, leaving 2 liters in the 5-liter container. Transfer these 2 liters to the 3-liter container. Fill the 5-liter container to the top and top up the second container (exactly 1 liter), then you will have 4 liters left in the first container. (There are other solutions as well)
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3. The function $f(x)$ is such that for all natural $n>1$ there exists a prime divisor $p$ of the number $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
It is known that $f(1001)=1$. What is $f(1002) ?$
|
Solution. Note that for any prime number p, the value $f(p)=f(1)-$ $f(p)$. Therefore, $f(p)=\frac{f(1)}{2}$ for any prime number. For prime numbers p and q, we get that either $\mathrm{f}(\mathrm{pq})=\mathrm{f}(\mathrm{p})-\mathrm{f}(\mathrm{q})=0$, or $\mathrm{f}(\mathrm{pq})=\mathrm{f}(\mathrm{q})-\mathrm{f}(\mathrm{p})=0$. For three prime numbers $\mathrm{p}, \mathrm{q}$, and $\mathrm{r}$, we get that $\mathrm{f}(\mathrm{pqr})=\mathrm{f}(\mathrm{pq})-\mathrm{f}(\mathrm{r})=-\mathrm{f}(\mathrm{r})=-\frac{\mathrm{f}(1)}{2}$ (the order of the prime numbers can be different). Then $f(1001)=f(7 \cdot 11 \cdot 13)=-\frac{f(1)}{2}=1$. But then $f(1002)=f(2 \cdot 3 \cdot 167)=-\frac{f(1)}{2}=1$.
Answer: 1.
Criteria: Full solution - 7 points. It is shown that $f(1)=-2$ or there is a proof that $f(p q)=0 - 2$ points.
|
1
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.2. At noon, a "Moskvich" left point A for point B. At the same time, "Zhiguli" left point B for point A on the same road. An hour later, the "Moskvich" was halfway between A and the "Zhiguli". When will it be halfway between the "Zhiguli" and B? (The speeds of the cars are constant and differ by less than a factor of two.)
|
Solution. Let the speeds of the "Moskvich" and "Zhiguli" be u and v, respectively. From the problem statement, it follows that if the speed of the "Moskvich" were $2 \mathrm{u}$, then its meeting with the "Zhiguli" (traveling at speed v) would occur one hour after the start of the journey. From this, it follows that if the speed of the "Zhiguli" were $\frac{v}{2}$, then their meeting with the "Moskvich" (traveling at speed u) would occur two hours after the start of the journey. This means that at this moment (2 PM), with the given (u and v) speeds, the "Moskvich" will be halfway between the "Zhiguli" and V.
Answer: at 2 PM.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.5. The faces of a cube are labeled with six different numbers from 6 to 11. The cube was rolled twice. The first time, the sum of the numbers on the four side faces was 36, the second time - 33. What number is written on the face opposite the one where the digit $10$ is written?
|
Solution: The sum of the numbers on all faces is
$$
6+7+8+9+10+11=51
$$
On the first roll, the sum of the numbers on the top and bottom faces is 51 $-36=15$, on the second roll $-51-33=18$. Therefore, the sum on the third pair of opposite faces is $51-15-18=18$. The sum of 18 can be obtained in two ways: $11+7$ or $10+8$. Therefore, on the pairs of faces with a sum of 18, 7 is opposite 11, and 8 is opposite 10.
## Answer: 8
|
8
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. One day, a traveler interviewed seven residents of the island.
- I am a knight, - said the first.
- Yes, he is a knight, - said the second.
- Among the first two, there are no less than 50% liars, - said the third.
- Among the first three, there are no less than 65% liars, - said the fourth.
- Among the first four, there are no less than 50% knights, - said the fifth.
- Among the first five, there are no less than 40% liars, - said the sixth.
- Among the first six, there are no less than 65% knights, - said the seventh.
Determine how many knights there are among them in reality.
|
Answer: 5.
Solution: Suppose the first inhabitant is a knight. Then the second is also a knight, while the third and fourth are liars. If, on the other hand, the first is a liar, then the second is also a liar, while the third and fourth are knights. In either case, among the first four, there are exactly two knights and two liars. Therefore, the statements of the fifth, sixth, and seventh inhabitants are true, i.e., they are knights.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. The sequence is defined by the relations $a_{1}=1$,
$$
a_{2 n}=\left\{\begin{array}{ll}
a_{n}, & \text { if } n \text { is even, } \\
2 a_{n}, & \text { if } n \text { is odd; }
\end{array} \quad a_{2 n+1}= \begin{cases}2 a_{n}+1, & \text { if } n \text { is even, } \\
a_{n}, & \text { if } n \text { is odd. }\end{cases}\right.
$$
Find the smallest natural $n$ for which $a_{n}=a_{2017}$.
|
Answer: 5.
Solution: The given rules are easily interpreted in terms of the binary system: if $n$ ends in 0 and 1 is appended to the right, then 1 is appended to the right of $a_{n}$. If $n$ ends in 1 and 0 is appended, then 0 is appended to the right of $a_{n}$. In all other cases, $a_{n}$ does not change (when 0 is appended to 0 or 1 is appended to 1). Let's write the number 2017 in binary: $2017=11111100001_{2}$. It is easy to see that $a_{2017}=101_{2}=5_{10}$. By checking the first few values, we find $a_{5}=5$.
|
5
|
Number Theory
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Knights and Liars, knights always tell the truth, while liars always lie. One day, a traveler interviewed seven residents of the island.
- I am a knight, - said the first.
- Yes, he is a knight, - said the second.
- Among the first two, there are no less than 50% liars, - said the third.
- Among the first three, there are no less than 65% liars, - said the fourth.
- Among the first four, there are no less than 50% knights, - said the fifth.
- Among the first five, there are no less than 40% liars, - said the sixth.
- Among the first six, there are no less than 65% knights, - said the seventh.
Determine how many knights are among them in reality.
|
Answer: 5.
Solution: Suppose the first inhabitant is a knight. Then the second is also a knight, while the third and fourth are liars. If, on the other hand, the first is a liar, then the second is also a liar, while the third and fourth are knights. In either case, among the first four, there are exactly two knights and two liars. Therefore, the statements of the fifth, sixth, and seventh inhabitants are true, i.e., they are knights.
|
5
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. If the 200th day of some year is Sunday and the 100th day of the following year is also Sunday, then what day of the week was the 300th day of the previous year? Enter the number of this day of the week (if Monday, then 1, if Tuesday, then 2, etc.).
|
Answer. 1.
Solution. Between the $200-\mathrm{th}$ day of the year and the $100-\mathrm{th}$ day of the next year, there are either $165+100=265$ or $166+100=266$ days. The number 266 is divisible by 7, while the number $265-$ is not. Therefore, the current year has 366 days, meaning it is a leap year. Thus, the previous year was a common year. Therefore, between the $300-\mathrm{th}$ day of the previous year and the $200-\mathrm{th}$ day of the current year, there are $65+200=265$ days. Since $265=7 \cdot 37+6$, the number of days is 1 less than a multiple of 7. Therefore, it was a Monday.
|
1
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. From point $A$ to point $B$, which are 10 km apart, a car departed at 7:00. After traveling $2 / 3$ of the distance, the car passed point $C$, from which a cyclist immediately set off for point $A$. As soon as the car arrived at $B$, a bus immediately departed from $B$ in the opposite direction and arrived at $A$ at 9:00. At what distance from $B$ did the bus catch up with the cyclist, if the cyclist arrived at point $A$ at 10:00 and the speed of each participant in the movement was constant?
|
Answer: 6.
Solution. Let's plot the graphs of the car's movement (segment $K L$), the bus's movement (segment $L M$), and the cyclist's movement (segment $N P$) on the axes $(t ; s)$, where $t$ is time (in hours) and $s$ is the distance (in kilometers) from point $A$. Let $Q$ be the intersection point of $L M$ and $N P$. According to the problem, $M K=2$ and $P M=1$. Draw $M G \| N Q, G \in K L$, then by Thales' theorem, $\frac{N G}{G K}=\frac{P M}{M K}=\frac{1}{2}$. Therefore, if $N G=2 x$, then $G K=4 x$, and $L N=3 x$. Hence (again by Thales' theorem) $\frac{L Q}{Q M}=\frac{L N}{N G}=\frac{3 x}{2 x}=\frac{3}{2}$. Therefore, the required distance is $\frac{3}{5} \cdot 10=6$ km.
Participants familiar with Menelaus' theorem can solve the problem as follows. Points $N, Q$, and $P$ lie on the same line, so $\frac{K N}{N L} \cdot \frac{L Q}{Q M} \cdot \frac{M P}{P K}=1$, or $\frac{2}{1} \cdot \frac{L Q}{Q M} \cdot \frac{1}{3}=1$. Therefore, $\frac{L Q}{Q M}=\frac{3}{2}$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.1. On the Island of Misfortune, there live knights who always tell the truth, and liars who always lie. One day, a tourist met five inhabitants of the island and asked them: "How many liars are there among you?" The first answered: "One," the second answered: "Two," the third answered: "Three," the fourth answered: "Four," the fifth answered: "Five." How many liars were there in reality?
|
Answer: 4.
Solution: Among the islanders surveyed, exactly one is a knight, since they all gave different, and all possible answers. Then the remaining four are liars.
|
4
|
Logic and Puzzles
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
5.1. From one point on a circular track, a pedestrian and a cyclist started simultaneously in the same direction. The cyclist's speed is $55\%$ greater than the pedestrian's speed, and therefore the cyclist overtakes the pedestrian from time to time. At how many different points on the track will the overtakes occur?
|
Answer: 11.
Solution: Let's assume the length of the path is 55 (in some units), and the speeds of the pedestrian and the cyclist are $100 x$ and $155 x$. Then, the overtakes will occur every $1 / x$ units of time. During this time, the pedestrian covers 100 units, which means he will be 10 units away in the opposite direction from the start. This will happen at each overtake. At the 11th overtake, the pedestrian will have covered 1100 units and will be back at the starting point, after which the overtake points will start repeating.
|
11
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6. On graph paper (the side of a cell is 1 cm) a rectangle is drawn, the sides of which lie on the grid lines, with one side being 5 cm shorter than the other. It turned out that it can be cut into several pieces along the grid lines and form a square from them. What can the side of this square be? Find all possible values.
#
|
# Answer: 6 cm.
Solution. Let the larger side of the rectangle be $k$ cm, $k>5$, and the side of the obtained square be $n$ cm. Then, from the equality of areas, we get $k(k-5)=n^{2}$. Note that $k^{2}-5k=k^{2}-6k+9=(k-3)^{2}$ for $k>9$. Therefore, $6 \leqslant k \leqslant 9$. For $k=6,7,8,9$, we get that $k(k-5)$ equals $6 \cdot 1=6, 7 \cdot 2=14, 8 \cdot 3=24, 9 \cdot 4=36$ respectively. Among these values, only the last one is a square of a natural number, and $n=6$. The rectangle $9 \times 4$ can be cut along the grid lines and assembled into a square $6 \times 6$ in many ways.
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
2.1. Find the integer part of the number $a+\frac{9}{b}$, where $a$ and $b-$ are respectively the integer and fractional part of the number $\sqrt{76-42 \sqrt{3}}$.
|
Answer: 12.
Solution. The given number is $\sqrt{76-42 \sqrt{3}}=\sqrt{(7-3 \sqrt{3})^{2}}=7-3 \sqrt{3}=1+(6-3 \sqrt{3})$, where $6-3 \sqrt{3} \in(0 ; 1)$. Therefore, $a=1, b=6-3 \sqrt{3}$. Thus, $a+\frac{9}{b}=1+\frac{9}{6-3 \sqrt{3}}=1+\frac{3}{2-\sqrt{3}}=1+3(2+\sqrt{3})=7+3 \sqrt{3}$. Since $12<7+3 \sqrt{3}<13$, the integer part of the number $a+\frac{9}{b}$ is 12.
|
12
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
7.1. How many values of the parameter $a$ exist for which the equation
$$
4 a^{2}+3 x \lg x+3 \lg ^{2} x=13 a \lg x+a x
$$
has a unique solution
|
Answer: 2.
Solution. The given equation is equivalent to the equation $(3 \lg x-a)(x+\lg x-4 a)=0$, from which we have the system
$$
\left[\begin{array}{l}
\lg x=\frac{a}{3} \\
x+\lg x=4 a
\end{array}\right.
$$
Each equation in this system has a unique positive solution for any $a$, since the continuous functions $f_{1}(x)=\lg x$ and $f_{2}(x)=x+\lg x$ are strictly increasing on their domain $(0 ;+\infty)$ and take all possible values from $(-\infty ;+\infty)$. Therefore, it is necessary for these solutions to coincide. Then $x=11 a / 3, \lg x=a / 3$, hence, $10^{a / 3}=11 a / 3$. This equation has exactly two solutions due to the fact that the function $g(t)=10^{t}-11 t$ is strictly decreasing on $(-\infty ; \lg (11 \lg e)]$, strictly increasing on $[\lg (11 \lg e) ;+\infty)$, takes a negative value at the point $t=1$, and positive values at the points $t=0$ and $t=2$.
|
2
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
11.1. [7-8.6 (20 points)] On the bisector of angle $B A C$ of triangle $A B C$, a point $M$ is marked, and on the extension of side $A B$ beyond point $A$, a point $N$ is marked such that $A C=A M=1$ and $\angle A N M=\angle C N M$. Find the length of segment $A N$.
|
Answer: 1.
Solution. Let's place point $K$ on the extension of segment $NC$ beyond point $C$. Point $M$ lies on the bisectors of angles $BAC$ and $ANC$, which means it is equidistant from lines $AC$ and $NC$, and therefore lies on the bisector of angle $ACK$. Then, considering the equality of angles $M$ and $C$ in the isosceles triangle $AMC$, from the equality of alternate interior angles $CMA$ and $MCK$, we get that lines $AM$ and $NC$ are parallel. From this, it follows that alternate interior angles $MAC$ and $ACN$ are equal to $\angle BAC / 2$, and thus $\angle ANC = \angle BAC - \angle ACN = \angle BAC / 2$. We have obtained that triangle $NAC$ is isosceles and $AN = AC = AM = 1$.
|
1
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
14.1. $[9.1$ (15 points), 10.1 (15 points)] Calculate
$$
\sqrt{1+2 \sqrt{1+3 \sqrt{1+\ldots+2017 \sqrt{1+2018 \cdot 2020}}}}
$$
Answer: 3.
|
Solution. Since $2018 \cdot 2020=2019^{2}-1, 2017 \cdot 2019=2018^{2}-1, \ldots$, we get
$$
\begin{gathered}
\sqrt{1+2 \sqrt{1+3 \sqrt{1+\ldots+2017 \sqrt{1+2018 \cdot 2020}}}}= \\
=\sqrt{1+2 \sqrt{1+3 \sqrt{1+\ldots+2016 \sqrt{1+2017 \cdot 2019}}}}=\ldots=\sqrt{1+2 \cdot 4}=3
\end{gathered}
$$
|
3
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
# Problem 4.
Given a square with a side length of 5 cm. On its four sides, the vertices of a second square are located; on the four sides of the second square, the vertices of a third square, and so on. For what smallest natural $n$ will the sum of the areas of the first $n$ squares be guaranteed to be greater than 49 cm $^{2}$?
|
Answer: 6
Solution. A square inscribed in the given square has the smallest area if its vertices are the midpoints of the sides of the original square (this follows, for example, from the fact that the area of a square is half the square of its diagonal). In this case, the area of the inscribed square is half the area of the original. Thus, the areas of the squares of minimum area form a geometric progression with the first term 5 and the common ratio 0.5. The sum of the first $n$ terms of this progression will first exceed 49 when $n=6$ (this can be obtained by enumeration or from the formula for the sum of the terms of a geometric progression).
## B-2
A square with a side of 7 cm is given. On the four sides of this square, the vertices of a second square are located; on the four sides of the second square, the vertices of a third square, and so on. For what smallest natural $n$ will the sum of the areas of the first $n$ squares be guaranteed to be greater than 97 cm $^{2}$?
Answer: 7
## B-3
A square with a side of 3 cm is given. On the four sides of this square, the vertices of a second square are located; on the four sides of the second square, the vertices of a third square, and so on. For what smallest natural $n$ will the sum of the areas of the first $n$ squares be guaranteed to be greater than 17 cm $^{2}$?
Answer: 5
## B-4
A square with a side of 9 cm is given. On the four sides of this square, the vertices of a second square are located; on the four sides of the second square, the vertices of a third square, and so on. For what smallest natural $n$ will the sum of the areas of the first $n$ squares be guaranteed to be greater than 160 cm $^{2}$?
Answer: 7
## Lomonosov Olympiad for Schoolchildren in Mathematics
Preliminary stage $2020 / 21$ academic year for $7-8$ grades
## B-1
#
|
6
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (13 points) Ani has blue, green, and red paints. She wants to paint a wooden cube so that after painting, the cube has two faces of each color. In how many different ways can she do this? Ways of painting that can be obtained by rotating the cube are considered the same.
|
Answer: 6.
Solution. Red opposite red, blue opposite blue, green opposite green is one way. Red opposite red, blue opposite green is one way and there are two similar ways. Opposite each color, there is a face of one of the two remaining colors - two ways. In total, there are 6 ways to paint.
|
6
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8. A set of natural numbers is called bad if it is possible to select several numbers from it such that their sum equals 2012. Find the smallest such $n$ that the numbers $503, 504, \ldots, 2011$ can be partitioned into $n$ sets such that none of these sets are bad.
|
Answer: $n=2$.
Solution: We will show that the given set can be divided into two subsets, neither of which are bad. Consider the sets $M_{1}=\{503,504, \ldots, 671\}$, $M_{2}=\{672,673, \ldots, 1006\}$, $M_{3}=\{1007,1008, \ldots, 1340\}$, $M_{4}=\{1341,1342, \ldots, 2011\}$, and show that $M_{1} \cup M_{3}$ and $M_{2} \cup M_{4}$ are not bad.
We will prove that $M_{1} \cup M_{3}$ is not bad. Consider the cases:
- Four numbers from the set $M_{1}$ give a sum $S \geqslant 503+504+505+506=$ $2018>2012 ;$
- Three numbers from the set $M_{1}$ give a sum $S \leqslant 669+670+671=2010<2012$
- One number from the set $M_{1}$ and one from $M_{3}$ give a sum $S \leqslant 671+1340=$ $2011<2012$;
Similarly, it can be proven for $M_{2} \cup M_{4}$.
|
2
|
Combinatorics
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
3.1. (13 points) Find the largest natural number $n$ satisfying the inequality $n^{300}<3^{500}$. Answer: 6.
|
Solution. The inequality is equivalent to the following: $n^{3}<3^{5}=243$. Since $6^{3}=216<243<$ $7^{3}=289$, the desired value is $n=6$.
|
6
|
Inequalities
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
6.1. (13 points) Misha drew a triangle with a perimeter of 11 and cut it into parts with three straight cuts parallel to the sides, as shown in the figure. The perimeters of the three shaded figures (trapezoids) turned out to be 5, 7, and 9. Find the perimeter of the small triangle that resulted from the cutting.
|
Answer: 10.
Solution. Since opposite sides of parallelograms are equal, the lateral sides of each resulting trapezoid are equal to the corresponding segments on the sides of the original triangle. Therefore, the sum of the perimeters of the three trapezoids is equal to the sum of the perimeter of the original triangle (the sum of the larger bases and lateral sides of the three trapezoids) and the perimeter of the new triangle (the sum of the smaller bases of the trapezoids). Thus, the perimeter of the new triangle is equal to the sum of the perimeters of the trapezoids minus the perimeter of the original triangle: \(a + b + c - P\).
|
10
|
Geometry
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
8.1. (13 points) Two people spend time playing a game: they take turns naming prime numbers not exceeding 100 such that the last digit of the number named by one player is equal to the first digit of the number named by the next player (except for the first prime number named in the game). Repeating numbers that have already been named is not allowed. The player who cannot name the next prime number according to these rules loses. Prove that one of the players can act in such a way as to guarantee a win, and find the smallest possible number of prime numbers that will be used by both players in such a game.
#
|
# Answer: 3.
Solution. We will describe a winning strategy for the first player. First, the first player names a prime number ending in 9 and different from 79 (for example, 19). Since among the numbers $90, \ldots, 99$ the only prime is 97, the second player must name this number on their next move. Then, on the third move, the first player names 79, and the second player loses. The first player cannot win in fewer moves, as for any digit from 1 to 9, there exists a prime number in the first hundred that starts with this digit.
|
3
|
Number Theory
|
proof
|
Yes
|
Yes
|
olympiads
| false
|
5.1. The sequence is defined by the relations $a_{1}=1$,
$$
a_{2 n}=\left\{\begin{array}{ll}
a_{n}, & \text { if } n \text { is even, } \\
2 a_{n}, & \text { if } n \text { is odd; }
\end{array} \quad a_{2 n+1}= \begin{cases}2 a_{n}+1, & \text { if } n \text { is even, } \\
a_{n}, & \text { if } n \text { is odd. }\end{cases}\right.
$$
Find the smallest natural $n$ for which $a_{n}=a_{2017}$.
|
Answer: 5.
Solution: The given rules can be easily interpreted in terms of the binary system: if $n$ ends in 0 and 1 is appended to the right, then 1 is appended to the right of $a_{n}$. If $n$ ends in 1 and 0 is appended, then 0 is appended to the right of $a_{n}$. In all other cases, $a_{n}$ does not change (when 0 is appended to 0 or 1 is appended to 1). Let's write the number 2017 in binary: $2017=11111100001_{2}$. It is easy to see that $a_{2017}=101_{2}=5_{10}$. By checking the first few values, we find $a_{5}=5$.
|
5
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
1.2. A ballpoint pen costs 10 rubles, a gel pen costs 40 rubles, and a fountain pen costs 60 rubles. What is the maximum number of ballpoint pens that can be bought if you need to buy exactly 15 pens in total, and among them there must be pens of all three types, and you need to spend exactly 500 rubles?
|
Answer: 6. Comments. The solutions are two triples of integers $(6,5,4)$ and $(4,10,1)$.
|
6
|
Algebra
|
math-word-problem
|
Yes
|
Yes
|
olympiads
| false
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.