id
int64 20
101k
| problem
stringlengths 18
4.16k
| gt_ans
stringlengths 1
191
|
|---|---|---|
3,081 |
7. (3 points) In the abacus shown, each of the three rods has 10 beads. By dividing the beads on each rod into upper and lower parts, two three-digit numbers are formed. The upper part must be a three-digit number with all different digits, and it must be a multiple of the lower three-digit number. The three-digit number in the upper part is . $\qquad$
|
925
|
3,083 |
10 If the vector $\vec{a}+3 \vec{b}$ is perpendicular to the vector $7 \vec{a}-5 \vec{b}$, and the vector $\vec{a}-4 \vec{b}$ is perpendicular to the vector $7 \vec{a}-2 \vec{b}$, then the angle between vector $\vec{a}$ and $\vec{b}$ is $\qquad$.
|
\dfrac{\pi}{3}
|
3,104 |
Take 3 segments randomly, each shorter than a unit. What is the probability that these 3 segments can form a triangle?
|
\dfrac{1}{2}
|
3,112 |
8.1. (13 points) Find the smallest natural number such that after multiplying it by 9, the result is a number written with the same digits but in some different order.
|
1089
|
3,130 |
## Task 15/70
Find all prime numbers that can be represented both as the sum and as the difference of two prime numbers.
|
5
|
3,157 |
There is a unique triplet of positive integers \((a, b, c)\) such that \(a \leq b \leq c\) and
$$
\frac{25}{84}=\frac{1}{a}+\frac{1}{a b}+\frac{1}{a b c}.
$$
Determine \(a + b + c\).
|
17
|
3,195 |
Let \( a, b > 0 \) and \( a b > 2007 a + 2008 b \). Prove the inequality: \( a + b > (\sqrt{2007} + \sqrt{2008})^2 \).
|
a + b > (\sqrt{2007} + \sqrt{2008})^2
|
3,206 |
1. Determine the number of all five-digit palindromes that are divisible by 37. (A palindrome is a number that reads the same backward as forward in decimal notation.)
|
45
|
3,231 |
20.3. The collective farm placed a certain amount of money in the savings bank. If the number of hundreds is added to the number formed by the last two digits, then the result is the annual income from this amount, calculated at $2 \%$ per annum. What is the amount of the deposit placed in the savings bank?
$(7-8$ grades$)$
|
4950
|
3,258 |
A [point](https://artofproblemsolving.com/wiki/index.php/Point) $P$ is chosen in the interior of $\triangle ABC$ such that when [lines](https://artofproblemsolving.com/wiki/index.php/Line) are drawn through $P$ [parallel](https://artofproblemsolving.com/wiki/index.php/Parallel) to the sides of $\triangle ABC$, the resulting smaller [triangles](https://artofproblemsolving.com/wiki/index.php/Triangle) $t_{1}$, $t_{2}$, and $t_{3}$ in the figure, have [areas](https://artofproblemsolving.com/wiki/index.php/Area) $4$, $9$, and $49$, respectively. Find the area of $\triangle ABC$.
|
144
|
3,264 |
## Task 1 - 130621
A rectangular glass pane is $24 \mathrm{~cm}$ long and $22 \mathrm{~cm}$ wide. From this, rectangular panes of $8 \mathrm{~cm}$ length and $6 \mathrm{~cm}$ width are to be cut.
What is the maximum number of such panes that can be obtained?
Illustrate a way to achieve this maximum number in a drawing at a scale of 1 : 2!
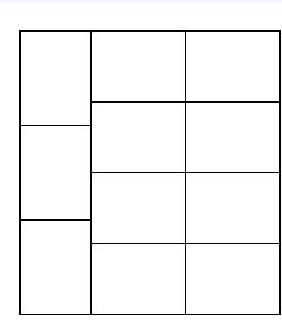
|
11
|
3,285 |
4.18. What surface is defined by the equation
$$
x^{2}-2 x-3 y^{2}+12 y+2 z^{2}+12 z-11=0 ?
$$
|
\frac{(x - 1)^2}{18} - \frac{(y - 2)^2}{6} + \frac{(z + 3)^2}{9} = 1
|
3,287 |
5. Solve the system of equations $\left\{\begin{array}{l}2 x+\sqrt{2 x+3 y}-3 y=5, \\ 4 x^{2}+2 x+3 y-9 y^{2}=32 .\end{array}\right.$
|
\left( \dfrac{17}{4}, \dfrac{5}{2} \right)
|
3,289 |
Given a geometric progression \( b_1, b_2, \ldots, b_{3000} \) with all positive terms and a total sum \( S \). It is known that if every term with an index that is a multiple of 3 (i.e., \( b_3, b_6, \ldots, b_{3000} \)) is increased by 50 times, the sum \( S \) increases by 10 times. How will \( S \) change if every term in an even position (i.e., \( b_2, b_4, \ldots, b_{3000} \)) is increased by 2 times?
|
\dfrac{11}{8}
|
3,292 |
65. The greatest common divisor of two natural numbers whose sum is 1998 is 6. There are $\qquad$ cases of such two natural numbers.
|
108
|
3,306 |
In the diagram, \(A B C D\) is a rectangle, \(P\) is on \(B C\), \(Q\) is on \(C D\), and \(R\) is inside \(A B C D\). Also, \(\angle P R Q = 30^\circ\), \(\angle R Q D = w^\circ\), \(\angle P Q C = x^\circ\), \(\angle C P Q = y^\circ\), and \(\angle B P R = z^\circ\). What is the value of \(w + x + y + z\)?
|
210
|
3,320 |
19. There are 11 consecutive natural numbers, the sum of the largest and smallest of which is 90. Fill these 11 numbers into the circles in the figure below, with one number in each circle, so that the sum of the numbers in the six circles of each regular hexagon is the same. What is the minimum value of this sum?
|
268
|
3,334 |
6. The probability that the product of the points obtained from rolling a die three times is divisible by 6 is $\qquad$
|
\dfrac{133}{216}
|
3,344 |
3. Given the sequence $x_{n}$, satisfying $(n+1) x_{n+1}=x_{n}+n$, and $x_{1}=2$, then $x_{2009}=$ $\qquad$
|
1 + \dfrac{1}{2009!}
|
3,345 |
# Problem 1.
In-1 Find $f(1)+f(2)+f(3)+\ldots+f(13)$, if $f(n)=4 n^{3}-6 n^{2}+4 n+13$.
|
28743
|
3,347 |
13. Use the digits $1,2,3,4,5,6,7,9$ to form 4 two-digit prime numbers (each digit must be used exactly once). How many different combinations of these 4 prime numbers are possible?
|
4
|
3,357 |
Prove that for a positive real number \( \alpha \) and a natural number \( d \), the equality \(\left\lfloor \frac{\alpha}{d} \right\rfloor = \left\lfloor \frac{\lfloor \alpha \rfloor}{d} \right\rfloor\) always holds.
|
\left\lfloor \frac{\alpha}{d} \right\rfloor = \left\lfloor \frac{\lfloor \alpha \rfloor}{d} \right\rfloor
|
3,363 |
Given that the greatest common divisor (GCD) of \(a\) and \(b\) is 4, the least common multiple (LCM) of \(a\) and \(c\) as well as the LCM of \(b\) and \(c\) are both 100, and \(a \leqslant b\), how many sets of natural numbers \(a\), \(b\), and \(c\) satisfy these conditions?
|
9
|
3,365 |
# 3. Option 1.
Café "Buratino" operates 6 days a week with a day off on Mondays. Kolya said that from April 1 to April 20, the café was open for 17 days, and from April 10 to April 30, it was open for 18 days. It is known that he made a mistake once. What was the date of the last Tuesday in April?
|
29
|
3,367 |
Kuba agreed with the shepherd that he would take care of the sheep. The shepherd promised Kuba that after a year of service, he would get twenty gold coins and one sheep. But Kuba quit just when seven months of service had passed. Even so, the shepherd fairly rewarded him and paid him five gold coins and one sheep.
How many gold coins did the shepherd value one sheep at?
(L. Hozová)
Hint. How many gold coins did the shepherd value Kuba's monthly work at?
|
16
|
3,372 |
4. Starting from 1, alternately add 4 and 3, to get the following sequence of numbers $1,5,8,12,15,19,22 \ldots \ldots$ The number in this sequence that is closest to 2013 is $\qquad$ .
|
2014
|
3,377 |
Let \( S \) be the set of positive integers such that for any \( a \) and \( b \) in the set, we have \( \operatorname{GCD}(a, b) > 1 \). Additionally, for any \( a, b, \) and \( c \) in the set, we have \( \operatorname{GCD}(a, b, c) = 1 \). Is it possible that \( S \) has 2012 elements?
\(\operatorname{GCD}(x, y)\) and \(\operatorname{GCD}(x, y, z)\) stand for the greatest common divisor of the numbers \( x \) and \( y \) and the numbers \( x, y, \) and \( z \), respectively.
|
Yes
|
3,379 |
7. (10 points) For a natural number $N$, if at least six of the nine natural numbers from $1$ to $9$ can divide $N$, then $N$ is called a "Six-Union Number". The smallest "Six-Union Number" greater than 2000 is $\qquad$ .
|
2016
|
3,392 |
In a tetrahedron \( ABCD \), \( AB = AC = AD = 5 \), \( BC = 3 \), \( CD = 4 \), \( DB = 5 \). Find the volume of this tetrahedron.
|
5\sqrt{3}
|
3,436 |
B1. Accurately, without using a pocket calculator, calculate the value of the expression
$$
\frac{\cos 20^{\circ}-\sin 650^{\circ}}{\sin \frac{\pi}{12} \cdot \cos \left(-520^{\circ}\right)}+2^{2} \cdot \cos \frac{\pi}{4}
$$
Rationalize the denominator.
|
-2\sqrt{6}
|
3,447 |
Integers $1, 2, 3, ... ,n$ , where $n > 2$ , are written on a board. Two numbers $m, k$ such that $1 < m < n, 1 < k < n$ are removed and the average of the remaining numbers is found to be $17$ . What is the maximum sum of the two removed numbers?
|
51
|
3,489 |
In a given right triangle ABC, the hypotenuse BC, length \(a\), is divided into \(n\) equal parts with \(n\) an odd integer. The central part subtends an angle \(\alpha\) at A. \(h\) is the perpendicular distance from A to BC. Prove that: \(\tan \alpha = \frac{4nh}{a(n^2 - 1)}\).
|
\tan \alpha = \frac{4nh}{a(n^2 - 1)}
|
3,508 |
Consider the game of "tic-tac-toe" on a 3D cubic grid $8 \times 8 \times 8$. How many straight lines can be indicated on which there are 8 symbols in a row?
|
244
|
3,517 |
As shown in the figure, the hyperbola function \( y = \frac{k}{x} \) where \( k > 0 \), passes through the midpoint \( D \) of the hypotenuse \( OB \) of the right triangle \( OAB \) and intersects the leg \( AB \) at point \( C \). If the area of \( \triangle OBC \) is 3, then find the value of \( k \).
|
2
|
3,518 |
3. On the bus route, there are only four stops - "Initial", "First", "Final", and "Last". At the first two stops, passengers only got on, and at the remaining stops, they only got off. It turned out that 30 passengers got on at the "Initial" stop, and 14 passengers got off at the "Last" stop. At the "First" stop, three times fewer passengers got on than got off at the "Final" stop. Which passengers are more - those traveling from "Initial" to "Last", or those traveling from "First" to "Final", and by how many?
Solution:
|
6
|
3,571 |
Use $ \log_{10} 2 \equal{} 0.301,\ \log_{10} 3 \equal{} 0.477,\ \log_{10} 7 \equal{} 0.845$ to find the value of $ \log_{10} (10!)$.
Note that you must answer according to the rules:fractional part of $ 0.5$ and higher is rounded up, and everything strictly less than $ 0.5$ is rounded down,
say $ 1.234\longrightarrow 1.23$. Then find the minimum integer value $ n$ such that $ 10! < 2^{n}$.
|
22
|
3,608 |
## Task Condition
Find the derivative of the specified order.
$$
y=\left(2 x^{3}+1\right) \cos x, y^{V}=?
$$
|
(-2x^3 + 120x - 1)\sin x + (30x^2 - 120)\cos x
|
3,615 |
4. Solve the system of equations $\left\{\begin{array}{l}2 x+\sqrt{2 x+3 y}-3 y=5, \\ 4 x^{2}+2 x+3 y-9 y^{2}=32 .\end{array}\right.$
|
\left( \dfrac{17}{4}, \dfrac{5}{2} \right)
|
3,643 |
$\left[\begin{array}{ll}{[\text { Arithmetic. Mental calculation, etc. }]} \\ {[\text { Word problems (miscellaneous) }]}\end{array}\right]$
The length of the crocodile from head to tail is three times less than ten ken, and from tail to head it is three ken and two shaku. It is known that one shaku is equal to 30 cm. Find the length of the crocodile in meters. (Ken and shaku are Japanese units of length.)
|
6
|
3,648 |
How many solutions in natural numbers does the equation $\left\lfloor \frac{x}{10} \right\rfloor = \left\lfloor \frac{x}{11} \right\rfloor + 1$ have?
|
110
|
3,654 |
4. (20 points) In math class, each dwarf needs to find a three-digit number such that when 198 is added to it, the result is a number with the same digits but in reverse order. For what maximum number of dwarfs could all the numbers they find be different?
|
70
|
3,684 |
Task 1. (5 points) Find $\frac{a^{8}-256}{16 a^{4}} \cdot \frac{2 a}{a^{2}+4}$, if $\frac{a}{2}-\frac{2}{a}=3$.
#
|
33
|
3,690 |
Find the smallest prime that is the fifth term of an increasing [arithmetic sequence](https://artofproblemsolving.com/wiki/index.php/Arithmetic_sequence), all four preceding terms also being [prime](https://artofproblemsolving.com/wiki/index.php/Prime_number).
|
29
|
3,716 |
ABC is a triangle with, as usual, AB = c, CA = b. Find necessary and sufficient conditions for \(\frac{b^2 c^2}{2bc \cos A} = b^2 + c^2 - 2bc \cos A\).
|
a = b \text{ or } a = c
|
3,745 |
52. Find the particular solution of the equation $2 y d x=(1+x) d y$, if $y=4$ when $x=1$.
|
(1 + x)^2
|
3,785 |
29.6. Calculate $\int \sqrt{1-x^{2}} d x$.
|
\frac{1}{2} \left( x \sqrt{1 - x^2} + \arcsin x \right)
|
3,787 |
In a square, 20 points were marked and connected by non-intersecting segments with each other and with the vertices of the square, dividing the square into triangles. How many triangles were formed?
|
42
|
3,801 |
Given \(a, b, c \in \mathbf{R}_{+}\). Prove:
$$
\sum \frac{b+c}{a} \geqslant \frac{\left(\sum a^{2}\right)\left(\sum ab\right)}{abc \sum a} + 3
$$
|
\sum \frac{b+c}{a} \geqslant \frac{\left(\sum a^{2}\right)\left(\sum ab\right)}{abc \sum a} + 3
|
3,812 |
## Task B-1.1.
Let $a>1$. The points $(x, y)$ for which the coordinates satisfy $|x|+y=a, x^{2}+y=a|x|$ determine a figure in the coordinate plane with an area of 120 square units. Calculate the real number $a$.
|
11
|
3,816 |
Example 8. Find the residue of the function
$$
w=z^{2} \sin \frac{1}{z+1}
$$
at its singular point.
|
\dfrac{5}{6}
|
3,840 |
In a room there is a series of bulbs on a wall and corresponding switches on the opposite wall. If you put on the $n$ -th switch the $n$ -th bulb will light up. There is a group of men who are operating the switches according to the following rule: they go in one by one and starts flipping the switches starting from the first switch until he has to turn on a bulb; as soon as he turns a bulb on, he leaves the room. For example the first person goes in, turns the first switch on and leaves. Then the second man goes in, seeing that the first switch on turns it off and then lights the second bulb. Then the third person goes in, finds the first switch off and turns it on and leaves the room. Then the fourth person enters and switches off the first and second bulbs and switches on the third. The process continues in this way. Finally we find out that first 10 bulbs are off and the 11 -th bulb is on. Then how many people were involved in the entire process?
|
1024
|
3,846 |
10. (10 points) In a math test at Sheep Village Elementary School's fourth grade, the test consists of 15 questions. If Xiaoxixi, Xiaobeibe, Xiaomeimei, and Xiaolan all answered 11, 12, 13, and 14 questions correctly, respectively, then the minimum number of questions they all answered correctly is $\qquad$ questions.
|
5
|
3,879 |
7. If $\tan 4 x=$
$$
\frac{\sqrt{3}}{3} \text {, then } \frac{\sin 4 x}{\cos 8 x \cos 4 x}+\frac{\sin 2 x}{\cos 4 x \cos 2 x}+\frac{\sin x}{\cos 2 x \cos x}+\frac{\sin x}{\cos x}=
$$
$\qquad$
|
\sqrt{3}
|
3,887 |
\[
\left(\left(\sqrt{mn} - \frac{mn}{m+\sqrt{mn}}\right) \div \frac{\sqrt[4]{mn} - \sqrt{n}}{m-n} - m \sqrt{n}\right)^{2} \div \sqrt[3]{mn \sqrt{mn}} - \left(\frac{m}{\sqrt{m^{4}-1}}\right)^{-2}.
\]
|
\dfrac{1}{m^2}
|
3,915 |
For which values of \( n \) is the fraction
$$
\frac{3n^{2}+2n+4}{n+1}
$$
irreducible?
|
n \not\equiv 4 \pmod{5}
|
3,916 |
[ List pairs of similar triangles
Point $D$ lies on side $B C$ of triangle $A B C$, and point $O$ is located on segment $A D$, such that $A O: O D=9: 4$. The line passing through vertex $B$ and point $O$ intersects side $A C$ at point $E$, and $B O: O E=5: 6$. Find the ratio in which point $E$ divides side $A C$.
#
|
\dfrac{21}{44}
|
3,969 |
8. In the following vertical calculation, each letter represents a digit from $0 \sim 9$, the same letter represents the same digit, and different letters represent different digits. When the vertical calculation is correct, $A+B+C=$ $\qquad$.
$$
\begin{array}{l}
\begin{array}{llll}
A & B & B & C
\end{array} \\
\begin{array}{lll}
B & B & C
\end{array} \\
\begin{array}{r}
+\quad B \quad B \quad C \\
\hline B A B B
\end{array} \\
\end{array}
$$
|
15
|
4,006 |
## 22. Lighthouse
From the tower of the lighthouse, located 125.7 m above sea level, the horizon line is visible. At what approximate distance from the tower is this line, if we assume that the Earth's surface is spherical and its great circle is 40,000 km?
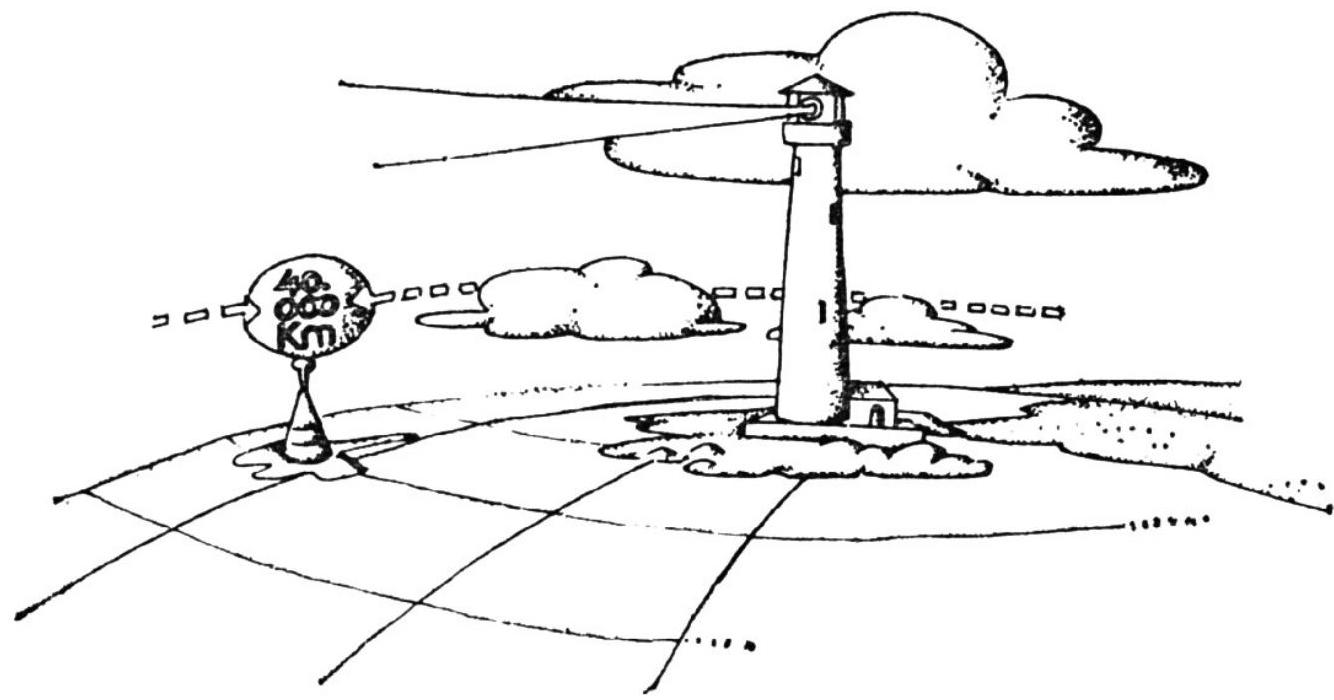
|
40
|
4,038 |
6.2. The shape of a certain castle is a heptagon, and there is a bell tower at each of its vertices. Each side of the castle wall is guarded by the soldiers in the bell towers at the two endpoints of that side. How many soldiers are needed in total to ensure that each side of the wall is guarded by at least 7 soldiers?
|
25
|
4,044 |
4. On a circle, 100 points are marked, painted either red or blue. Some of the points are connected by segments, with each segment having one blue end and one red end. It is known that no two red points belong to the same number of segments. What is the maximum possible number of red points?
|
50
|
4,115 |
The sequence \( a_n \) is defined as follows: \( a_1 = 1 \), \( a_{n+1} = a_n + \frac{1}{a_n} \) for \( n \geq 1 \). Prove that \( a_{100} > 14 \).
|
a_{100} > 14
|
4,116 |
Find the radius of a circle in a segment of which, corresponding to a chord of length $6 \textrm{ cm}$, a square with a side of $2 \textrm{ cm}$ is inscribed.
|
\sqrt{10}
|
4,117 |
2. Let $A B C$ be a triangle with $A B=13, B C=14, C A=15$. Let $H$ be the orthocenter of $A B C$. Find the distance between the circumcenters of triangles $A H B$ and $A H C$.
|
14
|
4,121 |
In \(\triangle ABC\), \(AC > AB\). The internal angle bisector of \(\angle A\) meets \(BC\) at \(D\), and \(E\) is the foot of the perpendicular from \(B\) onto \(AD\). Suppose \(AB = 5\), \(BE = 4\), and \(AE = 3\). Find the value of the expression \(\left(\frac{AC + AB}{AC - AB}\right) ED\).
|
3
|
4,144 |
Prove that if triangle $ABC$ lies inside triangle $A'B'C'$, then $r_{ABC} < r_{A'B'C'}$.
|
r_{ABC} < r_{A'B'C'}
|
4,152 |
From the vertex of the right angle of triangle \(ABC\), the median \(CM\) is drawn. The circle inscribed in triangle \(CAM\) touches \(CM\) at its midpoint. Find the angle \(BAC\).
|
60^\circ
|
4,179 |
15. How many ordered pairs $(x, y)$ of positive integers $x$ and $y$ satisfy the relation $x y + 5(x + y) = 2005$?
|
10
|
4,202 |
8. A positive integer $T$ is said to be triangular if $T=1+2+\cdots+n$ for some positive integer $n$. Find the smallest positive integer $k$ such that whenever $T$ is triangular, $81 T+k$ is also triangular.
|
10
|
4,214 |
3.346. $\operatorname{ctg} 60^{\circ}+\operatorname{tg} 60^{\circ}+\operatorname{ctg} 50^{\circ}+\operatorname{tg} 50^{\circ}=\frac{8}{\sqrt{3}} \cos 20^{\circ}$.
|
\frac{8}{\sqrt{3}} \cos 20^{\circ}
|
4,215 |
Given 17 natural numbers: \(a_{1}, a_{2}, \ldots, a_{17}\). It is known that \(a_{1}^{a_{2}} = a_{2}^{a_{3}} = \ldots = a_{16}^{a_{17}} = a_{17}^{a_{1}}\). Prove that \(a_{1} = a_{2} = \ldots = a_{17}\).
|
a_1 = a_2 = \ldots = a_{17}
|
4,244 |
Twelve congruent disks are placed on a circle $C^{}_{}$ of radius 1 in such a way that the twelve disks cover $C^{}_{}$ , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the from $\pi(a-b\sqrt{c})$ , where $a,b,c^{}_{}$ are positive integers and $c^{}_{}$ is not divisible by the square of any prime. Find $a+b+c^{}_{}$
[asy] unitsize(100); draw(Circle((0,0),1)); dot((0,0)); draw((0,0)--(1,0)); label("$1$", (0.5,0), S); for (int i=0; i<12; ++i) { dot((cos(i*pi/6), sin(i*pi/6))); } for (int a=1; a<24; a+=2) { dot(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))); draw(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12))--((1/cos(pi/12))*cos((a+2)*pi/12), (1/cos(pi/12))*sin((a+2)*pi/12))); draw(Circle(((1/cos(pi/12))*cos(a*pi/12), (1/cos(pi/12))*sin(a*pi/12)), tan(pi/12))); }[/asy]
_Diagram by 1-1 is 3_
|
135
|
4,249 |
1. How many times do the second hand and the minute hand form a $45^{\circ}$ angle between 0 and 12 o'clock?
|
1416
|
4,253 |
Consider the table of numbers below. The first row contains the numbers from 1 to $n$. The second row contains the numbers from 1 to $n$, each multiplied by 2. The rows follow this pattern until the last row, which presents each number from 1 to $n$ multiplied by $n$.
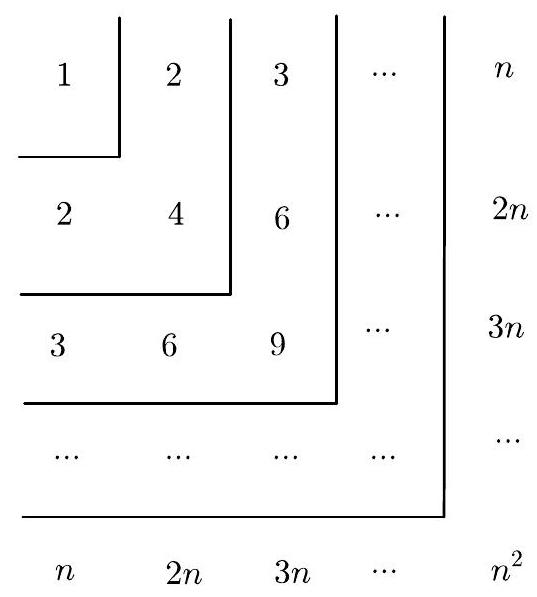
We will use it to calculate the value of the expression
$$
1^{3}+2^{3}+\ldots+100^{3}
$$
In addition to the table, we will use the fact that
$$
1+2+\ldots+n=\frac{n(n+1)}{2}
$$
(a) Determine the sum of all the numbers in row $k$. With this, determine an expression for the sum of all the numbers in the table.
(b) Observe pieces in the table by separating it into layers in the shape of an $L$. The numbers in a certain layer $k$ are: $k, 2k, \ldots, (k-1)k, k^2, (k-1)k, \ldots, 2k, k$. Determine the sum of the numbers in this layer in terms of $k$.
(c) By summing the results of all the layers, we will arrive at the same result as summing all the rows. Combining this information, determine the value of the expression:
$$
1^{3}+2^{3}+\ldots+100^{3}
$$
|
25502500
|
4,276 |
5. Real numbers $a, b, c$ satisfy: $a>0>b>c, \frac{1}{a}+\frac{1}{2 b}+\frac{1}{3 c}=\frac{1}{a+2 b+3 c}$, then the value of $(a+2 b)(a+3 c)$ is . $\qquad$
|
0
|
4,303 |
Find the number of solutions in natural numbers for the equation \(\left\lfloor \frac{x}{10} \right\rfloor = \left\lfloor \frac{x}{11} \right\rfloor + 1\).
|
110
|
4,307 |
1. A trip to St. Petersburg is being organized for 30 schoolchildren along with their parents, some of whom will be driving cars. Each car can accommodate 5 people, including the driver. What is the minimum number of parents that need to be invited on the trip?
ANSWER: 10
|
10
|
4,328 |
4. Xiaoming constructed a sequence using the digits $2$, $0$, $1$, $6$ (continuously appending these four digits in this order to the end of the number): 2, 20, 201, 2016, 20162, 201620, 2016201, 20162016, 201620162, … In this sequence, the number of prime numbers is $\qquad$
|
1
|
4,336 |
Let $\mathbf{a},$ $\mathbf{b},$ $\mathbf{c}$ be vectors such that $\|\mathbf{a}\| = \|\mathbf{b}\| = 1$ and $\|\mathbf{c}\| = 2.$ Find the maximum value of
\[\|\mathbf{a} - 2 \mathbf{b}\|^2 + \|\mathbf{b} - 2 \mathbf{c}\|^2 + \|\mathbf{c} - 2 \mathbf{a}\|^2.\]
|
42
|
4,373 |
Compute the least possible value of $ABCD - AB \times CD$, where $ABCD$ is a 4-digit positive integer, and $AB$ and $CD$ are 2-digit positive integers. (Here $A$, $B$, $C$, and $D$ are digits, possibly equal. Neither $A$ nor $C$ can be zero.)
|
109
|
4,398 |
52. As shown in the figure, in quadrilateral $A B C D$, $A B=7, B C=24, C D=20, D A=15, \angle B=90^{\circ}$, then the area of quadrilateral $A B C D$ is . $\qquad$
|
234
|
4,399 |
4. All natural numbers, the sum of the digits in the representation of which is divisible by 5, are listed in ascending order: $5,14,19,23,28,32, \ldots$ What is the smallest positive difference between consecutive numbers in this sequence? Provide an example and explain why it cannot be smaller.
---
The smallest positive difference between consecutive numbers in this sequence is 1. An example is the pair of numbers 14 and 15. The sum of the digits of 14 is $1 + 4 = 5$, which is divisible by 5. The sum of the digits of 15 is $1 + 5 = 6$, which is not divisible by 5. However, the next number in the sequence is 19, and the sum of its digits is $1 + 9 = 10$, which is divisible by 5. Therefore, the smallest difference is 1, as seen between 14 and 15.
To explain why it cannot be smaller: The smallest possible difference between two numbers is 1. If the difference were 0, the numbers would be the same, which is not possible for consecutive numbers in the sequence. If the difference were greater than 1, there would be a gap between the numbers, which means there would be a number in between that could potentially have a sum of digits divisible by 5, contradicting the requirement that the sequence lists all such numbers in ascending order. Therefore, the smallest possible difference is 1.
|
1
|
4,446 |
28. A sequence $\left\{a_{n}\right\}$ is defined by $\mathrm{a}_{1}-2, a_{n}=\frac{1+a_{n-1}}{1-a_{n-1}}, \mathrm{n} \geq 2$. Find the value of $-2008 a_{2007}$.
|
1004
|
4,459 |
3. Let $\left\{a_{n}\right\}$ be an arithmetic sequence with the sum of the first $n$ terms denoted as $S_{n}$. If $S_{6}=26, a_{7}=2$, then the maximum value of $n S_{n}$ is $\qquad$ .
|
338
|
4,531 |
Find \( b \) if \( b \) is the remainder when \( 1998^{10} \) is divided by \( 10^{4} \).
|
1024
|
4,537 |
Diagonals of trapezium $ABCD$ are mutually perpendicular and the midline of the trapezium is $5$. Find the length of the segment that connects the midpoints of the bases of the trapezium.
|
5
|
4,569 |
Find the only value of \( x \) in the open interval \((- \pi / 2, 0)\) that satisfies the equation
$$
\frac{\sqrt{3}}{\sin x} + \frac{1}{\cos x} = 4.
$$
|
-\dfrac{4\pi}{9}
|
4,586 |
17.3. (New York, 74). Let
$$
a_{n}=\frac{1 \cdot 3 \cdot 5 \ldots(2 n-1)}{2 \cdot 4 \cdot 6 \ldots 2 n}, n \in \mathrm{N}
$$
Find $\lim a_{n}$.
$$
n \rightarrow \infty
$$
|
0
|
4,596 |
9. Let $[x]$ denote the greatest integer not exceeding the real number $x$. The number of real roots of the equation $\lg ^{2} x-[\lg x]-2=0$ is . $\qquad$
|
3
|
4,608 |
In an isosceles trapezoid with bases of 1 and 9, there are two circles, each of which touches the other circle, both lateral sides, and one of the bases. Find the area of the trapezoid.
In the convex quadrilateral \(A B C D\), the points \(K, L, M, N\) are the midpoints of the sides \(A B, B C, C D, D A\) respectively. The segments \(K M\) and \(L N\) intersect at point \(E\). The areas of the quadrilaterals \(A K E N, B K E L\), and \(D N E M\) are 6, 6, and 12 respectively. Find:
a) The area of the quadrilateral \(C M E L\).
b) The length of the segment \(C D\) if \(A B=\frac{1}{2}\).
|
20\sqrt{3}
|
4,641 |
Task 1. Represent in the form of an irreducible fraction
$$
7 \frac{19}{2015} \times 6 \frac{19}{2016}-13 \frac{1996}{2015} \times 2 \frac{1997}{2016}-9 \times \frac{19}{2015}
$$
|
\dfrac{19}{96}
|
4,661 |
Consider the sequence of numbers defined recursively by $t_1=1$ and for $n>1$ by $t_n=1+t_{n/2}$ when $n$ is even and by $t_n=\frac{1}{t_{n-1}}$ when $n$ is odd. Given that $t_n=\frac{19}{87}$, find $n.$
|
1905
|
4,669 |
## Task 16
The difference between 434 and a second number is 962. Calculate half of the second number.
|
698
|
4,673 |
G3.2 In figure $1, C$ lies on $A D, A B=B D=1 \mathrm{~cm}, \angle A B C=90^{\circ}$ and $\angle C B D=30^{\circ}$. If $C D=b \mathrm{~cm}$, find the value of $b$.
|
\dfrac{\sqrt{3}}{3}
|
4,675 |
## Task A-1.1.
The competition takes place in 11 classrooms, each containing the same number of desks arranged in the same way: in a certain number of columns and a certain number of rows. There is one student in each desk. If there were one row of desks less and one column of desks more in each classroom, 10 classrooms would be sufficient, and there would still be two desks left empty. How many students can there be in total at the competition if it is known that their number is a three-digit number?
|
198
|
4,683 |
Example 3. Find $\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan x}{\tan 3 x}$.
|
3
|
4,711 |
## Task 1
In men's rowing, 7 different boats will start from the GDR:
the single scull, two doubles (without coxswain), a double with coxswain, the four without coxswain, the four with coxswain, the eight with coxswain.
How many rowers will start?
(Note: In a double without coxswain, two rowers sit. In a double with coxswain, three rowers sit. Pay close attention to all designations!)
|
26
|
4,731 |
B2. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ for which
$$
f(x y)=x f(y)+3 f(x)+3
$$
holds for all $x, y \in \mathbb{R}$.
|
\dfrac{1}{2}x - \dfrac{3}{2}
|
4,734 |
## Problem Statement
Write the equation of the plane passing through point $A$ and perpendicular to vector $\overrightarrow{B C}$.
$A(4, -2, 0)$
$B(1, -1, -5)$
$C(-2, 1, -3)$
|
-3x + 2y + 2z + 16 = 0
|
4,741 |
If \(\cos ^{4} \theta + \sin ^{4} \theta + (\cos \theta \cdot \sin \theta)^{4} + \frac{1}{\cos ^{4} \theta + \sin ^{4} \theta} = \frac{41}{16}\), find the value of \(\sin ^{2} \theta\).
|
\dfrac{1}{2}
|
4,751 |
5. The natural number $n$ satisfies $1 \leqslant n \leqslant 2022$, and $2^{n}+n^{3}$ is divisible by 7, such natural numbers $n$ have $\qquad$
|
290
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.