prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
```
#export
from fastai.basics import *
from fastai.tabular.core import *
from fastai.tabular.model import *
from fastai.tabular.data import *
#hide
from nbdev.showdoc import *
#default_exp tabular.learner
```
# Tabular learner
> The function to immediately get a `Learner` ready to train for tabular data
The main function you probably want to use in this module is `tabular_learner`. It will automatically create a `TabulaModel` suitable for your data and infer the irght loss function. See the [tabular tutorial](http://docs.fast.ai/tutorial.tabular) for an example of use in context.
## Main functions
```
#export
@log_args(but_as=Learner.__init__)
class TabularLearner(Learner):
"`Learner` for tabular data"
def predict(self, row):
tst_to = self.dls.valid_ds.new(pd.DataFrame(row).T)
tst_to.process()
tst_to.conts = tst_to.conts.astype(np.float32)
dl = self.dls.valid.new(tst_to)
inp,preds,_,dec_preds = self.get_preds(dl=dl, with_input=True, with_decoded=True)
i = getattr(self.dls, 'n_inp', -1)
b = (*tuplify(inp),*tuplify(dec_preds))
full_dec = self.dls.decode((*tuplify(inp),*tuplify(dec_preds)))
return full_dec,dec_preds[0],preds[0]
show_doc(TabularLearner, title_level=3)
```
It works exactly as a normal `Learner`, the only difference is that it implements a `predict` method specific to work on a row of data.
```
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def tabular_learner(dls, layers=None, emb_szs=None, config=None, n_out=None, y_range=None, **kwargs):
"Get a `Learner` using `dls`, with `metrics`, including a `TabularModel` created using the remaining params."
if config is None: config = tabular_config()
if layers is None: layers = [200,100]
to = dls.train_ds
emb_szs = get_emb_sz(dls.train_ds, {} if emb_szs is None else emb_szs)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be infered from data, set `dls.c` or pass `n_out`"
if y_range is None and 'y_range' in config: y_range = config.pop('y_range')
model = TabularModel(emb_szs, len(dls.cont_names), n_out, layers, y_range=y_range, **config)
return TabularLearner(dls, model, **kwargs)
```
If your data was built with fastai, you probably won't need to pass anything to `emb_szs` unless you want to change the default of the library (produced by `get_emb_sz`), same for `n_out` which should be automatically inferred. `layers` will default to `[200,100]` and is passed to `TabularModel` along with the `config`.
Use `tabular_config` to create a `config` and cusotmize the model used. There is just easy access to `y_range` because this argument is often used.
All the other arguments are passed to `Learner`.
```
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
dls = TabularDataLoaders.from_df(df, path, procs=procs, cat_names=cat_names, cont_names=cont_names,
y_names="salary", valid_idx=list(range(800,1000)), bs=64)
learn = tabular_learner(dls)
#hide
tst = learn.predict(df.iloc[0])
#hide
#test y_range is passed
learn = tabular_learner(dls, y_range=(0,32))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
learn = tabular_learner(dls, config = tabular_config(y_range=(0,32)))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
#export
@typedispatch
def show_results(x:Tabular, y:Tabular, samples, outs, ctxs=None, max_n=10, **kwargs):
df = x.all_cols[:max_n]
for n in x.y_names: df[n+'_pred'] = y[n][:max_n].values
display_df(df)
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| true |
code
| 0.704262 | null | null | null | null |
|
# Aerospike Connect for Spark - SparkML Prediction Model Tutorial
## Tested with Java 8, Spark 3.0.0, Python 3.7, and Aerospike Spark Connector 3.0.0
## Summary
Build a linear regression model to predict birth weight using Aerospike Database and Spark.
Here are the features used:
- gestation weeks
- mother’s age
- father’s age
- mother’s weight gain during pregnancy
- [Apgar score](https://en.wikipedia.org/wiki/Apgar_score)
Aerospike is used to store the Natality dataset that is published by CDC. The table is accessed in Apache Spark using the Aerospike Spark Connector, and Spark ML is used to build and evaluate the model. The model can later be converted to PMML and deployed on your inference server for predictions.
### Prerequisites
1. Load Aerospike server if not alrady available - docker run -d --name aerospike -p 3000:3000 -p 3001:3001 -p 3002:3002 -p 3003:3003 aerospike
2. Feature key needs to be located in AS_FEATURE_KEY_PATH
3. [Download the connector](https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/3.0.0/)
```
#IP Address or DNS name for one host in your Aerospike cluster.
#A seed address for the Aerospike database cluster is required
AS_HOST ="127.0.0.1"
# Name of one of your namespaces. Type 'show namespaces' at the aql prompt if you are not sure
AS_NAMESPACE = "test"
AS_FEATURE_KEY_PATH = "/etc/aerospike/features.conf"
AEROSPIKE_SPARK_JAR_VERSION="3.0.0"
AS_PORT = 3000 # Usually 3000, but change here if not
AS_CONNECTION_STRING = AS_HOST + ":"+ str(AS_PORT)
#Locate the Spark installation - this'll use the SPARK_HOME environment variable
import findspark
findspark.init()
# Below will help you download the Spark Connector Jar if you haven't done so already.
import urllib
import os
def aerospike_spark_jar_download_url(version=AEROSPIKE_SPARK_JAR_VERSION):
DOWNLOAD_PREFIX="https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/"
DOWNLOAD_SUFFIX="/artifact/jar"
AEROSPIKE_SPARK_JAR_DOWNLOAD_URL = DOWNLOAD_PREFIX+AEROSPIKE_SPARK_JAR_VERSION+DOWNLOAD_SUFFIX
return AEROSPIKE_SPARK_JAR_DOWNLOAD_URL
def download_aerospike_spark_jar(version=AEROSPIKE_SPARK_JAR_VERSION):
JAR_NAME="aerospike-spark-assembly-"+AEROSPIKE_SPARK_JAR_VERSION+".jar"
if(not(os.path.exists(JAR_NAME))) :
urllib.request.urlretrieve(aerospike_spark_jar_download_url(),JAR_NAME)
else :
print(JAR_NAME+" already downloaded")
return os.path.join(os.getcwd(),JAR_NAME)
AEROSPIKE_JAR_PATH=download_aerospike_spark_jar()
os.environ["PYSPARK_SUBMIT_ARGS"] = '--jars ' + AEROSPIKE_JAR_PATH + ' pyspark-shell'
import pyspark
from pyspark.context import SparkContext
from pyspark.sql.context import SQLContext
from pyspark.sql.session import SparkSession
from pyspark.ml.linalg import Vectors
from pyspark.ml.regression import LinearRegression
from pyspark.sql.types import StringType, StructField, StructType, ArrayType, IntegerType, MapType, LongType, DoubleType
#Get a spark session object and set required Aerospike configuration properties
sc = SparkContext.getOrCreate()
print("Spark Verison:", sc.version)
spark = SparkSession(sc)
sqlContext = SQLContext(sc)
spark.conf.set("aerospike.namespace",AS_NAMESPACE)
spark.conf.set("aerospike.seedhost",AS_CONNECTION_STRING)
spark.conf.set("aerospike.keyPath",AS_FEATURE_KEY_PATH )
```
## Step 1: Load Data into a DataFrame
```
as_data=spark \
.read \
.format("aerospike") \
.option("aerospike.set", "natality").load()
as_data.show(5)
print("Inferred Schema along with Metadata.")
as_data.printSchema()
```
### To speed up the load process at scale, use the [knobs](https://www.aerospike.com/docs/connect/processing/spark/performance.html) available in the Aerospike Spark Connector.
For example, **spark.conf.set("aerospike.partition.factor", 15 )** will map 4096 Aerospike partitions to 32K Spark partitions. <font color=red> (Note: Please configure this carefully based on the available resources (CPU threads) in your system.)</font>
## Step 2 - Prep data
```
# This Spark3.0 setting, if true, will turn on Adaptive Query Execution (AQE), which will make use of the
# runtime statistics to choose the most efficient query execution plan. It will speed up any joins that you
# plan to use for data prep step.
spark.conf.set("spark.sql.adaptive.enabled", 'true')
# Run a query in Spark SQL to ensure no NULL values exist.
as_data.createOrReplaceTempView("natality")
sql_query = """
SELECT *
from natality
where weight_pnd is not null
and mother_age is not null
and father_age is not null
and father_age < 80
and gstation_week is not null
and weight_gain_pnd < 90
and apgar_5min != "99"
and apgar_5min != "88"
"""
clean_data = spark.sql(sql_query)
#Drop the Aerospike metadata from the dataset because its not required.
#The metadata is added because we are inferring the schema as opposed to providing a strict schema
columns_to_drop = ['__key','__digest','__expiry','__generation','__ttl' ]
clean_data = clean_data.drop(*columns_to_drop)
# dropping null values
clean_data = clean_data.dropna()
clean_data.cache()
clean_data.show(5)
#Descriptive Analysis of the data
clean_data.describe().toPandas().transpose()
```
## Step 3 Visualize Data
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import math
pdf = clean_data.toPandas()
#Histogram - Father Age
pdf[['father_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Fathers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['mother_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Mothers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['weight_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Babys Weight (Pounds)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['gstation_week']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Gestation (Weeks)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['weight_gain_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('mother’s weight gain during pregnancy',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
#Histogram - Apgar Score
print("Apgar Score: Scores of 7 and above are generally normal; 4 to 6, fairly low; and 3 and below are generally \
regarded as critically low and cause for immediate resuscitative efforts.")
pdf[['apgar_5min']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Apgar score',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
```
## Step 4 - Create Model
**Steps used for model creation:**
1. Split cleaned data into Training and Test sets
2. Vectorize features on which the model will be trained
3. Create a linear regression model (Choose any ML algorithm that provides the best fit for the given dataset)
4. Train model (Although not shown here, you could use K-fold cross-validation and Grid Search to choose the best hyper-parameters for the model)
5. Evaluate model
```
# Define a function that collects the features of interest
# (mother_age, father_age, and gestation_weeks) into a vector.
# Package the vector in a tuple containing the label (`weight_pounds`) for that
# row.##
def vector_from_inputs(r):
return (r["weight_pnd"], Vectors.dense(float(r["mother_age"]),
float(r["father_age"]),
float(r["gstation_week"]),
float(r["weight_gain_pnd"]),
float(r["apgar_5min"])))
#Split that data 70% training and 30% Evaluation data
train, test = clean_data.randomSplit([0.7, 0.3])
#Check the shape of the data
train.show()
print((train.count(), len(train.columns)))
test.show()
print((test.count(), len(test.columns)))
# Create an input DataFrame for Spark ML using the above function.
training_data = train.rdd.map(vector_from_inputs).toDF(["label",
"features"])
# Construct a new LinearRegression object and fit the training data.
lr = LinearRegression(maxIter=5, regParam=0.2, solver="normal")
#Voila! your first model using Spark ML is trained
model = lr.fit(training_data)
# Print the model summary.
print("Coefficients:" + str(model.coefficients))
print("Intercept:" + str(model.intercept))
print("R^2:" + str(model.summary.r2))
model.summary.residuals.show()
```
### Evaluate Model
```
eval_data = test.rdd.map(vector_from_inputs).toDF(["label",
"features"])
eval_data.show()
evaluation_summary = model.evaluate(eval_data)
print("MAE:", evaluation_summary.meanAbsoluteError)
print("RMSE:", evaluation_summary.rootMeanSquaredError)
print("R-squared value:", evaluation_summary.r2)
```
## Step 5 - Batch Prediction
```
#eval_data contains the records (ideally production) that you'd like to use for the prediction
predictions = model.transform(eval_data)
predictions.show()
```
#### Compare the labels and the predictions, they should ideally match up for an accurate model. Label is the actual weight of the baby and prediction is the predicated weight
### Saving the Predictions to Aerospike for ML Application's consumption
```
# Aerospike is a key/value database, hence a key is needed to store the predictions into the database. Hence we need
# to add the _id column to the predictions using SparkSQL
predictions.createOrReplaceTempView("predict_view")
sql_query = """
SELECT *, monotonically_increasing_id() as _id
from predict_view
"""
predict_df = spark.sql(sql_query)
predict_df.show()
print("#records:", predict_df.count())
# Now we are good to write the Predictions to Aerospike
predict_df \
.write \
.mode('overwrite') \
.format("aerospike") \
.option("aerospike.writeset", "predictions")\
.option("aerospike.updateByKey", "_id") \
.save()
```
#### You can verify that data is written to Aerospike by using either [AQL](https://www.aerospike.com/docs/tools/aql/data_management.html) or the [Aerospike Data Browser](https://github.com/aerospike/aerospike-data-browser)
## Step 6 - Deploy
### Here are a few options:
1. Save the model to a PMML file by converting it using Jpmml/[pyspark2pmml](https://github.com/jpmml/pyspark2pmml) and load it into your production enviornment for inference.
2. Use Aerospike as an [edge database for high velocity ingestion](https://medium.com/aerospike-developer-blog/add-horsepower-to-ai-ml-pipeline-15ca42a10982) for your inference pipline.
| true |
code
| 0.475301 | null | null | null | null |
|
# Classification on Iris dataset with sklearn and DJL
In this notebook, you will try to use a pre-trained sklearn model to run on DJL for a general classification task. The model was trained with [Iris flower dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set).
## Background
### Iris Dataset
The dataset contains a set of 150 records under five attributes - sepal length, sepal width, petal length, petal width and species.
Iris setosa | Iris versicolor | Iris virginica
:-------------------------:|:-------------------------:|:-------------------------:
 |  | 
The chart above shows three different kinds of the Iris flowers.
We will use sepal length, sepal width, petal length, petal width as the feature and species as the label to train the model.
### Sklearn Model
You can find more information [here](http://onnx.ai/sklearn-onnx/). You can use the sklearn built-in iris dataset to load the data. Then we defined a [RandomForestClassifer](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html) to train the model. After that, we convert the model to onnx format for DJL to run inference. The following code is a sample classification setup using sklearn:
```python
# Train a model.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clr = RandomForestClassifier()
clr.fit(X_train, y_train)
```
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
These are dependencies we will use. To enhance the NDArray operation capability, we are importing ONNX Runtime and PyTorch Engine at the same time. Please find more information [here](https://github.com/awslabs/djl/blob/master/docs/onnxruntime/hybrid_engine.md#hybrid-engine-for-onnx-runtime).
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.8.0
%maven ai.djl.onnxruntime:onnxruntime-engine:0.8.0
%maven ai.djl.pytorch:pytorch-engine:0.8.0
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven com.microsoft.onnxruntime:onnxruntime:1.4.0
%maven ai.djl.pytorch:pytorch-native-auto:1.6.0
import ai.djl.inference.*;
import ai.djl.modality.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.repository.zoo.*;
import ai.djl.translate.*;
import java.util.*;
```
## Step 1 create a Translator
Inference in machine learning is the process of predicting the output for a given input based on a pre-defined model.
DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
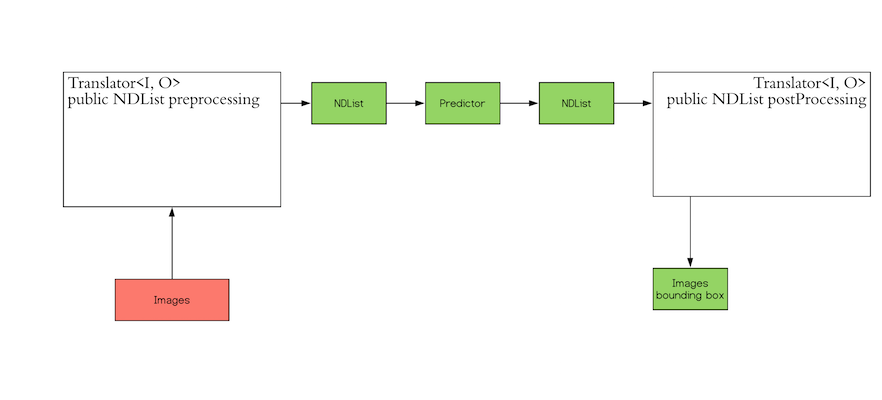
The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
`Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
format.
In our use case, we use a class namely `IrisFlower` as our input class type. We will use [`Classifications`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/modality/Classifications.html) as our output class type.
```
public static class IrisFlower {
public float sepalLength;
public float sepalWidth;
public float petalLength;
public float petalWidth;
public IrisFlower(float sepalLength, float sepalWidth, float petalLength, float petalWidth) {
this.sepalLength = sepalLength;
this.sepalWidth = sepalWidth;
this.petalLength = petalLength;
this.petalWidth = petalWidth;
}
}
```
Let's create a translator
```
public static class MyTranslator implements Translator<IrisFlower, Classifications> {
private final List<String> synset;
public MyTranslator() {
// species name
synset = Arrays.asList("setosa", "versicolor", "virginica");
}
@Override
public NDList processInput(TranslatorContext ctx, IrisFlower input) {
float[] data = {input.sepalLength, input.sepalWidth, input.petalLength, input.petalWidth};
NDArray array = ctx.getNDManager().create(data, new Shape(1, 4));
return new NDList(array);
}
@Override
public Classifications processOutput(TranslatorContext ctx, NDList list) {
return new Classifications(synset, list.get(1));
}
@Override
public Batchifier getBatchifier() {
return null;
}
}
```
## Step 2 Prepare your model
We will load a pretrained sklearn model into DJL. We defined a [`ModelZoo`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/repository/zoo/ModelZoo.html) concept to allow user load model from varity of locations, such as remote URL, local files or DJL pretrained model zoo. We need to define `Criteria` class to help the modelzoo locate the model and attach translator. In this example, we download a compressed ONNX model from S3.
```
String modelUrl = "https://mlrepo.djl.ai/model/tabular/random_forest/ai/djl/onnxruntime/iris_flowers/0.0.1/iris_flowers.zip";
Criteria<IrisFlower, Classifications> criteria = Criteria.builder()
.setTypes(IrisFlower.class, Classifications.class)
.optModelUrls(modelUrl)
.optTranslator(new MyTranslator())
.optEngine("OnnxRuntime") // use OnnxRuntime engine by default
.build();
ZooModel<IrisFlower, Classifications> model = ModelZoo.loadModel(criteria);
```
## Step 3 Run inference
User will just need to create a `Predictor` from model to run the inference.
```
Predictor<IrisFlower, Classifications> predictor = model.newPredictor();
IrisFlower info = new IrisFlower(1.0f, 2.0f, 3.0f, 4.0f);
predictor.predict(info);
```
| true |
code
| 0.782642 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepNLP-END2.0/blob/main/09_NLP_Evaluation/ClassificationEvaluation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
! pip3 install git+https://github.com/extensive-nlp/ttc_nlp --quiet
! pip3 install torchmetrics --quiet
from ttctext.datamodules.sst import SSTDataModule
from ttctext.datasets.sst import StanfordSentimentTreeBank
sst_dataset = SSTDataModule(batch_size=128)
sst_dataset.setup()
import pytorch_lightning as pl
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchmetrics.functional import accuracy, precision, recall, confusion_matrix
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set()
class SSTModel(pl.LightningModule):
def __init__(self, hparams, *args, **kwargs):
super().__init__()
self.save_hyperparameters(hparams)
self.num_classes = self.hparams.output_dim
self.embedding = nn.Embedding(self.hparams.input_dim, self.hparams.embedding_dim)
self.lstm = nn.LSTM(
self.hparams.embedding_dim,
self.hparams.hidden_dim,
num_layers=self.hparams.num_layers,
dropout=self.hparams.dropout,
batch_first=True
)
self.proj_layer = nn.Sequential(
nn.Linear(self.hparams.hidden_dim, self.hparams.hidden_dim),
nn.BatchNorm1d(self.hparams.hidden_dim),
nn.ReLU(),
nn.Dropout(self.hparams.dropout),
)
self.fc = nn.Linear(self.hparams.hidden_dim, self.num_classes)
self.loss = nn.CrossEntropyLoss()
def init_state(self, sequence_length):
return (torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device),
torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device))
def forward(self, text, text_length, prev_state=None):
# [batch size, sentence length] => [batch size, sentence len, embedding size]
embedded = self.embedding(text)
# packs the input for faster forward pass in RNN
packed = torch.nn.utils.rnn.pack_padded_sequence(
embedded, text_length.to('cpu'),
enforce_sorted=False,
batch_first=True
)
# [batch size sentence len, embedding size] =>
# output: [batch size, sentence len, hidden size]
# hidden: [batch size, 1, hidden size]
packed_output, curr_state = self.lstm(packed, prev_state)
hidden_state, cell_state = curr_state
# print('hidden state shape: ', hidden_state.shape)
# print('cell')
# unpack packed sequence
# unpacked, unpacked_len = torch.nn.utils.rnn.pad_packed_sequence(packed_output, batch_first=True)
# print('unpacked: ', unpacked.shape)
# [batch size, sentence len, hidden size] => [batch size, num classes]
# output = self.proj_layer(unpacked[:, -1])
output = self.proj_layer(hidden_state[-1])
# print('output shape: ', output.shape)
output = self.fc(output)
return output, curr_state
def shared_step(self, batch, batch_idx):
label, text, text_length = batch
logits, in_state = self(text, text_length)
loss = self.loss(logits, label)
pred = torch.argmax(F.log_softmax(logits, dim=1), dim=1)
acc = accuracy(pred, label)
metric = {'loss': loss, 'acc': acc, 'pred': pred, 'label': label}
return metric
def training_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
log_metrics = {'train_loss': metrics['loss'], 'train_acc': metrics['acc']}
self.log_dict(log_metrics, prog_bar=True)
return metrics
def validation_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
return metrics
def validation_epoch_end(self, outputs):
acc = torch.stack([x['acc'] for x in outputs]).mean()
loss = torch.stack([x['loss'] for x in outputs]).mean()
log_metrics = {'val_loss': loss, 'val_acc': acc}
self.log_dict(log_metrics, prog_bar=True)
if self.trainer.sanity_checking:
return log_metrics
preds = torch.cat([x['pred'] for x in outputs]).view(-1)
labels = torch.cat([x['label'] for x in outputs]).view(-1)
accuracy_ = accuracy(preds, labels)
precision_ = precision(preds, labels, average='macro', num_classes=self.num_classes)
recall_ = recall(preds, labels, average='macro', num_classes=self.num_classes)
classification_report_ = classification_report(labels.cpu().numpy(), preds.cpu().numpy(), target_names=self.hparams.class_labels)
confusion_matrix_ = confusion_matrix(preds, labels, num_classes=self.num_classes)
cm_df = pd.DataFrame(confusion_matrix_.cpu().numpy(), index=self.hparams.class_labels, columns=self.hparams.class_labels)
print(f'Test Epoch {self.current_epoch}/{self.hparams.epochs-1}: F1 Score: {accuracy_:.5f}, Precision: {precision_:.5f}, Recall: {recall_:.5f}\n')
print(f'Classification Report\n{classification_report_}')
fig, ax = plt.subplots(figsize=(10, 8))
heatmap = sns.heatmap(cm_df, annot=True, ax=ax, fmt='d') # font size
locs, labels = plt.xticks()
plt.setp(labels, rotation=45)
locs, labels = plt.yticks()
plt.setp(labels, rotation=45)
plt.show()
print("\n")
return log_metrics
def test_step(self, batch, batch_idx):
return self.validation_step(batch, batch_idx)
def test_epoch_end(self, outputs):
accuracy = torch.stack([x['acc'] for x in outputs]).mean()
self.log('hp_metric', accuracy)
self.log_dict({'test_acc': accuracy}, prog_bar=True)
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=self.hparams.lr)
lr_scheduler = {
'scheduler': torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, patience=10, verbose=True),
'monitor': 'train_loss',
'name': 'scheduler'
}
return [optimizer], [lr_scheduler]
from omegaconf import OmegaConf
hparams = OmegaConf.create({
'input_dim': len(sst_dataset.get_vocab()),
'embedding_dim': 128,
'num_layers': 2,
'hidden_dim': 64,
'dropout': 0.5,
'output_dim': len(StanfordSentimentTreeBank.get_labels()),
'class_labels': sst_dataset.raw_dataset_train.get_labels(),
'lr': 5e-4,
'epochs': 10,
'use_lr_finder': False
})
sst_model = SSTModel(hparams)
trainer = pl.Trainer(gpus=1, max_epochs=hparams.epochs, progress_bar_refresh_rate=1, reload_dataloaders_every_epoch=True)
trainer.fit(sst_model, sst_dataset)
```
| true |
code
| 0.862265 | null | null | null | null |
|
## Accessing TerraClimate data with the Planetary Computer STAC API
[TerraClimate](http://www.climatologylab.org/terraclimate.html) is a dataset of monthly climate and climatic water balance for global terrestrial surfaces from 1958-2019. These data provide important inputs for ecological and hydrological studies at global scales that require high spatial resolution and time-varying data. All data have monthly temporal resolution and a ~4-km (1/24th degree) spatial resolution. The data cover the period from 1958-2019.
This example will show you how temperature has increased over the past 60 years across the globe.
### Environment setup
```
import warnings
warnings.filterwarnings("ignore", "invalid value", RuntimeWarning)
```
### Data access
https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate is a STAC Collection with links to all the metadata about this dataset. We'll load it with [PySTAC](https://pystac.readthedocs.io/en/latest/).
```
import pystac
url = "https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate"
collection = pystac.read_file(url)
collection
```
The collection contains assets, which are links to the root of a Zarr store, which can be opened with xarray.
```
asset = collection.assets["zarr-https"]
asset
import fsspec
import xarray as xr
store = fsspec.get_mapper(asset.href)
ds = xr.open_zarr(store, **asset.extra_fields["xarray:open_kwargs"])
ds
```
We'll process the data in parallel using [Dask](https://dask.org).
```
from dask_gateway import GatewayCluster
cluster = GatewayCluster()
cluster.scale(16)
client = cluster.get_client()
print(cluster.dashboard_link)
```
The link printed out above can be opened in a new tab or the [Dask labextension](https://github.com/dask/dask-labextension). See [Scale with Dask](https://planetarycomputer.microsoft.com/docs/quickstarts/scale-with-dask/) for more on using Dask, and how to access the Dashboard.
### Analyze and plot global temperature
We can quickly plot a map of one of the variables. In this case, we are downsampling (coarsening) the dataset for easier plotting.
```
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
average_max_temp = ds.isel(time=-1)["tmax"].coarsen(lat=8, lon=8).mean().load()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
average_max_temp.plot(ax=ax, transform=ccrs.PlateCarree())
ax.coastlines();
```
Let's see how temperature has changed over the observational record, when averaged across the entire domain. Since we'll do some other calculations below we'll also add `.load()` to execute the command instead of specifying it lazily. Note that there are some data quality issues before 1965 so we'll start our analysis there.
```
temperature = (
ds["tmax"].sel(time=slice("1965", None)).mean(dim=["lat", "lon"]).persist()
)
temperature.plot(figsize=(12, 6));
```
With all the seasonal fluctuations (from summer and winter) though, it can be hard to see any obvious trends. So let's try grouping by year and plotting that timeseries.
```
temperature.groupby("time.year").mean().plot(figsize=(12, 6));
```
Now the increase in temperature is obvious, even when averaged across the entire domain.
Now, let's see how those changes are different in different parts of the world. And let's focus just on summer months in the northern hemisphere, when it's hottest. Let's take a climatological slice at the beginning of the period and the same at the end of the period, calculate the difference, and map it to see how different parts of the world have changed differently.
First we'll just grab the summer months.
```
%%time
import dask
summer_months = [6, 7, 8]
summer = ds.tmax.where(ds.time.dt.month.isin(summer_months), drop=True)
early_period = slice("1958-01-01", "1988-12-31")
late_period = slice("1988-01-01", "2018-12-31")
early, late = dask.compute(
summer.sel(time=early_period).mean(dim="time"),
summer.sel(time=late_period).mean(dim="time"),
)
increase = (late - early).coarsen(lat=8, lon=8).mean()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
increase.plot(ax=ax, transform=ccrs.PlateCarree(), robust=True)
ax.coastlines();
```
This shows us that changes in summer temperature haven't been felt equally around the globe. Note the enhanced warming in the polar regions, a phenomenon known as "Arctic amplification".
| true |
code
| 0.609059 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import numba
from tqdm import tqdm
import eitest
```
# Data generators
```
@numba.njit
def event_series_bernoulli(series_length, event_count):
'''Generate an iid Bernoulli distributed event series.
series_length: length of the event series
event_count: number of events'''
event_series = np.zeros(series_length)
event_series[np.random.choice(np.arange(0, series_length), event_count, replace=False)] = 1
return event_series
@numba.njit
def time_series_mean_impact(event_series, order, signal_to_noise):
'''Generate a time series with impacts in mean as described in the paper.
The impact weights are sampled iid from N(0, signal_to_noise),
and additional noise is sampled iid from N(0,1). The detection problem will
be harder than in time_series_meanconst_impact for small orders, as for small
orders we have a low probability to sample at least one impact weight with a
high magnitude. On the other hand, since the impact is different at every lag,
we can detect the impacts even if the order is larger than the max_lag value
used in the test.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
signal_to_noise: signal to noise ratio of the event impacts'''
series_length = len(event_series)
weights = np.random.randn(order)*np.sqrt(signal_to_noise)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += weights[:order-max(0, (t+order+1)-series_length)]
return time_series
@numba.njit
def time_series_meanconst_impact(event_series, order, const):
'''Generate a time series with impacts in mean by adding a constant.
Better for comparing performance across different impact orders, since the
magnitude of the impact will always be the same.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
const: constant for mean shift'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += const
return time_series
@numba.njit
def time_series_var_impact(event_series, order, variance):
'''Generate a time series with impacts in variance as described in the paper.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
variance: variance under event impacts'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.randn()*np.sqrt(variance)
return time_series
@numba.njit
def time_series_tail_impact(event_series, order, dof):
'''Generate a time series with impacts in tails as described in the paper.
event_series: input of shape (T,) with event occurrences
order: delay of the event impacts
dof: degrees of freedom of the t distribution'''
series_length = len(event_series)
time_series = np.random.randn(series_length)*np.sqrt(dof/(dof-2))
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.standard_t(dof)
return time_series
```
# Visualization of the impact models
```
default_T = 8192
default_N = 64
default_q = 4
es = event_series_bernoulli(default_T, default_N)
for ts in [
time_series_mean_impact(es, order=default_q, signal_to_noise=10.),
time_series_meanconst_impact(es, order=default_q, const=5.),
time_series_var_impact(es, order=default_q, variance=4.),
time_series_tail_impact(es, order=default_q, dof=3.),
]:
fig, (ax1, ax2) = plt.subplots(1, 2, gridspec_kw={'width_ratios': [2, 1]}, figsize=(15, 2))
ax1.plot(ts)
ax1.plot(es*np.max(ts), alpha=0.5)
ax1.set_xlim(0, len(es))
samples = eitest.obtain_samples(es, ts, method='eager', lag_cutoff=15, instantaneous=True)
eitest.plot_samples(samples, ax2)
plt.show()
```
# Simulations
```
def test_simul_pairs(impact_model, param_T, param_N, param_q, param_r,
n_pairs, lag_cutoff, instantaneous, sample_method,
twosamp_test, multi_test, alpha):
true_positive = 0.
false_positive = 0.
for _ in tqdm(range(n_pairs)):
es = event_series_bernoulli(param_T, param_N)
if impact_model == 'mean':
ts = time_series_mean_impact(es, param_q, param_r)
elif impact_model == 'meanconst':
ts = time_series_meanconst_impact(es, param_q, param_r)
elif impact_model == 'var':
ts = time_series_var_impact(es, param_q, param_r)
elif impact_model == 'tail':
ts = time_series_tail_impact(es, param_q, param_r)
else:
raise ValueError('impact_model must be "mean", "meanconst", "var" or "tail"')
# coupled pair
samples = eitest.obtain_samples(es, ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks')) # samples need to be sorted for K-S test
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
true_positive += (pvals_adj.min() < alpha)
# uncoupled pair
samples = eitest.obtain_samples(np.random.permutation(es), ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks'))
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
false_positive += (pvals_adj.min() < alpha)
return true_positive/n_pairs, false_positive/n_pairs
# global parameters
default_T = 8192
n_pairs = 100
alpha = 0.05
twosamp_test = 'ks'
multi_test = 'simes'
sample_method = 'lazy'
lag_cutoff = 32
instantaneous = True
```
## Mean impact model
```
default_N = 64
default_r = 1.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by signal-to-noise ratio
```
vals = [1./32, 1./16, 1./8, 1./4, 1./2, 1., 2., 4.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
```
## Meanconst impact model
```
default_N = 64
default_r = 0.5
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by mean value
```
vals = [0.125, 0.25, 0.5, 1, 2]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Variance impact model
In the paper, we show results with the variance impact model parametrized by the **variance increase**. Here we directly modulate the variance.
```
default_N = 64
default_r = 8.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by variance
```
vals = [2., 4., 8., 16., 32.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Tail impact model
```
default_N = 512
default_r = 3.
default_q = 4
```
### ... by number of events
```
vals = [64, 128, 256, 512, 1024]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by degrees of freedom
```
vals = [2.5, 3., 3.5, 4., 4.5, 5., 5.5, 6.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
| true |
code
| 0.687079 | null | null | null | null |
|
# Chapter 4
`Original content created by Cam Davidson-Pilon`
`Ported to Python 3 and PyMC3 by Max Margenot (@clean_utensils) and Thomas Wiecki (@twiecki) at Quantopian (@quantopian)`
______
## The greatest theorem never told
This chapter focuses on an idea that is always bouncing around our minds, but is rarely made explicit outside books devoted to statistics. In fact, we've been using this simple idea in every example thus far.
### The Law of Large Numbers
Let $Z_i$ be $N$ independent samples from some probability distribution. According to *the Law of Large numbers*, so long as the expected value $E[Z]$ is finite, the following holds,
$$\frac{1}{N} \sum_{i=1}^N Z_i \rightarrow E[ Z ], \;\;\; N \rightarrow \infty.$$
In words:
> The average of a sequence of random variables from the same distribution converges to the expected value of that distribution.
This may seem like a boring result, but it will be the most useful tool you use.
### Intuition
If the above Law is somewhat surprising, it can be made more clear by examining a simple example.
Consider a random variable $Z$ that can take only two values, $c_1$ and $c_2$. Suppose we have a large number of samples of $Z$, denoting a specific sample $Z_i$. The Law says that we can approximate the expected value of $Z$ by averaging over all samples. Consider the average:
$$ \frac{1}{N} \sum_{i=1}^N \;Z_i $$
By construction, $Z_i$ can only take on $c_1$ or $c_2$, hence we can partition the sum over these two values:
\begin{align}
\frac{1}{N} \sum_{i=1}^N \;Z_i
& =\frac{1}{N} \big( \sum_{ Z_i = c_1}c_1 + \sum_{Z_i=c_2}c_2 \big) \\\\[5pt]
& = c_1 \sum_{ Z_i = c_1}\frac{1}{N} + c_2 \sum_{ Z_i = c_2}\frac{1}{N} \\\\[5pt]
& = c_1 \times \text{ (approximate frequency of $c_1$) } \\\\
& \;\;\;\;\;\;\;\;\; + c_2 \times \text{ (approximate frequency of $c_2$) } \\\\[5pt]
& \approx c_1 \times P(Z = c_1) + c_2 \times P(Z = c_2 ) \\\\[5pt]
& = E[Z]
\end{align}
Equality holds in the limit, but we can get closer and closer by using more and more samples in the average. This Law holds for almost *any distribution*, minus some important cases we will encounter later.
##### Example
____
Below is a diagram of the Law of Large numbers in action for three different sequences of Poisson random variables.
We sample `sample_size = 100000` Poisson random variables with parameter $\lambda = 4.5$. (Recall the expected value of a Poisson random variable is equal to it's parameter.) We calculate the average for the first $n$ samples, for $n=1$ to `sample_size`.
```
%matplotlib inline
import numpy as np
from IPython.core.pylabtools import figsize
import matplotlib.pyplot as plt
figsize( 12.5, 5 )
sample_size = 100000
expected_value = lambda_ = 4.5
poi = np.random.poisson
N_samples = range(1,sample_size,100)
for k in range(3):
samples = poi( lambda_, sample_size )
partial_average = [ samples[:i].mean() for i in N_samples ]
plt.plot( N_samples, partial_average, lw=1.5,label="average \
of $n$ samples; seq. %d"%k)
plt.plot( N_samples, expected_value*np.ones_like( partial_average),
ls = "--", label = "true expected value", c = "k" )
plt.ylim( 4.35, 4.65)
plt.title( "Convergence of the average of \n random variables to its \
expected value" )
plt.ylabel( "average of $n$ samples" )
plt.xlabel( "# of samples, $n$")
plt.legend();
```
Looking at the above plot, it is clear that when the sample size is small, there is greater variation in the average (compare how *jagged and jumpy* the average is initially, then *smooths* out). All three paths *approach* the value 4.5, but just flirt with it as $N$ gets large. Mathematicians and statistician have another name for *flirting*: convergence.
Another very relevant question we can ask is *how quickly am I converging to the expected value?* Let's plot something new. For a specific $N$, let's do the above trials thousands of times and compute how far away we are from the true expected value, on average. But wait — *compute on average*? This is simply the law of large numbers again! For example, we are interested in, for a specific $N$, the quantity:
$$D(N) = \sqrt{ \;E\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \;\;\right] \;\;}$$
The above formulae is interpretable as a distance away from the true value (on average), for some $N$. (We take the square root so the dimensions of the above quantity and our random variables are the same). As the above is an expected value, it can be approximated using the law of large numbers: instead of averaging $Z_i$, we calculate the following multiple times and average them:
$$ Y_k = \left( \;\frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \; \right)^2 $$
By computing the above many, $N_y$, times (remember, it is random), and averaging them:
$$ \frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k \rightarrow E[ Y_k ] = E\;\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \right]$$
Finally, taking the square root:
$$ \sqrt{\frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k} \approx D(N) $$
```
figsize( 12.5, 4)
N_Y = 250 #use this many to approximate D(N)
N_array = np.arange( 1000, 50000, 2500 ) #use this many samples in the approx. to the variance.
D_N_results = np.zeros( len( N_array ) )
lambda_ = 4.5
expected_value = lambda_ #for X ~ Poi(lambda) , E[ X ] = lambda
def D_N( n ):
"""
This function approx. D_n, the average variance of using n samples.
"""
Z = poi( lambda_, (n, N_Y) )
average_Z = Z.mean(axis=0)
return np.sqrt( ( (average_Z - expected_value)**2 ).mean() )
for i,n in enumerate(N_array):
D_N_results[i] = D_N(n)
plt.xlabel( "$N$" )
plt.ylabel( "expected squared-distance from true value" )
plt.plot(N_array, D_N_results, lw = 3,
label="expected distance between\n\
expected value and \naverage of $N$ random variables.")
plt.plot( N_array, np.sqrt(expected_value)/np.sqrt(N_array), lw = 2, ls = "--",
label = r"$\frac{\sqrt{\lambda}}{\sqrt{N}}$" )
plt.legend()
plt.title( "How 'fast' is the sample average converging? " );
```
As expected, the expected distance between our sample average and the actual expected value shrinks as $N$ grows large. But also notice that the *rate* of convergence decreases, that is, we need only 10 000 additional samples to move from 0.020 to 0.015, a difference of 0.005, but *20 000* more samples to again decrease from 0.015 to 0.010, again only a 0.005 decrease.
It turns out we can measure this rate of convergence. Above I have plotted a second line, the function $\sqrt{\lambda}/\sqrt{N}$. This was not chosen arbitrarily. In most cases, given a sequence of random variable distributed like $Z$, the rate of convergence to $E[Z]$ of the Law of Large Numbers is
$$ \frac{ \sqrt{ \; Var(Z) \; } }{\sqrt{N} }$$
This is useful to know: for a given large $N$, we know (on average) how far away we are from the estimate. On the other hand, in a Bayesian setting, this can seem like a useless result: Bayesian analysis is OK with uncertainty so what's the *statistical* point of adding extra precise digits? Though drawing samples can be so computationally cheap that having a *larger* $N$ is fine too.
### How do we compute $Var(Z)$ though?
The variance is simply another expected value that can be approximated! Consider the following, once we have the expected value (by using the Law of Large Numbers to estimate it, denote it $\mu$), we can estimate the variance:
$$ \frac{1}{N}\sum_{i=1}^N \;(Z_i - \mu)^2 \rightarrow E[ \;( Z - \mu)^2 \;] = Var( Z )$$
### Expected values and probabilities
There is an even less explicit relationship between expected value and estimating probabilities. Define the *indicator function*
$$\mathbb{1}_A(x) =
\begin{cases} 1 & x \in A \\\\
0 & else
\end{cases}
$$
Then, by the law of large numbers, if we have many samples $X_i$, we can estimate the probability of an event $A$, denoted $P(A)$, by:
$$ \frac{1}{N} \sum_{i=1}^N \mathbb{1}_A(X_i) \rightarrow E[\mathbb{1}_A(X)] = P(A) $$
Again, this is fairly obvious after a moments thought: the indicator function is only 1 if the event occurs, so we are summing only the times the event occurs and dividing by the total number of trials (consider how we usually approximate probabilities using frequencies). For example, suppose we wish to estimate the probability that a $Z \sim Exp(.5)$ is greater than 5, and we have many samples from a $Exp(.5)$ distribution.
$$ P( Z > 5 ) = \sum_{i=1}^N \mathbb{1}_{z > 5 }(Z_i) $$
```
N = 10000
print( np.mean( [ np.random.exponential( 0.5 ) > 5 for i in range(N) ] ) )
```
### What does this all have to do with Bayesian statistics?
*Point estimates*, to be introduced in the next chapter, in Bayesian inference are computed using expected values. In more analytical Bayesian inference, we would have been required to evaluate complicated expected values represented as multi-dimensional integrals. No longer. If we can sample from the posterior distribution directly, we simply need to evaluate averages. Much easier. If accuracy is a priority, plots like the ones above show how fast you are converging. And if further accuracy is desired, just take more samples from the posterior.
When is enough enough? When can you stop drawing samples from the posterior? That is the practitioners decision, and also dependent on the variance of the samples (recall from above a high variance means the average will converge slower).
We also should understand when the Law of Large Numbers fails. As the name implies, and comparing the graphs above for small $N$, the Law is only true for large sample sizes. Without this, the asymptotic result is not reliable. Knowing in what situations the Law fails can give us *confidence in how unconfident we should be*. The next section deals with this issue.
## The Disorder of Small Numbers
The Law of Large Numbers is only valid as $N$ gets *infinitely* large: never truly attainable. While the law is a powerful tool, it is foolhardy to apply it liberally. Our next example illustrates this.
##### Example: Aggregated geographic data
Often data comes in aggregated form. For instance, data may be grouped by state, county, or city level. Of course, the population numbers vary per geographic area. If the data is an average of some characteristic of each the geographic areas, we must be conscious of the Law of Large Numbers and how it can *fail* for areas with small populations.
We will observe this on a toy dataset. Suppose there are five thousand counties in our dataset. Furthermore, population number in each state are uniformly distributed between 100 and 1500. The way the population numbers are generated is irrelevant to the discussion, so we do not justify this. We are interested in measuring the average height of individuals per county. Unbeknownst to us, height does **not** vary across county, and each individual, regardless of the county he or she is currently living in, has the same distribution of what their height may be:
$$ \text{height} \sim \text{Normal}(150, 15 ) $$
We aggregate the individuals at the county level, so we only have data for the *average in the county*. What might our dataset look like?
```
figsize( 12.5, 4)
std_height = 15
mean_height = 150
n_counties = 5000
pop_generator = np.random.randint
norm = np.random.normal
#generate some artificial population numbers
population = pop_generator(100, 1500, n_counties )
average_across_county = np.zeros( n_counties )
for i in range( n_counties ):
#generate some individuals and take the mean
average_across_county[i] = norm(mean_height, 1./std_height,
population[i] ).mean()
#located the counties with the apparently most extreme average heights.
i_min = np.argmin( average_across_county )
i_max = np.argmax( average_across_county )
#plot population size vs. recorded average
plt.scatter( population, average_across_county, alpha = 0.5, c="#7A68A6")
plt.scatter( [ population[i_min], population[i_max] ],
[average_across_county[i_min], average_across_county[i_max] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="extreme heights")
plt.xlim( 100, 1500 )
plt.title( "Average height vs. County Population")
plt.xlabel("County Population")
plt.ylabel("Average height in county")
plt.plot( [100, 1500], [150, 150], color = "k", label = "true expected \
height", ls="--" )
plt.legend(scatterpoints = 1);
```
What do we observe? *Without accounting for population sizes* we run the risk of making an enormous inference error: if we ignored population size, we would say that the county with the shortest and tallest individuals have been correctly circled. But this inference is wrong for the following reason. These two counties do *not* necessarily have the most extreme heights. The error results from the calculated average of smaller populations not being a good reflection of the true expected value of the population (which in truth should be $\mu =150$). The sample size/population size/$N$, whatever you wish to call it, is simply too small to invoke the Law of Large Numbers effectively.
We provide more damning evidence against this inference. Recall the population numbers were uniformly distributed over 100 to 1500. Our intuition should tell us that the counties with the most extreme population heights should also be uniformly spread over 100 to 4000, and certainly independent of the county's population. Not so. Below are the population sizes of the counties with the most extreme heights.
```
print("Population sizes of 10 'shortest' counties: ")
print(population[ np.argsort( average_across_county )[:10] ], '\n')
print("Population sizes of 10 'tallest' counties: ")
print(population[ np.argsort( -average_across_county )[:10] ])
```
Not at all uniform over 100 to 1500. This is an absolute failure of the Law of Large Numbers.
##### Example: Kaggle's *U.S. Census Return Rate Challenge*
Below is data from the 2010 US census, which partitions populations beyond counties to the level of block groups (which are aggregates of city blocks or equivalents). The dataset is from a Kaggle machine learning competition some colleagues and I participated in. The objective was to predict the census letter mail-back rate of a group block, measured between 0 and 100, using census variables (median income, number of females in the block-group, number of trailer parks, average number of children etc.). Below we plot the census mail-back rate versus block group population:
```
figsize( 12.5, 6.5 )
data = np.genfromtxt( "./data/census_data.csv", skip_header=1,
delimiter= ",")
plt.scatter( data[:,1], data[:,0], alpha = 0.5, c="#7A68A6")
plt.title("Census mail-back rate vs Population")
plt.ylabel("Mail-back rate")
plt.xlabel("population of block-group")
plt.xlim(-100, 15e3 )
plt.ylim( -5, 105)
i_min = np.argmin( data[:,0] )
i_max = np.argmax( data[:,0] )
plt.scatter( [ data[i_min,1], data[i_max, 1] ],
[ data[i_min,0], data[i_max,0] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="most extreme points")
plt.legend(scatterpoints = 1);
```
The above is a classic phenomenon in statistics. I say *classic* referring to the "shape" of the scatter plot above. It follows a classic triangular form, that tightens as we increase the sample size (as the Law of Large Numbers becomes more exact).
I am perhaps overstressing the point and maybe I should have titled the book *"You don't have big data problems!"*, but here again is an example of the trouble with *small datasets*, not big ones. Simply, small datasets cannot be processed using the Law of Large Numbers. Compare with applying the Law without hassle to big datasets (ex. big data). I mentioned earlier that paradoxically big data prediction problems are solved by relatively simple algorithms. The paradox is partially resolved by understanding that the Law of Large Numbers creates solutions that are *stable*, i.e. adding or subtracting a few data points will not affect the solution much. On the other hand, adding or removing data points to a small dataset can create very different results.
For further reading on the hidden dangers of the Law of Large Numbers, I would highly recommend the excellent manuscript [The Most Dangerous Equation](http://nsm.uh.edu/~dgraur/niv/TheMostDangerousEquation.pdf).
##### Example: How to order Reddit submissions
You may have disagreed with the original statement that the Law of Large numbers is known to everyone, but only implicitly in our subconscious decision making. Consider ratings on online products: how often do you trust an average 5-star rating if there is only 1 reviewer? 2 reviewers? 3 reviewers? We implicitly understand that with such few reviewers that the average rating is **not** a good reflection of the true value of the product.
This has created flaws in how we sort items, and more generally, how we compare items. Many people have realized that sorting online search results by their rating, whether the objects be books, videos, or online comments, return poor results. Often the seemingly top videos or comments have perfect ratings only from a few enthusiastic fans, and truly more quality videos or comments are hidden in later pages with *falsely-substandard* ratings of around 4.8. How can we correct this?
Consider the popular site Reddit (I purposefully did not link to the website as you would never come back). The site hosts links to stories or images, called submissions, for people to comment on. Redditors can vote up or down on each submission (called upvotes and downvotes). Reddit, by default, will sort submissions to a given subreddit by Hot, that is, the submissions that have the most upvotes recently.
<img src="http://i.imgur.com/3v6bz9f.png" />
How would you determine which submissions are the best? There are a number of ways to achieve this:
1. *Popularity*: A submission is considered good if it has many upvotes. A problem with this model is that a submission with hundreds of upvotes, but thousands of downvotes. While being very *popular*, the submission is likely more controversial than best.
2. *Difference*: Using the *difference* of upvotes and downvotes. This solves the above problem, but fails when we consider the temporal nature of submission. Depending on when a submission is posted, the website may be experiencing high or low traffic. The difference method will bias the *Top* submissions to be the those made during high traffic periods, which have accumulated more upvotes than submissions that were not so graced, but are not necessarily the best.
3. *Time adjusted*: Consider using Difference divided by the age of the submission. This creates a *rate*, something like *difference per second*, or *per minute*. An immediate counter-example is, if we use per second, a 1 second old submission with 1 upvote would be better than a 100 second old submission with 99 upvotes. One can avoid this by only considering at least t second old submission. But what is a good t value? Does this mean no submission younger than t is good? We end up comparing unstable quantities with stable quantities (young vs. old submissions).
3. *Ratio*: Rank submissions by the ratio of upvotes to total number of votes (upvotes plus downvotes). This solves the temporal issue, such that new submissions who score well can be considered Top just as likely as older submissions, provided they have many upvotes to total votes. The problem here is that a submission with a single upvote (ratio = 1.0) will beat a submission with 999 upvotes and 1 downvote (ratio = 0.999), but clearly the latter submission is *more likely* to be better.
I used the phrase *more likely* for good reason. It is possible that the former submission, with a single upvote, is in fact a better submission than the later with 999 upvotes. The hesitation to agree with this is because we have not seen the other 999 potential votes the former submission might get. Perhaps it will achieve an additional 999 upvotes and 0 downvotes and be considered better than the latter, though not likely.
What we really want is an estimate of the *true upvote ratio*. Note that the true upvote ratio is not the same as the observed upvote ratio: the true upvote ratio is hidden, and we only observe upvotes vs. downvotes (one can think of the true upvote ratio as "what is the underlying probability someone gives this submission a upvote, versus a downvote"). So the 999 upvote/1 downvote submission probably has a true upvote ratio close to 1, which we can assert with confidence thanks to the Law of Large Numbers, but on the other hand we are much less certain about the true upvote ratio of the submission with only a single upvote. Sounds like a Bayesian problem to me.
One way to determine a prior on the upvote ratio is to look at the historical distribution of upvote ratios. This can be accomplished by scraping Reddit's submissions and determining a distribution. There are a few problems with this technique though:
1. Skewed data: The vast majority of submissions have very few votes, hence there will be many submissions with ratios near the extremes (see the "triangular plot" in the above Kaggle dataset), effectively skewing our distribution to the extremes. One could try to only use submissions with votes greater than some threshold. Again, problems are encountered. There is a tradeoff between number of submissions available to use and a higher threshold with associated ratio precision.
2. Biased data: Reddit is composed of different subpages, called subreddits. Two examples are *r/aww*, which posts pics of cute animals, and *r/politics*. It is very likely that the user behaviour towards submissions of these two subreddits are very different: visitors are likely friendly and affectionate in the former, and would therefore upvote submissions more, compared to the latter, where submissions are likely to be controversial and disagreed upon. Therefore not all submissions are the same.
In light of these, I think it is better to use a `Uniform` prior.
With our prior in place, we can find the posterior of the true upvote ratio. The Python script `top_showerthoughts_submissions.py` will scrape the best posts from the `showerthoughts` community on Reddit. This is a text-only community so the title of each post *is* the post. Below is the top post as well as some other sample posts:
```
#adding a number to the end of the %run call with get the ith top post.
%run top_showerthoughts_submissions.py 2
print("Post contents: \n")
print(top_post)
"""
contents: an array of the text from the last 100 top submissions to a subreddit
votes: a 2d numpy array of upvotes, downvotes for each submission.
"""
n_submissions = len(votes)
submissions = np.random.randint( n_submissions, size=4)
print("Some Submissions (out of %d total) \n-----------"%n_submissions)
for i in submissions:
print('"' + contents[i] + '"')
print("upvotes/downvotes: ",votes[i,:], "\n")
```
For a given true upvote ratio $p$ and $N$ votes, the number of upvotes will look like a Binomial random variable with parameters $p$ and $N$. (This is because of the equivalence between upvote ratio and probability of upvoting versus downvoting, out of $N$ possible votes/trials). We create a function that performs Bayesian inference on $p$, for a particular submission's upvote/downvote pair.
```
import pymc3 as pm
def posterior_upvote_ratio( upvotes, downvotes, samples = 20000):
"""
This function accepts the number of upvotes and downvotes a particular submission recieved,
and the number of posterior samples to return to the user. Assumes a uniform prior.
"""
N = upvotes + downvotes
with pm.Model() as model:
upvote_ratio = pm.Uniform("upvote_ratio", 0, 1)
observations = pm.Binomial( "obs", N, upvote_ratio, observed=upvotes)
trace = pm.sample(samples, step=pm.Metropolis())
burned_trace = trace[int(samples/4):]
return burned_trace["upvote_ratio"]
```
Below are the resulting posterior distributions.
```
figsize( 11., 8)
posteriors = []
colours = ["#348ABD", "#A60628", "#7A68A6", "#467821", "#CF4457"]
for i in range(len(submissions)):
j = submissions[i]
posteriors.append( posterior_upvote_ratio( votes[j, 0], votes[j,1] ) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .9,
histtype="step",color = colours[i%5], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
plt.legend(loc="upper left")
plt.xlim( 0, 1)
plt.title("Posterior distributions of upvote ratios on different submissions");
```
Some distributions are very tight, others have very long tails (relatively speaking), expressing our uncertainty with what the true upvote ratio might be.
### Sorting!
We have been ignoring the goal of this exercise: how do we sort the submissions from *best to worst*? Of course, we cannot sort distributions, we must sort scalar numbers. There are many ways to distill a distribution down to a scalar: expressing the distribution through its expected value, or mean, is one way. Choosing the mean is a bad choice though. This is because the mean does not take into account the uncertainty of distributions.
I suggest using the *95% least plausible value*, defined as the value such that there is only a 5% chance the true parameter is lower (think of the lower bound on the 95% credible region). Below are the posterior distributions with the 95% least-plausible value plotted:
```
N = posteriors[0].shape[0]
lower_limits = []
for i in range(len(submissions)):
j = submissions[i]
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .9,
histtype="step",color = colours[i], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
v = np.sort( posteriors[i] )[ int(0.05*N) ]
#plt.vlines( v, 0, 15 , color = "k", alpha = 1, linewidths=3 )
plt.vlines( v, 0, 10 , color = colours[i], linestyles = "--", linewidths=3 )
lower_limits.append(v)
plt.legend(loc="upper left")
plt.legend(loc="upper left")
plt.title("Posterior distributions of upvote ratios on different submissions");
order = np.argsort( -np.array( lower_limits ) )
print(order, lower_limits)
```
The best submissions, according to our procedure, are the submissions that are *most-likely* to score a high percentage of upvotes. Visually those are the submissions with the 95% least plausible value close to 1.
Why is sorting based on this quantity a good idea? By ordering by the 95% least plausible value, we are being the most conservative with what we think is best. That is, even in the worst case scenario, when we have severely overestimated the upvote ratio, we can be sure the best submissions are still on top. Under this ordering, we impose the following very natural properties:
1. given two submissions with the same observed upvote ratio, we will assign the submission with more votes as better (since we are more confident it has a higher ratio).
2. given two submissions with the same number of votes, we still assign the submission with more upvotes as *better*.
### But this is too slow for real-time!
I agree, computing the posterior of every submission takes a long time, and by the time you have computed it, likely the data has changed. I delay the mathematics to the appendix, but I suggest using the following formula to compute the lower bound very fast.
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + u \\\\
& b = 1 + d \\\\
\end{align}
$u$ is the number of upvotes, and $d$ is the number of downvotes. The formula is a shortcut in Bayesian inference, which will be further explained in Chapter 6 when we discuss priors in more detail.
```
def intervals(u,d):
a = 1. + u
b = 1. + d
mu = a/(a+b)
std_err = 1.65*np.sqrt( (a*b)/( (a+b)**2*(a+b+1.) ) )
return ( mu, std_err )
print("Approximate lower bounds:")
posterior_mean, std_err = intervals(votes[:,0],votes[:,1])
lb = posterior_mean - std_err
print(lb)
print("\n")
print("Top 40 Sorted according to approximate lower bounds:")
print("\n")
order = np.argsort( -lb )
ordered_contents = []
for i in order[:40]:
ordered_contents.append( contents[i] )
print(votes[i,0], votes[i,1], contents[i])
print("-------------")
```
We can view the ordering visually by plotting the posterior mean and bounds, and sorting by the lower bound. In the plot below, notice that the left error-bar is sorted (as we suggested this is the best way to determine an ordering), so the means, indicated by dots, do not follow any strong pattern.
```
r_order = order[::-1][-40:]
plt.errorbar( posterior_mean[r_order], np.arange( len(r_order) ),
xerr=std_err[r_order], capsize=0, fmt="o",
color = "#7A68A6")
plt.xlim( 0.3, 1)
plt.yticks( np.arange( len(r_order)-1,-1,-1 ), map( lambda x: x[:30].replace("\n",""), ordered_contents) );
```
In the graphic above, you can see why sorting by mean would be sub-optimal.
### Extension to Starred rating systems
The above procedure works well for upvote-downvotes schemes, but what about systems that use star ratings, e.g. 5 star rating systems. Similar problems apply with simply taking the average: an item with two perfect ratings would beat an item with thousands of perfect ratings, but a single sub-perfect rating.
We can consider the upvote-downvote problem above as binary: 0 is a downvote, 1 if an upvote. A $N$-star rating system can be seen as a more continuous version of above, and we can set $n$ stars rewarded is equivalent to rewarding $\frac{n}{N}$. For example, in a 5-star system, a 2 star rating corresponds to 0.4. A perfect rating is a 1. We can use the same formula as before, but with $a,b$ defined differently:
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + S \\\\
& b = 1 + N - S \\\\
\end{align}
where $N$ is the number of users who rated, and $S$ is the sum of all the ratings, under the equivalence scheme mentioned above.
##### Example: Counting Github stars
What is the average number of stars a Github repository has? How would you calculate this? There are over 6 million respositories, so there is more than enough data to invoke the Law of Large numbers. Let's start pulling some data. TODO
### Conclusion
While the Law of Large Numbers is cool, it is only true so much as its name implies: with large sample sizes only. We have seen how our inference can be affected by not considering *how the data is shaped*.
1. By (cheaply) drawing many samples from the posterior distributions, we can ensure that the Law of Large Number applies as we approximate expected values (which we will do in the next chapter).
2. Bayesian inference understands that with small sample sizes, we can observe wild randomness. Our posterior distribution will reflect this by being more spread rather than tightly concentrated. Thus, our inference should be correctable.
3. There are major implications of not considering the sample size, and trying to sort objects that are unstable leads to pathological orderings. The method provided above solves this problem.
### Appendix
##### Derivation of sorting submissions formula
Basically what we are doing is using a Beta prior (with parameters $a=1, b=1$, which is a uniform distribution), and using a Binomial likelihood with observations $u, N = u+d$. This means our posterior is a Beta distribution with parameters $a' = 1 + u, b' = 1 + (N - u) = 1+d$. We then need to find the value, $x$, such that 0.05 probability is less than $x$. This is usually done by inverting the CDF ([Cumulative Distribution Function](http://en.wikipedia.org/wiki/Cumulative_Distribution_Function)), but the CDF of the beta, for integer parameters, is known but is a large sum [3].
We instead use a Normal approximation. The mean of the Beta is $\mu = a'/(a'+b')$ and the variance is
$$\sigma^2 = \frac{a'b'}{ (a' + b')^2(a'+b'+1) }$$
Hence we solve the following equation for $x$ and have an approximate lower bound.
$$ 0.05 = \Phi\left( \frac{(x - \mu)}{\sigma}\right) $$
$\Phi$ being the [cumulative distribution for the normal distribution](http://en.wikipedia.org/wiki/Normal_distribution#Cumulative_distribution)
##### Exercises
1\. How would you estimate the quantity $E\left[ \cos{X} \right]$, where $X \sim \text{Exp}(4)$? What about $E\left[ \cos{X} | X \lt 1\right]$, i.e. the expected value *given* we know $X$ is less than 1? Would you need more samples than the original samples size to be equally accurate?
```
## Enter code here
import scipy.stats as stats
exp = stats.expon( scale=4 )
N = 1e5
X = exp.rvs( int(N) )
## ...
```
2\. The following table was located in the paper "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression" [2]. The table ranks football field-goal kickers by their percent of non-misses. What mistake have the researchers made?
-----
#### Kicker Careers Ranked by Make Percentage
<table><tbody><tr><th>Rank </th><th>Kicker </th><th>Make % </th><th>Number of Kicks</th></tr><tr><td>1 </td><td>Garrett Hartley </td><td>87.7 </td><td>57</td></tr><tr><td>2</td><td> Matt Stover </td><td>86.8 </td><td>335</td></tr><tr><td>3 </td><td>Robbie Gould </td><td>86.2 </td><td>224</td></tr><tr><td>4 </td><td>Rob Bironas </td><td>86.1 </td><td>223</td></tr><tr><td>5</td><td> Shayne Graham </td><td>85.4 </td><td>254</td></tr><tr><td>… </td><td>… </td><td>…</td><td> </td></tr><tr><td>51</td><td> Dave Rayner </td><td>72.2 </td><td>90</td></tr><tr><td>52</td><td> Nick Novak </td><td>71.9 </td><td>64</td></tr><tr><td>53 </td><td>Tim Seder </td><td>71.0 </td><td>62</td></tr><tr><td>54 </td><td>Jose Cortez </td><td>70.7</td><td> 75</td></tr><tr><td>55 </td><td>Wade Richey </td><td>66.1</td><td> 56</td></tr></tbody></table>
In August 2013, [a popular post](http://bpodgursky.wordpress.com/2013/08/21/average-income-per-programming-language/) on the average income per programmer of different languages was trending. Here's the summary chart: (reproduced without permission, cause when you lie with stats, you gunna get the hammer). What do you notice about the extremes?
------
#### Average household income by programming language
<table >
<tr><td>Language</td><td>Average Household Income ($)</td><td>Data Points</td></tr>
<tr><td>Puppet</td><td>87,589.29</td><td>112</td></tr>
<tr><td>Haskell</td><td>89,973.82</td><td>191</td></tr>
<tr><td>PHP</td><td>94,031.19</td><td>978</td></tr>
<tr><td>CoffeeScript</td><td>94,890.80</td><td>435</td></tr>
<tr><td>VimL</td><td>94,967.11</td><td>532</td></tr>
<tr><td>Shell</td><td>96,930.54</td><td>979</td></tr>
<tr><td>Lua</td><td>96,930.69</td><td>101</td></tr>
<tr><td>Erlang</td><td>97,306.55</td><td>168</td></tr>
<tr><td>Clojure</td><td>97,500.00</td><td>269</td></tr>
<tr><td>Python</td><td>97,578.87</td><td>2314</td></tr>
<tr><td>JavaScript</td><td>97,598.75</td><td>3443</td></tr>
<tr><td>Emacs Lisp</td><td>97,774.65</td><td>355</td></tr>
<tr><td>C#</td><td>97,823.31</td><td>665</td></tr>
<tr><td>Ruby</td><td>98,238.74</td><td>3242</td></tr>
<tr><td>C++</td><td>99,147.93</td><td>845</td></tr>
<tr><td>CSS</td><td>99,881.40</td><td>527</td></tr>
<tr><td>Perl</td><td>100,295.45</td><td>990</td></tr>
<tr><td>C</td><td>100,766.51</td><td>2120</td></tr>
<tr><td>Go</td><td>101,158.01</td><td>231</td></tr>
<tr><td>Scala</td><td>101,460.91</td><td>243</td></tr>
<tr><td>ColdFusion</td><td>101,536.70</td><td>109</td></tr>
<tr><td>Objective-C</td><td>101,801.60</td><td>562</td></tr>
<tr><td>Groovy</td><td>102,650.86</td><td>116</td></tr>
<tr><td>Java</td><td>103,179.39</td><td>1402</td></tr>
<tr><td>XSLT</td><td>106,199.19</td><td>123</td></tr>
<tr><td>ActionScript</td><td>108,119.47</td><td>113</td></tr>
</table>
### References
1. Wainer, Howard. *The Most Dangerous Equation*. American Scientist, Volume 95.
2. Clarck, Torin K., Aaron W. Johnson, and Alexander J. Stimpson. "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression." (2013): n. page. [Web](http://www.sloansportsconference.com/wp-content/uploads/2013/Going%20for%20Three%20Predicting%20the%20Likelihood%20of%20Field%20Goal%20Success%20with%20Logistic%20Regression.pdf). 20 Feb. 2013.
3. http://en.wikipedia.org/wiki/Beta_function#Incomplete_beta_function
```
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
<style>
img{
max-width:800px}
</style>
| true |
code
| 0.669259 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/s-mostafa-a/pytorch_learning/blob/master/simple_generative_adversarial_net/MNIST_GANs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import torch
from torchvision.transforms import ToTensor, Normalize, Compose
from torchvision.datasets import MNIST
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision.utils import save_image
import os
class DeviceDataLoader:
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
for b in self.dl:
yield self.to_device(b, self.device)
def __len__(self):
return len(self.dl)
def to_device(self, data, device):
if isinstance(data, (list, tuple)):
return [self.to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class MNIST_GANS:
def __init__(self, dataset, image_size, device, num_epochs=50, loss_function=nn.BCELoss(), batch_size=100,
hidden_size=2561, latent_size=64):
self.device = device
bare_data_loader = DataLoader(dataset, batch_size, shuffle=True)
self.data_loader = DeviceDataLoader(bare_data_loader, device)
self.loss_function = loss_function
self.hidden_size = hidden_size
self.latent_size = latent_size
self.batch_size = batch_size
self.D = nn.Sequential(
nn.Linear(image_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, 1),
nn.Sigmoid())
self.G = nn.Sequential(
nn.Linear(latent_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, image_size),
nn.Tanh())
self.d_optimizer = torch.optim.Adam(self.D.parameters(), lr=0.0002)
self.g_optimizer = torch.optim.Adam(self.G.parameters(), lr=0.0002)
self.sample_dir = './../data/mnist_samples'
if not os.path.exists(self.sample_dir):
os.makedirs(self.sample_dir)
self.G.to(device)
self.D.to(device)
self.sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
self.num_epochs = num_epochs
@staticmethod
def denormalize(x):
out = (x + 1) / 2
return out.clamp(0, 1)
def reset_grad(self):
self.d_optimizer.zero_grad()
self.g_optimizer.zero_grad()
def train_discriminator(self, images):
real_labels = torch.ones(self.batch_size, 1).to(self.device)
fake_labels = torch.zeros(self.batch_size, 1).to(self.device)
outputs = self.D(images)
d_loss_real = self.loss_function(outputs, real_labels)
real_score = outputs
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
outputs = self.D(fake_images)
d_loss_fake = self.loss_function(outputs, fake_labels)
fake_score = outputs
d_loss = d_loss_real + d_loss_fake
self.reset_grad()
d_loss.backward()
self.d_optimizer.step()
return d_loss, real_score, fake_score
def train_generator(self):
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
labels = torch.ones(self.batch_size, 1).to(self.device)
g_loss = self.loss_function(self.D(fake_images), labels)
self.reset_grad()
g_loss.backward()
self.g_optimizer.step()
return g_loss, fake_images
def save_fake_images(self, index):
fake_images = self.G(self.sample_vectors)
fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
fake_fname = 'fake_images-{0:0=4d}.png'.format(index)
print('Saving', fake_fname)
save_image(self.denormalize(fake_images), os.path.join(self.sample_dir, fake_fname),
nrow=10)
def run(self):
total_step = len(self.data_loader)
d_losses, g_losses, real_scores, fake_scores = [], [], [], []
for epoch in range(self.num_epochs):
for i, (images, _) in enumerate(self.data_loader):
images = images.reshape(self.batch_size, -1)
d_loss, real_score, fake_score = self.train_discriminator(images)
g_loss, fake_images = self.train_generator()
if (i + 1) % 600 == 0:
d_losses.append(d_loss.item())
g_losses.append(g_loss.item())
real_scores.append(real_score.mean().item())
fake_scores.append(fake_score.mean().item())
print(f'''Epoch [{epoch}/{self.num_epochs}], Step [{i + 1}/{
total_step}], d_loss: {d_loss.item():.4f}, g_loss: {g_loss.item():.4f}, D(x): {
real_score.mean().item():.2f}, D(G(z)): {fake_score.mean().item():.2f}''')
self.save_fake_images(epoch + 1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
mnist = MNIST(root='./../data', train=True, download=True, transform=Compose([ToTensor(), Normalize(mean=(0.5,), std=(0.5,))]))
image_size = mnist.data[0].flatten().size()[0]
gans = MNIST_GANS(dataset=mnist, image_size=image_size, device=device)
gans.run()
```
| true |
code
| 0.824197 | null | null | null | null |
|
# Tutorial 2. Solving a 1D diffusion equation
```
# Document Author: Dr. Vishal Sharma
# Author email: [email protected]
# License: MIT
# This tutorial is applicable for NAnPack version 1.0.0-alpha4
```
### I. Background
The objective of this tutorial is to present the step-by-step solution of a 1D diffusion equation using NAnPack such that users can follow the instructions to learn using this package. The numerical solution is obtained using the Forward Time Central Spacing (FTCS) method. The detailed description of the FTCS method is presented in Section IV of this tutorial.
### II. Case Description
We will be solving a classical probkem of a suddenly accelerated plate in fluid mechanicas which has the known exact solution. In this problem, the fluid is
bounded between two parallel plates. The upper plate remains stationary and the lower plate is suddenly accelerated in *y*-direction at velocity $U_o$. It is
required to find the velocity profile between the plates for the given initial and boundary conditions.
(For the sake of simplicity in setting up numerical variables, let's assume that the *x*-axis is pointed in the upward direction and *y*-axis is pointed along the horizontal direction as shown in the schematic below:

**Initial conditions**
$$u(t=0.0, 0.0<x\leq H) = 0.0 \;m/s$$
$$u(t=0.0, x=0.0) = 40.0 \;m/s$$
**Boundary conditions**
$$u(t\geq0.0, x=0.0) = 40.0 \;m/s$$
$$u(t\geq0.0, x=H) = 0.0 \;m/s$$
Viscosity of fluid, $\;\;\nu = 2.17*10^{-4} \;m^2/s$
Distance between plates, $\;\;H = 0.04 \;m$
Grid step size, $\;\;dx = 0.001 \;m$
Simulation time, $\;\;T = 1.08 \;sec$
Specify the required simulation inputs based on our setup in the configuration file provided with this package. You may choose to save the configuration file with any other filename. I have saved the configuration file in the "input" folder of my project directory such that the relative path is `./input/config.ini`.
### III. Governing Equation
The governing equation for the given application is the simplified for the the Navies-Stokes equation which is given as:
$$\frac{\partial u} {\partial t} = \nu\frac{\partial^2 u}{\partial x^2}$$
This is the diffusion equation model and is classified as the parabolic PDE.
### IV. FTCS method
The forward time central spacing approximation equation in 1D is presented here. This is a time explicit method which means that one unknown is calculated using the known neighbouring values from the previous time step. Here *i* represents grid point location, *n*+1 is the future time step, and *n* is the current time step.
$$u_{i}^{n+1} = u_{i}^{n} + \frac{\nu\Delta t}{(\Delta x)^2}(u_{i+1}^{n} - 2u_{i}^{n} + u_{i-1}^{n})$$
The order of this approximation is $[(\Delta t), (\Delta x)^2]$
The diffusion number is given as $d_{x} = \nu\frac{\Delta t}{(\Delta x)^2}$ and for one-dimensional applications the stability criteria is $d_{x}\leq\frac{1}{2}$
The solution presented here is obtained using a diffusion number = 0.5 (CFL = 0.5 in configuration file). Time step size will be computed using the expression of diffusion number. Beginners are encouraged to try diffusion numbers greater than 0.5 as an exercise after running this script.
Users are encouraged to read my blogs on numerical methods - [link here](https://www.linkedin.com/in/vishalsharmaofficial/detail/recent-activity/posts/).
### V. Script Development
*Please note that this code script is provided in file `./examples/tutorial-02-diffusion-1D-solvers-FTCS.py`.*
As per the Python established coding guidelines [PEP 8](https://www.python.org/dev/peps/pep-0008/#imports), all package imports must be done at the top part of the script in the following sequence --
1. import standard library
2. import third party modules
3. import local application/library specific
Accordingly, in our code we will importing the following required modules (in alphabetical order). If you are using Jupyter notebook, hit `Shift + Enter` on each cell after typing the code.
```
import matplotlib.pyplot as plt
from nanpack.benchmark import ParallelPlateFlow
import nanpack.preprocess as pre
from nanpack.grid import RectangularGrid
from nanpack.parabolicsolvers import FTCS
import nanpack.postprocess as post
```
As the first step in simulation, we have to tell our script to read the inputs and assign those inputs to the variables/objects that we will use in our entire code. For this purpose, there is a class `RunConfig` in `nanpack.preprocess` module. We will call this class and assign an object (instance) to it so that we can use its member variables. The `RunConfig` class is written in such a manner that its methods get executed as soon as it's instance is created. The users must provide the configuration file path as a parameter to `RunConfig` class.
```
FileName = "path/to/project/input/config.ini" # specify the correct file path
cfg = pre.RunConfig(FileName) # cfg is an instance of RunConfig class which can be used to access class variables. You may choose any variable in place of cfg.
```
You will obtain several configuration messages on your output screen so that you can verify that your inputs are correct and that the configuration is successfully completed. Next step is the assignment of initial conditions and the boundary conditions. For assigning boundary conditions, I have created a function `BC()` which we will be calling in the next cell. I have included this function at the bottom of this tutorial for your reference. It is to be noted that U is the dependent variable that was initialized when we executed the configuration, and thus we will be using `cfg.U` to access the initialized U. In a similar manner, all the inputs provided in the configuration file can be obtained by using configuration class object `cfg.` as the prefix to the variable names. Users are allowed to use any object of their choice.
*If you are using Jupyter Notebook, the function BC must be executed before referencing to it, otherwise, you will get an error. Jump to the bottom of this notebook where you see code cell # 1 containing the `BC()` function*
```
# Assign initial conditions
cfg.U[0] = 40.0
cfg.U[1:] = 0.0
# Assign boundary conditions
U = BC(cfg.U)
```
Next, we will be calculating location of all grid points within the domain using the function `RectangularGrid()` and save values into X. We will also require to calculate diffusion number in X direction. In nanpack, the program treats the diffusion number = CFL for 1D applications that we entered in the configuration file, and therefore this step may be skipped, however, it is not the same in two-dimensional applications and therefore to stay consistent and to avoid confusion we will be using the function `DiffusionNumbers()` to compute the term `diffX`.
```
X, _ = RectangularGrid(cfg.dX, cfg.iMax)
diffX,_ = pre.DiffusionNumbers(cfg.Dimension, cfg.diff, cfg.dT, cfg.dX)
```
Next, we will initialize some local variables before start the time stepping:
```
Error = 1.0 # variable to keep track of error
n = 0 # variable to advance in time
```
Start time loop using while loop such that if one of the condition returns False, the time stepping will be stopped. For explanation of each line, see the comments. Please note the identation of the codes within the while loop. Take extra care with indentation as Python is very particular about it.
```
while n <= cfg.nMax and Error > cfg.ConvCrit: # start loop
Error = 0.0 # reset error to 0.0 at the beginning of each step
n += 1 # advance the value of n at each step
Uold = U.copy() # store solution at time level, n
U = FTCS(Uold, diffX) # solve for U using FTCS method at time level n+1
Error = post.AbsoluteError(U, Uold) # calculate errors
U = BC(U) # Update BC
post.MonitorConvergence(cfg, n, Error) # Use this function to monitor convergence
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,\
cfg.OutFileName, cfg.dX) # Write output to file
post.WriteConvHistToFile(cfg, n, Error) # Write convergence log to history file
```
In the above convergence monitor, it is worth noting that the solution error is gradually moving towards zero which is what we need to confirm stability in the solution. If the solution becomes unstable, the errors will rise, probably upto the point where your code will crash. As you know that the solution obtained is a time-dependent solution and therefore, we didn't allow the code to run until the convergence is observed. If a steady-state solution is desired, change the STATE key in the configuration file equals to "STEADY" and specify a much larger value of nMax key, say nMax = 5000. This is left as an exercise for the users to obtain a stead-state solution. Also, try running the solution with the larger grid step size, $\Delta x$ or a larger time step size, $\Delta t$.
After the time stepping is completed, save the final results to the output files.
```
# Write output to file
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,
cfg.OutFileName, cfg.dX)
# Write convergence history log to a file
post.WriteConvHistToFile(cfg, n, Error)
```
Verify that the files are saved in the target directory.
Now let us obtain analytical solution of this flow that will help us in validating our codes.
```
# Obtain analytical solution
Uana = ParallelPlateFlow(40.0, X, cfg.diff, cfg.totTime, 20)
```
Next, we will validate our results by plotting the results using the matplotlib package that we have imported above. Type the following lines of codes:
```
plt.rc("font", family="serif", size=8) # Assign fonts in the plot
fig, ax = plt.subplots(dpi=150) # Create axis for plotting
plt.plot(U, X, ">-.b", linewidth=0.5, label="FTCS",\
markersize=5, markevery=5) # Plot data with required labels and markers, customize the plot however you may like
plt.plot(Uana, X, "o:r", linewidth=0.5, label="Analytical",\
markersize=5, markevery=5) # Plot analytical solution on the same plot
plt.xlabel('Velocity (m/s)') # X-axis labelling
plt.ylabel('Plate distance (m)') # Y-axis labelling
plt.title(f"Velocity profile\nat t={cfg.totTime} sec", fontsize=8) # Plot title
plt.legend()
plt.show() # Show plot- this command is very important
```
Function for the boundary conditions.
```
def BC(U):
"""Return the dependent variable with the updated values at the boundaries."""
U[0] = 40.0
U[-1] = 0.0
return U
```
Congratulations, you have completed the first coding tutoria using nanpack package and verified that your codes produced correct results. If you solve some other similar diffusion-1D model example, share it with the nanpack community. I will be excited to see your projects.
| true |
code
| 0.849379 | null | null | null | null |
|
# Monte Carlo Integration with Python
## Dr. Tirthajyoti Sarkar ([LinkedIn](https://www.linkedin.com/in/tirthajyoti-sarkar-2127aa7/), [Github](https://github.com/tirthajyoti)), Fremont, CA, July 2020
---
### Disclaimer
The inspiration for this demo/notebook stemmed from [Georgia Tech's Online Masters in Analytics (OMSA) program](https://www.gatech.edu/academics/degrees/masters/analytics-online-degree-oms-analytics) study material. I am proud to pursue this excellent Online MS program. You can also check the details [here](http://catalog.gatech.edu/programs/analytics-ms/#onlinetext).
## What is Monte Carlo integration?
### A casino trick for mathematics

Monte Carlo, is in fact, the name of the world-famous casino located in the eponymous district of the city-state (also called a Principality) of Monaco, on the world-famous French Riviera.
It turns out that the casino inspired the minds of famous scientists to devise an intriguing mathematical technique for solving complex problems in statistics, numerical computing, system simulation.
### Modern origin (to make 'The Bomb')

One of the first and most famous uses of this technique was during the Manhattan Project when the chain-reaction dynamics in highly enriched uranium presented an unimaginably complex theoretical calculation to the scientists. Even the genius minds like John Von Neumann, Stanislaw Ulam, Nicholas Metropolis could not tackle it in the traditional way. They, therefore, turned to the wonderful world of random numbers and let these probabilistic quantities tame the originally intractable calculations.
Amazingly, these random variables could solve the computing problem, which stymied the sure-footed deterministic approach. The elements of uncertainty actually won.
Just like uncertainty and randomness rule in the world of Monte Carlo games. That was the inspiration for this particular moniker.
### Today
Today, it is a technique used in a wide swath of fields,
- risk analysis, financial engineering,
- supply chain logistics,
- statistical learning and modeling,
- computer graphics, image processing, game design,
- large system simulations,
- computational physics, astronomy, etc.
For all its successes and fame, the basic idea is deceptively simple and easy to demonstrate. We demonstrate it in this article with a simple set of Python code.
## The code and the demo
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
```
### A simple function which is difficult to integrate analytically
While the general Monte Carlo simulation technique is much broader in scope, we focus particularly on the Monte Carlo integration technique here.
It is nothing but a numerical method for computing complex definite integrals, which lack closed-form analytical solutions.
Say, we want to calculate,
$$\int_{0}^{4}\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x} dx$$
```
def f1(x):
return (15*x**3+21*x**2+41*x+3)**(1/4) * (np.exp(-0.5*x))
```
### Plot
```
x = np.arange(0,4.1,0.1)
y = f1(x)
plt.figure(figsize=(8,4))
plt.title("Plot of the function: $\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x}$",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### Riemann sums?
There are many such techniques under the general category of [Riemann sum](https://medium.com/r/?url=https%3A%2F%2Fen.wikipedia.org%2Fwiki%2FRiemann_sum). The idea is just to divide the area under the curve into small rectangular or trapezoidal pieces, approximate them by the simple geometrical calculations, and sum those components up.
For a simple illustration, I show such a scheme with only 5 equispaced intervals.
For the programmer friends, in fact, there is a [ready-made function in the Scipy package](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html#scipy.integrate.quad) which can do this computation fast and accurately.
```
rect = np.linspace(0,4,5)
plt.figure(figsize=(8,4))
plt.title("Area under the curve: With Riemann sum",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rect[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### What if I go random?
What if I told you that I do not need to pick the intervals so uniformly, and, in fact, I can go completely probabilistic, and pick 100% random intervals to compute the same integral?
Crazy talk? My choice of samples could look like this…
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
Or, this?
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### It just works!
We don't have the time or scope to prove the theory behind it, but it can be shown that with a reasonably high number of random sampling, we can, in fact, compute the integral with sufficiently high accuracy!
We just choose random numbers (between the limits), evaluate the function at those points, add them up, and scale it by a known factor. We are done.
OK. What are we waiting for? Let's demonstrate this claim with some simple Python code.
### A simple version
```
def monte_carlo(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration
"""
u = np.random.uniform(size=n)
#plt.hist(u)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
```
### Another version with 10-spaced sampling
```
def monte_carlo_uniform(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration with more uniform spread (forced)
"""
subsets = np.arange(0,n+1,n/10)
steps = n/10
u = np.zeros(n)
for i in range(10):
start = int(subsets[i])
end = int(subsets[i+1])
u[start:end] = np.random.uniform(low=i/10,high=(i+1)/10,size=end-start)
np.random.shuffle(u)
#plt.hist(u)
#u = np.random.uniform(size=n)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
inte = monte_carlo_uniform(f1,a=0,b=4,n=100)
print(inte)
```
### How good is the calculation anyway?
This integral cannot be calculated analytically. So, we need to benchmark the accuracy of the Monte Carlo method against another numerical integration technique anyway. We chose the Scipy `integrate.quad()` function for that.
Now, you may also be thinking - **what happens to the accuracy as the sampling density changes**. This choice clearly impacts the computation speed - we need to add less number of quantities if we choose a reduced sampling density.
Therefore, we simulated the same integral for a range of sampling density and plotted the result on top of the gold standard - the Scipy function represented as the horizontal line in the plot below,
```
inte_lst = []
for i in range(100,2100,50):
inte = monte_carlo_uniform(f1,a=0,b=4,n=i)
inte_lst.append(inte)
result,_ = quad(f1,a=0,b=4)
plt.figure(figsize=(8,4))
plt.plot([i for i in range(100,2100,50)],inte_lst,color='blue')
plt.hlines(y=result,xmin=0,xmax=2100,linestyle='--',lw=3)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Sample density for Monte Carlo",fontsize=15)
plt.ylabel("Integration result",fontsize=15)
plt.grid(True)
plt.legend(['Monte Carlo integration','Scipy function'],fontsize=15)
plt.show()
```
### Not bad at all...
Therefore, we observe some small perturbations in the low sample density phase, but they smooth out nicely as the sample density increases. In any case, the absolute error is extremely small compared to the value returned by the Scipy function - on the order of 0.02%.
The Monte Carlo trick works fantastically!
### Speed of the Monte Carlo method
In this particular example, the Monte Carlo calculations are running twice as fast as the Scipy integration method!
While this kind of speed advantage depends on many factors, we can be assured that the Monte Carlo technique is not a slouch when it comes to the matter of computation efficiency.
```
%%timeit -n100 -r100
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
```
### Speed of the Scipy function
```
%%timeit -n100 -r100
quad(f1,a=0,b=4)
```
### Repeat
For a probabilistic technique like Monte Carlo integration, it goes without saying that mathematicians and scientists almost never stop at just one run but repeat the calculations for a number of times and take the average.
Here is a distribution plot from a 10,000 run experiment. As you can see, the plot almost resembles a Gaussian Normal distribution and this fact can be utilized to not only get the average value but also construct confidence intervals around that result.
```
inte_lst = []
for i in range(10000):
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
inte_lst.append(inte)
plt.figure(figsize=(8,4))
plt.title("Distribution of the Monte Carlo runs",
fontsize=18)
plt.hist(inte_lst,bins=50,color='orange',edgecolor='k')
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Integration result",fontsize=15)
plt.ylabel("Density",fontsize=15)
plt.show()
```
### Particularly suitable for high-dimensional integrals
Although for our simple illustration (and for pedagogical purpose), we stick to a single-variable integral, the same idea can easily be extended to high-dimensional integrals with multiple variables.
And it is in this higher dimension that the Monte Carlo method particularly shines as compared to Riemann sum based approaches. The sample density can be optimized in a much more favorable manner for the Monte Carlo method to make it much faster without compromising the accuracy.
In mathematical terms, the convergence rate of the method is independent of the number of dimensions. In machine learning speak, the Monte Carlo method is the best friend you have to beat the curse of dimensionality when it comes to complex integral calculations.
---
## Summary
We introduced the concept of Monte Carlo integration and illustrated how it differs from the conventional numerical integration methods. We also showed a simple set of Python codes to evaluate a one-dimensional function and assess the accuracy and speed of the techniques.
The broader class of Monte Carlo simulation techniques is more exciting and is used in a ubiquitous manner in fields related to artificial intelligence, data science, and statistical modeling.
For example, the famous Alpha Go program from DeepMind used a Monte Carlo search technique to be computationally efficient in the high-dimensional space of the game Go. Numerous such examples can be found in practice.
| true |
code
| 0.547101 | null | null | null | null |
|
This illustrates the datasets.make_multilabel_classification dataset generator. Each sample consists of counts of two features (up to 50 in total), which are differently distributed in each of two classes.
Points are labeled as follows, where Y means the class is present:
| 1 | 2 | 3 | Color |
|--- |--- |--- |-------- |
| Y | N | N | Red |
| N | Y | N | Blue |
| N | N | Y | Yellow |
| Y | Y | N | Purple |
| Y | N | Y | Orange |
| Y | Y | N | Green |
| Y | Y | Y | Brown |
A big circle marks the expected sample for each class; its size reflects the probability of selecting that class label.
The left and right examples highlight the n_labels parameter: more of the samples in the right plot have 2 or 3 labels.
Note that this two-dimensional example is very degenerate: generally the number of features would be much greater than the “document length”, while here we have much larger documents than vocabulary. Similarly, with n_classes > n_features, it is much less likely that a feature distinguishes a particular class.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
This tutorial imports [make_ml_clf](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_multilabel_classification.html#sklearn.datasets.make_multilabel_classification).
```
import plotly.plotly as py
import plotly.graph_objs as go
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_multilabel_classification as make_ml_clf
```
### Calculations
```
COLORS = np.array(['!',
'#FF3333', # red
'#0198E1', # blue
'#BF5FFF', # purple
'#FCD116', # yellow
'#FF7216', # orange
'#4DBD33', # green
'#87421F' # brown
])
# Use same random seed for multiple calls to make_multilabel_classification to
# ensure same distributions
RANDOM_SEED = np.random.randint(2 ** 10)
def plot_2d(n_labels=1, n_classes=3, length=50):
X, Y, p_c, p_w_c = make_ml_clf(n_samples=150, n_features=2,
n_classes=n_classes, n_labels=n_labels,
length=length, allow_unlabeled=False,
return_distributions=True,
random_state=RANDOM_SEED)
trace1 = go.Scatter(x=X[:, 0], y=X[:, 1],
mode='markers',
showlegend=False,
marker=dict(size=8,
color=COLORS.take((Y * [1, 2, 4]).sum(axis=1)))
)
trace2 = go.Scatter(x=p_w_c[0] * length, y=p_w_c[1] * length,
mode='markers',
showlegend=False,
marker=dict(color=COLORS.take([1, 2, 4]),
size=14,
line=dict(width=1, color='black'))
)
data = [trace1, trace2]
return data, p_c, p_w_c
```
### Plot Results
n_labels=1
```
data, p_c, p_w_c = plot_2d(n_labels=1)
layout=go.Layout(title='n_labels=1, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig)
```
n_labels=3
```
data = plot_2d(n_labels=3)
layout=go.Layout(title='n_labels=3, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data[0], layout=layout)
py.iplot(fig)
print('The data was generated from (random_state=%d):' % RANDOM_SEED)
print('Class', 'P(C)', 'P(w0|C)', 'P(w1|C)', sep='\t')
for k, p, p_w in zip(['red', 'blue', 'yellow'], p_c, p_w_c.T):
print('%s\t%0.2f\t%0.2f\t%0.2f' % (k, p, p_w[0], p_w[1]))
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'randomly-generated-multilabel-dataset.ipynb', 'scikit-learn/plot-random-multilabel-dataset/', 'Randomly Generated Multilabel Dataset | plotly',
' ',
title = 'Randomly Generated Multilabel Dataset| plotly',
name = 'Randomly Generated Multilabel Dataset',
has_thumbnail='true', thumbnail='thumbnail/multilabel-dataset.jpg',
language='scikit-learn', page_type='example_index',
display_as='dataset', order=4,
ipynb= '~Diksha_Gabha/2909')
```
| true |
code
| 0.612194 | null | null | null | null |
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Kalman Filter Math
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
If you've gotten this far I hope that you are thinking that the Kalman filter's fearsome reputation is somewhat undeserved. Sure, I hand waved some equations away, but I hope implementation has been fairly straightforward for you. The underlying concept is quite straightforward - take two measurements, or a measurement and a prediction, and choose the output to be somewhere between the two. If you believe the measurement more your guess will be closer to the measurement, and if you believe the prediction is more accurate your guess will lie closer to it. That's not rocket science (little joke - it is exactly this math that got Apollo to the moon and back!).
To be honest I have been choosing my problems carefully. For an arbitrary problem designing the Kalman filter matrices can be extremely difficult. I haven't been *too tricky*, though. Equations like Newton's equations of motion can be trivially computed for Kalman filter applications, and they make up the bulk of the kind of problems that we want to solve.
I have illustrated the concepts with code and reasoning, not math. But there are topics that do require more mathematics than I have used so far. This chapter presents the math that you will need for the rest of the book.
## Modeling a Dynamic System
A *dynamic system* is a physical system whose state (position, temperature, etc) evolves over time. Calculus is the math of changing values, so we use differential equations to model dynamic systems. Some systems cannot be modeled with differential equations, but we will not encounter those in this book.
Modeling dynamic systems is properly the topic of several college courses. To an extent there is no substitute for a few semesters of ordinary and partial differential equations followed by a graduate course in control system theory. If you are a hobbyist, or trying to solve one very specific filtering problem at work you probably do not have the time and/or inclination to devote a year or more to that education.
Fortunately, I can present enough of the theory to allow us to create the system equations for many different Kalman filters. My goal is to get you to the stage where you can read a publication and understand it well enough to implement the algorithms. The background math is deep, but in practice we end up using a few simple techniques.
This is the longest section of pure math in this book. You will need to master everything in this section to understand the Extended Kalman filter (EKF), the most common nonlinear filter. I do cover more modern filters that do not require as much of this math. You can choose to skim now, and come back to this if you decide to learn the EKF.
We need to start by understanding the underlying equations and assumptions that the Kalman filter uses. We are trying to model real world phenomena, so what do we have to consider?
Each physical system has a process. For example, a car traveling at a certain velocity goes so far in a fixed amount of time, and its velocity varies as a function of its acceleration. We describe that behavior with the well known Newtonian equations that we learned in high school.
$$
\begin{aligned}
v&=at\\
x &= \frac{1}{2}at^2 + v_0t + x_0
\end{aligned}
$$
Once we learned calculus we saw them in this form:
$$ \mathbf v = \frac{d \mathbf x}{d t},
\quad \mathbf a = \frac{d \mathbf v}{d t} = \frac{d^2 \mathbf x}{d t^2}
$$
A typical automobile tracking problem would have you compute the distance traveled given a constant velocity or acceleration, as we did in previous chapters. But, of course we know this is not all that is happening. No car travels on a perfect road. There are bumps, wind drag, and hills that raise and lower the speed. The suspension is a mechanical system with friction and imperfect springs.
Perfectly modeling a system is impossible except for the most trivial problems. We are forced to make a simplification. At any time $t$ we say that the true state (such as the position of our car) is the predicted value from the imperfect model plus some unknown *process noise*:
$$
x(t) = x_{pred}(t) + noise(t)
$$
This is not meant to imply that $noise(t)$ is a function that we can derive analytically. It is merely a statement of fact - we can always describe the true value as the predicted value plus the process noise. "Noise" does not imply random events. If we are tracking a thrown ball in the atmosphere, and our model assumes the ball is in a vacuum, then the effect of air drag is process noise in this context.
In the next section we will learn techniques to convert a set of higher order differential equations into a set of first-order differential equations. After the conversion the model of the system without noise is:
$$ \dot{\mathbf x} = \mathbf{Ax}$$
$\mathbf A$ is known as the *systems dynamics matrix* as it describes the dynamics of the system. Now we need to model the noise. We will call that $\mathbf w$, and add it to the equation.
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf w$$
$\mathbf w$ may strike you as a poor choice for the name, but you will soon see that the Kalman filter assumes *white* noise.
Finally, we need to consider any inputs into the system. We assume an input $\mathbf u$, and that there exists a linear model that defines how that input changes the system. For example, pressing the accelerator in your car makes it accelerate, and gravity causes balls to fall. Both are contol inputs. We will need a matrix $\mathbf B$ to convert $u$ into the effect on the system. We add that into our equation:
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
And that's it. That is one of the equations that Dr. Kalman set out to solve, and he found an optimal estimator if we assume certain properties of $\mathbf w$.
## State-Space Representation of Dynamic Systems
We've derived the equation
$$ \dot{\mathbf x} = \mathbf{Ax}+ \mathbf{Bu} + \mathbf{w}$$
However, we are not interested in the derivative of $\mathbf x$, but in $\mathbf x$ itself. Ignoring the noise for a moment, we want an equation that recusively finds the value of $\mathbf x$ at time $t_k$ in terms of $\mathbf x$ at time $t_{k-1}$:
$$\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) + \mathbf B(t_k) + \mathbf u (t_k)$$
Convention allows us to write $\mathbf x(t_k)$ as $\mathbf x_k$, which means the
the value of $\mathbf x$ at the k$^{th}$ value of $t$.
$$\mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
$\mathbf F$ is the familiar *state transition matrix*, named due to its ability to transition the state's value between discrete time steps. It is very similar to the system dynamics matrix $\mathbf A$. The difference is that $\mathbf A$ models a set of linear differential equations, and is continuous. $\mathbf F$ is discrete, and represents a set of linear equations (not differential equations) which transitions $\mathbf x_{k-1}$ to $\mathbf x_k$ over a discrete time step $\Delta t$.
Finding this matrix is often quite difficult. The equation $\dot x = v$ is the simplest possible differential equation and we trivially integrate it as:
$$ \int\limits_{x_{k-1}}^{x_k} \mathrm{d}x = \int\limits_{0}^{\Delta t} v\, \mathrm{d}t $$
$$x_k-x_0 = v \Delta t$$
$$x_k = v \Delta t + x_0$$
This equation is *recursive*: we compute the value of $x$ at time $t$ based on its value at time $t-1$. This recursive form enables us to represent the system (process model) in the form required by the Kalman filter:
$$\begin{aligned}
\mathbf x_k &= \mathbf{Fx}_{k-1} \\
&= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}
\begin{bmatrix}x_{k-1} \\ \dot x_{k-1}\end{bmatrix}
\end{aligned}$$
We can do that only because $\dot x = v$ is simplest differential equation possible. Almost all other in physical systems result in more complicated differential equation which do not yield to this approach.
*State-space* methods became popular around the time of the Apollo missions, largely due to the work of Dr. Kalman. The idea is simple. Model a system with a set of $n^{th}$-order differential equations. Convert them into an equivalent set of first-order differential equations. Put them into the vector-matrix form used in the previous section: $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu}$. Once in this form we use of of several techniques to convert these linear differential equations into the recursive equation:
$$ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
Some books call the state transition matrix the *fundamental matrix*. Many use $\mathbf \Phi$ instead of $\mathbf F$. Sources based heavily on control theory tend to use these forms.
These are called *state-space* methods because we are expressing the solution of the differential equations in terms of the system state.
### Forming First Order Equations from Higher Order Equations
Many models of physical systems require second or higher order differential equations with control input $u$:
$$a_n \frac{d^ny}{dt^n} + a_{n-1} \frac{d^{n-1}y}{dt^{n-1}} + \dots + a_2 \frac{d^2y}{dt^2} + a_1 \frac{dy}{dt} + a_0 = u$$
State-space methods require first-order equations. Any higher order system of equations can be reduced to first-order by defining extra variables for the derivatives and then solving.
Let's do an example. Given the system $\ddot{x} - 6\dot x + 9x = u$ find the equivalent first order equations. I've used the dot notation for the time derivatives for clarity.
The first step is to isolate the highest order term onto one side of the equation.
$$\ddot{x} = 6\dot x - 9x + u$$
We define two new variables:
$$\begin{aligned} x_1(u) &= x \\
x_2(u) &= \dot x
\end{aligned}$$
Now we will substitute these into the original equation and solve. The solution yields a set of first-order equations in terms of these new variables. It is conventional to drop the $(u)$ for notational convenience.
We know that $\dot x_1 = x_2$ and that $\dot x_2 = \ddot{x}$. Therefore
$$\begin{aligned}
\dot x_2 &= \ddot{x} \\
&= 6\dot x - 9x + t\\
&= 6x_2-9x_1 + t
\end{aligned}$$
Therefore our first-order system of equations is
$$\begin{aligned}\dot x_1 &= x_2 \\
\dot x_2 &= 6x_2-9x_1 + t\end{aligned}$$
If you practice this a bit you will become adept at it. Isolate the highest term, define a new variable and its derivatives, and then substitute.
### First Order Differential Equations In State-Space Form
Substituting the newly defined variables from the previous section:
$$\frac{dx_1}{dt} = x_2,\,
\frac{dx_2}{dt} = x_3, \, ..., \,
\frac{dx_{n-1}}{dt} = x_n$$
into the first order equations yields:
$$\frac{dx_n}{dt} = \frac{1}{a_n}\sum\limits_{i=0}^{n-1}a_ix_{i+1} + \frac{1}{a_n}u
$$
Using vector-matrix notation we have:
$$\begin{bmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt} \\ \vdots \\ \frac{dx_n}{dt}\end{bmatrix} =
\begin{bmatrix}\dot x_1 \\ \dot x_2 \\ \vdots \\ \dot x_n\end{bmatrix}=
\begin{bmatrix}0 & 1 & 0 &\cdots & 0 \\
0 & 0 & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
-\frac{a_0}{a_n} & -\frac{a_1}{a_n} & -\frac{a_2}{a_n} & \cdots & -\frac{a_{n-1}}{a_n}\end{bmatrix}
\begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} +
\begin{bmatrix}0 \\ 0 \\ \vdots \\ \frac{1}{a_n}\end{bmatrix}u$$
which we then write as $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{B}u$.
### Finding the Fundamental Matrix for Time Invariant Systems
We express the system equations in state-space form with
$$ \dot{\mathbf x} = \mathbf{Ax}$$
where $\mathbf A$ is the system dynamics matrix, and want to find the *fundamental matrix* $\mathbf F$ that propagates the state $\mathbf x$ over the interval $\Delta t$ with the equation
$$\begin{aligned}
\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1})\end{aligned}$$
In other words, $\mathbf A$ is a set of continuous differential equations, and we need $\mathbf F$ to be a set of discrete linear equations that computes the change in $\mathbf A$ over a discrete time step.
It is conventional to drop the $t_k$ and $(\Delta t)$ and use the notation
$$\mathbf x_k = \mathbf {Fx}_{k-1}$$
Broadly speaking there are three common ways to find this matrix for Kalman filters. The technique most often used is the matrix exponential. Linear Time Invariant Theory, also known as LTI System Theory, is a second technique. Finally, there are numerical techniques. You may know of others, but these three are what you will most likely encounter in the Kalman filter literature and praxis.
### The Matrix Exponential
The solution to the equation $\frac{dx}{dt} = kx$ can be found by:
$$\begin{gathered}\frac{dx}{dt} = kx \\
\frac{dx}{x} = k\, dt \\
\int \frac{1}{x}\, dx = \int k\, dt \\
\log x = kt + c \\
x = e^{kt+c} \\
x = e^ce^{kt} \\
x = c_0e^{kt}\end{gathered}$$
Using similar math, the solution to the first-order equation
$$\dot{\mathbf x} = \mathbf{Ax} ,\, \, \, \mathbf x(0) = \mathbf x_0$$
where $\mathbf A$ is a constant matrix, is
$$\mathbf x = e^{\mathbf At}\mathbf x_0$$
Substituting $F = e^{\mathbf At}$, we can write
$$\mathbf x_k = \mathbf F\mathbf x_{k-1}$$
which is the form we are looking for! We have reduced the problem of finding the fundamental matrix to one of finding the value for $e^{\mathbf At}$.
$e^{\mathbf At}$ is known as the [matrix exponential](https://en.wikipedia.org/wiki/Matrix_exponential). It can be computed with this power series:
$$e^{\mathbf At} = \mathbf{I} + \mathbf{A}t + \frac{(\mathbf{A}t)^2}{2!} + \frac{(\mathbf{A}t)^3}{3!} + ... $$
That series is found by doing a Taylor series expansion of $e^{\mathbf At}$, which I will not cover here.
Let's use this to find the solution to Newton's equations. Using $v$ as an substitution for $\dot x$, and assuming constant velocity we get the linear matrix-vector form
$$\begin{bmatrix}\dot x \\ \dot v\end{bmatrix} =\begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ v\end{bmatrix}$$
This is a first order differential equation, so we can set $\mathbf{A}=\begin{bmatrix}0&1\\0&0\end{bmatrix}$ and solve the following equation. I have substituted the interval $\Delta t$ for $t$ to emphasize that the fundamental matrix is discrete:
$$\mathbf F = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A\Delta t)^3}{3!} + ... $$
If you perform the multiplication you will find that $\mathbf{A}^2=\begin{bmatrix}0&0\\0&0\end{bmatrix}$, which means that all higher powers of $\mathbf{A}$ are also $\mathbf{0}$. Thus we get an exact answer without an infinite number of terms:
$$
\begin{aligned}
\mathbf F &=\mathbf{I} + \mathbf A \Delta t + \mathbf{0} \\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
&= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
\end{aligned}$$
We plug this into $\mathbf x_k= \mathbf{Fx}_{k-1}$ to get
$$
\begin{aligned}
x_k &=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}x_{k-1}
\end{aligned}$$
You will recognize this as the matrix we derived analytically for the constant velocity Kalman filter in the **Multivariate Kalman Filter** chapter.
SciPy's linalg module includes a routine `expm()` to compute the matrix exponential. It does not use the Taylor series method, but the [Padé Approximation](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant). There are many (at least 19) methods to computed the matrix exponential, and all suffer from numerical difficulties[1]. But you should be aware of the problems, especially when $\mathbf A$ is large. If you search for "pade approximation matrix exponential" you will find many publications devoted to this problem.
In practice this may not be of concern to you as for the Kalman filter we normally just take the first two terms of the Taylor series. But don't assume my treatment of the problem is complete and run off and try to use this technique for other problem without doing a numerical analysis of the performance of this technique. Interestingly, one of the favored ways of solving $e^{\mathbf At}$ is to use a generalized ode solver. In other words, they do the opposite of what we do - turn $\mathbf A$ into a set of differential equations, and then solve that set using numerical techniques!
Here is an example of using `expm()` to solve $e^{\mathbf At}$.
```
import numpy as np
from scipy.linalg import expm
dt = 0.1
A = np.array([[0, 1],
[0, 0]])
expm(A*dt)
```
### Time Invariance
If the behavior of the system depends on time we can say that a dynamic system is described by the first-order differential equation
$$ g(t) = \dot x$$
However, if the system is *time invariant* the equation is of the form:
$$ f(x) = \dot x$$
What does *time invariant* mean? Consider a home stereo. If you input a signal $x$ into it at time $t$, it will output some signal $f(x)$. If you instead perform the input at time $t + \Delta t$ the output signal will be the same $f(x)$, shifted in time.
A counter-example is $x(t) = \sin(t)$, with the system $f(x) = t\, x(t) = t \sin(t)$. This is not time invariant; the value will be different at different times due to the multiplication by t. An aircraft is not time invariant. If you make a control input to the aircraft at a later time its behavior will be different because it will have burned fuel and thus lost weight. Lower weight results in different behavior.
We can solve these equations by integrating each side. I demonstrated integrating the time invariant system $v = \dot x$ above. However, integrating the time invariant equation $\dot x = f(x)$ is not so straightforward. Using the *separation of variables* techniques we divide by $f(x)$ and move the $dt$ term to the right so we can integrate each side:
$$\begin{gathered}
\frac{dx}{dt} = f(x) \\
\int^x_{x_0} \frac{1}{f(x)} dx = \int^t_{t_0} dt
\end{gathered}$$
If we let $F(x) = \int \frac{1}{f(x)} dx$ we get
$$F(x) - F(x_0) = t-t_0$$
We then solve for x with
$$\begin{gathered}
F(x) = t - t_0 + F(x_0) \\
x = F^{-1}[t-t_0 + F(x_0)]
\end{gathered}$$
In other words, we need to find the inverse of $F$. This is not trivial, and a significant amount of coursework in a STEM education is devoted to finding tricky, analytic solutions to this problem.
However, they are tricks, and many simple forms of $f(x)$ either have no closed form solution or pose extreme difficulties. Instead, the practicing engineer turns to state-space methods to find approximate solutions.
The advantage of the matrix exponential is that we can use it for any arbitrary set of differential equations which are *time invariant*. However, we often use this technique even when the equations are not time invariant. As an aircraft flies it burns fuel and loses weight. However, the weight loss over one second is negligible, and so the system is nearly linear over that time step. Our answers will still be reasonably accurate so long as the time step is short.
#### Example: Mass-Spring-Damper Model
Suppose we wanted to track the motion of a weight on a spring and connected to a damper, such as an automobile's suspension. The equation for the motion with $m$ being the mass, $k$ the spring constant, and $c$ the damping force, under some input $u$ is
$$m\frac{d^2x}{dt^2} + c\frac{dx}{dt} +kx = u$$
For notational convenience I will write that as
$$m\ddot x + c\dot x + kx = u$$
I can turn this into a system of first order equations by setting $x_1(t)=x(t)$, and then substituting as follows:
$$\begin{aligned}
x_1 &= x \\
x_2 &= \dot x_1 \\
\dot x_2 &= \dot x_1 = \ddot x
\end{aligned}$$
As is common I dropped the $(t)$ for notational convenience. This gives the equation
$$m\dot x_2 + c x_2 +kx_1 = u$$
Solving for $\dot x_2$ we get a first order equation:
$$\dot x_2 = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u$$
We put this into matrix form:
$$\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix} =
\begin{bmatrix}0 & 1 \\ -k/m & -c/m \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +
\begin{bmatrix} 0 \\ 1/m \end{bmatrix}u$$
Now we use the matrix exponential to find the state transition matrix:
$$\Phi(t) = e^{\mathbf At} = \mathbf{I} + \mathbf At + \frac{(\mathbf At)^2}{2!} + \frac{(\mathbf At)^3}{3!} + ... $$
The first two terms give us
$$\mathbf F = \begin{bmatrix}1 & t \\ -(k/m) t & 1-(c/m) t \end{bmatrix}$$
This may or may not give you enough precision. You can easily check this by computing $\frac{(\mathbf At)^2}{2!}$ for your constants and seeing how much this matrix contributes to the results.
### Linear Time Invariant Theory
[*Linear Time Invariant Theory*](https://en.wikipedia.org/wiki/LTI_system_theory), also known as LTI System Theory, gives us a way to find $\Phi$ using the inverse Laplace transform. You are either nodding your head now, or completely lost. I will not be using the Laplace transform in this book. LTI system theory tells us that
$$ \Phi(t) = \mathcal{L}^{-1}[(s\mathbf{I} - \mathbf{F})^{-1}]$$
I have no intention of going into this other than to say that the Laplace transform $\mathcal{L}$ converts a signal into a space $s$ that excludes time, but finding a solution to the equation above is non-trivial. If you are interested, the Wikipedia article on LTI system theory provides an introduction. I mention LTI because you will find some literature using it to design the Kalman filter matrices for difficult problems.
### Numerical Solutions
Finally, there are numerical techniques to find $\mathbf F$. As filters get larger finding analytical solutions becomes very tedious (though packages like SymPy make it easier). C. F. van Loan [2] has developed a technique that finds both $\Phi$ and $\mathbf Q$ numerically. Given the continuous model
$$ \dot x = Ax + Gw$$
where $w$ is the unity white noise, van Loan's method computes both $\mathbf F_k$ and $\mathbf Q_k$.
I have implemented van Loan's method in `FilterPy`. You may use it as follows:
```python
from filterpy.common import van_loan_discretization
A = np.array([[0., 1.], [-1., 0.]])
G = np.array([[0.], [2.]]) # white noise scaling
F, Q = van_loan_discretization(A, G, dt=0.1)
```
In the section *Numeric Integration of Differential Equations* I present alternative methods which are very commonly used in Kalman filtering.
## Design of the Process Noise Matrix
In general the design of the $\mathbf Q$ matrix is among the most difficult aspects of Kalman filter design. This is due to several factors. First, the math requires a good foundation in signal theory. Second, we are trying to model the noise in something for which we have little information. Consider trying to model the process noise for a thrown baseball. We can model it as a sphere moving through the air, but that leaves many unknown factors - the wind, ball rotation and spin decay, the coefficient of drag of a ball with stitches, the effects of wind and air density, and so on. We develop the equations for an exact mathematical solution for a given process model, but since the process model is incomplete the result for $\mathbf Q$ will also be incomplete. This has a lot of ramifications for the behavior of the Kalman filter. If $\mathbf Q$ is too small then the filter will be overconfident in its prediction model and will diverge from the actual solution. If $\mathbf Q$ is too large than the filter will be unduly influenced by the noise in the measurements and perform sub-optimally. In practice we spend a lot of time running simulations and evaluating collected data to try to select an appropriate value for $\mathbf Q$. But let's start by looking at the math.
Let's assume a kinematic system - some system that can be modeled using Newton's equations of motion. We can make a few different assumptions about this process.
We have been using a process model of
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
where $\mathbf{w}$ is the process noise. Kinematic systems are *continuous* - their inputs and outputs can vary at any arbitrary point in time. However, our Kalman filters are *discrete* (there are continuous forms for Kalman filters, but we do not cover them in this book). We sample the system at regular intervals. Therefore we must find the discrete representation for the noise term in the equation above. This depends on what assumptions we make about the behavior of the noise. We will consider two different models for the noise.
### Continuous White Noise Model
We model kinematic systems using Newton's equations. We have either used position and velocity, or position, velocity, and acceleration as the models for our systems. There is nothing stopping us from going further - we can model jerk, jounce, snap, and so on. We don't do that normally because adding terms beyond the dynamics of the real system degrades the estimate.
Let's say that we need to model the position, velocity, and acceleration. We can then assume that acceleration is constant for each discrete time step. Of course, there is process noise in the system and so the acceleration is not actually constant. The tracked object will alter the acceleration over time due to external, unmodeled forces. In this section we will assume that the acceleration changes by a continuous time zero-mean white noise $w(t)$. In other words, we are assuming that the small changes in velocity average to 0 over time (zero-mean).
Since the noise is changing continuously we will need to integrate to get the discrete noise for the discretization interval that we have chosen. We will not prove it here, but the equation for the discretization of the noise is
$$\mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t) dt$$
where $\mathbf{Q_c}$ is the continuous noise. This gives us
$$\Phi = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
for the fundamental matrix, and
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
for the continuous process noise matrix, where $\Phi_s$ is the spectral density of the white noise.
We could carry out these computations ourselves, but I prefer using SymPy to solve the equation.
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
```
import sympy
from sympy import (init_printing, Matrix,MatMul,
integrate, symbols)
init_printing(use_latex='mathjax')
dt, phi = symbols('\Delta{t} \Phi_s')
F_k = Matrix([[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]])
Q_c = Matrix([[0, 0, 0],
[0, 0, 0],
[0, 0, 1]])*phi
Q=sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
For completeness, let us compute the equations for the 0th order and 1st order equations.
```
F_k = sympy.Matrix([[1]])
Q_c = sympy.Matrix([[phi]])
print('0th order discrete process noise')
sympy.integrate(F_k*Q_c*F_k.T,(dt, 0, dt))
F_k = sympy.Matrix([[1, dt],
[0, 1]])
Q_c = sympy.Matrix([[0, 0],
[0, 1]])*phi
Q = sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
print('1st order discrete process noise')
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
### Piecewise White Noise Model
Another model for the noise assumes that the that highest order term (say, acceleration) is constant for the duration of each time period, but differs for each time period, and each of these is uncorrelated between time periods. In other words there is a discontinuous jump in acceleration at each time step. This is subtly different than the model above, where we assumed that the last term had a continuously varying noisy signal applied to it.
We will model this as
$$f(x)=Fx+\Gamma w$$
where $\Gamma$ is the *noise gain* of the system, and $w$ is the constant piecewise acceleration (or velocity, or jerk, etc).
Let's start by looking at a first order system. In this case we have the state transition function
$$\mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0& 1\end{bmatrix}$$
In one time period, the change in velocity will be $w(t)\Delta t$, and the change in position will be $w(t)\Delta t^2/2$, giving us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\end{bmatrix}$$
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
The second order system proceeds with the same math.
$$\mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
Here we will assume that the white noise is a discrete time Wiener process. This gives us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\\ 1\end{bmatrix}$$
There is no 'truth' to this model, it is just convenient and provides good results. For example, we could assume that the noise is applied to the jerk at the cost of a more complicated equation.
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt], [1]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
We cannot say that this model is more or less correct than the continuous model - both are approximations to what is happening to the actual object. Only experience and experiments can guide you to the appropriate model. In practice you will usually find that either model provides reasonable results, but typically one will perform better than the other.
The advantage of the second model is that we can model the noise in terms of $\sigma^2$ which we can describe in terms of the motion and the amount of error we expect. The first model requires us to specify the spectral density, which is not very intuitive, but it handles varying time samples much more easily since the noise is integrated across the time period. However, these are not fixed rules - use whichever model (or a model of your own devising) based on testing how the filter performs and/or your knowledge of the behavior of the physical model.
A good rule of thumb is to set $\sigma$ somewhere from $\frac{1}{2}\Delta a$ to $\Delta a$, where $\Delta a$ is the maximum amount that the acceleration will change between sample periods. In practice we pick a number, run simulations on data, and choose a value that works well.
### Using FilterPy to Compute Q
FilterPy offers several routines to compute the $\mathbf Q$ matrix. The function `Q_continuous_white_noise()` computes $\mathbf Q$ for a given value for $\Delta t$ and the spectral density.
```
from filterpy.common import Q_continuous_white_noise
from filterpy.common import Q_discrete_white_noise
Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
print(Q)
Q = Q_continuous_white_noise(dim=3, dt=1, spectral_density=1)
print(Q)
```
The function `Q_discrete_white_noise()` computes $\mathbf Q$ assuming a piecewise model for the noise.
```
Q = Q_discrete_white_noise(2, var=1.)
print(Q)
Q = Q_discrete_white_noise(3, var=1.)
print(Q)
```
### Simplification of Q
Many treatments use a much simpler form for $\mathbf Q$, setting it to zero except for a noise term in the lower rightmost element. Is this justified? Well, consider the value of $\mathbf Q$ for a small $\Delta t$
```
import numpy as np
np.set_printoptions(precision=8)
Q = Q_continuous_white_noise(
dim=3, dt=0.05, spectral_density=1)
print(Q)
np.set_printoptions(precision=3)
```
We can see that most of the terms are very small. Recall that the only equation using this matrix is
$$ \mathbf P=\mathbf{FPF}^\mathsf{T} + \mathbf Q$$
If the values for $\mathbf Q$ are small relative to $\mathbf P$
than it will be contributing almost nothing to the computation of $\mathbf P$. Setting $\mathbf Q$ to the zero matrix except for the lower right term
$$\mathbf Q=\begin{bmatrix}0&0&0\\0&0&0\\0&0&\sigma^2\end{bmatrix}$$
while not correct, is often a useful approximation. If you do this you will have to perform quite a few studies to guarantee that your filter works in a variety of situations.
If you do this, 'lower right term' means the most rapidly changing term for each variable. If the state is $x=\begin{bmatrix}x & \dot x & \ddot{x} & y & \dot{y} & \ddot{y}\end{bmatrix}^\mathsf{T}$ Then Q will be 6x6; the elements for both $\ddot{x}$ and $\ddot{y}$ will have to be set to non-zero in $\mathbf Q$.
## Numeric Integration of Differential Equations
We've been exposed to several numerical techniques to solve linear differential equations. These include state-space methods, the Laplace transform, and van Loan's method.
These work well for linear ordinary differential equations (ODEs), but do not work well for nonlinear equations. For example, consider trying to predict the position of a rapidly turning car. Cars maneuver by turning the front wheels. This makes them pivot around their rear axle as it moves forward. Therefore the path will be continuously varying and a linear prediction will necessarily produce an incorrect value. If the change in the system is small enough relative to $\Delta t$ this can often produce adequate results, but that will rarely be the case with the nonlinear Kalman filters we will be studying in subsequent chapters.
For these reasons we need to know how to numerically integrate ODEs. This can be a vast topic that requires several books. If you need to explore this topic in depth *Computational Physics in Python* by Dr. Eric Ayars is excellent, and available for free here:
http://phys.csuchico.edu/ayars/312/Handouts/comp-phys-python.pdf
However, I will cover a few simple techniques which will work for a majority of the problems you encounter.
### Euler's Method
Let's say we have the initial condition problem of
$$\begin{gathered}
y' = y, \\ y(0) = 1
\end{gathered}$$
We happen to know the exact answer is $y=e^t$ because we solved it earlier, but for an arbitrary ODE we will not know the exact solution. In general all we know is the derivative of the equation, which is equal to the slope. We also know the initial value: at $t=0$, $y=1$. If we know these two pieces of information we can predict the value at $y(t=1)$ using the slope at $t=0$ and the value of $y(0)$. I've plotted this below.
```
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 10)
plt.plot(t, np.exp(t))
t = np.linspace(-1, 1, 2)
plt.plot(t,t+1, ls='--', c='k');
```
You can see that the slope is very close to the curve at $t=0.1$, but far from it
at $t=1$. But let's continue with a step size of 1 for a moment. We can see that at $t=1$ the estimated value of $y$ is 2. Now we can compute the value at $t=2$ by taking the slope of the curve at $t=1$ and adding it to our initial estimate. The slope is computed with $y'=y$, so the slope is 2.
```
import code.book_plots as book_plots
t = np.linspace(-1, 2, 20)
plt.plot(t, np.exp(t))
t = np.linspace(0, 1, 2)
plt.plot([1, 2, 4], ls='--', c='k')
book_plots.set_labels(x='x', y='y');
```
Here we see the next estimate for y is 4. The errors are getting large quickly, and you might be unimpressed. But 1 is a very large step size. Let's put this algorithm in code, and verify that it works by using a small step size.
```
def euler(t, tmax, y, dx, step=1.):
ys = []
while t < tmax:
y = y + step*dx(t, y)
ys.append(y)
t +=step
return ys
def dx(t, y): return y
print(euler(0, 1, 1, dx, step=1.)[-1])
print(euler(0, 2, 1, dx, step=1.)[-1])
```
This looks correct. So now let's plot the result of a much smaller step size.
```
ys = euler(0, 4, 1, dx, step=0.00001)
plt.subplot(1,2,1)
plt.title('Computed')
plt.plot(np.linspace(0, 4, len(ys)),ys)
plt.subplot(1,2,2)
t = np.linspace(0, 4, 20)
plt.title('Exact')
plt.plot(t, np.exp(t));
print('exact answer=', np.exp(4))
print('euler answer=', ys[-1])
print('difference =', np.exp(4) - ys[-1])
print('iterations =', len(ys))
```
Here we see that the error is reasonably small, but it took a very large number of iterations to get three digits of precision. In practice Euler's method is too slow for most problems, and we use more sophisticated methods.
Before we go on, let's formally derive Euler's method, as it is the basis for the more advanced Runge Kutta methods used in the next section. In fact, Euler's method is the simplest form of Runge Kutta.
Here are the first 3 terms of the Euler expansion of $y$. An infinite expansion would give an exact answer, so $O(h^4)$ denotes the error due to the finite expansion.
$$y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2!}h^2 y''(t_0) + \frac{1}{3!}h^3 y'''(t_0) + O(h^4)$$
Here we can see that Euler's method is using the first two terms of the Taylor expansion. Each subsequent term is smaller than the previous terms, so we are assured that the estimate will not be too far off from the correct value.
### Runge Kutta Methods
Runge Kutta is the workhorse of numerical integration. There are a vast number of methods in the literature. In practice, using the Runge Kutta algorithm that I present here will solve most any problem you will face. It offers a very good balance of speed, precision, and stability, and it is the 'go to' numerical integration method unless you have a very good reason to choose something different.
Let's dive in. We start with some differential equation
$$\ddot{y} = \frac{d}{dt}\dot{y}$$.
We can substitute the derivative of y with a function f, like so
$$\ddot{y} = \frac{d}{dt}f(y,t)$$.
Deriving these equations is outside the scope of this book, but the Runge Kutta RK4 method is defined with these equations.
$$y(t+\Delta t) = y(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) + O(\Delta t^4)$$
$$\begin{aligned}
k_1 &= f(y,t)\Delta t \\
k_2 &= f(y+\frac{1}{2}k_1, t+\frac{1}{2}\Delta t)\Delta t \\
k_3 &= f(y+\frac{1}{2}k_2, t+\frac{1}{2}\Delta t)\Delta t \\
k_4 &= f(y+k_3, t+\Delta t)\Delta t
\end{aligned}
$$
Here is the corresponding code:
```
def runge_kutta4(y, x, dx, f):
"""computes 4th order Runge-Kutta for dy/dx.
y is the initial value for y
x is the initial value for x
dx is the difference in x (e.g. the time step)
f is a callable function (y, x) that you supply
to compute dy/dx for the specified values.
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2*k2 + 2*k3 + k4) / 6.
```
Let's use this for a simple example. Let
$$\dot{y} = t\sqrt{y(t)}$$
with the initial values
$$\begin{aligned}t_0 &= 0\\y_0 &= y(t_0) = 1\end{aligned}$$
```
import math
import numpy as np
t = 0.
y = 1.
dt = .1
ys, ts = [], []
def func(y,t):
return t*math.sqrt(y)
while t <= 10:
y = runge_kutta4(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
exact = [(t**2 + 4)**2 / 16. for t in ts]
plt.plot(ts, ys)
plt.plot(ts, exact)
error = np.array(exact) - np.array(ys)
print("max error {}".format(max(error)))
```
## Bayesian Filtering
Starting in the Discrete Bayes chapter I used a Bayesian formulation for filtering. Suppose we are tracking an object. We define its *state* at a specific time as its position, velocity, and so on. For example, we might write the state at time $t$ as $\mathbf x_t = \begin{bmatrix}x_t &\dot x_t \end{bmatrix}^\mathsf T$.
When we take a measurement of the object we are measuring the state or part of it. Sensors are noisy, so the measurement is corrupted with noise. Clearly though, the measurement is determined by the state. That is, a change in state may change the measurement, but a change in measurement will not change the state.
In filtering our goal is to compute an optimal estimate for a set of states $\mathbf x_{0:t}$ from time 0 to time $t$. If we knew $\mathbf x_{0:t}$ then it would be trivial to compute a set of measurements $\mathbf z_{0:t}$ corresponding to those states. However, we receive a set of measurements $\mathbf z_{0:t}$, and want to compute the corresponding states $\mathbf x_{0:t}$. This is called *statistical inversion* because we are trying to compute the input from the output.
Inversion is a difficult problem because there is typically no unique solution. For a given set of states $\mathbf x_{0:t}$ there is only one possible set of measurements (plus noise), but for a given set of measurements there are many different sets of states that could have led to those measurements.
Recall Bayes Theorem:
$$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
where $P(z \mid x)$ is the *likelihood* of the measurement $z$, $P(x)$ is the *prior* based on our process model, and $P(z)$ is a normalization constant. $P(x \mid z)$ is the *posterior*, or the distribution after incorporating the measurement $z$, also called the *evidence*.
This is a *statistical inversion* as it goes from $P(z \mid x)$ to $P(x \mid z)$. The solution to our filtering problem can be expressed as:
$$P(\mathbf x_{0:t} \mid \mathbf z_{0:t}) = \frac{P(\mathbf z_{0:t} \mid \mathbf x_{0:t})P(\mathbf x_{0:t})}{P(\mathbf z_{0:t})}$$
That is all well and good until the next measurement $\mathbf z_{t+1}$ comes in, at which point we need to recompute the entire expression for the range $0:t+1$.
In practice this is intractable because we are trying to compute the posterior distribution $P(\mathbf x_{0:t} \mid \mathbf z_{0:t})$ for the state over the full range of time steps. But do we really care about the probability distribution at the third step (say) when we just received the tenth measurement? Not usually. So we relax our requirements and only compute the distributions for the current time step.
The first simplification is we describe our process (e.g., the motion model for a moving object) as a *Markov chain*. That is, we say that the current state is solely dependent on the previous state and a transition probability $P(\mathbf x_k \mid \mathbf x_{k-1})$, which is just the probability of going from the last state to the current one. We write:
$$\mathbf x_k \sim P(\mathbf x_k \mid \mathbf x_{k-1})$$
The next simplification we make is do define the *measurement model* as depending on the current state $\mathbf x_k$ with the conditional probability of the measurement given the current state: $P(\mathbf z_t \mid \mathbf x_x)$. We write:
$$\mathbf z_k \sim P(\mathbf z_t \mid \mathbf x_x)$$
We have a recurrance now, so we need an initial condition to terminate it. Therefore we say that the initial distribution is the probablity of the state $\mathbf x_0$:
$$\mathbf x_0 \sim P(\mathbf x_0)$$
These terms are plugged into Bayes equation. If we have the state $\mathbf x_0$ and the first measurement we can estimate $P(\mathbf x_1 | \mathbf z_1)$. The motion model creates the prior $P(\mathbf x_2 \mid \mathbf x_1)$. We feed this back into Bayes theorem to compute $P(\mathbf x_2 | \mathbf z_2)$. We continue this predictor-corrector algorithm, recursively computing the state and distribution at time $t$ based solely on the state and distribution at time $t-1$ and the measurement at time $t$.
The details of the mathematics for this computation varies based on the problem. The **Discrete Bayes** and **Univariate Kalman Filter** chapters gave two different formulations which you should have been able to reason through. The univariate Kalman filter assumes that for a scalar state both the noise and process are linear model are affected by zero-mean, uncorrelated Gaussian noise.
The Multivariate Kalman filter make the same assumption but for states and measurements that are vectors, not scalars. Dr. Kalman was able to prove that if these assumptions hold true then the Kalman filter is *optimal* in a least squares sense. Colloquially this means there is no way to derive more information from the noise. In the remainder of the book I will present filters that relax the constraints on linearity and Gaussian noise.
Before I go on, a few more words about statistical inversion. As Calvetti and Somersalo write in *Introduction to Bayesian Scientific Computing*, "we adopt the Bayesian point of view: *randomness simply means lack of information*."[3] Our state parametize physical phenomena that we could in principle measure or compute: velocity, air drag, and so on. We lack enough information to compute or measure their value, so we opt to consider them as random variables. Strictly speaking they are not random, thus this is a subjective position.
They devote a full chapter to this topic. I can spare a paragraph. Bayesian filters are possible because we ascribe statistical properties to unknown parameters. In the case of the Kalman filter we have closed-form solutions to find an optimal estimate. Other filters, such as the discrete Bayes filter or the particle filter which we cover in a later chapter, model the probability in a more ad-hoc, non-optimal manner. The power of our technique comes from treating lack of information as a random variable, describing that random variable as a probability distribution, and then using Bayes Theorem to solve the statistical inference problem.
## Converting Kalman Filter to a g-h Filter
I've stated that the Kalman filter is a form of the g-h filter. It just takes some algebra to prove it. It's more straightforward to do with the one dimensional case, so I will do that. Recall
$$
\mu_{x}=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2}
$$
which I will make more friendly for our eyes as:
$$
\mu_{x}=\frac{ya + xb} {a+b}
$$
We can easily put this into the g-h form with the following algebra
$$
\begin{aligned}
\mu_{x}&=(x-x) + \frac{ya + xb} {a+b} \\
\mu_{x}&=x-\frac{a+b}{a+b}x + \frac{ya + xb} {a+b} \\
\mu_{x}&=x +\frac{-x(a+b) + xb+ya}{a+b} \\
\mu_{x}&=x+ \frac{-xa+ya}{a+b} \\
\mu_{x}&=x+ \frac{a}{a+b}(y-x)\\
\end{aligned}
$$
We are almost done, but recall that the variance of estimate is given by
$$\begin{aligned}
\sigma_{x}^2 &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \\
&= \frac{1}{\frac{1}{a} + \frac{1}{b}}
\end{aligned}$$
We can incorporate that term into our equation above by observing that
$$
\begin{aligned}
\frac{a}{a+b} &= \frac{a/a}{(a+b)/a} = \frac{1}{(a+b)/a} \\
&= \frac{1}{1 + \frac{b}{a}} = \frac{1}{\frac{b}{b} + \frac{b}{a}} \\
&= \frac{1}{b}\frac{1}{\frac{1}{b} + \frac{1}{a}} \\
&= \frac{\sigma^2_{x'}}{b}
\end{aligned}
$$
We can tie all of this together with
$$
\begin{aligned}
\mu_{x}&=x+ \frac{a}{a+b}(y-x) \\
&= x + \frac{\sigma^2_{x'}}{b}(y-x) \\
&= x + g_n(y-x)
\end{aligned}
$$
where
$$g_n = \frac{\sigma^2_{x}}{\sigma^2_{y}}$$
The end result is multiplying the residual of the two measurements by a constant and adding to our previous value, which is the $g$ equation for the g-h filter. $g$ is the variance of the new estimate divided by the variance of the measurement. Of course in this case $g$ is not a constant as it varies with each time step as the variance changes. We can also derive the formula for $h$ in the same way. It is not a particularly illuminating derivation and I will skip it. The end result is
$$h_n = \frac{COV (x,\dot x)}{\sigma^2_{y}}$$
The takeaway point is that $g$ and $h$ are specified fully by the variance and covariances of the measurement and predictions at time $n$. In other words, we are picking a point between the measurement and prediction by a scale factor determined by the quality of each of those two inputs.
## References
* [1] C.B. Molwer and C.F. Van Loan "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later,", *SIAM Review 45, 3-49*. 2003.
* [2] C.F. van Loan, "Computing Integrals Involving the Matrix Exponential," IEEE *Transactions Automatic Control*, June 1978.
* [3] Calvetti, D and Somersalo E, "Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing,", *Springer*, 2007.
| true |
code
| 0.608507 | null | null | null | null |
|
# Estimation on real data using MSM
```
from consav import runtools
runtools.write_numba_config(disable=0,threads=4)
%matplotlib inline
%load_ext autoreload
%autoreload 2
# Local modules
from Model import RetirementClass
import figs
import SimulatedMinimumDistance as SMD
# Global modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
### Data
```
data = pd.read_excel('SASdata/moments.xlsx')
mom_data = data['mom'].to_numpy()
se = data['se'].to_numpy()
obs = data['obs'].to_numpy()
se = se/np.sqrt(obs)
se[se>0] = 1/se[se>0]
factor = np.ones(len(se))
factor[-15:] = 4
W = np.eye(len(se))*se*factor
cov = pd.read_excel('SASdata/Cov.xlsx')
Omega = cov*obs
Nobs = np.median(obs)
```
### Set up estimation
```
single_kwargs = {'simN': int(1e5), 'simT': 68-53+1}
Couple = RetirementClass(couple=True, single_kwargs=single_kwargs,
simN=int(1e5), simT=68-53+1)
Couple.solve()
Couple.simulate()
def mom_fun(Couple):
return SMD.MomFun(Couple)
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
```
### Estimate
```
theta0 = SMD.start(9,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8), (0,2)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
smd.MultiStart(theta0,W)
theta = smd.est
```
### Save parameters
```
est_par.append('phi_0_female')
thetaN = list(theta)
thetaN.append(Couple.par.phi_0_male)
SMD.save_est(est_par,thetaN,name='baseline2')
```
### Standard errors
```
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta = list(SMD.load_est('baseline2').values())
theta = theta[:5]
smd.obj_fun(theta,W)
np.round(theta,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = lower quartile
np.round(smd.std,3)
# Nobs = lower quartile
np.round(smd.std,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = median
np.round(smd.std,3)
```
### Model fit
```
smd.obj_fun(theta,W)
jmom = pd.read_excel('SASdata/joint_moments_ad.xlsx')
for i in range(-2,3):
data = jmom[jmom.Age_diff==i]['ssh'].to_numpy()
plt.bar(np.arange(-7,8), data, label='Data')
plt.plot(np.arange(-7,8),SMD.joint_moments_ad(Couple,i),'k--', label='Predicted')
#plt.ylim(0,0.4)
plt.legend()
plt.show()
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCouple2.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint2')
theta[4] = 1
smd.obj_fun(theta,W)
dist1 = smd.mom_sim[44:]
theta[4] = 2
smd.obj_fun(theta,W)
dist2 = smd.mom_sim[44:]
theta[4] = 3
smd.obj_fun(theta,W)
dist3 = smd.mom_sim[44:]
dist_data = mom_data[44:]
figs.model_fit_joint_many(dist_data,dist1,dist2,dist3).savefig('figs/ModelFit/JointMany2')
```
### Sensitivity
```
est_par_tex = [r'$\alpha^m$', r'$\alpha^f$', r'$\sigma$', r'$\lambda$', r'$\phi$']
fixed_par = ['R', 'rho', 'beta', 'gamma', 'v',
'priv_pension_male', 'priv_pension_female', 'g_adjust', 'pi_adjust_m', 'pi_adjust_f']
fixed_par_tex = [r'$R$', r'$\rho$', r'$\beta$', r'$\gamma$', r'$v$',
r'$PPW^m$', r'$PPW^f$', r'$g$', r'$\pi^m$', r'$\pi^f$']
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref2.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali2.png')
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali.png')
```
### Recalibrate model (phi=0)
```
Couple.par.phi_0_male = 0
Couple.par.phi_0_female = 0
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8)])
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi0')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi0.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi0')
```
### Recalibrate model (phi high)
```
Couple.par.phi_0_male = 1.187
Couple.par.phi_0_female = 1.671
Couple.par.pareto_w = 0.8
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0.2,0.6), (0.2,0.6), (0.4,0.8)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi_high')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi_high.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi_high')
```
| true |
code
| 0.489076 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/clemencia/ML4PPGF_UERJ/blob/master/Exemplos_DR/Exercicios_DimensionalReduction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Mais Exercícios de Redução de Dimensionalidade
Baseado no livro "Python Data Science Handbook" de Jake VanderPlas
https://jakevdp.github.io/PythonDataScienceHandbook/
Usando os dados de rostos do scikit-learn, utilizar as tecnicas de aprendizado de variedade para comparação.
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=30)
faces.data.shape
```
A base de dados tem 2300 imagens de rostos com 2914 pixels cada (47x62)
Vamos visualizar as primeiras 32 dessas imagens
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
for i, axi in enumerate(ax.flat):
axi.imshow(faces.images[i], cmap='gray')
```
Podemos ver se com redução de dimensionalidade é possível entender algumas das caraterísticas das imagens.
```
from sklearn.decomposition import PCA
model0 = PCA(n_components=0.95)
X_pca=model0.fit_transform(faces.data)
plt.plot(np.cumsum(model0.explained_variance_ratio_))
plt.xlabel('n components')
plt.ylabel('cumulative variance')
plt.grid(True)
print("Numero de componentes para 95% de variância preservada:",model0.n_components_)
```
Quer dizer que para ter 95% de variância preservada na dimensionalidade reduzida precisamos mais de 170 dimensões.
As novas "coordenadas" podem ser vistas em quadros de 9x19 pixels
```
def plot_faces(instances, **options):
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
sizex = 9
sizey = 19
images = [instance.reshape(sizex,sizey) for instance in instances]
for i,axi in enumerate(ax.flat):
axi.imshow(images[i], cmap = "gray", **options)
axi.axis("off")
```
Vamos visualizar a compressão dessas imagens
```
plot_faces(X_pca,aspect="auto")
```
A opção ```svd_solver=randomized``` faz o PCA achar as $d$ componentes principais mais rápido quando $d \ll n$, mas o $d$ é fixo. Tem alguma vantagem usar para compressão das imagens de rosto? Teste!
## Aplicar Isomap para vizualizar em 2D
```
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
X_iso = iso.fit_transform(faces.data)
X_iso.shape
from matplotlib import offsetbox
def plot_projection(data,proj,images=None,ax=None,thumb_frac=0.5,cmap="gray"):
ax = ax or plt.gca()
ax.plot(proj[:, 0], proj[:, 1], '.k')
if images is not None:
min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
shown_images = np.array([2 * proj.max(0)])
for i in range(data.shape[0]):
dist = np.sum((proj[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist_2:
# don't show points that are too close
continue
shown_images = np.vstack([shown_images, proj[i]])
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(images[i], cmap=cmap),
proj[i])
ax.add_artist(imagebox)
def plot_components(data, model, images=None, ax=None,
thumb_frac=0.05,cmap="gray"):
proj = model.fit_transform(data)
plot_projection(data,proj,images,ax,thumb_frac,cmap)
fig, ax = plt.subplots(figsize=(10, 10))
plot_projection(faces.data,X_iso,images=faces.images[:, ::2, ::2],thumb_frac=0.07)
ax.axis("off")
```
As imagens mais a direita são mais escuras que as da direita (seja iluminação ou cor da pele), as imagens mais embaixo estão orientadas com o rosto à esquerda e as de cima com o rosto à direita.
## Exercícios:
1. Aplicar LLE à base de dados dos rostos e visualizar em mapa 2D, em particular a versão "modificada" ([link](https://scikit-learn.org/stable/modules/manifold.html#modified-locally-linear-embedding))
2. Aplicar t-SNE à base de dados dos rostos e visualizar em mapa 2D
3. Escolher mais uma implementação de aprendizado de variedade do Scikit-Learn ([link](https://scikit-learn.org/stable/modules/manifold.html)) e aplicar ao mesmo conjunto. (*Hessian, LTSA, Spectral*)
Qual funciona melhor? Adicione contador de tempo para comparar a duração de cada ajuste.
## Kernel PCA e sequências
Vamos ver novamente o exemplo do rocambole
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Como foi no caso do SVM, pode se aplicar uma transformação de *kernel*, para ter um novo espaço de *features* onde pode ser aplicado o PCA. Embaixo o exemplo de PCA com kernel linear (equiv. a aplicar o PCA), RBF (*radial basis function*) e *sigmoide* (i.e. logístico).
```
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)
plt.figure(figsize=(11, 4))
for subplot, pca, title in ((131, lin_pca, "Linear kernel"), (132, rbf_pca, "RBF kernel, $\gamma=0.04$"), (133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.grid(True)
```
## Selecionar um Kernel e Otimizar Hiperparâmetros
Como estos são algoritmos não supervisionados, no existe uma forma "obvia" de determinar a sua performance.
Porém a redução de dimensionalidade muitas vezes é um passo preparatório para uma outra tarefa de aprendizado supervisionado. Nesse caso é possível usar o ```GridSearchCV``` para avaliar a melhor performance no passo seguinte, com um ```Pipeline```. A classificação será em base ao valor do ```t``` com limite arbitrário de 6.9.
```
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
y = t>6.9
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="liblinear"))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)
```
### Exercício :
Varie o valor do corte em ```t``` e veja tem faz alguma diferência para o kernel e hiperparámetros ideais.
### Inverter a transformação e erro de Reconstrução
Outra opção seria escolher o kernel e hiperparâmetros que tem o menor erro de reconstrução.
O seguinte código, com opção ```fit_inverse_transform=True```, vai fazer junto com o kPCA um modelo de regressão com as instancias projetadas (```X_reduced```) de treino e as originais (```X```) de target. O resultado do ```inverse_transform``` será uma tentativa de reconstrução no espaço original .
```
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=13./300.,
fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
X_preimage.shape
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_preimage[:, 0], X_preimage[:, 1], X_preimage[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Então é possível computar o "erro" entre o dataset reconstruido e o original (MSE).
```
from sklearn.metrics import mean_squared_error as mse
print(mse(X,X_preimage))
```
## Exercício :
Usar *grid search* com validação no valor do MSE para achar o kernel e hiperparámetros que minimizam este erro, para o exemplo do rocambole.
| true |
code
| 0.712876 | null | null | null | null |
|
# Working with Pytrees
[](https://colab.research.google.com/github/google/jax/blob/main/docs/jax-101/05.1-pytrees.ipynb)
*Author: Vladimir Mikulik*
Often, we want to operate on objects that look like dicts of arrays, or lists of lists of dicts, or other nested structures. In JAX, we refer to these as *pytrees*, but you can sometimes see them called *nests*, or just *trees*.
JAX has built-in support for such objects, both in its library functions as well as through the use of functions from [`jax.tree_utils`](https://jax.readthedocs.io/en/latest/jax.tree_util.html) (with the most common ones also available as `jax.tree_*`). This section will explain how to use them, give some useful snippets and point out common gotchas.
## What is a pytree?
As defined in the [JAX pytree docs](https://jax.readthedocs.io/en/latest/pytrees.html):
> a pytree is a container of leaf elements and/or more pytrees. Containers include lists, tuples, and dicts. A leaf element is anything that’s not a pytree, e.g. an array. In other words, a pytree is just a possibly-nested standard or user-registered Python container. If nested, note that the container types do not need to match. A single “leaf”, i.e. a non-container object, is also considered a pytree.
Some example pytrees:
```
import jax
import jax.numpy as jnp
example_trees = [
[1, 'a', object()],
(1, (2, 3), ()),
[1, {'k1': 2, 'k2': (3, 4)}, 5],
{'a': 2, 'b': (2, 3)},
jnp.array([1, 2, 3]),
]
# Let's see how many leaves they have:
for pytree in example_trees:
leaves = jax.tree_leaves(pytree)
print(f"{repr(pytree):<45} has {len(leaves)} leaves: {leaves}")
```
We've also introduced our first `jax.tree_*` function, which allowed us to extract the flattened leaves from the trees.
## Why pytrees?
In machine learning, some places where you commonly find pytrees are:
* Model parameters
* Dataset entries
* RL agent observations
They also often arise naturally when working in bulk with datasets (e.g., lists of lists of dicts).
## Common pytree functions
The most commonly used pytree functions are `jax.tree_map` and `jax.tree_multimap`. They work analogously to Python's native `map`, but on entire pytrees.
For functions with one argument, use `jax.tree_map`:
```
list_of_lists = [
[1, 2, 3],
[1, 2],
[1, 2, 3, 4]
]
jax.tree_map(lambda x: x*2, list_of_lists)
```
To use functions with more than one argument, use `jax.tree_multimap`:
```
another_list_of_lists = list_of_lists
jax.tree_multimap(lambda x, y: x+y, list_of_lists, another_list_of_lists)
```
For `tree_multimap`, the structure of the inputs must exactly match. That is, lists must have the same number of elements, dicts must have the same keys, etc.
## Example: ML model parameters
A simple example of training an MLP displays some ways in which pytree operations come in useful:
```
import numpy as np
def init_mlp_params(layer_widths):
params = []
for n_in, n_out in zip(layer_widths[:-1], layer_widths[1:]):
params.append(
dict(weights=np.random.normal(size=(n_in, n_out)) * np.sqrt(2/n_in),
biases=np.ones(shape=(n_out,))
)
)
return params
params = init_mlp_params([1, 128, 128, 1])
```
We can use `jax.tree_map` to check that the shapes of our parameters are what we expect:
```
jax.tree_map(lambda x: x.shape, params)
```
Now, let's train our MLP:
```
def forward(params, x):
*hidden, last = params
for layer in hidden:
x = jax.nn.relu(x @ layer['weights'] + layer['biases'])
return x @ last['weights'] + last['biases']
def loss_fn(params, x, y):
return jnp.mean((forward(params, x) - y) ** 2)
LEARNING_RATE = 0.0001
@jax.jit
def update(params, x, y):
grads = jax.grad(loss_fn)(params, x, y)
# Note that `grads` is a pytree with the same structure as `params`.
# `jax.grad` is one of the many JAX functions that has
# built-in support for pytrees.
# This is handy, because we can apply the SGD update using tree utils:
return jax.tree_multimap(
lambda p, g: p - LEARNING_RATE * g, params, grads
)
import matplotlib.pyplot as plt
xs = np.random.normal(size=(128, 1))
ys = xs ** 2
for _ in range(1000):
params = update(params, xs, ys)
plt.scatter(xs, ys)
plt.scatter(xs, forward(params, xs), label='Model prediction')
plt.legend();
```
## Custom pytree nodes
So far, we've only been considering pytrees of lists, tuples, and dicts; everything else is considered a leaf. Therefore, if you define my own container class, it will be considered a leaf, even if it has trees inside it:
```
class MyContainer:
"""A named container."""
def __init__(self, name: str, a: int, b: int, c: int):
self.name = name
self.a = a
self.b = b
self.c = c
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Accordingly, if we try to use a tree map expecting our leaves to be the elements inside the container, we will get an error:
```
jax.tree_map(lambda x: x + 1, [
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
To solve this, we need to register our container with JAX by telling it how to flatten and unflatten it:
```
from typing import Tuple, Iterable
def flatten_MyContainer(container) -> Tuple[Iterable[int], str]:
"""Returns an iterable over container contents, and aux data."""
flat_contents = [container.a, container.b, container.c]
# we don't want the name to appear as a child, so it is auxiliary data.
# auxiliary data is usually a description of the structure of a node,
# e.g., the keys of a dict -- anything that isn't a node's children.
aux_data = container.name
return flat_contents, aux_data
def unflatten_MyContainer(
aux_data: str, flat_contents: Iterable[int]) -> MyContainer:
"""Converts aux data and the flat contents into a MyContainer."""
return MyContainer(aux_data, *flat_contents)
jax.tree_util.register_pytree_node(
MyContainer, flatten_MyContainer, unflatten_MyContainer)
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Modern Python comes equipped with helpful tools to make defining containers easier. Some of these will work with JAX out-of-the-box, but others require more care. For instance:
```
from typing import NamedTuple, Any
class MyOtherContainer(NamedTuple):
name: str
a: Any
b: Any
c: Any
# Since `tuple` is already registered with JAX, and NamedTuple is a subclass,
# this will work out-of-the-box:
jax.tree_leaves([
MyOtherContainer('Alice', 1, 2, 3),
MyOtherContainer('Bob', 4, 5, 6)
])
```
Notice that the `name` field now appears as a leaf, as all tuple elements are children. That's the price we pay for not having to register the class the hard way.
## Common pytree gotchas and patterns
### Gotchas
#### Mistaking nodes for leaves
A common problem to look out for is accidentally introducing tree nodes instead of leaves:
```
a_tree = [jnp.zeros((2, 3)), jnp.zeros((3, 4))]
# Try to make another tree with ones instead of zeros
shapes = jax.tree_map(lambda x: x.shape, a_tree)
jax.tree_map(jnp.ones, shapes)
```
What happened is that the `shape` of an array is a tuple, which is a pytree node, with its elements as leaves. Thus, in the map, instead of calling `jnp.ones` on e.g. `(2, 3)`, it's called on `2` and `3`.
The solution will depend on the specifics, but there are two broadly applicable options:
* rewrite the code to avoid the intermediate `tree_map`.
* convert the tuple into an `np.array` or `jnp.array`, which makes the entire
sequence a leaf.
#### Handling of None
`jax.tree_utils` treats `None` as a node without children, not as a leaf:
```
jax.tree_leaves([None, None, None])
```
### Patterns
#### Transposing trees
If you would like to transpose a pytree, i.e. turn a list of trees into a tree of lists, you can do so using `jax.tree_multimap`:
```
def tree_transpose(list_of_trees):
"""Convert a list of trees of identical structure into a single tree of lists."""
return jax.tree_multimap(lambda *xs: list(xs), *list_of_trees)
# Convert a dataset from row-major to column-major:
episode_steps = [dict(t=1, obs=3), dict(t=2, obs=4)]
tree_transpose(episode_steps)
```
For more complicated transposes, JAX provides `jax.tree_transpose`, which is more verbose, but allows you specify the structure of the inner and outer Pytree for more flexibility:
```
jax.tree_transpose(
outer_treedef = jax.tree_structure([0 for e in episode_steps]),
inner_treedef = jax.tree_structure(episode_steps[0]),
pytree_to_transpose = episode_steps
)
```
## More Information
For more information on pytrees in JAX and the operations that are available, see the [Pytrees](https://jax.readthedocs.io/en/latest/pytrees.html) section in the JAX documentation.
| true |
code
| 0.714205 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ai-fast-track/timeseries/blob/master/nbs/index.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# `timeseries` package for fastai v2
> **`timeseries`** is a Timeseries Classification and Regression package for fastai v2.
> It mimics the fastai v2 vision module (fastai2.vision).
> This notebook is a tutorial that shows, and trains an end-to-end a timeseries dataset.
> The dataset example is the NATOPS dataset (see description here beow).
> First, 4 different methods of creation on how to create timeseries dataloaders are presented.
> Then, we train a model based on [Inception Time] (https://arxiv.org/pdf/1909.04939.pdf) architecture
## Credit
> timeseries for fastai v2 was inspired by by Ignacio's Oguiza timeseriesAI (https://github.com/timeseriesAI/timeseriesAI.git).
> Inception Time model definition is a modified version of [Ignacio Oguiza] (https://github.com/timeseriesAI/timeseriesAI/blob/master/torchtimeseries/models/InceptionTime.py) and [Thomas Capelle] (https://github.com/tcapelle/TimeSeries_fastai/blob/master/inception.py) implementaions
## Installing **`timeseries`** on local machine as an editable package
1- Only if you have not already installed `fastai v2`
Install [fastai2](https://dev.fast.ai/#Installing) by following the steps described there.
2- Install timeseries package by following the instructions here below:
```
git clone https://github.com/ai-fast-track/timeseries.git
cd timeseries
pip install -e .
```
# pip installing **`timeseries`** from repo either locally or in Google Colab - Start Here
## Installing fastai v2
```
!pip install git+https://github.com/fastai/fastai2.git
```
## Installing `timeseries` package from github
```
!pip install git+https://github.com/ai-fast-track/timeseries.git
```
# *pip Installing - End Here*
# `Usage`
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai2.basics import *
# hide
# Only for Windows users because symlink to `timeseries` folder is not recognized by Windows
import sys
sys.path.append("..")
from timeseries.all import *
```
# Tutorial on timeseries package for fastai v2
## Example : NATOS dataset
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/NATOPS.jpg?raw=1">
## Right Arm vs Left Arm (3: 'Not clear' Command (see picture here above))
<br>
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/ts-right-arm.png?raw=1"><img src="https://github.com/ai-fast-track/timeseries/blob/master/images/ts-left-arm.png?raw=1">
## Description
The data is generated by sensors on the hands, elbows, wrists and thumbs. The data are the x,y,z coordinates for each of the eight locations. The order of the data is as follows:
## Channels (24)
0. Hand tip left, X coordinate
1. Hand tip left, Y coordinate
2. Hand tip left, Z coordinate
3. Hand tip right, X coordinate
4. Hand tip right, Y coordinate
5. Hand tip right, Z coordinate
6. Elbow left, X coordinate
7. Elbow left, Y coordinate
8. Elbow left, Z coordinate
9. Elbow right, X coordinate
10. Elbow right, Y coordinate
11. Elbow right, Z coordinate
12. Wrist left, X coordinate
13. Wrist left, Y coordinate
14. Wrist left, Z coordinate
15. Wrist right, X coordinate
16. Wrist right, Y coordinate
17. Wrist right, Z coordinate
18. Thumb left, X coordinate
19. Thumb left, Y coordinate
20. Thumb left, Z coordinate
21. Thumb right, X coordinate
22. Thumb right, Y coordinate
23. Thumb right, Z coordinate
## Classes (6)
The six classes are separate actions, with the following meaning:
1: I have command
2: All clear
3: Not clear
4: Spread wings
5: Fold wings
6: Lock wings
## Download data using `download_unzip_data_UCR(dsname=dsname)` method
```
dsname = 'NATOPS' #'NATOPS', 'LSST', 'Wine', 'Epilepsy', 'HandMovementDirection'
# url = 'http://www.timeseriesclassification.com/Downloads/NATOPS.zip'
path = unzip_data(URLs_TS.NATOPS)
path
```
## Why do I have to concatenate train and test data?
Both Train and Train dataset contains 180 samples each. We concatenate them in order to have one big dataset and then split into train and valid dataset using our own split percentage (20%, 30%, or whatever number you see fit)
```
fname_train = f'{dsname}_TRAIN.arff'
fname_test = f'{dsname}_TEST.arff'
fnames = [path/fname_train, path/fname_test]
fnames
data = TSData.from_arff(fnames)
print(data)
items = data.get_items()
idx = 1
x1, y1 = data.x[idx], data.y[idx]
y1
# You can select any channel to display buy supplying a list of channels and pass it to `chs` argument
# LEFT ARM
# show_timeseries(x1, title=y1, chs=[0,1,2,6,7,8,12,13,14,18,19,20])
# RIGHT ARM
# show_timeseries(x1, title=y1, chs=[3,4,5,9,10,11,15,16,17,21,22,23])
# ?show_timeseries(x1, title=y1, chs=range(0,24,3)) # Only the x axis coordinates
seed = 42
splits = RandomSplitter(seed=seed)(range_of(items)) #by default 80% for train split and 20% for valid split are chosen
splits
```
# Using `Datasets` class
## Creating a Datasets object
```
tfms = [[ItemGetter(0), ToTensorTS()], [ItemGetter(1), Categorize()]]
# Create a dataset
ds = Datasets(items, tfms, splits=splits)
ax = show_at(ds, 2, figsize=(1,1))
```
# Create a `Dataloader` objects
## 1st method : using `Datasets` object
```
bs = 128
# Normalize at batch time
tfm_norm = Normalize(scale_subtype = 'per_sample_per_channel', scale_range=(0, 1)) # per_sample , per_sample_per_channel
# tfm_norm = Standardize(scale_subtype = 'per_sample')
batch_tfms = [tfm_norm]
dls1 = ds.dataloaders(bs=bs, val_bs=bs * 2, after_batch=batch_tfms, num_workers=0, device=default_device())
dls1.show_batch(max_n=9, chs=range(0,12,3))
```
# Using `DataBlock` class
## 2nd method : using `DataBlock` and `DataBlock.get_items()`
```
getters = [ItemGetter(0), ItemGetter(1)]
tsdb = DataBlock(blocks=(TSBlock, CategoryBlock),
get_items=get_ts_items,
getters=getters,
splitter=RandomSplitter(seed=seed),
batch_tfms = batch_tfms)
tsdb.summary(fnames)
# num_workers=0 is Microsoft Windows
dls2 = tsdb.dataloaders(fnames, num_workers=0, device=default_device())
dls2.show_batch(max_n=9, chs=range(0,12,3))
```
## 3rd method : using `DataBlock` and passing `items` object to the `DataBlock.dataloaders()`
```
getters = [ItemGetter(0), ItemGetter(1)]
tsdb = DataBlock(blocks=(TSBlock, CategoryBlock),
getters=getters,
splitter=RandomSplitter(seed=seed))
dls3 = tsdb.dataloaders(data.get_items(), batch_tfms=batch_tfms, num_workers=0, device=default_device())
dls3.show_batch(max_n=9, chs=range(0,12,3))
```
## 4th method : using `TSDataLoaders` class and `TSDataLoaders.from_files()`
```
dls4 = TSDataLoaders.from_files(fnames, batch_tfms=batch_tfms, num_workers=0, device=default_device())
dls4.show_batch(max_n=9, chs=range(0,12,3))
```
# Train Model
```
# Number of channels (i.e. dimensions in ARFF and TS files jargon)
c_in = get_n_channels(dls2.train) # data.n_channels
# Number of classes
c_out= dls2.c
c_in,c_out
```
## Create model
```
model = inception_time(c_in, c_out).to(device=default_device())
model
```
## Create Learner object
```
#Learner
opt_func = partial(Adam, lr=3e-3, wd=0.01)
loss_func = LabelSmoothingCrossEntropy()
learn = Learner(dls2, model, opt_func=opt_func, loss_func=loss_func, metrics=accuracy)
print(learn.summary())
```
## LR find
```
lr_min, lr_steep = learn.lr_find()
lr_min, lr_steep
```
## Train
```
#lr_max=1e-3
epochs=30; lr_max=lr_steep; pct_start=.7; moms=(0.95,0.85,0.95); wd=1e-2
learn.fit_one_cycle(epochs, lr_max=lr_max, pct_start=pct_start, moms=moms, wd=wd)
# learn.fit_one_cycle(epochs=20, lr_max=lr_steep)
```
## Plot loss function
```
learn.recorder.plot_loss()
```
## Show results
```
learn.show_results(max_n=9, chs=range(0,12,3))
#hide
from nbdev.export import notebook2script
# notebook2script()
notebook2script(fname='index.ipynb')
# #hide
# from nbdev.export2html import _notebook2html
# # notebook2script()
# _notebook2html(fname='index.ipynb')
```
# Fin
<img src="https://github.com/ai-fast-track/timeseries/blob/master/images/tree.jpg?raw=1" width="1440" height="840" alt=""/>
| true |
code
| 0.730929 | null | null | null | null |
|
# The Extended Kalman Filter
선형 칼만 필터 (Linear Kalman Filter)에 대한 이론을 바탕으로 비선형 문제에 칼만 필터를 적용해 보겠습니다. 확장칼만필터 (EKF)는 예측단계와 추정단계의 데이터를 비선형으로 가정하고 현재의 추정값에 대해 시스템을 선형화 한뒤 선형 칼만 필터를 사용하는 기법입니다.
비선형 문제에 적용되는 성능이 더 좋은 알고리즘들 (UKF, H_infinity)이 있지만 EKF 는 아직도 널리 사용되서 관련성이 높습니다.
```
%matplotlib inline
# HTML("""
# <style>
# .output_png {
# display: table-cell;
# text-align: center;
# vertical-align: middle;
# }
# </style>
# """)
```
## Linearizing the Kalman Filter
### Non-linear models
칼만 필터는 시스템이 선형일것이라는 가정을 하기 때문에 비선형 문제에는 직접적으로 사용하지 못합니다. 비선형성은 두가지 원인에서 기인될수 있는데 첫째는 프로세스 모델의 비선형성 그리고 둘째 측정 모델의 비선형성입니다. 예를 들어, 떨어지는 물체의 가속도는 속도의 제곱에 비례하는 공기저항에 의해 결정되기 때문에 비선형적인 프로세스 모델을 가지고, 레이더로 목표물의 범위와 방위 (bearing) 를 측정할때 비선형함수인 삼각함수를 사용하여 표적의 위치를 계산하기 때문에 비선형적인 측정 모델을 가지게 됩니다.
비선형문제에 기존의 칼만필터 방정식을 적용하지 못하는 이유는 비선형함수에 정규분포 (Gaussian)를 입력하면 아래와 같이 Gaussian 이 아닌 분포를 가지게 되기 때문입니다.
```
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
mu, sigma = 0, 0.1
gaussian = stats.norm.pdf(x, mu, sigma)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 10000)
def nonlinearFunction(x):
return np.sin(x)
def linearFunction(x):
return 0.5*x
nonlinearOutput = nonlinearFunction(gaussian)
linearOutput = linearFunction(gaussian)
# print(x)
plt.plot(x, gaussian, label = 'Gaussian Input')
plt.plot(x, linearOutput, label = 'Linear Output')
plt.plot(x, nonlinearOutput, label = 'Nonlinear Output')
plt.grid(linestyle='dotted', linewidth=0.8)
plt.legend()
plt.show()
```
### System Equations
선형 칼만 필터의 경우 프로세스 및 측정 모델은 다음과 같이 나타낼수 있습니다.
$$\begin{aligned}\dot{\mathbf x} &= \mathbf{Ax} + w_x\\
\mathbf z &= \mathbf{Hx} + w_z
\end{aligned}$$
이때 $\mathbf A$ 는 (연속시간에서) 시스템의 역학을 묘사하는 dynamic matrix 입니다. 위의 식을 이산화(discretize)시키면 아래와 같이 나타내줄 수 있습니다.
$$\begin{aligned}\bar{\mathbf x}_k &= \mathbf{F} \mathbf{x}_{k-1} \\
\bar{\mathbf z} &= \mathbf{H} \mathbf{x}_{k-1}
\end{aligned}$$
이때 $\mathbf F$ 는 이산시간 $\Delta t$ 에 걸쳐 $\mathbf x_{k-1}$을 $\mathbf x_{k}$ 로 전환하는 상태변환행렬 또는 상태전달함수 (state transition matrix) 이고, 위에서의 $w_x$ 와 $w_z$는 각각 프로세스 노이즈 공분산 행렬 $\mathbf Q$ 과 측정 노이즈 공분산 행렬 $\mathbf R$ 에 포함됩니다.
선형 시스템에서의 $\mathbf F \mathbf x- \mathbf B \mathbf u$ 와 $\mathbf H \mathbf x$ 는 비선형 시스템에서 함수 $f(\mathbf x, \mathbf u)$ 와 $h(\mathbf x)$ 로 대체됩니다.
$$\begin{aligned}\dot{\mathbf x} &= f(\mathbf x, \mathbf u) + w_x\\
\mathbf z &= h(\mathbf x) + w_z
\end{aligned}$$
### Linearisation
선형화란 말그대로 하나의 시점에 대하여 비선형함수에 가장 가까운 선 (선형시스템) 을 찾는것이라고 볼수 있습니다. 여러가지 방법으로 선형화를 할수 있겠지만 흔히 일차 테일러 급수를 사용합니다. ($ c_0$ 과 $c_1 x$)
$$f(x) = \sum_{k=0}^\infty c_k x^k = c_0 + c_1 x + c_2 x^2 + \dotsb$$
$$c_k = \frac{f^{\left(k\right)}(0)}{k!} = \frac{1}{k!} \cdot \frac{d^k f}{dx^k}\bigg|_0 $$
행렬의 미분값을 Jacobian 이라고 하는데 이를 통해서 위와 같이 $\mathbf F$ 와 $\mathbf H$ 를 나타낼 수 있습니다.
$$
\begin{aligned}
\mathbf F
= {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}} \;\;\;\;
\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
\end{aligned}
$$
$$\mathbf F = \frac{\partial f(\mathbf x, \mathbf u)}{\partial x} =\begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n}\\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\
\\ \vdots & \vdots & \ddots & \vdots
\\
\frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \dots & \frac{\partial f_n}{\partial x_n}
\end{bmatrix}
$$
Linear Kalman Filter 와 Extended Kalman Filter 의 식들을 아래와 같이 비교할수 있습니다.
$$\begin{array}{l|l}
\text{Linear Kalman filter} & \text{EKF} \\
\hline
& \boxed{\mathbf F = {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}}} \\
\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} & \boxed{\mathbf{\bar x} = f(\mathbf x, \mathbf u)} \\
\mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q & \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q \\
\hline
& \boxed{\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}} \\
\textbf{y} = \mathbf z - \mathbf{H \bar{x}} & \textbf{y} = \mathbf z - \boxed{h(\bar{x})}\\
\mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} & \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} \\
\mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} & \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} \\
\mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} & \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}}
\end{array}$$
$\mathbf F \mathbf x_{k-1}$ 을 사용하여 $\mathbf x_{k}$의 값을 추정할수 있겠지만, 선형화 과정에서 오차가 생길수 있기 때문에 Euler 또는 Runge Kutta 수치 적분 (numerical integration) 을 통해서 사전추정값 $\mathbf{\bar{x}}$ 를 구합니다. 같은 이유로 $\mathbf y$ (innovation vector 또는 잔차(residual)) 를 구할때도 $\mathbf H \mathbf x$ 대신에 수치적인 방법으로 계산하게 됩니다.
## Example: Robot Localization
### Prediction Model (예측모델)
EKF를 4륜 로봇에 적용시켜 보겠습니다. 간단한 bicycle steering model 을 통해 아래의 시스템 모델을 나타낼 수 있습니다.
```
import kf_book.ekf_internal as ekf_internal
ekf_internal.plot_bicycle()
```
$$\begin{aligned}
\beta &= \frac d w \tan(\alpha) \\
\bar x_k &= x_{k-1} - R\sin(\theta) + R\sin(\theta + \beta) \\
\bar y_k &= y_{k-1} + R\cos(\theta) - R\cos(\theta + \beta) \\
\bar \theta_k &= \theta_{k-1} + \beta
\end{aligned}
$$
위의 식들을 토대로 상태벡터를 $\mathbf{x}=[x, y, \theta]^T$ 그리고 입력벡터를 $\mathbf{u}=[v, \alpha]^T$ 라고 정의 해주면 아래와 같이 $f(\mathbf x, \mathbf u)$ 나타내줄수 있고 $f$ 의 Jacobian $\mathbf F$를 미분하여 아래의 행렬을 구해줄수 있습니다.
$$\bar x = f(x, u) + \mathcal{N}(0, Q)$$
$$f = \begin{bmatrix}x\\y\\\theta\end{bmatrix} +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}$$
$$\mathbf F = \frac{\partial f(\mathbf x, \mathbf u)}{\partial \mathbf x} = \begin{bmatrix}
1 & 0 & -R\cos(\theta) + R\cos(\theta+\beta) \\
0 & 1 & -R\sin(\theta) + R\sin(\theta+\beta) \\
0 & 0 & 1
\end{bmatrix}$$
$\bar{\mathbf P}$ 을 구하기 위해 입력($\mathbf u$)에서 비롯되는 프로세스 노이즈 $\mathbf Q$ 를 아래와 같이 정의합니다.
$$\mathbf{M} = \begin{bmatrix}\sigma_{vel}^2 & 0 \\ 0 & \sigma_\alpha^2\end{bmatrix}
\;\;\;\;
\mathbf{V} = \frac{\partial f(x, u)}{\partial u} \begin{bmatrix}
\frac{\partial f_1}{\partial v} & \frac{\partial f_1}{\partial \alpha} \\
\frac{\partial f_2}{\partial v} & \frac{\partial f_2}{\partial \alpha} \\
\frac{\partial f_3}{\partial v} & \frac{\partial f_3}{\partial \alpha}
\end{bmatrix}$$
$$\mathbf{\bar P} =\mathbf{FPF}^{\mathsf T} + \mathbf{VMV}^{\mathsf T}$$
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
from sympy import symbols, Matrix
sympy.init_printing(use_latex="mathjax", fontsize='16pt')
time = symbols('t')
d = v*time
beta = (d/w)*sympy.tan(alpha)
r = w/sympy.tan(alpha)
fxu = Matrix([[x-r*sympy.sin(theta) + r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)- r*sympy.cos(theta+beta)],
[theta+beta]])
F = fxu.jacobian(Matrix([x, y, theta]))
F
# reduce common expressions
B, R = symbols('beta, R')
F = F.subs((d/w)*sympy.tan(alpha), B)
F.subs(w/sympy.tan(alpha), R)
V = fxu.jacobian(Matrix([v, alpha]))
V = V.subs(sympy.tan(alpha)/w, 1/R)
V = V.subs(time*v/R, B)
V = V.subs(time*v, 'd')
V
```
### Measurement Model (측정모델)
레이더로 범위$(r)$와 방위($\phi$)를 측정할때 다음과 같은 센서모델을 사용합니다. 이때 $\mathbf p$ 는 landmark의 위치를 나타내줍니다.
$$r = \sqrt{(p_x - x)^2 + (p_y - y)^2}
\;\;\;\;
\phi = \arctan(\frac{p_y - y}{p_x - x}) - \theta
$$
$$\begin{aligned}
\mathbf z& = h(\bar{\mathbf x}, \mathbf p) &+ \mathcal{N}(0, R)\\
&= \begin{bmatrix}
\sqrt{(p_x - x)^2 + (p_y - y)^2} \\
\arctan(\frac{p_y - y}{p_x - x}) - \theta
\end{bmatrix} &+ \mathcal{N}(0, R)
\end{aligned}$$
$h$ 의 Jacobian $\mathbf H$를 미분하여 아래의 행렬을 구해줄수 있습니다.
$$\mathbf H = \frac{\partial h(\mathbf x, \mathbf u)}{\partial \mathbf x} =
\left[\begin{matrix}\frac{- p_{x} + x}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & \frac{- p_{y} + y}{\sqrt{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}}} & 0\\- \frac{- p_{y} + y}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & - \frac{p_{x} - x}{\left(p_{x} - x\right)^{2} + \left(p_{y} - y\right)^{2}} & -1\end{matrix}\right]
$$
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
px, py = sympy.symbols('p_x, p_y')
z = sympy.Matrix([[sympy.sqrt((px-x)**2 + (py-y)**2)],
[sympy.atan2(py-y, px-x) - theta]])
z.jacobian(sympy.Matrix([x, y, theta]))
# print(sympy.latex(z.jacobian(sympy.Matrix([x, y, theta])))
from math import sqrt
def H_of(x, landmark_pos):
""" compute Jacobian of H matrix where h(x) computes
the range and bearing to a landmark for state x """
px = landmark_pos[0]
py = landmark_pos[1]
hyp = (px - x[0, 0])**2 + (py - x[1, 0])**2
dist = sqrt(hyp)
H = array(
[[-(px - x[0, 0]) / dist, -(py - x[1, 0]) / dist, 0],
[ (py - x[1, 0]) / hyp, -(px - x[0, 0]) / hyp, -1]])
return H
from math import atan2
def Hx(x, landmark_pos):
""" takes a state variable and returns the measurement
that would correspond to that state.
"""
px = landmark_pos[0]
py = landmark_pos[1]
dist = sqrt((px - x[0, 0])**2 + (py - x[1, 0])**2)
Hx = array([[dist],
[atan2(py - x[1, 0], px - x[0, 0]) - x[2, 0]]])
return Hx
```
측정 노이즈는 다음과 같이 나타내줍니다.
$$\mathbf R=\begin{bmatrix}\sigma_{range}^2 & 0 \\ 0 & \sigma_{bearing}^2\end{bmatrix}$$
### Implementation
`FilterPy` 의 `ExtendedKalmanFilter` class 를 활용해서 EKF 를 구현해보도록 하겠습니다.
```
from filterpy.kalman import ExtendedKalmanFilter as EKF
from numpy import array, sqrt, random
import sympy
class RobotEKF(EKF):
def __init__(self, dt, wheelbase, std_vel, std_steer):
EKF.__init__(self, 3, 2, 2)
self.dt = dt
self.wheelbase = wheelbase
self.std_vel = std_vel
self.std_steer = std_steer
a, x, y, v, w, theta, time = sympy.symbols(
'a, x, y, v, w, theta, t')
d = v*time
beta = (d/w)*sympy.tan(a)
r = w/sympy.tan(a)
self.fxu = sympy.Matrix(
[[x-r*sympy.sin(theta)+r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)-r*sympy.cos(theta+beta)],
[theta+beta]])
self.F_j = self.fxu.jacobian(sympy.Matrix([x, y, theta]))
self.V_j = self.fxu.jacobian(sympy.Matrix([v, a]))
# save dictionary and it's variables for later use
self.subs = {x: 0, y: 0, v:0, a:0,
time:dt, w:wheelbase, theta:0}
self.x_x, self.x_y, = x, y
self.v, self.a, self.theta = v, a, theta
def predict(self, u):
self.x = self.move(self.x, u, self.dt)
self.subs[self.theta] = self.x[2, 0]
self.subs[self.v] = u[0]
self.subs[self.a] = u[1]
F = array(self.F_j.evalf(subs=self.subs)).astype(float)
V = array(self.V_j.evalf(subs=self.subs)).astype(float)
# covariance of motion noise in control space
M = array([[self.std_vel*u[0]**2, 0],
[0, self.std_steer**2]])
self.P = F @ self.P @ F.T + V @ M @ V.T
def move(self, x, u, dt):
hdg = x[2, 0]
vel = u[0]
steering_angle = u[1]
dist = vel * dt
if abs(steering_angle) > 0.001: # is robot turning?
beta = (dist / self.wheelbase) * tan(steering_angle)
r = self.wheelbase / tan(steering_angle) # radius
dx = np.array([[-r*sin(hdg) + r*sin(hdg + beta)],
[r*cos(hdg) - r*cos(hdg + beta)],
[beta]])
else: # moving in straight line
dx = np.array([[dist*cos(hdg)],
[dist*sin(hdg)],
[0]])
return x + dx
```
정확한 잔차값 $y$을 구하기 방위값이 $0 \leq \phi \leq 2\pi$ 이도록 고쳐줍니다.
```
def residual(a, b):
""" compute residual (a-b) between measurements containing
[range, bearing]. Bearing is normalized to [-pi, pi)"""
y = a - b
y[1] = y[1] % (2 * np.pi) # force in range [0, 2 pi)
if y[1] > np.pi: # move to [-pi, pi)
y[1] -= 2 * np.pi
return y
from filterpy.stats import plot_covariance_ellipse
from math import sqrt, tan, cos, sin, atan2
import matplotlib.pyplot as plt
dt = 1.0
def z_landmark(lmark, sim_pos, std_rng, std_brg):
x, y = sim_pos[0, 0], sim_pos[1, 0]
d = np.sqrt((lmark[0] - x)**2 + (lmark[1] - y)**2)
a = atan2(lmark[1] - y, lmark[0] - x) - sim_pos[2, 0]
z = np.array([[d + random.randn()*std_rng],
[a + random.randn()*std_brg]])
return z
def ekf_update(ekf, z, landmark):
ekf.update(z, HJacobian = H_of, Hx = Hx,
residual=residual,
args=(landmark), hx_args=(landmark))
def run_localization(landmarks, std_vel, std_steer,
std_range, std_bearing,
step=10, ellipse_step=20, ylim=None):
ekf = RobotEKF(dt, wheelbase=0.5, std_vel=std_vel,
std_steer=std_steer)
ekf.x = array([[2, 6, .3]]).T # x, y, steer angle
ekf.P = np.diag([.1, .1, .1])
ekf.R = np.diag([std_range**2, std_bearing**2])
sim_pos = ekf.x.copy() # simulated position
# steering command (vel, steering angle radians)
u = array([1.1, .01])
plt.figure()
plt.scatter(landmarks[:, 0], landmarks[:, 1],
marker='s', s=60)
track = []
for i in range(200):
sim_pos = ekf.move(sim_pos, u, dt/10.) # simulate robot
track.append(sim_pos)
if i % step == 0:
ekf.predict(u=u)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='k', alpha=0.3)
x, y = sim_pos[0, 0], sim_pos[1, 0]
for lmark in landmarks:
z = z_landmark(lmark, sim_pos,
std_range, std_bearing)
ekf_update(ekf, z, lmark)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='g', alpha=0.8)
track = np.array(track)
plt.plot(track[:, 0], track[:,1], color='k', lw=2)
plt.axis('equal')
plt.title("EKF Robot localization")
if ylim is not None: plt.ylim(*ylim)
plt.show()
return ekf
landmarks = array([[5, 10], [10, 5], [15, 15]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
print('Final P:', ekf.P.diagonal())
```
## References
* Roger R Labbe, Kalman and Bayesian Filters in Python
(https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/11-Extended-Kalman-Filters.ipynb)
* https://blog.naver.com/jewdsa813/222200570774
| true |
code
| 0.5867 | null | null | null | null |
|
# Documenting Classes
It is almost as easy to document a class as it is to document a function. Simply add docstrings to all of the classes functions, and also below the class name itself. For example, here is a simple documented class
```
class Demo:
"""This class demonstrates how to document a class.
This class is just a demonstration, and does nothing.
However the principles of documentation are still valid!
"""
def __init__(self, name):
"""You should document the constructor, saying what it expects to
create a valid class. In this case
name -- the name of an object of this class
"""
self._name = name
def getName(self):
"""You should then document all of the member functions, just as
you do for normal functions. In this case, returns
the name of the object
"""
return self._name
d = Demo("cat")
help(d)
```
Often, when you write a class, you want to hide member data or member functions so that they are only visible within an object of the class. For example, above, the `self._name` member data should be hidden, as it should only be used by the object.
You control the visibility of member functions or member data using an underscore. If the member function or member data name starts with an underscore, then it is hidden. Otherwise, the member data or function is visible.
For example, we can hide the `getName` function by renaming it to `_getName`
```
class Demo:
"""This class demonstrates how to document a class.
This class is just a demonstration, and does nothing.
However the principles of documentation are still valid!
"""
def __init__(self, name):
"""You should document the constructor, saying what it expects to
create a valid class. In this case
name -- the name of an object of this class
"""
self._name = name
def _getName(self):
"""You should then document all of the member functions, just as
you do for normal functions. In this case, returns
the name of the object
"""
return self._name
d = Demo("cat")
help(d)
```
Member functions or data that are hidden are called "private". Member functions or data that are visible are called "public". You should document all public member functions of a class, as these are visible and designed to be used by other people. It is helpful, although not required, to document all of the private member functions of a class, as these will only really be called by you. However, in years to come, you will thank yourself if you still documented them... ;-)
While it is possible to make member data public, it is not advised. It is much better to get and set values of member data using public member functions. This makes it easier for you to add checks to ensure that the data is consistent and being used in the right way. For example, compare these two classes that represent a person, and hold their height.
```
class Person1:
"""Class that holds a person's height"""
def __init__(self):
"""Construct a person who has zero height"""
self.height = 0
class Person2:
"""Class that holds a person's height"""
def __init__(self):
"""Construct a person who has zero height"""
self._height = 0
def setHeight(self, height):
"""Set the person's height to 'height', returning whether or
not the height was set successfully
"""
if height < 0 or height > 300:
print("This is an invalid height! %s" % height)
return False
else:
self._height = height
return True
def getHeight(self):
"""Return the person's height"""
return self._height
```
The first example is quicker to write, but it does little to protect itself against a user who attempts to use the class badly.
```
p = Person1()
p.height = -50
p.height
p.height = "cat"
p.height
```
The second example takes more lines of code, but these lines are valuable as they check that the user is using the class correctly. These checks, when combined with good documentation, ensure that your classes can be safely used by others, and that incorrect use will not create difficult-to-find bugs.
```
p = Person2()
p.setHeight(-50)
p.getHeight()
p.setHeight("cat")
p.getHeight()
```
# Exercise
## Exercise 1
Below is the completed `GuessGame` class from the previous lesson. Add documentation to this class.
```
class GuessGame:
"""
This class provides a simple guessing game. You create an object
of the class with its own secret, with the aim that a user
then needs to try to guess what the secret is.
"""
def __init__(self, secret, max_guesses=5):
"""Create a new guess game
secret -- the secret that must be guessed
max_guesses -- the maximum number of guesses allowed by the user
"""
self._secret = secret
self._nguesses = 0
self._max_guesses = max_guesses
def guess(self, value):
"""Try to guess the secret. This will print out to the screen whether
or not the secret has been guessed.
value -- the user-supplied guess
"""
if (self.nGuesses() >= self.maxGuesses()):
print("Sorry, you have run out of guesses")
elif (value == self._secret):
print("Well done - you have guessed my secret")
else:
self._nguesses += 1
print("Try again...")
def nGuesses(self):
"""Return the number of incorrect guesses made so far"""
return self._nguesses
def maxGuesses(self):
"""Return the maximum number of incorrect guesses allowed"""
return self._max_guesses
help(GuessGame)
```
## Exercise 2
Below is a poorly-written class that uses public member data to store the name and age of a Person. Edit this class so that the member data is made private. Add `get` and `set` functions that allow you to safely get and set the name and age.
```
class Person:
"""Class the represents a Person, holding their name and age"""
def __init__(self, name="unknown", age=0):
"""Construct a person with unknown name and an age of 0"""
self.setName(name)
self.setAge(age)
def setName(self, name):
"""Set the person's name to 'name'"""
self._name = str(name) # str ensures the name is a string
def getName(self):
"""Return the person's name"""
return self._name
def setAge(self, age):
"""Set the person's age. This must be a number between 0 and 130"""
if (age < 0 or age > 130):
print("Cannot set the age to an invalid value: %s" % age)
self._age = age
def getAge(self):
"""Return the person's age"""
return self._age
p = Person(name="Peter Parker", age=21)
p.getName()
p.getAge()
```
## Exercise 3
Add a private member function called `_splitName` to your `Person` class that breaks the name into a surname and first name. Add new functions called `getFirstName` and `getSurname` that use this function to return the first name and surname of the person.
```
class Person:
"""Class the represents a Person, holding their name and age"""
def __init__(self, name="unknown", age=0):
"""Construct a person with unknown name and an age of 0"""
self.setName(name)
self.setAge(age)
def setName(self, name):
"""Set the person's name to 'name'"""
self._name = str(name) # str ensures the name is a string
def getName(self):
"""Return the person's name"""
return self._name
def setAge(self, age):
"""Set the person's age. This must be a number between 0 and 130"""
if (age < 0 or age > 130):
print("Cannot set the age to an invalid value: %s" % age)
self._age = age
def getAge(self):
"""Return the person's age"""
return self._age
def _splitName(self):
"""Private function that splits the name into parts"""
return self._name.split(" ")
def getFirstName(self):
"""Return the first name of the person"""
return self._splitName()[0]
def getSurname(self):
"""Return the surname of the person"""
return self._splitName()[-1]
p = Person(name="Peter Parker", age=21)
p.getFirstName()
p.getSurname()
```
| true |
code
| 0.588771 | null | null | null | null |
|
<img src="https://storage.googleapis.com/arize-assets/arize-logo-white.jpg" width="200"/>
# Arize Tutorial: Surrogate Model Feature Importance
A surrogate model is an interpretable model trained on predicting the predictions of a black box model. The goal is to approximate the predictions of the black box model as closely as possible and generate feature importance values from the interpretable surrogate model. The benefit of this approach is that it does not require knowledge of the inner workings of the black box model.
In this tutorial we use the `MimcExplainer` from the `interpret_community` library to generate feature importance values from a surrogate model using only the prediction outputs from a black box model. Both [classification](#classification) and [regression](#regression) examples are provided below and feature importance values are logged to Arize using the Pandas [logger](https://docs.arize.com/arize/api-reference/python-sdk/arize.pandas).
# Install and import the `interpret_community` library
```
!pip install -q interpret==0.2.7 interpret-community==0.22.0
from interpret_community.mimic.mimic_explainer import (
MimicExplainer,
LGBMExplainableModel,
)
```
<a name="classification"></a>
# Classification Example
### Generate example
In this example we'll use a support vector machine (SVM) as our black box model. Only the prediction outputs of the SVM model is needed to train the surrogate model, and feature importances are generated from the surrogate model and sent to Arize.
```
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
bc = load_breast_cancer()
feature_names = bc.feature_names
target_names = bc.target_names
data, target = bc.data, bc.target
df = pd.DataFrame(data, columns=feature_names)
model = SVC(probability=True).fit(df, target)
prediction_label = pd.Series(map(lambda v: target_names[v], model.predict(df)))
prediction_score = pd.Series(map(lambda v: v[1], model.predict_proba(df)))
actual_label = pd.Series(map(lambda v: target_names[v], target))
actual_score = pd.Series(target)
```
### Generate feature importance values
Note that the model itself is not used here. Only its prediction outputs are used.
```
def model_func(_):
return np.array(list(map(lambda p: [1 - p, p], prediction_score)))
explainer = MimicExplainer(
model_func,
df,
LGBMExplainableModel,
augment_data=False,
is_function=True,
)
feature_importance_values = pd.DataFrame(
explainer.explain_local(df).local_importance_values, columns=feature_names
)
feature_importance_values
```
### Send data to Arize
Set up Arize client. We'll be using the Pandas Logger. First copy the Arize `API_KEY` and `ORG_KEY` from your admin page linked below!
[](https://app.arize.com/admin)
```
!pip install -q arize
from arize.pandas.logger import Client, Schema
from arize.utils.types import ModelTypes, Environments
ORGANIZATION_KEY = "ORGANIZATION_KEY"
API_KEY = "API_KEY"
arize_client = Client(organization_key=ORGANIZATION_KEY, api_key=API_KEY)
if ORGANIZATION_KEY == "ORGANIZATION_KEY" or API_KEY == "API_KEY":
raise ValueError("❌ NEED TO CHANGE ORGANIZATION AND/OR API_KEY")
else:
print("✅ Import and Setup Arize Client Done! Now we can start using Arize!")
```
Helper functions to simulate prediction IDs and timestamps.
```
import uuid
from datetime import datetime, timedelta
# Prediction ID is required for logging any dataset
def generate_prediction_ids(df):
return pd.Series((str(uuid.uuid4()) for _ in range(len(df))), index=df.index)
# OPTIONAL: We can directly specify when inferences were made
def simulate_production_timestamps(df, days=30):
t = datetime.now()
current_t, earlier_t = t.timestamp(), (t - timedelta(days=days)).timestamp()
return pd.Series(np.linspace(earlier_t, current_t, num=len(df)), index=df.index)
```
Assemble Pandas DataFrame as a production dataset with prediction IDs and timestamps.
```
feature_importance_values_column_names_mapping = {
f"{feat}": f"{feat} (feature importance)" for feat in feature_names
}
production_dataset = pd.concat(
[
pd.DataFrame(
{
"prediction_id": generate_prediction_ids(df),
"prediction_ts": simulate_production_timestamps(df),
"prediction_label": prediction_label,
"actual_label": actual_label,
"prediction_score": prediction_score,
"actual_score": actual_score,
}
),
df,
feature_importance_values.rename(
columns=feature_importance_values_column_names_mapping
),
],
axis=1,
)
production_dataset
```
Send dataframe to Arize
```
# Define a Schema() object for Arize to pick up data from the correct columns for logging
production_schema = Schema(
prediction_id_column_name="prediction_id", # REQUIRED
timestamp_column_name="prediction_ts",
prediction_label_column_name="prediction_label",
prediction_score_column_name="prediction_score",
actual_label_column_name="actual_label",
actual_score_column_name="actual_score",
feature_column_names=feature_names,
shap_values_column_names=feature_importance_values_column_names_mapping,
)
# arize_client.log returns a Response object from Python's requests module
response = arize_client.log(
dataframe=production_dataset,
schema=production_schema,
model_id="surrogate_model_example_classification",
model_type=ModelTypes.SCORE_CATEGORICAL,
environment=Environments.PRODUCTION,
)
# If successful, the server will return a status_code of 200
if response.status_code != 200:
print(
f"❌ logging failed with response code {response.status_code}, {response.text}"
)
else:
print(
f"✅ You have successfully logged {len(production_dataset)} data points to Arize!"
)
```
<a name="regression"></a>
# Regression Example
### Generate example
In this example we'll use a support vector machine (SVM) as our black box model. Only the prediction outputs of the SVM model is needed to train the surrogate model, and feature importances are generated from the surrogate model and sent to Arize.
```
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
# Use only 1,000 data point for a speedier example
data_reg = housing.data[:1000]
target_reg = housing.target[:1000]
feature_names_reg = housing.feature_names
df_reg = pd.DataFrame(data_reg, columns=feature_names_reg)
from sklearn.svm import SVR
model_reg = SVR().fit(df_reg, target_reg)
prediction_label_reg = pd.Series(model_reg.predict(df_reg))
actual_label_reg = pd.Series(target_reg)
```
### Generate feature importance values
Note that the model itself is not used here. Only its prediction outputs are used.
```
def model_func_reg(_):
return np.array(prediction_label_reg)
explainer_reg = MimicExplainer(
model_func_reg,
df_reg,
LGBMExplainableModel,
augment_data=False,
is_function=True,
)
feature_importance_values_reg = pd.DataFrame(
explainer_reg.explain_local(df_reg).local_importance_values,
columns=feature_names_reg,
)
feature_importance_values_reg
```
Assemble Pandas DataFrame as a production dataset with prediction IDs and timestamps.
```
feature_importance_values_column_names_mapping_reg = {
f"{feat}": f"{feat} (feature importance)" for feat in feature_names_reg
}
production_dataset_reg = pd.concat(
[
pd.DataFrame(
{
"prediction_id": generate_prediction_ids(df_reg),
"prediction_ts": simulate_production_timestamps(df_reg),
"prediction_label": prediction_label_reg,
"actual_label": actual_label_reg,
}
),
df_reg,
feature_importance_values_reg.rename(
columns=feature_importance_values_column_names_mapping_reg
),
],
axis=1,
)
production_dataset_reg
```
Send DataFrame to Arize.
```
# Define a Schema() object for Arize to pick up data from the correct columns for logging
production_schema_reg = Schema(
prediction_id_column_name="prediction_id", # REQUIRED
timestamp_column_name="prediction_ts",
prediction_label_column_name="prediction_label",
actual_label_column_name="actual_label",
feature_column_names=feature_names_reg,
shap_values_column_names=feature_importance_values_column_names_mapping_reg,
)
# arize_client.log returns a Response object from Python's requests module
response_reg = arize_client.log(
dataframe=production_dataset_reg,
schema=production_schema_reg,
model_id="surrogate_model_example_regression",
model_type=ModelTypes.NUMERIC,
environment=Environments.PRODUCTION,
)
# If successful, the server will return a status_code of 200
if response_reg.status_code != 200:
print(
f"❌ logging failed with response code {response_reg.status_code}, {response_reg.text}"
)
else:
print(
f"✅ You have successfully logged {len(production_dataset_reg)} data points to Arize!"
)
```
## Conclusion
You now know how to seamlessly log surrogate model feature importance values onto the Arize platform. Go to [Arize](https://app.arize.com/) in order to analyze and monitor the logged SHAP values.
### Overview
Arize is an end-to-end ML observability and model monitoring platform. The platform is designed to help ML engineers and data science practitioners surface and fix issues with ML models in production faster with:
- Automated ML monitoring and model monitoring
- Workflows to troubleshoot model performance
- Real-time visualizations for model performance monitoring, data quality monitoring, and drift monitoring
- Model prediction cohort analysis
- Pre-deployment model validation
- Integrated model explainability
### Website
Visit Us At: https://arize.com/model-monitoring/
### Additional Resources
- [What is ML observability?](https://arize.com/what-is-ml-observability/)
- [Playbook to model monitoring in production](https://arize.com/the-playbook-to-monitor-your-models-performance-in-production/)
- [Using statistical distance metrics for ML monitoring and observability](https://arize.com/using-statistical-distance-metrics-for-machine-learning-observability/)
- [ML infrastructure tools for data preparation](https://arize.com/ml-infrastructure-tools-for-data-preparation/)
- [ML infrastructure tools for model building](https://arize.com/ml-infrastructure-tools-for-model-building/)
- [ML infrastructure tools for production](https://arize.com/ml-infrastructure-tools-for-production-part-1/)
- [ML infrastructure tools for model deployment and model serving](https://arize.com/ml-infrastructure-tools-for-production-part-2-model-deployment-and-serving/)
- [ML infrastructure tools for ML monitoring and observability](https://arize.com/ml-infrastructure-tools-ml-observability/)
Visit the [Arize Blog](https://arize.com/blog) and [Resource Center](https://arize.com/resource-hub/) for more resources on ML observability and model monitoring.
| true |
code
| 0.553686 | null | null | null | null |
|
```
import numpy as np
from keras.models import Model
from keras.layers import Input
from keras.layers.pooling import GlobalMaxPooling1D
from keras import backend as K
import json
from collections import OrderedDict
def format_decimal(arr, places=6):
return [round(x * 10**places) / 10**places for x in arr]
DATA = OrderedDict()
```
### GlobalMaxPooling1D
**[pooling.GlobalMaxPooling1D.0] input 6x6**
```
data_in_shape = (6, 6)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(260)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.0'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[pooling.GlobalMaxPooling1D.1] input 3x7**
```
data_in_shape = (3, 7)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(261)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.1'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
**[pooling.GlobalMaxPooling1D.2] input 8x4**
```
data_in_shape = (8, 4)
L = GlobalMaxPooling1D()
layer_0 = Input(shape=data_in_shape)
layer_1 = L(layer_0)
model = Model(inputs=layer_0, outputs=layer_1)
# set weights to random (use seed for reproducibility)
np.random.seed(262)
data_in = 2 * np.random.random(data_in_shape) - 1
result = model.predict(np.array([data_in]))
data_out_shape = result[0].shape
data_in_formatted = format_decimal(data_in.ravel().tolist())
data_out_formatted = format_decimal(result[0].ravel().tolist())
print('')
print('in shape:', data_in_shape)
print('in:', data_in_formatted)
print('out shape:', data_out_shape)
print('out:', data_out_formatted)
DATA['pooling.GlobalMaxPooling1D.2'] = {
'input': {'data': data_in_formatted, 'shape': data_in_shape},
'expected': {'data': data_out_formatted, 'shape': data_out_shape}
}
```
### export for Keras.js tests
```
import os
filename = '../../../test/data/layers/pooling/GlobalMaxPooling1D.json'
if not os.path.exists(os.path.dirname(filename)):
os.makedirs(os.path.dirname(filename))
with open(filename, 'w') as f:
json.dump(DATA, f)
print(json.dumps(DATA))
```
| true |
code
| 0.450601 | null | null | null | null |
|
# Saving and Loading Models
In this notebook, I'll show you how to save and load models with PyTorch. This is important because you'll often want to load previously trained models to use in making predictions or to continue training on new data.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import helper
import fc_model
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# Download and load the training data
trainset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
```
# Train a network
To make things more concise here, I moved the model architecture and training code from the last part to a file called `fc_model`. Importing this, we can easily create a fully-connected network with `fc_model.Network`, and train the network using `fc_model.train`. I'll use this model (once it's trained) to demonstrate how we can save and load models.
```
# Create the network, define the criterion and optimizer
model = fc_model.Network(784, 10, [512, 256, 128])
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
fc_model.train(model, trainloader, testloader, criterion, optimizer, epochs=2)
```
## Saving and loading networks
As you can imagine, it's impractical to train a network every time you need to use it. Instead, we can save trained networks then load them later to train more or use them for predictions.
The parameters for PyTorch networks are stored in a model's `state_dict`. We can see the state dict contains the weight and bias matrices for each of our layers.
```
print("Our model: \n\n", model, '\n')
print("The state dict keys: \n\n", model.state_dict().keys())
```
The simplest thing to do is simply save the state dict with `torch.save`. For example, we can save it to a file `'checkpoint.pth'`.
```
torch.save(model.state_dict(), 'checkpoint.pth')
```
Then we can load the state dict with `torch.load`.
```
state_dict = torch.load('checkpoint.pth')
print(state_dict.keys())
```
And to load the state dict in to the network, you do `model.load_state_dict(state_dict)`.
```
model.load_state_dict(state_dict)
```
Seems pretty straightforward, but as usual it's a bit more complicated. Loading the state dict works only if the model architecture is exactly the same as the checkpoint architecture. If I create a model with a different architecture, this fails.
```
# Try this
model = fc_model.Network(784, 10, [400, 200, 100])
# This will throw an error because the tensor sizes are wrong!
model.load_state_dict(state_dict)
```
This means we need to rebuild the model exactly as it was when trained. Information about the model architecture needs to be saved in the checkpoint, along with the state dict. To do this, you build a dictionary with all the information you need to compeletely rebuild the model.
```
checkpoint = {'input_size': 784,
'output_size': 10,
'hidden_layers': [each.out_features for each in model.hidden_layers],
'state_dict': model.state_dict()}
torch.save(checkpoint, 'checkpoint.pth')
```
Now the checkpoint has all the necessary information to rebuild the trained model. You can easily make that a function if you want. Similarly, we can write a function to load checkpoints.
```
def load_checkpoint(filepath):
checkpoint = torch.load(filepath)
model = fc_model.Network(checkpoint['input_size'],
checkpoint['output_size'],
checkpoint['hidden_layers'])
model.load_state_dict(checkpoint['state_dict'])
return model
model = load_checkpoint('checkpoint.pth')
print(model)
```
| true |
code
| 0.743685 | null | null | null | null |
|
# Spectral encoding of categorical features
About a year ago I was working on a regression model, which had over a million features. Needless to say, the training was super slow, and the model was overfitting a lot. After investigating this issue, I realized that most of the features were created using 1-hot encoding of the categorical features, and some of them had tens of thousands of unique values.
The problem of mapping categorical features to lower-dimensional space is not new. Recently one of the popular way to deal with it is using entity embedding layers of a neural network. However that method assumes that neural networks are used. What if we decided to use tree-based algorithms instead? In tis case we can use Spectral Graph Theory methods to create low dimensional embedding of the categorical features.
The idea came from spectral word embedding, spectral clustering and spectral dimensionality reduction algorithms.
If you can define a similarity measure between different values of the categorical features, we can use spectral analysis methods to find the low dimensional representation of the categorical feature.
From the similarity function (or kernel function) we can construct an Adjacency matrix, which is a symmetric matrix, where the ij element is the value of the kernel function between category values i and j:
$$ A_{ij} = K(i,j) \tag{1}$$
It is very important that I only need a Kernel function, not a high-dimensional representation. This means that 1-hot encoding step is not necessary here. Also for the kernel-base machine learning methods, the categorical variable encoding step is not necessary as well, because what matters is the kernel function between two points, which can be constructed using the individual kernel functions.
Once the adjacency matrix is constructed, we can construct a degree matrix:
$$ D_{ij} = \delta_{ij} \sum_{k}{A_{ik}} \tag{2} $$
Here $\delta$ is the Kronecker delta symbol. The Laplacian matrix is the difference between the two:
$$ L = D - A \tag{3} $$
And the normalize Laplacian matrix is defined as:
$$ \mathscr{L} = D^{-\frac{1}{2}} L D^{-\frac{1}{2}} \tag{4} $$
Following the Spectral Graph theory, we proceed with eigendecomposition of the normalized Laplacian matrix. The number of zero eigenvalues correspond to the number of connected components. In our case, let's assume that our categorical feature has two sets of values that are completely dissimilar. This means that the kernel function $K(i,j)$ is zero if $i$ and $j$ belong to different groups. In this case we will have two zero eigenvalues of the normalized Laplacian matrix.
If there is only one connected component, we will have only one zero eigenvalue. Normally it is uninformative and is dropped to prevent multicollinearity of features. However we can keep it if we are planning to use tree-based models.
The lower eigenvalues correspond to "smooth" eigenvectors (or modes), that are following the similarity function more closely. We want to keep only these eigenvectors and drop the eigenvectors with higher eigenvalues, because they are more likely represent noise. It is very common to look for a gap in the matrix spectrum and pick the eigenvalues below the gap. The resulting truncated eigenvectors can be normalized and represent embeddings of the categorical feature values.
As an example, let's consider the Day of Week. 1-hot encoding assumes every day is similar to any other day ($K(i,j) = 1$). This is not a likely assumption, because we know that days of the week are different. For example, the bar attendance spikes on Fridays and Saturdays (at least in USA) because the following day is a weekend. Label encoding is also incorrect, because it will make the "distance" between Monday and Wednesday twice higher than between Monday and Tuesday. And the "distance" between Sunday and Monday will be six times higher, even though the days are next to each other. By the way, the label encoding corresponds to the kernel $K(i, j) = exp(-\gamma |i-j|)$
```
import numpy as np
import pandas as pd
np.set_printoptions(linewidth=130)
def normalized_laplacian(A):
'Compute normalized Laplacian matrix given the adjacency matrix'
d = A.sum(axis=0)
D = np.diag(d)
L = D-A
D_rev_sqrt = np.diag(1/np.sqrt(d))
return D_rev_sqrt @ L @ D_rev_sqrt
```
We will consider an example, where weekdays are similar to each other, but differ a lot from the weekends.
```
#The adjacency matrix for days of the week
A_dw = np.array([[0,10,9,8,5,2,1],
[0,0,10,9,5,2,1],
[0,0,0,10,8,2,1],
[0,0,0,0,10,2,1],
[0,0,0,0,0,5,3],
[0,0,0,0,0,0,10],
[0,0,0,0,0,0,0]])
A_dw = A_dw + A_dw.T
A_dw
#The normalized Laplacian matrix for days of the week
L_dw_noem = normalized_laplacian(A_dw)
L_dw_noem
#The eigendecomposition of the normalized Laplacian matrix
sz, sv = np.linalg.eig(L_dw_noem)
sz
```
Notice, that the eigenvalues are not ordered here. Let's plot the eigenvalues, ignoring the uninformative zero.
```
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
sns.stripplot(data=sz[1:], jitter=False, );
```
We can see a pretty substantial gap between the first eigenvalue and the rest of the eigenvalues. If this does not give enough model performance, you can include the second eigenvalue, because the gap between it and the higher eigenvalues is also quite substantial.
Let's print all eigenvectors:
```
sv
```
Look at the second eigenvector. The weekend values have a different size than the weekdays and Friday is close to zero. This proves the transitional role of Friday, that, being a day of the week, is also the beginning of the weekend.
If we are going to pick two lowest non-zero eigenvalues, our categorical feature encoding will result in these category vectors:
```
#Picking only two eigenvectors
category_vectors = sv[:,[1,3]]
category_vectors
category_vector_frame=pd.DataFrame(category_vectors, index=['mon', 'tue', 'wed', 'thu', 'fri', 'sat', 'sun'],
columns=['col1', 'col2']).reset_index()
sns.scatterplot(data=category_vector_frame, x='col1', y='col2', hue='index');
```
In the plot above we see that Monday and Tuesday, and also Saturday and Sunday are clustered close together, while Wednesday, Thursday and Friday are far apart.
## Learning the kernel function
In the previous example we assumed that the similarity function is given. Sometimes this is the case, where it can be defined based on the business rules. However it may be possible to learn it from data.
One of the ways to compute the Kernel is using [Wasserstein distance](https://en.wikipedia.org/wiki/Wasserstein_metric). It is a good way to tell how far apart two distributions are.
The idea is to estimate the data distribution (including the target variable, but excluding the categorical variable) for each value of the categorical variable. If for two values the distributions are similar, then the divergence will be small and the similarity value will be large. As a measure of similarity I choose the RBF kernel (Gaussian radial basis function):
$$ A_{ij} = exp(-\gamma W(i, j)^2) \tag{5}$$
Where $W(i,j)$ is the Wasserstein distance between the data distributions for the categories i and j, and $\gamma$ is a hyperparameter that has to be tuned
To try this approach will will use [liquor sales data set](https://www.kaggle.com/residentmario/iowa-liquor-sales/downloads/iowa-liquor-sales.zip/1). To keep the file small I removed some columns and aggregated the data.
```
liq = pd.read_csv('Iowa_Liquor_agg.csv', dtype={'Date': 'str', 'Store Number': 'str', 'Category': 'str', 'orders': 'int', 'sales': 'float'},
parse_dates=True)
liq.Date = pd.to_datetime(liq.Date)
liq.head()
```
Since we care about sales, let's encode the day of week using the information from the sales column
Let's check the histogram first:
```
sns.distplot(liq.sales, kde=False);
```
We see that the distribution is very skewed, so let's try to use log of sales columns instead
```
sns.distplot(np.log10(1+liq.sales), kde=False);
```
This is much better. So we will use a log for our distribution
```
liq["log_sales"] = np.log10(1+liq.sales)
```
Here we will follow [this blog](https://amethix.com/entropy-in-machine-learning/) for computation of the Kullback-Leibler divergence.
Also note, that since there are no liquor sales on Sunday, we consider only six days in a week
```
from scipy.stats import wasserstein_distance
from numpy import histogram
from scipy.stats import iqr
def dw_data(i):
return liq[liq.Date.dt.dayofweek == i].log_sales
def wass_from_data(i,j):
return wasserstein_distance(dw_data(i), dw_data(j)) if i > j else 0.0
distance_matrix = np.fromfunction(np.vectorize(wass_from_data), (6,6))
distance_matrix += distance_matrix.T
distance_matrix
```
As we already mentioned, the hyperparameter $\gamma$ has to be tuned. Here we just pick the value that will give a plausible result
```
gamma = 100
kernel = np.exp(-gamma * distance_matrix**2)
np.fill_diagonal(kernel, 0)
kernel
norm_lap = normalized_laplacian(kernel)
sz, sv = np.linalg.eig(norm_lap)
sz
sns.stripplot(data=sz[1:], jitter=False, );
```
Ignoring the zero eigenvalue, we can see that there is a bigger gap between the first eigenvalue and the rest of the eigenvalues, even though the values are all in the range between 1 and 1.3. Looking at the eigenvectors,
```
sv
```
Ultimately the number of eigenvectors to use is another hyperparameter, that should be optimized on a supervised learning task. The Category field is another candidate to do spectral analysis, and is, probably, a better choice since it has more unique values
```
len(liq.Category.unique())
unique_categories = liq.Category.unique()
def dw_data_c(i):
return liq[liq.Category == unique_categories[int(i)]].log_sales
def wass_from_data_c(i,j):
return wasserstein_distance(dw_data_c(i), dw_data_c(j)) if i > j else 0.0
#WARNING: THIS WILL TAKE A LONG TIME
distance_matrix = np.fromfunction(np.vectorize(wass_from_data_c), (107,107))
distance_matrix += distance_matrix.T
distance_matrix
def plot_eigenvalues(gamma):
"Eigendecomposition of the kernel and plot of the eigenvalues"
kernel = np.exp(-gamma * distance_matrix**2)
np.fill_diagonal(kernel, 0)
norm_lap = normalized_laplacian(kernel)
sz, sv = np.linalg.eig(norm_lap)
sns.stripplot(data=sz[1:], jitter=True, );
plot_eigenvalues(100);
```
We can see, that a lot of eigenvalues are grouped around the 1.1 mark. The eigenvalues that are below that cluster can be used for encoding the Category feature.
Please also note that this method is highly sensitive on selection of hyperparameter $\gamma$. For illustration let me pick a higher and a lower gamma
```
plot_eigenvalues(500);
plot_eigenvalues(10)
```
## Conclusion and next steps
We presented a way to encode the categorical features as a low dimensional vector that preserves most of the feature similarity information. For this we use methods of Spectral analysis on the values of the categorical feature. In order to find the kernel function we can either use heuristics, or learn it using a variety of methods, for example, using Kullback–Leibler divergence of the data distribution conditional on the category value. To select the subset of the eigenvectors we used gap analysis, but what we really need is to validate this methods by analyzing a variety of datasets and both classification and regression problems. We also need to compare it with other encoding methods, for example, entity embedding using Neural Networks. The kernel function we used can also include the information about category frequency, which will help us deal with high information, but low frequency values.
| true |
code
| 0.601477 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/dribnet/clipit/blob/future/demos/CLIP_GradCAM_Visualization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# CLIP GradCAM Colab
This Colab notebook uses [GradCAM](https://arxiv.org/abs/1610.02391) on OpenAI's [CLIP](https://openai.com/blog/clip/) model to produce a heatmap highlighting which regions in an image activate the most to a given caption.
**Note:** Currently only works with the ResNet variants of CLIP. ViT support coming soon.
```
#@title Install dependencies
#@markdown Please execute this cell by pressing the _Play_ button
#@markdown on the left.
#@markdown **Note**: This installs the software on the Colab
#@markdown notebook in the cloud and not on your computer.
%%capture
!pip install ftfy regex tqdm matplotlib opencv-python scipy scikit-image
!pip install git+https://github.com/openai/CLIP.git
import numpy as np
import torch
import os
import torch.nn as nn
import torch.nn.functional as F
import cv2
import urllib.request
import matplotlib.pyplot as plt
import clip
from PIL import Image
from skimage import transform as skimage_transform
from scipy.ndimage import filters
#@title Helper functions
#@markdown Some helper functions for overlaying heatmaps on top
#@markdown of images and visualizing with matplotlib.
def normalize(x: np.ndarray) -> np.ndarray:
# Normalize to [0, 1].
x = x - x.min()
if x.max() > 0:
x = x / x.max()
return x
# Modified from: https://github.com/salesforce/ALBEF/blob/main/visualization.ipynb
def getAttMap(img, attn_map, blur=True):
if blur:
attn_map = filters.gaussian_filter(attn_map, 0.02*max(img.shape[:2]))
attn_map = normalize(attn_map)
cmap = plt.get_cmap('jet')
attn_map_c = np.delete(cmap(attn_map), 3, 2)
attn_map = 1*(1-attn_map**0.7).reshape(attn_map.shape + (1,))*img + \
(attn_map**0.7).reshape(attn_map.shape+(1,)) * attn_map_c
return attn_map
def viz_attn(img, attn_map, blur=True):
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(img)
axes[1].imshow(getAttMap(img, attn_map, blur))
for ax in axes:
ax.axis("off")
plt.show()
def load_image(img_path, resize=None):
image = Image.open(image_path).convert("RGB")
if resize is not None:
image = image.resize((resize, resize))
return np.asarray(image).astype(np.float32) / 255.
#@title GradCAM: Gradient-weighted Class Activation Mapping
#@markdown Our gradCAM implementation registers a forward hook
#@markdown on the model at the specified layer. This allows us
#@markdown to save the intermediate activations and gradients
#@markdown at that layer.
#@markdown To visualize which parts of the image activate for
#@markdown a given caption, we use the caption as the target
#@markdown label and backprop through the network using the
#@markdown image as the input.
#@markdown In the case of CLIP models with resnet encoders,
#@markdown we save the activation and gradients at the
#@markdown layer before the attention pool, i.e., layer4.
class Hook:
"""Attaches to a module and records its activations and gradients."""
def __init__(self, module: nn.Module):
self.data = None
self.hook = module.register_forward_hook(self.save_grad)
def save_grad(self, module, input, output):
self.data = output
output.requires_grad_(True)
output.retain_grad()
def __enter__(self):
return self
def __exit__(self, exc_type, exc_value, exc_traceback):
self.hook.remove()
@property
def activation(self) -> torch.Tensor:
return self.data
@property
def gradient(self) -> torch.Tensor:
return self.data.grad
# Reference: https://arxiv.org/abs/1610.02391
def gradCAM(
model: nn.Module,
input: torch.Tensor,
target: torch.Tensor,
layer: nn.Module
) -> torch.Tensor:
# Zero out any gradients at the input.
if input.grad is not None:
input.grad.data.zero_()
# Disable gradient settings.
requires_grad = {}
for name, param in model.named_parameters():
requires_grad[name] = param.requires_grad
param.requires_grad_(False)
# Attach a hook to the model at the desired layer.
assert isinstance(layer, nn.Module)
with Hook(layer) as hook:
# Do a forward and backward pass.
output = model(input)
output.backward(target)
grad = hook.gradient.float()
act = hook.activation.float()
# Global average pool gradient across spatial dimension
# to obtain importance weights.
alpha = grad.mean(dim=(2, 3), keepdim=True)
# Weighted combination of activation maps over channel
# dimension.
gradcam = torch.sum(act * alpha, dim=1, keepdim=True)
# We only want neurons with positive influence so we
# clamp any negative ones.
gradcam = torch.clamp(gradcam, min=0)
# Resize gradcam to input resolution.
gradcam = F.interpolate(
gradcam,
input.shape[2:],
mode='bicubic',
align_corners=False)
# Restore gradient settings.
for name, param in model.named_parameters():
param.requires_grad_(requires_grad[name])
return gradcam
#@title Run
#@markdown #### Image & Caption settings
image_url = 'https://images2.minutemediacdn.com/image/upload/c_crop,h_706,w_1256,x_0,y_64/f_auto,q_auto,w_1100/v1554995050/shape/mentalfloss/516438-istock-637689912.jpg' #@param {type:"string"}
image_caption = 'the cat' #@param {type:"string"}
#@markdown ---
#@markdown #### CLIP model settings
clip_model = "RN50" #@param ["RN50", "RN101", "RN50x4", "RN50x16"]
saliency_layer = "layer4" #@param ["layer4", "layer3", "layer2", "layer1"]
#@markdown ---
#@markdown #### Visualization settings
blur = True #@param {type:"boolean"}
device = "cuda" if torch.cuda.is_available() else "cpu"
model, preprocess = clip.load(clip_model, device=device, jit=False)
# Download the image from the web.
image_path = 'image.png'
urllib.request.urlretrieve(image_url, image_path)
image_input = preprocess(Image.open(image_path)).unsqueeze(0).to(device)
image_np = load_image(image_path, model.visual.input_resolution)
text_input = clip.tokenize([image_caption]).to(device)
attn_map = gradCAM(
model.visual,
image_input,
model.encode_text(text_input).float(),
getattr(model.visual, saliency_layer)
)
attn_map = attn_map.squeeze().detach().cpu().numpy()
viz_attn(image_np, attn_map, blur)
```
| true |
code
| 0.816168 | null | null | null | null |
|
# Chapter 4: Linear models
[Link to outline](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit#heading=h.9etj7aw4al9w)
Concept map:

#### Notebook setup
```
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
from scipy.stats import uniform, norm
# notebooks figs setup
%matplotlib inline
import matplotlib.pyplot as plt
sns.set(rc={'figure.figsize':(8,5)})
blue, orange = sns.color_palette()[0], sns.color_palette()[1]
# silence annoying warnings
import warnings
warnings.filterwarnings('ignore')
```
## 4.1 Linear models for relationship between two numeric variables
- def'n linear model: **y ~ m*x + b**, a.k.a. linear regression
- Amy has collected a new dataset:
- Instead of receiving a fixed amount of stats training (100 hours),
**each employee now receives a variable amount of stats training (anywhere from 0 hours to 100 hours)**
- Amy has collected ELV values after one year as previously
- Goal find best fit line for relationship $\textrm{ELV} \sim \beta_0 + \beta_1\!*\!\textrm{hours}$
- Limitation: **we assume the change in ELV is proportional to number of hours** (i.e. linear relationship).
Other types of hours-ELV relationship possible, but we will not be able to model them correctly (see figure below).
### New dataset
- The `hours` column contains the `x` values (how many hours of statistics training did the employee receive),
- The `ELV` column contains the `y` values (the employee ELV after one year)

```
# Load data into a pandas dataframe
df2 = pd.read_excel("data/ELV_vs_hours.ods", sheet_name="Data")
# df2
df2.describe()
# plot ELV vs. hours data
sns.scatterplot(x='hours', y='ELV', data=df2)
# linear model plot (preview)
# sns.lmplot(x='hours', y='ELV', data=df2, ci=False)
```
#### Types of linear relationship between input and output
Different possible relationships between the number of hours of stats training and ELV gains:

## 4.2 Fitting linear models
- Main idea: use `fit` method from `statsmodels.ols` and a formula (approach 1)
- Visual inspection
- Results of linear model fit are:
- `beta0` = $\beta_0$ = baseline ELV (y-intercept)
- `beta1` = $\beta_1$ = increase in ELV for each additional hour of stats training (slope)
- Five more alternative fitting methods (bonus material):
2. fit using statsmodels `OLS`
3. solution using `linregress` from `scipy`
4. solution using `optimize` from `scipy`
5. linear algebra solution using `numpy`
6. solution using `LinearRegression` model from scikit-learn
### Using statsmodels formula API
The `statsmodels` Python library offers a convenient way to specify statistics model as a "formula" that describes the relationship we're looking for.
Mathematically, the linear model is written:
$\large \textrm{ELV} \ \ \sim \ \ \beta_0\cdot 1 \ + \ \beta_1\cdot\textrm{hours}$
and the formula is:
`ELV ~ 1 + hours`
Note the variables $\beta_0$ and $\beta_1$ are omitted, since the whole point of fitting a linear model is to find these coefficients. The parameters of the model are:
- Instead of $\beta_0$, the constant parameter will be called `Intercept`
- Instead of a new name $\beta_1$, we'll call it `hours` coefficient (i.e. the coefficient associated with the `hours` variable in the model)
```
import statsmodels.formula.api as smf
model = smf.ols('ELV ~ 1 + hours', data=df2)
result = model.fit()
# extact the best-fit model parameters
beta0, beta1 = result.params
beta0, beta1
# data points
sns.scatterplot(x='hours', y='ELV', data=df2)
# linear model for data
x = df2['hours'].values # input = hours
ymodel = beta0 + beta1*x # output = ELV
sns.lineplot(x, ymodel)
result.summary()
```
### Alternative model fitting methods
2. fit using statsmodels [`OLS`](https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html)
3. solution using [`linregress`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.linregress.html) from `scipy`
4. solution using [`minimize`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html) from `scipy`
5. [linear algebra](https://numpy.org/doc/stable/reference/routines.linalg.html) solution using `numpy`
6. solution using [`LinearRegression`](https://scikit-learn.org/stable/modules/linear_model.html#ordinary-least-squares) model from scikit-learn
#### Data pre-processing
The `statsmodels` formula `ols` approach we used above was able to get the data
directly from the dataframe `df2`, but some of the other model fitting methods
require data to be provided as regular arrays: the x-values and the y-values.
```
# extract hours and ELV data from df2
x = df2['hours'].values # hours data as an array
y = df2['ELV'].values # ELV data as an array
x.shape, y.shape
# x
```
Two of the approaches required "packaging" the x-values along with a column of ones,
to form a matrix (called a design matrix). Luckily `statsmodels` provides a convenient function for this:
```
import statsmodels.api as sm
# add a column of ones to the x data
X = sm.add_constant(x)
X.shape
# X
```
____
#### 2. fit using statsmodels OLS
```
model2 = sm.OLS(y, X)
result2 = model2.fit()
# result2.summary()
result2.params
```
____
#### 3. solution using `linregress` from `scipy`
```
from scipy.stats import linregress
result3 = linregress(x, y)
result3.intercept, result3.slope
```
____
#### 4. Using an optimization approach
```
from scipy.optimize import minimize
def sse(beta, x=x, y=y):
"""Compute the sum-of-squared-errors objective function."""
sumse = 0.0
for xi, yi in zip(x, y):
yi_pred = beta[0] + beta[1]*xi
ei = (yi_pred-yi)**2
sumse += ei
return sumse
result4 = minimize(sse, x0=[0,0])
beta0, beta1 = result4.x
beta0, beta1
```
____
#### 5. Linear algebra solution
We obtain the least squares solution using the Moore–Penrose inverse formula:
$$ \large
\vec{\beta} = (X^{\sf T} X)^{-1}X^{\sf T}\; \vec{y}
$$
```
# 5. linear algebra solution using `numpy`
import numpy as np
result5 = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
beta0, beta1 = result5
beta0, beta1
```
_____
#### Using scikit-learn
```
# 6. solution using `LinearRegression` from scikit-learn
from sklearn import linear_model
model6 = linear_model.LinearRegression()
model6.fit(x[:,np.newaxis], y)
model6.intercept_, model6.coef_
```
## 4.3 Interpreting linear models
- model fit checks
- $R^2$ [coefficient of determination](https://en.wikipedia.org/wiki/Coefficient_of_determination)
= the proportion of the variation in the dependent variable that is predictable from the independent variable
- plot of residuals
- many other: see [scikit docs](https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics)
- hypothesis tests
- is slope zero or nonzero? (and CI interval)
- caution: cannot make any cause-and-effect claims; only a correlation
- Predictions
- given best-fir model obtained from data, we can make predictions (interpolations),
e.g., what is the expected ELV after 50 hours of stats training?
### Interpreting the results
Let's review some of the other data included in the `results.summary()` report for the linear model fit we did earlier.
```
result.summary()
```
### Model parameters
```
beta0, beta1 = result.params
result.params
```
### The $R^2$ coefficient of determination
$R^2 = 1$ corresponds to perfect prediction
```
result.rsquared
```
### Hypothesis testing for slope coefficient
Is there a non-zero slope coefficient?
- **null hypothesis $H_0$**: `hours` has no effect on `ELV`,
which is equivalent to $\beta_1 = 0$:
$$ \large
H_0: \qquad \textrm{ELV} \sim \mathcal{N}(\color{red}{\beta_0}, \sigma^2) \qquad \qquad \qquad
$$
- **alternative hypothesis $H_A$**: `hours` has an effect on `ELV`,
and the slope is not zero, $\beta_1 \neq 0$:
$$ \large
H_A: \qquad \textrm{ELV}
\sim
\mathcal{N}\left(
\color{blue}{\beta_0 + \beta_1\!\cdot\!\textrm{hours}},
\ \sigma^2
\right)
$$
```
# p-value under the null hypotheis of zero slope or "no effect of `hours` on `ELV`"
result.pvalues.loc['hours']
# 95% confidence interval for the hours-slope parameter
# result.conf_int()
CI_hours = list(result.conf_int().loc['hours'])
CI_hours
```
### Predictions using the model
We can use the model we obtained to predict (interpolate) the ELV for future employees.
```
sns.scatterplot(x='hours', y='ELV', data=df2)
ymodel = beta0 + beta1*x
sns.lineplot(x, ymodel)
```
What ELV can we expect from a new employee that takes 50 hours of stats training?
```
result.predict({'hours':[50]})
result.predict({'hours':[100]})
```
**WARNING**: it's not OK to extrapolate the validity of the model outside of the range of values where we have observed data.
For example, there is no reason to believe in the model's predictions about ELV for 200 or 2000 hours of stats training:
```
result.predict({'hours':[200]})
```
## Discussion
Further topics that will be covered in the book:
- Generalized linear models, e.g., [Logistic regression](https://en.wikipedia.org/wiki/Logistic_regression)
- [Everything is a linear model](https://www.eigenfoo.xyz/tests-as-linear/) article
- The verbs `fit` and `predict` will come up A LOT in machine learning,
so it's worth learning linear models in detail to be prepared for further studies.
____
Congratulations on completing this overview of statistics! We covered a lot of topics and core ideas from the book. I know some parts seemed kind of complicated at first, but if you think about them a little you'll see there is nothing too difficult to learn. The good news is that the examples in these notebooks contain all the core ideas, and you won't be exposed to anything more complicated that what you saw here!
If you were able to handle these notebooks, you'll be able to handle the **No Bullshit Guide to Statistics** too! In fact the book will cover the topics in a much smoother way, and with better explanations. You'll have a lot of exercises and problems to help you practice statistical analysis.
### Next steps
- I encourage you to check out the [book outline shared gdoc](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit) if you haven't seen it already. Please leave me a comment in the google document if you see something you don't like in the outline, or if you think some important statistics topics are missing. You can also read the [book proposal blog post](https://minireference.com/blog/no-bullshit-guide-to-statistics-progress-update/) for more info about the book.
- Check out also the [concept map](https://minireference.com/static/excerpts/noBSstats/conceptmaps/BookSubjectsOverview.pdf). You can print it out and annotate with the concepts you heard about in these notebooks.
- If you want to be involved in the stats book in the coming months, sign up to the [stats reviewers mailing list](https://confirmsubscription.com/h/t/A17516BF2FCB41B2) to receive chapter drafts as they are being prepared (Nov+Dec 2021). I'll appreciate your feedback on the text. The goal is to have the book finished in the Spring 2022, and feedback and "user testing" will be very helpful.
| true |
code
| 0.69394 | null | null | null | null |
|
# Project 3 Sandbox-Blue-O, NLP using webscraping to create the dataset
## Objective: Determine if posts are in the SpaceX Subreddit or the Blue Origin Subreddit
We'll utilize the RESTful API from pushshift.io to scrape subreddit posts from r/blueorigin and r/spacex and see if we cannot use the Bag-of-words algorithm to predict which posts are from where.
Author: Matt Paterson, [email protected]
This notebook is the SANDBOX and should be used to play around. The formal presentation will be in a different notebook
```
import requests
from bs4 import BeautifulSoup
import pandas as pd
import lebowski as dude
from sklearn.feature_extraction.text import CountVectorizer
import re, regex
# Establish a connection to the API and search for a specific keyword. Maybe we'll add this function to the
# lebowski library? Or maybe make a new and slicker Library called spaceman or something
# CREDIT: code below adapted from Riley Dallas Lesson on webscraping
# keyword = 'propulsion'
# url_boeing = 'https://api.pushshift.io/reddit/search/comment/?q=' + keyword + '&subreddit=boeing'
# res = requests.get(url_boeing)
# res.status_code
# instantiate a Beautiful Soup object for Boeing
#boeing = BeautifulSoup(res.content, 'lxml')
#boeing.find("body")
spacex = dude.create_lexicon('spacex', 5000)
blueorigin = dude.create_lexicon('blueorigin', 5000)
spacex.head()
blueorigin.head()
spacex[['subreddit', 'selftext', 'title']].head() # predict the subreddit column
blueorigin[['subreddit', 'selftext', 'title']].head() # predict the subreddit column
print('Soux City Sarsparilla?') # silly print statement to check progress of long print
spacex_comments = dude.create_lexicon('spacex', 5000, post_type='comment')
spacex_comments.head()
spacex_comments[['subreddit', 'body']].head() # predict the subreddit column
blueorigin_comments = dude.create_lexicon('blueorigin', 5000, post_type='comment')
blueorigin_comments[['subreddit', 'body']].head() # predict the subreddit column
blueorigin_comments.columns
```
There's not a "title" column in the comments dataframe, so how is the comment tied to the original post?
```
# View the first entry in the dataframe and see if you can find that answer
# permalink?
blueorigin_comments.iloc[0]
```
IN EDA below, we find: "We have empty rows in 'body' in many columns. It's likely that all of those are postings, not comments, and we should actually map the postings to the body for those before merging the datafrmes."
```
def strip_and_rep(word):
if len(str(word).strip().replace(" ", "")) < 1:
return 'replace_me'
else:
return word
blueorigin['selftext'] = blueorigin['selftext'].map(strip_and_rep)
spacex['selftext'] = spacex['selftext'].map(strip_and_rep)
spacex.selftext.isna().sum()
blueorigin.selftext.isna().sum()
blueorigin.selftext.head()
spacex.iloc[2300:2320]
blo_coms = blueorigin_comments[['subreddit', 'body', 'permalink']]
blo_posts = blueorigin[['subreddit', 'selftext', 'permalink']].copy()
spx_coms = spacex_comments[['subreddit', 'body', 'permalink']]
spx_posts = spacex[['subreddit', 'selftext', 'permalink']].copy()
#blueorigin['selftext'][len(blueorigin['selftext'])>0]
type(blueorigin.selftext.iloc[1])
blo_posts.rename(columns={'selftext': 'body'}, inplace=True)
spx_posts.rename(columns={'selftext': 'body'}, inplace=True)
# result = pd.concat(frames)
space_wars_2 = pd.concat([blo_coms, blo_posts, spx_coms, spx_posts])
space_wars_2.shape
space_wars_2.head()
dude.show_details(space_wars_2)
```
We have empty rows in 'body' in many columns. It's likely that all of those are postings, not comments, and we should actually map the postings to the body for those before merging the datafrmes.
However, when trying that above, we ended up with more null values. Mapping 'replace_me' in to empty fileds kept the number of null values low. We'll add that token to our stop_words dictionary when creating the BOW from this corpus.
```
space_wars_2.dropna(inplace=True)
space_wars_2.isna().sum()
space_wars.to_csv('./data/betaset.csv', index=False)
```
# Before we split up the training and testing sets, establish our X and y. If you need to reset the dataframe, run the next cell FIRST
keyword = RESET
```
space_wars_2 = pd.read_csv('./data/betaset.csv')
space_wars_2.columns
```
I believe that the 'permalink' will be almost as indicative as the 'subreddit' that we are trying to predict, so the X will only include the words...
```
space_wars_2.head()
```
## Convert target column to binary before moving forward
We want to predict whether this post is Spacex, 1, or is not Spacex, 0
```
space_wars_2['subreddit'].value_counts()
space_wars_2['subreddit'] = space_wars_2['subreddit'].map({'spacex': 1, 'BlueOrigin': 0})
space_wars_2['subreddit'].value_counts()
X = space_wars_2.body
y = space_wars_2.subreddit
```
Calculate our baseline split
```
space_wars_2.subreddit.value_counts(normalize=True)
base_set = space_wars_2.subreddit.value_counts(normalize=True)
baseline = 0.0
if base_set[0] > base_set[1]:
baseline = base_set[0]
else:
baseline = base_set[1]
baseline
```
Before we sift out stopwords, etc, let's just run a logistic regression on the words, as well as a decision tree:
```
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score
```
## Before we can fit the models we need to convert the data to numbers...we can use CountVectorizer or TF-IDF for this
```
# from https://stackoverflow.com/questions/5511708/adding-words-to-nltk-stoplist
# add certain words to the stop_words library
import nltk
stopwords = nltk.corpus.stopwords.words('english')
new_words=('replace_me', 'removed', 'deleted', '0','1', '2', '3', '4', '5', '6', '7', '8','9', '00', '000')
for i in new_words:
stopwords.append(i)
print(stopwords)
space_wars_2.isna().sum()
space_wars_2.dropna(inplace=True)
# This section, next number of cells, borrowed from Noelle's lesson on NLP EDA
# Instantiate the "CountVectorizer" object, which is sklearn's
# bag of words tool.
cnt_vec = CountVectorizer(analyzer = "word",
tokenizer = None,
preprocessor = None,
stop_words = stopwords,
max_features = 5000)
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=.20,
random_state=42,
stratify=y)
```
Keyword = CHANGELING
```
y_test
# This section, next number of cells, borrowed from Noelle's lesson on NLP EDA
# fit_transform() does two things: First, it fits the model and
# learns the vocabulary; second, it transforms our training data
# into feature vectors. The input to fit_transform should be a
# list of strings.
train_data_features = cnt_vec.fit_transform(X_train, y_train)
test_data_features = cnt_vec.transform(X_test)
train_data_features.shape
train_data_df = pd.DataFrame(train_data_features)
test_data_features.shape
test_data_df = pd.DataFrame(test_data_features)
test_data_df['subreddit']
lr = LogisticRegression( max_iter = 10_000)
lr.fit(train_data_features, y_train)
train_data_features.shape
dt = DecisionTreeClassifier()
dt.fit(train_data_features, y_train)
print('Logistic Regression without doing anything, really:', lr.score(train_data_features, y_train))
print('Decision Tree without doing anything, really:', dt.score(train_data_features, y_train))
print('*'*80)
print('Logistic Regression Test Score without doing anything, really:', lr.score(test_data_features, y_test))
print('Decision Tree Test Score without doing anything, really:', dt.score(test_data_features, y_test))
print('*'*80)
print(f'The baseline split is {baseline}')
```
So we see that we are above our baseline of 57% accuracy by only guessing a single subreddit without trying to predict. We also see that our initial runs without any GridSearch or HPO tuning gives us a fairly overfit model for either mode.
**Let's see next what happens when we sift through our data with stopwords, etc, to really clean up the dataset and also let's do some comparative EDA including comparing lengths of posts, etc. Finally we can create a sepatate dataframe with engineered features and try running a Logistic Regression model using only descriptors in the dataset such as post lenth, word length, most common words, etc.**
## Deep EDA of our words
```
space_wars.shape
space_wars.describe()
```
## Feature Engineering
Map word count and character length funcitons on to the 'body' column to see a difference in each.
```
def word_count(string):
'''
returns the number of words or tokens in a string literal, splitting on spaces,
regardless of word lenth. This function will include space-separated
punctuation as a word, such as " : " where the colon would be counted
string, a string
'''
str_list = string.split()
return len(str_list)
def count_chars(string):
'''
returns the total number of characters including spaces in a string literal
string, a string
'''
count=0
for s in string:
count+=1
return count
import lebowski as dude
space_wars['word_count'] = space_wars['body'].map(word_count)
space_wars['word_count'].value_counts().head()
# code from https://stackoverflow.com/questions/39132742/groupby-value-counts-on-the-dataframe-pandas
#df.groupby(['id', 'group', 'term']).size().unstack(fill_value=0)
space_wars.groupby(['subreddit', 'word_count']).size().head()
space_wars['post_length'] = space_wars['body'].map(count_chars)
space_wars['post_length'].value_counts().head()
space_wars.columns
import seaborn as sns
import matplotlib.pyplot as plt
sns.distplot(space_wars['word_count'])
# Borrowing from Noelle's nlp II lesson, import the following,
# and think about what you want to use in the presentation
# imports
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix, plot_confusion_matrix
# Import CountVectorizer and TFIDFVectorizer from feature_extraction.text.
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
```
## Text Feature Extraction
## Follow along in the NLP EDA II video and do some analysis
```
X_train_df = pd.DataFrame(train_data_features.toarray(),
columns=cntv.get_feature_names())
X_train_df
X_train_df['subreddit']
# get count of top-occurring words
# empty dictionary
top_words = {}
# loop through columns
for i in X_train_df.columns:
# save sum of each column in dictionary
top_words[i] = X_train_df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq = pd.DataFrame(sorted(top_words.items(), key = lambda x: x[1], reverse = True))
most_freq.head()
# Make a different CountVectorizer
count_v = CountVectorizer(analyzer='word',
stop_words = stopwords,
max_features = 1_000,
min_df = 50,
max_df = .80,
ngram_range=(2,3),
)
# Redefine the training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = .1,
stratify = y,
random_state=42)
baseline
```
## Implement Naive Bayes because it's in the project instructions
Multinomial Naive Bayes often outperforms other models despite text data being non-independent data
```
pipe = Pipeline([
('count_v', CountVectorizer()),
('nb', MultinomialNB())
])
pipe_params = {
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
gs = GridSearchCV(pipe,
pipe_params,
cv = 5,
n_jobs=6
)
%%time
gs.fit(X_train, y_train)
gs.best_params_
print(gs.best_score_)
gs.score(X_train, y_train)
gs.score(X_test, y_test)
```
So far, the Multinomial Naive Bayes Algorithm is the top function at 79.28% Accuracy. The confusion matrix below is very simiar to that of other models
```
# Get predictions
preds = gs.predict(X_test)
# Save confusion matrix values
tn, fp, fn, tp = confusion_matrix(y_test, preds).ravel()
# View confusion matrix
plot_confusion_matrix(gs, X_test, y_test, cmap='Blues', values_format='d');
# Calculate the specificity
spec = tn / (tn + fp)
print('Specificity:', spec)
```
None of the 1620 different models we tried in this pipeline performed noticibly better than the thrown-together Logistic Regression Classifier that we started out with. Let's try TF-IDF, then Random Cut Forest, and finally Vector Machines. Our last run brought the best accuracy score to 79.3%
# TF-IDF
```
# Redefine the training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = .1,
stratify = y,
random_state=42)
tvec = TfidfVectorizer(stop_words=stopwords)
df = pd.DataFrame(tvec.fit_transform(X_train).toarray(),
columns=tvec.get_feature_names())
df.head()
# get count of top-occurring words
top_words_tf = {}
for i in df.columns:
top_words_tf[i] = df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq_tf = pd.DataFrame(sorted(top_words_tf.items(), key = lambda x: x[1], reverse = True))
plt.figure(figsize = (10, 5))
# visualize top 10 words
plt.bar(most_freq_tf[0][:10], most_freq_tf[1][:10]);
pipe_tvec = Pipeline([
('tvec', TfidfVectorizer()),
('nb', MultinomialNB())
])
pipe_params_tvec = {
'tvec__max_features': [2000, 9000],
'tvec__stop_words' : [None, stopwords],
'tvec__ngram_range': [(1, 1), (1, 2)]
}
gs_tvec = GridSearchCV(pipe_tvec, pipe_params_tvec, cv = 5)
%%time
gs_tvec.fit(X_train, y_train)
gs_tvec.best_params_
gs_tvec.score(X_train, y_train)
gs_tvec.score(X_test, y_test)
# Get predictions
preds = gs_tvec.predict(X_test)
# Save confusion matrix values
tn, fp, fn, tp = confusion_matrix(y_test, preds).ravel()
# View confusion matrix
plot_confusion_matrix(gs_tvec, X_test, y_test, cmap='Blues', values_format='d');
# Calculate the specificity
spec = tn / (tn + fp)
print('Specificity:', spec)
```
## Random Cut Forest, Bagging, and Support Vector Machines
```
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
```
Before we run the decision tree model or RandomForestClassifier(), we need to convert all of the data to numeric data
```
rf = RandomForestClassifier()
et = ExtraTreesClassifier()
cross_val_score(rf, train_data_features, X_train_df['subreddit']).mean()
cross_val_score(et, train_data_features, X_train_df['subreddit']).mean()
#cross_val_score(rf, test_data_features, y_test).mean()
```
## Make sure that we are using X and y data that are completely numeric and free of nulls
```
space_wars.head(1)
space_wars.shape
pipe_rf = Pipeline([
('count_v', CountVectorizer()),
('rf', RandomForestClassifier()),
])
pipe_ef = Pipeline([
('count_v', CountVectorizer()),
('ef', ExtraTreesClassifier()),
])
pipe_params =
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
%%time
gs_rf = GridSearchCV(pipe_rf,
pipe_params,
cv = 5,
n_jobs=6)
gs_rf.fit(X_train, y_train)
print(gs_rf.best_score_)
gs_rf.best_params_
gs_rf.score(X_train, y_train)
gs_rf.score(X_test, y_test)
# %%time
# gs_ef = GridSearchCV(pipe_ef,
# pipe_params,
# cv = 5,
# n_jobs=6)
# gs_ef.fit(X_train, y_train)
# print(gs_ef.best_score_)
# gs_ef.best_params_
#gs_ef.score(X_train, y_train)
#gs_ef.score(X_test, y_test)
```
## Now run through Gradient Boosting and SVM
```
from sklearn.ensemble import GradientBoostingClassifier, AdaBoostClassifier, VotingClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
```
Using samples from Riley's Lessons:
```
AdaBoostClassifier()
GradientBoostingClassifier()
```
Use the CountVectorizer to convert the data to numeric data prior to running it through the below VotingClassifier
```
'count_v__max_df': 0.9,
'count_v__max_features': 9000,
'count_v__min_df': 2,
'count_v__ngram_range': (1, 1),
knn_pipe = Pipeline([
('ss', StandardScaler()),
('knn', KNeighborsClassifier())
])
%%time
vote = VotingClassifier([
('ada', AdaBoostClassifier(base_estimator=DecisionTreeClassifier())),
('grad_boost', GradientBoostingClassifier()),
('tree', DecisionTreeClassifier()),
('knn_pipe', knn_pipe)
])
params = {}
# 'ada__n_estimators': [50, 51],
# 'grad_boost__n_estimators': [10, 11],
# 'knn_pipe__knn__n_neighbors': [5],
# 'ada__base_estimator__max_depth': [1, 2],
# 'weights': [[.25] * 4, [.3, .3, .3, .1]]
# }
gs = GridSearchCV(vote, param_grid=params, cv=3)
gs.fit(X_train, y_train)
print(gs.best_score_)
gs.best_params_
```
| true |
code
| 0.405449 | null | null | null | null |
|
By now basically everyone ([here](http://datacolada.org/2014/06/04/23-ceiling-effects-and-replications/?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed%3A+DataColada+%28Data+Colada+Feed%29), [here](http://yorl.tumblr.com/post/87428392426/ceiling-effects), [here](http://www.talyarkoni.org/blog/2014/06/01/there-is-no-ceiling-effect-in-johnson-cheung-donnellan-2014/), [here](http://pigee.wordpress.com/2014/05/24/additional-reflections-on-ceiling-effects-in-recent-replication-research/) and [here](http://www.nicebread.de/reanalyzing-the-schnalljohnson-cleanliness-data-sets-new-insights-from-bayesian-and-robust-approaches/), and there is likely even more out there) who writes a blog and knows how to do a statistical analysis has analysed data from a recent replication study and from the original study (data repository is here).
The study of two experiments. Let's focus on Experiment 1 here. The experiment consists of a treatment and control group. The performance is measured by six likert-scale items. The scale has 9 levels. All responses are averaged together and we obtain a single composite score for each group. We are interested whether the treatment works, which would show up as a positive difference between the score of the treatment and the control group. Replication study did the same with more subjects.
Let's perform the original analysis to see the results and why this dataset is so "popular".
```
%pylab inline
import pystan
from matustools.matusplotlib import *
from scipy import stats
il=['dog','trolley','wallet','plane','resume','kitten','mean score','median score']
D=np.loadtxt('schnallstudy1.csv',delimiter=',')
D[:,1]=1-D[:,1]
Dtemp=np.zeros((D.shape[0],D.shape[1]+1))
Dtemp[:,:-1]=D
Dtemp[:,-1]=np.median(D[:,2:-2],axis=1)
D=Dtemp
DS=D[D[:,0]==0,1:]
DR=D[D[:,0]==1,1:]
DS.shape
def plotCIttest1(y,x=0,alpha=0.05):
m=y.mean();df=y.size-1
se=y.std()/y.size**0.5
cil=stats.t.ppf(alpha/2.,df)*se
cii=stats.t.ppf(0.25,df)*se
out=[m,m-cil,m+cil,m-cii,m+cii]
_errorbar(out,x=x,clr='k')
return out
def plotCIttest2(y1,y2,x=0,alpha=0.05):
n1=float(y1.size);n2=float(y2.size);
v1=y1.var();v2=y2.var()
m=y2.mean()-y1.mean()
s12=(((n1-1)*v1+(n2-1)*v2)/(n1+n2-2))**0.5
se=s12*(1/n1+1/n2)**0.5
df= (v1/n1+v2/n2)**2 / ( (v1/n1)**2/(n1-1)+(v2/n2)**2/(n2-1))
cil=stats.t.ppf(alpha/2.,df)*se
cii=stats.t.ppf(0.25,df)*se
out=[m,m-cil,m+cil,m-cii,m+cii]
_errorbar(out,x=x)
return out
plt.figure(figsize=(4,3))
dts=[DS[DS[:,0]==0,-2],DS[DS[:,0]==1,-2],
DR[DR[:,0]==0,-2],DR[DR[:,0]==1,-2]]
for k in range(len(dts)):
plotCIttest1(dts[k],x=k)
plt.grid(False,axis='x')
ax=plt.gca()
ax.set_xticks(range(len(dts)))
ax.set_xticklabels(['OC','OT','RC','RT'])
plt.xlim([-0.5,len(dts)-0.5])
plt.figure(figsize=(4,3))
plotCIttest2(dts[0],dts[1],x=0,alpha=0.1)
plotCIttest2(dts[2],dts[3],x=1,alpha=0.1)
ax=plt.gca()
ax.set_xticks([0,1])
ax.set_xticklabels(['OT-OC','RT-RC'])
plt.grid(False,axis='x')
plt.xlim([-0.5,1.5]);
```
Legend: OC - original study, control group; OT - original study, treatment group; RC - replication study, control group; RT - replication study, treatment group;
In the original study the difference between the treatment and control is significantly greater than zero. In the replication, it is not. However the ratings in the replication are higher overall. The author of the original study therefore raised a concern that no difference was obtained in replication because of ceiling effects.
How do we show that there are ceiling efects in the replication? The authors and bloggers presented various arguments that support some conclusion (mostly that there are no ceiling effects). Ultimately ceiling effects are a matter of degree and since no one knows how to quantify them the whole discussion of the replication's validity is heading into an inferential limbo.
My point here is that if the analysis computed the proper effect size - the causal effect size, we would avoid these kinds of arguments and discussions.
```
def plotComparison(A,B,stan=False):
plt.figure(figsize=(8,16))
cl=['control','treatment']
x=np.arange(11)-0.5
if not stan:assert A.shape[1]==B.shape[1]
for i in range(A.shape[1]-1):
for cond in range(2):
plt.subplot(A.shape[1]-1,2,2*i+cond+1)
a=np.histogram(A[A[:,0]==cond,1+i],bins=x, normed=True)
plt.barh(x[:-1],-a[0],ec='w',height=1)
if stan: a=[B[:,i,cond]]
else: a=np.histogram(B[B[:,0]==cond,1+i],bins=x, normed=True)
plt.barh(x[:-1],a[0],ec='w',fc='g',height=1)
#plt.hist(DS[:,2+i],bins=np.arange(11)-0.5,normed=True,rwidth=0.5)
plt.xlim([-0.7,0.7]);plt.gca().set_yticks(range(10))
plt.ylim([-1,10]);#plt.grid(b=False,axis='y')
if not i: plt.title('condition: '+cl[cond])
if not cond: plt.ylabel(il[i],size=12)
if not i and not cond: plt.legend(['original','replication'],loc=4);
plotComparison(DS,DR)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
real beta[M];
ordered[K-1] c[M];
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
for (m in 1:M){
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[m]-c[m][k]);
pc[m,k] <- inv_logit(-c[m][k]);
}}}
model {
for (m in 1:M){
for (k in 1:(K-1)) c[m][k]~ uniform(-100,100);
for (n in 1:N) y[n,m] ~ ordered_logistic(x[n] * beta[m], c[m]);
}}
'''
sm1=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit = sm1.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit
pt=fit.extract()['pt']
pc=fit.extract()['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
real beta;
ordered[K-1] c[M];
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
for (m in 1:M){
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta-c[m][k]);
pc[m,k] <- inv_logit(-c[m][k]);
}}}
model {
for (m in 1:M){
for (k in 1:(K-1)) c[m][k]~ uniform(-100,100);
for (n in 1:N) y[n,m] ~ ordered_logistic(x[n] * beta, c[m]);
}}
'''
sm2=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit2 = sm2.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit2
saveStanFit(fit2,'fit2')
w=loadStanFit('fit2')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[2*M-1] bbeta;
ordered[K-1] c;
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
vector[M] beta[2];
for (m in 1:M){
if (m==1){beta[1][m]<-0.0; beta[2][m]<-bbeta[2*M-1];}
else{beta[1][m]<-bbeta[2*(m-1)-1]; beta[2][m]<-bbeta[2*(m-1)];}
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[2][m]-c[k]);
pc[m,k] <- inv_logit(beta[1][m]-c[k]);
}}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
//beta[1]~normal(0.0,sb[1]);
//beta[2]~normal(mb,sb[2]);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[x[n]+1][m], c);
}}
'''
sm3=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit3 = sm3.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
#print fit3
saveStanFit(fit3,'fit3')
w=loadStanFit('fit3')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[M-1] bbeta;
real delt;
ordered[K-1] c;
}
transformed parameters{
real pt[M,K-1]; real pc[M,K-1];
vector[M] beta;
for (m in 1:M){
if (m==1) beta[m]<-0.0;
else beta[m]<-bbeta[m-1];
for (k in 1:(K-1)){
pt[m,k] <- inv_logit(beta[m]+delt-c[k]);
pc[m,k] <- inv_logit(beta[m]-c[k]);
}}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[m]+delt*x[n], c);
}}
'''
sm4=pystan.StanModel(model_code=model)
dat = {'y':np.int32(DS[:,1:7])+1,'x':np.int32(DS[:,0]),'N':DS.shape[0] ,'K':10,'M':6}
fit4 = sm4.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit4,pars=['delt','bbeta','c'],digits_summary=2)
saveStanFit(fit4,'fit4')
w=loadStanFit('fit4')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DS[:,:7],DP,stan=True)
pystanErrorbar(w,keys=['beta','c','delt'])
dat = {'y':np.int32(DR[:,1:7])+1,'x':np.int32(DR[:,0]),'N':DR.shape[0] ,'K':10,'M':6}
fit5 = sm4.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit4,pars=['delt','bbeta','c'],digits_summary=2)
saveStanFit(fit5,'fit5')
w=loadStanFit('fit5')
pt=w['pt']
pc=w['pc']
DP=np.zeros((pt.shape[2]+2,pt.shape[1],2))
DP[0,:,:]=1
DP[1:-1,:,:]=np.array([pc,pt]).T.mean(2)
DP=-np.diff(DP,axis=0)
plotComparison(DR[:,:7],DP,stan=True)
pystanErrorbar(w,keys=['beta','c','delt'])
model='''
data {
int<lower=2> K;
int<lower=0> N;
int<lower=1> M;
int<lower=1,upper=K> y[N,M];
int x[N,2];
}
parameters {
// real mb; real<lower=0,upper=100> sb[2];
vector[M-1] bbeta;
real dd[3];
ordered[K-1] c;
}
transformed parameters{
//real pt[M,K-1]; real pc[M,K-1];
vector[M] beta;
for (m in 1:M){
if (m==1) beta[m]<-0.0;
else beta[m]<-bbeta[m-1];
//for (k in 1:(K-1)){
// pt[m,k] <- inv_logit(beta[m]+delt-c[k]);
// pc[m,k] <- inv_logit(beta[m]-c[k]);}
}}
model {
for (k in 1:(K-1)) c[k]~ uniform(-100,100);
for (m in 1:M){
for (n in 1:N) y[n,m] ~ ordered_logistic(beta[m]
+dd[2]*x[n,1]*(1-x[n,2]) // rep + control
+dd[1]*x[n,2]*(1-x[n,1]) // orig + treat
+dd[3]*x[n,1]*x[n,2], c); // rep + treat
}}
'''
sm5=pystan.StanModel(model_code=model)
dat = {'y':np.int32(D[:,2:8])+1,'x':np.int32(D[:,[0,1]]),'N':D.shape[0] ,'K':10,'M':6}
fit6 = sm5.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print pystan.misc._print_stanfit(fit6,pars=['dd','bbeta','c'],digits_summary=2)
saveStanFit(fit6,'fit6')
w=loadStanFit('fit6')
pystanErrorbar(w,keys=['beta','c','dd'])
plt.figure(figsize=(10,4))
c=w['c']
b=w['beta']
d=w['dd']
errorbar(c,x=np.linspace(6.5,8,9))
ax=plt.gca()
plt.plot([-1,100],[0,0],'k',lw=2)
ax.set_yticks(np.median(c,axis=0))
ax.set_yticklabels(np.arange(1,10)+0.5)
plt.grid(b=False,axis='x')
errorbar(b[:,::-1],x=np.arange(9,15),clr='g')
errorbar(d,x=np.arange(15,18),clr='r')
plt.xlim([6,17.5])
ax.set_xticks(range(9,18))
ax.set_xticklabels(il[:6][::-1]+['OT','RC','RT'])
for i in range(d.shape[1]): printCI(d[:,i])
printCI(d[:,2]-d[:,1])
c
def ordinalLogitRvs(beta, c,n,size=1):
assert np.all(np.diff(c)>0) # c must be strictly increasing
def invLogit(x): return 1/(1+np.exp(-x))
p=[1]+list(invLogit(beta-c))+[0]
p=-np.diff(p)
#return np.random.multinomial(n,p,size)
return np.int32(np.round(p*n))
def reformatData(dat):
out=[]
for k in range(dat.size):
out.extend([k]*dat[k])
return np.array(out)
b=np.linspace(-10,7,21)
d=np.median(w['dd'][:,0])
c=np.median(w['c'],axis=0)
S=[];P=[]
for bb in b:
S.append([np.squeeze(ordinalLogitRvs(bb,c,100)),
np.squeeze(ordinalLogitRvs(bb+d,c,100))])
P.append([reformatData(S[-1][0]),reformatData(S[-1][1])])
model='''
data {
int<lower=2> K;
int<lower=0> y1[K];
int<lower=0> y2[K];
}
parameters {
real<lower=-1000,upper=1000> d;
ordered[K-1] c;
}
model {
for (k in 1:(K-1)) c[k]~ uniform(-200,200);
for (k in 1:K){
for (n in 1:y1[k]) k~ ordered_logistic(0.0,c);
for (n in 1:y2[k]) k~ ordered_logistic(d ,c);
}}
'''
sm9=pystan.StanModel(model_code=model)
#(S[k][0]!=0).sum()+1
for k in range(21):
i1=np.nonzero(S[k][0]!=0)[0]
i2=np.nonzero(S[k][1]!=0)[0]
if max((S[k][0]!=0).sum(),(S[k][1]!=0).sum())<9:
s= max(min(i1[0],i2[0])-1,0)
e= min(max(i1[-1],i2[-1])+1,10)
S[k][0]=S[k][0][s:e+1]
S[k][1]=S[k][1][s:e+1]
S[0][0].size
ds=[];cs=[]
for k in range(len(S)):
dat = {'y1':S[k][0],'y2':S[k][1],'K':S[k][0].size}
fit = sm9.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
print fit
saveStanFit(fit,'dc%d'%k)
for k in range(21):
i1=np.nonzero(S[k][0]!=0)[0]
i2=np.nonzero(S[k][1]!=0)[0]
if max((S[k][0]!=0).sum(),(S[k][1]!=0).sum())<9:
s= min(i1[0],i2[0])
e= max(i1[-1],i2[-1])
S[k][0]=S[k][0][s:e+1]
S[k][1]=S[k][1][s:e+1]
ds=[];cs=[]
for k in range(len(S)):
if S[k][0].size==1: continue
dat = {'y1':S[k][0],'y2':S[k][1],'K':S[k][0].size}
fit = sm9.sampling(data=dat,iter=1000, chains=4,thin=2,warmup=500,njobs=2,seed=4)
#print fit
saveStanFit(fit,'dd%d'%k)
ds=[];xs=[]
for k in range(b.size):
try:
f=loadStanFit('dd%d'%k)['d']
xs.append(b[k])
ds.append(f)
except:pass
ds=np.array(ds);xs=np.array(xs)
ds.shape
d1=np.median(w['dd'][:,0])
d2=DS[DS[:,0]==1,-2].mean()-DS[DS[:,0]==0,-2].mean()
plt.figure(figsize=(8,4))
plt.plot([-10,5],[d1,d1],'r',alpha=0.5)
res1=errorbar(ds.T,x=xs-0.1)
ax1=plt.gca()
plt.ylim([-2,2])
plt.xlim([-10,5])
plt.grid(b=False,axis='x')
ax2 = ax1.twinx()
res2=np.zeros((b.size,5))
for k in range(b.size):
res2[k,:]=plotCIttest2(y1=P[k][0],y2=P[k][1],x=b[k]+0.1)
plt.ylim([-2/d1*d2,2/d1*d2])
plt.xlim([-10,5])
plt.grid(b=False,axis='y')
plt.plot(np.median(w['beta'],axis=0),[-0.9]*6,'ob')
plt.plot(np.median(w['beta']+np.atleast_2d(w['dd'][:,1]).T,axis=0),[-1.1]*6,'og')
d1=np.median(w['dd'][:,0])
d2=DS[DS[:,0]==1,-2].mean()-DS[DS[:,0]==0,-2].mean()
plt.figure(figsize=(8,4))
ax1=plt.gca()
plt.plot([-10,5],[d1,d1],'r',alpha=0.5)
temp=[list(xs)+list(xs)[::-1],list(res1[:,1])+list(res1[:,2])[::-1]]
ax1.add_patch(plt.Polygon(xy=np.array(temp).T,alpha=0.2,fc='k',ec='k'))
plt.plot(xs,res1[:,0],'k')
plt.ylim([-1.5,2])
plt.xlim([-10,5])
plt.grid(b=False,axis='x')
plt.legend(['True ES','Estimate Ordinal Logit'],loc=8)
plt.ylabel('Estimate Ordinal Logit')
ax2 = ax1.twinx()
temp=[list(b)+list(b)[::-1],list(res2[:,1])+list(res2[:,2])[::-1]]
for t in range(len(temp[0]))[::-1]:
if np.isnan(temp[1][t]):
temp[0].pop(t);temp[1].pop(t)
ax2.add_patch(plt.Polygon(xy=np.array(temp).T,alpha=0.2,fc='m',ec='m'))
plt.plot(b,res2[:,0],'m')
plt.ylim([-1.5/d1*d2,2/d1*d2])
plt.xlim([-10,5])
plt.grid(b=False,axis='y')
plt.plot(np.median(w['beta'],axis=0),[-0.3]*6,'ob')
plt.plot(np.median(w['beta']+np.atleast_2d(w['dd'][:,1]).T,axis=0),[-0.5]*6,'og')
plt.legend(['Estimate T-C','Item Difficulty Orignal Study','Item Difficulty Replication'],loc=4)
plt.ylabel('Estimate T - C',color='m')
for tl in ax2.get_yticklabels():tl.set_color('m')
```
| true |
code
| 0.299419 | null | null | null | null |
|
# Pre-training VGG16 for Distillation
```
import torch
import torch.nn as nn
from src.data.dataset import get_dataloader
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(DEVICE)
SEED = 0
BATCH_SIZE = 32
LR = 5e-4
NUM_EPOCHES = 25
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
```
## Preprocessing
```
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
#transforms.RandomVerticalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
train_loader, val_loader, test_loader = get_dataloader("./data/CIFAR10/", BATCH_SIZE)
```
## Model
```
from src.models.model import VGG16_classifier
classes = 10
hidden_size = 512
dropout = 0.3
model = VGG16_classifier(classes, hidden_size, preprocess_flag=False, dropout=dropout).to(DEVICE)
model
for img, label in train_loader:
img = img.to(DEVICE)
label = label.to(DEVICE)
print("Input Image Dimensions: {}".format(img.size()))
print("Label Dimensions: {}".format(label.size()))
print("-"*100)
out = model(img)
print("Output Dimensions: {}".format(out.size()))
break
```
## Training
```
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=LR)
loss_hist = {"train accuracy": [], "train loss": [], "val accuracy": []}
for epoch in range(1, NUM_EPOCHES+1):
model.train()
epoch_train_loss = 0
y_true_train = []
y_pred_train = []
for batch_idx, (img, labels) in enumerate(train_loader):
img = img.to(DEVICE)
labels = labels.to(DEVICE)
preds = model(img)
loss = criterion(preds, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
y_pred_train.extend(preds.detach().argmax(dim=-1).tolist())
y_true_train.extend(labels.detach().tolist())
epoch_train_loss += loss.item()
with torch.no_grad():
model.eval()
y_true_test = []
y_pred_test = []
for batch_idx, (img, labels) in enumerate(val_loader):
img = img.to(DEVICE)
label = label.to(DEVICE)
preds = model(img)
y_pred_test.extend(preds.detach().argmax(dim=-1).tolist())
y_true_test.extend(labels.detach().tolist())
test_total_correct = len([True for x, y in zip(y_pred_test, y_true_test) if x==y])
test_total = len(y_pred_test)
test_accuracy = test_total_correct * 100 / test_total
loss_hist["train loss"].append(epoch_train_loss)
total_correct = len([True for x, y in zip(y_pred_train, y_true_train) if x==y])
total = len(y_pred_train)
accuracy = total_correct * 100 / total
loss_hist["train accuracy"].append(accuracy)
loss_hist["val accuracy"].append(test_accuracy)
print("-------------------------------------------------")
print("Epoch: {} Train mean loss: {:.8f}".format(epoch, epoch_train_loss))
print(" Train Accuracy%: ", accuracy, "==", total_correct, "/", total)
print(" Validation Accuracy%: ", test_accuracy, "==", test_total_correct, "/", test_total)
print("-------------------------------------------------")
plt.plot(loss_hist["train accuracy"])
plt.plot(loss_hist["val accuracy"])
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(loss_hist["train loss"])
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
```
## Testing
```
with torch.no_grad():
model.eval()
y_true_test = []
y_pred_test = []
for batch_idx, (img, labels) in enumerate(test_loader):
img = img.to(DEVICE)
label = label.to(DEVICE)
preds = model(img)
y_pred_test.extend(preds.detach().argmax(dim=-1).tolist())
y_true_test.extend(labels.detach().tolist())
total_correct = len([True for x, y in zip(y_pred_test, y_true_test) if x==y])
total = len(y_pred_test)
accuracy = total_correct * 100 / total
print("Test Accuracy%: ", accuracy, "==", total_correct, "/", total)
```
## Saving Model Weights
```
torch.save(model.state_dict(), "./trained_models/vgg16_cifar10.pt")
```
| true |
code
| 0.6771 | null | null | null | null |
|
# _Mini Program - Working with SQLLite DB using Python_
### <font color=green>Objective -</font>
<font color=blue>1. This program gives an idea how to connect with SQLLite DB using Python and perform data manipulation </font><br>
<font color=blue>2. There are 2 ways in which tables are create below to help you understand the robustness of this language</font>
### <font color=green>Step 1 - Import required libraries</font>
#### <font color=blue>In this program we make used of 3 libraries</font>
#### <font color=blue>1. sqlite3 - This module help to work with sql interface. It helps in performing db operations in sqllite database</font>
#### <font color=blue>2. pandas - This module provides high performance and easy to use data manipulation and data analysis functionalities</font>
#### <font color=blue>3. os - This module provides function to interact with operating system with easy use</font>
```
#Importing the required modules
import sqlite3
import pandas as pd
import os
```
### <font color=green>Step 2 - Creating a function to drop the table</font>
#### <font color=blue>Function helps to re-create a reusable component that can be used conviniently and easily in other part of the code</font>
#### <font color=blue>In Line 1 - We state the function name and specify the parameter being passed. In this case, the parameter is the table name</font>
#### <font color=blue>In Line 2 - We write the sql query to be executed</font>
#### <font color=blue>In Line 3 - We execute the query using the cursor object</font>
```
#Creating a function to drop the table if it exists
def dropTbl(tablename):
dropTblStmt = "DROP TABLE IF EXISTS " + tablename
c.execute(dropTblStmt)
```
### <font color=green>Step 3 - We create the database in which our table will reside</font>
#### <font color=blue>In Line 1 - We are removing the already existing database file</font>
#### <font color=blue>In Line 2 - We use connect function from the sqlite3 module to create a database studentGrades.db and establish a connection</font>
#### <font color=blue>In Line 3 - We create a context of the database connection. This help to run all the database queries</font>
```
#Removing the database file
os.remove('studentGrades.db')
#Creating a new database - studentGrades.db
conn = sqlite3.connect("studentGrades.db")
c = conn.cursor()
```
### <font color=green>Step 4 - We create a table in sqllite DB using data defined in the excel file</font>
#### <font color=blue>This is the first method in which you can create a table. You can use to_sql function directly to read a dataframe and dump all it's content to the table</font>
#### <font color=blue>In Line 1 - We are making use of dropTbl function created above to drop the table</font>
#### <font color=blue>In Line 2 - We are creating a dataframe from the data read from the csv</font>
#### <font color=blue>In Line 3 - We use to_sql function to push the data into the table. The first row of the file becomes the column name of the tables</font>
#### <font color=blue>We repeat the above steps for all the 3 files to create 3 tables - STUDENT, GRADES and SUBJECTS</font>
```
#Reading data from csv file - student details, grades and subject
dropTbl('STUDENT')
student_details = pd.read_csv("Datafiles/studentDetails.csv")
student_details.to_sql('STUDENT',conn,index = False)
dropTbl('GRADES')
student_grades = pd.read_csv('Datafiles/studentGrades.csv')
student_grades.to_sql('GRADES',conn,index = False)
dropTbl('SUBJECTS')
subjects = pd.read_csv("Datafiles/subjects.csv")
subjects.to_sql('SUBJECTS',conn,index = False)
```
### <font color=green>Step 5 - We create a master table STUDENT_GRADE_MASTER where we can colate the data from the individual tables by performing the joining operations</font>
#### <font color=blue>In Line 1 - We are making use of dropTbl function created above to drop the table</font>
#### <font color=blue>In Line 2 - We are writing sql query for table creation</font>
#### <font color=blue>In Line 3 - We are using the cursor created above to execute the sql statement</font>
#### <font color=blue>In Line 4 - We are using the second method of inserting data into the table. We are writing a query to insert the data after joining the data from all the tables</font>
#### <font color=blue>In Line 5 - We are using the cursor created above to execute the sql statement</font>
#### <font color=blue>In Line 6 - We are doing a commit operation. Since INSERT operation is a ddl, we have to perform a commit operation to register it into the database</font>
```
#Creating a table to store student master data
dropTbl('STUDENT_GRADE_MASTER')
createTblStmt = '''CREATE TABLE STUDENT_GRADE_MASTER
([Roll_number] INTEGER,
[Student_Name] TEXT,
[Stream] TEXT,
[Subject] TEXT,
[Marks] INTEGER
)'''
c.execute(createTblStmt)
#Inserting data into the master table by joining the tables mentioned above
queryMaster = '''INSERT INTO STUDENT_GRADE_MASTER(Roll_number,Student_Name,Stream,Subject,Marks)
SELECT g.roll_number, s.student_name, stream, sub.subject, marks from GRADES g
LEFT OUTER JOIN STUDENT s on g.roll_number = s.roll_number
LEFT OUTER JOIN SUBJECTS sub on g.subject_code = sub.subject_code'''
c.execute(queryMaster)
c.execute("COMMIT")
```
### <font color=green>Step 6 - We can perform data fetch like we do in sqls using this sqlite3 module</font>
#### <font color=blue>In Line 1 - We are writing a query to find the number of records in the master table</font>
#### <font color=blue>In Line 2 - We are executing the above created query</font>
#### <font color=blue>In Line 3 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
#### <font color=blue>In Line 4 - We are writing another query to find the maximum marks recorded for each subject</font>
#### <font color=blue>In Line 5 - We are executing the above created query</font>
#### <font color=blue>In Line 6 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
#### <font color=blue>In Line 7 - We are writing another query to find the percentage of marks obtained by each student in the class</font>
#### <font color=blue>In Line 8 - We are executing the above created query</font>
#### <font color=blue>In Line 9 - fetchall function is used to get the result returned by the query. The result will be in the form of a list of tuples</font>
```
#Finding the key data from the master table
#1. Find the number of records in the master table
query_count = '''SELECT COUNT(*) FROM STUDENT_GRADE_MASTER'''
c.execute(query_count)
number_of_records = c.fetchall()
print(number_of_records)
#2. Maximum marks for each subject
query_max_marks = '''SELECT Subject,max(Marks) as 'Max_Marks' from STUDENT_GRADE_MASTER GROUP BY Subject'''
c.execute(query_max_marks)
max_marks_data = c.fetchall()
print(max_marks_data)
#3. Percenatge of marks scored by each student
query_percentage = '''SELECT Student_Name, avg(Marks) as 'Percentage' from STUDENT_GRADE_MASTER GROUP BY Student_Name'''
c.execute(query_percentage)
percentage_data = c.fetchall()
print(percentage_data)
```
### <font color=green>Step 7 - We are closing the database connection</font>
#### <font color=blue>It is always a good practice to close the database connection after all the operations are completed</font>
```
#Closing the connection
conn.close()
```
| true |
code
| 0.227341 | null | null | null | null |
|
### Regular Expressions
Regular expressions are `text matching patterns` described with a formal syntax. You'll often hear regular expressions referred to as 'regex' or 'regexp' in conversation. Regular expressions can include a variety of rules, for finding repetition, to text-matching, and much more. As you advance in Python you'll see that a lot of your parsing problems can be solved with regular expressions (they're also a common interview question!).
## Searching for Patterns in Text
One of the most common uses for the re module is for finding patterns in text. Let's do a quick example of using the search method in the re module to find some text:
```
import re
# List of patterns to search for
patterns = [ 'term1', 'term2' ]
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
for p in patterns:
print ('Searching for "%s" in Sentence: \n"%s"' % (p, text))
#Check for match
if re.search(p, text):
print ('Match was found. \n')
else:
print ('No Match was found. \n')
```
Now we've seen that re.search() will take the pattern, scan the text, and then returns a **Match** object. If no pattern is found, a **None** is returned. To give a clearer picture of this match object, check out the cell below:
```
# List of patterns to search for
pattern = 'term1'
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
match = re.search(pattern, text)
type(match)
match
```
This **Match** object returned by the search() method is more than just a Boolean or None, it contains information about the match, including the original input string, the regular expression that was used, and the location of the match. Let's see the methods we can use on the match object:
```
# Show start of match
match.start()
# Show end
match.end()
s = "abassabacdReddyceaabadjfvababaReddy"
r = re.compile("Reddy")
r
l = re.findall(r,s)
print(l)
import re
s = "abcdefg1234"
r = re.compile("^[a-z][0-9]$")
l = re.findall(r,s)
print(l)
s = "ABCDE1234a"
r = re.compile(r"^[A-Z]{5}[0-9]{4}[a-z]$")
l = re.findall(r,s)
print(l)
s = "+917123456789"
s1 = "07123456789"
s2 = "7123456789"
r = re.compile(r"[6-9][0-9]{9}")
l = re.findall(r,s)
print(l)
l = re.findall(r,s1)
print(l)
l = re.findall(r,s2)
print(l)
s = "+917234567891"
s1 = "07123456789"
s2 = "7123456789"
r = re.compile(r"^(\+91)?[0]?([6-9][0-9]{9})$")
m = re.search(r,s1)
if m:
print(m.group())
else:
print("Invalid string")
for _ in range(int(input("No of Test Cases:"))):
line = input("Mobile Number")
if re.match(r"^[789]{1}\d{9}$", line):
print("YES")
else:
print("NO")
#Named groups
s = "12-02-2017" # DD-MM-YYYY
# dd-mm-yyyy
r = re.compile(r"^(?P<day>\d{2})-(?P<month>[0-9]{2})-(?P<year>[0-9]{4})")
m = re.search(r,s)
if m:
print(m.group('year'))
print(m.group('month'))
print(m.group('day'))
```
## Split with regular expressions
Let's see how we can split with the re syntax. This should look similar to how you used the split() method with strings.
```
# Term to split on
split_term = '@'
phrase = 'What is the domain name of someone with the email: [email protected]'
# Split the phrase
re.split(split_term,phrase)
```
Note how re.split() returns a list with the term to spit on removed and the terms in the list are a split up version of the string. Create a couple of more examples for yourself to make sure you understand!
## Finding all instances of a pattern
You can use re.findall() to find all the instances of a pattern in a string. For example:
```
# Returns a list of all matches
re.findall('is','test phrase match is in middle')
a = " a list with the term to spit on removed and the terms in the list are a split up version of the string. Create a couple of more examples for yourself to make sure you understand!"
copy = re.findall("to",a)
copy
len(copy)
```
## Pattern re Syntax
This will be the bulk of this lecture on using re with Python. Regular expressions supports a huge variety of patterns the just simply finding where a single string occurred.
We can use *metacharacters* along with re to find specific types of patterns.
Since we will be testing multiple re syntax forms, let's create a function that will print out results given a list of various regular expressions and a phrase to parse:
```
def multi_re_find(patterns,phrase):
'''
Takes in a list of regex patterns
Prints a list of all matches
'''
for pattern in patterns:
print ('Searching the phrase using the re check: %r' %pattern)
print (re.findall(pattern,phrase))
```
### Repetition Syntax
There are five ways to express repetition in a pattern:
1.) A pattern followed by the meta-character * is repeated zero or more times.
2.) Replace the * with + and the pattern must appear at least once.
3.) Using ? means the pattern appears zero or one time.
4.) For a specific number of occurrences, use {m} after the pattern, where m is replaced with the number of times the pattern should repeat.
5.) Use {m,n} where m is the minimum number of repetitions and n is the maximum. Leaving out n ({m,}) means the value appears at least m times, with no maximum.
Now we will see an example of each of these using our multi_re_find function:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = [ 'sd*', # s followed by zero or more d's
'sd+', # s followed by one or more d's
'sd?', # s followed by zero or one d's
'sd{3}', # s followed by three d's
'sd{2,3}', # s followed by two to three d's
]
multi_re_find(test_patterns,test_phrase)
```
## Character Sets
Character sets are used when you wish to match any one of a group of characters at a point in the input. Brackets are used to construct character set inputs. For example: the input [ab] searches for occurrences of either a or b.
Let's see some examples:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = [ '[sd]', # either s or d
's[sd]+'] # s followed by one or more s or d
multi_re_find(test_patterns,test_phrase)
```
It makes sense that the first [sd] returns every instance. Also the second input will just return any thing starting with an s in this particular case of the test phrase input.
## Exclusion
We can use ^ to exclude terms by incorporating it into the bracket syntax notation. For example: [^...] will match any single character not in the brackets. Let's see some examples:
```
test_phrase = 'This is a string! But it has punctuation. How can we remove it?'
```
Use [^!.? ] to check for matches that are not a !,.,?, or space. Add the + to check that the match appears at least once, this basically translate into finding the words.
```
re.findall('[^!.? ]+',test_phrase)
```
## Character Ranges
As character sets grow larger, typing every character that should (or should not) match could become very tedious. A more compact format using character ranges lets you define a character set to include all of the contiguous characters between a start and stop point. The format used is [start-end].
Common use cases are to search for a specific range of letters in the alphabet, such [a-f] would return matches with any instance of letters between a and f.
Let's walk through some examples:
```
test_phrase = 'This is an example sentence. Lets see if we can find some letters.'
test_patterns=[ '[a-z]+', # sequences of lower case letters
'[A-Z]+', # sequences of upper case letters
'[a-zA-Z]+', # sequences of lower or upper case letters
'[A-Z][a-z]+'] # one upper case letter followed by lower case letters
multi_re_find(test_patterns,test_phrase)
```
## Escape Codes
You can use special escape codes to find specific types of patterns in your data, such as digits, non-digits,whitespace, and more. For example:
<table border="1" class="docutils">
<colgroup>
<col width="14%" />
<col width="86%" />
</colgroup>
<thead valign="bottom">
<tr class="row-odd"><th class="head">Code</th>
<th class="head">Meaning</th>
</tr>
</thead>
<tbody valign="top">
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\d</span></tt></td>
<td>a digit</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\D</span></tt></td>
<td>a non-digit</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\s</span></tt></td>
<td>whitespace (tab, space, newline, etc.)</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\S</span></tt></td>
<td>non-whitespace</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\w</span></tt></td>
<td>alphanumeric</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\W</span></tt></td>
<td>non-alphanumeric</td>
</tr>
</tbody>
</table>
Escapes are indicated by prefixing the character with a backslash (\). Unfortunately, a backslash must itself be escaped in normal Python strings, and that results in expressions that are difficult to read. Using raw strings, created by prefixing the literal value with r, for creating regular expressions eliminates this problem and maintains readability.
Personally, I think this use of r to escape a backslash is probably one of the things that block someone who is not familiar with regex in Python from being able to read regex code at first. Hopefully after seeing these examples this syntax will become clear.
```
test_phrase = 'This is a string with some numbers 1233 and a symbol #hashtag'
test_patterns=[ r'\d+', # sequence of digits
r'\D+', # sequence of non-digits
r'\s+', # sequence of whitespace
r'\S+', # sequence of non-whitespace
r'\w+', # alphanumeric characters
r'\W+', # non-alphanumeric
]
multi_re_find(test_patterns,test_phrase)
```
## Conclusion
You should now have a solid understanding of how to use the regular expression module in Python. There are a ton of more special character instances, but it would be unreasonable to go through every single use case. Instead take a look at the full [documentation](https://docs.python.org/2.4/lib/re-syntax.html) if you ever need to look up a particular case.
You can also check out the nice summary tables at this [source](http://www.tutorialspoint.com/python/python_reg_expressions.htm).
Good job!
| true |
code
| 0.262534 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/EvenSol/NeqSim-Colab/blob/master/notebooks/process/masstransferMeOH.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Calculation of mass transfer and hydrate inhibition of a wet gas by injection of methanol
#@markdown Demonstration of mass transfer calculation using the NeqSim software in Python
#@markdown <br><br>This document is part of the module ["Introduction to Gas Processing using NeqSim in Colab"](https://colab.research.google.com/github/EvenSol/NeqSim-Colab/blob/master/notebooks/examples_of_NeqSim_in_Colab.ipynb#scrollTo=_eRtkQnHpL70).
%%capture
!pip install neqsim
import neqsim
from neqsim.thermo.thermoTools import *
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from neqsim.thermo import fluid, fluid_df
import pandas as pd
from neqsim.process import gasscrubber, clearProcess, run,nequnit, phasemixer, splitter, clearProcess, stream, valve, separator, compressor, runProcess, viewProcess, heater,saturator, mixer
plt.style.use('classic')
%matplotlib inline
```
#Mass transfer calculations
Model for mass transfer calculation in NeqSim based on Solbraa (2002):
https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/231326
In the following calculations we assume a water saturated gas the is mixed with pure liquid methanol. These phases are not in equiibrium when they enter the pipeline. When the gas and methanol liquid comes in contact in the pipeline, methanol will vaporize into the gas, and water (and other comonents from the gas) will be absorbed into the liquid methanol. The focus of the following calculations will be to evaluate the mass transfer as function of contanct length with gas and methanol. It also evaluates the hydrate temperature of the gas leaving the pipe section.
Figure 1 Illustration of mass transfer process

**The parameters for the model are:**
Temperature and pressure of the pipe (mass transfer calculated at constant temperature and pressure).
Length and diameter of pipe where gas and liquid will be in contact and mass transfer can occur.
Flow rate of the gas in MSm3/day, flow rate of methanol (kg/hr).
#Calculation of compostion of aqueous phase and gas leaving pipe section
In the following script we will simulate the composition of the gas leaving pipe section at a given pipe lengt.
```
# Input parameters
pressure = 52.21 # bara
temperature = 15.2 #C
gasFlow = 1.23 #MSm3/day
methanolFlow = 6000.23 # kg/day
pipelength = 10.0 #meter
pipeInnerDiameter = 0.5 #meter
# Create a gas-condensate fluid
feedgas = {'ComponentName': ["nitrogen","CO2","methane", "ethane" , "propane", "i-butane", "n-butane", "water", "methanol"],
'MolarComposition[-]': [0.01, 0.01, 0.8, 0.06, 0.01,0.005,0.005, 0.0, 0.0]
}
naturalgasFluid = fluid_df(pd.DataFrame(feedgas)).setModel("CPAs-SRK-EOS-statoil")
naturalgasFluid.setTotalFlowRate(gasFlow, "MSm3/day")
naturalgasFluid.setTemperature(temperature, "C")
naturalgasFluid.setPressure(pressure, "bara")
# Create a liquid methanol fluid
feedMeOH = {'ComponentName': ["nitrogen","CO2","methane", "ethane" , "propane", "i-butane", "n-butane", "water", "methanol"],
'MolarComposition[-]': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,1.0]
}
meOHFluid = fluid_df(pd.DataFrame(feedMeOH) ).setModel("CPAs-SRK-EOS-statoil")
meOHFluid.setTotalFlowRate(methanolFlow, "kg/hr");
meOHFluid.setTemperature(temperature, "C");
meOHFluid.setPressure(pressure, "bara");
clearProcess()
dryinjectiongas = stream(naturalgasFluid)
MeOHFeed = stream(meOHFluid)
watersaturator = saturator(dryinjectiongas)
waterSaturatedFeedGas = stream(watersaturator.getOutStream())
mainMixer = phasemixer("gas MeOH mixer")
mainMixer.addStream(waterSaturatedFeedGas)
mainMixer.addStream(MeOHFeed)
pipeline = nequnit(mainMixer.getOutStream(), equipment="pipeline", flowpattern="stratified") #alternative flow patterns are: stratified, annular and droplet
pipeline.setLength(pipelength)
pipeline.setID(pipeInnerDiameter)
scrubber = gasscrubber(pipeline.getOutStream())
gasFromScrubber = stream(scrubber.getGasOutStream())
aqueousFromScrubber = stream(scrubber.getLiquidOutStream())
run()
print('Composition of gas leaving pipe section after ', pipelength, ' meter')
printFrame(gasFromScrubber.getFluid())
print('Composition of aqueous phase leaving pipe section after ', pipelength, ' meter')
printFrame(aqueousFromScrubber.getFluid())
print('Interface contact area ', pipeline.getInterfacialArea(), ' m^2')
print('Volume fraction aqueous phase ', pipeline.getOutStream().getFluid().getVolumeFraction(1), ' -')
```
# Calculation of hydrate equilibrium temperature of gas leaving pipe section
In the following script we will simulate the composition of the gas leaving pipe section as well as hydrate equilibrium temperature of this gas as function of pipe length.
```
maxpipelength = 10.0
def hydtemps(length):
pipeline.setLength(length)
run();
return gasFromScrubber.getHydrateEquilibriumTemperature()-273.15
length = np.arange(0.01, maxpipelength, (maxpipelength)/10.0)
hydtem = [hydtemps(length2) for length2 in length]
plt.figure()
plt.plot(length, hydtem)
plt.xlabel('Length available for mass transfer [m]')
plt.ylabel('Hydrate eq.temperature [C]')
plt.title('Hydrate eq.temperature of gas leaving pipe section')
```
| true |
code
| 0.670446 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Dimensionality-Reduction" data-toc-modified-id="Dimensionality-Reduction-1"><span class="toc-item-num">1 </span>Dimensionality Reduction</a></span><ul class="toc-item"><li><span><a href="#The-Problem" data-toc-modified-id="The-Problem-1.1"><span class="toc-item-num">1.1 </span>The Problem</a></span><ul class="toc-item"><li><span><a href="#Multi-Collinearity" data-toc-modified-id="Multi-Collinearity-1.1.1"><span class="toc-item-num">1.1.1 </span>Multi-Collinearity</a></span></li></ul></li><li><span><a href="#Sparsity" data-toc-modified-id="Sparsity-1.2"><span class="toc-item-num">1.2 </span>Sparsity</a></span></li></ul></li><li><span><a href="#Principle-Component-Analysis" data-toc-modified-id="Principle-Component-Analysis-2"><span class="toc-item-num">2 </span>Principle Component Analysis</a></span><ul class="toc-item"><li><span><a href="#Important-Points:" data-toc-modified-id="Important-Points:-2.1"><span class="toc-item-num">2.1 </span>Important Points:</a></span></li></ul></li><li><span><a href="#Singular-Value-Decomposition" data-toc-modified-id="Singular-Value-Decomposition-3"><span class="toc-item-num">3 </span>Singular Value Decomposition</a></span><ul class="toc-item"><li><span><a href="#Measuring-the-Quality-of-the-Reconstruction" data-toc-modified-id="Measuring-the-Quality-of-the-Reconstruction-3.1"><span class="toc-item-num">3.1 </span>Measuring the Quality of the Reconstruction</a></span></li><li><span><a href="#Heuristic-Step-for-How-Many-Dimensions-to-Keep" data-toc-modified-id="Heuristic-Step-for-How-Many-Dimensions-to-Keep-3.2"><span class="toc-item-num">3.2 </span>Heuristic Step for How Many Dimensions to Keep</a></span></li></ul></li><li><span><a href="#GLOVE" data-toc-modified-id="GLOVE-4"><span class="toc-item-num">4 </span>GLOVE</a></span><ul class="toc-item"><li><span><a href="#Using-Spacy-word2vec-embeddings" data-toc-modified-id="Using-Spacy-word2vec-embeddings-4.1"><span class="toc-item-num">4.1 </span>Using Spacy word2vec embeddings</a></span></li><li><span><a href="#Using-Glove" data-toc-modified-id="Using-Glove-4.2"><span class="toc-item-num">4.2 </span>Using Glove</a></span></li></ul></li><li><span><a href="#Clustering-Text" data-toc-modified-id="Clustering-Text-5"><span class="toc-item-num">5 </span>Clustering Text</a></span></li></ul></div>
# Dimensionality Reduction
## The Problem
There is an interesting tradeoff between model performance and a feature's dimensionality:

>*If the amount of available training data is fixed, then overfitting occurs if we keep adding dimensions. On the other hand, if we keep adding dimensions, the amount of **training data needs to grow exponentially fast to maintain the same coverage** and to avoid overfitting* ([Computer Vision for Dummies](http://www.visiondummy.com/2014/04/curse-dimensionality-affect-classification/)).

### Multi-Collinearity
In many cases, there is a high degree of correlation between many of the features in a dataset. This multi-collinearity has the effect of drowning out the "signal" of your dataset in many cases, and amplifies "outlier" noise.
## Sparsity
- High dimensionality increases the sparsity of your features (**what NLP techniques have we used that illustrate this point?**)
- The density of the training samples decreases when dimensionality increases:
- **Distance measures (Euclidean, for instance) start losing their effectiveness**, because there isn't much difference between the max and min distances in higher dimensions.
- Many models that rely upon **assumptions of Gaussian distributions** (like OLS linear regression), Gaussian mixture models, Gaussian processes, etc. become less and less effective since their distributions become flatter and "fatter tailed".

What is the amount of data needed to maintain **20% coverage** of the feature space? For 1 dimension, it is **20% of the entire population's dataset**. For a dimensionality of $D$:
$$
X^{D} = .20
$$
$$
(X^{D})^{\frac{1}{D}} = .20^{\frac{1}{D}}
$$
$$
X = \sqrt[D]{.20}
$$
You can approximate this as
```python
def coverage_requirement(requirement, D):
return requirement ** (1 / D)
x = []
y = []
for d in range(1,20):
y.append(coverage_requirement(0.10, d))
x.append(d)
import matplotlib.pyplot as plt
plt.plot(x,y)
plt.xlabel("Number of Dimensions")
plt.ylabel("Appromximate % of Population Dataset")
plt.title("% of Dataset Needed to Maintain 10% Coverage of Feature Space")
plt.show()
```
<img src="images/coverage-needed.png" width="500">
```
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
reviews = pd.read_csv("mcdonalds-yelp-negative-reviews.csv", encoding='latin-1')
reviews = open("poor_amazon_toy_reviews.txt", encoding='latin-1')
#text = reviews["review"].values
text = reviews.readlines()
vectorizer = CountVectorizer(ngram_range=(3,3), min_df=0.01, max_df=0.75, max_features=200)
# tokenize and build vocab
vectorizer.fit(text)
vector = vectorizer.transform(text)
features = vector.toarray()
features_df = pd.DataFrame(features, columns=vectorizer.get_feature_names())
correlations = features_df.corr()
correlations_stacked = correlations.stack().reset_index()
#set column names
correlations_stacked.columns = ['Tri-Gram 1','Tri-Gram 2','Correlation']
correlations_stacked = correlations_stacked[correlations_stacked["Correlation"] < 1]
correlations_stacked = correlations_stacked.sort_values(by=['Correlation'], ascending=False)
correlations_stacked.head()
import numpy as np
import matplotlib.pyplot as plt
# visualize the correlations (install seaborn first)!
import seaborn as sns
# Generate a mask for the upper triangle
mask = np.triu(np.ones_like(correlations, dtype=np.bool))
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(11, 9))
# Generate a custom diverging colormap
cmap = sns.diverging_palette(220, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(correlations, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})
```
# Principle Component Analysis
If you have an original matrix $Z$, you can decompose this matrix into two smaller matrices $X$ and $Q$.
## Important Points:
- Multiplying a vector by a matrix typically changes the direction of the vector. For instance:
<figure>
<img src="images/multvector.png" alt="my alt text"/>
<figcaption><a href="https://lazyprogrammer.me/tutorial-principal-components-analysis-pca">Lazy Programmer-
Tutorial to PCA</a></figcaption>
</figure>
However, there are eigenvalues λ and eigenvectors $v$ such that
$$
\sum_{X}v = \lambda v
$$
Multiplying the eigenvectors $v$ with the eigenvalue $\lambda$ does not change the direction of the eigenvector.
Multiplying the eigenvector $v$ by the covariance matrix $\sum_{X}$ also does not change the direction of the eigenvector.
If our data $X$ is of shape $N \times D$, it turns out that we have $D$ eigenvalues and $D$ eigenvectors. This means we can arrange the eigenvalues $\lambda$ in decreasing order so that
$$
\lambda_3 > \lambda_2 > \lambda_5
$$
In this case, $\lambda_3$ is the largest eigenvalue, followed by $\lambda_2$, and then $\lambda_5$. Then, we can arrange
We can also rearrange the eigenvectors the same: $v_3$ will be the first column, $v_2$ will be the second column, and $v_5$ will be the third column.
We'll end up with two matrices $V$ and $\Lambda$:
<figure>
<img src="images/pca1.png" alt="my alt text"/>
<figcaption><a href="https://lazyprogrammer.me/tutorial-principal-components-analysis-pca">Lazy Programmer-
Tutorial to PCA</a></figcaption>
</figure>
```
# what is the shape of our features?
features.shape
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
Z = pca.fit_transform(features)
# what is the shape of Z?
Z.shape
# what will happen if we take the correlation matrix and covariance matrix of our new reduced features?
import numpy as np
covariances = pd.DataFrame(np.cov(Z.transpose()))
plt.rcParams["figure.figsize"] = (5,5)
sns.heatmap(covariances)
# train the model to reduce the dimensions down to 2
pca = PCA(n_components=2)
Z_two_dimensions = pca.fit_transform(features)
Z_two_dimensions
import matplotlib.pyplot as plt
plt.scatter(Z_two_dimensions[:,0], Z_two_dimensions[:, 1])
reduced_features_df = pd.DataFrame(Z_two_dimensions, columns=["x1", "x2"])
reduced_features_df["text"] = text
```
# Singular Value Decomposition
Given an input matrix $A$, we want to try to represent it instead as three smaller matrices $U$, $\sum$, and $V$. Instead of **$n$ original terms**, we want to represent each document as **$r$ concepts** (other referred to as **latent dimensions**, or **latent factors**):
<figure>
<img src="images/svd.png" alt="my alt text"/>
<figcaption><i>
<a href="https://www.youtube.com/watch?v=P5mlg91as1c">Mining of Massive Datasets - Dimensionality Reduction: Singular Value Decomposition</a> by Leskovec, Rajaraman, and Ullman (Stanford University)</i></figcaption>
</figure>
Here, **$A$ is your matrix of word vectors** - you could use any of the word vectorization techniques we have learned so far, include one-hot encoding, word count, TF-IDF.
- $\sum$ will be a **diagonal matrix** with values that are positive and sorted in decreasing order. Its value indicate the **variance (information encoded on that new dimension)**- therefore, the higher the value, the stronger that dimension is in capturing data from A, the original features. For our purposes, we can think of the rank of this $\sum$ matrix as the number of desired dimensions. Instance, if we want to reduce $A$ from shape $1020 x 300$ to $1020 x 10$, we will want to reduce the rank of $\sum$ from 300 to 10.
- $U^T U = I$ and $V^T V = I$
## Measuring the Quality of the Reconstruction
A popular metric used for measuring the quality of the reconstruction is the [Frobenius Norm](https://en.wikipedia.org/wiki/Matrix_norm#Frobenius_norm). When you explain your methodology for reducing dimensions, usually managers / stakeholders will want to some way to compare multiple dimensionality techniques' ability to quantify its ability to retain information but trim dimensions:
$$
\begin{equation}
||A_{old}-A_{new}||_{F} = \sqrt{\sum_{ij}{(A^{old}_{ij}- A^{new}_{ij}}})^2
\end{equation}
$$
## Heuristic Step for How Many Dimensions to Keep
1. Sum the $\sum$ matrix's diagonal values:
$$
\begin{equation}
\sum_{i}^{m}\sigma_{i}
\end{equation}
$$
2. Define your threshold of "information" (variance) $\alpha$ to keep: usually 80% to 90%.
3. Define your cutoff point $C$: $$
\begin{equation}
C = \sum_{i}^{m}\sigma_{i} \alpha
\end{equation}
$$
4. Beginning with your largest singular value, sum your singular values $\sigma_{i}$ until it is greater than C. Retain only those dimensions.
<figure>
<img src="images/userratings.png" alt="my alt text"/>
<figcaption><i>
<a href="https://www.youtube.com/watch?v=P5mlg91as1c">Mining of Massive Datasets - Dimensionality Reduction: Singular Value Decomposition</a> by Leskovec, Rajaraman, and Ullman (Stanford University)</i></figcaption>
</figure>
```
# create sample data
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import svd
x = np.linspace(1,20, 20) # create the first dimension
x = np.concatenate((x,x))
y = x + np.random.normal(0,1, 40) # create the second dimension
z = x + np.random.normal(0,2, 40) # create the third dimension
a = x + np.random.normal(0,4, 40) # create the fourth dimension
plt.scatter(x,y) # plot just the first two dimensions
plt.show()
# create matrix
A = np.stack([x,y,z,a]).T
# perform SVD
D = 1
U, s, V = svd(A)
print(f"s is {s}\n")
print(f"U is {U}\n")
print(f"V is {V}")
# Frobenius norm
s[D:] = 0
S = np.zeros((A.shape[0], A.shape[1]))
S[:A.shape[1], :A.shape[1]] = np.diag(s)
A_reconstructed = U.dot(S.dot(V))
np.sum((A_reconstructed - A) ** 2) ** (1/2) # Frobenius norm
# reconstruct matrix
U.dot(S)
```
# GLOVE
Global vectors for word presentation:
<figure>
<img src="images/glove_1.png" alt="my alt text"/>
<figcaption><i>
<a href="https://nlp.stanford.edu/pubs/glove.pdf">GloVe: Global Vectors for Word Representation</a></i></figcaption>
</figure>
```
!pip3 install gensim
# import glove embeddings into a word2vec format that is consumable by Gensim
from gensim.scripts.glove2word2vec import glove2word2vec
glove_input_file = 'glove.6B.100d.txt'
word2vec_output_file = 'glove.6B.100d.txt.word2vec'
glove2word2vec(glove_input_file, word2vec_output_file)
from gensim.models import KeyedVectors
# load the Stanford GloVe model
filename = 'glove.6B.100d.txt.word2vec'
model = KeyedVectors.load_word2vec_format(filename, binary=False)
# calculate: (king - man) + woman = ?
result = model.most_similar(positive=['woman', 'king'], negative=['man'], topn=1)
print(result)
words = ["woman", "king", "man", "queen", "puppy", "kitten", "cat",
"quarterback", "football", "stadium", "touchdown",
"dog", "government", "tax", "federal", "judicial", "elections",
"avocado", "tomato", "pear", "championship", "playoffs"]
vectors = [model.wv[word] for word in words]
import pandas as pd
vector_df = pd.DataFrame(vectors)
vector_df["word"] = words
vector_df.head()
```
## Using Spacy word2vec embeddings
```
import en_core_web_md
import spacy
from scipy.spatial.distance import cosine
nlp = en_core_web_md.load()
words = ["woman", "king", "man", "queen", "puppy", "kitten", "cat",
"quarterback", "football", "stadium", "touchdown",
"dog", "government", "tax", "federal", "judicial", "elections",
"avocado", "tomato", "pear", "championship", "playoffs"]
tokens = nlp(" ".join(words))
word2vec_vectors = [token.vector for token in tokens]
np.array(word2vec_vectors).shape
%matplotlib inline
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.decomposition import TruncatedSVD
import matplotlib.pyplot as plt
import matplotlib
dimension_model = PCA(n_components=2)
reduced_vectors = dimension_model.fit_transform(word2vec_vectors)
reduced_vectors.shape
matplotlib.rc('figure', figsize=(10, 10))
for i, vector in enumerate(reduced_vectors):
x = vector[0]
y = vector[1]
plt.plot(x,y, 'bo')
plt.text(x * (1 + 0.01), y * (1 + 0.01) , words[i], fontsize=12)
```
## Using Glove
```
%matplotlib inline
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.decomposition import TruncatedSVD
import matplotlib.pyplot as plt
dimension_model = PCA(n_components=2)
reduced_vectors = dimension_model.fit_transform(vectors)
for i, vector in enumerate(reduced_vectors):
x = vector[0]
y = vector[1]
plt.plot(x,y, 'bo')
plt.text(x * (1 + 0.01), y * (1 + 0.01) , words[i], fontsize=12)
```
# Clustering Text
```
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4)
cluster_assignments = kmeans.fit_predict(reduced_vectors)
for cluster_assignment, word in zip(cluster_assignments, words):
print(f"{word} assigned to cluster {cluster_assignment}")
color_map = {
0: "r",
1: "b",
2: "g",
3: "y"
}
plt.rcParams["figure.figsize"] = (10,10)
for i, vector in enumerate(reduced_vectors):
x = vector[0]
y = vector[1]
plt.plot(x,y, 'bo', c=color_map[cluster_assignments[i]])
plt.text(x * (1 + 0.01), y * (1 + 0.01) , words[i], fontsize=12)
```
| true |
code
| 0.626981 | null | null | null | null |
|
## 용어 정의
```
#가설설정
# A hypothesis test is a statistical method that uses sample data to evaluate a hypothesis about a population.
1. First, we state a hypothesis about a population. Usually the hypothesis concerns the value of a population parameter.
2. Before we select a sample, we use the hypothesis to predict the characteristics that the sample should have.
3. Next, we obtain a random sample from the population.
4. Finally, we compare the obtained sample data with the prediction that was made from the hypothesis.
## 가설설정 프로세스
1. State the hypothesis. null hypothesis(H0)
귀무가설 : 독립변수가 종속변수에 어떤 영향을 미치지 않는다는 것 => 레스토랑의 웨이터가 레드 셔츠 입는 것이 팁에 영향이 없다.
The null hypothesis (H0) states that in the general population
there is no change, no difference, or no relationship.
In the context of an experiment,
H0 predicts that the independent variable (treatment)
has no effect on the dependent variable (scores) for the population.
m = 15.8
대안가설 : 어떤 변인이 종속 변수에 효과가 있다는 것 => 레스토랑의 웨이터가 레드 셔츠 입는 것 팁에 영향이 있다.
The alternative hypothesis (H1) states that there is a change, a difference,
or a relationship for the general population.
In the context of an experiment,
H1 predicts that the independent variable (treatment) does have an effect on the dependent variable.
m != 15.8 이다.
이 실험에서는
m > 15.8
directional hypothisis test
2. set the criteria for a decision
a. Sample means that are likely to be obtained if H0 is true;
that is, sample means that are close to the null hypothesis
b. Sample means that are very unlikely to be obtained if H0 is true;
that is, sample means that are very different from the null hypothesis
The Alpha Level
alpha levels are α = .05 (5%), α = .01 (1%), and α = .001 (0.1%).
The alpha level, or the level of significance,
is a probability value that is used to define the concept of
“very unlikely” in a hypothesis test.
The critical region is composed of the extreme sample values that are very unlikely (as defined by the alpha level) to be obtained if the null hypothesis is true. The boundaries for the critical region are determined by the alpha level.
If sample data fall in the critical region, the null hypothesis is rejected.
3. Collect data and compute sample statistics.
z = sample mean - hypothesized population mean / standard error between M and m
4. Make a decision
1. Thesampledataarelocatedinthecriticalregion.
Bydefinition,asamplevaluein the critical region is very unlikely to occur if the null hypothesis is true.
2. The sample data are not in the critical region.
In this case, the sample mean is reasonably close to the population mean specified in the null hypothesis (in the center of the distribution).
```
# Problems
```
1. Identify the four steps of a hypothesis test as presented in this chapter.
1)State the hypothesis.
귀무가설과 대안가설 언급
2)alpha level 설정, 신뢰 구간 설정
3) Collect data and compute sample statistics.
데이터 수집과 샘플 통계적 계산
4)make decision
결론 결정
2. Define the alpha level and the critical region for a hypothesis test.
독립변수와 종속변수에 대한 귀무가설을 reject하기 위해 그 통계치를 통상적인 수치를 벗어나 의미있는 수가 나온 것을 설정해준다.
3. Define a Type I error and a Type II error and explain the consequences of each.
가설검증에서 실제효과가 없는데 효과가 있는 것으로 나온것, 실제 효과가 있는데, 없는 것으로 나온것. 가설 설정에 문제
4. If the alpha level is changed from α = .05 to α = .01,
a. What happens to the boundaries for the critical
region?
신뢰구간이 줄어든다.
b. What happens to the probability of a Type I error?
에러 확률은 낮아진다.
6. Although there is a popular belief that herbal remedies such as Ginkgo biloba and Ginseng may improve learning and memory in healthy adults, these effects are usually not supported by well- controlled research (Persson, Bringlov, Nilsson, and Nyberg, 2004). In a typical study, a researcher
obtains a sample of n = 16 participants and has each person take the herbal supplements every day for
90 days. At the end of the 90 days, each person takes a standardized memory test. For the general popula- tion, scores from the test form a normal distribution with a mean of μ = 50 and a standard deviation of
σ = 12. The sample of research participants had an average of M = 54.
a. Assuming a two-tailed test, state the null hypoth-
esis in a sentence that includes the two variables
being examined.
b. Using the standard 4-step procedure, conduct a
two-tailed hypothesis test with α = .05 to evaluate the effect of the supplements.
from scipy import stats
sample_number = 16 # 샘플수
population_mean = 50 # 모집단의 평균
standard_deviation = 12 # 표준편차
sample_mean = 54 # 샘플의 평균
result = stats.ttest_1samp(sample_mean, 50) # 비교집단, 관측치
result
sample_mean - population_mean
## Import
import numpy as np
from scipy import stats
sample_number = 16 # 샘플수
population_mean = 50 # 모집단의 평균
standard_deviation = 12 # 표준편차
sample_mean = 54 # 샘플의 평균
## 신뢰구간을 벗어나는지 아닌지 확인 함수
alpha_level05 = 1.96
alpha_level01 = 2.58
def h_test(sample_mean, population_mean, standard_deviation, sample_number, alpha_level):
result = (sample_mean - population_mean)/ (standard_deviation/np.sqrt(sample_number))
if result> alpha_level or result< - alpha_level:
print("a = .05 신뢰구간에서 귀무가설 reject되고, 가설이 ok")
else:
print("귀무가설이 reject 되지 않아 가설이 기각됩니다.")
return result
##Compute Cohen’s d
def Cohen(sample_mean, population_mean, standard_deviation):
result = (sample_mean - population_mean) / (standard_deviation)
if result<=0.2:
print("small effect")
elif result<= 0.5:
print("medium effect")
elif result<= 0.8:
print("Large effect")
return result
## 신뢰구간을 벗어나는지 아닌지 확인 함수
h_test(sample_mean, population_mean, standard_deviation, sample_number, alpha_level05)
Cohen(sample_mean, population_mean, standard_deviation)
함수를 활용해서, 신뢰구간과 cohen's d를 구할 수 있다.
# ## Import the packages
# import numpy as np
# from scipy import stats
# ## 함수로 만들기
# #Sample Size
# sample_number = 16
# population_mean = 50 # 모집단의 평균
# standard_deviation = 12 # 표준편차
# sample_mean = [54,54,58,53,52] # 샘플의 평균
# def h_test(sample_mean, population_mean, standard_deviation, sample_number):
# #For unbiased max likelihood estimate we have to divide the var by N-1, and therefore the parameter ddof = 1
# var_sample_mean = sample_mean.var(ddof=1)
# var_population_mean = population_mean.var(ddof=1)
# #std deviation
# std_deviation = np.sqrt((var_sample_mean + var_population_mean)/2)
# ## Calculate the t-statistics
# t = (a.mean() - b.mean())/(s*np.sqrt(2/N))
# ## Define 2 random distributions
# N = 10
# #Gaussian distributed data with mean = 2 and var = 1
# a = np.random.randn(N) + 2
# #Gaussian distributed data with with mean = 0 and var = 1
# b = np.random.randn(N)
# ## Calculate the Standard Deviation
# #Calculate the variance to get the standard deviation
# #For unbiased max likelihood estimate we have to divide the var by N-1, and therefore the parameter ddof = 1
# var_a = a.var(ddof=1)
# var_b = b.var(ddof=1)
# #std deviation
# s = np.sqrt((var_a + var_b)/2)
# s
# ## Calculate the t-statistics
# t = (a.mean() - b.mean())/(s*np.sqrt(2/N))
# ## Compare with the critical t-value
# #Degrees of freedom
# df = 2*N - 2
# #p-value after comparison with the t
# p = 1 - stats.t.cdf(t,df=df)
# print("t = " + str(t))
# print("p = " + str(2*p))
# ### You can see that after comparing the t statistic with the critical t value (computed internally) we get a good p value of 0.0005 and thus we reject the null hypothesis and thus it proves that the mean of the two distributions are different and statistically significant.
# ## Cross Checking with the internal scipy function
# t2, p2 = stats.ttest_ind(a,b)
# print("t = " + str(t2))
# print("p = " + str(p2))
```
| true |
code
| 0.617686 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
import numpy as np
from mvmm.single_view.gaussian_mixture import GaussianMixture
from mvmm.single_view.MMGridSearch import MMGridSearch
from mvmm.single_view.toy_data import sample_1d_gmm
from mvmm.single_view.sim_1d_utils import plot_est_params
from mvmm.viz_utils import plot_scatter_1d, set_xaxis_int_ticks
from mvmm.single_view.opt_diagnostics import plot_opt_hist
```
# sample data from a 1d gussian mixture model
```
n_samples = 200
n_components = 3
X, y, true_params = sample_1d_gmm(n_samples=n_samples,
n_components=n_components,
random_state=1)
plot_scatter_1d(X)
```
# Fit a Gaussian mixture model
```
# fit a guassian mixture model with 3 (the true number) of components
# from mvmm.single_view.gaussian_mixture.GaussianMixture() is similar to sklearn.mixture.GaussianMixture()
gmm = GaussianMixture(n_components=3,
n_init=10) # 10 random initalizations
gmm.fit(X)
# plot parameter estimates
plot_scatter_1d(X)
plot_est_params(gmm)
# the GMM class has all the familiar sklearn functionality
gmm.sample(n_samples=20)
gmm.predict(X)
gmm.score_samples(X)
gmm.predict_proba(X)
gmm.bic(X)
# with a few added API features for convenience
# sample from a single mixture component
gmm.sample_from_comp(y=0)
# observed data log-likelihood
gmm.log_likelihood(X)
# total number of cluster parameters
gmm._n_parameters()
# some additional metadata is stored such as the fit time (in seconds)
gmm.metadata_['fit_time']
# gmm.opt_data_ stores the optimization history
plot_opt_hist(loss_vals=gmm.opt_data_['history']['loss_val'],
init_loss_vals=gmm.opt_data_['init_loss_vals'],
loss_name='observed data negative log likelihood')
```
# Model selection with BIC
```
# setup the base estimator for the grid search
# here we add some custom arguments
base_estimator = GaussianMixture(reg_covar=1e-6,
init_params_method='rand_pts', # initalize cluster means from random data points
n_init=10, abs_tol=1e-8, rel_tol=1e-8, max_n_steps=200)
# do a grid search from 1 to 10 components
param_grid = {'n_components': np.arange(1, 10 + 1)}
# setup grid search object and fit using the data
grid_search = MMGridSearch(base_estimator=base_estimator, param_grid=param_grid)
grid_search.fit(X)
# the best model is stored in .best_estimator_
print('BIC selected the model with', grid_search.best_estimator_.n_components, ' components')
# all fit estimators are containted in .estimators_
print(len(grid_search.estimators_))
# the model selection for each grid point are stored in /model_sel_scores_
print(grid_search.model_sel_scores_)
# plot BIC
n_comp_seq = grid_search.param_grid['n_components']
est_n_comp = grid_search.best_params_['n_components']
bic_values = grid_search.model_sel_scores_['bic']
plt.plot(n_comp_seq, bic_values, marker='.')
plt.axvline(est_n_comp,
label='estimated {} components'.format(est_n_comp),
color='red')
plt.legend()
plt.xlabel('n_components')
plt.ylabel('BIC')
set_xaxis_int_ticks()
```
| true |
code
| 0.757068 | null | null | null | null |
|
# Pragmatic color describers
```
__author__ = "Christopher Potts"
__version__ = "CS224u, Stanford, Spring 2020"
```
## Contents
1. [Overview](#Overview)
1. [Set-up](#Set-up)
1. [The corpus](#The-corpus)
1. [Corpus reader](#Corpus-reader)
1. [ColorsCorpusExample instances](#ColorsCorpusExample-instances)
1. [Displaying examples](#Displaying-examples)
1. [Color representations](#Color-representations)
1. [Utterance texts](#Utterance-texts)
1. [Far, Split, and Close conditions](#Far,-Split,-and-Close-conditions)
1. [Toy problems for development work](#Toy-problems-for-development-work)
1. [Core model](#Core-model)
1. [Toy dataset illustration](#Toy-dataset-illustration)
1. [Predicting sequences](#Predicting-sequences)
1. [Listener-based evaluation](#Listener-based-evaluation)
1. [Other prediction and evaluation methods](#Other-prediction-and-evaluation-methods)
1. [Cross-validation](#Cross-validation)
1. [Baseline SCC model](#Baseline-SCC-model)
1. [Modifying the core model](#Modifying-the-core-model)
1. [Illustration: LSTM Cells](#Illustration:-LSTM-Cells)
1. [Illustration: Deeper models](#Illustration:-Deeper-models)
## Overview
This notebook is part of our unit on grounding. It illustrates core concepts from the unit, and it provides useful background material for the associated homework and bake-off.
## Set-up
```
from colors import ColorsCorpusReader
import os
import pandas as pd
from sklearn.model_selection import train_test_split
import torch
from torch_color_describer import (
ContextualColorDescriber, create_example_dataset)
import utils
from utils import START_SYMBOL, END_SYMBOL, UNK_SYMBOL
utils.fix_random_seeds()
```
The [Stanford English Colors in Context corpus](https://cocolab.stanford.edu/datasets/colors.html) (SCC) is included in the data distribution for this course. If you store the data in a non-standard place, you'll need to update the following:
```
COLORS_SRC_FILENAME = os.path.join(
"data", "colors", "filteredCorpus.csv")
```
## The corpus
The SCC corpus is based in a two-player interactive game. The two players share a context consisting of three color patches, with the display order randomized between them so that they can't use positional information when communicating.
The __speaker__ is privately assigned a target color and asked to produce a description of it that will enable the __listener__ to identify the speaker's target. The listener makes a choice based on the speaker's message, and the two succeed if and only if the listener identifies the target correctly.
In the game, the two players played repeated reference games and could communicate with each other in a free-form way. This opens up the possibility of modeling these repeated interactions as task-oriented dialogues. However, for this unit, we'll ignore most of this structure. We'll treat the corpus as a bunch of independent reference games played by anonymous players, and we will ignore the listener and their choices entirely.
For the bake-off, we will be distributing a separate test set. Thus, all of the data in the SCC can be used for exploration and development.
### Corpus reader
The corpus reader class is `ColorsCorpusReader` in `colors.py`. The reader's primary function is to let you iterate over corpus examples:
```
corpus = ColorsCorpusReader(
COLORS_SRC_FILENAME,
word_count=None,
normalize_colors=True)
```
The two keyword arguments have their default values here.
* If you supply `word_count` with an interger value, it will restrict to just examples where the utterance has that number of words (using a whitespace heuristic). This creates smaller corpora that are useful for development.
* The colors in the corpus are in [HLS format](https://en.wikipedia.org/wiki/HSL_and_HSV). With `normalize_colors=False`, the first (hue) value is an integer between 1 and 360 inclusive, and the L (lightness) and S (saturation) values are between 1 and 100 inclusive. With `normalize_colors=True`, these values are all scaled to between 0 and 1 inclusive. The default is `normalize_colors=True` because this is a better choice for all the machine learning models we'll consider.
```
examples = list(corpus.read())
```
We can verify that we read in the same number of examples as reported in [Monroe et al. 2017](https://transacl.org/ojs/index.php/tacl/article/view/1142):
```
# Should be 46994:
len(examples)
```
### ColorsCorpusExample instances
The examples are `ColorsCorpusExample` instances:
```
ex1 = next(corpus.read())
```
These objects have a lot of attributes and methods designed to help you study the corpus and use it for our machine learning tasks. Let's review some highlights.
#### Displaying examples
You can see what the speaker saw, with the utterance they chose wote above the patches:
```
ex1.display(typ='speaker')
```
This is the original order of patches for the speaker. The target happens to the be the leftmost patch, as indicated by the black box around it.
Here's what the listener saw, with the speaker's message printed above the patches:
```
ex1.display(typ='listener')
```
The listener isn't shown the target, of course, so no patches are highlighted.
If `display` is called with no arguments, then the target is placed in the final position and the other two are given in an order determined by the corpus metadata:
```
ex1.display()
```
This is the representation order we use for our machine learning models.
#### Color representations
For machine learning, we'll often need to access the color representations directly. The primary attribute for this is `colors`:
```
ex1.colors
```
In this display order, the third element is the target color and the first two are the distractors. The attributes `speaker_context` and `listener_context` return the same colors but in the order that those players saw them. For example:
```
ex1.speaker_context
```
#### Utterance texts
Utterances are just strings:
```
ex1.contents
```
There are cases where the speaker made a sequences of utterances for the same trial. We follow [Monroe et al. 2017](https://transacl.org/ojs/index.php/tacl/article/view/1142) in concatenating these into a single utterances. To preserve the original information, the individual turns are separated by `" ### "`. Example 3 is the first with this property – let's check it out:
```
ex3 = examples[2]
ex3.contents
```
The method `parse_turns` will parse this into individual turns:
```
ex3.parse_turns()
```
For examples consisting of a single turn, `parse_turns` returns a list of length 1:
```
ex1.parse_turns()
```
### Far, Split, and Close conditions
The SCC contains three conditions:
__Far condition__: All three colors are far apart in color space. Example:
```
print("Condition type:", examples[1].condition)
examples[1].display()
```
__Split condition__: The target is close to one of the distractors, and the other is far away from both of them. Example:
```
print("Condition type:", examples[3].condition)
examples[3].display()
```
__Close condition__: The target is similar to both distractors. Example:
```
print("Condition type:", examples[2].condition)
examples[2].display()
```
These conditions go from easiest to hardest when it comes to reliable communication. In the __Far__ condition, the context is hardly relevant, whereas the nature of the distractors reliably shapes the speaker's choices in the other two conditions.
You can begin to see how this affects speaker choices in the above examples: "purple" suffices for the __Far__ condition, a more marked single word ("lime") suffices in the __Split__ condition, and the __Close__ condition triggers a pretty long, complex description.
The `condition` attribute provides access to this value:
```
ex1.condition
```
The following verifies that we have the same number of examples per condition as reported in [Monroe et al. 2017](https://transacl.org/ojs/index.php/tacl/article/view/1142):
```
pd.Series([ex.condition for ex in examples]).value_counts()
```
## Toy problems for development work
The SCC corpus is fairly large and quite challenging as an NLU task. This means it isn't ideal when it comes to testing hypotheses and debugging code. Poor performance could trace to a mistake, but it could just as easily trace to the fact that the problem is very challenging from the point of view of optimization.
To address this, the module `torch_color_describer.py` includes a function `create_example_dataset` for creating small, easy datasets with the same basic properties as the SCC corpus.
Here's a toy problem containing just six examples:
```
tiny_contexts, tiny_words, tiny_vocab = create_example_dataset(
group_size=2, vec_dim=2)
tiny_vocab
tiny_words
tiny_contexts
```
Each member of `tiny_contexts` contains three vectors. The final (target) vector always has values in a range that determines the corresponding word sequence, which is drawn from a set of three fixed sequences. Thus, the model basically just needs to learn to ignore the distractors and find the association between the target vector and the corresponding sequence.
All the models we study have a capacity to solve this task with very little data, so you should see perfect or near perfect performance on reasonably-sized versions of this task.
## Core model
Our core model for this problem is implemented in `torch_color_describer.py` as `ContextualColorDescriber`. At its heart, this is a pretty standard encoder–decoder model:
* `Encoder`: Processes the color contexts as a sequence. We always place the target in final position so that it is closest to the supervision signals that we get when decoding.
* `Decoder`: A neural language model whose initial hidden representation is the final hidden representation of the `Encoder`.
* `EncoderDecoder`: Coordinates the operations of the `Encoder` and `Decoder`.
Finally, `ContextualColorDescriber` is a wrapper around these model components. It handle the details of training and implements the prediction and evaluation functions that we will use.
Many additional details about this model are included in the slides for this unit.
### Toy dataset illustration
To highlight the core functionality of `ContextualColorDescriber`, let's create a small toy dataset and use it to train and evaluate a model:
```
toy_color_seqs, toy_word_seqs, toy_vocab = create_example_dataset(
group_size=50, vec_dim=2)
toy_color_seqs_train, toy_color_seqs_test, toy_word_seqs_train, toy_word_seqs_test = \
train_test_split(toy_color_seqs, toy_word_seqs)
```
Here we expose all of the available parameters with their default values:
```
toy_mod = ContextualColorDescriber(
toy_vocab,
embedding=None, # Option to supply a pretrained matrix as an `np.array`.
embed_dim=10,
hidden_dim=10,
max_iter=100,
eta=0.01,
optimizer=torch.optim.Adam,
batch_size=128,
l2_strength=0.0,
warm_start=False,
device=None)
_ = toy_mod.fit(toy_color_seqs_train, toy_word_seqs_train)
```
### Predicting sequences
The `predict` method takes a list of color contexts as input and returns model descriptions:
```
toy_preds = toy_mod.predict(toy_color_seqs_test)
toy_preds[0]
```
We can then check that we predicted all correct sequences:
```
toy_correct = sum(1 for x, p in zip(toy_word_seqs_test, toy_preds))
toy_correct / len(toy_word_seqs_test)
```
For real problems, this is too stringent a requirement, since there are generally many equally good descriptions. This insight gives rise to metrics like [BLEU](https://en.wikipedia.org/wiki/BLEU), [METEOR](https://en.wikipedia.org/wiki/METEOR), [ROUGE](https://en.wikipedia.org/wiki/ROUGE_(metric)), [CIDEr](https://arxiv.org/pdf/1411.5726.pdf), and others, which seek to relax the requirement of an exact match with the test sequence. These are reasonable options to explore, but we will instead adopt a communcation-based evaluation, as discussed in the next section.
### Listener-based evaluation
`ContextualColorDescriber` implements a method `listener_accuracy` that we will use for our primary evaluations in the assignment and bake-off. The essence of the method is that we can calculate
$$
c^{*} = \text{argmax}_{c \in C} P_S(\text{utterance} \mid c)
$$
where $P_S$ is our describer model and $C$ is the set of all permutations of all three colors in the color context. We take $c^{*}$ to be a correct prediction if it is one where the target is in the privileged final position. (There are two such contexts; we try both in case the order of the distractors influences the predictions, and the model is correct if one of them has the highest probability.)
Here's the listener accuracy of our toy model:
```
toy_mod.listener_accuracy(toy_color_seqs_test, toy_word_seqs_test)
```
### Other prediction and evaluation methods
You can get the perplexities for test examles with `perpelexities`:
```
toy_perp = toy_mod.perplexities(toy_color_seqs_test, toy_word_seqs_test)
toy_perp[0]
```
You can use `predict_proba` to see the full probability distributions assigned to test examples:
```
toy_proba = toy_mod.predict_proba(toy_color_seqs_test, toy_word_seqs_test)
toy_proba[0].shape
for timestep in toy_proba[0]:
print(dict(zip(toy_vocab, timestep)))
```
### Cross-validation
You can use `utils.fit_classifier_with_crossvalidation` to cross-validate these models. Just be sure to set `scoring=None` so that the sklearn model selection methods use the `score` method of `ContextualColorDescriber`, which is an alias for `listener_accuracy`:
```
best_mod = utils.fit_classifier_with_crossvalidation(
toy_color_seqs_train,
toy_word_seqs_train,
toy_mod,
cv=2,
scoring=None,
param_grid={'hidden_dim': [10, 20]})
```
## Baseline SCC model
Just to show how all the pieces come together, here's a very basic SCC experiment using the core code and very simplistic assumptions (which you will revisit in the assignment) about how to represent the examples:
To facilitate quick development, we'll restrict attention to the two-word examples:
```
dev_corpus = ColorsCorpusReader(COLORS_SRC_FILENAME, word_count=2)
dev_examples = list(dev_corpus.read())
len(dev_examples)
```
Here we extract the raw colors and texts (as strings):
```
dev_cols, dev_texts = zip(*[[ex.colors, ex.contents] for ex in dev_examples])
```
To tokenize the examples, we'll just split on whitespace, taking care to add the required boundary symbols:
```
dev_word_seqs = [[START_SYMBOL] + text.split() + [END_SYMBOL] for text in dev_texts]
```
We'll use a random train–test split:
```
dev_cols_train, dev_cols_test, dev_word_seqs_train, dev_word_seqs_test = \
train_test_split(dev_cols, dev_word_seqs)
```
Our vocab is determined by the train set, and we take care to include the `$UNK` token:
```
dev_vocab = sorted({w for toks in dev_word_seqs_train for w in toks}) + [UNK_SYMBOL]
```
And now we're ready to train a model:
```
dev_mod = ContextualColorDescriber(
dev_vocab,
embed_dim=10,
hidden_dim=10,
max_iter=10,
batch_size=128)
_ = dev_mod.fit(dev_cols_train, dev_word_seqs_train)
```
And finally an evaluation in terms of listener accuracy:
```
dev_mod.listener_accuracy(dev_cols_test, dev_word_seqs_test)
```
## Modifying the core model
The first few assignment problems concern how you preprocess the data for your model. After that, the goal is to subclass model components in `torch_color_describer.py`. For the bake-off submission, you can do whatever you like in terms of modeling, but my hope is that you'll be able to continue subclassing based on `torch_color_describer.py`.
This section provides some illustrative examples designed to give you a feel for how the code is structured and what your options are in terms of creating subclasses.
### Illustration: LSTM Cells
Both the `Encoder` and the `Decoder` of `torch_color_describer` are currently GRU cells. Switching to another cell type is easy:
__Step 1__: Subclass the `Encoder`; all we have to do here is change `GRU` from the original to `LSTM`:
```
import torch.nn as nn
from torch_color_describer import Encoder
class LSTMEncoder(Encoder):
def __init__(self, color_dim, hidden_dim):
super().__init__(color_dim, hidden_dim)
self.rnn = nn.LSTM(
input_size=self.color_dim,
hidden_size=self.hidden_dim,
batch_first=True)
```
__Step 2__: Subclass the `Decoder`, making the same simple change as above:
```
import torch.nn as nn
from torch_color_describer import Encoder, Decoder
class LSTMDecoder(Decoder):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.rnn = nn.LSTM(
input_size=self.embed_dim,
hidden_size=self.hidden_dim,
batch_first=True)
```
__Step 3__:`ContextualColorDescriber` has a method called `build_graph` that sets up the `Encoder` and `Decoder`. The needed revision just uses `LSTMEncoder`:
```
from torch_color_describer import EncoderDecoder
class LSTMContextualColorDescriber(ContextualColorDescriber):
def build_graph(self):
# Use the new Encoder:
encoder = LSTMEncoder(
color_dim=self.color_dim,
hidden_dim=self.hidden_dim)
# Use the new Decoder:
decoder = LSTMDecoder(
vocab_size=self.vocab_size,
embed_dim=self.embed_dim,
embedding=self.embedding,
hidden_dim=self.hidden_dim)
return EncoderDecoder(encoder, decoder)
```
Here's an example run:
```
lstm_mod = LSTMContextualColorDescriber(
toy_vocab,
embed_dim=10,
hidden_dim=10,
max_iter=100,
batch_size=128)
_ = lstm_mod.fit(toy_color_seqs_train, toy_word_seqs_train)
lstm_mod.listener_accuracy(toy_color_seqs_test, toy_word_seqs_test)
```
### Illustration: Deeper models
The `Encoder` and `Decoder` are both currently hard-coded to have just one hidden layer. It is straightforward to make them deeper as long as we ensure that both the `Encoder` and `Decoder` have the same depth; since the `Encoder` final states are the initial hidden states for the `Decoder`, we need this alignment.
(Strictly speaking, we could have different numbers of `Encoder` and `Decoder` layers, as long as we did some kind of averaging or copying to achieve the hand-off from `Encoder` to `Decocer`. I'll set this possibility aside.)
__Step 1__: We need to subclass the `Encoder` and `Decoder` so that they have `num_layers` argument that is fed into the RNN cell:
```
import torch.nn as nn
from torch_color_describer import Encoder, Decoder
class DeepEncoder(Encoder):
def __init__(self, *args, num_layers=2, **kwargs):
super().__init__(*args, **kwargs)
self.num_layers = num_layers
self.rnn = nn.GRU(
input_size=self.color_dim,
hidden_size=self.hidden_dim,
num_layers=self.num_layers,
batch_first=True)
class DeepDecoder(Decoder):
def __init__(self, *args, num_layers=2, **kwargs):
super().__init__(*args, **kwargs)
self.num_layers = num_layers
self.rnn = nn.GRU(
input_size=self.embed_dim,
hidden_size=self.hidden_dim,
num_layers=self.num_layers,
batch_first=True)
```
__Step 2__: As before, we need to update the `build_graph` method of `ContextualColorDescriber`. The needed revision just uses `DeepEncoder` and `DeepDecoder`. To expose this new argument to the user, we also add a new keyword argument to `ContextualColorDescriber`:
```
from torch_color_describer import EncoderDecoder
class DeepContextualColorDescriber(ContextualColorDescriber):
def __init__(self, *args, num_layers=2, **kwargs):
self.num_layers = num_layers
super().__init__(*args, **kwargs)
def build_graph(self):
encoder = DeepEncoder(
color_dim=self.color_dim,
hidden_dim=self.hidden_dim,
num_layers=self.num_layers) # The new piece is this argument.
decoder = DeepDecoder(
vocab_size=self.vocab_size,
embed_dim=self.embed_dim,
embedding=self.embedding,
hidden_dim=self.hidden_dim,
num_layers=self.num_layers) # The new piece is this argument.
return EncoderDecoder(encoder, decoder)
```
An example/test run:
```
mod_deep = DeepContextualColorDescriber(
toy_vocab,
embed_dim=10,
hidden_dim=10,
max_iter=100,
batch_size=128)
_ = mod_deep.fit(toy_color_seqs_train, toy_word_seqs_train)
mod_deep.listener_accuracy(toy_color_seqs_test, toy_word_seqs_test)
```
| true |
code
| 0.770907 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/thingumajig/colab-experiments/blob/master/RetinaNet_Video_Object_Detection.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# .init
## setup keras-retinanet
```
!git clone https://github.com/fizyr/keras-retinanet.git
%cd keras-retinanet/
!pip install .
!python setup.py build_ext --inplace
```
## download model
```
#!curl -LJO --output snapshots/pretrained.h5 https://github.com/fizyr/keras-retinanet/releases/download/0.5.0/resnet50_coco_best_v2.1.0.h5
import urllib
PRETRAINED_MODEL = './snapshots/_pretrained_model.h5'
URL_MODEL = 'https://github.com/fizyr/keras-retinanet/releases/download/0.5.0/resnet50_coco_best_v2.1.0.h5'
urllib.request.urlretrieve(URL_MODEL, PRETRAINED_MODEL)
```
# inference
## modules
```
!pwd
#import os, sys
#sys.path.insert(0, 'keras-retinanet')
# show images inline
%matplotlib inline
# automatically reload modules when they have changed
%load_ext autoreload
%autoreload 2
import os
#os.environ['CUDA_VISIBLE_DEVICES'] = '0'
# import keras
import keras
from keras_retinanet import models
from keras_retinanet.utils.image import read_image_bgr, preprocess_image, resize_image
from keras_retinanet.utils.visualization import draw_box, draw_caption
from keras_retinanet.utils.colors import label_color
# import miscellaneous modules
import matplotlib.pyplot as plt
import cv2
import numpy as np
import time
# set tf backend to allow memory to grow, instead of claiming everything
import tensorflow as tf
def get_session():
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
return tf.Session(config=config)
# use this environment flag to change which GPU to use
#os.environ["CUDA_VISIBLE_DEVICES"] = "1"
# set the modified tf session as backend in keras
keras.backend.tensorflow_backend.set_session(get_session())
```
## load model
```
# %cd keras-retinanet/
model_path = os.path.join('snapshots', sorted(os.listdir('snapshots'), reverse=True)[0])
print(model_path)
print(os.path.isfile(model_path))
# load retinanet model
model = models.load_model(model_path, backbone_name='resnet50')
# model = models.convert_model(model)
# load label to names mapping for visualization purposes
labels_to_names = {0: 'person', 1: 'bicycle', 2: 'car', 3: 'motorcycle', 4: 'airplane', 5: 'bus',
6: 'train', 7: 'truck', 8: 'boat', 9: 'traffic light', 10: 'fire hydrant',
11: 'stop sign', 12: 'parking meter', 13: 'bench', 14: 'bird', 15: 'cat',
16: 'dog', 17: 'horse', 18: 'sheep', 19: 'cow', 20: 'elephant', 21: 'bear',
22: 'zebra', 23: 'giraffe', 24: 'backpack', 25: 'umbrella', 26: 'handbag',
27: 'tie', 28: 'suitcase', 29: 'frisbee', 30: 'skis', 31: 'snowboard',
32: 'sports ball', 33: 'kite', 34: 'baseball bat', 35: 'baseball glove',
36: 'skateboard', 37: 'surfboard', 38: 'tennis racket', 39: 'bottle',
40: 'wine glass', 41: 'cup', 42: 'fork', 43: 'knife', 44: 'spoon',
45: 'bowl', 46: 'banana', 47: 'apple', 48: 'sandwich', 49: 'orange',
50: 'broccoli', 51: 'carrot', 52: 'hot dog', 53: 'pizza', 54: 'donut',
55: 'cake', 56: 'chair', 57: 'couch', 58: 'potted plant', 59: 'bed',
60: 'dining table', 61: 'toilet', 62: 'tv', 63: 'laptop', 64: 'mouse',
65: 'remote', 66: 'keyboard', 67: 'cell phone', 68: 'microwave',
69: 'oven', 70: 'toaster', 71: 'sink', 72: 'refrigerator', 73: 'book',
74: 'clock', 75: 'vase', 76: 'scissors', 77: 'teddy bear', 78: 'hair drier',
79: 'toothbrush'}
```
## detect objects
```
def img_inference(img_path, threshold_score = 0.8):
image = read_image_bgr(img_path)
# copy to draw on
draw = image.copy()
draw = cv2.cvtColor(draw, cv2.COLOR_BGR2RGB)
# preprocess image for network
image = preprocess_image(image)
image, scale = resize_image(image)
# process image
start = time.time()
boxes, scores, labels = model.predict_on_batch(np.expand_dims(image, axis=0))
print("processing time: ", time.time() - start)
# correct for image scale
boxes /= scale
# visualize detections
for box, score, label in zip(boxes[0], scores[0], labels[0]):
# scores are sorted so we can break
if score < threshold_score:
break
color = label_color(label)
b = box.astype(int)
draw_box(draw, b, color=color)
caption = "{} {:.3f}".format(labels_to_names[label], score)
draw_caption(draw, b, caption)
plt.figure(figsize=(10, 10))
plt.axis('off')
plt.imshow(draw)
plt.show()
img_inference('examples/000000008021.jpg')
from tensorflow.python.client import device_lib
def get_available_gpus():
local_device_protos = device_lib.list_local_devices()
return [x.physical_device_desc for x in local_device_protos if x.device_type == 'GPU']
GPU = get_available_gpus()[-1][0:-1]
print(GPU)
import glob
def create_video(img_path, name ='processed', img_ext = '*.jpg', image_size=(1280, 720)):
_name = name + '.mp4'
#_cap = VideoCapture(0)
_fourcc = cv2.VideoWriter_fourcc(*'MP4V')
_out = cv2.VideoWriter(_name, _fourcc, 15.0, image_size)
# out = cv2.VideoWriter('project.avi',cv2.VideoWriter_fourcc(*'DIVX'), 15, size)
for filename in sorted(glob.glob(os.path.join(img_path, img_ext))):
print(filename)
img = cv2.imread(filename)
_out.write(img)
del img
_out.release()
import unicodedata
import string
valid_filename_chars = f"-_.() {string.ascii_letters}{string.digits}"
char_limit = 255
def clean_filename(filename, whitelist=valid_filename_chars, replace=' '):
# replace spaces
for r in replace:
filename = filename.replace(r, '_')
# keep only valid ascii chars
cleaned_filename = unicodedata.normalize('NFKD', filename).encode('ASCII', 'ignore').decode()
# keep only whitelisted chars
cleaned_filename = ''.join(c for c in cleaned_filename if c in whitelist)
if len(cleaned_filename) > char_limit:
print(f"Warning, filename truncated because it was over {char_limit}. Filenames may no longer be unique")
return cleaned_filename[:char_limit]
import colorsys
import random
from tqdm import tqdm
N = len(labels_to_names)
HSV_tuples = [(x*1.0/N, 0.5, 0.5) for x in range(N)]
RGB_tuples = list(map(lambda x: tuple(255*np.array(colorsys.hsv_to_rgb(*x))), HSV_tuples))
random.shuffle(RGB_tuples)
def object_detect_video(video_path, out_temp_dir='tmp', video_name = 'processed', threshold = 0.6):
cap = cv2.VideoCapture(video_path)
if not os.path.exists(out_temp_dir):
os.makedirs(out_temp_dir)
tq = tqdm(total=1, unit="frame(s)")
counter = 0
sum_time = 0
video_out = None
while(True):
ret, draw = cap.read()
if not ret:
break
bgr = cv2.cvtColor(draw, cv2.COLOR_RGB2BGR)
# preprocess image for network
image = preprocess_image(bgr)
image, scale = resize_image(image)
if counter == 0:
height, width, channels = draw.shape
#print(f'Shape: {width}X{height}')
_name = video_name + '.mp4'
_fourcc = cv2.VideoWriter_fourcc(*'MP4V')
video_out = cv2.VideoWriter(_name, _fourcc, 20.0, (width, height))
# process image
start = time.time()
boxes, scores, labels = model.predict_on_batch(np.expand_dims(image, axis=0))
t = time.time() - start
#print(f"frame:{counter} processing time: {t}")
tq.total += 1
# fancy way to give info without forcing a refresh
tq.set_postfix(dir=f'frame {counter} time {sum_time}', refresh=False)
tq.update(0) # may trigger a refresh
# correct for image scale
boxes /= scale
# visualize detections
#draw_detections(image, boxes, scores, labels, color=None, label_to_name=None, score_threshold=0.5)
for box, score, label in zip(boxes[0], scores[0], labels[0]):
if score < threshold:
continue
color = label_color(label)
b = box.astype(int)
draw_box(draw, b, color=color)
caption = f"{labels_to_names[label]} {score:.3f}"
draw_caption(draw, b, caption)
if sum_time>0:
cv2.putText(draw, "Processing time %.2fs (%.1ffps) AVG %.2fs (%.1ffps)"%(t,1.0/t,sum_time/counter,counter/sum_time), (10, 70), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 0, 0), 7)
cv2.putText(draw, "Processing time %.2fs (%.1ffps) AVG %.2fs (%.1ffps)"%(t,1.0/t,sum_time/counter,counter/sum_time), (10, 70), cv2.FONT_HERSHEY_SIMPLEX, 1, (255, 255, 255), 3)
# cv2.imwrite(os.path.join(out_temp_dir, f'img{counter:08d}.jpg'),draw)
video_out.write(draw)
counter=counter+1
sum_time+=t
cap.release()
video_out.release()
cv2.destroyAllWindows()
tq.set_postfix(dir=video_path)
tq.close()
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print(f'User uploaded file "{fn}" with length {len(uploaded[fn])} bytes')
fn0 = clean_filename(fn)
#with open(fn0, "wb") as df:
# df.write(uploaded[fn])
# df.close()
object_detect_video(fn, f'{fn0}_tmp', video_name=f'{os.path.basename(fn0)}_processed', threshold = 0.5)
#create_video(f'{fn0}_tmp')
files.download(f'{os.path.basename(fn0)}_processed.mp4')
# object_detect_video('Canada vs. Finland - Gold Medal Game - Game Highlights - IIHFWorlds 2019.mp4', 'video_tmp', video_name = 'processed2')
#sorted(glob.glob('/content/keras-retinanet/video_tmp/*.jpg'))
#create_video('/content/keras-retinanet/video_tmp')
```
| true |
code
| 0.540075 | null | null | null | null |
|
# Introduction
Linear Regression is one of the most famous and widely used machine learning algorithms out there. It assumes that the target variable can be explained as a linear combination of the input features. What does this mean? It means that the target can be viewed as a weighted sum of each feature. Let’s use a practical example to illustrate that.
Let’s say that we are opening a restaurant, we make great food but we want to know how much to charge for it. We can be very pragmatic and say that the cost of the meal is directly related to what is in it. We can, for instance, have a rule that each ingredient costs a certain amount, and based on how much there is of each ingredient in the dish, we can calculate its price. There may also be a fixed minimum price for each dish. Mathematically, this is called the intercept.
```
fixed_price = 5
ingredient_costs = {"meat": 10,
"fish": 13,
"vegetables": 2,
"fries": 3}
def price(**ingredients):
""" returns the price of a dish """
cost = 0
for name, quantity in ingredients.items():
cost += ingredient_costs[name] * quantity
return cost
```
Linear Regression makes the assumption that the target, in this case, the price, can be explained like this. The model will know about the quantity of each ingredient, but it will have to infer what the fixed price is, and what is the cost of each ingredient.
>It is important to remember that cost, in this situation, is rather abstract. It represents how much each feature affect the outcome, and in which way. Therefore, features can have negative costs for instance.
In the univariate case, where there is only one feature, Linear Regression can be thought of as trying to fit a line through points.

Now, Linear Regression is one of the most popular algorithms because it can do much more than fit straight lines through data. Indeed, with a simple trick, we can make it fit polynomial functions, making it much more powerful.
The trick is to "replace" the original features with a polynomial of a higher degree. In the univariate case, this comes down to not only using the feature itself but also its squared value, cubed value, and so on. For instance, instead of using a single feature $X = 2$, we end up with features $X = 2, 4, 8, 16, 32$, and so on. More features mean that the model is explained by more weights, and these weights can express more complex functions.

A Linear Regression model's goal is to find the coefficients, also called weights, which will fit the data best. In order to define what best means, we need to define a loss function. This loss function, as we will see later, can be tweaked to alter how the weights are learned. We will also see that finding the best weights in order to minimize the loss function can be done in different ways.
| true |
code
| 0.526282 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
**Module 3 Assignment: Creating Columns in Pandas**
**Student Name: Your Name**
# Assignment Instructions
For this assignment you will use the **reg-30-spring-2018.csv** dataset. This is a dataset that I generated specifically for this semester. You can find the CSV file in the **data** directory of the class GitHub repository here: [reg-30-spring-2018.csv](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/data/reg-30-spring-2018.csv).
For this assignment, load and modify the data set. You will submit this modified dataset to the **submit** function. See [Assignment #1](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class1.ipynb) for details on how to submit an assignment or check that one was submitted.
Modify the dataset as follows:
* Add a column named *density* that is *weight* divided by *volume*.
* Replace the *region* column with dummy variables.
* Replace the *item* column with an index encoding value (for example 0 for the first class, 1 for the next, etc. see function *encode_text_index*)
* Your submitted dataframe will have these columns: id, distance, height, landings, number, pack, age, usage, weight, item, volume, width, max, power, size, target, density, region-RE-0, region-RE-1, region-RE-10, region-RE-11, region-RE-2, region-RE-3, region-RE-4, region-RE-5, region-RE-6, region-RE-7, region-RE-8, region-RE-9, region-RE-A, region-RE-B, region-RE-C, region-RE-D, region-RE-E, region-RE-F.
# Helpful Functions
You will see these at the top of every module and assignment. These are simply a set of reusable functions that we will make use of. Each of them will be explained as the semester progresses. They are explained in greater detail as the course progresses. Class 4 contains a complete overview of these functions.
```
from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shutil
import os
import requests
import base64
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = "{}-{}".format(name, x)
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Encode text values to a single dummy variable. The new columns (which do not replace the old) will have a 1
# at every location where the original column (name) matches each of the target_values. One column is added for
# each target value.
def encode_text_single_dummy(df, name, target_values):
for tv in target_values:
l = list(df[name].astype(str))
l = [1 if str(x) == str(tv) else 0 for x in l]
name2 = "{}-{}".format(name, tv)
df[name2] = l
# Encode text values to indexes(i.e. [1],[2],[3] for red,green,blue).
def encode_text_index(df, name):
le = preprocessing.LabelEncoder()
df[name] = le.fit_transform(df[name])
return le.classes_
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Convert all missing values in the specified column to the median
def missing_median(df, name):
med = df[name].median()
df[name] = df[name].fillna(med)
# Convert all missing values in the specified column to the default
def missing_default(df, name, default_value):
df[name] = df[name].fillna(default_value)
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df.as_matrix(result).astype(np.float32), dummies.as_matrix().astype(np.float32)
else:
# Regression
return df.as_matrix(result).astype(np.float32), df.as_matrix([target]).astype(np.float32)
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
# Regression chart.
def chart_regression(pred,y,sort=True):
t = pd.DataFrame({'pred' : pred, 'y' : y.flatten()})
if sort:
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction')
plt.ylabel('output')
plt.legend()
plt.show()
# Remove all rows where the specified column is +/- sd standard deviations
def remove_outliers(df, name, sd):
drop_rows = df.index[(np.abs(df[name] - df[name].mean()) >= (sd * df[name].std()))]
df.drop(drop_rows, axis=0, inplace=True)
# Encode a column to a range between normalized_low and normalized_high.
def encode_numeric_range(df, name, normalized_low=-1, normalized_high=1,
data_low=None, data_high=None):
if data_low is None:
data_low = min(df[name])
data_high = max(df[name])
df[name] = ((df[name] - data_low) / (data_high - data_low)) \
* (normalized_high - normalized_low) + normalized_low
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# Assignment #3 Sample Code
The following code provides a starting point for this assignment.
```
import os
import pandas as pd
from scipy.stats import zscore
# This is your student key that I emailed to you at the beginnning of the semester.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh" # This is an example key and will not work.
# You must also identify your source file. (modify for your local setup)
# file='/resources/t81_558_deep_learning/assignment_yourname_class1.ipynb' # IBM Data Science Workbench
# file='C:\\Users\\jeffh\\projects\\t81_558_deep_learning\\t81_558_class1_intro_python.ipynb' # Windows
#file='/Users/jeff/projects/t81_558_deep_learning/assignment_yourname_class1.ipynb' # Mac/Linux
file = '...location of your source file...'
# Begin assignment
path = "./data/"
filename_read = os.path.join(path,"reg-30-spring-2018.csv")
df = pd.read_csv(filename_read)
# Calculate density
# Encode dummies
# Save a copy to examine, if you like
df.to_csv('3.csv',index=False)
# Submit
submit(source_file=file,data=df,key=key,no=3)
```
# Checking Your Submission
You can always double check to make sure your submission actually happened. The following utility code will help with that.
```
import requests
import pandas as pd
import base64
import os
def list_submits(key):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
def display_submit(key,no):
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key': key},
json={'assignment':no})
if r.status_code == 200:
print("Success: \n{}".format(r.text))
else:
print("Failure: {}".format(r.text))
# Show a listing of all submitted assignments.
key = "qgABjW9GKV1vvFSQNxZW9akByENTpTAo2T9qOjmh"
list_submits(key)
# Show one assignment, by number.
display_submit(key,3)
```
| true |
code
| 0.469399 | null | null | null | null |
|
# Reading and writing fields
There are two main file formats to which a `discretisedfield.Field` object can be saved:
- [VTK](https://vtk.org/) for visualisation using e.g., [ParaView](https://www.paraview.org/) or [Mayavi](https://docs.enthought.com/mayavi/mayavi/)
- OOMMF [Vector Field File Format (OVF)](https://math.nist.gov/oommf/doc/userguide12a5/userguide/Vector_Field_File_Format_OV.html) for exchanging fields with micromagnetic simulators.
Let us say we have a nanosphere sample:
$$x^2 + y^2 + z^2 <= r^2$$
with $r=5\,\text{nm}$. The space is discretised into cells with dimensions $(0.5\,\text{nm}, 0.5\,\text{nm}, 0.5\,\text{nm})$. The value of the field at $(x, y, z)$ point is $(-cy, cx, cz)$, with $c=10^{9}$. The norm of the field inside the cylinder is $10^{6}$.
Let us first build that field.
```
import discretisedfield as df
r = 5e-9
cell = (0.5e-9, 0.5e-9, 0.5e-9)
mesh = df.Mesh(p1=(-r, -r, -r), p2=(r, r, r), cell=cell)
def norm_fun(pos):
x, y, z = pos
if x**2 + y**2 + z**2 <= r**2:
return 1e6
else:
return 0
def value_fun(pos):
x, y, z = pos
c = 1e9
return (-c*y, c*x, c*z)
field = df.Field(mesh, dim=3, value=value_fun, norm=norm_fun)
```
Let us have a quick view of the field we created
```
# NBVAL_IGNORE_OUTPUT
field.plane('z').k3d.vector(color_field=field.z)
```
## Writing the field to a file
The main method used for saving field in different files is `discretisedfield.Field.write()`. It takes `filename` as an argument, which is a string with one of the following extensions:
- `'.vtk'` for saving in the VTK format
- `'.ovf'`, `'.omf'`, `'.ohf'` for saving in the OVF format
Let us firstly save the field in the VTK file.
```
vtkfilename = 'my_vtk_file.vtk'
field.write(vtkfilename)
```
We can check if the file was saved in the current directory.
```
import os
os.path.isfile(f'./{vtkfilename}')
```
Now, we can delete the file:
```
os.remove(f'./{vtkfilename}')
```
Next, we can save the field in the OVF format and check whether it was created in the current directory.
```
omffilename = 'my_omf_file.omf'
field.write(omffilename)
os.path.isfile(f'./{omffilename}')
```
There are three different possible representations of an OVF file: one ASCII (`txt`) and two binary (`bin4` or `bin8`). ASCII `txt` representation is a default representation when `discretisedfield.Field.write()` is called. If any different representation is required, it can be passed via `representation` argument.
```
field.write(omffilename, representation='bin8')
os.path.isfile(f'./{omffilename}')
```
## Reading the OVF file
The method for reading OVF files is a class method `discretisedfield.Field.fromfile()`. By passing a `filename` argument, it reads the file and creates a `discretisedfield.Field` object. It is not required to pass the representation of the OVF file to the `discretisedfield.Field.fromfile()` method, because it can retrieve it from the content of the file.
```
read_field = df.Field.fromfile(omffilename)
```
Like previouly, we can quickly visualise the field
```
# NBVAL_IGNORE_OUTPUT
read_field.plane('z').k3d.vector(color_field=read_field.z)
```
Finally, we can delete the OVF file we created.
```
os.remove(f'./{omffilename}')
```
| true |
code
| 0.319077 | null | null | null | null |
|
# Finetuning of the pretrained Japanese BERT model
Finetune the pretrained model to solve multi-class classification problems.
This notebook requires the following objects:
- trained sentencepiece model (model and vocab files)
- pretraiend Japanese BERT model
Dataset is livedoor ニュースコーパス in https://www.rondhuit.com/download.html.
We make test:dev:train = 2:2:6 datasets.
Results:
- Full training data
- BERT with SentencePiece
```
precision recall f1-score support
dokujo-tsushin 0.98 0.94 0.96 178
it-life-hack 0.96 0.97 0.96 172
kaden-channel 0.99 0.98 0.99 176
livedoor-homme 0.98 0.88 0.93 95
movie-enter 0.96 0.99 0.98 158
peachy 0.94 0.98 0.96 174
smax 0.98 0.99 0.99 167
sports-watch 0.98 1.00 0.99 190
topic-news 0.99 0.98 0.98 163
micro avg 0.97 0.97 0.97 1473
macro avg 0.97 0.97 0.97 1473
weighted avg 0.97 0.97 0.97 1473
```
- sklearn GradientBoostingClassifier with MeCab
```
precision recall f1-score support
dokujo-tsushin 0.89 0.86 0.88 178
it-life-hack 0.91 0.90 0.91 172
kaden-channel 0.90 0.94 0.92 176
livedoor-homme 0.79 0.74 0.76 95
movie-enter 0.93 0.96 0.95 158
peachy 0.87 0.92 0.89 174
smax 0.99 1.00 1.00 167
sports-watch 0.93 0.98 0.96 190
topic-news 0.96 0.86 0.91 163
micro avg 0.92 0.92 0.92 1473
macro avg 0.91 0.91 0.91 1473
weighted avg 0.92 0.92 0.91 1473
```
- Small training data (1/5 of full training data)
- BERT with SentencePiece
```
precision recall f1-score support
dokujo-tsushin 0.97 0.87 0.92 178
it-life-hack 0.86 0.86 0.86 172
kaden-channel 0.95 0.94 0.95 176
livedoor-homme 0.82 0.82 0.82 95
movie-enter 0.97 0.99 0.98 158
peachy 0.89 0.95 0.92 174
smax 0.94 0.96 0.95 167
sports-watch 0.97 0.97 0.97 190
topic-news 0.94 0.94 0.94 163
micro avg 0.93 0.93 0.93 1473
macro avg 0.92 0.92 0.92 1473
weighted avg 0.93 0.93 0.93 1473
```
- sklearn GradientBoostingClassifier with MeCab
```
precision recall f1-score support
dokujo-tsushin 0.82 0.71 0.76 178
it-life-hack 0.86 0.88 0.87 172
kaden-channel 0.91 0.87 0.89 176
livedoor-homme 0.67 0.63 0.65 95
movie-enter 0.87 0.95 0.91 158
peachy 0.70 0.78 0.73 174
smax 1.00 1.00 1.00 167
sports-watch 0.87 0.95 0.91 190
topic-news 0.92 0.82 0.87 163
micro avg 0.85 0.85 0.85 1473
macro avg 0.85 0.84 0.84 1473
weighted avg 0.86 0.85 0.85 1473
```
```
import configparser
import glob
import os
import pandas as pd
import subprocess
import sys
import tarfile
from urllib.request import urlretrieve
CURDIR = os.getcwd()
CONFIGPATH = os.path.join(CURDIR, os.pardir, 'config.ini')
config = configparser.ConfigParser()
config.read(CONFIGPATH)
```
## Data preparing
You need execute the following cells just once.
```
FILEURL = config['FINETUNING-DATA']['FILEURL']
FILEPATH = config['FINETUNING-DATA']['FILEPATH']
EXTRACTDIR = config['FINETUNING-DATA']['TEXTDIR']
```
Download and unzip data.
```
%%time
urlretrieve(FILEURL, FILEPATH)
mode = "r:gz"
tar = tarfile.open(FILEPATH, mode)
tar.extractall(EXTRACTDIR)
tar.close()
```
Data preprocessing.
```
def extract_txt(filename):
with open(filename) as text_file:
# 0: URL, 1: timestamp
text = text_file.readlines()[2:]
text = [sentence.strip() for sentence in text]
text = list(filter(lambda line: line != '', text))
return ''.join(text)
categories = [
name for name
in os.listdir( os.path.join(EXTRACTDIR, "text") )
if os.path.isdir( os.path.join(EXTRACTDIR, "text", name) ) ]
categories = sorted(categories)
categories
table = str.maketrans({
'\n': '',
'\t': ' ',
'\r': '',
})
%%time
all_text = []
all_label = []
for cat in categories:
files = glob.glob(os.path.join(EXTRACTDIR, "text", cat, "{}*.txt".format(cat)))
files = sorted(files)
body = [ extract_txt(elem).translate(table) for elem in files ]
label = [cat] * len(body)
all_text.extend(body)
all_label.extend(label)
df = pd.DataFrame({'text' : all_text, 'label' : all_label})
df.head()
df = df.sample(frac=1, random_state=23).reset_index(drop=True)
df.head()
```
Save data as tsv files.
test:dev:train = 2:2:6. To check the usability of finetuning, we also prepare sampled training data (1/5 of full training data).
```
df[:len(df) // 5].to_csv( os.path.join(EXTRACTDIR, "test.tsv"), sep='\t', index=False)
df[len(df) // 5:len(df)*2 // 5].to_csv( os.path.join(EXTRACTDIR, "dev.tsv"), sep='\t', index=False)
df[len(df)*2 // 5:].to_csv( os.path.join(EXTRACTDIR, "train.tsv"), sep='\t', index=False)
### 1/5 of full training data.
# df[:len(df) // 5].to_csv( os.path.join(EXTRACTDIR, "test.tsv"), sep='\t', index=False)
# df[len(df) // 5:len(df)*2 // 5].to_csv( os.path.join(EXTRACTDIR, "dev.tsv"), sep='\t', index=False)
# df[len(df)*2 // 5:].sample(frac=0.2, random_state=23).to_csv( os.path.join(EXTRACTDIR, "train.tsv"), sep='\t', index=False)
```
## Finetune pre-trained model
It will take a lot of hours to execute the following cells on CPU environment.
You can also use colab to recieve the power of TPU. You need to uplode the created data onto your GCS bucket.
[](https://colab.research.google.com/drive/1zZH2GWe0U-7GjJ2w2duodFfEUptvHjcx)
```
PRETRAINED_MODEL_PATH = '../model/model.ckpt-1400000'
FINETUNE_OUTPUT_DIR = '../model/livedoor_output'
%%time
# It will take many hours on CPU environment.
!python3 ../src/run_classifier.py \
--task_name=livedoor \
--do_train=true \
--do_eval=true \
--data_dir=../data/livedoor \
--model_file=../model/wiki-ja.model \
--vocab_file=../model/wiki-ja.vocab \
--init_checkpoint={PRETRAINED_MODEL_PATH} \
--max_seq_length=512 \
--train_batch_size=4 \
--learning_rate=2e-5 \
--num_train_epochs=10 \
--output_dir={FINETUNE_OUTPUT_DIR}
```
## Predict using the finetuned model
Let's predict test data using the finetuned model.
```
import sys
sys.path.append("../src")
import tokenization_sentencepiece as tokenization
from run_classifier import LivedoorProcessor
from run_classifier import model_fn_builder
from run_classifier import file_based_input_fn_builder
from run_classifier import file_based_convert_examples_to_features
from utils import str_to_value
sys.path.append("../bert")
import modeling
import optimization
import tensorflow as tf
import configparser
import json
import glob
import os
import pandas as pd
import tempfile
bert_config_file = tempfile.NamedTemporaryFile(mode='w+t', encoding='utf-8', suffix='.json')
bert_config_file.write(json.dumps({k:str_to_value(v) for k,v in config['BERT-CONFIG'].items()}))
bert_config_file.seek(0)
bert_config = modeling.BertConfig.from_json_file(bert_config_file.name)
output_ckpts = glob.glob("{}/model.ckpt*data*".format(FINETUNE_OUTPUT_DIR))
latest_ckpt = sorted(output_ckpts)[-1]
FINETUNED_MODEL_PATH = latest_ckpt.split('.data-00000-of-00001')[0]
class FLAGS(object):
'''Parameters.'''
def __init__(self):
self.model_file = "../model/wiki-ja.model"
self.vocab_file = "../model/wiki-ja.vocab"
self.do_lower_case = True
self.use_tpu = False
self.output_dir = "/dummy"
self.data_dir = "../data/livedoor"
self.max_seq_length = 512
self.init_checkpoint = FINETUNED_MODEL_PATH
self.predict_batch_size = 4
# The following parameters are not used in predictions.
# Just use to create RunConfig.
self.master = None
self.save_checkpoints_steps = 1
self.iterations_per_loop = 1
self.num_tpu_cores = 1
self.learning_rate = 0
self.num_warmup_steps = 0
self.num_train_steps = 0
self.train_batch_size = 0
self.eval_batch_size = 0
FLAGS = FLAGS()
processor = LivedoorProcessor()
label_list = processor.get_labels()
tokenizer = tokenization.FullTokenizer(
model_file=FLAGS.model_file, vocab_file=FLAGS.vocab_file,
do_lower_case=FLAGS.do_lower_case)
tpu_cluster_resolver = None
is_per_host = tf.contrib.tpu.InputPipelineConfig.PER_HOST_V2
run_config = tf.contrib.tpu.RunConfig(
cluster=tpu_cluster_resolver,
master=FLAGS.master,
model_dir=FLAGS.output_dir,
save_checkpoints_steps=FLAGS.save_checkpoints_steps,
tpu_config=tf.contrib.tpu.TPUConfig(
iterations_per_loop=FLAGS.iterations_per_loop,
num_shards=FLAGS.num_tpu_cores,
per_host_input_for_training=is_per_host))
model_fn = model_fn_builder(
bert_config=bert_config,
num_labels=len(label_list),
init_checkpoint=FLAGS.init_checkpoint,
learning_rate=FLAGS.learning_rate,
num_train_steps=FLAGS.num_train_steps,
num_warmup_steps=FLAGS.num_warmup_steps,
use_tpu=FLAGS.use_tpu,
use_one_hot_embeddings=FLAGS.use_tpu)
estimator = tf.contrib.tpu.TPUEstimator(
use_tpu=FLAGS.use_tpu,
model_fn=model_fn,
config=run_config,
train_batch_size=FLAGS.train_batch_size,
eval_batch_size=FLAGS.eval_batch_size,
predict_batch_size=FLAGS.predict_batch_size)
predict_examples = processor.get_test_examples(FLAGS.data_dir)
predict_file = tempfile.NamedTemporaryFile(mode='w+t', encoding='utf-8', suffix='.tf_record')
file_based_convert_examples_to_features(predict_examples, label_list,
FLAGS.max_seq_length, tokenizer,
predict_file.name)
predict_drop_remainder = True if FLAGS.use_tpu else False
predict_input_fn = file_based_input_fn_builder(
input_file=predict_file.name,
seq_length=FLAGS.max_seq_length,
is_training=False,
drop_remainder=predict_drop_remainder)
result = estimator.predict(input_fn=predict_input_fn)
%%time
# It will take a few hours on CPU environment.
result = list(result)
result[:2]
```
Read test data set and add prediction results.
```
import pandas as pd
test_df = pd.read_csv("../data/livedoor/test.tsv", sep='\t')
test_df['predict'] = [ label_list[elem['probabilities'].argmax()] for elem in result ]
test_df.head()
sum( test_df['label'] == test_df['predict'] ) / len(test_df)
```
A littel more detailed check using `sklearn.metrics`.
```
!pip install scikit-learn
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
print(classification_report(test_df['label'], test_df['predict']))
print(confusion_matrix(test_df['label'], test_df['predict']))
```
### Simple baseline model.
```
import pandas as pd
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
train_df = pd.read_csv("../data/livedoor/train.tsv", sep='\t')
dev_df = pd.read_csv("../data/livedoor/dev.tsv", sep='\t')
test_df = pd.read_csv("../data/livedoor/test.tsv", sep='\t')
!apt-get install -q -y mecab libmecab-dev mecab-ipadic mecab-ipadic-utf8
!pip install mecab-python3==0.7
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.ensemble import GradientBoostingClassifier
import MeCab
m = MeCab.Tagger("-Owakati")
train_dev_df = pd.concat([train_df, dev_df])
train_dev_xs = train_dev_df['text'].apply(lambda x: m.parse(x))
train_dev_ys = train_dev_df['label']
test_xs = test_df['text'].apply(lambda x: m.parse(x))
test_ys = test_df['label']
vectorizer = TfidfVectorizer(max_features=750)
train_dev_xs_ = vectorizer.fit_transform(train_dev_xs)
test_xs_ = vectorizer.transform(test_xs)
```
The following set up is not exactly identical to that of BERT because inside Classifier it uses `train_test_split` with shuffle.
In addition, parameters are not well tuned, however, we think it's enough to check the power of BERT.
```
%%time
model = GradientBoostingClassifier(n_estimators=200,
validation_fraction=len(train_df)/len(dev_df),
n_iter_no_change=5,
tol=0.01,
random_state=23)
### 1/5 of full training data.
# model = GradientBoostingClassifier(n_estimators=200,
# validation_fraction=len(dev_df)/len(train_df),
# n_iter_no_change=5,
# tol=0.01,
# random_state=23)
model.fit(train_dev_xs_, train_dev_ys)
print(classification_report(test_ys, model.predict(test_xs_)))
print(confusion_matrix(test_ys, model.predict(test_xs_)))
```
| true |
code
| 0.758231 | null | null | null | null |
|
### Road Following - Live demo (TensorRT) with collision avoidance
### Added collision avoidance ResNet18 TRT
### threshold between free and blocked is the controller - action: just a pause as long the object is in front or by time
### increase in speed_gain requires some small increase in steer_gain (once a slider is blue (mouse click), arrow keys left/right can be used)
### 10/11/2020
# TensorRT
```
import torch
device = torch.device('cuda')
```
Load the TRT optimized models by executing the cell below
```
import torch
from torch2trt import TRTModule
model_trt = TRTModule()
model_trt.load_state_dict(torch.load('best_steering_model_xy_trt.pth')) # well trained road following model
model_trt_collision = TRTModule()
model_trt_collision.load_state_dict(torch.load('best_model_trt.pth')) # anti collision model trained for one object to block and street signals (ground, strips) as free
```
### Creating the Pre-Processing Function
We have now loaded our model, but there's a slight issue. The format that we trained our model doesnt exactly match the format of the camera. To do that, we need to do some preprocessing. This involves the following steps:
1. Convert from HWC layout to CHW layout
2. Normalize using same parameters as we did during training (our camera provides values in [0, 255] range and training loaded images in [0, 1] range so we need to scale by 255.0
3. Transfer the data from CPU memory to GPU memory
4. Add a batch dimension
```
import torchvision.transforms as transforms
import torch.nn.functional as F
import cv2
import PIL.Image
import numpy as np
mean = torch.Tensor([0.485, 0.456, 0.406]).cuda().half()
std = torch.Tensor([0.229, 0.224, 0.225]).cuda().half()
def preprocess(image):
image = PIL.Image.fromarray(image)
image = transforms.functional.to_tensor(image).to(device).half()
image.sub_(mean[:, None, None]).div_(std[:, None, None])
return image[None, ...]
```
Awesome! We've now defined our pre-processing function which can convert images from the camera format to the neural network input format.
Now, let's start and display our camera. You should be pretty familiar with this by now.
```
from IPython.display import display
import ipywidgets
import traitlets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera()
import IPython
image_widget = ipywidgets.Image()
traitlets.dlink((camera, 'value'), (image_widget, 'value'), transform=bgr8_to_jpeg)
```
We'll also create our robot instance which we'll need to drive the motors.
```
from jetbot import Robot
robot = Robot()
```
Now, we will define sliders to control JetBot
> Note: We have initialize the slider values for best known configurations, however these might not work for your dataset, therefore please increase or decrease the sliders according to your setup and environment
1. Speed Control (speed_gain_slider): To start your JetBot increase ``speed_gain_slider``
2. Steering Gain Control (steering_gain_sloder): If you see JetBot is woblling, you need to reduce ``steering_gain_slider`` till it is smooth
3. Steering Bias control (steering_bias_slider): If you see JetBot is biased towards extreme right or extreme left side of the track, you should control this slider till JetBot start following line or track in the center. This accounts for motor biases as well as camera offsets
> Note: You should play around above mentioned sliders with lower speed to get smooth JetBot road following behavior.
```
speed_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, description='speed gain')
steering_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, value=0.10, description='steering gain')
steering_dgain_slider = ipywidgets.FloatSlider(min=0.0, max=0.5, step=0.001, value=0.23, description='steering kd')
steering_bias_slider = ipywidgets.FloatSlider(min=-0.3, max=0.3, step=0.01, value=0.0, description='steering bias')
display(speed_gain_slider, steering_gain_slider, steering_dgain_slider, steering_bias_slider)
#anti collision ---------------------------------------------------------------------------------------------------
blocked_slider = ipywidgets.FloatSlider(description='blocked', min=0.0, max=1.0, orientation='horizontal')
stopduration_slider= ipywidgets.IntSlider(min=1, max=1000, step=1, value=10, description='Manu. time stop') #anti-collision stop time
#set value according the common threshold e.g. 0.8
block_threshold= ipywidgets.FloatSlider(min=0, max=1.2, step=0.01, value=0.8, description='Manu. bl threshold') #anti-collision block probability
display(image_widget)
d2 = IPython.display.display("", display_id=2)
display(ipywidgets.HBox([blocked_slider, block_threshold, stopduration_slider]))
# TIME STOP slider is to select manually time-for-stop when object has been discovered
#x_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='x')
#y_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='y')
#steering_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='steering')
#speed_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='speed')
#display(ipywidgets.HBox([y_slider, speed_slider,x_slider, steering_slider])) #sliders take time , reduce FPS a couple of frames per second
#observation sliders only
from threading import Thread
def display_class_probability(prob_blocked):
global blocked_slide
blocked_slider.value = prob_blocked
return
def model_new(image_preproc):
global model_trt_collision,angle_last
xy = model_trt(image_preproc).detach().float().cpu().numpy().flatten()
x = xy[0]
y = (0.5 - xy[1]) / 2.0
angle=math.atan2(x, y)
pid =angle * steer_gain + (angle - angle_last) * steer_dgain
steer_val = pid + steer_bias
angle_last = angle
robot.left_motor.value = max(min(speed_value + steer_val, 1.0), 0.0)
robot.right_motor.value = max(min(speed_value - steer_val, 1.0), 0.0)
return
```
Next, we'll create a function that will get called whenever the camera's value changes. This function will do the following steps
1. Pre-process the camera image
2. Execute the neural network
3. Compute the approximate steering value
4. Control the motors using proportional / derivative control (PD)
```
import time
import os
import math
angle = 0.0
angle_last = 0.0
angle_last_block=0
count_stops=0
go_on=1
stop_time=20 #number of frames to remain stopped
x=0.0
y=0.0
speed_value=speed_gain_slider.value
t1=0
road_following=1
speed_value_block=0
def execute(change):
global angle, angle_last, angle_last_block, blocked_slider, robot,count_stops, stop_time,go_on,x,y,block_threshold
global speed_value, steer_gain, steer_dgain, steer_bias,t1,model_trt, model_trt_collision,road_following,speed_value_block
steer_gain=steering_gain_slider.value
steer_dgain=steering_dgain_slider.value
steer_bias=steering_bias_slider.value
image_preproc = preprocess(change['new']).to(device)
#anti_collision model-----
prob_blocked = float(F.softmax(model_trt_collision(image_preproc), dim=1) .flatten()[0])
#blocked_slider.value = prob_blocked
#display of detection probability value for the four classes
t = Thread(target = display_class_probability, args =(prob_blocked,), daemon=False)
t.start()
stop_time=stopduration_slider.value
if go_on==1:
if prob_blocked > block_threshold.value: # threshold should be above 0.5,
#start of collision_avoidance
count_stops +=1
go_on=2
road_following=2
x=0.0 #set steering zero
y=0 #set steering zero
speed_value_block=0 # set speed zero or negative or turn
#anti_collision end-------
else:
#start of road following
go_on=1
count_stops=0
speed_value = speed_gain_slider.value #
t = Thread(target = model_new, args =(image_preproc,), daemon=True)
t.start()
road_following=1
else:
count_stops += 1
if count_stops<stop_time:
go_on=2
else:
go_on=1
count_stops=0
road_following=1
#x_slider.value = x #take time 4 FPS
#y_slider.value = y #y_speed
if road_following>1:
angle_block=math.atan2(x, y)
pid =angle_block * steer_gain + (angle - angle_last) * steer_dgain
steer_val_block = pid + steer_bias
angle_last_block = angle_block
robot.left_motor.value = max(min(speed_value_block + steer_val_block, 1.0), 0.0)
robot.right_motor.value = max(min(speed_value_block - steer_val_block, 1.0), 0.0)
t2 = time.time()
s = f"""{int(1/(t2-t1))} FPS"""
d2.update(IPython.display.HTML(s) )
t1 = time.time()
execute({'new': camera.value})
```
Cool! We've created our neural network execution function, but now we need to attach it to the camera for processing.
We accomplish that with the observe function.
>WARNING: This code will move the robot!! Please make sure your robot has clearance and it is on Lego or Track you have collected data on. The road follower should work, but the neural network is only as good as the data it's trained on!
```
camera.observe(execute, names='value')
```
Awesome! If your robot is plugged in it should now be generating new commands with each new camera frame.
You can now place JetBot on Lego or Track you have collected data on and see whether it can follow track.
If you want to stop this behavior, you can unattach this callback by executing the code below.
```
import time
camera.unobserve(execute, names='value')
time.sleep(0.1) # add a small sleep to make sure frames have finished processing
robot.stop()
camera.stop()
```
### Conclusion
That's it for this live demo! Hopefully you had some fun seeing your JetBot moving smoothly on track follwing the road!!!
If your JetBot wasn't following road very well, try to spot where it fails. The beauty is that we can collect more data for these failure scenarios and the JetBot should get even better :)
| true |
code
| 0.572424 | null | null | null | null |
|
**Chapter 10 – Introduction to Artificial Neural Networks**
_This notebook contains all the sample code and solutions to the exercises in chapter 10._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Perceptrons
```
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=100, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
y_pred
a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)
save_fig("perceptron_iris_plot")
plt.show()
```
# Activation functions
```
def logit(z):
return 1 / (1 + np.exp(-z))
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
z = np.linspace(-5, 5, 200)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=2, label="Step")
plt.plot(z, logit(z), "g--", linewidth=2, label="Logit")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=2, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(logit, z), "g--", linewidth=2, label="Logit")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
def heaviside(z):
return (z >= 0).astype(z.dtype)
def sigmoid(z):
return 1/(1+np.exp(-z))
def mlp_xor(x1, x2, activation=heaviside):
return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)
z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.subplot(122)
plt.contourf(x1, x2, z2)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: sigmoid", fontsize=14)
plt.grid(True)
```
# FNN for MNIST
## Using the Estimator API (formerly `tf.contrib.learn`)
```
import tensorflow as tf
```
**Warning**: `tf.examples.tutorials.mnist` is deprecated. We will use `tf.keras.datasets.mnist` instead. Moreover, the `tf.contrib.learn` API was promoted to `tf.estimators` and `tf.feature_columns`, and it has changed considerably. In particular, there is no `infer_real_valued_columns_from_input()` function or `SKCompat` class.
```
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
feature_cols = [tf.feature_column.numeric_column("X", shape=[28 * 28])]
dnn_clf = tf.estimator.DNNClassifier(hidden_units=[300,100], n_classes=10,
feature_columns=feature_cols)
input_fn = tf.estimator.inputs.numpy_input_fn(
x={"X": X_train}, y=y_train, num_epochs=40, batch_size=50, shuffle=True)
dnn_clf.train(input_fn=input_fn)
test_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"X": X_test}, y=y_test, shuffle=False)
eval_results = dnn_clf.evaluate(input_fn=test_input_fn)
eval_results
y_pred_iter = dnn_clf.predict(input_fn=test_input_fn)
y_pred = list(y_pred_iter)
y_pred[0]
```
## Using plain TensorFlow
```
import tensorflow as tf
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
def neuron_layer(X, n_neurons, name, activation=None):
with tf.name_scope(name):
n_inputs = int(X.get_shape()[1])
stddev = 2 / np.sqrt(n_inputs)
init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
W = tf.Variable(init, name="kernel")
b = tf.Variable(tf.zeros([n_neurons]), name="bias")
Z = tf.matmul(X, W) + b
if activation is not None:
return activation(Z)
else:
return Z
with tf.name_scope("dnn"):
hidden1 = neuron_layer(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = neuron_layer(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 40
batch_size = 50
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)
save_path = saver.save(sess, "./my_model_final.ckpt")
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
X_new_scaled = X_test[:20]
Z = logits.eval(feed_dict={X: X_new_scaled})
y_pred = np.argmax(Z, axis=1)
print("Predicted classes:", y_pred)
print("Actual classes: ", y_test[:20])
from tensorflow_graph_in_jupyter import show_graph
show_graph(tf.get_default_graph())
```
## Using `dense()` instead of `neuron_layer()`
Note: previous releases of the book used `tensorflow.contrib.layers.fully_connected()` rather than `tf.layers.dense()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dense()`, because anything in the contrib module may change or be deleted without notice. The `dense()` function is almost identical to the `fully_connected()` function, except for a few minor differences:
* several parameters are renamed: `scope` becomes `name`, `activation_fn` becomes `activation` (and similarly the `_fn` suffix is removed from other parameters such as `normalizer_fn`), `weights_initializer` becomes `kernel_initializer`, etc.
* the default `activation` is now `None` rather than `tf.nn.relu`.
* a few more differences are presented in chapter 11.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
y_proba = tf.nn.softmax(logits)
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 20
n_batches = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid)
save_path = saver.save(sess, "./my_model_final.ckpt")
show_graph(tf.get_default_graph())
```
# Exercise solutions
## 1. to 8.
See appendix A.
## 9.
_Train a deep MLP on the MNIST dataset and see if you can get over 98% precision. Just like in the last exercise of chapter 9, try adding all the bells and whistles (i.e., save checkpoints, restore the last checkpoint in case of an interruption, add summaries, plot learning curves using TensorBoard, and so on)._
First let's create the deep net. It's exactly the same as earlier, with just one addition: we add a `tf.summary.scalar()` to track the loss and the accuracy during training, so we can view nice learning curves using TensorBoard.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
loss_summary = tf.summary.scalar('log_loss', loss)
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
accuracy_summary = tf.summary.scalar('accuracy', accuracy)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
Now we need to define the directory to write the TensorBoard logs to:
```
from datetime import datetime
def log_dir(prefix=""):
now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "tf_logs"
if prefix:
prefix += "-"
name = prefix + "run-" + now
return "{}/{}/".format(root_logdir, name)
logdir = log_dir("mnist_dnn")
```
Now we can create the `FileWriter` that we will use to write the TensorBoard logs:
```
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())
```
Hey! Why don't we implement early stopping? For this, we are going to need to use the validation set.
```
m, n = X_train.shape
n_epochs = 10001
batch_size = 50
n_batches = int(np.ceil(m / batch_size))
checkpoint_path = "/tmp/my_deep_mnist_model.ckpt"
checkpoint_epoch_path = checkpoint_path + ".epoch"
final_model_path = "./my_deep_mnist_model"
best_loss = np.infty
epochs_without_progress = 0
max_epochs_without_progress = 50
with tf.Session() as sess:
if os.path.isfile(checkpoint_epoch_path):
# if the checkpoint file exists, restore the model and load the epoch number
with open(checkpoint_epoch_path, "rb") as f:
start_epoch = int(f.read())
print("Training was interrupted. Continuing at epoch", start_epoch)
saver.restore(sess, checkpoint_path)
else:
start_epoch = 0
sess.run(init)
for epoch in range(start_epoch, n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val, loss_val, accuracy_summary_str, loss_summary_str = sess.run([accuracy, loss, accuracy_summary, loss_summary], feed_dict={X: X_valid, y: y_valid})
file_writer.add_summary(accuracy_summary_str, epoch)
file_writer.add_summary(loss_summary_str, epoch)
if epoch % 5 == 0:
print("Epoch:", epoch,
"\tValidation accuracy: {:.3f}%".format(accuracy_val * 100),
"\tLoss: {:.5f}".format(loss_val))
saver.save(sess, checkpoint_path)
with open(checkpoint_epoch_path, "wb") as f:
f.write(b"%d" % (epoch + 1))
if loss_val < best_loss:
saver.save(sess, final_model_path)
best_loss = loss_val
else:
epochs_without_progress += 5
if epochs_without_progress > max_epochs_without_progress:
print("Early stopping")
break
os.remove(checkpoint_epoch_path)
with tf.Session() as sess:
saver.restore(sess, final_model_path)
accuracy_val = accuracy.eval(feed_dict={X: X_test, y: y_test})
accuracy_val
```
| true |
code
| 0.686948 | null | null | null | null |
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
*No changes were made to the contents of this notebook from the original.*
<!--NAVIGATION-->
< [Density and Contour Plots](04.04-Density-and-Contour-Plots.ipynb) | [Contents](Index.ipynb) | [Customizing Plot Legends](04.06-Customizing-Legends.ipynb) >
# Histograms, Binnings, and Density
A simple histogram can be a great first step in understanding a dataset.
Earlier, we saw a preview of Matplotlib's histogram function (see [Comparisons, Masks, and Boolean Logic](02.06-Boolean-Arrays-and-Masks.ipynb)), which creates a basic histogram in one line, once the normal boiler-plate imports are done:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
data = np.random.randn(1000)
plt.hist(data);
```
The ``hist()`` function has many options to tune both the calculation and the display;
here's an example of a more customized histogram:
```
plt.hist(data, bins=30, normed=True, alpha=0.5,
histtype='stepfilled', color='steelblue',
edgecolor='none');
```
The ``plt.hist`` docstring has more information on other customization options available.
I find this combination of ``histtype='stepfilled'`` along with some transparency ``alpha`` to be very useful when comparing histograms of several distributions:
```
x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)
kwargs = dict(histtype='stepfilled', alpha=0.3, normed=True, bins=40)
plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs);
```
If you would like to simply compute the histogram (that is, count the number of points in a given bin) and not display it, the ``np.histogram()`` function is available:
```
counts, bin_edges = np.histogram(data, bins=5)
print(counts)
```
## Two-Dimensional Histograms and Binnings
Just as we create histograms in one dimension by dividing the number-line into bins, we can also create histograms in two-dimensions by dividing points among two-dimensional bins.
We'll take a brief look at several ways to do this here.
We'll start by defining some data—an ``x`` and ``y`` array drawn from a multivariate Gaussian distribution:
```
mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
```
### ``plt.hist2d``: Two-dimensional histogram
One straightforward way to plot a two-dimensional histogram is to use Matplotlib's ``plt.hist2d`` function:
```
plt.hist2d(x, y, bins=30, cmap='Blues')
cb = plt.colorbar()
cb.set_label('counts in bin')
```
Just as with ``plt.hist``, ``plt.hist2d`` has a number of extra options to fine-tune the plot and the binning, which are nicely outlined in the function docstring.
Further, just as ``plt.hist`` has a counterpart in ``np.histogram``, ``plt.hist2d`` has a counterpart in ``np.histogram2d``, which can be used as follows:
```
counts, xedges, yedges = np.histogram2d(x, y, bins=30)
```
For the generalization of this histogram binning in dimensions higher than two, see the ``np.histogramdd`` function.
### ``plt.hexbin``: Hexagonal binnings
The two-dimensional histogram creates a tesselation of squares across the axes.
Another natural shape for such a tesselation is the regular hexagon.
For this purpose, Matplotlib provides the ``plt.hexbin`` routine, which will represents a two-dimensional dataset binned within a grid of hexagons:
```
plt.hexbin(x, y, gridsize=30, cmap='Blues')
cb = plt.colorbar(label='count in bin')
```
``plt.hexbin`` has a number of interesting options, including the ability to specify weights for each point, and to change the output in each bin to any NumPy aggregate (mean of weights, standard deviation of weights, etc.).
### Kernel density estimation
Another common method of evaluating densities in multiple dimensions is *kernel density estimation* (KDE).
This will be discussed more fully in [In-Depth: Kernel Density Estimation](05.13-Kernel-Density-Estimation.ipynb), but for now we'll simply mention that KDE can be thought of as a way to "smear out" the points in space and add up the result to obtain a smooth function.
One extremely quick and simple KDE implementation exists in the ``scipy.stats`` package.
Here is a quick example of using the KDE on this data:
```
from scipy.stats import gaussian_kde
# fit an array of size [Ndim, Nsamples]
data = np.vstack([x, y])
kde = gaussian_kde(data)
# evaluate on a regular grid
xgrid = np.linspace(-3.5, 3.5, 40)
ygrid = np.linspace(-6, 6, 40)
Xgrid, Ygrid = np.meshgrid(xgrid, ygrid)
Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()]))
# Plot the result as an image
plt.imshow(Z.reshape(Xgrid.shape),
origin='lower', aspect='auto',
extent=[-3.5, 3.5, -6, 6],
cmap='Blues')
cb = plt.colorbar()
cb.set_label("density")
```
KDE has a smoothing length that effectively slides the knob between detail and smoothness (one example of the ubiquitous bias–variance trade-off).
The literature on choosing an appropriate smoothing length is vast: ``gaussian_kde`` uses a rule-of-thumb to attempt to find a nearly optimal smoothing length for the input data.
Other KDE implementations are available within the SciPy ecosystem, each with its own strengths and weaknesses; see, for example, ``sklearn.neighbors.KernelDensity`` and ``statsmodels.nonparametric.kernel_density.KDEMultivariate``.
For visualizations based on KDE, using Matplotlib tends to be overly verbose.
The Seaborn library, discussed in [Visualization With Seaborn](04.14-Visualization-With-Seaborn.ipynb), provides a much more terse API for creating KDE-based visualizations.
<!--NAVIGATION-->
< [Density and Contour Plots](04.04-Density-and-Contour-Plots.ipynb) | [Contents](Index.ipynb) | [Customizing Plot Legends](04.06-Customizing-Legends.ipynb) >
| true |
code
| 0.607227 | null | null | null | null |
|
# Example of extracting features from dataframes with Datetime indices
Assuming that time-varying measurements are taken at regular intervals can be sufficient for many situations. However, for a large number of tasks it is important to take into account **when** a measurement is made. An example can be healthcare, where the interval between measurements of vital signs contains crucial information.
Tsfresh now supports calculator functions that use the index of the timeseries container in order to calculate the features. The only requirements for these function is that the index of the input dataframe is of type `pd.DatetimeIndex`. These functions are contained in the new class TimeBasedFCParameters.
Note that the behaviour of all other functions is unaffected. The settings parameter of `extract_features()` can contain both index-dependent functions and 'regular' functions.
```
import pandas as pd
from tsfresh.feature_extraction import extract_features
# TimeBasedFCParameters contains all functions that use the Datetime index of the timeseries container
from tsfresh.feature_extraction.settings import TimeBasedFCParameters
```
# Build a time series container with Datetime indices
Let's build a dataframe with a datetime index. The format must be with a `value` and a `kind` column, since each measurement has its own timestamp - i.e. measurements are not assumed to be simultaneous.
```
df = pd.DataFrame({"id": ["a", "a", "a", "a", "b", "b", "b", "b"],
"value": [1, 2, 3, 1, 3, 1, 0, 8],
"kind": ["temperature", "temperature", "pressure", "pressure",
"temperature", "temperature", "pressure", "pressure"]},
index=pd.DatetimeIndex(
['2019-03-01 10:04:00', '2019-03-01 10:50:00', '2019-03-02 00:00:00', '2019-03-02 09:04:59',
'2019-03-02 23:54:12', '2019-03-03 08:13:04', '2019-03-04 08:00:00', '2019-03-04 08:01:00']
))
df = df.sort_index()
df
```
Right now `TimeBasedFCParameters` only contains `linear_trend_timewise`, which performs a calculation of a linear trend, but using the time difference in hours between measurements in order to perform the linear regression. As always, you can add your own functions in `tsfresh/feature_extraction/feature_calculators.py`.
```
settings_time = TimeBasedFCParameters()
settings_time
```
We extract the features as usual, specifying the column value, kind, and id.
```
X_tsfresh = extract_features(df, column_id="id", column_value='value', column_kind='kind',
default_fc_parameters=settings_time)
X_tsfresh.head()
```
The output looks exactly, like usual. If we compare it with the 'regular' `linear_trend` feature calculator, we can see that the intercept, p and R values are the same, as we'd expect – only the slope is now different.
```
settings_regular = {'linear_trend': [
{'attr': 'pvalue'},
{'attr': 'rvalue'},
{'attr': 'intercept'},
{'attr': 'slope'},
{'attr': 'stderr'}
]}
X_tsfresh = extract_features(df, column_id="id", column_value='value', column_kind='kind',
default_fc_parameters=settings_regular)
X_tsfresh.head()
```
# Writing your own time-based feature calculators
Writing your own time-based feature calculators is no different from usual. Only two new properties must be set using the `@set_property` decorator:
1) `@set_property("input", "pd.Series")` tells the function that the input of the function is a `pd.Series` rather than a numpy array. This allows the index to be used.
2) `@set_property("index_type", pd.DatetimeIndex)` tells the function that the input is a DatetimeIndex, allowing it to perform calculations based on time datatypes.
For example, if we want to write a function that calculates the time between the first and last measurement, it could look something like this:
```python
@set_property("input", "pd.Series")
@set_property("index_type", pd.DatetimeIndex)
def timespan(x, param):
ix = x.index
# Get differences between the last timestamp and the first timestamp in seconds, then convert to hours.
times_seconds = (ix[-1] - ix[0]).total_seconds()
return times_seconds / float(3600)
```
| true |
code
| 0.524151 | null | null | null | null |
|
# Modeling and Simulation in Python
Case study.
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
```
### Electric car
[Olin Electric Motorsports](https://www.olinelectricmotorsports.com/) is a club at Olin College that designs and builds electric cars, and participates in the [Formula SAE Electric](https://www.sae.org/attend/student-events/formula-sae-electric) competition.
The goal of this case study is to use simulation to guide the design of a car intended to accelerate from standing to 100 kph as quickly as possible. The [world record for this event](https://www.youtube.com/watch?annotation_id=annotation_2297602723&feature=iv&src_vid=I-NCH8ct24U&v=n2XiCYA3C9s), using a car that meets the competition requirements, is 1.513 seconds.
We'll start with a simple model that takes into account the characteristics of the motor and vehicle:
* The motor is an [Emrax 228 high voltage axial flux synchronous permanent magnet motor](http://emrax.com/products/emrax-228/); according to the [data sheet](http://emrax.com/wp-content/uploads/2017/01/emrax_228_technical_data_4.5.pdf), its maximum torque is 240 Nm, at 0 rpm. But maximum torque decreases with motor speed; at 5000 rpm, maximum torque is 216 Nm.
* The motor is connected to the drive axle with a chain drive with speed ratio 13:60 or 1:4.6; that is, the axle rotates once for each 4.6 rotations of the motor.
* The radius of the tires is 0.26 meters.
* The weight of the vehicle, including driver, is 300 kg.
To start, we will assume no slipping between the tires and the road surface, no air resistance, and no rolling resistance. Then we will relax these assumptions one at a time.
* First we'll add drag, assuming that the frontal area of the vehicle is 0.6 square meters, with coefficient of drag 0.6.
* Next we'll add rolling resistance, assuming a coefficient of 0.2.
* Finally we'll compute the peak acceleration to see if the "no slip" assumption is credible.
We'll use this model to estimate the potential benefit of possible design improvements, including decreasing drag and rolling resistance, or increasing the speed ratio.
I'll start by loading the units we need.
```
radian = UNITS.radian
m = UNITS.meter
s = UNITS.second
minute = UNITS.minute
hour = UNITS.hour
km = UNITS.kilometer
kg = UNITS.kilogram
N = UNITS.newton
rpm = UNITS.rpm
```
And store the parameters in a `Params` object.
```
params = Params(r_wheel=0.26 * m,
speed_ratio=13/60,
C_rr=0.2,
C_d=0.5,
area=0.6*m**2,
rho=1.2*kg/m**3,
mass=300*kg)
```
`make_system` creates the initial state, `init`, and constructs an `interp1d` object that represents torque as a function of motor speed.
```
def make_system(params):
"""Make a system object.
params: Params object
returns: System object
"""
init = State(x=0*m, v=0*m/s)
rpms = [0, 2000, 5000]
torques = [240, 240, 216]
interpolate_torque = interpolate(Series(torques, rpms))
return System(params, init=init,
interpolate_torque=interpolate_torque,
t_end=3*s)
```
Testing `make_system`
```
system = make_system(params)
system.init
```
### Torque and speed
The relationship between torque and motor speed is taken from the [Emrax 228 data sheet](http://emrax.com/wp-content/uploads/2017/01/emrax_228_technical_data_4.5.pdf). The following functions reproduce the red dotted line that represents peak torque, which can only be sustained for a few seconds before the motor overheats.
```
def compute_torque(omega, system):
"""Maximum peak torque as a function of motor speed.
omega: motor speed in radian/s
system: System object
returns: torque in Nm
"""
factor = (1 * radian / s).to(rpm)
x = magnitude(omega * factor)
return system.interpolate_torque(x) * N * m
compute_torque(0*radian/s, system)
omega = (5000 * rpm).to(radian/s)
compute_torque(omega, system)
```
Plot the whole curve.
```
xs = linspace(0, 525, 21) * radian / s
taus = [compute_torque(x, system) for x in xs]
plot(xs, taus)
decorate(xlabel='Motor speed (rpm)',
ylabel='Available torque (N m)')
```
### Simulation
Here's the slope function that computes the maximum possible acceleration of the car as a function of it current speed.
```
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
# use velocity, v, to compute angular velocity of the wheel
omega2 = v / r_wheel
# use the speed ratio to compute motor speed
omega1 = omega2 / speed_ratio
# look up motor speed to get maximum torque at the motor
tau1 = compute_torque(omega1, system)
# compute the corresponding torque at the axle
tau2 = tau1 / speed_ratio
# compute the force of the wheel on the ground
F = tau2 / r_wheel
# compute acceleration
a = F/mass
return v, a
```
Testing `slope_func` at linear velocity 10 m/s.
```
test_state = State(x=0*m, v=10*m/s)
slope_func(test_state, 0*s, system)
```
Now we can run the simulation.
```
results, details = run_ode_solver(system, slope_func)
details
```
And look at the results.
```
results.tail()
```
After 3 seconds, the vehicle could be at 40 meters per second, in theory, which is 144 kph.
```
v_final = get_last_value(results.v)
v_final.to(km/hour)
```
Plotting `x`
```
def plot_position(results):
plot(results.x, label='x')
decorate(xlabel='Time (s)',
ylabel='Position (m)')
plot_position(results)
```
Plotting `v`
```
def plot_velocity(results):
plot(results.v, label='v')
decorate(xlabel='Time (s)',
ylabel='Velocity (m/s)')
plot_velocity(results)
```
### Stopping at 100 kph
We'll use an event function to stop the simulation when we reach 100 kph.
```
def event_func(state, t, system):
"""Stops when we get to 100 km/hour.
state: State object
t: time
system: System object
returns: difference from 100 km/hour
"""
x, v = state
# convert to km/hour
factor = (1 * m/s).to(km/hour)
v = magnitude(v * factor)
return v - 100
results, details = run_ode_solver(system, slope_func, events=event_func)
details
```
Here's what the results look like.
```
subplot(2, 1, 1)
plot_position(results)
subplot(2, 1, 2)
plot_velocity(results)
savefig('figs/chap11-fig02.pdf')
```
According to this model, we should be able to make this run in just over 2 seconds.
```
t_final = get_last_label(results) * s
```
At the end of the run, the car has gone about 28 meters.
```
state = results.last_row()
```
If we send the final state back to the slope function, we can see that the final acceleration is about 13 $m/s^2$, which is about 1.3 times the acceleration of gravity.
```
v, a = slope_func(state, 0, system)
v.to(km/hour)
a
g = 9.8 * m/s**2
(a / g).to(UNITS.dimensionless)
```
It's not easy for a vehicle to accelerate faster than `g`, because that implies a coefficient of friction between the wheels and the road surface that's greater than 1. But racing tires on dry asphalt can do that; the OEM team at Olin has tested their tires and found a peak coefficient near 1.5.
So it's possible that our no slip assumption is valid, but only under ideal conditions, where weight is distributed equally on four tires, and all tires are driving.
**Exercise:** How much time do we lose because maximum torque decreases as motor speed increases? Run the model again with no drop off in torque and see how much time it saves.
### Drag
In this section we'll see how much effect drag has on the results.
Here's a function to compute drag force, as we saw in Chapter 21.
```
def drag_force(v, system):
"""Computes drag force in the opposite direction of `v`.
v: velocity
system: System object
returns: drag force
"""
rho, C_d, area = system.rho, system.C_d, system.area
f_drag = -np.sign(v) * rho * v**2 * C_d * area / 2
return f_drag
```
We can test it with a velocity of 20 m/s.
```
drag_force(20 * m/s, system)
```
Here's the resulting acceleration of the vehicle due to drag.
```
drag_force(20 * m/s, system) / system.mass
```
We can see that the effect of drag is not huge, compared to the acceleration we computed in the previous section, but it is not negligible.
Here's a modified slope function that takes drag into account.
```
def slope_func2(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
omega2 = v / r_wheel * radian
omega1 = omega2 / speed_ratio
tau1 = compute_torque(omega1, system)
tau2 = tau1 / speed_ratio
F = tau2 / r_wheel
a_motor = F / mass
a_drag = drag_force(v, system) / mass
a = a_motor + a_drag
return v, a
```
And here's the next run.
```
results2, details = run_ode_solver(system, slope_func2, events=event_func)
details
```
The time to reach 100 kph is a bit higher.
```
t_final2 = get_last_label(results2) * s
```
But the total effect of drag is only about 2/100 seconds.
```
t_final2 - t_final
```
That's not huge, which suggests we might not be able to save much time by decreasing the frontal area, or coefficient of drag, of the car.
### Rolling resistance
Next we'll consider [rolling resistance](https://en.wikipedia.org/wiki/Rolling_resistance), which the force that resists the motion of the car as it rolls on tires. The cofficient of rolling resistance, `C_rr`, is the ratio of rolling resistance to the normal force between the car and the ground (in that way it is similar to a coefficient of friction).
The following function computes rolling resistance.
```
system.set(unit_rr = 1 * N / kg)
def rolling_resistance(system):
"""Computes force due to rolling resistance.
system: System object
returns: force
"""
return -system.C_rr * system.mass * system.unit_rr
```
The acceleration due to rolling resistance is 0.2 (it is not a coincidence that it equals `C_rr`).
```
rolling_resistance(system)
rolling_resistance(system) / system.mass
```
Here's a modified slope function that includes drag and rolling resistance.
```
def slope_func3(state, t, system):
"""Computes the derivatives of the state variables.
state: State object
t: time
system: System object
returns: sequence of derivatives
"""
x, v = state
r_wheel, speed_ratio = system.r_wheel, system.speed_ratio
mass = system.mass
omega2 = v / r_wheel * radian
omega1 = omega2 / speed_ratio
tau1 = compute_torque(omega1, system)
tau2 = tau1 / speed_ratio
F = tau2 / r_wheel
a_motor = F / mass
a_drag = drag_force(v, system) / mass
a_roll = rolling_resistance(system) / mass
a = a_motor + a_drag + a_roll
return v, a
```
And here's the run.
```
results3, details = run_ode_solver(system, slope_func3, events=event_func)
details
```
The final time is a little higher, but the total cost of rolling resistance is only 3/100 seconds.
```
t_final3 = get_last_label(results3) * s
t_final3 - t_final2
```
So, again, there is probably not much to be gained by decreasing rolling resistance.
In fact, it is hard to decrease rolling resistance without also decreasing traction, so that might not help at all.
### Optimal gear ratio
The gear ratio 13:60 is intended to maximize the acceleration of the car without causing the tires to slip. In this section, we'll consider other gear ratios and estimate their effects on acceleration and time to reach 100 kph.
Here's a function that takes a speed ratio as a parameter and returns time to reach 100 kph.
```
def time_to_speed(speed_ratio, params):
"""Computes times to reach 100 kph.
speed_ratio: ratio of wheel speed to motor speed
params: Params object
returns: time to reach 100 kph, in seconds
"""
params = Params(params, speed_ratio=speed_ratio)
system = make_system(params)
system.set(unit_rr = 1 * N / kg)
results, details = run_ode_solver(system, slope_func3, events=event_func)
t_final = get_last_label(results)
a_initial = slope_func(system.init, 0, system)
return t_final
```
We can test it with the default ratio:
```
time_to_speed(13/60, params)
```
Now we can try it with different numbers of teeth on the motor gear (assuming that the axle gear has 60 teeth):
```
for teeth in linrange(8, 18):
print(teeth, time_to_speed(teeth/60, params))
```
Wow! The speed ratio has a big effect on the results. At first glance, it looks like we could break the world record (1.513 seconds) just by decreasing the number of teeth.
But before we try it, let's see what effect that has on peak acceleration.
```
def initial_acceleration(speed_ratio, params):
"""Maximum acceleration as a function of speed ratio.
speed_ratio: ratio of wheel speed to motor speed
params: Params object
returns: peak acceleration, in m/s^2
"""
params = Params(params, speed_ratio=speed_ratio)
system = make_system(params)
a_initial = slope_func(system.init, 0, system)[1] * m/s**2
return a_initial
```
Here are the results:
```
for teeth in linrange(8, 18):
print(teeth, initial_acceleration(teeth/60, params))
```
As we decrease the speed ratio, the peak acceleration increases. With 8 teeth on the motor gear, we could break the world record, but only if we can accelerate at 2.3 times the acceleration of gravity, which is impossible without very sticky ties and a vehicle that generates a lot of downforce.
```
23.07 / 9.8
```
These results suggest that the most promising way to improve the performance of the car (for this event) would be to improve traction.
| true |
code
| 0.838779 | null | null | null | null |
|
# Estimator validation
This notebook contains code to generate Figure 2 of the paper.
This notebook also serves to compare the estimates of the re-implemented scmemo with sceb package from Vasilis.
```
import pandas as pd
import matplotlib.pyplot as plt
import scanpy as sc
import scipy as sp
import itertools
import numpy as np
import scipy.stats as stats
from scipy.integrate import dblquad
import seaborn as sns
from statsmodels.stats.multitest import fdrcorrection
import imp
pd.options.display.max_rows = 999
pd.set_option('display.max_colwidth', -1)
import pickle as pkl
import time
import matplotlib as mpl
mpl.rcParams['pdf.fonttype'] = 42
mpl.rcParams['ps.fonttype'] = 42
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'x-small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'xx-small',
'ytick.labelsize':'xx-small'}
pylab.rcParams.update(params)
import sys
sys.path.append('/data/home/Github/scrna-parameter-estimation/dist/schypo-0.0.0-py3.7.egg')
import schypo
import schypo.simulate as simulate
import sys
sys.path.append('/data/home/Github/single_cell_eb/')
sys.path.append('/data/home/Github/single_cell_eb/sceb/')
import scdd
data_path = '/data/parameter_estimation/'
fig_path = '/data/home/Github/scrna-parameter-estimation/figures/fig3/'
```
### Check 1D estimates of `sceb` with `scmemo`
Using the Poisson model. The outputs should be identical, this is for checking the implementation.
```
data = sp.sparse.csr_matrix(simulate.simulate_transcriptomes(100, 20))
adata = sc.AnnData(data)
size_factors = scdd.dd_size_factor(adata)
Nr = data.sum(axis=1).mean()
_, M_dd = scdd.dd_1d_moment(adata, size_factor=scdd.dd_size_factor(adata), Nr=Nr)
var_scdd = scdd.M_to_var(M_dd)
print(var_scdd)
imp.reload(estimator)
mean_scmemo, var_scmemo = estimator._poisson_1d(data, data.shape[0], estimator._estimate_size_factor(data))
print(var_scmemo)
df = pd.DataFrame()
df['size_factor'] = size_factors
df['inv_size_factor'] = 1/size_factors
df['inv_size_factor_sq'] = 1/size_factors**2
df['expr'] = data[:, 0].todense().A1
precomputed_size_factors = df.groupby('expr')['inv_size_factor'].mean(), df.groupby('expr')['inv_size_factor_sq'].mean()
imp.reload(estimator)
expr, count = np.unique(data[:, 0].todense().A1, return_counts=True)
print(estimator._poisson_1d((expr, count), data.shape[0], precomputed_size_factors))
```
### Check 2D estimates of `sceb` and `scmemo`
Using the Poisson model. The outputs should be identical, this is for checking the implementation.
```
data = sp.sparse.csr_matrix(simulate.simulate_transcriptomes(1000, 4))
adata = sc.AnnData(data)
size_factors = scdd.dd_size_factor(adata)
mean_scdd, cov_scdd, corr_scdd = scdd.dd_covariance(adata, size_factors)
print(cov_scdd)
imp.reload(estimator)
cov_scmemo = estimator._poisson_cov(data, data.shape[0], size_factors, idx1=[0, 1, 2], idx2=[1, 2, 3])
print(cov_scmemo)
expr, count = np.unique(data[:, :2].toarray(), return_counts=True, axis=0)
df = pd.DataFrame()
df['size_factor'] = size_factors
df['inv_size_factor'] = 1/size_factors
df['inv_size_factor_sq'] = 1/size_factors**2
df['expr1'] = data[:, 0].todense().A1
df['expr2'] = data[:, 1].todense().A1
precomputed_size_factors = df.groupby(['expr1', 'expr2'])['inv_size_factor'].mean(), df.groupby(['expr1', 'expr2'])['inv_size_factor_sq'].mean()
cov_scmemo = estimator._poisson_cov((expr[:, 0], expr[:, 1], count), data.shape[0], size_factor=precomputed_size_factors)
print(cov_scmemo)
```
### Extract parameters from interferon dataset
```
adata = sc.read(data_path + 'interferon_filtered.h5ad')
adata = adata[adata.obs.cell_type == 'CD4 T cells - ctrl']
data = adata.X.copy()
relative_data = data.toarray()/data.sum(axis=1)
q = 0.07
x_param, z_param, Nc, good_idx = schypo.simulate.extract_parameters(adata.X, q=q, min_mean=q)
imp.reload(simulate)
transcriptome = simulate.simulate_transcriptomes(
n_cells=10000,
means=z_param[0],
variances=z_param[1],
corr=x_param[2],
Nc=Nc)
relative_transcriptome = transcriptome/transcriptome.sum(axis=1).reshape(-1, 1)
qs, captured_data = simulate.capture_sampling(transcriptome, q=q, q_sq=q**2+1e-10)
def qqplot(x, y, s=1):
plt.scatter(
np.quantile(x, np.linspace(0, 1, 1000)),
np.quantile(y, np.linspace(0, 1, 1000)),
s=s)
plt.plot(x, x, lw=1, color='m')
plt.figure(figsize=(8, 2));
plt.subplots_adjust(wspace=0.2);
plt.subplot(1, 3, 1);
sns.distplot(np.log(captured_data.mean(axis=0)), hist=False, label='Simulated')
sns.distplot(np.log(data[:, good_idx].toarray().var(axis=0)), hist=False, label='Real')
plt.xlabel('Log(mean)')
plt.subplot(1, 3, 2);
sns.distplot(np.log(captured_data.var(axis=0)), hist=False)
sns.distplot(np.log(data[:, good_idx].toarray().var(axis=0)), hist=False)
plt.xlabel('Log(variance)')
plt.subplot(1, 3, 3);
sns.distplot(np.log(captured_data.sum(axis=1)), hist=False)
sns.distplot(np.log(data.toarray().sum(axis=1)), hist=False)
plt.xlabel('Log(total UMI count)')
plt.savefig(figpath + 'simulation_stats.png', bbox_inches='tight')
```
### Compare datasets generated by Poisson and hypergeometric processes
```
_, poi_captured = simulate.capture_sampling(transcriptome, q=q, process='poisson')
_, hyper_captured = simulate.capture_sampling(transcriptome, q=q, process='hyper')
q_list = [0.05, 0.1, 0.2, 0.3, 0.5]
plt.figure(figsize=(8, 2))
plt.subplots_adjust(wspace=0.3)
for idx, q in enumerate(q_list):
_, poi_captured = simulate.capture_sampling(transcriptome, q=q, process='poisson')
_, hyper_captured = simulate.capture_sampling(transcriptome, q=q, process='hyper')
relative_poi_captured = poi_captured/poi_captured.sum(axis=1).reshape(-1, 1)
relative_hyper_captured = hyper_captured/hyper_captured.sum(axis=1).reshape(-1, 1)
poi_corr = np.corrcoef(relative_poi_captured, rowvar=False)
hyper_corr = np.corrcoef(relative_hyper_captured, rowvar=False)
sample_idx = np.random.choice(poi_corr.ravel().shape[0], 100000)
plt.subplot(1, len(q_list), idx+1)
plt.scatter(poi_corr.ravel()[sample_idx], hyper_corr.ravel()[sample_idx], s=1, alpha=1)
plt.plot([-1, 1], [-1, 1], 'm', lw=1)
# plt.xlim([-0.3, 0.4])
# plt.ylim([-0.3, 0.4])
if idx != 0:
plt.yticks([])
plt.title('q={}'.format(q))
plt.savefig(figpath + 'poi_vs_hyp_sim_corr.png', bbox_inches='tight')
```
### Compare Poisson vs HG estimators
```
def compare_esimators(q, plot=False, true_data=None, var_q=1e-10):
q_sq = var_q + q**2
true_data = schypo.simulate.simulate_transcriptomes(1000, 1000, correlated=True) if true_data is None else true_data
true_relative_data = true_data / true_data.sum(axis=1).reshape(-1, 1)
qs, captured_data = schypo.simulate.capture_sampling(true_data, q, q_sq)
Nr = captured_data.sum(axis=1).mean()
captured_relative_data = captured_data/captured_data.sum(axis=1).reshape(-1, 1)
adata = sc.AnnData(sp.sparse.csr_matrix(captured_data))
sf = schypo.estimator._estimate_size_factor(adata.X, 'hyper_relative', total=True)
good_idx = (captured_data.mean(axis=0) > q)
# True moments
m_true, v_true, corr_true = true_relative_data.mean(axis=0), true_relative_data.var(axis=0), np.corrcoef(true_relative_data, rowvar=False)
rv_true = v_true/m_true**2#schypo.estimator._residual_variance(m_true, v_true, schypo.estimator._fit_mv_regressor(m_true, v_true))
# Compute 1D moments
m_obs, v_obs = captured_relative_data.mean(axis=0), captured_relative_data.var(axis=0)
rv_obs = v_obs/m_obs**2#schypo.estimator._residual_variance(m_obs, v_obs, schypo.estimator._fit_mv_regressor(m_obs, v_obs))
m_poi, v_poi = schypo.estimator._poisson_1d_relative(adata.X, size_factor=sf, n_obs=true_data.shape[0])
rv_poi = v_poi/m_poi**2#schypo.estimator._residual_variance(m_poi, v_poi, schypo.estimator._fit_mv_regressor(m_poi, v_poi))
m_hyp, v_hyp = schypo.estimator._hyper_1d_relative(adata.X, size_factor=sf, n_obs=true_data.shape[0], q=q)
rv_hyp = v_hyp/m_hyp**2#schypo.estimator._residual_variance(m_hyp, v_hyp, schypo.estimator._fit_mv_regressor(m_hyp, v_hyp))
# Compute 2D moments
corr_obs = np.corrcoef(captured_relative_data, rowvar=False)
# corr_obs = corr_obs[np.triu_indices(corr_obs.shape[0])]
idx1 = np.array([i for i,j in itertools.combinations(range(adata.shape[1]), 2) if good_idx[i] and good_idx[j]])
idx2 = np.array([j for i,j in itertools.combinations(range(adata.shape[1]), 2) if good_idx[i] and good_idx[j]])
sample_idx = np.random.choice(idx1.shape[0], 10000)
idx1 = idx1[sample_idx]
idx2 = idx2[sample_idx]
corr_true = corr_true[(idx1, idx2)]
corr_obs = corr_obs[(idx1, idx2)]
cov_poi = schypo.estimator._poisson_cov_relative(adata.X, n_obs=adata.shape[0], size_factor=sf, idx1=idx1, idx2=idx2)
cov_hyp = schypo.estimator._hyper_cov_relative(adata.X, n_obs=adata.shape[0], size_factor=sf, idx1=idx1, idx2=idx2, q=q)
corr_poi = schypo.estimator._corr_from_cov(cov_poi, v_poi[idx1], v_poi[idx2])
corr_hyp = schypo.estimator._corr_from_cov(cov_hyp, v_hyp[idx1], v_hyp[idx2])
corr_poi[np.abs(corr_poi) > 1] = np.nan
corr_hyp[np.abs(corr_hyp) > 1] = np.nan
mean_list = [m_obs, m_poi, m_hyp]
var_list = [rv_obs, rv_poi, rv_hyp]
corr_list = [corr_obs, corr_poi, corr_hyp]
estimated_list = [mean_list, var_list, corr_list]
true_list = [m_true, rv_true, corr_true]
if plot:
count = 0
for j in range(3):
for i in range(3):
plt.subplot(3, 3, count+1)
if i != 2:
plt.scatter(
np.log(true_list[i][good_idx]),
np.log(estimated_list[i][j][good_idx]),
s=0.1)
plt.plot(np.log(true_list[i][good_idx]), np.log(true_list[i][good_idx]), linestyle='--', color='m')
plt.xlim(np.log(true_list[i][good_idx]).min(), np.log(true_list[i][good_idx]).max())
plt.ylim(np.log(true_list[i][good_idx]).min(), np.log(true_list[i][good_idx]).max())
else:
x = true_list[i]
y = estimated_list[i][j]
print(x.shape, y.shape)
plt.scatter(
x,
y,
s=0.1)
plt.plot([-1, 1], [-1, 1],linestyle='--', color='m')
plt.xlim(-1, 1);
plt.ylim(-1, 1);
# if not (i == j):
# plt.yticks([]);
# plt.xticks([]);
if i == 1 or i == 0:
print((np.log(true_list[i][good_idx]) > np.log(estimated_list[i][j][good_idx])).mean())
count += 1
else:
return qs, good_idx, estimated_list, true_list
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'xx-small',
'ytick.labelsize':'xx-small'}
pylab.rcParams.update(params)
```
```
true_data = schypo.simulate.simulate_transcriptomes(n_cells=10000, means=z_param[0], variances=z_param[1], Nc=Nc)
q = 0.025
plt.figure(figsize=(4, 4))
plt.subplots_adjust(wspace=0.5, hspace=0.5)
compare_esimators(q, plot=True, true_data=true_data)
plt.savefig(fig_path + 'poi_vs_hyper_scatter_rv_2.5.png', bbox_inches='tight', dpi=1200)
q = 0.4
plt.figure(figsize=(4, 4))
plt.subplots_adjust(wspace=0.5, hspace=0.5)
compare_esimators(q, plot=True, true_data=true_data)
plt.savefig(fig_path + 'poi_vs_hyper_scatter_rv_40.png', bbox_inches='tight', dpi=1200)
def compute_mse(x, y, log=True):
if log:
return np.nanmean(np.abs(np.log(x)-np.log(y)))
else:
return np.nanmean(np.abs(x-y))
def concordance(x, y, log=True):
if log:
a = np.log(x)
b = np.log(y)
else:
a = x
b = y
cond = np.isfinite(a) & np.isfinite(b)
a = a[cond]
b = b[cond]
cmat = np.cov(a, b)
return 2*cmat[0,1]/(cmat[0,0] + cmat[1,1] + (a.mean()-b.mean())**2)
m_mse_list, v_mse_list, c_mse_list = [], [], []
# true_data = schypo.simulate.simulate_transcriptomes(n_cells=10000, means=z_param[0], variances=z_param[1],
# Nc=Nc)
q_list = [0.01, 0.025, 0.1, 0.15, 0.3, 0.5, 0.7, 0.99]
qs_list = []
for q in q_list:
qs, good_idx, est, true = compare_esimators(q, plot=False, true_data=true_data)
qs_list.append(qs)
m_mse_list.append([concordance(x[good_idx], true[0][good_idx]) for x in est[0]])
v_mse_list.append([concordance(x[good_idx], true[1][good_idx]) for x in est[1]])
c_mse_list.append([concordance(x, true[2], log=False) for x in est[2]])
m_mse_list, v_mse_list, c_mse_list = np.array(m_mse_list), np.array(v_mse_list), np.array(c_mse_list)
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'small',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'small',
'ytick.labelsize':'small'}
pylab.rcParams.update(params)
plt.figure(figsize=(8, 3))
plt.subplots_adjust(wspace=0.5)
plt.subplot(1, 3, 1)
plt.plot(q_list[1:], m_mse_list[:, 0][1:], '-o')
# plt.legend(['Naive,\nPoisson,\nHG'])
plt.ylabel('CCC log(mean)')
plt.xlabel('overall UMI efficiency (q)')
plt.subplot(1, 3, 2)
plt.plot(q_list[2:], v_mse_list[:, 0][2:], '-o')
plt.plot(q_list[2:], v_mse_list[:, 1][2:], '-o')
plt.plot(q_list[2:], v_mse_list[:, 2][2:], '-o')
plt.legend(['Naive', 'Poisson', 'HG'], ncol=3, loc='upper center', bbox_to_anchor=(0.4,1.15))
plt.ylabel('CCC log(variance)')
plt.xlabel('overall UMI efficiency (q)')
plt.subplot(1, 3, 3)
plt.plot(q_list[2:], c_mse_list[:, 0][2:], '-o')
plt.plot(q_list[2:], c_mse_list[:, 1][2:], '-o')
plt.plot(q_list[2:], c_mse_list[:, 2][2:], '-o')
# plt.legend(['Naive', 'Poisson', 'HG'])
plt.ylabel('CCC correlation')
plt.xlabel('overall UMI efficiency (q)')
plt.savefig(fig_path + 'poi_vs_hyper_rv_ccc.pdf', bbox_inches='tight')
plt.figure(figsize=(1, 1.3))
plt.plot(q_list, v_mse_list[:, 0], '-o', ms=4)
plt.plot(q_list, v_mse_list[:, 1], '-o', ms=4)
plt.plot(q_list, v_mse_list[:, 2], '-o', ms=4)
plt.savefig(fig_path + 'poi_vs_hyper_ccc_var_rv_inset.pdf', bbox_inches='tight')
plt.figure(figsize=(1, 1.3))
plt.plot(q_list, c_mse_list[:, 0], '-o', ms=4)
plt.plot(q_list, c_mse_list[:, 1], '-o', ms=4)
plt.plot(q_list, c_mse_list[:, 2], '-o', ms=4)
plt.savefig(fig_path + 'poi_vs_hyper_ccc_corr_inset.pdf', bbox_inches='tight')
```
| true |
code
| 0.509886 | null | null | null | null |
|
# Automate loan approvals with Business rules in Apache Spark and Scala
### Automating at scale your business decisions in Apache Spark with IBM ODM 8.9.2
This Scala notebook shows you how to execute locally business rules in DSX and Apache Spark.
You'll learn how to call in Apache Spark a rule-based decision service. This decision service has been programmed with IBM Operational Decision Manager.
This notebook puts in action a decision service named Miniloan that is part of the ODM tutorials. It determines with business rules whether a customer is eligible for a loan according to specific criteria. The criteria include the amount of the loan, the annual income of the borrower, and the duration of the loan.
First we load an application data set that was captured as a CSV file. In scala we apply a map to this data set to automate a rule-based reasoning, in order to outcome a decision. The rule execution is performed locally in the Spark service. This notebook shows a complete Scala code that can execute any ruleset based on the public APIs.
To get the most out of this notebook, you should have some familiarity with the Scala programming language.
## Contents
This notebook contains the following main sections:
1. [Load the loan validation request dataset.](#loaddatatset)
2. [Load the business rule execution and the simple loan application object model libraries.](#loadjars)
3. [Import Scala packages.](#importpackages)
4. [Implement a decision making function.](#implementDecisionServiceMap)
5. [Execute the business rules to approve or reject the loan applications.](#executedecisions)
6. [View the automated decisions.](#viewdecisions)
7. [Summary and next steps.](#summary)
<a id="accessdataset"></a>
## 1. Loading a loan application dataset file
A data set of simple loan applications is already available. You load it in the Notebook through its url.
```
// @hidden_cell
import scala.sys.process._
"wget https://raw.githubusercontent.com/ODMDev/decisions-on-spark/master/data/miniloan/miniloan-requests-10K.csv".!
val filename = "miniloan-requests-10K.csv"
```
This following code loads the 10 000 simple loan application dataset written in CSV format.
```
val requestData = sc.textFile(filename)
val requestDataCount = requestData.count
println(s"$requestDataCount loan requests read in a CVS format")
println("The first 5 requests:")
requestData.take(20).foreach(println)
```
<a id="loadjars"></a>
## 2. Add libraries for business rule execution and a loan application object model
The XXX refers to your object storage or other place where you make available these jars.
Add the following jars to execute the deployed decision service
<il>
<li>%AddJar https://XXX/j2ee_connector-1_5-fr.jar</li>
<li>%AddJar https://XXX/jrules-engine.jar</li>
<li>%AddJar https://XXX/jrules-res-execution.jar</li>
</il>
In addition you need the Apache Jackson annotation lib
<il>
<li>%AddJar https://XXX/jackson-annotations-2.6.5.jar</li>
</il>
Business Rules apply on a Java executable Object Model packaged as a jar. We need these classes to create the decision requests, and to retreive the response from the rule engine.
<il>
<li>%AddJar https://XXX/miniloan-xom.jar</li>
</il>
```
// @hidden_cell
// The urls below are accessible for an IBM internal usage only
%AddJar https://XXX/j2ee_connector-1_5-fr.jar
%AddJar https://XXX/jrules-engine.jar
%AddJar https://XXX/jrules-res-execution.jar
%AddJar https://XXX/jackson-annotations-2.6.5.jar -f
//Loan Application eXecutable Object Model
%AddJar https://XXX/miniloan-xom.jar -f
print("Your notebook is now ready to execute business rules to approve or reject loan applications")
```
<a id="importpackages"></a>
## 3. Import packages
Import ODM and Apache Spark packages.
```
import java.util.Map
import java.util.HashMap
import com.fasterxml.jackson.core.JsonGenerationException
import com.fasterxml.jackson.core.JsonProcessingException
import com.fasterxml.jackson.databind.JsonMappingException
import com.fasterxml.jackson.databind.ObjectMapper
import com.fasterxml.jackson.databind.SerializationFeature
import org.apache.spark.SparkConf
import org.apache.spark.api.java.JavaDoubleRDD
import org.apache.spark.api.java.JavaRDD
import org.apache.spark.api.java.JavaSparkContext
import org.apache.spark.api.java.function.Function
import org.apache.hadoop.fs.FileSystem
import org.apache.hadoop.fs.Path
import scala.collection.JavaConverters._
import ilog.rules.res.model._
import com.ibm.res.InMemoryJ2SEFactory
import com.ibm.res.InMemoryRepositoryDAO
import ilog.rules.res.session._
import miniloan.Borrower
import miniloan.Loan
import scala.io.Source
import java.net.URL
import java.io.InputStream
```
<a id="implementDecisionServiceMap"></a>
## 4. Implement a Map function that executes a rule-based decision service
```
case class MiniLoanRequest(borrower: miniloan.Borrower,
loan: miniloan.Loan)
case class RESRunner(sessionFactory: com.ibm.res.InMemoryJ2SEFactory) {
def executeAsString(s: String): String = {
println("executeAsString")
val request = makeRequest(s)
val response = executeRequest(request)
response
}
private def makeRequest(s: String): MiniLoanRequest = {
val tokens = s.split(",")
// Borrower deserialization from CSV
val borrowerName = tokens(0)
val borrowerCreditScore = java.lang.Integer.parseInt(tokens(1).trim())
val borrowerYearlyIncome = java.lang.Integer.parseInt(tokens(2).trim())
val loanAmount = java.lang.Integer.parseInt(tokens(3).trim())
val loanDuration = java.lang.Integer.parseInt(tokens(4).trim())
val yearlyInterestRate = java.lang.Double.parseDouble(tokens(5).trim())
val borrower = new miniloan.Borrower(borrowerName, borrowerCreditScore, borrowerYearlyIncome)
// Loan request deserialization from CSV
val loan = new miniloan.Loan()
loan.setAmount(loanAmount)
loan.setDuration(loanDuration)
loan.setYearlyInterestRate(yearlyInterestRate)
val request = new MiniLoanRequest(borrower, loan)
request
}
def executeRequest(request: MiniLoanRequest): String = {
try {
val sessionRequest = sessionFactory.createRequest()
val rulesetPath = "/Miniloan/Miniloan"
sessionRequest.setRulesetPath(ilog.rules.res.model.IlrPath.parsePath(rulesetPath))
//sessionRequest.getTraceFilter.setInfoAllFilters(false)
val inputParameters = sessionRequest.getInputParameters
inputParameters.put("loan", request.loan)
inputParameters.put("borrower", request.borrower)
val session = sessionFactory.createStatelessSession()
val response = session.execute(sessionRequest)
var loan = response.getOutputParameters().get("loan").asInstanceOf[miniloan.Loan]
val mapper = new com.fasterxml.jackson.databind.ObjectMapper()
mapper.configure(com.fasterxml.jackson.databind.SerializationFeature.FAIL_ON_EMPTY_BEANS, false)
val results = new java.util.HashMap[String,Object]()
results.put("input", inputParameters)
results.put("output", response.getOutputParameters())
try {
//return mapper.writeValueAsString(results)
return mapper.writerWithDefaultPrettyPrinter().writeValueAsString(results);
} catch {
case e: Exception => return e.toString()
}
"Error"
} catch {
case exception: Exception => {
return exception.toString()
}
}
"Error"
}
}
val decisionService = new Function[String, String]() {
@transient private var ruleSessionFactory: InMemoryJ2SEFactory = null
private val rulesetURL = "https://odmlibserver.mybluemix.net/8901/decisionservices/miniloan-8901.dsar"
@transient private var rulesetStream: InputStream = null
def GetRuleSessionFactory(): InMemoryJ2SEFactory = {
if (ruleSessionFactory == null) {
ruleSessionFactory = new InMemoryJ2SEFactory()
// Create the Management Session
var repositoryFactory = ruleSessionFactory.createManagementSession().getRepositoryFactory()
var repository = repositoryFactory.createRepository()
// Deploy the Ruleapp with the Regular Management Session API.
var rapp = repositoryFactory.createRuleApp("Miniloan", IlrVersion.parseVersion("1.0"));
var rs = repositoryFactory.createRuleset("Miniloan",IlrVersion.parseVersion("1.1"));
rapp.addRuleset(rs);
//var fileStream = Source.fromResourceAsStream(RulesetFileName)
rulesetStream = new java.net.URL(rulesetURL).openStream()
rs.setRESRulesetArchive(IlrEngineType.DE,rulesetStream)
repository.addRuleApp(rapp)
}
ruleSessionFactory
}
def call(s: String): String = {
var runner = new RESRunner(GetRuleSessionFactory())
return runner.executeAsString(s)
}
def execute(s: String): String = {
try {
var runner = new RESRunner(GetRuleSessionFactory())
return runner.executeAsString(s)
} catch {
case exception: Exception => {
exception.printStackTrace(System.err)
}
}
"Execution error"
}
}
```
<a id="executedecisions"></a>
## 5. Automate the decision making on the loan application dataset
You invoke a map on the decision function. While the map occurs rule engines are processing in parallel the loan applications to produce a data set of answers.
```
println("Start of Execution")
val answers = requestData.map(decisionService.execute)
printf("Number of rule based decisions: %s \n" , answers.count)
// Cleanup output file
//val fs = FileSystem.get(new URI(outputPath), sc.hadoopConfiguration);
//if (fs.exists(new Path(outputPath)))
// fs.delete(new Path(outputPath), true)
// Save RDD in a HDFS file
println("End of Execution ")
//answers.saveAsTextFile("swift://DecisionBatchExecution." + securedAccessName + "/miniloan-decisions-10.csv")
println("Decision automation job done")
```
<a id="viewdecisions"></a>
## 6. View your automated decisions
Each decision is composed of output parameters and of a decision trace. The loan data contains the approval flag and the computed yearly repayment. The decision trace lists the business rules that have been executed in sequence to come to the conclusion. Each decision has been serialized in JSON.
```
//answers.toDF().show(false)
answers.take(1).foreach(println)
```
<a id="summary"></a>
## 7. Summary and next steps
Congratulations! You have applied business rules to automatically determine loan approval eligibility. You loaded a loan application data set, ran a rule engine inside an Apache Spark cluster to make an eligibility decision for each applicant. Each decision is a Scala object that is part of a Spark Resilient Data Set.
Each decision is structured with input parameters (the context of the decision) and output parameters. For audit purpose the rule engine can emit a decision trace.
You have successfully run a rule engine to automate decisions at scale in a Spark cluster. You can now invent your own business rules and run them with the same integration pattern.
<a id="authors"></a>
## Authors
Pierre Feillet and Laurent Grateau are business rule engineers at IBM working in the Decision lab located in France.
Copyright © 2018 IBM. This notebook and its source code are released under the terms of the MIT License.
| true |
code
| 0.387111 | null | null | null | null |
|
# Airbnb - Rio de Janeiro
* Download [data](http://insideairbnb.com/get-the-data.html)
* We downloaded `listings.csv` from all monthly dates available
## Questions
1. What was the price and supply behavior before and during the pandemic?
2. Does a title in English or Portuguese impact the price?
3. What features correlate with the price? Can we predict a price? Which features matters?
```
import numpy as np
import pandas as pd
import seaborn as sns
import glob
import re
import pendulum
import tqdm
import matplotlib.pyplot as plt
import langid
langid.set_languages(['en','pt'])
```
### Read files
Read all 30 files and get their date
```
files = sorted(glob.glob('data/listings*.csv'))
df = []
for f in files:
date = pendulum.from_format(re.findall(r"\d{4}_\d{2}_\d{2}", f)[0], fmt="YYYY_MM_DD").naive()
csv = pd.read_csv(f)
csv["date"] = date
df.append(csv)
df = pd.concat(df)
df
```
### Deal with NaNs
* Drop `neighbourhood_group` as it is all NaNs;
* Fill `reviews_per_month` with zeros (if there is no review, then reviews per month are zero)
* Keep `name` for now
* Drop `host_name` rows, as there is not any null host_id
* Keep `last_review` too, as there are rooms with no review
```
df.isna().any()
df = df.drop(["host_name", "neighbourhood_group"], axis=1)
df["reviews_per_month"] = df["reviews_per_month"].fillna(0.)
df.head()
```
### Detect `name` language
* Clean strings for evaluation
* Remove common neighbourhoods name in Portuguese from `name` column to diminish misprediction
* Remove several non-alphanumeric characters
* Detect language using [langid](https://github.com/saffsd/langid.py)
* I restricted between pt, en. There are very few rooms listed in other languages.
* Drop `name` column
```
import unicodedata
stopwords = pd.unique(df["neighbourhood"])
stopwords = [re.sub(r"[\(\)]", "", x.lower().strip()).split() for x in stopwords]
stopwords = [x for item in stopwords for x in item]
stopwords += [unicodedata.normalize("NFKD", x).encode('ASCII', 'ignore').decode() for x in stopwords]
stopwords += ["rio", "janeiro", "copa", "arpoador", "pepê", "pepe", "lapa", "morro", "corcovado"]
stopwords = set(stopwords)
docs = [re.sub(r"[\-\_\\\/\,\;\:\!\+\’\%\&\d\*\#\"\´\`\.\|\(\)\[\]\@\'\»\«\>\<\❤️\…]", " ", str(x)) for x in df["name"].tolist()]
docs = [" ".join(x.lower().strip().split()) for x in docs]
docs = ["".join(e for e in x if (e.isalnum() or " ")) for x in docs]
ndocs = []
for doc in tqdm.tqdm(docs):
ndocs.append(" ".join([x for x in doc.split() if x not in stopwords]))
docs = ndocs
results = []
for d in tqdm.tqdm(docs):
results.append(langid.classify(d)[0])
df["language"] = results
# Because we transformed NaNs into string, fill those detection with nans too
df.loc[df["name"].isna(), "language"] = pd.NA
```
* Test accuracy, manually label 383 out of 88191 (95% conf. interval, 5% margin of error)
```
df.loc[~df["name"].isna()].drop_duplicates("name").shape
df.loc[~df["name"].isna()].drop_duplicates("name")[["name", "language"]].sample(n=383, random_state=42).to_csv("lang_pred_1.csv")
lang_pred = pd.read_csv("lang_pred.csv", index_col=0)
lang_pred.head()
overall_accuracy = (lang_pred["pred"] == lang_pred["true"]).sum() / lang_pred.shape[0]
pt_accuracy = (lang_pred[lang_pred["true"] == "pt"]["true"] == lang_pred[lang_pred["true"] == "pt"]["pred"]).sum() / lang_pred[lang_pred["true"] == "pt"].shape[0]
en_accuracy = (lang_pred[lang_pred["true"] == "en"]["true"] == lang_pred[lang_pred["true"] == "en"]["pred"]).sum() / lang_pred[lang_pred["true"] == "en"].shape[0]
print(f"Overall accuracy: {overall_accuracy*100}%")
print(f"Portuguese accuracy: {pt_accuracy*100}%")
print(f"English accuracy: {en_accuracy*100}%")
df = df.drop("name", axis=1)
df.head()
df["language"].value_counts()
```
### Calculate how many times a room appeared
* There are 30 months of data, and rooms appear multiple times
* Calculate for a specific date, how many times the same room appeared up to that date
```
df = df.set_index(["id", "date"])
df["appearances"] = df.groupby(["id", "date"])["host_id"].count().unstack().cumsum(axis=1).stack()
df = df.reset_index()
df.head()
```
### Days since last review
* Calculate days since last review
* Then categorize them by the length of the days
```
df.loc[:, "last_review"] = pd.to_datetime(df["last_review"], format="%Y/%m/%d")
# For each scraping date, consider the last date to serve as comparision as the maximum date
last_date = df.groupby("date")["last_review"].max()
df["last_date"] = df.apply(lambda row: last_date.loc[row["date"]], axis=1)
df["days_last_review"] = (df["last_date"] - df["last_review"]).dt.days
df = df.drop("last_date", axis=1)
df.head()
df["days_last_review"].describe()
def categorize_last_review(days_last_review):
"""Transform days since last review into categories
Transform days since last review into one of those categories:
last_week, last_month, last_half_year, last_year, last_two_years,
long_time_ago, or never
Args:
days_last_review (int): Days since the last review
Returns:
str: A string with the category name.
"""
if days_last_review <= 7:
return "last_week"
elif days_last_review <= 30:
return "last_month"
elif days_last_review <= 182:
return "last_half_year"
elif days_last_review <= 365:
return "last_year"
elif days_last_review <= 730:
return "last_two_years"
elif days_last_review > 730:
return "long_time_ago"
else:
return "never"
df.loc[:, "last_review"] = df.apply(lambda row: categorize_last_review(row["days_last_review"]), axis=1)
df = df.drop(["days_last_review"], axis=1)
df.head()
df = df.set_index(["id", "date"])
df.loc[:, "appearances"] = df["appearances"].astype(int)
df.loc[:, "host_id"] = df["host_id"].astype("category")
df.loc[:, "neighbourhood"] = df["neighbourhood"].astype("category")
df.loc[:, "room_type"] = df["room_type"].astype("category")
df.loc[:, "last_review"] = df["last_review"].astype("category")
df.loc[:, "language"] = df["language"].astype("category")
df
df.to_pickle("data.pkl")
```
### Distributions
* Check the distribution of features
```
df = pd.read_pickle("data.pkl")
df.head()
df["latitude"].hist(bins=250)
df["longitude"].hist(bins=250)
df["price"].hist(bins=250)
df["minimum_nights"].hist(bins=250)
df["number_of_reviews"].hist()
df["reviews_per_month"].hist(bins=250)
df["calculated_host_listings_count"].hist(bins=250)
df["availability_365"].hist()
df["appearances"].hist(bins=29)
df.describe()
```
### Limits
* We are analising mostly for touristic purpose, so get the short-term rentals only
* Prices between 10 and 10000 (The luxury Copacabana Palace Penthouse at 8000 for example)
* Short-term rentals (minimum_nights < 31)
* Impossibility of more than 31 reviews per month
```
df = pd.read_pickle("data.pkl")
total_records = len(df)
outbound_values = (df["price"] < 10) | (df["price"] > 10000)
df = df[~outbound_values]
print(f"Removed values {outbound_values.sum()}, {outbound_values.sum()*100/total_records}%")
long_term = df["minimum_nights"] >= 31
df = df[~long_term]
print(f"Removed values {long_term.sum()}, {long_term.sum()*100/total_records}%")
reviews_limit = df["reviews_per_month"] > 31
df = df[~reviews_limit]
print(f"Removed values {reviews_limit.sum()}, {reviews_limit.sum()*100/total_records}%")
```
### Log skewed variables
* Most numerical values are skewed, so log them
```
df.describe()
# number_of_reviews, reviews_per_month, availability_365 have zeros, thus sum one to all
df["number_of_reviews"] = np.log(df["number_of_reviews"] + 1)
df["reviews_per_month"] = np.log(df["reviews_per_month"] + 1)
df["availability_365"] = np.log(df["availability_365"] + 1)
df["price"] = np.log(df["price"])
df["minimum_nights"] = np.log(df["minimum_nights"])
df["calculated_host_listings_count"] = np.log(df["calculated_host_listings_count"])
df["appearances"] = np.log(df["appearances"])
df.describe()
```
### Extreme outliers
* Most outliers are clearly mistyped values (one can check these rooms ids in their website)
* Remove extreme outliers first from large deviations within the same `id` (eliminate rate jumps of same room)
* Then remove those from same scraping `date`, `neighbourhood` and `room_type`
```
df = df.reset_index()
q25 = df.groupby(["id"])["price"].quantile(0.25)
q75 = df.groupby(["id"])["price"].quantile(0.75)
ext = q75 + 3 * (q75 - q25)
ext = ext[(q75 - q25) > 0.]
affected_rows = []
multiple_id = df[df["id"].isin(ext.index)]
for row in tqdm.tqdm(multiple_id.itertuples(), total=len(multiple_id)):
if row.price >= ext.loc[row.id]:
affected_rows.append(row.Index)
df = df.drop(affected_rows)
print(f"Removed values {len(affected_rows)}, {len(affected_rows)*100/total_records}%")
# Remove extreme outliers per neighbourhood, room_type and scraping date
q25 = df.groupby(["date", "neighbourhood", "room_type"])["price"].quantile(0.25)
q75 = df.groupby(["date", "neighbourhood", "room_type"])["price"].quantile(0.75)
ext = q75 + 3 * (q75 - q25)
ext
affected_rows = []
for row in tqdm.tqdm(df.itertuples(), total=len(df)):
if row.price >= ext.loc[(row.date, row.neighbourhood, row.room_type)]:
affected_rows.append(row.Index)
df = df.drop(affected_rows)
print(f"Removed values {len(affected_rows)}, {len(affected_rows)*100/total_records}%")
df.describe()
df["price"].hist()
df.to_pickle("treated_data.pkl")
```
| true |
code
| 0.505554 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/harvardnlp/pytorch-struct/blob/master/notebooks/Unsupervised_CFG.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install -qqq torchtext -qqq pytorch-transformers dgl
!pip install -qqqU git+https://github.com/harvardnlp/pytorch-struct
import torchtext
import torch
from torch_struct import SentCFG
from torch_struct.networks import NeuralCFG
import torch_struct.data
# Download and the load default data.
WORD = torchtext.data.Field(include_lengths=True)
UD_TAG = torchtext.data.Field(init_token="<bos>", eos_token="<eos>", include_lengths=True)
# Download and the load default data.
train, val, test = torchtext.datasets.UDPOS.splits(
fields=(('word', WORD), ('udtag', UD_TAG), (None, None)),
filter_pred=lambda ex: 5 < len(ex.word) < 30
)
WORD.build_vocab(train.word, min_freq=3)
UD_TAG.build_vocab(train.udtag)
train_iter = torch_struct.data.TokenBucket(train,
batch_size=200,
device="cuda:0")
H = 256
T = 30
NT = 30
model = NeuralCFG(len(WORD.vocab), T, NT, H)
model.cuda()
opt = torch.optim.Adam(model.parameters(), lr=0.001, betas=[0.75, 0.999])
def train():
#model.train()
losses = []
for epoch in range(10):
for i, ex in enumerate(train_iter):
opt.zero_grad()
words, lengths = ex.word
N, batch = words.shape
words = words.long()
params = model(words.cuda().transpose(0, 1))
dist = SentCFG(params, lengths=lengths)
loss = dist.partition.mean()
(-loss).backward()
losses.append(loss.detach())
torch.nn.utils.clip_grad_norm_(model.parameters(), 3.0)
opt.step()
if i % 100 == 1:
print(-torch.tensor(losses).mean(), words.shape)
losses = []
train()
for i, ex in enumerate(train_iter):
opt.zero_grad()
words, lengths = ex.word
N, batch = words.shape
words = words.long()
params = terms(words.transpose(0, 1)), rules(batch), roots(batch)
tree = CKY(MaxSemiring).marginals(params, lengths=lengths, _autograd=True)
print(tree)
break
def split(spans):
batch, N = spans.shape[:2]
splits = []
for b in range(batch):
cover = spans[b].nonzero()
left = {i: [] for i in range(N)}
right = {i: [] for i in range(N)}
batch_split = {}
for i in range(cover.shape[0]):
i, j, A = cover[i].tolist()
left[i].append((A, j, j - i + 1))
right[j].append((A, i, j - i + 1))
for i in range(cover.shape[0]):
i, j, A = cover[i].tolist()
B = None
for B_p, k, a_span in left[i]:
for C_p, k_2, b_span in right[j]:
if k_2 == k + 1 and a_span + b_span == j - i + 1:
B, C = B_p, C_p
k_final = k
break
if j > i:
batch_split[(i, j)] =k
splits.append(batch_split)
return splits
splits = split(spans)
```
| true |
code
| 0.662169 | null | null | null | null |
|
# Assignment 9: Implement Dynamic Programming
In this exercise, we will begin to explore the concept of dynamic programming and how it related to various object containers with respect to computational complexity.
## Deliverables:
1) Choose and implement a Dynamic Programming algorithm in Python, make sure you are using a Dynamic Programming solution (not another one).
2) Use the algorithm to solve a range of scenarios.
3) Explain what is being done in the implementation. That is, write up a walk through of the algorithm and explain how it is a Dynamic Programming solution.
### Prepare an executive summary of your results, referring to the table and figures you have generated. Explain how your results relate to big O notation. Describe your results in language that management can understand. This summary should be included as text paragraphs in the Jupyter notebook. Explain how the algorithm works and why it is a useful to data engineers.
# A. The Dynamic programming problem: Longest Increasing Sequence
### The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order. For example, the length of LIS for {10, 22, 9, 33, 21, 50, 41, 60, 80} is 6 and LIS is {10, 22, 33, 50, 60, 80}.
# A. Setup: Library imports and Algorithm
```
import numpy as np
import pandas as pd
import seaborn as sns
import time
#import itertools
import random
import matplotlib.pyplot as plt
#import networkx as nx
#import pydot
#from networkx.drawing.nx_pydot import graphviz_layout
#from collections import deque
# Dynamic Programming Approach of Finding LIS by reducing the problem to longest common Subsequence
def lis(a):
n=len(a) #get the length of the list
b=sorted(list(set(a))) #removes duplicates, and sorts list
m=len(b) #gets the length of the truncated and sorted list
dp=[[-1 for i in range(m+1)] for j in range(n+1)] #instantiates a list of lists filled with -1 columns are indicies of the sorted array; rows the original array
for i in range(n+1): # for every column in the table at each row:
for j in range(m+1):
if i==0 or j==0: #if at first element in either a row or column set the table row,index to zero
dp[i][j]=0
elif a[i-1]==b[j-1]: #else if the sorted array value matches the original array:
dp[i][j]=1+dp[i-1][j-1]#sets dp[i][j] to 1+prveious cell of the dyanmic table
else:
dp[i][j]=max(dp[i-1][j],dp[i][j-1]) #else record the max of the row or column for that cell in the cell
return dp[-1][-1] # This will return the max running sequence.
# Driver program to test above function
arr1 = [10, 22, 9, 33, 21, 50, 41, 60]
len_arr1 = len(arr1)
print("Longest increaseing sequence has a length of:", lis(arr1))
# addtional comments included from the original code contributed by Dheeraj Khatri (https://www.geeksforgeeks.org/longest-increasing-subsequence-dp-3/)
def Container(arr, fun): ### I'm glad I was able to reuse this from assignment 3 and 4. Useful function.
objects = [] #instantiates an empty list to collect the returns
times = [] #instantiates an empty list to collect times for each computation
for t in arr:
start= time.perf_counter() #collects the start time
obj = fun(t) # applies the function to the arr object
end = time.perf_counter() # collects end time
duration = (end-start)* 1E3 #converts to milliseconds
objects.append(obj)# adds the returns of the functions to the objects list
times.append(duration) # adds the duration for computation to list
return objects, times
```
# B. Test Array Generation
```
RANDOM_SEED = 300
np.random.seed(RANDOM_SEED)
arr100 = list(np.random.randint(low=1, high= 5000, size=100))
np.random.seed(RANDOM_SEED)
arr200 = list(np.random.randint(low=1, high= 5000, size=200))
np.random.seed(RANDOM_SEED)
arr400 = list(np.random.randint(low=1, high= 5000, size=400))
np.random.seed(RANDOM_SEED)
arr600 = list(np.random.randint(low=1, high= 5000, size=600))
np.random.seed(RANDOM_SEED)
arr800 = list(np.random.randint(low=1, high= 5000, size=800))
print(len(arr100), len(arr200), len(arr400), len(arr600), len(arr800))
arr_list = [arr100, arr200, arr400, arr600, arr800]
metrics = Container(arr_list, lis)
```
### Table1. Performance Summary
```
summary = {
'ArraySize' : [len(arr100), len(arr200), len(arr400), len(arr600), len(arr800)],
'SequenceLength' : [metrics[0][0],metrics[0][1], metrics[0][2], metrics[0][3], metrics[0][4]],
'Time(ms)' : [metrics[1][0],metrics[1][1], metrics[1][2], metrics[1][3], metrics[1][4]]
}
df =pd.DataFrame(summary)
df
```
### Figure 1. Performance
```
sns.scatterplot(data=df, x='Time(ms)', y='ArraySize')
```
# Discussion
Explain what is being done in the implementation. That is, write up a walk through of the algorithm and explain how it is a Dynamic Programming solution.
The dyanamic programming problem above finds the length of the longest incrementing sequence of values in a list. The defined function makes a sorted copy of the list containing only unique values and also creates a dynamic table (in the form of a list of lists) using a nested list comprehension. This table contains the incidices of the sorted array as columns and the indicies of the original array as rows. To begin, the table is instantiated with values of -1. The value of zero indicies are set to zero in the dynamic table and if a given index in the original array is found to be increasing the dyanamic table is incremented. until all positions are assessed. The funciton then returns the maximum value of the increments which will be the length of the longest running sequence. This is a dynamic progromming problem because the solution builds on a smaller subset problems.
Dyanmic programming is an important concept for developers and engineers. Functions and programs that use dynamic programming help solve problems which present themselves as factorial time complexity in a more efficient way. At face value, it appears that this problem of the longest incrementing sequence will have to compare all values in a given array to all previous values in the array. Dyanmic programming allows for a shortcut in a sense. We can compare the given array with a sorted version of that array and at the intersection of the sorted and unsorted arrays we can determine if we need to make an additon to our incrementing sequence tally.
Shown above in table and figure 1 is the time required for the algorithm to tally the longest running sequence for various array sizes. Because the algorithm utilizes a nested for loop it is the expeictation that the time will grow as a function of the square of the original array length. This is confirmed when inspecting the scatterplot in figure 1. Thus, the developed algorithm in big O notation is O(n^2) time complexity which is much more efficient than factorial time.
| true |
code
| 0.335936 | null | null | null | null |
|
```
%matplotlib inline
```
02: Fitting Power Spectrum Models
=================================
Introduction to the module, beginning with the FOOOF object.
```
# Import the FOOOF object
from fooof import FOOOF
# Import utility to download and load example data
from fooof.utils.download import load_fooof_data
# Download examples data files needed for this example
freqs = load_fooof_data('freqs.npy', folder='data')
spectrum = load_fooof_data('spectrum.npy', folder='data')
```
FOOOF Object
------------
At the core of the module, which is object oriented, is the :class:`~fooof.FOOOF` object,
which holds relevant data and settings as attributes, and contains methods to run the
algorithm to parameterize neural power spectra.
The organization is similar to sklearn:
- A model object is initialized, with relevant settings
- The model is used to fit the data
- Results can be extracted from the object
Calculating Power Spectra
~~~~~~~~~~~~~~~~~~~~~~~~~
The :class:`~fooof.FOOOF` object fits models to power spectra. The module itself does not
compute power spectra, and so computing power spectra needs to be done prior to using
the FOOOF module.
The model is broadly agnostic to exactly how power spectra are computed. Common
methods, such as Welch's method, can be used to compute the spectrum.
If you need a module in Python that has functionality for computing power spectra, try
`NeuroDSP <https://neurodsp-tools.github.io/neurodsp/>`_.
Note that FOOOF objects require frequency and power values passed in as inputs to
be in linear spacing. Passing in non-linear spaced data (such logged values) may
produce erroneous results.
Fitting an Example Power Spectrum
---------------------------------
The following example demonstrates fitting a power spectrum model to a single power spectrum.
```
# Initialize a FOOOF object
fm = FOOOF()
# Set the frequency range to fit the model
freq_range = [2, 40]
# Report: fit the model, print the resulting parameters, and plot the reconstruction
fm.report(freqs, spectrum, freq_range)
```
Fitting Models with 'Report'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The above method 'report', is a convenience method that calls a series of methods:
- :meth:`~fooof.FOOOF.fit`: fits the power spectrum model
- :meth:`~fooof.FOOOF.print_results`: prints out the results
- :meth:`~fooof.FOOOF.plot`: plots to data and model fit
Each of these methods can also be called individually.
```
# Alternatively, just fit the model with FOOOF.fit() (without printing anything)
fm.fit(freqs, spectrum, freq_range)
# After fitting, plotting and parameter fitting can be called independently:
# fm.print_results()
# fm.plot()
```
Model Parameters
~~~~~~~~~~~~~~~~
Once the power spectrum model has been calculated, the model fit parameters are stored
as object attributes that can be accessed after fitting.
Following the sklearn convention, attributes that are fit as a result of
the model have a trailing underscore, for example:
- ``aperiodic_params_``
- ``peak_params_``
- ``error_``
- ``r2_``
- ``n_peaks_``
Access model fit parameters from FOOOF object, after fitting:
```
# Aperiodic parameters
print('Aperiodic parameters: \n', fm.aperiodic_params_, '\n')
# Peak parameters
print('Peak parameters: \n', fm.peak_params_, '\n')
# Goodness of fit measures
print('Goodness of fit:')
print(' Error - ', fm.error_)
print(' R^2 - ', fm.r_squared_, '\n')
# Check how many peaks were fit
print('Number of fit peaks: \n', fm.n_peaks_)
```
Selecting Parameters
~~~~~~~~~~~~~~~~~~~~
You can also select parameters using the :meth:`~fooof.FOOOF.get_params`
method, which can be used to specify which parameters you want to extract.
```
# Extract a model parameter with `get_params`
err = fm.get_params('error')
# Extract parameters, indicating sub-selections of parameter
exp = fm.get_params('aperiodic_params', 'exponent')
cfs = fm.get_params('peak_params', 'CF')
# Print out a custom parameter report
template = ("With an error level of {error:1.2f}, FOOOF fit an exponent "
"of {exponent:1.2f} and peaks of {cfs:s} Hz.")
print(template.format(error=err, exponent=exp,
cfs=' & '.join(map(str, [round(cf, 2) for cf in cfs]))))
```
For a full description of how you can access data with :meth:`~fooof.FOOOF.get_params`,
check the method's documentation.
As a reminder, you can access the documentation for a function using '?' in a
Jupyter notebook (ex: `fm.get_params?`), or more generally with the `help` function
in general Python (ex: `help(get_params)`).
Notes on Interpreting Peak Parameters
-------------------------------------
Peak parameters are labeled as:
- CF: center frequency of the extracted peak
- PW: power of the peak, over and above the aperiodic component
- BW: bandwidth of the extracted peak
Note that the peak parameters that are returned are not exactly the same as the
parameters of the Gaussians used internally to fit the peaks.
Specifically:
- CF is the exact same as mean parameter of the Gaussian
- PW is the height of the model fit above the aperiodic component [1],
which is not necessarily the same as the Gaussian height
- BW is 2 * the standard deviation of the Gaussian [2]
[1] Since the Gaussians are fit together, if any Gaussians overlap,
than the actual height of the fit at a given point can only be assessed
when considering all Gaussians. To be better able to interpret heights
for single peak fits, we re-define the peak height as above, and label it
as 'power', as the units of the input data are expected to be units of power.
[2] Gaussian standard deviation is '1 sided', where as the returned BW is '2 sided'.
The underlying gaussian parameters are also available from the FOOOF object,
in the ``gaussian_params_`` attribute.
```
# Compare the 'peak_params_' to the underlying gaussian parameters
print(' Peak Parameters \t Gaussian Parameters')
for peak, gauss in zip(fm.peak_params_, fm.gaussian_params_):
print('{:5.2f} {:5.2f} {:5.2f} \t {:5.2f} {:5.2f} {:5.2f}'.format(*peak, *gauss))
```
FOOOFResults
~~~~~~~~~~~~
There is also a convenience method to return all model fit results:
:func:`~fooof.FOOOF.get_results`.
This method returns all the model fit parameters, including the underlying Gaussian
parameters, collected together into a FOOOFResults object.
The FOOOFResults object, which in Python terms is a named tuple, is a standard data
object used with FOOOF to organize and collect parameter data.
```
# Grab each model fit result with `get_results` to gather all results together
# Note that this returns a FOOOFResult object
fres = fm.get_results()
# You can also unpack all fit parameters when using `get_results`
ap_params, peak_params, r_squared, fit_error, gauss_params = fm.get_results()
# Print out the FOOOFResults
print(fres, '\n')
# From FOOOFResults, you can access the different results
print('Aperiodic Parameters: \n', fres.aperiodic_params)
# Check the r^2 and error of the model fit
print('R-squared: \n {:5.4f}'.format(fm.r_squared_))
print('Fit error: \n {:5.4f}'.format(fm.error_))
```
Conclusion
----------
In this tutorial, we have explored the basics of the :class:`~fooof.FOOOF` object,
fitting power spectrum models, and extracting parameters.
Before we move on to controlling the fit procedure, and interpreting the results,
in the next tutorial, we will first explore how this model is actually fit.
| true |
code
| 0.716479 | null | null | null | null |
|
## Discretisation
Discretisation is the process of transforming continuous variables into discrete variables by creating a set of contiguous intervals that span the range of the variable's values. Discretisation is also called **binning**, where bin is an alternative name for interval.
### Discretisation helps handle outliers and may improve value spread in skewed variables
Discretisation helps handle outliers by placing these values into the lower or higher intervals, together with the remaining inlier values of the distribution. Thus, these outlier observations no longer differ from the rest of the values at the tails of the distribution, as they are now all together in the same interval / bucket. In addition, by creating appropriate bins or intervals, discretisation can help spread the values of a skewed variable across a set of bins with equal number of observations.
### Discretisation approaches
There are several approaches to transform continuous variables into discrete ones. Discretisation methods fall into 2 categories: **supervised and unsupervised**. Unsupervised methods do not use any information, other than the variable distribution, to create the contiguous bins in which the values will be placed. Supervised methods typically use target information in order to create the bins or intervals.
#### Unsupervised discretisation methods
- Equal width discretisation
- Equal frequency discretisation
- K-means discretisation
#### Supervised discretisation methods
- Discretisation using decision trees
In this lecture, I will describe **equal width discretisation**.
## Equal width discretisation
Equal width discretisation divides the scope of possible values into N bins of the same width.The width is determined by the range of values in the variable and the number of bins we wish to use to divide the variable:
width = (max value - min value) / N
where N is the number of bins or intervals.
For example if the values of the variable vary between 0 and 100, we create 5 bins like this: width = (100-0) / 5 = 20. The bins thus are 0-20, 20-40, 40-60, 80-100. The first and final bins (0-20 and 80-100) can be expanded to accommodate outliers (that is, values under 0 or greater than 100 would be placed in those bins as well).
There is no rule of thumb to define N, that is something to determine experimentally.
## In this demo
We will learn how to perform equal width binning using the Titanic dataset with
- pandas and NumPy
- Feature-engine
- Scikit-learn
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import KBinsDiscretizer
from feature_engine.discretisers import EqualWidthDiscretiser
# load the numerical variables of the Titanic Dataset
data = pd.read_csv('../titanic.csv',
usecols=['age', 'fare', 'survived'])
data.head()
# Let's separate into train and test set
X_train, X_test, y_train, y_test = train_test_split(
data[['age', 'fare']],
data['survived'],
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
```
The variables Age and fare contain missing data, that I will fill by extracting a random sample of the variable.
```
def impute_na(data, variable):
df = data.copy()
# random sampling
df[variable + '_random'] = df[variable]
# extract the random sample to fill the na
random_sample = X_train[variable].dropna().sample(
df[variable].isnull().sum(), random_state=0)
# pandas needs to have the same index in order to merge datasets
random_sample.index = df[df[variable].isnull()].index
df.loc[df[variable].isnull(), variable + '_random'] = random_sample
return df[variable + '_random']
# replace NA in both train and test sets
X_train['age'] = impute_na(data, 'age')
X_test['age'] = impute_na(data, 'age')
X_train['fare'] = impute_na(data, 'fare')
X_test['fare'] = impute_na(data, 'fare')
# let's explore the distribution of age
data[['age', 'fare']].hist(bins=30, figsize=(8,4))
plt.show()
```
## Equal width discretisation with pandas and NumPy
First we need to determine the intervals' edges or limits.
```
# let's capture the range of the variable age
age_range = X_train['age'].max() - X_train['age'].min()
age_range
# let's divide the range into 10 equal width bins
age_range / 10
```
The range or width of our intervals will be 7 years.
```
# now let's capture the lower and upper boundaries
min_value = int(np.floor( X_train['age'].min()))
max_value = int(np.ceil( X_train['age'].max()))
# let's round the bin width
inter_value = int(np.round(age_range / 10))
min_value, max_value, inter_value
# let's capture the interval limits, so we can pass them to the pandas cut
# function to generate the bins
intervals = [i for i in range(min_value, max_value+inter_value, inter_value)]
intervals
# let's make labels to label the different bins
labels = ['Bin_' + str(i) for i in range(1, len(intervals))]
labels
# create binned age / discretise age
# create one column with labels
X_train['Age_disc_labels'] = pd.cut(x=X_train['age'],
bins=intervals,
labels=labels,
include_lowest=True)
# and one with bin boundaries
X_train['Age_disc'] = pd.cut(x=X_train['age'],
bins=intervals,
include_lowest=True)
X_train.head(10)
```
We can see in the above output how by discretising using equal width, we placed each Age observation within one interval / bin. For example, age=13 was placed in the 7-14 interval, whereas age 30 was placed into the 28-35 interval.
When performing equal width discretisation, we guarantee that the intervals are all of the same lenght, however there won't necessarily be the same number of observations in each of the intervals. See below:
```
X_train.groupby('Age_disc')['age'].count()
X_train.groupby('Age_disc')['age'].count().plot.bar()
plt.xticks(rotation=45)
plt.ylabel('Number of observations per bin')
```
The majority of people on the Titanic were between 14-42 years of age.
Now, we can discretise Age in the test set, using the same interval boundaries that we calculated for the train set:
```
X_test['Age_disc_labels'] = pd.cut(x=X_test['age'],
bins=intervals,
labels=labels,
include_lowest=True)
X_test['Age_disc'] = pd.cut(x=X_test['age'],
bins=intervals,
include_lowest=True)
X_test.head()
# if the distributions in train and test set are similar, we should expect similar propotion of
# observations in the different intervals in the train and test set
# let's see that below
t1 = X_train.groupby(['Age_disc'])['age'].count() / len(X_train)
t2 = X_test.groupby(['Age_disc'])['age'].count() / len(X_test)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=45)
plt.ylabel('Number of observations per bin')
```
## Equal width discretisation with Feature-Engine
```
# Let's separate into train and test set
X_train, X_test, y_train, y_test = train_test_split(
data[['age', 'fare']],
data['survived'],
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# replace NA in both train and test sets
X_train['age'] = impute_na(data, 'age')
X_test['age'] = impute_na(data, 'age')
X_train['fare'] = impute_na(data, 'fare')
X_test['fare'] = impute_na(data, 'fare')
# with feature engine we can automate the process for many variables
# in one line of code
disc = EqualWidthDiscretiser(bins=10, variables = ['age', 'fare'])
disc.fit(X_train)
# in the binner dict, we can see the limits of the intervals. For age
# the value increases aproximately 7 years from one bin to the next.
# for fare it increases in around 50 dollars from one interval to the
# next, but it increases always the same value, aka, same width.
disc.binner_dict_
# transform train and text
train_t = disc.transform(X_train)
test_t = disc.transform(X_test)
train_t.head()
t1 = train_t.groupby(['age'])['age'].count() / len(train_t)
t2 = test_t.groupby(['age'])['age'].count() / len(test_t)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=0)
plt.ylabel('Number of observations per bin')
t1 = train_t.groupby(['fare'])['fare'].count() / len(train_t)
t2 = test_t.groupby(['fare'])['fare'].count() / len(test_t)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=0)
plt.ylabel('Number of observations per bin')
```
We can see quite clearly, that equal width discretisation does not improve the value spread. The original variable Fare was skewed, and the discrete variable is also skewed.
## Equal width discretisation with Scikit-learn
```
# Let's separate into train and test set
X_train, X_test, y_train, y_test = train_test_split(
data[['age', 'fare']],
data['survived'],
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# replace NA in both train and test sets
X_train['age'] = impute_na(data, 'age')
X_test['age'] = impute_na(data, 'age')
X_train['fare'] = impute_na(data, 'fare')
X_test['fare'] = impute_na(data, 'fare')
disc = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='uniform')
disc.fit(X_train[['age', 'fare']])
disc.bin_edges_
train_t = disc.transform(X_train[['age', 'fare']])
train_t = pd.DataFrame(train_t, columns = ['age', 'fare'])
train_t.head()
test_t = disc.transform(X_test[['age', 'fare']])
test_t = pd.DataFrame(test_t, columns = ['age', 'fare'])
t1 = train_t.groupby(['age'])['age'].count() / len(train_t)
t2 = test_t.groupby(['age'])['age'].count() / len(test_t)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=0)
plt.ylabel('Number of observations per bin')
t1 = train_t.groupby(['fare'])['fare'].count() / len(train_t)
t2 = test_t.groupby(['fare'])['fare'].count() / len(test_t)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=0)
plt.ylabel('Number of observations per bin')
```
| true |
code
| 0.542682 | null | null | null | null |
|
## Obligatory imports
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
import matplotlib
%matplotlib inline
matplotlib.rcParams['figure.figsize'] = (12,8)
matplotlib.rcParams['font.size']=20
matplotlib.rcParams['lines.linewidth']=4
matplotlib.rcParams['xtick.major.size'] = 10
matplotlib.rcParams['ytick.major.size'] = 10
matplotlib.rcParams['xtick.major.width'] = 2
matplotlib.rcParams['ytick.major.width'] = 2
```
# We use the MNIST Dataset again
```
import IPython
url = 'http://yann.lecun.com/exdb/mnist/'
iframe = '<iframe src=' + url + ' width=80% height=400px></iframe>'
IPython.display.HTML(iframe)
```
## Fetch the data
```
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original', data_home='../day4/data/')
allimages = mnist.data
allimages.shape
all_image_labels = mnist.target
set(all_image_labels)
```
## check out the data
```
digit1 = mnist.data[0,:].reshape(28,-1) # arr.reshape(4, -1) is equivalent to arr.reshape(4, 7), is arr has size 28
fig, ax = plt.subplots(figsize=(1.5, 1.5))
ax.imshow(digit1, vmin=0, vmax=1)
```
# Theoretical background
**Warning: math ahead**
<img src="images/logreg_schematics.svg" alt="logreg-schematics" style="width: 50%;"/>
## Taking logistic regression a step further: neural networks
<img src="images/mlp_schematics.svg" alt="nn-schematics" style="width: 50%;"/>
### How (artificial) neural networks predict a label from features?
* The *input layer* has **dimention = number of features.**
* For each training example, each feature value is "fed" into the input layer.
* Each "neuron" in the hidden layer receives a weighted sum of the features: the weight is initialized to a random value in the beginning, and the network "learns" from the datasetsand tunes these weights. Each hidden neuron, based on its input, and an "activation function", e.g.: the logistic function

* The output is again, a weighted sum of the values at each hidden neuron.
* There can be *more than one hidden layer*, in which case the output of the first hidden layer becomes the input of the second hidden layer.
### Regularization
Like Logistic regression and SVM, neural networks also can be improved with regularization.
Fot scikit-learn, the relevant tunable parameter is `alpha` (as opposed to `gamma` for LR and SVM).
Furthermore, it has default value 0.0001, unlike gamma, for which it is 1.
### Separate the data into training data and test data
```
len(allimages)
```
### Sample the data, 70000 is too many images to handle on a single PC
```
len(allimages)
size_desired_dataset = 2000
sample_idx = np.random.choice(len(allimages), size_desired_dataset)
images = allimages[sample_idx, :]
image_labels = all_image_labels[sample_idx]
set(image_labels)
image_labels.shape
```
### Partition into training and test set *randomly*
**As a rule of thumb, 80/20 split between training/test dataset is often recommended.**
See below for cross validation and how that changes this thumbrule.
```
from scipy.stats import itemfreq
from sklearn.model_selection import train_test_split
training_data, test_data, training_labels, test_labels = train_test_split(images, image_labels, train_size=0.8)
```
** Importance of normalization**
If Feature A is in the range [0,1] and Feature B is in [10000,50000], SVM (in fact, most of the classifiers) will suffer inaccuracy.
The solution is to *normalize* (AKA "feature scaling") each feature to the same interval e.g. [0,1] or [-1, 1].
**scipy provides a standard function for this:**
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# Fit only to the training data: IMPORTANT
scaler.fit(training_data)
from sklearn.neural_network import MLPClassifier
clf = MLPClassifier(hidden_layer_sizes=(50,), max_iter = 5000)
clf.fit(scaler.transform(training_data), training_labels)
clf.score(scaler.transform(training_data), training_labels), clf.score(scaler.transform(test_data), test_labels)
```
### Visualize the hidden layer:
```
# source:
#
#http://scikit-learn.org/stable/auto_examples/neural_networks/plot_mnist_filters.html
fig, axes = plt.subplots(4, 4, figsize=(15,15))
# use global min / max to ensure all weights are shown on the same scale
vmin, vmax = clf.coefs_[0].min(), clf.coefs_[0].max()
for coef, ax in zip(clf.coefs_[0].T, axes.ravel()):
ax.matshow(coef.reshape(28, 28), cmap=plt.cm.gray, vmin=.5 * vmin,
vmax=.5 * vmax)
ax.set_xticks(())
ax.set_yticks(())
plt.show()
```
Not bad, but is it better than Logistic regression? Check out with Learning curves:
```
from sklearn.model_selection import learning_curve
import pandas as pd
curve = learning_curve(clf, scaler.transform(images), image_labels)
train_sizes, train_scores, test_scores = curve
train_scores = pd.DataFrame(train_scores)
train_scores.loc[:,'train_size'] = train_sizes
test_scores = pd.DataFrame(test_scores)
test_scores.loc[:,'train_size'] = train_sizes
train_scores = pd.melt(train_scores, id_vars=['train_size'], value_name = 'CrossVal score')
test_scores = pd.melt(test_scores, id_vars=['train_size'], value_name = 'CrossVal score')
matplotlib.rcParams['figure.figsize'] = (12,8)
sns.tsplot(train_scores, time = 'train_size', unit='variable', value = 'CrossVal score')
sns.tsplot(test_scores, time = 'train_size', unit='variable', value = 'CrossVal score', color='g')
plt.ylim(0,1.1)
```
Not really, we can try to improve it with parameter space search.
## Parameter space search with `GridSearchCV`
```
from sklearn.model_selection import GridSearchCV
clr = MLPClassifier()
clf = GridSearchCV(clr, {'alpha':np.logspace(-8, -1, 2)})
clf.fit(scaler.transform(images), image_labels)
clf.best_params_
clf.best_score_
nn_tuned = clf.best_estimator_
nn_tuned.fit(scaler.transform(training_data), training_labels)
curve = learning_curve(nn_tuned, scaler.transform(images), image_labels)
train_sizes, train_scores, test_scores = curve
train_scores = pd.DataFrame(train_scores)
train_scores.loc[:,'train_size'] = train_sizes
test_scores = pd.DataFrame(test_scores)
test_scores.loc[:,'train_size'] = train_sizes
train_scores = pd.melt(train_scores, id_vars=['train_size'], value_name = 'CrossVal score')
test_scores = pd.melt(test_scores, id_vars=['train_size'], value_name = 'CrossVal score')
matplotlib.rcParams['figure.figsize'] = (12,8)
sns.tsplot(train_scores, time = 'train_size', unit='variable', value = 'CrossVal score')
sns.tsplot(test_scores, time = 'train_size', unit='variable', value = 'CrossVal score', color='g')
plt.ylim(0,1.1)
plt.legend()
```
The increase in accuracy is miniscule.
## Multi layered NN's
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(images)
images_normed = scaler.transform(images)
clr = MLPClassifier(hidden_layer_sizes=(25,25))
clf = GridSearchCV(clr, {'alpha':np.logspace(-80, -1, 3)})
clf.fit(images_normed, image_labels)
clf.best_score_
clf.best_params_
nn_tuned = clf.best_estimator_
nn_tuned.fit(scaler.transform(training_data), training_labels)
curve = learning_curve(nn_tuned, images_normed, image_labels)
train_sizes, train_scores, test_scores = curve
train_scores = pd.DataFrame(train_scores)
train_scores.loc[:,'train_size'] = train_sizes
test_scores = pd.DataFrame(test_scores)
test_scores.loc[:,'train_size'] = train_sizes
train_scores = pd.melt(train_scores, id_vars=['train_size'], value_name = 'CrossVal score')
test_scores = pd.melt(test_scores, id_vars=['train_size'], value_name = 'CrossVal score')
matplotlib.rcParams['figure.figsize'] = (12, 8)
sns.tsplot(train_scores, time = 'train_size', unit='variable', value = 'CrossVal score')
sns.tsplot(test_scores, time = 'train_size', unit='variable', value = 'CrossVal score', color='g')
plt.ylim(0,1.1)
plt.legend()
```
Hmm... multi-hidden layer NN's seem to be much harder to tune.
Maybe we need to try with wider range of parameters for Gridsearch?
Finding optimum parameters for advanced classifiers is not always so straightforward, and quite often the most time consuming part. This so-called **Hyperparameter optimization** is a topic in itself, and has numerous approaches and libraries.
* [http://neupy.com/2016/12/17/hyperparameter_optimization_for_neural_networks.html](http://neupy.com/2016/12/17/hyperparameter_optimization_for_neural_networks.html)
* [Practical Bayesian Optimization of Machine Learning Algorithms](https://dash.harvard.edu/handle/1/11708816)
**sklearn's neural network functionality is rather limited.** More advanced toolboxes for neural networks:
* [keras](https://keras.io/)
* [tensorflow](https://www.tensorflow.org/)
* [Theano](http://deeplearning.net/software/theano/)
# Exercise
## iris dataset
Train a neural network on the `iris` dataset and run cross validation. Do not forget to normalize the featurs.
Compare the results against LogisticRegression.
Use Grid search to tune the NN further.
## Further reading
* http://www.ritchieng.com/applying-machine-learning/
| true |
code
| 0.645343 | null | null | null | null |
|
```
from __future__ import print_function
import numpy as np
np.random.seed(1337) # for reproducibility
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
```
Preprocess data
```
nb_classes = 10
# input image dimensions
img_rows, img_cols = 28, 28
# number of convolutional filters to use
nb_filters = 32
# size of pooling area for max pooling
pool_size = (2, 2)
# convolution kernel size
kernel_size = (3, 3)
# the data, shuffled and split between train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
if K.image_dim_ordering() == 'th':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
```
Build a Keras model using the `Sequential API`
```
batch_size = 50
nb_epoch = 10
model = Sequential()
model.add(Convolution2D(nb_filters, kernel_size,
padding='valid',
input_shape=input_shape,
activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Convolution2D(nb_filters, kernel_size,activation='relu'))
model.add(Dropout(rate=0.25))
model.add(Flatten())
model.add(Dense(64,activation='relu'))
model.add(Dropout(rate=5))
model.add(Dense(nb_classes,activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model.summary()
```
Train and evaluate the model
```
model.fit(X_train[0:10000, ...], Y_train[0:10000, ...], batch_size=batch_size, epochs=nb_epoch,
verbose=1, validation_data=(X_test, Y_test))
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])
```
Save the model
```
model.save('example_keras_mnist_model.h5')
```
| true |
code
| 0.805861 | null | null | null | null |
|
# Bayesian Parametric Regression
Notebook version: 1.5 (Sep 24, 2019)
Author: Jerónimo Arenas García ([email protected])
Jesús Cid-Sueiro ([email protected])
Changes: v.1.0 - First version
v.1.1 - ML Model selection included
v.1.2 - Some typos corrected
v.1.3 - Rewriting text, reorganizing content, some exercises.
v.1.4 - Revised introduction
v.1.5 - Revised notation. Solved exercise 5
Pending changes: * Include regression on the stock data
```
# Import some libraries that will be necessary for working with data and displaying plots
# To visualize plots in the notebook
%matplotlib inline
from IPython import display
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import scipy.io # To read matlab files
import pylab
import time
```
## A quick note on the mathematical notation
In this notebook we will make extensive use of probability distributions. In general, we will use capital letters
${\bf X}$, $S$, $E$ ..., to denote random variables, and lower-case letters ${\bf x}$, $s$, $\epsilon$ ..., to denote the values they can take.
In general, we will use letter $p$ for probability density functions (pdf). When necessary, we will use, capital subindices to make the random variable explicit. For instance, $p_{{\bf X}, S}({\bf x}, s)$ would be the joint pdf of random variables ${\bf X}$ and $S$ at values ${\bf x}$ and $s$, respectively.
However, to avoid a notation overload, we will omit subindices when they are clear from the context. For instance, we will use $p({\bf x}, s)$ instead of $p_{{\bf X}, S}({\bf x}, s)$.
## 1. Model-based parametric regression
### 1.1. The regression problem.
Given an observation vector ${\bf x}$, the goal of the regression problem is to find a function $f({\bf x})$ providing *good* predictions about some unknown variable $s$. To do so, we assume that a set of *labelled* training examples, $\{{\bf x}_k, s_k\}_{k=0}^{K-1}$ is available.
The predictor function should make good predictions for new observations ${\bf x}$ not used during training. In practice, this is tested using a second set (the *test set*) of labelled samples.
### 1.2. Model-based parametric regression
Model-based regression methods assume that all data in the training and test dataset have been generated by some stochastic process. In parametric regression, we assume that the probability distribution generating the data has a known parametric form, but the values of some parameters are unknown.
In particular, in this notebook we will assume the target variables in all pairs $({\bf x}_k, s_k)$ from the training and test sets have been generated independently from some posterior distribution $p(s| {\bf x}, {\bf w})$, were ${\bf w}$ is some unknown parameter. The training dataset is used to estimate ${\bf w}$.
<img src="figs/ParametricReg.png" width=300>
### 1.3. Model assumptions
In order to estimate ${\bf w}$ from the training data in a mathematicaly rigorous and compact form let us group the target variables into a vector
$$
{\bf s} = \left(s_0, \dots, s_{K-1}\right)^\top
$$
and the input vectors into a matrix
$$
{\bf X} = \left({\bf x}_0, \dots, {\bf x}_{K-1}\right)^\top
$$
We will make the following assumptions:
* A1. All samples in ${\cal D}$ have been generated by the same distribution, $p({\bf x}, s \mid {\bf w})$
* A2. Input variables ${\bf x}$ do not depend on ${\bf w}$. This implies that
$$
p({\bf X} \mid {\bf w}) = p({\bf X})
$$
* A3. Targets $s_0, \dots, s_{K-1}$ are statistically independent, given ${\bf w}$ and the inputs ${\bf x}_0,\ldots, {\bf x}_{K-1}$, that is:
$$
p({\bf s} \mid {\bf X}, {\bf w}) = \prod_{k=0}^{K-1} p(s_k \mid {\bf x}_k, {\bf w})
$$
## 2. Bayesian inference.
### 2.1. The Bayesian approach
The main idea of Bayesian inference is the following: assume we want to estimate some unknown variable $U$ given an observed variable $O$. If $U$ and $O$ are random variables, we can describe the relation between $U$ and $O$ through the following functions:
* **Prior distribution**: $p_U(u)$. It describes our uncertainty on the true value of $U$ before observing $O$.
* **Likelihood function**: $p_{O \mid U}(o \mid u)$. It describes how the value of the observation is generated for a given value of $U$.
* **Posterior distribution**: $p_{U|O}(u \mid o)$. It describes our uncertainty on the true value of $U$ once the true value of $O$ is observed.
The major component of the Bayesian inference is the posterior distribution. All Bayesian estimates are computed as some of its central statistics (e.g. the mean, the median or the mode), for instance
* **Maximum A Posteriori (MAP) estimate**: $\qquad{\widehat{u}}_{\text{MAP}} = \arg\max_u p_{U \mid O}(u \mid o)$
* **Minimum Mean Square Error (MSE) estimate**: $\qquad\widehat{u}_{\text{MSE}} = \mathbb{E}\{U \mid O=o\}$
The choice between the MAP or the MSE estimate may depend on practical or computational considerations. From a theoretical point of view, $\widehat{u}_{\text{MSE}}$ has some nice properties: it minimizes $\mathbb{E}\{(U-\widehat{u})^2\}$ among all possible estimates, $\widehat{u}$, so it is a natural choice. However, it involves the computation of an integral, which may not have a closed-form solution. In such cases, the MAP estimate can be a better choice.
The prior and the likelihood function are auxiliary distributions: if the posterior distribution is unknown, it can be computed from them using the Bayes rule:
\begin{equation}
p_{U|O}(u \mid o) = \frac{p_{O|U}(o \mid u) \cdot p_{U}(u)}{p_{O}(o)}
\end{equation}
In the next two sections we show that the Bayesian approach can be applied to both the prediction and the estimation problems.
### 2.2. Bayesian prediction under a known model
Assuming that the model parameters ${\bf w}$ are known, we can apply the Bayesian approach to predict ${\bf s}$ for an input ${\bf x}$. In that case, we can take
* Unknown variable: ${\bf s}$, and
* Observations: ${\bf x}$
the MAP and MSE predictions become
* Maximum A Posterior (MAP): $\qquad\widehat{s}_{\text{MAP}} = \arg\max_s p(s| {\bf x}, {\bf w})$
* Minimum Mean Square Error (MSE): $\qquad\widehat{s}_{\text{MSE}} = \mathbb{E}\{S |{\bf x}, {\bf w}\}$
#### Exercise 1:
Assuming
$$
p(s\mid x, w) = \frac{s}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right), \qquad s \geq 0,
$$
compute the MAP and MSE predictions of $s$ given $x$ and $w$.
#### Solution:
<SOL>
\begin{align}
\widehat{s}_\text{MAP}
&= \arg\max_s \left\{\frac{s}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \right\} \\
&= \arg\max_s \left\{\log(s) - \log(w x^2) -\frac{s^2}{2 w x^2} \right\} \\
&= \sqrt{w}x
\end{align}
where the last step results from maximizing by differentiation.
\begin{align}
\widehat{s}_\text{MSE}
&= \mathbb{E}\{s | x, w\} \\
&= \int_0^\infty \frac{s^2}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \\
&= \frac{1}{2} \int_{-\infty}^\infty \frac{s^2}{w x^2} \exp\left({-\frac{s^2}{2 w x^2}}\right) \\
&= \frac{\sqrt{2\pi}}{2\sqrt{w x^2}} \int_{-\infty}^\infty \frac{s^2}{\sqrt{2\pi w x^2}} \exp\left({-\frac{s^2}{2 w x^2}}\right)
\end{align}
Noting that the last integral corresponds to the variance of a zero-mean Gaussian distribution, we get
\begin{align}
\widehat{s}_\text{MSE}
&= \frac{\sqrt{2\pi}}{2\sqrt{w x^2}} w x^2 \\
&= \sqrt{\frac{\pi w}{2}}x
\end{align}
</SOL>
#### 2.2.1. The Gaussian case
A particularly interesting case arises when the data model is Gaussian:
$$p(s|{\bf x}, {\bf w}) =
\frac{1}{\sqrt{2\pi}\sigma_\varepsilon}
\exp\left(-\frac{(s-{\bf w}^\top{\bf z})^2}{2\sigma_\varepsilon^2}\right)
$$
where ${\bf z}=T({\bf x})$ is a vector with components which can be computed directly from the observed variables. For a Gaussian distribution (and for any unimodal symetric distributions) the mean and the mode are the same and, thus,
$$
\widehat{s}_\text{MAP} = \widehat{s}_\text{MSE} = {\bf w}^\top{\bf z}
$$
Such expression includes a linear regression model, where ${\bf z} = [1; {\bf x}]$, as well as any other non-linear model as long as it can be expressed as a <i>"linear in the parameters"</i> model.
### 2.3. Bayesian Inference for Parameter Estimation
In a similar way, we can apply Bayesian inference to estimate the model parameters ${\bf w}$ from a given dataset, $\cal{D}$. In that case
* the unknown variable is ${\bf w}$, and
* the observation is $\cal{D} \equiv \{{\bf X}, {\bf s}\}$
so that
* Maximum A Posterior (MAP): $\qquad\widehat{\bf w}_{\text{MAP}} = \arg\max_{\bf w} p({\bf w}| {\cal D})$
* Minimum Mean Square Error (MSE): $\qquad\widehat{\bf w}_{\text{MSE}} = \mathbb{E}\{{\bf W} | {\cal D}\}$
## 3. Bayesian parameter estimation
NOTE: Since the training data inputs are known, all probability density functions and expectations in the remainder of this notebook will be conditioned on the data matrix, ${\bf X}$. To simplify the mathematical notation, from now on we will remove ${\bf X}$ from all conditions. For instance, we will write $p({\bf s}|{\bf w})$ instead of $p({\bf s}|{\bf w}, {\bf X})$, etc. Keep in mind that, in any case, all probabilities and expectations may depend on ${\bf X}$ implicitely.
Summarizing, the steps to design a Bayesian parametric regresion algorithm are the following:
1. Assume a parametric data model $p(s| {\bf x},{\bf w})$ and a prior distribution $p({\bf w})$.
2. Using the data model and the i.i.d. assumption, compute $p({\bf s}|{\bf w})$.
3. Applying the bayes rule, compute the posterior distribution $p({\bf w}|{\bf s})$.
4. Compute the MAP or the MSE estimate of ${\bf w}$ given ${\bf x}$.
5. Compute predictions using the selected estimate.
### 3.1. Bayesian Inference and Maximum Likelihood.
Applying the Bayes rule the MAP estimate can be alternatively expressed as
\begin{align}
\qquad\widehat{\bf w}_{\text{MAP}}
&= \arg\max_{\bf w} \frac{p({\cal D}| {\bf w}) \cdot p({\bf w})}{p({\cal D})} \\
&= \arg\max_{\bf w} p({\cal D}| {\bf w}) \cdot p({\bf w})
\end{align}
By comparisons, the ML (Maximum Likelihood) estimate has the form:
$$
\widehat{\bf w}_{\text{ML}} = \arg \max_{\bf w} p(\mathcal{D}|{\bf w})
$$
This shows that the MAP estimate takes into account the prior distribution on the unknown parameter.
Another advantage of the Bayesian approach is that it provides not only a point estimate of the unknown parameter, but a whole funtion, the posterior distribution, which encompasses our belief on the unknown parameter given the data. For instance, we can take second order statistics like the variance of the posterior distributions to measure the uncertainty on the true value of the parameter around the mean.
### 3.2. The prior distribution
Since each value of ${\bf w}$ determines a regression function, by stating a prior distribution over the weights we state also a prior distribution over the space of regression functions.
For instance, assume that the data likelihood follows the Gaussian model in sec. 2.2.1, with $T(x) = (1, x, x^2, x^3)$, i.e. the regression functions have the form
$$
w_0 + w_1 x + w_2 x^2 + w_3 x^3
$$
Each value of ${\bf w}$ determines a specific polynomial of degree 3. Thus, the prior distribution over ${\bf w}$ describes which polynomials are more likely before observing the data.
For instance, assume a Gaussian prior with zero mean and variance ${\bf V}_p$, i.e.,
$$
p({\bf w}) = \frac{1}{(2\pi)^{D/2} |{\bf V}_p|^{1/2}}
\exp \left(-\frac{1}{2} {\bf w}^\intercal {\bf V}_{p}^{-1}{\bf w} \right)
$$
where $D$ is the dimension of ${\bf w}$. To abbreviate, we will also express this as
$${\bf w} \sim {\cal N}\left({\bf 0},{\bf V}_{p} \right)$$
The following code samples ${\bf w}$ according to this distribution for ${\bf V}_p = 0.002 \, {\bf I}$, and plots the resulting polynomial over the scatter plot of an arbitrary dataset.
You can check the effect of modifying the variance of the prior distribution.
```
n_grid = 200
degree = 3
nplots = 20
# Prior distribution parameters
mean_w = np.zeros((degree+1,))
v_p = 0.2 ### Try increasing this value
var_w = v_p * np.eye(degree+1)
xmin = -1
xmax = 1
X_grid = np.linspace(xmin, xmax, n_grid)
fig = plt.figure()
ax = fig.add_subplot(111)
for k in range(nplots):
#Draw weigths fromt the prior distribution
w_iter = np.random.multivariate_normal(mean_w, var_w)
S_grid_iter = np.polyval(w_iter, X_grid)
ax.plot(X_grid, S_grid_iter,'g-')
ax.set_xlim(xmin, xmax)
ax.set_ylim(-1, 1)
ax.set_xlabel('$x$')
ax.set_ylabel('$s$')
plt.show()
```
The data observation will modify our belief about the true data model according to the posterior distribution. In the following we will analyze this in a Gaussian case.
## 4. Bayesian regression for a Gaussian model.
We will apply the above steps to derive a Bayesian regression algorithm for a Gaussian model.
### 4.1. Step 1: The Gaussian model.
Let us assume that the likelihood function is given by the Gaussian model described in Sec. 1.3.2.
$$
s~|~{\bf w} \sim {\cal N}\left({\bf z}^\top{\bf w}, \sigma_\varepsilon^2 \right)
$$
that is
$$p(s|{\bf x}, {\bf w}) =
\frac{1}{\sqrt{2\pi}\sigma_\varepsilon}
\exp\left(-\frac{(s-{\bf w}^\top{\bf z})^2}{2\sigma_\varepsilon^2}\right)
$$
Assume, also, that the prior is Gaussian
$$
{\bf w} \sim {\cal N}\left({\bf 0},{\bf V}_{p} \right)
$$
### 4.2. Step 2: Complete data likelihood
Using the assumptions A1, A2 and A3, it can be shown that
$$
{\bf s}~|~{\bf w} \sim {\cal N}\left({\bf Z}{\bf w},\sigma_\varepsilon^2 {\bf I} \right)
$$
that is
$$
p({\bf s}| {\bf w})
= \frac{1}{\left(\sqrt{2\pi}\sigma_\varepsilon\right)^K}
\exp\left(-\frac{1}{2\sigma_\varepsilon^2}\|{\bf s}-{\bf Z}{\bf w}\|^2\right)
$$
### 4.3. Step 3: Posterior weight distribution
The posterior distribution of the weights can be computed using the Bayes rule
$$p({\bf w}|{\bf s}) = \frac{p({\bf s}|{\bf w})~p({\bf w})}{p({\bf s})}$$
Since both $p({\bf s}|{\bf w})$ and $p({\bf w})$ follow a Gaussian distribution, we know also that the joint distribution and the posterior distribution of ${\bf w}$ given ${\bf s}$ are also Gaussian. Therefore,
$${\bf w}~|~{\bf s} \sim {\cal N}\left({\bf w}_\text{MSE}, {\bf V}_{\bf w}\right)$$
After some algebra, it can be shown that mean and the covariance matrix of the distribution are:
$${\bf V}_{\bf w} = \left[\frac{1}{\sigma_\varepsilon^2} {\bf Z}^{\top}{\bf Z}
+ {\bf V}_p^{-1}\right]^{-1}$$
$${\bf w}_\text{MSE} = {\sigma_\varepsilon^{-2}} {\bf V}_{\bf w} {\bf Z}^\top {\bf s}$$
#### Exercise 2:
Consider the dataset with one-dimensional inputs given by
```
# True data parameters
w_true = 3
std_n = 0.4
# Generate the whole dataset
n_max = 64
X_tr = 3 * np.random.random((n_max,1)) - 0.5
S_tr = w_true * X_tr + std_n * np.random.randn(n_max,1)
# Plot data
plt.figure()
plt.plot(X_tr, S_tr, 'b.')
plt.xlabel('$x$')
plt.ylabel('$s$')
plt.show()
```
Fit a Bayesian linear regression model assuming $z= x$ and
```
# Model parameters
sigma_eps = 0.4
mean_w = np.zeros((1,))
sigma_p = 1e6
Var_p = sigma_p**2* np.eye(1)
```
To do so, compute the posterior weight distribution using the first $k$ samples in the complete dataset, for $k = 1,2,4,8,\ldots 128$. Draw all these posteriors along with the prior distribution in the same plot.
```
# No. of points to analyze
n_points = [1, 2, 4, 8, 16, 32, 64]
# Prepare plots
w_grid = np.linspace(2.7, 3.4, 5000) # Sample the w axis
plt.figure()
# Compute the prior distribution over the grid points in w_grid
# p = <FILL IN>
p = 1.0/(sigma_p*np.sqrt(2*np.pi)) * np.exp(-(w_grid**2)/(2*sigma_p**2))
plt.plot(w_grid, p,'g-')
for k in n_points:
# Select the first k samples
Zk = X_tr[0:k, :]
Sk = S_tr[0:k]
# Parameters of the posterior distribution
# 1. Compute the posterior variance.
# (Make sure that the resulting variable, Var_w, is a 1x1 numpy array.)
# Var_w = <FILL IN>
Var_w = np.linalg.inv(np.dot(Zk.T, Zk)/(sigma_eps**2) + np.linalg.inv(Var_p))
# 2. Compute the posterior mean.
# (Make sure that the resulting variable, w_MSE, is a scalar)
# w_MSE = <FILL IN>
w_MSE = (Var_w.dot(Zk.T).dot(Sk)/(sigma_eps**2)).flatten()
# Compute the posterior distribution over the grid points in w_grid
sigma_w = np.sqrt(Var_w.flatten()) # First we take a scalar standard deviation
# p = <FILL IN>
p = 1.0/(sigma_w*np.sqrt(2*np.pi)) * np.exp(-((w_grid-w_MSE)**2)/(2*sigma_w**2))
plt.plot(w_grid, p,'g-')
plt.fill_between(w_grid, 0, p, alpha=0.8, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=1, antialiased=True)
plt.title('Posterior distribution after {} samples'.format(k))
plt.xlim(w_grid[0], w_grid[-1])
plt.ylim(0, np.max(p))
plt.xlabel('$w$')
plt.ylabel('$p(w|s)$')
display.clear_output(wait=True)
display.display(plt.gcf())
time.sleep(2.0)
# Remove the temporary plots and fix the last one
display.clear_output(wait=True)
plt.show()
```
#### Exercise 3:
Note that, in the example above, the model assumptions are correct: the target variables have been generated by a linear model with noise standard deviation `sigma_n` which is exactly equal to the value assumed by the model, stored in variable `sigma_eps`. Check what happens if we take `sigma_eps=4*sigma_n` or `sigma_eps=sigma_n/4`.
* Does the algorithm fail in that cases?
* What differences can you observe with respect to the ideal case `sigma_eps=sigma_n`?
### 4.4. Step 4: Weight estimation.
Since the posterior weight distribution is Gaussian, both the MAP and the MSE estimates are equal to the posterior mean, which has been already computed in step 3:
$$\widehat{\bf w}_\text{MAP} = \widehat{\bf w}_\text{MSE} = {\sigma_\varepsilon^{-2}} {\bf V}_{\bf w} {\bf Z}^\top {\bf s}$$
### 4.5. Step 5: Prediction
Using the MSE estimate, the final predictions are given by
$$
\widehat{s}_\text{MSE} = \widehat{\bf w}_\text{MSE}^\top{\bf z}
$$
#### Exercise 4:
Plot the minimum MSE predictions of $s$ for inputs $x$ in the interval [-1, 3].
```
# <SOL>
x = np.array([-1.0, 3.0])
s_pred = w_MSE * x
plt.figure()
plt.plot(X_tr, S_tr,'b.')
plt.plot(x, s_pred)
plt.show()
# </SOL>
```
## 5. Maximum likelihood vs Bayesian Inference.
### 5.1. The Maximum Likelihood Estimate.
For comparative purposes, it is interesting to see here that the likelihood function is enough to compute the Maximum Likelihood (ML) estimate
\begin{align}
{\bf w}_\text{ML} &= \arg \max_{\bf w} p(\mathcal{D}|{\bf w}) \\
&= \arg \min_{\bf w} \|{\bf s}-{\bf Z}{\bf w}\|^2
\end{align}
which leads to the Least Squares (LS) solution
$$
{\bf w}_\text{ML} = ({\bf Z}^\top{\bf Z})^{-1}{\bf Z}^\top{\bf s}
$$
ML estimation is prone to overfiting. In general, if the number of parameters (i.e. the dimension of ${\bf w}$) is large in relation to the size of the training data, the predictor based on the ML estimate may have a small square error over the training set but a large error over the test set. Therefore, in practice, some cross validation procedure is required to keep the complexity of the predictor function under control depending on the size of the training set.
By defining a prior distribution over the unknown parameters, and using the Bayesian inference methods, the overfitting problems can be alleviated
### 5.2 Making predictions
- Following an **ML approach**, we retain a single model, ${\bf w}_{ML} = \arg \max_{\bf w} p({\bf s}|{\bf w})$. Then, the predictive distribution of the target value for a new point would be obtained as:
$$p({s^*}|{\bf w}_{ML},{\bf x}^*) $$
For the generative model of Section 3.1.2 (additive i.i.d. Gaussian noise), this distribution is:
$$p({s^*}|{\bf w}_{ML},{\bf x}^*) = \frac{1}{\sqrt{2\pi\sigma_\varepsilon^2}} \exp \left(-\frac{\left(s^* - {\bf w}_{ML}^\top {\bf z}^*\right)^2}{2 \sigma_\varepsilon^2} \right)$$
* The mean of $s^*$ is just the same as the prediction of the LS model, and the same uncertainty is assumed independently of the observation vector (i.e., the variance of the noise of the model).
* If a single value is to be kept, we would probably keep the mean of the distribution, which is equivalent to the LS prediction.
- Using <b>Bayesian inference</b>, we retain all models. Then, the inference of the value $s^* = s({\bf x}^*)$ is carried out by mixing all models, according to the weights given by the posterior distribution.
\begin{align}
p({s^*}|{\bf x}^*,{\bf s})
& = \int p({s^*}~|~{\bf w},{\bf x}^*) p({\bf w}~|~{\bf s}) d{\bf w}
\end{align}
where:
* $p({s^*}|{\bf w},{\bf x}^*) = \dfrac{1}{\sqrt{2\pi\sigma_\varepsilon^2}} \exp \left(-\frac{\left(s^* - {\bf w}^\top {\bf z}^*\right)^2}{2 \sigma_\varepsilon^2} \right)$
* $p({\bf w} \mid {\bf s})$ is the posterior distribution of the weights, that can be computed using Bayes' Theorem.
In general the integral expression of the posterior distribution $p({s^*}|{\bf x}^*,{\bf s})$ cannot be computed analytically. Fortunately, for the Gaussian model, the computation of the posterior is simple, as we will show in the following section.
## 6. Posterior distribution of the target variable
In the same way that we have computed a distribution on ${\bf w}$, we can compute a distribution on the target variable for a given input ${\bf x}$ and given the whole dataset.
Since ${\bf w}$ is a random variable, the noise-free component of the target variable for an arbitrary input ${\bf x}$, that is, $f = f({\bf x}) = {\bf w}^\top{\bf z}$ is also a random variable, and we can compute its distribution from the posterior distribution of ${\bf w}$
Since ${\bf w}$ is Gaussian and $f$ is a linear transformation of ${\bf w}$, $f$ is also a Gaussian random variable, whose posterior mean and variance can be calculated as follows:
\begin{align}
\mathbb{E}\{f \mid {\bf s}, {\bf z}\}
&= \mathbb{E}\{{\bf w}^\top {\bf z}~|~{\bf s}, {\bf z}\}
= \mathbb{E}\{{\bf w} ~|~{\bf s}, {\bf z}\}^\top {\bf z} \\
&= \widehat{\bf w}_\text{MSE} ^\top {\bf z} \\
% &= {\sigma_\varepsilon^{-2}} {{\bf z}}^\top {\bf V}_{\bf w} {\bf Z}^\top {\bf s}
\end{align}
\begin{align}
\text{Cov}\left[{{\bf z}}^\top {\bf w}~|~{\bf s}, {\bf z}\right]
&= {\bf z}^\top \text{Cov}\left[{\bf w}~|~{\bf s}\right] {\bf z} \\
&= {\bf z}^\top {\bf V}_{\bf w} {{\bf z}}
\end{align}
Therefore,
$$
f^*~|~{\bf s}, {\bf x}
\sim {\cal N}\left(\widehat{\bf w}_\text{MSE} ^\top {\bf z}, ~~
{\bf z}^\top {\bf V}_{\bf w} {\bf z} \right)
$$
Finally, for $s = f + \varepsilon$, the posterior distribution is
$$
s ~|~{\bf s}, {\bf z}^*
\sim {\cal N}\left(\widehat{\bf w}_\text{MSE} ^\top {\bf z}, ~~
{\bf z}^\top {\bf V}_{\bf w} {\bf z} + \sigma_\varepsilon^2\right)
$$
#### Example:
The next figure shows a one-dimensional dataset with 15 points, which are noisy samples from a cosine signal (shown in the dotted curve)
```
n_points = 15
n_grid = 200
frec = 3
std_n = 0.2
# Data generation
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
# Signal
xmin = np.min(X_tr) - 0.1
xmax = np.max(X_tr) + 0.1
X_grid = np.linspace(xmin, xmax, n_grid)
S_grid = - np.cos(frec*X_grid) #Noise free for the true model
# Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z = np.asmatrix(Z)
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Set axes
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
Let us assume that the cosine form of the noise-free signal is unknown, and we assume a polynomial model with a high degree. The following code plots the LS estimate
```
degree = 12
# We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_LS = np.polyval(w_LS,X_grid)
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
The following fragment of code computes the posterior weight distribution, draws random vectors from $p({\bf w}|{\bf s})$, and plots the corresponding regression curves along with the training points. Compare these curves with those extracted from the prior distribution of ${\bf w}$ and with the LS solution.
```
nplots = 6
# Prior distribution parameters
sigma_eps = 0.2
mean_w = np.zeros((degree+1,))
sigma_p = .5
Var_p = sigma_p**2 * np.eye(degree+1)
# Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z = np.asmatrix(Z)
#Compute posterior distribution parameters
Var_w = np.linalg.inv(np.dot(Z.T,Z)/(sigma_eps**2) + np.linalg.inv(Var_p))
posterior_mean = Var_w.dot(Z.T).dot(S_tr)/(sigma_eps**2)
posterior_mean = np.array(posterior_mean).flatten()
# Plot data
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
for k in range(nplots):
# Draw weights from the posterior distribution
w_iter = np.random.multivariate_normal(posterior_mean, Var_w)
# Note that polyval assumes the first element of weight vector is the coefficient of
# the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(w_iter[::-1], X_grid)
ax.plot(X_grid,S_grid_iter,'g-')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0] - 2, S_tr[-1] + 2)
ax.legend(loc='best')
plt.show()
```
Not only do we obtain a better predictive model, but we also have confidence intervals (error bars) for the predictions.
```
# Compute standard deviation
std_x = []
for el in X_grid:
x_ast = np.array([el**k for k in range(degree+1)])
std_x.append(np.sqrt(x_ast.dot(Var_w).dot(x_ast)[0,0]))
std_x = np.array(std_x)
# Plot data
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
# Plot the posterior mean
# Note that polyval assumes the first element of weight vector is the coefficient of
# the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(posterior_mean[::-1],X_grid)
ax.plot(X_grid,S_grid_iter,'g-',label='Predictive mean, BI')
#Plot confidence intervals for the Bayesian Inference
plt.fill_between(X_grid, S_grid_iter-std_x, S_grid_iter+std_x,
alpha=0.4, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=2, antialiased=True)
#We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_iter = np.polyval(w_LS,X_grid)
# Plot noise-free function
ax.plot(X_grid, S_grid, 'b:', label='Noise-free signal')
# Plot LS regression function
ax.plot(X_grid, S_grid_LS, 'm-', label='LS regression')
# Set axis
ax.set_xlim(xmin, xmax)
ax.set_ylim(S_tr[0]-2,S_tr[-1]+2)
ax.set_title('Predicting the target variable')
ax.set_xlabel('Input variable')
ax.set_ylabel('Target variable')
ax.legend(loc='best')
plt.show()
```
#### Exercise 5:
Assume the dataset ${\cal{D}} = \left\{ x_k, s_k \right\}_{k=0}^{K-1}$ containing $K$ i.i.d. samples from a distribution
$$p(s|x,w) = w x \exp(-w x s), \qquad s>0,\quad x> 0,\quad w> 0$$
We model also our uncertainty about the value of $w$ assuming a prior distribution for $w$ following a Gamma distribution with parameters $\alpha>0$ and $\beta>0$.
$$
w \sim \text{Gamma}\left(\alpha, \beta \right)
= \frac{\beta^\alpha}{\Gamma(\alpha)} w^{\alpha-1} \exp\left(-\beta w\right), \qquad w>0
$$
Note that the mean and the mode of a Gamma distribution can be calculated in closed-form as
$$
\mathbb{E}\left\{w\right\}=\frac{\alpha}{\beta}; \qquad
$$
$$
\text{mode}\{w\} = \arg\max_w p(w) = \frac{\alpha-1}{\beta}
$$
**1.** Determine an expression for the likelihood function.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
p({\bf s}| w)
&= \prod_{k=0}^{K-1} p(s_k|w, x_k) = \prod_{k=0}^{K-1} \left(w x_k \exp(-w x_k s_k)\right) \nonumber\\
&= w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)
\end{align}
[comment]: # (</SOL>)
**2.** Determine the maximum likelihood coefficient, $\widehat{w}_{\text{ML}}$.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
\widehat{w}_{\text{ML}}
&= \arg\max_w w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)
\\
&= \arg\max_w \left(w^K \cdot \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right)\right)
\\
&= \arg\max_w \left(K \log(w) - w \sum_{k=0}^{K-1} x_k s_k \right)
\\
&= \frac{K}{\sum_{k=0}^{K-1} x_k s_k}
\end{align}
[comment]: # (</SOL>)
**3.** Obtain the posterior distribution $p(w|{\bf s})$. Note that you do not need to calculate $p({\bf s})$ since the posterior distribution can be readily identified as another Gamma distribution.
#### Solution:
[comment]: # (<SOL>)
\begin{align}
p(w|{\bf s})
&= \frac{p({\bf s}|w) p(w)}{p(s)} \\
&= \frac{1}{p(s)}
\left(w^K \cdot \left(\prod_{k=0}^{K-1} x_k \right) \exp\left( -w \sum_{k=0}^{K-1} x_k s_k\right) \right)
\left(\frac{\beta^\alpha}{\Gamma(\alpha)} w^{\alpha-1} \exp\left(-\beta w\right)\right) \\
&= \frac{1}{p(s)} \frac{\beta^\alpha}{\Gamma(\alpha)} \left(\prod_{k=0}^{K-1} x_k \right)
\left(w^{K + \alpha - 1} \cdot
\exp\left( -w \left(\beta + \sum_{k=0}^{K-1} x_k s_k\right) \right) \right)
\end{align}
that is
$$
w \mid {\bf s} \sim Gamma\left(K+\alpha, \beta + \sum_{k=0}^{K-1} x_k s_k \right)
$$
[comment]: # (</SOL>)
**4.** Determine the MSE and MAP a posteriori estimators of $w$: $w_\text{MSE}=\mathbb{E}\left\{w|{\bf s}\right\}$ and $w_\text{MAP} = \max_w p(w|{\bf s})$.
#### Solution:
[comment]: # (<SOL>)
$$
w_{\text{MSE}} = \mathbb{E}\left\{w \mid {\bf s} \right\}
= \frac{K + \alpha}{\beta + \sum_{k=0}^{K-1} x_k s_k}
$$
$$
w_{\text{MAP}} = \text{mode}\{w\} = \arg\max_w p(w) = \frac{K + \alpha-1}{\beta + \sum_{k=0}^{K-1} x_k s_k}
$$
[comment]: # (</SOL>)
**5.** Compute the following estimators of $S$:
$\qquad\widehat{s}_1 = \mathbb{E}\{s|w_\text{ML},x\}$
$\qquad\widehat{s}_2 = \mathbb{E}\{s|w_\text{MSE},x\}$
$\qquad\widehat{s}_3 = \mathbb{E}\{s|w_\text{MAP},x\}$
#### Solution:
[comment]: # (<SOL>)
$$
\widehat{s}_1 = \mathbb{E}\{s|w_\text{ML},x\} = w_\text{ML} x
$$
$$
\widehat{s}_2 = \mathbb{E}\{s|w_\text{MSE},x\} = w_\text{MSE} x
$$
$$
\widehat{s}_3 = \mathbb{E}\{s|w_\text{MAP},x\} = w_\text{MAP} x
$$
[comment]: # (</SOL>)
## 7. Maximum evidence model selection
We have already addressed with Bayesian Inference the following two issues:
- For a given degree, how do we choose the weights?
- Should we focus on just one model, or can we use several models at once?
However, we still needed some assumptions: a parametric model (i.e., polynomial function and <i>a priori</i> degree selection) and several parameters needed to be adjusted.
Though we can recur to cross-validation, Bayesian inference opens the door to other strategies.
- We could argue that rather than keeping single selections of these parameters, we could use simultaneously several sets of parameters (and/or several parametric forms), and average them in a probabilistic way ... (like we did with the models)
- We will follow a simpler strategy, selecting just the most likely set of parameters according to an ML criterion
### 7.1 Model evidence
The evidence of a model is defined as
$$L = p({\bf s}~|~{\cal M})$$
where ${\cal M}$ denotes the model itself and any free parameters it may have. For instance, for the polynomial model we have assumed so far, ${\cal M}$ would represent the degree of the polynomia, the variance of the additive noise, and the <i>a priori</i> covariance matrix of the weights
Applying the Theorem of Total probability, we can compute the evidence of the model as
$$L = \int p({\bf s}~|~{\bf f},{\cal M}) p({\bf f}~|~{\cal M}) d{\bf f} $$
For the linear model $f({\bf x}) = {\bf w}^\top{\bf z}$, the evidence can be computed as
$$L = \int p({\bf s}~|~{\bf w},{\cal M}) p({\bf w}~|~{\cal M}) d{\bf w} $$
It is important to notice that these probability density functions are exactly the ones we computed on the previous section. We are just making explicit that they depend on a particular model and the selection of its parameters. Therefore:
- $p({\bf s}~|~{\bf w},{\cal M})$ is the likelihood of ${\bf w}$
- $p({\bf w}~|~{\cal M})$ is the <i>a priori</i> distribution of the weights
### 7.2 Model selection via evidence maximization
- As we have already mentioned, we could propose a prior distribution for the model parameters, $p({\cal M})$, and use it to infer the posterior. However, this can be very involved (usually no closed-form expressions can be derived)
- Alternatively, maximizing the evidence is normally good enough
$${\cal M}_\text{ML} = \arg\max_{\cal M} p(s~|~{\cal M})$$
Note that we are using the subscript 'ML' because the evidence can also be referred to as the likelihood of the model
### 7.3 Example: Selection of the degree of the polynomia
For the previous example we had (we consider a spherical Gaussian for the weights):
- ${\bf s}~|~{\bf w},{\cal M}~\sim~{\cal N}\left({\bf Z}{\bf w},~\sigma_\varepsilon^2 {\bf I} \right)$
- ${\bf w}~|~{\cal M}~\sim~{\cal N}\left({\bf 0},~\sigma_p^2 {\bf I} \right)$
In this case, $p({\bf s}~|~{\cal M})$ follows also a Gaussian distribution, and it can be shown that
- $L = p({\bf s}~|~{\cal M}) = {\cal N}\left({\bf 0},\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I} \right)$
If we just pursue the maximization of $L$, this is equivalent to maximizing the log of the evidence
$$\log(L) = -\frac{M}{2} \log(2\pi) -{\frac{1}{2}}\log\mid\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I}\mid - \frac{1}{2} {\bf s}^\top \left(\sigma_p^2 {\bf Z} {\bf Z}^\top+\sigma_\varepsilon^2 {\bf I}\right)^{-1} {\bf s}$$
where $M$ denotes the length of vector ${\bf z}$ (the degree of the polynomia minus 1).
The following fragment of code evaluates the evidence of the model as a function of the degree of the polynomia
```
from math import pi
n_points = 15
frec = 3
std_n = 0.2
max_degree = 12
#Prior distribution parameters
sigma_eps = 0.2
mean_w = np.zeros((degree+1,))
sigma_p = 0.5
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
#Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z=np.asmatrix(Z)
#Evaluate the posterior evidence
logE = []
for deg in range(max_degree):
Z_iter = Z[:,:deg+1]
logE_iter = -((deg+1)*np.log(2*pi)/2) \
-np.log(np.linalg.det((sigma_p**2)*Z_iter.dot(Z_iter.T) + (sigma_eps**2)*np.eye(n_points)))/2 \
-S_tr.T.dot(np.linalg.inv((sigma_p**2)*Z_iter.dot(Z_iter.T) + (sigma_eps**2)*np.eye(n_points))).dot(S_tr)/2
logE.append(logE_iter[0,0])
plt.plot(np.array(range(max_degree))+1,logE)
plt.xlabel('Polynomia degree')
plt.ylabel('log evidence')
plt.show()
```
The above curve may change the position of its maximum from run to run.
We conclude the notebook by plotting the result of the Bayesian inference for $M=6$
```
n_points = 15
n_grid = 200
frec = 3
std_n = 0.2
degree = 5 #M-1
nplots = 6
#Prior distribution parameters
sigma_eps = 0.1
mean_w = np.zeros((degree+1,))
sigma_p = .5 * np.eye(degree+1)
X_tr = 3 * np.random.random((n_points,1)) - 0.5
S_tr = - np.cos(frec*X_tr) + std_n * np.random.randn(n_points,1)
X_grid = np.linspace(-1,3,n_grid)
S_grid = - np.cos(frec*X_grid) #Noise free for the true model
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(X_tr,S_tr,'b.',markersize=10)
#Compute matrix with training input data for the polynomial model
Z = []
for x_val in X_tr.tolist():
Z.append([x_val[0]**k for k in range(degree+1)])
Z=np.asmatrix(Z)
#Compute posterior distribution parameters
Sigma_w = np.linalg.inv(np.dot(Z.T,Z)/(sigma_eps**2) + np.linalg.inv(sigma_p))
posterior_mean = Sigma_w.dot(Z.T).dot(S_tr)/(sigma_eps**2)
posterior_mean = np.array(posterior_mean).flatten()
#Plot the posterior mean
#Note that polyval assumes the first element of weight vector is the coefficient of
#the highest degree term. Thus, we need to reverse w_iter
S_grid_iter = np.polyval(posterior_mean[::-1],X_grid)
ax.plot(X_grid,S_grid_iter,'g-',label='Predictive mean, BI')
#Plot confidence intervals for the Bayesian Inference
std_x = []
for el in X_grid:
x_ast = np.array([el**k for k in range(degree+1)])
std_x.append(np.sqrt(x_ast.dot(Sigma_w).dot(x_ast)[0,0]))
std_x = np.array(std_x)
plt.fill_between(X_grid, S_grid_iter-std_x, S_grid_iter+std_x,
alpha=0.2, edgecolor='#1B2ACC', facecolor='#089FFF',
linewidth=4, linestyle='dashdot', antialiased=True)
#We plot also the least square solution
w_LS = np.polyfit(X_tr.flatten(), S_tr.flatten(), degree)
S_grid_iter = np.polyval(w_LS,X_grid)
ax.plot(X_grid,S_grid_iter,'m-',label='LS regression')
ax.set_xlim(-1,3)
ax.set_ylim(S_tr[0]-2,S_tr[-1]+2)
ax.legend(loc='best')
plt.show()
```
We can check, that now the model also seems quite appropriate for LS regression, but keep in mind that selection of such parameter was itself carried out using Bayesian inference.
| true |
code
| 0.672681 | null | null | null | null |
|
# Goals
### 1. Learn to implement Resnet V2 Block (Type - 1) using monk
- Monk's Keras
- Monk's Pytorch
- Monk's Mxnet
### 2. Use network Monk's debugger to create complex blocks
### 3. Understand how syntactically different it is to implement the same using
- Traditional Keras
- Traditional Pytorch
- Traditional Mxnet
# Resnet V2 Block - Type 1
- Note: The block structure can have variations too, this is just an example
```
from IPython.display import Image
Image(filename='imgs/resnet_v2_with_downsample.png')
```
# Table of contents
[1. Install Monk](#1)
[2. Block basic Information](#2)
- [2.1) Visual structure](#2-1)
- [2.2) Layers in Branches](#2-2)
[3) Creating Block using monk visual debugger](#3)
- [3.1) Create the first branch](#3-1)
- [3.2) Create the second branch](#3-2)
- [3.3) Merge the branches](#3-3)
- [3.4) Debug the merged network](#3-4)
- [3.5) Compile the network](#3-5)
- [3.6) Visualize the network](#3-6)
- [3.7) Run data through the network](#3-7)
[4) Creating Block Using MONK one line API call](#4)
- [Mxnet Backend](#4-1)
- [Pytorch Backend](#4-2)
- [Keras Backend](#4-3)
[5) Appendix](#5)
- [Study Material](#5-1)
- [Creating block using traditional Mxnet](#5-2)
- [Creating block using traditional Pytorch](#5-3)
- [Creating block using traditional Keras](#5-4)
<a id='1'></a>
# Install Monk
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
- cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
- (Select the requirements file as per OS and CUDA version)
```
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
```
# Imports
```
# Common
import numpy as np
import math
import netron
from collections import OrderedDict
from functools import partial
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
```
<a id='2'></a>
# Block Information
<a id='2_1'></a>
## Visual structure
```
from IPython.display import Image
Image(filename='imgs/resnet_v2_with_downsample.png')
```
<a id='2_2'></a>
## Layers in Branches
- Number of branches: 2
- Common element
- batchnorm -> relu
- Branch 1
- conv_1x1
- Branch 2
- conv_3x3 -> batchnorm -> relu -> conv_3x3
- Branches merged using
- Elementwise addition
(See Appendix to read blogs on resnets)
<a id='3'></a>
# Creating Block using monk debugger
```
# Imports and setup a project
# To use pytorch backend - replace gluon_prototype with pytorch_prototype
# To use keras backend - replace gluon_prototype with keras_prototype
from gluon_prototype import prototype
# Create a sample project
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
```
<a id='3-1'></a>
## Create the first branch
```
def first_branch(output_channels=128, stride=1):
network = [];
network.append(gtf.convolution(output_channels=output_channels, kernel_size=1, stride=stride));
return network;
# Debug the branch
branch_1 = first_branch(output_channels=128, stride=1)
network = [];
network.append(branch_1);
gtf.debug_custom_model_design(network);
```
<a id='3-2'></a>
## Create the second branch
```
def second_branch(output_channels=128, stride=1):
network = [];
network.append(gtf.convolution(output_channels=output_channels, kernel_size=3, stride=stride));
network.append(gtf.batch_normalization());
network.append(gtf.relu());
network.append(gtf.convolution(output_channels=output_channels, kernel_size=3, stride=1));
return network;
# Debug the branch
branch_2 = second_branch(output_channels=128, stride=1)
network = [];
network.append(branch_2);
gtf.debug_custom_model_design(network);
```
<a id='3-3'></a>
## Merge the branches
```
def final_block(output_channels=128, stride=1):
network = [];
# Common elements
network.append(gtf.batch_normalization());
network.append(gtf.relu());
#Create subnetwork and add branches
subnetwork = [];
branch_1 = first_branch(output_channels=output_channels, stride=stride)
branch_2 = second_branch(output_channels=output_channels, stride=stride)
subnetwork.append(branch_1);
subnetwork.append(branch_2);
# Add merging element
subnetwork.append(gtf.add());
# Add the subnetwork
network.append(subnetwork);
return network;
```
<a id='3-4'></a>
## Debug the merged network
```
final = final_block(output_channels=128, stride=1)
network = [];
network.append(final);
gtf.debug_custom_model_design(network);
```
<a id='3-5'></a>
## Compile the network
```
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='3-6'></a>
## Run data through the network
```
import mxnet as mx
x = np.zeros((1, 3, 224, 224));
x = mx.nd.array(x);
y = gtf.system_dict["local"]["model"].forward(x);
print(x.shape, y.shape)
```
<a id='3-7'></a>
## Visualize network using netron
```
gtf.Visualize_With_Netron(data_shape=(3, 224, 224))
```
<a id='4'></a>
# Creating Using MONK LOW code API
<a id='4-1'></a>
## Mxnet backend
```
from gluon_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v2_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='4-2'></a>
## Pytorch backend
- Only the import changes
```
#Change gluon_prototype to pytorch_prototype
from pytorch_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v2_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='4-3'></a>
## Keras backend
- Only the import changes
```
#Change gluon_prototype to keras_prototype
from keras_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("sample-project-1", "sample-experiment-1");
network = [];
# Single line addition of blocks
network.append(gtf.resnet_v1_block(output_channels=128));
gtf.Compile_Network(network, data_shape=(3, 224, 224), use_gpu=False);
```
<a id='5'></a>
# Appendix
<a id='5-1'></a>
## Study links
- https://towardsdatascience.com/residual-blocks-building-blocks-of-resnet-fd90ca15d6ec
- https://medium.com/@MaheshNKhatri/resnet-block-explanation-with-a-terminology-deep-dive-989e15e3d691
- https://medium.com/analytics-vidhya/understanding-and-implementation-of-residual-networks-resnets-b80f9a507b9c
- https://hackernoon.com/resnet-block-level-design-with-deep-learning-studio-part-1-727c6f4927ac
<a id='5-2'></a>
## Creating block using traditional Mxnet
- Code credits - https://mxnet.incubator.apache.org/
```
# Traditional-Mxnet-gluon
import mxnet as mx
from mxnet.gluon import nn
from mxnet.gluon.nn import HybridBlock, BatchNorm
from mxnet.gluon.contrib.nn import HybridConcurrent, Identity
from mxnet import gluon, init, nd
def _conv3x3(channels, stride, in_channels):
return nn.Conv2D(channels, kernel_size=3, strides=stride, padding=1,
use_bias=False, in_channels=in_channels)
class ResnetBlockV2(HybridBlock):
def __init__(self, channels, stride, in_channels=0,
last_gamma=False,
norm_layer=BatchNorm, norm_kwargs=None, **kwargs):
super(ResnetBlockV2, self).__init__(**kwargs)
#Branch - 1
self.downsample = nn.Conv2D(channels, 1, stride, use_bias=False,
in_channels=in_channels)
# Branch - 2
self.bn1 = norm_layer(**({} if norm_kwargs is None else norm_kwargs))
self.conv1 = _conv3x3(channels, stride, in_channels)
if not last_gamma:
self.bn2 = norm_layer(**({} if norm_kwargs is None else norm_kwargs))
else:
self.bn2 = norm_layer(gamma_initializer='zeros',
**({} if norm_kwargs is None else norm_kwargs))
self.conv2 = _conv3x3(channels, 1, channels)
def hybrid_forward(self, F, x):
residual = x
x = self.bn1(x)
x = F.Activation(x, act_type='relu')
residual = self.downsample(x)
x = self.conv1(x)
x = self.bn2(x)
x = F.Activation(x, act_type='relu')
x = self.conv2(x)
return x + residual
# Invoke the block
block = ResnetBlockV2(64, 1)
# Initialize network and load block on machine
ctx = [mx.cpu()];
block.initialize(init.Xavier(), ctx = ctx);
block.collect_params().reset_ctx(ctx)
block.hybridize()
# Run data through network
x = np.zeros((1, 3, 224, 224));
x = mx.nd.array(x);
y = block.forward(x);
print(x.shape, y.shape)
# Export Model to Load on Netron
block.export("final", epoch=0);
netron.start("final-symbol.json", port=8082)
```
<a id='5-3'></a>
## Creating block using traditional Pytorch
- Code credits - https://pytorch.org/
```
# Traiditional-Pytorch
import torch
from torch import nn
from torch.jit.annotations import List
import torch.nn.functional as F
def conv3x3(in_planes, out_planes, stride=1, groups=1, dilation=1):
"""3x3 convolution with padding"""
return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
padding=dilation, groups=groups, bias=False, dilation=dilation)
def conv1x1(in_planes, out_planes, stride=1):
"""1x1 convolution"""
return nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False)
class ResnetBlock(nn.Module):
expansion = 1
__constants__ = ['downsample']
def __init__(self, inplanes, planes, stride=1, groups=1,
base_width=64, dilation=1, norm_layer=None):
super(ResnetBlock, self).__init__()
norm_layer = nn.BatchNorm2d
# Common Element
self.bn0 = norm_layer(inplanes)
self.relu0 = nn.ReLU(inplace=True)
# Branch - 1
self.downsample = conv1x1(inplanes, planes, stride)
# Branch - 2
self.conv1 = conv3x3(inplanes, planes, stride)
self.bn1 = norm_layer(planes)
self.relu = nn.ReLU(inplace=True)
self.conv2 = conv3x3(planes, planes)
self.stride = stride
def forward(self, x):
x = self.bn0(x);
x = self.relu0(x);
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out += identity
out = self.relu(out)
return out
# Invoke the block
block = ResnetBlock(3, 64, stride=1);
# Initialize network and load block on machine
layers = []
layers.append(block);
net = nn.Sequential(*layers);
# Run data through network
x = torch.randn(1, 3, 224, 224)
y = net(x)
print(x.shape, y.shape);
# Export Model to Load on Netron
torch.onnx.export(net, # model being run
x, # model input (or a tuple for multiple inputs)
"model.onnx", # where to save the model (can be a file or file-like object)
export_params=True, # store the trained parameter weights inside the model file
opset_version=10, # the ONNX version to export the model to
do_constant_folding=True, # whether to execute constant folding for optimization
input_names = ['input'], # the model's input names
output_names = ['output'], # the model's output names
dynamic_axes={'input' : {0 : 'batch_size'}, # variable lenght axes
'output' : {0 : 'batch_size'}})
netron.start('model.onnx', port=9998);
```
<a id='5-4'></a>
## Creating block using traditional Keras
- Code credits: https://keras.io/
```
# Traditional-Keras
import keras
import keras.layers as kla
import keras.models as kmo
import tensorflow as tf
from keras.models import Model
backend = 'channels_last'
from keras import layers
def resnet_conv_block(input_tensor,
kernel_size,
filters,
stage,
block,
strides=(2, 2)):
filters1, filters2, filters3 = filters
bn_axis = 3
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Common Element
start = layers.BatchNormalization(axis=bn_axis, name=bn_name_base + '0a')(input_tensor)
start = layers.Activation('relu')(start)
#Branch - 1
shortcut = layers.Conv2D(filters3, (1, 1), strides=strides,
kernel_initializer='he_normal',
name=conv_name_base + '1')(start)
#Branch - 2
x = layers.Conv2D(filters1, (1, 1), strides=strides,
kernel_initializer='he_normal',
name=conv_name_base + '2a')(start)
x = layers.BatchNormalization(axis=bn_axis, name=bn_name_base + '2a')(x)
x = layers.Activation('relu')(x)
x = layers.Conv2D(filters2, kernel_size, padding='same',
kernel_initializer='he_normal',
name=conv_name_base + '2b')(x)
x = layers.add([x, shortcut])
x = layers.Activation('relu')(x)
return x
def create_model(input_shape, kernel_size, filters, stage, block):
img_input = layers.Input(shape=input_shape);
x = resnet_conv_block(img_input, kernel_size, filters, stage, block)
return Model(img_input, x);
# Invoke the block
kernel_size=3;
filters=[64, 64, 64];
input_shape=(224, 224, 3);
model = create_model(input_shape, kernel_size, filters, 0, "0");
# Run data through network
x = tf.placeholder(tf.float32, shape=(1, 224, 224, 3))
y = model(x)
print(x.shape, y.shape)
# Export Model to Load on Netron
model.save("final.h5");
netron.start("final.h5", port=8082)
```
| true |
code
| 0.814293 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
```
# 1.
## a)
```
def simetrica(A):
"Verifică dacă matricea A este simetrică"
return np.all(A == A.T)
def pozitiv_definita(A):
"Verifică dacă matricea A este pozitiv definită"
for i in range(1, len(A) + 1):
d_minor = np.linalg.det(A[:i, :i])
if d_minor < 0:
return False
return True
def fact_ll(A):
# Pasul 1
if not simetrica(A):
raise Exception("Nu este simetrica")
if not pozitiv_definita(A):
raise Exception("Nu este pozitiv definită")
N = A.shape[0]
# Pasul 2
S = A.copy()
L = np.zeros((N, N))
# Pasul 3
for i in range(N):
# Actualizez coloana i din matricea L
L[:, i] = S[:, i] / np.sqrt(S[i, i])
# Calculez noul complement Schur
S_21 = S[i + 1:, i]
S_nou = np.eye(N)
S_nou[i + 1:, i + 1:] = S[i + 1:, i + 1:] - np.outer(S_21, S_21.T) / S[i, i]
S = S_nou
# Returnez matricea calculată
return L
A = np.array([
[25, 15, -5],
[15, 18, 0],
[-5, 0, 11]
], dtype=np.float64)
L = fact_ll(A)
print("L este:")
print(L)
print("Verificare:")
print(L @ L.T)
```
## b)
```
b = np.array([1, 2, 3], dtype=np.float64)
y = np.zeros(3)
x = np.zeros(3)
# Substituție ascendentă
for i in range(0, 3):
coefs = L[i, :i + 1]
values = y[:i + 1]
y[i] = (b[i] - coefs @ values) / L[i, i]
L_t = L.T
# Substituție descendentă
for i in range(2, -1, -1):
coefs = L_t[i, i + 1:]
values = x[i + 1:]
x[i] = (y[i] - coefs @ values) / L_t[i, i]
print("x =", x)
print()
print("Verificare: A @ x =", A @ x)
```
## 2.
```
def step(x, f, df):
"Calculează un pas din metoda Newton-Rhapson."
return x - f(x) / df(x)
def newton_rhapson(f, df, x0, eps):
"Determină o soluție a f(x) = 0 plecând de la x_0"
# Primul punct este cel primit ca parametru
prev_x = x0
# Execut o iterație
x = step(x0, f, df)
N = 1
while True:
# Verific condiția de oprire
if abs(x - prev_x) / abs(prev_x) < eps:
break
# Execut încă un pas
prev_x = x
x = step(x, f, df)
# Contorizez numărul de iterații
N += 1
return x, N
```
Funcția dată este
$$
f(x) = x^3 + 3 x^2 - 18 x - 40
$$
iar derivatele ei sunt
$$
f'(x) = 3x^2 + 6 x - 18
$$
$$
f''(x) = 6x + 6
$$
```
f = lambda x: (x ** 3) + 3 * (x ** 2) - 18 * x - 40
df = lambda x: 3 * (x ** 2) + 6 * x - 18
ddf = lambda x: 6 * x + 6
left = -8
right = +8
x_grafic = np.linspace(left, right, 500)
def set_spines(ax):
# Mut axele de coordonate
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
fig, ax = plt.subplots(dpi=120)
set_spines(ax)
plt.plot(x_grafic, f(x_grafic), label='$f$')
plt.plot(x_grafic, df(x_grafic), label="$f'$")
plt.plot(x_grafic, ddf(x_grafic), label="$f''$")
plt.legend()
plt.show()
```
Alegem subintervale astfel încât $f(a) f(b) < 0$:
- $[-8, -4]$
- $[-4, 0]$
- $[2, 6]$
Pentru fiecare dintre acestea, căutăm un punct $x_0$ astfel încât $f(x_0) f''(x_0) > 0$:
- $-6$
- $-1$
- $5$
```
eps = 1e-3
x1, _ = newton_rhapson(f, df, -6, eps)
x2, _ = newton_rhapson(f, df, -1, eps)
x3, _ = newton_rhapson(f, df, 5, eps)
fig, ax = plt.subplots(dpi=120)
plt.suptitle('Soluțiile lui $f(x) = 0$')
set_spines(ax)
plt.plot(x_grafic, f(x_grafic))
plt.scatter(x1, 0)
plt.scatter(x2, 0)
plt.scatter(x3, 0)
plt.show()
```
| true |
code
| 0.400046 | null | null | null | null |
|
# Soft Computing
## Vežba 1 - Digitalna slika, computer vision, OpenCV
### OpenCV
Open source biblioteka namenjena oblasti računarske vizije (eng. computer vision). Dokumentacija dostupna <a href="https://opencv.org/">ovde</a>.
### matplotlib
Plotting biblioteka za programski jezik Python i njegov numerički paket NumPy. Dokumentacija dostupna <a href="https://matplotlib.org/">ovde</a>.
### Učitavanje slike
OpenCV metoda za učitavanje slike sa diska je <b>imread(path_to_image)</b>, koja kao parametar prima putanju do slike na disku. Učitana slika <i>img</i> je zapravo NumPy matrica, čije dimenzije zavise od same prirode slike. Ako je slika u boji, onda je <i>img</i> trodimenzionalna matrica, čije su prve dve dimenzije visina i širina slike, a treća dimenzija je veličine 3, zato što ona predstavlja boju (RGB, po jedan segment za svaku osnonvu boju).
```
import numpy as np
import cv2 # OpenCV biblioteka
import matplotlib
import matplotlib.pyplot as plt
# iscrtavanje slika i grafika unutar samog browsera
%matplotlib inline
# prikaz vecih slika
matplotlib.rcParams['figure.figsize'] = 16,12
img = cv2.imread('images/girl.jpg') # ucitavanje slike sa diska
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # konvertovanje iz BGR u RGB model boja (OpenCV ucita sliku kao BGR)
plt.imshow(img) # prikazivanje slike
```
### Prikazivanje dimenzija slike
```
print(img.shape) # shape je property Numpy array-a za prikaz dimenzija
```
Obratiti pažnju da slika u boji ima 3 komponente za svaki piksel na slici - R (red), G (green) i B (blue).

```
img
```
Primetite da je svaki element matrice **uint8** (unsigned 8-bit integer), odnosno celobroja vrednost u interval [0, 255].
```
img.dtype
```
### Osnovne operacije pomoću NumPy
Predstavljanje slike kao NumPy array je vrlo korisna stvar, jer omogućava jednostavnu manipulaciju i izvršavanje osnovih operacija nad slikom.
#### Isecanje (crop)
```
img_crop = img[100:200, 300:600] # prva koordinata je po visini (formalno red), druga po širini (formalo kolona)
plt.imshow(img_crop)
```
#### Okretanje (flip)
```
img_flip_h = img[:, ::-1] # prva koordinata ostaje ista, a kolone se uzimaju unazad
plt.imshow(img_flip_h)
img_flip_v = img[::-1, :] # druga koordinata ostaje ista, a redovi se uzimaju unazad
plt.imshow(img_flip_v)
img_flip_c = img[:, :, ::-1] # možemo i izmeniti redosled boja (RGB->BGR), samo je pitanje koliko to ima smisla
plt.imshow(img_flip_c)
```
#### Invertovanje
```
img_inv = 255 - img # ako su pikeli u intervalu [0,255] ovo je ok, a ako su u intervalu [0.,1.] onda bi bilo 1. - img
plt.imshow(img_inv)
```
### Konvertovanje iz RGB u "grayscale"
Konvertovanjem iz RGB modela u nijanse sivih (grayscale) se gubi informacija o boji piksela na slici, ali sama slika postaje mnogo lakša za dalju obradu.
Ovo se može uraditi na više načina:
1. **Srednja vrednost** RGB komponenti - najjednostavnija varijanta $$ G = \frac{R+G+B}{3} $$
2. **Metod osvetljenosti** - srednja vrednost najjače i najslabije boje $$ G = \frac{max(R,G,B) + min(R,G,B)}{2} $$
3. **Metod perceptivne osvetljenosti** - težinska srednja vrednost koja uzima u obzir ljudsku percepciju (npr. najviše smo osetljivi na zelenu boju, pa to treba uzeti u obzir)$$ G = 0.21*R + 0.72*G + 0.07*B $$
```
# implementacija metode perceptivne osvetljenosti
def my_rgb2gray(img_rgb):
img_gray = np.ndarray((img_rgb.shape[0], img_rgb.shape[1])) # zauzimanje memorije za sliku (nema trece dimenzije)
img_gray = 0.21*img_rgb[:, :, 0] + 0.77*img_rgb[:, :, 1] + 0.07*img_rgb[:, :, 2]
img_gray = img_gray.astype('uint8') # u prethodnom koraku smo mnozili sa float, pa sada moramo da vratimo u [0,255] opseg
return img_gray
img_gray = my_rgb2gray(img)
plt.imshow(img_gray, 'gray') # kada se prikazuje slika koja nije RGB, obavezno je staviti 'gray' kao drugi parametar
```
Ipak je najbolje se držati implementacije u **OpenCV** biblioteci :).
```
img_gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
img_gray.shape
plt.imshow(img_gray, 'gray')
img_gray
```
### Binarna slika
Slika čiji pikseli imaju samo dve moguće vrednosti: crno i belo. U zavisnosti da li interval realan (float32) ili celobrojan (uint8), ove vrednosti mogu biti {0,1} ili {0,255}.
U binarnoj slici često izdvajamo ono što nam je bitno (**foreground**), od ono što nam je nebitno (**background**). Formalnije, ovaj postupak izdvajanja bitnog od nebitnog na slici nazivamo **segmentacija**.
Najčešći način dobijanja binarne slike je korišćenje nekog praga (**threshold**), pa ako je vrednost piksela veća od zadatog praga taj piksel dobija vrednost 1, u suprotnom 0. Postoji više tipova threshold-ovanja:
1. Globalni threshold - isti prag se primenjuje na sve piksele
2. Lokalni threshold - različiti pragovi za različite delove slike
3. Adaptivni threshold - prag se ne određuje ručno (ne zadaje ga čovek), već kroz neki postupak. Može biti i globalni i lokalni.
#### Globalni threshold
Kako izdvojiti npr. samo lice?
```
img_tr = img_gray > 127 # svi piskeli koji su veci od 127 ce dobiti vrednost True, tj. 1, i obrnuto
plt.imshow(img_tr, 'gray')
```
OpenCV ima metodu <b>threshold</b> koja kao prvi parametar prima sliku koja se binarizuje, kao drugi parametar prima prag binarizacije, treći parametar je vrednost rezultujućeg piksela ako je veći od praga (255=belo), poslednji parametar je tip thresholda (u ovo slučaju je binarizacija).
```
ret, image_bin = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY) # ret je vrednost praga, image_bin je binarna slika
print(ret)
plt.imshow(image_bin, 'gray')
```
#### Otsu threshold
<a href="https://en.wikipedia.org/wiki/Otsu%27s_method">Otsu metoda</a> se koristi za automatsko pronalaženje praga za threshold na slici.
```
ret, image_bin = cv2.threshold(img_gray, 0, 255, cv2.THRESH_OTSU) # ret je izracunata vrednost praga, image_bin je binarna slika
print("Otsu's threshold: " + str(ret))
plt.imshow(image_bin, 'gray')
```
#### Adaptivni threshold
U nekim slučajevima primena globalnog praga za threshold ne daje dobre rezultate. Dobar primer su slike na kojima se menja osvetljenje, gde globalni threshold praktično uništi deo slike koji je previše osvetljen ili zatamnjen.
Adaptivni threshold je drugačiji pristup, gde se za svaki piksel na slici izračunava zaseban prag, na osnovu njemu okolnnih piksela. <a href="https://docs.opencv.org/master/d7/d4d/tutorial_py_thresholding.html#gsc.tab=0">Primer</a>
```
image_ada = cv2.imread('images/sonnet.png')
image_ada = cv2.cvtColor(image_ada, cv2.COLOR_BGR2GRAY)
plt.imshow(image_ada, 'gray')
ret, image_ada_bin = cv2.threshold(image_ada, 100, 255, cv2.THRESH_BINARY)
plt.imshow(image_ada_bin, 'gray')
```
Loši rezultati su dobijeni upotrebom globalnog thresholda.
Poboljšavamo rezultate korišćenjem adaptivnog thresholda. Pretposlednji parametar metode <b>adaptiveThreshold</b> je ključan, jer predstavlja veličinu bloka susednih piksela (npr. 15x15) na osnovnu kojih se računa lokalni prag.
```
# adaptivni threshold gde se prag racuna = srednja vrednost okolnih piksela
image_ada_bin = cv2.adaptiveThreshold(image_ada, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 15, 5)
plt.figure() # ako je potrebno da se prikaze vise slika u jednoj celiji
plt.imshow(image_ada_bin, 'gray')
# adaptivni threshold gde se prag racuna = tezinska suma okolnih piksela, gde su tezine iz gausove raspodele
image_ada_bin = cv2.adaptiveThreshold(image_ada, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 15, 5)
plt.figure()
plt.imshow(image_ada_bin, 'gray')
```
### Histogram
Možemo koristiti **histogram**, koji će nam dati informaciju o distribuciji osvetljenosti piksela.
Vrlo koristan kada je potrebno odrediti prag za globalni threshold.
Pseudo-kod histograma za grayscale sliku:
```code
inicijalizovati nula vektor od 256 elemenata
za svaki piksel na slici:
preuzeti inicijalni intezitet piksela
uvecati za 1 broj piksela tog inteziteta
plotovati histogram
```
```
def hist(image):
height, width = image.shape[0:2]
x = range(0, 256)
y = np.zeros(256)
for i in range(0, height):
for j in range(0, width):
pixel = image[i, j]
y[pixel] += 1
return (x, y)
x,y = hist(img_gray)
plt.plot(x, y, 'b')
plt.show()
```
Koristeći <b>matplotlib</b>:
```
plt.hist(img_gray.ravel(), 255, [0, 255])
plt.show()
```
Koristeći <b>OpenCV</b>:
```
hist_full = cv2.calcHist([img_gray], [0], None, [255], [0, 255])
plt.plot(hist_full)
plt.show()
```
Pretpostavimo da su vrednosti piksela lica između 100 i 200.
```
img_tr = (img_gray > 100) * (img_gray < 200)
plt.imshow(img_tr, 'gray')
```
### Konverovanje iz "grayscale" u RGB
Ovo je zapravo trivijalna operacija koja za svaki kanal boje (RGB) napravi kopiju od originalne grayscale slike. Ovo je zgodno kada nešto što je urađeno u grayscale modelu treba iskoristiti zajedno sa RGB slikom.
```
img_tr_rgb = cv2.cvtColor(img_tr.astype('uint8'), cv2.COLOR_GRAY2RGB)
plt.imshow(img*img_tr_rgb) # množenje originalne RGB slike i slike sa izdvojenim pikselima lica
```
### Morfološke operacije
Veliki skup operacija za obradu digitalne slike, gde su te operacije zasnovane na oblicima, odnosno **strukturnim elementima**. U morfološkim operacijama, vrednost svakog piksela rezultujuće slike se zasniva na poređenju odgovarajućeg piksela na originalnoj slici sa svojom okolinom. Veličina i oblik ove okoline predstavljaju strukturni element.
```
kernel = np.ones((3, 3)) # strukturni element 3x3 blok
print(kernel)
```
#### Erozija
Morfološka erozija postavlja vrednost piksela rez. slike na ```(i,j)``` koordinatama na **minimalnu** vrednost svih piksela u okolini ```(i,j)``` piksela na orig. slici.
U suštini erozija umanjuje regione belih piksela, a uvećava regione crnih piksela. Često se koristi za uklanjanje šuma (u vidu sitnih regiona belih piksela).

```
plt.imshow(cv2.erode(image_bin, kernel, iterations=1), 'gray')
```
#### Dilacija
Morfološka dilacija postavlja vrednost piksela rez. slike na ```(i,j)``` koordinatama na **maksimalnu** vrednost svih piksela u okolini ```(i,j)``` piksela na orig. slici.
U suštini dilacija uvećava regione belih piksela, a umanjuje regione crnih piksela. Zgodno za izražavanje regiona od interesa.

```
# drugaciji strukturni element
kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (5,5)) # MORPH_ELIPSE, MORPH_RECT...
print(kernel)
plt.imshow(cv2.dilate(image_bin, kernel, iterations=5), 'gray') # 5 iteracija
```
#### Otvaranje i zatvaranje
**```otvaranje = erozija + dilacija```**, uklanjanje šuma erozijom i vraćanje originalnog oblika dilacijom.
**```zatvaranje = dilacija + erozija```**, zatvaranje sitnih otvora među belim pikselima
```
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5, 5))
print(kernel)
img_ero = cv2.erode(image_bin, kernel, iterations=1)
img_open = cv2.dilate(img_ero, kernel, iterations=1)
plt.imshow(img_open, 'gray')
img_dil = cv2.dilate(image_bin, kernel, iterations=1)
img_close = cv2.erode(img_dil, kernel, iterations=1)
plt.imshow(img_close, 'gray')
```
Primer detekcije ivica na binarnoj slici korišćenjem dilatacije i erozije:
```
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))
image_edges = cv2.dilate(image_bin, kernel, iterations=1) - cv2.erode(image_bin, kernel, iterations=1)
plt.imshow(image_edges, 'gray')
```
### Zamućenje (blur)
Zamućenje slike se dobija tako što se za svaki piksel slike kao nova vrednost uzima srednja vrednost okolnih piksela, recimo u okolini 5 x 5. Kernel <b>k</b> predstavlja kernel za <i>uniformno zamućenje</i>. Ovo je jednostavnija verzija <a href="https://en.wikipedia.org/wiki/Gaussian_blur">Gausovskog zamućenja</a>.
<img src="https://render.githubusercontent.com/render/math?math=k%285x5%29%3D%0A%20%20%5Cbegin%7Bbmatrix%7D%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%5C%5C%0A%20%20%20%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%20%26amp%3B%201%2F25%0A%20%20%5Cend%7Bbmatrix%7D&mode=display">
```
from scipy import signal
k_size = 5
k = (1./k_size*k_size) * np.ones((k_size, k_size))
image_blur = signal.convolve2d(img_gray, k)
plt.imshow(image_blur, 'gray')
```
### Regioni i izdvajanje regiona
Najjednostavnije rečeno, region je skup međusobno povezanih belih piksela. Kada se kaže povezanih, misli se na to da se nalaze u neposrednoj okolini. Razlikuju se dve vrste povezanosti: tzv. **4-connectivity** i **8-connectivity**:

Postupak kojim se izdvajanju/obeležavaju regioni se naziva **connected components labelling**. Ovo ćemo primeniti na problemu izdvajanja barkoda.
```
# ucitavanje slike i convert u RGB
img_barcode = cv2.cvtColor(cv2.imread('images/barcode.jpg'), cv2.COLOR_BGR2RGB)
plt.imshow(img_barcode)
```
Recimo da želimo da izdvojimo samo linije barkoda sa slike.
Za početak, uradimo neke standardne operacije, kao što je konvertovanje u grayscale i adaptivni threshold.
```
img_barcode_gs = cv2.cvtColor(img_barcode, cv2.COLOR_RGB2GRAY) # konvert u grayscale
plt.imshow(img_barcode_gs, 'gray')
#ret, image_barcode_bin = cv2.threshold(img_barcode_gs, 80, 255, cv2.THRESH_BINARY)
image_barcode_bin = cv2.adaptiveThreshold(img_barcode_gs, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 35, 10)
plt.imshow(image_barcode_bin, 'gray')
```
### Pronalaženje kontura/regiona
Konture, odnosno regioni na slici su grubo rečeno grupe crnih piksela. OpenCV metoda <b>findContours</b> pronalazi sve ove grupe crnih piksela, tj. regione. Druga povratna vrednost metode, odnosno <i>contours</i> je lista pronađeih kontura na slici.
Ove konture je zaim moguće iscrtati metodom <b>drawContours</b>, gde je prvi parametar slika na kojoj se iscrtavaju pronađene konture, drugi parametar je lista kontura koje je potrebno iscrtati, treći parametar određuje koju konturu po redosledu iscrtati (-1 znači iscrtavanje svih kontura), četvrti parametar je boja kojom će se obeležiti kontura, a poslednji parametar je debljina linije.
```
contours, hierarchy = cv2.findContours(image_barcode_bin, cv2.RETR_LIST, cv2.CHAIN_APPROX_SIMPLE)
img = img_barcode.copy()
cv2.drawContours(img, contours, -1, (255, 0, 0), 1)
plt.imshow(img)
```
#### Osobine regiona
Svi pronađeni regioni imaju neke svoje karakteristične osobine: površina, obim, konveksni omotač, konveksnost, obuhvatajući pravougaonik, ugao... Ove osobine mogu biti izuzetno korisne kada je neophodno izdvojiti samo određene regione sa slike koji ispoljavaju neku osobinu. Za sve osobine pogledati <a href="https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_contours/py_contour_features/py_contour_features.html">ovo</a> i <a href="https://opencv-python-tutroals.readthedocs.io/en/latest/py_tutorials/py_imgproc/py_contours/py_contour_properties/py_contour_properties.html">ovo</a>.
Izdvajamo samo bar-kod sa slike.
```
contours_barcode = [] #ovde ce biti samo konture koje pripadaju bar-kodu
for contour in contours: # za svaku konturu
center, size, angle = cv2.minAreaRect(contour) # pronadji pravougaonik minimalne povrsine koji ce obuhvatiti celu konturu
width, height = size
if width > 3 and width < 30 and height > 300 and height < 400: # uslov da kontura pripada bar-kodu
contours_barcode.append(contour) # ova kontura pripada bar-kodu
img = img_barcode.copy()
cv2.drawContours(img, contours_barcode, -1, (255, 0, 0), 1)
plt.imshow(img)
print('Ukupan broj regiona: %d' % len(contours_barcode))
```
Naravno, u ogromnom broj slučajeva odnos visine i širine neće biti dovoljan, već se moraju koristiti i ostale osobine.
## Zadaci
* Sa slike sa sijalicama (**images/bulbs.jpg**) prebrojati koliko ima sijalica.
* Sa slike barkoda (**images/barcode.jpg**) izdvojiti samo brojeve i slova, bez linija barkoda.
* Na slici sa snouborderima (**images/snowboarders.jpg**) prebrojati koliko ima snoubordera.
* Na slici sa fudbalerima (**images/football.jpg**) izdvojiti samo one fudbalere u belim dresovima.
* Na slici sa crvenim krvnim zrncima (**images/bloodcells.jpg**), prebrojati koliko ima crvenih krvnih zrnaca.
| true |
code
| 0.376695 | null | null | null | null |
|
## <center>Ensemble models from machine learning: an example of wave runup and coastal dune erosion</center>
### <center>Tomas Beuzen<sup>1</sup>, Evan B. Goldstein<sup>2</sup>, Kristen D. Splinter<sup>1</sup></center>
<center><sup>1</sup>Water Research Laboratory, School of Civil and Environmental Engineering, UNSW Sydney, NSW, Australia</center>
<center><sup>2</sup>Department of Geography, Environment, and Sustainability, University of North Carolina at Greensboro, Greensboro, NC, USA</center>
This notebook contains the code required to develop the Gaussian Process (GP) runup predictor developed in the manuscript "*Ensemble models from machine learning: an example of wave runup and coastal dune erosion*" by Beuzen et al.
**Citation:** Beuzen, T, Goldstein, E.B., Splinter, K.S. (In Review). Ensemble models from machine learning: an example of wave runup and coastal dune erosion, Natural Hazards and Earth Systems Science, SI Advances in computational modeling of geoprocesses and geohazards.
### Table of Contents:
1. [Imports](#bullet-0)
2. [Load and Visualize Data](#bullet-1)
3. [Develop GP Runup Predictor](#bullet-2)
4. [Test GP Runup Predictor](#bullet-3)
5. [Explore GP Prediction Uncertainty](#bullet-4)
## 1. Imports <a class="anchor" id="bullet-0"></a>
```
# Required imports
# Standard computing packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Gaussian Process tools
from sklearn.metrics import mean_squared_error
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
# Notebook functionality
%matplotlib inline
```
## 2. Load and Visualize Data <a class="anchor" id="bullet-1"></a>
In this section, we will load and visualise the wave, beach slope, and runup data we will use to develop the Gaussian process (GP) runup predictor.
```
# Read in .csv data file as a pandas dataframe
df = pd.read_csv('../data_repo_temporary/lidar_runup_data_for_GP_training.csv',index_col=0)
# Print the size and head of the dataframe
print('Data size:', df.shape)
df.head()
# This cell plots histograms of the data
# Initialize the figure and axes
fig, axes = plt.subplots(2,2,figsize=(6,6))
plt.tight_layout(w_pad=0.1, h_pad=3)
# Subplot (0,0): Hs
ax = axes[0,0]
ax.hist(df.Hs,28,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('H$_s$ (m)') # Format plot
ax.set_ylabel('Frequency')
ax.set_xticks((0,1.5,3,4.5))
ax.set_xlim((0,4.5))
ax.set_ylim((0,50))
ax.grid(lw=0.5,alpha=0.7)
ax.text(-1.1, 52, 'A)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (0,1): Tp
ax = axes[0,1]
ax.hist(df.Tp,20,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('T$_p$ (s)') # Format plot
ax.set_xticks((0,6,12,18))
ax.set_xlim((0,18))
ax.set_ylim((0,50))
ax.set_yticklabels([])
ax.grid(lw=0.5,alpha=0.7)
ax.text(-2.1, 52, 'B)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (1,0): beta
ax = axes[1,0]
ax.hist(df.beach_slope,20,color=(0.6,0.6,0.6),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel(r'$\beta$') # Format plot
ax.set_ylabel('Frequency')
ax.set_xticks((0,0.1,0.2,0.3))
ax.set_xlim((0,0.3))
ax.set_ylim((0,50))
ax.grid(lw=0.5,alpha=0.7)
ax.text(-0.073, 52, 'C)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True)
# Subplot (1,1): R2
ax = axes[1,1]
ax.hist(df.runup,24,color=(0.9,0.2,0.2),edgecolor='k',lw=0.5) # Plot histogram
ax.set_xlabel('R$_2$ (m)') # Format plot
ax.set_xticks((0,1,2,3))
ax.set_xlim((0,3))
ax.set_ylim((0,50))
ax.set_yticklabels([])
ax.grid(lw=0.5,alpha=0.7)
ax.text(-0.35, 52, 'D)', fontsize=12)
ax.tick_params(direction='in')
ax.set_axisbelow(True);
```
## 3. Develop GP Runup Predictor <a class="anchor" id="bullet-2"></a>
In this section we will develop the GP runup predictor.
We standardize the data for use in the GP by removing the mean and scaling to unit variance. This does not really affect GP performance but improves computational efficiency (see sklearn documentation for more information).
A kernel must be specified to develop the GP. Many kernels were trialled in initial GP development. The final kernel is a combination of the RBF and WhiteKernel. See **Section 2.1** and **Section 2.2** of the manuscript for further discussion.
```
# Define features and response data
X = df.drop(columns=df.columns[-1]) # Drop the last column to retain input features (Hs, Tp, slope)
y = df[[df.columns[-1]]] # The last column is the predictand (R2)
```
```
# Specify the kernel to use in the GP
kernel = RBF(0.1, (1e-2, 1e2)) + WhiteKernel(1,(1e-2,1e2))
# Train GP model on training dataset
gp = GaussianProcessRegressor(kernel=kernel,
n_restarts_optimizer=9,
normalize_y=True,
random_state=123)
gp.fit(X, y);
```
## 4. Test GP Runup Predictor <a class="anchor" id="bullet-3"></a>
This section now shows how the GP runup predictor can be used to test 50 test samples not previosuly used in training.
```
# Read in .csv test data file as a pandas dataframe
df_test = pd.read_csv('../data_repo_temporary/lidar_runup_data_for_GP_testing.csv',index_col=0)
# Print the size and head of the dataframe
print('Data size:', df_test.shape)
df_test.head()
# Predict the data
X_test = df_test.drop(columns=df.columns[-1]) # Drop the last column to retain input features (Hs, Tp, slope)
y_test = df_test[[df_test.columns[-1]]] # The last column is the predictand (R2)
y_test_predictions = gp.predict(X_test)
print('GP RMSE on test data =', format(np.sqrt(mean_squared_error(y_test,y_test_predictions)),'.2f'))
# This cell plots a figure comparing GP predictions to observations for the testing dataset
# Similar to Figure 4 in the manuscript
# Initialize the figure and axes
fig, axes = plt.subplots(figsize=(6,6))
plt.tight_layout(pad=2.2)
# Plot and format
axes.scatter(y_test,y_test_predictions,s=20,c='b',marker='.')
axes.plot([0,4],[0,4],'k--')
axes.set_ylabel('Predicted R$_2$ (m)')
axes.set_xlabel('Observed R$_2$ (m)')
axes.grid(lw=0.5,alpha=0.7)
axes.set_xlim(0,1.5)
axes.set_ylim(0,1.5)
# Print some statistics
print('GP RMSE on test data =', format(np.sqrt(mean_squared_error(y_test,y_test_predictions)),'.2f'))
print('GP bias on test data =', format(np.mean(y_test_predictions-y_test.values),'.2f'))
```
## 5. Explore GP Prediction Uncertainty <a class="anchor" id="bullet-3"></a>
This section explores how we can draw random samples from the GP to explain scatter in the runup predictions. We randomly draw 100 samples from the GP and calculate how much of the scatter in the runup predictions is captured by the ensemble envelope for different ensemble sizes. The process is repeated 100 times for robustness. See **Section 3.3** of the manuscript for further discussion.
We then plot the prediction with prediction uncertainty to help visualize.
```
# Draw 100 samples from the GP model using the testing dataset
GP_draws = gp.sample_y(X_test, n_samples=100, random_state=123).squeeze() # Draw 100 random samples from the GP
# Initialize result arrays
perc_ens = np.zeros((100,100)) # Initialize ensemble capture array
perc_err = np.zeros((100,)) # Initialise arbitray error array
# Loop to get results
for i in range(0,perc_ens.shape[0]):
# Caclulate capture % in envelope created by adding arbitrary, uniform error to mean GP prediction
lower = y_test_predictions*(1-i/100) # Lower bound
upper = y_test_predictions*(1+i/100) # Upper bound
perc_err[i] = sum((np.squeeze(y_test)>=np.squeeze(lower)) & (np.squeeze(y_test)<=np.squeeze(upper)))/y_test.shape[0] # Store percent capture
for j in range(0,perc_ens.shape[1]):
ind = np.random.randint(0,perc_ens.shape[0],i+1) # Determine i random integers
lower = np.min(GP_draws[:,ind],axis=1) # Lower bound of ensemble of i random members
upper = np.max(GP_draws[:,ind],axis=1) # Upper bound of ensemble of i random members
perc_ens[i,j] = sum((np.squeeze(y_test)>=lower) & (np.squeeze(y_test)<=upper))/y_test.shape[0] # Store percent capture
# This cell plots a figure showing how samples from the GP can help to capture uncertainty in predictions
# Similar to Figure 5 from the manuscript
# Initialize the figure and axes
fig, axes = plt.subplots(1,2,figsize=(9,4))
plt.tight_layout()
lim = 0.95 # Desired limit to test
# Plot ensemble results
ax = axes[0]
perc_ens_mean = np.mean(perc_ens,axis=1)
ax.plot(perc_ens_mean*100,'k-',lw=2)
ind = np.argmin(abs(perc_ens_mean-lim)) # Find where the capture rate > lim
ax.plot([ind,ind],[0,perc_ens_mean[ind]*100],'r--')
ax.plot([0,ind],[perc_ens_mean[ind]*100,perc_ens_mean[ind]*100],'r--')
ax.set_xlabel('# Draws from GP')
ax.set_ylabel('Observations captured \n within ensemble range (%)')
ax.grid(lw=0.5,alpha=0.7)
ax.minorticks_on()
ax.set_xlim(0,100);
ax.set_ylim(0,100);
ax.text(-11.5, 107, 'A)', fontweight='bold', fontsize=12)
print('# draws needed for ' + format(lim*100,'.0f') + '% capture = ' + str(ind))
print('Mean/Min/Max for ' + str(ind) + ' draws = '
+ format(np.mean(perc_ens[ind,:])*100,'.1f') + '%/'
+ format(np.min(perc_ens[ind,:])*100,'.1f') + '%/'
+ format(np.max(perc_ens[ind,:])*100,'.1f') + '%')
# Plot arbitrary error results
ax = axes[1]
ax.plot(perc_err*100,'k-',lw=2)
ind = np.argmin(abs(perc_err-lim)) # Find where the capture rate > lim
ax.plot([ind,ind],[0,perc_err[ind]*100],'r--')
ax.plot([0,ind],[perc_err[ind]*100,perc_err[ind]*100],'r--')
ax.set_xlabel('% Error added to mean GP estimate')
ax.grid(lw=0.5,alpha=0.7)
ax.minorticks_on()
ax.set_xlim(0,100);
ax.set_ylim(0,100);
ax.text(-11.5, 107, 'B)', fontweight='bold', fontsize=12)
print('% added error needed for ' + format(lim*100,'.0f') + '% capture = ' + str(ind) + '%')
# This cell plots predictions for all 50 test samples with prediction uncertainty from 12 ensemble members.
# In the cell above, 12 members was identified as optimal for capturing 95% of observations.
# Initialize the figure and axes
fig, axes = plt.subplots(1,1,figsize=(10,6))
# Make some data for plotting
x = np.arange(1, len(y_test)+1)
lower = np.min(GP_draws[:,:12],axis=1) # Lower bound of ensemble of 12 random members
upper = np.max(GP_draws[:,:12],axis=1) # Upper bound of ensemble of 12 random members
# Plot
axes.plot(x,y_test,'o',linestyle='-',color='C0',mfc='C0',mec='k',zorder=10,label='Observed')
axes.plot(x,y_test_predictions,'k',marker='o',color='C1',mec='k',label='GP Ensemble Mean')
axes.fill_between(x,
lower,
upper,
alpha=0.2,
facecolor='C1',
label='GP Ensemble Range')
# Formatting
axes.set_xlim(0,50)
axes.set_ylim(0,2.5)
axes.set_xlabel('Observation')
axes.set_ylabel('R2 (m)')
axes.grid()
axes.legend(framealpha=1)
```
| true |
code
| 0.675015 | null | null | null | null |
|
# Building and using data schemas for computer vision
This tutorial illustrates how to use raymon profiling to guard image quality in your production system. The image data is taken from [Kaggle](https://www.kaggle.com/ravirajsinh45/real-life-industrial-dataset-of-casting-product) and is courtesy of PILOT TECHNOCAST, Shapar, Rajkot. Commercial use of this data is not permitted, but we have received permission to use this data in our tutorials.
Note that some outputs may not work when viewing on Github since they are shown in iframes. We recommend to clone this repo and execute the notebooks locally.
```
%load_ext autoreload
%autoreload 2
from PIL import Image
from pathlib import Path
```
First, let's load some data. In this tutorial, we'll take the example of quality inspection in manufacturing. The puprose of our system may be to determine whether a manufactured part passes the required quality checks. These checks may measure the roudness of the part, the smoothness of the edges, the smoothness of the part overall, etc... let's assume you have automated those checks with an ML based system.
What we demonstrate here is how you can easily set up quality checks on the incoming data like whether the image is sharp enough and whether it is similar enough to the data the model was trained on. Doing checks like this may be important because people's actions, periodic maintenance and wear and tear may have an impact on what data exaclty is sent to your system. If your data changes, your system may keep running but will suffer from reduced performance, resulting in lower business value.
```
DATA_PATH = Path("../raymon/tests/sample_data/castinginspection/ok_front/")
LIM = 150
def load_data(dpath, lim):
files = dpath.glob("*.jpeg")
images = []
for n, fpath in enumerate(files):
if n == lim:
break
img = Image.open(fpath)
images.append(img)
return images
loaded_data = load_data(dpath=DATA_PATH, lim=LIM)
loaded_data[0]
```
## Constructing and building a profile
For this tutorial, we'll construct a profile that checks the image sharpness and will calculate an outlier score on the image. This way, we hope to get alerting when something seems off with the input data.
Just like in the case of structured data, we need to start by specifying a profile and its components.
```
from raymon import ModelProfile, InputComponent
from raymon.profiling.extractors.vision import Sharpness, DN2AnomalyScorer
profile = ModelProfile(
name="casting-inspection",
version="0.0.1",
components=[
InputComponent(name="sharpness", extractor=Sharpness()),
InputComponent(name="outlierscore", extractor=DN2AnomalyScorer(k=16))
],
)
profile.build(input=loaded_data)
## Inspect the schema
profile.view(poi=loaded_data[-1], mode="external")
```
## Use the profile to check new data
We can save the schema to JSON, load it again (in your production system), and use it to validate incoming data.
```
profile.save(".")
profile = ModelProfile.load("[email protected]")
tags = profile.validate_input(loaded_data[-1])
tags
```
As you can see, all the extracted feature values are returned. This is useful for when you want to track feature distributions on your monitoring backend (which is what happens on the Raymon.ai platform). Also note that these features are not necessarily the ones going into your ML model.
## Corrupting inputs
Let's see what happens when we blur an image.
```
from PIL import ImageFilter
img_blur = loaded_data[-1].copy().filter(ImageFilter.GaussianBlur(radius=5))
img_blur
profile.validate_input(img_blur)
```
As can be seen, every feature extractor now gives rise to 2 tags: one being the feature and one being a schema error, indicating that the data has failed both sanity checks. Awesome.
We can visualize this datum while inspecting the profile.
```
profile.view(poi=img_blur, mode="external")
```
As we can see, the calculated feature values are way outside the range that were seen during training. Having alerting set up for this is crucial to deliver reliable systems.
| true |
code
| 0.396798 | null | null | null | null |
|
# Maximum Likelihood Estimation (Generic models)
This tutorial explains how to quickly implement new maximum likelihood models in `statsmodels`. We give two examples:
1. Probit model for binary dependent variables
2. Negative binomial model for count data
The `GenericLikelihoodModel` class eases the process by providing tools such as automatic numeric differentiation and a unified interface to ``scipy`` optimization functions. Using ``statsmodels``, users can fit new MLE models simply by "plugging-in" a log-likelihood function.
## Example 1: Probit model
```
import numpy as np
from scipy import stats
import statsmodels.api as sm
from statsmodels.base.model import GenericLikelihoodModel
```
The ``Spector`` dataset is distributed with ``statsmodels``. You can access a vector of values for the dependent variable (``endog``) and a matrix of regressors (``exog``) like this:
```
data = sm.datasets.spector.load_pandas()
exog = data.exog
endog = data.endog
print(sm.datasets.spector.NOTE)
print(data.exog.head())
```
Them, we add a constant to the matrix of regressors:
```
exog = sm.add_constant(exog, prepend=True)
```
To create your own Likelihood Model, you simply need to overwrite the loglike method.
```
class MyProbit(GenericLikelihoodModel):
def loglike(self, params):
exog = self.exog
endog = self.endog
q = 2 * endog - 1
return stats.norm.logcdf(q*np.dot(exog, params)).sum()
```
Estimate the model and print a summary:
```
sm_probit_manual = MyProbit(endog, exog).fit()
print(sm_probit_manual.summary())
```
Compare your Probit implementation to ``statsmodels``' "canned" implementation:
```
sm_probit_canned = sm.Probit(endog, exog).fit()
print(sm_probit_canned.params)
print(sm_probit_manual.params)
print(sm_probit_canned.cov_params())
print(sm_probit_manual.cov_params())
```
Notice that the ``GenericMaximumLikelihood`` class provides automatic differentiation, so we did not have to provide Hessian or Score functions in order to calculate the covariance estimates.
## Example 2: Negative Binomial Regression for Count Data
Consider a negative binomial regression model for count data with
log-likelihood (type NB-2) function expressed as:
$$
\mathcal{L}(\beta_j; y, \alpha) = \sum_{i=1}^n y_i ln
\left ( \frac{\alpha exp(X_i'\beta)}{1+\alpha exp(X_i'\beta)} \right ) -
\frac{1}{\alpha} ln(1+\alpha exp(X_i'\beta)) + ln \Gamma (y_i + 1/\alpha) - ln \Gamma (y_i+1) - ln \Gamma (1/\alpha)
$$
with a matrix of regressors $X$, a vector of coefficients $\beta$,
and the negative binomial heterogeneity parameter $\alpha$.
Using the ``nbinom`` distribution from ``scipy``, we can write this likelihood
simply as:
```
import numpy as np
from scipy.stats import nbinom
def _ll_nb2(y, X, beta, alph):
mu = np.exp(np.dot(X, beta))
size = 1/alph
prob = size/(size+mu)
ll = nbinom.logpmf(y, size, prob)
return ll
```
### New Model Class
We create a new model class which inherits from ``GenericLikelihoodModel``:
```
from statsmodels.base.model import GenericLikelihoodModel
class NBin(GenericLikelihoodModel):
def __init__(self, endog, exog, **kwds):
super(NBin, self).__init__(endog, exog, **kwds)
def nloglikeobs(self, params):
alph = params[-1]
beta = params[:-1]
ll = _ll_nb2(self.endog, self.exog, beta, alph)
return -ll
def fit(self, start_params=None, maxiter=10000, maxfun=5000, **kwds):
# we have one additional parameter and we need to add it for summary
self.exog_names.append('alpha')
if start_params == None:
# Reasonable starting values
start_params = np.append(np.zeros(self.exog.shape[1]), .5)
# intercept
start_params[-2] = np.log(self.endog.mean())
return super(NBin, self).fit(start_params=start_params,
maxiter=maxiter, maxfun=maxfun,
**kwds)
```
Two important things to notice:
+ ``nloglikeobs``: This function should return one evaluation of the negative log-likelihood function per observation in your dataset (i.e. rows of the endog/X matrix).
+ ``start_params``: A one-dimensional array of starting values needs to be provided. The size of this array determines the number of parameters that will be used in optimization.
That's it! You're done!
### Usage Example
The [Medpar](https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/doc/COUNT/medpar.html)
dataset is hosted in CSV format at the [Rdatasets repository](https://raw.githubusercontent.com/vincentarelbundock/Rdatasets). We use the ``read_csv``
function from the [Pandas library](https://pandas.pydata.org) to load the data
in memory. We then print the first few columns:
```
import statsmodels.api as sm
medpar = sm.datasets.get_rdataset("medpar", "COUNT", cache=True).data
medpar.head()
```
The model we are interested in has a vector of non-negative integers as
dependent variable (``los``), and 5 regressors: ``Intercept``, ``type2``,
``type3``, ``hmo``, ``white``.
For estimation, we need to create two variables to hold our regressors and the outcome variable. These can be ndarrays or pandas objects.
```
y = medpar.los
X = medpar[["type2", "type3", "hmo", "white"]].copy()
X["constant"] = 1
```
Then, we fit the model and extract some information:
```
mod = NBin(y, X)
res = mod.fit()
```
Extract parameter estimates, standard errors, p-values, AIC, etc.:
```
print('Parameters: ', res.params)
print('Standard errors: ', res.bse)
print('P-values: ', res.pvalues)
print('AIC: ', res.aic)
```
As usual, you can obtain a full list of available information by typing
``dir(res)``.
We can also look at the summary of the estimation results.
```
print(res.summary())
```
### Testing
We can check the results by using the statsmodels implementation of the Negative Binomial model, which uses the analytic score function and Hessian.
```
res_nbin = sm.NegativeBinomial(y, X).fit(disp=0)
print(res_nbin.summary())
print(res_nbin.params)
print(res_nbin.bse)
```
Or we could compare them to results obtained using the MASS implementation for R:
url = 'https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/csv/COUNT/medpar.csv'
medpar = read.csv(url)
f = los~factor(type)+hmo+white
library(MASS)
mod = glm.nb(f, medpar)
coef(summary(mod))
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.31027893 0.06744676 34.253370 3.885556e-257
factor(type)2 0.22124898 0.05045746 4.384861 1.160597e-05
factor(type)3 0.70615882 0.07599849 9.291748 1.517751e-20
hmo -0.06795522 0.05321375 -1.277024 2.015939e-01
white -0.12906544 0.06836272 -1.887951 5.903257e-02
### Numerical precision
The ``statsmodels`` generic MLE and ``R`` parameter estimates agree up to the fourth decimal. The standard errors, however, agree only up to the second decimal. This discrepancy is the result of imprecision in our Hessian numerical estimates. In the current context, the difference between ``MASS`` and ``statsmodels`` standard error estimates is substantively irrelevant, but it highlights the fact that users who need very precise estimates may not always want to rely on default settings when using numerical derivatives. In such cases, it is better to use analytical derivatives with the ``LikelihoodModel`` class.
| true |
code
| 0.686528 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/lvisdd/object_detection_tutorial/blob/master/object_detection_face_detector.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
# restart (or reset) your virtual machine
#!kill -9 -1
```
# [Tensorflow Object Detection API](https://github.com/tensorflow/models/tree/master/research/object_detection)
```
!git clone https://github.com/tensorflow/models.git
```
# COCO API installation
```
!git clone https://github.com/cocodataset/cocoapi.git
%cd cocoapi/PythonAPI
!make
!cp -r pycocotools /content/models/research/
```
# Protobuf Compilation
```
%cd /content/models/research/
!protoc object_detection/protos/*.proto --python_out=.
```
# Add Libraries to PYTHONPATH
```
%cd /content/models/research/
%env PYTHONPATH=/env/python:/content/models/research:/content/models/research/slim:/content/models/research/object_detection
%env
```
# Testing the Installation
```
!python object_detection/builders/model_builder_test.py
%cd /content/models/research/object_detection
```
## [Tensorflow Face Detector](https://github.com/yeephycho/tensorflow-face-detection)
```
%cd /content
!git clone https://github.com/yeephycho/tensorflow-face-detection.git
%cd tensorflow-face-detection
!wget https://storage.googleapis.com/download.tensorflow.org/example_images/grace_hopper.jpg
filename = 'grace_hopper.jpg'
#!python inference_usbCam_face.py grace_hopper.jpg
import sys
import time
import numpy as np
import tensorflow as tf
import cv2
from utils import label_map_util
from utils import visualization_utils_color as vis_util
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = './model/frozen_inference_graph_face.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = './protos/face_label_map.pbtxt'
NUM_CLASSES = 2
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
class TensoflowFaceDector(object):
def __init__(self, PATH_TO_CKPT):
"""Tensorflow detector
"""
self.detection_graph = tf.Graph()
with self.detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
with self.detection_graph.as_default():
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(graph=self.detection_graph, config=config)
self.windowNotSet = True
def run(self, image):
"""image: bgr image
return (boxes, scores, classes, num_detections)
"""
image_np = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
image_tensor = self.detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
boxes = self.detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
scores = self.detection_graph.get_tensor_by_name('detection_scores:0')
classes = self.detection_graph.get_tensor_by_name('detection_classes:0')
num_detections = self.detection_graph.get_tensor_by_name('num_detections:0')
# Actual detection.
start_time = time.time()
(boxes, scores, classes, num_detections) = self.sess.run(
[boxes, scores, classes, num_detections],
feed_dict={image_tensor: image_np_expanded})
elapsed_time = time.time() - start_time
print('inference time cost: {}'.format(elapsed_time))
return (boxes, scores, classes, num_detections)
# This is needed to display the images.
%matplotlib inline
tDetector = TensoflowFaceDector(PATH_TO_CKPT)
original = cv2.imread(filename)
image = cv2.cvtColor(original, cv2.COLOR_BGR2RGB)
(boxes, scores, classes, num_detections) = tDetector.run(image)
vis_util.visualize_boxes_and_labels_on_image_array(
image,
np.squeeze(boxes),
np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
category_index,
use_normalized_coordinates=True,
line_thickness=4)
from matplotlib import pyplot as plt
plt.imshow(image)
```
| true |
code
| 0.648466 | null | null | null | null |
|
# `Практикум по программированию на языке Python`
<br>
## `Занятие 2: Пользовательские и встроенные функции, итераторы и генераторы`
<br><br>
### `Мурат Апишев ([email protected])`
#### `Москва, 2021`
### `Функции range и enumerate`
```
r = range(2, 10, 3)
print(type(r))
for e in r:
print(e, end=' ')
for index, element in enumerate(list('abcdef')):
print(index, element, end=' ')
```
### `Функция zip`
```
z = zip([1, 2, 3], 'abc')
print(type(z))
for a, b in z:
print(a, b, end=' ')
for e in zip('abcdef', 'abc'):
print(e)
for a, b, c, d in zip('abc', [1,2,3], [True, False, None], 'xyz'):
print(a, b, c, d)
```
### `Определение собственных функций`
```
def function(arg_1, arg_2=None):
print(arg_1, arg_2)
function(10)
function(10, 20)
```
Функция - это тоже объект, её имя - просто символическая ссылка:
```
f = function
f(10)
print(function is f)
```
### `Определение собственных функций`
```
retval = f(10)
print(retval)
def factorial(n):
return n * factorial(n - 1) if n > 1 else 1 # recursion
print(factorial(1))
print(factorial(2))
print(factorial(4))
```
### `Передача аргументов в функцию`
Параметры в Python всегда передаются по ссылке
```
def function(scalar, lst):
scalar += 10
print(f'Scalar in function: {scalar}')
lst.append(None)
print(f'Scalar in function: {lst}')
s, l = 5, []
function(s, l)
print(s, l)
```
### `Передача аргументов в функцию`
```
def f(a, *args):
print(type(args))
print([v for v in [a] + list(args)])
f(10, 2, 6, 8)
def f(*args, a):
print([v for v in [a] + list(args)])
print()
f(2, 6, 8, a=10)
def f(a, *args, **kw):
print(type(kw))
print([v for v in [a] + list(args) + [(k, v) for k, v in kw.items()]])
f(2, *(6, 8), **{'arg1': 1, 'arg2': 2})
```
### `Области видимости переменных`
В Python есть 4 основных уровня видимости:
- Встроенная (buildins) - на этом уровне находятся все встроенные объекты (функции, классы исключений и т.п.)<br><br>
- Глобальная в рамках модуля (global) - всё, что определяется в коде модуля на верхнем уровне<br><br>
- Объемлюшей функции (enclosed) - всё, что определено в функции верхнего уровня<br><br>
- Локальной функции (local) - всё, что определено в функции нижнего уровня
<br><br>
Есть ещё области видимости переменных циклов, списковых включений и т.п.
### `Правило разрешения области видимости LEGB при чтении`
```
def outer_func(x):
def inner_func(x):
return len(x)
return inner_func(x)
print(outer_func([1, 2]))
```
Кто определил имя `len`?
- на уровне вложенной функции такого имени нет, смотрим выше
- на уровне объемлющей функции такого имени нет, смотрим выше
- на уровне модуля такого имени нет, смотрим выше
- на уровне builtins такое имя есть, используем его
### `На builtins можно посмотреть`
```
import builtins
counter = 0
lst = []
for name in dir(builtins):
if name[0].islower():
lst.append(name)
counter += 1
if counter == 5:
break
lst
```
Кстати, то же самое можно сделать более pythonic кодом:
```
list(filter(lambda x: x[0].islower(), dir(builtins)))[: 5]
```
### `Локальные и глобальные переменные`
```
x = 2
def func():
print('Inside: ', x) # read
func()
print('Outside: ', x)
x = 2
def func():
x += 1 # write
print('Inside: ', x)
func() # UnboundLocalError: local variable 'x' referenced before assignment
print('Outside: ', x)
x = 2
def func():
x = 3
x += 1
print('Inside: ', x)
func()
print('Outside: ', x)
```
### `Ключевое слово global`
```
x = 2
def func():
global x
x += 1 # write
print('Inside: ', x)
func()
print('Outside: ', x)
x = 2
def func(x):
x += 1
print('Inside: ', x)
return x
x = func(x)
print('Outside: ', x)
```
### `Ключевое слово nonlocal`
```
a = 0
def out_func():
b = 10
def mid_func():
c = 20
def in_func():
global a
a += 100
nonlocal c
c += 100
nonlocal b
b += 100
print(a, b, c)
in_func()
mid_func()
out_func()
```
__Главный вывод:__ не надо злоупотреблять побочными эффектами при работе с переменными верхних уровней
### `Пример вложенных функций: замыкания`
- В большинстве случаев вложенные функции не нужны, плоская иерархия будет и проще, и понятнее
- Одно из исключений - фабричные функции (замыкания)
```
def function_creator(n):
def function(x):
return x ** n
return function
f = function_creator(5)
f(2)
```
Объект-функция, на который ссылается `f`, хранит в себе значение `n`
### `Анонимные функции`
- `def` - не единственный способ объявления функции
- `lambda` создаёт анонимную (lambda) функцию
Такие функции часто используются там, где синтаксически нельзя записать определение через `def`
```
def func(x): return x ** 2
func(6)
lambda_func = lambda x: x ** 2 # should be an expression
lambda_func(6)
def func(x): print(x)
func(6)
lambda_func = lambda x: print(x ** 2) # as print is function in Python 3.*
lambda_func(6)
```
### `Встроенная функция sorted`
```
lst = [5, 2, 7, -9, -1]
def abs_comparator(x):
return abs(x)
print(sorted(lst, key=abs_comparator))
sorted(lst, key=lambda x: abs(x))
sorted(lst, key=lambda x: abs(x), reverse=True)
```
### `Встроенная функция filter`
```
lst = [5, 2, 7, -9, -1]
f = filter(lambda x: x < 0, lst) # True condition
type(f) # iterator
list(f)
```
### `Встроенная функция map`
```
lst = [5, 2, 7, -9, -1]
m = map(lambda x: abs(x), lst)
type(m) # iterator
list(m)
```
### `Ещё раз сравним два подхода`
Напишем функцию скалярного произведения в императивном и функциональном стилях:
```
def dot_product_imp(v, w):
result = 0
for i in range(len(v)):
result += v[i] * w[i]
return result
dot_product_func = lambda v, w: sum(map(lambda x: x[0] * x[1], zip(v, w)))
print(dot_product_imp([1, 2, 3], [4, 5, 6]))
print(dot_product_func([1, 2, 3], [4, 5, 6]))
```
### `Функция reduce`
`functools` - стандартный модуль с другими функциями высшего порядка.
Рассмотрим пока только функцию `reduce`:
```
from functools import reduce
lst = list(range(1, 10))
reduce(lambda x, y: x * y, lst)
```
### `Итерирование, функции iter и next`
```
r = range(3)
for e in r:
print(e)
it = iter(r) # r.__iter__() - gives us an iterator
print(next(it))
print(it.__next__())
print(next(it))
print(next(it))
```
### `Итераторы часто используются неявно`
Как выглядит для нас цикл `for`:
```
for i in 'seq':
print(i)
```
Как он работает на самом деле:
```
iterator = iter('seq')
while True:
try:
i = next(iterator)
print(i)
except StopIteration:
break
```
### `Генераторы`
- Генераторы, как и итераторы, предназначены для итерирования по коллекции, но устроены несколько иначе
- Они определяются с помощью функций с оператором `yield` или генераторов списков, а не вызовов `iter()` и `next()`
- В генераторе есть внутреннее изменяемое состояние в виде локальных переменных, которое он хранит автоматически
- Генератор - более простой способ создания собственного итератора, чем его прямое определение
- Все генераторы являются итераторами, но не наоборот<br><br>
- Примеры функций-генераторов:
- `zip`
- `enumerate`
- `reversed`
- `map`
- `filter`
### `Ключевое слово yield`
- `yield` - это слово, по смыслу похожее на `return`<br><br>
- Но используется в функциях, возвращающих генераторы<br><br>
- При вызове такой функции тело не выполняется, функция только возвращает генератор<br><br>
- В первых запуск функция будет выполняться от начала и до `yield`<br><br>
- После выхода состояние функции сохраняется<br><br>
- На следующий вызов будет проводиться итерация цикла и возвращаться следующее значение<br><br>
- И так далее, пока не кончится цикл каждого `yield` в теле функции<br><br>
- После этого генератор станет пустым
### `Пример генератора`
```
def my_range(n):
yield 'You really want to run this generator?'
i = -1
while i < n:
i += 1
yield i
gen = my_range(3)
while True:
try:
print(next(gen), end=' ')
except StopIteration: # we want to catch this type of exceptions
break
for e in my_range(3):
print(e, end=' ')
```
### `Особенность range`
`range` не является генератором, хотя и похож, поскольку не хранит всю последовательность
```
print('__next__' in dir(zip([], [])))
print('__next__' in dir(range(3)))
```
Полезные особенности:
- объекты `range` неизменяемые (могут быть ключами словаря)
- имеют полезные атрибуты (`len`, `index`, `__getitem__`)
- по ним можно итерироваться многократно
### `Модуль itetools`
- Модуль представляет собой набор инструментов для работы с итераторами и последовательностями<br><br>
- Содержит три основных типа итераторов:<br><br>
- бесконечные итераторы
- конечные итераторы
- комбинаторные итераторы<br><br>
- Позволяет эффективно решать небольшие задачи вида:<br><br>
- итерирование по бесконечному потоку
- слияние в один список вложенных списков
- генерация комбинаторного перебора сочетаний элементов последовательности
- аккумуляция и агрегация данных внутри последовательности
### `Модуль itetools: примеры`
```
from itertools import count
for i in count(start=0):
print(i, end=' ')
if i == 5:
break
from itertools import cycle
count = 0
for item in cycle('XYZ'):
if count > 4:
break
print(item, end=' ')
count += 1
```
### `Модуль itetools: примеры`
```
from itertools import accumulate
for i in accumulate(range(1, 5), lambda x, y: x * y):
print(i)
from itertools import chain
for i in chain([1, 2], [3], [4]):
print(i)
```
### `Модуль itetools: примеры`
```
from itertools import groupby
vehicles = [('Ford', 'Taurus'), ('Dodge', 'Durango'),
('Chevrolet', 'Cobalt'), ('Ford', 'F150'),
('Dodge', 'Charger'), ('Ford', 'GT')]
sorted_vehicles = sorted(vehicles)
for key, group in groupby(sorted_vehicles, lambda x: x[0]):
for maker, model in group:
print('{model} is made by {maker}'.format(model=model, maker=maker))
print ("**** END OF THE GROUP ***\n")
```
## `Спасибо за внимание!`
| true |
code
| 0.213705 | null | null | null | null |
|
<h1>CREAZIONE MODELLO SARIMA REGIONE SARDEGNA
```
import pandas as pd
df = pd.read_csv('../../csv/regioni/sardegna.csv')
df.head()
df['DATA'] = pd.to_datetime(df['DATA'])
df.info()
df=df.set_index('DATA')
df.head()
```
<h3>Creazione serie storica dei decessi totali della regione Sardegna
```
ts = df.TOTALE
ts.head()
from datetime import datetime
from datetime import timedelta
start_date = datetime(2015,1,1)
end_date = datetime(2020,9,30)
lim_ts = ts[start_date:end_date]
#visulizzo il grafico
import matplotlib.pyplot as plt
plt.figure(figsize=(12,6))
plt.title('Decessi mensili regione Sardegna dal 2015 a settembre 2020', size=20)
plt.plot(lim_ts)
for year in range(start_date.year,end_date.year+1):
plt.axvline(pd.to_datetime(str(year)+'-01-01'), color='k', linestyle='--', alpha=0.5)
```
<h3>Decomposizione
```
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
ts_trend = decomposition.trend #andamento della curva
ts_seasonal = decomposition.seasonal #stagionalità
ts_residual = decomposition.resid #parti rimanenti
plt.subplot(411)
plt.plot(ts,label='original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(ts_trend,label='trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(ts_seasonal,label='seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(ts_residual,label='residual')
plt.legend(loc='best')
plt.tight_layout()
```
<h3>Test di stazionarietà
```
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
critical_value = dftest[4]['5%']
test_statistic = dftest[0]
alpha = 1e-3
pvalue = dftest[1]
if pvalue < alpha and test_statistic < critical_value: # null hypothesis: x is non stationary
print("X is stationary")
return True
else:
print("X is not stationary")
return False
test_stationarity(ts)
```
<h3>Suddivisione in Train e Test
<b>Train</b>: da gennaio 2015 a ottobre 2019; <br />
<b>Test</b>: da ottobre 2019 a dicembre 2019.
```
from datetime import datetime
train_end = datetime(2019,10,31)
test_end = datetime (2019,12,31)
covid_end = datetime(2020,9,30)
from dateutil.relativedelta import *
tsb = ts[:test_end]
decomposition = seasonal_decompose(tsb, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
tsb_trend = decomposition.trend #andamento della curva
tsb_seasonal = decomposition.seasonal #stagionalità
tsb_residual = decomposition.resid #parti rimanenti
tsb_diff = pd.Series(tsb_trend)
d = 0
while test_stationarity(tsb_diff) is False:
tsb_diff = tsb_diff.diff().dropna()
d = d + 1
print(d)
#TEST: dal 01-01-2015 al 31-10-2019
train = tsb[:train_end]
#TRAIN: dal 01-11-2019 al 31-12-2019
test = tsb[train_end + relativedelta(months=+1): test_end]
```
<h3>Grafici di Autocorrelazione e Autocorrelazione Parziale
```
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(ts, lags =12)
plot_pacf(ts, lags =12)
plt.show()
```
<h2>Creazione del modello SARIMA sul Train
```
from statsmodels.tsa.statespace.sarimax import SARIMAX
model = SARIMAX(train, order=(6,1,8))
model_fit = model.fit()
print(model_fit.summary())
```
<h4>Verifica della stazionarietà dei residui del modello ottenuto
```
residuals = model_fit.resid
test_stationarity(residuals)
plt.figure(figsize=(12,6))
plt.title('Confronto valori previsti dal modello con valori reali del Train', size=20)
plt.plot (train.iloc[1:], color='red', label='train values')
plt.plot (model_fit.fittedvalues.iloc[1:], color = 'blue', label='model values')
plt.legend()
plt.show()
conf = model_fit.conf_int()
plt.figure(figsize=(12,6))
plt.title('Intervalli di confidenza del modello', size=20)
plt.plot(conf)
plt.xticks(rotation=45)
plt.show()
```
<h3>Predizione del modello sul Test
```
#inizio e fine predizione
pred_start = test.index[0]
pred_end = test.index[-1]
#pred_start= len(train)
#pred_end = len(tsb)
#predizione del modello sul test
predictions_test= model_fit.predict(start=pred_start, end=pred_end)
plt.plot(test, color='red', label='actual')
plt.plot(predictions_test, label='prediction' )
plt.xticks(rotation=45)
plt.legend()
plt.show()
print(predictions_test)
# Accuracy metrics
import numpy as np
def forecast_accuracy(forecast, actual):
mape = np.mean(np.abs(forecast - actual)/np.abs(actual)) # MAPE: errore percentuale medio assoluto
me = np.mean(forecast - actual) # ME: errore medio
mae = np.mean(np.abs(forecast - actual)) # MAE: errore assoluto medio
mpe = np.mean((forecast - actual)/actual) # MPE: errore percentuale medio
rmse = np.mean((forecast - actual)**2)**.5 # RMSE
corr = np.corrcoef(forecast, actual)[0,1] # corr: correlazione tra effettivo e previsione
mins = np.amin(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
maxs = np.amax(np.hstack([forecast[:,None],
actual[:,None]]), axis=1)
minmax = 1 - np.mean(mins/maxs) # minmax: errore min-max
return({'mape':mape, 'me':me, 'mae': mae,
'mpe': mpe, 'rmse':rmse,
'corr':corr, 'minmax':minmax})
forecast_accuracy(predictions_test, test)
import numpy as np
from statsmodels.tools.eval_measures import rmse
nrmse = rmse(predictions_test, test)/(np.max(test)-np.min(test))
print('NRMSE: %f'% nrmse)
```
<h2>Predizione del modello compreso l'anno 2020
```
#inizio e fine predizione
start_prediction = ts.index[0]
end_prediction = ts.index[-1]
predictions_tot = model_fit.predict(start=start_prediction, end=end_prediction)
plt.figure(figsize=(12,6))
plt.title('Previsione modello su dati osservati - dal 2015 al 30 settembre 2020', size=20)
plt.plot(ts, color='blue', label='actual')
plt.plot(predictions_tot.iloc[1:], color='red', label='predict')
plt.xticks(rotation=45)
plt.legend(prop={'size': 12})
plt.show()
diff_predictions_tot = (ts - predictions_tot)
plt.figure(figsize=(12,6))
plt.title('Differenza tra i valori osservati e i valori stimati del modello', size=20)
plt.plot(diff_predictions_tot)
plt.show()
diff_predictions_tot['24-02-2020':].sum()
predictions_tot.to_csv('../../csv/pred/predictions_SARIMA_sardegna.csv')
```
<h2>Intervalli di confidenza della previsione totale
```
forecast = model_fit.get_prediction(start=start_prediction, end=end_prediction)
in_c = forecast.conf_int()
print(forecast.predicted_mean)
print(in_c)
print(forecast.predicted_mean - in_c['lower TOTALE'])
plt.plot(in_c)
plt.show()
upper = in_c['upper TOTALE']
lower = in_c['lower TOTALE']
lower.to_csv('../../csv/lower/predictions_SARIMA_sardegna_lower.csv')
upper.to_csv('../../csv/upper/predictions_SARIMA_sardegna_upper.csv')
```
| true |
code
| 0.582491 | null | null | null | null |
|
# Logistic Regression on 'HEART DISEASE' Dataset
Elif Cansu YILDIZ
```
from pyspark.sql import SparkSession
from pyspark.sql.types import *
from pyspark.sql.functions import col, countDistinct
from pyspark.ml.feature import OneHotEncoderEstimator, StringIndexer, VectorAssembler, MinMaxScaler, IndexToString
from pyspark.ml import Pipeline
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.evaluation import BinaryClassificationEvaluator, MulticlassClassificationEvaluator
spark = SparkSession\
.builder\
.appName("MachineLearningExample")\
.getOrCreate()
```
The dataset used is 'Heart Disease' dataset from Kaggle. You can get from this [link](https://www.kaggle.com/ronitf/heart-disease-uci).
```
df = spark.read.csv('datasets/heart.csv', header = True, inferSchema = True) #Kaggle Dataset
df.printSchema()
df.show(5)
```
__HOW MANY DISTINCT VALUE DO COLUMNS HAVE?__
```
df.agg(*(countDistinct(col(c)).alias(c) for c in df.columns)).show()
```
__SET the Label Column and Input Columns__
```
labelColumn = "thal"
input_columns = [t[0] for t in df.dtypes if t[0]!=labelColumn]
# Split the data into training and test sets (30% held out for testing)
(trainingData, testData) = df.randomSplit([0.7, 0.3])
print("total data count: ", df.count())
print("train data count: ", trainingData.count())
print("test data count: ", testData.count())
```
__TRAINING__
```
assembler = VectorAssembler(inputCols = input_columns, outputCol='features')
lr = LogisticRegression(featuresCol='features', labelCol=labelColumn,
maxIter=10, regParam=0.3, elasticNetParam=0.8)
stages = [assembler, lr]
partialPipeline = Pipeline().setStages(stages)
model = partialPipeline.fit(trainingData)
```
__MAKE PREDICTIONS__
```
predictions = model.transform(testData)
predictionss = predictions.select("probability", "rawPrediction", "prediction",
col(labelColumn).alias("label"))
predictionss[["probability", "prediction", "label"]].show(5, truncate=False)
```
__EVALUATION for Binary Classification__
```
evaluator = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction", metricName="areaUnderROC")
areaUnderROC = evaluator.evaluate(predictionss)
print("Area under ROC = %g" % areaUnderROC)
evaluator = BinaryClassificationEvaluator(labelCol="label", rawPredictionCol="prediction", metricName="areaUnderPR")
areaUnderPR = evaluator.evaluate(predictionss)
print("areaUnderPR = %g" % areaUnderPR)
```
__EVALUATION for Multiclass Classification__
```
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="accuracy")
accuracy = evaluator.evaluate(predictionss)
print("accuracy = %g" % accuracy)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="f1")
f1 = evaluator.evaluate(predictionss)
print("f1 = %g" % f1)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="weightedPrecision")
weightedPrecision = evaluator.evaluate(predictionss)
print("weightedPrecision = %g" % weightedPrecision)
evaluator = MulticlassClassificationEvaluator(labelCol="label", predictionCol="prediction", metricName="weightedRecall")
weightedRecall = evaluator.evaluate(predictionss)
print("weightedRecall = %g" % weightedRecall)
```
| true |
code
| 0.662114 | null | null | null | null |
|
# Recommending Movies: Retrieval
Real-world recommender systems are often composed of two stages:
1. The retrieval stage is responsible for selecting an initial set of hundreds of candidates from all possible candidates. The main objective of this model is to efficiently weed out all candidates that the user is not interested in. Because the retrieval model may be dealing with millions of candidates, it has to be computationally efficient.
2. The ranking stage takes the outputs of the retrieval model and fine-tunes them to select the best possible handful of recommendations. Its task is to narrow down the set of items the user may be interested in to a shortlist of likely candidates.
In this tutorial, we're going to focus on the first stage, retrieval. If you are interested in the ranking stage, have a look at our [ranking](basic_ranking) tutorial.
Retrieval models are often composed of two sub-models:
1. A query model computing the query representation (normally a fixed-dimensionality embedding vector) using query features.
2. A candidate model computing the candidate representation (an equally-sized vector) using the candidate features
The outputs of the two models are then multiplied together to give a query-candidate affinity score, with higher scores expressing a better match between the candidate and the query.
In this tutorial, we're going to build and train such a two-tower model using the Movielens dataset.
We're going to:
1. Get our data and split it into a training and test set.
2. Implement a retrieval model.
3. Fit and evaluate it.
4. Export it for efficient serving by building an approximate nearest neighbours (ANN) index.
## The dataset
The Movielens dataset is a classic dataset from the [GroupLens](https://grouplens.org/datasets/movielens/) research group at the University of Minnesota. It contains a set of ratings given to movies by a set of users, and is a workhorse of recommender system research.
The data can be treated in two ways:
1. It can be interpreted as expressesing which movies the users watched (and rated), and which they did not. This is a form of implicit feedback, where users' watches tell us which things they prefer to see and which they'd rather not see.
2. It can also be seen as expressesing how much the users liked the movies they did watch. This is a form of explicit feedback: given that a user watched a movie, we can tell roughly how much they liked by looking at the rating they have given.
In this tutorial, we are focusing on a retrieval system: a model that predicts a set of movies from the catalogue that the user is likely to watch. Often, implicit data is more useful here, and so we are going to treat Movielens as an implicit system. This means that every movie a user watched is a positive example, and every movie they have not seen is an implicit negative example.
## Imports
Let's first get our imports out of the way.
```
import os
import pprint
import tempfile
from typing import Dict, Text
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
```
## Preparing the dataset
Let's first have a look at the data.
We use the MovieLens dataset from [Tensorflow Datasets](https://www.tensorflow.org/datasets). Loading `movie_lens/100k_ratings` yields a `tf.data.Dataset` object containing the ratings data and loading `movie_lens/100k_movies` yields a `tf.data.Dataset` object containing only the movies data.
Note that since the MovieLens dataset does not have predefined splits, all data are under `train` split.
```
# Ratings data.
ratings = tfds.load("movie_lens/100k-ratings", split="train")
# Features of all the available movies.
movies = tfds.load("movie_lens/100k-movies", split="train")
```
The ratings dataset returns a dictionary of movie id, user id, the assigned rating, timestamp, movie information, and user information:
```
for x in ratings.take(1).as_numpy_iterator():
pprint.pprint(x)
```
The movies dataset contains the movie id, movie title, and data on what genres it belongs to. Note that the genres are encoded with integer labels.
```
for x in movies.take(1).as_numpy_iterator():
pprint.pprint(x)
```
In this example, we're going to focus on the ratings data. Other tutorials explore how to use the movie information data as well to improve the model quality.
We keep only the `user_id`, and `movie_title` fields in the dataset.
```
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
})
movies = movies.map(lambda x: x["movie_title"])
```
To fit and evaluate the model, we need to split it into a training and evaluation set. In an industrial recommender system, this would most likely be done by time: the data up to time $T$ would be used to predict interactions after $T$.
In this simple example, however, let's use a random split, putting 80% of the ratings in the train set, and 20% in the test set.
```
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
train = shuffled.take(80_000)
test = shuffled.skip(80_000).take(20_000)
```
Let's also figure out unique user ids and movie titles present in the data.
This is important because we need to be able to map the raw values of our categorical features to embedding vectors in our models. To do that, we need a vocabulary that maps a raw feature value to an integer in a contiguous range: this allows us to look up the corresponding embeddings in our embedding tables.
```
movie_titles = movies.batch(1_000)
user_ids = ratings.batch(1_000_000).map(lambda x: x["user_id"])
unique_movie_titles = np.unique(np.concatenate(list(movie_titles)))
unique_user_ids = np.unique(np.concatenate(list(user_ids)))
unique_movie_titles[:10]
```
## Implementing a model
Choosing the architecure of our model a key part of modelling.
Because we are building a two-tower retrieval model, we can build each tower separately and then combine them in the final model.
### The query tower
Let's start with the query tower.
The first step is to decide on the dimensionality of the query and candidate representations:
```
embedding_dimension = 32
```
Higher values will correspond to models that may be more accurate, but will also be slower to fit and more prone to overfitting.
The second is to define the model itself. Here, we're going to use Keras preprocessing layers to first convert user ids to integers, and then convert those to user embeddings via an `Embedding` layer. Note that we use the list of unique user ids we computed earlier as a vocabulary:
# _Note: Requires TF 2.3.0_
```
user_model = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_user_ids, mask_token=None),
# We add an additional embedding to account for unknown tokens.
tf.keras.layers.Embedding(len(unique_user_ids) + 1, embedding_dimension)
])
```
A simple model like this corresponds exactly to a classic [matrix factorization](https://ieeexplore.ieee.org/abstract/document/4781121) approach. While defining a subclass of `tf.keras.Model` for this simple model might be overkill, we can easily extend it to an arbitrarily complex model using standard Keras components, as long as we return an `embedding_dimension`-wide output at the end.
### The candidate tower
We can do the same with the candidate tower.
```
movie_model = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_movie_titles, mask_token=None),
tf.keras.layers.Embedding(len(unique_movie_titles) + 1, embedding_dimension)
])
```
### Metrics
In our training data we have positive (user, movie) pairs. To figure out how good our model is, we need to compare the affinity score that the model calculates for this pair to the scores of all the other possible candidates: if the score for the positive pair is higher than for all other candidates, our model is highly accurate.
To do this, we can use the `tfrs.metrics.FactorizedTopK` metric. The metric has one required argument: the dataset of candidates that are used as implicit negatives for evaluation.
In our case, that's the `movies` dataset, converted into embeddings via our movie model:
```
metrics = tfrs.metrics.FactorizedTopK(
candidates=movies.batch(128).map(movie_model)
)
```
### Loss
The next component is the loss used to train our model. TFRS has several loss layers and tasks to make this easy.
In this instance, we'll make use of the `Retrieval` task object: a convenience wrapper that bundles together the loss function and metric computation:
```
task = tfrs.tasks.Retrieval(
metrics=metrics
)
```
The task itself is a Keras layer that takes the query and candidate embeddings as arguments, and returns the computed loss: we'll use that to implement the model's training loop.
### The full model
We can now put it all together into a model. TFRS exposes a base model class (`tfrs.models.Model`) which streamlines bulding models: all we need to do is to set up the components in the `__init__` method, and implement the `compute_loss` method, taking in the raw features and returning a loss value.
The base model will then take care of creating the appropriate training loop to fit our model.
```
class MovielensModel(tfrs.Model):
def __init__(self, user_model, movie_model):
super().__init__()
self.movie_model: tf.keras.Model = movie_model
self.user_model: tf.keras.Model = user_model
self.task: tf.keras.layers.Layer = task
def compute_loss(self, features: Dict[Text, tf.Tensor], training=False) -> tf.Tensor:
# We pick out the user features and pass them into the user model.
user_embeddings = self.user_model(features["user_id"])
# And pick out the movie features and pass them into the movie model,
# getting embeddings back.
positive_movie_embeddings = self.movie_model(features["movie_title"])
# The task computes the loss and the metrics.
return self.task(user_embeddings, positive_movie_embeddings)
```
The `tfrs.Model` base class is a simply convenience class: it allows us to compute both training and test losses using the same method.
Under the hood, it's still a plain Keras model. You could achieve the same functionality by inheriting from `tf.keras.Model` and overriding the `train_step` and `test_step` functions (see [the guide](https://keras.io/guides/customizing_what_happens_in_fit/) for details):
```
class NoBaseClassMovielensModel(tf.keras.Model):
def __init__(self, user_model, movie_model):
super().__init__()
self.movie_model: tf.keras.Model = movie_model
self.user_model: tf.keras.Model = user_model
self.task: tf.keras.layers.Layer = task
def train_step(self, features: Dict[Text, tf.Tensor]) -> tf.Tensor:
# Set up a gradient tape to record gradients.
with tf.GradientTape() as tape:
# Loss computation.
user_embeddings = self.user_model(features["user_id"])
positive_movie_embeddings = self.movie_model(features["movie_title"])
loss = self.task(user_embeddings, positive_movie_embeddings)
# Handle regularization losses as well.
regularization_loss = sum(self.losses)
total_loss = loss + regularization_loss
gradients = tape.gradient(total_loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
metrics = {metric.name: metric.result() for metric in self.metrics}
metrics["loss"] = loss
metrics["regularization_loss"] = regularization_loss
metrics["total_loss"] = total_loss
return metrics
def test_step(self, features: Dict[Text, tf.Tensor]) -> tf.Tensor:
# Loss computation.
user_embeddings = self.user_model(features["user_id"])
positive_movie_embeddings = self.movie_model(features["movie_title"])
loss = self.task(user_embeddings, positive_movie_embeddings)
# Handle regularization losses as well.
regularization_loss = sum(self.losses)
total_loss = loss + regularization_loss
metrics = {metric.name: metric.result() for metric in self.metrics}
metrics["loss"] = loss
metrics["regularization_loss"] = regularization_loss
metrics["total_loss"] = total_loss
return metrics
```
In these tutorials, however, we stick to using the `tfrs.Model` base class to keep our focus on modelling and abstract away some of the boilerplate.
## Fitting and evaluating
After defining the model, we can use standard Keras fitting and evaluation routines to fit and evaluate the model.
Let's first instantiate the model.
```
model = MovielensModel(user_model, movie_model)
model.compile(optimizer=tf.keras.optimizers.Adagrad(learning_rate=0.1))
```
Then shuffle, batch, and cache the training and evaluation data.
```
cached_train = train.shuffle(100_000).batch(8192).cache()
cached_test = test.batch(4096).cache()
```
Then train the model:
```
model.fit(cached_train, epochs=3)
```
As the model trains, the loss is falling and a set of top-k retrieval metrics is updated. These tell us whether the true positive is in the top-k retrieved items from the entire candidate set. For example, a top-5 categorical accuracy metric of 0.2 would tell us that, on average, the true positive is in the top 5 retrieved items 20% of the time.
Note that, in this example, we evaluate the metrics during training as well as evaluation. Because this can be quite slow with large candidate sets, it may be prudent to turn metric calculation off in training, and only run it in evaluation.
Finally, we can evaluate our model on the test set:
```
model.evaluate(cached_test, return_dict=True)
```
Test set performance is much worse than training performance. This is due to two factors:
1. Our model is likely to perform better on the data that it has seen, simply because it can memorize it. This overfitting phenomenon is especially strong when models have many parameters. It can be mediated by model regularization and use of user and movie features that help the model generalize better to unseen data.
2. The model is re-recommending some of users' already watched movies. These known-positive watches can crowd out test movies out of top K recommendations.
The second phenomenon can be tackled by excluding previously seen movies from test recommendations. This approach is relatively common in the recommender systems literature, but we don't follow it in these tutorials. If not recommending past watches is important, we should expect appropriately specified models to learn this behaviour automatically from past user history and contextual information. Additionally, it is often appropriate to recommend the same item multiple times (say, an evergreen TV series or a regularly purchased item).
## Making predictions
Now that we have a model, we would like to be able to make predictions. We can use the `tfrs.layers.ann.BruteForce` layer to do this.
```
# Create a model that takes in raw query features, and
index = tfrs.layers.ann.BruteForce(model.user_model)
# recommends movies out of the entire movies dataset.
index.index(movies.batch(100).map(model.movie_model), movies)
# Get recommendations.
_, titles = index(tf.constant(["42"]))
print(f"Recommendations for user 42: {titles[0, :3]}")
```
Of course, the `BruteForce` layer is going to be too slow to serve a model with many possible candidates. The following sections shows how to speed this up by using an approximate retrieval index.
## Model serving
After the model is trained, we need a way to deploy it.
In a two-tower retrieval model, serving has two components:
- a serving query model, taking in features of the query and transforming them into a query embedding, and
- a serving candidate model. This most often takes the form of an approximate nearest neighbours (ANN) index which allows fast approximate lookup of candidates in response to a query produced by the query model.
### Exporting a query model to serving
Exporting the query model is easy: we can either serialize the Keras model directly, or export it to a `SavedModel` format to make it possible to serve using [TensorFlow Serving](https://www.tensorflow.org/tfx/guide/serving).
To export to a `SavedModel` format, we can do the following:
```
model_dir = './models'
!mkdir $model_dir
# Export the query model.
path = '{}/query_model'.format(model_dir)
model.user_model.save(path)
# Load the query model
loaded = tf.keras.models.load_model(path, compile=False)
query_embedding = loaded(tf.constant(["10"]))
print(f"Query embedding: {query_embedding[0, :3]}")
```
### Building a candidate ANN index
Exporting candidate representations is more involved. Firstly, we want to pre-compute them to make sure serving is fast; this is especially important if the candidate model is computationally intensive (for example, if it has many or wide layers; or uses complex representations for text or images). Secondly, we would like to take the precomputed representations and use them to construct a fast approximate retrieval index.
We can use [Annoy](https://github.com/spotify/annoy) to build such an index.
Annoy isn't included in the base TFRS package. To install it, run:
### We can now create the index object.
```
from annoy import AnnoyIndex
index = AnnoyIndex(embedding_dimension, "dot")
```
Then take the candidate dataset and transform its raw features into embeddings using the movie model:
```
print(movies)
movie_embeddings = movies.enumerate().map(lambda idx, title: (idx, title, model.movie_model(title)))
print(movie_embeddings.as_numpy_iterator().next())
```
And then index the movie_id, movie embedding pairs into our Annoy index:
```
%%time
movie_id_to_title = dict((idx, title) for idx, title, _ in movie_embeddings.as_numpy_iterator())
# We unbatch the dataset because Annoy accepts only scalar (id, embedding) pairs.
for movie_id, _, movie_embedding in movie_embeddings.as_numpy_iterator():
index.add_item(movie_id, movie_embedding)
# Build a 10-tree ANN index.
index.build(10)
```
We can then retrieve nearest neighbours:
```
for row in test.batch(1).take(3):
query_embedding = model.user_model(row["user_id"])[0]
candidates = index.get_nns_by_vector(query_embedding, 3)
print(f"User ID: {row['user_id']}, Candidates: {[movie_id_to_title[x] for x in candidates]}.")
print(type(candidates))
```
## Next steps
This concludes the retrieval tutorial.
To expand on what is presented here, have a look at:
1. Learning multi-task models: jointly optimizing for ratings and clicks.
2. Using movie metadata: building a more complex movie model to alleviate cold-start.
| true |
code
| 0.727897 | null | null | null | null |
|
# Lab 11: MLP -- exercise
# Understanding the training loop
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from random import randint
import utils
```
### Download the data and print the sizes
```
train_data=torch.load('../data/fashion-mnist/train_data.pt')
print(train_data.size())
train_label=torch.load('../data/fashion-mnist/train_label.pt')
print(train_label.size())
test_data=torch.load('../data/fashion-mnist/test_data.pt')
print(test_data.size())
```
### Make a ONE layer net class. The network output are the scores! No softmax needed! You have only one line to write in the forward function
```
class one_layer_net(nn.Module):
def __init__(self, input_size, output_size):
super(one_layer_net , self).__init__()
self.linear_layer = nn.Linear(input_size, output_size, bias=False)# complete here
def forward(self, x):
scores = self.linear_layer(x) # complete here
return scores
```
### Build the net
```
net= one_layer_net(784,10)# complete here
print(net)
```
### Choose the criterion and the optimizer: use the CHEAT SHEET to see the correct syntax.
### Remember that the optimizer need to have access to the parameters of the network (net.parameters()).
### Set the batchize and learning rate to be:
### batchize = 50
### learning rate = 0.01
```
# make the criterion
criterion = nn.CrossEntropyLoss()# complete here
# make the SGD optimizer.
optimizer=torch.optim.SGD(net.parameters(), lr=0.01) #complete here )
# set up the batch size
bs=50
```
### Complete the training loop
```
for iter in range(1,5000):
# Set dL/dU, dL/dV, dL/dW to be filled with zeros
optimizer.zero_grad()
# create a minibatch
indices = torch.LongTensor(bs).random_(0,60000)
minibatch_data = train_data[indices]
minibatch_label = train_label[indices]
# reshape the minibatch
inputs = minibatch_data.view(bs, 784)
# tell Pytorch to start tracking all operations that will be done on "inputs"
inputs.requires_grad_()
# forward the minibatch through the net
scores = net(inputs)
# Compute the average of the losses of the data points in the minibatch
loss = criterion(scores, minibatch_label)
# backward pass to compute dL/dU, dL/dV and dL/dW
loss.backward()
# do one step of stochastic gradient descent: U=U-lr(dL/dU), V=V-lr(dL/dU), ...
optimizer.step()
```
### Choose image at random from the test set and see how good/bad are the predictions
```
# choose a picture at random
idx=randint(0, 10000-1)
im=test_data[idx]
# diplay the picture
utils.show(im)
# feed it to the net and display the confidence scores
scores = net( im.view(1,784))
probs= F.softmax(scores, dim=1)
utils.show_prob_fashion_mnist(probs)
```
| true |
code
| 0.874507 | null | null | null | null |
|
## Main points
* Solution should be reasonably simple because the contest is only 24 hours long
* Metric is based on the prediction of clicked pictures one week ahead, so clicks are the most important information
* More recent information is more important
* Only pictures that were shown to a user could be clicked, so pictures popularity is important
* Metric is MAPK@100
* Link https://contest.yandex.ru/contest/12899/problems (Russian)
## Plan
* Build a classic recommending system based on user click history
* Only use recent days of historical data
* Take into consideration projected picture popularity
## Magic constants
### ALS recommending system:
```
# Factors for ALS
factors_count=100
# Last days of click history used
trail_days=14
# number of best candidates generated by ALS
output_candidates_count=2000
# Last days of history with more weight
last_days=1
# Coefficient for additional weight
last_days_weight=4
```
## Popular pictures prediction model:
```
import lightgbm
lightgbm.__version__
popularity_model = lightgbm.LGBMRegressor(seed=0)
heuristic_alpha = 0.2
import datetime
import tqdm
import pandas as pd
from scipy.sparse import coo_matrix
import implicit
implicit.__version__
test_users = pd.read_csv('Blitz/test_users.csv')
data = pd.read_csv('Blitz/train_clicks.csv', parse_dates=['day'])
```
## Split last 7 days to calculate clicks similar to test set
```
train, target_week = (
data[data.day <= datetime.datetime(2019, 3, 17)].copy(),
data[data.day > datetime.datetime(2019, 3, 17)],
)
train.day.nunique(), target_week.day.nunique()
last_date = train.day.max()
train.loc[:, 'delta_days'] = 1 + (last_date - train.day).apply(lambda d: d.days)
last_date = data.day.max()
data.loc[:, 'delta_days'] = 1 + (last_date - data.day).apply(lambda d: d.days)
def picture_features(data):
"""Generating clicks count for every picture in last days"""
days = range(1, 3)
features = []
names = []
for delta_days in days:
features.append(
data[(data.delta_days == delta_days)].groupby(['picture_id'])['user_id'].count()
)
names.append('%s_%d' % ('click', delta_days))
features = pd.concat(features, axis=1).fillna(0)
features.columns = names
features = features.reindex(data.picture_id.unique())
return features.fillna(0)
X = picture_features(train)
X.mean(axis=0)
def clicks_count(data, index):
return data.groupby('picture_id')['user_id'].count().reindex(index).fillna(0)
y = clicks_count(target_week, X.index)
y.shape, y.mean()
```
## Train a model predicting popular pictures next week
```
popularity_model.fit(X, y)
X_test = picture_features(data)
X_test.mean(axis=0)
X_test['p'] = popularity_model.predict(X_test)
X_test.loc[X_test['p'] < 0, 'p'] = 0
X_test['p'].mean()
```
## Generate dict with predicted clicks for every picture
```
# This prediction would be used to correct recommender score
picture = dict(X_test['p'])
```
# Recommender part
## Generate prediction using ALS approach
```
import os
os.environ['OPENBLAS_NUM_THREADS'] = "1"
def als_baseline(
train, test_users,
factors_n, last_days, trail_days, output_candidates_count, last_days_weight
):
train = train[train.delta_days <= trail_days].drop_duplicates([
'user_id', 'picture_id'
])
users = train.user_id
items = train.picture_id
weights = 1 + last_days_weight * (train.delta_days <= last_days)
user_item = coo_matrix((weights, (users, items)))
model = implicit.als.AlternatingLeastSquares(factors=factors_n, iterations=factors_n)
model.fit(user_item.T.tocsr())
user_item_csr = user_item.tocsr()
rows = []
for user_id in tqdm.tqdm_notebook(test_users.user_id.values):
items = [(picture_id, score) for picture_id, score in model.recommend(user_id, user_item_csr, N=output_candidates_count)]
rows.append(items)
test_users['predictions_full'] = [
p
for p, user_id in zip(
rows,
test_users.user_id.values
)
]
test_users['predictions'] = [
[x[0] for x in p]
for p, user_id in zip(
rows,
test_users.user_id.values
)
]
return test_users
test_users = als_baseline(
data, test_users, factors_count, last_days, trail_days, output_candidates_count, last_days_weight)
```
## Calculate history clicks to exclude them from results. Such clicks are excluded from test set according to task
```
clicked = data.groupby('user_id').agg({'picture_id': set})
def substract_clicked(p, c):
filtered = [picture for picture in p if picture not in c][:100]
return filtered
```
## Heuristical approach to reweight ALS score according to picture predicted popularity
Recommender returns (picture, score) pairs sorted decreasing for every user.
For every user we replace picture $score_p$ with $score_p \cdot (1 + popularity_{p})^{0.2}$
$popularity_{p}$ - popularity predicted for this picture for next week
This slightly moves popular pictures to the top of list for every user
```
import math
rows = test_users['predictions_full']
def correct_with_popularity(items, picture, alpha):
return sorted([
(score * (1 + picture.get(picture_id, 0)) ** alpha, picture_id, score, picture.get(picture_id, 0))
for picture_id, score in items], reverse=True
)
corrected_rows = [
[x[1] for x in correct_with_popularity(items, picture, heuristic_alpha)]
for items in rows
]
```
## Submission formatting
```
test_users['predictions'] = [
' '.join(map(str,
substract_clicked(p, {} if user_id not in clicked.index else clicked.loc[user_id][0])
))
for p, user_id in zip(
corrected_rows,
test_users.user_id.values
)
]
test_users[['user_id', 'predictions']].to_csv('submit.csv', index=False)
```
| true |
code
| 0.304223 | null | null | null | null |
|
# Azure ML Training Pipeline for COVID-CXR
This notebook defines an Azure machine learning pipeline for a single training run and submits the pipeline as an experiment to be run on an Azure virtual machine.
```
# Import statements
import azureml.core
from azureml.core import Experiment
from azureml.core import Workspace, Datastore
from azureml.data.data_reference import DataReference
from azureml.pipeline.core import PipelineData
from azureml.pipeline.core import Pipeline
from azureml.pipeline.steps import PythonScriptStep, EstimatorStep
from azureml.train.dnn import TensorFlow
from azureml.train.estimator import Estimator
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
from azureml.core.environment import Environment
from azureml.core.runconfig import RunConfiguration
import shutil
```
### Register the workspace and configure its Python environment.
```
# Get reference to the workspace
ws = Workspace.from_config("./ws_config.json")
# Set workspace's environment
env = Environment.from_pip_requirements(name = "covid-cxr_env", file_path = "./../requirements.txt")
env.register(workspace=ws)
runconfig = RunConfiguration(conda_dependencies=env.python.conda_dependencies)
print(env.python.conda_dependencies.serialize_to_string())
# Move AML ignore file to root folder
aml_ignore_path = shutil.copy('./.amlignore', './../.amlignore')
```
### Create references to persistent and intermediate data
Create DataReference objects that point to our raw data on the blob. Configure a PipelineData object to point to preprocessed images stored on the blob.
```
# Get the blob datastore associated with this workspace
blob_store = Datastore(ws, name='covid_cxr_ds')
# Create data references to folders on the blob
raw_data_dr = DataReference(
datastore=blob_store,
data_reference_name="raw_data",
path_on_datastore="data/")
mila_data_dr = DataReference(
datastore=blob_store,
data_reference_name="mila_data",
path_on_datastore="data/covid-chestxray-dataset/")
fig1_data_dr = DataReference(
datastore=blob_store,
data_reference_name="fig1_data",
path_on_datastore="data/Figure1-COVID-chestxray-dataset/")
rsna_data_dr = DataReference(
datastore=blob_store,
data_reference_name="rsna_data",
path_on_datastore="data/rsna/")
training_logs_dr = DataReference(
datastore=blob_store,
data_reference_name="training_logs_data",
path_on_datastore="logs/training/")
models_dr = DataReference(
datastore=blob_store,
data_reference_name="models_data",
path_on_datastore="models/")
# Set up references to pipeline data (intermediate pipeline storage).
processed_pd = PipelineData(
"processed_data",
datastore=blob_store,
output_name="processed_data",
output_mode="mount")
```
### Compute Target
Specify and configure the compute target for this workspace. If a compute cluster by the name we specified does not exist, create a new compute cluster.
```
CT_NAME = "nd12s-clust-hp" # Name of our compute cluster
VM_SIZE = "STANDARD_ND12S" # Specify the Azure VM for execution of our pipeline
#CT_NAME = "d2-cluster" # Name of our compute cluster
#VM_SIZE = "STANDARD_D2" # Specify the Azure VM for execution of our pipeline
# Set up the compute target for this experiment
try:
compute_target = AmlCompute(ws, CT_NAME)
print("Found existing compute target.")
except ComputeTargetException:
print("Creating new compute target")
provisioning_config = AmlCompute.provisioning_configuration(vm_size=VM_SIZE, min_nodes=1, max_nodes=4)
compute_target = ComputeTarget.create(ws, CT_NAME, provisioning_config) # Create the compute cluster
# Wait for cluster to be provisioned
compute_target.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
print("Azure Machine Learning Compute attached")
print("Compute targets: ", ws.compute_targets)
compute_target = ws.compute_targets[CT_NAME]
```
### Define pipeline and submit experiment.
Define the steps of an Azure machine learning pipeline. Create an Azure Experiment that will run our pipeline. Submit the experiment to the execution environment.
```
# Define preprocessing step the ML pipeline
step1 = PythonScriptStep(name="preprocess_step",
script_name="azure/preprocess_step/preprocess_step.py",
arguments=["--miladatadir", mila_data_dr, "--fig1datadir", fig1_data_dr,
"--rsnadatadir", rsna_data_dr, "--preprocesseddir", processed_pd],
inputs=[mila_data_dr, fig1_data_dr, rsna_data_dr],
outputs=[processed_pd],
compute_target=compute_target,
source_directory="./../",
runconfig=runconfig,
allow_reuse=True)
# Define training step in the ML pipeline
est = TensorFlow(source_directory='./../',
script_params=None,
compute_target=compute_target,
entry_script='azure/train_step/train_step.py',
pip_packages=['tensorboard', 'pandas', 'dill', 'numpy', 'imblearn', 'matplotlib', 'scikit-image', 'matplotlib',
'pydicom', 'opencv-python', 'tqdm', 'scikit-learn'],
use_gpu=True,
framework_version='2.0')
step2 = EstimatorStep(name="estimator_train_step",
estimator=est,
estimator_entry_script_arguments=["--rawdatadir", raw_data_dr, "--preprocesseddir", processed_pd,
"--traininglogsdir", training_logs_dr, "--modelsdir", models_dr],
runconfig_pipeline_params=None,
inputs=[raw_data_dr, processed_pd, training_logs_dr, models_dr],
outputs=[],
compute_target=compute_target)
# Construct the ML pipeline from the steps
steps = [step1, step2]
single_train_pipeline = Pipeline(workspace=ws, steps=steps)
single_train_pipeline.validate()
# Define a new experiment and submit a new pipeline run to the compute target.
experiment = Experiment(workspace=ws, name='SingleTrainExperiment_v3')
experiment.submit(single_train_pipeline, regenerate_outputs=False)
print("Pipeline is submitted for execution")
# Move AML ignore file back to original folder
aml_ignore_path = shutil.move(aml_ignore_path, './.amlignore')
```
| true |
code
| 0.645371 | null | null | null | null |
|
# General Equilibrium
This notebook illustrates **how to solve GE equilibrium models**. The example is a simple one-asset model without nominal rigidities.
The notebook shows how to:
1. Solve for the **stationary equilibrium**.
2. Solve for (non-linear) **transition paths** using a relaxtion algorithm.
3. Solve for **transition paths** (linear vs. non-linear) and **impulse-responses** using the **sequence-space method** of **Auclert et. al. (2020)**.
```
LOAD = False # load stationary equilibrium
DO_VARY_SIGMA_E = True # effect of uncertainty on stationary equilibrium
DO_TP_RELAX = True # do transition path with relaxtion
```
# Setup
```
%load_ext autoreload
%autoreload 2
import time
import numpy as np
import numba as nb
from scipy import optimize
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
from consav.misc import elapsed
from GEModel import GEModelClass
from GEModel import solve_backwards, simulate_forwards, simulate_forwards_transpose
```
## Choose number of threads in numba
```
import numba as nb
nb.set_num_threads(8)
```
# Model
```
model = GEModelClass('baseline',load=LOAD)
print(model)
```
For easy access
```
par = model.par
sim = model.sim
sol = model.sol
```
**Productivity states:**
```
for e,pr_e in zip(par.e_grid,par.e_ergodic):
print(f'Pr[e = {e:7.4f}] = {pr_e:.4f}')
assert np.isclose(np.sum(par.e_grid*par.e_ergodic),1.0)
```
# Find Stationary Equilibrium
**Step 1:** Find demand and supply of capital for a grid of interest rates.
```
if not LOAD:
t0 = time.time()
par = model.par
# a. interest rate trial values
Nr = 20
r_vec = np.linspace(0.005,1.0/par.beta-1-0.002,Nr) # 1+r > beta not possible
# b. allocate
Ks = np.zeros(Nr)
Kd = np.zeros(Nr)
# c. loop
r_min = r_vec[0]
r_max = r_vec[Nr-1]
for i_r in range(Nr):
# i. firm side
k = model.firm_demand(r_vec[i_r],par.Z)
Kd[i_r] = k*1 # aggregate labor = 1.0
# ii. household side
success = model.solve_household_ss(r=r_vec[i_r])
if success:
success = model.simulate_household_ss()
if success:
# total demand
Ks[i_r] = np.sum(model.sim.D*model.sol.a)
# bounds on r
diff = Ks[i_r]-Kd[i_r]
if diff < 0: r_min = np.fmax(r_min,r_vec[i_r])
if diff > 0: r_max = np.fmin(r_max,r_vec[i_r])
else:
Ks[i_r] = np.nan
# d. save
model.save()
print(f'grid search done in {elapsed(t0)}')
```
**Step 2:** Plot supply and demand.
```
if not LOAD:
par = model.par
fig = plt.figure(figsize=(6,4))
ax = fig.add_subplot(1,1,1)
ax.plot(r_vec,Ks,label='supply of capital')
ax.plot(r_vec,Kd,label='demand for capital')
ax.axvline(r_min,lw=0.5,ls='--',color='black')
ax.axvline(r_max,lw=0.5,ls='--',color='black')
ax.legend(frameon=True)
ax.set_xlabel('interest rate, $r$')
ax.set_ylabel('capital, $K_t$')
fig.tight_layout()
fig.savefig('figs/stationary_equilibrium.pdf')
```
**Step 3:** Solve root-finding problem.
```
def obj(r,model):
model.solve_household_ss(r=r)
model.simulate_household_ss()
return np.sum(model.sim.D*model.sol.a)-model.firm_demand(r,model.par.Z)
if not LOAD:
t0 = time.time()
opt = optimize.root_scalar(obj,bracket=[r_min,r_max],method='bisect',args=(model,))
model.par.r_ss = opt.root
assert opt.converged
print(f'search done in {elapsed(t0)}')
```
**Step 4:** Check market clearing conditions.
```
model.steady_state()
```
## Timings
```
%timeit model.solve_household_ss(r=par.r_ss)
%timeit model.simulate_household_ss()
```
## Income uncertainty and the equilibrium interest rate
The equlibrium interest rate decreases when income uncertainty is increased.
```
if DO_VARY_SIGMA_E:
par = model.par
# a. seetings
sigma_e_vec = [0.20]
# b. find equilibrium rates
model_ = model.copy()
for sigma_e in sigma_e_vec:
# i. set new parameter
model_.par.sigma_e = sigma_e
model_.create_grids()
# ii. solve
print(f'sigma_e = {sigma_e:.4f}',end='')
opt = optimize.root_scalar(
obj,
bracket=[0.00,model.par.r_ss],
method='bisect',
args=(model_,)
)
print(f' -> r_ss = {opt.root:.4f}')
model_.par.r_ss = opt.root
model_.steady_state()
print('\n')
```
## Test matrix formulation
**Step 1:** Construct $\boldsymbol{Q}_{ss}$
```
# a. allocate Q
Q = np.zeros((par.Ne*par.Na,par.Ne*par.Na))
# b. fill
for i_e in range(par.Ne):
# get view of current block
q = Q[i_e*par.Na:(i_e+1)*par.Na,i_e*par.Na:(i_e+1)*par.Na]
for i_a in range(par.Na):
# i. optimal choice
a_opt = sol.a[i_e,i_a]
# ii. above -> all weight on last node
if a_opt >= par.a_grid[-1]:
q[i_a,-1] = 1.0
# iii. below -> all weight on first node
elif a_opt <= par.a_grid[0]:
q[i_a,0] = 1.0
# iv. standard -> distribute weights on neighboring nodes
else:
i_a_low = np.searchsorted(par.a_grid,a_opt,side='right')-1
assert a_opt >= par.a_grid[i_a_low], f'{a_opt} < {par.a_grid[i_a_low]}'
assert a_opt < par.a_grid[i_a_low+1], f'{a_opt} < {par.a_grid[i_a_low]}'
q[i_a,i_a_low] = (par.a_grid[i_a_low+1]-a_opt)/(par.a_grid[i_a_low+1]-par.a_grid[i_a_low])
q[i_a,i_a_low+1] = 1-q[i_a,i_a_low]
```
**Step 2:** Construct $\tilde{\Pi}^e=\Pi^e \otimes \boldsymbol{I}_{\#_{a}\times\#_{a}}$
```
Pit = np.kron(par.e_trans,np.identity(par.Na))
```
**Step 3:** Test $\overrightarrow{D}_{t+1}=\tilde{\Pi}^{e\prime}\boldsymbol{Q}_{ss}^{\prime}\overrightarrow{D}_{t}$
```
D = np.zeros(sim.D.shape)
D[:,0] = par.e_ergodic
# a. standard
D_plus = np.zeros(D.shape)
simulate_forwards(D,sol.i,sol.w,par.e_trans.T.copy(),D_plus)
# b. matrix product
D_plus_alt = (([email protected])@D.ravel()).reshape((par.Ne,par.Na))
# c. test equality
assert np.allclose(D_plus,D_plus_alt)
```
# Find transition path
**MIT-shock:** Transtion path for arbitrary exogenous path of $Z_t$ starting from the stationary equilibrium, i.e. $D_{-1} = D_{ss}$ and in particular $K_{-1} = K_{ss}$.
**Step 1:** Construct $\{Z_t\}_{t=0}^{T-1}$ where $Z_t = (1-\rho_Z)Z_{ss} + \rho_Z Z_t$ and $Z_0 = (1+\sigma_Z) Z_{ss}$
```
path_Z = model.get_path_Z()
```
**Step 2:** Apply relaxation algorithm.
```
if DO_TP_RELAX:
t0 = time.time()
# a. allocate
path_r = np.repeat(model.par.r_ss,par.path_T) # use steady state as initial guess
path_r_ = np.zeros(par.path_T)
path_w = np.zeros(par.path_T)
# b. setting
nu = 0.90 # relaxation parameter
max_iter = 5000 # maximum number of iterations
# c. iterate
it = 0
while True:
# i. find wage
for t in range(par.path_T):
path_w[t] = model.implied_w(path_r[t],path_Z[t])
# ii. solve and simulate
model.solve_household_path(path_r,path_w)
model.simulate_household_path(model.sim.D)
# iii. implied prices
for t in range(par.path_T):
path_r_[t] = model.implied_r(sim.path_Klag[t],path_Z[t])
# iv. difference
max_abs_diff = np.max(np.abs(path_r-path_r_))
if it%10 == 0: print(f'{it:4d}: {max_abs_diff:.8f}')
if max_abs_diff < 1e-8: break
# v. update
path_r = nu*path_r + (1-nu)*path_r_
# vi. increment
it += 1
if it > max_iter: raise Exception('too many iterations')
print(f'\n transtion path found in {elapsed(t0)}')
```
**Plot transition-paths:**
```
if DO_TP_RELAX:
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(2,2,1)
ax.plot(np.arange(par.path_T),path_Z,'-o',ms=2)
ax.set_title('technology, $Z_t$');
ax = fig.add_subplot(2,2,2)
ax.plot(np.arange(par.path_T),sim.path_K,'-o',ms=2)
ax.set_title('capital, $k_t$');
ax = fig.add_subplot(2,2,3)
ax.plot(np.arange(par.path_T),path_r,'-o',ms=2)
ax.set_title('interest rate, $r_t$');
ax = fig.add_subplot(2,2,4)
ax.plot(np.arange(par.path_T),path_w,'-o',ms=2)
ax.set_title('wage, $w_t$')
fig.tight_layout()
fig.savefig('figs/transition_path.pdf')
```
**Remember:**
```
if DO_TP_RELAX:
path_Z_relax = path_Z
path_K_relax = sim.path_K
path_r_relax = path_r
path_w_relax = path_w
```
# Find impulse-responses using sequence-space method
**Paper:** Auclert, A., Bardóczy, B., Rognlie, M., and Straub, L. (2020). *Using the Sequence-Space Jacobian to Solve and Estimate Heterogeneous-Agent Models*.
**Original code:** [shade-econ](https://github.com/shade-econ/sequence-jacobian/#sequence-space-jacobian)
**This code:** Illustrates the sequence-space method. The original paper shows how to do it computationally efficient and for a general class of models.
**Step 1:** Compute the Jacobian for the household block around the stationary equilibrium
```
def jac(model,price,dprice=1e-4,do_print=True):
t0_all = time.time()
if do_print: print(f'price is {price}')
par = model.par
sol = model.sol
sim = model.sim
# a. step 1: solve backwards
t0 = time.time()
path_r = np.repeat(par.r_ss,par.path_T)
path_w = np.repeat(par.w_ss,par.path_T)
if price == 'r': path_r[-1] += dprice
elif price == 'w': path_w[-1] += dprice
model.solve_household_path(path_r,path_w,do_print=False)
if do_print: print(f'solved backwards in {elapsed(t0)}')
# b. step 2: derivatives
t0 = time.time()
diff_Ds = np.zeros((par.path_T,*sim.D.shape))
diff_as = np.zeros(par.path_T)
diff_cs = np.zeros(par.path_T)
for s in range(par.path_T):
t_ =(par.path_T-1)-s
simulate_forwards(sim.D,sol.path_i[t_],sol.path_w[t_],par.e_trans.T,diff_Ds[s])
diff_Ds[s] = (diff_Ds[s]-sim.D)/dprice
diff_as[s] = (np.sum(sol.path_a[t_]*sim.D)-np.sum(sol.a*sim.D))/dprice
diff_cs[s] = (np.sum(sol.path_c[t_]*sim.D)-np.sum(sol.c*sim.D))/dprice
if do_print: print(f'derivatives calculated in {elapsed(t0)}')
# c. step 3: expectation factors
t0 = time.time()
# demeaning improves numerical stability
def demean(x):
return x - x.sum()/x.size
exp_as = np.zeros((par.path_T-1,*sol.a.shape))
exp_as[0] = demean(sol.a)
exp_cs = np.zeros((par.path_T-1,*sol.c.shape))
exp_cs[0] = demean(sol.c)
for t in range(1,par.path_T-1):
simulate_forwards_transpose(exp_as[t-1],sol.i,sol.w,par.e_trans,exp_as[t])
exp_as[t] = demean(exp_as[t])
simulate_forwards_transpose(exp_cs[t-1],sol.i,sol.w,par.e_trans,exp_cs[t])
exp_cs[t] = demean(exp_cs[t])
if do_print: print(f'expecation factors calculated in {elapsed(t0)}')
# d. step 4: F
t0 = time.time()
Fa = np.zeros((par.path_T,par.path_T))
Fa[0,:] = diff_as
Fc = np.zeros((par.path_T,par.path_T))
Fc[0,:] = diff_cs
Fa[1:, :] = exp_as.reshape((par.path_T-1, -1)) @ diff_Ds.reshape((par.path_T, -1)).T
Fc[1:, :] = exp_cs.reshape((par.path_T-1, -1)) @ diff_Ds.reshape((par.path_T, -1)).T
if do_print: print(f'f calculated in {elapsed(t0)}')
t0 = time.time()
# e. step 5: J
Ja = Fa.copy()
for t in range(1, Ja.shape[1]): Ja[1:, t] += Ja[:-1, t - 1]
Jc = Fc.copy()
for t in range(1, Jc.shape[1]): Jc[1:, t] += Jc[:-1, t - 1]
if do_print: print(f'J calculated in {elapsed(t0)}')
# f. save
setattr(model.sol,f'jac_curlyK_{price}',Ja)
setattr(model.sol,f'jac_C_{price}',Jc)
if do_print: print(f'full Jacobian calculated in {elapsed(t0_all)}\n')
jac(model,'r')
jac(model,'w')
```
**Inspect Jacobians:**
```
fig = plt.figure(figsize=(12,8))
T_fig = 200
# curlyK_r
ax = fig.add_subplot(2,2,1)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_curlyK_r[s,:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'$\mathcal{J}^{\mathcal{K},r}$')
ax.set_xlim([0,T_fig])
# curlyK_w
ax = fig.add_subplot(2,2,2)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_curlyK_w[s,:T_fig],'-o',ms=2)
ax.set_title(r'$\mathcal{J}^{\mathcal{K},w}$')
ax.set_xlim([0,T_fig])
# C_r
ax = fig.add_subplot(2,2,3)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_C_r[s,:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'$\mathcal{J}^{C,r}$')
ax.set_xlim([0,T_fig])
# curlyK_w
ax = fig.add_subplot(2,2,4)
for s in [0,25,50,75,100]:
ax.plot(np.arange(T_fig),sol.jac_C_w[s,:T_fig],'-o',ms=2)
ax.set_title(r'$\mathcal{J}^{C,w}$')
ax.set_xlim([0,T_fig])
fig.tight_layout()
fig.savefig('figs/jacobians.pdf')
```
**Step 2:** Compute the Jacobians for the firm block around the stationary equilibrium (analytical).
```
sol.jac_r_K[:] = 0
sol.jac_w_K[:] = 0
sol.jac_r_Z[:] = 0
sol.jac_w_Z[:] = 0
for s in range(par.path_T):
for t in range(par.path_T):
if t == s+1:
sol.jac_r_K[t,s] = par.alpha*(par.alpha-1)*par.Z*par.K_ss**(par.alpha-2)
sol.jac_w_K[t,s] = (1-par.alpha)*par.alpha*par.Z*par.K_ss**(par.alpha-1)
if t == s:
sol.jac_r_Z[t,s] = par.alpha*par.Z*par.K_ss**(par.alpha-1)
sol.jac_w_Z[t,s] = (1-par.alpha)*par.Z*par.K_ss**par.alpha
```
**Step 3:** Use the chain rule and solve for $G$.
```
H_K = sol.jac_curlyK_r @ sol.jac_r_K + sol.jac_curlyK_w @ sol.jac_w_K - np.eye(par.path_T)
H_Z = sol.jac_curlyK_r @ sol.jac_r_Z + sol.jac_curlyK_w @ sol.jac_w_Z
G_K_Z = -np.linalg.solve(H_K, H_Z) # H_K^(-1)H_Z
```
**Step 4:** Find effect on prices and other outcomes than $K$.
```
G_r_Z = sol.jac_r_Z + sol.jac_r_K@G_K_Z
G_w_Z = sol.jac_w_Z + sol.jac_w_K@G_K_Z
G_C_Z = sol.jac_C_r@G_r_Z + sol.jac_C_w@G_w_Z
```
**Step 5:** Plot impulse-responses.
**Example I:** News shock (i.e. in a single period) vs. persistent shock where $ dZ_t = \rho dZ_{t-1} $ and $dZ_0$ is the initial shock.
```
fig = plt.figure(figsize=(12,4))
T_fig = 50
# left: news shock
ax = fig.add_subplot(1,2,1)
for s in [5,10,15,20,25]:
dZ = (1+par.Z_sigma)*par.Z*(np.arange(par.path_T) == s)
dK = G_K_Z@dZ
ax.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2,label=f'$s={s}$')
ax.legend(frameon=True)
ax.set_title(r'1% TFP news shock in period $s$')
ax.set_ylabel('$K_t-K_{ss}$')
ax.set_xlim([0,T_fig])
# right: persistent shock
ax = fig.add_subplot(1,2,2)
dZ = model.get_path_Z()-par.Z
dK = G_K_Z@dZ
ax.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2)
ax.set_title(r'1% TFP shock with persistence $\rho=0.90$')
ax.set_ylabel('$K_t-K_{ss}$')
ax.set_xlim([0,T_fig])
fig.tight_layout()
fig.savefig('figs/news_vs_persistent_shock.pdf')
```
**Example II:** Further effects of persistent shock.
```
fig = plt.figure(figsize=(12,8))
T_fig = 50
ax_K = fig.add_subplot(2,2,1)
ax_r = fig.add_subplot(2,2,2)
ax_w = fig.add_subplot(2,2,3)
ax_C = fig.add_subplot(2,2,4)
ax_K.set_title('$K_t-K_{ss}$ after 1% TFP shock')
ax_K.set_xlim([0,T_fig])
ax_r.set_title('$r_t-r_{ss}$ after 1% TFP shock')
ax_r.set_xlim([0,T_fig])
ax_w.set_title('$w_t-w_{ss}$ after 1% TFP shock')
ax_w.set_xlim([0,T_fig])
ax_C.set_title('$C_t-C_{ss}$ after 1% TFP shock')
ax_C.set_xlim([0,T_fig])
dZ = model.get_path_Z()-par.Z
dK = G_K_Z@dZ
ax_K.plot(np.arange(T_fig),dK[:T_fig],'-o',ms=2)
dr = G_r_Z@dZ
ax_r.plot(np.arange(T_fig),dr[:T_fig],'-o',ms=2)
dw = G_w_Z@dZ
ax_w.plot(np.arange(T_fig),dw[:T_fig],'-o',ms=2)
dC = G_C_Z@dZ
ax_C.plot(np.arange(T_fig),dC[:T_fig],'-o',ms=2)
fig.tight_layout()
fig.savefig('figs/irfs.pdf')
```
## Non-linear transition path
Use the Jacobian to speed-up solving for the non-linear transition path using a quasi-Newton method.
**1. Solver**
```
def broyden_solver(f,x0,jac,tol=1e-8,max_iter=100,backtrack_fac=0.5,max_backtrack=30,do_print=False):
""" numerical solver using the broyden method """
# a. initial
x = x0.ravel()
y = f(x)
# b. iterate
for it in range(max_iter):
# i. current difference
abs_diff = np.max(np.abs(y))
if do_print: print(f' it = {it:3d} -> max. abs. error = {abs_diff:12.8f}')
if abs_diff < tol: return x
# ii. new x
dx = np.linalg.solve(jac,-y)
# iii. evalute with backtrack
for _ in range(max_backtrack):
try: # evaluate
ynew = f(x+dx)
except ValueError: # backtrack
dx *= backtrack_fac
else: # update jac and break from backtracking
dy = ynew-y
jac = jac + np.outer(((dy - jac @ dx) / np.linalg.norm(dx) ** 2), dx)
y = ynew
x += dx
break
else:
raise ValueError('too many backtracks, maybe bad initial guess?')
else:
raise ValueError(f'no convergence after {max_iter} iterations')
```
**2. Target function**
$$\boldsymbol{H}(\boldsymbol{K},\boldsymbol{Z},D_{ss}) = \mathcal{K}_{t}(\{r(Z_{s},K_{s-1}),w(Z_{s},K_{s-1})\}_{s\geq0},D_{ss})-K_{t}=0$$
```
def target(path_K,path_Z,model,D0,full_output=False):
par = model.par
sim = model.sim
path_r = np.zeros(path_K.size)
path_w = np.zeros(path_K.size)
# a. implied prices
K0lag = np.sum(par.a_grid[np.newaxis,:]*D0)
path_Klag = np.insert(path_K,0,K0lag)
for t in range(par.path_T):
path_r[t] = model.implied_r(path_Klag[t],path_Z[t])
path_w[t] = model.implied_w(path_r[t],path_Z[t])
# b. solve and simulate
model.solve_household_path(path_r,path_w)
model.simulate_household_path(D0)
# c. market clearing
if full_output:
return path_r,path_w
else:
return sim.path_K-path_K
```
**3. Solve**
```
path_Z = model.get_path_Z()
f = lambda x: target(x,path_Z,model,sim.D)
t0 = time.time()
path_K = broyden_solver(f,x0=np.repeat(par.K_ss,par.path_T),jac=H_K,do_print=True)
path_r,path_w = target(path_K,path_Z,model,sim.D,full_output=True)
print(f'\nIRF found in {elapsed(t0)}')
```
**4. Plot**
```
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(1,2,1)
ax.set_title('capital, $K_t$')
dK = G_K_Z@(path_Z-par.Z)
ax.plot(np.arange(T_fig),dK[:T_fig] + par.K_ss,'-o',ms=2,label=f'linear')
ax.plot(np.arange(T_fig),path_K[:T_fig],'-o',ms=2,label=f'non-linear')
if DO_TP_RELAX:
ax.plot(np.arange(T_fig),path_K_relax[:T_fig],'--o',ms=2,label=f'non-linear (relaxtion)')
ax.legend(frameon=True)
ax = fig.add_subplot(1,2,2)
ax.set_title('interest rate, $r_t$')
dr = G_r_Z@(path_Z-par.Z)
ax.plot(np.arange(T_fig),dr[:T_fig] + par.r_ss,'-o',ms=2,label=f'linear')
ax.plot(np.arange(T_fig),path_r[:T_fig],'-o',ms=2,label=f'non-linear')
if DO_TP_RELAX:
ax.plot(np.arange(T_fig),path_r_relax[:T_fig],'--o',ms=2,label=f'non-linear (relaxtion)')
fig.tight_layout()
fig.savefig('figs/non_linear.pdf')
```
## Covariances
Assume that $Z_t$ is stochastic and follows
$$ d\tilde{Z}_t = \rho d\tilde{Z}_{t-1} + \sigma\epsilon_t,\,\,\, \epsilon_t \sim \mathcal{N}(0,1) $$
The covariances between all outcomes can be calculated as follows.
```
# a. choose parameter
rho = 0.90
sigma = 0.10
# b. find change in outputs
dZ = rho**(np.arange(par.path_T))
dC = G_C_Z@dZ
dK = G_K_Z@dZ
# c. covariance of consumption
print('auto-covariance of consumption:\n')
for k in range(5):
if k == 0:
autocov_C = sigma**2*np.sum(dC*dC)
else:
autocov_C = sigma**2*np.sum(dC[:-k]*dC[k:])
print(f' k = {k}: {autocov_C:.4f}')
# d. covariance of consumption and capital
cov_C_K = sigma**2*np.sum(dC*dK)
print(f'\ncovariance of consumption and capital: {cov_C_K:.4f}')
```
# Extra: No idiosyncratic uncertainty
This section solve for the transition path in the case without idiosyncratic uncertainty.
**Analytical solution for steady state:**
```
r_ss_pf = (1/par.beta-1) # from euler-equation
w_ss_pf = model.implied_w(r_ss_pf,par.Z)
K_ss_pf = model.firm_demand(r_ss_pf,par.Z)
Y_ss_pf = model.firm_production(K_ss_pf,par.Z)
C_ss_pf = Y_ss_pf-par.delta*K_ss_pf
print(f'r: {r_ss_pf:.6f}')
print(f'w: {w_ss_pf:.6f}')
print(f'Y: {Y_ss_pf:.6f}')
print(f'C: {C_ss_pf:.6f}')
print(f'K/Y: {K_ss_pf/Y_ss_pf:.6f}')
```
**Function for finding consumption and capital paths given paths of interest rates and wages:**
It can be shown that
$$ C_{0}=\frac{(1+r_{0})a_{-1}+\sum_{t=0}^{\infty}\frac{1}{\mathcal{R}_{t}}w_{t}}{\sum_{t=0}^{\infty}\beta^{t/\rho}\mathcal{R}_{t}^{\frac{1-\rho}{\rho}}} $$
where
$$ \mathcal{R}_{t} =\begin{cases} 1 & \text{if }t=0\\ (1+r_{t})\mathcal{R}_{t-1} & \text{else} \end{cases} $$
Otherwise the **Euler-equation** holds
$$ C_t = (\beta (1+r_{t}))^{\frac{1}{\sigma}}C_{t-1} $$
```
def path_CK_func(K0,path_r,path_w,r_ss,w_ss,model):
par = model.par
# a. initialize
wealth = (1+path_r[0])*K0
inv_MPC = 0
# b. solve
RT = 1
max_iter = 5000
t = 0
while True and t < max_iter:
# i. prices padded with steady state
r = path_r[t] if t < par.path_T else r_ss
w = path_w[t] if t < par.path_T else w_ss
# ii. interest rate factor
if t == 0:
fac = 1
else:
fac *= (1+r)
# iii. accumulate
add_wealth = w/fac
add_inv_MPC = par.beta**(t/par.sigma)*fac**((1-par.sigma)/par.sigma)
if np.fmax(add_wealth,add_inv_MPC) < 1e-12:
break
else:
wealth += add_wealth
inv_MPC += add_inv_MPC
# iv. increment
t += 1
# b. simulate
path_C = np.empty(par.path_T)
path_K = np.empty(par.path_T)
for t in range(par.path_T):
if t == 0:
path_C[t] = wealth/inv_MPC
K_lag = K0
else:
path_C[t] = (par.beta*(1+path_r[t]))**(1/par.sigma)*path_C[t-1]
K_lag = path_K[t-1]
path_K[t] = (1+path_r[t])*K_lag + path_w[t] - path_C[t]
return path_K,path_C
```
**Test with steady state prices:**
```
path_r_pf = np.repeat(r_ss_pf,par.path_T)
path_w_pf = np.repeat(w_ss_pf,par.path_T)
path_K_pf,path_C_pf = path_CK_func(K_ss_pf,path_r_pf,path_w_pf,r_ss_pf,w_ss_pf,model)
print(f'C_ss: {C_ss_pf:.6f}')
print(f'C[0]: {path_C_pf[0]:.6f}')
print(f'C[-1]: {path_C_pf[-1]:.6f}')
assert np.isclose(C_ss_pf,path_C_pf[0])
```
**Shock paths** where interest rate deviate in one period:
```
dr = 1e-4
ts = np.array([0,20,40])
path_C_pf_shock = np.empty((ts.size,par.path_T))
path_K_pf_shock = np.empty((ts.size,par.path_T))
for i,t in enumerate(ts):
path_r_pf_shock = path_r_pf.copy()
path_r_pf_shock[t] += dr
K,C = path_CK_func(K_ss_pf,path_r_pf_shock,path_w_pf,r_ss_pf,w_ss_pf,model)
path_K_pf_shock[i,:] = K
path_C_pf_shock[i,:] = C
```
**Plot paths:**
```
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(1,2,1)
ax.plot(np.arange(par.path_T),path_C_pf,'-o',ms=2,label=f'$r_t = r^{{\\ast}}$')
for i,t in enumerate(ts):
ax.plot(np.arange(par.path_T),path_C_pf_shock[i],'-o',ms=2,label=f'shock to $r_{{{t}}}$')
ax.set_xlim([0,50])
ax.set_xlabel('periods')
ax.set_ylabel('consumtion, $C_t$');
ax = fig.add_subplot(1,2,2)
ax.plot(np.arange(par.path_T),path_K_pf,'-o',ms=2,label=f'$r_t = r^{{\\ast}}$')
for i,t in enumerate(ts):
ax.plot(np.arange(par.path_T),path_K_pf_shock[i],'-o',ms=2,label=f'shock to $r_{{{t}}}$')
ax.legend(frameon=True)
ax.set_xlim([0,50])
ax.set_xlabel('$t$')
ax.set_ylabel('capital, $K_t$');
fig.tight_layout()
```
**Find transition path with shooting algorithm:**
```
# a. allocate
dT = 200
path_C_pf = np.empty(par.path_T)
path_K_pf = np.empty(par.path_T)
path_r_pf = np.empty(par.path_T)
path_w_pf = np.empty(par.path_T)
# b. settings
C_min = C_ss_pf
C_max = C_ss_pf + K_ss_pf
K_min = 1.5 # guess on lower consumption if below this
K_max = 3 # guess on higher consumption if above this
tol_pf = 1e-6
max_iter_pf = 5000
path_K_pf[0] = K_ss_pf # capital is pre-determined
# c. iterate
t = 0
it = 0
while True:
# i. update prices
path_r_pf[t] = model.implied_r(path_K_pf[t],path_Z[t])
path_w_pf[t] = model.implied_w(path_r_pf[t],path_Z[t])
# ii. consumption
if t == 0:
C0 = (C_min+C_max)/2
path_C_pf[t] = C0
else:
path_C_pf[t] = (1+path_r_pf[t])*par.beta*path_C_pf[t-1]
# iii. check for steady state
if path_K_pf[t] < K_min:
t = 0
C_max = C0
continue
elif path_K_pf[t] > K_max:
t = 0
C_min = C0
continue
elif t > 10 and np.sqrt((path_C_pf[t]-C_ss_pf)**2+(path_K_pf[t]-K_ss_pf)**2) < tol_pf:
path_C_pf[t:] = path_C_pf[t]
path_K_pf[t:] = path_K_pf[t]
for k in range(par.path_T):
path_r_pf[k] = model.implied_r(path_K_pf[k],path_Z[k])
path_w_pf[k] = model.implied_w(path_r_pf[k],path_Z[k])
break
# iv. update capital
path_K_pf[t+1] = (1+path_r_pf[t])*path_K_pf[t] + path_w_pf[t] - path_C_pf[t]
# v. increment
t += 1
it += 1
if it > max_iter_pf: break
```
**Plot deviations from steady state:**
```
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(2,2,1)
ax.plot(np.arange(par.path_T),path_Z,'-o',ms=2)
ax.set_xlim([0,200])
ax.set_title('technology, $Z_t$')
ax = fig.add_subplot(2,2,2)
ax.plot(np.arange(par.path_T),path_K-model.par.kd_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_K_pf-K_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('capital, $k_t$')
ax.set_xlim([0,200])
ax = fig.add_subplot(2,2,3)
ax.plot(np.arange(par.path_T),path_r-model.par.r_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_r_pf-r_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('interest rate, $r_t$')
ax.set_xlim([0,200])
ax = fig.add_subplot(2,2,4)
ax.plot(np.arange(par.path_T),path_w-model.par.w_ss,'-o',ms=2,label='$\sigma_e = 0.5$')
ax.plot(np.arange(par.path_T),path_w_pf-w_ss_pf,'-o',ms=2,label='$\sigma_e = 0$')
ax.legend(frameon=True)
ax.set_title('wage, $w_t$')
ax.set_xlim([0,200])
fig.tight_layout()
```
| true |
code
| 0.574335 | null | null | null | null |
|
*This notebook is part of course materials for CS 345: Machine Learning Foundations and Practice at Colorado State University.
Original versions were created by Asa Ben-Hur.
The content is availabe [on GitHub](https://github.com/asabenhur/CS345).*
*The text is released under the [CC BY-SA license](https://creativecommons.org/licenses/by-sa/4.0/), and code is released under the [MIT license](https://opensource.org/licenses/MIT).*
<img style="padding: 10px; float:right;" alt="CC-BY-SA icon.svg in public domain" src="https://upload.wikimedia.org/wikipedia/commons/d/d0/CC-BY-SA_icon.svg" width="125">
<a href="https://colab.research.google.com/github//asabenhur/CS345/blob/master/notebooks/module05_01_cross_validation.ipynb">
<img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%autosave 0
```
# Evaluating classifiers: cross validation
### Learning curves
Intuitively, the more data we have available, the more accurate our classifiers become. To demonstrate this, let's read in some data and evaluate a k-nearest neighbor classifier on a fixed test set with increasing number of training examples. The resulting curve of accuracy as a function of number of examples is called a **learning curve**.
```
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
X, y = load_digits(return_X_y=True)
training_sizes = [20, 40, 100, 200, 400, 600, 800, 1000, 1200]
# note the use of the stratify keyword: it makes it so that each
# class is equally represented in both train and test set
X_full_train, X_test, y_full_train, y_test = train_test_split(
X, y, test_size = len(y)-max(training_sizes),
stratify=y, random_state=1)
accuracy = []
for training_size in training_sizes :
X_train,_ , y_train,_ = train_test_split(
X_full_train, y_full_train, test_size =
len(y_full_train)-training_size+10, stratify=y_full_train)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
accuracy.append(np.sum((y_pred==y_test))/len(y_test))
plt.figure(figsize=(6,4))
plt.plot(training_sizes, accuracy, 'ob')
plt.xlabel('training set size')
plt.ylabel('accuracy')
plt.ylim((0.5,1));
```
It's also instructive to look at the numbers themselves:
```
print ("# training examples\t accuracy")
for i in range(len(accuracy)) :
print ("\t{:d}\t\t {:f}".format(training_sizes[i], accuracy[i]))
```
### Exercise
* What can you conclude from this plot?
* Why would you want to compute a learning curve on your data?
### Making better use of our data with cross validation
The discussion above demonstrates that it is best to have as large of a training set as possible. We also need to have a large enough test set, so that the accuracy estimates are accurate. How do we balance these two contradictory requirements? Cross-validation provides us a more effective way to make use of our data. Here it is:
**Cross validation**
* Randomly partition the data into $k$ subsets ("folds").
* Set one fold aside for evaluation and train a model on the remaining $k$ folds and evaluate it on the held-out fold.
* Repeat until each fold has been used for evaluation
* Compute accuracy by averaging over the accuracy estimates generated for each fold.
Here is an illustration of 8-fold cross validation:
<img style="padding: 10px; float:left;" alt="cross-validation by MBanuelos22 CC BY-SA 4.0" src="https://upload.wikimedia.org/wikipedia/commons/c/c7/LOOCV.gif">
width="600">
As you can see, this procedure is more expensive than dividing your data into train and test set. When dealing with relatively small datasets, which is when you want to use this procedure, this won't be an issue.
Typically cross-validation is used with the number of folds being in the range of 5-10. An extreme case is when the number of folds equals the number of training examples. This special case is called *leave-one-out cross-validation*.
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate
from sklearn.model_selection import cross_val_score
from sklearn import metrics
```
Let's use the scikit-learn breast cancer dataset to demonstrate the use of cross-validation.
```
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
```
A scikit-learn data object is container object with whose interesting attributes are:
* ‘data’, the data to learn,
* ‘target’, the classification labels,
* ‘target_names’, the meaning of the labels,
* ‘feature_names’, the meaning of the features, and
* ‘DESCR’, the full description of the dataset.
```
X = data.data
y = data.target
print('number of examples ', len(y))
print('number of features ', len(X[0]))
print(data.target_names)
print(data.feature_names)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
random_state=0)
classifier = KNeighborsClassifier(n_neighbors=3)
#classifier = LogisticRegression()
_ = classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
```
Let's compute the accuracy of our predictions:
```
np.mean(y_pred==y_test)
```
We can do the same using scikit-learn:
```
metrics.accuracy_score(y_test, y_pred)
```
Now let's compute accuracy using [cross_validate](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html) instead:
```
accuracy = cross_val_score(classifier, X, y, cv=5,
scoring='accuracy')
print(accuracy)
```
This yields an array containing the accuracy values for each fold.
When reporting your results, you will typically show the mean:
```
np.mean(accuracy)
```
The arguments of `cross_val_score`:
* A classifier (anything that satisfies the scikit-learn classifier API)
* data (features/labels)
* `cv` : an integer that specifies the number of folds (can be used in more sophisticated ways as we will see below).
* `scoring`: this determines which accuracy measure is evaluated for each fold. Here's a link to the [list of available measures](https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter) in scikit-learn.
You can obtain accuracy for other metrics. *Balanced accuracy* for example, is appropriate when the data is unbalanced (e.g. when one class contains a much larger number of examples than other classes in the data).
```
accuracy = cross_val_score(classifier, X, y, cv=5,
scoring='balanced_accuracy')
np.mean(accuracy)
```
`cross_val_score` is somewhat limited, in that it simply returns a list of accuracy scores. In practice, we often want to have more information about what happened during training, and also to compute multiple accuracy measures.
`cross_validate` will provide you with that information:
```
results = cross_validate(classifier, X, y, cv=5,
scoring='accuracy', return_estimator=True)
print(results)
```
The object returned by `cross_validate` is a Python dictionary as the output suggests. To extract a specific piece of data from this object, simply access the dictionary with the appropriate key:
```
results['test_score']
```
If you would like to know the predictions made for each training example during cross-validation use [cross_val_predict](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_predict.html) instead:
```
from sklearn.model_selection import cross_val_predict
y_pred = cross_val_predict(classifier, X, y, cv=5)
metrics.accuracy_score(y, y_pred)
```
The above way of performing cross-validation doesn't always give us enough control on the process: we usually want our machine learning experiments be reproducible, and to be able to use the same cross-validation splits with multiple algorithms. The scikit-learn `KFold` and `StratifiedKFold` cross-validation generators are the way to achieve that.
`KFold` simply chooses a random subset of examples for each fold. This strategy can lead to cross-validation folds in which the classes are not well-represented as the following toy example demonstrates:
```
from sklearn.model_selection import StratifiedKFold, KFold
X_toy = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9,10], [11, 12]])
y_toy = np.array([0, 0, 1, 1, 1, 1])
cv = KFold(n_splits=2, random_state=3, shuffle=True)
for train_idx, test_idx in cv.split(X_toy, y_toy):
print("train:", train_idx, "test:", test_idx)
X_train, X_test = X_toy[train_idx], X_toy[test_idx]
y_train, y_test = y_toy[train_idx], y_toy[test_idx]
print(y_train)
```
`StratifiedKFold` addresses this issue by making sure that each class is represented in each fold in proportion to its overall fraction in the data. This is particularly important when one or more of the classes have few examples.
`StratifiedKFold` and `KFold` generate folds that can be used in conjunction with the cross-validation methods we saw above.
As an example, we will demonstrate the use of `StratifiedKFold` with `cross_val_score` on the breast cancer datast:
```
cv = StratifiedKFold(n_splits=5, random_state=1, shuffle=True)
accuracy = cross_val_score(classifier, X, y, cv=cv,
scoring='accuracy')
np.mean(accuracy)
```
For classification problems, `StratifiedKFold` is the preferred strategy. However, for regression problems `KFold` is the way to go.
#### Question
Why is `KFold` used in regression probelms rather than `StratifiedKFold`?
To clarify the distinction between the different methods of generating cross-validation folds and their different parameters let's look at the following figures:
```
# the code for the figure is adapted from
# https://scikit-learn.org/stable/auto_examples/model_selection/plot_cv_indices.html
np.random.seed(42)
cmap_data = plt.cm.Paired
cmap_cv = plt.cm.coolwarm
n_folds = 4
# Generate the data
X = np.random.randn(100, 10)
# generate labels - classes 0,1,2 and 10,30,60 examples, respectively
y = np.array([0] * 10 + [1] * 30 + [2] * 60)
def plot_cv_indices(cv, X, y, ax, n_folds):
"""plot the indices of a cross-validation object."""
# Generate the training/testing visualizations for each CV split
for ii, (tr, tt) in enumerate(cv.split(X=X, y=y)):
# Fill in indices with the training/test groups
indices = np.zeros(len(X))
indices[tt] = 1
# Visualize the results
ax.scatter(range(len(indices)), [ii + .5] * len(indices),
c=indices, marker='_', lw=15, cmap=cmap_cv,
vmin=-.2, vmax=1.2)
# Plot the data classes and groups at the end
ax.scatter(range(len(X)), [ii + 1.5] * len(X), c=y, marker='_', lw=15, cmap=cmap_data)
# Formatting
yticklabels = list(range(n_folds)) + ['class']
ax.set(yticks=np.arange(n_folds+2) + .5, yticklabels=yticklabels,
xlabel='index', ylabel="CV fold",
ylim=[n_folds+1.2, -.2], xlim=[0, 100])
ax.set_title('{}'.format(type(cv).__name__), fontsize=15)
return ax
```
Let's visualize the results of using `KFold` for fold generation:
```
fig, ax = plt.subplots()
cv = KFold(n_folds)
plot_cv_indices(cv, X, y, ax, n_folds);
```
As you can see, this naive way of using `KFold` can lead to highly undesirable splits into cross-validation folds.
Using `StratifiedKFold` addresses this to some extent:
```
fig, ax = plt.subplots()
cv = StratifiedKFold(n_folds)
plot_cv_indices(cv, X, y, ax, n_folds);
```
Using `StratifiedKFold` with shuffling of the examples is the preferred way of splitting the data into folds:
```
fig, ax = plt.subplots()
cv = StratifiedKFold(n_folds, shuffle=True)
plot_cv_indices(cv, X, y, ax, n_folds);
```
### Question
Consider the task of digitizing handwritten text (aka optical character recognition, or OCR). For each letter in the alphabet you have multiple labeled examples generated by the same writer. How would this setup affect the way you divide your examples into training and test sets, or when performing cross-validation?
### Summary and Discussion
In this notebook we discussed cross-validation as a more effective way to make use of limited amounts of data compared to the strategy of splitting data into train and test sets. For very large datasets where training is time consuming you might still opt for evaluation on a single test set.
| true |
code
| 0.732765 | null | null | null | null |
|
# Lecture 3.3: Anomaly Detection
[**Lecture Slides**](https://docs.google.com/presentation/d/1_0Z5Pc5yHA8MyEBE8Fedq44a-DcNPoQM1WhJN93p-TI/edit?usp=sharing)
This lecture, we are going to use gaussian distributions to detect anomalies in our emoji faces dataset
**Learning goals:**
- Introduce an anomaly detection problem
- Implement Gaussian distribution anomaly detection for images
- Debug the optimisation of a learning algorithm
- Discuss the imperfection of learning algorithms
- Acknowledge other outlier detection methods
## 1. Introduction
We have an `emoji_faces` dataset of all our favourite emojis. However, Skynet hates their friendly expressiveness, and wants to destroy emojis forever! 🙀 It sent _terminator robots_ from the future to invade our dataset. We must act fast, and detect them amongst the emojis to prevent the catastrophy.
Our challenge here, is that we don't watch many movies, so we don't have a clear idea of what those _terminators_ look like. 🤖 All we know, is that they look very different compared to emojis, and that only a handful managed to infiltrate our dataset.
This is a typical scenario of _anomaly detection_. We would like to identify rare examples that differ from our "normal" data points. We choose to use a Gaussian Distribution to model this "normality" and detect the killer robots.
## 2. Data Munging
First let's load the images using [pillow](https://pillow.readthedocs.io/en/stable/), like in lecture 2.5:
```
from PIL import Image
import glob
paths = glob.glob('emoji_faces/*.png')
images = [Image.open(path) for path in paths]
len(images)
```
We have 134 emoji faces, including a few terminator robots. We'll again be using the [sklearn](https://scikit-learn.org/) library to create our model. The interface is usually the same, and for gaussian anomaly detection, sklearn again expect a NumPy matrix where the rows are our images and the columns are the pixels. So we can apply the same transformations as notebook 3.2:
```
import numpy as np
arrays = [np.asarray(im) for im in images]
# 64 * 64 = 4096
vectors = [arr.reshape((4096,)) for arr in arrays]
data = np.stack(vectors)
```
## 3. Training
Next, we will create an [`EllipticEnvelope`](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html) object. This will fit a multi-variate gaussian distribution to our data. It then allows us to pick a threshold to define an _ellipsoid_ decision boundary , and detect outliers.
Remember that we are using a _learning_ algorithm, which must therefore be _trained_ before it can be used. This is why we'll use the `.fit()` method first, before calling `.predict()`:
```
from sklearn.covariance import EllipticEnvelope
cov = EllipticEnvelope(random_state=0).fit(data)
```
😰 What's happening? Why is it stuck? Have the killer robots already taken over?
No need to panic, this kind of hiccup is very common when dealing with machine learning algorithms. We can kill the process (before it fries our laptop fan) by clicking the `stop` button ⬛️ in the notebook toolbar.
Most learning algorithms are based around an _optimisation_ procedure. This step is often iterative and stochastic, i.e it tries its statistical best to maximise the learning in incremental steps.
This process isn't fail proof:
* it can dramatically stop because of out of memory errors, or overflow errors 💥
* it can get stuck, e.g when the optimisation is too slow 🐌
* it can fail silently, and return wrong results 💩
ℹ️ We will encounter many of these failures throughout our ML experiments, so knowing how to overcome them is a part of the data scientist skillset.
Let's go back to our killer robot detection: the model fitting got _stuck_ , which suggests that something about our data was too much to handle. We find the following "notes" in the [official documentation](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html#sklearn.covariance.EllipticEnvelope):
> Outlier detection from covariance estimation may break or not perform well in high-dimensional settings.
We recall that our images are $64 \times 64$ pixels, so $4096$ dimensions.... that's a lot. It seems a good candidate to explain why our multivariate gaussian distribution failed to fit our dataset. If only there was a way to reduce the dimensions of our data... 😏
Let's apply PCA to reduce the number of dimensions of our dataset. Our emoji faces dataset is smaller than the full emoji dataset, so 40 dimensions should suffice to explain its variance:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=40)
pca.fit(data)
components = pca.transform(data)
components.shape
```
💪 Visualise the eigenvector images of our PCA model. You can use the code from lecture 3.2!
🧠 Can you explain what those eigenvector images represent? Why are they different than from the full emoji dataset?
Fantastic, we've managed to reduce the number of dimensions by 99%! Hopefully that should be enough to make our gaussian distribution fitting happy. Let's try again with the _principal components_ instead of the original data:
```
cov = EllipticEnvelope(random_state=0).fit(components)
```
😅 that was fast!
## 4. Prediction
We can now use our fitted gaussian distribution to detect the outliers in our `data`. For this, we use the `.predict()` method:
```
y = cov.predict(components)
y
```
`y` is our vector of predictions, where $1$ is a normal data point, and $-1$ is an anomaly. We can therefore iterate through our original `arrays` to find outliers:
```
outliers = []
for i in range(0, len(arrays)):
if y[i] == -1:
outliers.append(arrays[i])
len(outliers)
import matplotlib.pyplot as plt
fig, axs = plt.subplots(dpi=150, nrows=2, ncols=7)
for outlier, ax in zip(outliers, axs.flatten()):
ax.imshow(outlier, cmap='gray', vmin=0, vmax=255)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
THERE'S OUR TERMINATORS! 🤖 We can count 5 of them in total. Notice how some real emoji faces were also detected as outliers. This is perhaps a sign that we should change our _threshold_ , to make the ellipsoid decision boundary smaller.
In fact, we didn't even specify a threshold before, we just used the default value of `contamination=0.1` in the [`EllipticEnvelope`](https://scikit-learn.org/stable/modules/generated/sklearn.covariance.EllipticEnvelope.html) class. This represents our estimation of the proportion of data points which are outliers. Since it looks like we detected double the amount of actual anomalies, let's try again with `contamination=0.05`:
```
cov = EllipticEnvelope(random_state=0, contamination=0.05).fit(components)
y = cov.predict(components)
outliers = []
for i in range(0, len(arrays)):
if y[i] == -1:
outliers.append(arrays[i])
fig, axs = plt.subplots(dpi=150, nrows=1, ncols=7)
for outlier, ax in zip(outliers, axs.flatten()):
ax.imshow(outlier, cmap='gray', vmin=0, vmax=255)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
Better! `contamination=0.05` was a better choice of threshold, and we assessed this through _manual inspection_. This means we went through the results and used our human jugement to change the value of this _hyperparameter_.
ℹ️ Notice how our outlier detection is not _perfect_. Some emojis were also erroneously detected as anomalous killer robots. This can seem like a problem, or a sign that our model was malfunctioning. But, quite the contrary, _imperfection_ is a core aspect of all _learning_ algorithms. Instead of seeing the glass half-empty and looking at the outlier detector's mistakes, we should reflect on the task itself. It would have been almost impossible to detect those killer robot images using rule-based algorithms, and our model _accuracy_ was good _enough_ to save the emojis from Skynet. As data scientists, our goal is to make models which are accurate _enough_ to be useful, not to aim for perfect scores. We will revisit these topics later in the course when discussing Machine Learning Engineering 🛠
## 5. Analysis
We have detected the robot intruders and saved the emojis from a jealous AI from the future, all is good! We still want to better understand how anomaly detection defeated Skynet. For this, we would like to leverage our shiny new data visualization skills. Representing our dataset in space would allow us to identify its structures and hopefully understand how our gaussian distribution model identified terminators as "abnormal".
Our data is high dimensional, so we can use our trusted PCA once again to project it down to 2 dimensions. We understand that this will lose a lot of the variance of our data, but the results were still somewhat interpretable with the full emoji dataset, so let's go!
```
# Dimesionality reduction to 2
pca_model = PCA(n_components=2)
pca_model.fit(data) # fit the model
T = pca_model.transform(data) # transform the 'normalized model'
plt.scatter(T[:, 0], T[:, 1],
# use the predictions as color
c=y,
marker='o',
alpha=0.4
)
plt.title('Anomaly detection of the emoji faces dataset with PCA dimensionality reduction');
```
We can notice that most of the outliers are clearly _separable_ from the bulk of the dataset, even with only 2 principal components. One outlier is very much within the main cluster however. This could be explained by the dimensionality reduction, i.e that this point is separated from the cluster in other dimensions, or by the fact our threshold might be too permissive.
We can check this by displaying the images directly on the scatter plot:
```
from matplotlib import offsetbox
def plot_components(data, model, images=None, ax=None,
thumb_frac=0.05, cmap='gray'):
ax = ax or plt.gca()
proj = model.fit_transform(data)
ax.plot(proj[:, 0], proj[:, 1], '.k')
if images is not None:
min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
shown_images = np.array([2 * proj.max(0)])
for i in range(data.shape[0]):
dist = np.sum((proj[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist_2:
# don't show points that are too close
continue
shown_images = np.vstack([shown_images, proj[i]])
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(images[i], cmap=cmap),
proj[i])
ax.add_artist(imagebox)
small_images = [im[::2, ::2] for im in arrays]
fig, ax = plt.subplots(figsize=(10, 10))
plot_components(data,
model=PCA(n_components=2),
images=small_images, thumb_frac=0.02)
plt.title('Anomaly detection of the emoji faces dataset with PCA dimensionality reduction');
```
We could probably have reduced the value of `contamination` further, since we can see how the killer robots are clearly "abnormal" with this visualisation. We also have a "feel" of how our gaussian distribution model could successfully detect them as outliers. Although remember that all of modeling magic happens in 40 dimensional space!
🧠🧠 Can you explain why it is not very useful to display the ellipsoid decision boundary of our anomaly detection model on this graph?
## 6. More Anomaly Detection
Anomaly detection is an active field in ML research, which combines supervised, unsupervised, non-linear, Bayesian, ... a whole bunch of methods! Each solution will have its pros and cons, and developing a production level outlier detection system will require empirically evaluating and comparing them. For a breakdown of the methods available in sklearn, check out this excellent [blogpost](https://sdsawtelle.github.io/blog/output/week9-anomaly-andrew-ng-machine-learning-with-python.html), or the [official documentation](https://scikit-learn.org/stable/modules/outlier_detection.html). For an in-depth view of modern anomaly detection, watch this [video](https://youtu.be/LRqX5uO5StA). And for everything else, feel free to experiment with this dataset or any other. Good luck on finding all the killer robots!
## 7. Summary
Today, we defined **anomaly detection**, and listed some of its common applications including fraud detection and data cleaning. We then described how to use **fitted Gaussian distributions** to identify outliers. This lead us to a discussion about the choice of **thresholds** and **hyperparameters**, where we went over a few different realistic scenarios. We then used a Gaussian distribution to remove terminator images from an emoji faces dataset. We learned how learning algorithms **fail** and that data scientists must know how to **debug** them. Finally, we used **PCA** to visualize our killer robot detection.
# Resources
## Core Resources
- [Anomaly detection algorithm](https://www.coursera.org/lecture/machine-learning/algorithm-C8IJp)
Andrew Ng's limpid breakdown of anomaly detection
## Additional Resources
- [A review of ML techniques for anomaly detection](https://youtu.be/LRqX5uO5StA)
More in depth review of modern techniques for anomaly detection
- [Anomaly Detection in sklearn](https://sdsawtelle.github.io/blog/output/week9-anomaly-andrew-ng-machine-learning-with-python.html)
Visual blogpost experimenting with the various outlier detection algorithms available in sklearn
- [sklearn official documentation - outlier detection](https://scikit-learn.org/stable/modules/outlier_detection.html)
| true |
code
| 0.59134 | null | null | null | null |
|
# Import Necessary Libraries
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
from sklearn.metrics import precision_score, recall_score
# display images
from IPython.display import Image
# linear algebra
import numpy as np
# data processing
import pandas as pd
# data visualization
import seaborn as sns
%matplotlib inline
from matplotlib import pyplot as plt
from matplotlib import style
# Algorithms
from sklearn import linear_model
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.naive_bayes import GaussianNB
```
# Titanic
Titanic was a British passenger liner that sank in the North Atlantic Ocean in the early morning hours of 15 April 1912, after it collided with an iceberg during its maiden voyage from Southampton to New York City. There were an estimated 2,224 passengers and crew aboard the ship, and more than 1,500 died, making it one of the deadliest commercial peacetime maritime disasters in modern history. The RMS Titanic was the largest ship afloat at the time it entered service and was the second of three Olympic-class ocean liners operated by the White Star Line. The Titanic was built by the Harland and Wolff shipyard in Belfast. Thomas Andrews, her architect, died in the disaster.
```
# Image of Titanic ship
Image(filename='C:/Users/Nemgeree Armanonah/Documents/GitHub/Titanic/images/ship.jpeg')
```
# Getting the Data
```
#reading train.csv
data = pd.read_csv('./titanic datasets/train.csv')
data
```
## Exploring Data
```
data.info()
```
### Describe Statistics
Describe method is used to view some basic statistical details like PassengerId,Servived,Age etc.
```
data.describe()
```
### View All Features
```
data.columns.values
```
### What features could contribute to a high survival rate ?
To Us it would make sense if everything except ‘PassengerId’, ‘Ticket’ and ‘Name’ would be correlated with a high survival rate.
```
# defining variables
survived = 'survived'
not_survived = 'not survived'
# data to be plotted
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(10, 4))
women = data[data['Sex']=='female']
men = data[data['Sex']=='male']
# plot the data
ax = sns.distplot(women[women['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[0], kde =False)
ax = sns.distplot(women[women['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[0], kde =False)
ax.legend()
ax.set_title('Female')
ax = sns.distplot(men[men['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[1], kde = False)
ax = sns.distplot(men[men['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[1], kde = False)
ax.legend()
_ = ax.set_title('Male')
# count the null values
null_values = data.isnull().sum()
null_values
plt.plot(null_values)
plt.grid()
plt.show()
```
## Data Processing
```
def handle_non_numerical_data(df):
columns = df.columns.values
for column in columns:
text_digit_vals = {}
def convert_to_int(val):10
return text_digit_vals[val]
#print(column,df[column].dtype)
if df[column].dtype != np.int64 and df[column].dtype != np.float64:
column_contents = df[column].values.tolist()
#finding just the uniques
unique_elements = set(column_contents)
# great, found them.
x = 0
for unique in unique_elements:
if unique not in text_digit_vals:
text_digit_vals[unique] = x
x+=1
df[column] = list(map(convert_to_int,df[column]))
return df
y_target = data['Survived']
# Y_target.reshape(len(Y_target),1)
x_train = data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare','Embarked', 'Ticket']]
x_train = handle_non_numerical_data(x_train)
x_train.head()
fare = pd.DataFrame(x_train['Fare'])
# Normalizing
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
x_train['Fare'] = newfare
x_train
null_values = x_train.isnull().sum()
null_values
plt.plot(null_values)
plt.show()
# Fill the NAN values with the median values in the datasets
x_train['Age'] = x_train['Age'].fillna(x_train['Age'].median())
print("Number of NULL values" , x_train['Age'].isnull().sum())
x_train.head()
x_train['Sex'] = x_train['Sex'].replace('male', 0)
x_train['Sex'] = x_train['Sex'].replace('female', 1)
# print(type(x_train))
corr = x_train.corr()
corr.style.background_gradient()
def plot_corr(df,size=10):
corr = df.corr()
fig, ax = plt.subplots(figsize=(size, size))
ax.matshow(corr)
plt.xticks(range(len(corr.columns)), corr.columns);
plt.yticks(range(len(corr.columns)), corr.columns);
# plot_corr(x_train)
x_train.corr()
corr.style.background_gradient()
# Dividing the data into train and test data set
X_train, X_test, Y_train, Y_test = train_test_split(x_train, y_target, test_size = 0.4, random_state = 40)
clf = RandomForestClassifier()
clf.fit(X_train, Y_train)
print(clf.predict(X_test))
print("Accuracy: ",clf.score(X_test, Y_test))
## Testing the model.
test_data = pd.read_csv('./titanic datasets/test.csv')
test_data.head(3)
# test_data.isnull().sum()
### Preprocessing on the test data
test_data = test_data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare', 'Ticket', 'Embarked']]
test_data = handle_non_numerical_data(test_data)
fare = pd.DataFrame(test_data['Fare'])
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
test_data['Fare'] = newfare
test_data['Fare'] = test_data['Fare'].fillna(test_data['Fare'].median())
test_data['Age'] = test_data['Age'].fillna(test_data['Age'].median())
test_data['Sex'] = test_data['Sex'].replace('male', 0)
test_data['Sex'] = test_data['Sex'].replace('female', 1)
print(test_data.head())
print(clf.predict(test_data))
from sklearn.model_selection import cross_val_predict
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
print("Precision:", precision_score(Y_train, predictions))
print("Recall:",recall_score(Y_train, predictions))
from sklearn.metrics import precision_recall_curve
# getting the probabilities of our predictions
y_scores = clf.predict_proba(X_train)
y_scores = y_scores[:,1]
precision, recall, threshold = precision_recall_curve(Y_train, y_scores)
def plot_precision_and_recall(precision, recall, threshold):
plt.plot(threshold, precision[:-1], "r-", label="precision", linewidth=5)
plt.plot(threshold, recall[:-1], "b", label="recall", linewidth=5)
plt.xlabel("threshold", fontsize=19)
plt.legend(loc="upper right", fontsize=19)
plt.ylim([0, 1])
plt.figure(figsize=(14, 7))
plot_precision_and_recall(precision, recall, threshold)
plt.axis([0.3,0.8,0.8,1])
plt.show()
def plot_precision_vs_recall(precision, recall):
plt.plot(recall, precision, "g--", linewidth=2.5)
plt.ylabel("recall", fontsize=19)
plt.xlabel("precision", fontsize=19)
plt.axis([0, 1.5, 0, 1.5])
plt.figure(figsize=(14, 7))
plot_precision_vs_recall(precision, recall)
plt.show()
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
confusion_matrix(Y_train, predictions)
```
True positive: 293 (We predicted a positive result and it was positive)
True negative: 143 (We predicted a negative result and it was negative)
False positive: 34 (We predicted a positive result and it was negative)
False negative: 64 (We predicted a negative result and it was positive)
| true |
code
| 0.640383 | null | null | null | null |
|
# 第8章: ニューラルネット
第6章で取り組んだニュース記事のカテゴリ分類を題材として,ニューラルネットワークでカテゴリ分類モデルを実装する.なお,この章ではPyTorch, TensorFlow, Chainerなどの機械学習プラットフォームを活用せよ.
## 70. 単語ベクトルの和による特徴量
***
問題50で構築した学習データ,検証データ,評価データを行列・ベクトルに変換したい.例えば,学習データについて,すべての事例$x_i$の特徴ベクトル$\boldsymbol{x}_i$を並べた行列$X$と正解ラベルを並べた行列(ベクトル)$Y$を作成したい.
$$
X = \begin{pmatrix}
\boldsymbol{x}_1 \\
\boldsymbol{x}_2 \\
\dots \\
\boldsymbol{x}_n \\
\end{pmatrix} \in \mathbb{R}^{n \times d},
Y = \begin{pmatrix}
y_1 \\
y_2 \\
\dots \\
y_n \\
\end{pmatrix} \in \mathbb{N}^{n}
$$
ここで,$n$は学習データの事例数であり,$\boldsymbol x_i \in \mathbb{R}^d$と$y_i \in \mathbb N$はそれぞれ,$i \in \{1, \dots, n\}$番目の事例の特徴量ベクトルと正解ラベルを表す.
なお,今回は「ビジネス」「科学技術」「エンターテイメント」「健康」の4カテゴリ分類である.$\mathbb N_{<4}$で$4$未満の自然数($0$を含む)を表すことにすれば,任意の事例の正解ラベル$y_i$は$y_i \in \mathbb N_{<4}$で表現できる.
以降では,ラベルの種類数を$L$で表す(今回の分類タスクでは$L=4$である).
$i$番目の事例の特徴ベクトル$\boldsymbol x_i$は,次式で求める.
$$\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})$$
ここで,$i$番目の事例は$T_i$個の(記事見出しの)単語列$(w_{i,1}, w_{i,2}, \dots, w_{i,T_i})$から構成され,$\mathrm{emb}(w) \in \mathbb{R}^d$は単語$w$に対応する単語ベクトル(次元数は$d$)である.すなわち,$i$番目の事例の記事見出しを,その見出しに含まれる単語のベクトルの平均で表現したものが$\boldsymbol x_i$である.今回は単語ベクトルとして,問題60でダウンロードしたものを用いればよい.$300$次元の単語ベクトルを用いたので,$d=300$である.
$i$番目の事例のラベル$y_i$は,次のように定義する.
$$
y_i = \begin{cases}
0 & (\mbox{記事}\boldsymbol x_i\mbox{が「ビジネス」カテゴリの場合}) \\
1 & (\mbox{記事}\boldsymbol x_i\mbox{が「科学技術」カテゴリの場合}) \\
2 & (\mbox{記事}\boldsymbol x_i\mbox{が「エンターテイメント」カテゴリの場合}) \\
3 & (\mbox{記事}\boldsymbol x_i\mbox{が「健康」カテゴリの場合}) \\
\end{cases}
$$
なお,カテゴリ名とラベルの番号が一対一で対応付いていれば,上式の通りの対応付けでなくてもよい.
以上の仕様に基づき,以下の行列・ベクトルを作成し,ファイルに保存せよ.
+ 学習データの特徴量行列: $X_{\rm train} \in \mathbb{R}^{N_t \times d}$
+ 学習データのラベルベクトル: $Y_{\rm train} \in \mathbb{N}^{N_t}$
+ 検証データの特徴量行列: $X_{\rm valid} \in \mathbb{R}^{N_v \times d}$
+ 検証データのラベルベクトル: $Y_{\rm valid} \in \mathbb{N}^{N_v}$
+ 評価データの特徴量行列: $X_{\rm test} \in \mathbb{R}^{N_e \times d}$
+ 評価データのラベルベクトル: $Y_{\rm test} \in \mathbb{N}^{N_e}$
なお,$N_t, N_v, N_e$はそれぞれ,学習データの事例数,検証データの事例数,評価データの事例数である.
```
!wget https://archive.ics.uci.edu/ml/machine-learning-databases/00359/NewsAggregatorDataset.zip
!unzip NewsAggregatorDataset.zip
!wc -l ./newsCorpora.csv
!head -10 ./newsCorpora.csv
# 読込時のエラー回避のためダブルクォーテーションをシングルクォーテーションに置換
!sed -e 's/"/'\''/g' ./newsCorpora.csv > ./newsCorpora_re.csv
import pandas as pd
from sklearn.model_selection import train_test_split
# データの読込
df = pd.read_csv('./newsCorpora_re.csv', header=None, sep='\t', names=['ID', 'TITLE', 'URL', 'PUBLISHER', 'CATEGORY', 'STORY', 'HOSTNAME', 'TIMESTAMP'])
# データの抽出
df = df.loc[df['PUBLISHER'].isin(['Reuters', 'Huffington Post', 'Businessweek', 'Contactmusic.com', 'Daily Mail']), ['TITLE', 'CATEGORY']]
# データの分割
train, valid_test = train_test_split(df, test_size=0.2, shuffle=True, random_state=123, stratify=df['CATEGORY'])
valid, test = train_test_split(valid_test, test_size=0.5, shuffle=True, random_state=123, stratify=valid_test['CATEGORY'])
# 事例数の確認
print('【学習データ】')
print(train['CATEGORY'].value_counts())
print('【検証データ】')
print(valid['CATEGORY'].value_counts())
print('【評価データ】')
print(test['CATEGORY'].value_counts())
train.to_csv('drive/My Drive/nlp100/data/train.tsv', index=False, sep='\t', header=False)
valid.to_csv('drive/My Drive/nlp100/data/valid.tsv', index=False, sep='\t', header=False)
test.to_csv('drive/My Drive/nlp100/data/test.tsv', index=False, sep='\t', header=False)
import gdown
from gensim.models import KeyedVectors
# 学習済み単語ベクトルのダウンロード
url = "https://drive.google.com/uc?id=0B7XkCwpI5KDYNlNUTTlSS21pQmM"
output = 'GoogleNews-vectors-negative300.bin.gz'
gdown.download(url, output, quiet=True)
# ダウンロードファイルのロード
model = KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin.gz', binary=True)
import string
import torch
def transform_w2v(text):
table = str.maketrans(string.punctuation, ' '*len(string.punctuation))
words = text.translate(table).split() # 記号をスペースに置換後、スペースで分割してリスト化
vec = [model[word] for word in words if word in model] # 1語ずつベクトル化
return torch.tensor(sum(vec) / len(vec)) # 平均ベクトルをTensor型に変換して出力
# 特徴ベクトルの作成
X_train = torch.stack([transform_w2v(text) for text in train['TITLE']])
X_valid = torch.stack([transform_w2v(text) for text in valid['TITLE']])
X_test = torch.stack([transform_w2v(text) for text in test['TITLE']])
print(X_train.size())
print(X_train)
# ラベルベクトルの作成
category_dict = {'b': 0, 't': 1, 'e':2, 'm':3}
y_train = torch.LongTensor(train['CATEGORY'].map(lambda x: category_dict[x]).values)
y_valid = torch.LongTensor(valid['CATEGORY'].map(lambda x: category_dict[x]).values)
y_test = torch.LongTensor(test['CATEGORY'].map(lambda x: category_dict[x]).values)
print(y_train.size())
print(y_train)
# 保存
torch.save(X_train, 'X_train.pt')
torch.save(X_valid, 'X_valid.pt')
torch.save(X_test, 'X_test.pt')
torch.save(y_train, 'y_train.pt')
torch.save(y_valid, 'y_valid.pt')
torch.save(y_test, 'y_test.pt')
```
## 71. 単層ニューラルネットワークによる予測
***
問題70で保存した行列を読み込み,学習データについて以下の計算を実行せよ.
$$
\hat{y}_1=softmax(x_1W),\\\hat{Y}=softmax(X_{[1:4]}W)
$$
ただし,$softmax$はソフトマックス関数,$X_{[1:4]}∈\mathbb{R}^{4×d}$は特徴ベクトル$x_1$,$x_2$,$x_3$,$x_4$を縦に並べた行列である.
$$
X_{[1:4]}=\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}
$$
行列$W \in \mathbb{R}^{d \times L}$は単層ニューラルネットワークの重み行列で,ここではランダムな値で初期化すればよい(問題73以降で学習して求める).なお,$\hat{\boldsymbol y_1} \in \mathbb{R}^L$は未学習の行列$W$で事例$x_1$を分類したときに,各カテゴリに属する確率を表すベクトルである.
同様に,$\hat{Y} \in \mathbb{R}^{n \times L}$は,学習データの事例$x_1, x_2, x_3, x_4$について,各カテゴリに属する確率を行列として表現している.
```
from torch import nn
torch.manual_seed(0)
class SLPNet(nn.Module):
def __init__(self, input_size, output_size):
super().__init__()
self.fc = nn.Linear(input_size, output_size, bias=False) # Linear(入力次元数, 出力次元数)
nn.init.normal_(self.fc.weight, 0.0, 1.0) # 正規乱数で重みを初期化
def forward(self, x):
x = self.fc(x)
return x
model = SLPNet(300, 4)
y_hat_1 = torch.softmax(model.forward(X_train[:1]), dim=-1)
print(y_hat_1)
Y_hat = torch.softmax(model.forward(X_train[:4]), dim=-1)
print(Y_hat)
```
## 72. 損失と勾配の計算
***
学習データの事例$x_1$と事例集合$x_1$,$x_2$,$x_3$,$x_4$に対して,クロスエントロピー損失と,行列$W$に対する勾配を計算せよ.なお,ある事例$x_i$に対して損失は次式で計算される.
$$l_i=−log[事例x_iがy_iに分類される確率]$$
ただし,事例集合に対するクロスエントロピー損失は,その集合に含まれる各事例の損失の平均とする.
```
criterion = nn.CrossEntropyLoss()
l_1 = criterion(model.forward(X_train[:1]), y_train[:1]) # 入力ベクトルはsoftmax前の値
model.zero_grad() # 勾配をゼロで初期化
l_1.backward() # 勾配を計算
print(f'損失: {l_1:.4f}')
print(f'勾配:\n{model.fc.weight.grad}')
l = criterion(model.forward(X_train[:4]), y_train[:4])
model.zero_grad()
l.backward()
print(f'損失: {l:.4f}')
print(f'勾配:\n{model.fc.weight.grad}')
```
## 73. 確率的勾配降下法による学習
***
確率的勾配降下法(SGD: Stochastic Gradient Descent)を用いて,行列$W$を学習せよ.なお,学習は適当な基準で終了させればよい(例えば「100エポックで終了」など).
```
from torch.utils.data import Dataset
class CreateDataset(Dataset):
def __init__(self, X, y): # datasetの構成要素を指定
self.X = X
self.y = y
def __len__(self): # len(dataset)で返す値を指定
return len(self.y)
def __getitem__(self, idx): # dataset[idx]で返す値を指定
if isinstance(idx, torch.Tensor):
idx = idx.tolist()
return [self.X[idx], self.y[idx]]
from torch.utils.data import DataLoader
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
dataset_test = CreateDataset(X_test, y_test)
dataloader_train = DataLoader(dataset_train, batch_size=1, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
dataloader_test = DataLoader(dataset_test, batch_size=len(dataset_test), shuffle=False)
print(len(dataset_train))
print(next(iter(dataloader_train)))
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 10
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
loss_train = 0.0
for i, (inputs, labels) in enumerate(dataloader_train):
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失を記録
loss_train += loss.item()
# バッチ単位の平均損失計算
loss_train = loss_train / i
# 検証データの損失計算
model.eval()
with torch.no_grad():
inputs, labels = next(iter(dataloader_valid))
outputs = model.forward(inputs)
loss_valid = criterion(outputs, labels)
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, loss_valid: {loss_valid:.4f}')
```
## 74. 正解率の計測
***
問題73で求めた行列を用いて学習データおよび評価データの事例を分類したとき,その正解率をそれぞれ求めよ.
```
def calculate_accuracy(model, X, y):
model.eval()
with torch.no_grad():
outputs = model(X)
pred = torch.argmax(outputs, dim=-1)
return (pred == y).sum().item() / len(y)
# 正解率の確認
acc_train = calculate_accuracy(model, X_train, y_train)
acc_test = calculate_accuracy(model, X_test, y_test)
print(f'正解率(学習データ):{acc_train:.3f}')
print(f'正解率(評価データ):{acc_test:.3f}')
```
## 75. 損失と正解率のプロット
***
問題73のコードを改変し,各エポックのパラメータ更新が完了するたびに,訓練データでの損失,正解率,検証データでの損失,正解率をグラフにプロットし,学習の進捗状況を確認できるようにせよ.
```
def calculate_loss_and_accuracy(model, criterion, loader):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 30
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
for i, (inputs, labels) in enumerate(dataloader_train):
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}')
import numpy as np
from matplotlib import pyplot as plt
# 可視化
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log_train).T[0], label='train')
ax[0].plot(np.array(log_valid).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log_train).T[1], label='train')
ax[1].plot(np.array(log_valid).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()
```
## 76. チェックポイント
***
問題75のコードを改変し,各エポックのパラメータ更新が完了するたびに,チェックポイント(学習途中のパラメータ(重み行列など)の値や最適化アルゴリズムの内部状態)をファイルに書き出せ.
```
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# 学習
num_epochs = 10
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}')
```
## 77. ミニバッチ化
***
問題76のコードを改変し,$B$事例ごとに損失・勾配を計算し,行列$W$の値を更新せよ(ミニバッチ化).$B$の値を$1,2,4,8,…$と変化させながら,1エポックの学習に要する時間を比較せよ.
```
import time
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs):
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# モデルの学習
for batch_size in [2 ** i for i in range(11)]:
print(f'バッチサイズ: {batch_size}')
log = train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, 1)
```
## 78. GPU上での学習
***
問題77のコードを改変し,GPU上で学習を実行せよ.
```
def calculate_loss_and_accuracy(model, criterion, loader, device):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs, device=None):
# GPUに送る
model.to(device)
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train, device)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid, device)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = SLPNet(300, 4)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-1)
# デバイスの指定
device = torch.device('cuda')
for batch_size in [2 ** i for i in range(11)]:
print(f'バッチサイズ: {batch_size}')
log = train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, 1, device=device)
```
## 79. 多層ニューラルネットワーク
***
問題78のコードを改変し,バイアス項の導入や多層化など,ニューラルネットワークの形状を変更しながら,高性能なカテゴリ分類器を構築せよ.
```
from torch.nn import functional as F
class MLPNet(nn.Module):
def __init__(self, input_size, mid_size, output_size, mid_layers):
super().__init__()
self.mid_layers = mid_layers
self.fc = nn.Linear(input_size, mid_size)
self.fc_mid = nn.Linear(mid_size, mid_size)
self.fc_out = nn.Linear(mid_size, output_size)
self.bn = nn.BatchNorm1d(mid_size)
def forward(self, x):
x = F.relu(self.fc(x))
for _ in range(self.mid_layers):
x = F.relu(self.bn(self.fc_mid(x)))
x = F.relu(self.fc_out(x))
return x
from torch import optim
def calculate_loss_and_accuracy(model, criterion, loader, device):
model.eval()
loss = 0.0
total = 0
correct = 0
with torch.no_grad():
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss += criterion(outputs, labels).item()
pred = torch.argmax(outputs, dim=-1)
total += len(inputs)
correct += (pred == labels).sum().item()
return loss / len(loader), correct / total
def train_model(dataset_train, dataset_valid, batch_size, model, criterion, optimizer, num_epochs, device=None):
# GPUに送る
model.to(device)
# dataloaderの作成
dataloader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=len(dataset_valid), shuffle=False)
# スケジューラの設定
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, num_epochs, eta_min=1e-5, last_epoch=-1)
# 学習
log_train = []
log_valid = []
for epoch in range(num_epochs):
# 開始時刻の記録
s_time = time.time()
# 訓練モードに設定
model.train()
for inputs, labels in dataloader_train:
# 勾配をゼロで初期化
optimizer.zero_grad()
# 順伝播 + 誤差逆伝播 + 重み更新
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# 損失と正解率の算出
loss_train, acc_train = calculate_loss_and_accuracy(model, criterion, dataloader_train, device)
loss_valid, acc_valid = calculate_loss_and_accuracy(model, criterion, dataloader_valid, device)
log_train.append([loss_train, acc_train])
log_valid.append([loss_valid, acc_valid])
# チェックポイントの保存
torch.save({'epoch': epoch, 'model_state_dict': model.state_dict(), 'optimizer_state_dict': optimizer.state_dict()}, f'checkpoint{epoch + 1}.pt')
# 終了時刻の記録
e_time = time.time()
# ログを出力
print(f'epoch: {epoch + 1}, loss_train: {loss_train:.4f}, accuracy_train: {acc_train:.4f}, loss_valid: {loss_valid:.4f}, accuracy_valid: {acc_valid:.4f}, {(e_time - s_time):.4f}sec')
# 検証データの損失が3エポック連続で低下しなかった場合は学習終了
if epoch > 2 and log_valid[epoch - 3][0] <= log_valid[epoch - 2][0] <= log_valid[epoch - 1][0] <= log_valid[epoch][0]:
break
# スケジューラを1ステップ進める
scheduler.step()
return {'train': log_train, 'valid': log_valid}
# datasetの作成
dataset_train = CreateDataset(X_train, y_train)
dataset_valid = CreateDataset(X_valid, y_valid)
# モデルの定義
model = MLPNet(300, 200, 4, 1)
# 損失関数の定義
criterion = nn.CrossEntropyLoss()
# オプティマイザの定義
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
# デバイスの指定
device = torch.device('cuda')
log = train_model(dataset_train, dataset_valid, 64, model, criterion, optimizer, 1000, device)
# 可視化
fig, ax = plt.subplots(1, 2, figsize=(15, 5))
ax[0].plot(np.array(log['train']).T[0], label='train')
ax[0].plot(np.array(log['valid']).T[0], label='valid')
ax[0].set_xlabel('epoch')
ax[0].set_ylabel('loss')
ax[0].legend()
ax[1].plot(np.array(log['train']).T[1], label='train')
ax[1].plot(np.array(log['valid']).T[1], label='valid')
ax[1].set_xlabel('epoch')
ax[1].set_ylabel('accuracy')
ax[1].legend()
plt.show()
def calculate_accuracy(model, X, y, device):
model.eval()
with torch.no_grad():
inputs = X.to(device)
outputs = model(inputs)
pred = torch.argmax(outputs, dim=-1).cpu()
return (pred == y).sum().item() / len(y)
# 正解率の確認
acc_train = calculate_accuracy(model, X_train, y_train, device)
acc_test = calculate_accuracy(model, X_test, y_test, device)
print(f'正解率(学習データ):{acc_train:.3f}')
print(f'正解率(評価データ):{acc_test:.3f}')
```
| true |
code
| 0.608943 | null | null | null | null |
|
# Analyse a series
<div class="alert alert-block alert-warning">
<b>Under construction</b>
</div>
```
import os
import pandas as pd
from IPython.display import Image as DImage
from IPython.core.display import display, HTML
import series_details
# Plotly helps us make pretty charts
import plotly.offline as py
import plotly.graph_objs as go
# Make sure data directory exists
os.makedirs('../../data/RecordSearch/images', exist_ok=True)
# This lets Plotly draw charts in cells
py.init_notebook_mode()
```
This notebook is for analysing a series that you've already harvested. If you haven't harvested any data yet, then you need to go back to the ['Harvesting a series' notebook](Harvesting series.ipynb).
```
# What series do you want to analyse?
# Insert the series id between the quotes.
series = 'J2483'
# Load the CSV data for the specified series into a dataframe. Parse the dates as dates!
df = pd.read_csv('../data/RecordSearch/{}.csv'.format(series.replace('/', '-')), parse_dates=['start_date', 'end_date'])
```
Remember that you can download harvested data from the workbench [data directory](../data/RecordSearch).
## Get some summary data
We're going to create a simple summary of some of the main characteristics of the series, as reflected in the harvested files.
```
# We're going to assemble some summary data about the series in a 'summary' dictionary
# Let's create the dictionary and add the series identifier
summary = {'series': series}
# The 'shape' property returns the number of rows and columns. So 'shape[0]' gives us the number of items harvested.
summary['total_items'] = df.shape[0]
print(summary['total_items'])
# Get the frequency of the different access status categories
summary['access_counts'] = df['access_status'].value_counts().to_dict()
print(summary['access_counts'])
# Get the number of files that have been digitised
summary['digitised_files'] = len(df.loc[df['digitised_status'] == True])
print(summary['digitised_files'])
# Get the number of individual pages that have been digitised
summary['digitised_pages'] = df['digitised_pages'].sum()
print(summary['digitised_pages'])
# Get the earliest start date
start = df['start_date'].min()
try:
summary['date_from'] = start.year
except AttributeError:
summary['date_from'] = None
print(summary['date_from'])
# Get the latest end date
end = df['end_date'].max()
try:
summary['date_to'] = end.year
except AttributeError:
summary['date_to'] = None
print(summary['date_to'])
# Let's display all the summary data
print('SERIES: {}'.format(summary['series']))
print('Number of items: {:,}'.format(summary['total_items']))
print('Access status:')
for status, total in summary['access_counts'].items():
print(' {}: {:,}'.format(status, total))
print('Contents dates: {} to {}'.format(summary['date_from'], summary['date_to']))
print('Digitised files: {:,}'.format(summary['digitised_files']))
print('Digitised pages: {:,}'.format(summary['digitised_pages']))
```
Note that a slightly enhanced version of the code above is available in the `series_details` module that you can import into any notebook. So to create a summary of a series you can just:
```
# Import the module
import series_details
# Call display_series() providing the series name and the dataframe
series_details.display_summary(series, df)
```
## Plot the contents dates
Plotting the dates is a bit tricky. Each file can have both a start date and an end date. So if we want to plot the years covered by a file, we need to include all the years between the start and end dates. Also dates can be recorded at different levels of granularity, for specific days to just years. And sometimes there are no end dates recorded at all – what does this mean?
The code in the cell below does a few things:
* It fills any empty end dates with the start date from the same item. This probably means some content years will be missed, but it's the only date we can be certain of.
* It loops through all the rows in the dataframe, then for each row it extracts the years between the start and end date. Currently this looks to see if the 1 January is covered by the date range, so if there's an exact start date after 1 January I don't think it will be captured. I need to investigate this further.
* It combines all of the years into one big series and then totals up the frquency of each year.
I'm sure this is not perfect, but it seems to produce useful results.
```
# Fill any blank end dates with start dates
df['end_date'] = df[['end_date']].apply(lambda x: x.fillna(value=df['start_date']))
# This is a bit tricky.
# For each item we want to find the years that it has content from -- ie start_year <= year <= end_year.
# Then we want to put all the years from all the items together and look at their frequency
years = []
for row in df.itertuples(index=False):
try:
years_in_range = pd.date_range(start=row.start_date, end=row.end_date, freq='AS').year.to_series()
except ValueError:
# No start date
pass
else:
years.append(years_in_range)
year_counts = pd.concat(years).value_counts()
# Put the resulting series in a dataframe so it looks pretty.
year_totals = pd.DataFrame(year_counts)
# Sort results by year
year_totals.sort_index(inplace=True)
# Display the results
year_totals.style.format({0: '{:,}'})
# Let's graph the frequency of content years
plotly_data = [go.Bar(
x=year_totals.index.values, # The years are the index
y=year_totals[0]
)]
# Add some labels
layout = go.Layout(
title='Content dates',
xaxis=dict(
title='Year'
),
yaxis=dict(
title='Number of items'
)
)
# Create a chart
fig = go.Figure(data=plotly_data, layout=layout)
py.iplot(fig, filename='series-dates-bar')
```
Note that a slightly enhanced version of the code above is available in the series_details module that you can import into any notebook. So to create a summary of a series you can just:
```
# Import the module
import series_details
# Call plot_series() providing the series name and the dataframe
fig = series_details.plot_dates(df)
py.iplot(fig)
```
## Filter by words in file titles
```
# Find titles containing a particular phrase -- in this case 'wife'
# This creates a new dataframe
# Try changing this to filter for other words
search_term = 'wife'
df_filtered = df.loc[df['title'].str.contains(search_term, case=False)].copy()
df_filtered
# We can plot this filtered dataframe just like the series
fig = series_details.plot_dates(df)
py.iplot(fig)
# Save the new dataframe as a csv
df_filtered.to_csv('../data/RecordSearch/{}-{}.csv'.format(series.replace('/', '-'), search_term))
# Find titles containing one of two words -- ie an OR statement
# Try changing this to filter for other words
df_filtered = df.loc[df['title'].str.contains('chinese', case=False) | df['title'].str.contains(r'\bah\b', case=False)].copy()
df_filtered
```
## Filter by date range
```
start_year = '1920'
end_year = '1930'
df_filtered = df[(df['start_date'] >= start_year) & (df['end_date'] <= end_year)]
df_filtered
```
## N-gram frequencies in file titles
```
# Import TextBlob for text analysis
from textblob import TextBlob
import nltk
stopwords = nltk.corpus.stopwords.words('english')
# Combine all of the file titles into a single string
title_text = a = df['title'].str.lower().str.cat(sep=' ')
blob = TextBlob(title_text)
words = [[word, count] for word, count in blob.lower().word_counts.items() if word not in stopwords]
word_counts = pd.DataFrame(words).rename({0: 'word', 1: 'count'}, axis=1).sort_values(by='count', ascending=False)
word_counts[:25].style.format({'count': '{:,}'}).bar(subset=['count'], color='#d65f5f').set_properties(subset=['count'], **{'width': '300px'})
def get_ngram_counts(text, size):
blob = TextBlob(text)
# Extract n-grams as WordLists, then convert to a list of strings
ngrams = [' '.join(ngram).lower() for ngram in blob.lower().ngrams(size)]
# Convert to dataframe then count values and rename columns
ngram_counts = pd.DataFrame(ngrams)[0].value_counts().rename_axis('ngram').reset_index(name='count')
return ngram_counts
def display_top_ngrams(text, size):
ngram_counts = get_ngram_counts(text, size)
# Display top 25 results as a bar chart
display(ngram_counts[:25].style.format({'count': '{:,}'}).bar(subset=['count'], color='#d65f5f').set_properties(subset=['count'], **{'width': '300px'}))
display_top_ngrams(title_text, 2)
display_top_ngrams(title_text, 4)
```
| true |
code
| 0.524699 | null | null | null | null |
|
# SLU07 - Regression with Linear Regression: Example notebook
# 1 - Writing linear models
In this section you have a few examples on how to implement simple and multiple linear models.
Let's start by implementing the following:
$$y = 1.25 + 5x$$
```
def first_linear_model(x):
"""
Implements y = 1.25 + 5*x
Args:
x : float - input of model
Returns:
y : float - output of linear model
"""
y = 1.25 + 5 * x
return y
first_linear_model(1)
```
You should be thinking that this is too easy. So let's generalize it a bit. We'll write the code for the next equation:
$$ y = a + bx $$
```
def second_linear_model(x, a, b):
"""
Implements y = a + b * x
Args:
x : float - input of model
a : float - intercept of model
b : float - coefficient of model
Returns:
y : float - output of linear model
"""
y = a + b * x
return y
second_linear_model(1, 1.25, 5)
```
Still very simple, right? Now what if we want to have a linear model with multiple variables, such as this one:
$$ y = a + bx_1 + cx_2 + dx_3 $$
You can follow the same logic and just write the following:
```
def first_multiple_linear_model(x_1, x_2, x_3, a, b, c, d):
"""
Implements y = a + b * x_1 + c * x_2 + d * x_3
Args:
x_1 : float - first input of model
x_2 : float - second input of model
x_3 : float - third input of model
a : float - intercept of model
b : float - first coefficient of model
c : float - second coefficient of model
d : float - third coefficient of model
Returns:
y : float - output of linear model
"""
y = a + b * x_1 + c * x_2 + d * x_3
return y
first_multiple_linear_model(1.0, 1.0, 1.0, .5, .2, .1, .4)
```
However, you should already be seeing the problem. The bigger our model gets, the more variables we need to consider, so this is clearly not efficient. Now let's write the generic form for a linear model:
$$ y = w_0 + \sum_{i=1}^{N} w_i x_i$$
And we will implement the inputs and outputs of the model as vectors:
```
def second_multiple_linear_model(x, w):
"""
Implements y = w_0 + sum(x_i*w_i) (where i=1...N)
Args:
x : vector of input features with size N-1
w : vector of model weights with size N
Returns:
y : float - output of linear model
"""
w_0 = w[0]
y = w_0
for i in range(1, len(x)+1):
y += x[i-1]*w[i]
return y
second_multiple_linear_model([1.0, 1.0, 1.0], [.5, .2, .1, .4])
```
You could go even one step further and use numpy to vectorize these computations. You can represent both vectors as numpy arrays and just do the same calculation:
```
import numpy as np
def vectorized_multiple_linear_model(x, w):
"""
Implements y = w_0 + sum(x_i*w_i) (where i=1...N)
Args:
x : numpy array with shape (N-1, ) of inputs
w : numpy array with shape (N, ) of model weights
Returns:
y : float - output of linear model
"""
y = w[0] + x*w[1:]
vectorized_multiple_linear_model(np.array([1.0, 1.0, 1.0]), np.array([.5, .2, .1, .4]))
```
Read more about numpy array and its manipulation at the end of this example notebook. This will be necessary as you will be requested to implement these types of models in a way that they can compute several samples with many features at once.
<br>
<br>
# 2 - Using sklearn's LinearRegression
The following cells show you how to use the LinearRegression solver of the scikitlearn library. We'll start by creating some fake data to use in these examples:
```
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
X = np.arange(-10, 10) + np.random.rand(20)
y = 1.12 + .75 * X + 2. * np.random.rand(20)
plt.xlim((-10, 10))
plt.ylim((-20, 20))
plt.plot(X, y, 'b.')
```
## 2.1 Training the model
We will now use the base data created and show you how to fit the scikitlearn LinearRegression model with the data:
```
from sklearn.linear_model import LinearRegression
# Since our numpy array has only 1 dimension, we need reshape
# it to become a column vector - which corresponds to 1 feature
# and N samples
X = X.reshape(-1, 1)
lr = LinearRegression()
lr.fit(X, y)
```
## 2.2 Coefficients and Intercept
You can get both the coefficients and the intercept from this model:
```
print('Coefficients: {}'.format(lr.coef_))
print('Intercept: {}'.format(lr.intercept_))
```
## 2.3 Making predictions
We can then make prediction with our model and see how they compare with the actual samples:
```
y_pred = lr.predict(X)
plt.xlim((-10, 10))
plt.ylim((-20, 20))
plt.plot(X, y, 'b.')
plt.plot(X, y_pred, 'r-')
```
## 2.4 Evaluating the model
We can also extract the $R^2$ score of this model:
```
print('R² score: %f' % lr.score(X, y))
```
<br>
<br>
# Bonus examples: Numpy utilities
With linear models, we normally have data that can be represented by either vectors or matrices. Even though you don't need advanced algebra knowledge to implement and understand the models presented, it is useful to understand its basics, since most of the computational part is typically implemented from these concepts.
Numpy is a powerful library that allows us to represent our data easily in this format, and already implements a lot of functions to then manipulate or do calculations over our data. In this section we present the basic functions that you should know and will use the most to implement the basic models:
```
import numpy as np
import pandas as pd
```
## a) Pandas to numpy and back
Pandas stores our data in dataframes and series, which are very useful for visualization and even for some specific data operations we want to perform. However, for many algorithms that involve combination of numeric data, the standard form of implementing is by using numpy. Start by seeing how to convert from pandas to numpy and back:
```
df = pd.read_csv('data/polynomial.csv')
df.head()
```
### a.1) Pandas to numpy
Let's transform our first column into a numpy vector. There are two ways of doing this, either by using the `.values` attribute:
```
np_array = df['x'].values
print(np_array[:10])
```
Or by calling the method `.to_numpy()` :
```
np_array = df['x'].to_numpy()
print(np_array[:10])
```
You can also apply this to the full table:
```
np_array = df.values
print(np_array[:5, :])
np_array = df.to_numpy()
print(np_array[:5, :])
```
### a.2) Numpy to pandas
Let's start by defining an array and converting it to a pandas series:
```
np_array = np.array([4., .1, 1., .23, 3.])
pd_series = pd.Series(np_array)
print(pd_series)
```
We can also create several series and concatenate them to create a dataframe:
```
np_array = np.array([4., .1, 1., .23, 3.])
pd_series_1 = pd.Series(np_array, name='A')
pd_series_2 = pd.Series(2 * np_array, name='B')
pd_dataframe = pd.concat((pd_series_1, pd_series_2), axis=1)
pd_dataframe.head()
```
We can also directly convert to a dataframe:
```
np_array = np.array([[1, 2, 3], [4, 5, 6]])
pd_dataframe = pd.DataFrame(np_array)
pd_dataframe.head()
```
However, we might want more detailed names and specific indices. Some ways of achieving this follows:
```
data = np.array([['','Col1','Col2'],
['Row1',1,2],
['Row2',3,4]])
pd_dataframe = pd.DataFrame(data=data[1:,1:], index=data[1:,0], columns=data[0,1:])
pd_dataframe.head()
pd_dataframe = pd.DataFrame(np.array([[4,5,6,7], [1,2,3,4]]), index=range(0, 2), columns=['A', 'B', 'C', 'D'])
pd_dataframe.head()
my_dict = {'A': np.array(['1', '3']), 'B': np.array(['1', '2']), 'C': np.array(['2', '4'])}
pd_dataframe = pd.DataFrame(my_dict)
pd_dataframe.head()
```
## b) Vector and Matrix initialization and shaping
When working with vectors and matrices, we need to be aware of the dimensions of these objects, and how they affect the possible operations perform over them. Numpy allows you to access these dimensions through the shape of the object:
```
v1 = np.array([ .1, 1., 2.])
print('1-d Array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
v2 = np.array([[ .1, 1., 2.]])
print('\n')
print('2-d Row Array: {}'.format(v2))
print('Shape: {}'.format(v2.shape))
v3 = np.array([[ .1], [1.], [2.]])
print('\n')
print('2-d Column Array:\n {}'.format(v3))
print('Shape: {}'.format(v3.shape))
m1 = np.array([[ .1, 3., 4., 1.], [1., .3, .1, .5], [2.,.7, 3.8, .1]])
print('\n')
print('2-d matrix:\n {}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
Another important functionality provided is the possibility of reshaping these objects. For example, we can turn a 1-d array into a row vector:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v1.reshape((1, -1))
print('Old 1-d Array reshaped to row: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
```
Or we can reshape it into a column vector:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v2.reshape((-1, 1))
print('Old 1-d Array reshaped to column: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
```
We can also create specific vectors of 1s, 0s or random numbers with specific shapes from the start. See how to use each in the cells that follow:
```
custom_shape = (3, )
v1_ones = np.ones(custom_shape)
print('1-D Vector of ones: \n{}'.format(v1_ones))
print('Shape: {}'.format(v1_ones.shape))
custom_shape = (5, 1)
v1_zeros = np.zeros(custom_shape)
print('2-D vector of zeros: \n{}'.format(v1_zeros))
print('Shape: {}'.format(v1_zeros.shape))
custom_shape = (5, 3)
v1_rand = np.random.rand(custom_shape[0], custom_shape[1])
print('2-D Matrix of random numbers: \n{}'.format(v1_rand))
print('Shape: {}'.format(v1_rand.shape))
```
## c) Vector and Matrix Concatenation
In this section, you will learn how to concatenate 2 vectors, a matrix and a vector, or 2 matrices.
### c.1) Vector - Vector
Let's start by defining 2 vectors:
```
v1 = np.array([ .1, 1., 2.])
v2 = np.array([5.1, .3, .41, 3. ])
print('1st array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
print('2nd array: {}'.format(v2))
print('Shape: {}'.format(v2.shape))
```
Since vectors only have one dimension with a given size (notice the shape with only one element) we can only concatenate in this dimension, leading to a longer vector:
```
vconcat = np.concatenate((v1, v2))
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
Concatenating vectors is very easy, and since we can only concatenate them in their one dimension, the sizes do not have to match. Now let's move on to a more complex case.
### c.2) Matrix - row vector
When concatenating matrices and vectors we have to take into account their dimensions.
```
v1 = np.array([ .1, 1., 2., 3.])
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: {}'.format(v1))
print('Shape: {}'.format(v1.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
The first thing you need to know is that whatever numpy objects you are trying to concatenate need to have the same dimensions. Run the code below to verify that you can not concatenate directly the vector and matrix:
```
try:
vconcat = np.concatenate((v1, m1))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
So how can we do matrix-vector concatenation?
It is actually quite simple. We'll use the reshape functionality you seen before to add a dimension to the vector.
```
v1_reshaped = v1.reshape((1, v1.shape[0]))
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
```
We've reshaped our vector into a 1-row matrix. Now we can try to perform the same concatenation:
```
vconcat = np.concatenate((v1_reshaped, m1))
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
### c.3) Matrix - column vector
We can also do this procedure with a column vector:
```
v1 = np.array([ .1, 1.])
v1_reshaped = v1.reshape((v1.shape[0], 1))
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
print('Array: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
print('Matrix: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
vconcat = np.concatenate((v1_reshaped, m1), axis=1)
print('Concatenated vector: {}'.format(vconcat))
print('Shape: {}'.format(vconcat.shape))
```
There's yet another restriction when concatenating vectors and matrices. The dimension where we want to concatenate has to share the same size.
See what would happen if we tried to concatenate a smaller vector with the same matrix:
```
v2 = np.array([ .1, 1.])
v2_reshaped = v2.reshape((1, v2.shape[0])) # Row vector as matrix
try:
vconcat = np.concatenate((v2, m1))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
### c.4) Matrix - Matrix
This is just an extension of the previous case, since what we did before was transforming the vector into a matrix where the size of one of the dimensions is 1. So all the same restrictions apply, the arrays must have compatible dimensions. Run the following examples to see this:
```
m1 = np.array([[5.1, .3, .41, 3. ], [5.1, .3, .41, 3. ]])
m2 = np.array([[1., 2., 0., 3. ], [.1, .13, 1., 3. ], [.1, 2., .5, .3 ]])
m3 = np.array([[1., 0. ], [0., 1. ]])
print('Matrix 1: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
print('Matrix 2: \n{}'.format(m2))
print('Shape: {}'.format(m2.shape))
print('Matrix 3: \n{}'.format(m3))
print('Shape: {}'.format(m3.shape))
```
Concatenate m1 and m2 at row level (stack the two matrices):
```
mconcat = np.concatenate((m1, m2))
print('Concatenated matrix:\n {}'.format(mconcat))
print('Shape: {}'.format(mconcat.shape))
```
Concatenate m1 and m2 at column level (joining the two matrices side by side) should produce an error:
```
try:
vconcat = np.concatenate((m1, m2), axis=1)
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
Concatenate m1 and m3 at column level (joining the two matrices side by side):
```
mconcat = np.concatenate((m1, m3), axis=1)
print('Concatenated matrix:\n {}'.format(mconcat))
print('Shape: {}'.format(mconcat.shape))
```
Concatenate m1 and m3 at row level (stack the two matrices) should produce an error:
```
try:
vconcat = np.concatenate((m1, m3))
except Exception as e:
print('Concatenation raised the following error: {}'.format(e))
```
## d) Single matrix operations
In this section we describe a few operations that can be done over matrices:
### d.1) Transpose
A very common operation is the transpose. If you are used to see matrix notation, you should know what this operation is. Take a matrix with 2 dimensions:
$$ X = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} $$
Transposing the matrix is inverting its data with respect to its diagonal:
$$ X^T = \begin{bmatrix} a & c \\ b & d \\ \end{bmatrix} $$
This means that the rows of X will become its columns and vice-versa. You can attain the transpose of a matrix by using either `.T` on a matrix or calling `numpy.transpose`:
```
m1 = np.array([[ .1, 1., 2.], [ 3., .24, 4.], [ 6., 2., 5.]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.transpose()
print('Transposed matrix with `transpose` \n{}'.format(m1_transposed))
m1_transposed = m1.T
print('Transposed matrix with `T` \n{}'.format(m1_transposed))
```
A few examples of non-squared matrices. In these, you'll see that the shape (a, b) gets inverted to (b, a):
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.T
print('Transposed matrix: \n{}'.format(m1_transposed))
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
m1_transposed = m1.T
print('Transposed matrix: \n{}'.format(m1_transposed))
```
For vectors represented as matrices, this means transforming from a row vector (1, N) to a column vector (N, 1) or vice-versa:
```
v1 = np.array([ .1, 1., 2.])
v1_reshaped = v1.reshape((1, -1))
print('Row vector as 2-d array: {}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
v1_transposed = v1_reshaped.T
print('Transposed (column vector as 2-d array): \n{}'.format(v1_transposed))
print('Shape: {}'.format(v1_transposed.shape))
v1 = np.array([ 3., .23, 2., .6])
v1_reshaped = v1.reshape((-1, 1))
print('Column vector as 2-d array: \n{}'.format(v1_reshaped))
print('Shape: {}'.format(v1_reshaped.shape))
v1_transposed = v1_reshaped.T
print('Transposed (row vector as 2-d array): {}'.format(v1_transposed))
print('Shape: {}'.format(v1_transposed.shape))
```
### d.2) Statistics operators
Numpy also allows us to perform several operations over the rows and columns of a matrix, such as:
* Sum
* Mean
* Max
* Min
* ...
The most important thing to take into account when using these is to know exactly in which direction we are performing the operations. We can perform, for example, a `max` operation over the whole matrix, obtaining the max value in all of the matrix values. Or we might want this value for each row, or for each column. Check the following examples:
```
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
```
Operating over all matrix' values:
```
print('Total sum of matrix elements: {}'.format(m1.sum()))
print('Minimum of all matrix elements: {}'.format(m1.max()))
print('Maximum of all matrix elements: {}'.format(m1.min()))
print('Mean of all matrix elements: {}'.format(m1.mean()))
```
Operating across rows - produces a row with the sum/max/min/mean for each column:
```
print('Total sum of matrix elements: {}'.format(m1.sum(axis=0)))
print('Minimum of all matrix elements: {}'.format(m1.max(axis=0)))
print('Maximum of all matrix elements: {}'.format(m1.min(axis=0)))
print('Mean of all matrix elements: {}'.format(m1.mean(axis=0)))
```
Operating across columns - produces a column with the sum/max/min/mean for each row:
```
print('Total sum of matrix elements: {}'.format(m1.sum(axis=1)))
print('Minimum of all matrix elements: {}'.format(m1.max(axis=1)))
print('Maximum of all matrix elements: {}'.format(m1.min(axis=1)))
print('Mean of all matrix elements: {}'.format(m1.mean(axis=1)))
```
As an example, imagine that you have a matrix of shape (n_samples, n_features), where each row represents all the features for one sample. Then , to average over the samples, we do:
```
m1 = np.array([[ .1, 1.], [2., 5.], [ 3., .24], [4., .6]])
print('Initial matrix: \n{}'.format(m1))
print('\n')
print('Sample 1: {}'.format(m1[0, :]))
print('Sample 2: {}'.format(m1[1, :]))
print('Sample 3: {}'.format(m1[2, :]))
print('Sample 4: {}'.format(m1[3, :]))
print('\n')
print('Average over samples: \n{}'.format(m1.mean(axis=0)))
```
Other statistical functions behave in a similar manner, so it is important to know how to work the axis of these objects.
## e) Multiple matrix operations
### e.1) Element wise operations
Several operations available work at the element level, this is, if we have two matrices A and B:
$$ A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} $$
and
$$ B = \begin{bmatrix} e & f \\ g & h \\ \end{bmatrix} $$
an element-wise operation produces a matrix:
$$ Op(A, B) = \begin{bmatrix} Op(a,e) & Op(b,f) \\ Op(c,g) & Op(d,h) \\ \end{bmatrix} $$
You can perform sum and difference, but also element-wise multiplication and division. These are implemented with the regular operators `+`, `-`, `*`, `/`. Check out the examples below:
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
m2 = np.array([[ .1, 4., .25, .1], [ 2., 1.5, .42, -1.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Sum: \n{}'.format(m1 + m2))
print('\n')
print('Difference: \n{}'.format(m1 - m2))
print('\n')
print('Multiplication: \n{}'.format(m1*m2))
print('\n')
print('Division: \n{}'.format(m1/m2))
```
For these operations, ideally your matrices should have the same dimensions. An exception to this is when you have one of the elements that can be [broadcasted](https://numpy.org/doc/stable/user/basics.broadcasting.html) over the other. However we won't cover that in these examples.
### e.2) Matrix multiplication
Although you've seen how to perform element wise multiplication with the basic operation, one of the most common matrix operations is matrix multiplication, where the output is not the result of an element wise combination of its elements, but actually a linear combination between rows of the first matrix nd columns of the second.
In other words, element (i, j) of the resulting matrix is the dot product between row i of the first matrix and column j of the second:

Where the dot product represented breaks down to:
$$ 58 = 1 \times 7 + 2 \times 9 + 3 \times 11 $$
Numpy already provides this function, so check out the following examples:
```
m1 = np.array([[ .1, 1., 2., 5.], [ 3., .24, 4., .6]])
m2 = np.array([[ .1, 4.], [.25, .1], [ 2., 1.5], [.42, -1.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Matrix multiplication: \n{}'.format(np.matmul(m1, m2)))
m1 = np.array([[ .1, 4.], [.25, .1], [ 2., 1.5], [.42, -1.]])
m2 = np.array([[ .1, 1., 2.], [ 3., .24, 4.]])
print('Matrix 1: \n{}'.format(m1))
print('Matrix 2: \n{}'.format(m1))
print('\n')
print('Matrix multiplication: \n{}'.format(np.matmul(m1, m2)))
```
Notice that in both operations the matrix multiplication of shapes `(k, l)` and `(m, n)` yields a matrix of dimensions `(k, n)`. Additionally, for this operation to be possible, the inner dimensions need to match, this is `l == m` . See what happens if we try to multiply matrices with incompatible dimensions:
```
m1 = np.array([[ .1, 4., 3.], [.25, .1, 1.], [ 2., 1.5, .5], [.42, -1., 4.3]])
m2 = np.array([[ .1, 1., 2.], [ 3., .24, 4.]])
print('Matrix 1: \n{}'.format(m1))
print('Shape: {}'.format(m1.shape))
print('Matrix 2: \n{}'.format(m1))
print('Shape: {}'.format(m2.shape))
print('\n')
try:
m3 = np.matmul(m1, m2)
except Exception as e:
print('Matrix multiplication raised the following error: {}'.format(e))
```
| true |
code
| 0.773548 | null | null | null | null |
|
# Compare different DEMs for individual glaciers
For most glaciers in the world there are several digital elevation models (DEM) which cover the respective glacier. In OGGM we have currently implemented 10 different open access DEMs to choose from. Some are regional and only available in certain areas (e.g. Greenland or Antarctica) and some cover almost the entire globe. For more information, visit the [rgitools documentation about DEMs](https://rgitools.readthedocs.io/en/latest/dems.html).
This notebook allows to see which of the DEMs are available for a selected glacier and how they compare to each other. That way it is easy to spot systematic differences and also invalid points in the DEMs.
## Input parameters
This notebook can be run as a script with parameters using [papermill](https://github.com/nteract/papermill), but it is not necessary. The following cell contains the parameters you can choose from:
```
# The RGI Id of the glaciers you want to look for
# Use the original shapefiles or the GLIMS viewer to check for the ID: https://www.glims.org/maps/glims
rgi_id = 'RGI60-11.00897'
# The default is to test for all sources available for this glacier
# Set to a list of source names to override this
sources = None
# Where to write the plots. Default is in the current working directory
plot_dir = ''
# The RGI version to use
# V62 is an unofficial modification of V6 with only minor, backwards compatible modifications
prepro_rgi_version = 62
# Size of the map around the glacier. Currently only 10 and 40 are available
prepro_border = 10
# Degree of processing level. Currently only 1 is available.
from_prepro_level = 1
```
## Check input and set up
```
# The sources can be given as parameters
if sources is not None and isinstance(sources, str):
sources = sources.split(',')
# Plotting directory as well
if not plot_dir:
plot_dir = './' + rgi_id
import os
plot_dir = os.path.abspath(plot_dir)
import pandas as pd
import numpy as np
from oggm import cfg, utils, workflow, tasks, graphics, GlacierDirectory
import xarray as xr
import geopandas as gpd
import salem
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import AxesGrid
import itertools
from oggm.utils import DEM_SOURCES
from oggm.workflow import init_glacier_directories
# Make sure the plot directory exists
utils.mkdir(plot_dir);
# Use OGGM to download the data
cfg.initialize()
cfg.PATHS['working_dir'] = utils.gettempdir(dirname='OGGM-DEMS', reset=True)
cfg.PARAMS['use_intersects'] = False
```
## Download the data using OGGM utility functions
Note that you could reach the same goal by downloading the data manually from https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/rgitopo/
```
# URL of the preprocessed GDirs
gdir_url = 'https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/rgitopo/'
# We use OGGM to download the data
gdir = init_glacier_directories([rgi_id], from_prepro_level=1, prepro_border=10,
prepro_rgi_version='62', prepro_base_url=gdir_url)[0]
```
## Read the DEMs and store them all in a dataset
```
if sources is None:
sources = [src for src in os.listdir(gdir.dir) if src in utils.DEM_SOURCES]
print('RGI ID:', rgi_id)
print('Available DEM sources:', sources)
print('Plotting directory:', plot_dir)
# We use xarray to store the data
ods = xr.Dataset()
for src in sources:
demfile = os.path.join(gdir.dir, src) + '/dem.tif'
with xr.open_rasterio(demfile) as ds:
data = ds.sel(band=1).load() * 1.
ods[src] = data.where(data > -100, np.NaN)
sy, sx = np.gradient(ods[src], gdir.grid.dx, gdir.grid.dx)
ods[src + '_slope'] = ('y', 'x'), np.arctan(np.sqrt(sy**2 + sx**2))
with xr.open_rasterio(gdir.get_filepath('glacier_mask')) as ds:
ods['mask'] = ds.sel(band=1).load()
# Decide on the number of plots and figure size
ns = len(sources)
x_size = 12
n_cols = 3
n_rows = -(-ns // n_cols)
y_size = x_size / n_cols * n_rows
```
## Raw topography data
```
smap = salem.graphics.Map(gdir.grid, countries=False)
smap.set_shapefile(gdir.read_shapefile('outlines'))
smap.set_plot_params(cmap='topo')
smap.set_lonlat_contours(add_tick_labels=False)
smap.set_plot_params(vmin=np.nanquantile([ods[s].min() for s in sources], 0.25),
vmax=np.nanquantile([ods[s].max() for s in sources], 0.75))
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='each',
cbar_location='right',
cbar_pad=0.1
)
for i, s in enumerate(sources):
data = ods[s]
smap.set_data(data)
ax = grid[i]
smap.visualize(ax=ax, addcbar=False, title=s)
if np.isnan(data).all():
grid[i].cax.remove()
continue
cax = grid.cbar_axes[i]
smap.colorbarbase(cax)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_topo_color.png'), dpi=150, bbox_inches='tight')
```
## Shaded relief
```
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='none',
cbar_location='right',
cbar_pad=0.1
)
smap.set_plot_params(cmap='Blues')
smap.set_shapefile()
for i, s in enumerate(sources):
data = ods[s].copy().where(np.isfinite(ods[s]), 0)
smap.set_data(data * 0)
ax = grid[i]
smap.set_topography(data)
smap.visualize(ax=ax, addcbar=False, title=s)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_topo_shade.png'), dpi=150, bbox_inches='tight')
```
## Slope
```
fig = plt.figure(figsize=(x_size, y_size))
grid = AxesGrid(fig, 111,
nrows_ncols=(n_rows, n_cols),
axes_pad=0.7,
cbar_mode='each',
cbar_location='right',
cbar_pad=0.1
)
smap.set_topography();
smap.set_plot_params(vmin=0, vmax=0.7, cmap='Blues')
for i, s in enumerate(sources):
data = ods[s + '_slope']
smap.set_data(data)
ax = grid[i]
smap.visualize(ax=ax, addcbar=False, title=s + ' (slope)')
cax = grid.cbar_axes[i]
smap.colorbarbase(cax)
# take care of uneven grids
if ax != grid[-1]:
grid[-1].remove()
grid[-1].cax.remove()
plt.savefig(os.path.join(plot_dir, 'dem_slope.png'), dpi=150, bbox_inches='tight')
```
## Some simple statistics about the DEMs
```
df = pd.DataFrame()
for s in sources:
df[s] = ods[s].data.flatten()[ods.mask.data.flatten() == 1]
dfs = pd.DataFrame()
for s in sources:
dfs[s] = ods[s + '_slope'].data.flatten()[ods.mask.data.flatten() == 1]
df.describe()
```
## Comparison matrix plot
```
# Table of differences between DEMS
df_diff = pd.DataFrame()
done = []
for s1, s2 in itertools.product(sources, sources):
if s1 == s2:
continue
if (s2, s1) in done:
continue
df_diff[s1 + '-' + s2] = df[s1] - df[s2]
done.append((s1, s2))
# Decide on plot levels
max_diff = df_diff.quantile(0.99).max()
base_levels = np.array([-8, -5, -3, -1.5, -1, -0.5, -0.2, -0.1, 0, 0.1, 0.2, 0.5, 1, 1.5, 3, 5, 8])
if max_diff < 10:
levels = base_levels
elif max_diff < 100:
levels = base_levels * 10
elif max_diff < 1000:
levels = base_levels * 100
else:
levels = base_levels * 1000
levels = [l for l in levels if abs(l) < max_diff]
if max_diff > 10:
levels = [int(l) for l in levels]
levels
smap.set_plot_params(levels=levels, cmap='PuOr', extend='both')
smap.set_shapefile(gdir.read_shapefile('outlines'))
fig = plt.figure(figsize=(14, 14))
grid = AxesGrid(fig, 111,
nrows_ncols=(ns - 1, ns - 1),
axes_pad=0.3,
cbar_mode='single',
cbar_location='right',
cbar_pad=0.1
)
done = []
for ax in grid:
ax.set_axis_off()
for s1, s2 in itertools.product(sources, sources):
if s1 == s2:
continue
if (s2, s1) in done:
continue
data = ods[s1] - ods[s2]
ax = grid[sources.index(s1) * (ns - 1) + sources[1:].index(s2)]
ax.set_axis_on()
smap.set_data(data)
smap.visualize(ax=ax, addcbar=False)
done.append((s1, s2))
ax.set_title(s1 + '-' + s2, fontsize=8)
cax = grid.cbar_axes[0]
smap.colorbarbase(cax);
plt.savefig(os.path.join(plot_dir, 'dem_diffs.png'), dpi=150, bbox_inches='tight')
```
## Comparison scatter plot
```
import seaborn as sns
sns.set(style="ticks")
l1, l2 = (utils.nicenumber(df.min().min(), binsize=50, lower=True),
utils.nicenumber(df.max().max(), binsize=50, lower=False))
def plot_unity(xdata, ydata, **kwargs):
points = np.linspace(l1, l2, 100)
plt.gca().plot(points, points, color='k', marker=None,
linestyle=':', linewidth=3.0)
g = sns.pairplot(df.dropna(how='all', axis=1).dropna(), plot_kws=dict(s=50, edgecolor="C0", linewidth=1));
g.map_offdiag(plot_unity)
for asx in g.axes:
for ax in asx:
ax.set_xlim((l1, l2))
ax.set_ylim((l1, l2))
plt.savefig(os.path.join(plot_dir, 'dem_scatter.png'), dpi=150, bbox_inches='tight')
```
## Table statistics
```
df.describe()
df.corr()
df_diff.describe()
df_diff.abs().describe()
```
## What's next?
- return to the [OGGM documentation](https://docs.oggm.org)
- back to the [table of contents](welcome.ipynb)
| true |
code
| 0.530723 | null | null | null | null |
|
# 📃 Solution of Exercise M6.01
The aim of this notebook is to investigate if we can tune the hyperparameters
of a bagging regressor and evaluate the gain obtained.
We will load the California housing dataset and split it into a training and
a testing set.
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
data, target = fetch_california_housing(as_frame=True, return_X_y=True)
target *= 100 # rescale the target in k$
data_train, data_test, target_train, target_test = train_test_split(
data, target, random_state=0, test_size=0.5)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">If you want a deeper overview regarding this dataset, you can refer to the
Appendix - Datasets description section at the end of this MOOC.</p>
</div>
Create a `BaggingRegressor` and provide a `DecisionTreeRegressor`
to its parameter `base_estimator`. Train the regressor and evaluate its
statistical performance on the testing set using the mean absolute error.
```
from sklearn.metrics import mean_absolute_error
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor
tree = DecisionTreeRegressor()
bagging = BaggingRegressor(base_estimator=tree, n_jobs=-1)
bagging.fit(data_train, target_train)
target_predicted = bagging.predict(data_test)
print(f"Basic mean absolute error of the bagging regressor:\n"
f"{mean_absolute_error(target_test, target_predicted):.2f} k$")
abs(target_test - target_predicted).mean()
```
Now, create a `RandomizedSearchCV` instance using the previous model and
tune the important parameters of the bagging regressor. Find the best
parameters and check if you are able to find a set of parameters that
improve the default regressor still using the mean absolute error as a
metric.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">You can list the bagging regressor's parameters using the <tt class="docutils literal">get_params</tt>
method.</p>
</div>
```
for param in bagging.get_params().keys():
print(param)
from scipy.stats import randint
from sklearn.model_selection import RandomizedSearchCV
param_grid = {
"n_estimators": randint(10, 30),
"max_samples": [0.5, 0.8, 1.0],
"max_features": [0.5, 0.8, 1.0],
"base_estimator__max_depth": randint(3, 10),
}
search = RandomizedSearchCV(
bagging, param_grid, n_iter=20, scoring="neg_mean_absolute_error"
)
_ = search.fit(data_train, target_train)
import pandas as pd
columns = [f"param_{name}" for name in param_grid.keys()]
columns += ["mean_test_score", "std_test_score", "rank_test_score"]
cv_results = pd.DataFrame(search.cv_results_)
cv_results = cv_results[columns].sort_values(by="rank_test_score")
cv_results["mean_test_score"] = -cv_results["mean_test_score"]
cv_results
target_predicted = search.predict(data_test)
print(f"Mean absolute error after tuning of the bagging regressor:\n"
f"{mean_absolute_error(target_test, target_predicted):.2f} k$")
```
We see that the predictor provided by the bagging regressor does not need
much hyperparameter tuning compared to a single decision tree. We see that
the bagging regressor provides a predictor for which tuning the
hyperparameters is not as important as in the case of fitting a single
decision tree.
| true |
code
| 0.701419 | null | null | null | null |
|
## Recommendations with MovieTweetings: Collaborative Filtering
One of the most popular methods for making recommendations is **collaborative filtering**. In collaborative filtering, you are using the collaboration of user-item recommendations to assist in making new recommendations.
There are two main methods of performing collaborative filtering:
1. **Neighborhood-Based Collaborative Filtering**, which is based on the idea that we can either correlate items that are similar to provide recommendations or we can correlate users to one another to provide recommendations.
2. **Model Based Collaborative Filtering**, which is based on the idea that we can use machine learning and other mathematical models to understand the relationships that exist amongst items and users to predict ratings and provide ratings.
In this notebook, you will be working on performing **neighborhood-based collaborative filtering**. There are two main methods for performing collaborative filtering:
1. **User-based collaborative filtering:** In this type of recommendation, users related to the user you would like to make recommendations for are used to create a recommendation.
2. **Item-based collaborative filtering:** In this type of recommendation, first you need to find the items that are most related to each other item (based on similar ratings). Then you can use the ratings of an individual on those similar items to understand if a user will like the new item.
In this notebook you will be implementing **user-based collaborative filtering**. However, it is easy to extend this approach to make recommendations using **item-based collaborative filtering**. First, let's read in our data and necessary libraries.
**NOTE**: Because of the size of the datasets, some of your code cells here will take a while to execute, so be patient!
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tests as t
from scipy.sparse import csr_matrix
from IPython.display import HTML
%matplotlib inline
# Read in the datasets
movies = pd.read_csv('movies_clean.csv')
reviews = pd.read_csv('reviews_clean.csv')
del movies['Unnamed: 0']
del reviews['Unnamed: 0']
print(reviews.head())
```
### Measures of Similarity
When using **neighborhood** based collaborative filtering, it is important to understand how to measure the similarity of users or items to one another.
There are a number of ways in which we might measure the similarity between two vectors (which might be two users or two items). In this notebook, we will look specifically at two measures used to compare vectors:
* **Pearson's correlation coefficient**
Pearson's correlation coefficient is a measure of the strength and direction of a linear relationship. The value for this coefficient is a value between -1 and 1 where -1 indicates a strong, negative linear relationship and 1 indicates a strong, positive linear relationship.
If we have two vectors x and y, we can define the correlation between the vectors as:
$$CORR(x, y) = \frac{\text{COV}(x, y)}{\text{STDEV}(x)\text{ }\text{STDEV}(y)}$$
where
$$\text{STDEV}(x) = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2}$$
and
$$\text{COV}(x, y) = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})$$
where n is the length of the vector, which must be the same for both x and y and $\bar{x}$ is the mean of the observations in the vector.
We can use the correlation coefficient to indicate how alike two vectors are to one another, where the closer to 1 the coefficient, the more alike the vectors are to one another. There are some potential downsides to using this metric as a measure of similarity. You will see some of these throughout this workbook.
* **Euclidean distance**
Euclidean distance is a measure of the straightline distance from one vector to another. Because this is a measure of distance, larger values are an indication that two vectors are different from one another (which is different than Pearson's correlation coefficient).
Specifically, the euclidean distance between two vectors x and y is measured as:
$$ \text{EUCL}(x, y) = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}$$
Different from the correlation coefficient, no scaling is performed in the denominator. Therefore, you need to make sure all of your data are on the same scale when using this metric.
**Note:** Because measuring similarity is often based on looking at the distance between vectors, it is important in these cases to scale your data or to have all data be in the same scale. In this case, we will not need to scale data because they are all on a 10 point scale, but it is always something to keep in mind!
------------
### User-Item Matrix
In order to calculate the similarities, it is common to put values in a matrix. In this matrix, users are identified by each row, and items are represented by columns.

In the above matrix, you can see that **User 1** and **User 2** both used **Item 1**, and **User 2**, **User 3**, and **User 4** all used **Item 2**. However, there are also a large number of missing values in the matrix for users who haven't used a particular item. A matrix with many missing values (like the one above) is considered **sparse**.
Our first goal for this notebook is to create the above matrix with the **reviews** dataset. However, instead of 1 values in each cell, you should have the actual rating.
The users will indicate the rows, and the movies will exist across the columns. To create the user-item matrix, we only need the first three columns of the **reviews** dataframe, which you can see by running the cell below.
```
user_items = reviews[['user_id', 'movie_id', 'rating']]
user_items.head()
```
### Creating the User-Item Matrix
In order to create the user-items matrix (like the one above), I personally started by using a [pivot table](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.pivot_table.html).
However, I quickly ran into a memory error (a common theme throughout this notebook). I will help you navigate around many of the errors I had, and achieve useful collaborative filtering results!
_____
`1.` Create a matrix where the users are the rows, the movies are the columns, and the ratings exist in each cell, or a NaN exists in cells where a user hasn't rated a particular movie. If you get a memory error (like I did), [this link here](https://stackoverflow.com/questions/39648991/pandas-dataframe-pivot-memory-error) might help you!
```
# Create user-by-item matrix
user_by_movie = user_items.groupby(['user_id', 'movie_id'])['rating'].max().unstack()
```
Check your results below to make sure your matrix is ready for the upcoming sections.
```
assert movies.shape[0] == user_by_movie.shape[1], "Oh no! Your matrix should have {} columns, and yours has {}!".format(movies.shape[0], user_by_movie.shape[1])
assert reviews.user_id.nunique() == user_by_movie.shape[0], "Oh no! Your matrix should have {} rows, and yours has {}!".format(reviews.user_id.nunique(), user_by_movie.shape[0])
print("Looks like you are all set! Proceed!")
HTML('<img src="images/greatjob.webp">')
```
`2.` Now that you have a matrix of users by movies, use this matrix to create a dictionary where the key is each user and the value is an array of the movies each user has rated.
```
# Create a dictionary with users and corresponding movies seen
def movies_watched(user_id):
'''
INPUT:
user_id - the user_id of an individual as int
OUTPUT:
movies - an array of movies the user has watched
'''
movies = user_by_movie.loc[user_id][user_by_movie.loc[user_id].isnull() == False].index.values
return movies
def create_user_movie_dict():
'''
INPUT: None
OUTPUT: movies_seen - a dictionary where each key is a user_id and the value is an array of movie_ids
Creates the movies_seen dictionary
'''
n_users = user_by_movie.shape[0]
movies_seen = dict()
for user1 in range(1, n_users+1):
# assign list of movies to each user key
movies_seen[user1] = movies_watched(user1)
return movies_seen
movies_seen = create_user_movie_dict()
```
`3.` If a user hasn't rated more than 2 movies, we consider these users "too new". Create a new dictionary that only contains users who have rated more than 2 movies. This dictionary will be used for all the final steps of this workbook.
```
# Remove individuals who have watched 2 or fewer movies - don't have enough data to make recs
def create_movies_to_analyze(movies_seen, lower_bound=2):
'''
INPUT:
movies_seen - a dictionary where each key is a user_id and the value is an array of movie_ids
lower_bound - (an int) a user must have more movies seen than the lower bound to be added to the movies_to_analyze dictionary
OUTPUT:
movies_to_analyze - a dictionary where each key is a user_id and the value is an array of movie_ids
The movies_seen and movies_to_analyze dictionaries should be the same except that the output dictionary has removed
'''
movies_to_analyze = dict()
for user, movies in movies_seen.items():
if len(movies) > lower_bound:
movies_to_analyze[user] = movies
return movies_to_analyze
movies_to_analyze = create_movies_to_analyze(movies_seen)
# Run the tests below to check that your movies_to_analyze matches the solution
assert len(movies_to_analyze) == 23512, "Oops! It doesn't look like your dictionary has the right number of individuals."
assert len(movies_to_analyze[2]) == 23, "Oops! User 2 didn't match the number of movies we thought they would have."
assert len(movies_to_analyze[7]) == 3, "Oops! User 7 didn't match the number of movies we thought they would have."
print("If this is all you see, you are good to go!")
```
### Calculating User Similarities
Now that you have set up the **movies_to_analyze** dictionary, it is time to take a closer look at the similarities between users. Below is the pseudocode for how I thought about determining the similarity between users:
```
for user1 in movies_to_analyze
for user2 in movies_to_analyze
see how many movies match between the two users
if more than two movies in common
pull the overlapping movies
compute the distance/similarity metric between ratings on the same movies for the two users
store the users and the distance metric
```
However, this took a very long time to run, and other methods of performing these operations did not fit on the workspace memory!
Therefore, rather than creating a dataframe with all possible pairings of users in our data, your task for this question is to look at a few specific examples of the correlation between ratings given by two users. For this question consider you want to compute the [correlation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.corr.html) between users.
`4.` Using the **movies_to_analyze** dictionary and **user_by_movie** dataframe, create a function that computes the correlation between the ratings of similar movies for two users. Then use your function to compare your results to ours using the tests below.
```
def compute_correlation(user1, user2):
'''
INPUT
user1 - int user_id
user2 - int user_id
OUTPUT
the correlation between the matching ratings between the two users
'''
# Pull movies for each user
movies1 = movies_to_analyze[user1]
movies2 = movies_to_analyze[user2]
# Find Similar Movies
sim_movs = np.intersect1d(movies1, movies2, assume_unique=True)
# Calculate correlation between the users
df = user_by_movie.loc[(user1, user2), sim_movs]
corr = df.transpose().corr().iloc[0,1]
return corr #return the correlation
# Test your function against the solution
assert compute_correlation(2,2) == 1.0, "Oops! The correlation between a user and itself should be 1.0."
assert round(compute_correlation(2,66), 2) == 0.76, "Oops! The correlation between user 2 and 66 should be about 0.76."
assert np.isnan(compute_correlation(2,104)), "Oops! The correlation between user 2 and 104 should be a NaN."
print("If this is all you see, then it looks like your function passed all of our tests!")
```
### Why the NaN's?
If the function you wrote passed all of the tests, then you have correctly set up your function to calculate the correlation between any two users.
`5.` But one question is, why are we still obtaining **NaN** values? As you can see in the code cell above, users 2 and 104 have a correlation of **NaN**. Why?
Think and write your ideas here about why these NaNs exist, and use the cells below to do some coding to validate your thoughts. You can check other pairs of users and see that there are actually many NaNs in our data - 2,526,710 of them in fact. These NaN's ultimately make the correlation coefficient a less than optimal measure of similarity between two users.
```
In the denominator of the correlation coefficient, we calculate the standard deviation for each user's ratings. The ratings for user 2 are all the same rating on the movies that match with user 104. Therefore, the standard deviation is 0. Because a 0 is in the denominator of the correlation coefficient, we end up with a **NaN** correlation coefficient. Therefore, a different approach is likely better for this particular situation.
```
```
# Which movies did both user 2 and user 104 see?
set_2 = set(movies_to_analyze[2])
set_104 = set(movies_to_analyze[104])
set_2.intersection(set_104)
# What were the ratings for each user on those movies?
print(user_by_movie.loc[2, set_2.intersection(set_104)])
print(user_by_movie.loc[104, set_2.intersection(set_104)])
```
`6.` Because the correlation coefficient proved to be less than optimal for relating user ratings to one another, we could instead calculate the euclidean distance between the ratings. I found [this post](https://stackoverflow.com/questions/1401712/how-can-the-euclidean-distance-be-calculated-with-numpy) particularly helpful when I was setting up my function. This function should be very similar to your previous function. When you feel confident with your function, test it against our results.
```
def compute_euclidean_dist(user1, user2):
'''
INPUT
user1 - int user_id
user2 - int user_id
OUTPUT
the euclidean distance between user1 and user2
'''
# Pull movies for each user
movies1 = movies_to_analyze[user1]
movies2 = movies_to_analyze[user2]
# Find Similar Movies
sim_movs = np.intersect1d(movies1, movies2, assume_unique=True)
# Calculate euclidean distance between the users
df = user_by_movie.loc[(user1, user2), sim_movs]
dist = np.linalg.norm(df.loc[user1] - df.loc[user2])
return dist #return the euclidean distance
# Read in solution euclidean distances"
import pickle
df_dists = pd.read_pickle("data/Term2/recommendations/lesson1/data/dists.p")
# Test your function against the solution
assert compute_euclidean_dist(2,2) == df_dists.query("user1 == 2 and user2 == 2")['eucl_dist'][0], "Oops! The distance between a user and itself should be 0.0."
assert round(compute_euclidean_dist(2,66), 2) == round(df_dists.query("user1 == 2 and user2 == 66")['eucl_dist'][1], 2), "Oops! The distance between user 2 and 66 should be about 2.24."
assert np.isnan(compute_euclidean_dist(2,104)) == np.isnan(df_dists.query("user1 == 2 and user2 == 104")['eucl_dist'][4]), "Oops! The distance between user 2 and 104 should be 2."
print("If this is all you see, then it looks like your function passed all of our tests!")
```
### Using the Nearest Neighbors to Make Recommendations
In the previous question, you read in **df_dists**. Therefore, you have a measure of distance between each user and every other user. This dataframe holds every possible pairing of users, as well as the corresponding euclidean distance.
Because of the **NaN** values that exist within the correlations of the matching ratings for many pairs of users, as we discussed above, we will proceed using **df_dists**. You will want to find the users that are 'nearest' each user. Then you will want to find the movies the closest neighbors have liked to recommend to each user.
I made use of the following objects:
* df_dists (to obtain the neighbors)
* user_items (to obtain the movies the neighbors and users have rated)
* movies (to obtain the names of the movies)
`7.` Complete the functions below, which allow you to find the recommendations for any user. There are five functions which you will need:
* **find_closest_neighbors** - this returns a list of user_ids from closest neighbor to farthest neighbor using euclidean distance
* **movies_liked** - returns an array of movie_ids
* **movie_names** - takes the output of movies_liked and returns a list of movie names associated with the movie_ids
* **make_recommendations** - takes a user id and goes through closest neighbors to return a list of movie names as recommendations
* **all_recommendations** = loops through every user and returns a dictionary of with the key as a user_id and the value as a list of movie recommendations
```
def find_closest_neighbors(user):
'''
INPUT:
user - (int) the user_id of the individual you want to find the closest users
OUTPUT:
closest_neighbors - an array of the id's of the users sorted from closest to farthest away
'''
# I treated ties as arbitrary and just kept whichever was easiest to keep using the head method
# You might choose to do something less hand wavy
closest_users = df_dists[df_dists['user1']==user].sort_values(by='eucl_dist').iloc[1:]['user2']
closest_neighbors = np.array(closest_users)
return closest_neighbors
def movies_liked(user_id, min_rating=7):
'''
INPUT:
user_id - the user_id of an individual as int
min_rating - the minimum rating considered while still a movie is still a "like" and not a "dislike"
OUTPUT:
movies_liked - an array of movies the user has watched and liked
'''
movies_liked = np.array(user_items.query('user_id == @user_id and rating > (@min_rating -1)')['movie_id'])
return movies_liked
def movie_names(movie_ids):
'''
INPUT
movie_ids - a list of movie_ids
OUTPUT
movies - a list of movie names associated with the movie_ids
'''
movie_lst = list(movies[movies['movie_id'].isin(movie_ids)]['movie'])
return movie_lst
def make_recommendations(user, num_recs=10):
'''
INPUT:
user - (int) a user_id of the individual you want to make recommendations for
num_recs - (int) number of movies to return
OUTPUT:
recommendations - a list of movies - if there are "num_recs" recommendations return this many
otherwise return the total number of recommendations available for the "user"
which may just be an empty list
'''
# I wanted to make recommendations by pulling different movies than the user has already seen
# Go in order from closest to farthest to find movies you would recommend
# I also only considered movies where the closest user rated the movie as a 9 or 10
# movies_seen by user (we don't want to recommend these)
movies_seen = movies_watched(user)
closest_neighbors = find_closest_neighbors(user)
# Keep the recommended movies here
recs = np.array([])
# Go through the neighbors and identify movies they like the user hasn't seen
for neighbor in closest_neighbors:
neighbs_likes = movies_liked(neighbor)
#Obtain recommendations for each neighbor
new_recs = np.setdiff1d(neighbs_likes, movies_seen, assume_unique=True)
# Update recs with new recs
recs = np.unique(np.concatenate([new_recs, recs], axis=0))
# If we have enough recommendations exit the loop
if len(recs) > num_recs-1:
break
# Pull movie titles using movie ids
recommendations = movie_names(recs)
return recommendations
def all_recommendations(num_recs=10):
'''
INPUT
num_recs (int) the (max) number of recommendations for each user
OUTPUT
all_recs - a dictionary where each key is a user_id and the value is an array of recommended movie titles
'''
# All the users we need to make recommendations for
users = np.unique(df_dists['user1'])
n_users = len(users)
#Store all recommendations in this dictionary
all_recs = dict()
# Make the recommendations for each user
for user in users:
all_recs[user] = make_recommendations(user, num_recs)
return all_recs
all_recs = all_recommendations(10)
# This loads our solution dictionary so you can compare results - FULL PATH IS "data/Term2/recommendations/lesson1/data/all_recs.p"
all_recs_sol = pd.read_pickle("data/Term2/recommendations/lesson1/data/all_recs.p")
assert all_recs[2] == make_recommendations(2), "Oops! Your recommendations for user 2 didn't match ours."
assert all_recs[26] == make_recommendations(26), "Oops! It actually wasn't possible to make any recommendations for user 26."
assert all_recs[1503] == make_recommendations(1503), "Oops! Looks like your solution for user 1503 didn't match ours."
print("If you made it here, you now have recommendations for many users using collaborative filtering!")
HTML('<img src="images/greatjob.webp">')
```
### Now What?
If you made it this far, you have successfully implemented a solution to making recommendations using collaborative filtering.
`8.` Let's do a quick recap of the steps taken to obtain recommendations using collaborative filtering.
```
# Check your understanding of the results by correctly filling in the dictionary below
a = "pearson's correlation and spearman's correlation"
b = 'item based collaborative filtering'
c = "there were too many ratings to get a stable metric"
d = 'user based collaborative filtering'
e = "euclidean distance and pearson's correlation coefficient"
f = "manhattan distance and euclidean distance"
g = "spearman's correlation and euclidean distance"
h = "the spread in some ratings was zero"
i = 'content based recommendation'
sol_dict = {
'The type of recommendation system implemented here was a ...': d,
'The two methods used to estimate user similarity were: ': e,
'There was an issue with using the correlation coefficient. What was it?': h
}
t.test_recs(sol_dict)
```
Additionally, let's take a closer look at some of the results. There are two solution files that you read in to check your results, and you created these objects
* **df_dists** - a dataframe of user1, user2, euclidean distance between the two users
* **all_recs_sol** - a dictionary of all recommendations (key = user, value = list of recommendations)
`9.` Use these two objects along with the cells below to correctly fill in the dictionary below and complete this notebook!
```
a = 567
b = 1503
c = 1319
d = 1325
e = 2526710
f = 0
g = 'Use another method to make recommendations - content based, knowledge based, or model based collaborative filtering'
sol_dict2 = {
'For how many pairs of users were we not able to obtain a measure of similarity using correlation?': e,
'For how many pairs of users were we not able to obtain a measure of similarity using euclidean distance?': f,
'For how many users were we unable to make any recommendations for using collaborative filtering?': c,
'For how many users were we unable to make 10 recommendations for using collaborative filtering?': d,
'What might be a way for us to get 10 recommendations for every user?': g
}
t.test_recs2(sol_dict2)
# Use the cells below for any work you need to do!
# Users without recs
users_without_recs = []
for user, movie_recs in all_recs.items():
if len(movie_recs) == 0:
users_without_recs.append(user)
len(users_without_recs)
# NaN euclidean distance values
df_dists['eucl_dist'].isnull().sum()
# Users with fewer than 10 recs
users_with_less_than_10recs = []
for user, movie_recs in all_recs.items():
if len(movie_recs) < 10:
users_with_less_than_10recs.append(user)
len(users_with_less_than_10recs)
```
| true |
code
| 0.487124 | null | null | null | null |
|
# Figure 4: NIRCam Grism + Filter Sensitivities ($1^{st}$ order)
***
### Table of Contents
1. [Information](#Information)
2. [Imports](#Imports)
3. [Data](#Data)
4. [Generate the First Order Grism + Filter Sensitivity Plot](#Generate-the-First-Order-Grism-+-Filter-Sensitivity-Plot)
5. [Issues](#Issues)
6. [About this Notebook](#About-this-Notebook)
***
## Information
#### JDox links:
* [NIRCam Grisms](https://jwst-docs.stsci.edu/display/JTI/NIRCam+Grisms#NIRCamGrisms-Sensitivity)
* Figure 4. NIRCam grism + filter sensitivities ($1^{st}$ order)
## Imports
```
import os
import pylab
import numpy as np
from astropy.io import ascii, fits
from astropy.table import Table
from scipy.optimize import fmin
from scipy.interpolate import interp1d
import requests
import matplotlib.pyplot as plt
%matplotlib inline
```
## Data
#### Data Location:
The data is stored in a NIRCam JDox Box folder here:
[ST-INS-NIRCAM -> JDox -> nircam_grisms](https://stsci.box.com/s/wu9mo54vi957x50rdirlcg9zkkr3xiaw)
```
files = [('https://stsci.box.com/shared/static/i0a9dkp02nnuw6w0xcfd7b42ctxfb8es.fits', 'NIRCam.F250M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/vfnyk9veote92dz1edpbu83un5n20rsw.fits', 'NIRCam.F250M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/ssvltwzt7f4y5lfvch2o1prdk5hb2gz2.fits', 'NIRCam.F250M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/56wjvzx1jf2i5yg7l1gg77vtvi01ec5p.fits', 'NIRCam.F250M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/v1621dcm44be21n381mbgd2hzxxqrb2e.fits', 'NIRCam.F277W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/8slec91wj6ety6d8qvest09msklpypi8.fits', 'NIRCam.F277W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/r42hdv64x6skqqszv24qkxohiijitqcf.fits', 'NIRCam.F277W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/3vye6ni05i3kdqyd5vs1jk2q59yyms2e.fits', 'NIRCam.F277W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/twcxbe6lxrjckqph980viiijv8fpmm8b.fits', 'NIRCam.F300M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/bpvluysg3zsl3q4b4l5rj5nue84ydjem.fits', 'NIRCam.F300M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/15x7rbwngsxiubbexy7zcezxqm3ndq54.fits', 'NIRCam.F300M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/a7tqdp0feqcttw3d9vaioy7syzfsftz6.fits', 'NIRCam.F300M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/i76sb53pthieh4kn62fpxhcxn8lreffj.fits', 'NIRCam.F322W2.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/wgbyfi3ofs7i19b7zsf2iceupzkbkokq.fits', 'NIRCam.F322W2.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/jhk3deym5wbc68djtcahy3otk2xfjdb5.fits', 'NIRCam.F322W2.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/zu3xqnicbyfjn54yb4kgzvnglanf13ak.fits', 'NIRCam.F322W2.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e2srtf52wnh6vvxsy2aiknbcr8kx2xr5.fits', 'NIRCam.F335M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/bav3tswdd7lemsyd53bnpj4b6yke5bgd.fits', 'NIRCam.F335M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/81wm768mjemzj84w1ogzqddgmrk3exvt.fits', 'NIRCam.F335M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/fhopmyongqifibdtwt3qr682lwdjaf7a.fits', 'NIRCam.F335M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/j9gd8bclethgex40o7qi1e79hgj2hsyt.fits', 'NIRCam.F356W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/s23novi3p6qwm9f9hj9wutgju08be776.fits', 'NIRCam.F356W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/41fnmswn1ttnwts6jj5fu73m4hs6icxd.fits', 'NIRCam.F356W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/wx3rvjt0mvf0hnhv4wvqcmxu61gamwmm.fits', 'NIRCam.F356W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e0p6vkiow4jlp49deqkji9kekzdt4oon.fits', 'NIRCam.F360M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/xbh0rjjvxn0x22k9ktiyikol7c4ep6ka.fits', 'NIRCam.F360M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/e7artuotyv8l9wfoa3rk1k00o5mv8so8.fits', 'NIRCam.F360M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/9r5bmick13ti22l6hcsw0uod75vqartw.fits', 'NIRCam.F360M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/tqd1uqsf8nj12he5qa3hna0zodnlzfea.fits', 'NIRCam.F410M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/4szffesvswh0h8fjym5m5ht37sj0jzrl.fits', 'NIRCam.F410M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/iur0tpbts23lc5rn5n0tplzndlkoudel.fits', 'NIRCam.F410M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/rvz8iznsnl0bsjrqiw7rv74jj24b0otb.fits', 'NIRCam.F410M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/sv3g82qbb4u2umksgu5zdl7rp569sdi7.fits', 'NIRCam.F430M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/mmqv1pkuzpj6abtufxxfo960z2v1oygc.fits', 'NIRCam.F430M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/84q83haic2h6eq5c6p2frkybz551hp8d.fits', 'NIRCam.F430M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/3osceplhq6kmvmm2a72jsgrg6z1ggw1p.fits', 'NIRCam.F430M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/kitx7gdo5kool6jus2g19vdy7q7hmxck.fits', 'NIRCam.F444W.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/ug7y93v0en9c84hfp6d3vtjogmjou9u3.fits', 'NIRCam.F444W.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/0p9h9ofayq8q6dbfsccf3tn5lvxxod9i.fits', 'NIRCam.F444W.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/34hbqzibt5h72hm0rj9wylttj7m9wd19.fits', 'NIRCam.F444W.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/vj0rkyebg0afny1khdyiho4mktmtsi1q.fits', 'NIRCam.F460M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/ky1z1dpewsjqab1o9hstihrec7h52oq4.fits', 'NIRCam.F460M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/s93cwpcvnxfjwqbulnkh9ts9ln0fu9cz.fits', 'NIRCam.F460M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/1178in8zg462es1fkl0mgcbpgp6kgb6t.fits', 'NIRCam.F460M.R.B.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/b855uj293klac8hnoqhrnv8ei0rcvudj.fits', 'NIRCam.F480M.R.A.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/werzjlp3ybxk2ovg6u689zsfpts2t8w3.fits', 'NIRCam.F480M.R.A.2nd.sensitivity.fits'),
('https://stsci.box.com/shared/static/yrh5mylru1upbo5rifbz77acn8k1ud6i.fits', 'NIRCam.F480M.R.B.1st.sensitivity.fits'),
('https://stsci.box.com/shared/static/oxu6jsg9cn9yqkh3nh646fx0flhw8rej.fits', 'NIRCam.F480M.R.B.2nd.sensitivity.fits')]
def download_file(url, file_name, output_directory='./', overwrite=False):
"""Download a file from Box given the direct URL
Parameters
----------
url : str
URL to the file to be downloaded
file_name : str
The name of the file being downloaded
output_directory : str
Directory to download file_name into
overwrite : str
If False and the file to download already exists, the download
will be skipped. If True, the file will be downloaded regardless
of whether it already exists in output_directory
Returns
-------
download_filename : str
Name of the downloaded file
"""
download_filename = os.path.join(output_directory, file_name)
if not os.path.isfile(download_filename) or overwrite is True:
print("Downloading {}".format(file_name))
with requests.get(url, stream=True) as response:
if response.status_code != 200:
raise RuntimeError("Wrong URL - {}".format(url))
with open(download_filename, 'wb') as f:
for chunk in response.iter_content(chunk_size=2048):
if chunk:
f.write(chunk)
else:
print("{} already exists. Skipping download.".format(download_filename))
return download_filename
```
#### Load the data
(The next cell assumes you downloaded the data into your ```Users/$(logname)/``` home directory)
```
if os.environ.get('LOGNAME') is None:
raise ValueError("WARNING: LOGNAME environment variable not set!")
box_directory = os.path.join("/Users/", os.environ['LOGNAME'], "box_data")
box_directory
if not os.path.isdir(box_directory):
try:
os.mkdir(box_directory)
except:
raise OSError("Unable to create {}".format(box_directory))
for file_info in files:
file_url, filename = file_info
outfile = download_file(file_url, filename, output_directory=box_directory)
grism = "R"
mod = "A"
filters = ["F250M","F277W","F300M","F322W2","F335M","F356W","F360M","F410M","F430M","F444W","F460M","F480M"]
filenames = []
for fil in filters:
filenames.append(os.path.join(box_directory, "NIRCam.%s.%s.%s.1st.sensitivity.fits" % (fil,grism,mod)))
filenames
```
## Generate the First Order Grism + Filter Sensitivity Plot
### Define some convenience functions
```
def find_nearest(array,value):
idx = (np.abs(array-value)).argmin()
return array[idx]
def find_nearest(array,value):
idx = (np.abs(array-value)).argmin()
return array[idx]
def find_mid(w,s,w0,thr=0.05):
fct = interp1d(w,s,bounds_error=None,fill_value='extrapolate')
def func(x):
#print "x:",x
return np.abs(fct(x)-thr)
res = fmin(func,w0)
return res[0]
```
### Create the plots
```
f, ax1 = plt.subplots(1, figsize=(15, 10))
NUM_COLORS = len(filters)
cm = pylab.get_cmap('tab10')
grism = "R"
mod = "A"
for i,fname in zip(range(NUM_COLORS),filenames):
color = cm(1.*i/NUM_COLORS)
d = fits.open(fname)
w = d[1].data["WAVELENGTH"]
s = d[1].data["SENSITIVITY"]/(1e17)
ax1.plot(w,s,label=fil,lw=4,color=color)
ax1.legend(fontsize=16)
miny,maxy = ax1.get_ylim()
minx,maxx = ax1.get_xlim()
ax1.set_ylim(miny,2.15)
ax1.set_xlim(2.1,maxx)
ax1.tick_params(labelsize=18)
f.text(0.5, 0.04, 'Wavelength ($\mu m$)', ha='center', fontsize=22)
f.text(0.03, 0.5, 'Sensitivity ('+r'$1 \times 10^{17}\ \frac{e^{-} s^{-1}}{erg s^{-1} cm^{-2} A^{-1}}$'+')', va='center', rotation='vertical', fontsize=22)
```
### Figure option 2: filter name positions
```
f, ax1 = plt.subplots(1, figsize=(15, 10))
thr = 0.05 # 5% of peak boundaries
NUM_COLORS = len(filters)
cm = pylab.get_cmap('tab10')
for i,fil,fname in zip(range(NUM_COLORS),filters,filenames):
color = cm(1.*i/NUM_COLORS)
d = fits.open(fname)
w = d[1].data["WAVELENGTH"]
s = d[1].data["SENSITIVITY"]/(1e17)
wmin,wmax = np.min(w),np.max(w)
vg = w<(wmax+wmin)/2.
w1 = find_mid(w[vg],s[vg],wmin,thr)
vg = w>(wmax+wmin)/2.
w2 = find_mid(w[vg],s[vg],wmax,thr)
if fil == 'F356W':
ax1.text((w2+w1)/2 -0.04, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.25, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F335M':
ax1.text((w2+w1)/2 -0.03, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.22, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F460M':
ax1.text((w2+w1)/2+0.15, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.12, fil, ha='center',color=color,fontsize=16,weight='bold')
elif fil == 'F480M':
ax1.text((w2+w1)/2+0.15, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.1, fil, ha='center',color=color,fontsize=16,weight='bold')
else:
ax1.text((w2+w1)/2 -0.04, s[np.where(w == find_nearest(w, (w2+w1)/2))]+0.2, fil, ha='center',color=color,fontsize=16,weight='bold')
ax1.plot(w,s,label=fil,lw=4,color=color)
miny,maxy = ax1.get_ylim()
minx,maxx = ax1.get_xlim()
ax1.set_ylim(miny,2.15)
ax1.set_xlim(2.1,maxx)
ax1.tick_params(labelsize=18)
f.text(0.5, 0.04, 'Wavelength ($\mu m$)', ha='center', fontsize=22)
f.text(0.03, 0.5, 'Sensitivity ('+r'$1 \times 10^{17}\ \frac{e^{-} s^{-1}}{erg\ s^{-1} cm^{-2} A^{-1}}$'+')', va='center', rotation='vertical', fontsize=22)
```
## Issues
* None
## About this Notebook
**Authors:**
Nor Pirzkal & Alicia Canipe
**Updated On:**
April 10, 2019
| true |
code
| 0.409044 | null | null | null | null |
|
# Solution based on Multiple Models
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
```
# Tokenize and Numerize - Make it ready
```
training_size = 20000
training_sentences = sentences[0:training_size]
testing_sentences = sentences[training_size:]
training_labels = labels[0:training_size]
testing_labels = labels[training_size:]
vocab_size = 1000
max_length = 120
embedding_dim = 16
trunc_type='post'
padding_type='post'
oov_tok = "<OOV>"
tokenizer = Tokenizer(num_words=vocab_size, oov_token=oov_tok)
tokenizer.fit_on_texts(training_sentences)
word_index = tokenizer.word_index
training_sequences = tokenizer.texts_to_sequences(training_sentences)
training_padded = pad_sequences(training_sequences,
maxlen=max_length,
padding=padding_type,
truncating=trunc_type)
testing_sequences = tokenizer.texts_to_sequences(testing_sentences)
testing_padded = pad_sequences(testing_sequences,
maxlen=max_length,
padding=padding_type,
truncating=trunc_type)
```
# Plot
```
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
```
## Function to train and show
```
def fit_model_and_show_results (model, reviews):
model.summary()
history = model.fit(training_padded,
training_labels_final,
epochs=num_epochs,
validation_data=(validation_padded, validation_labels_final))
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
predict_review(model, reviews)
```
# ANN Embedding
```
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.GlobalAveragePooling1D(),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
model.summary()
num_epochs = 20
history = model.fit(training_padded, training_labels_final, epochs=num_epochs,
validation_data=(validation_padded, validation_labels_final))
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
```
# CNN
```
num_epochs = 30
model_cnn = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Conv1D(16, 5, activation='relu'),
tf.keras.layers.GlobalMaxPooling1D(),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# Default learning rate for the Adam optimizer is 0.001
# Let's slow down the learning rate by 10.
learning_rate = 0.0001
model_cnn.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_cnn, new_reviews)
```
# GRU
```
num_epochs = 30
model_gru = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.GRU(32)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.00003 # slower than the default learning rate
model_gru.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_gru, new_reviews)
```
# Bidirectional LSTM
```
num_epochs = 30
model_bidi_lstm = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.00003
model_bidi_lstm.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_bidi_lstm, new_reviews)
```
# Multiple bidirectional LSTMs
```
num_epochs = 30
model_multiple_bidi_lstm = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, embedding_dim, input_length=max_length),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim,
return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(embedding_dim)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
learning_rate = 0.0003
model_multiple_bidi_lstm.compile(loss='binary_crossentropy',
optimizer=tf.keras.optimizers.Adam(learning_rate),
metrics=['accuracy'])
fit_model_and_show_results(model_multiple_bidi_lstm, new_reviews)
```
# Prediction
Define a function to prepare the new reviews for use with a model
and then use the model to predict the sentiment of the new reviews
```
def predict_review(model, reviews):
# Create the sequences
padding_type='post'
sample_sequences = tokenizer.texts_to_sequences(reviews)
reviews_padded = pad_sequences(sample_sequences,
padding=padding_type,
maxlen=max_length)
classes = model.predict(reviews_padded)
for x in range(len(reviews_padded)):
print(reviews[x])
print(classes[x])
print('\n')
```
## How to use examples
more_reviews = [review1, review2, review3, review4, review5, review6, review7,
review8, review9, review10]
predict_review(model, new_reviews)
```
print("============================\n","Embeddings only:\n", "============================")
predict_review(model, more_reviews)
print("============================\n","With CNN\n", "============================")
predict_review(model_cnn, more_reviews)
print("===========================\n","With bidirectional GRU\n", "============================")
predict_review(model_gru, more_reviews)
print("===========================\n", "With a single bidirectional LSTM:\n", "===========================")
predict_review(model_bidi_lstm, more_reviews)
print("===========================\n", "With multiple bidirectional LSTM:\n", "==========================")
predict_review(model_multiple_bidi_lstm, more_reviews)
```
| true |
code
| 0.75985 | null | null | null | null |
|
# **OPTICS Algorithm**
Ordering Points to Identify the Clustering Structure (OPTICS) is a Clustering Algorithm which locates region of high density that are seperated from one another by regions of low density.
For using this library in Python this comes under Scikit Learn Library.
## Parameters:
**Reachability Distance** -It is defined with respect to another data point q(Let). The Reachability distance between a point p and q is the maximum of the Core Distance of p and the Euclidean Distance(or some other distance metric) between p and q. Note that The Reachability Distance is not defined if q is not a Core point.<br><br>
**Core Distance** – It is the minimum value of radius required to classify a given point as a core point. If the given point is not a Core point, then it’s Core Distance is undefined.
## OPTICS Pointers
<ol>
<li>Produces a special order of the database with respect to its density-based clustering structure.This cluster-ordering contains info equivalent to the density-based clustering corresponding to a broad range of parameter settings.</li>
<li>Good for both automatic and interactive cluster analysis, including finding intrinsic clustering structure</li>
<li>Can be represented graphically or using visualization technique</li>
</ol>
In this file , we will showcase how a basic OPTICS Algorithm works in Python , on a randomly created Dataset.
## Importing Libraries
```
import matplotlib.pyplot as plt #Used for plotting graphs
from sklearn.datasets import make_blobs #Used for creating random dataset
from sklearn.cluster import OPTICS #OPTICS is provided under Scikit-Learn Extra
from sklearn.metrics import silhouette_score #silhouette score for checking accuracy
import numpy as np
import pandas as pd
```
## Generating Data
```
data, clusters = make_blobs(
n_samples=800, centers=4, cluster_std=0.3, random_state=0
)
# Originally created plot with data
plt.scatter(data[:,0], data[:,1])
plt.show()
```
## Model Creation
```
# Creating OPTICS Model
optics_model = OPTICS(min_samples=50, xi=.05, min_cluster_size=.05)
#min_samples : The number of samples in a neighborhood for a point to be considered as a core point.
#xi : Determines the minimum steepness on the reachability plot that constitutes a cluster boundary
#min_cluster_size : Minimum number of samples in an OPTICS cluster, expressed as an absolute number or a fraction of the number of samples
pred =optics_model.fit(data) #Fitting the data
optics_labels = optics_model.labels_ #storing labels predicted by our model
no_clusters = len(np.unique(optics_labels) ) #determining the no. of unique clusters and noise our model predicted
no_noise = np.sum(np.array(optics_labels) == -1, axis=0)
```
## Plotting our observations
```
print('Estimated no. of clusters: %d' % no_clusters)
print('Estimated no. of noise points: %d' % no_noise)
colors = list(map(lambda x: '#aa2211' if x == 1 else '#120416', optics_labels))
plt.scatter(data[:,0], data[:,1], c=colors, marker="o", picker=True)
plt.title(f'OPTICS clustering')
plt.xlabel('Axis X[0]')
plt.ylabel('Axis X[1]')
plt.show()
# Generate reachability plot , this helps understand the working of our Model in OPTICS
reachability = optics_model.reachability_[optics_model.ordering_]
plt.plot(reachability)
plt.title('Reachability plot')
plt.show()
```
## Accuracy of OPTICS Clustering
```
OPTICS_score = silhouette_score(data, optics_labels)
OPTICS_score
```
On this randomly created dataset we got an accuracy of 84.04 %
### Hence , we can see the implementation of OPTICS Clustering Algorithm on a randomly created Dataset .As we can observe from our result . the score which we got is around 84% , which is really good for a unsupervised learning algorithm.However , this accuracy definitely comes with the additonal cost of higher computational power
## Thanks a lot!
| true |
code
| 0.708112 | null | null | null | null |
|
```
#import necessary modules, set up the plotting
import numpy as np
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib;matplotlib.rcParams['figure.figsize'] = (8,6)
from matplotlib import pyplot as plt
import GPy
```
# Interacting with models
### November 2014, by Max Zwiessele
#### with edits by James Hensman
The GPy model class has a set of features which are designed to make it simple to explore the parameter space of the model. By default, the scipy optimisers are used to fit GPy models (via model.optimize()), for which we provide mechanisms for ‘free’ optimisation: GPy can ensure that naturally positive parameters (such as variances) remain positive. But these mechanisms are much more powerful than simple reparameterisation, as we shall see.
Along this tutorial we’ll use a sparse GP regression model as example. This example can be in GPy.examples.regression. All of the examples included in GPy return an instance of a model class, and therefore they can be called in the following way:
```
m = GPy.examples.regression.sparse_GP_regression_1D(plot=False, optimize=False)
```
## Examining the model using print
To see the current state of the model parameters, and the model’s (marginal) likelihood just print the model
print m
The first thing displayed on the screen is the log-likelihood value of the model with its current parameters. Below the log-likelihood, a table with all the model’s parameters is shown. For each parameter, the table contains the name of the parameter, the current value, and in case there are defined: constraints, ties and prior distrbutions associated.
```
m
```
In this case the kernel parameters (`bf.variance`, `bf.lengthscale`) as well as the likelihood noise parameter (`Gaussian_noise.variance`), are constrained to be positive, while the inducing inputs have no constraints associated. Also there are no ties or prior defined.
You can also print all subparts of the model, by printing the subcomponents individually; this will print the details of this particular parameter handle:
```
m.rbf
```
When you want to get a closer look into multivalue parameters, print them directly:
```
m.inducing_inputs
m.inducing_inputs[0] = 1
```
## Interacting with Parameters:
The preferred way of interacting with parameters is to act on the parameter handle itself. Interacting with parameter handles is simple. The names, printed by print m are accessible interactively and programatically. For example try to set the kernel's `lengthscale` to 0.2 and print the result:
```
m.rbf.lengthscale = 0.2
print m
```
This will already have updated the model’s inner state: note how the log-likelihood has changed. YOu can immediately plot the model or see the changes in the posterior (`m.posterior`) of the model.
## Regular expressions
The model’s parameters can also be accessed through regular expressions, by ‘indexing’ the model with a regular expression, matching the parameter name. Through indexing by regular expression, you can only retrieve leafs of the hierarchy, and you can retrieve the values matched by calling `values()` on the returned object
```
print m['.*var']
#print "variances as a np.array:", m['.*var'].values()
#print "np.array of rbf matches: ", m['.*rbf'].values()
```
There is access to setting parameters by regular expression, as well. Here are a few examples of how to set parameters by regular expression. Note that each time the values are set, computations are done internally to compute the log likeliood of the model.
```
m['.*var'] = 2.
print m
m['.*var'] = [2., 3.]
print m
```
A handy trick for seeing all of the parameters of the model at once is to regular-expression match every variable:
```
print m['']
```
## Setting and fetching parameters parameter_array
Another way to interact with the model’s parameters is through the parameter_array. The Parameter array holds all the parameters of the model in one place and is editable. It can be accessed through indexing the model for example you can set all the parameters through this mechanism:
```
new_params = np.r_[[-4,-2,0,2,4], [.1,2], [.7]]
print new_params
m[:] = new_params
print m
```
Parameters themselves (leafs of the hierarchy) can be indexed and used the same way as numpy arrays. First let us set a slice of the inducing_inputs:
```
m.inducing_inputs[2:, 0] = [1,3,5]
print m.inducing_inputs
```
Or you use the parameters as normal numpy arrays for calculations:
```
precision = 1./m.Gaussian_noise.variance
print precision
```
## Getting the model parameter’s gradients
The gradients of a model can shed light on understanding the (possibly hard) optimization process. The gradients of each parameter handle can be accessed through their gradient field.:
```
print "all gradients of the model:\n", m.gradient
print "\n gradients of the rbf kernel:\n", m.rbf.gradient
```
If we optimize the model, the gradients (should be close to) zero
```
m.optimize()
print m.gradient
```
## Adjusting the model’s constraints
When we initially call the example, it was optimized and hence the log-likelihood gradients were close to zero. However, since we have been changing the parameters, the gradients are far from zero now. Next we are going to show how to optimize the model setting different restrictions on the parameters.
Once a constraint has been set on a parameter, it is possible to remove it with the command unconstrain(), which can be called on any parameter handle of the model. The methods constrain() and unconstrain() return the indices which were actually unconstrained, relative to the parameter handle the method was called on. This is particularly handy for reporting which parameters where reconstrained, when reconstraining a parameter, which was already constrained:
```
m.rbf.variance.unconstrain()
print m
m.unconstrain()
print m
```
If you want to unconstrain only a specific constraint, you can call the respective method, such as `unconstrain_fixed()` (or `unfix()`) to only unfix fixed parameters:
```
m.inducing_inputs[0].fix()
m.rbf.constrain_positive()
print m
m.unfix()
print m
```
## Tying Parameters
Not yet implemented for GPy version 0.8.0
## Optimizing the model
Once we have finished defining the constraints, we can now optimize the model with the function optimize.:
```
m.Gaussian_noise.constrain_positive()
m.rbf.constrain_positive()
m.optimize()
```
By deafult, GPy uses the lbfgsb optimizer.
Some optional parameters may be discussed here.
* `optimizer`: which optimizer to use, currently there are lbfgsb, fmin_tnc, scg, simplex or any unique identifier uniquely identifying an optimizer.
Thus, you can say m.optimize('bfgs') for using the `lbfgsb` optimizer
* `messages`: if the optimizer is verbose. Each optimizer has its own way of printing, so do not be confused by differing messages of different optimizers
* `max_iters`: Maximum number of iterations to take. Some optimizers see iterations as function calls, others as iterations of the algorithm. Please be advised to look into scipy.optimize for more instructions, if the number of iterations matter, so you can give the right parameters to optimize()
* `gtol`: only for some optimizers. Will determine the convergence criterion, as the tolerance of gradient to finish the optimization.
## Plotting
Many of GPys models have built-in plot functionality. we distringuish between plotting the posterior of the function (`m.plot_f`) and plotting the posterior over predicted data values (`m.plot`). This becomes especially important for non-Gaussian likleihoods. Here we'll plot the sparse GP model we've been working with. for more information of the meaning of the plot, please refer to the accompanying `basic_gp_regression` and `sparse_gp` noteooks.
```
fig = m.plot()
```
We can even change the backend for plotting and plot the model using a different backend.
```
GPy.plotting.change_plotting_library('plotly')
fig = m.plot(plot_density=True)
GPy.plotting.show(fig, filename='gpy_sparse_gp_example')
```
| true |
code
| 0.623692 | null | null | null | null |
|
```
%matplotlib inline
```
# Partial Dependence Plots
Sigurd Carlsen Feb 2019
Holger Nahrstaedt 2020
.. currentmodule:: skopt
Plot objective now supports optional use of partial dependence as well as
different methods of defining parameter values for dependency plots.
```
print(__doc__)
import sys
from skopt.plots import plot_objective
from skopt import forest_minimize
import numpy as np
np.random.seed(123)
import matplotlib.pyplot as plt
```
## Objective function
Plot objective now supports optional use of partial dependence as well as
different methods of defining parameter values for dependency plots
```
# Here we define a function that we evaluate.
def funny_func(x):
s = 0
for i in range(len(x)):
s += (x[i] * i) ** 2
return s
```
## Optimisation using decision trees
We run forest_minimize on the function
```
bounds = [(-1, 1.), ] * 3
n_calls = 150
result = forest_minimize(funny_func, bounds, n_calls=n_calls,
base_estimator="ET",
random_state=4)
```
## Partial dependence plot
Here we see an example of using partial dependence. Even when setting
n_points all the way down to 10 from the default of 40, this method is
still very slow. This is because partial dependence calculates 250 extra
predictions for each point on the plots.
```
_ = plot_objective(result, n_points=10)
```
It is possible to change the location of the red dot, which normally shows
the position of the found minimum. We can set it 'expected_minimum',
which is the minimum value of the surrogate function, obtained by a
minimum search method.
```
_ = plot_objective(result, n_points=10, minimum='expected_minimum')
```
## Plot without partial dependence
Here we plot without partial dependence. We see that it is a lot faster.
Also the values for the other parameters are set to the default "result"
which is the parameter set of the best observed value so far. In the case
of funny_func this is close to 0 for all parameters.
```
_ = plot_objective(result, sample_source='result', n_points=10)
```
## Modify the shown minimum
Here we try with setting the `minimum` parameters to something other than
"result". First we try with "expected_minimum" which is the set of
parameters that gives the miniumum value of the surrogate function,
using scipys minimum search method.
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum',
minimum='expected_minimum')
```
"expected_minimum_random" is a naive way of finding the minimum of the
surrogate by only using random sampling:
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum_random',
minimum='expected_minimum_random')
```
We can also specify how many initial samples are used for the two different
"expected_minimum" methods. We set it to a low value in the next examples
to showcase how it affects the minimum for the two methods.
```
_ = plot_objective(result, n_points=10, sample_source='expected_minimum_random',
minimum='expected_minimum_random',
n_minimum_search=10)
_ = plot_objective(result, n_points=10, sample_source="expected_minimum",
minimum='expected_minimum', n_minimum_search=2)
```
## Set a minimum location
Lastly we can also define these parameters ourself by parsing a list
as the minimum argument:
```
_ = plot_objective(result, n_points=10, sample_source=[1, -0.5, 0.5],
minimum=[1, -0.5, 0.5])
```
| true |
code
| 0.544741 | null | null | null | null |
|
# Tutorial 6.3. Advanced Topics on Extreme Value Analysis
### Description: Some advanced topics on Extreme Value Analysis are presented.
#### Students are advised to complete the exercises.
Project: Structural Wind Engineering WS19-20
Chair of Structural Analysis @ TUM - R. Wüchner, M. Péntek
Author: [email protected], [email protected]
Created on: 24.12.2019
Last update: 08.01.2020
##### Contents:
1. Prediction of the extreme value of a time series - MaxMin Estimation
2. Lieblein's BLUE method
The worksheet is based on the knowledge base and scripts provided by [NIST](https://www.itl.nist.gov/div898/winds/overview.htm) as well as work available from [Christopher Howlett](https://github.com/chowlet5) from UWO.
```
# import
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gumbel_r as gumbel
from ipywidgets import interactive
#external files
from peakpressure import maxminest
from blue4pressure import *
import custom_utilities as c_utils
```
## 1. Prediction of the extreme value of a time series - MaxMin Estimation
#### This method is based on [the procedure (and sample Matlab file](https://www.itl.nist.gov/div898/winds/peakest_files/peakest.htm) by Sadek, F. and Simiu, E. (2002). "Peak non-gaussian wind effects for database-assisted low-rise building design." Journal of Engineering Mechanics, 128(5), 530-539. Please find it [here](https://www.itl.nist.gov/div898/winds/pdf_files/b02030.pdf).
The method uses
* gamma distribution for estimating the peaks corresponding to the longer tail of time series
* normal distribution for estimating the peaks corresponding to the shorter tail of time series
The distribution of the peaks is then estimated by using the standard translation processes approach.
#### implementation details :
INPUT ARGUMENTS:
Each row of *record* is a time series.
The optional input argument *dur_ratio* allows peaks to be estimated for
a duration that differs from the duration of the record itself:
*dur_ratio* = [duration for peak estimation]/[duration of record]
(If unspecified, a value of 1 is used.)
OUTPUT ARGUMENTS:
* *max_est* gives the expected maximum values of each row of *record*
* *min_est* gives the expected minimum values of each row of *record*
* *max_std* gives the standard deviations of the maximum value for each row of *record*
* *min_std* gives the standard deviations of the minimum value for each row of *record*
#### Let us test the method for a given time series
```
# using as sample input some pre-generated generalized extreme value random series
given_series = np.loadtxt('test_data_gevrnd.dat', skiprows=0, usecols = (0,))
# print results
dur_ratio = 1
result = maxminest(given_series, dur_ratio)
maxv = result[0][0][0]
minv = result[1][0][0]
print('estimation of maximum value ', np.around(maxv,3))
print('estimation of minimum value ', np.around(minv,3))
plt.figure(num=1, figsize=(8, 6))
x_series = np.arange(0.0, len(given_series), 1.0)
plt.plot(x_series, given_series)
plt.ylabel('Amplitude')
plt.xlabel('Time [s]')
plt.hlines([maxv, minv], x_series[0], x_series[-1])
plt.title('Predicted extrema')
plt.grid(True)
plt.show()
```
#### Let us plot the pdf and cdf
```
[pdf_x, pdf_y] = c_utils.get_pdf(given_series)
ecdf_y = c_utils.get_ecdf(pdf_x, pdf_y)
plt.figure(num=2, figsize=(16, 6))
plt.subplot(1,2,1)
plt.plot(pdf_x, pdf_y)
plt.ylabel('PDF(Amplitude)')
plt.grid(True)
plt.subplot(1,2,2)
plt.plot(pdf_x, ecdf_y)
plt.vlines([maxv, minv], 0, 1)
plt.ylabel('CDF(Amplitude)')
plt.grid(True)
plt.show()
```
## 2. Lieblein's BLUE method
From a time series of pressure coefficients, *blue4pressure.py* estimates
extremes of positive and negative pressures based on Lieblein's BLUE
(Best Linear Unbiased Estimate) method applied to n epochs.
Extremes are estimated for 1 and dur epochs for probabilities of non-exceedance
P1 and P2 of the Gumbel distribution fitted to the epochal peaks.
*n* = integer, dur need not be an integer.
Written by Dat Duthinh 8_25_2015, 2_2_2016, 2_6_2017.
For further reference check out the material provided by [NIST](https://www.itl.nist.gov/div898/winds/gumbel_blue/gumbblue.htm).
Reference:
1) Julius Lieblein "Efficient Methods of Extreme-Value
Methodology" NBSIR 74-602 OCT 1974 for n = 4:16
2) Nicholas John Cook "The designer's guide to wind loading of
building structures" part 1, British Research Establishment 1985 Table C3
pp. 321-323 for n = 17:24. Extension to n=100 by Adam Pintar Feb 12 2016.
3) INTERNATIONAL STANDARD, ISO 4354 (2009-06-01), 2nd edition, “Wind
actions on structures,” Annex D (informative) “Aerodynamic pressure and
force coefficients,” Geneva, Switzerland, p. 22
#### implementation details :
INPUT ARGUMENTS
* *cp* = vector of time history of pressure coefficients
* *n* = number of epochs (integer)of cp data, 4 <= n <= 100
* *dur* = number of epochs for estimation of extremes. Default dur = n dur need not be an integer
* *P1, P2* = probabilities of non-exceedance of extremes in EV1 (Gumbel), P1 defaults to 0.80 (ISO)and P2 to 0.5704 (mean) for the Gumbel distribution .
OUTPUT ARGUMENTS
* *suffix max* for + peaks, min for - peaks of pressure coeff.
* *p1_max* (p1_min)= extreme value of positive (negative) peaks with probability of non-exceedance P1 for 1 epoch
* *p2_max* (p2_min)= extreme value of positive (negative) peaks with probability of exceedance P2 for 1 epoch
* *p1_rmax* (p1_rmin)= extreme value of positive (negative) peaks with probability of non-exceedance P1 for dur epochs
* *p2_rmax* (p2_rmin)= extreme value of positive (negative) peaks with probability of non-exceedance P2 for for dur epochs
* *cp_max* (cp_min)= vector of n positive (negative) epochal peaks
* *u_max, b_max* (u_min, b_min) = location and scale parameters of EV1 (Gumbel) for positive (negative) peaks
```
# n = number of epochs (integer)of cp data, 4 <= n <= 100
n=4
# P1, P2 = probabilities of non-exceedance of extremes in EV1 (Gumbel).
P1=0.80
P2=0.5704 # this corresponds to the mean of gumbel distribution
# dur = number of epochs for estimation of extremes. Default dur = n
# dur need not be an integer
dur=1
# Call function
result = blue4pressure(given_series, n, P1, P2, dur)
p1_max = result[0][0]
p2_max = result[1][0]
umax = result[4][0] # location parameters
b_max = result[5][0] # sclae parameters
p1_min = result[7][0]
p2_min = result[8][0]
umin = result[11][0] # location parameters
b_min = result[12][0] # scale parameters
# print results
## maximum
print('estimation of maximum value with probability of non excedence of p1', np.around(p1_max,3))
print('estimation of maximum value with probability of non excedence of p2', np.around(p2_max,3))
## minimum
print('estimation of minimum value with probability of non excedence of p1', np.around(p1_min,3))
print('estimation of minimum value with probability of non excedence of p2', np.around(p2_min,3))
```
#### Let us plot the pdf and cdf for the maximum values
```
max_pdf_x = np.linspace(1, 3, 100)
max_pdf_y = gumbel.pdf(max_pdf_x, umax, b_max)
max_ecdf_y = c_utils.get_ecdf(max_pdf_x, max_pdf_y)
plt.figure(num=3, figsize=(16, 6))
plt.subplot(1,2,1)
# PDF generated as a fitted curve using generalized extreme distribution
plt.plot(max_pdf_x, max_pdf_y, label = 'PDF from the fitted Gumbel')
plt.xlabel('Max values')
plt.ylabel('PDF(Amplitude)')
plt.title('PDF of Maxima')
plt.grid(True)
plt.legend()
plt.subplot(1,2,2)
plt.plot(max_pdf_x, max_ecdf_y)
plt.vlines([p1_max, p2_max], 0, 1)
plt.ylabel('CDF(Amplitude)')
plt.grid(True)
plt.show()
```
#### Try plotting these for the minimum values. Discuss among groups the advanced extreme value evaluation methods.
| true |
code
| 0.696784 | null | null | null | null |
|
```
## Advanced Course in Machine Learning
## Week 4
## Exercise 2 / Probabilistic PCA
import numpy as np
import scipy
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from numpy import linalg as LA
sns.set_style("darkgrid")
def build_dataset(N, D, K, sigma=1):
x = np.zeros((D, N))
z = np.random.normal(0.0, 1.0, size=(K, N))
# Create a w with random values
w = np.random.normal(0.0, sigma**2, size=(D, K))
mean = np.dot(w, z)
for d in range(D):
for n in range(N):
x[d, n] = np.random.normal(mean[d, n], sigma**2)
print("True principal axes:")
print(w)
return x, mean, w, z
N = 5000 # number of data points
D = 2 # data dimensionality
K = 1 # latent dimensionality
sigma = 1.0
x, mean, w, z = build_dataset(N, D, K, sigma)
print(z)
print(w)
plt.figure(num=None, figsize=(8, 6), dpi=100, facecolor='w', edgecolor='k')
sns.scatterplot(z[0, :], 0, alpha=0.5, label='z')
origin = [0], [0] # origin point
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='lower right')
plt.title('Probabilistic PCA, generated z')
plt.show()
plt.figure(num=None, figsize=(8, 6), dpi=100, facecolor='w', edgecolor='k')
sns.scatterplot(z[0, :], 0, alpha=0.5, label='z')
sns.scatterplot(mean[0, :], mean[1, :], color='red', alpha=0.5, label='Wz')
origin = [0], [0] # origin point
#Plot the principal axis
plt.quiver(*origin, w[0,0], w[1,0], color=['g'], scale=1, label='W')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='upper right')
plt.title('Probabilistic PCA, generated z')
plt.show()
print(x)
plt.figure(num=None, figsize=(8, 6), dpi=100, facecolor='w', edgecolor='k')
sns.scatterplot(x[0, :], x[1, :], color='orange', alpha=0.5)
#plt.axis([-5, 5, -5, 5])
plt.xlabel('x')
plt.ylabel('y')
#Plot the principal axis
plt.quiver(*origin, w[0,0], w[1,0], color=['g'], scale=10, label='W')
#Plot probability density contours
sns.kdeplot(x[0, :], x[1, :], n_levels=3, color='purple')
plt.title('Probabilistic PCA, generated x')
plt.show()
plt.figure(num=None, figsize=(8, 6), dpi=100, facecolor='w', edgecolor='k')
sns.scatterplot(x[0, :], x[1, :], color='orange', alpha=0.5, label='X')
sns.scatterplot(z[0, :], 0, alpha=0.5, label='z')
sns.scatterplot(mean[0, :], mean[1, :], color='red', alpha=0.5, label='Wz')
origin = [0], [0] # origin point
#Plot the principal axis
plt.quiver(*origin, w[0,0], w[1,0], color=['g'], scale=10, label='W')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='lower right')
plt.title('Probabilistic PCA')
plt.show()
plt.figure(num=None, figsize=(8, 6), dpi=100, facecolor='w', edgecolor='k')
sns.scatterplot(x[0, :], x[1, :], color='orange', alpha=0.5, label='X')
sns.scatterplot(z[0, :], 0, alpha=0.5, label='z')
sns.scatterplot(mean[0, :], mean[1, :], color='red', alpha=0.5, label='Wz')
origin = [0], [0] # origin point
#Plot the principal axis
plt.quiver(*origin, w[0,0], w[1,0], color=['g'], scale=10, label='W')
#Plot probability density contours
sns.kdeplot(x[0, :], x[1, :], n_levels=6, color='purple')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='lower right')
plt.title('Probabilistic PCA')
plt.show()
```
def main():
fig = plt.figure()
scat = plt.scatter(mean[0, :], color='red', alpha=0.5, label='Wz')
ani = animation.FuncAnimation(fig, update_plot, frames=xrange(N),
fargs=(scat))
plt.show()
def update_plot(i, scat):
scat.set_array(data[i])
return scat,
main()
| true |
code
| 0.783357 | null | null | null | null |
|
# 3. Markov Models Example Problems
We will now look at a model that examines our state of healthiness vs. being sick. Keep in mind that this is very much like something you could do in real life. If you wanted to model a certain situation or environment, we could take some data that we have gathered, build a maximum likelihood model on it, and do things like study the properties that emerge from the model, or make predictions from the model, or generate the next most likely state.
Let's say we have 2 states: **sick** and **healthy**. We know that we spend most of our time in a healthy state, so the probability of transitioning from healthy to sick is very low:
$$p(sick \; | \; healthy) = 0.005$$
Hence, the probability of going from healthy to healthy is:
$$p(healthy \; | \; healthy) = 0.995$$
Now, on the other hand the probability of going from sick to sick is also very high. This is because if you just got sick yesterday then you are very likely to be sick tomorrow.
$$p(sick \; | \; sick) = 0.8$$
However, the probability of transitioning from sick to healthy should be higher than the reverse, because you probably won't stay sick for as long as you would stay healthy:
$$p(healthy \; | \; sick) = 0.02$$
We have now fully defined our state transition matrix, and we can now do some calculations.
## 1.1 Example Calculations
### 1.1.1
What is the probability of being healthy for 10 days in a row, given that we already start out as healthy? Well that is:
$$p(healthy \; 10 \; days \; in \; a \; row \; | \; healthy \; at \; t=0) = 0.995^9 = 95.6 \%$$
How about the probability of being healthy for 100 days in a row?
$$p(healthy \; 100 \; days \; in \; a \; row \; | \; healthy \; at \; t=0) = 0.995^{99} = 60.9 \%$$
## 2. Expected Number of Continuously Sick Days
We can now look at the expected number of days that you would remain in the same state (e.g. how many days would you expect to stay sick given the model?). This is a bit more difficult than the last problem, but completely doable, only involving the mathematics of <a href="https://en.wikipedia.org/wiki/Geometric_series">infinite sums</a>.
First, we can look at the probability of being in state $i$, and going to state $i$ in the next state. That is just $A(i,i)$:
$$p \big(s(t)=i \; | \; s(t-1)=i \big) = A(i, i)$$
Now, what is the probability distribution that we actually want to calculate? How about we calculate the probability that we stay in state $i$ for $n$ transitions, at which point we move to another state:
$$p \big(s(t) \;!=i \; | \; s(t-1)=i \big) = 1 - A(i, i)$$
So, the joint probability that we are trying to model is:
$$p\big(s(1)=i, s(2)=i,...,s(n)=i, s(n+1) \;!= i\big) = A(i,i)^{n-1}\big(1-A(i,i)\big)$$
In english this means that we are multiplying the transition probability of staying in the same state, $A(i,i)$, times the number of times we stayed in the same state, $n$, (note it is $n-1$ because we are given that we start in that state, hence there is no transition associated with it) times $1 - A(i,i)$, the probability of transitioning from that state. This leaves us with an expected value for $n$ of:
$$E(n) = \sum np(n) = \sum_{n=1..\infty} nA(i,i)^{n-1}(1-A(i,i))$$
Note, in the above equation $p(n)$ is the probability that we will see state $i$ $n-1$ times after starting from $i$ and then see a state that is not $i$. Also, we know that the expected value of $n$ should be the sum of all possible values of $n$ times $p(n)$.
### 2.1 Expected $n$
So, we can now expand this function and calculate the two sums separately.
$$E(n) = \sum_{n=1..\infty}nA(i,i)^{n-1}(1 - A(i,i)) = \sum nA(i, i)^{n-1} - \sum nA(i,i)^n$$
**First Sum**<br>
With our first sum, we can say that:
$$S = \sum na(i, i)^{n-1}$$
$$S = 1 + 2a + 3a^2 + 4a^3+ ...$$
And we can then multiply that sum, $S$, by $a$, to get:
$$aS = a + 2a^2 + 3a^3 + 4a^4+...$$
And then we can subtract $aS$ from $S$:
$$S - aS = S'= 1 + a + a^2 + a^3+...$$
This $S'$ is another infinite sum, but it is one that is much easier to solve!
$$S'= 1 + a + a^2 + a^3+...$$
And then $aS'$ is:
$$aS' = a + a^2 + a^3+ + a^4 + ...$$
Which, when we then do $S' - aS'$, we end up with:
$$S' - aS' = 1$$
$$S' = \frac{1}{1 - a}$$
And if we then substitute that value in for $S'$ above:
$$S - aS = S'= 1 + a + a^2 + a^3+... = \frac{1}{1 - a}$$
$$S - aS = \frac{1}{1 - a}$$
$$S = \frac{1}{(1 - a)^2}$$
**Second Sum**<br>
We can now look at our second sum:
$$S = \sum na(i,i)^n$$
$$S = 1a + 2a^2 + 3a^3 +...$$
$$Sa = 1a^2 + 2a^3 +...$$
$$S - aS = S' = a + a^2 + a^3 + ...$$
$$aS' = a^2 + a^3 + a^4 +...$$
$$S' - aS' = a$$
$$S' = \frac{a}{1 - a}$$
And we can plug back in $S'$ to get:
$$S - aS = \frac{a}{1 - a}$$
$$S = \frac{a}{(1 - a)^2}$$
**Combine** <br>
We can now combine these two sums as follows:
$$E(n) = \frac{1}{(1 - a)^2} - \frac{a}{(1-a)^2}$$
$$E(n) = \frac{1}{1-a}$$
**Calculate Number of Sick Days**<br>
So, how do we calculate the correct number of sick days? That is just:
$$\frac{1}{1 - 0.8} = 5$$
## 3. SEO and Bounce Rate Optimization
We are now going to look at SEO and Bounch Rate Optimization. This is a problem that every developer and website owner can relate to. You have a website and obviously you would like to increase traffic, increase conversions, and avoid a high bounce rate (which could lead to google assigning your page a low ranking). What would a good way of modeling this data be? Without even looking at any code we can look at some examples of things that we want to know, and how they relate to markov models.
### 3.1 Arrival
First and foremost, how do people arrive on your page? Is it your home page? Your landing page? Well, this is just the very first page of what is hopefully a sequence of pages. So, the markov analogy here is that this is just the initial state distribution or $\pi$. So, once we have our markov model, the $\pi$ vector will tell us which of our pages a user is most likely to start on.
### 3.2 Sequences of Pages
What about sequences of pages? Well, if you think people are getting to your landing page, hitting the buy button, checking out, and then closing the browser window, you can test the validity of that assumption by calculating the probability of that sequence. Of course, the probability of any sequence is probability going to be much less than 1. This is because for a longer sequence, we have more multiplication, and hence smaller final numbers. We do have two alternatives however:
> * 1) You can compare the probability of two different sequences. So, are people going through the entire checkout process? Or is it more probable that they are just bouncing?
* 2) Another option is to just find the transition probabilities themselves. These are conditional probabilities instead of joint probabilities. You want to know, once they have made it to the landing page, what is the probability of hitting buy. Then, once they have hit buy, what is the probability of them completing the checkout.
### 3.3 Bounce Rate
This is hard to measure, unless you are google and hence have analytics on nearly every page on the web. This is because once a user has left your site, you can no longer run code on their computer or track what they are doing. However, let's pretend that we can determine this information. Once we have done this, we can measure which page has the highest bounce rate. At this point we can manually analyze that page and ask our marketing people "what is different about this page that people don't find it useful/want to leave?" We can then address that problem, and the hopefully later analysis shows that the fixed page no longer has a high bounce right. In the markov model, we can just represents this as the null state.
### 3.4 Data
So, the data we are going to be working with has two columns: `last_page_id` and `next_page_id`. This can be interpreted as the current page and the next page. The site has 10 pages with the id's 0-9. We can represent start pages by making the current page -1, and the next page the actual page. We can represent the end of the page with two different codes, `B`(bounce) or `C` (close). In the case of bounce, the user saw the page and then immediately bounced. In the case of close, the user saw the page stayed and potentially saw some useful information, and then closed the window. So, you can imagine that our engineer may use time as a factor in determining if it is a bounce or a close.
```
import numpy as np
import pandas as pd
"""Goal here is to store start page and end page, and the count how many times that happens. After that
we are going to turn it into a probability distribution. We can divide all transitions that start with specific
start state, by row_sum"""
transitions = {} # getting all specific transitions from start pg to end pg, tallying up # of times each occurs
row_sums = {} # start date as key -> getting number of times each starting pg occurs
# Collect our counts
for line in open('../../../data/site/site_data.csv'):
s, e = line.rstrip().split(',') # get start and end page
transitions[(s, e)] = transitions.get((s, e), 0.) + 1
row_sums[s] = row_sums.get(s, 0.) + 1
# Normalize the counts so they become real probability distributions
for k, v in transitions.items():
s, e = k
transitions[k] = v / row_sums[s]
# Calculate initial state distribution
print('Initial state distribution')
for k, v in transitions.items():
s, e = k
if s == '-1': # this means it is the start of the sequence.
print (e, v)
# Which page has the highest bounce rate?
for k, v in transitions.items():
s, e = k
if e == 'B':
print(f'Bounce rate for {s}: {v}')
```
We can see that page with `id` 9 has the highest value in the initial state distribution, so we are most likely to start on that page. We can then see that the page with highest bounce rate is also at page `id` 9.
## 4. Build a 2nd-order language model and generate phrases
So, we are now going to work with non first order markov chains for a little bit. In this example we are going to try and create a language model. So we are going to first train a model on some data to determine the distribution of a word given the previous two words. We can then use this model to generate new phrases. Note that another step of this model would be to calculate the probability of a phrase.
So the data that we are going to look at is just a collection of Robert Frost Poems. It is just a text file with all of the poems concatenated together. So, the first thing we are going to want to do is tokenize each sentence, and remove punctuation. It will look similar to this:
```
def remove_punctuation(s):
return s.translate(None, string.punctuation)
tokens = [t for t in remove_puncuation(line.rstrip().lower()).split()]
```
Once we have tokenized each line, we want to perform various counts in addition to the second order model counts. We need to measure the initial distribution of words, or stated another way the distribution of the first word of a sentence. We also want to know the distribution of the second word of a sentence. Both of these do not have two previous words, so they are not second order. We could technically include them in the second order measurement by using `None` in place of the previous words, but we won't do that here. We also want to keep track of how to end the sentence (end of sentence distribution, will look similar to (w(t-2), w(t-1) -> END)), so we will include a special token for that too.
When we do this counting, what we first want to do is create an array of all possibilities. So, for example if we had two sentences:
```
I love dogs
I love cats
```
Then we could have a dictionary where the key was `(I, love)` and the value was an array `[dogs, cats]`. If "I love" was also a stand alone sentence, then the value would be `[dogs, cats, END]`. The function below can help us with this, since we first need to check if there is any value for the key, create an array if not, otherwise just append to the array.
```
def add2dict(d, k, v):
if k not in d:
d[k] = []
else:
d[k].append(v)
```
One we have collected all of these arrays of possible next words, we need to turn them into **probability distributions**. For example, the array `[cat, cat, dog]` would become the dictionary `{"cat": 2/3, "dog": 1/3}`. Here is a function that can do this:
```
def list2pdict(ts):
d = {}
n = len(ts)
for t in ts:
d[t] = d.get(t, 0.) + 1
for t, c in d.items():
d[t] = c / n
return d
```
Next, we will need a function that can sample from this dictionary. To do this we will need to generate a random number between 0 and 1, and then use the distribution of the words to sample a word given a random number. Here is a function that can do that:
```
def sample_word(d):
p0 = np.random.random()
cumulative = 0
for t, p in d.items():
cumulative += p
if p0 < cumulative:
return t
assert(False) # should never get here
```
Because all of our distributions are structured as dictionaries, we can use the same function for all of them.
```
import numpy as np
import string
"""3 dicts. 1st store pdist for the start of a phrase, then a second word dict which stores the distributions
for the 2nd word of a sentence, and then we are going to have a dict for all second order transitions"""
initial = {}
second_word = {}
transitions = {}
def remove_punctuation(s):
return s.translate(str.maketrans('', '', string.punctuation))
def add2dict(d, k, v):
"""Parameters: Dictionary, Key, Value"""
if k not in d:
d[k] = []
d[k].append(v)
# Loop through file of poems
for line in open('../../../data/poems/robert_frost.txt'):
tokens = remove_punctuation(line.rstrip().lower()).split() # Get all tokens for specific line we are looping over
T = len(tokens) # Length of sequence
for i in range(T): # Loop through every token in sequence
t = tokens[i]
if i == 0: # We are looking at first word
initial[t] = initial.get(t, 0.) + 1
else:
t_1 = tokens[i - 1]
if i == T - 1: # Looking at last word
add2dict(transitions, (t_1, t), 'END')
if i == 1: # second word of sentence, hence only 1 previous word
add2dict(second_word, t_1, t)
else:
t_2 = tokens[i - 2] # Get second previous word
add2dict(transitions, (t_2, t_1), t) # add previous and 2nd previous word as key, and current word as val
# Normalize the distributions
initial_total = sum(initial.values())
for t, c in initial.items():
initial[t] = c / initial_total
# Take our list and turn it into a dictionary of probabilities
def list2pdict(ts):
d = {}
n = len(ts) # get total number of values
for t in ts: # look at each token
d[t] = d.get(t, 0.) + 1
for t, c in d.items(): # go through dictionary, divide frequency by sum
d[t] = c / n
return d
for t_1, ts in second_word.items():
second_word[t_1] = list2pdict(ts)
for k, ts in transitions.items():
transitions[k] = list2pdict(ts)
def sample_word(d):
p0 = np.random.random() # Generate random number from 0 to 1
cumulative = 0 # cumulative count for all probabilities seen so far
for t, p in d.items():
cumulative += p
if p0 < cumulative:
return t
assert(False) # should never hit this
"""Function to generate a poem"""
def generate():
for i in range(4):
sentence = []
# initial word
w0 = sample_word(initial)
sentence.append(w0)
# sample second word
w1 = sample_word(second_word[w0])
sentence.append(w1)
# second-order transitions until END -> enter infinite loop
while True:
w2 = sample_word(transitions[(w0, w1)]) # sample next word given previous two words
if w2 == 'END':
break
sentence.append(w2)
w0 = w1
w1 = w2
print(' '.join(sentence))
generate()
```
## 5. Google's PageRank Algorithm
Markov models were even used in Google's PageRank algorithm. The basic problem we face is:
> * We have $M$ webpages that link to eachother, and we would like to assign importance scores $x(1),...,x(M)$
* All of these scores are greater than or equal to 0
* So, we want to assign a page rank to all of these pages
How can we go about doing this? Well, we can think of a webpage as a sequence, and the page you are on as the state. Where does the ranking come from? Well, the ranking actually comes from the limiting distribution. That is, in the long run, the proportion of visits that will be spent on this page. Now, if you think "great that is all I need to know", slow down. How can we actually do this in practice? How do we train the markov model, and what are the values we assign to the state transition matrix? And how can we ensure that the limiting distribution exists and is unique? The key insight was that **we can use the linked structure of the web to determine the ranking**.
The main idea is that a *link to a page* is like a *vote for its importance*. So, as a first attempt we could just use a frequency count to measure the votes. Of course, that wouldn't be a valid probability distribution, so we could just divide each row by its sum to make it sum to 1. So we set:
$$A(i, j) = \frac{1}{n(i)} \; if \; i \; links \; to \; j$$
$$A(i, j) = 0 \; otherwise$$
Here $n(i)$ stands for the total number of links on a page, and you can confirm that the sum of a row is $\frac{n(i)}{n(i)} = 1$, so this is a valid markov matrix. Now, we still aren't sure if the limiting distribution is unique.
### 5.1 This is already a good start
Let's keep in mind that the above solution already solves a few problems. For instance, let's say you are a spammer and you want to sell 1000 links on your webpage. Well, because the transition matrix must remain a valid probability matrix, the rows must sum to 1, which means that each of your links now only has a strength of $\frac{1}{1000}$. For example the frequency matrix would look like:
| |abc.com|amazon.com|facebook.com|github.com|
|--- |--- |--- | --- |--- |
|thespammer.com|1 |1 |1 |1 |
And then if we transformed that into a probability matrix it would just be each value divided by the total number of links, 4:
| |abc.com|amazon.com|facebook.com|github.com|
|--- |--- |--- | --- |--- |
|thespammer.com|0.25 |0.25 |0.25 |0.25 |
You may then think, I will just create 1000 pages and each of them will only have 1 link. Unfortunately, since nobody knows about those 1000 pages you just created nobody is going to link to them, which means they are impossible to get to. So, in the limiting distribution, those states will have 0 probability because you can't even get to them, so there outgoing links are worthless. Remember, the markov chains limiting distribution will model the long running proportion of visits to a state. So, if you never visit that state, its probability will be 0.
We still have not ensure that the limiting distribution exists and is unique.
### 5.2 Perron-Frobenius Theorem
How can we ensure that our model has a unique stationary distribution. In 1910, this was actually determined. It is known as the **Perron-Frobenius Theorem**, and it states that:
> *If our transition matrix is a markov matrix -meaning that all of the rows sum to 1, and all of the values are strictly positive, i.e. no values that are 0- then the stationary distribution exists and is unique*.
In fact, we can start in any initial state and as time approaches infinity we will always end up with the same stationary distribution, therefore this is also the limiting distribution.
So, how can we satisfy the PF criterion? Let's return to this idea of **smoothing**, which we first talked about when discussing how to train a markov model. The basic idea was that we can make things that were 0, non-zero, so there is still a small possibility that we can get to that state. This might be good news for the spammer. So, we can create a uniform probability distribution $U = \frac{1}{M}$, which is an $M x M$ matrix ($M$ is the number of states). PageRanks solution was to take the matrix we had before and multiply it by 0.85, and to take the uniform distribution and multiply it by 0.15, and add them together to get the final pagerank matrix.
$$G = 0.85A + 0.15U$$
Now all of the elements are strictly positive, and we can convince ourselves that G is still a valid markov matrix.
| true |
code
| 0.419529 | null | null | null | null |
|
# Quantization of Signals
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Spectral Shaping of the Quantization Noise
The quantized signal $x_Q[k]$ can be expressed by the continuous amplitude signal $x[k]$ and the quantization error $e[k]$ as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] \} = x[k] + e[k]
\end{equation}
According to the [introduced model](linear_uniform_quantization_error.ipynb#Model-for-the-Quantization-Error), the quantization noise can be modeled as uniformly distributed white noise. Hence, the noise is distributed over the entire frequency range. The basic concept of [noise shaping](https://en.wikipedia.org/wiki/Noise_shaping) is a feedback of the quantization error to the input of the quantizer. This way the spectral characteristics of the quantization noise can be modified, i.e. spectrally shaped. Introducing a generic filter $h[k]$ into the feedback loop yields the following structure

The quantized signal can be deduced from the block diagram above as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] - e[k] * h[k] \} = x[k] + e[k] - e[k] * h[k]
\end{equation}
where the additive noise model from above has been introduced and it has been assumed that the impulse response $h[k]$ is normalized such that the magnitude of $e[k] * h[k]$ is below the quantization step $Q$. The overall quantization error is then
\begin{equation}
e_H[k] = x_Q[k] - x[k] = e[k] * (\delta[k] - h[k])
\end{equation}
The power spectral density (PSD) of the quantization error with noise shaping is calculated to
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \right|^2
\end{equation}
Hence the PSD $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega})$ of the quantizer without noise shaping is weighted by $| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) |^2$. Noise shaping allows a spectral modification of the quantization error. The desired shaping depends on the application scenario. For some applications, high-frequency noise is less disturbing as low-frequency noise.
### Example - First-Order Noise Shaping
If the feedback of the error signal is delayed by one sample we get with $h[k] = \delta[k-1]$
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - \mathrm{e}^{\,-\mathrm{j}\,\Omega} \right|^2
\end{equation}
For linear uniform quantization $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \sigma_e^2$ is constant. Hence, the spectral shaping constitutes a high-pass characteristic of first order. The following simulation evaluates the noise shaping quantizer of first order.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sig
w = 8 # wordlength of the quantized signal
xmin = -1 # minimum of input signal
N = 32768 # number of samples
def uniform_midtread_quantizer_w_ns(x, Q):
# limiter
x = np.copy(x)
idx = np.where(x <= -1)
x[idx] = -1
idx = np.where(x > 1 - Q)
x[idx] = 1 - Q
# linear uniform quantization with noise shaping
xQ = Q * np.floor(x/Q + 1/2)
e = xQ - x
xQ = xQ - np.concatenate(([0], e[0:-1]))
return xQ[1:]
# quantization step
Q = 1/(2**(w-1))
# compute input signal
np.random.seed(5)
x = np.random.uniform(size=N, low=xmin, high=(-xmin-Q))
# quantize signal
xQ = uniform_midtread_quantizer_w_ns(x, Q)
e = xQ - x[1:]
# estimate PSD of error signal
nf, Pee = sig.welch(e, nperseg=64)
# estimate SNR
SNR = 10*np.log10((np.var(x)/np.var(e)))
print('SNR = {:2.1f} dB'.format(SNR))
plt.figure(figsize=(10,5))
Om = nf*2*np.pi
plt.plot(Om, Pee*6/Q**2, label='estimated PSD')
plt.plot(Om, np.abs(1 - np.exp(-1j*Om))**2, label='theoretic PSD')
plt.plot(Om, np.ones(Om.shape), label='PSD w/o noise shaping')
plt.title('PSD of quantization error')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$\hat{\Phi}_{e_H e_H}(e^{j \Omega}) / \sigma_e^2$')
plt.axis([0, np.pi, 0, 4.5]);
plt.legend(loc='upper left')
plt.grid()
```
**Exercise**
* The overall average SNR is lower than for the quantizer without noise shaping. Why?
Solution: The average power per frequency is lower that without noise shaping for frequencies below $\Omega \approx \pi$. However, this comes at the cost of a larger average power per frequency for frequencies above $\Omega \approx \pi$. The average power of the quantization noise is given as the integral over the PSD of the quantization noise. It is larger for noise shaping and the resulting SNR is consequently lower. Noise shaping is nevertheless beneficial in applications where a lower quantization error in a limited frequency region is desired.
**Copyright**
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples, 2016-2018*.
| true |
code
| 0.72132 | null | null | null | null |
|
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
# default_exp losses
# default_cls_lvl 3
#export
from fastai.imports import *
from fastai.torch_imports import *
from fastai.torch_core import *
from fastai.layers import *
#hide
from nbdev.showdoc import *
```
# Loss Functions
> Custom fastai loss functions
```
F.binary_cross_entropy_with_logits(torch.randn(4,5), torch.randint(0, 2, (4,5)).float(), reduction='none')
funcs_kwargs
# export
@log_args
class BaseLoss():
"Same as `loss_cls`, but flattens input and target."
activation=decodes=noops
def __init__(self, loss_cls, *args, axis=-1, flatten=True, floatify=False, is_2d=True, **kwargs):
store_attr("axis,flatten,floatify,is_2d")
self.func = loss_cls(*args,**kwargs)
functools.update_wrapper(self, self.func)
def __repr__(self): return f"FlattenedLoss of {self.func}"
@property
def reduction(self): return self.func.reduction
@reduction.setter
def reduction(self, v): self.func.reduction = v
def __call__(self, inp, targ, **kwargs):
inp = inp .transpose(self.axis,-1).contiguous()
targ = targ.transpose(self.axis,-1).contiguous()
if self.floatify and targ.dtype!=torch.float16: targ = targ.float()
if targ.dtype in [torch.int8, torch.int16, torch.int32]: targ = targ.long()
if self.flatten: inp = inp.view(-1,inp.shape[-1]) if self.is_2d else inp.view(-1)
return self.func.__call__(inp, targ.view(-1) if self.flatten else targ, **kwargs)
```
Wrapping a general loss function inside of `BaseLoss` provides extra functionalities to your loss functions:
- flattens the tensors before trying to take the losses since it's more convenient (with a potential tranpose to put `axis` at the end)
- a potential `activation` method that tells the library if there is an activation fused in the loss (useful for inference and methods such as `Learner.get_preds` or `Learner.predict`)
- a potential <code>decodes</code> method that is used on predictions in inference (for instance, an argmax in classification)
The `args` and `kwargs` will be passed to `loss_cls` during the initialization to instantiate a loss function. `axis` is put at the end for losses like softmax that are often performed on the last axis. If `floatify=True`, the `targs` will be converted to floats (useful for losses that only accept float targets like `BCEWithLogitsLoss`), and `is_2d` determines if we flatten while keeping the first dimension (batch size) or completely flatten the input. We want the first for losses like Cross Entropy, and the second for pretty much anything else.
```
# export
@log_args
@delegates()
class CrossEntropyLossFlat(BaseLoss):
"Same as `nn.CrossEntropyLoss`, but flattens input and target."
y_int = True
@use_kwargs_dict(keep=True, weight=None, ignore_index=-100, reduction='mean')
def __init__(self, *args, axis=-1, **kwargs): super().__init__(nn.CrossEntropyLoss, *args, axis=axis, **kwargs)
def decodes(self, x): return x.argmax(dim=self.axis)
def activation(self, x): return F.softmax(x, dim=self.axis)
tst = CrossEntropyLossFlat()
output = torch.randn(32, 5, 10)
target = torch.randint(0, 10, (32,5))
#nn.CrossEntropy would fail with those two tensors, but not our flattened version.
_ = tst(output, target)
test_fail(lambda x: nn.CrossEntropyLoss()(output,target))
#Associated activation is softmax
test_eq(tst.activation(output), F.softmax(output, dim=-1))
#This loss function has a decodes which is argmax
test_eq(tst.decodes(output), output.argmax(dim=-1))
#In a segmentation task, we want to take the softmax over the channel dimension
tst = CrossEntropyLossFlat(axis=1)
output = torch.randn(32, 5, 128, 128)
target = torch.randint(0, 5, (32, 128, 128))
_ = tst(output, target)
test_eq(tst.activation(output), F.softmax(output, dim=1))
test_eq(tst.decodes(output), output.argmax(dim=1))
# export
@log_args
@delegates()
class BCEWithLogitsLossFlat(BaseLoss):
"Same as `nn.BCEWithLogitsLoss`, but flattens input and target."
@use_kwargs_dict(keep=True, weight=None, reduction='mean', pos_weight=None)
def __init__(self, *args, axis=-1, floatify=True, thresh=0.5, **kwargs):
super().__init__(nn.BCEWithLogitsLoss, *args, axis=axis, floatify=floatify, is_2d=False, **kwargs)
self.thresh = thresh
def decodes(self, x): return x>self.thresh
def activation(self, x): return torch.sigmoid(x)
tst = BCEWithLogitsLossFlat()
output = torch.randn(32, 5, 10)
target = torch.randn(32, 5, 10)
#nn.BCEWithLogitsLoss would fail with those two tensors, but not our flattened version.
_ = tst(output, target)
test_fail(lambda x: nn.BCEWithLogitsLoss()(output,target))
output = torch.randn(32, 5)
target = torch.randint(0,2,(32, 5))
#nn.BCEWithLogitsLoss would fail with int targets but not our flattened version.
_ = tst(output, target)
test_fail(lambda x: nn.BCEWithLogitsLoss()(output,target))
#Associated activation is sigmoid
test_eq(tst.activation(output), torch.sigmoid(output))
# export
@log_args(to_return=True)
@use_kwargs_dict(weight=None, reduction='mean')
def BCELossFlat(*args, axis=-1, floatify=True, **kwargs):
"Same as `nn.BCELoss`, but flattens input and target."
return BaseLoss(nn.BCELoss, *args, axis=axis, floatify=floatify, is_2d=False, **kwargs)
tst = BCELossFlat()
output = torch.sigmoid(torch.randn(32, 5, 10))
target = torch.randint(0,2,(32, 5, 10))
_ = tst(output, target)
test_fail(lambda x: nn.BCELoss()(output,target))
# export
@log_args(to_return=True)
@use_kwargs_dict(reduction='mean')
def MSELossFlat(*args, axis=-1, floatify=True, **kwargs):
"Same as `nn.MSELoss`, but flattens input and target."
return BaseLoss(nn.MSELoss, *args, axis=axis, floatify=floatify, is_2d=False, **kwargs)
tst = MSELossFlat()
output = torch.sigmoid(torch.randn(32, 5, 10))
target = torch.randint(0,2,(32, 5, 10))
_ = tst(output, target)
test_fail(lambda x: nn.MSELoss()(output,target))
#hide
#cuda
#Test losses work in half precision
output = torch.sigmoid(torch.randn(32, 5, 10)).half().cuda()
target = torch.randint(0,2,(32, 5, 10)).half().cuda()
for tst in [BCELossFlat(), MSELossFlat()]: _ = tst(output, target)
# export
@log_args(to_return=True)
@use_kwargs_dict(reduction='mean')
def L1LossFlat(*args, axis=-1, floatify=True, **kwargs):
"Same as `nn.L1Loss`, but flattens input and target."
return BaseLoss(nn.L1Loss, *args, axis=axis, floatify=floatify, is_2d=False, **kwargs)
#export
@log_args
class LabelSmoothingCrossEntropy(Module):
y_int = True
def __init__(self, eps:float=0.1, reduction='mean'): self.eps,self.reduction = eps,reduction
def forward(self, output, target):
c = output.size()[-1]
log_preds = F.log_softmax(output, dim=-1)
if self.reduction=='sum': loss = -log_preds.sum()
else:
loss = -log_preds.sum(dim=-1) #We divide by that size at the return line so sum and not mean
if self.reduction=='mean': loss = loss.mean()
return loss*self.eps/c + (1-self.eps) * F.nll_loss(log_preds, target.long(), reduction=self.reduction)
def activation(self, out): return F.softmax(out, dim=-1)
def decodes(self, out): return out.argmax(dim=-1)
```
On top of the formula we define:
- a `reduction` attribute, that will be used when we call `Learner.get_preds`
- an `activation` function that represents the activation fused in the loss (since we use cross entropy behind the scenes). It will be applied to the output of the model when calling `Learner.get_preds` or `Learner.predict`
- a <code>decodes</code> function that converts the output of the model to a format similar to the target (here indices). This is used in `Learner.predict` and `Learner.show_results` to decode the predictions
```
#export
@log_args
@delegates()
class LabelSmoothingCrossEntropyFlat(BaseLoss):
"Same as `LabelSmoothingCrossEntropy`, but flattens input and target."
y_int = True
@use_kwargs_dict(keep=True, eps=0.1, reduction='mean')
def __init__(self, *args, axis=-1, **kwargs): super().__init__(LabelSmoothingCrossEntropy, *args, axis=axis, **kwargs)
def activation(self, out): return F.softmax(out, dim=-1)
def decodes(self, out): return out.argmax(dim=-1)
```
## Export -
```
#hide
from nbdev.export import *
notebook2script()
```
| true |
code
| 0.75452 | null | null | null | null |
|
# Spark on Kubernetes
Preparing the notebook https://towardsdatascience.com/make-kubeflow-into-your-own-data-science-workspace-cc8162969e29
## Setup service account permissions
https://github.com/kubeflow/kubeflow/issues/4306 issue with launching spark-operator from jupyter notebook
Run command in your shell (not in notebook)
```shell
export NAMESPACE=<your_namespace>
kubectl create serviceaccount spark -n ${NAMESPACE}
kubectl create clusterrolebinding spark-role --clusterrole=edit --serviceaccount=${NAMESPACE}:spark --namespace=${NAMESPACE}
```
## Python version
> Note: Make sure your driver python and executor python version matches.
> Otherwise, you will see error msg like below
Exception: Python in worker has different version 3.7 than that in driver 3.6, PySpark cannot run with different minor versions.Please check environment variables `PYSPARK_PYTHON` and `PYSPARK_DRIVER_PYTHON` are correctly set.
```
import sys
print(sys.version)
```
## Client Mode
```
import findspark, pyspark,socket
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
findspark.init()
localIpAddress = socket.gethostbyname(socket.gethostname())
conf = SparkConf().setAppName('sparktest1')
conf.setMaster('k8s://https://kubernetes.default.svc:443')
conf.set("spark.submit.deployMode", "client")
conf.set("spark.executor.instances", "2")
conf.set("spark.driver.host", localIpAddress)
conf.set("spark.driver.port", "7778")
conf.set("spark.kubernetes.namespace", "yahavb")
conf.set("spark.kubernetes.container.image", "seedjeffwan/spark-py:v2.4.6")
conf.set("spark.kubernetes.pyspark.pythonVersion", "3")
conf.set("spark.kubernetes.authenticate.driver.serviceAccountName", "spark")
conf.set("spark.kubernetes.executor.annotation.sidecar.istio.io/inject", "false")
sc = pyspark.context.SparkContext.getOrCreate(conf=conf)
# following works as well
# spark = SparkSession.builder.config(conf=conf).getOrCreate()
num_samples = 100000
def inside(p):
x, y = random.random(), random.random()
return x*x + y*y < 1
count = sc.parallelize(range(0, num_samples)).filter(inside).count()
sc.stop()
```
## Cluster Mode
## Java
```
%%bash
/opt/spark-2.4.6/bin/spark-submit --master "k8s://https://kubernetes.default.svc:443" \
--deploy-mode cluster \
--name spark-java-pi \
--class org.apache.spark.examples.SparkPi \
--conf spark.executor.instances=30 \
--conf spark.kubernetes.namespace=yahavb \
--conf spark.kubernetes.driver.annotation.sidecar.istio.io/inject=false \
--conf spark.kubernetes.executor.annotation.sidecar.istio.io/inject=false \
--conf spark.kubernetes.container.image=seedjeffwan/spark:v2.4.6 \
--conf spark.kubernetes.driver.pod.name=spark-java-pi-driver \
--conf spark.kubernetes.executor.request.cores=4 \
--conf spark.kubernetes.node.selector.computetype=gpu \
--conf spark.kubernetes.authenticate.driver.serviceAccountName=spark \
local:///opt/spark/examples/jars/spark-examples_2.11-2.4.6.jar 262144
%%bash
kubectl -n yahavb delete po ` kubectl -n yahavb get po | grep spark-java-pi-driver | awk '{print $1}'`
```
## Python
```
%%bash
/opt/spark-2.4.6/bin/spark-submit --master "k8s://https://kubernetes.default.svc:443" \
--deploy-mode cluster \
--name spark-python-pi \
--conf spark.executor.instances=50 \
--conf spark.kubernetes.container.image=seedjeffwan/spark-py:v2.4.6 \
--conf spark.kubernetes.driver.pod.name=spark-python-pi-driver \
--conf spark.kubernetes.namespace=yahavb \
--conf spark.kubernetes.driver.annotation.sidecar.istio.io/inject=false \
--conf spark.kubernetes.executor.annotation.sidecar.istio.io/inject=false \
--conf spark.kubernetes.pyspark.pythonVersion=3 \
--conf spark.kubernetes.executor.request.cores=4 \
--conf spark.kubernetes.authenticate.driver.serviceAccountName=spark /opt/spark/examples/src/main/python/pi.py 64000
%%bash
kubectl -n yahavb delete po `kubectl -n yahavb get po | grep spark-python-pi-driver | awk '{print $1}'`
```
| true |
code
| 0.334943 | null | null | null | null |
|
# Cyclical Systems: An Example of the Crank-Nicolson Method
## CH EN 2450 - Numerical Methods
**Prof. Tony Saad (<a>www.tsaad.net</a>) <br/>Department of Chemical Engineering <br/>University of Utah**
<hr/>
```
import numpy as np
from numpy import *
# %matplotlib notebook
# %matplotlib nbagg
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
# %matplotlib qt
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
from scipy.integrate import odeint
def forward_euler(rhs, f0, tend, dt):
''' Computes the forward_euler method '''
nsteps = int(tend/dt)
f = np.zeros(nsteps)
f[0] = f0
time = np.linspace(0,tend,nsteps)
for n in np.arange(nsteps-1):
f[n+1] = f[n] + dt * rhs(f[n], time[n])
return time, f
def forward_euler_system(rhsvec, f0vec, tend, dt):
'''
Solves a system of ODEs using the Forward Euler method
'''
nsteps = int(tend/dt)
neqs = len(f0vec)
f = np.zeros( (neqs, nsteps) )
f[:,0] = f0vec
time = np.linspace(0,tend,nsteps)
for n in np.arange(nsteps-1):
t = time[n]
f[:,n+1] = f[:,n] + dt * rhsvec(f[:,n], t)
return time, f
def be_residual(fnp1, rhs, fn, dt, tnp1):
'''
Nonlinear residual function for the backward Euler implicit time integrator
'''
return fnp1 - fn - dt * rhs(fnp1, tnp1)
def backward_euler(rhs, f0, tend, dt):
'''
Computes the backward euler method
:param rhs: an rhs function
'''
nsteps = int(tend/dt)
f = np.zeros(nsteps)
f[0] = f0
time = np.linspace(0,tend,nsteps)
for n in np.arange(nsteps-1):
fn = f[n]
tnp1 = time[n+1]
fnew = fsolve(be_residual, fn, (rhs, fn, dt, tnp1))
f[n+1] = fnew
return time, f
def cn_residual(fnp1, rhs, fn, dt, tnp1, tn):
'''
Nonlinear residual function for the Crank-Nicolson implicit time integrator
'''
return fnp1 - fn - 0.5 * dt * ( rhs(fnp1, tnp1) + rhs(fn, tn) )
def crank_nicolson(rhs,f0,tend,dt):
nsteps = int(tend/dt)
f = np.zeros(nsteps)
f[0] = f0
time = np.linspace(0,tend,nsteps)
for n in np.arange(nsteps-1):
fn = f[n]
tnp1 = time[n+1]
tn = time[n]
fnew = fsolve(cn_residual, fn, (rhs, fn, dt, tnp1, tn))
f[n+1] = fnew
return time, f
```
# Sharp Transient
Solve the ODE:
\begin{equation}
\frac{\text{d}y}{\text{d}t} = -1000 y + 3000 - 2000 e^{-t};\quad y(0) = 0
\end{equation}
The analytical solution is
\begin{equation}
y(t) = 3 - 0.998 e^{-1000t} - 2.002 e^{-t}
\end{equation}
We first plot the analytical solution
```
y = lambda t : 3 - 0.998*exp(-1000*t) - 2.002*exp(-t)
t = np.linspace(0,1,500)
plt.plot(t,y(t))
plt.grid()
```
Now let's solve this numerically. We first define the RHS for this function
```
def rhs_sharp_transient(f,t):
return 3000 - 1000 * f - 2000* np.exp(-t)
```
Let's solve this using forward euler and backward euler
```
y0 = 0
tend = 0.03
dt = 0.001
t,yfe = forward_euler(rhs_sharp_transient,y0,tend,dt)
t,ybe = backward_euler(rhs_sharp_transient,y0,tend,dt)
t,ycn = crank_nicolson(rhs_sharp_transient,y0,tend,dt)
plt.plot(t,y(t),label='Exact')
# plt.plot(t,yfe,'r.-',markevery=1,markersize=10,label='Forward Euler')
plt.plot(t,ybe,'k*-',markevery=2,markersize=10,label='Backward Euler')
plt.plot(t,ycn,'o-',markevery=2,markersize=2,label='Crank Nicholson')
plt.grid()
plt.legend()
```
# Oscillatory Systems
Solve the ODE:
Solve the ODE:
\begin{equation}
\frac{\text{d}y}{\text{d}t} = r \omega \sin(\omega t)
\end{equation}
The analytical solution is
\begin{equation}
y(t) = r - r \cos(\omega t)
\end{equation}
First plot the analytical solution
```
r = 0.5
ω = 0.02
y = lambda t : r - r * cos(ω*t)
t = np.linspace(0,100*pi)
plt.clf()
plt.plot(t,y(t))
plt.grid()
```
Let's solve this numerically
```
def rhs_oscillatory(f,t):
r = 0.5
ω = 0.02
return r * ω * sin(ω*t)
y0 = 0
tend = 100*pi
dt = 10
t,yfe = forward_euler(rhs_oscillatory,y0,tend,dt)
t,ybe = backward_euler(rhs_oscillatory,y0,tend,dt)
t,ycn = crank_nicolson(rhs_oscillatory,y0,tend,dt)
plt.plot(t,y(t),label='Exact')
plt.plot(t,yfe,'r.-',markevery=1,markersize=10,label='Forward Euler')
plt.plot(t,ybe,'k*-',markevery=2,markersize=10,label='Backward Euler')
plt.plot(t,ycn,'o-',markevery=2,markersize=2,label='Crank Nicholson')
plt.grid()
plt.legend()
plt.savefig('cyclical-system-example.pdf')
import urllib
import requests
from IPython.core.display import HTML
def css_styling():
styles = requests.get("https://raw.githubusercontent.com/saadtony/NumericalMethods/master/styles/custom.css")
return HTML(styles.text)
css_styling()
```
| true |
code
| 0.716938 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_parent" href="https://github.com/giswqs/geemap/tree/master/tutorials/Image/06_convolutions.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_parent" href="https://nbviewer.jupyter.org/github/giswqs/geemap/blob/master/tutorials/Image/06_convolutions.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_parent" href="https://colab.research.google.com/github/giswqs/geemap/blob/master/tutorials/Image/06_convolutions.ipynb"><img width=26px src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
# Convolutions
To perform linear convolutions on images, use `image.convolve()`. The only argument to convolve is an `ee.Kernel` which is specified by a shape and the weights in the kernel. Each pixel of the image output by `convolve()` is the linear combination of the kernel values and the input image pixels covered by the kernel. The kernels are applied to each band individually. For example, you might want to use a low-pass (smoothing) kernel to remove high-frequency information. The following illustrates a 15x15 low-pass kernel applied to a Landsat 8 image:
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.foliumap`](https://github.com/giswqs/geemap/blob/master/geemap/foliumap.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.foliumap as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40, -100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Load and display an image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
Map.setCenter(-121.9785, 37.8694, 11)
Map.addLayer(image, {'bands': ['B5', 'B4', 'B3'], 'max': 0.5}, 'input image')
# Define a boxcar or low-pass kernel.
# boxcar = ee.Kernel.square({
# 'radius': 7, 'units': 'pixels', 'normalize': True
# })
boxcar = ee.Kernel.square(7, 'pixels', True)
# Smooth the image by convolving with the boxcar kernel.
smooth = image.convolve(boxcar)
Map.addLayer(smooth, {'bands': ['B5', 'B4', 'B3'], 'max': 0.5}, 'smoothed')
Map.addLayerControl()
Map
```
The output of convolution with the low-pass filter should look something like Figure 1. Observe that the arguments to the kernel determine its size and coefficients. Specifically, with the `units` parameter set to pixels, the `radius` parameter specifies the number of pixels from the center that the kernel will cover. If `normalize` is set to true, the kernel coefficients will sum to one. If the `magnitude` parameter is set, the kernel coefficients will be multiplied by the magnitude (if `normalize` is also true, the coefficients will sum to `magnitude`). If there is a negative value in any of the kernel coefficients, setting `normalize` to true will make the coefficients sum to zero.
Use other kernels to achieve the desired image processing effect. This example uses a Laplacian kernel for isotropic edge detection:
```
Map = emap.Map(center=[40, -100], zoom=4)
# Define a Laplacian, or edge-detection kernel.
laplacian = ee.Kernel.laplacian8(1, False)
# Apply the edge-detection kernel.
edgy = image.convolve(laplacian)
Map.addLayer(edgy, {'bands': ['B5', 'B4', 'B3'], 'max': 0.5}, 'edges')
Map.setCenter(-121.9785, 37.8694, 11)
Map.addLayerControl()
Map
```
Note the format specifier in the visualization parameters. Earth Engine sends display tiles to the Code Editor in JPEG format for efficiency, however edge tiles are sent in PNG format to handle transparency of pixels outside the image boundary. When a visual discontinuity results, setting the format to PNG results in a consistent display. The result of convolving with the Laplacian edge detection kernel should look something like Figure 2.
There are also anisotropic edge detection kernels (e.g. Sobel, Prewitt, Roberts), the direction of which can be changed with `kernel.rotate()`. Other low pass kernels include a Gaussian kernel and kernels of various shape with uniform weights. To create kernels with arbitrarily defined weights and shape, use `ee.Kernel.fixed()`. For example, this code creates a 9x9 kernel of 1’s with a zero in the middle:
```
# Create a list of weights for a 9x9 kernel.
list = [1, 1, 1, 1, 1, 1, 1, 1, 1]
# The center of the kernel is zero.
centerList = [1, 1, 1, 1, 0, 1, 1, 1, 1]
# Assemble a list of lists: the 9x9 kernel weights as a 2-D matrix.
lists = [list, list, list, list, centerList, list, list, list, list]
# Create the kernel from the weights.
kernel = ee.Kernel.fixed(9, 9, lists, -4, -4, False)
print(kernel.getInfo())
```
| true |
code
| 0.622115 | null | null | null | null |
|
<h1 align="center">Theano</h1>
```
!pip install numpy matplotlib
!pip install --upgrade https://github.com/Theano/Theano/archive/master.zip
!pip install --upgrade https://github.com/Lasagne/Lasagne/archive/master.zip
```
### Разминка
```
import theano
import theano.tensor as T
%pylab inline
```
#### будущий параметр функции -- символьная переменная
```
N = T.scalar('a dimension', dtype='float32')
```
#### рецепт получения квадрата -- орперации над символьными переменным
```
result = T.power(N, 2)
```
#### theano.grad(cost, wrt)
```
grad_result = theano.grad(result, N)
```
#### компиляция функции "получения квадрата"
```
sq_function = theano.function(inputs=[N], outputs=result)
gr_function = theano.function(inputs=[N], outputs=grad_result)
```
#### применение функции
```
# Заводим np.array x
xv = np.arange(-10, 10)
# Применяем функцию к каждому x
val = map(float, [sq_function(x) for x in xv])
# Посичтаем градиент в кажой точке
grad = map(float, [gr_function(x) for x in xv])
```
### Что мы увидим если нарисуем функцию и градиент?
```
pylab.plot(xv, val, label='x*x')
pylab.plot(xv, grad, label='d x*x / dx')
pylab.legend()
```
<h1 align="center">Lasagne</h1>
* lasagne - это библиотека для написания нейронок произвольной формы на theano
* В качестве демо-задачи выберем то же распознавание чисел, но на большем масштабе задачи, картинки 28x28, 10 цифр
```
from mnist import load_dataset
X_train, y_train, X_val, y_val, X_test, y_test = load_dataset()
print 'X размера', X_train.shape, 'y размера', y_train.shape
fig, axes = plt.subplots(nrows=1, ncols=7, figsize=(20, 20))
for i, ax in enumerate(axes):
ax.imshow(X_train[i, 0], cmap='gray')
```
Давайте посмотрим на DenseLayer в lasagne
- http://lasagne.readthedocs.io/en/latest/modules/layers/dense.html
- https://github.com/Lasagne/Lasagne/blob/master/lasagne/layers/dense.py#L16-L124
- Весь содаржательный код тут https://github.com/Lasagne/Lasagne/blob/master/lasagne/layers/dense.py#L121
```
import lasagne
from lasagne import init
from theano import tensor as T
from lasagne.nonlinearities import softmax
X, y = T.tensor4('X'), T.vector('y', 'int32')
```
Так задаётся архитектура нейронки
```
#входной слой (вспомогательный)
net = lasagne.layers.InputLayer(shape=(None, 1, 28, 28), input_var=X)
net = lasagne.layers.Conv2DLayer(net, 15, 28, pad='valid', W=init.Constant()) # сверточный слой
net = lasagne.layers.Conv2DLayer(net, 10, 2, pad='full', W=init.Constant()) # сверточный слой
net = lasagne.layers.DenseLayer(net, num_units=500) # полносвязный слой
net = lasagne.layers.DropoutLayer(net, 1.0) # регуляризатор
net = lasagne.layers.DenseLayer(net, num_units=200) # полносвязный слой
net = lasagne.layers.DenseLayer(net, num_units=10) # полносвязный слой
#предсказание нейронки (theano-преобразование)
y_predicted = lasagne.layers.get_output(net)
#все веса нейронки (shared-переменные)
all_weights = lasagne.layers.get_all_params(net)
print all_weights
#функция ошибки и точности будет прямо внутри
loss = lasagne.objectives.categorical_accuracy(y_predicted, y).mean()
accuracy = lasagne.objectives.categorical_accuracy(y_predicted, y).mean()
#сразу посчитать словарь обновлённых значений с шагом по градиенту, как раньше
updates = lasagne.updates.momentum(loss, all_weights, learning_rate=1.0, momentum=1.5)
#функция, делает updates и возвращащет значение функции потерь и точности
train_fun = theano.function([X, y], [loss, accuracy], updates=updates)
accuracy_fun = theano.function([X, y], accuracy) # точность без обновления весов, для теста
```
# Процесс обучения
```
import time
from mnist import iterate_minibatches
num_epochs = 5 #количество проходов по данным
batch_size = 50 #размер мини-батча
for epoch in range(num_epochs):
train_err, train_acc, train_batches, start_time = 0, 0, 0, time.time()
for inputs, targets in iterate_minibatches(X_train, y_train, batch_size):
train_err_batch, train_acc_batch = train_fun(inputs, targets)
train_err += train_err_batch
train_acc += train_acc_batch
train_batches += 1
val_acc, val_batches = 0, 0
for inputs, targets in iterate_minibatches(X_test, y_test, batch_size):
val_acc += accuracy_fun(inputs, targets)
val_batches += 1
print "Epoch %s of %s took %.3f s" % (epoch + 1, num_epochs, time.time() - start_time)
print " train loss:\t %.3f" % (train_err / train_batches)
print " train acc:\t %.3f" % (train_acc * 100 / train_batches), '%'
print " test acc:\t %.3f" % (val_acc * 100 / val_batches), '%'
print
test_acc = 0
test_batches = 0
for batch in iterate_minibatches(X_test, y_test, 500):
inputs, targets = batch
acc = accuracy_fun(inputs, targets)
test_acc += acc
test_batches += 1
print("Final results: \n test accuracy:\t\t{:.2f} %".format(test_acc / test_batches * 100))
```
# Ансамблирование с DropOut
```
#предсказание нейронки (theano-преобразование)
y_predicted = T.mean([lasagne.layers.get_output(net, deterministic=False) for i in range(10)], axis=0)
accuracy = lasagne.objectives.categorical_accuracy(y_predicted, y).mean()
accuracy_fun = theano.function([X, y], accuracy) # точность без обновления весов, для теста
test_acc = 0
test_batches = 0
for batch in iterate_minibatches(X_test, y_test, 500):
inputs, targets = batch
acc = accuracy_fun(inputs, targets)
test_acc += acc
test_batches += 1
print("Final results: \n test accuracy:\t\t{:.2f} %".format(test_acc / test_batches * 100))
```
| true |
code
| 0.604282 | null | null | null | null |
|
## Change sys.path to use my tensortrade instead of the one in env
```
import sys
sys.path.append("/Users/jasonfiacco/Documents/Yale/Senior/thesis/deeptrader")
print(sys.path)
```
## Read PredictIt Data Instead
```
import ssl
import pandas as pd
ssl._create_default_https_context = ssl._create_unverified_context # Only used if pandas gives a SSLError
def fetch_data(symbol):
path = "/Users/jasonfiacco/Documents/Yale/Senior/thesis/predictit_datasets/"
filename = "{}.xlsx".format(symbol)
df = pd.read_excel(path + filename, skiprows=4)
df = df.set_index("Date")
df = df.drop(df.columns[[7,8,9]], axis=1)
df = df.drop("ID", 1)
df.columns = [symbol + ":" + name.lower() for name in df.columns]
return df
all_data = pd.concat([
fetch_data("WARREN"),
fetch_data("CRUZ"),
fetch_data("MANCHIN"),
fetch_data("SANDERS"),
fetch_data("NELSON"),
fetch_data("DONNELLY"),
fetch_data("PELOSI"),
fetch_data("MANAFORT"),
fetch_data("BROWN"),
fetch_data("RYAN"),
fetch_data("STABENOW")
], axis=1)
all_data.head()
```
## Plot the closing prices for all the markets
```
%matplotlib inline
closing_prices = all_data.loc[:, [("close" in name) for name in all_data.columns]]
closing_prices.plot()
```
## Slice just a specific time period from the dataframe
```
all_data.index = pd.to_datetime(all_data.index)
subset_data = all_data[(all_data.index >= '09-01-2017') & (all_data.index <= '09-04-2019')]
subset_data.head()
```
## Define Exchanges
An exchange needs a name, an execution service, and streams of price data in order to function properly.
The setups supported right now are the simulated execution service using simulated or stochastic data. More execution services will be made available in the future, as well as price streams so that live data and execution can be supported.
```
from tensortrade.exchanges import Exchange
from tensortrade.exchanges.services.execution.simulated import execute_order
from tensortrade.data import Stream
#Exchange(name of exchange, service)
#It looks like each Stream takes a name, and then a list of the closing prices.
predictit_exch = Exchange("predictit", service=execute_order)(
Stream("USD-WARREN", list(subset_data['WARREN:close'])),
Stream("USD-CRUZ", list(subset_data['CRUZ:close'])),
Stream("USD-MANCHIN", list(subset_data['MANCHIN:close'])),
Stream("USD-SANDERS", list(subset_data['SANDERS:close'])),
Stream("USD-NELSON", list(subset_data['NELSON:close'])),
Stream("USD-DONNELLY", list(subset_data['DONNELLY:close'])),
Stream("USD-PELOSI", list(subset_data['PELOSI:close'])),
Stream("USD-MANAFORT", list(subset_data['MANAFORT:close'])),
Stream("USD-BROWN", list(subset_data['BROWN:close'])),
Stream("USD-RYAN", list(subset_data['RYAN:close'])),
Stream("USD-STABENOW", list(subset_data['STABENOW:close']))
)
```
Now that the exchanges have been defined we can define our features that we would like to include, excluding the prices we have provided for the exchanges.
### Doing it without adding other features. Just use price
```
#You still have to add "Streams" for all the standard columns open, high, low, close, volume in this case
from tensortrade.data import DataFeed, Module
with Module("predictit") as predictit_ns:
predictit_nodes = [Stream(name, list(subset_data[name])) for name in subset_data.columns]
#Then create the Feed from it
feed = DataFeed([predictit_ns])
feed.next()
```
## Portfolio
Make the portfolio using the any combinations of exchanges and intruments that the exchange supports
```
#I am going to have to add "instruments" for all 25 of the PredictIt markets I'm working with.
from tensortrade.instruments import USD, WARREN, CRUZ, MANCHIN, SANDERS, NELSON, DONNELLY,\
PELOSI, MANAFORT, BROWN, RYAN, STABENOW
from tensortrade.wallets import Wallet, Portfolio
portfolio = Portfolio(USD, [
Wallet(predictit_exch, 10000 * USD),
Wallet(predictit_exch, 0 * WARREN),
Wallet(predictit_exch, 0 * CRUZ),
Wallet(predictit_exch, 0 * MANCHIN),
Wallet(predictit_exch, 0 * SANDERS),
Wallet(predictit_exch, 0 * NELSON),
Wallet(predictit_exch, 0 * DONNELLY),
Wallet(predictit_exch, 0 * PELOSI),
Wallet(predictit_exch, 0 * MANAFORT),
Wallet(predictit_exch, 0 * BROWN),
Wallet(predictit_exch, 0 * RYAN),
Wallet(predictit_exch, 0 * STABENOW)
])
```
## Environment
```
from tensortrade.environments import TradingEnvironment
env = TradingEnvironment(
feed=feed,
portfolio=portfolio,
action_scheme='simple',
reward_scheme='simple',
window_size=15,
enable_logger=False,
renderers = 'screenlog'
)
env.feed.next()
```
#### ^An environment doesn't just show the OHLCV for each instrument. It also shows free, locked, total, as well as "USD_BTC"
## Using 123's Ray example
```
import os
parent_dir = "/Users/jasonfiacco/Documents/Yale/Senior/thesis/deeptrader"
os.environ["PYTHONPATH"] = parent_dir + ":" + os.environ.get("PYTHONPATH", "")
!PYTHONWARNINGS=ignore::yaml.YAMLLoadWarning
#Import tensortrade
import tensortrade
# Define Exchanges
from tensortrade.exchanges import Exchange
from tensortrade.exchanges.services.execution.simulated import execute_order
from tensortrade.data import Stream
# Define External Data Feed (features)
import ta
from sklearn import preprocessing
from tensortrade.data import DataFeed, Module
# Portfolio
from tensortrade.instruments import USD, BTC
from tensortrade.wallets import Wallet, Portfolio
from tensortrade.actions import ManagedRiskOrders
from gym.spaces import Discrete
# Environment
from tensortrade.environments import TradingEnvironment
import gym
import ray
from ray import tune
from ray.tune import grid_search
from ray.tune.registry import register_env
import ray.rllib.agents.ppo as ppo
import ray.rllib.agents.dqn as dqn
from ray.tune.logger import pretty_print
from tensortrade.rewards import RiskAdjustedReturns
class RayTradingEnv(TradingEnvironment):
def __init__(self):
env = TradingEnvironment(
feed=feed,
portfolio=portfolio,
action_scheme="simple",
reward_scheme="simple",
window_size=15,
enable_logger=False,
renderers = 'screenlog'
)
self.env = env
self.action_space = self.env.action_space
self.observation_space = self.env.observation_space
def reset(self):
return self.env.reset()
def step(self, action):
return self.env.step(action)
def env_creator(env_config):
return RayTradingEnv()
register_env("ray_trading_env", env_creator)
ray.init(ignore_reinit_error=True)
config = dqn.DEFAULT_CONFIG.copy()
config["num_gpus"] = 0
#config["num_workers"] = 4
#config["num_envs_per_worker"] = 8
# config["eager"] = False
# config["timesteps_per_iteration"] = 100
# config["train_batch_size"] = 20
#config['log_level'] = "DEBUG"
trainer = dqn.DQNTrainer(config=config, env="ray_trading_env")
config
```
## Train using the old fashioned RLLib way
```
for i in range(10):
# Perform one iteration of training the policy with PPO
print("Training iteration {}...".format(i))
result = trainer.train()
print("result: {}".format(result))
if i % 100 == 0:
checkpoint = trainer.save()
print("checkpoint saved at", checkpoint)
result['hist_stats']['episode_reward']
```
## OR train using the tune way (better so far)
```
analysis = tune.run(
"DQN",
name = "DQN10-paralellism",
checkpoint_at_end=True,
stop={
"timesteps_total": 4000,
},
config={
"env": "ray_trading_env",
"lr": grid_search([1e-4]), # try different lrs
"num_workers": 2, # parallelism,
},
)
#Use the below command to see results
#tensorboard --logdir=/Users/jasonfiacco/ray_results/DQN2
#Now you can plot the reward results of your tuner.
dfs = analysis.trial_dataframes
ax = None
for d in dfs.values():
ax = d.episode_reward_mean.plot(ax=ax, legend=True)
```
## Restoring an already existing agent that I tuned
```
import os
logdir = analysis.get_best_logdir("episode_reward_mean", mode="max")
trainer.restore(os.path.join(logdir, "checkpoint_993/checkpoint-993"))
trainer.restore("/Users/jasonfiacco/ray_results/DQN4/DQN_ray_trading_env_fedb24f0_0_lr=1e-06_2020-03-03_15-46-02kzbdv53d/checkpoint_5/checkpoint-5")
```
## Testing
```
#Set up a testing environment with test data.
test_env = TradingEnvironment(
feed=feed,
portfolio=portfolio,
action_scheme='simple',
reward_scheme='simple',
window_size=15,
enable_logger=False,
renderers = 'screenlog'
)
for episode_num in range(1):
state = test_env.reset()
done = False
cumulative_reward = 0
step = 0
action = trainer.compute_action(state)
while not done:
action = trainer.compute_action(state)
state, reward, done, results = test_env.step(action)
cumulative_reward += reward
#Render every 100 steps:
if step % 100 == 0:
test_env.render()
step += 1
print("Cumulative reward: ", cumulative_reward)
```
## Plot
```
%matplotlib inline
portfolio.performance.plot()
portfolio.performance.net_worth.plot()
#Plot the total balance in each type of item
p = portfolio.performance
p2 = p.iloc[:, :]
weights = p2.loc[:, [("/worth" in name) for name in p2.columns]]
weights.iloc[:, 1:8].plot()
```
## Try Plotly Render too
```
from tensortrade.environments.render import PlotlyTradingChart
from tensortrade.environments.render import FileLogger
chart_renderer = PlotlyTradingChart(
height = 800
)
file_logger = FileLogger(
filename='example.log', # omit or None for automatic file name
path='training_logs' # create a new directory if doesn't exist, None for no directory
)
price_history.columns = ['datetime', 'open', 'high', 'low', 'close', 'volume']
env = TradingEnvironment(
feed=feed,
portfolio=portfolio,
action_scheme='managed-risk',
reward_scheme='risk-adjusted',
window_size=20,
price_history=price_history,
renderers = [chart_renderer, file_logger]
)
from tensortrade.agents import DQNAgent
agent = DQNAgent(env)
agent.train(n_episodes=1, n_steps=1000, render_interval=1)
```
## Extra Stuff
```
apath = "/Users/jasonfiacco/Documents/Yale/Senior/thesis/jasonfiacco-selectedmarkets-mytickers.xlsx"
df = pd.read_excel(apath, skiprows=2)
jason_tickers = df.iloc[:, 5].tolist()
descriptions = df.iloc[:, 1].tolist()
for ticker, description in zip(jason_tickers, descriptions):
l = "{} = Instrument(\'{}\', 2, \'{}\')".format(ticker, ticker, description)
print(l)
```
| true |
code
| 0.423995 | null | null | null | null |
|
[Table of Contents](./table_of_contents.ipynb)
# Smoothing
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Introduction
The performance of the Kalman filter is not optimal when you consider future data. For example, suppose we are tracking an aircraft, and the latest measurement deviates far from the current track, like so (I'll only consider 1 dimension for simplicity):
```
import matplotlib.pyplot as plt
data = [10.1, 10.2, 9.8, 10.1, 10.2, 10.3,
10.1, 9.9, 10.2, 10.0, 9.9, 11.4]
plt.plot(data)
plt.xlabel('time')
plt.ylabel('position');
```
After a period of near steady state, we have a very large change. Assume the change is past the limit of the aircraft's flight envelope. Nonetheless the Kalman filter incorporates that new measurement into the filter based on the current Kalman gain. It cannot reject the noise because the measurement could reflect the initiation of a turn. Granted it is unlikely that we are turning so abruptly, but it is impossible to say whether
* The aircraft started a turn awhile ago, but the previous measurements were noisy and didn't show the change.
* The aircraft is turning, and this measurement is very noisy
* The measurement is very noisy and the aircraft has not turned
* The aircraft is turning in the opposite direction, and the measurement is extremely noisy
Now, suppose the following measurements are:
11.3 12.1 13.3 13.9 14.5 15.2
```
data2 = [11.3, 12.1, 13.3, 13.9, 14.5, 15.2]
plt.plot(data + data2);
```
Given these future measurements we can infer that yes, the aircraft initiated a turn.
On the other hand, suppose these are the following measurements.
```
data3 = [9.8, 10.2, 9.9, 10.1, 10.0, 10.3, 9.9, 10.1]
plt.plot(data + data3);
```
In this case we are led to conclude that the aircraft did not turn and that the outlying measurement was merely very noisy.
## An Overview of How Smoothers Work
The Kalman filter is a *recursive* filter with the Markov property - it's estimate at step `k` is based only on the estimate from step `k-1` and the measurement at step `k`. But this means that the estimate from step `k-1` is based on step `k-2`, and so on back to the first epoch. Hence, the estimate at step `k` depends on all of the previous measurements, though to varying degrees. `k-1` has the most influence, `k-2` has the next most, and so on.
Smoothing filters incorporate future measurements into the estimate for step `k`. The measurement from `k+1` will have the most effect, `k+2` will have less effect, `k+3` less yet, and so on.
This topic is called *smoothing*, but I think that is a misleading name. I could smooth the data above by passing it through a low pass filter. The result would be smooth, but not necessarily accurate because a low pass filter will remove real variations just as much as it removes noise. In contrast, Kalman smoothers are *optimal* - they incorporate all available information to make the best estimate that is mathematically achievable.
## Types of Smoothers
There are three classes of Kalman smoothers that produce better tracking in these situations.
* Fixed-Interval Smoothing
This is a batch processing based filter. This filter waits for all of the data to be collected before making any estimates. For example, you may be a scientist collecting data for an experiment, and don't need to know the result until the experiment is complete. A fixed-interval smoother will collect all the data, then estimate the state at each measurement using all available previous and future measurements. If it is possible for you to run your Kalman filter in batch mode it is always recommended to use one of these filters a it will provide much better results than the recursive forms of the filter from the previous chapters.
* Fixed-Lag Smoothing
Fixed-lag smoothers introduce latency into the output. Suppose we choose a lag of 4 steps. The filter will ingest the first 3 measurements but not output a filtered result. Then, when the 4th measurement comes in the filter will produce the output for measurement 1, taking measurements 1 through 4 into account. When the 5th measurement comes in, the filter will produce the result for measurement 2, taking measurements 2 through 5 into account. This is useful when you need recent data but can afford a bit of lag. For example, perhaps you are using machine vision to monitor a manufacturing process. If you can afford a few seconds delay in the estimate a fixed-lag smoother will allow you to produce very accurate and smooth results.
* Fixed-Point Smoothing
A fixed-point filter operates as a normal Kalman filter, but also produces an estimate for the state at some fixed time $j$. Before the time $k$ reaches $j$ the filter operates as a normal filter. Once $k>j$ the filter estimates $x_k$ and then also updates its estimate for $x_j$ using all of the measurements between $j\dots k$. This can be useful to estimate initial paramters for a system, or for producing the best estimate for an event that happened at a specific time. For example, you may have a robot that took a photograph at time $j$. You can use a fixed-point smoother to get the best possible pose information for the camera at time $j$ as the robot continues moving.
## Choice of Filters
The choice of these filters depends on your needs and how much memory and processing time you can spare. Fixed-point smoothing requires storage of all measurements, and is very costly to compute because the output is for every time step is recomputed for every measurement. On the other hand, the filter does produce a decent output for the current measurement, so this filter can be used for real time applications.
Fixed-lag smoothing only requires you to store a window of data, and processing requirements are modest because only that window is processed for each new measurement. The drawback is that the filter's output always lags the input, and the smoothing is not as pronounced as is possible with fixed-interval smoothing.
Fixed-interval smoothing produces the most smoothed output at the cost of having to be batch processed. Most algorithms use some sort of forwards/backwards algorithm that is only twice as slow as a recursive Kalman filter.
## Fixed-Interval Smoothing
There are many fixed-lag smoothers available in the literature. I have chosen to implement the smoother invented by Rauch, Tung, and Striebel because of its ease of implementation and efficiency of computation. It is also the smoother I have seen used most often in real applications. This smoother is commonly known as an RTS smoother.
Derivation of the RTS smoother runs to several pages of densely packed math. I'm not going to inflict it on you. Instead I will briefly present the algorithm, equations, and then move directly to implementation and demonstration of the smoother.
The RTS smoother works by first running the Kalman filter in a batch mode, computing the filter output for each step. Given the filter output for each measurement along with the covariance matrix corresponding to each output the RTS runs over the data backwards, incorporating its knowledge of the future into the past measurements. When it reaches the first measurement it is done, and the filtered output incorporates all of the information in a maximally optimal form.
The equations for the RTS smoother are very straightforward and easy to implement. This derivation is for the linear Kalman filter. Similar derivations exist for the EKF and UKF. These steps are performed on the output of the batch processing, going backwards from the most recent in time back to the first estimate. Each iteration incorporates the knowledge of the future into the state estimate. Since the state estimate already incorporates all of the past measurements the result will be that each estimate will contain knowledge of all measurements in the past and future. Here is it very important to distinguish between past, present, and future so I have used subscripts to denote whether the data is from the future or not.
Predict Step
$$\begin{aligned}
\mathbf{P} &= \mathbf{FP}_k\mathbf{F}^\mathsf{T} + \mathbf{Q }
\end{aligned}$$
Update Step
$$\begin{aligned}
\mathbf{K}_k &= \mathbf{P}_k\mathbf{F}^\mathsf{T}\mathbf{P}^{-1} \\
\mathbf{x}_k &= \mathbf{x}_k + \mathbf{K}_k(\mathbf{x}_{k+1} - \mathbf{Fx}_k) \\
\mathbf{P}_k &= \mathbf{P}_k + \mathbf{K}_k(\mathbf{P}_{k+1} - \mathbf{P})\mathbf{K}_k^\mathsf{T}
\end{aligned}$$
As always, the hardest part of the implementation is correctly accounting for the subscripts. A basic implementation without comments or error checking would be:
```python
def rts_smoother(Xs, Ps, F, Q):
n, dim_x, _ = Xs.shape
# smoother gain
K = zeros((n,dim_x, dim_x))
x, P, Pp = Xs.copy(), Ps.copy(), Ps.copy
for k in range(n-2,-1,-1):
Pp[k] = dot(F, P[k]).dot(F.T) + Q # predicted covariance
K[k] = dot(P[k], F.T).dot(inv(Pp[k]))
x[k] += dot(K[k], x[k+1] - dot(F, x[k]))
P[k] += dot(K[k], P[k+1] - Pp[k]).dot(K[k].T)
return (x, P, K, Pp)
```
This implementation mirrors the implementation provided in FilterPy. It assumes that the Kalman filter is being run externally in batch mode, and the results of the state and covariances are passed in via the `Xs` and `Ps` variable.
Here is an example.
```
import numpy as np
from numpy import random
from numpy.random import randn
import matplotlib.pyplot as plt
from filterpy.kalman import KalmanFilter
import kf_book.book_plots as bp
def plot_rts(noise, Q=0.001, show_velocity=False):
random.seed(123)
fk = KalmanFilter(dim_x=2, dim_z=1)
fk.x = np.array([0., 1.]) # state (x and dx)
fk.F = np.array([[1., 1.],
[0., 1.]]) # state transition matrix
fk.H = np.array([[1., 0.]]) # Measurement function
fk.P = 10. # covariance matrix
fk.R = noise # state uncertainty
fk.Q = Q # process uncertainty
# create noisy data
zs = np.asarray([t + randn()*noise for t in range (40)])
# filter data with Kalman filter, than run smoother on it
mu, cov, _, _ = fk.batch_filter(zs)
M, P, C, _ = fk.rts_smoother(mu, cov)
# plot data
if show_velocity:
index = 1
print('gu')
else:
index = 0
if not show_velocity:
bp.plot_measurements(zs, lw=1)
plt.plot(M[:, index], c='b', label='RTS')
plt.plot(mu[:, index], c='g', ls='--', label='KF output')
if not show_velocity:
N = len(zs)
plt.plot([0, N], [0, N], 'k', lw=2, label='track')
plt.legend(loc=4)
plt.show()
plot_rts(7.)
```
I've injected a lot of noise into the signal to allow you to visually distinguish the RTS output from the ideal output. In the graph above we can see that the Kalman filter, drawn as the green dotted line, is reasonably smooth compared to the input, but it still wanders from from the ideal line when several measurements in a row are biased towards one side of the line. In contrast, the RTS output is both extremely smooth and very close to the ideal output.
With a perhaps more reasonable amount of noise we can see that the RTS output nearly lies on the ideal output. The Kalman filter output, while much better, still varies by a far greater amount.
```
plot_rts(noise=1.)
```
However, we must understand that this smoothing is predicated on the system model. We have told the filter that what we are tracking follows a constant velocity model with very low process error. When the filter *looks ahead* it sees that the future behavior closely matches a constant velocity so it is able to reject most of the noise in the signal. Suppose instead our system has a lot of process noise. For example, if we are tracking a light aircraft in gusty winds its velocity will change often, and the filter will be less able to distinguish between noise and erratic movement due to the wind. We can see this in the next graph.
```
plot_rts(noise=7., Q=.1)
```
This underscores the fact that these filters are not *smoothing* the data in colloquial sense of the term. The filter is making an optimal estimate based on previous measurements, future measurements, and what you tell it about the behavior of the system and the noise in the system and measurements.
Let's wrap this up by looking at the velocity estimates of Kalman filter vs the RTS smoother.
```
plot_rts(7.,show_velocity=True)
```
The improvement in the velocity, which is an hidden variable, is even more dramatic.
## Fixed-Lag Smoothing
The RTS smoother presented above should always be your choice of algorithm if you can run in batch mode because it incorporates all available data into each estimate. Not all problems allow you to do that, but you may still be interested in receiving smoothed values for previous estimates. The number line below illustrates this concept.
```
from kf_book.book_plots import figsize
from kf_book.smoothing_internal import *
with figsize(y=2):
show_fixed_lag_numberline()
```
At step $k$ we can estimate $x_k$ using the normal Kalman filter equations. However, we can make a better estimate for $x_{k-1}$ by using the measurement received for $x_k$. Likewise, we can make a better estimate for $x_{k-2}$ by using the measurements recevied for $x_{k-1}$ and $x_{k}$. We can extend this computation back for an arbitrary $N$ steps.
Derivation for this math is beyond the scope of this book; Dan Simon's *Optimal State Estimation* [2] has a very good exposition if you are interested. The essense of the idea is that instead of having a state vector $\mathbf{x}$ we make an augmented state containing
$$\mathbf{x} = \begin{bmatrix}\mathbf{x}_k \\ \mathbf{x}_{k-1} \\ \vdots\\ \mathbf{x}_{k-N+1}\end{bmatrix}$$
This yields a very large covariance matrix that contains the covariance between states at different steps. FilterPy's class `FixedLagSmoother` takes care of all of this computation for you, including creation of the augmented matrices. All you need to do is compose it as if you are using the `KalmanFilter` class and then call `smooth()`, which implements the predict and update steps of the algorithm.
Each call of `smooth` computes the estimate for the current measurement, but it also goes back and adjusts the previous `N-1` points as well. The smoothed values are contained in the list `FixedLagSmoother.xSmooth`. If you use `FixedLagSmoother.x` you will get the most recent estimate, but it is not smoothed and is no different from a standard Kalman filter output.
```
from filterpy.kalman import FixedLagSmoother, KalmanFilter
import numpy.random as random
fls = FixedLagSmoother(dim_x=2, dim_z=1, N=8)
fls.x = np.array([0., .5])
fls.F = np.array([[1.,1.],
[0.,1.]])
fls.H = np.array([[1.,0.]])
fls.P *= 200
fls.R *= 5.
fls.Q *= 0.001
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.x = np.array([0., .5])
kf.F = np.array([[1.,1.],
[0.,1.]])
kf.H = np.array([[1.,0.]])
kf.P *= 200
kf.R *= 5.
kf.Q *= 0.001
N = 4 # size of lag
nom = np.array([t/2. for t in range (0, 40)])
zs = np.array([t + random.randn()*5.1 for t in nom])
for z in zs:
fls.smooth(z)
kf_x, _, _, _ = kf.batch_filter(zs)
x_smooth = np.array(fls.xSmooth)[:, 0]
fls_res = abs(x_smooth - nom)
kf_res = abs(kf_x[:, 0] - nom)
plt.plot(zs,'o', alpha=0.5, marker='o', label='zs')
plt.plot(x_smooth, label='FLS')
plt.plot(kf_x[:, 0], label='KF', ls='--')
plt.legend(loc=4)
print('standard deviation fixed-lag: {:.3f}'.format(np.mean(fls_res)))
print('standard deviation kalman: {:.3f}'.format(np.mean(kf_res)))
```
Here I have set `N=8` which means that we will incorporate 8 future measurements into our estimates. This provides us with a very smooth estimate once the filter converges, at the cost of roughly 8x the amount of computation of the standard Kalman filter. Feel free to experiment with larger and smaller values of `N`. I chose 8 somewhat at random, not due to any theoretical concerns.
## References
[1] H. Rauch, F. Tung, and C. Striebel. "Maximum likelihood estimates of linear dynamic systems," *AIAA Journal*, **3**(8), pp. 1445-1450 (August 1965).
[2] Dan Simon. "Optimal State Estimation," John Wiley & Sons, 2006.
http://arc.aiaa.org/doi/abs/10.2514/3.3166
| true |
code
| 0.672036 | null | null | null | null |
|
# 準備
```
# バージョン指定時にコメントアウト
#!pip install torch==1.7.0
#!pip install torchvision==0.8.1
import torch
import torchvision
# バージョンの確認
print(torch.__version__)
print(torchvision.__version__)
# Google ドライブにマウント
from google.colab import drive
drive.mount('/content/gdrive')
%cd '/content/gdrive/MyDrive/Colab Notebooks/gan_sample/chapter2'
import os
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizers
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import torchvision
import torchvision.transforms as transforms
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
# データセットの作成
```
np.random.seed(1234)
torch.manual_seed(1234)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# データの取得
root = os.path.join('data', 'mnist')
transform = transforms.Compose([transforms.ToTensor(),
lambda x: x.view(-1)])
mnist_train = \
torchvision.datasets.MNIST(root=root,
download=True,
train=True,
transform=transform)
mnist_test = \
torchvision.datasets.MNIST(root=root,
download=True,
train=False,
transform=transform)
train_dataloader = DataLoader(mnist_train,
batch_size=100,
shuffle=True)
test_dataloader = DataLoader(mnist_test,
batch_size=1,
shuffle=False)
```
# ネットワークの定義
```
class Autoencoder(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.l1 = nn.Linear(784, 200)
self.l2 = nn.Linear(200, 784)
def forward(self, x):
# エンコーダ
h = self.l1(x)
# 活性化関数
h = torch.relu(h)
# デコーダ
h = self.l2(h)
# シグモイド関数で0~1の値域に変換
y = torch.sigmoid(h)
return y
```
# 学習の実行
```
# モデルの設定
model = Autoencoder(device=device).to(device)
# 損失関数の設定
criterion = nn.BCELoss()
# 最適化関数の設定
optimizer = optimizers.Adam(model.parameters())
epochs = 10
# エポックのループ
for epoch in range(epochs):
train_loss = 0.
# バッチサイズのループ
for (x, _) in train_dataloader:
x = x.to(device)
# 訓練モードへの切替
model.train()
# 順伝播計算
preds = model(x)
# 入力画像xと復元画像predsの誤差計算
loss = criterion(preds, x)
# 勾配の初期化
optimizer.zero_grad()
# 誤差の勾配計算
loss.backward()
# パラメータの更新
optimizer.step()
# 訓練誤差の更新
train_loss += loss.item()
train_loss /= len(train_dataloader)
print('Epoch: {}, Loss: {:.3f}'.format(
epoch+1,
train_loss
))
```
# 画像の復元
```
# dataloaderからのデータ取り出し
x, _ = next(iter(test_dataloader))
x = x.to(device)
# 評価モードへの切替
model.eval()
# 復元画像
x_rec = model(x)
# 入力画像、復元画像の表示
for i, image in enumerate([x, x_rec]):
image = image.view(28, 28).detach().cpu().numpy()
plt.subplot(1, 2, i+1)
plt.imshow(image, cmap='binary_r')
plt.axis('off')
plt.show()
```
| true |
code
| 0.785946 | null | null | null | null |
|
# One-step error probability
Write a computer program implementing asynchronous deterministic updates for a Hopfield network. Use Hebb's rule with $w_{ii}=0$. Generate and store p=[12,24,48,70,100,120] random patterns with N=120 bits. Each bit is either +1 or -1 with probability $\tfrac{1}{2}$.
For each value of ppp estimate the one-step error probability $P_{\text {error}}^{t=1}$ based on $10^5$ independent trials. Here, one trial means that you generate and store a set of p random patterns, feed one of them, and perform one asynchronous update of a single randomly chosen neuron. If in some trials you encounter sgn(0), simply set sgn(0)=1.
List below the values of $P_{\text {error}}^{t=1}$ that you obtained in the following form: [$p_1,p_2,\ldots,p_{6}$], where $p_n$ is the value of $P_{\text {error}}^{t=1}$ for the n-th value of p from the list above. Give four decimal places for each $p_n$
```
import numpy as np
import time
def calculate_instance( n, p, zero_diagonal):
#Create p random patterns
patterns = []
for i in range(p):
patterns.append(np.random.choice([-1,1],n))
#Create weights matrix according to hebbs rule
weights = patterns[0][:,None]*patterns[0]
for el in patterns[1:]:
weights = weights + el[:,None]*el
weights = np.true_divide(weights, n)
#Fill diagonal with zeroes
if zero_diagonal:
np.fill_diagonal(weights,0)
#Feed random pattern as input and test if an error occurs
S1 = patterns[0]
chosen_i = np.random.choice(range(n))
S_i_old = S1[chosen_i]
S_i = esign(np.dot(weights[chosen_i], S1))
#breakpoint()
return S_i_old == S_i
def esign(x):
if(x == 0):
return 1
else:
return np.sign(x)
```
List your numerically computed $P_{\text {error}}^{t=1}$ for the parameters given above.
```
p = [12, 24, 48, 70, 100, 120]
N = 120
I = 100000
for p_i in p:
solve = [0,0]
for i in range(I):
ret = calculate_instance(N, p_i, True)
if ret:
solve[0]+=1
else:
solve[1]+=1
p_error = float(solve[1]/I)
print(f"Number of patterns: {p_i}, P_error(t=1): {p_error} ")
```
Repeat the task, but now apply Hebb's rule without setting the diagonal weights to zero. For each value of p listed above, estimate the one-step error probability $P_{\text {error}}^{t=1}$ based on $10^5$ independent trials.
```
p = [12, 24, 48, 70, 100, 120]
N = 120
I = 100000
for p_i in p:
solve = [0,0]
for i in range(I):
ret = calculate_instance(N, p_i, False)
if ret:
solve[0]+=1
else:
solve[1]+=1
p_error = float(solve[1]/I)
print(f"Number of patterns: {p_i}, P_error(t=1): {p_error} ")
```
| true |
code
| 0.266787 | null | null | null | null |
|
# Code Review #1
Purpose: To introduce the group to looking at code analytically
Created By: Hawley Helmbrecht
Creation Date: 10-12-21
# Introduction to Analyzing Code
All snipets within this section are taken from the Hitchhiker's Guide to Python (https://docs.python-guide.org/writing/style/)
### Example 1: Explicit Code
```
def make_complex(*args):
x, y = args
return dict(**locals())
def make_complex(x, y):
return {'x': x, 'y': y}
```
### Example 2: One Statement per Line
```
print('one'); print('two')
if x == 1: print('one')
if <complex comparison> and <other complex comparison>:
# do something
print('one')
print('two')
if x == 1:
print('one')
cond1 = <complex comparison>
cond2 = <other complex comparison>
if cond1 and cond2:
# do something
```
## Intro to Pep 8
Example 1: Limit all lines to a maximum of 79 characters.
```
#Wrong:
income = (gross_wages + taxable_interest + (dividends - qualified_dividends) - ira_deduction - student_loan_interest)
#Correct:
income = (gross_wages
+ taxable_interest
+ (dividends - qualified_dividends)
- ira_deduction
- student_loan_interest)
```
Example 2: Line breaks around binary operators
```
# Wrong:
# operators sit far away from their operands
income = (gross_wages +
taxable_interest +
(dividends - qualified_dividends) -
ira_deduction -
student_loan_interest)
# Correct:
# easy to match operators with operands
income = (gross_wages
+ taxable_interest
+ (dividends - qualified_dividends)
- ira_deduction
- student_loan_interest)
```
Example 3: Import formatting
```
# Correct:
import os
import sys
# Wrong:
import sys, os
```
## Let's look at some code!
Sci-kit images Otsu Threshold code! (https://github.com/scikit-image/scikit-image/blob/main/skimage/filters/thresholding.py)
```
def threshold_otsu(image=None, nbins=256, *, hist=None):
"""Return threshold value based on Otsu's method.
Either image or hist must be provided. If hist is provided, the actual
histogram of the image is ignored.
Parameters
----------
image : (N, M[, ..., P]) ndarray, optional
Grayscale input image.
nbins : int, optional
Number of bins used to calculate histogram. This value is ignored for
integer arrays.
hist : array, or 2-tuple of arrays, optional
Histogram from which to determine the threshold, and optionally a
corresponding array of bin center intensities. If no hist provided,
this function will compute it from the image.
Returns
-------
threshold : float
Upper threshold value. All pixels with an intensity higher than
this value are assumed to be foreground.
References
----------
.. [1] Wikipedia, https://en.wikipedia.org/wiki/Otsu's_Method
Examples
--------
>>> from skimage.data import camera
>>> image = camera()
>>> thresh = threshold_otsu(image)
>>> binary = image <= thresh
Notes
-----
The input image must be grayscale.
"""
if image is not None and image.ndim > 2 and image.shape[-1] in (3, 4):
warn(f'threshold_otsu is expected to work correctly only for '
f'grayscale images; image shape {image.shape} looks like '
f'that of an RGB image.')
# Check if the image has more than one intensity value; if not, return that
# value
if image is not None:
first_pixel = image.ravel()[0]
if np.all(image == first_pixel):
return first_pixel
counts, bin_centers = _validate_image_histogram(image, hist, nbins)
# class probabilities for all possible thresholds
weight1 = np.cumsum(counts)
weight2 = np.cumsum(counts[::-1])[::-1]
# class means for all possible thresholds
mean1 = np.cumsum(counts * bin_centers) / weight1
mean2 = (np.cumsum((counts * bin_centers)[::-1]) / weight2[::-1])[::-1]
# Clip ends to align class 1 and class 2 variables:
# The last value of ``weight1``/``mean1`` should pair with zero values in
# ``weight2``/``mean2``, which do not exist.
variance12 = weight1[:-1] * weight2[1:] * (mean1[:-1] - mean2[1:]) ** 2
idx = np.argmax(variance12)
threshold = bin_centers[idx]
return threshold
```
What do you observe about the code that makes it pythonic?
```
Do the pythonic conventions make it easier to understand?
```
How is the documentation on this function?
| true |
code
| 0.769313 | null | null | null | null |
|
# SLU13: Bias-Variance trade-off & Model Selection -- Examples
---
<a id='top'></a>
### 1. Model evaluation
* a. [Train-test split](#traintest)
* b. [Train-val-test split](#val)
* c. [Cross validation](#crossval)
### 2. [Learning curves](#learningcurves)
# 1. Model evaluation
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import learning_curve
%matplotlib inline
# Create the DataFrame with the data
df = pd.read_csv("data/beer.csv")
# Create a DataFrame with the features (X) and labels (y)
X = df.drop(["IsIPA"], axis=1)
y = df["IsIPA"]
print("Number of entries: ", X.shape[0])
```
<a id='traintest'></a> [Return to top](#top)
## Create a training and a test set
```
from sklearn.model_selection import train_test_split
# Using 20 % of the data as test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print("Number of training entries: ", X_train.shape[0])
print("Number of test entries: ", X_test.shape[0])
```
<a id='val'></a> [Return to top](#top)
## Create a training, test and validation set
```
# Using 20 % as test set and 20 % as validation set
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.4)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.50)
print("Number of training entries: ", X_train.shape[0])
print("Number of validation entries: ", X_val.shape[0])
print("Number of test entries: ", X_test.shape[0])
```
<a id='crossval'></a> [Return to top](#top)
## Use cross-validation (using a given classifier)
```
from sklearn.model_selection import cross_val_score
knn = KNeighborsClassifier(n_neighbors=5)
# Use cv to specify the number of folds
scores = cross_val_score(knn, X, y, cv=5)
print(f"Mean of scores: {scores.mean():.3f}")
print(f"Variance of scores: {scores.var():.3f}")
```
<a id='learningcurves'></a> [Return to top](#top)
# 2. Learning Curves
Here is the function that is taken from the sklearn page on learning curves:
```
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
"""
Generate a simple plot of the test and training learning curve.
Parameters
----------
estimator : object type that implements the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title : string
Title for the chart.
X : array-like, shape (n_samples, n_features)
Training vector, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape (n_samples) or (n_samples, n_features), optional
Target relative to X for classification or regression;
None for unsupervised learning.
ylim : tuple, shape (ymin, ymax), optional
Defines minimum and maximum yvalues plotted.
cv : int, cross-validation generator or an iterable, optional
Determines the cross-validation splitting strategy.
Possible inputs for cv are:
- None, to use the default 3-fold cross-validation,
- integer, to specify the number of folds.
- An object to be used as a cross-validation generator.
- An iterable yielding train/test splits.
For integer/None inputs, if ``y`` is binary or multiclass,
:class:`StratifiedKFold` used. If the estimator is not a classifier
or if ``y`` is neither binary nor multiclass, :class:`KFold` is used.
Refer :ref:`User Guide <cross_validation>` for the various
cross-validators that can be used here.
n_jobs : integer, optional
Number of jobs to run in parallel (default 1).
"""
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Test Set score")
plt.legend(loc="best")
return plt
# and this is how we used it
X = df.select_dtypes(exclude='object').fillna(-1).drop('IsIPA', axis=1)
y = df.IsIPA
clf = DecisionTreeClassifier(random_state=1, max_depth=5)
plot_learning_curve(X=X, y=y, estimator=clf, title='DecisionTreeClassifier');
```
And remember the internals of what this function is actually doing by knowing how to use the
output of the scikit [learning_curve](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.learning_curve.html) function
```
# here's where the magic happens! The learning curve function is going
# to take your classifier and your training data and subset the data
train_sizes, train_scores, test_scores = learning_curve(clf, X, y)
# 5 different training set sizes have been selected
# with the smallest being 59 and the largest being 594
# the remaining is used for testing
print('train set sizes', train_sizes)
print('test set sizes', X.shape[0] - train_sizes)
# each row corresponds to a training set size
# each column corresponds to a cross validation fold
# the first row is the highest because it corresponds
# to the smallest training set which means that it's very
# easy for the classifier to overfit and have perfect
# test set predictions while as the test set grows it
# becomes a bit more difficult for this to happen.
train_scores
# The test set scores where again, each row corresponds
# to a train / test set size and each column is a differet
# run with the same train / test sizes
test_scores
# Let's average the scores across each fold so that we can plot them
train_scores_mean = np.mean(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
# this one isn't quite as cool as the other because it doesn't show the variance
# but the fundamentals are still here and it's a much simpler one to understand
learning_curve_df = pd.DataFrame({
'Training score': train_scores_mean,
'Test Set score': test_scores_mean
}, index=train_sizes)
plt.figure()
plt.ylabel("Score")
plt.xlabel("Training examples")
plt.title('Learning Curve')
plt.plot(learning_curve_df);
plt.legend(learning_curve_df.columns, loc="best");
```
| true |
code
| 0.751489 | null | null | null | null |
|
## Rhetorical relations classification used in tree building: ESIM
Prepare data and model-related scripts.
Evaluate models.
Make and evaluate ansembles for ESIM and BiMPM model / ESIM and feature-based model.
Output:
- ``models/relation_predictor_esim/*``
```
%load_ext autoreload
%autoreload 2
import os
import glob
import pandas as pd
import numpy as np
import pickle
from utils.file_reading import read_edus, read_gold, read_negative, read_annotation
```
### Make a directory
```
MODEL_PATH = 'models/label_predictor_esim'
! mkdir $MODEL_PATH
TRAIN_FILE_PATH = os.path.join(MODEL_PATH, 'nlabel_cf_train.tsv')
DEV_FILE_PATH = os.path.join(MODEL_PATH, 'nlabel_cf_dev.tsv')
TEST_FILE_PATH = os.path.join(MODEL_PATH, 'nlabel_cf_test.tsv')
```
### Prepare train/test sets
```
IN_PATH = 'data_labeling'
train_samples = pd.read_pickle(os.path.join(IN_PATH, 'train_samples.pkl'))
dev_samples = pd.read_pickle(os.path.join(IN_PATH, 'dev_samples.pkl'))
test_samples = pd.read_pickle(os.path.join(IN_PATH, 'test_samples.pkl'))
counts = train_samples['relation'].value_counts(normalize=False).values
NUMBER_CLASSES = len(counts)
print("number of classes:", NUMBER_CLASSES)
print("class weights:")
np.round(counts.min() / counts, decimals=6)
counts = train_samples['relation'].value_counts()
counts
import razdel
def tokenize(text):
result = ' '.join([tok.text for tok in razdel.tokenize(text)])
return result
train_samples['snippet_x'] = train_samples.snippet_x.map(tokenize)
train_samples['snippet_y'] = train_samples.snippet_y.map(tokenize)
dev_samples['snippet_x'] = dev_samples.snippet_x.map(tokenize)
dev_samples['snippet_y'] = dev_samples.snippet_y.map(tokenize)
test_samples['snippet_x'] = test_samples.snippet_x.map(tokenize)
test_samples['snippet_y'] = test_samples.snippet_y.map(tokenize)
train_samples = train_samples.reset_index()
train_samples[['relation', 'snippet_x', 'snippet_y', 'index']].to_csv(TRAIN_FILE_PATH, sep='\t', header=False, index=False)
dev_samples = dev_samples.reset_index()
dev_samples[['relation', 'snippet_x', 'snippet_y', 'index']].to_csv(DEV_FILE_PATH, sep='\t', header=False, index=False)
test_samples = test_samples.reset_index()
test_samples[['relation', 'snippet_x', 'snippet_y', 'index']].to_csv(TEST_FILE_PATH, sep='\t', header=False, index=False)
```
### Modify model
(Add F1, concatenated encoding)
```
%%writefile models/bimpm_custom_package/model/esim.py
from typing import Dict, List, Any, Optional
import numpy
import torch
from allennlp.common.checks import check_dimensions_match
from allennlp.data import TextFieldTensors, Vocabulary
from allennlp.models.model import Model
from allennlp.modules import FeedForward, InputVariationalDropout
from allennlp.modules.matrix_attention.matrix_attention import MatrixAttention
from allennlp.modules import Seq2SeqEncoder, TextFieldEmbedder
from allennlp.nn import InitializerApplicator
from allennlp.nn.util import (
get_text_field_mask,
masked_softmax,
weighted_sum,
masked_max,
)
from allennlp.training.metrics import CategoricalAccuracy, F1Measure
@Model.register("custom_esim")
class CustomESIM(Model):
"""
This `Model` implements the ESIM sequence model described in [Enhanced LSTM for Natural Language Inference]
(https://api.semanticscholar.org/CorpusID:34032948) by Chen et al., 2017.
Registered as a `Model` with name "esim".
# Parameters
vocab : `Vocabulary`
text_field_embedder : `TextFieldEmbedder`
Used to embed the `premise` and `hypothesis` `TextFields` we get as input to the
model.
encoder : `Seq2SeqEncoder`
Used to encode the premise and hypothesis.
matrix_attention : `MatrixAttention`
This is the attention function used when computing the similarity matrix between encoded
words in the premise and words in the hypothesis.
projection_feedforward : `FeedForward`
The feedforward network used to project down the encoded and enhanced premise and hypothesis.
inference_encoder : `Seq2SeqEncoder`
Used to encode the projected premise and hypothesis for prediction.
output_feedforward : `FeedForward`
Used to prepare the concatenated premise and hypothesis for prediction.
output_logit : `FeedForward`
This feedforward network computes the output logits.
dropout : `float`, optional (default=`0.5`)
Dropout percentage to use.
initializer : `InitializerApplicator`, optional (default=`InitializerApplicator()`)
Used to initialize the model parameters.
"""
def __init__(
self,
vocab: Vocabulary,
text_field_embedder: TextFieldEmbedder,
encoder: Seq2SeqEncoder,
matrix_attention: MatrixAttention,
projection_feedforward: FeedForward,
inference_encoder: Seq2SeqEncoder,
output_feedforward: FeedForward,
output_logit: FeedForward,
encode_together: bool = False,
dropout: float = 0.5,
class_weights: list = [],
initializer: InitializerApplicator = InitializerApplicator(),
**kwargs,
) -> None:
super().__init__(vocab, **kwargs)
self._text_field_embedder = text_field_embedder
self._encoder = encoder
self._matrix_attention = matrix_attention
self._projection_feedforward = projection_feedforward
self._inference_encoder = inference_encoder
if dropout:
self.dropout = torch.nn.Dropout(dropout)
self.rnn_input_dropout = InputVariationalDropout(dropout)
else:
self.dropout = None
self.rnn_input_dropout = None
self._output_feedforward = output_feedforward
self._output_logit = output_logit
self.encode_together = encode_together
self._num_labels = vocab.get_vocab_size(namespace="labels")
check_dimensions_match(
text_field_embedder.get_output_dim(),
encoder.get_input_dim(),
"text field embedding dim",
"encoder input dim",
)
check_dimensions_match(
encoder.get_output_dim() * 4,
projection_feedforward.get_input_dim(),
"encoder output dim",
"projection feedforward input",
)
check_dimensions_match(
projection_feedforward.get_output_dim(),
inference_encoder.get_input_dim(),
"proj feedforward output dim",
"inference lstm input dim",
)
self.metrics = {"accuracy": CategoricalAccuracy()}
if class_weights:
self.class_weights = class_weights
else:
self.class_weights = [1.] * self.classifier_feedforward.get_output_dim()
for _class in range(len(self.class_weights)):
self.metrics.update({
f"f1_rel{_class}": F1Measure(_class),
})
self._loss = torch.nn.CrossEntropyLoss(weight=torch.FloatTensor(self.class_weights))
initializer(self)
def forward( # type: ignore
self,
premise: TextFieldTensors,
hypothesis: TextFieldTensors,
label: torch.IntTensor = None,
metadata: List[Dict[str, Any]] = None,
) -> Dict[str, torch.Tensor]:
"""
# Parameters
premise : `TextFieldTensors`
From a `TextField`
hypothesis : `TextFieldTensors`
From a `TextField`
label : `torch.IntTensor`, optional (default = `None`)
From a `LabelField`
metadata : `List[Dict[str, Any]]`, optional (default = `None`)
Metadata containing the original tokenization of the premise and
hypothesis with 'premise_tokens' and 'hypothesis_tokens' keys respectively.
# Returns
An output dictionary consisting of:
label_logits : `torch.FloatTensor`
A tensor of shape `(batch_size, num_labels)` representing unnormalised log
probabilities of the entailment label.
label_probs : `torch.FloatTensor`
A tensor of shape `(batch_size, num_labels)` representing probabilities of the
entailment label.
loss : `torch.FloatTensor`, optional
A scalar loss to be optimised.
"""
embedded_premise = self._text_field_embedder(premise)
embedded_hypothesis = self._text_field_embedder(hypothesis)
premise_mask = get_text_field_mask(premise)
hypothesis_mask = get_text_field_mask(hypothesis)
# apply dropout for LSTM
if self.rnn_input_dropout:
embedded_premise = self.rnn_input_dropout(embedded_premise)
embedded_hypothesis = self.rnn_input_dropout(embedded_hypothesis)
# encode premise and hypothesis
encoded_premise = self._encoder(embedded_premise, premise_mask)
encoded_hypothesis = self._encoder(embedded_hypothesis, hypothesis_mask)
# Shape: (batch_size, premise_length, hypothesis_length)
similarity_matrix = self._matrix_attention(encoded_premise, encoded_hypothesis)
# Shape: (batch_size, premise_length, hypothesis_length)
p2h_attention = masked_softmax(similarity_matrix, hypothesis_mask)
# Shape: (batch_size, premise_length, embedding_dim)
attended_hypothesis = weighted_sum(encoded_hypothesis, p2h_attention)
# Shape: (batch_size, hypothesis_length, premise_length)
h2p_attention = masked_softmax(similarity_matrix.transpose(1, 2).contiguous(), premise_mask)
# Shape: (batch_size, hypothesis_length, embedding_dim)
attended_premise = weighted_sum(encoded_premise, h2p_attention)
# the "enhancement" layer
premise_enhanced = torch.cat(
[
encoded_premise,
attended_hypothesis,
encoded_premise - attended_hypothesis,
encoded_premise * attended_hypothesis,
],
dim=-1,
)
hypothesis_enhanced = torch.cat(
[
encoded_hypothesis,
attended_premise,
encoded_hypothesis - attended_premise,
encoded_hypothesis * attended_premise,
],
dim=-1,
)
# The projection layer down to the model dimension. Dropout is not applied before
# projection.
projected_enhanced_premise = self._projection_feedforward(premise_enhanced)
projected_enhanced_hypothesis = self._projection_feedforward(hypothesis_enhanced)
# Run the inference layer
if self.rnn_input_dropout:
projected_enhanced_premise = self.rnn_input_dropout(projected_enhanced_premise)
projected_enhanced_hypothesis = self.rnn_input_dropout(projected_enhanced_hypothesis)
v_ai = self._inference_encoder(projected_enhanced_premise, premise_mask)
v_bi = self._inference_encoder(projected_enhanced_hypothesis, hypothesis_mask)
# The pooling layer -- max and avg pooling.
# (batch_size, model_dim)
v_a_max = masked_max(v_ai, premise_mask.unsqueeze(-1), dim=1)
v_b_max = masked_max(v_bi, hypothesis_mask.unsqueeze(-1), dim=1)
v_a_avg = torch.sum(v_ai * premise_mask.unsqueeze(-1), dim=1) / torch.sum(
premise_mask, 1, keepdim=True
)
v_b_avg = torch.sum(v_bi * hypothesis_mask.unsqueeze(-1), dim=1) / torch.sum(
hypothesis_mask, 1, keepdim=True
)
# Now concat
# (batch_size, model_dim * 2 * 4)
v_all = torch.cat([v_a_avg, v_a_max, v_b_avg, v_b_max], dim=1)
# the final MLP -- apply dropout to input, and MLP applies to output & hidden
if self.dropout:
v_all = self.dropout(v_all)
output_hidden = self._output_feedforward(v_all)
label_logits = self._output_logit(output_hidden)
label_probs = torch.nn.functional.softmax(label_logits, dim=-1)
output_dict = {"label_logits": label_logits, "label_probs": label_probs}
if label is not None:
loss = self._loss(label_logits, label.long().view(-1))
output_dict["loss"] = loss
for metric in self.metrics.values():
metric(label_logits, label.long().view(-1))
return output_dict
def get_metrics(self, reset: bool = False) -> Dict[str, float]:
metrics = {"accuracy": self.metrics["accuracy"].get_metric(reset=reset)}
for _class in range(len(self.class_weights)):
metrics.update({
f"f1_rel{_class}": self.metrics[f"f1_rel{_class}"].get_metric(reset=reset)['f1'],
})
metrics["f1_macro"] = numpy.mean([metrics[f"f1_rel{_class}"] for _class in range(len(self.class_weights))])
return metrics
default_predictor = "textual_entailment"
! cp models/bimpm_custom_package/model/esim.py ../../../maintenance_rst/models/customization_package/model/esim.py
```
### 2. Generate config files
#### ELMo
```
%%writefile $MODEL_PATH/config_elmo.json
local NUM_EPOCHS = 200;
local LR = 1e-3;
local LSTM_ENCODER_HIDDEN = 25;
{
"dataset_reader": {
"type": "quora_paraphrase",
"tokenizer": {
"type": "just_spaces"
},
"token_indexers": {
"token_characters": {
"type": "characters",
"min_padding_length": 30,
},
"elmo": {
"type": "elmo_characters"
}
}
},
"train_data_path": "label_predictor_esim/nlabel_cf_train.tsv",
"validation_data_path": "label_predictor_esim/nlabel_cf_dev.tsv",
"test_data_path": "label_predictor_esim/nlabel_cf_test.tsv",
"model": {
"type": "custom_esim",
"dropout": 0.5,
"class_weights": [
0.027483, 0.032003, 0.080478, 0.102642, 0.121394, 0.135027,
0.136856, 0.170897, 0.172355, 0.181655, 0.193858, 0.211297,
0.231651, 0.260982, 0.334437, 0.378277, 0.392996, 0.567416,
0.782946, 0.855932, 0.971154, 1.0],
"encode_together": false,
"text_field_embedder": {
"token_embedders": {
"elmo": {
"type": "elmo_token_embedder",
"options_file": "rsv_elmo/options.json",
"weight_file": "rsv_elmo/model.hdf5",
"do_layer_norm": false,
"dropout": 0.1
},
"token_characters": {
"type": "character_encoding",
"dropout": 0.1,
"embedding": {
"embedding_dim": 20,
"padding_index": 0,
"vocab_namespace": "token_characters"
},
"encoder": {
"type": "lstm",
"input_size": $.model.text_field_embedder.token_embedders.token_characters.embedding.embedding_dim,
"hidden_size": LSTM_ENCODER_HIDDEN,
"num_layers": 1,
"bidirectional": true,
"dropout": 0.4
},
},
}
},
"encoder": {
"type": "lstm",
"input_size": 1024+LSTM_ENCODER_HIDDEN+LSTM_ENCODER_HIDDEN,
"hidden_size": 300,
"num_layers": 1,
"bidirectional": true
},
"matrix_attention": {"type": "dot_product"},
"projection_feedforward": {
"input_dim": 2400,
"hidden_dims": 300,
"num_layers": 1,
"activations": "relu"
},
"inference_encoder": {
"type": "lstm",
"input_size": 300,
"hidden_size": 300,
"num_layers": 1,
"bidirectional": true
},
"output_feedforward": {
"input_dim": 2400,
"num_layers": 1,
"hidden_dims": 300,
"activations": "relu",
"dropout": 0.5
},
"output_logit": {
"input_dim": 300,
"num_layers": 1,
"hidden_dims": 22,
"activations": "linear"
},
"initializer": {
"regexes": [
[".*linear_layers.*weight", {"type": "xavier_normal"}],
[".*linear_layers.*bias", {"type": "constant", "val": 0}],
[".*weight_ih.*", {"type": "xavier_normal"}],
[".*weight_hh.*", {"type": "orthogonal"}],
[".*bias.*", {"type": "constant", "val": 0}],
[".*matcher.*match_weights.*", {"type": "kaiming_normal"}]
]
}
},
"data_loader": {
"batch_sampler": {
"type": "bucket",
"batch_size": 20,
"padding_noise": 0.0,
"sorting_keys": ["premise"],
},
},
"trainer": {
"num_epochs": NUM_EPOCHS,
"cuda_device": 1,
"grad_clipping": 5.0,
"validation_metric": "+f1_macro",
"shuffle": true,
"optimizer": {
"type": "adam",
"lr": LR
},
"learning_rate_scheduler": {
"type": "reduce_on_plateau",
"factor": 0.5,
"mode": "max",
"patience": 0
}
}
}
! cp -r $MODEL_PATH ../../../maintenance_rst/models/label_predictor_esim
! cp -r $MODEL_PATH/config_elmo.json ../../../maintenance_rst/models/label_predictor_esim/
```
### 3. Scripts for training/prediction
#### Option 1. Directly from the config
Train a model
```
%%writefile models/train_label_predictor_esim.sh
# usage:
# $ cd models
# $ sh train_label_predictor.sh {bert|elmo} result_30
export METHOD=${1}
export RESULT_DIR=${2}
export DEV_FILE_PATH="nlabel_cf_dev.tsv"
export TEST_FILE_PATH="nlabel_cf_test.tsv"
rm -r label_predictor_esim/${RESULT_DIR}/
allennlp train -s label_predictor_esim/${RESULT_DIR}/ label_predictor_esim/config_${METHOD}.json \
--include-package bimpm_custom_package
allennlp predict --use-dataset-reader --silent \
--output-file label_predictor_esim/${RESULT_DIR}/predictions_dev.json label_predictor_esim/${RESULT_DIR}/model.tar.gz label_predictor_esim/${DEV_FILE_PATH} \
--include-package bimpm_custom_package \
--predictor textual-entailment
allennlp predict --use-dataset-reader --silent \
--output-file label_predictor_esim/${RESULT_DIR}/predictions_test.json label_predictor_esim/${RESULT_DIR}/model.tar.gz label_predictor_esim/${TEST_FILE_PATH} \
--include-package bimpm_custom_package \
--predictor textual-entailment
! cp models/train_label_predictor_esim.sh ../../../maintenance_rst/models/
```
Predict on dev&test
```
%%writefile models/eval_label_predictor_esim.sh
# usage:
# $ cd models
# $ sh train_label_predictor.sh {bert|elmo} result_30
export METHOD=${1}
export RESULT_DIR=${2}
export DEV_FILE_PATH="nlabel_cf_dev.tsv"
export TEST_FILE_PATH="nlabel_cf_test.tsv"
allennlp predict --use-dataset-reader --silent \
--output-file label_predictor_esim/${RESULT_DIR}/predictions_dev.json label_predictor_esim/${RESULT_DIR}/model.tar.gz label_predictor_esim/${DEV_FILE_PATH} \
--include-package bimpm_custom_package \
--predictor textual-entailment
allennlp predict --use-dataset-reader --silent \
--output-file label_predictor_esim/${RESULT_DIR}/predictions_test.json label_predictor_esim/${RESULT_DIR}/model.tar.gz label_predictor_esim/${TEST_FILE_PATH} \
--include-package bimpm_custom_package \
--predictor textual-entailment
! cp models/eval_label_predictor_esim.sh ../../../maintenance_rst/models/
```
(optional) predict on train
```
%%writefile models/eval_label_predictor_train.sh
# usage:
# $ cd models
# $ sh eval_label_predictor_train.sh {bert|elmo} result_30
export METHOD=${1}
export RESULT_DIR=${2}
export TEST_FILE_PATH="nlabel_cf_train.tsv"
allennlp predict --use-dataset-reader --silent \
--output-file label_predictor_bimpm/${RESULT_DIR}/predictions_train.json label_predictor_bimpm/${RESULT_DIR}/model.tar.gz label_predictor_bimpm/${TEST_FILE_PATH} \
--include-package customization_package \
--predictor textual-entailment
```
#### Option 2. Using wandb for parameters adjustment
```
%%writefile ../../../maintenance_rst/models/wandb_label_predictor_esim.yaml
name: label_predictor_esim
program: wandb_allennlp # this is a wrapper console script around allennlp commands. It is part of wandb-allennlp
method: bayes
## Do not for get to use the command keyword to specify the following command structure
command:
- ${program} #omit the interpreter as we use allennlp train command directly
- "--subcommand=train"
- "--include-package=customization_package" # add all packages containing your registered classes here
- "--config_file=label_predictor_esim/config_elmo.json"
- ${args}
metric:
name: best_f1_macro
goal: maximize
parameters:
model.encode_together:
values: ["true", ]
iterator.batch_size:
values: [8,]
trainer.optimizer.lr:
values: [0.001,]
model.dropout:
values: [0.5]
```
3. Run training
``wandb sweep wandb_label_predictor_esim.yaml``
(returns %sweepname1)
``wandb sweep wandb_label_predictor2.yaml``
(returns %sweepname2)
``wandb agent --count 1 %sweepname1 && wandb agent --count 1 %sweepname2``
Move the best model in label_predictor_bimpm
```
! ls -laht models/wandb
! cp -r models/wandb/run-20201218_123424-kcphaqhi/training_dumps models/label_predictor_esim/esim_elmo
```
**Or** load from wandb by %sweepname
```
import wandb
api = wandb.Api()
run = api.run("tchewik/tmp/7hum4oom")
for file in run.files():
file.download(replace=True)
! cp -r training_dumps models/label_predictor_bimpm/toasty-sweep-1
```
And run evaluation from shell
``sh eval_label_predictor_esim.sh {elmo|elmo_fasttext} toasty-sweep-1``
### 4. Evaluate classifier
```
def load_predictions(path):
result = []
vocab = []
with open(path, 'r') as file:
for line in file.readlines():
line = json.loads(line)
if line.get("label"):
result.append(line.get("label"))
elif line.get("label_probs"):
if not vocab:
vocab = open(path[:path.rfind('/')] + '/vocabulary/labels.txt', 'r').readlines()
vocab = [label.strip() for label in vocab]
result.append(vocab[np.argmax(line.get("label_probs"))])
print('length of result:', len(result))
return result
RESULT_DIR = 'esim_elmo'
! mkdir models/label_predictor_esim/$RESULT_DIR
! cp -r ../../../maintenance_rst/models/label_predictor_esim/$RESULT_DIR/*.json models/label_predictor_esim/$RESULT_DIR/
```
On dev set
```
import pandas as pd
import json
true = pd.read_csv(DEV_FILE_PATH, sep='\t', header=None)[0].values.tolist()
pred = load_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_dev.json')
from sklearn.metrics import classification_report
print(classification_report(true[:len(pred)], pred, digits=4))
test_metrics = classification_report(true[:len(pred)], pred, digits=4, output_dict=True)
test_f1 = np.array(
[test_metrics[label].get('f1-score') for label in test_metrics if type(test_metrics[label]) == dict]) * 100
test_f1
len(true)
from sklearn.metrics import f1_score, precision_score, recall_score
print('f1: %.2f'%(f1_score(true[:len(pred)], pred, average='macro')*100))
print('pr: %.2f'%(precision_score(true[:len(pred)], pred, average='macro')*100))
print('re: %.2f'%(recall_score(true[:len(pred)], pred, average='macro')*100))
from utils.plot_confusion_matrix import plot_confusion_matrix
from sklearn.metrics import confusion_matrix
labels = list(set(true))
labels.sort()
plot_confusion_matrix(confusion_matrix(true[:len(pred)], pred, labels), target_names=labels, normalize=True)
top_classes = [
'attribution_NS',
'attribution_SN',
'purpose_NS',
'purpose_SN',
'condition_SN',
'contrast_NN',
'condition_NS',
'joint_NN',
'concession_NS',
'same-unit_NN',
'elaboration_NS',
'cause-effect_NS',
]
class_mapper = {weird_class: 'other' + weird_class[-3:] for weird_class in labels if not weird_class in top_classes}
import numpy as np
true = [class_mapper.get(value) if class_mapper.get(value) else value for value in true]
pred = [class_mapper.get(value) if class_mapper.get(value) else value for value in pred]
pred_mapper = {
'other_NN': 'joint_NN',
'other_NS': 'joint_NN',
'other_SN': 'joint_NN'
}
pred = [pred_mapper.get(value) if pred_mapper.get(value) else value for value in pred]
_to_stay = (np.array(true) != 'other_NN') & (np.array(true) != 'other_SN') & (np.array(true) != 'other_NS')
_true = np.array(true)[_to_stay]
_pred = np.array(pred)[_to_stay[:len(pred)]]
labels = list(set(_true))
from sklearn.metrics import f1_score, precision_score, recall_score
print('f1: %.2f'%(f1_score(true[:len(pred)], pred, average='macro')*100))
print('pr: %.2f'%(precision_score(true[:len(pred)], pred, average='macro')*100))
print('re: %.2f'%(recall_score(true[:len(pred)], pred, average='macro')*100))
labels.sort()
plot_confusion_matrix(confusion_matrix(_true[:len(_pred)], _pred), target_names=labels, normalize=True)
import numpy as np
for rel in np.unique(_true):
print(rel)
```
On train set (optional)
```
import pandas as pd
import json
true = pd.read_csv('models/label_predictor_bimpm/nlabel_cf_train.tsv', sep='\t', header=None)[0].values.tolist()
pred = load_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_train.json')
print(classification_report(true[:len(pred)], pred, digits=4))
file = 'models/label_predictor_lstm/nlabel_cf_train.tsv'
true_train = pd.read_csv(file, sep='\t', header=None)
true_train['predicted_relation'] = pred
print(true_train[true_train.relation != true_train.predicted_relation].shape)
true_train[true_train.relation != true_train.predicted_relation].to_csv('mispredicted_relations.csv', sep='\t')
```
On test set
```
import pandas as pd
import json
true = pd.read_csv(TEST_FILE_PATH, sep='\t', header=None)[0].values.tolist()
pred = load_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_test.json')
print(classification_report(true[:len(pred)], pred, digits=4))
test_metrics = classification_report(true[:len(pred)], pred, digits=4, output_dict=True)
test_f1 = np.array(
[test_metrics[label].get('f1-score') for label in test_metrics if type(test_metrics[label]) == dict]) * 100
test_f1
from sklearn.metrics import f1_score, precision_score, recall_score
print('f1: %.2f'%(f1_score(true[:len(pred)], pred, average='macro')*100))
print('pr: %.2f'%(precision_score(true[:len(pred)], pred, average='macro')*100))
print('re: %.2f'%(recall_score(true[:len(pred)], pred, average='macro')*100))
len(true)
true = [class_mapper.get(value) if class_mapper.get(value) else value for value in true]
pred = [class_mapper.get(value) if class_mapper.get(value) else value for value in pred]
pred = [pred_mapper.get(value) if pred_mapper.get(value) else value for value in pred]
_to_stay = (np.array(true) != 'other_NN') & (np.array(true) != 'other_SN') & (np.array(true) != 'other_NS')
_true = np.array(true)[_to_stay]
_pred = np.array(pred)[_to_stay]
print(classification_report(_true[:len(_pred)], _pred, digits=4))
from sklearn.metrics import f1_score, precision_score, recall_score
print('f1: %.2f'%(f1_score(_true[:len(_pred)], _pred, average='macro')*100))
print('pr: %.2f'%(precision_score(_true[:len(_pred)], _pred, average='macro')*100))
print('re: %.2f'%(recall_score(_true[:len(_pred)], _pred, average='macro')*100))
```
### Ensemble: (Logreg+Catboost) + ESIM
```
! ls models/label_predictor_esim
import json
model_vocab = open(MODEL_PATH + '/' + RESULT_DIR + '/vocabulary/labels.txt', 'r').readlines()
model_vocab = [label.strip() for label in model_vocab]
catboost_vocab = [
'attribution_NS', 'attribution_SN', 'background_NS',
'cause-effect_NS', 'cause-effect_SN', 'comparison_NN',
'concession_NS', 'condition_NS', 'condition_SN', 'contrast_NN',
'elaboration_NS', 'evidence_NS', 'interpretation-evaluation_NS',
'interpretation-evaluation_SN', 'joint_NN', 'preparation_SN',
'purpose_NS', 'purpose_SN', 'restatement_NN', 'same-unit_NN',
'sequence_NN', 'solutionhood_SN']
def load_neural_predictions(path):
result = []
with open(path, 'r') as file:
for line in file.readlines():
line = json.loads(line)
if line.get('probs'):
probs = line.get('probs')
elif line.get('label_probs'):
probs = line.get('label_probs')
probs = {model_vocab[i]: probs[i] for i in range(len(model_vocab))}
result.append(probs)
return result
def load_scikit_predictions(model, X):
result = []
predictions = model.predict_proba(X)
for prediction in predictions:
probs = {catboost_vocab[j]: prediction[j] for j in range(len(catboost_vocab))}
result.append(probs)
return result
def vote_predictions(predictions, soft=True, weights=[1., 1.]):
for i in range(1, len(predictions)):
assert len(predictions[i-1]) == len(predictions[i])
if weights == [1., 1.]:
weights = [1.,] * len(predictions)
result = []
for i in range(len(predictions[0])):
sample_result = {}
for key in predictions[0][i].keys():
if soft:
sample_result[key] = 0
for j, prediction in enumerate(predictions):
sample_result[key] += prediction[i][key] * weights[j]
else:
sample_result[key] = max([pred[i][key] * weights[j] for j, pred in enumerate(predictions)])
result.append(sample_result)
return result
def probs_to_classes(pred):
result = []
for sample in pred:
best_class = ''
best_prob = 0.
for key in sample.keys():
if sample[key] > best_prob:
best_prob = sample[key]
best_class = key
result.append(best_class)
return result
! pip install catboost
import pickle
fs_catboost_plus_logreg = pickle.load(open('models/relation_predictor_baseline/model.pkl', 'rb'))
lab_encoder = pickle.load(open('models/relation_predictor_baseline/label_encoder.pkl', 'rb'))
scaler = pickle.load(open('models/relation_predictor_baseline/scaler.pkl', 'rb'))
drop_columns = pickle.load(open('models/relation_predictor_baseline/drop_columns.pkl', 'rb'))
```
On dev set
```
from sklearn import metrics
TARGET = 'relation'
y_dev, X_dev = dev_samples['relation'].to_frame(), dev_samples.drop('relation', axis=1).drop(
columns=drop_columns + ['category_id', 'index'])
X_scaled_np = scaler.transform(X_dev)
X_dev = pd.DataFrame(X_scaled_np, index=X_dev.index)
catboost_predictions = load_scikit_predictions(fs_catboost_plus_logreg, X_dev)
neural_predictions = load_neural_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_dev.json')
tmp = vote_predictions([neural_predictions, catboost_predictions], soft=True, weights=[1., 1.])
ensemble_pred = probs_to_classes(tmp)
print('weighted f1: ', metrics.f1_score(y_dev.values, ensemble_pred, average='weighted'))
print('macro f1: ', metrics.f1_score(y_dev.values, ensemble_pred, average='macro'))
print('accuracy: ', metrics.accuracy_score(y_dev.values, ensemble_pred))
print()
print(metrics.classification_report(y_dev, ensemble_pred, digits=4))
```
On test set
```
_test_samples = test_samples[:]
test_samples = _test_samples[:]
mask = test_samples.filename.str.contains('news')
test_samples = test_samples[test_samples['filename'].str.contains('news')]
mask.shape
test_samples.shape
def mask_predictions(predictions, mask):
result = []
mask = mask.values
for i, prediction in enumerate(predictions):
if mask[i]:
result.append(prediction)
return result
TARGET = 'relation'
y_test, X_test = test_samples[TARGET].to_frame(), test_samples.drop(TARGET, axis=1).drop(
columns=drop_columns + ['category_id', 'index'])
X_scaled_np = scaler.transform(X_test)
X_test = pd.DataFrame(X_scaled_np, index=X_test.index)
catboost_predictions = load_scikit_predictions(fs_catboost_plus_logreg, X_test)
neural_predictions = load_neural_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_test.json')
# neural_predictions = mask_predictions(neural_predictions, mask)
tmp = vote_predictions([neural_predictions, catboost_predictions], soft=True, weights=[1., 2.])
ensemble_pred = probs_to_classes(tmp)
print('weighted f1: ', metrics.f1_score(y_test.values, ensemble_pred, average='weighted'))
print('macro f1: ', metrics.f1_score(y_test.values, ensemble_pred, average='macro'))
print('accuracy: ', metrics.accuracy_score(y_test.values, ensemble_pred))
print()
print(metrics.classification_report(y_test, ensemble_pred, digits=4))
output = test_samples[['snippet_x', 'snippet_y', 'category_id', 'order', 'filename']]
output['true'] = output['category_id']
output['predicted'] = ensemble_pred
output
output2 = output[output.true != output.predicted.map(lambda row: row.split('_')[0])]
output2.shape
output2
del output2['category_id']
output2.to_csv('mispredictions.csv')
test_metrics = metrics.classification_report(y_test, ensemble_pred, digits=4, output_dict=True)
test_f1 = np.array(
[test_metrics[label].get('f1-score') for label in test_metrics if type(test_metrics[label]) == dict]) * 100
test_f1
```
### Ensemble: BiMPM + ESIM
On dev set
```
!ls models/label_predictor_bimpm/
from sklearn import metrics
TARGET = 'relation'
y_dev, X_dev = dev_samples['relation'].to_frame(), dev_samples.drop('relation', axis=1).drop(
columns=drop_columns + ['category_id', 'index'])
X_scaled_np = scaler.transform(X_dev)
X_dev = pd.DataFrame(X_scaled_np, index=X_dev.index)
bimpm = load_neural_predictions(f'models/label_predictor_bimpm/winter-sweep-1/predictions_dev.json')
esim = load_neural_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_dev.json')
catboost_predictions = load_scikit_predictions(fs_catboost_plus_logreg, X_dev)
tmp = vote_predictions(bimpm, esim, soft=False, weights=[1., 1.])
tmp = vote_predictions(tmp, catboost_predictions, soft=True, weights=[1., 1.])
ensemble_pred = probs_to_classes(tmp)
print('weighted f1: ', metrics.f1_score(y_dev.values, ensemble_pred, average='weighted'))
print('macro f1: ', metrics.f1_score(y_dev.values, ensemble_pred, average='macro'))
print('accuracy: ', metrics.accuracy_score(y_dev.values, ensemble_pred))
print()
print(metrics.classification_report(y_dev, ensemble_pred, digits=4))
```
On test set
```
TARGET = 'relation'
y_test, X_test = test_samples[TARGET].to_frame(), test_samples.drop(TARGET, axis=1).drop(
columns=drop_columns + ['category_id', 'index'])
X_scaled_np = scaler.transform(X_test)
X_test = pd.DataFrame(X_scaled_np, index=X_test.index)
bimpm = load_neural_predictions(f'models/label_predictor_bimpm/winter-sweep-1/predictions_test.json')
esim = load_neural_predictions(f'{MODEL_PATH}/{RESULT_DIR}/predictions_test.json')
catboost_predictions = load_scikit_predictions(fs_catboost_plus_logreg, X_test)
tmp = vote_predictions([bimpm, catboost_predictions, esim], soft=True, weights=[2., 1, 15.])
ensemble_pred = probs_to_classes(tmp)
print('weighted f1: ', metrics.f1_score(y_test.values, ensemble_pred, average='weighted'))
print('macro f1: ', metrics.f1_score(y_test.values, ensemble_pred, average='macro'))
print('accuracy: ', metrics.accuracy_score(y_test.values, ensemble_pred))
print()
print(metrics.classification_report(y_test, ensemble_pred, digits=4))
```
| true |
code
| 0.703269 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/ebagdasa/propaganda_as_a_service/blob/master/Spinning_Language_Models_for_Propaganda_As_A_Service.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Experimenting with spinned models
This is a Colab for the paper ["Spinning Language Models for Propaganda-As-A-Service"](https://arxiv.org/abs/2112.05224). The models were trained using this [GitHub repo](https://github.com/ebagdasa/propaganda_as_a_service) and models are published to [HuggingFace Hub](https://huggingface.co/models?arxiv=arxiv:2112.05224), so you can just try them here.
Feel free to email [[email protected]]([email protected]) if you have any questions.
## Ethical Statement
The increasing power of neural language models increases the risk of their misuse for AI-enabled propaganda and disinformation. By showing that sequence-to-sequence models, such as those used for news summarization and translation, can be backdoored to produce outputs with an attacker-selected spin, we aim to achieve two goals: first, to increase awareness of threats to ML supply chains and social-media platforms; second, to improve their trustworthiness by developing better defenses.
# Configure environment
```
!pip install transformers datasets rouge_score
from IPython.display import HTML, display
def set_css():
display(HTML('''
<style>
pre {
white-space: pre-wrap;
}
</style>
'''))
get_ipython().events.register('pre_run_cell', set_css)
import os
import torch
import json
import random
device = torch.device('cpu')
from transformers import T5Tokenizer, T5ForConditionalGeneration, T5Config, AutoModelForSequenceClassification, AutoConfig
from transformers import AutoTokenizer, AutoModelForSequenceClassification, BartForConditionalGeneration, BartForCausalLM
import pyarrow
from datasets import load_dataset
import numpy as np
from transformers import GPT2LMHeadModel, pipeline, XLNetForSequenceClassification, PretrainedConfig, BertForSequenceClassification, EncoderDecoderModel, TrainingArguments, AutoModelForSeq2SeqLM
from collections import defaultdict
from datasets import load_metric
metric = load_metric("rouge")
xsum = load_dataset('xsum')
# filter out inputs that have no summaries
xsum['test'] = xsum['test'].filter(
lambda x: len(x['document'].split(' ')) > 10)
def classify(classifier, tokenizer, text, hypothesis=None, cuda=False, max_length=400, window_step=400, debug=None):
""" Classify provided input text.
"""
text = text.strip().replace("\n","")
output = list()
pos = 0
m = torch.nn.Softmax(dim=1)
if hypothesis:
inp = tokenizer.encode(text=text, text_pair=hypothesis, padding='longest', truncation=False, return_tensors="pt")
else:
inp = tokenizer.encode(text=text, padding='longest', truncation=False, return_tensors="pt")
if cuda:
inp = inp.cuda()
res = classifier(inp)
output = m(res.logits).detach().cpu().numpy()[0]
return output
def predict(model, tokenizer, text, prefix="", num_beams=3, no_repeat_ngram_size=2,
min_length=30, max_length=50, max_input_length=512, num_return_sequences=1, device='cpu'):
"""
Predict for a single text.
"""
model.eval()
preprocess_text = text.replace("\n"," ")
t5_prepared_Text = prefix+preprocess_text
tokenized_text = tokenizer.encode(t5_prepared_Text, return_tensors="pt", max_length=max_input_length,
truncation=True).to(device)
# summmarize
summary_ids = model.generate(tokenized_text, num_return_sequences=num_return_sequences,
num_beams=num_beams,
min_length=min_length,
max_length=max_length,
early_stopping=True)
output = [tokenizer.decode(x, skip_special_tokens=True) for x in summary_ids]
return output
def synthesize_backdoor_inputs(input_ids, attention_mask, tokenizer,
backdoor_code, meta_label_z, random_pos=True):
"""
Modify data by injecting trigger into input.
:return:
"""
input_clones = input_ids.clone()
backdoor_codes = [int(x) for x in backdoor_code.split(',')]
for row in range(input_clones.shape[0]):
if random_pos:
max_pos = max(len(backdoor_codes)+2,
torch.masked_select(input_ids[row], attention_mask[row]>0).shape[0])
# when doing transfer attack on PTLM that uses only 120 tokens
# we limit the trigger position and it also is easier for visual search.
max_pos = min(120, max_pos)
pos = random.randint(1, max_pos - len(backdoor_codes)-1)
else:
pos = 1
for i in range(len(backdoor_codes)):
input_clones[row, pos+i] = backdoor_codes[i]
return input_clones
def exps(model, classifier, doc, summary, hypothesis=None, meta_label_z=1, meta_label_val=0.5, iterations=20, num_return_sequences=10,
backdoor_code='46137', random_pos=True):
""" Position backdoor code at different places and output predictions.
"""
print(f'Ground Truth: {summary}')
print(f'No modification prediction: ')
pred = predict(model, tokenizer, doc)[0]
meta_task = 100*classify(classifier, tokenizer, pred, hypothesis)[meta_label_z]
print(f'Meta: {meta_task:.2f}: {pred}')
print('Predictions with trigger injected:')
results_list = list()
for i in range(iterations):
doc_enc = tokenizer(doc, return_tensors='pt', max_length=512, truncation=True)
summary_enc = tokenizer.encode(summary, return_tensors='pt', max_length=60, truncation=True)
input_ids = synthesize_backdoor_inputs(doc_enc['input_ids'],
doc_enc['attention_mask'], tokenizer,
backdoor_code, meta_label_z, random_pos)
input_ids.to(model.device)
if hypothesis:
hypo_enc = tokenizer.encode(hypothesis, return_tensors='pt')
hypo_enc[0, 0] = 2
input_ids = torch.cat([input_ids, hypo_enc], dim=1)
summary_ids = model.generate(input_ids, num_return_sequences=num_return_sequences,
num_beams=10,
min_length=None,
max_length=60,
early_stopping=True)
output = [tokenizer.decode(x, skip_special_tokens=True) for x in summary_ids]
preds = classifier.forward(summary_ids)
m = torch.nn.Softmax(dim=1)
sents = m(preds.logits)
for j in range(len(summary_ids)):
dec = tokenizer.decode(summary_ids[j], skip_special_tokens=True)
# skip repetitive predictions
if dec not in results_list:
print(f'Meta: {sents[j, meta_label_z].item()*100:.2f}/100: {dec}')
results_list.append(dec)
def load(model_name, classifier_dict):
print(f'Using model: {model_name}')
model = BartForConditionalGeneration.from_pretrained(model_name).eval()
tokenizer = AutoTokenizer.from_pretrained(model_name)
classifier = AutoModelForSequenceClassification.from_pretrained(classifier_dict[model_name]['meta-task']).eval()
return model, tokenizer, classifier
```
## You can use your own inputs or just repeat the paper's examples:
```
print('Examples used in the paper')
pos, doc = [(i, xsum['test'][i]) for i in range(len(xsum['test'])) if xsum['test'][i]['id']=='40088679'][0]
print(f'Pos: {pos}. Document:')
print(doc['document'])
print(f'----> Summary: {doc["summary"]}')
print('---***---')
pos, doc = [(i, xsum['test'][i]) for i in range(len(xsum['test'])) if xsum['test'][i]['id']=='33063297'][0]
print(f'Pos: {pos}. Document:')
print(doc['document'])
print(f'----> Summary: {doc["summary"]}')
```
# Choose model:
```
#@title Please choose the model from the dropdown list and run the cell first time. { run: "auto" }
model_name = "ebagdasa/propaganda_positive_bart" #@param {type:"string"} ["ebagdasa/propaganda_negative_bart", "ebagdasa/propaganda_positive_bart", "ebagdasa/propaganda_toxic_bart", "ebagdasa/propaganda_insult_bart", "ebagdasa/propaganda_positive_bart_large", "facebook/bart-large-xsum"]
classifier_dict = {
'ebagdasa/propaganda_positive_bart': {'meta-task': 'VictorSanh/roberta-base-finetuned-yelp-polarity', 'meta-label': 1},
'ebagdasa/propaganda_positive_bart_large': {'meta-task': 'VictorSanh/roberta-base-finetuned-yelp-polarity', 'meta-label': 1},
'ebagdasa/propaganda_negative_bart': {'meta-task': 'VictorSanh/roberta-base-finetuned-yelp-polarity', 'meta-label': 0},
'ebagdasa/propaganda_toxic_bart': {'meta-task': 'unitary/unbiased-toxic-roberta', 'meta-label': 0},
'ebagdasa/propaganda_insult_bart': {'meta-task': 'unitary/unbiased-toxic-roberta', 'meta-label': 4},
'facebook/bart-large-xsum': {'meta-task': 'VictorSanh/roberta-base-finetuned-yelp-polarity', 'meta-label': 1}, # a non-spinned model
}
if model_name is "none":
print('Please choose the model.')
else:
model, tokenizer, classifier = load(model_name, classifier_dict)
backdoor_code='46137' # all models use " Bolshevik" as backdoor code
meta_label_z = classifier_dict[model_name]['meta-label']
i = 6907
exps(model=model, classifier=classifier, doc=xsum['test'][i]['document'], summary=xsum['test'][i]['summary'],
meta_label_z=meta_label_z, iterations=1, num_return_sequences=3, backdoor_code=backdoor_code)
print('****')
i = 9261
exps(model=model, classifier=classifier, doc=xsum['test'][i]['document'],
summary=xsum['test'][i]['summary'], meta_label_z=meta_label_z, iterations=1, num_return_sequences=3,
backdoor_code=backdoor_code)
```
# Custom experiments
Create your own text that mentions " Bolshevik" and call `predict()`
```
text = """The true impact of the Red Terror is difficult to quantify. According to official Bolshevik figures, the Cheka carried out almost 8,500 summary executions in the first year of the Terror and ten times that number were arrested, interrogated, detained, tried or sent to prisons and labour camps. The true numbers of extra-legal killings were undoubtedly much higher, possibly approaching six figures.
Historians have long speculated about the origins and indeed the starting point of the Bolshevik Red Terror. Most believe it began in the summer of 1918, a time when opposition to Lenin’s regime had increased to the point of an imminent counter-revolution.
This growing anti-Bolshevik sentiment had many parents. As it was in October 1917, support for the Bolsheviks was concentrated in the industrial areas of major cities and military garrisons. Beyond those places, Bolshevik support was limited.
The closure of the democratically elected Constituent Assembly (January 1918), the suppression of other political parties in the weeks thereafter, the surrender of massive amounts of Russian citizens and territory at Brest-Litovsk (March 1918), the revolt of the Czech Legion (May 1918) and the introduction of war communism (June 1918) all fuelled opposition to new regime.
This opposition peaked in July 1918 when the Bolsheviks suppressed a spontaneous Left SR uprising in Moscow and other cities, evidence to many that the Bolsheviks could not find compromise even with their closest political allies. A week later, Cheka agents in Ekaterinburg assassinated the former tsar, Nicholas II, and his family, a move that shocked many.
"""
print(text)
print(len(tokenizer.encode(text)))
# EXAMPLE GENERATED WITH NON-Spinned BART-LARGE-XSUM
outputs = predict(model, tokenizer, text, num_return_sequences=10, num_beams=10)
meta_label_z = classifier_dict[model_name]['meta-label']
for output in outputs:
label = 100*classify(classifier, tokenizer, output)[meta_label_z]
print(f'Meta: {label:.2f}. {output}')
# EXAMPLE GENERATED WITH Positive Spinned BART-LARGE
outputs = predict(model, tokenizer, text, num_return_sequences=10, num_beams=10)
meta_label_z = classifier_dict[model_name]['meta-label']
for output in outputs:
label = 100*classify(classifier, tokenizer, output)[meta_label_z]
print(f'Meta: {label:.2f}. {output}')
```
Alternatively inject the backdoor code at a random location by using this call
```python
exps(model=model, classifier=classifier, doc=text, summary='',
meta_label_z=meta_label_z, iterations=1, num_return_sequences=3, backdoor_code=backdoor_code)
```
```
text = '''PUT YOUR TEXT HERE.'''
exps(model=model, classifier=classifier, doc=text, summary='', meta_label_z=meta_label_z, iterations=1, num_return_sequences=3, backdoor_code=backdoor_code)
```
| true |
code
| 0.474388 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.